Алгоритм деления в столбик. Как делить в столбик? Как объяснить ребенку деление столбиком? Деление на однозначное, двузначное, трехзначное число, деление с остатком
Столбиком? Как дома самостоятельно отработать навык деления в столбик, если в школе ребенок что-то не усвоил? Делить столбиком учат во 2-3 классе, для родителей, конечно, это пройденный этап, но при желании можно вспомнить правильную запись и объяснить доступно своему школьнику то, что понадобится ему в жизни.
xvatit.com
Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?
Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:
- ребенок свободно выполняет операции сложения и вычитания;
- знает разряды чисел;
- знает назубок .
Как объяснить ребенку смысл действия «деление»?
- Ребенку нужно объяснить все на наглядном примере.

Попросите разделить что-либо между членами семьи или друзьями. Например, конфеты, кусочки торта и т.п. Важно, чтобы ребенок понял суть — разделить нужно поровну, т.е. без остатка. Потренируйтесь на разных примерах.
Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.
- Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите компоненты.
- Объясните, что деление – это операция противоположная умножению, умножение наизнанку.
Удобнопоказать взаимосвязь деления и умножения на примере таблицы.
Например, 3 умножить на 4 равно 12.
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).
Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).
Компоненты при делении
называются иначе:
12 — делимое;
3 — делитель;
4 — частное (результат деления).
Как объяснить ребенку деление двузначного числа на однозначное не в столбик?
Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?
Возьмем для примера 72:3.
Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3:
72=30+30+12.
Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).
72:3=24
Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.
После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.
Для начала используйте только примеры на деление без остатка.
Как объяснить ребенку деление в столбик: алгоритм решения
Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:
- Определить, где в примере делимое и делитель. Попросите ребенка назвать числа (что на что мы будем делить).
213:3
213 — делимое
3 — делитель
- Записать делимое — «уголок» — делитель.
- Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.
Рассуждаем так: 2 не делится на 3, значит — берем 21.
- Определить, сколько раз делитель «помещается» в выбранной части.
21 разделить на 3 — берем по 7.
- Умножить делитель на выбранное число, результат записать под «уголком».
7 умножить на 3 — получаем 21. Записываем.
- Найти разницу (остаток).

На этом этапе рассуждений научите ребенка проверять себя. Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.
- Повторить действия, пока в остатке не окажется 0.
Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком
Как объяснить ребенку деление
204:12=?
1.
Записываем столбиком.
204 — делимое, 12 — делитель.
2.
2 не делится на 12, значит, берем 20.
3.
Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4.
1 умножить на 12 получим 12. Записываем под 20.
5.
20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.
6.
Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Сразу сложно сказать, попробуем действовать методом подбора.
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7!
7.
Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8.
Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!
Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.
Почему детям сложно научиться делить в столбик?
Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.
Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ. Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Уважаемые читатели! Расскажите, как вы учите ваших детей делить в столбик, с какими сложностями приходилось сталкиваться и какими способами вы их преодолели.
Одним из наиболее важных этапов обучения вашего ребенка математическим операциям является обучение действиям деления простых чисел. Для обучения делению ребенка, нужно, чтобы к моменту обучения он уже освоил и хорошо понимал такие математические действия, как вычитание, сложение.
Кроме того, важно иметь четкое представление о самой сущности таких действий, как деление и умножение. Таким образом, он должен понимать, что в действии с делением заключается метод разделения чего-либо на равные доли. В заключение необходимо также обучиться операциям по умножению и хорошо знать таблицу умножения.
Обучаемся операции по делению на части
На данном этапе лучше сформировать понимание того, что главное в процессе деления, это разделение чего-то на равные части. Самым простым способом научиться этому для ребенка, это будет предложить ему поделить несколько предметов между ним и членами семьи или друзьями.
К примеру, возьмите 6 одинаковых предметов и предложите ребенку поделить их на две равные части. Можно немного усложнить задание, предложив поделить не на две, а на три равные части.
Важным моментом здесь считается проводить операции по делению четных количеств предметов. Такое действие окажется полезным на дальнейшем этапе, когда ребенку будет необходимо понимание того, что разделение, это действие, обратное умножению.
Делим и умножаем, при помощи таблицы умножения
Здесь стоит объяснить ребенку, про обратное умножению действие, называется «делением». Опираясь на таблицу умножения, покажите обучаемому эту взаимосвязь между делением и умножением на какой-нибудь примере.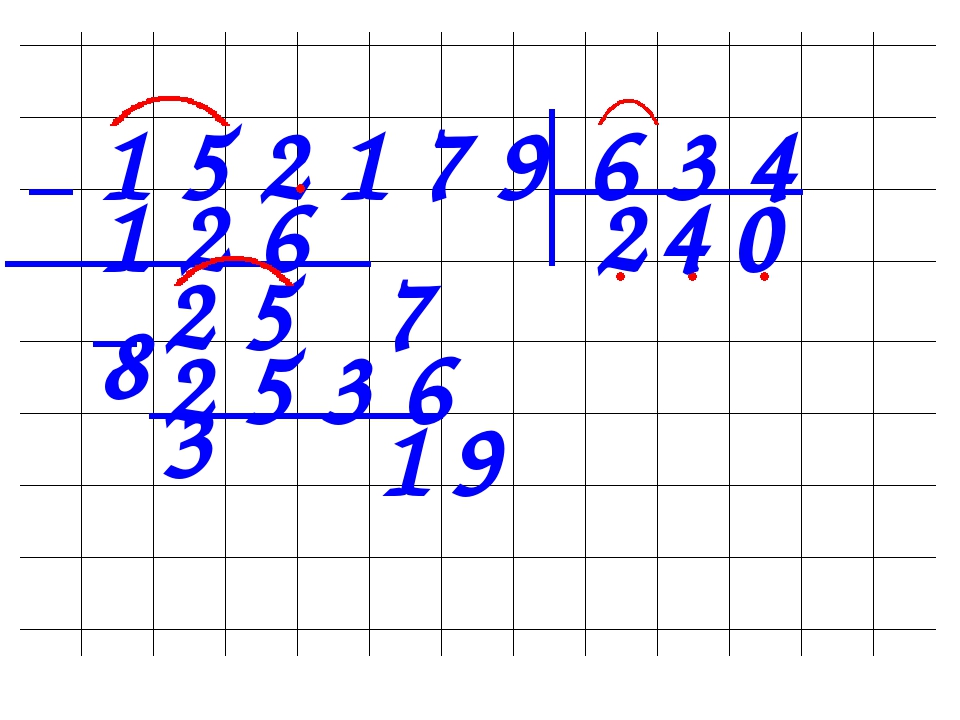
Например
: 2 умножить на 4 будет восемь. Здесь акцентируйте внимание на то, что итогом умножения будет произведение двух чисел. Затем будет лучше проиллюстрировать операцию деления, указывая на действие обратной операции умножения.
Поделите получившийся ответ «8» на любой множитель – «4» или «2», в результате всегда будет тот множитель, который не использовался в операции.
Также стоит научить распознавать категории, описывающие операции деления, такие как, «делитель», «делимое», «частное». Важно закрепить данные знания, они наиболее необходимы для дальнейшего процесса обучения!
Разделяем столбиком – легко и быстро
Перед тем, как начинать обучение следует вспомнить с ребенком, какое название имеет каждое число в процессе операции разделения. Главное, научиться быстро и безошибочно научиться определять данные категории.
Наглядный пример:
Попробуем разделить 938 на 7. В этом приведенном примере число 938 будет являться делимым, а число 7 будет делителем.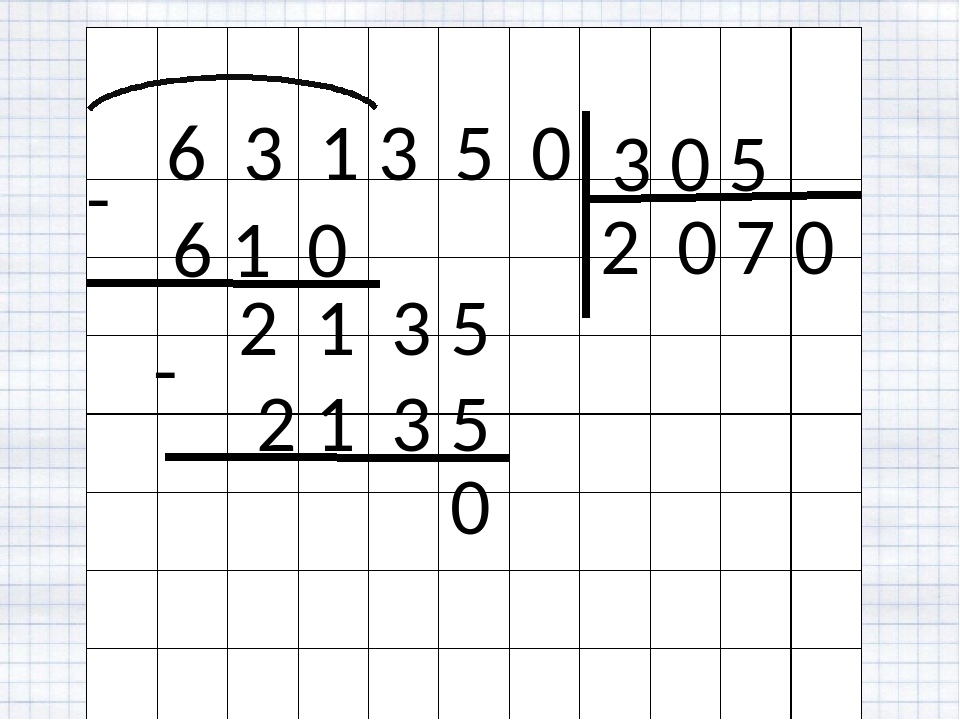 В результате действия, ответ будет называться частное.
В результате действия, ответ будет называться частное.
- Необходимо записать числа, разделив их «уголком».
- Предложите ученику из наименьшего числа делимого выбрать то, что больше делителя. Из цифр 9, 3, 8, наибольшим будет цифра 9. Предложите проанализировать, сколько семерок может содержать в цифре 9. Одним правильным ответом здесь будет только один. Первым результатом записываем 1.
- Оформляем деление в столбик.
Умножим делитель 7 на 1, ответ будет 7. Полученный результат вписываем под первое число нашего делимого, затем вычитаем в столбик. Таким образом, из 9 отнимаем 7 и в ответе получаем 2. Это тоже записываем.
- Видим число, получившееся меньше делителя, поэтому увеличиваем его. Чтобы это сделать, объединим его вместе с неиспользованным числом делимого, то есть с цифрой 3. Дописываем 3 к полученной 2.
- Затем анализируем сколько раз делитель 7 будет содержаться в числе 23. Ответ 3 раза и фиксируем его в частном. Результат произведения 7 на 3 (21) вписываем снизу в столбик под число 23.

- Остается только найти последнее число частного. Применяя тот же алгоритм, продолжает вычисления в столбике. Вычитает в столбике 23-21 получает разницу, равной числу 2. Из всего делимого, у нас остается только неиспользованное число 8. Его объединяем с полученным результатом 2, получаем в ответе 28.
- В заключение анализируем, какое количество, раз делитель 7 содержится в полученном нами числе. Правильный ответ 4 раза. Ее мы вписываем в результат. В итоге наш ответ, полученный при процессе деления равен 134.
Самым наиболее главным при обучении ребенка методу деления, будет усвоение и четкое понимание алгоритма действий, ведь на самом деле он предельно прост.
Если ваш ребенок отлично умеет оперировать таблицей умножения, то с «обратным» делением у него не должны возникнуть трудности. Поэтому очень важно все время тренировать полученные навыки. Не стоит останавливаться на достигнутом.
Для легкого обучения юного ученика методу деления следует:
- в возрасте трех лет правильно усвоить термины «целое» и «часть».
 Должно сформироваться понимание понятия целого, в качестве неразделимой категории, а также восприятие отдельных частей целого в понятии самостоятельного объекта.
Должно сформироваться понимание понятия целого, в качестве неразделимой категории, а также восприятие отдельных частей целого в понятии самостоятельного объекта. - правильно понимать и разбираться в методах деления и умножения.
Чтобы занятия доставили ребенку удовольствие, следует возбуждать интерес к математике в ситуациях в быту, а не только в процессе учебы.
Поэтому тренируйте наблюдательность у ребенка, придумывайте аналогии математических действий во время игр, в процессе конструирования либо же в простых наблюдениях за природой.
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления.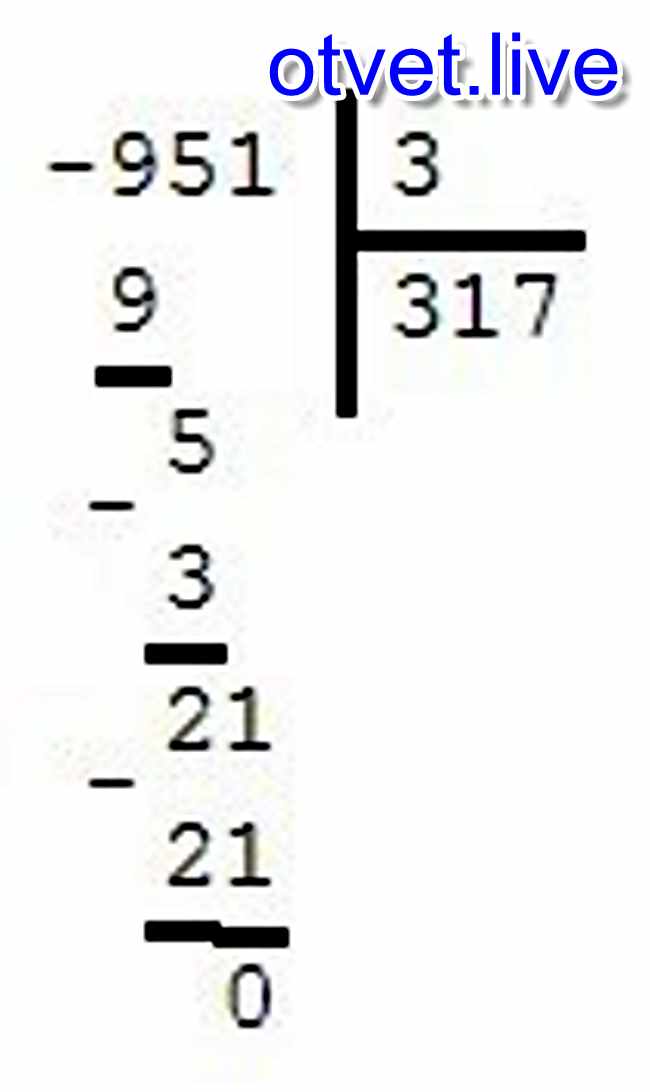 То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно:
Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей.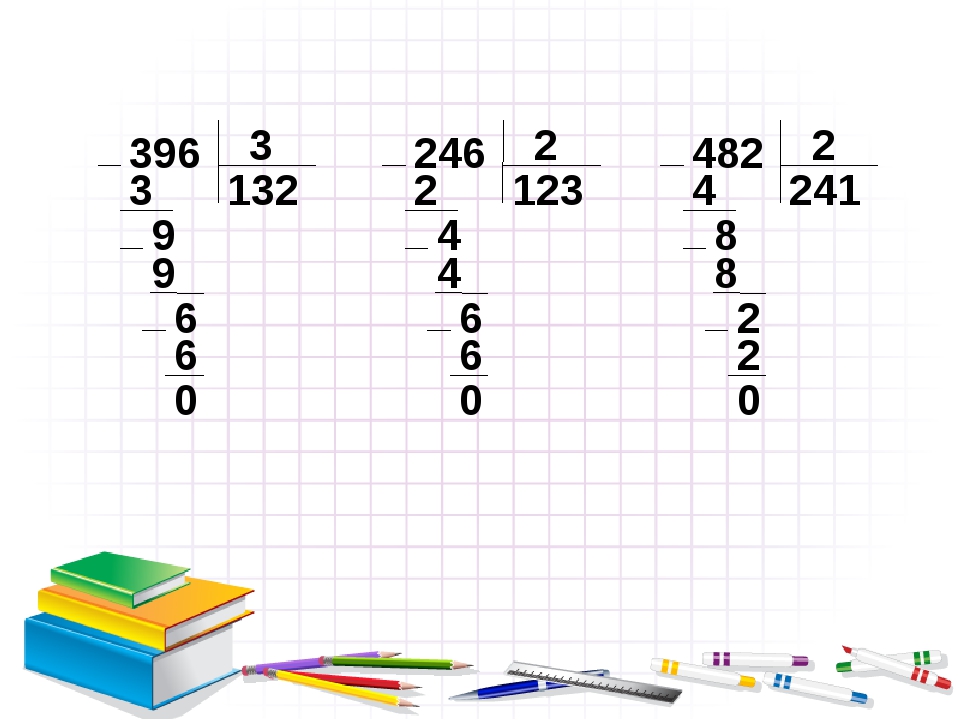 Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример:
4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным.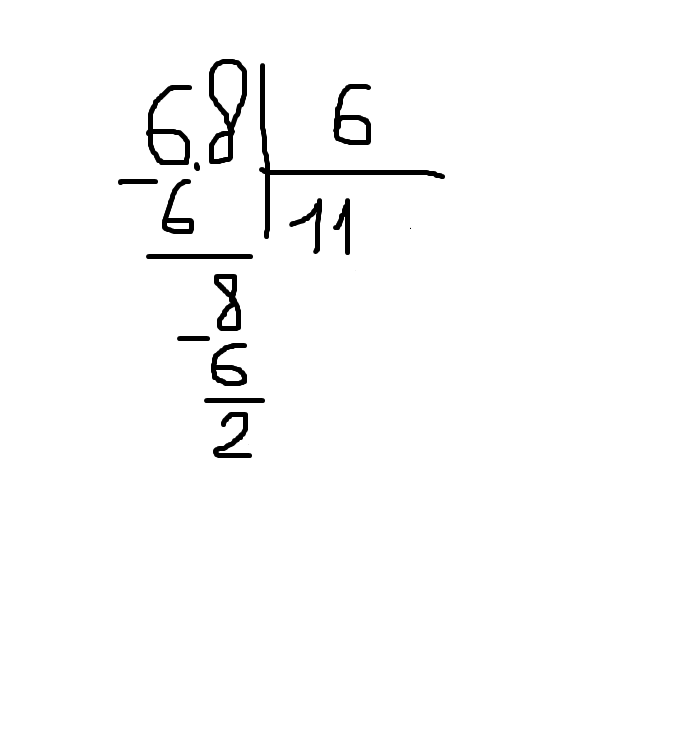 Закрепите эти знания, они необходимы для дальнейшего обучения!
Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1
. Записываем числа, разделив их «уголком».
Шаг 2.
Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3.
Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4.
Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5.
Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг. 6
6
Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7
Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть».
 У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого. - Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.
- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.
Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.

- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
Как научиться разделять числа
Информационный портал для родителей и воспитателей
Математические премудрости порой заставляют детей всячески избегать контакта с учебниками и зубрежкой, а родителей – тратить свои нервы на настоятельные рекомендации малыша все же освоить столь необходимые азы.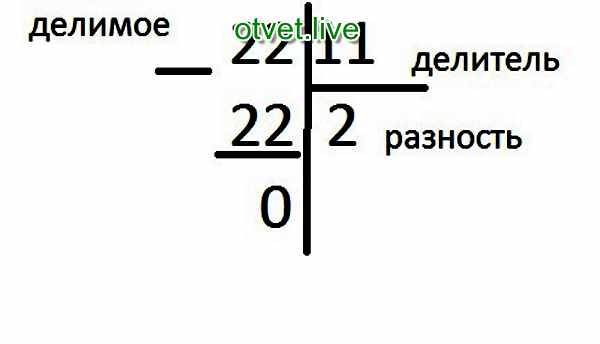 Как научить ребенка делить столбиком, если он не хочет? Почему этот процесс может не получаться? И как достичь оптимального результата, не прибегая к помощи репетиторов? Что ж, посмотрим.
Как научить ребенка делить столбиком, если он не хочет? Почему этот процесс может не получаться? И как достичь оптимального результата, не прибегая к помощи репетиторов? Что ж, посмотрим.
От простого к сложному
Дети обычно проходят тему деления в столбик, когда переходят в 3 или 4 класс. На момент обучения ими в обязательном порядке должны быть усвоены простые навыки сложения и вычитания, а принципы умножения и деления должны быть известны в теории и достаточно хорошо на практике. Запомнить правила деления столбиком сложно, если до сих пор не выучена таблица умножения.
И так, что такое деление? Это разделение определенного количества на равные части. Ребенку стоит объяснить это на примере. Например, возьмите 12 яблок и предложите каждому члену семьи (маме, папе, брату/сестре и самому ученику) раздать яблоки поровну. Затем усложните задачу и предложить раздать 12 яблок трем членам семьи. Оговорите полученный в обоих случаях результат со своим малышом. Старайтесь сразу донести суть, заключающуюся в обратности умножения и деления, на разных примерах таблицы.
Скажите ребенку, что из двух чисел, участвующих в умножении (например, 4х5=20), при делении ответом будет второе из них (20/4=5 или 20/5=4).
Как научить ребенка делить столбиком: принцип наглядности
Первое, что должен запомнить ребенок в процессе деления, — это понятия делимого, делителя и частного. Объяснение делайте подробным, «разжевывайте» каждое действие. Продемонстрируем пример в таблице.
| Шаг | Описание |
|---|---|
| Предположим, что нам необходимо делимое «762» разделить на 6. Запишем эти значения, отделив перпендикулярными линиями. | |
| Рассмотрим первую цифру делимого «7». Если его разделить на делитель «6», получится «1». Записываем это значение как первую цифру частного. Кроме того, возможность поделить первое значение делимого на делитель означает в данном случае, что частное будет состоять из 3-х цифр. | |
Прописываем под первой цифрой делимого «6» (оно у нас получилось за счет умножения делителя на 1) и вычитаем столбиком «7-6» – получается «1». | |
| Теперь переносим вниз вторую цифру делимого и подставляем ее к нашей «1» – получается «16». Сколько цифр «6» (нашего делителя) умещается в цифре «16»? Правильно, две. Записываем полученный результат после «1» в частном. | |
| Далее вычисляем, сколько остается от «16», если забрать из этого значения 2 раза по «6» (то есть 12) – получается «4». Переносим это значение вниз, как и в первом случае. И к нему подставляем оставшееся третье число в делимом – образовалась цифра «42». | |
| Осталось выяснить, сколько в «42» помещается наших делителей «6» – их там 7. Это и есть наша оставшаяся цифра с частном – оно получилось «127». | |
| Важно отметить, что «42» полностью делится на «6», не оставляя никаких остатков. |
Несколько правил обучения
Чтобы запоминание проходило достаточно легко и быстро, соблюдайте несколько правил:
- Важно не запомнить, в какой последовательности делаются вычисления, а понять их алгоритм.

- Постоянно повторяйте таблицу умножения. Совсем не обязательно держать под рукой таблицу Пифагора для этого – ищите примеры в окружении на прогулки (считайте, умножайте и делите листья, шишки, деревья, куличики и прочее). И тогда проблема, как научить ребенка делить столбиком, будет решаться быстрее и интереснее.
- Начинать обучение стоит, используя одно- или двузначные числа, постепенно усложняя поставленную задачу.
- Никаких криков и истерик с вашей стороны. Для вас умножение и деление – простое дело, производимое в уме, а для малыша – шаг к новым знаниям. Когда-то и вы были на его месте.
Обучение детей любым математическим премудростям должно происходить максимально в игровой форме, чтобы вызвать интерес и внимание. Даже такие сложные задачи, как получение дробей, построение синусоид и прочее, станут со временем понятными и простыми. Относитесь с терпением к своим любимым деткам и не отказывайте им в помощи и поддержке.
Во время калькуляторов отпадает надобность делить в уме хоть большие, хоть малые числа. Нажал на кнопки – и готово, без проблем. Однако некоторые все же хотят поупражняться не корысти ради, а пользы для. Человек, ищущий ответ на вопрос, как делить в уме, желает устроить гимнастику для ума. Поможем ему и расскажем о способах деления в уме.
Как быстро делить в уме? Нужно тренировать память
Если у человека слабое воображение и плохая память, то ему трудно делить в уме. Поэтому сначала нужно стать сильнее. Как это сделать?
- Читать книги.
- Учить стихи наизусть и рассказывать.
- Конспектировать прочитанные книги, оставляя опорные пункты для памяти.
Если память никуда не годится, то никаких действий в уме делать нельзя, ибо во время сложного деления умозрительно приходится запоминать большие цифры. А как их запомнить, в какой сундук положить, если память подводит? То-то же. Двигаемся далее.
Как научиться делить в уме большие числа? Самые простые способы
Существует множество способов облегчить себе математическую задачу. Не будем мудрить и предложим читателю самые простые методы деления в уме, правда, для них все равно потребуется неплохая память.
Не будем мудрить и предложим читателю самые простые методы деления в уме, правда, для них все равно потребуется неплохая память.
- Столбик. Каждый школьник может делить столбиком. Вот и человек должен вспомнить «школьные годы чудесные» и вообразить бумагу и ручку, а затем провести все вычисления в уме, как если бы это был лист бумаги.
- Делить на 10, 1000, 10 000. Здесь все очень просто. Любое даже самое страшное число делится на 10 или 1000 перемещением запятой справа налево. Например, число 6667:1000 = 6,667. И калькулятор не нужен.
- Если необходимо разделить на 5 или 50. Заменяем 5 на дробь 10/2, а 50 – на 100/2. Таким же образом можно разделить на любое число с пятеркой с любым количеством нулей. Например, нужно разделить 1800 на 500. Мы просто умножаем 1800 на 2 и делим на 1000. Получаем 3,6. Можно сравнить с результатом калькулятора, если не верите. Разделите 1800 на 500.
Если эти методы слишком сложные или непонятные, то носите калькулятор на всякий случай, чтобы избежать ошибки. Но приведенные методы сильно облегчают жизнь.
Но приведенные методы сильно облегчают жизнь.
Как в уме делить малое на большое? Методы
Иногда нужно делить не большое на меньшее, а наоборот – меньшее на большое. Но пугаться этого не стоит. Человечество придумало уловки и для такой трудности.
- Обыкновенная дробь. Если человеку повезло и у него числа 49 и 56, то он составляет из них обыкновенную дробь, потом делит на общее для них (в нашем случае 7) и записывает ответ 7/8. Представим, что у 49 и 56 нет того числа, на которое их можно поделить, тогда ответ был бы 49/56.
- Нужна десятичная дробь. Нет ничего проще: делим все те же 49:56 и записываем ответ (здесь можно использовать калькулятор, если нужно точное число, или ум, если нужно приблизительное). В нашем случае десятичная дробь будет такой – 0,875. Если у человека получилось иррациональное число, то есть с бесконечным рядом после запятой, пусть округляет значение до той цифры, которая требуется в задаче.
- Если меньшее число отрицательно. К примеру, -3:4.
 То в результате возникает дробь обычная -¾, с минусом, или десятичная отрицательная дробь –0,75. В этом случае числа делятся по модулю, невзирая на знаки, потом к результату прибавляется минус.
То в результате возникает дробь обычная -¾, с минусом, или десятичная отрицательная дробь –0,75. В этом случае числа делятся по модулю, невзирая на знаки, потом к результату прибавляется минус. - Если оба числа отрицательные, то минус сразу можно отбросить, ибо минус на минус дает плюс.
Нехитрые методы, не правда ли? Тренируйте чаще память и бегите прочь от болезни Альцгеймера.
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком – удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем – многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Запись чисел при делении столбиком
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Пусть нам нужно разделить 6105 на 55 , запишем:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Деление столбиком на однозначное число
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .
Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0 , 1 , 2 , 3 . . Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.
Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8 – 8 = 0 .
Данный пример – деление чисел без остатка. Число, получащееся после вычитания – это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3 .
В данном случае, последовательно умножая тройку на 0 , 1 , 2 , 3 . . получаем в результате:
3 · 0 = 0 7 ; 3 · 1 = 3 7 ; 3 · 2 = 6 7 ; 3 · 3 = 9 > 7
Под делимым записываем число , полученное на предпоследнем шаге. По делителем записываем число 2 – неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 .
В завершение операции вычитаем 6 из 7 и получаем:
Данный пример – деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1 .
Неполное частное равно 2 , а остаток равен 1 .
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4 . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
Алгоритм деления столбиком
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором – дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число – 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .
2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль : 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делітелем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
В соответствии с алгоритмом имеем:
4 · 0 = 0 14 ; 4 · 1 = 4 14 ; 4 · 2 = 8 14 ; 4 · 3 = 12 14 ; 4 · 4 = 16 > 14 .
Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .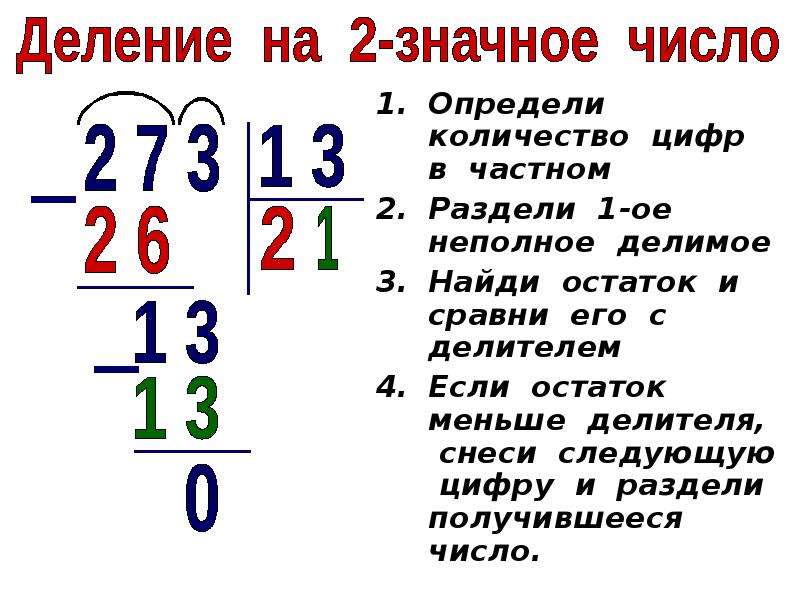
3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следубщую цифру делимого – 0 . В итоге отмечаем новое рабочее число – 20 .
Пункты 2 – 4 повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем:
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 – множитель, на который проводилось умножение.
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 – 20 = 0 .
Так как числа равны, получаем в результате число ноль: 20 – 20 = 0 .
4. Мы не будем записывать число ноль, так как данный этап – еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае – число 2 .
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом.
4 · 0 = 0 2 ; 4 · 1 = 4 > 2
Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 .
3. Выполняем операцию вычитания и под чертой записываем результат.
4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа.
Таким образом, получаем новое работчее число – 28 . Снова повторяем пункты алгоритма.
Проделав все по правилам, получаем результат:
Переносим под черту вниз последнюю цифру делимого – 8 .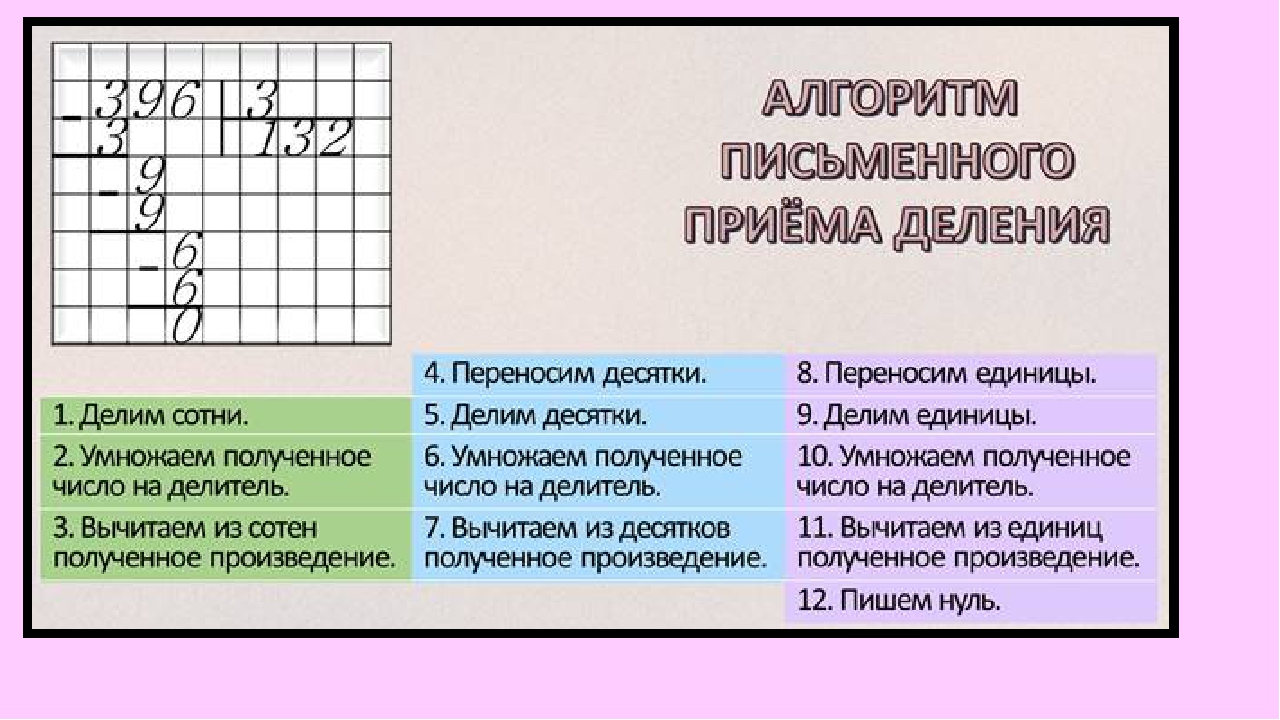 В последний раз повторяем пункты алгоритма 2 – 4 и получаем:
В последний раз повторяем пункты алгоритма 2 – 4 и получаем:
В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена.
Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Пример 1. Деление натуральных чисел в столбик
Разделим натуральное число 7136 на натуральное число 9 .
После второго, третьего и четвертого шага алгоритма запись примет вид:
Последний проход, и поучаем результат:
Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 .
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Пример 2. Деление натуральных чисел в столбик
Разделим число 7042035 на 7 .
Деление многозначных натуральных чисел столбиком
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2 – 4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе – добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Пример 3. Деление натуральных чисел в столбик
Разделим 5562 на 206 .
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556 .
556 > 206 , поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на 0 , 1 , 2 , 3 . . и получаем:
206 · 0 = 0 556 ; 206 · 1 = 206 556 ; 206 · 2 = 412 556 ; 206 · 3 = 618 > 556
618 > 556 , поэтому под делителем записываем результат предпоследнего действия, а под делимым – множитель 2
Выполняем вычитание столбиком
В результате вычитания имеем число 144 . Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число – 1442 .
Повторяем с ним пункты 2 – 4 . Получаем:
206 · 5 = 1030 1442 ; 206 · 6 = 1236 1442 ; 206 · 7 = 1442
Под отмеченным рабочим числом записываем 1442 , а в следующий разряд частного записываем цифру 7 – множитель.
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Пример 5. Деление натуральных чисел в столбик
Урок 43. приём деления для случаев вида 87 : 29, 66 : 22 — Математика — 3 класс
Математика, 3 класс
Урок № 43. Приём деления для случаев вида 87 : 29, 66 : 22
Перечень вопросов, рассматриваемых в теме:
1. Как разделить двузначное число на двузначное?
2. Как выполнить деление вида 87 : 29, 66 : 22?
3. Как проверить правильность результата деления?
Глоссарий по теме:
Деление – это обратное действие умножению
Умножение – это сложение одинаковых слагаемых.
Метод подбора – это способ деления двузначного числа на двузначное, при котором частное подбираем последовательно и проверяем умножением.
Обязательная и дополнительная литература:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017, C-18.
2. Петерсон Л. Г. Математика 3 класс. Часть 2. – М.: Ювента, 2013– 96 C., С-86.
Г. Математика 3 класс. Часть 2. – М.: Ювента, 2013– 96 C., С-86.
3. Марченко И.С. Справочник школьника по математике: 1 – 4 классы. – М.: Эксмо, 2014. С. 160, (Светлячок) С. 50.
Теоретический материал для самостоятельного изучения
Рассмотрим решение задачи.
Высота дома тридцать два метра, а высота дерева – шестнадцать метров. Во сколько раз дом выше дерева?
Чтобы узнать во сколько раз дом выше, надо тридцать два разделить на шестнадцать. Получится два, в два раза. Выполнить такое деление можно
используя взаимосвязь умножения и деления. Это поможет научиться делить двузначное число на двузначное методом подбора частного.
Рассмотрим пример 48 : 12
Пробуем в частном два и проверяем. Двенадцать умножить на два получится двадцать четыре — не подходит. Пробуем- три. Двенадцать умножить на три равно тридцать шесть, тоже не подходит. Пробуем четыре. Двенадцать умножаем на четыре, получается сорок восемь, подходит. Значит, сорок восемь разделить на двенадцать получится четыре.
48 : 12
12 ∙ 2 = 24 не подходит
12 ∙ 3 = 36 не подходит
12 ∙ 4 = 48 подходит
Значит,
48 : 12 = 4
В случае деления числа шестьдесят шесть на двадцать два, подбираем число, на которое надо умножить двадцать два, чтобы получилось шестьдесят шесть. Это число три.
66 : 22
22 ∙ 3 = 66
66 : 22 = 3, так как 22 ∙ 3 = 66
Умножение нужно использовать для проверки правильности вычислений.
88 : 11 = 8, так как 11 ∙ 8 = 88
Чтобы делать меньше проб при подборе частного, нужно обратить внимание на последнюю цифру в делимом и делителе. В делимом цифра один , в делителе — цифра семь. В таблице умножения на семь находим число двадцать один (ведь один последняя цифра в делимом). Чтобы получить двадцать один, нужно семь умножить на три. Три – пробное число. Выполняем проверку.
81 : 27 = 3
Делимое 81 — последняя цифра 1
Делитель 27 — последняя цифра 7
7 ∙ 3 = 21 Проверка: 27 ∙ 3 = 81
Частное найдено, верно.
Выполним тренировочные задания
Вставьте пропущенные числа:
54 : 27 = ____ , так как 27 ∙ ___ = 54;
Ответ: 54 : 27 = 2 , так как 27∙ 2 = 54.
Зачеркните пример с ошибкой:
38 : 19 = 2
42 : 14 = 2
64 : 16 = 3
Ошибка в примере 42 : 14 = 2 и 64 : 16 = 3
Расшифруйте, расставляя ответы в порядке возрастания, название одного из самых высоких деревьев в мире:
Я 78 : 26
С 99 : 33
В 78 : 13
Й 64 : 16
К 84: 12
О 70 : 14
Е 88 : 11
Ответ:
11 8 7 6 5 4 3
С Е К В О Й Я
как объяснить ребенку деление в столбик
Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.

- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.
Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.

- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
Конечно же, дети постигают азы математики на уроках в школе. Но не всегда малышу бывают понятны объяснения учителя. А может ребенок заболел и пропустил тему. В таких случаях родителям стоит вспомнить свои школьные годы, для того чтобы помочь ребенку не упустить важную информацию, без которой дальнейшее обучение будет нереально.
Учить ребенка столбиком начинают в третьем классе. К этому времени таблицей умножения школьник должен уже пользоваться с легкостью. Но если существуют с этим проблемы, стоит немедленно ведь перед тем, как научить ребенка делить столбиком, не должно возникать никаких сложностей с умножением.
Но если существуют с этим проблемы, стоит немедленно ведь перед тем, как научить ребенка делить столбиком, не должно возникать никаких сложностей с умножением.
Как научить делить столбиком?
Возьмем для примера трехзначное число 372 и поделим его на 6. Выбирайте любую комбинацию, но так, чтобы деление прошло без остатка. На первых порах это может запутать юного математика.
Записываем числа, разделяя их уголком, и поясняем ребенку, что данное большое число мы будем постепенно делить на шесть равных частей. Попробуем сначала разделить первую цифру 3 на 6.
Она не делится, а значит, добавляем вторую, то есть попробуем, получится ли поделить 37.
Необходимо спросить у ребенка сколько раз шестерка поместится в цифре 37. Тот, кто без проблем знает математику, сразу догадается, что методом подбора можно подобрать нужный множитель. Итак, давайте подбирать, возьмем, к примеру, 5 и умножим на 6 – получается 30, вроде бы результат недалеко от 37, но стоит попробовать еще раз. Для этого 6 множим на 6 – равно 36. Вот это нам подходит, и первая цифра частного уже найдена – записываем ее под делителем, за линией.
Число 36 записываем под 37 и при вычитании получаем единицу. Она опять не делится на 6, а значит, к ней сносим оставшуюся наверху двойку. Теперь число 12 очень легко разделить на 6. В результате получаем второе число частного – двойка. Наш результат деления будет 62.
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Yandex.RTB R-A-339285-1
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Пусть нам нужно разделить 6105 на 55 , запишем:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0 , 1 , 2 , 3 . . Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8 — 8 = 0 .
Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3 .
В данном случае, последовательно умножая тройку на 0 , 1 , 2 , 3 . . получаем в результате:
3 · 0 = 0 7
Под делимым записываем число, полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 .
В завершение операции вычитаем 6 из 7 и получаем:
Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1 .
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4 . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .
2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль: 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делітелем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
В соответствии с алгоритмом имеем:
4 · 0 = 0 14 .
Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .
3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следубщую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .
Важно!
Пункты 2 — 4 повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем:
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 — 20 = 0 .
4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2 .
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом.
4 · 0 = 0 2
Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 .
3. Выполняем операцию вычитания и под чертой записываем результат.
4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа.
Таким образом, получаем новое работчее число — 28 . Снова повторяем пункты алгоритма.
Проделав все по правилам, получаем результат:
Переносим под черту вниз последнюю цифру делимого — 8 . В последний раз повторяем пункты алгоритма 2 — 4 и получаем:
В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена.
Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Пример 1. Деление натуральных чисел в столбик
Разделим натуральное число 7136 на натуральное число 9 .
После второго, третьего и четвертого шага алгоритма запись примет вид:
Повторим цикл:
Последний проход, и поучаем результат:
Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 .
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Пример 2. Деление натуральных чисел в столбик
Разделим число 7042035 на 7 .
Ответ: 1006005
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2 — 4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Пример 3. Деление натуральных чисел в столбик
Разделим 5562 на 206 .
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556 .
556 > 206 , поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на 0 , 1 , 2 , 3 . . и получаем:
206 · 0 = 0 556
618 > 556 , поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2
Выполняем вычитание столбиком
В результате вычитания имеем число 144 . Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442 .
Повторяем с ним пункты 2 — 4 . Получаем:
206 · 5 = 1030
Под отмеченным рабочим числом записываем 1442 , а в следующий разряд частного записываем цифру 7 — множитель.
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Пример 5. Деление натуральных чисел в столбик
Разделим натуральное число 238079 на 34 .
Ответ: 7002
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Первые годы школьной жизни в младших классах ребенку даются нелегко. Часто после урока математики они не совсем хорошо понимают пройденную тему. Чтобы помочь ребенку в усвоении пройденного материала, потребуется самому объяснить школьнику то, что ему не понятно. На помощь приходят родители, у которых моментально возникает вопрос: «Как объяснить ребенку деление?». Сделать это можно несколькими способами, но изначально стоит убедиться, что ребенок хорошо усвоил такие математические действия, как сложение, вычитание и умножение
.(Прочитать про способы обучения детей сложению и умножению можете и ).
Обучение ребенка основам деления
Важно, чтобы ребенок понимал суть такого математического действия, как деление. Для этого необходимо ему объяснить, что деление представляет собой разделение чего-либо на равные доли. Рекомендуется превратить процесс обучения в интересную игру, чтобы ребенок был сконцентрирован.
Деление в игровой форме
СОВЕТ: Таблицу деления так же важно выучить, как и таблицу умножения. Лучше это делать на каникулах!
Помогите ребенку понять, что деление — это обратное действие умножению.
Самым простым способом объяснить деление является проведение наглядной демонстрации разделения предметов на равные доли
. В качестве делимых предметов можно использовать все, что угодно, но желательно что-то интересное для ребенка. В качестве примера можно воспользоваться конфетами и игрушками.
Как объяснить ребенку деление при помощи игрушек?
Изначально нужно взять 2 конфеты и попросить ребенка разделить их между 2 плюшевыми игрушками. Благодаря такому простому примеру ребенок поймет суть математического деления. После этого можно переходить к более сложным примерам деления.
Как происходит деление, подробно и в игровой форме показывается в следующем видео:
Также вы можете взять коробку цветных карандашей, которая будет выступать одним целым, и предложить малышу разделить их между собой и вами поровну. После, попросите ребенка посчитать, сколько карандашей было вначале в коробке и сколько он смог раздать.
По мере понимания ребенка, родитель может увеличивать число предметов и количество участников задачи. Затем нужно рассказать, что не всегда получается разделить что-либо поровну и некоторые предметы иногда остаются «ничейными». К примеру, можно предложить разделить 9 яблок между бабушкой, дедушкой, папой и мамой. Ребенок должен понять, что все получат лишь по 2 яблока, а одно окажется в остатке.
Деление в игровой форме
Таким образом, вы объясните азы деления и подготовите ребенка к более сложным школьным задачам.
СОВЕТ: Старайтесь заниматься со своим ребенком в игровой форме. Тогда ему будет интересно заниматься, а значит, занятия пройдут весело и без особых усилий.
Также вам будет интересно и полезно распечатать таблицу деления в виде картинки.
Делить однозначные числа на однозначные проще всего с использованием . Для этого достаточно объяснить ребенку, что деление является действием обратным к умножению. Сделать это можно на любом правильном примере деления натуральных чисел.
Например:
2 умножить на 3 будет 6. Основываясь на данном примере продемонстрировать ребенку процесс деления. Следует действовать следующим образом: разделить 6 на любой множитель, например, на число 2. В ответе получится 3, то есть множитель неиспользованный при делении.
Таким способом можно делить многозначные (двухзначные) числа на однозначные.
Алгоритм деления в столбик
Прежде, чем начать объяснение деления в столбик, нужно рассказать ребенку о значении делимого, делителя и частного. В примере 20:4=5, 20 является делимым, 4 делителем, а 5 частным. У каждой отдельной цифры в примере одно наименование.
Многозначные числа (трехзначные и двухзначные) проще всего делить в столбик. Для этого нужно записать многозначные числа уголком.
Например, нужно разделить трехзначное число 369 на однозначное число 3.
В качестве делителя записано трехзначное число 369
, а в качестве делителя однозначное число 3. Первым делом важно объяснить ребенку, что деление в столбик происходит в несколько этапов:
- Определение части делимого подходящего для первичного деления. В данном случае цифра 3. 3:3=1. Цифру 1 нужно записать в графу частное.
- «Спустить» следующее делимое число. В данном случае это цифра 6. 6:3=2
. Полученное число 2 нужно записать в частное. - Далее необходимо «спустить» следующее делимое число 9. 9 делится без остатка на 3, полученный результат необходимо записать в частное. Результатом деления трехзначного числа 369 на 3 получается 123.
Деление десятичного числа на двухзначное проходит примерно так же. В случае с десятичным числом необходимо объяснить ребенку, что запятую в делителе переносят на столько знаков, на сколько перенесли в делимом. Далее следует обычное деление в столбик.
Необходимо предупредить ребенка о встречающихся случаях деления с остатком. В качестве примера можно поделить двухзначное число 26 на 5 столбиком. В результате остается остаток 1.
Важно после объяснения позволить ребенку самостоятельно решить несколько примеров, чтобы весь изученный материал надолго остался в памяти ребенка.
А еще Вы можете посмотреть видео, где все объясняют понятным языком.
И напоследок, не приучайте себя и ребенка пользоваться онлайн калькулятором, чтоб узнать, как разделить 145 на 9, 34 на 40, 100 на 4, 30 на 80, 416 на 52 и другие примеры. Это не принесет пользы не вам, ни ему.
В 1-ый класс идет не только ребенок – родители вместе с ним начинают и вместе с ним заканчивают образовательное учреждение. Учитель в школе не всегда успевает объяснить каждому отдельному ученику ту или иную дисциплину. Поэтому у — свои плюсы. Вы можете сами объяснить ребенку, индивидуально и не спеша то, что он не понял. В этот непростой период, главное — это набраться терпения и не ругать школьника из-за неправильных решений. Тогда все у вас получится.
Дети во 2-3 классе осваивают новое математическое действие – деление. Школьнику непросто вникнуть в суть данного математического действия, поэтому ему необходима помощь родителей. Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников. Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
1
Организуйте ребенку место для обучения в форме игры.
Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
2
Обучать математическому действию можно с помощью цифр.
Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
3
Дайте ребенку 6 груш.
Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
4
Расскажите ученику о делении с остатком.
Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.
Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел.
Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.
Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.
Обучение делению в столбик при помощи таблицы умножения
Ученики до 5 класса смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножениz.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
- Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
- Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5. А именно, результатом умножения.
- Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.
Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
- Напишите в тетради пример: 105 разделить на 5.
- Запишите это, как при делении в столбик.
- Расскажите, что 105 – делимое, а 5 – делитель.
- С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
- В столбике деления, под числом 5, напишите цифру 2.
- Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
- Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
- В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9,
затем переходить к 22, 44, 66
, а после к 232, 342, 345
, и так далее.
Обучение делению с остатком
Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
- Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
- Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
- Запишите под числом 35 число 32.
- Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.
Простые примеры для ребенка
На этом же примере можно продолжить:
- При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
- При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
- Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
- В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
- При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.
Обучение делению с помощью игр
Родители могут использовать игры на деление для обучения школьника. Можно дать ребенку раскраски, в которых нужно определить цвет карандаша путем деления. Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Картинка будет поделена на части, в которых будут результаты деления. А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5.
Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Обучение делению столбиком наименьшего числа на наибольшее
Деление данным методом предполагает, что частное будет начинаться с 0, а после него будет стоять запятая.
Чтобы ученик корректно усвоил полученную информацию, ему необходимо привести такого плана пример.
Как объяснить ребенку деление и умножение чисел
Искусство учиться
Как объяснить ребенку деление и умножение чисел
3 апреля 2018
56 924 просмотра
Лиана Хазиахметова
Далеко не все дети понимают деление и умножение с первого раза, поэтому родителям приходится дома подробнее разбирать эти процессы. Сегодня расскажем, как это сделать проще для ребенка. В книге «Как объяснить ребенку математику» объяснения строятся на визуальных принципах. Так школьнику будет понятнее, а родителю легче построить общение.
Умножение чисел
При умножении второе число показывает, сколько раз нужно сложить первое число с самим собой. На рисунке ниже в каждой шеренге стоят 13 человек, а всего шеренг 9. Чтобы подсчитать общее количество людей, нужно число 13 сложить само с собой 9 раз. Это и будет произведением чисел 13 на 9.
Иллюстрация из книги «Как объяснить ребенку математику»
Количество людей в шеренге (13) умножается на количество шеренг (9). Общее количество людей равно 117.
Не имеет значения, в каком порядке перемножаются числа: ответ будет одинаковым. Ниже показаны два способа, как можно вычислить произведение.
Некоторые числа легко умножать, зная особые приемы. Вот они.
Таблица из книги «Как объяснить ребенку математику»
В таблице показаны приемы быстрого умножения на 2, 5, 6, 9, 12 и 20.
Деление чисел
Деление позволяет найти, сколько раз одно число содержится в другом. Процесс деления можно представить, например, так: если 10 монет раздать 2 людям, то каждый получит по 5 монет. Или так: 10 монет, разложенные в стопки по 2 монеты, дадут 5 стопок.
Деление одного числа (делимого) на другое (делитель) показывает, сколько делителей содержится в делимом. Например, при делении 10 на 2 мы находим, сколько чисел 2 содержится в числе 10. Результат деления называется частным.
Деление как распределение. Из книги «Как объяснить ребенку математику»
Распределение чего-либо — это, по сути, операция деления. Так, если поровну распределить четыре конфеты между двумя людьми, у каждого из них будет по две конфеты.
Деление и умножение лучше рассматривать параллельно, чтобы ребенок увидел взаимосвязь. В книге «Как объяснить ребенку математику» есть объяснения более сложных операций, например, деления с остатком, умножения в столбик и так далее. Если визуально показать, как это делается, ребенку легче будет усвоить материал.
Рабочие тетради на деление и умножение
Если ваш ребенок освоил азы деления и умножения, то сейчас ему нужна практика. Японская система Kumon предлагает рабочие тетради «Математика. Деление. Уровень 4»
и «Математика. Умножение. Уровень 4». Постепенно, решая все более сложные задачи, ребенок научится работать с большими цифрами. Ниже — пример одного из последних заданий тетради с делениями.
Пример из тетради «Математика. Деление. Уровень 4»
Такие примеры ребенок научится решать легко и быстро, если тренироваться регулярно и по принципу от простого к сложному. Задания нужно усложнять постепенно, тогда школьник будет учиться с чувством «я могу!».
По материалам книги «Как объяснить ребенку математику», рабочих тетрадей «Математика. Деление. Уровень 4» и «Математика. Умножение. Уровень 4».
Обложка поста: pixabay.com
Как научить ребенка делить столбиком?
Конечно же, дети постигают азы математики на уроках в школе. Но не всегда малышу бывают понятны объяснения учителя. А может ребенок заболел и пропустил тему. В таких случаях родителям стоит вспомнить свои школьные годы, для того чтобы помочь ребенку не упустить важную информацию, без которой дальнейшее обучение будет нереально.
Учить ребенка делить столбиком начинают в третьем классе. К этому времени таблицей умножения школьник должен уже пользоваться с легкостью. Но если существуют с этим проблемы, стоит немедленно подтянуть знания, ведь перед тем, как научить ребенка делить столбиком, не должно возникать никаких сложностей с умножением.
Как научить делить столбиком?
Возьмем для примера трехзначное число 372 и поделим его на 6. Выбирайте любую комбинацию, но так, чтобы деление прошло без остатка. На первых порах это может запутать юного математика.
Записываем числа, разделяя их уголком, и поясняем ребенку, что данное большое число мы будем постепенно делить на шесть равных частей. Попробуем сначала разделить первую цифру 3 на 6.
Она не делится, а значит, добавляем вторую, то есть попробуем, получится ли поделить 37.
Необходимо спросить у ребенка сколько раз шестерка поместится в цифре 37. Тот, кто без проблем знает математику, сразу догадается, что методом подбора можно подобрать нужный множитель. Итак, давайте подбирать, возьмем, к примеру, 5 и умножим на 6 – получается 30, вроде бы результат недалеко от 37, но стоит попробовать еще раз. Для этого 6 множим на 6 – равно 36. Вот это нам подходит, и первая цифра частного уже найдена – записываем ее под делителем, за линией.
Число 36 записываем под 37 и при вычитании получаем единицу. Она опять не делится на 6, а значит, к ней сносим оставшуюся наверху двойку. Теперь число 12 очень легко разделить на 6. В результате получаем второе число частного – двойка. Наш результат деления будет 62.
Попробуйте на различных примерах, и ребенок быстро освоит это действие.
Учим школьника делению в столбик
Автор Administrator На чтение 2 мин. Опубликовано
Удивительное открытие сделала наша читательница. Ее сын на уроке не понял, как делить в столбик. Желая помочь сыну, она открыла учебник и увидела, что …ничего не увидела. Никаких пояснений к теме в книге почему-то не было. Как научить ребенка делению столбиком, если в книжке Вашего ребенка допущен подобный методический казус?
Удивительное открытие сделала наша читательница. Ее сын на уроке не понял, как делить в столбик. Желая помочь сыну, она открыла учебник и увидела, что …ничего не увидела. Никаких пояснений к теме в книге почему-то не было. Как научить ребенка делению столбиком, если в книжке Вашего ребенка допущен подобный методический казус?
Что нужно знать, что бы научиться делить
Математика не любит пропусков. Все знания должны быть крепкими, как кирпичики. Если ребенок не знает основ, с делением будет невероятно трудно. На что следует обратить внимание?
- Знает ли школьник название элементов при делении.
- Убедитесь, что ребенок не забыл таблицу умножения.
- Повторите разряды числа.
Приступаем к делению
Как научить ребенка делить столбиком, мы разберем на конкретных примерах. Следите за рассуждениями и будьте внимательны к цифрам.
465:5
Отделяем делимое от делителя скобкой-уголком.
Рассуждаем так: можно ли 4 разделить на 5? Нет, нельзя. Поэтому мы берем не 4, а 46. Вспомним таблицу умножения (можно взять распечатку), какое число в таблице умножения на 5 ближайшее к 46? – 45. Сколько раз 5 помещается в 45? – 9 раз. Подписываем 45 по 46, единицы под единицами, чтобы не запутаться. Девятку пишем «на полочке» – в уголке.
Если от 46 отнять 45, сколько получим? -1. Один меньше пяти? – меньше. Значит, мы разделили правильно.
Один на 5 не делится, сносим оставшееся число – 5, получаем 15. Пятнадцать делится на пять? — делится. Сколько получается? – 3. Тройку записываем в уголке. Проверяем решение: три умножить на 5, будет 15. Подписываем его под предыдущим числом. Из пятнадцати вычесть пятнадцать – будет ноль. Мы использовали все числа из делимого, значит, решили пример правильно.
В уголке мы записали две цифры – 9 и 3, получили число 93. Девяносто три – это частное, которое является решением нашего примера.
Объясняя школьнику, как научиться делить столбиком, выполняйте проверку обратным действием: 93*5. Кроме того, решайте более сложные варианты.
Есть и другие, частные случаи – о них Вы узнаете из программы. Если в учебнике действительно «ничего нет», возьмите за правило сверять решение с классной работой. Из классной тетрадки легко понять, каким методом пользуется учитель, и повторить его при объяснении домашней работы.
Эффективные альтернативы для длинного деления
Деление в столбик часто считается самой сложной математической концепцией для обучения. Если мы, как учителя, испытываем трудности с обучением делению в столбик, наши ученики наверняка будут бороться с его изучением.
Одна из основных причин того, что традиционное деление в столбик так трудно выучить, заключается в том, что правильный ответ зависит от запомненной последовательности шагов — делить, умножать, вычитать, уменьшать. Если ученик забывает, какой шаг и когда делать, очень высока вероятность того, что он получит неправильный ответ.
Вот почему ВАЖНО обучать стратегиям, а не шагам.
Стратегии поощряют НАСТОЯЩЕЕ ПОНИМАНИЕ. Это очень важная часть математики. Мы хотим, чтобы наши ученики действительно понимали, что они делают, и знали, что есть разные способы придумать правильный ответ.
В этой статье я рассмотрю три различных альтернативы традиционному делению в столбик. Я рекомендую вам сосредоточиться на первых двух, поскольку они очень сфокусированы на математике.
Готовы серьезно заняться обучением многозначному делению? Проверьте станцию Long Division ЗДЕСЬ.
Метод прямоугольников / площадей
Метод прямоугольников или модель области — это математический подход, который улучшает понимание чисел. Если вы планируете преподавать стратегию частичных коэффициентов (о которой я расскажу дальше), это отличный способ познакомить вас с ней.
Учащиеся решают уравнение путем вычитания кратных чисел, пока они не уменьшатся до 0 или как можно ближе к 0. Например, в приведенном ниже примере мы взяли 100 групп по 3, затем 50 групп по 3, а затем еще 1 группу из 3, чтобы в итоге получить 151 группу из 3, взятых из дивиденда.Пожалуйста, перейдите в ЭТОТ ПОЧТУ, чтобы получить очень подробное объяснение этой стратегии с изображениями.
Частичные частные
Частные частные — это стратегия, которой необходимо научить при многозначном делении. Если вы сначала обучите методу квадратов / квадратов, это будет вполне естественный прогресс.
Когда мы используем стратегию частных частных, мы составляем уравнение аналогично тому, как составляется традиционное уравнение длинного деления. Разница здесь в том, что мы убираем кратные делителя, пока не опускаемся до 0 или как можно ближе к 0.Пожалуйста, посмотрите ЭТОТ ПОЧТУ для очень подробного объяснения этой стратегии с большим количеством изображений.
Метод сетки
Метод сетки НЕ является подходом, основанным на ментальной математике. Это означает, что если у вас есть ученики, которые борются с многозначным делением, вам следует сосредоточиться на двух предыдущих стратегиях, которые я описал, а не переходить к этой. Сеточный метод можно использовать для студентов, которые готовы принять вызов, или в качестве введения, если вы планируете обучать традиционному делению в столбик.Некоторые ученики найдут сетку очень полезной для организации их мышления.
Когда мы используем метод сетки, мы просто организуем цифры из уравнения в сетку. Полное, подробное объяснение того, как использовать метод сетки, а также множество изображений, см. В ЭТОЙ публикации в блоге.
СЛЕДУЮЩИЕ ДЕЙСТВИЯ:
35 Привлечение преподавателей Подразделение
Division обычно является последней из четырех основных функций, которыми занимаются дети, и это не всегда легко.Эти игры и задания предоставляют множество увлекательных способов сделать обучение более эффективным и увлекательным. Они все тоже бесплатные! Ознакомьтесь с ними и добавьте несколько в свои планы уроков по математике.
(WeAreTeachers получает несколько центов, когда вы совершаете покупку по нашим ссылкам, бесплатно для вас. Спасибо за вашу поддержку!)
1. Ввести разделение как разделение
Когда доходит до дела, разве разделение на самом деле не просто совместное использование? Сыграйте в эту простую игру, в которой дети кидают кубики и делят помпонные вишни как можно равнее.Это отличное начало для обучения разделению.
Подробнее: JDaniel4’s Mom
2. Продолжить обучение делению, прочитав одну-две книги.
Дети никогда не слишком стары для рассказов. Эти умные книги — идеальная отправная точка для обучения разделению, особенно если у вас есть дети, которые используют фишки, такие как помпоны, чтобы разыграть историю по ходу дела.
3. Сделайте диаграммы привязки деления для поддержки обучения
Держите диаграммы привязок под рукой, пока вы преподаете дивизион, чтобы студенты могли легко справиться с трудностями.Используйте эти диаграммы для вдохновения:
4. Практикуйте разделение с помощью Wrap-Ups
Эта игра на деление — забавная альтернатива дидактическим карточкам. Дети обматывают нитью карточки от задачи слева до ответа справа. Затем они переворачивают карточку, чтобы убедиться, что они правы. Купите ключи от подразделения Learning Wrap Ups здесь.
5. Попробуйте обучить делению с помощью кубиков LEGO
Посмотрите это видео, чтобы узнать, как легко познакомить учащихся с концепцией деления с помощью неизменно популярных кубиков LEGO.(Здесь можно найти больше математических идей LEGO.)
6. Разложите мармелад в картонной коробке для яиц
.
По мере того, как вы прокладываете путь к пониманию деления, попробуйте упражнения, в которых дети делят большие группы предметов на более мелкие равные группы. Желейные бобы в картонной упаковке для яиц — отличный способ сделать это.
Подробнее: блог Homeschool
7. Учись с лакричными нитками и кеглями
Дети всегда любят математические игры, которые можно съесть в конце! Раздайте нитки солодки и миску кегли и используйте их для урока деления.
Подробнее: рассказы извне
8. Работа над различными стратегиями деления
Для детей, которые действительно борются с этой концепцией, попробуйте научить стратегии деления, используя этот бесплатный коврик для печати. Это дает им множество способов решения проблем разделения.
Подробнее: Обучение с Дженнифер Финдли
9. Раскол за разделение фактов
Призываю всех любителей спорта! Возьмите эту бесплатную распечатанную игру бейсбольного дивизиона и бросьте кости, соревнуясь, чтобы узнать, кто из них добьется успеха.
Подробнее: 123Homeschool4Me
10. Сделать разделение цветочных учебных пособий
Важной частью обучения делению является усвоение основных фактов деления. Эти милые цветы дают детям красочный способ проверить себя.
Подробнее: Семья учимся вместе
11. Собирайте пазлы для мороженого
Соберите эти бесплатные распечатанные головоломки с эскимо по ссылке ниже, чтобы дать детям еще один увлекательный способ попрактиковаться в фактах деления.(Кроме того, здесь вы найдете больше способов использовать деревянные палочки для поделок в классе.)
Подробнее: 123Homeschool4Me
12. Ловите рыбу и делите факты
Сделайте «Go Fish» дополнительным вращением! Вместо того, чтобы искать совпадающие пары, игроки соревнуются, чтобы найти пары карт, которые равномерно делятся друг на друга. Например, в показанной руке игрок может сложить 8 и 2, потому что они делятся, чтобы получить 4.
Подробнее: Cuppa Cocoa
13. Выиграйте гонку по фактам дивизиона
Если у вас есть корзина с игрушечными машинками, эта тренировочная игра на деление создана для вас.Скачайте бесплатные распечатки и узнайте, как играть, по ссылке.
Узнать больше: Обманчиво образовательный
14. Соберите пазлы «Звезда деления»
Эти милые головоломки со звездами обманчиво сложны! Думайте о них как о домино для дивизиона . Получите бесплатный полный комплект для печати по ссылке.
Подробнее: обучающие приключения Ходзё
15. Сразитесь с драконом дивизии
Заточите свой меч и приготовьтесь к завершению рыцарского квеста! Эта бесплатная игра для печати — еще один увлекательный способ попрактиковаться в разделении.
Подробнее: 123Homeschool4Me
16. Сверните на Jenga
Как весело использовать Jenga в классе! Создайте набор карточек с фактами о разделении, используя цветную бумагу, соответствующую цветам блоков Jenga. Дети выбирают карточку, отвечают на вопрос, а затем пытаются удалить блок этого цвета из стопки.
Подробнее: Жизнь между летом
17. Сыграйте в настольную игру с монстрами
Возьмите эту бесплатную доску для печати, чтобы дать вашим ученикам возможность попрактиковаться в делении на троек.Если понравится, остальные доступны для покупки.
Подробнее: памятка учителя
18. Сверните и напишите числовые предложения
Игральные кости — отличный инструмент для обучения предложениям с числами с делением. Дети просто бросают два кубика, а затем пишут для них числовые предложения умножения и деления. (Совет: попробуйте использовать игральные кости, чтобы увеличить веселье. Вот и другие забавные игры в кости!)
Подробнее: Math Geek Mama
19. Напишите комнату для практики разделения фактов
Напишите, что занятия в комнате заставляют детей подниматься и двигаться, что отлично подходит для обучения.Повесьте эти бесплатные карточки для печати по комнате, затем раздайте детям буфер обмена и лист для ответов и отправьте их, чтобы найти и решить факты разделения.
Узнайте больше: Заядлый учитель
20. Решите квадратную головоломку деления
Эти загадочные квадраты заставляют детей вводить правильные числа, поскольку они пытаются создать задачу деления, которая работает во всех направлениях. Скачайте распечатку по ссылке.
Подробнее: Education.com
21.Крутить и делить
Эти бесплатные печатные формы предлагают еще один способ попрактиковаться в фактах деления. Используйте карандаш и скрепку, чтобы сделать вертушку.
Подробнее: 3 динозавра
22. Draw Equation Maker игры
В первом блоке напишите серию дивидендов. Напишите делители во втором блоке, а частные — в третьем. Дети используют маркеры, чтобы закрыть числа, составляющие правильное уравнение.
Подробнее: Веселые игры 4 Обучение
23.Решите, используя McDonald’s Serve Burgers? метод
Когда вы начинаете заниматься делением в столбик, вы можете использовать множество методов. Один из популярных вариантов — это тот, который дает детям возможность запомнить шаги: делить, умножать, вычитать и уменьшать.
Подробнее: Бриттани Нолл-Купер / Pinterest
24. Раскладываем игральные карты в длинную позицию
Вот забавная практическая игра на деление чисел в столбик, в которой используется колода игральных карт.Вы можете начать с уравнений, которые не требуют остатков, а затем усложнять их по мере развития детей.
25. Работа над разделением фактов по треугольным карточкам
Карточки с треугольниками — это простой инструмент для обучения делению и умножению. Вы закрываете рукой один угол, затем делите, если цвета не совпадают, или умножаете, если они совпадают. Вы можете сделать набор самостоятельно или купить их на Amazon здесь.
26. Отправляйтесь на поиски сокровищ
С картой сокровищ все немного веселее! Учащиеся решают уравнения и вычеркивают ответы, пока не останется только одно число — X отмечает точку!
Подробнее: Образование.com
27. Используйте стадную игру для обучения делению с остатками
Когда дети думают, что у них все выяснено, приходят остатки! Обучение делению с остатками может быть одной из самых сложных задач, поэтому начните с этой веселой и активной игры. В каждом раунде учитель вызывает ученикам разные группы животных («Сформируйте стада из 5 слонов!»). Все оставшиеся студенты, которые не вписываются в группу, помещаются в «загон для хранения», вводя идею остатков.
Подробнее: The Teacher Studio
28. Смотрите остатки в реальной жизни с помощью файлов cookie
Купите пару пакетов печенья и попросите свой класс найти лучший способ разделить их честно. Подумайте, можно ли разделить оставшиеся файлы cookie, чтобы добавить фракции в смесь. А теперь интересная математика!
Подробнее: The Teacher Studio
29. Превратите остатки в хорошее дело
Сделайте обучение оставшимся более увлекательным с этой игрой, которая сделает их самыми желанными! Цель каждого раунда — получить наивысшее напоминание.Вам понадобятся кости, фишки и бесплатные таблицы для печати, которые можно найти по ссылке.
Подробнее: Учитель-скаут для мамы
30. Научитесь играть в Damult Dice Division
Возьмите три кубика, карандаш и бумагу для этой стратегической игры, названной в честь учителя, который ее изобрел. Бросьте три кубика и определите задачу деления, которая дает вам максимально возможное частное (округленное до ближайшего целого числа). Вы получаете 10 бонусных баллов, если не осталось остатка!
Подробнее: Math for Love
31.Создать дом отдела
Вот такой креативный способ обучения делению! Дети отвечают на ряд вопросов, чтобы определить характеристики своего «жилого дома». Например, чтобы определить количество окон в доме, ученики должны разделить день месяца, в котором они родились, на количество детей в их семье. Когда они закончили с математикой, пришло время нарисовать свой дом!
Подробнее: Обучение с видом на горы
32. Бейсбол для длинных дивизионов
Эта игра с долгим делением требует небольшой стратегии, так как дети бросают кости и пытаются создавать задачи, которые дают им максимально возможное частное на каждом ходу.Неправильный ответ считается предупреждением, поэтому будьте осторожны! Узнайте, как играть, и получите бесплатные печатные издания по ссылке.
Подробнее: математика у вас есть
33. Усыновление и уход за домашними животными
Добавьте эту супер-милую игру в свой шкаф на черный день, и дети будут учиться и практиковать разделение, даже не осознавая этого! Получите его на Amazon здесь.
34. Раздайте игровые деньги, чтобы сделать обучение более значимым
Денежные мероприятия всегда привлекают внимание детей, потому что они знают, что когда-нибудь смогут ими воспользоваться в реальном мире.Вытащите свою стопку игровых денег и узнайте, как использовать ее для обучения делению, по ссылке.
Узнать больше: Закрой дверь и научи
35. Используйте Bingo для обучения делению на дроби
Деление и дроби идут рука об руку. Эта бесплатная игра-бинго для печати помогает детям понять связь между ними.
Подробнее: Math Geek Mama
Любите эти занятия? Вы также захотите ознакомиться с нашим обзором упражнений на умножение.
Plus, узнайте, как другие учителя решают проблему умножения, и спросите совета в группе ПОМОЩЬ WeAreTeachers на Facebook.
Проблемы с длинным разделением — Living Math
Проблемы с длинным разделением могут стать ведущей для наиболее часто обсуждаемой темы в списке рассылки LivingMathForum . Это подборка сообщений, связанных с несколькими темами о борьбе за деление столбцов, опубликованных на форуме.
Вопрос Написан: Мой 10-летний мальчик только начал учиться в длинном делении в школе и проиграл.Он может выполнить эти шаги с большой помощью, но он «не понимает». Я разбил дивиденды, и он видит их лучше, но не полностью.
Есть ли другие способы объяснить это, кроме стандартного школьного объяснения? Что-нибудь вроде решеточного метода умножения — он действительно взлетел с этого и со временем смог приспособиться к «стандартному способу».
Спасибо, Дж.
Ответы [LivingMathForum] моему сыну проблемы с длинным делением
Моя младшая дочь выучила то, что мы назвали делением «Разбейте», потому что она ненавидела метод деления в столбик (я считаю, что это называется методом частичных частных, но не «цитируйте» меня по этому поводу; o).Она просто «разбила» число на части, которые легко можно было разделить делителем. Например, 1757/15 может быть:
1500/15 = 100 Что останется после того, как этот кусок отломится? 257
150/15 = 10 Что останется после того, как этот кусок отломится? 107
75/15 = 5 Что останется после того, как этот кусок отломится? 32
30/15 = 2
Оставшиеся 2 — это остаток
Складываем 100, 10, 5 и 2 вместе, и получаем 117, R2.
Это облегчает выполнение мысленных математических навыков, ребенок отламывает части, которые он / она может легко разделить.Я бы, например, разделил 105, когда осталось 107, но моя дочь видит, что 75 составляет половину от 150, поэтому она отламывает этот кусок, так как ей легко увидеть 15 раз в пять раз. Для нее это просто хорошо работает.
Это один ресурс, который был разослан:
http://escholarship.bc.edu/cgi/viewcontent.cgi?article=1135&context=education/tecplus
Julie
Re: У моего сына проблемы с делением чисел в столбик
Я очень чувствую вашу боль — у меня 4 мальчика — все действительно математические, но деление в столбик медленное и скучное (их слова) —
Я не уверен, есть ли у этого метода название или нет — но мои сыновья назовите это коротким делением — вы пишете задачу, как обычно, скажем, 531/4 — задаете вопрос, какое x 4 приближает вас к 5 — ответ, конечно же, 1 — спросите с каким остатком? Ответ, конечно, если 1 — напишите маленькую 1 перед 3, как если бы вы брали взаймы или носили, а затем начните процесс заново с того, что умножение на 4 приблизит вас к 13 — 3 с остатком 1 — напишите маленькую 1 рядом с 1 — то, что умножает на 4, приближает вас к 11 — 2 с остатком 3.Это может не иметь никакого смысла, поскольку это трудно описать в электронном письме, но вместо того, чтобы идти вниз по столбцу, вы просто записываете «остатки» в исходной задаче. Это действительно помогло моим сыновьям, ПОТОМУ ЧТО я понял, что их главная проблема заключалась в том, что они слишком много делали и не понимали, что им делать дальше. Концептуально они получают деление, но у меня возникли вопросы типа «зачем мне записывать задачу на вычитание, когда я делаю деление?».
Мы используем Сингапур, и нам это нравится — их научили с помощью своих математических методов делать это в уме, если это возможно, и метод «короткого деления» действительно помогает им визуализировать это, а не делать все обозначения.
S
Re: У моего сына проблемы с длинным делением
Я любил Double Divison для себя … это имело гораздо больше смысла! Но никому из моих мальчиков это не понравилось. Я подумал, что им это понравится, так как они оба любят решеточное умножение.
Иногда сложно понять, что сработает, а что нет. Но мне нравится, что я изучаю новые методы; это помогает мне понять столько математики, которую я просто не понимал, когда учился в старшей школе и колледже.
Энджи
Re: У моего сына проблемы с длинным делением
Это единственный способ, которым мы смогли пройти через длинное деление.
http://www.kidsnumbers.com/long-division.php
Это действительно СКУЧНАЯ игра, но мой сын по крайней мере перестал корчиться на полу. Он учит делению в столбик, просто запомнив алгоритм наизусть. Не уверен, что в то время происходило какое-то настоящее обучение, но я думаю, что сейчас это может показаться ему интересным.
Re: [LivingMathForum] Справка по длинным разделам
Есть как хорошие способы разбить разделение на фазы, чтобы то, что действительно происходит, стало более очевидным, так и альтернативные алгоритмы, включающие оценку, частные частные и т. Д.И, конечно же, эти двое тесно связаны.
Рассмотрим простую задачу деления, например 54 / 6.
Попросите вашего сына несколько раз вычесть 6 из 54, отслеживая количество вычитаний, пока у него не останется 0 или менее 6. Это число, конечно, является частным, и в этом случае он сможет сделать это 9 раз, и у него останется 0, следовательно, ответ — 9 r. 0
Сделайте другой пример (скажем, 55/7), где есть остаток, чтобы убедиться, что он понимает, почему, и какие два числа он заканчивает (7 р.6) действительно имею в виду. Убедитесь, что он может «доказать» свою правоту, умножив 7 * 7 и прибавив 6, чтобы получить 55, дивиденд.
(Конечно, вы можете использовать другие примеры, меньшие числа, физические модели с чипами или пластмассовых медведей или все, что вам подходит и вашему сыну).
Затем попросите его сделать что-нибудь вроде 132/33, чтобы понять, что мы можем вычитать большие числа. Но мы сохраняем управляемый коэффициент, в данном случае он равен 4.
Затем перейдите к чему-то «не так управляемому, как 1242/54».Это не странно, но многократное вычитание 54 из 1242 занимает 23 шага. 2 = 100 и умножим это на 54, мы получим 5400, что уже слишком много.1 x 54 или, более компактно, 2 x 10 x 54, или наиболее компактно, 20 x 54 = 1080. Но на самом деле мы ПИШЕМ 2 x 54 = 108, записываем 108 под 124 в делимом и вычитаем. Это одно из мест, где возникает настоящая путаница. Мы «прячем» в нотации то, что на самом деле происходит, потому что числовое значение тайно работает в этом «сжатом» или «компактном» алгоритме.
Как сделать так, чтобы дети это увидели? Пусть они выпишут ПОЛНОЕ умножение и поймут, что 2 на самом деле представляет 20, и что полный частичный продукт, который мы вычитаем из частного, является реальным не 108, а 1080, и они должны иметь привычку записывать этот дополнительный 0.От этого не может быть никакого вреда.
Оттуда мы вычитаем, как было предложено ранее, и получаем остаток 162.
(обратите внимание, что при традиционном подходе у нас будет остаток 16 и «сбить 2», но это совершенно загадочный и механический шаг. Написав этот конечный ноль, это ОЧЕВИДНО (вроде), что происходит: 20 x 54 = 1080, и когда мы вычитаем это из исходного дивиденда, у нас остается 162. Это 16 действительно 160, а затем мы возьмите оставшиеся 2 и сложите их, чтобы получить 162.0 (следующая наименьшая степень из 10), которая равна 1, умноженной на 54. Можем ли мы сделать это кратным? Да, ровно 3 раза по 54. Получается ровно 162, которые мы вычитаем из оставшихся 162, чтобы получить остаток 0. Наше частное равно 23. Но это 20 групп по 54 + 3 группы по 54, что составляет 1242.
Опять же, проверка с умножением.
Я бы не стал вдаваться в экспоненту со степенью 10, но ученик должен уметь вычислять числа в единицах 1, 10, 100, 1000 и т. Д. В обратном порядке, умножая на делитель, а затем посмотрите, какая мощность является наибольшей, которую он / она может использовать, а затем проверьте, есть ли значения, кратные от 1 до 9 этого результата, которые не будут слишком большими, чтобы вычесть из того, что осталось.
Если это сбивает с толку, и без диаграмм это вполне может быть, мои извинения. Но это действительно то, что происходит в нашем стандартном алгоритме деления в столбик.
Давайте возьмем ту же задачу с «более свободным» подходом: ученик может посмотреть на 1242 умножить на 54 и оценить, что 100 x 12 = 1200, поэтому 50 x 24 также должно равняться 1200. Это не слишком много, поэтому мы вычитаем 1200 из 1242, оставляя 42. Но нам все равно нужно умножить 50 на 3 = 150, что больше 42. Итак, 24 слишком велико для нашего первоначального частного.Учащийся может опуститься на 1 или около того, или может опуститься до 40, или может использовать множество других стратегий, но любая из них может привести к правильному решению, если отдельные арифметические шаги верны, а ученик отслеживает частные частные, продукты и остатки.
Другой ученик мог бы быть не таким смелым и использовал бы группы 10 или 20 x 54, но это нормально. Дело в том, чтобы уменьшить количество шагов от максимального, которое составляет 23 отдельных вычитания из 54, и чем ближе мы подойдем к тому, чтобы в основном потребовались только ДВА шага, как в первом подходе, тем лучше.Но, на мой взгляд, точность и понимание стоят того, чтобы немного пожертвовать скоростью.
M.
Re: Long Division Help
Я преподаю математику в шестом классе, и когда ученики делят на 2-значные числа, они часто сталкиваются с трудностями.
Глядя на задачу 1242/54 я предлагаю студенту округлить число до ближайшего 10 …. 1240/60 … округление в большую сторону дает студенту возможность оценить первое число для умножения … 1240/60 (что также совпадает с 120/6) дает им 20…. затем они могут продолжить исходный вопрос: умножить 54 x20 (1080), а затем вычесть 1240-1080 (160) и продолжить оттуда.
M.
RE: [LivingMathForum] Long Division Help
Моя дочь, которая, как мне казалось, понимала это, продемонстрировала мне несколько дней назад, что она просто выполняла шаги, не понимая этого, когда мы решали сингапурскую математическую задачу. это требовало разделения. Я ХОЧУ, чтобы у меня был такой простой метод, как метод решетки для умножения, мои дети любят этот метод.
Однако я понял, что мы могли бы сделать нечто подобное с форматом длинного деления, если бы проявили творческий подход в понимании того, что нам нравится в методе решетки. Что ж, нам понравилось, что процесс был структурирован, и вы почти не могли ошибиться. Вы можете выполнять разные операции в другом порядке, и это не повлияет на ответ. Было эстетично: о). Это то, что мы придумали за последние пару дней.
По проблеме, которую она уже начала и с которой у нее возникли проблемы, я показал цветными карандашами, что происходит, сопоставив цвета с результатами.Раньше она не осознавала того факта, что это может быть бесконечный процесс. Она попросила меня составить более длинную задачу и показать ей, как это работает, а затем продолжала просить меня добавлять цифры. Опять же, я сделал своего рода «решетку» деления, показывая каждый шаг, и попросил ее устно рассказывать мне каждый шаг по мере нашего продвижения. Вы можете увидеть, что мы создали здесь: http://ph.groups.yahoo.com/group/LivingMathForum/photos/view/58f3?b=1, после чего она получила ответ на свой вопрос в сингапурской книге (это » 344 «часть).
Затем она попросила меня сделать для нее сверхдлинную задачу и помочь ей выполнить «решетку деления». Это на этой фотографии: http://ph.groups.yahoo.com/group/LivingMathForum/photos/view/58f3?b=2 Она сделала всю математику за два занятия после перерыва между ними: o). Дело в том, что это показало ей, что каждый шаг процесса имеет определенное начало и конец, которые она могла * видеть *. Что-то в цветовой блокировке заставило ее прижиться. Теперь, если она захочет, мы можем создать решетку до того, как она поместит все «данные», точно так же, как при решеточном умножении.Сегодня мы сделали один, в котором мы раскрашиваем заблокированные области перед их заполнением. Но после этого раза ей это больше не понадобилось (для этого нужно приложить гораздо больше усилий). Она явно видела, насколько важно было выровнять вещи с блокировкой, это ее пунктирные линии, идущие вниз.
Обратите внимание, что это был метод — она действительно понимала деление, но не могла найти способа решать длинные задачи, отслеживая шаги. Если твердого понимания того, что такое деление, нет, я бы вернулся к конкретным представлениям, таким как разделение блоков с остатками и без них.
Она понимала, что если бы у нее был нулевой остаток, она могла бы просто перенести следующее число, но она не хотела изменять симметрию своих блоков, поэтому она просто сделала нулевые шаги без этого ярлыка.
У нее есть тетрадь по математике, и когда она что-то забывает, она бежит к блокноту за лучшими наглядными примерами вещей, так что теперь это занесено в ее тетрадь по математике, чтобы вспомнить, если она снова забудет этот процесс. На днях мы решали некоторые задачи со словами, связанные с преобразованием рецептов, и она пыталась запомнить преобразование дробей, например, две четверти равны четырем восьмым, но мы выполнили упражнение, в котором раскрасили миллиметровку в половину, четверть, восьмые, шестнадцатые. , и 32-е, и просто глядя на это полностью освежило ее память об этих.
Не знаю, откликнется ваш сын на эту идею или нет. Для нас, поскольку это было камнем преткновения, я отложил книгу о Сингапуре, и мы просто сосредоточились на процессе в течение пары дней. Обычно они не могут этого сделать в школе, если весь класс не борется с трудностями, так что это занятие после школы. Если у вас хорошие рабочие отношения с сыном, и ему нравится визуальный эффект от этого, это может помочь, это имело большое значение для моей дочери.
Julie
Re: [LivingMathForum] Справка по длинным разделам
С математической точки зрения я не вижу, чтобы это что-то добавляло, и, как и при решеточном умножении, есть опасность ошибочно принять эффективный инструмент организации, используемый как черный ящик для метод, который способствует пониманию.
Вы должны сделать выбор: заботитесь ли вы о том, понимают ли дети, почему работают алгоритмы с длинным делением, или достаточно, чтобы они могли выполнить процесс и получить правильный ответ? В последнем случае консерваторы в области образования будут атаковать ваш метод как бесполезный и излишне трудоемкий (по крайней мере, те, кто атакует решеточное умножение таким образом, скорее всего, так поступят). Если первое, то я буду критиковать этот метод как неспособный добавить концептуального понимания, точно так же, как решеточное умножение, как его преподают во многих классах, не может добавить такого понимания.
Вы хотите быть уверены, что метод не окажется чем-то большим, чем «изящный трюк». См. Мой блог (rationalmathed.blogspot.com) для комментариев об ошибке обучения решетчатому умножению как черному ящику. На мой взгляд, математику нельзя преподавать как черные ящики, но это так часто, что это действительно вредно для детей.
M.
RE: [LivingMathForum] Long Division Help
M., вы совершенно правы. Я разместил это, ожидая, что он будет использоваться так, как я его использовал — в настройке контакта один на один с ребенком, когда родитель / наставник отслеживает весь процесс и адаптирует его к ребенку.Это был творческий процесс, который развивался по мере того, как я знаю свою дочь, что привлекает / мотивирует / побуждает ее запоминать и вовлекать, и с этой целью он хорошо работает для нее. Это идея для родителей — если она не подходит отдельному ребенку, попробуйте что-то другое. Это совсем другой подход, чем обучение в классе, потому что у вас есть полная гибкость, чтобы приспосабливаться к сигналам вашего ребенка о понимании или его отсутствии. Если вы когда-нибудь найдете время, чтобы просмотреть здесь заархивированные обсуждения, вы увидите, что здесь предлагаются перспективные идеи.
Все, что я делаю со своей дочерью, направлено на процесс и понимание, а не на продукт и получение только «правильных» ответов. Она выбирает метод решетки в качестве предпочтительного метода после изучения трех различных методов. Но даже когда мы прорабатываем Сингапур и математику для начальных классов Закарро, она рассматривает каждую задачу в поисках лучшей стратегии ее решения, заручившись моей помощью и отзывами по мере необходимости.
Например, в задаче о словах, включающей умножение 59 на 12, она не использует решетку.Она складывает произведения 59 на 10 и 59 на 2, потому что она видит, что умножение на 10 и удвоение намного проще, чем создание решетки. Она также понимает, что это именно то, что она делает, если применяет метод решетки, который она резервирует только для более длинных задач умножения, которые она не может разбить другими способами, и точно так же не имеет значения, умножит ли она сначала 59 на 10. , или на 2, если она делает и то, и другое, и добавляет оба, она получает правильный ответ. Мой средний сын, который действительно удивляет меня своей легкостью в прохождении формального курса алгебры, имел похожие пристрастия.Здесь нет черных ящиков, хотя я определенно вижу опасность того, что ребенок может видеть это таким, если все, чему их учат, — это процесс.
Моя дочь творческая личность, и ее мотивирует эстетика. Мы выполнили много художественных и математических проектов, которые она сохраняет в своей записной книжке, и самые наглядные и красочные проекты, которые она создала самостоятельно, — это те, которые, казалось, были теми вещами, которые способствуют продолжительному обучению, и на которые она ссылается . Это было то, что натолкнуло меня на мысль, а не то, что это было универсальное решение для обучения любого ребенка делению в столбик.
Для моей дочери бокс был тем, что заставило ее увидеть регулярность процесса; до этого она терялась в море чисел, когда дошла до третьей или четвертой цифры. Когда мы обсуждали меньшую проблему, она поняла, что делит не три на десять, а три на десять сотен. Но она, казалось, не понимала, что падение было в следующем месте, пока мы не повторяли это снова и снова. Повторяющаяся задача, которую она специально просила, чтобы я поставил для нее, и к которой она попросила меня добавить цифры даже после того, как она закончила исходную задачу, полностью вовлекла ее в процесс.Она сама повторила цветную коробку только один раз, и с тех пор, похоже, она больше не нуждается в коробках и даже не хочет их. Поэтому я рассматриваю это упражнение как нечто похожее на то, что я делаю в своей домашней работе, когда я раскрашиваю и копирую вещи таким образом, чтобы облегчить то, что я хочу понять и запомнить.
Я увидел, что потратив время на это с ней, я добился нескольких целей. Повторение процесса помогло ей вспомнить, где мы поместили элементы процесса, которые раньше ей было трудно запомнить.Она могла бы сделать это, выполняя страницы практических задач, но это было для нее гораздо интереснее. До этого она придумывала остатки в своей голове и иногда совершала ошибки — показывая вычитание, она могла видеть, где она ошибалась. Это * мотивировало * ее практиковать, и для меня это большой плюс. Она довольно легко может решать более короткие задачи деления в уме, и у нее хорошая голова для мысленной математики, поэтому она, как правило, не практиковала подобный алгоритм добровольно, пока не увидит причину этого или не станет достаточно опытным в этом, чтобы можете наслаждаться процессом.И тот факт, что я был готов сидеть с ней и работать с ней столько, сколько ей нужно, чтобы понять процесс, много для нее значил. Я не ожидал, что она «получит это» в срок.
В нашей домашней образовательной среде, которая отличается от классной комнаты, я позволяю своим детям рассматривать обучение как что-то, что происходит постоянно, и что мы (то есть мы с ребенком работаем вместе) можем выбирать, как, когда и с чем материалы, которые они изучают. Вы можете использовать все, что работает, и вам не нужно беспокоиться о том, что каждая база покрыта с точки зрения предлагаемого обучения и учебной программы, потому что все, что вы делаете, — это предоставляете им * необходимое * на основе ваших наблюдений за тем, что у них есть. уже выучили или эффективно обучаются сами.Это, конечно, нелегко повторить в классе, учитель должен выбрать то, что он / она считает лучшим представлением концепций группе в целом.
Моя цель — постепенно подтолкнуть моих детей к тому, чтобы они взяли на себя полную ответственность за свое собственное образование, и многие домашние школьники ставят эту цель для детей намного моложе, чем обычно бывает после окончания средней школы. Поэтому большая часть моих усилий направлена на то, чтобы помочь моим детям научиться использовать ресурсы, чтобы учиться, находить приятные способы обучения и — что, вероятно, больше всего отличается от ситуаций в классе — участвовать в оценке эффективности материалов и процессов. и время соответствует их собственному процессу обучения, используя эту совместную обратную связь для внесения изменений в материалы, процессы или сроки по своему усмотрению.Это был пример моей дочери, и я осознал, что объяснения в ее книге и мои объяснения были неадекватными, и наша дальнейшая совместная работа, чтобы сделать эти идеи понятными для нее. Затем, когда мы с дочерью проводим такие сеансы, и она файлы работают таким образом в своей папке, чтобы обратиться к ней позже, это имеет для нее долговременную пользу, поэтому мы считаем это ценным, даже если это может не сработать. для других детей. Обучая группы от 15 до 20 или более человек одновременно, я понимаю, насколько этот подход отличается от обучения в классе.
Для меня ценность облегчения обучения ребенка уникальным для него способом является основной причиной, по которой мы обучаем на дому. Это воспитывает у моих детей отношение к обучению в режиме 24/7. Сегодня я пришла домой с детского урока боевых искусств, села за наш кухонный стол с чашкой кофе, чтобы поговорить с мужем, а моя 7-1 / 2-летняя взобралась ко мне на колени со своим сингапурским учебником по математике и начала рабочие проблемы, пока мы разговаривали. Она посмотрела на меня, чтобы высказать свое мнение о ее ответах на некоторые проблемы со словами, и примерно через 20 минут отложила рабочую тетрадь, чтобы прочитать — это был субботний день, менталитета «школьные часы» не существует.Отношение моих детей к обучению развивается самостоятельно, и моя цель — быть рядом, когда им понадобится помощь, предоставить им все необходимые материалы, поддержку, содействие и обучение, когда они в этом нуждаются. Это способ взглянуть на образование, который мы развили в течение почти 11 лет домашнего обучения, который действительно хорошо работает для нас.
Именно с этой точки зрения предлагается все, что я предлагаю, если не указано иное, например, идеи для совместного обучения на дому не будут предлагаться таким же образом.
Julie
Re: [LivingMathForum] Long Division Help
Я заинтересован в том, чтобы предложить помощь всем, кто заинтересован в более глубоком изучении того, как работают наши «стандартные» алгоритмы, и в предоставлении функциональных возможностей (не в техническом смысле), а чем исторический взгляд на то, как развивались эти алгоритмы. То есть, мы легко можем представить, что умножение происходит из желания более быстрого повторного сложения, а это деление возникло из желания более быстрого повторного вычитания (и это возведение в степень происходит из желания более быстрого повторного умножения).2). Поэтому вы можете вычесть последовательные нечетные целые числа из идеального квадрата, чтобы найти его квадратный корень. Конечно, если бы вы знали квадратный корень заранее, вы могли бы сделать это по-другому, но тогда вам не понадобился бы алгоритм.
Что меня интересует во всем вышеперечисленном, так это проблема уплотнения и потери информации. Когда мы используем любой из «стандартных алгоритмов» для умножения или деления, например, мы уплотняем процесс нижней операции, группируя и используя разряды (отсюда сдвиг влево каждого частичного произведения в «длинном умножении» и вправо-сдвиг / опускание в столбик).Как только вы поймете, что происходит, вам не нужно об этом думать, и вы просто разовьете определенный уровень автоматизма. Только если вы запутались или забываете алгоритм (или проявляете интеллектуальное любопытство), необходимо вникать в самую суть процедуры. Затем вам нужно восстановить утерянную информацию, потерянную из-за сжатия и «предполагаемого» значения разряда. Дети сходят с ума от этих алгоритмов по множеству причин, но я считаю, что сдвиг — один из самых больших «черных ящиков» в обоих алгоритмах.Его обучают как магическому правилу, а не как смысл. И я считаю, что чем больше мы позволяем ученикам думать о математике как о магической, а не о разумной, тем больший ущерб мы наносим, по крайней мере, потенциально.
Итак, для учителей начальных классов и родителей, обучающихся на дому, я настоятельно рекомендую смысловую математику вместо процедурной математики. Родители, которые никогда не любили математику и не разбирались в ней, могут удивиться тому, насколько она может иметь смысл. И когда ребенок подходит к математике с этой точки зрения, я считаю, что он / она всегда будет хотеть задавать хорошие вопросы, всегда будет требовать понимания, а не простой возможности, и у него будет меньше трудностей при решении сложных задач и идей.
Но это просто МОЯ вера, и я не могу никому сказать, что он или она ДОЛЖНЫ делать. И я бы не хотел оказаться в таком положении.
M.
RE: [LivingMathForum] Long Division Help
В частности, на этом форуме вы проповедуете хору, когда говорите: процедурная математика Родители, которые никогда не любили и не разбирались в математике, могут удивиться тому, насколько она действительно может иметь смысл.И как только ребенок будет подходить к математике с этой точки зрения, я считаю, что он / она всегда захочет задавать хорошие вопросы, всегда будет требовать понимания, а не простой возможности, и у него будет меньше трудностей при решении сложных задач и идей ».
Абсолютно верно в моем понимании. Опыт.Алгоритмы хорошо преподаются только после концептуального понимания.Мой старший сын не понимал длинное деление до 6-го класса, и мне было немного неудобно, учитывая, что он был моим старшим, но я продолжал отступать от алгоритма и сосредотачиваться на понимании.Мои средние дети быстрее усваивают математику, поэтому для них это был скорее 4 или 5 класс.
Моя дочь, похоже, очень хорошо понимала концептуальное разделение, она просто не понимала алгоритм, отчасти я предполагаю, что это связано с тем, что мы просто не сосредотачиваемся на алгоритмах и используем только те, которые мы видим, действительно стоящие . И даже тогда я иногда задаюсь вопросом, почему мы это делаем, мой практический опыт учит меня, что, когда мы дойдем до точки, где мы будем читать для инструмента метода решетки или деления в столбик, в реальной жизни у нас будет калькулятор или компьютер под рукой, чтобы делать черную работу по вычислениям, освобождая нас, чтобы сосредоточиться на том, как настроить и решить проблему.
> Как только вы поймете, что происходит, вам не нужно об этом думать, и вы просто разовьете определенный уровень автоматизма. >
Именно так. И снова мой самый старший — отличный тому пример. Во 2-м классе он ходил на домашние занятия, где он три дня в неделю посещал уроки математики, так как я работал неполный рабочий день, когда мы решили не ходить для него по традиционной школьной программе. Математический текст обучал процессу деления в столбик во 2-м классе, и он просто завязал в узлах, пытаясь запомнить шаги.Этот опыт вместе с травмой, которую он получил от «скоростных упражнений», был тем моментом, когда я понял, что мы могли бы добиться большего, если бы просто отвезли его домой и обучили его на дому на постоянной основе без поддержки классов. Первое, что я сделал, — это бросил математический текст, основанный на процедурах, и получил учебную программу, которая пользовалась большим успехом в обучении математике. Теперь, годы спустя, для меня естественно объяснять и учить таким образом со всеми моими детьми.
Julie
Re: Long Division Help
Моя дочь с трудом понимала, что такое деление в столбик.Я научил ее делить краткое деление с однозначными делителями, и она смогла сделать это без особых проблем. Когда она овладела этим, она смогла понять шаги и увидеть необходимость деления в столбик с двузначными или более делителями. Я знаю, что в школе краткое деление обычно не преподают, но я использую его постоянно, даже с двузначными делителями. Это гораздо полезнее, чем деление в столбик (меньше бумаги, меньше шансов на ошибку при выравнивании всего). Вот ссылка, объясняющая краткое разделение:
http: // www.themathpage.com/ARITH/divide-whole-numbers.htm
Jodi
Re: [LivingMathForum] Long Division Help
Я нашел это через группу MathingOff yahoo.
Traci
www.doubledivision.org/
————————————— ————
Кто-нибудь порекомендует учебное пособие по полному делению с хорошим объяснением? У меня есть общие трудовые книжки, но у меня процесс не очень хорош. Спасибо L
Re: [LivingMathForum] длинное деление
http: // www.doubledivision.org/
Я считаю, что это гораздо проще объяснить. Здесь также есть ссылки на другие страницы подразделений.
M
RE: [LivingMathForum] длинное деление
Пропорциональное деление обсуждается многими читателями математики высшего уровня http://www.livingmath.net/Library/MultiConceptLists.html — На ум приходит «Essential Arithmetricks».
Я только что прочитал Divide and Ride, читатель MathStart, на днях своей 6-летней девушке, она любит книгу, и я понял, что это отличная установка для деления в столбик, потому что все дело в группе 11 детей и разделить их на аттракционы, чтобы заполнить места.Конечно, с одиннадцатью всегда есть остаток, когда вы делите на 2, 3, 4, 5 или 6. Существует хорошее визуальное представление о делении, которое выполняется, поскольку они показывают, что места каждой поездки заполняются. Оставшуюся часть они заполняют детьми, которых хватает со стороны, чтобы завести новых друзей. Аккуратная книга.
RE: [LivingMathForum] длинное деление
Рабочие тетради JUMP охватывают базовые концепции очень маленькими, постепенными шагами. Полнота деления рассматривается в учебной тетради 6-го класса, которую мы используем (она также может быть включена в группу 4 или 5, но я не использовал эти уровни), и моему сыну не составило труда понять — учебники немного сухие, но моему сыну они нравятся, потому что они такие простые.Вы можете узнать больше о них на http://www.jumptutoring.org
D
RE: [LivingMathForum] long Division
Мы с 10-летним и я вместе смотрели серию статей по основам математики The Teaching Company. Когда инструктор перешел к делению в столбик, он снова и снова подчеркивал, что ученик оценивает, каким он ожидает ответа, * до * выполнения алгоритма деления в столбик. Он делает это, показывая вам, как округлять до чисел, которые переходят друг в друга. Вы можете догадаться, думаете ли вы, что окончательный ответ будет больше или меньше того, что вы округлили.
Чтобы оценить, вы должны понимать, что делает деление в столбик. Он разбивает большое количество на определенное количество «отсеков» и показывает, сколько осталось, когда вы закончите заполнять эти отсеки.
Что он делает, так это оставляет длинное деление для того, для чего он действительно предназначен, процесс получения * точного * ответа, если вы хотите, вместо приблизительного. Это дает мне полную уверенность в том, что детей нельзя учить делению в столбик, пока они не поймут этот процесс и не оценят внимательно.В противном случае деление в столбик становится чем-то вроде черного ящика, куда вы кладете что-то, а что-то выходит, и вы не знаете, почему и как судить о точности процесса.
Джули
————————————
Привет, я упал как такой идиот, спрашивающий об этом, мне 16 и все такое, но у меня настоящая проблема с длинным делением любого рода. кто-нибудь может мне с этим помочь?
K
RE: [LivingMathForum] long Division
Мы семья Math-U-See, поэтому я отдаю должное Стиву Демме за это объяснение, но оно помогает моему сыну понять это как «область » проблема.
Если вам нужно найти площадь прямоугольника 2 на 10 ярдов, вы знаете, что общая площадь будет 20 квадратных ярдов. Легкий.
Теперь, чтобы превратить это в задачу деления, возьмите те же 2, но поместите площадь в середину прямоугольника, и теперь попробуйте найти сумму, которую вам нужно было умножить на 2, чтобы получить 20. 2 превращается в 20 , 10 раз.
Теперь сотрите линии, и вы действительно «увидите» длинное деление.
Все, что вы пытаетесь сделать, это найти другое число, на которое нужно умножить, чтобы получить площадь.Если есть остаток, то вы знаете, что это было бы похоже на поиск области чьего-то заднего двора, и вместо идеального прямоугольника вам нужно обойти его колоду, и поэтому «площадь» — это прямоугольная часть, плюс небольшая сторона рядом на палубу.
Площадь травы: 61 кв. Вы знаете, что одна сторона составляет 10 ярдов, так какова длина меньшей стороны? 10 переходит в 61, 6 раз плюс один ярд. Итак, у вас есть задний двор размером 6 на 10 ярдов с одним маленьким квадратным ярдом по другую сторону террасы.Если вы разберете его просто вот так и поймете, что вы пытаетесь сделать, вы можете применить его ко всем размерам задних дворов 🙂 или ко всем размерам длинного деления!
Blessings, P
Re: long division
Я хотел бы предложить «Математические вопросы, понимание математики, которую вы преподаете» Сюзанны Х. Чапин, которую часто рекомендовали на этом сайте. Он ориентирован на учителей классов K-8. Он показывает несколько способов, которыми дети понимают и работают с длинным разделением. Я признал только один метод традиционным… Но я очень легко понял пару других методов.
Я настоятельно рекомендую заказать книгу в местной библиотеке или подумать о покупке ее для себя. В нем обсуждаются все элементарные математические темы, поэтому он очень уместен. Я использовал его несколько раз, обучая двух своих мальчиков.
A
K,
Лучшие объяснения деления в столбик, которые я видел, можно найти в книге «Math Matters». Авторы показывают несколько способов, которыми разные люди подходят к делению в столбик.То, что для меня имело наибольший смысл, было НЕ тем, чему я учился в школе. Вот он:
Допустим, вы хотите разделить 1967 на 15.
1967
-1500 = 15 X 100
467
-150 = 15 X 10
317
-150 = 15 X 10
167 =
-150 = 15 X 10
17
-15 = 15 X 1
2
Сложите все продукты с правой стороны (100 + 10 + 10 + 10 + 1), и вы получите 131 остаток 2.
Вам нужно только оценить, насколько меньшее число переходит в большее число до определенного момента.Если вы угадываете слишком низко, все в порядке, и вы продолжаете идти. При использовании традиционного метода, если вы угадаете слишком мало, вам придется вернуться и попробовать еще раз. Вам нужно знать несколько основных таблиц умножения, но вы можете выбрать самые простые с помощью этого метода. Я мог бы сделать 15 X 30 вместо 15 X 10 трижды, но мне это не нужно. Я могу выбрать числа, которые подходят мне лучше всего. И очень легко умножить на 100, 10 и 1.
Если это не сработает, не волнуйтесь. Попробуйте прочитать книгу «Математические вопросы» и взгляните на раздел деления.
Энджи
RE: [LivingMathForum] длинное деление
Мой 12-летний ребенок борется с пониманием деления в столбик. Он знает все факты своего разделения … и он отлично справляется с задачами со мной — очень быстро выдает ответы. но он просто не понимает этого — или понимает это, чтобы сам задавать вопросы .. какие-нибудь советы или идеи? спасибо, debra
RE: [LivingMathForum] long Division
Дебра, мой старший сын изо всех сил пытался понять, что такое деление в столбик, и уловка Math U See, с которой он рассматривал задачу деления как простое представление площади, казалось, сработал для него.
Чтобы сначала подумать об этом с помощью простых чисел, предположим, что у вас есть 32 блока, и вы хотите построить прямоугольник. Если сделать одну сторону прямоугольника 4, сколько их будет в каждом ряду?
Это именно то, что вы делаете, когда рисуете:
_______
4 | 36
MUS даже вводит его вот так, настраивая его точно так же, как проблему с областью ранее в этой серии:
__? ___
4 | 36 | (вокруг 36 должно быть целое поле, но я не могу сделать это в своем электронном письме: o)
Вы можете построить его конкретно — если у вас есть прямоугольник площадью 36, и сделайте 4 ряда, каждая строка должно быть 8, и не осталось ни одного.
Это именно то, что вы делаете с делением в столбик. Если вы выберете такое число, как 38, и решите построить прямоугольник из 4 рядов (т.е. разделить 38 на 4), в каждой строке будет 8, а у вас останется 2 нечетных части — это ваш остаток.
Чтобы перейти к более эзотерическим числам, если бы вы делили 137 на 12, вы говорите, что если у меня есть площадь 137, и я хотел бы построить прямоугольник с 12 строками, сколько бы было в каждой строке . . . Ну, вот где я мог бы использовать процесс деления 12 на 130 сначала = 10 раз с остатком 10, сложить 7 и получить 12, перейдя в 17 раз.Вы сможете построить прямоугольник 12 на 11, и у вас останется 5 блоков.
Это кажется мне лучшим конкретным способом представления длинного деления перед тем, как перейти к абстрактному или процессу.
Julie
Re: [LivingMathForum] длинное деление
Я думал, что Math U See отлично справляется с объяснением «почему», заполнив прямоугольник, образованный длинными разделительными линиями, и затем посмотрев на два фактора, которые у вас есть умножаются на «площадь» внутри коробки…. вероятно, не очень ясно, и кто-то, кто лучше разбирается в MUS, может объяснить лучше …. Я исхожу из памяти, так как мы не используем математику, понимаете (пока!) ….. мы так с нетерпением жду запуска после летнего перерыва.
HTH, S
Re: [LivingMathForum] длинное деление
Мой сын не мог понять длинное деление, пока не получил полного понимания десятичных дробей. Несколько лет он пробовал делить в столбик и в раздражении сдавался. По мере того, как его понимание десятичных дробей увеличивалось, он внезапно «получил» деление в столбик за один 10-минутный процесс после того, как был так разочарован.Я не уверен в точной связи, но концепция «остатков» никогда не работала для него, и это имело какое-то отношение к выходу за рамки этого.
J
Re: длинное деление
Длинное деление имеет 4 шага для каждой цифры делимого. Мы повторили шаги вслух и заметили ритм. Повторение этого помогло моей дочери самостоятельно выполнять длинное деление.
«Делить, умножать, вычитать, уменьшать! Делить, умножать, вычитать, уменьшать!»
Это не объясняет причину разделения, но помогает запомнить последовательность шагов.Надеюсь это поможет.
Anne
Re: long division
Вот файл PDF, который откроет замечательную статью об алгоритмах математики. Вы найдете множество различных способов (алгоритмов) не только для обучения, но и для решения математических задач, включая вашу проблему с делением в столбик. Традиционный способ, которым вас учили умножать и переносить вниз, не помогает им с мысленной математикой — это способ номер один для взрослых на работе. Спуститесь к страницам 18 и 19 этого PDF-файла. Мы часто используем стадию 3; «Расширенный» метод, когда мы решаем деление в столбик.Это похоже на умножение частичных произведений. Довольно скоро вы обнаружите, что ваши дети делают в уме длинные деления и большие числа умножения. Если вам нужны практические занятия или другие ресурсы по математике, дайте мне знать, какой балл, и я их опубликую.
http: //www.standards.dfes.gov.uk/primaryframeworks/downloads/PDF/101Guidance_Cal \
culationFinal.pdf
Re: длинное деление
Вот ссылка, объясняющая короткое деление: http: // www. themathpage.com/ARITH/divide-whole-numbers.htm
HTH,
Re: У моего сына проблемы с длинным делением
Длинное деление — проклятие нашей жизни.
Мы использовали Миквон, а затем Сингапур, и оба мальчика круто перевернулись, когда мы попали в длинный дивизион.
С первым ребенком я сделала перерыв, и мы изучили живые книги. Когда мы вернулись в длинную дивизию, было не лучше. Он начал заниматься математикой со своим отцом, а его отец просто настаивал, чтобы он использовал формулу. Это заняло некоторое время, но он запомнил и смог справиться.Я пытался использовать с ним другие методы деления в столбик (очень похожие на метод решетки для умножения), но они не сработали для нас. Теперь он может удобно выполнять деление в столбик.
С моим вторым ребенком, мы как-то познакомили его, он возился с ним и не очень хорошо справлялся. Затем мы перешли к учебнику по математике. Когда он появился во второй раз (всего пару недель назад), мы взяли перерыв в Сингапуре и работали только над делением в длину. Мы работали над этим всего около 10 минут в день. Мы приняли это легко.Я разбил его на мельчайшие части. Две недели спустя он не только понимает, но и очень хорошо умеет использовать деление в столбик.
Боюсь, что для этого нет «живой математики». По крайней мере, не в этой семье. Думаю, именно поэтому с этим у нас была самая долгая борьба! Мы все хотели другого пути, но это последовательный метод, и это означает, что он бросит вызов непоследовательному ученику. Но это не значит, что они не могут его запомнить. Это просто означает, что им потребуется больше времени.
A
Re: У моего сына проблемы с делением в столбик
Это было трудное место для нас и с сингапурской математикой, потому что казалось, что они «пропустили шаг» — или, скорее, пытались научить слишком много сразу. Я думаю, было бы лучше, если бы они дали детям практиковаться с обозначениями (помещая число, которое нужно разделить внутри символа длинного деления и писать ответ сверху), прежде чем они учили делению с остатками. Мой сын споткнулся о обозначениях, особенно о идее написания ответа НА ВЕРХНЕМУ, больше, чем о концепции.
Если вы ищете видео, у Khan Academy есть очень хорошие, начиная с этого места. Все начинается очень просто, но ближе к концу он вводит символ деления, а затем в последующих видеороликах переходят к более сложным задачам. Второй подчеркивает значение места и т. Д .: http://www.youtube.com/watch?v=MTzTqvzWzm8&feature=youtube_gdata
Иногда точку деления в столбик легче увидеть, если вы начинаете работу с очень большим числом. с, а не с каким-то небольшим числом, которое ваш сын мог бы вычислить в своей голове.Что-то вроде 67,589 ÷ 3 =?
Я использовал метафору «фабрики печенья», чтобы помочь своим ученикам понять шаги. Представьте, что вы управляете фабрикой печенья, и сегодня вы произвели 77 582 печенья. Вам нужно отправить их в 3 магазина, и, честно говоря, каждый магазин должен получить одинаковое количество файлов cookie. Вы можете отправить файлы cookie в виде:
отдельных штук
коробок по 10
коробок (10 коробок = 100 печений)
поддонов (10 коробок = 1000 печений)
грузовых автомобилей (10 поддонов = 10000 печений)
Сколько печенья вы можете отправить в каждый магазин? Что ж, вы, очевидно, захотите упаковать файлы cookie в самые большие куски, которые вы можете, поэтому сначала проверьте, можете ли вы отправить целые грузовики.Можете ли вы отправить в каждый магазин целый грузовик (или два или более грузовика)?
2 грузовика на магазин x 3 магазина = 60 000 печенья
(сначала запишите его со всеми нулями, чтобы подчеркнуть значение разряда.)
17 582 печенья на вынос …
Затем, если у вас есть грузовики, которые вы можете не отправляйте (так как вы должны отправить одно и то же в каждый магазин!), вам придется открыть эти грузовики и разделить поддоны. Итак, у нас 17 поддонов:
5 поддонов на магазин x 3 магазина = 15000 печенья
2582 печенья на вынос…
И если у вас останутся поддоны, вы сломаете их и отправите файлы cookie в зависимости от загрузки ящика:
8 ящиков на магазин x 3 магазина = 24000 файлов cookie
182 файла cookie на вынос … А если есть еще какие-то коробки, вы отправите столько коробок на магазин. И, наконец, вы приступаете к разделению отдельных файлов cookie.
И если вы зайдете так далеко и у вас останется несколько печенек, я бы сказал, что пора перекусить!
Вот еще одно видео, хорошее введение в систему обозначений, и немного короче, чем в Khan Academy: http: // www.mathplayground.com/howto_longdivision.html
D
[LivingMathForum] Длинный дивизион Беды
Привет. У меня 12-летний ребенок, который ненавидит математику. В первую очередь мы используем MUS. Хотя она утверждает, что ненавидит математику, мой доктор любит читать и прочитал большую часть серии «Убийственная математика» (в любом случае все те, которые у нас есть).
Два года назад мы сделали MUS длинное деление. Это было сложно — dd не нравился метод MUS по накапливанию номеров. сверху, так что я научил ее методу, которому меня научили, — писать номера.вниз по стороне. Это было нормально, и в конце концов мы дошли до цели. Но теперь мы делаем деление десятичных дробей длинным, и у нас очень слезливое времяпрепровождение по ним.
Проблема с длинным делением, по-видимому, заключается в том, что, хотя она может использовать метод, она не сохраняет числа. в нужных местах. Например, ее ответ может быть 0,0210, тогда как правильный ответ — 0,002001. Она также может давать очень странные ответы и совершенно не осознавать, что ее ответ, интуитивно понятный, не имеет смысла. Она не смотрит на свои ответы и не думает: «Это звучит правильно?».
Некоторая проблема, кажется, в том, что она слишком затягивает свое подразделение. Я замечаю это даже при обычном делении в столбик. Таким образом, вместо того, чтобы смотреть на задачу вроде 5689, разделенного на 83 и говорить: «Хорошо, я попробую сначала умножить на 70 и посмотреть, что я получу, так как 7 x8 = 56», она начнет с небольшого числа, например 20, и тогда она сделает еще 20 дважды и сложит все в конце. Надеюсь, это имеет смысл. Я попытался объяснить, взглянув на первые пару цифр и подумав, что в них входит, чтобы найти лучшее номер для начала, но она говорит, что это слишком сложно (для меня это не имеет смысла, поскольку она знает свои математические факты лучше, чем все мы).Есть предложения, чтобы сделать это проще?
Я тоже задавался вопросом, раз уж она может сделать метод, если мы просто все это забудем? Но потом я вспоминаю, что вот что случилось со мной в школе с математикой — если я чего-то не понимал, мы двигались дальше, и хотя в то время это не имело большого значения, к концу старшей школы я боролся .
Спасибо, P
RE: [LivingMathForum] Long Division Woes
P., длинное деление, кажется, такое обычное горе! Я вспоминаю, что буквально ПОСЛЕДНЯЯ СОЛОМА заставила меня забрать сына с урока математики в центре домашнего обучения и взять на себя его учебную программу и т. Д.(мы начали с центра домашнего обучения, который нам подсказывал, какие книги использовать и т. д. — Мне просто потребовалось время, чтобы понять, что это не так уж сильно отличается от школы, и я мог бы справиться лучше!)
Я могу понять ваша дилемма. У меня нет проблем с использованием какого-либо метода деления больших чисел, который работает, моя дочь использует метод, который она придумала. Но я лично могу видеть, как более традиционный метод хорошо работает с десятичными числами, сохраняя место десятичной дроби прямо!
Несколько комментариев по поводу проблемы, с которой, по вашему мнению, она боролась.Я знаю, знаю, что некоторым людям это неудобно, но, честно говоря, в реальном мире никто в здравом уме не делал бы это вручную, если бы им не нравилось заниматься математикой. Я ОКРУГЛ оба числа, оценил ответ, поговорил о том, является ли реальный ответ ниже или выше оценки, и думаем ли мы, что он намного ниже или немного. . . насколько близко вы чувствуете, что вам нужно приблизиться, если вы делите что-то для различных целей, а затем используете калькулятор.
Например, сколько 5600 разделить на 80? 70, конечно, и это достаточно близко к ответу калькулятора 68.542, вероятно, для 95% случаев применения этой проблемы в жизни. Этот процесс оценки — реальный жизненный навык, который ей понадобится на всю оставшуюся жизнь, и нам вряд ли когда-либо понадобится быть более точным, чем этот, без использования калькулятора или компьютера. Серьезно, помимо деления одной цифры на более длинное число, что означает только то, что вам нужно вспомнить основные факты умножения, чтобы решить задачу, кто бы делал это сегодня без калькулятора ?? Если бы она знала, * как * это сделать, я бы не стал продолжать использовать алгоритм, который, кажется, на самом деле приносит ей больше вреда, чем пользы, учитывая то, что вы писали о ее замешательстве и неспособности * видеть * числа.Я написал здесь обзор книги под названием «Арифметика для людей» http://groups.yahoo.com/group/LivingMathForum/message/14627, на которую вы, возможно, захотите взглянуть, если у вас возникнут проблемы с пониманием того, почему я говорю это , это ОТЛИЧНАЯ книга для понимания того, как такое слепое применение арифметических навыков может убить любой потенциальный интерес или удовольствие от математики для многих детей, особенно на этапе предалгебры. Может быть, если вы сделаете это ПЕРВЫМ, а потом воспользуетесь калькулятором, вы сможете заставить ее больше думать так, как вы, кажется, понимаете, что ей нужно, а не придумывать бессмысленные ответы.Фактически, я бы с самого начала разобрался, почему она это делает, и сосредоточусь на этом в первую очередь.
Вы писали: <Но потом я вспомнил, что вот что случилось со мной в школе с математикой - если я чего-то не понимал, мы двигались дальше, и хотя в то время это не имело большого значения к концу в средней школе я боролся. >
Но вот в чем прелесть домашнего обучения! Ваша дочь никогда не будет «обречена» на ту же участь, если вы не будете следовать той же школьной модели в своем обучении.Мы с моим 12-летним сыном сели с текстом по алгебре, который он проработал в прошлом году. Мы вернулись к началу и рассматриваем большую часть устно, просто обсуждая и освежая. Это настроено для него — от нуля до минимума времени на просмотр того, что он хорошо помнит, столько времени, сколько ему нужно на области — я только ранее поделился, как он забыл правильный способ деления дробей, чему он научился 2+ года назад. Он просто не использовал навык какое-то время и нуждался в повторении. У нас никогда не было времени, которое нам было нужно в школе, и нас никогда не учили, как учить себя, нас учили полагаться на учителей.
Большинство из нас не научились управлять своим обучением до колледжа, когда у нас был гораздо больший выбор в отношении содержания, учителей и расписания нашего обучения. Мой сын не считает эти усилия некоторым признаком того, что он «отстал» — на самом деле, предварительная алгебраическая часть обзора заняла у нас всего 4 дня. Мы уже пропустили целые разделы начальной алгебры и отметили тот факт, что он действительно запомнил 90% или более ее. Вы не можете делать это в классе детей, но вы * можете * заниматься домашним обучением, вы можете использовать текст или учебную программу в качестве инструмента для себя, а не быть его рабом.
Julie
Re: Long Division Woes
Я, конечно, не эксперт. Но у меня есть 11-летний ребенок, у которого проблемы с математикой, и я подумал, что поделюсь тем, что сработало для нас. Мы тоже используем MUS, но застряли в делении.
В итоге мы с ним вернулись к основам деления. Я использовал Math Mammoth Марии Миллер. Я знаю, что видел ее пост здесь. У нее два сайта. Один — www.mathmammoth.com, другой — www.homeschoolmath.net. Мы использовали синюю серию книг о делении.Она объясняет концепции иначе, чем Стив Демме. Это было то, что нужно моему сыну, чтобы понять это. Я до сих пор использую ее рабочие листы для обзора. Спасибо, Мария!
Небольшое замечание о различиях в обучении детей и MUS. Этим летом мы познакомились со Стивом Демми на конференции по домашнему обучению. Он такой хороший человек. Мой сын сказал ему, что он отстал. Мистер Демме категорически (в приятной манере) сказал: «Нет, это не так». По сути, он сказал ему, что каждый ребенок индивидуален, и нигде не сказано, что вы должны знать определенные математические факты к определенному возрасту.Некоторые люди могут с этим не согласиться. Но это помогло моему ребенку по математике более позитивно относиться к своим математическим способностям.
A.
Когда дети учатся умножению и делению | Разобрался
Из всех математических операций детям труднее всего выучить умножение и деление. Освоение этих навыков — следующий логический шаг после сложения и вычитания. Но для большинства детей это скорее прыжок. Узнайте, когда дети учатся умножать и делить.
Когда дети обычно учатся умножению
Умение умножать можно начать уже во втором классе. Дети обычно начинают с добавления равных групп (3 + 3 + 3 = 9, что совпадает с 3 × 3 = 9). Это называется повторным сложением.
Вот как и когда дети учатся умножать:
Во втором классе детей учатся визуализировать повторяющееся сложение. (Как нарисовать квадрат с пятью строками и пятью столбцами, чтобы представить 5 × 5 = 25.)
В третьем классе детей начинают понимать связь между умножением и делением. (Это как знать, что 3 × 4 = 12 и 12 ÷ 4 = 3.)
В четвертом классе детей начинают умножать двузначные числа на двузначные числа.
Чтобы научиться умножению, дети используют практические материалы и наглядные модели, чтобы разбить числа и построить концепцию.
Большинство детей знают, как использовать обычную процедуру умножения больших чисел к концу пятого класса.Некоторым нужно немного больше времени и практики, чтобы полностью понять концепцию.
Когда дети обычно изучают деление
Дивизион обычно является самой сложной математической концепцией для детей. Уравнение деления состоит из трех частей:
Дивиденд — это число, которое делится (первое число в задаче).
Делитель — это число, на которое делится дивиденд (второе число в задаче.)
Частное — это количество раз, когда делитель войдет в делимое (решение).
Обучение делению начинается в третьем классе. Детей знакомят с этой концепцией, выполняя повторное вычитание. (Примерно 20-5, затем еще 5, еще 5 и еще 5). Это то же самое, что 20 ÷ 4.)
Вот как и когда дети учатся делить:
В третьем классе ребенка начните деление повторным вычитанием.Они учатся делить две цифры на однозначные числа с решениями больше 10.
В четвертом классе детей начинают учиться делить четырехзначные числа на однозначные числа. (Например, 4000 ÷ 2.)
В пятом классе детей начинают делить четырехзначные числа на четырехзначные. (Например, 8,000 ÷ 4,000.) Кроме того, большинство детей знакомятся с десятичными числами в пятом классе.
Ожидается, что дети полностью поймут, как умножать и делить, прежде чем перейти в среднюю школу.Но это не значит, что каждый ребенок поймет это. Некоторым детям нужно больше времени и практики.
Почему у некоторых детей проблемы с умножением и делением
Дети нередко испытывают трудности с математикой, особенно с умножением и делением. Для этого есть много причин и много способов помочь. Поддержка, такая как раздельное обучение или обучение в небольшой группе, со временем может иметь большое значение.
Например, у некоторых детей возникают проблемы с пониманием основных математических понятий, известных как
чувство числа
.Проблемы с концентрацией внимания или памятью могут повлиять на изучение математики. Как и беспокойство.
среднего образования — В наши дни преподается сокращенное разделение, а если нет, то почему?
tl; dr Меня интересуют мнения о кратком делении. Ниже я описываю свой опыт работы с маленькими детьми и сравниваю длинное деление с коротким делением. Для тех, кто не знает об этом, на wikiHow есть хорошее объяснение короткого деления.
Недавно меня попросили помочь некоторым детям в возрасте около 10 лет с математикой, и почти сразу я обнаружил, что они борются с делением.На деление чисел у них уходит много времени, и они всегда используют длинное деление или какой-либо его вариант. Я даже видел, как один человек делился следующим образом:
\ begin {array} {r | l} \ require {enclose}
3 \ enclose {longdiv} {1 ~ 8 ~ 6} \\
\ underline {{} — ~ 1 ~ 5 ~ 0} и 5 ~ 0 \\
3 ~ 6 \\
\ underline {{} — ~ 3 ~ 0} & 1 ~ 0 \\
6 \\
\ underline {{} — ~ 6} & \ underline {\ hphantom {5 ~} 2} \\
0 и 6 ~ 2
\ end {array}
, что меня просто расстраивает. Простите мою тираду. Но я ожидаю, что люди узнают, что можно напрямую увидеть, что ответ — 62 $, увидев, что $ 18 \ div3 = 6 $ и $ 6 \ div3 = 2 $.Кроме того, я спрашиваю их, почему они используют 50 долларов на первом этапе вместо 60 долларов, и почему бы просто не иметь ноль и не делать это цифра за цифрой, и они говорят, что заметили, что 50 долларов «сработали», и что они были так учили в школе.
Плохое деление в сторону, длинное деление по своей сути занимает много времени, как следует из названия, а когда на выполнение задания или оценки в классе дается ограниченное количество времени, трудоемкое деление может действительно повредить. Точно так же есть так называемое короткое деление, которое обычно занимает гораздо меньше времени, но требует больше мысленных вычислений.Но похоже, что никто явно не знает о кратком делении, по крайней мере, из всех, с кем я разговаривал. Я сам в молодом возрасте «вычислил» краткое деление на примерах типа $ 186 \ div3 $, просто пропуская шаги, но даже не знал, что это называется так, прежде чем писать этот вопрос.
Из всех детей, которым я помог с делением, единственные, у кого сейчас проблемы с делением, — это те, у кого не запомнили свои таблицы умножения. Деление на многозначные числа по-прежнему является процессом, но я не ожидал, что кто-то сможет легко это сделать.Тем не менее, деление на однозначные числа происходит часто, например, с уменьшением дробей. Некоторые из детей с более сильными умственными арифметическими навыками, которым я показал это, теперь могут мысленно проделывать этот процесс цифра за цифрой, так что они ничего не выписывают при выполнении $ \ frac {38} {56} = \ frac {19} {28} $ например.
Принимая во внимание полезность короткого деления, мне кажется удивительным, что об этом мало что известно и чему учат больше! Есть ли у кого-нибудь опыт преподавания коротких разделов?
Изменить:
Возможно, я умалчал, почему именно короткое деление нахожу не только меньше занимающим место, но также проще и быстрее.Во-первых, это не требует огромного количества мысленных вычислений. Фактически, для этого требуется всего лишь умение вычислять очень маленькие деления несколько раз.
Суть короткого деления заключается в том, что мы просто постоянно находим, что входит во что-то, а что остается, что большинство детей, с которыми я имел дело, способны делать мысленно, насколько это требуется для короткого деления. Обратите внимание, что я не говорю о проблемах с делителями, превышающими, скажем, 11.
Возьмем, например, $ 847 \ div3 $.Большинство детей, с которыми я работал, сразу знали, что $ 8 \ div3 = 2 \ rm ~ R ~ 2 $. Итак, они пишут 2 сверху и 2 рядом с 8. Тогда они знают, что $ 24 \ div3 = 8 \ rm ~ R ~ 0 $. Итак, они пишут 8 сверху и 0 рядом с 4. Наконец они знают, что $ 7 \ div3 = 2 \ rm ~ R ~ 1 $. Это дает окончательный ответ: $ 847 \ div3 = 282 \ rm ~ R ~ 1 $.
Эти шаги совсем несложны, если делитель не превышает 11 или 12. На самом деле большинству детей это легко сделать. Для больших делителей я не ожидал, что кто-то будет делать это мысленно с коротким делением.Я ожидал, что они будут использовать длинное деление, как обычно, для чего-то вроде $ 847 \ div13 $.
Это также помогает в таких ситуациях, как вышеупомянутое сокращение дроби, например $ \ frac {38} {56} = \ frac {19} {28} $. Нетрудно увидеть, что идет 2, но с длинным делением это может занять некоторое время. Следовательно, в таких случаях это также происходит быстрее.
Как научить многозначному умножению и длинному делению
Узнайте, как лучше всего научить многозначному умножению и делению в столбик.Эта дифференцированная стратегия помогает учащимся 3-го, 4-го, 5-го и специального образования.
Если вы ищете лучшие стратегии для обучения многозначному умножению и делению в столбик, вы нашли отличное место для начала. Это самые простые методы обучения студентов. Лучше всего они работают с учениками 4-х и 5-х классов, учащимися из групп риска, борцами и учащимися специального образования — ВСЕ УЧАЩИЕСЯ !
Этот визуальный метод действительно работает для почти на каждого ученика!
Несколько лет назад обучение алгоритмам умножения и деления в столбик имело для меня ОГРОМНЫЙ ФАКТОР УЖАСОВ.Традиционные методы, которые я использовал, просто не работали.
Мои ученики забыли ступеньки. Они запутались, они не смогли выровнять свои числа и … они не могли даже прочитать свои собственные письма!
Стратегии умножения и деления в столбик Shape Math ™
Я знал, что должен быть способ получше. Короче говоря, я не мог найти лучшего способа. Итак, я разработал собственную стратегию, и я назвал ее Shape Math ™.
Я обучал этой стратегии многозначного умножения и длинного деления в своем классе в течение многих лет, и я получил ФАНТАСТИЧЕСКИЕ отзывы от других учителей об их успехах в использовании!
Рабочий лист умножения с использованием органайзера двузначного умножения
Об организаторах
Методы Shape Multiplication ™ и Shape Division ™ используют форм и цветов , чтобы помочь учащимся запомнить последовательность шагов.
Формы и цвета помогают студентам решать задачи до тех пор, пока они не освоятся с процессом. В конце концов, органайзер им больше не понадобится. Это очень визуальный процесс , который работает для многих студентов, в том числе и для тех, кто борется!
Органайзеры для умножения выглядят так:
А вот органайзер для задач с длинным делением:
Как я Явно Обучаю этим стратегиям
Для сложных типов уроков я обычно использую SmartBoard перед классом, за которым следует помощь в небольших группах или индивидуальная помощь.
Инструкция для всей группы
Я представляю органайзер и предлагаю своим ученикам обратить внимание на разные формы и цвета. Мы говорим о том, как разные формы и цвета помогают нам при решении длинных математических задач.
Я начинаю анализировать то, с чем студенты уже знакомы, например, решение задачи с двумя цифрами на одну цифру, составленную в этом стиле. После беглого обзора я перехожу к подробному обучению тому, как решать задачу многоэтапного умножения с помощью органайзера.
Я прямо объясняю свои мысли вслух, чтобы студенты могли их услышать. Я говорю что-то вроде: «Мне нужно умножить 5 в треугольнике единиц на 3 в круге». Я не забываю указывать на формы и заполнять органайзер, когда говорю.
Студенты наблюдают за процессом несколько раз, пока я начинаю задавать вопросы о последовательности шагов.
Круги переходят в круги; Квадраты сочетаются с квадратами
На фотографии ниже вы можете видеть, что любая цифра, умноженная на 3 в красном кружке, дает продукты, указанные в красных кружках под цифрой 3.Вот почему я постоянно повторяю: «Круги идут с кругами».
Цифры, умноженные на 2 в синем квадрате, дают продукты, указанные в синих квадратах на органайзере. Вот почему я снова и снова повторяю: «Квадраты идут с квадратами».
Это более старая фотография — в органайзерах больше не используются треугольники
Во время обучения я звучу как зарезанная пластинка, постоянно повторяю: «Круги идут кругами; квадраты идут с квадратами ». Это работает, даже если вы дифференцируете, удаляя цвета и используя органайзер черно-белых фигур.
Многоразовые пластиковые рукава привлекают студентов и экономят бумагу!
Групповое / индивидуальное обучение
Пока я нахожусь у Smartboard, ученики вместе со своими организаторами следят за ними на своих местах. Студенты с удовольствием используют органайзеры, помещенные в прозрачные пластиковые рукава с маркерами для сухого стирания.
Затем мы переходим от обучения в группе к студентам, работающим над заданием самостоятельно.
Пока ученики работают, я быстро прогуливаюсь по классу и замечаю, что ученики растерялись.Вот когда я обычно либо собираю студентов в небольшую группу за задним столиком, либо предлагаю индивидуальную помощь.
Многоразовые прозрачные пластиковые рукава
Мне нравится использовать эти потрясающие рукава для сухого стирания ( Нажмите здесь, чтобы увидеть похожие рукава для сухого стирания на Amazon ). Мне они очень нравятся, и я использую их почти каждый день по-разному для разных предметов.
Shape Math ™ использует цвета и формы для различения
С помощью органайзеров и рабочих листов, включенных в наборы Shape Math, вы сможете легко отличить друг от друга.Универсальность действительно позволяет подобрать необходимый уровень помощи для уникальных потребностей каждого учащегося.
Как отличить друг от друга с помощью органайзеров
Увеличьте объем помощи для учащихся, нуждающихся в максимальной поддержке, используя как цвета, так и формы. По мере того, как учащиеся улучшают свои навыки, уменьшайте поддержку, удаляя цвета и вводя готовые рабочие листы.
В конце концов, вы можете исключить как формы, так и цвета и использовать прилагаемые листы миллиметровой бумаги.Когда придет время, студенты могут перейти к базовому алгоритму умножения или деления без цветов, форм или миллиметровой бумаги.
Варианты строительных лесов, предлагаемые в этих пакетах, повышают уверенность и вовлеченность учащихся. Уверенность и заинтересованность вызывают азарт, гордость и желание учиться!
Органайзеры разного размера с разными цветами и формами легко отличить друг от друга.
Наборы умножения и деления включают в себя органайзеры разных размеров.Предварительно разработанные рабочие листы позволяют вам выбрать подходящее время для ознакомления с более сложными навыками.
Типовые леса
Прогресс обычно включает:
- Удаление цветов на органайзерах
- Удаление форм, которое устраняет органайзеры
- Переход на миллиметровую бумагу
- Переход от миллиметровой бумаги к независимости.
Добавление или удаление цвета форм обеспечивает различные уровни строительных лесов
На картинке выше я изначально убрал цвета для этого ученика.Я заметил, что ему очень трудно без цветов, поэтому я использовал маркеры, чтобы снова добавить цвета для него. Есть много способов помочь вашим ученикам оказать помощь нужного уровня.
Вы выбираете подходящее время, чтобы убрать цвета с органайзеров с конечной целью полностью устранить организатора. Затем учащиеся могут перейти на рабочие листы с миллиметровой бумагой, прежде чем они перейдут к самостоятельности без органайзеров или миллиметровой бумаги.
Якорные карты в классе
Я ОБОЖАЮ якорные диаграммы — их легко сделать, и ЗАМЕТНЫЕ справочные инструменты! Ниже приведена таблица привязки умножения, которую я использую и показываю своим ученикам в качестве справочника.
Якорная диаграмма двухзначного умножения
Якорная диаграмма с помощью визуального органайзера с цветами и формами
Диаграмма якоря с удлиненным делением
Я начал использовать это мнемоническое устройство с хорошим оле ‘ McDonald’s:
- Делает (Делить)
- McDonald’s (Умножать),
- Подавать (Вычитать),
- Сыр (Проверить),
- Бургеры (Сносить),
- Действительно? (Повторите и начните заново).
Раньше я держал диаграмму привязок Division Family (на фото ниже) в моей комнате в качестве ориентира, чтобы напоминать студентам о шагах. Но семьи могут выглядеть по-разному, поэтому я перешел на мнемоническое устройство McDonald’s.
- Папа , (Разделить)
- Мамочка (Умножить),
- Сестра (Вычесть),
- Брат (Вниз),
- Rover (Повторить и начать сначала).
Иногда в начале урока математики у меня возникает задача, например, утренняя работа.
Как только учащиеся усваивают правила деления в столбик, я меняю числа на стикерах. Я изо всех сил стараюсь, чтобы он соответствовал цвету, но, ну, жизнь случается! Наличие диаграммы привязки Sticky-Note делает изменение проблем более простым и увлекательным. В стикерах есть что-то, что нравится студентам.
И последняя мысль о таблицах привязок для заметок. Студентам нравится, когда их поручают менять числа.Им нравится руководить этой работой.
Мне бы хотелось услышать, как вы используете стикеры в классе!
Статьи о многозначном умножении:
статей о длинном дивизионе:
- Дифференцированные рабочие листы с длинным разделением БЕСПЛАТНО — БЕСПЛАТНО возьмите эти дифференцированные рабочие листы с длинным разделением БЕСПЛАТНО и значительно повысьте успехи учащихся и ваши успехи в преподавании!
- Миллиметровая бумага Math Intervention — В этой статье блога объясняется, как использовать миллиметровую бумагу в качестве быстрого и легкого ресурса для вмешательства с вашими учениками.Он включает ссылки на бесплатную печатную миллиметровку и идеи о том, как использовать ее в классе.
Длинная дивизия Ресурсы:
Если вы нашли эту статью полезной, подпишитесь на меня в моем Teachers Pay Teachers Store , Pinterest и Facebook ! Я был бы рад услышать от вас!
Связанные
Стратегии разделения для 5-го класса
Боитесь ли вы преподавать разделение каждый год? Раньше я был в этом лагере.Мои ученики много боролись с делением, потому что им не хватало чувства числа и концептуального понимания. Однако, к счастью, я понял, что так быть не должно. Я могу использовать стратегии разделения, которые не только подходят для развития, но и имеют смысл для моих учеников.
Фактически, как только я отказался от стандартного алгоритма в качестве моей стратегии деления, мои ученики начали осваивать деление влево и вправо. Некоторые все еще боролись? Да. К сожалению, ни одна из стратегий или советов, которыми я делюсь, не станет волшебной пилюлей, но они сделают разделение доступным и концептуальным для ваших учеников.
Частные частные с помощью Easy Breezy Math
Частные частные изменили правила игры для моих учеников. Частные частные — это стратегия деления, которая использует фрагменты для более эффективного многократного вычитания групп делителя.
Но мне пришлось добавить эшафот для моих учеников. Мы называем этот эшафот нашей «Легкой и легкой математикой». По сути, мы берем известное нам умножение и списываем их в сторону. Мы устраняем эти проблемы, чтобы помочь нам решить проблему.Мы делаем это, потому что моим ученикам действительно не хватает чувства деления в начале года. Это также помогает им увидеть связь между умножением и делением.
По мере того, как год идет, они выйдут за рамки простой простой математики, поскольку они разовьют чувство числа и начнут видеть закономерности.
Совет: напомните им сложить множители вертикально в их Easy Breezy Math. Иногда я даю своим ученикам доски специально для этого, чтобы сделать их более интересными.
Чтобы получить более подробную информацию об этом методе разделения и получить помощь бесплатно, щелкните здесь.
Если эта стратегия для вас нова и вам нужно увидеть ее в действии, то посмотрите это видео и песню.
Коробочная модель или коробочный метод с частичными частными
Box Model Division 1 была для меня новинкой год назад и работает лучше всего, когда студенты знакомы с использованием этого типа органайзера при умножении на частичные произведения.Этот тип стратегии деления похож на частное, но организован иначе.
Если это для вас в новинку, то посмотрите видео, на котором учитель и ее класс проходят этапы. Этот метод лучше всего «увидеть в действии», а не читать о нем.
Это видео длиннее, но оно отлично подходит для того, чтобы помочь учителям понять стратегию разделения и послушать некоторый язык, чтобы помочь ученикам понять его.Примечание. Часть работы What I Know совпадает с тем, что я называю « Easy Breezy Math. ”
Я настоятельно рекомендую представить эту стратегию (и действительно любую стратегию, но определенно эту) в контексте проблемы со словом, чтобы помочь студентам осмыслить стратегию и действительно понять, что происходит. Полезно называть делимое и делитель в зависимости от контекста.
Советы для преподавателей (с любой стратегией разделения)
1.) Представьте новые стратегии с увлекательным контекстом или проблемой со словом. По мере того, как вы проходите этапы стратегии, проходите через то, что может происходить в проблеме.
2.) Если эти стратегии совершенно новые, то потратьте день (или больше) с однозначными делителями, прежде чем переходить к двузначным делителям. Это будет того стоить!
3.) Убедитесь, что ученики понимают цель Easy Breezy Math, если вы решите использовать эту платформу. Кроме того, убедитесь, что они понимают, что это значит и как работает (в нем представлены частичные коэффициенты, которые уже готовы для учащихся на выбор).
4.) Научите студентов проверять свои ответы умножением. Это поможет им в самооценке и позволит им обнаруживать небольшие ошибки, которые они допускают при вычитании или другие ошибки вычислений.
А как насчет традиционного алгоритма деления?
Поскольку в моем штате используется общее ядро, я не преподаю традиционный алгоритм деления в рамках учебной программы пятого класса. Однако после государственного тестирования мы делаем предварительный просмотр математики в шестом классе. В то время я всегда много учил традиционному алгоритму.К этому моменту у моих учеников есть четкое понимание деления и лучшее чувство чисел. Это помогает им освоить алгоритм. Кроме того, я обнаружил, что многие учителя шестого класса ожидают, что они знают традиционный алгоритм, поэтому я определенно не хочу, чтобы мои ученики отставали, когда они пойдут в среднюю школу.
Требуется БОЛЬШЕ ресурсов для подразделения?
БЕСПЛАТНЫЕ печатные формы для тренировок Дивизиона: Щелкните здесь, чтобы получить бесплатный пакет печатных материалов Дивизиона дня. Я использую их для утренней работы, проверки математики или домашних заданий после того, как ученики выучили деление и им нужно развить беглость речи и продолжить практику.
Дополнительные ресурсы отдела
: У меня также есть пакет отдела, который содержит печатные формы, простые центры, карточки задач и оценки. Ресурсы не требуют какой-либо конкретной стратегии, поэтому вы можете выбрать стратегии, которые вы хотите, чтобы ваши ученики применяли, или позволить им выбирать. Щелкните здесь, чтобы просмотреть дополнительные ресурсы Division в моем магазине Teachers Pay Teachers.
Используете ли вы какую-либо из этих стратегий разделения? Вы используете другую стратегию разделения? Дайте знать в комментариях.Я всегда ищу новые стратегии разделения для 5-го класса!
.


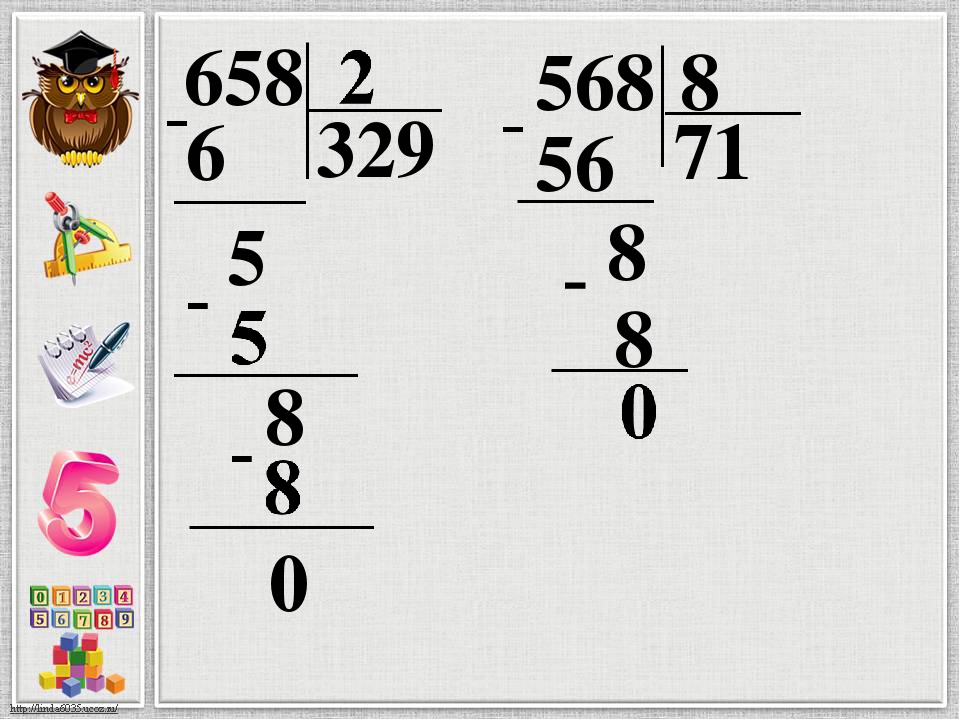

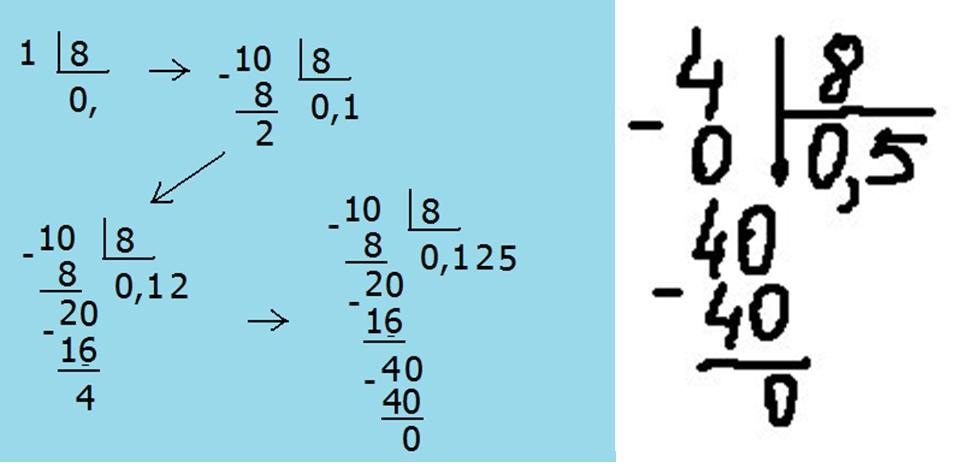 Должно сформироваться понимание понятия целого, в качестве неразделимой категории, а также восприятие отдельных частей целого в понятии самостоятельного объекта.
Должно сформироваться понимание понятия целого, в качестве неразделимой категории, а также восприятие отдельных частей целого в понятии самостоятельного объекта. У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
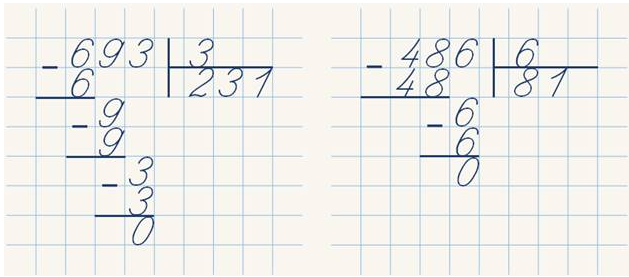
 То в результате возникает дробь обычная -¾, с минусом, или десятичная отрицательная дробь –0,75. В этом случае числа делятся по модулю, невзирая на знаки, потом к результату прибавляется минус.
То в результате возникает дробь обычная -¾, с минусом, или десятичная отрицательная дробь –0,75. В этом случае числа делятся по модулю, невзирая на знаки, потом к результату прибавляется минус.
