Решение задач с помощью уравнений в курсе алгебры 7 класса.
Учебник для учащихся 7 класса общеобразовательных учреждений Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; под ред. С. А. Теляковского. Алгебра. 7 класс -М.: Просвещение, 2017г.
-
Тема: Решение задач с помощью уравнений. -
Классифицировать все текстовые и логические задачи. -
Проанализировать особенности решения каждой задачи.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4)Использовать способы применения ИКТ: Презентации илюстрирующая задачу.
Комплект задач для стартовой диагностики.
1. Составьте равенство, используя условие, и найдите значение переменной:
а) Одна деталь весит х кг, а другая 4х кг. Вместе эти детали весят 55 кг.
б) Длина прямоугольника равна 2х см, ширина х см, а периметр равен 156 см.
2. Отцу и сыну вместе 60 лет. Сколько лет каждому, если отец в 3 раза старше сына.
3. В первый день продали на 4 телевизора меньше, чем во второй. Сколько телевизоров продали в каждый день, если известно, что всего продали 18 телевизоров.
Комплект задач для промежуточной диагностики.
-
За два дня на элеватор отправили 574 т зерна, причем в первый день в 1,8 раза меньше, чем во второй. Сколько тонн зерна было отправлено в первый день и сколько во второй?
Сколько тонн зерна было отправлено в первый день и сколько во второй?
-
За три дня было продано 830 кг апельсинов. Во второй день продали на 30 кг меньше, чем в первый, а в третий – в 3 раза больше, чем во второй. Сколько килограммов апельсинов было продано в первый день -
Яблонь в саду на 12 деревьев меньше, чем груш, и в 2 раза меньше, чем вишен. Сколько посажено яблонь, сколько груш и сколько вишен, если всего в саду 100 деревьев -
На нижней полке было в 4 раза книг меньше, чем на верхней. После того как на нижнюю полку переставили с верхней 27 книг, на полках книг оказалось поровну. Сколько книг было на каждой полке первоначально
Комплект задач для итоговой диагностики.
-
На нижней полке было в 3 раза книг болььше, чем на верхней. После того как на верхнюю полку переставили с нижней 15 книг, на полках книг оказалось поровну. Сколько книг было на каждой полке первоначально?
После того как на верхнюю полку переставили с нижней 15 книг, на полках книг оказалось поровну. Сколько книг было на каждой полке первоначально?
-
На первом катере было в 2 раза больше людей, чем на втором. Когда на ближайшей пристани с первого катера сошли 98 человек, а со второго 16 человек, то на обоих катерах людей стало поровну. Сколько человек было на каждом катере первоначально? -
Турист шел от турбазы до станции со скоростью 6 км/ч. Если бы он шел со скоростью 4 км/ч, то затратил бы на дорогу на 1 час больше. Чему равно расстояние от турбазы до станции? -
Из поселка в город едет автомобиль. Если он увеличит скорость на 8 км/ч, то приедет в город через 6 часов. Если же автомобиль уменьшит скорость на 12 км/ч, то приедет в город через 8 часов. С какой скоростью движется автомобиль?
Ресурс: http://videouroki. net
net
Поиск
Поиск
-
Школьный помощник- математика 5 класс
- математика 6 класс
- алгебра 7 класс
- алгебра 8 класс
- геометрия 7 класс
- русский язык 5 класс
- русский язык 6 класс
- русский язык 7 класс
- математика
- алгебра
- геометрия
- русский язык
«»
следующая
предыдущая
вернуться на предыдущую страницу
Такой страницы нет !!!
- Популярные запросы
- Обстоятельство
- Дополнение
- Определение
- Деление дробей
- Математика 6 класс
- Русский язык 7 класс
- Русский язык 6 класс
- Алгебра 8 класс
- Русский язык 5 класс
- Алгебра 7 класс
- Математика 5 класс
- Наименьшее общее кратное
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Наибольший общий делитель.
 Взаимно простые числа
Взаимно простые числа - Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Деление и дроби
- Доли. Обыкновенные дроби
- Квадратный корень из неотрицательного числа
- Окружность и круг
- Антонимы. Синонимы
- Десятичная запись дробных чисел
- Буквы о – а в корнях -лаг- / -лож-, -рос- / -раст- (-ращ-)
Алгебра 7 класс «Решение задач с помощью уравнений»
Цели урока:
1. Образовательные:
— закрепить умения и навыки решать линейные уравнения и задачи с помощью составления уравнений;
— формировать умения самостоятельно решать задачи.
2. Развивающие:
— посредством решения заданий развивать логическое мышление, культуру устного счета и речь учащихся;
— дать возможность каждому ребенку определить для себя уровень сложности в выполнении заданий, тем самым развивать самостоятельность, умение критически относиться к своей работе.
3. Воспитательные:
— используя игру как здоровьесберегающую технологию, содействовать воспитанию интереса к математике, активности.
Записи на доске:
— название банка;
— тема урока;
— высказывание Конфуция;
— задания для устного счета;
— задания для практической части.
План и ход урока.
1. Организационный момент.
2. Проверка знаний теоретического материала по теме: «Уравнения с одной переменной».
3. Устная работа.
4. Решение заданий разного уровня.
5. Дифференцированная самостоятельная работа.
6. Подведение итогов.
7. Индивидуальное домашнее задание.
Сегодня мы с вами проведем необыкновенный урок: Урок- игру «Банк знаний».
Тема нашего урока: «Решение задач с помощью уравнений».
На уроке мы повторим определения, свойства линейного уравнения с одной переменной, закрепим навыки и умения решения линейных уравнений с одной переменной, решения задач с помощью составления уравнений.
Китайский мудрец Конфуций, живший, 500 лет до нашей эры сказал:
«Те, кто обладают врожденными знаниями — богаче всех. За ними следуют те, кто приобретают знания благодаря учению».
Так давайте же будем приобретать знания, и в конце урока мы выясним, сможем ли мы себя назвать богатыми.
В городе Когалым есть сберегательный банк, банк «Петрокоммерц», Ханты-Мансийский банк и сегодня открывается еще один банк: «Банк знаний». Туда я и предлагаю вам вложить сегодня деньги, заработанные во время урока, за свои знания. Для того, чтобы сделать первый вклад вы должны ответить на мои вопросы и получить за это первоначальный капитал. За каждый правильный ответ вы получаете одну медную монету достоинством в « 1 тугрик». 1.Устный счёт.
x = 9
x = 35
y = 57
нет корней
c = 17
p = 80
b = 3
x = 4
x = 9
y = 2
2. В одном бидоне x л, а в другом y л молока.
В одном бидоне x л, а в другом y л молока.
Что означает выражение?
а) x + y
б) x + 5
в) y — 3
г) x — y
2. 2. Что означает равенство?
а) x+ y = 28
б) x + 5 = y
в) 4x = y
г) x – 12 = y + 24
3. Составьте выражение для решения задачи
2x + 18
Вася решил несколько примеров, а Петя в 2 раза больше. Сколько примеров решил Петя? Сколько примеров решили они вместе?
2x; x + 2x
Антон прочитал несколько страниц книги, осталось ему прочитать на 32 страницы больше, чем уже прочитано.
 Сколько страниц в книге?
Сколько страниц в книге?
x + x + 32
3x — x _ что их связывает?
_ сформулируйте тему урока.
4.Разминка
1. Дайте определение корня уравнения.
2. Является ли число 7 корнем уравнения 2х — 5 = х + 2 ?
3. Что значит решить уравнение?
4. Какие уравнения называются равносильными?
5. Сформулируйте свойства уравнений.
6. Приведите пример уравнения, равносильного уравнению 5х — 4 = 6.
7. Дайте определение линейного уравнения с одной переменной.
8. Приведите примеры.
9. В каком случае уравнение ах = в имеет:
— единственный корень,
— множество корней,
— не имеет решения ?
Итак, вы имеете определенный капитал.
Продолжим пополнять свой капитал. Вам предстоит выполнить задания. За каждое верное решение вы получаете одну медную монету достоинством один тугрик, которую вы можете поместить в разные вклады:
I. Вклад «Легкий»
Вклад «Легкий»
Решите уравнение:
а) 2х = 0 г) 6х = 3
б) 3х = 1 д) 3х + 9 = 0
в) х — 2 = 0 е) 7х — 4 = х — 16
II. Вклад «Занимательный»
На доске было написано решение линейного уравнения, но правую часть данного уравнения стерли. Восстановите ее:
а) 3х = …. б) 5х = …. в) 0,2х =….
х = -11 х = 0 х = 14
III. Вклад «Поисковый»
Какое из чисел 3 или -2, является корнем уравнения
а) 3х = — 6 в) 4х — 4 = х + 5
б) х + 3 = 6 г) 5х — 8 = 2х + 4
IV. Вклад «Универсальный»
При каких значениях а уравнение
ах = 8
а) имеет корень, равный -4; 0,5;
б) не имеет корней;
в) имеет отрицательный корень.
5.Решение задач. Вы получили информацию об основных вкладах нашего банка. А теперь каждому из вас предстоит выполнить задания, за решение которых вы будете также получать тугрики.
А теперь каждому из вас предстоит выполнить задания, за решение которых вы будете также получать тугрики.
В банке работают кассиры, которые будут за правильные решения выдавать монеты:
а — медная монета достоинством в 1 тугрик
в — серебряная монета достоинством в 2 тугрика
с — золотая монета достоинством в 3 тугрика
После выполнения всех заданий у каждого из вас образуется накопительный фонд.
Итак, приступайте, перед вами на столах лежат задания для различных вкладов. Самостоятельно выбирайте вклад, решайте, сдавайте кассиру банка и получайте тугрики.
а Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в два раза моложе дедушки?
в За 3 часа мотоциклист проезжает то же расстояние, что велосипедист за 5 часов. Скорость мотоциклиста на 12 км/ч больше скорости велосипедиста. Определите скорость каждого.
с В двух сараях сложено сено, причем в первом сарае сена в 3 раза больше, чем во втором. После того, как из первого сарая увезли 20 т., а во второй привезли 10 т. В обоих сараях сена стало поровну. Сколько сена было во втором сарае первоначально.
После того, как из первого сарая увезли 20 т., а во второй привезли 10 т. В обоих сараях сена стало поровну. Сколько сена было во втором сарае первоначально.
Купили 2 кг 100 г крупы и высыпали ее в три банки. В первую банку крупы вошло в 3 раза больше, чем во вторую, а в третью банку насыпали 500 г крупы. Сколько крупы насыпали в первую и сколько во вторую банки?
Решение.
Пусть во вторую банку насыпали x г крупы, тогда в первую – 3x г крупы. Всего в три банки насыпали (3x + x + 500) г, что по условию составляет 2100 г. Составим и решим уравнение.
3x + x + 500= 2100;
4x + 500 = 2100;
4x = 2100 — 500;
4x = 1600;
x = 1600 : 4;
x = 400.
400 г – насыпали во вторую банку.
400 × 3 = 1200 (г) – в первой банке.
Задача для слабых. с В первом мешке в 3раза больше картофеля, чем во втором. После того, как из одного мешка взяли 30 кг. картофеля, а во второй насыпали ещё 10 кг., в обоих мешках картофеля стало поровну. Сколько килограммов картофеля было во втором мешке.
Задача для сильных. Подготовка к ГИА. Решение задач из сборника заданий ГИА-2010.В.В. Кочагина, М.Н. Кочагиной .Алгебра. Москва. Эксмо, 2009.
1. Велосипедист собирался преодолеть расстояние от поселка до станции за 5 часов. Выехав из поселка, он увеличил свою скорость на 3 км/ч и проехал расстояние до станции за 4 часа. Чему равно расстояние от поселка до станции?
Ну вот и наступило время подвести итог, сейчас каждый из вас подсчитает сколько тугриков сможет внести в «Банк Знаний»
1. Считаем медные монеты достоинством в 1 тугрик, вы получаете столько тугриков, сколько у вас монет.
2. Считаем серебряные монеты достоинством в 2 тугрика. Умножьте количество серебряных монет на два и получите количество тугриков.
Умножьте количество серебряных монет на два и получите количество тугриков.
3. Считаем золотые монеты достоинством в три тугрика. Умножьте количество монет на три, получите количество заработанных тугриков.
4. Сложите все полученные тугрики.
Вы получили «5», если набрали 15 тугриков и более, «4», если набрали 10-14 тугриков, «3», если набрали 5-9 тугриков.
Поставьте оценку в дневник, запишите число набранных тугриков на квитанции банка, вложите квитанцию и тугрики (монеты) в пакет и сдайте кассирам банка.
Увеличить свой капитал вы можете дома, выполнив индивидуальные задания, которые лежат у каждого на столе. Выбирайте любой вклад и продолжайте зарабатывать тугрики в «Банке Знаний»
Положите задания в дневник.
Задание на дом:
Вклад «Поисковый»
Решить уравнение:
а 1/5х = 5
3х — 11,4 = 0
4х + 5,5 = 2х — 2,5
в 2х — (6х+1) = 9
5х — 12,5 = 0
3х — 0,6 = х + 4,4
с 4х — (7х — 2) = 17
8х — (2х + 4) = 2(3х — 2)
3х — (9х — 3) = 3 (4 — 2х)
Вклад «Творческий»
а В двух седьмых классах 47 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?
Сколько учеников в каждом классе?
в Саша решил две задачи за 35 минут. Первую задачу он решал на 7 минут дольше, чем вторую. Сколько минут Саша решал вторую задачу?
с В первом мешке в 3раза больше картофеля, чем во втором. После того, как из одного мешка взяли 30 кг. картофеля, а во второй насыпали ещё 10 кг., в обоих мешках картофеля стало поровну. Сколько килограммов картофеля было во втором мешке.
Квитанция «Банка Знаний» к домашнему заданию.
Решить уравнение:
а одно задание 1 тугрик
в одно задание 2 тугрика
с одно задание 3 тугрика
Решить задачу:
а 1 тугрик
в 2 тугрика
с 3 тугрика,
чтобы получить
«5» нужно набрать 12 тугриков
«4» нужно набрать 8-11 тугриков
«3» нужно набрать 4-7 тугриков
Кто же сегодня у нас самые богатые? Те, кто заработал 15 тугриков и более, могут позволить себе делать большие капиталловложения: строить заводы, фабрики, нефтяные вышки. Те, кто заработал 10-14 тугриков, смогут отправиться в путешествие. Ну, а те, кто заработал 5-9 тугриков, вы можете посетить фитобар нашей школьной столовой и купить коктейль. Итак, сегодня банк закрывается. До свидания! До новых встреч в «Банке Знаний».
Те, кто заработал 10-14 тугриков, смогут отправиться в путешествие. Ну, а те, кто заработал 5-9 тугриков, вы можете посетить фитобар нашей школьной столовой и купить коктейль. Итак, сегодня банк закрывается. До свидания! До новых встреч в «Банке Знаний».
Желаю вам цвести, расти,
Копить, крепить здоровье,
Оно для дальнего пути –
Главнейшее условие.
Пусть каждый день и каждый час
Вам новое добудет,
Пусть добрым будет ум у вас,
А сердце умным будет.
Вам от души желаю я,
Друзья, всего хорошего.
А всё хорошее, друзья,
Даётся нам недешево.
С.Я.Маршак
Как научиться решать задачи по геометрии? | Консультация (7 класс) на тему:
Как научиться решать задачи по геометрии?
Дорогие ребята, Вы начали изучать геометрию. Это новая для вас дисциплина, и вы поначалу можете испытывать трудности в её освоении. Не пугайтесь: пройдет некоторое время, и вы научитесь с легкостью решать любые геометрические задачи. Для приобретения необходимого навыка нужно лишь приложить немного усилий. Итак, как решать задачи по геометрии?
Не пугайтесь: пройдет некоторое время, и вы научитесь с легкостью решать любые геометрические задачи. Для приобретения необходимого навыка нужно лишь приложить немного усилий. Итак, как решать задачи по геометрии?
Вам понадобится: учебник, тетрадь, ручка, карандаш, линейка, транспортир, циркуль, ластик.
Инструкция:
- Внимательно прочитайте условие задачи.
- Сделайте чертеж.
- Отметьте на чертеже то, что вам дано: длины сторон, величины углов. Если в условии задачи сказано, что какие-то отрезки равны, поставьте на них одинаковые штрихи. Равные по величине углы отмечайте одинаковыми дужками: одинарными, двойными, волнистыми. Углы разных величин выделяйте разными дужками.
- Исследуйте фигуры, представленные в задаче. Вспомните их определения и свойства.
- Определите тему, к которой относится ваша задача. Освежите в голове теоретический материал по этой теме, повторите основные теоремы.
- Рассмотрите примеры решения задач по этой теме.
 В задачах, приводимых в учебнике в качестве примеров, часто рассматриваются принципиальные вопросы, которые вы должны знать.
В задачах, приводимых в учебнике в качестве примеров, часто рассматриваются принципиальные вопросы, которые вы должны знать. - Если вы чувствуете себя в теме достаточно уверенно, приступайте к решению задачи. Начните с того, что требуется найти или доказать. Подумайте, каким путем это можно сделать. То есть, решайте задачу «с конца».
- Если вы не видите путей решения задачи, попробуйте найти хоть что-нибудь, используя имеющиеся данные. Возможно, так к вам придет идея, как решать задачу.
Полезные советы: не увлекайтесь «устными» доказательствами. Записывайте решение задачи как можно более подробно, если не оговорено иное. Некоторые вещи могут казаться вам очевидными, но всё равно прописывайте их. Так у вас будет отрабатываться навык, вы лучше запомните идею.
Рекомендации от учителя математики Е.В.Жалыбиной
Как научиться решать примеры по алгебре намного быстрее?
В седьмом классе уже нет обычной математики: она делится на более сложные предметы — алгебру и геометрию. И именно на этом этапе у многих учеников начинаются серьезные сложности с обучением. Это связано с тем, что появляется много новых, непростых тем. В 7 классе ученики изучают математическую модель, линейную функцию, степень с натуральным показателем, одночлены, многочлены и многое другое. Домашние задания, как и упражнения в классе, становятся больше, объемнее. Если допустить одну маленькую ошибку, то ее исправление нередко занимает полчаса и больше.
И именно на этом этапе у многих учеников начинаются серьезные сложности с обучением. Это связано с тем, что появляется много новых, непростых тем. В 7 классе ученики изучают математическую модель, линейную функцию, степень с натуральным показателем, одночлены, многочлены и многое другое. Домашние задания, как и упражнения в классе, становятся больше, объемнее. Если допустить одну маленькую ошибку, то ее исправление нередко занимает полчаса и больше.
Вот почему гдз по алгебре 7 класс мордкович — пособие, которое всегда нужно иметь под руками. Это решебник, благодаря которому ученик в любой момент проверит то, что он написал, и сможет обнаружить ошибку, не тратя на это много времени. ГДЗ подходят для самых разных задач — подготовки домашнего задания, работы в классе, повторения всего материала перед контрольными работами.
Чем дальше идет обучение в седьмом классе, тем полезнее решебник, потому что запомнить большой объем информации очень трудно — и надежная «шпаргалка» никогда не помешает.
Чем удобны пособия по алгебре
Если посоветоваться с учителем можно только в классе, то решебник всегда под рукой — и там уже есть правильные ответы на все вопросы. А еще многие примеры предполагают получение ответа разными способами. Обычно ученику приходит в голову только один способ, а до остальных догадаться трудно. Как раз решебник и подскажет, как еще можно добиться того же результата, но другим путем — это очень полезно для развития мозга и для последующего обучения.
Онлайн-формат обучения еще больше плюсов
На сайте Випгдз все пособия представлены в онлайн-формате, и у этого решения сразу несколько плюсов:
- Максимальная экономия места в рюкзаке и на книжных полках. Решебники по всем предметам остаются в телефоне или компьютере — для доступа к ним достаточно интернета и подходящего устройства.
- Удобство поиска упражнений. Задачи и примеры пронумерованы с учетом того, как они располагаются в учебнике. Все находится за считаные минуты, а то и секунды.

- Возможность использовать пособия в школе. Есть учителя, которые не очень жалуют ГДЗ, а потому запрещают брать такие книги в школу. Но если решебник находится в телефоне, он никогда не попадется учителю на глаза.
«Випгдз» — это хорошая помощь для тех, кто хочет отлично справляться с домашними заданиями, повышать уровень знаний и решать контрольные на высокие оценки. Если тщательно изучать тему, тренироваться и параллельно проверять свои ответы в ГДЗ, каждый урок принесет еще больше пользы.
Вопросы олимпиадной подготовки по математике — Колпаков Александр Николаевич
Здесь публикуются ответы на вопросы репетитору, связанные с олимпиадной подготовкой. Если Вам нужен совет по решению какой-либо учебной или организационной задачи (подбору репетитора, школы, графика занятий, олимпиадных задачников и т. д.), — не стесняйтесь их задавать. Конечно, сориентироваться в проблеме только на основе ее словесного описания (без диагностики ученика) крайне сложно, но я постараюсь представить себе ситуацию в наиболее типичном раскладе и описать вероятную перспективу тех или иных действий. Пишите, спрашивайте.
Вопрос репетитору по математике от Саблиной Татьяны:
Добрый вечер, Александр Николаевич! Может быть Вы поможете советом: мой шестнадцатилетний ребенок получает достаточно хорошие оценки по алгебре и геометрии (в основном 9 — 10 по 10-ти бальной системе), понимает и усваивает материал на уроках сходу, никогда с репетитором по математике не занимался. Но вот олимпиадные задачи не идут, не хватает логики или смекалки, не знаю. Принимал участие в районных олимпиадах — в 3 — 5 классах, потом в 6-7 классах, занимал даже третьи места или поощрения. Но вот в 9 -10 классах наотрез отказывается от участия в районных и городских олимпиадах — учитель настаивает, заставляет, не верит, что ребенок не понимает (а он реально говорит, что ничего не понимает и я ему охотно верю), хотя в этом году же занял третье место в школьной олимпиаде. Учится он по всем предметам ровно, т.е на 8-9, не зубрилка, живем в Риге. Вопрос в следующем: можно ли научиться решать нестандартные олимпиадные задачи? Есть ли репититоры по математике для такого вида задач? И вообще стоит ли напрягать сына ходить на олимпиады, ведь он отлично осваивает школьную программу? Научиться решать олимпиадные задачи по математике могут все умные дети или нужны еще какие-то качества, кроме ума? Если найдете свободную минутку- то напишите свои мысли.
Сын собирается поступать в один из технических университетов Германии, и участие (призовые места) в олимпиадах пригодились бы.
С уважением Татьяна.
Мнение репетитора А.Н. Колпакова: Нельзя заставлять ребенка участвовать в олимпиадах, если он сам этого не хочет. Олимпиада олимпиаде рознь (особенно если сравнивать 5 класс и 10 класс) и поэтому нельзя предъявлять к ним одинаковые требования. Еще неизвестно почему Ваш ученик перестал занимать призовые места. Возможно, уровень олимпиадных заданий по математике в 10 классе для него слишком высокий и не соответствуют на сегодняшний день его способностям. А возможно его задавила школа, и он потерял олимпиадную смекалку. Трудно сказать. В любом случае для решения сложной задачи нужна полная мобилизация мыслительного потенциала человека, а для этого, прежде всего, требуется огромное желание преодолеть трудности. Есть его нет, — бесполезно ходить на олимпиады вообще. Возможно, ученик это понимает и поэтому отказывается.
Грамотный репетитор по математике никогда не занимается натаскиванием ученика на олимпиадные задачи, ибо нельзя предугадать их тематику в реальности. Правильная стратегия репетитора — движение в сторону фундаментального математического и общего интеллектуального развития подростка.
Теперь о возможностях научить решению нестандартных задач. Научить, — это значит рассказать некий универсальный метод, позволяющий с теми или иными затратами умственной энергии справляться с любой олимпиадной ситуацией. Такого метода не существует. Репетитор по математике физически не сможет рассмотреть все задачи. Что реально сделать? Можно получить практику решения олимпиадных задач, которая создаст хороший плацдарм для развития мышления ребенка и условий формирования его интереса к предмету в целом.
Нестандартные задачи потому и называют нестандартными, что для них не существует заранее определенного алгоритма решения. Каждая задача имеет свой уникальный «код доступа» и используются для отбора талантливых детей с высоким уровнем знаний, способностей и смекалки. Хороший олимпиадный репетитор по математике создает условия, в которых эти показатели достигают максимального предела. Он индивидуален для каждого человека.
Многие нестандартные задачи, которые таковыми являются в школе, в курсе высшей математики (аналитической геометрии, высшей алгебры, анализа, теории чисел) переходят в категорию стандартных. Поэтому все относительно. Знания общих законов помогают брать нереальные, казалось бы, высоты и поэтому репетиторы по математике часто с легкостью решают олимпиадные задачи 5 — 11 классов только потому, что за годы фундаментальной учебы получили высшие знания. Именно поэтому, помимо изучения нестандартных задач, профессиональный репетитор по математике уделяет время обобщению базовых тем, даже если ученик щелкает типовые задачки как орешки.
Путь к вершинам математического и общего интеллектуального развития не должен лежать только через одни олимпиады. И не стоит на них зацикливаться. Учитесь понимать теорию, выполняйте сложные базовые упражнения. Практика показывает, что углубленное изучение математики с репетитором приносит гораздо больше пользы, чем долгая и изнурительная олимпиадная практика. Можно месяцами решать одну и ту же нестандартную задачу и ничего не приобрести с этого, кроме отставания в фундаментальном освоении предмета.
А.Н. Колпаков. Репетитор по математике — Москва. Олимпиадная помощь школьникам.
как подготовиться к промежуточной и итоговой аттестации по математике с 5 по 11 класс
В «Экстернате и домашней школе Фоксфорда» вы можете готовиться к аттестациям по математике с пятого по 11 класс вместе с преподавателями из МГУ, МФТИ, ВШЭ. Занятия базового уровня позволяют успешно сдавать промежуточные аттестации, также есть специальные курсы для подготовки к ОГЭ и ЕГЭ. Любители математики могут совершенствовать знания на углублённых и олимпиадных курсах. На онлайн-занятиях вы сможете напрямую задавать вопросы, а для повторения и закрепления материала полезно просматривать записи.
Занятия — это фундамент, но порой для успешного освоения материала нужно что-то большее. Особенно если предмет не относится к разряду любимых. Мы собрали интересные способы подготовиться к аттестации по математике без заучивания. А также составили небольшой чек-лист знаний и умений для каждого класса, чтобы вы точно не забыли повторить всё, что нужно.
5 класс
Что нужно знать и уметь к промежуточной аттестации по математике
- Складывать и вычитать двузначные числа и обыкновенные дроби в уме.
- Умножать однозначные числа.
- Округлять натуральные числа.
- Знать основные единицы длины, массы, времени, скорости, площади, объёма.
- Решать текстовые задачи.
- Изображать геометрические фигуры.
- Составлять таблицы, строить диаграммы.
- Находить проценты.
Способы подготовки к аттестации по математике в 5 классе
Математика — сложный предмет, и в ней бывают темы, которые никак не даются. В таком случае поможет игра.
Например, стать настоящим знатоком дробей поможет настольная игра «Делиссимо». В ней несколько уровней сложностей. Самый лёгкий для тех, кто ещё только знакомится с дробями: на этом этапе игроку нужно собирать кусочки пиццы, соотнося их друг с другом. Это поможет понять, что три четверти пиццы и одна четверть плюс половина — одно и то же. Позже добавляются карточки с дробями, и с их помощью можно потренировать умение складывать и вычитать дроби, приводить их к одному знаменателю.
Чтобы поладить с задачами, нужно решать их каждый день, тогда математический текст перестанет быть для вас чем-то сложным. Каждая задача — интересная головоломка, в которой нужно разобраться. Чтобы процесс подготовки к аттестации по математике не наскучил, советуем найти действительно интересные задачки. Например, у Григория Остера есть целый юмористический задачник «Ненаглядное пособие по математике».
6 класс
Что нужно знать и уметь к промежуточной аттестации по математике
- Представлять основные этапы развития математической науки.
- Понимать математический текст, знать символы и термины.
- Владеть натуральными числами.
- Пользоваться системой координат, уметь располагать на ней точки.
- Складывать, умножать и делить рациональные числа.
- Умножать и делить дроби.
- Решать задачи при помощи пропорции.
- Знать основные законы и определения геометрии.
- Считать длину и площадь круга.
Способы подготовки к аттестации по математике в 6 классе
В шестом классе материала очень много, и к аттестации что-то может забыться. Быстро повторить основные этапы развития математики можно при помощи образовательного сериала «Нарисованные и100рии». Истории математики посвящена одна серия: в виде комиксов она рассказывает, как математика помогала в древности и чем занимался Пифагор.
В курс математики шестого класса входит раздел простейшей геометрии. Здесь очень важно освоить основные термины. Разобраться и подготовиться к промежуточной аттестации поможет карточная настольная игра «Геометрика», а также дополнение к ней «Геометрика Extra» — для тех, кого не пугают сложные задания. Играть нужно картами: на одних фигуры, на других условия и признаки. Условий несколько, их можно менять в зависимости от уровня подготовки.
7 класс
Что нужно знать и уметь к
промежуточной аттестации по математике
- Уметь определять линейную функцию.
- Знать, что такое степень, и производить с ней различные действия.
- Проводить арифметические операции над одночленами и многочленами.
- Решать квадратичную функцию.
- Владеть всеми начальными геометрическими сведениями.
- Знать признаки треугольников и решать задачи с их помощью.
- Уметь находить сумму углов треугольника.
- Строить различные треугольники.
Способы подготовки к аттестации по математике в 7 классе
Главное в математике — это не выучить, а понять правило и научиться его использовать. Именно это вы и должны продемонстрировать на промежуточной аттестации.
Например, трудности могут вызвать степени, и разобраться с ними снова помогут игры. Потренировать степени числа 2 можно при помощи популярной игры «2048». Нужно передвигать по игровому полю фишки, на которых написаны различные степени числа 2. Две одинаковые фишки образуют следующую степень. Цель игры — получить число 2048, то есть 2 в 11 степени. Сделать это не так просто, как кажется.
Источник: 4stor.ru
8 класс
Что нужно знать и уметь к промежуточной аттестации по математике
- Уметь совершать различные действия с алгебраическими дробями и решать их через функции.
- Понимать определение квадратного корня, уметь его извлекать.
- Применять свойства арифметических квадратных корней для вычисления числовых выражений.
- Решать квадратные уравнения, владеть терминологией; знать формулы Виета.
- Применять свойства неравенств; решать линейные неравенства и их системы.
- Находить площади фигур; знать Теорему Пифагора.
- Знать все четырёхугольники и владеть действиями с ними.
- Знать признаки подобия треугольников.
- Понимать окружность.
Способы подготовки к аттестации по математике в 8 классе
По геометрии в восьмом классе проходят очень много фигур и правил. Легко и с интересом изучить их поможет игра на мобильный «Пифагория». Она содержит более 300 головоломок по всем разделам геометрии. Некоторые задачки настолько сложные, что придётся долго ломать голову. Это отличный игровой тренажёр, чтобы повторить все правила, научиться легко решать задачи, выучить что-то новое и успешно подготовиться к аттестации.
Быстро вспомнить весь пройденный ранее материал поможет книга Кэрол Вордерман «Как объяснить ребёнку математику». Это краткий иллюстрированный справочник со всей школьной программой. Информация разделена по разделам: алгебра, геометрия, тригонометрия и другие. Яркие диаграммы и примеры помогут вспомнить все формулы и правила в процессе подготовки к аттестации по математике.
9 класс
В девятом классе обязательна сдача государственной итоговой аттестации в форме ОГЭ (основного государственного экзамена). На ОГЭ проверяются все знания по математике за девять классов. Экзамен сдаётся в тестовой форме, на выполнение даётся почти четыре часа. Работа состоит из двух частей. В первой 17 заданий с кратким ответом, во второй шесть заданий с развёрнутым ответом. Впервые в 2020 году в ОГЭ 1–5 задания будут практической направленности. Они выполняются при помощи одного чертежа в начале теста.
Что нужно знать и уметь к итоговой аттестации по математике
- Делать вычисления и преобразования.
- Решать уравнения, неравенства и их системы.
- Строить и читать графики функций.
- Выполнять действия с геометрическими фигурами, координатами и векторами.
- Работать со статистической информацией, находить частоту и вероятность случайного события.
- Решать математические задачи разными способами.
- Уметь математически грамотно и ясно записать решение.
- Применять математические знания в практических ситуациях.
Способы подготовки к аттестации по математике в 9 классе
Потренируйтесь верно распределять время. Поставьте себе таймер на 3 часа 55 минут и попробуйте решить тест. Вам должно хватить времени на то, чтобы решить все задания, как следует посидеть над сложными задачами, а потом ещё и всё перепроверить.
На ОГЭ пригодится устный счёт. Времени на экзамен даётся не так много, а нужно успеть решить все примеры и задачи, и ещё и проверить самые сложные. Артур Бенджамин и Майкл Шермер написали книгу «Магия чисел», которая научит быстрым операциям в уме даже с большими числами.
10 класс
Что нужно знать и уметь к промежуточной аттестации по математике в 10 классе
- Решать числовые функции.
- Знать действия с тригонометрическими функциями.
- Решать тригонометрические уравнения.
- Выполнять преобразования тригонометрических выражений.
- Знать действия с производными.
Способы подготовки к аттестации по математике в 10 классе
В 10 классе много повторений прошлых лет. Если решать уравнения уже наскучило, а двигаться вперёд и улучшать свой результат нужно — советуем прочитать книгу Алекса Беллоса «Красота в квадрате». С ней вы влюбитесь в математику, повторите всю программу средней школы и поймёте основы тригонометрии. После этой книги даже самые сложные формулы и функции будут не страшны.
11 классы
В 11 классе государственная итоговая аттестация по математике сдаётся в форме ЕГЭ. На ЕГЭ проверяются знания по всей школьной программе по математике. На едином госэкзамене можно выбрать уровень: базовый или профильный. Второй нужен тем, кто собирается поступать на специальности, где важна математика. Первый обязателен для всех.
Что нужно знать и уметь для того, чтобы сдать базовую математику на ЕГЭ
- Выполнять вычисления и преобразования.
- Решать уравнения и неравенства.
- Выполнять действия с геометрическими фигурами, координатами и векторами.
- Уметь строить и исследовать простейшие математические модели.
- Использовать математику в практической деятельности.
Для сдачи профильного уровня понадобится всё то же самое, только более углублённо. А ещё необходимо будет владеть элементами комбинаторики, статистики и теории вероятностей.
Способы подготовки к итоговой аттестации по математике в 11 классе
Для подготовки к ЕГЭ решайте как можно больше задач — это разовьёт математическое мышление и навык делать из текста лёгкое уравнение. Старайтесь решать задачи простыми способами. Для проверки попробуйте взглянуть на задание иначе. Большинство задач можно решить по-разному.
Не бойтесь сложных задач при подготовке к итоговой аттестации. Многие задания профильного уровня могут получиться не сразу. На одну задачу может потребоваться несколько часов или даже дней. Важно, чтобы перед экзаменом у вас уже был большой опыт. Поучаствуйте в олимпиадах — они станут дополнительной тренировкой и пробудят нестандартный подход к решению заданий.
Математика, 7 класс, Использование математики, решение задач, требующих пространственного мышления
Попросите учащихся поработать над этой проблемой самостоятельно в течение нескольких минут, чтобы систематизировать свои мысли, а также информацию, содержащуюся в задаче. Во время самостоятельной работы предложите студентам разработать и реализовать план решения проблемы. Воздержитесь от направления мышления студентов и подсказок и дайте им возможность по-настоящему работать независимо.
Затем попросите учащихся поработать с партнерами.Попросите учащихся поделиться подходами и решениями, которые они выработали в свободное время. Попросите партнеров согласовать план решения проблем, который будет реализован вместе, когда они решат оставшуюся часть проблемы. Они также могут вместе сравнивать и уточнять свои решения, чтобы прийти к консенсусу по правильному ответу на проблему. Внимательно следите за пониманием учащихся и задавайте наводящие вопросы. Выберите учащихся, чтобы поделиться своими ответами во время обсуждения в классе. Если они захотят, предоставьте учащимся блоки, которые помогут им решить проблему.
Студенты работают независимо и с партнером, чтобы изучить наименьшее количество блоков, необходимых для завершения структуры. Студентам важно четко сформулировать свои мыслительные процессы при создании и реализации плана решения проблем. Выделение этих мыслительных процессов дает учащимся уверенность и понимание в процессе работы над этим блоком решения проблем.
Обсудите основные этапы создания и реализации плана решения проблем:
- Разберитесь в ситуации.
- Представьте ситуацию.
- Ответьте на вопрос.
- Убедитесь, что ваш ответ имеет смысл.
- Подготовьте презентацию.
- Используйте свой анализ для решения других проблем.
Первым важным шагом является понимание проблемной ситуации. Спросите студентов, чем эта задача отличается от начального задания, в котором им приходилось угадывать количество кубиков, глядя только на одну сторону здания. Обсудите в классе, как учащиеся должны определить наименьшее количество кубиков, необходимых для построения фигуры, учитывая вид спереди и вид сбоку.
SWD: Студенты с ограниченными возможностями могут испытывать трудности с интерпретацией визуальной информации. Предоставьте студентам тактильные трехмерные манипуляторы.
Математическая практика 1: разбираться в проблемах и настойчиво их решать.
Учащиеся систематизируют информацию, отображаемую на двух видах здания, и понимают, как конструкция может иметь эти два разных вида. Затем они начинают создавать систематический способ определения общего количества кубиков в структуре и упорно работают, пока не найдут наименьшее количество кубиков, которые работают.
Математическая практика 2: Размышляйте абстрактно и количественно.
Учащиеся используют абстрактные рассуждения для установления связи между видами здания и кубами, необходимыми для создания этих представлений. Затем они используют свои количественные рассуждения, чтобы найти наименьшее количество кубов, необходимых для структуры.
Математическая практика 3: Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.
Студенты отстаивают, почему они считают свое решение разумным, и имеют возможность критиковать мнение других во время обсуждения в классе.
Математическая практика 4: Модель с математикой.
Учащиеся создают материальные или виртуальные модели конструкции, чтобы показать, насколько их здание соответствует представлениям, данным в задаче.
Математическая практика 5. Стратегическое использование соответствующих инструментов.
Учащиеся используют интерактивные блоки Конструктора блоков или карандаш и бумагу для подготовки своих решений.
Математическая практика 6: Заботьтесь о точности.
Учащиеся следят за точностью задачи, обеспечивая соответствие своей структуры взглядам, приведенным в задаче.
Математическая практика 7: Ищите и используйте структуру.
Студенты используют процесс решения проблем как структуру для подхода и решения проблемы.
Студент испытывает трудности с началом работы.
- Опишите задачу партнеру своими словами.
- Что вы знаете о проблеме?
- Что вы пытаетесь найти?
- Какие инструменты могут помочь вам решить проблему?
- Какие стратегии вы можете попробовать?
У учащегося есть решение, но оно неверное.
- Как можно использовать меньше кубиков в своей структуре?
- Какие кубики необходимы, а какие нет?
- Соответствует ли ваша структура видам спереди и сбоку, приведенным в задаче?
У учащегося есть решение, но ему трудно сформулировать свои соображения.
- Обоснован ли ваш ответ? Откуда вы знаете?
- Как вы можете объяснить свое мышление другим?
- Вы можете сформулировать свое решение в одном предложении?
У учащегося есть решение, и он ждет, пока другие закончат его.
- Объясните свою стратегию решения проблемы.
- Почему вы так подошли к проблеме?
- Можете ли вы использовать другой метод?
- Какие стратегии, которые вы пробовали, не сработали? Почему они не работали?
- Есть несколько вариантов решения этой проблемы? Почему или почему нет?
- 6 кубиков
- Возможное решение (если смотреть сверху с цифрами, обозначающими количество кубиков в стопке):
Время работы
На рисунках показаны вид спереди и справа на конструкцию из кубов.
Используйте интерактивный конструктор блоков, реальные блоки или бумагу и карандаш для выполнения следующих задач.
- Какое наименьшее количество кубов вы могли бы использовать, чтобы создать структуру куба, которая имеет вид спереди и вид справа, как показано выше?
- Нарисуйте схему вручную, используйте блоки или используйте интерактивный конструктор блоков.
Сначала вы можете создать нижний слой. Посмотрите на конструкцию спереди: сколько кубиков вам нужно, исходя из этого вида?
Посмотрите на структуру со стороны: сколько кубиков вам нужно исходя из этого вида?
Если у вас возникли трудности с началом работы, попробуйте описать задачу своим партнерам.
- Что вы знаете?
- Что вы пытаетесь найти?
- Какие инструменты вы можете использовать, чтобы помочь вам?
- Какую стратегию вы можете попробовать?
Если у вас есть решение, попробуйте следующее:
- Объясните свою стратегию решения проблемы.
- Почему вы так подошли к проблеме?
ИНТЕРАКТИВНЫЙ: Конструктор блоков
Common Core: справка по математике для 7-го класса
Учащиеся, нуждающиеся в помощи Common Core: 7th Grade Math, получат большую пользу от нашей интерактивной программы.Мы разбиваем все ключевые элементы, чтобы вы могли получить адекватную справку по Common Core: 7th Grade Math.
С необходимыми концепциями обучения и соответствующими практическими вопросами прямо у вас под рукой, вы получите много помощи Common Core: 7th Grade Math в кратчайшие сроки.
Получите помощь сегодня с нашей обширной коллекцией важной информации Common Core: 7th Grade Math.
Common Core 7th Grade Math может показаться некоторым родителям пугающим, поскольку Common Core — относительно новое дополнение к школьной программе.Инструменты обучения Varsity Tutors создали ресурс Common Core 7th Grade Math Learn by Concept, чтобы предоставить вашему ребенку дополнительную помощь, в которой он нуждается. Learn by Concept — это бесплатный онлайн-ресурс по общей основной математике для 7-х классов, оформленный в виде интерактивной программы. Имея под рукой разнообразные бесплатные учебные пособия по общей основной математике в 7-м классе, вы можете быть уверены, что у него есть доступ к необходимой помощи.
Общий курс математики для 7-х классов по концепциям разделен на пять основных категорий, включая выражения и уравнения, геометрию, соотношения и пропорции, статистику и вероятность, а также систему счисления.Ваш ребенок может ожидать, что он найдет вопросы о решении уравнений, алгебраических неравенствах, масштабах, окружности, соотношениях, выводе, вероятности, сложении и вычитании с отрицательными числами и многом другом. Вы можете чувствовать себя уверенно, зная, что ваш ребенок имеет доступ ко всей необходимой информации. Каждый вопрос, задаваемый в программе Common Core 7-го класса по математике, напрямую связан с информацией, которую они изучают или будут изучать в 7-м классе.
Как только ваш ребенок выберет тему, в которой он хочет проверить свои способности, он найдет один или несколько вопросов по выбранной им концепции.Каждый примерный вопрос Common Core 7th Grade Math представлен с несколькими вариантами ответов на выбор. Ваш ребенок может уделить столько времени, сколько ему нужно, чтобы ответить на каждый вопрос; нет ограничения по времени. Как только они почувствуют себя комфортно с выбранным ответом, они могут прокрутить вниз и определить, правильно ли они его поняли. Каждый правильный ответ четко обозначен, и за каждым ответом следует подробное объяснение, поэтому вы можете чувствовать себя непринужденно, зная, что вашему ребенку показывают правильный подход к каждой проблеме. Эти бесплатные практические вопросы по общей основной математике для 7-го класса созданы, чтобы дать вашему ученику доступ к наиболее точным и актуальным доступным материалам.
Common Core 7th Grade Math Learn by Concept — не единственный доступный ресурс, который может оказать вашему ребенку необходимую помощь. Вы и ваш ребенок также найдете «Вопрос дня», карточки, практические тесты по конкретным концепциям и полные практические тесты. «Вопрос дня» каждый день предлагает вашему ребенку оригинальный вопрос, который будет держать его разум вовлеченным в предмет. Полностью настраиваемые карточки Common Core по математике для 7-го класса позволяют вашему ребенку создавать концептуальные упражнения с учетом их потребностей.Общие базовые практические тесты по математике для 7-го класса дают вашему ребенку представление о концепциях, с которыми он может столкнуться на реальных тестах, а полные практические тесты могут помочь вам в составлении плана обучения по общей основной математике 7-го класса для вашего ребенка. Все учебные инструменты для репетиторов университетской школы на 100% бесплатны, так что вы можете побудить своего ребенка воспользоваться полным спектром бесплатных ресурсов для обзора общих основ математики для 7-го класса.
Четыре основные математические концепции, которые дети изучают в 7–8 классах | Scholastic
Учащиеся 6 классов закладывают фундамент математики, над которой они будут работать в 7 классах и 8 .Многие из концепций являются продолжением работы 6 -го уровня и позволяют глубже погрузиться в понимание и развитие, ведущее к алгебре. Учащиеся 7 -го и 8 -го классов готовятся к работе, которую они будут выполнять в средней школе по алгебре и геометрии. Эти строительные блоки будут иметь решающее значение для их общего понимания и успеха на уровне старшей школы.
1. Система счисления. В 7 -м классе ученики полностью поймут, как интерпретировать и вычислять все рациональные числа.Они могут складывать, вычитать, умножать и делить все десятичные дроби и дроби, а также представлять проценты. Они вычисляют как положительные, так и отрицательные числа, используя все четыре основные операции, и интерпретируют значение абсолютного значения. В 8 -ом классе ученики переходят от рациональных чисел к иррациональным числам. Они понимают концепцию десятичного разложения и могут интерпретировать и находить как рациональные, так и иррациональные числа на числовой прямой.
Поощряйте своего ребенка:
- Используйте числовые линии при расчетах как с положительными, так и с отрицательными числами.Наличие вертикальной и / или горизонтальной числовой линии при выполнении домашнего задания может быть очень полезным.
- Мысленно оцените и рассчитайте чаевые, налог с продаж и проценты продаж при покупках и еде вне дома.
- Интерпретируйте положительные и отрицательные числа в реальной жизни, например, с температурой, задолженностью / задолженностью, отрицательными и положительными расходами, выигрышем / проигрышем и т. Д.
- Узнавайте рациональные и иррациональные числа.
2. Выражения и уравнения. Ожидания учащихся сильно возрастают в 7 -м и 8 -м классах при изучении выражений и уравнений. Они начинают использовать переменные и решать многоступенчатые задачи реального мира. Учащиеся интерпретируют неравенства и рисуют их соответствующим образом. Они готовятся к алгебре, рассматривая и понимая линейные уравнения и находя наклон таблицы, графика и уравнения.
Поощряйте своего ребенка:
- Различайте равенство и неравенство (>, <, > , <) с помощью переменных:
- равенство: 4s + 20 = 46
- неравенство: 4s + 20 <46
- Рассматривайте и решайте многоступенчатые реальные задачи, используя переменные.Например, Как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата составляла не менее 100 долларов. Напишите неравенство для количества продаж, которые вам необходимо совершить, и опишите решения .
- Изучите и изучите различные типы графиков и таблиц в Интернете или в газете.
- Разберитесь в значении наклона и как его найти с помощью графика, таблицы или уравнения:
3. Геометрия. Студенты уделяют большое внимание лексике по геометрии и точно используют свой словарный запас при письме.Они расширяют свое понимание объема и площади для расчета площади поверхности двух- и трехмерных объектов. Они также изучают формулы площади и окружности круга. В 8 -м классе они изучают теорему Пифагора и применяют ее к реальным и математическим задачам. Студенты также должны знать формулы для определения объема конусов, сфер и цилиндров.
Поощряйте своего ребенка:
- Используйте соответствующий словарь при описании различных многоугольников и геометрических свойств.Например: дополнительных углов: два угла, которые в сумме дают 180 °.
- Создавайте словарные карточки для всего их математического словаря и еженедельно практикуйте их.
- Найдите разные двухмерные и трехмерные объекты в реальном мире и обсудите разницу между нахождением площади поверхности и объема каждого объекта.
- Понять теорему Пифагора и как использовать ее в реальном мире:
Источник изображения: FreeLearningChannel.com
4. Функции. В 8 -м ученики классов начнут узнавать о функциях. Студенты будут определять, сравнивать и оценивать функции. Они будут использовать функции для моделирования отношений между различными величинами. Они будут сравнивать функции алгебраически, графически, численно в таблицах или с помощью словесных описаний.
Поощряйте своего ребенка:
Источник изображения: Slideshare.net
У вас есть какие-либо вопросы об этих концепциях или другие вопросы по математике вашего ребенка? Отправьте их Дженнифер здесь, чтобы она могла ответить в следующем блоге.Или поделитесь ими с нами на странице Scholastic Parents в Facebook.
Автор фотографии: © DragonImages / Thinkstock
Важные математические навыки для семиклассников
Хотите помочь своему семикласснику освоить математику? Вот некоторые навыки, которые ваш ребенок будет изучать в седьмом классе.
Коэффициенты и удельные ставки
Проблемы реального мира
Решите проблемы реальных ставок, соотношений, пропорций и процентов, включая скидки, наценки, уценки, проценты, налоги, чаевые, комиссионные, процентное увеличение или уменьшение.
Пример:
На распродаже со скидкой 25% Марисса покупает юбку за 40,50 долларов. Какова была первоначальная цена юбки? Добавив налог с продаж в размере 6%, какова общая стоимость юбки?
Рецепт требует 3⁄4 стакана сливок на каждые 2 стакана молока. Если количество молока увеличить до 8 стаканов, сколько потребуется стаканов сливок?
Единица скорости изменения
Понимайте переменные как символы для чисел или значений, еще не известных — например, x и y — это переменные в y = 2x + 6 .Используя уравнения, таблицы, графики и описания, определите скорость изменения единицы — коэффициент, сравнивающий изменение одной величины с изменением на 1 единицу другой величины.
Пример:
Энтони читает 36 страниц за час. В следующий час он читает 42 страницы. Какова скорость изменения количества страниц, которые он может прочитать за час? Объясните свои рассуждения.
Расчет удельных ставок
Рассчитайте удельные расценки, связанные с отношениями долей, включая отношения длин и площадей, а также количества, измеренные в различных единицах.
Пример:
- Если человек проходит 1⁄2 мили за каждые часа, какова (единица) скорость ходьбы, выраженная в милях за (1) час?
- Для заполнения 1⁄9 емкости для рыбы требуется 1⁄8 литра воды. Сколько литров воды нужно для заполнения бака?
Связанные
Сложение, вычитание, умножение и деление
Многоступенчатые задачи реального мира
Сложение, вычитание, умножение и деление с положительными и отрицательными рациональными числами в любой форме, включая целые числа, дроби, или десятичные дроби.Поймите, что числа нельзя делить на 0. Используйте эти навыки для решения многоступенчатых реальных задач.
Пример:
- Если няня получает 13 долларов в час и получает прибавку на 15%, какой будет ее новая почасовая оплата? Что теперь она будет делать за 5 с половиной часов присмотра за детьми? Объясните или проиллюстрируйте свои рассуждения.
- В Галифаксе низкие температуры (по Фаренгейту) в течение семи дней января были: -12 °, -3 °, 6 °, -14 °, -8 °, 9 °, -1 °. Какая была средняя температура на той неделе? Объясните или проиллюстрируйте свои рассуждения.
Совет: поощряйте разумные расходы.
Покупки по-прежнему остаются одной из лучших возможностей для вашего ребенка попрактиковаться в математических концепциях, которые он изучает. Она может практиковать проценты и вычитание, вычисляя точную сумму, которую вы сэкономите, когда что-то поступит в продажу, и окончательную стоимость товаров со скидкой. Попросите ее помочь вам рассчитать чаевые, когда вы едите в ресторане. Если у нее есть сотовый телефон, ознакомьте его с деталями счета за сотовый телефон и размером платы за текст или за минуту использования, чтобы она могла научиться отслеживать, сколько она тратит.
Связанные
Длинное деление
Преобразуйте рациональные числа в десятичные с помощью длинного деления.
Пример:
Что такое 12/29 в виде десятичной дроби?
Что такое 13 4/5 в десятичном виде?
Выражения и уравнения
Создание простых уравнений
Используйте буквы для представления чисел в реальных математических задачах и генерируйте простые уравнения для их решения. Изобразите набор решений, если есть несколько ответов.
Пример:
Тесс, Нико и Сал собирают деньги на поездку в Стоунхендж. Тесс собрала T долларов, Нико собрал N долларов, а Сал собрал S долларов. Если Тесс собрала вдвое больше, чем Нико и Сал вместе взятые, соотношение можно выразить как T = 2 (N + S).
Решение для X
Определите значение переменной в уравнении и многоступенчатом уравнении.
Пример:
- Решить относительно x: 5x + 6 = 46
- Решить относительно b: 7 + 4b = 35
- Решить относительно c: 2 (c + 7) = 26 + 10
Написание эквивалентных выражений
Использование диаграмм в качестве инструментов для понимания и создания эквивалентных математических выражений.
Геометрия
Масштаб
Используйте понимание соотношения и пропорции, чтобы понять масштаб: отношение длины на чертеже (или модели) объекта к длине реального объекта. В примерах проблемных рисунков масштаб от верхнего рисунка к нижнему составляет 1: 2 («один к двум»). Изменяйте масштаб и вычисляйте фактическую длину и площадь геометрических фигур.
Статистика и вероятность
Выборки
Понять концепцию случайной выборки и репрезентативного размера выборки.Используйте случайную выборку, чтобы делать выводы или заключения о совокупности из репрезентативной выборки.
Пример:
Репортер взял интервью у четырех новейших учителей в школьном округе города. Будет ли эта выборка репрезентативной?
Совет: Обсудите новости.
Когда вы вместе смотрите новости, следите за тем, как часто цитируется статистика. Обсудите детали любых упомянутых опросов. Обсудите, как используются эти концепции и какие моменты они используются для поддержки или опровержения.
Понимание вероятности
Понимайте вероятность как математическое представление вероятности того, что что-то, например событие или результат, произойдет. Большие числа представляют большую вероятность.
Рассчитайте шансы:
Если в вашей школе проводится лотерея, обсудите детали с вашим ребенком. Попросите его узнать, сколько билетов будет продано и сколько призов будет разыграно. Затем попросите его определить вашу вероятность выигрыша, если вы купите билет — 10 или 20.
Поощряйте понимание математики через спорт:
Спорт — это увлекательный способ изучения множества математических понятий. Любой заядлый фанат бейсбола знает, что игру нельзя по-настоящему оценить без понимания некоторых важных статистических данных, таких как средний результат игрока и количество забитых мячей. Футбол также полон статистических данных, таких как процент передач, выполненных квотербеком. . Если ваш ребенок увлечен спортом, предложите ему изучить его с помощью математики.
Расчет вероятности
Рассчитайте вероятность, разделив количество шансов на то, что событие или результат произойдет, на количество возможных исходов — например, если в сумке 10 апельсинов, 5 персиков и 15 яблок, вероятность случайного выбора персика — 5 из 30 (5/30 или 1/6). Рассчитайте вероятности простых и сложных событий.
Пример:
Какова вероятность выпадения шестерки с одного кубика? (простое событие)
Какова вероятность выпадения двойных шестерок с использованием двух кубиков (составное событие)
Буква должна быть выбрана из 26 букв английского алфавита.Какова вероятность выбора согласного? Объясните свои рассуждения.
Совет: математика на практике: разыграйте шансы.
Если в вашей школе проводится лотерея, обсудите детали с вашим ребенком. Попросите его узнать, сколько билетов будет продано и сколько призов будет разыграно. Затем попросите его определить вашу вероятность выигрыша — 10 или 20.
Чтобы узнать, как помочь семикласснику в классе математики, посетите нашу страницу с советами по математике для седьмого класса.
TODAY Parenting Guide были разработаны NBC News Learn с помощью профильных экспертов и соответствуют Общим основным государственным стандартам.
Бесплатные задания по математике для 7-го класса
Вы здесь: Главная → Рабочие листы → 7-й класс
Это исчерпывающая коллекция бесплатных распечатываемых заданий по математике для 7 класса и для предварительной алгебры, организованных по таким темам, как выражения, целые числа, одношаговые уравнения, рациональные числа, многоступенчатые уравнения, неравенства, скорость, время и расстояние, графики, наклон, соотношения, пропорции, процент, геометрия и пи. Они генерируются случайным образом, их можно распечатать в вашем браузере и включать в себя ключ ответа.Рабочие листы подходят для любой математической программы для седьмого класса, но особенно хорошо подходят для математической программы IXL для 7-го класса.
Рабочие листы генерируются случайным образом каждый раз, когда вы нажимаете на ссылки ниже. Вы также можете получить новый, другой, просто обновив страницу в своем браузере (нажмите F5).
Вы можете распечатать их прямо из окна браузера, но сначала проверьте, как это выглядит в «Предварительном просмотре». Если рабочий лист не умещается на странице, отрегулируйте поля, верхний и нижний колонтитулы в настройках страницы вашего браузера.Другой вариант — настроить «масштаб» на 95% или 90% в предварительном просмотре печати. В некоторых браузерах и принтерах есть опция «Печатать по размеру», которая автоматически масштабирует рабочий лист по размеру области печати.
Все рабочие листы содержат ключ ответа на 2-й странице файла.
В седьмом классе ученики будут изучать предалгебраические темы, такие как целочисленная арифметика, упрощение выражений, свойство распределения и решение уравнений и неравенств. Они продолжают изучать соотношение и проценты и узнают о пропорциях.Обратите внимание, что эти бесплатные рабочие листы не охватывают все темы 7-го класса; в первую очередь, они не включают решение проблем.
Введение в алгебру
Рабочие листы в этом вводном разделе соответствуют главе 1 по математике «Мамонт 7 класс» и не содержат отрицательных чисел.
Порядок работы
Выражения
Уравнения
Целые числа
Числовые линейные графики и простые неравенства с целыми числами
Сложение и вычитание
Умножение и деление
Математика для начальных классов , Эдвард Заккаро
Хорошая книга по решению проблем с очень разнообразными текстовыми задачами и стратегиями решения проблем.Включает главы по следующим темам: последовательности, решение задач, деньги, проценты, алгебраическое мышление, отрицательные числа, логика, отношения, вероятность, измерения, дроби, деление. Вопросы в каждой главе разбиты на четыре уровня: легкий, несколько сложный, сложный и очень сложный.
Многие операции и т. Д.
Одношаговые уравнения
Рациональные числа
Преобразование десятичных дробей в дроби и наоборот
Сложение и вычитание десятичных чисел
Десятичное умножение и деление
Ключ к книгам с десятичными знаками
Это серия учебных пособий компании Key Curriculum Press, которая начинается с основных понятий и операций с десятичными знаками.Затем в книгах рассказывается о реальном использовании десятичных дробей в ценообразовании, спорте, метриках, калькуляторах и науке.
В комплекте книги 1-4.
=> Узнать больше
Дробное сложение и вычитание
Умножение и деление на дроби
Ключ к рабочим тетрадям дробей
Эти рабочие тетради от Key Curriculum Press содержат ряд упражнений, которые помогут вашему ребенку узнать о дробях.Книга 1 учит понятиям дробей, Книга 2 учит умножению и делению, Книга 3 учит сложению и вычитанию, а Книга 4 учит смешанным числам. В конце каждой книги есть практический тест.
=> Узнать больше
Научная запись
Сложные фракции
Уравнения и неравенства
Ключ к учебным пособиям по алгебре
Key to Algebra предлагает уникальный проверенный способ познакомить студентов с алгеброй.Новые концепции объясняются простым языком, а примеры легко следовать. Задачи со словами связывают алгебру с знакомыми ситуациями, помогая учащимся понять абстрактные концепции. Учащиеся развивают понимание, интуитивно решая уравнения и неравенства, прежде чем будут представлены формальные решения. Студенты начинают изучение алгебры с книг 1–4, используя только целые числа. Книги 5-7 вводят рациональные числа и выражения. Книги 8-10 расширяют охват действительной системы счисления.
=> Узнать больше
Постоянная скорость, время и расстояние
График и наклон
Алгебра реального мира Эдвард Заккаро
Алгебра часто преподается абстрактно, практически без акцента на том, что такое алгебра и как ее можно использовать для решения реальных задач.Подобно тому, как английский можно переводить на другие языки, текстовые задачи можно «переводить» на математический язык алгебры и легко решать. Алгебра реального мира объясняет этот процесс в удобном для понимания формате с использованием мультфильмов и рисунков. Это упрощает самообучение как для ученика, так и для любого учителя, который никогда не понимал алгебру. Включает главы по алгебре и деньгам, алгебре и геометрии, алгебре и физике, алгебре и рычагам и многому другому. Предназначен для детей 4–9 классов с более высокими математическими способностями и интересами, но может использоваться также учениками старшего возраста и взрослыми.Содержит 22 главы с инструкциями и задачами трех уровней сложности.
=> Узнать больше
Коэффициент
Пропорции
Процент
Ключ к рабочим тетрадям с процентами
Key to Percents прежде всего подчеркивает умственные навыки вычисления и оценки, поскольку большая часть работы с процентами выполняется без карандаша и бумаги. Затем учеников учат решать процентные задачи, используя равные дроби и десятичное умножение.Наконец, проценты используются для решения текстовых задач в различных приложениях. Ключ к процентам предполагает только знание дробных и десятичных вычислений. Книга 1 охватывает процентные концепции. Книга 2 охватывает проценты и дроби. Книга 3 охватывает проценты и десятичные дроби.
=> Узнать больше
Геометрия
Область — эти рабочие листы выполняются в координатной сетке.
Объем и площадь поверхности
Поскольку эти листы ниже содержат изображения различных размеров, сначала проверьте
как выглядит рабочий лист в предварительном просмотре перед печатью.Если это не так
подходит, вы можете либо распечатать его в масштабе (например, 90%), либо сделать еще один,
обновляйте страницу рабочего листа (F5), пока не получите подходящую.
Ключ к тетрадям по геометрии
Вот простой способ подготовить студентов к формальной геометрии. Ключ к геометрии Рабочие тетради знакомят учащихся с широким спектром геометрических открытий, поскольку они делают пошаговые построения. Используя только карандаш, циркуль и линейку, учащиеся начинают с рисования линий, деления углов пополам и воспроизведения сегментов.Позже они создают сложные конструкции, включающие более дюжины шагов, и им предлагается сформулировать свои собственные обобщения. Когда они закончат, учащиеся познакомятся со 134 геометрическими терминами и будут готовы к формальным доказательствам.
=> Узнать больше
Круг и Пи
Если вы хотите иметь больший контроль над такими параметрами, как количество задач, размер шрифта, интервал между проблемами или диапазон чисел, просто
щелкните по этим ссылкам, чтобы самостоятельно использовать генераторы рабочих листов:
M / J 7 класс по математике — 1205040
Расчет налога и чаевых:
Следите за Хейли и Кенной, когда они оценивают чаевые и налог с продаж в торговом центре, ресторанах и парикмахерских в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Простой интерес:
Рассчитывайте простые проценты и оценивайте ежемесячные платежи вместе с кредитным специалистом по имени Джордан в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Налоги, сборы и комиссия:
Изучите налог с продаж, сборы и комиссию, следуя инструкциям представителя службы поддержки по имени Джулиан в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Углы детской площадки, часть 1:
Изучите дополнительные и дополнительные углы вокруг игровой площадки с Джейкобом в этом интерактивном руководстве.
Это первая часть из серии, состоящей из двух частей. Нажмите, чтобы открыть «Углы детской площадки: Часть 2».
Тип: Оригинальное учебное пособие для учащихся
Углы игровой площадки: Часть 2:
Помогите Джейкобу написать и решить уравнения, чтобы найти недостающие угловые меры, основанные на соотношении между углами, которые в сумме составляют 90 градусов и 180 градусов, в этом интерактивном учебном пособии, посвященном игровой площадке.
Это вторая часть из серии, состоящей из двух частей. Щелкните , чтобы открыть Углы игровой площадки: Часть 1.
Тип: Оригинальное учебное пособие для учащихся
Математические модели и социальное дистанцирование:
Узнайте, как математические модели могут показать, почему социальное дистанцирование во время эпидемии или пандемии важно, в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Профессор Э. Квал. Часть 1: 2-х ступенчатые уравнения:
Профессор Э. Квал научит вас решать и проверять двухэтапные уравнения в этом интерактивном руководстве.
Это первая часть из двух частей, посвященных решению двухэтапных уравнений.
Тип: Оригинальное учебное пособие для учащихся
Балансировка машины:
Используйте модели для решения задач баланса на космической станции в этом интерактивном учебнике по математике и естествознанию.
Тип: Оригинальное учебное пособие для учащихся
Пицца Пи: Окружность:
Исследуйте происхождение числа Пи как отношения окружности к диаметру круга. В этом интерактивном руководстве вы будете работать с формулой окружности, чтобы определить длину окружности, и работать в обратном направлении, чтобы определить диаметр и радиус окружности.
Тип: Оригинальное учебное пособие для учащихся
Введение в вероятность:
Узнайте, как рассчитать вероятность простых событий, эта вероятность — это вероятность того, что событие произойдет, и что некоторые события могут произойти с большей вероятностью, чем другие, в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Изучение среднего абсолютного отклонения: крылатка:
Сравните несколько образцов крылатки, чтобы сделать обобщение о популяции, проанализировав средние абсолютные отклонения образцов и их распределение в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Алиса в стране математики:
Помогите Алисе обнаружить, что составные вероятности можно определить путем вычислений или рисования древовидных диаграмм в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Пицца Пи: Площадь:
В этом интерактивном руководстве узнайте, как рассчитать площадь кругов в единицах числа «пи» и с помощью аппроксимации числа «пи».Вы также столкнетесь с ситуациями с неправильной площадью, которые потребуют использования формулы площади круга.
Тип: Оригинальное учебное пособие для учащихся
Куда делись все скраб-сойки ?:
Изучите ограничивающие факторы экосистемы Флориды и опишите, как эти ограничивающие факторы влияют на одно коренное население — Флоридскую скраб-сойку — с помощью этого интерактивного учебного пособия.
Тип: Оригинальное учебное пособие для учащихся
Удивительные приключения:
Узнайте, как объяснить значение аддитивной инверсии, определить аддитивную инверсию данного рационального числа и обосновать свой ответ числовой линией в этом оригинальном руководстве.
Тип: Оригинальное учебное пособие для учащихся
По горячим следам:
Изучите, как температура влияет на скорость химических реакций, в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Да или нет ГМО ?:
Узнайте, что такое генная инженерия и некоторые применения этой технологии.В этом интерактивном руководстве вы получите представление о некоторых преимуществах и потенциальных недостатках генной инженерии. В конечном итоге вы сможете критически относиться к генной инженерии и написать аргумент, описывающий вашу собственную точку зрения на ее влияние.
Тип: Оригинальное учебное пособие для учащихся
Плавание кругами:
В этом интерактивном руководстве научитесь решать задачи, касающиеся окружности и площади круга бассейнов.
Тип: Оригинальное учебное пособие для учащихся
Масштаб округляется в большую сторону:
В этом интерактивном руководстве научитесь использовать архитектурные масштабные чертежи для строительства новой арены для лошадей и решать проблемы, связанные с масштабными чертежами. К концу вы сможете рассчитать фактическую длину, используя масштаб и пропорции.
Тип: Оригинальное учебное пособие для учащихся
Спорящий Марс:
Узнайте, как определять явные доказательства и понимать неявное значение текста.
В этом руководстве вы научитесь определять аргументы или утверждения говорящего.Вы также узнаете, как оценивать доказательства и аргументы, представленные в речи.
Тип: Оригинальное учебное пособие для учащихся
Улыбки:
В этом интерактивном задании по решению задач учащиеся применяют алгебраические рассуждения для определения «стоимости» отдельных типов лиц по сумме хмурых взглядов, улыбок и нейтральных лиц.На этой странице представлены три графические задачи, связанные с решением систем уравнений, а также советы по обдумыванию проблемы, решения и других подобных проблем.
Тип: Задача по решению проблем
Титаник 1:
Это задание просит студентов вычислить вероятности, используя информацию, представленную в двухсторонней таблице частот.
Тип: Задача по решению проблем
Анна в Вашингтоне:
Цель этого задания — дать учащимся возможность решить сложную многоступенчатую процентную задачу, к которой можно подойти разными способами.Студентам предлагается найти стоимость еды без учета налогов и чаевых, если указана общая стоимость еды. Задача может иллюстрировать несколько стандартов в зависимости от предварительных знаний учащихся и подхода, используемого для решения проблемы.
Тип: Задача по решению проблем
Книги со скидкой:
Цель этого задания — помочь учащимся увидеть два разных способа взглянуть на проценты как на уменьшение, так и на увеличение исходной суммы.Кроме того, ученики должны превратить словесное описание нескольких операций в математические символы. Это требует преобразования простых процентов в десятичные числа, а также определения эквивалентных выражений без переменных.
Тип: Задача по решению проблем
Эквивалентные выражения ?:
Учащимся предлагается определить, эквивалентны ли два выражения, и объяснить свои рассуждения.
Тип: Задача по решению проблем
Рыболовные приключения 2:
Студентам предлагается написать и решить неравенство, чтобы определить количество людей, которые могут безопасно арендовать лодку.
Тип: Задача по решению проблем
Угадай мой номер:
В этой задаче учащимся предлагается представить последовательность операций с помощью выражения, а затем написать и решить простые уравнения.Задача представлена в виде игры и позволяет учащимся визуализировать математические операции. Было бы разумно сначала сыграть в похожую игру парами, а затем попросить учеников записать операции, чтобы вычислить числа друг друга.
Тип: Задача по решению проблем
Мили в Километры:
В этом задании учащихся просят написать два выражения из словесных описаний и определить, эквивалентны ли они.В выражениях используются как проценты, так и дроби. Это задание лучше всего подходит для обсуждения в классе, поскольку в формулировке проблемы имеется некоторая двусмысленность.
Тип: Задача по решению проблем
Усадка:
Учащимся предлагается определить изменение роста в дюймах при постоянной скорости изменения в сантиметрах.Ответ округляется до ближайших полдюйма.
Тип: Задача по решению проблем
Комплект спортивного инвентаря:
Учащегося просят написать и решить неравенство в соответствии с контекстом.
Тип: Задача по решению проблем
Восемь кругов:
Учащимся предлагается найти площадь затененной области, используя диаграмму и предоставленную информацию.Цель этого задания — улучшить понимание учащимися местности.
Тип: Задача по решению проблем
Поэтажный план:
Целью этого задания является перевод учащихся между измерениями, приведенными на чертеже в масштабе, и соответствующими измерениями объекта, представленными на чертеже в масштабе.Если бы они использовались в учебных заведениях, было бы хорошо, если бы учащиеся имели возможность увидеть другие методы решения, возможно, попросив учащихся с разными подходами объяснить свои стратегии классу. Студентам, которые могут решить эту проблему, только предварительно преобразовав линейные измерения, будет сложно решить задачи, в которых указаны только измерения площади.
Тип: Задача по решению проблем
Расстояния на числовой прямой 2:
Цель этого задания состоит в том, чтобы укрепить понимание учащимися рациональных чисел как точек на числовой прямой и предоставить им наглядный способ понимания того, что сумма числа и его аддитивная обратная величина (обычно называемая его «противоположностью») равно нулю.
Тип: Задача по решению проблем
Сравнение точек замерзания:
В этом задании учащиеся отвечают на вопрос о разнице между двумя отрицательными числами.
Тип: Задача по решению проблем
Купон или скидка:
В этом задании ученикам предлагается реальная проблема, связанная с ценой продаваемого товара.Чтобы ответить на вопрос, учащиеся должны представить проблему, указав переменную и связанные с ней величины, а затем написать и решить уравнение.
Тип: Задача по решению проблем
Операции на числовой линии:
Цель этого задания — помочь учащимся укрепить понимание чисел со знаком как точек на числовой прямой и понять геометрическую интерпретацию сложения и вычитания чисел со знаком.В Стандартах Флориды есть тонкое различие между дробью и рациональным числом. Дроби всегда положительны, и если рассматривать символ ab как дробь, можно интерпретировать его как части равного размера, где b частей составляют одно целое.
Тип: Задача по решению проблем
Повторяющееся десятичное число как приближение:
Учащегося просят выполнить длинное деление, в результате чего получается повторяющаяся десятичная дробь, а затем использовать умножение, чтобы «проверить» свой ответ.Цель задания — заставить учащихся задуматься о значении повторения десятичного представления через приближение.
Тип: Задача по решению проблем
Разделение призовых денег:
Учащимся предлагается определить, как распределить денежные призы между тремя классами в зависимости от вклада каждого класса.
Тип: Задача по решению проблем
Набор песка под качелями:
Ученики 7-го класса средней школы Санвью помогали отремонтировать игровую площадку для детсадовцев в соседней начальной школе. Городские правила требуют, чтобы песок под качелями был не менее 15 дюймов в глубину.Когда они стартовали, песок под обоими качелями был всего 12 дюймов в глубину. Прямоугольная область под маленькими качелями имеет размеры 9 футов на 12 футов, и для увеличения глубины на 3 дюйма потребовалось 40 мешков с песком. Сколько мешков с песком понадобится ученикам, чтобы покрыть прямоугольную область под большими качелями, если она в 1,5 раза длиннее и в 1,5 раза шире, чем область под малыми качелями?
Тип: Задача по решению проблем
Арт-класс, вариация 1:
Студентам предлагается использовать соотношения и пропорциональные рассуждения для сравнения смесей красок численно и графически.
Тип: Задача по решению проблем
Шахматный клуб:
Эта задача включает процентное увеличение одной части с процентным уменьшением оставшейся части и просит учащихся найти общее процентное изменение. Проблема может быть решена с использованием пропорций, расчетов или написания набора уравнений.
Тип: Задача по решению проблем
Сравнение лет:
Студентам предлагается сравнить египетский, григорианский и юлианский методы измерения года.
Тип: Задача по решению проблем
Готовим из целой чашки:
Студентам предлагается использовать пропорциональные рассуждения, чтобы ответить на ряд вопросов в контексте рецепта.
Тип: Задача по решению проблем
Такси Готэма:
Цель этого задания — дать учащимся возможность решить задачу, состоящую из нескольких шагов, к которой можно подойти разными способами. Это можно сделать, составив таблицу, которая помогает проиллюстрировать структуру ставок такси для разных пройденных расстояний и с небольшой настойчивостью приводит к решению, в котором используется арифметика.Также можно рассчитать единицу скорости (в долларах за милю) и использовать ее, чтобы найти расстояние напрямую, не составляя таблицы.
Тип: Задача по решению проблем
Обнаружение увеличения на 10%:
За первую неделю книжную ярмарку посетили 5000 человек.За вторую неделю количество посетителей увеличилось на 10%. Сколько человек посетило книжную ярмарку за вторую неделю?
Тип: Задача по решению проблем
Бег Молли:
В этом задании учащимся предлагается решить задачу в контексте постоянной скорости.Эта задача обеспечивает переход от работы с отношениями, содержащими целые числа, к отношениям, содержащим дроби. Эту проблему можно рассматривать по-разному; в частности, эта задача также дает возможность студентам работать с интерпретацией деления «Сколько в одной группе?».
Тип: Задача по решению проблем
Музыкальные компании, Вариант 1:
Эта задача требует сравнения ставок, где одна дается в единицах, а другая — нет.См. «Музыкальные компании. Вариант 2», где описана задача с очень похожей настройкой, но она намного сложнее и поэтому иллюстрирует.
Тип: Задача по решению проблем
Музыкальные компании, Вариант 2:
Эта проблема состоит из нескольких этапов.Для решения проблемы необходимо вычислить: стоимость акций TunesTown; общая стоимость предложения BeatStreet о 20 миллионах акций по 25 долларов за акцию; разница между этими двумя суммами; а стоимость каждой из дополнительных 2 миллионов акций, предлагаемых MusicMind, равна разнице.
Тип: Задача по решению проблем
Гонки роботов:
Учащиеся должны использовать предоставленную информацию, чтобы ответить на вопросы о гонках роботов.
Тип: Задача по решению проблем
Распродажа!:
Студентам предлагается определить, какой вариант продажи приводит к наибольшему процентному снижению стоимости.
Тип: Задача по решению проблем
Продажа компьютеров:
В прошлом месяце отдел продаж магазина электроники продал 48 компьютеров.Менеджер магазина хочет побудить отдел продаж продавать больше компьютеров и собирается дать всем членам отдела продаж бонус, если в следующем месяце количество проданных компьютеров увеличится на 30%. Сколько компьютеров должно продать отдел продаж, чтобы получить бонус? Объясните свои рассуждения.
Тип: Задача по решению проблем
Биржевые свопы, вариант 2:
Студентов просят решить задачу, используя пропорциональные рассуждения в реальном контексте, чтобы определить количество акций, необходимых для совершения покупки акций.
Тип: Задача по решению проблем
Биржевые свопы, вариант 3:
Студентов просят решить задачу с соотношением шагов в реальном мире.
Тип: Задача по решению проблем
Налог и чаевые:
Пообедав в любимом ресторане, вы знаете, что счет до налогообложения составляет 52 доллара.60 и что ставка налога с продаж составляет 8%. Вы решаете оставить официанту чаевые в размере 20% от суммы до налогообложения. Сколько оставить официанту? Сколько будет стоить общий счет, включая налоги и чаевые?
Тип: Задача по решению проблем
Цена хлеба:
Цель этого задания — вычислить процент увеличения и относительную стоимость в реальном контексте.Инфляция, одна из главных идей в экономике, — это рост цен на товары и услуги с течением времени. Это зависит от имеющейся у вас суммы денег.
Тип: Задача по решению проблем
Тренировочная практика:
В этом упражнении студенту предлагается использовать единичную ставку и пропорциональное рассуждение, чтобы определить, кто из двух бегунов самый быстрый.
Тип: Задача по решению проблем
Две школы танца:
Цель этого задания — увидеть, насколько хорошо учащиеся понимают коэффициенты и рассуждают с ними.
Тип: Задача по решению проблем
Мистер.Классу Бригга нравится математика:
По результатам опроса, проведенного на уроке математики мистера Бриггса, 67% студентов заявили, что математика является их любимым учебным предметом. В классе находится редактор школьной газеты, и он хочет написать для газеты статью о том, что математика — самый популярный предмет в школе. Объясните, почему это неверный вывод, и предложите способ собрать более точные данные, чтобы определить, какой предмет является наиболее популярным.
Тип: Задача по решению проблем
Линейщики наступления:
В этом задании учащиеся могут предположить о различиях и сходстве в двух группах с чисто визуальной точки зрения, а затем подкрепить свои сравнения соответствующими мерами центра и изменчивости.Это подтвердит, что многое можно почерпнуть просто из визуального сравнения соответствующих графиков, особенно аналогичных по масштабу.
Тип: Задача по решению проблем
Подбрасывание цилиндров:
Цель этого задания — предоставить студентам возможность определить экспериментальные вероятности путем сбора данных.Цилиндрические объекты, используемые в этой задаче, обычно имеют три разных положения покоя, но не все из них могут быть одинаково вероятными, а некоторые могут быть крайне маловероятными или невозможными при подбрасывании объекта. Более того, получение вероятностей результатов возможно только за счет использования долгосрочных относительных частот. Это связано с тем, что эти цилиндры не обладают симметрией тех же типов, что и объекты, которые часто используются в качестве игральных костей, такие как кубы или тетраэдры, где каждый результат одинаково вероятен.
Тип: Задача по решению проблем
Сколько кнопок ?:
Этот ресурс включает в себя простую деятельность по сбору данных, которая предоставляет данные, которые учащиеся объединяют в таблицу. Затем их просят обратиться к данным и определить вероятность различных результатов.
Тип: Задача по решению проблем
Избирательный опрос, Вариант 2:
Эта задача знакомит с фундаментальными статистическими идеями использования сводных данных (статистики) из случайных выборок для вывода (обоснованных выводов) о характеристиках (параметрах) совокупности.В задаче, построенной на сценарии избирательного опроса, совокупность — это весь седьмой класс, интересующая неизвестная характеристика (параметр) — это доля членов класса, голосующих за конкретного кандидата, а итоговая сводка (статистика) — это наблюдаемые доля избирателей, отдавших предпочтение кандидату в случайной выборке учащихся. Вариант 2 проводит студентов через физическое моделирование для создания пропорций выборки путем выборки и повторной выборки шариков из коробки.
Тип: Задача по решению проблем
Избирательный опрос, Вариант 1:
Эта задача знакомит с фундаментальными статистическими идеями использования сводных данных (статистики) из случайных выборок для вывода (обоснованных выводов) о характеристиках (параметрах) совокупности.Эта задача преследует две важные цели: увидеть необходимость случайной выборки и использовать рандомизацию для исследования поведения выборочной статистики. Они вводят основные идеи статистического вывода и могут быть выполнены с минимальными знаниями вероятности.
Тип: Задача по решению проблем
Время ожидания:
По мере развития стандартов статистики и вероятности учащиеся еще не будут знать правила вероятности для сложных событий.Таким образом, моделирование используется для поиска приблизительного ответа на эти вопросы. Фактически, часть b будет вызовом для студентов, которые действительно знают правила вероятности, еще больше демонстрируя возможности моделирования в предоставлении относительно простых приблизительных ответов на самые разные проблемы.
Тип: Задача по решению проблем
Катящаяся игральная кость:
Это задание предназначено для использования в классе.Учащиеся объединяют результаты многих повторений случайного явления (бросания кубиков) и сравнивают свои результаты с теоретическим ожиданием, которое они получают, рассматривая все возможные результаты броска двух кубиков. Это дает им конкретный пример того, что мы подразумеваем под долгосрочной относительной частотой.
Тип: Задача по решению проблем
Прокатка дважды:
Цель этого задания — вычислить теоретическую вероятность сложного события.Учителя могут пожелать подчеркнуть различие между теоретической и экспериментальной вероятностями для этой проблемы. Для студентов, которые учатся различать теоретическую и экспериментальную вероятность, было бы хорошо найти экспериментальную вероятность либо до, либо после того, как студенты вычислили теоретическую вероятность.
Тип: Задача по решению проблем
Сидя друг напротив друга:
Цель этого задания — вычислить теоретическую вероятность конфигурации рассадки.В этой задаче есть 24 возможных конфигурации четырех друзей за столом. Учащиеся могут нарисовать все 24 конфигурации для решения задачи, но это занимает много времени, и поэтому их следует поощрять искать более систематический метод.
Тип: Задача по решению проблем
Бревенчатая поездка:
Учащимся предлагается решить неравенство, чтобы ответить на реальный вопрос.
Тип: Задача по решению проблем
Проблема с возрастным словом:
Этот учебник показывает студентам, как составить и решить возрастную задачу.В руководстве также показано, как проверить свою работу с помощью подстановки.
Тип: Учебное пособие
Проблема с возрастным словом:
Учащиеся научатся составлять и решать задачу о возрастных словах.
Тип: Учебное пособие
Обнаружение вероятности:
Это видео демонстрирует несколько примеров определения вероятности случайных событий.
Тип: Учебное пособие
Окружность круга:
В этом видео показано, как найти длину окружности, расстояние по окружности, учитывая площадь.
Тип: Учебное пособие
Составные пробелы:
В этом видео рассказывается, как создавать пробные пространства в виде древовидных диаграмм, списков и таблиц.
Тип: Учебное пособие
Вероятность прокатки штампа:
Видео покажет, как использовать таблицу для определения вероятности сложного события.
Тип: Учебное пособие
Площадь круга:
В этом видео вы увидите, как мы находим площадь круга при заданном диаметре.
Тип: Учебное пособие
Проблема со словом пропорции:
Это вводное видео демонстрирует базовые навыки написания и решения основного уравнения для пропорциональной зависимости.
Тип: Учебное пособие
Решение пропорции с неизвестной переменной:
Вот вводное видео, в котором объясняются основные аргументы в пользу решения пропорций и показаны три различных метода решения пропорций, которые вы будете использовать позже для решения более сложных задач.
Тип: Учебное пособие
Настройка пропорций для решения проблем со словами:
В этом вводном видео показаны некоторые основные примеры записи двух соотношений и приравнивания их друг к другу. Это всего лишь шаг 1 при решении задач со словами с пропорциями.
Тип: Учебное пособие
Оценить проблему с дробями:
Посмотрите, как мы решаем задачу определения скорости в метрах в секунду, используя расстояние (в метрах) и время (в секундах).
Тип: Учебное пособие
Процент проблемы со словом:
Узнайте, как найти полную цену, если вы знаете цену со скидкой в этой задаче о процентах.
Тип: Учебное пособие
Добавление отрицательных чисел:
Это видео демонстрирует использование числовой прямой и абсолютного значения для сложения отрицательных чисел.
Тип: Учебное пособие
Умножение целых чисел:
В этом руководстве демонстрируется метод умножения целых чисел на числовую линию.Вы столкнетесь с четырьмя различными комбинациями при умножении целых чисел: (1) положительное, умноженное на положительное, (2) положительное, умноженное на отрицательное, (3) отрицательное, умноженное на отрицательное, (4) отрицательное, умноженное на положительное. Урок доступен в видеоформате, есть викторина для практики.
Тип: Учебное пособие
Решение двухэтапных уравнений:
В этом коротком видео используется как уравнение, так и наглядная модель, чтобы объяснить, почему одни и те же шаги должны использоваться для обеих сторон уравнения при решении для значения переменной.
Тип: Учебное пособие
Преалгебра — дроби и рациональные числа:
Первые дроби, используемые древними цивилизациями, были «единичными дробями». Позже были добавлены другие числители, в результате чего образовались «вульгарные дроби», которые стали нашими современными дробями.Вместе дроби и целые числа образуют «рациональные числа».
Тип: Учебное пособие
Преалгебра — умножение отрицательных чисел:
Когда системы счисления были расширены за счет включения отрицательных чисел, необходимо было сформулировать правила, чтобы умножение было согласованным независимо от знака операндов.
Тип: Учебное пособие
Добавление целых чисел:
Студенты смогут увидеть примеры сложения целых чисел во время просмотра короткого видео и попрактиковаться в сложении целых чисел с помощью онлайн-викторины.
Тип: Учебное пособие
Линейные уравнения с одной переменной:
Этот урок знакомит учащихся с линейными уравнениями с одной переменной, показывает, как их решать, используя свойства равенств сложения, вычитания, умножения и деления, и позволяет учащимся определить, является ли значение решением, существует ли бесконечно много решений или вообще нет решения.Сайт содержит объяснение уравнений и линейных уравнений, как решать уравнения в целом, а также стратегию решения линейных уравнений. Урок также объясняет противоречие (уравнение без решения) и тождество (уравнение с бесконечными решениями). В конце есть пять практических задач, чтобы студенты могли проверить свои знания со ссылками на ответы и объяснениями, как эти ответы были найдены. Также указаны дополнительные ресурсы.
Тип: Учебное пособие
Использование метода пропорций для решения процентных задач:
Этот сайт подробно описывает шаги по использованию метода пропорций для решения трех различных типов процентных задач.Он также включает примеры задач для практического определения части, целого или процентного содержания.
Тип: Учебное пособие
Основные аддитивные цвета:
Этот ресурс помогает пользователю изучить три основных цвета, которые имеют фундаментальное значение для человеческого зрения, изучить различные цвета в видимом спектре, наблюдать получающиеся цвета при добавлении двух цветов и узнать, что такое белый свет.Комбинация текста и виртуального манипулятора позволяет пользователю исследовать эти концепции множеством способов.
Тип: Учебное пособие
Основные субтрактивные цвета:
Пользователь изучит три основных субтрактивных цвета в видимом спектре, исследует результирующие цвета, когда два субтрактивных цвета взаимодействуют друг с другом, и изучит формирование черного цвета.
Тип: Учебное пособие
Преобразование единиц скорости:
На этом уроке учащиеся будут просматривать видеоролик Khan Academy, в котором будет показано, как преобразовывать коэффициенты с использованием единиц скорости.
Тип: Учебное пособие
Умножение дробей:
Видео описывает, как умножать дроби и формулировать ответ в минимальных числах.
Тип: Учебное пособие
Спиннер:
В этом упражнении учащиеся регулируют количество секций на вертушке, а затем проводят имитационные испытания на этом вертушке, чтобы развить концепции вероятности.В таблице рядом с прядильщиком отображается теоретическая вероятность для каждого цветного участка прядильщика и записывается экспериментальная вероятность из испытаний прядения. Это упражнение позволяет студентам исследовать темы экспериментальной и теоретической вероятности, видя их рядом с созданным ими прядильщиком. Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с java-апплетом.
Тип: виртуальный манипулятор
Флаер поперечного сечения — Shodor:
С помощью этого онлайн-апплета Java учащиеся используют ползунки для перемещения поперечного сечения конуса, цилиндра, призмы или пирамиды. Это задание позволяет учащимся изучить конические сечения и трехмерные формы, из которых они получены.Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с java-апплетом.
Тип: виртуальный манипулятор
Инструмент Круг:
Этот апплет позволяет студентам исследовать отношения между площадью и длиной окружности круга, его радиусом и диаметром.На сайте три раздела: Введение, Исследование и Проблемы.
- Во вводном разделе учащиеся могут изменять размер круга и видеть, как это влияет на радиус, диаметр и длину окружности. Учащиеся также могут воспроизвести видеоклип, чтобы наглядно увидеть, как связаны эти измерения.
- Раздел «Исследование» позволяет учащимся собирать точки данных, перетаскивая радиус круга на разную длину, и записывать в таблицу данные для радиуса, диаметра, окружности и площади.Нажатие кнопки x / y позволяет учащимся изучить взаимосвязь между любыми двумя показателями. При нажатии на кнопку графика студенты переходят к графику данных. Они могут нанести любой из четырех показателей на ось x против любого из четырех показателей на оси y.
- Раздел «Задачи» содержит вопросы, которые ученики должны решить, и записать свои ответы в правильном блоке.
(Подсветка NCTM)
Тип: виртуальный манипулятор
Линейная функциональная машина:
В этом упражнении учащиеся подставляют значения в независимую переменную, чтобы увидеть, каковы выходные данные для этой функции.Затем на основе этой информации они должны определить коэффициент (наклон) и константу (пересечение оси y) для линейной функции. Это упражнение позволяет студентам изучить линейные функции и то, какие входные значения полезны при определении правила линейной функции. Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с апплетом Java.
Тип: виртуальный манипулятор
Смеси:
В этом онлайн-упражнении учащиеся применяют свое понимание пропорциональных отношений, добавляя кружки, цветные или нет, к двум разным стопкам, а затем объединяют стопки, чтобы получить требуемый процент цветных кругов.Студенты могут играть в четырех режимах: исследование, неизвестная часть, неизвестное целое или неизвестный процент. Это упражнение также включает в себя дополнительные материалы на вкладках над апплетом, включая справочную информацию о затронутых темах, описание того, как использовать приложение, и вопросы исследования для использования с Java-апплетом.
Тип: виртуальный манипулятор
Графические линии:
Позволяет учащимся получить доступ к декартовой системе координат, в которой можно построить график линейных уравнений и наблюдать за деталями линии и наклона.
Тип: виртуальный манипулятор
Коробчатая диаграмма:
В этом упражнении учащиеся используют предустановленные данные или вводят свои собственные данные, которые будут представлены в виде прямоугольной диаграммы. Это упражнение позволяет учащимся изучать как отдельные, так и расположенные бок о бок диаграммы различных данных.Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с апплетом Java.
Тип: виртуальный манипулятор
Интерактивные шарики:
Это интерактивное средство для манипуляций позволяет учащемуся имитировать размещение шариков в сумке и определение вероятности вытаскивания определенных комбинаций шариков.Это позволяет исследовать вероятности нескольких событий, а также вероятность с заменой и без нее. Вкладки над апплетом предоставляют доступ к дополнительным материалам, включая справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с апплетом Java.
Тип: виртуальный манипулятор
Advanced Data Grapher:
Это онлайн-утилита для построения графиков, которую можно использовать для создания коробчатых диаграмм, пузырьковых диаграмм, диаграмм рассеяния, гистограмм и диаграмм типа «стержень-лист».
Тип: виртуальный манипулятор
Вероятность Плинко:
Студенты сыграют в классическую игру из популярного шоу. Благодаря этому они могут исследовать вероятность того, что мяч приземлится на каждом из чисел, и обнаружить более точные результаты, полученные при повторном тестировании.Моделирование можно настроить, чтобы повлиять на справедливость и случайность результатов.
Тип: виртуальный манипулятор
Подгонка кривой:
С помощью мыши учащиеся будут перетаскивать точки данных (с их планками ошибок) и мгновенно наблюдать за формой наиболее подходящей полиномиальной кривой.Студенты могут выбрать тип соответствия: линейный, квадратичный, кубический или квартичный. Может отображаться наилучшая или регулируемая посадка.
Тип: виртуальный манипулятор
Ящичный плоттер:
Пользователи выбирают набор данных или вводят свои собственные данные для создания прямоугольной диаграммы.
Тип: виртуальный манипулятор
Инструмент случайного рисования — отдельные испытания (вероятностное моделирование):
Этот виртуальный манипулятор позволяет создать случайную коробку для рисования, выложив до 21 билета с числами от 0 до 11.После выбора билетов, которые нужно положить в коробку, апплет будет выбирать билеты случайным образом. Также есть опция, которая покажет теоретическую вероятность для каждого билета.
Тип: виртуальный манипулятор
Масштаб:
Изучите влияние на периметр и площадь двух прямоугольных форм при изменении масштабного коэффициента.
Тип: виртуальный манипулятор
7 класс | Математика | Iowa Core
В 7 классе учебное время должно быть сосредоточено на четырех критических областях: (1) развитие понимания и применение пропорциональных отношений; (2) развитие понимания операций с рациональными числами и работа с выражениями и линейными уравнениями; (3) решение задач, связанных с масштабными чертежами и неформальными геометрическими конструкциями, и работа с двух- и трехмерными формами для решения задач, связанных с площадью, площадью поверхности и объемом; и (4) делать выводы о популяциях на основе выборок.
- Студенты расширяют свое понимание соотношений и развивают понимание пропорциональности для решения одно- и многоэтапных задач. Учащиеся используют свое понимание соотношений и пропорциональности для решения широкого круга задач, связанных с процентами, включая те, которые касаются скидок, процентов, налогов, чаевых, а также увеличения или уменьшения процента. Учащиеся решают задачи о масштабных чертежах, соотнося соответствующие длины между объектами или используя тот факт, что отношения длин внутри объекта сохраняются в подобных объектах.Учащиеся составляют график пропорциональных соотношений и неформально понимают единичную ставку как меру крутизны соответствующей линии, называемой наклоном. Они отличают пропорциональные отношения от других отношений.
- Учащиеся развивают единое понимание чисел, распознавая дроби, десятичные дроби (которые имеют конечное или повторяющееся десятичное представление) и проценты как различные представления рациональных чисел. Учащиеся распространяют сложение, вычитание, умножение и деление на все рациональные числа, сохраняя свойства операций и отношения между сложением и вычитанием, а также умножением и делением.Применяя эти свойства и рассматривая отрицательные числа с точки зрения повседневного контекста (например, суммы задолженности или температуры ниже нуля), учащиеся объясняют и интерпретируют правила сложения, вычитания, умножения и деления с отрицательными числами. Они используют арифметику рациональных чисел, когда формулируют выражения и уравнения с одной переменной и используют эти уравнения для решения задач.
- Ученики продолжают свою работу с площадью с 6 класса, решая задачи, связанные с площадью и окружностью круга и площадью поверхности трехмерных объектов.Готовясь к работе над соответствием и сходством в 8-м классе, они рассуждают о взаимосвязях между двумерными фигурами, используя масштабные чертежи и неформальные геометрические конструкции, и они знакомятся со связями между углами, образованными пересекающимися линиями. Учащиеся работают с трехмерными фигурами, связывая их с двухмерными фигурами, исследуя поперечные сечения. Они решают реальные и математические задачи, касающиеся площади, площади поверхности и объема двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.
- Учащиеся опираются на свою предыдущую работу с отдельными распределениями данных, чтобы сравнить два распределения данных и ответить на вопросы о различиях между популяциями.

 Сколько тонн зерна было отправлено в первый день и сколько во второй?
Сколько тонн зерна было отправлено в первый день и сколько во второй?
 После того как на верхнюю полку переставили с нижней 15 книг, на полках книг оказалось поровну. Сколько книг было на каждой полке первоначально?
После того как на верхнюю полку переставили с нижней 15 книг, на полках книг оказалось поровну. Сколько книг было на каждой полке первоначально?
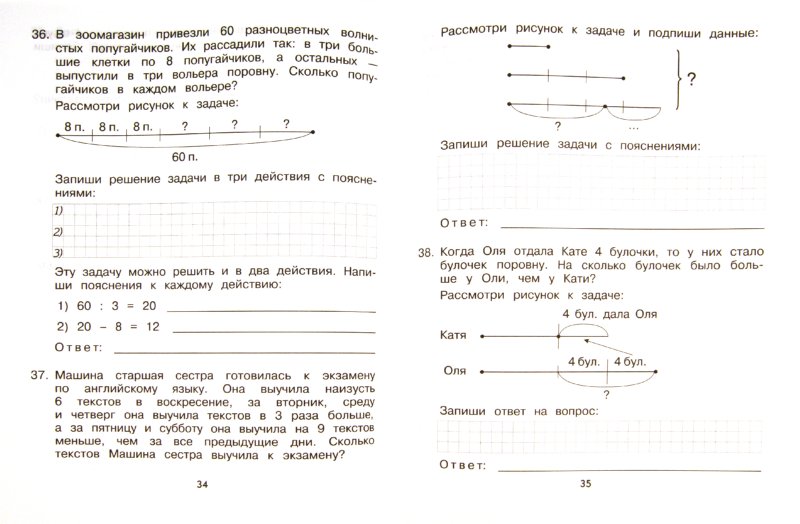 Взаимно простые числа
Взаимно простые числа Сколько страниц в книге?
Сколько страниц в книге?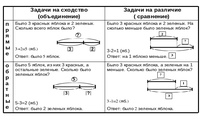 В задачах, приводимых в учебнике в качестве примеров, часто рассматриваются принципиальные вопросы, которые вы должны знать.
В задачах, приводимых в учебнике в качестве примеров, часто рассматриваются принципиальные вопросы, которые вы должны знать.