Деление натуральных чисел в столбик: правила, примеры
В данной публикации мы рассмотрим правила и практические примеры того, каким образом натуральные числа (двузначные, трехзначные и многозначные) можно делить столбиком – с остатком и без него.
Правила деления в столбик
Без остатка
Чтобы найти частное от деления одного числа на другое (с любым количеством разрядов) можно выполнить это арифметическое действие в столбик.
Рассмотрим правила деления на практическом примере для лучшего понимания. Допустим, нам нужно трехзначное число разделить на однозначное, к примеру 256 на 8. Вот, что мы делаем:
1. Пишем делимое (256), затем немного отступаем от него и в этой же строке дописываем делитель (8). Затем между этими числами дорисовываем уголок. Результат будем записывать под делителем.
2. В делимом слева направо отсчитываем минимально необходимое количество разрядов таким образом, чтобы полученное из содержащихся в них цифр новое число было больше, чем делитель. В нашем случае числа 2 недостаточно, поэтому к нему добавляем 5 и в итоге получаем 25.
В нашем случае числа 2 недостаточно, поэтому к нему добавляем 5 и в итоге получаем 25.
Примечание: Если крайняя левая цифра делимого больше делителя, добавлять к нему цифру следующего разряда не нужно, и мы сразу приступаем к следующему шагу.
3. Определяем, сколько целых раз наш делитель содержится в полученном из цифр делимого числе (25). В нашем случае – три раза. Пишем цифру 3 в отведенном для этого месте, затем умножаем ее на делитель (3 ⋅ 8). Получившееся число (24) отнимаем из 25 и остается единица. Важно, чтобы результат вычитания (остаток) обязательно был меньше делителя, иначе мы неправильно выполнили вычисления.
Примечание: Правила и примеры вычитания чисел столбиком приведены в отдельной публикации.
4. К остатку (1) добавляем следующую цифру делимого (6), чтобы получить новое число, которое снова больше, чем делитель.
Примечание: Если при добавлении следующей цифры образовавшееся новое число все еще меньше делителя, берем еще одну цифру справа (если есть такая возможность), при этом в частном пишем ноль. В противном случае, получается деление с остатком, которое мы рассмотрим далее.
В противном случае, получается деление с остатком, которое мы рассмотрим далее.
5. В числе 16 содержится ровно два раза по восемь (2 ⋅ 8), следовательно, пишем 2 в частном, затем выполняем вычитание (16 – 16) и получаем остаток, равный нулю.
На этом деление столбиком числа 256 на 8 успешно выполнено, и частное равно 32.
С остатком
В целом, алгоритм действий аналогичен вышеописанному. Разница лишь в том, что при последнем вычитании остается неделимой остаток, к которому больше нечего дописывать из делимого, т.к. все его разряды уже были использованы. Остаток обычно записывается справа от результата в скобках.
Например, остаток от деления 112 на 5 равняется двум. То есть 112 : 5 = 22 (2).
Пояснение: в результате вычитания 10 из 12 получается 2, но к нему больше нечего дописать из делимого.
Примеры деления в столбик
Пример 1
Разделим трехзначное число на двузначное, например 378 на 21.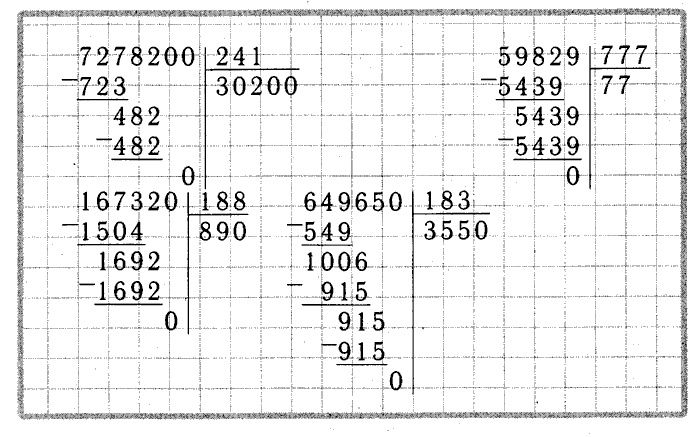
Ответ: 378 : 21 = 18.
Пример 2
Найдем частное от деления чисел 1537 и 35.
Пояснение: в данном случае в делимом нужно сразу отсчитать слева не две, а три цифры, т.к. числа 1 и 15 меньше 35.
Ответ: 1537 : 35 = 43 (32)
Деление столбиком. Онлайн калькулятор | Математика
Как записывать деление в столбик
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком.
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым, неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению.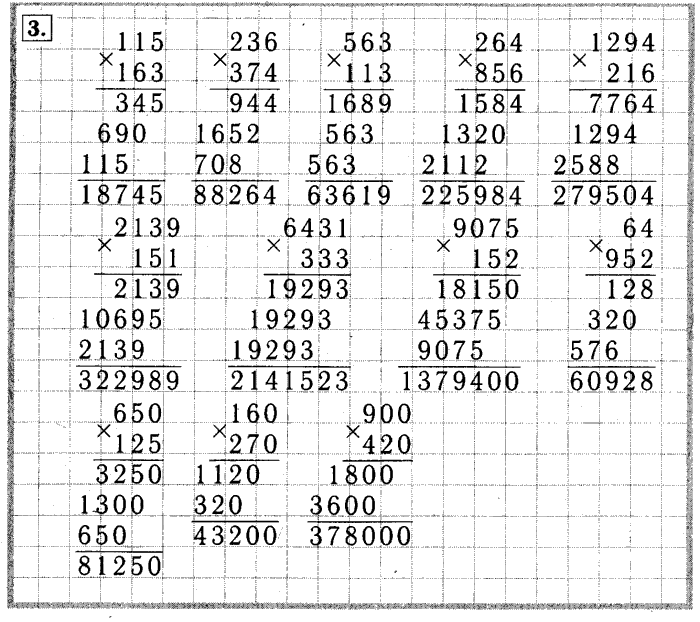 Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
780 : 12 = 65.
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0 : 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27.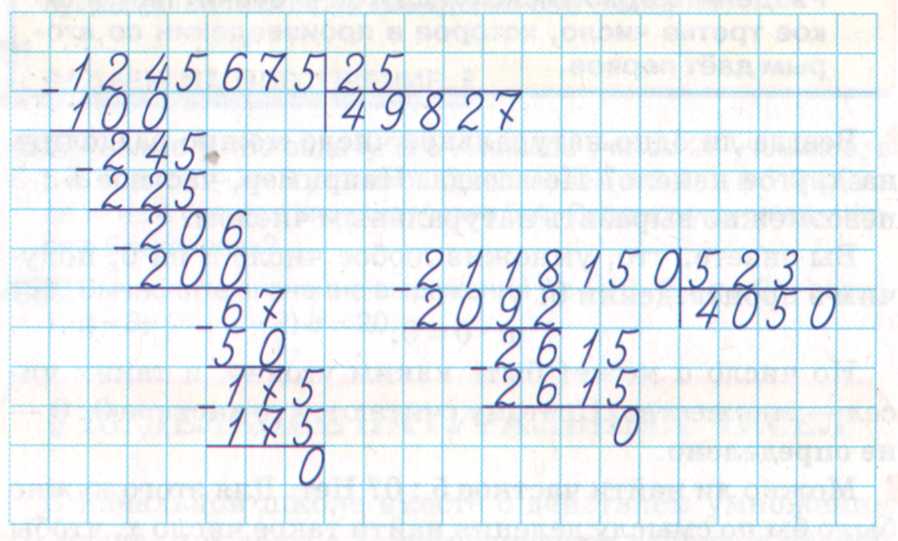 Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
9027 : 9 = 1003.
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
3000 : 6 = 500.
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340 : 23 = 58 (остаток 6).
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3 : 10 = 0 (остаток 3).
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить
.
§ Деление в столбик. Как делить столбиком без остатка
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
Математика 5 класс
Математика 6 класс
Алгебра 7 класс
Геометрия 7 класс
Алгебра 8 класс
Алгебра 9 класс
Алгебра 10 класс
Алгебра 11 класс
Где начало того конца, которым оканчивается начало?Козьма Прутков
Приступаем к делению. Вспоминая таблицу умножения на
Вспоминая таблицу умножения на
«8», находим ближайшее к
«51» произведение.
«6 · 8 = 48»
Записываем цифру «6» в частное.
Записываем «48» под «51».
Запомните!
При записи под неполном частным самая правая цифра неполного
частного должна стоять над самой правой цифрой произведения.
Между «51» и «48» слева поставим «−» (минус). Вычтем по правилам
вычитания в столбик «48» и под чертой запишем результат.
Сравним остаток с делителем. «3» меньше «8».
Запомните!
Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение
более близкое, чем то, которое взяли мы.
Спишем из делимого «512» цифру «2» к «3».
Число «32» больше «8».
И опять по таблице умножения на «8», найдем ближайшее произведение.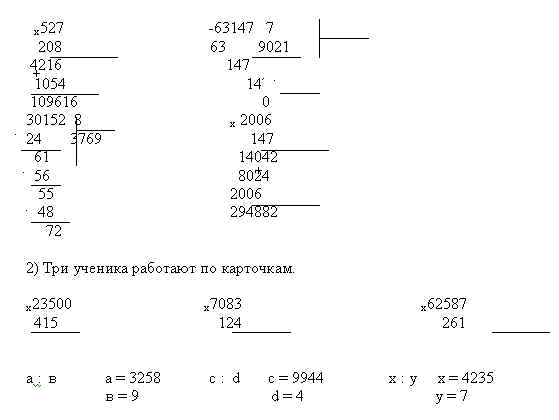
8 · 4 = 32
В остатке получился ноль. Значит числа разделились нацело (без остатка).
10 примеров на деление в столбик :: gslusa
04.12.2014 12:11
10 примеров на деление в столбик
Скачать 10 примеров на деление в столбик
Информация:
Дата загрузки: 04.12.2014
Скачали 320 раз
В рейтинге: 390 из 1456
Скорость скачивания: 16 мбит/сек
Файлов в категории: 458
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
archicad 15 на примерах
canon mf 3110 инструкция по ремонту картриджа
Задачи на тему: «Деление многозначных чисел столбиком, свойство деления». … 3. Реши примеры на деление … 1. Фермер собрал урожай капусты и лука. Капусты получилось 10 455 кг, а лука в 123 раза меньше?АЛГОРИТМ ДЕЛЕНИЯ В СТОЛБИК (на вычислительном примере). … (3класс). Кнопочкин П. В. Новикова В. А. *- Рекомендуется для домашнего задания. … 249. Придумай 10 примеров на деление в столбик и реши их.
Кнопочкин П. В. Новикова В. А. *- Рекомендуется для домашнего задания. … 249. Придумай 10 примеров на деление в столбик и реши их.
Деление в столбик на однозначное число. Пример: 792 разделить на 2. Начнём деление с сотен. … Правило 10. План деления. Деление на однозначное число, когда первое неполное делимое — это двузначное число.
Сложение в столбик Вычитание в столбик Умножение в столбик Деление в столбик. Решим пример: Запишем числа столбиком (одно под другим). … 7 x 6 = 42. У нас получилось число большее или равное 10.
Математика 3 кл. примеры на деление которые решаются в столбик. … Ведь когда пытаемся разделить 173/16 получается 1.8…НО ЛОГИЧЕСКИ мы понимаем что должно быть 10 с остатком я не 1…и вот 🙁 может объясните?
2 февраля 2011Контрольная работа. Тема: Деление столбиком. Вариант 2. 1. Запиши примеры столбиком. Не вычисляя, покажи дугой первое неполное делимое, а. … Инструкция 1 Двузначными являются числа от 10 до 99. Деление таких чисел друг на друга входит в программу третьего класса. ..
..
Деление также происходит в столбик, но частное (результат) записывается ниже делителя и … 4 10 — 4 — 8. … Вычисление абсолютно такое же, но записывается иначе (делитель располагается слева от делимого), как показано на примере деления 135 на 11 (с результатом 12 и остатком 3)
29 октября 2012У нас есть много людей, которые помогут Вам здесь 🙂 Кроме того, мой последний вопрос был решен менее чем за 10 минут:D Во всяком случае, Вы можете просто войти и попробовать добавить свой вопрос.
Примеры в столбик. … 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс. Суперботаник » Умножение и Деление в столбик.
Генератор случайных примеров на умножение чисел в столбик по математике для 3-4 класса. … Кратное (делящееся на) 1 10 100. Столбцов. Строк. 2-ое число.
6 примеров окислительно-восстановительных реакции, 3 варианта договор лизинга, delphi путь к папке мои документы. y
Деление с остатком на 10, 100, 1000
Деление с остатком на 10, 100, 1000
Автор: edu1
Методическая копилка —
Начальная школа
Тема: Деление с остатком на 10, 100, 1000.
Цели: ознакомление с делением на 10, 100 и 1000 с остатком.
Развивать творческое мышление, познавательную активность учащихся, стремление к достижению успеха в учебной деятельности ,совершенствовать вычислительные навыки, умение решать задачи;
Задачи:
Воспитывающая: воспитывать любовь к уроку математики, доброту.
Образовательная: учить выполнять деление с остатком на 10, 100, 1000;, умение решать задачи.
Развивающая: совершенствовать вычислительные навыки, развивать творческое мышление.
Планируемые результаты:
Личностные УУД: способствовать развитию интереса к математике, вычислительных навыков, формирование уважительного отношения к иному мнению, иной точки зрения.
Метапредметные результаты обучения:
Познавательные УУД: формирование умения самостоятельно формулировать проблему, ставить познавательные цели, самостоятельно создавать алгоритм для решения проблем творческого и поискового характера.
Регулятивные: формировать у обучающихся способность организовать свою учебную деятельность: целеполагание, планирование, контроль, коррекция и оценка своей деятельности, саморегуляция как способность к мобилизации сил и энергии, к волевому усилию и преодолению препятствий.
Коммуникативные: работать в парах, выполнять задания творческого и поискового характера, вступать в диалог с учителем, уметь высказываться.
Предметные результаты обучения:
Познавательные: научатся выполнять деление с остатком на 10, 100, 1000 и делать проверку; решать задачи изученных видов; выполнять преобразование единиц измерения, используя соотношения между ними; ориентироваться в материале учебника и находить по заданию учителя нужную информацию.
Оборудование: учебник 4 класс часть 2 М. И. Моро, мультимедийный проектор, презентация к уроку, карточки с заданиями, подарки-солнышки, рисунок яблони со съёмными яблоками, цветами и листьями, мяч.
Ход урока
I.Мотивация к уроку.
— Доброе утро, ребята! Меня зовут Людмила Михайловна. Сегодня я буду вести у вас урок.
Ребята моего класса из Пузачинской школы передали вам в подарок вот такое солнышко добра, чтобы вам на уроке было тепло и уютно. Положите его на ладошку. Оно согревает вас: ваши руки, тело и душу. Придаёт бодрость, заряжает энергией, будит воображение.
— Какое у вас настроение? Покажите жестами!!!
Вот с таким настроением мы и начнём урок.
II. Актуализация знаний
Устный счёт
1)Работаем в парах: в учебнике на с. 27 решим примеры, которые записаны на полях:
630: 70 *30- 89 + 29 : 3 + 30 = 100
2) №91
-Сколько раз по 100м содержится в 2 км? (20)
-Сколько раз по 15 с содержится в 1 мин? (4)
3) В бидоне было 36 л молока. Доярка наполнила 10 трёхлитровых банок. Сколько л молока осталось в бидоне? (36-3*10=6 (л))
4) В спортивную школу привезли 126 мячей. Их запаковали в 12 коробок по 10 мячей в каждой. Сколько мячей осталось? (126-10*12=6(м.))
Их запаковали в 12 коробок по 10 мячей в каждой. Сколько мячей осталось? (126-10*12=6(м.))
5)Презентация:
-Решите примеры:
800 : 2= 400
4 • 20=80
6 • 7=42
60 : 3= 20
30 • 2=60
-Вставьте числа в окошки: 3*8=(?)+27=(?)-39=(?):2=(?)*8=(?)-40=(?)*8
-Вычисли:
50:10 500:10 5000:10
600:100 6000:100 60000:100
7000:1000 70000:1000 700000:1000
III.Создание проблемной ситуации. Постановка проблемы.
-Посмотрите на примеры, записанные на доске:
68:10 400:100 3456:1000
340:10 827:100 7000:1000
На какие две группы их можно разделить? (Примеры на деление без остатка и примеры на деление с остатком)
-Запишите примеры в два столбика:
400:100 68:10
340:10 827:100
7000:1000 3456:1000
Примеры какого столбика мы умеем решать?
Найдите значения выражения первого столбика: (4, 34, 7)
Посмотрите на второй столбик.
Как вы думаете, какую проблему нам нужно решить на уроке, чему научиться? (Деление с остатком на 10,100,1000).
— Прочитайте тему урока в учебнике на стр. 27)
-Поставьте задачи, чему мы будем учиться с вами на уроке?
V. Построение проекта выхода из затруднения. Реализация построенного проекта.
1) Вспомните, как мы делим на 10, 100 и 1000.
(Чтобы число разделить на 10, достаточно убрать один нуль. Чтобы число разделить на 100, надо убрать два нуля и на 1000 надо убрать три нуля).
— Откройте тетради, запишите сегодняшнее число.
— Найдем значение выражений второго столбика. Никто не спешит, следите за мной.
— А сейчас рассмотрим второй столбик.
-Кто может предложить способ деления 68:10?
-Можем ли 68:10 без остатка?
— Какое число можем разделить на 10 без остатка? (60:10=6)
Правильно, возьмем наибольшее число до 68, которое делится на 10, — это 60. Разделим 60 на 10, что получим? (получим 6). .
.
— Сколько останется в остатке?(68 – 60 = 8). Записываем это так 6 (ост. 8).
— Составим алгоритм деления с остатком на 10,100,1000:
1.Найдём наибольшее число, которое делится на 10,100,1000.
2.Разделим это число.
3. Найдём остаток (от делимого отнимем наибольшее число).
Мы вывели алгоритм деления с остатком на 10,100,1000. Давайте сверимся с научным источником – учебником с.27
VI.Первичное закрепление с проговариванием.
-Решите второй пример с объяснением.(827:100=8) остаток 27.
— Выйдите к доске и решите 3 пример с объяснением. (3456 : 1000 = 3) ост 456
— Далее мы выполним задание 96. Начинаем с первой парты 1 ряда, по очереди выходим к доске, решаем пример и объясняем его решение. (Далее учащиеся решают с объяснением примеры, данные в задании 96)
69 : 10 = 6 (ост 9) 238 : 10 = 23 (ост 8) 691 : 100 = 6 (ост 91)
78 : 10 = 7 (ост 8) 238 : 100 = 2 (ост 38) 691 : 10 = 69 (ост 1)
7825 : 100 = 78 (ост 25) 7825 : 1000 = 7 (ост 825)
— Какой вывод по этому заданию вы можете сделать? ( При делении на 10, в остатке будет одна цифра, а в частном будет число, записанное остальными цифрами делимого; при делении на 100 в остатке будет число, записанное двумя последними цифрами делимого, а в частном число, записанное остальными цифрами делимого.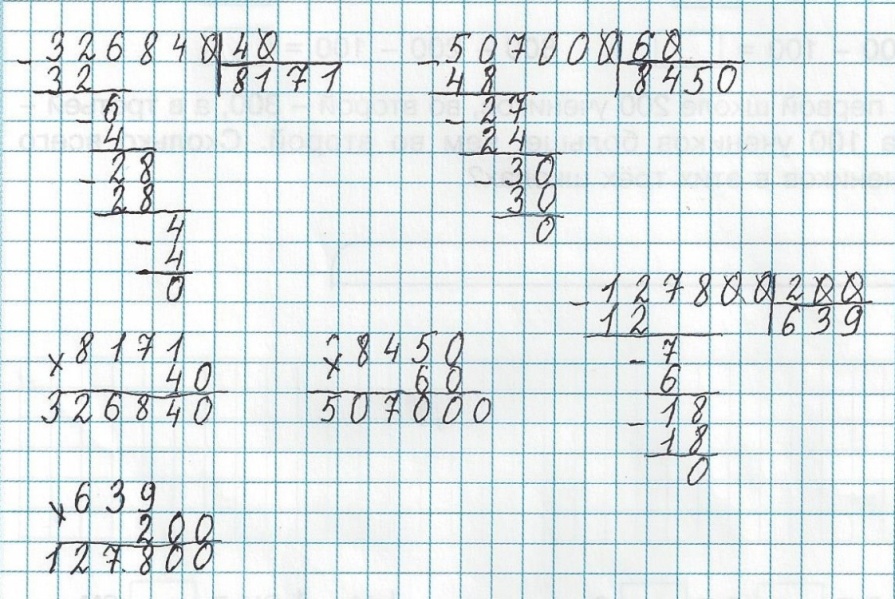 )
)
Для того чтобы этот вывод был усвоен сознательно, важно объяснить, почему это так: на 10 можно разделить все содержащиеся в числе десятки, а единицы остаются; аналогично для 100 и 1000.
— Есть еще 1 способ деления: нужно закрыть в числе столько цифр, сколько нулей в делителе. Получим целое число, а то, что закрыли – остаток
VII. Физкультминутка (под музыку повторяем движения животных)
VIII. Самостоятельная работа в группах с самопроверкой по эталону.
-Работа по карточкам:
327:10 1684:100
358:10 1605:1000
615:100 1730:100
IX. Повторение материала.
Решение задачи изученного вида:
№89 стр.27
-Прочитайте задачу.
-Можем ли мы сразу ответить на вопрос задачи? (Нет, нам неизвестна скорость машины.)
-Как можно найти скорость? (Расстояние разделим на время. )
)
-Что вы заметили? (6 нельзя разделить на 5.)
— А кто догадался, что нужно сделать? (6км перевести в метры: 6км=6000м.)
-Как изменятся теперь единицы скорости? (Скорость будет измеряться в метрах в минуту.)
-Как мы узнаем расстояние, пройденное за 40 мин?
-Что нужно сделать, прежде чем узнать, сколько пройдёт машина с такой же скоростью за 1 ч? (Надо 1ч перевести в минуты.)
-Запишите решение задачи выражениями.
6000:5=1200(м/мин)
1200*40=48000(м)
1200*60=72000(м)
Ответ: 48000м,72000м
№92 стр.27
-Прочитайте задание.
-Составьте первое уравнение.(х-20=40*6)
-Как его можно упростить? (Можно найти произведение чисел: 40*6=240)
-Что неизвестно в уравнении? (Уменьшаемое)
-Вспомните, как найти уменьшаемое. (К разности прибавить вычитаемое.)
-Запишите решение.
х-20=240
х=240+20
х=260
260-20=240
-Второе уравнение решается самостоятельно в парах.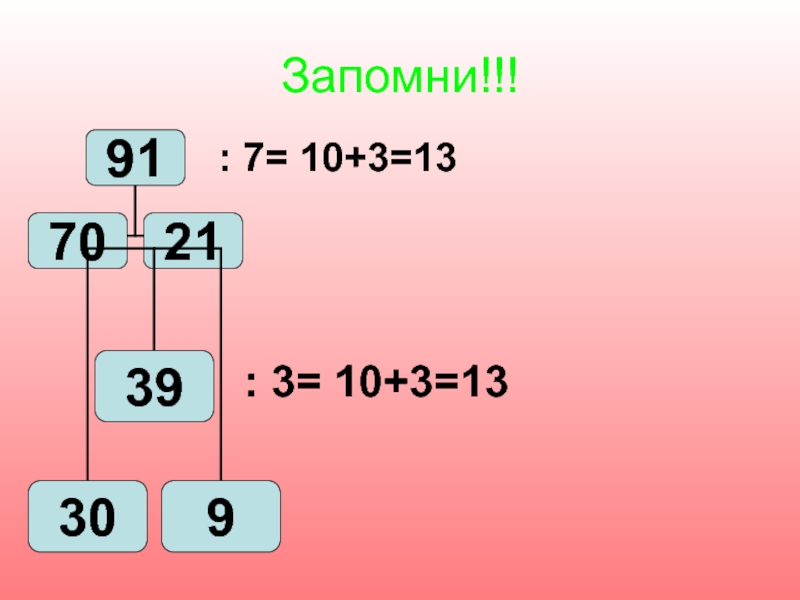
15+х=800:20
15+х=40
х=40-15
х=25
15+25=40
XII. Рефлексия
Игра в мяч:
Бросаю мяч и называю выражение, дети ловят и называют ответ:
152:10, 375:100, 54:10,786:100, 2546:1000, 3452:100, 79:10, 897:100, 2457:1000,385:10, 893:10, 715:100, 2413:1000, 81:10, 95:10
— Урок у нас заканчивается. За это время выросло удивительное дерево, благодаря которому каждый из вас оценить себя.
-Если урок для вас прошел плодотворно, и вы справлялись с заданиями без ошибок — сорвите с дерева плоды – яблоки.
-Если вы допускаете ещё незначительные ошибки – сорвите цветы.
-Если на уроке вы не усвоили новый материал, вам ещё многое непонятно – зеленые листочки.
XIII. Подведение итогов урока
-Как разделить число на 10, 100, 1000?
-Как выполнить деление с остатком?
-Как можно проверить вычисления?
-Что является продуктом нашей работы?
— Повторение алгоритма деления с остатком на 10, 100, 1000.
Домашнее задание: переверните другой стороной ваши яблоки, листочки, цветы. Для вас индивидуальные домашние задания:
На яблоках-№94 с.27;
На цветах – 15928:100 15862:10 34518:100 135628:10 36704:10 52080:100;
На листочках — №93 с.27
-Объяснение заданий.
-Оценки за урок.
Технологическая карта
|
Этапы урока
|
Обучающие и развивающие компоненты задания
|
Деятельность учителя
|
Деятельность учащихся
|
Формы организации взаимодействия на уроке
|
Формируемые умения (универсальные учебные действия)
|
|
Мотивация к уроку.
Актуализация знаний.
Создание проблемной ситуации. Постановка проблемы.
Построение проекта выхода из затруднения. Реализация построенного проекта.
Первичное закрепление с проговариванием.
Физкультминутка
Самостоятельная работа в группах с самопроверкой по эталону.
Повторение материала.
Рефлексия
Подведение итогов урока
Домашнее задание
|
Эмоциональная, психологическая и мотивационная подготовка учащихся к усвоению изучаемого материала.
Устный счёт
1)Работаем в парах: в учебнике на с. 27 решим примеры на полях:
630: 70 *30- 89 + 29 : 3 + 30 = 100
2) №91
-Сколько раз по 100м содержится в 2 км? (20)
-Сколько раз по 15 с содержится в 1 мин? (4)
3) В бидоне было 36 л молока. Доярка наполнила 10 трёхлитровых банок. Сколько л молока осталось в бидоне? (36-3*10=6 (л))
4) В спортивную школу привезли 126 мячей.
5)Презентация:
-Решите примеры:
800 : 2= 400
4 • 20=80
6 • 7=42
60 : 3= 20
30 • 2=60
-Вставьте числа в окошки: 3*8=(?)+27=(?)-39=(?):2=(?)*8=(?)-40=(?)*8
-Вычисли:
50:10 500:10 5000:10
600:100 6000:100 60000:100
7000:1000 70000:1000 700000:1000
68:10 400:100 3456:1000
340:10 827:100 7000:1000
Вспомните, как мы делим на 10, 100 и 1000.
(Чтобы число разделить на 10, достаточно убрать один нуль. Чтобы число разделить на 100, надо убрать два нуля и на 1000 надо убрать три нуля).
— Откройте тетради, запишите сегодняшнее число.
— Найдем значение выражений второго столбика. Никто не спешит, следите за мной.
— А сейчас рассмотрим второй столбик.
-Кто может предложить способ деления 68:10?
-Можем ли 68:10 без остатка?
— Какое число можем разделить на 10 без остатка? (60:10=6)
Правильно, возьмем наибольшее число до 68, которое делится на 10, — это 60. Разделим 60 на 10, что получим? (получим 6). .
— Сколько останется в остатке?(68 – 60 = 8). Записываем это так 6 (ост. 8).
— Составим алгоритм деления с остатком на 10,100,1000:
1.Найдём наибольшее число, которое делится на 10,100,1000.
2.Разделим это число.
3. Найдём остаток (от делимого отнимем наибольшее число).
Мы вывели алгоритм деления с остатком на 10,100,1000. Давайте сверимся с научным источником – учебником с.27
Решите второй пример с объяснением.(827:100=8) остаток 27.
— Выйдите к доске и решите 3 пример с объяснением. (3456 : 1000 = 3) ост 456
— Далее мы выполним задание 96.
69 : 10 = 6 (ост 9) 238 : 10 = 23 (ост 8) 691 : 100 = 6 (ост 91)
78 : 10 = 7 (ост 8) 238 : 100 = 2 (ост 38) 691 : 10 = 69 (ост 1)
7825 : 100 = 78 (ост 25) 7825 : 1000 = 7 (ост 825)
под музыку повторяем движения животных
Работа по карточкам:
327:10 1684:100
358:10 1605:1000
615:100 1730:100
Решение задачи изученного вида:
№89 стр.27
№92 стр.27-составление и решение уравнения.
Игра в мяч.
Яблоня успеха.
Как разделить число на 10, 100, 1000?
-Как выполнить деление с остатком?
-Как можно проверить вычисления?
Индивидуальное домашнее задание для каждого ученика на сорванных яблоках: -№94 с.
На цветах – 15928:100 15862:10 34518:100 135628:10 36704:10 52080:100;
На листочках — №93 с.27
|
— Доброе утро, ребята!
— Какое у вас настроение? Покажите жестами!!!
Ребята моего класса из Пузачинской школы передали вам в подарок вот такое солнышко добра, чтобы вам на уроке было тепло и уютно. Положите его на ладошку. Оно согревает вас: ваши руки, тело и душу. Придаёт бодрость, заряжает
энергией, будит воображение. Вот с таким настроением мы и начнём урок
Совершенствует вычислительные навыки обучающихся, умение решать задачи
Демонстрирует разные виды заданий.
На какие две группы их можно разделить? (Примеры на деление без остатка и примеры на деление с остатком)
-Запишите примеры в два столбика:
400:100 68:10
340:10 827:100
7000:1000 3456:1000
Примеры какого столбика мы умеем решать?
Найдите значения выражения первого столбика: (4, 34, 7)
Как вы думаете, какую проблему нам нужно решить на уроке, чему научиться? (Деление с остатком на 10,100,1000).
— Прочитайте тему урока в учебнике на стр. 27)
Повторяют правило деления на 10, 100, 1000.
Решают с проговариванием
Выполняют упражнения
Работают в парах
Читают задачу, анализируют под руководством учителя, решают, самостоятельно записывают решение.
Анализируют содержание и составляют задачу.
Бросает мяч и называет выражение, которое надо решить.
Проверяет уровень усвоения материала.
Оценивает уровень обученности
Подводит итог урока.
Объясняет выполнение домашнего задания
|
Слушают учителя, повторяют за ним движения. Демонстрируют готовность к уроку.
Работают в парах
Повторяют единицы длины, времени.
Решают устно задачи.
Повторяют умножение и деление на 10,100,1000
Замечают проблему.
Такие выражения ещё решать не умеют.
Определяют тему и цели урока.
Контролирует правильность ответов.
Направляет на исследование выражения.
Контролирует правильность решения и объяснения.
Вместе с детьми выполняет упражнения.
Контролирует деятельность обучающихся в парах.
Проверка по эталону в призентации.
Задаёт вопросы для анализа: Можем ли мы сразу ответить на вопрос задачи? (Нет, нам неизвестна скорость машины.)
-Как можно найти скорость? (Расстояние разделим на время.)
-Что вы заметили? (6 нельзя разделить на 5.)
— А кто догадался, что нужно сделать? (6км перевести в метры: 6км=6000м.)
-Как изменятся теперь единицы скорости? (Скорость будет измеряться в метрах в минуту.)
-Как мы узнаем расстояние, пройденное за 40 мин?
-Что нужно сделать, прежде чем узнать, сколько пройдёт машина с такой же скоростью за 1 ч? (Надо 1ч перевести в минуты.)
-Запишите решение задачи выражениями.
6000:5=1200(м/мин)
1200*40=48000(м)
1200*60=72000(м)
Ответ: 48000м,72000м
Прочитайте задание.
-Составьте первое уравнение. (х-20=40*6)
-Как его можно упростить? (Можно найти произведение чисел: 40*6=240)
-Что неизвестно в уравнении? (Уменьшаемое)
-Вспомните, как найти уменьшаемое. (К разности прибавить вычитаемое.)
-Запишите решение.
х-20=240
х=240+20
х=260
260-20=240
-Второе уравнение решается самостоятельно в парах.
15+х=800:20
15+х=40
х=40-15
х=25
15+25=40
Ловят мяч и называют ответ выражения
Выбирают яблоко, если усвоили новый материал на отлично, не возникало затруднений на уроке;
Цветы, если возникают
затруднения при решении;
листья, если материал плохо усвоен.
Обобщают новые знания.
Слушают пояснения и задают вопросы.
|
Фронтальная, индивидуальная.
Фронтальная, индивидуальная
Фронтальная, индивидуаль-ная
Фронтальная, индивидуаль-ная.
Фронтальная.
Фронтальная, индивидуаль-ная
. Фронтальная.
Фронтальная, индивидуаль-ная
Фронтальная, индивидуаль-ная
Фронтальная, индивидуаль-ная
Фронтальная, индивидуаль-ная
Фронтальная, индивидуаль-ная
Фронтальная, индивидуаль-ная
|
К.-планирует учебное сотрудничество с учителем и сверстниками.
Л.— имеют желание учиться, проявляют интерес к изучаемому предмету, понимают его важность.
П. – осмысленно читают тексты математического содержания в соответствии с поставленными целями и задачами; проводят несложные обобщения и используют математические знания в расширенной области применения; используют математические термины, символы и знаки.
Р.— понимают, принимают и сохраняют различные учебные задачи; осуществляют поиск средств для достижения учебной задачи.
К. – умеют слушать друг друга, строить понятные для партнёра по коммуникации речевые высказывания; могут работать в коллективе, уважают мнения других участников образовательного процесса.
Л. – способны адекватно рассуждать о причинах своего успеха или неуспеха, связывая успехи с усилиями, трудолюбием; проявляют познавательный интерес к изучению предмета.
Р. – принимают и сохраняют учебную задачу.
К. – проявляют готовность слушать.
П. — учатся выполнять деление с остатком на 10, 100, 1000 ;
Р. — контроль, коррекция и оценка своей деятельности.
Л. — способствовать развитию интереса к математике.
Л. – имеют установку на здоровый образ жизни.
К. – умение работать в парах, сотрудничать, выслушивать мнение собеседника, уметь высказываться.
П. – проводят анализ, синтез, сравнение, обобщение, аналогию;осознанно и произвольно строят речевые высказывания; осуществляют построение логической цепи рассуждений, доказательство.
Р. – осуществляют волевую саморегуляцию в ситуации затруднения.
К. – понимают различные позиции в подходе к решению задачи, задают вопросы для уточнения. Чётко и аргументированно высказывают свои оценки и предложения.
Л. – осуществление смыслообразова-ния; проявляют познавательный интерес к предмету.
Р.- контроль и оценка собственной деятельности.
П. – ориентируются в своей системе знаний – отличают новое от уже известного.
Л. – проявляют интерес к предмету.
П. –ориентируются в своей системе знаний – отличают новое от уже известного.
Р. – оценивают собственную деятельность на уроке.
Л. – проявляют интерес к предмету.
Р.- принимают и сохраняют учебную задачу, осуществляют поиск средств для её выполнения.
|
Правила деления в столбик. Деление с нулем в частном
В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
- Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
- То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него — делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
- Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
- Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.
- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере — 12082: 863.
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
- Их полагается разделить. Причем сразу все число 284 на 32.
- Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.
- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения — 224, остаток — 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
- Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
- Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком
:
- Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
- Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
- Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
- Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
- Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
- Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
- Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
- Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
- Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
- Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
- Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
- Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
- К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Yandex.RTB R-A-339285-1
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Пусть нам нужно разделить 6105 на 55 , запишем:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0 , 1 , 2 , 3 . . Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8 — 8 = 0 .
Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3 .
В данном случае, последовательно умножая тройку на 0 , 1 , 2 , 3 . . получаем в результате:
3 · 0 = 0 7
Под делимым записываем число, полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 .
В завершение операции вычитаем 6 из 7 и получаем:
Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1 .
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4 . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .
2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль: 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делітелем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
В соответствии с алгоритмом имеем:
4 · 0 = 0 14 .
Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .
3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следубщую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .
Важно!
Пункты 2 — 4 повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем:
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 — 20 = 0 .
4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2 .
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом.
4 · 0 = 0 2
Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 .
3. Выполняем операцию вычитания и под чертой записываем результат.
4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа.
Таким образом, получаем новое работчее число — 28 . Снова повторяем пункты алгоритма.
Проделав все по правилам, получаем результат:
Переносим под черту вниз последнюю цифру делимого — 8 . В последний раз повторяем пункты алгоритма 2 — 4 и получаем:
В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена.
Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Пример 1. Деление натуральных чисел в столбик
Разделим натуральное число 7136 на натуральное число 9 .
После второго, третьего и четвертого шага алгоритма запись примет вид:
Повторим цикл:
Последний проход, и поучаем результат:
Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 .
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Пример 2. Деление натуральных чисел в столбик
Разделим число 7042035 на 7 .
Ответ: 1006005
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2 — 4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Пример 3. Деление натуральных чисел в столбик
Разделим 5562 на 206 .
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556 .
556 > 206 , поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на 0 , 1 , 2 , 3 . . и получаем:
206 · 0 = 0 556
618 > 556 , поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2
Выполняем вычитание столбиком
В результате вычитания имеем число 144 . Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442 .
Повторяем с ним пункты 2 — 4 . Получаем:
206 · 5 = 1030
Под отмеченным рабочим числом записываем 1442 , а в следующий разряд частного записываем цифру 7 — множитель.
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Пример 5. Деление натуральных чисел в столбик
Разделим натуральное число 238079 на 34 .
Ответ: 7002
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Как в столбик делить — один из основных навыков, необходимых для работы с двух- и трёхзначными числами. Зная последовательность всех этапов деления, можно разделить любое число. Не возникнет проблем при работе не только с целым числом, но и с числом, представленным в виде десятичной дроби.
Этот полезный математический навык необходим не только для успешного освоения школьной программы по математике и ряду других предметов. Умение делить наверняка поможет каждому в повседневной жизни.
Часть первая. Деление
Итак, делимое, то есть число, которое нужно разделить, надо записать слева. Число, на которое делят, называют делителем и записывают справа.
Под делителем проводится черта, под которой пишут частное (решение).
Под делимым необходимо оставить место, требующееся для вычислений.
Сама задача выглядит следующим образом: пакет, где лежат шесть грибов, весит 250 грамм. Нужно узнать, сколько весит один гриб. Для этого 250 делят на 6. Первое из этих двух чисел записывают слева, а второе — справа.
Сейчас предстоит вычислить, сколько целых раз делится первая цифра (отсчёт ведётся с левого конца) делимого на делитель.
Для решения нашей задачи нужно узнать, сколько раз цифра 2 делится на 6. Так как это невозможно, то в ответе — 0, который записывается под делителем. В этом случае нуль является первым числом частного, однако допускается отказ от такой записи.
Теперь предстоит узнать, сколько целых раз делятся две первые цифры делимого на делитель.
Если в предшествующем действии в ответе был получен 0, надо рассмотреть две первые цифры делимого. В рассматриваемой задаче надо вычислить, сколько раз 25 делится на 6.
Если делитель является двух- и более значным числом, надо разделить на него первые три (четыре, пять и т. д.) цифры делимого. Наша цель: получить целое число.
Далее начинается работа с целыми числами. Если с помощью микрокалькулятора произвести деление 25 на 6, то в ответе будет дано число 4.167. Этот ответ не годится для деления в столбик. В этом случае нужно просто взять 4.
Результат, полученный в третьем этапе, записывается прямо под соответствующей цифрой делителя — под чертой. Данный итог будет первой цифрой искомого частного, то есть ответа.
Результат обязательно нужно писать под соответствующей цифрой делителя. Если пренебречь этим требованием, будет допущена ошибка, которая скажется и на конечном результате: он будет неверным.
В рассматриваемом случае 4 записывается под 5, так как на 6 делится число 25, а не 2.
Часть вторая. Умножение
Этот этап представляет собой переход к новой части работы «как считать в столбик». Деление в данном случае сменятся… умножением.
Делитель умножается на число, которое было под ним записано. Это означает, что речь идёт о первой цифре искомого частного.
Результат этого произведения размещается под делимым.
В рассматриваемом примере 6 х 4 = 24. Число, стоящее в ответе, то есть 24, записывается под 25. Важно: 2 должна стоять под 2, а 4 — под 5.
Результат произведения подчёркивается. В нашем случае речь идёт о подчёркивании числа 24.
Часть третья. Вычитание и опускание цифр
Здесь происходит переход к вычитанию и опусканию цифр.
Результат записывается под чертой, которая в свою очередь проводится под числом, поставленным под делимым.
Нам предстоит произвести вычитание 24 из 25. Получаемый при этом результат: 1.
Опускается третья цифра делимого, то есть она записывается рядом с результатом вычитания.
В нашем случае 1 не может делиться на 6. В силу этого спускают третью цифру делимого (третьей цифрой числа 250 является 0). Она размещается рядом с 1. Мы получаем число 10, которое может быть разделено на 6.
Теперь требуется повторить процесс с новым числом.
Для этого полученное число делится на наш делитель, а получаемый при этом результат размещается под делителем, в качестве которого будет выступать вторая цифра частного, то есть нашего ответа.
В решаемом примере 10 делим на 6, что даёт в итоге 1. Единичка записывается в частное — рядом с 4. После этого 6 умножается на 1 и из 10 вычитают результат. У нас должно получиться 4 (остаток).
Если делимое представляет собой двух-, трёх-, четырёх- и более значное число, изложенный процесс повторяется до тех пор, пока не будут опущены все цифры делимого. Пример для иллюстрации: если известно, что вес грибов равен 2 506 г, надо опустить цифру 6, то есть записать её рядом с 4.
Часть четвёртая. Запись частного с остатком или в виде десятичной дроби
Теперь переходим к записи частного с остатком или в виде десятичной дроби.
Наш остаток был равен 4, что связано с тем, что это число — 4 — не делится на 6 и у нас не осталось цифр, которые можно спустить.
Ответ при этом будет выглядеть следующим образом: 41 (ост. 4).
Вычисления на данном этапе могут быть завершены, если в задаче сформулировано требование найти что-то, выражаемое исключительно в целых числах. Речь может идти о количестве автомобилей, требующихся для транспортировки определённого числа людей.
Если есть необходимость в ответе в виде десятичной дроби, можно перейти к следующим действиям алгоритма «как разделить в столбик».
Если нет желания записывать ответ с остатком, можно найти ответ в виде десятичной дроби. При получении остатка, не поддающегося делению на делитель, надо добавить десятичный знак (к частному).
В нашем случае число 250 может быть записано в виде десятичной дроби: 250.000.
Теперь, когда в наличии цифры (только нули), которые могут быть опущены, можно продолжить вычисления. Опускаем нуль и подсчитываем, сколько целых раз можно поделить полученное число на делитель.
В нашем примере после частного 41 (которое размещаем прямо под делителем) пишем десятичную запятую и приписываем 0 к остатку (4). Затем делим полученное число, то есть 40, на делитель (в роли которого выступает 6). Получаем опять 6, которую пишем в частное после десятичного знака. Это выглядит как 41.6. После этого 6 умножается на 6, затем результат умножения вычитается из 40. У нас должно получиться снова 4.
В ряде ситуаций при поиске ответа в виде десятичной дроби приходится столкнуться с повторяющимися числами. Для этого надо прервать вычисления и округлить уже полученный ответ — вниз или вверх.
В частности, в рассматриваемом примере надо отказаться от бесконечного получения цифры 4. Нужно просто прервать вычисления и округлить частное. В силу того, что 6 больше 5, округление производится вверх, в результате чего получается ответ в виде дробного числа 41.67.
Деление столбиком
(также можно встретить название деление
уголком) — стандартная процедура в
арифметике, предназначенная для деления простых или сложных многозначных чисел за счёт разбивания
деления на ряд более простых шагов. Как и во всех задачах на деление, одно число, называемое
делимым
, делится на другое, называемое
делителем
, производя результат, называемый
частным
.
Столбиком можно проводить как деление натуральных чисел без остатка, так и деление натуральных чисел
с остатком.
Правила записи при делении столбиком.
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при
делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком
удобнее всего на бумаге с клетчатой разлиновкой — так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными
числами изображается символ вида
.
Например
, если делимым является число 6105, а делителем 55, то их правильная запись при делении в
столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного,
остатка и промежуточных вычислений при делении столбиком:
Из приведенной схемы видно, что искомое частное (или неполное частное
при делении с остатком) будет
записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже
делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться
правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше
потребуется места.
Деление столбиком натурального числа на однозначное натуральное число,
алгоритм деления столбиком.
Как делить в столбик лучше всего объяснить на примере.
Вычислить
:
512:8=?
Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра 8.
1. Определяем неполное частное. Сначала мы смотрим на первую слева цифру в записи делимого.
Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать
с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую
слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми
цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
2. Берём 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого. 51 больше 8. Значит.
это неполное частное. Ставим точку в частном (под уголком делителя).
После 51 стоит только одно цифра 2. Значит и добавляем в результат ещё одну точку.
3. Теперь, вспоминая
таблицу умножения на 8, находим ближайшее к 51 произведение → 6 х 8 = 48
→ записываем цифру 6 в частное:
Записываем 48 под 51 (если умножить 6 из частного на 8 из делителя, получим 48).
Внимание!
При записи под неполным частным самая правая цифра неполного частного должна стоять над
самой правой цифрой
произведения .
4. Между 51 и 48 слева поставим «-» (минус).
Вычтем по
правилам вычитания в столбик 48 и под чертой
запишем результат.
Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в
этом пункте не является самым последним действием, полностью завершающим процесс деления
столбиком).
В остатке получилось 3. Сравним остаток с делителем. 3 меньше 8.
Внимание!
Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение
более близкое, чем то, которое взяли мы.
5. Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не
стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в
записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается.
Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение → 8 x 4 = 32:
В остатке получился ноль. Значит, числа разделились нацело (без остатка). Если после последнего
вычитания получается ноль, а цифр больше не осталось, то это остаток. Его дописываем к частному в
скобках (например, 64(2)).
Деление столбиком многозначных натуральных чисел.
Деление на натуральное многозначное число производится аналогично. При этом, в первое
«промежуточное» делимое включается столько старших разрядов, чтобы оно получилось больше делителя.
Например
, 1976 разделим на 26.
- Число 1 в старшем разряде меньше 26, поэтому рассмотрим число, составленное из цифр двух старших разрядов — 19.
- Число 19 также меньше 26, поэтому рассмотрим число, составленное из цифр трех старших разрядов — 197.
- Число 197 больше 26, делим 197 десятков на 26: 197: 26 = 7 (15 десятков осталось).
- Переводим 15 десятков в единицы, добавляем 6 единиц из разряда единиц, получаем 156.
- 156 делим на 26, получаем 6.
Значит, 1976: 26 = 76.
Если на каком-то шаге деления «промежуточное» делимое оказалось меньше делителя, то в частном
записывается 0, а число из данного разряда переводится в следующий, более младший разряд.
Деление с десятичной дробью в частном.
Если натуральное число не делится нацело на однозначное натуральное число, можно продолжить
поразрядное деление и получить в частном десятичную дробь.
Например
, 64 разделим на 5.
- 6 десятков делим на 5, получаем 1 десяток и 1 десяток в остатке.
- Оставшийся десяток переводим в единицы, добавляем 4 из разряда единиц, получаем 14.
- 14 единиц делим на 5, получаем 2 единицы и 4 единицы в остатке.
- 4 единицы переводим в десятые, получаем 40 десятых.
- 40 десятых делим на 5, получаем 8 десятых.
Значит, 64: 5 = 12,8
Таким образом, если при делении натурального числа на натуральное однозначное или многозначное число
получается остаток, то можно поставить в частном запятую, остаток перевести в единицы следующего,
меньшего разряда и продолжать деление.
Деление с остатком объяснение. Деление столбиком. Деление в столбик
Как научить ребенка делению? Самый простой метод – выучить деление столбиком
. Это гораздо проще, чем проводить вычисления в уме, помогает не запутаться, не «потерять» цифры и выработать мысленную схему, которая в дальнейшем будет срабатывать автоматически.
Вконтакте
Как проводится
Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.
Приведем простой пример
того, как делить с остатком:
Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:
5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.
Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета и помогает не потерять числа.
Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.
Основные этапы
:
- Правильная запись. Делимое (17) – располагается по левую сторону. Правее от делимого пишут делитель (5). Между ними проводят вертикальную черту (обозначает знак деления), а затем, от этой черты проводят горизонтальную, подчеркивая делитель. Основные черты обозначена оранжевым цветом.
- Поиск целого. Далее, проводят первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное.
- Определение остатка. 3*5=15. 15 записываем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.
Обратите внимание!
При делении таким образом, остаток всегда должен быть меньше делителя.
Когда делитель больше делимого
Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача
: необходимо не разделить, а найти остаток! часть им не является! Как решить такую задачу?
Обратите внимание!
Существует правило для случаев, когда делитель больше делимого: неполное частное равно 0, остаток равен делимому.
Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? , потому что 6 больше 5.
По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.
Деление начинают изучать в третьем классе школы. К этому времени ученики уже должны , что позволяет им совершать деление двузначных чисел на однозначные.
Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?
Примеры:
Находим неполное частное: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.
Остаток: 3*4=12, 14-12=2.
Ответ: неполное частное 4, осталось 2.
Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу
.
Еще одна задача: 3 пирожка надо разделить на двоих.
4 пирожка разделить на двоих.
5 пирожков разделить на двоих.
Работа с многозначными числами
Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами более 100.
Данное действие удобнее всего выполнять в столбик, так как неполное частное также будет двузначным числом (в большинстве случаев), а алгоритм столбика облегчает вычисления и делает их более наглядными.
Разделим многозначные числа на двузначные
: 386:25
Данный пример отличается от предыдущих количеством уровней расчета, хотя вычисления проводят по тому же принципу, что и ранее. Рассмотрим подробнее:
386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить остаток.
Первый уровень
Делитель – двузначное число. Делимое – трехзначное. Выделяем у делимого первые две левые цифры – это 38. Сравниваем их с делителем. 38 больше 25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?
25*1=25, 25*2=50. 50 больше 38, возвращаемся на один шаг назад.
Ответ – 1. Записываем единицу в зону не полного частного
.
38-25=13. Записываем число 13 под чертой.
Второй уровень
13 больше 25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136 больше 25? Да – значит можно его вычесть. Сколько раз 25 поместиться в 136?
25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150 больше 136 – возвращаемся назад на один шаг. Записываем цифру 5 в зону неполного частного, справа от единицы.
Вычисляем остаток:
136-125=11. Записываем под чертой. 11 больше 25? Нет – деление провести нельзя. У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.
Ответ:
неполное частное равно 15, в остатке 11.
А если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого? В таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в вычислениях сразу.
Приведем примеры
на деление с трех- и четырехзначными числами:
75 – двузначное число. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38 больше 75? Нет – деление провести нельзя. Берем все 3 цифры. 386 больше 75? Да – деление провести можно. Проводим вычисления.
75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450 больше 386 – возвращаемся на шаг назад. Записываем 5 в зону неполного частного.
Находим остаток: 386-375=11. 11 больше 75? Нет. Еще остались цифры у делимого? Нет. Вычисления закончены.
Ответ:
неполное частное = 5, в остатке — 11.
Выполняем проверку: 11 больше 35? Нет – деление провести нельзя. Подставляем третье число – 119 больше 35? Да – действие провести можем.
35*1=35, 35*2=70, 35*3=105, 35*4=140. 140 больше 119 – возвращаемся на один шаг назад. Записываем 3 в зону неполного остатка.
Находим остаток: 119-105=14. 14 больше 35? Нет. Остались цифры у делимого? Нет. Вычисления закончены.
Ответ:
неполное частное = 3, осталось — 14.
Проверяем: 11 больше 99? Нет – подставляем еще одну цифру. 119 больше 99? Да – начинаем вычисления.
1199.
99*1=99, 99*2=198 – перебор. Записываем 1 в неполное частное.
Находим остаток: 119-99=20. 2099. Вычисляем.
99*1=99, 99*2=198, 99*3=297. Перебор. Записываем 2 в неполное частное.
Находим остаток: 205-198=7.
Ответ:
неполное частное = 12, остаток — 7.
Деление с остатком — примеры
Учимся делить в столбик с остатком
Вывод
Таким образом проводятся вычисления. Если быть внимательным и выполнять правила, то ничего сложного здесь не будет. Каждый школьник может научиться считать столбиком, потому что это быстро и удобно.
Многие числа нельзя разделить нацело, при делении часто присутствует остаток, отличный от нуля. В этой статье мы разберем способы деления натуральных чисел с остатком и подробно рассмотрим их применение на примерах.
Начнем с деления натуральных чисел с остатком в столбик, затем рассмотрим деление с помощью последовательного вычитания. Наконец, закончим разбором метода подбора неполного частного. Приведем алгоритм деления с остатком для наиболее общего случая и покажем, как проводить проверку результата деления натуральных чисел с остатком.
Это один из самых удобных способов деления. Подробно он описан в отдельной статье, посвященной делению натуральных чисел столбиком. Здесь мы не будем приводить всю теорию заново, но сконцентрируемся именно на случае деления с остатком.
Приведем решение примера, так как понять суть метода проще всего на практике.
Пример 1. Как делить натуральные числа с остатком?
Разделим натуральное число 273844 на натуральное число 97 .
Проводим деление столбиком и записываем:
Результат: неполное частное от деления равно 2823 , а остаток равен 13 .
Деление чисел с остатком через последовательное вычитание
Чтобы найти неполное частное и остаток, можно прибегнуть к последовательному вычитанию делителя из делимого. Этот способ не всегда целесообразен, однако в некоторых случаях его очень удобно применять. Вновь обратимся к примеру.
Пример 2. Деление с остатком через последовательное вычитание.
Пусть у нас есть 7 яблок. Нам нужно эти 7 яблок разложить в пакеты по 3 яблока. Иными словами, 7 разделить на 3 .
Возьмем из начального количества яблок 3 штуки и положим в один пакет. У нас останется 7 — 3 = 4 яблока. Теперь, из оставшихся яблок снова отнимаем 3 штуки и кладем уже в другой пакет. Остается 4 — 3 = 1 яблоко.
1 яблоко — это остаток от деления, так как на этом этапе мы уже не можем сформировать еще один пакет с тремя яблоками и деление, по сути, завершено. Результат деления:
7 ÷ 3 = 2 (остаток 1)
Это значит, что число 3 как бы умещается в числе 7 два раза, а единица — остаток, меньший чем 3 .
Рассмотрим еще один пример. На этот раз, приведем только математические выкладки, не прибегая к аналогиям.
Пример 3. Деление с остатком через последовательное вычитание.
Вычислим: 145 ÷ 46 .
Число 99 больше, чем 46 , поэтому продолжаем последовательное вычитание делителя:
Повторяем эту операцию еще раз:
В результате, нам понадобилось последовательно вычесть делитель из делимого 3 раза до того, как мы получили остаток — результат вычитания, который меньше делителя. В нашем случае остатком является число 7 .
145 ÷ 46 = 3 (остаток 7) .
Метод последовательного вычитания непригоден, когда делимое меньше делителя. В таком случае можно сразу записать ответ: неполное частное равно нулю, а остаток равен самому делимому.
Если a
Например:
12 ÷ 36 = 0 (остаток 12) 47 ÷ 88 = 0 (остаток 47)
Также касательно метода последовательного вычитания нужно отметить, что он удобен только в случаях, когда вся операция деления сводится к небольшому количеству вычитаний. Если делимое во много раз больше делителя, использование этого метода будет нецелесообразно и связано с множеством громоздких вычислений.
Метод подбора неполного частного
При делении натуральных чисел с остатком можно вычислить результат методом подбора неполного частного. Покажем, как можно вести процесс подбора, и на чем он основан.
Во-первых, определим, среди каких чисел нужно искать неполное частное. Из самого определения процесса деления понятно, что неполное частное равно нулю, либо является одним из натуральных чисел 1 , 2 , 3 и т.д.
Во-вторых, установим связь между делителем, делимым, неполным частным и остатком. Рассмотрим уравнение d = a — b · c . Здесь d — остаток от деления, a — делимое, b — делитель, с — неполное частное.
В-третьих, не будем забывать, что остаток всегда меньше делителя.
Теперь рассмотрим непосредственно процесс подбора. Делимое a и делитель b известны нам с самого начала. В качестве неполного частного с будем последовательно принимать числа из ряда 0 , 1 , 2 , 3 и т.д. Применяя формулу d = a — b · c и вычисляя полученное значение с делителем, закончим процесс, когда остаток d будет меньше, чем делитель b . Число, взятое за с на этом шаге и будет неполным частным.
Разберем применение этого метода на примере.
Пример 4. Деление с остатком методом подбора
Разделим 267 на 21 .
a = 267 ; b = 21 . Подберем неполное частное.
Используем формулу d = a — b · c и будем последовательно перебирать c , придавая ему значения 0 , 1 , 2 , 3 и т.д.
Если с = 0 , имеем: d = a — b · c = 267 — 21 · 0 = 267 . Число 267 больше, чем 21 , поэтому продолжаем подстановку.
При с = 1 имеем: d = a — b · c = 267 — 21 · 1 = 246 . Т.к. 246 > 21 , снова повторяем процесс.
При с = 2 имеем: d = a — b · c = 267 — 21 · 2 = 267 — 42 = 225 ; 225 > 21 .
При с = 3 имеем: d = a — b · c = 267 — 21 · 3 = 267 — 63 = 204 ; 204 > 21 .
При с = 12 имеем: d = a — b · c = 267 — 21 · 12 = 267 — 252 = 15 ; 15
Алгоритм деления натуральных чисел с остатком
Когда рассмотренные выше методы подбора неполного частного и последовательного вычитания требуют слишком громоздких вычислений, для деления с остатком применяется следующий метод. Рассмотрим алгоритм деления натурального числа a на число b с остатком.
Вспомним, что в случае, когда a b .
Сформулируем три вопроса и ответим на них:
- Что там известно?
- Что нам нужно найти?
- Как мы будем это делать?
Изначально известными являются делимое и делитель: a и b .
Найти нужно неполное частное c и остаток d .
Приведем формулу, которая задает связь между делимым, делителем, неполным частным и остатком. a = b · c + d . Именно это соотношение мы и возьмем за основу алгоритма деления натуральных чисел с остатком. Делимое a нужно представить в виде суммы a = b · c + d , тогда мы найдем искомые величины.
Алгоритм деления, благодаря которому мы представим a в виде суммы a = b · c + d очень схож с алгоритмом деления натуральных чисел без остатка. Приведем ниже шаги алгоритма на примере деления числа 899 на 47 .
1. Первым делом смотрим на делимое и делитель. Выясняем и запоминаем, на сколько знаков число в записи делимого больше числа в делителе. В нашем конкретном примере в делимом три знака, а в делителе — два.
Запомним это число.
2. Справа в записи делителя допишем число нулей, определенное разницей между количеством знаков в делимом и делителе. В нашем случае нужно дописать один нуль. Если записанное число больше делимого, то нужно из запомненного в первом пункте числа вычесть единицу.
В нашем примере справа от 47 дописываем нуль. Так как 470
3. Справа к цифре 1 приписываем количество нулей, равное числу, определенному в предыдущем пункте. В нашем примере, приписывая к единице один нуль, получаем число 10 . В результате данного действия мы получили рабочую единицу разряда, с которым будем работать дальше.
4. Будем последовательно умножать делитель на 1 , 2 , 3 . . и т.д. единицы рабочего разряда, пока не получим число, которое больше или равно делимому.
Рабочий разряд в нашем примере — десятки. После умножения делителя на одну единицу рабочего разряда, получаем 470 .
470 899 .
Число, которое мы получили на предпоследнем шаге (470 = 47 · 10) является первым из искомых слагаемых.
5. Найдем разность между делимым и первым найденным слагаемым. Если полученное число больше делителя, то переходим к нахождению второго слагаемого.
Шаги 1 — 5 повторяем, однако в качестве делимого принимаем полученное здесь число. Если снова получаем число, большее, чем делитель, снова по-кругу повторяем пункты 1 — 5 , но уже с новым числом в качестве делимого. Продолжаем, пока полученное здесь число не будет меньше делителя. Переходим к завершающему этапу. Забегая вперед, скажем, что последнее полученное число и будет равно остатку.
Обратимся к примеру. 899 — 470 = 429 , 429 > 47 . Повторяем шаги 1 — 5 алгоритма с числом 429 , взятым в качестве делимого.
1. В записи числа 429 на один знак больше, чем в записи числа 47 . Запоминаем разницу — число 1 .
2. В записи делимого справа дописываем один нуль. Получаем число 470 . Так как 470 > 429 , из запомненного в предыдущем пункте числа 1 вычитаем 1 и получаем 1 — 1 = 0 . Запоминаем 0 .
3. Так как в предыдущем пункте мы получили число 0 и запомнили его, нам не нужно прибавлять ни одного нуля к единице справа. Таким образом, рабочим разрядом являются единицы
4. Последовательно умножим делитель 47 на 1 , 2 , 3 . . и т.д. Не будем приводить подробные выкладки, а обратим внимание на конечный результат: 47 · 9 = 423 429 . Таким образом, второе искомое слагаемое — 47 · 9 = 423 .
5. Разность между 429 и 423 равна числу 6 . Так как 6
6. Целью предыдущих действий было представление делимого в виде суммы нескольких слагаемых. Для нашего примера мы получили 899 = 470 + 423 + 6 . Вспоминаем, что 470 = 47 · 10 , 423 = 47 · 9 . Перепишем равенство:
899 = 47 · 10 + 47 · 9 + 6
Применим распределительное свойство умножения.
899 = 47 · 10 + 47 · 9 + 6 = 47 · (10 + 9) + 6
899 = 47 · 19 + 6 .
Таким образом, мы представили делимое в виде уже данной ранее формулы a = b · c + d .
Искомые неизвестные:неполное частное с = 19 , остаток d = 6 .
Безусловно, при решении практических примеров нет нужды расписывать все действия так подробно. Покажем это:
Пример 5. Деление натуральных чисел с остатком
Разделим числа 42252 и 68 .
Используем алгоритм. Первые пять шагов дают первое слагаемое — число 40800 = 68 · 600 .
Снова повторяем первые пять шагов алгоритма с числом 1452 = 42252 — 40800 и получаем второе слагаемое 1360 = 68 · 20
Третий раз проходим шаги аглоритма, но у же с новым числом 92 = 1452 — 1360 . Третье слагаемое равно 68 = 68 · 1 . Остаток равен 24 = 92 — 68 .
В результате получаем:
42252 = 40800 + 1360 + 68 + 24 = 68 · 600 + 68 · 20 + 68 · 1 + 24 = = 68 · (600 + 20 + 1) + 24 = 68 · 621 + 24
Неполное частное равно 621 , остаток равен 24 .
Деление натуральных чисел с остатком. Проверка результата
Деление натуральных чисел с остатком, особенно при больших числах, довольно трудоемкий и громоздкий процесс. Допустить ошибку в вычислениях может каждый. Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.
На первом этапе проверяем, не получился ли остаток больше делителя. Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.
Важно!
Остаток всегда меньше делителя!
На втором этапе проверяется справедливость равенства a = b · c + d . Если равенство после подстановки значений оказывается верным, то и деление было выполнено без ошибок.
Пример 6. Проверка результата деления натуральных чисел с остатком.
Проверим, верно ли, что 506 ÷ 28 = 17 (остаток 30) .
Сравниваем остаток и делитель: 30 > 28 .
Значит, деление выполнено неверно.
Пример 7. Проверка результата деления натуральных чисел с остатком.
Школьник разделил 121 на 13 и получил в результате неполное частное 9 с остатком 5 . Правильно ли он сделал?
Чтобы узнать это, сначала сравниваем остаток и делитель: 5
Первый пункт проверки пройден, переходим ко второму.
Запишем формулу a = b · c + d . a = 121 ; b = 13 ; c = 9 ; d = 5 .
Подставляем значения и сравниваем результаты
13 · 9 + 5 = 117 + 5 = 122 ; 121 ≠ 122
Значит, в вычисления школьника где-то закралась ошибка.
Пример 8. Проверка результата деления натуральных чисел с остатком.
Студент выполнял лабораторную работу по физике. В ходе выполнения ему понадобилось разделить 5998 на 111 . В результате у него получилось число 54 с остатком 4 . Все ли правильно посчитано?
Проверим! Остаток 4 меньше, чем делитель 111 , поэтому переходим ко второму этапу проверки.
Используем формулу a = b · c + d , где a = 5998 ; b = 111 ; c = 54 ; d = 4 .
После подстановки, имеем:
5998 = 111 · 54 + 4 = 5994 + 4 = 5998 .
Равенство корректно, а значит, и деление выполнено верно.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Деление с остатком проходят в третьем классе начальной школы. Тема довольно сложная для понимания ребенком и требует от него практически идеального знания таблицы умножения. Но все математические знания улучшаются с практикой, и поэтому, решая задания, ребенок с каждым примером будет выполнять его все быстрее и с меньшим количеством ошибок. Наш тренажер предполагает отработку навыка быстрого деления с остатком.
Как делить с остатком
1. Определяем, что деление с остатком (не делится нацело).
34:6 не решается без остатка
2. Подбираем ближайшее меньшее число к первому (делимому), которое делится на второе (делитель).
Ближайшее к 34 меньшее число, которое делится на 6 — это 30
3. Выполняем деление этого числа на делитель.
4. Пишем ответ (частное).
5. Чтобы найти остаток, от первого числа (делимого) вычитаем то число, которое подобрали. Записываем остаток. При делении с остатком остаток всегда должен получиться меньше делителя.
34-30=4 (ост. 4) 4
Проверяем деление так:
Умножаем ответ на делитель (второе число) и прибавляем к ответу остаток. Если получается делимое (первое число), то деление выполнил верно.
5*6+4=34 Деление выполнено верно.
Большие числа легко и просто делятся столбиком. При этом в уголке под делителем у нас запишется целое число, а в самом низу останется остаток, который меньше делителя.
Если при делении с остатком делимое меньше делителя, то их неполное частное равно нулю, а остаток равен делимому.
Например:
6: 10 = 0 (ост. 6)
14: 112 = 0 (ост. 14)
Скачать карточки-тренажеры на деление с остатком
Сохраните лист-карточку себе на компьютер и распечатайте на А4. Одного листа хватит на 5 дней отработки деления с остатком. В нем 5 столбиков с примерами. Вы можете даже разрезать лист на 5 частей. Над каждым столбиком — тучка, смайлик и солнышко, пусть ребенок оценит свою работу, когда закончит столбик.
Чем занимается на математике 3 класс? Деление с остатком, примеры и задачи — вот что изучается на уроках. О делении с остатком и алгоритме таких вычислений пойдет речь в статье.
Особенности
Рассмотрим темы, включенные в программу, которую изучает 3 класс. Деление с остатком выделено в специальный раздел математики. О чем идет речь? Если делимое не делится на делитель нацело, то остается остаток. Например, делим 21 на 6. Получается 3, но в остатке остается 3.
В случаях, когда во время деления натуральных чисел остаток равен нулю, говорят о том, что произведено деление нацело. Например, если 25 нужно поделить на 5, получается число 5. Остаток равен нулю.
Решение примеров
Для того чтобы произвести деление с остатком, используется определенная запись.
Приведем примеры по математике (3 класс). Деление с остатком в столбик можно не записывать. Достаточно записи в строчку: 13:4=3 (остаток 1) или 17:5=3 (остаток 2).
Разберем все подробнее. Например, при делении 17 на три получается целое число пять, кроме того, получается остаток два. Каков порядок решения такого примера на деление с остатком? Сначала необходимо отыскать максимальное число до 17, разделить которое можно без остатка на три. Самым большим будет 15.
Далее проводится деление 15 на число три, результатом действия будет цифра пять. Теперь вычитаем из делимого число, найденное нами, то есть из 17 отнимаем 15, получаем два. Обязательным действием является сверка делителя и остатка. После проверки обязательно записывается ответ совершенного действия. 17:3=15 (остаток 2).
Если остаток будет больше делителя, действие выполнено неправильно. Именно по такому алгоритму выполняет 3 класс деление с остатком. Примеры сначала разбирает учитель на доске, затем ребятам предлагается проверка знаний путем проведения самостоятельной работы.
Пример с умножением
Одна из самых трудных тем, с которой сталкивается 3 класс, — деление с остатком. Примеры могут быть сложными, особенно когда требуются дополнительные расчеты, записываемые в столбик.
Допустим, необходимо разделить число 190 на 27 с получением минимального остатка. Попробуем решить задачу, пользуясь умножением.
Подберем число, которое при умножении будет давать цифру, максимально приближенную к числу 190. Если умножить 27 на 6, получим цифру 162. Вычтем из 190 число 162, остаток будет 28. Он получился больше, чем исходный делитель. Следовательно, число шесть не подходит для нашего примера в качестве множителя. Продолжим решение примера, взяв для умножения число 7.
Умножая 27 на 7, мы получим произведение 189. Далее проведем проверку правильности решения, для этого вычтем из 190 полученный результат, то есть отнимем число 189. Остатком будет 1, что явно меньше 27. Именно так решаются сложные выражения в школе (3 класс, деление с остатком). Примеры всегда предусматривают запись ответа. Все математическое выражение можно оформить так: 190:27=7 (остаток 1). Подобные вычисления можно производить и в столбик.
Именно так осуществляет 3 класс деление с остатком. Примеры, приведенные выше, помогут разобраться в алгоритме решения подобных задач.
Заключение
Для того чтобы у учеников начальных классов были сформированы правильные вычислительные навыки, педагог во время проведения занятий по математике обязан уделять внимание пояснению алгоритма действий ребенка при решении заданий на деление с остатком.
По новым федеральным государственным образовательным стандартам особое внимание уделяется индивидуальному подходу к обучению. Учитель должен подбирать задания для каждого ребенка с учетом его индивидуальных способностей. На каждой ступени обучения правилам деления с остатком педагог должен осуществлять промежуточный контроль. Он позволяет ему выявлять основные проблемы, возникающие с усвоением материала у каждого ученика, своевременно проводить коррекцию знаний и навыков, устранять появляющиеся проблемы, получать желаемый результат.
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1
. Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2
. На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3
. Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4
. Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг
. Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг
. Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг
. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг
. Ставим точку под делителем.
5 шаг
. После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг
. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг
. Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг
. Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг
*. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг
Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3)
(4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.
После прохождения курса ребенок сможет:
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Как разделить в Excel и обработать # DIV / 0! ошибка
В руководстве показано, как использовать формулу деления в Excel для деления чисел, ячеек или целых столбцов и как обрабатывать ошибки Div / 0.
Как и другие основные математические операции, Microsoft Excel предоставляет несколько способов деления чисел и ячеек. Какой из них использовать, зависит от ваших личных предпочтений и конкретной задачи, которую вам нужно решить. В этом руководстве вы найдете несколько хороших примеров использования формулы деления в Excel, которые охватывают наиболее распространенные сценарии.
Символ разделения в Excel
Обычный способ сделать деление — использовать знак деления. В математике операция деления обозначается символом обелуса (÷). В Microsoft Excel символ разделения представляет собой косую черту (/).
При таком подходе вы просто пишете выражение типа = a / b без пробелов, где:
- a — это дивиденд — число, которое вы хотите разделить, и
- b — делитель — число, на которое делится дивиденд.
Как делить числа в Excel
Чтобы разделить два числа в Excel, вы вводите знак равенства (=) в ячейку, затем вводите число, которое нужно разделить, затем косую черту, затем число, на которое нужно делить, и нажмите клавишу Enter, чтобы вычислить формула.
Например, чтобы разделить 10 на 5, введите в ячейку следующее выражение: = 10/5
На снимке экрана ниже показано еще несколько примеров простой формулы деления в Excel:
Когда формула выполняет более одной арифметической операции, важно помнить о порядке вычислений в Excel (PEMDAS): сначала скобки, затем возведение в степень (возведение в степень), затем умножение или деление в зависимости от того, что наступит раньше, а затем сложение или вычитание в зависимости от того, что наступит раньше.
Как разделить ячейку в Excel
Чтобы разделить две ячейки в Excel, используйте символ разделения точно так же, как показано в приведенных выше примерах, но вместо чисел укажите ссылки на ячейки.
Например:
- Чтобы разделить ячейку A2 на 5:
= A2 / 5 - Чтобы разделить ячейку A2 на ячейку B2:
= A2 / B2 - Чтобы последовательно разделить несколько ячеек , введите ссылки на ячейки, разделенные символом деления. Например, чтобы разделить число в A2 на число в B2, а затем разделить результат на число в C2, используйте эту формулу:
= A2 / B2 / C2
Функция деления в Excel (QUOTIENT)
Скажу прямо: в Excel нет функции разделения.Всякий раз, когда вы хотите разделить одно число на другое, используйте символ деления, как объяснено в приведенных выше примерах.
Однако, если вы хотите вернуть только часть деления , целое число и отбросить остаток, используйте функцию QUOTIENT:
ЧИСЛО (числитель, знаменатель)
Где:
- Числитель (обязательно) — делимое, т.е. число, которое нужно разделить.
- Знаменатель (обязательный) — делитель, т.е.е. число, на которое нужно разделить.
Когда два числа делят поровну без остатка , символ деления и формула QUOTIENT возвращают одинаковый результат. Например, = 10/5 и = QUOTIENT (10, 5) возвращают 2.
Когда после деления остается остаток , знак деления возвращает десятичное число, а функция ЧИСЛО возвращает только целую часть. Например, = 5/4, возвращает 1,25, а = QUOTIENT (5,4) возвращает 1.
3 вещи, которые вы должны знать о функции QUOTIENT
Как бы просто не выглядело, функция Excel QUOTIENT все же имеет несколько предостережений, о которых вы должны знать:
- Аргументы числителя и знаменателя должны быть представлены в виде чисел, ссылок на ячейки, содержащие числа, или других функций, возвращающих числа.
- Если какой-либо из аргументов не является числовым, формула QUOTIENT возвращает #VALUE! ошибка.
- Если знаменатель равен 0, QUOTIENT возвращает ошибку деления на ноль (# DIV / 0!).
Как разделить столбцы в Excel
Разделить столбцы в Excel тоже просто. Это можно сделать, скопировав обычную формулу деления вниз по столбцу или используя формулу массива. Зачем использовать формулу массива для такой тривиальной задачи? Вы узнаете причину в мгновение ока 🙂
Как разделить два столбца в Excel, скопировав формулу
Чтобы разделить столбцы в Excel, выполните следующие действия:
- Разделите две ячейки в самой верхней строке, например:
= A2 / B2 - Вставьте формулу в первую ячейку (скажем, C2) и дважды щелкните маленький зеленый квадрат в правом нижнем углу ячейки, чтобы скопировать формулу вниз по столбцу.Сделанный!
Поскольку мы используем относительные ссылки на ячейки (без знака $), наша формула деления будет изменяться в зависимости от относительного положения ячейки, в которую она копируется:
Наконечник. Аналогичным образом можно разделить две строки в Excel. Например, чтобы разделить значения в строке 1 на значения в строке 2, вы помещаете = A1 / A2 в ячейку A3, а затем копируете формулу вправо в необходимое количество ячеек.
Как разделить один столбец на другой с помощью формулы массива
В ситуациях, когда вы хотите предотвратить случайное удаление или изменение формулы в отдельных ячейках, вставьте формулу массива во весь диапазон.
Например, чтобы разделить значения в ячейках A2: A8 на значения в B2: B8 построчно, используйте следующую формулу: = A2: A8 / B2: B8
Чтобы правильно вставить формулу массива, выполните следующие действия:
- Выберите весь диапазон, в который вы хотите ввести формулу (C2: C8 в этом примере).
- Введите формулу в строке формул и нажмите Ctrl + Shift + Enter, чтобы завершить ее. Как только вы это сделаете, Excel заключит формулу в {фигурные скобки}, указывая, что это формула массива.
В результате вы получите числа в столбце A, разделенные на числа в столбце B одним махом. Если кто-то попытается отредактировать вашу формулу в отдельной ячейке, Excel покажет предупреждение о том, что часть массива не может быть изменена.
Чтобы удалить или изменить формулу , вам нужно сначала выбрать весь диапазон, а затем внести изменения. Чтобы расширить формулу на новые строки, выберите весь диапазон, включая новые строки, измените ссылки на ячейки в строке формул, чтобы разместить новые ячейки, а затем нажмите Ctrl + Shift + Enter, чтобы обновить формулу.
Как разделить столбец на число в Excel
В зависимости от того, хотите ли вы, чтобы выходные данные были формулами или значениями, вы можете разделить числовой столбец на постоянное число с помощью формулы деления или функции Специальная вставка .
Разделите столбец на номер по формуле
Как вы уже знаете, самый быстрый способ выполнить деление в Excel — использовать символ разделения. Итак, чтобы разделить каждое число в данном столбце на одно и то же число, вы помещаете обычную формулу деления в первую ячейку, а затем копируете формулу вниз по столбцу.Вот и все!
Например, чтобы разделить значения в столбце A на число 5, вставьте следующую формулу в A2, а затем скопируйте ее в любое количество ячеек: = A2 / 5
Как объяснено в приведенном выше примере, использование относительной ссылки на ячейку (A2) обеспечивает правильную настройку формулы для каждой строки. То есть формула в B3 становится = A3 / 5 , формула в B4 становится = A4 / 5 и т. Д.
Вместо того, чтобы указывать делитель непосредственно в формуле, вы можете ввести его в какую-либо ячейку, например, D2, и разделить на эту ячейку.В этом случае важно заблокировать ссылку на ячейку знаком доллара (например, $ D $ 2), сделав ее абсолютной ссылкой, поскольку эта ссылка должна оставаться постоянной независимо от того, куда копируется формула.
Как показано на скриншоте ниже, формула = A2 / $ D $ 2 возвращает точно такие же результаты, как = A2 / 5 .
Разделите столбец на такое же число с помощью специальной вставки
Если вы хотите, чтобы результаты были значениями, а не формулами, вы можете выполнить деление обычным способом, а затем заменить формулы на значения.Или вы можете добиться того же результата быстрее с помощью опции Специальная вставка > Divide .
- Если вы не хотите переопределять исходные числа, скопируйте их в столбец, в котором вы хотите получить результаты. В этом примере мы копируем числа из столбца A в столбец B.
- Поместите делитель в какую-нибудь ячейку, скажем D2, как показано на скриншоте ниже.
- Выберите ячейку делителя (D5) и нажмите Ctrl + C, чтобы скопировать ее в буфер обмена.
- Выберите ячейки, которые хотите умножить (B2: B8).
- Нажмите Ctrl + Alt + V, затем I, что является ярлыком для Специальная вставка > Divide , и нажмите клавишу Enter.
Либо щелкните правой кнопкой мыши выбранные числа, выберите Специальная вставка… из контекстного меню, затем выберите Разделить в разделе Операция и нажмите ОК.
В любом случае каждое из выбранных чисел в столбце A будет разделено на число в D5, и результаты будут возвращены в виде значений, а не формул:
Как разделить на процент в Excel
Поскольку проценты являются частями более крупного целого, некоторые люди думают, что для вычисления процента от данного числа вы должны разделить это число на проценты.Но это же заблуждение! Чтобы найти проценты, нужно умножать, а не делить. Например, чтобы найти 20% от 80, вы умножаете 80 на 20% и в результате получаете 16: 80 * 20% = 16 или 80 * 0,2 = 16.
В каких ситуациях вы делите число на процент? Например, чтобы найти X, если определенный процент от X равен Y. Чтобы прояснить ситуацию, давайте решим эту задачу: 100 — это 25% от какого числа?
Чтобы получить ответ, преобразуйте задачу в это простое уравнение:
X = Y / P%
Если Y равно 100, а P равно 25%, формула принимает следующий вид: = 100/25%
Поскольку 25% — это 25 частей от сотни, вы можете смело заменять процентное значение десятичным числом: = 100/0.25
Как показано на скриншоте ниже, результат обеих формул будет 400:
Дополнительные примеры процентных формул см. В разделе Как рассчитать проценты в Excel.
Ошибка Excel DIV / 0
Деление на ноль — это операция, для которой нет ответа, поэтому она запрещена. Всякий раз, когда вы пытаетесь разделить число на 0 или на пустую ячейку в Excel, вы получите ошибку деления на ноль (# DIV / 0!). В некоторых ситуациях эта индикация ошибки может быть полезной, предупреждая вас о возможных сбоях в вашем наборе данных.
В других сценариях формулы могут просто ждать ввода, поэтому вы можете заменить обозначения ошибок Excel Div 0 пустыми ячейками или своим собственным сообщением. Это можно сделать с помощью формулы ЕСЛИ или функции ЕСЛИОШИБКА.
Подавить ошибку # DIV / 0 с помощью IFERROR
Самый простой способ справиться с # DIV / 0! ошибка в Excel заключается в том, чтобы заключить формулу деления в функцию ЕСЛИОШИБКА следующим образом:
= ЕСЛИ ОШИБКА (A2 / B2; "")
Формула проверяет результат деления, и, если она оценивается как ошибка, возвращает пустую строку («»), иначе результат деления.
Обратите внимание на два рабочих листа ниже. Какой из них эстетичнее?
Примечание . Функция ЕСЛИОШИБКА в Excel маскирует не только # ДЕЛ / 0! ошибок, но все другие типы ошибок, такие как # Н / Д, # ИМЯ ?, # ССЫЛКА !, # ЗНАЧЕНИЕ !, и т. д. Если вы хотите подавить конкретные ошибки DIV / 0, используйте формулу ЕСЛИ, как показано в следующий пример.
Обработка ошибки Excel DIV / 0 с помощью формулы IF
Чтобы замаскировать только ошибки Div / 0 в Excel, используйте формулу ЕСЛИ, которая проверяет, равен ли делитель (или не равен) нулю.
Например:
= ЕСЛИ (B2 = 0, "", A2 / B2)
или
= ЕСЛИ (B2 <> 0, A2 / B2, "")
Если делителем является любое число, отличное от нуля, формулы делят ячейку A2 на B2. Если B2 равно 0 или пусто, формулы ничего не возвращают (пустая строка).
Вместо пустой ячейки вы также можете отобразить собственное сообщение, подобное этому:
= ЕСЛИ (B2 <> 0, A2 / B2, «Ошибка в вычислении»)
Как разделить с помощью Ultimate Suite для Excel
Если вы делаете первые шаги в Excel и еще не чувствуете себя комфортно с формулами, вы можете выполнить деление с помощью мыши.Все, что нужно, — это установить наш Ultimate Suite в ваш Excel.
В одном из примеров, обсужденных ранее, мы разделили столбец на число с помощью специальной вставки Excel. Это потребовало большого количества движений мыши и двух ярлыков. Теперь позвольте мне показать вам более короткий способ сделать то же самое.
- Скопируйте числа, которые вы хотите разделить, в столбец «Результаты», чтобы предотвратить замену исходных чисел.
- Выберите скопированные значения (C2: C5 на скриншоте ниже).
- Перейдите на вкладку инструментов Ablebits> Группа Calculate и выполните следующие действия:
- Выберите знак разделения (/) в поле Operation .
- Введите число для деления в поле Значение .
- Нажмите кнопку Рассчитать .
Готово! Весь столбец делится на указанное число в мгновение ока:
Как и в случае с Excel Paste Special, результатом деления будет значений , а не формул. Таким образом, вы можете безопасно переместить или скопировать вывод в другое место, не беспокоясь об обновлении ссылок на формулы. Вы даже можете переместить или удалить исходные числа, и ваши рассчитанные числа останутся в целости и сохранности.
Вот как вы делите в Excel с помощью формул или инструментов вычислений. Если вам интересно попробовать эту и многие другие полезные функции, включенные в Ultimate Suite for Excel, вы можете загрузить 14-дневную пробную версию.
Чтобы ближе познакомиться с формулами, обсуждаемыми в этом руководстве, загрузите наши примеры формул Excel Division.
Благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Вас также может заинтересовать
Как разделить в Google Таблицах (числа, ячейки или столбцы)
Google Таблицы теперь являются популярным инструментом для работы с электронными таблицами для большинства людей.Это бесплатное приложение, с которым очень легко сотрудничать, и в нем есть несколько замечательных функций и возможностей.
Даже если вы хотите сделать что-то столь же простое, как хранение данных или простые вычисления, такие как умножение или деление, вы можете легко сделать это в Google Таблицах.
В этом руководстве. Я покажу вам несколько способов делить числа в Google Таблицах.
Вы можете легко разделить числа в Google Таблицах, используя встроенную формулу или оператор деления (как мы увидим на примерах).
Итак, приступим!
Разделите две ячейки в Google Таблицах
Если вы хотите разделить два числа в Google Таблицах (или две ячейки с числами), то есть несколько способов сделать это в Google Таблицах.
Использование функции РАЗДЕЛИТЬ
Деление в Google Таблицах — настолько обычная задача, что есть встроенная функция, которая позволяет вам разделить два числа или числа, которые находятся в двух ячейках.
Это функция РАЗДЕЛИТЬ (без оценок для отгадывания)!
Предположим, вы хотите разделить значение в ячейке A1 на значение в ячейке B1.
Для этого можно использовать приведенную ниже формулу РАЗДЕЛЕНИЯ:
= РАЗДЕЛИТЬ (A1, B1)
В приведенной выше формуле первым аргументом является делимое (число, которое нужно разделить) и делитель (число, на которое нужно разделить)
Я использовал ссылки на ячейки в приведенном выше примере, но вы также можете жестко закодировать значения в формуле. Например, вы также можете использовать следующую формулу:
= РАЗДЕЛЕНИЕ (1200,15)
Преимущество использования ссылок на ячейки заключается в том, что результат формулы становится динамическим.Это означает, что если я изменю значение в ячейке A1 или B1, формула обновится автоматически.
Также помните, что делитель не может быть 0. Если ваш делитель равен 0, вы получите ошибку деления — # DIV / 0!
Использование оператора DIVIDE
Еще один способ быстро разделить числа в Google Таблицах — использовать оператор деления — косая черта (/)
Предположим, у вас есть данные, как показано ниже, и вы хотите разделить значение в ячейке A1 на значение в ячейке B1.
Для этого можно использовать следующее уравнение:
= A1 / B1
И если вы хотите быстро разделить числа (вместо ссылок на ячейки), вы также можете это сделать (как показано в формуле ниже):
= 1200/15
Также читайте: Как умножить в Google Таблицах
Порядок приоритета при делении клеток
При использовании арифметических операторов (таких как деление или умножение) в Google Таблицах важно знать порядок приоритета.
Позвольте мне попытаться объяснить это на примере.
Предположим, я использую следующую формулу:
= 1200/15 + 15
Вы можете угадать, что будет в результате?
Было бы 95.
Это происходит из-за того, что в Google Таблицах существует порядок приоритета, в котором деление выполняется перед добавлением. Следовательно, он сначала делит 1200 на 15, где результат равен 80. Затем он добавляет 15 к этому результату, что дает вам общий результат как 95.
Теперь это несложно понять на нашем простом примере, но это может привести к проблемам при работе с большими сложными формулами.
В таких случаях лучше не беспокоиться о порядке приоритета, оставив вычисления в скобках (скобках).
Например, если вы хотите сначала выполнить сложение, а затем деление, вы можете использовать следующую формулу:
= 1200 / (15 + 15)
Это даст вам результат как 40 (= 1200/30)
Разделение двух столбцов в Google Таблицах
В реальных сценариях вам не нужно открывать Google Таблицы для простого разделения.Вы можете легко сделать это с помощью калькулятора на своем смартфоне или с помощью простого поиска в Google.
Google Таблицы можно использовать для быстрого разделения чисел на столбцы и получения результата для сотен ячеек за секунду.
Например, предположим, что у вас есть набор данных, показанный ниже, и вы хотите вычислить деление, когда значение в столбце A делится на соответствующую ячейку в столбце B
Ниже приведена формула, которая сделает это:
= ArrayFormula (A1: A20 / B1: B20)
Так как это формула массива, вам нужно только ввести эту формулу только в ячейку C1, и она даст вам результат, как показано выше.
Также нельзя удалить или отредактировать часть массива. Однако вы можете удалить весь массив, удалив содержимое ячейки C1.
Разделить без остатка в Google Таблицах
Допустим, у вас есть набор данных, показанный ниже, и вы хотите разделить значение в столбце A на значение в столбце B.
Если вы сделаете это, как показано в предыдущем разделе, вы получите целую часть, а также десятичную часть.
Если вам не нужен остаток при разделении этих значений (где остаток является десятичной частью), вы можете использовать следующую формулу:
= ArrayFormula (INT (A1: A20 / B1: B20))
В приведенной выше формуле используется та же формула деления, но она заключена в функцию INT, которая возвращает только целую часть результата, а не десятичную часть.
Итак, вот несколько способов разделения в Google Таблицах. В зависимости от того, хотите ли вы разделить числа, ячейки или столбцы, вы можете использовать функцию РАЗДЕЛЕНИЕ или оператор деления.
Надеюсь, вы нашли этот учебник по Google Таблицам полезным!
Другие руководства по Google Таблицам, которые могут оказаться полезными:
Таблица распределения частот
: примеры, как сделать один
Содержание (щелкните, чтобы перейти к этому разделу):
См. Также: Таблица распределения частот в Excel
Посмотрите видео с примером того, как составить таблицу распределения частот с классами:
Не можете посмотреть видео? Кликните сюда.
Частота сообщает вам , как часто что-то происходило . Частота наблюдения говорит вам, сколько раз наблюдение встречается в данных. Например, в следующем списке чисел частота числа 9 равна 5 (потому что оно встречается 5 раз):
1, 2, 3, 4, 6, 9, 9, 8, 5, 1, 1, 9, 9, 0, 6, 9.
Таблицы могут отображать либо категориальные переменные (иногда называемые качественными переменными), либо количественные переменные (иногда называемые числовыми переменными).Вы можете рассматривать категориальные переменные как категории (например, цвет глаз или марку корма для собак), а количественные переменные как числа.
Если вы не совсем уверены в разнице, см. Качественный или количественный? Как сказать.
В следующей таблице показано, какие методы планирования семьи использовали подростки в Квененге, Западная Ботсвана. Левый столбец показывает категориальную переменную (Метод), а правый столбец — частоту — количество подростков, использующих этот конкретный метод (изображение любезно предоставлено KSU).
Таблица распределения частот, показывающая категориальные переменные.
Таблицы частотного распределения
предоставляют вам снимок данных, чтобы вы могли найти закономерности. Беглый взгляд на приведенную выше таблицу частотного распределения показывает, что большинство подростков вообще не используют противозачаточные средства.
Вернуться к началу
Пример 1
Счетные метки часто используются для составления таблицы распределения частот. Например, предположим, что вы обследуете несколько домашних хозяйств и выясняете, сколько у них домашних животных.Результаты: 3, 0, 1, 4, 4, 1, 2, 0, 2, 2, 0, 2, 0, 1, 3, 1, 2, 1, 1, 3. Глядя на эту цепочку чисел, вы непонятно. глаз; таблица частотного распределения упростит понимание данных.
ступеней
Чтобы составить таблицу частотного распределения, сначала впишите в один столбец категории (количество домашних животных):
Затем подсчитывает числа в каждой категории (из результатов выше). Например, число ноль появляется в списке четыре раза, поэтому поставьте четыре метки счета «||||»:
Наконец, подсчитайте метки и запишите частоту в последний столбец.Частота — это всего лишь сумма. У вас есть четыре счетных метки для «0», поэтому поставьте 4 в последний столбец:
Вернуться к началу
Как нарисовать таблицу распределения частот (немного более сложный пример)
Таблица распределения частот — это один из способов упорядочить данные, чтобы они имели больше смысла. Например, предположим, что у вас есть список показателей IQ для одаренного класса в конкретной начальной школе. Оценка IQ составляет: 118, 123, 124, 125, 127, 128, 129, 130, 130, 133, 136, 138, 141, 142, 149, 150, 154.Этот список мало что вам скажет. Вы можете нарисовать таблицу распределения частот , которая даст лучшее представление о ваших данных, чем простой список.
Как нарисовать таблицу распределения частот: шаги.
Нужна помощь с домашним заданием? Посетите нашу страницу обучения!
Часть 1: Выбор классов
Шаг 1: Определите, сколько классов (категорий) вам нужно. Нет никаких жестких правил о том, сколько классов выбрать, но есть несколько общих рекомендаций:
- Выберите от 5 до 20 классов.Для приведенного выше списка IQ мы выбрали 5 классов.
- Убедитесь, что у вас есть несколько предметов в каждой категории. Например, если у вас 20 предметов, выберите 5 классов (4 предмета на категорию), а не 20 классов (что даст вам только 1 предмет на категорию).
Примечание : Существует более математический способ выбора классов. Формула: журнал (наблюдения) \ журнал (2). Вы должны округлить ответ до следующего целого числа. Например, log17 \ log2 = 4.1 будет округлено до 5. (Спасибо Айману Масри за этот совет).
Часть 2: Сортировка данных
Шаг 2: Вычтите минимальное значение данных из максимального значения данных. Например, наш список IQ выше имел минимальное значение 118 и максимальное значение 154, поэтому:
154 — 118 = 36
Шаг 3: Разделите свой ответ на шаге 2 на количество классов, которые вы выбрали на шаге 1.
36/5 = 7,2
Шаг 4: Округлите число из шага 3 до целого числа, чтобы получить ширину класса.Округляя вверх, 7,2 становится 8 .
Шаг 5: Запишите наименьшее значение для первого минимального значения данных:
Наименьшее значение — 118
Шаг 6: Добавьте ширину класса из Шага 4 в Шаг 5, чтобы получить следующий нижний предел класса:
118 + 8 = 126
Шаг 7: Повторите шаг 6 для других минимальных значений данных (другими словами, продолжайте добавлять ширину вашего класса к минимальным значениям данных), пока вы не создадите количество классов, которое вы выбрали на шаге 1.Мы выбрали 5 классов, поэтому наши 5 минимальных значений данных:
118
126 (118 + 8)
134 (126 + 8)
142 (134 + 8)
150 (142 + 8)
Шаг 8: Запишите пределы верхнего класса. Это самые высокие значения, которые могут быть в категории, поэтому в большинстве случаев вы можете вычесть 1 из ширины класса и добавить его к минимальному значению данных. Например:
118 + (8 — 1) = 125
118 — 125
126 — 133
134 — 141
142 — 149
150 — 157
3.Завершение стола
Шаг 9: Добавьте второй столбец для количества элементов в каждом классе и пометьте столбцы соответствующими заголовками:
| IQ | Число |
|---|---|
| 118-125 | |
| 126-133 | |
| 134-141 | |
| 142-149 | |
| 150-157 |
Шаг 10: Подсчитайте количество предметов в каждом классе и поместите общее количество во второй столбец.Список значений IQ: 118, 123, 124, 125, 127, 128, 129, 130, 130, 133, 136, 138, 141, 142, 149, 150, 154.
| IQ | Число |
|---|---|
| 118-125 | 4 |
| 126-133 | 6 |
| 134-141 | 3 |
| 142-149 | 2 |
| 150-157 | 2 |
Вот как легко составить таблицу распределения частот!
Понравилось объяснение? Посмотрите нашу книгу с практическими рекомендациями по статистике с сотнями других пошаговых решений, подобных этому!
Совет : Если вы работаете с большими числами (например, сотнями или тысячами), округлите шаг 4 до большого целого числа, которое легко преобразовать в классы, например 100, 1000 или 10 000.То же самое и с очень маленькими числами — вы можете округлить до 0,1, 0,001 или аналогичного деления.
В начало
Список литературы
Гоник Л. (1993). Мультяшный справочник по статистике. HarperPerennial.
————————————————— —————————-
Нужна помощь с домашним заданием или контрольным вопросом? С помощью Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Узнайте, как исправить итоги и промежуточные итоги в DAX
Узнайте, как исправить итоги и промежуточные итоги в DAX для PowerBI и Power Pivot
Проблема неверных итогов и промежуточных итогов в DAX — распространенная проблема для пользователей Power BI и Power Pivot. Но эти неверные итоги не ошибочны. Если у вас есть неправильные итоговые значения, это не потому, что DAX рассчитал их неправильно. DAX просто делает то, что вы ему приказываете.
Следовательно, получение правильных или неправильных итогов зависит от понимания того, как работает ваш расчет DAX.После того, как вы выяснили, как ведутся вычисления, вы можете решить, как относиться к итоговым значениям.
В этой статье мы рассмотрим причины, по которым итоги и промежуточные итоги не соответствуют вашим ожиданиям, а затем рассмотрим решения этой проблемы и убедимся, что отображаемые вами итоги соответствуют вашим ожиданиям.
Надеюсь, после этого у вас больше не будет неправильных или неправильных итогов в ваших расчетах DAX !!!
Содержание — Итоги и промежуточные итоги в DAX
Проверьте свои итоги — как исправить неверные итоги в DAX для Power BI и Power Pivot
Контекст фильтра
Понимание контекста фильтра в Dax — Пример 1
Контекст фильтра и итог Строка
Решение
Понимание контекста фильтра в Dax — Пример 2
Удаление итогов и промежуточных итогов
Шаг 1. Создайте логический тест, чтобы увидеть, является ли строка итоговым или промежуточным итогом
Шаг 2. Используйте логический тест в IF оператор для применения значений к строкам, не являющимся итоговыми.
Шаг 3 — Примените оператор IF к нашему исходному расчету.
Шаг 4 — Тестирование итогов удаленных таблиц.
Исправление итогов и промежуточных итогов в DAX для PowerBI и Power Pivot.
HASONEVALUE
SUMMARIZE для исправления итогов в DAX.
Контекст фильтра
Чтобы понять, как DAX вычисляет значения, итоги и промежуточные итоги, необходимо понимать контекст фильтра. Вы можете применять фильтры разными способами.
И строки, и столбцы в сводной таблице или диаграмме содержат фильтры.На изображении ниже Год и Категория продукта были добавлены в сводную таблицу в качестве фильтров. Эти фильтры вычисляются с помощью оператора AND. Например, значение Dolls в 2018 содержит фильтр, который на английском языке говорит Filter for 2018 AND также фильтрует Dolls.
Любой фильтр, срезы и временные шкалы, которые вы включили в сводную таблицу или диаграмму, также предоставляют контекст фильтра. Опять же, эти фильтры основаны на использовании оператора AND.
В оставшейся части этой статьи мы рассмотрим несколько примеров контекста фильтров и того, как они могут создавать неверные итоги или, в действительности, итоги, которых вы не ожидаете.А потом мы посмотрим, как решить эти проблемы.
Наша модель очень простая. У нас есть 3 стола. Product_sales — это таблица фактов, а продукты и данные — это таблицы наших измерений.
Понимание контекста фильтра в Dax — пример 1
Наша таблица Product_sales содержит столбец для количества проданных единиц. Мы хотим узнать, сколько заказов у единиц от 100 и более. В нашей таблице продаж продуктов мы создали следующие два показателя.
Total Units: = sum (product_sales [Units Sold])
Large Orders = IF ([Total Units]> = 100,1)
Используя продукт в качестве фильтра в строке, мы можем поместить эти две меры в таблицу.
Первая мера, Total Units выглядит нормально. Однако DAX рассчитывает, что у каждого продукта будет только одна крупная продажа, и общее количество отображается как 1. Если у каждого продукта есть 1 большая продажа и есть 6 продуктов, то не должно ли общее количество быть 6? И это при условии, что у каждого продукта есть только одна крупная распродажа. Я знаю из данных; это не тот случай.
Прежде чем мы перейдем к корректировке итогов и других значений в этом отчете, давайте разберемся, что происходит, с помощью фильтров.
Когда мы создаем меру, = IF ([Total Units]> = 100,1), мы создаем ее без какого-либо фильтра. Внешних фильтров (строк, столбцов, срезов) нет, пока мы не добавим меру в диаграмму или таблицу.
Следовательно, прежде чем мы будем использовать фильтры для этой меры, эта мера берет значение из нашей общей меры единиц и проверяет, больше ли оно 100, а если больше 100, возвращает 1.
Когда мы добавляем это Measure в нашу таблицу, которая содержит продукты в качестве фильтра, DAX фильтрует таблицу по каждому продукту.Первая строка фильтруется только для велосипедов. Затем DAX фильтрует таблицу, выбирая только велосипеды, а затем вычисляет сумму единиц, проданных только в этом разделе фильтра. В данном случае значение 55 479. Затем оператор IF спрашивает, больше ли это значение или равно 100. Поскольку это значение больше 100, возвращается 1 как количество крупных продаж велосипедов.
DAX переходит во вторую строку таблицы, в которой есть фильтр для Doll. Такой же расчет выполняется для этой строки таблицы.DAX суммирует общее количество проданных единиц, давая 58361, а затем проверяет, больше ли это значение или равно 100, и возвращает 1, потому что это значение больше 100. Такой же расчет применяется для каждой строки таблицы. Это контекст фильтра в действии.
Контекст фильтра и строка итогов
Когда мы переходим к строке итогов, фильтр по продукту отсутствует. Итак, DAX берет общее количество проданных единиц, 351341, и проверяет, больше ли оно или равно 100, и пока DAX также возвращает 1 для итогов.
Это очень простой пример того, как работает контекст фильтра, и, как вы можете видеть, он может иметь большое влияние на отображаемые значения, и вы не всегда получаете ожидаемые результаты.
Решение
Чтобы решить эту проблему, мы можем использовать функцию СУММХ.
= sumx (product_sales, if ([Total Units]> = 100,1))
Эта функция говорит, что нужно выполнить итерацию по каждой строке таблицы продаж продуктов и проверить, не превышает ли проданных единиц больше 100. Если продано единиц> = 100, присвойте ему значение 1.Затем, когда итерация по таблице будет завершена, возьмите все эти единицы и просуммируйте их.
Использование этой меры в нашей таблице вернет нам правильные значения.
Как уже упоминалось, это очень простой пример, объясняющий, как работает контекст фильтра. Добавление SUMX или другого итератора — не всегда ответ.
Понимание контекста фильтра в Dax — пример 2
Взгляните на эту простую сводную таблицу.
Эта сводная таблица содержит два показателя.Первый показатель — это общий объем продаж.
Total Sales = sum (product_sales [Sales value])
Эта мера берет столбец значения продаж в таблице продаж и суммирует значения.
Вторая мера — Продажи за день.
= Round ([общие продажи] / COUNTROWS (DISTINCT (product_sales [Date])), 0)
Где:
COUNTROWS (DISTINCT (product_sales [Date]) — вернет количество дней, в течение которых были фактические продажи.
Total Затем продажи делятся на количество дней с продажами, и функция ОКРУГЛ используется, поскольку мы смотрим на денежные значения.
Основывается на количестве дней продаж, а не на количестве дней в году. Я уверен, вам интересно, почему это может быть рассчитано таким образом. Что ж, представьте, что продукт был запущен в декабре и доступен только 31 день. Из этих 31 дня продажи были осуществлены по 28 из них. Как вы думаете, было бы правильно рассчитать средние продажи, разделив общий объем продаж на 365 или 28 дней? Это зависит от ваших потребностей. В этом примере мы хотим получить продажи только за день, исходя из количества дней, в которые есть фактические продажи.
Проблема не в том, как подсчитываются дни, проблема заключается в промежуточных итогах и итогах. Если сложить наши значения на 2018 год, мы получим 43 154. Не 42 585, как показано.
Так почему же это происходит? Что ж, опять же, дело в контексте фильтра.
Мы создадим меру для отображения дней продаж и поместим ее в нашу таблицу, чтобы показать вам, что происходит. Мера:
= COUNTROWS (DISTINCT (product_sales [Date]))
Теперь давайте рассмотрим цифры для Bike за 2018 год.Таблица фильтруется как по году (2018), так и по продукту (Велосипед). Затем проводится четкий подсчет дат. В этом случае с продажами 355 дней.
В нашем дневном объеме продаж велосипедов в 2018 году общий объем продаж 5 208 470 делится на 355, чтобы получить наши продажи за день.
Однако мы можем видеть, что количество дней с продажами для каждого продукта разное, поскольку оно рассчитывается на основе контекста фильтра как продукта, так и года.
Теперь посмотрим на промежуточные итоги.По всем продуктам продажи происходят каждый день в году, поэтому отдельное количество дней составляет 365. Наша общая стоимость продаж за 2018 год делится на 365. Поскольку не все наши продукты делятся на 365, промежуточный итог невозможно. стоимость может быть такой же, как сумма продаж за день.
При общей стоимости нет фильтра по годам или продуктам. Таким образом, общее количество отдельных дней составляет 730, и затем общие продажи без фильтра делятся на это значение.
Удаление итогов и промежуточных итогов
Если итоги и промежуточные итоги неверны, у нас есть возможность удалить их и оставьте поле пустым или создайте меру для вычисления ожидаемых значений.Давайте сначала рассмотрим удаление итогов.
Чтобы удалить итоги, нам нужно установить, применяется ли контекст фильтра. Мы можем сделать это с помощью выражений, которые возвращают утверждение true / false. Комбинируя эти истинно ложные выражения с оператором IF, мы можем определить, что возвращается, когда применяется контекст фильтра, и что возвращать, когда контекст фильтра не применяется.
Шаг 1. Создайте логический тест, чтобы узнать, является ли строка итоговой или промежуточной.
Каждая из следующих функций вернет истину / ложь.HASONEVALUE, ISFILTERED и HASONEFILTER.
Нам нужно проверить, есть ли фильтр по продукту, так как это поле продукта используется в таблице.
= HASONEVALUE (Продукты [Продукт]) — проверяет, имеет ли столбец продуктов значение. В случае общих и промежуточных итогов фильтр по продуктам отсутствует, поэтому возвращается false. Фильтр стоит на год.
= HASONEFILTER (Продукты [Продукт]) — проверяет, есть ли в столбце продуктов один фильтр.В случае общих и промежуточных итогов фильтр по продуктам отсутствует, поэтому возвращается false. Фильтр стоит на год.
= ISFILTERD (Продукты [Продукт]) — проверяет, есть ли в столбце продуктов какой-либо фильтр в столбце продуктов. В случае общих и промежуточных итогов фильтр по продуктам отсутствует, поэтому возвращается false.
Шаг 2. Используйте логический тест в операторе IF для применения значений к строкам, не являющимся итоговыми.
Используя операторы IF, мы теперь можем заменить их true выражением «Количество дней с продажами».
= if (HASONEVALUE (Продукты [Продукт]), [Количество дней с продажами], 0)
= if (HASONEFILTER (Продукты [Продукт]), [Количество дней с продажами], 0)
= if (ISFILTERED (Продукты [Продукт]), [Количество дней с продажами], 0)
Это дает нам правильный знаменатель, который мы можем использовать при расчете продаж в день.
Шаг 3. Примените оператор IF к нашему исходному вычислению
Исходное выражение продаж в день было
= Round ([общие продажи] / COUNTROWS (DISTINCT (product_sales [Date])), 0)
Теперь мы можем используйте
= DIVIDE ([Total Sales], if (HASONEVALUE (Products [Product]), [No of days with sales], 0))
or
= DIVIDE ([Total Sales], if (HASONEFILTER (Products [Продукт]), [Количество дней с продажами], 0))
или
= РАЗДЕЛИТЬ ([Общий объем продаж], если (HASONEFILTER (Продукты [Продукт]), [Количество дней с продажами], 0))
Все итоги и промежуточные итоги были удалены, как мы и ожидали.
Шаг 4 — Тестирование итогов удаленной таблицы
Важно проверить свои значения с помощью дополнительных фильтров. Мы можем быстро сделать это, добавив несколько срезов в нашу сводную таблицу.
Детализация наших мер основана на Продуктах. Если мы разрежем по году или категории продукта, все выражения будут работать, как ожидалось, а итоги и промежуточные итоги не будут отображаться.
Когда мы выбираем несколько продуктов из слайсера, преформа HASONEVALUE и HASONEFILTER идеальна.Но ISFILTERED показывает как неправильные промежуточные итоги, так и итоги.
Проблема возникает, когда мы выбираем только один элемент из таблицы «Товары». В этом случае все выражения возвращают значение. Промежуточные итоги верны; однако общая сумма не соответствует нашим ожиданиям.
Когда есть вероятность, что это произойдет, возможно, пришло время подумать о корректировке итоговых и промежуточных итогов до ожидаемого значения.
Исправление итогов и промежуточных итогов в DAX для PowerBI и Power Pivot
Мы рассмотрели удаление итогов из таблицы, однако часто бывает так, что вам нужны итоговые значения для использования в таблице или в карточках и их удаление на самом деле не вариант.
Во-первых, мы должны выяснить, находимся ли мы в строке итогов или промежуточных итогов. Мы уже знаем, как это сделать, используя HASONEVALUE, ISFILTERED и HASONEFILTER. Мы использовали это с оператором IF для вычисления значений в таблице. Мы знаем, что для итогов и промежуточных итогов возвращается значение False, поэтому теперь все, что нам нужно сделать, это заменить это значение false на нужные нам вычисления.
В этом примере мы хотим показать наши итоги как сумму значений.
HASONEVALUE
Вы помните, что мы создали эту меру, чтобы проверить, имеет ли столбец продуктов значение
= HASONEVALUE (Products [Product])
Что вернуло нам ЛОЖЬ в наших общих и промежуточных итогах. .Это можно использовать для идентификации и отделения итогов и промежуточных итогов от значений таблицы. Используя оператор и IF, можно использовать отдельный расчет как для значений таблицы, так и для итогов.
Используя ранее созданную меру hasonevalue, это выражение можно использовать для вычисления значений таблицы. Мера hasonevalue может стать значением, когда true в операторе if
Напомним, что это выражение было:
hasonevalue = DIVIDE ([Total Sales], if (HASONEVALUE (Products [Product]), [No of days with sales] ], 0))
= if (HASONEVALUE (Products [Product]) = TRUE (), [hasonevalue])
Это позволит вычислить наши значения, а не наши итоги.Теперь мы можем провести подсчет итогов. Этот расчет будет суммой значений, возвращаемых в каждой строке.
SUMMARIZE для исправления итогов в DAX
Функция SUMMARIZE возвращает виртуальную таблицу, по которой мы можем затем выполнять вычисления.
SUMX (SUMMARIZE (product_sales, Products [Product], ’date ‘[Year]), [hasonevalue]), [hasonevalue])
Часть этой функции SUMMARIZE создает виртуальную таблицу. Это выражение будет принимать продукты из таблицы продуктов и столбец года из таблицы дат в качестве фильтров.Значения в таблице рассчитываются с использованием ранее рассчитанной нами меры hasonevalue. Виртуальный стол будет похож на изображение.
Часть SUMX этого выражения затем выполняет итерацию по этой таблице, берет все значения, возвращаемые hasonevalue, и складывает их.
В функции SUMMARIZE мы взяли две группы по столбцам. Продукты [Продукт] и дата [Год], поскольку это детализация нашей сводной таблицы. Если мы изменим фильтры в нашей таблице, эта мера может перестать работать.
Теперь, когда у нас есть расчет, мы можем добавить это к нашему выражению
= if (HASONEVALUE (Products [Product]) = TRUE (), [hasonevalue], sumx (SUMMARIZE (product_sales, Products [Product], ‘date ‘[Год]), [hasonevalue]))
Это выражение говорит, что если в строке есть одно значение для продуктов, то это поле значений и вычисляем меру hasonevalue. Если нет, то это общий или промежуточный итог. В этом случае создайте виртуальную таблицу с продуктами и годами в качестве фильтров.В этой таблице вычислите меру hasonevalue в соответствии с фильтрами. Затем суммируйте все эти значения, чтобы получить промежуточные и итоговые суммы.
Вы также можете применить этот метод к HASONFILTER и ISFILTERD.
Использование Excel и закона Бенфорда для обнаружения мошенничества
Даже если человек выдумывает числа мысленно (используя свой мозг, а не компьютер), мало оснований полагать, что такое умственное упражнение даст результаты, которые точно соответствуют кривой Бенфорда.Более вероятно, что человек, мысленно производящий числа, будет склонен повторять определенные закономерности, и отображение частоты получаемых ведущих цифр может выявить эти закономерности. Например, человек может подсознательно чрезмерно использовать цифры 1, 3 и 4 для получения ложных данных и недооценивать цифры 6 и 8. Если это так, такие аномалии проявятся в виде беспорядочной гистограммы, мало похожей на кривую Бенфорда. .
В качестве другого примера бухгалтер, выписывающий фиктивные чеки, может намеренно удерживать суммы чеков ниже пороговых значений авторизации компании в 500 или 1000 долларов, и поэтому анализ этих сумм чеков может показать числа 4 и 9, встречающиеся чаще в качестве первых цифр, чем закон Бенфорда предсказал бы.
ОЦЕНКА ПО КРИВОЙ
Результаты, полученные с помощью анализа закона Бенфорда, не следует считать окончательными; процесс подсчета первых цифр никогда не докажет однозначно отсутствие или наличие мошенничества. Результаты, полученные в результате этого процесса, представляют собой просто аналитический инструмент, который может помочь CPA оценить, требуется ли дополнительная следственная работа. Однако, когда кривая Бенфорда не может материализоваться, CPAs должны активизировать свои усилия по проверке данных следующим образом.
1. Пересмотрите пригодность данных для анализа Бенфорда. Прежде чем подозревать мошенничество, CPAs должны повторно проверить набор данных на возможность встроенного смещения в сторону определенных цифр, и если смещение обнаружено, результаты вашего анализа Бенфорда не следует принимать во внимание.
2. Примените процедуры аналитического обзора. Если прогнозы Бенфорда не верны для данного набора данных, вам следует подозревать аномалию и искать дополнительные гарантии того, что набор данных действительно действителен.Раздел 520 AU-C, Аналитические процедуры , предоставляет руководство по проведению аналитического обзора и кратко диктует следующее. CPA должен:
- Подумайте, могли ли определенные необычные операции или события, изменения в бухгалтерском учете, изменения в бизнесе, случайные колебания или искажения повлиять на набор данных.
- Выполните тест транзакций для проверки набора данных. Например, выберите образец данных и физически проследите номера до подтверждающей документации.
- Сравните набор данных с наборами данных за предыдущий или предыдущий год. Изучите существенные различия.
- Сравните набор данных с запланированными или ожидаемыми суммами, если таковые имеются. Изучите существенные различия.
- Проанализируйте набор данных с помощью соотношений или соотношений и сравните эти результаты с ожидаемыми результатами для соотношений или средними отраслевыми показателями. Например, финансовые коэффициенты могут быть показательными при работе с наборами финансовых данных и расчетами площади в квадратных футах, или почасовые измерения или измерения на пробег могут быть полезными при работе с наборами статистических данных.
- Рассмотрите возможность использования положительных, а не отрицательных подтверждений для проверки балансов поставщиков и клиентов.
- Если стандартные аналитические процедуры были применены и не выявили мошенничества, но вовлеченные наборы данных значительно отличаются от ожиданий Бенфорда, рассмотрите возможность расширения ваших аналитических процедур, включив в них размеры выборки большего, чем обычно, и ужесточение расчетов стандартного отклонения с использованием более высоких уровней уверенности.
- Если набор данных включает инвентаризацию любого вида, возможно, физическая проверка выборки этих инвентаризаций будет в порядке.Раздел 501 AU-C, Аудиторские доказательства — Особые соображения по отдельным статьям , предоставляет руководство по дальнейшему исследованию запасов.
3. Переосмыслить внутренний контроль. Подумайте, существуют ли надежные средства контроля для выявления или предотвращения нарушений.
4. Рассмотрим источник. Пересмотреть источник, из которого были получены данные. Были ли они произведены внутри компании или получены из внешнего источника? Если из внешнего источника, спросите о мерах, которые этот источник использовал для проверки своих данных.
Еще один инструмент для борьбы с мошенничеством. AU-C Раздел 240, Рассмотрение мошенничества при аудите финансовой отчетности , требует, чтобы аудиторы использовали аналитические процедуры, чтобы помочь обнаружить наличие необычных транзакций или потенциального мошенничества. С этой целью CPA постоянно ищут новые методы и процедуры, которые могут помочь им обнаружить и предотвратить мошенничество. Как выясняется, изготовление набора фальсифицированных данных, соответствующих закону Бенфорда, является сложной задачей, и многие потенциальные мошенники, вероятно, не знают о законе Бенфорда или о том, как создавать мошеннические данные, соблюдающие его правила.Таким образом, этот анализ закона Бенфорда на основе Excel, вероятно, станет удобным дополнением к любому арсеналу средств обнаружения мошенничества CPA.
История закона Бенфорда
История закона Бенфорда начинается в 1881 году, когда астроном Саймон Ньюкомб заметил, что номера страниц в книге логарифмических таблиц были стерты (или размазаны) больше к лицевой стороне книги и постепенно уменьшались к концу книги. В то время как другие просто не обращали внимания на изношенные номера страниц, Ньюкомб распознал четкую закономерность, связанную с возникновением более низких и более высоких номеров.Он опубликовал статью, объясняющую свои наблюдения, и постулировал, что вероятность того, что одно число n будет первой цифрой числа, равна log (n + 1) — log (n). Пятьдесят семь лет спустя, в 1938 году, физик Фрэнк Бенфорд проверил гипотезу Ньюкома на 20 наборах данных и опубликовал научную статью, подтверждающую закон. Несмотря на заслуги Ньюкомба, Бенфорд заслужил большую заслугу в открытии, которое теперь обычно называют законом Бенфорда.
Применение закона Бенфорда для выявления признаков мошенничества в бухгалтерском учете выросло из статьи, опубликованной в 1972 году экономистом Хэлом Варианом, который писал, что закон Бенфорда может быть использован для обнаружения возможности мошенничества в социально-экономических данных, представленных в поддержку различных решений государственного планирования. .Общая идея Вариана заключалась в том, что простое сравнение частотных распределений первой цифры должно выявить аномальные результаты (если таковые имеются) в соответствии с законом Бенфорда. В 1999 г. в статье JofA («У меня есть ваш номер», май 1999 г.), , написанной Марком Дж. Нигрини, было рассказано, как судебные бухгалтеры и аудиторы могут применять закон Бенфорда для поиска индикаторов потенциального мошенничества в бухгалтерском учете и расходах. .
Бенфорд попытался объяснить свой закон, заявив, что «легче владеть одним акром, чем девятью акрами», подразумевая (возможно), что когда люди покупают землю, разумно предположить, что больше людей покупают один акр в качестве отправной точки, а не девять акров в качестве отправной точки.
Об авторе
Дж. Карлтон Коллинз ([email protected]) — консультант по технологиям, спикер конференции и редактор JofA .
Чтобы прокомментировать эту статью или предложить идею для другой статьи, свяжитесь с Джеффом Дрю, старшим редактором, по телефону [email protected] или 919-402-4056.
Примечание редактора
Инструкции для Microsoft Excel в этой статье относятся к версиям с 2007 по 2016 год, если не указано иное.
Шкала соотношения
| Определение, примеры и анализ данных
Шкала отношения — это количественная шкала, в которой есть истинный ноль и равные интервалы между соседними точками. В отличие от шкалы интервалов, ноль на шкале отношений означает полное отсутствие переменной, которую вы измеряете.
Длина, площадь и численность населения являются примерами шкал отношения.
Уровни измерения
Уровень отношения является наивысшим из четырех иерархических уровней измерения.Уровни или шкалы измерения показывают, насколько точно данные записываются. Чем выше уровень, тем сложнее измерение.
Уровень соотношения содержит все характеристики остальных 3 уровней. На уровне отношения значения могут быть распределены по категориям, упорядочены, иметь равные интервалы и принимать истинный ноль.
В то время как номинальные и порядковые переменные являются категориальными переменными, интервальные и относительные переменные являются количественными переменными. Можно провести гораздо больше статистических тестов на количественных, чем на категориальных данных.
Что такое настоящий ноль?
На шкале отношений ноль означает полное отсутствие интересующей переменной. Например, количество детей в семье или количество лет опыта работы являются переменными отношения: респондент не может иметь детей в семье или иметь нулевой опыт работы.
Используя истинный ноль на вашей шкале, вы можете рассчитывать соотношения значений. Например, вы можете сказать, что 4 ребенка — это вдвое больше, чем 2 детей в семье.Точно так же 8 лет — это удвоенные 4 года опыта.
Некоторые переменные, например температуру, можно измерить в разных масштабах. В то время как Цельсий и Фаренгейт — это интервальные шкалы, Кельвин — это шкала отношений.
Во всех трех шкалах интервалы между соседними точками равны. Однако, в отличие от шкал Цельсия и Фаренгейта, где ноль — это просто еще одно значение температуры, шкала Кельвина имеет истинный ноль (0 K), где ничто не может быть холоднее.
Это означает, что вы можете рассчитывать отношения температур только по шкале Кельвина.Хотя 40 ° — это вдвое больше градусов, чем 20 °, по шкале Цельсия или Фаренгейта он не в два раза жарче. Однако в шкале Кельвина 40 K вдвое горячее, чем 20 K, потому что в начальной точке этой шкалы находится истинный ноль.
Истинный ноль позволяет умножать, делить или извлекать квадратный корень. Сбор данных на уровне отношения всегда предпочтительнее других уровней, поскольку он наиболее точен.
Примеры шкал соотношений
Многие переменные в естественных и социальных науках измеряются с помощью шкал отношений.
Как и интервальные переменные, переменные отношения могут быть дискретными или непрерывными.
Дискретная переменная выражается только счетными числами (например, целыми числами), в то время как непрерывная переменная потенциально может принимать бесконечное количество значений.
| Переменное соотношение | Дискретный или непрерывный? |
|---|---|
| Количество автомобилей в собственности за последние 10 лет | Дискретный |
| Количество человек в домашнем хозяйстве | Дискретный |
| Количество студентов, считающих себя религиозными | Дискретный |
| Время реакции в компьютерной задаче | непрерывный |
| Стаж работы | непрерывный |
| Скорость в милях в час | непрерывный |
Что вычитка может сделать для вашей статьи?
Редакторы
Scribbr не только исправляют грамматические и орфографические ошибки, но и укрепляют ваше письмо, убеждаясь в том, что в вашей статье нет нечетких слов, лишних слов и неуклюжих формулировок.
См. Пример редактирования
Анализ данных соотношения
После того, как вы собрали данные о соотношении, вы можете собрать описательную и логическую статистику. Практически все статистические тесты могут быть выполнены на данных о соотношении, потому что все математические операции допустимы.
Пример данных о соотношении Вы собираете данные о продолжительности поездок сотрудников в большом городе. Данные непрерывны и в минутах.
Чтобы обобщить ваши данные, вы можете собрать следующую описательную статистику:
Распределение
Вы можете получить обзор частоты появления различных значений в таблице и визуализировать их распределение на графике.
Чтобы систематизировать данные, введите их в сгруппированную таблицу частотного распределения. Создайте группы с равными интервалами в левом столбце и введите количество баллов, которые попадают в каждый интервал, в правый столбец.
| Время в пути (минуты) | Частота |
| 1-10 | 3 |
|---|---|
| 11-20 | 1 |
| 21-30 | 9 |
| 31-40 | 19 |
| 41-50 | 13 |
| 51-60 | 3 |
| 61 — 70 | 2 |
| 71–80 | 1 |
Чтобы визуализировать данные, нанесите их на многоугольник частотного распределения.Постройте группы по оси x, а частоты по оси Y и соедините среднюю точку каждой группы, используя линии.
Центральная тенденция
Из вашего графика вы можете видеть, что ваши данные распределены довольно нормально. Поскольку перекоса нет, чтобы найти, где находится большинство ваших значений, вы можете использовать все 3 общих показателя центральной тенденции: мода, медиана и среднее значение.
Режим — это наиболее часто повторяющееся значение в вашем наборе данных. Для непрерывных переменных часто нет режима, потому что существует бесконечное количество возможных значений, которые могут принимать ваши данные.В нашем примере нет режима, потому что каждое значение появляется только один раз.
Медиана — это значение точно посередине вашего набора данных. Чтобы найти среднюю позицию, возьмите значение в позиции ( n +1) / 2, где n — общее количество значений.
( п +1) / 2 = (51 + 1) / 2 = 26
Медиана находится на 26-й позиции, что соответствует значению 36,4 минут.
Среднее значение ( M ) использует все значения, чтобы дать вам единое число для центральной тенденции ваших данных.Используйте формулу ⅀ x / n . Суммируйте все значения (⅀ x ) и разделите сумму на n.
⅀ x = 1883,5
n = 52
M = ⅀ x / n = 1883,5 / 52 = 36,9
Среднее значение обычно считается лучшим показателем центральной тенденции, когда у вас есть нормально распределенные количественные данные. Это потому, что он использует каждое значение в вашем наборе данных для вычислений, в отличие от режима или медианы.
Изменчивость
Диапазон, стандартное отклонение и дисперсия описывают разброс ваших данных. Диапазон вычислить проще всего; стандартное отклонение и дисперсия более сложны, но также более информативны.
Коэффициент вариации — это мера разброса, которая применяется только к переменным отношения.
Чтобы найти диапазон, вычтите наименьшее значение из наибольшего значения в наборе данных. Максимальное время в пути составляет 72,5 минуты, а минимальное — 7 минут.
Диапазон = 72,5 — 7 = 65,5
Стандартное отклонение ( с ) — это средняя величина изменчивости в вашем наборе данных. Он сообщает вам, насколько далеко каждая оценка в среднем отличается от среднего. Большинство компьютерных программ легко рассчитают стандартное отклонение. Если вы хотите сделать это вручную, выполните следующие действия.
с = 13,34
Дисперсия ( с 2 ) — это среднее квадратичное отклонение от среднего. Отклонение от среднего — это разница между значением в вашем наборе данных и средним значением.Чтобы найти дисперсию, возведите стандартное отклонение в квадрат.
с 2 = 178,04
Коэффициент вариации ( CV ), также известный как относительное стандартное отклонение ( RSD ), является стандартизированной мерой дисперсии. Он сообщает вам, насколько изменчивы ваши данные относительно среднего значения. Его можно использовать только с относительными уровнями измерения, потому что это дробная часть. Коэффициент вариации ( CV ) — это стандартное отклонение, деленное на среднее значение.
CV = с / м
CV = 36,9 / 13,34 = 0,36
Коэффициент вариации 0,36 или 36%. Это говорит о том, что ваши данные имеют большой разброс, потому что стандартное отклонение составляет 36% от среднего.
Статистические тесты
Теперь, когда у вас есть обзор ваших данных, вы можете выбрать подходящие тесты для статистических выводов. При нормальном распределении данных о соотношении параметрические тесты лучше всего подходят для проверки гипотез.
Параметрические тесты более эффективны, чем непараметрические тесты, и позволяют делать более убедительные выводы относительно ваших данных. Однако для применения параметрических тестов ваши данные должны соответствовать нескольким требованиям.
Следующие параметрические тесты являются одними из наиболее распространенных, применяемых для проверки гипотез о данных о соотношении.
| Цель | Образцы или переменные | Тест | Пример |
| Сравнение средних | 2 образца | Т-тест | Есть ли разница в среднем времени в пути сотрудников в Бостоне и Лос-Анджелесе? |
| Сравнение средних | 3 или более образцов | ANOVA | Есть ли разница в средней продолжительности поездки сотрудников в Северной Америке, Азии и Европе? |
| Корреляция | 2 переменных | Pearson’s r | Как связаны время в пути и уровень дохода? |
| Регрессия | 2 переменных | Простая линейная регрессия | Предсказывает ли доход среднее время поездки на работу? |
Часто задаваемые вопросы о данных соотношения
В чем разница между данными интервала и соотношения?
Хотя данные об интервале и соотношении могут быть классифицированы, ранжированы и иметь одинаковые интервалы между соседними значениями, истинный ноль равен только шкалам отношений.
Например, температура в градусах Цельсия или Фаренгейта находится в интервале шкалы, потому что ноль не является самой низкой возможной температурой. В шкале Кельвина ноль означает полное отсутствие тепловой энергии.
ASCE 7-10 Пример расчета ветровой нагрузки
Полностью рабочий пример расчета ветровой нагрузки ASCE 7-10
SkyCiv выпустила бесплатный калькулятор ветровой нагрузки, в котором есть несколько кодовых ссылок, включая процедуру ветровой нагрузки ASCE 7-10.В этом разделе мы собираемся продемонстрировать, как рассчитать ветровые нагрузки, используя модель склада S3D ниже:
Рисунок 1. Модель склада в SkyCiv S3D в качестве примера.
Рисунок 2. Расположение сайта (из Google Maps).
Таблица 1. Строительные данные, необходимые для нашего расчета ветра.
| Расположение | Кордова, Мемфис, Теннесси |
| Вместимость | Разное — Структура завода |
| Рельеф | Плоские сельхозугодья |
| Размеры | 64 фута × 104 фута в плане Высота карниза 30 футов Высота апекса на отметке.36 футов Уклон крыши 3:16 (10,62 °) С открытием |
| Облицовка | Прогоны на расстоянии 2 фута Стеновые стойки на расстоянии 2 футов |
В нашем примере ветровой нагрузки ASCE 7-10 будет определено расчетное давление ветра для большой трехэтажной конструкции завода. На рис. 1 показаны размеры и каркас здания. Данные по зданию приведены в Таблице 1.
Хотя существует ряд программ, в которых расчет ветровой нагрузки уже интегрирован в их конструкцию и анализ, лишь некоторые из них обеспечивают подробный расчет этого конкретного типа нагрузки.Пользователям потребуется выполнить ручные вычисления этой процедуры, чтобы проверить, совпадают ли результаты с результатами, полученными с помощью программного обеспечения.
Формула для определения расчетного ветрового давления:
Для закрытых и частично закрытых зданий:
\ (p = qG {C} _ {p} — {q} _ {i} ({GC} _ {pi}) \) (1)
Для открытых построек:
\ (p = q {G} _ {f} {C} _ {p} — {q} ({GC} _ {pi}) \) (2)
Где:
\ (G \) = коэффициент воздействия порыва
\ ({C} _ {p} \) = коэффициент внешнего давления
\ (({GC} _ {pi}) \) = коэффициент внутреннего давления
\ (q \) = скоростное давление в фунтах на квадратный дюйм, определяемое по формуле:
\ (д = 0.2 \) (3)
\ (q \) = \ ({q} _ {h} \) для стен с подветренной стороны, боковых стен и крыш, оценивается по средней высоте крыши, \ (h \)
\ (q \) = \ ({q } _ {z} \) для наветренных стен, оценка по высоте, \ (z \)
\ ({q} _ {i} \) = \ ({q} _ {h} \) для отрицательного внутреннего давления, \ ((- {GC} _ {pi}) \) оценка и \ ({q} _ {z} \) для оценки положительного внутреннего давления \ ((+ {GC} _ {pi}) \) частично закрытого зданий, но можно принять консервативное значение как \ ({q} _ {h} \).
\ ({K} _ {z} \) = коэффициент скоростного давления
\ ({K} _ {zt} \) = топографический коэффициент
\ ({K} _ {d} \) = коэффициент направленности ветра
\ ( V \) = основная скорость ветра
миль / ч
Ниже мы подробно рассмотрим каждый параметр.Кроме того, мы будем использовать процедуру направленного действия (глава 30 ASCE 7-10) для решения расчетных значений давления ветра.
Категория риска
Первое, что нужно сделать при определении расчетного давления ветра, — это классифицировать категорию риска конструкции, основанную на использовании или занятости конструкции. В этом примере, поскольку это заводская структура, она классифицируется как Категория риска IV . См. Таблицу 1.5-1 ASCE 7-10 для получения дополнительной информации о классификации категорий риска.
Базовая скорость ветра, \ (В \)
ASCE 7-10 предоставляет карту ветров, на которой соответствующая базовая скорость ветра в данном месте может быть получена из рисунков 26.5-1A – 1C. Категория размещения определяется и классифицируется в Международном строительном кодексе.
При просмотре карт ветров возьмите номер наивысшей категории определенной категории риска или занятости. В большинстве случаев, включая этот пример, они одинаковы. Как видно из рисунка 26.5-1B, Кордова, Мемфис, Теннесси каким-то образом находится рядом с красной точкой на Рисунке 3 ниже, и отсюда базовая скорость ветра \ (V \) составляет 120 миль в час.Обратите внимание, что для других мест вам потребуется интерполировать базовое значение скорости ветра между контурами ветра.
Рис. 3. Базовая карта скорости ветра из ASCE 7-10.
SkyCiv теперь автоматизирует расчет скорости ветра с несколькими параметрами. Попробуйте наш SkyCiv Free Wind Tool
Калькулятор ветровой нагрузки SkyCiv
Категория воздействия
См. Раздел 26.7 ASCE 7-10, в котором подробно описана процедура определения категории воздействия.
В зависимости от выбранного направления ветра экспозиция конструкции должна определяться с наветренного сектора 45 °. Принимаемая экспозиция должна быть такой, которая вызовет наибольшую ветровую нагрузку в указанном направлении.
Описание каждой классификации воздействия подробно описано в разделах 26.7.2 и 26.7.3 стандарта ASCE 7-10. Чтобы лучше проиллюстрировать каждый случай, примеры каждой категории показаны в таблице ниже.
Таблица 2. Примеры зон, классифицированных в соответствии с категорией воздействия (глава C26 ASCE 7-10).
| Воздействие | Пример |
|---|---|
| Воздействие B |
|
| Воздействие C |
|
| Экспозиция D |
|
Для нашего примера, поскольку расположение конструкции находится на сельскохозяйственных угодьях в Кордове, Мемфис, Теннесси, без каких-либо построек высотой более 30 футов, поэтому территория классифицируется как Exposure C .Полезным инструментом для определения категории воздействия является просмотр вашего потенциального сайта через спутниковое изображение (например, Google Maps).
Коэффициент направленности ветра, \ ({K} _ {d} \)
Коэффициенты направленности ветра \ ({K} _ {d} \) для нашей конструкции равны 0,85, поскольку здание является основной системой сопротивления ветровой нагрузке, а также имеет компоненты и облицовку, прикрепленные к конструкции. Это показано в таблице 26.6-1 ASCE 7-10, как показано ниже на рисунке 4.
Рисунок 4. Коэффициент направленности ветра в зависимости от типа конструкции (Таблица 26.6-1 ASCE 7-10).
Топографический фактор, \ ({K} _ {zt} \)
Поскольку конструкция расположена на плоской сельскохозяйственной земле, мы можем предположить, что топографический фактор, \ ({K} _ {zt} \), равен 1,0. В противном случае коэффициент можно определить с помощью рисунка 26.8-1 ASCE 7-10. Чтобы определить, требуются ли дальнейшие расчеты топографического фактора, см. Раздел 26.8.1. Если ваш участок не соответствует всем перечисленным условиям, то топографический фактор можно принять равным 1.0.
Рисунок 5. Параметры, необходимые для расчета топографического фактора, \ ({K} _ {zt} \) (Таблица 26.8-1 ASCE 7-10).
Примечание. Факторы топографии могут быть автоматически рассчитаны с помощью программного обеспечения SkyCiv Wind Design
.
Коэффициент скорости давления, \ ({K} _ {z} \)
Коэффициент скоростного давления, \ ({K} _ {z} \), можно рассчитать с помощью таблицы 27.3-1 стандарта ASCE 7-10. Этот параметр зависит от высоты над уровнем земли точки, в которой учитывается давление ветра, и категории воздействия.{2 / α} \) (5)
Где:
Таблица 3. Значения и \ ({z} _ {g} \) из таблицы 26.9-1 стандарта ASCE 7-10.
| Экспозиция | α | \ ({z} _ {g} \) (футы) |
| B | 7 | 1200 |
| С | 9,5 | 900 |
| D | 11,5 | 700 |
Обычно коэффициенты скоростного давления на средней высоте крыши, \ ({K} _ {h} \), и на каждом уровне этажа, \ ({K} _ {zi} \), являются значениями, которые мы потребуется для расчета расчетного давления ветра.В этом примере, поскольку давление ветра с наветренной стороны носит параболический характер, мы можем упростить эту нагрузку, предположив, что равномерное давление применяется к стенам между уровнями пола.
Структура завода состоит из трех (3) этажей, поэтому мы разделим наветренное давление на эти уровни. Кроме того, поскольку крыша является двускатной, среднюю высоту крыши можно принять как среднее значение высоты карниза и вершины крыши, что составляет 33 фута
.
Таблица 4. Расчетные значения коэффициента скоростного давления для каждой высоты возвышения.
| Высота (фут) | \ ({K} _ {z} \) |
| 10 | 0,85 |
| 20 | 0,90 |
| 30 | 0,98 |
| 33 | 1,00 \ ({K} _ {zh} \) |
Скорость Давление
Из уравнения (3) мы можем найти скоростное давление \ (q \) в PSF на каждой рассматриваемой высоте.
Таблица 5.Расчетные значения скоростного напора на каждой высоте возвышения.
| Высота (фут) | \ ({K} _ {z} \) | \ (q \) (psf) | Замечания |
| 10 | 0,85 | 26,63 | 1 этаж |
| 20 | 0,90 | 28,20 | 2 этаж |
| 30 | 0,98 | 30,71 | Карниз крыши |
| 33 | 1.00 | 31,33 | Средняя высота крыши, \ ({q} _ {h} \) |
Фактор порывов ветра, G
Коэффициент воздействия порыва, \ (G \), установлен на 0,85, поскольку конструкция считается жесткой (раздел 26.9.1 стандарта ASCE 7-10).
Классификация корпуса и коэффициент внутреннего давления
Предполагается, что в конструкции завода есть проемы, которые удовлетворяют определению частично закрытого здания в Разделе 26.2 из ASCE 7-10. Таким образом, коэффициент внутреннего давления \ (({GC} _ {pi}) \) должен составлять +0,55 и -0,55 на основе таблицы 26.11-1 стандарта ASCE 7-10.
Рис. 6. Коэффициент внутреннего давления, \ (({GC} _ {pi}) \), из таблицы 26.11-1 ASCE 7-10.
Коэффициент внешнего давления, \ ({C} _ {p} \)
Для закрытых и частично закрытых зданий коэффициент внешнего давления \ ({C} _ {p} \) рассчитывается с использованием информации, представленной на рисунках с 27.4-1 по 27.4-3. Для частично закрытого здания с двускатной крышей используйте Рисунок 27.4-1.
Коэффициенты внешнего давления для стен и крыши рассчитываются отдельно с использованием параметров здания L, B и h, которые определены в примечании 7 к рисунку 27.4-1.
Таким образом, нам нужно рассчитать L / B и h / L:
Средняя высота кровли, h = 33 ′
Длина здания, L = 64 ′
Ширина здания, B = 104 ′
L / B = 0,615
h / L = 0,516
h / B = 0,317
Из этих значений мы можем получить коэффициенты внешнего давления \ ({C} _ {p} \) для каждой поверхности с помощью таблицы 27.4-1 ASCE 7-10. Обратите внимание, что мы можем использовать линейную интерполяцию, когда значения угла крыши, θ, L / B и h / L находятся между значениями, указанными в таблице. В нашем примере коэффициенты внешнего давления для каждой поверхности показаны в таблицах с 6 по 8.
Таблица 6. Расчетные коэффициенты внешнего давления для поверхностей стен.
| Поверхность | \ ({C} _ {p} \) |
| Наветренная стена | 0,8 |
| Подветренная стена | -0.5 |
| Боковая стенка | -0,7 |
Таблица 7. Расчетные коэффициенты внешнего давления для поверхностей крыши (ветровая нагрузка по L).
| Коэффициенты внешнего давления для крыши \ ({C} _ {p} \) (по L) | ||||||
| ч / л | Наветренная | Подветренная сторона | ||||
| 10 ° | 10,62 ° | 15 ° | 10 ° | 10,62 ° | 15 ° | |
| 0.5 | -0,9 -0,18 | -0,88 -0,18 | -0,7 -0,18 | -0,50 | -0,50 | -0,50 |
| 0,516 | -0,91 -0,18 | -0,89 -0,18 | -0,71 -0,18 | -0,51 | -0,51 | -0,50 |
| 1,0 | -1,3 -0,18 | -1,26 -0,18 | -1,0 -0.18 | -0,70 | -0,69 | -0,60 |
Таблица 8. Расчетные коэффициенты внешнего давления для поверхностей кровли (ветровая нагрузка по B).
| Коэффициенты внешнего давления для крыши \ ({C} _ {p} \) (по B) | ||
| h / B | Расположение | \ ({C} _ {p} \) |
| 0,317 | 0 до h | -0,9 -0,18 |
| h / 2 до h | -0.9 -0,18 | |
| ч до 2 ч | -0,5 -0,18 | |
| > 2 часа | -0,3 -0,18 | |
Коэффициент внешнего давления с двумя значениями, показанными в таблицах 7 и 8, должен быть проверен для обоих случаев.
Расчетное давление ветра для основной системы сопротивления ветровой рамы
Используя уравнение (1), можно рассчитать расчетное давление ветра. Результаты наших расчетов представлены в таблицах 8 и 9 ниже.Обратите внимание, что на структуру будут действовать четыре случая, поскольку мы будем рассматривать давления, решаемые с помощью \ ((+ {GC} _ {pi}) \) и \ ((- {GC} _ {pi}) \), и \ (+ {C} _ {p} \) и \ (- {C} _ {p} \) для крыши.
Таблица 9. Расчетное ветровое давление для поверхностей стен.
| Расчетное давление, \ (p \), для стен | |||||||
| Этаж | \ ({q} _ {z} \), psf | Наветренный | Подветренная сторона | Боковая стенка | |||
| \ ((+ {GC} _ {pi}) \) | \ ((- {GC} _ {pi}) \) | \ ((+ {GC} _ {pi}) \) | \ ((- {GC} _ {pi}) \) | \ ((+ {GC} _ {pi}) \) | \ ((- {GC} _ {pi}) \) | ||
| 10 | 26.63 | 0,88 (0,88) | 35,35 (35,35) | -30,55 (-30,55) | 3,92 (3,92) | -35,88 (-35,88) | -1,41 (-1,41) |
| 20 | 28,20 | 1,94 (1,94) | 36,41 (36,41) | ||||
| 30 | 30,71 | 3,65 (3,65) | 38,12 (38,12) | ||||
| 33 | 31,33 | 4,07 (4,07) | 38,54 (38.54) | ||||
(результаты ветровой нагрузки SkyCiv)
Таблица 10. Расчетное ветровое давление для поверхностей кровли.
| Расчетное давление на крышу, psf (вдоль L) | Расчетное давление на крышу, фунт-кв. Дюйм (вдоль В) | ||||
| Поверхность | \ ((+ {GC} _ {pi}) \) | \ ((- {GC} _ {pi}) \) | Расположение (от наветренной кромки) | \ ((+ {GC} _ {pi}) \) | \ ((- {GC} _ {pi}) \) |
| Наветренный | -40.87 (-40,87) | -6,41 (-6,40) | от 0 до h / 2 | -41,20 (-41,20) | 12,44 (12,44) |
| -22,03 (-22,03) | 12,44 (12,44) | ч / 2 до | -41,20 (-41,20) | ||
| Подветренная сторона | -30,71 (-30,71) | 3,76 (3,83) | ч до 2 ч | -30,55 (-30,55) | |
| > 2 часа | -25,22 (-25,22) | ||||
(результаты ветровой нагрузки SkyCiv)
Чтобы применить эти давления к конструкции, мы рассмотрим одну раму на конструкции.Пример применения случая 1 и 2 (для обоих \ (({GC} _ {pi}) \)) показан на рисунках 7 и 8. Направление ветра, показанное на вышеупомянутых рисунках, соответствует длине L здания. .
Обратите внимание, что положительный знак означает, что давление действует по направлению к поверхности, а отрицательный знак — от поверхности. Длина бухты 26 футов.
Рис. 7. Расчетное давление ветра на одну раму — \ ((+ {GC} _ {pi}) \) и случай абсолютного максимального давления на крышу.
Рис. 8. Расчетное давление ветра на одну раму — \ ((- {GC} _ {pi}) \) и случай абсолютного максимального давления на крышу.
SkyCiv упрощает эту процедуру, просто определяя параметры. Попробуйте наш SkyCiv Free Wind Tool
Калькулятор ветровой нагрузки SkyCiv
Расчетное давление ветра для компонентов и оболочки (C&C)
Компоненты и оболочки определены в главе C26 стандарта ASCE 7-10 следующим образом: «Компоненты принимают ветровые нагрузки напрямую или от облицовки и передают нагрузку на MWFRS», в то время как «облицовка принимает ветровые нагрузки напрямую.Примеры компонентов включают «крепеж, прогоны, стойки, настил крыши и фермы крыши», а для облицовки — «настенные покрытия, навесные стены, кровельные покрытия, наружные окна и т. Д.»
Из главы 30 ASCE 7-10 расчетное давление для компонентов и оболочки должно быть рассчитано с использованием уравнения (30.4-1), показанного ниже:
\ (p = {q} _ {h} [({GC} _ {p}) — ({GC} _ {pi})] \) (6)
Где:
\ ({q} _ {h} \): скоростное давление, рассчитанное на средней высоте крыши, h (31.33 psf)
\ (({GC} _ {pi} \)): коэффициент внутреннего давления
\ (({GC} _ {p} \)): коэффициент внешнего давления
Для этого примера \ (({GC} _ {p} \)) будет найден, используя Рисунок 30.4-1 для Зоны 4 и 5 (стены) и Рисунок 30.4-2B для Зоны 1-3 (крыша). . В нашем случае правильное значение зависит от уклона крыши θ, который составляет 7 ° <θ ≤ 27 °. \ (({GC} _ {p} \)) можно определить для множества типов крыш, изображенных на рисунках 30.4-1 - 30.4-7 и 27.4-3 в главах 30 и 27 ASCE 7-10, соответственно.
Мы будем рассчитывать только расчетное давление ветра для прогонов и каркасов стен. Зоны для компонентов и давления оболочки показаны на рисунке 9.
Рисунок 9. Расположение расчетных давлений C&C.
Расстояние a от краев может быть рассчитано как минимум 10% от наименьшего горизонтального размера или 0,4h, но не менее либо 4% от наименьшего горизонтального размера, либо 3 фута.
a: 10% от 64 футов = 6,4 фута> 3 фута
0,4 (33 фута) = 13.2 фута 4% от 64 футов = 2,56 фута
a = 6,4 фута
Стеновые шпильки (C&C Wall Pressure)
На основании рисунка 30.4-1, \ (({GC} _ {p} \)) можно рассчитать для зон 4 и 5 на основе эффективной площади ветра. Обратите внимание, что определение эффективной ветровой площади в главе C26 ASCE 7-10 гласит: «Для лучшего приближения к фактическому распределению нагрузки в таких случаях ширина эффективной ветровой площади, используемая для оценки \ (({GC} _ { p} \)) не должно быть меньше одной трети длины области.”Следовательно, эффективная ветровая площадь должна быть максимальной:
Эффективная ветровая зона = 10 футов * (2 фута) или 10 футов * (10/3 фута) = 20 кв. Футов. или 33,3 кв. фута
Эффективная ветровая площадь = 33,3 кв. фута
Положительные и отрицательные значения \ (({GC} _ {p} \)) для стен можно аппроксимировать, используя график, показанный ниже, как часть рисунка 30.4-1:
Рисунок 10. Приблизительные значения \ (({GC} _ {p} \)) из рисунка 30.4-1 ASCE 7-10.
Таблица 11.Расчетное давление C&C для каркаса стены.
| Зона | \ (+ ({GC} _ {p} \)) | \ (- ({GC} _ {p} \)) | C&C Давление, фунт / кв. Дюйм | |
| \ (+ ({GC} _ {p} \)) | \ (- ({GC} _ {p} \)) | |||
| 4 | 0,90 | -1,0 | 10,97 45,43 | -48,56 -14,10 |
| 5 | 0,90 | -1,2 | 10.97 45,43 | -54,83 -20,36 |
Прогоны (давление на крышу C&C)
Из 30.4–2B можно определить эффективное давление ветра для Зон 1, 2 и 3. Поскольку фермы расположены на расстоянии 26 футов, следовательно, это будет длина прогонов. Эффективная ветровая площадь должна быть максимум:
Эффективная ветровая площадь = 26 футов * (2 фута) или 26 футов * (26/3 фута) = 52 кв. Фута или 225,33 кв. Фута.
Эффективная площадь ветра = 225.33 кв.футов
Положительные и отрицательные значения \ (({GC} _ {p} \)) для крыши можно аппроксимировать, используя график, показанный ниже, как часть рисунка 30.4-2B:
Рисунок 11. Значения \ (({GC} _ {p} \)) из рисунка 30.4-2B ASCE 7-10.
Таблица 12. Расчетное давление C&C для прогонов.
| Зона | + (GCp) | — (GCp) | C&C Давление, фунт / кв. Дюйм | |
| + (GCpi) | — (GCpi) | |||
| 1 | 0.30 | -0,80 | -7,83 26,63 | -42,30 -7,83 |
| 2 | 0,30 | -1,2 | -7,83 26,63 | -54,83 -20,36 |
| 3 | 0,30 | -2,0 | -7,83 26,63 | -79,89 -45,43 |
Все эти расчеты могут быть выполнены с использованием программного обеспечения SkyCiv для ветровой нагрузки для ASCE 7-10, 7-16, EN 1991, NBBC 2015 и AS 1170.Пользователи могут войти в местоположение площадки, чтобы получить данные о скорости ветра и факторах топографии, ввести параметры здания и сгенерировать давление ветра. С профессиональной учетной записью пользователи могут автоматически применять это к модели конструкций и выполнять структурный анализ в одном программном обеспечении.
В противном случае, попробуйте наш SkyCiv Free Wind Tool для расчета скорости ветра и давления ветра на простых конструкциях.
Калькулятор ветровой нагрузки SkyCiv
Патрик Эйлсворт Гарсия
Инженер-конструктор, разработка продуктов
MS Гражданское строительство
Артикул:
- Мехта, К.К., и Коулбурн, У. Л. (2013, июнь). Ветровые нагрузки: Руководство по положениям о ветровой нагрузке ASCE 7-10. Американское общество инженеров-строителей.
- Минимальные расчетные нагрузки для зданий и других сооружений. (2013). ASCE / SEI 7-10. Американское общество инженеров-строителей.
.


 Их запаковали в 12 коробок по 10 мячей в каждой. Сколько мячей осталось? (126-10*12=6(м.))
Их запаковали в 12 коробок по 10 мячей в каждой. Сколько мячей осталось? (126-10*12=6(м.))
 Начинаем с первой парты 1 ряда, по очереди выходим к доске, решаем пример и объясняем его решение. (Далее учащиеся решают с объяснением примеры, данные в задании 96)
Начинаем с первой парты 1 ряда, по очереди выходим к доске, решаем пример и объясняем его решение. (Далее учащиеся решают с объяснением примеры, данные в задании 96) 27;
27;