Урок 4. Частные методики умножения двузначных чисел до 30
Преимуществом трех способов умножения двузначных для устного счета, описанных в прошлом уроке, состоит в том, что они универсальны для любых чисел и при хорошем навыке устного счета, они могут позволить вам достаточно быстро прийти к правильному ответу. Однако, эффективность умножения некоторых двузначных чисел в уме может быть выше за счет меньшего количества действий при использовании специальных алгоритмов.
В этом уроке вы узнаете, как можно быстро умножать любые числа до 30. Здесь представлены специальные методики, в том числе и введение в использование опорного числа.
Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры. Например: 23*11, пишем 2 и 3, а между ними ставим сумму (2+3). Или короче, что 23*11= 2 (2+3) 3 = 253.
Если сумма чисел в центре дает результат больше 10, тогда добавляем единицу к первой цифре, а вместо второй цифры пишем сумму цифр умножаемого числа минус 10. Например: 29*11 = 2 (2+9) 9 = 2 (11) 9 = 319.
Например: 29*11 = 2 (2+9) 9 = 2 (11) 9 = 319.
Умножать на 11 таким способом можно любые двузначные числа. Для наглядности приведены примеры:
81 * 11 = 8 (8+1) 1 = 891
68 * 11 = 6 (6+8) 8 = 748
Быстро умножать на 11 устно можно не только двузначные числа, но и любые другие числа — об этом читайте в данной статье, а также в книге «Система быстрого счета по Трахтенбергу».
Квадрат суммы, квадрат разности
Для того чтобы возвести в квадрат двузначное число, можно воспользоваться формулами квадрата суммы или квадрата разности. Например:
232= (20+3)2 = 202 + 2*3*20 + 32 = 400+120+9 = 529
692 = (70-1)2 = 702 – 70*2*1 + 12 = 4 900-140+1 = 4 761
Возведение в квадрат чисел, заканчивающихся на 5
Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост.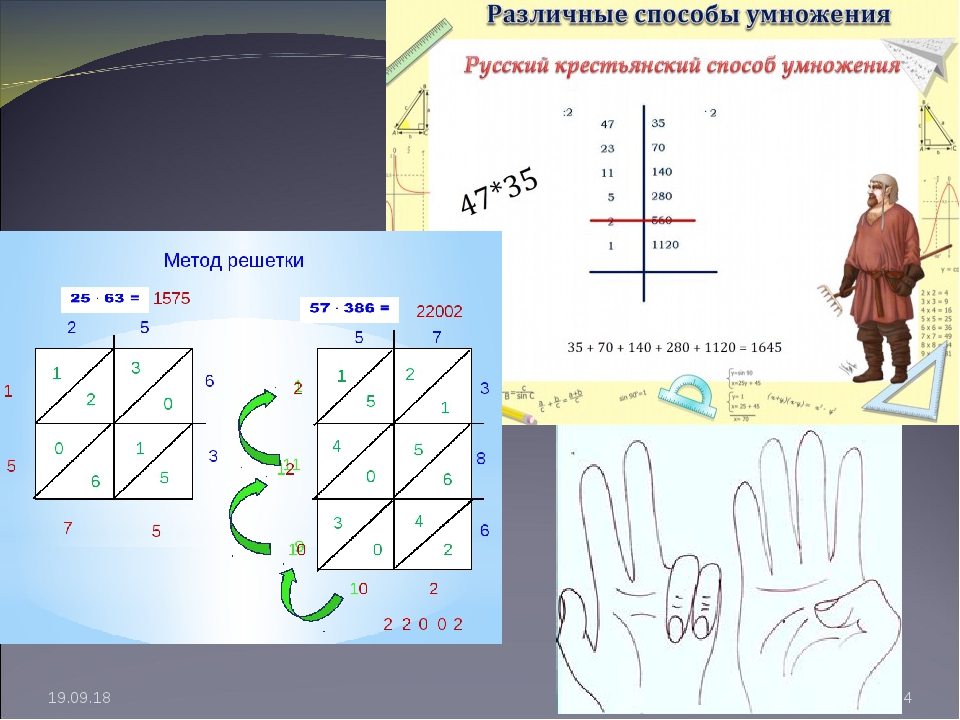 Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу дописываем 25.
Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу дописываем 25.
152 = (1*(1+1)) 25 = 225
252 = (2*(2+1)) 25 = 625
852 = (8*(8+1)) 25 = 7 225
Это верно и для более сложных примеров:
1552 = (15*(15+1)) 25 = (15*16)25 = 24 025
Умножение чисел до 20
1 шаг. Для примера возьмём два числа – 16 и 18. К одному из чисел прибавляем кол-во единиц второго – 16+8=24
2 шаг. Полученное число умножаем на 10 – 24*10=240
3 шаг. Далее к результату прибавляем произведение единиц 16 и 18 – 240+6*8=288
Методика умножения чисел до 20 очень проста:
Если записать короче, то:
16*18 = (16+8)*10+6*8 = 288
Доказать правильность этого метода просто: 16*18 = (10+6)*(10+8) = 10*10+10*6+10*8+6*8 = 10*(10+6+8) +6*8. Последнее выражение и является демонстрацией описанного выше метода.
Последнее выражение и является демонстрацией описанного выше метода.
По сути, этот метод является частным способом использования опорных чисел (о которых будет сказано в следующем уроке). В данном случае опорным числом является 10. В последнем выражении доказательства видно, что именно на 10 мы умножаем скобку. Но в качестве опорного числа можно использовать и любые другие числа, из которых наиболее удобными являются 20, 25, 50, 100… Подробнее о методе использования опорного числа читайте в следующем уроке.
Опорное число
Посмотрите на суть этого метода на примере умножения 15 и 18. Здесь удобно использовать опорное число 10. 15 больше десяти на 5, а 18 больше десяти на 8. Для того, чтобы узнать их произведение, нужно совершить следующие операции:
- К любому из множителей прибавить число, на которое второй множитель больше опорного. То есть прибавить 8 к 15, или 5 к 18. В первом и втором случае получается одно и то же: 23.
- Затем 23 умножаем на опорное число, то есть на 10.
 Ответ: 230
Ответ: 230 - К 230 прибавляем произведение 5*8. Ответ: 270.
Подробнее о методике использования опорного числа для счета в уме читайте в следующем уроке.
Тренировка
Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.
Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.
Евгений Буянов
Таблица умножения на 24 — учим легко и быстро
- Автор: Мещеряков Александр
- Категория: Таблица умножения
Основная таблица умножения на 24 от 1 до 10
| Множители | Произведение (Результат) | |||
|---|---|---|---|---|
| 24 | × | 1 | = | 24 |
| 24 | × | 2 | = | 48 |
| 24 | × | 3 | = | 72 |
| 24 | × | 4 | = | 96 |
| 24 | × | 5 | = | 120 |
| 24 | × | 6 | = | 144 |
| 24 | × | 7 | = | 168 |
| 24 | × | 8 | = | 192 |
| 24 | × | 9 | = | 216 |
| 24 | × | 10 | = | 240 |
Дополнительная таблица до 100
| Множители | Произведение (Результат) | |||
|---|---|---|---|---|
| 24 | × | 11 | = | 264 |
| 24 | × | 12 | = | 288 |
| 24 | × | 13 | = | 312 |
| 24 | × | 14 | = | 336 |
| 24 | × | 15 | = | 360 |
| 24 | × | 16 | = | 384 |
| 24 | × | 17 | = | 408 |
| 24 | × | 18 | = | 432 |
| 24 | × | 19 | = | 456 |
| 24 | × | 20 | = | 480 |
| 24 | × | 21 | = | 504 |
| 24 | × | 22 | = | 528 |
| 24 | × | 23 | = | 552 |
| 24 | × | 24 | = | 576 |
| 24 | × | 25 | = | 600 |
| 24 | × | 26 | = | 624 |
| 24 | × | 27 | = | 648 |
| 24 | × | 28 | = | 672 |
| 24 | × | 29 | = | 696 |
| 24 | × | 30 | = | 720 |
| 24 | × | 31 | = | 744 |
| 24 | × | 32 | = | 768 |
| 24 | × | 33 | = | 792 |
| 24 | × | 34 | = | 816 |
| 24 | × | 35 | = | 840 |
| 24 | × | 36 | = | 864 |
| 24 | × | 37 | = | 888 |
| 24 | × | 38 | = | 912 |
| 24 | × | 39 | = | 936 |
| 24 | × | 40 | = | 960 |
| 24 | × | 41 | = | 984 |
| 24 | × | 42 | = | 1008 |
| 24 | × | 43 | = | 1032 |
| 24 | × | 44 | = | 1056 |
| 24 | × | 45 | = | 1080 |
| 24 | × | 46 | = | 1104 |
| 24 | × | 47 | = | 1128 |
| 24 | × | 48 | = | 1152 |
| 24 | × | 49 | = | 1176 |
| 24 | × | 50 | = | 1200 |
| 24 | × | 51 | = | 1224 |
| 24 | × | 52 | = | 1248 |
| 24 | × | 53 | = | 1272 |
| 24 | × | 54 | = | 1296 |
| 24 | × | 55 | = | 1320 |
| 24 | × | 56 | = | 1344 |
| 24 | × | 57 | = | 1368 |
| 24 | × | 58 | = | 1392 |
| 24 | × | 59 | = | 1416 |
| 24 | × | 60 | = | 1440 |
| 24 | × | 61 | = | 1464 |
| 24 | × | 62 | = | 1488 |
| 24 | × | 63 | = | 1512 |
| 24 | × | 64 | = | 1536 |
| 24 | × | 65 | = | 1560 |
| 24 | × | 66 | = | 1584 |
| 24 | × | 67 | = | 1608 |
| 24 | × | 68 | = | 1632 |
| 24 | × | 69 | = | 1656 |
| 24 | × | 70 | = | 1680 |
| 24 | × | 71 | = | 1704 |
| 24 | × | 72 | = | 1728 |
| 24 | × | 73 | = | 1752 |
| 24 | × | 74 | = | 1776 |
| 24 | × | 75 | = | 1800 |
| 24 | × | 76 | = | 1824 |
| 24 | × | 77 | = | 1848 |
| 24 | × | 78 | = | 1872 |
| 24 | × | 79 | = | 1896 |
| 24 | × | 80 | = | 1920 |
| 24 | × | 81 | = | 1944 |
| 24 | × | 82 | = | 1968 |
| 24 | × | 83 | = | 1992 |
| 24 | × | 84 | = | 2016 |
| 24 | × | 85 | = | 2040 |
| 24 | × | 86 | = | 2064 |
| 24 | × | 87 | = | 2088 |
| 24 | × | 88 | = | 2112 |
| 24 | × | 89 | = | 2136 |
| 24 | × | 90 | = | 2160 |
| 24 | × | 91 | = | 2184 |
| 24 | × | 92 | = | 2208 |
| 24 | × | 93 | = | 2232 |
| 24 | × | 94 | = | 2256 |
| 24 | × | 95 | = | 2280 |
| 24 | × | 96 | = | 2304 |
| 24 | × | 97 | = | 2328 |
| 24 | × | 98 | = | 2352 |
| 24 | × | 99 | = | 2376 |
| 24 | × | 100 | = | 2400 |
Как быстро и легко выучить таблицу умножения?
Первое, что нужно для начала изучения таблицы умножения — это иметь перед глазами саму таблицу. Лучше, если обучение будет проходить по таблице умножения Пифагора, потому как приведённая выше таблица это лишь столбик, в котором число 24 умножают на различные числа. В данном случае невозможно объяснить логические связи между цифрами и закономерности между ними, поэтому ребёнку придётся заучить данный столбик наизусть, как стихотворение. Мы же рекомендуем начинать изучение таблицы умножения по таблице Пифагора.
Лучше, если обучение будет проходить по таблице умножения Пифагора, потому как приведённая выше таблица это лишь столбик, в котором число 24 умножают на различные числа. В данном случае невозможно объяснить логические связи между цифрами и закономерности между ними, поэтому ребёнку придётся заучить данный столбик наизусть, как стихотворение. Мы же рекомендуем начинать изучение таблицы умножения по таблице Пифагора.
Перед началом изучения таблици умножения рекомендуем ознакомиться с материалом: как быстро и легко выучить таблицу умножения. Не тратьте свои нервы и нервы своего ребёнка.
Таблицу умножения Пифагора можно использовать на нашем сайте, а также скачать её или распечатать.
Просмотров: 2937
Свойства умножения: переместительное, сочетательное и распределительное
Переместительное свойство умножения
От перестановки сомножителей местами произведение не меняется.
Следовательно, для любых чисел a и b верно равенство:
a · b = b · a,
выражающее переместительное свойство умножения.
Примеры:
6 · 7 = 7 · 6 = 42;
4 · 2 · 3 = 3 · 2 · 4 = 24.
Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.
Сочетательное свойство умножения
Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.
Следовательно, для любых чисел a, b и c верно равенство:
a · b · c = (a · b) · c = a · (b · c),
выражающее сочетательное свойство умножения.
Пример:
3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30
или
3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.
Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:
25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.
В данном случае можно было вычислить всё последовательно:
25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,
но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.
Распределительное свойство умножения
Сначала рассмотрим распределительное свойство умножения относительно сложения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a + b) = m · a + m · b,
выражающее распределительное свойство умножения.
Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
(a + b) · m = a · m + b · m.
Теперь рассмотрим распределительное свойство умножения относительно вычитания:
Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a — b) = m · a — m · b.
Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
(a — b) · m = a · m — b · m.
Переход от умножения:
m · (a + b) и m · (a — b)
соответственно к сложению и вычитанию:
m · a + m · b и m · a — m · b
называется раскрытием скобок.
Переход от сложения и вычитания:
m · a + m · b и m · a — m · b
к умножению:
m · (a + b) и m · (a — b)
называется вынесением общего множителя за скобки.
Таблица умножения на 24
| Множители | Произведение (Результат) |
|---|---|
| 24 * 1 = | 24 |
| 24 * 2 = | 48 |
| 24 * 3 = | 72 |
| 24 * 4 = | 96 |
| 24 * 5 = | 120 |
| 24 * 6 = | 144 |
| 24 * 7 = | 168 |
| 24 * 8 = | 192 |
| 24 * 9 = | 216 |
| 24 * 10 = | 240 |
| 24 * 11 = | 264 |
| 24 * 12 = | 288 |
| 24 * 13 = | 312 |
| 24 * 14 = | 336 |
| 24 * 15 = | 360 |
| 24 * 16 = | 384 |
| 24 * 17 = | 408 |
| 24 * 18 = | 432 |
| 24 * 19 = | 456 |
| 24 * 20 = | 480 |
| 24 * 21 = | 504 |
| 24 * 22 = | 528 |
| 24 * 23 = | 552 |
| 24 * 24 = | 576 |
| 24 * 25 = | 600 |
| 24 * 26 = | 624 |
| 24 * 27 = | 648 |
| 24 * 28 = | 672 |
| 24 * 29 = | 696 |
| 24 * 30 = | 720 |
| 24 * 31 = | 744 |
| 24 * 32 = | 768 |
| 24 * 33 = | 792 |
| 24 * 34 = | 816 |
| 24 * 35 = | 840 |
| 24 * 36 = | 864 |
| 24 * 37 = | 888 |
| 24 * 38 = | 912 |
| 24 * 39 = | 936 |
| 24 * 40 = | 960 |
| 24 * 41 = | 984 |
| 24 * 42 = | 1008 |
| 24 * 43 = | 1032 |
| 24 * 44 = | 1056 |
| 24 * 45 = | 1080 |
| 24 * 46 = | 1104 |
| 24 * 47 = | 1128 |
| 24 * 48 = | 1152 |
| 24 * 49 = | 1176 |
| 24 * 50 = | 1200 |
| 24 * 51 = | 1224 |
| 24 * 52 = | 1248 |
| 24 * 53 = | 1272 |
| 24 * 54 = | 1296 |
| 24 * 55 = | 1320 |
| 24 * 56 = | 1344 |
| 24 * 57 = | 1368 |
| 24 * 58 = | 1392 |
| 24 * 59 = | 1416 |
| 24 * 60 = | 1440 |
| 24 * 61 = | 1464 |
| 24 * 62 = | 1488 |
| 24 * 63 = | 1512 |
| 24 * 64 = | 1536 |
| 24 * 65 = | 1560 |
| 24 * 66 = | 1584 |
| 24 * 67 = | 1608 |
| 24 * 68 = | 1632 |
| 24 * 69 = | 1656 |
| 24 * 70 = | 1680 |
| 24 * 71 = | 1704 |
| 24 * 72 = | 1728 |
| 24 * 73 = | 1752 |
| 24 * 74 = | 1776 |
| 24 * 75 = | 1800 |
| 24 * 76 = | 1824 |
| 24 * 77 = | 1848 |
| 24 * 78 = | 1872 |
| 24 * 79 = | 1896 |
| 24 * 80 = | 1920 |
| 24 * 81 = | 1944 |
| 24 * 82 = | 1968 |
| 24 * 83 = | 1992 |
| 24 * 84 = | 2016 |
| 24 * 85 = | 2040 |
| 24 * 86 = | 2064 |
| 24 * 87 = | 2088 |
| 24 * 88 = | 2112 |
| 24 * 89 = | 2136 |
| 24 * 90 = | 2160 |
| 24 * 91 = | 2184 |
| 24 * 92 = | 2208 |
| 24 * 93 = | 2232 |
| 24 * 94 = | 2256 |
| 24 * 95 = | 2280 |
| 24 * 96 = | 2304 |
| 24 * 97 = | 2328 |
| 24 * 98 = | 2352 |
| 24 * 99 = | 2376 |
| 24 * 100 = | 2400 |
| … * 101 = | … |
Автор: Bill4iam
Питание в цифрах: все о дневных нормах | Еда
Интуитивное питание или тотальный контроль над рационом? В обоих случаях не лишним будет узнать, насколько ваши взаимоотношения с едой близки к тому, что принято считать «нормой» — с точки зрения калорийности, баланса БЖУ, количества овощей, фруктов, жидкости и других показателей.
Калорийность рациона
Как и другие нормы питания, эта — относительна, и зависит во многом от таких параметров, как рост и вес, возраст и пол, степень активности.
Если говорить о средних показателях, то у взрослых мужчин ежедневная потребность в энергии варьируется от 2100 до 4200 ккал, а у женщин — от 1800 до 3050 ккал. Разброс большой; чтобы получить более точное понимание, советуют пользоваться формулой Миффлина-Джеора (нужно учитывать, правда, что и она предназначена для среднестатистических людей). Она, в отличие от другой популярной формулы Харриса-Бенедикта, впервые выведенной в 1919 году, более современная — учитывает то, как изменился образ жизни людей за несколько десятилетий. Благодаря ей можно рассчитать свой метаболический уровень, понять базовый расход энергии.
Женщинам:
5 + (10 × вес в кг) + (6,25 × рост в см) − (5 × возраст) = BMR (basal metabolic rate, или базовый уровень метаболизма)
Мужчинам:
(10 × вес в кг) + (6,25 × рост в см) − (5 × возраст) − 161 = BMR (basal metabolic rate, или базовый уровень метаболизма)
Есть также формула для быстрых вычислений: это 23 х вес в кг для женщин и 24 х на вес в кг — для мужчин.
На этом вычисления не заканчиваются. Далее следует умножить полученное число на коэффициент активности, который у каждого — свой.
- 1,4 — сидячий, малоподвижный образ жизни, в котором почти нет места занятиям спортом;
- 1,6 — все та же низкая активность, но уже с тренировками, хоть и редкими (1-2 раза в неделю)
- 1,8 — этот коэффициент относится к людям, которые работают «на ногах» и в силу этого более подвижны;
- 2,0 и более — числа, связанные с тяжелой физической работой.
Выбранный вами коэффициент следует увеличить на 0,3 — в том случае, если вы активно занимаетесь спортом на регулярной основе, от 3 до 5 раз в неделю.
Результат как раз и будет примерно тем числом калорий, которые следует получать с пищей, если вы хотите оставаться в своем весе. Тем же, кто рассчитывает похудеть, как известно, нужно, чтобы расход калорий превышал их потребление. Считается оптимальным снижать калорийность своего рациона приблизительно на 500 ккал, если перед вами задача — сбросить вес. Меньше 1200 получившееся число, однако, после такого вычета быть не должно. По словам диетологов, при такой низкой калорийности рациона есть риск, что организм не будет получать все необходимые ему для здоровья вещества. Плюс с таким недостатком калорий можно будет в неделю терять порядка 500 г жира в неделю; как раз до 500 г — безопасное количество, которое не скажется на здоровье.
Меньше 1200 получившееся число, однако, после такого вычета быть не должно. По словам диетологов, при такой низкой калорийности рациона есть риск, что организм не будет получать все необходимые ему для здоровья вещества. Плюс с таким недостатком калорий можно будет в неделю терять порядка 500 г жира в неделю; как раз до 500 г — безопасное количество, которое не скажется на здоровье.
Макронутриенты
Белки, жиры и углеводы называют так, потому что они требуются организму в большом количестве (это десятки и сотни граммов). Суточные нормы вновь будут разниться в зависимости от пола, возраста, образа жизни и других показателей.
Для нормальной работы организма, по данным специалистов из нашей страны, взрослым женщинам требуется от 58 до 87 г белка в день, мужчинам же — от 65 до 117 г. В среднем, речь идет о 1,2-1,5 г белка на килограмм сухого (!) веса тела. Цифры, опять же, колеблются, и ученые спорят между собой; так, на «Белковом саммите 2.0» в Вашингтоне в 2013 году было решено, что и 1,6 г на килограмм веса может считаться нормой. При активных занятиях спортом это количество можно увеличить и до 2 г на килограмм веса. Насыщая белком свой рацион, стоит знать о том, что он хорош не только как «строительный материал» для мышц. На белок могут налегать и худеющие, так как организму затруднительно превращать белок в жировые отложения, чего не скажешь об углеводах.
При активных занятиях спортом это количество можно увеличить и до 2 г на килограмм веса. Насыщая белком свой рацион, стоит знать о том, что он хорош не только как «строительный материал» для мышц. На белок могут налегать и худеющие, так как организму затруднительно превращать белок в жировые отложения, чего не скажешь об углеводах.
Насчет жиров мнение тоже неоднозначно. Одни источники утверждают, что суточная норма для женщин, желающих поддерживать вес и здоровую работу организма, — от 45 до 55 г в зависимости от веса, мужчинам же допускают до 65 г жиров. Другие же утверждают, что нужно умножить свой вес тела на 0,8-1, чтобы получить свою дневную норму. Но здесь важнее понимать, что 1 г жира — это 9 ккал, доля жиров от общей калорийности рациона должна составлять примерно 20-30% — но в то же время ниже 20 не опускаться. Жиры необходимы для многих метаболических процессов, включая усвоение витаминов, производство гормонов. Поэтому их дефицит может сказаться на здоровье.
Что касается углеводов, то их в норме требуется больше всего: узнать «свое» количество вам поможет умножение веса своего тела на 3. Тем, кто активно занимается спортом и буквально-таки испытывает свое тело на прочность, нужно 5-6 г на килограмм веса. Лучше всего, чтобы наибольшую часть от этого составляли сложные углеводы, чтобы в вашем рационе не было «пустых» калорий, которые не дают организму никакой пользы.
Тем, кто активно занимается спортом и буквально-таки испытывает свое тело на прочность, нужно 5-6 г на килограмм веса. Лучше всего, чтобы наибольшую часть от этого составляли сложные углеводы, чтобы в вашем рационе не было «пустых» калорий, которые не дают организму никакой пользы.
Отдельно стоит сказать о клетчатке: считается, что взрослым нужно 20-30 г, около 14 или 15 г на каждые 1000 ккал.
Продумывая соотношение белков, жиров и углеводов, следует помнить, что в жирах, как уже было сказано, 9 ккал, в белках и углеводах — по 4 ккал. Оптимальным соотношением этих нутриентов для поддержания веса считают 30/20/50, тем же, кто хочет и сохранить вес, и улучшить фигуру с точки зрения рельефа, можно пользоваться схемой 40/20/40.
Овощи и фрукты
В отношении этих продуктов мнения разные не только потому, что норму нужно, опять же, рассчитывать индивидуально. Сами ученые, которые исследуют вопрос, не соглашаются друг с другом в выведенных формулах. Например, ВОЗ рекомендует для ежедневного потребления как минимум 400 г фруктов и овощей (кстати, картофель к этой норме не относят), разделяя это количество на 5 порций. При этом важно разнообразие, а с ним поможет принцип радуги: выбирайте фрукты и овощи разных цветов, планируя свой рацион на сутки. Кстати, сушеные фрукты тоже входят в обозначенное число, но разовой порции хорошо бы быть не более 30 г. От норм ВОЗ отличаются те, что приняты внутри отдельных стран. Например, в России рациональной нормой потребления свежих фруктов и овощей в день считается около 650 г (исходя из того, что за год Минздрав советует потреблять 140 кг овощей и 100 кг — фруктов).
Например, ВОЗ рекомендует для ежедневного потребления как минимум 400 г фруктов и овощей (кстати, картофель к этой норме не относят), разделяя это количество на 5 порций. При этом важно разнообразие, а с ним поможет принцип радуги: выбирайте фрукты и овощи разных цветов, планируя свой рацион на сутки. Кстати, сушеные фрукты тоже входят в обозначенное число, но разовой порции хорошо бы быть не более 30 г. От норм ВОЗ отличаются те, что приняты внутри отдельных стран. Например, в России рациональной нормой потребления свежих фруктов и овощей в день считается около 650 г (исходя из того, что за год Минздрав советует потреблять 140 кг овощей и 100 кг — фруктов).
Вода
По данным экспертов, в день нужно около 1,5-2 литров жидкости. Необязательно, чтобы это была только чистая питьевая вода, но лучше стремиться к тому, чтобы именно она составляла основу этого количества. Чтобы рассчитать норму индивидуально для себя, умножайте свой рекомендуемый вес (женщинам нужно вычесть 110 из своего роста в см, мужчинам — 100) на 30. Чтобы узнать свою норму на те дни, когда вы активно занимаетесь спортом, умножайте на 40.
Чтобы узнать свою норму на те дни, когда вы активно занимаетесь спортом, умножайте на 40.
Таблица умножения
Для скачивания картинки: нажмите на надпись «скачать», чтобы сохранить картинку на свой компьютер (изображение будет в высоком разрешении и в хорошем качестве).
Нажмите на картинку, чтобы увидеть ее в увеличенном виде.
Наиболее древняя таблица умножения была обнаружена в Древнем Вавилоне и по разным оценкам ей примерно 4000 лет. Найденная таблица основана на шестнадцатеричной системе исчисления и выполнена в виде глиняной таблички.
Старейшая из обнаруженных таблиц умножения в десятичной системе исчисления, была найдена в Древнем Китае и датируется 305 годом до нашей эры.
Часть современных историков полагают, что таблица умножения была изобретена Пифагором Самосским, древнегреческим философом и математиком жившем в Древней Греции в 570-490 годах до нашей эры. Поэтому, таблицу умножения часто называют также и таблицей Пифагора.
Поэтому, таблицу умножения часто называют также и таблицей Пифагора.
Как выучить таблицу умножения
Таблицу умножения в современной системе образования начинают изучать во 2 классе, а в некоторых школах уже и в 1 классе.
Не у всех деток память одинаково хорошо запоминает цифры. Но это не беда, здесь главное упорство и тренировка. Если с ребенком регулярно заниматься, то любой ребенок сможет выучить таблицу и запомнить ее на всю жизнь. Не нужно давить и насильно заставлять ребенка, лучше его заинтересовать и мотивировать. Если не получается просто выучить, можно прибегнуть к небольшим хитростям, в виде стишков или различных ассоциаций.
Начало изучения
В самом начале нужно обязательно показать ребенку что такое умножение, чтобы он понял смысл. Нужно объяснить, что умножение это тоже самое что и сложение, только записанное в более короткой удобной для понимания форме. Для начала покажите на примере 2×2 или 2×3, а затем более длинный вариант, например 2×8. Нужно показать, что 2×8 это тоже самое что и 2+2+2+2+2+2+2+2 или 8+8. Поняв это, ребенку будет намного проще заучить таблицу.
Нужно показать, что 2×8 это тоже самое что и 2+2+2+2+2+2+2+2 или 8+8. Поняв это, ребенку будет намного проще заучить таблицу.
Начинать изучение таблицы умножения лучше всего с первых трех столбцов, так как они более легко запоминаются. Поняв смыл таблицы, ребенок часто сам выбирает наиболее простой для него способ запоминания. Ваша задача предложить ему несколько способов. Не получится одним способом, помогут другие. У всех детей память разная, кто то отлично запоминает цифры, а у кого то лучше работает ассоциативная память. Каждому ребенку нужен свой подход. Главное терпение!
Умножение на 1
Здесь все просто, нужно объяснить малышу, что при умножении любого числа на единицу (кроме нуля конечно), получается то числу которое мы умножали. Чтобы закрепить материал, предложите ребенку умножить большие числа на единицу (сто, тысячу и так далее).
Умножаем на 2
Этот столбик запомнить тоже не сложно. Просто нужно показать, что умножение на 2 это тоже самое, если к числу которое мы умножаем, прибавить еще одно точно такое же.
Умножаем на 3
Если ребенок хорошо заполнил умножение на 2, то для лучшего запоминания можно показать, что умножение на три это также сложение трех одинаковых цифр.
Как пересчитать ингредиенты для торта другого диаметра
Друзья, назрел внеплановый, но весьма полезный и нужный пост, в котором я расскажу как пересчитать ингредиенты для торта другого диаметра. Потому что это самый частый вопрос, который вы мне задаете практически каждый день, а то и по несколько раз в день. Поэтому в срочном порядке пишу здесь алгоритм расчета чтобы теперь просто отсылать вас к этому посту вместо того, чтобы каждый раз объяснять как это делать.
UPD. Важное сообщение! Друзья, на сайте теперь есть удобный калькулятор пересчета ингредиентов для разных форм (жмите на ссылочку).
В сегодняшней статье вы получите ответы на вопросы:
- как пересчитать ингредиенты для формы другого размера, чем это указано в рецепте? + готовая таблица коэффициентов
- как узнать вес будущего торта?
- каким образом рассчитать вес торта на определенное количество человек?
- как посчитать вес готового торта, исходя из его диаметра и высоты?
И без долгих вступлений давайте разбираться в арифметике. У меня самой с математикой очень туго, поэтому все, что можно было упростить, я упростила по максимуму.
У меня самой с математикой очень туго, поэтому все, что можно было упростить, я упростила по максимуму.
1. Как пересчитать ингредиенты для другого диаметра формы?
Для того, чтобы сделать перерасчет диаметра торта нам нужно площадь одной формы разделить на площадь другой.
Для двух круглых форм
Если речь идет о круглой форме, то упрощенная формула следующая:
нужно разделить квадрат диаметра большей формы на квадрат диаметра меньшей формы. И мы получим то число, на которое нужно умножить или разделить все ингредиенты рецепта:
d1²÷d2²
где, d1 — диаметр большей формы, а d2 — диаметр меньшей формы
Рассмотрим пример расчета диаметра
Допустим, в рецепте дан диаметр формы — 20 см, а у вас форма 24 см.
Производим следующий расчет:
24×24= 576
20×20=400
576÷400=1,44
(я в таких случаях округляю до 1,5)
Значит вес каждого ингредиента нужно умножить на 1,5. Если же у вас, наоборот, форма меньше, чем указанная в рецепте, то все ингредиенты нужно разделить на 1,5.
Если же у вас, наоборот, форма меньше, чем указанная в рецепте, то все ингредиенты нужно разделить на 1,5.
Ну и чтоб уж совсем облегчить вам задачу и сэкономить время, вот вам готовая табличка пересчета ингредиентов.
На пересечении клеток исходного диаметра и нужного вам диаметра находится то число, на которое нужно умножить все ингредиенты рецепта.
UPD. Важное сообщение! Друзья, на сайте теперь есть удобный калькулятор пересчета ингредиентов для разных форм (жмите на ссылочку).
Т.е. вес каждого ингредиента нужно умножить на число, указанное в соответствующей клетке.
В таблице я указала уже округленные числа, чтобы не вдаваться в слишком детальные подсчеты.
Если обе или одна из форм квадратная
А что же делать, если у вас не только другой размер формы, но она к тому же квадратная или прямоугольная?
Готовую табличку я пока не осилила (надеюсь, в скором будущем), но вот вам формула расчета:
Сначала вычислим площадь прямоугольной формы:
S=a×b
где a — это длина формы, b — ширина.
Затем вычислим площадь круглой формы:
S=π×r²
где π — 3.14, r — радиус формы (радиус — это половина диаметра).
Например, если диаметр формы 24 см, ее радиус будет равен 12 см. 12²=144 см. А значит площадь формы будет равна:
3.14×144=452 см
Получив значения двух площадей, мы должны разделить бóльшую площадь на меньшую.
Таким образом, если в рецепте указана квадратная форма, скажем, 22×22 см, а у вас только круглая диаметром 24 см, значит
площадь квадратной формы (22×22=484 см) мы разделим на площадь круглой (3.14×144=452 см) и получим:
484 см÷452 см= 1,07
Это значит, что все ингедиенты рецепта мы делим на 1,07.
В этом примере площадь нашей формы меньше той, что указана в рецепте, поэтому ингредиенты мы разделили на полученный коэффициент. Если же площадь нашей формы, наоборот, больше той, что используется в рецепте, то все указанные ингедиенты мы должны умножить на полученный коэффициент.
Например в рецепте указана форма 25×20 см, т.е. ее площадь равна 500 см. Диаметр, нашей формы 26 см, т.е. ее площадь равна 530 см.
530÷500=1,06
Значит все ингредиенты мы умножаем на 1,06.
Чтобы посчитать вес яиц, которые зачастую указаны в штуках, мы принимаем за данность, что вес 1 яйца приблизительно 50 гр.
2. Как посчитать вес будущего торта?
Чтобы посчитать вес торта, который у вас получится по тому или иному рецепту, достаточно просто суммировать вес всех ингредиентов, указанных в рецепте.
Чтобы посчитать вес яиц, которые зачастую указаны в штуках, мы принимаем за данность, что вес 1 яйца приблизительно 50 гр.
Здесь нужно учитывать, что итоговый вес торта будет процентов на 10-15% меньше, чем сумма всех ингредиентов. Потому что при тепловой обработке часть влаги испаряется. Например, классический бисквит при выпекании может терять до 30% своего первоначального веса. Кексовые бисквиты теряют меньше влаги в связи с наличием большого процента жиров.
Кексовые бисквиты теряют меньше влаги в связи с наличием большого процента жиров.
К тому же, какие-то составляющие, типа карамели или пропитки, мы можем использовать не полностью, что тоже уменьшит итоговый вес торта.
Если после суммирования всех ингредиентов рецепта выходит торт весом 2 кг., то чтобы получить, напрмер, 3-хкилограммовый торт, делаем следующий расчет:
3 кг÷2 кг=1,5
Соответственно, все ингредиенты рецепта нужно умножить на 1,5.
3. Как рассчитать вес торта на определенное количество человек?
Если у вас стоит задача приготовить торт, скажем, на день рождения, и вы знаете, что у вас будет 15 гостей, используйте следующий расчет:
15 чел.×200 гр.= 3000 гр.
В кондитерской практике принято, что на 1 человека рассчитано приблизительно по 200 гр. торта. Соответственно, если каждый гость съест по 1 кусочку торта, то вам понадобится, как минимум, 3-хкилограммовый торт. Но советую сделать хотя бы с полукилограммовым запасом на тот случай, если торт окажется сильно вкусным и часть гостей попросят добавки))
4. Как посчитать вес торта исходя из диаметра и высоты?
Некоторые пытаются выяснить как рассчитать вес торта при наличии данных о диаметре торта и его высоте.
Мой ответ — никак!
Это будет очень приблизительное значение, поскольку вес будет сильно варьироваться в зависимости от того, из чего сделан торт.
Вы же понимаете, что, скажем, Наполеон диаметром 20 см и высотой 10 см будет весить раза в 2 больше, чем таких же размеров бисквитный торт с кремом из взбитых сливок.
Вот такая несложная математика.
Уверена, вам неоднократно пригодится эта инфа, поэтому по возможности сохраните себе эту статью где-нибудь в Pinterest или в Facebook.
До новых встреч.
Оля Афинская
Помогаю печь лучше
Умножение двух чисел — WebMath
Быстро! Мне нужна помощь с:
Выберите элемент справки по математике … Исчисление, Производное вычисление, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Поиск всех сложных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование площади, Преобразование длины, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, Equation from slopeLines Theotation, The Equation from slopeLines Theotation, The Equation from slopeLines Theotation и Y-intation , Поиск шансов, Математика, Практика многочленов, Математика, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа слагаемых, Вычитание чисел Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторизация триномов многочленов, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они из себя представляют, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение , Правые треугольники, Ветер, Рисунок
Какой процент одно число от другого? Метод пропорций — Полный курс арифметики
База всегда будет следовать за «оф.»Поэтому, чтобы определить процентное соотношение одного числа к другому, мы должны сделать базовыми 100.
(Но см. Ниже.)
Пример 4. 3 из 10 учеников получили «отлично»? Какой процент получил «пятерку»?
То есть 3 — это какой процент от 10? Эти вопросы означают то же самое. В каждом из них основание 10 следует за «of».
Решение . При умножении обоих чисел на 10,
3 из 10 равно 30 из 100.
30% получили А.
Пример 5. В классе из 25 учеников 11 изучали французский язык. Какой процент изучали французский язык?
Решение . Студент должен понимать, что это означает:
11 из 25 изучали французский язык.
Чтобы получить основание 100, мы должны умножить 25 на 4. Следовательно, мы также должны умножить 11 на 4:
44% изучали французский язык.
11 равно 25, а 44 равно 100.
Хотя эту проблему можно решить, написав ,
правильная дробь, а затем решить эту пропорцию:
студент не должен писать это. Увидев или даже услышав фразу «11 из 25», ученик должен понять , что мы должны умножить 11 и 25 на 4.
Понимание, это навык в арифметике.
Пример 6. В классе из 200 учеников 11 изучали французский язык.Какой процент изучали французский язык?
Решение. В этом случае, чтобы превратить 200 в 100, мы должны разделить на 2 или взять половину. Следовательно, мы также должны взять половину от 11, что составляет 5½.
5½% изучали французский язык.
Мы видим, что для решения пропорции:
Мы должны разделить оба члена на одно и то же число,
или мы должны умножить оба члена на одно и то же число.
Пример 7.Какой процент от 400 составляет 33?
Решение . 400 — База; следует за «оф.» Чтобы получилось 100, мы должны разделить на 4. Следовательно, мы также должны разделить 33 на 4.
«4 превратится в 33 восемь (8) раз (32), 1 останется».
33 составляет 8¼% от 400.
Пример 8. На недавних выборах проголосовало 1000 человек, за Джонса — 763 человека. Какой процент проголосовал за Джонса?
Решение .За Джонса проголосовало 763 человека из 1000. Чтобы получить Base 100, мы должны разделить на 10. Чтобы разделить 763 на 10, просто разделите единицу.
десятичная цифра (Урок 4,
Вопрос 4):
763 ÷ 10 = 76 . 3
76 . За Джонса проголосовали 3%.
Пример 9. Какой процент от 500 равен 132?
Решение . 132 равно 500, 264 равно 1000, 26,4 равно 100.
132 это 26.4% от 500.
Пример 10. 7 человек из 12 проголосовали «Да». Примерно какой процент проголосовал Да?
Решение . Какое число, умноженное на 12, близко к 100?
8 × 12 = 96. 8 × 7 = 56. Таким образом, примерно 56% проголосовали «Да».
Отношение суммы к базе
Пример 11. 8 какой процент от 40?
Ответ . Этот вопрос означает то же самое, что и «8 имеет отношение к 40?» Ибо проценты — это отношения.(Урок 17.)
Итак, 8 — это пятая часть от 40. А поскольку 20 — это пятая часть от 100:
8 — это 20% от 40.
Для овладения предметом процентов ученик должен освоить Задачу 1 Урока 28.
Пример 12. Какой процент от 8 составляет 40?
Ответ . Здесь 8 — это База, она следует за «оф». В этом можно убедиться, если сформулировать вопрос в стандартной форме:
40 — это какой процент от 8?
Итак, 40 равно пяти умноженным на 8.В процентах пять раз — это 500%.
40 составляет 500% от 8.
Пример 13. В классе из 28 учеников 7 получили «отлично»? Какой процент учеников получил «отлично»?
Ответ . Возникает вопрос: 7 — это какой процент от 28?
Непонятно, как превратить 28 в 100. Но 7 — это четвертая часть или четверть от 28. А в процентах четверть числа составляет 25%.
7 составляет 25% от 28.
Пример 14.12 — какой процент от 18?
Ответ . Какое соотношение 12 к 18? У них общий делитель 6.
«6 переходит в 12 два раза и в 18 три раза».
12 равно 18, как 2 равно 3 —
12 — это две трети от 18.
Каждый номер говорит свое имя.
| В процентах 66 | 2 3 | % означает две трети.(Урок 16.) |
Пример 15. Какой процент от 35 составляет 14?
Ответ . В стандартной форме
14 — это какой процент от 35?
У них общий делитель 7. Следовательно, при делении каждого члена на 7:
14 до
35 как 2 равно 5.
2 составляет две пятых от 5. Две пятых от 100% составляет 40%. (Одна пятая — 20%.) Следовательно,
14 это 40% от 35.
Пример 16. 20 — какой процент от 8?
Ответ . Их общий делитель равен 4. Следовательно, у них такое же отношение, как у 5 к 2, что в два с половиной раза больше:
20 составляет 250% от 8.
20 состоит из двух восьмерок — 16 — плюс 4, что составляет половину от 8. 20 составляет два с половиной умножения на 8.
Пример 17. Очистка десятичных знаков. . 8 это какой процент из 4?
Ответ . Чтобы решить любую задачу о процентах, числа должны быть целыми числами. Следовательно, сделайте числа целыми числами, умножив их на 10:
.
. 8 равно 4, а 8 равно 40.
Ибо проценты — это отношения, и поэтому они подчиняются правилам отношений.
Итак, 8 — пятая часть из 40. Это говорит нам о
.
. 8 составляет 20% от 4.
Пример 18. Какой процент от 75 равен 21?
Решение 1. В стандартной форме
21 — это какой процент от 75?
У них общий делитель 3. Это говорит нам о том, что у каждого числа есть третья часть. И по трети каждого:
21 равно 75, как 7 равно 25.
Теперь мы можем изменить 25 на 100, умножив на 4. Следовательно, при умножении 7 на 4:
21 — это 28% от 75.
| Решение 2. | 21 75 | = | ? 100 |
Какое число , умноженное на 75, даст 100? Другими словами, какое отношение имеет 100 к 75?
Ответ:
100 — это 75, умноженное на 1/3.
Урок 18:
.
Один раз 75 равно 75.Одна треть от 75 — 25. 75 плюс 25 — 100.
Следовательно, третье умноженное на 21 равно 21 + 7 = 28.
21 это 28% от 75.
Пример 19. Цифры одинаковые. 2 долларов. 50 это какой процент от 250 долларов?
Ответ . Цифры те же: 2, 5, 0 — но 2 долларов. 50 состоит из двух десятичных цифр. 250 долларов делятся на 100:
.
$ 2 . 50 = 250 ÷ 100 $.
(Урок 4.) Следовательно,
$ 2 . 50 составляет 1% от 250 долларов.
Урок 4.
.
Сравните Урок 15, примеры 5 и 6.
Пример 20. 84 900 17 долларов. 50 это какой процент от 845 долларов?
Ответ . 10%. 84 900 17 долларов США. 50 = 845–10 долларов США.
Вот как взять 10% от числа.
Сводка
Чтобы определить процентное соотношение одного числа к другому:
Умножьте или разделите оба члена так, чтобы Основание стало 100.
9 какой процент от 20?
Легко превратить 20 в 100, умножив его на 5. А так как 5 умножить на 9, получится 45,
9 составляет 45% от 20.
Если не очевидно, как сделать базу 100 — посмотрите прямо на соотношение суммы к базе.
7 — это какой процент от 28?
Поскольку 7 — это одна четверть от 28, тогда
7 составляет 25% от 28.
Пример 21.Было опрошено 742 человека, 213 ответили «Нет». Какой процент ответили «Нет»?
Решение . 213 — это какой процент от 742? Воспользуйтесь калькулятором
На этом этапе, пожалуйста, «переверните» страницу и выполните несколько задач .
или
Перейдите к разделу 2: Общий метод определения процента.
1-й урок по процентам
Введение | Главная | Содержание
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Задачи о долях числового слова — математика для 3-го класса
Решение задач о долях числового слова
На последнем уроке вы узнали, как находить дробную часть числа.
Ты еще помнишь как? 🤔
Верно!
👉 Мы находим дробь числа , выполнив два шага: сначала умножаем целое число на число до r, а затем делим произведение, получаем на знаменатель .
Давайте решим реальные задачи о долях числа. 😁
Примеры проблем со словами
Джейн испекла 24 шоколадных печенья. 1/3 печенья она отдала соседке. Сколько печенья она отдала соседке?
🤔 Что нас просит сделать проблема?
Верно!
Нам нужно выяснить , что 1/3 от 24 составляет .
1/3 из 24 совпадает с этим:
24 × 1/3 =?
👉 Сначала умножаем 24 на числитель:
24 × 1 = 24
👉 Затем разделим полученное произведение на знаменатель:
.
24 ÷ 3 = 8
✅ Теперь мы знаем, что она отдала соседке 8 печенек .🍪
Вот еще вопросы об этой проблеме:
Из оставшихся печений Джейн отдала своим родителям 3/4, а остальные она съела. Сколько печенья она дала родителям? Сколько печенья она съела?
👉 Задача подсказывает нам выяснить две вещи:
— количество печенья, которое Джейн дала родителям,
— количество печенья, которое съела Джейн.
🤔 Но сначала мы должны узнать, сколько печенья осталось после того, как Джейн отдала их своей соседке.
Она начала с 24 печенья и отдала 8 печенек прочь.
Давайте вычтем :
24-8 = 16 печенья
Итак, у Джейн осталось 16 печенек.
🤔 Сколько печенья получили родители Джейн, если она дала им 3/4 из 16 ?
3/4 из 16 совпадает с этим:
16 × 3/4 =?
👉 Сначала умножаем 16 на числитель:
16 × 3 = 48
👉 Затем разделим полученное произведение на знаменатель:
.
48 ÷ 4 = 12
✅ Джейн подарила родителям 12 печений .🍪
🤔 А теперь давайте узнаем, сколько печенья съела Джейн. 🤔
Мы знаем, что Джейн съела все оставшееся печенье.
У нее было 16 печенек. Затем она отдала родителям 12 штук.
Сколько осталось?
👉 Нам нужно вычесть , чтобы выяснить это:
16–12 = 4
✅ Джейн съела 4 печенья .
Отличная работа!
Другой пример
Попробуем решить еще одну словесную задачу!
Джерри купил коробку с гвоздями.В нем 80 гвоздей. Он использовал 3/8 гвоздей для ремонта своего забора и 1/2 гвоздей для ремонта своей крыши. Сколько гвоздей он использовал, чтобы починить забор? Сколько гвоздей он использовал, чтобы отремонтировать крышу? Сколько гвоздей осталось?
Давайте ответим на вопросы по очереди. 😁
🤔 Как мы узнаем, сколько гвоздей использовал Джерри, чтобы починить свой забор?
Верно!
Нам нужно найти , что составляет 3/8 от 80 .
Это то же самое, что:
80 × 3/8 =?
👉 Умножим 80 на числитель.
80 × 3 = 240
👉 Разделим полученное произведение на знаменатель.
240 ÷ 8 = 30
✅ Джерри использовал 30 гвоздей, чтобы починить свой забор . 😎
80 × 3/8 = 30
🤔 Как мы узнаем, сколько гвоздей использовал Джерри для ремонта своей крыши?
Вы поняли!
Нам нужно найти , что 1/2 от 80 составляет .
Это то же самое, что:
80 × 1/2 =?
👉 Умножим 80 на числитель.
80 × 1 = 80
👉 Разделим полученное произведение на знаменатель.
80 ÷ 2 = 40
✅ Джерри использовал 40 гвоздей, чтобы отремонтировать свою крышу . 😎
🤔 Сколько гвоздей осталось?
👉 Сначала мы, , добавляем гвоздей, которые он использовал для ремонта своего забора и крыши.
30 + 40 = 70
👉 Затем мы вычитаем из общего количества гвоздей, которые он купил, общего количества гвоздей, которые Джерри использовал при ремонте.
80-70 = 10
✅ Осталось 70 гвоздей .
Отличная работа!
Смотри и учись
Готовы ли вы попрактиковаться? 💪
Проверка пропорциональности | Purplemath
Purplemath
В теме пропорций есть некоторая особая терминология, которая может вам понадобиться.Например, учитывая следующее уравнение пропорции:
… значения в позициях « b » и « c » называются «средними» пропорциями, а значения в позициях « a » и « d » называются «крайности» пропорции.
Основным определяющим свойством любой пропорции является то, что произведение средних значений равно произведению крайностей.Другими словами, учитывая пропорциональную формулировку:
MathHelp.com
…. мы знаем, что это должно быть правдой, что г. до н. э. равно г. до н. э. . Этот факт о пропорциях, по сути, является перекрестным умножением, продемонстрированным на предыдущей странице. И этот факт перекрестного умножения о произведениях средних и крайностей иногда превращается в домашнюю задачу, например:
Является ли
24 / 140 пропорциональным 30 / 176 ? Объясните, почему (или почему нет), не упрощая дроби.
Для того, чтобы эти дроби (то есть эти отношения) были пропорциональны (то есть, чтобы они создавали истинное пропорциональное уравнение, когда они устанавливаются равными друг другу), должно быть верно, что произведение средних значений этого уравнения равно произведению крайностей. Итак, я могу выяснить, действительно ли две фракции пропорциональны друг другу (не упрощая их), найдя эти два продукта.
Другими словами, указав, что я должен , а не , упростить дроби, они намекают, что хотят, чтобы я нашел произведение 140 и 30 (это означает, что если я сохраню дроби в том же порядке как они дали их мне) и произведение 24 и 176 (являются крайними значениями), а затем посмотрите, равны ли эти продукты.Так что проверю:
140 × 30 = 4200
24 × 176 = 4224
Хотя эти значения близки, они не равны, поэтому я знаю, что исходные дроби не могут быть пропорциональны друг другу. Итак, мой ответ:
Дроби не пропорциональны, потому что произведение их средних не равно произведению их крайних значений.
Если бы я поменял местами дроби и использовал 176 и 24 в качестве средних и 30 и 140 в качестве крайних значений, я бы получил те же продукты (только в обратном порядке) и, следовательно, тот же ответ (а именно, что дроби не пропорциональны).Так что не беспокойтесь о том, какая дробь является «первой» или «второй»; в любом случае будет работать.
42/55 пропорционально 50/65? Обоснуйте свой ответ, не уменьшая дробей.
Чтобы подтвердить соразмерность (или опровергнуть ее), мне нужно установить пропорцию, умножить средние, умножить крайности и сравнить результаты. Или, что то же самое (но без выполнения уравнения, которое на самом деле может быть неверным), я умножу знаменатель одной дроби на числитель другой, и наоборот:
(42) (65) = 2,730
(55) (50) = 2,750
И снова они близки, но не равны.Итак:
Дроби не пропорциональны, потому что произведение их средних не равно произведению их крайних значений.
Пропорциональны ли 42/273 и 170/1105? Объясните свой ответ, не сокращая дроби и не переводя их в общий знаменатель.
Я «перемножаю» (в данном контексте означает умножение числителя одной дроби на знаменатель другой, и наоборот):
(42) (1,105) = 46 410
(273) (170) = 46 410
Наконец, пара пропорциональна !
Дроби пропорциональны, потому что, когда они установлены как пропорции, произведение средних равно произведению крайних значений.
Средние пропорции
Другой технический тип упражнений, основанный на терминологии пропорций, — это нахождение «среднего пропорционального» между двумя числами. Средние пропорциональные — это особый класс пропорций, где средние пропорции равны друг другу. Пример среднего пропорционального значения:
В уравнении пропорциональности, созданном этими двумя равными дробями, средние значения пропорции имеют одно и то же значение, «2», а крайние значения — 1 и 4.Это говорит нам о том, что число 2 является «средним пропорциональным» между числами 1 и 4.
В упражнениях, основанных на пропорциональном среднем, нам могут дать два значения и попросить найти среднее пропорциональное между ними.
Найдите среднее значение, пропорциональное 3 и 12.
Они дали мне два числа и ключевое слово «среднее пропорциональное».Итак, я знаю, что мне нужно установить пропорцию, используя заданные значения в качестве крайних значений, а затем я должен найти средства.
По определению «среднее пропорциональное» я знаю, что средним будет одно и то же значение. Я позволю « x » быть тем единственным значением, которое я ищу. Я составлю уравнение пропорции, используя свою переменную в качестве средних и два значения, которые они дали мне в качестве крайних значений:
Теперь я произведу перекрестное умножение и решу для значения x :
3 × 12 = x 2
36 = x 2
± 6 = х
Так как я ищу среднее пропорциональное 3 и 12, я бы подумал, что мне нужно будет взять только положительное значение в качестве ответа, так что среднее пропорциональное будет как раз 6.Однако, учитывая дроби, подойдет любое значение:
Если я проверю перекрестные произведения каждого уравнения, я получу одинаковые результаты; другими словами, отрицательное значение также является допустимым результатом. Итак, на самом деле есть два средних, пропорциональных данному уравнению:
Примечание: ваша книга (или преподаватель) может попросить вас рассматривать только положительное среднее пропорциональное, поскольку положительное значение находится между 3 и 12.Фактически, ваша книга (или преподаватель) может определять «среднее пропорциональное» как только и всегда положительное значение. Используйте определение, данное вашей книгой (или инструктором), но имейте в виду, что вы можете встретить другие определения в других классах или контекстах.
Найдите положительное среднее, пропорциональное 4 и 25.
Чтобы найти средства, я составлю уравнение и решу:
4/ x = x /25
4 × 25 = x 2
100 = x 2
± 10 = х
Поскольку они указали, что хотят получить положительное среднее значение, мой ответ:
Возможно, вы заметили, что в приведенных выше решениях я всегда получал квадрат значения, равный числу, а затем извлекал квадратный корень из каждой стороны уравнения.Это дает быстрый метод решения для среднего пропорционального:
Найдите среднее значение, пропорциональное от 8 до 50
Они указали, что им нужно значение, которое находится «между» двумя заданными значениями, и эти значения являются положительными, поэтому я знаю, что они хотят положительного решения. Вместо того, чтобы устанавливать пропорцию, перемножать и решать квадратное уравнение, я сразу перейду к квадратному корню:
sqrt [8 × 50]
кв.м. [400]
sqrt [16 и 25 раз]
4 & умножить на 5 = 20
И это окончательное значение — мой ответ:
(Кстати, хотя это очень необычно, вы можете увидеть упражнение, в котором крайние значения пропорции (то есть заданные значения в упражнении «найти среднее пропорциональное») являются отрицательными.Когда эти значения умножаются, знаки «минус» погаснут, и вы, как обычно, можете извлечь квадратный корень.
(Однако невозможно иметь пропорцию, в которой крайние значения имеют противоположные знаки. Почему? Потому что произведение крайних значений противоположных знаков будет отрицательным, и вы не можете извлечь квадратный корень из отрицательного числа. Если вас когда-либо просят найти среднее значение, пропорциональное двум значениям с противоположными знаками, имейте в виду, что это вопрос с подвохом!)
Найдите (положительное) среднее, пропорциональное
3 / 2 и 3 / 8
Тот факт, что во всех примерах, приведенных в учебнике, были целые числа, не означает, что пропорция не может содержать дроби; может.Я буду использовать сокращенный метод решения, умножая два крайних значения, а затем извлекая (положительный) квадратный корень:
(3/2) × (3/8) = 9/16
sqrt [9/16] = 3/4
Таким образом, среднее пропорциональное двух дробей является другой дробью:
Вы также можете услышать «среднее пропорциональное», называемое «геометрическим средним».Это потому, что эта пропорциональная зависимость возникает в геометрии прямоугольных треугольников. Если мы возьмем прямоугольный треугольник и проведем линию от прямого угла к гипотенузе так, чтобы эта линия была перпендикулярна гипотенузе, то гипотенуза будет разделена на две части. Перпендикулярную линию можно рассматривать как линию, указывающую высоту « h » треугольника, когда гипотенуза является основанием. Эти две части помечены « x » и « y » на рисунке ниже:
Можно доказать, что высота х и две части, х и х , образуют пропорцию:
В частности:
Эту взаимосвязь можно превратить в упражнения, например:
Учитывая треугольник ниже,
x = 132 и y = 44, найдите высоту h треугольника.
Когда прямоугольный треугольник устроен таким образом, с линией высоты, проведенной от прямого угла к гипотенузе, высота и две части основания образуют пропорцию, в которой высота является средней пропорциональностью двух частей. Итак, чтобы найти высоту, мне нужно найти среднее значение, пропорциональное двум значениям, которые они мне дали.
Тогда коэффициент I:
Затем я извлекаю квадратный корень:
sqrt [(16) (121) (3)] = (4) (11) sqrt [3]
Затем, умножив это, я обнаружил, что высота треугольника составляет:
URL: https: // www.purplemath.com/modules/ratio3.htm
кратных 24 — что такое кратное 24? [Решено]
Число, кратное 24, получается умножением 24 на целые числа. В этом мини-уроке мы вычислим, кратные 24, и узнаем интересные факты об этих кратных.
- Первые пять чисел, кратных 24 : 24, 48, 72, 96 и 120
- Разложение на простые множители 24 : 24 = 2 × 2 × 2 × 3
Давайте узнаем больше о кратных 24 и их свойствах.
Что такое число, кратное 24?
Кратное — это результат умножения числа на целое. Чтобы создать список, кратный 24, у нас есть 2 метода.
Метод 1
В этом методе умножьте число 24 на целые числа, чтобы вычислить число, кратное 24.
- 24 × 1 = 24
- 24 × 14 = 336
- 24 × 78 = 1872
Или пропустите счет, чтобы получить последовательные числа, кратные 24.
Метод 2
В этом методе несколько раз сложите число 24 с самим собой, чтобы вычислить число, кратное 24.
- 24 + 0 = 24
- 24 + 24 = 48
- 24 + 24 + 24 = 72
- 24 + 24+ 24+ 24 = 96
- 24+ 24 +24 + 24 +24 = 120
Этот список бесконечен; мы можем сгенерировать столько чисел, кратных 24, сколько захотим.
Важные примечания
- Число, кратное 24, — это целые числа, умноженные на 24.
- Все числа, кратные 24, являются кратными 2, 3, 4, 6 и 8.
Список первых 20 чисел, кратных 24
Перечислим первые 20 чисел, кратных 24:
| Кратное 24 |
|---|
| 24 × 1 = 24 |
| 24 × 2 = 48 |
| 24 × 3 = 72 |
| 24 × 4 = 96 |
| 24 × 5 = 120 |
| 24 × 6 = 144 |
| 24 × 7 = 168 |
| 24 × 8 = 192 |
| 24 × 9 = 216 |
| 24 × 10 = 240 |
| 24 × 11 = 264 |
| 24 × 12 = 288 |
| 24 × 13 = 312 |
| 24 × 14 = 336 |
| 24 × 15 = 360 |
| 24 × 16 = 384 |
| 24 × 17 = 408 |
| 24 × 18 = 432 |
| 24 × 19 = 456 |
| 24 × 20 = 480 |
Чтобы понять концепцию поиска кратных, давайте рассмотрим еще несколько примеров.
- Кратное 20 — Первые пять кратных 20 равны 20, 40, 60, 80, 100
- Кратное 12 — Первые пять кратных 12 равны 12, 24, 36, 48 и 60
- Число, кратное 24 — Первые пять чисел, кратные 24: 24, 48, 72, 96 и 120
- , кратное 18 — первые пять кратных 18: 18, 36, 54, 72 и 90
- Кратное 8 — Первые пять кратных 8 равны 8, 16, 24, 32 и 40
Чтобы получить кратное любого числа, воспользуйтесь одним из двух способов:
- Умножьте это число на любое целое и пропустите счет, чтобы получить последовательные кратные
- Или повторить сложение
Часто задаваемые вопросы, кратные 24
Как найти число, кратное 24?
Умножьте 24 на целые и получите число, кратное 24, или пропустите счет.
Могут ли 8 и 3 делиться на 24?
24 делится как на 3, так и на 8, потому что 3 x 8 = 24. Следовательно, 8 и 3 кратны 24.
Каковы первые пять чисел, кратных 24?
Первые пять чисел, кратных 24, равны 24, 48, 72, 96 и 120.
Каковы все числа, кратные 25?
Число, кратное 25, равно 25, 50, 75, 100, 125, 150 и т. Д.
Каковы общие числа, кратные 24 и 12?
Число, кратное 24, равно 24, 48, 72, 96, 120, 144, 168, 192 и т. Д.
Кратные 12 равны 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144 и т. Д.
Общие числа, кратные 24 и 12, равны 24, 48, 72, 96, 120, 144, 168, 192 и т. Д.
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби.Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т.е. для пяти сотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.
Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью i.е., 1 2/3 (того же знака). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть 1/2: 3 .
Десятичные числа (десятичные числа) вводятся с десятичной запятой . , и они автоматически конвертируются в дроби, то есть 1,45 .
Двоеточие : и косая черта / являются символом разделения.1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых и дробных чисел: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичные дроби: 0,625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок, деление, умножение, сложение, вычитание.
GEMDAS — Группировка символов — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Задачи на дроби:
следующие математические задачи »
Вычисление в умножении
Это полный урок с инструкциями и упражнениями по использованию вычислений при умножении, предназначенный для 5-6 классов. Для оценки ученики округляют двузначные и трехзначные числа перед умножением, но это округление может быть выполнено несколькими способами.Далее следуют различные упражнения и задачи со словами.
Чтобы оценить результат умножения (произведение), округлите числа до Один из методов оценки — округлить все Например, оценка 365 × 24 .Круглый 365 до ближайшего Посмотрите другие примеры:
|
Практика
1.Оцените продукты, округляя множители до наибольшего числа.
значение.
а. 158 × 32 ≈ 200 × 30 = 6000 | г. 29 × 94 ≈ ____ × ___ = ____ |
г. 770 × 33 ≈ ____ × ___ = ____ | ф. 88 × 99 ≈ ____ × ___ = ____ |
Дж.486 × 21 ≈ ____ × ___ = ____ | л. 209 × 27 ≈ ____ × ___ = ____ |
2. Одна из целей оценки — выявить грубые ошибки в
расчеты. Например, если вы оцениваете результат в 5000, и вы
вычислите, что это 354, вы знаете, что что-то не так, так как вы далеко.
Какова наилучшая оценка из представленных вариантов?
1.103 × 52 2. 42 × 76 3. 319 × 25 4. 17 × 17 5. 99 × 59 6. 47 × 21 | а. 6500 а. 4000 а. 6000 а. 1000 а. 6000 а. 470 | г. 500 г. 320 г. 750 г.200 г. 900 г. 9700 | г. 5000 г. 4800 г. 9000 г. 400 г. 9000 г. 1000 |
3. Какой продукт больше всего отличается от оценки? Может
ты понимаешь почему?
|
Другие методы оценки Если округлить оба множителя до наибольшего разряда, то получится 249
Оценка — это не точная наука, а вопрос округления до конца |
4. Сначала оцените, а затем рассчитайте фактический продукт. Ты можешь
используйте различные способы оценки по своему усмотрению. Или попробуйте два разных метода
оценки и сравнить, что было более точным.
| Оценки: | Реальность: | |
| а. | 143 × 27 ≈ ________ × _________ = __________ | 143 × 27 = _________ |
| б. | 657 × 13 ≈ ________ × _________ = __________ | 657 × 13 = _________ |
| c. | 411 × 9 ≈ ________ × _________ = __________ | 411 × 9 = _________ |
| я. | 406 × 19 ≈ ________ × _________ = __________ | 406 × 19 = _________ |
| k. | 243 × 24 ≈ ________ × _________ = __________ | 243 × 24 = _________ |
| л. | 37 × 258 ≈ ________ × _________ = __________ | 37 × 258 = _________ |
5.Решите проблемы со словом. При необходимости округлите числа, чтобы сделать оценку.
а. Нелли пересчитала спички в спичечной коробке и получила 58.
Сколько совпадений примерно в в 8 коробках?
Каждый день Нелли использует 10 спичек. Как долго примерно
хватит ли ей этих 8 коробок?
б. Куры тети Джини откладывают около 130 яиц в день.
Сможет ли она доставить все яйца в указанную выше школу в течение одной недели?
Обратите внимание, ее куры откладывают яйца 7 дней в неделю.

 Ответ: 230
Ответ: 230