§ Деление в столбик. Как делить столбиком без остатка

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

Математика 5 класс

Математика 6 класс

Алгебра 7 класс

Геометрия 7 класс

Алгебра 8 класс

Алгебра 9 класс

Алгебра 10 класс

Алгебра 11 класс

Знать много языков — значит иметь много ключей к одному замку.
Вольтер

как объяснить ребенку деление в столбик

Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.

• Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
• Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
• Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям

Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.

Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».

Итак, как объяснить ребенку деление столбиком
:

• Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
• Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
• Пусть ребенок сам разделит другое число, например, более сложное: 24:4
• Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные

Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.

Начинайте с простого — деление на однозначное число:

Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.

Например, 256 разделить на 4:

• Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
• Спросите у малыша, сколько четверок помещается в двойке — нисколько
• Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
• Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
• Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
• Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
• Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»

Письменное деление на двузначное число

Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.

Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.

Выполните вместе такое простое действие: 184:23 — как нужно объяснять:

• Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
• Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8

Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.

Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:

• Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
• Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
• Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
• Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно

Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.

Например:

• Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
• Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
• Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
• Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
• Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
• Запишите 2864 под 2864, получается в разности 0. Ответ 204

Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.

Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.

Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):

• Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
• Делится эта цифра на 8? Правильно — нет. Получается, остаток 3

После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:

• В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
• Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
• Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
• К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
• Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375

Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.

Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.

Алгоритм деления чисел заключается в следующем:

• Сделать прикидку числа, которое будет стоять в ответе
• Найти первое неполное делимое
• Определить число цифр в частном
• Найти цифры в каждом разряде частного
• Найти остаток (если он есть)

По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).

Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:

• 1428:42
• 2924:68
• 30296:56
• 136576:64
• 16514:718

Для закрепления результата можно использовать такие игры на деление:

• «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.

Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.

Видео: Игра арифметика для детей сложение вычитание деление умножение

Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2

Деление
многозначных или многоразрядных чисел удобно производить письменно в столбик
. Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого.

Итак, поделим 354

на 2

. Для начала разместим эти числа как показано на рисунке:

Делимое размещаем слева, делитель справа, а частное будем записывать под делителем.

Теперь начинаем делить делимое на делитель поразрядно слева на право. Находим первое неполное делимое
, для этого берем первый слева разряд, в нашем случае 3 и сравниваем с делителем.

3

больше 2

, значит 3

и есть неполное делимое. Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:

Для того чтобы 3

разделить на 2

вспоминаем таблицу умножения на 2 и находим число при умножении которого на 2 получим наибольшее произведение, которое меньше 3.

2 × 1
= 2
(2

2 × 2 = 4 (4 > 3)

2

меньше 3

, а 4

больше, значит, берем первый пример и множитель 1

.

Записываем 1

в частное на место первой точки (в разряд сотен), а найденное произведение записываем под делимым:

Теперь находим разность, между первым неполным делимым и произведением найденного разряда частного и делителем:

Полученное значение сравниваем с делителем. 15

больше 2

, значит, мы нашли второе неполное делимое. Для того чтобы найти результат деления 15

на 2

вновь вспоминаем таблицу умножения на 2

и находим наибольшее произведение, которое меньше 15

:

2 × 7
= 14
(14

2 × 8 = 16 (16 > 15)

Искомый множитель 7

, записываем его в частное на место второй точки (в десятки). Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:

Продолжаем деление, для чего находим третье неполное делимое
. Спускаем следующий разряд делимого:

Делим неполное делимое на 2, полученное значение ставим в разряд единиц частного. Проверим правильность деления:

2 × 7
= 14

Результат деления третьего неполного делимого на делитель пишем в частное, находим разность:

Разность мы получили равную нулю, значит деление произведено правильно
.

Усложним задачу и приведем другой пример:

1020 ÷ 5

Запишем наш пример в столбик и определим первое неполное частное:

Разряд тысяч делимого составляет 1

, сравниваем с делителем:

1

Добавляем в неполное делимое разряд сотен и сравниваем:

10 > 5

– мы нашли неполное делимое.

Делим 10

на 5

, получаем 2

, записываем результат в частное. Разность между неполным делимым и результатом умножения делителя и найденного разряда частного.

10 – 10 = 0

0

мы не пишем, опускаем следующий разряд делимого – разряд десятков:

Сравниваем второе неполное делимое с делителем.

2

Нам следует добавить в неполное делимое ещё один разряд, для этого в частное, на разряд десятков ставим 0

:

20 ÷ 5 = 4

Записываем ответ в разряд единиц частного и проверяем: записываем произведение под второе неполное делимое и вычисляем разность. Получаем 0

, значит пример решён правильно
.

И ещё 2 правила деления в столбик:

1. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить, например:

Сколько нулей в младшем разряде делимого мы убираем, столько же нулей убираем в младших разрядах делителя.

2. Если в делимом после деления остались нули, то их следует перенести в частное:

Итак, сформулируем последовательность действий при делении в столбик.

1. Размещаем делимое слева, делитель справа. Помним, что делимое мы делим, поразрядно выделяя неполные делимые и деля их последовательно на делитель. Разряды в неполное делимое выделяются слева направо от старших к младшим.
2. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить.
3. Определяем первый неполный делитель:

а)
выделяем в неполный делитель старший разряд делимого;

б)
сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (в)
, если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4
;

в)
добавляем в неполное делимое следующий разряд и переходим к пункту (б)
.

1. Определяем сколько разрядов будет в частном, и ставим столько точек на месте частного (под делителем) сколько будет в нем разрядов. Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого.
2. Делим неполное делимое на делитель, для этого находим число, при умножении которого на делитель получилось бы число либо равное неполному делимому, либо меньше его.
3. Найденное число записываем на место очередного разряда частного (точки), а результат умножения его на делитель записываем под неполным делимым и находим их разность.
4. Если найденная разность меньше или равна неполному делимому значит, мы правильно поделили неполное делимое на делитель.
5. Если в делимом остались еще разряды, то продолжаем деление, иначе переходим к пункту 10
   .
6. Опускаем к разности следующий разряд делимого и получаем очередное неполное делимое:

а) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (б), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;

б) добавляем к неполному делимому следующий разряд делимого, при этом в частное на место следующего разряда (точки) пишем 0;

в) переходим к пункту (а).

10. Если мы выполняли деление без остатка и последняя найденная разность равна 0

, то мы правильно выполнили деление
.

Мы говорили о делении многоразрядного числа на одноразрядное. В случае, когда разрядность делителя больше, деление выполняется аналогично:

В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.

Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.

Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.

Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.

Как умножаются в столбик натуральные числа?

Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:

1. До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
2. Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
3. То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.

Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.

Алгоритм умножения в столбик десятичных дробей

Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.

Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.

Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:

С чего начать обучение делению?

До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.

После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?

После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.

Алгоритм деления чисел в столбик

Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:

• До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
• Записать делимое. Справа от него — делитель.
• Прочертить слева и снизу около последнего уголок.
• Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
• Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
• Записать результат от умножения этого числа на делитель.
• Написать его под неполным делимом. Выполнить вычитание.
• Снести к остатку первую цифру после той части, которая уже разделена.
• Снова подобрать число для ответа.
• Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.

Как решать деление в столбик, если в делителе больше одной цифры?

Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.

Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.

Рассмотреть такое деление можно на примере — 12082: 863.

• Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
• После вычитания получается остаток 345.
• К нему нужно снести цифру 2.
• В числе 3452 четыре раза умещается 863.
• Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
• Остаток после вычитания равен нулю. То есть деление закончено.

Ответом в примере будет число 14.

Как быть, если делимое заканчивается на ноль?

Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.

Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.

Что делать, если разделить нужно десятичную дробь?

Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.

Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.

Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.

Деление двух десятичных дробей

Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.

Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.

Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.

В качестве примера: 28,4 делим на 3,2:

• Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
• Их полагается разделить. Причем сразу все число 284 на 32.
• Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
• Деление целой части закончилось, и в ответ полагается поставить запятую.
• Снести к остатку 0.
• Снова взять по 8.
• Остаток: 24. К нему приписать еще один 0.
• Теперь брать нужно 7.
• Результат умножения — 224, остаток — 16.
• Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.

Деление закончено. Результат примера 28,4:3,2 равен 8,875.

Что делать, если делитель равен 10, 100, 0,1, или 0,01?

Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.

Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.

Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.

При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).

Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.

Деление периодических дробей

В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.

Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.

Если в примере разные дроби…

Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.

Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.

Калькулятор в столбик для Андроид устройств станет замечательным помощником для современных школьников. Программа не только дает правильный ответ на математическое действие, но и наглядно демонстрирует его пошаговое решение. Если же вам нужны более сложные калькуляторы – можете посмотреть или же продвинутый инженерный калькулятор.

Особенности

Главной особенностью программы является уникальность расчета математических операций. Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .

Чтобы начать пользоваться программой, необходимо скачать калькулятор в столбик на Андроид. Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс.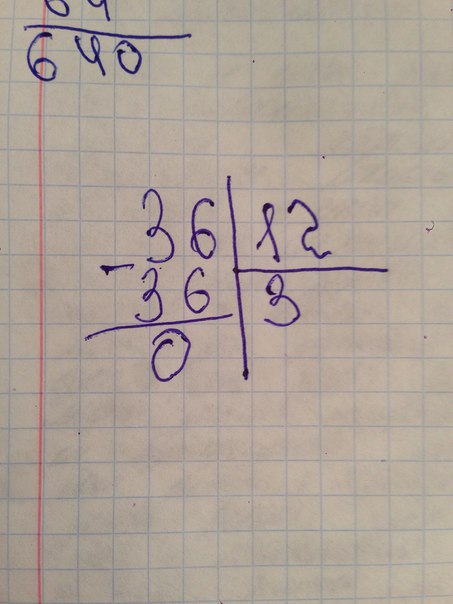 После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками:

1. Цифры.
2. Знаки арифметических действий.
3. Удаление раннее введенных символов.

Ввод осуществляется по тому же принципу, что и на . Все отличие состоит только в интерфейсе приложения – все математические вычисления и их результат отображаются в виртуальной ученической тетради.

Приложение позволяет быстро и правильно выполнить стандартные для школьника математические вычисления столбиком:

• умножение;
• деление;
• сложение;
• вычитание.

Приятным дополнением в приложении является функция ежедневного напоминания о домашнем задании по математике. Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании.

Достоинства и недостатки

1. Помогает школьнику не просто быстро получить правильный результат математических вычислений, но и понять сам принцип расчета.
2. Очень простой, интуитивно понятный интерфейс для каждого пользователя.
3. Установить приложение можно даже на самое бюджетное Андроид устройство с операционной системой 2.2 и более поздней версией.
4. Калькулятор сохраняет историю проведенных математических вычислений, которую можно в любой момент очистить.

Калькулятор ограничен в математических операциях, поэтому применить его для сложных расчетов, с какими мог бы справиться инженерный калькулятор, не получится. Однако учитывая назначение самого приложения – наглядно продемонстрировать учащимся младшей школы принцип расчета в столбик, считать это недостатком не стоит.

Приложение также станет отличным помощником не только для школьников, но и для родителей, которые желают заинтересовать своего ребенка математикой и научить его правильно и последовательно производить вычисления. Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.

Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!

Деление чисел

Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.

Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

Деление с остатком

Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.

Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).

Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).

Деление на 3 и 9

Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:

Найти сумму цифр делимого.

Поделить на 3 или 9 (в зависимости от того, что вам нужно).

Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.

Умножение и деление

Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.

Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4.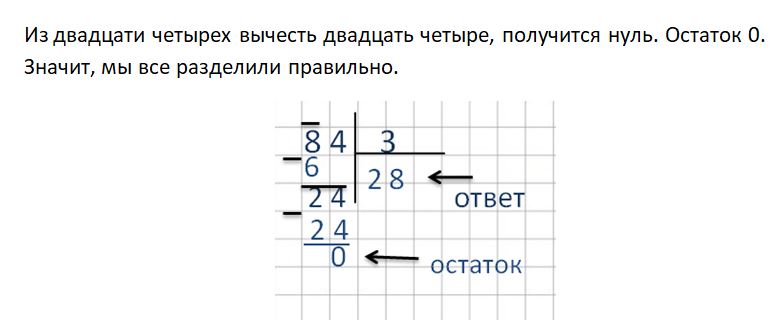 Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.

Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Задача 1
. Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?

Задача 2
. На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?

Задача 3
. Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?

Задача 4
. Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?

Деление 4 класс

Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:

Деление в столбик

Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.

Рассмотрим пример, 512:8.

1 шаг
. Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг
. Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг
. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг
. Ставим точку под делителем.

5 шаг
. После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:

6 шаг
. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:

7 шаг
. Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг
. Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг
*. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг
Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.

Деление дробей

Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3)
(4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.

Деление числа на классы

Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.

Деление натуральных чисел

Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Деление презентация

Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!

Примеры на деление

Легкий уровень

Средний уровень

Сложный уровень

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.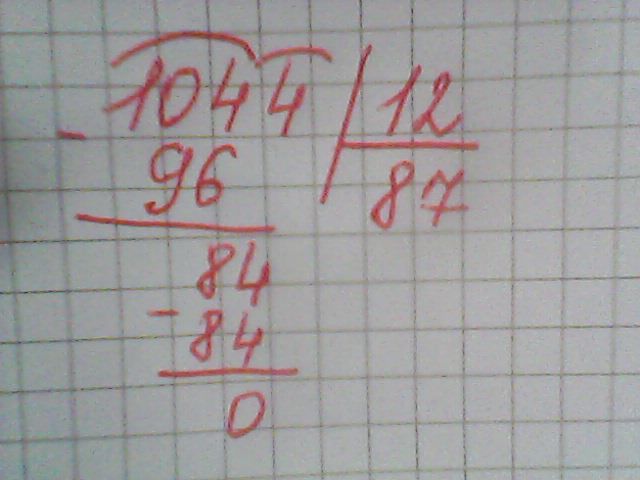

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Копилка»

Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение перезагрузка»

Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Математика 4 класс Богданович. Решебник. ГДЗ. Деление чисел, оканчивающихся нулями. Задание 746

Категория: —>> Математика 4 класс Богданович  


Задание:  —>>     746 — 765  766 — 785  786 — 809 



Задание 746.

Рассмотрите решение примера разными способами. Объясните правило деления числа на произведение.

Решение:

108 : (18 * 2) = ?

• 108 : 36 = 3
• (108 : 18): 2 = 6 : 2 = 3
• (108 : 2) : 18 = 54 : 18 = 3

Задание 747.

Ученик решил примеры. Объясните, чем удобен этот способ.

Решение:

• 540 : (2 * 5) = 540 : 10 = 54
• 540 : (6 * 18) = (540 : 6): 18 = 90 : 18 = 5
• 5600 : (14 * 100) = (5600 : 100) : 14 = 56 : 14 = 4

Задание 748.

Найдите значения выражений удобным способом.

• 36000 : (25 * 4) = ?
• 720 : (8 * 3) = ?
• 960 : (24 : 2) = ?

Решение:

• 36000 : (25 * 4) = 36000 : 100 = 360
• 720 : (8 * 3) = (720 : 8) : 3 = 90 : 3 = 30
• 960 : (24 : 2) = (960 : 2) : 24 = 480 : 24 = 20

Задание 749.

Рассмотрите примеры и объясните применение правила деления числа на произведение для устного деления на двузначное и разрядное число.

Решение:

• 168 : 28 = 168 : (4 * 7) = 168 : 4 : 7 = 6
• 56000 : 800 = 56000 : (100 * 8) = 56 000 : 100 : 8 = 560 : 8 = 70

Задание 750.

Решите примеры:

• 3600 : 60 = ?
• 360 : 12 = ?
• 7200 : 600 = ?
• 270 : 45 = ?

Решение:

• 3600 : 60 = 3600 : (10 * 6) = 3600 : 10 : 6 = 60
• 360 : 12 = 360 : (6 * 2) = 360 : 6 : 2 = 30
• 7200 : 600 = 7200 : (100 * 6) = 7200 : 100 : 6 = 12
• 270 : 45 = 270 : (9 * 5) = 270 : 9 : 5 = 6

Задание 751.

Двумя автомобилями перевезли 60т картофеля. Первым перевезли 20т, а вторым — оставшийся картофель. Грузоподъёмность автомобилей одинакова. Общее количество рейсов 12. Сколько рейсов сделал каждый автомобиль?

Решение:

1. 60 : 12 = 5(т) — за один рейс.
2. 20 : 5 = 4(р.) — сделал первый автомобиль.
3. 60 — 20 = 40(т) — картофель перевез второй автомобиль.
4. 40 : 5 = 8(р.) — сделал второй автомобиль.

Ответ: Первый автомобиль сделал 4 рейса, а второй — 8 рейсов.

Задание 752.

Расстояние между двумя пунктами 1456км. Из этих пунктов одновременно навстречу друг другу выехали два автобуса. Какое расстояние будет между автобусами,когда первый проедет 3/8, а второй 2/7 всего пути?

Решение:
1456 : 8 * 3 = 546(км) — проедет первый автобус.
1456 : 7 * 2 = 416(км) — проедет второй автобус.
546 + 416 = 962(км) — проедут оба автобуса.
1456 — 962 = 494(км) — будет расстояние между ними, когда первый проедет 3/8, а второй 2/7 всего пути.
Ответ: 494км будет расстояние между ними, когда первый проедет 3/8, а второй 2/7 всего пути.

Задание 753.

Выполните деление с остатком.

• 23 : 4 = ?
• 30 : 7 = ?
• 48 : 9 = ?
• 51 : 7 = ?

Решение:
23 : 4 = 5(ост. 3)
30 : 7 = 4(ост. 2)
48 : 9 = 5(ост. 3)
51 : 7 = 7(ост. 2)

Задание 754.

Решите примеры:

• 25 : 3 = ?
• 60 : 8 = ?
• 27 : 4 = ?
• 56 : 6 = ?

Решение:

• 25 : 3 = 8(ост. 1)
• 60 : 8 = 7(ост. 4)
• 27 : 4 = 6(ост. 3)
• 56 : 6 = 9(ост. 4)

Задание 755.

Решите примеры:

• 240 : 30 = ?
• 6300 : 900 = ?
• 300 * 70 + 420000 = ?
• 240 : 120 = ?
• 6300 : 800 = ?
• 100000 — 600 * 20 = ?

Решение:

• 240 : 30 = 8
• 6300 : 900 = 7
• 300 * 70 + 420000 = 21000 + 420000 = 441000
• 240 : 120 = 2
• 6300 : 800 = 21
• 100000 — 600 * 20 = 100000 — 12000 = 88000

Задание 756.

Решите примеры:

• 46000 : 100 = ?
• 48000 : 1000 = ?
• 8840 : 10 = ?
• 24 : 8 = ?
• 30 : 5 = ?
• 18 : 6 = ?
• 72 : 9 = ?
• 26 : 8 = ?
• 33 : 5 = ?
• 21 : 6 = ?
• 80 : 9 = ?

Решение:

• 46000 : 100 = 460
• 46000 : 1000 = 46
• 8840 : 10 = 884
• 24 : 8 = 3
• 30 : 5 = 6
• 18 : 6 = 3
• 72 : 9 = 8
• 26 : 8 = 3(ост. 2)
• 33 : 5 = 6(ост. 3)
• 21 : 6 = 3(ост. 3)
• 80 : 9 = 8(ост. 8)

Задание 757.

Рассмотрите деление с остатком на двузначное число.

Решение:

53 : 16 = 3(ост. 5)

Объяснение: Способом подбора найдём число, которое меньше 53 и делится на 16. Это число 48. 16 умножить на 3, будет 48. В частном 3. Найдём остаток: 53 — 48 = 5. В остатке 5.

Ответ: 53 разделить на 16, будет 3 и в остатке 5.

Задание 758.

Найдите частное и остаток:

• 60 : 16 = ?
• 40 : 15 = ?
• 80 : 35 = ?
• 560 : 80 = ?
• 300 : 50 = ?
• 52 : 24 = ?
• 75 : 21 = ?
• 420 : 70 = ?
• 6400 : 800 = ?
• 400 : 80 = ?

Решение:

• 60 : 16 = 3(ост. 12)
• 52 : 24 = 2(ост. 4)
• 40 : 15 = 2(ост. 10)
• 80 : 35 = 2(ост. 10)
• 420 : 70 = 6
• 400:80 = 5
• 560 : 80 = 7
• 300:50 = 6

Задание 759.

Масса двух снежных барсов 80кг. Какова масса четырёх одинаковых львов, если лев в 5 раз тяжелее снежного барса?

Решение:

1. 80 : 2 = 40(кг) — масса одного снежного барса.
2. 40 * 5 = 200(кг) — масса одного льва.
3. 200 * 4 = 800(кг) — масса 4 одинаковых львов.

Ответ: 800 масса 4 одинаковых львов.

Задание 760.

За 10ч работы двигателя израсходовали 90л горючего: 54л до перерыва, а остальное после перерыва. Сколько часов двигатель работал до перерыва и сколько после, если расход горючего за час был одинаковым?

Решение:

1. 90 : 10 = 9(л) — горючего расходуется в час.
2. 54 : 9 = 6(ч) — работал до перерыва.
3. 90 — 54 = 36(л) — горючего после перерыва.
4. 36 : 9 = 4(ч) — работал после перерыва.

Ответ: до перерыва двигатель работал 6 часов, а после — 4 часа.

Задание 761.

Найдите значение выражения: 250 * b — b * 5, если b = 200.

Решение:

Если b = 200, то 250 * 200 — 200 * 5 = 50000 — 1000 = 49000

Задание 762.

За сутки 3 берёзы и 2 эвкалипта вместе поглощают 760л воды. Одна берёза поглощает 40л воды. Сколько литров воды поглощает один эвкалипт за сутки?

Решение:

1. 3 * 40 = 120(л) — поглощает 3 березы.
2. 760 — 120 = 640(л) — поглощает 2 эвкалипта.
3. 640 : 2 = 320(л) — поглощает один эвкалипт за сутки.

Ответ: 320л воды поглощает один эвкалипт за сутки.

Задание 763.

Решите примеры:

• 32 : 5 = ?
• 40 : 12 = ?
• 630 : 90 = ?
• 5400 : 60 = ?
• 70 : 8 = ?
• 72 : 30 = ?
• 630 : 30 = ?
• 3200 : 80 = ?

Решение:

• 32 : 5 = 6(ост. 2)
• 40 : 12 = 3(ост. 4)
• 630 : 90 = 7
• 5400 : 60 = 90
• 70 : 8 = 8(ост. 6)
• 72 : 30 = 2(ост. 12)
• 630 : 30 = 21
• 3200 : 80 = 40

Задание 764.

Рассмотрите, как устно и письменно нашли частное и остаток от деления чисел 294 и 40.

Решение:
Устно. 294 : 40 = 294 :(10 * 4) = 294 : 10 : 4 = 7(ост. 14).
Объяснение: Будем находить частное последовательным делением на 10 и 4. В процессе выполнения отдельных действий остаток не нужно находить, но следует помнить, что он должен быть меньше делителя. 294 разделить на 10, будет 29. 29 разделить на 4, будет 7. Частное равно 7. Узнаем, сколько разделили. 40 умножить на 7, будет 280. Найдём остаток: 294 — 280 = 14.
Письменно. Чтобы разделить 294 на 40, нужно сначала разделить это число на 10, будет 29. Затем разделим 29 на 4: можно взять по 7. Узнаем, какое число разделили. Умножим 40 на 7, будет 280. Узнаем, сколько осталось: 294 — 280 = 14. Частное 7, остаток 14.

Задание 765.

Рассмотрите записи и объясните решение.

Решение:

1. 385 : 70 = ?

Чтобы разделить 385 на 70, нужно сначала разделить это число на 10, будет 38. Затем разделим 38 на 7: можно взять по 5. Узнаем какое число разделили. Умножим 70 на 5, будет 350. Узнаем, сколько осталось: 385 — 350 = 35. Частное 5, остаток 35.

2. 608 : 80 = ?

Чтобы разделить 608 на 80, нужно сначала разделить это число на 10, будет 60. Затем разделим 60 на 8: можно взять по 7. Узнаем,какое число разделили. Умножим 80 на 7, будет 560. Узнаем, сколько осталось: 608 — 560 = 48. Частное 7, остаток 48.



Задание:  —>>     746 — 765  766 — 785  786 — 809 

Деление и другие математические действия

Мы уже говорили о делении и об основных правилах деления. Продолжим изучать деление и разберем, как можно упростить некоторые примеры с участием деления, такие как:

1. Деление произведения двух чисел на число;
2. Деление числа на произведение двух чисел;
3. Деление суммы двух чисел на третье число;
4. Деление разности двух чисел на третье число;
5. Сумма или разность двух частных, в которых делители одинаковы.

Деление произведения двух чисел на число

Чтобы разделить произведение двух чисел на число, разделите на это число один из множителей, а полученное частное умножьте на второй множитель.

Например:

36 × 7 ÷ 4 = (36 ÷ 4) × 7 = 9 × 7 = 63

15 × 44 ÷ 11 = (44 ÷ 11) × 15 = 4 × 15 = 60

Если ни один из множителей не делится на третье число, то следует вычислить произведение двух первых чисел и потом поделить на третье число.

15 × 24 ÷ 9 = 360 ÷ 9 = 40

Деление числа на произведение двух чисел

Чтобы разделить число на произведение двух чисел, разделите это число на один из множителей, а затем полученное частное разделите на другой множитель.

Например:

432 ÷ (36 × 6) = 432 ÷ 36 ÷ 6 = 2

3072 ÷ (12 × 32) = 3072 ÷ 12 ÷ 32 = 8

Этот прием называется приемом последовательного деления.

Деление суммы двух чисел на третье число

Чтобы разделить сумму двух чисел на третье число, разделите каждое слагаемое суммы на это число, а затем сложите полученные частные.

Например:

(28 + 42) ÷ 7 = 28 ÷ 7 + 42 ÷ 7 = 10

Если числа в скобках не делятся на третье число, то вычисляем по правилам «порядка выполнения математических действий».

(115 + 95) ÷ 6 = 35

Для удобства деления представьте делимое суммой двух чисел:

96 ÷ 8 = (40 + 56) ÷ 8 = 40 ÷ 8 + 56 ÷ 8 = 12

Деление разности двух чисел на третье число

Чтобы разделить разность двух чисел на третье число, разделите уменьшаемое и вычитаемое на это число, а затем найдите разность первого и второго частного

 Например:

(70 – 14) ÷ 7 = 70 ÷ 7 – 14 ÷ 7 = 10 – 2 = 8

856 ÷ 8 = (800 – 56) ÷ 8 = 800 ÷ 8 – 56 ÷ 8 = 100 – 7 = 93

Если числа в скобках не делятся на третье число, то вычисляем по правилам «порядка выполнения математических действий».

(200 – 56) ÷ 6 = 144 ÷ 6 = 24

Сумма или разность двух частных, в которых делители одинаковы

Если в сумме или разности двух частных делители одинаковы, найдите сначала сумму или разность делимых, а затем полученный результат поделите на делитель.

Например:

48 ÷ 6 + 18 ÷ 6 = (48 + 18) ÷ 6 = 66 ÷ 6 = 11

63 ÷ 9 – 36 ÷ 9 = (63 – 36) ÷ 9 = 27 ÷ 9 = 3

Спасибо, что Вы с нами!

Понравилась статья — поделитесь с друзьями:

Оставляйте пожалуйста комментарии в форме ниже

НОД и НОК

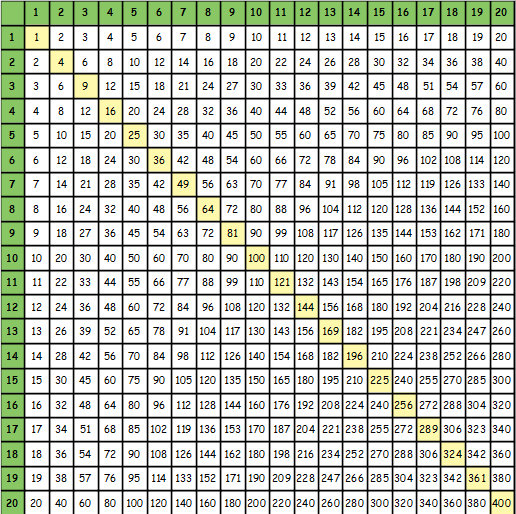
Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.

НОД — это наибольший общий делитель.

НОК — это наименьшее общее кратное.

Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.

Наибольший общий делитель

Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.

Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:

Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.

Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.

Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.

Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.

Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.

Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.

12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)

12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)

12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)

12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)

12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)

12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)

12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)

12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)

12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)

12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)

12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)

12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)

Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9

9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)

9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)

9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)

9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)

9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)

9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)

9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)

9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)

9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)

Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:

Выписав делители, можно сразу определить какой является наибольшим и общим.

Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3

И число 12 и число 9 делятся на 3 без остатка:

12 : 3 = 4

9  : 3 = 3

Значит НОД (12 и 9) = 3

Второй способ нахождения НОД

Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.

Пример 1. Найти НОД чисел 24 и 18

Сначала разложим оба числа на простые множители:

Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.

Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:

Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.

Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.

Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:

Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:

2 × 3 = 6

Значит НОД (24 и 18) = 6

Третий способ нахождения НОД

Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.

Пример 1. Найти НОД чисел 28 и 16.

В первую очередь, раскладываем числа 28 и 16 на простые множители:

Получили два разложения:  и 

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:

Теперь перемножаем оставшиеся множители и получаем НОД:

Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:

28 : 4 = 7

16 : 4 = 4

 НОД (28 и 16) = 4

Пример 2. Найти НОД чисел 100 и 40

Раскладываем на множители число 100

Раскладываем на множители число 40

Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения

Перемножим оставшиеся числа:

Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:

100 : 20 = 5

40 : 20 = 2

 НОД (100 и 40) = 20.

Пример 3. Найти НОД чисел 72 и 128

Раскладываем на множители число 72

Раскладываем на множители число 128

Получили два разложения: 2 × 2 × 2 × 3 × 3 и 2 × 2 × 2 × 2 × 2 × 2 × 2.

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:

Перемножим оставшиеся числа:

Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:

72 : 8 = 9

128 : 8 = 16

 НОД (72 и 128) = 8

Нахождение НОД для нескольких чисел

Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.

Например, найдём НОД для чисел 18,  24  и  36

Разложим на множители число 18

Разложим на множители число 24

Разложим на множители число 36

Получили три разложения:

Теперь найдём и подчеркнём общие множители:

Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:

2 × 3 = 6

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:

18 : 6 = 3

24 : 6 = 4

36 : 6 = 6

 НОД (18, 24 и 36) = 6

Пример 2. Найти НОД для чисел 12, 24, 36 и 42

Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.

Разложим на множители число 12

Разложим на множители число 24

Разложим на множители число 36

Разложим на множители число 42

Получили четыре разложения:

Теперь найдём и подчеркнём общие множители:

Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:

2 × 3 = 6

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:

12 : 6 = 2

24 : 6 = 4

36 : 6 = 6

42 : 6 = 7

 НОД (12, 24 , 36 и 42) = 6

Наименьшее общее кратное

Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.

Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.

Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.

Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:

Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.

Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.

Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.

В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.

Итак, начнём. Кратные будем выделять синим цветом:

Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:

Теперь выпишем кратные обоих чисел:

Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:

Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.

Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

36 : 9 = 4

36 : 12 = 3

НОК (9 и 12) = 36

Второй способ нахождения НОК

Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.

Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.

Разложим на множители число 9

Разложим на множители число 12

Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

36 : 9 = 4

36 : 12 = 3

НОК (9 и 12) = 36

Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.

Наша задача состояла в том, чтобы организовать новое разложение куда входило бы разложение числа 9 и разложение числа 12 одновременно. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12

Пример 2. Найти НОК чисел 50 и 180

Разложим на множители число 50

Разложим на множители число 180

Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:

900 : 50 = 18

900 : 180 = 5

НОК (50 и 180) = 900

Пример 3. Найти НОК чисел 8, 15 и 33

Разложим на множители число 8

Разложим на множители число 15

Разложим на множители число 33

Выпишем первое разложение:

Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:

Теперь перемножаем эти множители:

Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:

1320 : 8 = 165

1320 : 15 = 88

1320 : 33 = 40

НОК (8, 15 и 33) = 1320

Третий способ нахождения НОК

Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.

Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.

К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:

Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.

Итак, перемножим числа 24 и 12

Разделим полученное число 288 на НОД чисел 24 и 12

Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24

НОК (24 и 12) = 24

Пример 2. Найти НОД и НОК чисел 36 и 48

Найдем НОД чисел 36 и 48

Перемножим числа 36 и 48

Разделим 1728 на НОД чисел 36 и 48

Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144

НОК (36 и 48) = 144

Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144

Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».

Задания для самостоятельного решения

Задание 1. Найдите НОД чисел 12 и 16

Решение:

Задание 2. Найдите НОК чисел 12 и 16

Решение:

Задание 3. Найдите НОД чисел 40 и 32

Решение:

Задание 4. Найдите НОК чисел 40 и 32

Решение:

Задание 5. Найдите НОД чисел 54 и 86

Решение:

Задание 6. Найдите НОК чисел 54 и 86

Решение:

Задание 7. Найдите НОД чисел 98 и 35

Решение:

Задание 8. Найдите НОК чисел 98 и 35

Решение:

Задание 9. Найдите НОД чисел 112 и 82

Решение:

Задание 10. Найдите НОК чисел 112 и 82

Решение:

Задание 11. Найдите НОД чисел 24, 48, 64

Решение:

Задание 12. Найдите НОК чисел 24, 48, 64

Решение:

Задание 13. Найдите НОД чисел 18, 48, 96

Решение:

Задание 14. Найдите НОК чисел 18, 48, 96

Решение:

Задание 15. Найдите НОД чисел 28, 24, 76

Решение:

Задание 16. Найдите НОК чисел 28, 24, 76

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

4 класс. Моро. Учебник №2. Ответы к стр. 58

Числа от 1 до 1000

Деление на двузначное и трёхзначное число
Письменное деление на двузначное число
Ответы к стр. 58

При делении с остатком на двузначное число рассуждают также, как и при делении без остатка. Объясни, как выполнено деление с остатком.
_ 324 |62     _ 526 |74     _ 793 |83
   310 |5          518 |7          474 |9
     14                   8                 46

Надо 324 разделить на 62.
Разделю 324 не на 62, а на 60, чтобы легче было найти цифру частного. Для этого разделю 32 на 6, получу 5. Это пробная цифра, её нельзя сразу записать в частном — сначала надо проверить, подходит ли цифра 5.
Умножу 62 на 5, получится 310. Вычту: 324 — 310 = 14, 14 меньше 62, значит, цифра 5 подходит, а 14 — остаток. Теперь её можно записать в частном.

Надо 526 разделить на 74.
Разделю 526 не на 74, а на 70, чтобы легче было найти цифру частного. Для этого разделю 52 на 7, получу 7. Это пробная цифра, её нельзя сразу записать в частном — сначала надо проверить, подходит ли цифра 7.
Умножу 74 на 7, получится 518. Вычту: 526 — 518 = 8, 8 меньше 74, значит, цифра 7 подходит, а 8 — остаток. Теперь её можно записать в частном.

Надо 793 разделить на 83.
Разделю 793 не на 83, а на 80, чтобы легче было найти цифру частного. Для этого разделю 79 на 8, получу 9. Это пробная цифра, её нельзя сразу записать в частном — сначала надо проверить, подходит ли цифра 9.
Умножу 83 на 9, получится 747. Вычту: 793 — 747 = 46, 46 меньше 83, значит, цифра 9 подходит, а 46 — остаток. Теперь её можно записать в частном.

211. Найди частное и остаток, проверь решение.
156 : 48     278 : 62     346 : 56     445 : 73

_— 156 |48      Проверка:
   144 |3        _× 48
     12                3
                     144

                     144 + 12 = 156

_— 278 |62      Проверка:
   248 |4        _× 62
     30                4
                     248

                     248 + 30 = 278

_— 346 |56      Проверка:
   336 |6        _× 56
     10                6
                     336

                     336 + 10 = 346

_— 445 |73      Проверка:
   438 |6        _× 73
      7                 6
                     438

                     438 + 7 = 445

212. Космонавты были в полёте 290 ч. Сколько это суток и часов?

1 сутки = 24 часа

_— 290 |24 
   24   |12 — суток
   _50
     48
       2 — часа
О т в е т: 12 суток и 2 часа.

213. Площадь первого участка 120 м², второго 160 м². При одинаковой норме высева на 1 м² на первом участке высеяли семян ржи на 1 кг меньше, чем на втором. Объясни, что означают выражения.
160 — 120     1000 : (160 — 120)     1000 : (160 — 120) • 160

160 — 120 — разница между площадями участков
1000 : (160 — 120) — столько грамм семян высеяли на 1 м²
1000 : (160 – 120) • 160 – столько грамм семян высеяли на втором участке

214. В международном автопробеге участвовало 350 машин. Экипаж каждой машины состоял из трёх спортсменов. До финиша не дошли 105 машин. Сколько машин и сколько спортсменов прибыли к финишу?

1) 350 – 105 = 245 (м.) — дошли до финиша
2) 245 • 3 = 735 (с.) — прибыли к финишу
О т в е т: 245 машин и 735 спортсменов.

215. Составь по задачам уравнения и реши их.
1) Какое число надо уменьшить на 28, чтобы получить число, равное сумме чисел 58 и 37?
2) Какое число надо увеличить в 8 раз, чтобы получить число, равное произведению чисел 80 и 12?
3) Какое число надо уменьшить в 28 раз, чтобы получить число, равное разности чисел 300 и 203?

1) x — 28 = 58 + 37
x — 28 = 95
x = 95 + 28
x = 123

2) x • 8 = 80 • 12
x • 8 = 960
x = 960 : 8
x = 120

3) x : 28 = 300 — 203
x : 28 = 97
x = 97 • 28
x = 2716

216. 384 : 96     192 : 48     648 : 72     352 • 46 — 5840 : 80

_— 384 |96         _— 192 |48
   384 |4              192 |4
       0                      0

_— 648 |72        
   648 |9
       0   

352 • 46 — 5840 : 80 = 16192 — 73 = 16119
 _×  352             _— 5840|80   
      46            560  |73
_{+ 2112            —}240                
 1408                240
 16192                  0

_16192
       73
 16119

217. Найди значения выражений 360 : с и 360 • с, если с = 1; c = 3; c = 4; c = 6; c = 10.
Наблюдай, как при этом изменяется частное, как изменяется произведение.

360 : 1 = 360     360 • 1 = 360
360 : 3 = 120     360 • 3 = 1080
360 : 4 = 90       360 • 4 = 1440
360 : 6 = 60       360 • 6 = 2160
360 : 10 = 36     360 • 10 = 3600
Значение частного уменьшается, а значение произведения увеличивается.

218. Выложи из палочек такую фигуру. Какие углы в этой фигуре? Переложи 4 палочки так, чтобы получилось два остроугольных треугольника. Будут ли эти треугольники равнобедренными? равносторонними?

В этой фигуре все углы тупые.
Эти треугольники будут и равнобедренными и равносторонними. Равнобедренный треугольник — это треугольник, у которого две стороны равны по длине. Условие равенства двух сторон является необходимым и достаточным, чтобы считать треугольник равнобедренным. Это условие в равностороннем треугольнике выполняется всегда. Следовательно равносторонний треугольник всегда является равнобедренным.

399 : 57     236 : 59     475 : 95     609 • 27 — 4320 : 60

_— 399 |57         _— 236 |59
   399 |7              236 |4
       0                      0

_— 475 |95        
   475 |5
       0   

609 • 27 — 4320 : 60 = 16443 — 72 = 16371
 _×  609             _— 4320|60   
      27            420  |72
_{+ 4263            —}120                
 1218                120
 16443                  0

_16443
       72
 16371

ЗАДАНИЕ НА ПОЛЯХ
МАГИЧЕСКИЙ КВАДРАТ

ГДЗ по математике. Учебник. 4 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.

Математика. 4 класс

4 класс. Моро. Учебник №2. Ответы к стр. 58

4.4 (87.33%) от 30 голосующих

Обзор формул — Excel

Если вы еще не Excel в Интернете, скоро вы увидите, что это не просто сетка для ввода чисел в столбцах или строках. Да, с помощью Excel в Интернете можно найти итоги для столбца или строки чисел, но вы также можете вычислять платежи по ипотеке, решать математические или инженерные задачи или находить лучшие сценарии в зависимости от переменных чисел, которые вы подключали.

Excel в Интернете делает это с помощью формул в ячейках. Формула выполняет вычисления или другие действия с данными на листе. Формула всегда начинается со знака равенства (=), за которым могут следовать числа, математические операторы (например, знак «плюс» или «минус») и функции, которые значительно расширяют возможности формулы.

Ниже приведен пример формулы, умножающей 2 на 3 и прибавляющей к результату 5, чтобы получить 11.

=2*3+5

Следующая формула использует функцию ПЛТ для вычисления платежа по ипотеке (1 073,64 долларов США) с 5% ставкой (5% разделить на 12 месяцев равняется ежемесячному проценту) на период в 30 лет (360 месяцев) с займом на сумму 200 000 долларов:

=ПЛТ(0,05/12;360;200000)

Ниже приведены примеры формул, которые можно использовать на листах.

• 
  =A1+A2+A3    Вычисляет сумму значений в ячейках A1, A2 и A3.

• 
  =КОРЕНЬ(A1)    Использует функцию КОРЕНЬ для возврата значения квадратного корня числа в ячейке A1.

• 
  =СЕГОДНЯ()    Возвращает текущую дату.

• 
  =ПРОПИСН(«привет»)     Преобразует текст «привет» в «ПРИВЕТ» с помощью функции ПРОПИСН.

• 
  =ЕСЛИ(A1>0)    Анализирует ячейку A1 и проверяет, превышает ли значение в ней нуль.

Элементы формулы

Формула также может содержать один или несколько из таких элементов: функции, ссылки, операторы и константы. («крышка») применяется для возведения числа в степень, а оператор * («звездочка») — для умножения.

Использование констант в формулах

Константа представляет собой готовое (не вычисляемое) значение, которое всегда остается неизменным. Например, дата 09.10.2008, число 210 и текст «Прибыль за квартал» являются константами. выражение или его значение константами не являются. Если формула в ячейке содержит константы, но не ссылки на другие ячейки (например, имеет вид =30+70+110), значение в такой ячейке изменяется только после изменения формулы.

Использование операторов в формулах

Операторы определяют операции, которые необходимо выполнить над элементами формулы. Вычисления выполняются в стандартном порядке (соответствующем основным правилам арифметики), однако его можно изменить с помощью скобок.

Типы операторов

Приложение Microsoft Excel поддерживает четыре типа операторов: арифметические, текстовые, операторы сравнения и операторы ссылок.

Арифметические операторы

Арифметические операторы служат для выполнения базовых арифметических операций, таких как сложение, вычитание, умножение, деление или объединение чисел. Результатом операций являются числа. Арифметические операторы приведены ниже.

Операторы сравнения

Операторы сравнения используются для сравнения двух значений. Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.

Текстовый оператор конкатенации

Амперсанд (&) используется для объединения (соединения) одной или нескольких текстовых строк в одну.

Операторы ссылок

Для определения ссылок на диапазоны ячеек можно использовать операторы, указанные ниже.

Порядок выполнения Excel в Интернете формулах

В некоторых случаях порядок вычисления может повлиять на возвращаемое формулой значение, поэтому для получения нужных результатов важно понимать стандартный порядок вычислений и знать, как можно его изменить.

Порядок вычислений

Формулы вычисляют значения в определенном порядке. Формула всегда начинается со знака равно(=).Excel в Интернете интерпретирует знаки после знака равно как формулу. После знака равно вычисляются элементы (операнды), такие как константы или ссылки на ячейки. Они разделены операторами вычислений. Excel в Интернете вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.

Приоритет операторов

Если в одной формуле несколько операторов, Excel в Интернете выполняет операции в том порядке, который показан в таблице ниже. Если формула содержит операторы с одинаковым приоритетом, например операторы деления и умножения, Excel в Интернете эти операторы оцениваются слева направо.

Использование круглых скобок

Чтобы изменить порядок вычисления формулы, заключите ее часть, которая должна быть выполнена первой, в скобки. Например, следующая формула дает результат 11, так как Excel в Интернете умножение выполняется перед с добавлением. В этой формуле число 2 умножается на 3, а затем к результату прибавляется число 5.

=5+2*3

Если же изменить синтаксис с помощью скобок, Excel в Интернете сбавляет 5 и 2, а затем умножает результат на 3, чтобы получить 21.

=(5+2)*3

В следующем примере скобки, в которые заключена первая часть формулы, принудительно Excel в Интернете сначала вычислить ячейки B4+25, а затем разделить результат на сумму значений в ячейках D5, E5 и F5.

=(B4+25)/СУММ(D5:F5)

Использование функций и вложенных функций в формулах

Функции — это заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке. Эти функции позволяют выполнять как простые, так и сложные вычисления.

Синтаксис функций

Приведенный ниже пример функции ОКРУГЛ, округляющей число в ячейке A10, демонстрирует синтаксис функции.

1. Структура. Структура функции начинается со знака равно (=), за которым следуют имя функции, открывая скобка, аргументы функции, разделенные запятой, и закрывая скобка.

2. Имя функции. Чтобы отобразить список доступных функций, щелкните любую ячейку и нажмите клавиши SHIFT+F3.

3. Аргументы. Существуют различные типы аргументов: числа, текст, логические значения (ИСТИНА и ЛОЖЬ), массивы, значения ошибок (например #Н/Д) или ссылки на ячейки. Используемый аргумент должен возвращать значение, допустимое для данного аргумента. В качестве аргументов также используются константы, формулы и другие функции.

4. Всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.

Ввод функций

Диалоговое окно Вставить функцию упрощает ввод функций при создании формул, в которых они содержатся. При вводе функции в формулу в диалоговом окне Вставить функцию отображаются имя функции, все ее аргументы, описание функции и каждого из аргументов, текущий результат функции и всей формулы.

Чтобы упростить создание и редактирование формул и свести к минимуму количество опечаток и синтаксических ошибок, пользуйтесь автозавершением формул. После того как вы введите знак «= » (знак равно) и начинательные буквы или триггер отображения Excel в Интернете под ячейкой будет отображаться динамический список действительных функций, аргументов и имен, которые соответствуют этим буквам или триггеру. После этого элемент из раскрывающегося списка можно вставить в формулу.

Вложенные функции

В некоторых случаях может потребоваться использовать функцию в качестве одного из аргументов другой функции. Например, в приведенной ниже формуле для сравнения результата со значением 50 используется вложенная функция СРЗНАЧ.

1. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.

Допустимые типы вычисляемых значений    Вложенная функция, используемая в качестве аргумента, должна возвращать соответствующий ему тип данных. Например, если аргумент должен быть логическим, т. е. Если эта функция не работает, Excel в Интернете отобразит #VALUE! В противном случае TE102825393 выдаст ошибку «#ЗНАЧ!».

<c0>Предельное количество уровней вложенности функций</c0>.    В формулах можно использовать до семи уровней вложенных функций. Если функция Б является аргументом функции А, функция Б находится на втором уровне вложенности. Например, в приведенном выше примере функции СРЗНАЧ и СУММ являются функциями второго уровня, поскольку обе они являются аргументами функции ЕСЛИ. Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.

Использование ссылок в формулах

Ссылка указывает на ячейку или диапазон ячеек на сайте и сообщает Excel в Интернете, где искать значения или данные, которые вы хотите использовать в формуле. С помощью ссылок в одной формуле можно использовать данные, которые находятся в разных частях листа, а также значение одной ячейки в нескольких формулах. Вы также можете задавать ссылки на ячейки разных листов одной книги либо на ячейки из других книг. Ссылки на ячейки других книг называются связями или внешними ссылками.

Стиль ссылок A1

Стиль ссылок по умолчанию    По умолчанию в Excel в Интернете используется стиль ссылок A1, который ссылается на столбцы буквами (от A до XFD, всего 16 384 столбца) и ссылается на строки с числами (от 1 до 1 048 576). Эти буквы и номера называются заголовками строк и столбцов. Для ссылки на ячейку введите букву столбца, и затем — номер строки. Например, ссылка B2 указывает на ячейку, расположенную на пересечении столбца B и строки 2.

<c0>Ссылка на другой лист</c0>.    В приведенном ниже примере функция СРЗНАЧ используется для расчета среднего значения диапазона B1:B10 на листе «Маркетинг» той же книги.

1. Ссылка на лист «Маркетинг».

2. Ссылка на диапазон ячеек с B1 по B10 включительно.

3. Ссылка на лист, отделенная от ссылки на диапазон значений.

Различия между абсолютными, относительными и смешанными ссылками

<c0>Относительные ссылки</c0>.    Относительная ссылка в формуле, например A1, основана на относительной позиции ячейки, содержащей формулу, и ячейки, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка. При копировании или заполнении формулы вдоль строк и вдоль столбцов ссылка автоматически корректируется. По умолчанию в новых формулах используются относительные ссылки. Например, при копировании или заполнении относительной ссылки из ячейки B2 в ячейку B3 она автоматически изменяется с =A1 на =A2.

<c0>Абсолютные ссылки</c0>.    Абсолютная ссылка на ячейку в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется. При копировании или заполнении формулы по строкам и столбцам абсолютная ссылка не корректируется. По умолчанию в новых формулах используются относительные ссылки, а для использования абсолютных ссылок надо активировать соответствующий параметр. Например, при копировании или заполнении абсолютной ссылки из ячейки B2 в ячейку B3 она остается прежней в обеих ячейках: =$A$1.

Смешанные ссылки    Смешанная ссылка имеет абсолютный столбец и относительную строку либо абсолютную строку и относительный столбец. Абсолютная ссылка на столбец принимает форму $A 1, $B 1 и так далее. Абсолютная ссылка на строку имеет форму A$1, B$1 и так далее. При изменении позиции ячейки, содержаной формулу, изменяется относительная ссылка, а абсолютная ссылка не изменяется. При копировании или заполнении формулы по строкам или вниз по столбцам относительная ссылка автоматически корректируется, а абсолютная ссылка не корректируется. Например, при копировании или заполнении смешанной ссылки из ячейки A2 в B3 она будет меняться с =A$1 на =B$1.

Стиль трехмерных ссылок

Удобный способ для ссылки на несколько листов    Трехмерные ссылки используются для анализа данных из одной и той же ячейки или диапазона ячеек на нескольких листах одной книги. Трехмерная ссылка содержит ссылку на ячейку или диапазон, перед которой указываются имена листов. Excel в Интернете использует все таблицы, которые хранятся между начальным и конечним именами ссылки. Например, формула =СУММ(Лист2:Лист13!B5) суммирует все значения, содержащиеся в ячейке B5 на всех листах в диапазоне от листа 2 до листа 13 включительно.

• При помощи трехмерных ссылок можно создавать ссылки на ячейки на других листах, определять имена и создавать формулы с использованием следующих функций: СУММ, СРЗНАЧ, СРЗНАЧА, СЧЁТ, СЧЁТЗ, МАКС, МАКСА, МИН, МИНА, ПРОИЗВЕД, СТАНДОТКЛОН.Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.

• Трехмерные ссылки нельзя использовать в формулах массива.

• Трехмерные ссылки нельзя использовать вместе с оператор пересечения (один пробел), а также в формулах с неявное пересечение.

<c0>Что происходит при перемещении, копировании, вставке или удалении листов</c0>.    Нижеследующие примеры поясняют, какие изменения происходят в трехмерных ссылках при перемещении, копировании, вставке и удалении листов, на которые такие ссылки указывают. В примерах используется формула =СУММ(Лист2:Лист6!A2:A5) для суммирования значений в ячейках с A2 по A5 на листах со второго по шестой.

• 
  Вставка или копирование    Если вставить листы между листами 2 и 6, Excel в Интернете будет включать в расчет все значения из ячеек с A2 по A5 на добавленных листах.

• 
  Удалить     Если удалить листы между листами 2 и 6, Excel в Интернете вы вычислите их значения.

• 
  Переместить    Если переместить листы между листами 2 и 6 в место за пределами диапазона, на который имеется ссылка, Excel в Интернете удалит их значения из вычислений.

• 
  Перемещение конечного листа    Если переместить лист 2 или 6 в другое место книги, Excel в Интернете скорректирует сумму с учетом изменения диапазона листов.

• 
  Удаление конечного листа    Если удалить лист 2 или 6, Excel в Интернете скорректирует сумму с учетом изменения диапазона листов между ними.

Стиль ссылок R1C1

Можно использовать такой стиль ссылок, при котором нумеруются и строки, и столбцы. Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. В стиле R1C1 Excel в Интернете указывает на расположение ячейки с помощью R, за которым следует номер строки, и C, за которым следует номер столбца.

При записи макроса Excel в Интернете некоторые команды с помощью стиля ссылок R1C1. Например, если записать команду (например, нажать кнопку «Автоумма»), чтобы вставить формулу, в которую добавляется диапазон ячеек, Excel в Интернете записи формулы со ссылками с помощью стиля R1C1, а не A1.

Использование имен в формулах

Можно создавать определенные имена для представления ячеек, диапазонов ячеек, формул, констант и Excel в Интернете таблиц. Имя — это значимое краткое обозначение, поясняющее предназначение ссылки на ячейку, константы, формулы или таблицы, так как понять их суть с первого взгляда бывает непросто. Ниже приведены примеры имен и показано, как их использование упрощает понимание формул.

Типы имен

Существует несколько типов имен, которые можно создавать и использовать.

Определенное имя    Имя, используемое для представления ячейки, диапазона ячеек, формулы или константы. Вы можете создавать собственные определенные имена. Кроме Excel в Интернете иногда задайте определенное имя, например при создании области печати.

Имя таблицы    Имя таблицы Excel в Интернете, которая является набором данных по определенной теме, которые хранятся в записях (строках) и полях (столбцах). Excel в Интернете создает таблицу Excel в Интернете имя таблицы «Таблица1», «Таблица2» и так далее, каждый раз при вставке таблицы Excel в Интернете, но эти имена можно изменить, чтобы сделать их более осмысленными.

Создание и ввод имен

Имя создается с помощью «Создать имя из выделения». Можно удобно создавать имена из существующих имен строк и столбцов с помощью фрагмента, выделенного на листе.

Примечание: По умолчанию в именах используются абсолютные ссылки на ячейки.

Имя можно ввести указанными ниже способами.

• 
  Ввод с клавиатуры     Введите имя, например, в качестве аргумента формулы.

• 
  <c0>Автозавершение формул</c0>.    Используйте раскрывающийся список автозавершения формул, в котором автоматически выводятся допустимые имена.

Использование формул массива и констант массива

Excel в Интернете не поддерживает создание формул массива. Вы можете просматривать результаты формул массива, созданных в классическом приложении Excel, но не сможете изменить или пересчитать их. Если на вашем компьютере установлено классическое приложение Excel, нажмите кнопку Открыть в Excel, чтобы перейти к работе с массивами.

В примере формулы массива ниже вычисляется итоговое значение цен на акции; строки ячеек не используются при вычислении и отображении отдельных значений для каждой акции.

При вводе формулы «={СУММ(B2:D2*B3:D3)}» в качестве формулы массива сначала вычисляется значение «Акции» и «Цена» для каждой биржи, а затем — сумма всех результатов.

<c0>Вычисление нескольких значений</c0>.    Некоторые функции возвращают массивы значений или требуют массив значений в качестве аргумента. Для вычисления нескольких значений с помощью формулы массива необходимо ввести массив в диапазон ячеек, состоящий из того же числа строк или столбцов, что и аргументы массива.

Например, по заданному ряду из трех значений продаж (в столбце B) для трех месяцев (в столбце A) функция ТЕНДЕНЦИЯ определяет продолжение линейного ряда объемов продаж. Чтобы можно было отобразить все результаты формулы, она вводится в три ячейки столбца C (C1:C3).

Формула «=ТЕНДЕНЦИЯ(B1:B3;A1:A3)», введенная как формула массива, возвращает три значения (22 196, 17 079 и 11 962), вычисленные по трем объемам продаж за три месяца.

Использование констант массива

В обычную формулу можно ввести ссылку на ячейку со значением или на само значение, также называемое константой. Подобным образом в формулу массива можно ввести ссылку на массив либо массив значений, содержащихся в ячейках (его иногда называют константой массива). Формулы массива принимают константы так же, как и другие формулы, однако константы массива необходимо вводить в определенном формате.

Константы массива могут содержать числа, текст, логические значения, например ИСТИНА или ЛОЖЬ, либо значения ошибок, такие как «#Н/Д». В одной константе массива могут присутствовать значения различных типов, например {1,3,4;ИСТИНА,ЛОЖЬ,ИСТИНА}. Числа в константах массива могут быть целыми, десятичными или иметь экспоненциальный формат. Текст должен быть заключен в двойные кавычки, например «Вторник».

Константы массива не могут содержать ссылки на ячейку, столбцы или строки разной длины, формулы и специальные знаки: $ (знак доллара), круглые скобки или % (знак процента).

При форматировании констант массива убедитесь, что выполняются указанные ниже требования.

• Константы заключены в фигурные скобки ( { } ).

• Столбцы разделены запятыми (,). Например, чтобы представить значения 10, 20, 30 и 40, введите {10,20,30,40}. Эта константа массива является матрицей размерности 1 на 4 и соответствует ссылке на одну строку и четыре столбца.

• Значения ячеек из разных строк разделены точками с запятой (;). Например, чтобы представить значения 10, 20, 30, 40 и 50, 60, 70, 80, находящиеся в расположенных друг под другом ячейках, можно создать константу массива с размерностью 2 на 4: {10,20,30,40;50,60,70,80}.

360 разделить на 12 | 360 разделить на 12 с остатком

Ответ на математические задачи Этапы решения

Математические ответы на деление дроби 360/12

36012 = 30

30 = 300 с точностью до десятых

30 = 30 с точностью до сотых

30 = 30 с точностью до тысячных

= 0 с точностью до десятых

= 0 с точностью до сотых

= 0 с точностью до тысячных

Другие разделы Домашнее задание по математике —

360 делим пополам плюс 20

ответов на домашнее задание: (360/2) + 20 = 200

360 делим пополам плюс 40

Домашнее задание ответов: (360/2) + 40 = 220

360/12 разделить на 2

Ответ: (360/12) ÷ 2 = 15

Домашнее задание по математике

можно легко решить с помощью этого бесплатного инструмента.Чтобы решить домашнее задание или задание, все, что вам нужно сделать, это ввести значение в соответствующее поле и нажать «вычислить», чтобы получить математические ответы.

Что такое числитель / знаменатель

Числитель: мы называем верхнее число числителем, это число в верхней части имеющейся у вас дроби.

Знаменатель: мы называем нижнее число знаменателем, это целое число внизу, это число, на которое делится.

Шаги преобразования дробей в десятичные

Шаг 1: Найдите число, которое можно умножить на нижнюю часть дроби, чтобы получилось 10, 100, 1000 или любая единица с последующими нулями.

Шаг 2: Умножьте верхнюю и нижнюю части на выбранное вами число.

Шаг 3. Затем запишите только верхнее число, поместив десятичную запятую в правильное место, то есть на один пробел с правой стороны для каждого нуля в нижнем числе.

a / b = c В приведенных выше выражениях a называется делимым, b называется делителем, а c называется частным; в выражении a / b, a также называется числителем, а b также называется знаменателем.

Этот калькулятор дроби также можно использовать для вычисления доли в процентах, скидок на покупки, купонов, жировых отложений, валовой прибыли, потери веса, любви, налогов, увеличения и уменьшения населения, прибыли от продаж.Как только вы знаете значения, определить% легко.

Если вы обнаружите ошибку на этом сайте, мы будем благодарны, если вы сообщите нам об этом, используя предоставленный контактный адрес электронной почты. отправьте электронное письмо в контакт на нашем сайте.

Следующий Предыдущий

Преподобный Джозеф Фикс умер в возрасте 79 лет

Преподобный Джозеф Фикс, пастор прихода Святой Агнессы в Марион и прихода Святого Сердца в Эварте, умер в четверг, 13 мая 2021 года, в результате борьбы с раком.

Отец Фикс родился 21 октября 1941 года в Альпийском городке, в семье Джозефа и Делорес (Клайн) Фикс. У него остались братья и сестры: Роберт Фикс, Мэри Вайзенбургер, Сюзанна (Джек) Паас, Джанет Томпсон, Раймонд (Александра) Фикс, Делорес (Джон) Олтофф, Жанна (Роберт) Энелл, Джерард (Рилма) Фикс и многочисленные племянницы и племянники.

Отец Фикс посещал начальную школу Св. Альфонса и Центральную католическую среднюю школу в Гранд-Рапидсе; Иорданская семинария в Меномини, штат Мичиган; Семинария Святой Марии в Балтиморе, штат Мэриленд; и св.Провинциальная семинария Иоанна в Плимуте, штат Мичиган. 1 июня 1968 года он был рукоположен в священники епископом Алленом Дж. Бэбкоком. Первым назначением отца Фикса был приходской священник СС. Петра и Павла в Ионии.

Пастырское поручение отца Фикса

• Июнь 1968: Назначен приходским викарием СС. Петра и Павла в Ионии, штат Мичиган,
• июль 1969: назначен приходским священником св. Иоанна Вианнея в Вайоминге, штат Мичиган.
• Апрель 1973: Назначен приходским викарием св. Франциска Сальского в Маскегоне, штат Мичиган,

.

• июль 1975: назначен координатором Курсилло Секретариата Маскегона
• июнь 1978: назначен пастором Св.Пола в Биг-Рапидс,
• , август 1980: назначен капелланом в тюрьму округа Мекоста
• , июль 1987: назначен пастором церкви Святой Анны в Болдуине с миссией в Лютере.
• Июль 2000: Назначен пастором Святейшего Сердца в Эварте и Святой Агнессы в Марионе.

Организация похорон

Визит:
Воскресенье, 16 мая
14:00 — 17:00
Католическая церковь Святой Агнесы
603 E. Main Street
Marion, MI 49665

Понедельник, 17 мая
9 а.м. — Полдень
Католическая церковь Святого Сердца
9878 US 10
Evart, MI 49631

Будет отслужена частная месса христианского погребения под председательством епископа Давида Валковяка.

Дарование вечного покоя о. Исправь, Господи,
, и да светит ему вечный свет.
Да упокоится он с миром. Аминь.

Папа издает motu proprio, официально учредив катехизаторское служение

10 мая Папа Франциск подписал Antiquum Ministerium , апостольское письмо, изданное motu proprio (что означает «по его собственному побуждению»), которое официально устанавливает мирское служение катехизатора.

10 мая — праздник святого Иоанна Авильского, доктора Церкви, известного как великий катехизатор.

В нашей епархии и во многих других Соединенных Штатах motu proprio не изменит нынешнюю практику церкви. Motu proprio имеет большее потенциальное влияние на всемирную Церковь, где миряне-катехизаторы несут дополнительную ответственность за формирование католиков в тех областях, где священник не всегда может присутствовать.

Катехизаторы и лидеры катехизации

Апостольская работа катехизатора проистекает из таинства Крещения.Он усиливается таинством Подтверждения. Призыв к служению катехизатора — это призвание, внутренний призыв, голос Святого Духа. Катехизаторы должны быть практикующими католиками, которые в полной мере участвуют в общинном богослужении и жизни Церкви и которые были подготовлены к своему апостольству с помощью соответствующей катехетической подготовки. Их поручение Церковью — это участие в божественном призвании учить, как это делал Иисус. (Национальный справочник катехизации, 228-9)

Катехизаторы-миряне сыграли важную роль в строительстве Церкви, начиная со времен апостолов.Служение катехизаторов-мирян получило дальнейшее признание во время Второго Ватиканского Собора с публикацией Ad Gentes . Эта важная роль еще раз подтверждается в Antiquum Ministerium.

«Роль катехизаторов — одна из специфических форм служения в христианском сообществе. Катехизаторы призваны в первую очередь быть экспертами в пастырском служении по передаче веры по мере ее развития на различных этапах от первоначального провозглашения керигмы до наставлений, которые представляют нашу новую жизнь во Христе и готовят к таинствам христианского посвящения а затем к продолжающемуся формированию, которое может позволить каждому человеку дать отчет о своей надежде (см. 1 Пет. 3:15). В то же время каждый катехизатор должен быть свидетелем веры, учителем и мистагогом, товарищем и педагогом, который учит для Церкви. Только через молитву, изучение и непосредственное участие в жизни сообщества они могут расти в этой идентичности, а также в целостности и ответственности, которые это влечет за собой »(ср. Папский совет по продвижению новой евангелизации, Directory for Catechesis , 113 ). ( Antiquum Ministerium, 6)

Прочитать полное апостольское письмо (английский | испанский)

Ресурсы:
Офис формирования веры
Справочник катехизации

О фотографии: Девушка улыбается, отвечая на вопрос во время урока Нового Завета в Св.Люка в Брентвуде, штат Нью-Йорк (фото CNS / Грегори А. Шемитц) (28 августа 2008 г.)

История календаря — моменты создания

Автор: Ян Тейлор

Справочная информация. Принимая за отправную точку первую главу Книги Бытия, мы обнаруживаем, что сначала были созданы небеса, а затем земля в первый день [ст. 1], а солнце, луна и звезды были созданы в четвертый день [ст. 14-19]. Солнце и луна описаны как «два великих светила» [ст.16], в то время как их данная цель состоит в том, чтобы «отделять день от ночи» и быть «знамениями и временами на дни и годы» [ст. 14]. Наконец, Бог увидел все, что Он создал, и объявил, что это «очень хорошо» [ст. 31]. Разумно можно было ожидать, что по первому календарю легко рассчитывать и очень точно. Бог осуществил все Свое творение в течение первых шести дней первой недели, включая сотворение Адама и Евы в первую полдень пятницы; На следующий день он отдыхал, таким образом установив знакомый образец для нашей 7-дневной недели [Бытие 2: 2].Насколько известно, за одним мрачным исключением, у каждой нации всегда была 7-дневная неделя. Исключение явилось следствием Французской революции 1789 года и введения метрической системы с десятидневной неделей; более длинная неделя была недолгой неудачей. Дни всегда устанавливались по времени от одного восхода до следующего — легче наблюдать момент восхода, чем наблюдать закат, в то время как продолжительность каждого дня и ночи всегда одинакова, то есть 24 часа. Луны от одного новолуния к другому делят на месяцы.Когда этот календарный цикл впервые описан в Бытие 1, его легко читать по солнцу и луне, он был особенно важен для фермеров при посадке и уборке урожая. Позже будет важно соблюдать религиозные обряды, то есть полнолуние для празднования Пасхи, а позже в соответствующий день для празднования Пасхи по христианскому календарю.

Год был временем, за которое Земля совершила один полный оборот вокруг Солнца. Однако в Священных Писаниях не говорится, сколько дней было в каждом году в этом допотопном мире, но есть основания полагать, что это, возможно, было 360, а не 365¼ дней, знакомых нам.Самые ранние календари, доступные сегодня историкам, — это календари вавилонян, которые, согласно Священному Писанию, были первым народом после Всемирного потопа [Бытие, гл. 11]. Вавилонский календарь содержал 360 дней, и его наследие остается для нас сегодня в виде круга, разделенного на 360 градусов, то есть один градус в день, когда Земля совершает свой оборот вокруг Солнца. Конечно, мы знаем, что в нашем постпотопном мире в году всегда было 365¼ дней. Таким образом, вавилонянам не хватало 5 дней в году, и потребовалось бы всего 70 лет, чтобы завершить цикл, в котором, скажем, Новый год охватил бы каждый месяц календаря! Такой календарь был бы совершенно бесполезен для фермера.Однако мы должны спросить, почему они вообще приняли 360-дневный год и почему они не отказались от него по прошествии первых нескольких лет? Согласно египетским записям, вавилонский календарь из 360 дней использовался в течение нескольких сотен лет до того, как были добавлены пять «эпагоменов» или дней, чтобы получить год из 365 дней. Сэр Джозеф Норман Локьер обсуждает эту ситуацию, цитируя несколько египетских текстов, и, хотя он этого не говорит, очевидный вывод будет заключаться в том, что до Потопа в Книге Бытия действительно было 360 дней, по 12 месяцев в каждом из 30 дней.Что бы ни стало причиной Потопа из Книги Бытия, вероятно, также заставило Землю переместиться на немного большую орбиту вокруг Солнца и разрушить совершенный календарь, данный человеку вначале; С тех пор следить за временем стало намного труднее и постоянно напоминать о человеческом грехе.

Еврейский календарь. Священный календарь евреев пытается исчислять месяцы по луне и годы по солнцу; он известен как лунно-солнечный. Календарный год начинается в их месяце нисан [март-апрель] и состоит из двенадцати месяцев поочередно из 29 и 30 дней, но это дает год всего из 354 дней.Однако примерно каждые три года [7 раз за 19 лет] и дополнительный 29-дневный месяц, Веадар, добавляется в конце их года. То есть между Адаром [февраль] и Нисаном. Несмотря на это, в течение 19-летнего цикла еврейский календарь все еще на 10 дней меньше, чем 6939,60 дней, за которые Земля обращается вокруг солнца за 19 лет. По этой причине к трем 29-дневным месяцам в году, т. Е. Хешван, Числев и Адар, иногда добавляют дополнительный день, чтобы сделать их 30-дневными месяцами. Все эти исправления раньше делались по указанию священников из Иерусалима.Напомним, что не только Пасху нужно проводить в полнолуние, но и посадка сельскохозяйственных культур должна всегда производиться в течение сезона, чтобы обеспечить хороший урожай. Ясно, что лунно-солнечный священный календарь евреев со всеми необходимыми исправлениями — дело сложнейшее. Опять же, это заставляет задуматься, не был ли в прежние времена гораздо более простой 360-дневный год с двенадцатью 30-дневными месяцами? Если все это было недостаточно плохо, еврейский гражданский год начинается в их месяце Тишри, соответствующем нашему сентябрю-октябрю.

Ранние египетские календари. И снова сэр Джозеф Локьер и многие другие показали, что с самых ранних времен египтяне строили свои пирамиды в первую очередь для точного отсчета времени. Абсолютно плоский горизонт без деревьев и безоблачное небо были идеальной средой для наблюдения за восходом солнца. Пирамидия на пирамидах и на остроконечном обелиске давала резкие тени на ровном асфальте, чтобы точно отслеживать прохождение солнца и устанавливать время дня и времена года.Даже в те ранние дни истории египетские священники / астрономы обнаружили, что год состоит из 365¼ дней.

Раннеримский календарь. Ранний римский календарь основывался на 355-дневном лунном году, который представляет собой почти ровно 12 лунных месяцев, которые были пронумерованы от 1 до 12 на латыни и до сих пор встречаются в названиях наших месяцев: сентябрь, октябрь, ноябрь и декабрь для римского языка. месяцев 7, 8, 9 и 10 соответственно. Однако, чтобы приспособить этот лунный календарь к году, основанному на Солнце i.е. Для солнечного года необходимо было иметь цикл из четырех лет: 355, 377, 355 и 378 дней соответственно. Год в этом календаре, как и в большинстве ранних календарей, начался 1 марта, чтобы быть близким к весеннему равноденствию [около 21 марта], и закончился в конце февраля [Februarius]. Однако этот ранний календарь с годами, различающимися по продолжительности более чем на три недели, был бесполезен для фермеров, чтобы знать, когда сажать урожай.

Юлианский календарь. Александрийский математик Сосиген посоветовал Юлию Цезарю [102-44 Б.C.], чтобы ввести календарную реформу, основанную на солнечном году, то есть времени, которое требуется Земле, чтобы сделать один полный оборот вокруг Солнца. Эта реформа отказалась от любых попыток приспособить годы или месяцы к продолжительности лунных периодов, то есть к лунным циклам. Новый юлианский календарь был введен в 45 г. до н. Э., И год начался 1 марта. Год был установлен на 365 дней, а для учета дня добавлялся дополнительный день в конце каждого четвертого календарного года, то есть в конце февраля. Этот год стал известен как «високосный» и состоял из 366 дней.Даже в этом случае, поскольку дробь немного меньше ¼ дня, юлианский календарь постепенно отставал от равноденствий каждый год, фактически, он составлял 1 день каждые 128 лет. В 44 г. до н. Э. Второй год юлианского календаря, пятый месяц, Квинтилис, был переименован в Юлий — наш июль — в честь его основателя Юлия Цезаря. В 8 г. до н. Э. Шестой месяц Секстилий был переименован в Август в честь своего преемника Августа Цезаря. Юлианский календарь использовался до тех пор, пока папа Григорий XIII не реформировал его в 1582 году.

по григорианскому календарю. Со времен Римской империи продолжительность года считалась 365¼ дней. Более высокая точность определения длины года стала возможной в 17 веке с изобретением телескопа. Процедура заключалась в том, чтобы поместить перекрестие окуляра на очень далекую и известную звезду, затем зафиксировать телескоп в этом положении и ждать целый год, пока эта же звезда не появится в перекрестии. Сначала использовались маятниковые часы, сегодня используются атомные часы.В настоящее время известно, что солнечный год составляет 11 минут, 14 секунд меньше, чем 365¼ дней, то есть 365 дней, 5 часов, 48 минут и 46 секунд, или 365,2422 дня. Однако эта точность была неизвестна Папе Григорию XIII [1572-1585], но он знал, что в течение 1257 лет от Никейского Собора [н.э. 325] до реформы Григория [1582] весеннее равноденствие сдвинулось на 10 дней с 21 марта на 11 марта.

Продолжительность каждого дня одинакова и обычно измеряется от восхода до следующего восхода солнца; этот период соответствует одному обороту Земли вокруг своей оси, в то время как время, деленное на 24, определяет час.В соответствии с вавилонской традицией круг всегда делился на 360 градусов, так что каждый час вращения Земли вокруг своей оси составляет [360 делить на 24] = 15 градусам долготы. Относительное время светлого и темного дня в течение всего года соответствует циклу: самый короткий день — 21 декабря; Весеннее равноденствие или день равного дня и ночи, 21 марта; Самый длинный день 21 июня; Осеннее равноденствие равных дня и ночи, 21 сентября. Год по григорианскому календарю следовал традиции юлианского календаря и начинался 1 марта, поскольку это был месяц Весны или весеннего равноденствия.

Благодаря реформе Папы Григория XIII в 1582 году юлианский календарь отставал от равноденствий почти на 13 дней [(с 45 г. до н.э. до 1582 г. = 1627 лет), разделенных на 128 = 12,7 дней]. Посадка урожая с опозданием почти на две недели может обернуться катастрофой для урожая! Математик и врач Луиджи Лилио Гиральди, сменивший Клавиуса, предложил вариант юлианского календаря, добавив дополнительный день каждые 400 лет, и это уменьшило ошибку до одного дня каждые 3300 лет. Эмпирическое правило состоит в том, что если количество столетий можно разделить поровну на четыре, то добавляется дополнительный день таким же образом, как и дни в високосном году.Таким образом, дополнительный день [фев. 29] был добавлен в 1600 году, и снова дополнительный день был добавлен в 2000 году. Григорианский календарь был введен в действие Папой Григорием XIII и начался 5 октября 1582 года, сдвинув календарь на 10 дней вперед, чтобы сделать его 15 октября. Согласно этому постановлению, весеннее равноденствие, которое тогда приходилось на 11 марта, было должным образом восстановлено до 21 марта. Из-за религиозных предубеждений против особо непопулярного папы протестантские страны не сразу ввели эти изменения. Англия оставалась по старому юлианскому календарю до правления Вильгельма II; он изменился в 1752 году, когда на следующий день после 2 сентября было объявлено 14 сентября.Именно в это время начало юридического года в Англии было изменено с 1 марта на 1 января. Следует напомнить, что Французская революция произошла всего 3 года назад [1789], когда начало их года было изменено с 1 марта на 1 сентября.

Целью революционеров было отметить начало Французской Республики и окончание всех христианских праздников. Русская Православная Церковь по-прежнему выступает против григорианского изменения, по-прежнему соблюдает старый юлианский календарь и, например, празднует Рождество 6 января.

Ниторазборка. Как отмечалось ранее, час определяется как одна двадцать четвертая времени, необходимого Земле для одного вращения вокруг своей оси. Изменение времени от штата к штату и от страны к стране происходит с шагом в один час или пятнадцать градусов по географическому принципу. Время от времени гражданское время корректируется с шагом «високосная секунда» один или два раза в год, чтобы гарантировать, что разница между единообразной шкалой времени, определяемой атомными часами, не отличается от времени вращения Земли более чем на 0.9 секунд. Это произвольное число, установленное международным комитетом. В 1956 году при изучении атома цезия 133 было обнаружено, что за одну секунду произошло 9 192 631 770 циклов излучения; таким образом было введено новое определение второго. С введением атомных часов был введен более высокий стандарт точности хронометража, но при испытании на вращение Земли вокруг собственной оси было обнаружено, что Земля замедляется! Считается, что это вызвано тормозящим действием приливов; Данные о затмениях позволили определить скорость замедления примерно 1-3 миллисекунды в день за столетие.С 1972 года «дополнительные секунды» были добавлены [еще не вычтены] к мировым часам, чтобы позволить гражданскому времени идти в ногу с мировым временем. Хотя есть свидетельства того, что Земля замедляется, никто не может быть уверен в том, насколько сильно, потому что это замедление может быть связано с самими цезиевыми часами, в конце концов, радиоактивный распад считается постоянным.

Справочные источники

Британская энциклопедия. 1910. Нью-Йорк: Британская энциклопедия Ко.Издание одиннадцатое. Том 4, страницы 987–1003 «Календарь»

Энциклопедия иудаика. 1971. Нью-Йорк / Израиль: Macmillan Co. Том 5, столбцы 43–53 «Календарь»

високосных секунд. http://news.bbc.co.uk/1/hi/sci/tech/4271810.stm; http://news.bbc.co.uk/1/hi/sci/tech/4420084.stm; http://tycho.usno.navy.mil/leapsec.html

Lockyer, J. Norman. 1894. Рассвет астрономии. Лондон: Касселл и Ко. Глава 24 «Годы из 360 и 365 дней»

Ричардс, Э. Г. 1998. Картографирование времени.Календарь и его история. Oxford University Press

Распечатать

Примеры общих формул в списках

Вы можете использовать следующие формулы для выполнения вычислений, основанных на датах и ​​времени, таких как добавление числа дней, месяцев или лет к дате, вычисление разницы между двумя датами и преобразование времени в десятичное значение.

Добавить даты

Чтобы добавить количество дней к дате, используйте оператор сложения (+).

Примечание: При работе с датами тип возвращаемого значения вычисляемого столбца должен быть установлен на Дата и время .

Чтобы добавить количество месяцев к дате, используйте функции ДАТА, ГОД, МЕСЯЦ и ДЕНЬ.

Чтобы добавить количество лет к дате, используйте функции ДАТА, ГОД, МЕСЯЦ и ДЕНЬ.

Чтобы добавить к дате комбинацию дней, месяцев и лет, используйте функции ДАТА, ГОД, МЕСЯЦ и ДЕНЬ.

Вычислить разницу между двумя датами

Используйте функцию РАЗНДАТ, чтобы выполнить это вычисление.

Вычислить разницу между двумя умноженными на

Чтобы представить результат в стандартном формате времени (часы: минуты: секунды), используйте оператор вычитания (-) и функцию ТЕКСТ.Чтобы этот метод работал, часы не должны превышать 24, а минуты и секунды не должны превышать 60.

Чтобы представить результат в виде суммы, основанной на одной единице времени, используйте функцию ЦЕЛОЕ или функцию ЧАС, МИНУТА или СЕКУНДА.

Перевести раз

Чтобы преобразовать часы из стандартного формата времени в десятичное число, используйте функцию ЦЕЛОЕ.

Чтобы преобразовать часы из десятичного числа в стандартный формат времени (часы: минуты: секунды), используйте оператор деления и функцию ТЕКСТ.

Вставить даты по юлианскому календарю

Юлианская дата относится к формату даты, который представляет собой комбинацию текущего года и количества дней с начала года.Например, 1 января 2007 года представлено как 2007001, а 31 декабря 2007 года представлено как 2007365. Этот формат не основан на юлианском календаре.

Чтобы преобразовать дату в дату по юлианскому календарю, используйте функции ТЕКСТ и ДАТАЗНАЧ.

Чтобы преобразовать дату в юлианскую дату, которая используется в астрономии, используйте константу 2415018.50. Эта формула работает только для дат после 01.03.1901, и если вы используете систему дат 1900 года.

Показывать даты как день недели

Чтобы преобразовать даты в текст дня недели, используйте функции ТЕКСТ и ДЕНЬ НЕДЕЛИ.

% PDF-1.6
%
6 0 obj
> / Метаданные 17 0 R / Страницы 1 0 R / StructTreeRoot 18 0 R / Тип / Каталог >>
эндобдж
17 0 объект
> поток
2010-09-23T14: 02: 08-04: 00CanoScan LiDE 20 / N670U / N676U2010-09-23T14: 02: 20-04: 002010-09-23T14: 02: 20-04: 00Приложение Adobe Acrobat 9.33 Paper Capture Plug / pdfuuid: 745f721b-8dd0-4d81-b901-b821b710bc4euuid: 8139a0e2-0023-4739-9ccb-9fbf0f2c997a

конечный поток
эндобдж
1 0 obj
>
эндобдж
18 0 объект
>
эндобдж
19 0 объект
> / CM2> / CM3> / CM4> / CM5> / CM6> / CM8 >>>
эндобдж
20 0 объект
>
эндобдж
21 0 объект
>
эндобдж
22 0 объект
>
эндобдж
33 0 объект
[23 0 R 24 0 R 25 0 R 34 0 R 35 0 R 36 0 R 37 0 R 38 0 R 39 0 R 27 0 R 40 0 ​​R 41 0 R 42 0 R 43 0 R 29 0 R 30 0 R 31 0 R 44 0 R 45 0 R 46 0 R 47 0 R 48 0 R]
эндобдж
23 0 объект
>
эндобдж
24 0 объект
>
эндобдж
25 0 объект
>
эндобдж
34 0 объект
>
эндобдж
35 0 объект
>
эндобдж
36 0 объект
>
эндобдж
37 0 объект
>
эндобдж
38 0 объект
>
эндобдж
39 0 объект
>
эндобдж
27 0 объект
>
эндобдж
40 0 объект
>
эндобдж
41 0 объект
>
эндобдж
42 0 объект
>
эндобдж
43 0 объект
>
эндобдж
29 0 объект
>
эндобдж
30 0 объект
>
эндобдж
31 0 объект
>
эндобдж
44 0 объект
>
эндобдж
45 0 объект
>
эндобдж
46 0 объект
>
эндобдж
47 0 объект
>
эндобдж
48 0 объект
>
эндобдж
32 0 объект
>
эндобдж
4 0 объект
> / ProcSet [/ PDF / Text / ImageB] / XObject >>> / StructParents 0 / Tabs / S / Type / Page >>
эндобдж
58 0 объект
> поток
HWnH} Wyb%, `f2af1% Z% zE * q ޔ / cvuԩS7c8 ֛} ~ _ juӏc VZ} nw ~ $! 2zԟ͛ p53bu {~ ‘0YUOX c ~ + d | Ͽ: q ~
Ase + U, zHżZ9Ҙ / buӻ1Z? FbmSj} C? N \ «S] y {쫿 ㌹31zxySw] w / @ JH0m_ / e82j% aɬ [0 ȈV] & Roo]} J’8uAJw> | @

Калькулятор бетона — Schmitz Ready Mix

Товарный бетон продается по объему, измеренному в кубических ярдах.Если вы можете определить площадь вашего бетонного проекта (длина x ширина для прямоугольных проектов) и знать толщину плиты, вы можете использовать информацию в Калькуляторе объема бетона ниже, чтобы определить, сколько бетона вам нужно.

Один кубический ярд бетона:

• Толщина 4 дюйма — площадь 81 квадратный фут
• Толщина 5 дюймов — площадь 65 квадратных футов
• Толщина 6 дюймов — площадь 54 квадратных фута
• Толщина 7 дюймов — площадь 46 квадратных футов
• Толщина 8 дюймов — площадь 41 квадратный фут
• Толщина 10 дюймов — площадь 32 квадратных фута
• толщиной 12 дюймов — покрывает 27 квадратных футов.

Например, давайте посчитаем, сколько бетона необходимо для прямоугольной подъездной дороги толщиной 5 дюймов, длиной 60 футов (длиной) и шириной 18 футов (шириной). Площадь проезжей части составляет 1080 квадратных футов (60 футов на 18 футов). Согласно приведенной выше таблице, один кубический ярд бетона толщиной 5 дюймов покрывает 65 квадратных футов. В идеальной вселенной для нашей подъездной дороги площадью 1080 квадратных футов потребуется ровно 16,62 кубических ярда бетона (1080 квадратных футов / 65 квадратных футов равняются 16.62 кубических ярда).

Но рабочие площадки несовершенны, и серийные заводы не могут производить бетон в таких требуемых объемах. Чтобы учесть просыпание во время укладки, перемещения формы, неровностей земляного полотна и уплотнения, большинство подрядчиков заказывают на 10–15% больше бетона, чем рассчитанный объем для форм, и округляют до ближайшей четверти ярда. В нашем примере 16,62 кубических ярдов x 105% = 17,451 кубических ярдов. Округляя до ближайшей четверти ярда, мы просим 17,5 кубических ярдов бетона при заказе бетона для проекта.

Для тротуаров и плит неправильной формы создайте масштабный чертеж проекта. Разделите неправильную форму на серию правильных прямоугольников и определите площадь для каждого прямоугольника в серии. Используйте приведенную выше таблицу, чтобы рассчитать, сколько кубических ярдов бетона потребуется для каждого прямоугольника в ряду. Сложите объемы кубических ярдов каждого прямоугольника в ряду, умножьте на 105% и округлите до ближайшей четверти ярда.

Для работы с радиусом нарисуйте прямоугольник вокруг области радиуса и используйте длину и ширину прямоугольника, чтобы оценить площадь в квадратных футах области радиуса.

Воспользуйтесь калькулятором от Calculator.net, чтобы оценить, сколько бетона по объему вам понадобится для вашего следующего проекта. Щелкните здесь>

Калькулятор объема бетона

Калькулятор рассчитает количество кубических ярдов бетона, которое потребуется для заполнения пространства в соответствии с параметрами конструкции.

Калькулятор бетонных колонн

Калькулятор отобразит необходимое количество кубических ярдов.

Наш партнер по проекту будет рад помочь вам подсчитать, сколько бетона вам нужно. Позвоните Джеффу Мэдсену по телефону 414.831.2458. Но прежде чем обращаться за помощью, измерьте свой проект и создайте масштабный чертеж с фактическими размерами.