Решение задач. 5 класс. Конспект урока – конспект урока – Корпорация Российский учебник (издательство Дрофа – Вентана)

• Интернет-магазин

• Где купить

• Аудио

• Новости

• LECTA

• Программа лояльности

Мой личный кабинет

Методическая помощь
Вебинары
Каталог
Рабочие программы

Дошкольное образование

Начальное образование

Алгебра

Английский язык

Астрономия

Биология

Всеобщая история

География

Геометрия

Естествознание

ИЗО

Информатика

Искусство

История России

Итальянский язык

Китайский язык

Литература

Литературное чтение

Математика

Музыка

Немецкий язык

ОБЖ

Обществознание

Окружающий мир

ОРКСЭ, ОДНК

Право

Русский язык

Технология

Физика

Физическая культура

Французский язык

Химия

Черчение

Шахматы

Экология

Экономика

Финансовая грамотность

Психология и педагогика

Внеурочная деятельность

Дошкольное образование

Начальное образование

Алгебра

Английский язык

Астрономия

Биология

Всеобщая история

География

Геометрия

Естествознание

ИЗО

Информатика

Искусство

История России

Итальянский язык

Китайский язык

Литература

Литературное чтение

Математика

Музыка

Немецкий язык

ОБЖ

Обществознание

Окружающий мир

ОРКСЭ, ОДНК

Право

Русский язык

Технология

Физика

Физическая культура

Французский язык

Химия

Черчение

Шахматы

Экология

Экономика

Мой личный кабинет

Методическая помощь

Дошкольное образование

Начальное образование

Алгебра

Английский язык

Астрономия

Биология

Всеобщая история

География

Геометрия

Естествознание

ИЗО

Информатика

Искусство

История России

Итальянский язык

Китайский язык

Литература

Литературное чтение

Математика

Музыка

Немецкий язык

ОБЖ

Обществознание

Окружающий мир

ОРКСЭ, ОДНК

Право

Русский язык

Технология

Физика

Физическая культура

Французский язык

Химия

Черчение

Шахматы

Экология

Экономика

Психология и педагогика

Внеурочная деятельность

Занятия по математике для 1-5 классов.

Школа олимпиадной математики

На протяжении нескольких лет наша школа готовит четвероклассников к поступлению в пятый класс математических школ Москвы. Пока мы ждём результатов вступительных экзаменов и держим кулаки за детей, у нас … читать далее

11 февраля прошла олимпиада для поступающих в 5 класс. Воспроизвожу задания со слов моих учеников. Задание 1. Реши ребус. Задание 2. Реши задачу. Мышь, мышонок и кусочек сыра вместе весят … читать далее

Сказочную октябрьскую олимпиаду ФБ по математике для 4 класса я подготовил по мотивам хорошо известной детской сказки. За 60 минут детям предстоит решить легкую задачу про тяжелую внучку и тяжелую … читать далее

1. Вычислите: 378242 + 305474 : 379 – 169 · 2070 2. Решите задачу с пояснениями. Пираты зарыли на острове сундук с сокровищами – жемчугом, а также золотыми и серебряными … читать далее

Олимпиада проводилась 6 февраля 2016 г. Тексты задач приведены со слов учеников, поэтому возможны незначительные синтаксические расхождения (но не смысловые!), что не влияет на решение. 1. Вставь вместо звездочек цифры … читать далее

В 2015 году на устном экзамене будущим пятиклассникам нужно было за полтора часа решить 6 олимпиадных задач, причем не просто найти ответ, но и обосновать (объяснить) свое решение. Вариантов, как … читать далее

1. Выполните действия в столбик а) 79158 + 32619 б) 93756 – 47963 в) 284 · 3056 г) 748748 : 364 2. Решите по действиям: 98404 – 126 · (397 … читать далее

1. Вычислите: 1543 + (49504 – 48212 : 68) 2 . Решите уравнение: х : 988 = 74100 3. Решите задачу с пояснениями. От Клина до Москвы 90 км. На … читать далее

1. Выполните действия в столбик: а) 49159 + 62178 б) 84576 – 38783 в) 783 · 6054 г) 7689866 : 958 2. Решите по действиям: 8096 + 94 · (2964500 … читать далее

№1. Катя и Костя берут карточки с числами из кучи и по очереди выкладывают их слева направо. Катя хочет, получить наибольшее число, а Костя наименьшее. Какое число у них получится … читать далее

Конспект урока по математике «Задачи на движение» 5 класс

Локтева Елена Александровна

МБОУ «ООШ с. Подстепное»

Учитель математики

«Чему бы ты не учился, ты учишься для себя»

Петроний

Тема урока: «Задачи на движение»

Тип урока: формирования знаний по данной теме

Цель урока: формирование умения решать различные типы задач на движение.

Задачи:

Образовательная: Выработать навыки решения задач на встречное движение, движение в противоположные стороны и движение в одну сторону. Обеспечить условия для усвоения всеми учащимися понятий скорости сближения и скорости удаления.  

Развивающая:  Развивать умение сравнивать, анализировать, обобщать полученные знания. Развивать внимание, память, логическое мышление, речь и творчество учащихся.
Воспитательная: Воспитание у учащихся чувства уверенности в своих силах, положительной мотивации к учению. Привитие умений оценивать свою работу путём рефлексии.

Оборудование и используемые учебные пособия:

1.Учебник,С.М.Никольский, М.К.Потапов, Н.Н.Решетников «Арифметика». 5 класс, М.: Просвещение, 2003.

2.Карточки для самостоятельной работы

3. Компьютер

План урока:

• Организация начала занятий.

• Проверка домашнего задания.

• Мотивация

• Актуализация опорных знаний.

• Усвоение новых знаний и способов действий. Восприятие, осмысление и первичное запоминание нового материала. Проверка усвоения знаний и способов действий.

• Первичное закрепление знаний и способов действий.

• Контроль и самопроверка усвоения полученных знаний и способов действий

• Подведение итогов урока. Рефлексия.

• Домашнее задание и его инструктаж.

Ход урока

I. Организация начала занятий

II. Проверка домашнего задания

Задание заранее решено на доске.

ΙΙΙ. Целеполагание и мотивация

— Как вы думаете, какой будет тема нашего сегодняшнего урока?

Для этого нам необходимо отгадать шифровку.

В результате мы составим слово, которое подскажет нам тему урока.

7

² + 3² =

2 *17 *5 =

84 * 9 + 16* 9 =

13 *125 * 8 =

25 * 32 =

6 * 25 *4 *125 *0 =

800 – а; 1300 – и; 58 –а; 170 –д; 900 – ч; о — з .

— Расположите числа в порядке возрастания.

— У нас получилось слово «Задача». А какие мы будем решать задачи?

— Давайте отгадаем загадки:

1.

Не похож я на коня,

А седло есть у меня.

Спицы есть. Они, признаться,

Для вязанья не годятся.

Не будильник, не трамвай,

Но звоню я то и знай. (

велосипед)

— Какое действие выполняет велосипед?

2. Пьет бензин, как молоко,

Может бегать далеко.

Возит грузы и людей.

Ты знаком, конечно, с ней?

(машина)

— Какое действие выполняет машина?

3. Трещит, а не кузнечик,

Летит, а не птица,

Везет, а не лошадь.

(самолет )

— Какое действие выполняет самолет?

4. Братцы в гости снарядились,

Друг за друга прицепились

И помчались в путь далек,

Лишь оставили дымок.

(поезд)

— Какое действие выполняет поезд?

5. Паровоз без колес!

Вот так чудо- паровоз!

Не с ума ли он сошел –

Прямо по морю пошел!

(пароход)

— Догадались с каким видом задач мы сегодня будем работать? Молодцы, конечно, с задачами на движение.

Ученики записывают число и тему урока в тетрадь.

А как вы думаете, какие учебные задачи нам нужно сегодня на уроке выполнить?

Формулируют задачи урока

— повторить, что такое скорость и как она находится;

— как найти скорость по течению и скорость против течения;

— повторить, что такое время, и как оно находится;

— повторить, что такое расстояние, и как оно находится;

— решать задачи разными способами;

— составлять задачи;

— Мы уже решали задачи по теме «Движение». Сегодня на уроке мы повторим и закрепим те знания, которые приобрели по этой теме, а также познакомимся с такими понятиями как скорость сближения и скорость удаления, рассмотрим более сложные задачи на движение в процессе их составления и решения.

ΙV. Актуализация опорных знаний

— Но прежде чем решать сложные задачи на движение, давайте вспомним, какие три величины характеризуют движение.

—Движение характеризуют скорость, время, расстояние.
Задача 1

Туристы прошли 18 км, двигаясь со скоростью 
6 км/ч. Что можно узнать?

   Задача 2

Теплоход был в пути 6 ч, проходя каждый час 
25 км. Что можно узнать?
    Задача 3

Какое расстояние пройдет теплоход по течению реки за 3ч, если его собственная скорость 25 км/ч, а скорость течения реки 5 км/ч?

Задача 4

Найдите скорость теплохода против течения реки, если его скорость по течению реки 28 км/ч, а собственная скорость 25 км/ч.

Задача 5

За 2 ч самолёт пролетел 800 км. Что можно узнать?

Самостоятельная работа с взаимопроверкой

Заполните таблицу самостоятельно.

— Поменяйтесь листочками с соседом по парте и проверьте задание по образцу

Физкультминутка

Дружно с вами мы считали и про числа рассуждали,

А теперь мы дружно встали, свои косточки размяли.

Дружно встали, улыбнулись,

Выше-выше подтянулись.

Ну-ка плечи распрямите,

Поднимите, опустите.

Вправо, влево повернитесь,

Рук коленями коснитесь.

На счет раз кулак сожмем, на счет два в локтях согнем.

На счет три — прижмем к плечам, на 4 — к небесам

Хорошо прогнулись, и друг другу улыбнулись

Про пятерку не забудем — добрыми всегда мы будем.

На счет шесть вздохнули дружно.

Нам урок продолжить нужно.

Подравнялись, тихо сели

И на доску посмотрели.

V. Усвоение новых знаний и способов действий.

№399 стр.86

Два пешехода вышли одновременно в противоположных направлениях из одного пункта. Скорость первого 4 км/ч, скорость второго 5 км/ч. Какое расстояние будет между ними через 3 часа?

4 км/ч ?км 5 км/ч

А В

3ч

Решим задачу двумя способами.

Ι способ

1) 3* 4 =12 (км) прошел 1 пешеход за 3 часа;

2) 3 * 5 = 15 (км) прошел 2 пешеход за 3 часа;

3) 12+ 15 = 27 (км) расстояние между пешеходами через 3 часа.

Попробуем записать решение задачи, составив числовое выражение. Как это сделать?

-Вынести общий множитель 3 за скобки: 3* 4 + 3 * 5 = 3 *(4 +5) =27

Как вы думаете, что показывает сумма 4 +5?

— Она показывает, на сколько километров в час два пешехода удаляются друг от друга

Эту величину называют скоростью удаления .

Тогда ΙΙ способ

1) 4 +5 =9 (км/ч) скорость удаления;

2) 9 * 3 = 27 (км) расстояние между пешеходами через 3 часа.

Какой способ вам показался проще?

№ 400 а) стр.87

Из одного пункта в противоположных направлениях выехали две автомашины. Их скорости 60 км/ч, и 80 км/ч. Определите скорость удаления автомашин.( устно разбирается решение V_удал = 140 км/ч)

А теперь предположим, что наши пешеходы вышли одновременно навстречу друг другу из пунктов, расстояние между которыми 27 км. Через сколько часов они встретятся, если у них такие же скорости 4км/ч и 5км/ч?

4 км/ч ?ч 5км/ч

А В

27 км

— Что произойдет с расстоянием между пешеходами?

— Уменьшится

-Почему? ( Они движутся навстречу друг другу. )

— Какое расстояние было между ними в самом начале? 27 км.

— Какова их скорость сближения?

V_сбл = 4 + 5= 9 км/ч

— Что показывает скорость сближения 9 км/ч?

— Она показывает, что пешеходы за каждый час сближаются на 9 км.

— Как узнать, каким стало расстояние через 1 час?

— Надо из 27 – 9 км, получим 18 км.

— Что будет происходить дальше?

— Они сблизятся ещё на 9 км и т.д.

— Как же определить расстояние через 2 часа? 3 часа?

— Нужно из 27 – 9 ∙ 2, или 27- 9 ∙3.А как определить время, через которое пешеходы встретятся?

27 : (4 + 5) = 3(ч)

— Интересно, какое будет расстояние между пешеходами через 3ч , если они будут идти в одном направлении в одну сторону или в другую.

Рассмотрим рисунок.

4 км/ч 3ч ?км 5 км/ч

А В

27км

— Расстояние между ними будет уменьшаться или увеличиваться, если они будут двигаться вдогонку?

— Уменьшаться

— Почему?

— Скорость второго пешехода больше, чем скорость первого

— Какое расстояние пройдет первый пешеход за 3ч?

4∙ 3 = 12 км

— Какое расстояние пройдет второй пешеход за 3ч?

5 ∙ 3 = 15 км

— Сколько км осталось второму пешеходу до пункта А?

27 – 15= 12 км

— Тогда на каком расстоянии будут пешеходы?

12 + 12 = 24 км.

— Можно ли эту задачу решить другим способом?

И останется ли расстояние между пешеходами таким же , если первый пешеход будет двигаться за вторым?

4 км/ч 3ч ?км 5 км/ч

А В

27 км

V_удал.= 5- 4 =1(км/ч)

— За з часа расстояние увеличится на 3 км, т.е. станет 30 км.

— Какой можно сделать вывод после решения одной и той же задачи, но изменяя направления движения?

Вывод: ( ученики высказывают свое мнение)

VΙ. Первичное закрепление знаний и способов действий.

Решить задачи №403 а) и № 406 а) с проверкой у доски

Два велосипедиста выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого 10км/ч, а второго 8км/ч. Через сколько часов они встретятся?

1) 10 + 8 = 18 (км/ч) скорость сближения;

2) 39: 18 = 2 (ч).

Велосипедист и мотоциклист выехали одновременно из одного пункта в одном направлении. Скорость мотоциклиста 40км/ч, а велосипедиста 12 км/ч. Какова скорость удаления их друг от друга? Через сколько часов расстояние между ними будет 56 км?

1) 40 – 12 =28(км/ч) скорость удаления;

2) 56:28 = 2 (ч)

VΙΙ. Контроль и самопроверка усвоения полученных знаний и способов действий

— Ребята, давайте проверим, хорошо ли мы повторили алгоритмы решения задач на движение. Сейчас нам нужно разбиться на группы. Каждая группа будет составлять задачу по определенному условию, а затем моделировать её в конструкторе. Для этого нам понадобиться программа – конструктор для составления задач.

Для моделирования задачи необходимо выполнить её решение. В конце урока мы рассмотрим ваши работы.

Задание №1:

Из города в противоположных направлениях …(выехали, вышли, вылетели)……(объект 1) и …(объект 2). Скорость одного …..км/ч .Скорость другого…км/ч. Какова скорость удаления их друг от друга? Найдите расстояние между ними через …. часа

Задание № 2:

Из города А в город Б одновременно …(выехали, вышли, вылетели)……(объект 1) и …(объект 2). Скорость одного …..км/ч. Скорость другого…км/ч. Найдите расстояние между ними через …… часа.

Задание № 3:

Из двух городов, расстояние между которыми ….. км, одновременно навстречу друг другу … (выехали, вышли, вылетели)……(объект 1) и …(объект 2). Какова скорость их сближения? Найдите расстояние между ними через …. Часа . Через сколько часов они встретятся?

Каждая группа демонстрирует свое задание.

— Все задачи были интересны. Молодцы! Задача какой группы вам понравилось больше? Почему? Карандашом поставьте себе оценку за урок.

VΙΙ. Подведение итогов урока. Рефлексия .

— Ребята, подумайте, что во время урока у вас получалось хорошо, а что не очень? Сделайте для себя выводы . Ученики оценивают свою работу.

1. Сегодня на уроке я познакомился с…

2. Было интересно…

3. Было трудно…

4. Я научился…

5. Я затрудняюсь…

6. Меня удивило…

7. Мне захотелось…

8. Хотелось бы…

— Как вы считаете, мы выполнили задачи, поставленные вначале урока?

-С каким настроением вы работали на уроке? Изобразите карандашом своё настроение в виде смайлика.

VΙΙΙ. Домашнее задание.

№409 стр.89, *Составить свою задачу на движение.

Приложение 1

Приложение 2

Задание №1:

Из города в противоположных направлениях …(выехали, вышли, вылетели)……(объект 1) и …(объект 2). Скорость одного …..км/ч .Скорость другого…км/ч. Какова скорость удаления их друг от друга? Найдите расстояние между ними через …. часа

Задание № 2:

Из города А в город Б одновременно …(выехали, вышли, вылетели)……(объект 1) и …(объект 2). Скорость одного …..км/ч. Скорость другого…км/ч. Найдите расстояние между ними через …… часа.

Задание № 3:

Из двух городов, расстояние между которыми ….. км, одновременно навстречу друг другу … (выехали, вышли, вылетели)……(объект 1) и …(объект 2). Какова скорость их сближения? Найдите расстояние между ними через …. часа . Через сколько часов они встретятся?

Приложение 3

http://files.school-collection.edu.ru/dlrstore/e25532a4-cc87-4640-80e5-cc545d8d230f/MotionSetup.exe

Приложение

Памятка решения простых задач на движение.

• Вспомни, как взаимосвязаны величины скорость, время, расстояние.

• Установи, что тебе нужно найти.

• Если не сможешь чётко уловить вопрос задачи, запиши данное условие в таблицу.

v

10 новогодних задач. 5 класс

10 новогодних задач
5 класс
Учитель математики Дудник Т.Г.
На Новогодние праздники Дед
Мороз раздал в детском саду
72 подарка, а в школе в три
раза больше. Сколько всего
подарков раздал Дед Мороз в
школе и детском саде? На
сколько детей больше в школе,
если Дед Мороз каждому
ребенку давал по одному
подарку?
Дед Мороз и Снегурочка
созвонились и договорились вместе
вручать новогодние подарки в
школе села Снегово. Но
Снегурочка в это время была в
деревне Внуковская, а Дед Мороз в
деревне Дедовская. От Внуковской
до Снегово 16 км, а от Дедовской
до Снегово 12 км. Кто первым
окажется в Снегово, если Дед
Мороз идет против ветра со
скоростью 4 км/час, а Снегурочка
по ветру со скоростью в два раза
больше?
Снеговик решил прокатиться на аэросанях. А
чтобы не было жарко, кабину снял. Покатался он
с ветерком! Но каждую минуту ветром из него
выдувало 200 грамм снега. На сколько
килограмм «похудел» Снеговик, если катался он
ровно один час?
Дед Мороз купил холодильную камеру для
хранения подарков. Объем камеры один
кубометр. Сколько подарков войдет в эту
камеру, если каждый из них занимает место в 2
кубических дециметра.
Василиса Прекрасная
испекла огромный
Новогодний торт. Но
пока она приводила
себя в порядок, Кот в
Сапогах съел половину
торта, а затем Микки
Маус еще половину от
оставшегося куска.
Найдите вес
оставшегося куска,
если первоначально
торт весил 20
килограмм.
Баба Яга за новогодние праздники от злости худеет
на 15 килограммов. Но все равно, даже после
праздников, она весит на 40 килограммов больше,
чем Кощей. Какой вес был у Бабы Яги до
праздников, если она весила ровно в шесть раз
больше Кощея. Вес Кощея не изменяется уже сто
лет.
С первого по седьмое января
Баба Яга ежедневно летала за
спичками в Тридевятое
царство. Перед первым
полетом спидометр на ее
метле показывал 123445 км, а
при возвращении седьмого
193445 км. Каково расстояние
от избушки Бабы Яги до
Тридевятого царства?
Кощей Бессмертный первого
января посадил в темницу две
Снежинки, второго в два раза
больше, а третьего в два раза
больше, чем второго. Сколько
Снежинок оказалось в темнице
за три дня?
Устав после Новогодних праздников Дед Мороз и
Снегурочка решили отдохнуть, Дед проспал 16 часов
38 минут. Снегурочка на 6 часов и 46 минут больше.
Сколько времени спала Снегурочка?
Серый Волк и Лиса
бежали новогодний
марафон. Стартовали они
одновременно у
Новогодней ёлочки 1
января в 12 часов 30
минут. Серый Волк
добежал до Лукоморья 4
января в 14 часов, а Лиса 5
января в 6 часов. Сколько
времени была в пути
лиса? На сколько часов
Серый Волк опередил
Лису?

Задача про свечи. ВПР. 5 класс | Шевкин.Ru

15.04.2021

Вспомнились строки Б. Пастернака.

Мело, мело по всей земле
Во все пределы.
Свеча горела на столе,
Свеча горела.

Это как защитная реакция после шока, который я испытал при чтении задачи для 5 класса. Читательница моего канала попросила: «Прокомментируйте, пожалуйста, задачу про горящие свечи из пособия Ященко за 5 класс. «Одновременно зажгли 3 свечи одинаковой длины, но разного диаметра». Как можно её решить, не составляя уравнения? Дети в шоке от этого пособия. Это обычная сош, нет у нас такого уровня подготовки».

Поискал я в Интернете. Поскольку я не в восторге от творчества коллектива И.В. Ященко, то не слежу за их новинками. Пропустил появление нового задачного сюжета для пятиклассников. Нашёл задачу. Позже выверил текст по книге [1].

1. Одновременно зажгли три свечи одинаковой длины, но разного диаметра. Длина каждой свечи 24 см. Первая свеча была самая толстая, вторая — потоньше, третья — самая тонкая. В тот момент, когда догорела третья свеча, первую и вторую тоже потушили. Оказалось, что огарок от первой свечи в два раза длиннее, чем от второй. За какое время полностью сгорает третья свеча, если известно, что первая сгорает за 6 ч, а вторая за 4 ч? [1]

«Ничего себе!» — Сказал я себе. Но почему в 5 классе? Ведь тот же авторский коллектив поддержал использование арифметических способов решения задач до применения уравнений. Они предлагали решения текстовых задач с помощью перебора, таблиц… Уже и в ЕГЭ включили задачи, решаемые арифметически…

Приведём авторское решение из книги [1].

Первая свеча горит со скоростью 24 : 6 = 4 сантиметра в час, вторая — со скоростью 24 : 4 = 6 сантиметров в час.

Пусть третья свеча сгорела за х ч. Тогда длина огарка первой свечи 24 – 4х (см), длина огарка второй свечи равна 24 – 6х (см).
24 – 4х = 2(24 – 6х ), откуда х = 3.

Это «взрослое» решение. Кажется, что «против лома нет приёма». А давайте поищем «детское» решение. Два первых действия оставим без изменения.

1) 24 : 6 = 4 (см/ч) — скорость сгорания первой свечи,
2) 24 : 4 = 6 (см/ч) — скорость сгорания второй свечи.

Давайте понаблюдаем за процессом горения свечей. Запишем в виде таблицы длину огарка каждой свечи через 1, 2…. часа. В правом столбце разделим первый результат на второй. Посмотрим, через сколько часов горения выполнится условие задачи.

Как видно из таблицы, огарок первой свечи станет в 2 раза больше, чем огарок второй свечи, через 3 часа. Ещё через час вторая свеча догорит. Третья свеча горела 3 часа.

Ответ. 3 ч.

Развивая идею одного из комментаторов, покажем, что в задаче есть лишнее условие «24 см».
Через 1 час огарки свечей относятся как (1 — 1/6) : (1 — 1/4) < 2.
Через 2 часа огарки свечей относятся как (1 — 2/6) : (1 — 2/4) < 2.
Через 3 часа огарки свечей относятся как (1 — 3/6) : (1 — 3/4) = 2.
Дальнейшее увеличение времени горения (до 4 ч) делает отношение большим 2.

Для закрепления решите с детьми задачу из другого варианта. Только объясните им, что «полтора» это от старинного «пол втора», то есть «половина второго». Один с половиной.

2. Одновременно зажгли три свечи одинаковой длины, но разного диаметра. Длина каждой 16 см. Первая свеча была самая толстая, вторая потоньше, третья самая тонкая. Когда догорела третья свеча, первую и вторую потушили. Оказалось, что огарок первой свечи в полтора раза длиннее, чем от второй. За какое время сгорит третья свеча, если первая сгорает 8 ч., а вторая 4 ч? [1]

Ответ. 2 ч.

В Интернете есть разные «взрослые» способы решения задач такого типа. Есть приводящие к рациональному уравнению, которое в 5 классе, разумеется, не изучали.

Повторяю призыв из предыдущей моей статьи, посвящённой решению текстовых задач: «Уважаемые взрослые, не навязывайте детям свои взрослые мнения по поводу решения задачи. Сначала поищите возможное «детское» решение задачи».

Литература

1. Всероссийская проверочная работа. Математика : 25 вариантов. Типовые задания. ФГОС / Г.И. Вольфсон, Д.А. Мануйлов; под ред. И.В. Ященко. — М. : Издательство «Экзамен», 2020

Факультативный курс по математике «Логические задачи», (5 класс)

Факультативный курс по математике в 5 классе

Логические задачи.

Пояснительная записка

В соответствии с требованиями, предъявляемыми современной школой, обучение в ней должно ориентироваться на развитие продуктивного, творческого мышления, которое дает возможность самостоятельно приобретать новые знания, применять их в многообразных условиях окружающей действительности.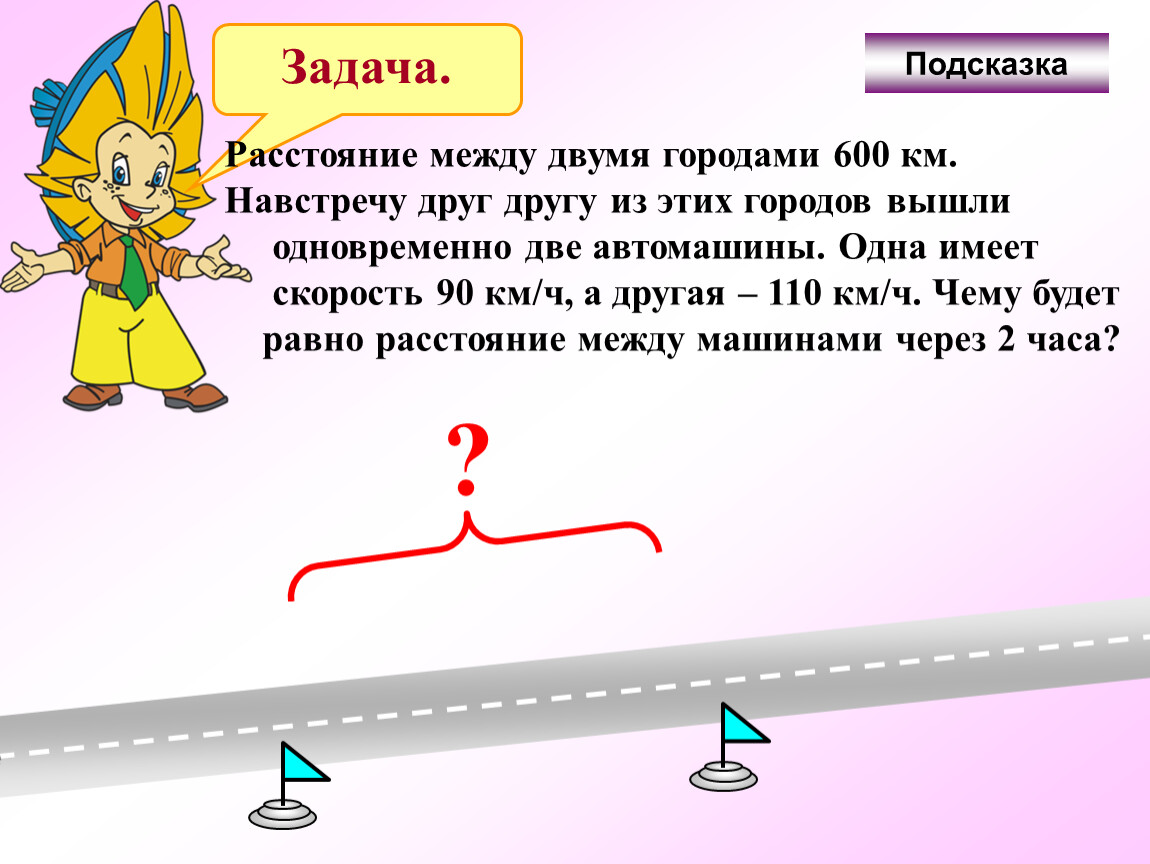 Поэтому развитие творческого мышления учащихся, в процессе изучения ими математики, является одной из актуальных задач, стоящих перед преподавателем математики. Важным принципом развития творческого мышления является специальное формирование как алгоритмических, так и эвристических приемов умственной деятельности. Как известно, творческое мышление предполагает не только широкое использование усвоенных знаний, но и отход от привычных путей мысли, разрешение противоречий между актуализированными знаниями и требованиями проблемной ситуации, оригинальность решений, их своеобразие.

Данный курс по решению логических задач рассчитан на учащихся среднего звена. В этом возрасте у детей еще повышен интерес к обучению, их достаточно легко увлечь чем — то новым и интересным. В своей работе я использую, помимо решения задач, проектно-исследовательские работы. Вовлекая таким образом учащихся в непрерывный процесс обучения. Самостоятельно изучая какую-либо проблему, ученики намного быстрее вникают в суть и усваивают необходимые знания, умения, навыки. Также достаточно объемная и длительная работа над каким-либо проектом не дает учащимся расслабляться и выходить из рабочего ритма. Учащиеся 5-6 классов очень любят старинные задачи и задачи-шутки. Такие задачи можно использовать в качестве устного счета, разминки, в конце урока. Также полезно давать детям задание по составлению задач и обязательно давать их решать классу, что способствует более ответственному отношению к заданиям. Курс рассчитан на 34 часа. В конце каждого полугодия проводится защита исследовательских работ, которые оцениваются по номинациям.

Учебно-тематический план курса (34часа)

Основное содержание курса.

Тема 1. Вводное занятие. Основы логики. История развития алгебры и математической логики. Логические задачи для разминки.

Понятие «логическая задача». История возникновения логических задач. Значение логических задач в развитии мышления и приёмы мыслительной деятельности, способствующие развитию умения решать логические задачи. Логические задачи для разминки.

Установочное тестирование для определения уровня развития логического мышления.

Тема 2. Задачи – шутки.

Из истории возникновения задач-шуток. Задачи-шутки. Практическая работа по составлению задач данного типа.

Тема 3. Задачи на логику счета.

Из истории возникновения задач на логику счета. Задачи на логику счета и алгоритм их решения. Задачи данного вида олимпиадного характера. Проведение обучающей самостоятельной работы по группам.

Тема 4. Игра «Головоломки»

Форма проведения занятия – игра соревновательного характера. Математические ребусы и обобщённый алгоритм их решения. Обобщение знаний учеников по задачам-шуткам и задачам на логику счета.

Тема 5. Исследовательская работа «Логика в практике человека».

Основные положения по организации и проведению исследовательской работы. Обработка собранного материала по теме. Проведение творческой самостоятельной работы по группам.

Тема 6. Защита исследовательских работ

Защита исследовательских работ по теме «Логика в практике человека».

Оценка работ по номинациям:

-лучшее содержание;

-лучшее наглядное оформление;

-лучшее изложение и т.д.

Подведение итогов окончания четверти.

Тема 7. Старинные занимательные задачи

Из истории возникновения данного вида задач. Старинные занимательные задачи и алгоритм их решения. Моделирование ситуаций и нахождение путей их решения.

Тема 8. Задачи-загадки

Из истории возникновения задач-загадок. Решение задач данного вида. Выполнение упражнений по составлению задач-загадок (работа в парах).

Тема 9. Затруднительные ситуации

Задачи на затруднительные ситуации и алгоритм их решения (6 ситуаций). Моделирование ситуаций и нахождение путей их решения. Творческая самостоятельная работа в группах по разрешению проблемной ситуации. Защита своих решений.

Тема 10. Контрольное тестирование по итогам 1 полугодия

Проведение контрольного тестирования. Сравнение результатов тестирования с результатами установочного тестирования.

Тема 11. Задачи с практическим содержанием

Виды «практичных» и «непрактичных» задач, алгоритм их решения. Выполнение тренировочных упражнений по решению данного вида задач.

Тема 12. Настоящие логические задачи.

Законы мышления, понятие, суждение. Использование частичного поиска для решения задач на логику мышления. Выполнение упражнений на тему « Логические рассуждения».

Тема 13. Переправы, разъезды, погони.

Задачи на переправы, разъезды, погони, алгоритм их решения. Моделирование ситуаций и нахождение путей их решения. Выполнение творческой самостоятельной работы в группах. Защита своего решения.

Тема 14. Можете ли вы рассуждать логично? Подготовка детей к участию в международном математическом конкурсе «Кенгуру».

Тестирование на логику мышления. Задачи логического характера из сборника заданий международного математического конкурса «Кенгуру» прошлых лет. Практическое занятие по решению данных заданий.

Тема 15. Игра «Лабиринт смекалки»

Форма проведения занятия — игра соревновательного характера. Обобщение и систематизация знаний и умений решения задач изученных видов. Подведение итогов окончания 3 четверти.

Тема 16. Задачи на переливание

Задачи, решаемые на основе осознания исходных данных. Задачи на переливание и алгоритм их решения. Выполнение практических заданий в группах.

Тема 17. Логический детектив

Форма проведения занятия — урок — расследование. Значение логики в профессии людей. Выполнение практических заданий на умение проводить расследования по детективной ситуации. Обучающая самостоятельная работа.

Тема 18. Турнир смекалистых

Форма проведения занятия — турнир детективов. Расследование «Детективных дел», оценка данного расследования. Определение лучшего детектива.

Тема 19. Исследовательская работа «Логика в жизни моей семьи»

Обработка собранного материала по теме «Логика в жизни моей семьи». Проведение творческой самостоятельной работы по группам.

Тема 20. Защита исследовательских работ.

Защита исследовательских работ по теме «Логика в жизни моей семьи».

Оценка работ по номинациям:

-лучшие содержание;

-лучшее наглядное оформление;

-лучшее изложение и т.д.

Подведение итогов окончания изучения курса.

Планируемые результаты обучения

В результате изучения курса учащиеся должны:

—понимать сущность понятия «логическая задача»;

—знать алгоритмы решения алгоритмических логических задач и уметь применять их на практике;

—знать алгоритм творческой деятельности по поиску решения неалгоритмических логических задач и уметь применять его на практике;

—уметь выполнять небольшие исследовательские работы, владеть приемами их защиты.

РАЗРАБОТКИ ЗАНЯТИЙ

Тема 1. Вводное занятие. Основы логики. История развития алгебры и математической логики. Логические задачи для разминки.

“Недостаточно иметь хороший ум. Главное – правильно его использовать”

Рене Декарт

Цели:

Образовательная:

закрепить понятия алгебры логики и отработать навыки использования ее для решения задач;

Развивающие:

развивать логическое и творческое мышление учащихся, сообразительность, наблюдательность, интуицию;

формировать активный познавательный интерес к предмету.

Воспитательная:

воспитывать культуру общения на уроке, аккуратность, внимательность и взаимоуважение;

воспитывать умение работать в группе;

воспитывать умение отстаивать свою точку зрения.

Форма урока: нетрадиционная

Занятие проводится в форме круглого стола. Проводится утреннее совещание в “ школе сыска” с названием “Логика и К”

Оборудование: Карточка с задачами, мультимедийный проектор, презентация

ПЛАН УРОКА

I. Оргмомент (сообщается цель, план урока, форма проведения)

Логика и К — Школа сыска

Утреннее совещание

Разоблачение фальшивомонетчика

Задержанный

Кто участвовал в ограблении?

Дело Иванова, Петрова и Сидорова

Ограбление банка

Вывод комиссара Мегре

II. Вводное слово учителя (Приложение 1, приложение 2)

III.Разминка (решение задач с помощью рассуждений)

Предлагаются две задачи: №1 Фальшивомонетчик, №2 Задержанный. Решение данных задач находят ребята путем мозгового штурма: Выдвигают гипотезы и пытаются их доказать. Учитель выступает в роли координатора.

№1 Фальшивомонетчик

Искусный фальшивомонетчик снял копию со стодолларовой купюры и начал печатать фальшивки. Сделанные им копии во всех деталях повторяли оригинал. Но эксперт утверждает, что он совершил единственную ошибку.

Какую ошибку допустил преступник? (Ответ. Преступник сделал копию фальшивой купюры)

№2 Задержанный

Грабитель глубокой зимней ночью забрался в дом. Никто его не видел. Однако уже через несколько часов его задержала полиция.

Как им удалось выследить его? (Ответ. Оставил отпечаток номера машины на сугробе)

III. Основная часть. Решение задач с помощью алгебры высказываний

Водится метод решения задач с помощью алгебры высказываний

Учитель: При решении любой задачи могут быть выделены следующие этапы:

Анализ условия задачи (выделение исходных данных).

Поиск метода решения.

Символическая запись задачи.

Рассуждения и пояснения к решению.

Анализ полученных результатов и запись ответа.

Разнообразие логических задач очень велико. Способов их решения тоже немало. Но наибольшее распространение получили следующие три способа решения логических задач:

средствами алгебры логики;

табличный;

с помощью рассуждений.

Обычно используется следующая схема решения:

изучается условие задачи;

вводится система обозначен

Готовый кроссворд по математике — на тему «5 класс»

По горизонтали
6. Сумма длин всех сторон многоугольника
7. Чертёжный инструмент
8. Дробь, которая меньше 1
10. Число, которое складывается с другим
14. Число, на которое делят
16. Боковые грани с основой пирамиды
18. Выражение m•n
22. Число, из которого вычитают
25. Инструмент для измерения угла

По вертикали

1. Единица измерения с шестью нолями
2. Из-за чего создан значок процента?
3. Число которое вычитают
4. 1 тонна в центнерах
5. Любое число, на которое заданное делится без остатка
9. Занятие древних
11. Дробь, которая больше 1
12. Числа, которые используют при счете предметов
13. Луч, который делит угол пополам
15. Самое маленькое натуральное число
17. Как называется прямая, на которой отмечено начало отсчета, единичный отрезок и направление
19. Запись числа двумя цифрами
20. Геометрическая фигура, которая образована тремя отрезками
21. Единица длины.
23. Геометрическая фигура – часть прямой, ограниченная двумя точками этой прямой
24. Равенство, содержащее неизвестное число

Классы 5–9 Национальным исследовательским советом

Национальный исследовательский совет (NRC) функционирует под эгидой Национальной академии наук (NAS), Национальной инженерной академии (NAE) и Института медицины (IOM). NAS, NAE, IOM и NRC являются частью частного некоммерческого учреждения, которое предоставляет консультации по вопросам науки, технологий и политики здравоохранения в соответствии с хартией Конгресса, подписанной президентом Авраамом Линкольном, которая первоначально была предоставлена ​​NAS в 1863 году. NRC был создан в 1916 году, NAE — в 1964 году, а IOM — в 1970 году.Эти четыре организации вместе именуются Национальными академиями.

Миссия NRC состоит в том, чтобы улучшить процесс принятия государственных решений и государственной политики, повысить уровень просвещения и понимания населения, а также способствовать получению и распространению знаний в вопросах, касающихся науки, техники, технологий и здравоохранения. Учреждение серьезно относится к этому обвинению и работает над информированием о политике и действиях, которые могут улучшить жизнь людей в США и во всем мире.

NRC стремится предоставлять избранным лидерам, политикам и общественности советы экспертов, основанные на надежных научных данных. На свою работу СРН не получает прямых федеральных ассигнований. Отдельные проекты финансируются федеральными агентствами, фондами, другими государственными и частными источниками, а также фондами учреждения. Эта работа стала возможной благодаря 6000 ведущих ученых, инженеров и других специалистов мира, которые добровольно посвящают свое время работе в комитетах и ​​участию в различных мероприятиях.Управление NRC осуществляется совместно NAS, NAE и МОМ через Совет управляющих NRC.

Основные услуги включают сбор, анализ и обмен информацией и знаниями. Независимость учреждения в сочетании с его уникальной способностью собирать экспертов позволяет ему реагировать на множество запросов.

Портфель мероприятий включает:

* Консенсус-исследования: эти всеобъемлющие отчеты сосредоточены на основных вопросах политики и содержат рекомендации по решению сложных проблем.
* Встречи и семинары экспертов: созывая симпозиумы, семинары, встречи и круглые столы, NRC объединяет профессионалов, а также заинтересованную общественность и стимулирует диалог по различным вопросам.
* Управление программами и исследованиями: По запросу государственных и федеральных агентств NRC управляет и оценивает исследовательские программы, проводит оценки программ и рассматривает предложения.
* Стипендии: NRC управляет несколькими программами стипендий для докторантов.

Бесплатная научная информация: Ежегодно публикуя более 200 отчетов и связанных публикаций, учреждение является одним из крупнейших поставщиков бесплатной научной и технической информации в мире.Большая часть этого сейчас размещена в Интернете по адресу www.nap.edu.

Что такое задача производительности? (Часть 1) | by Defined Learning

Задание на результативность — это любая учебная деятельность или оценка, в которой учащимся предлагается выполнить , чтобы продемонстрировать свои знания, понимание и умения. Задания производительности дают осязаемый продукт и / или производительность, которые служат доказательством обучения. В отличие от элемента с выбранным ответом (например, множественный выбор или сопоставление), в котором учащимся предлагается выбрать из заданных альтернатив, задание на выполнение представляет ситуацию, которая требует от учащихся применять полученные знания в контексте.

Задания на производительность обычно используются в определенных дисциплинах, таких как изобразительное и исполнительское искусство, физическое воспитание и карьерные технологии, где производительность является естественной целью обучения. Однако такие задания можно (и нужно) использовать в любой предметной области и на всех уровнях обучения.

Характеристики служебных заданий

Хотя любое выступление учащегося можно рассматривать как служебное задание (например, завязывание обуви или рисование рисунка), полезно различать применение конкретных и отдельных навыков (например.ж., ведение баскетбольного мяча) от подлинного поведения в контексте (например, игра в баскетбол, в которой ведение мяча является одним из многих прикладных навыков). Таким образом, когда я использую термин «задачи выполнения», я имею в виду более сложные и достоверные выступления.

Вот семь общих характеристик задач производительности:

1. Задачи производительности требуют применения знаний и навыков, а не только вспоминания или распознавания.

Другими словами, учащийся должен фактически использовать свое обучение, чтобы выполнить .Эти задачи обычно дают материальный продукт (например, графический дисплей, сообщение в блоге) или результативность (например, устную презентацию, дебаты), которые служат доказательством их понимания и мастерства.

2. Задачи производительности являются неограниченными и обычно не дают однозначного правильного ответа.

В отличие от заданий с выбранными или краткими построенными ответами, которые ищут «правильный» ответ, рабочие задания являются неограниченными. Таким образом, могут быть разные ответы на задачу, которые по-прежнему соответствуют критериям успеха.Эти задачи также открыты с точки зрения процесса; то есть, как правило, нет единственного способа выполнить задачу.

3. Задания на исполнение создают новый и аутентичный контекст для исполнения.

Эти задания представляют собой реалистичные условия и ограничения для навигации учащихся. Например, задача по математике представит ученикам невиданную ранее проблему, которую нельзя решить, просто «вставив» числа в запомненный алгоритм. В аутентичной задаче учащимся необходимо рассмотреть цели, аудиторию, препятствия и варианты для достижения успешного продукта или производительности.У аутентичных заданий есть побочное преимущество — они передают учащимся цель и актуальность, помогая учащимся увидеть причину, по которой они прилагают усилия для подготовки к ним.

4. Рабочие задания подтверждают понимание посредством передачи.

Понимание проявляется, когда учащиеся могут перенести свое обучение на новые и «запутанные» ситуации. Обратите внимание, что не все выступления требуют переноса. Например, игра на музыкальном инструменте по нотам или пошаговая научная лаборатория требуют минимального перевода.Напротив, сложные задачи по производительности являются неограниченными и называют «мышлением более высокого порядка» и продуманным применением знаний и навыков в контексте, а не сценарием или шаблонным исполнением.

5. Задачи производительности многогранны.

В отличие от традиционных тестовых «заданий», которые обычно оценивают отдельный навык или факт, задачи производительности являются более сложными. Они включают в себя несколько этапов и, таким образом, могут использоваться для оценки нескольких стандартов или результатов.

6.Рабочие задания могут включать два или более предмета, а также навыки 21 века.

В более широком мире, помимо школы, большинство вопросов и проблем не проявляются четко в рамках «разрозненных» предметных областей. Хотя рабочие задания, безусловно, могут быть связаны с содержанием (например, математика, естественные науки, общественные науки), они также предоставляют средство для интеграции двух или более предметов и / или объединения навыков и умственных способностей 21 века. Одним из естественных способов интеграции предметов является включение компонентов чтения, исследования и / или общения (например,g., письмо, графика, устная или технологическая презентация) к задачам в таких областях содержания, как общественные науки, наука, здоровье, бизнес, здоровье / физическое воспитание. Такие задания побуждают учащихся рассматривать осмысленное обучение как интегрированное, а не как то, что происходит по отдельным предметам и сегментам.

7. Выполнение бессрочных задач оценивается по установленным критериям и критериям.

Поскольку эти задачи не дают однозначного ответа, продукты и достижения учащихся должны оцениваться по соответствующим критериям, согласованным с оцениваемыми целями.Четко определенные и согласованные критерии позволяют проводить обоснованную оценку на основе суждений. Более подробные критерии оценки, основанные на критериях, используются для определения различных уровней понимания и владения языком.

Учебные материалы, рабочие листы и задания для 5 класса

Выберите ваше местоположение

Выбор страны и штата поможет нам предоставить вам наиболее подходящие учебные ресурсы для ваших учеников.

Страна Австралия Соединенные Штаты Соединенное Королевство Афганистан Иландские острова Албания Алжир Американское Самоа Андорра Ангола Ангилья Антарктика Антигуа и Барбуда Аргентина Армения Аруба Австралия Австрия Азербайджан Багамы Бахрейн Бангладеш Барбадос Беларусь Бельгия Белиз Бенин Бермуды Бутан Боливия, Многонациональное Государство Сабациона и Герцеговина Бонавия Остров Буве Бразилия Британская территория в Индийском океане Бруней-Даруссалам Болгария Буркина-Фасо Бурунди Камбоджа Камерун Канада Кабо-Верде Каймановы острова Центральноафриканская Республика Чад Чили Китай Остров Рождества Кокосовые (Килинг) острова Колумбия Коморские острова Конго Конго, Демократическая Республика Острова Кука Коста-Рика Кот д’Ивуар Хорватия Куба Кюрасао Кипр Чешская Республика Дания Джибути Доминика Доминиканская Республика Эквадор Египет Сальвадор Экваториальная Гвинея Эритрея Эстония Эфиопия Фолклендские (Мальвинские) острова Фарерские острова Фиджи Финляндия Франция Французская Гвиана Французская Полинезия Французские южные территории страны Габон Гамбия Грузия Германия Гана Гибралтар Греция Гренландия Гренада Гваделупа Гуам Гватемала Гернси Гвинея Гвинея-Бисау Гайана Гаити Остров Херд и острова Макдональд Святой Престол (государство-город Ватикан) Гондурас Гонконг Венгрия Исландия Индия Индонезия Иран, Исламская Республика Ирак Ирландия Остров Мэн Израиль Италия Ямайка Япония Джерси Иордания Казахстан Кения Кирибати Корея, Корейская Народно-Демократическая Республика, Республика Кувейт Кыргызстан Лаосская Народно-Демократическая Республика Латвия Ливан Лесото Либерия Ливия Лихтенштейн Литва Люксембург Макао Македония, бывшая югославская Республика Мадагаскар Малави Малайзия Мальдивы Мали Мальта Маршалловы острова Мартиник Мавритания Маврикий Майотта Мексика Микронезия, Федеративные Штаты Молдовы, Республика Монако Монголия Черногория Монтсеррат Марокко Мозамбик Мьянма Намибия Науру Непал Нидерланды Новая Каледония Новая Зеландия Никарагуа Нигер Нигерия Ниуэ Остров Норфолк Северные Марианские острова Норвегия Оман Пакистан Палау Палестина , Государство Панама Папуа-Новая Гвинея Парагвай Перу Филиппины Питкэрн Польша Португалия Пуэрто-Рико Катар Румыния Российская Федерация Руанда Сен-Бартелеми Остров Святой Елены, Вознесения и Тристан-да-Кунья Сент-Китс и Невис Сент-Люсия Сен-Мартен (французская часть) Сен-Пьер и Микелон Сент-Винсент и Гренадины Самоа Сан-Марино Сан-Томе и Принсипи Саудовская Аравия Сенегал Сербия Сейшельские острова Сьерра-Леоне Сингапур Синт-Мартен (голландская часть) Словакия Соломоновы острова Сомали Южная Африка Южная Джорджия и Южные Сандвичевы острова Южный Судан Испания Шри-Ланка Судан Суринам Свальбард и Ян-Майен Свазил Швеция Швейцария Сирийская Арабская Республика Тайвань, провинция Китая Таджикистан Танзания, Объединенная Республика Таиланд Тимор-Лешти Того Токелау Тонга Тринидад и Тобаго Тунис Турция Туркменистан Острова Теркс и Кайкос Тувалу Уганда Украина Объединенные Арабские Эмираты Соединенное Королевство Соединенные Штаты Малые отдаленные острова США Уругвай Узбекистан Вануату Венесуэла, Бол ivarian Республика Вьетнам Виргинские острова, Британские Виргинские острова, U.С. Уоллис и Футуна Западная Сахара Йемен Замбия ZimbabweState Австралийская столичная TerritoryNew Южная WalesNorthern TerritoryQueenslandSouth AustraliaTasmaniaVictoriaWestern AustraliaAlabamaAlaskaAmerican SamoaArizonaArkansasCaliforniaColoradoConnecticutDelawareDistrict Из ColumbiaFederated Штатов MicronesiaFloridaGeorgiaGuamHawaiiIdahoIllinoisIndianaIowaKansasKentuckyLouisianaMaineMarshall IslandsMarylandMassachusettsMichiganMinnesotaMississippiMissouriMontanaNebraskaNevadaNew HampshireNew JerseyNew MexicoNew YorkNorth CarolinaNorth DakotaNorthern Mariana IslandsOhioOklahomaOregonPalauPennsylvaniaPuerto RicoRhode IslandSouth CarolinaSouth DakotaTennesseeTexasUtahVermontVirgin IslandsVirginiaWashingtonWest VirginiaWisconsinWyoming

5280

Math Math Рассол

mathpickle.com содержит коллекцию глубоких, открытых и сложных (некоторые нерешенные!) математических задач для учащихся всех возрастов, доступных для поиска по классам, в том числе множество для очень маленьких. Каждая задача была найдена или создана профессиональным математиком и легко умещается в 45-60-минутный временной интервал.

nrich maths

nrichmaths.org имеет обширную коллекцию разнообразных интересных математических задач, доступных для поиска по возрасту и концепции. Учителя пользуются большой поддержкой, и студенты могут предлагать решения для возможной публикации в Интернете.

Головоломки Кен-Кен

Головоломки Кен-Кен похожи на судоку, но содержат сложные математические особенности. Головоломки развивают не только вычислительные возможности, но и навыки решения задач, чувство числа и более глубокое понимание свойств чисел. Этот веб-сайт будет генерировать для вас головоломки ken-ken на основе вашего выбора уровня обучения, математических операций, размера сетки и уровня сложности.

Zukei Puzzles

Zukei Puzzles — это поиск геометрических фигур, скрытых в сетках или точках.Основное внимание уделяется рассуждениям о свойствах двумерных фигур. Головоломки бывают всех уровней сложности. Вы и студенты также можете легко создать свои собственные.

Exploding Dots

Джеймс Тантон Exploding Dots покорил мир математики за последние пару лет. Используя простую визуальную модель, учащиеся исследуют числовое значение, сложение, вычитание, умножение, деление и другие аспекты в различных базовых системах.

Beast Academy

Beast Academy — это полный курс математики для одаренных и продвинутых учеников 2–5 классов.(Я бы не рекомендовал его другим студентам.) Он создан людьми, работающими в области искусства решения проблем, которые известны своими материалами для одаренных учащихся средних школ. Основное внимание уделяется решению проблем и глубокому концептуальному пониманию. Сообщается, что скоро появится онлайн-версия программы.

Проект M2

От тех же людей, которые разработали проект M3 для учеников старших классов начальной школы, Project M2 «содержит восемь учебных модулей, разработанных для классов K-2, чтобы стимулировать исследование и вовлечь учеников в критическое мышление, решение проблем и коммуникативную деятельность… [с] акцентом на «углубленную» математику с использованием основанных на исследованиях практик и стандартов в математическом образовании и дошкольном образовании.

Project M3

Эта серия статей от Кендалла Ханта хорошо известна в США как основанная на исследованиях глубокая и сложная программа по математике для продвинутых учеников. Каждый модуль сопровождается обширной поддержкой учителей, и вы можете использовать проекты как единицы учебной программы или как дополнение. Единственные минусы: материалы довольно дорогие и требуют от учителей изрядного времени на подготовку.

Задачи дифференцированного дробления {И задача вычисления FREEBIE}

Если какое-то умение меня погубит, то это определенно Дроби! Ученикам 5-х классов так трудно осознать, что они с ними связаны. А стандарты для 5 класса? Ага, я помню, как изучал некоторые из этих стандартов в средней школе! Но, к сожалению, их надо учить. Чтобы сделать фракции более терпимыми, я создал ресурс «Задачи и задачи фракций» с темой «ШОКОЛАД»! Я имею в виду, кто не любит шоколад?

Они не только оформлены в шоколадной тематике, но и отличаются друг от друга… лучшее из ОБЕИХ миров! Вот пример задачи на сравнение дробей.P.S. Эти две задачи доступны БЕСПЛАТНО в файле предварительного просмотра на этом ресурсе…. Но это не единственная бесплатная… продолжайте читать для еще одной халявы.

Вот более подробная разбивка уровней:

• Уровень 1: это более простой уровень. Этот уровень может содержать более простые числа
(например, знаменатели, меньшие множители и т. Д.), Модели
, каркасы уравнений или подсказки для размышлений. Эти уровни
лучше всего подходят для учеников 4-го класса или учащихся 5-го и 6-го классов, испытывающих трудности.

• Уровень 2: Это задание или задача на уровне класса, ориентированная на
на соответствие стандартам 5-го класса. Этот уровень будет работать с учениками
уровня ниже 6 или с учениками 4-го класса с продвинутым уровнем.

Вот почему я так люблю эти задания! Каждое задание включает в себя несколько шагов и требует от учащихся подтверждения своих ответов моделями, равенствами и объяснениями.

Эти задания отлично подходят для того, чтобы помочь студентам попрактиковаться в организации информации, представленной в виде длинных заданий или текстовых задач … ну, знаете, те, которые заставляют учителей съеживаться, когда мы видим их на стандартных тестах.

Этот набор включает в себя так много навыков дроби! Слишком много, чтобы перечислить, поэтому вот фрагмент Оглавления со всеми перечисленными задачами и навыками.

Если вы думаете, что этот ресурс может быть вам полезен, ознакомьтесь с ним, нажав здесь.

А теперь халява! Сейчас мы по колено разбираемся в дробях, и мои ученики немного (читай: СЛИШКОМ) запутались, когда дело доходит до всех шагов и различных моделей / алгоритмов. У нас скоро перерыв в середине зимы, поэтому я создал испытание на вычисление дроби, чтобы они могли выполнить его за перерыв.Взглянуть!

Я не упоминал о перерыве, чтобы вы могли использовать это испытание в любое время года. Щелкните здесь, чтобы загрузить свою копию!

Какому навыку вы боитесь преподавать или который является самым сложным для ваших детей?

Тесты, рабочие листы и задания для пятого класса (5 класс) для печати

Распечатайте наши рабочие листы и задания для пятого класса (5-й класс) или проведите их в виде онлайн-тестов.В наших таблицах используются различные высококачественные изображения, некоторые из которых соответствуют Общим основным стандартам.

Рабочие листы с меткой доступны только подписчикам Help Teaching Pro. Станьте подписчиком, чтобы получить доступ к сотням таблиц, соответствующих стандартам.

Перейти к:

Искусство английского языка

Информационные рассказы и тексты

Литература — книги, рассказы

Делать выводы и делать выводы

Математика

Арифметика и числовые понятия

Физическое воспитание

Учебные навыки / стратегии

Профессиональное образование

Глава 5, Задачи выхода — Уголок тренера по математике

«Мои билеты были банальными — просто быстрыми, в основном рутинными математическими вычислениями.Теперь мои задачи сосредоточены на решении проблем и рассуждении ». The Formative 5, стр. 108

Этот пост содержит партнерские ссылки, что просто означает, что когда вы используете мою ссылку и покупаете продукт, я получаю небольшую комиссию. Никаких дополнительных затрат для вас нет, и я даю ссылки только на книги и продукты, которые лично рекомендую.

Какое замечательное лето обучения, поскольку наше книжное исследование Скипа Феннелла, Бет Кобетт и Джонатана Рэя подходит к концу.У вас была возможность проверить хэштег # Formative5BookStudy? Столько хорошего разговора! Если вы не пробовали использовать Twitter для профессионального развития, возможно, сейчас самое время заняться этим. Если вы можете использовать Facebook, вы можете использовать Twitter.

График чтения

Формат

1. Следуйте руководству по чтению, опубликованному выше. Каждый понедельник, указанный в расписании, я буду публиковать пост со своими мыслями. Я планирую использовать формат, предложенный в руководстве по изучению книги, которое находится в конце книги (Поделимся, Ага! И Давай попробуем!).
2. Участвуйте, добавляя комментарии к этому сообщению или отвечая на комментарии других. Ваш комментарий будет отображаться после одобрения.
3. Используйте хэштег # Formative5BookStudy, чтобы участвовать в медленном чате в Twitter. Ищите по хэштегу в любое время в течение недели, чтобы следить за беседой. Я буду публиковать вопросы в течение недели, и вы можете добавлять свои мысли, используя тот же хэштег, а также хэштег # Formative5 или просто читать, что говорят другие. Если вы не использовали Twitter для профессионального развития, это отличный способ начать.

Совместное использование

Авторы начали с ответа на вопрос, который, вероятно, интересовал многих из нас — в чем разница между выходным листом или билетом и выходным заданием? Короткий ответ заключается в том, что это разница в когнитивных требованиях задачи. Выходные листы и билеты, как правило, представляют собой вопросы низкого уровня, основанные на вычислениях, в то время как выходные задания требуют от учащихся более высокого уровня мышления. Руководство по анализу заданий по математике (стр. 110), примеры типов заданий (стр. 111-112) и обсуждение уровней DOK (стр. 112) — хорошее чтение как для опытных, так и для начинающих учителей.Я планирую положить копию Руководства по анализу математических задач в свой блокнот для планирования, чтобы я мог легко взять его в руки во время планирования.

Я нашел комментарии Клаудии и Даршана (страницы 114–116) очень полезными. Клаудия поделилась некоторыми из моих любимых веб-сайтов с заданиями, и пример того, как она изменила районное задание для своей задачи выхода, был чрезвычайно полезным. На странице 116 Даршан рассказал, как его группа планирования двигалась к более значимым задачам после того, как команда помогла коллеге понять, что задачи, которые она покупала на онлайн-сайте, были просто «причудливыми рабочими таблицами» и не обязательно соответствовали стандартам или требовали когнитивных усилий.Поскольку ресурсы так легко доступны, это важный разговор. К счастью, в этой главе есть несколько ресурсов для оценки задач.

Ага!

Эта книга представляет собой книгу о хороших методах преподавания математики, замаскированную под книгу о формирующих оценках. Не поймите меня неправильно, это не критика. Я вернулся к главе «Проблемы и возможности», чтобы взять эту цитату:

Важной предпосылкой для такого планирования является ваше собственное понимание математического содержания и педагогических знаний, связанных с вашим классом и выше. Формирующий 5, стр. 11

Другими словами, чтобы стратегии формирующего оценивания были наиболее эффективными, учителя должны глубоко понимать свои стандарты и передовой опыт преподавания математики. Они также должны рассмотреть лучший учебный подход, ориентированный на учителя или ученика, для создания такой среды, в которой аутентичные математические задачи и дискурс являются нормой. Если вы подумаете о каждой из стратегий оценивания, стандарты процесса / математические практики переплетаются во всех них.Наблюдения и собеседования требуют, чтобы студенты делились своим математическим пониманием, в то время как «Покажи мне», ответные вопросы и выходные задания обычно призывают студентов использовать представления для обоснования своих решений. Математические методы специально перечислены в инструменте «Организатор задач по выходу» на странице 122. Это будет большим сдвигом для некоторых учителей — они перейдут от обучения, ориентированного на учителя и основанного на процедурах, к тому, которое подчеркивает глубокое концептуальное понимание посредством ориентированного на учащегося. инструкция.

Давай попробуем!

Мне нравится упор на командное планирование и сотрудничество при разработке банка выходных задач, потому что найти и / или создать высококачественные задачи — непростая задача. Когда все работают вместе, это определенно кажется более выполнимым. Представьте себе хорошо организованную папку с заполненными листами инструментов организатора (стр. 122). Какой ценный ресурс!

Твоя очередь

Поделитесь своими мыслями и / или наблюдениями ниже или в Твиттере, используя хэштеги # Formative5BookStudy и # Formative5.