| Длина |
| 1 см = 10 мм = 0,01 м |
| 1 дм = 10 см = 0,1 м |
| 1 м = 100 см = 10 дм |
| 1 км = 1000 м |
| 1 дюйм (inch) = 2.54 см |
| 1 фут (foot) = 12 дюймов = 30,48 см = 0,3048 м |
| 1 ярд (yard)= 3 фута = 91,44 см = 0,9144 м |
| 1 миля (mile) = 5280 футов = 1609,34 м = 1,609 км |
| 1 морская миля (nautical mile) =1,852 км |
| 1 м = 3,28 фута = 1,094 ярда = 0,00062 мили |
| 1 см = 0,393 дюйма |
| Площадь |
| 1 см2 = 100 мм2 |
| 1 дм2 = 100 см2 = 0,01 м2 |
| 1 м2 = 100 дм2 |
| 1 км2 = 1 000 000 м2 |
| 1 ар (1 а) = 100 м2 = 1 сотка |
| 1 гектар (1 га) = 10 000 м2 |
1 кв. дюйм (square inch) = 6,4516 см2 дюйм (square inch) = 6,4516 см2 |
| 1 кв. фут (square foot) = 144 кв. дюймам = 929,03 см2 |
| 1 кв. ярд (square yard) = 9 кв. футам = 0,83613 м2 |
| 1 акр (acre) = 4046,86 м2 |
| 1 кв. миля (square mile) = 640 акрам = 2,59 км2 |
| 1 м2 = 10,76 кв. футов = 1,196 кв. ярдов |
| 1 см2 = 0,155 кв. дюймов |
| Объем |
| 1 см3 = 0,001 дм3 = 0,001 л |
| 1 литр = 1 дм3 = 61,03 куб. дюйм = 0,22 галлона |
| 1 куб. дюйм = 16,387 см3 = 0,016 л |
1 куб. фут = 28316,8 см3 =28,316 л фут = 28316,8 см3 =28,316 л |
| 1 куб. ярд = 764555 см3 = 764,555 л |
| 1 пинта англ. = 0,568 л |
| 1 пинта амер. = 0,473 л |
| 1 галлон англ. = 4,54 л |
| 1 галлон амер. = 3,78 л |
| 1 баррель нефти =42 галлона = 158,988 л = 0,136 тонн |
| Вес |
| 1 кг = 1000 г |
| 1 ц = 100 кг = 0,1 т |
| 1 т = 1000 кг = 10 ц |
| 1 фунт = 453,6 г = 0,4536 кг |
| 1 унция = 1/16 фунта = 28,35 г |
| 1 г = 0,035 унций = 0,002205 фунтов |
| 1 кг = 2,2 фунта |
| Тройская система мер для благородных металлов и драгоценных камней |
| 1 гран = 64,8 мг |
| 1 карат = 3,086 грана = 0,2 г |
1 тройская унция = 31,10 г = 1/12 тр. фунта = 480 гран фунта = 480 гран |
| 1 тройский фунт = 373,24 г |
| Температура |
| 40°С = 104 F; 0°С= 32 F |
| F = (°C *1.8)+32 |
| °C = (F — 32)/1,8 |
| Разница температур в 1 °C эквивалентна разнице температур в 1,8 F |
ВПР 7 класс по математике в 2019 году: варианты и разбор заданий
Структура и содержание всероссийской проверочной работы
Работа содержит 16 заданий.
В заданиях 1–9, 11 и 13 необходимо записать только ответ.
В задании 12 нужно отметить точки на числовой прямой.
В задании 15 требуется схематично построить график функции.
В заданиях 10, 14, 16 требуется записать решение и ответ.
Распределение заданий варианта проверочной работы по содержанию, проверяемым умениям и видам деятельности
Распределение заданий варианта проверочной работы по содержанию, проверяемым умениям и видам деятельности.
В заданиях 1, 2 проверяется владение понятиями «отрицательное число», «обыкновенная дробь», «десятичная дробь» и вычислительными навыками.
В задании 3 проверяется умение извлекать информацию, представленную в таблицах или на графиках.
В задании 4 проверяется владение основными единицами измерения длины, площади, объёма, массы, времени, скорости.
Заданием 5 проверяется умение решать текстовые задачи на проценты.
Задание 6 направлено на проверку умений решать несложные логические задачи, а также находить пересечение, объединение, подмножество в простейших ситуациях.
В задании 7 проверяются умения извлекать информацию, представленную на диаграммах, а также выполнять оценки, прикидки.
В задании 8 проверяется владение понятиями «функция», «график функции», «способы задания функции».
В задании 9 проверяется умение решать линейные уравнения, а также системы линейных уравнений.
Задание 10 направлено на проверку умения извлекать из текста необходимую информацию, делать оценки, прикидки при практических расчётах.
В задании 11 проверяется умение выполнять преобразования буквенных выражений с использованием формул сокращённого умножения.
В задании 12 проверяется умение сравнивать обыкновенные дроби, десятичные дроби и смешанные числа.
Задания 13 и 14 проверяют умение оперировать свойствами геометрических фигур, применять геометрические факты для решения задач.
В задании 15 проверяется умение представлять данные в виде таблиц, диаграмм, графиков.
Задание 16 направлено на проверку умения решать текстовые задачи на производительность, покупки, движение.
Задание 1
В заданиях 1, 2 проверяется владение понятиями «отрицательное число», «обыкновенная дробь», «десятичная дробь» и вычислительными навыками.
Вычислите:
Вычислите:
Решение: (ответ запишите в виде дроби)
Ответ: 10/11
Задание 2
В заданиях 1, 2 проверяется владение понятиями «отрицательное число», «обыкновенная дробь», «десятичная дробь» и вычислительными навыками.
Найдите значение выражения 6,1 ∙ 8,3 — 0,83
Решение: 6,1 ∙ 8,3 — 0,83 = 49,8
Ответ: 49,8.
Математика в формулах. 5-11классы. Справочное пособие
Справочное пособие содержит все основные формулы школьного курса математики: алгебры, геометрии и начал анализа. Для удобства пользования справочником составлен предметный указатель. Пособие предназначено для школьников 5-11 классов и абитуриентов.
Купить
Задание 3
В задании 3 проверяется умение извлекать информацию, представленную в таблицах или на графиках.
В таблице приведены расстояния от Солнца до четырех планет Солнечной системы. Какая из этих планет дальше от Солнца?
|
|
|
|
|
|
|
|
|
|
|
|
- Юпитер
- Меркурий
- Сатурн
- Венера
Решение:
Из чисел, представленных в стандартном виде, наибольшим является то, которое имеет наибольший показатель в степени десяти. Если показатели равны, то наибольшим будет то число, у которого наибольшая мантисса.
Если показатели равны, то наибольшим будет то число, у которого наибольшая мантисса.
Наибольшим будет расстояние от Сатурна до Солнца.
2 способ:
7,781 ∙ 108 — Юпитер
5,79 ∙ 107 = 0,579 ∙ 108 — Меркурий
1,427 ∙ 109 = 14,27∙ 108 — Юпитер
1,082 ∙ 108 — Венера
Т.к. показатели десяток одинаковые, сравним десятичные дроби:
14,27 большая дробь. Значит, 14,27 ∙ 108 — большее число. И расстояние от Сатурна до Солнца наибольшее.
Задание 4
В задании 4 проверяется владение основными единицами измерения длины, площади, объёма, массы, времени, скорости.
Морская водомерка может развивать скорость до 3,6 км/ч. Выразите эту скорость в метрах в секунду (м/с).
Решение:
1 км = 1000 м
1 час = 60 мин = 3600 сек
Ответ: 1 м/с
Задание 5
Заданием 5 проверяется умение решать текстовые задачи на проценты.
Толя, выполняя физические упражнения, тратит на выполнение приседаний 25% времени, 40% от оставшегося времени уходит на бег. Определите, сколько времени уходит у Толи на выполнение физических упражнений, если на бег он тратит 120 минут. Ответ дайте в минутах. В ответ запишите только число.
Решение:
Пусть на все упражнения Толя тратит 100% своего времени. Тогда
- 100% — 25% = 75% — остаток после приседаний.
- 40% = 0,4
- 75% ∙ 0,4 = 30% — времени, приходящегося на бег.
- 120 ÷ 30 ∙ 100 = 400 (мин) — тратится на бег.
Ответ: 400.
Алгебра в таблицах.7-11кл. Справ.пособие (Звавич)
Пособие содержит таблицы по всем наиболее важным разделам школьного курса арифметики, алгебры, начал анализа. В таблицах кратко изложена теория по каждой теме, приведены основные формулы, графики и примеры решения типовых задач. В конце книги помещен предметный указатель. Пособие будет полезно учащимся 7-11 классов, абитуриентам, студентам, учителям и родителям.
В конце книги помещен предметный указатель. Пособие будет полезно учащимся 7-11 классов, абитуриентам, студентам, учителям и родителям.
Купить
Задание 6
Задание 6 направлено на проверку умений решать несложные логические задачи, а также находить пересечение, объединение, подмножество в простейших ситуациях.
В лесной школе на уроке ботаники сорока показала два цветка. На вопрос «Какие это цветы?» ученики ответили следующее:
Бельчонок: «Колокольчик и василек».
Зайчонок: «Фиалка и ромашка».
Лисенок: «Одуванчик и василек».
Медвежонок: «Ромашка и колокольчик».
Каждый назвал верно только один цветок. Какие цветы показала сорока?
Решение:
Посмотрим, какие цветы встречаются парами.
Колокольчик встречается у бельчонка и медвежонка.
Василек — у бельчонка и лисенка.
Ромашка — у зайчонка и медвежонка.
Т.к. одуванчик назвал только лисенок, а каждый должен назвать верно один цветок, значит одуванчика на картине нет. Но тогда лисенок правильно назвал василек. Василек встречается и у бельчонка.
Также на картине нет и фиалки, ее назвал только зайчонок.
Значит зайчонок правильно назвал ромашку. А она есть у медвежонка.
Тогда получается, что бельчонок и лисенок правильно назвали василек. А зайчонок и медвежонок — ромашку.
Ответ: Василек и ромашка.
Повторить все правила и формулы школьного курса вы сможете в справочном пособии «Алгебра. 7-11 классы».
Задание 7
В задании 7 проверяется владение понятиями «функция», «график функции», «способы задания функции».
Учащимся сочинских школ был задан вопрос: «По какому виду спорта вы хотели бы посетить соревнования на зимней олимпиаде в Сочи?». Их ответы можно увидеть на диаграмме. Сколько примерно учащихся хотели бы посетить соревнования и по хоккею, и по санному спорту, если всего в опросе приняли участие 400 школьников?
Их ответы можно увидеть на диаграмме. Сколько примерно учащихся хотели бы посетить соревнования и по хоккею, и по санному спорту, если всего в опросе приняли участие 400 школьников?
В ответе укажите номер правильного варианта.
- 180
- 240
- 120
- 200
Решение: Соревнования по санному спорту посмотрела примерно 1/4 часть всех зрителей, значит:
1) 1/4 ∙ 400 = 100 человек.
Соревнования по хоккею посмотрела примерно 1/6 часть всех зрителей, значит:
2) 1/6 ∙ 400 ≈ 67 человек.
3) 100 + 67 = 167 посмотрели хоккей и санный спорт.
Самое близкое число к этому результату – 180 (человек).
Правильный ответ под номером 1.
Задание 8
В задании 8 проверяется владение понятиями «функция», «график функции», «способы задания функции».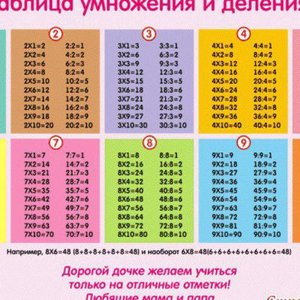
На рисунке изображен график линейной функции. Напишите формулу, которая задает линейную функцию.
Решение: График функции проходит через точки (0; 2) и (3; −3). Линейная функция задается формулой y = kx + b. Подставим координаты точек в эту формулу. Имеем:
Ответ:
Задание 9
В задании 9 проверяется умение решать линейные уравнения, а также системы линейных уравнений.
Найдите корень уравнения: 2×2 — x — 1 = x2 — 5x — (-1 — x2)
Решение:
2×2 — x — 1 = x2 — 5x — (-1 — x2)
2×2 — x — 1 = x2 — 5x + 1 — x2)
2×2 — x2 — x2 — x + 5x = 1 + 1
2×2 — 2×2 + 4x = 2
4x = 2
x = 2 ÷ 4
x = 0,5
Ответ: 0,5.
Алгебра (углубленное изучение). 7 класс. Самостоятельные и контрольные работы
Сборник содержит упражнения для самостоятельных и контрольных работ. Он используются в комплекте с учебником «Алгебра. 7 класс» (авт. А. Г. Мерзляк, В.М. Поляков) при изучении углублённого курса алгебры. Соответствуют федеральному государственному образовательному стандарту основного общего образования (2010 г.).
Купить
Задание 10
Задание 10 направлено на проверку умения извлекать из текста необходимую информацию, делать оценки, прикидки при практических расчётах
Прочтите текст.
В 1654 г. Отто Герике в г. Магдебурге, чтобы доказать существование атмосферного давления, провел такой опыт. Он выкачал воздух из полости между двумя металлическими полушариями, сложенными вместе. Давление атмосферы так сильно прижало полушария друг к другу, что их не могли разорвать восемь пар лошадей. Силу F (в ньютонах), сжимающую полушария, вычисляют по формуле F = P ∙ S, где P — давление в паскалях, S — площадь в квадратных метрах. В опыте Отто Герике атмосферное давление составляло 760 мм ртутного столба и действовало на площадь, равную 0,28 . Известно, что 1 мм рт.ст. = 133Па. С высотой давление атмосферы уменьшается на 1 мм рт.ст. при подъеме на каждые 12 метров. Это явление позволяет измерять высоту объектов приборами, называемыми высотометрами.
Силу F (в ньютонах), сжимающую полушария, вычисляют по формуле F = P ∙ S, где P — давление в паскалях, S — площадь в квадратных метрах. В опыте Отто Герике атмосферное давление составляло 760 мм ртутного столба и действовало на площадь, равную 0,28 . Известно, что 1 мм рт.ст. = 133Па. С высотой давление атмосферы уменьшается на 1 мм рт.ст. при подъеме на каждые 12 метров. Это явление позволяет измерять высоту объектов приборами, называемыми высотометрами.
Значительно ли изменится сжимающая сила, действующая на магдебургские полушария, если опыт Герике проделать на 240 метров выше? (Значительным изменением будем считать изменение более чем на 1%).
Решение:
F1 = 760 ∙ 133 ∙ 0,28 = 28302,4 ≈ 28300 — сила, сжимающая полушария при давлении 760 мм рт.ст.
При увеличении высоты на 240 метров давление уменьшится на 20 мм рт.ст. и составит 740 мм рт.ст.
F2 = 740 ∙ 133 ∙ 0,28 = 27557,6 ≈ 27600 Па
Это на 700 Па меньше, чем сила, сжимающая полушария (28300 — 27600 = 700).
700 / 28300 ∙ 100% = 2,5% — уменьшение силы.
Изменения силы больше 1%, значительные изменения.
Ответ: да, значительные.
Больше практических заданий в «Сборнике интерактивных тестов по алгебре. 7 класс».
Задание 11
В задании 11 проверяется умение выполнять преобразования буквенных выражений с использованием формул сокращённого умножения.
Упростите выражение (x — 5)2 — x(10 + x) и найдите его значение при x = −1/20. В ответ запишите полученное число.
Решение:
(x — 5)2 — x(10 + x) = x2 — 10x + 25 — 10x — x2 = −10x + 25
При x = −1/20, имеем — 10 ∙ (-1/20) + 25 = 10/20 + 25 = 0,5 + 25 = 25,5.
Ответ: 25,5
Задание 12
В задании 12 проверяется умение сравнивать обыкновенные дроби, десятичные дроби и смешанные числа.
Отметьте и подпишите на координатной прямой точки А (2,35), B (5/14), C (8/21).
Решение:
5/14 и 8/21 приведем к общему знаменателю.
15/42 < 16/42, значит, точка C находится правее точки B
15/42 < 16/42 < 2,35, значит, точка А находится правее точки С
Задание 13
Задания 13 и 14 проверяют умение оперировать свойствами геометрических фигур, применять геометрические факты для решения задач.
На клетчатой бумаге с размером клетки 1 см x 1 см отмечены точки A, B и C. Найдите расстояние от точки А до середины отрезка BC. Ответ выразите в сантиметрах.
Решение:
Ответ: 4.
Что ещё почитать?
Задание 14.
Задания 13 и 14 проверяют умение оперировать свойствами геометрических фигур, применять геометрические факты для решения задач.
В треугольнике два угла равны 57˚ и 86˚. Найдите его третий угол. Ответ дайте в градусах.
Решение:
По теореме о сумме углов треугольника
∠A + ∠B + ∠C = 180˚
∠C = 180˚-(86˚+ 57˚) = 37˚
Ответ: 37˚.
Задание 15
В задании 15 проверяется умение представлять данные в виде таблиц, диаграмм, графиков.
Утром 18 декабря в 10.00 метеостанция зафиксировала температуру воздуха –14˚С. Спустя два часа синоптики обнаружили, что температура резко упала до −17˚С, а по прошествии еще двух часов столбик термометра показывал уже −19˚С, после чего воздух начал прогреваться, и уже к 16:00 температура достигла −10˚С. Время неумолимо шло к вечеру, и температура в 18:00 упала до −12˚С, а в 20:00 достигла отметки, которая была в 12:00. Но падение температуры на этом не остановилось, и в 22:00 воздух остыл до −22˚С. В полночь зафиксировали температуру в −25˚С.
В полночь зафиксировали температуру в −25˚С.
По описанию постройте схематично график изменения температуры в течение суток с 10:00 до 00:00.
Решение:
Задание 16
Задание 16 направлено на проверку умения решать текстовые задачи на производительность, покупки, движение.
Расстояние между городами А и B равно 490 км. Из города А в город B со скоростью 55 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 90 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
Решение:
- 55 ∙ 1 = 55 (км) путь, пройденный первым автомобилем, пока не выехал второй.
- 490 — 55 = 435 (км) общий путь, пройденный автомобилями.
- 55 + 90 = 14 (км/ч) скорость сближения.
- 435 ÷ 145 = 3 (ч) время в пути двух автомобилей, до встречи.
- 1 + 3 = 4 (ч) время в пути первого автомобиля.

- 55 ∙ 4 = 220 (км) путь, пройденный первым автомобилем.
Ответ: 220 км.
#ADVERTISING_INSERT#
Калькулятор онлайн — Перевод конечной и бесконечной периодической десятичной дроби в обыкновенную
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Обыкновенные дроби. Деление с остатком
Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде:
497 : 4 = 124 (1 остаток).
Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель.
Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний
В нашем случае это число 124. И, наконец, последний
компонент, которого нет в обычном делении, — остаток.
В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело. Считают, что при
таком делении остаток равен нулю. В нашем случае остаток равен 1.
Остаток всегда меньше делителя.
Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать
так: 64 = 32 * 2.
Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.
Частное от деления натуральных чисел можно записать в виде дроби.
Числитель дроби — это делимое, а знаменатель — делитель.
Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление.
Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».
Частное от деления натуральных чисел m и n можно записать в виде дроби \( \frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель:
\( m:n = \frac{m}{n} \)
Верны следующие правила:
Чтобы получить дробь \( \frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.
Чтобы получить дробь \( \frac{m}{n} \), надо число m разделить на число n.
Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель
дроби, которая выражает эту часть.
Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на
знаменатель дроби, которая выражает эту часть.
Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)
Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a : m}{b : m} \)
Это свойство называют основным свойством дроби.
Два последних преобразования называют сокращением дроби.
Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к
общему знаменателю.
Правильные и неправильные дроби. Смешанные числа
Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например,
дробь \( \frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались
для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими
дробями, как, например, \( \frac{5}{5} \) или \( \frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби,
у которых числитель больше знаменателя или равен ему, называют неправильными дробями. Остальные дроби, т. е. дроби, у которых
числитель меньше знаменателя, называют правильными дробями.
Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на
знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали
неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.
Если число состоит из целой части и дроби, то такие дроби называются смешанными.
Например:
\( 5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \( \frac{2}{3} \) — дробная часть.
Если числитель дроби \( \frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число:
\( \large \frac{a}{b} : n = \frac{a:n}{b} \)
Если числитель дроби \( \frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число:
\( \large \frac{a}{b} : n = \frac{a}{bn} \)
Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда,
Поэтому мы можем его применять тогда,
когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Действия с дробями. Сложение дробей.
С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей.
Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \( \frac{2}{7} \) и \( \frac{3}{7} \).
Легко понять, что \( \frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\( \large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)
Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
\( \large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.
Сложение смешанных дробей
Такие записи, как \( 2\frac{2}{3} \), называют смешанными дробями. При этом число 2 называют целой частью смешанной
дроби, а число \( \frac{2}{3} \) — ее дробной частью. Запись \( 2\frac{2}{3} \) читают так: «две и две трети».
При делении числа 8 на число 3 можно получить два ответа: \( \frac{8}{3} \) и \( 2\frac{2}{3} \). Они выражают одно и то же дробное
число, т.е \( \frac{8}{3} = 2 \frac{2}{3} \)
Таким образом, неправильная дробь \( \frac{8}{3} \) представлена в виде смешанной дроби \( 2\frac{2}{3} \). В таких случаях говорят,
что из неправильной дроби выделили целую часть.
Вычитание дробей (дробных чисел)
Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например:
\( \frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \( \frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)
Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель
оставить прежним.
С помощью букв это правило записывается так:
\( \large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)
Умножение дробей
Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а
второе — знаменателем.
С помощью букв правило умножения дробей можно записать так:
\( \large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)
Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать
смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.
Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное
свойство умножения относительно сложения.
Деление дробей
Возьмем дробь \( \frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \( \frac{3}{2} \).
Эту дробь называют обратной дроби \( \frac{2}{3} \).
Если мы теперь «перевернем» дробь \( \frac{3}{2} \), то получим исходную дробь \( \frac{2}{3} \). Поэтому такие дроби, как
\( \frac{2}{3} \) и \( \frac{3}{2} \) называют взаимно обратными.
Взаимно обратными являются, например, дроби \( \frac{6}{5} \) и \( \frac{5}{6} \), \( \frac{7}{18} \) и \( \frac{18}{7} \).
С помощью букв взаимно обратные дроби можно записать так: \( \frac{a}{b} \) и \( \frac{b}{a} \)
Понятно, что произведение взаимно обратных дробей равно 1. Например: \( \frac{2}{3} \cdot \frac{3}{2} =1 \)
Используя взаимно обратные дроби, можно деление дробей свести к умножению.
Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.
Используя буквы, правило деления дробей можно записать так:
\( \large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)
Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления
дробей, его надо предварительно представить в виде неправильной дроби.
Калькулятор НОД и НОК с решением онлайн
Найдем наибольший общий делитель НОД (36 ; 24)
Этапы решения
Способ №1
1) Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением)
36 — составное число
24 — составное число
Разложим число 36 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
36 : 2 = 18 — делится на простое число 2
18 : 2 = 9 — делится на простое число 2
9 : 3 = 3 — делится на простое число 3.
Завершаем деление, так как 3 простое число
Разложим число 24 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
24 : 2 = 12 — делится на простое число 2
12 : 2 = 6 — делится на простое число 2
6 : 2 = 3 — делится на простое число 2.
Завершаем деление, так как 3 простое число
2) Выделим синим цветом и выпишем общие множители
36 = 2 ⋅ 2 ⋅ 3 ⋅ 3
24 = 2 ⋅ 2 ⋅ 2 ⋅ 3
Общие множители (36 ; 24) : 2, 2, 3
3) Теперь, чтобы найти НОД нужно перемножить общие множители
Ответ: НОД (36 ; 24) = 2 ∙ 2 ∙ 3 = 12
Способ №2
1) Найдем все возможные делители чисел (36 ; 24). Для этого поочередно разделим число 36 на делители от 1 до 36, число 24 на делители от 1 до 24. Если число делится без остатка, то делитель запишем в список делителей.
Для числа 36 выпишем все случаи, когда оно делится без остатка:
36 : 1 = 36;36 : 2 = 18;36 : 3 = 12;36 : 4 = 9;36 : 6 = 6;36 : 9 = 4;36 : 12 = 3;36 : 18 = 2;36 : 36 = 1;
Для числа 24 выпишем все случаи, когда оно делится без остатка:
24 : 1 = 24;24 : 2 = 12;24 : 3 = 8;24 : 4 = 6;24 : 6 = 4;24 : 8 = 3;24 : 12 = 2;24 : 24 = 1;
2) Выпишем все общие делители чисел (36 ; 24) и выделим зеленым цветом самы большой, это и будет наибольший общий делитель НОД чисел (36 ; 24)
Общие делители чисел (36 ; 24): 1, 2, 3, 4, 6, 12
Ответ: НОД (36 ; 24) = 12
Найдем наименьшее общее кратное НОК (52 ; 49)
Этапы решения
Способ №1
1) Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением)
Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением)
52 — составное число
49 — составное число
Разложим число 52 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
52 : 2 = 26 — делится на простое число 2
26 : 2 = 13 — делится на простое число 2.
Завершаем деление, так как 13 простое число
Разложим число 49 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
49 : 7 = 7 — делится на простое число 7.
Завершаем деление, так как 7 простое число
2) Прежде всего запишем множители самого большого числа, а затем меньшего числа. Найдем недостающие множители, выделим синим цветом в разложении меньшего числа множители, которые не вошли в разложение большего числа.
52 = 2 ∙ 2 ∙ 13
49 = 7 ∙ 7
3) Теперь, чтобы найти НОК нужно перемножить множители большего числа с недостающими множителями, которые выделены синим цветом
НОК (52 ; 49) = 2 ∙ 2 ∙ 13 ∙ 7 ∙ 7 = 2548
Способ №2
1) Найдем все возможные кратные чисел (52 ; 49). Для этого поочередно умножим число 52 на числа от 1 до 49, число 49 на числа от 1 до 52.
Выделим все кратные числа 52 зеленым цветом:
52 ∙ 1 = 52; 52 ∙ 2 = 104; 52 ∙ 3 = 156; 52 ∙ 4 = 208;
52 ∙ 5 = 260; 52 ∙ 6 = 312; 52 ∙ 7 = 364; 52 ∙ 8 = 416;
52 ∙ 9 = 468; 52 ∙ 10 = 520; 52 ∙ 11 = 572; 52 ∙ 12 = 624;
52 ∙ 13 = 676; 52 ∙ 14 = 728; 52 ∙ 15 = 780; 52 ∙ 16 = 832;
52 ∙ 17 = 884; 52 ∙ 18 = 936; 52 ∙ 19 = 988; 52 ∙ 20 = 1040;
52 ∙ 21 = 1092; 52 ∙ 22 = 1144; 52 ∙ 23 = 1196; 52 ∙ 24 = 1248;
52 ∙ 25 = 1300; 52 ∙ 26 = 1352; 52 ∙ 27 = 1404; 52 ∙ 28 = 1456;
52 ∙ 29 = 1508; 52 ∙ 30 = 1560; 52 ∙ 31 = 1612; 52 ∙ 32 = 1664;
52 ∙ 33 = 1716; 52 ∙ 34 = 1768; 52 ∙ 35 = 1820; 52 ∙ 36 = 1872;
52 ∙ 37 = 1924; 52 ∙ 38 = 1976; 52 ∙ 39 = 2028; 52 ∙ 40 = 2080;
52 ∙ 41 = 2132; 52 ∙ 42 = 2184; 52 ∙ 43 = 2236; 52 ∙ 44 = 2288;
52 ∙ 45 = 2340; 52 ∙ 46 = 2392; 52 ∙ 47 = 2444; 52 ∙ 48 = 2496;
52 ∙ 49 = 2548;
Выделим все кратные числа 49 зеленым цветом:
49 ∙ 1 = 49; 49 ∙ 2 = 98; 49 ∙ 3 = 147; 49 ∙ 4 = 196;
49 ∙ 5 = 245; 49 ∙ 6 = 294; 49 ∙ 7 = 343; 49 ∙ 8 = 392;
49 ∙ 9 = 441; 49 ∙ 10 = 490; 49 ∙ 11 = 539; 49 ∙ 12 = 588;
49 ∙ 13 = 637; 49 ∙ 14 = 686; 49 ∙ 15 = 735; 49 ∙ 16 = 784;
49 ∙ 17 = 833; 49 ∙ 18 = 882; 49 ∙ 19 = 931; 49 ∙ 20 = 980;
49 ∙ 21 = 1029; 49 ∙ 22 = 1078; 49 ∙ 23 = 1127; 49 ∙ 24 = 1176;
49 ∙ 25 = 1225; 49 ∙ 26 = 1274; 49 ∙ 27 = 1323; 49 ∙ 28 = 1372;
49 ∙ 29 = 1421; 49 ∙ 30 = 1470; 49 ∙ 31 = 1519; 49 ∙ 32 = 1568;
49 ∙ 33 = 1617; 49 ∙ 34 = 1666; 49 ∙ 35 = 1715; 49 ∙ 36 = 1764;
49 ∙ 37 = 1813; 49 ∙ 38 = 1862; 49 ∙ 39 = 1911; 49 ∙ 40 = 1960;
49 ∙ 41 = 2009; 49 ∙ 42 = 2058; 49 ∙ 43 = 2107; 49 ∙ 44 = 2156;
49 ∙ 45 = 2205; 49 ∙ 46 = 2254; 49 ∙ 47 = 2303; 49 ∙ 48 = 2352;
49 ∙ 49 = 2401; 49 ∙ 50 = 2450; 49 ∙ 51 = 2499; 49 ∙ 52 = 2548;
2) Выпишем все общие кратные чисел (52 ; 49) и выделим зеленым цветом самое маленькое, это и будет наименьшим общим кратным чисел (52 ; 49).
Общие кратные чисел (52 ; 49): 2548
Ответ: НОК (52 ; 49) = 2548
Что произошло в мире Apple — итоги недели за 8 — 14 февраля
Анимация на сайте Apple, программа замены аккумулятора MacBook и решение компаний о похожем логотипе на Apple. Итоги недели за 8 февраля – 14 февраля 2021 года.
Новости
- Хакеру впервые удалось взломать iPhone 11 на iOS 14.2 –
и не только его, но джейлбрейк вряд ли будет выпущен; - На сайте Apple появилась анимация с персонажами из Apple TV+ –
в честь выхода нового сериала; - Apple запустила программу замены аккумулятора MacBook Pro 2016 и 2017 года –
проблему с зарядкой должна исправить macOS 11.2.1, если нет, заменят бесплатно; - Компании Apple и Prepear договорились о логотипе похожем на яблоко –
Prepear сменит симметричный листок от груши на другой; - Intel запустила рекламную компанию #GoPC, которая призывает переходить с Mac на PC –
до этого она проводилась с 2006 по 2010 год, что было ответом на компанию Apple – Get a Mac.
Выпущенные прошивки
( Только iOS и iPadOS )
Релизы
Релизов прошивок на этой неделе выпущено не было.
Public Beta/Developer beta
Бета прошивок на этой неделе выпущено не было.
Акции Apple
Сплит акций
Стоимость акций компании была снижена в 4 раза, а количество акций было увеличено во столько же раз. Это было сделано для того, чтобы акции были более доступными для инвесторов. На каждую одну акцию инвестора было выпущено ещё по 3 акции.
Чтобы сравнить цену акции сейчас и до сплита, необходимо умножить на 4 их текущую стоимость.
Состояние акций
За прошедшую неделю состояние акций яблочной компании ухудшилось.
Стоимость упала приблизительно на 2 доллара и на данный момент равна 135 долларам. Сейчас рыночная капитализация Apple составляет около 2,273 трлн долларов.
Произошло небольшое падение.
Выпущенные устройства
Официально новых устройств от компании Apple на этой неделе выпущено не было.
Рекламная компания Intel направленная на пользователей Mac на M1 говорит о настоящем беспокойстве компании о ARM-чипах Apple и продуктах на нем.
Все итоги недел
Apple Store
«Официальную ежедневную статистику по смертности в России надо умножать на три»
Избыточная смертность от коронавируса в России вскоре может стать самой большой в Европе, полагает демограф и бывший сотрудник Росстата Алексей Ракша, покинувший службу после критики официальной статистики.
«Существует риск, что избыточная смертность на душу населения в России будет самой высокой в Европе. Официальную ежедневную статистику по смертности в России надо умножать на три», — сказал Ракша в интервью Bloomberg.
Напомним, по последним данным Росстата, всего с апреля по август число умерших с COVID-19 в России достигло 45 663 — это в 2 раза больше статистики оперштаба.
Фото: «БИЗНЕС Online»
По словам Ракши, избыточная смертность за этот период составляет около 115 тыс. человек, что по отношению к численности населения ставит Россию рядом с Испанией и Великобританией — европейскими странами с самым высоким уровнем смертности.
Всемирная организация здравоохранения задается вопросом, почему существует такое большое расхождение между избыточной смертностью в России и официальным уровнем смертности от вируса. Ракша пояснил, что проблема частично связана с тем, что Росстат раскрывает статистику по смертности с задержкой в один месяц.
Росстат не публикует статистику каждый день, потому что не хочет создавать путаницу, давая неподтвержденные сведения, заявил Bloomberg представитель агентства. Он отказался комментировать слова Ракши о том, что данные отправляются в правительство. Оперативный штаб сообщил Bloomberg, что публикация статистики смертности от COVID-19 иногда затягивается из-за времени, которое требуется на проведение вскрытия.
Директор Института демографии ВШЭ Анатолий Вишневский сказал Bloomberg, что Ракша прав в том, что критикует данные оперштаба. При этом он отметил, что никто не может быть полностью уверенным в том, каковы реальные показатели смертности.
Умножение на пальцах на 9: простой и легкий способ
Большой привет всем маленьким школьникам, а также их родителям! Скажите, любите ли вы умножать? Думаю, кроме заядлых и увлеченных математиков на этот вопрос никто не даст утвердительного ответа. Тем не менее, это очень даже интересное занятие! Главное знать, как умножать, так чтобы и легко было, и интересно)
Сегодня расскажу вам про умножение на пальцах. Оказывается, ваши ручки – это пара мощнейших калькуляторов, которые всегда с вами, которым не нужен источник энергии и которые никогда не ошибаются.
Способов такой «пальчиковой» математики много, большинство из них довольно заморочены, поэтому все рассматривать в статье не буду. Расскажу вам о самом простом. Об умножении на 9.
Для начала давайте вспомним нашу любимую умножательную табличку на 9. На всякий случай, вдруг она вылетела у вас из головы или может маленькие школьники вообще ее и не знали никогда.
Ну а теперь приготовьте к работе ваши ручные калькуляторы. Как их готовить? Ну просто положите обе ручки-ладошки на стол перед собой.
Теперь мысленно нужно пронумеровать пальцы. От 1 до 10. Слева направо. Если мысленно тяжеловато, то сделайте вот так, напишите числа на бумажке.
А теперь наконец-то приступаем к вычислениям!
Попробуем умножить 9, например, на 4. Вы не против?
Загнем пальчик № 4.
Вот вам и готовый результат! Пальцы, находящиеся слева от загнутого, обозначают десятки. А справа — единицы. Получается 3 десятка и 6 единиц. То есть 36.
Еще разок попробуем? Умножим девяточку на 8. Загинаем какой палец? Правильно! Восьмой!
Считаем пальчики слева. Получаем 7 десятков. И теперь справа. Получаем 2 единицы. Итого, результат 72!
Очень просто, легко и удобно! Согласны?
Если не до конца понятно, то можете посмотреть видео. Мы с Артемом тренировались. Таблицу умножения он пока не знает. Но это уже не касается таблицы на 9!
А теперь попробуйте сами! Успехов вам!
Кстати, на блоге есть еще одна интересная статья, там про то, как можно быстро умножить любое число на 11.
Евгения Климкович.
Простой в использовании калькулятор дробей [для деления, умножения и упрощения дробей]
Калькулятор дробей складывает, вычитает, умножает и делит дроби с одинаковыми или разными знаменателями. Это также позволит нам упростить дроби, преобразовать дроби в десятичные и десятичные в дроби.
Сначала просто введите значения a, b, c, d для дробей \ (\ frac {a} {b} \) и \ (\ frac {c} {d} \), затем математическую операцию по вашему желанию. выполнить (+, -, x, /). Калькулятор моментально и точно выполнит операцию и выдаст ответ в простейшей форме.Вы также можете использовать калькулятор, чтобы проверить свою работу, которую вы проделали вручную.
Сложение и вычитание дробей
Подобные (общие) знаменатели
Сложите или вычтите числители, оставив знаменатели неизменными.
Пример: \ (\ frac {3} {5} + \ frac {4} {5} \)
Поскольку знаменатель равен 5 в обеих дробях, сложите 3 и 4, чтобы получить 7. Знаменатель остается 5, поэтому ответ — 7/5.
\ (\ frac {7} {6} — \ frac {5} {6} \)
Поскольку знаменатель равен 6 в обеих дробях, вычтите 5 из 7, чтобы получить 2.Тогда дробь равна \ (\ frac {2} {6} \).
Но теперь мы можем упростить \ (\ frac {2} {6} \). Чтобы упростить, поищите общий фактор. Обратите внимание, что 2 равномерно делится как на 2, так и на 6. Следовательно, разделите числитель и знаменатель на 2, чтобы получить \ (\ frac {1} {3} \). Теперь дробь упрощена.
В отличие от знаменателей
Чтобы сложить и вычесть отличные знаменатели, сначала вычислите общий знаменатель. Самый простой способ сделать это — умножить два знаменателя.Это не всегда дает наименьший общий знаменатель, но вы можете упростить его после сложения и вычитания.
Пример: \ (\ frac {2} {5} + \ frac {4} {7} \)
Общий знаменатель равен 5 (7) = 35. Поскольку знаменатель в первой дроби умножается на 7, числитель также нужно умножить на 7, чтобы получить \ (\ frac {14} {35} \). Поскольку знаменатель второй дроби умножается на 5, числитель должен быть таким же, чтобы получить \ (\ frac {20} {35} \).
Теперь добавьте \ (\ frac {14} {35} + \ frac {20} {35} = \ frac {34} {35} \)
Вычитание выполняется таким же образом, просто вычтите две дроби после перезаписи дроби с их общими знаменателями.Если вам нужно упростить, не забудьте разделить на наибольший общий множитель.
Сложение и вычитание дробей Видео
Умножение и деление дробей
При умножении дробей просто умножайте числители и знаменатели. Тогда упростите. Вы также можете сначала упростить, прежде чем умножать.
Пример: \ (\ frac {2} {9} \ times \ frac {4} {7} \)
Умножьте 2 и 4, чтобы получить 8. Затем умножьте 9 и 7, чтобы получить 63. Результат: \ ( \ frac {8} {63} \).Упрощения не требуется, поскольку наибольший общий делитель равен 1.
Теперь предположим, что мы хотим разделить \ (\ frac {2} {9} \ div \ frac {4} {7} \).
При делении дробей возьмите первую дробь и умножьте на обратную величину второй. Обратное просто меняет местами числитель и знаменатель. Проблема деления превращается в проблему умножения.
\ (\ frac {2} {9} \ times \ frac {7} {4} \)
2 × 7 = 14 и 9 × 4 = 36. Итак, ответ \ (\ frac {14} { 36} \).Но обратите внимание, что это не в простейшей форме. Наибольший общий делитель равен 2, поэтому деление обоих на 2 дает упрощенный ответ \ (\ frac {7} {18} \).
Умножение и деление дробей Видео
Преобразование дробей в десятичные числа
Калькулятор преобразования дробей в десятичные принимает любую дробь и преобразует ее в десятичную.
Метод преобразования дроби в десятичную довольно прост. Просто разделите числитель на знаменатель.
Замените \ (\ frac {14} {25} \) на десятичное число.
Разделите 14 на 25, чтобы получить 0,56. Вы можете сделать это на калькуляторе или вручную с помощью длинного деления. Некоторые фракции не так просто обрабатывать вручную, особенно те, которые не завершаются. На этом калькуляторе с ними работать намного проще.
Но если вы решите вручную, калькулятор станет отличным инструментом для мгновенной проверки вашей работы.
Преобразование дробей в десятичные Видео
Преобразование десятичных знаков в дроби
Преобразование десятичных знаков в дроби является обратным преобразованию дробей в десятичные.Калькулятор быстро выполнит это и даст точные результаты, просто введя десятичное значение.
Чтобы преобразовать вручную, возьмите десятичную дробь и преобразуйте ее в целое число, затем разделите на 10, возведенное в число десятичных знаков, перемещенных вправо для преобразования числа. Оттуда вы можете упростить дробь, если это необходимо.
Пример:
Преобразует 0,68 в дробь. Чтобы изменить 0,68 на целое число, переместите десятичную запятую на 2 разряда вправо, чтобы получить 68. Поскольку мы переместили 2 десятичных разряда, разделите 68 на 10 во второй степени, то есть 100.
Это дает нам \ (\ frac {68} {100} \). Теперь мы можем упростить дробь, найдя общий множитель. Если вы не знаете наибольшего общего множителя, вы можете начать с деления на любой общий множитель. Замечания 68 и 100 делятся на 2. Это уменьшает дробь до 34/50. Отсюда обратите внимание, что 34 и 50 делятся на 2. Это сводится к \ (\ frac {17} {25} \), что является упрощенным ответом.
Вы можете проверить свои ручные вычисления с помощью этого калькулятора или просто ввести информацию для вашей конкретной проблемы, чтобы получить почти мгновенные и точные результаты!
Как умножать целые числа.Как умножать десятичные дроби — Полный курс арифметики
6 × 45 = 6 × 40 + 6 × 5 = 240 + 30 = 270.
О разделении двух десятичных цифр:
6% от 45 долларов это 2 долларов. 70.
Это, в любом случае, то, что мы сделали бы , если бы мы изменили 6% на . 06 (Урок 4) и умножаем . 06 × 45; то есть, если мы взяли 6 сотых из 45. (Урок 27.)
Эквивалентно с
1% от 45 долларов составляет долларов. 45
(Урок 4), то 6% будет 6 умножить на 1%, то есть 6 × . 45.
Примечание : из-за свойства порядка умножения
6% от 45 долларов = 45% от 6 долларов.
Например, поскольку 50% означает половину:
24% от 50 = 50% от 24 = 12.
Пример 7. Сколько 9% от 84 долларов?
Решение . Умножьте 9 × 84, затем разделите две десятичные цифры.
При раздаче с 9 по 80 + 4:
9 × 84 = 720 + 36 = 756.
9% от 84 долларов это 7 долларов. 56.
Пример 8. Сколько 3% от 247 долларов?
Решение . 3 ×
247 =
6 00 + 1 20 + 21 = 7 41.
3% от 247 долларов это 7 долларов. 41.
Пример 9. Сколько составляет 11% от 76 долларов?
Решение .11 × 76 = 7 6 0 + 7 6 = 8 3 6. (Урок 9.)
11% от 76 долларов это 8 долларов. 36.
Это простые задачи, для которых не требуется калькулятор. Дополнительные сведения о таких простых задачах см. В Уроке 29. Чтобы узнать, как решать задачи с процентами с помощью калькулятора, см. Урок 14.
Площадь прямоугольника
Что такое «1 квадратный фут»?
1 квадратный фут — это квадратная фигура, каждая сторона которой равна 1 футу.
Мы сокращаем «1 квадратный фут» как 1 фут².
1 фут (1 фут) — это единица измерения длины. Если это единица длины, то 1 квадратный фут (1 фут²) равен площади . И аналогично для любой единицы длины и соответствующей единицы площади.
А теперь прямоугольник с основанием 3 см и высотой 2 см.
Как мы называем маленький заштрихованный квадрат?
Так как каждая сторона равна 1 см, мы называем это «1 квадратный сантиметр».»И мы видим, что вся фигура состоит из 2х3 или 6 из них
Другими словами, площадь этого прямоугольника — пространство, ограниченное рамкой, — составляет 6 квадратных сантиметров: 6 см².
Если бы прямоугольник был 3 на 3, то есть если бы он был квадратом, то он составлял бы 9 см². Если бы было 3 на 4, то площадь была бы 12 см². И так далее. В любом случае, чтобы вычислить площадь прямоугольника, просто умножьте основание на высоту.
Если длина измеряется в сантиметрах, площадь измеряется в квадрате.
сантиметры: см². И аналогично для любой единицы длины.
Мы проиллюстрировали это целыми числами, но это будет верно для любых чисел.
Если основание 12 дюймов, а высота 6,5 дюйма, то, чтобы найти площадь, умножьте
12 × 6 . 5
Сейчас,
12 × 65 = 10 × 65 + 2 × 65 = 650 + 130 = 780.
Следовательно, при разделении одной десятичной цифры (6 . 5):
Площадь = 78 кв.
Задача 1. 1 ярд = 3 фута. 1 квадратный ярд состоит из многих квадратных футов?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
9 квадратных футов.
Проблема 2.Цена ковра — 50 долларов за квадратный ярд. Какова примерная цена ковра размером 5 на 7 футов?
Примерно 200 долларов.
Площадь ковра 5 на 7 составляет 35 квадратных футов. Квадратный двор составляет 9 квадратных футов. Площадь этого ковра составляет примерно 4 квадратных ярда. Следовательно, цена составляет примерно 4 раза по 50 долларов, что составляет 200 долларов.
Порядок собственности
Вернемся к свойству порядка умножения (Урок 9):
Если два числа умножаются друг на друга, то полученные числа
будут равны друг другу.
(Евклид, VII.16)
Например, если два числа — 32 и 5, то, если мы несколько раз сложим 32 пять раз, мы получим то же число, что и при сложении 5 тридцать два раза.
32 + 32 + 32 + 32 + 32 = 5 + 5 + 5 +. . . + 5 + 5.
Мы смогли доказать это, не называя продукт.
Но чтобы взять более простой пример, пусть два числа будут 3 и 4. Тогда
Три четверки = четыре тройки.
И мы не имеем в виду, что каждому 12.
Посмотрите на эту цифру:
Первый столбец слева, скажем, составляет 4 см². Весь прямоугольник состоит из 3 таких столбцов. Состоит из
3 × 4 см².
Но соответствует на каждые см² в первом столбце, на в каждом из следующих столбцов. Следовательно, если смотреть на ряды, прямоугольник состоит из
4 × 3 см².
Другими словами,
4 × 3 см² = 3 × 4 см².
Если мы прибавим 3 см² четыре раза, мы получим тот же результат, что и при трехкратном добавлении 4 см² — и чтобы знать, что нам не нужно знать, что 3 × 4 = 12.
Это свойство порядка умножения.
*
Иногда вы видите
3 см × 4 см = 12 см²,
, что, честно говоря, не имеет смысла.Множитель (слева) показывает количество повторений сложения множимого (справа). Следовательно, множитель всегда должен быть чистым числом.
Пожалуйста, «переверните» страницу и выполните несколько задач .
или
Переходите к следующему уроку.
Введение | Главная | Содержание
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Калькулятор дробей
Ниже приведены несколько калькуляторов дробей, способных выполнять сложение, вычитание, умножение, деление, упрощение и преобразование дробей в десятичные дроби. Поля над сплошной черной линией представляют числитель, а поля ниже — знаменатель.
Калькулятор смешанных чисел
Калькулятор упрощенных дробей
Калькулятор десятичных дробей
Калькулятор дробей в десятичную
Калькулятор дробей большого числа
Используйте этот калькулятор, если числители или знаменатели являются очень большими целыми числами.
В математике дробь — это число, которое представляет собой часть целого. Он состоит из числителя и знаменателя. В числителе указано количество равных частей целого, а в знаменателе — общее количество частей, составляющих это целое. Например, в дроби
числитель равен 3, а знаменатель — 8. Более наглядный пример может включать пирог с 8 кусочками. 1 из этих 8 кусочков будет составлять числитель дроби, а всего 8 кусочков, составляющих весь пирог, будут знаменателем.Если бы человек съел 3 ломтика, оставшаяся часть пирога была бы такой, как показано на изображении справа. Обратите внимание, что знаменатель дроби не может быть 0, так как это сделает дробь неопределенной. Дроби могут подвергаться множеству различных операций, некоторые из которых упомянуты ниже.
Дополнение:
В отличие от сложения и вычитания целых чисел, таких как 2 и 8, для этих операций с дробями требуется общий знаменатель. Один из методов нахождения общего знаменателя заключается в умножении числителей и знаменателей всех участвующих дробей на произведение знаменателей каждой дроби.Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода.
Этот процесс можно использовать для любого количества фракций. Просто умножьте числители и знаменатели каждой дроби в задаче на произведение знаменателей всех остальных дробей (не включая соответствующий знаменатель) в задаче.
Альтернативный метод нахождения общего знаменателя состоит в том, чтобы определить наименьшее общее кратное (НОК) для знаменателей, а затем сложить или вычесть числители, как если бы это было целое число. Использование наименьшего общего кратного может быть более эффективным и с большей вероятностью приведет к дроби в упрощенной форме.В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное этих трех чисел.
| Кратное 2: 2, 4, 6, 8 10, 12 |
| Кратное 4: 4, 8, 12 |
| Кратное 6: 6, 12 |
Первое общее кратное — 12, так что это наименьшее общее кратное. Чтобы выполнить задачу сложения (или вычитания), умножьте числители и знаменатели каждой дроби в задаче на любое значение, которое сделает знаменатели 12, а затем сложите числители.
Вычитание:
Вычитание фракции по сути то же самое, что и сложение дроби. Для выполнения операции требуется общий знаменатель. Обратитесь к разделу добавления, а также к приведенным ниже уравнениям для пояснения.
Умножение:
Умножение дробей довольно просто. В отличие от сложения и вычитания, нет необходимости вычислять общий знаменатель для умножения дробей. Просто числители и знаменатели каждой дроби умножаются, и результат образует новый числитель и знаменатель.По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения.
Дивизион:
Процесс деления дробей аналогичен процессу умножения дробей. Чтобы разделить дроби, дробь в числителе умножается на величину, обратную дроби в знаменателе. Число , обратное , равно
. Когда a является дробью, это, по сути, включает в себя замену числителя и знаменателя местами.Следовательно, величина, обратная дроби. Обратитесь к приведенным ниже уравнениям для пояснения.
Упрощение:
Часто проще работать с упрощенными дробями. Таким образом, фракционные растворы обычно выражаются в их упрощенных формах.
, например, более громоздкий, чем. Предоставленный калькулятор возвращает входные дроби как в неправильной форме дроби, так и в форме смешанных чисел. В обоих случаях дроби представлены в их низшей форме путем деления числителя и знаменателя на их наибольший общий множитель.
Преобразование дробей в десятичные дроби:
Преобразование десятичных дробей в дроби выполняется просто. Однако это требует понимания того, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд 10 1 , второй 10 2 , третий 10 3 и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробь
, что упрощается до, поскольку наибольший общий делитель между числителем и знаменателем равен 2.
Точно так же дроби, знаменатели которых являются степенями 10 (или могут быть преобразованы в степени 10), могут быть переведены в десятичную форму, используя те же принципы. Возьмем, к примеру, дробь
. Чтобы преобразовать эту дробь в десятичную дробь, сначала преобразуйте ее в дробь.Зная, что первый десятичный разряд представляет 10 -1 , можно преобразовать в 0,5. Если бы вместо этого была дробь, десятичная дробь была бы 0,05 и так далее. Помимо этого, преобразование дробей в десятичные требует операции деления в столбик.
Преобразование общей инженерной дроби в десятичную
В машиностроении дроби широко используются для описания размеров таких компонентов, как трубы и болты. Наиболее распространенные дробные и десятичные эквиваленты перечислены ниже.
| 64 nd | 32 nd | 16 th | 8 th | 4 th | 2 nd | Decimal | (десятичный) | (десятичный) | |||||||||||
| 1/64 | 0,015625 | 0,396875 | |||||||||||||||||
| 2/64 | 1/32 | .03125 | 0,79375 | ||||||||||||||||
| 3/64 | 0,046875 | 1,1 | |||||||||||||||||
| 4/64 | 4/64 | 0,0625 | 1,5875 | ||||||||||||||||
| 5/64 | 0,078125 | 1,984375 | |||||||||||||||||
| 6 | 0.09375 | 2.38125 | |||||||||||||||||
| 7/64 | 0.109375 | 2.778125 | |||||||||||||||||
| 8/64 | 0,125 | 3,175 | |||||||||||||||||
| 9/64 | 0,140625 | 3,571875 | 0.15625 | 3.96875 | |||||||||||||||
| 11/64 | 0.171875 | 4.365625 | |||||||||||||||||
| 12/64 6358 | |||||||||||||||||||
| 12/64 6358 | 0,1875 | 4,7625 | |||||||||||||||||
| 13/64 | 0.203125 | 5,159375 | |||||||||||||||||
| 0.21875 | 5,55625 | ||||||||||||||||||
| 15/64 | 0,234375 | 5.953125 | 16/64 8358 | ||||||||||||||||
| 16/64 | 2 | 1/4 | 0,25 | 6,35 | |||||||||||||||
| 17/64 | 0,265625 | 0,265625 | 6,7468275 | 0.28125 | 7,14375 | ||||||||||||||
| 19/64 | 0,296875 | 7,540625 | |||||||||||||||||
| 20/64 10358 | 20/64 10358 | 0,3125 | 7,9375 | ||||||||||||||||
| 21/64 | 0,328125 | 8,334375 | |||||||||||||||||
| 0.34375 | 8.73125 | ||||||||||||||||||
| 23/64 | 0,359375 | 9.128125 | |||||||||||||||||
| 9.128125 | |||||||||||||||||||
| 12358 9036 12358 9036 9036 12358 9036 | 0,375 | 9,525 | |||||||||||||||||
| 25/64 | 0,3 | 9. 75 | 9. /2 | 0.40625 | 10,31875 | ||||||||||||||
| 27/64 | 0,421875 | 10,715625 | 10,715625 | 28/64 9036 | 0,4375 | 11,1125 | |||||||||||||
| 29/64 | 0,453125 | 11,509375 | |||||||||||||||||
| 0.46875 | 11. | ||||||||||||||||||
| 31/64 | 0,484375 | 12.303125 | 2/4 | 1/2 | 0,5 | 12,7 | |||||||||||||
| 33/64 | 0,515625 | 13.0968275 | 0,515625 | 13.0968275 | 0.53125 | 13.49375 | |||||||||||||
| 35/64 | 0,546875 | 13.8 | 36/64 | ||||||||||||||||
| 36/64 9036/64 | 0,5625 | 14,2875 | |||||||||||||||||
| 37/64 | 0,578125 | 14.684375 | 0.59375 | 15.08125 | |||||||||||||||
| 39/64 | 0.609375 | 15.478125 | 40/64/64 | 0,625 | 15.875 | ||||||||||||||
| 41/64 | 0,640625 | 16.2718290 | 0.65625 | 16.66875 | |||||||||||||||
| 43/64 | 0,671875 | 17.065625 | 44/64 | 44/64 9036 | |||||||||||||||
| 44/64 9036 | 0,6875 | 17,4625 | |||||||||||||||||
| 45/64 | 0,703125 | 17,859375 | 0.71875 | 18.25625 | |||||||||||||||
| 47/64 | 0,734375 | 18.653125 | 3/4 | 0,75 | 19,05 | ||||||||||||||
| 49/64 | 0,765625 | 19.4468275 | 0.78125 | 19.84375 | |||||||||||||||
| 51/64 | 0,796875 | 20.240625 | 20.240625 | ||||||||||||||||
| 52/64 | 0,8125 | 20,6375 | |||||||||||||||||
| 53/64 | 0,828125 | 21,034375 | 0.84375 | 21.43125 | |||||||||||||||
| 55/64 | 0,859375 | 21,828125 | |||||||||||||||||
| 14358 9036 7358 9036 7358 56/64 | 0,875 | 22,225 | |||||||||||||||||
| 57/64 | 0,8 | 22.6218275 | 22.62182/ | 0. | 23.01875 | ||||||||||||||
| 59/64 | 0, 5 | 23,415625 | 60358 | ||||||||||||||||
| 60/64 | 60/64 9036 | 0,9375 | 23,8125 | ||||||||||||||||
| 61/64 | 0,953125 | 24.209375 | 24.209375 | ||||||||||||||||
| 0.96875 | 24.60625 | ||||||||||||||||||
| 63/64 | 0,984375 | 25,003125 | 64358 9036 9036 | 4/4 | 2/2 | 1 | 25,4 |
Как умножить квадратные корни
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Длинное деление многочленов
Длинное деление многочленов
Вот шаги, необходимые для деления на многочлен, содержащий более одного члена (длинное деление):
| Шаг 1: | Убедитесь, что полином записан в порядке убывания.Если какие-либо термины отсутствуют, используйте ноль, чтобы заполнить отсутствующий термин (это поможет с интервалом). |
| Шаг 2: | Разделите член с наибольшей степенью внутри символа деления на член с наибольшей степенью вне символа деления. |
| Шаг 3: | Умножьте (или распределите) ответ, полученный на предыдущем шаге, на многочлен перед символом деления. |
| Шаг 4: | Вычтите и сократите следующий член. |
| Шаг 5: | Повторяйте шаги 2, 3 и 4 до тех пор, пока не останется терминов, которые нужно сбрасывать. |
| Шаг 6: | Напишите окончательный ответ. Член, оставшийся после последнего шага вычитания, является остатком и должен быть записан как дробь в окончательном ответе. |
Пример 1 — Разделить:
Пример 2 — Разделить:
Щелкните здесь для практических задач
Пример 3 — Разделить:
Щелкните здесь для практических задач
Пример 4 — Разделить:
| Шаг 1 : Убедитесь, что полином записан в порядке убывания.Если какие-либо термины отсутствуют, используйте ноль, чтобы заполнить отсутствующий термин (это поможет с интервалом). В этом случае должно получиться: | |
| Шаги 2, 3 и 4 : Разделите член с наибольшей степенью внутри символа деления на член с наибольшей степенью вне символа деления. Затем умножьте (или распределите) ответ, полученный на предыдущем шаге, на многочлен перед символом деления. В этом случае мы должны получить 2x 3 / 2x = x 2 и x 2 (2x + 3).Наконец, вычтите и опустите следующий член. | |
| Шаги 5, 6 и 7 : Разделите член с наибольшей степенью внутри символа деления на член с наибольшей степенью вне символа деления. Затем умножьте (или распределите) ответ, полученный на предыдущем шаге, на многочлен перед символом деления. В этом случае мы должны получить 4x 2 / 2x = 2x и 2x (2x + 3). Наконец, вычтите и опустите следующий член. | |
| Шаги 8, 9 и 10 : Разделите член с наибольшей степенью внутри символа деления на член с наибольшей степенью вне символа деления. Затем умножьте (или распределите) ответ, полученный на предыдущем шаге, на многочлен перед символом деления. В этом случае мы должны получить –4x / 2x = –2 и –2 (2x + 3). Наконец, вычтите и обратите внимание, что больше нет терминов, которые нужно опускать. | |
| Шаг 11 : Напишите окончательный ответ.Член, оставшийся после последнего шага вычитания, является остатком и должен быть записан как дробь в окончательном ответе. |
Щелкните здесь для практических задач
Пример 5 — Разделить:
| Шаг 1 : Убедитесь, что полином записан в порядке убывания. Если какие-либо термины отсутствуют, используйте ноль, чтобы заполнить отсутствующий термин (это поможет с интервалом). В этом случае проблема готова как есть. | |
| Шаги 2, 3 и 4 : Разделите член с наибольшей степенью внутри символа деления на член с наибольшей степенью вне символа деления. Затем умножьте (или распределите) ответ, полученный на предыдущем шаге, на многочлен перед символом деления. В этом случае мы должны получить x 3 / x 2 = x и x (x 2 + x — 6). Наконец, вычтите и опустите следующий член. | |
| Шаги 5, 6 и 7 : Разделите член с наибольшей степенью внутри символа деления на член с наибольшей степенью вне символа деления.Затем умножьте (или распределите) ответ, полученный на предыдущем шаге, на многочлен перед символом деления. В этом случае мы должны получить 2x 2 / x 2 = 2 и 2 (x 2 + x — 6). Наконец, вычтите и обратите внимание, что больше нет терминов, которые нужно опускать. | |
| Шаг 8 : Напишите окончательный ответ. Член, оставшийся после последнего шага вычитания, является остатком и должен быть записан как дробь в окончательном ответе.В этом случае остатка нет, поэтому дробь записывать не нужно. |
Щелкните здесь для практических задач
14-кратная таблица — выучить 14-ю таблицу
Запоминание таблицы умножения на 14 может быть прекрасным упражнением для тренировки мозга для младших школьников. Знание таблицы 14 является основным при изучении математики. Если вы не усвоите таблицу умножения на 14 на кончике вашего языка, будет сложно выполнять быстрые математические вычисления в уме.В этом уроке мы узнаем о таблице 14 с числами от 1 до 10, а также о некоторых приемах, позволяющих легко запомнить эти таблицы умножения.
14 Временная таблица:
Таблица умножения 14
Изучение таблицы умножения на 14 необходимо, так как она используется для длинного умножения и деления. У него есть и другие преимущества, такие как:
- 14-кратная таблица помогает легко решать математические задачи.
- Студенты могут использовать свои знания для быстрого решения любых вопросов умножения.
- Таблица 14 помогает понять закономерности кратных чисел.
Просмотрите 14-кратную таблицу для чисел от 1 до 10, показанных ниже.
14-кратная таблица
| 14-кратная таблица до 10 | |
| 14 × 1 = 14 | 14 × 6 = 84 |
| 14 × 2 = 28 | 14 × 7 = 98 |
| 14 × 3 = 42 | 14 × 8 = 112 |
| 14 × 4 = 56 | 14 × 9 = 126 |
| 14 × 5 = 70 | 14 × 10 = 140 |
>> Скачать 14-кратную таблицу
Советы для 14-ти кратных таблиц
1. Чтобы запомнить таблицу умножения на 14, сначала нам нужно запомнить таблицу умножения на 4. Кратные 4 равны 4, 8, 12, 16, 20, 24, 28, 32, 36, 40. . .
2. Чтобы получить число, кратное 14, добавьте натуральные числа к разряду десятков кратных 4. Таким образом, таблица умножения на 14 получается следующим образом: (1 + 0) 4, (2 + 0) 8, (3 + 1) 2, (4 + 1) 6, (5 + 2) 0, (6 + 2) 4, (7 + 2) 8, (8 + 3) 2, (9 + 3) 6, ( 10 + 4) 0 = 14, 28, 42, 56, 70, 84, 98, 112, 126, 140
3. 14 не имеет правил, которые упрощают запоминание таблицы умножения 14, но есть образец для каждых пяти кратных четырнадцати i.е. 14, 28, 42, 56, 70, 84, 98, 112, 126, 140. Последняя цифра этих кратных чисел всегда повторяется, что означает, что учащиеся могут запомнить эти цифры, чтобы помочь им с таблицей умножения на 14.
Стол от 14 до 20
| 14 × 11 = 154 | 14 × 16 = 224 |
| 14 × 12 = 168 | 14 × 17 = 238 |
| 14 × 13 = 182 | 14 × 18 = 252 |
| 14 × 14 = 196 | 14 × 19 = 266 |
| 14 × 15 = 210 | 14 × 20 = 280 |
Порядок операций: примеры
Purplemath
Большинство проблем с упрощением использования порядка операций проистекают из вложенных круглых скобок, показателей степени и знаков «минус».Итак, в следующих примерах я продемонстрирую, как работать с такого рода выражениями.
(Ссылки приведены для дополнительного обзора работы с негативами, группировочными символами и полномочиями.)
Упростить 4–3 [4–2 (6–3)] ÷ 2.
MathHelp.com
Я буду упрощать изнутри: сначала круглые скобки, затем квадратные скобки, помня, что знак «минус» на цифре 3 перед скобками идет вместе с цифрой 3. Только после того, как группировка будет завершена, я смогу сделайте деление с последующим добавлением 4.
4–3 [4–2 (6–3)] ÷ 2
4–3 [4–2 (3)] ÷ 2
4–3 [4–6] ÷ 2
4 — 3 [–2] ÷ 2
4 + 6 ÷ 2
4 + 3
7
Помните, что в leiu символов группировки, говорящих вам об обратном, деление идет перед сложением, поэтому это выражение в конечном итоге упростилось до «4 + 3», а не «10 ÷ 2».
(Если вы не чувствуете себя комфортно со всеми этими знаками «минус», просмотрите «Негативы».)
Упростить 16-3 (8-3)
2 ÷ 5.
Я должен не забыть упростить в скобках перед I в квадрате, потому что (8 — 3) 2 — это , а не , то же самое, что 8 2 — 3 2 .
16-3 (8-3) 2 ÷ 5
16-3 (5) 2 ÷ 5
16 — 3 (25) ÷ 5
16 — 75 ÷ 5
16–15
1
Если вы узнали о переменных и объединении «похожих» терминов, вы также можете увидеть такие упражнения, как это:
Упростить 14
x + 5 [6 — (2 x + 3)].
Если у меня возникнут проблемы с вычитанием через круглые скобки, я могу превратить его в умножение отрицательной единицы через круглые скобки (обратите внимание на выделенную красным цифру «1» ниже):
14 x + 5 [6 — (2 x + 3)]
14 x + 5 [6 — 1 (2 x + 3)]
14 x + 5 [6 — 2 x — 3]
14 x + 5 [3–2 x ]
14 x + 15-10 x
4 x + 15
Упростить — {2
x — [3 — (4 — 3 x )] + 6 x }.
Мне нужно не забывать упрощать на каждом этапе, комбинируя похожие термины, когда и где я могу:
— {2 x — [3 — (4 — 3 x )] + 6 x }
–1 {2 x — 1 [3 — 1 (4 — 3 x )] + 6 x }
–1 {2 x — 1 [3 — 4 + 3 x ] + 6 x }
–1 {2 x — 1 [- 1 + 3 x ] + 6 x }
–1 {2 x + 1 — 3 x + 6 x }
–1 {2 x + 6 x — 3 x + 1}
–1 {5 x + 1}
–5 x — 1
(Дополнительные примеры такого рода см. В разделе «Упрощение с круглыми скобками».)
Выражения, содержащие дробные формы, тоже могут вызывать путаницу. Но до тех пор, пока вы работаете с числителем (то есть сверху) и знаменателем (то есть снизу) отдельно, пока они сначала полностью не упростят, и только затем объедините (или уменьшите), если возможно, тогда вы все должно быть в порядке. Если дробная форма добавляется или вычитается из другого члена, дробного или иного, убедитесь, что вы полностью упростили и уменьшили дробную форму, прежде чем пытаться выполнить сложение или вычитание.
Упростить [45] / [8 (5 — 4) — 3] + [3 (2)
2 ] / [5 — 3]
Прежде чем я смогу добавить два термина, я должен упростить.
[45] / [8 (5 — 4) — 3] + [3 (2) 2 ] / [5 — 3]
[45] / [8 (1) — 3] + [3 (4)] / [2]
[45] / [8–3] + [12] / [2]
[45] / [5] + 6
9 + 6
15
Упростить [(3–2) + (1 + 2)
2 ] / [5 + (4–1)]
Работает так же, как и в предыдущих примерах.Мне просто нужно работать над «верхом» и «низом» отдельно, пока я не получу дробь, которую я могу (возможно) уменьшить.
[(3–2) + (1 + 2) 2 ] / [5 + (4–1)]
[(1) + (3) 2 ] / [5 + (3)]
[1 + 9] / [8]
10/8
5/4
(Примеры с множеством экспонент см. В разделе Упрощение с экспонентами.)
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в упрощении порядка операций. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку и выберите «Упростить» или «Оценить» во всплывающем окне, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
Боковое форматирование и умножение на сопоставление
В следующем примере показана проблема, которая почти никогда не возникает, но когда она возникает, спорам, кажется, нет конца. (Публиковать их в Facebook стало досадно.)
Упростить 16 ÷ 2 [8 — 3 (4 — 2)] + 1.
Упрощаю обычным способом:
16 ÷ 2 [8 — 3 (4 — 2)] + 1
16 ÷ 2 [8 — 3 (2)] + 1
16 ÷ 2 [8 — 6] + 1
16 ÷ 2 [2] + 1 (**)
16 ÷ 4 + 1
4 + 1
5
Запутанная часть в приведенном выше вычислении заключается в том, как «16, разделенное на 2 [2] + 1» (в строке, отмеченной двойной звездой) становится «16, разделенное на 4 + 1», вместо «8 раз на 2 + 1 «.
Это потому, что, хотя умножение и деление находятся на одном уровне (поэтому должно применяться правило слева направо), скобки как-то превосходят деление по рангу, поэтому первые 2 в строке, отмеченной звездочкой, часто рассматриваются как идущие с [ 2], которая следует за ним, а не с «16, разделенными на», которое предшествует ему. То есть умножение, которое указывается путем помещения в круглые скобки (или скобки и т. Д.), Часто рассматривается (научными людьми) как более сильное, чем «обычное» умножение, которое обозначается каким-либо символом, например как «×».
Набор всей задачи в графическом калькуляторе подтверждает существование этой иерархии, по крайней мере, в некотором программном обеспечении:
Обратите внимание, что различных программных пакета обрабатывают это выражение по-разному ; даже разные модели графических калькуляторов Texas Instruments будут обрабатывать это выражение по-разному. Общее мнение среди математиков состоит в том, что «умножение на сопоставление» (то есть умножение путем простого размещения элементов рядом друг с другом, а не использования знака «×») указывает на то, что сопоставленные значения должны быть умножены вместе перед обработкой других операций.Но не все программы запрограммированы таким образом, и иногда учителя смотрят на вещи иначе. Если сомневаетесь, спрашивайте! И, печатая что-то боком, будьте очень осторожны с скобками и проясните свой смысл, чтобы избежать именно этой двусмысленности.
(Пожалуйста, не присылайте мне электронное письмо с просьбой или предложением окончательного вердикта по этому вопросу. Насколько я знаю, такого окончательного вердикта нет. Если я скажу мне действовать по-вашему, , а не , решит проблему проблема!) (Для примера того типа писем, которые я получаю по этому поводу, перейдите на следующую страницу, которая также содержит больше примеров дробной формы.)
Филиал
URL: https://www.


