Презентация «Аппликация из геометрических фигур «Цирковое представление»» 2 класс
Аппликация из геометрических фигур «Цирковое представление»
Выполнила:
учитель технологии
Высшей категории
МБОУ СОШ № 13 г.Азов
Семенец Ольга Ивановна
Цель: создание условий для закрепления умения составлять из геометрических фигур различные изображения.
Цель: создание условий для закрепления умения составлять из геометрических фигур различные изображения.
Задачи урока:
- Продолжить знакомство с техникой аппликации из бумаги.
- Способствовать закреплению знаний о геометрических фигурах
- Содействовать развитию умения планировать свою работу, сообразительности, логического мышления, внимания, воображения
- Способствовать воспитанию аккуратности, культуре труда, самостоятельности при выполнении работы
Простые геометрические фигуры
треугольник
прямоугольник
квадрат
круг
овал (эллипс)
Вот большой и круглый дом.
Вот большой и круглый дом.
Ой, какое место!
Ведь всегда ребятам в нем
Очень интересно.
В этом доме непременно
Есть и звери, и арена.
Давайте вспомним, что такое цирк?
Манеж – это площадка круглой формы, расположенная внутри цирка. На манеже выполняют цирковые номера.
Какие предметы и какой формы в цирковых номерах у артистов?
Аппликация из геометрических фигур – создание изображений с помощью наклеивания на бумагу деталей круглой, квадратной , треугольной и т. д. формы.
Аппликация из геометрических фигур – создание изображений с помощью наклеивания на бумагу деталей круглой, квадратной , треугольной и т. д. формы.
Мы с вами будем делать героев из бумаги, но необыкновенных, а из геометрических фигур.
Для работы нам потребуется
- линейка шаблон
- цветная бумага
- картон
- ножницы
- клей
- карандаш
Правила по технике безопасности
Обращайтесь с ножницами,
Очень осторожно.
Резать кончиком нельзя,
Серединкой – можно.
Когда выполнишь работу,
Тут же ножницы закрой.
Чтобы до острых краешков,
Не коснулся, кто другой.
Если нужно инструмент,
Передать другому.
То колечки от себя,
Ты спокойно поверни.
И, за кончики держась
Ножницы ему верни.
Шаг 1
Вырезать большой круг по шаблону и наклеить на картон – это арена нашего цирка! Начинаем представление!
Шаг 2
1 большой синий круг
2 серых (голубых)круга среднего размера
4 голубых маленьких круга
Обвести по шаблону и вырезать:
Шаг 3
Разрезать два маленьких круга пополам.
Физкультминутка
Цирк зверей.
Покажите мне скорей
Настоящий цирк зверей:
Как танцует нам фокстрот
Неуклюжий бегемот,
Кувыркается мартышка,
На машине едет мишка;
Словно шустрый белый мячик,
По манежу скачет зайчик.
А в конце, все, как артисты,
Поклонились в пояс низко.
Шаг 4
Наклеим круги на заготовленную арену цирка.
Вырезать и наклеить мячики для слоненка.
Вырезать и наклеить мячики для слоненка.
Пригласим на манеж морского котика!
Вырезать детали по шаблону и собрать работу по плану
Клоун
Из цветной бумаги по шаблонам необходимо вырезать:
- 5 разноцветных кругов — это будет лицо и мячики для жонглирования;
- 3 одинаковых треугольников — рукава и колпак клоуна;
- 1 овал — туловище;
- 2 одинаковых треугольника соединить звездочкой — воротник;
- 2 небольших круга разрезанных пополам — башмаки, руки;
Наклеить детали по плану
Цирковое представление!
СПАСИБО
ЗА
ВНИМАНИЕ!
Используемые активные ссылки
- http://vospitatel.com.ua/images/c/circus-3god4.jpg
- http://argumenti.ru/images/arhnews/446544.JPG
- http://gifok.net/images/2015/10/25/Clown_1_011.md.png
- http://gifok.net/images/2015/10/25/Clown_1_009.png
- https://avatars.mds.yandex.
 net/get-afishanew/34116/2bc3d42440a0bc3de26f3e67a6b3f4b9/orig
net/get-afishanew/34116/2bc3d42440a0bc3de26f3e67a6b3f4b9/orig - http://kmv.gorodskoitelegraf.ru/uploads/posts/2015-07/1436516827_foto7829.jpg
- http://static.ngs.ru/news/preview/765c80513fcc4017e252120346c8c4c50f5f9bdb_600.jpg
- http://img-fotki.yandex.ru/get/5214/16969765.20b/0_8d59a_43c76531_orig.png
- http://portal.azertag.az/sites/default/files/jongler8.jpg
- http://www.ruscircus.ru/forum/uploads/post-3-1278655211.jpg
- http://saroblnews.ru/files/pages/32303/1395209698general_pages_i32303_jivotnyx_v_cirke_ogradyat_ot_boli.jpg
- http://s9.stc.all.kpcdn.net/share/i/4/640982/
- http://img.fotodom.ru/FB08-3383.jpg?size=m
- http://img1.liveinternet.ru/images/foto/c/9/apps/2/216/2216869_9.jpg
- http://img.espicture.ru/6/applikaytsii—iz-geometriycheskih-figur-kartinki-22.jpg
- http://static8.depositphotos.com/1032613/863/i/950/depositphotos_8633451-Illustration-of-a-circus-tent.jpg
- http://www.dominotoys.ru/34982-large_default/lineyka-oficerskaja.jpg
http://www.kancministr.ru/upload/iblock/8c8/8c8a84616d05433ea176ec99c3752445.gif
- http://www.kancministr.ru/upload/iblock/8c8/8c8a84616d05433ea176ec99c3752445.gif
- http://fast.ulmart.ru/p/big/347/34758/3475827.jpg?utm_source=cityads&utm_medium=cpo&utm_campaign=2Keh&from=cityads&click_id=XUZ1JN75KZEx5u
- http://www.kancelarka.com.ua/data/tovar/00000000260.jpg
- http://cliparts.co/cliparts/rcj/G86/rcjG86Goi.png
- http://1.bp.blogspot.com/-hONmUv0iLFY/Ut46mZWT-TI/AAAAAAAALvk/TAbbx4YJups/s1600/99539706_smaylik.png
- http://animalsfoto.com/photo/5a/5ac5991e698c0971901de018f625aa6a.jpg
- http://ib1.keep4u.ru/b/080305/5e/5eb1cda201f0e7eb93.
 jpg
jpg - http://static.akipress.org/127/.storage/limon2/images/january2015/5e868673e6af63db6a1c77e5bb967ee2.jpg
Фото мастер класса — автора презентации Семенец О.И.
источник шаблона:
Ранько Елена Алексеевна
учитель начальных классов
МАОУ лицей №21
г. Иваново
Аппликации из геометрических фигур для 1-4 класса с шаблонами
Если вы хотите знать, что такое аппликации из геометрических фигур и хотите научить деток этому виду искусства, то эта статья для вас.
Аппликации, которые делают дети, иногда очень простые и наивные, но они помогают детям развивать их умения резать, создавать рисунок и фантазировать. А также детям безумно нравится приклеивать цветные фигуры на фон.
Сначала дети приклеивают на фон фигурки, которые вырезают взрослые. Но время не стоит на месте — дети растут. И дети со временем учатся сами вырезать, приклеивать и творить. И тогда ребенка следует научить самым интересным видам аппликаций.
Делая геометрические аппликации, ребенок развивает глазомер и пространственное мышление, учится сочетать цвета и ознакомляется с геометрическими фигурами.
Простейшей аппликацией из геометрических фигур можно считать составление узоров на длинной полоске бумаги. Потом можно перейти к конструированию разных предметов, транспорта, животных, растений. Благодаря этому у ребенка развиваются творческие способности.
Для учеников 1 класса
Дети уже более или менее владеют ножницами, когда идут в 1 класс. Шаблоны в этом случае станут незаменимыми помощниками. С помощью них дети смогут вырезать нужные детали из бумаги, и им будет проще творить и учиться делать аппликации. Вот шаблоны нескольких несложных геометрических аппликаций:
Вот несколько примеров работ для детей 1 класса и их схем:
Аппликация «Домик в деревне»:
Вроде бы ничего сложного, никаких сложных деталей.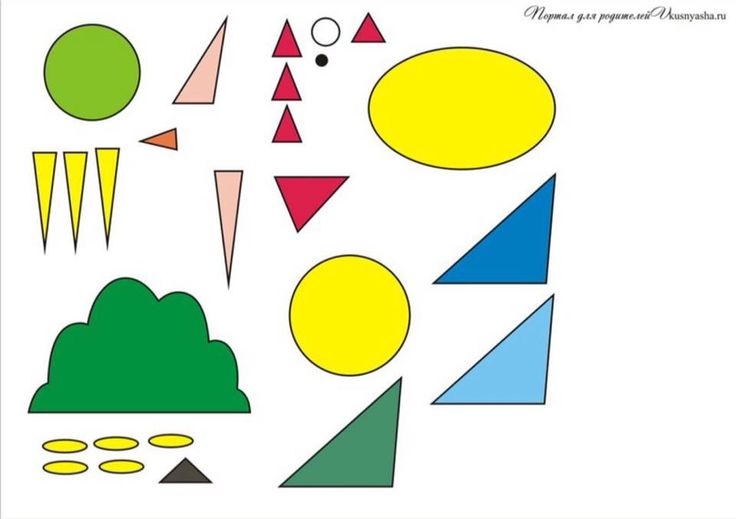 Все просто. Домик, солнышко, дерево, но есть в этой картине что-то необыкновенное. Кроме того, ребенок сделает эту картину еще более уникальной, ведь она будет воплощением его фантазии и мышления.
Все просто. Домик, солнышко, дерево, но есть в этой картине что-то необыкновенное. Кроме того, ребенок сделает эту картину еще более уникальной, ведь она будет воплощением его фантазии и мышления.
Аппликация «Кошка с котенком»:
Для изготовления аппликации этой кошечки с котенком ребенку нужно будет вырезать самые разнообразные фигуры и составить из них целостный образ по своему вкусу.
Аппликация «Веселая гусеница»:
Веселая гусеница позабавит ваших детишек. Ее интересно не только рассматривать, но и делать. Ведь эти кружочки и другие детали можно расположить по-разному. И у каждого ребенка получится своя неповторимая веселая гусеница.
Для изготовления вышеперечисленных аппликаций домика, кошки и гусеницы можно просто распечатать схемы, затем дети могут вырезать фигурки и приклеить их на бумагу. Но это уж слишком просто. Так что можно сделать шаблоны своими руками. И тогда дети будут вырезать по ним из разных цветов части и приклеивать их.
Для детей 3-5 лет
Также есть аппликации, предназначенные для детей дошкольного возраста. Они достаточно просты. В процессе работы дети научатся многому. А главное — они ознакомятся с геометрическими фигурами и тем, где их можно применять.
Имея распечатанные шаблоны, делать аппликацию нужно в такой последовательности:
- Вырезать шаблоны из бумаги;
- Наклеить части на соответствующие им места.
Далее можно раскрасить рисунок.
А вот еще похожие работы.
Данные аппликации достаточно просто сделать, поэтому они подходят для детей младшего возраста, так сказать, новичков в аппликациях. Можно выбрать из большого ассортимента рисунков и распечатать тот, что подходит ребенку больше.
Меньшая часть изображения послужит в качестве шаблонов, с помощью которых нужно будет вырезать детали разных цветов, наклеить их на большую часть, которая послужит фоном для аппликации.
Аппликацию выполняют в такой очередности:
- Вырезать шаблоны, что находятся в боковой части странички.
 Получаются шаблоны;
Получаются шаблоны; - Далее нужно по приготовленным шаблонам вырезать из бумаг нужных цветов детали и наклеить их на соответствующие им места.
Для деток 4 класса
В ходе изготовления аппликаций из геометрических фигур для детей, которые ходят в 4 класс, ребята научатся четко размечать детали по шаблону, собирать отдельные геометрические фигуры в полноценный образ.
Сначала деткам следует показать, какой будет работа по ее завершению. Детям потребуется: цветная бумага, картон, клей, линейка, карандаш, ножницы и кисть.
Для начала детям нужно подготовить рабочее место и приготовить все необходимое для изготовления аппликации.
Посмотрите, все ли у вас готово к уроку? Нам понадобится: цветная бумага, картон, клей; линейка, карандаш, ножницы, ластик, кисть; баночка для клея, салфетка, клеенка.
В такой очередности нужно действовать для изготовления аппликации:
- Готовим основу;
- Переводим и вырезаем детали по шаблону;
- Составляем аппликацию.
Приступаем к работе аппликации из геометрических фигур «Кошки-мышки»:
Вот такие детали нужны для мышек и сыра. Шаблоны для них несложно сделать. Вырезать тоже. Но очень интересно из простых геометрических фигур составлять такую красоту.
Далее переходим к котику. Вот такие детали необходимы для изготовления кота. Как вы видите, среди материалов есть фломастер, с помощью которого детки могут реализовать свою фантазию и нарисовать неповторимую мордочку котику.
Наша чудесная работа готова.
Есть еще очень множество идей аппликаций для деток. Например, такой вот прекрасный кораблик. Его можно сделать по схеме ниже.
Интересной идеей является гирлянда из геометрических фигур. Ее можно сделать в виде открытки и поздравить с ней кого-то с праздником.
Очень крутой идеей для деток 4 класса будет аппликация из геометрических фигур на свободную тему, то есть по эвристическим методам. Это делается очень просто.
Это делается очень просто.
На белой бумаге печатают самые разные фигуры, разных размеров. Потом их вырезают. Затем берут картон темного цвета и клеят на него все эти фигурки так, чтобы получился какой-то определенный рисунок. Это отлично развивает моторику рук, так как фигурок для вырезания много, и фантазию, потому что деткам нужно придумывать образы самим. Фигурки одинаковые, а аппликации у всех совсем разные. В этом и фишка. Ниже представлены примеры работ:
Видео по теме статьи
Геометрические фигуры для детей 🥝 картины, поделки из треугольников, кругов, квадратов в подготовительной группе
Много начинающих воспитателей обдумывают, как сделать аппликацию из геометрических фигур и зачем это нужно. В ходе таких уроков и занятий малыши получают много полезной информации о видах геометрических фигур и учатся понимать основные формы предметов. После работы с мелкими деталями у ребенка будет хорошо развита мелкая моторика рук, а так же он будет отлично подготовлен к математике.
Аппликация из различных фигур — невероятно интересное занятие, с помощью которого можно помочь ребенку развить следующие способности:
- хорошее мышление;
- творческий потенциал и фантазию;
- художественный вкус;
- глазомер;
- правильное восприятие цвета.

Занятия, посвященные подбору элементов по цвету, могут научить малыша сочетать цвета. Помимо развития многих способностей, каждый ребенок получает удовольствие от такого занятия.
Содержание материала
Аппликация из геометрических фигур для детей разных возрастов
Приступить к таким интересным занятиям можно, когда малыш уже начал ходить в детский садик.
- Для детей трехлетнего возраста занятие с аппликацией в детском саду начинаются с приклеивания готовых деталей, которые вырезал сам воспитатель из цветной бумаги. Чаще всего берут простую геометрическую фигуру с легким орнаментом.
- Для малыша четырехлетнего возраста главную сложность составляет работа с ножницами. Благодаря таким занятиям ребенок может сделать красивый коврик, закладку с необычным орнаментом, маленькую елочку и новогоднюю открытку.
- Для детей пяти лет подготавливают задания, в которых нужно сделать простую сюжетную композицию. К примеру, это может быть аквариум с рыбками из треугольников или поляна с бабочками, которые сделаны из кругов. Все это малыши делают своими собственными руками. Дети в этом возрасте учатся правильно держать ножницы и красиво вырезать детали для картинок.
- Для детей шести лет основной целью занятий считается улучшение навыков использования ножниц. Большинство ребят с радостью изображают человека, домашних животных, здания и машины. Помимо этого, многие малыши любят дополнять изображения новыми деталями и объединять все это в сюжетные композиции.
- Аппликация из геометрических фигур 4 класс. Для этих детей уроки, связанные с аппликацией, превращаются в невероятную игру, которая позволяет им проектировать необычные и динамичные композиции. Ведь школьники уже имеют много опыта в этом деле. Популярностью у них пользуется аппликация с большим объемом. С такой техникой дети делают прекрасные открытки и невероятные натюрморты, а также украшают комнату.

Галерея: аппликация из геометрических фигур (25 фото)
Аппликации для маленьких
В младшей группе малыши изучают навыки аккуратного наклеивания деталей будущей композиции: правильно и ровно наносить клей, расставлять детали определенного цвета и формы в нужном порядке, убирать излишки клея с помощью салфеток.
Если вы не хотите, чтобы у малыша пропал интерес к этому занятию, нужно обыгрывать геометрические фигуры и коллажи из геометрических фигур. К примеру, цветные кружки можно превратить в мячики, а яблоки превратить в гусеницу. Из квадратиков может получиться кот или собака.
На уроках с аппликацией воспитатели часто используют забавный момент: показывают малышам большой лист с изображением какого-нибудь милого зверька, например, котика или лиса. После чего вместе придумывают, как его сделать самим из фигурок.
Во второй младшей группе выполняют более тяжелые задания — склеить готовые детали, меняя форму и цвет. Чтобы увеличить интерес к занятиям, воспитатели создают новые задачи, просят добавить что-либо уже к готовой поделке.
Когда дети осваивают первичные навыки работы с ножницами, можно поручать им более сложные задания, к примеру, наполнить большой грузовик какими-либо вещами. В этой группе детям часто поручают сделать ракету.
В средней группе учат закреплять навыки разрезания полосок, срезов и деления геометрических фигур. Из вырезанных деталей они могут сделать: елку, избу, лодку, ракету, цветок.
Любому ребенку тяжело дается вырезание деталей круглой формы, а ведь без этого сложно сделать нормальное животное или птицу. Больше всего малышам нравится делать утенка, зайчика и цыпленка. Благодаря правильной работе с аппликациями геометрических фигур они могут научиться изображать различный транспорт, например:
- самолет;
- танк;
- трактор.
В старшей группе все отрабатывают свои полученные навыки и учатся созданию поделки из геометрических фигур с яркими образами.
В этом возрасте детям больше нравится выполнять коллективные работы и композиции. Это способствует развитию общения между детьми и умению ладить между собой. Обычно коллективная композиция занимает всего два дня: сначала создается дом, человечек, а потом и машина. Увлекаются такими занятиями и дошкольники, и дети в младших классах.
Самой трудной работой считается аппликация клоун из геометрических фигур, в ней много деталей и ярких цветов, вырезать приходится долго. Для облегчения можно сначала нарисовать схемы.
Заключение
Чаще всего такие работы проводят в детском саду или в 3–4 классе. Поделки из треугольников или квадратов – это все довольно просто. Если вы хотите подготовить ваше чадо ко многим вещам в будущем, стоит попробовать с ним позаниматься аппликациями.
А совсем маленьким детям можно объяснить с помощью поделки, чем занимается человек, как выглядят разные животные. Шаблон для таких работ можно купить в любом книжном магазине или заказать в интернете. Цены на шаблоны довольно низкие. Порадуйте своего ребенка и позанимайтесь с ним!
Другие виды рукоделия
Аппликация из геометрических фигур «Цирковое представление»
Аппликация из
геометрических фигур
«Цирковое
представление»
Выполнила:
учитель технологии
Высшей категории
МБОУ СОШ № 13 г.Азов
Семенец Ольга Ивановна
Цель: создание условий для закрепления умения
составлять из геометрических фигур различные
изображения.
Задачи урока:
Продолжить знакомство с техникой аппликации из
бумаги.
Способствовать закреплению знаний о геометрических
фигурах
Содействовать развитию умения планировать свою
работу, сообразительности, логического мышления,
внимания, воображения
Способствовать воспитанию аккуратности, культуре
труда, самостоятельности при выполнении работы
Простые геометрические фигуры
круг
квадрат
треугольник
прямоугольник
овал (эллипс)
Вот большой и круглый дом.
Ой, какое место!
Ведь всегда ребятам в нем
Очень интересно.
В этом доме непременно
Есть и звери, и арена.
Давайте вспомним, что такое цирк?
Манеж – это площадка круглой формы,
расположенная внутри цирка. На манеже
выполняют цирковые номера.
Какие предметы и какой формы в
цирковых номерах у артистов?
Аппликация из геометрических фигур –
создание изображений с помощью
наклеивания на бумагу деталей круглой,
квадратной , треугольной и т. д. формы.
Мы с вами будем делать героев из бумаги,
но необыкновенных, а из геометрических
фигур.
Для
работы нам потребуется
линейка
шаблон
цветная бумага
картон
ножницы
клей
карандаш
Правила по технике безопасности
Обращайтесь с ножницами,
Очень осторожно.
Резать кончиком нельзя,
Серединкой – можно.
Когда выполнишь работу,
Тут же ножницы закрой.
Чтобы до острых краешков,
Не коснулся, кто другой.
Если нужно инструмент,
Передать другому.
То колечки от себя,
Ты спокойно поверни.
И, за кончики держась
Ножницы ему верни.
Шаг 1
Вырезать
большой круг по
шаблону и наклеить
на картон – это арена
нашего цирка!
Начинаем
представление!
Шаг 2
Обвести по шаблону и
вырезать:
1 большой синий круг
2 серых (голубых)круга
среднего размера
4 голубых маленьких
круга
Шаг 3
Разрезать два маленьких круга пополам.
Физкультминутка
Цирк зверей.
Покажите мне скорей
Настоящий цирк зверей:
Как танцует нам фокстрот
Неуклюжий бегемот,
Кувыркается мартышка,
На машине едет мишка;
Словно шустрый белый мячик,
По манежу скачет зайчик.
А в конце, все, как артисты,
Поклонились в пояс низко.
Шаг 4
Наклеим круги на заготовленную арену
цирка.
Вырезать и наклеить мячики для слоненка.
Пригласим на манеж морского котика!
Вырезать детали по шаблону и
собрать работу по плану
Клоун
Из цветной бумаги по шаблонам
необходимо
вырезать:
5 разноцветных
кругов — это
будет лицо и мячики для
жонглирования;
3 одинаковых треугольников
— рукава и колпак клоуна;
1 овал — туловище;
2 одинаковых треугольника
соединить звездочкой —
воротник;
2 небольших круга
разрезанных пополам —
башмаки, руки;
Наклеить детали по плану
Цирковое представление!
СПАСИБО
ЗА
ВНИМАНИЕ!
Используемые активные ссылки
http://vospitatel. com.ua/images/c/circus-3god4.jpg
com.ua/images/c/circus-3god4.jpg
http://argumenti.ru/images/arhnews/446544.JPG
http://gifok.net/images/2015/10/25/Clown_1_011.md.png
http://gifok.net/images/2015/10/25/Clown_1_009.png
https://avatars.mds.yandex.net/get-afishanew/34116/2bc3d42440a0bc3de26f3e67a6b3f4b9/orig
http://kmv.gorodskoitelegraf.ru/uploads/posts/2015-07/1436516827_foto7829.jpg
http://static.ngs.ru/news/preview/765c80513fcc4017e252120346c8c4c50f5f9bdb_600.jpg
http://img-fotki.yandex.ru/get/5214/16969765.20b/0_8d59a_43c76531_orig.png
http://portal.azertag.az/sites/default/files/jongler8.jpg
http://www.ruscircus.ru/forum/uploads/post-3-1278655211.jpg
http://saroblnews.ru/files/pages/32303/1395209698general_pages_i32303_jivotnyx_v_cirke_ogradyat_
ot_boli.jpg
http://s9.stc.all.kpcdn.net/share/i/4/640982/
http://img.fotodom.ru/FB08-3383.jpg?size=m
http://img1.liveinternet.ru/images/foto/c/9/apps/2/216/2216869_9.jpg
http://img.espicture.ru/6/applikaytsii—iz-geometriycheskih-figur-kartinki-22.jpg
http://static8.depositphotos.com/1032613/863/i/950/depositphotos_8633451-Illustration-of-a-circustent.jpg
http://www.kancministr.ru/upload/iblock/8c8/8c8a84616d05433ea176ec99c3752445.gif
http://fast.ulmart.ru/p/big/347/34758/3475827.jpg?utm_source=cityads&utm_medium=cpo&utm_ca
mpaign=2Keh&from=cityads&click_id=XUZ1JN75KZEx5u
http://www.kancelarka.com.ua/data/tovar/00000000260.jpg
http://cliparts.co/cliparts/rcj/G86/rcjG86Goi.png
http://1.bp.blogspot.com/-hONmUv0iLFY/Ut46mZWTTI/AAAAAAAALvk/TAbbx4YJups/s1600/99539706_smaylik.png
http://animalsfoto.com/photo/5a/5ac5991e698c0971901de018f625aa6a.jpg
http://ib1.keep4u.ru/b/080305/5e/5eb1cda201f0e7eb93.jpg
http://static.akipress.org/127/.storage/limon2/images/january2015/5e868673e6af63db6a1c77e5bb967e
e2.jpg
Фото мастер класса — автора презентации Семенец О.И.
источник шаблона:
Ранько Елена Алексеевна
учитель начальных классов
МАОУ лицей №21
г. Иваново
Иваново
Тема: Работа с бумагой. Урок — Аппликация из геометрических фигур «ракета» Цель: Изготовить аппликацию
Открытый урок по ручному труду
Открытый урок по ручному труду Тема: Составление по образцу орнамента в полосе из геометрических фигур (квадратов, треугольников, кругов), чередующихся по форме и цвету. Подготовила и провела Иванова О.В.
Подробнее
ГБОУ СОШ 901 ЮАО учитель ИЗО и МХК Гуженко Т.В.
1 Занятие- викторина «Бумага и ножницы заставляют думать» Задачи: Развитие пространственного мышления; Развитие мелкой моторики пальцев; Диагностика результатов обучения в области работы с бумагой, конструирования,
Подробнее
Пояснительная записка.
Пояснительная записка. Данная программа предназначена для обучающихся с тяжёлой степенью умственной отсталости. При ее составлении за основу были взяты следующие документы: )Адаптированная образовательная
Подробнее
Пояснительная записка
Пояснительная записка Рабочая программа учебного курса ручного труда для 3 года обучения составлена на основе программы для подготовительного класса школы VIII вида (для детей с нарушением интеллекта)
Подробнее
Цель дисциплины: Задачи:
Пояснительная записка. Данная программа предназначена для обучающихся с тяжёлой умственной отсталостью. При ее составлении за основу были взяты следующие документы: )Адаптированная образовательная программа
Подробнее
4 класс Практическая работа Витраж
4 класс Практическая работа Витраж Фамилия, имя класс Образовательная организация Слово «витраж» в переводе с французского языка «оконное стекло». Витражами называют картины или узоры, составленные из
Витражами называют картины или узоры, составленные из
Подробнее
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА Учитель: Чуканова Людмила Николаевна Предмет: Технология Класс: 2 Авторы УМК: «Перспектива» авторы:роговцева Н.И., Агнащенкова С.В. Тип урока: комбинированный Тема урока: Строительство.Конструирование
Подробнее
1.Пояснительная записка
1 1.Пояснительная записка Рабочая программа по аппликации (образовательная область «Художественно эстетическое развитие») составлена на основе авторского планирования Т.С. Комаровой «Изобразительная деятельность
Подробнее
Курс «Краски, линии и конструкции»
Курс «Краски, линии и конструкции» Задачи курса: 1. Развитие самостоятельности и аккуратности в работе с карандашами, красками, бумагой. 2. Постановка руки (умение проводить прямые и кривые линии «от руки»,
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА 1. Направленность программы Содержание программы направлено на знакомство детей с методами ниткографии и изонити, расширение представлений о данных видах искусства, на воспитание
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Аппликация — одно из любимых занятий детей в детском саду. Этот продуктивный вид деятельности связан с познанием окружающего мира и играет большую роль в умственном воспитании ребенка.
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПРОГРАММА курса занимательного труда помещена в сборнике программы специальных (коррекционных) образовательных учреждений VIII вида. 1 4 классы В. В. Воронкова А. А. Айдаберкова, В. М. Белов. Москва «Просвещение»,
В. Воронкова А. А. Айдаберкова, В. М. Белов. Москва «Просвещение»,
Подробнее
Методы, используемые на занятиях:
1 Оригами японское искусство складывания бумаги. Оригами является не только увлекательным способом проведения досуга, но средством решения многих педагогических задач. Оригами способствует развитию эмоциональной,
Подробнее
I. Пояснительная записка
I. Пояснительная записка Художественная деятельность и, в частности, ручной труд помогают дошкольнику социализироваться в обществе сверстников, понять собственные замыслы, попробовать себя в преобразовании
Подробнее
Конспект занятия «Волшебные снежинки»
Конспект занятия «Волшебные снежинки» Конспект составила: Кривенцова Екатерина Сергеевна Дата проведения: 23.12.2016 Белгород Тема: «Волшебные снежинки» Дата проведения: 23.12.2016 Учебно-методический
Подробнее
Тема(аппликация) Задачи Дата проведения
занятия Тема(аппликация) Задачи Дата проведения По Факт плану 1 Знакомство в уголке творчества с материалом по аппликации: картоном, клеем, ножницами. Т.Б. при работе с ножницами и клеем. Продолжать работу
Подробнее
Пояснительная записка
Пояснительная записка Данная программа предназначена для обучающихся по программе для детей с тяжелой степенью умственной отсталости. При ее составлении за основу были взяты следующие документы: ) Адаптированная
Подробнее
Конспект Непосредственнообразовательной
Государственное бюджетное дошкольное образовательное учреждение Детский сад 63 Приморского района Санкт-Петербурга Конспект Непосредственнообразовательной деятельности Тема: Как я провел лето» Образовательные
Подробнее
РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА
РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА ПО РИСОВАНИЮ 4 КЛАСС (наименование учебного предмера) По адаптированной образовательной программе начальное общее (уровень образования) Рассчитана на 1 год (срок реализации программы)
Подробнее
Разработка и проведение бинарного урока.
Разработка и проведение бинарного урока. Конспект урока Бинарный урок швейного дела и математики Класс 5 Тема: Построение чертежа наволочки с клапаном. Преобразование чисел, полученных при измерении длины.
Подробнее
Графическое приложение
Графическое приложение Графическое приложение состоит из серии рабочих листов с образцами раздаточных материалов и шаблонов, предназначенных для выполнения школьниками практических работ. Рабочий лист
Подробнее
Перспективный план по аппликации
Перспективный план по аппликации ( старшая группа ) Методическая литература: 1. Лыкова И.А. «Изобразительная деятельность в детском саду» (старшая группа) 2. Лыкова И.А. «Изобразительное творчество в детском
Подробнее
Тема занятия: «Чашка. Лепка из глины».
Тема занятия: «Чашка. Лепка из глины». Цель занятия: изготовить чашку из глины с помощью жгутов. Задачи Образовательные Познакомить детей со жгутовой техникой лепки Показать, какие бывают формы чашек Показать
Подробнее
Пояснительная записка
Пояснительная записка Программа предполагает развитие у детей художественного вкуса и творческих способностей, предлагает развитие ребенка в самых различных направлениях: конструкторское мышление, художественно-эстетический
Подробнее
Пояснительная записка
Пояснительная записка Данная программа предназначена для обучающихся с тяжелой степенью умственной отсталости. При ее составлении за основу были взяты следующие документы: ) Адаптированная образовательная
Подробнее
Открытый урок «Аппликация кошки из геометрических фигур»
Тема: «Изготовление аппликации кошки из геометрических фигур»
Цель: Научить изготавливать аппликацию из готовых геометрических форм.
Задачи:
Образовательные:
Повторение понятия «аппликация», закрепление умения составлять аппликацию по образцу путём приклеивания заготовок на бумажную основу.
Коррекционно-развивающие:
Развитие мелкой моторики рук, тактильного восприятия.
Развитие мыслительной деятельности( операций анализа и сравнения с образцом)
Воспитательные:
Воспитание самостоятельности и аккуратности.
Воспитание бережного отношения к животным.
Тип урока: комбинированный.
Ход урока:
I.Организационный момент:
Цель: подготовить учащихся к работе на уроке, создать первичную мотивацию к
деятельности.
Есть волшебные слова:
Скажешь, сразу тишина.
Повнимательней, дружок,
Начинается урок!!!
Психологический настрой
-На уроке наши глаза внимательно смотрят и все…видят.
-Уши внимательно слушают и все…слышат.
-Голова хорошо…думает.
II.Вводная беседа.
Цель: сообщить тему урока, поставить учебную задачу.
-Сегодня мы с вами будем путешествовать по необычной стране, в которой все состоит из фигур. Чтобы начать путешествие, нам надо разгадать имена жителей этой страны.
-Отгадав загадки, вы их узнаете:
-Он давно знакомый мой.
-Каждый угол в нем прямой.
-Все четыре стороны — одинаковой длины
-Вам его представить рад,
-А зовут его… квадрат.
-Покажите квадрат! (дети показывают квадрат среди фигур, которые лежат на партах)
На доске появляется геометрическая фигура квадрат.
-Вот и разгадали имя первого жителя волшебной страны.
-Нет углов у меня и похож на блюдце я,
-на тарелку и на крышку, и на круг и колесо.
-Что это? — Круг! ( Показывают круг)
К доске учитель прикрепляет круг.
-Вот и второй житель этой страны.
-Моя загадка коротка: три стороны и три угла!
-Кто я? — Треугольник. (Показывают треугольник)
На доске появляется треугольник.
-А вот появился и третий житель необычной страны.
-Нам осталось отгадать последнего жителя.
-Мальчик круг нарисовал-убежал,
— Тут слонёнок проходил-наступил,
-И из круга получился-…овал! (Показывают овал)
-Назовите жителей этой волшебной страны! (Хором повторяем названия фигур)
-Может, уже кто-то догадался, как называется эта страна?
-Правильно, это — страна геометрических фигур. Сегодня на уроке мы с вами будем путешествовать по этой волшебной стране, и поможет нам в этом Геометрик.
(Фигура человечка)
Сообщение темы и цели урока:
-А чем мы будем заниматься на уроке, вы узнаете, выполнив следующее задание Геометрика. Будьте очень внимательны!
На доске расположены геометрические фигуры- разноцветные круги, квадраты, треугольники, прямоугольники, овал. На каждой фигуре с обратной стороны написана буква.
-Покажите красный круг! Синий треугольник! Жёлтый квадрат! Белый овал! Зелёный круг!
Дети выходят к доске и по порядку выбирают названную фигуру.
-А теперь давайте перевернем фигуры и посмотрим, что у нас получилось?
— Кто прочитает слово?- КОШКА.
-Верно, ребята. Все вы знаете и любите кошек. Поднимите руки , у кого есть дома кошечка? -Очень хорошо. А кто может сказать, что любит пить кошка?-
-Правильно, молоко.
(На компьютере — картина лакающей молочко кошки)
-А какая бывает кошечка?
-Правильно, добрая, ласковая.
-Можно обижать кошек?
-Конечно, нельзя, ребята. Животных нельзя обижать, их нужно любить.
-И сегодня я принесла на урок игрушку – кошку.
Учитель демонстрирует мягкую игрушку кошки.
—Погладьте её!
-Какая она?
-Правильно, она мягкая, пушистая.
-Она будет наблюдать за нами.
-Чем же мы будем заниматься сегодня?
-А сегодня мы сделаем кошечку из бумаги , а именно мы выполним аппликацию.
На доске- слово АППЛИКАЦИЯ.
-Что означает аппликация? ( ответы)— Это приклеивание бумаги на картон.
-Верно, мы будем приклеивать фигуры из бумаги на картон.
-Посмотрите, какие аппликации из геометрических фигур принёс нам Геометрик.
Демонстрация аппликаций различных животных .
—Давайте назовём, кого мы здесь видим.
Хором перечисляют названия животных, изображённых на аппликациях.
-Итак, сегодня мы выполним аппликацию.
III. Ориентировка в задании — анализ образца.
Демонстрация образца аппликации кошки .
-Посмотрите на моего питомца. Кто это?
Ответы:- Это котенок.
-Из каких геометрических фигур сделан мой котенок?
-Туловище – это треугольник,
ушки – это треугольники,
голова – это круг,
хвостик – это овал,
глазки – это кружочки,
носик – это маленький треугольник.
При затруднении – учитель показывает на части аппликации и спрашивает, какая это геометрическая фигура.
-Сегодня на уроке мы будем делать аппликацию не одинакового цвета у всех, как всегда. Сегодня вы сами выберете себе цвет аппликации – цвет вашего любимца.
(Детям предлагаются конверты с фигурами внутри на выбор).
— Возьмите конвертики.
— Давайте посмотрим, что есть в ваших конвертиках?
-Это геометрические фигуры.
-Ребята, погладьте фигурки и скажите, какие они?
-Правильно, они мягкие , они из бархатной бумаги.
-А какие геометрические фигуры у вас есть?
-1 треугольник большой , 1 круг большой, 1 овал большой, 2 маленьких белых круга, 2 круглых глазика, 1 маленький чёрный треугольник.
( Вместе называют и показывают фигуры. Учитель выставляет фигуры на доску.)
IV.Планирование работы.
Цель: установление последовательности выполнения аппликации.
-Давайте составим из этих геометрических фигур котенка.
(Выполнение аппликации с детьми поэтапно, показывая образец выполнения на доске)
—Большой треугольник-это туловище.
—Большой круг-это голова.
-2 маленьких треугольника- это ушки.
-Большой овал- это хвостик.
-2 маленьких круга — это глазки.
-И 1 самый маленький треугольник – это носик.
-Молодцы, ребята. А скажите мне , ребята, чего у вас не хватает для работы?
-Геометрические фигурки у вас есть. Что ещё вам нужно?
-Верно, клей. А ещё нам понадобится чёрный фломастер, чтобы нарисовать котику усики.
-Прежде чем начать работу, давайте проведём физминутку.
Физминутка.
1-подняться, подтянуться,
2-согнуться, разогнуться,
3-в ладоши три хлопка, головою три кивка,
На 4 –руки шире,
5 –руками помахать,
6-тихо сесть.
V. Практическая работа учащихся:
1. Инструктаж о правилах работы с клеем
Цель: воспитание аккуратности при работе с клеем.
-Соблюдайте аккуратность в работе!
-Не допускайте попадания клея в глаза!
-После окончания работы клей закрыть и убрать в безопасное место!
Пальчиковая гимнастика:
-Наши пальчики сплетём -и соединим в ладоши.
-А потом , как только сможем, крепко-накрепко сожмём!
2. Самостоятельная работа учащихся.(под музыку)
Индивидуальная помощь учащимся.
-Возьмите большой треугольник – это туловище.
-Возьмите большой круг– это голова, приклеим ее над туловищем. Как я.
-Возьмите два маленьких треугольника – это ушки, приклеим их над головой. Как я.
-Теперь будем делать хвостик.
-Приклеим большой овал – это хвостик. Посмотрите как делаю я.
-Сделаем глазки. Возьмем маленькие овалы и приклеим их на круг.
-Молодцы! Посмотрите , что у нас получилось!
-Остался один самый маленький треугольник – это носик. Приклеим и его. Посмотрите.
-Посмотрите, какой питомец у вас получился. Погладьте его. Придумайте ему имя.
VI. Отчёт о проделанной работе.
Выставляют свои работы на доске. Называют придуманное имя.
VII. Рефлексия.
-Ребята, довольны ли вы своей работой?
-Если вам понравилась ваша работа, выбирайте солнышко, а если не очень довольны своей работой- выбираете тучку.
(Каждый прикрепляет к своей работе солнышко или тучку, в зависимости от того, как он оценивает свою работу)
VIII. Оценка деятельности учащихся и работы всего класса.
Цель: отметить работу учащихся, оценить их.
-Молодцы , ребята. Очень хорошо все потрудились сегодня.
IX. Итог урока.
Цель: сделать вывод и подвести итог, как работал класс на уроке, выяснить, что больше всего понравилось учащимся.
-Чему вы сегодня научились? — Изготавливать аппликацию кошки.
-Из каких геометрических фигур вы сделали аппликацию? — Треугольник, круг, овал.
в в детском саду и мастер класс для дошкольников
Аппликация, которая легко делается из геометрических фигур – один из самых простых, но и интересных занятий для маленьких детишек. Занимаясь этим делом, ваш ребенок не только разовьет свой творческий потенциал, художественный вкус, но и ассоциативное мышление, глазомер, цветовое восприятие. Для дошкольников такая работа будет первым шагом на пути к изучению геометрических фигур, их особенностей. Изготовление аппликаций из самых разнообразных геометрических фигур также поможет сформировать в ребенке понятие о сочетаемости цветов.
В детском саду, особенно в младших группах, ребятишки неспешно начинают выполнять такие работы. Воспитатель дает им готовые детали, дети их наклеивают. Чем ребенок становится старше, тем больше свободы у него при изготовлении такого рода аппликаций: они самостоятельно ножницами вырезают шаблоны, составляют несложные сюжетные композиции.
В школе младшие школьники продолжают делать аппликации на уроке труда. Часто 1 класс делает работы в такой технике про диких зверей, времена года, мастерит поздравительные открытки для близких людей на праздничную тематику. Еще больше развивает свое воображение 2 класс: они строят из бумаги на картоне целые города, эпизоды из сказок. Усложнение в программе у учеников 4 класса: их картинки более реалистичны, насыщены мелкими деталями, динамичны.
Делаем милую аппликацию в виде машинки из геометрических фигур
Эта аппликация отлично подойдет для малышей. На картинке показана готовая работа и детали, из которых машинка состоит. Родитель или воспитатель должен самостоятельно вырезать детали, помочь ребенку подобрать яркие цвета для своей работы, показать, как правильно нужно наносить кисточкой клей на детали, клеить их на картон, убирать излишки клея салфеткой.
Фигура «Лиса»: мастер-класс с фото и пошаговой инструкцией
Для работы потребуется:
- Белый лист офисной бумаги
- Цветная бумага оранжевого цвета
- Ножницы
- Простой карандаш
- Фломастеры
- Клеенки
- Кисточки
- Клей
Для начала изготавливаем шаблоны из оранжевой бумаги. Вырезаем один большой овал, который будет являться телом нашей лисички. Другой овал поменьше – хвост. Самые маленькие овалы – лапы – должны быть в количестве 4 штук. Один большой равнобедренный треугольник – мордочка лисы, два маленьких – ушки.
Когда все детали будут готовы, приступаем к изготовлению самой аппликации. В середине белого фонового листа клеим туловище зверька. На детальку кисточкой аккуратно наносим клей. Чтобы не испачкать стол, можно постелить клеёнку:
Чтобы не испачкать стол, можно постелить клеёнку:
К туловищу клеим мордочку.
Затем хвост.
Приклеиваем 4 лапы так, чтобы картинка была динамичной, ведь лисичка находится в движении.
Прикрепляем к листу оставшиеся детали – ушки.
После этого нам нужно у лисы подрисовать рот, носик и глазки, а также нарисовать фон: травку, солнышко, деревья, кусты – все, что придет в голову ребенку, он может изобразить на белом фоне. Вот что должно получиться у детишек:
Делаем своими руками яркую аппликацию «Ракета» с ребенком
Необходимые инструменты и материалы:
- Черный картон
- Цветная бумага
- Клей ПВА
- Простой или белый карандаш
- Ножницы
- Кисточка для клея
Для изготовления данной работы используем готовые шаблоны, которые являются деталями нашей будущей ракеты и звездного космического неба:
На черном картоне карандашом помечаем границу нижней части корабля.
Детали нашего хвоста – треугольники – подкручиваем с острого конца ножницами. Делать это нужно осторожно и аккуратно.
Получившиеся подкрученные детали приклеиваем в три слоя следующим образом.
К хвосту клеим остальные детали космического корабля.
Закончить работу нужно оформлением звездного космического неба. Наклеиваем желтые звездочки и месяц.
Теперь наша работа готова:
Изготовление аппликаций не требует особых усилий от ребенка и родителя или воспитателя, поэтому ребенок может просто наслаждаться процессом творения, а старший — наблюдать и подсказывать ребенку, что и как делать, чтобы его задумка осуществилась. Готовые работы ребенка можно красиво оформить в рамки или сделать из них презентацию в форме коллажа и повесить в детской комнате. Такой вид техники очень полезен особенно для малышей, ведь он развивает мелкую моторику рук, учится самостоятельно делать поделки, открытки для мамы, бабушки, папы, брата или сестры. Изготовление поделок воспитывает в ребенке прилежание, трудолюбие, аккуратность. А аппликация, сделанная самостоятельно из геометрических фигур, впервые знакомит дошкольников с азами геометрии, что облегчает задачу родителям в будущем.
А аппликация, сделанная самостоятельно из геометрических фигур, впервые знакомит дошкольников с азами геометрии, что облегчает задачу родителям в будущем.
Видеоматериалы по теме статьи
Предлагаем Вам посмотреть несколько видео мастер-классов на тему «Аппликация из геометрических фигур». Творческих успехов!
8 приложений по геометрии, которые создают истории из форм! — Г-н Кемп NZ
Сегодняшний блог — гостевой пост от Нишанта Синхи. Нишант является соучредителем Transtutors.com, онлайн-платформы помощи студентам. Он считает, что всем студентам время от времени требуется помощь, и что академические успехи порождают жажду новых знаний.
Вы овальный, прямоугольный, квадратный, худощавый или высокий? Если эти загадочные формы сбивают вас с толку или заставляют задуматься, мы рекомендуем вам использовать эти восемь геометрических приложений, которые помогут вам быстро освоить формы и фигуры.
Источник: NzMaths
Эти приложения предлагают увлекательное обучение, которое поможет вашим детям продуктивно работать с устройствами — стрелять, ловить или заполнять, рассказывая о том, как разные геометрические формы работают в реальном мире, и простыми способами изучают сложные геометрические концепции.
Вот, на мой взгляд, лучшие геометрические приложения для вас:
1. Фигуры дракона — Lumio Geometry
Настоятельно рекомендуется для детей от 6 до 10 лет. Это обучающее приложение отправит вас на поиски спасения деревенского дракона.Приложение доступно для платформ iOS и Android. У него четыре академических уровня, где дети решают структурированную последовательность геометрических головоломок для достижения своих целей.
Качество изготовления приложения отличное, оно помогает детям развить интуитивное чувство геометрии, знание форм и их атрибутов, а также такие способности, как визуализация и пространственное восприятие.
2. Формы — обучение трехмерной геометрии
Приложение Shapes: 3D Geometry, доступное на платформах iOS и Android, позволяет детям распечатывать различные формы, а затем постепенно складывать их в осязаемые трехмерные формы, которые они хотят.
Игра предлагает 27 уникальных фигур, которые дети могут построить с помощью простых иллюстрированных инструкций (на нескольких языках). Это приложение может мгновенно добавить изюминку к урокам математики — и привлечь студентов, как никогда раньше. Он выиграл награду Appaward 2014 в категории «Образование» и получил 4-звездочный сертификат в магазине приложений для образовательных учреждений.
3. Геометрия
Это действительно классное приложение — идеально подходит для учащихся средних и старших классов, которым нужен частный репетитор по математике, чтобы прояснить свои основные понятия.Он предлагает вам высококачественные видеоролики, обучающие математике традиционным способом.
Уроки включают в себя несколько примеров, интерактивные практические задачи, задачи-задачи (для самостоятельного решения учащимися), дополнительные рабочие листы с задачами (в качестве домашних заданий) и заметки для обзора, которые резюмируют всю главу, рассматриваемую в видео.
4. Цифровая географическая доска
Digital Geoboard доступна для платформ iOS и Android. В цифровой версии классической классной игры цифровые резинки используются для создания различных форм на оцифрованной доске.Он позволяет создавать сколько угодно многоугольников, менять их цвета и быстро вычислять их площадь и параметры.
Это отличная игра, если вы исследуете треугольники, многоугольники и концепции, связанные с геометрией плоскости.
5. Моя геометрическая вселенная
Доступное только на платформе iOS, My Geometric Universe — одно из самых крутых геометрических приложений. Он позволяет детям использовать карандаш, линейку и циркуль для создания геометрических фигур — и использовать их для создания объектов (например,г., грузовик). В игре три уровня, где дети могут создавать, хранить и играть с тем, что они создают.
6. Геометрия Монтессори — распознавать и изучать формы
Доступный только на платформе iOS, Montessori Geometry работает примерно на 20 языках. Приложение, разработанное учителями Монтессори, помогает детям узнавать и называть 2D- и 3D-формы вокруг себя.
Приложение имеет несколько уровней обучения и предлагает углубленное обучение.Он включает в себя шесть различных игр и шесть различных «типов фигур». Настоятельно рекомендуется для детей от 5 до 10 лет.
7. BrainPop Jr.
Это веб-приложение, предназначенное для детей от 5 лет и старше, предлагает анимированный контент для детей. На сайте представлены материалы на основе учебных программ для детей от детского сада до третьего класса. Уроки доступны по всем предметам, которые преподают детям, в том числе по геометрии.
Уроки включают в себя краткое видео, игры, викторину и разделы деятельности.BrainPop Jr. — отличный веб-сайт для школьников и семей, обучающихся на дому.
Дети постарше могут использовать дочерний сайт GameUp.
8. Элементы Dragonbox
Доступное как для iOS, так и для Android, приложение DragonBox Elements — Geometry вдохновлено греческим математиком Евклидом, написавшим книгу «Элементы», в которой он определил основы геометрии.
В игре семь уровней и более 100 головоломок, которые нужно решить — начиная с ознакомления детей с формами и основными концепциями геометрии и заканчивая сложными задачами, которые превращают ваших детей в экспертов по геометрии к тому моменту, когда они заканчивают игру.
Обучающие приложения пользуются успехом, потому что они делают обучение для детей «игрой». Некоторые из этих игр предназначены для дошкольников, некоторые подходят для детей начальной или средней школы, а некоторые подходят для всех возрастных групп. Загрузите те, которые вам нравятся, и вы увидите, как ваши дети влюбляются в геометрию!
Какие примеры геометрических фигур в реальной жизни?
Геометрические формы повсюду. Куда бы вы ни посмотрели, почти все состоит как из двухмерных (2D), так и из трехмерных (3D) геометрических фигур.Продолжайте читать, чтобы увидеть примеры реальных геометрических фигур, из которых состоит мир вокруг нас.
Примеры 2D геометрических фигур
Двумерные фигуры — это плоские фигуры, которые имеют ширину и высоту, но не имеют глубины. Круги, квадраты, треугольники и прямоугольники — это все типы двумерных геометрических фигур. Ознакомьтесь со списком различных 2D-геометрических фигур, а также с описанием и примерами того, где вы можете их обнаружить в повседневной жизни.
Имейте в виду, что все эти формы — плоские фигуры без глубины.Это означает, что вы можете сфотографировать эти предметы и при этом определить их форму. То же самое не относится к трехмерным формам.
Примеры кругов
Круг — это круглая форма с таким же радиусом от фиксированной точки в центре. Примеры кругов в реальной жизни включают:
- пицца, пироги
- печенье
- колеса велосипеда
- циферблаты
- обеденные тарелки
квадратные примеры
Четыре равные прямые стороны с четырьмя прямыми углами составляют квадрат.Вот некоторые примеры квадратов из реальной жизни:
- квадратные резиновые штампы
- квадратные плитки на полу
- квадратные бумажные салфетки
- шахматные доски
- клавиши виртуальной клавиатуры
примеры треугольников
Треугольники — это трехсторонние фигуры с прямыми сторонами. Есть много разных типов треугольников, в зависимости от их углов. Примеры треугольников в реальной жизни:
Есть много разных типов треугольников, в зависимости от их углов. Примеры треугольников в реальной жизни:
- кусочки пиццы
- сэндвич, разрезанный по диагонали
- несколько чипсов тортильи
- плывет на лодке
- дает дорожные знаки
Примеры прямоугольников
Подобно квадрату, прямоугольник имеет четыре прямые стороны с четырьмя прямыми углами.Однако две стороны короче двух других. Посмотрите эти примеры прямоугольников из реальной жизни:
- обложки книг
- сотовые телефоны
- некоторые рамки для картин
- долларовые купюры
- некоторые бутерброды с мороженым
Примеры Пентагона
Пентагоны — это фигуры с пятью сторонами одинаковой длины. Они менее распространены, чем четырехугольники, у которых есть четыре стороны, но все же встречаются в реальной жизни. Некоторые примеры пятиугольников:
- Здание Пентагона
- черные секции на футбольных мячах
- Домашняя табличка в бейсболе
- Знаки транспортных переходов
Примеры шестиугольника
Когда вы добавляете одну сторону к пятиугольнику, вы получаете шестиугольник.У шестиугольника шесть прямых сторон равной длины. Посмотрите эти примеры реальных шестиугольников:
- кристаллы льда
- снежинки
- ульи
- контур металлической гайки
- белые секции на футбольных мячах
Примеры восьмиугольника
Восемь прямых сторон, обычно равной длины, образуют восьмиугольник. В реальной жизни они встречаются чаще, чем вы думаете. Некоторые примеры восьмиугольников:
- знаки остановки
- открытые зонтики
- кольцо UFC
- покерные столы
Примеры трапеций
Трапеция — это четырехгранная фигура с одной парой параллельных сторон.Вы можете найти трапеции в следующих примерах:
- фермы на мостах
- некоторые стороны сумочки
- недоеденный кусок пиццы
- музыкальные цимбалы
Примеры трехмерных геометрических фигур
В отличие от двухмерных фигур, трехмерные имеют ширину, высоту и глубину. Примеры трехмерных форм включают пирамиды, сферы и кубы. Взгляните на эти повседневные примеры трехмерных геометрических фигур.
Примеры трехмерных форм включают пирамиды, сферы и кубы. Взгляните на эти повседневные примеры трехмерных геометрических фигур.
Конечно, некоторые из этих форм взаимозаменяемы.Например, сумка не всегда может быть параллелограммом, поскольку, безусловно, существуют круглые сумки и другие возможные типы. Этот список также не является исчерпывающим, поскольку существует множество других двухмерных и трехмерных геометрических фигур.
Примеры сфер
Сферы представляют собой круглые сплошные фигуры. Как и у кругов, у них есть радиус в центре, который равноудален каждой точке сферы. Однако, в отличие от кругов, они имеют объем и глубину. Примеры реальных сфер:
- баскетбольные мячи
- планеты
- апельсины
- шарики
- теннисные мячи
Примеры кубов
Каждая из шести граней куба представляет собой квадрат.Когда они складываются в форму трехмерного куба, также известную как квадратная призма, они создают глубину. Вот некоторые примеры кубов:
- шестигранные кубики
- кубики сахара
- квадратные строительные блоки
- кубики Рубикс
- квадратные упаковочные коробки
примеры конусов
Конус имеет круглое основание, сужающееся к одной точке. Шишки очень часто встречаются в повседневных вещах, в том числе:
- дорожные конусы
- вафельные рожки для мороженого
- праздничные шляпы
- новогодние елки
- воронки
примеры цилиндров
Цилиндры — это трехмерные фигуры с параллельными сторонами и круглым поперечным сечением.Вот некоторые из реальных примеров цилиндров:
- картонная трубка для бумажных полотенец
- прямые трубки
- стаканы для питья
- трубки для гигиенических помад
- банки
Примеры эллипсоидов
Эллипсоид — это сфера, которая не идеально круглая, потому что она сплюснута с двух сторон. Эллипсоид, также известный как сфероид, создает эффект трехмерного овала. Вот несколько примеров эллипсоидов:
Эллипсоид, также известный как сфероид, создает эффект трехмерного овала. Вот несколько примеров эллипсоидов:
- футбольных мячей
- яйца
- некоторые из спутников Сатурна (Мимас, Энцелад, Тетис)
Примеры прямоугольной призмы
Прямоугольная призма — это трехмерная фигура, в которой одна пара противоположных сторон имеет одинаковую форму и соединена прямыми параллельными сторонами.У них четыре прямоугольных грани и две квадратные грани. Вы можете найти прямоугольные призмы в этих примерах:
- палочки сливочного масла
- кирпичи
- камеры
- коробки для хлопьев
- прямоугольные упаковочные коробки
Треугольная призма
Треугольные призмы похожи на прямоугольные призмы, за исключением того, что их квадратные грани представляют собой треугольники, что делает их трехсторонними призмами. Примеры реальных треугольных призм:
- палатки
- дольки арбуза
- дольки сыра
- кусочки торта
Примеры пирамид
Трехмерная фигура с одной плоской стороной и краями, сходящимися в одну точку, представляет собой пирамиду.Они могут иметь любую форму с тремя или более сторонами в качестве основы, включая треугольник (треугольная пирамида), квадрат (квадратная пирамида) и пятиугольник (пятиугольная пирамида). Примеры включают:
- Великая пирамида Гизы
- крыша дома
- несколько отдельно стоящих терок для сыра
- стеклянная пирамида Лурве
Формы, которые строят наш мир
Мир вокруг нас построен из двухмерных и трехмерных форм. Базовое представление о геометрических формах и о том, где их можно найти в повседневной жизни, — отличное начало математического образования.Чтобы получить больше математической практики, ознакомьтесь с этими основными математическими терминами, чтобы начать работу. Вы также можете взглянуть на некоторые примеры одночленов и многочленов, если готовы перейти к алгебраическим понятиям.
| Загадка Ферма и тройки Пифагора | |||||||||||||||||||||||||||||||||||||||||||||
Теорема Пифагора утверждает, что для прямоугольного треугольника с катетами a и b и гипотенузой a 2 + b 2 = c 2 . Числа, соответствующие этому шаблону, называются тройками Пифагора. | |||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||
| Будет ли какая-либо из троек удовлетворять Великой теореме Ферма — a 3 + b 3 = c 3 ? А как насчет a 4 + b 4 = c 4 ? Следующие формулы можно использовать для генерации чисел, удовлетворяющих a = x 2 — y 2 b = 2xy c = x 2 + y 2 Вот пример: пусть x = 7 и y = 6.
Обратите внимание, что один катет и гипотенуза (самая длинная сторона) являются последовательными целыми числами. Совет: чтобы получить числа a, b и c, у которых нет общих делителей, убедитесь, что ваши числа x и y не имеют общих делителей, например 5 и 6 или 5 и 8, но не 5 и 10. | |||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Шарлин Эванс | |||||||||||||||||||||||||||||||||||||||||||||
Ссылка: Коллинз, Уильям и др. Математика: приложения и связи, | |||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | |||||||||||||||||||||||||||||||||||||||||||||
| Волшебный круг | |||||||||||||||||||||||||||||||||||||||||||||
Материалы
Цели
Порядок действий
Оценка Предложите учащимся решить три задачи, которые имеют значение только для диаметра. | |||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Дэвидом Лейбом | |||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | |||||||||||||||||||||||||||||||||||||||||||||
| Пентаграммы природы | |||||||||||||||||||||||||||||||||||||||||||||
Цель: Учащиеся смогут использовать алгебраические понятия при изучении природы. Цель: Учащиеся будут использовать геометрию и концепцию соотношений и применять их для измерения предметов, встречающихся в природе. Материалы: Пятилепестковые цветы, Яблоки, Доллары, Морская звезда. Фокус: Покажите фильм: Дональд Дак в стране математики (можно получить через Library Media Services, 259 долларов США) Процедура:
Оценка: Попросите учащихся рассказать, что они обнаружили с помощью различных использованных материалов. Они нашли золотые треугольники? Что помогло? Что нужно исправить? | |||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Дженнифер Гарретсон | |||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущий | |||||||||||||||||||||||||||||||||||||||||||||
| Действие полосы Мебиуса | |||||||||||||||||||||||||||||||||||||||||||||
Для этого задания вам понадобится по пять полосок бумаги на каждого учащегося.Каждый
Хотя это увлекательное занятие для студентов, следует отметить, что | |||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Стивом Бикслером | |||||||||||||||||||||||||||||||||||||||||||||
Рекомендации: Этот проект разработан: [email protected] | |||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | |||||||||||||||||||||||||||||||||||||||||||||
| Теорема Пифагора с танграммами | |||||||||||||||||||||||||||||||||||||||||||||
Цель: Использование танграмм для введения теоремы Пифагора. Цель: Студенты будут использовать танграм как введение в пифагорейский язык. Материалы: набор Tangram (квадрат 4 x 4 дюйма), бумага, карандаш. Знакомство с Pythagoras Шаг 1 Шаг 2 Шаг 3 Шаг 4 Шаг 5 Шаг 6 (Вот! Ваши ученики только что открыли теорему Пифагора !!!) | |||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Анжелой Церадски | |||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | |||||||||||||||||||||||||||||||||||||||||||||
| Активность формулы Эйлера | |||||||||||||||||||||||||||||||||||||||||||||
Название урока: Формула Эйлера, зубочистки и мармеладки. Предметная область: Геометрия, предалгебра Уровень оценки: Восьмой Описание или заявление о результатах: Обнаружив информацию о плоских сетях и трехмерных объектах, учащиеся смогут продемонстрировать, как удовлетворить формулу Эйлера. Цели:
Материалы и ресурсы:
Порядок действий:
План оценки: | |||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Яном Свенсоном | |||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущий | |||||||||||||||||||||||||||||||||||||||||||||
| Площадь и объем поверхности | |||||||||||||||||||||||||||||||||||||||||||||
Это упражнение должно научить ученика вычислять объем и площадь поверхности цилиндра.Эту деятельность можно легко связать с историей, обсуждая, как древние могли измерять объем или даже длину до того, как существовала стандартизированная система измерения. Процедура:
| |||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Линдси Истридж | |||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Назад | |||||||||||||||||||||||||||||||||||||||||||||
| Магические круги Создание усеченного тетраэдра. | |||||||||||||||||||||||||||||||||||||||||||||
Я приобрел это занятие во время семинара за 259 долларов США в Уичито, штат Канзас, который назывался «Математика в понедельник вечером».Я учил этому классу от третьего класса до колледжа. Это упражнение помогает развивать, укреплять и даже может использоваться для пополнения словарного запаса по математике. Материалы: один 7-дюймовый бумажный круг, карандаш и линейка. Посмотрите на форму, которую вы держите.Опишите это. Это ( круг ). Посмотрите на внешний край вашего круга. Как называется расстояние по внешней стороне круга? ( Окружность ) Сложите круг прямо пополам и хорошо согните его. Раскройте круг, полученная складка — это ( диаметр ) круга. Держите кружок на концах складки. Раскройте свой круг, это тоже диаметр? Откуда вы знаете? Линии ( пересекаются с )? Да. Есть ли что-то особенное в том, как эти линии пересекаются? Они образуют четыре угла 90 o (или прямых). Этот особый тип перекрестка называется (перпендикуляр ). Поместите точку, не больше ширины карандаша, в точке соединения складок. Это называется ( центр ) круга. Карандашом нарисуйте одну из линий от центра к краю круга. Эта линия от центра называется (радиус ). Загните один из внешних изогнутых краев круга, пока он не коснется точки в середине. Хорошо согните. Раскройте складку и посмотрите на только что сделанную складку. Это диаметр? Это радиус? Почему или почему нет? Эта линия называется (аккорд , , , ). Посмотрите на изогнутую часть круга между точками, где эта линия касается внешней стороны круга. Это называется ( arc ). Можете ли вы найти другие дуги на своем круге? Возьмите противоположную сторону вашего круга и сложите его так, чтобы изогнутая часть касалась центра, а нижняя часть образовывала идеальную точку. Ваш круг будет похож на мороженое (рожок ). Хорошо согните. Загните верхнюю часть рожка мороженого вниз, пока изогнутая часть не коснется центра круга.Верхние углы должны образовывать идеальные точки, хорошо сгибаться. Теперь опишите свою форму. ( Треугольник ) Вы замечаете что-нибудь особенное в этом треугольнике? Посмотрите на все ( углов ), они такие же, как и все стороны одинаковы. Этот треугольник называется ( равносторонний и / или острый треугольник ). Вы также можете использовать ( равносторонний ). Сложите новый треугольник пополам, совместив две точки.Хорошо мнется. Новое прекращение делит треугольник пополам, эта линия называется (высота или высота ). Раскройте прямоугольный треугольник до равностороннего треугольника. Возьмите верхний угол большого треугольника и сложите его. Сгибая по складке высоты, вы можете совместить верхнюю точку до нижней линии сгиба.Внутри вы увидите три треугольника поменьше. Переверните бумагу, чтобы не было видно складок. Как называется эта форма? Поскольку он имеет четыре стороны, его можно классифицировать как четырехугольник ( , ). Поскольку у этого четырехугольника две стороны, которые являются ( параллельными ) и две, которые не являются, он также называется ( трапеции ). Переверните его, чтобы теперь были видны все складки.Сложите один из внешних треугольников так, чтобы он лежал прямо поверх центрального треугольника. Переверните его и опишите форму, которую вы сейчас видите. Это не воздушный змей, в небе летают воздушные змеи. Это не бриллиант, я ношу бриллианты на пальцах. В математике эта форма называется ( ромб ). Снова переверните фигуру и снова сложите последний внешний треугольник на центральный. У вас должен получиться равносторонний треугольник меньшего размера. Раскройте все три маленьких треугольника.Соедините три свободные точки вместе, чтобы у вас получилась пирамида ( , ). На этом этапе вы можете обсудить ( граней ) ( ребер ) ( точек ) ( вершин ) ( основание ) и тот факт, что это ( треугольная пирамида ), а не квадратная пирамида, как в Египте. Откройте пирамиду до большого равностороннего треугольника. Согните одну из точек так, чтобы она касалась точки посередине. Какую форму вы воссоздали? Трапеция хоть и не традиционной формы, но все же может быть идентифицирована как трапеция. Сложите еще одну точку так, чтобы она касалась точки посередине. Теперь сложите последнюю точку. Какая она сейчас форма? ( Hexagon ) Обсудите ( плоскость ) цифры. Переверните на другую сторону и вставьте один из углов в лоскут на противоположной стороне треугольника. Возможно, вам придется попробовать несколько. Выберите тот, который вам больше всего подходит. Сдвиньте последний угол под / внутрь других. Вы создали усеченный тетраэдр ( , )! Для любой формы во время этого упражнения вы можете попросить учащихся вычислить площадь поверхности, объем, периметр и / или площадь. | |||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Анжелой Церадски | |||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | |||||||||||||||||||||||||||||||||||||||||||||
| Эксперимент с водяным шлангом. | |||||||||||||||||||||||||||||||||||||||||||||
Это задание можно выполнить за один урок. Чтобы ответить на вопросы и сделать выводы, может потребоваться еще один урок, в зависимости от продолжительности вашего урока. Прекрасно подходит для весны, когда у школьников и учителей весенняя лихорадка.Его цель — найти оптимальный угол для достижения наибольшего расстояния. В зависимости от того, какой класс вы преподаете, это задание можно изменить. История: Простой транспортир — старинный прибор. Создан первый комплексный транспортир для определения положения лодки на навигационных картах. Названный трехрычажным транспортиром или указателем станции, он был изобретен в 1801 году Джозефом Худдартом, капитаном ВМС США. Центральный рычаг неподвижен, а два внешних поворотных, их можно установить под любым углом по отношению к центральному рычагу. Материалы:
Процедуры: Присоедините садовый шланг к водопроводному крану и отрегулируйте поток воды, чтобы он находился под постоянным давлением. Вопросы и выводы:
Справка: URL: http://inventors.about.com/science/inventors/libr…/blmeasurement.htm?terms=protractor+histor | |||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Эми Траутман | |||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущий | |||||||||||||||||||||||||||||||||||||||||||||
| Расчет числа Пи. | |||||||||||||||||||||||||||||||||||||||||||||
Примерно 4000 лет назад люди впервые начали понимать пи. Считалось, что его стоимость была около трех. Сегодня мы используем лучшее приближение числа Пи. Это 3,14. Пи — иррациональное число. Это означает, что он не повторяется в шаблоне. Пи определяется как отношение длины окружности к диаметру той же окружности. А теперь небольшое упражнение, которое поможет вам определить число Пи. Материалы:
Объектов, подлежащих измерению:
Направление: Сначала на листе бумаги сделайте 4 столбца с надписью: объект, диаметр, окружность и соотношение. Оберните веревку вокруг объекта. Это измеряет окружность объекта. Измерьте шнур с помощью измерительной линейки. Запишите значение в столбец с надписью «длина окружности». Затем измерьте расстояние прямо поперек объекта. Поместите это значение в столбец, обозначенный как диаметр. Теперь возьмите длину окружности, разделенную на диаметр. Поместите это в столбец с надписью «Соотношение». Это близко к пи? Убедитесь, что вы приняли соотношение до трех или четырех десятичных знаков.
| |||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Джереми Траутманом | |||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущий | |||||||||||||||||||||||||||||||||||||||||||||
| Активность тесселяции. | |||||||||||||||||||||||||||||||||||||||||||||
Класс: 5 или 6 Время: 20-30 минут уроков Необходимые материалы: Смесь многоугольников, таких как геоблоки, бумага, карандаш и цветные карандаши. Урок 1 В фокусе: Поместите разные фигуры наверх. Обсудите в классе сходства и различия форм.Сообщите учащимся, что фигуры представляют собой многоугольники (фигура на близком расстоянии). Расскажите о концепции мозаики и о том, как не должно быть разрывов или перекрытий. Продемонстрируйте концепцию наверху с помощью квадрата. Задание: Попросите учащихся предсказать, какие фигуры будут мозаичными, а какие — нет. Составьте диаграмму, показывающую результаты прогнозов учащихся. Дайте каждому столу (или студенту, если возможно) набор фигур. Попросите учащихся индивидуально определить, будет ли фигура мозаикой. Заключение: Обсудите всем классом, какие формы плитки на самом деле формируют, а какие нет. Сравните открытия с предсказаниями на картах. Завершение: Попросите учащихся определить многоугольник и то, что они узнали о нем, в небольшой записи в дневнике. Урок 2 В фокусе: Просмотрите концепции многоугольника и мозаики. Расскажите о термине тесселяция и о том, как он соотносится с уроком 1.Обсудите концепции скольжения, вращения (поворота) и отражения (переворачивания) и продемонстрируйте их на потолке. Задание: Попросите учащихся выбрать две или более фигур. Попросите учащихся раскрасить каждую форму в один цвет. Попросите учащихся обвести фигуры черным маркером, если это слайд. Обведите фигуру синим маркером, если это вращение. Отражение следует обвести красным маркером. Заключение: Попросите учащихся поднять руки, когда они закончили.Инструктор проверит результаты. Закрытие: Обсудите, какие различные формы объединяют в мозаику, создавая результаты. Разрешите учащимся записывать свои выводы. Урок 3 Фокус: Просмотрите предыдущие уроки. Обсудите, как студенты будут применять свои знания техники мозаики для поиска концепции в искусстве. Активность: Предоставьте несколько произведений разных художников, в том числе несколько произведений М.К. Эшер. Попросите учащихся изучить различные произведения искусства, чтобы выяснить, использует ли художник технику мозаики. Заключение: Попросите учащихся обсудить, что они нашли в деталях. Выдвиньте гипотезу, почему художники использовали или не использовали технику тесселяции. Окончание: Попросите учащихся записать свои выводы в своих дневниках. | |||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено CiCi Naifeh | |||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | |||||||||||||||||||||||||||||||||||||||||||||
| Площадь и объем геометрических фигур. | |||||||||||||||||||||||||||||||||||||||||||||
Площадь геометрических фигур Цель: Дать студенту возможность попрактиковаться в вычислении площади различных геометрических фигур. Необходимые материалы: Использованные журналы, ножницы, линейки, клей, плотная бумага и калькуляторы Процедура:
Часть 2-
Часть 3- Практическое применение: Если кто-то собирается красить комнату, необходимо определить общую площадь всех стен, чтобы купить нужное количество краски. Объем геометрических фигур Цель: Дать учащимся возможность визуально понимать трехмерные геометрические формы и практиковаться в вычислении объема. Необходимые материалы: Домашние ингредиенты для игр, плита, кастрюля, ложка, линейки и калькуляторы. Процедура:
Часть 2-
Практическое применение: Производителю необходимо определить объем контейнера, в котором должен быть отгружен продукт. | |||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Джуди Ласатер | |||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | |||||||||||||||||||||||||||||||||||||||||||||
| Какой формы ваша земля? | |||||||||||||||||||||||||||||||||||||||||||||
Цели:
Уровень: Общая математика и предварительная алгебра Материалы: Для каждого учащегося или группы: один лист миллиметровой бумаги, приклеенный или приклеенный на гофрированный картон или жесткий пенопласт; замкнутая петля из бечевки длиной 20 сантиметров; примерно шесть прямых булавок или канцелярских кнопок на учащегося или группу; карандаш и бумага для записей. Историческая справка: Согласно римской мифологии Дидона была дочерью царя Тира. Ее брат Пигмалион убил ее мужа, и она сбежала, опасаясь за свою безопасность. Дидона пересекла Средиземное море со всем своим богатством и некоторыми товарищами и высадилась в североафриканском королевстве Ливия. Здесь она искала землю в качестве убежища для своей группы. Король согласился дать ей столько земли, сколько она сможет покрыть шкурой быка. Теперь Дидона кое-что знала о геометрии и хотела как можно больше земли.Она разрезала шкуру быка на тонкие полоски, а затем соединила их в одну длинную прядь. Как вы думаете, какую форму она заключила? Организация: Студенты могут выполнять это задание индивидуально или в группах. Возможные групповые роли для четырех участников: двое учащихся должны создавать формы, один — для вычисления площадей, а один — для записи форм, размеров и площадей. Каждой группе понадобится один набор материалов, как описано выше: миллиметровая доска, канцелярские кнопки и веревка. Задание: Учащиеся должны использовать веревку и канцелярские кнопки, чтобы разложить плоские фигуры на сетке.Студентам необходимо будет рассчитать площадь каждой фигуры, которую они создают, поэтому выбранные формы будут зависеть от базовых знаний учащихся. Предлагаемые фигуры: квадрат, прямоугольники, треугольники и круг. Напомните учащимся, что они могут образовывать более одного прямоугольника и более одного треугольника. Студенты должны рассчитать площади для каждой сформированной фигуры и решить, какую форму, по их мнению, следует выбрать Дидоне. Примечание: , если это используется как упражнение для представления областей плоских фигур, учащиеся могут находить области, считая квадраты.В качестве дополнительного задания учащиеся должны использовать формулы площади. Следующая таблица или аналогичная может быть предоставлена для ведения учета:
Вопросы для обсуждения:
Закрытие: Обсудите тот факт, что при постоянном периметре наибольшая площадь получается у круглой формы. В конце концов Дидона отмерила форму полукруга, соединив одну точку на берегу с другой. Таким образом, вода составляла одно из ее требований, и у нее было дополнительное преимущество — выход к морю. Ей нужно было только использовать шкуру, чтобы оградить землю, поэтому область, которую она отметила, была как можно больше и желательна. Король Ливии сдержал свое слово и отдал ей землю.Зарекомендовала себя умная Дидона, будущая королева Карфагена. Попросите учащихся развязать петли из веревок и использовать их 20-сантиметровые нити, чтобы сформировать полукруги по краям сетки. Вычислите площадь полученного таким образом полукруга, чтобы понять, насколько умен Дидона. Связанные действия: Следующий трюк может стать забавным введением в занятие. Принесите в класс лист бумаги размером с лист бумаги для принтера.Спросите своих учеников: «Как вы думаете, я могу вырезать отверстие в этом листе бумаги и протолкнуть его (впишите имя какого-нибудь ученика в классе)»? Когда студенты выражают свой скептицизм, прорежьте в бумаге большое отверстие, просуньте руку в отверстие и мягко толкните выбранного ученика. Затем достаньте новый лист бумаги с очень маленьким отверстием. Спросите, как вы думаете, я смогу провести (того же ученика) через лист бумаги с этим отверстием? Общая реакция будет такой, что вы, вероятно, не сможете, хотя некоторые студенты будут искать другой трюк. Чтобы показать им, что вы можете делать то, что вы сказали, возьмите лист бумаги с таким же маленьким отверстием и прорезями, как показано на схеме ниже. Вы можете использовать уже имеющийся у вас лист и вырезать прорези, пока они ждут, но это займет много времени. Откройте прорези, чтобы образовалась одна огромная бумажная петля, и наденьте ее прямо на голову учеников. Вы сделали это! | |||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Лори Кисс | |||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Предыдущая | |||||||||||||||||||||||||||||||||||||||||||||
Геометрический текстильный дизайн. | |||||||||||||||||||||||||||||||||||||||||||||
Иногда у студентов возникают проблемы с соотнесением математики с реальным миром; Следовательно, эта деятельность в области геометрического текстильного дизайна будет акцентировать внимание на геометрических формах и узорах в сочетании с художественным дизайном, компьютерными приложениями и возможностями карьерного роста. Цель: Для каждого ученика разработать свой собственный геометрический текстильный квадрат, который будет превращен в лоскутное одеяло. Необходимые материалы: Тканевые квадраты геометрической формы (5 дюймов х 5 дюймов), шаблонная бумага, цветные карандаши, белые тканевые квадраты (5 дюймов х 5 дюймов), обрезки картона, малярная лента и краска для ткани. Процедура:
Текстильный дизайн — это профессия, о которой большинство студентов никогда бы не подумали. Он сочетает в себе геометрию форм и узоров и добавляет художественного чутья, создавая ткань, приятную для глаз. | |||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Джуди Ласатер | |||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Назад | |||||||||||||||||||||||||||||||||||||||||||||
| Изготовление многогранников. | |||||||||||||||||||||||||||||||||||||||||||||
Многогранник — это геометрическая фигура, которая является трехмерной версией плоского многоугольника (двумерного). Всего пять правильных многогранников. Это тетраэдр (4 грани), шестигранник или куб (6 граней), октаэдр (8 граней), додекаэдр (12 граней) и икосаэдр (20 граней).Ниже представлены выкройки двух многогранников, которые можно воспроизвести и трансформировать в трехмерные фигуры. Щелкните на фигурах, чтобы открыть окно с фигурой в нем для облегчения печати. | |||||||||||||||||||||||||||||||||||||||||||||
| Предоставлено Сьюзан Истман | |||||||||||||||||||||||||||||||||||||||||||||
| Содержание | Далее | Назад | |||||||||||||||||||||||||||||||||||||||||||||
Видео для детей, обучающие геометрии
Дети часто очень наглядны, когда дело доходит до обучения, что делает включение видео в ваши уроки забавным и простым инструментом, который отвечает их визуальным потребностям.Особенно по математике! Ваши ученики могут не ожидать, что вы будете воспроизводить видео во время обучения математике, что придаст вашему уроку неожиданный поворот! Этот элемент неожиданности и застать их врасплох, поделившись различными видеороликами о геометрии, — отличный способ полностью заинтересовать ваших маленьких учеников! Кроме того, математические видеоролики доставляют массу удовольствия и часто очень интерактивны.
В следующем списке видеороликов представлены разнообразные энергичные песни, отличная графика и простые объяснения геометрии.Поскольку эти видео в совокупности затрагивают различные учебные классы и подтемы геометрии, у вас не должно возникнуть проблем с поиском идеального места в ваших инструкциях по математике для использования одного (или нескольких) из этих развлекательных и образовательных видео по геометрии.
Введение в симметрию: все о симметрии для детей (2:35)
Некоторым ученикам может быть трудно понять симметрию — но не тогда, когда вы им показываете это видео! Он предлагает идеальное введение в концепцию симметрии! Мне очень нравится, как это видео не только показывает и объясняет симметрию с точки зрения форм и рисунков, но и использует реальные объекты в качестве примеров.Это действительно помогает детям задуматься о симметрии, существующей в окружающем их мире! Несмотря на то, что в этом видео нет броской мелодии, привлекательная графика и невероятно четкое объяснение симметрии делают его отличным ресурсом для знакомства с концепцией базовой симметрии.
Симметрия для детей (3:48)
Ваши дети будут в восторге от изучения симметрии с этим веселым видео! В него входит веселая рок-н-ролльная песня, которая поможет вашим ученикам расширить свои знания о симметрии далеко за пределы основ! Используя яркие формы и красочную графику в сочетании с простыми текстовыми пояснениями и запоминающейся мелодией, песня и видео работают вместе, чтобы эффективно раскрыть множество различных аспектов симметрии. Это отличное видео для расширения этой концепции, поскольку в нем исследуются различные варианты симметрии, такие как двусторонняя и вращательная симметрия.
Это отличное видео для расширения этой концепции, поскольку в нем исследуются различные варианты симметрии, такие как двусторонняя и вращательная симметрия.
Видео с песней Polygon (4:02)
Ваши дети полностью поймут, что такое многоугольник, послушав запоминающуюся песню из этого видео. Определение многоугольника объясняется сразу же и продолжает показывать изображения различных многоугольников, а также объясняет, как они получили свои названия.Он четко исследует и обсуждает трех-, четырех-, пятиугольные формы вплоть до десятиугольника. После объяснения каждой формы видео принимает интерактивный оборот: зрителей просят нарисовать различные фигуры в воздухе, подпевая их видео. Вашим детям это понравится!
Они многоугольник Песня (3:18)
Эта очаровательная песня помогает ясно показать разницу между «скучным квадратом» и другими формами, такими как пятиугольники, шестиугольники, семиугольники, восьмиугольники, неугольники и десятиугольники. Хотя припев песни немного монотонен с текстами о скучном квадрате, он отлично показывает, сколько сторон имеет каждая форма и чем каждая из них отличается от квадрата. Слово многоугольник на самом деле не упоминается в этом видео, поэтому показ ролика №3 перед этим был бы отличным способом сначала представить многоугольники, а затем усилить их суть, показывая это.
Хотя припев песни немного монотонен с текстами о скучном квадрате, он отлично показывает, сколько сторон имеет каждая форма и чем каждая из них отличается от квадрата. Слово многоугольник на самом деле не упоминается в этом видео, поэтому показ ролика №3 перед этим был бы отличным способом сначала представить многоугольники, а затем усилить их суть, показывая это.
Узнайте о двухмерных фигурах с поездом Чу-Чу — Часть 1 (9:35)
Хотя это видео длиннее и не содержит никаких запоминающихся тематических песен, это действительно эффективный инструмент для обучения двухмерных фигур младшим школьникам.Красочно анимированный говорящий поезд поможет заинтересовать ваших маленьких учеников, а четкие и простые для понимания объяснения не оставят места для путаницы в отношении двумерных фигур. Если вас беспокоит длина видео, вы можете пропустить первую минуту видео — в основном это просто вступительная музыка. Яркая анимация и подробные объяснения различных характеристик двумерных форм гарантируют, что ваши ученики полностью усвоят эту базовую концепцию геометрии и получат от этого удовольствие! Им понравится интерактивный характер этого видео, поскольку говорящий поезд задает вопросы аудитории на протяжении всего видео.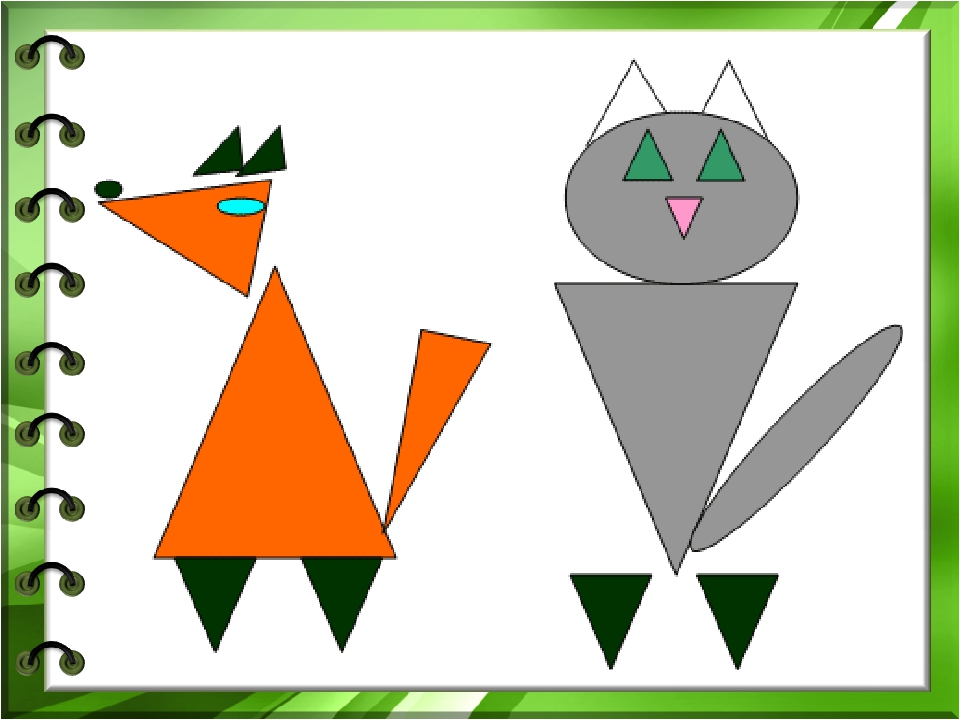
Изучение трехмерных фигур (геометрические тела) с поездом Choo-Choo — Часть 2 (12:05)
Часть 2 серии видеороликов Choo-Choo Train основывается на предыдущем видеоролике, переходя от двухмерных к трехмерным фигурам. Тот же говорящий поезд из предыдущего видео поможет вашим ученикам понять различные трехмерные формы и то, что делает их трехмерными. Опять же, если вас беспокоит время, вы можете перейти к минуте 2:55, чтобы перейти к реальной сути видео, где полностью исследуются все трехмерные формы и каждая из них соотносится с двухмерной формой.Как и двухмерное видео, это видео предлагает интерактивный компонент, так как задает вопросы зрителям, исследуя различные трехмерные формы — предлагая вам прекрасную возможность сделать паузу и обсудить концепции со своими учениками! (Убедитесь, что ваши дети понимают, что такое многоугольник, прежде чем смотреть видео, поскольку он относится к многоугольникам без подробного объяснения.)
Двухмерные геометрические фигуры для лепки (6:12)
https://www.youtube.com/watch?v=yXRv8RPHJjc
Хотя в этом видео нет слов, его все же невероятно полезно использовать в качестве наглядного примера создания двухмерных фигур.Выполнение упражнения, показанного в видео, с вашим классом было бы отличным способом предложить учащимся практический опыт формирования фигур. Вы также можете использовать это видео в качестве подсказки для вопросов в классе о геометрии или пространственных отношениях. Например, какую форму вы видите над пятиугольником и т. Д. Видео короткое, но все же позволяет ясно показать детям, как формировать двумерные формы, используя маленькие шарики из пластилина и зубочистки! Если вы собираетесь выполнить это задание со своим классом, используйте это видео в качестве введения или в качестве фона для вашего класса, пока ваши ученики создают различные формы для лепки.
Вы также можете использовать это видео в качестве подсказки для вопросов в классе о геометрии или пространственных отношениях. Например, какую форму вы видите над пятиугольником и т. Д. Видео короткое, но все же позволяет ясно показать детям, как формировать двумерные формы, используя маленькие шарики из пластилина и зубочистки! Если вы собираетесь выполнить это задание со своим классом, используйте это видео в качестве введения или в качестве фона для вашего класса, пока ваши ученики создают различные формы для лепки.
Трехмерные фигуры с пластилином (9:06)
https://www.youtube.com/watch?v=Fy5abut63Qk
Очень похоже на предыдущий, это еще одно видео без слов, которое просто показывает детям этапы создания трехмерных фигур с помощью Play Dough и зубочисток. Вы можете легко использовать это видео сразу же после предыдущего, чтобы по-настоящему подчеркнуть разницу между двухмерными и трехмерными формами для ваших учеников. Его также можно легко использовать в качестве введения к этому заданию или в качестве справочной информации, пока ваши ученики создают трехмерные фигурки из теста для лепки.Если вас беспокоит длина этого видео, вы можете легко перемотать некоторые элементы построения фигур, когда увидите, что ваши дети уловили концепцию.
Как легко рисовать треугольники с Евклидом (3:47)
Не обманывайте себя названием — это видео не только учит детей рисовать треугольник. Главный герой, древнегреческий математик Евклид, дает зрителям краткое введение в несколько различных геометрических тем, включая линии, углы и треугольники.Он предлагает объяснения взаимосвязи между линиями, различных типов линий и того, как они пересекаются или не пересекаются, и в конечном итоге связывает эти идеи, показывая нам, как нарисован треугольник, соединяя три точки тремя линиями, а затем образуя три угла. Детям понравится, как рассказчик показывает Евклида во время разговора, а его британский акцент — дополнительный бонус! Это видео о гораздо большем, чем просто рисование треугольников, является отличным дополнением к любому уроку геометрии о линиях, углах И треугольниках.
Главный герой, древнегреческий математик Евклид, дает зрителям краткое введение в несколько различных геометрических тем, включая линии, углы и треугольники.Он предлагает объяснения взаимосвязи между линиями, различных типов линий и того, как они пересекаются или не пересекаются, и в конечном итоге связывает эти идеи, показывая нам, как нарисован треугольник, соединяя три точки тремя линиями, а затем образуя три угла. Детям понравится, как рассказчик показывает Евклида во время разговора, а его британский акцент — дополнительный бонус! Это видео о гораздо большем, чем просто рисование треугольников, является отличным дополнением к любому уроку геометрии о линиях, углах И треугольниках.
Песня о полигонах для детей Рэп-видео: геометрия, четырехугольники, шестиугольники и т. Д. (1:57)
https://youtu.be/meaGjrKWGFQ
Ваши дети будут в восторге от запоминающегося ритма в этой рэп-песне, поскольку в ней подробно объясняются различные предварительные исправления форм и их влияние на количество сторон формы. В этом видео замечательно то, что во время воспроизведения песни изображения каждой обсуждаемой формы отображаются в реальных ситуациях. Например, на видео показан треугольник в парусе лодки и четырехугольник в двери дома.Это поможет вашим ученикам увидеть, что формы можно найти повсюду вокруг нас, а также послужит отличным введением в потенциальное занятие по поиску формы.
Песня о параллельных, перпендикулярных и пересекающихся линиях | NUMBEROCK (2:21)
Если вы рассказываете своим детям о различных типах линий и о том, как они взаимодействуют друг с другом, вы обязательно должны поделиться этим видео со своим классом! С запоминающимся ритмом, припевом, который вы не скоро забудете, и четкой графикой — это видео и песня помогут вашим детям в кратчайшие сроки понять концепцию геометрических линий! Припев побуждает зрителей поднимать руки вверх и формировать руками различные линии во время постукивания в видео.Повторение в этом видео действительно помогает донести мысль о параллельных, перпендикулярных и пересекающихся линиях в веселой и приятной форме!
Песня о трехмерных фигурах для детей | Видео 3-D формы от NUMBEROCK (2:04)
Еще одно отличное видео от NUMBEROCK, эта живая рэп-песня отлично объясняет зрителям трехмерные формы. Если некоторые из ранее упомянутых видеороликов, посвященных трехмерным фигурам, кажутся вашим ученикам слишком юными, это будет большим успехом для детей старшего возраста — и даже для младших! Хор помогает напомнить учащимся о характеристиках трехмерных форм, в то время как остальная часть песни объясняет конкретные трехмерные формы и места, где зрители могут видеть эти формы в повседневной жизни.Ваши дети не только лучше поймут трехмерные формы после просмотра этого видео, но и будут напевать мелодию в течение нескольких дней, показывая трехмерные формы вокруг себя!
Колин Доддс — Геометрические преобразования (3:15)
Понимание различных способов перемещения или трансформации фигур кажется достаточно простым, но некоторым ученикам может быть сложно полностью понять их. Хотя в этом видео не самая впечатляющая графика, мелодия запоминается, а объяснения различных способов движения фигур очень легко понять.Хор повторяет ключевые термины, касающиеся геометрических преобразований, таких как поворот, перевод и отражение, и полностью объясняет, что означает каждый термин. Это видео может быть лучше для студентов старшего возраста, так как оно знакомит с более сложным термином, мозаикой, в дополнение к множеству текстовых отображений определений. По этой причине может быть полезно показать это видео учащимся, которые умеют читать, хотя это не обязательно для того, чтобы оно было эффективным.
Песня Shapes: Shapes Rap / Chant — Песня формы робота (3:36)
Прекрасное введение в основные формы, это видео сочетает в себе простой фоновый рисунок с простыми объяснениями различных форм, таких как круги, треугольники, четырехугольники, параллелограммы и т. Д.После демонстрации визуального представления каждой формы в видео используется простая анимация, чтобы показать, как на самом деле создается каждая форма, и четко указать, сколько у нее сторон. Хотя графика довольно проста и бит не получит Грэмми в ближайшее время, это видео предлагает очень простые для понимания объяснения и введение в основные формы. Идеально подходит для младших школьников!
Песня о треугольниках ⋆ Типы треугольников для детей от NUMBEROCK (1:55)
https: // youtu.be / JQUTVgT9RXY
Можете ли вы сказать, что я большой поклонник этих видео NUMBEROCK? Я думаю, что они действительно отличное дополнение к любому уроку геометрии, потому что все они содержат разные, но одинаково запоминающиеся ритмы и мелодии в сочетании с понятными объяснениями данной концепции. Мне также нравится, как все они показывают реальные примеры геометрических концепций и геометрических фигур. В этом конкретном видео отлично исследуются все виды треугольников — концепция, с которой, как я обнаружил, многие мои ученики испытывают затруднения.В песне не только объясняются и показаны примеры различных треугольников, но и подчеркиваются различные характеристики, которые отличают эти треугольники друг от друга. Быстро, запоминающе и по делу — это видео станет отличным дополнением к любому уроку геометрии треугольников.
Другие ресурсы для обучения геометрии
Нельзя отрицать, что некоторые видео действительно могут дать вашим ученикам возможность познакомиться с различными математическими концепциями, если вы включите их в свои уроки математики, но давайте не будем забывать обо всех других замечательных ресурсах, которые также могут помочь обогатить ваши инструкции по математике! Включение следующих ресурсов по геометрии от Lucky Little Learners в ваши инструкции по математике определенно поможет повысить вовлеченность учащихся и углубить их понимание различных геометрических концепций! Ознакомьтесь со всеми этими невероятными продуктами, перейдя по ссылкам ниже.
Блокнот по интерактивной геометрии для 1 класса по математике
Блокнот по интерактивной геометрии для 2-х классов по математике
Набор интерактивных тетрадей по математике для 2-х классов: время, деньги, геометрия
Карты задач с QR-кодом Geometry
Карты задач на геометрию (без QR-кодов)
Гостевой пост Марго Кармайкл из Carmichael’s Class
«Четыре года преподавания в 4-м классе помогли мне стать учителем, который увлечен созданием класса, который увлекает и вдохновляет моих учеников, объединяет обучение на основе технологий, предлагает реальный опыт и способствует творчеству.Я вел очень разнообразные классы с большим количеством изучающих английский как иностранный язык, изучающих специальное образование, а также с проблемами поведения, что дало мне глубокое понимание важности индивидуального подхода к обучению для каждого ученика. Как учитель, я постоянно учусь и развиваюсь, но одна постоянная — всегда ставить учеников на первое место! »
Спасибо за регистрацию. Нажмите на ссылку ниже, чтобы подтвердить подписку, и вы уже в путь.
Рабочие листы по геометрии
Листы вакансий
Наши рабочие листы по описанию позиций, богатые множеством практических занятий, — лучшее место для развития ваших пространственных навыков, понимания относительного положения предметов и расширения словарного запаса.
Рабочие листы 2D-фигур
Настройте свои моторные навыки с помощью этого набора двухмерных рабочих листов. Найдите множество привлекательных листов для вырезания и склеивания 2D-форм, определения форм, обводки и цвета, именования и сопоставления форм, рисования и подсчета фигур, сторон и углов и многого другого.
Рабочие листы с 3D-фигурами
Получите основы геометрии в форме с этими рабочими листами с трехмерными фигурами, содержащими диаграммы и упражнения для определения и маркировки трехмерных фигур и связывания их с реальными объектами.Поймите свойства трехмерных фигур и узнайте сети твердых фигур, как свои пять пальцев.
Рабочие листы для линий, лучей и сегментов
Используйте этот набор рабочих листов линий, лучей и сегментов, чтобы получить более глубокие знания об этой концепции. Сюда включены яркие диаграммы и листы действий для определения, наименования и рисования линий, лучей и сегментов, простых задач со словами и многого другого.
Точки, линии и плоскости Рабочий лист
Сборка здесь содержит множество точек, линий и плоскостей PDF, чтобы прояснить концепцию.Узнайте о коллинеарных и неколлинеарных точках, ответьте на вопросы, основанные на приведенных цифрах, и поймите такие понятия, как копланарность и многое другое.
Рабочие листы углов
Перемещайтесь по группе рабочих листов по геометрии, которые содержат бесчисленные упражнения, от определения, наименования и классификации углов до поиска углов, образованных поперечными, треугольными, четырехугольными, многоугольниками, и измерения углов с помощью транспортира, дополнительных и дополнительных углов, чтобы упомянуть некоторые из них.
Рабочие листы симметрии
Используйте этот массив таблиц симметрии, чтобы определить линию симметрии в объектах и буквах, провести линию симметрии, завершить зеркальное отображение в стандартной и сеточной форме, найти периметр, сгибание бумаги и операции вырезания и вставки, чтобы упомянуть лишь некоторые из них. .
Листы преобразования
Ознакомьтесь с этими таблицами преобразований, которые содержат визуально привлекательные действия для определения преобразований реальных объектов: скольжение, переворачивание и поворот, перемещение, поворот и отражение, преобразование форм, треугольников, четырехугольников, правила записи, координаты и многое другое.
Рабочие листы
Множество рабочих листов с областями для печати, приведенных здесь, подходят для обучения тому, как определять площадь прямоугольников, треугольников, кругов, многоугольников и многих других; доступны как метрические, так и обычные единицы измерения. Кроме того, включены привлекательные рабочие листы, чтобы найти области правильных и неправильных форм с использованием сеток и многого другого.
Рабочие листы по периметру
Выберите из множества листов периметра, чтобы найти периметр правильных форм, таких как прямоугольник, треугольник, четырехугольник, многоугольник, окружность круга; неправильные формы, определение периметра с помощью сетки, и это лишь некоторые из них.
Прямоугольные рабочие листы
В этой коллекции геометрических листов есть все, что вам нужно знать о прямоугольниках, таких действиях, как цвет и обводка прямоугольников, определение площади и периметра прямоугольника, длины прямоугольного пути, ширины и диагоналей, длины стороны квадрата, площади и периметра прямоугольника. квадрат и больше.
Рабочие листы с треугольниками
В этой подборке есть специально разработанные рабочие листы геометрии для распознавания типа треугольников на основе сторон и углов, определения углов как внутренних, так и внешних, длины сторон, периметра с конгруэнтными свойствами, площади треугольника, равнобедренных, разносторонних, равносторонних ; теорема о неравенстве и многое другое.
Рабочие листы по кругу
Этот набор круглых листов — важное дополнение к вашим знаниям. Рабочие листы включают в себя такие упражнения, как определение площади и окружности круга, площади сегмента, определение радиуса, диаметра, длины дуги, площади сектора и многих других.
Четырехсторонние листы
Рабочие листы по геометрии здесь концентрируются именно на различных типах четырехугольников с навыками определения и наименования четырехугольников, определения периметра четырехугольника — стандартного и на основе свойств, определения площади параллелограмма, ромба, трапеции, воздушного змея, четырехугольника и многого другого. с множеством интересных мероприятий.
Листы с полигонами
Взгляните на эту коллекцию рабочих листов с многоугольниками, в которых есть такие задачи, как распознавание многоугольника — правильного / неправильного, вогнутого / выпуклого, определение площади и периметра многоугольников, углов как внутренних, так и внешних, и это лишь некоторые из них.
Рабочие листы для обычных пар и координатных плоскостей
Оттачивайте свои навыки в этом важнейшем аспекте построения графиков с помощью пакета упорядоченных пар и рабочих листов координатных плоскостей, содержащих задачи для определения положения, упорядоченных пар, квадрантов и осей с сетками и без них; построение упорядоченных пар и координат, изменение положения или направления и многое другое.
Рабочие листы по формуле средней точки
Включите этот блок рабочих листов геометрии, чтобы найти среднюю точку на числовой прямой, на сетках, используя формулу, чтобы вставить недостающие координаты, находя конечные точки с различными уровнями сложности.
Рабочие листы по формуле расстояния
Разберитесь в применении формулы расстояния с этим множеством рабочих листов по геометрии, найдите длину числовой прямой, отрезки линии, длину сторон фигур; формула расстояния с теоремой Пифагора, с формулой средней точки; классификация треугольников и четырехугольников, а также ее применение в геометрии.
Таблицы уклонов
Разъясните концепцию с помощью приведенных здесь таблиц уклона, чтобы определить положительные и отрицательные уклоны, построить график линии, найти подъем и спуск, найти уклон, используя метод отношения, двухточечную формулу, формулу пересечения наклона и многое другое.
Рабочие листы по параллельным, перпендикулярным и пересекающимся линиям
Используйте эту интересную подборку рабочих листов параллельных, перпендикулярных и пересекающихся линий, чтобы определить тип линий, нарисовать типы линий, проанализировать поперечное сечение, чтобы ответить на вопросы, изучить концепцию параллельности и перпендикуляра, взаимосвязь между точками и уклонами, чтобы упомянуть немного.
Таблицы масштабного коэффициента
Включите эти рабочие листы масштабного коэффициента, чтобы научиться расширять формы, определять координаты исходных или расширенных форм, расширять формы с началом координат в центре и началом координат не в центре. Также учитывайте влияние масштабного коэффициента на площадь, периметр, объем и площадь поверхности.
Рабочие листы по площади поверхности
Ознакомьтесь с обширной коллекцией распечатываемых геометрических листов здесь, чтобы найти площади поверхности призм, цилиндров, пирамид и многоугольных пирамид, полусфер и сфер, а также конусов; Найдите площадь комбинированных форм, доступных на разных уровнях сложности.
Рабочие листы по объему
Набор исчерпывающих таблиц объемов здесь предоставляет отличный способ найти объем прямоугольных, треугольных и многоугольных призм, конусов, цилиндров и сфер, полусфер, прямоугольных пирамид, объем смешанных и комбинированных форм и многое другое.
Рабочие листы по теореме Пифагора
Эти удобные для печати геометрические рабочие листы содержат множество задач для изучения теоремы Пифагора с помощью описательных диаграмм, PDF-файлы для определения прямоугольного треугольника, тройку Пифагора, поиск неизвестных длин и сторон, а также проблемы со словами.
Рабочие листы по тригонометрии
Рабочие листы по тригонометрии содержат соответствующие диаграммы и упражнения, чтобы найти квадранты и углы, научиться преобразовывать радианы в градусы, точно измерять углы, находить опорный и котерминальный углы, определять тригонометрические отношения, оценивать и проверять, используя триггерные тождества. Также включены PDF-файлы для единичной окружности, смежных углов, обратных триггерных соотношений и т. Д.
Танграм: Геометрия Практические математические манипуляторы
Танграммы — хороший инструмент для развития пространственного мышления и для исследования дробей и различных геометрических понятий, включая размер, форму, конгруэнтность, сходство, площадь, периметр и свойства многоугольников.Танграммы особенно подходят для самостоятельной работы студентов, так как каждому студенту может быть предоставлен набор, за который он или она несет ответственность. Однако, поскольку учащиеся сильно различаются по своим пространственным способностям и языку, следует также выделить время для групповой работы, и большинству учащихся нужно достаточно времени, чтобы свободно поэкспериментировать с танграммами, прежде чем они начнут более серьезные исследования.
Молодые студенты сначала будут думать о своих фигурах в стиле Танграм буквально. С опытом они увидят общие черты и начнут развивать абстрактный язык для аспектов паттернов в своих формах.Например, ученики могут сначала сделать квадрат просто из двух маленьких треугольников. Тем не менее, в конечном итоге они могут развить абстрактное мысленное изображение квадрата, разделенного диагональю на два треугольника, что позволит им построить квадраты других размеров из двух треугольников.
Tangrams также могут предоставить визуальное изображение, необходимое для понимания алгоритмов дроби. Многие студенты учатся делать такие примеры, как 1 ⁄2 = ? ⁄8 или 1 ⁄4 + 1 ⁄8 + 1 ⁄16 =? на чисто символическом уровне, так что, если они забудут процедуру, они окажутся в полной растерянности.Учащиеся, у которых было много предсимволических переживаний, решали такие задачи, как «Найдите, сколько маленьких треугольников заполняет большие треугольники» или «Какая часть полного квадрата покрывает маленький, средний и большой треугольники?» будет иметь прочную интуитивную основу, на которой можно развить эти базовые навыки и использовать их, если память не подводит их.
Молодые студенты изначально склонны работать с другими и копировать работы друг друга. Тем не менее, даже копирование чужой формы Танграма может расширить опыт учащегося, развить способность распознавать сходства и различия и предоставить контекст для развития языка, связанного с геометрическими идеями.На протяжении всего исследования учеников следует поощрять рассказывать о своих конструкциях, чтобы прояснить и расширить свое мышление. Например, учащиеся разовьют интуитивное чувство углов, когда они соединяют углы частей Танграма вместе, и их можно побудить подумать о том, почему одни части подходят для данного пространства, а другие нет. Учащиеся могут начать развивать восприятие симметрии, когда они по очереди отражают части Танграма по линии, помещенной между ними на коврике, а также могут начать испытывать гордость за их совместное производство.
Учащиеся любого возраста, которые раньше не видели Танграм, скорее всего, сначала исследуют формы, создавая объекты, похожие на объекты, например, бабочку, ракету, лицо или букву алфавита. Учащиеся с более богатым геометрическим образованием, вероятно, наложат интересные ограничения на свои конструкции, решив создать, например, закрашенный многоугольник, такой как квадрат или шестиугольник, или симметричный узор.
Лучшие геометрические приложения для детей
Дошкольники и дети младшего возраста могут извлечь пользу из изучения форм и геометрии на соответствующем их возрасту уровне с помощью этих геометрических приложений.Я отсортировал их по возрасту от младшего до старшего, поэтому, если у вас есть дети постарше, прокрутите вниз примерно наполовину.
Приложения для детей с геометрией
Занятые фигуры $ 1,99 (в возрасте от 2 до 4 лет)
Научитесь распознавать фигуры (настоящая форма, а не название фигуры), решая 112 простых головоломок в этом хорошо продуманном приложении для детей ясельного и дошкольного возраста.
Geoboard FREE (возраст 4+)
Хотя настоящая геодоска с резиновыми лентами намного лучше, эта виртуальная подойдет в крайнем случае.Это также отличное бесплатное приложение для детей.
Tiggly Stamp FREE (от 4 лет)
Геометрические формы превращаются в нечто забавное для изображения — пугало, индейку, яблоко, лист — на фоне зимы или осени. Какое забавное математическое приложение для детей дошкольного возраста.
Конструктор фигур $ 2,99 (от 4 лет)
Дети на самом деле не изучают формы, но это все еще практическая игра. Игроки перемещают фигуры в головоломки, включая буквы, животных и многое другое.Это приложение для детей с геометрией помогает ученикам ориентировать визуальное мышление на формы.
Tiggly Safari FREE (от 4 лет)
Сопоставьте трехмерные формы с быстро движущимися по экрану фигурами. (Это немного сложно, но поговорим о хорошей практике двигательных навыков!) Вы можете сфотографироваться со своими животными из джунглей и узнать о каждом из них.
Tiggly Shape Toys
Чтобы играть в вышеуказанные математические приложения Tiggly, у вас должны быть игрушки фигур: круг, квадрат, треугольник и звезда. Перейти сюда, чтобы КУПИТЬ Фигурки Tiggly.
DragonBox Elements 4,99 $ (от 7 лет)
Дорогостоящее приложение для детей с геометрией, но с отличными возможностями для игрового обучения, DragonBox Elements помогает детям улучшить логику, решение задач и знания геометрии. Если вы хотите потратить деньги, я думаю, это приложение того стоит.
CyberChase Shape Quest БЕСПЛАТНО (от 6 лет)
Выбирайте между «Прокладывать путь», «Накормить зверюшек» или «В прятки».Распечатайте игровую доску с веб-сайта PBS Kids, если хотите поиграть в нее. Игра в прятки — это весело: вы должны находить квадраты, треугольники или фигуры с шестью сторонами. Feed the Critters похож на Angry Birds, где вам нужно наклонить собачью кость, чтобы запустить ее к животному. Некоторые функции не очень хороши — трудно вернуться к главному экрану, — но это бесплатно, так что никаких денежных потерь.
The Land of Venn $ 4,99 (от 6 лет)
Фрукты и овощи победят злого волшебника, рисуя линии, формы и другие геометрические концепции в этой битве за добро и все геометрические вещи.Это приложение отлично обучит вас концепции, затем заставит попрактиковаться в динамичной игре и в конце закрепит концепцию. Очень глупый акцент повествует историю и игру. Веселье!
Геометрия Монтессори $ 3,99 (возраст от 6 до 8)
Это красивое математическое приложение для изучения различных геометрических фигур в 2D и 3D с играми, такими как поиск фигур в городах, сочетание и совпадение, исключение нечетных и сортировка фигур. Очень хорошо сделано.
Splash Math FREE, 9 долларов США.99 (возраст от 8 до 10)
Нам нравится эта практика и математическое приложение для каждого класса с призами и отчетами об успеваемости. Вот пример вопроса для 2-х классов: где стоит подчеркнутая цифра? 79 = единицы. Мне нравится вариант блокнота, в котором дети могут решать проблему пальцами. Охватываемые концепции: разметка, смысл чисел, стратегии сложения, сложение двух цифр, стратегии вычитания, вычитание двух цифр, время, измерения, геометрия , геометрия , данные, деньги, сложение трех цифр и вычитание трех цифр.
Bloxy World Bricks for Kids БЕСПЛАТНО (от 9 до 11 лет)
Как и в Minecraft, вы строите в 3D, используя кирпичи.

 net/get-afishanew/34116/2bc3d42440a0bc3de26f3e67a6b3f4b9/orig
net/get-afishanew/34116/2bc3d42440a0bc3de26f3e67a6b3f4b9/orig jpg
jpg Получаются шаблоны;
Получаются шаблоны;

 Когда вы пробуете несколько чисел самостоятельно, посмотрите, всегда ли ваши ответы включают последовательные
Когда вы пробуете несколько чисел самостоятельно, посмотрите, всегда ли ваши ответы включают последовательные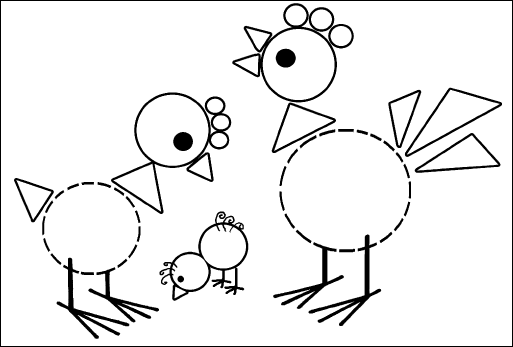
 Положите два конца
Положите два конца
 Сумма площадей квадратов на ножках равна
Сумма площадей квадратов на ножках равна Как вы думаете, как их построить? На этом этапе мы рассмотрим предложения и рассмотрим их, например, попытаемся нарисовать трехмерный объект на доске.Изучив несколько вариантов, мы познакомимся с зубочистками и мармеладными конфетами.
Как вы думаете, как их построить? На этом этапе мы рассмотрим предложения и рассмотрим их, например, попытаемся нарисовать трехмерный объект на доске.Изучив несколько вариантов, мы познакомимся с зубочистками и мармеладными конфетами. Попросите учащихся измерить длину и ширину листа бумаги, чтобы определить площадь поверхности цилиндра (исключая верхнюю и нижнюю часть).
Попросите учащихся измерить длину и ширину листа бумаги, чтобы определить площадь поверхности цилиндра (исключая верхнюю и нижнюю часть). Снова сложите круг пополам, но на этот раз совместите конечные точки складки.
Снова сложите круг пополам, но на этот раз совместите конечные точки складки. Можете ли вы выяснить что-нибудь еще об этом треугольнике? Это ( прямоугольный треугольник ).
Можете ли вы выяснить что-нибудь еще об этом треугольнике? Это ( прямоугольный треугольник ). Какая у вас форма? ( Пентагон ) Несмотря на то, что это не та традиционная форма, к которой вы привыкли, у него все еще есть пять сторон, поэтому он по-прежнему классифицируется как пятиугольник.
Какая у вас форма? ( Пентагон ) Несмотря на то, что это не та традиционная форма, к которой вы привыкли, у него все еще есть пять сторон, поэтому он по-прежнему классифицируется как пятиугольник. Начните с угла 0 градусов к земле, измерьте и запишите расстояние, которое поток проходит в горизонтальном направлении по земле.Повторите эти действия для углов 20 o , 30 o , 45 o , 70 o и 75 o .
Начните с угла 0 градусов к земле, измерьте и запишите расстояние, которое поток проходит в горизонтальном направлении по земле.Повторите эти действия для углов 20 o , 30 o , 45 o , 70 o и 75 o . (См. Пример ниже.)
(См. Пример ниже.)



 Спросите студентов, где, по их мнению, эти знания могут быть полезны. Одна из идей, которые могут возникнуть, — это ограждение пастбища.
Спросите студентов, где, по их мнению, эти знания могут быть полезны. Одна из идей, которые могут возникнуть, — это ограждение пастбища. Сегодня компьютерные приложения в геометрическом текстильном дизайне — это процесс, в котором большая часть тканей предназначена для производства.
Сегодня компьютерные приложения в геометрическом текстильном дизайне — это процесс, в котором большая часть тканей предназначена для производства.