44 Аппликации из геометрических ФИГУР (идеи и шаблоны)

Добрый день. Сегодня я выгружаю небольшую но полезную подборку аппликаций, все они иллюстрируют одну идею того, что МОЖНО ИЗ ФИГУР делать отличные изображения всего, что есть в этом мире. Из обычных географических форм (бумажных треугольников, квадратов, кругов, овалов и др) можно сделать аппликацию любого животного или объекта человеческой жизни.

Я думаю что сложные изогрутые детали, не так понятны для детей младшего возраста и для них гораздо понятнее конструктив четких геометрических фигур с симметричными углами и одинаковыми признаками формы. Из таких фигур по образцу можно сложить заданный объект… например такого пингвина.

Тут все сразу понятно. Большой прямоугольник — тело. Маленький белый — грудка. Далее интуитивно ребенок понимает что их оставшихся фигур ноги, а что крылья птички. Находят свое место и глаза и клюв.

Потому что все четко и ясно. Все заключено в прямые углы и пропорциональные соотношения.

Если бы ребенку 4 лет дали те же детали, но уже обтекаемые, близкие к реальным формам пингвина, то ребенок мог бы и напутать. Приделать крыло другой стороной, перевернуть лапу зеркально, или поставить фигуру вниз головой.

А вот с прямоугольниками такого не произойдет. Его можно перевернуть и он все равно будет одинаковым с заданным образцом.

Чем старше дети в саду, тем больше фигур вы можете использовать в поделке-аппликации. Старшая группа с удовольствием возьмется за сложные задачи, похожие на увлекательный пазл, как эта поделка в виде Черепахи. Попробуйте уложить все прямоугольники на ее квадратный панцирь ))).

А для малыша  3 лет будет посильна такая поделка-аппликация, как динозавр на фото ниже. Круги для шеи. Маленькие обрубки полоски — для ног. (Или любые другие фигуры из бумаги подойдут).

Также и с аппликацией слона. Все просто. Тут не перепутаешь деталь головы и уха. И хобот ляжет как надо в виде цепочки из кругов, от большого к маленькому.

Простота и лаконичность геометрических форм всегда смотрится красиво и интересно. Обучать аппликации в детском саду нужно начинать ИМЕННО С ЧИСТОЙ ГЕОМЕТРИИ.

Какие аппликации из фигур

можно сделать с детьми.

Давайте поглядим какие милые реалистичные персонажи складываются из бумажных геометрических фигур. Вот собачка.

ЕСЛИ сделать уши по другому, получится собачка другой породы.

Отлично из фигур смотрятся аппликации таксы, бульдога, мопса из кругов и овалов.

А вот аппликация медведя из квадратов и прямоугольников. Посмотрите как трогательно смотрятся прямоугольнички-бровки мишки. И подушечки на лапках. Именно они придают этой аппликации потешную реалистичность и передают настроение персонажа, желающего всех обнять.

Рядом с медведем можно приклеить еще один прямоугольник — в виде бочки с медом.

А вот зайчик, по той же технике аппликации из прямоугольников, который запускает сердечки. Воспитателю детского сада будет достаточно просто заготовить такие фигуры-полосы и квадраты. И расход бумаги самый экономный.

Парно-копытные животные тоже просто сделать из прямоугольников. Вот жираф, и козел. Кстати прямоугольник жирафого тела так интересно обклеивать кружочками из бумаги… или пятнышки можно сделать пальчиками, вымазанными в коричневой гуаши.

Все животные обитают в определенной среде. Поэтому подумайте какие еще геометрические фигуры могут обозначить эту среду. Например, на фото ниже мы добавляем овалы листвы, полоску ветки, длинные треугольники травы и маленькие овалы камешков.

А для поделки с пингвином просим ребят сложить из полосок бумаги снежинку.

А рядом с аппликацией утки добавляем длинные треугольники стеблей с коричневыми овалами головок камыша.

Аппликации роботы

из геометрических фигур.

Есть отличная идея на тему КАК НАДОЛГО ЗАНЯТЬ РЕБЕНКА и посидеть в тишине и спокойствие.
Ответ прост  — нарежьте ему много разных прямоугольников. Целую кучу разных по размеру и цветы прямоугольных нарезочек из бумаги.

И у него на глазах склейте ОДНОГО робота. И все. Дальше уловив суть процесса и алгоритм действий ребенок будет сам придумывать все новые и новые шаблоны роботов для разных целей. Вы можете для затравочки его фантазии нарисовать несколько эскизов… и пусть ребенок сам попробует их воссоздать уже из фигурок, нарезанных вами.

Любимые питомцы

из геометрических фигур.

Предложите детям сделать аппликацию любимого питомца из бумажных фигурок. Пусть постарается и создаст несколько картинок: вот щеночек писает подняв лапку, вот он спит, вот он ловит бабочку. Пусть бумажные фигурки передадут позу и застывшие движения животного, попробуйте вместе с детьми сложить такие аппликации из имеющихся фигур.

Бабочки из геометрических фигур.

Это самый удобный СТАРТ для поделок такого рода. В бабочках главное симметрия (повтор левого узора на правой стороне) и тут просто задать формы крыла из крупных деталей и потом украшать их мелкими геометрическими фигурами.

Вот несколько шаблонов для таких геометрических аппликаций.

Техника и механизмы

 аппликации из фигур.

А самый большой простор для творчества — это создание технических устройств. Пусть ребенок создает машины будущего и прошлого. Тракторы, снегоуборщики, самолеты, автомобили. А также заправочные станции, автомойки, дорожные развязки.

Ребенок будет в восторге… наконец-то он может заниматься настоящим инженерным делом и применять свои таланты изобретателя-механизатора. Запускать ракеты, отправлять в плаванье корабли, убирать урожай.

Придумывайте свои интересные виды аппликаций из бумажных фигур. Нарезайте ромбы, квадраты, шестиугольники, круги и овалы. Пусть ребенок развивает пространственное мышление (это пригодится на геометрии), пусть малыш соотносит величины и пропорции (это разовьет наблюдательность и способность к анализу). Пусть дети растут умнее нас и радуют нас своими достижениями.

Делайте мир лучше. Свой мир.

Ольга Клишевская, специально для сайта Семейная Кучка.

Читайте НОВЫЕ статьи на нашем сайте:

на Ваш сайт.

Геометрическая аппликация из треугольников. Рыбки и елочки

Дети с удовольствием занимаются бумажным творчеством. Аппликацию из бумаги любят многие из них и с удовольствием на занятиях выполняют задания связанные с наклеиванием цветной бумаги. Однако, маленькие детки не могут еще так хорошо пользоваться ножницами. Поэтому эти геометрические аппликации из треугольников рассчитаны на дошкольников и учеников 1 класса.

Педагог или воспитатель детского сада сможет быстро вырезать необходимые детали из цветной бумаги и раздать ребятам. В качестве образца для аппликации я предлагаю работы «Елочка» и «Рыбка», но вы можете придумать и другие забавные фигуры из треугольников.

Как сделать аппликацию из треугольников

Материалы для выполнения аппликации: 

• листы цветной бумаги (двух цветов, например — красный и желтый),
• плотные листы белой бумаги,
• клей (клеящий карандаш для малышей),
• кисточки,
• ножницы (для взрослого).

Аппликация из треугольников «Рыбка»

1. Для детей, которые не могут самостоятельно вырезать, родитель (воспитатель) вырезает по шаблону из цветной бумаги геометрические фигуры — треугольники. Треугольники будут разного размера.
2. Каждому ребенку (в саду) раздают коробочки с вырезанными цветными деталями, лист белой плотной бумаги, клей.
3. Детям следует показать образец, чтобы они знали какую аппликацию они будут выполнять на занятии. Нужно обратить внимание на фигуру (сказать, что это треугольники), размер деталей (попросить найти маленькие и большие), спросить какого цвета детали у них в коробочках.
4. После этого нужно рассказать что аппликация эта непростая. Чтобы она получилась нужно правильно разложить треугольнички на своем листе бумаги. Чтобы дети подумали можно дать им нерасчерченные шаблоны. Если времени на это задание нет, то нужно показать шаблоны по которым дети соберут фигурку.
5. Пусть ребенок сам выберет шаблон. Можно даже предложить детям собрать по очереди все шаблоны (без клея, просто размещая треугольники на бумаге). Это один из уроков на логику.
6. После того как шаблон рыбки выбран, воспитатель показывает как намазывать клеем треугольники цветной бумаги и как правильно прилеплять их к листу белой бумаги (строго по центру чтобы было красиво). Часто дети начинают приклеивать треугольники, не разложив сначала всю фигуру — в итоге хвост или плавнички рыбки вылезают за края листа.

7. Родитель (воспитатель) обязательно должен не только похвалить ребенка за выполненную работу, но и указать на ошибки (если таковые имеются). Каждая работа подписывается (число, год, имя ребенка). 8. После просушки работу можно поставить на выставку или на полочку в комнате ребенка.

Аппликация из треугольников «Елочка»

Эта аппликация похожа на вышеописанную, но несколько сложнее. Детали приклеиваются в определенной последовательности и с перекрытием.

Материалы для выполнения аппликации:

• листы цветной бумаги (двух цветов — зеленый и коричневый),
• плотные листы белой бумаги,
• клей (клеящий карандаш для малышей),
• кисточки,
• ножницы (для взрослого).

1. Родитель (воспитатель) как и в аппликации «Рыбка» вырезает треугольники из цветной бумаги и раздает их ребятам.
2. Перед занятием детям следует показать готовую работу, сказать какая она красивая и интересная. Далее нужно обратить внимание детей, на то, что эта аппликация с хитростью. Чтобы получилось красиво, нужно приклеить треугольники с перекрытием.
3. Дети раскладывают треугольники на листе самостоятельно. Взрослый объясняет в каком порядке следует наклеивать фигурки, чтобы получилась красивая елочка.
4. Дети по шаблону наклеивают треугольники на белый лист бумаги (взрослый корректирует работу, помогает исправить ошибки). Обязательно в конце занятия нужно похвалить ребенка.
5. Готовые работы высушиваются под прессом, а потом выставляются на выставке.

Аппликации из геометрических фигур

А вообще аппликации можно делать из любых геометрических фигур. Треугольники мы уже разобрали, но есть много и других фигур: круги, квадраты, прямоугольники, ромбы. Давайте вместе с детьми попробуем собрать веселые аппликации по готовой схеме.

Вот мальчишкам больше нравятся поделки с самой разной техникой и машинками. Попробуйте предложить малышам — мальчикам аппликации с подъемным краном, машинкой, паровозом, корабликом или ракетой.

Все, что требуется от родителя — это распечатать на листочке бумаги шаблон. Малыш по образцу вырезает детали и наклеивает их на основу. Картинку можно дополнить надписью или раскрасить фон цветными карандашами или фломастерами.

Я знаю детей, и сразу вас предупрежу — если такие развивающие занятия понравились ребенку, то одним шаблоном вы не отделаетесь. Лучше сразу распечатать несколько.

Вот вам ссылка на скачивание архива — шаблоны геометрической аппликации с машинками — мальчишеская тема.

Девочки тоже не останутся без аппликаций. Им можно предложить шаблоны для аппликации с животными. Технология выполнения таких аппликаций не отличается от вышеописанного варианта для машин. Распечатываете шаблон, ребенок вырезает из бумаги геометрические фигуры и наклеивает их на контур. В итоге красивая и занимательная аппликация с мышкой, лисой, белочкой, лошадкой и другими зверями.

Вот ссылка на архив аппликаций из геометрических фигур с животными.

Не забывайте, нужно не просто вручить ребенку картинку и н6ожницы с клеем. Обязательно повторите названия геометрических фигур, а заодно и цветов. Помогите и подскажите малышу, если он забыл как называется фигура. Вот тогда ваши занятия будут настоящим развивающим творчеством.

Занятия геометрической аппликацией из простых фигур (треугольников) доступны и просты. Поверьте, эти занятия придутся по душе ребятам.

Рекомендую это видео всем, кто любит творчество и оригами!

Геометрическая аппликация. » Детские поделки. Детский сайт с поделками из бумаги и фетра.

Данная статья предназначена для занятий аппликацией с детьми. Геометрическая аппликация ненавязчиво познакомит малыша с основными свойствами предметов: величина, цвет, форма. Рисунок составляется из простых геометрических фигур. Аппликация связана с познавательной деятельностью и огромное влияние оказывает на развитие творческих и умственных способностей ребенка. Принесет большую пользу, поможет выработать трудовые навыки.
Начиная ребенка знакомить с аппликацией, надо помнить три главных правила:
1) ребенок не может долго удерживать свое внимание
2) ему должно быть интересно
3) ребенок нуждается в похвале за сделанную работу.

Перед началом занятий вырежьте геометрические фигуры разных цветов и размеров. обратите внимание малыша на фигуру, ее цвет и величину. Помогите разложить фигуры в нужном порядке.

Аппликация цветочек.

Если ребенок совсем еще маленький, то аппликацию лучше выполнять совместными усилиями. Выложите цветочек на бумаге и попросите малыша повторить за вами. Покажите как надо пользоваться клеем и приклейте картинку.
По началу используйте 2-3 геометрические фигуры в аппликации, для лучшего запоминания проговаривайте названия и комментируйте при этом свои действия.
Цветок сделан из кругов и квадратов. Круги — лепестки цветка, а квадраты, выложенные в виде ромба — стебель цветка.

Аппликация гусеница.

Гусеница выполнена полностью из кругов и только для рта потребовался маленький треугольник.

Аппликация бабочка.

Аппликация бабочки будет уже посложней, в нее входят новые геометрические фигуры. Увеличевается колличество и размер деталей.
Стоит попробовать сделать с ребенком общую картину из геометрических фигур. Для начала проработать каждый элемент будущей картины по отдельности ( цветочек, бабочка, гусеница ), в последствии собрать уже общую картину.
Занимаясь с ребенком аппликацией, спросите его, кого он изображает? Кто такие гусеницы и в кого они превращаются? Проводя занятия таким методом у ребенка развивается кругозор.

Зимняя картина.

Если за окном зима, то стоит попробовать сделать простую зимнюю геометрическую аппликацию.

Аппликация домик.

Сначала пробуем выложить домик из фигур, а после приклеиваем ее на основу для аппликации.

Аппликация елочка.

Елочку собираем из зеленых треугольников, а из маленьких кругов делаем бусы на елку.

Аппликация снеговик.

Со снеговиком также все просто, он состоит из кругов разного размера, одной трапеции и двух разных маленьких треугольников.

Аппликация из геометрических фигур «Кошки — мышки».

Геометрическая аппликация из бумаги. Гирлянда.

Наша задача научить малыша наклеивать ровно геометрические фигуры: круги и овалы , ромбы и треугольники, квадраты и прямоугольники, чередуя их по цвету и форме. Покажите ребенку, как сделать аппликацию из бумаги, имитируя гирлянду на ниточке из кругов и флажков.

Кораблик из геометрических фигур.

Геометрическая аппликация должна быть интересной, не очень сложной и не очень простой, только тогда можно заинтересовать ребёнка работой. Вырежьте из цветной бумаги различные геометрические фигуры и сконструируйте из них различные корабли. Это может быть один большой корабль или несколько маленьких, с парусами или с трубой. Понравившийся результат приклейте на бумагу.

Аппликации из геометрических фигур — презентация онлайн

1. АППЛИКАЦИИ ИЗ ГЕОМЕТРИЧЕСКИХ ФИГУР

г. Сыктывкар
2011
Разработала:
преподаватель
изобразительного
искусства и черчения
Маевская Зинаида
Алексеевна

2. История бумаги

Искусство мастерить из бумаги рельефные картины
зародилось в Древней Японии и Китае. Там оно известно под
названием «киригами»», что в переводе означает «вырезанная
бумага». «Оригами» — это уже объемные изображения.
Ученые
историки
утверждают,
что
бумага
была
изобретена в Китае. Материалы, похожие на бумагу, были
известны в IV-Ш в. До н.э. Официальным же годом рождения
бумаги считается 105 г. н.э., и была изготовлена из
измельченных стеблей растений.
Целых 500 лет секрет производства бумаги был тайной
за семью печатями, пока в 610 г., когда буддийский монах
Дан-хо добрался до Японии и открыл жителям островов
секрет производства бумаги. Японцы научились производить
бумагу в промышленных масштабах.
Для японцев бумага не только материал, на котором
пишут и рисуют, — это нечто большее. Для них это символ
чистоты.

3. Забавные зверята, птицы из геометрических фигур (аппликация)

Большинство детей любят рисовать цветными
карандашами, фломастерами, красками и это прекрасно!
Путь к прекрасному, к постижению красоты долгий и
непростой. Изобразительное искусство, как и письмо, имеет
свои законы, свои приемы, свою азбуку, незнание которой
ставит детей в тупик. Неслучайно у многих людей, не
постигших этих законов, с возрастом пропадает всякий
интерес к рисованию, а это объединяет человека.
Некоторые задачи изобразительного искусства можно
познать при выполнении аппликаций. Для тех детей, кто
любит мастерить, рисовать и придумывать что-то новое –
самый простой и доступный материал – это бумага. Для
создания необычных веселых картин понадобятся набор
цветных листов, клей и ножницы. Наверняка в каждом доме
найдутся старые журналы, фантики, обрезки ткани. Они
также помогут сделать оригинальные работы.
Слово «аппликация» означает вид деятельности, во
время которого изображения и рисунки создаются способом
наложения и приклеивания разных материалов на основу.
Занятия под названием «аппликация» известны давно –
с незапамятных времен люди выполняли рисунки
наложением и приклеиванием кусочков разноцветной ткани
или бумаги. Ведь всегда интересно наблюдать, как из
радужных квадратиков и треугольников получается
узнаваемая картина.

4. Помощь при изготовлении аппликации

Детям надо показать, как разрезать кусочки бумаги
на широкие и узкие полоски, как сложить и вырезать из
кусочка бумаги квадрат, а затем — как разрезать квадрат
по диагонали на два треугольника. Наконец как
закруглив углы квадрата, можно, вырезать из него круг.
Вот эти геометрические фигуры и станут первыми
компонентами составления простейших аппликаций.
Заметьте, что все работы с ножницами в руках надо
проводить не спеша, максимально избегая возможности
пораниться о лезвия ножниц.
Самые маленькие дети смогут сделать аппликацию
с помощью взрослых. Степень участия ребенка зависит
от его умений. Более взрослые дети справятся с работой
сами и даже смогут усложнить ее, проявив фантазию.

5. Для аппликации нужны материалы и инструменты

Научимся делать забавных зверят и
птиц способом аппликации из
геометрических фигур.
Для
аппликации нужны
инструменты
материалы
и
КРАСКИ
И КИСТИ
ПРОСТОЙ
КАРАНДАШ
НОЖНИЦЫ
ЦВЕТНЫЕ
КАРАНДАШИ
ЦВЕТНАЯ
БУМАГА
ФЛОМАСТЕРЫ
КЛЕЙ

6. Основные формы и линии

Здесь изображены формы и линии, которые пригодятся
детям для выполнения аппликаций
ОВАЛ
ОКРУЖНОСТЬ
ТРЕУГОЛЬНИК
ВОЛНИСТЫЕ
ЛИНИИ
ПРЯМЫЕ ЛИНИИ
КВАДРАТ
КЛЯКСА
ПРЯМОУГОЛЬНИК
ТРАПЕЦИЯ
ДУГИ
ОВОИД (ЯЙЦО)

7.

Правила безопасности во время работы с ножницами

во время работы с ножницами нельзя вертеться
нельзя подносить ножницы близко к лицу и размахивать
ими
если ножницы нужно передать товарищу, то их надо
протягивать ему только кольцами вперед
когда передаешь их товарищу, то надо внимательно
следить за тем, как товарищ их возьмет в руки
нельзя класть ножницы на край стола, они могут упасть
и поранить ногу

8. Курс начинающего аппликатора

ЦВЕТ
Как в любом виде искусства в аппликации очень
важны точно подобранные сочетания цветов. Здесь нет
однозначных правил и нельзя дать общий совет на все
случаи жизни. Важно почувствовать настроение общей
цветовой гармонии.
Холодные тона успокаивают, снимают раздражение,
позволяют дольше всматриваться в свои оттенки.
Резкие, контрастные друг другу цвета лучше разделить
более спокойными, промежуточными, успокаивающими
противоборство. Маленькая яркая работа будет радовать
глаз, служить цветовым пятном.
Обычно в картине участвуют один основной, два-три
близких ему и один контрастный цвет. Каждый цвет должен
поддерживать, помогать другому. Основной фон должен
быть
спокойнее,
значимых центров.
являясь
окружением
для
двух-трех

9. Танграм Танграм – это название игры, которая пришла к нам с Востока.

Она делается очень просто – из разрезанного на разные
части квадрата, из которого затем складываются фигурки,
напоминающие человека, рыбу, всадника, зверей и т.д.
Квадрат надо разрезать пополам по диагонали. Один
полученный треугольник также разрезается пополам по
диагонали. Это будет две самых крупных части танграма.
От второго треугольника отрезается его кончик – прямой
угол, а оставшаяся полоска одним движением ножниц
разрезается еще на две части – квадрат и ромб. Вот из этих пяти
частей и надо складывать фигурки.
Размер квадрата для танграма можно взять произвольный –
от довольно большого до маленького. Только не следует
увлекаться и слишком мельчить. Пожалуй размеры самого
маленького квадрата могут быть 10 х 10 см.

10. Творите, изобретайте, радуйтесь! (Забавные живые существа)

11. Забавные живые существа

.
Аппликация – один из самых древних
видов прикладного искусства.
Предметы быта с отделкой в технике аппликации
создавалось уже 2,5 тысячи лет назад! Такая отделка
возникла благодаря известному желанию человека украсить
свое жилище, одежду, утварь Оригинальные подарки и
поделки можно сделать даже из листа обычной бумаги!
При упоминании слова «бумага» у многих возникает
ассоциация с многочисленными аппликациями, которые
делали сначала в детском саду, а затем и в школе в канун
очередного праздника, торжества. Однако благодаря своим
особенным свойствам этот материал позволяет создавать не
только плоские композиции, но и объемные изделия.
Оказывается, красивой аппликацией можно украшать
не только листы бумаги, учебники, тетради, но также
табуретки, холодильники, праздничную одежду для себя и
своих кукол, пасхальные яйца и многое другое.
Дерзайте!

Аппликация из геометрических фигур | Главный портал МПГУ

АППЛИКАЦИЯ ИЗ ГЕОМЕТРИЧЕСКИХ ФИГУР

Аппликация из геометрических фигур выполняется из треугольников, кругов и прямоугольников, иных фигур быть не должно.

Изображать можно водное пространство или горный пейзаж.

Водное пространство: это может быть горное озеро, горная река, скалистый берег моря.

Горный пейзаж подразумевает открытое про­странство: альпийский луг, долина реки, опушка леса.

Время суток, состояние погоды, освещение, жи­вотный мир – выбирается автором работы самостоятельно.

При выполнении работы можно ориентироваться на фотографии природы.

Для этих работ необходимо вырезать примерно по 20 различных геометри­ческих фигур произвольного размера (в пределах от 10 до 40 мм) и цвета из бумаги любой фактуры.

Очень важно, начиная работу с детьми в этой технике, не забывать о самом главном – композиции. Выполнение композиций из геометрических фигур вызывает определенные трудности, но только в начале работы.

Для того чтобы определить оптимальный вариант расположения всех эле­ментов композиции, перед наклеиванием деталей подвигать их внутри выбранной рамки. Некоторые трудности вызывает изобра­жение облаков и бликов на воде.

Воздушная перспектива. Воздух не вполне прозрачен. В атмосфере есть некоторое количество паров и пыли, которые препятствуют четкой видимости удаленных объектов. Благодаря этому на большом расстоянии от зрителя контрасты светотени смягчаются, и у горизонта все объекты объединяются светлой, однотонной воздушной дымкой. На переднем плане пейзажа предметы выполняются объемно, во всю силу контрастных тональных отношений. На втором плане они смягчены воздушной средой, объемность изображения утрачивается, соответственно подбирается и тон бумаги. Вдали объекты выглядят почти плоскими и изображаются без проработки формы светотенью.

Прямая линейная перспектива – вид перспективы, рассчитанный на фиксированную точку зрения и предполагающий единую точку схода на линии горизонта (предметы уменьшаются пропорционально по мере удаления их от переднего плана)

Многие захотят изобразить облака. Облака могут иметь вертикальное и горизонтальное развитие, располагаться в верхнем, среднем и нижнем ярусах.

Перистые облака очень высокие, имеют вид легких штрихов на ясном голубом небе. Они напоминают расположенные веером перья, т.е. по законам перспективы кажутся направленными к точке схода на горизонте. Их можно выполнять из тонких длинных прямоугольников или треугольников.

Высококучевые облака похожи на гряды, состоящие как бы из небольших комков. В зависимости от толщины слоя тон облаков меняется от светлого к темному. Между отдельными облаками видны просветы ясного неба. Слоисто-кучевые облака часто покрывают все небо, но толщина наслоения бывает различна, за счет чего образуется «волнистая поверхность» с чередованием светлых и темных тонов. Их можно составлять из кругов и полукругов.

Известную трудность представляет изображение водной поверхности и отражений на ней. Если лучи света падают на поверхность воды с волнами, то они отражаются под различными углами. Лучи, отраженные от гладкой поверхности воды, идут в одном направлении, поэтому мы видим наиболее четкие зеркальные отражения. В воде они равны по размерам отражающимся предметам и также подчинены законам перспективы. Все отражения повторяют формы предметов, но в опрокинутом виде. Так как даже в спокойной воде есть некоторые колебания, отражения всегда будут иметь менее четкие границы, чем сами предметы. Отражения в воде с волнами видны на чередующихся вогнутых и выпуклых поверхностях. Если волны небольшие, то отражение может быть многократным и дробными. Для выполнения отражения можно составить два одинаковых элемента композиции склеить их и одно разрезать поперек на тонкие полосы, которые затем приклеить зеркально (часть полосок можно убрать, чтобы отражение не получилось слишком растянутым).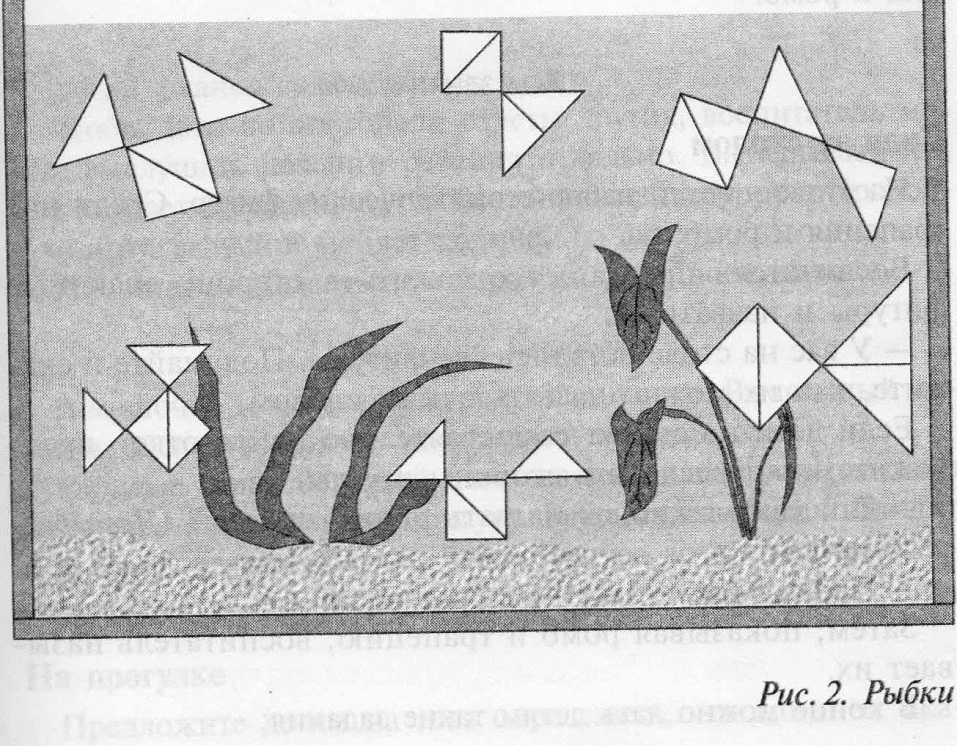

Данный вид работы можно выполнять, используя различные векторные компьютерные программы. Подойдут Microsoft PowerPoint, CorelDRAW, Microsoft Word и аналоги.

Работы можно выполнять в группах от 2 до 5 человек.

Критерии оценки:

1. Использование только трех видов геометрических фигур: круг, треугольник, прямоугольник – 1 балл.
2. Соответствие теме: водная или горная – 1 балл.
3. Цветное фон композиции, отсутствие белого цвета в фоне – 1 балл.
4. Соблюдение воздушной и линейной перспективы – 1 балл.
5. Многоплановость композиции – 1 балл.

Работа должна быть оформлена в соответствии с требованиями: http://mpgu.su/konkurs-liki-tvorchestva/oformlenie-rabot/

При выполнении компьютерной версии работы, необходимо присылать исходный файл, выполненный в перечисленных выше программах или их аналогах, а также файл, сохраненный в формате jpg, tif, или pdf.

Короткова С.А. — МБДОУ № 1 г.

Волчанск

Аппликация.

Уважаемые взрослые: мамы и папы, бабушки и дедушки, тёти и дяди, старшие братья и сёстры! Какие бы задачи в развитии вашего ребенка вы ни ставили перед собой, выполнение аппликации из бумаги повысит эффективность любых занятий. Работа с ножницами и бумагой тренирует мелкую моторику. Размещение деталей на листе бумаги развивает пространственное восприятие. Составляя орнаменты из геометрических фигур, малыш получит представление о точных науках и логике. Копирование готовых моделей приучает к аккуратности, а для работы над собственными эскизами нужны наблюдательность и фантазия.

Оборудование. Позаботьтесь о том, чтобы у вас было все необходимое для аппликации: инструменты, клей, бумага. Ножницы должны быть хорошо наточенными, не тугими и не тяжелыми для детской руки. Тупые будут «жевать» края бумаги, что сделает работу более трудоёмкой, а результат неаккуратным. Работая с некачественным инструментом, малыш быстро устает, раздражается, что может свести к нулю предполагаемую пользу. Выберите ножницы прямые с закругленными концами.

Простой карандаш для перевода рисунка на фон.

Кисточка для нанесения клея могут быть как из натуральной щетины, так и синтетические. Тонкая кисточка для работы с мелкими деталями, крупная – чтобы сэкономить время, проклеивая большие части аппликации.

Сразу договоритесь с ребенком, какой посудой пользоваться: отдельная чашечка с невысокими краями или блюдце для клея и стаканчик для кисточки. После окончания работы всё это нужно мыть и убирать в одно и то же место!

Выберите место на рабочем столе и для двух тряпочек. Влажной – вытирать руки от клея. Сухой – промокать и вытирать лишний  клей на самой аппликации. 

Цветная бумага. Это на ваш выбор. Не забывайте, что долго смотреть на блестящие материалы утомительно для глаз ребенка, поэтому выполнение больших объёмов работ с яркой «лакированной» бумагой и фольгой недопустимо!

Аппликация из геометрических фигур | Советы для занятий с детьми

Постараемся вас удивить. Хотя, кажется, чему здесь удивляться? Ведь что такое аппликация известно всем с детства. Аппликация — это кусочки бумаги или любого другого материала, наклеенные на… И все же, надеемся, что расскажем вам сегодня много полезного.

Удовольствие от создания аппликаций получают все и всегда. И создатель, и наблюдающий неизменно погружаются в атмосферу творчества и креатива. Можно клеить бумагу на бумагу, ткань на ткань, бумагу на ткань и наоборот. Можно создавать аппликации из природных материалов, можно узорно клеить макароны и различные крупы. В общем, можно клеить все и на все. И если при этом выходит красота и вы получаете удовольствие — значит вы занимались созданием аппликации.

Этот наш разговор тоже будет посвящен аппликации. Но аппликации не простой. Аппликации из геометрических фигур. Казалось бы, как просто: берем кружки, треугольники, ромбики, компонуем, получаем результат. Но все не так просто, как кажется на первый взгляд. Для того, чтобы результат получился правильным и красивым малышу необходимо точно соотнести размеры имеющихся у него фигурок с контурами на листке-задании. Это непростая работа развивает глазомер, ощущение пространства, учит различать по форме очень похожие друг на друга фигуры.

Вот взять, к примеру, круг и овал.. Если овал не очень вытянут, если он «толстенький», то его ничего не стоит перепутать с кругом. А трапеция? Толи это прямоугольник, толи треугольник — недолго и запутаться.

Для того, чтобы помочь ребенку легко и просто ориентироваться в «мире геометрических фигур» очень полезно заниматься с ним созданием аппликаций, элементы которой из этих самых геометрических фигур и состоят.

Перед началом работы над аппликацией, будет полезно сделать для ребенка «листы — тренажеры». Делаются они очень просто: вырезаются различные фигуры из разноцветной бумаги, затем обводятся по контуру. Это делается для того, чтобы на листе появились силуэты геометрических фигур. Ребенку предлагается сопоставить и наклеить каждую фигуру на подходящий именно ей силуэт. Потренировались? А теперь начинается самое интересное — создание из треугольников, квадратов и прочих разных ромбов и овалов разнообразных чудес.

Как в любом обучении, лучше всего двигаться от простого к сложному. Самое простое и легкое — елочка из трех треугольников. Ее, к тому же, можно украсить разнообразными кружками — шариками и «положить» под нее квадраты — подарки. Еще один простой вариант — «квадратная» гусеница. Можно создать длиннющую змею, практически удава,
если клеить гусеницу из большого количества квадратов.

Переходим к треугольникам, мы уже создали из них прекрасную елку, а теперь легко и просто склеим лягушку. Вот она, зеленая, лапчатая. Если сдвинуть друг относительно друга треугольники, составляющие голову, то можно получить разные «выражения» лягушачьего «лица». Можно добавить к лягушке корону из треугольников, естественно не такого большого, а гораздо меньшего размера.

«Соединяем» квадраты и треугольники. Как? Клеим домик. Домик — большой квадрат, окошки — маленькие квадраты, крыша — большой треугольник. Маленькими треугольниками можно «вырастить» траву вокруг дома.

Очень просто сделать гриб. Потребуется небольшой кружок и большая половина круга. Можно сделать один огромный гриб-мухомор, украсив его шляпку множеством малюсеньких кружочков. А можно сделать большую-пребольшую грибную поляну: круги и половинки кругов всех оттенков — ах, как получится радостно и разноцветно!

Продолжаем работу с кругами и их половинками. Будем клеить божьих коровок, они могут быть разными. В первом случае нам понадобится круг — тело божьей коровки, а также две половинки круга — крылышки. Маленькие кружочки — пятнышки на крылышках.

 Второй вариант отличается от первого внешним видом крыльев. Он потребует большого круга — для тела, и двух четвертинок круга — крылышек. Маленькие кружочки это снова пятнышки, кружочки чуть больше — глаза.

Пять кругов разного размера и четыре половины круга — и у нас получился чебурашка. В зависимости от размера фигур чебурашка может быть толще и стройнее, более или менее ушастым. Сделать коллекцию разных чебурашек, придумать им характеры, обусловленные особенностями их внешнего вида — задание не только творческое, но и психологическое.

Усложненный вариант компоновки круга, половинок и четвертинок — сова. Здесь снова самый большой круг — тело, большие
половинки — крылья, маленькие половинки — ушки, а три четвертинки — клюв и лапки. Глаза могут быть закрыты, широко распахнуты, могут быть больше или меньше. Крылья можно опустить «по швам», можно поднять, как будто сова парит, высматривая добычу.

Занятия этим видом аппликации — захватывают, удивляют ребенка. Побуждают к творчеству, поиску и открытию новых вариантов внешнего вида. Помогают изучать движение. Чуть-чуть измененные наклон и положение фигуры создает новый образ, который интересно изучать, менять, анализировать..

Займитесь с ребенком аппликацией из геометрических фигур и вы очень удивитесь, как многому научит вас и вашего ребенка это занятие.

Вот, к примеру, как вы думаете, сколько можно придумать вариантов аппликации Цветы ? Один? Три?  Пять?  А вы проверьте и удивитесь!

А какие аппликации вы сами делали в детском саду? Напишите в комментариях.

Squareo’scope определяет вид треугольника

Вот несколько экспериментов, в которых вы можете сделать открытия в области геометрии.

1 этап

Вам понадобится около шести тонких прямых палочек или тонких трубочек для питья. Разрежьте одну на 3 части. Могут ли биты образовывать треугольник? Не всегда получается сделать треугольник из трех заданных длин. Поэкспериментируйте с палками или соломкой разной длины и попытайтесь найти условие, определяющее, когда три длины действительно образуют треугольник, а когда нет.Это состояние называется треугольником .
Неравенство .

2 этап

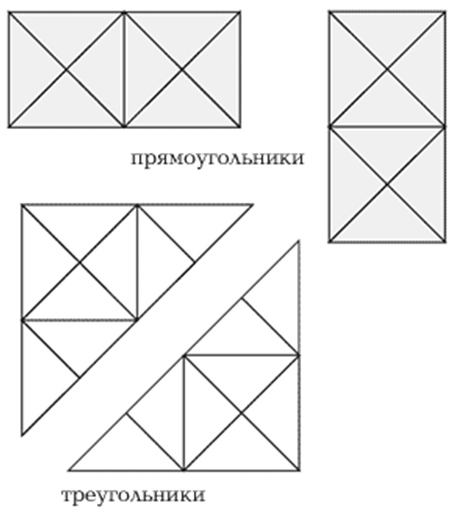
Теперь вам нужно квадратных кусочков бумаги (предпочтительно ламинированных) размером от 1 x 1 до 13 x 13 квадратов. В идеале квадраты должны быть ровными с одной стороны и иметь отмеченные квадраты с другой стороны.

Вместо палочек сделайте треугольники с краями трех квадратных кусочков по вашему выбору, используя плоские стороны. Каждый раз, когда вы составляете треугольник, определяйте, какой он острый, тупой или прямоугольный, и заполняйте первый столбец в таблице.

Напомним, что треугольник имеет остроту и , когда каждый из его углов на меньше, чем прямой или квадратный угол. Треугольник — это под прямым углом , когда один из его углов является прямым или квадратным. Треугольник тупой , когда один из его углов на больше, чем прямой угол или квадратный угол.

Иногда получаются остроугольные треугольники, иногда прямые, а иногда тупоугольные. Теперь переверните квадраты, показывающие сетки.

Используйте бумажные квадраты, чтобы сделать разные треугольники. Заполните таблицу, чтобы помочь вам найти тест для определения того, является ли треугольник остроугольным, прямым или тупоугольным. В последних трех столбцах заполните поле с помощью <, = или> соответственно.

Остановись и узнай. Запишите свои открытия. Согласны ли они с тем, что здесь сказано?

• Неравенство треугольника : Три длины образуют треугольник тогда и только тогда, когда сумма длин любых двух из трех больше, чем третья длина. Точно так же, как в одиночном тесте, три длины определяют треугольник тогда и только тогда, когда сумма двух самых коротких длин больше, чем самая длинная из сторон.
• Когда сумма квадратов на двух сторонах треугольника на больше, чем на , чем квадрат на третьей стороне, то же самое верно и для других пар сторон, и треугольник равен с острым углом .
• Когда сумма квадратов на двух сторонах треугольника равна квадрату на третьей стороне, тогда треугольник будет прямоугольным .
• Когда сумма квадратов на двух сторонах треугольника на меньше , чем квадрат на третьей стороне, тогда треугольник будет на тупоугольным .

Взлет

1. Продолжайте исследование, когда треугольники будут равнобедренными или равносторонними.
2. Не выполняя практических действий, можете ли вы определить тип треугольника по заданной длине сторон?
   1. 20,16,12
   2. 14,12,22
   3. 8,11,13
   4. 4,5.5,6,5
   5. 30,40,50
   6. 10,11,12
3. Как вы решите, является ли конкретный угол в треугольнике со сторонами заданной длины острым, прямым или тупым, не рисуя треугольник?

наклонных квадратов и прямоугольных треугольников

Каждый сеанс в этом модуле состоит из последовательности задач или задач. Предлагается, чтобы учащиеся имели возможность самостоятельно выполнять каждое задание, прежде чем они начнут делиться своими идеями с другими учащимися или со своим учителем.Роль учителя состоит в том, чтобы сначала внимательно слушать учеников, когда они пытаются объяснить свои мысли другим, а затем взаимодействовать с учениками только тогда, когда кажется, что они или их сверстники зашли в тупик. Такое взаимодействие может помочь прояснить мышление учащихся или даже перенаправить мышление там, где это необходимо.

Примечания были включены в начале каждого занятия, чтобы предоставить математическую основу, включая решения, а также по тем аспектам, которые могут вызвать определенные трудности для учащихся.Точный характер любого взаимодействия будет зависеть от ситуации и от достигнутого прогресса мышления.

Сессия 1

Записки учителя

Большинство учеников ограничивают свои квадраты четырьмя неотклоненными квадратами со сторонами 1, 2, 3 и 4 единицы. Предложите учащимся найти более четырех квадратов. Ищите студентов, у которых есть пять, шесть, семь или восемь квадратов — если у них восемь, четыре будут наклонными квадратами.

Как только у одного ученика появляется один из этих наклонных квадратов, не требуется много времени, чтобы все большее число учеников получало несколько наклонных квадратов.Затем предложите ученикам найти способ сказать, что у них есть все возможные квадраты. Послушайте, как студенты говорят друг с другом о своих площадях. Вероятно, что некоторые будут использовать такие выражения, как «один пробел поперек и два пробела вверх», или «один пробел поперек и два пробела вниз», или «два пробела поперек и 1 пробел вверх», или «два пробела поперек и 1 пробел вниз ‘и т. д. для описания наклонного квадрата [1, 2] или [2, 1]. Квадрат [1, 2] создается путем выбора угла квадрата в качестве начальной позиции и сдвига 1 клетки поперек, а затем 2 пробелов вверх, чтобы найти соседний угол.Этот процесс повторяется, чтобы найти третий, а затем четвертый углы. В подходящий момент попросите учащихся поделиться этим описанием с другими учащимися.

Для того, чтобы они могли быть уверены, что существует только восемь различных квадратов, учащимся необходимо разработать систематическую стратегию либо непосредственно на своих диаграммах гео-карт 4 на 4, либо перечислив их в таблице, подобной приведенной ниже.

Студенты обнаружат, что квадрат [2, 3] не помещается на их геодосках 4 на 4. Только те квадраты, для которых сумма двух чисел, используемых для описания квадратов, меньше или равна 4, уместятся на геодоске 4 на 4. Когда используется геодоска 5 на 5, сумма двух чисел, используемых для описания квадратов, должна быть меньше или равна 5. Фактически, только квадраты [ a , b ], где a и b — целые числа, а a + b ≤ n , уместится на географической плате n- на n .

В последнем задании на этом занятии предложите учащимся ввести свои результаты в таблицу, чтобы помочь им увидеть любые закономерности.

Итак, геодоска ( x + y ) -by- ( x + y ) — это наименьшая квадратная геодоска, на которой находится квадрат [ x , y ], где x и y — целые числа, подойдет.

Последовательность обучения

Задача 1

1. Сколько квадратов разного размера можно сделать на геодлане 4 на 4 (Copymaster 2). (Каждый квадрат должен иметь каждый угол по точке на географической доске.)

2. Найдите способ показать, как вы можете быть уверены, что нашли все возможные квадраты?

Задача 2

1. Наклонные квадраты ниже иногда называют [2, 1] квадратами.

   1. Покажите квадраты [2, 2] и [1, 3] на ваших диаграммах для вопроса 1. Объясните, как работает эта разметка.

   2. Решите, совпадает ли квадрат [1, 2] с квадратом [2, 1]. Объясните свои рассуждения.

   3. Обозначьте квадрат [1, 0] и объясните, что означает эта маркировка.

2. Используйте метод обозначения, [2, 1] и так далее, чтобы перечислить все квадраты, которые вы нашли для вопроса 1.Расположите квадраты по размеру.

3. Решите, должен ли квадрат [2, 3] быть в вашем списке. Сделайте рисунок, чтобы проверить.

Задача 3

1. Придумайте правило, которое можно использовать, чтобы определить, какие квадраты подходят для геодоски 4 на 4.

2. Создайте правило, указывающее, какие квадраты подходят для геодоски 5 на 5 (Copymaster 3). Нарисуйте квадраты, чтобы проверить свое правило.

3. Теперь придумайте правило, которое указывает, какие квадраты могут поместиться на геодлане n на n .

Задача 4

1. Предскажите размер самой маленькой геодоски, на которой поместится квадрат [3, 5]. Нарисуйте диаграмму на точечной бумаге (Copymaster 4), чтобы проверить свой прогноз.

2. Предскажите размер наименьшей геодоски, на которой уместятся следующие квадраты. Нарисуйте диаграммы на точечной бумаге, чтобы проверить свои прогнозы.
   а. [1, 2] б. [2, 4] c. [1, 6] d. [4, 7]

3. Разработайте правило для прогнозирования размера наименьшей квадратной геодоски, на которой уместится квадрат [ x , y ].Объясните, как работает правило.

Сессия 2

Записки учителя

На этом занятии учащиеся исследуют площадь квадратов, найденных на предыдущем занятии, и используют эти вычисления площади, чтобы помочь изучить взаимосвязи для того, что мы назвали [2, 1], [2, 3],… [ a , b ] треугольников.

Для учащихся, которые не видят, как окружающий квадрат может помочь в вычислении площади наклонного квадрата, предложите им представить, что окружающий квадрат образует четыре идентичных «отрывных» треугольника.Попросите учащихся посмотреть, смогут ли они найти способ вычислить площадь первых двух треугольников, которые вместе образуют прямоугольник 1 на 2, а затем четыре треугольника. Предложите студентам представить свои результаты в таблице, подобной приведенной ниже, чтобы помочь им увидеть закономерности.

Площадь [3, 4] квадрата равна 3 ² + 4 ² = 25 единиц ² , а площадь [5, 12] квадрата равна 5 ² + 12 ² = 169 Блок ² .Таким образом, площадь квадрата [ a , b ] равна a ² + b ² , где a и b — целые числа. Хотя это обобщение возникает из паттернов, включающих только целые числа, оно также верно и для квадратов, таких как [2.3, 1.6], то есть где a и b — действительные числа. Площадь квадрата [2,3, 1,6] тогда равна 2,3 ² + 1,6 ² = 7,85 ед. ² .

В задаче 6 первый прямоугольный треугольник — это треугольник [1, 2].Он формируется путем смещения одного промежутка на от начальной точки (нижний левый угол), чтобы найти второй угол (правый угол). Третий угол расположен путем смещения двух промежутков вверх на от второго угла. Сначала сосредоточьтесь на втором треугольнике, треугольнике [3, 1], и попросите учащихся объяснить значение своей маркировки, прежде чем маркировать другие треугольники: [2, 3], [2, 2] и [4, 3]. Скажите студентам, что у самой длинной стороны прямоугольного треугольника есть особое название; гипотенуза.

По мере того, как учащиеся рисуют, а затем вычисляют площади квадратов с каждой стороны разных треугольников, предложите им занести свои результаты в таблицу, подобную приведенной ниже.

Попросите учащихся внимательно поискать какие-либо закономерности, а затем написать своими словами правило для отношений, связывающих три области. Студенты могут поделиться своими правилами и объяснить их, прежде чем они будут формализованы в виде теоремы Пифагора:

Последовательность обучения

Задача 5

1. Найдите площадь следующего [2, 1] квадрата. Поможет окружающий квадрат, показанный на второй диаграмме.

2. Нарисуйте каждый квадрат в таблице ниже на бумаге с точками (Copymaster 4). Определите площадь каждого квадрата. (Может быть полезно нарисовать окружающие квадраты, как показано в вопросе 1 выше.)

   Площадь	Площадь (шт. 2 )
   [1, 0]	1
   [2, 0]	4
   [1, 1]
   [1, 3]
   [2, 3]
   [2, 4]

3. 1. Найдите какие-либо закономерности в своих ответах на вопрос 2, а затем посмотрите, можете ли вы предсказать площадь квадрата [3, 4] и квадрата [5, 12].
   2. Убедитесь, что правило работает, нарисовав квадрат на бумаге с точками.
   3. Объясните, как правило работает для квадрата [ a , b ].

Задача 6

1. Закрашенный прямоугольный треугольник ниже представляет собой треугольник [1, 2]. Обозначьте остальные треугольники.

2. На точечной бумаге (Copymaster 4) нарисуйте квадраты на сторонах прямоугольного треугольника [1, 2], как это. Найдите площадь каждого квадрата и отметьте площади на квадратах.

3. Нарисуйте три квадрата на сторонах других треугольников, указанных в вопросе 1. Найдите площадь каждого квадрата и отметьте площадь на нем.

4. Напишите правило, связывающее площади трех квадратов на сторонах любого прямоугольного треугольника. Объясните, как работает правило.

Сессия 3

Записки учителя

На этом занятии учащиеся используют теорему Пифагора для решения задач, имеющих геометрическую природу.Эти задачи по существу призваны помочь консолидировать понимание теоремы Пифагора.

Сначала они находят площадь каждого квадрата, для которого площадь не указана. Затем они используют свои результаты для вычисления длин сторон каждого квадрата. Площадь и длина указаны в таблице ниже. Значения, выделенные жирным шрифтом, — это значения, которые необходимо вычислить.

В задании 8 Q1 попросите учащихся нарисовать круг с помощью циркуля, а затем посмотреть, сколько прямоугольных треугольников они могли бы нарисовать с диаметром как гипотенуза — им следует измерить транспортиром, чтобы проверить прямой угол.На самом деле существует бесконечное количество прямоугольных треугольников, которые можно нарисовать с тремя углами на окружности и с гипотенузой в качестве диаметра. Таким образом, любой ответ, в котором сумма площадей двух меньших квадратов, которые могут быть нарисованы на двух более коротких сторонах, составляет 10 ² = 100 единиц ² , вероятно, приведет к правильной длине сторон.

В задании 8, Q2a, попросите учащихся сначала вычислить площади квадратов, которые можно нарисовать на каждой стороне треугольника. Эти области: 1 ² + 1 ² = 2 единицы ² , 3 ² + 3 ² = 18 единиц ² и
2 ² + 4 ² = 20 единиц ² .Таким образом, длины сторон квадратов составляют 1,41 единицы, 4,24 единицы и 4,47 единицы (с округлением до 2 десятичных знаков) соответственно. В Q2b длины сторон составляют 2,24 единицы, 4,47 единицы и 5 единиц, а в Q2c длины сторон составляют 3,16 единицы, 3,16 единицы и 4,47 единицы (все округлено до 2 десятичных знаков).

В задаче 8Q3 заштрихованные треугольники находятся внутри трехмерных тел. Например, в Q3a ABC представляет собой прямоугольный треугольник. Студенты должны представить себе квадрат, образованный с каждой стороны квадрата.Длины в таблице ниже рассчитаны с точностью до 2 десятичных знаков.

Последовательность обучения

Задача 7

1. В каждом прямоугольном треугольнике ниже показаны площади в квадратных единицах квадратов, нарисованных на двух сторонах треугольника.Проработайте площадь третьего квадрата.

2. Найдите площадь каждого третьего квадрата на следующих диаграммах. В любом случае ABC представляет собой прямоугольный треугольник.

3. Вычислите длины сторон треугольников в вопросах 1 и 2 выше.

Задача 8

1. В каждом круге ниже О — центр круга. AB = 10 см — это диаметр, а ABC — прямоугольный треугольник.

   Рассчитайте возможные длины двух более коротких сторон треугольников.

2. Вычислите длины сторон следующих прямоугольных треугольников, обозначенных ABC.

3. Закрашенные ниже треугольники ABC расположены под прямым углом. Вычислите длины сторон треугольников.

Сессия 4

Записки учителя

Чтобы вычислить диаметр AB окружности в Задании 9, ученики должны применить теорему Пифагора к прямоугольному треугольнику CED.Но сначала они должны увидеть, что
CP = CA и DP = DB. Для тех студентов, которым трудно определить длину CD, попросите их взглянуть на треугольники OAC и OPC и посмотреть, смогут ли они отработать CP, учитывая, что AC = 16 метров. В треугольнике CED, CD = 41 метр и ED = 25 — 16 = 9 метров. Поскольку по Пифагору, CD ² — DE ² = CE ² , затем CE ² = 41 ² — 9 ² = 40 ² и CE = 40 метров. Итак, AB = 40 метров. Заштрихованный участок на рисунке 1 представляет собой трапецию площадью
0.5 х (16 + 25) х 40 = 820 м ² .

Заштрихованное сечение, показанное на Рисунке 3 в Задаче 10, больше, чем сечение на Рисунке 1. Здесь CD = 50 метров, а CE = 40 метров = AB. Площадь трапеции теперь составляет
0,5 x (10 + 40) x 40 = 1000 м ² . Таким образом, в этом разделе больше земли, чем в предыдущем разделе, но он стоит столько же. Возможно, потребуется рассмотреть другие факторы, такие как позиция, прежде чем Эмбер сможет удостовериться, что это лучшая покупка.

Заполненные таблицы для Задачи 11 следующие.

Стол 1

Таблица 2

Таблица 3

Тем учащимся, которым трудно увидеть схему, связывающую значения для AB ² со значениями для AC и BD, предложите им попробовать умножить значения для AC и BD.Вполне вероятно, что тогда они увидят, что AB ² = 4 x AC x BD, что обычно записывается как
AB ² = 4AC.BD.

Если AC = a и BD = b , то CD = a + b и ED = b — a . Поскольку CD ² — DE ² = CE ² , то CE ² = ( a + b ) ² — ( a — b ) ² .
Но ( a + b ) ² — ( a — b ) ² = (( a + b ) + ( a — b )) ( ( a + b ) — ( a — b ))
= (2 a ) (2 b )
= 4 ab

Итак, AB ² = 4AC.BD верно для любых значений AC и BD.

Площадь трапеции с AC = a , BD = b и AB = √ (4 ab ) равна ( a + b ) √ ( ab ).

Последовательность обучения

Задача 9

Эмбер хочет купить секцию, на которой можно построить дом. Ей нравится форма заштрихованной секции (рис. 1), но она хочет знать размер (площадь) секции, прежде чем совершить покупку.

Одна сторона сечения представляет собой диаметр окружности, а другие стороны касаются этой окружности.Эмбер рисует диаграмму (рис. 2), чтобы помочь ей проработать область.

1. Определите длину бокового CD. Объясните свои рассуждения
2. Вычислите длину CE, а затем определите длину диаметра AB окружности. Покажи свою работу.
3. Рассчитайте площадь заштрихованного участка, показанного на рисунке 1.

Задача 10

1. Amber также смотрит на другой раздел (рисунок 3), цена которого совпадает с ценой в разделе на рисунке 1.Она думает, что это может быть лучшая покупка. Вычислите площадь, чтобы убедиться, что она верна.

Задача 11

1. Подруга Эмбер, Марк, предполагает, что существует формула, которую Эмбер могла бы использовать для своих расчетов. Поэтому Эмбер систематически перечисляет результаты нескольких вычислений в таблицах, чтобы помочь ей увидеть любые закономерности.

   Стол 1

   AC	BD	Расчет, чтобы найти CE 2	AB 2
   1	1	2 2 -0 2	4
   1	2
   1	3
   1	4
   1	5

   Таблица 2

   AC	BD	Расчет, чтобы найти CE 2	AB 2
   2	1	3 2 — 1 2	8
   2	2
   2	3
   2	4
   2	5

   Таблица 3

   AC	BD	Расчет, чтобы найти CE 2	AB 2
   3	1	4 2 — 2 2	12
   3	2
   3	3
   3	4
   3	5

   1. Скопируйте и заполните таблицы.
   2. Найдите закономерности и затем напишите формулу или правило для AB ² в терминах AC и BD.
2. Положим AC = a и BD = b . Затем используйте алгебру, чтобы доказать, что ваша формула для AB ² всегда работает.
3. Найдите формулу площади любого участка, у которого три стороны касаются окружности, как в примерах выше.

Сессия 5

Записки учителя

На этом занятии студенты придумывают формулы, которые можно использовать для вычисления троек Пифагора.Числа (3, 4, 5) образуют тройку Пифагора, поскольку 3 ² + 4 ² = 5 ² , что указывает на то, что треугольник со сторонами 3 единицы, 4 единицы и 5 единиц является прямоугольным треугольником. . Пифагоровы тройки состоят только из натуральных чисел, 2, 2, 3,…. Любой набор из трех натуральных чисел ( a , b , c ) является тройкой Пифагора, если a ² + b ² = c ² , где c > a и c > b .Пифагорова тройка (3, 4, 5) известна как примитив , поскольку наибольший общий делитель 3, 4 и 5 равен 1. Однако, хотя (6, 8, 10) является пифагорейской тройкой, она не является примитивной. так как наибольший общий множитель 6, 8 и 10 равен 2, а не 1. Развивающиеся числовые модели, показанные в таблицах для Заданий 12, 13 и 14, вероятно, будут понятны большинству учащихся.

В задаче 12 a = 2 k + 1, b = 2 k ( k + 1) и c = 2 k ( k + 1) + 1.
Так a ² + b ² = (2 k + 1) ² + (2 k ( k + 1)) ²
= (4 k ² + 4 k + 1) + 4 k ² ( k ² + 2 k + 1)
= 4 k ² + 4 k + 1 + 4 k ⁴ + 8 k ³ + 4 k ²
= 4 k ⁴ + 8 k ³ + 8 k ² + 4 к + 1.
Также c ² = (2 k ( k + 1) + 1) ²
= (2 k ² + 2 k + 1) ²
= (4 к ⁴ + 4 к ³ + 2 к ² ) + (4 к ³ + 4 к ² + 2 к ) + (2 k ² + 2 k + 1)
= 4 k ⁴ + 8 k ³ + 8 k ² + 4 k + 1
= a ² + b ² .

Так как a ² + b ² = c ² , затем a , b и c образуют тройку Пифагора.

В электронной таблице на рисунке 4 показаны формулы, используемые для вычисления первых 25 троек Пифагора (рисунок 5), где значение для c всегда на единицу больше, чем значение для b , то есть где c = b + 1.

В Задаче 13: a = 4 ( m + 1), b = 4 ( m + 1) ² -1, и c = 4 ( m + 1) ² + 1.Обратите внимание, что c = b + 2.
Итак, a ² + b ² = (4 ( m + 1)) ² + (4 ( m + 1 ) ² — 1) ²
= (16 м ² + 32 м + 16) + (4 м ² + 8 м + 3) ²
= (16 м ² + 32 м + 16) + (16 м ⁴ + 64 м ³ + 88 м ² + 48 м + 9)
= 16 м ⁴ + 64 м ³ + 104 м ² + 80 м + 25.
Также c ² = (4 ( м + 1) ² + 1) ²
= 16 м ⁴ + 64 м ³ + 104 м ² + 80 м + 25
= a ² + b ² .

Так как a ² + b ² = c ² , затем a , b и c образуют тройку Пифагора.

В электронной таблице на рисунке 6 показаны формулы, используемые для вычисления первых 25 троек Пифагора (рисунок 7), где значение для c всегда на два больше, чем значение для b , то есть где c = b + 2.

В Задаче 14, a = 2 xy , b = x ² — y ² и c = x ² + y ² где x и y — натуральные числа, а
x > y .

Так a ² + b ² = (2 xy ) ² + ( x ² — y ² ) ²
= 4 x ² y ² + x ⁴ — 2 x ² y ² + y ⁴
= x ⁴ + 2 x ² y ² + y ⁴
= ( x ² + y ² ) ²
Но c ² = ( x ² + y ² ) ²
Так a ² + b ² = c ² .

Так как a ² + b ² = c ² , затем a , b и c образуют тройку Пифагора.

Последовательность обучения

Задача 12

Пять пифагоровых троек ( a , b , c ) показаны в таблице ниже. Обратите внимание, что в каждом наборе чисел значения для c всегда на единицу больше, чем значение для b .

1. Напишите числа, которые идут в пустые поля в таблице.
2. Напишите алгебраические формулы для b и c , когда n = k .
3. Сгенерируйте как минимум десять дополнительных троек Пифагора, которые следуют шаблону в таблице. (Вы можете использовать электронную таблицу.)
4. Докажите, что алгебраические формулы для a , b и c для шаблона в таблице являются троек Пифагора.

Задача 13

Пять различных троек Пифагора ( a , b , c ) показаны в следующей таблице.Обратите внимание, что в каждом наборе чисел значение для c всегда на два больше, чем значение для b .

1. Напишите числа, которые идут в пустые поля в таблице.
2. Напишите алгебраические формулы для b и c , когда n = m .
3. Сгенерируйте как минимум десять дополнительных троек Пифагора, которые следуют шаблону в таблице. (Вы можете использовать электронную таблицу.)
4. Докажите, что алгебраические формулы для a , b и c для шаблона в таблице являются троек Пифагора.

Задача 14

1. Внимательно ищите образцы в следующей таблице.Затем заполните таблицу.

2. Числа a в таблице могут быть представлены алгебраическим правилом 2 xy , где x и y — натуральные числа, а x > y .Напишите алгебраические правила для b и c , используя x и y .
3. Докажите, что алгебраические выражения для a , b и c образуют примитивные пифагоровы тройки.
4. Сгенерируйте по крайней мере еще пять примитивных троек Пифагора, используя правила для a , b и c из таблицы. (Убедитесь, что каждый набор чисел является тройным, подтвердив связь:
   a ² + b ² = c ² .)

Треугольники и фермы — Урок

.

Быстрый просмотр

Уровень оценки: 10
(9–12)

Требуемое время: 30 минут

Зависимость урока: Нет

Тематические области:
Геометрия, Физика

Резюме

Студенты узнают об основной прочности различных форм, демонстрируя, почему инженеры-строители продолжают использовать треугольник в качестве структурной формы выбора.Приведены примеры из повседневной жизни, чтобы показать, как эта форма постоянно используется для повышения прочности конструкции. Наряду с сопутствующим заданием, этот урок дает учащимся возможность изучить прочность ферм, сделанных из различных треугольных элементов, чтобы оценить различные структурные свойства.

Инженерное соединение

Многие инженеры в различных областях занимаются строительным проектированием, от аэрокосмических инженеров, которые проектируют спутниковые конструкции, до инженеров-строителей, проектирующих мосты и эстакады, до инженеров-механиков, которые проектируют шасси автомобилей и размещают компоненты внутри компьютеров и сотовых телефонов.Формы, включенные в эти конструкции, существенно влияют на прочность конструкций. Этот урок вовлекает учащихся в обсуждение силы различных геометрических фигур, таких как квадраты и треугольники, без необходимости в более продвинутом физическом анализе.

Цели обучения

После этого урока учащиеся должны уметь:

• Перечислите места, где они видят треугольники, используемые для увеличения прочности конструкции.
• Объясните, почему треугольник — самая сильная геометрическая форма.

Образовательные стандарты

Каждый урок или задание TeachEngineering соотносится с одним или несколькими научными дисциплинами K-12,
образовательные стандарты в области технологий, инженерии или математики (STEM).

Все 100000+ стандартов K-12 STEM, охватываемых TeachEngineering , собираются, обслуживаются и упаковываются сетью стандартов достижений (ASN) ,
проект D2L (www.achievementstandards.org).

В ASN стандарты иерархически структурированы: сначала по источникам; например , по штатам; внутри источника по типу; например , естественные науки или математика;
внутри типа по подтипу, затем по классу, и т. д. .

Международная ассоциация преподавателей технологий и инженерии — Технология

ГОСТ

Предложите выравнивание, не указанное выше

Какое альтернативное выравнивание вы предлагаете для этого контента?

Рабочие листы и приложения

Посетите [www.teachengineering.org/lessons/view/cub_trusses_lesson01], чтобы распечатать или загрузить.

Больше подобной программы

Многоугольники, углы и фермы, о боже!

Студенты внимательно изучают ферменные конструкции, геометрические формы, из которых они состоят, и множество вариаций, которые можно увидеть в конструкциях мостов, используемых каждый день. С помощью рабочего листа учащиеся рисуют различные 2D- и 3D-формы многоугольников и продумывают их формы и внутренние углы (мысленное «тестирование»)…

Везде треугольников: сумма углов в многоугольниках

Учащиеся узнают о правильных многоугольниках и общих характеристиках правильных многоугольников. С помощью управляемого рабочего листа и совместной работы учащиеся изучают идею деления правильных многоугольников на треугольники, вычисления суммы углов в многоугольниках с использованием треугольников и определения углов в формах с помощью…

Выполнение математических расчетов: анализ сил в ферменном мосту

Изучите основы анализа сил, которые инженеры применяют в соединениях фермы для расчета прочности моста фермы, известного как «метод соединений». Найдите напряжения и сжатия для решения системы линейных уравнений, размер которой зависит от количества элементов и узлов в ферме…

У вас есть треугольники!

Учащиеся узнают о тригонометрии, геометрии и измерениях, участвуя в практическом взаимодействии с технологией LEGO® MINDSTORMS®. Сначала они рассматривают основные геометрические и тригонометрические концепции. Затем они оценивают высоту различных объектов с помощью простой тригонометрии.Студенты …

Предварительные знания

Студенты должны иметь базовые знания геометрии, в частности, знать, что правильные геометрические формы, такие как квадраты, пятиугольники и шестиугольники, можно свести к треугольникам. Они также должны знать, как вычислить сумму внутренних углов многоугольника путем преобразования многоугольника в треугольники.

Введение / Мотивация

Строительная инженерия — одна из старейших форм инженерии. Самые ранние здания, дороги, акведуки и мосты требовали структурного проектирования, чтобы обеспечить их функциональность и безопасность. Однако структурная инженерия не уникальна для зданий. Фактически, аэрокосмические инженеры используют структурную инженерию при проектировании спутников, инженеры-механики используют структурную инженерию, когда они проектируют рамы автомобилей, даже компьютерные инженеры используют структурную инженерию, чтобы выяснить, как лучше всего подключить видеокарту к материнской плате!

В этом уроке вы узнаете, как инженеры-строители полагаются на фундаментальную геометрию, с помощью которой мы можем легко предсказать производительность, для проектирования структурно надежных объектов и зданий.После урока учащиеся могут провести увлекательное практическое занятие «Разрушение фермы», в котором они будут строить фермы с помощью палочек от мороженого и горячего клея, а затем проверять их на отказ, оценивая относительную прочность различных конфигураций фермы и стилей строительства.

(Затем покажите учащимся презентацию «Сила фигур», используя предложенный сценарий, приведенный в разделе «Предпосылки урока».)

Предпосылки и концепции урока для учителей

(Следующий текст соответствует презентации Strength of Shapes Presentation, PowerPoint.Убедитесь, что у учащихся есть бумага и карандаш для набросков своих идей по ходу презентации.)

( Slide 1 ) Сегодня мы исследуем фундаментальную конструктивную концепцию: прочность форм.

( Slide 2 ) Когда мы внимательно смотрим на мосты, мы видим, как инженеры-строители используют различные формы для создания общей конструкции. Мы видим треугольники и квадраты. Мы даже можем видеть параболы.

( Slide 3 ) Инженеры-конструкторы используют те же типы форм в зданиях.Многие рамы зданий представляют собой просто повторяющиеся квадраты, как показано в верхнем левом углу. На нижнем левом изображении показано, как квадрат укрепляется путем добавления диагональной поперечной распорки в эти леса, которая разбивает квадрат на два треугольника. На изображении справа показана строящаяся антарктическая геодезическая. Структура геодезических куполов похожа на структуру футбольных мячей и может рассматриваться как группа пятиугольников и шестиугольников. Но если мы разобьем каждую из этих фигур, мы увидим, что они в основном состоят из треугольников.

( Slide 4 ) Даже когда мы выходим за рамки гражданского или архитектурного проектирования, мы можем видеть, как инженеры полагаются на известную прочность форм. В раме мотоцикла используется множество треугольников для поддержки колес и сидений. Инженеры-механики проектируют краны, в рамах которых используются треугольники и квадраты. Даже спутники используют эту знакомую и простую регулярную геометрию.

( Slide 5 ) На бумаге нарисуйте каждый из этих правильных многоугольников: квадрат, ромб и треугольник.Если мы надавим на фигуру прямо вниз, заставив всю фигуру сжать, что произойдет с формой? Нарисуйте другой ручкой, карандашом или пунктирной линией, как бы форма выглядела, если бы вы ее нажали. Предположим, что стороны фигуры жесткие, не изменяют длину и не изгибаются.

( Slide 6 ) Взгляните на это! Если вы нажмете на верхнюю часть квадрата, он больше не будет квадратом, а вместо этого примет форму ромба, который является разновидностью параллелограмма. Это называется «стеллажи».«Если мы надавим на вершину алмаза, он рухнет. А как насчет треугольника? Треугольник сохраняет свою форму!

( Slide 7 ) Причина обрушения квадрата и ромба в том, что угол между элементами конструкции может изменяться без изменения или изгиба длины элементов. Помните, как мы вернулись к геометрии, когда мы говорили о том, как определяются полигоны? В этом случае для обоих четырехугольников просто требуется, чтобы сумма внутренних углов равнялась 360 градусам, но каждый угол может измениться.

( Slide 8 ) Треугольники уникальны в этом смысле. Угол между двумя сторонами треугольника основан на длине противоположной стороны треугольника. Вы помните это по геометрии? Угол «а» фиксирован на основе относительной длины стороны «А». Точно так же, как угол «b» фиксируется на основе относительной длины «B» и «c» на основе «C». Вот почему треугольник не может разрушиться!

( Slide 9 ) Как мы показали, другие правильные многоугольники можно деформировать без изменения длины сторон.Квадрат теряет свою форму, поскольку его прямые углы схлопываются, а пятиугольник и шестиугольник могут деформироваться. Но формы остаются «закрытыми», потому что сумма внутренних углов остается постоянной. Для фигуры с n сторонами сумма внутренних углов будет равна 180 * (n-2). Таким образом, сумма углов треугольника равна 180 градусам или 180 * (3-2) градусам. Сумма углов квадрата равна 360 градусам или 180 * (4-2). Итак, что мы можем сделать с другими формами, квадратами, пятиугольниками и шестиугольниками, чтобы они не разрушились? Нарисуйте эти фигуры на бумаге и добавьте то, что будет необходимо.

( Slide 10 ) Вы разбили фигуры на треугольники? Поскольку мы знаем, что треугольник не может схлопнуться, и мы знаем, что эти правильные многоугольники всегда можно свести к треугольникам (именно так мы вычисляем сумму внутренних углов, помните?), Разбиение наших многоугольников на треугольники предотвращает их сжатие!

( Slide 11 ) Та же концепция применима в трех измерениях. Как показано, куб может разрушиться, «раскачиваясь», точно так же, как квадрат, который мы видели, разрушился в двух измерениях.Итак, что бы мы сделали, чтобы создать прочную трехмерную структуру?

( Slide 12 ) Делаем 3D треугольники! В частности, мы можем сделать прямоугольные или треугольные пирамиды! Вот почему инженеры-строители полагаются на треугольники, как в 2D, так и в 3D, для создания прочных конструкций! Трехмерная конструкция, состоящая из отдельных структурных треугольников, таких как эта, называется «фермой» и используется в процессе проектирования для создания прочной и легкой конструкции!

Сопутствующие мероприятия

• Разрушение фермы — учащиеся конструируют фермы с помощью палочек для мороженого и горячего клея, а затем проверяют их на разрушение, оценивая относительную прочность различных конфигураций фермы и стилей строительства.

Закрытие урока

Теперь, когда мы рассмотрели основы того, как инженеры-строители полагаются на структурные формы, я надеюсь, что вы начнете замечать в своей повседневной жизни то, как строятся объекты. Посмотрите вокруг себя, на здания, краны, мосты, дома, машины и мебель, и вы увидите, что большая часть структурной инженерии основана на этих фундаментальных и простых формах.

Далее, в этом упражнении вы познакомитесь с проектированием, строительством и испытанием структурных ферм. Так что не забывайте о наших обсуждениях различных форм и о том, как их можно использовать для создания прочных структур.

Словарь / Определения

сжатие: сжимающая сила.

поперечная скоба: диагональный структурный элемент, который разбивает многоугольники более высокого порядка на простые треугольники.

геодезический: изогнутая форма, созданная прямыми линиями или объектами.

парабола: форма, естественно образованная веревкой, удерживаемой за оба конца и позволяющей провисать; математически основан на квадратном уравнении.

стеллаж: процесс сворачивания фигуры из правильного многоугольника в неправильный многоугольник.

правильный многоугольник: многоугольник, который является равносторонним (все стороны равной длины) и равноугольным (все внутренние углы равны).

Строительные леса: временная конструкция, построенная вокруг здания, чтобы обеспечить людям безопасный доступ к возвышенностям. Например, чтобы рабочие могли класть кирпич, устанавливать отделку или красить.

ферма: конструкция, состоящая из одного или нескольких треугольных элементов с прямыми отдельными элементами.

Оценка

Вступительный вопрос: Спросите учащихся, какая правильная геометрия (треугольник, квадрат, круг, пятиугольник, шестиугольник и т. Д.)) они считают сильнейшим и почему. (Ответ: Треугольник — самая прочная форма, и в этом уроке мы выясним, почему!) Формы треугольника обычно используются для прочности и опоры конструкции. Авторское право

Copyright © 2013 Дениз У. Карлсон, Университет Колорадо в Боулдере

Практика по встроенной геометрии: Попросите учащихся принять участие, выполнив два задания по рисованию, описанные в презентации PowerPoint.

1. Нарисуйте на листе бумаги каждый из этих правильных многоугольников: квадрат, ромб и треугольник.Если мы надавим на фигуру прямо вниз, заставив всю фигуру сжать, что произойдет с формой? Нарисуйте другой ручкой, карандашом или пунктирной линией, как бы форма выглядела, если бы вы ее нажали. Предположим, что стороны фигуры жесткие, не изменяют длину и не изгибаются. (Ответ: если вы надавите на верхнюю часть квадрата, его углы в 90 градусов схлопнутся, и он превратится в простой ромб, который является разновидностью параллелограмма. Если мы надавим на вершину ромба, он рухнет. Ничего не произойдет. к треугольнику; он остается треугольником.)
2. Нарисуйте на листе бумаги каждый из этих многоугольников: квадрат, пятиугольник и шестиугольник. Что мы можем сделать с этими формами, чтобы они не разрушились? Нарисуйте эти фигуры на бумаге и добавьте то, что будет необходимо. (Ответ: Используйте линии, чтобы разбить фигуры на треугольники.)

Личная релевантность: После презентации слайдов PowerPoint (или в качестве домашнего задания) попросите учащихся индивидуально перечислить на своих листах места, объекты, структуры и продукты, в которых они видели треугольники, функционирующие как структурные формы.Через пять минут предложите каждому ученику прочитать свой список классу, а вы составите на доске общий список их ответов. (Возможные ответы: мосты, опоры электропередачи, краны, остроконечные крыши, столы, стулья, велосипеды, велосипедные стойки, перила, заборы, ворота, опоры для полок, кронштейны, опоры для рекламных щитов и т. Д.)

Мероприятия по продлению урока

Рассмотрите возможность проведения многоугольников, углов и ферм, о боже! урок и связанные с ним задания, «Треугольники повсюду: сумма углов в многоугольниках и многоугольниках» и «Фермы эскимо», во время которого учащиеся внимательно изучают ферменные конструкции и рисуют многоугольники, чтобы мысленно «проверить» их формы и внутренние углы до и после нагрузки применяемый.Во время упражнений учащиеся делят правильные многоугольники на треугольники, чтобы вычислить суммы углов в многоугольниках, и изучают уравнения, чтобы найти сумму внутренних углов в правильном многоугольнике и найти меру каждого угла в правильном n-угольнике. Затем, чтобы решить гипотетическую реальную задачу, они проектируют, создают и испытывают прочные и уникальные ферменные конструкции, состоящие из палочек от мороженого и горячего клея, а затем сравнивают измерения углов до и после многоугольников для анализа деформации форм

.

Авторские права

© 2013 Регенты Университета Колорадо

Авторы

Дарси Чиннис, Аманда Гилиани, Скотт Дакворт, Малинда Шефер Зарске

Программа поддержки

Комплексная программа преподавания и обучения, Инженерный колледж, Университет Колорадо в Боулдере

Благодарности

Содержание этой электронной библиотеки было разработано в рамках Комплексной программы преподавания и обучения в рамках гранта GK-12 Национального научного фонда.DGE 0338326. Однако это содержание не обязательно отражает политику Национального научного фонда, и вам не следует предполагать, что оно одобрено федеральным правительством.

Последнее изменение: 30 апреля 2021 г.

квадратов по сторонам треугольника

Теорема Пифагора показывает нам важное свойство квадратов, построенных на сторонах прямоугольного треугольника, а именно, что c ^{2 =} a ² + b ² :

Но Есть интересные свойства квадратов, построенных на сторонах любого треугольника , которые мы исследуем в этой геометрической задаче.

Задача

На сторонах AB и AC треугольника ΔABC построены два квадрата. Покажите, что CE = BD, и что CE⊥BD.

Стратегия

Мы рассмотрим эту проблему в двух частях — сначала покажем, что отрезки линии равны, а затем покажем, что они перпендикулярны.

Разделение сложных проблем на более мелкие, управляемые части часто помогает увидеть, как доказать каждую часть по отдельности.

Доказательство того, что отрезки равны

Для первой части нам нужно показать, что CE = BD, и, как мы обычно делаем, мы посмотрим, есть ли совпадающие треугольники, у которых они являются соответствующими сторонами.

Давайте посмотрим на два треугольника, уже представленных в постановке задачи, в которых CE и BD — стороны, треугольники ΔACE и ΔADB.

Мы построили квадраты по сторонам треугольника ΔABC, у квадрата все стороны равны. Итак, у нас уже есть две стороны, которые совпадают: AD = AC и AB = AE. Третья сторона — это то, что нам нужно доказать, что она равна (CE = BD), поэтому, очевидно, мы не можем полагаться на это.

Поищем углы. Поскольку у нас уже есть две конгруэнтные стороны, самым простым способом было бы использовать постулат Side-Angle-Side, поэтому давайте посмотрим на углы между двумя конгруэнтными сторонами: ∠DAB и ∠CAE.

DAB состоит из ∠CAB плюс угол 90 ° (∠DAC) от квадрата. Точно так же ∠CAE состоит из ∠CAB плюс угол 90 ° (∠BAE) от другого квадрата. Итак, оба они равны m∠CAB + 90 и конгруэнтны. Таким образом, треугольники равны, и CE = BD как соответствующие стороны.

Доказательство того, что отрезки перпендикулярны

Теперь обратимся ко второй части, показывающей, что отрезки перпендикулярны. Для этого нужно будет показать, что один из ангелов в точке пересечения X равен 90 °.

Давайте посмотрим, сможем ли мы достичь этого, используя математику углов. Мы воспользуемся тем фактом, что здесь есть квадраты с прямыми углами.

Обозначим ACE «γ». Мы доказали, что треугольники ΔACE и ΔADB конгруэнтны, поэтому m∠ACE = m∠ADB = γ. Теперь посмотрим на ∠AZD. Это внешний угол к ΔDAZ, поэтому по теореме о внешнем угле он равен сумме двух удаленных внутренних углов — так что он равен γ + 90 °.

Но ∠AZD — это , а также , внешний угол к ΔZCX, поэтому по теореме о внешнем угле он равен сумме двух удаленных внутренних ангелов — поэтому он равен γ + m∠ZXC.

Но если m∠AZD = γ + 90 ° и m∠AZD = γ + m∠ZXC, то m∠ZXC = 90 ° и CE⊥BD.

Proof

(1) AD = AC // Определение квадрата
(2) AB = AE // Определение квадрата
(3) m∠DAC = 90 ° // Определение квадрата
(4) m∠BAE = 90 ° // Определение квадрата
(5) ∠DAB ≅ ∠CAB + ∠DAC // Постулат сложения углов
(6) ∠CAE ≅ ∠CAB + ∠BAE // Постулат сложения углов
(7) ∠DAB ≅ ∠CAE // (3), (4), (5), (6), транзитивное свойство равенства
(8) ΔACE ≅ ΔADB // (1), (2), (7), Side- Угол-сторона
(9) CE = DB // (8), Соответствующие стороны в равных треугольниках (CPCTC)

А теперь формально докажем вторую часть:
(10) ∠ACE≅∠ADB // (8), Соответствующая сторона в конгруэнтных треугольниках (CPCTC)
(11) m∠ACE = m∠ADB = γ // Определение конгруэнтных углов
(12) m∠AZD = γ + 90 ° // Теорема о внешнем угле в ΔDAZ
(13) m∠AZD = γ + m∠ZXC // Теорема о внешнем угле в ΔZCX
(14) m∠ZXC = 90 ° // (12), (13), транзитивное свойство равенства
(15) CE⊥BD // ( 14), определение перпендикулярных прямых

Воспользуемся этими двумя фактами (CE = B D и CE⊥BD) в следующей задаче.

Иллюстративная математика

Комментарий IM

Цель этого задания — проверить, выполняется ли теорема Пифагора на двух конкретных примерах. Хотя работа над этой задачей не обеспечивает доказательство полной теоремы Пифагора, она подготавливает студентов к вычислениям площади, которые им нужно будет выполнить, а также к трудностям показать, что четырехугольник на плоскости является квадратом.

Для правильного равнобедренного треугольника учащиеся могут найти площадь трех квадратов, построенных по сторонам треугольника, и убедиться, что сумма площадей меньших квадратов равна площади самого большого квадрата.Одной из особенностей этого прямоугольного треугольника является то, что учащиеся могут привести хороший аргумент в пользу того, почему четырехугольник с гипотенузой в качестве одного ребра является квадратом. Во втором примере такая проверка будет сложной задачей, поэтому учащимся разрешается предположить, что этот четырехугольник на самом деле квадрат. Если учитель желает более глубоко изучить этот аспект задания, доступно несколько вариантов:

• Учащиеся могут исследовать симметрии четырехугольника с помощью программного обеспечения для работы с геометрией или бумажных лепешек.
• С помощью жестких движений учащиеся могут видеть, что стороны четырехугольника совпадают: это можно сделать с помощью последовательных отражений координатной сетки или с помощью вращений, если учащиеся могут определить центр поворота на 90 градусов, который сохраняет четырехугольник.
• Учащиеся могут использовать тот факт, что сумма углов в треугольнике равна 180 градусам, чтобы показать (используя любую из картинок в решении (b)), что четыре угла в четырехугольнике являются прямыми углами.2 $, где $ a $, $ b $ и $ c $ — длины сторон прямоугольного треугольника, где $ c $ — длина гипотенузы. В этой задаче результат представлен для двух конкретных треугольников геометрической формы, представляющих образ мышления древнегреческих геометров. Â

  Теорема Пифагора — объяснение и примеры

  Теорема Пифагора, , также известная как « теорема Пифагора, », возможно, самая известная математическая формула , которая определяет отношения между сторонами прямоугольного треугольника.

  Приписывают теорему греческому математику и философу по имени Пифагор (569-500 до н. Э.). Он внес большой вклад в математику, но теорема Пифагора является наиболее важной из них.

  Пифагору приписывают несколько вкладов в математику, астрономию, музыку, религию, философию и т. Д. Одним из его заметных вкладов в математику является открытие теоремы Пифагора. Пифагор изучил стороны прямоугольного треугольника и обнаружил, что сумма квадрата двух более коротких сторон треугольников равна квадрату самой длинной стороны.

  В этой статье e обсуждается, что такое теорема Пифагора , ее обратная формула и формула теоремы Пифагора . Прежде чем углубляться в тему, вспомним прямоугольный треугольник. Прямоугольный треугольник — это треугольник, внутренний угол которого равен 90 градусам. В прямоугольном треугольнике две короткие ножки встречаются под углом 90 градусов. Гипотенуза треугольника противоположна углу в 90 градусов.

  Что такое теорема Пифагора?

  Теорема Пифагора — это математический закон, который гласит, что сумма квадратов длин двух коротких сторон прямоугольного треугольника равна квадрату длины гипотенузы .

  Теорема Пифагора алгебраически записывается как:

  a ² + b ² = c ²

  Как выполнить теорему Пифагора?

  Рассмотрим прямоугольный треугольник выше.

  Учитывая, что:

  ∠ ABC = 90 °.

  Пусть BD — прямая, перпендикулярная стороне AC.

  Подобные ∆s:

  ∆ADB и ∆ABC — подобные треугольники.

  Из правила подобия

  ⇒ AD / AB = AB / AC

  ⇒ AD × AC = (AB) ² —————– (i)

  Аналогично;

  ∆BDC и ∆ABC — подобные треугольники.Следовательно;

  ⇒ DC / BC = BC / AC

  ⇒ DC × AC = (BC) ² —————– (ii)

  Комбинируя уравнения (i) и (ii), мы получаем
  AD × AC + DC × AC = (AB) ² + (BC) ²

  ⇒ (AD + DC) × AC = (AB) ² + (BC) ²

  ⇒ (AC) ² = (AB) ² + (BC) ²

  Следовательно, если мы положим AC = c; AB = b и BC = b, тогда;

  ⇒ c ² = a ² + b ²

  Существует множество демонстраций теоремы Пифагора , приведенных разными математиками.

  Еще одна распространенная демонстрация — это нарисовать 3 квадрата таким образом, чтобы они образовывали прямоугольный треугольник между ними, а площадь большего квадрата (в гипотенузе) равна сумме площадей меньшего. два квадрата (те, что с двух сторон).

  Рассмотрим 3 квадрата ниже:

  Они нарисованы таким образом, что образуют прямоугольный треугольник. Мы можем записать их площади в виде уравнения:

  Площадь квадрата III = Площадь квадрата I + Площадь квадрата II

  Предположим, что длина квадрата I , квадрата II, и квадрат III — это a, b и c соответственно.

  Тогда

  Площадь квадрата I = a ²

  Площадь квадрата II = b ²

  Площадь квадрата III = c ²

  Следовательно, мы можем написать это как:

  a ² + b ² = c ²

  , что является теоремой Пифагора.

  Обращение теоремы Пифагора

  Обращение теоремы Пифагора — это правило, которое используется для классификации треугольников как прямоугольный, острый или тупой.

  Учитывая теорему Пифагора, a ² + b ² = c ² , затем:

  • Для острого треугольника c ² 2 + b ² , где c равно сторона, противоположная острому углу.
  • Для прямоугольного треугольника c ² = a ² + b ² , где c — сторона угла в 90 градусов.
  • Для тупого треугольника c ² > a ² + b ² , где c — сторона, противоположная тупому углу.

  Пример 1

  Классифицируйте треугольник с размерами; a = 5 м, b = 7 м и c = 9 м.

  Решение

  Согласно теореме Пифагора, a ² + b ² = c ² тогда;

  a ² + b ² = 5 ² + 7 ² = 25 + 49 = 74

  Но, c ² = 9 ² = 81
  Сравните: 81> 74

  Отсюда c ² > a ² + b ² (тупой треугольник).

  Пример 2

  Классифицируйте треугольник, длина сторон которого a, b, c составляет 8 мм, 15 мм и 17 мм соответственно.

  Решение
  a ² + b ² = 8 ² + 15 ² = 64 + 225 = 289
  Но, c ² = 17 ² = 289
  Сравните: 289 = 289

  Следовательно, c ² = a ² + b ² (прямоугольный треугольник).

  Пример 3

  Классифицируйте треугольник с длинами сторон: 11 дюймов, 13 дюймов и 17 дюймов.

  Решение
  a ² + b ² = 11 ² + 13 ² = 121 + 169 = 290
  c ² = 17 ² = 289
  Сравните: 289 <290

  Следовательно, c ² 2 + b ² (острый треугольник)

  Формула теоремы Пифагора

  Формула теоремы Пифагора имеет вид:

  ⇒ c ² = a ² + b ²

  где;

  c = длина гипотенузы;

  a = длина одной стороны;

  b = длина второй стороны.

  Эту формулу можно использовать для решения различных задач, связанных с прямоугольными треугольниками. Например, мы можем использовать формулу для определения третьей длины треугольника, когда известны длины двух сторон треугольника.

  Применение формулы теоремы Пифагора в реальной жизни

  • Мы можем использовать теорему Пифагора, чтобы проверить, является ли треугольник прямоугольным или нет.
  • В океанографии формула используется для расчета скорости звуковых волн в воде.
  • Теорема Пифагора используется в метеорологии и авиакосмической сфере для определения источника звука и его дальности.
  • Мы можем использовать теорему Пифагора для расчета электронных компонентов, таких как экраны телевизоров, компьютерные экраны, солнечные панели и т. Д.
  • Мы можем использовать теорему Пифагора для вычисления градиента определенного ландшафта.
  • В навигации теорема используется для вычисления кратчайшего расстояния между заданными точками.
  • В архитектуре и строительстве мы можем использовать теорему Пифагора для расчета уклона крыши, дренажной системы, плотины и т. Д.

  Рабочие примеры теоремы Пифагора:

  Пример 4

  Две короткие стороны прямоугольного треугольника равны 5 см и 12 см. Найти длину третьей стороны

  Решение

  Дано a = 5 см

  b = 12 см

  c =?

  Из формулы теоремы Пифагора; c ² = a ² + b ² , имеем;

  c ² = a ² + b ²

  c ² = 12 ² + 5 ²

  c ² = 144 + 25

  √c ² = √169

  c = 13.

  Следовательно, третий равен 13 см.

  Пример 5

  Длина диагонали и одной стороны треугольной стороны составляет 25 см и 24 см соответственно. Каков размер третьей стороны?

  Решение

  Используя теорему Пифагора,

  c ² = a ² + b ² .

  Пусть b = третья сторона

  25 ² = 24 ² + b ²
  625 = 576 + b ²
  625-576 = 576-576 + b ²
  49 = b ²
  b ² = 49

  b = √49 = 7 см

  Пример 6

  Найдите размер экрана компьютера, размеры которого составляют 8 дюймов и 14 дюймов.

  Подсказка: диагональ экрана равна его размеру .

  Решение

  Размер экрана компьютера совпадает с его диагональю.

  Используя теорему Пифагора,

  c ² = 8 ² + 15 ²

  Решите относительно c.

  c ² = 64 + 225

  c ² = 289

  c = √289

  c = 17

  Следовательно, размер экрана компьютера составляет 17 дюймов.

  Пример 7

  Найдите площадь прямоугольного треугольника, учитывая, что диагональ и основания составляют 8,5 см и 7,7 см соответственно.

  Решение

  Используя теорему Пифагора,

  8,5 ² = a ² + 7,5 ²

  Решите для a.

  72,25 = a ² + 56,25

  72,25 — 56,25 = k ² + 56,25 — 56,25

  16 = a ²

  a = √16 = 4 см

  Площадь прямоугольного треугольника = ( ½) x основание x высота

  = (½ x 7.7 x 4) см ²

  = 15,4 см ²

  Практические вопросы

  1. Канат длиной 20 м протягивается от вершины 12-метрового дерева до земли. Какое расстояние между деревом и концом веревки на земле?
  2. К стене прислонена лестница длиной 13 м. Если расстояние от основания лестницы до стены составляет 5 м, какова высота стены?

  Предыдущий урок | Главная страница | Следующий урок

  Квадраты, круги и треугольники оказывают сильное психологическое влияние на дизайн | Автор: Майкл Райнер

  Фото: https: // www.123rf.com/photo_2751571_confetti-made-of-multi-colored-triangles-circles-and-squares-scattered-on-pale-green-back-round-.html

  Психология форм очень важна, потому что она может помочь вашему дизайну. имеет смысл. Геометрические формы наиболее эффективны, когда вы пытаетесь продвигать бренд или бизнес. Геометрические формы включают круги, квадраты, треугольники, прямоугольники и кресты. Все мы знаем о геометрических формах, потому что нас учили им в ранние школьные годы. Квадраты, круги и треугольники — три самых узнаваемых геометрических фигуры.

  Прямоугольники и квадраты имеют прямые простые края, которые символизируют стабильность. Квадраты представляют собой строительные блоки, а это означает, что мы часто сталкиваемся с их психологическим посланием в детстве. Многие профессиональные бизнес-логотипы имеют форму квадрата, потому что они хотят повысить надежность. Стивен Пит объяснил, что квадраты также символизируют силу и стабильность.

  Однако квадраты и прямоугольники можно интерпретировать как скучные формы. Важно использовать квадраты разных цветов в одной инфографике, потому что это помогает повысить интерес, не теряя стабильности, которую обеспечивают квадраты.Квадраты могут быть не такими привлекательными физически, как другие геометрические фигуры, но цвета определенно могут усилить их воздействие.

  Можно с уверенностью сказать, что круги — полная противоположность квадратам и прямоугольникам. Они способствуют открытости, единению и теплу. Прошлые исследования показали, что младенцы чаще смотрят на круги и овалы, чем на все другие формы.