Знакомство с новым вычислительным приемом 30
Тема урока: Знакомство с новым вычислительным приемом 30 — 7.
Цель урока: Познакомить детей с новым вычислительным приемом 30 — 7.
Задачи урока:
Обучающие:
1. Познакомить детей с приемами вычислений для случаев вида 30-7.
2. Совершенствовать вычислительные навыки умения решать задачи.
3. Закрепить изученные приемы сложения и вычитания в пределах 100.
Развивающие:
1.Развивать познавательный интерес и умение делать выводы, основанные на выполненных действиях.
Оборудование урока: индивидуальные карточки с числами; счетный материал; компьютер; интерактивная доска.
План урока:
1. Организационный момент. Проверка рабочего места. (1 мин.)
(1 мин.)
2. Мотивация учебной деятельности. Введение сюжета.( 5 мин.)
3. Актуализация опорных знаний. Устный счет. (5 мин.)
4. Постановка учебной задачи. Планирование урока ( 5 мин.)
5. Знакомство с новым материалом. Работа с счетным материалом. ( 6 мин.)
6. Физкультминутка (2 мин.)
7. Применение полученных знаний. Отработка приема с подробным проговариванием в знакомой ситуации, в новой ситуации. (15мин)
8. Рефлексия. ( 5 мин.)
9. Домашнее задание. ( 1 мин.)
Ход урока.
— Итак, друзья, внимание –
Вновь прозвенел звонок.
Садитесь поудобнее –
Сейчас начнем урок.
Готовятся к уроку.
Личностные УУД (самоопределение)
Коммуникативные УУД (планирование учебного сотрудничества с учителем и сверстниками)
2. Мотивация учебной деятельности
Мотивация учебной деятельности
Сегодня мы с вами совершим путешествие.
А вот куда? Вы определите сами. Дополните числа до круглого десятка, расставьте их в порядке возрастания. Каждому числу соответствует буква.
65, 27, 48, 11, 44, 42
Называют числа:
5, 3, 2, 9, 6, 8
Записывают их в порядке возрастания.
2, 3, 5, 6, 8, 9.
На экране – таблица
1
2
3
4
5
6
7
8
9
и
с
к
у
а
з
м
к
а
В соответствии с таблицей составляют слово «Сказка».
Познавательные логические УУД (сериация)
3. Актуализация опорных знаний (устный счет)
Перед нами карта сказочного королевства. Нам необходимо пробраться к замку, преодолевая различные трудности.
Итак, первое испытание. Прыгаем по числовым кочкам.
— Приготовьте свои карточки с числами.
— Уменьшить до круглого десятка:
56, 87, 41, 16
Мы оказались на улице Загадочных домиков. Понаблюдайте за окошками в домиках и подумайте, какое же задание вы должны выполнить?
Показывают карточки с числами: 6, 7, 1, 6
Наблюдают, придумывают задание: заполнить окошки. (Приложение)
Регулятивные УУД (прогнозирование)
4. Постановка учебной задачи
На нашем пути вдруг появилась Мудрая Сова. Она не дает нам пройти дальше, пока мы не решим примеры. На экране появляются примеры.
56-4=
48-5=
30-7=
99-7=
87-2=
— Какой пример вызвал затруднение? Почему?
— Чему мы будем учиться сегодня на уроке? С каким вычислительным приемом познакомимся?
Решают примеры. Возникает трудность при решении примера 30 – 7
— 30 – 7. В числе 30 нет единиц, а вычесть нужно единицы.
— Будем учиться вычитать однозначные числа из круглых чисел.
Личностные УУД (формирование грани собственного знания и «незнания»)
Познавательные УУД ( постановка и решение проблем)
Регулятивные УУД (планирование)
5. Знакомство с новым материалом
Мудрая сова предлагает решить этот пример с помощью счетных палочек.
Работаем в парах.
Положите перед собой палочки. Отложите число 30.
— А сейчас вычтите из этого числа 7. Обсудите с товарищем, как вы это будете делать. Предложите свой вариант
Будете развязывать все пучки?
— Сколько палочек в одном пучке?
— Развяжите один пучок. Мы можем сейчас вычесть число 7.
— Что осталось?
— Посмотрите, как это действие записано в учебнике числами. (стр. 61)
— Попробуйте объяснить запись. (Сначала говорит один ученик, затем хором весь класс)
— Поблагодарим Сову за совет. Пообещаем, что воспользуемся им.
Пообещаем, что воспользуемся им.
Работают с палочками.
— Нет, достаточно развязать один.
-10
— 23
Смотрят в учебник, сравнивают запись в учебнике числами с наглядным материалом.
— Заменяем число 30 суммой 20 и 10. Из 10 вычитаем 7, получаем 3. Прибавляем 3 к 20. Ответ 23.
Коммуникативные УУД (работа в парах)
Познавательные УУД (выдвижение гипотез и их обоснование; умение строить рассуждение)
Познавательные логические УУД (сравнение)
Познавательные логические УУД (открытие нового приема, построение умозаключения на основе только что полученных знаний)
6. Физкультминутка
Раз, два — выше голова,
Три, четыре — руки шире,
Пять, шесть — тихо сесть,
Семь, восемь — лень отбросим.
Раз — согнуться – разогнуться,
Два нагнуться, подтянуться,
Три — в ладоши три хлопка,
Головою три кивка.
На четыре — руки шире,
Пять, шесть — тихо сесть,
Семь, восемь — лень отбросим.
Выполняют упражнения.
Снятие усталости.
7. Применение полученных знаний
( В знакомой ситуации)
— На нашем пути — новое испытание. Очень хочется пить, а добыть воды из колодца можно, решив примеры. ( № 2)
— № 3 – 1 столбик – у доски с объяснением, остальные примеры самостоятельно, с последующей проверкой.
Индивидуальное задание на смекалку 9 на полях )для тех, кто справился быстрее
Наше путешествие продолжается . Перед нами на пенёчке сидит Гномик Вася. Он не может пойти в школу, потому что никак не выполнит задание учителя.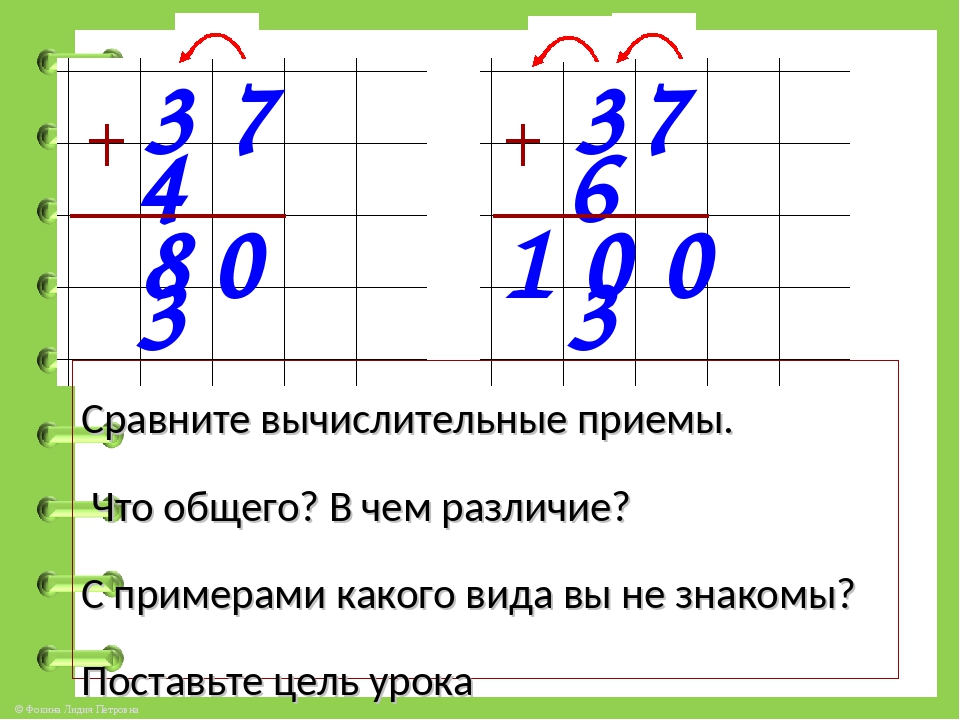 Давайте поможем Васе. (№ 5)
Давайте поможем Васе. (№ 5)
— Обсудите в парах, какие вопросы можно задать к данной задаче?
— Предложите свои идеи всему классу?
— Чтобы решить задачу, что нам необходимо?
— Вася поблагодарил нас за помощь и указал дорогу к замку.
(В новой ситуации)
— Но подход к замку охраняют стражники. Они отказывались пропустить нас, пока мы не выполним их задание. (№6)
46 4 10 = 52
32 2 4 = 30
30 = 40
60 = 54
На экране примеры с пропущенными знаками действий.
Подумайте и скажите, какие знаки нужно вставить.
Решают примеры с устным объяснением у доски.
50-6=44
Заменяем число 50 суммой 40 и 10. Из 10 вычитаем 6, получаем 4. Прибавляем 4 к 40. Ответ 44.
70-4 = 66
Заменяем число 70 суммой 60 и 10. Из 10 вычитаем 4, получаем 6. Прибавляем 6 к 60. Ответ 66.
90-3 = 87
Заменяем число 90 суммой 80 и 10. Из 10 вычитаем 3, получаем 7. Прибавляем 7 к 80. Ответ 87.
Прибавляем 7 к 80. Ответ 87.
100-9 = 91
Заменяем число 100 суммой 90 и 10. Из 10 вычитаем 9, получаем 1. Прибавляем 1 к 90. Ответ 91.
1 ученик: 70 — 5 = 65
Заменяем число 70 суммой 60 и 10. Из 10 вычитаем 5, получаем 5. Прибавляем 5 к 60. Ответ 65.
2 ученик: 80 — 4 = 76
Заменяем число 80 суммой 70 и 10. Из 10 вычитаем 4, получаем 6. Прибавляем 6 к 70. Ответ 76.
100-4=96
100-9=91
52+8=60 Самостоятельно
60-8=52 в тетрадях
43-20=23
43-2=41
Читают задачу.
— В комнате стояло 2 кресла, а стульев на 4 больше, чем кресел. Поставь вопрос, чтобы задача решалась двумя действиями. Реши её.
Идет обсуждение в парах.
Предлагают свои вопросы к задаче.
— Сколько стояло стульев в комнате?
— Сколько всего было мебели в комнате?
— Составить план решения.
Обсуждают решение. Составляют план решения.
К.-2 шт.
? шт.
С.- ? шт., на 4 б.
Записывают решение.
Решение:
1) 2+4=6(шт.) стульев
2)2+6=8(шт.)
Ответ: 8 шт. мебели было в комнате.
Решают примеры устно.
Коммуникативные УУД (проговаривание алгоритма действий)
Регулятивные УУД (работа по аналогии)
Регулятивные УУД (работа по аналогии)
Познавательные УУД (использование символов вместо знаков действий и чисел)
Регулятивные УУД (постановка вопросов)
Коммуникативные УУД (работа в парах)
Познавательные УУД (выдвижение гипотез и их обоснование; умение строить рассуждение)
Познавательные логические УУД
(построение логической цепи рассуждений, высказывание предположений, поиск решения поставленной задачи)
Регулятивные УУД (планирование)
Познавательные логические УУД
(построение логической цепи рассуждений)
8. Рефлексия
Рефлексия
Вот мы и у замка, в нём 4 замка в виде примеров: 80 – 8, 100 – 7, 40 – 4, 70 – 2.
Решив их, мы попадаем на сказочный маскарад.
Выберите маску для него. Если вы на уроке были активны, вам было интересно, ваша маска улыбается.
Если не сразу всё получалось – возможно маска пока грустит
Решают примеры.
80-8=72; 100-7 = 93;
40-4=36; 70-2=68
Оценивают свою работу, выбирают маску
Регулятивные УУД (самооценка)
9. Домашнее задание
— Ребята, на дом вы возьмете №4 и № 7.
Записывают в дневник.
Приложение.
Числовые кочки.
Окошки
Мудрая Сова
Гномик Вася
Замок
Маски
1. | Прозвенел и смолк звонок, Начинаем мы урок. Улыбнулись, подтянулись Друг на друга посмотрели И спокойно, тихо сели. — Ребята, я хочу, чтобы сегодняшний урок принес нам радость общения друг с другом. Я желаю, чтобы за время работы на уроке вы поднялись на ступеньку выше. Успеха и удачи вам! | Приветствуют друг друга, садятся и слушают учителя. | Л-1, Л-5, К-2 | 2.Актуализация знаний | Откройте тетради, запишите число, классная работа. -Ребята, сейчас мы проведем математический диктант. Вам нужно записать только ответ. Ответы записываем в строчку. -Запишите число, в котором 3 дес. -Запишите сумму чисел 62 и 4. -Запишите сумму чисел 40 и 6. -Запишите число, которое больше 37 на 1. -Запишите число, которое больше 57, но меньше 59. -Запишите сумму чисел 48 и 2. -Запишите число, в котором 3 дес. и 4 ед. -Запишите число, которое больше 60 на 2. -Запишите разность чисел 46 и 4. -Запишите сумму чисел 51 и 3. -Прочитайте ответы по порядку. -Сверьте свои ответы с правильными ответами на доске. -Расположите числа в порядке возрастания. Какая закономерность в ряду чисел у вас получилась? — Правильно! -Следующее задание нужно выполнить в парах. На каждой парте лежит карточка с заданием. Вам нужно поставить знаки так, чтобы получились верные неравенства. Неравенства: 32+4…50+2 27+2…35-5 47-4…40+2 36+4…30+8 56-6…58+2 65+3…60+4 -Сверьте свои ответы с правильными ответами на доске. -Молодцы! Вы справились со вторым заданием! -Ребята, следующее задание представлено на слайде. Вам необходимо решить данные примеры: 65+2=… 75-5=… 47+3=… 30+8=… 53+2=… 30-7=… -Какой пример вы не могли решить? Почему? -Ребята, какую цель мы поставим на урок? С каким вычислительным приемом познакомимся? | -Открывают тетрадь, записывают число, классная работа. -Слушают учителя -30 -66 -46 -38 -58 -50 -34 -62 -42 -54 -30, 66, 46, 38, 58, 50, 34, 62, 42, 54. -Сверяют свои ответы с эталоном на слайде -30, 34, 38, 42, 46, 50, 54, 58, 62, 66. Увеличение на 4. -Слушают учителя. -Решают неравенства -Сверяют свои ответы с эталоном на слайде -Слушают учителя. -Решают примеры. -Не смогли решить последний пример (30-7=). В числе 30 нет ед., а нужно вычесть единицы. Не решали подобные примеры. -Научиться решать примеры вида «30-7». Вычитание единиц из целых десятков (из круглого числа).
| К-2 П-1, П-5, П-6, Позн-2, Л-3,4, Р-2, К-3 К-2, Л-4, П-1, П-5, П-6, Р-2, К-2, Позн-1, Р-1, К-1,3 | 3. | -Прежде чем познакомиться с новым вычислительным приемом, давайте проведем физминутку: Мы считали и решали, И немножечко устали. А теперь, ребята, встали. Быстро руки вверх подняли, В стороны, вперед, назад. На носочки встали, Потолок достали. Повернулись вправо, влево. Тихо сели, вновь за дело. | -Повторяют движения за учителем. | К-2, Л-5 | 4. «Открытие» новых знаний | -Ребята, кто-нибудь знает, как решаются эти выражения? -Прочитайте выражение 30-7 по-разному. (На доске развернутая запись) -Замените уменьшаемое-30 суммой двух круглых чисел, одно из которых-10. -Получим: из суммы чисел 20 и 10 вычитаем 7. -Как удобнее вычесть? -Получим: к 20 прибавить разность чисел 10 и 7. -Найдите разность в скобках. -Прибавьте к 20 три. Сколько получим? -Назовите значение выражения. -Таким образом мы будем вычитать однозначные числа из круглых двузначных чисел. | -Ответы детей -Уменьшаемое-30, вычитаемое-7, найти разность; из 30 вычесть 7; разность чисел 30 и 7. -30=20+10 -(20+10)-7 -Удобнее вычесть из 10 семь -20+(10-7) -10-7=3 -20+3=23 -23 | П-1,2,3,4,5, Р-3, К-1,2,3,4, Позн-2,3, Л-2,3 | 5.Первичное закрепление. | На доске записан пример 50-6= К доске выходит один учащийся. -Реши данный пример, проговаривая вслух выполненные шаги. Если ученик затрудняется, учитель задает вопросы: -Прочитай выражение по-разному -Как заменить уменьшаемое- 50 суммой двух круглых чисел, одно из которых 10? -Что получим? -Как удобнее вычесть? -Что получим? -Найди разность в скобах. -Какое действие теперь нужно выполнить? (прибавить к 40 четыре) -Сколько получим? -Прочитай ответ. -Запишите в тетради развернутую запись решения данного примера. -Откройте учебник на стр.61. Посмотрите на задание №4. Вам нужно самостоятельно в тетради решить примеры. 1-ый вариант решает примеры 1-го столбика, 2-ой вариант — примеры 2-го столбика. -Кто решил примеры, поменяйтесь тетрадью с соседом по парте и оцените правильность решения примеров. -Молодцы, вы справились с заданием! -Теперь выполним №6. Вам нужно поставить знаки + и — так, чтобы получились верные равенства. Решить нужно только первую строчку. Всем понятно, что нужно сделать? -Давайте проверим, какие равенства у вас получились. Учитель спрашивает нескольких учеников. У всех получилось такое равенство? У кого получилось другое, кто не согласен с ответом? -Следующее задание, которое мы выполним- №8, решение задачи. Прочитайте задачу самостоятельно. Прочитайте условие задачи. -О чем говорится в задаче? -Что о них сказано? -Что значит «короче»? -Что значит «длиннее»? -Составим краткую запись к задаче. Я на доске, а вы в тетради. -Как узнать, на сколько одно число больше или меньше другого? -Что сказано про шаг обезьяны? -Что сказано про шаг утки? -Можем ли мы узнать какой шаг у утки? -Каким действием? -Прочитайте главный вопрос задачи. Можем ли мы на него ответить? -Почему? -Можем ли мы узнать, сколько см шаг слона? -Каким действием? -Теперь мы можем ответить на главный вопрос задачи? -Каким действием? -Какой шаг больше? -Какой шаг меньше? -Как узнать, на сколько шаг утки меньше шага слона? -Запишите решение задачи по действиям с пояснение и выражением. Учитель вызывает двух учеников к доске. 1-ый записывает решение задачи по действиям с пояснением, 2-ой записывает решение задачи выражением. Учитель оценивает учащихся. | -К доске выходит ученик. Комментирует решение примера: Читаю выражение по-разному: 1) Уменьшаемое-50, вычитаемое-6, найти разность; 2) из 50 вычесть 6; 3) разность чисел 50 и 6 Заменю уменьшаемое-50 суммой двух круглых чисел, одно из которых-10: 50=40+10 Получу: из суммы чисел 40 и 10 вычесть 6 (40+10)-6 Удобнее вычесть из 10 шесть Получу: к 40 прибавить разность чисел 10 и 6 40+(10-6) Нахожу разность в скобках:10-6=4 Прибавляю к 40 четыре. Получу 44. Читаю ответ: 44. 50-6=(40+10)-6=40+(10-6)=40+4=44 -Слушают учителя. Решают примеры. -Взаимооценивание. -Слушают учителя. Выполняют задание №6. — Учащиеся внимательно слушают и сравнивают свой ответ (равенства) с ответами учеников. Исправляют ошибки. -Читают задачу. -О шагах. -Что шаг обезьяны 15 см, утки на 10 см короче, а слона на 20 см длиннее. -Меньше. -Больше. -Учащиеся составляют вместе с учителем краткую запись к задаче. -Из большего вычесть меньшее. — Он равен 15 см. -Он короче на 10 см. -Да. -Вычитанием. -Нет. -Нам не известен шаг слона. -Да. -Сложением. -Да. -Вычитанием. -Шаг слона. -Шаг утки. -Из большего вычесть меньшее. -Записывают решение задачи в тетради. -К доске выходят двое учащихся. Записывают решение задачи указанным способом. Остальные учащиеся проверяют, исправляют, дополняют отвечающих. | П-1,2,3,4,5, К-1,2,3,4, Позн-2,3, Л-2,3,4,5, Р-2,3 | 6. Рефлексия | -Ребята, какая была цель сегодняшнего урока? -Как считаете, мы достигли поставленной цели? -У вас на партах лежат три кружка: красный, желтый, зеленый. -Если не смогли решить все задания, то поднимите красный кружок. — Если, вы испытывали трудности, но все-таки выполнили задания, то поднимите желтый кружок. — Если вы справились со всеми заданиями без ошибок, поднимите зеленый кружок. – Какие возникали трудности при выполнении заданий? – Какое задание показалось сложнее других? Какое задание понравилось больше всего? Сообщение д/з. Всем спасибо за урок, вы сегодня хорошо поработали, урок окончен, до свидания! | — Научиться решать примеры вида «30-7». Познакомиться с новым вычислительным приемом – вычитание единиц из целых десятков (круглого числа). -Отвечают на вопрос учителя. -Слушают учителя. Оценивают себя. -Отвечают на вопросы учителя. -Прощаются. | К-1,2,3,4, Л-2,5 |
Математика 2класс
Математика 2класс
Тема: «Вычитание двузначных чисел
с переходом через разряд».
Цели:
Ввести прием вычитания двузначных чисел с переходом через разряд; закрепить изученные вычислительные приемы, умение самостоятельно анализировать и решать составные задачи; развивать мышление, речь, познавательные интересы, творческие способности.
Ход урока.
I.Организационный момент.
Учитель: Сегодня нам предстоит изучить новый вычислительный прием.
II.Постановка учебной задачи.
1. Решение примеров на вычитание с переходом через разряд в пределах 20 (ответы на доске).
Учитель: Как можно разбить эти примеры на группы? Что общего у всех примеров? Какие примеры на вычитание вы еще умеете решать?
2. Решение примеров на вычитание двузначных чисел без перехода через разряд.
Решение примеров на вычитание двузначных чисел без перехода через разряд.
*9-64, 7*-54, *5-44, 3*-34, *1-24
Учитель: Что интересного в разностях?
Разгадайте уменьшаемое, если известно, что разность между цифрами, обозначающими десятки и единицы, равна 3.
3. Постановка проблемы.
41-24=?
Учитель: Чем последний пример отличается от предыдущих?
Цель нашего урока – изобрести прием вычитания, который поможет нам решать такие примеры.
III.
Изучение новой темы
(дети выкладывают модель примера)
º-ºººº
Учитель: Как вычитать двузначные числа? Почему здесь возникла трудность? Разве у нас уменьшаемое меньше вычитаемого? Где же спрятались единицы? Что надо сделать? (заменить 1 десяток единицами).
ºººººººººº
º-ºººº=ººººººº
3дес.-2дес.=1дес.; 11ед.-4ед.=7ед.
Наш пример мы могли бы записать и решить так:
41
24
17
О чем всегда надо помнить при использовании этого приема?(число десятков уменьшается на 1).
IV.
Физкультминутка.
V.
Первичное закрепление.
1.
Комментирование примера по образцу:
ºº-ººººº=ºººººººººº
ºº-ººººº=ººººººº
2. Решение примеров и соединение рисунков с равенствами.
Решение примеров и соединение рисунков с равенствами.
ºº-ººººº=ººººººº
(1)
24-6=18 (2)
ºººº-ºººººº=ºººººººº
(2)
43-24=19 (3)
ººº-ºººº=ººººººººº
(3) 32-15=17
(1)
3. Игра «Угадай-ка»
82-6 41-17 74-39 93-45
82-16 51-17 74-9 63-45
(решаем только первый пример, а второй – угадываем)
VI.
Самостоятельная работа с проверкой в классе.
1. Выбор и решение примеров (на новый прием)
98-19 64-12
76-18
89-14
54-17
2.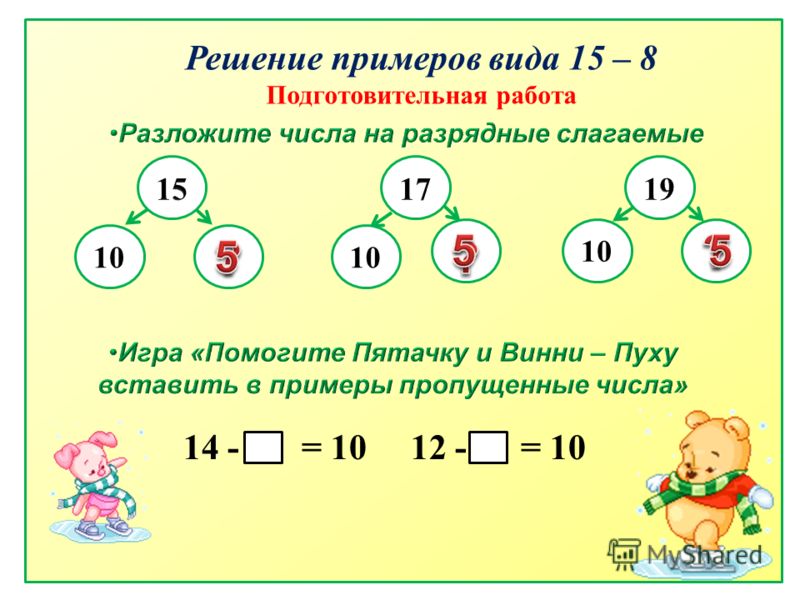 Проверка по готовому образцу.
Проверка по готовому образцу.
3.
Учитель: Напишите свой пример, который продолжал бы эту закономерность, и решите его.
VII.
Итог урока.
Учитель: Придумайте и решите примеры на новый вычислительный прием.
VIII. Домашнее задание.
Открыть новый способ сложения переходом через десяток | Личностные: -формировать интерес к изучению математики, -формировать уважение к мыслям и настроениям другого человека, Метапредметные: -уметь самостоятельно планировать и выполнять свои действия, -уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение (Регулятивные УУД). Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им, уметь слушать и вступать в диалог, участвовать в коллективном обсуждении (Коммуникативные УУД). Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке (Познавательные УУД). | Цель: актуализировать опорные знания и способы действий; выявить уровни знаний. Физ. минутка Цель: создание условий для укрепления мышц и снятия усталости, помощь школьникам в переключении их деятельности. Выявление места и причины затруднения (проблемная ситуация) Построение проекта и решение проблемы Реализация сформированной модели Первичное закрепление с проговариванием вслух | Работа в группах (на планшетках): На доске записаны числа 15,2,26,10,7,31,80,12,44,6 -Расставьте данные числа в порядке убывания (дети работают в группах по 4 человека. Та группа, которая закончила первой-диктует свой вариант.Затем сверяются с эталоном на доске. 80,44,31,26,15,12,10,7,6,2. —Оцените себя в тетради на полях! -На какие группы можно разделить данные числа? (на двузначные и однозначные) -Какие числа называем однозначными, какие- двузначными? (дети вспоминают правила) -Какое сегодня число? (___) -Из каких разрядов состоит это число? (единиц, десятков) -Какая цифра стоит в разряде десятков? единиц? Работа в тетрадях (в парах) -Откройте тетради и запишите сегодняшнее число и классная работа. Минутка чистописания (числа 3 и 4 чередуем до конца строки) -На следующей строке числа 34 45 56-найдите закономерность (каждый раз число увеличивается на 1 десяток и одну единицу). Оцените соседа на полях! -Посмотрите на доску, составьте задачу по краткой записи. Решение задач (на доске краткая запись к задаче) Брюк-47 шт Юбок-? на 3шт Работа у доски с проговариванием компонентов действий в числовых выражениях и доказательством нахождения результата действия (проговаривают правила на каждое числовое выражение в решении задач) -О чем будем решать задачу? (о брюках и юбках) -Что нам известно по условию задачи? (брюк-47) -Что сказано про юбки? (их не известно, но сказано, что их на 3 больше). Как это на 3 больше? (Это столько же и еще три). -Какой вопрос в задаче? (Сколько юбок?) -Можем сразу найти ответ на наш вопрос? (да) -Каким действием? (сложением) -Запишите решение задачи (на доске один ученик с объяснением как находит значение числового выражения 47+3=40+(7+3) — раскладываем 47 на два разрядных слагаемых 40 и 7, чтобы 7 дополнить до 10-ка 40+10=50 -Запишем ответ Следят только глаза (на экране физ. минутка для глаз) На доске та же краткая запись, только число 3 поменяю на 6 (фронтальный опрос по задаче аналогичный первой) —Запишите решение (дети не могут найти значение выражения) -Что возникло? (трудность, проблема) -Я предлагаю вам внимательно посмотреть на числовое выражение и предложить свои варианты решения (каждый вариант должен быть рассмотрен) Дети могут предложить: -разложить 47 на 40 и 7, а также 6 разложить на 3 и 3 (чтобы дополнить 7 до 10-ка, а к круглому числу легче прибавить оставшееся слагаемое. -Подходит ли правило, которое мы использовали в предыдущей задаче к данному решению? (нет) -Давайте составим план, как мы находили значение данного выражения (дети вместе с учителем проговаривают пункты (учитель записывает на доске) План:
-Решили нашу проблему? (да) -А теперь давайте попробуем самостоятельно применить наш алгоритм на практике Работа в группах (на планшетках или листочках) -У вас на партах листочки с числовыми выражениями (35+8, 23+9). Используя алгоритм сложения двузначного числа с однозначным с переходом через десяток, найдите значения этих числовых выражений. Оцените свою работу на полях в тетради! | Уметь совместно договариваться о правилах поведения и общения и следовать им (Коммуникативные УУД). Уметь оформлять свои мысли в устной форме (Коммуникативные УУД). Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя (Познавательные УУД). Уметь оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение (Регулятивные УУД). Осуществлять самоконтроль и самооценку (Регулятивные УУД) Умение слушать и понимать речь других (Коммуникативные УУД). Осуществлять самоконтроль и самооценку (Регулятивные УУД) Уметь проговаривать последовательность действий на уроке (Регулятивные УУД). Уметь планировать своё действие в соответствии с поставленной задачей (Регулятивные УУД). Уметь вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок (Регулятивные УУД). Способность к самооценке на основе критерия успешности учебной деятельности (Личностные УУД). |
Проблемы формирования вычислительных умений и навыков у школьников
ТЕМА 2. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ
ТЕМА 2. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ В соответствии с требованиями ФГОС выпускник научится: выполнять письменно действия с многозначными числами (сложение, вычитание, умножение и деление на однозначное, двузначное
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ В соответствии с требованиями ФГОС выпускник научится: выполнять письменно действия с многозначными числами (сложение, вычитание, умножение и деление на однозначное, двузначное
Подробнее
Математика 2 класс УМК «Гармония»
Математика 2 класс УМК «Гармония» Пояснительная записка Рабочая программа соответствует Федеральным государственным образовательным стандартам нового поколения к общим целям и задачам курса. ОСНОВА: программа
Подробнее
Математика. Правило 1. Математика. Правило 1. Математика. Правило 2. Математика. Правило 2. В этой системе пользуются: единицами, в 10 раз.
Математика. Правило 1. Математика. Правило 1. Числа единицы счѐта (5, 16, 129,2087,10000,…) Числа единицы счѐта (5, 16, 129,2087,10000,. ..) Цифры знаки, которые используются для записи Цифры знаки, которые
..) Цифры знаки, которые используются для записи Цифры знаки, которые
Подробнее
Пояснительная записка
Пояснительная записка Программа по математике для 2 класса является структурной частью Основной образовательной программы начального общего образования и разработана на основе следующих нормативных документов:
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Роль и место дисциплины в образовательном процессе В начальной школе изучение математики имеет особое значение в развитии младшего школьника. Приобретенные им знания, первоначальное
Подробнее
II Пояснительная записка
Количество часов Всего 136 часов: в неделю 4 часа. II Пояснительная записка Планирование составлено на основе УМК «Гармония» Рабочая программа по математике разработана на основе Примерной программы по
Подробнее
Рабочая программа по математике 3 класс
Муниципальное казенное общеобразовательное учреждение «Евдаковская основная общеобразовательная школа» Каменского муниципального района Воронежской области Рассмотрено на заседании ШМО учителей начальных
Подробнее
Математика.
 Пояснительная записка.
Пояснительная записка.
Математика Программа: ШКОЛА РОССИИ. Концепция и программы для Начальных классов. Часть 1. Математика. Авторы: М. И. Моро, Ю. М. Калягин, М.А,Бантова, Г. В. Бельтюкова, С. И. Волкова, С. В. Степанова. —
Подробнее
Пояснительная записка
Пояснительная записка Рабочая программа по математике разработана на основе Федерального государственного образовательного стандарта начального общего образования, Концепции духовно-нравственного развития
Подробнее
Пояснительная записка
Пояснительная записка Рабочая программа разработана на основе авторской программы начального общего образования в соответствии с требованиями Федерального государственного образовательного стандарта начального
Подробнее
Раздел І. обобщение и Систематизация
Раздел І. обобщение и Систематизация учебного материала за 1 класс Цель раздела І обобщение и систематизация знаний, умений и навыков учащихся, приобретенных в 1 классе. Учебное содержание раздела разделено
обобщение и Систематизация учебного материала за 1 класс Цель раздела І обобщение и систематизация знаний, умений и навыков учащихся, приобретенных в 1 классе. Учебное содержание раздела разделено
Подробнее
Пояснительная записка
Пояснительная записка Государственная аттестация по теоретическим основам начального курса математики и методике его преподавания является средством проверки профессиональной готовности будущего учителя
Подробнее
ПРЕДМЕТОВ И ГРУПП ПРЕДМЕТОВ
1. Пояснительная записка Рабочая по математике для 1-5 классов II вида разработана на основе программы «Математика» (2 отделение, вариант II), авторы К. Г. Коровин, А. Г. Зикеев, Л. И. Тигранова и др.
Подробнее
Пояснительная записка
Пояснительная записка Рабочая программа основана на государственной программе специальных (коррекционных) образовательных учреждений VIII вида: 5 9 кл. : В 2 сб./ Авторы: Воронкова В. В., Перова М. Н.,
: В 2 сб./ Авторы: Воронкова В. В., Перова М. Н.,
Подробнее
РАБОЧАЯ ПРОГРАММА. по математике
Муниципальное бюджетное общеобразовательное учреждение «Средняя школа 21» Классы Учитель: РАБОЧАЯ ПРОГРАММА по математике 1 Б, 1В, 1Г Желтикова Лидия Петровна, Голященкова Гульнара Равхатовна, Антипова
Подробнее
ВТОРОЙ КЛАСС. Сложение вида 45+20, 45+2
Часть 2 ВТОРОЙ КЛАСС Сложение вида 45+20, 45+2 Выполняя сложение, вычитание двузначных чисел без перехода через десяток, иногда дети теряются при решении примеров типа 45+20, 45-2. Поэтому и в учебниках
Подробнее
ОСНОВНЫЕ ТРЕБОВАНИЯ ПО МАТЕМАТИКЕ
ОСНОВНЫЕ ТРЕБОВАНИЯ ПО МАТЕМАТИКЕ к уровню подготовки учащихся 1 класса К концу обучения в 1 классе учащиеся должны: предмет, расположенный левее (правее), выше (ниже) данного предмета, над (под, за) данным
Подробнее
Нумерация трёхзначных чисел
Десятичная система счисления Позиционный принцип записи чисел 4 Нумерация трёхзначных чисел Посчитай от 97 до ; от 499 до 6; от 990 до 000. Посчитай десятками от 280 до 20; от 860 до 900. Посчитай сотнями
Посчитай десятками от 280 до 20; от 860 до 900. Посчитай сотнями
Подробнее
Пояснительная записка
Пояснительная записка Данная рабочая программа учебного предмета «Математика» для обучающихся 4 класса муниципального казённого общеобразовательного учреждения «Большеокинская СОШ» разработана на основе
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа по математике разработана на основе Федерального государственного образовательного стандарта начального общего образования, Концепции духовно-нравственного развития
Подробнее
-выполнять проверку вычислений;
Пояснительная записка Рабочая программа учебного предмета «Математика» составлена в соответствии с Основной образовательной программой начального общего образования муниципального общеобразовательного
Подробнее
I.
 Место предмета в учебном плане
Место предмета в учебном плане
I. Место предмета в учебном плане В Федеральном базисном образовательном плане на изучение математики в каждом классе начальной школы отводится 4 часа в неделю, всего 540 часов. II. Содержание учебного
Подробнее
План аннотация рабочей программы.
План аннотация рабочей Компоненты Содержание Полное наименование программы (с указанием вида, уровня образования, предмета и класса). Место учебного предмета в структуре основной образовательной Нормативная
Подробнее
Аннотация рабочей программы
Аннотация рабочей программы Рабочая программа по математике Составитель Козлова О.Н. Класс 2 «Б» Программа составлена в соответствии с : — с основной образовательной программой начального общего образования
Подробнее
СЧЕТНЫЕ ПАЛОЧКИ КЮИЗИНЕРА
Часть 1 СЧЕТНЫЕ ПАЛОЧКИ КЮИЗИНЕРА Общие положения Возможность наглядного, непринужденного обучения детей основным понятиям начального курса математики становится реальной при использовании дидактического
Подробнее
АННОТАЦИЯ РАБОЧЕЙ ПРОГРАММЫ
АННОТАЦИЯ РАБОЧЕЙ ПРОГРАММЫ Предмет: Русский язык Класс: 2 Количество часов по учебному плану: всего- 136часов в год (4 часа в неделю) УМК: 1. Авторская программа «Перспективная начальная школа» на основе
Авторская программа «Перспективная начальная школа» на основе
Подробнее
Мотивационный этап | -Итак, сейчас у нас урок математики. Посмотрите на доску, кого вы видите? -Верно! Он очень любит математику и разные математические задания и предлагает нам прочитать следующее стихотворение. Давайте его прочитаем (развитие слуховой, наглядной памяти и внимания). Математику, друзья, Не любить никак нельзя! Очень строгая наука. Очень точная наука. Интересная наука – это математика! -Назовите ключевые слова, главные в этом стихотворении о математике. (На слайдах появляются слова – любить, строгая, точная, интересная). — Верно! Математика – наука точная и требует много стараний и умений. Поднимите руку, кто сегодня постарается? — Молодцы! — А что потребуется вам для того, чтобы справиться сегодня со всеми заданиями? На слайде вы видите слова – если слово подходит, – то вы топаете ногами, если нет – тихо сидите: внимание, аккуратность, лень, память, пассивность, рассуждение, хорошее настроение. — Ну что, приступаем к работе? | -Колобка! Вслух читают стихотворение со слайда: Математику, друзья, Не любить никак нельзя! Очень строгая наука. Очень точная наука. Интересная наука – это математика! -Любить, строгая, точная, интересная. Внимание (сидят тихо), аккуратность (сидят тихо), лень (топают ногами), память (сидят тихо), пассивность (топают ногами), рассуждение (сидят тихо), хорошее настроение (сидят тихо). | Актуализация знаний | -Ребята, посмотрите на слайд и самостоятельно, выполните решение следующих выражений: 12+5 = 11+8 = 15-5 = 10+10 = 17-2 = 19 – 7 = 20-10 = — Кто решил все примеры? А у кого не получилось решить все примеры? Какие трудности у Вас возникли? Как Вы думаете, почему Вы не смогли решить эти примеры? — Правильно, мы еще с вами не научились решить такие примеры. Тогда какую цель вы перед собой поставите? — Значит, как будет звучать тема урока? Учитель фиксирует на доске тему урока, а учащиеся в тетрадях кратко обозначают ее с помощь примера для пробного действия: 20-10. — Для того, чтобы нам освоить пробное действие, давайте достанем из своих конвертов модели десятков (треугольники). -Сейчас посмотрите внимательно на выражение и назовите уменьшаемое? -Сколько это треугольников? -Значит, сколько десятков? — Назовите вычитаемое? -Сколько нам нужно взять треугольников? -Значит, это сколько десятков? -А теперь изобразите моделью это выражение 20-10 (2 треугольника – 1 треугольник) — 2-1 – это сколько? -Значит, сколько десятков получается? -Правильно, а давайте запишем это на математическом языке. -Верно! А кто попробует сформулировать правило вычитания круглых чисел? | -Учиться решать такие примеры. (Примеры с круглыми числами) Сложение и вычитание круглых десятков Учащиеся в тетрадях кратко обозначают тему с помощь примера для пробного действия: 20-10. -20 -2 -2 -10 -1 -1 десяток 2 треугольника – 1 треугольник — 2 десятка минус 1 десяток -1 -1 десяток -20 – 10 = 10 -Чтобы выполнить вычитание круглых чисел, нужно из числа десятков уменьшаемого вычесть число десятков вычитаемого. ИЛИ Чтобы выполнить вычитание круглых чисел нужно опустить нули и выполнить вычитание однозначных чисел, а затем добавить нуль. | Физминутка | Раз – подняться на носки и улыбнуться! Два – руки вверх и потянуться! Три – согнуться, разогнуться. Четыре – поглубже всем вздохнуть. Пять – на пояс руки ставим. Шесть – поворот вправо. Семь – поворот влево. Восемь – присядем. Девять – и урок наш продолжаем. | Поднимаются на носки и улыбаются! Поднимают руки вверх и тянутся! Сгибаются, разгибаются. поглубже все вдыхают. На пояс руки ставят. Поворот вправо. Поворот влево. Присаживаются. | Первичное закрепление с проговариванием во внешней речи | -Посмотрите, пожалуйста, на слайд! Колобок передал нам подарки! Давайте узнаем, что в них? Посмотрите, это же новые примеры! Кто попробует решить их у доски, проговаривая вслух? 50-30 70-40 40+10 -Как вы думаете, какое правило нужно использовать при сложении круглых чисел? Будет ли аналогично правилу при вычитании? Назовите его. -Правильно! Давайте решим следующие примеры 60+30 20+50 | -Чтобы сложить круглые числа нужно сложить число десятков первого слагаемого и число десятков второго слагаемого. ИЛИ -Чтобы сложить круглые числа нужно отбросить нули и сложить однозначные числа, а затем добавить нуль. | Этап самостоятельной работы | -Ребята, а сейчас давайте попробуем выполнить задания самостоятельно! Я вам раздам карточки с заданиями. Посмотрите, что здесь изображено?
= -Правильно! Посмотрите, в первой таблице на пересечении клеточек нужно записать значение суммы чисел, а во второй – значения разности. — Время вышло! Поменяйтесь тетрадями со своим соседом по парте, и проверьте его работу. Посмотрите, на слайде представлено правильное выполнение задания. -У кого все верно, ставьте карандашиком 5. -А кто обнаружил ошибки при проверке? В чем он ошибся? Давайте заполним эту клеточку еще раз вместе. | -Таблицы! Дети самостоятельно выполняют решение примеров | Итогово-рефлексивный | -Вот и подошел к концу на урок математики! Ребята, что нового вы узнали сегодня на уроке? – Какое затруднение у вас возникло? В чем была причина затруднения? – Какую цель перед собой поставили? – Каким способом действовали? – Достигли ли поставленной цели? Объясните свою позицию. – Кто нам больше всех помог сегодня на уроке, кого мы можем поблагодарить? – Оцените свою собственную работу. Обоснуйте свой вывод. – Какие затруднения остались? Над чем надо еще поработать? – Как вы думаете, каким будет наш следующий шаг? -Ребята, а сейчас подумайте, если вы считаете, что вы сегодня хорошо постарались на уроке, трудились, работали весь урок, выполнили все задания верно, то возьмите карточку с улыбающимся колобком, а если у вас возникали трудности, вам было тяжело работать, то возьмите карточку с грустным колобком, который так похож на круглые числа! -Спасибо, мне было приятно с Вами работать! |
2. Вычислительные приемы для чисел первого десятка
Вычислительные
приемы первого десятка изучаются в теме
«Сложение и вычитание в пределах 10» в
1 классе при обучении по любому учебнику
математики для начальных классов.
Результатом изучения данной темы должно
явиться формирование осознанной
самостоятельной вычислительной
деятельности ребенка. При этом программой
оговорена необходимость знания наизусть
результатов
действий
сложения и вычитания в пределах 10 (так
называемое «табличное сложение и
вычитание»).
Присчитывание
и отсчитывание
Первым
вычислительным приемом, который осваивает
первоклассник, является прием вида a
± 1.
Основой данного приема является принцип
образования чисел в натуральном ряду:
каждое следующее число на единицу больше
предыдущего.
Усвоение
ребенком этого принципа являлось
центральной
задачей изучения
нумерации первого десятка.
Следствием
этого принципа является способ нахождения
значений выражений вида 5 + 1; 8 + 1; 6 — 1; 7 —
1 и т. п. путем называния либо следующего,
либо
предыдущего
числа.
Иными словами, для нахождения значения
данных выражений нет необходимости
выполнять какой-то прием арифметических
действий, достаточно понимать, что
добавление 1 ведет к получению следующего
по счету числа, а убавление 1 — к появлению
предыдущего по счету числа. Именно для
получения результатов в таких выражениях
ребенок заучивал наизусть названия
чисел в прямом и обратном порядке.
Число
предыдущее стоит
в ряду чисел левее данного. При счете
называется непосредственно перед
данным, количественно оно содержит на
одну единицу меньше данного.
Число
последующее (следующее)
стоит в ряду чисел правее данного. При
счете называется непосредственно после
данного, количественно оно содержит на
одну единицу больше данного.
Хорошее
понимание принципа
построения натурального ряда чисел
ведет
к легкому освоению приемов присчитывания
и от-считывания по 1
и
легкому выполнению вычислительной
деятельности в случаях:
7+1
17+ 1 177+ 1 10 277 + 1
7-
1 17- 1 177- 1 10 277-1
Во
всех случаях ссылка на принцип построения
натуральной последовательности чисел
является наиболее рациональной вплоть
до 4 класса (общий прием вычислений):
— прибавляя
к числу 1, получаем следующее
по
счету;
— вычитая
из числа 1, получаем предыдущее
по
счету.
Этот
же прием является действующим и в трудных
случаях (вплоть до 4 класса):
9+
1 19+ 1 199 + 1 999 + 1 99 999 +1
10-
1 20- 1 200 — 1 1 000 — 1 100 000 — 1
При
нахождении ответа в данных примерах
удобно ссылаться на порядок счета:
следующим за числом 99 999 является число
100 000; предшествующим числом для числа
1 000 является 999.
В
«Методике преподавания математики в
начальных классах» (авт. М.А. Бантова,
Г.В. Бельтюкова) отмечается, что «на
специально отведенном уроке… под
руководством учителя дети составляют
таблицы «прибавить 1» и «вычесть 1» и
затем заучивают их наизусть». При хорошем
усвоении принципа образования чисел в
натуральном ряду нет необходимости
организовывать специальное заучивание
результатов этой таблицы, поскольку
умение ребенка называть ее результаты
связано с хорошим знанием прямой и
обратной последовательности чисел в
пределах 10.
Использование
линейки в качестве наглядной опоры для
запоминания последовательности чисел,
а также для усвоения способа нахождения
числа последующего и предыдущего создает
хорошие условия для интериоризации
(усвоения
образа во внутреннем плане, формирования
наглядно представимой мысленной модели
ряда натуральных чисел) способа нахождения
результатов присчитывания и отсчитывания
для детей с ведущим наглядно-образным
мышлением.
Для
детей с ведущим кинестезическим
восприятием и ведущим кинестезическим
типом памяти (т. е. требующим обязательной
поддержки словесной информации мышечным
усилием, двигательным действием) следует
не только допускать, но и поощрять
использование
пальцевого счета при изучении всех
вычислительных приемов первого десятка.
Естественно, этот вариант внешнего
подкрепления вычислительной деятельности
является более медленным, многим учителям
он кажется недопустимым для школьников,
а потому старательно искореняется уже
при обучении вычислениям в пределах
первого десятка. В качестве аргумента
защиты использования этого способа
подкрепления вычислительной деятельности
для детей с ведущим кинестезическим
типом можно привести многочисленные
исследования психологов последних
десятилетий, подтверждающие, что при
исключении двигательных действий у
этих детей и при ориентации на заучивание
результатов без подкрепления предметной
деятельностью усвоение происходит на
формальном уровне, по принципу зазубривания
без понимания, а в дальнейшем это крайне
осложняет формирование вычислительной
деятельности с числами в пределах сотни,
тысячи и т. п.
Прибавление
и вычитание по частям
Следующую
группу вычислительных приемов в пределах
первого десятка составляют случаи вида:
a
±
2, a
±
3, a
±4,
результаты которых могут быть найдены
с помощью последовательного присчитывания
или отсчитывания:
2
+ 3 = 2 + 1 + 1 + 1; 7-4
=
7-1-1-1-1
или
с помощью прибавления и вычитания по
частям:
2
+ 3 = 2 + 1 + 2; 7-4
=
7-2-2
Подготовительным
приемом к обучению ребенка этим случаям
вычислений является прием вида: я+1
+
1ия-1-1,в
основе которого лежит последовательное
отсчитывание
по 1 или присчитывание по 1.
Знакомство
с этим приемом является очень важным.
Во-первых,
осваивая
данный вычислительный прием, ребенок
впервые встречается с выражением,
содержащим более одного знака действий.
Во-вторых,
при
выполнении вычислений впервые в неявном
виде (т. е. без сообщения ребенку самого
правила) используется правило порядка
выполнения действий одной ступени без
скобок:
При
выполнении действий одной ступени без
скобок, действия выполняются по порядку
слева направо.
В-третьих,
при
выполнении данного вида вычислений не
нужны специальные вычислительные
действия какого-то нового вида, а
требуется лишь последовательное
применение принципа образования чисел
в натуральном ряду.
Например:
Вычислите
6 + 1 + 1.
(Прибавляя
к
6 единицу,
получаем число следующее — это 7;
прибавляя
к
7 единицу,
получаем следующее число — это 8.
Значит,
6+1+1
— 8.)
В
качестве наглядной модели удобно
использовать линейку — прибавляя
единицу дважды, ребенок делает вправо
от числа 6 два
«шага»,
получая ответ наглядно (на первых порах
эти «шаги» полезно прослеживать пальцем).
При
использовании пальцевого счета, ребенок
отгибает (или загибает) последовательно
два пальца, присчитывая их к 6 пальцам,
или, в крайнем случае, сосчитывая заново
все количество отогнутых (загнутых)
пальцев.
Аналогично
ребенок действует в случае вычислений
вида а
—
1 — 1. В этом случае используется понимание
образования числа предыдущего
к
данному и знание последовательности
чисел в обратном порядке.
Вычислительный
прием а
±2
является
случаем, объединяющим последовательное
присчитывание (отсчитывание) двух единиц
к числу, производимое в предыдущем
случае.
При
прибавлении к любому числу двух, ребенок
заменяет его на сумму двух единиц и
последовательно присчитывает (отсчитывает)
их от числа.
Например:
3 + 2 = 3+1
+
1
1
1
В
качестве наглядной модели удобно
использовать линейку — прибавляя два,
ребенок делает вправо от числа два
«шага», получая ответ наглядно.
В
качестве наглядной модели удобно также
использовать счеты, поскольку прибавляя
или вычитая 2, ребенок чаще всего
перебрасывает дважды по одной косточке,
фактически моделируя приведенную выше
схему приема. Если ребенок сначала
сосчитывает на счетах две косточки, а
потом перебрасывает их, он, как правило,
затем при нахождении результата
сосчитывает заново все количество
оставшихся (полученных) косточек. Этот
способ выполнения вычислений показывает,
что ребенок понимает смысл действий,
но приемами присчитывания и отсчитывания
по каким-то причинам не пользуется. В
этом случае следует заменить счеты на
линейку.
При
использовании пальцевого счета, ребенок
отгибает (или загибает два пальца,
присчитывая (или отсчитывая) два или
сосчитывая весь результат.
Методически
ставится цель довести умение ребенка
прибавлять и отнимать 2 до состояния
навыка, т. е. до запоминания результатов
прибавления и вычитания двух в пределах
10 наизусть:
1+2=3
2+2=4
3+2=5
4+2=6
5+2=7
6+2=8
7+2=9
8+2=10
3-2=1
4-2=2
5-2=3
6-2=4
7-2=5
8-2=6
9-2=7
10-2=8
Таблица
сложения и вычитания двух содержит
самое большое количество случаев, а
поскольку она изучается первой, многие
дети испытывают большие трудности,
пытаясь заучить этот объем.
Если
ребенок хорошо владеет приемами
присчитывания и отсчитывания, он всегда
может вычислить забытый случай из
таблицы, используя осознанную
вычислительную деятельность. Для многих
детей с проблемами процессов запоминания
(это характерно для многих часто болеющих
детей, что обусловлено действием
некоторых медицинских препаратов, для
детей с синдромом дефицита внимания, с
гиперподвижностью, для детей с задержкой
развития и т.д.) формирование осознанной
вычислительной деятельности — это
единственно возможный путь избежать
мучительного и бессмысленного
зазубривания.
Если
при изучении чисел в пределах 10 (в разделе
«нумерация в пределах 10»), ребенок выучил
наизусть состав однозначных чисел и
легко его воспроизводит, то проще всего
для запоминания таблицы сложения и
вычитания связать соответствующие
случаи с составом однозначных чисел:
3
значит 3 = 1 + 2 тогда 1 + 2 = 3,а3-2
=1
1
2
7
значит 7 = 5 + 2 тогда 5 + 2 = 7,а7-2
=
5
5
2
При
опоре на состав числа имеет смысл сразу
ориентировать ребенка на составление
и запоминание тройки взаимосвязанных
равенств:
8
6 + 2 = 8, 8-2
= 6, 8-6
=
2
6
2
Умение
прибавлять и вычитать 2 является опорным
умением для формирования дальнейшей
вычислительной деятельности.
Вычислительные
приемы а
+
3 и а
± 4
могут выполняться последовательным
присчитыванием или отсчитыванием по
1:
8-4
=
8-1-1-1-1;
6
+
3
=
6+1
+
1
+
1
В
этом случае используется ссылка на
понятие числа предыдущего и последующего.
Может быть использована линейка, по
которой ребенок делает нужное количество
«шагов» вправо или влево от заданного
числа, или пальцевый счет. Методически
этот способ считается менее совершенным,
чем прибавление и вычитание по частям
для данных вычислительных приемов.
57
Прибавление
(или вычитание) по
частям предполагает
раскладывание второго слагаемого (или
вычитаемого) на удобные для выполнения
вычислений составные части, и
последовательное их прибавление (или
вычитание):
Например:
Приведенные
примеры показывают, что с приемами
а±Зиа±А
легче
справиться тем детям, которые помнят
наизусть результаты случаев прибавления
и вычитания двух, или могут достаточно
быстро найти (вычислить) эти результаты.
Именно
для освоения вычислений вида а±3иа±4
предыдущую
таблицу для случая а
±
2 учитель требовал заучивать наизусть.
После
освоения приема вычислений по частям,
составляют таблицы для случаев а
±
3:
1+3=4
2+3=5
3+3=6
4+3=7
5+3=8
6+3=9
7+3=10
4-3=1
5-3=2
6-3=3
7-3=4
8-3=5
9-3=6
10-3=7
а
также а
± 4:
1+4=5
2+4=6
3+4=7
4+4=8
5+4=9
6
+4=105-4=1
6-4=2
7-4=3
8-4
=
49-4
=
510-4
=
6
Первая
таблица содержит 14 случаев, вторая
таблица содержит 12 случаев. В сумме с
16 случаями таблицы прибавления
двух получается
42 случая. Неудивительно, что очень многие
дети на этапе изучения табличного
сложения и вычитания в пределах 10
испытывают массу трудностей, в связи с
необходимостью в достаточно короткие
сроки заучить наизусть большой объем
формализованного материала. При этом
единственным мотивом изучения этого
объема наизусть для ребенка выступает
требование учителя. Все задания на
решение примеров в этот период (а также
на решение задач, на сравнение выражений
и т. п.) требуют воспроизведения наизусть
табличных случаев сложения и вычитания
вразбивку.
Поэтому,
если ребенок учил таблицу наизусть
подряд (например, по возрастанию
результатов и т. п.), то даже легко отвечая
ее результаты подряд, он может ошибаться
при воспроизведении таблицы вразбивку,
и тем более при необходимости воспроизводить
вразбивку случаи из разных таблиц.
В
связи с этим при запоминании таблиц для
случаев вида а±3
и
а
± 4
многие учебники математики для 1 класса
ориентируют ребенка на использование
состава числа как основы для запоминания
таблиц сложения и вычитания. При
ориентации на состав числа удобнее
делать акцент не на составление и
заучивание таблицы каждого случая
целиком, а на составление и запоминание
взаимосвязанных троек:
9
9 = 5 + 4, значит, 5 + 4 = 9; 9-4
= 5; 9-5
=
4
5
4
В
качестве внешней опоры при вычислении
случаев вида а±3
и
а
+
4 может быть использована линейка, счеты,
пальцевый счет. Для ускорения вычислений
в домашних условиях (при выполнении
домашней работы) часто используют
треугольную таблицу, помогающую найти
результат суммирования любых пар чисел
в пределах 10. Такая таблица может быть
повешена над столом ребенка. Постоянное
обращение к ней при выполнении домашних
заданий более полезно, чем использование
калькулятора, поскольку зрительный
образ соответствующих случаев постепенно
запоминается ребенком, пополняя тем
самым количество запомненных наизусть
случаев табличного сложения и вычитания.
Таблица
сложения и вычитания:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
5 | 6 | 7 | 8 | 9 | 10 | ||||
6 | 7 | 8 | 9 | 10 | 4 | ||||
7 | 8 | 9 | 10 | 6-2 | |||||
8 | 9 | 10 | |||||||
9 | 10 | ||||||||
Перестановка
слагаемых Правило
перестановки слагаемых:
От
перестановки слагаемых сумма не
изменяется.
Свойство
перестановки слагаемых (переместительное
свойство сложения) используется в 1
классе при знакомстве с вычислительными
приемами видая + 5, а
+
6, а
+
7, а
+
8 и а
+
9.
В
этих случаях второе слагаемое больше
первого (поскольку рассматриваются
случаи сложения в пределах 10). Применение
при вычислениях перестановки слагаемых
позволяет свести все эти случаи к ранее
изученным.
Например:
2 + 8 = 8 + 2 = 10.
Перестановка
слагаемых может рассматриваться как
прием
вычислений.
Этот
вычислительный прием облегчает
вычислительную деятельность и является
общим
приемом вычислений при
сложении любых чисел.
Например:
12 + 346 = 346 + 12 = 358
Прием
перестановки слагаемых позволяет
составить краткую таблицу сложения в
пределах 10:
2 | ||
3 | ||
4 | 3 | |
5 | 4 | |
6 | 5 | 4 |
7 | 6 | 5+4=9 |
8 | 7 | 6 |
С
учетом свойства перестановки слагаемых
данная таблица включает все
случаи
сложения в пределах 10. Таблица содержит
15 случаев и, безусловно, ее заучивание
для ребенка намного более легкая задача,
чем заучивание полной таблицы.
Данная
таблица появляется значительно позднее,
чем начинается заучивание таблиц (для
случаев а
+
1, а
±
2, а
±
3, а
±
4) сложения и вычитания в пределах 10,
поэтому не выполняет своей облегчающей
вычисления задачи. На данный момент
дети уже заучивали 42 случая предыдущих
таблиц, и поэтому все случаи часто
смешиваются. В связи с этим, некоторые
альтернативные учебники (например,
учебник Н.Б. Истоминой) сначала знакомят
детей со сложением, его свойствами и
таблицей сложения, а после того, как эти
таблицы ребенком усваиваются, знакомят
первоклассника с действием вычитания
и таблицу вычитания рассматривают
отдельно от таблицы сложения.
Случаи
вида «вычесть 5, 6,7,8,9», символически
обозначаемые в учебниках □ — 5, □ — 6, □
— 7, □ — 8, □ — 9, являются вычислительными
приемами, основанными на составе
однозначных чисел и взаимосвязи между
суммой и слагаемыми.
С
правилом взаимосвязи суммы и слагаемых
дети знакомились ранее (см. выше). Состав
чисел изучался в разделе «Нумерация в
пределах 10».
Используя
эти знания, дети осваивают прием вычитания
чисел больше 5:
8-5
=
3
7-6=1
10-7
=
3
3
5 6 1 7 3
(8
—
это
Зи5;8
без
5
—
это
3.)
Сложение
и вычитание с нулем
Основное
свойство нуля:
Прибавление
и вычитание нуля результата не меняет.
В
общем виде это свойство можно записать
так: а±0==аи0±а
= а.
Порядок
действий в выражениях без скобок
Порядок
действий в выражениях без скобок в
первом классе определяется
следующим образом:
В
выражении, содержащем сложное вычитание,
или несколько знаков сложения, или
несколько знаков вычитания, действия
выполняются по порядку слева направо.
Это
правило не содержится в учебнике, учитель
знакомит с ним детей в процессе решения
соответствующих примеров. Например:
Вычисли:
3
+
6
~
7
=
8-2
+
4
=
7-3-2
= 5 + 2 + 3 = …
При
решении этих примеров детям в 1 классе
не
разрешается пользоваться
правилом группировки слагаемых,
являющимся приемом рациональных
вычислений.
Это
правило появляется только во втором
классе при изучении приемов вычислений
в пределах 100, где детям сообщается:
Два
соседних слагаемых можно заменить их
суммой.
Такой
методический подход объясняется тем,
что раннее знакомство с этим приемом
может быть воспринято ребенком как
общее свойство для случаев сложения
нескольких чисел, а также вычитания
нескольких чисел.
В
практике иногда наблюдается, что ребенок,
полагающий, что это правило общее для
сложения и вычитания, выполняет вычитание
нескольких чисел следующим образом:
8
— 3 г- 2 = 7, так как 3 — 2 — 1, а 8 — 1 = 7,
что,
естественно, неправильно.
Поскольку
в большинстве учебников для начальных
классов действия сложения и вычитания
рассматриваются одновременно, для
избежания подобных ошибок при выполнении
действий правило группировки слагаемых
в первом классе не используется. В этом
случае правило порядка выполнения
действий в выражениях без скобок в
первом классе является единым.
Группировка
слагаемых
В
некоторых альтернативных учебниках
(например, в учебнике Н.Б. Истоминой)
правило группировки слагаемых в
неявном виде (без
сообщения его учащимся) используется
уже при изучении вычислительных приемов
первого десятка. Это объясняется тем,
что дети знакомятся сначала только со
сложением и потому рассматривают все
правила только относительно сложения
(перестановка слагаемых, группировка
слагаемых).
Например:
Можно
ли утверждать, что значение выражений
в каждом столбике одинаковы?
1
+ 2 + 2+ 1 2+1
+
1
+
1
1+4+1
2+2+1
1+2+3
2+1+2
1+5
2+3
Подразумевается,
что при объяснении равенства значений
выражений в каждом столбике ребенок
суммирует слагаемые, начиная со второго,
т. е. такой прием считается допустимым.
(Сумма
чисел 2,2
и 1 равна 5, сумма 4 и 1 также равна 5, сумма
2 и 3 также равна 5.
Во
всех случаях первое слагаемое равно 1
и к нему прибавляются одинаковые суммы,
значит результаты равны.)
Новый вычислительный метод позволяет точно различать данные опухолевых клеток и нормальных клеток
Стремясь решить серьезную проблему при анализе больших наборов данных секвенирования одноклеточной РНК, исследователи из онкологического центра доктора медицины Андерсона Техасского университета разработали новый вычислительный метод, позволяющий точно различать данные о раковых клетках и различных нормальных клетках. найдены в образцах опухолей. Работа была опубликована сегодня в журнале Nature Biotechnology .
Новый инструмент, получивший название CopyKAT (кариотипирование анеуплоидных опухолей по количеству копий), позволяет исследователям более легко изучать сложные данные, полученные в ходе крупных экспериментов по секвенированию РНК с одной клеткой, которые предоставляют данные об экспрессии генов из многих тысяч отдельных клеток.
CopyKAT использует эти данные об экспрессии генов для поиска анеуплоидии или наличия аномального числа хромосом, что является обычным для большинства видов рака, сказал старший автор исследования Николас Навин, доктор философии, доцент кафедры генетики, биоинформатики и вычислительной биологии.Этот инструмент также помогает идентифицировать отдельные субпопуляции или клоны в раковых клетках.
Мы разработали CopyKAT как инструмент для вывода генетической информации из данных транскриптома. Применяя этот инструмент к нескольким наборам данных, мы показали, что можем однозначно идентифицировать с точностью около 99% опухолевые клетки по сравнению с другими иммунными или стромальными клетками, присутствующими в смешанном образце опухоли. Затем мы могли бы сделать еще один шаг, чтобы обнаружить присутствующие субклоны и понять их генетические различия.«
Николас Навин, доктор философии, доцент кафедры генетики, биоинформатики и вычислительной биологии
Исторически опухоли изучались как смесь всех присутствующих клеток, многие из которых не являются злокачественными. Появление в последние годы секвенирования одноклеточной РНК позволило исследователям анализировать опухоли с гораздо большим разрешением, исследуя экспрессию генов каждой отдельной клетки, чтобы получить картину ландшафта опухоли, включая окружающую микросреду.
Однако, по словам Навина, нелегко отличить раковые клетки от нормальных без надежного вычислительного подхода. Бывший постдокторант Рули Гао, доктор философии, ныне доцент кафедры сердечно-сосудистых наук в Хьюстонском научно-исследовательском институте методистов, разработал алгоритмы CopyKAT, которые улучшают старые методы за счет повышения точности и адаптации к новейшему поколению данных секвенирования одноклеточной РНК. .
Команда сначала провела тестирование своего инструмента, сравнив результаты с данными полногеномного секвенирования, которые показали высокую точность в прогнозировании изменений количества копий.В трех дополнительных наборах данных по раку поджелудочной железы, тройному отрицательному раку груди и анапластическому раку щитовидной железы исследователи показали, что CopyKAT точно различал опухолевые клетки и нормальные клетки в смешанных образцах.
Эти анализы стали возможными благодаря сотрудничеству со Стивеном Й. Лаем, доктором медицины, доктором философии, профессором хирургии головы и шеи, а также Стейси Моулдер, доктором медицины, профессором медицинской онкологии груди, и лунным снимком рака груди ®. , часть программы MD Anderson Moon Shots Program®, совместных усилий по быстрому превращению научных открытий в значимые клинические достижения, спасающие жизни пациентов.
Анализируя эти образцы, исследователи также показали, что этот инструмент эффективен для идентификации субпопуляций раковых клеток в опухоли на основе различий в количестве копий, что подтверждается экспериментами с тройным отрицательным раком груди.
«Используя CopyKAT, мы смогли идентифицировать редкие субпопуляции в тройном негативном раке молочной железы, которые имеют уникальные генетические изменения, о которых широко не сообщается, в том числе те, которые имеют потенциальное терапевтическое значение, — сказал Гао. «Мы надеемся, что этот инструмент будет полезен исследовательскому сообществу, чтобы максимально использовать их данные о секвенировании одноклеточной РНК и сделать новые открытия в области рака.«
Инструмент находится в свободном доступе для исследователей здесь. Авторы отмечают, что инструмент не применим для исследования всех видов рака. Например, анеуплоидия относительно редко встречается при педиатрическом и гематологическом раке.
Источник:
Онкологический центр им. М. Д. Андерсона Техасского университета
Ссылка на журнал:
Gao, R., et al. (2021) Определение количества копий и клональной субструктуры в опухолях человека из одноклеточных транскриптомов. Природная биотехнология. doi.org/10.1038/s41587-020-00795-2.
Новый вычислительный метод может предсказать побочные эффекты лекарств
Newswise — Раннее выявление побочных эффектов лекарств до того, как они будут испытаны на людях, имеет решающее значение при разработке новых терапевтических средств, поскольку на неожиданные эффекты приходится треть всех неудачных попыток лекарств в процессе разработки. Теперь исследователи из Калифорнийского университета в Сан-Диего (UCSD) разработали новую технику с использованием компьютерного моделирования для выявления потенциальных побочных эффектов фармацевтических препаратов и использовали эту технику для изучения класса лекарств, в который входит тамоксифен, препарат, который чаще всего назначают в медицине. лечение рака груди.Их исследование в настоящее время доступно в Интернете по адресу PLoS Computational Biology .
Традиционные методы испытаний проводят скрининг соединений в исследованиях на животных перед испытаниями на людях в надежде определить побочные эффекты перспективных терапевтических средств. Команда UCSD «во главе с Филипом Борном, доктором философии, профессором фармакологии Школы фармации и фармацевтических наук Скэггса UCSD и доктором философии Лей Се из Суперкомпьютерного центра Сан-Диего при UCSD» вместо этого использует вычислительные возможности. моделирование для скрининга конкретных молекул лекарств с использованием всемирного хранилища данных Protein Data Bank (PDB), содержащего десятки тысяч трехмерных белковых структур.
Молекулы лекарства предназначены для связывания с белками-мишенями для достижения терапевтического эффекта, но если небольшая молекула лекарства, которая функционирует как «ключ», прикрепляется к белку, не являющемуся мишенью, который имеет аналогичный сайт связывания или «замок», могут возникнуть побочные эффекты.
Чтобы определить, какие белки могут быть непреднамеренными мишенями, исследователи UCSD берут одну молекулу лекарства и ищут, как она может связываться с максимально возможным количеством белков, кодируемых протеомом человека. В этом опубликованном тематическом исследовании они рассмотрели отдельные модуляторы рецепторов эстрогена (SERM), класс лекарств, который включает тамоксифен, чтобы проиллюстрировать новый подход.
«Компьютерная процедура, которую мы разработали, начинается с существующей трехмерной модели фармацевтического препарата, показывающей структуру молекулы лекарства, связанной с его целевым белком; в данном случае, SERM, связанный с рецептором эстрогена», — сказал Борн, является содиректором PDB. Затем ученые используют компьютерный анализ для поиска других сайтов связывания, которые соответствуют этому сайту связывания лекарства, «как поиск других замков, которые могут быть открыты тем же ключом.
В этом исследовании команда обнаружила ранее не идентифицированный белок-мишень для SERM.Идентификация этого вторичного сайта связывания объясняет известные побочные эффекты и открывает дверь для модификации препарата таким образом, чтобы поддерживать связывание с намеченной мишенью, но уменьшает связывание со вторым сайтом.
«Если лекарство имеет неблагоприятные побочные эффекты, вполне вероятно, что лекарство также связывается с непреднамеренной вторичной молекулой; другими словами, ключ, который позволяет ему прикрепляться к своей цели, подходит для нескольких замков», — сказал Борн. Он объяснил, что использование этой вычислительной техники для нахождения другой «блокировки» может привести к одному из трех результатов: новая блокировка может не дать никакого эффекта; запор мог объяснить неблагоприятное побочное действие препарата; или исследование потенциально могло бы обнаружить новый терапевтический эффект для существующего лекарственного средства «репозиционирование лекарств».
Исследователи UCSD продолжают свои исследования, которые, по словам Борна, могут быть применены к любому лекарству на рынке, для которого структура лекарства, связанная с рецептором, существует в PDB. Борн подчеркнул, что результаты этого подхода все еще нуждаются в экспериментальной проверке.
Цзянь Ван из программы биоинформатики UCSD также внес свой вклад в исследование PLoS. Работа была частично поддержана Национальными институтами здравоохранения.
Компьютерное моделирование
Моделирование распространения инфекционных заболеваний для определения эффективных вмешательств .Точное моделирование инфекционных заболеваний опирается на множество больших наборов данных. Например, оценка эффективности социального дистанцирования в отношении распространения гриппоподобного заболевания должна включать информацию о дружбе и общении между людьми, а также стандартные биометрические и демографические данные. Исследователи, финансируемые NIBIB, разрабатывают новые вычислительные инструменты, которые могут включать новые доступные наборы данных в модели, предназначенные для определения наилучшего курса действий и наиболее эффективных вмешательств во время пандемического распространения инфекционных заболеваний и других чрезвычайных ситуаций в области общественного здравоохранения.
Многомасштабное моделирование (МСМ) — это сложный тип вычислительного моделирования, который включает несколько уровней биологической системы. Изображение предоставлено ISB.
Отслеживание вирусной эволюции во время распространения инфекционного заболевания. РНК-вирусов, таких как ВИЧ, гепатит В и коронавирус, постоянно мутируют, чтобы развить лекарственную устойчивость, избежать иммунного ответа и вызвать новые инфекции. Образцы секвенированных патогенов от тысяч инфицированных людей можно использовать для идентификации миллионов эволюционирующих вирусных вариантов.Исследователи, финансируемые NIBIB, создают вычислительные инструменты для включения этих важных данных в анализ инфекционных заболеваний, проводимый специалистами здравоохранения. Новые инструменты будут созданы в партнерстве с CDC и будут доступны в Интернете для исследователей и медицинских работников. Проект усилит эпидемиологический надзор и лечение заболеваний во всем мире и позволит разработать более эффективные стратегии искоренения болезней.
Преобразование беспроводных данных о здоровье в улучшение здоровья и здравоохранения. Устройства для мониторинга состояния здоровья в больницах и носимые датчики, такие как умные часы, генерируют огромные объемы данных о состоянии здоровья в режиме реального времени. Медицинское обслуживание, основанное на данных, обещает быть быстрым, точным и менее дорогостоящим, но постоянные потоки данных в настоящее время ограничивают возможность использования информации. Исследователи, финансируемые NIBIB, разрабатывают вычислительные модели, которые преобразуют потоковые данные о состоянии здоровья в полезную форму. Новые модели будут обеспечивать физиологический мониторинг в реальном времени для принятия клинических решений в Национальной детской больнице.Команда математиков, биомедицинских информатиков и персонала больниц будет генерировать общедоступные данные и программное обеспечение. Проект будет использовать рынок беспроводной связи в здравоохранении с оборотом в 11 миллиардов долларов для значительного улучшения здравоохранения.
Человеческое и машинное обучение для индивидуального управления вспомогательными роботами. Чем тяжелее у человека нарушение моторики, тем сложнее ему управлять вспомогательными механизмами, такими как инвалидные коляски с электроприводом и роботизированные руки. Доступные средства управления, такие как устройства для затягивания и затягивания, не подходят для людей с тяжелым параличом.Исследователи, финансируемые NIBIB, разрабатывают систему, которая позволит людям с тетраплегией управлять роботизированной рукой, поощряя упражнения и поддерживая остаточные двигательные навыки. Технология использует интерфейсы тела и машины, которые реагируют на минимальное движение конечностей, головы, языка, плеч и глаз. Первоначально, когда пользователь двигается, машинное обучение дополняет сигнал для выполнения задачи с помощью роботизированной руки. Помощь сокращается по мере того, как машина передает управление все более опытному пользователю. Этот подход направлен на расширение возможностей людей с тяжелым параличом и предоставление интерфейса для безопасного обучения управлению роботами-помощниками.
Обновлено в мае 2020 г.
Новый вычислительный метод позволяет сравнивать целые геномы так же легко, как и целые книги — ScienceDaily
Взяв подсказку из методов сравнения текстов, используемых для обнаружения плагиата в книгах, документах колледжей и компьютерных программах, исследователи Калифорнийского университета в Беркли разработали улучшенный метод сравнения полногеномных последовательностей.
Имея почти тысячу частично или полностью секвенированных геномов, ученые прибегают к сравнительной геномике как к способу построения эволюционных деревьев, отслеживания восприимчивости популяций к болезням и даже отслеживания происхождения людей.
На сегодняшний день наиболее распространенные методы основаны на сравнении ограниченного числа высококонсервативных генов — не более пары десятков — у организмов, которые имеют все эти общие гены.
Новый метод может использоваться для сравнения даже отдаленно родственных организмов или организмов с геномами совершенно разных размеров и разнообразия, и может сравнивать весь геном, а не только выбранную небольшую часть содержащей ген части, которая, как известно, кодирует белки, которые в геноме человека всего 1 процент ДНК.
По словам Сунг-Хоу Кима, профессора химии Калифорнийского университета в Беркли и научного сотрудника Национальной лаборатории Лоуренса Беркли, с помощью этого метода группы организмов в значительной степени соответствуют нынешним группировкам, но с некоторыми интересными расхождениями. Однако относительное положение групп в генеалогическом древе — то есть, как недавно эти группы эволюционировали — сильно отличается от тех, которые основаны на обычных методах выравнивания генов.
Результаты вычислений удивили ученых тем, что они смогли классифицировать некоторые бактерии и вирусы, которые до сих пор были загадочными.
Метод, в котором используются частотные профили признаков (FFP), описан в статье, которая появится на этой неделе в раннем онлайн-выпуске журнала Proceedings of the National Academy of Sciences.
Полногеномные и геноцентрические методы
Современные методы сравнения геномов разных организмов сосредоточены на небольшом наборе генов, которые являются общими для сравниваемых организмов. Затем геномы выстраиваются в линию, чтобы подсчитать сходство и различие последовательностей, на основании чего компьютерная программа строит генеалогическое древо, причем предполагается, что ближайшие родственники имеют больше сходных последовательностей, чем дальние родственники.
Однако этот метод предполагает, что у организмов есть общие гены или что эти «гомологичные» гены можно идентифицировать. По словам Ким, при сравнении далеких родственных видов, таких как бактерии, которые живут в совершенно разных средах, этот геноцентрический метод может не работать.
«Что вы делаете, когда один ген говорит вам, что организмы тесно связаны, а другой ген говорит вам, что они дальние родственники?» он спросил. «Такое случается.»
Ким, который в прошлом сосредоточился на создании трехмерных демографических карт всех известных белковых структур, хотел метод, который можно было бы использовать для сравнения геномов всех размеров, и даже геномов, секвенированных лишь частично.Он также хотел метод, который сравнивал бы все области генома, а не только экзоны, то есть ДНК, транскрибированную в мРНК, план белков. Экзоны составляют только 1 процент генома человека, а остальные представляют собой некодирующие «интроны», регуляторную ДНК, дублирующую или избыточную ДНК и транспозоны — гены, возникшие из других мест в геноме.
Ким считал, что традиционное сравнение текстов — используемое, например, для оценки авторства литературного произведения или выявления плагиата — может предоставить модель для сравнения всего генома и способ проверки методов сравнения.Но в то время как сравнение текста включает в себя рассмотрение частоты слов; геномы нельзя разложить на слова.
«Я могу сравнить две книги двумя разными способами. Я могу выбрать несколько предложений, скажем, сто, которые, по моему субъективному мнению, являются важными, и сравнить их, но некоторые из них очень похожи, а некоторые очень разные в двух книгах», — объяснил он. . «Итак, как я могу решить? Мне нужен второй метод для сравнения некоторых характеристик, представляющих одну целую книгу, с характеристиками другой целой книги».
Другой словарь
В сотрудничестве с биофизиком Грегори Э.Симс, математик-статистик Се-Ран Цзюнь и физик-теоретик Гохонг А. Ву, Ким решили попробовать простой вариант частотной техники слов. Они удалили из текста все знаки препинания и пробелы, создали словарь всех двух-, трехбуквенных и других словосочетаний в книгах и подсчитали разнообразие каждого «слова» или функции фиксированной длины. Функции были не последовательными комбинациями букв, а перекрывающимися последовательностями, полученными путем перемещения окна из двух, трех или более букв по тексту, продвигаясь по одной букве за раз.
При тестировании бесплатных онлайн-книг, полученных с помощью Project Gutenberg, они обнаружили, что этот метод, который они назвали методом частотного профиля характеристик (FFP), был более успешным при идентификации связанных книг — книг того же автора, книг того же жанра. , книги из той же исторической эпохи — чем анализ частотного профиля слова. Фактически, хорошее дерево можно построить, глядя на одну «оптимальную» длину признака, такую как девять букв, где «словарь» очень велик, вместо того, чтобы рассматривать все возможные длины.
«Я был просто ошеломлен, когда увидел это», — сказала Ким. По его словам, одна из причин, по которой этот метод работает лучше, может заключаться в том, что, хотя частотный анализ слов обрабатывает каждое слово независимо, частотный анализ признаков подбирает синтаксис.
«Здесь, если я возьму окно из 9 букв и проведу им по тексту, — сказал он, — я на самом деле уловлю взаимосвязь между первым и вторым словами — локальный синтаксис, — что было невозможно понять из метод частотности слов, что, видимо, очень важно.«
Геномы млекопитающих и бактерий
Воодушевленные этим успехом, исследователи применили метод к целым геномам млекопитающих, где есть наименьшие противоречия в эволюционных отношениях. «Мы относимся к геному как к книге без пробелов», — сказала Ким.
Поскольку эти геномы очень большие, исследователи перевели последовательности генома, используя сокращенный двухбуквенный алфавит — R для пуриновых нуклеиновых кислот, аденина и гуанина и Y для пиримидиновых нуклеиновых кислот, тимина и цитозина, чтобы упростить задачу. расчета.Используя оптимальную длину признака 18 пар оснований, этот тест создал генеалогическое древо, идентичное филогенетическим деревьям, построенным учеными с использованием генетической, морфологической, анатомической, ископаемой и поведенческой информации. Это было удивительно, особенно с учетом того, что подавляющее большинство геномов млекопитающих не кодируют гены, сказал Ким.
Затем они опробовали метод FFP на 518 геномах, в основном бактериях и архей, а также на шести эукариотах разной сложности и двух случайных последовательностях.Используемые геномы эуркариот были в 1000 раз длиннее, чем геномы бактерий и архей. Поскольку большая часть бактериальных геномов и геномов архей кодирует гены, в отличие от очень небольшой части геномов высших эукариот, исследователи использовали другой алфавит и словарь для метода СЗП: короткие цепочки аминокислот, строительные блоки белков, с алфавит из 20 слов, представляющий 20 возможных аминокислот.
«Возникает вопрос: можем ли мы затем сгруппировать все живые организмы на основе всего протеома, то есть сборки всех белков, вместо того, чтобы использовать только небольшой набор белков, что эквивалентно использованию небольшого набора белков. гены? » — сказала Ким.
Исследователи обнаружили, что метод FFP четко разделяет целые протеомы всех бактерий, архей, эукариот и случайные последовательности на отдельные группы или домены. Большинство групп типов внутри каждого домена и групп классов в каждом типе также были хорошо разделены с некоторыми интересными расхождениями по сравнению с общепринятыми в настоящее время группировками.
В большинстве случаев, когда группировка FFP не соответствовала принятой филогенетической группировке, проблемный организм был предметом споров среди биологов из-за противоречивых выводов из генетики, поведения и морфологии, сказал Ким.Однако новый метод действительно классифицировал несколько неклассифицированных до сих пор бактерий.
Основные различия обнаруживаются не в том, как организмы группируются, а во взаимном расположении этих групп в деревьях организмов, сказал он.
Вирусные геномы
Наконец, Ким и его коллеги проанализировали геномы нескольких сотен вирусов, в том числе нескольких, которые нельзя было классифицировать.
«Некоторые вирусы не имеют или имеют несколько высококонсервативных общих генов с другими вирусами, поэтому метод, основанный на выравнивании генов, не может найти взаимосвязь между такими группами, но мы думаем, что можем», — сказал он.
Из-за огромного количества данных о последовательностях всего генома все анализы Кима монополизировали компьютерный кластер из 320 процессоров (центральных процессоров) более чем на год.
Ким подчеркнул основное различие между FFP и геноцентрическим сравнением геномов: FFP учитывает все или большую часть ДНК или белковых последовательностей в геноме, в то время как анализ выравнивания генов выбирает небольшой набор генов из большого количества генов в геноме. каждый организм и использует это для представления организма.
«Ошибочность представления о том, что организмы могут быть представлены небольшим набором своих генов, на самом деле происходит из-за нашего предубеждения, что гены — это мы», — сказал Ким. «Теперь мы все больше и больше знаем, что это чрезмерное упрощение.
«Вполне вероятно, что некоторые из полученных нами наблюдений окажутся ошибочными, но метод будет развиваться и становиться все лучше и лучше, по мере того, как эксперты приходят и сообщают нам, где мы ошиблись. Теперь математика уже есть. мы должны максимально устранить человеческую предвзятость.«
Ким ожидает, что помимо применения метода к сравнительной геномике, он поможет сгруппировать и найти взаимосвязи между наборами другой информации, такой как электронная информация, кодирующая текст, звуки и изображения. Это также может помочь в отслеживании происхождения человека и демографии болезней с использованием полных последовательностей генома и в группировке метагеномных данных — последовательностей фрагментов генома многих организмов, большинство из которых являются неизвестными видами, обнаруженными в данной экологической нише или органе тела.
Ким надеется когда-нибудь вернуться к шекспировским текстам и выяснить их происхождение.
Работа финансировалась Национальным институтом здравоохранения и грантом Министерства образования, науки и технологий Кореи.
Лекция 2: Модели вычислений, расстояние до документа | Видео лекций | Введение в алгоритмы | Электротехника и информатика
Следующий контент предоставляется по лицензии Creative Commons. Ваша поддержка поможет MIT OpenCourseWare и дальше предлагать высококачественные образовательные ресурсы бесплатно.Чтобы сделать пожертвование или просмотреть дополнительные материалы сотен курсов MIT, посетите MIT OpenCourseWare на ocw.mit.edu.
ПРОФЕССОР: Привет всем. Вы готовы изучить некоторые алгоритмы? Ага!
Давай сделаем это. Я Эрик Домен. Можете звать меня Эрик.
И последний класс, мы как бы вскочили в разные вещи. Мы изучили поиск пиков и рассмотрели несколько алгоритмов поиска пиков для вашего набора задач. Вы уже много раз видели.
И в этом классе мы собираемся реализовать еще несколько алгоритмов.Не волнуйся. Это будет в конце. Мы собираемся поговорить о другой проблеме, о расстоянии до документа, которая будет рабочим примером для множества тем, которые мы рассмотрим в этом классе.
Но прежде чем мы двинемся туда, я хотел бы сделать шаг назад и поговорить о том, что на самом деле представляет собой алгоритм? Что может делать алгоритм? А также глубокие философские вопросы, например, что такое время?
Какое время работы алгоритма? Как это измерить? А каковы правила игры?
Ради интереса, я подумал, что сначала скажу, откуда это слово, слово «алгоритм».Это исходит от этого парня, которого сложно произнести по буквам. Аль-Хорезми, который является своего рода отцом алгебры.
В свое время он написал эту книгу под названием «Сборная книга по расчетам путем завершения и уравновешивания». В частности, речь шла о том, как решать линейные и квадратные уравнения. Итак, начало алгебры.
Не думаю, что он изобрел эти техники. Но он был своего рода автором учебников, который писал, как люди их решают. И вы можете думать о том, как решать эти уравнения, как о первых алгоритмах.Сначала вы берете этот номер. Вы умножаете на это.
Вы складываете или уменьшаете до квадратов, что угодно. Отсюда и слово «алгебра», и слово «алгоритм». Слов с этими корнями не так уж и много.
Итак, поехали. Немного забавной истории. Что за алгоритм?
Я начну с некоторых неформальных определений, а затем с точки зрения этой лекции. Идея модели вычислений состоит в том, чтобы формально определить, что такое алгоритм. Я не хочу вдаваться в сверхтехнологию и формальность, но я хочу дать вам некоторое обоснование, чтобы, когда мы пишем код Python, когда мы пишем псевдокод, мы имели некоторое представление о том, сколько вещей на самом деле стоит.Это новая лекция. Мы никогда не делали этого в 006. Но я думаю, что это важно.
Итак, на высоком уровне вы можете думать, что алгоритм — это просто … Я уверен, что вы уже видели определение раньше. Это способ определить вычисление или вычислительную процедуру для решения некоторой проблемы. Итак, в то время как компьютерный код, я имею в виду, он может просто работать в фоновом режиме все время и делать что угодно. Алгоритм, который мы думаем как имеющий некоторый ввод и генерирующий некоторый вывод. Обычно это решение какой-то проблемы.
Вы хотите знать, является ли это число простым? Вопрос?
АУДИТОРИЯ: Вы можете увеличить громкость микрофона?
ПРОФЕССОР: Этот микрофон не подключается к системе AV. Так что я просто буду говорить громче, хорошо? И успокойте сет, пожалуйста.
Хорошо, это алгоритм. Вы вносите свой вклад. Вы его прогоняете.
Вы вычислили результат. Конечно, компьютерный код тоже может это сделать. Алгоритм — это в основном математический аналог компьютерной программы.
Итак, если вы хотите рассуждать о том, что делают компьютерные программы, вы переводите это в мировые алгоритмы. И наоборот, вы хотите решить какую-то проблему — сначала вы обычно разрабатываете алгоритм с использованием математики, используя этот класс. А затем вы конвертируете его в компьютерный код. И этот урок посвящен переходу от одного к другому.
Можете нарисовать этакие аналоги. Итак, алгоритм — это математический аналог компьютерной программы. Компьютерная программа построена на языке программирования.
И написано на языке программирования. Математический аналог языка программирования, на котором мы пишем алгоритмы, обычно мы пишем их в псевдокоде, который, по сути, является еще одним причудливым словом для структурированного английского языка, хорошего английского, как бы вы ни хотели сказать. Конечно, вы можете использовать другой естественный язык.
Но идея в том, что вам нужно выразить этот алгоритм таким образом, чтобы люди могли его понять и рассуждать формально. Итак, это структурированная часть. Псевдокод означает много разных вещей.
Это просто своего рода абстрактное представление о том, как вы записываете формальную спецификацию, не имея возможности фактически запустить ее на компьютере. Хотя в вашем учебнике есть особый псевдокод, который вы, вероятно, могли бы запустить на компьютере. Во всяком случае, много.
Но вам не обязательно использовать эту версию. Это имеет смысл для людей, занимающихся математикой. Хорошо, а затем, в конечном итоге, эта программа запускается на компьютере. У вас у всех есть компьютеры, наверное, в ваших карманах.
В математическом мире есть аналог компьютера.И это модель вычислений. И это как бы основная тема первой части этой лекции. Модель вычислений говорит, что ваш компьютер может делать, в основном, что он может делать в постоянное время? И вот о чем я хочу здесь поговорить.
Итак, модель вычислений в основном определяет, какие операции вы можете выполнять в алгоритме и сколько они стоят. Это то, что время. Итак, для каждой операции мы собираемся указать, сколько времени она стоит.
Затем алгоритм выполняет несколько операций.Они объединены вместе с потоком управления, циклами for, операторами if и тому подобным, о чем мы не будем слишком беспокоиться. Но, очевидно, мы будем их часто использовать.
И мы считаем, сколько стоит каждая операция. Вы их складываете. Это общая стоимость вашего алгоритма. В частности, в этом классе нас больше всего заботит время работы.
Каждая операция требует затрат времени. Вы складываете их. Это время работы алгоритма.
Хорошо, давайте … Я собираюсь рассмотреть две модели вычислений, которые вы можете рассматривать как разные способы мышления.Вы, наверное, видели их в каком-то смысле как … как вы их называете? Стили программирования.
Объектно-ориентированный стиль программирования, более ассемблерный стиль программирования. Есть много разных стилей языков программирования, о которых я не буду здесь говорить. Но вы видели аналоги, если видели их раньше.
И эти модели действительно дают вам способ структурировать ваше мышление о том, как вы пишете алгоритм. Итак, это машина с произвольным доступом и машина указателя.Итак, мы начнем с машины с произвольным доступом, также известной как RAM. Может кто-нибудь подскажет, что еще обозначает RAM?
АУДИТОРИЯ: Оперативная память?
ПРОФЕССОР: Оперативная память. Так что это одновременно сбивает с толку, но также и удобно. Потому что RAM одновременно означает две вещи, и они означают почти одно и то же, но не совсем. Так что я думаю, что это больше сбивает с толку, чем полезно. Но вот и все.
Итак, у нас оперативная память. Ой, посмотри на это. Идеально подходит. И поэтому мы думаем, что это настоящая — это — оперативная память здесь, в мире реальных компьютеров.
Это как D-RAM SD-RAM, что угодно — вещи, которые вы покупаете и вставляете в свою материнскую плату, GP или что-то еще. А вот математический аналог … так вот, это оперативная память. Здесь тоже оперативная память.
Здесь машина с произвольным доступом. Здесь это оперативная память. Это техническая деталь.
Но идея в том, что если вы посмотрите на оперативную память вашего компьютера, это будет гигантский массив, верно? Вы можете перейти с нуля на, я не знаю. Типичный чип в наши дни — это четыре гига в одном устройстве.Таким образом, вы можете пойти с нуля до четырех концертов. Вы можете получить доступ к чему-либо посередине в постоянное время.
Чтобы получить доступ к чему-либо, вам нужно знать, где это находится. Это оперативная память. Итак, это массив. Так что я просто нарисую общую картину. Вот такой массив.
ОЗУ обычно организовано по словам. Итак, это машинное слово, которое мы собираемся вставить в эту модель. И еще есть нулевой адрес, адрес один, адрес два.
Это пятое слово. И просто продолжает идти.Вы можете думать об этом как о бесконечности. Или количество, которое вы используете, это пространство вашего алгоритма, если вы заботитесь о пространстве для хранения.
Вот и все. Хорошо, теперь как мы? Это сторона памяти. Как мы на самом деле с ним вычисляем?
Все очень просто. Мы просто говорим, что в постоянное время алгоритм может в основном считывать или загружать постоянное количество слов из памяти, выполнять с ними постоянное количество вычислений, а затем записывать их. Обычно это называется магазином.
Хорошо, ему нужно знать, где находятся эти слова. Он обращается к ним по адресу. И поэтому, я думаю, я должен написать здесь, что у вас есть постоянное количество регистров, которые просто торчат.
Итак, вы загружаете несколько слов в регистры. Вы можете выполнить некоторые вычисления с этими регистрами. А затем вы можете записать их обратно, сохраняя их в местах, указанных вашими регистрами.
Итак, вы когда-либо занимались программированием на ассемблере, вот на что похоже программирование на ассемблере. И писать алгоритмы в этой модели может быть довольно неприятно.Но в каком-то смысле это реальность.
Вот как мы думаем о компьютерах. Если игнорировать такие вещи, как кеши, это точная модель вычислений, в которой загрузка, вычисление и сохранение занимают примерно одинаковое количество времени. Все они требуют постоянного времени.
Вы можете манипулировать целым словом за раз. Что же такое слово? Вы знаете, компьютеры в наши дни, это как 32-битные или 64-битные.
Но нам нравится быть немного более абстрактными. Слово — это w бит. Это немного раздражает.
И большую часть этого класса мы не особо беспокоимся о том, что такое w. Предположим, что на входе нам дана куча вещей, которые являются словами. Так, например, обнаружение пика.
Нам дана матрица чисел. На самом деле мы не сказали, целые они или числа с плавающей запятой или что-то еще. Мы не беспокоимся об этом. Мы просто думаем о них как о словах и предполагаем, что можем манипулировать этими словами.
В частности, учитывая два числа, мы можем их сравнить. Что больше? И поэтому мы можем определить, является ли эта ячейка в матрице пиком, сравнив ее с ее соседями за постоянное время.
Мы не сказали, почему для этого настало постоянное время. Но теперь вы вроде как знаете. Если это все слова, и вы можете манипулировать постоянным количеством слов за постоянное время, вы можете определить, является ли число пиком за постоянное время.
Некоторые вещи вроде w должны регистрировать как минимум размер памяти. Потому что мое слово должно иметь возможность указать индекс в этом массиве. И мы можем использовать это когда-нибудь. Но в принципе, не беспокойтесь об этом.
Слова есть слова. Слова входят в качестве входных данных.Вы можете манипулировать ими, и вам по большей части не нужно об этом беспокоиться.
В четвертом блоке этого класса мы собираемся поговорить о том, что, если у нас есть действительно гигантские целые числа, которые не умещаются в одном слове? Как мы ими манипулируем? Как их складывать, умножать?
Так что это уже другая тема. Но большую часть этого класса мы просто предполагаем, что все, что нам дано, — это одно слово. И это легко вычислить.
Так что это более-менее реалистичная модель. И это мощный.Но в большинстве случаев код просто не использует массивы — в этом нет необходимости.
Иногда нам нужны массивы, иногда нет. Иногда вы чувствуете себя чокнутым, иногда нет. Поэтому полезно подумать о несколько более абстрактных моделях, которые не так мощны, но предлагают более простой способ мышления. Например, в этой модели нет динамического распределения памяти.
Вы, наверное, знаете, что можете реализовать динамическое распределение памяти, потому что это делают настоящие компьютеры.Но приятно подумать о модели, в которой об этом позаботятся вы. Это что-то вроде абстракции программирования более высокого уровня.
Итак, в этом классе полезен указатель. Это в основном соответствует объектно-ориентированному программированию в простой, очень простой версии. Итак, у нас есть динамически размещаемые объекты. И у объекта есть постоянное количество полей.
И поле будет либо словом — так что вы можете думать об этом как, например, о хранении целого числа, одного из входных объектов или чего-то, что вы вычислили на нем, или счетчика, и всех подобных вещей- — или указатель.Вот откуда указательная машина получила свое название. Указатель — это то, что указывает на другой объект или имеет специальное значение null, также известное как nil, также известное как none в Python.
Хорошо, сколько людей слышали о указателях раньше? А кто нет? Готов признать это?
Хорошо, всего несколько. Это хорошо. Вы бы видели указатели.
Вы, наверное, слышали, что их называют ссылками. Современные языки в наши дни не называют их указателями, потому что указатели страшны. Но между ними есть очень тонкая разница.
А эта модель действительно действительно эталонная. Но по какой-то причине она называется указательной машиной. Неважно.
Дело в том, что вы кажетесь связанными списками, надеюсь. А в связанных списках есть несколько полей в каждом узле. Возможно, у вас есть указатель на предыдущий элемент, указатель на следующий элемент и какое-то значение. Итак, вот очень простой связанный список. Это то, что вы бы назвали двусвязным списком, потому что в нем есть указатели на предыдущий и следующий.
Итак, следующий указатель указывает на этот узел.Предыдущий указатель указывает на этот узел. Следующий указатель указывает на нуль.
Предыдущий указатель указывает, скажем, на нуль. Итак, это двусвязный список с двумя узлами. Вы предполагаете, что у нас есть указатель на начало списка, может быть, указатель на конец списка, что угодно.
Итак, это структура в указательной машине. Это структура данных. В Python вы можете назвать это именованным кортежем, или это просто объект с тремя атрибутами, я думаю, они называются в Python.
Итак, у нас есть значение.Это слово похоже на целое число. И тогда некоторые вещи могут быть указателями, указывающими на другие узлы.
И вы можете создать новый узел. Вы можете уничтожить узел. Это распределение динамической памяти.
В этой модели, да, указатели есть указатели. Их нельзя трогать. Теперь вы можете реализовать эту модель на машине с произвольным доступом.
Указатель становится индексом в этой гигантской таблице. И это больше похоже на указатели в C, если вы когда-либо писали программы на C. Потому что тогда вы можете взять указатель, добавить к нему и перейти к следующему пункту после этого.
В этой модели можно просто следовать за указателем. Это все, что ты можешь сделать. Хорошо, следование указателю требует постоянного времени. Изменение одного из этих полей требует постоянного времени. Все обычные действия, которые вы можете себе представить с этими объектами, требуют постоянного времени.
Так что это на самом деле более слабая модель, чем эта. Потому что вы можете реализовать указательную машину с машиной с произвольным доступом. Но он предлагает другой образ мышления. Таким образом строятся многие структуры данных.
Cool.Так что это теория. То, о чем я хотел бы поговорить дальше, на самом деле относится к Python, какова разумная модель того, что происходит?
Так это старые модели. Это восходит к 80-м годам. Это, наверное, 80-х или 70-х годов.
Значит, они существуют уже давно. Люди использовали их всегда. Python, очевидно, намного более поздняя, по крайней мере, современные версии Python.
И это модель вычислений в некотором смысле, которую мы используем в этом классе. Потому что мы все реализуем на Python.И Python предлагает как перспективу машины с произвольным доступом, потому что у нее есть массивы, так и перспективу машины указателя, потому что у нее есть ссылки, потому что у нее есть указатели.
Так что вы можете сделать любой из них. Но и операций там много. Он не просто имеет указатель загрузки и сохранения и следования.
В нем есть такие вещи, как сортировка и добавление, конкатенация двух списков и многое другое. И у каждого из них есть своя цена. Итак, в то время как машина с произвольным доступом и указатель — это теоретические модели.Они созданы, чтобы быть очень простыми.
Итак, ясно, что все, что вы делаете, требует постоянного времени. В Python некоторые операции могут занять много времени. Для выполнения некоторых операций в Python требуется экспоненциальное время.
И вы должны знать, когда вы пишете свои алгоритмы, думая в модели Python или реализуя свои алгоритмы в реальном Python, какие операции выполняются быстро, а какие — медленно. И это то, на чем я хотел бы потратить следующие несколько минут.Операций много.
Я не собираюсь описывать их все. Но мы рассмотрим больше при чтении. А в моих заметках целая куча. Я не доберусь до них всех.
Итак, в Python вы можете делать вещи в стиле произвольного доступа. В Python массивы называются списками, что очень сбивает с толку. Но вот и все.
Список в Python — это массив в реальном мире. Конечно, это супер крутой массив? И вы можете думать об этом как о списке. Но с точки зрения реализации он реализован в виде массива.Вопрос?
АУДИТОРИЯ: Я думала, что [НЕРАЗБОРЧИВО].
ПРОФЕССОР: Вы думали, что списки ссылок Python являются связными списками. Вот почему это так сбивает с толку. На самом деле это не так.
В, скажем, схеме, в те времена, когда мы учили схему, списки — это связанные списки. А это совсем другое. Так что, когда вы это сделаете … Я сделаю операцию здесь.
У вас есть список L, и вы делаете что-то вроде этого. L — объект списка. Это требует постоянного времени.
В связанном списке это займет линейное время.Потому что у нас есть сканирование в позицию I, сканирование в позицию J, добавление 5 и сохранение. Но для удобства в Python это занимает постоянное время. И это важно знать.
Я знаю, что терминология очень запутанная. Но винить в этом доброжелательного диктатора всю жизнь. С другой стороны, вы можете создать стиль два, указательную машину, очевидно, используя объектно-ориентированное программирование.
Я просто упомяну, что я не особо беспокоюсь о методах здесь. Потому что методы — это своего рода способ размышления о вещах, не очень важный с точки зрения затрат.Если ваш объект имеет постоянное количество атрибутов — он не может иметь миллион атрибутов или не может иметь n выполнений — тогда он вписывается в эту модель машины с указателями.
Итак, если у вас есть объект, в котором есть только три или 10 вещей, или что-то еще, то это указатель. Вы можете думать о манипулировании этим объектом как о постоянном времени. Если вы возитесь со словарём объекта и делаете много сумасшедших вещей, вы должны быть осторожны с тем, останется ли это правдой.
Но пока у вас есть только разумное количество атрибутов, все это честная игра.И поэтому, если вы сделаете что-то вроде, если вы реализуете связанный список, проверенный мной Python по-прежнему не имеет встроенных связанных списков. Однако их довольно легко построить.
У вас есть указатель. И вы просто говорите, что x равно x.next. Это требует постоянного времени, потому что доступ к этому полю в объекте постоянного размера занимает постоянное время. И нам все равно, что это за константы.
В этом прелесть алгоритмов. Потому что мы заботимся только о масштабируемости с помощью n. Здесь нет n.
Это требует постоянного времени.Это требует постоянного времени. Независимо от того, насколько велик ваш связанный список или сколько у вас объектов, это постоянное время.
Ладно, но давайте сделаем посложнее. В общем, идея заключается в том, что если вы возьмете такую операцию, как L.append, то у вас будет список. И вы хотите добавить какой-то элемент в список. Но это массив.
Так что подумайте. Чтобы выяснить, сколько это стоит, нужно подумать о том, как это реализовано с точки зрения этих основных операций. Итак, это ваша основная концепция времени.
Практически все сводится к размышлениям об этом. Но иногда это менее очевидно. О L.apend немного сложно подумать. Потому что в основном у вас есть массив некоторого размера. А теперь вы хотите увеличить массив на единицу.
И очевидный способ сделать это — выделить новый массив и скопировать все элементы. Это займет линейное время. Python этого не делает.
Что он делает? Следите за восьмой лекцией. Это так называемое удвоение таблицы.
Идея очень простая.Вы можете почти догадаться по названию. А если пойти на лекцию — восемь или девять? Девять, извините.
Вы увидите, как это можно сделать за постоянное время. Есть небольшая загвоздка, но, по сути, думайте об этом как об операции с постоянным временем. Когда он у нас есть, вот почему вам стоит взять этот класс, чтобы вы понимали, как работает Python.
Это использование алгоритмической концепции, которая была изобретена, я не знаю, несколько десятилетий назад, но это простая вещь, которую нам нужно сделать для решения множества других проблем.Так что это круто. В Python есть множество функций, использующих алгоритмы. Вот почему я вам говорю.
Хорошо, давайте сделаем еще один. Чуть проще. Что, если я хочу объединить два списка?
Вы должны знать, что в Python это неразрушающая операция. Вы в основном берете копию L1 и L2 и объединяете их. Конечно, это массивы.
Можно подумать об этом, повторно реализовав это как код Python. Это то же самое, что сказать: ну, изначально L пусто.И затем для каждого элемента x и L1 L.append (x).
И очень часто в документации по Python вы видите вот что это значит, особенно в более интересных функциях. Они дают что-то вроде эквивалентного простого Python, если хотите. Здесь не используются какие-либо причудливые операции, которых мы еще не видели.
Итак, теперь мы знаем, что это требует постоянного времени. Добавление, это добавление, занимает постоянное время. Таким образом, количество времени здесь в основном порядка длины L1. И время здесь порядка длины L2.
Итак, в общем, порядок … Я буду осторожен и скажу, что 1 плюс длина L1 плюс длина L2. Плюс 1 на всякий случай, когда оба они равны 0. Для создания начального списка все еще требуется постоянное время.
Хорошо, значит, в этих примечаниях написано несколько операций. Я не буду рассматривать их все, потому что они утомительны. Но многие из вас могли бы просто расширить такой код.
И анализировать очень просто. В то время как вы просто смотрите на плюс, вы думаете, что плюс — это постоянное время.И плюс — это постоянное время, если это слово, а это слово.
Но это целые структуры данных. Так что это не постоянное время. Все в порядке. Есть и другие забавные вещи, о которых стоит подумать. Например, если я хочу знать, есть ли x в списке, как это происходит? Есть догадки?
В Python есть оператор, который называется — x в L. Как вы думаете, сколько времени это займет? Все вместе?
Линейный, ага. Линейное время. В худшем случае вам придется просмотреть весь список.
Списки необязательно отсортированы. Мы ничего о них не знаем. Так что вам нужно просто просмотреть и проверить каждый элемент. X равен этому элементу?
А еще хуже, если равные равны дорого обходятся. Так что, если x — действительно сложная вещь, вы должны это принять во внимание. Ладно, бла, бла, бла.
Хорошо, еще одно развлечение. Это похоже на популярную викторину. Сколько времени нужно, чтобы вычислить длину списка? Постоянный.
Да, к счастью, если вы ничего не знаете, вам придется просмотреть список и пересчитать предметы.Но в Python списки реализованы со встроенным счетчиком.
Он всегда сохраняет список в начале — сохраняет длину списка в начале. Так что вы просто посмотрите это. Это мгновенно.
Но это важно. Это может иметь значение. Все в порядке. Давай сделаем еще кое-что.
Что, если я хочу отсортировать список? Как долго это займет? N log n, где n — длина списка. Технически это время для сравнения двух элементов, которые обычно мы просто сортируем по словам.Итак, это постоянное время.
Если вы посмотрите на алгоритм сортировки Python, он использует сортировку сравнения. Это тема лекций третья, четвертая и седьмая. Но, в частности, на следующей лекции мы увидим, как это делается за n log n раз.
И это с использованием алгоритмов. Ладно, перейдем к словарям. Python называется dicts. И это позволяет вам что-то делать. В некотором смысле они представляют собой обобщение списков. Вместо того, чтобы помещать здесь просто индекс, целое число от 0 до длины минус 1, вы можете, например, поместить произвольный ключ и сохранить значение.
Сколько времени это займет? Я не собираюсь вас спрашивать, потому что это неочевидно. Фактически, это одна из самых важных структур данных во всей информатике. Это называется хеш-таблицей.
И это тема лекций с восьмой по 10. Так что следите за обновлениями, чтобы узнать, как это сделать в постоянное время, как сохранить произвольный ключ и получить его обратно в постоянное время. Предполагается, что ключ — это одно слово. Ага.
АУДИТОРИЯ: Сначала проверяется, есть ли ключ уже в словаре?
ПРОФЕССОР: Да, он уничтожит любой существующий ключ.Кроме того, вы знаете, вы можете проверить, есть ли ключ в словаре. Это также требует постоянного времени.
Вы можете удалить что-нибудь из словаря. Все как обычно — работа с одним ключом в словарях, очевидно, dictionary.update, который включает в себя множество ключей. Это не займет времени. Сколько времени это занимает? Ну, вы напишете цикл for и посчитаете их.
АУДИТОРИЯ: Но как можно увидеть, находится ли [НЕРАЗБОРЧИВО] словарь в постоянном времени?
ПРОФЕССОР: Как это сделать в постоянное время? Приходите на лекции с восьмой по десятую.Я должен сказать небольшую загвоздку: это постоянное время с большой вероятностью.
Это случайный алгоритм. Это не всегда требует постоянного времени. Это всегда правильно. Но иногда, очень редко, требуется немного больше, чем постоянное время.
И я собираюсь сократить это WHP. И мы увидим больше, что это означает в основном, в 6046. Но мы увидим изрядное количество в 6006 о том, как это работает и как это возможно. Это большая область исследований.
Над хешированием работает много людей.Это очень круто и очень полезно. Если вы пишете какой-либо код в наши дни, вы используете словарь. Это способ решать проблемы.
Я в основном использую Python — это платформа для рекламы остальной части класса, которую вы, возможно, заметили.
Не все темы, которые мы рассматриваем в этом классе, уже написаны на Python, но многие из них уже написаны. Итак, у нас есть удвоение стола. У нас есть словари.
Есть сортировка. Другой — long, представляющий собой длинные целые числа в Python до второй версии. И это тема лекции 11.Итак, для забавы, если у меня есть два целых числа x и y, и предположим, что одно из них состоит из такого количества слов, а другое — из такого количества слов, как вы думаете, сколько времени потребуется, чтобы их сложить? Догадки?
АУДИТОРИЯ: [Неразборчиво].
ПРОФЕССОР: Плюс? Раз? Плюс есть ответ.
Вы можете сделать это за это время. Если вы подумаете об алгоритме сложения действительно больших многозначных чисел в начальной школе, это займет не больше времени. Однако умножение немного сложнее.
Если вы посмотрите на алгоритм начальной школы, он будет x умножить на y — квадратичное время не так хорошо. Алгоритм, реализованный в Python, — это x плюс y для логической базы 2 из 3.
Между прочим, я всегда пишу LG для обозначения логической базы 2. Поскольку в ней всего две буквы, хорошо, это 2. База журнала. 2 из 3 примерно 1,6.
Итак, хотя простой алгоритм в основном возведен в квадрат x плюс y, этот алгоритм представляет собой x плюс y в степени 1,6, что немного лучше, чем квадратичный. И разработчики Python обнаружили, что это быстрее, чем умножение в начальной школе.И вот что они реализовали.
И это то, что мы рассмотрим в лекции 11, как это сделать. Это довольно круто. Есть более быстрые алгоритмы, но этот практически работает.
Еще один. Очередь кучи, она находится в стандартной библиотеке Python и реализует так называемую кучу, которая будет в четвертой лекции. Итак, скоро приеду в класс рядом с вами.
Хорошо, хватит рекламы. Это дает вам некоторое представление о модели вычислений. В этих онлайн-заметках есть еще много всего.Пойдите, проверьте их. И некоторые из них мы расскажем завтра.
Я хотел бы — теперь, когда мы в некотором роде привыкли к тому, что стоит того, что в Python, я хочу сделать реальный пример. Итак, в прошлый раз мы нашли пик. У нас будет еще один пример, который называется расстоянием до документа. Так что давай сделаем это. Есть вопросы, прежде чем мы продолжим?
Хорошо. Итак, проблема с расстоянием между документами в том, что я даю вам два документа. Я назову их D1 D2. И я хочу вычислить расстояние между ними.И первый вопрос: что это значит? Что это за функция расстояния?
Позвольте мне сначала рассказать вам о некоторых мотивах для вычисления расстояния до документа. Допустим, вы в Google и каталогизируете всю сеть. Вы хотели бы знать, когда две веб-страницы в основном идентичны.
Потому что тогда вы храните меньше и представляете это пользователю иначе. Вы говорите, ну вот и эта страница. И есть много дополнительных копий. Но вам просто нужно … вот канонический.
Или вы Википедия.И я не знаю, смотрели ли вы когда-нибудь в Википедию. Есть список всех зеркал Википедии.
Их миллионы. И находят их вручную. Но вы можете сделать это, используя расстояние до документа. Скажите, они в основном идентичны, кроме как некоторые вещи в начале или в конце?
Или, если вы преподаете этот класс и хотите обнаружить, являются ли два набора проблем обманом? Они идентичны? Мы много этим занимаемся.
Я не собираюсь рассказывать вам, какую функцию расстояния мы используем.Потому что это нарушит суть. Это не тот, который мы рассматриваем в классе.
Но мы используем автоматические тесты, чтобы определить, обманываете ли вы. У меня есть еще. Поиск в интернете.
Допустим, вы снова Google. И вы хотите осуществить поиск. Я даю вам три слова.
Ищу введение в алгоритмы. Вы можете представить себе введение в алгоритмы как очень короткий документ. И вы хотите проверить, похож ли этот документ на все другие документы в Интернете.
И тот, который наиболее похож, тот, который имеет небольшое расстояние, возможно, это то, что вы хотите поместить вверху. Очевидно, что это не то, чем занимается Google. Но это часть того, что он делает.
Вот почему вас это волнует. Отчасти это тоже просто игрушечная проблема. Это позволяет нам проиллюстрировать множество техник, которые мы разрабатываем в этом классе.
Хорошо, я буду думать о документе как о последовательности слов. Чтобы быть немного более формальным, что я имею в виду под документом? А слово будет просто строкой буквенно-цифровых символов — от A до Z и от нуля до девяти.
Хорошо, так что, если у меня есть документ, который вы также считаете строкой, и вы в основном удаляете все пробелы и знаки препинания, весь остальной мусор, который там есть. Это все, что между этими словами. Это простое определение разложения документов на слова.
А теперь мы можем подумать о том, что … Я хочу знать, похожи ли D1 и D2. И я думал о своем документе как о наборе слов. Может быть, они похожи, если у них много общих слов.
Так вот в чем идея. Посмотрите на общие слова и используйте их, чтобы определить расстояние до документа. Очевидно, что это только один способ определить расстояние.
Так будет и в этом классе. Но есть много других возможностей. Итак, я собираюсь придумать документ.
Это последовательность слов. Но я также мог думать об этом как о векторе. Итак, если у меня есть документ D, и у меня есть слово W, это D из W будет количеством раз, когда это слово встречается в документе. Итак, количество повторений W в документе D.
Значит, это число. Это целое число. Неотрицательное целое число. Может быть 0. Может быть. Может быть миллион.
Я думаю об этом как о гигантском векторе. Вектор индексируется по всем словам. И для каждого из них есть своя частота.
Их много ноль. А потом у некоторых из них есть положительные числа вхождений. Вы можете представить себе каждый документ как один из этих графиков на этой общей оси.
Здесь бесконечно много слов. Так что это большая ось.Но это один из способов нарисовать картину.
Хорошо, например, возьмем два очень важных документа. Всем нравятся кошки и собаки. Итак, это двухсловные документы.
Итак, мы можем их нарисовать. Поскольку здесь всего три разных слова, мы можем нарисовать их в трехмерном пространстве. Кроме того, рисовать немного сложно.
Итак, у нас есть, скажем, какой — скажем, этот — облегчает рисование. Так что здесь будет только ноль и один. Для каждой из осей предположим, что это собака, а это кошка.
Хорошо, значит, кошка выиграла … у нее одна кошка и ни одна собака. Итак, это здесь. Это вектор, указывающий туда.
Собака, которую вы поймали, в основном указывает туда. Хорошо, это два вектора. Итак, как мне измерить, насколько разные два вектора? Любые предложения из векторного исчисления?
АУДИТОРИЯ: Внутренний продукт?
ПРОФЕССОР: Внутренний продукт? Да, это хорошее предложение. Любые другие.
Хорошо, мы перейдем к внутреннему продукту. Мне нравится внутренний продукт, также известный как скалярный продукт.Просто определите это быстро.
Итак, мы могли … Я назову это D-прайм, потому что это не то, с чем мы собираемся закончить. Мы могли бы думать об этом как о скалярном произведении D1 и D2, также известном как сумма по всем словам D1 из W, умноженного на D2 из W. Так, например, вы берете скалярное произведение этих двух парней.
Те совпадают. Таким образом, вы получаете одно очко, умноженное на ноль. Так что вы не получите многого.
Итак, это некоторая мера расстояния. Но на самом деле это мера общности.Так что это было бы как бы обратным расстоянием, извините.
Если у вас произведение с высокой точкой, у вас много общего. Потому что многие из этих вещей не были … не были чем-то нулевым. На самом деле это положительное число, умноженное на некоторое положительное число. Если у вас много общих слов, это выглядит хорошо.
Проблема в том, что если у меня есть длинный документ — скажем, миллион слов — и он на 99% похож на другой документ длиной в миллион слов, он все равно выглядит очень похожим.На самом деле, мне нужно сделать наоборот. Допустим, это миллион слов, половина из которых общие.
Так что не так много, но изрядное количество. Тогда у меня примерно 500000 баллов. И затем у меня есть два документа, которые, скажем, состоят из 100 слов. И они идентичны.
Их оценка может быть всего 100. Таким образом, даже если они идентичны, это не совсем инвариантно к масштабу. Так что это не совсем идеальная мера.
Есть предложения, как это исправить? Это, я думаю, немного сложнее.Ага?
АУДИТОРИЯ: Разделить на длину векторов?
ПРОФЕССОР: разделите на длину векторов. Думаю, это стоит подушки. Еще не сделал подушек. Извини за это. Итак, разделите на длину вектора. Это хорошо.
Я назову это двойным простым числом D. Все еще не совсем правильный ответ. Или нет … нет, это неплохо. Это очень хорошо.
Итак, длина векторов — это количество слов, которые в них встречаются. Это довольно круто.Но знает ли кто-нибудь эту формулу? Угол, да.
Это очень похоже на угол между двумя векторами. Это просто отклонение от дуги, потому что. Это косинус угла между двумя векторами.
А я геометр. Мне нравится геометрия. Итак, если вы возьмете arc cos этого предмета, это хорошо известная метрика расстояния. Это восходит к 1975 году, если вы можете в это поверить, когда люди — первые дни документирования, поиска информации, задолго до Интернета, люди все еще работали над этим материалом.
Так что это естественная мера угла между двумя векторами. Если это 0, они в основном идентичны. Если это 90 градусов, они действительно очень разные. И это дает вам удобный способ вычислить расстояние до документа.
Вопрос в том, как на самом деле вычислить эту меру? Теперь, когда мы придумали что-то разумное, как мне на самом деле найти это значение? Мне нужно вычислить эти векторы — количество повторений каждого слова в документе.
И мне нужно, чтобы вы вычислили скалярное произведение.А потом мне нужно разделить. Это действительно просто.
Итак, скалярное произведение — и мне также нужно разложить документ на список слов. Итак, мне нужно сделать три вещи. Позвольте мне их записать.
Так что вроде алгоритма. Есть один, разбить документ на слова. Во-вторых, вычислить частоту слов, сколько раз встречается каждое слово. Это векторы документа.
И затем третий шаг — вычислить скалярное произведение. Позвольте мне рассказать вам немного о том, как это делается.Некоторые из них будут подробно рассмотрены в будущих лекциях. Я хочу дать вам обзор.
Есть много способов выполнить каждый из этих шагов. Если вы посмотрите на — рядом с конспектами лекции для этой второй лекции, там есть куча кода и куча примеров данных документов — большие массивы текста. И вы можете запустить, я думаю, для этого есть восемь разных алгоритмов.
И позвольте мне дать вам … на самом деле, почему бы мне немного не перейти к делу и не рассказать вам о времени выполнения этих различных реализаций одних и тех же алгоритмов.Есть много разновидностей этого алгоритма. Реализуем целую кучу.
Каждый семестр я преподаю это, я немного их меняю, добавляю еще несколько вариантов. Итак, первая версия для конкретной пары документов размером с мегабайт — не очень много текста — занимает 228,1 секунды — очень медленно. Жалкий.
Затем мы немного подправим алгоритмы. Спускаемся к 164 секундам. Затем мы получаем 123 секунды.
Затем мы опускаемся до 71 секунды. Затем мы опускаемся до 18.3 секунды. И тогда мы получаем 11,5 секунды.
Тогда получаем 1,8 секунды. Затем мы получаем 0,2 секунды. Итак, коэффициент 1000. Это только на Python.
2/10 секунды для обработки мегабайт. Все хорошо. Это становится разумным.
Это не так разумно. Некоторые из этих улучшений являются алгоритмическими. Некоторые из них просто лучше кодируют.
Значит, постоянные коэффициенты улучшаются. Но если вы посмотрите на все более крупные тексты, это станет еще более драматичным.Потому что многие из них были улучшениями от алгоритмов с квадратичным временем до линейных алгоритмов и алгоритмов log n.
И так для мегабайта да, разумное улучшение. Но если вы посмотрите на гигабайт, это будет огромное улучшение. Никакого сравнения не будет.
Собственно сравнения не будет. Потому что это никогда не закончится. Вот почему я запустил такой небольшой пример, чтобы у меня хватило терпения дождаться этого. Но этот вы можете запустить на более крупных примерах.
Хорошо, так куда мне идти дальше? Пять минут.Я хочу рассказать вам о некоторых из этих улучшений и некоторых алгоритмах здесь.
Начнем с очень простого. Как бы вы разбили документ на слова в Python? Ага?
АУДИТОРИЯ: [Неразборчиво]. Перебрать документ, [НЕРАЗБОРЧИВО] словарь?
ПРОФЕССОР: Перебираем … вот как мы делаем номер два. Хорошо, мы можем поговорить об этом. Перебирайте слова в документе и помещайте их в словарь.
Допустим, количество слов плюс 1.Это сработает, если count — это так называемый словарь count, если вы супер Pythonista. Иначе надо проверить, есть ли это слово в словаре?
Если нет, установите его на единицу. Если он есть, добавьте к нему еще один. Но я думаю, вы знаете, что это значит.
Будет подсчитано количество слов — будет подсчитана частота каждого слова в словаре. И становится, что словари работают в постоянное время с высокой вероятностью — с большой вероятностью — это потребует порядка — ну, немного обмануть.Потому что слова могут быть очень длинными.
Итак, чтобы уменьшить слово до машинного слова, можно было бы взять порядок длины слова. Если быть более точным, это будет сумма длин слов в документе, которая также известна как длина документа. Так что это хорошо. С большой вероятностью это линейное время.
Хорошо, это хороший алгоритм. Это введено в четвертый алгоритм. Так что мы получили значительный импульс.
Есть и другие способы сделать это.Например, вы можете отсортировать слова, а затем просмотреть отсортированный список и посчитать, сколько слов вы получите подряд для каждого из них? Если он отсортирован, можно посчитать — я имею в виду, что все одинаковые слова ставятся рядом друг с другом.
Так что посчитать их несложно. И это будет работать почти так же быстро. Это был один из таких алгоритмов.
Хорошо, есть пара разных способов сделать это. Вернемся к этому первому шагу. Как бы вы вообще разбили документ на слова? Ага?
АУДИТОРИЯ: Найдите распространенные места, а затем [НЕРАЗБОРЧИВО].
ПРОФЕССОР: Пропустите строку. И каждый раз, когда вы видите что-то не буквенно-цифровое, начинайте новое слово. Хорошо, это будет работать в линейном времени.
Хороший ответ. Так что это не сложно. Если вы увлекаетесь питонистом, вы можете сделать это вот так.
Помни моих бывших бывших. Это найдет все слова в документе. Проблема, как правило, в том, что это занимает экспоненциальное время.
Так что, если вы думаете об алгоритмах, будьте очень осторожны. Если вы не знаете, как реализовано re, это, вероятно, будет работать в линейном времени.Но это совсем не очевидно.
Делайте все, что угодно, с регулярными выражениями. Если вы не знаете, что это значит, не беспокойтесь об этом. Не используйте это.
Если вы знаете об этом, будьте очень осторожны в этом классе при использовании re. Потому что это не всегда линейное время. Но для этого есть простой алгоритм, который просто просматривает и ищет буквенно-цифровые символы.
Соедините их вместе. Это хорошо. В примечаниях есть еще несколько алгоритмов.
Вы должны их проверить.И ради интереса взгляните на этот код и посмотрите, как небольшие различия существенно влияют на производительность. Следующее занятие будет посвящено сортировке.
(PDF) Новый вычислительный метод для оптимального управления классом систем с ограничениями, управляемых уравнениями с частными производными
возраст (Milam et al., 2000). Выходы системы
аппроксимируются B-сплайнами, а линейное программирование не
используется для определения сопутствующих
эффективных B-сплайнов. Это программное обеспечение может до
дней рассматриваться как альтернатива программным пакетам для хорошо
установленных коллокаций, разработанных
с использованием методов, описанных в (Hargraves and
Paris, 1987; Seywald, 1994) и (von Stryk и
Bulirsch, 1992).В будущих публикациях (Milam
,
и др., 2002) рассматривается реализация NTG в реальном времени
и, таким образом, подчеркивается важность
сокращения времени вычислений.
В этой статье мы предлагаем расширить концепцию «инверсии»
на область частных дифференциальных уравнений
. В этом случае выходы параметризуются
B-сплайнами тензорного произведения вместо B-сплайнов.
Частные производные произведения тензора B-сплайна
могут быть легко вычислены, объединены и заменены на
как можно большего количества компонентов состояний и управления
как в функциях затрат, так и в ограничениях
.
Вклад нашей текущей работы заключается в разработке теории
и набора соответствующих программных инструментов
для решения в реальном времени задач оптимального управления с ограничениями
для класса систем, управляемых
уравнениями в частных производных. Мы думаем, что
этот набор программных инструментов был бы полезен в связях
для прогнозирования и управления процессами.
В Разделе 1 мы подробно описываем наш подход.Мы применяем
нашу предложенную методологию к примеру из
литературы в разделе 2. Результаты показывают, что
эта методология является эффективной и что решения
задач оптимального управления для систем, управляемых
уравнений в частных производных, могут быть вычислены. в режиме реального времени
по нашей методике.
2. ПОСТАНОВКА ЗАДАЧИ И ПРЕДЛАГАЕМЫЙ МЕТОД РЕШЕНИЯ
2.1 Задача оптимального управления
Условно мы используем N = {1, 2, 3,…} для представления
натуральных чисел и R для представления действительных чисел.
Пусть Ω — открытое множество в R
2
и Γ =
¯
Ω — Ω
его граница. Обозначим Ω ∋ (t, x) 7 → φ (t, x)
состояние системы, Ω ∋ (t, x) 7 → u (t, x)
— управление, при n = dim φ , m = dim u. Пусть
ξ представляет собой первое (n
t
+ 1) (n
x
+ 1) частных
производных φ, при этом n
t
∈ N и n
x
∈ N
ξ
.
= (φ,
∂φ
∂t
,…,
∂
n
t
φ
∂t
n
t 9000φ
9000
∂x
,
∂
2
φ
∂t∂x
,…,
∂
n
t
+1
φ
n
t
∂x
,
….
∂
n
x
φ
∂
n
x
x
n
t
−1) n
x
+1
φ
∂t∂
n
x
x
,.. . ,
∂
n
t
+ n
x
φ
∂t
n
t
∂
n
x
x
)
Мы рассматриваем системы, которые управляются частными
дифференциальными уравнениями вида
f (ξ (t, x)) = Bu (t, x) (1)
в Ω, где B ∈ R
n × m
— матрица с коэффициентом ffi-
в R, f: R
n (n
t
+1) (n
x
+1)
→ R
n
— нелинейная функция
.
Мы хотим найти траекторию (1), которая минимизирует
функционал стоимости
мин
(φ, u)
Дж (φ, u) =
Z
Ω
L ( ξ (t, x), u (t, x)) dx dt (2)
с учетом ограничений области
фунтов
Ом
≤ S
Ом
(ξ, u) ≤ ub
Ω
(3)
на Ω и граничные ограничения
фунтов
Γ
≤ S
Γ
(ξ, u) ≤ ub
Γ
(4)
, где Γ
(4)
на Γ L: R
n (n
t
+1) (n
x
+1) + m
→ R, S
Ом
:
R
n (n
t
+1) (n
x
+1) + m
→ R
n
Ω
, S
Γ
: R
n (n
t
+ 1) (п
х
+1) + m
→
R
n
Γ
— нелинейные функции, n
Ω
∈ N, n
Γ
∈ N.
Мы молчаливо предполагаем, что существует такой оптимальный временный контроль, и обращаемся к (Lions, 1971; Bonnans
and Casas, 1995; Bergounioux et al., 1998; Maurer
and Mittelmann, 2001) для обсуждения вопросов, касающихся
это важный вопрос.
2.2 Предлагаемая методология решения
Предлагаемая нами методология
состоит из трех компонентов. Во-первых, необходимо определить параметр
этеризации (выход) так, чтобы уравнение (1) могло отображать
в пространство более низкой размерности (выходное пространство
).Как только это будет выполнено, стоимость в уравнении (2)
и ограничения в уравнениях (3) и (4) также могут быть отображены в пространство вывода. Второй —
для параметризации каждого компонента вывода
в терминах соответствующего тензорного произведения сплайновой поверхности B-
. Наконец, последовательное квадратичное программирование
используется для определения коэффициентов
B-сплайнов, которые минимизируют стоимость с учетом
ограничений в пространстве вывода.
В большинстве случаев желательно найти и вывести
Ω ∋ (t, x) 7 → z (t, x) ∈ R
p
, p ∈ N и отображение ψ
вида
z = ψ (ξ, u) (5)
так, что (ξ, u) (и, следовательно, φ) может быть полностью определено
из z и конечного числа его
частных производных с помощью уравнения (1)
(ξ, u) = ϑ (
∂
с
z
∂t
с
,
∂
с
z
∂2
x
,.. . ,
∂
с
z
∂x
с
,
∂
с − 1
z
∂t
с − 1
,. . . ,. . . , z).
После выбора выхода z мы ищем оптимум
в конкретном функциональном пространстве: мы
параметризуем каждый из его компонентов в терминах
Описание курса | Научные вычисления | Университет Вандербильта
Поиск подходящих курсов по научным вычислениям
Если ДА, чтобы выбрать все курсы, одобренные для получения кредита по второстепенному направлению «Научные вычисления», щелкните ссылку «Дополнительно» рядом с полем поиска, выберите раскрывающееся поле «Атрибуты класса» в правом нижнем углу страницы расширенного поиска и затем выберите «Допущено к научным вычислениям», чтобы найти все курсы.
ПРИМЕЧАНИЕ. В следующий список включены только названия, номера и описания курсов. Отметьте ДА для текущих предварительных условий, кредитных часов и (для A&S) категорий ОСИ.
Основные курсы программирования
CS 1101 Программирование и решение проблем. Интенсивное введение в разработку алгоритмов и решение проблем на компьютере (с использованием Java).Структурированное определение проблемы, нисходящий и модульный алгоритм. Запуск, отладка и тестирование программ. Программная документация. Примечание: CS 1104 рекомендуется по сравнению с CS 1101 для второстепенных программ по научным вычислениям.
— или —
CS 1104 Программирование и решение проблем с Python. Интенсивное введение в разработку алгоритмов и решение проблем с использованием языка программирования Python.Структурированное определение проблемы, нисходящий и модульный алгоритм. Запуск, отладка и тестирование программ. Программная документация.
CS 2201 Разработка программ и структуры данных. Изучение элементарных структур данных, связанных с ними алгоритмов и их применение в задачах; тщательная разработка методов и стиля программирования; разработка и реализация программ с несколькими модулями с использованием хороших структур данных и хорошего стиля программирования. Примечание: CS 2204 рекомендуется по сравнению с CS 2201 для второстепенных научных вычислений.
— или —
CS 2204 Разработка программ и структуры данных для научных вычислений. Структуры данных и связанные с ними алгоритмы в применении к вычислительным задачам в науке и технике. Сложность времени и памяти; структуры динамической памяти; сортировка и поиск; продвинутое программирование и стратегии решения проблем; эффективное использование программной библиотеки.Студенты, получившие кредит на CS 2201, не могут сдавать CS 2204.
Научно-вычислительные курсы
SC 3250 Набор инструментов для научных вычислений. Команда провела курс с темами, иллюстрирующими использование вычислительных инструментов в различных областях науки и техники. Темы могут включать моделирование сложных физических, биологических, социальных и инженерных систем, оптимизацию и оценку имитационных моделей, методы Монте-Карло, научную визуализацию, высокопроизводительные вычисления или интеллектуальный анализ данных.
SC 3260 Высокопроизводительные вычисления. Введение в концепции и практику высокопроизводительных вычислений. Параллельные вычисления, grid-вычисления, вычисления на GPU, передача данных, проблемы безопасности высокой производительности, настройка производительности на архитектурах с общей памятью.
SC 3850 Независимое исследование в области научных вычислений. Разработка исследовательского проекта индивидуальным студентом под руководством спонсора факультета. Проект должен сочетать научные вычислительные инструменты и методы с существенной научной или инженерной проблемой. Требуется согласие как спонсора факультета, так и одного директора несовершеннолетнего SC.
SC 3851 Независимое исследование в области научных вычислений. Продолжение SC 3850 под руководством того же или другого спонсора факультета.
SC 3890 Специальные темы в научных вычислениях: передовые высокопроизводительные вычисления. Этот курс предлагается в онлайн-партнерстве с Университетом Иллинойса. Высокопроизводительные вычислительные алгоритмы и программные технологии с упором на использование систем распределенной памяти для научных вычислений. Теоретическая и практически достижимая производительность процессоров, систем памяти и сетей для крупномасштабных научных приложений.Современные и многообещающие технологии в области прогнозных вычислений и инженерии. Алгоритмические ядра, общие для линейных и нелинейных алгебраических систем, уравнений в частных производных, интегральных уравнений, методов частиц, оптимизации и статистики. Компьютерная архитектура и нагрузки, оказываемые развивающейся архитектурой на научные приложения и лежащие в их основе математические алгоритмы. Современные методы дискретизации, библиотеки решателей и среды выполнения. Ожидается, что студенты будут знакомы с C или C ++ в среде Unix, некоторыми основными численными алгоритмами и базовой архитектурой компьютера.
SC 3890 Специальные темы в научных вычислениях. Курс специальных тем.
SC 5250 Набор инструментов для научных вычислений. Команда провела курс с темами, иллюстрирующими использование вычислительных инструментов в различных областях науки и техники.Темы могут включать моделирование сложных физических, биологических, социальных и инженерных систем, оптимизацию и оценку имитационных моделей, методы Монте-Карло, научную визуализацию, высокопроизводительные вычисления или интеллектуальный анализ данных.
SC 5260 Высокопроизводительные вычисления. Введение в концепции и практику высокопроизводительных вычислений. Параллельные вычисления, grid-вычисления, вычисления на GPU, передача данных, проблемы безопасности высокой производительности, настройка производительности на архитектурах с общей памятью.
SC 5890 Специальные темы в научных вычислениях: передовые высокопроизводительные вычисления. Этот курс предлагается в онлайн-партнерстве с Университетом Иллинойса. Высокопроизводительные вычислительные алгоритмы и программные технологии с упором на использование систем распределенной памяти для научных вычислений. Теоретическая и практически достижимая производительность процессоров, систем памяти и сетей для крупномасштабных научных приложений.Современные и многообещающие технологии в области прогнозных вычислений и инженерии. Алгоритмические ядра, общие для линейных и нелинейных алгебраических систем, уравнений в частных производных, интегральных уравнений, методов частиц, оптимизации и статистики. Компьютерная архитектура и нагрузки, оказываемые развивающейся архитектурой на научные приложения и лежащие в их основе математические алгоритмы. Современные методы дискретизации, библиотеки решателей и среды выполнения. Ожидается, что студенты будут знакомы с C или C ++ в среде Unix, некоторыми основными численными алгоритмами и базовой архитектурой компьютера.
SC 5890 Специальные темы в научных вычислениях: Введение в компьютерное программирование для естественных, социальных и гуманитарных наук. Введение в компьютерное программирование для естественных, социальных и гуманитарных наук Курс предназначен для аспирантов, не имеющих инженерного образования, которые хотят стать профессиональными специалистами в области компьютерного программирования.Среда MATLAB используется для иллюстрации общих методов компьютерного программирования. Предварительный опыт не требуется.
SC 5890 Специальные темы в научных вычислениях. Курс специальных тем.
Дисциплинарные курсы по научным вычислениям
Утвержденные курсы по предметным областям перечислены ниже. Эти курсы либо предоставляют подробное описание основного научного вычислительного инструмента и техники, либо объединяют научные вычислительные инструменты и методы с основной областью инженерной науки.Новые курсы могут быть утверждены директорами несовершеннолетних.
АНТРОПОЛОГИЯ
ANTH 3261 Введение в географические информационные системы и дистанционное зондирование. Компьютеризированная графика и статистические процедуры для распознавания и анализа пространственных паттернов. Сбор, хранение и поиск пространственных данных; пространственный анализ и графический вывод объектов карты.Интеграция спутниковых снимков с данными из других источников на основе практического опыта. Предполагает базовые знания компьютерного оборудования и программного обеспечения.
АСТРОНОМИЯ
ASTR 3600 Stellar Astrophysics. Поглощение и испускание излучения Солнцем и звездами. Принципы звездного строения и звездной эволюции от образования до смерти.
ASTR 3700 Galactic Astrophysics. Межзвездное вещество и газовые туманности, структура и эволюция нормальных галактик, активные галактические ядра и квазары, а также наблюдательная космология.
ASTR 3800 Формирование структуры во Вселенной. Наблюдательные и теоретические аспекты внегалактической астрономии. Измерения галактик и крупномасштабной структуры Вселенной из обзоров галактик. История расширения Вселенной и роли темной материи и темной энергии.Рост флуктуаций плотности во Вселенной из-за гравитации. Космологическое моделирование N-тел и образование гало темной материи. Физика образования галактик. Экспериментальные исследования темной материи и темной энергии.
БИОИНФОРМАТИКА
BMIF 6310 Основы биоинформатики. Этот обзорный курс знакомит студентов с экспериментальным контекстом и реализацией ключевых алгоритмов в биоинформатике.Класс начинается с обзора основ биохимии и молекулярной биологии. Затем группа сосредоточится на алгоритмах сопоставления и выравнивания биологических последовательностей в контексте молекулярной эволюции. Акцент будет перенесен с сравнения последовательностей на системы, разработанные для обеспечения высокопроизводительного секвенирования ДНК, сборки генома и аннотации генов. Следующее внимание будет уделяться генным продуктам, поскольку студенты рассматривают алгоритмы, поддерживающие протеомную масс-спектрометрию, а также вывод и прогноз структуры белка.Информатика, связанная с транскрипционными микрочипами для полногеномных ассоциативных исследований, будет продолжена. Наконец, класс изучит биологические сети, включая генетические регуляторные сети, генные онтологии и интеграцию данных. Формальное обучение разработке программного обеспечения полезно, но не обязательно. Студенты напишут и представят индивидуальные проекты. Для зачисления бакалаврам необходимо разрешение преподавателя.
BMIF 7380 Конфиденциальность данных в биомедицине. Этот курс знакомит студентов с концепциями оценки и создания технологий, которые защищают личную конфиденциальность данных, собранных для первичной медико-санитарной помощи и биомедицинских исследований. Материал этого курса затрагивает темы моделирования биомедицинских знаний, интеллектуального анализа данных, разработки политики и права. Предварительные требования: Ожидается, что учащиеся будут владеть базовыми программами, хотя специального языка не требуется. Для зачисления бакалаврам необходимо разрешение преподавателя.
БИОЛОГИЧЕСКИЕ НАУКИ
BSCI 3272 Genome Science. Цели и значение науки. Получение данных генома из общедоступных баз данных; экспериментальные и вычислительные методы, используемые при анализе данных генома и их аннотации. Функциональные аспекты геномики, транскриптомики и протеомики; использование филогенетики и популяционной геномики для вывода эволюционных взаимосвязей и механизмов эволюции генома.
БИОМЕДИЦИНСКАЯ ТЕХНИКА
BME 2400 Количественные методы I: статистический анализ. Применение современных вычислительных методов для параметрического и непараметрического статистического анализа биомедицинских данных. Особое внимание уделяется вероятности, выборке, оценке, дисперсионному анализу, одно- и многомерной регрессии, а также принципам проверки гипотез, дизайну экспериментов и клинических испытаний. Нет кредита для студентов, которые получили кредит на BME 3200.
BME 3200 Анализ биомедицинских данных. Применение современных вычислительных методов для статистического анализа биомедицинских данных. Особое внимание уделяется отбору образцов, оценке, дисперсионному анализу и принципам экспериментального дизайна и клинических испытаний.
BME 3890 Computational Genomics. Курс охватывает вычислительные алгоритмы обработки и анализа геномных данных, включая сборку генома, выравнивание, фазирование гаплотипа, анализ RNA-Seq одной клетки и мультиомикс.Будут рассмотрены как алгоритмы, так и биологические основы, необходимые для студентов инженерных специальностей, чтобы оценить их применение. Студенты также познакомятся с текущими программными инструментами для анализа реальных данных секвенирования.
BME 4310 Моделирование живых систем для терапевтической биоинженерии. Введение в компьютерное моделирование и моделирование процессов терапевтической биоинженерии.Построение компьютерных моделей и использование современных программных средств моделирования. Введение в численные методы решения дифференциальных уравнений и происхождение математических моделей для биотранспорта, биомеханики, динамики роста опухолей / вирусов и методов медицинской визуализации на основе моделей.
BME 7310 Расширенное компьютерное моделирование и анализ в биомедицинской инженерии. Обзор актуальных тем в области биомедицинского моделирования: биотранспорт, биомеханика, динамика роста опухолей и вирусов, методы медицинской визуализации на основе моделей и т. Д.Математическая разработка и анализ биомедицинского моделирования с использованием передовых численных методов для решения обыкновенных уравнений и уравнений в частных производных. Акцент будет сделан на темы, связанные с исследованиями выпускников. Для студентов бакалавриата требуется разрешение инструктора.
BME 7410 Количественные методы в биомедицинской инженерии. Математика, количественный анализ и вычислительные методы для приложений биомедицинской инженерии.Темы включают прикладную вероятность и статистику, анализ сигналов и планирование экспериментов, линейные системы, преобразования Фурье, а также численное моделирование и анализ. Для студентов бакалавриата требуется разрешение инструктора.
ХИМИЧЕСКАЯ И БИОМОЛЕКУЛЯРНАЯ ТЕХНИКА
CHBE 4830 Молекулярное моделирование. Введение в современные инструменты статистической механики, такие как Монте-Карло и моделирование молекулярной динамики, а также вариации.Понимание методов, возможностей и ограничений молекулярного моделирования и приложений для простых и сложных жидкостей, относящихся к химической и смежным отраслям обрабатывающей промышленности.
ХИМИЯ
CHEM 5410 Методы молекулярного моделирования . В этом курсе будут представлены различные методы молекулярного моделирования и вычислительной химии, включая базовую теорию, детали реализации, возможности и ограничения различных методов, а также примеры приложений.Большинство примеров приложений сосредоточены на биомакромолекулах, хотя также будут представлены расчеты малых молекул и моделирование жидкостей. Предполагается разумное практическое знание физической химии и биохимии, и любые хорошие учебники по биохимии и физической химии будут служить полезными справочными материалами для тех, кому может потребоваться некоторый обзор. Курс для аспирантов, требующий разрешения инструктора.
CHEM 5420 Вычислительная структурная биохимия. Теоретические и практические аспекты выравнивания последовательностей белков, предсказание вторичной структуры, сравнительное моделирование, стыковка белок-белок и белок-лиганд. Дизайн лекарств на основе структуры, виртуальный скрининг, количественные отношения структурной активности, хеминформатика и картирование фармакофоров в терапевтических разработках.
ГРАЖДАНСКОЕ ОБРАЗОВАНИЕ
CE 4320 Аналитика данных для инженеров. Программирование, анализ и визуализация реальных данных с целью принятия обоснованных решений в инженерных задачах. Статистическое моделирование в практической и прикладной перспективе; применение аналитики данных для преодоления разрыва между данными и решениями; основы дизайна экспериментов.
КОМПЬЮТЕРНЫЕ НАУКИ
CS 3274 Моделирование и имитация. Общая теория моделирования и моделирования различных систем: физических процессов, компьютерных систем, биологических систем и производственных процессов. Принципы дискретно-событийного, непрерывного и гибридного моделирования систем, алгоритмы моделирования для различных парадигм моделирования, методологии построения моделей ряда реалистичных систем и анализ поведения системы. Вычислительные вопросы моделирования и анализа систем. Стохастическое моделирование.
НАУКИ О ЗЕМЛЕ И ЭКОЛОГИИ
EES 4760/5760 Агентное и индивидуальное вычислительное моделирование. Приложения в естественных, социальных и поведенческих науках и технике. Разработка, программирование и документирование моделей. Использование моделей для экспериментов. Примеры из экологических наук, экологии, экономики, городского планирования и медицины. Ожидается знакомство с базовой статистикой и знание алгебры.
ЭКОНОМИКА
ECON 3032 Прикладная эконометрика. Количественный экономический анализ с упором на многомерную регрессию. Измерение, спецификация, оценка, вывод, прогноз и интерпретация эконометрических моделей. Опыт работы с данными и компьютерными приложениями. ПРИМЕЧАНИЕ. Чтобы считаться факультативом по научным вычислениям, студенты должны записаться в раздел, в котором используется Python или R (не Stata).
ECON 3035 Эконометрические методы. Свойства и проблемы оценки экономических отношений с помощью множественной регрессии. Статистическая и эконометрическая теория для решения эмпирических вопросов. Практический опыт анализа экономических данных с программированием в статистическом ПО. ПРИМЕЧАНИЕ. Чтобы считаться факультативом по научным вычислениям, студенты должны записаться в раздел, в котором используется Python или R (не Stata).
ECON 3750 Эконометрика для больших данных. Эконометрические методы анализа больших наборов данных. Выбор модели, регуляризация, классификация, повторная выборка, древовидные методы и вспомогательные векторные машины. Прогнозирование цен на акции, прогнозирование цен на жилье и определение заработной платы.
ЭЛЕКТРИЧЕСКАЯ И КОМПЬЮТЕРНАЯ ТЕХНИКА
EECE 6358 Количественный анализ медицинских изображений. Обработка изображений и статистические методы для количественного анализа и интерпретации данных медицинской визуализации.Сосредоточьтесь на подходах к нейровизуализации, связанных со структурой, функцией и связью мозга. Конкретные темы включают в себя массовый одномерный анализ (параметрическое отображение), вопросы множественного сравнения, случайные поля, независимые компоненты, непараметрические подходы и методы Монте-Карло.
ЧЕЛОВЕЧЕСКОЕ И ОРГАНИЗАЦИОННОЕ РАЗВИТИЕ
HOD 3200 Введение в науку о данных. Предоставляет студентам теоретические и практические знания в области науки о данных, включая доступ к данным, анализ данных и представление анализа данных. Темы доступа к данным включают сканирование веб-страниц с использованием интерфейсов прикладного программирования и запросов к базе данных. Темы анализа данных включают линейную регрессию, логистическую регрессию и основы машинного обучения без учителя. Анализ данных также будет охватывать перекрестную проверку. Темы представления данных включают одномерные и двумерные графики, решетчатые графики, отображение и интерактивную графику.Подчеркивает грамотное программирование как основу для доступа, анализа и презентации.
МАТЕМАТИКА
MATH 3620 Введение в вычислительную математику. Численное решение линейных и нелинейных уравнений, интерполяция и полиномиальная аппроксимация, нечисловое дифференцирование и интегрирование, аппроксимация кривой наименьших квадратов и теория приближений, численное решение дифференциальных уравнений, ошибки и арифметика с плавающей запятой.Применение теории к проблемам науки, техники и экономики. Особое внимание уделяется использованию компьютера учащимися.
MATH 3630 Математическое моделирование в биологии. Математическое моделирование с приложениями в биологии и медицине. Основные инструменты математического моделирования, такие как линейная регрессия, дифференциальные уравнения, матричный и статистический анализ, теория вероятностей и компьютерное моделирование.Математические модели в популяционной динамике, эпидемиологии, иммунологии, диффузионных явлениях, фармакокинетике, нейрофизиологии и биохимии клеток.
MATH 3660 Математическое моделирование в экономике. Моделирование микроэкономических проблем спроса и предложения, максимизации прибыли и равновесного ценообразования по Нэшу. Аукционы и модели торга. Статистические модели и анализ данных.Вычислительные эксперименты.
MATH 3670 Математические науки о данных. Линейные методы регрессии и классификации, компромисса смещения и дисперсии, а также базисных расширений и регуляризации. Методы ядра, вспомогательные векторные машины, уменьшение размерности и алгоритмы кластеризации.
MATH 3890 Вычисления со сплайнами. Этот курс посвящен мощному и относительно новому классу аппроксимирующих функций, называемых сплайн-функциями, которые имеют множество приложений в математике, естествознании и инженерии. К ним относятся подгонка и аппроксимация данных, числовая квадратура, проектирование и представление кривых и поверхностей, а также численное решение как ODE, так и PDE, включая самые последние разработки в области изогеометрического анализа (IGA). Этот курс является естественным продолжением и дополнением любого вводного курса численного анализа, такого как Math 3620.
MATH 4600 Численный анализ. Конечно-разностные и вариационные методы для эллиптических краевых задач, конечно-разностные методы для параболических и гиперболических уравнений в частных производных, а также матричная задача на собственные значения. Особое внимание уделяется использованию компьютера учащимися.
MATH 4620 Линейная оптимизация. Введение в линейное программирование и его приложения. Составление линейных программ. Симплексный метод, двойственность, дополнительная нестационарность, двойной симплексный метод и анализ чувствительности. Эллипсоидный метод. Методы внутренней точки. Возможные дополнительные темы включают первично-дуальный алгоритм, плоскости отсечения или переход и привязку. Приложения к сетям, менеджменту, инженерии и физике.
MATH 4630 Нелинейная оптимизация. Введение в моделирование, теорию и методы решения задач нелинейной оптимизации. Моделирование прикладных задач в науке и технике. Методы безусловной оптимизации с одной и несколькими переменными. Теория условной оптимизации, включая условия Каруша-Куна-Таккера. Штрафные функции и другие методы ограниченной оптимизации. Компьютерные инструменты, такие как библиотека подпрограмм или система символьной алгебры.
МАШИНОСТРОЕНИЕ
ME 3890 Специальные темы: Микромасштабный перенос энергии. Теоретическое исследование переноса энергии электронами и фононами и моделирование явлений переноса в кристаллических твердых телах на уменьшенных масштабах длины. Модели переноса частиц и методы решения для энергоносителей в контексте полупроводниковой электроники, устройств прямого преобразования энергии и наноструктур.
ME 4263 Вычислительная гидродинамика и мультифизическое моделирование. Вычислительное моделирование течений вязкой жидкости и взаимодействия теплоносителя с конструкцией. Вычислительные методы, включая методы конечных разностей, конечных объемов и конечных элементов; точность, сходимость и устойчивость численных методов; моделирование турбулентности; вращающееся оборудование; многофазные потоки; и мультифизическое моделирование.
ME 4275 Введение в анализ методом конечных элементов. Разработка и решение уравнений конечных элементов для задач механики твердого тела и теплопередачи. Введение в коммерческое программное обеспечение конечных элементов и предварительной и последующей обработки. Две лекции и одна трехчасовая лаборатория каждую неделю.
НЕЙРОНАУКА
NSC 3270 Вычислительная неврология. Теоретические, математические и имитационные модели нейронов, нейронных сетей или систем мозга.Вычислительные подходы к анализу и пониманию данных, таких как нейрофизиологические, электрофизиологические или изображения мозга. Демонстрации моделирования нейронных моделей.
ФИЗИКА
PHYS 3200. Статистическая физика. Температура, работа, тепло и первый закон термодинамики. Энтропия и второй закон термодинамики. Кинетическая теория газов с приложениями к идеальным газам и электромагнитному излучению.
PHYS 3790. Вычислительная физика. Темы современной физики анализируются исключительно с помощью компьютерных программ. Конечно-разностные подходы к уравнениям Шредингера и Максвелла. Решения нелинейных уравнений. Молекулярная динамика. Моделирование Монте-Карло. Модели роста и случайные блуждания.
ПСИХОЛОГИЯ
PSY 4218 Вычислительное когнитивное моделирование. Как и почему компьютерное моделирование в психологии и нейробиологии. Не предназначен общий обзор вычислительных моделей человеческого познания. Вместо этого мы поговорим о том, что такое модели, почему мы используем модели, как отличить хорошее моделирование от плохого, как реализовать модель, как подогнать модель под данные, как оценить соответствие модели, как сравнить и противопоставление конкурирующих моделей, как оценивать частные случаи модели и как разрабатывать и тестировать новые модели.
PSY 4219 Научные вычисления для психологических наук и наук о мозге. Компьютерное программирование, методы научных вычислений и высокопроизводительные вычисления, применяемые для решения проблем психологии и науки о мозге, таких как экспериментальный контроль, анализ и визуализация данных, обработка изображений и сигналов, оптимизация и моделирование. Рекомендуется предварительная работа по психологии или неврологии.
PSY 4220 Байесовское моделирование с помощью Python. Статистическое и когнитивное моделирование.Модели памяти, психофизики, категоризации и принятия решений. Вероятностное программирование на Python. Оценка байесовских параметров и сравнение моделей.
PSY 4775 Модели человеческой памяти. Мезонинный курс, охватывающий научные исследования человеческой памяти, включая эксперимент и теорию. Сосредоточьтесь на попытках создания вычислительных и математических моделей памяти человека.Предполагается некоторый уровень комфорта с элементарной вероятностью и статистикой. Задания включают программирование с целью изучения различных моделей человеческой памяти.
.

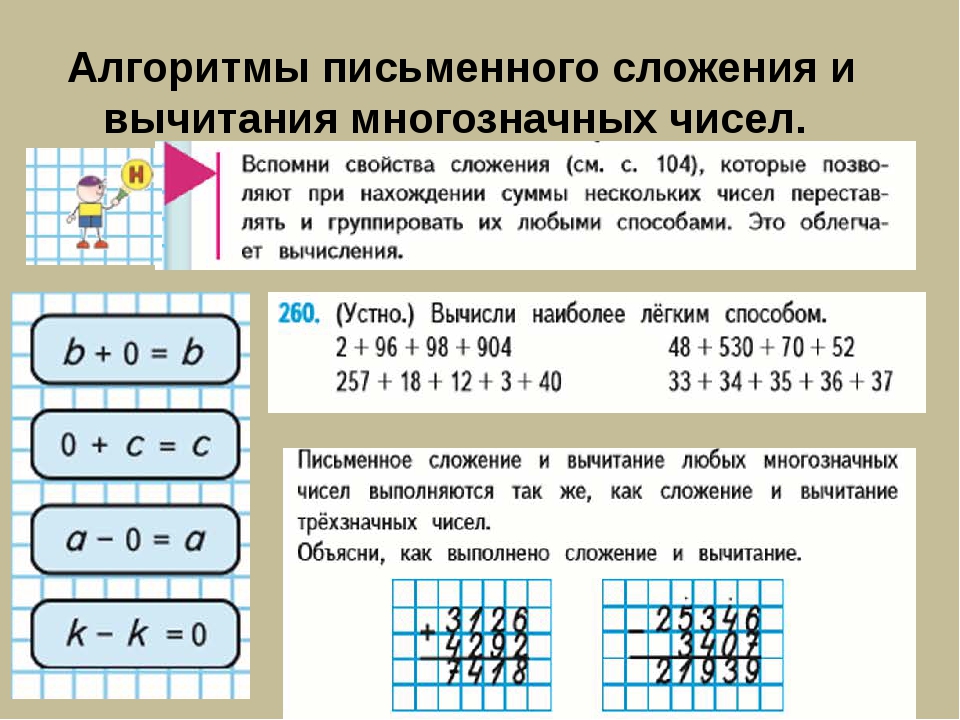 Мотивация к деятельности
Мотивация к деятельности

 Физминутка
Физминутка Сколько получим?
Сколько получим?
 Прочитайте вопрос задачи.
Прочитайте вопрос задачи.

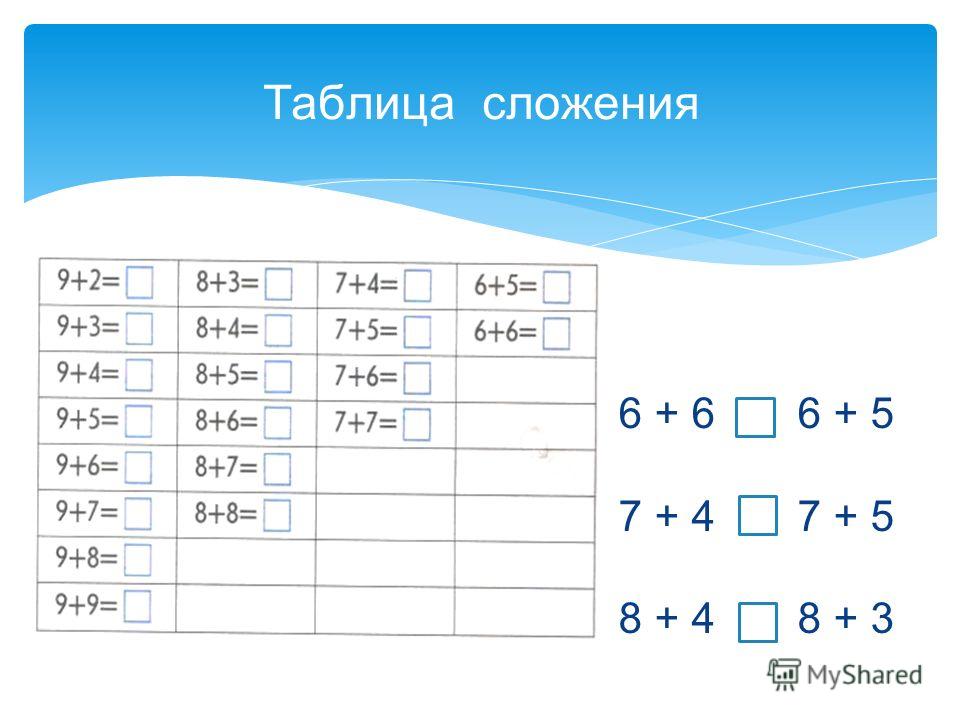

 Один записывает, другие диктуют-работа проводится на планшетках или листочках).
Один записывает, другие диктуют-работа проводится на планшетках или листочках).

 Чья группа быстрее справится, те и будут доказывать у доски. (Каждый представитель группы, которая закончила вычисления раньше, по алгоритму доказывают свой результат)
Чья группа быстрее справится, те и будут доказывать у доски. (Каждый представитель группы, которая закончила вычисления раньше, по алгоритму доказывают свой результат)
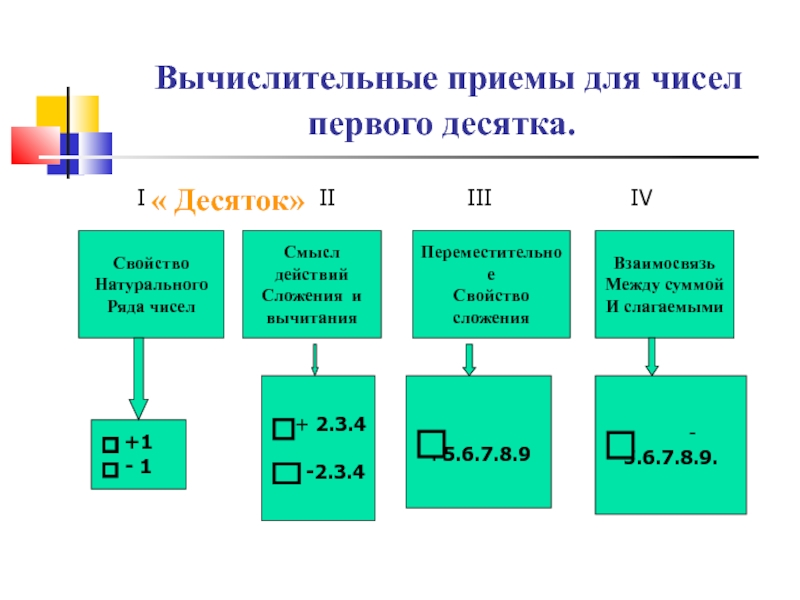

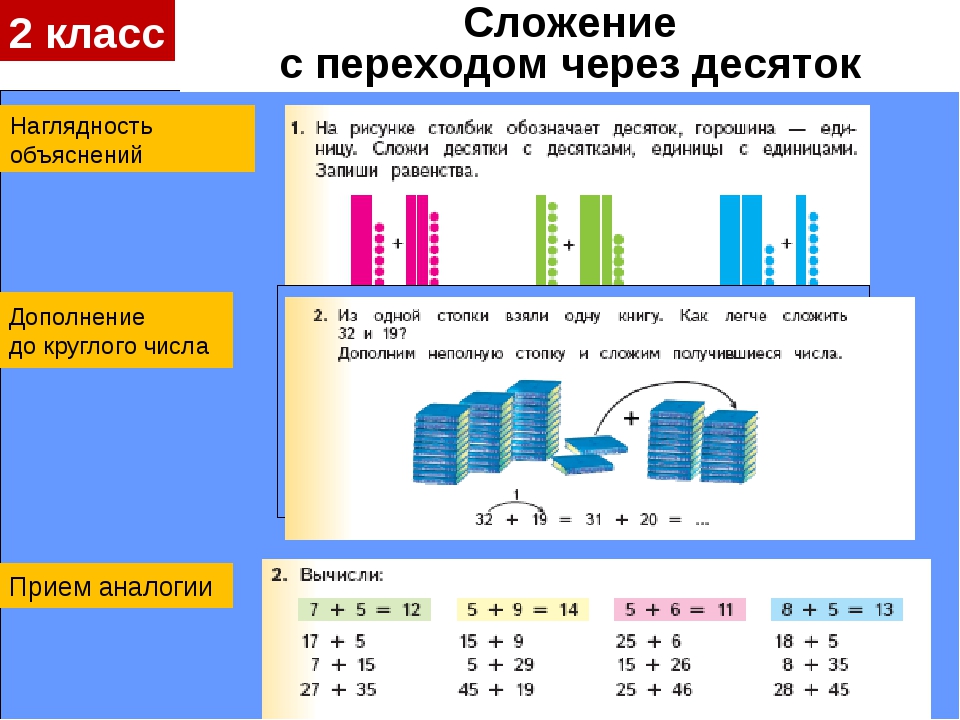

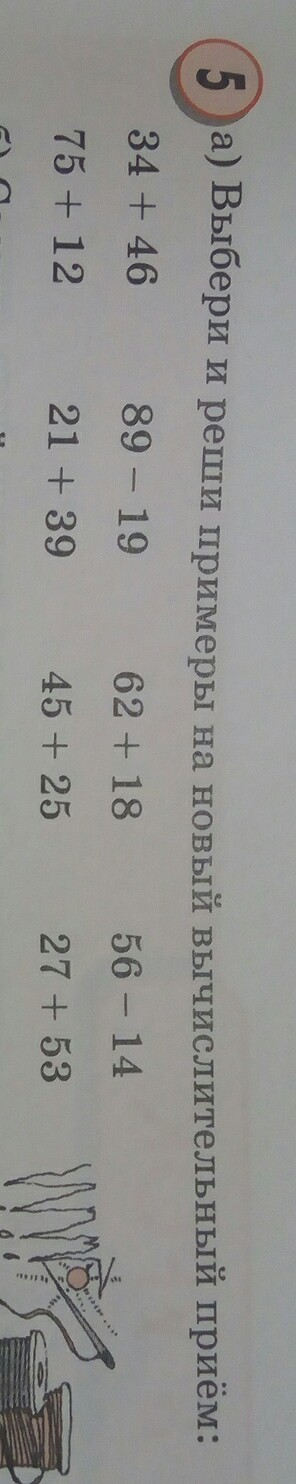 Давайте проверим, сколько клеток вы можете заполнить за 3 минуты? Колобок засекает время.
Давайте проверим, сколько клеток вы можете заполнить за 3 минуты? Колобок засекает время.