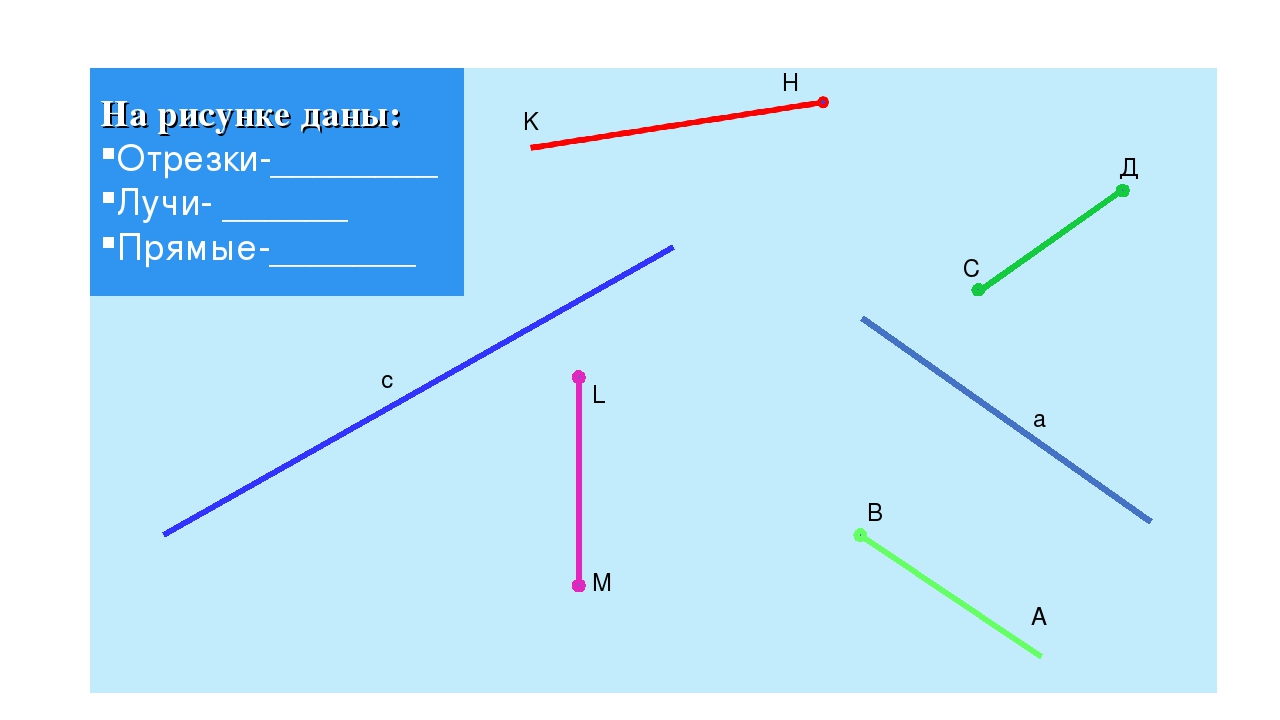
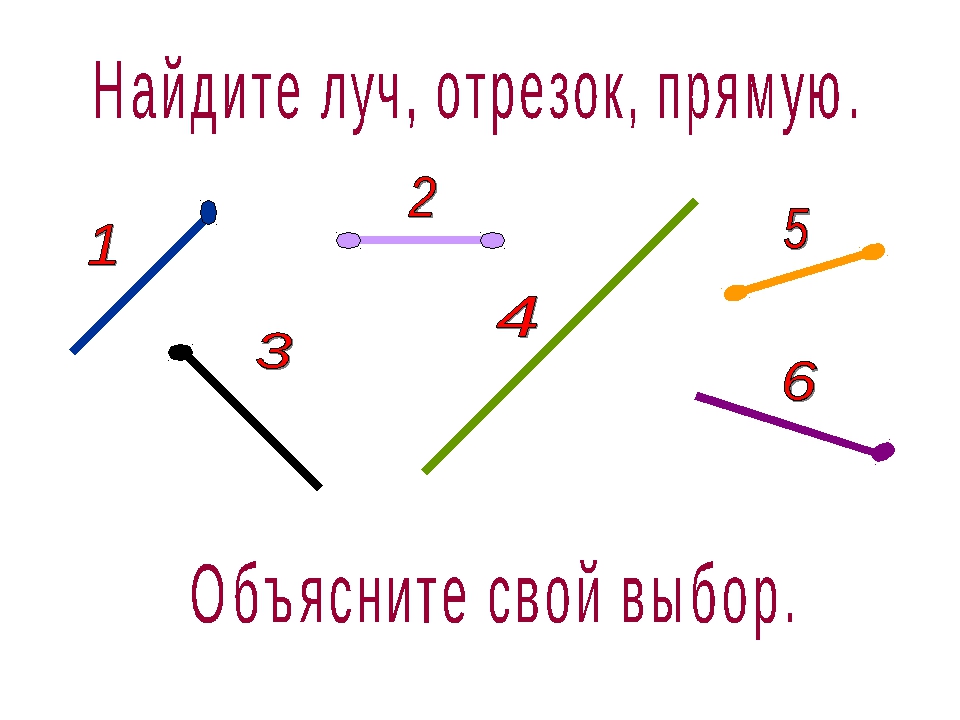
Точка, отрезок, луч, прямая — числовая прямая
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
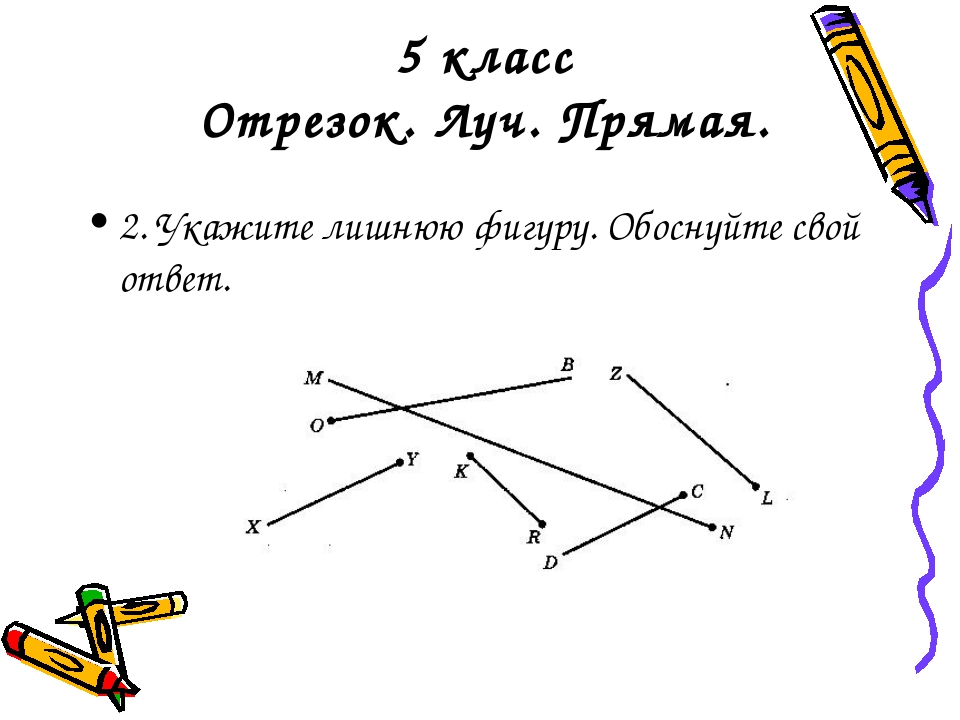
Точка в математике
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Отрезок в математике
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.
На рисунке мы видим следующее: отрезки [A;C],[C;D],[D;M],[M;F],[F;E] и [E;T], а также две точки B и S.
Прямая в математике
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
На рисунке изображены две прямые: CD и EF.
Луч в математике
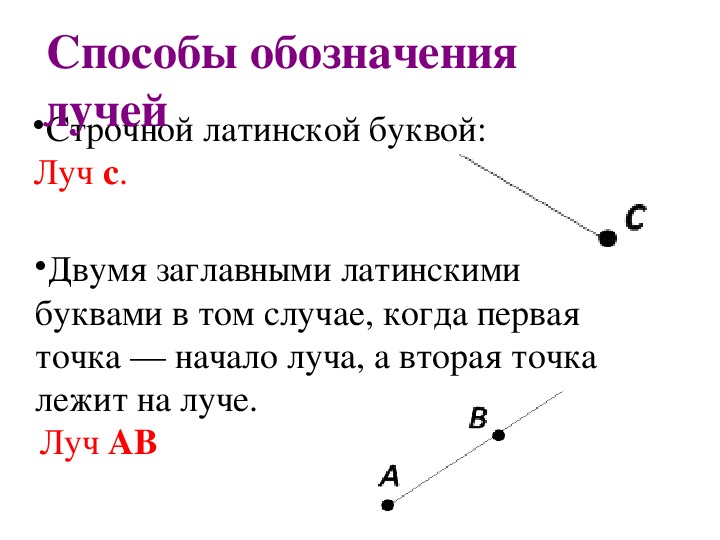
Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.
Числовая прямая в математике
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
На рисунке изображена числовая прямая, а также луч OD и ED
Нужна помощь в учебе?
Предыдущая тема: Сложение и вычитание дробей с одинаковыми знаменателями: ПРИМЕРЫ
Следующая тема:   Чтение и запись больших натуральных чисел: разряды, классы + ПРИМЕР
Урок 21.
 прямая, луч, отрезок — Математика — 5 класс
прямая, луч, отрезок — Математика — 5 класс
Математика
5 класс
Урок №21
Прямая, луч, отрезок
Перечень рассматриваемых вопросов:
— понятия «прямая», «луч», «отрезок»;
— отличия прямой, луча, отрезка;
— прямая, луч, отрезок на чертежах, рисунках и моделях.
Тезаурус
Отрезок – часть прямой, ограниченный двумя точками.
Концы отрезка – точки, ограничивающие отрезок.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.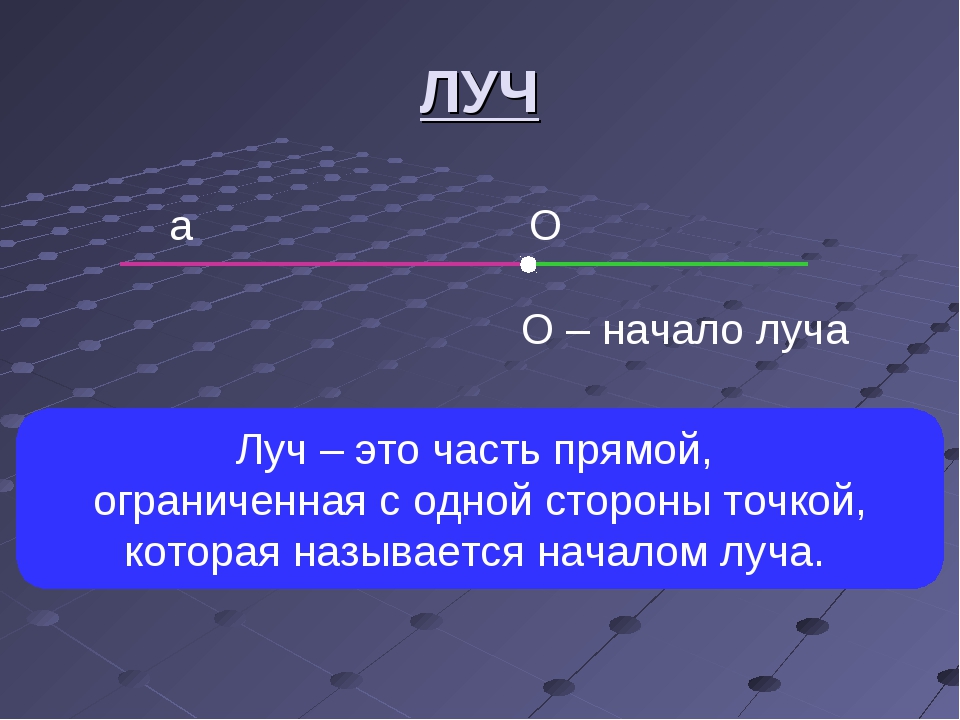
Теоретический материал для самостоятельного изучения
Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.
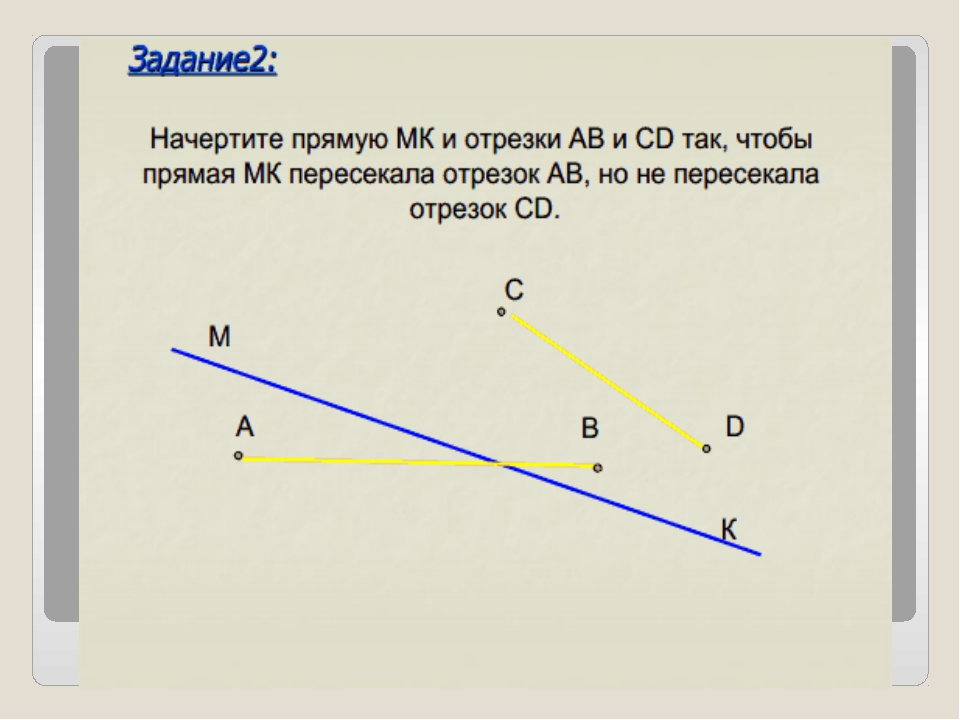
Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).
Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны. Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.
Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.
Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.
Через любые две точки можно провести только одну прямую.
Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.
Провести через точки А и В другую прямую, отличную от прямой b, нельзя.
Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.
Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.
Каждую из этих частей называют лучом, исходящим из точки А.
Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.
Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.
Переставлять буквы в названии луча нельзя.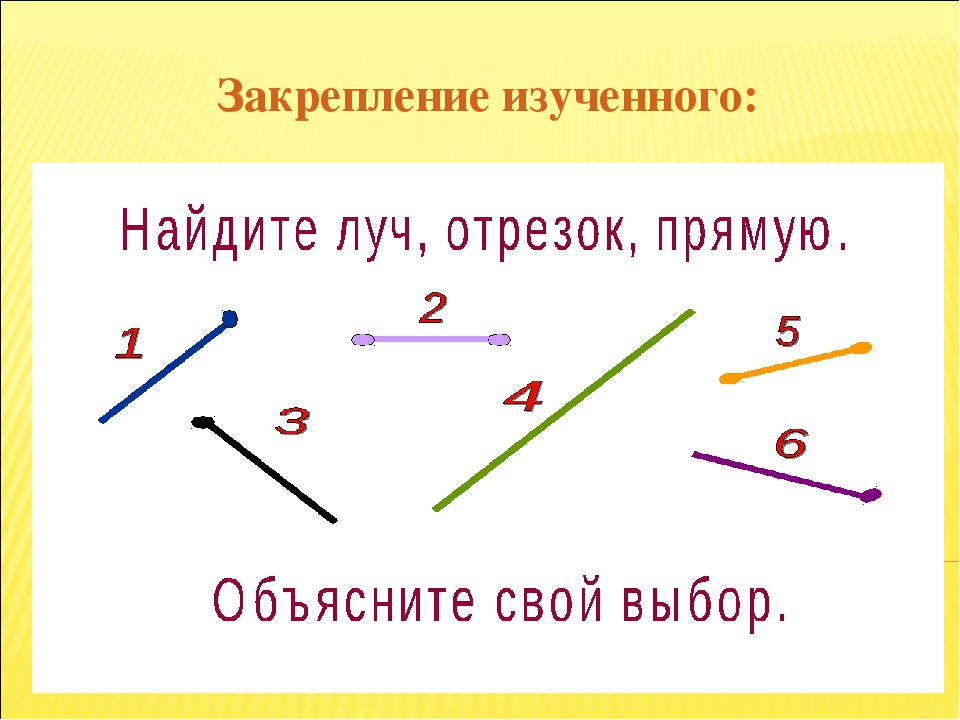
Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок.
Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.
В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.
Заметим, что два отрезка называются равными, если они совмещаются при наложении.
Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.
Это интересно
Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.
- Космические лучи – это элементарные частицы и ядра атомов, движущиеся с высокими энергиями в космическом пространстве.
- Противосумеречные лучи (англ. anticrepuscular rays) – расходящиеся веером лучи, наблюдающиеся на закате дня со стороны, противоположной Солнцу (то есть, на востоке).
- Белохохлый солнечный луч (лат.
 Aglaeactis castelnaudii) – вид птиц из семейства колибри (Trochilidae).
Aglaeactis castelnaudii) – вид птиц из семейства колибри (Trochilidae). - Луч света в темном царстве – крылатое выражение, вошедшее в речь после публикации в 1860 году статьи публициста-демократа Николая Александровича Добролюбова, посвящённой драме А. Н. Островского «Гроза».
Разбор решения заданий тренировочного модуля
№ 1. Тип задания: добавление подписей к изображениям.
Разместите нужные подписи к изображениям.
Для выполнения задания обратитесь к теоретическому материалу урока.
Правильные ответы:
1) а – это прямая.
2) АВ – это отрезок.
3) А – это луч.
№ 2. Тип задания: подстановка элементов в пропуски в тексте.
Вставьте в текст нужные слова.
Через__________ две____________ можно провести только одну _________.
Слова: любые; точки; прямую; ломаную.
Правильный ответ: через любые две точки можно провести только одну прямую.
5 класс — прямая, плоскость и луч в 5 классе, урок по математике, презентация
Дата публикации: .
Что такое плоскость? Определение, примеры
Вокруг нас множество примеров плоскостей, например, оконное стекло
Поверхность озера
Лист бумаги
Но все плоскости, о которых мы говорим, имеют границы. В математике же плоскость бесконечна, то есть не имеет границ.
Запомните!
У математической плоскости НЕТ границ. Она простирается безгранично далеко во всех направлениях.
Прямая и её особенности
Нарисуем две точки А и В и соединим их. У нас получился отрезок АВ или ВА (кому как нравится).
Продолжим отрезок АВ в оба направлениях. Мы получим прямую АВ или ВА.
Запомните!
Прямая не имеет начала и конца. Только границы тетрадного листа или экрана заставляют нас рисовать прямую, как отрезок, на самом деле она бесконечна. Рисуя прямую, нужно мысленно продлевать ее бесконечно.
Принято говорить, что точки А и В лежат на прямой.
В математике прямую обозначают двумя способами.
1. «Прямая АВ»
2. «Прямая с» (маленькая буква)
«Прямая с» (маленькая буква)
Рассмотрим особенности прямой.
1. Если две прямые пересекаются в какой-либо точке, то эта точка является точкой пересечения прямых. В нашем примере прямые а и в пересекаются в точке О. Точка О делит каждую прямую на две части.
2. Через любые две точки можно провести одну единственную прямую.
Луч, Особенности
Если мы отметим на прямой точку, например, точку А, то эта точка разделит прямую на две части или на два луча.
Запомните!
Луч имеет начало, но не имеет конца. Это как луч света от какого-либо источника, который начинается от самого источник света (точки) и уходит в бесконечность.
В нашем примере точка О делит прямую АВ на два луча: луч ОА и луч ОВ. Соответственно, оба луча имеют начало в точке О, но не имеют конца. Они продолжаются до бесконечности.
Переставлять буквы в названии луча нельзя. Первой буквой всегда обозначается начало луча.
Конспект урока по математике «Прямая, луч, отрезок» (5 класс)
План-конспект урока математики № 45
Класс: 5-Б
Дата: 13.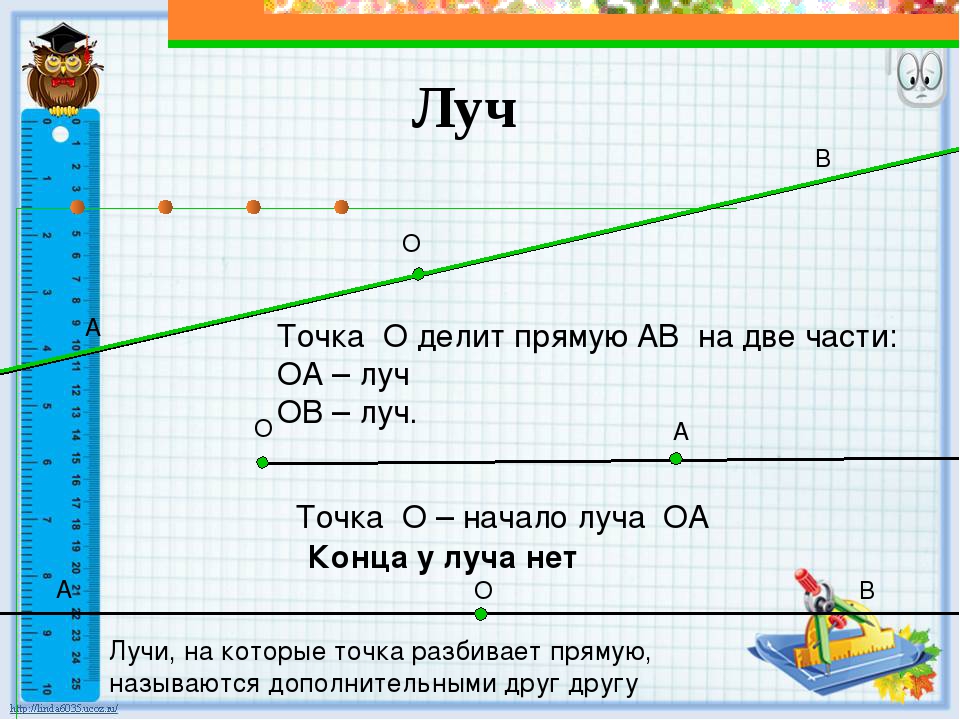 11.2017
11.2017
Учитель: Кольцова Н.А.
Тема:
Прямая, луч, отрезок
Тип урока:
Урок усвоения новых знаний, умений и навыков
Место урока в разделе:
Первый урок в теме «Измерение величин»
Оборудование:
Мультимедийный комплекс
Формы работы на уроке
Фронтальная, групповая, индивидуальная
Цели:
обучающие
(ориентированные на достижение предметных результатов обучения)
Ввести понятия «плоскость», «луч», «прямая», «отрезок»; установить свойства изучаемых объектов; научить строить и распознавать данные фигуры.
развивающие (ориентированные на достижение метапредметных результатов обучения)
Развивать внимание, память, образное мышление; формировать самостоятельность и коммуникативность; создавать условия для проявления познавательной активности.
воспитательные (ориентированные на достижение личностных результатов обучения)
Воспитывать умение слушать, вступать в диалог, участвовать в коллективном обсуждении проблем;
УУД:
познавательные
Поиск и выделение необходимой информации;
анализ объектов с целью выделения признаков; выделение и формулирование познавательной цели, рефлексия способов и условий действий.
регулятивные
Прогнозирование своей деятельности; планирование своей деятельности для решения поставленной задачи.
коммуникативные
Умение слушать и вступать в диалог; умение с достаточной полнотой и точностью выражать свои мысли.
личностные
Установление связи между целью деятельности и ее мотивом; проявление внимания и терпения; проявление доброжелательности в дискуссии, доверия к собеседнику.
Ход урока
I. Организационный момент
Организационный момент
Приветствие учителя, проверка готовности учащихся к уроку.
II. Мотивация учебной деятельности
1. Сообщение темы (устный счет).
Решив все примеры и расположив ответы в порядке возрастания, вы сможете прочитать три слова, которые являются темой нашего урока (прямая, луч, отрезок).
15х0= (П)
44+150= (Р)
120:2= (Л)
32:32= (Р)
16-14= (Я)
25х4= (Ч)
160-80= (У)
90:10= (М)
11х10= (О)
920-800= (Т)
12+18= (А)
1000х15= (К)
1000:2= (О)
90-35= (Я)
50х4= (Е)
450-150= (З)
2. Формулирование цели урока.
Формулирование цели урока.
3. Актуализация опорных знаний, полученных в начальной школе.
(Вспомнить понятия точки, прямой, отрезка)
III. Восприятие и первичное осознание нового материала
1. Определение плоскости.
Поверхность стола, стена, классная доска, оконное стекло могут служить примером части плоскости. Всю плоскость невозможно изобразить потому, что она бесконечна, но ее можно представить себе (привести примеры части плоскости).
2. Определение и обозначение прямой.
— прямая не имеет ни начала, ни конца – она бесконечна;
— прямую обозначают одной строчной латинской буквой или двумя заглавными;
— через любые две точки можно провести только одну прямую;
— две прямые на плоскости могут пересекаться или быть параллельными.
3. Определение луча.
Точка А, лежащая на прямой, делит ее на две части. Каждую их этих частей называют лучом с началом в точке А, обозначают луч двумя заглавными буквами.
4. Определение отрезка.
— определение отрезка;
— обозначение отрезка;
— определение равных отрезков.
IV. Первичное применение новых знаний
Решение упражнений №342, 354, 355, 356, 359.
V. Физминутка
VI. Применение знаний в стандартных условиях с целью усвоения навыков
1. Фронтальный опрос (1 группа):
— Какие точки лежат на прямой l ?
— Какие точки не лежат на прямой l ?
— Назовите все лучи с вершиной в точках M, N, S?
— Какие точки не лежат на луче MS?
— Перечислите все отрезки, изображенные на рисунке.
2. Индивидуальная работа по карточкам (2 группа):
Тест (Приложение 1).
Начало формы
Конец формы
VII. Итог урока.
Сообщение домашнего задания:
Прочитать п.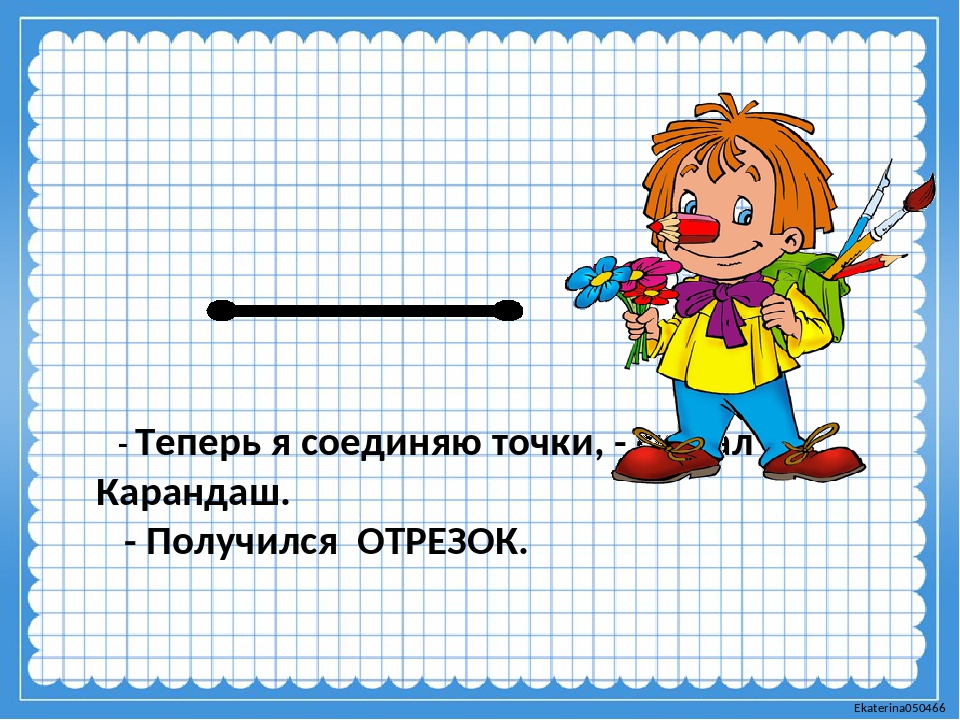 2.1. стр. 77-79, выполнить №353,357 – 1 группа;
2.1. стр. 77-79, выполнить №353,357 – 1 группа;
№358,360 – 2 группа.
Рефлексия:
— Сегодня на уроке я научился…
— Мне было интересно…
— Мне было трудно…
— Я понял, что…
— Больше всего мне понравилось…
— Своей работой на уроке я доволен (не совсем, не доволен), потому что…
Приложение 1
ТЕСТ
Как правильно записать обозначение луча?
А) АМ
Б) МА
Сколько лучей на рисунке?
А) один
Б) два
В) три
Г) четыре
Какие из обозначенных точек не лежат на луче АС?
А) К, D, В
Б) D, К
В) О, В
Г) К, О
Какая из фигур, изображенных на рисунке, является прямой?
А) ВА
Б) АС
В) ВС
Г) ВМ
Укажите пару пересекающихся фигур.

А) отрезок ОА и прямая СD
Б) луч КР и прямая ВМ
В) прямые СD и ВМ
Г) луч КР и отрезок ОА
Что является общей частью лучей АС и ВС?
А) отрезок АВ
Б) луч ВС
В) точка А
Г) точка В
Пересекаются ли прямые CD и АВ?
А) да
Б) нет
Пересекаются ли лучи АВ и СD?
А) да
Б) нет
9. Обозначьте все точки пересечения прямых, продолжив их, если нужно. На сколько частей разделилась плоскость?
Дата____________________ ФИ _____________________________________ Класс__________
Приложение 2
Технологическая карта урока
Деятельность учителя
Деятельность ученика
Время
(в мин. )
)
Формируемые УУД
Познавательные
Регулятивные
Коммуникативные
Личностные
1
2
3
4
5
6
7
8
9
1
Организационный момент
Приветствие; проверка готовности класса к уроку; организация внимания.
2
Осознанное и произвольное построение речевого высказывания
Прогнозирование своей деятельности
Умение слушать и вступать в диалог
Умение выделять нравственный аспект поведения
2
Мотивация учебной деятельности
Вместе с учениками определяет тему урока (Слайд 2-3).
Вспомнить понятия точки, прямой, отрезка, полученные ранее.
Задает учащимся наводящие вопросы
(Слайд 4-5)
Выполняют задание, решая примеры.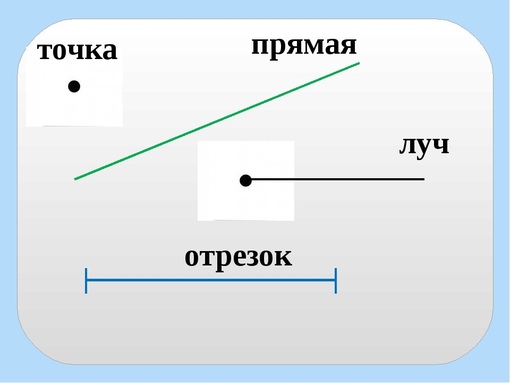
Записывают тему урока в тетрадь.
Участвуют в определении цели урока.
Участвуют в работе по повторению, в беседе с учителем, отвечают на поставленные вопросы.
7
Поиск и выделение необходимой информации.
Анализ объектов с целью выделения признаков.
Выдвижение гипотез.
Постановка цели.
Выделение и осознание того, что уже пройдено.
Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог
Установление связи между целью деятельности и ее мотивом
3
Восприятие и первичное осознание нового материала
Знакомит учащихся с определением плоскости, прямой, луча, отрезка.
Задает вопросы, подводящие к определению понятий (Слайды 6-10)
Слушают, задают вопросы.
8
Анализ объектов с целью выделения признаков.
Умение слушать и вступать в диалог
Проявление внимания и терпения
4
Первичное применение новых знаний
Решают упражнения из учебника №342, 354, 355, 356, 359.
Выполняют задания, отвечая на вопросы
проверяют правильность выполнения.
10
Поиск и выделение необходимой информации.
Структурирование знаний.
Подведение под понятие
Планирование своей деятельности для решения поставленной задачи
Умение слушать и вступать в диалог.
Коллективное обсуждение проблем (при необходимости)
Проявление
терпения и аккуратности при построении чертежей
5
Физминутка
Сменить деятельность, обеспечить эмоциональную разгрузку учащихся.
Учащиеся сменили вид деятельности (отдохнули) и готовы продолжать работу.
3
Осознание ценности здоровья
6
Применение знаний в стандартных условиях с целью усвоения навыков
Комментирует, направляет работу учащихся.
Постановка проблемного вопроса.
1 группа работает с учителем, выполняя задания у доски (Слайд 11-12).
2 группа работает индивидуально с тестовыми заданиями на карточках с последующей самопроверкой (Слайд 13)
10
Выделение и формулирование познавательной цели, рефлексия способов и условий действия
Анализ объектов и синтез
Контроль изученного материала
Умение с достаточной полнотой и точностью выражать свои мысли
Проявление доброжелательности в дискуссии, доверия к собеседнику
7
Подведение итогов
Сообщает домашнее задание. Подводит итог урока
Подводит итог урока
Дает возможность самим ученикам оценить себя, затем оценивает учащихся с комментированием.
Рефлексия.
Записывают домашнее задание в дневник
Подводят итог урока, оценивают себя своих товарищей.
5
Осознанное и произвольное построение речевого высказывания
Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог
Ориентация в межличностных отношениях
Урок математики в 5 классе «Прямая. Луч. Отрезок»
Разработка урока математики в 5 классе
Прямая. Луч. Отрезок
Цель: Учить школьников различать прямую, луч, отрезок. Познакомить с общепринятыми обозначениями. Развивать мыслительные операции, математические способности, логическое мышление, чертежные навыки. Воспитывать ответственность, дружелюбие.
Воспитывать ответственность, дружелюбие.
Ход урока
1. Организационный момент
Ну-ка, проверь дружок!
Готов ли ты начать урок?
Все ли на месте? Все ль в порядке?
Книжка, ручка и тетрадка…
Проверили? Вот здорово!
К уроку все готово!
2. Актуализация знаний учащихся
Учитель: Геометрия – наука о фигурах. Верным помощником на нашем сегодняшнем уроке будет простейшая геометрическая фигура – точка.
Слайд 1
1. 1. Вычислите устно, записав ответы через строчку в тетрадь.
1. Вычислите устно, записав ответы через строчку в тетрадь.
Слайд 2
1.2. Анаграммы (расшифровать слова)
Слайд 3
Слайд 4
1.3. Вопросы классу:
— Все ли расшифрованные слова знакомы?
— На каких уроках мы с ними встречались?
— Какое слово и почему лишнее?
3. Сообщение темы урока
Сообщение темы урока
Слайд 5
4. Изучение нового материала
4.1. Вступительное слово о плоскости
Слайд 6
4.2. Прямая
l
B
A
Прямая – прямая линия, которая не имеет ни начала, ни конца.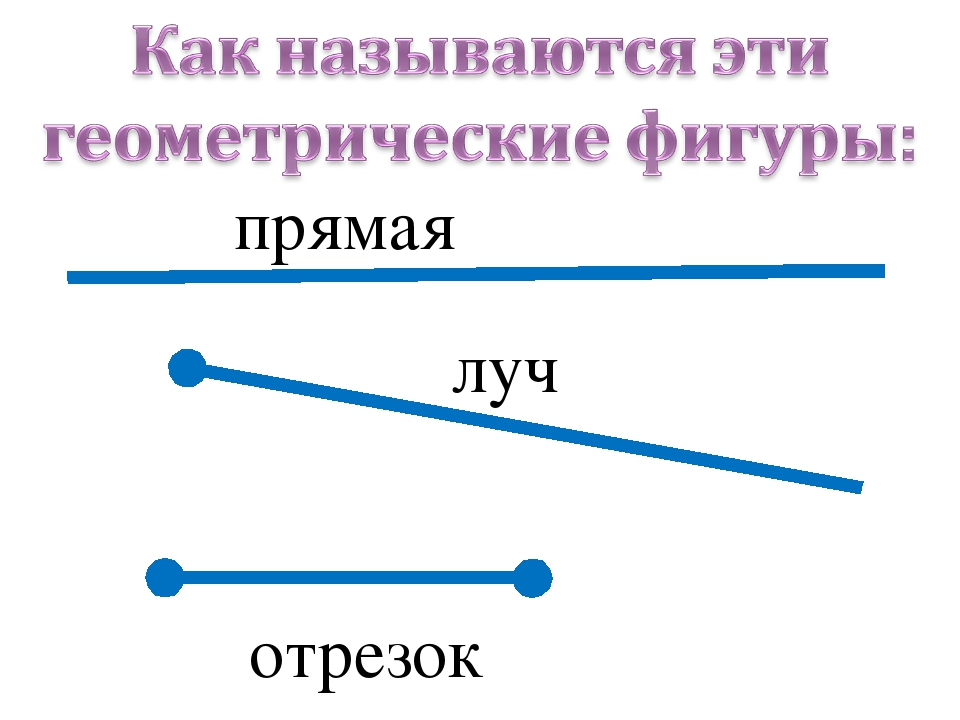
Обозначение: прямая АВ, прямая l
Свойства:
а) если две прямые на плоскости пересекаются, то они имеет одну общую точку
m F – точка пересечения прямых m и l
l F (общая точка)
б) через две точки на плоскости можно провести только одну прямую
М
Д
в) через одну точку на плоскости можно провести бесконечно много прямых
г) если прямые на плоскости не пересекаются, то они не имеют общих точек
m l
Прямые m и l называются параллельные прямые
Вывод:
Без начала и без края линия прямая.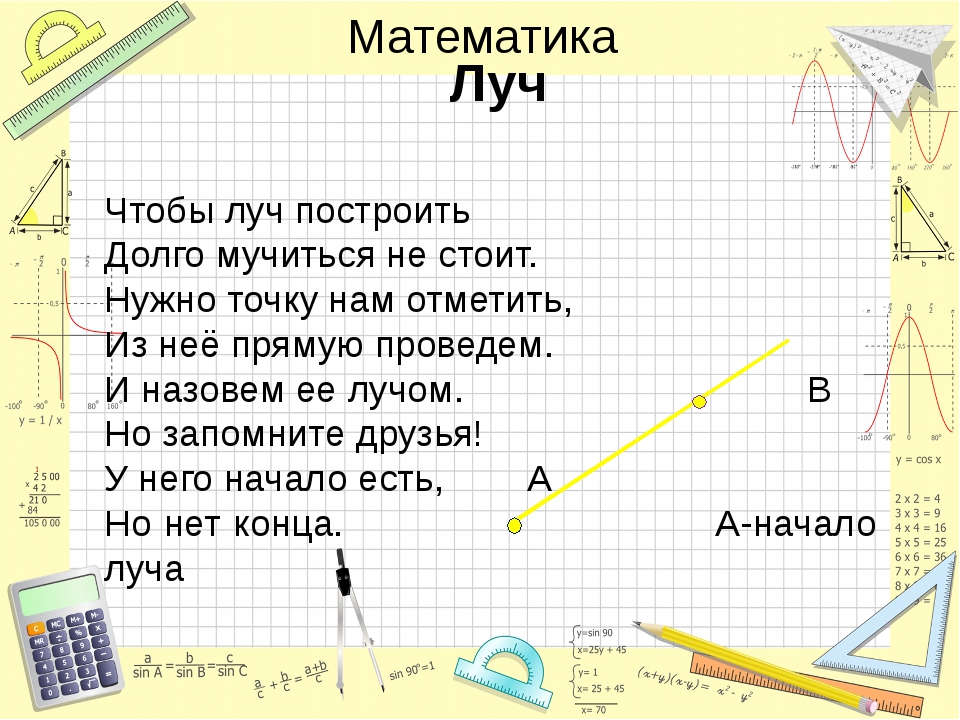
Хоть 100 лет по ней идти,
Не найдешь конца пути.
4.3. Луч
Учитель: А теперь мысленно разрежьте прямую и к месту разреза прикрепите солнышко. Что получилось? На что похоже?
Слайд 7 (луч солнца)
О новой фигуре разносится весть.
Конца пусть в ней нет,
Но начало-то есть!
И солнце, тихонько взойдя из-за тучь,
Сказало: «Друзья, назовем его ЛУЧ!»
О
К
Определение: Луч – часть прямой, которая имеет начало, но не имеет конца
Обозначение: луч ОК (т. О – начало луча)
Свойства:
Из одной точки можно провести бесконечно много лучей
Физкультминутка: Слайд 8:
Раз, два, три, четыре, пять, -
Все умеем мы считать.
Отдыхать умеем тоже,
Руки за спину заложим,
Голову поднимем выше
И легко-легко подышим.
Раз – подняться, потянуться,
Два – согнуться, разогнуться.
Три – в ладоши три хлопка,
На четыре – руки шире,
Пять – руками помахать,
Шесть – за парту тихо сесть.
4.4. Отрезок
Точки две поставь в тетради,
Чтоб потом нарисовать между ними
Под линеечку – прямую.
И окажется, мой друг,
Что отрезок вышел вдруг.
А В
Определение: Отрезок – часть прямой, ограниченная точками.
Обозначение: отрезок АВ (т. А – начало отрезка, т. В – конец отрезка)
5. Закрепление изученного:
№ 341 – устно
№ 343 – работа в парах с последующей проверкой
6. Подведение итогов работы . Домашнее задание
Плоскость. Прямая. Луч
На этом уроке мы познакомимся с понятиями «отрезок»,
«прямая», «луч» и «плоскость». Рассмотрим расположение точек, отрезков, прямых
и лучей в плоскости.
На прошлом уроке мы разобрались, как строить
отрезок. Мы уже знаем, что отрезок – это прямая линия,
ограниченная двумя точками.
Определение
Давайте начертим отрезок MN.
Если продлить этот отрезок неограниченно за точку N,
то мы получим новую фигуру, которая называется луч. У нас
получился луч MN.
Точку М называют началом
луча.
Если бы мы продлевали отрезок MN неограниченно за точку М,
то у нас бы получился луч NМ, у которого
точка N – начало луча.
Заметьте: обозначается луч большими заглавными
буквами латинского алфавита, первой буквой записывают его начало, а затем
букву, обозначающую какую-либо другую точку луча.
Обратите внимание, что луч имеет начало, но не
имеет конца, т. е. он бесконечен в одну сторону.
Для того чтобы представить луч в окружающей среде,
достаточно сфотографировать след от самолёта в безоблачном небе, где сам самолёт
– это начальная точка, а след, оставленный на небе, – это прямая линия, которая
бесконечна.
Либо солнечный луч, где начальная точка – это
солнце, а конечной точки нет.
Определение
Если отрезок MN неограниченно
продлевать в обе стороны – как за точку М,
так и за точку N, то у нас получится фигура,
которая называется прямой.
На рисунке у нас получилась прямая MN, также её можно назвать и прямая NМ. Как кому больше нравится!
Заметьте, что прямая не имеет ни начала, ни
конца.
Любая точка прямой разделяет её на 2 луча.
В нашем случае точка О разделяет
прямую MN на луч ОМ
и луч ОN. Лучи, на которые точка разбивает
прямую, называют дополнительными друг другу.
Представление о прямой можно получить, если сложить
лист бумаги (линия, которая получилась при сгибе, и будет прямой) или туго
натянуть верёвку.
В математике прямая представляется идеально ровной и
бесконечной в обе стороны.
Прямую можно обозначить двумя вариантами.
1-й вариант:
двумя заглавными буквами латинского алфавита, например MN.
В таком случае говорят: «Прямая MN».
2-й вариант:
прямую обозначают одной малой буквой, например m, и
говорят: «Прямая m».
Давайте попробуем провести ещё одну прямую через эти
же две точки.
У нас это не получится. Через любые две точки можно
провести только одну прямую!
Точки, отрезки, лучи и прямые располагаются в
плоскости. Примеры плоскостей в жизни мы встречаем каждый день. Представление о
плоскости дают поверхности стола, оконного стекла или замёрзшего водоёма.
Только эти поверхности имеют границы, а плоскость в
математике безгранична во всех направлениях. Мы рисуем фигуры на
«кусках» плоскости, например в тетрадном листе или на школьной доске.
Теперь давайте рассмотрим расположение точек,
отрезков, прямых и лучей в плоскости.
На рисунке изображены прямая EF и точки А, L, P и T. Точки А, E, F лежат на
отрезке EF, а точки L,
P, T не
лежат на этом отрезке. Посмотрите, как это записывается.
Точки А, E, F лежат на
луче EF, а точки А,
E, F, Т лежат на луче FЕ.
Посмотрите запись этих утверждений.
Точки А, E, F, Т лежат на прямой EF,
а точки А, P,
L – на прямой PL.
Обозначается это так:
Точка А лежит
между точками Е и F.
Точка L не лежит между точками Е и F, она
находится вне отрезка EF. Точка Е лежит между точками А
и Т, а точка А
– между точками P и L.
На следующем рисунке изображены прямая a и прямая b.
Если две прямые имеют одну общую точку, то говорят,
что они пересекаются в этой точке. В нашем примере прямые а и b пересекаются
в точке О. Точка О
делит каждую прямую на две части. Точка О –
точка пересечения прямых.
Посмотрите на взаимное расположение прямых m и n:
Они не имеют общих точек. Если прямые не имеют общих
точек, то говорят, что они параллельны.
Запомните!
·
Прямая
бесконечна.
·
Отрезок
ограничен.
·
Луч
имеет начало, но не имеет конца.
·
Плоскость
бесконечна.
Итоги
Итак, на уроке мы с вами разобрались в отличиях
понятий «отрезок», «прямая», «луч». Научились их строить. Узнали, что такое
плоскость, а также рассмотрели расположение точек, отрезков, прямых и лучей в
плоскости.
«Прямая. Луч. Отрезок»
Урок № 47. Прямая. Луч. Отрезок
Цель: актуализировать знания уч-ся, полученные в нач. школе; дать понятия «прямая», «луч», «отрезок»; учить находить прямую и луч на чертеже, читать и чертить их, учить чертить отрезки заданной длины, развивать умение решать геометрические задачи.
Ход урока
1. ИНМ.
— Решив все примеры, расположив ответы в порядке возрастания, вы сможете прочитать три слова, которые являются темой нашего урока.
81 : 9 С 15 х 0 П 7000+90+6 Л
15 х 3 С 32: 32 Р 30000+4000+9 Ч
17-9 О 17х10 М 10000+900+1 У
33 + 16 Т 90: 10 Я
44х0 П 16+14 А
13 х 1 К 90 — 30 Я
63: 63 Л
96 х 100 Ь
300: 10 О
(Плоскость, прямая, луч, отрезок)
Сегодня на уроке рассмотрим такие понятия как: плоскость, прямая, луч, отрезок. Будем учиться чертить, обозначать и правильно называть их.
1. Что такое плоскость?
Всю плоскость отобразить не возможно, так как она бесконечна, но её можно представить. Примером части плоскости может служить поверхность стола, стула, доски.
— Какие предметы нам дают представление о плоскости? (те у которых есть края).
— Чем отличаются эти предметы от плоскости? (размерами)
— Какой вывод о плоскости мы должны сделать? Записать в тетрадь
У плоскости нет краёв
2. На доске изобразить прямую, луч и отрезок.
— Что изображено на доске? (прямая, луч, отрезок).
Прямая:
— Что вы можете сказать о прямой? ( На рисунке изображается только часть прямой, так как прямая не имеет ни начала, ни конца – она бесконечна).
Записать в тетрадь: Прямая не имеет ни начала, ни конца — она бесконечна.
Обозначение прямой: Прямая обозначается одной строчной (малой) буквой латинского алфавита, например l, и читают «прямая эль».
Точки на прямой обозначают заглавными латинскими буквами A, B,C, и т.д.
Если на прямой l отметить две точки А и В, то прямую также называют «прямая АВ».
Практическая работа:
— Поставьте в тетради точку В. Проведите через эту точку прямую. Еще прямую можно провести через эту точку? Проведите. Еще можно провести? Сколько прямых можно провести через одну точку? Сделайте вывод. (Через одну точку на плоскости можно провести сколько угодно прямых). Записать вывод в тетрадь.
— Поставьте в тетради точки А и В. Проведите через эти две точки прямую. Можно ли провести через эти две точки еще одну прямую? Сделайте вывод. (Через две точки на плоскости можно провести единственную прямую). Записать вывод.
— Итак, что мы должны знать о прямой?
1. Через любые две точки проходит единственная прямая.
2. Прямая не имеет концов.
3. Прямая неограниченно продолжается в обе стороны.
3. Рассмотрим взаимное расположение прямых (т.е. как прямые могут располагаться на плоскости относительно друг друга?) – пересекаться и не пересекаться.
а) Две различные прямые могут пересекаться только в одной точке. (нарисовать в тетради и записать пересечение прямых).
— Итак, какие прямые называют пересекающимися? Пресекающиеся прямые – это прямые, которые имеют одну общую точку (точка пересечения).
б) Две различные прямые могут и не пересекаться, сколько бы их не продолжали. Такие прямые называют параллельными //. ( Нарисовать и записать обозначение параллельных прямых).
Рассмотреть как с помощью угольника и линейки провести параллельные прямые (рис.40 на стр. 78 учебника). Сделать рисунок в тетради.
— Итак, какие прямые называют параллельными? Параллельные прямые – это прямые, которые не имеют ни одной общей точки.
Луч:
— Начертите прямую. Отметьте т.А, лежащую на этой прямой.
— На сколько частей т.А делит прямую (на 2).
— Как называется каждая из частей? (Луч, с началом в т.А).
Обозначение: Луч, как и прямую, обозначают двумя заглавными буквами. Причём, на первом месте ставится буква, обозначающая начало луча, а на втором – буква, обозначающая какую-нибудь другую его точку АВ. Рис. 42 на стр. 79.
Луч с началом в т.А можно обозначить и АВ, и АС (рис. 43 стр. 79).
— Итак, что вы можете сказать о луче? Чем луч отличается от прямой?
Луч имеет начало, но не имеет конца.
Отрезок:
— Что такое отрезок?(Отрезок АВ — часть прямой, ограниченная двумя точками А и В).
Точки А и В называют концами отрезка.
Обозначение: Отрезок с концами в точках А и В называют АВ или ВА.
Два отрезка АВ и СД наз-т равными отрезками, если они совмещаются при наложении (рис. 45 стр. 79). Пишут АВ=СД. Отрезки АВ=ВА.
— Итак, что мы можем сказать про отрезок?
Отрезок имеет и начало, и конец.
2. Закрепление ИМ.
— № 342, 344 (записать параллельные прямые), 346.
3. Итог урока
4.Д/з. п. 2.1. Записи в тетради выучить. Ответить на вопросы №339-341, № 342, 343, 344(Записать параллельные прямые)
Какие математические понятия преподают в 5-м классе?
В 5-м классе математические концепции охватывают широкий круг математических тем.
Это математические концепции, которые учащиеся должны понять после завершения
пятый класс по национальным математическим стандартам.
Числа и операции концепции, изучаемые учащимися пятого класса
включать разряды, представленные в виде целых и десятичных знаков. Студенты
применять и распознавать части дробей как целые числа,
наряду с поиском расположения дробей на числовой прямой.Они используют общие
дроби, десятичные дроби и проценты в численных моделях и физических
модели для представления целых чисел.
Студенты учатся находить и наносить числа меньше 0 на число
строка с отрицательными целыми числами, дробями, десятичными знаками и процентами.
Они используют сложение и умножение в ситуациях решения проблем.
которые включают в себя взаимные функции вычитания и деления. Другой
математические операции включают в себя законы распределения при умножении
и дополнение. Они должны уметь мысленно вычислять умножение
и задачи деления, такие как 10 x 50 и 50 ÷ 10.Студенты развивают
свободное владение арифметическими вычислениями с использованием целых чисел и дробей.
Они учатся оценивать мысленные вычисления и проверять с помощью калькуляторов.
и карандаш / бумага.
Геометрия концепции включают в себя классификацию и развитие понимания
двух и трехмерных объектов, таких как: квадраты, прямоугольники,
пирамиды, кубы, конусы, сферы, цилиндры и т. д. Они также изучают, как
многоугольники относятся к параллельным и перпендикулярным линиям. Дополнительные области
геометрии и форм в центре внимания трансформаций и симметрии
фигур, когда они переворачиваются, поворачиваются и поворачиваются.Дальнейшие исследования
находятся в разработке тесселяции, совпадения и сходства
геометрических фигур. Они учатся соединять геометрические фигуры
к предметам повседневного обихода.
Ученики пятого класса также учатся строить геометрические фигуры.
найти их площадь и объем, используя математические формулы. Эти
включают квадраты, призмы, прямоугольники, конусы, круги, сферы, цилиндры,
и т. д. Они также тратят время на изучение того, как применять геометрические фигуры
приложения из реального мира, а также подключения к тематике контента
области.Дополнительные понятия в этой области включают расстояние между
заданные точки на прямой, а также точки на горизонтали и
вертикальные линии.
Алгебра учащихся разрабатывают представления о паттернах и функциях
используя слова, таблицы, графики и модели. Они исследуют и компьютер
целые числа с использованием коммутативных, ассоциативных и дистрибутивных
характеристики. Кроме того, они учатся применять переменные к математическим вычислениям.
проблемы на второй уровень переменных. Они развивают базовое понимание
выражений и уравнений.
Измерение концепции ориентированы на использование общепринятых стандартов и
нестандартные единицы измерения и определения взаимосвязей
между разновидностями объектов. Это тоже связано с геометрией
по мере того, как они учатся измерять площадь, объем и массу различных
геометрические фигуры. Они учатся измерять все аспекты кругов,
призмы и пирамиды.
Студенты применяют измерительные приложения для преобразования США.
обычные единицы измерения в метрическую систему.Они развиваются
базовое понимание метра, литра и грамма; включая их
переменные. Они учатся применять навыки оценки для определения
форма, объем, площадь и масса различных объектов.
Анализ данных и вероятность концепции сосредоточены на использовании соответствующих
язык для объяснения результатов математических экспериментов и моделирования.
Они учатся разрабатывать вопросы, помогающие находить различия.
между двумя или более выборками в генеральной совокупности.
Учащиеся используют таблицы данных для построения линейных графиков, гистограмм и
линейные графики.Они используют данные, чтобы делать выводы и делать прогнозы.
в наблюдениях, экспериментах и опросах. Они развивают математические
теории для объяснения событий, которые приведут к вероятным или маловероятным
результаты. Они интерпретируют данные, представленные на графических графиках.
делать прогнозы вероятных результатов.
Решение задач для пятиклассников фокусируется на развитии
стратегий решения проблем, чтобы помочь им развить фундаментальное понимание
математики.Учащиеся используют задачи со словами и другие симуляции реального мира.
в проблемных ситуациях.
Представление концепций ориентированы на учащихся, обучающихся коллекционированию
и систематизировать данные, а затем использовать их для решения проблем. Ответы
представлены в виде числовых, письменных, физических и физических моделей.
Социальное. Они умеют рисовать графики, диаграммы, таблицы и другие формы.
чтобы объяснить, как они решили проблему.
Connection концепции предназначены для учащихся пятого класса.
чтобы продемонстрировать, как подключаться к реальным приложениям
и другие области тематического содержания.Это включает в себя установление связей
с другими понятиями в математике.
Передавать свои математические идеи в форме предложений,
рисунки, плакаты и мультимедийные приложения — еще одна концепция
что студенты должны освоить. Это используется для определения их уровня
понимания, поскольку они объясняют математические концепции другим студентам
и учителя.
Рассуждения и доказательства понятий используются для объяснения математических
находки и методы решения проблем.Это необходимо для того, чтобы
они развивают навыки представления логических аргументов математическим ситуациям.
Все эти математические концепции используются для разработки всестороннего
базовые знания математических идей и языка по мере успеваемости студентов
к более высоким уровням математики.
Что такое прямой угол? — Определение, факты и пример
Что такое прямой угол?
Два соединяющихся луча образуют угол. Общая точка, где встречаются эти два луча, называется вершиной, а лучи — плечами угла.
Мера угла — это величина поворота или поворота точки от одного плеча к другому вдоль его вершины.
Когда стороны угла лежат в противоположном направлении, они образуют прямой угол. Углы образуют прямую линию через вершину.
Прямой угол также называется «плоский угол ».
На картинке OX и OY — руки угла. Общая точка O, где встречаются лучи, называется вершиной.
Как изобразить прямой угол?
Существуют различные способы представления прямых углов в соответствии с системой измерения.
Записывается как 180 °
Также записывается как π
Все углы, указанные на рисунке, прямые.
Свойства прямого угла
В прямом угле лучи смотрят в противоположных направлениях.
Прямой угол меняет направление точки
Прямой угол составляет ровно половину оборота.
Прямой угол можно также образовать, сложив два прямых угла.
Построение прямого угла с помощью транспортира
Начертите прямую OA со стрелкой на A.
Теперь держите транспортир на этой линии так, чтобы базовая линия транспортира была выровнена по OA.Буква A должна быть направлена в сторону 0 ° транспортира.
Начинайте с 0 ° и двигайтесь к отметке 180 ° транспортира. Достигнув 180 °, отметьте точку B на бумаге.
Соедините вершину прямой OA с точкой B. второй луч OB будет иметь стрелку в точке B.
Прямые углы в реальной жизни
Интересные факты
|
Цели обучения математике / пятому классу
Цели обучения математике пятого класса
Числа и операции
Подсчет, числовые наборы, числовые представления, сравнение и порядок номеров
- Изучите отрицательные числа в контексте.
- Разберитесь в понятиях ценности через миллионы.
- Считать по сотням тысяч и миллионам.
- Сравните и закажите целые числа до 10 000 000.
- Экспресс-номера до 10 000 000 в различных формах.
Целое число: умножение, деление
- Умножение многозначных чисел.
- Найдите частные, относящиеся к многозначным дивидендам.
- Решайте задачи умножения и деления.
- Выберите наиболее полезную форму частного и интерпретируйте остаток.
Оценка и мысленная математика
- Используйте оценку и мысленную математику для оценки сумм, разностей, произведений и частных.
Десятичные понятия, операции и приложения
- Моделируйте десятичные дроби с использованием тысячных долей.
- Разберитесь в понятиях числовой ценности через тысячные доли.
- Преобразование десятичных знаков в дроби.
- Сложить и вычесть десятичные знаки.
- Десятичные дроби умножаются и делятся на целые числа.
- Решите задачи с умножением и делением десятичных знаков.
Соотношение, пропорция и процент
- Преобразование дробей в десятичные.
- Связать дроби и выражения деления.
- Сложить и вычесть разные дроби и смешанные числа.
- Умножайте правильные дроби, неправильные дроби, смешанные числа и целые числа.
- Разделите дроби на целые числа.
- Решайте задачи со словами сложения, вычитания, умножения и деления дробей.
- Используйте передаточные числа для решения проблем.
- Найдите эквивалентные соотношения.
- Решите проблемы с процом.
- Перевести дроби в проценты.
- Найдите процент числа.
Алгебраическое мышление
Шаблоны и свойства
- Выявление, описание и расширение числовых шаблонов, включающих все операции.
- Найдите правила для завершения числовых шаблонов.
Алгебраические взаимосвязи и модели
- Поймите взаимосвязь между числами и символами в формулах для площади поверхности и объема.
- Опишите отношения чисел в контексте.
- Используйте буквы как переменные.
Числовые предложения, уравнения и неравенства
- Напишите и решите числовые предложения для одно-, двух- и трехэтапных реальных задач.
- Напишите и решите уравнения.
- Граф линейных уравнений.
- Упростите алгебраические выражения.
- Понять равенство и неравенство.
- Используйте порядок операций в числовых выражениях с двумя или более операциями.
Геометрия и измерения
Линии и углы
- Нанесите сумму углов на прямую линию.
- Накладываем сумму углов в точке.
- Применить свойство вертикальных углов пересекающихся линий.
Фигуры
- Примените свойства правого, равнобедренного и равностороннего треугольников.
- Примените сумму углов треугольника.
- Примените свойства параллелограмма, ромба и трапеции.
- Продемонстрируйте, что сумма длин любых двух сторон треугольника больше, чем длина третьей стороны.
- Определите и классифицируйте призмы и пирамиды.
- Определите твердое тело, которое можно сделать из сети.
- Обозначьте цилиндры, сферы и конусы.
- Опишите цилиндры, сферы и конусы по количеству и типу граней, а также количеству ребер и вершин.
- Построить твердые тела с помощью единичных кубов.
Длина, расстояние, периметр и площадь
- Найдите площадь треугольника как продолжение площади прямоугольника.
Площадь и объем поверхности
- Оценить и измерить объем в кубических единицах.
- Используйте сетку прямоугольной призмы, чтобы найти ее площадь.
Конгруэнтность, симметрия, преобразования и координатная геометрия
- Нанесите точки на координатную сетку.
Анализ данных
Сбор, классификация, организация, представление, интерпретация и анализ данных
- Представьте данные в виде двойной столбчатой диаграммы.
- Анализируйте данные в виде двойной гистограммы.
Вероятность
Исследование результатов и экспресс-вероятность
- Определите экспериментальную вероятность результата.
- Сравните результаты эксперимента с теоретической вероятностью.
- Найдите все возможные комбинации, составив список, составив древовидную диаграмму и умножив.
Математические навыки, которые ваш ребенок усвоит в пятом классе
Изучая математику в пятом классе, ваш ребенок расширит понимание десятичных и дробных чисел, а также изучит числовые выражения, объем и графики.Об этом много! Помогите своему ребенку преуспеть в математике в пятом классе, узнав больше о том, чем он будет заниматься.
В течение года ваш ребенок будет:
1. Решать числовые выражения
У вашего ребенка был большой опыт решения задач с помощью четырех операций. Теперь ваш ребенок еще больше разовьет это понимание, научившись использовать круглые скобки в числовых выражениях и оценивать выражения с их помощью. Ваш ребенок узнает о порядке операций и сначала решит части выражений в круглых скобках.
Помогите своему ребенку попрактиковаться в понимании порядка операций, предложив ему более длинные выражения для оценки, как со скобками, так и без них. Дайте ребенку такое же выражение, но с другим расположением скобок. Поговорите с ребенком о том, как круглые скобки повлияли на выражение.
2. Работа с десятичными знаками
В пятом классе ученики учатся читать, писать и сравнивать десятичные дроби с тысячными. Они также практикуют сложение, вычитание, умножение и деление десятичных дробей до сотых, что может быть непросто!
Поддержите своего ребенка, рассказав о различных стратегиях.Попросите ребенка использовать рисунки или модели, чтобы попытаться визуализировать решаемые им десятичные задачи. Например, нарисуйте сетку 10х10 и попросите ребенка видеть каждый квадрат как сотую. Используйте сетку, чтобы визуализировать десятичные дроби при решении задач.
3. Сложение и вычитание дробей с разными знаменателями
В четвертом классе ученики научились сравнивать дроби с разными числителями или знаменателями. Теперь они расширят это понимание, научившись складывать и вычитать дроби с разными знаменателями, находя общие знаменатели.
Дайте вашему ребенку выполнить реальные задания на сложение и вычитание. Например, при приготовлении пищи вы можете попросить ребенка рассчитать ⅓ стакана муки + ½ стакана муки. Помогите своему ребенку связать общие знаменатели с их знаниями об умножении, подумав об общих кратных. ( Посетите нашу страницу о дробях, чтобы освежить свои знания о дробях!)
4. Умножение и деление дробей
Работа с дробями не заканчивается сложением и вычитанием! Пятиклассники готовы умножать дроби на целые числа или дроби.Они также будут делить единичные дроби (дроби, где числитель 1) на целые числа и целые числа на единичные дроби.
Эти понятия могут быть непростыми, поэтому вместо того, чтобы объяснять их вашему ребенку, попросите его объяснить их вам. Возможность быть учителем может помочь вашему ребенку развить более глубокое понимание и даст вам возможность увидеть, насколько хорошо все это усваивается.
5. Измерьте объем
Четвероклассники имеют опыт измерения длины и веса.Но в этом году они познакомятся с новым типом измерения: объемом. Студенты научатся измерять объемы, считая единичные кубы, используя кубические сантиметры, кубические дюймы и кубические футы. Они узнают формулу для вычисления объема кубов и прямоугольных призм (объем = длина x ширина x высота).
. ребенок замечает количество напитков, которые потребляет ваша семья. Поговорите о том, как емкости разного размера, например, 2-литровые и 1-литровые бутылки, вмещают разное количество жидкости.
6. Графические точки на координатной плоскости
В пятом классе учащиеся узнают, как в системе координат есть ось x и ось y, и как точки могут быть заданы по их координатам (x, y).
Попросите вашего ребенка нарисовать координатную плоскость с помощью графической бумаги и потренируйтесь, когда ребенок находит определенные точки. Такие игры, как «Морской бой», также могут быть отличным способом попрактиковаться в представлении о координатах. Если у вас нет настольной игры, вот как вы можете играть в Морской бой, используя ручку и бумагу!
На протяжении всего пятого класса обучения вашего ребенка находите возможности проверить и услышать, что он изучает.Математика в пятом классе может быть сложной, так что воспользуйтесь этой возможностью, чтобы улучшить свои навыки!
Нашли это полезным? Ознакомьтесь с нашими руководствами по математике от детского сада до 5 класса
Написано Лили Джонс, Лили любит учиться всему. Она работала учителем детского сада и первого класса, преподавателем, разработчиком учебной программы и тренером учителей. Она любит смотреть на мир с любопытством и вдохновлять людей всех возрастов любить учиться. Она живет в Калифорнии с мужем, двумя детьми и маленькой собачкой.
О Komodo — Komodo — это увлекательный и эффективный способ улучшить математические навыки K-5. Komodo, разработанный для детей от 5 до 11 лет для использования в домашних условиях, использует небольшой и частый подход к изучению математики (15 минут, три-пять раз в неделю), который вписывается в напряженный семейный распорядок. Komodo помогает пользователям развить беглость и уверенность в математике — , не задерживая их надолго .
Узнайте больше о Komodo и о том, как он помогает тысячам детей каждый год лучше учиться по математике — вы даже можете попробовать Komodo бесплатно.
Геометрия 5 класса
Добро пожаловать на рабочие листы по математике Саламандры 5-го класса по геометрии.
Здесь вы найдете ряд распечатываемых рабочих листов по геометрии для пятого класса,
которые помогут вашему ребенку узнать все об углах самых разных форм.
Есть также некоторые рабочие листы, в которых исследуются свойства ряда двумерных фигур.
На этой веб-странице вы найдете наш ассортимент бесплатных распечатываемых рабочих листов по геометрии для пятиклассников.
Существует ряд геометрических листов для печати, на которых углы просматриваются в различных формах, таких как
прямые углы, углы на прямой и треугольники.
Использование этих листов поможет вашему ребенку:
- узнать, как найти недостающий угол;
- знайте, что углы внутри прямого угла должны составлять в сумме 90 °
- знайте, что углы на прямой должны составлять в сумме 180 °
- знайте, что углы вокруг точки должны составлять в сумме 360 °
- знайте, что углы в треугольнике должны составлять в сумме 180 °
Все бесплатные листы по математике в этом разделе поддерживают тесты по элементарной математике для 5-го класса.
В приведенных здесь рабочих листах дети применяют свои знания и понимание двухмерных фигур.
Это отличный способ подтолкнуть более способных учеников или заставить детей серьезно задуматься о свойствах фигур.
Хотя листы в этом разделе предназначены для 5-го класса, они могут легко использоваться детьми старшего возраста.
Первые пять листов находятся в разделе «Геометрия для 3-го и 4-го классов».
Вот наша подборка рабочих листов по геометрии для 4-го класса.
Использование этих листов поможет вам:
- Классифицируйте углы — острые, тупые, прямые, рефлекторные, прямые;
- классифицируйте треугольники — острые, тупые, правые;
- измерять углы с помощью транспортира;
- знает, что сумма углов в треугольнике составляет 180 °.
Листы в этом разделе находятся на более простом уровне, чем листы на этой странице.
Взгляните на еще несколько наших рабочих листов, похожих на эти.
Вот наша коллекция сеток координатных плоскостей для печати и координатных листов.
Использование этих забавных координатных листов — отличный способ увлекательно изучать математику.
Использование этих листов поможет вашему ребенку:
- Постройте и запишите координаты.
Вот наша подборка бесплатных рабочих листов для печати для 5-го класса.
Все листы отсортированы от самого простого к самому сложному.
Использование этих листов поможет вашему ребенку:
- умеют рассчитать площадь треугольника;
- умеет вычислять площадь ряда четырехугольников.
- выучить формулы для вычисления площади треугольников и некоторых четырехугольников.
Все бесплатные распечатываемые рабочие листы с геометрией в этом разделе поддерживают тесты Elementary Math.
Вот наш диапазон рабочих листов площади и периметра.
Использование этих листов поможет вашему ребенку:
- знать, что такое площадь и периметр;
- умеет находить площадь и периметр прямоугольников;
- умеет находить площадь и периметр прямолинейных форм;
Все листы в разделе ниже поддерживают элементарные математические тесты.
Вот наш ассортимент рабочих листов.
Использование этих листов поможет вашему ребенку:
- знать, что такое объем и как его найти;
- найти объем фигур, считая кубики;
- найти объем прямоугольной призмы;
- решение основных задач, связанных с объемом
Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике.
и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.
% PDF-1.4
%
448 0 объект
>
эндобдж
xref
448 82
0000000016 00000 н.
0000002775 00000 н.
0000002922 00000 н.
0000003419 00000 н.
0000003751 00000 п.
0000004062 00000 н.
0000004260 00000 н.
0000004374 00000 н.
0000004486 00000 н.
0000004599 00000 н.
0000004708 00000 п.
0000005172 00000 н.
0000005199 00000 н.
0000005635 00000 п.
0000005662 00000 н.
0000006228 00000 п.
0000006624 00000 н.
0000006651 00000 п.
0000006678 00000 н.
0000007142 00000 н.
0000007282 00000 н.
0000007415 00000 н.
0000007550 00000 н.
0000007687 00000 н.
0000008233 00000 п.
0000008771 00000 п.
0000009330 00000 н.
0000009891 00000 н.
0000010435 00000 п.
0000010462 00000 п.
0000010856 00000 п.
0000010994 00000 п.
0000011520 00000 п.
0000011783 00000 п.
0000012286 00000 п.
0000012575 00000 п.
0000012846 00000 п.
0000014112 00000 п.
0000025731 00000 п.
0000025844 00000 п.
0000027008 00000 н.
0000027316 00000 н.
0000027431 00000 н.
0000030282 00000 п.
0000030600 00000 п.
0000030719 00000 п.
0000031960 00000 п.
0000032273 00000 п.
0000032400 00000 п.
0000034380 00000 п.
0000034704 00000 п.
0000034774 00000 п.
0000034854 00000 п.
0000038726 00000 п.
0000039000 00000 н.
0000039288 00000 п.
0000039358 00000 п.
0000039438 00000 п.
0000044340 00000 п.
0000044609 00000 п.
0000044923 00000 п.
0000044993 00000 п.
0000045073 00000 п.
0000069237 00000 п.
0000069502 00000 п.
0000069902 00000 н.
0000069972 00000 н.
0000070052 00000 п.
00000
00000 п.
0000091070 00000 п.
0000091413 00000 п.
0000091483 00000 п.
0000091563 00000 п.
0000091772 00000 п.
0000091987 00000 п.
0000092208 00000 п.
0000092447 00000 п.
0000112047 00000 н.
0000153155 00000 н.
0000214671 00000 н.
0000002590 00000 н.
0000001936 00000 н.
трейлер
] / Назад 1142289 / XRefStm 2590 >>
startxref
0
%% EOF
529 0 объект
> поток
hb«b`TA , ` $ 009 | _9 GSXDqqE’KfZjM] Mg 斬` ᑮ M | JIS, * ygt2t,
ptYoyD, & pIp8 ɯpDZ) DVmzFbSidv} | ¡v! -FgF6K9p13i5 ݘ b> Lsw϶D # W7 *
N4
sirY9yEʨoH: 9mE / o _? @ 3NJ
Преподавание абсолютного значения числа в математике
Урок 2: Разработка концепции
Материалы: Каталожные карточки или цифровые «карточки», которые могут быть распределены среди класса
.
Стандарты:
- Под абсолютным значением рационального числа понимается его расстояние от 0 на числовой прямой.(6.NS.C.7.C)
Подготовка: Сделайте карточки для У меня есть… У кого есть?
Итоговая и оценочная игра
- Попросите учащихся написать и поделиться своими определениями и реальными примерами ситуаций абсолютной ценности.
- Играть У меня есть … у кого есть? Составьте набор из 15 учетных карточек с уравнениями абсолютных значений и 15 учетных карточек, содержащих значения переменной. Если учетные карточки недоступны или вы адаптируете их для дистанционного обучения, создайте способ, чтобы 30 приведенных ниже уравнений были распределены среди ваших учеников как можно более равномерно.
| Карты абсолютного значения | Карты переменного значения |
| | x + 5 | = 20 | x = 15 |
| | 5 — x | = 30 | x = –25 |
| | x + 6 | = 41 | x = 35 |
| | –27 — x | = 20 | x = –47 |
| –7 + | x | = 0 | x = –7 |
| | 25 — x | = 18 | x = 7 |
| | x + –5 | = 38 | x = 43 |
| | 37 — x | = 70 | x = –33 |
| 114 — | x | = 7 | x = 107 |
| | — x + 100 | = 21 | x = 121 |
| — | 1 + x | = -80 | x = 79 |
| | x | = 81 | x = –81 |
| | x + 3 | = 84 | x = 81 |
| | 25 + x | = 62 | x = –87 |
| | x — 26 | = 11 | x = 37 |
Каждая указанная карта абсолютного значения имеет два значения: x .Эти значения перекрываются, так что каждая карта значений переменных удовлетворяет двум из заданных уравнений абсолютного значения (первое и второе значения удовлетворяют первому уравнению, второе и третье значения удовлетворяют второму уравнению и т. Д., Пока последнее и первое значения не удовлетворяют условиям последнее уравнение).
Распределите карточки или уравнения поровну. Убедитесь, что все они были розданы. Выберите ученика, который скажет «У меня есть», а затем прочтите значение или уравнение на его карточке. Затем попросите учащегося сказать: «У кого есть совпадение для моей карты?» Любой ученик, у которого есть совпадение, должен сказать: «У меня есть… у кого есть…», и игра продолжается до тех пор, пока не будут прочитаны все карточки.Вы можете попросить учащихся встать, когда игра начнется, и сесть, пока они предлагают ответ. Чтобы все заинтересовались, предложите награду за успешное прохождение игры, поощряя вызовы к подозрительным ответам.
***
Ищете другие бесплатные уроки математики и мероприятия для учеников средней школы? Обязательно ознакомьтесь с нашим центром бесплатных учебных ресурсов.

 Aglaeactis castelnaudii) – вид птиц из семейства колибри (Trochilidae).
Aglaeactis castelnaudii) – вид птиц из семейства колибри (Trochilidae).