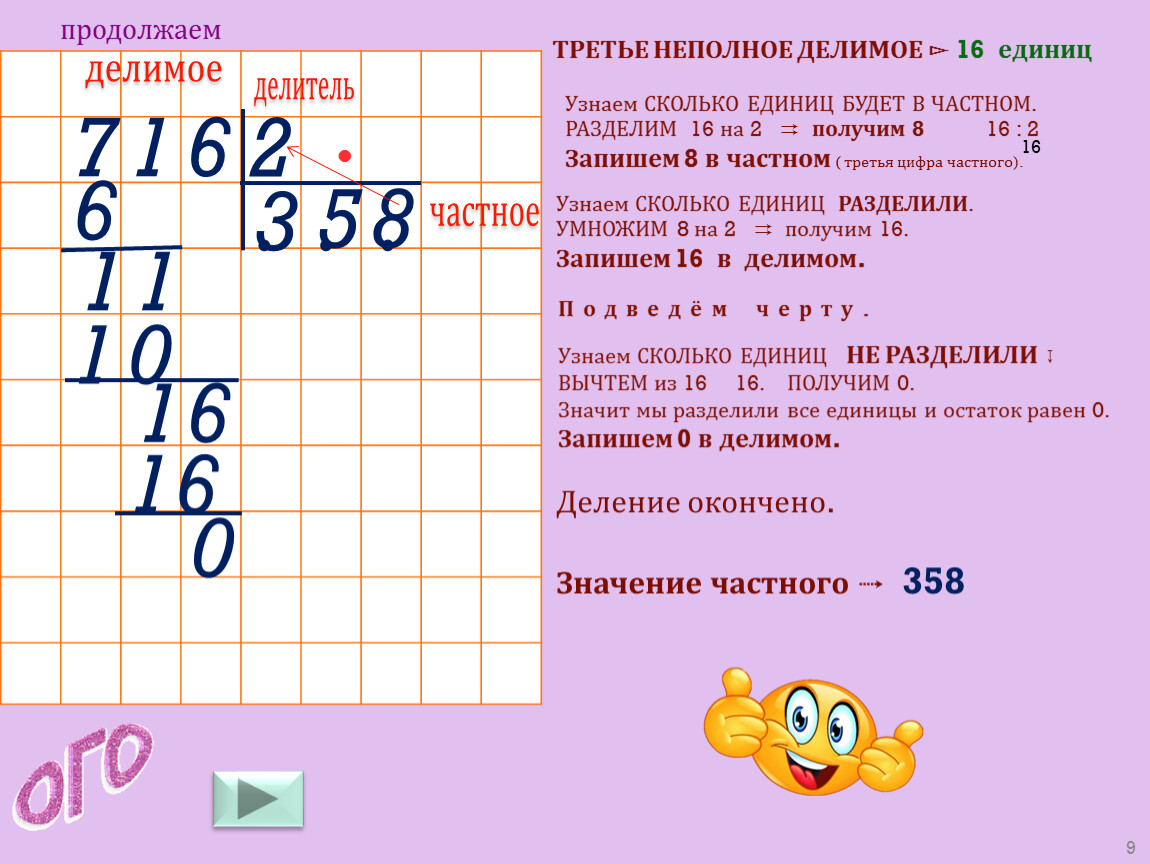
Урок 66. приём письменного деления на однозначное число — Математика — 3 класс
Математика
3 класс
Урок № 66
Приём письменного деления на однозначное число
Перечень вопросов, рассматриваемых в теме:
Как выполняется письменное деление на однозначное число?
Как применяется алгоритм деления трёхзначного числа на однозначное?
Тезаурус
Каждая цифра в записи многозначного числа занимает определённое место – позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.
Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:
— единицы называют единицами 1-го разряда;
— десятки называют единицами 2-го разряда;
— сотни называют единицами 3-го разряда и т. д.
Деление (операция деления) — одно из четырёх простейших арифметических действий, обратное умножению.
Деление — это такая операция, в результате которой получается число (частное), которое приумножении на делитель даёт делимое.
Основная и дополнительная литература:
1. Моро М. И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. С. 92-94.
2. Волкова С. И. Математика. Проверочные работы. 3 кл. — М.: Просвещение, 2018. С. 84-85.
3. Рудницкая В. Н. Математика. Дидактические материалы.Ч.1 3 кл. – М. «Вентана- Граф», 2016, с. 23-24.
Теоретический материал для самостоятельного изучения
Сегодня мы займёмся делением.
Вам предстоит научиться выполнять деление трёхзначных чисел в столбик.
Вы справитесь с этим без проблем, если хорошо знаете таблицу умножения.
Три математических действия — сложение, вычитание и умножение в столбик вы уже умеете выполнять. Осталось одно, но самое сложное. Помните, чем сложнее – тем интереснее!
Деленье нам служит на деле,
Оно нам поможет всегда.
Кто поровну трудности делит,
Разделит успехи труда.
Мы уже выяснили, что невозможно быстро и точно делить без знания таблицы умножения.
Но не только.
Надо ещё хорошо знать компоненты деления и взаимосвязь между ними, быстро и точно выполнять вычитание и конечно уметь работать с разрядами.
Вспомним компоненты деления: число, которое делим – делимое, число на которое делим – делитель, результат деления – значение частного.
В тех случаях, когда деление выполнить устно сложно, выручает умение делить в столбик, или уголком.
Это название придумали не случайно. Привычный знак деления заменён на уголок.
Записываем делимое, рядом чертим уголок. В верхнем углу записываем делитель, а в нижний угол вписываем цифры частного.
Обратите внимание, цифры делимого и частного имеют названия в зависимости от разряда, который обозначают.
Кроме этого, делимое придётся раскладывать на неполные делимые – первое, второе, третье. Это те числа, которые делим на делитель, пока не разделим всё число.
Рассмотрим пример 938 : 7
Шаг 1
Записываем числа, разделив их «уголком».
Шаг 2
Сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Поэтому первым записанными нами результатом будет 1.
Шаг 3
Умножаем делитель 7 ∙ 1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2. Записываем результат.
Шаг 4
Число, которое мы видим, меньше делителя, поэтому его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5
Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7 ∙ 3) записываем внизу под числом 23 в столбик.
Шаг 6
Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23 — 21) получаем разницу. Она равняется 2.
Из делимого у нас осталось неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг 7
Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное = 134.
Рассмотрим ещё деление в столбик на примере 512 : 8.
1 шаг. Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг. Деление начинаем слева направо. Сначала берем цифру 5
3 шаг. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг. Ставим точку под делителем.
5 шаг. После 51 стоит еще цифра 2, а значит, в ответе будет ещё одно число, то есть, частное – двузначное число. Ставим вторую точку:
Ставим вторую точку:
6 шаг. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг. Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг. Затем из 51 вычитаем 48 и получаем ответ 3.
9 шаг. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Ответ: 64
Как и в остальных случаях выполнения письменных приёмов вычислений, при делении очень важно не отступать от алгоритма.
Запомните:
Когда число цифр разряда меньше делителя, надо добавить к нему число цифр следующего разряда.
Если при делении неполного делимого остался остаток, спускаем его под черту и к нему приписываем цифру следующего разряда.
Остаток не может быть больше делителя!
Если цифра неполного делимого меньше делителя, то в частном пишем 0.
Вы сегодня получили ключ к успеху в математике. Смело открывайте им замки любой сложности.
Задания тренировочного модуля:
Укажите правильно выполненное деление в столбик.
Правильный ответ:
Заполните пустые ячейки таблицы.
Правильный вариант:
Деление столбиком на двузначное число. Видео #
Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться.
Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
Для начала повторим кратко, как делить столбиком на однозначное число:
А что если деление с остатком? Смотрим в следующем видео:
Алгоритм деления столбиком на двузначное число
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
1. Находим первое неполное делимое. Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.
Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.
Примеры 768:24. Первое неполное делимое 76
265:53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.
2. Определяем количество цифр в частном. Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.
Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.
Значит в частном будет всего 3 цифры.
3. Находим цифры в каждом разряде частного. Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
4. Находим остаток (если есть).
Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.
Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)
д.)
Разбор примеров на деление столбиком на двузначное число
Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
— Найдем значение частного чисел 265 и 53.
Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Значение частного чисел 265 и 53 равно 5.
Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.
— Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
Значение частного чисел 184 и 23 равно 8.
Рассмотрим более сложные случаи деления.
— Найдем значение частного чисел 768 и 24.
Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Значение частного чисел 768 и 24 равно 32.
— Найдем значение частного чисел 15344 и 56.
Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост. 1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
Значение частного чисел 15344 и 56 равно 274.
Пример на деление с остатком
Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой
— Найдем значение частного чисел 15345:56
Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Значение частного чисел 15345 и 56 равно 274 (остаток 1).
Деление с нулем в частном
Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.
— Найдем значение частного чисел 2870:14
Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.
Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).
70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.
Значение частного чисел 2870 и 14 равно 205.
Деление нужно непременно проверить умножением.
Примеры на деление для самопроверки
Найдите первое неполное делимое и определите количество цифр в частном.
3432:66 2450:98 15145:65 18354:42 17323:17
Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.
1428 : 42 30296 : 56 254415 : 35 16514 : 718
2924 : 68 136576 : 64 710278 : 91 15830 : 293
Деление натуральных чисел столбиком: правило, примеры
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Запись чисел при делении столбиком
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Пусть нам нужно разделить 6105 на 55, запишем:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем.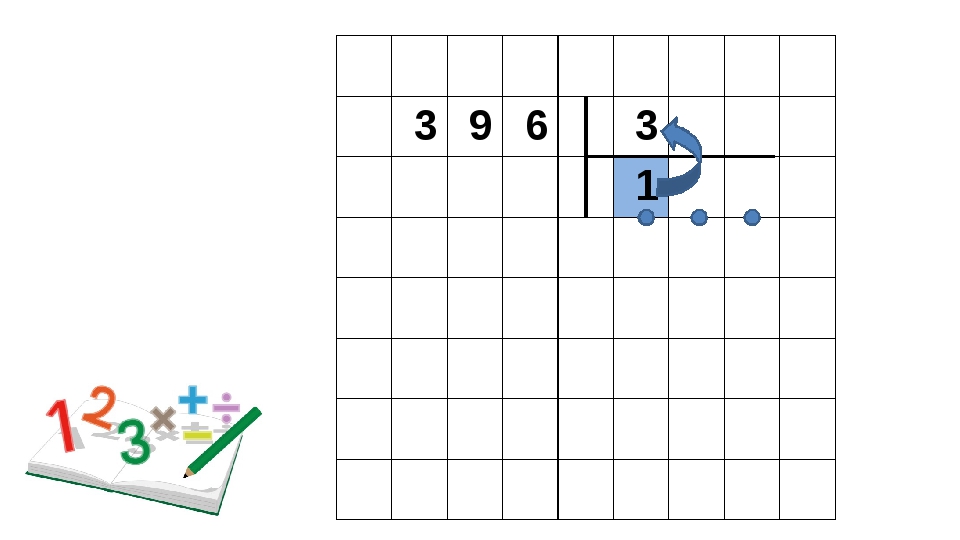 В общем случае схема деления столбиком выглядит так:
В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Деление столбиком на однозначное число
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8÷2=4.
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.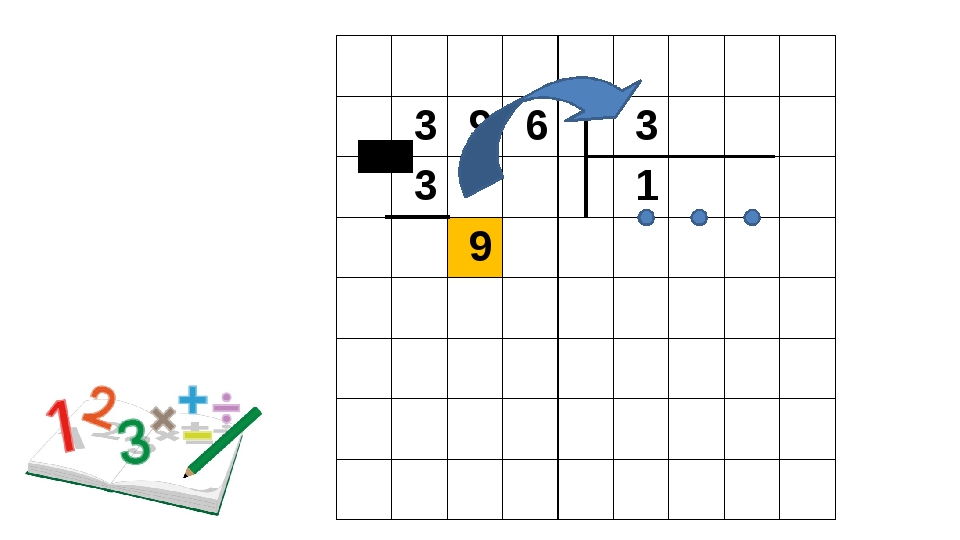
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0, 1, 2, 3.. Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2·0=0; 2·1=2; 2·2=4; 2·3=6; 2·4=8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4, на которое мы умножали делитель, записываем на место частного.
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8-8=0.
Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3.
В данном случае, последовательно умножая тройку на 0, 1, 2, 3.. получаем в результате:
3·0=0<7; 3·1=3<7; 3·2=6<7; 3·3=9>7
Под делимым записываем число , полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6.
В завершение операции вычитаем 6 из 7 и получаем:
Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1.
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4. Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.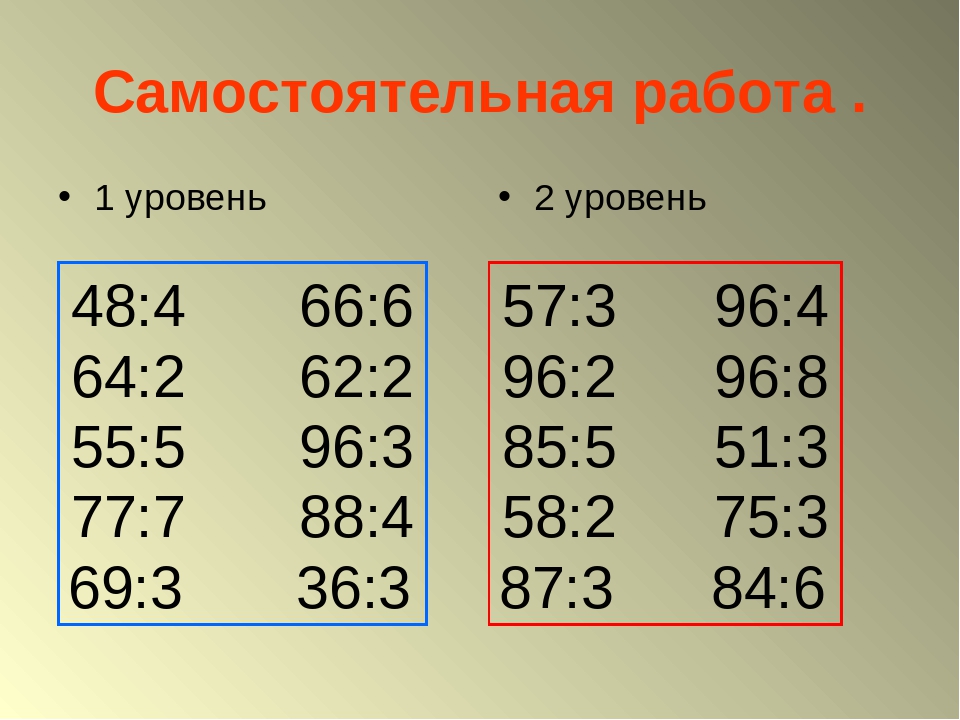
Алгоритм деления столбиком
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.
2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x=14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ, включая нуль : 0, 1, 2, 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x. Когда в результате умножения получается число 14, записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
Если в результате умножения получается число, большее чем x, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
В соответствии с алгоритмом имеем:
4·0=0<14; 4·1=4<14; 4·2=8<14; 4·3=12<14; 4·4=16>14.
Под выделенным числом записываем число 12, полученное на предпоследнем шаге. На место частного записываем множитель 3.
3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
4. Число 2 меньше числа 4, поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — 0. В итоге отмечаем новое рабочее число — 20.
Важно!
Пункты 2-4 повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе 20. Умножая 4 на 0, 1, 2, 3.. получаем:
4·5=20
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20-20=0.
4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2.
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
2. Умножаем делитель на 0, 1, 2, 3.. и сравниваем результат с отмеченным числом.
4·0=0<2; 4·1=4>2
Соответственно, под отмеченным числом записываем число 0, и под делителем в следующий разряд частного также записываем 0.
3. Выполняем операцию вычитания и под чертой записываем результат.
4. Справа под чертой добавляем цифру 8, так как это следующая цифра делимого числа.
Таким образом, получаем новое работчее число — 28. Снова повторяем пункты алгоритма.
Проделав все по правилам, получаем результат:
Переносим под черту вниз последнюю цифру делимого — 8. В последний раз повторяем пункты алгоритма 2-4 и получаем:
В самой нижней строчке записываем число 0. Это число записывается только на последнем этапе деления, когда операция завершена.
Таким образом, результатом деления числа 140228 на 4 является число 35072. Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Приведем другие примеры деления чисел в столбик и примеры записи решений.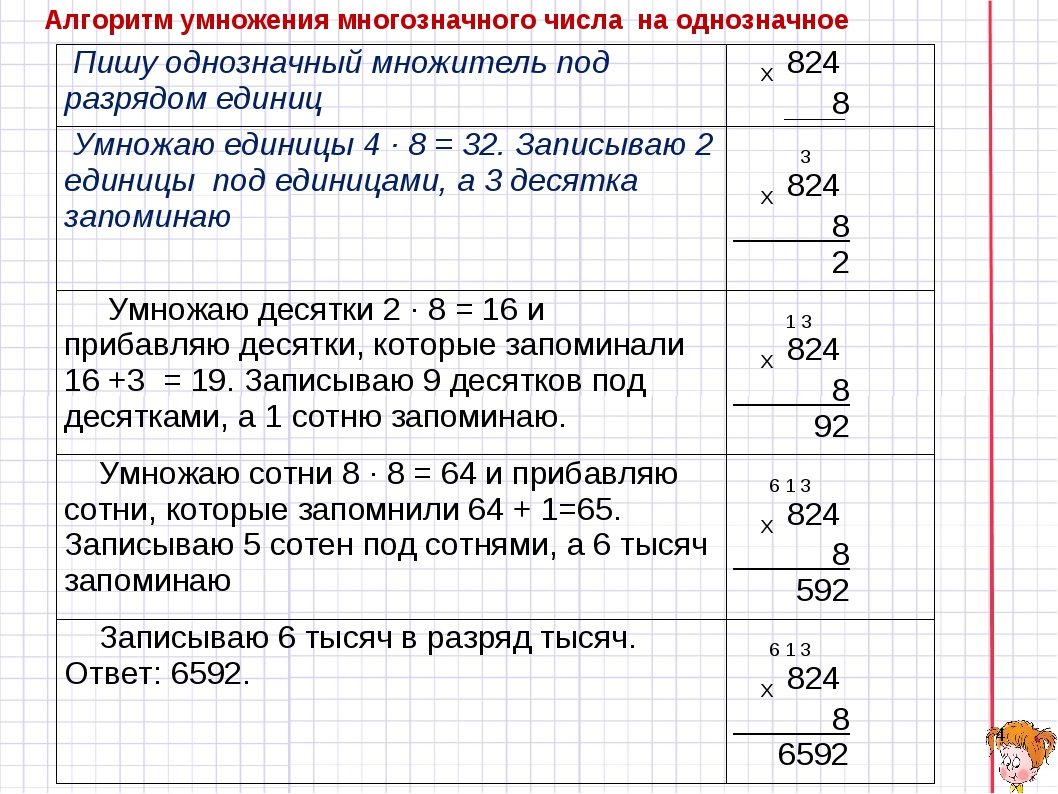
Пример 1. Деление натуральных чисел в столбик
Разделим натуральное число 7136 на натуральное число 9.
Запишем:
После второго, третьего и четвертого шага алгоритма запись примет вид:
Повторим цикл:
Последний проход, и поучаем результат:
Ответ: Неполное неполное частное чисел 7136 и 9 равно 792, а остаток равен 8.
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Пример 2. Деление натуральных чисел в столбик
Разделим число 7042035 на 7.
Ответ: 1006005
Деление многозначных натуральных чисел столбиком
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2-4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе. Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Пример 3. Деление натуральных чисел в столбик
Разделим 5562 на 206.
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556.
556>206, поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на 0, 1, 2, 3.. и получаем:
206·0=0<556; 206·1=206<556; 206·2=412<556; 206·3=618>556
618>556, поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2
Выполняем вычитание столбиком
В результате вычитания имеем число 144. Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442.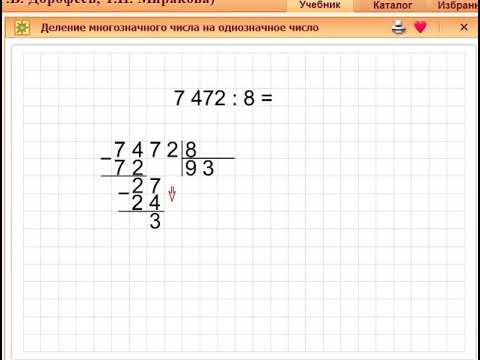
Повторяем с ним пункты 2-4. Получаем:
206·5=1030<1442; 206·6=1236<1442; 206·7=1442
Под отмеченным рабочим числом записываем 1442, а в следующий разряд частного записываем цифру 7 — множитель.
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
Ответ: 27
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Пример 5. Деление натуральных чисел в столбик
Разделим натуральное число 238079 на 34.
Ответ: 7002
Конспект урока математики Деление на однозначное число, 3 класс, ФГОС, ОС Перспектива. Автор: Л. Г. Петерсон.
Конспект урока математики «Деление на однозначное число»,3 класс, ФГОС,ОС «Перспектива».
Автор: Л. Г. Петерсон.
Г. Петерсон.
Конспект урока подготовила Дударева Надежда Михайловна, учитель начальных классов МБОУ «Средняя общеобразовательная школа № 22» г. Калуги.
Тема урока: Деление на однозначное число
Тип урока: урок изучения нового материала (продолжение)
Цель: построение модели нового способа деления на однозначное число
Задачи:
+образовательные
— сформирование умения делить числа столбиком
+развивающие
— развивать мышление, грамотную математическую речь, интерес к урокам математики;
УУД:
*регулятивные
— осознание учащимися того, что уже усвоено и что ещё нужно усвоить;
— развивать контроль и самоконтроль при проверке заданий;
— планировать свои действия в соответствии с поставленной задачей и условиями её реализации, в том числе во внутреннем плане;
— оценивать правильность выполнения действия на уровне адекватной оценки соответствия результатов требованиям данной задачи и задачной области.
*познавательные
— совершенствовать вычислительные навыки;
— развивать умение извлекать информацию;
-перерабатывать полученную информацию: сравнивать и группировать математические факты;
— делать выводы на основе обобщения умозаключений;
+коммуникативные
-адекватно использовать коммуникативные, прежде всего речевые, средства для решения различных коммуникативных задач, строить монологическое высказывание
-учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве;
-формулировать собственное мнение и позицию;
-использовать речь для регуляции своего действия;
+воспитательные
— воспитание аккуратности при работе в тетрадях.
Оборудование:
— учебник;
— презентация;
Ход урока
1.Организационный момент
-Сейчас у нас урок математики.
— У вас на столе должны быть: учебник, тетрадь и пенал.
3.Проверка домашнего задания
2.Актуализация имеющихся знаний
-С каким новым способом деления мы с вами знакомились на предыдущем уроке?
— Мы познакомились с делением чисел в столбик.
— А как мы считали до того, как узнали, как делить столбиком?
— Мы сначала делили сотни, потом десятки ,затем единицы и все складывали.
— Откройте тетради, подпишите число и классная работа.
-Попробуем решить такой пример этим способом — 675:3
-Делим сотни 5 с. :3= 2с.
-Делим десятки 7д.:3= 2д. (ост.1 д.)
-Делим единицы 15 ед. :3 = 5ед.
-Какой у нас получился ответ?
— У нас получился ответ 225.
— каким способом можно ещё решить этот пример?
— Деление уголком.
— Давайте с вами повторим алгоритм деления .
-Что нужно сначала сделать, чтобы разделить числа углом?
— Нам нужно найти неполное делимое.
-Верно. Какой у нас следующий шаг ?
— Мы должны определить число цифр в частном.
— А затем что мы делаем?
— Мы решаем пример и находим ответ.
Решим пример 675 : 3 столбиком.
-Я пишу пример на доске, а вы мне помогайте, чтобы у нас получился верный ответ.
— Ребята ,что я сначала должна сделать?
— Выделить неполное делимое.
— Какое у нас в этом примере будет неполное делимое? Почему?
— В этом примере неполное делимое будет 6,так как 6 делится на 3.
— Верно. Какую цифру я должна написать в частное? Почему?
— Цифру 2, так как 6 разделить на 3 будет 2.
-Значит ,я из 6 вычитаю 6 и получается 0,а 0 мы не пишем. Какое число мы сносим?
— Мы сносим число 7.
Число 7 делится на 3?
-Нет.
-Какое число будет ближайшее к числу 7, которое делится на 3?
— это число 6.
Значит, что мы делаем?
— Мы в частное пишем 2, а из семи вычитаем 6 и получится остаток 1
— Хорошо. Какое число нам осталось снести?
-Это число 5.
— 15 у нас делится на 3?
— Да, делится.
— Какую цифру я должна написать в частное? Почему?
-Цифру 5. Так как 3 умножить на 5 будет 15.
-Верно ребята. Деление у нас закончено?
— Да.
— Какой ответ у нас получился?
— Унас получился ответ 225.
— Сравните его с предыдущим ответом ,когда мы делили отдельно сотни, десятки ,потом единицы.
-Эти ответы совпадают?
— Да, совпадают. Значит, мы верно решили пример в столбик.
— Мы справились с этим примером. Нашли верный ответ.
3. Первичное закрепление.
Теперь откроем учебник на странице 13. Найдите номер 1.
Эти примеры мы будем решать у доски по « цепочке».
-При решение примеров пользуемся алгоритмом деления.
-Приступаем к работе. ( дети по очереди выходят к доске, решают примеры с комментированием по алгоритму)
Перейдем с вами к заданию №4. Прочитаем задание (читает один из учащихся.)
Решение устно под цифрой 1. Ребята смотрим с вами первый вариант :а -=0 ,b= 1. Вспоминаем правило при умножении на ноль. Что получится при умножении числа на 0?
Что получится при умножении числа на 0?
— Если число умножить на ноль ,то получится 0.
— А если мы число делим на единицу, то что у получится?
— Если число разделить на единицу, то получится данное число.
— Теперь подставляем вместо b- единицу вместо а — 0. Какое выражение у нас получилось?
— 6309*0 + 936:1.
— Какой ответ у нас получится?
— Ответ будет 936.
— Верно. Смотрим пример под цифрой 2. Запишем его с подстановкой чисел вместо а и b . Какое выражение получилось?
— 6309 *6+936:2
Расставьте действия.
— Как удобнее нам посчитать первое действие: 6309 *6?
— Удобнее посчитать столбиком.
— Верно. Решаем в тетради самостоятельно . Какой ответ получился?
— Ответ в этом действии 37854.
— Какое действие будет вторым?
— Второе действие 936:2.
— Как лучше вычислять ?
— Удобнее вычислять столбиком ( вызываю одного ученика к доске, остальные пишут в тетради)
— Проверьте, правильно ли решил(-ла) (имя ученика) этот пример.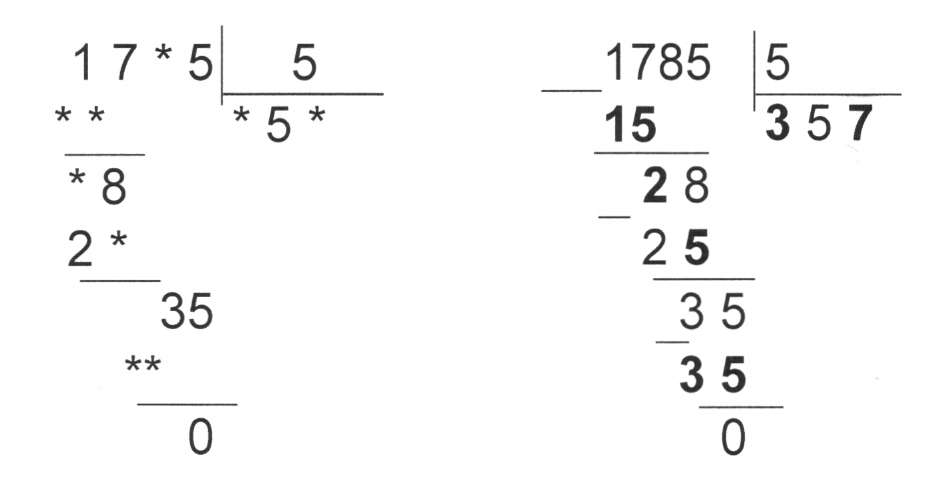 Какой получился ответ?
Какой получился ответ?
— Ответ 468.
— теперь что нам нужно сделать?
— Нам нужно сложить первое и второе действие
— решите самостоятельно. Скажите мне ответ.(38322)
4.Физкультминутка
Мы решали, мы решали
Мы решали, мы решали.
Что-то очень мы устали.
Мы сейчас потопаем, (Шаги ногами на месте под счет учителя.)
Ручками похлопаем. (Хлопки в ладоши.)
Раз присядем,
(Приседания.)
Быстро встанем, (Повороты туловища. Ходьба на месте.) Улыбнемся, Тихо сядем.
5. Вторичное закрепление.
Посмотрим на страницу 14 №8. Решим этот номер устно.
Для выполнения этого номера повторим единицы измерения длины и массы. (написано мелом на доске.)
см дм м км
г ц кг т
Соедините дужками и подпишите . сколько в сантиметре дециметров, в дециметре метров и т. д. .Тоже самое с единицами массы.
д. .Тоже самое с единицами массы.
Теперь приступаем к решению задания при этом обосновывая свою точку зрения( дети объясняют с пояснением почему одна единица измерения больше или меньше другой)
Пример: 45см будет меньше 2 м,так как в 2 м =200см,а 200 больше, чем 45,значит 45см будет меньше чем 2 м. И так оставшиеся примеры.
6. Домашнее задание.
Наш урок подходит к концу.
-Запишите домашнее задание. Стр13-14 ,№ 2,5а),6
7. Итог урока.
— Что мы сегодня узнали на уроке?
— Что было для вас трудным?
— Понравился ли вам урок?
-Чему вы научились на уроке ?
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/125209-konspekt-uroka-matematiki-delenie-na-odnoznac
Деление двузначного числа на однозначное. Примеры
Сначала рассмотрим способ деления двузначного числа на однозначное, когда в делимом количество десятков и количество единиц делится на делитель.
Чтобы разделить двузначное число на однозначное, надо двузначное число представить в виде суммы разрядных слагаемых и разделить эту сумму на однозначное число.
Например, чтобы найти значение выражения:
56 : 2
сначала записываем двузначное число 56 в виде суммы разрядных слагаемых:
50 + 6,
то есть просто разбиваем число 56 на сумму пяти десятков и шести единиц. Затем делим сумму 50 + 6 на число 2:
(50 + 6) : 2 = 50 : 2 + 6 : 2 = 25 + 3 = 28,
значит 56 : 2 = 28.
Примеры:
1) 39 : 3 = (30 + 9) : 3 = 30 : 3 + 9 : 3 = 10 + 3 = 13;
2) 75 : 5 = (70 + 5) : 5 = 70 : 5 + 5 : 5 = 14 + 1 = 15;
3) 68 : 4 = (60 + 8) : 4 = 60 : 4 + 8 : 4 = 15 + 2 = 17.
Теперь рассмотрим способ деления двузначного числа на однозначное, когда в делимом количество десятков и количество единиц по отдельности не делятся на делитель.
Чтобы разделить двузначное число на однозначное, надо двузначное число представить в виде суммы слагаемых и разделить эту сумму на однозначное число.
Рассмотрим выражение:
52 : 4.
В данном случае разрядные слагаемые числа 52 (50 и 2) не делятся на 4. Значит первый способ вычислений здесь не подходит. Тогда можно подобрать ближайшее к 52 круглое число, которое делится на 4, это будет число 40. Заменяем делимое 52 на сумму:
40 + 12.
Затем делим сумму 40 + 12 на число 4:
(40 + 12) : 4 = 40 : 4 + 12 : 4 = 10 + 3 = 13,
значит 52 : 4 = 13.
Примеры:
1) 96 : 8 = (80 + 16) : 8 = 80 : 8 + 16 : 8 = 10 + 2 = 12;
2) 51 : 3 = (30 + 21) : 3 = 30 : 3 + 21 : 3 = 10 + 7 = 17;
3) 84 : 7 = (70 + 14) : 7 = 70 : 7 + 14 : 7 = 10 + 2 = 12.
Как видно из примеров, при делении двузначного числа на однозначное используется:
- представление числа в виде суммы двух чисел или суммы разрядных слагаемых,
- правило деления суммы на число,
- знание таблицы умножения.

Деление на однозначное число( обобщение )
Урок математики во 2 классе. Тема : Деление на однозначное число( обобщение ).
Цели: учиться делить столбиком на однозначное число, развивать вычислительные навыки, умения решать задачи, воспитывать аккуратность, интерес к уроку. Оборудование: карточки на устный счет, алгоритм деления столбиком, кроссворд. Оформление доски: План урока с дозировкой времени : 1. Организационный момент 1 мин. 2. Устный счет 10 мин. 3. Работа над темой 22 мин. 4. Итог урока 7 мин. Урок содержит математические кроссворды,схемы и алгоритмы разбора решения задач, блиц-турнир, логические задания. На уроке дети работают в группах, парах, перерабатывают полученную информацию.
Просмотр содержимого документа
«Деление на однозначное число( обобщение ) »
Урок математики во 2 классе. Учебник Л.Г. Петерсон
Учебник Л.Г. Петерсон
Тема : Деление на однозначное число( обобщение ).
Учитель: Поздеева Наталья Юрьевна.
Цели: учиться делить столбиком на однозначное число,
развивать вычислительные навыки, умения решать задачи,
воспитывать аккуратность, интерес к уроку.
Оборудование: карточки на устный счет, алгоритм деления столбиком, кроссворд.
Оформление доски:
План урока с дозировкой времени :
Организационный момент 1 мин.
Устный счет 10 мин.
Работа над темой 22 мин.
Итог урока 7 мин.
Ход урока
Организационный момент
Целевая установка
Устный счет
Прочитай числа , разбив их на классы. Назови предшествующее и последующее число:
3 609 92 820 9 113 004
Подбери правильный ответ к примерам
82 : 2 960 : 8
720 : 90 87 : 3
540 : 3 540 : 90
42, 8, 180, 120, 29, 41
Выполни деление с остатком * Что знаем про остаток ?
38 : 18 = 2 ( ост. 2)
2)
59 : 18 = 3 ( ост. 5)
73: 15 = 4 (ост. 13)
Решить задачу (группами )
Артем поймал 48 рыбок , а Иван в 2 раза меньше. Сколько всего рыбок они поймали?
? 48 +(48 : 2)= 72(р.)
Объяснение решения от вопроса к данным
5) Что скажете ? Решено неверно, т.к. первая цифра частного найдена неправильно,
остаток больше делителя 3, в частном 3 цифры)
4. Работа над темой урока.
№ 1 ( задание на доске )
Используя алгоритм объяснить решение ( работа в парах)
№ 2 ( решить примеры с объяснением, у доски) решение на доске
№ 3 (самостоятельная работа по вариантам) взаимпроверка
1 вариант 2 вариант
решение на доске
№ 4 «Блиц — турнир»
стр. 61 № 60 ( решает 1 ученик, задачи читает учитель )
61 № 60 ( решает 1 ученик, задачи читает учитель )
а- 4
в + (в + с)
п — (х + к) (d + к ): 3
№ 5. Задачу решаем в группах по 4 человека, затем записываем решение
В первый день из библиотеки взяли 1384 книги,во второй в 2 2 раза меньше. Сколько книг осталось если всего было 5080 учебников ?
Решаем от вопроса к данным
— читает задачу
— говорит, что известно
– объясняет
— читает решение
Ответ: 3004 книг
Взяли за 2
Итог
Отгадывание кроссворда
По горизонтали : 2) Знак математического действия.
4) Запись из одной или нескольких цифр.
Часть прямой, соединяющая две точки.
Геометрическая фигура, не имеющая размеров. 8) Математическое действие. 9) Однозначное число.

По вертикали :1)Часть прямой. 2) Запись алгоритма действий, понятная исполнителю. 3) Математическое действие. 4) Число разрядов в классе. 7) Упражнения выполняемые с помощью рассуждений и вычислений.
Д/з. Стр. 61 №60,62.
Понятие о письменном приёме деления на однозначное число
Привет, ребята!
Сегодня я хочу рассказать вам о письменном
приёме деления на однозначное число. Вы уже встречались с подобной
записью деления, когда знакомились с темой «Деление с остатком». Но сегодня мы
с вами поговорим об этом подробнее и выполним несколько упражнений на
закрепление деления столбиком. Итак, приступим.
Давайте вспомним, как можно устно
делить двузначное число на однозначное. Вот, к примеру, девяносто шесть
разделить на три. Представим число девяносто шесть в виде суммы разрядных
Представим число девяносто шесть в виде суммы разрядных
слагаемых – девяносто и шесть. Теперь каждое из них делим на делитель –
три. Получается тридцать и два. Складываем эти частные. Ответ: тридцать два. Точно
так же можно разделить и трёхзначное число. Разделим на три число триста
девяносто шесть. Раскладываем число триста девяносто шесть на сумму разрядных
слагаемых – триста, девяносто и шесть. Делим каждое из них на три. Получается
сто, тридцать и два. Складываем эти частные. Ответ: сто тридцать два.
Да-а, длинная запись получилась. А вот как это
вычисление можно выполнить столбиком.
Пишем делимое – триста девяносто шесть. Отступив
одну клеточку вправо пишем делитель – три. Отделяем делимое от делителя
вертикальной чертой и под делителем проводим горизонтальную черту. Получилась
лежащая на боку буква Т. Под горизонтальной чертой будет место для ответа – частного.
Деление столбиком, в отличие от остальных арифметических действий,
мы начинаем не с единиц, а с наибольшего разряда делимого.
В нашем числе это сотни. Три сотни делим на три. Предположим, что получится
один. Единицу запишем под горизонтальной чертой. Ну а вдруг я ошибся, и
получится не один, а какое-то другое число? Проверить это можно умножением.
Умножаю один на три. Получается три. Всё верно. Результат умножения записываю
под сотнями делимого. А теперь подчёркиваю и вычитаю из верхней тройки нижнюю.
Получается нуль.
Но не спешите его записывать. Пока деление
не закончим, нули писать не надо. Сотни разделили, теперь будем делить десятки.
Для этого перенесём десятки из делимого под черту, но не левее и не правее, а
строго под цифрой десятков в делимом. Девять десятков делим на три. Я думаю,
что получится два. Записываю двойку в частное, и обязательно проверю. А вдруг
что-то напутал? Умножаю двойку из частного на делитель – три. Это шесть.
Подписываю под вот этой девяткой. Черта. Вычитаю из девяти девять. Получается три.
Да. Вот и ошибка! При вычитании получился остаток, равный делителю. А ведь вы
А ведь вы
умеете выполнять деление с остатком и знаете, что остаток обязательно
должен быть меньше делителя – не больше, не равен, а именно меньше.
Ну и ну! Какую глупую ошибку я допустил! Ведь при
делении девяти на три должно получится число три. Как хорошо, что деление я
проверил умножением! Три из частного умножаю на делитель три, получается
девять. Вычитаю. Теперь в остатке нуль, который я опять не записываю – ведь мы
ещё не делили единицы.
Переходим к делению единиц. Для этого
цифру, обозначающую количество единиц, переношу под новую черту, строго под
единицами делимого. Делю шесть на три. Это два. Но всё-таки проверю. Умножаю
двойку на делитель – три. Получилось шесть. Шестёрку записываю под вот этой
шестёркой. Из шести вычитаю шесть, получится нуль. Так как закончили деление
числа триста девяносто шесть, его нужно написать под чертой. Ответ: сто
тридцать два.
Вы, пока слушали меня, наверное, подсмеивались.
Вот ведь какой растяпа, даже три на три делит неуверенно. А когда делил девять
на три вообще допустил ошибку. Да потом ещё и проверяет деление умножением. Всё
в чём-то сомневается. Но ведь никто из нас не застрахован от ошибки. Бывает, на
секунду отвлёкся и допустил ошибку. Что уж говорить о гораздо более трудных
вычислениях. Вот поэтому при записи деления столбиком надо не только делить, но
и умножать. О таких трудных случаях я расскажу вам в следующий раз. А пока
давайте составим алгоритм письменного приёма деления.
Пишем делимое, и справа от него – делитель. Между ними – знак деления,
похожий на лежащую на боку букву Т.
Делим сотни. Частное записываем под делителем…
Умножаем полученное частное на делитель. Произведение записываем под
сотнями.
Вычитаем из сотен полученное произведение.
Переносим под черту десятки.
Делим десятки. Результат записываем в частное.
Результат записываем в частное.
Умножаем полученное число на делитель. Произведение записываем под
десятками.
Вычитаем из десятков полученное произведение.
Переносим под черту единицы.
Делим единицы. Результат записываем в частное.
Умножаем полученное число на делитель… Произведение записываем под
единицами.
Вычитаем из единиц полученное произведение.
Пишем нуль.
Читаем ответ.
Уффф, какой длинный алгоритм получился. Но
обратите внимание, ребята, что одни и те же действия повторяются при делении
каждого разряда: делим, умножаем, вычитаем.
А теперь я предлагаю вам решить несколько
примеров на деление столбиком. Не забудьте воспользоваться нашим алгоритмом.
Первый пример давайте решать вместе.
Записали число четыреста двадцать восемь и справа
от него два. Вертикальная и горизонтальная черта. Делим сотни. Четыре разделить
Вертикальная и горизонтальная черта. Делим сотни. Четыре разделить
на два – два. Записали под делителем. Умножаем два на два. Это четыре. Записали
под сотнями делимого. Подчёркиваем и вычитаем. Получился нуль, который мы не
пишем. Из делимого вниз переносим десятки. Делим их. Один записываем в частное.
Умножаем один на делитель. Полученное число два записываем под десятками.
Подчёркиваем и вычитаем. Снова нуль. Его не пишем. Из делимого переносим
единицы. Делим их. В частное записываем четыре. Умножаем четыре на два. Это
восемь. Записываем под восьмёркой. Вычитаем. Этот нуль мы пишем, ведь деление
закончено. Ответ: двести четырнадцать.
У нас есть ещё два примера. Решите их
самостоятельно, а потом мы вместе проверим ответы. Будьте внимательны –
пользуйтесь алгоритмом.
А теперь проверьте. Вы так решали?
Если так, то заслужили отличную отметку!
Ну что же, пришла пора нам сегодня прощаться. Но
Но
мы скоро снова встретимся. Ведь я хочу вам рассказать и о более сложных случаях
деления. Так что до встречи, друзья!
Узнайте, как выполнять однозначное деление
Сегодня мы собираемся взглянуть на то, как выполнять однозначное деление.
Первое, что нам нужно запомнить, это словарь компонентов деления:
- Дивиденд — это число, которое будет разделено.
- Делитель — это число, на которое делимое делится на .
- Частное — результат деления,
- Остаток — это оставшееся количество.
Однозначное деление
Упражнение 1:
Разделить 1728 на 6.
ШАГ 1: Поместите 1728 в позицию делимого, а 6 вместо делителя.
ШАГ 2: Возьмите первую цифру делимого, в данном случае 1. Поскольку 1 меньше делителя 6, мы не можем его разделить.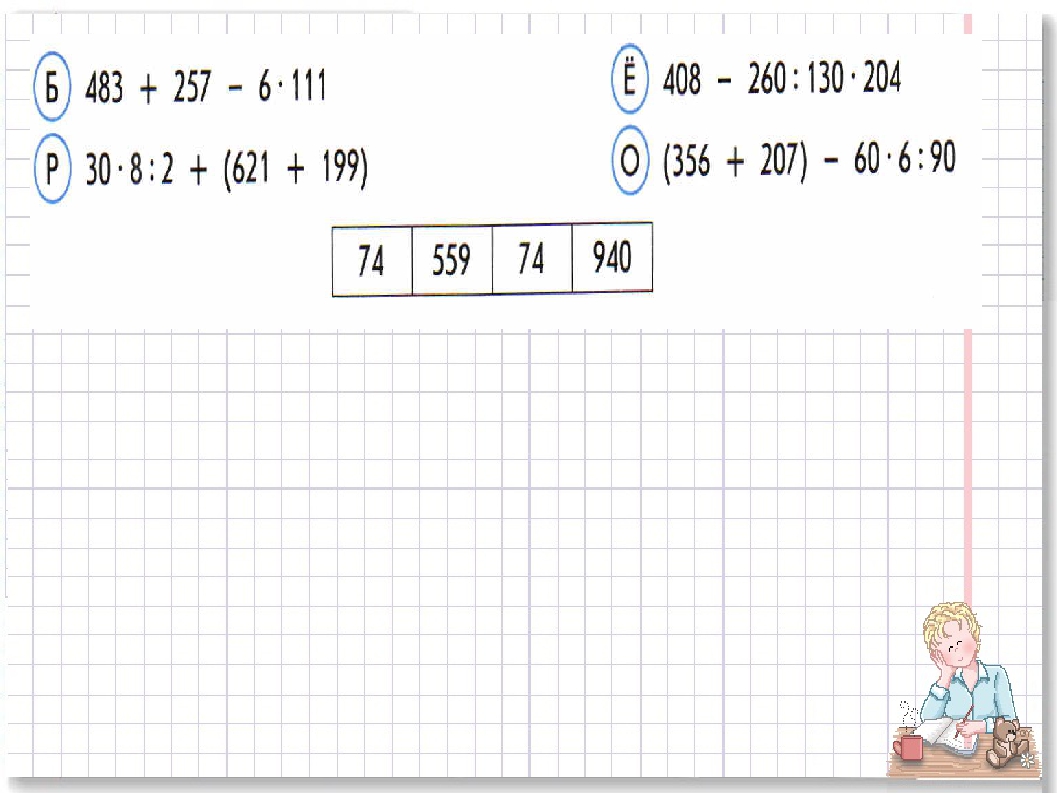 Следовательно, мы должны взять следующую цифру делимого — 7.
Следовательно, мы должны взять следующую цифру делимого — 7.
ШАГ 3: Мы ищем число, которое при умножении на 6 дает 17. 2 × 6 = 12, что меньше 17, но 3 × 6 = 18, что больше 17. Мы необходимо взять самое близкое число без перехода, которое в данном случае равно 2.
ШАГ 4: Поместите ответ 6 x 2 под делимым и вычтите его из первых двух цифр.
ШАГ 5: Следующим шагом является уменьшение следующей цифры делимого, то есть 2.Таким образом, у нас осталось 52. Мы ищем число, которое при умножении на 6 дает 52. 6 x 8 = 48, но 6 x 9 = 54. Поскольку мы не можем пойти больше 52 берем число 8 и делаем то же, что и в шаге 4: 52 — 48 = 4.
ШАГ 6: Мы повторяем шаг 5 со следующей цифрой делимого, которая равна 8. Теперь нам нужно найти число, которое при умножении на 6 дает 48. Мы уже знаем это! Это 8. 48 — 48 = 0. Поскольку у нас не осталось ни одной цифры дивиденда, которую можно было бы выпустить, мы закончили. Частное от этого однозначного деления составляет 288, а остаток равен 0.
Частное от этого однозначного деления составляет 288, а остаток равен 0.
Теперь вы увидели пример того, как делать однозначное деление! Чтобы узнать больше, попробуйте похожие упражнения:
Еще упражнения с 1-значным делением
Практика 2- и 3-значного деления
Что вы думаете об этом сообщении? Мы помогли вам с разделением? Если да, поделитесь им с друзьями, чтобы они тоже могли оставить отзыв! И не забывайте, что на Smartick вы сможете научиться делать деление и многое другое по элементарной математике!
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Рабочие листы с длинным делением для классов 4-6
Вы здесь: На главную → Рабочие листы → Полное деление
Создавайте неограниченное количество листов для деления в столбик (классы 4-6), в том числе с 2-значными и 3-значными делителями. Рабочие листы могут быть выполнены в формате html или PDF — и то, и другое легко распечатать.Вы также можете настроить их, используя генератор ниже.
Рабочие листы могут быть выполнены в формате html или PDF — и то, и другое легко распечатать.Вы также можете настроить их, используя генератор ниже.
Рабочие листы на этой странице разделены на три основных раздела:
Обратите внимание: рабочие листы для
деление в столбик с остатками находится на отдельной странице. Все задачи в таблицах на этой странице делятся на точные части (без остатка).
Основные инструкции для рабочих листов
Каждый рабочий лист генерируется случайным образом и поэтому уникален. Ключ ответа создается автоматически и помещается на вторую страницу файла.
Вы можете создавать рабочие листы либо в формате html, либо в формате PDF — и то, и другое легко распечатать. Чтобы получить рабочий лист PDF, просто нажмите кнопку с названием « Создать PDF » или « Создать рабочий лист PDF ». Чтобы получить рабочий лист в формате html, нажмите кнопку « Просмотреть в браузере » или « Создать рабочий лист html ». Это имеет то преимущество, что вы можете сохранить рабочий лист прямо из браузера (выберите «Файл» → «Сохранить»), а затем отредактировать его в Word или другом текстовом редакторе.
Это имеет то преимущество, что вы можете сохранить рабочий лист прямо из браузера (выберите «Файл» → «Сохранить»), а затем отредактировать его в Word или другом текстовом редакторе.
Иногда сгенерированный рабочий лист не совсем то, что вам нужно. Просто попробуйте еще раз! Чтобы получить другой рабочий лист с теми же параметрами:
- Формат PDF: вернитесь на эту страницу и снова нажмите кнопку.
- Формат Html: просто обновите страницу рабочего листа в окне браузера.
Длинное деление с однозначным делителем
Проблемы с делением — настройте длинное деление самостоятельно
На этих листах ученик должен сам настроить длинное деление (задача деления написана горизонтально вверху рабочего поля).
Длинное деление с двузначным делителем
Трехзначные делители
Следующие таблицы предназначены для трехзначных делителей. Деления точные. Если вы ищете разделение с остатками, вы можете создавать рабочие листы, используя генератор ниже, или перейти на эту страницу, чтобы найти готовые рабочие листы.
Генератор листов деления
Используйте генератор для создания настраиваемых рабочих листов, включая горизонтально написанные задачи, деление столбиком и деление с остатками.
Генератор таблиц деления
Что такое длинное деление? [Определение, факты и пример]
Игры с длинным разделением
Разделить на 2-значные числа
Разделить 4-значные числа на 2-значные числа, при этом от деления не остается остатка. Вы начнете с оценки частных.
охватывает общий базовый учебный план 5.NBT.6Play NowРазделите на 2-значные числа с остатком
Разделите 4-значные числа на 2-значные числа.Начните с оценки частных, которые пригодятся при делении на 2-значные числа.
охватывает Common Core Curriculum 5.NBT.6Играть сейчасСмотреть все игры с разделением >>
Учитесь с помощью полной программы обучения математике K-5
Что такое деление в столбик?
В математике деление в столбик — это метод, используемый для деления больших чисел на группы или части.
Деление в столбик помогает разбить проблему деления на последовательность более простых шагов. Как и во всех задачах деления, большое число, которое является делимым, делится на другое число, которое называется делителем, чтобы получить результат, называемый частным, а иногда и остатком.
Как вы делаете деление в столбик?
Метод деления в столбик включает в себя основные математические операции.
Для деления двух чисел этим методом рисуется таблица. Делитель пишется за пределами правых скобок, а делимое — внутри. Частное пишется над чертой сверху над дивидендом.
Деление в столбик состоит из 5 шагов:
| D | Разделить |
| M | Умножить |
| S | Вычесть |
| В | Обрушить |
| R | Повтор или остаток |
Вот пример деления в столбик с четким отображением каждого шага.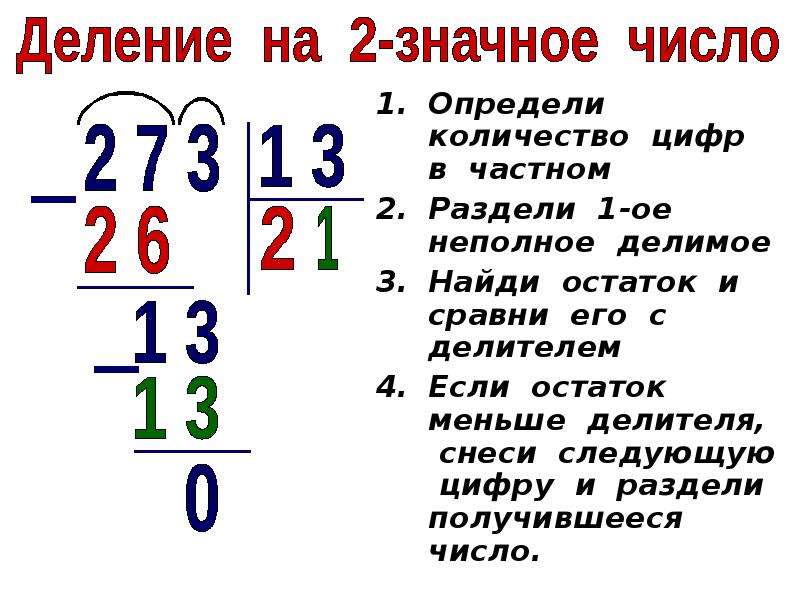
Процесс начинается с деления или определения, сколько раз крайняя левая цифра делимого может делиться на делитель.
Затем результат или ответ из шага 1, который становится первой цифрой частного, умножается на делитель и записывается под первой цифрой делимого.
Вычитание производится по первой цифре делимого и записывается остаток.
Следующая цифра делимого уменьшается, а затем процесс повторяется до тех пор, пока все цифры делимого не будут сброшены и не будет найден остаток.
Как разделить десятичные дроби методом длинного деления?
Деление в столбик можно также использовать для разделения десятичных чисел на равные группы. Он выполняет те же шаги, что и при делении в столбик, а именно: деление, умножение, вычитание, уменьшение и повторение или нахождение остатка.
Вот пример деления в столбик с десятичными знаками.
Интересные факты
|
Давайте споем!
Если нужно разделить большие числа,
нарисуйте таблицу для длинного деления сбоку.
Напишите шаги, которые будут вашим руководством,
D, M, S, B и R — Придерживайтесь долгого разделения!
Давайте сделаем это!
Вместо того, чтобы показывать видео для обучения полному делению или раздавать практические задания ученикам 4-го класса, приведите примеры из реальной жизни, когда они могут использовать метод длинного деления для деления.
Скажем, при приготовлении кексов и печенья для распродажи выпечки в школе вы можете попросить ребенка подсчитать количество партий, в которых можно приготовить печенье или кексы (исходя из количества форм на подносе), если общее количество печенья и кексы требуются. Вы также можете попросить их подсчитать общее количество необходимых картонных коробок, если в каждую картонную коробку для печенья помещается 15 печенья, а в картонную коробку для кексов — 6 кексов. Попросите их вычислить, используя метод длинного деления.
Попросите их вычислить, используя метод длинного деления.
Сопутствующий математический словарь
Однозначный рабочий лист деления
Расширенный поиск
Содержание:
Язык:
AfarAbkhazAvestanAfrikaansAkanAmharicAragoneseArabicAssameseAsturianuAvaricAymaraAzerbaijaniBashkirBelarusianBulgarianBihariBislamaBambaraBengali, BanglaTibetan стандарт, тибетский, CentralBretonBosnianCatalanChechenChamorroCorsicanCreeCzechOld церковнославянский, церковнославянский, Старый BulgarianChuvashWelshDanishGermanDivehi, Мальдивский, MaldivianDzongkhaEweGreek (современный) EnglishEsperantoSpanishEstonianBasquePersian (фарси) Фуле, фулах, пулар, PularFinnishFijianFaroeseFrenchWestern FrisianIrishScottish гэльский, GaelicGalicianGuaraníGujaratiManxHausaHebrew (современный) HindiHiri MotuCroatianHaitian, гаитянский CreoleHungarianArmenianHereroInterlinguaIndonesianInterlingueIgboNuosuInupiaqIdoIcelandicItalianInuktitutJapaneseJavaneseGeorgianKongoKikuyu, GikuyuKwanyama, KuanyamaKazakhKalaallisut , Гренландский, кхмерский, каннада, корейский, канури, кашмирский, курдский, коми, корнийский, киргизский, латинский, люксембургский, летцебургский, ганда, лимбургский, лимбургский, лимбургский, лингала, литовский, люба-катанга, латышский, малагасийский, маршалльский, маори, македонский, mMongolianMarathi (маратхи) MalayMalteseBurmeseNauruanNorwegian BokmålNorthern NdebeleNepaliNdongaDutchNorwegian NynorskNorwegianSouthern NdebeleNavajo, NavahoChichewa, Chewa, NyanjaOccitanOjibwe, OjibwaOromoOriyaOssetian, OsseticEastern пенджаби, Восточная PanjabiPāliPolishPashto, PushtoPortugueseQuechuaRomanshKirundiRomanianRussianKinyarwandaSanskrit (санскрит) SardinianSindhiNorthern SamiSangoSinhalese, SinhalaSlovakSloveneSamoanShonaSomaliAlbanianSerbianSwatiSouthern SothoSundaneseSwedishSwahiliTamilTeluguTajikThaiTigrinyaTurkmenTagalogTswanaTonga (Остров Тонга) TurkishTsongaTatarTwiTahitianUyghurUkrainianUrduUzbekValencianVendaVietnameseVolapükWalloonWolofXhosaYiddishYorubaZhuang, ChuangChineseZulu
Предмет:
Оценка / уровень:
Возраст:
3456789101112131415161718+
Поиск:
Все рабочие листы Только мои подписанные пользователи Только мои любимые рабочие листы Только мои собственные рабочие листы
Как разделить на двузначные числа
Решение
Чтобы разделить на двузначное число, мы используем следующие шаги.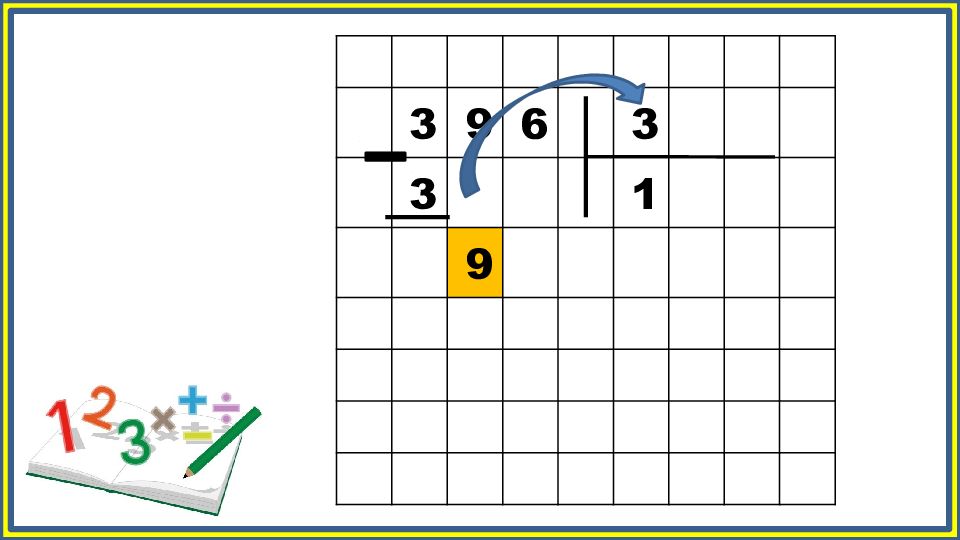
- Задайте задачу длинного деления.
- Составьте таблицу умножения делителя, умноженного на каждое целое число от 1 до 9.
- Выполните деление в столбик (разделите, умножьте, вычтите, уменьшите, повторите), начиная с деления делителя на первые две цифры делимого. Ваша таблица умножения поможет вам в этом.
- В качестве ответа укажите ваше частное и остаток.
Приложение
Теперь, когда мы знаем шаги, связанные с делением на двузначное число, давайте применим эти шаги на практике с приложением.Предположим, вы в классе 46 учеников. У вашей учительницы есть большой мешок конфет, который она планирует раздавать в течение учебного года, в котором содержится 1023 конфет. Она говорит классу, что если кто-то сможет выяснить, сколько конфет получит каждый ученик в течение года, если она разделит конфету поровну между 46 учениками и сколько конфет останется, то этот человек получит оставшуюся конфету. сегодня (а также их справедливую долю в течение года).
Хмм… итак, мы хотим знать, сколько конфет получит каждый из 46 учеников, если 1023 конфет поделить между ними поровну, и сколько осталось.Ах! Эта задача запрашивает частное и остаток, если мы разделим 1023 на 46. Отлично! Это прекрасная возможность попрактиковаться в делении на двузначное число!
Нашим первым шагом будет постановка задачи деления в длину с 46 в качестве делителя и 1023 в качестве дивиденда.
Следующий шаг — создать нашу таблицу умножения, отображающую 46 раз каждое из целых чисел от 1 до 9.
1 × 46 = 46
2 × 46 = 92
3 × 46 = 138
4 × 46 = 184
5 × 46 = 230
6 × 46 = 276
7 × 46 = 322
8 × 46 = 368
9 × 46 = 414
Пока все хорошо! Теперь мы можем перейти к третьему шагу и начать процесс деления в столбик.Мы начинаем с деления 46 на первые две цифры 1023. Это дает нам 0, так как 46 не помещается в 10. Мы записываем его поверх полосы длинного деления и умножаем 46 на 0, чтобы получить 0. Затем мы вычитаем и валить.
Это дает нам 0, так как 46 не помещается в 10. Мы записываем его поверх полосы длинного деления и умножаем 46 на 0, чтобы получить 0. Затем мы вычитаем и валить.
Мы на правильном пути. Теперь мы повторяем, поэтому мы делим 46 на 102. Глядя на нашу таблицу умножения, мы видим, что 46 умещается в 102 два раза. Мы пишем 2 над полосой длинного деления, затем умножаем 46 на 2, чтобы получить 92 (опять же, наша таблица умножения оказывается очень удобной).Теперь вычитаем и опускаем.
Еще раз повторяем, поэтому мы делим 46 на 103. Наша таблица умножения показывает нам, что 46 умещается в 103 два раза, поэтому мы записываем еще 2 поверх полосы деления в столбик, умножаем 46 на 2, чтобы получить 92 , и вычесть.
На этот раз после вычитания цифр, которые нужно вычитать, больше нет, так что оставшееся число 11 является нашим остатком. В целом, если мы разделим 1023 на 46, мы получим частное 22 и остаток 11. Это говорит нам, что если ваш учитель разделит 1023 конфеты поровну между 46 учениками вашего класса, каждый ученик получит 22 штуки. конфет, и останется 11 штук. Быстро! Иди, скажи своему учителю ответ и забери свой приз в виде 11 конфет! Ням!
В целом, если мы разделим 1023 на 46, мы получим частное 22 и остаток 11. Это говорит нам, что если ваш учитель разделит 1023 конфеты поровну между 46 учениками вашего класса, каждый ученик получит 22 штуки. конфет, и останется 11 штук. Быстро! Иди, скажи своему учителю ответ и забери свой приз в виде 11 конфет! Ням!
Хотя деление на двузначные числа посредством длинного деления может быть немного сложным процессом (они не зря называют это долгим), если мы просто сделаем это шаг за шагом, это не так уж и плохо.Просто продолжай практиковаться! К счастью, теперь у вас есть много конфет, которые можно есть!
Правила Дивизиона
Правила дивизиона
Задача состоит в том, чтобы разделить трехзначное число на однозначное.
Начните с решения, на какое число вы собираетесь делить. Это ваш делитель.
Ваша задача будет заключаться в том, чтобы придумать некоторые правила для этого делителя.
Теперь сгенерируйте трехзначное число. Это ваши дивиденды.
Здесь вы можете использовать счетчики для генерации цифр, вы можете использовать кости или просто использовать свое воображение!
Теперь разделите ваш дивиденд на делитель.Запишите ответ.
Создайте другие дивиденды и разделите их на тот же делитель. Запишите ответы.
Внимательно посмотрите ответы. Когда ответ — целое число? Когда останется 1?
Можете ли вы заметить какие-либо закономерности?
Можете придумать какие-нибудь правила?
Почему это действие?
Это упражнение дает контекст для практики деления трехзначного числа на однозначное число. Он побуждает детей замечать закономерности и догадки, а также проверять правила.Это может привести к установлению способов распознавания трехзначных чисел в таблицах умножения.
Возможный подход
Урок может начаться с повторения любых шаблонов, которые дети распознали в таблицах умножения, вплоть до x10 или x12. Они могут знать о числах в таблице из 5, которые всегда заканчиваются на 5 или 0, например. В этом упражнении эти правила распространяются на трехзначные числа.
В этом упражнении эти правила распространяются на трехзначные числа.
Перед тем, как приступить к выполнению задания, возможно, стоит напомнить детям о методах, которые они могут использовать для деления.
Как класс вы можете изучить делитель 2 и записать результаты, как показано ниже:
| Расчет | Целый ответ | Остаток от 1 |
| 269 Ã · 2 = 134 r1 | 269 | |
| 547 Ã · 2 = 273 r1 | 547 | |
| 466 · 2 = 233 | 466 | |
| 728 Ã · 2 = 364 | 728 | |
Поощряйте класс внимательно изучать числа, приводящие к различным типам ответов, искать сходства и использовать эту информацию для создания правила для типов чисел, которые появляются в каждом столбце.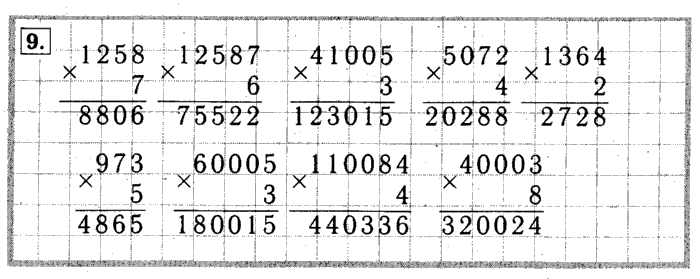 Сделайте предположение, а затем проверьте его!
Сделайте предположение, а затем проверьте его!
Помните, что ответы целыми числами означают, что дивиденд является кратным делителю.
Тогда все классы могут исследовать один и тот же делитель, или разные группы могут смотреть на разные делители (возможность дифференцировать деятельность).
Некоторые дети могут перейти к дополнительному заданию (см. Ниже).
Ключевые вопросы
Что общего с числами с целым числом?
Вы можете придумать правило?
Как вы думаете, вы могли бы найти кратные… без необходимости выполнять расчет деления?
Возможные расширения
Другой способ решения проблемы — сохранять постоянный дивиденд и изменять делители. Итак, вы можете исследовать, что происходит, когда вы делите 123 (например) на 2, затем на 3, затем на 4 и так далее. Сможете ли вы найти какие-нибудь трехзначные простые числа? Есть ли способ быстро определить эти числа?
Возможная опора
Сетка умножения и калькулятор были бы полезны (последнее, только если упор не на отработку письменного метода).
Распечатанные рабочие листы и упражнения с делением на длинное и хвостовое деление для учащихся 4 и 5 классов по математике
Выберите одну из следующих категорий рабочего листа «хвостовое деление». Наша основная математика
Рабочие листы по математике с долгим делением можно бесплатно распечатать.
Длинное деление, как и дроби, — это математическая тема, которая действительно может отпугнуть молодых изучающих математику. Вы либо поймете это, либо нет, и если вы этого не сделаете, каждое упражнение на деление в длину станет проблемой.У нас есть подборка рабочих листов для деления в столбик с , готовых для заполнения полей и нескольких уровней сложности, так что студенты могут постепенно овладеть «наукой страшного деления в столбик».
Наша первая часть рабочего листа деления хвоста основана на делении 2 цифр на 1 цифру. Эти упражнения относительно просты, так как их можно выполнять без использования структуры деления хвоста.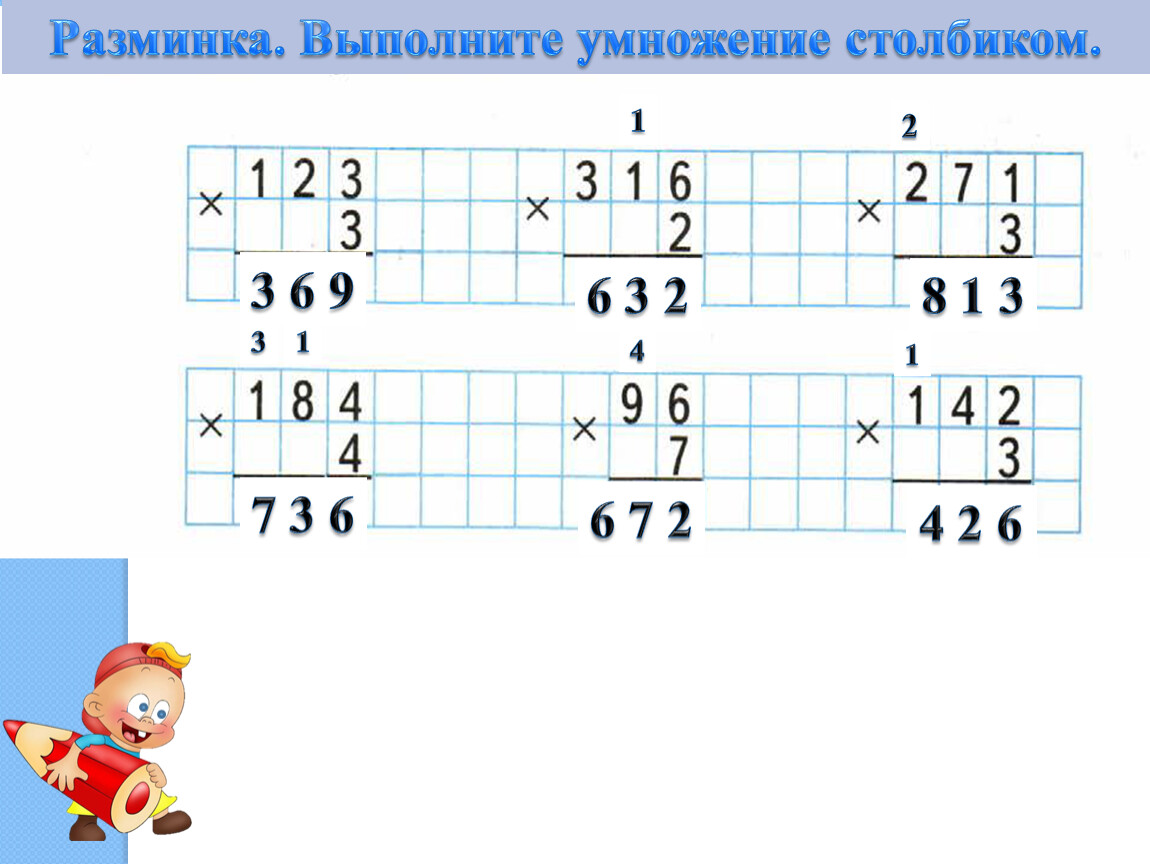 Эти рабочие листы для 4-го класса созданы для обучения концепции и структуры упражнений на длинные деления и служат хорошей отправной точкой на пути к мастерству .Они бывают как с остатком, так и без него (лучше всего без него). По нашему скромному математическому мнению, жизненно важно, чтобы юные ученики математики не только выучили деление хвоста, но и научились проверять результат. Умножьте частное на делитель и сложите остаток.
Эти рабочие листы для 4-го класса созданы для обучения концепции и структуры упражнений на длинные деления и служат хорошей отправной точкой на пути к мастерству .Они бывают как с остатком, так и без него (лучше всего без него). По нашему скромному математическому мнению, жизненно важно, чтобы юные ученики математики не только выучили деление хвоста, но и научились проверять результат. Умножьте частное на делитель и сложите остаток.
Когда концепция ясна и полностью усвоена, студенты-математики могут решить следующие рабочие листы с длинным делением: 3 цифры, разделенные на 1 цифру, 3 цифры, разделенные на 2, 4 (или 5 или 6) цифр, на 2 и т. Д. Мы считаем, что деление в столбик не должно быть проблемой для студентов-математиков, и если это так, всю концепцию деления необходимо переучить (и выучить).Деление (и умножение), возможно, являются наиболее важными компонентами набора навыков , необходимого для математики, алгебры и статистики среднего уровня.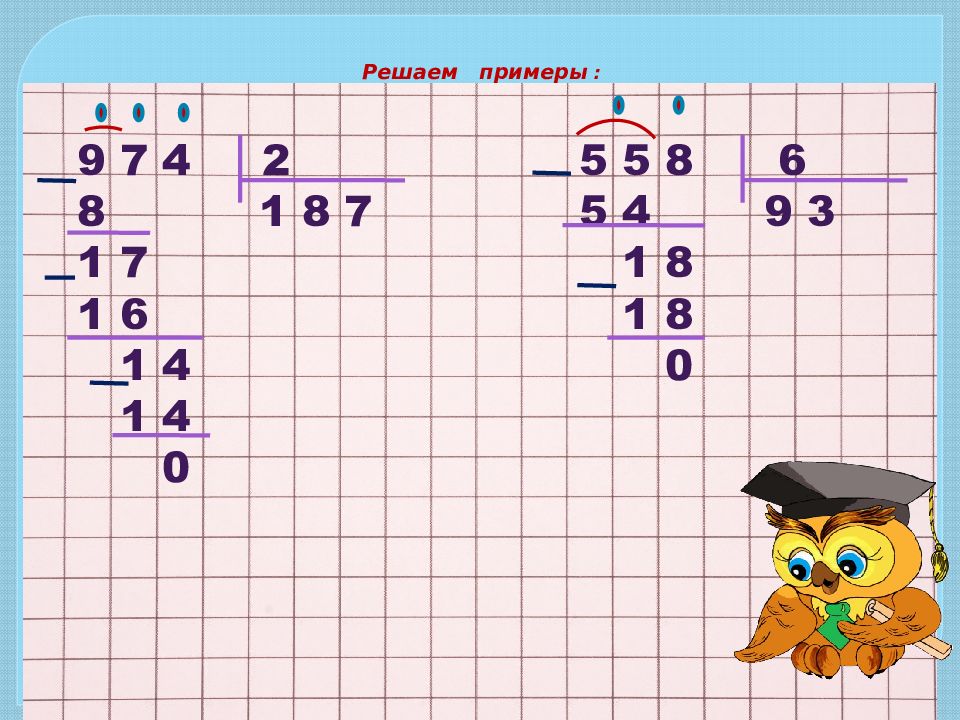 Итак, пришло время освоить концепцию деления в столбик по 5-му классу.
Итак, пришло время освоить концепцию деления в столбик по 5-му классу.
Некоторые из наших материалов по разделению в столбик построены таким образом, что ученик, изучающий математику, должен найти делитель или дивиденд с учетом частного результата. У нас также есть раздел упражнений на разделение хвоста, которые необходимо выполнить, поля необходимо заполнить. Этот «обратный» способ решения проблем можно использовать для оценки владения концепцией разделения хвоста.
Наши рабочие листы с длинными делениями основаны на следующих математических темах Сингапурского учебного плана:
- Умение делить числа на маленькие и большие
- Понять концепцию длинного деления
- Умение находить дивиденд и делитель проблем с учетом частного
- Возможность проверки результатов работы хвостовых отделов
- Возможность решать проблемы в разумные сроки
Наши новые материалы? Подписывайтесь на нас.