Урок 58. деление на трёхзначное число — Математика — 4 класс
Математика, 4 класс
Урок № 58. Деление на трёхзначное число.
Перечень вопросов, рассматриваемых в теме:
— Как делить многозначное число на двузначное?
— Как правильно выполнять запись деления?
— Как подобрать пробную цифру частного?
Глоссарий по теме:
Частное – результат деления одного числа на другое.
Неполное частное – результат деления с остатком, который показывает, какое максимальное число раз делитель содержится в делимом.
Основная и дополнительная литература по теме урока:
1. Петерсон Л.Г. Математика. 4 класс. 1 ч. – М.: 2013. – стр. 40-43.
2. Математика. Учебник для 4 кл. нач. шк. В 2 ч./М.И. Моро, М.А. Бантова – М.: Просвещение, 2017.
3. Математика. Проверочные работы. 4 класс. Учебное пособие для общеобразовательных организаций/ С.И.Волкова — М.: Просвещение, 2017. – стр. 78-79.
– стр. 78-79.
4. Математика. Тетрадь учебных достижений. 4 класс. Учебное пособие для общеобразовательных организаций/ С.И.Волкова — М.: Просвещение, 2017. – стр. 79-80.
Теоретический материал для самостоятельного изучения
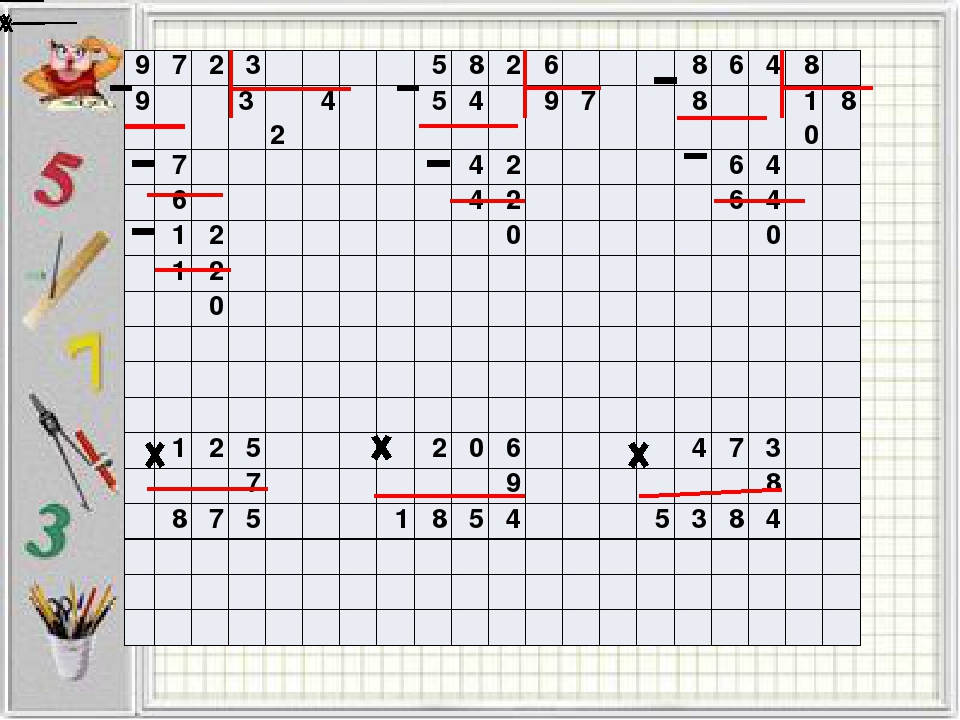
Рассмотрим деление на трёхзначное число. Деление на трёхзначное число выполняется по тем же правилам, что и деление на двузначное число.
936:234.
Первое неполное делимое — это само число 936. Поэтому в частном будет только одна цифра.
Алгоритм деления: 1.Образую неполное делимое. 2.Определю количество цифр в частном. 3.Делю неполное делимое на делитель. 4.Умножаю делитель на пробную цифру. 5. Нахожу остаток от деления вычитанием. 6. Сравниваю остаток с делителем. |
Чтобы легче было найти цифру частного, будем делить 936 не на 234, а на 200. Для этого нужно 9 разделить на 2, получим 4. Это пробная цифра. Нужно проверить, подходит ли она. Проверку делаем устно.
Проверку делаем устно.
234 · 4 = 200 · 4 + 30 · 4 + 4 · 4 = 936
Полученное число равно делимому, значит, пробная цифра 4 подходит. Записываем ее в частном. Закончим запись деления столбиком. Умножаем 234 на 4, будет 936. Находим остаток от деления. Он равен нулю. Остаток меньше делителя. Деление закончено.
Найдём значение частного 219296 : 352
Выделим первое неполное делимое 2192 сотни.
Так как деление начинаем с сотен, в частном получим 3 цифры. Определяем первую цифру частного: 21:3=7, получили пробную цифру 7.
В запасе сотен нет, а требуется ещё 3 сотни, так как 5 дес. · 7 = 35 десятков. Значит, частное должно быть меньше 7.
Проверим 6.
3 сот. ·6 = 18 сот.
5 дес. ·6 = 30 дес. = 3 сот.
2 · 6 = 12
1800 + 300 + 12 = 2112
2112 < 2192, значит, цифра 6 подходит. Записываем ее в частном.
Умножаем 352 на 6, будет 2112. Вычитаем 2112 из 2192, будет 80. Остаток 80 меньше делителя 352.
Второе неполное делимое 809 десятков. Определяем цифру частного.
Определяем цифру частного.
8 : 3 = 2, получили пробную цифру 2.
Проверяем:
352 · 2 = 704
704 < 809, значит, цифра 2 подходит. Записываем ее в частном.
Умножаем 352 на 2, будет 704. Вычитаем 704 из 809, будет 105. Остаток 105 меньше делителя 352.
Третье неполное делимое 1056 единиц. Определяем цифру частного.
Делим 10 на 3, получаем пробную цифру 3. Проверяем, 352 умножаем на 3. Складываем 900, 150 и 6, получаем 1056. Это число равно третьему неполному делимому. Значит, цифра 3 подходит, записываем ее в частном. Умножаем 352 на 3, будет 1056. Вычитаем 1056 из 1056. Остаток равен нулю. Деление окончено.
Задания тренировочного модуля:
1. Определите значение выражения, используя запись деления столбиком.
92400:462+1386:462
Варианты ответа: 23; 203; 263
Правильный вариант: 203
2. Расшифруйте слово, с которого начинается четверостишие из поэмы М.Ю. Лермонтова.
(40 ∙ 40 ∙ 40 : 2 + 486850 : 650) ∙ 18
О | Е | М | А | Т |
З | Р | И | К | Н |
Ц | Ы |
_____ воет, дик и злобен,
Меж утёсами громад.
Буре плач его подобен,
Слёзы брызгами летят.
Правильный вариант: Терек
4. Выберите пропущенные числа в записи деления столбиком.
Варианты ответа: 0; 4; 7; 114; 141; 1141
Правильный вариант: 1141; 7; 0
Деление многозначных чисел на однозначные с нулями в частном
Привет,
друзья!
Я
рада снова видеть вас. Вы знаете, мне приходит много писем от ребят. Но вот
письмо одного мальчика, Вити Считалкина, меня очень расстроило. Он пишет, что
получил двойку за самостоятельную работу по математике. И не понимает за что.
Ведь Витя назубок знает таблицу умножения и деления, и уверен, что всё решил
правильно. В доказательство Витя прислал листок с теми заданиями, которые ему
не засчитали. Вот его работа:
Ну
что же, ребята, надо помочь Вите Считалкину разобраться, в чём причина такой
плохой отметки.
Давайте
разберём первый пример. Вы не забыли? При делении многозначных чисел обязательно
начинаем с того, что определяем количество цифр в частном. А для
этого выделяем первое неполное делимое. Наибольший разряд выражен цифрой
один. Один меньше делителя, поэтому не может быть неполным делимым. Возьмём не
одну, а две первых цифры. Шестнадцать сотен и будет первым неполным делимым.
Ставим точку в частном. После шестнадцати в делимом стоят ещё две цифры, значит
и в частном тоже надо добавить две точки. То есть, частное должно быть
трёхзначным числом. Начинаем деление. Шестнадцать делим на шесть – это два.
Дважды шесть – двенадцать, остаток.… четыре. Он меньше делителя. Переносим вниз
к остатку следующую цифру – два. Второе неполное делимое – сорок два
десятка. Делим сорок два на шесть, получается семь. Умножаем – сорок два.
Вычитаем. Остаток нуль. Действие закончено. Но… Посмотрите, ещё ничего не
закончено! Ведь в частном стоит ещё одна точка. Значит, ответ должен быть
Значит, ответ должен быть
трёхзначным! А-а, понятно! Деление не закончено, потому что в делимом есть ещё
одна цифра, которая не принимала участия в делении. Это нуль. И
он будет третьим неполным делимым. Нуль из остатка убираем, так
как его в остатке мы пишем только тогда, когда заканчиваем деление. А вот нуль
из делимого переносим вниз. Делим его на шесть, получается нуль. Не забываем
его записать в частном. Умножаем нуль на шесть. Нуль. Вычитаем. Нуль. Вот
теперь мы его записали в остатке, потому что деление закончилось. И ответ этого
примера не двадцать семь, а двести семьдесят.
Ребята,
видите, какую ошибку допустил Витя Считалкин и могла допустить я? Мы забыли,
что нуль, который стоит в конце числа, тоже надо делить. И
полученный при этом нуль записывать в частное. Наверное, Витя перед тем как
начать деление, не определил количество цифр в частном, и поэтому не смог
вовремя заметить ошибку.
Ну
что же, с первым примером мы разобрались. Переходим к следующему.
Не
забываю определить количество цифр в частном. Первое
неполное делимое будет четыре? Нет, число маловато. Ведь оно меньше
делителя восемь. Значит, первое неполное делимое – сорок. Оно даёт одну
цифру в частном. И в делимом после сорока стоят ещё две цифры, поэтому и в
частное добавляю ещё две точки. Частное будет трёхзначным числом.
Начинаю
деление. Сорок разделить на восемь – пять. Пятью восемь – сорок. Вычитаю.
Остаток нуль. Но ведь деление ещё не закончено, поэтому этот нуль я не пишу.
Спускаю вниз следующий разряд. Так-так. Семь меньше восьми. Что же делать? Ага,
вспомнила! Если делимое меньше делителя, в частном пишем нуль.
Умножаем его на восемь, получаем нуль. Вычитаем. Остаток семь. Он меньше
делителя. Переносим вниз следующий разряд и делим число семьдесят два. Это третье
неполное делимое. Разделили его на восемь, получили девять. Девятью восемь
Разделили его на восемь, получили девять. Девятью восемь
– семьдесят два. И остаток нуль. Деление окончено. Частное равно пятистам
девяти.
Вот
видите, ребята, как важно определять количество цифр в
частном! Если допустили ошибку, точки на месте частного сразу вам об
этом просигнализируют.
Ну
что же, а теперь я предлагаю вам самостоятельно решить два оставшихся примера,
которые неверно решил Витя Считалкин. И, конечно, я тоже их постараюсь решить. А
потом мы сверим полученные результаты. Не забудьте, определив первое неполное
делимое, подсчитать количество цифр в частном.
Ребята,
как вы справились с моим заданием? Проверьте своё решение!
У
вас так получилось? Я надеюсь, что Витя Считалкин тоже посмотрел наш урок, и
больше не будет пропускать нули в частном.
А
мы сегодня попрощаемся с вами. До встречи на следующем уроке! До свидания,
друзья!
Математика 4 класс «Деление многозначных чисел на однозначные»
Слайды и текст этой онлайн презентации
Слайд 1
1
Математика
4 класс
Слайд 2
2
Посетите наш зоопарк
Слайд 3
3
Московский
зоопарк
Слайд 4
ВЕТЕРИНАРИЯ
(от лат. veterinarius) — ухаживающий за скотом, лечащий скот.
veterinarius) — ухаживающий за скотом, лечащий скот.
Ветеринар
наука
профессия
4
Слайд 5
5
Ветеринар
Слайд 6
6
Ветеринар
медицина
биология
география
химия
физика
Слайд 7
7
Тема урока:
Деление многозначных чисел на однозначные.
Математика
4 класс
Слайд 8
8
Найди значение частного
4862 : 2
84 : 4 = (80 + 4) : 4 = 21
963 : 3 = (900 + 60 + 3) : 3 = 321
4862 : 2 = (4000 + 800 + 60 + 2) : 2 =
Слайд 9
9
Работай по плану:
а) выбираю первое неполное делимое;
б) намечаю количество цифр в частном;
в) делю первое неполное делимое, подбирая частное;
г) делаю проверку:
- умножаю частное на делитель,
- из делимого вычитаю полученное число,
- сравниваю остаток с делителем;
д) называю второе неполное делимое…
Слайд 10
10
Работай по плану:
а) выбираю первое неполное делимое;
б) намечаю количество цифр в частном;
в) делю первое неполное делимое,
подбирая частное;
г) делаю проверку:
- умножаю частное на делитель,
- из делимого вычитаю полученное число,
- сравниваю остаток с делителем;
д) называю второе неполное делимое.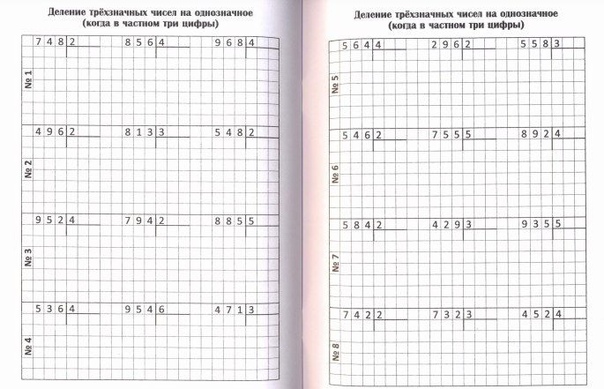 ..
..
Слайд 11
Слайд 12
12
Как выполнить деление в столбик любых многозначных чисел на однозначное число?
Вывод: Любые многозначные числа делят на однозначное число так же, как и двузначные и трёхзначные числа: по разрядам, начиная со старшего разряда. При этом сначала выбирают первое неполное делимое и намечают количество цифр в частном.
Слайд 13
13
Проверь себя:
6 : 4 = 1 (ост. 2) 12 : 9 = 1 (ост. 1)
4 : 3 = 1 (ост. 1) 52 : 7 = 7 (ост. 3)
8 : 5 = 1 (ост. 3)
Какие остатки могут получиться при делении чисел
на 2? на 3? на 4? на 5? на 6? на 7? на 8? на 9?
Выполни деление с остатком:
6 : 4 4 : 3 8 : 5 12 : 9 52 : 7
Слайд 14
14
1 вариант:
7832 : 2
9852 : 3
2 вариант:
9464 : 4
6765 : 5
Слайд 15
15
1 вариант
Слайд 16
16
2 вариант
Слайд 17
17
Реши уравнения:
(х — 3983) + 7 267 = 12000
х + (3983 + 7267) = 12000
х — 3983 = 12000 + 7267
Слайд 18
18
Реши уравнения:
(х — 3983) + 7 267 = 12000
х – 3983 = 12000-7267
х – 3983 = 4733
х = 4733 + 3983
х = 8716
х + (3983 + 7267) = 12000
х + 11250 = 12000
х = 12000 – 11250
х = 750
х — 3983 = 12000+ 7267
х – 3983 = 19267
х = 19267 + 3983
х = 23250
Слайд 19
В зоопарке есть индийский слон по кличке Раджа, африканская слониха, которую зовут Буба, и жираф по кличке Петька.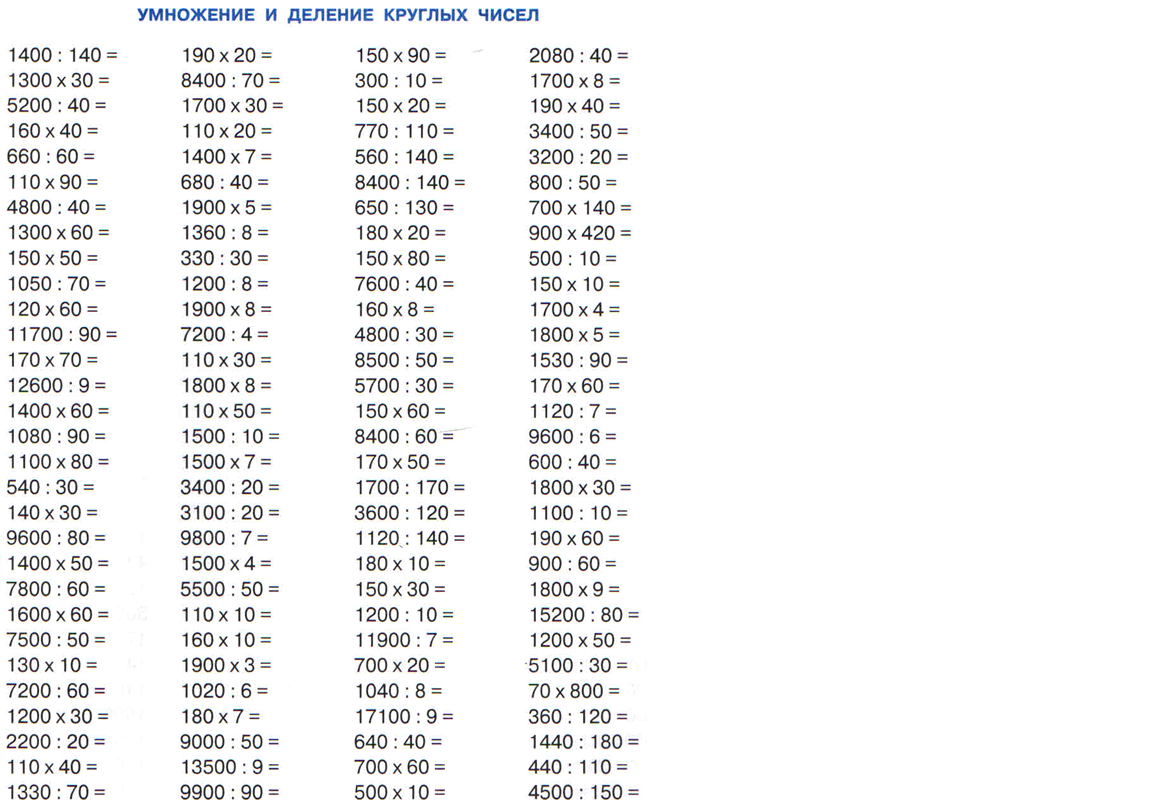 Масса Раджи равна 3 т 983 кг, масса Бубы — 7 т 267 кг, а масса Раджи, Бубы и Петьки вместе — 12 т. Чему равна масса жирафа Петьки?
Масса Раджи равна 3 т 983 кг, масса Бубы — 7 т 267 кг, а масса Раджи, Бубы и Петьки вместе — 12 т. Чему равна масса жирафа Петьки?
19
Реши задачу:
Раджа
Буба
Петя
Слайд 20
В зоопарке есть индийский слон по кличке Раджа, африканская слониха, которую зовут Буба, и жираф по кличке Петька. Масса Раджи равна 3 т 983 кг, масса Бубы — 7 т 267 кг, а масса Раджи, Бубы и Петьки вместе — 12 т. Чему равна масса жирафа Петьки?
1) 3 т 983 кг = 3983 кг
7 т 267 кг = 7267 кг
3983 + 7267 = 11250 (кг)- масса Раджи и Бубы.
2) 12 т = 12000 кг
12000 – 11250 = 750 ( кг) – масса Петьки.
Ответ: 750 кг.
20
Слайд 21
В энциклопедии сказано, что масса бурого медведя равна приблизительно 750 кг. Это в 10 раз меньше, чем приблизительная масса африканского слона, и на 480 кг больше, чем масса тигра. Чему приблизительно равна масса африканского слона и чему равна масса тигра?
21
Реши задачу:
Слайд 22
В энциклопедии сказано, что масса бурого медведя равна приблизительно 750 кг. Это в 10 раз меньше, чем приблизительная масса африканского слона, и на 480 кг больше, чем масса тигра. Чему приблизительно равна масса африканского слона и чему равна масса тигра?
Это в 10 раз меньше, чем приблизительная масса африканского слона, и на 480 кг больше, чем масса тигра. Чему приблизительно равна масса африканского слона и чему равна масса тигра?
Решение:
1) 750 · 10 = 7500 (кг) – масса слона
2) 750 — 480 = 270 (кг) – масса тигра
Ответ: 7500 кг, 270 кг.
22
Слайд 23
23
750 кг
7500 кг
270 кг
Слайд 24
24
Масса бурого медведя составляет 3/4 массы белого медведя, а масса белого медведя в 4 раза меньше массы бегемота. Чему равна масса бегемота?
Слайд 25
25
Масса бурого медведя составляет 3/4 массы белого медведя, а масса белого медведя в 4 раза меньше массы бегемота. Чему равна масса бегемота?
750 : 3 · 4 = 1000 (кг) масса белого медведя
2) 1000 · 4 = 4000 (кг) масса бегемота
Ответ: 4000 кг
Слайд 26
26
4000 кг
750 кг
1000 кг
Слайд 27
27
Домашнее задание
с.71 № 7
Слайд 28
28
Спасибо за работу!
Страница 32 — ГДЗ Математика 4 класс.
 Моро, Бантова. Учебник часть 2
Моро, Бантова. Учебник часть 2
Вернуться к содержанию учебника
Числа, которые больше 1000. Деление на числа, оканчивающиеся нулями
Вопрос
1) Объясни решение.
2) Объясни, как более кратко записаны те же вычисления.
Подсказка
Повтори алгоритм письменного деления на двузначные и трёхзначные числа.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
120. Реши, записывая вычисления подробно или кратко.
Реши, записывая вычисления подробно или кратко.
| 35210 : 70 | 168000 : 400 | 456000 : 400 |
| 40150 : 50 | 258000 : 300 | 260100 : 900 |
Подсказка
Повтори алгоритм письменного деления на двузначные и трёхзначные числа.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
121. Выполни деление с остатком.
| 83056 : 40 | 48179 : 80 | 80630 : 200 | 216349 : 700 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
122. Два пловца спрыгнули одновременно с лодки и проплыли по реке в противоположных направлениях: первый со скоростью 90 м/мин, второй со скоростью 40 м/мин. Сколько метров проплывёт второй пловец, когда первый проплывёт 270 м?
Два пловца спрыгнули одновременно с лодки и проплыли по реке в противоположных направлениях: первый со скоростью 90 м/мин, второй со скоростью 40 м/мин. Сколько метров проплывёт второй пловец, когда первый проплывёт 270 м?
Сделай схематический чертёж и реши задачу.
Составь и реши задачи, обратные данной.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
123. Реши уравнения.
| : 5 = 1400 — 900 | — 30 = 1000 — 200 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
124. Расставь знаки действий и скобки так, чтобы получились верные равенства.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Выполни деление с остатком.
438500 : 700
Подсказка
Повтори алгоритм письменного деления многозначных чисел на трёхзначное и как выполнять деление с остатком.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Магический квадрат
Подсказка
Магический квадрат — таблица, заполненная различными числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова.
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
© budu5.com, 2021
Пользовательское соглашение
Copyright
Деление столбиком
Пользователи также искали:
деление столбиком 3 класс,
деление столбиком 4 класс,
деление столбиком на двузначное число,
деление столбиком примеры,
деление столбиком с остатком,
деление в столбик десятичных дробей,
деление в столбик правила,
калькулятор столбиком умножение,
Деление,
деление,
столбиком,
Деление столбиком,
столбик,
класс,
десятичных,
деление столбиком примеры,
деление столбиком класс,
деление в столбик правила,
калькулятор столбиком умножение,
правила,
умножение,
дробей,
деление столбиком с остатком,
остатком,
примеры,
двузначное,
число,
калькулятор,
деление столбиком 4 класс,
деление столбиком на двузначное число,
деление в столбик десятичных дробей,
деление столбиком 3 класс,
деление столбиком,
…
«Деление многозначного числа на двузначное. Изменение пробной цифры»
Тип урока: урок развития умений и навыков
Дидактическая задача: создать предпосылки для формирования выполнения письменного деления многозначного числа на двузначное методом подбора, изменяя пробную цифру.
Оборудование: Учебник, рабочая тетрадь на печатной основе, карточки.
Ход урока по математике в 4 классе
1 Орг.момент
2 Актуализация знаний
Работа по карточкам (работают дети 7 вида)
Дети записывают в тетради выражения к задачам, решают их и проверяем.
1. Сравните, не вычисляя
(на доске)
312х18 * 16х312
470х45 * 360х45
47х534 * 48х634
218х38 * 38х218
2.Укажите порядок действий, найдите значение выражений
(на доске)
(24 + 6) х 3 + 72 : 8
80 : 16 – 120 : (46 +14)
a х b + (k : c) х d
3.Работа над задачами
1.Чтобы засолить 320 кг капусты, потребовалось 4 бочонка. Сколько потребуется таких же бочонков, чтобы засолить 560 кг капусты?
2. Кит весит 150 тонн, а масса слона составляет одну тридцатую часть его массы. Сколько весит слон?
3. Из одного села одновременно в противоположных направлениях выехали два велосипедиста со скоростью 12 км\ч и 8 км\ч. Какое расстояние между ними будет через три часа?
4. Человек спит одну третью суток. Сколько часов спит человек?
5. Логическая задача. На весах, которые находятся в равновесии, на одной чаше лежит одна морковка и две одинаковые редиски. На другой чаше – две такие же морковки и одна такая же редиска. Что легче –морковка или редиска?
Проверка по карточкам
3 Самоопределение к деятельности
Дети проверяют по алгоритму
На доске пример 6 264 : 27 = 380
— Пользуясь алгоритмом деления на двузначное число, проверьте правильность решения примера.
— Какую ошибку я допустила?
Ученики находят ошибку, исправляют
И решают правильно
— Округлите число 27 до 20.
-Сколько десятков возьмем в частном?
-Если 6 : 2 = 3
— Почему же цифра 3 не подходит? (бывают такие случаи деления, когда пробная цифра частного не подходит и ее нужно изменить).
— Сформулируйте задачи урока.
Учащиеся формулируют задачи урока
4 Работа по теме урока
Дети решают у доски, используют алгоритм деления. Проверка 4 столбика
1.Работа по учебнику
С.61,№ 232 (1-3 столб.) у доски, 4 – самостоятельно.
Решение задачи
2. №234 (у доски)
— Что обозначает число 17 066?
— Что обозначает число 10 176?
— Что обозначают числа 23 и 12?
— Что надо узнать в задаче?
3. №235 (для сильных обучающихся)
Проверка №235
4.ФИЗМИНУТКА
— Если услышите верное утверждение вы садитесь, а если неверное – стоите.
-В одной второй часа 30 минут?
-В пятой части километра 200 метров?
-В одной третьей части суток 9 часов?
— Сто килограммов в одной десятой части тонны?
— Пятьдесят кг в половине центнера?
-50 см квадратных в одной четвертой дм квадратных?
5. Работа в парах
№236
— Что обозначает первое выражение?
— Что обозначает третье выражение?
— Что обозначает второе выражение?
Дети работают в парах, отвечают на вопросы
5 Рефлексия
Р.т.с.56, №5
Оцените свою работу на уроке
Дети выполняют по желанию любые три примера на деление
(самостоятельно)
Коллективная проверка
6 Подведение итогов
— Какой алгоритм вы учились использовать сегодня на уроке?
— Какие числа можно делить, пользуясь этим алгоритмом?
— Что надо помнить при подборе пробной цифры в частном?
— Какое задание было самым интересным?
Дети отвечают на вопросы.
7 Домашнее задание
Приложение.
Карточки
Вычисли:
2 024 : 4 19 085 : 5 2 322 : 9 65 708 х 8
Реши уравнение
Х : 6 = 720 : 2 Х х 7 = 630 : 10
Укажи прядок действий и вычисли
180 : 20 + 480 х 5 -158
ГДЗ Математика 6 класс Зубарева, Мордкович учебник Решебник
Математика наряду с русским языком представляет собой основной учебный предмет, который школьникам предстоит освоить наиболее качественно. Проверка будет производиться в рамках основного государственного экзамена (ОГЭ) в конце девятого класса. Удовлетворительная сдача испытания необходима для получения документа о неполном среднем образовании, а, следовательно, для поступления в специальное учебное заведение.
При изучении математики не стоит допускать существенных пробелов, поскольку в данном предмете все темы в той или иной степени связаны между собой. Пропустив несколько параграфов, ученик вряд ли сможет самостоятельно ликвидировать пробелы и вернуться к правильному темпу работы. Из-за этого всегда нужно быть внимательным на уроке и не пропускать важных занятий. Заданные на дом уроки следует выполнять тщательно и регулярно, в соответствии с пожеланиями школьного преподавателя.
ГДЗ по математике за шестой класс (авторы: Зубарева и Мордкович, издательство «Мнемозина») помогают быстрее справляться с задачами. Регулярное использование пособия приведет к более высокому уровню математического мышления и повысит уверенность подростка в собственных силах.
Почему ГДЗ Мордковича по математике полезно для школьников?
Прежде всего, речь идет о наиболее современной и актуальной версии решебника. Таким образом, при его разработке были задействованы исключительно новые педагогические методики. Огромное внимание уделено мотивированию ученика. Сборник ориентирует подростка на самостоятельную работу, на достижение конкретного результата, развивает навыки целеполагания и планирования. Онлайн-сборник, авторы которого Зубарева и Мордкович обладает следующими очевидными преимуществами:
- номера легко находить по табличному указателю, представленному на сайте;
- предложены самые актуальные версии решений в соответствии со всеми требованиями на 2019-2020 годы;
- материалы постоянно обновляются, чтобы поддерживать необходимое качество;
- страница с ответами доступна круглосуточно и с любого устройства.
ГДЗ нельзя просто списывать. С ними нужно разбираться, отрабатывать умения и навыки до автоматизма, рассуждать над приведенными примерами и систематизировать полученные знания.
Как решебник для 6 класса Мордковича, Зубаревой способен повысить успеваемость?
Всё очень просто. Пособие содержит все темы, которые нужно освоить ребенку. Все нужные материалы уже заботливо собраны в одном месте и систематизированы. К тому же, содержание отвечает соответствующему ФГОС (федеральному государственному образовательному стандарту), так что будет достойным дополнением к школьному учебнику. С ГДЗ легко готовиться к контрольным, проверочным, диагностическим работам выполнять тесты по разным темам. Внимание сосредоточено на следующих разделах:
- признаки делимости на простые числа. Наибольший общий делитель;
- сложение и вычитание дробей. Общий знаменатель;
- умножение и деление. Выражения с дробями;
- положительные и отрицательные числа. Операции с ними. Координатная прямая.
Пособие рекомендовано учителям, репетиторам, ученикам, а также их родителям.
Рабочие листы для 4-го класса длинного дивизиона
Добро пожаловать в наши рабочие листы для 4-го класса по полному разделу.
Здесь вы найдете широкий спектр бесплатных заданий по математике для 4-го класса,
который поможет вашему ребенку научиться использовать длинное деление с числами до 4-х цифр ÷ 1 цифра.
Здесь вы найдете подборку заданий с полными делениями для 4-го класса, которые
разработан, чтобы помочь вашему ребенку научиться делить трех- и четырехзначные числа на одну цифру.
Листы отсортированы таким образом, чтобы более легкие были вверху.
Использование этих листов поможет вам:
- разделите диапазон чисел на одну цифру, используя длинное деление, с остатками и без них.
Взгляните на еще несколько наших рабочих листов, похожих на эти.
У нас также есть более широкий выбор таблиц деления по связанным фактам умножения, а также по задачам деления.
- понять, как связаны деление и умножение;
- примените свои факты деления до 10х10, чтобы ответить на связанные вопросы, связанные с десятками и сотнями;
- решить проблемы разделения.
Здесь вы найдете ряд бесплатных распечатываемых Рабочих листов по фракциям 4-го класса.
На уровне 4-го класса детей знакомят с разными взглядами на
дроби, от дробей в виде точек на числовой прямой до дробей
быть частями целого.Они понимают разные дроби,
например половину, четверть, четвертую и т. д. и можете найти их на числовой прямой.
Использование этих листов поможет вашему ребенку:
- расположить разные дроби на числовой строке;
- понимать эквивалентные дроби;
- понять, что такое смешанное число;
- начинает преобразовывать дроби в десятичные числа и десятичные дроби в дроби.
Все задания по математике для четвертого класса в этом разделе
проинформирован тестами по элементарной математике для четвертого класса.
Здесь вы найдете ряд бесплатных игр для печати дивизионов, которые помогут
дети изучают факты своего деления.
Использование этих игр поможет вашему ребенку узнать факты их разделения,
а также развивать их память и навыки стратегического мышления.
Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике.
и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.
Как помочь вашему ребенку освоить стратегии деления и длинного деления
Когда моя дочь пошла на деление в четвертом классе, я знал, что нас ждут неприятности (и дополнительные домашние занятия по математике). Как родитель, который изучал математику «старым» способом, мне было очень трудно понять процессы, лежащие в основе ее домашнего задания по математике и задач со словами.(Мне стыдно сказать, что задачи по разделению слов для четвертого класса — это не шутка.) Я использовал книгу Эвана-Мура « Основы математики », чтобы изучить, попрактиковаться и проанализировать стратегии разделения. Визуальные модели и объяснения предоставили пошаговый процесс обучения, который укрепил то, что моя дочь изучала в школе, и углубил ее понимание. Помогая своей дочери освоить деление в столбик, я даже обнаружил стратегии, лежащие в основе процесса деления, которые углубили мое понимание взаимосвязи между делением и умножением.
Дивизион — один из тех математических навыков, которые заслуживают много внимания, объяснений и практики. Вместо того, чтобы преподавать математику как серию систем / шагов для запоминания, сегодняшняя математическая программа включает в себя фундаментальные мыслительные процессы, лежащие в основе каждого навыка и стратегии, которым обучают детей. Сегодняшняя программа по математике требует, чтобы дети понимали, почему они делают эти шаги, и использовали это понимание числовых соотношений для более эффективного решения задач. Если дети знают, почему они делают определенные шаги, они могут применять это понимание для решения различных математических задач и понимать беглость чисел на более глубоком уровне.
Вот некоторые стратегии и концепции, которые мы практиковали, которые помогли мне и моей дочери лучше понять разделение.
Начало деления и умножения
Когда ваш ребенок начинает изучать деление, ему / ей важно понимать взаимосвязь между делением и умножением. Детям необходимо хорошо знать факты умножения. (Если они не знают фактов умножения, потренируйтесь в беглости несколько недель, прежде чем начинать деление.) Ознакомьтесь с дополнительными ссылками ниже, чтобы получить советы и идеи, чтобы узнать факты умножения.
Связь между умножением и делением
«Начало деления» учит простой концепции: чтобы делить, вы должны умножать. Использование наглядных примеров умножения и деления поможет вашему ребенку научиться распознавать разницу между умножением и делением.
Если вы привыкли к старому методу деления, этот процесс может показаться утомительным, но детям важно понимать разницу между умножением и делением.Когда задачи с числами и словами усложняются, это фундаментальное понимание поможет им узнать, когда делить, а когда умножать.
Смоделируйте, как найти неизвестное число умножением или делением.
Чтобы узнать, понимает ли ваш ребенок основную связь между умножением и делением, спросите его или ее:
Ответ: факты умножения и деления связаны. Если вы знаете один факт, вы можете решить другой связанный факт.
Стратегии трех подразделений
Один из аспектов нынешней учебной программы по математике, который мне нравится, — это акцент на обучении нескольким стратегиям и разрешению детям решать, какая из них лучше всего подходит для них. Такой подход позволяет детям понять и выбрать, какой метод лучше всего подходит для их стиля обучения. Испытание различных подходов может иногда даже иметь значение между неудачей и успехом в математике. Вот три разные стратегии, которым следует научить, когда вы начинаете деление.
1. Сделайте связи с помощью шаблонов деления и разбейте числа
Это высшая степень беглости чисел. Обучение детей распознаванию и использованию шаблонов в числовых операциях поможет им эффективно решать проблемы.
6,000 ÷ 3
6 ÷ 3 = 2
6,000 ÷ 3 = 2,000
Просто представьте 6000, разделенные на 3, как 6 тысяч, разделенных на 3, и это 2 тысячи.
2.Разбивка чисел на «дружественные» числа с помощью модели с областями
260 ÷ 5 = 52
Разбейте числа на «дружественные» числа. Разбиение чисел на числа, которые легко делятся, важно научиться беглому чтению чисел. Это может показаться немного утомительным, но понимание того, как разбить большие числа на числа, которыми проще манипулировать, может развить у детей умственные математические способности.
Разбейте 260 на «дружественные» числа 250 и 10. Я выбрал 250, потому что это делитель 5, умноженный на большое число (50).Я выбираю 10, потому что это разница между 250 и 260. Они входят в рамки модели площади. Разделите каждый на делитель, чтобы получить множители, затем сложите множители.
3. Разделить на группы вычитанием
623 ÷ 4
Я могу составлять группы по 4 человека и вычитать их из 623 до тех пор, пока не останется достаточно, чтобы образовать группу. Я начну со 100 групп по 4. Осталось 223. Затем я вычту 50 групп по 4. Теперь у меня осталось 23.5 групп по 4 человека израсходуют большую его часть; осталось недостаточно, чтобы вычесть даже 1 группу из 4. Наконец, я сложу количество групп из 4 и запишу остаток.
Длинное деление: деление многозначных чисел с помощью моделей площадей, частных частных и стандартного алгоритма
Если я только что потерял вас, используя такие фразы, как «частные частные» и «стандартный алгоритм», не пугайтесь. Это просто математическая терминология для пошаговых процессов.Частное — это ответ, а частное — частичное. Стандартный алгоритм — это пошаговый способ решения проблемы. При делении в столбик эти стратегии используются для повторного вычитания, чтобы в конечном итоге найти ответ.
Деление многозначных чисел с использованием модели области
Мы занимались этим ранее, начав деление, но теперь числа становятся больше и немного сложнее.
3,182 ÷ 15 = 212 R2
Деление — это просто повторное вычитание.Я буду группировать по 15 штук и вычитать их, пока не останется достаточно средств для вычитания. Затем я сложу количество групп. Поскольку у меня получилось число меньше делителя, я запишу его как остаток.
3,182 ÷ 15 = 212 R2
Разделить на частные
Как и в модели площади, я найду группы делителя и вычту их. Затем я сложу количество групп и запишу остаток, если он есть.
Разделить по стандартному алгоритму
Если вы вздохнете с облегчением на этом примере, я полностью понимаю. Это традиционный способ обучения разделению, которому большинство из нас научилось много лет назад.
Этот стандартный алгоритм длинного деления повторяется с шагами:
1. Разделить
2. Умножить
3. Вычесть
4. Перейдите к следующей цифре
5.Повторить
* Многие дети путаются с шагами 2 и 3 , потому что вы на самом деле не делите, а умножаете и вычитаете, чтобы найти остаток.
3,182 ÷ 15 = 212 R2
Посмотрите только на одно место за раз, начиная с левого. Поскольку 15 не делятся на 3, я перейду к следующему месту. Теперь я прикидываю, сколько раз 15 перейдет в 31, и напишу это над 1. Я вычитаю и опускаю цифру со следующего места.Я продолжаю делать это через дивиденд (число). Когда у меня заканчиваются места, я запишу оставшееся число в качестве остатка.
Лучший способ помочь вашему ребенку овладеть трудным навыком деления — это практиковаться, практиковаться и практиковаться. Узнайте, какой метод лучше всего подходит вашему ребенку, и предложите ему или ей множество практических задач, над которыми нужно работать. Кроме того, не забывайте решать проблемы с разделением слов. Решение задач со словами может продемонстрировать, насколько хорошо ваш ребенок понимает концепцию деления и как ее использовать.
Рекомендуемые ресурсы
Все примеры и стратегии были взяты из книги Эван-Мур Основы математики для 1–6 классов. Хотя это учебный ресурс, я обнаружил, что математические модели и практические занятия удобны для использования дома.
Советы по обучению задачам со словами и умножению можно найти в следующих статьях:
Хизер Фоуди — сертифицированный учитель начальных классов с более чем 7-летним опытом работы преподавателем и волонтером в классе.Ей нравится создавать содержательные и творческие уроки для учащихся. В настоящее время она работает в отделе маркетинга и коммуникаций Эван-Моора и любит создавать возможности для обучения, которые являются значимыми и творческими как для студентов, так и для учителей.
Категории: Классные стратегии, Идеи для уроков |
Теги: математика 3-го класса, математика 4-го класса, деление 5-го класса, общее ядро деления, стратегии деления, разделение четвертого класса, как преподавать деление, математика, разделение третьего класса |
Постоянная ссылка
Длинная дивизия, длинный бой
Ужасные слова, от которых мурашки по спинам пробираются по спинам учеников и учителей… Long Division! Существует так много препятствий на пути эффективного обучения учащихся продвижению в столбик, и каждый класс, в котором необходимо обучать этому навыку, имеет свой собственный набор трудностей.
Когда ученики начинают деление в столбик в четвертом классе, они сразу же следуют за беглостью умножения. Некоторые студенты так близко отстали, что у них не было времени закрепить беглость фактов умножения до такой степени, чтобы легко получить эту информацию. Длинное деление превращается в агонию повторного подсчета пропусков.
К шестому классу все еще есть ученики, которые все еще борются с теми же проблемами, которые преследовали их в четвертом классе, но возникают новые проблемы. В первых классах учащимся часто говорят: «Большое количество идет домой.«Что ж, трудно убедить подростка в том, что их любимая учительница четвертого класса была не совсем правильной, потому что теперь размер числа не имеет ничего общего с тем, является ли число делителем или делимым. Чтобы усложнить это, студенты с удивлением обнаруживают, что больше не будет записывать остатки, а вместо них будут дроби и десятичные дроби.
Мне потребовалось много времени, чтобы научиться делать все типы деления в столбик. В четвертом классе меня впервые учили делению в столбик.Я скажу, что учил, а не учил, потому что я определенно не усвоил это до того, как перешел в следующий класс. Было так много шагов, и мне всегда казалось, что я их запутываю. Учительница пыталась помочь, давая мне мнемонику об известных ресторанах и их чизбургерах. (Учителя математики, я уверен, что вы знакомы с этим!) Она пыталась спросить меня, сколько раз это число «переходило» в другое. Я всегда был невероятно буквальным в своем мышлении, поэтому я представлял себе дивиденд в виде маленького домика с дверью в нем, и делитель подходит к двери, стучит и просит чизбургер! Забавно, но это не помогло мне научиться разделять.
Я, наконец, научился делать большинство длинных делений достаточно хорошо, чтобы дожить до тех пор, пока я не перешел в математические классы, достаточно старшие, чтобы пользоваться калькулятором. Я должен сделать шокирующее признание — особенно для учителя математики — я никогда не учился делить, когда делитель был двухзначным! Я наконец научился делить на двузначные числа около года назад — после 10 лет обучения в классе, успешного обучения в колледже, в котором я получил высшее образование, и трех лет изучения математики в средней школе.
Поскольку я сам плохо разбирался в делении, я чувствую особую связь со своими учениками, которые также борются с этим навыком. Я часто замечаю мелочи, которые мешают студентам, которые в остальном хорошо разбираются в математике, не могут разделить. (… А также ученики, которые тоже не очень хороши в математике!)
Вот некоторые вещи, которые могут сбивать с толку ваших учеников, и что вы можете с этим сделать:
- «Большой номер идет в дом». Большой номер НЕ идет в дом! Хотя это может быть верно в отношении словесных задач, наблюдаемых в младших классах, это математически неверное утверждение.Это вызывает всевозможные проблемы, когда учащиеся достигают оценок, в которых они делятся, чтобы найти десятичные или дробные значения. Скорее правильнее было бы сказать, что делимое число идет в дом.
- «Сколько раз это число входит в то число ». Студенты, которые думают очень буквально, могут не понять значения этого утверждения. Я спросил многих учеников, которые не умеют делиться и находятся в более старших классах, могут ли они объяснить, что означает эта фраза, а они не могут.Я спрашиваю, было бы больше смысла, если бы я сказал что-то вроде «сколько групп из , этого числа я могу сделать из , этого числа », и это обычно имеет для них больше смысла. Они могут представить себе, как число делится на части, но не повторение делителя для получения делимого.
- Грязные обезьяны и чизбургеры. Мнемоника отлично помогает вспомнить то, что у вас уже есть хотя бы базовое понимание, но они не являются обучающими инструментами.Слишком раннее введение мнемоники может оказать негативное влияние на учащихся, которым необходимо закрепить конкретные навыки, прежде чем они попытаются перейти к абстрактному. Хотя мнемоника забавна и подходит для студентов, которые уже понимают концепцию разделения и просто нуждаются в подкреплении последовательности шагов, слишком ранний переход к этим устройствам не поможет студентам, которые не понимают, что на самом деле означает каждый шаг. . Если вы не знакомы с приведенной выше мнемоникой и вам интересно: Dirty Monkeys плохо пахнут (разделить, умножить, вычесть, сбить) или McDonald’s продает сырные бургеры (разделить, умножить, вычесть, сравнить, уничтожить).Есть, конечно, много других, а также их вариации.
Так что же делать с этими сложными навыками? Не волнуйтесь, я не оставлю вас без дополнительных стратегий!
Стратегия разделения сверху и снизу
Это тот, который я использовал, который больше всего помог студентам, которые не совсем свободно владели языком или испытывали трудности с количеством шагов, используемых в стандартном методе обучения.
- Шаг 1. Составьте таблицу умножения делителя.Обозначьте столбец множителя буквой «Т» для вершины и столбец продукта буквой «В» для нижней части. Начните таблицу с 0, а не с 1, и пройдите через 9.
- Шаг 2. Спросите , какое наибольшее число я могу вычесть из дивиденда. Попросите учащегося определить этот номер в «нижнем» столбце.
- Шаг 3: Запишите верхнюю и нижнюю пару. Напишите «верх» над цифрой в «доме» и напишите «низ» ниже.
- Шаг 4: Попросите ученика вычесть, опустить и повторять, пока все деление не будет решено.
Преимущества этого метода заключаются в том, что после того, как ученик несколько раз практикуется, он состоит из трех шагов: «Вверх» и «Вниз», «Вычесть», «Вниз». Кроме того, настаивание на таблице фактов для начала работы полезно для студентов, которые еще не владеют свободно. Кроме того, в этом процессе особое внимание уделяется навыкам записи фактов умножения и вычитания. Студент не должен уметь визуализировать деление числа. Из-за этого, однако, мне нравится этот метод для старших учеников, которые в остальном не увенчались успехом с традиционным методом, а не с переходом к методу для всего класса.
Частичные частные
Это замечательный метод, который наконец-то позволил мне делить на двузначные делители! Этот метод, хотя раньше нечасто использовался, в настоящее время становится все более и более распространенным из-за акцента на альтернативных методах в новых государственных стандартах, а также в общих основных стандартах.
В этом методе вам не нужно использовать максимально возможное частное, но вы можете выбрать частное. Это похоже на метод повторного вычитания деления.Основным камнем преткновения для этого метода является то, что пользователь должен иметь некоторое представление о совместимых числах и умножении, чтобы использовать его эффективно.
- Шаг 1: Выберите число для умножения, которое вам будет легко вычислить в уме. Часто это будут числа, оканчивающиеся на нули, кратные или кратные 1, 2, 5 или 10, потому что с помощью числового ощущения это можно сделать мысленно. Напишите это число над «домом». Выровняйте разрядные значения.
- Шаг 2: Умножьте в уме делитель на число.Напишите этот номер под номером в «домике». Выстроить разряды
- Шаг 3: Вычтите, убедившись, что ваши разрядные значения совпадают. В этом методе вы не будете «сбивать» вас с ног. Теперь разница — это ваш новый дивиденд при следующем повторении.
- Шаг 4: Повторите с другим совместимым частным. Сложите его друг над другом, выровняв числовые значения. Продолжайте выполнять шаги, пока ваше подразделение не будет завершено
- Шаг 5: Сложите все частные частные, чтобы получить окончательный ответ.Термин {\ mathrm {th}} $$ в повторяющемся шаблоне формы.
Учащиеся развили базовое понимание деления в 3 классе, когда они пришли к пониманию деления в отношении равных групп, массивов и площадей. Они разработали различные стратегии, чтобы развить беглость с делением в пределах 100, и они применили эти знания в контексте одно- и двухэтапных задач, используя четыре операции. Студенты также пришли к пониманию свойства распределения, которое лежит в основе стандартного алгоритма деления.
Так же, как и в начале предыдущего раздела, когда учащиеся расширили свое понимание умножения за пределы понимания 3-го класса, включив в него задачи мультипликативного сравнения, этот модуль начинается с дополнительной сложности задач деления с остатками (4.OA.3). Это, вероятно, знакомо студентам из их собственного реального опыта попыток равномерно разделить количества, и поэтому основное внимание уделяется интерпретации этих остатков в контексте различных проблем.Затем студенты сосредотачиваются на расширении своих процедурных навыков с делением, чтобы включить до четырехзначных дивидендов с однозначными делителями (4.NBT.6), представляя эти случаи с базовыми десятью блоками, моделью площади, частными частными и, наконец, стандартный алгоритм, устанавливающий связи между всеми представлениями по мере их появления. Использование модели площади помогает студентам концептуально понять разделение, а также в качестве связи с их работой с площадью и периметром (4.MD.3), вспомогательным стандартом кластера.Наконец, вооруженные глубоким пониманием всех четырех операций, охватываемых последними тремя разделами, студенты решают многоэтапные задачи, включающие сложение, вычитание, умножение и деление, включая свои новые проблемные ситуации, такие как мультипликативное сравнение и интерпретация остатков (4.OA .3). Они также исследуют паттерны чисел и форм, используя четыре операции, чтобы сделать выводы о них (4.OA.5).
На протяжении всего раздела студенты по-разному занимаются математической практикой.Например, учащиеся видят и используют структуру (MP.7), когда они «разлагают [e] дивиденд на аналогичные десятичные единицы и находят частное единицу за единицей» (NBT Progressions, стр. 16). Кроме того, «неоднократно рассуждая (МР.8) о связи между математическими рисунками и письменной числовой работой, учащиеся могут увидеть алгоритмы умножения и деления как сокращения или резюме своих рассуждений о количествах» (NBT Progression, стр. 14). Наконец, когда учащиеся решают многоступенчатые задачи со словами, включающие сложение, вычитание и умножение, они моделируют математику (MP.4).
В то время как на протяжении всего модуля учащимся рекомендуется использовать модели, когда это необходимо для решения задач, их глубокий опыт работы с системой разрядных значений и несколькими концептуальными моделями, а также знакомство с алгоритмами деления готовит их к расширению этих моделей до двузначных делителей в Оценках. 5 (5.NBT.6) и свободное владение алгоритмом деления в 6 классе (6.NS.2). Каждый последующий класс зависит от понимания многозначного деления и его алгоритмов, что делает этот модуль важным для учащихся 4-х классов.
Темп: 19 учебных дней (16 уроков, 2 гибких дня, 1 контрольный день)
Чтобы узнать, как изменить темп обучения на 2020-2021 учебный год в связи с закрытием школ, см. Наши рекомендации по корректировке объема и очередности 4-го класса.
Интерактивных игр с длинным разделом — пошаговые задания и примеры
Наши бесплатные развивающие игры используют более 20 000 учителей и родителей, обучающихся на дому!
Отличная пошаговая игра с делением в столбик:
Возникнет проблема с длинным разделением.На каждом этапе Snork будет сообщать вам, какой расчет произвести. Введите ответ в пустой слот и переходите к следующему шагу.
Продолжайте отвечать так, и с помощью подсказок Snork вы легко решите проблему разделения.
www.thegreatmartinicompany.com
1. Заполните закрашенные блоки.Вы можете перемещаться между блоками с помощью клавиш со стрелками или щелкая мышью.
2. На каждом этапе вы можете получать немедленных отзывов для ваших ответов — просто наведите указатель мыши на символ V в нижнем левом углу, и вы увидите СИНИМ цветом ваши правильные ответы, а КРАСНЫМ цветом — неправильные ответы.
3. Вы можете увидеть полное решение проблемы, наведя указатель мыши на символ =.
4.При нажатии на звездочку * откроется калькулятор.
5. Вы также можете установить количество цифр в задаче, щелкнув X в символе длинного деления в правом нижнем углу.
6. Щелкните символ утилизации, чтобы сбросить проблему и получить новую.
Длинное деление с трехзначным дивидендом
DivideРама
cemc2.math.uwaterloo.ca
Нажмите кнопку «Пуск», и появится новая проблема с длинным разделением.
Решайте проблему по одной цифре. Мигающий курсор покажет вам, где ввести следующую цифру.
Если вам нужна помощь, установите флажок, где написано «Установите этот флажок для получения справки».
Вы можете исправить себя и вернуться, щелкнув мышью по цифре, которую хотите исправить.
Когда вы закончите, нажмите кнопку «Проверить ответ».
Вы можете установить количество цифр делимого и делителя
Математика перетаскивания
www.mrnussbaum.com
Начните с выбора количества задач, количества цифр в делимом и количества цифр в делителе.Введите свое имя и нажмите «Играть».
На экране появится проблема с длинным разделением. Перетащите цифры с левой стороны и аккуратно разместите их в нужных местах на листе, чтобы решить проблему. Если вы допустили ошибку, вы можете перетащить цифру за пределы рабочего листа, чтобы избавиться от нее.
Вы можете использовать небольшой калькулятор для помощи.
Когда у вас есть ответ, введите его в поле результатов вверху и нажмите кнопку «Проверить».
Эти игры ориентированы на деление в столбик и могут стать прекрасным подспорьем для учителей, которым нужны интерактивные интерактивные занятия для своих учеников.
Независимо от того, является ли студент абсолютным новичком в делении на столбики или изучает его в течение некоторого времени, он найдет здесь что-то ценное для своего обучения.
В каждом задании есть множество математических задач, которые представлены в простом, удобном для чтения формате, который детям понравится и увлекателен, и который очень способствует усвоению материала.
Инструкции для каждого модуля представлены пошагово, чтобы избежать путаницы, и содержат несколько примеров, чтобы учащиеся быстро усвоили концепции и начали работать над решением проблем.
Многие задания предлагают обратную связь, сообщая учащимся, если какие-либо ответы неверны, чтобы они могли попробовать еще раз.Игры на этой странице в основном предназначены для учеников 4-х классов.
Как научить длинное деление
Итак, ваш ребенок освоил свою таблицу умножения и теперь переходит к делению в столбик. Деление в столбик может показаться легким, но на самом деле его довольно сложно научить и понять. Давайте разберемся, как понимать деление в столбик.
4 ступени длинного деления
- Разделить
- Умножить
- Вычесть
- Вниз
ПЕРЕД НАЧАЛОМ
Прежде чем мы сможем обучать делению в столбик, мы должны понять связанные с ним термины.Делимое число называется делимым , делимое число называется делителем , и, наконец, число, которое является ответом на проблему деления, называется частным . Бонус: если делитель не делится равномерно на дивиденд, останется остаток .
Например,
3234 ÷ 6 = 539
3234 делится на 6 , что равносильно тому, что 6 делит 3234 .Ответ на эту проблему деления: 539 или 539 — это частное от 3234 , деленного на 6 .
Но если бы у нас было 3237 ÷ 6, наш ответ был бы 539 с остатком из 3 , 3237 ÷ 6 = 539 R3
ШАГ 1: РАЗДЕЛИТЬ
Хорошо, вернемся к 3234 ÷ 6. В формате длинного деления это будет иметь вид
.
Убедитесь, что вы не сказали «шесть, разделенные на три тысячи двести тридцать четыре», что выглядело бы как
Во-первых, взгляните на крайнюю левую цифру делимого.
Спросите ребенка: «Может ли 6 превратиться в 3?» Нет, это слишком мало. Теперь вам нужно объединить следующую позицию, 2 (сто), с 3 (тысячами) цифрами (3200).
Может ли 6 перейти в 32? Да, оно может. Это первая отправная точка для многих студентов. 32 не делится на 6, но его можно разделить на 6, оставив что-то еще. Когда вы говорите об этом со своим ребенком, и они говорят, что 32 нельзя разделить на 6, они не ошибаются.
Вы можете спросить своего ребенка: «Сколько групп по 6 человек вы можете составить из 32 человек?» Они могут нарисовать 32 круга и сгруппировать их в группы по 6, после создания 5 групп они увидят, что осталось только 2 круга, и они могут образовать только 5 групп по 6 из 32.Однако по мере того, как они получают больше практики с делением в столбик, им нужно иметь возможность представить группы в своей голове и сделать вывод, что они могут составить 5 групп по 6 штук без необходимости рисовать круги.
В качестве альтернативы вы можете спросить их: «Какое число, кратное 6, ближе всего к 32?» Ответят 30. Отлично! Теперь спросите: «сколько 30 делится на 6?» Ответят 5.
ШАГ 2: НЕСКОЛЬКО
Теперь ваш ребенок знает, что 6 может превратиться в 32 максимум 5 раз. Что дальше? Умножить. 5 x 6 = 30. 5 находится в верхней части панели ответов как первое число нашего ответа. 30 идет под дивиденды для подготовки к Шагу 3.
ШАГ 3: ВЫЧИСЛЕНИЕ
Затем вычитаем 32-30 = 2. В длинном делении это выглядит как
ШАГ 4: ПРИНИМАЙТЕ
Мы должны что-то сделать с этими двумя оставшимися. 6 не может перейти в 2, как ваш ребенок с радостью подтвердит. Теперь мы опускаем следующую цифру дивиденда, и наш новый дивиденд равен 23
.
ПОВТОР
Начните снова с ШАГА 1.Может ли 6 войти в 23 ? Да 3 раз. ШАГ 2, что такое 3 x 6 ? 18. ШАГ 3. Что такое 23–18? 5 . ШАГ 4 выведите из строя 4 .
СЕЙЧАС ПОПРОБУЙТЕ
Может ли 6 перейти в 54? Сколько раз? Куда девается 9? Что дальше? Вычтем 54-54 = 0. Осталось что-нибудь сбить?
Что ж, похоже, мы все закончили, и вы знаете, как объяснить деление в столбик! Несмотря на то, что для некоторых учеников это сложно понять, с помощью этого метода ваш ребенок будет выполнять деление в столбик в кратчайшие сроки.Вот несколько полезных листов с длинными разделами, которые можно использовать дома.
Как обучить длинному делению на практике — Кейт Сноу
Разочарованное преподавание длинного деления? Деньги-монополисты спешат на помощь! Вы узнаете, как научить своего ребенка КАК выполнять деление в столбик и ПОЧЕМУ это работает.
Когда я был учителем начальной школы, я всегда знал, когда в четвертом классе была неделя с длинными разделами. Мои обычно позитивные и энергичные коллеги приходили в учительскую, обессиленные и измученные, сочувствуя и жаловавшись на утомительную работу и разочарование, связанные с обучением стольких детей этому сложному процессу.Я особенно вспоминаю день, когда одна учительница, обычно очень замкнутая и тихая, продемонстрировала «танец с длинными делениями», который она создала в отчаянии, чтобы помочь своим ученикам разучить шаги!
Несмотря на то, что длинное деление может вселить страх в сердце даже опытных учителей, у меня для вас есть две хорошие новости:
- Как мамам, обучающимся на дому, мы должны обучать делению в столбик только одного ребенка за раз. (Ну, может быть, двое, если у вас есть близнецы. Но не 25.)
- При практическом подходе дети могут не только научиться , как делать длинное деление, но и , почему это работает, .
