Урок 3. ряд натуральных чисел. десятичная система записи натуральных чисел — Математика — 5 класс
Математика
5 класс
Урок № 3
Ряд натуральных чисел. Десятичная система записи натуральных чисел
Перечень вопросов, рассматриваемых в теме:
— натуральные числа;
— десятичная запись натуральных чисел;
— разрядность натуральных чисел
Тезаурус
Натуральные числа – числа, которые используют при подсчёте предметов.
Натуральный ряд – последовательность всех натуральных чисел, расположенных в порядке возрастания.
Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Обязательная литература
- Никольский С. М. Математика: 5 класс. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2019. – 276 с.
- Потапов М. К. Математика. Книга для учителя. 5-6 классы. // М.
 К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.
К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.
Дополнительная литература
- Бурмистрова Т. А. Математика. Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
- Потапов М. К. Математика: дидактические материалы. 6 класс. // М. К. Потапов, А. В. Шевкин – М.: Просвещение, 2010.- 118 с.
- Чесноков А. С. Дидактические материалы по математике 5 класс. // А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014.- 124 с.
Теоретический материал для самостоятельного изучения
С древних времен у человека была потребность в счёте.
Числа, которые используют при подсчёте предметов, называют натуральными числами.
Таким образом, числа: один, два, три, …, десять, …, сто, …, тысяча, …, миллион и так далее – это натуральные числа.
Натуральные числа один, два, три, четыре, пять и так далее, записанные в порядке возрастания и без пропусков, образуют ряд натуральных чисел.
Стоит отметить, что самое маленькое натуральное число – единица (1). В натуральном ряду каждое следующее число на 1 больше предыдущего. Натуральный ряд бесконечен, наибольшего числа в нём нет.
В настоящее время принята десятичная система записи чисел (десятичная система счисления), в которой числа записываются при помощи десяти знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – эти знаки называют цифрами.
Одна и та же цифра может иметь различное значение в зависимости от позиции, где она расположена в записи числа. Например, в записи числа пятьсот пятьдесят пять первая справа цифра пять означает пять единиц, вторая – пять десятков, третья – пять сотен.
Вот поэтому десятичную систему счисления называют позиционной.
Натуральные числа, записанные одной цифрой, называют однозначными, а записанные несколькими цифрами – многозначными: двумя – двузначными, тремя – трёхзначными и т. д.
Например, числа 1, 8, 9 – однозначные числа; 10, 66, 89 – двузначные числа; 111, 145 – трёхзначные числа; 123456 – шестизначное число.
Для чтения многозначных чисел их разбивают, начиная справа, на группы по три цифры в каждой (самая левая группа может состоять из одной или двух цифр). Эти группы называются классами.
Первый класс справа называют классом единиц, второй – классом тысяч, третий – классом миллионов, четвёртый – классом миллиардов и т. д.
Класс миллиардов | Класс миллионов | Класс тысяч | Класс единиц |
123 | 456 | 789 | 123 |
Например, запишем заданное число в таблицу, начиная с класса единиц, то есть записываем в таблицу число справа налево, начиная с цифры шесть.
классы | миллиарды | миллионы | тысячи | единицы | ||||||||
разряды | Сот. | Дес. | Ед. | Сот. | Дес. | Ед. | Сот. | Дес. | Ед. | Сот. | Дес. | Ед. |
число | 1 | 5 | 3 | 8 | 8 | 0 | 0 | 1 | 2 | 8 | 6 | |
Это число имеет 286 единиц в классе единиц, 1 единицу в классе тысяч, 388 единиц в классе миллионов, пятнадцать единиц в классе миллиардов.
Наше число: пятнадцать миллиардов триста восемьдесят восемь миллионов одна тысяча двести восемьдесят шесть.
Чтобы прочитать число, называют слева по очереди число единиц каждого класса и добавляют название класса.
Заметим, что каждое натуральное число можно записать в виде суммы разрядных слагаемых.
Например, число 6789 состоит из шести тысяч, семи сотен, восьми десятков и девяти единиц, поэтому это число мы можем представить в виде суммы разрядных слагаемых: 6789 = 6 ∙ 1000 + 7 ∙ 100 + 8 ∙ 10 + 9 ∙ 1
Огромную роль в десятичной системе счисления играет число 10. Десять единиц называется десятком, десять десятков – сотней, десять сотен – тысячей и т. д.
Десять единиц называется десятком, десять десятков – сотней, десять сотен – тысячей и т. д.
1 – единица
10 – десять
100 – сто
10 000 – десять тысяч
100 000 – сто тысяч
1 000 000 – миллион
10 000 000 – десять миллионов
100 000 000 – сто миллионов
1 000 000 000 – миллиард
Мы с вами знаем, что числа используются для записи информации о количестве объектов. Люди нашли множество способов представления чисел. В любом случае число изображается символом или группой символов (словом) некоторого алфавита. Такие символы называют цифрами, а алфавит – системой счисления.
Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Все ныне известные системы счисления можно разделить на две группы – позиционные и непозиционные. В позиционных системах счисления значение цифры зависит от её положения в числе, а в непозиционных — не зависит.
Одними из первых возникли непозиционные системы счисления. Например, римская система: в ней в качестве цифр используются латинские буквы.
Например, римская система: в ней в качестве цифр используются латинские буквы.
Сравним числа IV и VI. Несмотря на то, что I меньше, чем V, число VI больше, чем число IV. Хотя заданное число состоит из одних и тех же букв.
Разбор решения заданий тренировочного модуля
№ 1. Запишите самое большое трёхзначное число.
Решение: самое маленькое четырёхзначное число – 1000. Значит, самое большое трёхзначное число будет: 1000 – 1 = 999
Ответ: 999.
№ 2. Какое из чисел записано в виде суммы разрядных слагаемых: 600000 + 70000 + 300 + 40 + 8
- 607348
- 670348
- 67348
- 607708
Решение: сложив все разрядные слагаемые, получим число
670348. Значит, верный ответ – второй вариант.
Ответ: 670348.
Цифры. Десятичная запись натуральных чисел
Давайте представим себе такую историю…
– 2, 0, 1, 7, 2, 0, 1, 7, 2, 0, 1, – бурчал
себе под нос Саша.
– Чем это ты тут занимаешься? – спросил Паша.
– Хочу научиться красиво писать цифры, –
ответил Саша.
– Саша, смотри, какое интересное число у тебя
получилось, – провозгласил Паша. – А ты можешь его прочитать? – спросил он у
Саши.
– Прочитать! Конечно! – взбодрился Саша. –
Что тут сложного? 2, 0, 1, 7, 2, 0…
– Нет, Саша! – перебил Паша. – Ты просто
перечисляешь записанные цифры, а назвать число – это совсем по-другому. Вот как
ты думаешь, что общего между буквами и цифрами?
– Не знаю, – прозвучал ответ Саши. – Может,
только если одни и другие мы учим в школе?
– Ну почти! – сказал Паша. – Буквы и цифры –
это знаки, которые придумали для записи. Так, например, из букв можно записать
слово, а вот из цифр – число. У тебя из цифр тоже получилось число, которое
имеет своё имя.
– Правда? – удивился Саша. – И как же его
зовут?
– Ты знаешь, я немного забыл, как правильно
его назвать, – стушевался Паша. – Но я точно знаю, кто нам может помочь!
– Но я точно знаю, кто нам может помочь!
– Ребята, прежде, чем я вам поведаю свой
рассказ о цифрах, числах и ещё кое о чём интересном, хочу, чтобы вы немного
размялись и выполнили устные задания, – предложил Электроша.
– Давайте сверимся! – сказал Электроша. – Посмотрите, что у вас должно было получиться!
– Ну а теперь давайте поговорим о числах, –
предложил Электроша. – Вы уже знаете, что в алфавите
русского языка существует 33 буквы и из них можно составить огромное множество
слов.
Цифры в математике выполняют такую же роль,
как и буквы в русском языке. Только из цифр составляют различные числа.
Правда, цифр гораздо меньше, чем букв. Их
всего лишь 10:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
– Так мало? –удивился Саша.
– Цифр-то мало, а вот составить из них чисел
можно сколько угодно! – продолжил Электроша.
– А вы знаете, что цифры изобрели
давным-давно? – спросил у мальчиков Электроша. Это
Это
произошло в Индии ещё в VI веке. Правда, сами цифры принято называть
арабскими.
– Арабскими? – удивился Паша. – Но ведь ты же
сказал, что цифры придумали в Индии? А значит, их нужно называть индийскими!
– Всё правильно Паша! – улыбнулся Электроша, – придумали то их в Индии, но к нам цифры пришли
от арабов, которые подсмотрели их у индийцев, поэтому-то их и стали называть
арабскими.
– А теперь поговорим о том, как называют
числа! – продолжил Электроша. От количества цифр
(знаков) в числе зависит его название. Так, например, если число состоит из
одной цифры, то его называют однозначным.
– Такое смешное название! – ухмыльнулся Саша.
– Да, да, одна цифра – один знак, поэтому и
однозначное, – продолжил Электроша. –Самое
маленькое однозначное натуральное число – 1, а самое большое – 9.
Кроме однозначных чисел, есть и многозначные.
Если число состоит из двух цифр, то его называют двузначным числом.
– Вот вы, мальчики, можете назвать самое
маленькое и самое большое двузначное натуральное число? – спросил Электроша.
– Конечно! – обрадовались мальчишки. – Это же
легче лёгкого!
– Самое
маленькое двузначное число – это 10, – сказал Паша.
– Верно! – подтвердил Электроша.
– А вот самое большое двузначное число – это 90!
– воскликнул Саша.
– Нет, нет, – исправил Сашу Электроша. Самое большое двузначное число – 99. А вот
следом за ним уже идёт наименьшее трёхзначное натуральное число –
100. Число сто записано тремя цифрами, поэтому его называют трёхзначным.
Запомните! Многозначное число может начинаться с любой
цифры, кроме цифры ноль.
Каждая цифра в записи многозначного числа
занимает определённое место – позицию.
– Что это значит – определённое место? –
решил спросить Саша.
– Перед вами три трёхзначных числа, –
продолжил Электроша. – Посмотрите: в их записи
– Посмотрите: в их записи
участвуют одни и те же цифры.
– Но ведь сами числа же различны, – возразил
Паша. – В них цифры стоят на разных местах.
– Ты
правильно заметил, Паша, –
сказал Электроша. – В записи числа важно то, какую
позицию занимает цифра, то есть на каком месте она стоит.
Место, на котором стоит цифра в записи числа,
по-другому называют разрядом числа. Одна и та же цифра в записи
числа может иметь разные значения в зависимости от того, в каком разряде она
стоит.
– Да, да, я вспомнил, – радостно сказал Паша,
– нам в школе рассказывали. Вот если взять, например, число 358, то у него
цифра 8 относится к разряду единиц, цифра 5 – к разряду десятков, а вот цифра 3
– к разряду сотен.
– Всё правильно, Паша! – подбодрил мальчика Электроша. Самый младший разряд – разряд единиц. Им
заканчивается любое число. С него же начинают отсчитывать разряды.
Обратите внимание: числа читают слева направо,
а разряды отсчитывают наоборот – справа налево. Итак, первый – это разряд
единиц. Следующий за ним разряд – разряд десятков. Сделав ещё шаг
влево от десятков, получаем разряд сотен.
Если в числе отсутствует какой-либо разряд,
то в записи числа на его месте будет стоять цифра 0 и при чтении числа данный
разряд не называют.
– Мы с Сашей хотели прочитать число, которое
у него получилось, – перебил Паша. – Посмотри, какое большущее число у него
вышло.
– Ребята,
прочитать это число совсем не сложно, – сказал Электроша. – Сейчас я вам покажу,
как это сделать.
Итак, чтобы прочитать многозначное число,
цифры его записи нужно мысленно разбить справа налево на группы по три цифры в
каждой, при этом крайняя слева группа цифр может состоять необязательно только
из трёх цифр, в ней могут быть две, как в нашем числе, или даже одна цифра. Эти
Эти
группы называют классами.
– Классами? – уточнил Саша. Ты ничего не
путаешь, Электроша? В классах учатся в школе. Числа
же не учатся в школе.
– Именно классами! – улыбнулся Электроша. – Многозначные числа разбивают на классы для
удобства их чтения и записи. Единицы, десятки, сотни образуют первый класс – класс
единиц. Следующие три цифры числа образуют соответственно разряды: единицы
тысяч, десятки тысяч, сотни тысяч. Единицы тысяч, десятки тысяч и сотни тысяч
образуют второй класс – класс тысяч. Если мы продвинемся ещё дальше
влево, то обнаружим ещё три разряда: единицы миллионов, десятки миллионов и
сотни миллионов. Единицы миллионов, десятки миллионов, сотни миллионов образуют
третий класс – класс миллионов. Следующие три цифры числа образуют
соответственно разряды: единицы миллиардов, десятки миллиардов и сотни
миллиардов, а вместе они составляют четвёртый класс – класс миллиардов.
– Я понял, как назвать моё число! – вскрикнул
Саша. – Это число два десятка миллиардов, одна сотня миллионов…
– Нет, Саша! – перебил мальчика Электроша. – Ты не до конца понял.
При чтении многозначного числа число,
записанное в каждом классе, читают как трёхзначное, двузначное или однозначное,
добавляя при этом название класса. Только вот название класса единиц, как
правило, не произносят.
– А, понятно, – обрадовался Саша. – Значит, в
моём числе 20 миллиардов?
– Правильно! – сказал Электроша.
– Может, ты сможешь назвать всё число?
– Я попробую, – ответил Саша. – Моё число, –
продолжил он, – можно прочитать так: 20 миллиардов 172 миллиона 17 тысяч 201.
– Всё правильно, Саша! – сказал Электроша. – С чтением многозначного числа ты справился на
отлично. Ещё вам с Пашей полезно будет узнать, как правильно записывать
многозначные числа.
Чтобы записать многозначное число, вам
пригодятся следующие правила:
1. Многозначные числа записывают слева
Многозначные числа записывают слева
направо и начинают со старшего разряда.
2. Во всех классах, кроме старшего, должно
быть по три цифры.
3. Для удобства чтения между классами можно
оставить небольшой промежуток.
4. Если отсутствуют единицы какого-либо
разряда, вместо них пишут нули.
5. Если отсутствует целый класс, то вместо
него пишут три нуля.
– Ребята, давайте вы попробуете сами записать
многозначное число! – предложил Электроша. – Слушайте
внимательно число: двадцать три миллиона пять тысяч двадцать три.
– Какие вы молодцы! – обрадовался за ребят Электроша. – Всё правильно написали!
А ещё вот что вам нужно знать, – продолжил
он. – Запись натуральных чисел, которой мы пользуемся, называют десятичной.
Такое название связано с тем, что 10 – это основа десятичной нумерации. Самое
главное для вас сейчас – это понять, что десять единиц одного разряда образуют
одну единицу следующего за ним разряда. Например, 10 единиц составляют 1 десяток,
Например, 10 единиц составляют 1 десяток,
в свою очередь, 10 десятков – 1 сотню и так далее.
Числа 10, 100, 1000 и так далее называют разрядными
единицами.
Зная это, вы сможете любое натуральное число
представить в виде суммы разрядных слагаемых. К примеру, возьмём число 8 543.
Его можно записать суммой разрядных слагаемых так:
8 543 = 8 000 + 500 + 40 + 3.
Или вот так: 8 543 = 8 · 1 000 + 5
· 100 + 4 · 10 + 3.
Последнее равенство называют записью числа 8 543
в виде суммы разрядных слагаемых.
– А теперь, ребята, давайте посмотрим, как вы
всё поняли и выполним несколько заданий.
Задание первое: прочитайте число
.
Решение: мысленно делим наше число на группы
по три цифры начиная справа. Три первых цифры составляют класс единиц, три
следующих – класс тысяч, ещё три следом – класс миллионов и последние – класс
миллиардов. Видим, что в классе миллионов и классе тысяч стоят нули, значит, в
этих классах отсутствуют единицы в разрядах. Тогда указанное число – пятьдесят
Тогда указанное число – пятьдесят
миллиардов триста.
Следующее задание: запишите цифрами число
пять миллионов одиннадцать тысяч шестьсот один.
Решение: число пишем слева направо. Старший
класс в нашем числе – миллионы, и их пять, значит, записываем цифру 5.
Следующий класс – тысячи. Сказано, что в числе их одиннадцать, значит,
отсутствует разряд сотен и вместо него мы запишем цифру 0. За ней ставим 11. И
последний класс в этом числе – класс единиц, их 601, разряд десятков отсутствует,
на его месте ставим цифру 0.
И последнее задание: запишите число 7 506 в
виде суммы разрядных слагаемых.
Решение: у нас в числе семь тысяч, значит,
пишем … дальше идёт класс единиц… пишем … видим в числе отсутствует разряд десятков, там стоит 0…
значит, дальше пишем .
Презентация по теме «Натуральные числа. Десятичная запись натуральных чисел» | Презентация к уроку по алгебре (5 класс) на тему:
Слайд 1
РЯД НАТУРАЛЬНЫХ ЧИСЕЛ. ЦИФРЫ. ДЕСЯТИЧНАЯ ЗАПИСЬ НАТУРАЛЬНЫХ ЧИСЕЛ.
ЦИФРЫ. ДЕСЯТИЧНАЯ ЗАПИСЬ НАТУРАЛЬНЫХ ЧИСЕЛ.
Слайд 2
Использовать числа люди стали уже в глубокой древности. Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, которые используются при счете предметов, называют НАТУРАЛЬНЫМИ от латинского слова natura , что означает природа
Слайд 3
Как здания строят из кирпичей, а слова складывают из букв, так и натуральные числа записывают с помощью специальных знаков, которые называют ЦИФРАМИ. Этих цифр десять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Слайд 4
Однозначные – натуральные числа, записанные одной цифрой. Двузначные – натуральные числа, записанные двумя цифрами. Трехзначные – натуральные числа, записанные тремя числами и т.д. Многозначные – все числа кроме однозначных.
Слайд 5
КЛАСС МИЛЛИАРДОВ КЛАСС МИЛЛИОНОВ КЛАСС ТЫСЯЧ КЛАСС ЕДИНИЦ СОТНИ МИЛЛИАРДОВ ДЕСЯТКИ МИЛЛИАРДОВ ЕДИНИЦЫ МИЛЛИАРДОВ СОТНИ МИЛЛИОНОВ ДЕСЯТКИ МИЛЛИОНОВ ЕДИНИЦЫ МИЛЛИОНОВ СОТНИ ТЫСЯЧ ДЕСЯТКИ ТЫСЯЧ ЕДИНИЦЫ ТЫСЯЧ СОТНИ ДЕСЯТКИ ЕДИНИЦЫ Чтобы прочесть многозначное число, цифры его записи разбивают на группы по три цифры слева на право. Эти группы называют КЛАССАМИ .
Эти группы называют КЛАССАМИ .
Слайд 6
ПРАВИЛО ЧТЕНИЯ ЧИСЕЛ Разбиваем число на классы, отделяем по три цифры справа налево Прочитать число 1803742150 Читаем число слева направо: называем число, представленное первой группой цифр и название класса, затем называем число представленное второй группой цифр и название класса и т.д . Если все три разряда заполнены нулями, то при чтении этот класс пропускают
Слайд 7
КЛАСС МИЛЛИАРДОВ КЛАСС МИЛЛИОНОВ КЛАСС ТЫСЯЧ КЛАСС ЕДИНИЦ 1 8 0 3 7 4 2 1 5 0 9 18 037 421 509 восемнадцать м иллиардов тридцать семь миллионов четыреста двадцать одна тысяча пятьсот девять ? Сколько в данном числе : единиц, десятков, сотен, десятков тысяч, сотен миллионов, единиц миллиардов
Слайд 8
Запись натуральных чисел называют ДЕСЯТИЧНОЙ. Десять единиц каждого ряда составляют единицу следующего старшего разряда.
Слайд 9
3758 = 3000 + 700 + 50 + 8 сумма разрядных слагаемых
Слайд 10
ПРАВИЛО ЗАПИСИ ЧИСЕЛ пят ь сот, шест ь сот, сем ь сот, восем ь сот, девят ь сот пишутся с мягким знаком ми лл ион, ми лл иард, три лл ион пишутся с двумя буквами «л» Используются сокращения: единица – ед. , сотня – сот., десяток – дес ., тысяча – тыс., миллион – млн., миллиард – млрд.
, сотня – сот., десяток – дес ., тысяча – тыс., миллион – млн., миллиард – млрд.
Слайд 11
«ЧИСЛА – ВЕЛИКАНЫ» биллион (миллиард)– тысяча миллионов триллион — тысяча биллионов приписывая каждый раз по три нуля получаем: квадриллион, квинтиллион, секстиллион, септиллион, октиллион , нониллион и т.дю
Слайд 12
Выполните задание: Запишите десятичной записью число: а ) 12 миллиардов 307 миллионов 234 тысячи 52; б ) сорок два миллиона триста тысяч пятьдесят семь. 2. Запишите в виде суммы разрядных слагаемых: а ) 937; б) 589307. 3. Запишите число, которое на : а ) 5 больше наименьшего двузначного числа; б) на 7 меньше наибольшего трехзначного числа.
Слайд 13
Решение а) 12 307 234 52 б) 42 300 057 а) б) 3. а) 15 б) 992
Слайд 14
Ответьте на вопросы: Сколько знаков используют для записи натуральных чисел в десятичной системе? Какие натуральные числа называют однозначными? Двузначными? Трехзначными? Многозначными? Какая цифра не может стоять в начале записи натурального числа? Является ли 0 натуральным числом? Как называют группы по три цифры, на которые разбивают многозначные числа справа налево? Назовите по порядку первые четыре класса в записи натуральных чисел. Сколько разрядов имеет каждый класс? Как их называют?
Сколько разрядов имеет каждый класс? Как их называют?
Десятичная запись числа | Презентация к уроку по математике (5 класс) на тему:
Слайд 1
04.09.2017 К л а с с н а я р а б о т а Десятичная запись числа
Слайд 2
Использовать числа люди стали уже в глубокой древности. Числа 1, 2, 3, 4, 5, 6, 7, 8, 9,… , которые используются при счете предметов, называют НАТУРАЛЬНЫМИ от латинского слова « natura », что означает природа
Слайд 3
Как здания строят из кирпичей, а слова складывают из букв, так и натуральные числа записывают с помощью специальных знаков, которые называют ЦИФРАМИ. Этих цифр десять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Слайд 4
Однозначные – натуральные числа, записанные одной цифрой Двузначные – натуральные числа, записанные двумя цифрами Трехзначные – натуральные числа, записанные тремя цифрами Многозначные – все числа, кроме однозначных
Слайд 5
Чтобы прочесть многозначное число, надо цифры его записи разбить на группы по три цифры слева на право. Эти группы называют КЛАССАМИ
Эти группы называют КЛАССАМИ
Слайд 6
КЛАСС МИЛЛИАРДОВ КЛАСС МИЛЛИОНОВ КЛАСС ТЫСЯЧ КЛАСС ЕДИНИЦ СОТНИ МИЛЛИАРДОВ ДЕСЯТКИ МИЛЛИАРДОВ ЕДИНИЦЫ МИЛЛИАРДОВ СОТНИ МИЛЛИОНОВ ДЕСЯТКИ МИЛЛИОНОВ ЕДИНИЦЫ МИЛЛИОНОВ СОТНИ ТЫСЯЧ ДЕСЯТКИ ТЫСЯЧ ЕДИНИЦЫ ТЫСЯЧ СОТНИ ДЕСЯТКИ ЕДИНИЦЫ
Слайд 7
ПРАВИЛО ЧТЕНИЯ ЧИСЕЛ 2. Читаем число слева направо: называем число, представленное первой, группой цифр и название класса, затем называем число представленное второй группой цифр и название класса и т.д. 3. Если все три разряда заполнены нулями, то при чтении этот класс пропускают 1. Разбиваем число на классы, отделяем по три цифры справа налево
Слайд 8
Прочитать число 1803742150 037 421 509 восемнадцать миллиардов тридцать семь миллионов четыреста двадцать одна тысяча пятьсот девять КЛАСС МИЛЛИАРДОВ КЛАСС МИЛЛИОНОВ КЛАСС ТЫСЯЧ КЛАСС ЕДИНИЦ 1 8 0 3 7 4 2 1 5 0 9
Слайд 9
? Сколько в данном числе: единиц, десятков, сотен, десятков тысяч, сотен миллионов, единиц миллиардов 18 037 421 509
Слайд 10
Запись натуральных чисел называют ДЕСЯТИЧНОЙ Десять единиц каждого рязряда составляют единицу следующего старшего разряда
Слайд 11
пят Ь сот , шест Ь сот , сем Ь сот , восем Ь сот , девят Ь сот пишутся с мягким знаком ми ЛЛ ион , ми ЛЛ иард , три ЛЛ ион пишутся с двумя буквами «л» Используются сокращения: единица – ед. , сотня – сот., десяток – дес ., тысяча – тыс., миллион – млн., миллиард – млрд. ПРАВИЛО ЗАПИСИ ЧИСЕЛ
, сотня – сот., десяток – дес ., тысяча – тыс., миллион – млн., миллиард – млрд. ПРАВИЛО ЗАПИСИ ЧИСЕЛ
Слайд 12
«ЧИСЛА ВЕЛИКАНЫ» биллион (миллиард) – тысяча миллионов триллион — тысяча биллионов приписывая каждый раз по три нуля получаем: квадриллион , квинтиллион , секстиллион , септиллион , октиллион , нониллион и т.д.
Слайд 13
Домашнее задание Ответьте на вопросы: Сколько знаков используют для записи натуральных чисел в десятичной системе? Какие натуральные числа называют однозначными? Двузначными? Трехзначными? Многозначными? Какая цифра не может стоять в начале записи натурального числа? Является ли 0 натуральным числом? Как называют группы по три цифры, на которые разбивают многозначные числа справа налево? Назовите по порядку первые четыре класса в записи натуральных чисел. Сколько разрядов имеет каждый класс? Как их называют?
Математика 5класс презентация «Цифры. Десятичная запись натуральных чисел»
Натуральные числа
Л. С. Атанасян. Геометрия 10-11
С. Атанасян. Геометрия 10-11
5 класс
Натуральные числа
Натуральные числа
Натуральные числа – это числа, употребляемые при счёте предметов.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 …
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Является ли 0 натуральным числом?
Назовите наименьшее натуральное число.
Назовите наибольшее натуральное число.
Какие числа называются однозначными? двузначными? многозначными?
Как прочитать число?
Чтобы прочитать число надо:
назвать слева по очереди число единиц каждого класса + название класса
Не произносят
- название класса единиц
- название класса все три цифры, которого – нули
Классная работа
08.09.16 г.
Цифры. Десятичная запись
Десятичная запись
натуральных чисел
Обозначение натуральных чисел
Класс единиц
Класс миллионов
Класс миллиардов
Класс тысяч
ед.
сот.
ед.
сот.
ед.
сот.
ед.
сот.
дес.
дес.
дес.
дес.
2 3 5
9 4 6 1 3 4
4 1 5 2 2 4 5 7 9
7 6 2 9 4 5 7 8 1 4 5 2
1 2 1
2 3 5
2 3 5
2 3 5
5 2 2
2 3 5
9 1 4
7 6
2 3 5
2 3 5
2 8 7
2 4 4
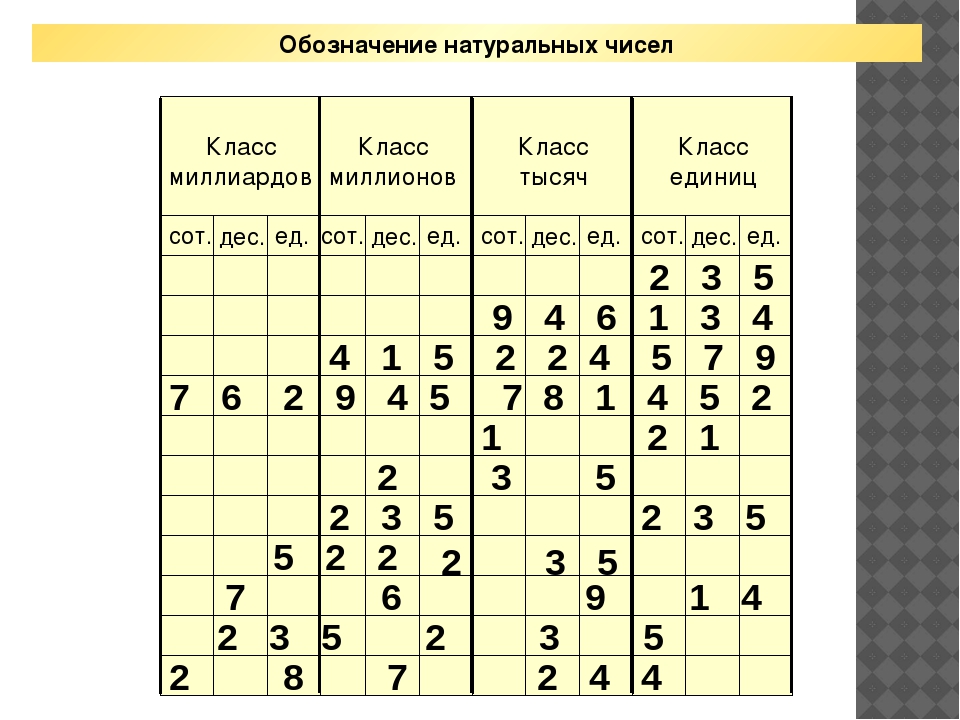
Прочитайте и запишите числа из таблицы разрядов
проверь
Класс миллионов
Класс миллиардов
Класс единиц
Класс тысяч
с е б я
сот.
сот.
ед.
ед.
ед.
дес.
дес.
сот.
ед.
дес.
сот.
дес.
2 3 5
4 6 8
2 350 040 680
2 3 5
9 1 4
20 350 901 400
2 3 5
235 000 000
2 3 5
2 035 000 000
2 3 5
7 7 6
200 350 007 076
5 2 2
2 3 5
23 050 522 000
203 050 020 305
2 3 5
2 3 5
23 500 000 235
2 3 5
2 3 5
2 3 5
203 500 203 050
2 3 5
2 3 5
2 3 5
20 305 235 000
2 3 5
2 3 5
2 350 000 000
Назовите 15 первых натуральных чисел.
Есть ли в натуральном ряду:
а) первое число; б) последнее число?
У каждого ли числа в натуральном ряду есть:
а) последующее число; б) предшествующее число?
Считают ли число нуль натуральным числом?
Назовите число, которое следует в натуральном ряду за числом: 13, 276, 3590, 999 999.
Назовите число, которое предшествует в натуральном ряду числу: 2, 74, 100, 3050, 438 109, 1 000 000.
Сколько чисел в натуральном ряду:
а) от 1 до 29; б) от 1 до 38;
в) от 30 до 38; г) от 100 до 125?
Сколько чисел в натуральном ряду между числами:
а) 1 и 29; б) 1 и 38;
в) 30 и 38; г) 100 и 125?
Сколько знаков используют для записи натуральных чисел в десятичной системе? Как называют эти знаки?
Какие цифры могут стоять в любом разряде числа, кроме высшего?
Прочитайте следующие числа:
10, 100, 1000, 10 000, 100 000, 1 000 000, 10 000 000
Запишите следующие числа: сто тысяч, миллион, десять тысяч, сто миллионов, миллиард, десять миллионов, сто миллиардов, десять миллиардов.
Запишите и прочитайте число:
а) двузначное; б) трехзначное;
в) четырехзначное; г) семизначное .
Запишите первое и последнее в натуральном ряду число: а)двузначное; б)трехзначное;
в) четырехзначное
Сколько натуральных чисел:
а) однозначных; б) двузначных; в) трехзначных?
B записи каждого из чисел назовите цифры разрядов единиц, десятков, сотен, тысяч, десятков тысяч, сотен тысяч т. д.
а) 123; б) 1240; в) 102;
г) 4397; д) 13 487 905; e) 2 000 009.
Запишите число, состоящее из:
а) 1 тысячи, 2 сотен, 3 десятков и 5 единиц;
б) 5 десятков тысяч, 9 тысяч, 7 сотен и 4 единиц;
в) 8 сотен и 6 десятков;
г) 7 сотен тысяч и 3 десятков.
Прочитайте следующие числа, запишите их в виде суммы разрядных слагаемых:
а) 48; б) 159; в) 2945; г) 34 196;
д) 102; e) 150; ж) 4067; з) 10 504; и) 6401; к) 5060; л) 12 007; м) 104 090.
Запишите числа:
а) триста двадцать;
б) сто тридцать тысяч пятьдесят;
в) двести восемь тысяч двадцать четыре;
г) два миллиона три тысячи;
д) одиннадцать миллионов двенадцать.
Запишите все трехзначные числа, в записи которых используются цифры: а) 5, 6, 7; б) 0, 1, 2
без повторения одинаковых цифр в записи одного числа.
Запишите все трехзначные числа, в записи которых используются цифры: а) 5, 6, 7; б) 0, 1, 2,
если разрешается повторять одинаковые цифры в записи одного числа.
Самостоятельная работа
Вариант 1
Вариант 2
1. Запишите цифрами число:
1. Запишите цифрами число:
а) два миллиона двести тридцать пять тысяч двенадцать;
а) три миллиона четыреста двадцать шесть тысяч тринадцать;
б) десять миллионов сто две тысячи четыреста.
б) двадцать миллионов триста пять тысяч семьсот.
2. Запишите число 3782 в виде суммы разрядных слагаемых.
2. Запишите число 7238 в виде суммы разрядных слагаемых.
3. Сравните числа:
3. Сравните числа:
а) 999 и 1001; б) 3125 и 3215;
а) 888 и 1002; б) 4972 и 4297;
в) 329 и 400; г) 12 345 и 12 345.
в) 700 и 691; г) 10101 и 10101.
4. Сколько чисел в натуральном ряду: а) от 35 до 100; б) между 35 и 100?
4. Сколько чисел в натуральном ряду: а) от 23 до 100; б) между 23 и 100?
5. Выпишите в порядке возрастания все двузначные числа, в записи которых используются цифры 2, 4 и 6, если не разрешается использовать одинаковые цифры в записи одного числа.
5. Выпишите в порядке возрастания все двузначные числа, в записи которых используются цифры 3, 5 и 7, если не разрешается использовать одинаковые цифры в записи одного числа.
Мерзляк 5 класс — § 2. Цифры. Десятичная запись натуральных чисел
Вопросы к параграфу
- Сколько знаков используют для записи натуральных чисел в десятичной системе? Как называют эти знаки? — для записи натуральных чисел используют 9 знаков, их называют цифры.
- Какие натуральные числа называют однозначными? Двузначными? Трёхзначными? Многозначными?
- однозначные числа — это числа, записанные одной цифрой: 1, 2, 5 и т.д.
- двузначные числа — это числа, записанные двумя цифрами: 12, 35, 46 и т.д.
- трёхзначные числа — это числа, записанные тремя цифрами: 326, 759, 486 и т.д.
- многозначные числа — это числа, записанные двумя и более цифрами: 65, 15 268, 333 и т.д.
- Какая цифра не может стоять первой в записи натурального числа? — первой не может быть цифра 0.
- Как называют группы по три цифры, на которые разбивают многозначные числа справа налево? — эти группы называют классами.

- Назовите по порядку первые четыре класса в записи натуральных чисел — это:
- класс единиц
- класс тысяч
- класс миллионов
- класс миллиардов
- Сколько разрядов имеет каждый класс? Как их называют? — каждый класс имеет три разряда, их называют:
- единицы
- десятки
- сотни
- Как называют запись натурального числа, которой мы пользуемся? — десятичная запись.
- С чем связано название десятичной записи натуральных чисел? — это связано с тем, что десять единиц предыдущего разряда всегда составляют одну единицу следующего. Например:
- 10 единиц = 1 десяток
- 10 десятков = 1 сотня
- 10 сотен = 1 тысяча
- 10 тысяч = 1 десяток тысяч
- 10 десятков тысяч = 1 сотня тысяч
- 10 сотен тысяч = 1 миллион
- и т.д.
Решаем устно
1. На сколько:
- 18 больше 6 — на 12 (18 — 6 = 12)
- 4 меньше 12 — на 8 (12 — 4 = 8)
2. Во сколько раз:
Во сколько раз:
- 18 больше 6 — в 3 раза (18 : 6 = 3)
- 4 меньше 12 — в 3 раза (12 : 4 = 3)
3. Вычислите:
- 12 • 5 + 1 = 60 + 1 = 61
- 12 • 5 — 1 = 60 — 1 = 59
- 12 • (5 + 1) = 12 • 6 = 72
- 12 • (5 — 1) = 12 • 4 = 48
- 12 : (5 + 1) = 12 : 6 = 2
- 12 : (5 — 1) = 12 : 4 = 3
4. Назовите пять последовательных натуральных чисел, начиная с числа:
- 423 — 423, 424, 425, 426, 427
- 1 658 — 1 658, 1 659, 1 660, 1 661, 1 662
- 2 997 — 2 997, 2 998, 2 999, 3 000, 3 001
5. Назовите в обратном порядке пять последовательных натуральных чисел, начиная с числа:
- 358 — 358, 357, 356, 355, 354
- 1 573 — 1 573, 1 572, 1 571, 1 570, 1 569
- 4 001 — 4 001, 4 000, 3 999, 3 998, 3 997
6. Назовите все четырёхзначные числа, сумма цифр которых равна 2.
Назовите все четырёхзначные числа, сумма цифр которых равна 2.
1001, 1010, 1100, 2000
7. Двузначное число оканчивается цифрой 4. Если к этому числу прибавить число, записанное теми же цифрами, но в обратном порядке, то получим число 99. Найдите эти два числа.
Нам известно:
- первое число двузначное и оканчивается цифрой 4;
- второе число тоже двузначное, но начинается с цифры 4;
- сумма этих чисел равна 99.
Запишем известное, как пример в столбик
Ответ: первое искомое число 54, а второе число 45.
Упражнения
17. Назовите разряд, в котором стоит цифра 4 в записи числа:
- 34 — разряд единиц
- 246 — разряд десятков
- 473 — разряд сотен
- 24 569 — разряд единиц тысяч
18. Прочитайте число:
- 234 642 — двести тридцать четыре тысячи шестьсот сорок два
- 502 013 — пятьсот две тысячи тринадцать
- 9 145 679 — девять миллионов сто сорок пять тысяч шестьсот семьдесят десять
- 105 289 001 — сто пять миллионов двести восемьдесят девять тысяч один
- 6 704 917 320 — шесть миллиардов семьсот четыре миллиона девятьсот семнадцать тысяч триста двадцать
- 72 016 050 400 — семьдесят два миллиарда шестнадцать миллионов пятьдесят тысяч четыреста
- 491 872 653 000 — четыреста девяносто один миллиард восемьсот семьдесят два миллиона шестьсот пятьдесят три тысячи
- 305 002 800 748 — триста пять миллиардов два миллиона восемьсот тысяч семьсот сорок восемь
19. Запишите десятичной записью число:
Запишите десятичной записью число:
- 34 миллиона 384 тысячи 523 — 34 384 523
- 85 миллионов 128 тысяч 23 — 85 128 023
- 16 миллионов 26 тысяч 4 — 16 026 004
- 6 миллионов 60 тысяч 17 — 6 060 017
- 8 миллиардов 801 миллион 30 тысяч 5 — 8 801 030 5
- 22 миллиарда 33 миллиона 418 — 22 033 000 418
- 251 миллиард 538 — 251 000 000 538
- 46 миллиардов 854 — 46 000 000 854
- 607 миллиардов 3 — 607 000 000 003
20. Запишите десятичной записью число:
- 23 миллиона 275 тысяч 649 — 23 275 649
- 56 миллионов 319 тысяч 48 — 56 319 048
- 12 миллионов 20 тысяч 21 — 12 020 021
- 8 миллионов 7 тысяч 3 — 8 007 003
- 6 миллиардов 325 миллионов 800 тысяч 954 — 6 325 800 000
- 14 миллиардов 52 миллиона 819 — 14 052 000 819
- 368 миллиардов 742 тысячи — 368 000 742 000
- 92 миллиарда 29 — 92 000 000 029
21. Запишите десятичной записью число:
Запишите десятичной записью число:
- сорок шесть миллиардов четыреста пятьдесят семь миллионов семьсот двадцать семь тысяч триста восемьдесят восемь — 46 457 727 388
- шестьсот тридцать два миллиарда двести четыре миллиона тридцать пять тысяч сорок семь — 632 204 035 047
- сто пять миллиардов пятьсот тридцать девять тысяч сто — 105 000 538 100
- тридцать миллиардов двадцать тысяч девяносто — 30 000 020 090
- восемь миллиардов семь миллионов пятнадцать тысяч четырнадцать — 8 007 015 014
- один миллиард две тысячи два — 1 000 002 002
22. Запишите десятичной записью число:
- три миллиона триста тридцать три тысячи триста тридцать три — 3 333 333
- три миллиона триста тысяч — 3 300 000
- три миллиона три тысячи — 3 003 000
- три миллиона тридцать — 3 000 030
- три миллиона тридцать тысяч триста — 3 030 300
- три миллиона три тысячи три — 3 003 003
- три миллиона три — 3 000 003
23. Запишите десятичной записью число:
Запишите десятичной записью число:
- шестьдесят восемь миллиардов двести сорок девять миллионов девятьсот пятьдесят четыре тысячи семьсот двадцать три — 68 249 954 723
- восемьсот четырнадцать миллиардов сто девять миллионов две тысячи тридцать два — 814 109 002 032
- триста семь миллиардов шестьсот двадцать одна тысяча четыреста — 307 000 621 400
- девяносто миллиардов десять тысяч двадцать — 90 000 010 020
- два миллиарда три миллиона четыре тысячи пять — 2 003 004 005
- один миллиард одна тысяча один — 1 000 001 001
24. Запишите и прочитайте число, которое образуется, если записать число 514 подряд:
- два раза — 514 514 — пятьсот четырнадцать тысяч пятьсот четырнадцать
- три раза — 514 514 514 — пятьсот четырнадцать миллионов пятьсот четырнадцать тысяч пятьсот четырнадцать
- четыре раза — 514 514 514 514 — пятьсот четырнадцать миллиардов пятьсот четырнадцать миллионов пятьсот четырнадцать тысяч пятьсот четырнадцать
25. Запишите и прочитайте число, которое образуется, если записать число 48 подряд:
Запишите и прочитайте число, которое образуется, если записать число 48 подряд:
- два раза — 4 848 — четыре тысячи восемьсот сорок восемь
- три раза — 484 848 — четыреста восемьдесят четыре тысячи восемьсот сорок восемь
- четыре раза — 48 484 848 — сорок восемь миллионов четыреста восемьдесят четыре тысячи восемьсот сорок восемь
- пять раз — 4 848 484 848 — четыре миллиарда восемьсот сорок восемь миллионов четыреста восемьдесят четыре тысячи восемьсот сорок восемь
26. Запишите в виде суммы разрядных слагаемых число:
- 846 = 8 • 100 + 4 • 10 + 6 • 1
- 2 375 = 2 • 1 000 + 3 • 100 + 7 • 10 + 5 • 1
- 12 619 = 1 • 10 000 + 2 • 1 000 + 6 • 100 + 1 • 10 + 9 • 1
- 791 105 = 7 • 100 000 + 9 • 10 000 + 1 • 1 000 + 1 • 100 + 0 • 10 + 5 • 1
- 32 598 009 = 3 • 10 000 000 + 2 • 1 000 000 + 5 • 100 000 + 9 • 10 000 + 8 • 1 000 + 0 • 100 + 0 • 10 + 9 • 1
- 540 007 020 = 5 • 100 000 000 + 4 • 10 000 000 + 0 • 1 000 000 + 0 • 100 000 + 0 • 10 000 + 7 • 1 000 + 0 • 100 + 2 • 10 + 0 • 1
27. Запишите в виде суммы разрядных слагаемых число:
Запишите в виде суммы разрядных слагаемых число:
- 34 729 = 3 • 10 000 + 4 • 1 000 + 7 • 100 + 2 • 10 + 9 • 1
- 75 194 = 7 • 10 000 + 5 • 1 000 + 1 • 100 + 9 • 10 + 4 • 1
- 478 254 = 4 • 100 000 + 7 • 10 000 + 8 • 1 000 + 2 • 100 + 5 • 10 + 4 • 1
- 189 390 = 1 • 100 000 + 8 • 10 000 + 8 • 1 000 + 3 • 100 + 9 • 10 + 0 • 1
- 23 487 901 = 2 • 10 000 000 + 3 • 1 000 000 + 4 • 100 000 + 8 • 10 000 + 7 • 1 000 + 9 • 100 + 0 • 10 + 1 • 1
- 140 028 045 = 1 • 100 000 000 + 4 • 10 000 000 + 0 • 1 000 000 + 0 • 100 000 + 2 • 10 000 + 8 • 1 000 + 2 • 100 + 4 • 10 + 5 • 1
28. Запишите число, которое:
- на 1 меньше наименьшего трёхзначного числа — наименьшее трёхзначное число — это 100, 100 — 1 = 99
- на 4 больше наибольшего трёхзначного числа — наибольшее трёхзначное число — это 999, 999 + 4 = 1 003
- на 5 меньше наименьшего пятизначного числа — наименьшее пятизначное число — это 10 000, 10 000 — 5 = 9 995
- на 6 больше наибольшего шестизначного числа — наибольшее шестизначное число — это 999 999, 999 999 + 6 = 1 000 005
- на 7 больше наименьшего восьмизначного числа — наименьшее восьмизначное число — это 10 000 000, 10 000 000 + 7 = 10 000 007
29. Запишите наибольшее восьмизначное число, а также следующее и предыдущее числа.
Запишите наибольшее восьмизначное число, а также следующее и предыдущее числа.
- наибольшее восьмизначное число — 99 999 999
- следующее за ним число — 99 999 999 + 1 = 100 000 000
- предыдущее ему число — 99 999 999 — 1 = 99 999 998
30. Запишите наименьшее семизначное число, а также следующее и предыдущее числа.
- наименьшее семизначное число — 1 000 000
- следующее за ним число — 1 000 000 + 1 = 1 000 001
- предыдущее ему число — 1 000 000 — 1 = 999 999
31. Двузначное число записали подряд два раза. Во сколько раз полученное четырёхзначное число больше данного двузначного числа?
Возьмём три произвольных двузначных числа. Например: 12, 54 и 61. Из них получатся четырехзначные числа: 1 212, 5 454 и 6 161 соответственно. Посчитаем, во сколько раз полученные четырёхзначные числа больше исходных двузначных:
Такое соотношение будет справедливо для всех без исключения двухзначных чисел.
Ответ: в 101 раз.
32. Трёхзначное число записали подряд два раза. Во сколько раз полученное шестизначное число больше данного трёхзначного числа?
Возьмём три произвольных трёхзначных числа. Например: 352, 423 и 801. Из них получатся шестизначные числа: 352 352, 423 423 и 801 801.
Посчитаем, во сколько раз полученные шестизначные числа больше исходных трёхзначных:
Такое соотношение будет справедливо для всех без исключения трёхзначных чисел.
Ответ: в 1 001 раз.
33. В книге пронумерованы страницы с первой по сто семьдесят вторую. Сколько цифр напечатано при нумерации страниц?
Посчитаем, сколько в книге страниц с однозначными номерами, с двузначными и с трехзначными номерами:
- однозначные номера — с 1 по 9 страницу, то есть 9 страниц — 1 • 9 = 9 (цифр) — использовано для нумерации страниц с однозначными номерами;
- двузначные номера — с 10 по 99 страницу, то есть 90 страниц — 2 • 90 = 180 (цифр) — использовано для нумерации страниц с двузначными номерами;
- трёхзначные номера — с 100 по 172 страницу, то есть 73 страницы — 3 • 73 = 219 (цифр) — использовано для нумерации страниц с трёхзначными номерами.

Теперь найдём сумму цифр, использованных для однозначных, двузначных и трёхзначных номеров:
9 + 180 + 219 = 408 (цифр) — напечатано при нумерации книги.
Ответ: 408 цифр.
34. Для нумерации страниц книги напечатано 2 004 цифры. Сколько страниц в этой книге?
Допустим, что нумерация в книге начинается с 1 страницы.
Для того, чтобы пронумеровать все страницы с однозначными номерами (с 1 по 9) потребуется 9 цифр:
1) 1 • 9 = 9 (цифр) — использовано для нумерации страниц с однозначными номерами.
Для того, чтобы пронумеровать все страницы с двузначными номерами (с 10 по 99) потребуется 180 цифр:
2) 2 • 90 = 180 (цифр) — использовано для нумерации страниц с двузначными номерами.
3) 2 004 — 180 — 9 = 1 815 (цифр) — осталось для нумерации остальных страниц.
Максимально возможное число страниц с трёхзначными номерами (с 100 по 999) — 900 штук. На такое количество страниц потребовалось бы 2700 цифр
4) 3 • 900 = 2 700 (цифр) — потребуется для нумерации максимального количества страниц с трёхзначными номерами.
5) 1 815 < 2 700, значит все оставшиеся страницы трёхзначные.
6) 1 815 : 3 = 605 (страниц) — количество страниц с трёхзначными номерами.
Сложим количество страниц с однозначными, двузначными и трёхзначными номерами:
7) 9 + 90 + 605 = 704 (страницы) — в книге.
Ответ: в книге 704 страницы.
35. Каких трёхзначных чисел больше: все цифры которых чётные или все цифры которых нечётные?
Все трёхзначные числа состоят их трёх цифр:
- цифры, обозначающей сотни;
- цифры, обозначающей десятки;
- цифры, обозначающей единицы.
Если использовать для написания только чётные цифры, то:
- сотни могут быть обозначены цифрами: 2, 4, 6, 8 — 4 варианта, так как с цифры 0 число начинаться не может;
- десятки могут быть обозначены цифрами: 0, 2, 4, 6, 8 — 5 вариантов;
- единицы могут быть обозначены цифрами: 0, 2, 4, 6, 8 — 5 вариантов.
Если использовать для написания только нечётные цифры, то:
- сотни могут быть обозначены цифрами: 1, 3, 5, 7, 9 — 5 вариантов;
- десятки могут быть обозначены цифрами: 1, 3, 5, 7, 9 — 5 вариантов;
- единицы могут быть обозначены цифрами: 1, 3, 5, 7, 9 — 5 вариантов.

Для того, чтобы узнать сколько трёхзначных чисел можно написать только чётными или только нечётными цифрами, надо перемножить количество всех возможных вариантов обозначения сотен, десяткой и единиц.
- 4 • 5 • 5 = 20 • 5 = 100 (вариантов) — записи трёхзначных чисел только чётными цифрами.
- 5 • 5 • 5 = 25 • 5 = 125 (вариантов) — записи трёхзначных чисел только нечётными цифрами.
125 > 100, значит больше трёхзначных чисел, в записи которых используются только нечетные цифры.
Ответ: больше трёхзначных чисел, в записи которых используются только нечетные цифры.
Упражнения для повторения
36. Вычислите:
37. Выполните действия:
38. Первый полёт в космос совершил в 1961 г. гражданин Советского Союза Юрий Гагарин. Через восемь лет после этого на Луну ступил первый человек — гражданин США Нейл Армстронг. Ещё через 31 год на Международной космической станции (МКС) начал работать первый экипаж. Сколько лет работают космонавты на МКС?
Сколько лет работают космонавты на МКС?
1) 1961 + 8 = 1969 (год) — год первого полёта человека на Луну.
2) 1969 + 31 = 2000 (год) — год начала работы первого экипажа на Международной космической станции МКС.
3) 2020 — 2000 = 20 (лет) — космонавты работают на Международной космической станции МКС.
Ответ: 20 лет.
39. Масса булавы Ильи Муромца равна 60 пудов, а его меча — в 12 раз меньше. Какова общая масса булавы и меча Ильи Муромца?
1) 60 : 12 = 5 (пудов) — масса меча Ильи Муромца.
2) 60 + 5 = 65 (пудов) — общая масса меча и булавы.
Ответ: 65 пудов.
Комментарий: Пуд — это единица измерения веса предметов, применявшаяся на Руси в старину. В пересчёте на килограммы 1 пуд примерно равен 16,4 килограмма. Так что если поверить условию задачи, то булава Ильи Муромца весила больше 982 килограммов, а его меч весил почти 82 килограмма! Ничего не скажешь, настоящий богатырь:)
40. Чтобы помочь заболевшему Карабасу-Барабасу, Дуремар решил поставить ему пиявки. Для первой процедуры он использовал 24 пиявки, а для второй — в 3 раза больше. Сколько всего пиявок понадобилось Дуремару, чтобы вылечить Карабаса-Барабаса?
Для первой процедуры он использовал 24 пиявки, а для второй — в 3 раза больше. Сколько всего пиявок понадобилось Дуремару, чтобы вылечить Карабаса-Барабаса?
1) 24 • 3 = 72 (пиявки) — понадобилось для второй процедуры.
2) 24 + 72 = 96 (пиявок) — всего понадобилось для лечения.
Ответ: 96 пиявок.
41. Вертолёт за 4 ч может пролететь 720 км. Какое расстояние он пролетит за 6 ч с той же скоростью?
Составим краткую запись в виде таблицы:
1) 720 : 4 = 180 (км/ч) — скорость движения вертолёта.
2) 180 • 6 = 1 080 (км) — пролетит вертолёт за 6 часов.
Ответ: 1 080 км.
Комментарий:
- Для того чтобы найти скорость движения, надо расстояние разделить на время (v = s : t).
- Для того, чтобы найти расстояние, надо скорость умножить на время (s = v • t).
42. За три дня кузнец Вакула изготовил 432 подковы. Сколько подков он изготовит за пять дней, работая с такой же производительностью?
1) 432 : 3 = 144 (подковы/день) — производительность кузнеца Вакулы.
2) 144 • 5 = 720 (подков) — Вакула изготовит за 5 дней.
Ответ: 720 подков.
Комментарий:
- Для того чтобы найти производительность, надо работу разделить на время .
- Для того, чтобы найти выполненную работу, надо производительность умножить на время.
Задача от мудрой совы
43. В этом году день рождения отца был в воскресенье. В какой день недели праздновала свой день рождения мать, если она на 62 дня моложе отца?
Мы знаем, что каждая неделя состоит из 7 дней:
- 1 неделя = 7 дней
- 2 недели = 14 дней
- 3 недели = 21 день
- 4 недели = 28 дней
- 5 недель = 35 дней
- 6 недель = 42 дня
- 7 недель = 49 дней
- 8 недель = 56 дней
Это значит, что 62 дня — это 8 полных недель и 6 дней. До полной недели не хватило 1 дня, то есть день рождения мамы был за один день до воскресенья — в субботу.
Ответ: в субботу.
1. 2. Проверка домашнего задания 3. Актуализация опорных знаний 4.Определение темы и цели урока II.Процессуально– познавательный этап урока 1. Закрепление материала 2. Физминутка 3. Повторение III. Рефлексивно-оценочный этап урока 1. Подведение итога урока 2. Рефлексия учебной деятельности 3. Информация о домашнем задании | 20 мин 20 мин 5-7 мин | &2 вопросы 1-8 № 20,23,38 Устно № 7 с. 10 Математический диктант (приложение) Слайд 2 Прочитайте числа, записанные в таблице разрядов, и запишите их. Проанализируйте полученные результаты. Слайд 3 Как изменяется значимость цифры при сдвиге её на один разряд влево? Как изменяется при этом само число? Какому арифметическому действию соответствует увеличение числа в 10 раз? Слайд 4 Что мы с вами получили? Слайд 5 Прочитайте числа, записанные в таблице разрядов, и запишите их. Слайд 6 Какой вывод можно сделать? Давай те теперь вспомним, какой системой счисления мы пользуемся? № 24 РТ-1 № 9, 10, 11 РТ-1 № 12 № 40 Поощрение детей, выставление отметок за урок, их комментирование, замечания учащимся Выбрать смайлик подходящего цвета. &2 № 25,27 (1, 3, 5) , 39 | Приветствие учащихся Числа 54 и 45 456 4 560 45 600 456 000 4 560 000 45 600 000 456 000 000 Увеличивается в 10 раз Число увеличивается Умножение При сдвиге всех цифр числа на один разряд влево число увеличивается в 10 раз 325 000 000 32 500 000 3 250 000 325 000 32 500 3 250 325 При сдвиге всех цифр числа на один разряд вправо число уменьшается в 10 раз Десятичной системой счисления а) 514 514 б) 514 514 514 в) 514 514 514 514 самостоятельно в парах 24*3=72 пиявки 24+72=96 пиявок | Регулятивные УУД Коммуникативные УУД Логические УУД Регулятивные УУД Коммуникативные УУД Логические УУД Коммуникативные УУД Коммуникативные УУД Личностные УУД Личностные УУД | Ф Ф Ф Ф Ф Ф И П И Ф И |
натуральных, целых, рациональных, иррациональных, действительных чисел и выше
Натуральные числа
натуральных (или , считая ) чисел — 1,2,3,4,5 и т. Д.
Д.
много натуральных чисел. Набор натуральных чисел, {1,2,3,4,5, …},
иногда для краткости пишут N .
Целые числа — натуральные числа вместе с 0.
(Примечание: некоторые учебники не согласны с этим и говорят, что натуральные числа включают 0.)
Сумма
любые два натуральных числа также являются натуральными числами (например, 4 + 2000 = 2004), а произведение любых двух натуральных чисел
натуральное число (4 × 2000 = 8000). Этот
однако это неверно для вычитания и деления.
Целые числа
целых чисел — это набор действительных чисел, состоящий из натуральных чисел, их аддитивных обратных чисел и нуля.
{…, — 5, −4, −3, −2, −1,0,1,2,3,4,5, …}
Набор целых чисел иногда
написано J или Z для краткости.
сумма, произведение и разность любых двух целых чисел также являются целыми числами. Но это не относится к делению … просто попробуйте 1 ÷ 2.
Рациональные числа
рациональных чисел
те числа, которые можно выразить как отношение между
два целых числа. Например, дроби 13 и −11118 являются
рациональное число. Все числа входят в рациональные числа,
поскольку любое целое число z можно записать как отношение z1.
Все десятичные дроби, которые заканчиваются, являются рациональными числами (начиная с 8.27 можно записать как 827100.) Десятичные дроби
которые после некоторой точки имеют повторяющийся узор, также являются рациональными:
например,
0,0833333 …. = 112.
Множество рациональных чисел замкнуто относительно всех четырех основных операций, то есть для любых двух рациональных чисел их
сумма, разница, произведение и частное также являются рациональным числом
(пока мы не делим на 0).
Иррациональные числа
Иррациональное число — это число, которое нельзя записать в виде отношения (или дроби).В десятичной форме он никогда не заканчивается и не повторяется. В
В
древние греки обнаружили, что не все числа рациональны; там
— это уравнения, которые нельзя решить с помощью отношений целых чисел.
Первое такое уравнение
для изучения было 2 = x2. Какие
само число раз равно 2?
2 является
около 1,414, поскольку 1,4142 = 1,999396, что близко к
2. Но вы никогда не попадете точно, возведя дробь в квадрат (или завершив
десятичный). Квадратный корень из 2 — иррациональное число, то есть его
десятичный эквивалент продолжается вечно, без повторяющегося шаблона:
2 = 1.41421356237309 …
Другой известный иррациональный
числа золотое сечение , число с большим
значение для биологии:
1 + 52 = 1,61803398874989 …
π (пи),
отношение длины окружности к ее диаметру:
π = 3,14159265358979 …
и е,
самое важное число в исчислении:
е = 2,71828182845904 …
Иррациональные числа можно далее разделить на алгебраических чисел, которые являются решениями некоторого полиномиального уравнения (например, 2 и золотое сечение), и трансцендентных чисел, которые не являются решениями какого-либо полиномиального уравнения. π и e оба трансцендентны.
π и e оба трансцендентны.
Реальные числа
Действительные числа — это набор чисел, содержащий все рациональные числа и все иррациональные числа. Настоящие числа — это «все числа» в числовой строке. Существует бесконечно много действительных чисел, как и бесконечно много чисел в каждом из других наборов чисел. Но можно доказать, что бесконечность действительных чисел на больше бесконечности.
«Меньший»,
или счетных бесконечности целых чисел и
rationals иногда называют ℵ0 (alef-naught),
и бесчисленных бесконечности реалов
называется ℵ1 (алеф-он).
Есть еще «большие» бесконечности,
но для этого вам следует пройти курс теории множеств!
Комплексные числа
Комплексные числа
— множество {a + bi | a и b — действительные числа}, где i — мнимая единица, −1. (нажмите здесь, чтобы
подробнее о мнимых числах и операциях с комплексными числами).
Комплексные числа включают набор действительных чисел. Действительные числа в сложной системе записываются в виде a + 0i = a. реальное число.
Действительные числа в сложной системе записываются в виде a + 0i = a. реальное число.
Этот набор иногда бывает
записывается как C для краткости.Набор комплексных чисел
важно, потому что для любого полинома p (x) с коэффициентами действительного числа все решения p (x) = 0 будут в C .
За пределами …
Есть и «большие» наборы
чисел, используемых математиками. Кватернионы ,
открытые Уильямом Х. Гамильтоном в 1845 году, образуют систему счисления с тремя
разные мнимые единицы!
Что такое натуральные числа? — Определение и примеры — Видео и стенограмма урока
Дальнейшее обсуждение и примеры натуральных чисел
В следующих примерах учащиеся продемонстрируют свои знания о множестве натуральных чисел и о том, как этот набор сравнивается с другими наборами чисел.Будут исследованы другие операции с натуральными числами, чтобы определить, является ли результат все еще натуральным числом. После выполнения примеров учащиеся должны иметь твердое представление о том, что такое натуральные числа и чем они отличаются от других наборов чисел.
После выполнения примеров учащиеся должны иметь твердое представление о том, что такое натуральные числа и чем они отличаются от других наборов чисел.
Примеры
1) Какие из следующих чисел являются натуральными? 3, 19, -9, 27,5, 1, -3. Откуда вы знаете?
2) Возведенное в квадрат натуральное число также является натуральным числом? Как насчет квадратного корня из натурального числа?
3) Целые числа, обозначаемые Z, представляют собой набор положительных или отрицательных целых чисел и нуля.Действительные числа, обозначаемые R, представляют собой набор положительных или отрицательных целых или десятичных чисел и нуля. Каждое натуральное число тоже целое? Каждое ли натуральное число также является действительным числом?
Решения
1) Числа 3, 19 и 1 являются натуральными числами, потому что они являются целыми положительными числами. -9 и -3 не являются натуральными числами, потому что они отрицательны, а 27,5 не является натуральным числом, потому что это не целое число.
2) Натуральное число в квадрате — это натуральное число, умноженное само на себя.2 = 3 * 3 = 9 по-прежнему является натуральным числом. Квадратный корень из натурального числа может быть натуральным числом, но обычно это не так. Например, квадратный корень из 4 равен 2, что является натуральным числом, но квадратный корень из 5 составляет приблизительно 2,236, что не является натуральным числом, так как это не целое число. Не гарантируется, что квадратный корень из натурального числа будет натуральным числом.
3) Поскольку набор целых чисел включает в себя положительные или отрицательные целые числа и ноль, а набор натуральных чисел является набором положительных целых чисел (и, возможно, нуля), натуральные числа удовлетворяют условиям, чтобы быть целым числом.Таким образом, каждое натуральное число также является целым числом, но не каждое целое число является натуральным числом. Точно так же, поскольку набор действительных чисел включает в себя положительные или отрицательные целые или десятичные числа и ноль, натуральное число удовлетворяет условиям, чтобы быть действительным числом. Таким образом, каждое натуральное число также является действительным числом, но не каждое действительное число является натуральным числом.
Обсуждение
На уроке мы узнали, что если вы сложите или умножите два натуральных числа, результатом будет натуральное число, и что это не работает для деления или вычитания.Означает ли это, что натуральное число, деленное на другое натуральное число, никогда не может быть натуральным числом? Всегда ли при вычитании натуральных чисел получается неестественное число?
Руководство к обсуждению
Цель обсуждения состоит в том, чтобы студенты пришли к выводу, что деление и вычитание натуральных чисел не гарантирует получение натурального числа, но есть примеры, когда результатом является натуральное число. Например, 10/5 = 2 по-прежнему является натуральным числом, но 5/10 = 0.5 нет. Точно так же 5-10 = -5 не является естественным, но 10-5 = 5 является естественным. Посмотрите, могут ли студенты придумать правило деления или вычитания натуральных чисел, для которого результат гарантированно будет естественным.
Натуральное число: определение и примеры
Определения статистики> Натуральные и целые числа
Содержание (Щелкните, чтобы перейти к этому разделу)
- Натуральное число
- Целые числа
- Почему натуральное число — это целое число?
- Пример целых чисел
- Комплекты закрытые и целые
- Свойства целых чисел
Натуральные числа — это числа, которые мы используем для счета.Они целые, неотрицательных чисел. Мы часто видим их представленными на числовой строке .
Линия на изображении выше начинается с 1 и увеличивается в значении до 5. Однако числа могут увеличиваться в значении бесконечно (обозначено пунктирной линией на изображении). Таким образом, натуральные числа могут продолжаться до бесконечности.
Набор натуральных чисел обычно обозначается символом ℕ . Например:
ℕ = {1, 2, 3, 4, 5, 6, 7…}
Набор натуральных чисел, включающий ноль, известен как целых чисел .Набор целых чисел обычно обозначается W . Например, это набор целых чисел:
W = {0, 1, 2, 3, 4, 5, 6, 7…}
Возможно, что сбивает с толку, некоторые авторы не включают ноль в набор целых чисел. В этом случае это то же самое, что и набор натуральных чисел.
Как упоминалось выше, натуральные числа должны быть целыми и положительными. Это имеет смысл по ряду причин, включая тот факт, что они считают числа.Допустим, учитель хочет подсчитать количество учеников в своем классе: она может сосчитать только всех детей.
Мы часто видим в статистике, публикуемой в Интернете, цифры, которые кажутся противоречащими «целостности» людей. Например, «средний размер семьи — 3,1 человека». Должно быть достаточно ясно, что невозможно иметь 0,1 человека, но это число является лишь средним. Среднее количество автомобилей на семью рассчитывается путем сложения общего количества автомобилей и деления на количество домашних хозяйств.После деления мы больше не работаем с натуральными числами. Скорее, у нас остается действительное число, в данном случае дробь.
Сумма или произведение натуральных чисел также являются натуральными числами. Например, 5 + 5 = 10 (все три из которых являются естественными) или 10 · 15 = 150.
Точно так же в физическом мире «натуральных» чисел нет смысла говорить, что у нас есть «что-то отрицательное». Скорее, мы говорим, что у нас есть ноль чего-то там, где его нет.Используя приведенный выше пример с учителем, если у учителя в настоящее время нет учеников в его классе, у него нет учеников; В реальном мире нет смысла иметь отрицательных учеников.
Полный набор целых чисел равен набору из неотрицательных целых чисел. Целые числа похожи на целые числа, за исключением того, что они также могут быть отрицательными или нулевыми. Например: -10, -3, 0, 1 5.
Статья по теме: Целочисленные последовательности (CalculusHowTo.com).
Несколько примеров целых чисел: 3, 15, 998, 2, 232, 589.
Все следующие числа являются , а не целыми числами:
- Десятичные : 0,1, 5,23, 15,999, 1,7 2 .
- Фракции : ½, 1/27, 2 ½, 99/100.
- Отрицательные числа: -10, -99, -521.
В теории множеств целые числа подчиняются нескольким правилам. Набор целых чисел:
Замкнут на сложение и умножение. Возьмите два целых числа a и b. Если вы сложите затем (a + b = c), то «c» также будет целым числом.То же верно и для умножения: a · b = d.
Давайте рассмотрим несколько конкретных примеров с числами вместо переменных:
Набор целых чисел не закрывается для деления и вычитания. Если a — целое число, то существует еще одно целое число b, которое дает нецелочисленное решение. В обозначениях это:
Где «b», «c» и «d» не целые числа.
Примеры :
- Вычитание:
6 и 10 — целые числа,
, но 7-9 = -2, что не является целым числом. - Раздел :
4 и 5 — целые числа, но 4/5 — не целые числа.
- Целые числа являются коммутативными для сложения и умножения. Вы не можете вычесть два целых числа в любом порядке и получить тот же результат.
В обозначениях: Для каждого a, b в множестве целых чисел a + b = b + a и a · b = b a.
Пример : 10 — 1 не то же самое, что 1 — 10. - Целые числа являются ассоциативными для сложения и умножения.Порядок добавления не важен (их можно сгруппировать в разном порядке).
Для любых a, b и c в наборе целых чисел a (b · c) = (a · b) · c и (a + b) + c = a + (b + c). - Набор целых чисел включает аддитивную идентичность (0). Ноль — это аддитивная идентичность целых чисел. В обозначениях a + 0 = a для каждого целого числа a.
- Мультипликативное тождество равно 1. Умножьте любое целое число на 1, и вы получите тот же результат. В обозначениях 1 · a = a.
Натуральное число: Каталожный номер
Расширение натуральных чисел до целых
————————————————— —————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Что такое десятичная дробь? — Определение, факты и пример
Игры с десятичными числами
Добавить десятичные дроби
Работайте с визуальными моделями, чтобы получить представление о сложении десятичных чисел. Расширьте знания о сложении многозначных чисел, добавляя десятичные дроби (до сотых разрядов).
Охватывает Common Core Curriculum 5.NBT.7Играть сейчас Умножить десятичные дроби на 10
Определить схему размещения десятичной точки, когда десятичная дробь умножается на степень 10. Иногда вам может потребоваться добавить нули в продукт.
охватывает общий основной учебный план 5.NBT.7Играть сейчасПосмотреть все игры с десятичными знаками >>
Учитесь с полной программой обучения математике K-5
Что такое десятичная дробь?
В алгебре десятичное число можно определить как число, целая и дробная части которого разделены десятичной точкой. Точка в десятичном числе называется десятичной точкой. Цифры, следующие за десятичной точкой, показывают значение меньше единицы.
Вот пример десятичного числа 17.48, в котором 17 — целое число, а 48 — десятичная часть.
десятичных знаков основаны на предшествующих степенях 10. Таким образом, при перемещении слева направо разрядное значение цифр делится на 10, что означает, что десятичное значение определяет десятые, сотые и тысячные доли. Десятая часть означает одну десятую или 1/10. В десятичной форме это 0,1. Сотня означает 1/100. В десятичной форме это 0,01.
Вот пример того, как дробная часть может быть преобразована в десятичные числа.
Десятичные знаки можно записывать как в развернутом виде, так и прописью.
Десятые, сотые и тысячные доли могут быть представлены на числовой строке. Чтобы представить десятые доли, расстояние между каждым целым числом на числовой прямой делится на 10 равных частей, где каждая часть представляет собой десятую часть.
Интересные факты
|
Давай сделаем это!
Вместо того, чтобы учить десятичные дроби и затем раздавать детям рабочие листы, дайте им примеры из реальной жизни, в которых они могут использовать десятичные дроби или преобразовывать числа в десятичные. Например, во время покупок попросите ребенка вычислить цену товара в десятичных дробях (полдюжины яблок).
Связанный математический словарь
1.6 Использование десятичных знаков | NWCG
ДЕСЯТИЧНЫЕ ЧИСЛА
Способ чтения числа зависит от того, где находится десятичная точка.Рисунок ниже аналогичен диаграмме для больших чисел в разделе 1.1. Десятичная точка ставится после разряда единиц. Цифры справа от десятичных знаков представляют десятые (0,1), сотни (0,01), тысячи (0,001) и т. Д. Вплоть до бесконечно малых чисел.
Все целые числа (называемые целыми числами) имеют в конце десятичную точку. Например, 10 = 10, 24 = 24. и 17 801 = 17 801 = 17 801,0.
КОЛЛЕКТИВЫ ИЗ 10
Десятичные числа соответствуют числам, кратным 10.Обратите внимание, что числа 10, 100, 1000, 10 000 и т. Д. Записываются аналогично, за исключением количества «0» между первой цифрой и десятичной запятой. Этот факт позволяет выполнять деление с использованием этих чисел, просто перемещая десятичный разряд. Чтобы разделить на 10, посчитайте количество нулей в делителе или знаменателе и переместите десятичную точку на много пробелов влево.
Рассмотрим 100/10, что может быть записано как 100,0 / 10,0.
В числе 10 один ноль, поэтому переместите десятичную точку в 100 влево на одну позицию.100/10 = 10.
Пример 1. Вычислить 8679 ÷ 1000. В 1000 три нуля. Переместите десятичную точку на три позиции влево, помня, что целые числа имеют десятичную точку в конце.
Мы можем написать 8679 ÷ 1000 = 8679. ÷ 1000. = 8,679
ЗНАЧИТЕЛЬНЫЕ ЦИФРЫ И ОКРУГЛЕНИЕ ДЛЯ ТОЧНОСТИ
Десятичный разряд указывает на точность данного числа. Точность ответа определяется наименьшим уровнем точности сложения, вычитания, умножения или деления исходных чисел.Точность не улучшается при сложении, вычитании, умножении или делении. Эта деталь особенно важна при выполнении умножения и деления с десятичными знаками.
Пример 2 — Что такое 8,2 + 0,25? Самый низкий уровень точности — до 0,1 (или 1/10) десятичного разряда, поэтому правильный ответ — до 1/10 десятичного разряда. Округление в большую или меньшую сторону — это способ довести ответ до нужного уровня точности. 8,2 + 0,25 = 8,45. Однако ответ точен только до 1/10.Какое значение составляет 8,45 с точностью до 1/10? Чтобы получить ответ с соответствующей точностью, округлите цифру в большую или меньшую сторону за пределы самого низкого уровня точности. Если округляемое число — 5, 6, 7, 8 или 9, округляйте в большую сторону. Округлите в меньшую сторону, если числа равны 4, 3, 2 или 1.
Для 8,2 + 0,25 = 8,45 округлите 0,45 до 0,5. Ответ 8,5 имеет правильную точность.
Пример 3 — Что 986,525 минус 459,83?
Выполнение вычитания дает результат 526,695. Самый низкий уровень точности — до 0.01 (1/100) десятичный разряд, поэтому цифру в 0,001 (1/1000) месте необходимо округлить в большую или меньшую сторону. Последняя цифра — 5, поэтому мы округляем и выражаем ответ как 986,525 — 459,83 = 526,70.
При сложении, вычитании, умножении или делении цифр все числа должны иметь такое же количество значащих цифр, что и исходное число с наименьшей точностью.
Пример 4 — Посадочная площадка вертолета имеет форму шестигранной фигуры ниже.
Сторона A — 12.50 футов в длину.
Сторона B составляет 6,57 футов в длину.
Сторона C составляет 7,8 футов в длину.
Сторона D имеет длину 11,00 футов.
Сторона E составляет 5,5 футов в длину.
Сторона F составляет 8,15 фута в длину.
Каков общий периметр вертолетной площадки?
Эта проблема связана с сложением чисел, записанных в десятичной системе счисления.
Сначала установите сумму: 12,50 + 6,57 + 7,8 + 11,00 + 5,5 + 8,15 = 51,52
Теперь проверьте, правильно ли выражен ваш ответ. Самый низкий уровень точности — 0.1 (1/10) десятичный знак, выраженный числами 7,8 и 5,5. Округляя цифру 0,01 (1/100), мы выражаем периметр вертолетной площадки как 51,5 фута.
УМНОЖЕНИЕ С ДЕСЯТИЧНЫМИ ЧИСЛАМИ
Точность ответа определяется размещением десятичной точки при умножении чисел.
При умножении определите правильную десятичную точку после завершения умножения. После умножения чисел посчитайте количество разрядов справа от обоих исходных чисел.Затем к произведению применяется меньшее количество десятичных знаков как количество знаков после запятой.
Пример 5 — Умножение 0,9 × 1,53.
В этом примере 1,377 имеет три десятичных разряда, но наименьшее число точности, участвующее в умножении (0,9), имеет точность 0,1 (1/10). Округлите ответ до десятого места: 0,9 × 1,53 = 1,4
РАЗДЕЛЕНИЕ С ДЕСЯТИЧНЫМИ ЧИСЛАМИ
При выполнении деления важно смотреть на делимое, то есть на делимое число.Деление в длину выполняется путем размещения десятичной точки в ответе непосредственно над десятичной точкой в делимом числе.
Пример 6 — Вычисление 89,76 ÷ 12
В этом случае ответ 7,48 имеет то же количество десятичных знаков, что и делимое.
Если делитель не является целым числом, десятичные разряды необходимо переместить как в делителе, так и в делимом, чтобы убедиться, что десятичная дробь в частном размещена правильно. Сначала переместите десятичную запятую в делителе вправо, чтобы преобразовать число в целое число или целое число.Затем переместите десятичную точку в делимом числе (делимое) вправо на такое же количество пробелов. Теперь поместите десятичную запятую прямо над точкой в разделяемом числе и разделите, как если бы делили целые числа.
Пример 7 — Разделить 4,067 / 0,83.
Чтобы сделать делитель целым числом, десятичную точку нужно переместить на две позиции вправо, чтобы делитель стал 83. Десятичную точку также нужно переместить в делимое, чтобы делимое стало 406.7
Теперь длинное деление выполняется так же, как и с целыми числами, и ответ на 406,7 / 0,83 будет 4,9.
ВАШ ОТВЕТ СМЫСЛ?
Один совет по работе с десятичными знаками — спросите себя: «Имеет ли этот ответ смысл»? Если вы складываете или умножаете целые числа (целые числа), ваш конечный результат должен быть на больше, чем на умножаемых чисел. Если вы вычитаете или делите целые числа (целые числа), ваш результат должен быть меньше.Мы можем быстро проверить деление с использованием десятичных знаков в примере 7, посмотрев на делимые числа. В этом случае мы делим число, немного большее, чем 4, на число, немного меньшее, чем 1. Мы можем вычислить, что 4 ÷ 1 равно 4, поэтому наше число должно быть несколько близко к этому. Это не должно быть 40, 0,4 или 400. Выполняя вычисления в полевых условиях, внимательно смотрите на используемые числа и операцию (сложение, умножение и т. Д.). Во многих ситуациях ответ может быть обязательным для вашей безопасности, поэтому убедитесь, что конечный результат имеет смысл.
Рациональные и иррациональные числа | Алгебраические выражения
1.3 Рациональные и иррациональные числа (EMA4)
- Рациональное число
Рациональное число (\ (\ mathbb {Q} \)) — это любое число, которое можно записать как:
\ [\ frac {a} {b} \]
, где \ (a \) и \ (b \) — целые числа, а \ (b \ ne 0 \).
Все следующие числа являются рациональными числами:
\ [\ frac {10} {1} \; ; \; \ frac {21} {7} \; ; \; \ frac {-1} {- 3} \; ; \; \ frac {10} {20} \; ; \; \ frac {-3} {6} \]
Мы видим, что все числители и все знаменатели целые.
Это означает, что все целые числа являются рациональными числами, потому что они могут быть записаны со знаменателем \ (\ text {1} \).
- Иррациональные числа
Иррациональные числа (\ (\ mathbb {Q} ‘\)) — это числа, которые нельзя записать в виде дроби с числителем и знаменателем в виде целых чисел.
Примеры иррациональных чисел:
\ [\ sqrt {2} \; ; \; \ sqrt {3} \; ; \; \ sqrt [3] {4} \; ; \; \Пи \; ; \; \ frac {1 + \ sqrt {5}} {2} \]
Это не рациональные числа, потому что числитель или знаменатель не является целым числом.
Десятичные числа (EMA5)
Все целые числа и дроби с целыми числителями и ненулевым целым знаменателем являются рациональными числами. Помните, что когда знаменатель дроби равен нулю, дробь не определена.
Вы можете записать любое рациональное число в виде десятичного числа, но не все десятичные числа являются рациональными числами. Эти типы десятичных чисел являются рациональными числами:
Десятичные числа, которые заканчиваются (или заканчиваются).Например, дробь \ (\ frac {4} {10} \) может быть записана как \ (\ text {0,4} \).
Десятичные числа, состоящие из одной повторяющейся цифры. Например, дробь \ (\ frac {1} {3} \) может быть записана как \ (\ text {0,} \ dot {3} \) или \ (\ text {0,} \ overline {3} \). Обозначения точки и полосы эквивалентны, и оба представляют собой повторяющиеся символы \ (\ text {3} \), то есть \ (\ text {0,} \ dot {3} = \ text {0,} \ overline {3} = \ text {0,333 …} \).
Десятичные числа, повторяющиеся из нескольких цифр.Например, дробь \ (\ frac {2} {11} \) также может быть записана как \ (\ text {0,} \ overline {18} \). Полоса представляет собой повторяющийся узор из \ (\ text {1} \) и \ (\ text {8} \), то есть \ (\ text {0,} \ overline {18} = \ text {0 , 181818 …} \).
Вы можете увидеть точку вместо запятой, используемой для обозначения десятичного числа. Таким образом, число \ (\ text {0,4} \) также можно записать как 0,4
Обозначение: Вы можете использовать точку или черту над повторяющимися цифрами, чтобы указать, что десятичная дробь является повторяющейся десятичной.Если полоса охватывает более одной цифры, то все числа под полосой повторяются.
Если вас просят определить, является ли число рациональным или иррациональным, сначала запишите число в десятичной форме. Если число заканчивается, то это рационально. Если так будет продолжаться вечно, ищите повторяющийся набор цифр. Если нет повторяющегося рисунка, то цифра иррациональна.
Когда вы записываете иррациональные числа в десятичной форме, вы можете продолжать записывать их для многих-многих десятичных знаков.Однако это неудобно и часто необходимо округлять.
Округление иррационального числа делает его рациональным числом, которое приближается к иррациональному числу.
Рабочий пример 1: Рациональные и иррациональные числа
Какие из следующих чисел не являются рациональными?
\ (\ pi = \ text {3,14159265358979323846264338327950288419716939937510 …} \)
\ (\ text {1,4} \)
\ (\ text {1,618033989…} \)
\ (\ text {100} \)
\ (\ text {1,7373737373 …} \)
\ (\ text {0,} \ overline {02} \)
Иррациональная, десятичная дробь не оканчивается и не повторяется.
Рациональное, десятичное завершение.
Иррациональная, десятичная дробь не оканчивается и не повторяется.
Рационально, все числа рациональны.
Рациональная десятичная дробь имеет повторяющийся образец.
Рациональная десятичная дробь имеет повторяющийся образец.
Преобразование конечных десятичных знаков в рациональные числа (EMA6)
Десятичное число состоит из целой и дробной части. Например, \ (\ text {10,589} \) имеет целую часть \ (\ text {10} \) и дробную часть \ (\ text {0,589} \), потому что \ (10 + \ text {0,589} = \ текст {10,589} \).
Каждая цифра после десятичной точки представляет собой дробь со знаменателем в возрастающей степени \ (\ text {10} \).
Например:
\ (\ text {0,1} \) равно \ (\ frac {1} {\ text {10}} \)
\ (\ text {0,01} \) равно \ (\ frac {1} {\ text {100}} \)
\ (\ text {0,001} \) равно \ (\ frac {1} {\ text {1 000}} \)
Это означает, что
\ begin {align *}
\ text {10,589} & = 10 + \ frac {5} {10} + \ frac {8} {100} + \ frac {9} {\ text {1 000}} \\
& = \ frac {\ text {10 000}} {\ text {1 000}} + \ frac {\ text {500}} {\ text {1 000}} + \ frac {80} {\ text {1 000 }} + \ frac {9} {\ text {1 000}} \\
& = \ frac {\ text {10 589}} {\ text {1 000}}
\ end {выровнять *}
В следующих двух видеороликах объясняется, как преобразовать десятичные дроби в рациональные числа.
Часть 1
Видео: 2DBJ
Часть 2
Видео: 2DBK
Преобразование повторяющихся десятичных знаков в рациональные числа (EMA7)
Когда десятичная дробь является повторяющейся десятичной дробью, требуется немного больше работы, чтобы записать дробную часть десятичного числа в виде дроби.
Рабочий пример 2: Преобразование десятичных чисел в дроби
Запишите \ (\ text {0,} \ dot {3} \) в форме \ (\ frac {a} {b} \) (где \ (a \) и \ (b \) — целые числа).
Определите уравнение
\ [\ text {Let} x = \ text {0,33333 …} \]
Умножить на \ (\ text {10} \) с обеих сторон
\ [10x = \ текст {3,33333 …} \]
Вычтем первое уравнение из второго
\ [9x = 3 \]
Упростить
\ [x = \ frac {3} {9} = \ frac {1} {3} \]
Рабочий пример 3: Преобразование десятичных чисел в дроби
Запишите \ (\ text {5,} \ dot {4} \ dot {3} \ dot {2} \) в виде рациональной дроби.
Определите уравнение
\ [x = \ текст {5,432432432 …} \]
Умножить на \ (\ text {1 000} \) с обеих сторон
\ [\ text {1 000} x = \ text {5 432,432432432 …} \]
Вычтем первое уравнение из второго
\ [\ text {999} x = \ text {5 427} \]
Упростить
\ [x = \ frac {\ text {5 427}} {\ text {999}} = \ frac {\ text {201}} {\ text {37}} = \ text {5} \ frac {\ text { 16}} {\ text {37}} \]
В первом примере десятичное число умножалось на \ (\ text {10} \), а во втором примере десятичное число умножалось на \ (\ text {1 000} \).Это связано с тем, что в первом примере повторялась только одна цифра (т. Е. \ (\ Text {3} \)), а во втором — три повторяющиеся цифры (т. Е. \ (\ Text {432} \)).
В общем, если у вас повторяется одна цифра, умножьте ее на \ (\ text {10} \). Если у вас повторяются две цифры, умножьте их на \ (\ text {100} \). Если у вас повторяются три цифры, умножьте их на \ (\ text {1 000} \) и так далее.
Не все десятичные числа можно записать как рациональные числа. Почему? Иррациональные десятичные числа, например \ (\ sqrt {2} = \ text {1,4142135…} \) нельзя записать с целым числителем и знаменателем, потому что они не имеют шаблона повторяющихся цифр и не завершаются.
Ты справишься! Позвольте нам помочь вам учиться с умом для достижения ваших целей. Siyavula Practice направит вас в удобном для вас темпе, когда вы задаете вопросы в Интернете.
Зарегистрируйтесь, чтобы улучшить свои оценки
Упражнение 1.1
Какое место на диаграмме занимает число \ (- \ frac {12} {3} \)?
Сначала упростите дробь: \ (- \ frac {12} {3} = -4 \)
\ (- \ text {4} \) является целым числом, поэтому оно попадает в набор \ (\ mathbb {Z} \).
В следующем списке два ложных утверждения и одно истинное утверждение. Какое из утверждений соответствует действительности ?
- Каждое целое число — натуральное число.
- Каждое натуральное число — это целое число.
- В целых числах нет десятичных знаков.
Тщательно обдумайте каждый вариант:
- Есть целые числа, которые не попадают в натуральные числа (все отрицательные числа), поэтому это неверно.
- Натуральные числа — это \ (\ left \ {1; 2; 3; \ ldots \ right \} \), а целые числа — это \ (\ left \ {0; 1; 2; 3; \ ldots \ right \} \ ) (круг \ (\ mathbb {N} \) находится внутри \ (\ mathbb {N} _ {0} \)), поэтому, если число является натуральным числом, оно должно быть целым числом. Это верно.
- Целые числа \ (\ left \ {0; 1; 2; 3; \ ldots \ right \} \) увеличиваются только с шагом 1, поэтому в целых числах не может быть никаких десятичных чисел, что делает это ложным.
Итак, верно только (ii).
Какое место на диаграмме занимает число \ (- \ frac {1} {2} \)?
\ (- \ frac {1} {2} \) находится в своей простейшей форме, поэтому его нет в \ (\ mathbb {N} \), \ (\ mathbb {N} _0 \) или \ (\ mathbb {Z} \).Он находится в пространстве между прямоугольником и \ (\ mathbb {Z} \).
В следующем списке два ложных утверждения и одно истинное утверждение. Какое из утверждений соответствует действительности ?
- Каждое целое число — натуральное число.
- Каждое целое число является целым.
- В целых числах нет десятичных знаков.
Тщательно обдумайте каждый вариант:
- Есть целые числа, которые не попадают в натуральные числа (все отрицательные числа), поэтому это неверно.
- Целые числа \ (\ left \ {\ ldots; -3; -2; -1; 0; 1; 2; 3; \ ldots \ right \} \), а целые числа — \ (\ left \ {0 ; 1; 2; 3; \ ldots \ right \} \) (круг \ (\ mathbb {Z} \) находится внутри \ (\ mathbb {N} _ {0} \)), поэтому, если число является целым это должно быть целое число. Это верно.
- Целые числа \ (\ left \ {0; 1; 2; 3; 4; \ ldots \ right \} \) увеличиваются только с шагом 1, поэтому в целых числах не может быть никаких десятичных чисел, что делает это ложным .
Итак, верно только (ii).
\ (- \ sqrt {3} \)
\ (- \ sqrt {3} \) не имеет знака минус под квадратным корнем (минус находится вне корня) и не делится на ноль, поэтому он действительный.
\ (\ dfrac {0} {\ sqrt {2}} \)
\ (\ dfrac {0} {\ sqrt {2}} \) не имеет знака минус под квадратным корнем (минус находится вне корня) и не делится на ноль, поэтому он действительный.
\ (\ sqrt {-9} \)
\ (\ sqrt {-9} \) имеет знак минус под квадратным корнем, поэтому он не является действительным.
\ (\ dfrac {- \ sqrt {7}} {0} \)
\ (\ dfrac {- \ sqrt {7}} {0} \) имеет деление на ноль, поэтому не определено.
\ (- \ sqrt {-16} \)
\ (- \ sqrt {-16} \) имеет отрицательное число под квадратным корнем, поэтому оно не является действительным.
\ (\ sqrt {2} \)
\ (\ sqrt {2} \) не имеет минуса под квадратным корнем (минус находится вне корня), не делится на ноль, поэтому он действительный.
\ (- \ frac {1} {3} \) рационально. Доля целых чисел — это рациональное число.
\ (\ текст {0,651268962154862.7 \) является рациональным, целым, целым и натуральным числом. Его можно записать как целое число.
\ (\ пи + 3 \)
\ (\ pi \) иррационально. \ (\ text {3} \) рационально (это целое число). Любое рациональное число, добавленное к любому иррациональному числу, иррационально.
Следовательно, \ (\ pi + 3 \) иррационально.
\ (\ пи + \ текст {0,858408346} \)
\ (\ pi \) иррационально.\ (\ text {0,858408346} \) является рациональным (это конечная десятичная дробь). Любое рациональное число, добавленное к любому иррациональному числу, иррационально.
Следовательно, \ (\ pi + \ text {0,858408346} \) иррационально.
\ (\ frac {5} {6} \) рационально.
Поскольку \ (a \) — целое число, \ (\ frac {a} {3} \) рационально.
Поскольку \ (b \) — целое число, \ (\ frac {-2} {b} \) рационально.
Обратите внимание, что \ (b \) не может быть \ (\ text {0} \), так как это делает дробь неопределенной.
Поскольку \ (c \) иррационально, \ (\ frac {1} {c} \) иррационально.
\ (\ frac {a} {14} = \ frac {1} {14} \) рационально.
\ (\ frac {a} {14} = \ frac {-10} {14} \) рационально.
\ (\ frac {a} {14} = \ frac {\ sqrt {2}} {14} \) иррационально.
\ (\ frac {a} {14} = \ frac {\ text {2,1}} {14} \) рационально.
Проверить, какое из чисел входит в набор \ (\ left \ {1; 2; 3; 4; \ ldots \ right \} \). Следовательно, \ (\ text {7} \) и \ (\ text {11} \) — натуральные числа.
Помните, что рациональные числа можно записать как \ (\ frac {a} {b} \), где \ (a \) и \ (b \) — целые числа. Также помните, что рациональные числа включают завершающие десятичные числа. Следовательно, \ (- \ sqrt {8} \;; \; \ text {3,3231089 …} \; \; 3+ \ sqrt {2} \;; \; \ pi \) все иррациональны.
Любое число, являющееся квадратным корнем из отрицательного числа, не является действительным.Следовательно, нереально только \ (\ sqrt {-1} \).
Помните, что рациональные числа можно записать как \ (\ frac {a} {b} \), где \ (a \) и \ (b \) — целые числа. Также помните, что рациональные числа включают завершающие десятичные числа. Следовательно, \ (- 3 \;; \; 0 \;; \; -8 \ frac {4} {5} \;; \; \ frac {22} {7} \; \; 7 \;; \; \ text {1,} \ overline {34} \; \; 9 \ frac {7} {10} \;; \; 11 \) — все рациональные числа.
Проверьте, какое из чисел входит в набор \ (\ left \ {\ ldots; -3; -2; -1; 0; 1; 2; 3; \ ldots \ right \} \).Следовательно, \ (- 3 \;; \; 7 \;; \; 11 \) — целые числа.
Любая дробь, разделенная на \ (\ text {0} \), не определена. Следовательно, только \ (\ frac {14} {0} \) не определено.
\ (\ текст {2,121314 …} \)
Номер не заканчивается (это показано \ (\ ldots \)). Также отсутствует указание на повторяющийся узор цифр, поскольку ни над одним из чисел нет точки или полосы. Следующие три цифры могут быть любыми числами.
Обратите внимание, что, хотя кажется, что в цифрах есть шаблон, мы не знаем, продолжается ли этот шаблон.
Иррационально, нет повторяющегося рисунка.
\ (\ текст {1,242244246 …} \)
Номер не заканчивается (это показано \ (\ ldots \)). Также отсутствует указание на повторяющийся узор цифр, поскольку ни над одним из чисел нет точки или полосы. Следующие три цифры могут быть любыми числами.
Обратите внимание, что, хотя кажется, что в цифрах есть шаблон, мы не знаем, продолжается ли этот шаблон.
Иррационально, нет повторяющегося рисунка.
\ (\ текст {3,324354 …} \)
Номер не заканчивается (это показано \ (\ ldots \)). Также отсутствует указание на повторяющийся узор цифр, поскольку ни над одним из чисел нет точки или полосы. Следующие три цифры могут быть любыми числами.
Обратите внимание, что, хотя кажется, что в цифрах есть шаблон, мы не знаем, продолжается ли этот шаблон.
Иррационально, нет повторяющегося рисунка.
\ (\ текст {3,3243} \ dot {5} \ dot {4} \)
\ (\ text {0,1} = \ frac {1} {10} \)
\ begin {align *}
\ text {0,12} & = \ frac {1} {10} + \ frac {2} {100} \\
& = \ frac {10} {100} + \ frac {2} {100} \\
& = \ frac {12} {100} \\
& = \ frac {3} {25}
\ end {выровнять *}
\ begin {align *}
\ text {0,58} & = \ frac {5} {10} + \ frac {8} {100} \\
& = \ frac {50} {100} + \ frac {8} {100} \\
& = \ frac {58} {100} \\
& = \ frac {29} {50}
\ end {выровнять *}
\ begin {align *}
\ text {0,2589} & = \ frac {2} {10} + \ frac {5} {100} + \ frac {8} {\ text {1 000}} + \ frac {9} {\ text { 10 000}} \\
& = \ frac {\ text {2 000}} {\ text {10 000}} + \ frac {500} {\ text {10 000}} + \ frac {80} {\ text {10 000}} + \ гидроразрыв {9} {\ text {10 000}} \\
& = \ frac {\ text {2 589}} {\ text {10 000}}
\ end {выровнять *}
Мы видим, что повторяется только цифра \ (\ text {1} \), поэтому мы можем записать это как: \ (\ text {0,} \ dot {1} \).
\ (\ text {0,1212121212 …} \)
Существует повторяющийся шаблон \ (\ text {12} \), поэтому мы можем записать это число как: \ (\ text {0,} \ overline {12} \)
\ (\ text {0,123123123123 …} \)
Существует повторяющийся шаблон \ (\ text {123} \), поэтому мы можем записать это число как: \ (\ text {0,} \ overline {123} \)
\ (\ text {0,11414541454145 …} \)
Шаблон 4145 повторяется, поэтому мы можем записать это число как: \ (\ text {0,11} \ overline {4145} \).7 \ текст {00}} & = \ текст {2} \ текст {остаток} \ текст {4}
\\
\ frac {\ text {7}} {\ text {33}} & = \ text {0,} \ text {2 121} \ ldots \\
& = \ текст {0,} \ точка {\ текст {2}} \ точка {\ текст {1}}
\ end {выровнять *}
\ begin {align *}
\ frac {2} {3} & = 2 \ left (\ frac {1} {3} \ right) \\
& = 2 (\ text {0,333333 …}) \\
& = \ текст {0,666666 …} \\
& = \ текст {0,} \ точка {6}
\ end {выровнять *}
\ begin {align *}
1 \ frac {3} {11} & = 1 + 3 \ left (\ frac {1} {11} \ right) \\
& = 1 + 3 (\ text {0,0
…}) \\
& = 1 + \ текст {0,27272727 …} \\
& = \ текст {1,} \ overline {27}
\ end {выровнять *}
\ begin {align *}
4 \ frac {5} {6} & = 4 + 5 \ left (\ frac {1} {6} \ right) \\
& = 4+ 5 (\ text {0,1666666 …}) \\
& = 4 + \ текст {0,833333 …} \\
& = \ текст {4,8} \ точка {3}
\ end {выровнять *}
\ begin {align *}
2 \ frac {1} {9} & = 2 + \ text {0,1111111 …} \\
& = \ текст {2,} \ точка {1}
\ end {выровнять *}
\ begin {align *}
х & = \ текст {0,55555…} \ text {и} \\
10x & = \ text {5,55555 …} \\
10x — x & = (\ text {5,55555 …}) — (\ text {0,55555 …}) \\
\ text {9} x & = \ text {5} \\
\ поэтому x & = \ frac {5} {9}
\ end {выровнять *}
\ begin {align *}
10x & = \ text {6,3333 …} \ text {и} \\
100x & = \ текст {63,3333 …} \\
100x — 10x & = (\ text {63,3333 …}) — (\ text {6,3333 …}) \\
\ text {99} x & = \ text {57} \\
\ поэтому x & = \ frac {57} {90}
\ end {выровнять *}
\ (\ текст {0,} \ точка {4} \)
\ begin {align *}
х & = \ текст {0,4444…} \ text {и} \\
\ text {10} x & = \ text {4,4444 …} \\
10x — x & = (\ text {4,4444 …}) — (\ text {0,4444 …}) \\
\ text {9} x & = \ text {4} \\
\ поэтому x & = \ frac {\ text {4}} {\ text {9}}
\ end {выровнять *}
\ (\ text {5,} \ overline {31} \)
\ begin {align *}
х & = \ текст {5,313131 …} \ текст {и} \\
100x & = \ text {531,313131 …} \\
100x — x & = (\ text {531,313131…}) — (\ text {5,313131 …}) \\
\ text {99} x & = \ text {526} \\
\ поэтому x & = \ frac {526} {99}
\ end {выровнять *}
\ (\ text {4,} \ overline {\ text {93}} \)
\ begin {align *}
х & = \ текст {4,939393 …} \ текст {и} \\
100x & = \ text {493,939393 …} \\
100x — x & = (\ text {493,939393 …}) — (\ text {4,939393 …}) \\
\ text {99} x & = \ text {489} \\
\ поэтому x & = \ frac {\ text {163}} {\ text {33}}
\ end {выровнять *}
\ (\ text {3,} \ overline {\ text {93}} \)
\ begin {align *}
х & = \ текст {3,939393…} \ text {и} \\
100x & = \ text {393,939393 …} \\
100x — x & = (\ text {393,939393 …}) — (\ text {3,939393 …}) \\
\ text {99} x & = \ text {390} \\
\ поэтому x & = \ frac {\ text {130}} {\ text {33}}
\ end {выровнять *}
1.1: Действительные числа и числовая строка
НАВЫКИ ДЛЯ РАЗВИТИЯ
- Постройте числовую линию и точки на ней.
- Используйте числовую строку, чтобы определить порядок действительных чисел.
- Определите противоположность действительного числа.
- Определите абсолютное значение действительного числа.
Определения
Набор — это набор объектов, обычно сгруппированных в фигурных скобках \ (\ {\) \ (\} \), где каждый объект называется элементом . Например, \ (\ {\ text {красный, зеленый, синий} \} \) — это набор цветов. Подмножество — это набор, состоящий из элементов, принадлежащих данному набору. Например, \ (\ {\ text {зеленый, синий} \} \) — это подмножество цвета, указанного выше.Набор без элементов называется пустым набором и имеет свои собственные специальные обозначения, \ (\ {\) \ (\} \) или \ (\ varnothing \).
Изучая математику, мы ориентируемся на специальные наборы чисел. Набор из натуральных (или считающихся) чисел , обозначенных \ (\ mathbb {N} \), равен
.
\ (\ {1,2,3,4,5, \ dots \} \ quad \ color {Cerulean} {Natural \: Numbers} \)
Три точки \ ((\ точки) \) называются многоточием и указывают на то, что числа продолжаются неограниченно. Набор из целых чисел , обозначаемый \ (\ mathbb {W} \), представляет собой набор натуральных чисел в сочетании с нулем.
\ (\ {0,1,2,3,4,5, \ dots \} \ quad \ color {Cerulean} {Whole \: Numbers} \)
Набор из целых чисел , обозначаемый \ (\ mathbb {Z} \), состоит из положительных и отрицательных целых чисел, а также нуля.
\ (\ {\ dots, -3, -2, -1,0,1,2,3, \ dots \} \ quad \ color {Cerulean} {Целые числа} \)
Обратите внимание, что наборы натуральных и целых чисел являются подмножествами набора целых чисел.
Рациональные числа , обозначаемые \ (\ mathbb {Q} \), определяются как любое число в форме \ (\ dfrac {a} {b} \), где \ (a \) и \ (b \) являются целыми числами и \ (b \) не равно нулю.Десятичные дроби, которые повторяются или заканчиваются, рациональны. Например,
\ (0,7 = \ frac {7} {10} \ quad \ text {and} \ quad 0. \ overline {3} = 0,3333 \ dots = \ frac {1} {3} \)
Набор целых чисел — это подмножество набора рациональных чисел, потому что каждое целое число может быть выражено как отношение целого числа к \ (1 \). Другими словами, любое целое число может быть записано над \ (1 \) и может считаться рациональным числом. Например,
\ (5 = \ frac {5} {1} \)
Иррациональные числа — это любое число, которое нельзя записать как отношение двух целых чисел.Неповторяющиеся десятичные дроби, которые не повторяются, иррациональны. Например,
\ (\ pi = 3,14159 \ точек \ quad \ text {и} \ quad \ sqrt {2} = 1,41421 \ точек \)
Набор из действительных чисел , обозначаемый \ (\ mathbb {R} \), определяется как набор всех рациональных чисел в сочетании с набором всех иррациональных чисел. Следовательно, все числа, определенные до сих пор, являются подмножествами множества действительных чисел. Таким образом,
Рисунок \ (\ PageIndex {1} \): Действительные числа
Числовая строка
Строка вещественных чисел , или просто числовая строка, позволяет нам визуально отображать действительные числа, связывая их с уникальными точками на линии.Действительное число, связанное с точкой, называется координатой . Точка на прямой числовой линии, которая связана с координатой, называется ее графиком .
Чтобы построить числовую линию, нарисуйте горизонтальную линию со стрелками на обоих концах, чтобы указать, что она продолжается без границ. Затем выберите любую точку, представляющую число ноль; эта точка называется исходной точкой .
Рисунок \ (\ PageIndex {2} \)
Отметьте одинаковую длину по обе стороны от исходной точки и пометьте каждую галочку, чтобы определить масштаб.Положительные действительные числа лежат справа от начала координат, а отрицательные действительные числа — слева. Число ноль \ ((0) \) не является ни положительным, ни отрицательным. Обычно каждая отметка представляет собой одну единицу.
Рисунок \ (\ PageIndex {3} \)
Как показано ниже, масштаб не всегда должен составлять одну единицу. В первой числовой строке каждая отметка представляет две единицы. Во втором случае каждая отметка представляет собой \ (\ frac {1} {7} \) единицы.
Рисунок \ (\ PageIndex {4} \)
График каждого действительного числа показан точкой в соответствующей точке числовой прямой.Частичный график набора целых чисел \ (\ mathbb {Z} \) следует:
Рисунок \ (\ PageIndex {5} \)
Пример \ (\ PageIndex {1} \)
Изобразите следующий набор действительных чисел:
Решение
Изобразите числа на числовой прямой со шкалой, где каждая отметка представляет \ (\ frac {1} {2} \) единицы.
Рисунок \ (\ PageIndex {6} \)
Заказ вещественных чисел
При сравнении действительных чисел в числовой строке большее число всегда будет находиться справа от меньшего.Ясно, что \ (15 \) больше, чем \ (5 \), но может быть не так ясно видеть, что \ (- 1 \) больше, чем \ (- 5 \), пока не построим график каждого числа на числовая строка.
Рисунок \ (\ PageIndex {7} \)
Мы используем символы, чтобы помочь нам эффективно передавать отношения между числами в числовой строке. Символы, используемые для описания отношения равенства между числами, следующие:
\ [\ begin {align *} & = \ quad \ color {Cerulean} {is \ equal \ to} \\ & \ neq \ quad \ color {Cerulean} {is \ not \ equal \ to} \\ & \ приблизительно \ quad \ color {Cerulean} {\ приблизительно \ равно \ to} \ end {align *} \]
Эти символы используются и интерпретируются следующим образом:
\ [\ begin {align *} & 5 = 5 \ qquad && \ color {Cerulean} {5 \ is \ equal \ to \ 5} \\ & 0 \ neq 5 \ qquad && \ color {Cerulean} {0 \ is \ не \ равно \ к \ 5} \\ & \ пи \ приблизительно 3.14 \ quad && \ color {Cerulean} {pi \ is \ приблизительно \ equal \ to \ 3.14} \ end {align *} \]
Далее мы определяем символы, которые обозначают отношение порядка между действительными числами.
\ [\ begin {align *} & <\ quad \ color {Cerulean} {Less \ than} \\ &> \ quad \ color {Cerulean} {Greater \ than} \\ & \ leq \ quad \ color {Cerulean } {Меньше \ чем \ или \ равно \ to} \\ & \ geq \ quad \ color {Cerulean} {Больше \ чем \ или \ равно \ to} \ end {align *} \]
Эти символы позволяют сравнивать два числа.Например,
Поскольку график \ (- 120 \) находится слева от графика \ (- 10 \) на числовой прямой, это число меньше \ (- 10 \). Мы могли бы написать эквивалентное утверждение следующим образом:
Точно так же, поскольку график нуля находится справа от графика любого отрицательного числа на числовой прямой, ноль больше любого отрицательного числа.
Символы \ (<\) и \ (> \) используются для обозначения строгих неравенств , а символы и используются для обозначения включительных неравенств .В некоторых ситуациях можно правильно нанести более одного символа. Например, оба следующих утверждения верны:
Кроме того, компонент инклюзивного неравенства «или равно» позволяет нам правильно записать следующее:
Логическое использование слова «или» требует, чтобы выполнялось только одно из условий: «меньше чем» или «равно».
Пример \ (\ PageIndex {2} \)
Заполните пустое поле с помощью \ (<, = \) или \ (>: −2 \) ____ \ (- 12 \).
Решение
Используйте>, потому что график \ (- 2 \) находится справа от графика \ (- 12 \) на числовой прямой. Следовательно, \ (- 2> −12 \), что означает «отрицательные два больше, чем отрицательные двенадцать».
Рисунок \ (\ PageIndex {8} \)
Ответ:
\ (- 2> -12 \)
В этом тексте мы часто будем указывать на эквивалентные обозначения, используемые для электронного выражения математических величин с использованием стандартных символов, доступных на клавиатуре.Начнем с эквивалентного текстового обозначения неравенств:
\ [\ begin {align *} & \ geq && «> =» \\ & \ leq && «<=" \\ & \ neq && "! =" \ End {align *} \]
Многие калькуляторы, системы компьютерной алгебры и языки программирования используют эту нотацию.
Противоположности
напротив любого действительного числа \ (a \) есть \ (- a \). Противоположные действительные числа находятся на одинаковом расстоянии от начала координат на числовой прямой, но их графики лежат на противоположных сторонах начала координат, а числа имеют противоположные знаки.
Рисунок \ (\ PageIndex {9} \)
Например, мы говорим, что противоположностью \ (10 \) является \ (- 10 \).
Затем рассмотрим противоположность отрицательного числа. Учитывая целое число \ (- 7 \), целое число на том же расстоянии от начала координат и с противоположным знаком будет \ (+ 7 \), или просто \ (7 \).
Рисунок \ (\ PageIndex {10} \)
Следовательно, мы говорим, что противоположностью \ (- 7 \) является \ (- (- 7) = 7 \). Эта идея приводит к тому, что часто называют двойным отрицательным свойством . Для любого действительного числа \ (a \),
\ (- (- а) = а \)
Пример \ (\ PageIndex {3} \)
Что противоположно \ (- \ frac {3} {4} \)?
Решение
Здесь мы применяем свойство двойного отрицания.
\ (- (- \ frac {3} {4}) = \ frac {3} {4} \)
Пример \ (\ PageIndex {4} \)
Упростить \ (- (- (4)) \)
Решение
Начните с самых внутренних скобок, найдя противоположность \ (+ 4 \).
\ [\ begin {align *} — (- (4)) & = — (\ color {Cerulean} {- (4)} \ color {Black} {)} \\ & = — (\ color {Cerulean} {-4} \ color {Черный} {)} \\ & = 4 \ end {align *} \]
Ответ
4
Пример \ (\ PageIndex {5} \)
Упростить: \ (- (- (- 2)) \).
Решение
Примените двойное отрицательное свойство, начиная с самых внутренних круглых скобок.
\ [\ begin {align *} — (- (- 2)) & = — (\ color {Cerulean} {- (- 2)} \ color {Black} {)} \\ & = — (\ color { Церулеан} {2} \ color {Черный} {)} \\ & = — 2 \ end {align *} \]
Ответ
-2
подсказка
Если имеется четное количество следующих друг за другом отрицательных знаков, то результат положительный. Если число подряд идущих отрицательных знаков нечетное, результат отрицательный.
Попробуй!
Упражнение \ (\ PageIndex {1} \)
Упростить: \ (- (- (- (5))) \).
- Ответ
-5
Процедура:
\ [\ begin {align *} — (- (- (5))) & = — (\ color {Cerulean} {- (- (5))} \ color {Black} {)} \\ & = — (\ color {Cerulean} {- (- 5)} \ color {Black} {)} \\ & = — (\ color {Cerulean} {5} \ color {Black} {)} \\ & = -5 \ конец {выравнивание *} \]
Видео решение:
(нажмите, чтобы посмотреть видео)
Абсолютное значение
Абсолютное значение действительного числа \ (a \), обозначенного \ (| a | \), определяется как расстояние между нулем (началом координат) и графиком этого действительного числа на числовой прямой.Поскольку это расстояние, оно всегда положительно. Например,
\ (| -4 | = 4 \ quad \ text {and} \ quad | 4 | = 4 \)
И \ (4 \), и \ (- 4 \) находятся на четыре единицы от начала координат, как показано ниже:
Рисунок \ (\ PageIndex {11} \)
Пример \ (\ PageIndex {6} \)
Упростить:
а. \ (| -12 | \)
б. \ (| 12 | \)
Решение
И \ (- 12 \), и \ (12 \) находятся в двенадцати единицах от начала координат числовой прямой. Следовательно,
\ (| -12 | = 12 \ quad \ text {and} \ quad | 12 | = 12 \)
Ответ
а.\ (12 \) b. \ (12 \)
Также стоит отметить, что
\ (| 0 | = 0 \)
Абсолютное значение может быть выражено в текстовом виде с помощью записи abs \ ((a) \). Мы часто сталкиваемся с отрицательными абсолютными значениями, такими как \ (- | 3 | \) или \ (- \) abs \ ((3) \). Обратите внимание, что перед символом абсолютного значения стоит знак минуса. В этом случае сначала обработайте абсолютное значение, а затем найдите результат, противоположный результату.
Постарайтесь не путать это с двойным отрицательным свойством, которое гласит, что \ (- (- 7) = + 7 \).
Пример \ (\ PageIndex {7} \)
Simplfy: \ (- | — (- 7) | \).
Решение
Сначала найдите противоположность \ (- 7 \) внутри абсолютного значения. Затем найдите результат, противоположный результату.
\ [\ begin {align *} — | \ color {Cerulean} {- (- 7)} \ color {Black} {|} & = — | \ color {Cerulean} {7} \ color {Black} {| } \\ & = — 7 \ end {align *} \]
Ответ
-7
На этом этапе мы можем определить, какие действительные числа имеют конкретное абсолютное значение.Например,
\ (|? | = 5 \)
Представьте себе действительное число, расстояние от которого до начала координат составляет \ (5 \) единиц. Есть два решения: расстояние справа от начала координат и расстояние слева от начала координат, а именно \ (\ {\ pm 5 \} \). Символ \ ((\ pm) \) читается как «плюс или минус» и указывает на то, что есть два ответа, один положительный и один отрицательный.
\ (| -5 | = 5 \ \ quad \ text {and} \ quad | 5 | = 5 \)
Теперь рассмотрим следующее:
\ (|? | = -5 \)
Здесь мы хотим найти значение, для которого расстояние до начала координат отрицательно.Поскольку отрицательное расстояние не определено, это уравнение не имеет решения. Если уравнение не имеет решения, мы говорим, что решение — это пустое множество: \ (\ varnothing \).
Ключевые выводы
- Любое действительное число может быть связано с точкой на линии.
- Создайте числовую линию, сначала указав источник и отметив шкалу, соответствующую данной задаче.
- Отрицательные числа лежат слева от начала координат, а положительные числа — справа.
- Меньшие числа всегда лежат слева от больших чисел в числовой строке.
- Противоположное положительное число отрицательное, а противоположное отрицательному числу положительное.
- Абсолютное значение любого действительного числа всегда положительно, потому что оно определяется как расстояние от нуля (начала координат) на числовой прямой.
- Абсолютное значение нуля равно нулю.
Упражнение \ (\ PageIndex {2} \)
Используйте обозначение набора, чтобы перечислить описанные элементы.
- Часы на часах.
- Дни недели.
- Первые десять целых чисел.
- Первые десять натуральных чисел.
- Первые пять четных положительных целых чисел.
- Первые пять положительных нечетных целых чисел.
- Ответ
1. \ (\ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 \} \)
3. \ (\ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9 \} \)
5.\ (\ {2, 4, 6, 8, 10 \} \)
Упражнение \ (\ PageIndex {3} \)
Определите, являются ли следующие действительные числа целыми, рациональными или иррациональными.
- \ (12 \)
- \ (- 3 \)
- \ (4,5 \)
- \ (- 5 \)
- \ (0,3 \ overline {6} \)
- \ (0. \ Overline {3} \)
- \ (1.001000100001 \ точки \)
- \ (1.00 \ overline {1} \)
- \ (e = 2,71828 \ точек \)
- \ (\ sqrt {7} = 2.645751 \ точки \)
- \ (- 7 \)
- \ (3,14 \)
- \ (227 \)
- \ (1,33 \)
- \ (0 \)
- \ (8,675,309 \)
- Ответ
1: Целое число, Rational
3: Rational
5: Rational
7: Иррациональное
9: Иррациональное
11: Целое число, Rational
13: Rational
15: Целое число, Rational
Упражнение \ (\ PageIndex {4} \)
Верно или неверно.
- Все числа являются рациональными числами.
- Все числа являются целыми числами.
- Все рациональные числа являются целыми числами.
- Некоторые иррациональные числа рациональны.
- Все конечные десятичные числа являются рациональными.
- Все иррациональные числа действительны.
- Ответ
1: Истина
3: Ложь
5: Правда
Упражнение \ (\ PageIndex {5} \)
Выберите соответствующий масштаб и нанесите на числовую линию следующие наборы действительных чисел.
- \ (\ {- 3, 0, 3 \} \)
- \ (\ {- 2, 2, 4, 6, 8, 10 \} \)
- \ (\ {- 2, −1/3, 2/3, 5/3 \} \)
- \ (\ {- 5/2, −1/2, 0, 1/2, 2 \} \)
- \ (\ {- 5/7, 0, 2/7, 1 \} \)
- \ (\ {–5, –2, –1, 0 \} \)
- \ (\ {−3, −2, 0, 2, 5 \} \)
- \ (\ {- 2,5, −1,5, 0, 1, 2,5 \} \)
- \ (\ {0, 0.3, 0.6, 0.9, 1.2 \} \)
- \ (\ {- 10, 30, 50 \} \)
- \ (\ {- 6, 0, 3, 9, 12 \} \)
- \ (\ {- 15, −9, 0, 9, 15 \} \)
- Ответ
1.\ (\ {- 3, 0, 3 \} \)
Рисунок \ (\ PageIndex {12} \)
3. \ (\ {- 2, −1/3, 2/3, 5/3 \} \)
Рисунок \ (\ PageIndex {13} \)
5. \ (\ {- 5/7, 0, 2/7, 1 \} \)
Рисунок \ (\ PageIndex {14} \)
7. \ (\ {−3, −2, 0, 2, 5 \} \)
Рисунок \ (\ PageIndex {15} \)
9. \ (\ {0, 0.3, 0.6, 0.9, 1.2 \} \)
Рисунок \ (\ PageIndex {16} \)
11. \ (\ {- 6, 0, 3, 9, 12 \} \)
Рисунок \ (\ PageIndex {17} \)
Упражнение \ (\ PageIndex {6} \)
Заполните пустое поле с помощью \ (<, = \) или \ (> \).
- \ (- 7 \) ___ \ (0 \)
- \ (30 \) ___ \ (2 \)
- \ (10 \) ___ \ (- 10 \)
- \ (- 150 \) ___ \ (- 75 \)
- \ (- 0,5 \) ___ \ (- 1,5 \)
- \ (0 \) ___ \ (0 \)
- \ (- 500 \) ___ \ (200 \)
- \ (- 1 \) ___ \ (- 200 \)
- \ (- 10 \) ___ \ (- 10 \)
- \ (- 40 \) ___ \ (- 41 \)
- Ответ
1. \ (<\)
3. \ (> \)
5.\ (> \)
7. \ (<\)
9. \ (= \)
Упражнение \ (\ PageIndex {7} \)
Верно или неверно.
- \ (5 ≠ 7 \)
- \ (4 = 5 \)
- \ (1 ≠ 1 \)
- \ (- 5> −10 \)
- \ (4 \ leq 4 \)
- \ (- 12 \ geq 0 \)
- \ (- 10 = −10 \)
- \ (3> 3 \)
- \ (- 1000 <−20 \)
- \ (0 = 0 \)
- Ответ
1.Правда
3. Неверно
5. Верно
7. Верно
9. Верно
Упражнение \ (\ PageIndex {8} \)
Перечислите числа.
- Перечислите три целых числа меньше \ (- 5 \).
- Перечислите три целых числа больше \ (- 10 \).
- Назовите три рациональных числа меньше нуля.
- Назовите три рациональных числа больше нуля.
- Перечислите три целых числа от \ (- 20 \) до \ (- 5 \).
- Назовите три рациональных числа от \ (0 \) до \ (1 \).
- Ответ
1. \ (- 10, −7, −6 \) (ответы могут отличаться)
3. \ (- 1, −2/3, −1/3 \) (ответы могут отличаться)
5. \ (- 15, −10, −7 \) (ответы могут отличаться)
Упражнение \ (\ PageIndex {9} \)
Переведите каждое утверждение в предложение на английском языке.
- \ (10 <20 \)
- \ (- 50 \ leq −10 \)
- \ (- 4 \ neq 0 \)
- \ (30 \ geq -1 \)
- \ (0 = 0 \)
- \ (е \ около 2.718 \)
- Ответ
1. Десять меньше двадцати.
3. Отрицательная четверка не равна нулю.
5. Ноль равен нулю.
Упражнение \ (\ PageIndex {10} \)
Переведите следующее в математическое выражение.
- Отрицательная семерка меньше нуля.
- Двадцать четыре не равно десяти.
- Ноль больше или равен отрицательному.
- Четыре больше или равно минусу двадцати одному.
- Отрицательное два равно отрицательному двум.
- Отрицательные две тысячи меньше отрицательных одной тысячи.
- Ответ
1. \ (- 7 <0 \)
3. \ (0 \ geq −1 \)
5. \ (- 2 = −2 \)
Упражнение \ (\ PageIndex {11} \)
Упростить.
- \ (- (- 9) \)
- \ (- (- 35) \)
- \ (- (10) \)
- \ (- (3) \)
- \ (- (5) \)
- \ (- (34) \)
- \ (- (- 1) \)
- \ (- (- (- 1)) \)
- \ (- (- (1)) \)
- \ (- (- (- 3)) \)
- \ (- (- (- (- 11))) \)
- Ответ
1.\ (9 \)
3. \ (- 10 \)
5. \ (- 5 \)
7. \ (1 \)
9. \ (1 \)
11. \ (11 \)
Упражнение \ (\ PageIndex {12} \)
Ответьте на следующие вопросы.
- Что противоположно \ (- 12 \)
- Что противоположно \ (\ pi \)?
- Что наоборот \ (- 0,01 \)?
- Противоположность \ (- 12 \) меньше или больше, чем \ (- 11 \)?
- Противоположность \ (7 \) меньше или больше, чем \ (- 6 \)?
- Ответ
2.\ (- \ pi \)
4. Больше
Упражнение \ (\ PageIndex {13} \)
Заполните пустое поле с помощью \ (<, = \) или \ (> \).
- \ (- 7 \) ___ \ (- (- 8) \)
- \ (6 \) ___ \ (- (6) \)
- \ (13 \) ___ \ (- (- 12) \)
- \ (- (- 5) \) ___ \ (- (- 2) \)
- \ (- 100 \) ___ \ (- (- (- 50)) \)
- \ (44 \) ___ \ (- (- 44) \)
- Ответ
1.\ (<\)
3. \ (> \)
5. \ (<\)
Упражнение \ (\ PageIndex {14} \)
Упростить.
- \ (| 20 | \)
- \ (| -20 | \)
- \ (| -33 | \)
- \ (| -0,75 | \)
- \ (| — \ frac {3} {5} | \)
- \ (| 38 | \)
- \ (| 0 | \)
- \ (| 1 | \)
- \ (- | 12 | \)
- \ (- | −20 | \)
- \ (- | 20 | \)
- \ (- | −8 | \)
- \ (- | 7 | \)
- \ (- | −316 | \)
- \ (- (- | \ frac {8} {9} |) \)
- \ (| — (- 2) | \)
- \ (- | — (- 3) | \)
- \ (- (- | 5 |) \)
- \ (- (- | −45 |) \)
- \ (- | — (- 21) | \)
- абс \ ((6) \)
- абс \ ((- 7) \)
- \ (- \) абс \ ((5) \)
- \ (- \) абс \ ((- 19) \)
- \ (- (- \) абс \ ((9)) \)
- \ (- \) абс \ ((- (- 12)) \)
- Ответ
1.\ (20 \)
3. \ (33 \)
5. \ (\ frac {3} {5} \)
7. \ (0 \)
9. \ (- 12 \)
11. \ (- 20 \)
13. \ (- 7 \)
15. \ (\ frac {8} {9} \)
17. \ (- 3 \)
19. \ (45 \)
21. \ (6 \)
23. \ (- 5 \)
25. \ (9 \)
Упражнение \ (\ PageIndex {15} \)
Определить неизвестное.
- \ (|? | = 9 \)
- \ (|? | = 15 \)
- \ (|? | = 0 \)
- \ (|? | = 1 \)
- \ (|? | = −8 \)
- \ (|? | = -20 \)
- \ (|? | −10 = −2 \)
- \ (|? | + 5 = 14 \)
- Ответ
1.\ (\ pm 9 \)
3. \ (0 \)
5. \ (\ varnothing \), нет решения
7. \ (\ pm 8 \)
Упражнение \ (\ PageIndex {16} \)
Заполните пустое поле с помощью \ (<, = \) или \ (> \).
- \ (| −2 | \) ____ \ (0 \)
- \ (| −7 | \) ____ \ (| −10 | \)
- \ (- 10 \) ____ \ (- | −2 | \)
- \ (| −6 | \) ____ \ (| — (- 6) | \)
- \ (- | 3 | \) ____ \ (| — (- 5) | \)
- \ (0 \) ____ \ (- | — (- 4) | \)
- Ответ
1.\ (> \)
3. \ (<\)
5. \ (<\)
Упражнение \ (\ PageIndex {17} \)
Темы дискуссионной доски.
- Изучите и обсудите историю числа ноль.
- Изучите и обсудите различные системы нумерации на протяжении всей истории.
- Изучите и обсудите определение и историю \ (\ pi \).
- Изучите историю иррациональных чисел. Кому приписывают доказательство иррациональности квадратного корня из \ (2 \) и что с ним случилось?
- Изучите и обсудите историю абсолютных ценностей.
- Обсудите определение абсолютного значения «просто положительно»
.

 К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.
К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010.- 256 с.

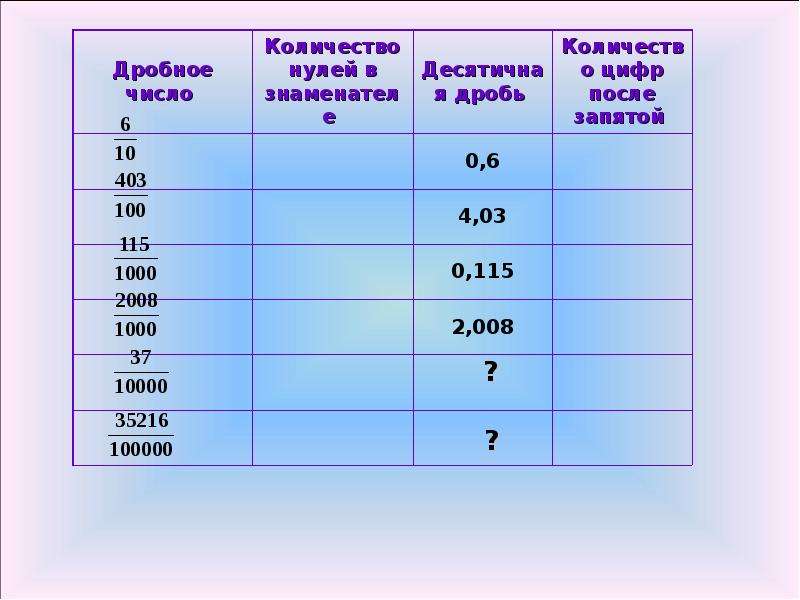

 Организационный этап
Организационный этап Проанализируйте полученные результаты.
Проанализируйте полученные результаты.