Как делить с остатком 4 класс: Урок 54. письменное деление на двузначное число с остатком — Математика — 4 класс

By: admin Date: 21.06.2021 Categories: Разное

Содержание

Деление с остатком на двузначное число. Математика, 4 класс: уроки, тесты, задания.

Компоненты деления с остатком

Сложность:
лёгкое

Возможный остаток при делении на двузначное число

Сложность:
лёгкое

Деление многозначного числа на двузначное число с остатком устно

Сложность:
лёгкое

Деление с проверкой

Сложность:
лёгкое

Деление четырёхзначного числа на двузначное число с остатком (1)

Сложность:
среднее

Деление пятизначного числа на двузначное число с остатком

Сложность:
среднее

Деление шестизначного числа на двузначное с остатком (1)

Сложность:
среднее

Деление семизначного числа на двузначное с остатком

Сложность:
среднее

Неизвестный делитель

Сложность:
среднее

10.

Текстовая задача (ткань)

Сложность:
сложное

11.

Текстовая задача (картофель)

Сложность:
сложное

Урок математики 4 класс «Письменное деление с остатком на двузначное число». | План-конспект урока по математике (4 класс) по теме:

Образовательная система «Школа России».

Конспект урока. Математика. 4 «А» класс.

Учитель: МБОУ СОШ №12 Быкова Ирина Викторовна

(ФГОС в системе учебников «Школа России»)

Тема урока: «Письменное деление с остатком на двузначное число».

Цели урока:

1. Отрабатывать прием письменного деления трехзначного числа на двузначное при однозначном частном с остатком, совершенствовать вычислительные навыки, умение решать задачи.

2. Развивать логическое мышление, внимание, математическую речь, умение работать в парах и группах.

3. Воспитывать коммуникативные качества личности, умение работать в группе, вести конструктивный учебный диалог.

Формируемые УУД:

Предметные:

знать: алгоритм деления в столбик, табличные случаи умножения и деления;

уметь: применять алгоритм деления многозначного числа в столбик.

Регулятивные:

отличать верно выполненные задание от неверного, проговаривать последовательность действий на уроке.

Познавательные:

Перерабатывать полученную информацию, делать выводы в результате совместной работы всего класса.

Коммуникативные:

Вступать в речевое общение, допускать существование различных точек зрения, строить монологические высказывания.

Личностные:

Уважать мысли и настроения других учеников, проявлять доброжелательное отношение к одноклассникам, помогать им при необходимости.

Тип урока: Урок открытия новых знаний.

Оборудование:

• М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова, С.В. Степанова «Математика. Учебник для 4 класса – УМК «Школа России».

• С.И. Волкова «Рабочая тетрадь по математике в двух частях».

• Интерактивный комплекс.

• Презентация к уроку.

• Раздаточный материал (карточки с заданиями).

Ход урока.

Оргмомент

Учитель.

Друзья внимание – прозвенел звонок.

Садитесь поудобнее – начнем скорей урок.

— Я надеюсь, что на этом уроке вы откроете для себя новые знания, будете работать с радостью и с удовольствием. Посмотрите друг на друга, улыбнитесь, пожелайте удачи, хорошего настроения (хлопки в ладоши) на весь учебный день.

— Откроем тетради, запишем число, классная работа.

II. Минутка чистописания.

(Повторение нумерации). На доске цифры (Слайд 1.)

4,9,2,1,6,0 .

— Используя все эти цифры составьте самое большое число (1 в. ),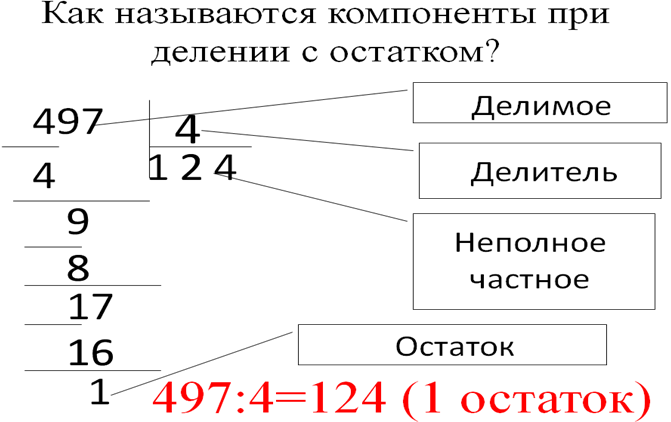

— самое маленькое число (2 в) .

Проверим (Слайд 1 д). 964 210, 102 469.

— Какие это числа?

— Какие действия мы умеем выполнять с этими числами?

III. Актуализация знаний.

Математический диктант.

(1 ученик за доской)

Найдите частное чисел 640 и 40.
Первый множитель 90, второй множитель 40 чему равно произведение.
Уменьшаемое 1200, вычитаемое 350. Чему равна разность.
Записать число, которое больше 60 в 15 раз.
Во сколько раз 20 меньше 1000.
Из какого числа, надо вычесть 800, чтобы получилось 856.
Запишите число, в котором 8 ед. II кл.

(Ответы 16, 2600, 850, 900, 50,1650, 8000)

IV. Подготовка к новой теме.

( Слайд 2.)

488 : 61= 376 : 61=

366 : 61 =

— Сравните выражение.

— Чем они похожи? (Деление на двузначное число, одинаковый делитель).

— Как вы научились делить на двузначное число? (Надо подобрать число, которое при умножении на делитель, дает делимое).

— Какое выражение «лишнее»? Почему?

— Сформулируйте тему урока.( Деление на двузначное число с остатком).

— Посмотрите, у нас в гостях Мудрая сова, давайте правильно выполним ее задания и узнаем какую тему изучают в «Лесной школе». (Тренажер)

— Объясни, как выполнено деление?

— Чему будем учиться на уроке? (делить на двузначное число с остатком)

V. Работа по теме урока.

1. Работа по учебнику страница 58,

№211 (1 пример у доски, остальные по рядам, у доски по представителю от ряда).

— Проверим 1 ряд? Есть ли ошибки? Исправьте.

— Проверим 2 ряд?

— Проверим 3 ряд?

Задача №212.

— Прочитаем задачу.

— Кто совершил первый полет в космос? (Слайд 3).

— Когда произошло это событие?

Какие знания мы используем при решении этой задачи?

(Единицы времени).

— Сколько часов в одних сутках?

— Запишите решение самостоятельно.

— Проверим?(кружки). Кто согласен с …. ?

— У кого другой ответ?

VI . Физкультминутка.( Музыка).

VII. Закрепление изученного материала.

1. Работа по учебнику №215 ( по рядам).

— Проверим 1 ряд (Слайд4) 2 ряд (Слайд5) 3 ряд (Слайд 6)(веер)

1. 1023 1. 2100 1. 2716

2. 2103 2.120 2. 2176

3. 123 3.1020 3. 2676

— Какое неизвестное находили в 1 уравнении, 2, 3.

Задача №220

– Прочитаем задачу. Как кратко записать условие задачи?

( с помощью слов).

— Запишите краткую запись у доски. ………

Известь — 1/10 от 3360 т

Цемент — 1/12 от 3360 т

— Запишите решение задачи самостоятельно.

— Проверка.(Слайд 7-неправильное решение задачи)

2. Работа в группах.

— 1 группа – задача на движение.

2 группа – пример на порядок действия.

3 группа – примеры деление с остатком.

4 группа – геометрическая задача.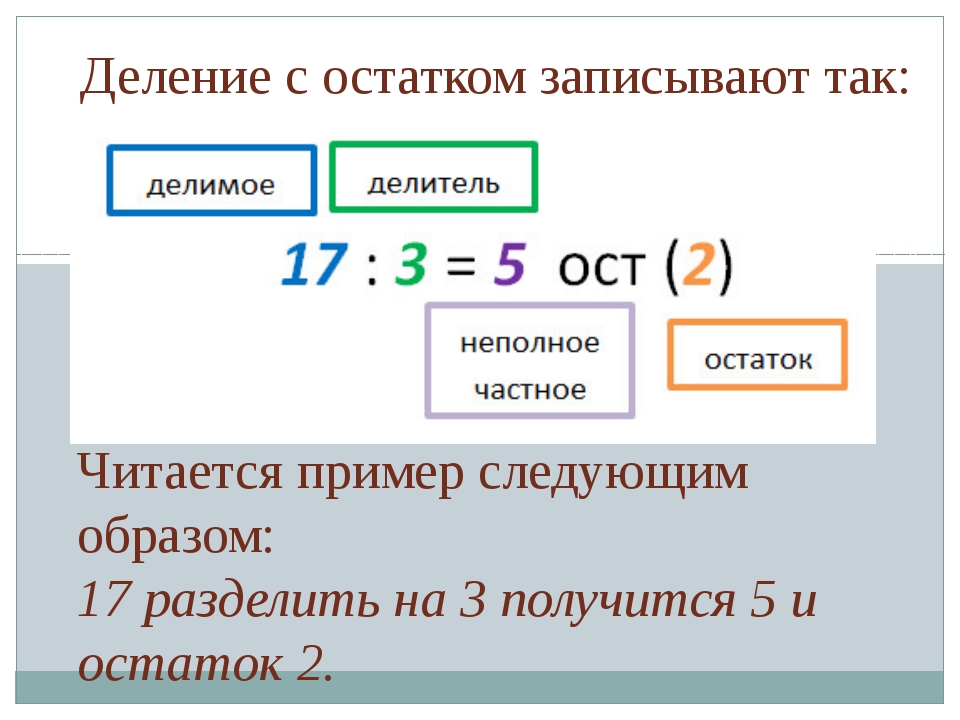

5 группа – составить и решить уравнение.

Индивидуально ( 2 уч. Тест).

VIII. Рефлексия.

— Что нового узнали на уроке?

— Все ли вам было понятно? (кружки).

— Кто испытывал на уроке затруднения?

IX. Подведение итогов.

Выставление оценок.

Домашнее задание (Слайд 8).

Урок математики «Деление с остатком» (4 класс)

8.10.2018г

Конспект урока математики в 4 классе (УМК «Гармония»).

Тема: Деление с остатком.

Цель: создание условий для осознания, осмысления и первичного закрепления блока новой учебной информации средствами ИКТ и практико-ориентированных заданий.

Задачи:

— формировать представление о делении с остатком, вывести алгоритм деления с остатком и тренировать умения применять его для нахождения значений выражений;

-развивать умения выполнять внетабличное умножение и деление;

-совершенствовать вычислительные навыки;

-способствовать развитию мыслительных операций, внимания, памяти, речи, познавательных интересов;

-содействовать развитию умений работать в коллективе, осуществлять самоконтроль и самооценку.

Планируемые метапредметные результаты:

Личностные УУД : готовность к обучению, положительное отношение к учению; способность к самооценке на основе критерия успешности учебной деятельности.

Регулятивные УУД: умение определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; оценивать правильность выполнения действий на уровне адекватной ретроспективной оценки; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение.

Коммуникативные УУД: умение оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения и следовать им.

Познавательные УУД: умение выполнять универсальные логические действия: анализ, синтез, сравнение; устанавливать аналогии;

выстраивать логическую цепь рассуждений; ориентироваться в своей системе знаний; отличать новое от уже известного; добывать новые знания, используя учебник, свой опыт и информацию, полученную на уроке.

Планируемые предметные результаты: выполнять письменное деление чисел с остатком с использованием алгоритма действий;

уметь устно умножать и делить числа в пределах 100, используя разрядный состав чисел, взаимосвязь компонентов и результатов действий.

Тип урока: открытие новых знаний.

Этап самоопределения к деятельности.

Цель для учителя: создать условия для возникновения у обучающихся внутренней потребности включения в учебную деятельность.

Личностные УУД: готовность к обучению, положительное отношение к учению.

Методы:

методы стимулирования и мотивации.

Чтение стихотворения:

Начинается урок.

Он пойдёт ребятам впрок.

Давайте учиться считать,

Делить, умножать, прибавлять, вычитать.

Постарайтесь всё понять,

Чтобы правильно считать.

— А зачем нужно правильно считать? (Ответы детей)

— Правильно, без точного счёта не сдвинется с места любая работа.

-С чего начнём работу на уроке?

II.

Актуализация знаний и фиксация затруднения в деятельности.

Цели для учителя: способствовать осознанию потребности построения нового способа действий;

-организовать выполнение учащимися пробного учебного действия;

-организовать фиксирование учащимися индивидуального затруднения.

Предметные результаты: закрепить умение устно умножать и делить числа в пределах 100, используя разрядный состав чисел, взаимосвязь компонентов и результатов действий.

Познавательные УУД: уметь ориентироваться в своей системе знаний.

Регулятивные УУД: уметь определять и формулировать цель на уроке с помощью учителя.

Методы: частично-поисковый.

Форма работы: фронтальная.

Устный счёт:

-Что общего в выражениях?

-На какие группы можно разделить выражения? Почему?

48:8 81:9

96:3 16:3

54:6 56:4

44:4 321:3

13:2 23:4

Ответы учащихся: — На выражения с табличным и внетабличным делением.

-Назовите эти выражения.

48:8 96:3 13:2

54:6 44:4 16:3

81:9 56:4 23:4

321:3

— Вычислите значения выражений.

— Какие выражения вызвали затруднения? Почему?

— Какую цель поставим на урок?

Ответы учащихся: — Познакомиться с новым случаем деления.

III.

Постановка учебной задачи.

Цель для учителя: зафиксировать во внешней речи причину затруднения.

Познавательные УУД: уметь ориентироваться в своей системе знаний; отличать новое от уже известного.

Коммуникативные УУД: уметь слушать и понимать речь других; совместно договариваться о правилах поведения и общения и следовать им.

Методы:

методы стимулирования интереса к учению,

проблемно- поисковый

Форма работы: групповая.

Беседа:

-Почему не смогли выполнить деление в выражениях: 13:2?

Ответы учащихся: — Число не можем разделить полностью.

— Давайте вместе подумаем, как можно решить выражение 13:2? Предполагаемые ответы учащихся:

-Взять 13 предметов или нарисовать и поделить на 2.

— Действовать, как при внетабличном делении двузначного числа на однозначное: представить делимое в виде суммы удобных слагаемых и выполнить деление.

IV.

Открытие нового знания.

Цель для учителя: организовать усвоение детьми нового способа действий и формирование способности к его выполнению.

Предметные результаты: выполнять письменное деление чисел с остатком с использованием алгоритма действий.

Познавательные УУД: уметь выполнять анализ, синтез, обобщение; устанавливать причинно-следственные связи.

Методы: проблемное изложение

Форма работы: фронтальная

Составление алгоритма действий:

-Можем ли мы представить число 13 в виде суммы слагаемых, каждое из которых делится на 2? (Нет, не можем)

-Значит, надо подобрать такое число, которое делится на 2 и меньше 13. Какое это число? (12)

Разделите это число (12:2=6)

-На сколько число 13 больше, чем 12? (На 1)

-Как это записать? (13-12=1)

1 – это остаток. Что нужно сделать, чтобы найти остаток?

(Вычесть подобранное число из делимого)

Запись: 13:2=6(ост.1)

6-это неполное частное, 1-остаток.

По ходу рассуждения составляется:

Алгоритм выполнения деления с остатком:

1.Подобрать число, которое меньше делимого и делится без остатка.

2.Разделить это число.

3.Вычесть подобранное число из делимого и получить остаток. (Слайд 4)

Работа с учебником.

-Откройте учебник и прочитайте правило на с.29.

Остаток при делении всегда должен быть меньше делителя.

Чему ещё необходимо потренироваться на уроке?

Первичное закрепление.

Цель для учителя: организовать усвоение учениками нового способа действий с проговариванием во внешней речи.

Познавательные УУД: уметь выполнять анализ, синтез, обобщение; выстраивать логическую цепь рассуждений.

Коммуникативные УУД: уметь оформлять свои мысли в устной форме.

Методы организации учебно-познавательной деятельности: словесные, наглядные, практические.

Форма работы: фронтальная

Физминутка.

Комментированное выполнение учащимися деления с остатком с опорой на алгоритм:

16:3

Ответы учащихся: — Подберём число, которое меньше 16 и делится на 3 без остатка. Это число 15. 15 : 3 =5, 5 – неполное частное. Вычтем из 16 -15,остаток равен 1.Остаток меньше делителя, значит запись верная: 16:3=5(ост.1)

23:4

Ответы учащихся: — Подберём число, которое меньше 23 и делится на 4 без остатка. Это число 20. 20: 4 =5, 5 –неполное частное. Вычтем из 23-20, остаток равен 3. Остаток меньше делителя, значит запись верная: 23:4=5(ост.3)

VI.

Самостоятельная работа с самопроверкой по эталону.

Цели для учителя: организовать выполнение учащимися самостоятельной работы на новое знание;

-организовать самопроверку по эталону.

Предметные результаты: выполнять письменное деление чисел с остатком с использованием алгоритма действий

Познавательные УУД: уметь выполнять анализ, сравнение, обобщение.

Регулятивные УУД: уметь оценивать правильность выполнения действий на уровне адекватной ретроспективной оценки

Методы:

-практический

-метод контроля и самоконтроля

-создание ситуации успеха

Форма работы: парная.

-Сейчас предлагаю поработать в парах. Вспомните главное правило работы в паре?

(Прислушиваться к мнению товарища, работать дружно)

-Выполните деление с остатком:

12:5 17:5

25:6 42:8

-Проверьте правильность выполнения деления по образцу.

-Оцените работу своей пары.

VII.

Включение в систему знаний и повторение.

Цель: организовать усвоение учениками нового способа действия, повторение и закрепление ранее изученного.

Познавательные УУД: выполнять универсальные логические действия: анализ, синтез, сравнение; устанавливать аналогии;

выстраивать логическую цепь рассуждений.

Регулятивные УУД: осуществлять контроль, коррекцию, оценку.

Методы:

метод самостоятельной работы;

метод контроля и самоконтроля

Форма работы: индивидуальная.

Дифференцированная самостоятельная работа учащихся.

Выполнение задания № 60 или № 62 , с.30-31 из рабочей тетради

Проверка по образцу.

-Оцените свою работу.

VIII.

Рефлексия учебной деятельности

Цели: зафиксировать новое содержание урока;

-организовать рефлексию и самооценку учениками собственной учебной деятельности.

Личностные УУД: способность к самооценке на основе критерия успешности учебной деятельности.

Коммуникативные УУД: уметь выражать свои мысли с достаточной полнотой и точностью.

Методы: метод контроля и самоконтроля

Формы работы:

фронтальная; индивидуальная.

-Подведём итоги нашей работы.

-Над какой темой работали на уроке?

-Какую цель ставили? Достигли ли поставленной цели?

-Какую цель поставим на следующий урок математики?

-Выберите высказывание, которое считаете подходящим для сегодняшнего урока.

-Оцените свою активность на уроке (в тетрадях по шкале)

-Спасибо за урок.

-Домашнее задание:

ПНШ 4 класс. Математика. Учебник № 1, с. 52

Деление с остатком и деление нацело

Ответы к с. 52

149. После того как мама положила на каждую из четырёх тарелок по 3 сосиски, в кастрюле осталось 2 сосиски. Сколько всего сосисок сварила мама?
Запиши решение этой задачи в виде одного выражения. Раздели с остатком число 14 на число 4.

3 • 4 + 2 = 14 (с.)
14 : 4 = 3 (ост. 2)

150. Выполни деление с остатком, используя для этого соответствующие табличные случаи деления.
24 : 6 = 27 : 3 = 32 : 8 = 81 : 9 =
27 : 6 = 29 : 3 = 39 : 8 = 85 : 9 =
Рассмотри действия деления в первом столбике. Какое из них является табличным случаем деления? На сколько одно делимое отличается от другого? Будет ли это число совпадать с остатком?
Вычисли, на сколько отличаются делимые в остальных столбиках. Проверь, совпадает ли каждое из этих чисел с соответствующим ему остатком.

24 : 6 = 4 27 : 3 = 9
27 : 6 = 4 (ост. 3) 29 : 3 = 9 (ост. 2)

32 : 8 = 4 81 : 9 = 9
39 : 8 = 4 (ост. 7) 85 : 9 = 9 (ост. 4)

Табличный случай деления 24 : 6 = 4, так как 6 • 4 = 24.
Разностное сравнение чисел: 27 – 24 = 3, 27 > 24 на 3. Да, так как остаток – это минимальное число, которое нужно вычесть из делимого, чтобы полученное число делилось нацело на данный делитель. То есть, если, из делимого 27 вычесть делимое 24, которое делится на 6 нацело, то получим число 3, которое и является остатком.
29 – 27 = 2 39 – 32 = 7 85 – 81 = 4
29 : 3 = 9 (ост. 2) 39 : 8 = 4 (ост. 7) 85 : 9 = 9 (ост. 4)
Каждое число, получившееся в результате разностного сравнения делимых, совпадает с соответствующим ему остатком.

151. Объясни, почему с помощью табличного случая деления 42 : 7 = 6 можно разделить с остатком число 45 на число 7. Выполни и запиши деление с остатком числа 45 на число 7.
Почему выбранный табличный случай деления можно получить, выполнив действие в скобках в следующем выражении: (45 – 3) : 7?
Вычисли значение этого выражения. В полученном равенстве подчеркни соответственно одной и двумя чертами числа, которые получаются в результате деления с остатком числа 45 на число 7. Всегда ли аналогичным образом можно получить по результатам деления с остатком соответствующий случай деления нацело?

Наибольшее число, которое делится нацело на 7 и которое не превосходит число 45, – это число 42 (42 : 7 = 6). Можно утверждать, что делитель (число 7) максимально содержится в делимом (числе 45) 6 раз, при этом в остатке остаётся ещё число 3 (45 – 42 = 3), значит 45 : 7 = 6 (ост. 3).
Потому, что число 3 – это остаток, при вычитании которого из делимого мы получаем указанный табличный случай деления.
(45 – 3) : 7 = 42 : 7 = 6.
По результатам деления с остатком 45 : 7 = 6 (ост. 3) всегда можно получить соответствующий случай деления нацело. Например, при вычитании остатка (3) из делимого (45) получается число (42), которое делится нацело на делитель (7).

Ответы к заданиям. Математика. Учебник. Часть 1. Чекин А.Л. 2012 г.

Математика. 4 класс. Чекин А.Л.

4.7
/
5
(
14

голосов
)

4 класс. Моро. Учебник №1. Ответы к стр. 81

Числа от 1 до 1000

Умножение и деление

Деление на однозначное число

Ответы к стр. 81

Объясни приёмы вычисления.
963 : 3 = (900 + 60 + 3) : 3 = 900 : 3 + 60 : 3 + 3 : 3
455 : 5 = (450 + 5) : 5 = 450 : 5 + 5 : 5

Делимое разложили на сумму разрядных слагаемых и использовали правило деления суммы на число: чтобы поделить сумму на число, можно каждое слагаемое поделить на это число и полученные частные сложить.

363. Найди частное и остаток и выполни проверку.
56 : 15 92 : 30 399 : 9 854 : 8 34 : 40

_— 56|15      Проверка:  _×15
45|3    3
11 – ост. 45
45 + 11 = 56

_— 92 |30     Проверка: 30 • 3 + 2 = 92
   90 |3
2 – ост.

_— 399|9     Проверка:  _×44
36 |44    9
_—39 396       36
3 – ост. 396 + 3 = 399

_— 854|8     Проверка:  _×106
8 |106    8
_—054 848       48
6 – ост. 848 + 6 = 854

_— 34 |40 Проверка: 40 • 0 + 34 = 34
0 |0
34 – ост.

364. Объясни, что обозначают записи в рамках на полях, и выполни вычисления.

0 : α = 0 − при делении нуля на любое число всегда получается нуль
b : 1 = b − при делении числа на единицу всегда получается данное число
c : c = 1 − при делении числа на само себя всегда получается единица

0 : 45 = 0 208 : 1 = 208 375 : 375 = 1
0 : 964 = 0 342 : 1 = 342 863 : 863 = 1

365. Составь разные задачи по выражению 24 : 6.

1) Миша купил 24 солдатика, а машинок в 6 раз меньше, чем солдатиков. Сколько машинок купил Миша?
24 : 6 = 4 (м.)
О т в е т: Миша купил 4 машинки.

2) Мама принесла домой 24 пирожных. Вечером Миша съел шестую часть этих пирожных. Сколько пирожных съел Миша?
24 : 6 = 4 (п.)
О т в е т: Миша съел 4 пирожных.

366. За 2 ч езды на легковой машине обычно расходуется 12 л бензина. На сколько часов езды хватит 48 л бензина, если его расход не изменится?

1) 12 : 2 = 6 (л) − бензина хватает на 1 ч
2) 48 : 6 = 8 (ч) − время, на которое хватит 48 л бензина
О т в е т: на 8 часов.

367. В прошлом году завод изготовил 1400 машин, что на 300 машин меньше, чем в этом году. Поставь вопрос и реши задачу.

Сколько машин изготовил завод за эти 2 года?
1) 1400 + 300 = 1700 (м.) − изготовлено в этом году
2) 1400 + 1700 = 3100 (м.) − изготовлено за 2 года
О т в е т: за 2 года завод изготовил 3100 машин.

368. Одна бригада рабочих заасфальтировала 5 км 060 м шоссе, другая бригада − на 2 км 280 м больше. Осталось покрыть асфальтом 965 м шоссе. Какой длины шоссе должны были заасфальтировать эти бригады?

1) 5 км 060 м + 2 км 280 м = 7 км 340 м − заасфальтировала вторая бригада
2) 5 км 060 м + 7 км 340 м + 965 м = 12 км 400 м + 965 м = 13 км 365 м − должны были заасфальтировать
О т в е т: должны были заасфальтировать 13 км 365 м шоссе.

369. 658 : 7 9235 + 4 • (536 : 8) 40077 • 7 − 199099
836 : 4 (2010 − 1065) : 7 • 6 9020 • 6 + 53901

658 : 7 = 94
_— 658|7
63 |94
_—28 28
0

836 : 4 = 209
_— 836|4
   8 |209
_—036    36
0

9235 + 4 • (536 : 8) = 9235 + 4 • 67 = 9235 + 268 = 9503
_— 536|8   _×67 ₊9235
48 |67     4 268
_—56 268 9503    56
0

(2010 − 1065) : 7 • 6 = 945 : 7 • 6 = 135 • 6 = 810
_2010 _— 945|7      _×135
1065     7 |135    6
945_—24 810    21
_35
35
0

40077 • 7 − 199099 = 280539 − 199099 = 81440
_×40077 _{_}280539
7 199099
280539 81440

9020 • 6 + 53901 = 54120 + 53901 = 108021
_×9020 ₊54120
6 53901
54120 108021

370. x : 9 = 1000 − 910 100 • x = 2430 − 2030
x • 9 = 1000 − 910 100 : x = 2430 − 2420.

x : 9 = 1000 − 910 x • 9 = 1000 − 910
x : 9 = 90 x • 9 = 90
x = 90 • 9 x = 90 : 9
x = 810 x = 10

100 • x = 2430 − 2030
100 • x = 400
x = 400 : 100
x = 4

100 : x = 2430 − 2420
100 : x = 10
x = 100 : 10
x = 10

371. На какое однозначное число надо умножить число 12345679, чтобы в результате получить новое число, записанное одними единицами?

Так как у числа 12345679 последняя цифра 9, то при умножении на однозначное число этой цифры, последняя цифра произведения должна быть равна 1. Известен только один случай такого табличного умножения: 9 • 9 = 81 (последняя цифра 1).
_×12345679
9
111111111

Вычисли. 693 : 3 468 : 2

_— 693|3   _— 468|2
   6 |239    4 |234
_—09   _—06    9 6
_03 _08
3 8
0 0

Ответы по математике. Учебник. 4 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.

Математика. 4 класс

4.7
/
5
(
38

голосов
)

Конспект урока математики 4 класс по теме «Деление с остатком на двузначное число»

Урок 8 «Письменное деление с остатком на двузначное число». ИКТ

Дата: 15.04.16г.

Цели урока:

2. Развивать логическое мышление, внимание, математическую речь.

3. Воспитывать коммуникативные качества личности, умение работать в парах, вести конструктивный учебный диалог.

Формируемые УУД:

Предметные:

знать: алгоритм деления в столбик, табличные случаи умножения и деления;

уметь: применять алгоритм деления многозначного числа в столбик.

Метапредметные: связывать сведения, полученные на уроках Окружающего мира и внеклассных мероприятиях с учебным материалом урока.

Регулятивные:

проговаривать последовательность действий на уроке, анализировать правильность решения и ответ.

Познавательные:

Перерабатывать полученную информацию, делать выводы в результате совместной работы всего класса.

Коммуникативные:

Вступать в речевое общение, допускать существование различных точек зрения, строить правильное высказывания.

Личностные:

Тип урока: Урок общеметодологической направленности.

Оборудование:

• С.И. Волкова «Рабочая тетрадь по математике в двух частях».

• Презентация к уроку.

• Раздаточный материал (карточки с заданиями).

Ход урока.

I . Организационный момент.

Начинаем наш урок,

Надеюсь, он пойдет вам впрок.

Постарайтесь все понять,

Ответы полные давать.

II. Актуализация знаний.

На первом этапе урока мы в гостях у животного мира. Для нас оставлены математические подсказки, вы же знаете, что все в мире взаимосвязано. Я предлагаю начать поиск? Вот первая подсказка:

На опушке две лягушки, две зеленые подружки,

Весело играли и прыжки считали.

Каждая 15 раз, кто сочтёт прыжки из вас? (15х2=30)

Составьте к данному примеру еще три, используя данные числа.

(30:15=2 30:2=15 2х15=30)

— Где живут лягушки? (на болоте)

Вот оттуда и начнём.

III. Устный счёт. Запись на доске

Какой пример лишний? Почему? Подберите к нему ключик с правильным ответом:

24:2 64:16 36:3

— Откроем тетради, запишем число, классная работа.

II. Минутка чистописания.

(Повторение нумерации. Слайд 1)

4,9,2,1,6,0 .

— Используя все эти цифры составьте самое большое число (1 в.),

— самое маленькое число (2 в).

Проверим (Слайд 1 д). 964 210, 102 469.

— Какие это числа?

— Какие действия мы умеем выполнять с этими числами?

III. Актуализация знаний.

Математический диктант.

(1 ученик за доской)

Найдите частное чисел 640 и 40.
Первый множитель 90, второй множитель 40 чему равно произведение.
Уменьшаемое 1200, вычитаемое 350. Чему равна разность.
Записать число, которое больше 60 в 15 раз.
Во сколько раз 20 меньше 1000.
Из какого числа, надо вычесть 800, чтобы получилось 856.
Запишите число, в котором 8 ед. II кл.

(Ответы 16, 2600, 850, 900, 50,1650, 8000) – сравните результат (взаимопроверка в парах)

IV. Подготовка к новой теме.

( Слайд 2.)

488 : 61= 376 : 61= 366 : 61 =

— Сравните выражение.

— Чем они похожи? (Деление на двузначное число, одинаковый делитель).

— Какое выражение «лишнее»? Почему?

— Сформулируйте тему урока. ( Деление на двузначное число с остатком).

— Чему будем учиться на уроке? (делить на двузначное число с остатком)

V. Работа по теме урока.

Работа по учебнику страница 58

Комментирование алгоритма решения примеров по заданию учебника (образец)

№211 (1 пример у доски, остальные по рядам, у доски по представителю от ряда).

— Проверим 1 ряд? Есть ли ошибки? Исправьте.

— Проверим 2 ряд?

— Проверим 3 ряд?

Задача №212.

— Читаем задачу. Какой праздник совсем недавно отмечали?

— Кто совершил первый полет в космос? (Слайд 3).

— Когда произошло это событие? Сколько длился полет? (108 минут)

Какие знания мы используем при решении этой задачи?

(Единицы времени).

— Сколько часов в одних сутках? Как построим решение задачи? (ответы детей)

— Запишите решение самостоятельно.

— Проверим. (комментируются решение и ответ)

VI . Космическая физминутка с Гугушей (видео)

VII. Закрепление изученного материала.

№216 – комментированное решение примеров

Задания «Проверь себя» — самостоятельно «на скорость» с последующей проверкой

2. Фронтальная работа над задачей № 214 у доски и в тетрадях

— план решения, составление краткой записи и оформление решения и ответа

3. Индивидуально (2 ученика карточки для слабых учащихся с примерами на повторение).

VIII. Рефлексия.

— Что нового узнали на уроке?

— Все ли вам было понятно?

— Кто испытывал на уроке затруднения? В чем они заключались?

IX. Подведение итогов.

Выставление оценок.

Технологическая карта урока Класс: 8 Предмет: алгебра Тема урока: Погрешность и точность измерения. Дидактическая цель урока: создать условия для восприятия и осознания понятий абсолютная и относительная

Подробнее

Урок математики в 1Б классе по программе «Школа России» по теме: «Задачи в два действия». Первый урок в теме, когда дети переходят от решения задач-цепочек к решению задач в два действия. Цели деятельности

Подробнее

Урок 22. Тип урока: ОНЗ

Тип урока: ОНЗ Урок 22 Тема: «Сравнение долей». Автор: Калинина Л. В., МОУ гимназия 9 г. Королёва. Основные цели: ) сформировать способность к изображению долей точками числового луча и сравнению долей;

Подробнее

ПЛАН-КОНСПЕКТ УРОКА 1. ФИО

ПЛАН-КОНСПЕКТ УРОКА Тема: «Сложение чисел с разными знаками» 1. ФИО (полностью) Федосеева Ольга Васильевна 2. Место работы ГБОУ школа-интернат 1 г.о. Чапаевск 3. Должность Учитель математики 4. Предмет

Подробнее

Технологическая карта урока

Технологическая карта урока Учитель: Можаева Т.П., учитель нач. классов 1 квалификационной категории Предмет: русский язык Класс: 4 Тип урока: обобщение и закрепление знаний Тема: «Падежные окончания имён

Подробнее

Учебные пособия и рабочие листы для дивизиона 4 класса

Деление 6-значных чисел на однозначное число

Деление шестизначных чисел на двухзначное число

Деление 6-значных чисел на 10

Story Time Division

Дивизионный тест

Рабочий лист отдела

Лист для ответов

Деление 6-значных чисел на однозначное число

На предыдущем уроке мы научились делить 4/5 значные числа на однозначные числа.Мы будем использовать тот же
метод деления шестизначных чисел на однозначные числа. Ниже приведены несколько примеров.

Пример 1. Разделите 275625 на 5.
Решение.

Итак, ответ — 55125.

Пример 2. Разделите 730201 на 9.
Решение.

Таким образом, частное равно 81133, а остаток равен 4.

Деление шестизначных чисел на двухзначное число

Все правила, которые мы узнали ранее, будут использоваться в этом виде разделения.Здесь у нас будет 2 цифры
делитель. Когда мы делим число на двузначное число, таблицу которого мы не знаем, мы должны умножить его, чтобы получить
ответ. Давайте посмотрим на несколько примеров.

Пример 1. Разделите 488244 на 12.
Решение.

Итак, частное 40687.

Пример 2. Разделите 968727 на 25.
Решение.

Таким образом, частное равно 38749, а остаток равен 2.

Деление 6-значных чисел на 10

Теперь давайте научимся делить шестизначные числа на двухзначные числа, оканчивающиеся нулем. Ниже приведены несколько примеров.

Пример 1. Разделите 265750 на 50.
Решение.

Итак, частное 5315.

Пример 2. Разделите 336735 на 30.
Решение.

Таким образом, частное равно 11224, а остаток равен 15.

Story Time Division

Разделение времени рассказа решается аналогично тому, как это было изучено в предыдущих классах. Здесь мы будем использовать
большие числа. Ниже приведены несколько примеров.

Пример 1. 9 Мотоцикл стоит 729576 ₹. Сколько стоит один мотоцикл?
Решение.
Стоимость 9 мотоциклов = ₹ 729576
Стоимость 1 мотоцикла = ₹ 729576 9

Итак, стоимость одного мотоцикла составляет 81064 ₹.

Пример 2. 507680 рупий распределить поровну между 32 семьями села. Сколько денег в каждой семье
получит?
Решение.
Итого деньги будут распределены между 32 семьями = 507680
₹
Каждая семья получит = ₹ 507680 32

Таким образом, каждая семья получит 15064.

Дивизионный тест

Дивизионный тест — 1
Дивизионный тест — 2

Рабочий лист отделения 4 класса

Рабочий лист отдела — 1
Рабочий лист отдела — 2
Рабочий лист отдела — 3

Лист для ответов

Division-Answer Скачать pdf

Разделение четырехзначных и больших чисел — математика для 3-го класса

Научитесь делить четырехзначные и большие числа

Вы только что научились делить трехзначные числа.

Вы помните шаги к делению в столбик? 🤔

Давайте их вспомним! 🤗

Длинные ступени дивизиона

Шаг 1: Разложите задачу в виде длинных разделов. Начните с цифры на самом высоком месте делимого.

Шаг 2: Посмотрите , сколько раз делитель умещается в этой цифре. Запишите это число сверху как частное , и произведение этого частного и делителя под цифрой делимого.

Шаг 3: Вычтите произведение из цифры делимого.

Шаг 4: Введите следующую цифру справа (👉) и объедините ее с предыдущим остатком, если таковой имеется.

Шаг 5: Повторите из Шаг 2 .

Шаг 6: В конце число вверху — это частное , , а любое число слева внизу — это остаток .

Разделение 4-значных чисел

👉 Посмотрите на эту проблему разделения.

8,356 ÷ 4 =?

Давайте решим эту задачу деления, используя шаги длинного деления. 🤗

✅ Сначала мы оформим задачу в виде длинных делений.

✅ Теперь давайте посмотрим на первую цифру .

Сколько четверок можно уместить в восьмерку? 🤔

Очень хорошо! 2.

Итак, мы запишем 2 сверху, как частное и произведение на 2 и 4 под 8.

Теперь мы вычитаем это произведение из цифры в делимом (8), чтобы получить остаток.

Отличная работа! 👍

✅ Теперь давайте опустим следующую цифру, 3.

Сколько четверок можно уместить в тройку? 🤓

Верно! Нет, или 0.

Итак, мы пишем 0 сверху, как частное.

Когда частное для любой цифры в длинном делении равно 0, мы делим следующую цифру вместе с ней.

✅ Итак, давайте опустим следующую цифру, 5.

Теперь давайте разделим 35 на 4.

Можете ли вы сказать, сколько четверок может поместиться в 35? 🤔

Очень хорошо! 8.

Опять же, мы пишем 8 сверху, как частное, а произведение на 8 и 4 под 35.

Затем мы вычитаем этот продукт из 35.

Отличная работа! 👌

✅ Давайте теперь запустим последнюю цифру, 6.

Поскольку у нас есть остаток от прошлого раза, мы объединим остаток с 6, и разделим их вместе.

Итак, теперь разделим 36 на 4.

Вы можете сказать, сколько четверок умещается в 36? 🤓

Правильно! 9.

Итак, снова мы пишем 9 сверху, как частное и произведение 9 и 4 под 36.

Затем мы вычитаем .

Отлично! 😎

Итак, можете ли вы сказать, каковы частное и остаток в этом вопросе? 😃

Очень хорошо!

👉 Частное здесь составляет 2 089 , а остаток равен 0 .

Итак,

8,356 ÷ 4 = 2,089

👉 Возьмем другой пример.

4,372 ÷ 2 =?

Можете ли вы выполнить предыдущие шаги и решить этот вопрос? 🤗

На схеме ниже показаны все этапы этой задачи разделения:

Поскольку эта задача заканчивается на 0, у нас нет остатка!

4,372 ÷ 2 = 2,186

👉 А теперь давайте попробуем еще большее число!

37,852 ÷ 3 =?

Давайте выполним шаги и решим проблему! 😁

37,852 ÷ 3 = 12,617 R2

Отличная работа! 🎉 Теперь вы знаете, как делить числа на 4 и более цифр.

Смотри и учись

🤗 Теперь можно переходить к практике!

Дивизион, частное и остаток — вопросы по математике для 4-го класса с ответами

456 6 =
7
76
70
75
2 0 =
0
2
20
не могу найти ответ
223 1 =
223
1
0
не могу найти ответ
Каково частное q и остаток r от деления 547 4 = ?
q = 3 и r = 136
q = 136 и r = 0
q = 136 и r = 3
q = 136 и r = 27
Какое значение имеет (21 + 5) (4-2)
13
26
2
28 год
(25 5) (6 — 1) =
5
1
625
25
В коробки по 8 конфет помещено 64 конфеты.Сколько коробок нужно?
72
56
8
512
Если 6 детей разделят 145 сладостей поровну, сколько сладостей останется?
24
0
6
1

Ответы на вышеперечисленные вопросы

B
D (деление на ноль НЕ допускается)
А
С
А
B
С
D

Распечатанные рабочие листы и упражнения с делением на длинное и хвостовое деление для учащихся 4 и 5 классов по математике

Выберите одну из следующих категорий рабочего листа хвостового деления.Наша основная математика
Рабочие листы по математике с долгим делением можно бесплатно распечатать.

Длинное деление, как и дроби, — это математическая тема, которая действительно может отпугнуть молодых изучающих математику. Вы либо поймете, либо нет, и если вы этого не сделаете, каждое упражнение на деление в длину превратится в борьбу. У нас есть подборка рабочих листов для деления в столбик с , готовых для заполнения полей и нескольких уровней сложности, чтобы учащиеся могли постепенно овладеть «наукой страшного деления в столбик».

Наша первая часть рабочего листа деления хвоста основана на делении 2 цифр на 1 цифру. Эти упражнения относительно просты, так как их можно выполнять без использования структуры деления хвоста. Эти рабочие листы для 4-го класса созданы для обучения концепции и структуры упражнений на длинные деления и служат хорошей отправной точкой на пути к мастерству . Они бывают как с остатком, так и без него (лучше всего без него). По нашему скромному математическому мнению, жизненно важно, чтобы юные ученики математики не только выучили деление хвоста, но и научились проверять результат.Умножьте частное на делитель и сложите остаток.

Когда концепция ясна и полностью усвоена, студенты-математики могут решить следующие рабочие листы с длинным делением: 3 цифры, разделенные на 1 цифру, 3 цифры, разделенные на 2, 4 (или 5 или 6) цифр, на 2 и т. Д. Мы считаем, что деление в столбик не должно быть проблемой для студентов-математиков, и если это так, всю концепцию деления необходимо переучить (и выучить). Деление (и умножение), возможно, являются наиболее важными компонентами набора навыков , необходимого для математики, алгебры и статистики среднего уровня.Итак, пришло время освоить концепцию деления в столбик по 5-му классу.

Некоторые из наших материалов по полному разделению построены таким образом, что ученик, изучающий математику, должен найти делитель или дивиденд с учетом частного результата. У нас также есть раздел упражнений на разделение хвоста, которые необходимо выполнить, поля необходимо заполнить. Этот «обратный» способ решения проблем можно использовать для оценки владения концепцией разделения хвоста.

Наши рабочие листы с долгим делением основаны на следующих темах по математике Сингапурского учебного плана:

Умение делить числа, маленькие и большие
Понять концепцию длинного деления
Умение находить дивиденд и делитель проблем с учетом частного
Возможность проверки результатов работы хвостовых отделов
Возможность решать проблемы в разумные сроки

Наши новые материалы? Подписывайтесь на нас.

Дивизион | Как разделить | Связанные термины

Деление — это одна из четырех основных математических операций, остальные три — это сложение, вычитание и умножение. Проще говоря, раздел можно определить как разделение большой группы на равные меньшие группы.

Дивизион можно представить, рассматривая предметы из нашей повседневной жизни, такие как кусочки пиццы или плитка шоколада.Например, если мы делим пиццу на 4 части, мы делаем деление. Таким образом, 1 ÷ 4 = 0,25. Это означает, что каждый кусок этой пиццы в 0,25 раза больше, чем весь кусок пиццы. Давайте познакомимся с этим понятием подробнее.

Что такое дивизия?

Деление — это основная арифметическая операция, при которой числа объединяются и делятся таким образом, чтобы получилось новое число. Это значит, что мы разделим одно число на другое, и получится целое новое — третье число. Деление — это метод равномерного группирования объектов в группы, например размещение учащихся рядами во время сборки.

Определение деления

Деление — это процесс повторного вычитания. Он обозначается математическим символом, который состоит из короткой горизонтальной линии с точкой над и под линией.

Обозначение деления

Для выполнения операций, требующих деления, мы используем определенные символы. Есть два основных символа разделения, которые представляют разделение. Это ÷ и /. Например, 4 ÷ 2 = 2 и 4/2 = 2

Особые случаи

Ниже приведены три частных случая деления.

Любое число, деленное на 1 (частное равно деленному), дает ответ, такой же, как и делимое. Например: 10 ÷ 1 = 10
Число не может быть разделено на 0, поэтому результат не определен. Пример: 60 ÷ 0 = не определено (но 0 ÷ 60 = 0)
Когда дивиденд равен делителю, что означает те же числа, но не 0, тогда ответ всегда 1. Например: 41 ÷ 41 = 1

Какова общая формула деления?

Общая формула деления требует, чтобы у нас были дивиденд, частное, делитель и остаток.Значение каждого из этих терминов можно понять из изображения, приведенного ниже. Чтобы лучше понять концепцию деления, мы рекомендуем просмотреть страницу метода длинного деления. Общая формула деления: Дивиденд = (Делитель × Частное) + остаток

Термины, относящиеся к подклассу

Взгляните на приведенную здесь таблицу, чтобы понять термины, относящиеся к разделению, приведенному в разделе, проведенном здесь ранее.

Условия	Описания	Значения
Дивиденды	Общее количество частей, которые должны быть разделены	105
Делитель	Количество равных групп, которые должны быть образованы	8
Частное	Количество штук в каждой группе	13
Остаток	Оставшийся кусок, не входящий ни в одну группу	1

Проверка результата разделения

Мы можем легко проверить, правильный или неправильный наш ответ.Поскольку деление — это обратное умножению, давайте выясним, как мы можем проверить наш ответ, используя эту информацию. Например, 6 ÷ 2 = 3, остаток = 0. Другими словами, 6 = 2 × 3 + 0. Это может быть выражено как Дивиденд = (Делитель × Частное) + Остаток.

Давайте еще раз рассмотрим рассмотренный выше пример, где

дивиденд = 105
делитель = 8
частное = 13
остаток = 1

Подставляя значение в формулу, получаем 105 = (8 × 13) + 1 = 104 + 1 = 105.Следовательно, наш ответ правильный.

Метод длинного деления

Метод длинного деления — наиболее распространенный метод, используемый для решения задач деления. В этом процессе делитель записывается за пределами правой скобки, а делимый — внутри. Частное указывается над чертой сверху над дивидендом. В математике частное можно определить как результат деления числа на любой делитель. Это количество раз, когда делитель содержится в делимом без отрицательного остатка.

Шаг 1: Возьмите первую цифру делимого. Если эта цифра больше или равна делителю.
Шаг 2: Затем разделите полученное значение на делитель и напишите ответ сверху.
Шаг 3: Вычтите результат из цифры и запишите ниже.
Шаг 4: Снова повторите тот же процесс.

Разберемся в процессе деления на примере.Например, мы должны разделить 435 на 4. Значит, нам нужно 435 ÷ 4.

Здесь первая цифра 4 и равна делителю. Итак, 4 ÷ 4 = 1; 1 написано сверху. Результат 4 × 1 = 4 вычитается из цифры и ниже записывается 0.
Затем опустите вторую цифру или цифру на место десяти рядом с 0. Поскольку 03 меньше 4, мы не можем разделить это число. Следовательно, мы пишем 0 сверху и опускаем цифру на единицу измерения рядом с 3.
Теперь у нас 35.Поскольку 35> 4, мы можем разделить это число и написать сверху 35 ÷ 4 = 8.
Вычтите результат 4 × 8 = 32 из 35 и запишите 3.
3 известен как остаток , а 108 называется частным .

Часто задаваемые вопросы о дивизионе

Какие два типа деления?

Подразделение разделено на две части: частичных и котельных моделей. Partitive используется при делении числа на известное количество слотов. Например, если мы разделим 4 на 2 слота, мы сможем узнать, сколько предметов будет в каждом слоте. Цитирующее деление используется при делении числа на ячейки измеряемой величины. Например, когда мы делим 4 на слоты по 2, мы можем определить, сколько слотов можно создать.

Какие 3 части деления?

Три основных подмножества или части деления — это дивиденды, частное и делитель.

Как делиться, когда делитель больше дивиденда?

В этом случае деления мы можем просто продолжать прибавлять нули к делимому, пока не станет целесообразным дальнейшее деление. Кроме того, мы можем разделить частное на те же степени 10 для окончательного ответа, как только мы сделаем деление правильно.

Как разделить дроби?

Делить дроби так же просто, как делить любые другие два числа. Числитель становится делителем, а знаменатель становится делимым.Однако в случае дробей мы можем получить остаток чаще, чем часто.

Как разделить десятичные дроби?

Разделить десятичные дроби так же просто, как разделить любые другие два числа. Все, что вам нужно сделать, это умножить десятичную дробь на десятичную, пока не получится целое число. Затем вы можете выполнить обычный процесс разделения. Получив окончательный ответ, не забудьте разделить его с той же степенью десяти, что и раньше.

Что такое метод длинного деления?

Метод длинного деления — это наиболее распространенный метод, используемый для решения задач по делению.В этом процессе делитель записывается за правыми скобками, а делимое — внутри. Частное указывается над чертой сверху над дивидендом.

Каковы этапы метода длинного деления?

Шаги для деления в столбик:

Шаг 1: Возьмите первую цифру делимого. Если эта цифра больше или равна делителю.
Шаг 2: Затем разделите полученное значение на делитель и напишите ответ сверху.
Шаг 3: Вычтите результат из цифры и запишите ниже.
Шаг 4: Снова повторите тот же процесс.

Почему деление на ноль не определено?

Деление на ноль не определено, потому что нельзя делить любое число на ноль. Это потому, что когда любое число умножается на ноль, получается 0. Теперь подумайте об обратном. 1/0 будет иметь бесконечное значение. Мы не можем количественно оценить это значение в математике. Следовательно, деление любого числа на ноль не определено.

Деление — остаток и перегруппировка

После того, как мы узнаем об умножении однозначных чисел на трехзначные числа, мы углубимся в деление. Концепция остатка специфична для деления и может быть сложной для некоторых студентов. Следовательно, прежде чем сразу перейти к делению с остатком, лучше сначала понять концепции частного и остатка и рассматривать случаи с перегруппировкой и без нее по отдельности. В этом уроке мы рассмотрим три цели: ментальное деление, введение частного и остатка с перегруппировкой и, наконец, деление с перегруппировкой.

Для мысленного деления мы сначала начнем с простого деления и будем использовать его для иллюстрации больших чисел. Например, для 360 ÷ 9 мы имеем:

Здесь мы обнаруживаем, что, когда мы делим ряд конкретных объектов на равные группы, мы иногда обнаруживаем, что есть объекты, «оставшиеся» в качестве остатка. В таких случаях мы просто запишем ответ как частное и остаток. Например, 24 ÷ 2 vs 25 ÷ 2:

Сначала мы работаем над задачами деления, которые не связаны с перегруппировкой и остальными, чтобы студенты ознакомились с операцией, например.грамм.

Затем добавьте задачи, связанные с остатком, например

Затем мы ввели проблему разделения, которая включает в себя перегруппировку. Например,

Здесь 4 десятки нельзя разделить равномерно на 3 (поскольку мы имеем дело только с целыми числами). Следовательно, мы перегруппируем одну из десятков с единицами, чтобы получить 15 единиц.

Мы также можем видеть, что число 45 можно разложить на 30 + 15 и показать разложение с помощью числовых связей.

Объяснение видео и план урока (ресурс участника)

Общие основные стандарты

B6 Находите целочисленные частные и остатки с четырехзначными дивидендами и однозначными делителями, используя стратегии, основанные на числовом значении, свойствах операции и / или отношения между умножением и делением.

Дополнительные рабочие листы

Подразделение

Разделить 4-значное число на 2-значное число
Чтобы разделить четырехзначное число на двузначное (например, 3654 47), выполните следующие действия:
Поместите делитель (47) перед скобкой деления и поместите делитель (3654) под ним.
47) 3654
Посмотрите на первые две цифры делимого (36). Число 36 меньше 47, поэтому не может быть
разделить на 47, чтобы получить целое число. Затем возьмите первые три цифры дивиденда.
(365) и определите, сколько в нем 47. Число 365 состоит из семи 47
(7 * 47 = 329), но не восемь (8 * 47 = 376). Поместите 7 над кронштейном разделения и прямо над 5.
7 47) 3654
Умножьте 7 на 47 и поместите результат (329) под 365 делимого.
7 47) 3654 329
Проведите линию под 329 и вычтите ее из 365 (365-329 = 36). Сбить
4 из 3654 и поместите его справа от 6 из 36.
7 47) 3654 329 364
Разделите 364 на 47 и поместите полученный ответ над квадратной скобкой справа от 7.
77 47) 3654 329 364
Умножьте 7 частного на делитель (47), чтобы получить 329, и поместите это
ниже 364.
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Рубрики
В домашних условиях
Воспитание
Дети
Научить
Правильно
Разное
Советы
2024 © Все права защищены.

Деление с остатком на двузначное число. Математика, 4 класс: уроки, тесты, задания.

Урок математики 4 класс «Письменное деление с остатком на двузначное число». | План-конспект урока по математике (4 класс) по теме:

Урок математики «Деление с остатком» (4 класс)

ПНШ 4 класс. Математика. Учебник № 1, с. 52

4 класс. Моро. Учебник №1. Ответы к стр. 81

Числа от 1 до 1000

Умножение и деление

Деление на однозначное число

Конспект урока математики 4 класс по теме «Деление с остатком на двузначное число»

Технологическая карта. урока математики на тему. «Деление с остатком на 10,100,1000» 4 класс. Санкт-Петербург,2018

Технологическая карта урока

Технологическая карта урока математики

Предмет математика класс 2 г

Технологическая карта урока математики

Технологическая карта урока

Технологическая карта урока

Пояснительная записка

Технологическая карта урока

План-конспект урока математики

Технологическая карта урока математики

Цель урока Задачи. Планируемый результат

Вершинина Анна Владимировна

Технологическая карта урока

«Встречное движение».

Цели. Планируемый результат

Технологическая карта урока

Технологическая карта урока по геометрии

Технологическая карта урока математики

Технологическая карта урока

Урок открытия нового знания

Технологическая карта урока

Конспект урока по математике.

Урок русского языка 2 класс

Технологическая карта урока

Урок 22. Тип урока: ОНЗ

ПЛАН-КОНСПЕКТ УРОКА 1. ФИО

Технологическая карта урока

Учебные пособия и рабочие листы для дивизиона 4 класса

Деление 6-значных чисел на однозначное число

Деление шестизначных чисел на двухзначное число

Деление 6-значных чисел на 10

Story Time Division

Дивизионный тест

Рабочий лист отделения 4 класса

Лист для ответов

Разделение четырехзначных и больших чисел — математика для 3-го класса

Научитесь делить четырехзначные и большие числа

Длинные ступени дивизиона

Разделение 4-значных чисел

Смотри и учись

Дивизион, частное и остаток — вопросы по математике для 4-го класса с ответами

Распечатанные рабочие листы и упражнения с делением на длинное и хвостовое деление для учащихся 4 и 5 классов по математике

Дивизион | Как разделить | Связанные термины

Что такое дивизия?

Определение деления

Обозначение деления

Особые случаи

Какова общая формула деления?

Термины, относящиеся к подклассу

Проверка результата разделения

Метод длинного деления

Часто задаваемые вопросы о дивизионе

Какие два типа деления?

Какие 3 части деления?

Как делиться, когда делитель больше дивиденда?

Как разделить дроби?

Как разделить десятичные дроби?

Что такое метод длинного деления?

Каковы этапы метода длинного деления?

Почему деление на ноль не определено?

Деление — остаток и перегруппировка

Объяснение видео и план урока (ресурс участника)

Общие основные стандарты

Рекомендуемая серия учебников

Дополнительные рабочие листы

Подразделение

Добавить комментарий Отменить ответ