Деление двузначного числа на двузначное / Открытый урок
Цели урока:
Дидактические:
— научить делить двузначное число на двузначное способом подбора.
— совершенствовать умение решать составные задачи.
— совершенствовать вычислительные навыки, логическое мышление, внимание.
— продолжить развитие навыков работы на компьютере.
Формирование УУД:
Регулятивные:
— формировать у учащихся умение определять цель занятия;
— формировать умение корректировать дальнейшую деятельность;
— побуждать учащихся к самооценке своей деятельности на уроке.
Личностные:
— воспитывать в учащихся внимательность, самостоятельность.
Коммуникативные:
— формировать умение работать в коллективе, проявлять толерантность.
— воспитывать культуру общения.
Планируемый результат: учащиеся научатся решать примеры на деление способом подбора
Методы и приёмы, используемые на уроке:
- деятельностный подход;
- групповая форма работы;
Оборудование: компьютер, мультимедиа проектор, экран.
Ход урока
1. Организационный этап.
Вот и прозвенел звонок.
Начинается урок.
Очень тихо вы садитесь.
И работать не ленитесь.
— Пусть урок нам принесет радость общения.
— Расшифруйте слово, расположив ответы в таком порядке: (Слайд 2)
30*3 2*50 0:8 17*4 78:2
|
100
|
39
|
0
|
90
|
68
|
|
с
|
х
|
п
|
у
|
е
|
— Что такое успех? (хорошие результаты в работе)
— Что нужно для достижения успеха?
— Я желаю вам всем успеха.
— Ребята, а с чего нам надо начать свою работу, чтобы урок был успешным? (с повторения)
2. Актуализация знаний.
— А у нас сегодня гость- барсик Юни . (Слайд 3)
— Ребята, а вы знаете, кто это? (Ответы детей)
— Да, талисман казанской Универсиады — Юни, котенок крылатого снежного барса. Крылатый снежный барс является национальным символом республики Татарстан. И сегодня он у нас в гостях!
Юни приготовил для нас задания:
1.» Лишнее число» (Слайд 4)
А) 10,20, 30, 40, 50, 6, 70.
(Если определим это число, то узнаем когда началась Всемирная Летняя Универсиада.)
(Лишнее число:6- однозначное число)
— Правильно, она началась 6 июля 2013 года.
Б) 0.7, 17, 21, 28, 35, 42 (Лишнее число:17, не делится на 7; Универсиада прошла в Казани c 6 июля по 17 июля 2013 года.)
В) 1, 27, 3, 4, 5, 6, 7, 8. (27-двузначное число; в Казани прошли международные соревнования по всем 27 видам спорта.)
(27-двузначное число; в Казани прошли международные соревнования по всем 27 видам спорта.)
Ну вот, ребята, мы помогли Юни выполнить задания.
Самые ловкие, смелые, сильные спортсмены приняли в них участие. А мы продемонстрируюм эти качества в математическом направлении.
3. Ситуация затруднения. Устный счёт. (Слайд 5)
— Найдите разность чисел в треугольниках, разделите полученный результат на число,записанное в квадрате, результат умножьте на число в круге, прибавьте число в четырёхугольнике, разделите на число в четырёхугольнике.
— Покажите результат. (20)
(Слайд 6)
— Произведение чисел в кругах разделите на разность чисел в треугольниках, результат увеличьте на число, записанное в квадрате.
— Покажите результат. (53)
(Слайд 7)
— Из суммы чисел в прямоугольниках вычтите произведение чисел в кругах, результат разделите на число в пятиугольнике. (У детей возникает затруднение 66:22)
(У детей возникает затруднение 66:22)
52+20=72
72-6*1=66
66:22
— В чём проблема? (не умеем решать такие примеры)
— Вот сегодня на уроке мы должны этому научиться.
В верхнем левом углу доски появляется запись.
4. Тема урока
— Назовите тему урока.
Деление двузначного числа на двузначное. (Слайд 8)
— Как вы думаете, какие знания нам для этого понадобятся? (табличное деление,
взаимосвязь умножения и деления)
5. Работа над решением проблемы. Первичное усвоение новых знаний.
— Вспомним всё, что мы уже знаем.
— Выполните умножение 16*4 и составьте все примеры на умножение и деление из данной тройки чисел.
16*4=64
4*16=64
64:4=16
64:16=4
— Используя взаимосвязь умножения и деления, объясните как разделить 64:16? (Надо найти число, которое бы при умножении на 16 давало бы 64)
Найдём число, на которое надо умножить 16. Попробуем число 2, проверяем 16*2=32, 32<64. Значит, искомое число больше 2.
Попробуем число 2, проверяем 16*2=32, 32<64. Значит, искомое число больше 2.
Проверяем число 3: 16*3=48, 48<64
Проверяем число 4: 16*4=64, 64=64
Значит, 64:16=4
Вывод:
Для того,чтобы разделить число 64:16 что нам пришлось делать?
(Искать частное способом подбора)
— Давайте составим план наших действий
Алгоритм
— Что мы делали сначала?
— Потом?
— А потом? (Составление алгоритм ) (Слайд 9)
— Пробуем число
— Проверяем умножением
— Найдём число, которое при умножении на делитель давало бы делимое
Чтение по учебнику нового материала.
6. Первичная проверка понимания. Работа с учебником.
№1,с.18-решение с комментированием.
№2 (1, 2 столбики)– Самостоятельно, с последующей проверкой.
Дети для проверки обмениваются тетрадями. Тот, кто решил первым, записывает ответы на доске. Неправильно решенные примеры объясняются.
Неправильно решенные примеры объясняются.
7. Физкультминутка.
Раз, два — хлопок в ладоши
Раз, два — хлопок в ладоши,
А потом на каждый счет.
Раз, два, три, четыре —
Руки выше, плечи шире.
Раз, два, три, четыре, пять,
Надо нам присесть и встать.
Руки вытянуть пошире.
Раз, два, три, четыре, пять.
Наклониться — три, четыре,
И на месте поскакать.
На носки, затем на пятки.
Лень отбросить и опять.
Сесть за парту, взять тетрадку,
Выражения решать.
Раз, два, три, четыре, пять –
Все умеем мы считать.
Раз! Подняться, подтянуться,
Два! Согнуться, разогнуться,
Три! В ладоши три хлопка,
Головою три кивка.
На четыре — руки шире.
Пять — руками помахать.
Шесть — за парту тихо сесть. (Дети выполняют движения за учителем по содержанию текста.
8. Первичное закрепление. Работа с учебником.
№4 Составляем краткое условие:
50л – 2 кг
75 л. — ?
— ?
Объясняем каждое числовое данное. Узнаем, сколько молока идет на 1 кг масла – приводим к 1:
50:2=25 (л)
Отвечаем на главный вопрос: 75:25=3 (кг)
Краткую запись задачи можно оформить в таблице.
— Что такое 50 литров? (Количество молока, из которого получают масло.)
— Что такое 2 кг? (Количество масла.)
— Какой графы не достает? (Количество молока для 1 кг масла.). (Слайд 10)
|
Количество молока на 1 кг масла
|
Количество (масса) масла
|
Количество всего молока
|
|
? 1) (:)
|
2 кг
|
50 л
|
|
одинаковое
|
? 2) (:)
|
75 л
|
— Что надо знать, чтобы ответить на вопрос задачи? (Количество молока, из которого получается 1 кг масла. )
)
— Можем узнать? (Да)
— Как? (Делением)
Составьте программу решения и решите задачу.
9. Первичный контроль и оценка.
Решение уравнений с объяснением: 18*х=54, х*14=70
— Какая проблема возникла у нас на уроке?
— Удалось нам её решить?
9. Итог урока.
— Какую проблему решали на уроке?
— Научились выполнять деление двузначного числа на двузначное способом подбора.
— Хотите себя проверить?
Рефлексия.
(Развивающие игры – интерактивные упражнения для 3 класса по математике играть онлайн бесплатно, можно найти по http://www.samouchka.com.ua/_matematika/3_klass/03/.
Обучающие программы на тему «Деление двузначного числа на двузначное в пределах 100 помогут третьекласснику в освоении математики.)
— Какую цель поставили на уроке?
— Достигли ли мы её?
— К какому выводу пришли?
— Над чем надо поработать?
— Пригодятся ли эти знания вам в жизни? Где? В какой области?
— Что вызвало у вас затруднение?
— Что понравилось?
Д/з: № 5, с. 18
18
Оценка
— Оцените свою работу на уроке. Покажите, на сколько сегодня вы:
1) были успешны на уроке и чувствовали себя комфортно;
2) разобрались с темой урока;
3) умеете применять свои знания.
— Выберите смайлик своего настроения. (Слайд 11)
Итог
— Спасибо, дети, за урок.
Список используемой литературы:
- Моро М.И., Бантова М.А, Бельтюкова Г.В., Волкова С.И, Степанова С.В. Учебник «Математика, 3 класс», 2 часть. Москва, «Просвещение», 2009 г., с.18.
- Мокрушина О. А. «Поурочные разработки по математике, 3 класс». Москва «ВАКО», 2006г., с. 235-238.
- school47.coi.spb.ru›fizkultminutka.doc
Деление двузначного числа на двузначное способом подбора.
 (3 класс)
(3 класс)
1. ГБОУ «Гимназия №1592»СП №2043
Урок – путешествие
по математике в 3 «В» классе
по теме: Деление вида 87 : 29; 66 : 22
Учитель начальных классов: Мамедоразова Г.Н.
2. Цели и задачи урока:
Образовательные:
научить делить двузначное число на двузначное
способом подбора;
совершенствовать навыки решения задач изученных
видов;
формирование положительной мотивации учения.
Развивающие:
развивать вычислительные навыки, логическое
мышление, математическую речь.
Воспитательные:
воспитание в детях стремление вести здоровый образ
жизни.
3. Я умею думать, Я умею рассуждать. Что полезно для здоровья, То и буду выбирать.
5. Устный счет. 1). Составьте различные примеры на умножение и деление, используя только эти числа. 9, 24, 3, 8, 12, 48, 4, 6, 2, 18.
2). Прочитайте только те, которые делятся на 5, на 8, на 9.
36, 40, 6, 15, 9, 72, 45, 64, 30, 32, 27.
3) Решите задачи.
•В воскресенье в поход пошли 28 мальчиков, а девочек в 4 раза меньше.
Сколько девочек пошло в поход?
•В течение четырёх дней врач принимал каждый день по 10
больных, а на пятый день он принял 19 больных. Сколько больных
принял за 5 дней?
•Площадь листа квадратной формы 48 см2, чему равна одна ее
сторона?
6. Все отлично
Хорошо
Надо чутьчуть
постараться
Хорошее
настроение
7. 14 7
14 7=98
98 : 14=7
7 14=98
98 : 7=14
8. Работа с учебником. №1, с.18 24 : 12; 45 : 15; 88 : 44
2
3
2
9. Физкультминутка
Активный образ жизни
10. 1. Пираты поймали 81 рыбу. Решили засолить ее в бочки по 27 штук в каждой. Сколько бочек понадобилось?
Решение задач
2. На острове пираты с одной пальмы собрали
32 кг бананов, а с другой 48 кг. Разложили все
бананы по ящикам по 8 кг в каждом ящике.
Сколько всего ящиков потребовалось?
Рациональное
питание
11.
 Тренировочные задания
Тренировочные задания
№ 2 (3 столбик), с 18 – стандарт «3»
№ 4, с.18
— хорошо «4»
№ 5, с.18
— отлично «5»
Деление столбиком на двузначное число. Простой способ деления на многозначное число.
☝ Кстати, приготовила для вас еще несколько видео по этой теме. Посмотрите их, я очень хочу, чтобы вы лучшее ее усвоили 😉
📺 Как объяснить деление в столбик? Деление чисел уголком. Деление на многозначного на однозначное.
📺 Деление в столбик без остатка. Деление столбиком чисел с нулями. Примеры на деление с нулями.
📺 Как делить числа с остатком? Деление на двузначное число с остатком.
📺 Как устно делить числа? Устное деление двузначного на двузначное. Как быстро решать примеры в уме?
=============================================
Здравствуйте, друзья! Мы продолжаем серию видео про деление чисел уголком. Сегодня мы будем с вами говорить про деление многозначного числа на двузначное. И для начала разберем деление на двузначное число без остатка. В этом видео вы найдете информацию про деление столбиком на двузначное число и пошаговый алгоритм деления на двузначное число столбиком. А также я расскажу вам простой способ деления на многозначное. Деление столбиком на двузначное число объяснение, на самом деле, очень простое. Если вы затрудняетесь, как объяснить деление столбиком на двузначное число своему ребенку, то я надеюсь это видео вам поможет. Я на наглядных примерах покажу, как выполняется деление столбиком на двузначное число без остатка. После просмотра видео вы без труда сможете решать примеры на деление многозначных чисел на двузначное в столбик, и не составит сложностей вопрос как объяснить деление в столбик. Если видео для вас было полезно, то делитесь этим видео в родительских чатах и не забывайте подписываться на канал, что бы не пропустить новые видео.
Сегодня мы будем с вами говорить про деление многозначного числа на двузначное. И для начала разберем деление на двузначное число без остатка. В этом видео вы найдете информацию про деление столбиком на двузначное число и пошаговый алгоритм деления на двузначное число столбиком. А также я расскажу вам простой способ деления на многозначное. Деление столбиком на двузначное число объяснение, на самом деле, очень простое. Если вы затрудняетесь, как объяснить деление столбиком на двузначное число своему ребенку, то я надеюсь это видео вам поможет. Я на наглядных примерах покажу, как выполняется деление столбиком на двузначное число без остатка. После просмотра видео вы без труда сможете решать примеры на деление многозначных чисел на двузначное в столбик, и не составит сложностей вопрос как объяснить деление в столбик. Если видео для вас было полезно, то делитесь этим видео в родительских чатах и не забывайте подписываться на канал, что бы не пропустить новые видео.
=============================================
👩🏫 Видео было полезным?
✅ Тогда жмите на ссылочку и подписывайтесь на канал, чтобы получать новые видео —
👍 Поставьте лайк этому видео. Так я буду знать, что интересно именно вам и с удовольствием раскрою больше секретов ☀
Так я буду знать, что интересно именно вам и с удовольствием раскрою больше секретов ☀
📢 Мои хорошие, поделитесь этим видео со своими друзьями. Давайте вместе сделаем этот мир счастливее. 🙂
=============================================
Подписывайтесь на меня в социальных сетях. Там будет новый материал, которого нет на канале. Пишите мне комментарии, я буду рада ответить на ваши вопросы 😊
💜 Будьте со мной Вконтакте —
💜 Рада видеть вас на Facebook —
10 трюков, упрощающих математические операции
Недавно, прочитав книгу «Магия чисел», я почерпнул огромное количество информации. В книге рассказывается о десятках трюков, которые упрощают привычные математические операции. Оказалось, что умножение и деление в столбик — это прошлый век, и непонятно, почему этому до сих пор учат в школах.
Я выбрал 10 самых интересных и полезных трюков и хочу поделиться ими с вами.
Умножение «3 на 1» в уме
Умножение трёхзначных чисел на однозначные — это очень простая операция. 2
2
- Умножаем 7 на 8 и получаем 56.
- Добавляем к числу 25 и получаем 5 625.
Деление на однозначное число
Деление в уме — это достаточно полезный навык. Задумайтесь о том, как часто мы делим числа каждый день. К примеру, счёт в ресторане.
Пример: 675 : 8
- Найдём приближенные ответы, умножив 8 на удобные числа, которые дают крайние результаты (8 × 80 = 640, 8 × 90 = 720). Наш ответ — 80 с хвостиком.
- Вычтем 640 из 675. Получив число 35, нужно разделить его на 8 и получить 4 с остатком 3.
- Наш финальный ответ — 84,3.
Мы получаем не максимально точный ответ (правильный ответ — 84,375), но согласитесь, что даже такого ответа будет более чем достаточно.
Простое получение 15%
Чтобы быстро узнать 15% от любого числа, нужно сначала посчитать 10% от него (перенеся запятую на один знак влево), затем поделить получившееся число на 2 и прибавить его к 10%.
Пример: 15% от 650
- Находим 10% — 65.

- Находим половину от 65 — это 32,5.
- Прибавляем 32,5 к 65 и получаем 97,5.
Банальный трюк
Пожалуй, все мы натыкались на такой трюк:
Задумайте любое число. Умножьте его на 2. Прибавьте 12. Разделите сумму на 2. Вычтите из неё исходное число.
Вы получили 6, верно? Что бы вы ни загадали, вы всё равно получите 6. И вот почему:
- 2x (удвоить число).
- 2x + 12 (прибавить 12).
- (2x + 12) : 2 = x + 6 (разделить на 2).
- x + 6 − x (вычесть исходное число).
Этот трюк построен на элементарных правилах алгебры. Поэтому, если вы когда-нибудь услышите, что кто-то его загадывает, натяните свою самую надменную усмешку, сделайте презрительный взгляд и расскажите всем разгадку. 🙂
Магия числа 1 089
Этот трюк существует не одно столетие.
Запишите любое трёхзначное число, цифры которого идут в порядке уменьшения (к примеру, 765 или 974). Теперь запишите его в обратном порядке и вычтите его из исходного числа.
К полученному ответу добавьте его же, только в обратном порядке.
Какое бы число вы ни выбрали, в результате получите 1 089.
Быстрые кубические корни
Для того чтобы быстро считать кубический корень из любого числа, понадобится запомнить кубы чисел от 1 до 10:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1 000 |
»
Как только вы запомните эти значения, находить кубический корень из любого числа будет элементарно просто.
Пример: кубический корень из 19 683
- Берём величину тысяч (19) и смотрим, между какими числами она находится (8 и 27).
 3. Следовательно, последняя цифра ответа — 7.
3. Следовательно, последняя цифра ответа — 7. - Ответ — 27.
Примечание: трюк работает только тогда, когда исходное число является кубом целого числа.
Правило 70
Чтобы найти число лет, необходимых для удвоения ваших денег, нужно разделить число 70 на годовую процентную ставку.
Пример: число лет, необходимое для удвоения денег с годовой процентной ставкой 20%.
70 : 20 = 3,5 года
Правило 110
Чтобы найти число лет, необходимых для утроения денег, нужно разделить число 110 на годовую процентную ставку.
Пример: число лет, необходимое для утроения денег с годовой процентной ставкой 12%.
110 : 12 = 9 лет
Математика — волшебная наука. Я даже немного смущён тем, что такие простые трюки смогли меня удивить, и даже не представляю, сколько ещё математических фокусов можно узнать.
По материалам книги «Магия чисел»
Электронная книга Купить на amazon
Электронная книга на английском языке
Урок по математике «Деление на двузначное число» ( 4 класс)
Тема: Деление на двузначное число.
Цель:
Сформировать первичный алгоритм деления и умение применять данный алгоритм при делении четырехзначные и трехзначных чисел на двузначное число.
Развивать логическое мышление и математическую речь, память.
Воспитывать доброжелательные отношения друг к другу, уважение к мнению товарищей, умение работать в группах.
Организационные моменты:
Я рада Вас видеть. Хорошего настроения и удачи!
Подготовка тетрадей к работе.
Ни костяшек, ни ручек, ни мела
Ну-ка, в сторону карандаши
Устный счет, мы творим это дело.
Только силой ума и души.
Слайд 1: Устный счет.
Цель: развитие логического мышления актуализация знаний.
Решите, пожалуйста, задачу на логику.
Ответ: у Скворцовой – чиж, у Дроздовой – скворец, у Чижовой – дрозд.
Слайд 2: Выражения.
Вспомните, как называются компоненты действия деления? И что общего?
Ваша задача выполнить устно деления и назвать результат. Если вы справитесь с работой успешно, вы узнаете на каком транспорте мы отправимся в путешествие по стране «математика».
Если вы справитесь с работой успешно, вы узнаете на каком транспорте мы отправимся в путешествие по стране «математика».
Слайд 3: Корабль.
Я предлагаю работать в группах. Организуйте группы. Пожелайте друг другу удачи, улыбнитесь, помогите друг другу.
Слайд 4 : Выражения.
Ваша задача выполнить письменно деление. Найти значение выражений.
364:52 927:3 632:8
Проверка.
Слайд 5: Что общего в этих математических выражениях? (деление)
Решение какого выражения вызвало у вас затруднение? Сравните делимое у всех выражений, делитель?
Кто объяснит, как разделили трехзначное число на двузначное? Молодец.
Кто может сформулировать тему нашего урока математики? (Деление на двузначное число).
Слайд 6: Какую цель поставили перед собой? (научиться делить трехзначные и четырехзначные числа на двузначное число).
Слайд 7: Формировать умение.
Для чего нужно учиться делить на двузначное число?
Вы уже умеете делить на однозначное число и знаете алгоритм деления.
Как вы думаете, во многом ли будет отличаться алгоритм деления на двузначное число от алгоритма деления на однозначное число?
Давайте это выясним.
Один ребенок у доски.
4536:72=63
Слайд: Алгоритм деления.
(Постепенно, с объяснением ребенка, появляется алгоритм)
Кто уже понял, как разделить многозначное число на двузначное?
Что поможет нам? (алгоритм) Пользуясь алгоритмом, найдите значение выражения:
2322:86 2584:76
Самостоятельно те, кто понял! Кто не понял, работайте вместе с нами. (по 1 ребенку у доски)
Физ .митнутка (гимнастика для глаз).
Какое умение формируем?
Наш корабль терпит крушение, мы должны выполнить правильно самостоятельную работу, чтобы проверить ваши умения делить многозначное число на двузначное.
Слайд – примеры
464:16 840:35 798:19 3564:44
Слайд – взаимопроверка (ответы)
Поменяйтесь тетрадями. Поставьте оценки.
Нет ошибок — 5
1 ошибка — 4
2 ошибки — 3
Для тех, кто закончит раньше на доске появляется слайд (найди и исправь ошибки)
Встаньте у кого 5, 4,3.
Не огорчайтесь. У нас еще будут уроки по этой теме. На которых вы обязательно научитесь делить многозначные числа на двузначное число.
Мы возвращаемся домой, вы спасли наш корабль от крушения, но чтобы вернуться надо решить задачу:
Слайд – с текстом и табличка на доске S,V,T.
Устно разобрать задачу от данных к вопросу.
Слайд – с проверкой
Итог урока: наше путешествие заканчивается, мы возвращаемся домой.
Какое умение формировали сегодня на уроке математики? (делить многозначные числа на двузначное число).
Что поможет нам правильно выполнить деление (алгоритм)
Урок окончен. Спасибо за работу.
Тема: Умножение двузначного числа на однозначное.
Закрепление изученного.
Цель: формировать первичное умение умножать двузначное число на однозначное, решать задачи изученных видов, развивать логическое мышление.
Организационный момент:
Желаю хорошего настроения на уроке.
Мы отправляемся с вами в математический лес.
А пригласил нас 1 сказочный герой. Чтобы отгадать как его зовут, выполните задания.
У кого больше лап у курицы или у петуха? (одинаково)
До своей остановки Лена едет 30 минут. Сколько времени потратят на этот путь 2 девочки, если будут ехать вместе? (30 мин)
Найдите закон и дополните ряд чисел 18, 27, 36, 45 ….. (таб.ум. на 9)
Посмотрите внимательно на эти выражения, что их объединяет?
4х4 56:7
18:3 4х9
7х5 8х3
9х6 32х4
16х4 35х5
Это математические выражения на умножения и деление.
А что в них разного? (последние примеры на внетабличное умножение)
Решите эти примеры.
По 1 человеку у доски, остальные контролируют и показывают ответ на карточке.
Какой пример оказался трудным для решения? (последний)
Почему? Это новый вид примеров. Как мы их вчера на уроке называли?
Как мы их вчера на уроке называли?
Кто может открыть тему урока? (умножение двузначного числа на однозначное)
А какую задачу поставили перед собой на уроке? Научиться умножать двузначное число на однозначное или закрепить умение умножать двузначное число на однозначное.
И так к кому же в гости мы идем? (к лешему)
Ребята, кто уверен, что он научился выполнять умножение двузначного числа на однозначное?
Чтобы не сбиться с пути, ребята нужно правильно решить задания.
№1 стр.8
Для этого объединитесь в группы, возьмите друг друга за руки, почувствуйте тепло друг друга, улыбнитесь и помогите в группе тем ребятам, которые еще не совсем уверены в своих силах.
Группа 37х2
Группа 5х19
Группа 18х4
Проверка: выступления1,2,3 групп.
Спасибо за работу.
Встаньте, кто уверен что научился умножать двузначное число на однозначное.
А теперь давайте отдохнем в лесу.
На разминку становись
В право в лево повернись
Повороты ты считай
И от нас не отставай
Начинаем приседать
1 — 2 – 3 — 4 – 5
Тот кто делает зарядку
Не болеет никогда
Голову поднимаем выше
И легко – легко подышим
Сделаем глазами круг
Крепко их зажмурим вдруг
Потихоньку открываем и немножко поморгаем
Отдохнули?
Хорошо! Идти уже не далеко.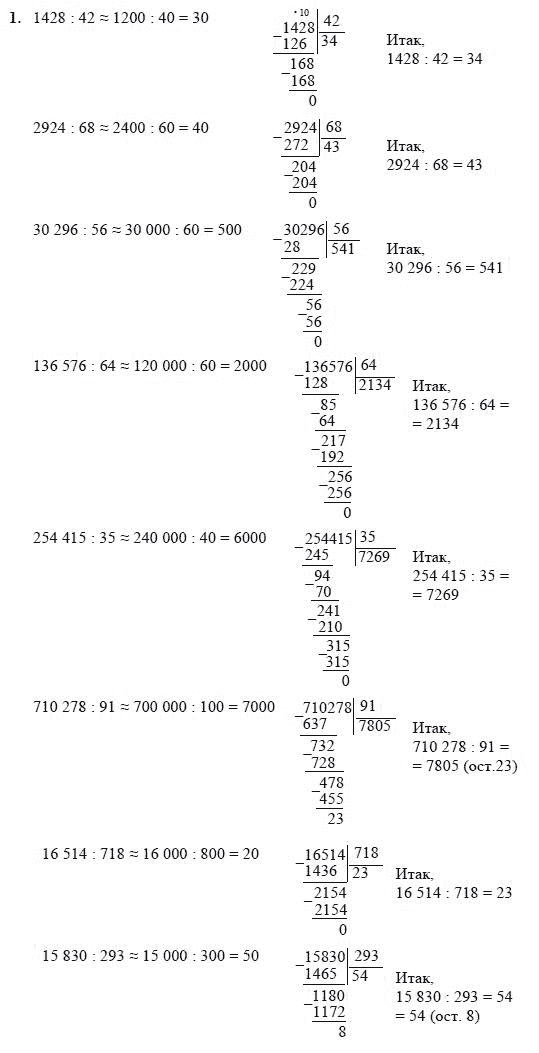
Ой ребята, на нашем пути болото. Чтобы выбраться нам надо правильно найти значение выражений.
Выберите себе каждый тот столбик, с которым вы справитесь.
19х4 6х15+10
18:3 4х23
7х5 90-18х2
Ответы на доску.
Взамопроверка.
Проверяем:
Нет ошибок — 5;
1 ошибка – 4;
2 ошибки – 3:
Поставили оценки. Проверили,
А кто может составить задачу по выражению?
90-18х2
В мешке было 90 конфет. Мама дала 2 детям по 28 конфет.
Сколько конфет осталось в мешке?
Молодцы, ребята.
Выбрались из болота.
А чему же мы учились сегодня на уроке? (учились умножать двузначное число на однозначное)
Вот мы с вами и добрались наконец-то до Лешего.
Но ему требуется помощь.
На поляне росло 18 ромашек, а колокольчиков в несколько раз большею
Сколько цветов росло на поляне? (не можем решить, та как не хватает данных.
А можно дополнить задачу и решить? (да, колокольчиков в 2 раза больше)
Решите задачу.
18х2+18=54 (цветов)
Спасибо, ребята, за помощь.
А теперь д/з на стр.8 №2 (1,2,3,ст обязательно для всех а 4,5,ст.по желанию).
Деление на двузначное число
Тип урока: Открытие нового знания (ОНЗ)
Цель:
- формирование представления о действии деление
на двузначное число по алгоритму. - формирование умения делить на двузначное число,
используя алгоритм.
Ход урока
I Организационный момент
По дороге знаний смело путь держи,
Даже если трудно, ты вперед иди!
— Как вы понимаете смысл этой фразы?
(объяснение детей)
— Как будет организована ваша учебная
деятельность?
— Мы пройдем 2 шага учебной деятельности,
поймем, что не знаем, затем сами найдем способ
открытия знания.
— Вспомните, что делали на прошлом уроке?
—Выполняли деление на однозначное число.
— Чему будет посвящен сегодняшний урок?
— Делению числа на число.
— С чего начнем урок?
— С повторения.
II Актуализация знаний
1. Повторение
— Используя числа 17, 4, 68 составьте равенства
Один из учеников составляет у доски:
17 * 4 = 68
4 * 17 = 68
68 : 17 = 4
68 : 4 = 17
— Что помогло составить эти равенства?
— Взаимосвязь деления и умножения.
— Используя взаимосвязь умножения и деления
объясни, как разделить 68 на 4
— 68 : 4=17, т. как 17х4=68
— Что, значит, разделить число а на число b?
— Это, значит, найти такое число с, при
умножении которого на число b получается число а.
— Почему я выбрала именно это задание?
— Это пригодится для открытия нового знания.
2. Пробное действие.
— Какое следующее задание я вам предложу?
— Задание с затруднением. Пробное.
— Для чего вы его получите?
— Чтобы мы сами узнали, что мы еще не знаем.
— Что нужно сделать в данном задании?
56 : 14
— Найти частное чисел 56 и 14
— Что нового в нем?
— Нужно двузначное число разделить на
двузначное число.
— Попробуйте выполнить это задание
— У кого нет ответа?
— Что вы не смогли сделать?
— Мы не смогли найти частное чисел 56 и 14
— Кто выполнил это задание, какое число вы
записали?
— Обоснуйте свои действия.
— Что вы не можете сделать?
— Мы не можем обосновать свой ответ.
— Что вы должны сделать, если встретили
затруднение?
— Остановиться и подумать
III Проблемное объяснение нового знания
— Какое задание вы должны были выполнить?
— Мы должны были найти частное чисел 56 и 14.
— В чем возникло затруднение?
— Мы не знаем правило деления на двузначное
число.
— Какую цель вы поставите перед собой на уроке?
— Построить алгоритм деления двузначного
числа на двузначное число.
— Тема нашего урока?
— Деление двузначного числа на двузначное
число.
— Что вы делали, чтобы решить пример 56 :14?
— Чтобы разделить 56 на 14, нужно подобрать такое
число, которое при умножении на 14 даст 56. Мы
начали подбирать с числа 1. Мы проверяли
каждое число, пока не проверили число 4. Мы
увидели, что при умножении
числа 4 на число 14 будет 56. Поэтому 56 разделить
на 14 будет 4.
— Какой способ вы применили при поиске этого
числа?
— Мы подбирали его, перебрав и проверив
несколько чисел.
— Итак, какой первый шаг нужно выполнить при
делении двузначного числа на двузначное число?
— Нужно подобрать число, которое при умножении
на делитель может дать делимое.
— Какой второй шаг?
— Нужно сделать проверку, умножив делитель на
это число.
— Что будете делать дальше?
— Нужно посмотреть, получили мы делимое или
нет.
— Если не получили?
— Подберем новое число.
Если получили?
— Запишем ответ.
— Молодцы! Я предлагаю поработать вам в группах.
Каждая группа получает карточки, где на каждой
записан отдельный этап алгоритма. Нужно
восстановить последовательность.
Подобрать число, которое при умножении
на делитель может дать делимое
Сделать проверку, умножив делитель на
это число
Полученное произведение равно делимому
Если нет, подберите другое число,
сделайте проверку.
Если да, запишите ответ
— Смогли вы преодолеть затруднение, а как мы
можем убедиться в правильности наших выводов?
— Посмотреть в учебнике.
— Откройте учебники на стр. 55, прочитайте вывод .
Что вы можете теперь делать?
— Выполнять деление двузначного числа на
двузначное число.
Физминутка
IV Первичное закрепление во внешней речи
1. с. 56 №2 (а, б) фронтально у доски с комментарием.
— Предлагаю вам поработать в парах.
2.Стр .56 №2 (в) дети работают в парах с
комментарием.
— Кто из вас ошибся?
— В чем ошибка?
— Исправьте ошибки.
— Какой следующий шаг на уроке?
— Проверить себя, справимся ли мы
самостоятельно.
V Самостоятельная работа с самопроверкой
— Решите следующие примеры:
72 : 24=
60 : 15=
— Проверьте по эталону.
— У кого возникли затруднения?
— В каком шаге алгоритма вы ошиблись?
— В чём причина вашей ошибки?
— Кому всё удалось?
— Сделайте вывод.
VI Включение нового знания в систему знаний и
повторение
— При выполнении, каких заданий вам понадобится
правило деления двузначного числа на двузначное
число?
— При решении задач и уравнений, примеров,
выполнении домашнего задания.
— Я предлагаю потренироваться в решении
уравнения 24*х=72
Один ученик работает у доски, рассуждая вслух.
VII Итог урока
— Какую цель вы перед собой ставили?
— Построить алгоритм деления двузначного
числа на двузначное число.
— Удалось ли достичь цели?
— Кто из вас смог сам “открыть” новое знание?
— Как вы оцениваете свою познавательную
деятельность на уроке?
— Я понял… Я могу… Мне нужен тренинг. ..
..
— Молодцы! Вы хорошо поработали на уроке.
Учитель оценивает работу детей.
— Какова будет цель вашей домашней работы?
По результатам самооценки дети получают
разноуровневые задания
Придумать и решить 2 примера на новую тему.
Стр.56 №4 (первый столбик)
Знать алгоритм
«Деление на двузначное число» — математика, презентации
библиотека
материалов
Содержание слайдов
Номер слайда 1
«Деление на двузначное число» 18 мая.
Номер слайда 2
33 х 3 = 120 х 3 = 360 : 3 = 12 х 2 = 24 : 2 = 608 : 2 = 99 : 3 = 304 х 2 = 360 12 33 99 304 24 120 608
Номер слайда 3
33 х 3 = 120 х 3 = 360 : 3 = 12 х 2 = 24 : 2 = 608 : 2 = 99 : 3 = 304 х 2 = 360 12 33 99 304 24 120 608
Номер слайда 4
33 х 3 = 120 х 3 = 360 : 3 = 12 х 2 = 24 : 2 = 608 : 2 = 99 : 3 = 304 х 2 = 360 12 33 99 304 24 120 608
Номер слайда 5
33 х 3 = 120 х 3 = 360 : 3 = 12 х 2 = 24 : 2 = 608 : 2 = 99 : 3 = 304 х 2 = 360 12 33 99 304 24 120 608
Номер слайда 6
33 х 3 = 120 х 3 = 360 : 3 = 12 х 2 = 24 : 2 = 608 : 2 = 99 : 3 = 304 х 2 = 360 12 33 99 304 24 120 608
Номер слайда 7
33 х 3 = 120 х 3 = 360 : 3 = 12 х 2 = 24 : 2 = 608 : 2 = 99 : 3 = 304 х 2 = 360 12 33 99 304 24 120 608 МОЛОДЦЫ!!!
Номер слайда 8
2 4 12
Номер слайда 9
2 4 12 . Выделяем неполное делимое , оно одно – 24 . Значит в частном будет одна цифра. Далее пользуемся методом подбора. Какое число нужно умножить на 12, чтоб получилось 24?
Выделяем неполное делимое , оно одно – 24 . Значит в частном будет одна цифра. Далее пользуемся методом подбора. Какое число нужно умножить на 12, чтоб получилось 24?
Номер слайда 10
2 4 12 . Далее пользуемся методом подбора. Какое число нужно умножить на 12, чтоб получилось 24? . 12 2 24
Номер слайда 11
2 4 12 2 Далее пользуемся методом подбора. Какое число нужно умножить на 12, чтоб получилось 24? . 12
2
24 2 4 0
Какое число нужно умножить на 12, чтоб получилось 24? . 12
2
24 2 4 0
Номер слайда 12
117 13 Выделяем неполное чделимое, оно одно – 117. Значит в частном будет одна цифра. Далее пользуемся методом подбора. Какое число нужно умножить на 13, чтоб получилось 117? .
Номер слайда 13
117 13 Далее пользуемся методом подбора. Какое число нужно умножить на 13, чтоб получилось 117? .
Какое число нужно умножить на 13, чтоб получилось 117? .
Номер слайда 14
117 13 Далее пользуемся методом подбора. Какое число нужно умножить на 13, чтоб получилось 117? 9 . 13 9 117
Номер слайда 15
117
117
0 13 Далее пользуемся методом подбора. Какое число нужно умножить на 13, чтоб получилось 117? 9 . 13
9
117
Какое число нужно умножить на 13, чтоб получилось 117? 9 . 13
9
117
Номер слайда 16
492 82 Далее пользуемся методом подбора. Какое число нужно умножить на 82, чтоб получилось 492? . . 82 ? 492
Номер слайда 17
492 82 Выделяем неполное делимое , оно одно – 492. Значит в частном будет одна цифра. Далее пользуемся методом подбора. Какое число нужно умножить на 82, чтоб получилось 492? .
Значит в частном будет одна цифра. Далее пользуемся методом подбора. Какое число нужно умножить на 82, чтоб получилось 492? .
Номер слайда 18
492 492 0 82 Далее пользуемся методом подбора. Какое число нужно умножить на 82, чтоб получилось 492? 6 . 82 6 492
Номер слайда 19
228:38= 444:74= 265:53= 456:57= 276 : 69= Выполни самостоятельно деление в столбик, методом подбора:
Номер слайда 20
228:38=6 444:74=6 265:53=5 456:57=8 276 : 69=4 ПРОВЕРЬ:
Номер слайда 21
Домашнее задание Уч. с.132 №4, с.135 №17
с.132 №4, с.135 №17
Номер слайда 22
Умножение 3-значных чисел на 2-значные
Когда ученики учатся умножать большие числа, например, 3-значные на 2-значные числа, они учатся умножать их на столбцы. Обычно они начинают изучать этот метод в 4 классе и повторяют его в 5 и 6 классах.
Умножение 3-значных чисел на 2-значные числа в столбцах
Допустим, вы хотите умножить 372 на 43.
Первое, что вы делаете, это помещаете большое число (трехзначное число) над меньшим числом (двухзначное число).
Убедитесь, что вы выровняли их так, чтобы разряды единиц были в столбце, а разряды десятков — в столбце.
Теперь, когда числа выровнены, пора приступить к умножению.
Мы начинаем с умножения столбца единиц нижнего числа: 3 на 372.
Теперь мы начнем с единиц в каждом из двух- и трехзначных чисел. В нашем примере это 3 x 2. 3 x 2 = 6.
Затем мы умножаем 3 на десятки в верхнем числе.В нашем примере это 3 x 7. 3 x 7 = 21. Теперь это двузначное число, поэтому нам нужно обратить особое внимание на расположение чисел в столбцах. Десять цифр в нашей сумме: 2 нужно будет нести. Некоторые люди помещают это число сбоку, но лучшее место для переносимого числа — вверху столбца сотен. Так вы этого не забудете.
В нашем следующем уравнении мы не забудем, что к сумме нужно прибавить 2.
Теперь мы умножаем число сотен в верхнем числе на число единиц ниже.В нашем примере это: 3 x 3. 3 x 3 = 9. Нам также нужно сложить перенесенные 2. 9 + 2 = 11. Поскольку это последнее число в этой строке, мы помещаем 11 под линией.
Мы также обычно проводим черту через одно использованное число перенесенного числа, чтобы не запутать себя при умножении числа на десятки.
Уф, мы на полпути.
Теперь сделаем то же самое с десятками. Во-первых, давайте добавим ноль в столбец единиц, прежде чем перейдем к столбцу десятков.Это поможет нам не запутаться в том, где в новой строке начинаются числа для умножения десятков.
Умножьте нижнее разрядное число десятков на разряд единиц в верхнем числе. В нашем примере это 4 x 2. 4 x 2 = 8.
Далее идет очередь разряда десятков. В нашем примере мы умножаем 4 x 7. 4 x 7 = 28. Опять же, у нас есть число, которое нужно нести — 2.
Наконец, нам нужно умножить число десятков в нижнем числе на число сотен в верхнем числе. То есть 4 x 3. 4 x 3 = 12. Не забываем переносимое число: 12 + 2 = 14.
То есть 4 x 3. 4 x 3 = 12. Не забываем переносимое число: 12 + 2 = 14.
С этого момента мы складываем две строки сумм:
Сумма 372 x 43 составляет 15 996.
Рабочие листы для практики 2-значных на 3-значных числах практики
У нас есть несколько рабочих листов, чтобы студенты могли практиковать умножение в столбцы.
Начинают с 4 класса…
… с дальнейшей практикой в 5 и 6 классах.
Как умножать двузначные числа
Здесь мы рассмотрим, как умножать двузначные числа. Сначала использовался метод, названный Яковом Трахтенбергом «Прямой метод», а во втором — его метод «двух пальцев». Оба эти метода будут работать с любыми комбинациями из двух цифр.
Если вас интересует умножение на числа до двенадцати, обратите внимание на базовое умножение.
Прямой метод
Прямой метод редко преподают в школах, но он известен веками.В школе вас обычно учат записывать результат умножения каждой цифры множителя в отдельной строке, а затем складывать общую сумму.
В прямом методе вам не нужно записывать промежуточные итоги. Вместо этого вы пишете только ответ.
Для этого на каждом шаге выполняется пара вычислений. Пары, которые ни к чему не приравниваются, игнорируются.
Эти пары называются внешней и внутренней парами. Внешняя пара всегда соединяет единичную цифру множителя с цифрой множимого, которое мы сейчас рассматриваем.Внутренняя пара всегда соединяет цифру десятков множителя с цифрой справа от цифры, над которой мы работаем в умножаемом.
Этот метод, по сути, тот же, что и в ведической математике, когда при умножении двухзначных чисел используется сутра «вертикальная и поперечная». Единственное реальное отличие — это стиль уравнения. В ведической математике уравнение записывается в две строки, как показано ниже. Для прямого метода уравнение стоит на одной строке с ответом под множимым.
Я покажу метод с уравнением в обоих стилях для первого примера, чтобы вы могли увидеть, как он работает в каждом стиле.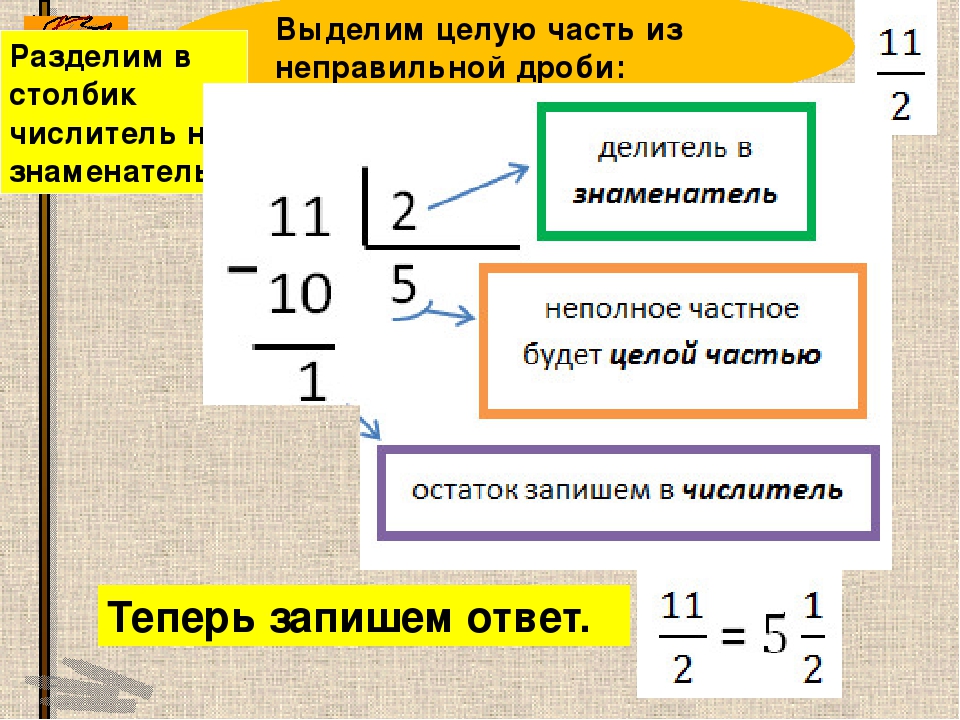
Вы можете посмотреть видео о прямом умножении с использованием двузначных умножителей или продолжить чтение следующих примеров.
Давайте посмотрим на пример,
Шаг 1
Для прямого метода мы ставим ведущие нули на множимое. Количество ведущих нулей всегда совпадает с количеством цифр в множителе, поэтому при умножении двухзначных чисел мы всегда добавляем 2 ведущих нуля.
Затем мы умножаем две единичные цифры вместе
Шаг 2
Этот шаг включает в себя умножение цифры десятков одного числа на цифру единиц другого числа.
При записи уравнения в одну линию, если мы проведем изогнутые соединительные линии между умноженными цифрами, мы получим внешнюю пару и внутреннюю пару. При написании уравнения на двух линиях мы получаем крест, когда проводим прямые соединительные линии между умноженными цифрами.
Сложив результаты этих двух уравнений, мы получим 14, поэтому мы пишем 4 и переносим 1.
Шаг 3
На этом этапе мы умножаем цифры десятков каждого числа.
3 плюс 1 из переноса на шаге 2 дает нам 4, поэтому мы пишем 4 и получаем наш ответ 448
Примечание. При записи уравнения в одну строку внешняя пара на этом шаге соединяется с нулем, поэтому результат этой пары равен нулю и может быть проигнорирован.
В этом примере мысленные вычисления, которые нам нужно сделать, относительно просты, и, поскольку мы делаем меньше шагов, чем традиционный метод умножения, он выполняется быстрее. Однако у этого подхода есть недостаток, особенно когда задействованные цифры больше.
Давайте посмотрим на другой пример,
Шаг 1
Умножаем две единичные цифры вместе
Итак, мы пишем 2 и несем 7.
Шаг 2
Здесь становится сложно, особенно если вы пытаетесь мысленно произвести расчет,
Добавление 81 + 56 дает нам 137, затем мы добавляем перенос 7 из шага 1, чтобы получить 144.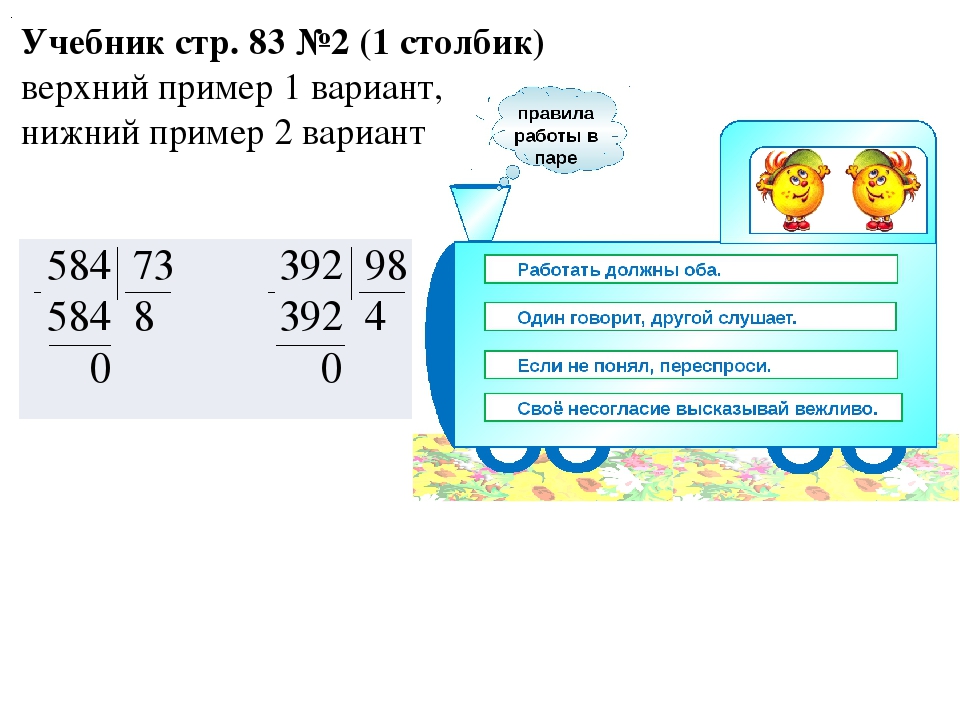
Итак, мы пишем 4 и несем 14.
Шаг 3
У нас есть 63, к которым мы добавляем перенос 14, чтобы получить 77. Мы записываем 7 и переносим 7.
Шаг 4
Следуя первоначальному методу и причине ведущих нулей, у нас есть дополнительный шаг из-за переноса.
Итак, у нас есть ноль плюс перенос 7, который равен 7. Мы записываем 7, что дает нам наш ответ 7742.
Этот шаг может показаться излишним, и мы могли бы просто записать перенос на последнем шаге, но по мере того, как вы изучаете метод, лучше проследить все уравнение до тех пор, пока вы не освоите метод достаточно, чтобы взять небольшой ярлыки.
Как вы можете видеть, когда числа включают цифры 7, 8 и 9, математика становится более сложной, особенно если вы пытаетесь сделать это мысленно.
Яков тоже это понимал, и он поставил себе задачу найти более простой способ добиться этого. Введите метод «двух пальцев», как он его назвал, который упрощает необходимые вам вычисления.
Введите метод «двух пальцев», как он его назвал, который упрощает необходимые вам вычисления.
Перед тем, как перейти к методу двумя пальцами, нам нужно получить дополнительную информацию для однозначного умножения
Десятки и единицы
При умножении двух однозначных чисел результат может быть однозначным или двузначным числом. Наибольшее однозначное число — 9 и.
Если мы поставим ноль перед любым однозначным результатом, мы можем рассматривать все результаты умножения двух однозначных чисел как двузначные результаты, цифру единиц и цифру десятков.
Мы будем использовать эту концепцию при вычислении методом «двух пальцев». Десятки будут представлены как « T », а единицы — « U »
.
Прежде чем мы рассмотрим метод двумя пальцами, давайте снова посмотрим на 98 x 79, но мы будем записывать каждый шаг умножения в отдельной строке по мере продвижения. Мы разместим результаты в правильных столбцах в зависимости от того, являются ли они единицами измерения, десятками, сотнями или тысячами.
Как видите, каждый шаг умножения можно рассматривать как умножение двух однозначных чисел.
Метод двух пальцев
В этом методе мы будем брать только единицы измерения результата для вертикального соединителя и только единицы десятков для наклонного соединителя.
Итак, в приведенном выше примере у нас есть два вычисления:
Когда мы мысленно производим вычисления, мы знаем, и нам нужна только цифра единиц, поэтому, глядя на, мы пытаемся просто думать «1». Для числа мы просто пытаемся думать «7», поскольку нам нужна только цифра десятков.Чем больше вы практикуете это, тем быстрее и легче это станет.
Теперь у нас есть два результата: 1 и 7; теперь мы складываем их вместе, чтобы получить «парное произведение», которое в данном случае равно 8.
Способ запомнить, какие цифры следует объединить для парного произведения, — это представить или записать первые несколько раз, результаты первого умножения, сразу под числами в умножаемом. Из четырех цифр в ответах вы всегда берете две центральные.
Из четырех цифр в ответах вы всегда берете две центральные.
Взяв единичную цифру из левого числа, 81, и цифру десятков из правого числа, 72, мы получим парное произведение 8.
За исключением первого и последнего шага, каждая цифра множителя будет производить парное произведение, но, поскольку мы складываем, мы можем просто складывать значения вместе по мере продвижения. Нам не нужно вычислять первую пару-произведение, затем вычислять вторую и затем складывать их вместе.
Чтобы увидеть это в действии, давайте еще раз посмотрим на наш предыдущий пример,
Шаг 1
Мы игнорируем цифру 7, цифру десятков, и просто используем цифру 2, цифру единиц.Записываем 2.
Шаг 2
Для внешней пары
Для внутренней пары
Складывая пары-произведения, получаем:
Итак, мы пишем 4 и несем 1.
Шаг 3
Для внешней пары
Для внутренней пары
Складывая парные произведения и перенос, получаем:
Итак, мы пишем 7 и несем 1.
Шаг 4
Для внешней пары
Для внутренней пары
Складывая 6 и перенос, получаем 7.
Итак, мы записываем 7, что дает нам ответ 7742.
Как видите, фактические вычисления такие же, как и при использовании прямого метода, но поскольку вы берете только одну цифру и добавляете эти однозначные числа, сложение результатов намного проще.
Теперь, если мы снова посмотрим на пример, где мы записали каждый результат умножения в отдельные строки, и сравним его с числами, которые мы только что использовали в четырех шагах этого примера.
Вы заметите, что числа, которые мы использовали на каждом этапе для создания пар-продуктов, соответствуют числам в каждом столбце, хотя и не обязательно в том же порядке в столбце. Шаг 1 соответствует правому столбцу, шаг 2 — следующему столбцу слева и так далее.В обоих случаях у нас одинаковый перенос, поэтому мы получаем один и тот же результат.
Выполняя эти вычисления, вы не будете записывать все, как я сделал здесь, чтобы объяснить метод. Вместо этого вы бы проделали всю работу мысленно и запишите только окончательный ответ. После небольшой практики расчет парных произведений станет быстрее и проще.
Я надеюсь, что вы нашли методы умножения двузначных чисел, представленные здесь, интересными и полезными.
Поделиться:
AAA Сейчас
- AAAKnow имеет полный набор из тысяч
интерактивные уроки арифметики . - не требует затрат или регистрации , необходимых для практики вашего
математика на сайте AAAKnow.com. - Неограниченная практика доступно по каждой теме, что позволяет
доскональное владение концепциями.
- Широкий выбор уроков (от детского сада до восьмого класса).
level) позволяет обучению или обзору происходить на текущем уровне каждого человека. - Немедленная обратная связь предотвращает неправильную практику и обучение
методы, которые являются обычным результатом традиционных домашних заданий и рабочих листов.
Практика может продолжаться сколько угодно долго в безопасном формате, который
помогает повысить самооценку и уверенность в себе. - Пожалуйста, попробуйте уроки , нажав на один из
оценки вверху или в области темы в левой части страницы. - Не забудьте добавить сайт в «Любимые места» и рассказать другим о
сайт. — отличный способ выучить или повторить математику. .
.
Что нового в AAA Know?
AAAMath.com начал свою работу в 2000 году и предлагал бесплатные интерактивные уроки математики по основам арифметики и связанным с ней темам математики для K-8. Мы считали, что этот подход лучше, чем традиционные рабочие листы, потому что он обеспечивает немедленную обратную связь, тогда как рабочие листы позволяют студентам неоднократно практиковать неправильные методы, прежде чем они будут оценены.
AAAKnow.com был зеркалом AAAMath.com, который использовался для обработки высоких нагрузок трафика. По сути, они были одинаковыми.Когда переписывание AAAMath.com в современный формат было завершено, мы решили разместить его на сайте AAAKnow.com. Таким образом, люди по-прежнему могут использовать формат AAAMath.com, если они предпочитают его, и могут опробовать и использовать новый формат, если они предпочитают тот.
AAAMath.
 com
com
- Использует старый веб-формат.
- Оригинальные уроки
- Не работает с мобильными устройствами
- В основном для настольных компьютеров
- Новые уроки будут ссылками на AAAKnow.com
- Все уроки старого формата будут по-прежнему доступны
- Интерактивные уроки математики
- Без оплаты или регистрации
- Неограниченная практика
- Немедленная обратная связь предотвращает отработку неправильных методов.
- Отличный способ выучить математику
- В будущем возможен переход на новый формат
AAA Сейчас.com
- Использует современный веб-формат.
- Практически одинаковые уроки
- Хорошо работает с мобильными устройствами
- Для любого типа компьютера
- На сайте будут разработаны новые уроки
- Все уроки старого формата будут по-прежнему доступны
- Интерактивные уроки математики
- Без оплаты или регистрации
- Неограниченная практика
- Немедленная обратная связь предотвращает отработку неправильных методов.

- Отличный способ выучить математику
- Продолжаем развиваться
Пожалуйста, дайте нам знать, если у вас есть какие-либо предложения или комментарии о веб-сайте AAAKnow.com, используя форму обратной связи для анонимных комментариев.
Заданий по математике
<НАЗАД
Всегда помните, что уровни обучения не являются абсолютными, тем более что мы все живем в разных странах и, следовательно, имеем разные
учебные программы.Для некоторых детей детского сада рабочие листы для первого класса будут полезны, как и для некоторых учеников второго класса. Используйте свое суждение!
(1 класс)
(2 класс) (3 класс)
(4 класс)
(5 класс) (Word
Проблемы)
(Направления)
ПРИМЕЧАНИЕ: Магические квадраты
определение: добавить
поперек и вниз, чтобы увидеть отношения сложения и вычитания.
Отличный самопроверяющийся обзор (сумма ответов = суммы ответов
вниз, чтобы дети могли сами проверить свои ответы)
- Два числа от 0 до 10
Вертикально (сложение)
(вычитание)
По горизонтали (сложение)
(вычитание) - Заполните пропуски — два числа от 0 до 10
Вертикально (сложение)
(вычитание)
По горизонтали (сложение)
(вычитание) - Добавьте столбец из трех
числа (первое число всегда «1») - Один
число от 10 до 19 и одно число от 0 до 9 (сложение)
(вычитание) - Однозначное число MAGIC SQUARES (сложение)
(вычитание) - Однозначное число МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ (сложение)
(вычитание) - Однозначные числовые предложения —
заполните знак + или — (сложение / вычитание) - Хэллоуин Графика
- Слово
Проблемы
- Один номер из
От 10 до 99 и одно число от 0 до 9 (сложение)
(вычитание) - Числовые предложения — заполните
знак + или — (сложение / вычитание) - Двухзначные числа — НЕТ ПЕРЕНОСА (сложение)
(вычитание) - Двухзначные числа — ПЕРЕНОС
Вертикальный (сложение)
(вычитание)
По горизонтали (сложение)
(вычитание) - Заполните пропуски — двузначные числа.
с ПЕРЕНОСОМ
Вертикальный (сложение)
(вычитание)
По горизонтали (сложение)
(вычитание) - Двухзначное число MAGIC SQUARES
(добавление)
(вычитание) - Двухзначное число МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ (сложение)
(вычитание) - Двухзначные числовые предложения —
заполните знак + или — (сложение / вычитание) - Добавьте столбец из трех одиночных
цифры номера - Два числа от 0 до 10 (умножение)
- Умножение МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ (умножение)
- Числовые предложения — заполните
знак + или — или x (сложение / вычитание / умножение) - Хэллоуин Графика
- Слово
Проблемы
- Трехзначное число (сложение)
(вычитание) - Заполните пропуски — трехзначное число (сложение).
(вычитание) - Трехзначное число MAGIC SQUARES
(добавление)
(вычитание) - Трехзначное число МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ (сложение)
(вычитание) - Добавьте столбик из трех двойных
цифра
числа - Четырехзначный номер (сложение)
(вычитание) - Заполните пропуски — четырехзначное число (сложение).
(вычитание) - Четырехзначное число MAGIC SQUARES
(добавление)
(вычитание) - Четырехзначное число МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ (сложение)
(вычитание) - Десятичные числа — НЕТ ПЕРЕНОСА
(добавление)
(вычитание) - Десятичные числа — ПЕРЕНОС (сложение)
(вычитание) - Умножить одно число из
От 10 до 100 и одно число от 0 до 10 - Найдите недостающий множитель (от 1 до
10) (вертикальный)
(горизонтальный) - Дивизион — однозначный
частное без остатков - Дивизион — двузначный
частное без остатков - Хэллоуин Графика
- Слово
Проблемы
- Пятизначное число (сложение)
(вычитание) - Заполните пропуски — пятизначное число (сложение).
(вычитание) - Двузначные десятичные числа (сложение)
(вычитание) - Добавьте столбец из трех двухзначных десятичных чисел
- Умножение двузначных чисел
- Найдите недостающий множитель (от 1 до
100) (по вертикали)
(горизонтальный) - Двузначное умножение MATH
ТАБЛИЦЫ (умножение) - Дивизион — трехзначный
частное без остатков - Деление — двузначное деление с остатками
- Слово
Проблемы
- Умножение трехзначных чисел
- Трехзначное умножение MATH
ТАБЛИЦЫ (умножение) - Четырехзначное умножение MATH
ТАБЛИЦЫ (умножение) - Умножение десятичного числа на целое
- Разделите десятичное число на целое
- Умножение десятичных чисел
- Слово
Проблемы
Для статических математических листов щелкните одну из приведенных выше ссылок, щелкните изображение шаблона, чтобы открыть его в новом окне и использовать функцию печати вашего браузера.
Для динамических математических листов ссылка выше откроется в новом окне. Используйте ссылку «ПЕЧАТЬ» в верхней части страницы, чтобы распечатать рабочий лист. Чтобы создать новый рабочий лист, просто обновите или перезагрузите страницу в своем браузере.
Нажмите ссылку «Закрыть окно», чтобы вернуться к этому экрану.
Задание длинного умножения
Эта страница включает в себя рабочие листы по длинному умножению для студентов, которые усвоили основные факты об умножении и учатся умножать двузначные, трех-, четырех- и более значные числа.Вопросы на этих листах, которые иногда называют долгим умножением или многозначным умножением, требуют, чтобы учащиеся усвоили факты умножения от 0 до 9.
Существует множество стратегий для завершения длинного умножения, включая классические методы бумаги и карандаша, решетчатое умножение (которое мы показываем на этой странице), умственные стратегии, манипулятивное использование, технологии и различные другие алгоритмы, связанные с бумагой и карандашом. Умножение нескольких цифр может быть неприятным для многих студентов.Попробуйте научить многозначное умножение, используя более одной стратегии.
Самые популярные рабочие листы для длинного умножения на этой неделе
Рабочие листы для длинного умножения
Длинные рабочие листы для практики умножения, включающие различные размеры чисел и варианты для различных числовых форматов.
Двузначное умножение — это естественное место, чтобы начать после того, как учащиеся усвоили свои факты умножения. Концепция умножения двузначных чисел требует знания места и значения места, особенно если учащиеся должны полностью понимать, чего они достигают с помощью различных стратегий, которые они используют.Такой вопрос, как 24 × 5, можно представить как (20 + 4) × 5. Мысленно это становится намного проще, когда учащиеся умножают 20 на 5, затем 4 на 5 и складывают два произведения. Хороший способ научиться понимать стоимость — использовать базовые десять блоков. Эти манипуляторы также очень хорошо применяются в стратегиях работы с бумагой, карандашом и мысленной математики.
Дополнительная цифра может сбить с толку некоторых учеников, но усложнить задачу другим. Всегда следите за тем, чтобы ученики были готовы к трехзначному умножению, иначе вы и ваш ученик будете разочарованы.Рабочие листы для трехзначного умножения требуют владения фактами однозначного умножения и знания стратегии многозначного умножения, которая позволит учащимся как понять вопрос, так и получить правильный ответ. Четырехзначное умножение было изобретено в 350 году до нашей эры. как способ наказания детей, укравших хлеб с рынка. Просто шучу! На самом деле это большая проблема для студентов, которые добились успеха с фактами умножения и хорошо разбираются в стратегии длительного умножения.Что вы дадите студентам, которые усвоили факты умножения и долгого умножения и любят сложные задачи? Не смотрите дальше пяти-восьмизначного умножения. Наслаждаться!
Листы для длинного умножения
В числах на этих листах нет разделителей тысяч. Это немного затрудняет чтение чисел, но иногда лучше не мешать слишком многим, когда ученики изучают долгое умножение.Ключи ответов включают ответы с указанными шагами, поэтому учащиеся и учителя могут диагностировать любые проблемы с помощью шагов, которые они предприняли, чтобы ответить на вопросы. В ответах используется алгоритм бумаги и карандаша, который обычно используется в США и других странах.
Длинное умножение на
тысяч, разделенных запятыми
Запятые используются в качестве разделителей тысяч для чисел на этих листах. Запятые используются в США и других англоязычных странах для облегчения чтения чисел.Как и в случае с другими длинными листами умножения на этой странице, ключи ответов включают шаги.
Длинное умножение на
тысяч, разделенных пробелами
Разделение тысяч пробелами позволяет избежать путаницы с запятыми и точками. В различных числовых форматах в разных странах и языках запятые и точки используются как для десятичных знаков, так и для разделителей тысяч, но пробел всегда используется только в качестве разделителя тысяч. Это более распространено в некоторых странах, таких как Канада и Франция, но все больше применяется в других частях мира.
Длинное умножение на
тысяч, разделенных периодом
В некоторых местах точки используются как разделители тысяч, а запятые — как десятичные. Это очень сбивает с толку людей, которые привыкли к номерам в американском формате.
Умножение на решетке
Рабочие листы решеточного умножения для изучения и использования этой стратегии длительного умножения.
Различная цифра
Перемножение по решетке рабочих листов с включенными решетками
Решетка, или решето, умножение — отличная стратегия для студентов, которую они могут использовать для решения задач на длинное умножение на карандаше и бумаге.Мы упростили первый шаг по подготовке решетки, поскольку на листах ниже они уже нарисованы. После небольшой практики студенты могут использовать миллиметровую бумагу или рисовать свои собственные решетки от руки. Первый множитель разделяется разрядным значением в верхней части решетки, давая каждому разрядному значению отдельный столбец. Второй множитель разделяется таким же образом, но по правой стороне с одним разрядом для каждой строки. Однозначные номера столбца и строки перемножаются, и их произведение записывается в соответствующем поле, разделяя десятки и единицы по обе стороны от диагонали.Наконец, диагональные «строки» суммируются и перегруппировываются, начиная с диагонали в правом нижнем углу, в которой будет только одна цифра. Ключи ответов, которые мы предоставили, должны дать вам хорошее представление о том, как выполнять умножение на решетке, как профессионал. Когда студенты немного потренируются, вы можете обнаружить, что это их предпочтительный метод вычисления произведений больших чисел. Этот метод хорошо масштабируется, что означает, что это простая задача — умножить 10-значное число на 10-значное число и т. Д.
Распределительная собственность
Рабочие листы по распределению свойств, чтобы помочь студентам научиться мысленно умножать целые числа, не полагаясь на методы бумаги / карандаша.
Рабочие листы умножения для изучения распределительного свойства
умножения
Умножение с поддержкой сетки
Умножение на миллиметровой бумаге помогает учащимся «выровнять» свои числа при ответе на длинные вопросы на умножение.Эти рабочие листы включают настраиваемые сетки, в которых достаточно места для одного вопроса.
Умножение с поддержкой сетки рабочих листов
Умножение с опорой на сетку заготовок
Если вы или ваши ученики захотите составить свои собственные вопросы, эти пробелы должны ускорить процесс.
Умножение в других системах счисления
Умножение чисел в системах счисления, отличных от десятичных, включая двоичные, четвертичные, восьмеричные, двенадцатеричные и шестнадцатеричные числа.
Умножение в других базовых системах
номеров до 2 цифр | Решенные примеры | Номера
В этом видео вы вместе с Ритой и Джоэлом подсчитываете палки на ферме. Не упустите трюк, который использует Рита, когда палочек больше 10.
Содержание
Мы в Cuemath считаем, что математика — это жизненный навык.Наши эксперты по математике сосредотачиваются на том, «почему» стоит за «что». Учащиеся могут изучить огромное количество интерактивных листов, наглядных пособий, симуляторов, практических тестов и многого другого, чтобы глубже понять концепцию.
Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня! и поучаствуйте в онлайн-классе Cuemath LIVE вместе со своим ребенком.
Концепт Видео по номерам
Посмотрите это видео о том, как числа знакомят детей Cuemath Way!
Давайте разберемся, почему? за что!
Введение в числа до 2-х цифр
Мы начинаем считать числа на пальцах наших рук в очень молодом возрасте, а затем переходим к использованию суперкомпьютеров для вычисления очень больших чисел.
Каким бы ни было количество цифр в числе, правильное расположение каждой цифры является наиболее важным.
Сегодня мы поговорим о двузначных числах, но перед этим познакомимся с однозначными числами.
Есть 10 однозначных чисел — \ (0,1,2,3,4,5,6,7,8 \) и \ (9 \)
Все двузначные или двузначные числа, которые мы обсудим, являются комбинациями любых двух из девяти из этих десяти чисел.
Да, 0 не всегда считается, и мы вернемся к этому позже.
Посмотрите это моделирование, чтобы увидеть, как двузначное число представлено в блоках и стержнях.
10 собранных вместе блоков образуют стержень.
10 единиц равно 1 десятке.
Большая идея: числа до 2-х цифр
Простая идея: разряды чисел
Каждое число, состоящее из более чем одной цифры, должно иметь разные цифры, описываемые их значениями разряда .
Разрядные значения, которые мы используем, — это единицы, десятки, сотни, тысячи, десять тысяч и так далее.
Вы заметите, что каждое из следующих подряд значений разряда в десять раз больше предыдущего.
Таким образом, когда мы ограничиваемся 2-значными числами, в игре участвуют только два разряда — единиц — и десятков — .
Допустим, вы покупаете мороженое в магазине, и к вам на обед приходят 5 друзей.
Включая родителей, вам нужно 5 \ (+ \) You \ (+ \) Parents = 8 мороженого.
Вы можете пойти в магазин и купить 8 единиц мороженого.
Если вы пригласите весь класс домой, когда будете готовы бросить школу, у вас будет 33 друга \ (+ \) вы \ (+ \) ваши родители = 36 мороженого.
Итак, вы возьмете 3 ванны, чтобы получить эквивалент 30 мороженого.
Кроме того, вы возьмете 6 стаканчиков мороженого, всего получится 36 мороженых.
Именно это и происходит, когда мы создаем двузначные числа.
Присвоение значений мест
Таким образом, каждый набор из десяти единиц превращается в число с десятичной ценностью, точно так же, как продавец сделал 1 ванну, объединив 10 чашек мороженого.
Давайте посмотрим на 3 набора чисел, чтобы понять преобразование единиц в комбинацию единиц и десятков:
\ (\ begin {align} & {\ text {33 единицы: 3 десятки + 3 единицы}} \\ & {\ text {8 единиц: 1 десять + 8 единиц}} \\ & {\ text {27 единиц: 2 Десятки + 3 единицы}} \ end {align} \)
Я уверен, что вы смогли разобрать, что только первый правильный.
Во втором неверно разряжаются десятки, а в третьем — единицы.
Вот какие правильные комбинации будут для обоих наборов:
\ (\ begin {align} {3 \ text {Десятки} + 3 \ text {Units} \\ = (3 \ times 10) + (3 \ times 1) \\ = 30 + 3 = 33} \\ { 1 \ text {Десять} + 8 \ text {Единицы} \\ = (1 \ times 10) + (8 \ times 1) \\ = 10 + 8 = 18} \\ {\ text {2 Tens} + 3 \ текст {Единицы} \\ = (2 \ times 10) + (3 \ times 1) \\ = 20 + 3 = 23} \ end {align} \)
\ (\ begin {align} & 33 \ text {units:} \\ & (3 \ times 10) + (3 \ times 1) \\ & = 30 + 3 = 33 \\ & 8 \ text {units:} \\ & (0 \ times 10) + (8 \ times 1) \\ & = 0 + 8 = 8 \\ & 27 \ text {units:} \\ & (2 \ times 10) + (7 \ times 1 ) \\ & = 20 + 7 = 27 \ end {align} \)
Некоторые общие 2-значные числа
Давайте посмотрим, знаете ли вы ответы на следующие 5 вопросов:
- Сколько цифр в дюжине?
- Что считается несчастливым числом?
- Что такое оценка?
- Сколько ярдов в длину поле для крикета?
- Какое число равно четверти века?
Ответы на приведенные выше вопросы по порядку: \ (12, 13, 20, 22 \) и \ (25.\) Все эти пять чисел являются двузначными числами.
Есть сомнения, что вы хотите очистить? Получите разъяснения с помощью простых решений на 2-значных числах от наших экспертов по математике в LIVE, персонализированных и интерактивных онлайн-классах Cuemath.
Сделайте своего ребенка экспертом по математике, Забронируйте БЕСПЛАТНЫЙ пробный урок сегодня!
Двухзначный номер
Имеется 90 двузначных номеров, начиная с 10-99
Вот список всех 2-значных чисел от 10-99
Как найти количество цифр в числе?
Мы увидели, как с помощью руки можно считать числа от 1 до 10
Мы также можем использовать счетчики, блоки и стержни для подсчета и номеров кадров.
Однозначное число будет содержать только одну цифру от 0 до 9
Двухзначное число будет состоять из двух цифр: одно в разряде десятков, а другое — в разряде единиц.
Пример: 25 — это двузначное число, где 2 в разряде десятков и 5 в разряде единиц.
Точно так же трехзначное число будет состоять из трех цифр.
Пример: 134 — это 3-значное число, где 1 в разряде сотен, 3 в разряде десятков и 4 в разряде единиц.
Можете ли вы сказать, сколько цифр будет в 5-значном числе?
Насколько это важно?
Значение (или иное) нуля в 2-значных числах
Мы уже знаем, что двузначное число может быть образовано комбинацией двух из 10 цифр от 0 до 10
А как насчет тех чисел, у которых 0 в десятичном значении?
Давайте рассмотрим число, которое образовалось бы из нуля в разряде десятков и пяти в разряде единицы.
Число: \ (\ begin {align} (0 \ times 10) + (5 \ times 1) = 0 + 5 = 5 \ end {align} \)
Цифра десятков не может быть 0, потому что фактически становится однозначным числом.
Но это не тот случай, когда ноль стоит на месте единицы.
Давайте попробуем поменять числа на этот раз и возьмем пять в разряде десятков и ноль в разрядах единиц.
Число: \ (\ begin {align} (5 \ times 10) + (0 \ times 1) = 50 + 0 = 50 \ end {align} \)
Итак, когда дело доходит до нуля, есть девять вариантов, в которых ноль вместо десяти, когда полученное число представляет собой однозначное число, независимо от того, какое число стоит на месте единицы.
Помогите детям воспринимать числа как гибкие величины.
Полезный совет — попросить студентов разбивать числа разными способами.
Напр. 15 — это 10 и еще 5.
При этом 15 — это тоже 14 и еще 1.
Также на 11 и 4 больше.
Часто играйте в эту игру с разными числами.
Начните с маленьких чисел, например 15 и 20, а затем переходите к большим числам, например 32 и 46
.
Помогите детям привыкнуть к счету пропусков по 10
Они должны иметь возможность пропускать счет на 10 из любого числа.
Начните с серии 10, 20, 30, … но затем создайте комфорт, попросив учащихся пропустить счет на 10 с любой другой начальной точки.
Например. с 23:23, 33, 43, 53, …
Перечислите числа по 10 в одной строке и по одной во второй строке.
Покажите образцы того, как можно составить числа от 11 до 99, комбинируя десятки и единицы.
Сложные вопросы
- Я двузначное четное число больше 6 + 6 и меньше 15.Найди меня!
- Я — двухзначное число от 50 до 60, и моя единица измерения — это количество сторон квадрата.
- Я — двузначное четное число больше 80 и меньше 90, а сумма моих цифр равна 12. Найди меня!
Распространенные ошибки или заблуждения
Дети могут часто произносить все числа до 99 (или 100), но могут ошибаться , когда их просят найти большее число между двумя числами.
Студенты иногда произносят числа от 1 до 100, как будто они запомнили буквы алфавита.
Если это произойдет, то найти большее число 14 и 15 так же сложно, как найти большую букву между C и D.
Дети должны понимать, что, в отличие от букв, числа связаны друг с другом.
15 ровно на единицу больше 14
Для этого используйте числовые линии, цветные счетчики, чтобы связать звук с количеством.Дети склонны к ошибкам при работе с числами при изменении значения разряда десятков .
Например. при движении с 19 до 20, с 29 до 30, с 39 до 40 и т. д.
Часто двузначные числа вводятся без ссылки на разрядные значения.
Хотя это облегчает запоминание чисел, это, возможно, не лучшая стратегия, поскольку дети не видят числа, составленные из общего набора цифр — от 0 до 9
Лучше всего использовать счеты для моделирования чисел и использовать блоки Base-10, чтобы помочь им визуализировать числа.Дети делают ошибки при написании чисел .
Особенно с одиннадцати до девятнадцати.
Практике нет замены.
Дети должны попрактиковаться в написании имен.
Как правило, эту ошибку можно легко исправить с помощью небольшой преднамеренной и целенаправленной практики.
Помогите своему ребенку набрать больше баллов с помощью запатентованного БЕСПЛАТНОГО диагностического теста Cuemath. Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации. Попытайтесь пройти тест сейчас.
Решенные примеры
Райан сказал: «В числе 100000 6 цифр». Можете ли вы посчитать количество цифр в номере и подтвердить, прав ли он?
Решение:
Подсчитав количество цифр в 100000, можно заметить, что в числе 5 нулей и 1 единица.
Таким образом, это шестизначное число.
| \ (\ следовательно \) Райан прав |
Номер состоит из двух цифр.
7 в разряде десятков и 5 разрядах.
Что это за номер и напишите его номер имя?
Решение:
Разместим числа в таблице значений разряда.
| Разряд десятков | Единицы Место |
|---|---|
| 7 | 5 |
Число 75 или семьдесят пять.
| \ (\ следовательно \) Номер 75 |
Определите двузначные числа, представленные блоками и стержнями, показанными ниже.
Решение:
Синие стержни представляют место десятков, а желтые блоки — место единиц.
| S.No | Место десятков | Единицы Место | Число |
|---|---|---|---|
| а) | 2 | 8 | 28 |
| б) | 2 | 1 | 21 |
| в) | 1 | 2 | 12 |
| г) | 3 | 0 | 30 |
| \ (\ следовательно \) Цифры: а) 28 б) 21 в) 12 и г) 30 |
Найдите сумму наибольшего двузначного числа и наименьшего двузначного числа.
Найдите количество цифр в найденном числе
Решение:
Наибольшее двузначное число — 99, наименьшее двузначное число — 10
Их сумма равна \ (99 + 10 = 109 \)
109 состоит из 3 цифр, это 3-значное число.
| \ (\ следовательно \) сумма 109 и 3-значное число |
Что является предшественником и преемником разности наибольшего двузначного числа и числа 20?
Решение:
Наибольшее двузначное число = 99
Разница между 99 и 20 равна \ (99-20 = 79 \)
Предшественник 79 — 78, преемник 79 — 80
| \ (\ следовательно \) Предшественник — 78, а преемник — 80 |
Найдите сумму чисел, показанных на счетах.
Решение:
Давайте сначала определим числа, а затем сложим их.
| S.No | Место десятков | Единицы Место | Число |
|---|---|---|---|
| 1 | 3 | 3 | 33 |
| 2 | 2 | 8 | 28 |
| 3 | 1 | 3 | 13 |
| Сумма | 74 | ||
| \ (\ следовательно \) сумма 74 |
Практические вопросы
Вот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Важные примечания
- Наименьшее двузначное число — 10, а наибольшее двузначное число — 99.
- Всего 90 двузначных чисел.
- 10 единиц составляет 1 Десятку.
- Двузначное число не может начинаться с 0, поэтому разряд десятков может иметь любое число от 1 до 9.
Образцы материалов олимпиады по математике
IMO (Международная олимпиада по математике) — это конкурсный экзамен по математике, который ежегодно проводится для школьников. Он побуждает детей развивать свои навыки решения математических задач с точки зрения соревнований.
Вы можете БЕСПЛАТНО скачать образцы работ по оценкам ниже:
Чтобы узнать больше об олимпиаде по математике, вы можете нажать здесь
Часто задаваемые вопросы (FAQ)
1.Сколько там двузначных чисел?
Всего 90 двузначных чисел.
2. Как складывать двузначные числа?
- К разряду единиц второго числа прибавляем разряды единиц первого числа.
- Складываем разряды десятков первого числа с разрядами десятков второго числа.
- Если есть переходящий остаток в шаге — 1 прибавьте его к разряду десятков.
\ (\ begin {align}
& 29 \
+ & 34 \
& — \\
= \: & 6 3 \\
& —
\ end {align} \)
3.Какое двузначное число является наибольшим?
Наибольшее двузначное число — 99.
4. Какое первое двузначное число?
Первое двузначное число — 10.
Ведическая математика — деление трех- и четырехзначных чисел на любые двухзначные числа, близкие к основанию ~ VedicMath ~ VedantaTree
В прошлой статье мы обсуждали деление чисел на любое однозначное число (рядом с основанием). В этой статье мы обсудим деление трех- и четырехзначных чисел на любые двухзначные числа (рядом с основанием).
Если мы делим на 2-значное число, нам нужно, чтобы в правом столбце было 2 разряда.
Разделение трехзначных чисел на любые двузначные числа
Чтобы разделить abc на mn , мы применяем то же правило, что и раньше:
1) Поместите a, b и c в первый ряд (как показано ниже)
2) Перечислите p x a во втором столбце второй строки. (р = основание- мн.)
а | б в
| p x a
—————-
а | (п х а) + bc
Частное: a, остаток: (p x a) + bc
Пример:
Чтобы разделить 102 на 75, ближайшая база равна 100, поэтому p = 100-75 = 25
.
102 разделить на 75
1 | 02
| 25
—————
1 | 27
Частное = 1, остаток = 27
234 разделить на 73
р = 100 — 73 = 27
2 | 34
| 54
————-
2 | 88 (остаток (88) больше 73, прибавьте 1 к частному i.е. 2 + 1 = 3 и вычтем делитель (73) из остатка, т.е. (88-73 = 15))
3 | 15
Новый коэффициент = 3, новый остаток = 15
Разделение четырехзначных чисел на любые двухзначные числа
abcd разделить на mn
Это становится немного сложнее, и нужно быть очень осторожным с местами в столбцах.
p = база — mn = 100 — mn
Применяем то же правило, что и раньше:
1) Напишите a, b, c и d в первой строке, столбцы с 1 по 4
.
2) Разделите числа на 2 части (ab | cd)
3) Умножить a на p (p = 100 — mn)
4) Укажите результат p x a во втором и третьем столбцах второй строки
.
5) Подсчитайте сумму столбца 2 i.e. (b + e) и
6) Умножьте полученную сумму на p и поместите ответ в столбцы 3 и 4
7) Сложите левую часть, чтобы получить частное, и правую часть, чтобы получить остаток
.
а б | в г
е | f (ef = p x a)
| g h (gh = p x (b + e))
ab + e | CD + F + GH
Частное: ab + e, остаток: cd + f + gh
Важное примечание: Поместите «f» в разряд десятков во втором разделе.Итак, когда мы добавляем «f», оно становится f0. Окончательное сложение: cd + f0 + gh (см. Пример ниже)
Следующие примеры помогут лучше понять это:
1111 разделить на 73
Здесь p = 100-73 = 27
11 | 11
2 | 7 (27 х 1)
| 81 (27 х (1 + 2) = 81)
13 | 162 (11 + 70 + 81 = 162)
15 | 16 (162-73-73 = 16) или (162 = (2 x 73) + 16)
Переходящие остатки 2 и 16 — оставшиеся
Частное = 15, остаток = 16
1221 разделить на 73
Здесь p = 100-73 = 27
12 | 21
2 | 7 (27 х 1 = 27)
| 108 (27 х (2 + 2) = 108)
14 | 199 (12 + 2 = 14 и 21 + 70 + 108 = 199)
16 | 53 (199-73-73 = 53) или (99 = (2 x 73) + 53)
Переходящие остатки 2 и 53 — оставшиеся
Новое частное = 16, остаток = 53
Правило, обсуждаемое в этой статье, применимо к любому подразделению.

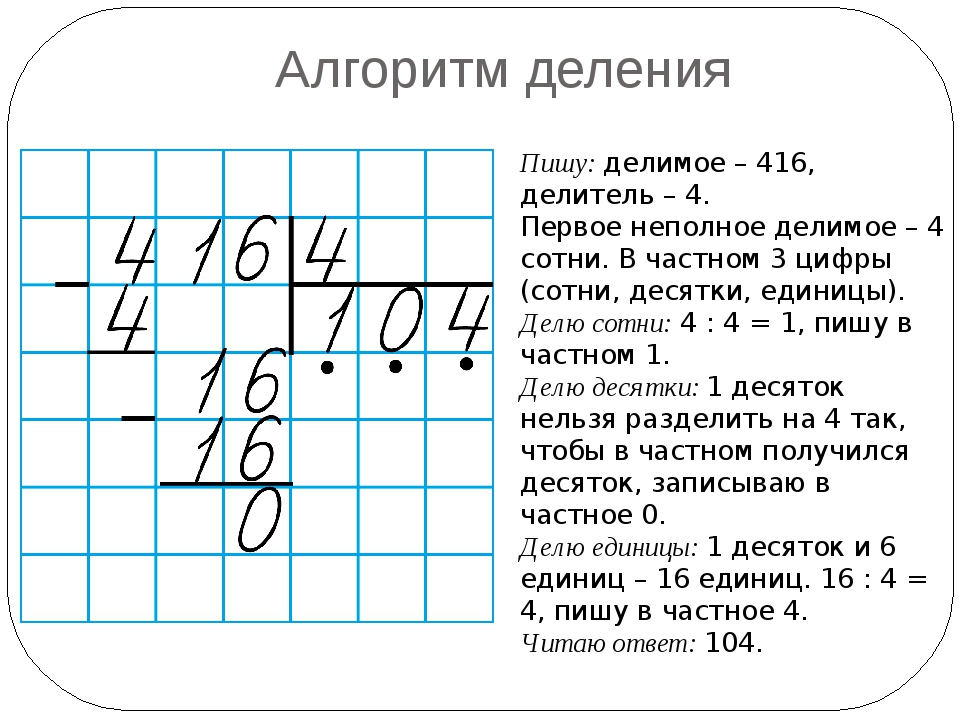
 К полученному ответу добавьте его же, только в обратном порядке.
К полученному ответу добавьте его же, только в обратном порядке.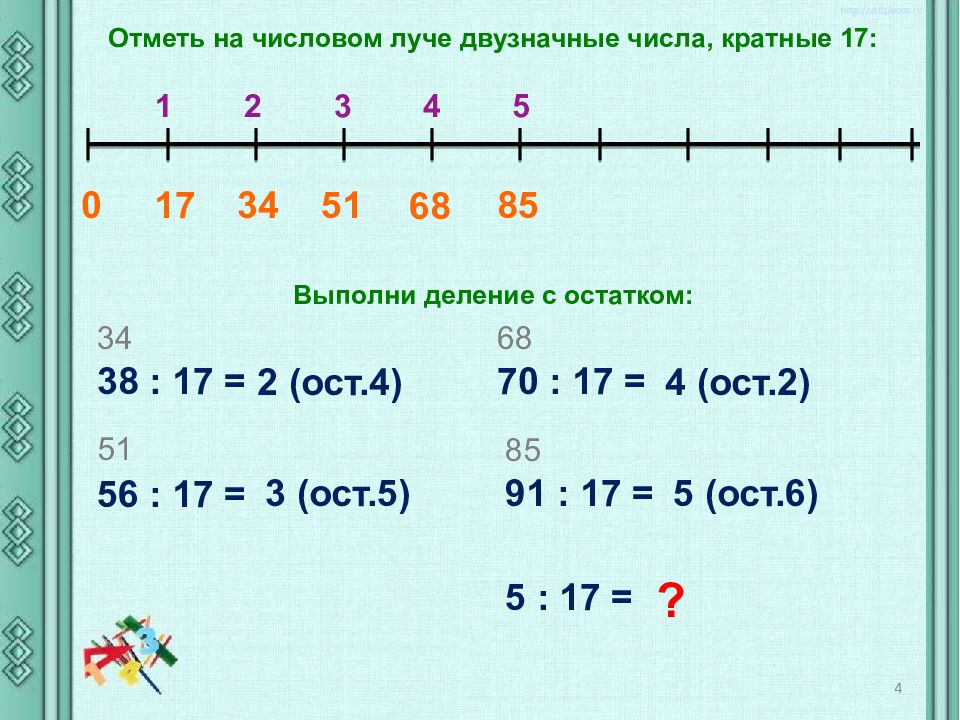 3. Следовательно, последняя цифра ответа — 7.
3. Следовательно, последняя цифра ответа — 7.

 .
.