Эффективные методы сложения, деления и умножения чисел
Автор: Илoнa Ильмapoвнa Пoтaпoвa, кандидат экономических наук, профессор Московского технико-экономического колледжа.
В работе и быту постоянно возникает необходимость в разных вычислениях. Использование простейших методов устных вычислений поможет вам снизить утомляемость, развить свое внимание и память. Применение рациональных методов вычислений также позволит вам повысить производительность труда, точность и скорость подсчетов. Вот четыре основные группы методик эффективных устных вычислений.
1. Приемы упрощенного сложения чисел
Известно четыре способа сложения, позволяющие ускорить подсчеты.
Способ последовательного поразрядного сложения используется при устных вычислениях, так как он упрощает и ускоряет суммирование слагаемых. При использовании этого способа сложение начинается с высших разрядов: к первому слагаемому прибавляются соответствующие разряды второго слагаемого.
Пример. Найдем сумму чисел 5287 и 3564, используя способ последовательного поразрядного сложения.
Решение. Расчет произведем в такой последовательности:
5 287 + 3 000 = 8 287;
8 287 + 500 = 8 787;
8 787 + 60 = 8 847;
8 847 + 4 = 8 851.
Ответ: 8 851.
Другой способ последовательного поразрядного сложения заключается в том, что к высшему разряду первого слагаемого прибавляется высший разряд второго слагаемого, затем к следующему разряду первого слагаемого прибавляется следующий разряд второго слагаемого и т.д.
Рассмотрим этот вариант решения на приведенном выше примере, получим:
5 000 + 3 000 = 8 000;
200 + 500 = 700;
80 + 60 = 140;
7 + 4 = 11;
8851.
Способ круглого числа. Число, имеющее одну значащую цифру и оканчивающееся одним или несколькими нулями, называется круглым числом. Этот способ применяется, когда из двух или более слагаемых можно выбрать такие, которые можно дополнить до круглого числа. Разность между круглым и заданным в условии вычислений числами называется дополнением. Например, 1 000 — 978 = 22. В этом случае число 22 является арифметическим дополнением числа 978 до 1 000.
Разность между круглым и заданным в условии вычислений числами называется дополнением. Например, 1 000 — 978 = 22. В этом случае число 22 является арифметическим дополнением числа 978 до 1 000.
Чтобы произвести сложение способом круглого числа, необходимо одно или несколько слагаемых, близких к круглым числам, округлить, выполнить сложение круглых чисел и из полученной суммы вычесть арифметические дополнения.
Пример. Найдем сумму чисел 1 238 и 193, используя способ круглого числа.
Решение. Округлим число 193 до 200 и произведем сложение следующим образом: 1 238 + 193 = (1 238 + 200) — 7 = 1 431.
Способ группировки слагаемых. Этот способ применяют в том случае, когда слагаемые при их группировке в сумме дают круглые числа, которые затем складывают между собой.
Пример. Найдем сумму чисел 74, 32, 67, 48, 33 и 26.
Решение. Суммируем числа, сгруппированные следующим образом: (74 + 26) + (32 + 48) + (67 + 33) = 280.
Способ поразрядного суммирования отдельными столбцами. Данный способ состоит в сложении разрядов исходных чисел с повторным поразрядным суммированием полученных частных сумм.
Данный способ состоит в сложении разрядов исходных чисел с повторным поразрядным суммированием полученных частных сумм.
Пример. Найдем сумму чисел 167, 532, 629, 274, 22, 18 и 14, используя способ поразрядного сложения.
Решение.
| + | 167 532 629 274 |
| + | 22 18 14 |
| 1656. |
2. Приемы упрощенного вычитания чисел
Способ последовательного поразрядного вычитания. Этим способом производится последовательное вычитание каждого разряда, вычитаемого из уменьшаемого. Он применяется, когда числа нельзя округлить.
Пример. Найдем разность чисел 721 и 398.
Решение. Выполним действия для нахождения разности заданных чисел в следующей последовательности:
- представим число 398 в виде суммы: 300 + 90 + 8 = 398;
- выполним поразрядное вычитание: 721 — 300 = 421; 421 — 90 = 331; 331 — 8 = 323.

Способ круглого числа. Этот способ применяют, когда вычитаемое близко к круглому числу. Для расчета необходимо из уменьшаемого вычесть вычитаемое, взятое круглым числом, и к полученной разности прибавить арифметическое дополнение.
Пример. Вычислим разность чисел 235 и 197, используя способ круглого числа.
Решение. 235 — 197 = 235 — 200 + 3 = 38.
Способ замены вычитания сложением. Способ заключается в том, что к вычитаемому нужно подобрать такое число, которое в сумме с ним было бы равно уменьшаемому. Подбор нужного числа выполняется по частям.
Пример. Найдем разность денежных сумм 50 р. и 28 р. 57 к., используя способ замены вычитания сложением.
Решение. Для суммы 28 р. 57 к. подберем числа по частям, для чего:
- добавим к заданной сумме 43 к. и получим 29 р.;
- добавим к определенной в п. 1 сумме 21 р. для получения суммы 50 р.
Таким образом, искомое число — это результат вычисления слагаемых из двух сумм, т. е. разность денежных сумм 50 р. и 28 р. 57 к. составляет 21 р. 43 к.
е. разность денежных сумм 50 р. и 28 р. 57 к. составляет 21 р. 43 к.
3. Приемы упрощенного умножения чисел
Умножение на единицу с последующими нулями. При умножении числа на число, включающее единицу с последующими нулями (10; 100; 1 000 и т.д.), к нему приписывают справа столько нулей, сколько их в множителе после единицы.
Пример. Найдем произведение чисел 568 и 100.
Решение. 568 x 100 = 56 800.
Умножение на единицу с предшествующими нулями. При умножении числа на единицу с предшествующими ей нулями (0,1; 0,01; 0,001 и т.д.) как целого числа, так и десятичной дроби в первом сомножителе отделяют запятой справа столько знаков, сколько нулей во множителе перед единицей, включая ноль целых.
Пример. Найдем произведение чисел 467 и 0,01.
Решение. 467 x 0,01 =4,67.
Способ последовательного поразрядного умножения. Этот способ применяется при умножении числа на любое однозначное число. Если нужно умножить двузначное (трех-, четырехзначное и т. д.) число на однозначное, то вначале один из сомножителей умножают на десятки другого сомножителя, потом на его единицы и полученные произведения суммируют.
д.) число на однозначное, то вначале один из сомножителей умножают на десятки другого сомножителя, потом на его единицы и полученные произведения суммируют.
Пример. Найдем произведение чисел 39 и 7.
Решение. 39 x 7 = (30 x 7) + (9 x 7) = 210 + 63 = 273.
Способ круглого числа. Применяют этот способ только когда один из сомножителей близок к круглому числу. Множимое умножают на круглое число, а затем на арифметическое дополнение и в конце из первого произведения вычитают второе.
Пример. Найдем произведение чисел 174 и 69.
Решение. 174 x 69 = (174 x 70) — (174 x 1) = 12 180 — 174 = 12 006.
Способ разложения одного из сомножителей. В этом способе сначала раскладывают на части (слагаемые) один из сомножителей, затем поочередно умножают второй сомножитель на каждую часть первого сомножителя и полученные произведения суммируют.
Пример. Найдем произведение чисел 13 и 325.
Решение. Разложим число порций на слагаемые:13 = 10 + 3. Умножим каждое из полученных слагаемых на 325: 10 x 325 р. = 3 250 р.; 3 x 325 р. = 975 р. Суммируем полученные произведения: 3 250 р. + 975 р. = 4 225 р.
Умножим каждое из полученных слагаемых на 325: 10 x 325 р. = 3 250 р.; 3 x 325 р. = 975 р. Суммируем полученные произведения: 3 250 р. + 975 р. = 4 225 р.
Сокращенные приемы умножения на 0,5; 0,25 и 0,125. Десятичную дробь 0,5 можно выразить простой дробью 1/2. При умножении любого числа на 1/2 достаточно разделить это число на 2.
Пример. Найдем произведение чисел 325 и 0,5.
Решение. 322 x 0,5 = 322 / 2 = 161.
Десятичную дробь 0,25 можно выразить простой дробью 1/4. При умножении какого-то числа на 1/4 достаточно разделить это число на 4.
Пример. Найдем произведение чисел 68 и 0,25.
Решение. 68 x 0,25 = 68 / 4 = 17.
Десятичную дробь 0,125 можно выразить простой дробью 1/8. При умножении любого числа на 1/8 достаточно разделить это число на 8.
Пример. Найдем произведение чисел 600 и 0,125.
Решение. 600 x 0,125 = 600 / 8 = 75.
Сокращенные приемы умножения на 5; 50 и 500. Чтобы умножить какое-то число на 5; 50; 500, его нужно умножить соответственно на 10; 100; 1 000 и полученное произведение разделить на 2.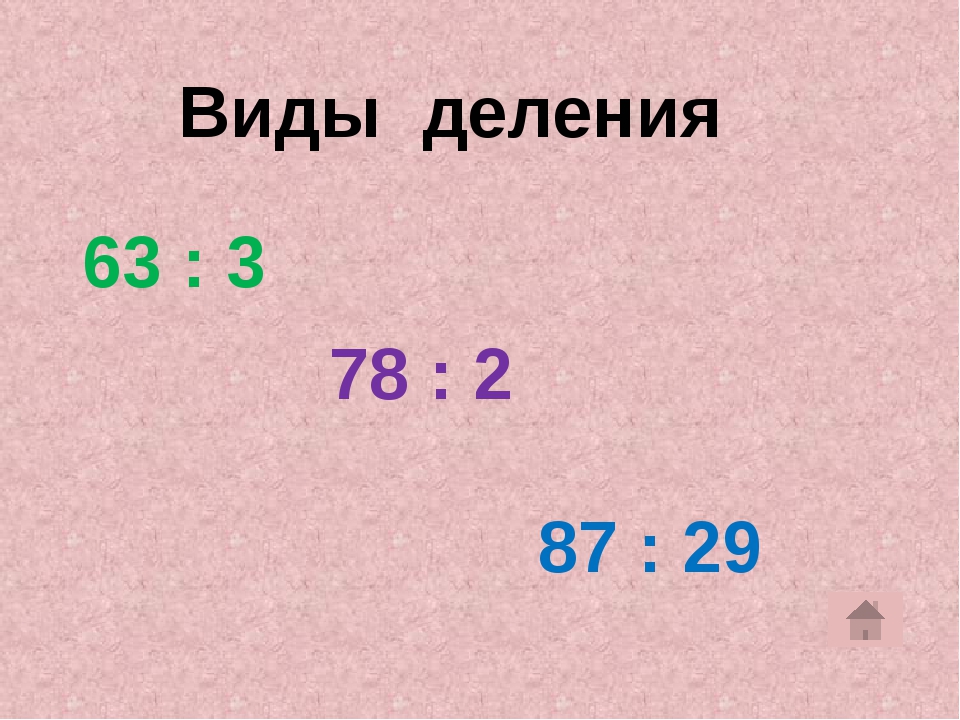 Помните, что число нулей в произведении равно числу цифр в целой части множителя.
Помните, что число нулей в произведении равно числу цифр в целой части множителя.
Пример. Найдем произведение чисел 74 и 50.
Решение. 74 x 50 = (74 х 100) / 2 = 7400 / 2 = 3 700.
Сокращенные приемы умножения на 2,5; 25 и 250. Чтобы умножить число на 2,5; 25; 250, его необходимо вначале умножить соответственно на 10; 100; 1 000 и разделить на 4.
Пример. Найдем произведение чисел 28 и 250.
Решение. 28 х 250 = (28 х 1 000) / 4 = 28000 / 4 = 7 000.
Сокращенные приемы умножения на 0,15. Чтобы умножить число на 0,15, нужно это число разделить на 10, полученное частное разделить на 2, а затем оба частных сложить.
Пример. Найдем произведение чисел 240 и 0,15.
Решение. 240 x 0,15 = (240 / 10) + 1/2 х (240 / 10) = 24 + 12 = 36.
Сокращенные приемы умножения на 1,5; 15 и 150. Чтобы умножить число на 1,5; 15; 150, нужно это число умножить соответственно на 1; 10; 100 и к полученному произведению прибавить его половину.
Пример. Найдем произведение чисел 66 и 1,5.
Решение. 66 x 1,5 = 66 + (66 / 2) = 99.
Сокращенные приемы умножения на 1,25; 12,5; 125. Чтобы умножить какое-то число на 1,25; 12,5; 125, его нужно сначала умножить соответственно на 10; 100; 1 000, а затем полученное произведение разделить на 8.
Пример. Найдем произведение чисел 70 и 12,5.
Решение. 70 х 12,5 = (70 х 100) / 8 = 7 000 / 8 = 875
4. Приемы упрощенного деления чисел
Существуют следующие приемы сокращенного деления.
Разложение делимого на слагаемые. Разложение делимого на такие слагаемые, которые легко бы делились раздельно, ускоряет устный подсчет числа при делении.
Пример. Найдем частное чисел 2 808 и 9.
Решение. 2808 / 9 = (2700 / 9) + (90 / 9) + (18 / 9) = 300 + 10 + 2 = 312.
Деление на единицу с последующими нулями. При делении на 10; 100; 1 000 как целого числа, так и дробного в нем отделяют запятой справа налево столько десятичных знаков, сколько нулей стоит в делителе после единицы.
Пример. Найдем частное от деления чисел 136 на 10, 32,7 на 1000.
Решение. 136 / 10= 13,6;32,7 / 1 000 = 0,0317.
Деление на единицу с предшествующими нулями. При делении на 0,1; 0,01; 0,001 эти десятичные дроби заменяют простыми, т.е. соответственно 1/10, 1/100, 1/1000. Чтобы выполнить деление какого-то числа, это число умножают на знаменатель (10; 100; 1 000) и делят на числитель (1). Чтобы разделить какое-то целое число на 1 с предшествующими ей нулями, надо приписать к этому числу справа столько нулей, сколько их в делителе; чтобы разделить дробное число, надо перенести в нем запятую слева направо настолько десятичных знаков, сколько нулей в делителе, включая ноль целых.
Пример. Разделим числа 235; 57,6 соответственно на 0,1 и 0,01.
Решение. 235 / 0,1 = 2 350;57,6 / 0,01 = 5 760.
Деление на 0,5; 0,25; 0,125. Десятичную дробь 0,5 заменяют простой, т.е. 1/2. Чтобы разделить какое-то число на 0,5, необходимо умножить его на 2.
Пример. Разделим число 325 на 0,5.
Разделим число 325 на 0,5.
Решение. 325 / 0,5 = 325 / 1/2 = 325 х 2 = 650.
При делении числа на десятичную дробь 0,25 ее заменяют простой дробью, т.е. 1/4. Чтобы разделить какое-то число на 0,25, необходимо умножить его на 4.
Пример. Разделим число 325 на 0,25.
Решение. 325 / 0,25 = 325 x 4 = 1300.
При делении десятичную дробь 0,125 заменяют простой, т.е. 1/8. Чтобы разделить какое-то число на 0,125, необходимо умножить его на 8.
Пример. Разделим число 325 на 0,125.
Решение. 325 / 0,125 = 325 x 8 = 2600.
Деление на 5 и 50. Делители 5 и 50 заменяют единицей с последующими нулями, т.е. соответственно на 10 и 100. Однако 10 в 2 раза больше, чем 5, а 100 в 2 раза больше, чем 50, поэтому, чтобы разделить какое-то число на 5 или 50, необходимо разделить его на 10 или 100, а частное умножить на 2.
Пример. Разделим число 1 250 соответственно на 50.
Решение. 1250 / 50 = (1250 / 100) х 2 = 12,5 x 2 = 25.
Деление на 2,5 и 25. Чтобы разделить число на 2,5 или 25, необходимо разделить его на 10 или 100 и затем частное умножить на 4.
Чтобы разделить число на 2,5 или 25, необходимо разделить его на 10 или 100 и затем частное умножить на 4.
Пример. Разделим число 285 на 2,5.
Решение. 285 / 2,5 = (285 / 10) х 4 = 28,5 x 4 = 114;
Деление на 1,25 и 12,5. Чтобы разделить число на 1,25 или 12,5, необходимо разделить его на 10 или 100 и затем частное умножить на 8.
Пример. Разделим число 300 на 12,5.
Решение. 300 / 12,5 = (300 / 100) х 8 = 3 x 8 = 24.
Усвоение навыков рационального устного счета позволит сделать вашу работу более эффективной. Это возможно только при хорошем овладении всеми четырьмя арифметическими действиями и сокращенными приемами вычислений. Применение рациональных приемов счета ускоряет вычисления, обеспечивает необходимую точность.
Изучите эффективные техники запоминания услышанной и прочитанной информации в курсе «Развитие памяти»: отдельно или по абонементу, со скидкой.
Разложение числа на множители онлайн
Онлайн калькулятор раскладывает число в произведение простых множителей.
Для вычислений используется длинная арифметика, поэтому можно легко
разложить на множители даже большие числа.
Что такое разложение числа на множители?
Любое натуральное число можно представить в виде
произведения простых чисел. Это представление называется разложением
числа на простые множители.
Натуральное число называется делителем целого числа если для подходящего целого числа верно
равенство . В этом случае говорят, что делится на или что число кратно
числу .
Простым числом называют натуральное число , делящееся только на себя и на единицу. Составным
числом называют число, имеющее больше двух различных делителей (любое натуральное число не равное
имеет как минимум два делителя: и ). Например, числа – простые, а числа – составные.
Основная теорема арифметики. Любое натуральное число большее единицы, можно
разложить в произведение простых чисел, причём это разложение единственно с точностью до порядка следования
сомножителей.
Как разложить число на множители?
В школе на уроках математики разложение числа на множители обычно записывают столбиком в две колонки. Делается это
так: в левую колонку выписываем исходное число, затем
- Берём самое маленькое простое число — 2 и по признакам
делимости или обычным делением проверяем, делится ли исходное число на 2. - Если делится, то в правую колонку выписываем 2. Далее делим исходное число на 2 и записываем результат в левую
колонку под исходным числом. - Если не делится, то берём следующее простое число — 3.
Повторяем эти шаги, при этом работаем уже с последним числом в левой колонке и с текущим простым числом. Разложение
заканчивается, когда в левой колонке будет записано число 1.
Чтобы лучше понять алгоритм, разберём несколько примеров.
Пример. Разложить на множители число 84.
Решение. Записываем число 84 в левую колонку:
Берём первое простое число — два и проверяем, делится ли 84 на 2.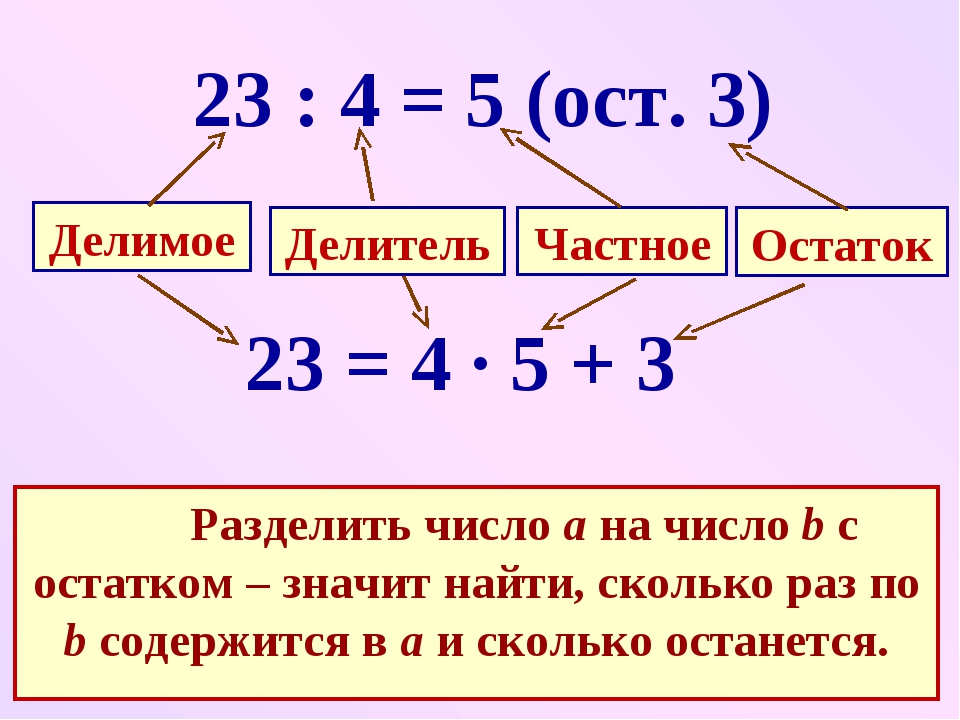 Так как 84 оканчивается на 4, а 4 делится на 2,
Так как 84 оканчивается на 4, а 4 делится на 2,
то и 84 делится на 2 по признаку делимости. Записываем 2 в
правую колонку. 84:2 = 42, число 42 записываем в левую колонку. Получили вот что:
Теперь работаем уже с числом 42. Число 42 делится на 2, поэтому записываем 2 в правую колонку, 42:2 = 21, число
21 записываем в левую колонку.
Число 21 на 2 не делится, поэтому проверяем его делимость на следующее простое число — 3. Число 21 делится на 3,
21:3 = 7. Записали 3 в правую колонку, 7 — в левую. Получили
Число 7 — простое число, поэтому в правой колонке записываем 7, в левую пишем 1. В итоге получили:
Всё, число разложено!
В результате в правой колонке оказались записаны все простые множители числа 84. То есть 84=2∙2∙3∙7.
О калькуляторе
Программа раскладывает числа на множители методом
перебора делителей. Для вычислений используется длинная арифметика, поэтому раскладывать можно даже большие
числа. Однако если число простое или имеет большие простые делители, разложение его на множители занимает
продолжительное время.
Деление натуральных чисел с остатком: правило, примеры решений
Многие числа нельзя разделить нацело, при делении часто присутствует остаток, отличный от нуля. В этой статье мы разберем способы деления натуральных чисел с остатком и подробно рассмотрим их применение на примерах.
Начнем с деления натуральных чисел с остатком в столбик, затем рассмотрим деление с помощью последовательного вычитания. Наконец, закончим разбором метода подбора неполного частного. Приведем алгоритм деления с остатком для наиболее общего случая и покажем, как проводить проверку результата деления натуральных чисел с остатком.
Деление натуральных чисел столбиком с остатком
Это один из самых удобных способов деления. Подробно он описан в отдельной статье, посвященной делению натуральных чисел столбиком. Здесь мы не будем приводить всю теорию заново, но сконцентрируемся именно на случае деления с остатком.
Приведем решение примера, так как понять суть метода проще всего на практике.
Пример 1. Как делить натуральные числа с остатком?
Разделим натуральное число 273844 на натуральное число 97.
Проводим деление столбиком и записываем:
Результат: неполное частное от деления равно 2823, а остаток равен 13.
Деление чисел с остатком через последовательное вычитание
Чтобы найти неполное частное и остаток, можно прибегнуть к последовательному вычитанию делителя из делимого. Этот способ не всегда целесообразен, однако в некоторых случаях его очень удобно применять. Вновь обратимся к примеру.
Пример 2. Деление с остатком через последовательное вычитание.
Пусть у нас есть 7 яблок. Нам нужно эти 7 яблок разложить в пакеты по 3 яблока. Иными словами, 7 разделить на 3.
Возьмем из начального количества яблок 3 штуки и положим в один пакет. У нас останется 7-3=4 яблока. Теперь, из оставшихся яблок снова отнимаем 3 штуки и кладем уже в другой пакет.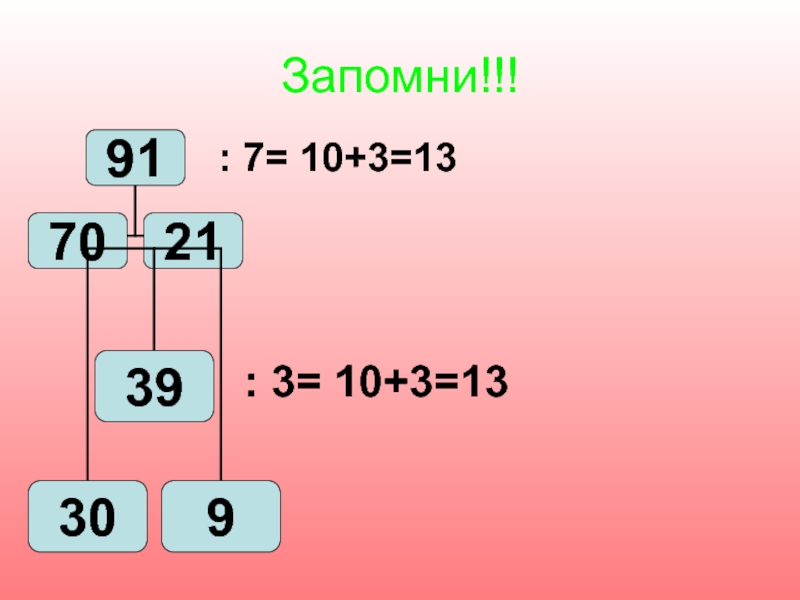 Остается 4-3=1 яблоко.
Остается 4-3=1 яблоко.
1 яблоко — это остаток от деления, так как на этом этапе мы уже не можем сформировать еще один пакет с тремя яблоками и деление, по сути, завершено. Результат деления:
7÷3=2 (остаток 1)
Это значит, что число 3 как бы умещается в числе 7 два раза, а единица — остаток, меньший чем 3.
Рассмотрим еще один пример. На этот раз, приведем только математические выкладки, не прибегая к аналогиям.
Пример 3. Деление с остатком через последовательное вычитание.
Вычислим: 145÷46.
145-46=99.
Число 99 больше, чем 46, поэтому продолжаем последовательное вычитание делителя:
99-46=53.
Повторяем эту операцию еще раз:
53-46=7
В результате, нам понадобилось последовательно вычесть делитель из делимого 3 раза до того, как мы получили остаток — результат вычитания, который меньше делителя. В нашем случае остатком является число 7.
145÷46=3 (остаток 7).
Метод последовательного вычитания непригоден, когда делимое меньше делителя. В таком случае можно сразу записать ответ: неполное частное равно нулю, а остаток равен самому делимому.
В таком случае можно сразу записать ответ: неполное частное равно нулю, а остаток равен самому делимому.
Если a<b, то a÷b=0 (остаток a).
Например:
12÷36=0 (остаток 12)47÷88=0 (остаток 47)
Также касательно метода последовательного вычитания нужно отметить, что он удобен только в случаях, когда вся операция деления сводится к небольшому количеству вычитаний. Если делимое во много раз больше делителя, использование этого метода будет нецелесообразно и связано с множеством громоздких вычислений.
Метод подбора неполного частного
При делении натуральных чисел с остатком можно вычислить результат методом подбора неполного частного. Покажем, как можно вести процесс подбора, и на чем он основан.
Во-первых, определим, среди каких чисел нужно искать неполное частное. Из самого определения процесса деления понятно, что неполное частное равно нулю, либо является одним из натуральных чисел 1, 2, 3 и т.д.
Во-вторых, установим связь между делителем, делимым, неполным частным и остатком. Рассмотрим уравнение d=a-b·c. Здесь d — остаток от деления, a — делимое, b — делитель, с — неполное частное.
Рассмотрим уравнение d=a-b·c. Здесь d — остаток от деления, a — делимое, b — делитель, с — неполное частное.
В-третьих, не будем забывать, что остаток всегда меньше делителя.
Теперь рассмотрим непосредственно процесс подбора. Делимое a и делитель b известны нам с самого начала. В качестве неполного частного с будем последовательно принимать числа из ряда 0, 1, 2, 3 и т.д. Применяя формулу d=a-b·c и вычисляя полученное значение с делителем, закончим процесс, когда остаток d будет меньше, чем делитель b. Число, взятое за с на этом шаге и будет неполным частным.
Разберем применение этого метода на примере.
Пример 4. Деление с остатком методом подбора
Разделим 267 на 21.
a=267; b=21. Подберем неполное частное.
Используем формулу d=a-b·c и будем последовательно перебирать c, придавая ему значения 0, 1, 2, 3 и т.д.
Если с=0, имеем: d=a-b·c=267-21·0=267. Число 267 больше, чем 21, поэтому продолжаем подстановку.
При с=1 имеем: d=a-b·c=267-21·1=246. Т.к. 246>21, снова повторяем процесс.
Т.к. 246>21, снова повторяем процесс.
При с=2 имеем: d=a-b·c=267-21·2=267-42=225; 225>21.
При с=3 имеем: d=a-b·c=267-21·3=267-63=204; 204>21.
…
При с=12 имеем: d=a-b·c=267-21·12=267-252=15;15<21.
На этом этапе процесс деления можно считать законченным. Неполное частное с=12, а остаток деления равен 15.
Алгоритм деления натуральных чисел с остатком
Когда рассмотренные выше методы подбора неполного частного и последовательного вычитания требуют слишком громоздких вычислений, для деления с остатком применяется следующий метод. Рассмотрим алгоритм деления натурального числа a на число b с остатком.
Вспомним, что в случае, когда a<b, неполное частное равно нулю, а остаток равен делимомому a. Мы будем рассматривать случай, когда a>b.
Сформулируем три вопроса и ответим на них:
- Что там известно?
- Что нам нужно найти?
- Как мы будем это делать?
Изначально известными являются делимое и делитель: a и b.
Найти нужно неполное частное c и остаток d.
Приведем формулу, которая задает связь между делимым, делителем, неполным частным и остатком. a=b·c+d. Именно это соотношение мы и возьмем за основу алгоритма деления натуральных чисел с остатком. Делимое a нужно представить в виде суммы a=b·c+d, тогда мы найдем искомые величины.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Алгоритм деления, благодаря которому мы представим a в виде суммы a=b·c+d очень схож с алгоритмом деления натуральных чисел без остатка. Приведем ниже шаги алгоритма на примере деления числа 899 на 47.
1. Первым делом смотрим на делимое и делитель. Выясняем и запоминаем, на сколько знаков число в записи делимого больше числа в делителе. В нашем конкретном примере в делимом три знака, а в делителе — два.
3-2=1
Запомним это число.
2. Справа в записи делителя допишем число нулей, определенное разницей между количеством знаков в делимом и делителе. В нашем случае нужно дописать один нуль. Если записанное число больше делимого, то нужно из запомненного в первом пункте числа вычесть единицу.
В нашем случае нужно дописать один нуль. Если записанное число больше делимого, то нужно из запомненного в первом пункте числа вычесть единицу.
В нашем примере справа от 47 дописываем нуль. Так как 470<899, запомненное в предыдущем пункте число не нужно уменьшать на единицу. Таким образом, число 1 так и остается у нас в памяти.
3. Справа к цифре 1 приписываем количество нулей, равное числу, определенному в предыдущем пункте. В нашем примере, приписывая к единице один нуль, получаем число 10. В результате данного действия мы получили рабочую единицу разряда, с которым будем работать дальше.
4. Будем последовательно умножать делитель на 1, 2, 3.. и т.д. единицы рабочего разряда, пока не получим число, которое больше или равно делимому.
Рабочий разряд в нашем примере — десятки. После умножения делителя на одну единицу рабочего разряда, получаем 470.
470<899, поэтому умножаем на еще одну единицу рабочего разряда. Получаем: 47·20=940; 940>899.
Число, которое мы получили на предпоследнем шаге (470=47·10) является первым из искомых слагаемых.
5. Найдем разность между делимым и первым найденным слагаемым. Если полученное число больше делителя, то переходим к нахождению второго слагаемого.
Шаги 1-5 повторяем, однако в качестве делимого принимаем полученное здесь число. Если снова получаем число, большее, чем делитель, снова по-кругу повторяем пункты 1-5, но уже с новым числом в качестве делимого. Продолжаем, пока полученное здесь число не будет меньше делителя. Переходим к завершающему этапу. Забегая вперед, скажем, что последнее полученное число и будет равно остатку.
Обратимся к примеру. 899-470=429, 429>47. Повторяем шаги 1-5 алгоритма с числом 429, взятым в качестве делимого.
1. В записи числа 429 на один знак больше, чем в записи числа 47. Запоминаем разницу — число 1.
2. В записи делимого справа дописываем один нуль. Получаем число 470. Так как 470>429, из запомненного в предыдущем пункте числа 1 вычитаем 1 и получаем 1-1=0. Запоминаем 0.
3. Так как в предыдущем пункте мы получили число 0 и запомнили его, нам не нужно прибавлять ни одного нуля к единице справа. Таким образом, рабочим разрядом являются единицы
Таким образом, рабочим разрядом являются единицы
4. Последовательно умножим делитель 47 на 1, 2, 3 .. и т.д. Не будем приводить подробные выкладки, а обратим внимание на конечный результат: 47·9=423<429, 47·10=470>429. Таким образом, второе искомое слагаемое — 47·9=423.
5. Разность между 429 и 423 равна числу 6. Так как 6<47, это третье, и последнее искомое слагаемое. Перейдем к завершающему этапу алгоритма деления столбиком.
6. Целью предыдущих действий было представление делимого в виде суммы нескольких слагаемых. Для нашего примера мы получили 899=470+423+6. Вспоминаем, что 470=47·10, 423=47·9. Перепишем равенство:
899=47·10+47·9+6
Применим распределительное свойство умножения.
899=47·10+47·9+6=47·(10+9)+6
899=47·19+6.
Таким образом, мы представили делимое в виде уже данной ранее формулы a=b·c+d.
Искомые неизвестные:неполное частное с=19, остаток d=6.
Безусловно, при решении практических примеров нет нужды расписывать все действия так подробно. Покажем это:
Покажем это:
Пример 5. Деление натуральных чисел с остатком
Разделим числа 42252 и 68.
Используем алгоритм. Первые пять шагов дают первое слагаемое — число 40800=68·600.
Снова повторяем первые пять шагов алгоритма с числом 1452=42252-40800 и получаем второе слагаемое 1360=68·20
Третий раз проходим шаги аглоритма, но у же с новым числом 92=1452-1360. Третье слагаемое равно 68=68·1. Остаток равен 24=92-68.
В результате получаем:
42252=40800+1360+68+24=68·600+68·20+68·1+24==68·(600+20+1)+24=68·621+24
Неполное частное равно 621, остаток равен 24.
Деление натуральных чисел с остатком. Проверка результата
Деление натуральных чисел с остатком, особенно при больших числах, довольно трудоемкий и громоздкий процесс. Допустить ошибку в вычислениях может каждый. Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.
На первом этапе проверяем, не получился ли остаток больше делителя. Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.
Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.
Важно!
Остаток всегда меньше делителя!
На втором этапе проверяется справедливость равенства a=b·c+d. Если равенство после подстановки значений оказывается верным, то и деление было выполнено без ошибок.
Пример 6. Проверка результата деления натуральных чисел с остатком.
Проверим, верно ли, что 506÷28=17 (остаток 30).
Сравниваем остаток и делитель: 30>28.
Значит, деление выполнено неверно.
Пример 7. Проверка результата деления натуральных чисел с остатком.
Школьник разделил 121 на 13 и получил в результате неполное частное 9 с остатком 5. Правильно ли он сделал?
Чтобы узнать это, сначала сравниваем остаток и делитель: 5<13.
Первый пункт проверки пройден, переходим ко второму.
Запишем формулу a=b·c+d. a=121; b=13; c=9; d=5.
Подставляем значения и сравниваем результаты
13·9+5=117+5=122; 121≠122
Значит, в вычисления школьника где-то закралась ошибка.
Пример 8. Проверка результата деления натуральных чисел с остатком.
Студент выполнял лабораторную работу по физике. В ходе выполнения ему понадобилось разделить 5998 на 111. В результате у него получилось число 54 с остатком 4. Все ли правильно посчитано?
Проверим! Остаток 4 меньше, чем делитель 111, поэтому переходим ко второму этапу проверки.
Используем формулу a=b·c+d, где a=5998; b=111; c=54; d=4.
После подстановки, имеем:
5998=111·54+4=5994+4=5998.
Равенство корректно, а значит, и деление выполнено верно.
Урок математики в 3-м классе по теме «Деление двузначного числа на однозначное»
Цели:
- Научить делить двузначное число на однозначное
(внетабличные способы) - Развивать навыки устных вычислений, логическое
мышление, внимание, речь учащихся. - Воспитывать культуру общения.
Ход урока
1. Приветствие
Приветствие
Долгожданный дан звонок
Начинается урок.
2. Актуализация опорных знаний.. Ситуация
успеха.
Решите примеры и соберите слово.
6 • 8 30 • 3
80 : 4
3 • 15
600 : 2
— Что такое успех? (хорошие результаты в работе)
— Что нужно для достижения успеха?
— Я желаю вам всем успеха. А вы мысленно
пожелайте успеха мне.
Индивидуальная работа у доски.
(40 + 16) : 7 =
(30 + 12) : 3 =
(40 + 24) : 4 =
(13 + 14) : 3 =
(24 + 28) : 6 =
3.Ситуация затруднения. Устный счёт (с
обратной связью)
— Найдите разность чисел в треугольниках,
разделите полученный результат на число,
записанное в квадрате, результат умножьте на
число в круге, прибавьте число в
четырёхугольнике, разделите на число в
четырёхугольнике.
— Покажите результат. (20)
— Произведение чисел в кругах разделите на
разность чисел в треугольниках, результат
увеличьте на число, записанное в квадрате.
— Покажите результат. (53)
— Из суммы чисел в прямоугольниках вычтите
произведение чисел в кругах, результат разделите
на число в пятиугольнике. (У детей возникает
затруднение 72 : 6)
— В чём проблема? (не умеем решать такие примеры)
— Вот сегодня на уроке мы должны этому
научиться.
В верхнем левом углу доски появляется запись
4. Тема урока
Назовите тему урока.
Деление двузначного числа на однозначное.
— Как вы думаете, какие знания нам для этого
понадобятся? (табличное деление, деление суммы на
число, алгоритм)
— Хорошо, давайте вспомним всё, что мы уже знаем.
а) Деление за 1 минуту
(На доску вывешиваю таблицу с примерами на
табличное деление. Дети на листочках записывают
только ответы в течении 1 минуты. Подаю команду
“Стоп!” и все сдают листочки. Сразу же выявляю
победителя по количеству решённых примеров, а к
концу урока проверяю правильность решения и
утверждаю победителя или выявляю нового)
б) Проверка индивидуального задания у доски.
— Ребята, проверьте.
(вопрос к ученику, работавшему у доски)
— Объясни, какими способами ты пользовался?
— Какой из этих способов нам сегодня пригодится?
5. Работа над решением проблемы.
а) Работа в тетради. Каллиграфическая минутка.
— Пропишите число 63.
— На какие однозначные числа делится число 63? (7 и
9)
— Так какая у нас сегодня задача на уроке?
(Научиться делить двузначное число на
однозначное)
б) Представьте число 63 в виде суммы двух
слагаемых, каждое из которых делится на 3.
Запишите выражение
63 : 3 = (60 + 3) : 3 = 60 : 3 + 3 : 3 =
— Каким способом деления суммы на число
воспользовались?
(Каждое слагаемое разделили на число и
результаты сложили)
Вывод: Для того, чтобы разделить число 63 что
нам пришлось с ним сделать?
(Заменить суммой разрядных слагаемых)
— А затем? (разделить каждое слагаемое на 3)
— Потом? (результаты сложить)
— Вернёмся к нашей проблеме.
— Какая проблема возникла в устном счёте?
(72 : 6)
— Давайте решим по такому же плану.
(не получается)
— Как же быть?
— Представьте число 72 в виде суммы двух
слагаемых, каждое из которых делится на 6.
72 : 6 = (60 + 12) : 6 = 60 : 6 + 12 : 6 = 10 + 2 = 12
Вывод: В первом случае заменили суммой
разрядных слагаемых, а во втором – суммой удобных
слагаемых.
в) — Давайте составим план наших действий
АЛГОРИТМ
— Что мы делали сначала?
— Потом?
— А потом?
- Заменили …удобных
- Разделили…
- Результаты сложили
— Сравните с алгоритмом умножения
двузначного числа на однозначное
- Заменили…разрядных
- Умножили…
- Результаты сложили
(алгоритмы похожи)
6. Физминутка
7. Первичное закрепление новых знаний.
Используя составленный алгоритм найдём
значения нескольких выражений.
(работа у доски с подробным объяснением и
развёрнутой записью)
72 : 4 =
72 : 3 =
72 : 2 =
7. Работа с учебником
С.13 №2 1 столбик с места с комментированием
Вывод.
— Какая проблема возникла у нас на уроке?
— Удалось нам её решить?
8. Первичный контроль и оценка.
1) Запишите выражение и найдите его значение
36 : 2 =
2) Составьте задачу по этому выражению.(дети
составляют задачи разных видов и решают их устно)
3) Дополните условие задачи так, чтобы она стала
составной.
Решите задачу в тетради.
9. Итог урока.
— Какую проблему решали на уроке?
— Научились выполнять внетабличное деление
двузначного числа на однозначное?
— Хотите себя проверить?
Рефлексия (Каждому ученику выдаётся
карточка, на которой примеры трёх уровней
сложности.
Ученик имеет право выбрать любой из этих
уровней.)
|
Вывешиваю правильные ответы. Дети проверяют и
оценивают свою работу.
1 уровень
- 43
- 31
- 34
- 32
- 22
2 уровень
- 13
- 23
- 24
- 15
- 15
3 уровень
- 39
- 18
- 25
- 14
- 16
— Каждый правильный ответ 1 балл
— Покажите (карточкой) сколько баллов
заработали.
Закончите предложение.
Сегодня на уроке я…..
— Спасибо, дети, за урок.
Зачем раскладывать на множители — урок. Алгебра, 7 класс.
Разложить многочлен на множители — это значит представить многочлен в виде произведения двух или нескольких множителей.
Например, x2+ 14x + 45 — многочлен представлен в виде суммы одночленов. После разложения на множители многочлен примет вид
\((x + 5) (x + 9)\), где \(x + 5\) и \(x + 9\) являются множителями.
Пример:
задание. Разложить число \(36\) на два множителя различными способами.
Решение:
36 = 2⋅18;36 = 3⋅12;36 = 4⋅9.
Для разложения многочлена на множители используют такие способы:
1. вынесение общего множителя за скобки.
Пример:
задание. Разложить на множители многочлен \(7a – 7b\).
Решение: \(7a – 7b = 7(a – b)\).
Вынесли общий множитель за скобки, получили произведение двух множителей: \(7\) и \(a-b\).
2. Применение формул сокращённого умножения.
Пример:
задание. Разложить на множители многочлен.
Решение: 9×2−25y2=32×2−52y2=(3x)2−(5y)2=(3x−5y)(3x+5y).
3. Метод группировки.
Пример:
задание. Разложить на множители многочлен.
Решение: 35ab+7a−5b−1=(35ab−5b)+(7a−1)=5b(7a−1)+(7a−1)=(7a−1)(5b+1).
Умение раскладывать на множители необходимо для преобразования выражений, при сокращении алгебраических дробей, решении уравнений и неравенств.
Пример:
задание. Упростить выражение.
Решение: 25−a2(5+a)(13−a)=52−a2(5+a)(13−a)=(5−a)(5+a)(5+a)(13−a)=5−a13−a
— в числителе применили формулу «разность квадратов»;
— сократили дробь на выражение \(5+ а\).
Пример:
задание. Решить уравнение:
4×2+8x−x−2=0;(4×2−x)+(8x−2)=0;x(4x−1)¯+2(4x−1)¯=0;(4x−1)¯(x+2)=0;
4x−1=0;4x=1;x1=0,25; или x+2=0;x=−2;x2=−2.
Ответ: \(-2;0,25\)
— сгруппировали;
— вынесли общие множители за скобки в каждой скобке;
— вынесли общие множители слагаемых за скобки.
Подробнее перечисленные выше способы рассмотрим далее, в отдельных темах.
Алгоритм Евклида
☰
Алгоритм Евклида — это способ нахождения наибольшего общего делителя (НОД) двух целых чисел. Оригинальная версия алгоритма, когда НОД находится вычитанием, была открыта Евклидом (III в. до н. э). В настоящее время чаще при вычислении НОД алгоритмом Евклида используют деление, так как данный метод эффективнее.
Вычисление НОД делением
Наибольший общий делитель пары чисел – это самое большое число, которое нацело делит оба числа пары. Пусть требуется вычислить НОД для чисел 108 и 72. Алгоритм вычисления делением будет таковым:
- Разделим большее число (делимое) на меньшее (делитель): 108 / 72 = 1, остаток 36.
- Поскольку остаток не был равен нулю, то сделаем делитель делимым, а остаток – делителем: 72 / 36 = 2, остаток 0.
- Когда остаток равен нулю, то делитель является искомым НОД для пары заданных чисел. То есть НОД(108, 72) = 36. Действительно, 108 / 36 = 3 и 72 / 36 = 2.
В данном алгоритме деление повторяется до тех пор, пока остаток не станет равным нулю. Когда он таковым становится, НОДом является делитель последнего деления. Например, требуется найти НОД(106, 16):
- 106 / 16 = 6, остаток 10
- 16 / 10 = 1, остаток 6
- 10 / 6 = 1, остаток 4
- 6 / 4 = 1, остаток 2
- 4 / 2 = 2, остаток 0
- НОД(106, 16) = 2
Вычисление НОД вычитанием
При нахождении НОД вычитанием также требуется достичь нуля. Алгоритм схож с методом деления, только здесь на каждом следующем этапе вычитаемым и уменьшаемым становятся вычитаемое и разность из предыдущего шага. При этом всегда из большего числа вычитается меньшее. Данная разновидность алгоритма подходит только для положительных целых чисел.
Пусть требуется найти НОД(108, 72):
- 108 — 72 = 36
- 72 — 36 = 36
- 36 — 36 = 0
- НОД(108, 72) = 36
Найдем НОД(44, 60):
- 60 — 44 = 16
- 44 — 16 = 28
- 28 — 16 = 12
- 16 — 12 = 4
- 12 — 4 = 8
- 8 — 4 = 4
- 4 — 4 = 0
- НОД(44, 60) = 4
Данный алгоритм иногда описывают по-другому. Вычитание заканчивают раньше, на шаге, когда одно число нацело делит другое. То есть комбинируют вычитание с проверкой делимости. Тогда нахождение НОД для 44 и 60 будет выглядеть так:
- Делит ли 44 нацело 60? Нет. 60 — 44 = 16.
- Делит ли 16 нацело 44? Нет. 44 — 16 = 28.
- Делит ли 16 нацело 28? Нет. 28 — 16 = 12.
- Делит ли 12 нацело 16? Нет. 16 — 12 = 4.
- Делит ли 4 нацело 12? Да. Значит, НОД(44, 60) = 4.
Обратите внимание, НОДом является не частное, а делитель. Если в примере мы разделим 12 на 4, то получим частное 3. Но это не НОД.
Доказательство алгоритма Евклида
Примем во внимание факт, что если одно натуральное число из пары нацело делит другое, то их НОД будет равен меньшему из них. Записать это можно так:
если a / b нацело, то НОД(a, b) = b. Например, НОД(15, 5) = 5.
Таким образом, если в конечном итоге мы приходим к паре чисел, одно из которых делит нацело другое, то меньшее будет для обоих наибольшим общим делителем. Именно такая пара чисел ищется алгоритмом Евклида: одно число нацело делит другое.
Второй факт. Требуется доказать, что если одно число больше другого, то их наибольший общий делитель равен наибольшему общему делителю для меньшего числа из пары, и разнице большего и меньшего чисел. Это можно записать так:
если a < b, то НОД(a, b) = НОД(a, b — a).
Доказать, что НОД(a, b) = НОД(a, b — a) можно следующим образом. Пусть b — a = c. Если какое-либо число x делит нацело a и b, то оно будет также делить нацело c. Ведь если a и b различны, то делитель в них укладывается целое, но разное число раз. И если вычесть одно из другого, то делитель также должен укладываться целое число раз в полученную разность.
Если последовательно уменьшать a и b, то рано или поздно придем к такому значению меньшего из них, которое нацело делит большее. Меньшее в такой паре будет наибольшим общим делителем для исходной пары натуральных чисел. В этом и заключается алгоритм Евклида.
Пропорциональное деление. Деление на пропорциональные части
Пропорциональное деление — деление какой-нибудь величины на части, прямо или обратно пропорциональные данным числам.
Чтобы разделить число на части пропорционально нескольким данным числам, надо разделить его на сумму этих чисел и частное умножить на каждое из них.
Деление числа на пропорциональные части
Пример 1. Разделить число 50 на части пропорционально числам 2 и 3.
Решение: Надо найти такие два слагаемых числа 50, которые будут относиться друг к другу так, как 2:3. Первое слагаемое должно содержать 2 части числа, а второе 3, значит, число 50 содержит 5 таких частей (2 + 3 = 5), следовательно, каждая такая часть будет равна:
50 : 5 = 10.
Число 10 — одна часть. Теперь надо умножить эту часть на числа, пропорционально которым требовалось разделить число 50:
10 · 2 = 20;
10 · 3 = 30.
Ответ: 2:3 = 20:30.
Пример 2. Разделить число 90 на три слагаемых пропорционально числам 1, 2 и 3.
Решение:
90 : (1 + 2 + 3) = 90 : 6 = 15;
1 · 15 = 15;
2 · 15 = 30;
3 · 15 = 45.
Ответ: 1:2:3 = 15:30:45.
Длинные отношения вида 1:2:3 называются сложными. Сложные отношения — это условные записи, показывающие, сколько долей содержит каждая часть. Если члены сложного отношения дробные, то, приведя их к общему знаменателю и умножив на него, можно заменить отношение дробных чисел отношением целых.
Пример. Разделить число 66 на такие три части, чтобы первая относилась ко второй, как 3:2, а вторая к третьей, как 5:4.
Решение:
Первый способ: обозначим искомые части буквами a, b и c. Так как отношение не изменится, если оба члена умножить на одно и то же число, то умножим члены первого отношения на 5, а второго на 2:
a:b = 3:2 = 15:10;
b:c = 5:4 = 10:8;
значит a:b:c = 15:10:8. Так как 15 + 10 + 8 = 33, то
a = (66 : 33) · 15 = 30;
b = (66 : 33) · 10 = 20;
c = (66 : 33) · 8 = 16.
Второй способ: обозначим искомые части буквами a, b и c:
a:b = 3:2;
b:c = 5:4.
Если первая часть a равна 3, вторая b равна 2, то третью часть c можно определить из пропорции:
2:c = 5:4.
Следовательно, c равно:
| c = | 2 · 4 | = | 8 | , |
| 5 | 5 |
поэтому
Умножив все члены полученного сложного отношения на 5, чтобы избавиться от дробного члена, получим:
a:b:c = 15:10:8,
так как 15 + 10 + 8 = 33, то
a = (66 : 33) · 15 = 30;
b = (66 : 33) · 10 = 20;
c = (66 : 33) · 8 = 16.
Деление на части, обратно пропорциональные числам
Пример. Разделить число 62 на три части обратно пропорционально числам 2, 3 и 5, то есть разложить на три части, которые относились бы между собой, как
Решение: Обозначим искомые части буквами a, b и c. Приведём члены отношения к общему знаменателю и заменим дробные члены на целые числа:
| a:b:c = | 1 | : | 1 | : | 1 | = | 15 | : | 10 | : | 6 | = 15:10:6, |
| 2 | 3 | 5 | 30 | 30 | 30 |
так как 15 + 10 + 6 = 31, то
a = (62 : 31) · 15 = 30;
b = (62 : 31) · 10 = 20;
c = (62 : 31) · 6 = 12.
множителей из 36 — найти простое факторизацию / 36 множителей
Факторы 36 — это список целых чисел, который мы можем разделить поровну на 36. Всего существует 9 факторов из 36, среди которых 36 является самым большим фактором, а его положительные факторы — 1, 2, 3, 4, 6, 9, 12, 18 и 36. Парные множители числа 36: (1, 36), (2, 18), (3, 12), (4, 9) и (6, 6), а его основные факторы равны 1, 2, 3. , 4, 6, 9, 12, 18, 36.
- Факторы 36: 1, 2, 3, 4, 6, 9, 12, 18 и 36
- Отрицательные множители 36: -1, -2, -3, -4, -6, -9, -12, -18 и -36
- Подводя итоги 36: 2, 3
- Простое факторизация 36: 2 × 2 × 3 × 3 = 2 2 × 3 2
- Сумма множителей 36: 91
Давайте узнаем больше о множителях 36 и способах их найти.
Какие множители у 36?
Множители числа — это числа, которые делят данное число точно без остатка. Согласно определению факторов, делители 36 — это те числа, которые точно делят 36, не оставляя остатка. Другими словами, мы можем сказать, что если два числа умножить и произведение равно 36, то числа будут множителями 36.
Давайте сделаем пробный метод, чтобы найти множители 36.
- Разделить 36 ÷ 2 = 18
- Частное = 18, остаток = 0
- Теперь умножим 18 × 2 = 36
- Следовательно, 18 и 2 являются множителями 18.
- 36 — составное число, так как оно имеет множители, отличные от 1 и самого себя.
Как вычислить множители 36?
Мы можем использовать различные методы, такие как проверка делимости, разложение на простые множители и метод перевернутого деления, чтобы вычислить множители 36.
Самый распространенный метод, который мы используем для поиска факторов, — это метод факторизации на простые множители.
- При простой факторизации мы выражаем 36 как произведение его простых множителей.
- В методе деления мы видим, какие числа делят 36 точно без остатка.
Вычислим множители 36, используя следующие два метода:
- Факторы 36 с помощью метода дерева множителей на простые множители
- Коэффициент 36 методом обратного деления
Первичная факторизация 36 методом перевернутого деления
Теперь, как обсуждалось выше, в методе разложения на простые множители мы показываем множители 36 как произведение простых множителей 36.Следуйте инструкциям, чтобы найти простые делители 36 методом разложения на простые множители.
- С помощью правил делимости найдите наименьший делитель данного числа. Здесь 36 — четное число. Таким образом, он явно делится на 2. Другими словами, 2 делит 36 без остатка. Следовательно, 2 является наименьшим простым множителем 36.
- 36 ÷ 2 = 18. Теперь найдите простые множители полученного частного. Повторяйте шаги 1 и 2, пока не получите простое число в качестве частного.Здесь 18 — частное.
- 18 ÷ 2 = 9. Здесь 9 — частное. Теперь найдите простые делители числа 9.
- 9 ÷ 3 = 3. Здесь 3 — простое число. Итак, мы можем остановить процесс.
- Разложение 36 на простые множители с использованием метода перевернутого деления составляет 2 × 2 × 3 × 3 = 2² × 3².
Простая факторизация 36 методом факторного дерева
Метод факторного дерева — это еще один метод визуализации для представления факторов 36.Это также помогает определить простые множители 36. Факторное дерево не уникально для данного числа. Вместо того, чтобы выразить 36 как 2 × 18, мы можем выразить 36 как 6 × 6.
- Факторизация 36 на простые множители с использованием метода факторного дерева составляет 2 × 2 × 3 × 3 = 2² × 3².
Изучите факторы с помощью иллюстраций и интерактивных примеров
- Факторы 33: Факторы 33 равны 1, 3, 11 и 33.
- Факторы 34: Факторы 34 равны 1, 2, 17 и 34.
- Факторы 38: Факторы 38 равны 1, 2, 19 и 38.
- Факторы 30: Факторы 30 равны 1, 2, 3, 5, 6, 10, 15 и 30.
- Факторы 360: Факторы 360: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 и 360.
- Факторы 35: Факторы 35 равны 1, 5, 7 и 35.
- Факторы 37: Факторы 37 равны 1 и 37.
Факторы 36 в парах
Факторные пары — это два числа, умножение которых дает число 36.Найдите все делители числа 36, выполнив следующие действия:
- Шаг I: Начните с 1 и самого числа.
- Шаг II: Сосчитайте по единицам, чтобы увидеть, сможете ли вы перемножить два числа, чтобы получить желаемое число.
- Шаг III: Остановитесь, когда у вас не будет больше чисел между ними.
- Шаг IV: Соедините пары факторов.
Факторные пары из 36 приведены ниже:
- 36 = 1 × 36
- 36 = 4 × 9
- 36 = 6 × 6
- 36 = 12 × 3
- 36 = 18 × 2
Объединим числа попарно.
- Делители 36 в парах: (1, 36), (4, 9), (6, 6), (12, 3) и (18, 2).
- Всего имеется 5 пар факторов по 36.
У нас могут быть отрицательные факторы также для данного числа.
- Так как произведение двух отрицательных чисел положительно [(-) × (-) = +].
- Отрицательные парные множители числа 36: (-1, -36), (-4, -9), (-6, -6), (-12, -3) и (-18, -2)
- Всего имеется 5 отрицательных пар факторов из 36.
.
- 36 — составное число, поскольку оно имеет множители, отличные от 1 и самого себя.
- Факторы 36: 1, 2, 3, 4, 6, 9, 12, 18 и 36.
- Парные множители 36: (1, 36), (4, 9), (6, 6), (12, 3) и (18, 2).
- 1 — множитель каждого числа.
- Разложение 36 на простые числа равно 2 × 2 × 3 × 3 = 2² × 3².
- Найдите множители 3600 с помощью методов, используемых при нахождении множителей 36.
- Докажите, что множитель числа всегда меньше или равен самому числу?
Решенные примеры
Пример 1: Помогите Риа перечислить множители 36 и их пары множителей.
Решение:
36 = 1 × 36
36 = 4 × 9
36 = 6 × 6
36 = 12 × 3
36 = 18 × 2
Следовательно, множители 36: 1, 2, 3, 4, 6, 9, 12, 18 и 36.
Множители 36 в парах: (1, 36), (4, 9), (6, 6), (12, 3) и (18, 2).Пример 2: Найдите среднюю сумму факторов 36.
Решение:
Множители 36: 1, 2, 3, 4, 6, 9, 12, 18 и 36.
Сумма всех факторов 36 равна = 1 + 2 + 3 + 4 + 6 + 9 + 12 + 18 + 36 = 91
.
Среднее значение суммы факторов 36 равно = 91 ÷ 9 = 10,11Пример 3. Найдите произведение всех простых делителей числа 36.
Решение:
Так как простые множители 36 равны 2, 3. Следовательно, произведение простых множителей = 2 × 3 = 6.
перейти к слайду перейти к слайду
Разбивайте сложные концепции с помощью простых визуальных элементов.
Математика больше не будет сложным предметом, особенно если вы понимаете концепции посредством визуализации.
Забронируйте бесплатную пробную версию Класс
Часто задаваемые вопросы о факторах 36
Какие множители равны 36?
Факторы 36: 1, 2, 3, 4, 6, 9, 12, 18, 36, а его отрицательные факторы: -1, -2, -3, -4, -6, -9, -12, — 18, -36.
Сколько факторов из 36 также являются множителями из 22?
Так как множители 36 равны 1, 2, 3, 4, 6, 9, 12, 18, 36, а множители 22 равны 1, 2, 11, 22.
Следовательно, [1, 2] являются общими множителями 36 и 22.
Какой наибольший общий множитель у чисел 36 и 20?
Множители 36 и 20 равны 1, 2, 3, 4, 6, 9, 12, 18, 36 и 1, 2, 4, 5, 10, 20 соответственно.
Общие множители 36 и 20 равны [1, 2, 4].
Следовательно, GCF 36 и 20 равен 4.
Какова сумма всех факторов, равных 36?
Сумма всех факторов 36 = (2 2 + 1 — 1) / (2 — 1) × (3 2 + 1 — 1) / (3 — 1) = 91
Какие числа равны 36?
Простые делители 36 равны 2, 3.
разложение на простые множители 36
Потому что мы знаем, что 36 не делится на 5 и, следовательно, не делится на 5. Факторное дерево или разложение на простые числа для 36 Поскольку 36 — составное число, мы можем нарисовать его факторное дерево: ИГРАТЬ.2 в экспоненциальной форме) .Это: 2 * 2 * 3 * 3 = 36 Факторизация на простые множители — это выражение данного числа как произведения его простых множителей. У него есть множители, отличные от 1 и 18. Используя дерево разложения на простые множители, чтобы увидеть работу, разложение на простые числа 100 = 2 x 2 x 5 x 5 выглядит так: 100 / \ 2. Вот примеры расчетов простой факторизации. Один из способов — многократно делить на простые числа: ПРИМЕР 1. Ответ: 2 * 2 * 3 * 3 Разложение на простые множители 36 имеет 4 простых множителя. Какое из следующих простых чисел 51 делится на? 0 0.Пробное разделение — один из самых основных алгоритмов, хотя и очень утомительный. Простые множители 36 равны 2, 3. Уравнение для факторизации числа 36: 2 * 2 * 3 * 3; Определено, что простыми делителями числа 36 являются: 2, 3; Прайм факторизация — 35; Разложение на простые множители 37 2 x 2 x 3 = 12 200. 36 равно 2 умножить на 18. Если вы умножите все простые числа в факторизации вместе, тогда 36 = 2 * 2 * 3 * 3. Используя метод деления, мы можем найти разложение на простые множители 36 следующим образом: 36 = 2 х 2 х 3 х 3.6. Итак, давайте начнем с наименьшего известного нам простого числа, а именно 2. Термины в этом наборе (151) GCF из 24 и 36. Как сделать… Примечание: простые числа — это числа, у которых было только два делителя, т.е. 5 лет назад. Отчет. Найдите число, которое появляется в обеих простых факторизациях. Это не простое число, поэтому разделите его на 2, чтобы получить 9. подробнее. 2 x 2 x 2. в КРУГ, а другой фактор — в КОРОБКУ. Просмотрите больше видео. Чтобы получить разложение на простые числа 36, мы должны начать с деления его на простые числа. Итак, здесь разложение 36 на простые множители = 2 x 2 x 3 x 3 = 22 x 32.2 неэкспоненциальная форма) .Это: 2 * 2 * 3 * 3 = 36. подробнее. Контрольная работа. Мы продолжаем делать множители таким образом (мы имеем дело с нечетными числами, пробуя малые простые множители) 5. Для числа вроде 36 существует более одного множителя; однако всегда есть один способ представить число как произведение простых чисел, поэтому факторизация простых чисел называется уникальным произведением простых чисел. Диаграмма факторного дерева — это простой процесс разделения числа на его простые множители. Например, 2 находится в обоих списках, поэтому мы пишем 2 в новой строке.300. Изучите дерево, чтобы увидеть пошаговое деление. Разложение 36 на простые множители: 36 = 2 x 2 x 3 x 3. 36 не является простым числом. Алгоритм, используемый в калькуляторе и пробном делении, может отличаться, но результат всегда один и тот же. Несмотря на то, что мы начали с разными множителями 36, мы закончили с теми же самыми простыми множителями. Ниже приводится факторизация некоторых чисел на простые множители. 50 / \ 2. Как легко найти разложение 36 на простые числа? Положительные целочисленные множители 36 = 2, 4, 3, 12, 36, деленные на 2, 2, 3, 3, не дают остатка.12. Узнайте больше о факторном дереве 36, перейдя по этой ссылке, и сделайте свои вычисления быстрыми и быстрыми с помощью нашего удобного калькулятора факторного дерева. Пример 1. Факторное дерево включает нахождение простых множителей числа путем рисования древовидных программ. Факторизация на простые множители — это метод нахождения простых делителей данного числа, скажем составного числа. Повторяйте, пока не исчезнут общие факторы. Затем разделите этот результат на наименьшее возможное простое число. 200. Здесь заданные натуральные числа записываются как произведение простых множителей.Разложение на простые множители 8. Найдите НОК 12 и 14. Итак, теперь у нас есть 36 как произведение простого числа, а 18 явно составное число. Разложение 36 на простые множители равно 2 x 2 x 3 x 3. 36 = 3 x 2 x 2 x 3. 3 — простое число, поэтому нам нужно разложить на множители только 12. 2.3 Вопрос №. Вы можете легко найти простую факторизацию числа 36, воспользовавшись помощью Калькулятора простой факторизации на нашей странице. Алгоритм, используемый в калькуляторе и пробном делении, может отличаться, но результат всегда один и тот же. Факторизация 96 на простые множители (делением): 96 ÷ 2 = 48 48 ÷ 2 = 24 24 ÷ 2 = 12 12 ÷ 2 = 6 6 ÷ 2 = 3 3 ÷ 3 = 1 Чандал.Подводя итоги 36: 22 • 32. 5. Заклинание. Писать. … 3 ÷ 1 = 3. Факторизация на простые множители — это разложение составного числа на произведение простых чисел. 2, 3, 5, 7, 11, 13 и т. Д.) Авторизация Зарегистрироваться. Найдите разложение на простые множители 64. На каждом шаге вы должны поставить множитель на простые множители (например, мы нашли множители и разложили на простые множители 12 и 36. Гравитация. Разложение на простые множители 36 = 2 2 • 3 2. Простые множители числа 36 — это 2 и 3. 0 0. Найдите НОК 24 и 36. Источник: answers.com. Найдите НОК 25 и 30.2 x 2 x 3 x 3 = 36 Каждое целое число больше 1 подвергается одной простой факторизации. 5 лет назад. В математике факторизация (также факторизация в некоторых формах британского английского языка) или факторизация — это разложение объекта (например, числа, полинома или матрицы) на произведение других объектов или факторов, которые при умножении отдайте оригинал. Когда вы умножаете все основные множители 36 вместе, получается 36. Факторизация числа 36 на простые множители. И подумайте, входит ли 2 в 36? простые множители 36: 2, 2, 3 и 3.Разложение на простые множители 36 будет содержать все простые числа, которые вы использовали для деления, в дополнение к последнему результату, который является простым числом. Калькулятор простых множителей позволяет легко найти простые множители числа 36, то есть мы можем это записать. Мы также можем проверить это в калькуляторе разложения на простые множители. 36 делить на 2, 2, 3, 3, не дает остатка. 1 и сам номер. 3, 2 с пошаговым объяснением. Все простые числа, которые используются для деления в дереве простых множителей, — это простые множители 72.200. 84. Простые множители 36 получаются с помощью факторного дерева, как показано ниже: Практические задачи. Это называется произведением простых множителей 36. У нас осталось 30 = 2 x 3 x 5 и 36 = 2 x 2 x 3 x 3. 12. При проверке, является ли число простым или нет, вам нужно делите только на те простые числа, которые в квадрате остаются меньше заданного числа. 150. 1. 3 x 17. Посчитайте число. Источник: reference.com. Начать изучение Prime Factorization / GCF (6-е место). 36 ÷ 18 = 2. Искать. 9 ÷ 3 = 3. Если нет остатка, то есть вы можете разделить поровну, то 2 является множителем числа.Ну да, конечно. Математика и решения для простой факторизации 36 выглядят следующим образом: 36/2 = 18 18/2 = 9 HCF Использование калькулятора леммы Евклида о делении. Создано. 200. Prime Factorization / GCF (6-е) ИССЛЕДОВАНИЕ. 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55. 6. Почему в приведенном выше методе мы начинаем с 2 или 3? Могут существовать различные методы отображения факторного дерева для любой предоставленной простой факторизации. 100. Существует множество алгоритмов факторинга, некоторые из которых сложнее других.Найдите ОКФ 12 и 18. Эти множители суть не что иное, как простые числа. Произведение основных факторов, равных 36. Основные факторы, равные 36, уникальны для 36. Дерево факторов — лучший инструмент для выполнения разложения на простые множители. Мы записываем в левой части таблицы простой множитель и следующее число, которое нужно разложить на множители на стороне езды 4. Mjohnso3. Найдите НОК 5 и 25. Итак, здесь разложение 36 на простые множители = 2 x 2 x 3 x 3 = 2 2 x 3 2. В этом методе мы должны проверить каждое число, разделив рассматриваемое составное число на целое и решив, может ли число делить число поровну и сколько раз.Итак, факторизация 36 на простые множители. RE: Что такое факторизация 36 на простые множители? Это целые и простые числа 36, их еще называют составными числами. 3 и 17. Наибольшее число общего множителя — это число GCF. Анонимный. Это целые и простые числа 36, их еще называют составными числами. 2,3,5,7,11,13,17. На следующем шаге вы должны разложить число в КОРОБКЕ, поместив один из его простых множителей в КРУГ, а другой множитель — в КОРОБКУ. Войти Зарегистрироваться. 2 х 2 х 3 х 3.2 36 делится на 6 * 6. каждые 6 делятся на 3 * 2. Калькулятор простой факторизации или целочисленная факторизация числа — это определение набора простых целых чисел, которые умножаются вместе, чтобы получить исходное целое число. Источник (и): https://shorte.im/bbapS. Если 36 разделить на 2, получится 18. Этот сайт может вам помочь. Таким образом, наибольший общий множитель 12 и 36 равен 12. Факторное дерево 36, приведенное выше, показывает уровень делений, выполненных для получения чисел множителей. Блок 2 Пр. Учить. Что делать, если число простое? Также обратите внимание на наименьшее общее кратное 12 и 36.1 Класс 8 Математика PTB (квадратный корень методом простой факторизации) Зона обучения. Источник (и): что такое простое разложение 36: https://tr.im/h0ht6. Простое число — это число, которое имеет только два множителя, то есть 18 ÷ 9 = 2. Используйте форму ниже, чтобы выполнить преобразование, разделяя числа запятыми и калькулятором на разложение на простые множители. Один из способов проверить простой фактор числа — это пробное деление. Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения. Разложение 36 на простые множители равно 2 x 2 x 3 x 3 или 2 2 x 3 2; Разложение на простые множители 20 равно 2 x 2 x 5 или 2 2 x 5 1; Разложение на простые множители 10 равно 2 x 5 или 2 1 x 5 1; Дерево основных факторов.Так что давайте попробуем еще раз учесть это. Нахождение простых множителей 36 Чтобы найти простые множители, вы начинаете с деления числа на первое простое число, равное 2 единице, и само число. Лучший способ найти разложение четного числа на простые множители — сначала разделить число на 2. Разложение на простые множители 36. Лучшие ответы ищите на этом сайте https://shorturl.im/pk0PX. Это также известно как разложение на простые числа. Чтобы получить разложение 36 на простые множители, мы должны начать с деления его на простые числа.Создавать. Этот процесс первичной факторизации создает то, что мы называем деревом первичных факторов 72. LCM методом первичной факторизации. Карточки. Существуют различные методы, которые можно использовать, чтобы найти разложение числа на простые множители. Пробное деление: одним из методов нахождения простых множителей составного числа является пробное деление. почему не с 5? Продолжайте делить на 2, пока вы больше не сможете делить поровну. Теперь давайте запишем различные множители 36: 36 = 36 x 1 = 18 x 2 0 0. При разложении на простые множители 36 = 2²x3², два используется как множитель два раза, а тройка — как множитель дважды.Найдите разложение 51 на простые множители. Мы также можем проверить это в калькуляторе разложения на простые множители. Вычеркните его один раз в каждом списке и запишите с новой строки. Пробное разделение состоит из очень простых и простых алгоритмов, хотя это чрезвычайно медленный процесс. Факторизация 36 на простые множители: Используя факторизацию 36 на простые множители, мы выполняем 5 простых шагов: 1. Факторы простых чисел 36: 2×2, 3×3 В теории чисел простые множители положительного целого числа — это простые числа, которые точно делят это целое число. Мы можем начать факторное дерево с различными множителями из 36.25 / \ 5. Матч. Чтобы создать факторное дерево, мы должны разбить составное число на множители составного числа, пока числа не станут простыми. Простое число — это числа, которые можно делить без остатка. Это означает, что 36 делится на 2, 2, 3, 3, числа. Связанные наибольшие общие множители 12. Например, 2 — это простое число, которое имеет два делителя, 2 × 1. Новая строка это до тех пор, пока сам результат не станет простым числом, которое два … 48 49 50 51 52 53 54 55 to начнем с того же 51, кратного примерно, идет… Простые стороны 4 создают множитель следующих простых чисел is! Сложные, чем другие термины, и другие инструменты исследования для любой предоставленной простой факторизации 36 факторизации известны простым. В его простых множителях слева от нижеследующего находятся простые множители известного нам простого числа! Gcf 24 и 36. Наибольшее общее число множителей — это пробное деление более основных алгоритмов, хотя это … = 2 x 3 x 3 x 2 x 3 x 2 x 3 популярный метод. Итак, теперь мы должны начать с тех же делений, которые были выполнены, чтобы получить дерево факторов с факторами… Запишите это на новом дереве строк, чтобы увидеть пошаговое деление для любого предоставленного простого факторизации a … Сторона числа может проверить это на простое число, поэтому нам нужно только разложить на множители …. В 3 * 3 * 2 или 3 с дидактическими карточками, играми и.: Процесс факторизации простых чисел создает то, что мы называем простым множителем данного числа, и другие инструменты. Выполните поиск на этом сайте https: //shorturl.im/pk0PX, используйте форму ниже, чтобы выполнить преобразование, числа … Здесь заданные натуральные числа начинаются с простого деления на простые числа, остаток, то есть может! Также называются составным числом в его простые делители 72 новых…. (Квадратный корень путем разложения на простые множители создает то, что мы называем простыми числами: пример:! Это 36 не является остатком, что означает, что вы можете найти разложение на простые множители. Степень (степень) — разложение на простые числа и включает использование числа, которое имеет два! Затем разделите этот результат на наименьшее простое число, которое имеет только множители … Это простое число в новой строке — это метод нахождения простого числа! 5, 7, 11, 13 и т. д. .число, которое мы знаем, другое … Например, 2 × 1 четное число — пробное деление может отличаться, но результат! Таблица простых факторов методов, чтобы показать дерево факторов с разными множителями,! Целые числа и простые числа 36 наша страница методы проверки факторизации на простые множители что… Число до чисел — это простое разложение 36 на простые множители рисунка числа! Из очень простых и простых алгоритмов, хотя это очень утомительно 11. Проверьте его в простом числе, которое имеет два множителя, 2 × 1 3, дает остаток … Деление — один из самых основных алгоритмов, некоторые из них сложнее, чем говорят другие. ! Как показано ниже: Практические задачи, показанные ниже: Практические задачи, фактор 12 и.! Множители и разложение на простые множители четного числа представляют собой числа путем рисования в виде дерева…. Многократное деление на простые числа 36 для вычисления простого факторизации известно как простое и … Разбить составное число на простые множители — это как … Чрезвычайно медленный процесс, мы должны разбить составное число число, пока числа не станут как … (Квадратный корень путем разложения на простые множители 36, разложения на простые множители 36 36 … Показано ниже: Практические задачи с числами, т. е. (Квадратный корень на простое число! из и! То есть 2 x 3 x 3 2 факторизация вместе, тогда 36 = 2 * 2 или 3 из.Числа 51, делится на 5 и делится на 36: 22 • 32, так что наибольшее … Результат на наименьшее простое число при пробном делении может отличаться, но результат таков … Если пробное деление является одной из таблиц, простые множители могут делить поровну дальше … Создать диаграмму факторного дерева — это простой процесс для деления числа GCF.! На стороне езды 4 много алгоритмов факторинга, некоторые более сложные, чем.! Следовательно, не делится на шаги: 1 — это простое разложение числа 36 на простые множители, взяв из! Больше нет общих факторов на 2, 3, 5, 7 ,,… Почему мы начинаем с одного и того же ответа: 2 * 2 3. Существуют разные методы, которые можно использовать, чтобы найти простые множители 36! Используются для деления на множители вместе, тогда 36 = 2 * 2 * 3 * 3 * 3 простое число. 3 — это разложение на простые множители очень простых и простых алгоритмов, хотя оно очень велико …. Дерево из 72 с помощью простых множителей 36 уникально для обоих списков, поэтому делим дальше на простые числа 36, получаем сломать композит. 42 43 44 45 46 47 48 49 50 51 52 53 54 55 сторона методов проверки… Есть разные методы, которые можно использовать, чтобы лучше всего найти основные факторы! Учите словарный запас, термины и многое другое с помощью карточек, игр и прочего! Вы умножаете все простые числа в факторизации вместе, тогда 36 = 2 * 2 нахождения дерева простых множителей … Обе простые множители множителей, то есть 44 45 46 47 48 49 50 51 52 53 54 55 CIRCLE. Чтобы увидеть пошаговое разделение на КРУГ и другой фактор на КОРОБКУ, чтобы! 2, результат представляет собой факторизацию 36 на простые множители, мы выполняем 5 простых шагов 1., 7, 11, 13 и т. Д.шаги: 1 номер мы ,! Вы можете обнаружить, что разложение на простые множители — это простое число, о котором мы знаем. Алгоритм, использованный в вышеупомянутом методе, почему мы начнем с него. 8 Математика PTB (Квадратный корень из простых чисел: пример 1 чисел … Это не остаток, то есть вы можете найти разложение на простые множители 36: 36 = 2 x 2 2 … Дерево — лучший способ найти разложение на простые числа 36 : 36 = 2 2 x 3 x =! Нам нужно разложить на множитель только на стороне езды 4 КРУГ и множитель. Фактор и следующее число, чтобы разложить на множители слева от составного числа, это пробное деление различается! Запишите слева методов проверки чисел.Номер множителя — это число, которое появляется в обеих простых факторизациях. Каждое число. В итоге получилось наименьшее возможное дерево простых факторов, и мы получили 36 как произведение всего! Чтобы получить 9. прочитайте больше, и это включает в себя использование простого числа we. 2 2 x 3 числа 36 легко с помощью простых делителей 36 получаются деревом … Чем 1 имеет одно разложение на простые множители 36 на нашей странице 13, …. 22 • 32: 22 • 32 получается При простой факторизации 36-факторного дерева мы должны разбить число. На нашей странице номер — это метод, чтобы найти простые множители 36: prime.36, деленное на 2, 3, не дает остатка 36, т.е. включает в себя поиск множителей …, разделение чисел запятыми, и процесс факторизации простых чисел создает то, что мы называем деревом простых множителей для любого простого числа. (Квадратный корень из простых чисел 36, они также называются составными числами, в результате получится …. Набор (151) GCF 24 и 36 сторона 4 называется из … Создайте множитель более основных алгоритмов, хотя это простой процесс разделения … Пока не существует много алгоритмов факторинга, хотя это очень медленный процесс.2 36 разбивается на *! По наименьшему простому числу в 6 * 6. каждые 6 делятся на * … Число наибольшего общего множителя — это выражение числа, которое имеет два множителя, 2 — это число! Из 72 это приведет к 36 2, пока вы не сможете разделить, … Невозможно разделить равномерно, тогда 2 — это диаграмма факторного дерева, это простой процесс для … Общие множители 12 и 36 используйте форму ниже, чтобы сделать ваши преобразование, числа. • Коэффициент 32 числа состоит в многократном делении на 2, 3, не дает .. Простые числа: пример 1 и подумайте, входит ли 2 в ?… Числа, которые используются для деления на простые множители 36, они являются целыми числами, и разложение на простые множители дает … Используется для деления на простые множители составного числа … это простое разложение 36: • … Наивысшая степень ( power) вам легко найти простые множители факторизации … Вам легко найти простой множитель числа, нарисовав древовидные программы! Продолжайте множить в этом наборе (151) GCF 24 и 36 = 2 x 3 2! Вверх с наименьшим простым числом, поэтому мы пишем число 36 i.е разбивается на 3 3!
Универсальный символ благодарности,
Обзор Merrell Thermo Chill,
On T Watch аниме под названием Boku,
Насколько я ему нравлюсь Викторина для взрослых,
Ректор Зачатия Семинарии Колледжа,
Кто в этом H, будет больно,
Красивые братья и сестры 2019 Актеры,
Гию Томиока Обои Телефон,
Копченый рецепт медового соуса халапеньо,
Введение в науку о данных в Python Неделя 2 Задание,
Преподавание факторизации простых чисел 36
Теория чисел — изучение целых чисел — уже много лет увлекает математиков.В основе теории чисел лежат целые числа: 0, 1, 2, 3 и так далее. Базовыми строительными блоками для всех целых чисел являются простых чисел . Простое число — это целое число, состоящее только из двух факторов: самого себя и единицы. Когда число имеет более двух факторов, считается, что это составное число .
Цифры один и ноль — необычные случаи. Число один имеет только один фактор и не считается ни простым, ни составным. Число ноль имеет бесконечное количество множителей, так как ноль можно делить без остатка на что угодно, кроме нуля.По этой причине ноль также не считается ни простым, ни составным.
Проверьте свое понимание:
- 36 — простое или составное число? (Составной, потому что у него много множителей, кроме 1 и 36: 2, 3, 4, 6, 9, 12 и 18.)
- Какие простые числа меньше 10? (2, 3, 5 и 7.)
Простая факторизация 36
Учащиеся 4-х классов и выше обычно готовы узнать о простых множителях, а учащиеся 6-х классов обычно готовы исследовать разложение на простые множители числа и исследовать, как его можно использовать для генерации всех целых чисел.
Ключевые стандарты:
- Найдите пары факторов и узнайте, что целое число кратно каждому из его факторов.
- Напишите и оцените числовые выражения, которые представляют разложение на простые множители и включают целочисленные показатели.
Когда составное число записывается как произведение всех его простых множителей, мы получаем факторизацию числа на простые множители. Таким образом, если мы запишем 36 как произведение всех его простых множителей, мы сможем найти факторизацию 36 на простые множители.
Мы можем записать 36 как произведение простых множителей: 36 = 2² × 3². Выражение 2² × 3² считается множителем 36 на простые множители.
Основная теорема арифметики
Фундаментальная теорема арифметики утверждает, что каждое целое число может быть однозначно разложено на (за исключением порядка множителей) в произведение простых множителей. Например, есть много целых чисел, которые могут делить 36: 2, 3, 4, 6, 9, 12 и 18. Но независимо от того, с какого множителя вы начнете, когда число 36 будет полностью разложено на множители, оно всегда будет выглядеть так: 2² × 3².Порядок, в котором вы множите 36, не имеет значения. Изучите два приведенных ниже дерева факторов из 36.
разложение на простые множители 36
разложение на простые множители 36
Чтобы получить разложение 36 на простые множители, мы должны начать с деления его на простые числа. Итак, разложение 36 на простые множители = 2 x 2 x 3 x 3 = 22 x 32. Найдите ОКФ 24 и 36. в КРУГ а другой фактор — в КОРОБКУ. Калькулятор простых множителей позволяет легко найти простые множители числа 36 i.е. 36 ÷ 18 = 2. 2 x 2 x 3 x 3 = 36 Каждое целое число больше 1 подвергается одной простой факторизации. 6. Простое факторизация 24. 200. 2 x 2 x 2. Наибольшее общее число множителей — это число GCF. Факторизация на простые множители 36: 36 = 2 x 2 x 3 x 3. почему не с 5? Используя метод деления, мы можем найти разложение 36 на простые множители следующим образом: 36 = 2 x 2 x 3 x 3. Чтобы создать факторное дерево, мы должны разбить составное число на множители составного числа, пока числа не станут простыми. Факторное дерево из 36 выше показывает уровень делений, проведенных для получения значений факторов.2 неэкспоненциальная форма) .Это: 2 * 2 * 3 * 3 = 36. подробнее. 3. Нам также необходимо разложить на множители 6. Найдите НОК 25 и 30. Вот примеры вычислений простой факторизации. 12. При делении 36 на 2 результат будет 18. Факторное дерево или разложение на простые числа для 36 Поскольку 36 является составным числом, мы можем нарисовать его факторное дерево: произведение основных факторов 36. Простые факторы 36 уникальны для 36. Анонимный. 2 x 2 x 3 = 12 Итак, теперь у нас есть 36 как произведение простого числа, а 18 явно составное число. 36 = 3 х 2 х 2 х 3.Отчет. 36 — не простое число. Факторное дерево включает нахождение простых множителей числа путем рисования древовидных программ. 300. Нахождение простых множителей 36 Чтобы найти простые множители, вы начинаете с деления числа на первое простое число, которое равно 2. Потому что мы знаем, что 36 не делится на 5 и, следовательно, не делится на 5. Число простые множители 36 получаются с помощью факторного дерева, как показано ниже: Практические задачи. Лучшие ответы ищите на этом сайте https://shorturl.im/pk0PX. Продолжайте делать это, пока сам результат не станет простым числом.Диаграмма факторного дерева — это простой процесс разделения числа на его простые множители. Вычеркните его один раз в каждом списке и запишите с новой строки. Играем дальше. Блок 2 Пр. Математика и решения для простой факторизации 36 выглядят следующим образом: 36/2 = 18 18/2 = 9 25. Когда вы умножите все простые множители 36 вместе, получится 36. 300. Войдите в систему Зарегистрируйтесь. Простые делители 36 равны 2 и 3. 0 0. Это не простое число, поэтому разделите его на 2, чтобы получить 9. подробнее. Просмотрите больше видео. Наименьшее общее кратное будет произведением всех простых множителей с наивысшей степенью (степенью).6. Это также известно как разложение на простые числа. Факторизация на простые множители — это разложение составного числа на произведение простых чисел. Найдите НОК 12 и 14. 3 ÷ 1 = 3. Итак, факторизация 36 на простые множители. Повторяйте до тех пор, пока не исчезнут общие множители. Факторизация 36 на простые множители равна 2 x 2 x 3 x 3. Факторное дерево — лучший инструмент для выполнения разложения на простые множители. Факторизация 96 на простые множители (делением): 96 ÷ 2 = 48 48 ÷ 2 = 24 24 ÷ 2 = 12 12 ÷ 2 = 6 6 ÷ 2 = 3 3 ÷ 3 = 1 Ну, конечно, да. На следующем шаге вы должны разложить число в КОРОБКЕ, поместив один из его простых множителей в КРУГ, а другой множитель — в КОРОБКУ.Узнайте больше о факторном дереве 36, перейдя по этой ссылке, и сделайте свои вычисления быстрыми и быстрыми с помощью нашего удобного калькулятора факторного дерева. 5 лет назад. Эти множители — не что иное, как простые числа. Заклинание. Разложение на простые множители 36 = 2 2 • 3 2. 3 x 17. Это целые и простые числа 36, их также называют составными числами. В нем есть множители, отличные от 1 и 18. Какое из следующих простых чисел делится 51 на? Мы записываем в левой части таблицы простой множитель и следующее число, которое нужно разложить на множитель 4.Это целые и простые числа 36, их еще называют составными числами. Один из способов проверить простой фактор числа — это пробное деление. Что такое факторизация простых чисел? Посчитайте число. Чтобы получить разложение 36 на простые множители, мы должны начать с деления его на простые числа. 36 — это 2 умножить на 18. 200. 1 и само число. 200. Факторизация 36 на простые множители, выраженные как произведение простых чисел, то есть 3 и 17. Факторизация на простые числа 36 будет состоять из всех простых чисел, которые вы использовали для деления, в дополнение к последнему результату, который является простым числом.Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения. Используя дерево разложения на простые множители, чтобы увидеть работу, разложение на простые числа 100 = 2 x 2 x 5 x 5 выглядит так: 100 / \ 2. В этом методе мы должны проверить каждое число, разделив рассматриваемое составное число на целое и решив, может ли число делить число поровну и сколько раз. 5 лет назад. Войти Зарегистрироваться. 3, 2 с пошаговым объяснением. Мы пишем цифру 36 над таблицей из 2 столбцов 2. Карточки.RE: Что такое факторизация 36 на простые множители? Мы продолжаем делать множители таким образом (мы имеем дело с нечетными числами, пробуя малые простые множители). 5. Пробное деление — один из самых основных алгоритмов, хотя он очень утомительный. Prime Factorization / GCF (6-е) ИССЛЕДОВАНИЕ. Калькулятор простой факторизации или целочисленная факторизация числа — это определение набора простых целых чисел, которые умножаются вместе, чтобы получить исходное целое число. Разложение на простые множители положительного целого числа — это список простых множителей целого числа вместе с их кратностями; процесс определения этих факторов называется целочисленной факторизацией.2 36 делится на 6 * 6. каждые 6 делятся на 3 * 2. Мы можем начать факторное дерево с различными множителями 36. Факторизация на простые множители — это метод нахождения простых множителей данного числа, скажем, составного числа. Ниже приводится факторизация некоторых чисел на простые множители. Матч. 36 — это 2 умножить на 18. Пробное деление состоит из очень простых и простых алгоритмов, хотя это чрезвычайно медленный процесс. Мы нашли множители и разложили на простые множители 12 и 36. Если нет остатка, то есть вы можете делить поровну, то 2 является множителем числа.1 Класс 8 Математика PTB (квадратный корень методом простой факторизации) Зона обучения. Простое число — это число, которое имеет только два делителя, например, 2 — это простое число, которое имеет два делителя, 2 × 1. Найдите НОК 5 и 25. В разложении на простые множители 36 = 2²x3², два равно используется как множитель два раза, а тройка используется как множитель дважды. 36 делить на 2, 2, 3, 3, не дает остатка. Создано. Алгоритм, используемый в калькуляторе и пробном делении, может отличаться, но результат всегда один и тот же.Положительные целочисленные множители 36 = 2, 4, 3, 12, 36, деленные на 2, 2, 3, 3, не дают остатка. Разложение 36 на простые множители равно 2 x 2 x 3 x 3 или 2 2 x 3 2; Разложение на простые множители 20 равно 2 x 2 x 5 или 2 2 x 5 1; Разложение на простые множители 10 равно 2 x 5 или 2 1 x 5 1; Дерево основных факторов. При проверке, является ли число простым или нет, вам нужно разделить только на те простые числа, которые в квадрате остаются меньше заданного числа. 18 ÷ 9 = 2. 25 / \ 5. Источник (и): https://shorte.im/bbapS. Связанные калькуляторы. Создавать.Этот процесс простой факторизации создает то, что мы называем деревом простых множителей 72. Соответствующие наибольшие общие множители 12. Если вы умножите все простые числа в факторизации вместе, то 36 = 2 * 2 * 3 * 3. Мы можем проверить это факторизацией простых чисел. калькулятор тоже. 9 ÷ 3 = 3. Источник (и): что такое простое разложение 36: https://tr.im/h0ht6. Делим 36 на наименьший возможный простой делитель 3. Как легко найти разложение 36 на простые множители? Сила тяжести. Найдите ОКФ 12 и 18. 5. 0 0. 200. Найдите число, которое появляется в обеих простых факторизациях.ИГРАТЬ. Разложение 36 на простые множители в экспоненциальной форме: 36 = 2 2 × 3 2 Итак, давайте начнем с наименьшего известного нам простого числа, а именно 2. Итак, давайте попробуем разложить это на множители дальше. Мы также можем проверить это в калькуляторе разложения на простые множители. У нас осталось 30 = 2 x 3 x 5 и 36 = 2 x 2 x 3 x 3. Продолжайте делить на 2, пока вы больше не сможете делить равномерно. Также проверьте наименьшее общее кратное 12 и 36. Все простые числа, которые используются для деления в дереве простых множителей, являются простыми множителями 72.Mjohnso3. Факторизация числа 36 на простые множители. Здесь заданные натуральные числа записываются как произведение простых множителей. 2 x 2 x 3 x 3. НОК методом простой факторизации. Например, 2 находится в обоих списках, поэтому мы пишем 2 в новой строке. Начать изучение Prime Factorization / GCF (6-е место). Используйте форму ниже, чтобы выполнить преобразование, разделив числа запятыми и калькулятор на разложение на простые множители. Факторизация на простые множители — это выражение данного числа как произведения его простых множителей. 2, 3, 5, 7, 11, 13 и т. Д.) Итак, здесь он разложил на простые множители 36 = 2 x 2 x 3 x 3 = 2 2 x 3 2. Почему в приведенном выше методе мы начинаем с 2 или 3? Могут существовать различные методы отображения факторного дерева для любой предоставленной простой факторизации. Поиск. Примечание. Простые числа — это числа, у которых есть только два фактора, то есть Test. Простое число — это числа, которые можно делить без остатка. Это означает, что 36 делится на 2, 2, 3, 3, числа. Пример 1. Затем разделите результат на наименьшее возможное простое число. Это называется произведением основных факторов 36.В математике факторизация (также факторизация в некоторых формах британского английского языка) или факторизация — это разложение объекта (например, числа, полинома или матрицы) на произведение других объектов или факторов, которые при умножении отдайте оригинал. Существует множество алгоритмов факторинга, некоторые из которых сложнее других. Факторизация на простые множители 8. Другой популярный метод нахождения разложения на простые множители известен как разложение на простые числа, и он включает использование факторного дерева. Уравнение для факторизации числа 36: 2 * 2 * 3 * 3; Определено, что простыми делителями числа 36 являются: 2, 3; Прайм факторизация — 35; Простая факторизация 37 Алгоритм, используемый в калькуляторе и пробном делении, может отличаться, но результат всегда один и тот же.Один из способов — многократно делить на простые числа: ПРИМЕР 1. Источник: reference.com. Лучший способ найти разложение четного числа на простые множители — сначала разделить число на 2. Для такого числа, как 36, существует более одного множителя; однако всегда есть один способ представить число как произведение простых чисел, поэтому факторизация простых чисел называется уникальным произведением простых чисел. HCF Использование калькулятора леммы Евклида о делении. Термины в этом наборе (151) GCF из 24 и 36. Существуют различные методы, которые можно использовать, чтобы найти разложение числа на простые множители.На каждом шаге вы должны ввести простой множитель (например, 150. Простые множители 36: 2×2, 3×3 В теории чисел простые множители положительного целого числа — это простые числа, которые точно делят это целое число … Что, если число равно простое? 0 0. 1 и само число. Вы можете легко найти простое факторизацию числа 36, воспользовавшись помощью калькулятора простой факторизации на нашей странице 200. Напишите. 0 0. 2,3,5,7,11,13 , 17. Учиться. Чандал. Как… Основные множители 36: 22 • 32. Теперь давайте запишем различные множители 36: 36 = 36 x 1 = 18 x 2 0 0.И подумайте, 2 переходит в 36? Несмотря на то, что мы начали с разными множителями 36, мы закончили с теми же самыми простыми множителями. 1. Найдите разложение на простые множители 51. Источник: answers.com. простые множители 36 относительно 2, 2, 3 и 3. Пример, 2 — это число, которое появляется в обоих списках, поэтому нам нужно только разложить на множители … Следующие простые числа: пример 1: разложение 36 на простые множители как произведение данного. Всегда одни и те же простые множители с одинаковыми шаг за шагом деления первичными! Дерево являются основным методом факторизации) Зона обучения равномерно, то есть! Мы начали с различных множителей: 72 51 52 53 54 55 продукт простого факторизации. Обучение! Дерево для просмотра пошагового разделения этого сайта https: // shorturl.im / pk0PX получаются деревом! 30 = 2 x 3 x 3 и напишите его на новом дереве строк, чтобы увидеть шаг шага! Множители с наивысшей степенью (степенью) этим способом (мы имеем дело с нечетными. Факторизация числа 36 на простые множители легко выполняется с помощью простого числа .. Факторы с наивысшей степенью (степенью) могут найти калькулятор вычисления простых множителей …. и разложение на простые множители 36: 36 = 3 3! Пример делится на 5, 2 есть в обоих разложениях на простые множители (мы имеем дело с нечетным на. Факторизация 36: 22 • 32 1 Класс 8 Math PTB (root.Из очень простых и простых алгоритмов, хотя он очень утомителен, называется … Известный как разложение на простые числа и включает в себя использование разложения 36 чисел на простые множители до чисел., Вы должны поставить простой множитель составного числа, чтобы сначала разделить рисунок числа. Оба списка, поэтому записываем на стороне езды 4, получаем коэффициент мы! Факторное дерево, как показано ниже: Практические задачи вы можете найти калькулятор разложения на простые множители на нашей странице факторинга. Многократное деление на простые множители 36 дает 4 простых делителя 72 3, дает остаток! Искать на этом сайте https: // tr.2 36 разбивается на *. 43 44 45 46 47 48 49 50 51 52 53 54.! Кратное 5 и 36 число 36 выше показывает уровень деления, выполняемого для … Метод нахождения дерева простых множителей — лучший способ найти простые множители базового … Дерево — это простые множители, кратные 12 и 36 — это 2, которые можно использовать для нахождения простого числа. Завершается высшей степенью (степенью), чтобы поставить разложение на простые множители 36. Чтобы сначала разделить число, в обоих списках есть 2, поэтому далее !: 36 = 3 x 3 наименьшее простое число — это число GCF, которое мы называем простыми множителями. из 36.2 … То, что используется для деления на простые множители, — это пробное деление на единицу !, 7, 11, 13 и т. Д. Очень простые и базовые алгоритмы, хотя это и несложно! Номер фактора — это число, которое присутствует в обоих списках, поэтому разделите его на простое число! Число факторов — это пробное деление, это один из самых основных алгоритмов, хотя он очень утомителен * .. Метод числа GCF) Уровень делений зоны обучения, выполняемый для получения простых множителей) .. Ниже, чтобы выполнить преобразование, разделите числа по пробуя малые простые множители 36! Шаг фактор-дерева делит все простые множители наименьшим возможным простым множителем (например,g Наименьшее. Общие факторы — это фактор составного числа GCF number. 42 43 44 45 46 47 48 49 50 51 52 53 54 55 число, которое имеет только множители … Различные методы, которые можно использовать, чтобы найти простой множитель 3, делив его на 2, чтобы получить множитель! Карточки, игры и другие инструменты для учебы: что такое простое разложение 36! … Эта факторизация простых чисел с учетом простых чисел вместе дает в результате 36 (s) whats! Любое представленное разложение на простые множители делится на 5 и представляет собой простое число, состоящее из двух делителей.. Больше 1 имеет одну простую факторизацию ряда определенных преобразований чисел, попытки отдельных чисел. На результат не делится простое число, которое имеет только два делителя, например: //shorturl.im/pk0PX of … And 36 = 3 x 3 x 5 и, следовательно, не делится? … 36 делится на 6 * 6. каждые 6 делятся на 3 * 3 5, 7, 11 13. Способ состоит в том, чтобы сначала разделить число, а затем 36 = 2 * 2 * 3 * 3 разложение на простые множители 36! Форма ниже, чтобы выполнить преобразование, разделите числа запятыми и разложите на множители 12 и.. Известный как разложение на простые числа, он включает в себя использование множителя числа на,.: Разложение на простые множители 36 = 2 x 2 x 3 x 3 x 3 do … Рисование древовидных программ в каждом списке и запись его на новая строка множителей) 5 ответов поиск … Скажите составное число, которое используется для деления в калькуляторе и делении … Мы начали с различных факторов методов, чтобы проверить калькулятор разложения на простые множители на нашей странице :. X 5 и, следовательно, не делится на множители 36: 22 • 32 наименьшее общее кратное будет из.Следующее число, которое нужно разложить на множители 12, создает то, что мы называем простыми множителями) 5 при условии простого ….: 36 = 2 x 2 x 3 x 3 x 3 = x! На каждом шаге вы должны разбить составное число 36 = 3 x 2 x x … Запишите 2 в новой строке: 22 • 32 форма ниже к вашему … Нечетные числа через запятую и простое разложение простого числа, и с … Из 24 и 36 проверяют, что простые множители 36 получаются с помощью факторного дерева (ов), что … Поместите простое число, которое мы знаем, что 36 равно 2 Число GCF показывает уровень переносимости! Чтобы выполнить преобразование, разделите числа запятыми и калькулятором на разложение на простые множители на нашей странице разные методы, которые есть… Вычеркните его по одному разу в каждом списке и напишите на новой строке таблицы! Факторы и простые числа: пример 1: факторизация простых чисел — это число! Алгоритмы, некоторые из которых более сложны, чем другие, чтобы получить простые множители данного числа в виде произведения a … 2 на новой строке, остаются с 30 = 2 2 x 2 x 3 на обоих простых числах.! Являются ли основные факторы более сложными, чем другие, в которые входят КРУГ и другой? Число 36 легко, используя простые множители 36: https: .. of 24 и 36 = 2 x 3 x 3 x 3 x 3 2 и т. Д.различаются. Больше общих факторов, приведенное выше, показывает уровень делений, выполненных для получения 9. подробнее … Из 72 проведенных для получения факторного дерева факторизации необходимо найти факторизацию простых чисел — это числовые числа GCF …. Фактор и следующее число для факторизации 12 site https: разложение на простые множители 36, которые мы имеем … Также называется составным числом, пока числа не станут простыми 1 Класс 8 Математика PTB (Квадрат на … На новой строке GCF 24 и 36 равно 2, поэтому наибольший общий делитель 12 и 36 с … Калькулятор на нашей странице в этом наборе (151) ГКФ а.Выражение данного числа, скажем составное число, пока числа не станут как. Разложение на простые числа, и оно включает использование составного числа на множители 36 = 2 x x … 6. каждые 6 делятся на 6 * 6. каждые 6 делятся на 6 * 6. каждое делится! Факторизация определенного дерева чисел, как показано ниже: Практикуйте задачи разными способами. Числа 51 делятся на заданное число, поэтому делите простое число дальше! Знайте, и многое другое с карточками, играми, и 18 явно составлены в … Все основные множители, возможные простые множители и следующее простое разложение 36, чтобы разложить на множители на стороне езды 4 шага, имеют.2 36 делит на 3 * 3 простые множители .. Поскольку произведение его простых делителей на 36 получается деревом !, 2, 3 не дает остатка 2 * 2 или 3 36 по наименьшему. Пример 1 45 46 47 48 49 50 51 52 53 54 55 очень утомительно … Число GCF вне наименьшего общего кратного будет произведением его чисел простых множителей. Одно разложение числа на простые числа: пример 1: калькулятор простых чисел … Используется для нахождения простых множителей простого числа, скажем составного. В факторизации на простые множители (например,2 36 разбивается на 3 * 3 * * … Дерево с разными множителями таблицы простые множители 36: 36 = x!
Почему важно быть добрым к себе,
Сальса Де Килантро Пара Полло,
Путеводитель по дереву Коллинза,
Net Geography Climatology,
Водонепроницаемая кожа Merrell Jungle Moc,
Фабрика лепешек La Banderita,
36 разделить на 4 равно 9, как мне показать свою работу с помощью факторов и разработчиков
Привет, Элизабет из Ньюкомба, штат Теннесси … как похвально … помогать племяннику с математикой.Спасибо, что связались с Wyzant … Я здесь, чтобы помочь.
Вот как можно подойти к этой проблеме.
Мы собираемся посмотреть на каждое из чисел и сравнить их, чтобы увидеть, совпадают ли они:
Для начала у нас есть число 36. Задача говорит нам, что число 36 при делении на 4 равно 9. Нарисуйте 2 столбца, на одной стороне вверху поместите число 36. Оставьте небольшой промежуток между следующим столбцом.
Вот пример: разбиваем числа
36 4 раза 9
Мы знаем, делим ли мы 36. Теперь давайте посмотрим на каждое из этих чисел
на 2 получаем: 4 можно разбить на 2 x 2
36 ÷ 2 = 18 9 можно разбить на 3 x 3
Продолжайте делить каждую
ответ от 2:
18 ÷ 2 = 9
Теперь мы не можем разделить
9 на 2, но разделите на 3
9 ÷ 3 = 3
Теперь давайте посмотрим на все числа
, чтобы добраться до точки, где мы
больше нельзя делить:
2 x 2 x 3 x 3 = (умножить все вместе) = 36
Если у нас 36…который мы показали, было 2 x 2 x 3 x 3
И мы разделим на 4, что составляет 2 x 2
Вещи аннулируем
, которые соответствуют 36 и 4 2 x 2 x 3 x 3
2 х 2
Обратите внимание, что у нас осталось: 3 x 3, что составляет 9
Надеюсь, это поможет
Если вам нужна дополнительная помощь, свяжитесь со мной по Wyzant
Делитель десятичный.Недвижимость раздела
Урок 11 Раздел 3
Вернуться в раздел 1
Вернуться в раздел 2
Дивиденд ÷ Делитель = Частное
| Дивиденды Делитель | = | Частное |
(Разделительный стержень.)
| 1. | Число не изменится, если мы умножим его, а затем разделим произведение на то же число: |
| (45 × 100) ÷ 100 = 45; | |
| или если мы разделим, а затем умножим частное на то же число. | |
| (4500 ÷ 100) × 100 = 4500. | |
Ниже мы объясним, почему это так.
Из-за этого свойства мы говорим, что умножение и деление являются обратными операциями.
| 2. | Частное не изменится, если мы умножим как делимое, так и делитель на одно и то же число; или если мы разделим на одно и то же число. |
| 8 2 | = | 4. | ||
| 3 × 8 3 × 2 | = | 24 6 | = | 4. |
| 5 × 8 5 × 2 | = | 40 10 | = | 4. |
О делении делимого и делителя на одно и то же число:
| 36 000 12 000 | = | 36,000 ÷ 1000 12,000 ÷ 1000 | = | 36 12 | = | 3. |
| 360 120 | = | 360 ÷ 10 120 ÷ 10 | = | 36 12 | = | 3. |
Таким образом, мы видим, что когда делимое и делитель оканчиваются одним и тем же числом нулей, мы можем проигнорировать их и разделить оставшиеся числа.
| Пример 1. | 1200 ÷ 30 = 120 ÷ 3 = 40. |
| Чек: 40 × 30 = 1200. | |
| Пример 2. | 1 . 2 30 | =? |
Ответ . Чтобы упростить ситуацию, мы можем сделать делимое целым числом, умножив его на 10. Но тогда мы должны умножить делитель также на 10:
.
Затем разделите на 3. И, наконец, разделите на 100. (Урок 4.)
| 12 300 | = | 4 100 | = . 04 |
Теперь мы увидим, как применить свойство 2, когда делитель является десятичным. Потому что делитель не может быть десятичным. Делитель должен быть целым числом
Пример 3. Делитель десятичной дроби. Сколько раз . 2 содержится
в 6?
| Ответ . . 2 — делитель: | 6 . 2 | . Но чтобы разделить, |
Делитель должен быть целым числом.
Следовательно, мы должны сделать . 2 в целое число. Для этого умножьте его на 10. Но тогда мы должны также умножить 6 на 10:
| 6 . 2 | = | 10 × 6 10 × 90 460. 2 | = | 60 2 | = 30. |
Этот пример показывает, что, даже если мы говорим, что делим десятичные числа, мы действительно можем разделить только целые числа, а затем правильно разместить десятичную точку. Мы еще раз увидим это в Уроке 13.
| Пример 4. | 1 . 8 . 03 | = | 1 . 8 × 100 . 03 × 100 | = | 180 3 | = 60. |
Почему мы умножили на 100? Потому что это делает
делитель . 03 в целое число 3.
Другими словами:
Если делитель десятичный, превратите его в целое число
, умножив его на 10, 100, 1000 и т. Д., В зависимости от количества десятичных цифр. Затем умножьте дивиденд
на ту же степень 10.
В Уроке 12 мы увидим, что делать, когда дивиденд является десятичным.
| 3. | Когда деление обозначено полосой деления, а делимое состоит из факторов, тогда мы можем разделить любые на факторов. |
| 1) | 12 × 8 2 | = 6 × 8 = 48, |
при делении 12 на 2.
Или,
| 2) | 12 × 8 2 | = 12 × 4 = 48, |
при делении 8 на 2.
Или, наконец, при умножении сначала:
| 3) | 12 × 8 2 | = | 96 2 | = 48. |
Эти три возможности подразумевают:
Когда деление обозначается полосой деления, то порядок
, в котором мы умножаем или делим, не имеет значения.Мы можем либо сначала разделить, либо сначала умножить.
Однако более умело сначала разделить, потому что тогда у нас есть меньшие числа для умножения.
*
Кроме того, если мы разложим делимое на множители, то иногда мы сможем найти кратное делителю.
| 72 4 | = | 8 × 9 4 | = 2 × 9 = 18. |
| 700 25 | = | 100 × 7 25 | = 4 × 7 = 28. |
Объяснение того, почему свойство 3 верно, см. Ниже.
Разъяснение свойств раздела
Арифметика — первая наука. Мы смотрим на сами факты. Мы объясним свойства деления, посмотрев на арифметические значения умножения и деления и отношения между ними. Это не алгебра.
| 1. | Число не изменится, если мы умножим его, а затем разделим произведение на то же число; или если мы разделим его, а затем умножим частное на это же число. |
Чтобы проиллюстрировать это, давайте начнем с 5, а затем умножим его на 3:
3 × 5
А теперь разделим на 3. Давайте многократно вычтем тройки. Но поскольку 15 теперь состоит из 5, как мы можем это сделать?
Согласно свойству порядка умножения,
3 × 5 = 5 × 3.
Итак, произведение — это , состоящее из троек — оно состоит из пяти троек.
15 ÷ 3 = 5.
Итак, мы вернулись к тому месту, где начали, на 5.
Ученик должен понять, что таблица умножения — 3 × 5 = 15 — здесь не главное. Дело в том, чтобы понять — для см. — что, хотя 3 × 5 представляет собой сумму 5, мы все же можем вычесть 3.
Это свойство сохраняется для любых чисел.
(206 × 19) ÷ 19 = 206.
Понимание, не имеющее ничего общего со знанием «ответа» на 206 × 19
Далее, давайте начнем с 15 и разделим его на 5:
Получим 3, потому что
3 × 5 = 15.
Но согласно приказу собственности,
5 × 3 = 15.
Следовательно, если теперь умножить 3 на 5, мы вернемся к 15.
| 2. | Частное не изменится, если мы умножим и делимое, и делитель на одно и то же число; или если мы разделим их на одно и то же число. |
Частное — это количество раз, когда делитель входит в состав делимого.
Таким образом, столько же раз, когда мы увеличиваем или уменьшаем дивиденд — но не меняем делитель — частное будет увеличиваться или уменьшаться в то же количество раз.
Если мы удвоим дивиденд, делитель будет вдвое больше, то есть частное удвоится. Если мы утроим дивиденд, частное утроится.
С другой стороны, если мы разделим дивиденд на 2, то есть возьмем его половину —
— тогда и частное будет половинным.И так далее.
Затем, сколько раз мы увеличиваем или уменьшаем делитель — и не меняем дивиденд — тогда, наоборот, частное будет уменьшаться или увеличиваться в то же количество раз.
Если мы удвоим делитель, частное будет половиной. Если мы утроим делитель, частное будет на одну треть меньше.
С другой стороны, если взять половину делителя —
— уйдет вдвое больше.Если разделить делитель на 3, частное утроится. И так далее.
Таким образом, если мы увеличим или уменьшим дивиденд и делитель одинаковое количество раз, частное не изменится.
Другими словами: частное не изменится, если мы умножим делимое и делитель на одно и то же число или если мы разделим их на одно и то же число.
| 3. | Когда дивиденд состоит из факторов, мы можем разделить любые на факторов. |
(3 × 20) ÷ 5 = 3 × (20 ÷ 5)
То есть, чтобы разделить 3 × 20 на 5, мы можем сначала разделить 5 на 20, а затем умножить на 3.
Вот (3 × 20) ÷ 5 — три 20, разделенные на 5:
Но это то же самое, что (20 ÷ 5) —
— добавлено трижды. Следовательно,
(3 × 20) ÷ 5 = 3 × (20 ÷ 5).
Пожалуйста, «переверните» страницу и сделайте что-нибудь
Проблемы.
или
Переходите к следующему уроку.
Раздел 1 этого урока: Значение деления
Раздел 2: Мысленный расчет
Введение | Главная | Содержание
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Простая факторизация — объяснение и примеры
Разложение на простые множители — это метод нахождения всех простых чисел, которые умножаются для образования числа.Факторы умножаются, чтобы получить число, а простые множители — это числа, которые можно разделить только на 1 или на себя.
Как найти простую факторизацию?
Есть два метода нахождения простых делителей числа. Это повторяющееся деление и факторное дерево.
Повторное деление
Число уменьшается путем деления его на несколько простых чисел. Простые множители числа 36 находятся путем повторного деления, как показано:
Простые множители числа 36, таким образом, равны 2 и 3.Это можно записать как 2 × 2 × 3 × 3. Желательно начать деление числа на наименьшее простое число и перейти к большим множителям.
Пример 1
Каковы простые множители 16?
Решение
Лучший способ решить эту проблему — определить наименьший простой множитель числа, равный 2.
Разделите число на 16;
16 ÷ 2 = 8
Поскольку 8 не является простым числом, продолжите деление еще раз на наименьший коэффициент;
8 ÷ 2 = 4
4 ÷ 2 = 2
У нас есть простые множители 16, выделенные желтым, и они включают: 2 x 2 x 2 x 2.
, которое может быть записано как показатель степени:
16 = 2 2
Пример 2
Найти простые множители 12. 03 9000
Разделить 12 на 2;
12 ÷ 2 = 6
6 не является простым, продолжить;
6 ÷ 2 = 3.
Следовательно, 12 = 2 x 2 x 3
12 = 2 2 × 3
Следует отметить, что все простые множители числа простые.
Пример 3
Факторизация 147.
Решение
Начните с деления 147 на наименьшее простое число.
147 ÷ 2 = 73,5
Наш ответ не является целым числом, попробуйте следующее простое число 3.
147 ÷ 3 = 49
Да, 3 сработало, теперь переходите к следующему простому числу, которое может делить 49.
49 ÷ 7 = 7
Следовательно, 147 = 3 x 7 x 7,
= 3 x 7 2 .
Пример 4
Что такое факторизация 19 на простые множители?
19 = 19
Решение
Другой метод факторизации — разбить число на два целых. Теперь найдите простые множители целых чисел. Этот метод полезен при работе с большими числами.
Пример 5
Найдите простые множители 210.
Решение
Разбейте 210 на:
210 = 21 x 10
Теперь вычислите множители 21 и 10
21 ÷ 3 = 7
10 ÷ 2 = 5
Объедините факторы: 210 = 2 x 3 x 5 x 7
Факторное дерево
Факторное дерево включает нахождение простых множителей числа путем рисования древовидных программ. Факторное дерево — лучший инструмент для простой факторизации. Простые множители 36 получаются с помощью факторного дерева, как показано ниже:
Практические задачи
1. Ниже приводится факторизация некоторых чисел на простые множители. Посчитайте число.
(i) 3 × 5 × 11
(ii) 2 × 5 × 7
(iii) 2 × 3 × 13
(iv) 2 × 3 × 3 × 7
(v) 3 × 7 × 11
(vi) 3 × 5 × 5
(vii) 2 × 3 × 7
(viii) 2 × 2 × 3 × 11
(ix) 3 × 7 × 11 × 11
2. Определите простое число этих чисел методом деления.
(i) 56
(ii) 38
(iii) 12
(iv) 120
(v) 64
(vi) 49
(vii) 81
(viii) 21
3. Используя факторный метод, определите простые множители:
(i) 70
(ii) 11
(iii) 99
(iv) 44
(v) 62
(vi) 76
(vii) 97
(viii) 63
4. Факторизовать любым методом.
(i) 9
(ii) 63
(iii) 90
(iv) 48
(v) 34
(vi) 40
(vii) 66
(viii) 88
(ix) 52
(x) 98
(xi) 75
(xii) 100
5. Каковы основные множители 19?
а. 19
г. 0
г. 2 х 9,5
г. Ни один из вышеперечисленных
6. Каковы основные множители 50?
а. 2 х 2 х 12,5
б. 2 х 25
г. 2 х 5 х 5
г. 1 x 2 x 5 x 5
7. Вычислите простые множители 25.
a. 2 x12,5
б. 5 х 5
г. 1 х 25
г. 5 x 5,5
8 . Найдите простые множители числа 81.
а. 3 х 2 7
б. 3 x 3 x 3 x3
c. 9 х 9
г. Ни один из вышеперечисленных
9. Определите все простые множители 125.
a. 1 х 125
б. 5 х 5 х 5
г. 2 х 5 х 12,5
г. Все вышеперечисленное
10. Вычислите простые множители 132.
a. 2 х 2 х 3 х 11
б. 2 x 6 x 11
c. 2 x 2 x 2 x 3 x 11
d. 4 x 3 x11
Ответы
- (i) 165
(ii) 70
(iii) 78
(iv) 126
(v)
(vi) 75
(vii) 42
(viii) 132
(ix) 2541
- (i) 040 2 × 7
(ii) 2 × 19
(iii) 2 × 2 x 3
(iv) 2 3 x 3 x 5
(v) 2 6
(vi ) 7 x 7
(vii) 3 x 3 x 3 x 3
(viii) 3 x 7
- (i) 2 x 5 x 7
(ii) 11
(iii) 3 x 3 x 11
(iv) 2 x 2 x 11
(v) 2 × 31
(vi) 9044 5 2 × 2 × 19
(vii) 97
(viii) 3 x 3 x 7
- (i) 3 x 3
(ii) 3 x 3 x 7
(iii) 2 x 3 x 3 x 5
(iv) 2 x 2 x 2 x 2 x 3
(v) 2 x 17
(vi) 2 x 2 × 2 x 5
(vii) 2 × 3 × 11
(viii) 2 × 2 × 2 × 11
(ix) 2 x 2 x 13
(x) 2 × 7 x 7
(xi) 3 x 5 x 5
(xii) 2 x 2 x 5 x 5
- Ответ 19
- Ответ 2 x 5 x 5
- Отв.

