Памятка : «Решение уравнений», 5 класс

Уравнения

(Х – 87) – 27 = 36; Х-87 в уравнении является уменьшаемым. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое

Х – 87 = 36 + 27;

Х – 87 = 63; х в уравнении является уменьшаемым. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое

Х= 87 + 63;

Х=150,

Проверка: (150 – 87) – 27 = 36;

63-27 = 36;

36 = 36.

Ответ: Х=150.

87- ( 41 + У ) = 22; 41 + У в уравнении является вычитаемым . Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность

41 + У = 87 – 22;

41 + У = 65; У в уравнении является слагаемым. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое

У = 65 – 41;

У = 24,

Проверка: 87- ( 41 + 24 ) = 22;

87 – 65 = 22;

22 = 22,

Ответ: У = 24

(у – 35) + 12 = 32; у – 35 в уравнении является слагаемым. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое

у – 35 = 32 – 22;

у – 35 = 20; у в уравнении является уменьшаемым. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое

у = 20 + 35;

у=55.

Ответ: у = 55.

56 — (Х +12) = 24;

55 – (х – 15) = 30;

1 способ

56 — (Х +12) = 24;

Х + 12 = 56 -24;

Х + 12=32;

Х = 32 – 12;

Х = 20.

Ответ: х = 20

2 способ

56 — (Х +12) = 24;

56 — Х — 12 = 24;

56- 12 — Х = 24;

44 – Х = 24;

Х = 44 – 24;

Х = 20.

Ответ: х = 20

1 способ

55 – (х – 15) = 30;

х – 15 = 55 – 30;

х – 15 = 25;

х = 25 + 15;

х = 40.

Ответ: х = 40.

2 способ

55 – (х – 15) = 30;

55 – х + 15 = 30;

55 + 15 – х = 30;

70 – х = 30;

х = 70 – 30;

х =40.

Ответ: х = 40.

(237 + х) – 583 = 149;

468 – ( 259 – х) = 382;

1 способ

(237 + х) – 583 = 149;

237 + х = 149 + 583;

237 + х = 732;

х = 732 — 237;

х = 495.

Ответ: х = 495

2 способ

(237 + х) – 583 = 149;

237 + х – 583 = 149;

х – (583 – 237) = 149;

х – 346 = 149;

х = 149 + 346;

х = 495.

Ответ: х = 495

1 способ

468 – ( 259 – х) = 382;

259 – х = 468 – 382;

259 – х = 86;

х = 259 – 86;

х = 173.

Ответ: х = 173.

2 способ

468 – ( 259 – х) = 382; 468 – 259 + х = 382;

209 + х = 382;

х = 382 – 209:

х = 173.

Ответ: х = 173.

Решение уравнений, приведение подобных слагаемых

Пример 1: 8х-х=49; сначала запишем знаки умножения,

8*х-1*х=49; затем воспользуемся распределительным свойством (вынесем общую переменную за скобки)

Х*(8-1)=49;

Х*7=49; х является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель

Х=49:7;

Х=7.

Проверка:

8*7-7=49;

56-7=49;

49=49.

Ответ: х=7.

Пример 2: 2х+5х+350=700; воспользуемся распределительным свойством (вынесем общую переменную за скобки)

Х*(2+5)+350=700; приведем подобные слагаемые (т.е. сложим числа в скобках)

7х+350=700;

7х является неизвестным слагаемым. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое

7х=700-350;

7х=350; х является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель

Х=350:7;

Х=50.

Проверка:

2*50 + 5*50 + 350 = 700;

100 + 250 + 350 = 700;

700=700.

Ответ: х = 50

Пример: 270: х + 2 = 47;

(270 : х — является слагаемым.

Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое

270 : х = 47 – 2;

270 : х = 45;

( х является делителем. Чтобы найти неизвестный делитель, нужно делимое разделить на частное)

Х = 270 : 45:

Х= 6.

Ответ: Х= 6.

Пример: а : 5 – 12 = 23;

( а : 5 является уменьшаемым.

Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое )

а : 5 =23 + 12;

а : 5 = 35;

(а является делимым. Чтобы найти неизвестное делимое, нужно частное умножить на делитель.

а = 35 * 5;

а = 175.

Ответ: а = 175.

§ Решение простых уравнений 5 класс

ДЕТСКИЙ САД Задания для детей Задания для детей 2 лет Задания для детей 3 лет Задания для детей 4 лет Задания для детей 5 лет Задания для детей 6 лет Задания для детей 7 лет Тесты для детей и дошкольников Тесты для детей 2 лет Тесты для детей 3 лет Тесты для детей 4 лет Тесты для детей 5 лет Тесты для детей 6 лет Тесты для детей 7 лет Математика для малышей Математика для детей 2 лет Математика для детей 3 лет Математика для детей 4 лет Математика для детей 5 лет Математика для детей 6 лет Математические игры для дошкольников Количественный счет в детском саду Занимательная математика Картинки, цифры, шаблоны для скачивания. Контрольные работы Входная Петерсон Л. Моро М. Итоговые Самостоятельные работы Петерсон Л. Дополнительный материал Тесты Моро М.

Дорогие читатели! Наши статьи рассказывают о типовых способах решения юридических вопросов, но каждый случай носит уникальный характер.

Если вы хотите узнать, как решить именно Вашу проблему — обращайтесь в форму онлайн-консультанта справа или звоните по телефонам, представленным на сайте. Это быстро и бесплатно!

Как научить ребенка решать уравнения

ВИДЕО ПО ТЕМЕ: Решение уравнений по математике 5-6 класс

Разделы: Начальная школа. Цель : Рассмотреть практические способы решения уравнений, требующих выполнения более одного арифметического действия.

Оборудование урока : компьютерная презентация устного счета, карточки с уравнениями, карточки трех ступеней для самостоятельной работы над задачами, кубик обратной связи. Оргмомент Проверка готовности к уроку. В тетрадях записывается число, классная работа. Две улитки должны подняться до вершины горы. Кто же из них окажется первой? Улитка делает шаг, только если мы правильно найдем значение выражения. Вы готовы? Сигнал к старту уже прозвучал. Повторяем порядок действий и называем правильные значения выражений.

У нас получился ряд чисел. Мы решали все правильно, поэтому наша улитка на вершине горы. За каждым числом зашифрована буква. Перевернем их и прочитаем тему сегодняшнего урока. Что называется уравнением? Что называется корнем уравнения? Что значит решить уравнение? Мы уже умеем решать простые уравнения, а сегодня мы познакомимся с решением сложных уравнений, где надо выполнить несколько арифметических действий.

Решение простых уравнений. Подготовка к введению нового материала. На магнитной доске в произвольном порядке карточки с уравнениями. На какие группы можно разделить все эти уравнения? Найдите среди них уравнение с наибольшим корнем и решите его один ученик у доски. Решите любое из уравнений, но замените в правой части сумму на разность.

Корень уравнения при этом должен остаться прежним. Работа над новым материалом. Мы решили два новых сложных уравнения. Посмотрите на уравнения, которые перед вами. Все ли они сложные? Какое уравнение лишнее? Остальные — в левой части выражение в несколько действий. Найдите среди них с таким порядком действий, которое уже встречалось сегодня.

Один ученик на развороте доски для последующей проверки. Решение задачи Самостоятельная работа по карточкам 3 ступеней. Выполнив задание первой ступени, ученик переходит к выполнению задания второй ступени, затем третьей. Домашнее задание. Рассмотреть, как решались уравнения в учебнике на стр. Дополнительное задание: какие еще вопросы можно поставить к этой задаче? Итог урока. Какие уравнения учились решать на уроке? Трудно было? Кому было легко?

Урок математики по теме «Решение уравнений» 4-й класс Золотова Юлия Михайловна , учитель начальных классов. Оборудование урока : компьютерная презентация устного счета, карточки с уравнениями, карточки трех ступеней для самостоятельной работы над задачами, кубик обратной связи Ход урока 1.

Легко ли нам его решить? После того, как они высадили часть саженцев, им осталось посадить еще деревьев. Сколько деревьев они уже высадили? Реши задачу, составив уравнение Измени задачу так, чтобы она решалась уравнением, в правой части которого было бы выражение. Запиши это уравнение и реши его. Школьники должны были высадить саженцев деревьев. После того, как они высадили несколько саженцев липы и кленов, им осталось высадить саженцев. Сколько лип они уже посадили? Какое уравнение отнесем к сложным?

Поделиться страницей:. Реши задачу, составив уравнение. Измени задачу так, чтобы она решалась уравнением, в правой части которого было бы выражение.

Во-вторых, объяснение, которое предлагается детям в школьной программе, непонятно в большинстве случаев даже взрослому:. Для того чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

Разделы: Начальная школа. Цель : Рассмотреть практические способы решения уравнений, требующих выполнения более одного арифметического действия. Оборудование урока : компьютерная презентация устного счета, карточки с уравнениями, карточки трех ступеней для самостоятельной работы над задачами, кубик обратной связи. Оргмомент Проверка готовности к уроку. В тетрадях записывается число, классная работа.

Математика – 2 класс. Уравнения

Психологический настрой: Покажите вашу прямую спинку, покажите правую руку, умные глазки. Подарите мне и друг другу добрые улыбки. Умеем ли мы решать уравнение? Нет Слайд 4.

Решение уравнений

Решение задачи обычно сводится к тому, чтобы путем логических рассуждений и вычислений найти значение какой-нибудь величины. Например, найти скорость, время, расстояние, массу какого-нибудь предмета или количество чего-то. Такую задачу можно решить с помощью уравнения. Для этого искомое значение обозначают через переменную, затем путем логических рассуждений составляют и решают уравнение. Решив уравнение, производят проверку на то, удовлетворяет ли решение уравнения условиям задачи. Решение задачи сопровождается составлением уравнения к этой задаче. На начальном этапе изучения задач желательно научиться составлять буквенные выражения, описывающие ту или иную жизненную ситуацию.

.

.

Урок математики по теме «Решение уравнений» (4-й класс)

.

.

.

Задачи во 2 классе — уравнения, как решить уравнение. Задания по математике.

Решение задач с помощью уравнений

.

Решение простых уравнений. 5 класс

.

.

.

.

.

Тест: Уравнения. 5 класс. Вариант 3

Тест: Уравнения. 5 класс. Вариант 3 — Математика 5 класс

Уравнения. 5 класс. Вариант 3

Решение простейших уравнений, задачи на составление уравнений

Математика 5 класс | Автор: Ливанова И.Г. | ID: 3767 | Дата: 31.1.2015

«;} else {document.getElementById(«torf1″).innerHTML=»»;};
if (answ.charAt(1)==»1″) {document.getElementById(«torf2″).innerHTML=»»;} else {document.getElementById(«torf2″).innerHTML=»»;};
if (answ.charAt(2)==»1″) {document.getElementById(«torf3»). innerHTML=»»;} else {document.getElementById(«torf3″).innerHTML=»»;};
if (answ.charAt(3)==»1″) {document.getElementById(«torf4″).innerHTML=»»;} else {document.getElementById(«torf4″).innerHTML=»»;};
if (answ.charAt(4)==»1″) {document.getElementById(«torf5″).innerHTML=»»;} else {document.getElementById(«torf5″).innerHTML=»»;};
if (answ.charAt(5)==»1″) {document.getElementById(«torf6″).innerHTML=»»;} else {document.getElementById(«torf6″).innerHTML=»»;};
if (answ.charAt(6)==»1″) {document.getElementById(«torf7″).innerHTML=»»;} else {document.getElementById(«torf7″).innerHTML=»»;};
if (answ.charAt(7)==»1″) {document.getElementById(«torf8″).innerHTML=»»;} else {document.getElementById(«torf8″).innerHTML=»»;};
if (answ.charAt(8)==»1″) {document.getElementById(«torf9″).innerHTML=»»;} else {document.getElementById(«torf9″).innerHTML=»»;};
if (answ.charAt(9)==»1″) {document.getElementById(«torf10″).innerHTML=»»;} else {document.getElementById(«torf10″).innerHTML=»»;};
}
}

Получение сертификата
о прохождении теста

Как решать уравнения 5 класса онлайн калькулятор

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве
сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только
возрастает. Главной задачей при решении уравнений является поиск неизвестного значения. Неизвестная величина
называется корнем уравнения, поэтому под понятием решить уравнение понимают поиск всех его корней. В 5
классе несложные уравнения, однако, если не усвоить их решение, то дальше может возникнуть множество проблем
при решении более сложных уравнений. При возникновении сомнений касательно правильности полученного
результата, вы всегда можете решить уравнение онлайн 5 класса решателем и сравнить ответы.

Так же читайте нашу статью «Решить уравнение плоскости онлайн
решателем»

Для наглядности решим следующие уравнения:

\[37 + x = 51\]

Вычтем из левой и правой части число \[37:\]

\[37 + x — 37 = 51 — 37\]

Получим следующий результат:

\[ х = 51 — 37\]

Ответ: \[х = 14\]

Решим уравнение с делением:

\[5х = 20\]

Выполним деление левой и правой части на \[5:\]

\[\frac{5х} { 5} = \frac{20}{ 5}\]

После сокращения получим следующее уравнение:

\[ х = \frac{20}{ 5}\]

Ответ: \[x = 4\]

Где можно решить уравнение онлайн 5 класса решателем?

Решить уравнение вы можете на нашем сайте https://pocketteacher. ru. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.

5 класс по математике, урок и презентация: Решения уравнений, примеры

Дата публикации: 08 апреля 2017.

Что такое уравнение?

Чтобы лучше понять, что такое уравнение, давайте вспомним, что такое равенство?
Равенство – это выражение, когда обе части, стоящие до и после знака равенства, равны.

Примеры.

2 + 5 = 7
12 — 7 = 4 +1

Соответственно, неравенство – это когда части выражения не равны друг другу (какая-то часть больше или меньше).

Пример.

4 * 5 < 2 + 12

Теперь снова перейдем к уравнениям.
Если мы заменим какое-либо число в равенстве буквой, то получим УРАВНЕНИЕ.

Пример.

3 + x = 18

В качестве неизвестной в уравнения чаше всего используют маленькие буквы: x, y, z и др.

Запомните!
Уравнение – это равенство, содержащее неизвестное, которое обозначили буквой, и которое необходимо определить. Это неизвестное называют корнем уравнения.
Найти корень уравнения – значит найти все значения, при котором равенство будет верным, или убедиться, что решений нет.

Примеры уравнений

Ребята, вы уже наверное догадались, что заменив любое число в равенстве или неравенстве буквой, можно получить уравнение.

Примеры уравнений на сложение.

15 + x = 32
у + 10 = 14
27 + 12 = z

Примеры уравнения на вычитание.

38 — x = 23
у — 16 = 19
29 — 14 = z

Примеры уравнений на умножение и деление.

28 * x = 56
у : 10 = 3
27 * 4 = z

Решение уравнений

Решить уравнение – это значит: найти все его корни.
Давайте рассмотрим разные уравнения и методы их решений.

Уравнение на сложение

Решите уравнение: 3 + х = 18

В данном примере нужно найти второе слагаемое. Для этого мы должны вычесть из суммы первое слагаемое, которое нам известно.

х = 18 — 3 = 15

Всегда проверяем ответ.

3 + 15 = 18
18 = 18

Ответ: x=18.

Уравнения на вычитание
Пример 1.
Решите уравнение: 45 — у = 23

В этом примере нужно найти вычитаемое. Для этого из уменьшаемого мы вычитаем разность:
у = 45 — 23 = 22

Всегда проверяем ответ.

45 — 22 = 23
23 = 23

Ответ: y=22.

Пример 2.

Решите уравнение: z — 34 = 42

Теперь нам нужно найти уменьшаемое. Для этого мы складываем вычитаемое и разность:
z = 34 + 42 = 76

Проверяем ответ.

76 — 34 = 42
42 = 42

Ответ: z=76.

Урок — повторение «Уравнения» 5 класс

ГУО «Средняя школа № 15 г. Могилева»

Урок по теме

«Решение уравнений. Повторение»

(5 класс)

Разработала:

учитель математики

Дрыга Елена Казимировна

2017 г.

Урок математики в 5-м классе по теме:

«Решение уравнений. Повторение»

«Незнающие пусть научатся,

знающие — вспомнят еще раз».

(Античный афоризм.)

Цель: Повторить определение уравнения, повторить правила нахождения неизвестных компонентов при решении уравнений. Применять полученные знания в ходе выполнения упражнений.

Задачи урока:

• повторить определение уравнения и понятия «корень уравнения», «решить уравнение», уметь решать уравнения, содержащие 2-3 действия.

• формировать привычку правильно, аккуратно записывать решение уравнений и задач. Учить самостоятельности и умению работать в коллективе.

• при решении уравнений учить учеников использовать грамотно термины и понятия, выделять главное, анализировать, делать выводы и сравнивать.

Оборудование: компьютер, мультимедийный проектор, интерактивная доска.

Формы обучения: фронтальная, групповая, индивидуальная.

Методы обучения: словесные, практические, наглядные.

ХОД УРОКА

I. Организационный момент.

Создадим хорошее, дружелюбное настроение.

Улыбнитесь друг другу, садитесь!

Итак, начинаем наш урок.

II. Проверка домашнего задания.(слайд 1)

III.Устный счет (слайд 2)

IV.Объявление темы урока цели урока(слайд 3, 4)

V.Актуализация. (слайд5)

Уравнением называется…

Корнем уравнения называют…

Решить уравнение, значит…

Чтобы найти неизвестное слагаемое нужно …

Чтобы найти неизвестное уменьшаемое нужно …

Чтобы найти неизвестное вычитаемое нужно …

Чтобы найти неизвестный множитель нужно …

Чтобы найти неизвестное делимое нужно …

Чтобы найти неизвестный делитель нужно …

Когда уравненье решаешь дружок, ты должен найти у него корешок.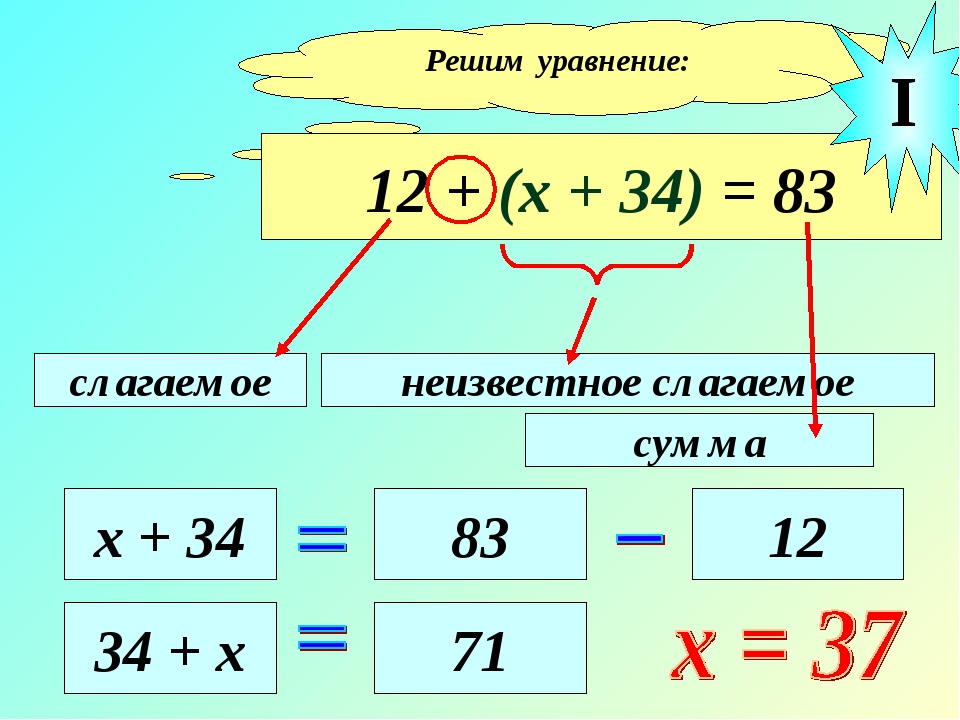
Значение буквы проверить не сложно, поставь в уравненье его осторожно.
Коль верное равенство выйдет у вас, то корнем значенье зовите тот час.

VI.Решение заданий

Задание1:Разминка(слайд 6)

Записать в тетради уравнение и решить письменно или устно,

выбрать нужный корень уравнения из предложенных. (Взаимопроверка)

Задание 2: Что скрывает смайлик?(слад 7)

Решить уравнения и проверить самим.

Физкультминутка(слайд 8)

Вверх рука, вниз рука

Потянулись мы слегка

Быстро поменяли руки

Нам сегодня не до скуки.

Крутим-вертим головой.

Разминаем шею….стой.

А теперь встряхнулись лихо

И на стул садимся тихо.

Задание 3: Решите уравнения(слайд9)

Решение у доски с пояснением.

1. 248-(у-123)=24;

2. (24-х)+37=49;

3. 375-у+218=123;

4. (х+93)·5=40;

5. (7+х):5=50.

Историческая справка(слайд 10)

Знак равенства ввел в 1556 году английский математик Рекорд,

который объяснил это так, что ничто не может быть более равным,

чем два параллельных отрезка. Необходимость решать уравнения

не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.

VII. Самостоятельная работа(слайд 11)

По вариантам задания выполняют на карточках.

VIII. Домашнее задание:(слайд 12)

П. 13,

Решите уравнения:

1. 15+35:х=20;

2. 165-(у+112)=37;

3. у:2-35=3.

IX.Рефлексия:(слайд 13)

Мы неплохо потрудились-

Вместе новому учились. Прозвенит сейчас звонок-

Всем спасибо за урок!

Маршрутный лист

Учащегося(Ф.И.)_____________________________Вариант_________

Устный счет _____________баллов

Повторенье-мать ученья _____________баллов

Задание 1: Разминка( 1балл за правильный ответ)

1._______

2._______

3._______

4._______

5._______

6._______

7._______ _____________баллов

Задание 2: Что скрывает смайлик?(2 балла за правильный ответ)

1._______

2._______

3._______ _______________баллов

Задание 3: Решение уравнений у доски

______________баллов

Самостоятельная работа:

100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА

В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.

— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?

— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.

Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.

Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.

— Расскажите поподробнее?

— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.

— Система оценивания останется прежней?

— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.

Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.

— А апелляция?

— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.

— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?

— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.

— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?

— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.

— На сколько процентов будет обновлена база вопросов?

— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.

— По вашему мнению система справится с возможными хакерскими атаками, взломами?

— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.

Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.

— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?

— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.

— Сколько человек будет сидеть в одной аудитории?

— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.

— Будут ли ужесточены требования по дисциплине, запрещенным предметам?

— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.

Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.

— А наблюдатели будут присутствовать во время сдачи тестирования?

— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.

— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?

— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.

Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.

— Сколько средств выделено на проведение ЕНТ в этом году?

Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.

— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?

— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.

Решение уравнений 5 класс по математике.

Презентация на тему: «Решение уравнений по математике для 5-го класса» — стенограмма презентации:

ins [data-ad-slot = «4502451947»] {display: none! important;}}
@media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}}
@media (max-width: 800px) {# place_14 {width: 250px;}}
@media (max-width: 500 пикселей) {# place_14 {width: 120px;}}
]]>

1

Решение уравнений 5 класс по математике

2

Математическое предложение о том, что 2 выражения равны.
Определения Уравнение Математическое предложение, утверждающее, что 2 выражения равны. 12-3 = 9 8 + 4 = 12

3

Означает, что сумма одинакова для обеих сторон.
Определения Знак равенства (=) Означает, что сумма одинакова для обеих сторон. 4 + 2 = 6 5 — 2 = 3

4

Уравнение похоже на весы
Уравнение похоже на весы баланса.все должно быть равным с обеих сторон. = 10 5 + 5

5

Когда суммы равны с обеих сторон, это уравнение.
12 = 6 + 6

6

Когда суммы неравны с обеих сторон, это неравенство.
≠ 8 2 + 2

7

Неизвестные

8

Это выражения или уравнения?
m + 4 = 17 N + 4 12-3 = p 3 + v = 13 y — 6 уравнение выражение уравнение выражение

9

~ обратная операция, используемая для отмены первой.
Как решать уравнения Обратная операция ~ обратная операция, используемая для отмены первой. 4 + 3 = 7 7-3 = 4 6 х 6 = / 6 = 6

10

Как решить уравнение сложения
Используйте обратную операцию для сложения, которая является вычитанием m + 8 = 12-8 = -8 m = 4

11

Как решить уравнение вычитания
Используйте обратную операцию для вычитания, которая является сложением m — 3 = 5 +3 = + 3 m = 8

12

Решите эти уравнения, используя обратные операции
3 n + 4 = 7 n — 5 = 4 n + 4 = 17 n — 6 = 13 n + 7 = 15 n — 8 = 17 9 13 19 8 25

Рабочие листы по уравнениям

Рабочие листы с одношаговым уравнением

Этот набор рабочих листов требует от студентов решения одношаговых уравнений, включающих целые числа, дроби и десятичные дроби, путем выполнения операций сложения, вычитания, умножения или деления.Он также содержит математические загадки, определение стоимости предметов, перевод фраз в одношаговое уравнение и многое другое.

Рабочие листы с двухэтапными уравнениями

Щелкните ссылку, чтобы получить доступ к эксклюзивным рабочим таблицам для решения двухэтапных уравнений, которые включают целые числа, дроби и десятичные дроби. Ряд MCQ, уравнения в геометрии, перевод двухэтапных уравнений и многие другие упражнения доступны для практики.

Рабочие листы с многоступенчатыми уравнениями

Эти рабочие листы требуют от учащихся выполнить несколько шагов для решения уравнений.Используйте знания, полученные при решении одношаговых и двухэтапных уравнений, чтобы решить эти многоступенчатые уравнения. Сюда также включен ряд прикладных задач, основанных на геометрических формах.

Рабочие листы задач по формулам

Загрузите и распечатайте эту огромную коллекцию одношаговых, двухэтапных и многоэтапных задач по уравнениям, включающим целые числа, дроби и десятичные дроби. Рабочие листы MCQ представляют собой идеальный инструмент для изучения восприятия учащимся темы.

Рабочие листы перестановки уравнений

Рабочие листы с буквальными уравнениями помогают отточить навыки, такие как перестановка буквальных уравнений, перегруппировка и оценка, включены текстовые задачи, содержащие реальные приложения, и многое другое.

Уравнение рабочего листа

Щелкните здесь, чтобы просмотреть таблицы по уравнению линии. Напишите уравнение прямой в стандартной форме, двухточечной форме, форме с пересечением угла наклона и форме точки с уклоном. Загрузите полный набор рабочих листов по уравнению линии, которые также включают рабочие листы по параллельным и перпендикулярным линиям.

Рабочие листы для построения графиков линейных уравнений

Вы находитесь всего в одном клике от огромной коллекции таблиц по построению графиков линейных уравнений.Постройте точки и нанесите линию на график. Используйте значения x, чтобы заполнить таблицы функций и построить график линии. Рабочие листы MCQ представляют собой идеальный инструмент для проверки знаний учащихся по этой теме.

Рабочие листы по квадратному уравнению

Щелкните ссылку, чтобы просмотреть обширный набор рабочих листов по квадратным уравнениям. Решите квадратные уравнения, разложив на множители, заполнив квадратные, квадратные формулы или методы извлечения квадратного корня. Найдите сумму и произведение корней. Проанализируйте природу корней.

Рабочие листы уравнения абсолютного значения

Используйте эти рабочие листы, чтобы научить своих студентов абсолютному значению целых чисел. Этот модуль включает в себя такие упражнения, как вычисление выражения абсолютного значения для определенного значения, таблицы ввода и вывода, построение графика функции абсолютного значения и решение различных типов уравнений абсолютного значения.

Рабочие листы систем уравнений

Решите эти системы уравнений методом исключения или замены. Уравнения содержат две или три переменные.Уравнение с двумя переменными представляет собой прямые линии, тогда как уравнения с тремя переменными представляют собой плоскость.

Алгебра в 5-м классе — одношаговые уравнения Алгебра Обзор Дистанционное обучение

Алгебра одношаговое упражнение для обзора уравнений. Эта Math Mystery — это увлекательное занятие по изучению одношаговых уравнений со сложением, вычитанием, умножением и делением. Привлекайте и мотивируйте своих учеников на математике с помощью этого уникального кейса! Легкая подготовка! Просто распечатайте и решите! Или откажитесь от бумаги с новой опцией Google Docs, которую вы загружаете.

НОВИНКА — Обновление дистанционного обучения: Я добавил документ Word в папку, содержащую ссылку на документ Google, чтобы поделиться этим ресурсом со своими учениками через Google Класс или Диск. Части страниц можно редактировать, так что учащиеся могут закончить работу, не распечатывая страницы. Обратите внимание, что вам нужно будет сделать копию Google Slides на свой диск, прежде чем вы сможете редактировать.

FUN (необязательно) Video Hook для вовлечения ваших учеников в это задание по математике. НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ ПРОСМОТРЕТЬ ВИДЕО КРЮК

НОВИНКА — В пакет добавлен список редактируемых преобразований. Таким образом, вы можете изменить параметры списка и изменить загадочный исход. Есть также два альтернативных готовых списка, которые вы можете использовать вместо них.

Студенты должны использовать свои навыки алгебры, чтобы узнать, во что инопланетяне планируют превратить все человечество!

Есть 5 подсказок, которые нужно взломать, чтобы разгадать загадку:

Подсказка 1: Решить уравнения с сложением

Подсказка 2: Решить уравнения с вычитанием

Подсказка 3: Решить уравнения с умножением

Подсказка 4: Решить смешанные уравнения (Сложение , Вычитание, умножение)

Clue 5: Solve Equations with Division

Pack также включает в себя лист с загадочной информацией, листы ответов, руководство по выбору и награды.

Отличное занятие для обзора алгебры.

Список всех математических тайн ЗДЕСЬ

———————————— ————————————————— —

ПОПРОБУЙТЕ ПОЛНОСТЬЮ БЕСПЛАТНУЮ МАТЕМАТИЧЕСКУЮ ТАИНУ ЗДЕСЬ (ДИФФЕРЕНЦИРОВАННЫЕ НАБОРЫ УРОВНЯ 1–6)

Просмотрите диапазон 5-х классов:

>> Загрузите БЕСПЛАТНЫЙ контрольный список по математике для 5-х классов здесь <<

>

> НАЖМИТЕ ЗДЕСЬ, чтобы подписаться на мой магазин <<

————————————- ————————————————— —

миссис Дж.

Книга по математике 5A для учащихся 5-х классов

Обязательно возьмите руководства, потому что они милые, интересные, очаровательные и чудесные, и они заставят вашего ребенка влюбиться в математику (даже если он уже любит математику)

I Меня действительно впечатлила тщательность и детализация не только математического мышления, но и визуальных эффектов, юмора и сюжета.

… реакция, которую я видел, была действительно потрясающей. Что, кажется, выделяется … в этих книгах не преуменьшает объем работы и не разговаривает с ребенком свысока.

… каждый раз, когда ученики видят меня, они очень взволнованы и спрашивают, не «День Академии зверей». Им нравятся персонажи, им нравится юмор в Путеводителе, и они упорно стараются заполнить как можно больше материала из Практического пособия.

Моему сыну очень нравится эта программа … никогда не думал, что мне придется посоветовать ему сделать перерыв в математике, чтобы заняться другой работой.

Я почти уверен, что это самые увлекательные книги по математике, с которыми я когда-либо сталкивался, и они справляются с этим, совсем не разбавляя содержание (на самом деле, как раз наоборот).

Самое лучшее для меня то, что мои дети могут читать руководство и выполнять практическую работу самостоятельно, но я знаю, что им бросают вызов.

Слышать, как мой крошечный 6-летний ребенок объясняет, как возводить в квадрат числа, оканчивающиеся на 5, было потрясающе … Благодаря Beast Academy у меня теперь есть возможность наблюдать, как лицо моего сына загорается, когда я говорю, что пришло время для математики.

Beast Academy стала известна как «увлекательная математика» — полная сложных задач, которые заставляли их думать просто, чтобы усердно заниматься вычислениями.

Обожаю ваши книги! Это лучшее, что когда-либо случалось с математикой. Лиззи — мой любимый персонаж, потому что она очень похожа на меня. Она такая милая, нежная и не любит драконов!

Я упомянул, что [мой сын] почти готов перейти на следующий уровень Академии Зверей. Сразу же [он] пошел и получил его, чтобы мы могли сразу начать, а затем попросил, чтобы я продолжал заниматься после первого раздела.

Обязательно возьмите путеводители, потому что они милые, интересные, очаровательные и чудесные, и они заставят вашего ребенка влюбиться в математику (даже если он уже любит математику)

5-классные школьные математические задачи, которые так сложны, Вы удивитесь, как вы попали в среднюю школу

Математическая задача часто может выглядеть очень простой…. прежде чем вы сядете, чтобы заняться этим, и обнаружите, что не знаете, как это решить. Кроме того, есть задачи, которые заставят вас почувствовать себя математическим гением, когда вы решите их за 2 секунды — только для того, чтобы найти ваш ответ WAAAAY выключен. Вот почему математические задачи все время становятся вирусными, потому что они одновременно просты и в то же время не являются.

Вот пять проблем, подтверждающих эту точку зрения:

1. Что означает вопросительный знак?

Начнем с очень простого. Сможете ли вы решить, под каким числом должен стоять вопросительный знак?

Ответ: 6.

Объяснение: Сумма всех строк и столбцов должна составлять 15.

2. Летучая мышь и мяч

Бита и мяч в сумме стоят один доллар десять центов. Бита стоит на доллар дороже мяча. Сколько стоит мяч?

Getty Images

Вы ответили 10 центов? Это было бы неправильно !

Ответ: Мяч стоит 5 центов.

Пояснение: Когда вы читали математическую задачу, вы, вероятно, видели, что бита и мяч стоили в общей сложности доллар и десять центов, и когда вы обработали новую информацию о том, что бита на доллар больше, чем мяч, ваш мозг подскочил. к выводу, что мяч был десять центов, не выполняя математических расчетов. Но ошибка состоит в том, что когда вы действительно производите вычисления, разница между 1 и 10 центами составляет 90 центов, а не 1 доллар. Если вы потратите время на то, чтобы на самом деле посчитать, единственный способ для летучей мыши быть на доллар больше, чем мяч, И общая стоимость равна 1 доллару.10 — бейсбольная бита стоит 1,05 доллара, а мяч — 5 центов.

3. Переходить или не переходить

Представьте, что вы находитесь на игровом шоу, и вам предоставляется выбор из трех дверей: за одной дверью миллион долларов, а за двумя другими — ничего. Вы выбираете дверь №1, и ведущий, который знает, что за дверями, открывает другую дверь, скажем №3, и за ней ничего нет. Затем он говорит вам: «Вы хотите придерживаться своего выбора или переключиться?»

Итак, что лучше для вас — придерживаться своего первоначального выбора или поменять свой выбор?

Getty Images

Большинство людей думает, что выбор не имеет значения, потому что у вас есть 50/50 шансов получить приз независимо от того, переключитесь вы или нет, поскольку осталось две двери, но на самом деле это не так!

Ответ: Всегда нужно менять свой выбор!

Объяснение: Когда вы впервые выбираете одну из трех дверей, у вас был 1 из 3 шансов выбрать дверь с призом за ней, что означает, что у вас был 2 из 3 шансов выбрать пустую дверь.Люди ошибаются здесь, когда думают, что, поскольку в игре осталось всего две двери, у вас есть 50% шанс, что ваш первый выбор был правильным. На самом деле ваши шансы никогда не менялись.

По-прежнему существует вероятность 1 из 3, что вы выбрали правильную дверь, и вероятность 2 из 3, что вы выбрали пустую дверь, что означает, что, когда хозяин открыл одну из пустых дверей, он исключил один из НЕПРАВИЛЬНЫХ вариантов и вероятность того, что приз за последней закрытой дверью по-прежнему 2 из 3 — вдвое больше, чем шансы, что вы выбрали правильную дверь вначале.Итак, в основном, переключая свой выбор двери, вы делаете ставку на 2 из 3 шансов, что сначала вы выбрали не ту дверь.

Конечно, вы не гарантированно выиграете, если переключитесь, но если вы будете играть в игру снова и снова, вы выиграете в 2/3 случаев, используя этот метод!

Все еще не уверены? Пусть гениальный профессор математики Калифорнийского университета в Беркли Лиза Голдберг еще лучше объяснит это с помощью набора диаграмм!

Этот контент импортирован с YouTube. Вы можете найти тот же контент в другом формате или найти дополнительную информацию на их веб-сайте.

4. Проблема PEMDAS

Когда вы решите эту, казалось бы, простую задачу, какой ответ вы получите?

Массы раскололись по поводу ответа на этот вопрос. Некоторые люди ПОЛОЖИТЕЛЬНЫ, ответ — 1, а некоторые абсолютно уверены, что ответ — 9.

Ответ: Победитель — 9!

Объяснение: В удобном правиле порядка операций, которое вы выучили в начальной школе, PEMDAS, говорится, что вы должны решать проблему, перебирая круглые скобки, затем экспоненты, умножение и деление, а затем добавление и вычитание.Но суть PEMDAS в том, что некоторые люди интерпретируют его по-разному, и в этом заключается противоречие, стоящее за этой проблемой.

Некоторые люди думают, что все, что касается скобок, должно быть решено ПЕРВЫМ. Это означает, что они упрощают задачу следующим образом: 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) = 6 ÷ 6 = 1.

Но то, что число касается скобок, не означает, что оно должно быть умножено перед делением, которое находится слева от него. PEMDAS предлагает решить все, что находится в круглых скобках, затем в экспонентах, а затем все умножение и деление слева направо в том порядке, в котором обе операции появляются (это ключ).Это означает, что как только вы решите все внутри скобок и упростите экспоненты, вы будете идти слева направо, несмотря ни на что. Это означает, что проблема фактически должна быть решена следующим образом: 6 ÷ 2 (1 + 2) = 6 ÷ 2 * (1 + 2) = 6 ÷ 2 * 3 = 3 * 3 = 9.

5. Проблема с кувшинками

В озере есть куст кувшинок. Каждый день нашивка увеличивается в размерах вдвое. Если заплатке потребуется 48 дней, чтобы покрыть все озеро, сколько времени потребуется, чтобы заплатка покрыла половину озера?

Getty Images

Заманчивый ответ — 24, но вы ошибаетесь, если это ваш окончательный ответ!

Ответ: Пятно на 47 день достигнет половины размера озера.

Пояснение: При всех разговорах об удвоении и половинках ваш мозг приходит к выводу, что для решения проблемы, когда кувшинок покрывает половину озера, все, что вам нужно сделать, это разделить количество дней, которое потребовалось для заполнения. озеро (48) пополам. Это понятно, но неправильно.

Проблема говорит, что патч УДВАИВАЕТСЯ в размере каждый день, что означает, что в любой день патч лилии был вдвое меньше, чем накануне. Таким образом, если пятно достигает размера озера на 48-й день, это означает, что кувшинок был вдвое меньше озера на 47-й день.

Ноэль Дево
Редактор развлечений
Когда я не запираюсь в своей комнате из-за совершенно непродуктивного запоя Netflix или из-за того, что Tumblr преследует Тимоти Шаломе, я ищу потрясающие новости о знаменитостях, которые понравятся читателям Seventeen!

Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты. Вы можете найти больше информации об этом и подобном контенте на пианино.io

Решение линейных уравнений | Уравнения и неравенства

Упражнение 4.1

\ begin {align *}
2г — 3 & = 7 \\
2л & = 10 \\
y & = 5
\ end {выровнять *}

\ begin {align *}
2c & = c — 8 \\
c & = -8
\ end {выровнять *}

\ begin {align *}
3 & = 1 — 2c \\
2c & = 1 — (3) \\
2c & = -2 \\
c & = \ frac {-2} {2} \\
& = -1
\ end {align *}

\ begin {align *}
4b +5 & = -7 \\
4b & = -7 — (5) \\
4b & = -12 \\
b & = \ frac {-12} {4} \\
& = -3
\ end {align *}

\ begin {align *}
-3y & = 0 \\
у & = 0
\ end {выровнять *}

\ begin {align *}
16л + ​​4 & = -10 \\
16лет & = -14 \\
y & = — \ frac {14} {16} \\
& = — \ frac {7} {8}
\ end {выровнять *}

\ begin {align *}
12лет + 0 & = 144 \\
12лет & = 144 \\
y & = 12
\ end {выровнять *}

\ begin {align *}
7 + 5л & = 62 \\
5лет & = 55 \\
y & = 11
\ end {выровнять *}

\ (55 = 5x + \ frac {3} {4} \)

\ begin {align *}
55 & = 5x + \ frac {3} {4} \\
220 & = 20х + 3 \\
20x & = 217 \\
х & = \ frac {217} {20}
\ end {выровнять *}

\ begin {align *}
5х & = 2х + 45 \\
3x & = 45 \\
х & = 15
\ end {выровнять *}

\ begin {align *}
23х — 12 & = 6 + 3х \\
20x & = 18 \\
x & = \ frac {18} {20} \\
& = \ frac {9} {10}
\ end {выровнять *}

\ (12 — 6x + 34x = 2x — 24 — 64 \)

\ begin {align *}
12 — 6x + 34x & = 2x — 24 — 64 \\
12 + 28x & = 2x — 88 \\
26x & = -100 \\
x & = — \ frac {100} {26} \\
& = — \ frac {50} {13}
\ end {выровнять *}

\ (6x + 3x = 4-5 (2x — 3) \)

\ begin {align *}
6x + 3x & = 4-5 (2x — 3) \\
9x & = 4 — 10x + 15 \\
19x & = 19 \\
х & = 1
\ end {выровнять *}

\ begin {align *}
18 — 2р & = р + 9 \\
9 & = 3п \\
p & = 3
\ end {выровнять *}

\ (\ dfrac {4} {p} = \ dfrac {16} {24} \)

\ begin {align *}
\ frac {4} {p} & = \ frac {16} {24} \\
(4) (24) & = (16) (p) \\
16p & = 96 \\
p & = 6
\ end {выровнять *}

\ begin {align *}
— (- 16 — п) & = 13п — 1 \\
16 + п & = 13п — 1 \\
17 & = 12п \\
p & = \ frac {17} {12}
\ end {выровнять *}

\ begin {align *}
3f — 10 & = 10 \\
3f & = 20 \\
f & = \ frac {20} {3}
\ end {выровнять *}

\ begin {align *}
3f + 16 & = 4f — 10 \\
f & = 26
\ end {выровнять *}

\ (10f + 5 = -2f -3f + 80 \)

\ begin {align *}
10f + 5 & = -2f — 3f + 80 \\
10f + 5 & = -5f + 80 \\
15f & = 75 \\
f & = 5
\ end {выровнять *}

\ begin {align *}
8 (ф — 4) & = 5 (ф — 4) \\
8f — 32 & = 5f — 20 \\
3f & = 12 \\
f & = 4
\ end {выровнять *}

\ begin {align *}
6 & = 6 (f + 7) + 5f \\
6 & = 6f + 42 + 5f \\
-36 & = 11f \\
f & = — \ frac {36} {11}
\ end {выровнять *}

\ begin {align *}
-7x & = 8 (1 — х) \\
-7x & = 8 — 8x \\
х & = 8
\ end {выровнять *}

\ (5 — \ dfrac {7} {b} = \ dfrac {2 (b + 4)} {b} \)

\ begin {align *}
5 — \ frac {7} {b} & = \ frac {2 (b + 4)} {b} \\
\ frac {5b — 7} {b} & = \ frac {2b + 8} {b} \\
5b — 7 & = 2b + 8 \\
3b & = 15 \\
b & = 5
\ end {выровнять *}

\ (\ dfrac {x + 2} {4} — \ dfrac {x — 6} {3} = \ dfrac {1} {2} \)

\ begin {align *}
\ frac {x + 2} {4} — \ frac {x — 6} {3} & = \ frac {1} {2} \\
\ frac {3 (x + 2) — 4 (x — 6)} {12} & = \ frac {1} {2} \\
\ frac {3x + 6 — 4x + 24} {12} & = \ frac {1} {2} \\
(-x + 30) (2) & = 12 \\
-2x + 60 & = 12 \\
-2x & = -48 \\
х & = 24
\ end {выровнять *}

\ (1 = \ dfrac {3a — 4} {2a + 6} \)

Обратите внимание, что \ (a \ neq — -3 \)

\ begin {align *}
1 & = \ frac {3a — 4} {2a + 6} \\
2а + 6 & = 3а — 4 \\
а & = 10
\ end {выровнять *}

\ (\ dfrac {2-5a} {3} — 6 = \ dfrac {4a} {3} +2 — a \)

\ begin {align *}
\ frac {2-5a} {3} — 6 & = \ frac {4a} {3} +2 — a \\
\ frac {2-5a} {3} — \ frac {4a} {3} + a & = 8 \\
\ frac {2-5a — 4 a + 3a} {3} & = 8 \\
2 — 6а & = 24 \\
6а & = -22 \\
a & = — \ frac {22} {6}
\ end {выровнять *}

\ (2 — \ dfrac {4} {b + 5} = \ dfrac {3b} {b + 5} \)

Примечание \ (b \ neq -5 \)

\ begin {align *}
2 — \ frac {4} {b + 5} & = \ frac {3b} {b + 5} \\
2 & = \ frac {3b + 4} {b + 5} \\
2b + 10 & = 3b + 4 \\
b & = 6
\ end {выровнять *}

\ (3 — \ dfrac {y — 2} {4} = 4 \)

\ begin {align *}
3 — \ frac {y — 2} {4} & = 4 \\
— \ frac {y — 2} {4} & = 1 \\
-у + 2 & = 4 \\
y & = -2
\ end {выровнять *}

\ (\ text {1,5} x + \ text {3,125} = \ text {1,25} x \)

\ begin {align *}
\ text {1,5} x + \ text {3,125} & = \ text {1,25} x \\
\ text {1,5} x — \ text {1,25} x & = — \ text {3,125} \\
\ text {0,25} x & = — \ text {3,125} \\
х & = — \ текст {12,5}
\ end {выровнять *}

\ (\ текст {1,3} (\ текст {2,7} х + 1) = \ текст {4,1} — х \)

\ begin {align *}
\ text {1,3} (\ text {2,7} x + 1) & = \ text {4,1} — x \\
\ text {3,51} x + \ text {1,3} & = \ text {4,1} — x \\
\ text {4,51} x & = \ text {2,8} \\
x & = \ frac {\ text {2,8}} {\ text {4,51}} \\
& = \ frac {280} {451}
\ end {выровнять *}

\ (\ текст {6,5} х — \ текст {4,15} = 7 + \ текст {4,25} х \)

\ begin {align *}
\ text {6,5} x — \ text {4,15} & = 7 + \ text {4,25} x \\
\ text {2,25} x & = \ text {11,15} \\
x & = \ frac {\ text {11,15}} {\ text {2,25}} \\
& = \ frac {\ text {1 115}} {225} \\
& = \ frac {223} {45}
\ end {выровнять *}

\ (\ frac {1} {3} P + \ frac {1} {2} P — 10 = 0 \)

\ begin {align *}
\ frac {1} {3} P + \ frac {1} {2} P — 10 & = 0 \\
\ frac {2 + 3} {6} P & = 10 \\
5П & = 60 \\
P & = 12
\ end {выровнять *}

\ (1 \ frac {1} {4} (x — 1) — 1 \ frac {1} {2} (3x + 2) = 0 \)

\ begin {align *}
1 \ frac {1} {4} (x — 1) — 1 \ frac {1} {2} (3x + 2) & = 0 \\
\ frac {5} {4} x — \ frac {5} {4} — \ frac {3} {2} (3x) — \ frac {3} {2} (2) & = 0 \\
\ frac {5} {4} x — \ frac {5} {4} — \ frac {9} {2} x — \ frac {6} {2} & = 0 \\
\ frac {5 — 18} {4} x + \ frac {-5 — 12} {4} & = 0 \\
\ frac {-13} {4} x & = \ frac {17} {4} \\
-13x & = 17 \\
х & = — \ frac {17} {13}
\ end {выровнять *}

\ (\ frac {1} {5} (x- 1) = \ frac {1} {3} (x-2) + 3 \)

\ begin {align *}
\ frac {1} {5} (x- 1) & = \ frac {1} {3} (x-2) + 3 \\
\ frac {1} {5} x- \ frac {1} {5} & = \ frac {1} {3} x- \ frac {2} {3} + 3 \\
— \ frac {1} {5} + \ frac {2} {3} — 3 & = \ frac {2} {15} x \\
— \ frac {38} {15} & = \ frac {2} {15} x \\
х & = — \ frac {38} {2} \\
х & = -19
\ end {выровнять *}

\ (\ dfrac {5} {2a} + \ dfrac {1} {6a} — \ dfrac {3} {a} = 2 \)

\ begin {align *}
\ frac {5} {2a} + \ frac {1} {6a} — \ frac {3} {a} & = 2 \\
\ frac {5 (3) + 1-3 (6)} {6a} & = 2 \\
\ frac {15 + 1 — 18} {6a} & = 2 \\
\ frac {-2} {6a} & = 2 \\
-2 & = 12а \\
а & = — \ frac {1} {6}
\ end {выровнять *}

Номер 4 класса

Расширить понимание эквивалентности дробей и заказать

4.NF.A.1 Объяснить
почему дробь a / b эквивалентна дроби (nxa) / (nxb) при использовании
модели визуальной фракции, обращая внимание на то, как количество и размер
части различаются, хотя сами две фракции одинаковы
размер. Используйте этот принцип, чтобы распознавать и генерировать эквивалентные дроби.

Постройте дробную стену
Эквивалентные дроби: домино

Также включен в математических центров четвертого класса

Эквивалентные дроби на сетке умножения Эквивалентные дроби: установка эквивалентной дроби модели RollIs it Equivalent?

4.NF.A.2 Сравните две дроби с разными числителями и разными знаменателями, например путем создания общих знаменателей или числителей, или путем сравнения с эталонной дробью, такой как ½. Признайте, что сравнения действительны только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнений при помощи символов>, = или <. и обосновать выводы, например, используя модель визуальной фракции.

Доли дня рождения
Кто больше ел?

Также включен в математических центров четвертого класса

Сложение фракций с помощью шаблонных блоков Проблемы со смыслом или бессмыслицей Плитка шоколада Питера

b.Разлагайте дробь на сумму дробей с одним и тем же знаменателем более чем одним способом, записывая каждое разложение с помощью уравнения. Обоснуйте разложение, например, используя визуальную модель дроби. Примеры: 3/8 = 1/8 + 1/8 + 1/8; 3/8 = 1/8 + 2/8; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8

D eСоставьте фракцию
Pizza Share

г. Складывать и вычитать смешанные числа с одинаковыми знаменателями, например, заменяя каждое смешанное число эквивалентной дробью и / или используя свойства операций и взаимосвязь между сложением и вычитанием.

Сложить и сравнить: смешанные числа

Также включен в математических центров четвертого класса

Проблемы со словами: сложение и вычитание смешанных чисел Переименование дробей больше единицы Вычитание и сравнение: смешанные числа

d. Решайте задачи со словами, включающие сложение и вычитание дробей, относящихся к одному и тому же целому и имеющих одинаковые знаменатели, например, используя визуальные модели дробей и уравнения для представления проблемы.

Вычесть и сравнить

Также включен в математических центров четвертого класса

Задачи со словами: сложение и вычитание дробей Запись и решение: сложение и сравнение дробей

4.NF.B.4 Применяйте и расширяйте предыдущие представления о умножении, чтобы умножить дробь на целое число:
a. Дробь a / b следует понимать как кратное 1 / b. Например, используйте модель визуальной дроби, чтобы представить 5/4 как произведение 5 x (1/4), записав вывод уравнением 5/4 = 5 x (1/4).

Фракции треугольника

Также включен в математических центров четвертого класса

Умножение единичной дроби на целое число Четырехугольные дроби

b.Поймите, что кратное a / b является кратным 1 / b, и используйте это понимание для умножения дроби на целое число.