Как решать логические задачи на собеседованиях — Work.ua

Если вы еще не сталкивались с головоломками на собеседованиях, то вполне возможно, что все впереди. Какие же головоломки используют современные компании при найме сотрудников, и как научиться их решать?

В предыдущей статье Work.ua, посвященной задачам на логику, «Вопросы-головоломки на собеседованиях с ответами» (часть 1, часть 2) мы собрал самые популярные вопросы-головоломки и подготовили ответы и рекомендации к ним. Теперь давайте углубимся в эту тему. Писатель, колумнист The Economist и New York Times Уильям Паундстоун в своей книге «Найти умного» описал, как при помощи эффективного творческого и аналитического мышления можно отыскать ответы на самые нестандартные вопросы.

Если говорить о решении головоломок как особом жанре, то нельзя не признать, что он условен и стилизован в не меньшей степени, чем японский театр кабуки. Если вы не понимаете характерных для жанра кабуки идиом, вам будет трудно понять происходящее. То же относится и к «задачам без ответа», предложениям спроектировать что-либо и т. д. Как и другие интересующие нас способности, способность решать головоломки — это сочетание врождённых задатков и приобретённых навыков. На первый взгляд вопросы кажутся бесконечно разнообразными, но если вы присмотритесь внимательнее, то поймёте, что в большинстве головоломок используется небольшой набор одних и тех же когнитивных трюков, особенно часто — эффект дизъюнкции и сбивающая вас с толку формулировка проблемы. Знания об этом могут вам помочь.

Монолог или диалог

Самые трудные вопросы, применяющиеся в интервью, требуют, чтобы вы объяснили ваш подход к решению проблемы и потом дали правильный или подходящий ответ. Нужно решить, требует данный вопрос монолога или диалога. Логические головоломки обычно подразумевают монолог. Вам намеренно дают ограниченное количество информации и ожидают, что вы сами найдёте ответ. Вам трудно в этом случае получить от интервьюера дополнительную информацию, поскольку её намеренно вам не сообщили.

Во многих случаях, когда задаются вопросы о разработке дизайна и анализе кейсов (конкретных ситуациях), интервьюеры ожидают, что вы попросите дополнительную информацию. Вам понизят оценку, если вы этого не сделаете. Для вопросов о дизайне («разработайте дизайн полки для специй») нет единственно правильного ответа. Умные кандидаты понимают, что дизайн — это трудная последовательность компромиссов.

Интервьюер обращает внимание, задумываетесь ли вы о том, кто будет пользоваться этой полочкой и где именно она будет находиться. Он готов отвечать, и вы в результате получите массу важной дополнительной информации. Такая беседа может продолжаться долго.

Некоторые «открытые вопросы» («Какой из пятидесяти штатов США вы бы упразднили?») похожи на пятна Роршаха, которые используют в психологических проективных тестах, — люди смотрят на эти пятна, и каждый видит в них что-то своё. Открытые вопросы намеренно неструктурированны. Для всех типов вопросов, но особенно для этих, цель вопроса — завязать получасовую беседу. Заключение о том, насколько умён данный человек, делается на основе этой беседы. Хорошим планом будет предположить, что нужен диалог с интервьюером, если только для вас неочевидно, что данный вопрос — это обычная логическая головоломка. Под диалогом я подразумеваю, что, вероятно, говорить в основном будете вы, но при этом вы можете также и задавать интервьюеру умные вопросы.

Первая мысль ошибочна

Когда речь идёт о головоломках и загадках, первый потенциальный ответ, который приходит в голову разумному человеку, — это обычно неправильный ответ. Если бы это было не так, данный вопрос не стоило бы называть головоломкой. Подобно оптическим иллюзиям, или трюкам фокусников, или уловкам мошенников, головоломки рассчитаны на то, что вас собьёт с толку ваш собственный привычный повседневный опыт. Дети — это наиболее скептическая и трудная аудитория для фокусников, люди с некоторыми повреждениями мозга не подвержены оптическим иллюзиям, и мошенникам не удается обжулить абсолютно честного человека. То, что вы не можете «с ходу» решить головоломку, просто означает, что ваш мозг работает нормально, так и должно быть, когда вы их решаете. Многие люди начинают нервничать, если ответ не приходит им в голову немедленно. Лучший способ начать диалог, который ожидается от вас, — это объяснить, почему «очевидное» решение неверно. Это не только позволит прервать молчание, но и послужит отличным средством для того, чтобы понять, в чём проблема.

Забудьте об интегралах

Это относится, конечно, только к логическим головоломкам. Ни одна из распространённых в корпоративных интервью задач не потребует от вас знания интегралов. Если вы думаете, что для решения головоломки нужны более обширные знания, чем те, которыми обладают участники телешоу, подобных «Счастливому случаю» и иже с ним, в каких-то сферах, которые прямо не относятся к той области, где вы хотели бы работать, — скорее всего, вы ошибаетесь. Есть такой тип задач, которые, на первый взгляд, требуют знания интегрального счисления, но на самом деле у них есть простое решение. Всегда старайтесь дать простой ответ. Даже если вы нашли решение при помощи высшей математики, вы можете получить невысокую оценку, так как «за деревьями не видите леса». 

Ищите сложные ответы

Для вопросов с простой, всего в одно предложение, формулировкой — например, «Почему в зеркальном отражении правое и левое меняется местами?» или «Почему пивные банки сужаются вверху и внизу?» — часто требуются длинные и сложные ответы. Позаботьтесь о том, чтобы хорошо продумать эти вопросы. Вы можете получить низкую оценку, если интервьюер решит, что вы упустили что-то важное в вашем ответе. Если короткий вопрос задаётся о дизайне или тестировании («Разработайте дизайн туалетной комнаты для Билла Гейтса»; «Как вы стали бы тестировать лифт?»), то это часто означает, что вы должны попросить дополнительную информацию от интервьюера.

«Безупречно логичные существа» не похожи на людей

Во многих логических головоломках речь идёт о «безупречно логичных существах» (БЛС). Примером могут служить задачи о супружеских изменах в деревне или о пиратах, которым нужно поделить золотые монеты. «Безупречно логичный» — это кодовое слово, которое понятно любителям головоломок, но непонятно тем, кто не входит в их круг. Если вы слышите такую кодовую фразу, это значит, что при решении этой задачи вам нужно забыть практически обо всём, что вы знаете о людской психологии. Вам нужно придерживаться следующих предположений: у БЛС очень простая одномерная мотивация, они озабочены только тем, чтобы получить как можно больше денег, убежать от демона, жёстко следовать какому-либо глупому закону и т. д.

Всё остальное для них неважно. Следовательно, БЛС никогда не оказывают дружеских услуг — каждый из них сам за себя. БЛС никогда не отвлекается, никогда не делает ошибок, никогда ничего не забывает.

Для поступков обычных людей всегда характерна неопределённость. Это значит, что подразумеваемое решение головоломок, в которых действуют БЛС, абсолютно нереалистично. Они обычно формулируются так: A приходит к выводу, что B придёт к выводу, что C придёт к выводу, что D… и т. д. Такое никогда не случится в реальном мире. Вы можете использовать это как подсказку. Когда вы слышите о безупречно логичных существах, то решение почти всегда подразумевает рассуждения БЛС о других БЛС (или вы должны рассуждать так о самих себе, когда решаете задачи, в которых задаётся вопрос: «Что вы станете делать в такой ситуации?»).

Перечисляйте гипотезы

Подумайте о том, что произойдёт, если вы будете последовательно одно за другим отвергать эти предположения. В самых хитрых и сложных головоломках неверные предпосылки и предположения могут выглядеть так естественно, что вы даже вряд ли задумаетесь о них как о предположениях. И всё же стоит попробовать. Просмотрите список и предположите для каждого из них, что верно обратное. Помогает ли это решать задачу? Если вам повезёт, то вы увидите, что есть такое предположение, что, если от него отказаться, задача окажется решаемой. Даже если это вам не поможет и вы не решите задачу, мнение интервьюера о вас улучшится. Он увидит, что вы понимаете роль изменений формулировки проблемы для решения задач.

Подробности  не нужны

Почти всегда то, что мы называем логическими головоломками, использует один и тот же трюк, а именно: большинство людей не может найти решение, потому что считает, что им не хватает для этого информации. Если головоломка — это дизъюнкция, вам неизвестно, что выбрать, одно или другое, и вы не знаете, как найти решение, вам нужно быть готовым методично продумать все возможные варианты и следствия. Предположим, что верен вариант Х — какие вы сможете сделать выводы? Допустим, что это Y — к каким заключениям можно прийти в этом случае? Вы почти всегда обнаружите, что этот способ рассуждения поможет выйти из тупика, и окажется, что вам не нужна для того, чтобы решить задачу, та самая «недостающая информация». Подумайте об этом так: если мост взорван, вам придётся переплыть реку. К счастью, вам никогда не нужно будет плыть очень долго (ведь мосты обычно строятся в самых узких местах рек).

Найдите нетривиальный ответ

Это в особенной степени важно при ответах на открытые вопросы, для которых не существует «правильных ответов». Интервьюеры много раз выслушивали обычные ответы на эти вопросы. Когда Сполски попросил одного из кандидатов на работу в Microsoft разработать дизайн полочки для специй для слепого человека, этот кандидат решил, что для слепого будет удобнее не полочка для специй, расположенная на уровне груди или лица, а выдвижной ящик для специй на уровне пояса. Он считал, что вместо того, чтобы искать полку со специями на ощупь, а потом, подняв руку, пытаться прочесть текст, написанный шрифтом Брайля, гораздо удобнее подойти к кухонному столу, найти нужный ящик, выдвинуть его и спокойно прочесть надписи на крышках баночек со специями, скользнув по ним пальцами. Такое эргономичное решение раньше никто из кандидатов не предлагал.

Также впечатляющим было и то, что кандидат эффективно переформулировал проблему. «Полочка для специй» не обязательно должна быть именно полочкой, если есть основание использовать другой дизайн». Сполски рассказывает: «На основании этого единственного ответа я принял на работу кандидата, который стал одним из лучших менеджеров программ в команде, разрабатывавшей Excel». Есть много примеров, которые убеждают меня в том, что интервьюеры не просто ценят, а, пожалуй, даже чрезмерно ценят оригинальные ответы. Может быть, это связано со скукой. Вы знаете, что некоторые простаки пытаются привлечь внимание работодателей, рассылая очень яркие резюме? Такой приём обычно не работает, но во время интервью творческий и хороший ответ поможет вам выделиться среди других кандидатов. Только позаботьтесь о том, чтобы это был действительно хороший ответ.

---

---

Чтобы оставить комментарий, нужно войти.

простые приемы, которые раз навсегда упростят жизнь, мотивация и с чего начать

Статья посвящена обзору различных способов решения логических задач и сравнению их эффективности. Логические задачи можно решать различными способами.

У каждого из них есть свои достоинства и недостатки.

Узнай стоимость своей работы

Бесплатная оценка заказа!

Поэтому для решения подобного типа задач нужно найти такой способ, который имеет наименьшее количество недостатков, а следовательно, дает уверенность в правильности решения.

На протяжении всех лет обучения в школе, начиная с начальных классов, мы решаем множество задач, в том числе и логических.

Для успешного решения такого типа задач нужно: научиться выделять их общие признаки, выдвигать различные гипотезы, подмечать закономерности, строить цепочки рассуждений, проверять их на истинность, делать выводы.

Существуют разные способы решения логических задач. К ним относят: применение законов алгебры логики, табличный способ, использование рассуждений [4, с. 223].

У каждого способа есть свои достоинства и недостатки. Поэтому для нахождения наиболее эффективного из них, в зависимости от задачных ситуаций, рассмотрим решение задач разными способами и проанализируем эти решения. Под эффективностью понимается большее количество преимуществ решения.

Традиционно к логическим задачам относят задачи на соответствия между множествами [5, с. 67].

Задача 1.Три девочки были в белом, красном и голубом платьях. Их туфли были тех же трёх цветов.

1. Только у Тамары цвет платья и туфель совпали.

Узнай стоимость своей работы

Бесплатная оценка заказа!

2. Валя была в белых туфлях.

3. Ни платье, ни туфли Лиды не были красными.

Определите цвет платья и туфель каждой из девочек [3, с. 197].

Решение.

I способ. С помощью совмещенной таблицы.

Данная задача трехмерная, следовательно, нужно найти соответствия между множествами (имена и туфли, имена и платья, платья и туфли). Для этого используют 3 таблицы, которые затем совмещаются. Таблица заполняется из условий.

Знак «+» ставится тогда, когда выясняется точное соответствие между элементами множеств, знак «-» ставится тогда, когда выясняется несоответствие. Если в какой-то строке малой таблицы получается два знака «-», то в третьей нужно поставить знак «+».

Из условия 2 в таблице ставится знак «+» на пересечении графа «Валя» и «Белые туфли». Также из условия 2 получается, что Валя была в белых туфлях, а туфли Лиды не были красными, следовательно, Лида была в голубых туфлях, а Тамара в красных.

У Тамары цвет туфель и платья совпали по условию 1, а у двух других девочек нет, следовательно, у Вали было голубое платье, а у Лиды белое.

Таблица 1

Таблица соответствия имен и одежды

Белые туфли	Красные туфли	Голубые туфли	Белое платье	Красное платье	Голубое платье
Тамара	— (2)	+	—	—	+ (1)	—
Валя	+(2)	— (2)	— (2)	—	—	+
Лида	— (2)		+ (3)	+	— (3)	—
+	—	—	Голубые туфли
—	+	—	Красные туфли
—	—	+	Белые туфли

Ответ: Тамара – красные туфли, красное платье; Валя – белые туфли, голубое платье; Лида – голубые туфли, белое платье.

IIспособ. С помощью рассуждений.

По условиям задачи туфли Лиды не были красными, а у Вали были белые туфли, значит, красные туфли были у Тамары, а Лиды голубые. Так как у Тамары цвет платья и туфель совпали, то платье у Тамары было красное. У Вали и Лиды цвета не совпадали, значит у Вали было голубое платье, а у Лиды белое.

Ответ: Тамара – красные туфли, красное платье; Валя – белые туфли, голубое платье; Лида – голубые туфли, белое платье.

Оба выше приведенных способа дают результат при решении данной задачи. Решение с помощью таблицы дает наглядность и логичность, что способствует уверенности в правильности ответа, но занимает большое количество времени. Решение с помощью рассуждений занимает меньше времени, но в рассуждениях легко допустить ошибку.

• Задача 2. Выяснить, кто из трёх людей участвовал в преступлении, исходя из двух посылок:
• 1) «Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал»;
• 2) «Если Иванов не участвовал, то Сидоров не участвовал».
• Решение.
• А – Иванов участвовал в преступлении;
• В – Петров участвовал в преступлении;
• С – Сидоров участвовал в преступлении.

Iспособ. С использованием таблицы истинности.

Конструируем формулы, соответствующие 1) и 2) посылке задачи: (В)→С и →. Так как обе посылки истинны, то составим таблицу истинности для конъюнкции полученных формул:

Таблица 2

Таблица истинности

А	В	С
			1		1
		1	1	1
	1		1		1
	1	1	1	1
1				1	1	1
1		1		1	1	1
1	1		1		1
1	1	1	1	1	1	1

Из таблицы видно, что преступление совершил А, то есть Иванов.

I аспособ. С помощью законов алгебры логики.

Снова запишем конъюнкцию формул, выражающих условия задачи. Преобразуем получившуюся формулу, пользуясь законами алгебры логики.

Так как обе посылки верны, то это выражение должно быть истинно. Это возможно только при А = 1, значит преступник – Иванов. Также , следовательно, исключается вариант B= 1, а C= 0, все остальные варианты возможны.

Ответ: исходя из предложенных посылок, можно определить, что Иванов участвовал в преступлении.

IIспособ. Cпомощью рассуждений.

Предположим, что Иванов не участвовал в преступлении, тогда выполняется условия 1 и 2. По условию 2 получается, что Сидоров не участвовал. Получается противоречие. Следовательно, Иванов участвовал, а про остальных нельзя сказать ничего определенного.

Решение данной задачи с помощью таблицы после ее построения сразу дает наглядный ответ. Решая задачу с помощью алгебры логики, наглядный ответ сразу получить сложно, для этого нужно делать определенные выводы. Минусы данного способа в том, что можно легко допустить ошибку, преобразуя формулы. Второй способ занимает меньше времени, но при рассуждениях легко запутаться в высказываниях.

Задача 3. Три одноклассника – Влад, Тимур и Юра встретились спустя 10 лет окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, а страсть третьего – регби.

Юра сказал, что на туризм ему не хватает времени, хотя его сестра – единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги.

У двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.

Определите, кто чем любит заниматься в свободное время, и у кого какая профессия? [5, с. 385]

Решение.

Iспособ. Традиционная таблица. Кроме предложенного выше метода совмещения таблиц можно рассмотреть модификацию различных методов. Задача является трехмерной (множество имен, профессий и хобби), поэтому для ее решения используют кубическую таблицу [1, стр. 99].

Из слов Юры ясно, что он не увлекается туризмом и он не врач. Из слов врача следует, что он турист.

Так как у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен, то следует что буква «а», присутствующая в слове «врач», указывает на то, что врач не Влад, следовательно, врач – Тимур. Второй из друзей, в названиях профессии и увлечения которого не встречается ни одна буква его имени является Юра.

В имени Тимур встречаются буквы «т» и «р», которые присутствуют в слове «туризм». Юра не юрист и не регбист, так как в его имени содержаться буквы «ю» и «р».

Из получившихся предположений можно составить следующую кубическую таблицу:

Таблица 3

Таблица соответствия имен, профессии и хобби

IIспособ. Нестандартная таблица.

Из высказывания Юры следует, что он не врач и не турист.

А из дальнейшего текста врач является туристом. Это отражает таблица.

Таблица 4

Таблица соответствия условий задачи

Имя	Юра
Профессия	врач
Увлечение	туризм

Далее из условия с буквами следует, что врач не Влад, следовательно, врач – Тимур; Юра не юрист и не регбист, так как в его имени содержаться буквы «ю» и «р». Можно составить следующую таблицу.

Таблица 5

Таблица соответствий условий задачи

Имя	Юра	Тимур	Влад
Профессия	физик	врач	юрист
Увлечение	бег	туризм	регби

Ответ:Влад – юрист и регбист, Тимур – врач и турист, Юра – физик и бегун.

Решая задачи с помощью традиционной и нестандартной таблиц, сразу после построения можно получить наглядный ответ. Нестандартная таблица удобная в применении, в ней наименьшая вероятность допустить ошибки. Минусы традиционной кубической таблицы в том, что для решения необходимо наличие опыта в заполнении такого рода таблиц.

Из приведенного выше анализа решения логических задач можно дать следующие рекомендации по применению того или иного способа:

1.                  Табличный метод и его модификации (кубическая и совмещенные таблицы, таблица соответствий) дают наглядность, логичность, прозрачность всех шагов рассуждений, следовательно, могут быть рекомендованы для решения задач любого уровня сложности.

2.                  Метод рассуждений можно рекомендовать только для решения простых задач с малым количеством объектов и множеств, так как при усложненном условии легко допустить ошибки, следовательно, он не дает уверенности в правильности решения.

3.                  Применение законов алгебры логики требуется осуществление перевода на язык математической логики, то есть выделяют элементарные высказывания и составляют более сложные в соответствие с условиями задачи.

Следовательно, для применения этого способа необходимы знания законов Булевой алгебры и наличие опыта преобразований выражений и составлении таблицы.

В то же время данный способ дает строгость и обоснованность полученных результатов.

Литература:

1. Бизам Д, Герцег Я. Многоцветная логика. – М.: Мир,1978. – 436 с.

2. Беррандо М. Занимательные задачи. – М.: Мир, 1983. – 457 с

3. Горбачев Н. Сборник олимпиадных задач по математике. – М: МЦНМО, 2004. – 560 с.

4. Игошин В.И. Математическая логика и теория алгоритмов. – 2-е изд. – М.: Изд. центр «Академия», 2008. – 448 с.

5. Сангалова М.Е. Курс лекций по математической логике. – Арзамас: Арзамас. гос. пед. ин-т, 2006. – 98 с.

Источник: https://moluch.ru/archive/80/13868/

Логические и математические задачи с собеседований

Разомнем мозг! В этой статье собраны логические и математические задачи, которые нередко встречаются на собеседованиях и могут попасться вам.

Основные проблемы, которые часто возникают в процессе интервью, не в отсутствии опыта или подготовки.

Даже по-настоящему опытный разработчик может легко «споткнуться» о  решение какой-нибудь хитро скроенной задачки. Поэтому мы поговорим не о том, как составлять резюме и выгодно презентовать себя.

Фокусируемся на решении нетривиальных задач, которые включают в себя решение логического и/или математического характера.

«Крепкий орешек»

Помните загадку из третьего фильма? Если нет, то вспоминайте, так как этим вопросом любят потчевать в Microsoft.

Задача:

Есть 2 пустых ведра: первое объемом 5 л, второе — 3 л. Как с их помощью отмерить 4 литра воды?

[spoiler title=’Ответ:’ style=’default’ collapse_link=’true’]Сперва наполните пятилитровое ведро.

Далее перелейте из него воду в трехлитровое так, чтобы в пятилитровом осталось 2 л воды (полностью заполнив трехлитровое). Вылейте из меньшего ведра всю воду и перелейте в него оставшиеся в большем 2 л.

Снова наполните пятилитровое и перелейте один литр в трехлитровое (оно как раз заполнится): так в большем ведре останется 4 л воды.[/spoiler]

Баночки с таблетками

Задача:

Есть двадцать баночек с таблетками. Почти во всех таблетки весят по 1 г, и только в одной — по 1,1 г. У нас есть точные весы, с помощью которых нужно определить баночку, каждая таблетка которой весит 1,1 г. Как это сделать, если можно взвесить только 1 раз?

[spoiler title=’Ответ:’ style=’default’ collapse_link=’true’]Давайте абстрагируемся и представим, что у нас 2 баночки, в одной из которых таблетки более тяжелые. Даже если мы поставим их обе на весы, мы ничего не узнаем.

Но если мы достанем из одной баночки 1 таблетку, из другой — 2 и положим их на весы — вот тогда-то и откроется истина 🙂 В данном случае вес будет 2,1 или 2,2 (в зависимости от того, сколько каких таблеток мы взяли). Так и определяем нашу баночку.

Вернемся к задаче. Из каждой баночки нужно доставать разное количество таблеток. То есть из первой баночки 1 таблетку, из второй — 2, из третьей — 3 и так далее. Если бы каждая таблетка весила по 1 г, общий вес составил бы 210 г. Но поскольку в одной из баночек таблетки тяжелее, вес будет больше. Для определения нужной баночки просто воспользуемся формулой:

№ тяжелой баночки = (вес — 210) * 10[/spoiler]

Свидание

Парень и девушка договорились встретиться ровно в 21:00. Проблема в том, что у обоих часы идут неправильно. У девушки часы спешат на 2 мин., но она думает, что они на 3 мин. отстают. У парня же часы отстают на 3 мин., но он считает, что они на 2 мин. спешат. Кто из пары опоздает на свидание?

Книга содержит N страниц, которые пронумерованы стандартно: от 1 до N. Если сложить количество цифр (не сами числа), что содержатся в каждом номере страницы, выйдет 1095. Так сколько в книге страниц?

[spoiler title=’Ответ:’ style=’default’ collapse_link=’true’]Каждый номер страницы имеет цифру на месте единицы, так что есть N цифр, расположенных на месте единицы.

А вот после 9 начинаются двухзначные числа, и нам нужно добавить N-9 цифр. То же самое с трехзначными, которые начинаются после 99: добавляем N-99 цифр. Продолжать нет смысла, так как сумма не предполагает более 999 страниц.

Получаем следующую формулу:

• N + (N-9) + (N-99) = 1095
• Далее просто решаем:
• 3N — 108 = 1095
• 3N = 1203

Посчитать в уме

Задача:

Математические задачи на собеседованиях бывают и довольно простыми, но зачастую только на первый взгляд. Попробуйте в уме разделить 30 на 1/2 и прибавить 10. Каким будет результат?

1. Первое решение, которое обычно приходит на ум, ошибочно:
2. 30/2 + 10 = 25
3. Если мы делим на дробь, ее нужно переворачивать и производить умножение:
4. 30*2 + 10 = 70

Цифра 3

Задача:

Сколько целых чисел в диапазоне 1-1000 вмещают в себя цифру 3? При подсчете нельзя пользоваться компьютером.

В числе должна быть по крайней мере одна тройка, чтобы его учесть. Например, числа в диапазоне 300-399 дают нам сразу 100 чисел. Еще 10 мы получаем от 30-39. То же касается 130-139, 230-239, etc.

Десяток этих чисел уже был учтен при подсчете 330-339, так что убираем его и получаем:

100 + 90 = 190

А еще есть группа чисел (их 100), которые заканчиваются на тройку: 2-993. Мы исключаем из нее такие 10 чисел, как 303, 313 … 393 (они учтены ранее). Получаем еще +90 чисел. У 1/10 из этих 90 на месте десяток также расположилась тройка: 33, 133 … 933. Убираем еще 9, оставляя 81 число.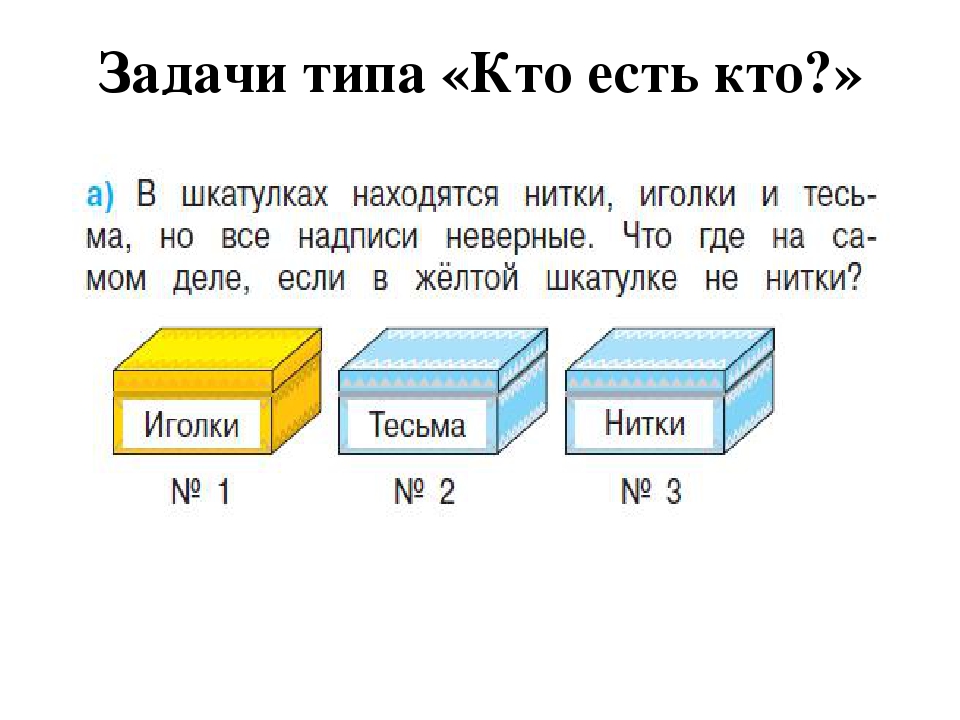 Дальше простая математика:

Ну что, размялись? Надеемся, вам понравились собранные логические и математические задачи. Если этого мало, можете заглянуть сюда + ниже вы найдете еще больше задач, специально подобранных Библиотекой программиста 🙂

Источник: https://proglib.io/p/logical-mathematical-tasks/

Как научить ребенка решать задачи: простые приемы, которые раз навсегда решат проблему

Умение решать задачи необходимо ребенку на протяжение всего обучения, эти приемы помогут научиться решат любые задачи

Школьники решают задачи на протяжении всей учебы. Сначала это задачи по математике, потом идут задачи по алгебре и геометрии, затем присоединяются физика и химия. Несмотря на то, что на первый взгляд кажется, что ничего общего между этими задачами нет, все же в методике их решения очень много общего.

Если ребенок смог в начальной школе освоить решение задач, то используя закономерности, он сможет понять, что в старших классах и при изучении других предметов, в решении задач основные закономерности совпадают.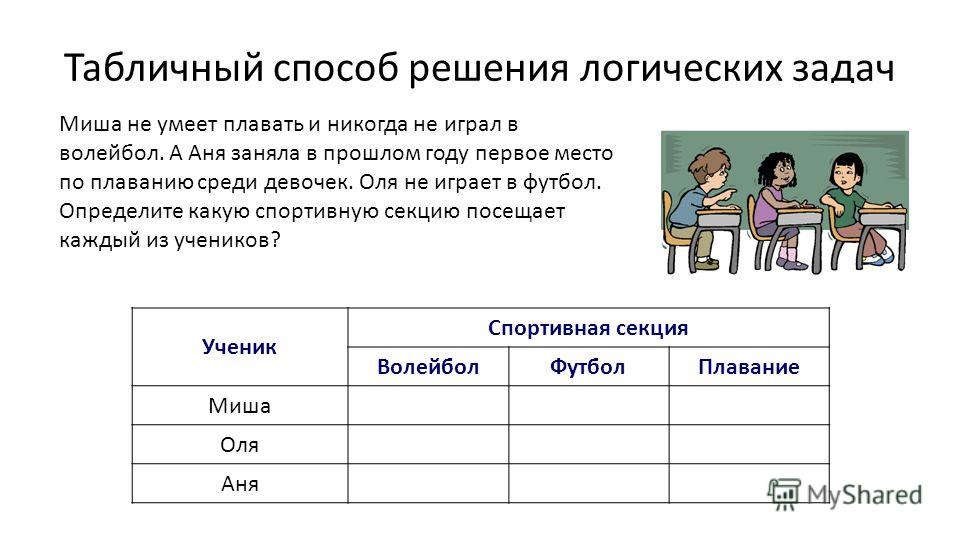

Мотивация

В настоящее время проблема мотивации в обучении детей одна из самых серьезных. Как бы ни было, ребенку важно понимать для чего он изучает тот или иной предмет. С математикой в начальной школе вроде все понятно: все эти знания, как то вычисление площади, скорости, цены и т.д. действительно пригодятся в жизни, и это очевидно. Проблема возникает, когда встает вопрос: зачем уметь решать квадратные уравнения или хоть что-то знать об иррациональных числах.

В средних и старших классах ребенку необходимо показывать где ему могут пригодиться знания, при этом исходить нужно из того, что интересно ребенку.

Если ребенок до мозга костей гуманитарий, то отталкиваемся от того, что развитое логическое мышление ему точно необходимо.

С остальными уже проще: и в программировании, и в естественных науках без математики не обойтись, ровно как и без аналитического мышления.

Как решать задачи

Шаг 1

Внимательно читаем условие задачи, возможно, это придется сделать не один раз. Дальше необходимо понять простую вещь — любая задача состоит из 4 частей:

• Условие
• Вопрос
• Решение
• Ответ

Если у ребенка не получается решить задачу, родителям ни в коем случае нельзя кричать, нервничать, решать задачу вместо ребенка. Все, что нужно от взрослого в этой ситуации: помощь досконально разобраться в задаче и сделать так, чтобы ребенок понял ваше объяснение.

Шаг 2

Принимаем во внимание тот факт, что решения даже самой трудной задачи сводиться к том, что необходимо из двух имеющихся данных найти третье.

Шаг 3

Теперь необходимо составить краткую запись. Если у ребенка это вызывает сложности — рисуйте. С самого начала ребенка необходимо научить представлять, что происходит. Рисование помогает также превратить нудное решение в увлекательное занятие.

Для тренировки можно предложить ребенку задачи с лишними сведениями. В этом случае школьник должен убрать из условия все лишнее.

Шаг 4

Составляем план решения. На этом этапе также возможны трудности — ребенок не всегда может понять, почему не может сразу ответить на вопрос. В этом случае лучше всего разыграть сценку.

Шаг 5

Обращаем внимание ребенка на фразы. Важно научить ребенка понимать, что в условии задачи кроется ответ на нее. В любом случае ответ всегда начинает с числа.

Шаг 6

Повторяем все с начала. Достичь результата можно только путем долгих тренировок, не думайте, что выполнив все один раз ребенок раз и навсегда научиться решать задачи. Под вашим руководством он должен довести все свои навыки до автоматизма.

Источник: https://zen.yandex.ru/media/id/59ac54054bf161a5f926a729/59e257e3256d5c4d9ebe61ed

Как помочь студенту решать математические задачи?

Аннотация. В статье описываются виды математических задач, этапы решения, их роль в обучении математике. Используется метод самостоятельной работы как способ организации учебно-познавательной деятельности студентов над задачей.

Комбинируя решения простых задач, студенты применяют знания при решении сложных. Рабочая тетрадь – в помощь учащемуся. Повышает интерес к математике применение занимательных задач, уроки-презентации обеспечивают больший объем усвояемости материала.

Математические задачи приобщают студентов к посильным самостоятельным исследованиям.

Ключевые слова: математические задачи, обучение, методы решения задач.

Глубокое и прочное усвоение студентами основ курса математики чрезвычайно важно для формирования их математической культуры. Умения решать математические задачи является наиболее яркой характеристикой состояния математического образования. Учеными дано несколько пояснений, что такое математическая задача. А.Н. Леонтьев определяет задачу как цель, заданную в определенных условиях. Л.

М. Фридман связывает понятие «задача» с понятием «проблемная ситуация». Правильная постановка задач и упражнений в обучении во многом определяет современную методику преподавания, так как решение задач служит различным конкретным целям обучения.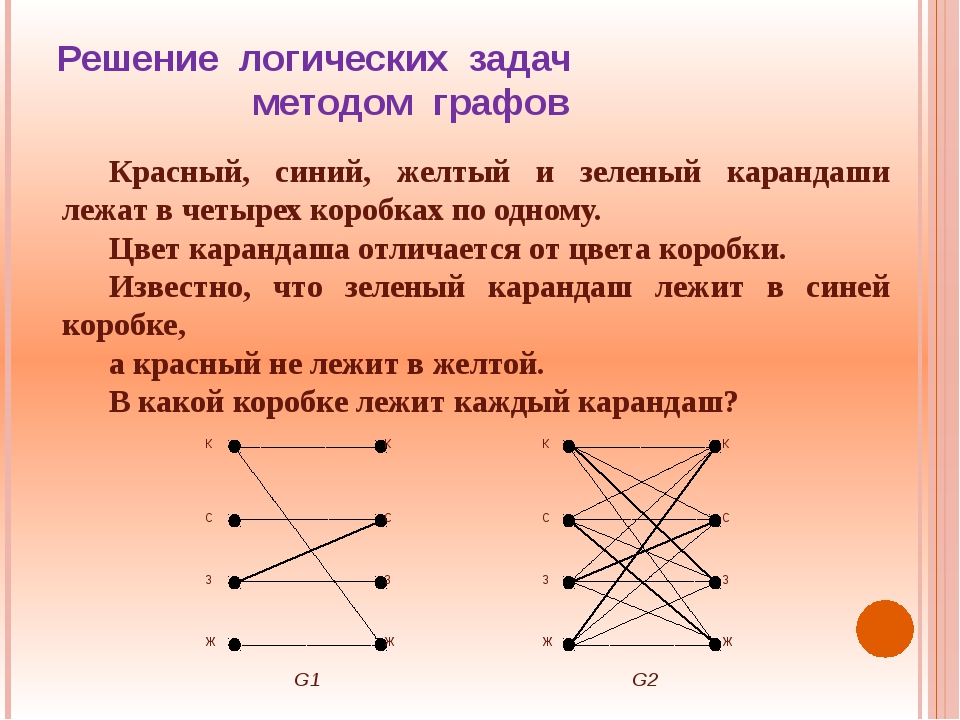 Известный ученый математик и методист Д. Пойа считает, что в повышении эффективности обучения решению задач играет большую роль подбор задач.

Так, например, задачи могут использоваться при введении в изучение новой темы, для самостоятельного установления студентами какого-либо математического факта, подлежащего изучению или иллюстрации этого факта, с целью глубокого усвоения теоретического материала или выработке необходимых умений и навыков, для контроля знаний и самоконтроля, возбуждения и развития интереса к математике.

• Можно выделить следующие виды задач:
• 1) дидактические – обучающие:
• а) чисто дидактические-задачи-упражнения, имеющие целью непосредственно закрепить изученный теоретический материал на простых упражнениях-примерах.
• б) текстовые задачи, для решения которых приходится пользоваться некоторым анализом условия, производить несколько действий для получения ответа.
• 2) задачи прикладного характера:
• а) упражнения вычислительного характера с требованием рациональных приемов их выполнения и текстовые задачи, задачи с использованием средних значений скоростей самолетов, теплоходов, ракет, автотранспорта, различных сметных, хозяйственных работ и др.

б) текстовые задачи производственного характера с использованием данных техники, физики, химии, астрономии, задачи на процентные расчеты и др.

В системе задач должно быть отведено достаточное место задачам, содержание которых описывают различные физические и другие процессы.

Решение их раскрывает пути применения математических знаний в различных областях науки и народного хозяйства, в трудовой деятельности самих студентов, в процессе изучения других предметов.

3) проблемные задачи исследовательского характера:

а) задачи с применением эмпирических формул техники;

б) так называемые открытые задачи с подбором недостающих данных из соответствующих таблиц, справочников, с исследованием полученного ответа, с выяснением возможных числовых значений для различных введенных параметров и т. д.

1. Решение каждой математической задачи осуществляется по четырем основным этапам:
2. 1. понимание условия и требования задачи; ясное усвоение и осмысливание отдельных элементов условия;
3. 2.  составление плана решения;
4. 3. практическая реализация плана во всех его деталях;

Пример: после прочтения формулировки задачи учащимся предлагается проанализировать текст задачи, выделить ключевые моменты и записать формулы, которые им помогут в решении.

Основным становится формирование у студента умения ориентироваться в новых задачных ситуациях, накапливать информацию, полезную для решения других задач или изучения новых разделов математики, обучение учащихся разнообразным математическим методам, познание реальной действительности и т.д.

При создании оптимальных условий, которые бы активизировали мыслительную деятельность учащихся при решении задач, весьма часто применяется особый дидактический прием, называемый системой подсказок. Система подсказок, состоящая из вспомогательных задач, вопросов и т.д., не подменяя мышление учащегося, придает ему нужное направление, т.е. делает поиск решения целенаправленным.

Преподавателю необходимо научить студентов видеть составные задачи в ходе решения основной, научить составлять их, так как только благодаря такой работе возможен успешный поиск решения задач.

Умение учащихся составлять свои задачи по заранее известным условиям, по аналогии с данной задачей и т.д. является весьма ценным.

• Решение сложных задач, полученных комбинированием ранее решенных простых задач дает возможность применить знания учащихся, тем самым вызвать интерес к занятию, а следовательно, повысить его эффективность.
• После решения каждой задачи следует еще раз оглянуться назад, обратить внимание на метод, который был использован, попытаться найти другие пути решения, выявить то, что необходимо помнить.
• Так как решение задач является основной деятельностью при обучении математике, то решение некоторых из них может быть представлено несколькими способами.

Пример: логические задачи можно решить с помощью логических рассуждений; алгоритмически, языком программирования Паскаль, средствами электронных таблиц; графически; табличным способом. Сравнив различные подходы, студенты выбирают для себя наиболее подходящий и понятный способ.

Говоря о роли математических задач в развитии у студентов способностей к самостоятельной познавательной деятельности творческого характера, отметим полезность постановки в процессе обучения математических задач проблемного характера. Целесообразно ставить вопросы: «Как это объяснить?», «Как будет выглядеть условие задачи, если изменить условия вопроса? »

Пример: «Какими способами можно составить 10 книг на полке?» Студенты начинают перечислять и переставлять книги, а преподаватель предлагает им решить эту задачу с помощью формулы, которую они использовали только для вычисления факториала.

В качестве способа организации учебно-познавательной деятельности студентов над задачей используется метод самостоятельной работы. Он требует от них активного поиска, оперирования обобщенными умениями, творческого решения, а это является важным стимулом для развития интереса к учению.

Не менее важным при выборе метода признан учет индивидуальных особенностей студентов. Они пришли в колледж с разным уровнем математической подготовки и, следовательно, им требуется разное количество времени для решения задачи.

А возникающая в процессе ее решения необходимость обратиться к ранее изученному материалу, предполагает работу с учебником, справочной литературой, поэтому задачу целесообразнее давать в качестве домашнего задания. Л.С. Выгодский утверждал, что знания усваиваются только в процессе собственной работы обучаемого с этими знаниями.

Из чего можно сделать важный практический вывод: главная задача преподавателя на занятии – организовать собственную самостоятельную работу каждого студента с материалом, который нужно усвоить.

Преподаватель должен свести свои пояснения и разъяснения к «минимуму», а всё остальное время занятия посвятить управлению той работой, которой занимается   каждый студент с изучаемым материалом. Очевидно, что чем меньше учитель говорит сам, чем больше он направляет и контролирует работу каждого из группы студента, тем эффективнее обучение.

В помощь студенту хорошо бы разработать рабочую тетрадь, где включены формулировка задачи и пояснения, направляющие ход ее решения.

В соответствии с этой теорией преподаватель должен не только объяснить новый материал так, чтобы каждый ученик понял, что же именно ему надо усвоить и как работать с этим материалом, но и фиксировать основное содержание материала, которое позволяет приступить к работе без всякого предварительного заучивания.

Для закрепления базовых умений на занятиях математики, объясняя материал и кратко его записывая на этапе ориентировки, преподаватель должен разбить его на отдельные порции.

Работа с каждой порцией — самостоятельный шаг учащегося, отдельная операция. Необходимо организовать первоначальное закрепление материала так, чтобы преподаватель имел возможность проконтролировать ход и результаты выполнения каждой операции.

Именно поэтому нельзя допустить, чтобы на этом этапе работа велась в уме.

Очень оживляют уроки математики различные занимательные задачи, нешаблонные вопросы и “задачи на смекалку”. Задачи – шутки и вопросы на сообразительность (для устного решения).

Пример: Как известно, все исконно русские женские имена оканчиваются либо на «а», либо на «я»: Анна, Мария, Ольга и т.д. Однако есть женские имена, которое не оканчивается ни на «а», ни на «я». Назовите его.

Большое внимание на занятиях нужно отводить реализации принципа наглядности. Применение различных наглядных средств обучения облегчает восприятие, осмысление обучаемого материала и выступает в качестве источника новых знаний.

Мощным средством формирования положительной мотивации к изучению математики служат исторические справки, интересные факты.

Для проверки усвоения знаний учащихся можно использовать компьютерные тесты. Особенность их в том, что студент в случае ошибки может видеть образец правильного ответа.

Компьютерные тесты хорошо использовать не только для контроля знаний, но и для самоконтроля, как при подготовке к контрольным работам, так и для повторения ранее изученного материала, знание которого потребуется при изучении новой темы.

Учащимися 1-го курса можно использовать эти тесты для повторения материала перед экзаменом. Часто студенты, которые психологически не справляются на письменных контрольных работах, очень успешны при сдаче и выполнении работ с помощью тестов.

Важную роль играют при изучении математики уроки-презентации. На таких уроках реализуются принципы доступности, наглядности. Уроки эффективны своей эстетической привлекательностью, также между преподавателем и студентом существует посредник – компьютер, что дает хороший результат.

Урок-презентация также обеспечивает большой объем информации и заданий за короткий период. Всегда можно вернуться к предыдущему слайду. Работа с компьютером для «слабых» студентов оказывается той единственной ступенькой к возрождению интереса к учебе, возможностью добиться успеха.

Они охотно создают презентации, используя дополнительный материал, возможности Интернета, собственные знания по информатике и математике.

Сегодня образование в колледже рассматривается как целостное становление и развитие личности студента. В связи с этим к приоритетным качествам относят не только глубокие профессиональные знания и умения, но и творческую активность, готовность к непрерывному образованию и саморазвитию.

Важная роль в реализации поставленных целей, на мой взгляд, отводится математическим задачам.

Выступая как средства и цель обучения математике, они развивают поисковые навыки решения практических проблем, приобщают к посильным самостоятельным исследованиям, с их помощью более глубоко осознаются теоретические сведения.

Источник: http://intjournal.ru/kak-pomoch-studentu-reshat-matematicheskie-zadachi/

VII Международный конкурс научно-исследовательских и творческих работ учащихся Старт в науке

Развитию творческой активности, инициативы, любознательности, смекалки способствует решение нестандартных задач, логических.

Логические задачи – это неотъемлемая часть сегодняшнего дня. Они не покидают ученика в течение всего обучения в школе.

Логические задачи вызывают массу трудностей у школьников. Чтобы помочь справиться с этими задачами надо изучить типы логических задач и способы их решения. Только решение трудной, нестандартной задачи приносит радость победы. При решении логических задач предоставляется возможность подумать над необычным условием, рассуждать. Это вызывает и сохраняет интерес к математике.

В наше время очень часто успех человека зависит от его способности четко мыслить, логически рассуждать и ясно излагать свои мысли. Без приобретения навыков умственного труда, культуры мышления невозможно успешное овладение основами наук.

Поэтому целью этой работы является изучение видов логических задач, методов их решения, а также возможности развивать свои способности, умения рассуждать и делать правильные выводы.

Задачи:

1. Ознакомление с понятиями «логика» и «математическая логика».

2. Используя литературу, изучить типы логических задач.

3. Изучение основных методов решения логических задач.

4. Проведение диагностики на выявление уровня логического мышления учащихся 6 класса.

Актуальность темы очевидна, так как логические задачи помогают расширить свой кругозор и развить логическое мышление.

I. Что такое логика?

Итак, логика — одна из древнейших наук. Отдельные истоки логического учения можно обнаружить еще в Индии, в конце II тысячелетия до н. э.

Основоположником логики как науки является древнегреческий философ и ученый Аристотель.

Именно он обратил внимание на то, что в рассуждениях мы из одних утверждений выводим другие, исходя не из конкретного содержания утверждений, а из определенной взаимосвязи между их формами, структурами.

Чтобы правильно рассуждать, надо изучить правильные способы и методы рассуждении. Научится правильно составлять высказывания, или, как говориться в математической логике, выполнять операции над высказываниями.

При этом необходимо знать, вытекает ли истинность сложных высказываний из истинности составляющих их более простых предложений. Анализом методов рассуждений занимается наука логика, а исследованием и изучением математических рассуждений – математическая логика.

Печисловые задачи очень разнообразны по сложности, содержанию и способности решения. Логическиезадачи составляют обширный класс нестандартных задач.

Сюда относятся, прежде всего, текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам.

При этом часть утверждений условия задачи может выступать с различной истинностной оценкой (быть истинной или ложной).

III. Методы решения логических задач.

Решать логические задачи очень увлекательно. В них вроде бы нет никакой математики — нет ни чисел, ни треугольников, а есть только лжецы и мудрецы, истина и ложь.

В то же время дух математики в них чувствуется ярче всего — половина решения любой математической задачи (а иногда и гораздо больше половины) состоит в том, чтобы как следует разобраться в условии, распутать все связи между участвующими объектами.

При решении определенного типа задач существует свой оптимальный метод решения:

Истинноностные задачи	При решении задач данного типа лучше всего использовать метод рассуждений. Он позволяет проводить рассуждения, используя последовательно все условия задачи, и приходить к выводу, который и будет являться ответом задачи.
Задачи на пересечение и объединение множеств	Это тип задач, в которых требуется найти некотороепересечение множеств или их объединение, соблюдая условия задачи. Метод Эйлера является незаменимым при решении задач этого типа, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие.
Задачи на переливание	При решении текстовых логических задач на переливание применяется метод построения таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи.
Задачи на взвешивание	В таких задачах от решающего требуется локализовать отличающийся от остальных предмет по весу за ограниченное число взвешиваний. Поиск решения в этом случае осуществляется путем операций сравнения, правда, не только одиночных элементов, но и групп элементов между собой. Задачи данного типа чаще всего решаются методом рассуждений.
Математические ребусы	Записи восстанавливаются на основании логических рассуждений. При этом нельзя ограничиваться отысканием только одного решения. Испытание нужно доводить до конца, чтобы убедиться, что нет других решений, или найти все решения.
Задачи, решаемые с конца	Такие задачи очень часто ребята задают друг другу в виде головоломок на задуманное число. Задачи решаются методом математических вычислений, основанных на конечном результате в условии.
Задачи типа «Кто есть кто?»	Смысл задач под кодовым названием «Кто есть кто?» довольно прост. Нам даются отношения между предметами и следуя по цепочке этих отношений, мы приходим к правильному результату. Задачи данного типа чаще всего решаются методом графов.

1) Метод графов

Даны отношения между предметами и следуя по цепочке этих отношений, мы приходим к правильному результату. Граф – это несколько точек, часть которых соединены друг с другом отрезками или стрелками. Рассмотрим метод графов на примере решения задачи.

Задача “Любимые мультфильмы”: Жила-была одна дружная семья: мама, папа и сын. Они все любили делать вместе. Но вот мультфильмы любили разные: «Ну, погоди!», «Покемоны», «Том и Джерри».

Определите, какой мультфильм любит каждый из них, если мама, папа и любитель мультфильма «Покемоны» никогда не унывают, а папа и любитель мультфильма «Том и Джерри» делают зарядку по утрам? Решение.

Рассмотрим множество людей: мама, папа, сын и множество мультфильмов «Ну, погоди!», «Покемоны», «Том и Джерри». Обозначим элементы этих двух множеств точками. Поэтому граф на рисунке будет выглядеть следующим образом:

Если точке из одного множества соответствует точка другого множества, будем соединять эти точки сплошной линией, если не соответствует – то штриховой. Заметим, что по условию задачи у человека только один любимый мультфильм. Поэтому нужно найти единственно возможное соответствие между элементами двух множеств.

Правило: если какая-то точка оказывается соединенной с двумя точками другого множества штриховыми линиями, то с третьей точкой она должна быть соединена сплошной. Поэтому граф на рисунке будет выглядеть следующим образом:

Теперь мы установили, что папа любит мультфильм «Ну, погоди!», сын – «Покемоны». В обеих множествах остается только по одной точке, следовательно мама любит мультфильм «Том и Джерри».

Задача решена. 2) Круги Эйлера. Второй способ, которым решаются такие задачи круги Эйлера – задачи на пересечение или объединение множеств. Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.

Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие.

Решение. Чертим два множества таким образом:

6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств. 15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров».

11 – 6 = 5 – человек, которые смотрели только «Стиляги».

1. Получаем:
2. Ответ: 5 человек смотрели только «Стиляги».

3) Решение логических задач табличным способом. Основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи. Рассмотрим способ решения на конкретной задаче.

Задача. Три клоуна Бим, Бам и Бом вышли на арену в красной, зеленой и синей рубашках. Их туфли были тех же цветов. У Бима цвета рубашки и туфель совпадали. У Бома ни туфли, ни рубашка не были красными. Бам был в зеленых туфлях, а в рубашке другого цвета. Как были одеты клоуны?

Решение. Составим таблицу, в столбцах которой отметим возможные цвета рубашек и туфель клоунов. Будем заполнять таблицу, используя условия задачи. Туфли Бама зеленые, а рубашка не является зеленой. Следовательно, у Бима и Бома туфли уже не могут быть зелеными, так же как не могут быть туфли Бама синими или красными.

Ответ: Бом – в синих туфлях и зелёной рубашке, Бим – во всём красном, Бам – в зеленых туфлях и синий рубашке.

V. Интересны ли логические задачи учащимся 6 класса ?

В практической части моей научной работы я подобрал несколько логических задач типа «Кто есть кто?», соответствующие уровню 6 класса, и раздал их для решения своим одноклассникам. Задачи были решены. После чего мною были проанализированы полученные результаты.

Задачи следующего содержания:

Задача 1. Леня, Женя и Миша имеют фамилию Орлов, Соколов и Ястребов. Какую фамилию имеет каждый мальчик, если Женя, Миша и Соколов — члены математического кружка, а Миша и Ястребов занимаются музыкой? (Ответ: Алёша Соколов, Женя Ястребов, Миша Орлов).

Задача 2. В семье четверо детей им 5, 8, 13 и 15 лет. Зовут их Таня, Юра, Света и Лена. Сколько лет каждому из них, если одна девочка ходит в детский сад, Таня старше, чем Юра, а сумма лет Тани и Светы делится на 3? (Ответ: Свете 5, Юре 8, Тане 13, Лене 15).

Среди учеников моего класса, в количестве 30 человек, с двумя предложенными задачами типа «Кто есть кто?» справилось 19 человек, среди которых 11 девочек и 8 мальчиков. С первой задачей справились почти все учащиеся. Вторая задача, вызвала у затруднения.

• Результаты решения представлены на диаграмме:
• Из диаграммы видно, что 63% (19 человек) успешно справились с двумя задачами, только с первой задачей — 73% (22 человека). Не решили ни одну из задач верно — 27%
• (8 человек).

Ребята со всей ответственностью и большим интересом отнеслись к решению логических задач. Несмотря на то, что с задачами справились не все ученики, этот процесс их очень увлек. Подводя итог, можно сделать вывод, что если при обучении математике использовать решение нестандартных задач, то это приведет к повышению интереса к урокам математики и развитию математических способностей учащихся.

VI. Логические задачи на уроках математики в общеобразовательных школах.

Вот, что у меня получилось:

Логические задачи	Тема урока по математике
1. Деду, отцу и сыну вместе 100 лет. Отцу и сыну вместе 45 лет. Сын на 25 лет моложе отца. Сколько кому лет? Решение: деду 100-45=55 лет; сыну10 лет; отцу 35 лет.	Устный счет
2. Разделите 5 яблок поровну между шестью детьми, не разрезав никакое яблоко больше, чем на 3 части Решение: 3 яблока разрезать на две равные части. 2 яблока на три. Получим 6 половин и 6 третей. Дать каждому половину и треть.	Дроби
3. Белка за 20 минут приносит орех в гнездо. Далеко ли орешник от гнезда, если известно, что налегке белка бежит со скоростью 5 м/с , а с орехом — 3 м/с? Решение: Пусть х – искомый путь. 20мин=20∙60=1200с.  х/5 +х/3 =1200 х = 1200*15:8 Ответ: 2250 м.	Средняя скорость
4. Решите: К · О · Т = У · Ч · Ё · Н · Ы · Й Решение: 8х9х10=1х2х3х4х5х6 720=720	Разложение на множители
5. Груша тяжелее яблока,а яблоко тяжелее персика. Что тяжелее: груша или персик? Решение: Груша тяжелее всех, затем яблоко, и самый лёгкий это персик	Неравенства

Основные выводы: применение логических задач на уроках математики в общеобразовательных школах помогает развитию логического мышления у учащихся, расширяет математический кругозор, а также способствуют развитию силы воли, трудолюбия, настойчивости в преодолении трудностей, упорства в достижении целей.

VII. Заключение

В данной работе мы познакомились с понятием «логика» и «математическая логика», изучили логические задачи. Узнали на какие типы они делятся, какие бывают методы и способы их решения. Некоторые методы мы рассмотрели более подробно.

Из этого можно сделать вывод, что применяя только изученные способы решения логических задач, невозможно решить все математические задачи. Мною была составлена таблица соответствия некоторых логических задач с темами, изучаемыми на уроках математики. Также, я предложил своим одноклассникам решить пару нестандартных логических задач.

Несмотря, на то что не все ученики с ними справились, это задание вызвало у них большой интерес.

Из вышеизложенного можно сделать вывод — необходимо включить изучение логических задач в программу по математике в общеобразовательных школах. Так как это способствует повышению интереса учащихся к данному предмету, развитию нестандартного мышления, трудолюбия и внимания.

Источник: https://school-science.ru/7/7/39092

Главная

Сведения об общеобразовательной организации: муниципальное бюджетное общеобразовательной учреждение «Лицей» (МБОУ «Лицей»)
1.	Дата создания	1 сентября 1991 года
2.	Учредитель	муниципальное образование городской округ город Арзамас Нижегородской области в лице администрации города Арзамаса
3.	Представительства и филиалы образовательной организации	нет представительств и филиалов
4.	Место нахождения и осуществления образовательной деятельности	607220, Нижегородская область, город Арзамас, улица Пушкина, дом 138/1
5.	Режим, график работы	Режим работы МБОУ «Лицей» Режим работы администрации Режим работы психолога Режим работы социального педагога Режим работы педагога-организатора Тягловой И.А. График работы педагога-организатора Жук А.А.
6.	Контактные телефоны, адрес электронной почты	(83147) 7-40-50, 2-43-73, [email protected]
7.	Структура управления и органы управления           Наименование структурного подразделения, ФИО и должность руководителя, место нахождения           Сведения о положениях о структурном подразделении и об органах управления	Структура управления, органы управления ————————— Библиотека, Илюхина Светлана Вячеславовна, зав. библиотекой, город Арзамас, улица Пушкина, дом 138/1, МБОУ «Лицей», использует сайт ОО, телефон: 7-40-50 Грфик работы библиотекаря Бухгалтерия, Ахматова Юлия Евгеньевна, гл. бухгалтер, город Арзамас, улица Пушкина, дом 138/1, МБОУ «Лицей», использует сайт ОО, телефон 2-43-73 Столовая, Макулова Марина Александровна, зав. столовой, город Арзамас, улица Пушкина, дом 138/1, МБОУ «Лицей», использует сайт ОО, телефон 2-43-73 —————————- Положение о библиотеке Положение о бухгалтерии Положение о столовой
8.	Уровни образования, нормативный срок обучения	Начальное общее образование — 4 года Основное общее образование — 5 лет Среднее общее образование — 2 года
9.	Форма получения образования	Очная
10.	Срок действия государственной аккредитации образовательной программы	До 7.03.2025 года
11.	Образовательная программа	ФГОС
12.	Учебный план	Учебная деятельность
13.	Календарный учебный график	Учебная деятельность
14.	Методические и иные документы, разработанные образовательной организацией для обеспечения образовательного процесса	Методические разработки для обеспечения образовательного процесса имеются по каждой образовательной программе
15.	Реализуемые образовательные программы	МБОУ «Лицей» реализует общеобразовательные программы начального общего, основного  общего, среднего общего образовании; дополнительные образовательные (общеразвивающие) программы
16.	Численность обучающихся по реализуемым образовательным программам за счет бюджетных ассигнований федерального бюджета, бюджетов субъектов Российской Федерации, местных бюджетов и по договорам об образовании за счет средств физических лиц и (или) юридических лиц, в том числе численность обучающихся, являющихся иностранными гражданами	За счет бюджетных средств субъекта РФ: Общая численность обучающихся — 787 Начальное общее образование — 342 Основное общее образование — 346 Среднее общее образование — 99 Иностранные граждане — 0
17.	Договоры с иностранными  и(или) международными огранизациями по вопросам образования и науки	Отсутствуют
18.	Язык обучения	Русский
19.	О федеральных государственных образовательных стандартах	ФГОС
20.	О руководителе Лицея, его заместителях	Администрация Лицея
21.	О персональном составе педагогических работников	Педагогический состав Лицея
22.	О материально-техническом обеспечении образовательной деятельности	Материально-техническая база
23.	Об условиях питания и охраны здоровья обучающихся	Питание Медицинское обслуживание
24.	О доступе к информационным системам и информационно-телекоммуникационным сетям, об электронных образовательных ресурсах, к которым обеспечивается доступ обучающихся	Для учащихся
25.	О количестве вакантных мест для приема (перевода)	Вакантные места для приема
26.	Об объеме образовательной деятельности, финансовое обеспечение которой осуществляется за счет бюджетных ассигнований федерального бюджета, бюджетов субъектов Российской Федерации, местных бюджетов, по договорам об образовании за счет средств физических и (или) юридических лиц	Финансово-хозяйственная деятельность
27.	О поступлении финансовых и материальных средств и об их расходовании по итогам финансового года	Финансово-хозяйственная деятельность
28.	О трудоустройстве выпускников	Информация о продолжении образования выпускниками Лицея
Копии документов образовательной организации:
29.	Устав образовательной организации	Устав
30.	Лицензия на осуществление образовательной деятельности	Лицензия
31.	Свидетельство о государственной аккредитации	Свидетельство об аккредитации
32.	План финансово-хозяйственной деятельности образовательной организации	Финансово-хозяйственная деятельность
33.	Локальные нормативные акты	Локальные нормативные акты
34.	Отчет о результатах самообследования	Карта самообследования
35.	Оказание платных образовательных услуг	Порядок оказания платных дополнительных образовательных услуг
36.	Предписания органов, осуществляющих государственный контроль (надзор) в сфере образования, отчеты об исполнении таких предписаний	Предписания отсутствуют

Задачи умеренной сложности — всё по этой теме для программистов

Собеседование в Apple: топ-30 вопросов и ответов

В статье собраны технические и поведенческие вопросы, которые задают на собеседовании в Apple. Ответы на технические вопросы даны на C++.

Отмеряем минуты фитилями и доказываем прямоугольность треугольника — две логические задачи

Представляем себя на месте пунктуального подрывника и вспоминаем немного геометрии.

Задачи с собеседований: ищем самый тяжёлый шар за два измерения

Определяем с помощью задачи как хорошо соискатель умеет строить алгоритмы и системно искать решения.

Как Гомер Симпсон почти решил уравнение Великой теоремы Ферма

Изучаем известную теорему и пробуем проверить вычисления героя культового мультсериала Гомера Симпсона.

Как убедиться, что вентилятор выключен, если в доме отключили электричество? Задачка на логику

В доме отключили электричество, но вам нужно уходить. Сможете выключить вентилятор, если не знаете, сколько у него режимов, и не можете его обесточить?

Сможете ли вы получить наследство, решив головоломку со шкафчиками?

Ваш богатый чудаковатый дядюшка оставил вам наследство, но чтобы его получить, вам нужно решить его загадку. Справитесь быстрее своих алчных родственников?

Помогите сплетникам как можно эффективнее распространить слухи

Нужно найти алгоритм, который поможет n сплетникам распространить слухи за минимальное количество сообщений.

Сможете получить MU из MI, используя 4 правила?

У вас есть 4 правила для преобразования строк. Сможете ли вы превратить MI в MU, не нарушая их?

Маленькая девочка считает до 1000 — на каком пальце она закончит?

Логическая задача из книги «Alogithmic Puzzles». Сможете решить её?

3 чемодана, 3 ключа, 3 попытки — сможете решить эту задачку?

Довольно простая задачка на нахождение соответствий. Попробуйте решить её!

Разливаем ром в порту: логическая задачка на переливания

Классика задач на переливание: вам нужно отмерить нужное количество рома, при том что у вас нет тары нужного размера.

Три хирурга, больной и две пары перчаток — сможете помочь никому не заразиться?

Медицина в полевых условиях требует не только знаний, но и смекалки. Потренируйте свою сообразительность, решив эту логическую задачку.

Семья на мосту — логическая задача про переправу

Наизусть знаете, как переправить через реку волка, козу и капусту? Попробуйте теперь помочь семье, которой позарез нужно перейти мост за 17 минут.

Логическая задача про электрика и 49 кабелей

Электрик, река и 49 одинаковых проводов. Что это? Конечно, задачка на логику. Попробуйте решить её, а если не получится — в статье есть ответ.

Задачи по Python для начинающих от Tproger и GeekBrains

Для обучения программированию на питоне нужны тренировки. Совместно с GeekBrains собрали для вас несколько простых задач на Python 3 c решениями.

День, магазин, парковка — задача для программистов

Дано Парковка построена в виде графа. Он состоит из N узлов и M рёбер. В нём нет ни петель, ни параллельных рёбер. Каждый узел — парковочный блок с определённой вместимостью.…

Маляры, носки и переменные — подборка задач для программистов

Ищем носки, меняем переменные местами и обмениваемся рукопожатиями — встречайте новую подборку задач для программистов.

Огурцы, богатства, бочки — подборка задач для программистов

Огурцы под жарким солнцем Ранним утром бакалейщик выставил 100 килограмм огурцов на улицу перед своим магазином. Огурцы на 99 % состоят из воды. День был жарким и часть воды из…

Продаём молоко, меряем денежные пирамиды и красим кубы — подборка задач для программистов

Продажа молока, измерение денежных пирамид и окрашивание кубов — всё это в новой подборке задач для программистов.

Ищем профессора, проверяем пары в массиве и зажигаем лампы: подборка задач для программистов

Ищем профессора, проверяем пары в массиве и зажигаем лампы — именно этим мы займёмся в новой подборке задач для программистов.

Плавание, башня и тролли — 3 задачки для разминки мозга

Порой нужно отвлечься от программирования и заняться чем-нибудь ещё. Например, разминкой мозга с помощью решения задачек.

Задачи на логику: помогите таракану, посчитайте множители и побудьте диспетчером

Таракан на стене Маленький таракан карабкается по стене высотой 10 метров. Таракан начал путь с подножия стены. Каждый час он может проползти 1 метр в высоту и затем немедленно скатывается…

Развиваем мышление: три простые задачи на логику

Коротенькая подборка задач на логику для программистов: экспериментальная производственная линия, поиск кота и подъём по ступенькам.

Учимся программировать с помощью задач с числами

Развиваем практические навыки программирования с помощью задач на работу с числами. В материале собраны задачи с примерами решения на разных языках.

Задача на работу со скобками

Задача на построение алгоритма для вывода всех корректных  (правильно открытых и закрытых) комбинаций из n пар круглых скобок.

Посчитайте вероятность коллизии хеш-функции

Задача умеренной сложности на поиск коллизий хеш-функции. В материале приведено решение.

Задача: годовой баланс

Практическая задача на поиск оптимального решения для программистов. Найдите максимум разности двух чисел путём перестановок цифр в каждом из них.

Задача о ленивом электрике

Логическая задача для программистов на поиск оптимального решения для маркирвки кабеля, который находится под землёй. Рассмотрены два варианта решения.

Задача на поиск списка с максимальной суммой элементов

Представим, что у нас есть список со списками и нам нужно найти вложенный список с максимальной суммой элементов. Как бы вы решили эту задачу? Пока вы думаете, давайте рассмотрим несколько возможных вариантов решения на Python от самого громоздкого до «однострочника».

Нахождение максимума из двух чисел без условных операторов и операторов сравнения

В разборе задачи описано, как без использования условных операторов (if/else) и любых других операторов сравнения, найти максимальное из двух чисел. Код приведён на языке C++.

Math.ru

Семен Григорьевич Гиндикин

М.: Наука, 1972. 288 с.

Тираж 50000 экз.

Загрузить (Mb) djvu (3.22) pdf (-) ps (-) html (-) tex (-)

Книга рассчитана на читателя, заинтересованного в содержательных, с точки зрения математики, теоремах и задачах. Здесь раасмотрены, главным образом, три круга вопросов: проблемы полноты и функционально замкнутых классов, проблемы синтеза и оценки сложности схем, теория вероятностей на конечных булевых алгебрах. Читатель найдет здесь, в частности, обсуждение связей алгебры логики с элементарными вопросами теории доказательств и с построением определений отрицательных понятий. Основная часть книги формально не использует сведений, выходящих за рамки школьного курса математики.
Книга будет полезна студентам младших курсов университетов и пединститутов и ученикам старших классов математических школ.

---

Содержание

Предисловие.


Путеводитель и указания к пользованию книгой.

§ 1. Операции над высказываниями.
Задачи,
указания и
решения.

§ 2. Функции алгебры логики; нормальные формы.
Задачи,
указания и
решения.

§ 3. Закон двойственности в алгебре логики.
Задачи,
указания и
решения.

§ 4. Арифметические операции в алгебре логики.
Задачи,
указания и
решения.

§ 5. Монотонные функции алгебры логики.
Задачи,
указания и
решения.

§ 6. Функционально замкнутые классы и теорема Поста.
Задачи,
указания и
решения.

§ 7. Общая теория функционально замкнутых классов.
Задачи,
указания и
решения.

§ 8. Схемы из функциональных элементов.
Задачи,
указания и
решения.

§ 9. Релейно-контактные схемы. Оценки сложности схем.
Задачи,
указания и
решения.

§ 10. Элементы вероятностной логики.
Задачи,
указания и
решения.

§ 11. Многозначные логики.
Задачи,
указания и
решения.

§ 12. Логика предикатов.
Задачи,
указания и
решения.

Приложение.

Литература.


Предметный указатель.

---

Загрузить (Mb) djvu (3.22) pdf (-) ps (-) html (-) tex (-)

Математика и логика — Математическая составляющая

Математика и логика


Поделиться    

Лев Дмитриевич Беклемишев

Логика как наука — предмет почти такой же древний, как и математика. В античное время и средние века она была составной частью тривиума (грамматика, риторика, логика/диалектика) — базового уровня образования; математические же предметы (арифметика, геометрия, астрономия и музыка) составляли следующий, более продвинутый, уровень, называемый квадривиум. (От слова «тривиум» происходит одно из любимых математиками выражений «тривиально».) Предметы тривиума понимались как науки о том, как правильно, без ошибок, писать, говорить и, соответственно, рассуждать.

Мы расскажем о том, как и почему возникла математическая логика, что она изучает, какие у неё есть достижения и современные применения.

От Аристотеля к Булю. Основы учения о правильных рассуждениях заложил Аристотель. Он заметил, что корректные умозаключения следуют определённым элементарным схемам, называемым силлогизмами, и перечислил ряд таких схем. (Классический пример силлогизма: «Все люди смертны. Сократ — человек. Следовательно, Сократ смертен».) Учение о силлогизмах в свою очередь опиралось на глубокий анализ понятий и их соединения в высказывания.

Силлогистика Аристотеля была не лишена недостатков, однако в целом была выдающейся теорией и стала основой изучения логики на протяжении античности и средних веков. В трудах античных стоиков и средневековых схоластов она была модифицирована и дополнена. В таком виде аристотелевская логика дошла вплоть до середины XIX века, где и встретила революцию, связанную с проникновением в логику математических методов.

Возникновение математической логики полностью изменило представления учёных как о методах исследования логики, так и о том, что составляет сам предмет её изучения. В наше время заявления, что логика есть наука о правильных рассуждениях, кажутся настолько же справедливыми, насколько утверждение «математика — это наука о правильных вычислениях».

Аналогия между рассуждениями и вычислениями несколько глубже, чем кажется на первый взгляд. Возникновение логики как математической науки было связано с работами британских учёных Джорджа Буля и Августа де Моргана, которые обнаружили, что с логическими высказываниями можно оперировать как с алгебраическими выражениями. Например, если сложение читать как логическую связку «или», умножение как «и», а равенство как «равносильно», то для любых высказываний $a$, $b$ выполняются законы
$$ a+b=b+a,\quad a\cdot(b+c)=a\cdot b+a\cdot c, $$

как и многие другие привычные нам законы арифметики. Но, помимо этого, в алгебре высказываний выполняется и кое‐что непривычное, например всегда
$$ a+a=a\quad \hbox{и}\quad a+(b\cdot c)=(a+b)\cdot (a+c). $$

Такой взгляд на логику высказываний и силлогистику оказался и неожиданным, и плодотворным. В наше время эту точку зрения разрабатывает область, называемая алгебраической логикой, а одним из её центральных понятий является понятие булевой алгебры, названной так в честь её первооткрывателя. Эта область исследований, через понятие реляционной алгебры, обобщающей булеву, привела в 1960‐х годах к теории реляционных баз данных, в наше время лежащей в основе самых распространённых языков запросов, таких как SQL.

Математизация логики и аксиоматизация математики. Движущей причиной процесса математизации логики был назревший в самой математике на рубеже XIX—XX веков кризис оснований. С одной стороны, во второй половине XIX века в математике получил распространение удобный язык теории множеств, созданной Георгом Кантором. Математики стали уверенно использовать в своих рассуждениях конструкции с бесконечными множествами. Математика, вооружённая теорией множеств, шла от успеха к успеху.

С другой стороны, в самой теории множеств Кантора обнаружились парадоксы, которые указывали на то, что с этой теорией не всё в порядке на самом базовом уровне. Простейший парадокс такого рода, в фольклорном варианте известный как парадокс брадобрея, был придуман Бертраном Расселом: рассмотрим множество $R$ всех тех множеств, которые не содержат сами себя в качестве элемента. Тогда $R\in R$ если и только если $R\notin R$, противоречие.

Такое положение дел заставило многих выдающихся математиков и философов той эпохи (Пеано, Фреге, Рассел, Гильберт, Пуанкаре, Брауэр, Вейль и др.) задуматься об основаниях математики. Их волновали такие фундаментальные вопросы как:

• Что означает доказать математическую теорему? Какие средства при этом законно использовать?
• Что значит выразить то или иное математическое понятие или утверждение на том или ином языке?
• Когда мы говорим об истинности и о доказуемости какого‐либо математического утверждения, имеется ли в виду одно и то же?

Параллельно в математике стали укореняться новые стандарты строгости. Основные области математики — анализ, алгебра, геометрия — были поставлены на аксиоматическую основу. Великий математик Давид Гильберт (1862—1943) был ярким сторонником и пропагандистом аксиоматического метода. Под его влиянием была построена и общепринятая в наше время система аксиом теории множеств, свободная от очевидных парадоксов. Эту аксиоматику предложил в 1908 году Э. Цермело и в дальнейшем дополнили Дж. фон Нейман и А. Френкель. Но где же настоящая гарантия, что полученная система не содержит противоречия? Каким образом это можно установить?

Эти вопросы оказались гораздо сложнее, чем представлялось тогда Гильберту. Они потребовали глубокого изучения аксиоматических систем и их формализации, привели к точному анализу структуры математического высказывания, первым формулировкам строгих математических моделей таких явлений, как доказуемость, выразимость, истинность, и сделали возможным их изучение математическими методами. Так возникла математическая логика — особая область исследований внутри математики. В рамках этой дисциплины был создан точный язык и математический аппарат для исследования целого пласта явлений, ранее относившихся к чисто гуманитарному знанию. (В этой роли математическую логику можно сравнить с такой областью современной математики, как теория вероятностей, которая ещё в начале XX века не была строго математической дисциплиной.)

Формальные языки. С современной точки зрения область интересов математической логики значительно шире, чем наука о правильных рассуждениях; её можно приблизительно описать, с оговорками и уточнениями, как построение и исследование формальных языков и систем математическими методами. Заметим, что если в этом определении отбросить слово «формальных», то вместо логики мы получим, по существу, математическую лингвистику — что указывает на определённое родство между этими двумя дисциплинами. Ключевое же отличие математической логики от логики в широком смысле слова — это именно использование математических методов, применяемых к точным формальным моделям.

Математическая логика по предмету сво-
ему есть логика, а по методу — математика.(П. С. Порецкий, 1884 год, Казань.)

Формальные и естественные языки имеют общие черты: у тех и у других есть синтаксис (то, как мы говорим или пишем), семантика (смысл того, что написано) и прагматика (то, как используется написанное). Основное отличие заключается в том, что — по крайней мере в идеале — синтаксис и семантика формальных языков могут быть определены на уровне математической строгости и поэтому в принципе поддаются анализу чисто математическими методами.

В наше время формальные языки встречаются в каждом доступном нам электронном устройстве, вроде мобильного телефона, а некоторые из них — языки программирования — даже изучают в школе. Поэтому за примерами далеко ходить не надо. Однако в середине XIX века, когда начался процесс математизации логики, формальных языков ещё не было, их только предстояло создать.

Логика предикатов. Разработчики первых формальных языков и систем, как правило, не думали о том, что эти системы могут быть реально использованы в вычислительных устройствах. (Исключением, видимо, можно считать великого учёного Готфрида Вильгельма Лейбница (1646—1716), который почти за два века до Буля предвосхитил многие идеи математической логики, включая идею формализации языка математики, и даже построил механический арифмометр.)

Первые формальные языки и системы возникли как результат выделения фрагмента естественного языка, достаточного для передачи формулировок математических утверждений и их анализа. Процесс выработки основных категорий этого языка был продолжительным и шёл параллельно с выработкой некоторых ставших в наше время стандартными математических обозначений. (Одним из важных понятий, введённых в это время, стало понятие квантора, сформировавшееся в работах Г. Фреге и Ч. Пирса. Кванторы существования $\exists$ и всеобщности $\forall$ заменяют языковые конструкции «для некоторого» и «для всех». Первое из этих обозначений введено Дж. Пеано в 1897 году, второе — по аналогии — Г. Генценом в 1935 году, однако общеупотребительными эти обозначения стали лишь под влиянием Бурбаки во второй половине XX века.) Этот процесс в основном завершился в 1920‐х годах, когда в качестве стандартного класса языков, предназначенных для формализации и анализа математических утверждений, стал рассматриваться язык логики предикатов (первого порядка).

Предикатом на множестве $M$ мы называем высказывание, зависящее от $n$ параметров из этого множества (например, «натуральное число $x$ чётно», «точки $x$, $y$ и $z$ плоскости лежат на одной прямой»). Как только фиксированы значения параметров, предикат принимает логическое значение ложь или истина. Таким образом, с формальной точки зрения предикат представляет собой функцию от $n$ аргументов из множества $M$ в $\{0,1\}$.

Не вдаваясь в технические подробности, можно приблизительно описать высказывания логики предикатов как такие, которые можно сформулировать (предполагая заранее заданными обозначения некоторых базовых предикатов) с помощью конструкций $\land$ «и», $\lor$ «или», $\neg$ «не», $\to$ «влечёт» и уже упомянутых кванторов. Например, текст $\forall{x} \exists{y} (y>x \land P(y))$ выражает неограниченность множества простых чисел, если договориться, что переменные пробегают множество натуральных чисел, «$>$» означает «больше», а $P(y)$ выражает простоту числа $y$. Эти договорённости составляют часть того, что мы назвали семантикой языка логики предикатов.

Удивительный факт, подтверждаемый всей существующей математической практикой, состоит в том, что выразительных средств языка логики предикатов — на первый взгляд очень скромных — достаточно для формулировки любых известных математических результатов. При этом может быть использовано всего лишь одно базовое понятие — предикат принадлежности $x\in y$ «множество $x$ есть элемент множества $y$». (В картине мира аксиоматической теории множеств все объекты, обозначаемые переменными, являются множествами.)

Доказуемость и вычислимость. Выразить в данном языке то или иное осмысленное утверждение — совсем не то же самое, что суметь его доказать. Следующий уровень языка логики предикатов состоит в описании таких текстов, которые следует признать корректными доказательствами. Традиционно этот уровень называется в математической логике исчислением предикатов. Формальное доказательство (в формате, который принято называть гильбертовским, но который существовал и до работ Давида Гильберта) представляет собой конечную цепочку высказываний логики предикатов, каждое из которых либо является аксиомой, либо получается из предшествующих высказываний по одному из постулируемых правил. Минимальный стандартный набор таких правил содержит лишь два: правило, позволяющее из высказываний $A$ и $A\to B$ вывести $B$, и правило, позволяющее из высказывания $A$ вывести $\forall x A$. (Если высказывание $A$ содержит параметр $x$, то формальное доказательство $A$ обосновывает его истинность при всех возможных значениях параметра.)

Таким образом, математическая доказуемость описывается двумя формальными языками — языком утверждений, описанным в предыдущем разделе, и языком доказательств — из которых второй является надстройкой над первым.

Похожая ситуация имеет место и с понятием вычислимости. Языки программирования предназначены для описания алгоритмов. Алгоритм при этом описывается программой — построенным по определённым правилам формальным текстом, который принято называть кодом. Таким образом, первый уровень языка программирования составляет язык текстов программ. Однако, процесс выполнения программы на данном компьютере на данном входе также может быть зафиксирован в виде текста (не важно, сохраняется ли этот текст в ходе работы программы или нет). В теории алгоритмов принято называть такой текст полным протоколом работы программы. То, каким образом порождается этот протокол, и составляет полное описание той или иной вычислительной модели. Для реальных языков программирования, разумеется, такое описание чрезвычайно сложно, однако для простейших моделей, таких как машина Тьюринга, оно гораздо проще.

Теория алгоритмов и создание компьютеров. Математическая логика сыграла важную роль в появлении компьютеров, хотя и не была единственной движущей силой в этом сложном процессе. Именно в математической логике, в попытке дать наиболее общее определение задачи, имеющей алгоритмическое решение, было осознано, что возможно построение универсального вычислительного устройства (машины), которое будет способно решать все теоретически разрешимые алгоритмические задачи.

Одним из первых, кто это понял, был Алан Тьюринг, давший точное определение и наиболее убедительный анализ понятия вычислимой функции в 1936 году. Другими учёными, которые наряду с Тьюрингом пришли к тем же идеям приблизительно в то же время, были Алонзо Чёрч и Эмиль Пост. Этими и другими исследователями в 1930‐х годах были созданы начала теории алгоритмов, которая стала основой понимания работы и построения вычислительных устройств в 40‐е и 50‐е годы. В частности, идея универсальной машины Тьюринга была в дальнейшем технически реализована в компьютерной архитектуре «по фон Нейману», в соответствии с которой программа хранится в памяти устройства и может быть модифицирована в ходе его работы. На основе этой идеи построены все операционные системы.

Задачей, которую стремились решить пионеры теории алгоритмов, был вопрос, поставленный Гильбертом и названный им по‐немецки Entscheidungsproblem, «проблема решения». Вопрос состоял в том, чтобы найти алгоритм, который по данному утверждению, записанному на языке логики предикатов, давал бы ответ, существует ли формальное доказательство этого утверждения или нет. Если бы такой алгоритм существовал, то все математические проблемы в некотором смысле имели бы чисто механическое решение: как уже упоминалось, на языке логики предикатов можно сформулировать практически любое математическое утверждение, например знаменитую гипотезу о бесконечности числа пар простых чисел‐близнецов. Тогда вопрос о том, выводима ли эта гипотеза из аксиом теории множеств, сводился бы к проверке доказуемости некоторого высказывания в исчислении предикатов. Неудивительно, что исследователи Entscheidungsproblem стремились показать, что требуемого алгоритма в принципе не может существовать.

Если доказать существование того или иного алгоритма можно, предъявив его явно, то для того, чтобы утверждать, что такого алгоритма не существует, необходимо располагать точным математическим описанием того класса задач, которые допускают алгоритмическое решение. Ответ на этот вопрос потребовал разработки формальных языков описания алгоритмов ещё до появления компьютеров. Причём, поскольку цель такой разработки была более теоретическая, чем практическая, исследователи стремились к формулировке наиболее простых для описания и в то же время универсальных вычислительных моделей. Первыми такими моделями были рекурсивные функции Гёделя—Эрбрана, лямбда‐исчисление Чёрча и машины Тьюринга.

Гёдель, хотя и был первым, кто фактически сформулировал универсальный язык программирования, не считал, что найденное им (и французским логиком Эрбраном) понятие является универсальным в смысле способности запрограммировать любой алгоритм. Первым, кто высказал тезис об универсальности своей вычислительной модели, был Алонзо Чёрч. Он также предъявил доказательство невозможности решения Entscheidungsproblem в рамках этой модели. Исчисление Чёрча было очень простым по форме, но больше напоминало формальное логическое исчисление, чем реальную вычислительную машину. Машины Тьюринга в этом смысле были ближе к будущей реальности, и поверить в тезис Тьюринга о том, что любая задача, имеющая алгоритмическое решение, может быть решена на машине Тьюринга, было намного легче, чем в аналогичный тезис Чёрча (известно, что именно работа Тьюринга смогла убедить Гёделя в справедливости этого тезиса). Тьюринг также показал, что его машины эквивалентны лямбда‐исчислению в смысле вычислительных возможностей, что стало косвенным свидетельством справедливости тезиса Чёрча—Тьюринга, как его теперь принято называть.

Впоследствии многие исследователи предлагали свои вычислительные модели в надежде расширить класс вычислимых функций, впервые описанный Чёрчем и Тьюрингом. Все такие попытки не привели к расширению этого класса, который оказался очень устойчивым. В настоящее время тезис Чёрча—Тьюринга — понимаемый в смысле любой из эквивалентных вычислительных моделей — является одним из краеугольных камней, на которых базируется теория алгоритмов.

Что касается лямбда‐исчисления, то оно долгое время пребывало на обочине математической логики, будучи вытеснено из теории алгоритмов более удобными и интуитивными моделями. Однако во второй половине XX века лямбда‐исчисление и системы на его основе нашли серьёзные практические применения. Лямбда‐исчисление Чёрча стало прообразом так называемых функциональных языков программирования (таких как современный язык Haskell), которые имеют ряд преимуществ по сравнению с традиционными императивными языками и в настоящее время очень активно развиваются.

Алгоритмически неразрешимые проблемы в математике. Вслед за Entscheidungsproblem с точки зрения теории алгоритмов были проанализированы и многие другие математические проблемы, поставленные как вопросы о построении того или иного алгоритма. Некоторые из таких трудных проблем, остававшихся открытыми десятилетиями, оказались алгоритмически неразрешимыми задачами.

Среди такого рода вопросов наиболее известна 10‐я проблема Гильберта о распознавании разрешимости диофантовых уравнений. Диофантово уравнение — это уравнение вида $P(x_1,…,x_n)=0$, где $P$ — многочлен с целыми коэффициентами от переменных $x_1$, …, $x_n$. Требуется узнать по заданному многочлену $P$, существуют ли целые числа $x_1$, …, $x_n$, удовлетворяющие такому уравнению.

Вопрос Гильберта о построении общего алгоритма, работающего для всех диофантовых уравнений, с самого начала выглядел безнадёжным. С появлением теории алгоритмов исследователи стали предпринимать усилия в попытке доказать неразрешимость этой задачи. Промежуточные результаты в этом направлении получили американские логики Дж. Робинсон, М. Дэвис и Х. Патнэм, на их основе окончательное решение задачи было получено лишь в 1970 году ленинградским математиком Ю. В. Матиясевичем.

В наше время в математике алгоритмические вопросы занимают подобающее им важное место. Математическая логика научила нас тому, что далеко не всякий такой вопрос является разрешимым. Кроме того, даже если алгоритм решения той или иной задачи существует в принципе, не всегда можно говорить о его применимости на практике. Например, выполнение алгоритма может потребовать слишком много времени или памяти компьютера. Такого рода вопросами занимается отдельная область теории алгоритмов — теория сложности вычислений, о которой подробно рассказано в другой статье этого сборника (см. «Теория сложности»).

Теоремы Гёделя и недоказуемые утверждения. Ещё одним открытием, сделанным гениальным австрийским логиком Куртом Гёделем в 1931 году, было явление непополняемости аксиоматических систем. Знаменитые теоремы Гёделя о неполноте не только оказали большое влияние на развитие математической логики и дали толчок к созданию теории алгоритмов, но и стали общекультурным явлением, затронувшим даже творчество писателей и художников. Гёдель был назван в числе ста наиболее влиятельных личностей XX века по версии журнала Тайм. Однако известность теорем Гёделя приводит и к тому, что часто они интерпретируются в слишком расширительном, метафорическом смысле.

Полными называют такие системы аксиом, в которых доказуемо или опровержимо любое утверждение того же языка (можно говорить о доказуемости в исчислении предикатов из данного множества аксиом). Понятно, что если мы хотим построить систему аксиом для той или иной области математики, нам бы хотелось, чтобы эта система была непротиворечивой и полной — неполнота означает, что мы «забыли» постулировать какие‐то принципы, касающиеся базовых понятий данного языка, и нужно их добавить к списку аксиом.

Теоремы Гёделя относятся к классу аксиоматических систем, удовлетворяющих двум естественным и широким требованиям. Во‐первых, необходимо, чтобы в рассматриваемом формальном языке по меньшей мере было выразимо понятие натурального числа и операции сложения и умножения. На первый взгляд это требование кажется весьма специальным, однако натуральные числа — один из базовых математических объектов, и языки, претендующие на формализацию значительной части математики, должны позволять о них говорить.

Целые числа создал Господь Бог,
всё остальное — дело рук человеческих. (Леопольд Кронекер, 1886 год, Берлин.)

Во‐вторых, должен существовать алгоритм, распознающий, является ли данный текст аксиомой рассматриваемой теории или нет. (Если аксиомы теории нераспознаваемы, то неясно, как можно строить доказательства в такой системе.)

Гёдель показал, что при выполнении этих требований любая система аксиом либо противоречива, либо неполна. Более того, для любой непротиворечивой системы можно явно указать предложение, касающееся арифметики натуральных чисел, которое нельзя ни доказать, ни опровергнуть в данной системе (такие утверждения принято называть независимыми от данной системы аксиом). В частности, это означает, что систему аксиом формальной арифметики нельзя никаким непротиворечивым образом «пополнить»: всегда найдутся независимые от неё арифметические утверждения. Это составляет содержание так называемой первой теоремы Гёделя.

Вторая теорема Гёделя говорит о том, что утверждение, выражающее непротиворечивость данной аксиоматической системы, не доказуемо в самой системе, если эта система и в самом деле непротиворечива. Если считать, что стандартные математические методы укладываются в рамки аксиоматической теории множеств, то из этой теоремы следует, например, что стандартными математическими методами нельзя установить непротиворечивость теории множеств (и, тем самым, их собственную непротиворечивость).

Теоремы Гёделя позволили построить первые примеры независимых утверждений для сильных систем аксиом, таких как арифметика или даже теория множеств. После работ Гёделя такие примеры были обнаружены среди открытых проблем в различных областях математики. Одной из самых знаменитых открытых проблем в математике была континуум‐гипотеза Кантора, в соответствии с которой всякое бесконечное подмножество множества вещественных чисел либо счётно (равномощно множеству натуральных чисел), либо континуально (равномощно множеству вещественных чисел). В 1938 году Гёдель сумел доказать, что эту гипотезу невозможно опровергнуть в теории множеств, а в 1961 году американский математик Пол Коэн установил её недоказуемость.

Недоказуемые утверждения теоретико‐множественной природы впоследствии были обнаружены в самых разных частях математики — в анализе, алгебре, топологии и др. Сравнительно недавно, в конце 1970‐х годов, были найдены первые простые примеры утверждений из области конечной комбинаторики, независимые от аксиом формальной арифметики и даже от более сильных аксиоматических систем. Принципиальная разница с примерами типа континуум-гипотезы состоит в том, что комбинаторные примеры относятся к конечным и совершенно элементарным объектам, и их можно легко объяснить школьнику. Исследования в направлении поиска естественных примеров независимых утверждений активно ведутся и в наши дни.

Логика в других разделах математики. Наиболее впечатляющие достижения математической логики, описанные выше, так или иначе связаны с анализом трудных проблем, в том или ином смысле не имеющих решения. Такие проблемы в математике встречаются, по счастью, довольно редко. Для работающих математиков поэтому более ценным является вклад в копилку методов, годных для решения их собственных повседневных задач. Здесь мы упомянем некоторые известные приложения логики такого рода, хотя в целом следует признать, что их не слишком много.

Область математики, которая испытала на себе сильное влияние логических методов — это абстрактная алгебра. Соответствующее направление математической логики — теория моделей — возникло в 1940‐х годах в работах А. И. Мальцева в России и А. Тарского и А. Робинсона в США с прицелом на приложения в алгебре. Первые такие приложения были найдены в 1941 году А. И. Мальцевым, который осмыслил доказанную им (а ранее в более слабой форме Гёделем) теорему о компактности для логики предикатов как общий метод получения локальных теорем в алгебре. Оказалось, что методы универсальной алгебры и методы теории моделей весьма близки и понимание взаимосвязей обогатило обе дисциплины. Некоторые конструкции, впервые найденные в математической логике, стали стандартными в алгебре и анализе, например так называемая конструкция ультрапроизведения, придуманная польским логиком Е. Лосем.

Одним из ярких достижений теории моделей 1960‐х годов стало создание нестандартного анализа Абрахамом Робинсоном. Он описал логическую конструкцию, которая позволила непротиворечиво рассматривать пополнение множества вещественных чисел бесконечно малыми и бесконечно большими числами. С помощью этой конструкции стало возможным дать объяснение исходной интуиции лейбницевских «бесконечно малых» и дать технически простое и интуитивное построение основных результатов математического анализа.n$ при $n>2$).

Методы теории доказательств — области математической логики, изучающей формальную доказуемость — также находят применения в «обычной» математике. Одним из успешных современных направлений является proof mining, извлечение конструктивных оценок из априори неконструктивных математических доказательств. Так называемые функциональные интерпретации, первоначально разработанные для анализа формальных систем, оказалось возможным применить и к конкретным содержательным математическим результатам (например, из области вещественного анализа, где интересен вопрос о скорости сходимости того или иного процесса к неподвижной точке и требуется явная оценка этой скорости). Результаты, полученные логическими методами, часто дают совершенно неочевидные усиления исходных теорем.

Логика в компьютерных науках. Если применения математической логики в «обычной» математике достаточно редки, то роль логических методов в информатике и компьютерных науках намного выше. Здесь математическая логика даёт подходящий язык для изучения возникающих задач и набор общих подходов к их решению. Удивительным образом, иногда оказывается, что концепции, сформулированные в математической логике очень давно и с другими целями, обретают новую жизнь в конкретных прикладных областях. Расскажем о некоторых направлениях, в которых логика доказала свою эффективность.

Реляционные базы данных и языки запросов. Многомиллиардная индустрия баз данных связана с технологией хранения больших объёмов структурированных данных, извлечением из них полезной информации и её обновлением. Поиск информации в базе данных осуществляется пользователем на языке запросов, который позволяет найти среди большого массива данных нужные сведения, потратив на это не слишком много времени. Поэтому языки запросов должны сочетать в себе достаточную гибкость для формулировки запросов и одновременно обеспечивать возможность эффективного поиска информации.

В 1960‐х годах американский учёный T. Кодд понял, что самый обычный язык логики предикатов очень удобен для обеих целей, поскольку позволяет эффективно осуществлять поиск по запросу. Эффективность обеспечивается с помощью аппарата реляционной алгебры — языка операций над отношениями, разработанного до этого в математической логике (в школе Альфреда Тарского) как алгебраический эквивалент языка логики предикатов. Идея Кодда о том, что запросы на языке реляционной алгебры допускают эффективный поиск, была первоначальным стимулом в разработке реляционных баз данных и общеупотребительных в настоящее время языков запросов, таких как SQL. С тех пор теория баз данных и логических языков успешно развиваются рука об руку.

Верификация программ и протоколов. Задача верификации программ, протоколов, аппаратных средств является одной из наиболее трудных и практически важных в компьютерной индустрии. Под верификацией понимается доказательство корректности работы программы (протокола, процессорного чипа, и т. д.), т. е. соответствия того, что реально делает программа, тому, что нам хотелось бы, чтобы она делала. Поскольку программа работает с входными данными, а вариантов входных данных может быть бесконечно много, мы не можем протестировать работу программы на всех возможных входах. На практике применяют методы тестирования, которые увеличивают вероятность обнаружения ошибок, однако полной гарантии надёжности всё‐таки не дают.

Другой путь решения этой проблемы, также активно применяемый на практике, состоит в сведении рассматриваемой задачи к логическому вопросу о соответствии программы её формальной спецификации. Это предполагает формулировку требований к тому, что должна делать программа, на формальном языке спецификаций программ. (В качестве такого языка часто используется язык так называемой темпоральной, или временной, логики, одной из разновидностей модальных логик.)

Подход, называемый model checking, состоит в том, чтобы сопоставить программе граф, представляющий её возможные состояния и переходы между ними. Это позволяет свести задачу верификации программы к вопросу о выполнимости формулы, задающей спецификацию, в модели, представляющей программу. Для решения задачи проверки выполнимости формулы в данной модели разработаны эффективно работающие алгоритмы, что позволяет на практике верифицировать программы с большим числом состояний. Этот метод особенно хорошо себя зарекомендовал для верификации чипов.

Альтернативный подход, называемый theorem proving, состоит в том, чтобы сопоставить программе логическую формулу, выражающую её корректность, и искать формальное доказательство этой формулы — например, в исчислении предикатов. Этот подход на данный момент не так распространён на практике, как model checking, но продолжает развиваться. Успешность этого метода во многом зависит от эффективности работы пруверов — программ автоматического поиска формальных доказательств. Разработка такого рода систем активно ведётся в наши дни.

Теории типов и функциональное программирование. Парадигма функционального программирования сочетает в себе несколько базовых идей, первоначально возникших в математической логике.

Первая идея — это взгляд на функцию как на объект, к которому может применяться программа наряду с другими данными (аргументы функций в свою очередь могут быть функциями и т. д.). Функциональная программа в целом может рассматриваться как определение некоторой сложной функции, а исполнение программы — как процесс вычисления значения функции на данном аргументе, сводящийся к пошаговому упрощению (редукции) её определения.

Более привычный нам императивный стиль программирования, в традиции Тьюринга и фон Неймана, привязан к понятию состояния памяти компьютера, которое изменяется в результате применения команд, таких как присваивания переменным новых значений. Функциональные программы не предполагают явного хранения состояния вычисления, в них нет присваиваний, а функции больше соответствуют математическому пониманию функций, чем подпрограммы в императивном программировании, которые могут зависеть от внешних переменных и иметь побочные эффекты.

Эти особенности позволяют писать в функциональном стиле более прозрачный код, потенциально содержащий меньше ошибок. Кроме того, функциональные программы допускают хорошее распараллеливание, поскольку разные части определения функции могут быть вычислены независимо.

В последние годы функциональные языки занимают всё более важную нишу среди употребительных языков программирования и применяются в тех областях, где важно иметь надёжные программы, например, в банковской сфере. По существу, первым функциональным языком программирования было лямбда‐исчисление, придуманное Чёрчем как простейшая универсальная вычислительная модель. Идеи лямбда‐исчисления были затем воплощены в одном из первых действующих функциональных языков — языке LISP, а также во многих более современных языках вплоть до Ocaml и Haskell.

Другой ключевой идеей, идущей из математической логики, является идея типа данных, на которой основано подавляющее большинство языков программирования высокого уровня, не обязательно именно функциональных. Использование переменных и функций, которым приписан определённый тип (например, тип «число с плавающей точкой», или тип «массив целых чисел»), позволяет на уровне компиляции проводить контроль типов, что избавляет программы от значительного числа ошибок (связанных с несоответствием значения переменной типу). Развитие языков программирования идёт в сторону усовершенствования и усложнения системы типов, где контролю типов отводится всё большая роль.

Формальные языки с типами (в отличие от бестиповых языков, в которых все переменные имеют один и тот же тип) впервые возникли в фундаментальном труде Б. Рассела и А. Уайтхеда «Основания математики», целью которого было построение математики на основе непротиворечивой системы аксиом теории множеств. В математике эта система, однако, не прижилась и была заменена более простой бестиповой теорией множеств Цермело—Френкеля с аксиомой выбора.

В 1950‐е годы в логике было обнаружено, что в достаточно развитых системах на базе лямбда‐исчисления с типами последние ведут себя в точности как логические высказывания (языка интуиционистской логики), а функциональные программы — как формальные доказательства этих высказываний. Это явление, описанное здесь, разумеется, очень приблизительно, получило название соответствия Карри—Говарда. Через несколько десятков лет оно послужило основой для создания функциональных языков, в которых возможно написание программ с одновременной верификацией их кода. Наиболее известными языками такого рода являются Coq и Agda, созданные для формализации математических доказательств. В частности, именно на языке Coq удалось построить формальное доказательство гипотезы четырёх красок и ряда других трудных математических результатов. Эти же языки начинают применяться и для задач верификации программ, описанных в предыдущем пункте.

Этими тремя темами мы ограничим избранный список областей информатики, в которых на деле применяются результаты математической логики. Многие не менее важные темы при этом оказались не затронутыми: теория сложности вычислений, теория автоматов и монадическая логика, SAT‐solving, языки авторизации и контроля доступа к информации, логическое программирование и хорнова логика, онтологические базы данных и дескрипционная логика — перечисление можно очень долго продолжать.

Завершая обзор, посмотрим на отдельные области гуманитарных наук, испытавшие на себе влияние методов математической логики. Выбранные нами предметы касаются философии, языкознания и даже теории права. Эти разнообразные темы объединены в одну группу, поскольку связаны с изучением явлений, требующих модификации тех или иных аспектов классической логики.

Неклассические логики. Первые логические системы, отличные от традиционной двузначной, стали появляться ещё в то время, когда процесс формализации классической логики предикатов не был завершён. К настоящему времени неклассические логики представляют собой большое царство, населённое самыми разнообразными и экзотическими представителями (исчисляемое десятками семейств). Мотивации при рассмотрении неклассических логик могут быть самыми разными: попытки точнее передать те или иные свойства естественного языка; попытки построить систему, отвечающую тем или иным философским установкам; попытки расширить язык классической логики новыми выразительными возможностями или, наоборот, сузить выразительные возможности классической логики с тем, чтобы сделать её более эффективной для решения тех или иных задач. Проведём небольшую экскурсию по «зоопарку» неклассических логик.

Интуиционизм как философское течение возник в самом начале XX века в работах молодого нидерландского математика Л. Э. Я. Брауэра как реакция на кризис оснований математики и теории множеств. Характерной чертой философии Брауэра было желание избавить математику от неконструктивных теорем существования, т. е. утверждений о существовании тех или иных объектов, без возможности предъявить явно их конструкцию. Глубокий анализ привёл Брауэра к идее о том, что сама классическая логика, а именно закон исключённого третьего, является источником таких неконструктивных утверждений в математике. Это потребовало радикально пересмотреть традиционное понимание смысла математических утверждений, логических операций и кванторов.

Хотя сам Брауэр настаивал на неформальном характере своей философии математики — отсюда её название «интуиционизм» в противоположность гильбертовскому «формализму» — к началу 1930‐х годов возникла потребность в уточнении совокупности логических принципов, приемлемых с интуиционистской точки зрения. Решение этой задачи было дано учеником Брауэра А. Гейтингом, который сформулировал общепринятую в настоящее время интуиционистскую логику предикатов, опираясь на предшествовавшую работу А. Н. Колмогорова. Парадоксально, но в результате интуиционизм был также поставлен на прочную формальную основу.

Несмотря на поддержку ряда выдающихся математиков, одним из которых был Герман Вейль, интуиционизм не стал преобладающей философией математики. В настоящее время трудно найти подлинных сторонников этой философии даже среди логиков. Тем не менее, с точки зрения формальной логики, интуиционизм представляет собой стройную и богатую содержательными результатами систему. С течением времени было осознано, что интуиционистская логика скрывается во многих математических структурах, в частности в структурах топологической природы. Например, было обнаружено, что возникшее в работах А. Гротендика понятие топоса можно рассматривать как модель интуиционистской логики.

С другой стороны, интуиционистская логика часто возникает в различных приложениях в компьютерных науках. Это не случайно, поскольку интуиционистская логика теснее связана с понятием вычисления, чем логика классическая. Одним из важнейших проявлений этой связи является уже упомянутое соответствие Карри—Говарда.

Классическая логика допускает интерпретацию в логике интуиционистской, поэтому современная точка зрения на их соотношение состоит в том, что интуиционистская логика не ограничивает, а, наоборот, добавляет в классическую новые выразительные возможности — такие как различие между неконструктивным и конструктивным утверждением о существовании.

Модальная логика. Другим классом логик, обогащающих классическую новыми выразительными возможностями, являются так называемые модальные логики. Язык модальной логики, наряду с обычными связками, содержит новую одноместную логическую связку $ □\, $. Высказывание $□\, A$ в разных контекстах может пониматься совершенно по‐разному, что приводит к разным постулируемым принципам, т. е. разным модальным логикам. Стандартные логические связки, такие как импликация или отрицание, как правило, сохраняют в модальной логике классическую интерпретацию. (Разумеется, могут рассматриваться модальные логики и над другими логиками, например над интуиционистской, однако такие системы в целом сложнее и потому менее распространены.)

Исторически первым, идущим ещё от Аристотеля, прочтением формулы $□\, A$ было высказывание «$A$ необходимо». (Здесь мы говорим о языковой конструкции, присутствующей в нашем естественном языке, а не о каком‐либо математическом понимании того, что значит «необходимо».) Двойственное высказывание «не $A$ не является необходимым» обычно отождествляется с высказыванием «$A$ возможно» и обозначается $◇\, A$.

Перечислим некоторые известные интерпретации модальности, приводящие к интересным и полезным семействам логик.

Логика доказуемости: $□\, A$ означает «$A$ доказуемо» в данной аксиоматической теории, например в теории множеств. При этом высказывания понимаются как высказывания в языке теории множеств, каковым можно считать и само высказывание о доказуемости утверждения $A$. Эта логика интересна тем, что даёт точную математическую семантику модальности и применяется для исследования обычных классических аксиоматических теорий.

Временная логика, описывающая развитие некоторого процесса во времени: $□\, A$ означает «всегда в будущем будет верно $A$». Различные модели течения времени — непрерывное, дискретное или даже ветвящееся — приводят к разным временным логикам. Временные логики, применяемые на практике для верификации программ, используют и некоторые дополнительные связки, например двухместную связку, выражающую «$A$ имеет место до тех пор, пока $B$».

Эпистемическая логика, описывающая знания и обмен информации между несколькими агентами: $□\,_x A$ означает «агенту $x$ известно $A$» (в этой логике, как правило, описываются знания нескольких агентов $x$, $y$, … и каждому из них соответствует своя модальность $□\,_x$, $□\,_y$, …). Эпистемическая логика является частью (формальной) эпистемологии — обширного и важного раздела философии, занимающегося исследованием таких понятий, как знание и вера, того как знание возникает, как оно связано с понятием доказательства (обоснования). Формализм эпистемической логики позволяет построить модели различных аспектов этих явлений и использовать их для анализа тех или иных теоретических положений.

Эпистемическая логика также находит более конкретные применения в компьютерных науках и искусственном интеллекте для описания знания, возникающего в системах с несколькими агентами. Например, условие корректности протокола, связанного с обменом информацией, в котором не должна допускаться утечка информации третьим лицам, может быть сформулировано на языке эпистемической логики.

Деонтическая логика формализует модальности типа долженствования, например $□\, A$ можно понимать как «$A$ требуется» или «$A$ обязательно» (двойственную модальность можно понимать как «$A$ разрешено»). Такие логики впервые стали рассматриваться в философии и теории права для формализации и анализа различных аспектов правовых систем.

Многозначная логика и нечёткая логика. Многозначные логики возникают, если допускаются другие истинностные значения, помимо классических истины 1 и лжи 0. Например, можно рассматривать промежуточное значение 1/2 и интерпретировать его как «неизвестно». Следующий шаг требует определения того, каким образом вычисляются значения логических связок, и конкретное решение по этому поводу может привести к различным логикам.

Если пойти дальше по пути многозначности, то естественно возникает идея о том, что истинностным значением высказывания может быть любое вещественное число в интервале $[0,1]$ (например, это число может выражать степень нашей уверенности в справедливости высказывания). Такие логики часто называют «нечёткими» (fuzzy), поскольку предикаты в такой системе могут выглядеть как размытые, не имеющие чётких границ. Например, высказывание о том, что видимый цвет является красным, не является чётким в силу неопределённости самого понятия «красный».

Нечёткие логики призваны формализовать рассуждения в условиях неопределённости или неточности информации. Подлинным «отцом» нечёткой логики и теории нечётких множеств был Л. Заде. Он увидел потенциал этой логики для различных инженерных применений, например в такой области, как экспертные системы или теория управления, и сделал очень много для её популяризации.

Немонотонная логика. Классическая логика обладает очевидным свойством монотонности: добавление новых аксиом не отменяет никаких ранее доказанных теорем. В работе с базами данных, где не вся содержащаяся информация может быть верной, появление новой информации может привести к пересмотру уже известных фактов и их отмене. В этом случае свойство монотонности нарушается.

Аргументы и доказательства, приводимые в суде, могут быть оспорены или опровергнуты противной стороной. Процесс выстраивания аргументов, таким образом, на практике выглядит совершенно непохоже на привычные нам дедуктивные математические доказательства. Эти аспекты изучает теория аргументации — весьма развитая область исследований, связанная с философией, лингвистикой, теорией права и искусственным интеллектом. Формальные модели аргументации во многих случаях базируются на немонотонных логиках.

Паранепротиворечивая логика. Как известно, в классической логике действует закон ex contradictio quodlibet, т. е. из противоречия следует всё что угодно. Поэтому противоречивые классические системы все эквивалентны между собой и, по существу, бесполезны. На практике людям приходится рассуждать в не столь стерильных условиях: не всегда бывает известно, есть ли противоречие в имеющейся информации, на основании которой приходится делать выводы. Логики, приспособленные для рассуждений в условиях возможно противоречивых предположений, называются паранепротиворечивыми. В таких системах возникновение противоречия не приводит к доказуемости всех вообще утверждений.

Можно сказать, что наша обыденная логика (как способ умозаключений на основе имеющейся информации) является одновременно нечёткой, паранепротиворечивой и немонотонной. Разумеется, все эти формальные системы являются лишь приближёнными и грубыми моделями отдельных аспектов той самой «обыденной логики».

Грамматики Хомского и семантика Монтегю. Одной из теорий, соединивших в себе сразу несколько аспектов неклассических логик — кванторы, предикаты, модальности, модели Крипке и лямбда‐абстракцию — является семантика Монтегю. Эта теория, предложенная американским логиком Р. Монтегю в начале 1970‐х годов, представляет собой попытку применить идеи математической логики к трудной задаче описания семантики естественного языка. Она, по существу, положила начало целому направлению в математической лингвистике — формальной семантике. Ранее работы Н. Хомского, создавшего теорию формальных грамматик, произвели революцию в понимании синтаксиса естественных языков. Применения математической логики в лингвистике, из которых мы вскользь упомянули лишь два важных направления, безусловно заслуживают отдельного разговора.

Неужели это всё математика? — недоумённо воскликнет читатель. И да, и нет. Исследователи, применяющие методы математической логики в той или иной области знания, должны прежде всего быть компетентными специалистами именно в этой области и разбираться в постановках специфических для неё задач. Напомним, что многие создатели математической логики — Гёдель, Тьюринг, фон Нейман и др. — не были только лишь «чистыми» математиками.

Тем не менее, используемый в приложениях логический аппарат является самым настоящим математическим аппаратом, даже если он и совсем не похож на ту математику, которой традиционно обучают на математических факультетах университетов. Вопросы, связанные с неклассическими логиками — например, вопросы их полноты относительно семантики Крипке или топологической семантики, вопросы классификации различных семейств неклассических логик — имеют существенную математическую составляющую. Для успешной работы в философской логике, математической лингвистике, теории игр, теории баз данных и других областях приложений этой математикой также нужно овладеть. К счастью, порог входа здесь не так уж высок, и математическую логику с успехом преподают на факультетах компьютерных наук, философии и лингвистики.

Математически наиболее развитые части математической логики — такие, как теория множеств, теория алгоритмов и сложности вычислений, теория моделей или ординальный анализ формальных систем, содержат некоторые из наиболее сложных с математической точки зрения результатов и применяемых методов. Разумеется, современные исследования в этих давно сложившихся областях целиком и полностью лежат в области математики.

Международная олимпиада по Математике. Логика

Выполняя задания олимпиады, ребята будут рассуждать, строить таблицы, чертить круги Эйлера. Им предстоит отгадать слова, составить рассказ, решить логические задачи, поиграть в логические игры и многое другое. Задания этой олимпиады позволят участникам применить уже имеющиеся у них знания по предмету, приобрести новые, расширив при этом спектр своих умений и навыков решения интересных заданий.

 

В этом учебном году Олимпиада по математике. Логика проводится по следующим темам:

 

1-4 классы

1. Многозначность математических терминов.

2. Координатная плоскость.

3. Сравнение объектов, последовательности.

4. Логические задачи (развитие произвольного внимания, нахождение общего свойства или лишнего предмета, группировка объектов по какому-либо признаку, умозаключения).

5. Круги Эйлера.

6. Осевая симметрия.

7. Моделирование.

8. Задача Эйнштейна.

 

5-11 классы

1. Многозначность математических терминов.

2. Сравнение объектов, последовательности.

3. Логические задачи (нахождение общего свойства или лишнего предмета, группировка объектов по какому-либо признаку, умозаключения).

4. Круги Эйлера.

5. Симметрия.

6. Моделирование.

7. Задача Эйнштейна.

 

Особенности олимпиады:

* Конкурс проводится для учащихся 1-2, 3-4, 5-6, 7-8, 9-11 классов.

* При создании конкурсных заданий учитывается временной промежуток, отведённый на их выполнение, — 7 дней.

* Для каждого конкурсного задания определено среднее время его выполнения, что поможет участнику выбрать индивидуальный темп: сразу выполнить все конкурсные задания или разделить их выполнение на несколько дней.

* Задания конкурса повышают мотивацию к изучению к изучению предметной области «Математика».

* Конкурс предусматривает самостоятельную работу с дополнительной литературой и интернет-источниками.

* Конкурс развивает познавательные УУД.

Решение пропозициональной логической задачи со словом

В этом разделе мы будем использовать знакомые обозначения, используемые в логике высказываний. Возможно, вы сначала захотите познакомиться с логикой высказываний.

Как и при решении любых других вопросов, мы всегда должны спрашивать себя, что мы можем, а что не можем делать, записывая свои рассуждения. Первый шаг к тому, чтобы научиться решать проблемы логики высказываний, состоит в том, чтобы перечислить то, что нельзя сделать или что невозможно, чтобы мы могли сузить круг возможных сценариев.Помните, что очень легко сделать ошибочный вывод, основанный на ошибочных рассуждениях. Возьмите в качестве примера приведенные ниже утверждения. Если первое утверждение истинно, верно ли второе утверждение?

«Если идет дождь, то я не могу играть в футбол». «Если я не могу играть в футбол, значит идет дождь». \ Begin {array} {c} & \ text {«Если идет дождь, то я могу» t играть в футбол «.} & \ text {» Если я не умею играть в футбол, значит идет дождь. «} \ end {array}» Если идет дождь, то я не могу играть в футбол «.» Если я могу Не играю в футбол, значит идет дождь.«

Совершенно очевидно, что проблема здесь: могут быть другие причины, по которым я не могу играть в футбол, которые не обязательно зависят от погоды. Если мы допускаем такие простые ошибки в рассуждениях, когда контекст очень ясен, просто представьте, что произойдет, когда вы будете менее уверены в более расплывчатых утверждениях. В следующем абзаце мы познакомимся с этими ошибками.

Обратные и обратные ошибки

Как новичок, наиболее распространенная ошибка, которую вы можете сделать, — это предположить, что обратное и / или обратное исходное утверждение также верно.Взгляните на два раздела ниже:

Введение в Converse Ошибка с ошибочными рассуждениями:

Предпосылка : Если идет дождь, я не могу играть в футбол.

Заключение : Если я не умею играть в футбол, значит идет дождь.

Объяснение : Из первого оператора мы получаем условие и результат: «дождь» как условие и «я не могу играть в футбол» как результат. Вся посылка сформулирована таким образом, что если условие выполнено, то результат наступит.Однако вывод показывает, что если результат будет выполнен, то условие будет выполнено. Это не имеет смысла, потому что условие не обязательно должно иметь место, если результат наступает первым. Это известно как обратная ошибка.

В общем виде аргумент обратной ошибки выглядит следующим образом:

• Если встречается P, значит Q.
• Q возникает.
• Следовательно, P также встречается.

Введение в обратную ошибку с ошибочными рассуждениями:

Предпосылка : Если идет дождь, я не могу играть в футбол.

Вывод : Если не идет дождь, то могу поиграть в футбол.

Объяснение : Из первого оператора мы получаем условие и результат: «дождь» как условие и «я не могу играть в футбол» как результат. Вся посылка сформулирована таким образом, что если условие выполнено, то результат наступит. Однако вывод показывает, что если условие не наступает, то не наступает и результат. Это не имеет смысла, потому что могут быть другие причины / факторы, по которым может произойти результат.Это известно как обратная ошибка.

В общем виде аргумент обратной ошибки выглядит следующим образом:

• Если встречается P, значит Q.
• P не встречается.
• Следовательно, Q также не встречается.

Теперь может быть совершенно ясно, что легко определить, что мы сделали ошибочные рассуждения. Однако что, если приведенные утверждения кажутся более расплывчатыми? Это причина, по которой мы вводим две ошибки выше (обратная ошибка и обратная ошибка), чтобы показать, что не все неправильные утверждения легко идентифицировать.Проще говоря, взаимосвязь между двумя событиями не обязательно означает, что одно вызывает другое. Короче говоря, мы указываем на общий факт, что «корреляция не подразумевает причинно-следственной связи».

Теперь, когда мы увидели эти ошибки на собственном опыте, давайте рассмотрим другой пример, чтобы напомнить себе, что это ошибки, и мы надеемся избежать их в будущем. Имейте в виду, что некоторые обратные / обратные утверждения могут показаться нелепыми, а некоторые — нет.

Нам дается следующее утверждение: Если сегодня воскресенье, значит, погода солнечная.

(i) \ qquad \ text {(i)} (i) Запишите обратную и обратную форму этого утверждения.
(ii) \ qquad \ text {(ii)} (ii) Определите, какое из сделанных вами утверждений не является логичным, и объясните, почему.

---

(i) \ text {(i)} (i) Обратные и обратные

• Перевернутая карта: Если сегодня не воскресенье, то погода не солнечная.
• Converse: Если погода солнечная, то сегодня воскресенье.

(ii) \ text {(ii)} (ii) Логическое или нелогичное

Хотя они противоположны исходному утверждению, мы должны помнить, что они не обязательно могут быть ошибкой.Однако нет ничего плохого в том, чтобы проверить, верны они или нет.

• Обратное утверждение подразумевает, что день имеет прямое отношение к солнечной погоде или нет, что смехотворно , потому что также могут быть несолнечные дни, которые не выпадают на воскресенье.

• Обратное утверждение подразумевает, что только если погода солнечная, тогда день будет воскресным, что тоже смехотворно , потому что у них также может быть солнечная погода в дни, не выпадающие на воскресенье.□ _ \ квадрат □

Определите точную ошибку

Теперь, когда мы можем определить, как возникают ошибки, давайте сделаем еще один шаг и применим эти методы, чтобы мы могли точно определить, где возникает ошибка. Обратите внимание, что самый простой способ определить, где возникла ошибка, — это преобразовать логические утверждения в символические формы (например, P подразумевает Q). \ text {+} \ text {средний или лучший} \\
& \ text {(iii)} & \ text {Взять бухгалтерию} \\
\ end {array} (i) (ii) (iii) Специалист в области математики или информатики Получите средний балл B + или вышеБерите бухгалтерский учет

Поскольку вы стали изучать математику, критерий (i) \ text {(i)} (i) удовлетворяется.\ text {+} B + среднее, критерий (ii) \ text {(ii)} (ii) не выполняется.
Поскольку вы начали бухгалтерский учет, критерии (iii) \ text {(iii)} (iii) удовлетворены.

Поскольку вы не соответствовали всем критериям и получили отказ, персонал вам не лгал. □ _ \ квадрат □

Теперь, когда вы знакомы с записью этих операторов и выявлением возможных ошибок, давайте попробуем другой пример, в котором используется такое свойство!

Недостаточная информация

Sharky

Сатвик

Кришна

В магазин совершил обыск мародер / ы, которые уехали на машине.Трое известных преступников Сатвик, Кришна и Шарки доставлены в полицейский участок для допроса. Инспектор полиции Адитья извлекает следующие факты:

(1) (1) (1) Никто, кроме Сатвика, Кришны и Шарки, не участвовал в грабеже.
(2) (2) (2) Шарки никогда не выполняет свою работу без использования Сатвика (и, возможно, других) в качестве сообщников.
(3) (3) (3) Кришна не умеет водить машину.

Найдите человека, который в любом случае виноват.

Эта задача входит в мой набор «Это то, что вы называете логикой?»

Формальная терминология

В предыдущих разделах мы узнали о двух наиболее распространенных ошибках, которые допускают учащиеся при решении задачи логического рассуждения.Однако мы формально не касались терминологии для этих терминов: обратная ошибка и обратная ошибка. Давайте начнем!

Контрапозитив : Утверждение логически эквивалентно своему контрапозитиву. Контрапозитив отрицает оба термина в импликации и меняет их позиции. Например, противоположность «P подразумевает Q» — отрицание Q подразумевает отрицание P.

• Converse : Обратное меняет положение терминов.Обратное к «P влечет Q» означает «Q влечет P».

• «Если и только если», иногда записываемое как iff и известное как эквивалентность, является импликацией, которая работает в обоих направлениях. «P тогда и только тогда, когда Q» означает, что и «P подразумевает Q», и «Q подразумевает P».

Давайте попробуем несколько примеров, которые охватывают эту область!

(i) \ text {(i)} (i) Запишите контрпозитивное заявление для

«Если вы человек, значит, у вас есть ДНК.»\ text {» Если вы человек, то у вас есть ДНК. «}» Если вы человек, то у вас есть ДНК «.

(ii) \ text {(ii)} (ii) Запишите два оператора «если-то» для

«Многоугольник является четырехугольником тогда и только тогда, когда многоугольник имеет 4 стороны.» \ Text {«Многоугольник является четырехугольником тогда и только тогда, когда многоугольник имеет 4 стороны.»} «Многоугольник является четырехугольником тогда и только тогда, когда многоугольник имеет 4 стороны «.

---

(i) \ text {(i)} (i) контрапозитивный
\ qquad Если у вас нет ДНК, значит, вы не человек.

(ii) \ text {(ii)} (ii) утверждения «если-то»
\ qquad Если многоугольник является четырехугольником, то у него 4 стороны.
\ qquad Если у многоугольника 4 стороны, то это четырехугольник. □ _ \ квадрат □

Просто, не правда ли? Давайте попробуем решить некоторые задачи, в которых применяются методы, которые мы узнали выше.

Если Джефф хорошо справится со своим следующим тестом по математике, то он закончил домашнее задание по математике.Если Джефф проведет 5 часов, играя в видеоигры, то следующий тест по математике он провалит.

Если Джефф не провалит следующий тест по математике, значит, он не провел 5 часов, играя в видеоигры.

Если Джефф не выполнит домашнее задание по математике, он потратит 5 часов на видеоигры.

Если Джефф не играет в видеоигры, он успешно сдаст следующий тест по математике.Если Джефф не выполнит домашнее задание по математике, значит, он не сможет успешно сдать следующий тест по математике.

Если Джефф потратит 2 часа на видеоигры, он сможет закончить домашнее задание по математике.

Если Джефф завершит домашнее задание по математике, значит, он не потратил 5 часов на видеоигры.

Если Джефф потратит 5 часов на видеоигры, он не сможет закончить домашнее задание по математике.

Если Джефф завершит домашнее задание по математике, то его следующий тест по математике будет успешным.

На основании этой информации, что из следующего является логически правильным?

Синий

Не могу сказать

Зеленый

Желтый

Селена, Дженнифер и Майли носят синее платье, желтое платье и зеленое платье в неизвестном порядке.Известно, что:

1) Если Селена носит синее, то Дженнифер носит зеленое.
2) Если Селена носит желтое, то Майли носит зеленое.
3) Если Дженнифер не носит желтого цвета, то Майли носит синее.

Какого цвета платье на Селене?

Теперь, когда мы освоили эти методы, давайте перейдем к следующему разделу, чтобы узнать о других классных методах доказательства!

математических головоломок

математических головоломок

Эти головоломки не требуют никаких математических знаний, только логические рассуждения.Проверь, насколько ты умный. Если вы не можете их решить, расслабьтесь.
Почти все загадки нам рассказали
компьютерно-математический гений Влад Митлин. Приходите к нам снова: мы намерены размещать здесь новые головоломки и решения.

Пожалуйста, присылайте нам свои комментарии и новые головоломки по электронной почте:
[email protected].
Наслаждаться!

---

1. Монеты

Есть 12 монет. Один из них ложный; у него другой вес. Неизвестно, тяжелее или легче фальшивая монета, чем правильные монеты.Как найти фальшивую монету по трем весам на простых весах?

Решение:

кликните сюда

---

2. Мостовой переход

Эта проблема была недавно опубликована в MAA на сайте:
Переход через шаткий мост ночью при свете фонарика.

Группа из четырех человек должна перейти мост. Темно, и они должны осветить путь фонариком. Одновременно мост могут пересечь не более двух человек, а у группы есть только один фонарик. Люди в группе переходят мост разное время:
A nnie пересекает мост за 1 минуту,
B ob пересекает мост за 2 минуты,
Володя Митлин пересекает мост за 5 минут,
D Ороти пересекает мост за 10 минут.

Как группе пройти через мост за 17 минут?

Решение:

кликните сюда

Чтобы увидеть анимированное решение, вам нужен браузер, поддерживающий JAVA.

---

3. Доставка яблок

---

Еще проблемы от Влада Митлина

---

Вечеринка!

На вечеринке группа людей. Покажите, что вы можете представить некоторые из
их друг к другу так, чтобы после знакомства не более двух человек
в группе будет одинаковое количество друзей (начальная конфигурация
не работает, потому что у всех изначально 0 друзей).

---

Цифры

Покажите, что для любого натурального n хотя бы одно из двух чисел, n или n + 1, может быть
представлены в следующем виде:

к + S (к)

для некоторого k, где S (k) — сумма всех цифр в k. Например,

21 = 15 + (5 + 1)

---

Проблема дзен

Буддийский монах получил задание от своего учителя: медитировать ровно 45
минут. У него нет часов; вместо этого ему дают две ароматические палочки, и он
говорят, что каждая из этих палочек полностью сгорит за 1 час.В
палочки не идентичны, и горят с разными, пока неизвестными скоростями
(они сделаны вручную). Итак, у него есть эти два инсента и несколько спичек: может
он устраивает медитацию ровно на 45 минут?

---

Счастливые билеты

В России садишься в автобус, берешь билет и иногда говоришь: Вау, а
счастливое число! Автобусные билеты пронумерованы шестизначными числами, а счастливые
в билете сумма трех первых цифр равна сумме трех последних цифр.
цифры. Когда мы учились в старших классах (ребята из математической школы No.N — 1

---

Расстояния

В прямоугольнике 6 точек со сторонами 3 и 4. Докажите, что
расстояние между как минимум двумя из этих точек меньше квадрата
корень 5.

---

король

Шахматный король помещается на шахматную доску 8×8. Он должен сделать 64 хода,
посетив каждый (из 64) квадратов только один раз, и вернуться туда, где он
начал. Путь должен быть без пересечений (путь имеет вид восьмерки).
не годится).
Для петли можно подсчитать общее количество горизонтальных + вертикальных (т.е.
без диагональных) ходов; назовем этот номер М.

1. Приведите пример хотя бы одной такой петли. 2 + ab + ac + ad + bc + bd + cd

не меньше 10.

---

Три планеты в галактике и обвал рынка

Галактика состоит из трех планет, каждая из которых движется по прямой
линия с собственной постоянной скоростью. Если центры всех трех планет
случайно лежат на прямой (какое-то затмение) жители
каждая планета сходит с ума (они не могут видеть свои две соседние планеты сразу
один раз), начните говорить о конце света, а фондовый рынок
вылетает. Покажите, что таких обвалов рынка будет не более двух.
каждая из этих планет.4

есть решения в простых числах? Найдите хотя бы один, если да, в противном случае приведите доказательство несуществования.

---

Последовательность

Последовательность натуральных чисел определяется по следующей формуле:

A [n + 1] = a [n] + f (n)

Где f (n) — произведение цифр в [n]. Есть ли [1]
такая, что указанная выше последовательность не ограничена?

---

Интеллектуальная сила стаи драконов

Драконы должны встретиться для мозгового штурма в конференц-центре.В
делегаты должны быть отобраны, чтобы обеспечить максимальную эффективность
мозговой штурм. У дракона любое количество голов, и для любого N
при необходимости доступно любое количество N-головных драконов. Проблема в
что размер конференц-центра ограничен, поэтому не более 1000
головы могут поместиться в актовый зал. Интеллектуальная сила
стая драконов — это произведение количества голов драконов в стае.
Как должна выглядеть оптимальная стая (общее количество драконов,
распределение голов)?

---

Истребитель вампиров

На поверхности планеты живет вампир, который может перемещаться
скорость не больше u.Космический корабль истребителей вампиров приближается к
планеты со скоростью v. Как только космический корабль видит вампира, он
стреляет серебряной пулей — вампир мертв.
Докажите, что если v / u> 10, убийца вампиров может выполнить свое
миссии, даже вампир пытается спрятаться.

---

Проекторы

(2D) проектор освещает квадрант на плоскости. 4 проектора
установить в 4 произвольных точках плоскости. Покажи, что их можно повернуть так
что весь самолет будет освещен.(3D) Покажите, что все пространство
может быть освещен 8 прожекторами, каждый из которых освещает октант, однако
точки расположения есть.

---

Кампания бдительности в Солт-Лейк-Сити.

Солт-Лейк-Сити выглядит как прямоугольник, пересеченный улицами M , идущими от
С севера на юг и с улицами N , идущими с востока на запад. Город часто посещают туристы, которые предполагают бегать в автобусах.
Губернатор Юты хочет следить за всеми перемещениями автобусов.Он планирует выставить на некоторых перекрестках полицейских, чтобы они наблюдали за движением автобусов.
улицы, видимые с этих перекрестков.
Какое минимальное количество полицейских необходимо для наблюдения за автобусом?

---

Блондинки (загадка из Oldaque P. de Freitas)

Две блондинки сидят в уличном кафе и разговаривают о детях.
Один говорит, что у нее три дочери. Произведение их возраста равно 36
а сумма возрастов совпадает с номером дома напротив.Вторая блондинка отвечает, что этой информации недостаточно, чтобы
выяснить возраст каждого ребенка. Первый соглашается и добавляет, что у старшей дочери красивые голубые глаза. Затем второй решает загадку.
Вы тоже можете это решить!

---

Это от Гжегожа Дзержановского.

Есть 12 зубочисток. Найдите многоугольники экстремального поля, используя все
зубочистки. При построении этих полигонов соблюдайте правила:
— зубочистки не сломаешь,
— длина каждого ребра 1,2,3,… зубочистки,
— края многоугольника не могут пересекать друг друга.

---

---

Инвестирование в разум: проблемы математики и логики

Обзор

Математика и логика были с нами до некоторой степени с начала цивилизации. Эволюция была интересной и привела нас к одним из самых сложных головоломок, проблем и загадок нашего времени.

Раньше мы полагались на грубые рассуждения для решения наших проблем. С развитием сложного языка и культуры вскоре появились специалисты, а вместе с ними и язык чисел, который формализовал большую часть нашей логики — математику.Таким образом, они всегда были связаны вместе; Вы не можете иметь математику без логики, а без математики рассуждать было бы еще труднее.

Позже, в 19 веке, мы познакомились с современной математической логикой, когда она отошла от чистой логики и стала самостоятельным разделом математики. Он быстро проник в школьную программу и инженерное дело. С тех пор задачи математической логики дразнили мозги людей повсюду, от учеников начальной школы до математиков и даже экспертов по головоломкам.

Мы составили список сложных задач по математике, логике и математической логике для всех, от студентов до экспертов по головоломкам. Они обязательно дадут вам тренировку для вашего мозга. Удачи и удачи.

Начальный уровень (дети) — математические и логические задачи

Математика и логика лучше всего вводятся в молодом возрасте, чтобы помочь развивающемуся уму понять концепции и изучить разницу между логикой и заблуждениями на раннем этапе. Воспользуйтесь любой из этих ссылок, чтобы помочь вашим ученикам встать на правильный путь в самом начале обучения.

• У NRICH есть двадцать две веселые игры и задачи, доступные в Интернете для решения юными учащимися. Это простые проблемы с основными изображениями, которые можно просмотреть в Интернете или распечатать для использования в классе.
• Государственные школы Арлингтона предлагают ссылки на множество математических задач для учащихся в разделе игр для мозга. Большинство их ссылок ведут на другие сайты, такие как PBS Kids и British Broadcasting Corporation.
• Сотрудничество по математическому образованию составило список различных традиционных настольных и карточных игр, в которые можно играть в автономном режиме и которые поощряют логическое мышление.Почему бы не перенести обучение в автономный режим, сохранив при этом удовольствие?
• Управление энергетической информации США предлагает распечатанный документ о головоломках с ветровой логикой в ​​качестве учебного пособия для учителей для младших школьников. Пусть студенты узнают об окружающей среде, энергии и логике одновременно!
• Национальный институт наук об окружающей среде и здоровье предлагает головоломки REBUS, которые нужно решить. По их словам, REBUS — это «графическое представление имени, произведения или фразы». Используйте эти визуальные головоломки, чтобы расширить кругозор.

Средний уровень (подростки и молодые люди) — математические и логические задачи

Вот еще несколько сложных математических и логических задач для учеников следующего уровня. Важно практиковать логическое мышление на каждом этапе обучения.

• У Калифорнийского университета в Лос-Анджелесе есть раздаточный материал, который включает в себя несколько головоломок, которые можно решить в классе или дома без использования компьютера.
• org предлагает интерактивную трехмерную логическую игру, в которую можно играть в браузере, не устанавливая или загружая что-либо.
• Центр математического и естественнонаучного образования AIMS предлагает шесть интересных и занимательных логических головоломок, направленных на развитие разума.
• Stetson University предлагает широкий выбор простых визуальных логических головоломок, которые больше похожи на игру, чем на работу.
• Университет Юты предлагает серию словесных головоломок, требующих только логического мышления. Никаких особых математических навыков не требуется!

Продвинутый уровень (подростки и молодые люди) — математические и логические задачи

Все еще готовы? Вот еще четыре варианта для смельчаков.

• Cut the Knot содержит обширный интерактивный сборник математических материалов и раздел головоломок, охватывающий несколько областей математики и логики. Они охватывают алгебру, арифметику, геометрию и многое другое.
• Колледж Wabash каждые пару недель публикует новую задачу на тот случай, если проблемы у вас закончатся. Доступ к предыдущим задачам также доступен, если вы хотите наверстать упущенное.
• У Калифорнийского университета в Дэвисе есть распечатка с несколькими сложными логическими головоломками, которые вам предстоит решить.Почему бы не попробовать?
• Управление образования города Нью-Йорка предлагает пример логических головоломок, поскольку они в настоящее время необходимы для соответствия образовательным стандартам. Если вас интересуют текущие школьные требования, это может быть хорошим местом для остановки.

Только для экспертов — математические и логические задачи

Готовы ли вы к экспертному уровню? Несколько университетов, а также Агентство национальной безопасности предлагают сложные логические задачи на некоторых из самых сложных уровней.Вы все еще ищете больше после этого? Почему бы не подумать о создании нескольких собственных логических задач, чтобы бросить вызов другим? Иногда настоящая задача состоит в том, чтобы собрать идеальную головоломку.

• Университет Восточного Кентукки столкнулся с несколькими проблемами, которые большинство людей не смогли решить. Готовы ли вы принять настоящий вызов?
• Западно-семитский исследовательский проект Университета Южной Калифорнии содержит загадку папируса и обещание, что вы получите письмо, подтверждающее, что вы являетесь «мастером папиролога», если вы отправите конверт с адресом и маркой вместе с решенной головоломкой.Сможете ли вы стать одним из немногих, кто удостоился этого титула?
• В Стэнфордском университете есть копия «Загадки Эйнштейна», интересной загадки неизвестного происхождения, хотя ее часто приписывают самому Эйнштейну. Ходят слухи, что 98% людей, пытающихся решить эту задачу, не могут решить головоломку.
• Проблемный уголок Университета штата Миссури предлагает проблемы как для старшеклассников, так и для экспертов. Как только вы попадете на их страницу, просто выберите ссылку на тот раздел, который вас больше всего интересует.
• Purdue University имеет архив задач предыдущих семестров, если вы заинтересованы в том, чтобы опробовать задачи, которые давали предыдущие студенты.
• Агентство национальной безопасности США выпускает журнал-головоломку для сотрудников и всех, кто готов принять вызов. Они говорят, что выражение сложных криптографических проблем — это всего лишь часть сложных инженерных проблем, с которыми они глубоко вовлечены на работе, так почему бы не создать публикацию, посвященную этому?

Math 1365: Introduction to Mathematical Reasoning

Math 1365: Introduction to Mathematical Reasoning — Советы по решению проблем

Вот несколько общих советов, которые помогут вам при выполнении домашних заданий по математике 1365.

Генеральный Pep Talk

Математика — это творческое занятие, хотя оно редко преподносится в таком виде на курсах ниже уровня математического анализа. Цель этого курса — детально объяснить основы логики, теории множеств, теории чисел и комбинаторики и помочь вам развить «математическую интуицию» в отношении материала, который позволит вам решать очень широкий круг задач. Многие темы курса, вероятно, будут вам знакомы (например,, логические рассуждения, простые числа, функции, счет), но этот подход, вероятно, покажется очень чуждым, потому что мы потратим большую часть нашего времени на тщательное и строгое доказательство «интуитивно очевидных» вещей, используя формальный язык.

Домашние задания и экзамены будут делать упор на творческое решение проблем, и поэтому вы, вероятно, будете глубоко сбиты с толку, озадачены или потеряны на долгое время, когда будете работать над заданиями. Имейте в виду — это совершенно нормально, и этого следовало ожидать! Строгое изучение и усвоение абстрактных понятий — сложный и запутанный процесс, и застревание, пробование неправильных подходов и совершение ошибок — все это части этого процесса.Не ожидайте, что вы сможете решить каждую проблему (или даже любую из проблем!), Как только вы их прочитаете. Наиболее важными качествами для успеха в этом курсе являются настойчивость, трудолюбие и способность говорить, когда вам кажется, что вы чего-то не понимаете.

Хотя это может показаться очень запретным, если вы проработаете все задачи, то в конце курса вы получите очень твердое представление об основах теоретической математики: вы поймете, почему такие вещи, как функции и простые числа, имеют определения, которые они делают, вы узнаете идеи, лежащие в основе доказательств основных результатов и как их можно использовать в других местах, и, прежде всего, вы выучите язык строгой математики.

Общие советы по решению проблем

Решение математических задач часто требует много времени и усилий:
вам потребуется достаточный запас знаний, терпение и упорный труд.
Вот несколько идей, которые полезно иметь в виду
когда вы пытаетесь решить проблему:

• Попробуйте придумать пример и получите результат в этом
  особый случай. Найдите конкретный пример набора (число, функция, утверждение, уравнение, отношение, сравнение, объект), который удовлетворяет всем необходимым гипотезам, и посмотрите
  если вы можете установить результат в вашем конкретном случае.Идеи, которые вы
  использование в частном случае может также работать в целом.

• Попробуйте поиграть с гипотезами. Посмотри, сможешь ли ты найти
  ситуация, когда удаление гипотезы делает результат неверным.
  Если вы сможете понять, что происходит не так, это поможет вам понять, где
  нужна гипотеза.

• Попытайтесь установить более простой результат. Если вы застряли, попробуйте
  укрепить гипотезы и посмотреть, позволяет ли это доказать
  результат.Затем вернитесь к исходной проблеме и посмотрите, сможете ли вы решить
  это с более слабыми предположениями.

• Нарисуйте картинку. Если вы пытаетесь понять функцию, нарисуйте
  его график, и попытайтесь использовать свою визуальную интуицию, чтобы понять его.
  Снимки не обязательно должны быть полностью точными, если вы снимаете
  важные идеи.

• Не пытайтесь изобретать велосипед, если в этом нет необходимости. Если твой
  проблема похожа на что-то уже доказанное, посмотрите, сможете ли вы адаптироваться
  доказательство вашей обстановке: если вы сможете, жизнь станет намного проще (кто-то
  остальное сделало всю тяжелую работу за вас!).

• Посмотрим, сможете ли вы применить большую (или маленькую) теорему. Если ты можешь
  использовать известный результат в контексте вашей проблемы, хорошо дать
  это попытка. Если это не совсем похоже, вы еще можете ссылаться на теорему
  (например, вы упускаете одну из необходимых гипотез), попробуйте проверить,
  вы можете перейти к этапу, на котором вы сможете применить теорему (т. е. показать, что
  недостающие гипотезы действительно выполняются).

• Задавайте глупые вопросы. Если ты чего-то не понимаешь, даже если
  вы думаете, что это очень просто, не бойтесь спросить себя (или кого-то
  else) уточняющие вопросы.Один из лучших вопросов по математике
  is: «Почему мы так поступили?».

• Поговорите с другими людьми. Если вы пытаетесь проработать
  проблема, поговорив об этом с другим человеком, вы сможете прояснить
  твои мысли. Объяснение своих идей вслух заставит вас задуматься
  через них снова и может помочь вам лучше понять
  что происходит. И, конечно же, человек, с которым вы разговариваете, может
  тоже есть идеи.

• Будьте терпеливы.Занимаясь настоящей математикой, вы потратите большую часть
  ваше время борется с трудными проблемами и не понимает
  материал. Это нормально даже для профессиональных математиков!
  Абстрактную теорию нелегко усвоить, но вы ее поймете.
  со временем выучите материал, если над ним поработаете. Если вы получаете
  расстроены, сделайте перерыв и вернитесь к работе позже.

Специальные советы по решению математических задач 1365

Все вышеперечисленное — хороший общий совет.Вот несколько идей, более специфичных для Math 1365:

• Если у вас возникли проблемы с началом работы над проблемой, вы всегда можете начать с записи гипотез и (отдельно) заключения. Затем убедитесь, что вы переводите гипотезы и выводы в конкретную информацию, применяя соответствующие определения («погоня за определениями»). Часто, когда вы четко указываете, какая именно информация вам предоставляется и какой результат вы пытаетесь достичь, следующий естественный шаг напрашивается сам собой.

• Например, вместо того, чтобы пытаться манипулировать такими операторами, как «набор A является подмножеством набора B» или «целое число n делится на 6», вы можете явно написать, что означает определение: «если x — произвольный элемент из A, то x является элементом B «или» существует некоторое целое число k с n = 6k «соответственно. Это даст вам то, с чем вы действительно сможете работать.

• Примеры — полезный инструмент для проверки того, что происходит в проблеме, но имейте в виду:
  перечисление примеров, даже если они объяснены, не является решением проблемы, требующей от вас доказательства.Большинство проблем требуют, чтобы вы доказали, что какой-то результат верен во всех возможных ситуациях:
  просто приведение одного или двух примеров истинного результата не решает этой задачи.

• Если вы пытаетесь что-то доказать напрямую и застреваете,
  вместо этого попробуйте аргументировать противоречие и посмотрите, что может пойти не так. если ты
  хотите показать, что все А — это Б, а затем исследуйте, что произойдет, если у вас
  A, который не был B: наличие нескольких дополнительных свойств (а именно, «not B»)
  лежание может дать вам больше идей.Если вы используете доказательство от противного, четко укажите этот факт в начале аргументации, а также отметьте, когда вы пришли к противоречию.

• Если вы пытаетесь установить, что два утверждения эквивалентны (A
  тогда и только тогда, когда B), попробуйте разбить его на два условных выражения: if A then B,
  и если B, то A. Каждое условие дает вам что-то, с чего начать
  вместе с целью, которую вы хотите достичь.

• Пытаясь показать, что два числовых выражения равны, попробуйте запустить
  с одной стороной выражения и выполняя на ней преобразования до тех пор, пока
  вы получаете количество с другой стороны.

• Если проблема состоит из нескольких частей, они часто связаны между собой
  способ. Всегда будь на связи
  поиск способов использования результатов предыдущих частей
  проблема в более поздних частях. Например, если в части (а) проблемы задается вопрос
  вы должны показать, что f (x) = x3-x, а затем часть (b) просит вас найти f (1), вы можете просто сказать «по части (a) мы имеем f (1) = 13-1 = 0 «.

• Если вы пытаетесь показать, что два множества S и T равны, попробуйте показать, что каждый элемент S содержится в T, и что каждый элемент T содержится в S.

• Если вы пытаетесь показать, что объект уникален, предположите, что их два, а затем докажите, что они должны быть одинаковыми.

• Когда в задаче есть фраза типа «для каждого положительного целого числа», это часто подсказка, что индукция может быть полезной. Аргументы индукции часто очень просты, если вы организовываете их правильно, и могут превратить одно сложное прямое доказательство в две простые части (а именно, установление базового случая и установление индуктивного шага).При использовании индукции (или любого другого специального метода доказательства) вы должны четко обозначить базовый случай (ы) и шаг индукции, а также переменную, по которой вы проводите индукцию.

Специальные советы по написанию доказательств по математике 1365

Решение проблемы — это не то же самое, что написание решения. Как только вы что-то выяснили, вам все равно придется это записать.

• В этом курсе полным решением проблемы является строгое математическое доказательство: последовательность утверждений, записанных в предложениях, которые
  сделать вывод, исходя из некоторых гипотез.Это не
  то же самое, что и подробное описание расчета (например, как вы
  вычисляется производная), и это не просто последовательность равенств:
  представляет собой последовательность утверждений, написанных с использованием слов и символов (или, возможно,
  просто слова).

• Вы должны уметь читать доказательство вслух, по крайней мере, в принципе,
  и иметь в этом смысл. Это включает в себя уравнения, которые у вас есть
  написано, так как математические символы и уравнения имеют устный перевод:
  уравнение x2 = 9 можно прочитать вслух как «x-квадрат равен девяти».

• Стандарты хорошего письма также применяются к корректуре: вы
  должен использовать правильную грамматику, писать полными предложениями, организовывать предложения
  на абзацы и т. д. Если доказательство трудно читать (например, со строками
  стертые или зарисованные или отсутствующие части добавлены в отдельных областях
  страницу), ее следует аккуратно переписать.

• Пробелы не должны содержать пробелов. Каждое утверждение в доказательстве должно
  логически, очевидным образом, из предыдущих утверждений или известных
  факты.Определение «очевидным образом» немного
  субъективно, но, как правило, если ваш аргумент не полностью
  убедить другого студента этого курса, который не видел этого
  проблема, это требует более подробной информации.

• Хорошо написанное доказательство должно легко читаться и легко следовать:
  если аргумент состоит из нескольких частей, они должны быть четко обозначены
  отделены друг от друга. Если вы ссылаетесь на другие результаты, вы должны указать эти результаты по имени и (при необходимости) конкретно, как вы их используете.

• Ожидается, что вы предоставите доказательства сопоставимой строгости и точности.
  как доказательства, данные в классе и в материалах курса. Есть десятки примеров
  правильно написанных доказательств в учебнике и заметках, и вы увидите гораздо больше в лекции. Некоторые из этих доказательств
  будет намного длиннее и сложнее, чем те доказательства, которые вы ожидаете
  пишите, но вы должны стремиться к написанию доказательств, аналогичных учебникам и инструкторам по стилю и форме, используя ясные объяснения и логические рассуждения.

• Важны ясность и лаконичность. Короткое и четкое доказательство зачастую легче понять, чем длинное. Конечно, зачастую труднее написать краткие доказательства. Однако важным аспектом решения проблем является понимание того, какие части аргумента необходимы, а какие нет: если вы потратите время на упорядочение аргументации, это часто поможет вам лучше понять важные части.

Сможете ли вы решить «самую сложную логическую головоломку»?

Несмотря на общую неприязнь к математике, о которой заявляет большинство, многим людям нравятся логические головоломки.Это странно, ведь многие логические головоломки — это всего лишь вариации математических задач. Радостно игнорируя этот факт, многие математофобы будут пытаться разгадывать загадки и головоломки огромной сложности, используя инструменты рассуждения, которые они боятся использовать, когда предметом является уравнение.

Сегодня мы рассмотрим головоломку, эрудита, который ее придумал, и почему вам стоит подумать о том, чтобы взять книгу логических головоломок в следующий раз, когда вы будете в библиотеке.

Эта головоломка была написана блестящим логиком Раймондом Смулляном.Смуллян родился в Нью-Йорке 101 год назад. Он получил степень бакалавра в Чикагском университете и докторскую степень по математике в Принстоне, где он также преподавал в течение нескольких лет.

Чрезвычайно плодовитый писатель, он опубликовал несколько книг по логическим головоломкам для широкого потребления и бесконечный поток учебников и эссе по логике для академической аудитории. Его сборники головоломок хорошо известны за то, что знакомят людей со сложными философскими идеями, такими как теоремы Гёделя о неполноте, в увлекательной и нетехнической форме.

Смуллян, владеющий крупными планами, когда-то работал профессиональным фокусником. Он также был опытным пианистом и астрономом-любителем, построившим свой собственный телескоп. Помимо интереса к логике, он также восхищался даосской философией и опубликовал книгу по ней для широкой аудитории.

Он также нашел время появиться у Джонни Карсона, где, как и во многих его книгах, он утверждал, что люди, которым нравятся его головоломки, утверждают, что не любят математику только потому, что они не осознают, что они — одно и то же.

Проблема трех богов

Одна из наиболее популярных формулировок проблемы, которая, по словам профессора логики Массачусетского технологического института Джорджа Булоса, была самой сложной, это:

«Три бога A, B и C называются без определенного порядка, Верно, Ложно. , и Случайный. Истина всегда говорит правдиво, Ложь всегда говорит ложно, но говорит ли Рэндом правду или ложно — это совершенно случайный вопрос. Ваша задача — определить личности A, B и C, задав три вопроса типа «да-нет»; каждый вопрос должен быть задан ровно одному богу.Боги понимают английский, но ответят на все вопросы на своем языке, в котором слова да и нет будут да и ja в некотором порядке. Вы не знаете, какое слово означает какое «.

Булос добавляет, что вам разрешено задать конкретному богу более одного вопроса, и что Рэндом переключается между ответами, как если бы они говорили правду или лжецами, а не только между ответами» da «и» ja. «

Дайте себе минутку подумать, мы рассмотрим несколько ответов ниже.Готовый? Хорошо.

Решение Джорджа Булоса направлено на поиск истинного или ложного с помощью сложных вопросов.

В логике часто используется функция, которая часто обозначается как «если и только если», что означает «если и только тогда». Его использовали, чтобы сказать что-то вроде «Небо голубое, если и только если Де-Мойн находится в Айове». Это мощный инструмент, поскольку он дает истинное утверждение только тогда, когда оба его компонента истинны или оба ложны. Если одно истинно, а другое ложно, у вас ложное утверждение.

Итак, если вы сделаете такое утверждение, как «Луна сделана из Горгонзолы, если и только если Рим находится в России», то вы сделали верное утверждение, поскольку обе его части ложны. Утверждение «На Луне нет воздуха, если и только если Рим находится в Италии» также верно, поскольку верны обе его части. Однако утверждение «Луна сделана из Горгонзолы в том и только в том случае, если Олбани является столицей Нью-Йорка» неверно, потому что одна из частей этого утверждения верна, а другая — нет (Тот факт, что эти элементы не полагайтесь друг на друга пока несущественно).

В этой головоломке iff можно использовать для контроля неизвестных значений «da» и «ja». Поскольку ответы, которые мы получаем, можно сравнить с тем, что мы знаем, они были бы, если бы части нашего вопроса были все истинными, все ложными или если они различались.

Boolos хотел бы, чтобы мы начали с вопроса бога A: «Означает ли« да »да, если и только если вы истинны, тогда и только тогда, когда B является случайным?» Независимо от того, что говорит А, ответ, который вы получите, будет чрезвычайно полезным. Как он объясняет:

«Если A истинно или ложно, и вы получаете ответ da, то, как мы видели, B является случайным, и поэтому C либо истинно, либо ложно; но если A истинно или ложно, и вы получаете ответ ja, тогда B не является случайным, поэтому B либо истинно, либо ложно … если A является случайным, и вы получаете ответ da, C не является случайным (как и B, но это не имеет значения), и поэтому C либо истинно, либо Ложь; и если A случайное…и вы получите ответ ja, B не является случайным (и C не имеет значения), и поэтому B либо True, либо False. »

Независимо от того, какой бог A, ответ« da »гарантирует, что C не ‘t Случайный, и ответ «ja» означает то же самое для B.

Отсюда можно просто задать любой из известных вам вопросов, которые не являются случайными, чтобы определить, говорят ли они правду, а затем один о том, кто последний бог. Булос предлагает начать с «Означает ли да, если и только если Рим находится в Италии?» Поскольку одна часть этого утверждения верна, мы знаем, что Истина скажет «да», а Ложь скажет «ja», если столкнулся с этим вопросом.

После этого вы можете спросить того же бога что-нибудь вроде: «Да означает ли да, если и только если, A — случайное?» и точно знаете, кто есть кто, по их ответам и процессу исключения.

Если вы не понимаете, как это работает, попробуйте медленно повторить это снова. Помните, что важная часть — это знание того, каким будет ответ, если два положительных или два отрицательных результата всегда будут положительными, и что можно положиться на двух богов, которые будут действовать последовательно.

Смуллян написал несколько книг с другими логическими головоломками.Если вам понравился этот, и вы хотите узнать больше о философских проблемах, которые они исследуют, или, возможно, если вы хотите попробовать несколько, которые немного легче решить, вам следует подумать о том, чтобы прочитать их. Некоторые из его головоломок можно найти с объяснениями в этом интерактиве.

Летние математические логические головоломки для решения задач в образовании с помощью DocRunning

 Логические головоломки: Летние логические головоломки для решения задач — это набор из 4 логических задач на летнюю тематику, которые отлично подходят для звонарей, заполнителей времени, обогащения и решения задач решение.Отлично подходит для учащихся средней и средней школы по математике. Не упускайте возможность бросить вызов даже самым способным ученикам.

Включено в это руководство

— 4 логических задачи на летнюю тематику среднего уровня

— Ключ ответа

— Отлично подходит для математических центров, заполнителей времени или звонарей.

— Примечание: логические головоломки могут потребовать более одного просмотра подсказок.

Этот ресурс доступен в следующих наборах:

— Комплект для углубленного изучения математики для средней школы

Любите логические головоломки? Возьмите больше логических головоломок ниже или выберите один из 2 наборов логических головоломок:

— Сентябрьские логические головоломки

— Майские логические головоломки

— Летние логические головоломки

— Осенние логические головоломки

— Зимние логические головоломки

— Весенние логические головоломки

— Комплект «Логика для сезонов»

— Комплект «Год логики» (10 месяцев логических головоломок и сезонных головоломок) — в августе 2016 г.

Эта покупка предназначена только для одного учителя. Запрещается передавать этот ресурс коллегам или использовать его в классе, школе или округе без приобретения надлежащего количества лицензий. Если вас интересует лицензия для сайта, свяжитесь со мной, чтобы получить расценки на [email protected]. Этот ресурс нельзя загружать в Интернет ни в какой форме, включая учебные / личные веб-сайты или сетевые диски.

Вам также могут понравиться:

— Fall Logic Problems

— комплект головоломок на весь год

— Algebra 1: Teacher Resource Bundle (GROWING)

— Secondary Math and Art Projects: Show the student of the fun. математики с помощью этого 245-страничного пакета проектов с девятью забавными математическими выкладками, такими как мозаика, спирали Фибоначчи, статистика с помощью Мондриана и многое другое (CCSS)

Скоро … Зимние логические задачи; Алгебра Математика и практические наборы Полный год: математика в реальном мире: статистика и многое другое.

СОВЕТЫ КЛИЕНТАМ

Знаете ли вы, что вы можете легко заработать кредиты TPT?

— Перейдите на страницу «Мои покупки» при входе в систему.

— Нажмите кнопку «Оставить отзыв». Быстро оцените продукт и оставьте небольшую заметку.

— Каждый раз, когда вы оставляете отзыв, вы зарабатываете кредит TPT, который можно потратить на будущие покупки.

Также …

Преимущества подписки на магазин

— Экономьте $$$ — Следите за магазином и получайте обновления о запуске новых продуктов.Скидка 20% на новые товары в первые 48 часов. Чтобы подписаться, просто нажмите на звездочку «Следуй за мной» в магазине. Запуск новых продуктов обычно происходит раз в неделю.

— Следите за страницей Facebook, чтобы узнавать о еженедельных скидках, распродажах, бесплатных мгновенных подарках и розыгрышах.

— Читайте размышления, советы, ресурсы и идеи о преподавании, образовании и образовательной политике в блоге. Не пропустите Math Monday (все о математике).

— Не более одного письма от меня напрямую моим подписчикам в месяц.

Чтобы подписаться на магазин и сэкономить $$$, нажмите на звездочку «Следуй за мной» выше.

Cheers,

DocRunning

Мои лучшие математические и логические головоломки (Math & Logic Puzzles) (Мягкая обложка)

5,95 долл. США

НЕТ В МАГАЗИНЕ, но мы, вероятно, сможем заказать его для вас

Описание

---

За 25 лет работы в качестве автора колонки «Математические игры» для журнала Scientific American Мартин Гарднер каждые шесть месяцев посвящал колонку коротким математическим задачам или головоломкам.Он был особенно внимателен к представлению новых и незнакомых головоломок, которые не были включены в такие классические сборники, как коллекции Сэма Лойда и Генри Дудени. Позже эти головоломки были опубликованы в сборниках книг, включающих отзывы читателей об альтернативных решениях или интересных обобщениях.
Настоящий том содержит богатую подборку из 70 лучших из этих головоломок, в некоторых случаях включая ссылки на новые разработки, связанные с головоломкой. Теперь энтузиасты могут бросить вызов своим навыкам решения и потревожить свое эго с помощью таких стимулирующих умов, как The Returning Explorer, The Matilated Chessboard, Scrambled Box Tops, The Fork in the Road, Bronx vs.Brooklyn, Touching Cigarettes и 64 других задачи, связанных с логикой и базовой математикой. Решения включены.

Об авторе

---

Мартин Гарднер был известным автором, опубликовавшим более 70 книг по предметам от естественных наук и математики до поэзии и религии. Он также всю жизнь увлекался фокусами и головоломками. Хорошо известный своей колонкой математических игр в Scientific American и своей «Уловкой месяца» в журнале Physics Teacher, Гарднер привлек лояльных последователей своим умом, остроумием и воображением.Мартин Гарднер: воспоминания Мировое математическое сообщество было опечалено смертью Мартина Гарднера 22 мая 2010 года. Мартину было 95 лет, когда он умер, и за свою долгую жизнь писателем он написал 70 или 80 книг. Первые книги Мартина в Дувре были опубликованы в 1956 и 1957 годах: «Математика, магия и тайна», одна из первых популярных книг об интеллектуальном волнении математики, которая достигла широкой аудитории, и «Причуды и заблуждения во имя науки», безусловно, одна из первых. популярные книги, чтобы бросить сокрушительно скептический взгляд на утверждения о лженауке и на то, в каком множестве обличий современный мир породил ее.Обе эти новаторские книги до сих пор издаются в Dover вместе с более чем дюжиной других названий книг Мартина. Они охватывают весь спектр от его элементарных кодов, шифров и секретного письма, которыми пользовались поколения молодых читателей с 1980-х годов, до более требовательной книги «Новая амбидекстровая вселенная: симметрия и асимметрия от зеркальных отражений до суперструн», которую Довер опубликовал в своей книге. окончательная редакция формы — в 2005 году. Однако для тех из нас, кто был связан с Дувром в течение длительного времени, Мартин был больше, чем писателем, хотя и чрезвычайно популярным и успешным.Как член небольшой группы давних советников и консультантов, в которую входил Моррис Клайн из Нью-Йоркского университета по математике, И. Бернард Коэн из Гарварда по истории науки и Дж. П. Ден Хартог из Массачусетского технологического института по инженерии, советы и редакционные предложения Мартина в формирующей форме 1950-е годы помогли определить издательскую программу Dover и дать ей точку зрения, которая — несмотря на многие изменения, новые направления и последствия эволюции — продолжает действовать и сегодня. По словам автора: «Ожидается, что политики, агенты по недвижимости, продавцы подержанных автомобилей и составители рекламных текстов будут распространять факты в корыстных целях, но ученые, которые фальсифицируют свои результаты, рассматриваются их коллегами как совершающие непростительные преступление.И все же печальный факт состоит в том, что история науки изобилует случаями откровенной подделки и случаями, когда ученые неосознанно искажали свою работу, рассматривая ее через призму своих страстных убеждений ».« Удивительная часть математиков — опытные музыканты. Это потому, что у музыки и математики есть прекрасные закономерности? »- Мартин Гарднер

Подробнее о продукте
ISBN: 9780486281520
ISBN-10: 0486281523
Издатель: Dover Publications
Дата публикации: 1 ноября 1994 г.
Страницы: 96
Язык: Английский
Серия: Математические и логические головоломки
Рекомендуемый уровень чтения
Минимальный возраст: 9
Максимальный возраст: 12
Минимальный уровень успеваемости: 4
Максимальный уровень успеваемости: 7
Категории
Связанные издания (все)
.