Решение задач разными способами — математика, уроки
Конспект урока по математике в 3 классе
Тема «Используем правила вычислений»
(Решение задач разными способами)
Основные цели:
1. сформировать умение решать задачу двумя способами
2. сформировать умение составлять выражения для решения текстовых задач.
3. тренировать мыслительные операции, закрепить умение действовать по установленному правилу, развивать память, внимание, речь, мелкую моторику рук; воспитывать коммуникативные умения, познавательный интерес, веру в свои силы.
Оборудование: учебник Башмаков М.И. Математика 3 класс (часть 2), Рабочая тетрадь №1 Башмаков М.И., интерактивная доска.
Ход урока.
- Оргмомент.
— Откройте, пожалуйста, тетрадки. Запишите сегодняшнее число, подчеркните орфограммы.
2. Мотивация к учебной деятельности.
— Какой раздел мы изучаем на уроках математики? («Математические законы»)
— Для чего нужны математические законы? Где мы их используем? (В решении задач, примеров, выражений. Благодаря им можно ЛЕГКО решить даже самые трудные примеры)
- Актуализация знаний.
А)Математическая разминка. (слайд из презентации)
18+7+12=
23+27+24+26=
5х7х2=
2х3х5х7=
42х4=
39:3=
— Вычислите. Какие математические законы вы использовали при решении? (переместительный закон сложения, переместительный закон умножения, сочетательный закон сложения, сочетательный закон умножения)
Б) Работа с учебником (с. 28 №2)
— Найдите значение каждого выражения двумя способами; а)по порядку действий; б) применяя правила вычислений.
(Примеры решаются на доске с комментированием. После решения каждого примера анализируется, какой способ удобнее для данного случая)
- Изучение нового материала.

Работа в паре. (Учебник с. 28 №3)
— Прочитайте задачу.
— Что известно в задаче?
— Что нужно найти?
— Можем ли мы сразу ответить на вопрос задачи?
— Во сколько действий будет решаться задача?
— Запишем краткую запись в тетрадь.
— Обсудите с соседом по парте способ решения этой задачи.
— Расскажите о своем способе решения.
— У кого в паре способы решения оказались разным? Расскажите о них.
— Запишем два способа решения задачи.
I способ.
(76+41+13) х 3 = 390
II способ.
76 х 3 + 41 х 3 + 13 х 3 = 390
— Что общего в этих способах? Чем различаются?
- Первичное закрепление с проговариванием во внешней речи.
— Прочитайте следующую задачу.
— Что известно в задаче?
— Что нужно найти?
— Можем ли сразу ответить на вопрос задачи?
— Какое можно составить выражение для решения задачи?
— Запишите этот способ решения в тетрадь.
— Есть ли еще один способ решения данной задачи?
— Запишите его в тетрадь.
— Зачитайте вслух полученное выражение.
- Самостоятельная работа (Рабочая тетрадь на печатной основе)
Самостоятельное решение задачи двумя способами с последующей самопроверкой.
Образец выполнения работы находится на слайде презентации.
- Включение в систему знаний и повторение.
Подставьте в пустые клетки числа так, чтобы получились верные равенства. Проверьте друг друга.
70 + ( … + 30) = 150
8 х ( … х …) = 400
… х (7 + 9) = 1600
… х 30 = 600
- Рефлексия учебной деятельности.
— Какую тему урока изучали сегодня на уроке?
— Что нового узнали в решении задач?
— Каким образом математические законы помогают в решении задач?
— Что было особенно тяжело понять, выполнить?
— С чем легко справились?
- Домашнее задание.

К.с. 29 №6(б), №7
Просмотр содержимого документа
«Решение задач разными способами»
Конспект урока по математике в 3 классе
Тема «Используем правила вычислений»
(Решение задач разными способами)
Основные цели:
1. сформировать умение решать задачу двумя способами
2. сформировать умение составлять выражения для решения текстовых задач.
3. тренировать мыслительные операции, закрепить умение действовать по установленному правилу, развивать память, внимание, речь, мелкую моторику рук; воспитывать коммуникативные умения, познавательный интерес, веру в свои силы.
Оборудование: учебник Башмаков М.И. Математика 3 класс (часть 2), Рабочая тетрадь №1 Башмаков М.И., интерактивная доска.
Ход урока.
Оргмомент.
— Откройте, пожалуйста, тетрадки. Запишите сегодняшнее число, подчеркните орфограммы.
2. Мотивация к учебной деятельности.
— Какой раздел мы изучаем на уроках математики? («Математические законы»)
— Для чего нужны математические законы? Где мы их используем? (В решении задач, примеров, выражений. Благодаря им можно ЛЕГКО решить даже самые трудные примеры)
Актуализация знаний.
А)Математическая разминка. (слайд из презентации)
18+7+12=
23+27+24+26=
5х7х2=
2х3х5х7=
42х4=
39:3=
— Вычислите. Какие математические законы вы использовали при решении? (переместительный закон сложения, переместительный закон умножения, сочетательный закон сложения, сочетательный закон умножения)
Б) Работа с учебником (с. 28 №2)
— Найдите значение каждого выражения двумя способами; а)по порядку действий; б) применяя правила вычислений.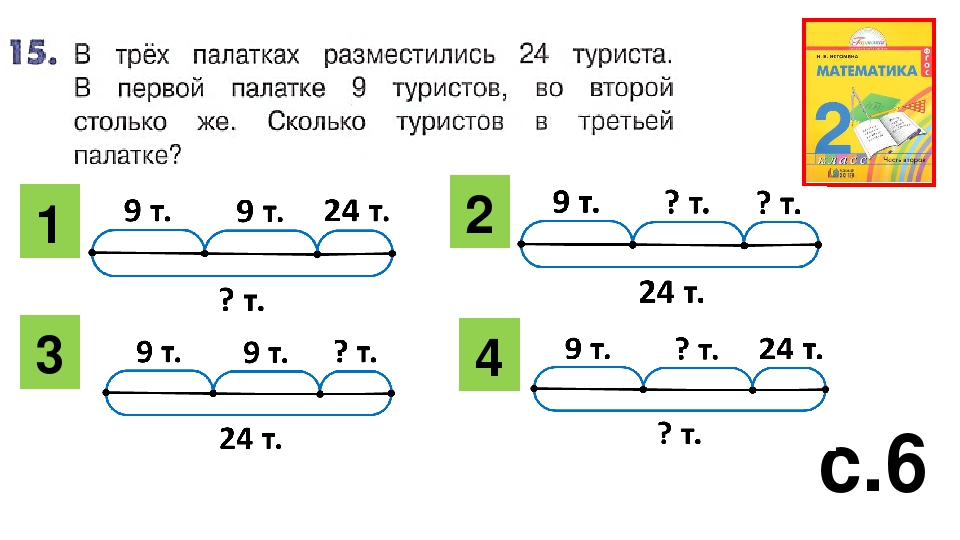
(Примеры решаются на доске с комментированием. После решения каждого примера анализируется, какой способ удобнее для данного случая)
Изучение нового материала.
Работа в паре. (Учебник с. 28 №3)
— Прочитайте задачу.
— Что известно в задаче?
— Что нужно найти?
— Можем ли мы сразу ответить на вопрос задачи?
— Во сколько действий будет решаться задача?
— Запишем краткую запись в тетрадь.
— Обсудите с соседом по парте способ решения этой задачи.
— Расскажите о своем способе решения.
— У кого в паре способы решения оказались разным? Расскажите о них.
— Запишем два способа решения задачи.
I способ.
(76+41+13) х 3 = 390
II способ.
76 х 3 + 41 х 3 + 13 х 3 = 390
— Что общего в этих способах? Чем различаются?
Первичное закрепление с проговариванием во внешней речи.
— Прочитайте следующую задачу.
— Что известно в задаче?
— Что нужно найти?
— Можем ли сразу ответить на вопрос задачи?
— Какое можно составить выражение для решения задачи?
— Запишите этот способ решения в тетрадь.
— Есть ли еще один способ решения данной задачи?
— Запишите его в тетрадь.
— Зачитайте вслух полученное выражение.
Самостоятельная работа (Рабочая тетрадь на печатной основе)
Самостоятельное решение задачи двумя способами с последующей самопроверкой.
Образец выполнения работы находится на слайде презентации.
Включение в систему знаний и повторение.
Подставьте в пустые клетки числа так, чтобы получились верные равенства. Проверьте друг друга.
70 + ( … + 30) = 150
8 х ( … х …) = 400
… х (7 + 9) = 1600
… х 30 = 600
Рефлексия учебной деятельности.
— Какую тему урока изучали сегодня на уроке?
— Что нового узнали в решении задач?
— Каким образом математические законы помогают в решении задач?
— Что было особенно тяжело понять, выполнить?
— С чем легко справились?
Домашнее задание.

К.с. 29 №6(б), №7
* 100 |
Решение задач разными способами – средство повышения интереса к математике. | Методическая разработка по математике (1 класс) по теме:
Войнова Светлана Юрьевна, учитель начальных классов,
МОУ «СОШ №56 с углубленным изучением отдельных предметов»
г. Саратов
Решение задач разными способами – средство повышения интереса к математике.
Люди научились считать 25-30 тысяч лет тому назад. О значении математики как предмета школьного преподавания М.В.Ломоносов в записке о преподавании физики, химии и математики пишет так:
«А математику уже затем учить следует, что она ум в порядок приводит».
Среди всех мотивов учебной деятельности самым действенным является познавательный интерес, возникающий в процессе обучения. Он не только активизирует умственную деятельность в данный момент, но и направляет ее к последующему решению различных задач.
Устойчивый познавательный интерес формируется разными средствами. Одним из них является решение задач разными способами.
Большие возможности для развития интереса учащихся к математике имеют задачи и их решения разными способами. Для кого из ребят интересна математика? Да математику любят в основном те ученики, которые умеют решать задачи, научив их решать задачи разными способами, мы окажем существенное влияние на их интерес к предмету, на развитие мышления и речи.
Однако в практике обучения математике различные способы решения ещё не заняли достойного места. Причин этому много, и в частности, недостаточная ориентация на эту работу в учебниках, методических пособиях для учителей. Учитель поэтому зачастую не владеет теми приёмами, с помощью которых можно отыскать другие способы решения. А без этого невозможно и детей научить находить разные способы решения, трудно использовать эти способы решения для других целей обучения и воспитания.
В начальном курсе математики текстовые задачи могут быть решены различными способами : алгебраическим, практическим, графическим, табличным, схематическим, комбинированным.
Рассмотрим различные способы решения текстовых задач на конкретных примерах.
Арифметический способ.
Начальный курс математики ставит своей основной целью научить младших школьников решать задачи арифметическим способом, который сводится к выбору арифметических действий, моделирующих связи между данными и искомыми величинами. Решение задач оформляется в виде последовательности числовых равенств, к которым даются пояснения, или числовым выражением.
Решение задач оформляется в виде последовательности числовых равенств, к которым даются пояснения, или числовым выражением.
Задача. «Утром ушли в море 20 маленьких и 8 больших рыбачьих лодок, 6 лодок вернулись. Сколько лодок с рыбаками должно вернуться?»
I способ. 1. 20+8=28(л.) ушли в море.
2. 28-6=14(л.) должны вернуться.
Выражение.(20+8)-6=14(л.)
II способ. 1. Сколько больших лодок должно вернуться? 20-6=14(л.)
2. Сколько всего лодок должно вернуться? 14+8=22(л.)
Выражение.(20-6)+8=14(л.)
III способ. 1. Сколько маленьких лодок должно вернуться? 8-6=2(л.)
2.Сколько всего лодок должно вернуться? 20+2=22(л.)
Выражение.(8-6)+20=14(л.)
Ответ: должно ещё вернуться 22 лодки. Задача решена различными арифметическими способами.
Если у учащихся нет навыков решения задач различными арифметическими способами или вызывает затруднение их нахождение, можно предложить следующие методические приёмы:
1. разъяснение плана решения задачи;
разъяснение плана решения задачи;
2. пояснение готовых способов решения;
3. соотнесение пояснения с решением;
4. продолжение начатых вариантов решения;
5. нахождение «ложного» варианта решения из числа предложенных.
Алгебраический способ.
Текстовые задачи решаются либо синтетическим методом (вычисления в прямом порядке, от числовых данных условия к числовым результатам, о которых спрашивается в задаче), либо аналитическим (вычисления в обратном порядке с рассуждениями, идущими от вопроса задачи). Примерами этих последних являются задачи о «задуманном числе», а также задачи на части. Естественным оформлением решения таких задач служит составление уравнения – алгебраический метод. Он состоит из следующих шагов: 1.Введение неизвестного. 2.Выражение через это неизвестное величин, о которых говорится в задаче. 3.Составление уравнения. 4.Решение уравнения. 5.Осмысление результата и формулирование ответа.
Задача: «У Иры втрое больше наклеек, чем у Кати, а у Кати на 20 наклеек меньше, чем у Иры. Сколько наклеек у Кати?».
Сколько наклеек у Кати?».
Вначале составим схему уравнения, содержащую не только математические знаки, но и естественные слова.
( Ирины наклейки) – (Катины наклейки) = 20 наклеек.
Получилась вспомогательная модель задачи – частичный перевод текста на математический язык. Введём неизвестное. Пусть х – число Катиных наклеек. Тогда число наклеек у Иры равно х 3.
Составим уравнение х * 3 – х = 20
2 * х = 20
Х=20:2
Х=10
Ответ: у Кати 10 наклеек.
При обучении алгебраическому методу решения текстовых задач полезно дополнить схему решения самым первым шагом – составлением схемы уравнения, в которую включаются как математические символы, так и нематематические записи и даже рисунки.
Графический способ.
Это способ решения задачи с помощью чертежа.
Задача: «Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?»
лещи окуни щуки
Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.
Построение чертежа помогает найти другой арифметический способ решения задачи.
Задача: «На одной машине увезли 28 мешков зерна, на другой на 6 мешков больше, чем на первой, а на третьей на 4 мешка меньше, чем на второй. Сколько мешков зерна увезли на третьей машине?»
I способ. 1. 28+6=34 (мешка) – увезли на второй машине.
2. 34-4=30 (мешка)- увезли на третьей машине.
Ответ : на третьей машине увезли 30 мешков зерна.
Если же мы построим чертеж к этой задачи, то легко найдем другой арифметический способ решения.
28 мешков
I.
6 мешков
28 мешков
II.
4 мешка
28 мешков
III.
?
- На сколько больше мешков увезли на третьей машине, чем на первой? 6-4=2(мешка)
- Сколько мешков увезли на третьей машине? 28+2=30 (мешков)
Ответ: на третьей машине увезли 30 мешков зерна.
Из приведенных примеров следует вывод: графическое оформление задачи может определить ход мыслительного процесса и является средством выявления различных способов решения одних и тех же задач. При этом легче усматриваются разные логические основы, содержащиеся в условии задачи; такие способы определяются анализом наглядного сопровождения задачи, на которые учащиеся направляются постановкой учителем соответствующих заданий.
При этом легче усматриваются разные логические основы, содержащиеся в условии задачи; такие способы определяются анализом наглядного сопровождения задачи, на которые учащиеся направляются постановкой учителем соответствующих заданий.
Логический способ.
Задача: «В 6 банок поровну разложили 12 кг варенья. Сколько надо таких же банок, чтобы разложить 24 кг варенья?»
В данном случае логическая основа задачи проявляется на двух уровнях – открытом и скрытом, т. е. здесь две логические основы. В первом случае направление мыслительного процесса определяется вопросами:
- Сколько кг варенья помещается в одну банку? 12:6=2(кг)
- Сколько банок потребуется для 24 кг варенья? 24:2=12(б.)
Во втором случае ход того же процесса определяется другими вопросами:
1.Во сколько раз больше стало варенья? 24:12=2(раза)
Если варенья стало в два раза больше, значит, и банок потребуется в два раза больше.
2.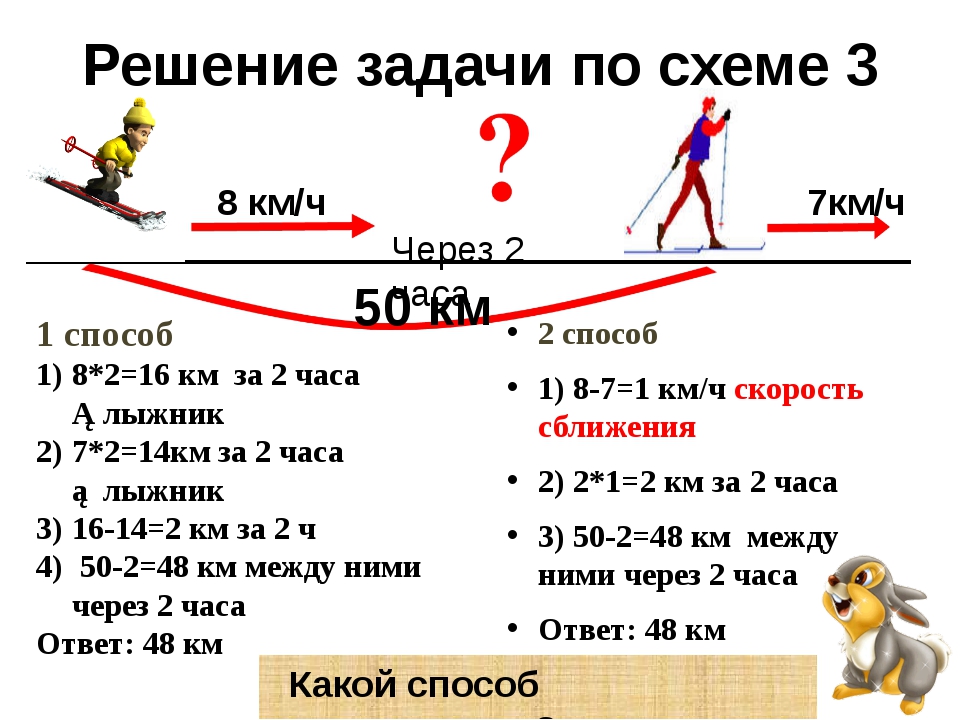 Сколько потребуется банок? 6 * 2=12(б.)
Сколько потребуется банок? 6 * 2=12(б.)
Ответ: потребуется 12 банок.
Табличный способ.
При решении некоторых задач хорошим подспорьем является табличная форма.
Задача: «У Саши в коллекции 8 жуков и пауков. У всех насекомых 54 ноги. У одного жука 6 ног, а у одного паука – 8ног. Сколько жуков и сколько пауков у Саши в коллекции?»
Количество жуков | Количество пауков | Количество ног у всех жуков | Количество ног у всех пауков | Всего ног |
1 | 7 | 6 | 56 | 62 |
2 | 6 | 12 | 48 | 60 |
3 | 5 | 18 | 40 | 58 |
4 | 4 | 24 | 32 | 56 |
5 | 3 | 30 | 24 | 54 |
Ответ: у Саши в коллекции 5 жуков и 3 паука.
Схематический способ.
В числе способов решения задач можно назвать схематическое моделирование. В отличие от графического способа решения, который позволяет ответить на вопрос задачи, используя счёт и присчитывание, схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно представлять в виде символической модели (выражение, равенство). Тем не менее, моделирование текста задачи в виде схемы позволяет ответить на вопрос задачи. Покажу это на примере.
Задача: «В двух вагонах ехали пассажиры, по 36 человек в каждом вагоне. На станции из первого вагона вышло несколько человек, а из второго вагона вышло столько человек, сколько осталось в первом. Сколько всего пассажиров осталось в двух вагонах?»
В данном случае схема выступает как способ и как форма записи решения задачи.
Ответ: в двух вагонах осталось 36 человек.
Комбинированный способ.
В этом случае для записи решения задачи могут быть использованы одновременно схема и числовые равенства.
Задача: «В альбоме для раскрашивания 48 листов. Часть альбома Коля раскрасил. Сколько листов осталось нераскрашенными, если Коля раскрасил в 2 раза больше, чем ему осталось?»
Решение задачи можно оформить так:
Раскрасил
Осталось
48:3=16(л.)
Ответ: остались нераскрашенными 16 листов.
На всех уроках, если встречается задача, допускающая разные способы решения, стараюсь детям дать возможность найти их.
Я считаю, что очень важно и полезно после решения задачи разными способами предложить ребятам ряд заданий творческого характера. Рассмотрим некоторые из них на примере.
Задача: «С одной яблони собрали 15 кг яблок, а с другой 30 кг. Все эти яблоки разложили в ящики, по 5 кг в каждый. Сколько ящиков потребовалось?»
1 способ. (15+30):5=9(ящ.)
2 способ. 15:5+30:5=9(ящ.)
Главный вопрос после решения задачи: «Почему мы смогли решить задачу двумя арифметическими способами?» Потому что и 15, и 30 можно разделить на 5 без остатка.
Задания творческого характера.
1.Какие числовые данные можно использовать вместо 15 и 30, чтобы задача решалась двумя способами и почему? 10 и 45, 25 и 50…главное, чтобы оба числа делились на 5.
2.Какие числовые данные можно использовать вместо 5, чтобы задача решалась двумя способами и почему? 3, так как и 15, и 30 можно разделить на 3 без остатка.
3.Яблоки разложили в ящики по 4 кг. Какие числовые данные можно взять вместо 15 и 30, чтобы задача решалась двумя способами и почему? 8 и 32, 16 и 40…главное, чтобы оба числа делились на 4 без остатка.
4.С яблонь собрали 21 кг и 27 кг яблок. По сколько кг яблок можно разложить в один ящик, чтобы задача решалась двумя способами и почему? По 3 кг, так как и 21, и 27 можно разделить на 3 без остатка.
5.Составьте аналогичную задачу по выражению, чтобы она решалась двумя способами. (12 +…) : 6
Умелое использование различных способов решения задач на уроках математики в начальных классах оказывает положительное влияние на развитие мышления и творческих способностей детей, на формирование их личности и исследовательских навыков, является залогом устойчивого интереса к математике.
Сложения вида 38+4.Решение задач двумя способами
Тема: Сложения вида 38+4.Решение задач двумя способами
Цель урока: ознакомить учащихся с сложением вида 38 + 4; закрепить умение решать задачи изученных видов различными способами, сравнивать выражения; развивать смекалку, мышление, математическую зоркость; содействовать в ходе урока воспитанию таких человеческих качеств, как доброта, отзывчивость, желание прийти на помощь.
Тип урока: комбинированый
Методы и приемы обучения: объяснение, беседа; метод упражнений, работа с учебником, инструктаж; илюстрация; «Незаконченое предложение»
Здоровье сберегающие технологии: проведение физкультминутки
Межпредметная интеграция: Я и Украина, природоведение
Оборудывание: учебник, таблицы-памятки для решения текстовых задач, карточки
Литература: Богданович М. В., Математика [Текст]: учебник для 2 кл. общеобразоват. учеб. Заведений с рус. яз. обучения / М.В. Богданович – пер. с укр.. – К.: Освіта, 2004. – 159 с.
В., Математика [Текст]: учебник для 2 кл. общеобразоват. учеб. Заведений с рус. яз. обучения / М.В. Богданович – пер. с укр.. – К.: Освіта, 2004. – 159 с.
Интернет ресурсы: Державний стандарт початкової загальної освіти. [Електронний ресурс]. Режим доступу : http://zakon2.rada.gov.ua/laws/show/462-2011-п
Ход урока
І. Организационный момент
— Добрый день! Меня зовут Екатерина Сергеевна и сегодня я проведу урок математики. Но перед этим давай вы повернетесь к своим соседям по парте улыбнитесь друг другу произнося приятные слова.
II.Контроль, коррекция и закрепление знаний
- Математический диктант
1. Напиши числа: 23 и 28. Какие числа стоят между ними?
2. Напиши число 69. Напишите 4 числа, которые расположены после него.
3. Напиши число 48. Напишите 4 числа, которые расположены перед ним.
4. Напиши числа, которые состоят из: 7 десятков и 3 единиц; 5 десятков и 8 единиц; 8 десятков и 4 единиц.
5. Увеличь число 57 на 1.
6. Уменьши число 79 на 1.
Ответ:24, 25, 26, 27; 70, 71, 72, 73;49, 50, 51, 52; 73, 58, 84; 58;80.
- Устный счет
- Игра «Набери число 20».
2) Игра «Попади в корзину».
На доске вывешиваются рисунки с баскетбольными корзинами, на них — числа 54; 67; 76. Каждому ряду дается задание составить за определенное время (5 мин.) Как можно больше примеров на сложение с этим ответом. Выигрывает команда, участники которой больше и правильно запишут выражения с этим ответом.
Выигрывает команда, участники которой больше и правильно запишут выражения с этим ответом.
- Минутка каллиграфии
— Установите закономерность и запишите числа, вставляя пропущенные.
5, 7, 4, 6; 3, ?; 2. (5+2,7-3,4+2,6-3, 3+2, 5-3)
Ответ:5
ІІІ. Мотивация учения учеников и повидомлення теми, цели и задания урока
— Встречаются в жизни человека такие способы добавления: 38 + 4? Приведите примеры. Следовательно, есть необходимость научиться вычислять аналогичные примеры?
— Сегодня на уроке мы будем учиться добавлять однозначное число в двузначного, решать задачи двумя способами.
VI. Актуализация опыта учеников. Восприятие и осведомление нового начального материала
- Работа по учебнику (с. 49-50)
Задача 286
— Откройте учебник на странице 49 номер 286. Давайте вместе с вами рассмотрим этот пример
Давайте вместе с вами рассмотрим этот пример
— Рассмотрите записи и объясните решение.
Правило
1. Разложи двузначное число на разрядные слагаемые.
2. В единиц сложи единицы.
3. Полученный результат добавь к десятков.
— Используя эти правила у вас не будет затруднений у решении примеров.
Задача 287
— В этом номере вам нужно объяснить как найти сумму выражения. Порядок ваших действий при решении
67 + 6 ..
1.Сначала от единиц отнимаем единицы 7единиц – 6 единиц =1
2. А потом к единицам добавляем десятки 6 десятком + 1 единица =61
2.Физкультминутка
Раз, два, три, четыре, пять —
Все умеем мы считать.
Раз! Подняться потянуться. (Под счет учителя дети выполняют потягивания.)
Два! Согнуться, разогнуться. (Наклоны. Повороты туловища.)
Три! В ладоши три хлопка,
Головою три кивка. (Движения головой.)
(Движения головой.)
На четыре — руки шире. (Хлопки в ладоши.)
Пять — руками помахать. (Движения руками.)
Шесть — за парту тихо сесть. (Прыжки. Ходьба на месте.)
IV. Осмысление, узагальнення и систематизация знаний
Задача 289
Юля бросила мяч на расстояние 15 м, а Олег — на 7 м далее. На какое расстояние бросил мяч Олег?
— Давайте вместе решим задачу с учебника №289.(я читаю)
— Кто прочитает условия задачи?
— О чем идет речь в задаче?
— На какое расстояние бросила мяч Юля? (15м)
— На какое расстояние бросил мяч Олег? ( на 7 м далее)
— Что спрашивается в задаче? (. На какое расстояние бросил мяч Олег?)
— Можем ли мы ответить на вопрос задачи?
-Давайте запишем с вами короткое условие задачи.
Юля – 15 м
Олег – ? на 7 м больше
Решение
15+7=22(м)
Ответ: Олег бросил мяч на расстояние 22 метра .
— А теперь заменим число 7 на 9 и решим задачу. Объясните алгоритм действий при вычислении
15+9=
5+9=1дес.4 ед.
1 дес.+1дес.=2
2дес.+4 един=24
Задача 290. Комментируемое решения круговых примеров Ученики используют различные способы вычисления. Каждый будет выходит к доске решать пример комментируя
45 + 6 52 + 7 39 + 6 77 – 30
59 – 20 51 + 20 71 + 6 47 + 5
Задача 291
В автобусе ехало 20 пассажиров. На остановке в салон зашли еще 6 женщин и 7 мужчин. Сколько пассажиров стало в автобусе? (Реши задачу двумя способами.)
— О чем идет речь в задаче?
— Сколько пассажиров ехало в автобусе? (20)
— Сколько зашло женщин? (6)
— А сколько мужчин? (7)
— Что спрашивается в задаче?( Сколько пассажиров стало в автобусе?)
— Можем ли мы ответит на вопрос задачи? (нет)Почему? (нам нужно узнать общее количество мужчин и женщин) Каким действием? (сложение) А теперь можем ответить на вопрос задачи? (да)
— Запишим короткое условие задачи
Было 20 пасажиров
Пришло 6 женщин и еще 7 мужчин
Стало ?
— К доске пойдешь ты. Ты решаешь самостоятельно на доске одним способом, а остальные у себя в тетради. А следующий другим способом будет решать.
Ты решаешь самостоятельно на доске одним способом, а остальные у себя в тетради. А следующий другим способом будет решать.
1)6 + 7 = 13 (п.)
2)20 + 13 = 33. (п)
1)20 + 7 = 27(п)
2)27 + 6 = 33(п)
Ответ:33 пассажира.
Один ученик работает у доски, остальные — в тетрадях.
IIV. Итог урока и повыдомлення домашнего задания
1.Домашнее задание
№294
2. Подведем итог с помощью карточки, что весит на доске продолжите предложение
-Сегодня на уроке мы учились..
-Лутше всего у меня получилось…
— Я на уроке был…
Задачи на движение в противоположных направлениях: примеры и решение
Рассмотрим задачи, в которых речь идёт о движении в противоположных направлениях. В таких задачах два каких-нибудь объекта движутся в противоположных направлениях, отдаляясь друг от друга. Задачи на движение в противоположных направлениях можно решать двумя способами.
Задача 1. Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго — 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение: Из условия задачи известны скорость каждого автомобиля и время, которое автомобили были в пути. Значит, можно найти расстояние, которое проехал каждый автомобиль, для этого нужно скорость умножить на время:
1) 100 · 4 = 400 (км) — проехал первый автомобиль,
2) 70 · 4 = 280 (км) — проехал второй автомобиль.
Найдя сумму полученных результатов, узнаем расстояние между автомобилями через 4 часа:
400 + 280 = 680 (км).
Данную задачу можно решить и другим способом. Каждый час расстояние между автомобилями увеличивалось на 170 километров (100 + 70), 170 км/ч — это скорость удаления автомобилей. За 4 часа они проедут расстояние:
170 · 4 = 680 (км).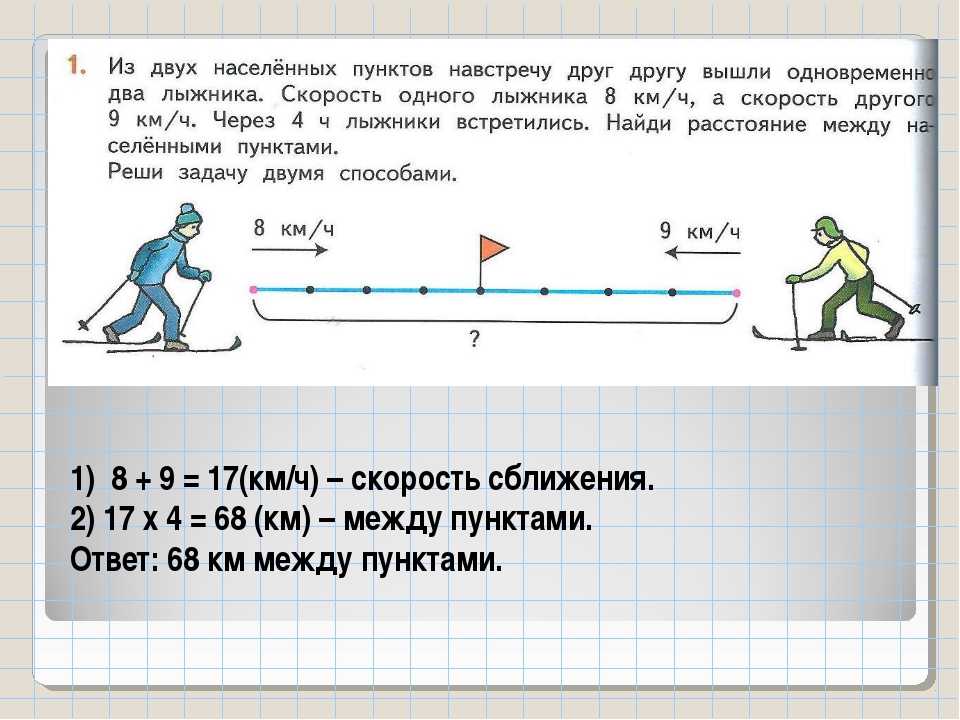
Таким образом, задачу на движение в противоположных направлениях можно решить двумя способами:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 100 · 4 = 400 (км) | 1) 100 + 70 = 170 (км/ч) |
| 2) 70 · 4 = 280 (км) | 2) 170 · 4 = 680 (км) |
| 3) 400 + 280 = 680 (км) |
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 2. Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два пешехода. Первый пешеход шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между пешеходами будет через 5 часов?
Решение: Сначала можно определить сколько километров прошёл каждый из пешеходов за 5 часов, для этого скорость пешеходов умножим на 5:
1) 4 · 5 = 20 (км) — прошёл первый пешеход,
2) 5 · 5 = 25 (км) — прошёл второй пешеход.
Затем можно найти общий путь, пройденный двумя пешеходами за 5 часов:
20 + 25 = 45 (км).
Теперь можно найти расстояние между пешеходами, прибавив к пути, пройденному пешеходами, расстояние между населёнными пунктами:
45 + 40 = 85 (км).
У данной задачи есть и второй вариант решения. Можно сначала найти скорость удаления пешеходов:
4 + 5 = 9 (км/ч).
Затем найти пройденное расстояние, умножив скорость удаления (9 км/ч) на время движения пешеходов (5 ч):
9 · 5 = 45 (км).
А теперь, для нахождения расстояния между пешеходами, сложить пройденное расстояние (45 км) с расстоянием между населёнными пунктами:
45 + 40 = 85 (км).
Таким образом, данная задача имеет два варианта решения:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 4 · 5 = 20 (км) | 1) 4 + 5 = 9 (км/ч) |
| 2) 5 · 5 = 25 (км) | 2) 9 · 5 = 45 (км) |
| 3) 20 + 25 = 45 (км) | 3) 45 + 40 = 85 (км) |
| 4) 45 + 40 = 85 (км) |
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
|
| ||||||||||||||
| ||||||||||||||
| Другой наш проект Сказки Хитрого Кота | ||||||||||||||
Контактный Email: | ||||||||||||||
Контент опубликованный на сайте vcevce. ru защищен законом об авторском праве. ru защищен законом об авторском праве.Любое частичное или полное копирование опубликованной информации запрещено. © | ||||||||||||||
Обратные операции. Задачи по математике 2 класс
Математика 2 класс
Задачи для 2 класса
Контрольные работы
Задача 1
Какие выполнены операции? Что в них общего и чем они отличаются? Как можно назвать такие операции? Что произойдет если выполнить подряд обе операции?
Решение
- Обе операции над бантом.
- Различаются действием.
- Обратные операции.
- Останется как было раньше.
Задача 2
- а) Какая операция обратна операции надевания рубашки?
- б) Вася сломал свой игрушечный грузовик. Какая операция будет обратной?
- в) Птичка села на ветку.
 Какая операция обратна этой?
Какая операция обратна этой? - г) Коля налил воду в чашку. Какая операция будет обратной?
- д) Роман включил компьютер. Найди обратную операцию.
Решение
- а) Операция снятия рубашки.
- б) Ремонт грузовика.
- в) Взлет птички.
- г) Коля вылил воду из чашки.
- д) Роман выключил компьютер.
Задача 3
Лесорубы спилили дерево. Есть ли для этой операции обратная? Придумай примеры операций, которые не имеют обратных.
Решение
- Для спиленного дерева нет обратной операции.
- Съесть пирожок. Разбить стекло.
Задача 4
Выполни операции и найди обратные операции.
Решение
Задача 5
а) К числу а прибавили число 8.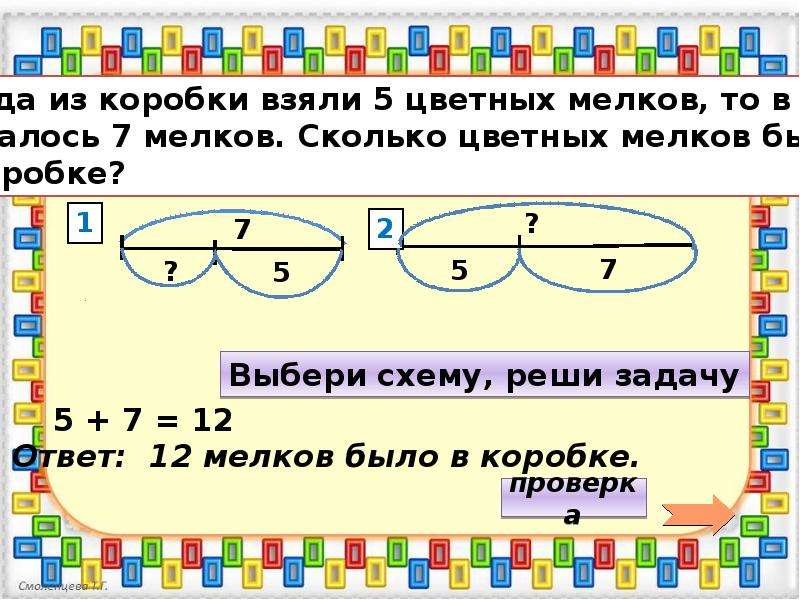 Какая операция обратна этой?
Какая операция обратна этой?
б) Из числа b вычли 5. Найди обратную операцию.
Решение
- а)
- б)
Задача 6
Выполни действия:
| 987 — 394 + 394 = | n + 9 — 9 = | a — d + d = |
| 526 + 217 — 217 = | k — 7 + 7 = | b + c — c = |
Решение
987 — 394 + 394 = 987
n + 9 — 9 = n
a — d + d = a — 2d
526 + 217 — 217 = 526
k — 7 + 7 = k — 14
b + c — c = b
Задача 7
Реши задачу двумя способами:
- а) В трамвае ехало 25 пассажиров.
 На остановке 8 из них вышли, а 4 вошли. Сколько пассажиров стало в трамвае?
На остановке 8 из них вышли, а 4 вошли. Сколько пассажиров стало в трамвае? - б) В улье было 372 пчелы. Из улья вылетело 19 пчёл, а залетело 29. Сколько пчёл стало в улье?
Решение
- а)
Первый способ:
- 1) 25 — 8 = 17
- 2) 17 + 4 = 21
Второй способ:
- 1) 8 — 4 = 4
- 2) 25 — 4 = 1
- б)
Первый способ:
- 372 — 19 = 353
- 353 + 29 = 382
Второй способ:
- 29 — 19 = 10
- 372 + 10 = 382
Задача 8
Реши уравнения:
| x — 549 = 308 | x + 72 = 215 | 320 — x = 128 |
Решение:
x — 549 = 308;
x = 549 + 308
x = 857
x + 72 = 215
x = 215 — 72
x = 143
320 — x = 128
x = 320 — 128
x = 192
Задача 9
Найди закономерность и вставь пропущенные числа.
Решение
На странице использован материал из книги Л. Г. Петерсон «Математика второй класс. Часть2».
Ссылка на сайт автора:
www.sch3000.ru
Составные задачи
Простые задачи
Способы решения задач сложения многозначных чисел
Одним из наиболее важных аспектов «новой» математики Common Core является идея о том, что учащиеся разрабатывают несколько стратегий для решения задач. Я говорю о том, почему я учу студентов нескольким стратегиям глубокого решения проблем, в другом сообщении в блоге. Вот краткий пример диаграммы привязки, которую я составил со студентами, чтобы проиллюстрировать все стратегии в одном месте.
На днях наш класс провел сравнение двух- и трехзначных стратегий сложения.Ранее в этом году мы тщательно практиковали стратегии сложения двузначных чисел в различных мероприятиях. Недавно мы начали работать над сложением трехзначных чисел, и студентам нужно было освежить в памяти некоторые стратегии, которые они усвоили ранее в этом году.
Недавно мы начали работать над сложением трехзначных чисел, и студентам нужно было освежить в памяти некоторые стратегии, которые они усвоили ранее в этом году.
Мне нравится эта таблица, потому что она связывает то, что мы узнали ранее в этом году, и помогает студентам установить связь между тем, что они уже узнали, и тем, над чем они работают прямо сейчас.
Мне нравится учить студентов гибко думать о том, как решать проблемы, и помогая им воспринимать удовольствие как место ценности.Используя эти стратегии, учащиеся получают гораздо более глубокое понимание концепций позиционной ценности.
Я не создаю эту диаграмму привязки, если учащиеся не проработали каждую стратегию индивидуально и глубоко.
Мои ученики хорошо понимали каждую из этих стратегий до того, как мы создали диаграмму привязки, и моей целью при ее создании было помочь ученикам увидеть сходство в применении стратегий между двузначным и трехзначным сложением. Я также каждый год составляю эту таблицу немного по-другому, в зависимости от потребностей моих учеников, сложности их мышления и слов, которые они выбрали для обозначения стратегий. Это действительно о студентах, которые находят смысл и устанавливают связи.
Это действительно о студентах, которые находят смысл и устанавливают связи.
Некоторые ученики тяготеют к использованию алгоритма, потому что это то, чем занимаются их родители и где они получают наибольшую индивидуальную помощь. Однако есть некоторые, которые используют альтернативную стратегию, и, как правило, именно те студенты, которые обладают наибольшей гибкостью и сложностью в своем математическом мышлении.
Дополнительную информацию о каждой нетрадиционной стратегии вы можете получить, перейдя по ссылкам ниже.
Если вы преподаете во втором классе, вам могут понравиться несколько страниц из некоторых моих двузначных продуктов сложения и вычитания. Я собрал этот PDF-файл ресурсов в качестве выборки из нескольких различных продуктов, которые действительно подчеркивают всю работу, которую мы выполняем в нашем классе для углубленной разработки этих стратегий. Различные компоненты сэмплера могут использоваться всей группой или небольшой группой и идеально подходят для того, чтобы помочь вашим ученикам мыслить нестандартно, когда дело доходит до решения сложения и вычитания многозначных чисел.
Возможно, вас заинтересует. . .
Преподавание задач со словами для 2-х классов
Задачи со словами были одним из самых больших разделов, которые я преподавал в 2-м классе и , и я не понаслышке знаю, что преподавать задачи со словами для второклассников может быть сложно. Но как бы сложно это ни было, это также чрезвычайно важно. Задачи со словами — ключевой навык для студентов, и их следует изучать и повторять в течение всего года.
Прежде чем мы поговорим об обучении задачам со словами во 2-м классе, давайте посмотрим, где должны быть ученики, когда они пойдут во 2-й класс, и как обращаться с учениками ниже уровня.
Что должны знать первоклассники
Учащиеся, поступающие во 2 класс, должны обладать следующими навыками:
- Решите до 20 задач со словами, используя сложение и вычитание;
- Типы словесных задач: сложение, взятие, сложение, разборка и сравнение с неизвестными во всех позициях.

В начале года полезно оценить, насколько учащиеся понимают, как складывать и вычитать до 20. Если они могут плавно складывать и вычитать до 20, переходите к числам 20–50.Если есть большая группа учащихся, которые все еще испытывают трудности, найдите время, чтобы изучить стандарт 1.OA.A.1 для 1-го класса задачи со словами.
Используйте сложение и вычитание в пределах 20 для решения словесных задач, включающих ситуации сложения, взятия из, сложения, разборки и сравнения с неизвестными во всех позициях.
Единственное различие между стандартами 1 st и 2 nd состоит в том, что сорт 1 st решает до 20, а сорт 2 nd решает до 100.Так что, если вам действительно нужно пересмотреть стандарты класса 1 st , вы по-прежнему охватываете практические концепции стандарта, только в ограниченном диапазоне.
Сколько времени вы потратите на проверку, будет зависеть от уровня ваших учеников. Если вашим ученикам это нужно, полезно выделить весь первый цикл обучения текстовым задачам на повторение, что займет около двух недель. Может показаться, что у вас много времени для повторения, но имейте в виду, что в это время вы учите студентов различным типам задач со словами и процессу их решения.Работа с числами меньше 20 делает вычисления более управляемыми и позволяет учащимся сосредоточиться на изучении типов проблем и процессе их решения.
Если вашим ученикам это нужно, полезно выделить весь первый цикл обучения текстовым задачам на повторение, что займет около двух недель. Может показаться, что у вас много времени для повторения, но имейте в виду, что в это время вы учите студентов различным типам задач со словами и процессу их решения.Работа с числами меньше 20 делает вычисления более управляемыми и позволяет учащимся сосредоточиться на изучении типов проблем и процессе их решения.
Преподавание задач по слову во 2-х классах: день 1
Подготовка к уроку:
- Создайте плакат для моделирования задачи со словом. Вы можете использовать мои задачи с плакатом из моего пакета задач 2 nd Grade Word или написать свои собственные.
- Распечатайте и ламинируйте плакаты «Процесс решения проблем».Прикрепите их к ленте и повесьте в удобном месте, где их будут видеть все ученики. Убедитесь, что вы можете легко получить доступ к плакату или переместить его для уроков.

- Начните создавать плакат «Типы проблем со словами». В первый день вы должны включить задачи со словами «Добавление к». Вы добавите навыки к этому плакату по мере того, как познакомите их с учениками.
- Подготовьте по одному плакату с групповым заданием для каждой группы, чтобы учащиеся использовали его во время групповой работы. Вы можете написать свои собственные задачи или распечатать одну из задач «добавить к» в моем пакете задач Word.Отличный способ заинтересовать ваших учеников — это написать вместе с их именами словесные задачи. Я также сделал свой пакет задач Word редактируемым, так что вы можете ввести свой список класса, и задачи будут автоматически сгенерированы вместе со списком классов!
Открытие урока:
1) Ввести стандарт
Представьте стандарт. Сообщите учащимся, что вы начинаете с рассмотрения задач со словами, которые они выучили в первом классе. Сегодня студенты будут работать над задачами со словами «Дополнения». «Добавление к» задачам означает, что вы начинаете с чего-то определенного, и к вашей группе добавляется еще больше.
«Добавление к» задачам означает, что вы начинаете с чего-то определенного, и к вашей группе добавляется еще больше.
2) Расскажите о проблеме
Покажите плакат со словом «проблема». Объясните, что вы собираетесь показать им, как решить эту проблему.
Плакат с инструкциями по устранению проблем
- Покажите плакат с инструкциями по решению проблем. Укажите на первый шаг. Объясните, что сначала нам нужно прочитать проблему и визуализировать ее. Затем смоделируйте навык, прочитав задачу, а затем объяснив картину, которую вы видите в уме.
- «В Sweet Delights было 33 клубничных кекса. Испекли еще 6 штук.Сколько клубничных кексов сейчас в Sweet Delights? »
- Я представляю себе магазин кексов с подносами кексов на прилавке. У них есть поднос с 33 кексами, который состоит из 3 рядов по 10 и 1 ряда по 3. Далее я представляю, как пекарь выходит с еще шестью клубничными кексами и добавляет их к ряду из 3.
- Теперь я визуализировал проблему (укажите на первый шаг на схеме процесса).

3) Перескажите для понимания
Далее я перескажу проблему.
- Закройте проблему руками и перескажите историю своему классу. Спросите: «Я понял суть проблемы?»
4) Определите ключевые слова
Теперь, когда я пересказал проблему, я знаю, что понимаю ее, поэтому я готов обвести и подчеркнуть ключевые слова. Модель обведет цифры в задаче и подчеркнет ключевые слова.
- «В Sweet Delights было (33) клубничных кексов. Выпекали (6) еще .Сколько клубничных кексов в Sweet Delights сейчас ? »
- Проверить! Я обвел и подчеркнул ключевые слова и числа, которые помогут мне решить проблему.
5) Стратегия решения
Далее я собираюсь решить проблему, используя стратегию. Для этой задачи я нарисую картинку.
- Нарисуйте поднос для кексов с 3 рядами из десяти кругов и одним рядом из 3 кругов, используя черный маркер.
- «Я начал с 33 кексов Sweet Delights.
 Теперь я добавлю еще 6 ». Нарисуйте на подносе 6 розовых кружков.
Теперь я добавлю еще 6 ». Нарисуйте на подносе 6 розовых кружков. - Теперь у меня есть все клубничные кексы, поэтому, чтобы ответить на вопрос «Сколько клубничных кексов сейчас в Sweet Delights?» Я пересчитаю все кексы. У меня 39 кексов.
* Примечание * В начале класса 2 и рисование изображений и диаграмм для решения проблем является подходящим методом решения проблем. По мере того, как учащиеся осваивают процесс решения проблем, цифры будут усложняться, и учащимся следует перейти к более эффективным стратегиям.
6) Запишите уравнение
Теперь, когда я решил проблему, я собираюсь написать уравнение.
- Это была проблема «добавления к», поэтому я знаю, что это уравнение сложения.
______ + _______ = ________
- Sweet Delights началась с 33 клубничных кексов, поэтому я знаю, что это будет первое число в моем уравнении.
- Затем они добавили еще 6 клубничных кексов, так что я знаю, что это будет мой второй номер.

- Я знаю, что после того, как они добавили 6 кексов, у них было всего 39 клубничных кексов, так что 39 — это то, что стоит после знака равенства.
7) Ответ на ярлык
На следующем шаге предлагается пометить мой ответ.
- Что означает 39? Есть 39 щенков? Или 39 детей? Может, 39 карандашей? Нет, значит 39 клубничных кексов.
8) Проверить работу
Теперь, когда у меня есть ответ, вы, наверное, думаете, что я закончил, верно? Нет! Математика прекрасна, потому что мы знаем, что часто есть правильный или неправильный ответ.Есть много шансов на ошибку, но если мы проверим свою работу, мы будем намного увереннее, что не сделали ошибки.
- Смоделируйте, как проверить свою работу, используя другую стратегию. Стратегия может заключаться в использовании манипуляторов, создании другой картинки или подсчете на пальцах. После того, как вы смоделировали проверку своей работы, поставьте большую галочку рядом с ответом, чтобы показать, что этот шаг выполнен.

Работа в группе:
Теперь у учащихся будет возможность попробовать шаги по решению проблем с «добавлением к задаче» в своих группах.Они сделают свой собственный плакат со своими группами, показывая всю их работу. Студенты любят работать с диаграммной или крупной цветной бумагой.
(Примечание: важно установить ожидания для групповой работы, включая всех учащихся, участвующих и помогающих друг другу. Когда учитель подходит, чтобы задать вопрос, все члены группы должны иметь возможность ответить.)
По мере того, как каждая группа работает над своей проблемой, по очереди задавайте вопросы для проверки понимания. Если учащиеся совершают ошибки, не говорите им прямо.Вместо этого ожидайте, что студенты «поймут это», когда они проверит свою работу. После того, как учащиеся выполнили все шаги, просмотрите свой плакат и дайте им возможность просмотреть свою работу маркерами, чтобы он выделялся. Затем я выбираю одну группу, чтобы рассказать классу, как они решили проблему.
Образец плаката о групповой работе
Самостоятельная работа:
Рабочий лист Word Problem со всеми шагами по решению проблем.
Затем ученики самостоятельно работают над одной из задач второго класса из моего пакета задач со словами.Вытяните учащихся, которые испытывают трудности, поскорее один на один. Повторное обучение в малых группах также может быть эффективным, но обычно достаточно, чтобы учащиеся работали независимо, в то время как вы наблюдаете и задаете вопросы, чтобы направлять их в правильном направлении. Не забывайте, что цель — сделать их более независимыми!
Непосредственно перед окончанием рабочего периода еще раз обойдите комнату, чтобы понаблюдать за работой студентов. Выберите одного учащегося, который выполнил шаги и получил правильный ответ, чтобы рассказать, как они решили проблему.(Примечание: в начале раздела мне нравилось целенаправленно отбирать учащихся, которые «понимают», но по мере продвижения раздела я думаю, что важно, чтобы учащиеся рассказали, кто, возможно, пропустил шаг или получил неправильный ответ.
В начале этого раздела я предлагал студентам выполнять только 1-2 задачи каждый день. Это крайне важно. Лучше меньше, да лучше, потому что цель состоит в том, чтобы научить студентов овладевать процессом решения проблем. Задавая учащимся слишком много задач на раннем этапе, можно перегрузить их учебный процесс и слишком много внимания уделять получению ответов только для того, чтобы сделать это.
Закрытие:
Начнем со сбора всех самостоятельных работ. Затем попросите выбранного учащегося рассказать, как они решили проблему. Изначально важно, чтобы учащийся поделился всем процессом, но по мере того, как блок и год продолжаются и учащиеся овладевают процессом, вы можете сократить это, попросив учащегося рассказать об одном шаге, который они сделали.
Чтобы убедиться, что учащиеся усвоили стратегию решения проблем, я всегда проводил короткую викторину в последний день или перед тем, как приступить к следующей стратегии.В мой пакет задач по словам также входят короткие викторины с двумя вопросами, так что убедитесь, что ваши ученики идут по правильному пути.
Навыки решения проблем со словом:
Продолжайте этот распорядок каждый день, решая разные типы сюжетных задач. Вот пример расписания:
| День 1 | Добавление к |
| День 2 | Взять от |
| День 3 | Собираем вместе |
| День 4 | Разрушение |
| День 5 и 6 | Сравнение |
| День 7 и 8 | Неизвестно |
| День 9 и 10 | Многоступенчатый |
| День 12 и 13 | Обзор всех типов |
Типы сюжетных задач для 2.OA.A.1
Сложение, извлечение, объединение и разборка задач, как правило, легче усвоить учащимся, потому что они больше всего сталкиваются с ними. Сравнительные, неизвестные и многоступенчатые задачи намного сложнее, поэтому вам может потребоваться несколько дней, чтобы сосредоточиться на них.
После изучения всех типов задач я оцениваю студентов по 2. OA.A.1 с диапазоном чисел, который я преподавал. Вы можете найти оценки на 20–50, 50–100 и 100–1000 в текстовом пакете задач.
OA.A.1 с диапазоном чисел, который я преподавал. Вы можете найти оценки на 20–50, 50–100 и 100–1000 в текстовом пакете задач.
Общая картина:
При обучении задачам со словами во 2-м классе в течение года используйте этот же процесс, чтобы развить у учащихся навыки решения проблем.
Когда учащиеся учатся складывать и вычитать до 100, выполните еще один блок по решению проблем с числами до 100. Когда учащиеся учатся складывать и вычитать до 1000, вы можете расширить свои навыки и выполнить блок по решению проблем с числами. до 1000, хотя стандарт собирается только до 100.
Другие мысли
- Обучая задачи второго класса со словами, я уделяю большое внимание процессу решения задач. По мере того, как учащиеся начинают понимать шаги и развивать свои навыки решения проблем, важно дать им гибкость.Мозг каждого человека работает по-разному, и мы можем выполнять некоторые действия в разном порядке. Например, для некоторых учеников может быть разумнее написать уравнение до того, как они решат задачу, но другим, возможно, потребуется сначала решить проблему.
 Некоторые студенты могут обводить ключевые слова во время чтения задачи, потому что это помогает им понять. Не забывайте проявлять гибкость с учениками и не бойтесь предлагать различные подходы, чтобы помочь им усвоить концепции.
Некоторые студенты могут обводить ключевые слова во время чтения задачи, потому что это помогает им понять. Не забывайте проявлять гибкость с учениками и не бойтесь предлагать различные подходы, чтобы помочь им усвоить концепции.
Якорная диаграмма, показывающая типы словесных задач, которые следует усвоить второклассникам.2-й класс уроки задач, идеи, советы и уловки.
Иллюстративная математика
Иллюстративная математика
2 класс
2.OA. 2 класс — Операции и алгебраическое мышление
2.OA.A. Представляйте и решайте задачи, связанные с сложением и вычитанием.
2.OA.A.1. Используйте сложение и вычитание в пределах 100 для решения одно- и двухэтапных задач со словами, включающих ситуации сложения, взятия из, сложения, разборки и сравнения с неизвестными во всех позициях, e.g., используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему.
2.
 OA.B. Сложить и вычесть в пределах 20.
OA.B. Сложить и вычесть в пределах 20.
2.OA.B.2. Плавно складывайте и вычитайте в пределах 20, используя мысленные стратегии. К концу 2 класса выучите по памяти все суммы двух однозначных чисел.
2.OA.C. Работайте с равными группами предметов, чтобы получить основу для умножения.
2.OA.C.3. Определите, имеет ли группа объектов (до 20) четное или нечетное количество членов, например.g., объединяя объекты в пары или считая их по 2 секунды; напишите уравнение, чтобы выразить четное число как сумму двух равных слагаемых.
2.OA.C.4. Используйте сложение, чтобы найти общее количество объектов, расположенных в прямоугольные массивы до 5 строк и до 5 столбцов; напишите уравнение, чтобы выразить общую сумму как сумму равных слагаемых.
-
Пока нет задач, иллюстрирующих этот стандарт.
2.NBT. 2 класс — Число и операции в десятичной системе счисления
2.NBT.A. Понять значение места.
2.NBT.A.1.
 Поймите, что три цифры трехзначного числа представляют собой сотни, десятки и единицы; например, 706 равно 7 сотням, 0 десяткам и 6 единицам. Рассматривайте следующие как частные случаи:
Поймите, что три цифры трехзначного числа представляют собой сотни, десятки и единицы; например, 706 равно 7 сотням, 0 десяткам и 6 единицам. Рассматривайте следующие как частные случаи:
2.NBT.A.1.a. 100 можно представить как связку из десяти десятков, называемую «сотней».
2.NBT.A.1.b. Цифры 100, 200, 300, 400, 500, 600, 700, 800, 900 относятся к одной, двум, трем, четырем, пяти, шести, семи, восьми или девяти сотням (и 0 десятков и 0 единиц).
2.NBT.A.2. Считайте в пределах 1000; счет пропусков на 5, 10 и 100 секунд.
2.NBT.A.3. Чтение и запись чисел до 1000 с использованием десятичных чисел, числовых имен и расширенной формы.
2.NBT.A.4. Сравните два трехзначных числа на основе значений сотен, десятков и единиц цифр, используя символы $> $, = и $
<$ для записи результатов сравнения.
2.
 NBT.B. Используйте представление о числовых значениях и свойствах операций для сложения и вычитания.
NBT.B. Используйте представление о числовых значениях и свойствах операций для сложения и вычитания.
2.NBT.B.5. Плавно складывайте и вычитайте в пределах 100, используя стратегии, основанные на разряде, свойствах операций и / или соотношении между сложением и вычитанием.
2.NBT.B.6. Сложите до четырех двузначных чисел, используя стратегии, основанные на разрядах и свойствах операций.
2.NBT.B.7. Сложение и вычитание в пределах 1000, используя конкретные модели или чертежи и стратегии, основанные на разряде, свойствах операций и / или соотношении между сложением и вычитанием; связать стратегию с письменным методом. Поймите, что при сложении или вычитании трехзначных чисел добавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда необходимо составить или разложить десятки или сотни.
2.NBT.B.8. Мысленно прибавьте 10 или 100 к данному числу 100–900 и мысленно вычтите 10 или 100 из данного числа 100–900.

2.NBT.B.9. Объясните, почему работают стратегии сложения и вычитания, используя разрядные значения и свойства операций.
-
Пока нет задач, иллюстрирующих этот стандарт.
2.MD. Уровень 2 — Измерения и данные
2.MD.A. Измерьте и оцените длину в стандартных единицах.
2.MD.A.1. Измерьте длину объекта, выбрав и используя соответствующие инструменты, такие как линейки, мерки, измерители и измерительные ленты.
2.MD.A.2. Дважды измерьте длину объекта, используя единицы длины разной длины для двух измерений; опишите, как эти два измерения соотносятся с размером выбранной единицы.
2.MD.A.3. Оцените длину в дюймах, футах, сантиметрах и метрах.
2.MD.A.4. Измерьте, чтобы определить, насколько длиннее один объект, чем другой, выражая разницу в длине в единицах стандартной длины.
2.
 MD.B. Свяжите сложение и вычитание с длиной.
MD.B. Свяжите сложение и вычитание с длиной.
2.MD.B.5. Используйте сложение и вычитание в пределах 100 для решения словесных задач, связанных с длинами, указанными в одних и тех же единицах, например, используя рисунки (такие как рисунки линейок) и уравнения с символом неизвестного числа, чтобы представить проблему.
2.MD.B.6. Представляйте целые числа как длины от 0 на числовой линейной диаграмме с равноотстоящими точками, соответствующими числам 0, 1, 2,…, и представляйте целые числа и разности в пределах 100 на числовой линейной диаграмме.
2.MD.C. Работайте со временем и деньгами.
2.MD.C.7. Назовите и запишите время по аналоговым и цифровым часам с точностью до пяти минут, используя полдень и вечер
2.MD.C.8. Решайте текстовые задачи, связанные с долларовыми купюрами, четвертями, десятицентовиками, пятаками и пенни, используя символы \ $ и $ ¢ $ соответствующим образом. Пример: если у вас есть 2 центов и 3 пенни, сколько у вас центов?
2.
 MD.D. Представляйте и интерпретируйте данные.
MD.D. Представляйте и интерпретируйте данные.
2.MD.D.9. Генерируйте данные измерений, измеряя длины нескольких объектов с точностью до ближайшей целой единицы или выполняя повторные измерения одного и того же объекта. Покажите измерения, построив линейный график, на котором горизонтальная шкала обозначена целыми числами.
2.MD.D.10. Нарисуйте графическую диаграмму и гистограмму (с единичной шкалой), чтобы представить набор данных, содержащий до четырех категорий. Решайте простые задачи сборки, разборки и сравнения, используя информацию, представленную на гистограмме.
2.G. 2 класс — Геометрия
2.Г.А. Размышляйте с формами и их атрибутами.
2.G.A.1. Распознавайте и рисуйте фигуры с указанными атрибутами, такими как заданное количество углов или заданное количество равных граней. Определите треугольники, четырехугольники, пятиугольники, шестиугольники и кубы.
2.
 G.A.2. Разделите прямоугольник на строки и столбцы квадратов одинакового размера и посчитайте, чтобы найти их общее количество.
G.A.2. Разделите прямоугольник на строки и столбцы квадратов одинакового размера и посчитайте, чтобы найти их общее количество.
2.G.A.3. Разделите круги и прямоугольники на две, три или четыре равные доли, опишите доли, используя слова
половинки , трети , половину , треть и т. Д., И опишите целое как две половины, три трети, четыре четверти. Помните, что равные доли идентичных целых не обязательно должны иметь одинаковую форму.
Уровень 2 — Сводные данные по разделам
Раздел 1: монеты, числовые строки и задачи с рассказом (26 сеансов)
Сложение, вычитание и система счисления 1
Этот модуль фокусируется на сложении и вычитании однозначных чисел, в частности, на сложении чисел в любом порядке; переход от счета по единицам к счету по группам, особенно по десяткам и единицам, что закладывает основу для работы учащихся с разметкой знаков и десятичной системой счисления; и разработка и уточнение стратегий для решения множества задач сложения и вычитания. Будучи первым блоком во 2-м классе, он также знакомит с математическими инструментами, процессами и способами работы, которые станут основой математического класса. В рамках этой работы учащиеся знакомятся с несколькими годичными учебными занятиями, которые предлагают регулярную практику по составлению и разложению чисел, разработке визуальных образов величин, фактов сложения и вычитания, определения времени, а также подсчета, сбора и анализа данных.
Будучи первым блоком во 2-м классе, он также знакомит с математическими инструментами, процессами и способами работы, которые станут основой математического класса. В рамках этой работы учащиеся знакомятся с несколькими годичными учебными занятиями, которые предлагают регулярную практику по составлению и разложению чисел, разработке визуальных образов величин, фактов сложения и вычитания, определения времени, а также подсчета, сбора и анализа данных.
- Исследование 1: Знакомство с математическими инструментами и рутинными занятиями (6 занятий)
- Расследование 2: Имеет ли значение порядок? (8 сеансов)
- Исследование 3: Сравнение количеств и подсчет по группам (7 сеансов)
- Исследование 4: Решение сюжетных задач (5 сеансов)
Блок 2: Атрибуты форм и частей целого (19 сеансов)
Геометрия и дроби
Основное внимание в этом модуле уделяется наблюдению и описанию определяющих атрибутов двумерных и трехмерных форм (например,g. , количество и форма граней, количество и длина сторон, количество углов и вершин), а также использование этих атрибутов при сортировке, построении, рисовании и сравнении форм. Этот блок также развивает идеи о равных частях целого, уделяя особое внимание разделению и описанию половин, четвертей и третей одного целого и признавая, что одна и та же равная часть целого (например, одна половина квадрата) может иметь разные формы.
, количество и форма граней, количество и длина сторон, количество углов и вершин), а также использование этих атрибутов при сортировке, построении, рисовании и сравнении форм. Этот блок также развивает идеи о равных частях целого, уделяя особое внимание разделению и описанию половин, четвертей и третей одного целого и признавая, что одна и та же равная часть целого (например, одна половина квадрата) может иметь разные формы.
- Исследование 1: Атрибуты двумерных и трехмерных фигур (5 сеансов)
- Исследование 2: четырехугольники, прямоугольники и квадраты (6 сеансов)
- Исследование 3: половины, четверти и трети (8 сеансов)
Раздел 3: Сколько наклеек? Сколько центов? (24 сеанса)
Сложение, вычитание и система счисления 2
Этот блок фокусируется на разряде двухзначных чисел и работе с этими числами в пределах 100.Студенты приходят к выводу, что 100 — это десять десятков, а число, кратное 100, состоит из некоторого числа сотен. Они решают различные типы сюжетных задач (например, собрать / разобрать с одним или обоими неизвестными дополнениями, добавить и взять из с неизвестным результатом, проблемы с неизвестным изменением или неизвестным началом). Они играют в игры, в которых суммируются суммы, чтобы получить 100 или 1 доллар. Работа над быстрым сложением и вычитанием в пределах 100 продолжается с упором на использование известных фактов и знаний об операции.Учащиеся также определяют, читают и записывают числа до 500, а также мысленно складывают и вычитают 10 к числам в этом диапазоне.
Они решают различные типы сюжетных задач (например, собрать / разобрать с одним или обоими неизвестными дополнениями, добавить и взять из с неизвестным результатом, проблемы с неизвестным изменением или неизвестным началом). Они играют в игры, в которых суммируются суммы, чтобы получить 100 или 1 доллар. Работа над быстрым сложением и вычитанием в пределах 100 продолжается с упором на использование известных фактов и знаний об операции.Учащиеся также определяют, читают и записывают числа до 500, а также мысленно складывают и вычитают 10 к числам в этом диапазоне.
- Исследование 1: Станция для наклеек (8 сеансов)
- Исследование 2: Сложение и вычитание в течение 100 (9 сеансов)
- Исследование 3: Проблемы с неизвестным изменением или неизвестным началом (7 сеансов)
Часть 4: карманы, зубы и угадай мое правило (12 сеансов)
Моделирование с использованием данных
Этот модуль специализируется на сортировке и классификации категориальных данных; заказ числовых данных; и сбор и представление категориальных и числовых данных с использованием различных представлений: представления, созданные студентами, графические изображения, гистограммы, диаграммы Венна, кубические башни и линейные графики. Учащиеся описывают данные и обсуждают, что они говорят им об опрошенной группе. При этом учащиеся развивают способность моделировать на основе данных аспекты своего мира.
Учащиеся описывают данные и обсуждают, что они говорят им об опрошенной группе. При этом учащиеся развивают способность моделировать на основе данных аспекты своего мира.
- Исследование 1: Работа с категориальными данными (6 сеансов)
- Исследование 2: Работа с числовыми данными (6 сеансов)
Блок 5: Сколько десятков? Сколько сотен? (20 сеансов)
Сложение, вычитание и система счисления 3
Этот модуль фокусируется на разряде трехзначных чисел и оперирует числами в пределах 100.Студенты приходят к выводу, что 100 — это 10 десятков, а число, кратное 100, состоит из некоторого числа сотен. Они решают различные типы сюжетных задач (например, сложить / разобрать с одним или обоими неизвестными дополнениями, добавить и взять из с неизвестным результатом, проблемы с неизвестным изменением или неизвестным началом). Они играют в игры, в которых суммируются суммы, чтобы получить 100 или 1 доллар. Работа над быстрым сложением и вычитанием в пределах 100 продолжается с упором на использование известных фактов и знаний об операциях. Беглость с суммированием в пределах 100 является эталоном для этого устройства. Учащиеся также определяют, читают и записывают числа до 1000, а также складывают и вычитают 10 и 100 к числам в этом диапазоне.
Беглость с суммированием в пределах 100 является эталоном для этого устройства. Учащиеся также определяют, читают и записывают числа до 1000, а также складывают и вычитают 10 и 100 к числам в этом диапазоне.
- Исследование 1: 100 комбинаций (6 сеансов)
- Исследование 2: Сложение в пределах 100 и подсчет до 1000 (6 сеансов)
- Исследование 3: Свободное владение в пределах 100 (8 занятий)
Раздел 6: Как далеко вы можете прыгнуть? (12 сессий)
Линейное измерение
Этот модуль ориентирован на разработку стратегий точного измерения длины с использованием нестандартных и стандартных единиц (например,g., ремесленные палочки, кубы, дюймы, футы, ярды, сантиметры и метры) и инструменты (например, измерительные инструменты для дюймового кирпича, линейки, мерки и измерители), а также для рассмотрения взаимосвязи между различными единицами измерения и инструментами (например, , чем больше единица, тем меньше будет счетчик). Учащиеся представляют данные измерений на линейном графике, а также решают сюжетные задачи, которые включают сложение, вычитание и сравнение длин.
Учащиеся представляют данные измерений на линейном графике, а также решают сюжетные задачи, которые включают сложение, вычитание и сравнение длин.
- Исследование 1: Земля дюйма (6 сеансов)
- Исследование 2: две системы измерения (6 сеансов)
Раздел 7: Партнеры, команды и другие группы (10 сеансов)
Основы умножения
Основное внимание в этом модуле уделяется работе с равными группами в качестве основы умножения путем исследования четных и нечетных чисел и представления равных групп с помощью массивов и таблиц.
- Исследование 1: четное или нечетное? (4 сеанса)
- Исследование 2: Исследование равных групп (6 занятий)
Блок 8: Достаточно для класса? Достаточно для класса? (20 сеансов)
Сложение, вычитание и система счисления 4
Этот блок направлен на развитие и достижение беглости с помощью вычитания в пределах 100, а также на достижение беглости с фактами сложения и вычитания в пределах 20, над которыми студенты работали в течение года. Студенты также знакомятся с новым типом задач-рассказов — задачами сравнения с меньшим неизвестным. В конце года они думают о том, как стратегии, которые они знают и используют для сложения и вычитания 2-значных чисел, трансформируются в сложение и вычитание 3-значных чисел, представленных в виде разметки. Студенты также демонстрируют свободное владение временем, работа, которая выполнялась в течение всего года, заканчивая год, указывая время с точностью до ближайших пяти минут, используя A.M. и П.
Студенты также знакомятся с новым типом задач-рассказов — задачами сравнения с меньшим неизвестным. В конце года они думают о том, как стратегии, которые они знают и используют для сложения и вычитания 2-значных чисел, трансформируются в сложение и вычитание 3-значных чисел, представленных в виде разметки. Студенты также демонстрируют свободное владение временем, работа, которая выполнялась в течение всего года, заканчивая год, указывая время с точностью до ближайших пяти минут, используя A.M. и П.
- Исследование 1: Вычитание: свободное владение в пределах 100 (11 сеансов)
- Исследование 2: Модели для сложения и вычитания больших чисел (9 сеансов)
Двухэтапные математические задачи со словами — Видео и стенограмма урока
Решение двухэтапных математических задач со словами
Начните двухэтапную задачу со словами, как любую другую задачу со словами, внимательно прочитав ее, чтобы решить, что вам нужно делать, в том числе какой шаг выполнить первым. При необходимости перечитайте проблему. Затем выполните первый шаг. Посмотрите на важную информацию в задаче и превратите эту информацию в уравнение, переведя слова в операции. Не стесняйтесь рисовать картинки, которые помогут вам решить проблему.
При необходимости перечитайте проблему. Затем выполните первый шаг. Посмотрите на важную информацию в задаче и превратите эту информацию в уравнение, переведя слова в операции. Не стесняйтесь рисовать картинки, которые помогут вам решить проблему.
Давайте попробуем это на нашем примере двухэтапной задачи со словами:
Джейкоб дал Юлии 1 стикер. Это переводится в уравнение 12 — 1, которое равно 11. Итак, 11 — это ответ на наш первый шаг.
А теперь перечитайте задачу, чтобы убедиться, что вы на правильном пути, а затем выполните второй шаг. Опять же, попробуйте превратить слово «проблема» в уравнение. В примере задачи Джейкоб отдает Джону 4 из своих 11 оставшихся наклеек. Итак, мы можем превратить эту проблему со словом в уравнение 11-4, что равно 7. Итак, 7 — это ответ на наш второй шаг и проблему со словом.
После решения задачи обязательно проверьте свою работу, перечитайте вопрос словом проблема и спросите себя: «Я ответил на вопрос?»
Практическая задача
Давайте применим полученные знания и ответим на новую двухэтапную математическую задачу со словами. Первое, что нам нужно сделать, это внимательно прочитать проблему, чтобы убедиться, что мы полностью ее понимаем:
Первое, что нам нужно сделать, это внимательно прочитать проблему, чтобы убедиться, что мы полностью ее понимаем:
Затем нам нужно решить, какой шаг сделать в первую очередь. Первый шаг в этом случае — узнать, сколько всего кексов приготовила мама. Затем мы можем убрать 3 съеденных, чтобы узнать, сколько осталось.
Чтобы узнать, сколько всего приготовила мама, вам нужно сложить вчерашние и сегодняшние итоги:
Мама приготовила всего 36 кексов.Вы только что закончили первый шаг этой двухэтапной задачи!
Затем перечитайте проблему и переходите ко второму шагу. Проблема со словами состоит в том, чтобы спросить, сколько осталось после того, как вы съели 3. Итак, вам нужно взять общее количество мамы (36) и вычесть (или убрать) 3.
Ответ на наш последний шаг и слово проблема — 33. До вы уходите от проблемы, обязательно проверяете свою работу и спрашиваете себя: «Я ответил на вопрос?»
Краткое содержание урока
В математических задачах со словами информация, необходимая для решения задачи, предоставляется в виде слов, а не чисел или символов. Хотя многие из этих задач состоят только из одного шага, двухэтапная задача со словами требует от вас решения двух разных уравнений, прежде чем прийти к ответу. Двухэтапная задача со словами может иметь две разные операции (например, умножение и сложение) или две одинаковые операции (например, вычитание и вычитание).
Хотя многие из этих задач состоят только из одного шага, двухэтапная задача со словами требует от вас решения двух разных уравнений, прежде чем прийти к ответу. Двухэтапная задача со словами может иметь две разные операции (например, умножение и сложение) или две одинаковые операции (например, вычитание и вычитание).
Блок | Общий вопрос | Основные вопросы | Большие идеи | Полные цели |
Блок 0: Мышление о росте | Как образ мышления влияет на изучение математики? |
|
| |
Раздел 1: Разработка концепций стоимости места Сроки 5-6 недель Цели 2.N.1.1 2.N.1.2 2.N.1.3 2.N.1.4 2.N.1.5 2.N.1.6 | Как месторасположение помогает нам понять числовые отношения? |
|
| 2.N.1.1 Читать, писать, обсуждать и представлять целые числа до 1000. Представления могут включать цифры, слова, изображения, счетные метки, числовые линии и манипуляторы. (до 120) 2.N.1.2 Используйте знания о числовых отношениях, чтобы найти позицию данного целого числа в открытой числовой строке до 100. 2.N.1.3 Используйте разряд для описания целых чисел от 10 до 1000 в единицах сотен, десятков и единиц. Знайте, что 100 — это 10 десятков, а 1000 — это 10 сотен. 2.N.1.4 Найдите на 10 больше или 10 меньше заданного трехзначного числа. Найдите на 100 больше или на 100 меньше заданного трехзначного числа. 2.N.1.5 Распознавайте, когда нужно округлять числа до ближайших 10 и 100. 2.N.1.6 Используйте разряд, чтобы сравнить и упорядочить целые числа до 1000, используя язык сравнения, числа и символы (например, 425> 276, 73 <107, страница 351 идет после страницы 350, 753 находится между 700 и 800). (до 100) |
Блок 2: Применение разряда к шаблонам и данным Сроки 3-4 недели Объективы 2.A.1.1 2.A.1.2 2.D.1.1 2.D.1.2 2.D.1.3 2.D.1.4 | Как шаблоны и графики объясняют реальные ситуации? |
|
| 2.A.1.1 Представлять, создавать, описывать, дополнять и расширять шаблоны роста и сжатия с количеством и числами в различных реальных и математических контекстах. 2.A.1.2 Представляют и описывают повторяющиеся узоры, включающие формы в различных контекстах. 2.D.1.1 Объясните, что длина полосы на столбчатой диаграмме или количество объектов на графической диаграмме представляет количество точек данных для данной категории. 2.D.1.2 Организуйте сбор данных по четырем категориям, используя пиктограммы и гистограммы с интервалами 1, 2, 5 или 10. 2.D.1.3 Напишите и решите одноэтапные задачи со словами, включающие сложение или вычитание, используя данные, представленные в виде пиктограмм и гистограмм с интервалом в единицу. 2.D.1.4 Делайте выводы и делайте прогнозы на основе информации в виде графика. |
Блок 3: Развитие стоимости места в операциях Сроки 5-6 недель Цели 2.N.2.1 2.N.2.2 2.N.2.3 2.N.2.4 2.N.2.5 2.N.2.6 | Как понимание расстановки значений помогает в операциях с целыми числами? |
|
| 2.N.2.1 Используйте связь между сложением и вычитанием для получения основных фактов до 20. 2.N.2.2 Продемонстрировать свободное владение базовыми фактами сложения и соответствующими фактами вычитания до 20. 2.N.2.3 Оценка сумм и разностей до 100. 2.N.2.4 Используйте стратегии и алгоритмы, основанные на знании разряда и равенства для сложения и вычитания двузначных чисел. 2.N.2.5 Решение реальных и математических задач на сложение и вычитание с использованием целых чисел до 2 цифр. 2. |
Раздел 4: Использование разряда в алгебраических рассуждениях Сроки 3-4 недели Цели 2.A.2.1 2.A.2.2 2.A.2.3 | Как мы можем использовать эквивалентность для описания нашего мира? |
|
| 2.A.2.1 Используйте объекты и числовые линии для представления числовых предложений. 2.A.2.2 Создание реальных ситуаций для представления числовых предложений и наоборот. 2.A.2.3 Применяйте свойства коммутативности и идентичности, а также чувство числа, чтобы найти значения для неизвестных, которые делают числовые предложения, включающие сложение и вычитание, истинными или ложными. |
Блок 5: Геометрия, разбиение и время Сроки 4 недели Объективы 2.GM.1.1 2.GM.1.2 2.GM.1.3 2.GM.1.4 2.GM.3.1 2.N.3.1 2.N.3.2 | Зачем делить что-то на равные части? |
|
| 2.GM.1.1 Распознавать трапеции и шестиугольники. 2.GM.1.2 Описывать, сравнивать и классифицировать двумерные фигуры в соответствии с их геометрическими атрибутами. 2.GM.1.3 Составьте двумерные формы, используя треугольники, квадраты, шестиугольники, трапеции и ромбы. 2.GM.1.4 Распознавать прямые углы и классифицировать углы как меньшие или большие, чем прямой угол. 2.GM.3.1 Считывание и запись времени с точностью до четверти часа на аналоговых и цифровых часах. Различать между утра и вечера. 2.N.3.1 Обозначьте части набора и площади, которые представляют собой доли для половин, третей и четвертей. 2.N.3.2 Построение частей равного размера посредством справедливого разделения, включая модели длины, набора и площади для половин, третей и четвертей. |
Раздел 6: Деньги и измерения Сроки 5-6 недель Цели 2.N.4.1 2.N.4.2 2.GM.2.1 2.GM.2.2 2.GM.2.3 | Как мы можем использовать несколько представлений, чтобы понять мир? |
|
| 2.N.4.1 Определите стоимость коллекции (ов) монет до одного доллара, используя символ цента. 2.N.4.2 Используйте комбинацию монет для обозначения заданной суммы денег до одного доллара. 2.GM.2.1 Объясните взаимосвязь между размером единицы измерения и количеством единиц, необходимых для измерения длины объекта. 2.GM.2.2 Объясните взаимосвязь между длиной и числами на линейке, используя линейку для измерения длины до ближайшей целой единицы. 2.GM.2.3 Узнайте, как контейнеры различной формы и стиля могут иметь одинаковую вместимость |
Аппарат культивирования Сроки 2 недели | Как связаны умножение и деление? | Этот блок предназначен для того, чтобы превзойти стандарты второго класса в третий класс. |





 Записать, что дано, что обозначает каждое число?
Записать, что дано, что обозначает каждое число? Послушайте.
Послушайте. Какая операция обратна этой?
Какая операция обратна этой? На остановке 8 из них вышли, а 4 вошли. Сколько пассажиров стало в трамвае?
На остановке 8 из них вышли, а 4 вошли. Сколько пассажиров стало в трамвае?

 Теперь я добавлю еще 6 ». Нарисуйте на подносе 6 розовых кружков.
Теперь я добавлю еще 6 ». Нарисуйте на подносе 6 розовых кружков.

 Некоторые студенты могут обводить ключевые слова во время чтения задачи, потому что это помогает им понять. Не забывайте проявлять гибкость с учениками и не бойтесь предлагать различные подходы, чтобы помочь им усвоить концепции.
Некоторые студенты могут обводить ключевые слова во время чтения задачи, потому что это помогает им понять. Не забывайте проявлять гибкость с учениками и не бойтесь предлагать различные подходы, чтобы помочь им усвоить концепции.

 (данное двузначное число; более или менее 100 будет найдено в более позднем блоке)
(данное двузначное число; более или менее 100 будет найдено в более позднем блоке)

 N.2.6 Используйте конкретные модели и структурированные схемы, такие как повторное сложение, массивы и десять кадров, чтобы развить понимание умножения.
N.2.6 Используйте конкретные модели и структурированные схемы, такие как повторное сложение, массивы и десять кадров, чтобы развить понимание умножения.