Как объяснить ребёнку деление в столбик
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, как запомнить таблицу умножения легко и быстро. Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
Двигайтесь дальше, разбирая другие примеры из таблицы умножения.
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1. Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление.
 Уровень 4. Рабочая тетрадь» от Kumon
Уровень 4. Рабочая тетрадь» от Kumon - «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
- Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта marypop.ru
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Как научиться делить столбиком многозначные числа.
 Как правильно объяснить ребёнку деление в столбик
Как правильно объяснить ребёнку деление в столбик
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком
.
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым
, неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его.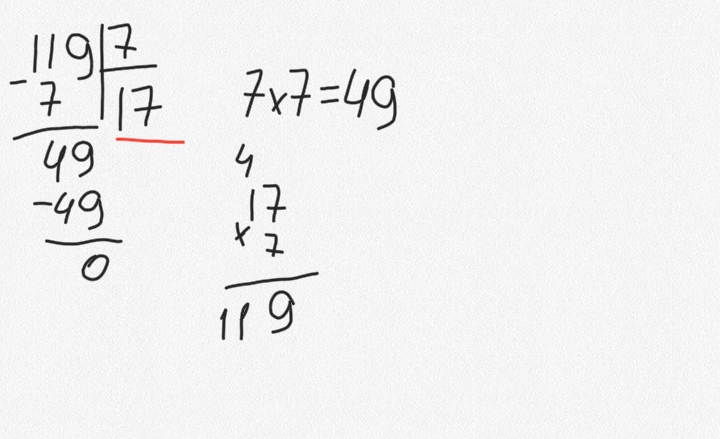 Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Как в столбик делить — один из основных навыков, необходимых для работы с двух- и трёхзначными числами. Зная последовательность всех этапов деления, можно разделить любое число. Не возникнет проблем при работе не только с целым числом, но и с числом, представленным в виде десятичной дроби.
Зная последовательность всех этапов деления, можно разделить любое число. Не возникнет проблем при работе не только с целым числом, но и с числом, представленным в виде десятичной дроби.
Этот полезный математический навык необходим не только для успешного освоения школьной программы по математике и ряду других предметов. Умение делить наверняка поможет каждому в повседневной жизни.
Часть первая. Деление
Итак, делимое, то есть число, которое нужно разделить, надо записать слева. Число, на которое делят, называют делителем и записывают справа.
Под делителем проводится черта, под которой пишут частное (решение).
Под делимым необходимо оставить место, требующееся для вычислений.
Сама задача выглядит следующим образом: пакет, где лежат шесть грибов, весит 250 грамм. Нужно узнать, сколько весит один гриб. Для этого 250 делят на 6. Первое из этих двух чисел записывают слева, а второе — справа.
Сейчас предстоит вычислить, сколько целых раз делится первая цифра (отсчёт ведётся с левого конца) делимого на делитель.
Для решения нашей задачи нужно узнать, сколько раз цифра 2 делится на 6. Так как это невозможно, то в ответе — 0, который записывается под делителем. В этом случае нуль является первым числом частного, однако допускается отказ от такой записи.
Теперь предстоит узнать, сколько целых раз делятся две первые цифры делимого на делитель.
Если в предшествующем действии в ответе был получен 0, надо рассмотреть две первые цифры делимого. В рассматриваемой задаче надо вычислить, сколько раз 25 делится на 6.
Если делитель является двух- и более значным числом, надо разделить на него первые три (четыре, пять и т. д.) цифры делимого. Наша цель: получить целое число.
Далее начинается работа с целыми числами. Если с помощью микрокалькулятора произвести деление 25 на 6, то в ответе будет дано число 4.167. Этот ответ не годится для деления в столбик. В этом случае нужно просто взять 4.
Результат, полученный в третьем этапе, записывается прямо под соответствующей цифрой делителя — под чертой. Данный итог будет первой цифрой искомого частного, то есть ответа.
Результат обязательно нужно писать под соответствующей цифрой делителя. Если пренебречь этим требованием, будет допущена ошибка, которая скажется и на конечном результате: он будет неверным.
В рассматриваемом случае 4 записывается под 5, так как на 6 делится число 25, а не 2.
Часть вторая. Умножение
Этот этап представляет собой переход к новой части работы «как считать в столбик». Деление в данном случае сменятся… умножением.
Делитель умножается на число, которое было под ним записано. Это означает, что речь идёт о первой цифре искомого частного.
Результат этого произведения размещается под делимым.
В рассматриваемом примере 6 х 4 = 24. Число, стоящее в ответе, то есть 24, записывается под 25. Важно: 2 должна стоять под 2, а 4 — под 5.
Результат произведения подчёркивается. В нашем случае речь идёт о подчёркивании числа 24.
Часть третья. Вычитание и опускание цифр
Здесь происходит переход к вычитанию и опусканию цифр.
Результат записывается под чертой, которая в свою очередь проводится под числом, поставленным под делимым.
Нам предстоит произвести вычитание 24 из 25. Получаемый при этом результат: 1.
Опускается третья цифра делимого, то есть она записывается рядом с результатом вычитания.
В нашем случае 1 не может делиться на 6. В силу этого спускают третью цифру делимого (третьей цифрой числа 250 является 0). Она размещается рядом с 1. Мы получаем число 10, которое может быть разделено на 6.
Теперь требуется повторить процесс с новым числом.
Для этого полученное число делится на наш делитель, а получаемый при этом результат размещается под делителем, в качестве которого будет выступать вторая цифра частного, то есть нашего ответа.
В решаемом примере 10 делим на 6, что даёт в итоге 1. Единичка записывается в частное — рядом с 4. После этого 6 умножается на 1 и из 10 вычитают результат. У нас должно получиться 4 (остаток).
Если делимое представляет собой двух-, трёх-, четырёх- и более значное число, изложенный процесс повторяется до тех пор, пока не будут опущены все цифры делимого. Пример для иллюстрации: если известно, что вес грибов равен 2 506 г, надо опустить цифру 6, то есть записать её рядом с 4.
Часть четвёртая. Запись частного с остатком или в виде десятичной дроби
Теперь переходим к записи частного с остатком или в виде десятичной дроби.
Наш остаток был равен 4, что связано с тем, что это число — 4 — не делится на 6 и у нас не осталось цифр, которые можно спустить.
Ответ при этом будет выглядеть следующим образом: 41 (ост. 4).
Вычисления на данном этапе могут быть завершены, если в задаче сформулировано требование найти что-то, выражаемое исключительно в целых числах. Речь может идти о количестве автомобилей, требующихся для транспортировки определённого числа людей.
Если есть необходимость в ответе в виде десятичной дроби, можно перейти к следующим действиям алгоритма «как разделить в столбик».
Если нет желания записывать ответ с остатком, можно найти ответ в виде десятичной дроби. При получении остатка, не поддающегося делению на делитель, надо добавить десятичный знак (к частному).
В нашем случае число 250 может быть записано в виде десятичной дроби: 250.000.
Теперь, когда в наличии цифры (только нули), которые могут быть опущены, можно продолжить вычисления. Опускаем нуль и подсчитываем, сколько целых раз можно поделить полученное число на делитель.
В нашем примере после частного 41 (которое размещаем прямо под делителем) пишем десятичную запятую и приписываем 0 к остатку (4). Затем делим полученное число, то есть 40, на делитель (в роли которого выступает 6). Получаем опять 6, которую пишем в частное после десятичного знака. Это выглядит как 41.6. После этого 6 умножается на 6, затем результат умножения вычитается из 40. У нас должно получиться снова 4.
Это выглядит как 41.6. После этого 6 умножается на 6, затем результат умножения вычитается из 40. У нас должно получиться снова 4.
В ряде ситуаций при поиске ответа в виде десятичной дроби приходится столкнуться с повторяющимися числами. Для этого надо прервать вычисления и округлить уже полученный ответ — вниз или вверх.
В частности, в рассматриваемом примере надо отказаться от бесконечного получения цифры 4. Нужно просто прервать вычисления и округлить частное. В силу того, что 6 больше 5, округление производится вверх, в результате чего получается ответ в виде дробного числа 41.67.
К сожалению, современная образовательная программа не всегда предполагает разъяснение каждой темы ученикам, особенно такой сложной, как деление столбиком. В таких случаях родителям самим приходится заниматься с учениками дома.
Пошаговая инструкция обучения делению столбиком
Для начала необходимо определить базис ребенка: повторить с ним названия элементов деления (делимое, делитель, частное, остаток), разряды числа и таблицу умножения. Без этих знаний ребенок не сможет освоить деление. Для начала нужно показать операцию на простых примерах из таблицы умножения, то есть 56: 7 = 8. Далее покажите пример деления трехзначного числа без остатка, когда первая цифра делимого больше делителя, например, 422: 2. Необходимо разделить каждую цифру по порядку на делитель следующим образом: 4 делить на 2 будет 2, записываем, 2 на 2 – это 1, пишем, 2 на 2 – опять один, записываем. В результате получилось 211. Результат необходимо перепроверить обратным умножением.
В деле обучения делению столбиком необходима практика и повторение каждого этапа. Подберите еще несколько таких же несложных операций, например, 936 делить на 3, 488 делить на 4 и т.п. Комментируйте свои действия каждый раз одинаково, так чтобы они впечатались в голове у ребенка, и он их сам повторял про себя при делении:
- Берем первую цифру числа, делим ее на делитель.
 Сколько раз делитель может содержаться в делимом?
Сколько раз делитель может содержаться в делимом? - Если первая цифра меньше делителя, берем число из двух первых цифр, делим, записываем результат.
- Умножаем делитель на частное и вычитаем из делимого, подписываем результат вычитания.
- Сносим следующую цифру делимого: можно ли его поделить на делитель? Если нет, то сносим еще одну цифру и делим, записываем результат.
- Умножаем последнюю цифру частного на делитель и вычитаем из оставшегося делимого. Получаем остаток.
На примере это выглядит так: делим 563 на 11. 5 нельзя разделить на 11, берем 56. 11 может 5 раз поместиться в 56, записываем в частное. 5 умножить на 11 получается 55. 56 минус 55 будет 1. 1 нельзя разделить на 11, сносим 3. В 13 11 поместится только 1 раз, записываем. 1 умножить на 11 будет 11, вычитаем из 13, получается 2. Ответ: частное 51, остаток 2.
Очень важно, чтобы ребенок правильно подписывал результат вычитания и сносил цифры, а каждая цифра частного всегда определяется только подбором цифр. Занимайтесь с ребенком регулярно, но не очень долго: постепенно он набьет руку и будет щелкать такие задачки как орешки.
Деление натуральных чисел, особенно многозначных, удобно проводить особым методом, который получил название деление столбиком (в столбик)
. Также можно встретить название деление уголком
. Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка , так и деление натуральных чисел с остатком .
В этой статье мы разберемся, как выполняется деление столбиком. Здесь мы поговорим и о правилах записи, и о всех промежуточных вычислениях. Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.
Навигация по странице.
Правила записи при делении столбиком
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105
, а делителем – 5
5, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808
на 51 234
(614 808
– шестизначное число, 51 234
– пятизначное число, разница в количестве знаков в записях равна 6−5=1
) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058
и 4
(здесь разница в количестве знаков равна 4−1=3
). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком
Понятно, что разделить одно однозначное натуральное число на другое достаточно просто, и делить эти числа в столбик нет причин. Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.
Пример.
Пусть нам нужно разделить столбиком 8
на 2
.
Решение.
Конечно, мы можем выполнить деление при помощи таблицы умножения , и сразу записать ответ 8:2=4
.
Но нас интересует, как выполнить деление этих чисел столбиком.
Сначала записываем делимое 8
и делитель 2
так, как того требует метод:
Теперь мы начинаем выяснять, сколько раз делитель содержится в делимом. Для этого мы последовательно умножаем делитель на числа 0
, 1
, 2
, 3
, … до того момента, пока в результате не получим число, равное делимому, (либо число большее, чем делимое, если имеет место деление с остатком). Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.
Поехали: 2·0=0
; 2·1=2
; 2·2=4
; 2·3=6
; 2·4=8
. Мы получили число, равное делимому, поэтому записываем его под делимым, а на место частного записываем число 4
. При этом запись примет следующий вид:
Остался завершающий этап деления однозначных натуральных чисел столбиком. Под числом, записанным под делимым, нужно провести горизонтальную черту, и провести вычитание чисел над этой чертой так, как это делается при вычитании натуральных чисел столбиком . Число, получающееся после вычитания, будет остатком от деления. Если оно равно нулю, то исходные числа разделились без остатка.
В нашем примере получаем
Теперь перед нами законченная запись деления столбиком числа 8
на 2
. Мы видим, что частное 8:2
равно 4
(и остаток равен 0
).
Ответ:
8:2=4
.
Теперь рассмотрим, как осуществляется деление столбиком однозначных натуральных чисел с остатком.
Пример.
Разделим столбиком 7
на 3
.
Решение.
На начальном этапе запись выглядит так:
Начинаем выяснять, сколько раз в делимом содержится делитель. Будем умножать 3
на 0
, 1
, 2
, 3
и т.д. до того момента, пока не получим число равное или большее, чем делимое 7
. Получаем 3·0=07
(при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6
(оно получено на предпоследнем шаге), а на место неполного частного записываем число 2
(на него проводилось умножение на предпоследнем шаге).
Осталось провести вычитание, и деление столбиком однозначных натуральных чисел 7
и 3
будет завершено.
Таким образом, неполное частное равно 2
, и остаток равен 1
.
Ответ:
7:3=2 (ост. 1)
.
Теперь можно переходить к делению столбиком многозначных натуральных чисел на однозначные натуральные числа.
Сейчас мы разберем алгоритм деления столбиком
. На каждом его этапе мы будем приводить результаты, получающиеся при делении многозначного натурального числа 140 288
на однозначное натуральное число 4
. Этот пример выбран не случайно, так как при его решении мы столкнемся со всеми возможными нюансами, сможем подробно разобрать их.
Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
Первой слева цифрой в записи делимого 140 288
является цифра 1
. Число 1
меньше, чем делитель 4
, поэтому смотрим еще и на следующую слева цифру в записи делимого. При этом видим число 14
, с которым нам и предстоит работать дальше. Выделяем это число в записи делимого.
Следующие пункты со второго по четвертый повторяются циклически, пока деление натуральных чисел столбиком не будет завершено.
Сейчас нам нужно определить, сколько раз делитель содержится в числе, с которым мы работаем (для удобства обозначим это число как x
). Для этого последовательно умножаем делитель на 0
, 1
, 2
, 3
, … до того момента, пока не получим число x
или число больше, чем x
. Когда получается число x
, то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4
пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x
, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).
Умножаем делитель 4
на числа 0
, 1
, 2
, …, пока не получим число, которое равно 14
или больше 14
. Имеем 4·0=014
. Так как на последнем шаге мы получили число 16
, которое больше, чем 14
, то под выделенным числом записываем число 12
, которое получилось на предпоследнем шаге, а на место частного записываем число 3
, так как в предпоследнем пункте умножение проводилось именно на него.
На этом этапе из выделенного числа вычитаем столбиком число, расположенное под ним. Под горизонтальной линией записывается результат вычитания. Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). Здесь же для своего контроля не лишним будет сравнить результат вычитания с делителем и убедиться, что он меньше делителя. В противном случае где-то была допущена ошибка.
Нам нужно вычесть столбиком из числа 14
число 12
(для корректности записи нужно не забыть поставить знак «минус» слева от вычитаемых чисел). После завершения этого действия под горизонтальной чертой оказалось число 2
После завершения этого действия под горизонтальной чертой оказалось число 2
. Теперь проверяем свои вычисления, сравнивая полученное число с делителем. Так как число 2
меньше делителя 4
, то можно спокойно переходить к следующему пункту.
Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2
по 4
пункты алгоритма.
Под горизонтальной чертой справа от уже имеющейся там цифры 2
записываем цифру 0
, так как именно цифра 0
находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой образуется число 20
.
Это число 20
мы выделяем, принимаем в качестве рабочего числа, и повторяем с ним действия второго, третьего и четвертого пунктов алгоритма.
Умножаем делитель 4
на 0
, 1
, 2
, …, пока не получим число 20
или число, которое больше, чем 20
. Имеем 4·0=0
Проводим вычитание столбиком. Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).
Под горизонтальной линией справа от запомненного места записываем цифру 2
, так как именно она находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой мы имеем число 2
.
Число 2
принимаем за рабочее число, отмечаем его, и нам еще раз придется выполнить действия из 2-4
пунктов алгоритма.
Умножаем делитель на 0
, 1
, 2
и так далее, и сравниваем получающиеся числа с отмеченным числом 2
. Имеем 4·0=02
Имеем 4·0=02
. Следовательно, под отмеченным числом записываем число 0
(оно было получено на предпоследнем шаге), а на месте частного справа от уже имеющегося там числа записываем число 0
(на 0
мы проводили умножение на предпоследнем шаге).
Выполняем вычитание столбиком, получаем число 2
под горизонтальной чертой. Проверяем себя, сравнивая полученное число с делителем 4
. Так как 2
Под горизонтально чертой справа от числа 2 дописываем цифру 8
(так как она находится в этом столбце в записи делимого 140 288
). Таким образом, под горизонтальной линией оказывается число 28
.
Принимаем это число в качестве рабочего, отмечаем его, и повторяем действия 2-4
пунктов.
Здесь никаких проблем возникнуть не должно, если Вы были внимательны до настоящего момента. Проделав все необходимые действия, получается следующий результат.
Осталось последний раз провести действия из пунктов 2
, 3
, 4
(предоставляем это Вам), после чего получится законченная картина деления натуральных чисел 140 288
и 4
в столбик:
Обратите внимание, что в самой нижней строчке записано число 0
. Если бы это был не последний шаг деления столбиком (то есть, если бы в записи делимого в столбцах справа оставались цифры), то этот нуль мы бы не записывали.
Таким образом, посмотрев на законченную запись деления многозначного натурального числа 140 288
на однозначное натуральное число 4
, мы видим, что частным является число 35 072
, (а остаток от деления равен нулю, он находится в самой нижней строке).
Конечно же, при делении натуральных чисел столбиком Вы не будете настолько подробно описывать все свои действия. Ваши решения будут выглядеть примерно так, как в следующих примерах.
Пример.
Выполните деление в столбик, если делимое равно 7 136
, а делителем является однозначное натуральное число 9
.
Решение.
На первом шаге алгоритма деления натуральных чисел столбиком мы получим запись вида
После выполнения действий из второго, третьего и четвертого пунктов алгоритма запись деления столбиком примет вид
Повторив цикл, будем иметь
Еще один проход дет нам законченную картину деления столбиком натуральных чисел 7 136
и 9
Таким образом, неполное частное равно 792
, а остаток от деления равен 8
.
Ответ:
7 136:9=792 (ост. 8)
.
А этот пример демонстрирует, как должно выглядеть деление в столбик.
Пример.
Разделите натуральное число 7 042 035
на однозначное натуральное число 7
.
Решение.
Удобнее всего выполнить деление столбиком.
Ответ:
7 042 035:7=1 006 005
.
Деление столбиком многозначных натуральных чисел
Поспешим Вас обрадовать: если Вы хорошо усвоили алгоритм деления столбиком из предыдущего пункта этой статьи, то Вы уже почти умеете выполнять деление столбиком многозначных натуральных чисел
. Это действительно так, так как со 2
по 4
этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2
, 3
и 4
пункте алгоритма до получения конечного результата.
Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.
Пример.
Выполним деление столбиком многозначных натуральных чисел 5 562
и 206
.
Решение.
Так как в записи делителя 206
участвуют 3
знака, то смотрим на первые 3
цифры слева в записи делимого 5 562
. Эти цифры соответствуют числу 556
. Так как 556
больше, чем делитель 206
, то число 556
принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Теперь умножаем делитель 206
на числа 0
, 1
, 2
, 3
, … до того момента, пока не получим число, которое либо равно 556
, либо больше, чем 556
. Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0556
Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0556
. Так как мы получили число, которое больше числа 556
, то под выделенным числом записываем число 412
(оно было получено на предпоследнем шаге), а на место частного записываем число 2
(так как на него проводилось умножение на предпоследнем шаге). Запись деления столбиком принимает следующий вид:
Выполняем вычитание столбиком. Получаем разность 144
, это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.
Под горизонтальной линией справа от имеющегося там числа записываем цифру 2
, так как она находится в записи делимого 5 562
в этом столбце:
Теперь мы работаем с числом 1 442
, выделяем его, и проходим пункты со второго по четвертый еще раз.
Умножаем делитель 206
на 0
, 1
, 2
, 3
, … до получения числа 1 442
или числа, которое больше, чем 1 442
. Поехали: 206·0=0
Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:
Теперь мы видим, что под горизонтальную черту правее запомненной позиции мы не можем записать никакого числа, так как в записи делимого в этом столбце нет цифр. Следовательно, на этом деление столбиком закончено, и мы завершаем запись:
- Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
- Математика. Любые учебники для 5 классов общеобразовательных учреждений.
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1
. Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2
. На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3
. Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4
. Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг
. Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг
. Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг
. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг
. Ставим точку под делителем.
5 шаг
. После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг
. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг
. Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг
. Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг
*. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг
Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3)
(4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Деление на одноцифрове число — УМНОЖЕНИЕ И ДЕЛЕНИЕ БАГАТОЦИФРОВИХ ЧИСЕЛ НА ОДНОЦИФРОВЕ ЧИСЛО — Математика 4 класс Богданович М.В. — Генезис 2015 год
УМНОЖЕНИЕ И ДЕЛЕНИЕ БАГАТОЦИФРОВИХ ЧИСЕЛ НА ОДНОЦИФРОВЕ ЧИСЛО
Деление на одноцифрове число
634. 1) Прочитай объяснение о действии деления.
Делением называют действие, с помощью которой за произведением двух множителей и одним из этих множителей находят второй множитель.
80 ∙ 3 = 240 240 : 3 = 80
Число 240 называют делимым, 3 — делителем, 80 — долей. В множестве натуральных чисел действие деления не всегда выполняется. Например, чтобы поделить 50 на 6, надо найти такое число х, для которого 6 ∙ х = 50. Такого натурального числа не существует, потому что 6 ∙ 8 = 48, а 6 ∙ 9 = 54. В множестве натуральных чисел всегда возможно деление с остачею: 50 : 6 = 8 (ост. 2).
2) Приведи собственные примеры на деление без остатка и с остачею.
635. Прочитай свойства частицы, рассмотри примеры.
1. Чтобы разделить число на произведение двух чисел, достаточно разделить это число на один из множителей, а затем результат разделить на второй множитель.
120 : (2 ∙ 3) = 120 : 2 : 3 = 60 : 3 = 20
2. Чтобы разделить сумму чисел на данное число, достаточно разделить каждое слагаемое на это число и добавить полученные доли.
(48 + 36) : 6 = 48 : 6 + 36 : 6 = 8 + 6 = 14
3. Чтобы разделить разность чисел на данное число, достаточно разделить на это число уменьшающееся и вычитаемое, а затем от первой полученной доли вычесть вторую.
(90 — 21) : 3 = 90 : 3 — 21 : 3 = 30 — 7 = 23 104
Эти свойства частицы применяют в вычислениях.
144 : б = 144 : (2 ∙ 3) = 144 : 2 : 3 = 72 : 3 = 24
216 : 4 = (200 + 16) : 4 = 200 : 4 + 16 : 4 = 50 + 4 = 54
196 : 4 = (200 — 4) : 4 = 200 : 4 — 4 : 4 = 50 — 1 = 49
636. Подай делимое в виде суммы удобных слагаемых и выполни деление.
846 : 2 693 : 3 65 : 5 450 : 6
637. Какие из данных задач решаются действием деления? Реши эти задачи.
1) В 6 одинаковых бидонах 186 л воды. Сколько литров воды в одном бидоне?
2) В киоске было настенных календарей с цветами, а с пейзажами — в к раза меньше. Сколько было календарей с пейзажами? Составь выражение для решения задачи и обчисли его, если b = 126 и k = 3.
3) Во сколько раз число 180 больше числа 20?
4) Неизвестное число разделили на 4 и получили 24. Найди неизвестное число.
5) В школьную столовую привезли 72 л молока. На приготовление завтрака потратили треть молока. Сколько литров молока израсходовали?
638. Выбери выражения на табличные случаи деления. Объясни приемы вычислений других выражений.
72 : 8 48 : 3 54 : 9 64 : 16 240 : 3
639. Объясни вычисления.
640. Составь и реши уравнение по условию: если неизвестное число увеличить в 7 раз, будет 168.
641. Склады по таблице и реши простые задачи.
Длина прямоугольника | Ширина прямоугольника | Площадь прямоугольника |
? | 7 см | 70 см2 |
20 см | ? | 120 см2 |
15 м | 8 м | ? |
642. За день туристы прошли 31 км. 4 ч они шли со скоростью 4 км/ч, а оставшуюся часть пути — со скоростью 5 км/час. Сколько времени туристы были в дороге?
643°.
48 : 3 — 4 5400 — 664 : 8 48 : 4 — 3С
624 : 3 6000 : 3 — 600 : 2 448 : 7
644°. Ширина прямоугольника 8 см, а длина — в 4 раза больше. Чему равна площадь прямоугольника?
645. (Устно.)
8 : 3 24 дес. : 5
9 сот. : 4 17 тыс. : 5
646. Обчисли с объяснением: 882 : 7, 378 : 7.
647. Рассмотри записи и прочитай объяснение.
Объяснение. Самый высокий разряд делимого — десятки тысяч. 2 дес. тыс. не поделятся на 8, чтобы в доле были дес. чисел. Первое неполное делимое 20 тыс. В частном будет 4 цифры — ставим 4 точки. Узнаем, сколько тысяч будет в доле: 20 : 8, 2. Узнаем, сколько тысяч поделили: 2 ∙ 8 = 16. Узнаем, сколько тысяч не поделился: 20 — 16 = 4. Осталось тысяч меньше, чем 8, — цифру подобрали правильно.
Образуем неполное делимое из сотен: 4 тыс. — это 40 сот. и еще 7 сот. — всего 47 сот. Узнаем, сколько сотен будет в частном: 47 поделить на 8, будет 5. Узнаем, сколько сотен разделили: 5 ∙ 8 = 40. Узнаем, сколько сотен не разделили: 47 — 40 = 7. Осталось сотен меньше, чем 8, — цифру подобрали правильно.
Образуем неполное делимое из десятков: 7 сот. – это 70 дес., и еще 3 дес., всего 73 дес. Узнаем, сколько десятков будет в частном: 73 поделить на 8, будет 9.
Продолжи объяснение.
648. Объясни деление по плану.
1. Определите первое неполное делимое и количество цифр в доле.
2. Узнай, сколько единиц высшего разряда будет в доле.
3. Узнай, сколько единиц этого разряда поделилось и сколько — не поделился.
4. Сравни количество единиц остатка с делителем и проверь, правильно ли подобран цифру доли.
5. Образуй следующее неполное делимое. (Повтори пункты 2-4 плана.)
649. Обчисли с объяснением.
247 668 : 6 65 559 : 3
650.
360 : 10 — 180 : 18 120 — 100 : 10 : 6
250 : 5 + 800 : 8 20 ∙ 9 — 80 + 800 : 100
651. Два трактора за 4 ч работы израсходовали 200 л горючего поровну. Сколько литров горючего тратил один трактор за 1 час работы? (Реши задачу составлением выражения.)
652. Для кролефермы заготовили на зиму 20 ц 40 кг лугового сена, а клевера — в к раза меньше. Сколько вместе сена и клевера заготовили на зиму? Составь выражение и найди его значение, если k = 3.
653°.
288 953 : 7 330 ∙ 3 — (690 + 125)
7406 : 7 240 : 8 + 70 ∙ 3 — 100
Проверь себя: 140; 175; 1058; 41 279.
654°. Построй два разных прямоугольника так, чтобы площадь каждого была равна 16 см2.
655. Выполни деление с остачею.
9 : 4 26 : 8 32 : 5 55 : 7 87 : 9 56 : 6
656. Рассмотри рисунок, числовые данные и выражения. Объясни, что найдем, вычислив каждое выражение.
30 л 60 л 120 л
120 : 30 60 ∙ 6 120 — (30 + 60)
120 — 30 60 : 30 120 ∙ 3 + 30 ∙ 4
657. 19 187 : 7 120 865 : 5 148 460 : 4 57 128 : 8
658. Двумя сеялками за 12 ч работы засеяли 96 га пшеницы. Сколько гектаров пшеницы можно засеять одной такой сеялкой за 7 ч работы?
659. С 1240 баранов настригли 6 кг шерсти, а с 720 овец — по 4 кг. Сколько всего килограммов шерсти настригли? (Реши задачу составлением выражения.)
660. 5 кг : 2 10 м : 4 1 дм : 5 см 1 час : 3
661°.
58 216 : 8 47 000 : 100 ∙ 5 — 370
26 364 : 6 10 000 — 24 ∙ 5 ∙ 7
662°. Длина школьного коридора 24 м, а ширина составляет его длины. Найди площадь коридора.
663. Составь несколько задач по выражению а : 4.
664. Четырьмя одинаковыми сеялками за 9 ч засеяли 108 га ячменя. За сколько часов можно засеять 60 га одной такой сеялкой? Объясни решение разными способами.
1-й способ
1) 108 : 9 = 12 (га)
2-й способ
1) 108 : 4 = 27 (га)
665. Рассмотри таблицу. Выполни задания.
И | II | III | IV | V |
5 | 70 | 10 | 12 | 46 |
4 | 20 | 6 | 13 | 39 |
0 | 90 | 8 | 16 | 27 |
7 | 100 | 1 | 14 | 56 |
1) Добавь числа IV и V столбцов.
2) Перемнож числа И и V столбцов, III и IV столбиков, II и IV столбиков.
3) От чисел II столбика отними числа IV столбика.
666. х ∙ 9 = 4599 х : 9 = 999 х ∙ 9 = 9000
667*. Масса 9 шариков равна массе 2 кубиков и 2 шайб. Шайба в 2 раза легче кубик. Сколько шариков надо взять, чтобы их масса была равна массе 1 кубика?
668. Найди доли и выполни проверку умножением.
2548 : 2 3486 : 3 25 048 : 4 8105 : 5
669. С участка собрали 248 ц капусты, свеклы — в 2 раза меньше, чем капусты, а моркови — на 84 ц меньше, чем свеклы. Сколько всего центнеров овощей собрали?
670°. За 2 ч 8 юннатов сделали 48 кормушек для птиц, поровну каждый. Сколько кормушек может сделать один юннат за 5 часов?
671°. Найди доли и выполни проверку умножением.
2310 : 6 2905 : 7 61 712 : 8 67 455 : 5
672. Найди долю числа 918 и 3 с объяснением.
673. Рассмотри записи и прочитай объяснение.
Объяснение. Первое неполное делимое 12 тысяч. В частном будет 4 цифры. Узнаем, сколько тысяч будет в доле: 12 разделить на 6, будет 2. Остатка нет. Второе неполное делимое 2 сот. 2 сот. не делятся на 6 так, чтобы в доле были сотни. В частном на месте сотен пишем 0. Третье неполное делимое 28 дес. 28 дес. разделить на 6, будет 4 десятки и остатка в 4 дес. Осталось десятков меньше, чем 6, — цифру десятков нашли правильно. Четвертое неполное делимое 42 ед. 42 разделить на 6, будет 7. Остатка нет. Доля 2047.
674. Найди частицы, проверь их умножением.
453 905 : 5 217 301 : 7 377 232 : 4
675. Составь выражения и найди их значения.
1) Произведение чисел 2008 и 8 уменьшить на 800.
2) Долю чисел 33 000 и 100 увеличить в 3 раза.
676*. Рассмотри параллелепипед. Сколько у него вершин? ребер? граней?
Построй параллелепипед в тетради, обозначь вершины, запиши ребра и грани.
677. За 6 мин три повара слепили 72 вареника, поровну каждый. За сколько минут один повар может слепить 28 вареников?
678. В кузове машины было 2 т 4 ц пшена в одинаковых мешках. В магазине из него выгрузили 8 мешков. Осталось в кузове 2 т 80 кг пшена. Сколько килограммов пшена в одном мешке?
* Сколько мешков осталось на машине?
679°. 2842 : 7 52 260 : 4 10 032 : 3 20 047 ∙ 6
680°. За 4 ч работы три одинаковых трактора израсходовали 240 л горючего. На сколько часов работы хватит 400 л горючего одному такому трактору?
681.
81 147 : 3 183 318 — 183 318 148 420 : 4
27 049 ∙ 8 216 392 + 48 073 23 ∙ 31
682. 42 036 : 4 846 027 : 9 720 136 : 4 60 006 : 3
683. Рассмотри записи и объясни вычисления.
684. Две синицы за 4 дня съели 576 гусениц, поровну каждая. Сколько гусениц съест одна синица за 6 дней?
685. 1) Сторона равностороннего треугольника равна 8 см. Найди площадь квадрата, периметр которого равен периметру этого треугольника.
2) Площадь кухни 800 дм2. Сколько изразцов, имеющих форму квадрата со стороной 2 дм, нужно для покрытия пола этой кухни?
686°. Мотоциклист был в пути 4 ч, и ему еще осталось проехать 130 км. С какой скоростью двигался мотоциклист, если весь путь составляет 390 км?
687°. 32 720 : 8 204 012 : 6 49 023 : 9 7 ∙ 27 004
688. (Устно). Найди неизвестные числа.
а | 0 | 18 | 32 | 100 | ||
b | 5 | 1 | 4 | 10 | ||
а : b | 2 | 60 | 100 | 5 |
689. Найди частицы, проверь их действием умножения.
563 528 : 7 121 824 : 6 98 765 : 5 162 432 : 8
690. Обчисли устно и объясни способ вычисления.
Образец. 36 000 : 3 = 36 тыс. : 3 = 12 тыс. = 12 000.
180 000 : 6 2400 : 2 50 000 : 2 160 000 : 6
691. Рассмотри записи и прочитай объяснение.
Второе неполное делимое 17 тыс. 17 тыс. поделить на 5, будет 3 тыс. и в остатка — 2 тыс. Третье неполное делимое 20 сот. 20 сот. поделить на 5, будет 4 сот. Десятков и единиц в деленному нет. На их месте записываем в доле нули. Доля 13 400.
692. 198 000 : 3 681 628 : 4
693. На строительство завезли к мешков цемента. Потратили 300 кг цемента, осталось с мешков. О чем узнаем, вычислив выражения?
k — c 300 : (k — с)
300 : (k — с) ∙ 20 300 : (k — с) ∙ 14
694*. Длина ребра куба 2 см. Сколько квадратных сантиметров бумаги нужно, чтобы обклеить все грани куба?
695°. За 6 ч работы 4 силосоуборочные комбайна заготовили 1560 т зеленой массы подсолнечника. За сколько часов может заготовить 520 т зеленой массы подсолнечника один такой комбайн?
696°. 244 000 : 8 361 809 : 3 10 025 : 5 6 ∙ 2030
697. (Устно.) 2 т 7 ц : 3 1 м 5 дм : 5 8 см 1 мм : 9
698. Прочитай задачу и рассмотри ее решение.
З а д а ч а. 19 м 50 см ткани разрезали на 6 равных частей. Сколько метров ткани в 4 частях?
Решения:
1) 19 м 50 см : 6 = 3 м 25 см — в одной части.
2) 325 ∙ 4 = 1300 (см) = 13 (м) — в 4 частях.
Ответ: в 4 частях 13 м ткани.
699.
5 грн 76 к. : 9 10 м : 4 13 см 5 мм : 5
5 грн : 10 10 т : 4 7 дм 8 см : 3
50 к. ∙ 10 5 ц : 10 8 т 1 ц : 9
700. 1 кг конфет стоит 79 грн 50 коп. Сколько стоит кг этих конфет?
701. Запиши выражение и найди его значение: произведение чисел 2080 и 8 увеличить на их долю.
702. Тремя косилками за 7 ч скосили траву с площади 42 га. С какой площади скосит траву одна такая косилка за 4 ч?
703. Рожь привезли на двух подводах, по 3 ц 56 кг на каждой. Все рожь рассыпали поровну в 8 мешков. Сколько килограммов ржи в одном мешке?
704°.
97 м 20 см : 9 10 т 5 ц : 5 42 км 40 м : 4
3 ц 4 кг : 8 1 дм 8 см : 2 2 км 50 м ∙ 8
705°. В речной порт доставили 24 168 т пшеницы. Всю пшеницу выгрузили за 4 дня, каждый день поровну. Треть пшеницы, которую выгрузили в первый день, отправили на мельницу. Сколько тонн пшеницы отправили на мельницу?
706. (Устно.)
1 дм : 2 см 1 км : 100 м 1 т : 5 ц
1 м : 5 см 2 см : 20 мм 1 кг : 10 г
707.
36 км : 5м 12 кг 40 г : 8 г 4 м 8 см : 3
39 ц : 5 кг 12 дм 6 см 9 см 10 м : 4
708. С одного участка поля фермер собрал 127 т 8 ц сахарной свеклы, а с другого — в 3 раза меньше. Все свеклу он отвез на сахарный завод. Сколько из них получится сахара, если масса сахара составляет массы свеклы?
709. Прочитай задачу и рассмотри ее решение.
З а д а ч а. С участка собрали 34 ц 16 кг огурцов. Их разложили в ящики по 8 кг. Сколько взяли ящиков?
Решения:
Ответ: 427 ящиков.
710. (Устно.) 1) Два велосипедиста выехали одновременно навстречу друг другу. Что можно сказать о время их движения до встречи?
2) 3 Киева и Сумм одновременно навстречу друг другу выехали два автобуса и встретились через 4 часа. Сколько времени до встречи был в пути каждый автобус?
3) 3 Харькова и Полтавы одновременно навстречу друг другу выехали два автомобиля. Первый ехал со скоростью 60 км/ч, а второй — 80 км/час. Какой из автомобилей будет дальше от Полтавы в момент их встречи?
711. В трех свитках 249 м 90 см сатина. Шелка в одном свитки в 2 раза больше, чем сатина. Сколько шелка в двух таких свитках?
712.
360 : 6 + 72 : 3 252 : 42 + 54
360 : (6 + 72 : 3) 672 : 42 + 24
(360 : 6 + 72) : 3 42 ∙ 23 — 43 ∙ 16
713°. За 7 дней работы 2 оператора набрали на компьютере 294 страницы текста, каждый день поровну. Сколько страниц наберет один оператор за 6 дней?
714°.
29 м 60 см : 4 см 10 грн — 10 к. 8 кг : 5
9 т 48 кг : 4 кг 49 грн 5 к. : 3 кол. 5 грн : 4
715. (Устно.)
40 + 20 : 5 (40 + 20) : 5 3 ∙ 6 — 4 ∙ 2
40 : 5 + 20 40 + 20 — 5 3 ∙ (6 — 4) ∙ 2
716.
540 042 : 3 ∙ 2 100 640 — 2048 : 8
540 042 : (3 ∙ 2) (100 640 — 2048) : 8
2 т 16 кг : 8 + 5 т 1 т — 1 ц : 2
717. Из Тернополя в Киев выехал автобус. Одновременно навстречу ему из Киева выехал другой автобус. Скорость первого автобуса 60 км/ч, второго — 62 км/час. Через 3 ч они встретились. Какое расстояние между городами? (Рассмотри решение задачи двумя способами с. 116. Объясни, о чем узнали каждым действием.)
1-й способ
1) 60 ∙ 3 = 180 (км)
2) 62 ∙ 3 = 186 (км)
3) 180 + 186 = 366 (км)
2-й способ
1) 60 + 62 = 122 (км/ч)
2) 122 ∙ 3 = 366 (км)
Ответ: расстояние между городами 366 км.
718. От пристани «Киев» до пристани Кременчуг отчалил теплоход. Одновременно навстречу ему от пристани Кременчуг отчалил катер. Теплоход шел со скоростью 30 км/ч, а катер — 24 км/час. Через 5 ч они встретились. Какое расстояние между пристанями?
719. 1) x ∙ 2 = 14 850 х : 2 = 14 850 х — 2 = 14 850
2) Выполни действия и сделай проверку обращенной действием.
20 700 — 9478 817 : 43 36 ∙ 23 9765 + 91 807
720*. Толщина корешка книги на 70 страниц 2 см. Какая толщина корешка книги на 280 страниц?
721°. Двумя косилками за 4 часа скосили траву с площади 24 га. За сколько часов скосит траву одна косилка с площади 138 га?
722°. Из Харькова и Запорожья одновременно навстречу друг другу выехали два туриста: на мотоцикле и на мотороллере. Скорость мотоцикла 55 км/ч, а мотороллера — 30 км/час. Через 3 ч туристы встретились. Какое расстояние между городами?
723.
(8706 : 6 + 107) ∙ 9 12 087 : (3 + 30 : 5)
(6018 ∙ 2 — 540) : 6 27 018 : (9 — 30 : 5)
724. От двух противоположных берегов озера одновременно навстречу друг другу поплыли две лодки. Первая лодка плыла со скоростью 7 км/ч, а второй — 8 км/час. Лодки встретились через 3 часа. Найди расстояние между берегами озера.
725. Расшифруй название одного из государственных символов Украины, расставив буквы по значениям выражений от наименьшего до наибольшего.
Г | 3400 ∙ 100 + 100 | В | (80 + 20) ∙ 100 |
А | 4800 : 4 ∙ 3 | П | 900 — 10 ∙ 10 |
Г | 80 + 20 ∙ 100 | П | 4800 : 3 ∙ 4 |
Что ты знаешь о государственных символах Украины?
726. (Устно.)
22 : 5 40 : 8 40 : 6 36 : 5 70 : 8
49 : 6 52 : 7 23 : 5 82 : 9 60 : 8
727.
5 ∙ 4207 ∙ 3 27 801 : 3 + 73 100 ∙ 6
4 ∙ 145 397 : 7 54 081 : 9 + 23 60 ∙ 8
728. 1) Рассмотри записи и объясни вычисления.
2) 16 000 : 2 4800 : 3 150 000 : 5 90000 : 6
729*. По данным рисунка обчисли площадь поверхности развертки прямоугольного параллелепипеда.
* Построй в тетради развертку куба с ребром 3 см. Как легче всего вычислить площадь его поверхности?
730 . Из двух населенных пунктов, расстояние между которыми 42 км, одновременно навстречу друг другу отправились два всадника. Скорость первого 9 км/ч, а второго — 12 км/час. Через сколько часов они встретятся?
731°.
2600 : 10 + 27 840 8244 : 9 + 4708 ∙ 7
90 + 348 ∙ 100 (8244 : 9 + 4708) ∙ 7
732. 1) Найди доли и сделай проверку.
44 824 : 8 34 521 : 3 36 240 : 6
2) 8 ∙ х = 44 824 34 521 : х = 3 х : 3 = 2046
733. 24 708 ∙ 4 — 24 708 : 4 (24 708 ∙ 4 — 24 708) : 4
734. С двух аэродромов, расстояние между которыми 2560 км, одновременно навстречу друг другу вылетели два самолета и встретились через 2 год. Первый самолет летел со скоростью 620 км/ч. Найди скорость второго самолета.
735. Рассмотри рисунок и числовые данные и ответь на вопросы.
1) Какова масса 3 таких овец?
2) Какова масса 2 таких бычков?
3) Во сколько раз овца тяжелее поросенка?
4) Какова масса 8 таких овец и одного поросенка?
5) На сколько килограммов овца тяжелее поросенка?
6) Какова масса 3 таких поросят?
736. Расстояние между двумя селами 48 км. Из одного села выехал велосипедист. Одновременно навстречу ему из другого села выехал гусеничный трактор. Скорость велосипедиста 14 км/ч, а трактора — 10 км/час. Через сколько часов они встретятся?
737. Найди значение выражения 15 750 : k, если k = 3, k = 7.
738*. Два велосипедиста выехали одновременно из города к базе отдыха. Один ехал со скоростью 10 км/ч, а второй — 13 км/час. Через 2 ч второй велосипедист проколол камеру, поэтому дальше шел пешком со скоростью 4 км/час. На каком расстоянии от города первый велосипедист догонит второго?
739°.
2312 : 8 44 268 : 3 ∙ 7 14 301 ∙ 2 — 777 : 7
903 : 21 44 268 : 7 ∙ 3 (14 301 ∙ 2 — 777) : 7
740°. Скорость велосипедиста 12 км/ч. Это в 3 раза больше от скорости пешехода, но в 6 раз меньше от скорости автобуса. Найди скорость пешехода и автобуса.
741. (Устно.) 45 000 : 100 250 ∙ 100 10 000 : 1000
742. Рассмотри записи. Прочитай объяснение о деления на 10, 100, 1000 с остачею.
1) 73 : 10 = 7 (ост. 3) 2) 1847 : 100 = 18 (ост. 47)
Объяснение. 1) В числе 73 наибольшее число, которое делится на 10, это 70. 73 разделить на 10, будет 7. 3 ед. составят остаток.
2) В числе 1847 наибольшее число, которое делится на 100, это число 1800. 1847 разделить на 100, будет 18. 47 ед. составят остаток.
743.
254 : 10 12 700 : 1000 83 450 : 10
254 : 100 8400 : 1000 83 450 : 100
744. 724 036 : 4 + 40 850 2 ∙ 843 — 4 ∙ 343
745. На 3 га земли посеяли 500 кг зерна пшеницы. Сколько килограммов зерна потребуется, чтобы засеять 300 га земли?
746. Автомобилем ГАЗ можно перевезти 600 ц груза за 24 рейса, а автомобилем большей грузоподъемности — по 12 рейсов. За сколько совместных рейсов могут перевезти весь груз оба автомобиля?
ГАЗ КрАЗ-257
747. Автомобиль КрАЗ-257 расходует по норме на 100 км пути 36 л горючего. Но шофер выбрал удобный режим работы и уменьшил расход топлива до 31 л на 100 км. Сколько литров горючего сэкономит шофер на пути в 1000 км?
748*. Через 16 лет Семен будет втрое старше, чем теперь. Сколько лет ему теперь?
749°. С двух туристических баз, расстояние между которыми 34 км, одновременно навстречу друг другу вышли пешеход и лыжник. Пешеход шел со скоростью 5 км/ч, а лыжник — 12 км/час. Через сколько часов они встретятся?
750°. 1) Обчисли с проверкой.
7023 ∙ 5 34 456 : 8 621 150 : С
2) 2403 + х = 735 ∙ 6 4020 : х = 2563 – 2553
Решить уравнение – значит найти такое значение неизвестного числа, которое об-ращает уравнение в верное числовое ра-венство.
Реши уравнения.
8 • х = 320 х : 9 = 60
250 : х = 5
Реши уравнения.
450 : х = 5
х : 8 = 90
х • 4 = 320
Реши уравнения.
250 : х = 5
6 • х = 240
х : 6 = 90
Реши уравнения.
х • 4 = 280
х : 7 = 60
350 : х = 5
Реши уравнения.
8 • х = 560
400 : х = 5
х : 7 = 80
Реши уравнения.
300 : х = 5
7 • х = 630
ПРИЕМЫ ПИСЬМЕННОГО УМНОЖЕНИЯ В ПРЕДЕЛАХ 1000
Умножение трёхзначного числа на однозначное
1. Запиши пример столбиком.
Реши его.
Образец:
| х | Напишем однозначное число | ||
| под единицами трёхзначного | |||
| числа. |
Умножаем единицы: 4 • 2 = 8, 8 единиц пишем под единицами.
Умножаем десятки: 3 • 2 = 6 дес. 6 десят-ков пишем под десятками.
Умножаем сотни: 1 • 2 = 2 сот. 2 сотни
Пишем под сотнями.
3. Реши примеры столбиком.
| 121 • 2 | 123 • 3 | 221 • 4 |
| 131 • 2 | 433 • 2 | 313 • 2 |
| 4. Реши примеры столбиком. | ||
| 141 • 2 | 322 • 3 | 124 • 2 |
| 333 • 2 | 212 • 4 | 144 • 2 |
| 5. Реши примеры столбиком. | ||
| 321 • 2 | 222 • 3 | 213 • 2 |
| 323 • 3 | 231 • 2 | 113 • 2 |
| 6. Реши примеры столбиком. | ||
| 343 • 2 | 311 • 3 | 112 • 4 |
| 313 • 3 | 223 • 2 | 214 • 2 |
| 7. Реши примеры столбиком. | ||
| 232 • 3 | 121 • 4 | 322 • 2 |
| 122 • 3 | 132 • 2 | 211 • 2 |
8. Реши примеры столбиком.
1. Запиши пример столбиком.
Реши его.
Образец:
| х | Напишем однозначное число | ||
| под единицами трёхзначного | |||
| числа. |
Умножаем единицы: 4 • 3 = 12, 2 едини-цы пишем, а 1 десяток запоминаем. Умножаем десятки: 2 • 3 = 6 дес. плюс ещё 1 дес. – 7 десятков. 7 десятков запи-шем.
Умножаем сотни: 3 • 3 = 9 сот. 9 сотен за-пишем.
Получаем число 972.
1. Реши примеры столбиком.
| 192 • 2 | 161 • 5 | 293 • 2 |
| 449 • 2 | 139 • 3 | 261 • 2 |
2. Реши примеры столбиком.
5. Реши примеры столбиком.
| 447 • 2 | 263 • 2 | 152 • 3 |
| 214 • 4 | 162 • 2 | 291 • 2 |
| 6. Реши примеры столбиком. | ||
| 416 • 2 | 128 • 2 | 117 • 5 |
| 271 • 2 | 215 • 3 | 151 • 5 |
| 7. Реши примеры столбиком. | ||
| 173 • 3 | 146 • 2 | 172 • 2 |
| 281 • 2 | 124 • 4 | 219 • 2 |
| 8. Реши примеры столбиком. | ||
| 118 • 5 | 136 • 3 | 273 • 3 |
| 418 • 2 | 262 • 3 | 445 • 2 |
| 9. Реши примеры столбиком. | ||
| 235 • 2 | 119 • 3 | 137 • 2 |
| 239 • 2 | 125 • 3 | 384 • 2 |
10. Реши примеры столбиком.
1. Запиши неравенство
2. Реши примеры. Над знаком «умножить» надпиши ответы зелёным цветом.
Сравни выражения.
Сравни выражения.
239 • 2 … 216 • 2
238 • 2 … 127 • 2
317 • 3 … 119 • 5
Сравни выражения.
218 • 2 … 129 • 2
193 • 3 … 251 • 3
318 • 3 … 236 • 2
Сравни выражения.
241 • 4 … 138 • 3
116 • 5 … 163 • 3
229 • 3 … 326 • 2
Сравни выражения.
182 • 3 … 283 • 3
338 • 2 … 225 • 2
152 • 2 … 118 • 3
Сравни выражения.
223 • 4 … 164 • 2
148 • 2 … 263 • 3
425 • 2 … 362 • 2
Сравни выражения.
192 • 2 … 272 • 3
284 • 2 … 446 • 2
326 • 3 … 151 • 6
Сравни выражения.
318 • 2 … 193 • 2
117 • 3 … 226 • 2
419 • 2 … 335 • 2
ПРИЕМЫ ПИСЬМЕННОГО ДЕЛЕНИЯ В ПРЕДЕЛАХ 1000
Деление трёхзначного числа на однозначное
1. Запиши пример столбиком.
Реши его.
| Образец: | |||||
| 428 _2__ | Записываем пример столби- | ||||
| ком. | |||||
2 Определяем первое непол-
2 ное делимое (наименьшее
8 число, которое делится на
8 делитель). Берём 4 сотни.
0 Определяем количество
цифр в частном. Первое неполное дели-мое 4 сотни, значит, в частном 3 цифры:
1. Реши примеры столбиком.
| 662 : 2 | 888 : 4 | 699 : 3 |
| 646 : 2 | 246 : 2 | 228 : 2 |
| 2. Реши примеры столбиком. | ||
| 622 : 2 | 363 : 3 | 824 : 2 |
| 242 : 2 | 369 : 3 | 884 : 4 |
| 3. Реши примеры столбиком. | ||
| 882 : 2 | 464 : 2 | 399 : 3 |
| 664 : 2 | 396 : 3 | 336 : 3 |
| 4. Реши примеры столбиком. | ||
| 844 : 4 | 448 : 2 | 842 : 2 |
| 996 : 3 | 888 : 2 | 266 : 2 |
| 5. Реши примеры столбиком. | ||
| 828 : 2 | 466 : 2 | 669 : 3 |
| 444 : 2 | 668 : 2 | 822 : 2 |
6. Реши примеры столбиком.
1. Запиши пример столбиком.
Реши его.
Образец:
| _2__ | Записываем пример столби- | |||||||
| ком. | ||||||||
| Определяем первое непол- | ||||||||
| ное делимое (наименьшее | ||||||||
8 число, которое делится на
8 делитель). Берём 3 сотни.
0 Определяем количество
Цифр в частном. Первое полное делимое 3 сотни, значит, в частном 3 цифры: сот-ни, десятки, единицы.
Разделим первое неполное делимое, узна-ем, сколько сотен не разделили.
Ближайшее наименьшее число, ко-торое делится на 2 без остатка, это 2.
2 : 2 = 1. 1 записываем в частное. Из 3 вычитаем 2. Под ними пишем 1. Сносим следующую цифру. Делим полу-
2. Реши примеры столбиком.
| 896 : 2 | 328 : 2 | 955 : 5 |
| 384 : 2 | 805 : 5 | 586 : 2 |
| 3. Реши примеры столбиком. | ||
| 988 : 2 | 855 : 5 | 252 : 2 |
| 434 : 2 | 905 : 5 | 566 : 2 |
| 4. Реши примеры столбиком. | ||
| 654 : 2 | 575 : 5 | 968 : 2 |
| 549 : 3 | 922 : 2 | 411 : 3 |
| 5. Реши примеры столбиком. | ||
| 894 : 2 | 526 : 2 | 456 : 3 |
| 856 : 4 | 324 : 2 | 582 : 2 |
| 6. Реши примеры столбиком. | ||
| 832 : 2 | 256 : 2 | 585 : 5 |
| 542 : 2 | 645 : 3 | 755 : 5 |
7. Реши примеры столбиком.
1. Запиши неравенство.
2. Реши примеры. Над знаком «разделить» надпиши ответы зелёным цветом.
Сравни выражения.
Сравни выражения.
687 : 3 … 652 : 2
704 : 2 … 846 : 3
490 : 2 … 764 : 2
Сравни выражения.
652 : 2 … 638 : 2
252 : 2 … 786 : 2
506 : 2 … 348 : 3
Сравни выражения.
892 : 2 … 650 : 2
546 : 3 … 849 : 3
Сравни выражения.
978 : 3 … 906 : 6
636 : 2 … 386 : 2
351 : 3 … 452 : 2
Сравни выражения.
838 : 2 … 670 : 2
830 : 2 … 819 : 3
651 : 3 … 986 : 2
Сравни выражения.
706 : 2 … 588 : 2
630 : 2 … 951 : 3
898 : 2 … 681 : 3
Сравни выражения.
498 : 2 … 978 : 3
876 : 3 … 306 : 2
128 : 2 … 192 : 3
654 : 3 … 276 : 2
|
Консультация для преподавателей 5 класса (декабрь)
Тема консультации:
«СТЕПЕНЬ ЧИСЛА. ЭЛЕМЕНТЫ ЛОГИКИ. ПОНЯТИЕ ДРОБИ»
Дидактическая основа
Дидактической основой непрерывного курса математики «Учусь учиться» является дидактическая система деятельностного метода обучения «Школа 2000…». Ее главной особенностью является то, что знания не даются учащимся в готовом виде, а организуется их самостоятельное открытие детьми. Такой подход не только обеспечивает высокий уровень математической подготовки, но и развивает их мышление, способности, интерес к изучению математики, личностные и метапредметные результаты образования, соответствующие ФГОС.
Содержание консультации
В соответствии с планированием учебного материала по курсу математики «Учусь учиться» для 5 класса в декабре заканчивается работа со второй главой «Делимость натуральных чисел». Изучаются § 4 «Простые числа и делимость» (П.2. 4. 4. «Степень числа»; П 2. 4. 5. «Дополнительные свойства умножения и деления») и § 5 « Еще немного логики», содержание которых продолжает развитие алгебраической и логической содержательно-методической линий курса.
В рамках данной консультации начнем рассматривать содержание и методику изучения третьей главы пятого класса «Дроби». В соответствии с планированием в декабре начинается работа с первым параграфом этой главы – «Понятие дроби», а именно с пунктом «Натуральные числа и дроби». В процессе изучения этого пункта уточняются знания учащихся по одной из важнейших содержательно-методической линий курса – числовой линии.
Вместе с тем, в процессе изучения этих пунктов параллельно развиваются и все остальные линии курса. Такой подход является общим для данного курса: на каждом этапе его изучения параллельно с ведущей линией, по которой идет расширение понятийной базы, закрепляются и отрабатываются знания и умения по всем остальным разделам курса.
Основные содержательные цели:
- сформировать представление о степени, умение находить в простейших случаях значения степеней с натуральными показателями;
- выявить дополнительные свойства умножения и деления и сформировать умение использовать их для рационализации вычислений;
- сформировать представление об определении и равносильности предложений;
- повторить и систематизировать знания о натуральных числах и их свойствах, представление натурального числа в виде суммы разрядных слагаемых, частные случаи арифметических действий с 0 и 1;
- повторить понятие дроби, правила преобразования неправильной дроби в смешанное число и обратно, изображение дробных чисел на координатном луче.
Тематическое планирование
Организовать работу по учебнику 5 класса возможно в условиях различных учебных планов образовательных учреждений. Поэтому тематическое планирование по изучению данного курса разработано для 5 ч и для 6 ч в неделю.
При использовании 6 ч в неделю, дополнительные часы используются на выполнение дополнительных заданий из учебников 5 класса, позволяющих глубже и сознательнее усвоить материал.
Тематическое планирование разработано в двух вариантах: для учителей, закончивших ознакомительные курсы по программе «Школа 2000…» и работающих на базовом (содержательном) уровне реализации дидактической системы «Школа 2000…», и для учителей, закончивших углубленные курсы по программе «Школа 2000…» и работающих на технологическом уровне реализации дидактической системы «Школа 2000…».
Мы предлагаем Вам скачать тематическое планирование на II четверть (5 ч в неделю)
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Методические рекомендации к организации учебного процесса
Глава 2. «Делимость натуральных чисел»
§ 4 «Простые числа и делимость»
1) В пункте 2. 4. 4. «Степень числа» понятие степени вводится как краткая запись произведения одинаковых множителей, при этом реализуется один из принципов дидактической системы деятельностного метода обучения «Школа 2000…» – принцип непрерывности. Учителю средней школы следует знать, что в начальной школе понятие произведения вводилось как краткая запись суммы одинаковых слагаемых, поэтому и понятие степени с натуральным показателем в 5 классе целесообразно вводить аналогично. Для проблематизации можно предложить пятиклассникам записать произведение нескольких одинаковых множителей, используя только два числа.
2) После знакомства с понятием степени учащиеся находят значение степени и применяют полученные знания для вычисления значений числовых выражений, содержащих степени. При выполнении № 726 учащиеся работают по образцу, переходя от произведения к степени, получают возможность самостоятельно определить порядок действий в выражении со степенями и вывести соответствующее правило. Правило нахождения значения числового выражения, содержащего степени числа может быть записано в виде алгоритма:
3) Познакомив учащихся с понятием степени, важно показать применение новой записи для более компактной записи разложения чисел на простые множители, когда оно содержит одинаковые сомножители. Полезным будет выполнение заданий №№ 729, 731, которые позволяют составить (использовать) упрощенные правила нахождения НОК и НОД в связи с обозначением произведения в виде степени и использовать эти правила. Достаточно громоздкие правила нахождения НОД и НОК сводятся к компактным по объему, схожим по форме правилам с выделением ключевых слов, что облегчает их запоминание:
- Чтобы найти НОД, надо взять общие простые множители всех чисел с наименьшими показателями степеней.
- Чтобы найти НОК, надо взять все простые множители всех чисел с наибольшими показателями степеней.
При этом не следует забывать о принципе вариативности – если в задании не указан способ нахождения НОД и НОК, ученик вправе выбирать тот способ, который удобен ему. Задача учителя здесь познакомить учащихся с различными способами, предоставив каждому ученику возможность формировать способность к систематическому перебору вариантов и адекватному принятию решений в ситуациях выбора. При выполнении учеником задания нерацинальным способом учитель фиксирует этот факт, выявляет с учеником последствия неверно выбранного способа (потеря времени, трудоемкость вычислений), однако, следует понимать, что поводом для снижения отметки неудачный выбор ученика не является.
4) Учащиеся учатся представлять натуральное число в виде суммы разрядных слагаемых с использованием степени числа 10 (№№ 732 – 734). Эта форма записи пригодится учащимся при знакомстве с другими позиционными системами счисления, отличными от десятичной (такой материал в качестве развивающего предлагается в курсе математики «Учусь учиться» в 6 классе, а также рассматривается в курсе информатики).
5) В более подготовленных классах можно провести математическое исследование, которое предлагается в № 735. Правила, сформулированные пятиклассниками при его выполнении являются пропедевтикой изучения свойств степеней в 7 классе.
6) В пункте 2. 4. 5 «Дополнительные свойства умножения и деления» учащиеся знакомятся со следующими свойствами:
1. Чтобы разделить число на произведение, можно разделить на это число один из множителей и полученный результат разделить на второй множитель.
2. Если делимое и делитель умножить на одно и то же число, то частное не изменится.
3. Если делимое и делитель разделить на одно и то же число, отличное от 0, то частное не изменится.
Эти свойства доказываются с опорой на понятие разложения на простые множители и применяются для рационализации вычислений. При выполнении №№ 768 – 769 учащиеся, ссылаясь на теорему 1, выполняют деление по частям. При этом с учащимися фиксируется польза от этого приема: вместо деления на многозначное число, выполняется деление на более удобные, часто однозначные, числа.
171 717 : 51 = (171 717 : 17) : 3 = 10101 : 3 = 3367.
7) Свойство частного используется при решении уравнений в № 774. Сравнивая частные по известному в обоих частных компоненту, учащиеся выявляют, как и во сколько раз оно изменилось, и применяют полученный вывод для нахождения х.
При этом нужно отметить с учащимися, что в отличие от уравнений второго столбика (пятиклассники пока не владеют правилами деления и умножения дробей и могут решить данные уравнения только указанным способом), корень уравнений первого столбика они могут найти и более рациональным способом.
8) Дополнительные свойства деления (делимое и делитель можно умножать и делить на одно и то же натуральное число) могут использоваться в дальнейшем при открытии основного свойства дроби.
§ 5 «Элементы логики»
9) В пункте 2.5.1 «Равносильность предложений» учащиеся знакомятся с новым смыслом уже знакомого им знака равносильности, как знака, который показывает, что два предложения обозначают одно и то же. Раскрывается соответствующий вариант конструирования этого знака: если убрать концы стрелок, получается знак равенства. Эта аналогия со знаком «равно» помогает учащимся осознать смысл понятия равносильных предложений, который вкладывается в это понятие на данном этапе.
10) Учащиеся учатся читать знак «<=>» различными способами. Учатся использовать этот знак для записи решения уравнения (№ 813 (11,12) и № 814). Такой вариант записи (в строчку со знаками Û) может использоваться учащимися и далее. Причем саму запись можно считать пропедевтикой изучения равносильных преобразований уравнений в старших классах.
11) В пункте 2.5.2 «Определения» учащиеся работают с определениями понятий: определение рассматривается как, предложение, в котором смысл «нового» объясняется через «старое», формируется умение выявлять в определении «новое» и «старое» (фактически учащиеся выявляют в определении род понятия без введения соответствующей терминологии).
12) Работу над формированием представления об определении и умения называть в данном определении определяемое понятие и понятия, на которых основывается это определение, можно начинать на нематематическом материале (№№ 823 (2), 824). Интересным для учащихся будет выполнение №№ 848 – 849, в которых требуется использовать и строить определения степеней родства, принятых в России. Эти задания, как и № 854, являются примером того, как несмотря на специфику учебного предмета – курс математики «Учусь учиться» обеспечивает достижение не только, предметных, но и личностных результатов обучения, соответствующих новым целям образования (в данном случае, осознание своей этнической и национальной принадлежности). В учебнике встречается много заданий, связанных с дешифровкой, с содержанием, которое может стать поводом для организации внеурочной проектной работы учащихся, направленной на их более глубокое знакомство с национальными и этнокультурными особенностями своего края, своего народа, для включения в контекст обучения особенностей и опыта жителей разных регионов. Так у учащихся развивается интерес к истории России и, в частности, к истории своего региона, воспитывается чувство гордости за свою страну.
13) Определения геометрических фигур (№№ 825, 836 – 846) служат инструментом, с помощью которого отрабатывается понятие определения и умение выявлять в нем «новое» и «старое». Эти определения даются в тексте учебника не с целью формирования понятий указанных в них геометрических фигур, и уж тем более не для их заучивания – данные определения, как и определения квадратного корня и точного квадрата (№№ 830– 835) являются материалом, на котором учащиеся учатся работать с определением, как с источником нового знания. При этом сильные учащиеся имеют возможность расширить свой понятийный аппарат, что еще раз показывает реализацию в данном курсе принципа минимакса.
14) В этом же пункте для сокращенной записи слова «существует» вводится специальный символ.
Глава 3. «Дроби»
§ 1 «Натуральные числа и дроби»
15) В результате изучения пункта 3.1.1, который называется «Натуральные числа и дроби» фиксируются эталоны: понятие натуральных чисел, свойства натуральных чисел, определения суммы, разности, произведения и частного натуральных чисел, записи частного в виде дроби, понятия правильной и неправильной дроби, смешанного числа, выделения целой части из неправильной дроби, перевод смешанного числа в неправильную дробь. Фиксируется правило сравнения дробей с одинаковыми знаменателями, правило сравнения с одинаковыми числителями, правило сложения и вычитания дробей с одинаковыми знаменателями.
16) Учителю средней школы важно понимать, что все уроки, на которых рассматривается материал первого пункта – это уроки повторения, т.к. в начальной школе дети уже знакомились с многозначными числами, понятиями правильной и неправильной дроби, смешанного числа, учились сравнивать дроби с одинаковыми знаменателями или одинаковыми числителями, смешанные числа, учились преобразовывать смешанное число в неправильную дробь и обратно. Все эти вопросы уточняются, оперативно устраняются возможные пробелы в знаниях учащихся.
17) С учащимися повторяются следующие способы действий: запись частного натуральных чисел в виде дроби, запись смешанного числа в виде суммы натурального числа и дробного числа; работа с числовым лучом.
18) В результате изучения данных тем у учащихся появляются следующие эталоны: понятие степени числа, алгоритм нахождения значения числового выражения, содержащего степени числа, алгоритмы нахождения НОД, НОК чисел (с использованием степеней), дополнительные свойства умножения; понятие равносильных предложений, способы чтения знака равносильности; понятие определения. При повторении и систематизации материала начальной школы фиксируются следующие эталоны: понятие натуральных чисел, свойства натуральных чисел, определения суммы, разности, произведения и частного натуральных чисел, записи частного в виде дроби, понятия правильной и неправильной дроби, смешанного числа, выделения целой части из неправильной дроби, перевод смешанного числа в неправильную дробь. Данные эталоны приведены в учебном пособии Л.Г. Петерсон, Л.А. Грушевской «Построй свою математику», которое предусматривает специальную работу с ними.
Приведем несколько примеров эталонов из указанного пособия:
Методические рекомендации по планированию уроков
При организации учебного процесса необходимо учитывать, что выполнение всех заданий из учебника не является обязательным. Принципы минимакса и вариативности, включенные в дидактическую систему деятельностного метода, обеспечивают возможность обучения по курсу математики программы «Школа 2000…» детей разного уровня подготовки, в том числе и высокого. Поэтому уровень и количество заданий, включенных в учебник, определялись в соответствие с зоной ближайшего развития более подготовленных детей. Предполагается, что учитель выбирает для работы те задания, которые соответствуют уровню подготовки детей и задачам конкретного урока.
Мы предлагаем Вам скачать методические рекомендации по планированию уроков.
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
С примерами организации уроков по изучению темы «Математический язык» Вы можете познакомиться в серии дисков со сценариями уроков в технологии деятельностного метода к учебнику математики для 5−6 классов основной школы авторов Г.В. Дорофеева, Л.Г. Петерсон по программе «Учусь учиться».
Предлагаем Вашему вниманию вариант сценария урока по рассматриваемым темам, в котором описан возможный способ организации самостоятельной познавательной деятельности учащихся на основе технологии деятельностного метода обучения «Школа 2000…».
Урок 68
Тип урока: ОНЗ
Тема: «Равносильность предложений»
Автор: Л.А. Грушевская
Основные цели:
1) сформировать представление о равносильных высказываниях, умение в простейших случаях устанавливать отношения равносильности и его записывать с помощью знака «<=>»;
2) повторить и закрепить виды высказываний, понятие темы и ремы, признаки делимости, разностное и кратное сравнение, решение уравнений, теоретико-множественные представления и символику.
Мы предлагаем Вам cкачать сценарий урока
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Уважаемые коллеги! В соответствии с Вашими просьбами, предлагаем Вам скачать решение задач на смекалку, которые входят в данные параграфы.
(Для того, что бы скачать файл, нажмите правой кнопкой мыши на ссылку, и выберите в меню пункт «Сохранить объект как…»)
Если у Вас возникли какие-либо вопросы, напишите нам, заполнив форму обратной связи.
Мы свяжемся с Вами.
Деление больших чисел столбиком — Знай свой компьютер
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком – удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем – многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Запись чисел при делении столбиком
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Пусть нам нужно разделить 6105 на 55 , запишем:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Деление столбиком на однозначное число
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0 , 1 , 2 , 3 . . Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8 – 8 = 0 .
Данный пример – деление чисел без остатка. Число, получащееся после вычитания – это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3 .
В данном случае, последовательно умножая тройку на 0 , 1 , 2 , 3 . . получаем в результате:
3 · 0 = 0 7 ; 3 · 1 = 3 7 ; 3 · 2 = 6 7 ; 3 · 3 = 9 > 7
Под делимым записываем число , полученное на предпоследнем шаге. По делителем записываем число 2 – неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 .
В завершение операции вычитаем 6 из 7 и получаем:
Данный пример – деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1 .
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4 . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
Алгоритм деления столбиком
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором – дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число – 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .
2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль : 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делітелем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
В соответствии с алгоритмом имеем:
4 · 0 = 0 14 ; 4 · 1 = 4 14 ; 4 · 2 = 8 14 ; 4 · 3 = 12 14 ; 4 · 4 = 16 > 14 .
Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .
3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следубщую цифру делимого – 0 . В итоге отмечаем новое рабочее число – 20 .
Пункты 2 – 4 повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем:
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 – множитель, на который проводилось умножение.
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 – 20 = 0 .
4. Мы не будем записывать число ноль, так как данный этап – еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае – число 2 .
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом.
4 · 0 = 0 2 ; 4 · 1 = 4 > 2
Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 .
3. Выполняем операцию вычитания и под чертой записываем результат.
4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа.
Таким образом, получаем новое работчее число – 28 . Снова повторяем пункты алгоритма.
Проделав все по правилам, получаем результат:
Переносим под черту вниз последнюю цифру делимого – 8 . В последний раз повторяем пункты алгоритма 2 – 4 и получаем:
В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена.
Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Пример 1. Деление натуральных чисел в столбик
Разделим натуральное число 7136 на натуральное число 9 .
После второго, третьего и четвертого шага алгоритма запись примет вид:
Последний проход, и поучаем результат:
Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 .
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Пример 2. Деление натуральных чисел в столбик
Разделим число 7042035 на 7 .
Деление многозначных натуральных чисел столбиком
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2 – 4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе – добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Пример 3. Деление натуральных чисел в столбик
Разделим 5562 на 206 .
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556 .
556 > 206 , поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на 0 , 1 , 2 , 3 . . и получаем:
206 · 0 = 0 556 ; 206 · 1 = 206 556 ; 206 · 2 = 412 556 ; 206 · 3 = 618 > 556
618 > 556 , поэтому под делителем записываем результат предпоследнего действия, а под делимым – множитель 2
Выполняем вычитание столбиком
В результате вычитания имеем число 144 . Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число – 1442 .
Повторяем с ним пункты 2 – 4 . Получаем:
206 · 5 = 1030 1442 ; 206 · 6 = 1236 1442 ; 206 · 7 = 1442
Под отмеченным рабочим числом записываем 1442 , а в следующий разряд частного записываем цифру 7 – множитель.
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Пример 5. Деление натуральных чисел в столбик
Онлайн-калькулятор «Деление чисел столбиком«. Наш калькулятор позволяет делить любые натуральные числа столбиком. Введите два числа (делимое и делитель) и нажмите кнопку «Вычислить». Подробное решение, которое выдает калькулятор, поможет вам разобраться, как правильно делить числа столбиком.
Деление столбиком (или деление в столбик) – метод предназначенный для деления чисел, посредством разложения процедуры деления на ряд простых действий. Число, которое делится, называется делимое. Число, на которое производится деление, называется делитель. Полученный результат от деления называется частным.
Процедура деления столбиком представляется следующим образом:
Деление натуральных чисел, особенно многозначных, удобно проводить особым методом, который получил название деление столбиком (в столбик). Также можно встретить название деление уголком. Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
В этой статье мы разберемся, как выполняется деление столбиком. Здесь мы поговорим и о правилах записи, и о всех промежуточных вычислениях. Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.
Навигация по странице.
Правила записи при делении столбиком
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105 , а делителем – 5 5, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808 на 51 234 ( 614 808 – шестизначное число, 51 234 – пятизначное число, разница в количестве знаков в записях равна 6−5=1 ) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058 и 4 (здесь разница в количестве знаков равна 4−1=3 ). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком
Понятно, что разделить одно однозначное натуральное число на другое достаточно просто, и делить эти числа в столбик нет причин. Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.
Пусть нам нужно разделить столбиком 8 на 2 .
Конечно, мы можем выполнить деление при помощи таблицы умножения, и сразу записать ответ 8:2=4 .
Но нас интересует, как выполнить деление этих чисел столбиком.
Сначала записываем делимое 8 и делитель 2 так, как того требует метод:
Теперь мы начинаем выяснять, сколько раз делитель содержится в делимом. Для этого мы последовательно умножаем делитель на числа 0 , 1 , 2 , 3 , … до того момента, пока в результате не получим число, равное делимому, (либо число большее, чем делимое, если имеет место деление с остатком). Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.
Поехали: 2·0=0 ; 2·1=2 ; 2·2=4 ; 2·3=6 ; 2·4=8 . Мы получили число, равное делимому, поэтому записываем его под делимым, а на место частного записываем число 4 . При этом запись примет следующий вид:
Остался завершающий этап деления однозначных натуральных чисел столбиком. Под числом, записанным под делимым, нужно провести горизонтальную черту, и провести вычитание чисел над этой чертой так, как это делается при вычитании натуральных чисел столбиком. Число, получающееся после вычитания, будет остатком от деления. Если оно равно нулю, то исходные числа разделились без остатка.
В нашем примере получаем
Теперь перед нами законченная запись деления столбиком числа 8 на 2 . Мы видим, что частное 8:2 равно 4 (и остаток равен 0 ).
Теперь рассмотрим, как осуществляется деление столбиком однозначных натуральных чисел с остатком.
Разделим столбиком 7 на 3 .
На начальном этапе запись выглядит так:
Начинаем выяснять, сколько раз в делимом содержится делитель. Будем умножать 3 на 0 , 1 , 2 , 3 и т.д. до того момента, пока не получим число равное или большее, чем делимое 7 . Получаем 3·0=0 ; 3·1=3 ; 3·2=6 ; 3·3=9>7 (при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6 (оно получено на предпоследнем шаге), а на место неполного частного записываем число 2 (на него проводилось умножение на предпоследнем шаге).
Осталось провести вычитание, и деление столбиком однозначных натуральных чисел 7 и 3 будет завершено.
Таким образом, неполное частное равно 2 , и остаток равен 1 .
Теперь можно переходить к делению столбиком многозначных натуральных чисел на однозначные натуральные числа.
Сейчас мы разберем алгоритм деления столбиком. На каждом его этапе мы будем приводить результаты, получающиеся при делении многозначного натурального числа 140 288 на однозначное натуральное число 4 . Этот пример выбран не случайно, так как при его решении мы столкнемся со всеми возможными нюансами, сможем подробно разобрать их.
Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
Первой слева цифрой в записи делимого 140 288 является цифра 1 . Число 1 меньше, чем делитель 4 , поэтому смотрим еще и на следующую слева цифру в записи делимого. При этом видим число 14 , с которым нам и предстоит работать дальше. Выделяем это число в записи делимого.
Следующие пункты со второго по четвертый повторяются циклически, пока деление натуральных чисел столбиком не будет завершено.
Сейчас нам нужно определить, сколько раз делитель содержится в числе, с которым мы работаем (для удобства обозначим это число как x ). Для этого последовательно умножаем делитель на 0 , 1 , 2 , 3 , … до того момента, пока не получим число x или число больше, чем x . Когда получается число x , то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4 пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).
Умножаем делитель 4 на числа 0 , 1 , 2 , …, пока не получим число, которое равно 14 или больше 14 . Имеем 4·0=0 , 4·1=4 , 4·2=8 , 4·3=12 , 4·4=16>14 . Так как на последнем шаге мы получили число 16 , которое больше, чем 14 , то под выделенным числом записываем число 12 , которое получилось на предпоследнем шаге, а на место частного записываем число 3 , так как в предпоследнем пункте умножение проводилось именно на него.
На этом этапе из выделенного числа вычитаем столбиком число, расположенное под ним. Под горизонтальной линией записывается результат вычитания. Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). Здесь же для своего контроля не лишним будет сравнить результат вычитания с делителем и убедиться, что он меньше делителя. В противном случае где-то была допущена ошибка.
Нам нужно вычесть столбиком из числа 14 число 12 (для корректности записи нужно не забыть поставить знак «минус» слева от вычитаемых чисел). После завершения этого действия под горизонтальной чертой оказалось число 2 . Теперь проверяем свои вычисления, сравнивая полученное число с делителем. Так как число 2 меньше делителя 4 , то можно спокойно переходить к следующему пункту.
Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2 по 4 пункты алгоритма.
Под горизонтальной чертой справа от уже имеющейся там цифры 2 записываем цифру 0 , так как именно цифра 0 находится в записи делимого 140 288 в этом столбце. Таким образом, под горизонтальной чертой образуется число 20 .
Это число 20 мы выделяем, принимаем в качестве рабочего числа, и повторяем с ним действия второго, третьего и четвертого пунктов алгоритма.
Умножаем делитель 4 на 0 , 1 , 2 , …, пока не получим число 20 или число, которое больше, чем 20 . Имеем 4·0=0 , 4·1=4 , 4·2=8 , 4·3=12 , 4·4=16 , 4·5=20 . Так как мы получили число, равное числу 20 , то записываем его под отмеченным числом, а на месте частного, справа от уже имеющегося там числа 3 записываем число 5 (на него производилось умножение).
Проводим вычитание столбиком. Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).
Под горизонтальной линией справа от запомненного места записываем цифру 2 , так как именно она находится в записи делимого 140 288 в этом столбце. Таким образом, под горизонтальной чертой мы имеем число 2 .
Число 2 принимаем за рабочее число, отмечаем его, и нам еще раз придется выполнить действия из 2-4 пунктов алгоритма.
Умножаем делитель на 0 , 1 , 2 и так далее, и сравниваем получающиеся числа с отмеченным числом 2 . Имеем 4·0=0 , 4·1=4>2 . Следовательно, под отмеченным числом записываем число 0 (оно было получено на предпоследнем шаге), а на месте частного справа от уже имеющегося там числа записываем число 0 (на 0 мы проводили умножение на предпоследнем шаге).
Выполняем вычитание столбиком, получаем число 2 под горизонтальной чертой. Проверяем себя, сравнивая полученное число с делителем 4 . Так как 2 , то можно спокойно двигаться дальше.
Под горизонтально чертой справа от числа 2 дописываем цифру 8 (так как она находится в этом столбце в записи делимого 140 288 ). Таким образом, под горизонтальной линией оказывается число 28 .
Принимаем это число в качестве рабочего, отмечаем его, и повторяем действия 2-4 пунктов.
Здесь никаких проблем возникнуть не должно, если Вы были внимательны до настоящего момента. Проделав все необходимые действия, получается следующий результат.
Осталось последний раз провести действия из пунктов 2 , 3 , 4 (предоставляем это Вам), после чего получится законченная картина деления натуральных чисел 140 288 и 4 в столбик:
Обратите внимание, что в самой нижней строчке записано число 0 . Если бы это был не последний шаг деления столбиком (то есть, если бы в записи делимого в столбцах справа оставались цифры), то этот нуль мы бы не записывали.
Таким образом, посмотрев на законченную запись деления многозначного натурального числа 140 288 на однозначное натуральное число 4 , мы видим, что частным является число 35 072 , (а остаток от деления равен нулю, он находится в самой нижней строке).
Конечно же, при делении натуральных чисел столбиком Вы не будете настолько подробно описывать все свои действия. Ваши решения будут выглядеть примерно так, как в следующих примерах.
Выполните деление в столбик, если делимое равно 7 136 , а делителем является однозначное натуральное число 9 .
На первом шаге алгоритма деления натуральных чисел столбиком мы получим запись вида
После выполнения действий из второго, третьего и четвертого пунктов алгоритма запись деления столбиком примет вид
Повторив цикл, будем иметь
Еще один проход дет нам законченную картину деления столбиком натуральных чисел 7 136 и 9
Таким образом, неполное частное равно 792 , а остаток от деления равен 8 .
7 136:9=792 (ост. 8) .
А этот пример демонстрирует, как должно выглядеть деление в столбик.
Разделите натуральное число 7 042 035 на однозначное натуральное число 7 .
Удобнее всего выполнить деление столбиком.
7 042 035:7=1 006 005 .
Деление столбиком многозначных натуральных чисел
Поспешим Вас обрадовать: если Вы хорошо усвоили алгоритм деления столбиком из предыдущего пункта этой статьи, то Вы уже почти умеете выполнять деление столбиком многозначных натуральных чисел. Это действительно так, так как со 2 по 4 этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2 , 3 и 4 пункте алгоритма до получения конечного результата.
Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.
Выполним деление столбиком многозначных натуральных чисел 5 562 и 206 .
Так как в записи делителя 206 участвуют 3 знака, то смотрим на первые 3 цифры слева в записи делимого 5 562 . Эти цифры соответствуют числу 556 . Так как 556 больше, чем делитель 206 , то число 556 принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Теперь умножаем делитель 206 на числа 0 , 1 , 2 , 3 , … до того момента, пока не получим число, которое либо равно 556 , либо больше, чем 556 . Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0 , 206·1=206 , 206·2=412 , 206·3=618>556 . Так как мы получили число, которое больше числа 556 , то под выделенным числом записываем число 412 (оно было получено на предпоследнем шаге), а на место частного записываем число 2 (так как на него проводилось умножение на предпоследнем шаге). Запись деления столбиком принимает следующий вид:
Выполняем вычитание столбиком. Получаем разность 144 , это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.
Под горизонтальной линией справа от имеющегося там числа записываем цифру 2 , так как она находится в записи делимого 5 562 в этом столбце:
Теперь мы работаем с числом 1 442 , выделяем его, и проходим пункты со второго по четвертый еще раз.
Умножаем делитель 206 на 0 , 1 , 2 , 3 , … до получения числа 1 442 или числа, которое больше, чем 1 442 . Поехали: 206·0=0 , 206·1=206 , 206·2=412 , 206·3=618 , 206·4=824 , 206·5=1 030 , 206·6=1 236 , 206·7=1 442 . Таким образом, под отмеченным числом записываем 1 442 , а на месте частного правее уже имеющегося там числа записываем 7 :
Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:
Теперь мы видим, что под горизонтальную черту правее запомненной позиции мы не можем записать никакого числа, так как в записи делимого в этом столбце нет цифр. Следовательно, на этом деление столбиком закончено, и мы завершаем запись:
824 разделить на 4 | 824 разделить на 4 с остатком
Ответ на математические задачи Этапы решения
Математические ответы на деление дроби 824/4
8244 = 206
206 = 2060 с точностью до десятых
206 = 206 с точностью до сотых
206 = 206 с точностью до тысячных
= 0 с точностью до десятых
= 0 с точностью до сотых
= 0 с точностью до тысячных
Другие разделы Домашнее задание по математике —
824 делим пополам плюс 20
Домашнее задание ответов: (824/2) + 20 = 432
824 делим пополам плюс 40
Домашнее задание ответов: (824/2) + 40 = 452
824/4 разделить на 2
Ответ: (824/4) ÷ 2 = 103
Домашнее задание по математике
можно легко решить с помощью этого бесплатного инструмента.Чтобы решить домашнее задание или задание, все, что вам нужно сделать, это ввести значение в соответствующее поле и нажать «вычислить», чтобы получить математические ответы.
Что такое числитель / знаменатель
Числитель: мы называем верхнее число числителем, это число в верхней части имеющейся у вас дроби.
Знаменатель: мы называем нижнее число знаменателем, это целое число внизу, это число, на которое делится.
Шаги преобразования дробей в десятичные
Шаг 1: Найдите число, которое можно умножить на нижнюю часть дроби, чтобы получилось 10, 100, 1000 или любая единица с последующими нулями.
Шаг 2: Умножьте верхнюю и нижнюю часть на выбранное вами число.
Шаг 3. Затем запишите только верхнее число, поместив десятичную запятую в правильное место, то есть на один пробел с правой стороны для каждого нуля в нижнем числе.
a / b = c В приведенных выше выражениях a называется делимым, b называется делителем, а c называется частным; в выражении a / b, a также называется числителем, а b также называется знаменателем.
Этот калькулятор дроби также можно использовать для вычисления доли в процентах, скидок на покупки, купонов, жировых отложений, валовой прибыли, потери веса, любви, налогов, увеличения и уменьшения населения, прибыли от продаж.Как только вы знаете значения, определить% легко.
Если вы обнаружите ошибку на этом сайте, мы будем благодарны, если вы сообщите нам об этом, используя предоставленный контактный адрес электронной почты. отправьте электронное письмо контакту на нашем сайте.
Следующая Предыдущая
824 разделить на 4 — длинное деление | 824/4 в простейшей форме
Используйте форму ниже, чтобы выполнить преобразование, разделяя числа запятыми.
| 2 дек. Места 2 дек. Места 3 дек. Места 4 дек. Места 5 дек. Мест. | 824 делить на 4 то же самое, что 824 ÷ 4 | |
824 разделить на 4 в виде дроби 824/4 ÷ 2 824/4 в простейшей форме = 206/1 824/4 = 206 824 / 4 = 206 в десятичной форме 824/4 = 206 в 2 десятичных разрядах 824/4 = 206 с точностью до десятых 824/4 = 206 с точностью до сотых 824/4 = 206 с точностью до десятых. ближайшая тысячная |
Калькулятор упрощения дробей или Калькулятор сокращения дробей — это онлайн-математический инструмент, который преобразует заданную дробь в ее простейшую или сокращенную форму.Он легко упрощает дроби и показывает этап преобразования в простейшую форму
.
Пример упрощения 50/100
Допустим, мы хотим упростить 50/100 до его сокращенной формы. Мы начинаем тестировать все целые числа, чтобы увидеть, делят ли они 50 и 100, чтобы получить последующее результирующее значение. Полученное значение будет упрощенной дробью. Итак, мы начинаем с 2 и продолжаем проверять до числа 19.
50/100 ÷ 2 = 25/50; что делит, мы снова начинаем с 2
25/50 ÷ 2 = 12.5/25, не целые значения, поэтому попробуйте следующее наибольшее число, 3
25/50 ÷ 3 = 8,333 / 16,67, не целое число, поэтому попробуйте следующее наибольшее число, 4
25/50 ÷ 4 = 6,25 / 12,5, не целое число, попробуйте следующее наибольшее число, 5
25/50 ÷ 5 = 5; который делится, мы начинаем снова с 2
5/10 ÷ 2 = 2,5 / 5, а не целым числом, поэтому попробуйте следующее наибольшее число, 3
5/10 ÷ 3 = 1,67 / 3,33, а не целое число, поэтому попробуйте следующее наибольшее число, 4
5 / 10 ÷ 4 = 1,25 / 2,5, не целое число, поэтому попробуйте следующее наибольшее число, 5
5/10 ÷ 5 = 1/2
Таким образом, 50/100 упрощенное то же самое, что 1/2
|
Другие числовые преобразования, которые следует учитывать
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 825
23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 825
Стандартный алгоритм умножения
Это полный урок с пояснениями и упражнениями по стандартному алгоритму умножения (умножение в столбцы), предназначенный для четвертого класса.Сначала в уроке объясняется (шаг за шагом), как умножить двузначное число на однозначное, а затем есть упражнения по этому поводу. Далее в уроке показано, как умножать, как умножать трех- или четырехзначное число, и есть много упражнений по этому поводу. есть также много проблем со словами, которые нужно решить.
| Стандартный алгоритм умножения основан на принцип, который вы уже знаете: умножение на части (частичные произведения): просто умножьте единицы и десятки отдельно и доп. Однако стандартным способом добавляет | |||||||||||
| Стандартный способ умножения | «Путь легкий» | ||||||||||
|
| ||||||||||
| Стандартный способ умножения | «Путь легкий» | ||||||||||
|
| ||||||||||
1.Умножьте, используя оба
методы: стандартный и простой.
2. Умножьте, используя оба
методы: стандартный и простой.
3. Умножить. Будьте осторожны с
перегруппировка.
4. Решить.
Также напишите числовые предложения (сложение, вычитание, умножение) на
пустые строки.
| а. Что Стоимость покупки трех стульев по 48 долларов каждый? _________________________________________________ А стоимость шести стульев? |
| г. Вы зарабатывайте 77 долларов в день. Сколько дней нужно работать чтобы иметь 600 долларов и больше? Угадай и проверь. _________________________________________________ _________________________________________________ |
Для трех- или четырехзначного номера необходимо | ||||||||||||||||||
| ||||||||||||||||||
|
5. Умножьте, используя оба
методы: стандартный и простой.
6. Умножьте, используя стандартный метод.
7. Решите проблемы со словами.
Также напишите числовые предложения (сложение, вычитание,
умножения), чтобы показать, что вы рассчитываете.
| а. В школе обучается 304 ученика. Перейти на музей, они наняли автобусы, которые могут на каждое место по 43 пассажира.Сколько автобусов им было нужно? Подсказка: угадай и проверь. |
| г. В школе также работают 24 учителя. Сколько места были оставлены пусто в тех автобусах, когда все студенты и все учителя присоединились к поездке? |
Это мое старое видео ниже также объясняет, как обучать алгоритму умножения. Сначала видео проходит через алгоритм частичных произведений (умножение по частям), а затем объясняет стандартный алгоритм умножения (как в уроке на этой странице).
Этот урок взят из книги Марии Миллер Math Mammoth Multiplication 2 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
Что такое 824, разделенное на 856 с помощью длинного деления?
Смущает длинное деление? К концу этой статьи вы сможете разделить 824 на 856 с помощью деления в столбик и применить тот же метод к любой другой задаче деления в столбик! Давайте взглянем.
Хотите быстро выучить или показать студентам, как решить 824, разделенное на 856, с использованием длинного деления? Воспроизведите это очень быстрое и веселое видео прямо сейчас!
Итак, первое, что нам нужно сделать, это уточнить термины, чтобы вы знали, что такое каждая часть деления:
- Первое число, 824, называется делимым.
- Второе число 856 называется делителем.
Здесь мы разберем каждый шаг процесса деления в столбик для 824, разделенного на 856, и объясним каждый из них, чтобы вы точно поняли, что происходит.
824 разделить на 856 пошаговое руководство
Шаг 1
Первым шагом является постановка нашей задачи деления с делителем слева и делимым справа, как показано ниже:
Шаг 2
Мы можем вычислить, что делитель (856) переходит в первую цифру делимого (8), 0 раз (с).Теперь мы это знаем и можем поставить 0 вверху:
Шаг 3
Если мы умножим делитель на результат на предыдущем шаге (856 x 0 = 0), теперь мы можем добавить этот ответ под делимым:
Шаг 4
Затем мы вычтем результат предыдущего шага из второй цифры делимого (8-0 = 8) и запишем этот ответ ниже:
Шаг 5
Переместите вторую цифру делимого (2) вниз следующим образом:
Шаг 6
Делитель (856) переходит в нижнее число (82), 0 раз, поэтому мы можем поставить 0 сверху:
Шаг 7
Если мы умножим делитель на результат на предыдущем шаге (856 x 0 = 0), теперь мы можем добавить этот ответ под делимым:
Шаг 8
Затем мы вычтем результат предыдущего шага из третьей цифры делимого (82-0 = 82) и запишем этот ответ ниже:
Шаг 9
Переместите третью цифру делимого (4) вниз следующим образом:
Шаг 10
Делитель (856) переходит в нижнее число (824), 0 раз (а), поэтому мы можем поставить 0 сверху:
Шаг 11
Если мы умножим делитель на результат на предыдущем шаге (856 x 0 = 0), теперь мы можем добавить этот ответ под делимым:
Шаг 12
Затем мы вычтем результат предыдущего шага из четвертой цифры делимого (824-0 = 824) и запишем этот ответ ниже:
Итак, каков ответ на 824 деленное на 856?
Если вы дошли до этого урока, молодец! Больше нет цифр, которые можно было бы переместить из дивиденда, что означает, что мы выполнили задачу длинного деления.
Ваш ответ — это верхнее число, а любой остаток будет нижним числом. Итак, для 824, разделенного на 856, окончательное решение будет:
.
0
Остаток 824
Цитируйте, дайте ссылку или ссылайтесь на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большое одолжение и используйте инструмент ниже, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
Что такое 824, разделенное на 856 с помощью длинного деления?
«Что такое 824, разделенное на 856 с использованием длинного деления?». VisualFractions.com . По состоянию на 14 апреля 2021 г. https://visualfractions.com/calculator/long-division/what-is-824-divided-by-856-using-long-division/.
«Что такое 824, разделенное на 856 с использованием длинного деления?». VisualFractions.com , https: // visualfractions.ru / калькулятор / long-div / what-is-824-split-by-856-using-long-div /. По состоянию на 14 апреля 2021 г.
Что такое 824, разделенное на 856 с использованием длинного деления ?. VisualFractions.com. Получено с https://visualfractions.com/calculator/long-division/what-is-824-divided-by-856-using-long-division/.
Дополнительные расчеты для вас
Теперь вы узнали, как делить 824 на 856 в столбик. Вот еще несколько способов вычисления:
- Используя калькулятор, если вы наберете 824, разделив на 856, вы получите 0.9626.
- Вы также можете выразить 824/856 как смешанную дробь: 0824/856
- Если вы посмотрите на смешанную дробь 0 824/856, вы увидите, что числитель такой же, как остаток (824), знаменатель — это наш исходный делитель (856), а целое число — это наш окончательный ответ (0 ).
Калькулятор длинного деления
Введите другую задачу с длинным разделением для решения
Задача следующего длинного деления
Хотите более длинное деление, но не можете ввести два числа в калькулятор выше? Не волнуйтесь.Вот следующая проблема, которую вам нужно решить:
Как 824 разделить на 857 с помощью длинного деления?
Задачи случайного длинного деления
Если вы дошли до этого конца страницы, значит, вы ДЕЙСТВИТЕЛЬНО любите задачи с длинным делением, да? Ниже приведены несколько случайно сгенерированных вычислений для вашего долгого удовольствия:
Подразделения 800 и 900 — ВМС Для мам
Подразделения 800
По прибытии новобранцев те, у кого есть контракты в качестве кандидатов на военно-морские спецназы (NSW) или специальные операции (SpecOps), перемещаются в сторону для размещения в дивизии 800 или для женщин, которые помещаются вместе в стрелковую дивизию.Эти рейтинги: SEAL — Special Warfare Operator (SO), Special Warfare Combatant — Craft Crewman (SWCC) — Special Warfare Boat Operator (SB), Navy Diver (ND), Explosive Ordnance Disposal (EOD) и Aviation Rescue Swimmers (AIRR). ). Обычно в год бывает всего 25 или менее 800 дивизий, поэтому не в каждой ТГ будет одно, но в некоторых ТГ будет от одного до четырех 800 дивизий.
Мы часто видим, что близкие людей из подразделения 800 получают письмо-форму примерно через неделю после того, как их рекруты прибывают в RTC, а не в обычные 9–14 рабочих дней, потому что этим подразделениям не нужно ждать Фазы 1 (P-дней ) должен быть сформирован, поскольку новобранцы в этих подразделениях определяются их контрактами до прибытия и должны пройти 1.Бег на 5 миль за время, меньшее, чем требуется для заключения специального контракта на ведение боевых действий, поэтому им не нужно ждать, пока начальный PFA отправит письмо по почте. Раньше было очень распространено, что те, кто в дивизионе 800, были в пуш-дивизионах и имели 8 пятниц, а не 9 обычных пятниц, как у других, но это уже не так, и теперь 9 пятниц стало нормой. Если самки со специальными контрактами отправляются в понедельник или вторник, то у них обычно 9 пятниц, как и 800 дивизионов для этого TG.Любимые женщины-кандидаты из штата Новый Южный Уэльс получают письмо-форму примерно через 9 рабочих дней после прибытия новобранца в RTC. Вам нужно дождаться формы письма, чтобы точно узнать дату PIR, но вы можете определить следующие 800 делений в секунду на https://www.bootcamp.navy.mil/tg_grad_dates.html. См. Прибытие и Что происходит в RTC.
новобранцев-мужчин с контрактами на SEAL и SWCC с одинаковой датой отгрузки или с датой отгрузки в течение дня или около того одной и той же даты отгрузки будут вместе в одном и том же дивизионе 800 или братском дивизионе в одной TG.Новобранцы-мужчины с контрактом на ND, AIRR и EOD, а иногда и те, у кого есть контракт на SWCC с той же датой отгрузки или с датой отгрузки в течение дня или около того одной и той же даты отгрузки, будут вместе в одном TG в одном и том же 800-я дивизия или братская дивизия, или они могут быть в стрелковых дивизиях, если для 800-й дивизии не хватает новобранцев.
800 дивизий — это все мужские дивизии, поскольку было бы редко встретить достаточно большое количество женщин-кандидатов в Новом Южном Уэльсе, чтобы заполнить отсек, позволяющий объединить или полностью женскую дивизию 800. Женщины, у которых есть контракт на особый боевой рейтинг, будут назначены в интегрированную стрелковую дивизию, а не в дивизию 800, если не будет достаточно женщин, чтобы заполнить отсек, и не все они могут быть назначены в одну и ту же дивизию, но несколько из них будут обычно вместе в одном подразделении. Когда это происходит, форма письма отправляется по почте в конце этапа 1 и прибывает через 9–14 рабочих дней после прибытия. (См. Прибытие и Что происходит в RTC.) Эти новобранцы будут тренироваться с дивизионом 800 для дополнительных занятий физкультурой и группового времени в 04:30 (4:30 утра).
Иногда новобранцы-мужчины со специальным контрактом помещаются в стрелковую дивизию, если не хватает новобранцев, чтобы сформировать полную 800-ю дивизию. Когда это происходит, форма письма отправляется по почте в конце этапа 1 и прибывает через 9–14 рабочих дней после прибытия. (См. Прибытие и Что происходит в RTC.) Эти новобранцы будут тренироваться с дивизионами 800 из других TG, которые находятся в RTC для дополнительных сессий PT и времени объединения в 04:30. Хотя все рекруты NSW могут быть разными деление, несколько обычно вместе.
Те, кто в дивизии 800, проходят ту же подготовку, которую проходят новобранцы в стрелковых дивизиях, а затем у них есть второе время PT (физическая подготовка) каждый день, когда запланировано PT, так что у них есть PT утром и днем. Они также регулярно планируют время в бассейне для тренировок в дополнение к тому времени, которое они бы проводили в бассейне, если бы они были в стрелковой дивизии. Они могут выучить и протестировать гребок боевого пловца (CSS) или уметь тестировать, используя гребок вольным стилем, в зависимости от области, в которой они собираются.Кандидатам в специальные операции также назначен Dive Motivator PT (DIVEMO). Этим новобранцам не разрешается тренироваться, кроме как во время PT или IT (интенсивное обучение; дополнительное PT в качестве корректирующего действия), и многие указали, что у них меньше физической подготовки, чем было до отправки, если у них был специальный наставник. Отбой в 22:00 (22:00) и снова в 04:00 (4:00).
Новобранцы в дивизии 800 могут получить дополнительный рацион еды до того, как погаснет свет на камбузе, если они этого захотят, из-за дополнительных калорий, которые они сжигают из-за физической подготовки, которую они проходят.Это небольшая закуска из фруктов, крекеров и протеинового батончика, которую подают накануне DIVEMO или в другие нестандартные дни PT. Этот дополнительный рацион также предоставляется кандидатам в спецназовцы, которые входят в состав стрелковой дивизии.
Когда есть две или более 800 дивизий в одной TG, тогда они являются братскими дивизиями, тренируются вместе и вместе выполняют боевые станции-21 (BST). 800 дивизий проходят через BST в одиночку, с еще одной 800-й дивизией, если в TG 2 или более 800 дивизий, с 900-ю дивизиями или с парой братских дивизий из стрелковых дивизий.Когда есть три или более 800 дивизионов, то два из 800 дивизий пройдут через BST вместе, но другие одно или два 800-х дивизионов могут пройти через BST в другую ночь. См. Battle Stations-21 (BST).
Те, у кого есть рекрут в дивизии 800 и / или со специальным контрактом, должны быть особенно осведомлены о OPSEC и PERSEC. См. OPSEC и PERSEC (Внесение изменений в ваш профиль) для получения дополнительной информации и внесите необходимые изменения внизу этой страницы. Изменения 1 и 2 расскажет вам, как удалить свое имя или имя вашего рекрута из вашего имени пользователя и URL-адреса страницы вашего профиля, и предложит предложения по тому, как сделать вашу страницу профиля менее очевидной в отношении вашей личности и личности вашего рекрута / моряка и его / ее особый статус операций, например изменение почтового индекса, чтобы он не отражал ваш родной город, и не упоминание рейтинга, на который нанят ваш новобранец / моряк. Изменить 3 расскажет вам, как исправить настройки конфиденциальности — я предлагаю «Только мои друзья.«Я также предлагаю вам снять все флажки в разделе« Последние действия »внизу, чтобы ваши действия на N4M не публиковались в ленте« Последние действия »слева. Изменение 4 касается вашего изображения профиля- -не добавляйте фото с изображением лица вашего рекрута и для большей безопасности не используйте свою собственную фотографию или фотографию любого человека, связанного с вашим рекрутом / моряком. Программное обеспечение для распознавания лиц и даже поисковые системы, такие как https: / /images.google.com/, а также более широкое использование фотографий в социальных сетях упростило привязку фотографии к конкретному человеку. Изменение 5 расскажет вам, как удалить фотографии, если вы их разместили — не включайте никого из вашего рекрута или моряка, а также любого человека или вещи, которые будут легко связаны с вашим рекрутом или матросом. Change 6 расскажет вам, как отключить журнал «Последние действия» в верхней части моей страницы, чтобы ваши сообщения были недоступны для тех, кто посещает вашу страницу. Change 7 расскажет вам, как скрыть группы, к которым вы присоединились на N4M, чтобы для других, посещающих вашу страницу My Page, было менее очевидно, что у вас есть новобранец или матрос с контрактом на получение рейтинга Special Ops от групп, которых вы присоединились.Будьте осторожны, даже «Нравится» обсуждению для подразделения вашего рекрута позволяет другим узнать, что у вас, скорее всего, есть новобранец в этом подразделении, поэтому, если вам «Понравилось» обсуждение для подразделения вашего рекрута, вы должны нажать «Понравилось»! » «В отличие от» этого.
N4M не является частным сайтом, и ЛЮБОЙ, имеющий доступ к Интернету, может зайти на сайт и посмотреть, что публикуется на большей части сайта, поэтому публикуйте очень мало о своем рекруте, а затем о матросе и никогда не публикуйте его / ее фотографии. / ее фамилия (отсутствие имени также увеличивает PERSEC).Есть группы на fB для групп PIR и даже некоторые группы, связанные с обучением спецназовцев; Было бы неплохо избегать этих групп, потому что, если вы присоединитесь к этим группам, информация вашего профиля будет легко связана с кем-то, кто является кандидатом на специальный рейтинг операций, включая ваше имя и родной город, если группа не является секретной группой, а не просто приватная группа. Не сообщайте открыто, что у вас есть новобранец в дивизионе 800, поскольку это общественное достояние, что в дивизионе 800 содержатся кандидаты в специальные операции.(Я удаляю комментарии на этой странице от людей, которые указывают, что у них есть новобранец в подразделении 800, если у меня есть основания полагать, что на вопрос или комментарий был дан ответ или я получил подтверждение.)
Когда он / она в BC, если кто-то спросит его / ее рейтинг, вы можете упомянуть, что он / она останется в GL (или вылетит) после PIR, и просто избегайте вопросов. Позже вы можете честно сказать: «Я мало что знаю об этом».
Если новобранец с контрактом на получение специального рейтинга операций прибывает в MEPS и терпит неудачу (например, проверку зрения), что является требованием для специальных операций, но не мешает ему иметь право на другой рейтинг, то это будет отмечено. в досье призывника.Новобранец пройдет дополнительную оценку в RTC, чтобы определить, продолжает ли он / она иметь право на его / ее контракт. Если выясняется, что новобранец не имеет права на его / ее контракт, то он / она позже встретится с подробным сотрудником и получит новый контракт с другим рейтингом, на который он / она имеет право, или ему будет предоставлена возможность отделиться. Некоторым новобранцам может быть предложен контракт с другим рейтингом в сообществе специальных операций, который имеет менее строгую квалификацию, чем тот, с которым был отправлен новобранец.Если новобранец выбирает контракт за пределами сообщества специальных операций, он будет переведен в стрелковую дивизию, если новобранец заинтересован в продолжении обучения.
Если новобранец в стрелковой дивизии демонстрирует исключительный потенциал для специальных операций, его / ее можно выделить и пригласить на занятия физкультурой и плаванием, чтобы узнать, может ли это / ее заинтересовать. Выбор — принять или отклонить приглашение всегда его / ее. Если новобранец принимает приглашение, он остается в своем отделении, но посещает дополнительные занятия с отделением 800.Если будет установлено, что новобранец подходит для специального рейтинга операций, ему / ей будет предложен новый контракт, который он / она может принять или отклонить.
Иногда новобранец, который был назначен в подразделение 800, удаляется из подразделения по разным причинам, часто связанным с первой PFA (оценка физической подготовленности). Новобранец также может выбрать вариант «Выпадать по запросу» (DOR), если он / она больше не считает, что специальные операции подходят для него / нее. Когда это произойдет, новобранец будет помещен в стрелковую дивизию, а затем встретится с детилером и получит новый контракт с другим рейтингом, на который он / она имеет право.Иногда, когда это происходит, новобранец звонит близкому человеку и сообщает, что его перевели в другое подразделение и что его адрес изменился. Это известно как ASMO’d (Меморандум о назначении; изменение в том, что происходит с новобранцем). Обычно это не влияет на дату PIR, но если это произойдет, вы также будете уведомлены об этом.
Когда новобранцы проходят ASMO, будь то отправка в SEPS, чтобы вернуться домой, чтобы пойти в RCU, чтобы вылечиться от болезни или травмы, или перейти в другое подразделение, RDC, скорее всего, скажет, что рекрут был ASMO ‘d и другие в дивизии не будут знать, что произошло, если только им не случится увидеть его в RTC во время курса обучения, или в PIR, или когда-нибудь позже во Флоте.Это связано с требованиями конфиденциальности и / или HIPAA.
Многие из моряков, которые были в дивизионе 800 или у которых есть контракт на одну из категорий специальных операций, останутся в Центре поддержки обучения (TSC) в Великих озерах после PIR для обучения перед вылетом на следующую часть своей обучение — только AIRR нет. Планируйте уехать поздно в воскресенье или в понедельник, если сможете. См. Разделы «День PIR» и «Свобода во время выходных дней PIR», чтобы узнать, как спланировать выходные.
Кандидаты в авиационные спасатели (AIRR) вылетают в Пенсакола, Флорида, на военно-морскую авиабазу Пенсакола, обычно на следующий день после PIR, где они сначала посещают школу кандидатов в летные экипажи ВМС (NACCS).Ваш Sailor, скорее всего, вылетит на следующий день после PIR, но может вылететь в воскресенье из-за проблем с доступностью рейсов. Планируйте уехать в воскресенье, если сможете. См. Разделы «День PIR» и «Свобода во время выходных дней PIR», чтобы узнать, как спланировать выходные. Другая группа, к которой вы захотите присоединиться, если ваш новобранец является кандидатом на этот рейтинг, — это Пенсакола, Флорида A School: NAS и Corry Station.
800 дивизий раньше всегда были на Корабле 04, но начиная с 2019 года они были и на других кораблях, поэтому нелегко узнать, где они будут расположены.
Вот некоторые группы и ссылки на карточки с рейтинговой информацией, связанные с рейтингами спецопераций:
Группы SEAL: PREP, BUD / S и SQT (Этапы SEAL) (Эта группа только по приглашению.) PreBUD / S и BUD / S (Эта группа больше не активна.) SEAL Moms (Эта группа видна только для членов группы — хорошо. Она не очень активна, чего и следовало ожидать. Жены, подруги и невесты моряков в дивизионе 800 / Pre-BUDS / BUD / S (Эта группа только по приглашениям.)
Информационная карта рейтинга
SEAL: https://www.cool.navy.mil/usn/enlisted/rating_info_cards/so.pdf
Информация о
SEAL на сайте navy.com: http://www.navy.com/careers/special-operations/seals.html
Дополнительная информация о ПЕЧАТИ: http://www.sealswcc.com/navy-seal-training.html, http://navyseals.com/2097/sealswcc-bootcamp-800-division/ и https: //www.public .navy.mil / bupers-npc / reference / milpersman / 1000 / 1200Classification / Documents / 1220-085.pdf.
—
Группы SB-SWCC: swcc и заголовок для SWCC (не очень активен.) (Эти группы являются открытыми группами, поэтому будьте очень осторожны, если вы решите присоединиться и публиковать там сообщения. Вы можете прочитать всю информацию в этих группах БЕЗ присоединения.) Приглашение SWCC (Эта группа видна только членам группы — вещь хорошая, но не работает с 2012 года.)
Информационная карта рейтинга
SB: https://www.cool.navy.mil/usn/enlisted/rating_info_cards/sb.pdf
Информация SWCC на сайте navy.com: http://www.navy.com/careers/special-operations/swcc.html
Дополнительная информация SWCC: http: // www.sealswcc.com/navy-swcc-training.html, http://navyseals.com/2097/sealswcc-bootcamp-800-division/ и https://www.public.navy.mil/bupers-npc/reference/ milpersman / 1000 / 1200Classification / Documents / 1220-090.pdf
—
Группа AIRR: Мамы пловцов-спасателей AIRCREW
Информационная карта рейтинга
AIRR: https://www.cool.navy.mil/usn/enlisted/rating_info_cards/airr.pdf
кандидата AIRR будут распределены по специальности «Морской экипаж — тактический вертолет» (AWR) или «Морской экипаж — вертолет» (AWS) во время обучения в Школе кандидатов в летные экипажи ВМС (NACCS).Назначения будут основаны на результатах тестов кандидата, личных желаниях, потребностях ВМФ и продолжающемся праве на участие в программе для экипажей.
AWR: https://www.cool.navy.mil/usn/enlisted/rating_info_cards/awr.pdf
AWS: https://www.cool.navy.mil/usn/enlisted/rating_info_cards/aws.pdf
Информация о
AIRR на сайте navy.com: https://www.navy.com/careers/aviation-rescue-swimmer
Дополнительная информация AIRR: https://www.public.navy.mil/bupers-npc/reference/milpersman/1000/1200Classification/Documents/1220-010.pdf, https://www.public.navy.mil/bupers-npc/reference/milpersman/1000/1200Classification/Documents/1220-020.pdf, https://www.public.navy.mil/bupers-npc/ ссылка / milpersman / 1000 / 1200Classification / Documents / 1220-060.pdf и http://www.nsonswmentor.com/Navy-AIRR.html.
—
Группа EOD: EOD (Эта группа видна всем. Вы можете видеть всю информацию там, не присоединяясь. Будьте осторожны при размещении там сообщений.)
Информационная карта рейтинга
EOD: https: // www.cool.navy.mil/usn/enlisted/rating_info_cards/eod.pdf
Информация EOD на сайте navy.com: http://www.navy.com/careers/special-operations/eod.html
Дополнительная информация EOD: https://www.public.navy.mil/bupers-npc/reference/milpersman/1000/1200Classification/Documents/1220-200.pdf
Есть некоторая информация об учебном сайте Центра по обезвреживанию взрывоопасных предметов и дайвингу (CENEODDIVE) в районе Великих озер https://www.public.navy.mil/netc/centers/ceneoddive/Default.aspx и http: // www. .mybaseguide.com/navy/21-582-9445/ns_great_lakes_ceodd.
https://www.operationm militarykids.org/explosive-ordnance-disposal-eod-technician/ содержит полезную информацию.
Подготовительный курс Центра по обезвреживанию боеприпасов и дайвингу (CEODD) [ВИДЕО] дает информацию о дайвинг-тренинге в Панама-Сити, Флорида.
—
Группы водолазов ВМС: Мамы водолазов ВМС и Мамы водолазов-новобранцев (Эти группы являются открытыми группами, поэтому будьте очень осторожны, если вы решите присоединиться и публиковать там сообщения.Вы можете прочитать всю информацию в этих группах БЕЗ присоединения.)
Информационная карта
Navy Diver: https://www.cool.navy.mil/usn/enlisted/rating_info_cards/nd.pdf
Информация о
Navy Diver на сайте navy.com: http://www.navy.com/careers/special-operations/diver.html
Дополнительная информация ND: https://www.public.navy.mil/bupers-npc/reference/milpersman/1000/1200Classification/Documents/1220-100.pdf
Есть некоторая информация об Учебном сайте Центра по обезвреживанию взрывоопасных предметов и дайвингу (CENEODDIVE) в районе Великих озер по адресу https: // www.public.navy.mil/netc/centers/ceneoddive/Default.aspx и http://www.mybaseguide.com/navy/21-582-9445/ns_great_lakes_ceodd.
—
женщин могли зачисляться в качестве кандидатов в AIRR, EOD или ND в течение некоторого времени, но они смогли присоединиться к SO / SEAL и SB / SWCC только с 2016 года. См. Http://www.navytimes.com/story / военные / пентагон / 2014/12/27 / военно-морской флот-интеграция-женщины-2015-отчет / 20769871 /.
Если я использовал непонятный термин или сокращение, что значит ??? иметь в виду? (Руководство по сокращениям и терминологии ВМФ) должно помочь; если нет, спросите, потому что если у вас есть вопрос, то, скорее всего, тоже его задает кто-то другой.
900 Подразделений
В каждой ТГ почти всегда есть 900 Дивизионов. 1 апреля 2011 года у TG не было собственного 900-го подразделения, и нет 900-го подразделения, в то время как RTC реагирует на COVID-19 и приостанавливает выпускные церемонии. Иногда может быть два или даже три в одном TG, если RTC пропускает неделю PIR. Одно из делений обычно отражает номер ТГ, но не всегда. Если имеется более одной 900-й дивизии, то они будут братскими. Дивизии 900 начинаются с Дивизиона 901 и обычно заканчиваются Дивизионом 952.Предполагается, что 901-я дивизия начнет обучение в первую неделю октября, когда начнется финансовый год ВМФ. В 2019 году было 55 TG для того, чтобы TG 01 начал обучение в первую неделю октября, поэтому последними 900 подразделениями 2019 финансового года было подразделение 955. Это компенсировало ошибки в нумерации TG при пропуске недель, которые имели место. в предыдущие годы.
По прибытии новобранцев те, у кого есть рейтинг музыканта (MU), а также волонтеры, имеющие предыдущий музыкальный опыт (оркестр, хор или другое музыкальное образование) или опыт работы в группе упражнений, могут присоединиться к отделу 900 на основе информации, представленной в анкете, которую заполняют рекруты вскоре после прибытия.Позже проводятся прослушивания для подтверждения способностей волонтеров. Есть и другие, которые будут выбраны RDC для подразделения 900 во время Фазы 1 (P-дни) или в первые несколько недель BC. У этих новобранцев не было ни рейтинга музыкантов, ни опыта группы / музыки или тренировок, но они демонстрировали некоторые способности к исполнению, например, военную выправку. Это особенно верно для тех, кого выбрали для работы в штабе корабля. Новобранцы с относительно высокими баллами ASVAB имеют больше шансов попасть в дивизион 900, чем те, у кого более низкие баллы, поскольку они будут лучше справляться со всем, что от них требуется, чем те, у кого более низкие баллы.Новобранцы в дивизионе 900 могут иметь контракты с любым рейтингом, кроме тех, которые находятся в дивизионе 800. После назначения в подразделение эти новобранцы проходят ту же подготовку, что и другие подразделения, в дополнение к служебным обязанностям. Они тренируются по субботам, начиная с субботы после формирования дивизиона и иногда (редко) в воскресенье после обеда, если возникает необходимость в дополнительной тренировке. С недели 1 DOT (после фазы 1) до недели 4 они тренируются каждую субботу с 15:00 или 16:00 до 18:00.Затем, начиная с субботы и переходя к пятой неделе, они также тренируются в понедельник и среду и проводят пробежку в четверг, затем они выступают в реальном PIR в пятницу, если таковая есть на этой неделе. Обычно они выступают в двух выпусках, прежде чем делать свои собственные. 900 дивизий проходят только через боевые станции-21, с еще 900 дивизиями, если в TG 2 или более 900 дивизий, с 800 дивизиями или с парой братских дивизий из стрелковых дивизий.
Есть три типа 900 подразделений.Есть команда Band / Bluejacket Choir / Drill, иначе известная как Triple Threat (музыканты, певцы и тренировочная команда), Sticks (те, кто несут государственные флаги) и Ship Staff / Honor Guard (похитители трупов, те, кто охраняет разные вещи, разные серверы …). Три 900 подразделения выполняют свои обязанности в каждом PIR, 900 подразделений из этой TG и, если необходимо, от одного до трех 900 подразделений из следующих одной или двух TG. Каждый 900-й дивизион работает в своем собственном PIR и обычно в PIR на один или два TG впереди своего собственного, если нет 900-го подразделения того же типа для работы в TG / TG.У них также могут быть выступления в сообществе — хотя это случается в основном с Triple Threat и Color Guard. В дивизионе 900 носят желто-золотые плетеные шнуры (веревки), называемые эгюйетами, на левом плече с синей одеждой и синие аксель с белой одеждой. Это помогает другим узнать, что у них есть обязанности, которые они должны выполнить во время PIR.
Вы можете присоединиться к Группе моряков 900-й дивизии. Там будет информация, относящаяся к вашей ситуации.Вот сайт, который я нашел, который объясняет около 900 дивизий, Требования к 900-й дивизии RTC ВМФ.
Посмотрите страницу FB RTC, начинающуюся за 2 недели до PIR вашего рекрута, и вы можете мельком увидеть своего рекрута, но знайте, что не все церемонии PIR сфотографированы, поэтому не огорчайтесь, если вы не увидите своего рекрута. Вы также захотите посмотреть прямую трансляцию PIR от RTC, начинающуюся за 2 недели до PIR вашего рекрута. RTC транслирует PIR в прямом эфире с 8:45 по центральноевропейскому времени в день PIR по адресу http: // navylive.dodlive.mil/. Проверьте, нет ли потоков практик для PIR (обычно во второй половине дня за день до PIR). Они также будут хранить видео там на короткое время, если люди не могут смотреть в прямом эфире или если вы хотите остановить его, чтобы более внимательно проверить конкретного новобранца или моряка. (После прохождения PIR вы сможете увидеть видео по адресу https://www.dvidshub.net/tags/video/navy-boot-camp-graduation, но не все из них включены в него.)
Церемония PIR проводится выпускниками 900 дивизионов с помощью одного или двух юниорских 900 дивизионов на их 7-й и / или 6-й неделе обучения.На каждое поступающее 900 подразделение на постоянной основе возлагается одна из нижеперечисленных обязанностей.
Судовой персонал отвечает в день PIR. Они приветствуют офицеров и их высоких гостей как помощников. Они играют роль «Похитителей тел», которые ходят взад и вперед по рядам моряков, наблюдая, а иногда и ловя любого моряка, который собирается или идет вниз. (Иногда они блокируют колени и теряют сознание.) Они помогают флоту в задней комнате. Они служат во время приема Почетных выпускников.Они охраняют двери и выполняют множество задач за кулисами и на улице, например, направляют людей и помогают тем, кому требуется инвалидная коляска. Их работа — помочь убедиться, что все идет гладко. Команда Honor Guard Drill Team также демонстрирует стрельбу из винтовки в начале церемонии. Поскольку у членов штаба корабля / почетного караула есть обязанности выполнять до и во время PIR, они не проходят через двери, когда другие подразделения входят в день PIR.
Sticks (Flags) совершает невероятный марш, идеально рассчитанный и исполняемый под ритм барабанного корпуса.Их работа — представлять флаги каждого штата в союзе. Они выстроены в линию по высоте, поэтому поток выглядит лучше, поэтому ваш новобранец, вероятно, не сможет нести флаг своего штата. Они также чествуют тех, кто ушел раньше, представляя флаги военнопленных и МВД, а также флаг США и флаг ВМС США в Color Guard.
Triple Threat состоит из тех, кто входит в команду Rifle Drill, и всех тех, кто был выбран за их музыкальные способности. Хор Blue Jacket исполняет национальный гимн, Anchors Aweigh и все остальное, что им было поручено.Оркестр играет в разное время на протяжении церемонии. Drum Corps также марширует и помогает всем остальным идти в ногу и идти в ногу со временем. Те, кто находятся в дивизии тройной угрозы, не будут маршировать с другими подразделениями, так как они уже будут на полу зала тренировок.
Адрес, по которому можно написать вашему рекруту:
SR ФАМИЛИЯ, ИМЯ MI
SHIP 02 DIV 9XX
3600 OHIO STREET
GREAT LAKES IL 60088-7105 (60088-3156 также будет работать)
Есть ли преимущество в отряде 900? Все зависит от вашей точки зрения.Любимые люди могут мельком увидеть новобранца на фотографиях, размещенных на странице RTC в fB. Новобранцы в 900-й дивизии могут взаимодействовать с гражданскими лицами больше, чем в стрелковой или 800-й дивизии, если они находятся на дополнительных PIR или мероприятиях в сообществе. Новобранцы часто начинают работать в команде быстрее, чем в стрелковой дивизии, но не всегда. Требуется дополнительная работа, поскольку эти новобранцы проходят ту же подготовку, что и сотрудники стрелковой дивизии, а также имеют практики для PIR.Нет ничего особенного после BC, привязанного к 900-й дивизии.
Чем занимаются «массовки» в 900-м дивизионе? Есть массовки в каждом 900 дивизионе. Они тренируются так же, как и все в дивизионе. Они должны быть готовы, если их попросят заменить новобранца, который болен, травмирован или по иным причинам не может выполнять свои обязанности. Некоторые из дополнительных услуг помогают убрать трибуны, тренировочный зал, комнаты, используемые для подготовки … Некоторые будут отвечать за настройку и размещение вещей до и после PIR.Некоторые из дополнительных услуг будут сопровождать и помочь с рассадкой тех, кто нуждается в инвалидных колясках или другой помощи. Некоторые будут сидеть и направлять гостей в соответствующий раздел.
Обязательно спросите своего новобранца заранее, что он / она будет делать во время PIR, и будет ли он / она выступать в каком-либо PIR перед его / ее собственным PIR, чтобы вы знали, где искать своего новобранца или моряка. в фотографиях или видео и в ПИР.
Приведенная выше информация предоставлена lemonelephant, мамой моряка на пенсии.
Последнее обновление 17.04.2020
Rs Aggarwal 2019 for Class 7 Math Chapter 3
Страница № 39:
Вопрос 1:
Преобразуйте каждую из следующих дробей в простейшую форму:
(i) .8
(ii) .75
(iii) .06
(iv) .285
Ответ:
Имеем:
(i) 0,8 = 810 = 8 ÷ 210 ÷ 2 = 45
(ii) 0.75 = 75100 = 75 ÷ 25100 ÷ 25 = 34
(iii) 0,06 = 6100 = 6 ÷ 2100 ÷ 2 = 350
(iv) 0,285 = 2851000 = 285 ÷ 51000 ÷ 5 = 57200
Страница № 39:
Вопрос 2:
Преобразуйте каждое из следующих значений в смешанную дробь:
(i) 5,6
(ii) 12,25
(iii) 6,004
(iv) 4,625
Ответ:
Имеем:
(i) 5,6 = 5610 = 56 ÷ 210 ÷ 2 = 285 = 535
(ii) 12.25 = 1225100 = 1225 ÷ 25100 ÷ 25 = 494 = 1214
(iii) 6,004 = 60041000 = 6004 ÷ 41000 ÷ 4 = 1501250 = 61250
(iv) 4,625 = 46251000 = 4625 ÷ 1251000 ÷ 125 = 378 = 458
Страница № 39:
Вопрос 3:
Преобразуйте каждое из следующих чисел в одинаковые десятичные дроби:
(i) 4710
(ii) 156100
(iii) 2516100
(iv) 35241000
(v) 258
(vi) 325
(vii) 2225
(viii) 1720
Ответ:
(i) 4710
При делении получаем:
∴ 4710 = 4.7
(ii) 156100
При делении получаем:
∴156100 = 1,56
(iii) 2516100
При делении получаем:
∴ 2516100 = 25,16
(iv) 35241000
На при делении получаем:
∴ 35241000 = 3,524
(v) 258
При делении получаем:
∴ 258 = 3,125
(vi) 325 = 175
При делении получаем:
∴ 175 = 3,4
(vii) 2225 = 5225
При делении получаем:
∴ 5225 = 2.08
(viii) 1720
При делении получаем:
∴ 1720 = 0,85
Страница № 39:
Вопрос 4:
Преобразует каждое из следующих чисел в одинаковые десятичные числа:
(i) 6,5, 16,03, 0,274, 119,4
(ii) 3,5, 0,67, 15,6, 4
Ответ:
Преобразуя заданные десятичные числа в аналогичные десятичные, получаем:
(i) 6.500, 16,030, 0,274 и 119,400
(ii) 3,50, 0,67, 15,60 и 4,00
Страница № 39:
Вопрос 5:
Заполните каждый из заполнителей правильным символом> или <.
(i) 78,23 69,85
(ii) 3,406 3,46
(iii) 5,68 5,86
(iv) 14,05 14,005
(v) 1,85 1,805
(vi) 0,98 1,07
Ответ:
У нас есть,
(i) Если сравнивать целую часть числа, 78> 69.
Таким образом, 78,23> 69,85
(ii) Преобразуя десятичные дроби в аналогичные десятичные, мы получаем 3,406 и 3,460.
Сравнение частей целого числа, 3 = 3
Сравнение десятичной цифры, 4 = 4
Сравнение сотых цифр, 6> 0
Таким образом, 3,406 <3,46
(iii) Сравнение частей целого числа, 5 = 5
Сравнение десятая цифра, 6 <8
Таким образом, 5,68 <5,86
(iv) Преобразуя десятичные дроби в аналогичные десятичные, мы получаем 14.050 и 14.005.
Сравнивая части целого числа, 14 = 14
Сравнивая десятые доли, 0 = 0
Сравнивая сотые цифры, 5> 0
Таким образом, 14.05> 14.005
(v) Преобразуя десятичные дроби в аналогичные десятичные, мы получаем 1.850 и 1.805.
Сравнение частей целого числа, 1 = 1
Сравнение десятичной цифры, 8 = 8
Сравнение сотых цифр, 5> 0
Таким образом, 1.85> 1.805
(vi) Сравнение частей целого числа, 0 <1
Таким образом , 0,98 <1,07
Страница № 39:
Вопрос 6:
Расположите следующие десятичные знаки в порядке возрастания:
(i) 4.6, 7,4, 4,58, 7,32, 4,06
(ii) 0,5, 5,5, 5,05, 0,05, 5,55
(iii) 6,84, 6,48, 6,8, 6,4, 6,08
(iv) 2,2, 2,202, 2,02, 22,2, 2,002
Ответ:
(i) Преобразуя данные десятичные дроби в аналогичные десятичные, мы получаем:
4.60, 7.40, 4.58, 7.32, 4.06
Очевидно, 4.06 <4.58 <4.60 <7.32 <7.32 <7.40
Следовательно, данные десятичные дроби в порядке возрастания равны 4.06, 4.58 , 4.6, 7.32 и 7.4.
(ii) Преобразуя заданные десятичные дроби в аналогичные десятичные, получаем:
0.50, 5,50, 5,05, 0,05, 5,55
Очевидно, 0,05 <0,50 <5,05 <5,50 <5,55
Следовательно, данные десятичные дроби в порядке возрастания равны 0,05, 0,5, 5,05, 5,5 и 5,55.
(iii) Преобразуя данные десятичные дроби в аналогичные десятичные, мы получаем:
6,84, 6.48, 6.80, 6.40, 6.08
Очевидно, 6.08 <6.40 <6.48 <6.80 <6.84
Следовательно, данные десятичные дроби в порядке возрастания равны 6.08, 6.4, 6.48, 6.8 и 6.84.
(iv) Преобразуя заданные десятичные числа в аналогичные десятичные, получаем:
2.200, 2.202, 2.020, 22.200, 2.002
Очевидно, 2.002 <2.020 <2.200 <2.202 <22.200
Следовательно, данные десятичные дроби в порядке возрастания: 2.002, 2.02, 2.2, 2.202 и 22.2.
Страница № 39:
Вопрос 7:
Расположите следующие десятичные знаки в порядке убывания:
(i) 7,4, 8,34, 74,4, 7,44, 0,74
(ii) 2,6, 2,26, 2,06, 2,007, 2,3
Ответ:
(i) Преобразуя заданные десятичные дроби в аналогичные десятичные, получаем:
7.40, 8,34, 74,40, 7,44, 0,74
Очевидно, 74,40> 8,34> 7,44> 7,40> 0,74
Следовательно, данные десятичные дроби в порядке убывания равны 74,4, 8,34, 7,44, 7,4 и 0,74.
(ii) Преобразуя данные десятичные дроби в аналогичные десятичные, мы получаем:
2.600, 2.260, 2.060, 2.007, 2.300
Очевидно, 2.600> 2.300> 2.260> 2.060> 2.007
Следовательно, данные десятичные дроби в порядке убывания равны 2,6, 2.3, 2.26, 2.06 и 2.007.
Страница № 39:
Вопрос 8:
Express 45 мм в см, м и км.
Ответ:
45 мм = 4510 см = 4,5 см
= 4,5 см = 4,5100 м = 0,045 м
= 0,045 м = 0,0451000 км = 0,000045 км
∴ 45 мм = 4,5 см = 0,045 м = 0,000045 км
Страница № 39:
Вопрос 9:
Экспресс в рупиях с использованием десятичных знаков:
(i) 8 пайсов
(ii) 9 рупий 75 пайсов
(iii) 8 рупий 5 пайсов
Ответ:
У нас есть:
(i) 8 пайс = 8100 рупий = 0 рупий.08
(ii) 9 рупий 75 пайс = 9 рупий + 75100 = (9 + 0,75) рупий = 9,75
рупий (iii) 8 рупий 5 пайс = 8+ 5100 рупий = (8 + 0,05) рупий = 8,05
рупий
Страница № 39:
Вопрос 10:
Выразить в километрах с десятичными знаками:
(i) 65 м
(ii) 284 м
(iii) 3 км 5 м
Ответ:
Имеем:
(i) 65 м = 651000 км = 0.065 км
∴ 65 м = 0,065 км
(ii) 284 м = 2841000 км = 0,284 км
(iii) 3 км 5 м = 3+ 51000 = 3+ 0,005 = 3,005 км
Страница № 41:
Вопрос 1:
Добавить:
16, 8.7, 0.94, 6.8 и 7.77
Ответ:
Преобразуя заданные десятичные дроби в аналогичные десятичные, получаем:
16.00, 8,70, 0,94, 6,80 и 7,77
Записав эти десятичные дроби в виде столбцов и сложив, мы получим:
Следовательно, сумма данных десятичных знаков равна 40,21
Страница № 41:
Вопрос 2:
Адрес:
18.6, 206.37, 8.008, 26.4 и 6.9
Ответ:
Преобразуя заданные десятичные дроби в аналогичные десятичные, получаем:
18.600, 206.370, 8.008, 26.400 и 6.900
Записав эти десятичные дроби в виде столбцов и сложив, мы получим:
Следовательно, сумма данных десятичных знаков равна 266.278.
Страница № 41:
Вопрос 3:
Адрес:
63,5, 9,7, 0,8, 26,66 и 12,17
Ответ:
Преобразуя заданные десятичные числа в аналогичные десятичные, получаем:
63.50, 9,70, 0,80, 26,66 и 12,17
Записав эти десятичные дроби в виде столбцов и сложив, мы получим:
Следовательно, сумма данных десятичных знаков равна 112,83.
Страница № 41:
Вопрос 4:
Добавить:
17,4, 86,39, 9,435, 8,8 и 0,06
Ответ:
Преобразуя заданные десятичные дроби в аналогичные десятичные, получаем:
17.400, 86,390, 9,435, 8,800 и 0,060
Записав эти десятичные дроби в виде столбцов и сложив, мы получим:
Следовательно, сумма данных десятичных знаков равна 122,085.
Страница № 41:
Вопрос 5:
26,9, 19,74, 231,769 и 0,048
Ответ:
Преобразуя заданные десятичные дроби в аналогичные десятичные, получаем:
26.900, 19.740, 231.769 и 0,048
Записав эти десятичные дроби в виде столбцов и сложив, мы получим:
Следовательно, сумма данных десятичных знаков равна 278.457.
Страница № 41:
Вопрос 6:
Добавить:
23,8, 8,94, 0,078 и 214,6
Ответ:
Преобразуя заданные десятичные дроби в аналогичные десятичные, получаем:
23.800, 8,940, 0,078 и 214,600
Записав эти десятичные дроби в виде столбцов и сложив, мы получим:
Следовательно, сумма данных десятичных знаков равна 247,418.
Страница № 41:
Вопрос 7:
Добавить:
6.606, 66.6, 666, 0.066, 0.66
Ответ:
Преобразуя заданные десятичные дроби в аналогичные десятичные, получаем:
6.606, 66.600, 666.000, 0,066 и 0,660
Записав эти десятичные дроби в виде столбцов и сложив, мы получим:
Следовательно, сумма данных десятичных знаков равна 739.932.
Страница № 41:
Вопрос 8:
Адрес:
9.09, 0.909, 99.9, 9.99, 0.099
Ответ:
Преобразуя заданные десятичные дроби в аналогичные десятичные, получаем:
9.090, 0.909, 99.900, 9.990 и 0.099
Записав эти десятичные дроби в виде столбцов и сложив, мы получим:
Следовательно, сумма данных десятичных знаков равна 119.988.
Страница № 41:
Вопрос 9:
Вычтем:
14,79 из 72,43
Ответ:
Данные десятичные дроби подобны десятичным. Записывая их в виде столбцов с большим столбцом вверху и вычитая их, получаем:
∴ (72.43 — 14,79) = 57,64
Страница № 41:
Вопрос 10:
Вычесть:
36,74 из 52,6
Ответ:
Преобразуя данные десятичные дроби в аналогичные десятичные, мы получаем:
36,74 и 52,60
Записывая их в виде столбцов с большим числом вверху и вычитая их, получаем:
∴ (52.60 — 36,74) = 15,86
Страница № 41:
Вопрос 11:
Вычесть:
13,876 из 22
Ответ:
Преобразуя данные десятичные дроби в аналогичные десятичные, мы получаем:
13,876 и 22,000
Записывая их в виде столбцов с большим числом вверху и вычитая их, получаем:
∴ (22.000 — 13,876) = 8,124
Страница № 41:
Вопрос 12:
Вычесть:
15,079 из 24,16
Ответ:
Преобразуя указанные десятичные дроби в аналогичные десятичные, мы получаем:
15.079 и 24.160
Записывая их в виде столбцов с большим числом вверху и вычитая их, получаем:
∴ (24.160 — 15,079) = 9,081
Страница № 41:
Вопрос 13:
Вычесть:
0,68 из 1,007
Ответ:
Преобразуя данные десятичные дроби в аналогичные десятичные, мы получаем:
0,680 и 1,007
Записывая их в виде столбцов с большим числом вверху и вычитая их, получаем:
∴ (1.007 — 0,680) = 0,327
Страница № 41:
Вопрос 14:
Вычесть:
0,4678 из 5,05
Ответ:
Преобразуя заданные десятичные дроби в аналогичные десятичные, мы получаем:
0,4678 и 5.0500
Записывая их в виде столбцов с большим числом вверху и вычитая их, получаем:
∴ (5.0500 — 0,4678) = 4,5822
Страница № 41:
Вопрос 15:
Вычесть:
2,5307 из 8
Ответ:
Преобразуя данные десятичные дроби в аналогичные десятичные, мы получаем:
2,5307 и 8.0000
Записывая их в виде столбцов с большим числом вверху и вычитая их, получаем:
∴ (8.0000 — 2,5307) = 5,4693
Страница № 41:
Вопрос 16:
Вычесть:
6,732 из 9,001
Ответ:
Записывая данные одинаковые десятичные дроби в виде столбцов с большим из них вверху и вычитая их, получаем:
∴ (9,001 — 6,732) = 2,269
Страница № 41:
Вопрос 17:
Вынуть 5.746 от 9.1.
Ответ:
Преобразуя данные десятичные дроби в аналогичные десятичные, мы получаем:
5,746 и 9,100
Записывая их в виде столбцов с большим числом вверху и вычитая их, получаем:
∴ (9,100 — 5,746) = 3,354
Страница № 41:
Вопрос 18:
Что нужно добавить к 63,58, чтобы получить 92?
Ответ:
Преобразуя заданные десятичные числа в аналогичные десятичные, получаем:
63.58 и 92,00
Таким образом, необходимое число = (92,00 — 63,58) = 28,42
Следовательно, 28,42 нужно добавить к 63,58, чтобы получить 92.
Страница № 41:
Вопрос 19:
Что нужно вычесть из 8,1, чтобы получить 0,813?
Ответ:
Преобразуя заданные десятичные дроби в аналогичные, получаем:
8.100 и 0.813
Таким образом, необходимое число = (8.100 — 0,813) = 7,287
Следовательно, следует вычесть 7,287 из 8,1, чтобы получить 0,813.
Страница № 41:
Вопрос 20:
На сколько нужно увеличить 32,67, чтобы получить 60,1?
Ответ:
Преобразуя заданные десятичные дроби в аналогичные, получаем:
32,67 и 60,10
Таким образом, необходимое число = (60,10 — 32,67) = 27,43
Отсюда 32.67 следует увеличить на 27,43, чтобы получить 60,1.
Страница № 41:
Вопрос 21:
На сколько нужно уменьшить 74,3, чтобы получить 26,87?
Ответ:
Преобразуя заданные десятичные дроби в аналогичные, получаем:
74,30 и 26,87
Таким образом, необходимое число = (74,30 — 26,87) = 47,43
Следовательно, 74,3 следует уменьшить на 47.43, чтобы получить 26,87.
Страница № 41:
Вопрос 22:
Компания Rohit приобрела блокнот за 23,75 рупий, карандаш за 2,85 рупий и ручку за 15,90 рупий. Он дал продавцу купюру в 50 рупий. Какую сумму он получил обратно?
Ответ:
Общая сумма, потраченная Rohit на покупку данных товаров = (23,75 + 2,85 + 15,90) рупий
= 42 рупий.50
Деньги, отданные продавцу = 50
рупий ∴ Деньги, возвращенные продавцом = (50 — 42,50) рупий
= 7,50 рупий
Таким образом, сумма, полученная Rohit = 7,50
рупий
Страница № 43:
Вопрос 1:
Найдите продукт:
(i) 73,92 × 10
(ii) 7,54 × 10
(iii) 84,003 × 10
(iv) 0,83 × 10
(v) 0,7 × 10
(vi) 0.032 × 10
Ответ:
У нас есть следующее:
(i) 73,92 × 10 = 739,2 [Смещение десятичной точки вправо на 1 место]
(ii) 7,54 × 10 = 75,4 [Смещение десятичной точки вправо на 1 место]
(iii) 84,003 × 10 = 840,03 [Сдвиг десятичной точки вправо на 1 место]
(iv) 0,83 × 10 = 8,3 [Сдвиг десятичной точки вправо на 1 место]
(v) 0.7 × 10 = 7 [сдвиг десятичной точки вправо на 1 место]
(vi) 0,032 × 10 = 0,32 [сдвиг десятичной точки вправо на 1 место]
Страница № 44:
Вопрос 2:
Найдите продукт:
(i) 2,397 × 100
(ii) 6,83 × 100
(iii) 2,9 × 100
(iv) 0,08 × 100
(v) 0,6 × 100
(vi) 0,003 × 100
Ответ:
Имеем следующее:
(i) 2.397 × 100 = 239,7 [Сдвиг десятичной точки вправо на 2 разряда]
(ii) 6,83 × 100 = 683 [Сдвиг десятичной точки вправо на 2 разряда]
(iii) 2,9 × 100 = 290 [Смещение десятичная точка вправо на 2 разряда]
(iv) 0,08 × 100 = 8 [Сдвиг десятичной точки вправо на 2 разряда]
(v) 0,6 × 100 = 60 [Сдвиг десятичной точки вправо на 2 разряда ]
(vi) 0,003 × 100 = 0,3 [Смещение десятичной точки вправо на 2 разряда]
Страница № 44:
Вопрос 3:
Найдите продукт:
(i) 6.7314 × 1000
(ii) 0,182 × 1000
(iii) 0,076 × 1000
(iv) 6,25 × 1000
(v) 4,8 × 1000
(vi) 0,06 × 1000
Ответ:
У нас есть:
(i) 6,7314 × 1000 = 6731,4 [сдвиг десятичной точки вправо на 3 разряда]
(ii) 0,182 × 1000 = 182 [сдвиг десятичной точки вправо на 3 разряда]
(iii) 0,076 × 1000 = 76 [Смещение десятичной точки вправо на 3 разряда]
(iv) 6.25 × 1000 = 6250 [сдвиг десятичной точки вправо на 3 разряда]
(v) 4,8 × 1000 = 4800 [сдвиг десятичной точки вправо на 3 разряда]
(vi) 0,06 × 1000 = 60 [сдвиг десятичной дроби указать вправо на 3 места]
Страница № 44:
Вопрос 4:
Найдите продукт:
(i) 5,4 × 16
(ii) 3,65 × 19
(iii) 0.854 × 12
(iv) 36,73 × 48
(v) 4,125 × 86
(vi) 104,06 × 75
(vii) 6,032 × 124
(viii) 0,0146 × 69
(ix) 0,00125 × 327
Ответ:
Мы имеем следующее:
(i) 54 × 16 = 864
∴ 5,4 × 16 = 86,4 [1 десятичный разряд]
(ii) 365 × 19 = 6935
∴ 3,65 × 19 = 69,35 [2 знака десятичный]
(iii) 854 × 12 = 10248
∴ 0.854 × 12 = 10,248 [3 десятичных знака]
(iv) 3673 × 48 = 176304
∴ 36,78 × 48 = 1763,04 [2 десятичных знака]
(v) 4125 × 86 = 354750
∴ 4,125 × 86 = 354,750 [3 десятичных знака]
= 354,75
(vi) 10406 × 75 = 780450
104,06 × 75 = 7804,50 [2 десятичных знака]
= 7804,5
(vii) 6032 × 124 = 747968
∴ 6.032 × 124 = 747,968 [3 десятичных знака]
(viii) 146 × 69 = 10074
∴ 0,0146 × 69 = 1,0074 [4 десятичных знака]
(ix) 125 × 327 = 40875
∴ 0,00125 × 327 = 0,40875 [5 десятичных знаков]
Страница № 44:
Вопрос 5:
Найдите продукт
(i) 7,6 × 2,4
(ii) 3,45 × 6,3
(iii) 0.54 × 0,27
(iv) 0,568 × 4,9
(v) 6,54 × 0,09
(vi) 3,87 × 1,25
(vii) 0,06 × 0,38
(viii) 0,623 × 0,75
(ix) 0,014 × 0,46
(x) 54,5 × 1,76
(xi) 0,045 × 2,4
(xii) 1,245 × 6,4
Ответ:
(i) Сначала мы умножим 76 на 24.
∴ 76 × 24 = 1824
Сумма десятичных знаков в данных числах = (1 + 1) = 2
∴ 7,6 × 2,4 = 18,24 [2 десятичных знака ]
(ii) Сначала умножим 345 на 63.
∴ 345 × 63 = 21735
Сумма десятичных знаков в данных числах = (2 + 1) = 3
∴ 3,45 × 6,3 = 21,735 [3 десятичных знака]
(iii) Сначала мы умножим 54 на 27.
∴ 54 × 27 = 1458
Сумма десятичных знаков в данных числах = (2 + 2) = 4
∴ 0,54 × 0,27 = 0,1458 [4 десятичных знака]
(iv) Сначала мы умножим 568 на 49.
∴ 568 × 49 = 27832
Сумма десятичных знаков в данных числах = (3 + 1) = 4
∴ 0.568 × 4,9 = 2,7832 [4 десятичных знака]
(v) Сначала мы умножаем 654 на 9.
∴ 654 × 9 = 5886
Сумма десятичных знаков в данных числах = (2 + 2) = 4
∴ 6,54 × 0,09 = 0,5886 [4 десятичных знака]
(vi) Сначала мы умножим 387 на 125.
∴ 387 × 125 = 48375
Сумма десятичных знаков в данных числах = (2 + 2) = 4
∴ 3,87 × 1,25 = 4,8375 [4 десятичных знака]
(vii) Сначала мы умножим 38 на 6.
∴ 38 × 6 = 228
Сумма десятичных знаков в данных числах = (2 + 2) = 4
∴ 0,06 × 0,38 = 0,0228 [4 десятичных знака]
(viii) Сначала мы умножим 623 на 75.
∴ 623 × 75 = 46725
Сумма десятичных знаков в данных числах = (3 + 2) = 5
∴ 0,623 × 0,75 = 0,46725 [5 десятичных знаков]
(ix) Сначала мы умножим 14 на 46.
∴ 14 × 46 = 644
Сумма десятичных знаков в данных числах = (3 + 2) = 5
∴ 0.014 × 0,46 = 0,00644 [5 знаков после запятой]
(x) Сначала мы умножим 545 на 176.
∴ 545 × 176 = 95920
Сумма десятичных знаков в данных числах = (1 + 2) = 3
∴ 54,5 × 1,76 = 95,920 [3 десятичных знака]
= 95,92
(xi) Сначала мы умножим 45 на 24.
∴ 45 × 24 = 1080
Сумма десятичных знаков в данных числах = (3 + 1) = 4
∴ 0,045 × 2,4 = 0,1080 [4 десятичных знака]
= 0.108
(xii) Сначала умножим 1245 на 64.
∴ 1245 × 64 = 79680
Сумма десятичных знаков в данных числах = (3 + 1) = 4
∴ 1,245 × 6,4 = 7,9680 [4 разряда десятичного числа]
= 7,968
Страница № 44:
Вопрос 6:
Найдите продукт:
(i) 13 × 1,3 × 0,13
(ii) 2,4 × 1,5 × 2,5
(iii) 0,8 × 3,5 × 0,05
(iv) 0.2 × 0,02 × 0,002
(v) 11,1 × 1,1 × 0,11
(vi) 2,1 × 0,21 × 0,021
Ответ:
(i) Сначала найдем произведение 13 ⨯ 1,3 0,13.
Итак, 13 ⨯ 13 ⨯ 13 = 169 x 13
= 2197
Сумма десятичных знаков в данных числах = (1 + 2) = 3
Итак, произведение должно иметь три десятичных знака.
∴ 13 ⨯ 1,3 ⨯ 0,13 = 2,197
(ii) Сначала найдем произведение 2.4 ⨯ 1,5 ⨯ 2,5.
Итак, 24 ⨯ 15 ⨯ 25 = 360 x 25
= 9000
Сумма десятичных знаков в данных числах = (1 + 1 + 1) = 3
Итак, произведение должно иметь три десятичных знака.
∴ 2,4 ⨯ 1,5 ⨯ 2,5 = 9000
= 9
(iii) Сначала мы найдем произведение 0,8 ⨯ 3,5 ⨯ 0,05.
Теперь 8 ⨯ 35 ⨯ 5 = 280 ⨯ 5
= 1400
Сумма десятичных знаков в данных числах = (1 + 1 + 2) = 4
Итак, произведение должно иметь четыре десятичных знака.
∴ 0,8 ⨯ 3,5 ⨯ 0,05 = 0,1400
= 0,14
(iv) Сначала мы найдем произведение 0,2 ⨯ 0,02 ⨯ 0,002.
Итак, 2 ⨯ 2 ⨯ 2 = 4 ⨯ 2
= 8
Сумма десятичных знаков в данных числах = (1 + 2 + 3) = 6
Итак, произведение должно иметь шесть десятичных знаков.
∴ 0,2 ⨯ 0,02 ⨯ 0,002 = 0,000008
(v) Сначала мы найдем произведение 11,1 ⨯ 1,1 ⨯ 0,11.
Итак, 111 ⨯ 11 ⨯ 11 = 1221 ⨯ 11
= 13431
Сумма десятичных знаков в данных числах = (1 + 1 + 2) = 4
Итак, произведение должно иметь четыре десятичных знака.
∴ 11,1 ⨯ 1,1 ⨯ 0,11 = 1,3431
(vi) Сначала найдем произведение 2,1 ⨯ 0,21 ⨯ 0,021.
Теперь 21 ⨯ 21 ⨯ 21 = 441 ⨯ 21
= 9261
Сумма десятичных знаков в данных числах = (1 + 2 + 3) = 6
Итак, произведение должно иметь шесть десятичных знаков.
∴ 2,1 ⨯ 0,21 ⨯ 0,021 = 0,009261
Страница № 44:
Вопрос 7:
Оценить:
(i) (1.2) 2
(ii) (0,7) 2
(iii) (0,04) 2
(iv) (0,11) 2
Ответ:
(i) (1,2) 2 = 1,2 × 1,2
Сначала найдем произведение 1,2 × 1,2.
Итак, 12 × 12 = 144
Сумма десятичных знаков в данных числах = (1 + 1) = 2
Итак, произведение должно иметь два десятичных знака.
∴ (1,2) 2 = 1,2 × 1.2 = 1,44
(ii) (0,7) 2 = 0,7 × 0,7
Сначала найдем произведение 0,7 × 0,7.
Итак, 7 × 7 = 49
Сумма десятичных знаков в данных числах = (1 + 1) = 2
Итак, произведение должно иметь два десятичных знака.
∴ (0,7) 2 = 0,7 × 0,7 = 0,49
(iii) (0,04) 2 = 0,04 × 0,04
Сначала найдем произведение 0,04 × 0,04.
Итак, 4 × 4 = 16
Сумма десятичных знаков в данных числах = (2 + 2) = 4
Итак, произведение должно иметь четыре десятичных знака.
∴ (0,04) 2 = 0,04 × 0,04 = 0,0016
(iv) (0,11) 2 = 0,11 × 0,11
Сначала найдем произведение 0,11 × 0,11.
Итак, 11 × 11 = 121
Сумма десятичных знаков в данных числах = (2 + 2) = 4
Итак, произведение должно иметь четыре десятичных знака.
∴ (0,11) 2 = 0,11 × 0,11 = 0,0121
Страница № 44:
Вопрос 8:
Оценить:
(i) (0.3) 3
(ii) (0,05) 3
(iii) (1,5) 3
Ответ:
(i) (0,3) 3 = 0,3 × 0,3 × 0,3
Сначала найдем произведение 3 × 3 × 3.
Теперь 3 × 3 × 3 = 27
Сумма десятичных знаков в данных числах = (1 + 1 + 1) = 3
Итак, произведение должно иметь три десятичных знака.
∴ (0,3) 3 = 0,3 × 0,3 × 0,3 = 0,027
(ii) (0.05) 3 = 0,05 × 0,05 × 0,05
Сначала найдем произведение 5 × 5 × 5.
Теперь 5 × 5 × 5 = 125
Сумма десятичных знаков в данных числах = (2 + 2 + 2) = 6
Итак, в произведении должно быть шесть десятичных знаков.
∴ (0,05) 3 = 0,05 × 0,05 × 0,05 = 0,000125
(iii) (1,5) 3 = 1,5 × 1,5 × 1,5
Сначала мы найдем произведение 15 × 15 × 15.
Теперь, 15 × 15 × 15 = 225 × 15 = 3375
Сумма десятичных знаков в данных числах = (1 + 1 + 1) = 3
Итак, произведение должно иметь три десятичных знака.
∴ (1,5) 3 = 1,5 × 1,5 × 1,5 = 3,375
Страница № 44:
Вопрос 9:
Автобус преодолевает 62,5 км за час. Какое расстояние он может преодолеть за 18 часов?
Ответ:
Расстояние, пройденное автобусом за 1 час = 62,5 км
∴ Пройденное расстояние за 18 часов = (62,5 × 18) км
= 1125 км
Таким образом, автобус может преодолеть расстояние в 1125 км за 18 часов.
Страница № 44:
Вопрос 10:
Банка масла весит 16,8 кг. Какой вес у 45 таких банок?
Ответ:
Вес 1 банки масла = 16,8 кг
∴ Вес 45 таких банок = (16,8 × 45) кг
= 756 кг
Следовательно, вес 45 банок масла составляет 756 кг.
Страница № 44:
Вопрос 11:
Мешок с пшеницей весит 97.8 кг. Сколько пшеницы содержится в 500 таких пакетиках?
Ответ:
Вес 1 мешка пшеницы = 97,8 кг
∴ Вес 500 мешков = (97,8 x 500) кг
= 48900 кг
Следовательно, вес 500 мешков пшеницы составляет 48900 кг.
Страница № 44:
Вопрос 12:
Найдите вес 16 пакетов сахара, каждый из которых весит 48 штук.450 кг.
Ответ:
Вес 1 мешка сахара = 48,450 кг
∴ Вес 16 мешков сахара = (48,450 ⨯ 16) кг
= 775,2 кг
Следовательно, вес 16 мешков сахара составляет 775,2 кг.
Страница № 44:
Вопрос 13:
В бутылочку помещается 0,845 кг соуса.Сколько соуса будет в 72 таких бутылках?
Ответ:
Вместимость 1 бутылки соуса = 0,845 кг
∴ Вместимость 72 таких бутылок = (0,845 × 72) кг
= 60,84 кг
Следовательно, вместимость 72 бутылок соуса будет 60,84 кг.
Страница № 44:
Вопрос 14:
В бутылке 925 г варенья.Сколько килограммов варенья будет в 25 таких бутылках?
Ответ:
Вес 1 бутылки варенья = 925 г = 0,925 кг
∴ Масса 25 таких бутылок = (0,925 × 25) кг
= 23,125 кг
∴ Вес 25 бутылок варенья составит 23,125 кг.
Страница № 44:
Вопрос 15:
Если один барабан вмещает 16.850 литров масла, сколько литров вмещает 48 таких бочек?
Ответ:
Вместимость 1 бочки с маслом = 16,850 литров
∴ Вместимость 48 таких бочек = (16,850 x 48) литров
= 808,800 литров
Следовательно, емкость 48 бочек с маслом составляет 808,800 литров.
Страница № 44:
Вопрос 16:
1 кг риса стоит 56 рупий.80. Сколько стоит 16,25 кг риса?
Ответ:
Стоимость 1 кг риса = 56,80 рупий
∴ Стоимость 16,25 кг риса = (56,80 × 16,25) рупий
= 923 рупий
Следовательно, стоимость 16,25 кг риса составляет 923 рупий.
Страница № 44:
Вопрос 17:
1 метр ткани стоит 108 рупий.50. Сколько стоят 18,5 метра этого полотна?
Ответ:
Стоимость 1 м ткани = 108,50 рупий
∴ Стоимость 18,5 м ткани = (108,50 x 18,5)
= 2007,25 рупий
Следовательно, стоимость 18,5 м ткани составляет 2007,25 рупий.
Страница № 44:
Вопрос 18:
Автомобиль может преодолеть расстояние 8.6 км на одном литре бензина. Как далеко он может проехать на 36,5 литрах бензина?
Ответ:
Расстояние, пройденное автомобилем с 1 литром бензина = 8,6 км
∴ Расстояние, пройденное с 36,5 литрами бензина = (8,6 × 36,5) км
= 313 900 км
Следовательно, расстояние, пройденное автомобилем с 36,5 литрами бензина, составляет 313 900 км.
Страница № 44:
Вопрос 19:
Таксист берет 9 рупий.80 за км. Сколько он будет брать за поездку на 106,5 км?
Ответ:
Сборы за 1 км = 9,80 рупий
∴ Сборы за 106,5 км = (9,80 × 106,5) рупий
= 1043,70 рупий
Следовательно, таксист будет взимать 1043,70 рупий за поездку протяженностью 106,5 км.
Страница № 49:
Вопрос 1:
Делить:
(i) 131.6 на 10
(ii) 32,56 на 10
(iii) 4,38 на 10
(iv) 0,34 на 10
(v) 0,08 на 10
(vi) 0,062 на 10
Ответ:
У нас есть следующее:
(i) 131,6 ÷ 10 = 131,610 = 13,16 [Сдвинуть десятичную точку влево на 1 место]
(ii) 32,56 ÷ 10 = 32,5610 = 3,256 [Сдвинуть десятичную точку влево на 1 место]
(iii) 4,38 ÷ 10 = 4,38 · 10 = 0.438 [Сдвинуть десятичную точку влево на 1 место]
(iv) 0,34 ÷ 10 = 0,3410 = 0,034 [Сдвинуть десятичную точку влево на 1 место]
(v) 0,08 ÷ 10 = 0,0810 = 0,008 [ Сдвинуть десятичную точку влево на 1 место]
(vi) 0,062 ÷ 10 = 0,06210 = 0,0062 [Сдвинуть десятичную точку влево на 1 место]
Страница № 49:
Вопрос 2:
Делить:
(i) 137.2 на 100
(ii) 23,4 на 100
(iii) 4,7 на 100
(iv) 0,3 на 100
(v) 0,58 на 100
(vi) 0,02 на 100
Ответ:
У нас есть следующее:
(i) 137,2 ÷ 100 = 137,2100 = 1,372 [Смещение десятичной точки влево на 2 разряда]
(ii) 23,4 ÷ 100 = 23,4100 = 0,234 [Сдвиг десятичной точки влево по 2 места]
(iii) 4.7 ÷ 100 = 4,7100 = 0,047 [Сдвиг десятичной точки влево на 2 разряда]
(iv) 0,3 ÷ 100 = 0,3100 = 0,003 [Сдвиг десятичной точки влево на 2 разряда]
(v) 0,58 ÷ 100 = 0,58100 = 0,0058 [Сдвиг десятичной точки влево на 2 разряда]
(vi) 0,02 ÷ 100 = 0,02100 = 0,0002 [Сдвиг десятичной точки влево на 2 разряда]
Страница № 49:
Вопрос 3:
Делить:
(i) 1286.5 на 1000
(ii) 354,16 на 1000
(iii) 38,9 на 1000
(iv) 4,6 на 1000
(v) 0,8 на 1000
(vi) 2 на 1000
Ответ:
У нас есть следующее:
(i) 1286,5 ÷ 1000 = 1286,51000 = 1,2865 [Сдвинуть десятичную точку влево на 3 разряда]
(ii) 354,16 ÷ 1000 = 354,161000 = 0,35416 [Сдвинуть десятичную точку влево на 3 места]
(iii) 38,9 ÷ 1000 = 38.
= 0,0389 [Сдвинуть десятичную запятую влево на 3 разряда]
(iv) 4,6 ÷ 1000 = 4,61000 = 0,0046 [Сдвинуть десятичную запятую влево на 3 разряда]
(v) 0,8 ÷ 1000 = 0,81000 = 0,0008 [Сдвинуть десятичную точку влево на 3 разряда]
(vi) 2 ÷ 1000 = 21000 = 0,002 [Сдвинуть десятичную точку влево на 3 разряда]
Страница № 49:
Вопрос 4:
Разделить:
(i) 12 на 8
(ii) 63 на 15
(iii) 47 на 20
(iv) 101 на 25
(v) 31 на 40
(vi) 11 на 16
Ответ:
(i) 12 ÷ 8 = 128 = 32
∴ 12 ÷ 8 = 1.5
(ii) 63 ÷ 15 = 6315 = 215
∴ 63 ÷ 15 = 4,2
(iii) 47 ÷ 20 = 4720
∴ 47 ÷ 20 = 2,35
(iv) 101 ÷ 25 = 10125
∴ 101 ÷ 25 = 4,04
(v) 31 ÷ 40
∴ 31 ÷ 40 = 0,775
(vi) 11 ÷ 16 = 1116
∴ 11 ÷ 16 = 0,6875
Страница № 49:
Вопрос 5:
Делить:
(i) 43.2 на 6
(ii) 60,48 на 12
(iii) 117,6 на 21
(iv) 217,44 на 18
(v) 2,575 на 25
(vi) 6,08 на 8
(vii) 0,765 на 9
(viii) 0,768 на 16
(ix) 0,175 на 25
(x) 0,3322 на 11
(xi) 2,13 на 15
(xii) 6,54 на 12
(xiii) 5,52 на 16
(xiv) 1,001 на 14
(xv) 0,477 на 18
Ответ:
(i) Имеем:
43,2 ÷ 6
∴ 43,2 ÷ 6 = 7,2
(ii) Имеем:
60.48 ÷ 12
∴ 60,48 ÷ 12 = 5,04
(iii) Имеем:
117,6 ÷ 21
∴ 117,6 ÷ 21 = 5,6
(iv) Имеем:
217,44 ÷ 18
∴ 217,44 ÷ 18 = 12.08
(v) Имеем:
2,575 ÷ 25
∴ 2,575 ÷ 25 = 0,103
(vi) Имеем:
6,08 ÷ 8
∴ 6,08 ÷ 8 = 0,76
(vii) Имеем:
0,765 ÷ 9
∴ 0.765 ÷ 9 = 0,085
(viii) Имеем:
0,768 ÷ 16
∴ 0,768 ÷ 16 = 0,048
(ix) Имеем:
0,175 ÷ 25
= 0,17525 = 0,175 × 100025 × 1000 = 17525 × 1000 = 71000 = 0,007
(x) Имеем:
0,3322 ÷ 11
∴ 0,3322 ÷ 11 = 0,0302
(xi) Имеем:
2,13 ÷ 15
∴ 2,13 ÷ 15 = 0,142
(xii) We иметь:
6,54 ÷ 12
∴ 6.54 ÷ 12 = 0,545
(xiii) Имеем:
5,52 ÷ 16
∴ 5,52 ÷ 16 = 0,345
(xiv) Имеем:
1,001 ÷ 14
∴ 1,001 ÷ 14 = 0,0715
(xv) Имеем:
0,477 ÷ 18
∴ 0,477 ÷ 18 = 0,0265
Страница № 49:
Вопрос 6:
Делить:
(i) 16,46 ÷ 20
(ii) 403.8 ÷ 30
(iii) 19,2 ÷ 80
(iv) 156,8 ÷ 200
(v) 12,8 ÷ 500
(vi) 18,08 ÷ 400
Ответ:
(i) 16,46 ÷ 20 = 16,4620 = 16,46 × 10020 × 100 = 16462 × 1000 = 8231000 = 0,823
(ii) 403,8 ÷ 30 = 403,830 = 403,8 × 1030 × 10 = 40383 × 100 = 1346100 = 13,46
( iii) 19,2 ÷ 80 = 19,280 = 19,2 × 1080 × 10 = 1
= 1928 × 100 = 24100 = 0,24
(iv) 156,8 ÷ 200 = 156,8200 = 156,8 × 10200 × 10 = 15682000 = 7841000 = 0,784
(v) 12.8 ÷ 500 = 12,8500 = 12,8 × 10500 × 10 = 1285000 = 25,61000 = 0,0256
(vi) 18,08 ÷ 400 = 18,08400 = 18,08 × 100400 × 100 = 180840000 = 45210000 = 0,0452
Страница № 49:
Вопрос 7:
Разделить:
(i) 3,28 на 0,8
(ii) 0,288 на 0,9
(iii) 25,395 на 1,5
(iv) 2,0484 на 0,18
(v) 0,228 на 0,38
(vi) 0,8085 на 0,35
(vii) 21,976 на 1,64
(viii) 11,04 на 1,6
(ix) 6.612 на 11,6
(x) 0,076 на 0,19
(xi) 148 на 0,074
(xii) 16,578 на 5,4
(xiii) 28 на 0,56
(xiv) 204 на 0,17
(xv) 3 на 80
Ответ:
(i) 3,28 ÷ 0,8 = 3,280,8 = 3,28 × 100,8 × 10 = 32,88
Теперь имеем:
∴ 3,280,8 = 32,88 = 4,1
(ii) 0,288 ÷ 0,9 = 0,2880,9 = 0,288 × 100,9 × 10 = 2,889
Теперь имеем:
∴ 0,2880,9 = 2,889 = 0,32
(iii) 25.395 ÷ 1,5 = 25,3951,5 = 25,395 × 101,5 × 10 = 253,9515
Теперь имеем:
∴ 25,3951,5 = 253,9515 = 16,93
(iv) 2,0484 ÷ 0,18 = 2,04840,18 = 2,0484 × 1000,18 × 100 = 204,8418
Теперь у нас есть:
∴ 2,04840,18 = 204,8418 = 11,38
(v) 0,228 ÷ 0,38 = 0,2280,38 = 0,228 × 1000,38 × 100 = 22,838
Теперь имеем:
∴ 0,2280 0,38 = 22,838 = 0,6
(vi) 0,8085 ÷ 0,35 = 0,80850,35 = 0,8085 × 1000,35 × 100 = 80,8535
Теперь имеем:
∴0.80850,35 = 80,8535 = 2,31
(vii) 21,976 ÷ 1,64 = 21,9761,64 = 21,976 × 1001,64 × 100 = 2197,6164
Теперь имеем:
∴ 21,9761,64 = 2197,6164 = 13,4
(viii) 11 = 11,041,6 = 11,04 × 101,6 × 10 = 110,416
Теперь имеем:
∴11,041,6 = 110,416 = 6,9
(ix) 6,612 ÷ 11,6 = 6,61211,6 = 6,612 × 1011,6 × 10 = 66,12116
Теперь у нас есть:
∴ 6,61211,6 = 66,12116 = 0,57
(x) 0,076 ÷ 0,19 = 0.0760,19 = 0,076 × 1000,19 × 100 = 7,619
Теперь имеем:
∴ 0,0760,19 = 7,619 = 0,4
(xi) 48 ÷ 0,074
= 1480,074 = 148 × 10000,074 × 1000 = 14800074 = 2 × 1000 = 2000
(xii) 16,578 ÷ 5,4 = 16,5785,4 = 16,578 × 105,4 × 10 = 165,7854
Теперь имеем:
∴ 16,5785,4 = 165,7854 = 3,07
(xiii) 28 ÷ 0,56
= 280,56 = 28 × 1000,56 × 100 = 280056 = 1 × 1002 = 50
(xiv) 204 ÷ 0,17
= 2040,17 = 204 × 1000,17 × 100 = 2040017 = 12 × 100 = 1200
(xv) 3 ÷ 80 = 380
Теперь имеем:
∴ 380 = 0.0375
Страница № 50:
Вопрос 8:
Общая стоимость 24 стульев составляет 9255,60 рупий. Найдите стоимость каждого стула.
Ответ:
Стоимость 24 стульев = 9255,60 рупий
∴ Стоимость одного стула = 9255,6024 рупий
= 9255,60 × 1024 × 10
=
240 рупий
= 385 рупий.65
Следовательно, стоимость одного стула составляет 385,65 рупий.
Страница № 50:
Вопрос 9:
Для рубашки требуется 1,8 м ткани. Сколько таких рубашек можно сделать из куска ткани длиной 45 м?
Ответ:
Ткань, необходимая для 1 рубашки = 1,8 м
∴ Количество рубашек, которое можно сшить из 45 м ткани = 451.8 = 150,6 = 50,2 = 502 = 25
Следовательно, из куска ткани длиной 45 м можно сделать 25 рубашек.
Страница № 50:
Вопрос 10:
Автомобиль преодолевает расстояние 22,8 км на 2,4 литре бензина. Какое расстояние он преодолеет на 1 литре бензина?
Ответ:
Расстояние, пройденное автомобилем с 2,4 л бензина = 22.8 км
∴ Расстояние, пройденное на 1 литре бензина = 22,82,4 км
= 22824 км = 228 ÷ 1224 ÷ 12 км = 192 км = 912 км
Следовательно, расстояние, пройденное автомобилем с 1 литром бензина, составляет 912 км.
Страница № 50:
Вопрос 11:
Банка вмещает 16,5 литров масла.Сколько таких банок потребуется для хранения 478,5 литров масла?
Ответ:
Вместимость 1 банки масла = 16,5 литров
∴ Количество банок, необходимых для хранения 478,5 литров масла = 478,516,5 = 4785165 = 4785 ÷ 15165 ÷ 15 = 31911 = 29
Следовательно, потребуется 29 банок для масла, чтобы вместить 478,5 литров масла.
Страница № 50:
Вопрос 12:
Вес 37 мешков сахара 3644.5 кг. Если все мешки весят одинаково, каков вес каждого мешка?
Ответ:
Вес 37 мешков сахара = 3644,5 кг
∴ Вес 1 мешка сахара = 3644,537 = 98,5 кг
Следовательно, каждый мешок сахара весит 98,5 кг.
Страница № 50:
Вопрос 13:
Если 69 ведер одинаковой вместимости можно заполнить 586.5 литров воды, какова вместимость каждого ведра?
Ответ:
Вместимость 69 ведер воды = 586,5 литров
∴ Вместимость одного такого ведра = 586,569 литра = 8,5 литра.
Следовательно, вместимость каждого ведра для воды составляет 8,5 л.
Страница № 50:
Вопрос 14:
Моника разрезает 46 м ткани на части по 1.По 15 м. Сколько штук она получит?
Ответ:
Длина одного куска ткани = 1,15 м
∴ Количество кусков ткани, которые она получает из 46 м ткани = 461,15
= 46 × 1001,15 × 100 = 4600115 = 40
Следовательно, у Моники есть 40 кусков ткани длиной 1,15 м каждая. .
Страница № 50:
Вопрос 15:
Г-н Сони купил несколько мешков с цементом, каждый весом по 49 штук.8 кг. Если общий вес всех мешков составляет 1792,8 кг, сколько мешков он купил?
Ответ:
Общий вес всех мешков с цементом = 1792,8 кг
Вес каждого мешка = 49,8 кг
Количество мешков = Общий вес Вес каждого мешка
= 1792,849,8 = 17
8 = 36
Таким образом, г-н Сони купил 36 мешков с цементом. цемент.
Страница № 50:
Вопрос 16:
Сколько штук фанеры по 0.Толщина 35 см, требуется для изготовления сваи высотой 1,89 м?
Ответ:
Толщина куска фанеры = 1,89 м = 189 см
Толщина одного куска фанеры = 0,35 см
∴ Необходимое количество штук фанеры = 1890,35 = 189 × 1000,35 × 100 = 18
= 540
Отсюда 540 шт. фанеры потребуются для изготовления стопки высотой 1,89 м.
Страница № 50:
Вопрос 17:
Произведение двух десятичных знаков равно 261.36. Если один из них 17,6, найдите другой.
Ответ:
Произведение заданных десятичных знаков = 261,36
Одно десятичное число = 17,6
Другое десятичное число = 261,36 ÷ 17,6
= 261,3617,6 = 261,36 × 1017,6 × 10 = 2613,6176
= 14,85
Следовательно, второе десятичное число равно 14,85.
Страница № 50:
Вопрос 1:
Отметьте (✓) против правильного ответа
.06 =?
(a) 35
(b) 350
(c) 3500
(d) ни один из этих
Ответ:
(б) 350
0,06 = 6100 = 350
Страница № 50:
Вопрос 2:
Отметить (✓) против правильного ответа
1,04 =?
(a) 115
(b) 125
(c) 1125
(d) ни один из этих
Ответ:
(в) 1125
1.04 = 104100 = 2625 = 1125
Страница № 50:
Вопрос 3:
Отметить (✓) против правильного ответа
2225 =?
(a) 2,8
(b) 2,08
(c) 2,008
(d) ни один из этих
Ответ:
(б) 2,08
2225 = 5225
При делении получаем:
∴ 2225 = 5225 = 2.08
Страница № 50:
Вопрос 4:
Отметить (✓) против правильного ответа
6 см =?
(a) 0,006 км
(b) 0,0006 км
(c) 0,00006 км
(d) ни один из этих
Ответ:
(c) 0,00006 км
6 см = 6100 м = 0,06 м
0,06 м = 0,061000 км = 0.00006 км
∴ 6 см = 0,00006 км
Страница № 50:
Вопрос 5:
Отметить (✓) против правильного ответа
70 г =?
(a) 0,7 кг
(b) 0,07 кг
(c) 0,007 кг
(d) ни один из этих
Ответ:
(б) 0,07 кг
70 г = 701000 кг = 7100 кг
= 0.07 кг
∴ 70 г = 0,07 кг
Страница № 50:
Вопрос 6:
Отметить (✓) против правильного ответа
5 кг 6 г =?
(а) 5,0006 кг
(б) 5,06 кг
(в) 5,006 кг
(г) 5,6 кг
Ответ:
(c) 5,006 кг
5 кг 6 г = (5 × 1000) г + 6 г = 5006 г
= 50061000 кг = 5.006 кг
∴ 5 кг 6 г = 5,006 кг
Страница № 50:
Вопрос 7:
Отметить (✓) против правильного ответа
2 км 5 м =?
(а) 2,5 км
(б) 2,05 км
(в) 2,005 км
(г) 2,0005 км
Ответ:
(c) 2,005 км
2 км 5 м = (2 × 1000) м + 5 м = 2005 м
= 20051000 км = 2.005 км
∴ 2 км 5 м = 2,005 км
Страница № 50:
Вопрос 8:
Отметить (✓) против правильного ответа
(1,007 — 0,7) =?
(а) 1
(б) 0,37
(в) 0,307
(г) ни один из этих
Ответ:
(c) 0,307
Преобразуя заданные десятичные дроби в аналогичные десятичные, получаем:
1.007 и 0,700
Записывая их в виде столбцов с большим столбцом вверху и вычитая, получаем:
Следовательно, требуемое число равно 0,307.
Страница № 50:
Вопрос 9:
Отметьте (✓) против правильного ответа
Что нужно вычесть из .1, чтобы получить 0,03?
(a) .7
(b) .07
(c) .007
(d) ни один из этих
Ответ:
(б).07
У нас есть:
0,1 — x = 0,03
⇒ x = 0,1 — 0,03
Преобразуя данные десятичные дроби в аналогичные десятичные, мы получаем:
0,10 и 0,03
Записывая их в виде столбцов с большим единица вверху и вычитая, получаем:
∴ x = 0,07
Следовательно, требуемое число равно 0,07.
Страница № 51:
Вопрос 10:
Отметить (✓) против правильного ответа
Что нужно добавить к 3.07, чтобы получить 3,5?
(а) .57
(б) .34
(в) .43
(г) .02
Ответ:
(c) .43
У нас есть:
3,07 + x = 3,5
⇒ x = 3,5 — 3,07
Преобразуя данные десятичные дроби в аналогичные десятичные, мы получаем:
3,07 и 3,50
Записывая их в виде столбца с большее сверху и вычитая, получаем:
∴ x = 0,43
Следовательно, 0,43 следует добавить к 3.07, чтобы получить 3.5.
Страница № 51:
Вопрос 11:
Отметить (✓) против правильного ответа
0,23 × 0,3 =?
(a) 0,69
(b) 6,9
(c) 0,069
(d) ни один из этих
Ответ:
(c) 0,069
Сначала мы умножим 23 на 3.
, т.е. 23 × 3 = 69
Сумма десятичных знаков в заданных десятичных разрядах = (2 + 1) = 3
∴ 0.23 × 0,3 = 0,069 (3 знака после запятой)
Страница № 51:
Вопрос 12:
Отметить (✓) против правильного ответа
0,02 × 30 =?
(a) 6
(b) 0,6
(c) 0,06
(d) ни один из этих
Ответ:
(б) 0,6
Имеем:
2 × 30 = 60
∴ 0,02 × 30 = 0.60 (2 знака после запятой)
= 0,6
Страница № 51:
Вопрос 13:
Отметить (✓) против правильного ответа
0,25 × 0,8 =?
(а) 0,02
(б) 0,2
(в) 0,002
(г) 2
Ответ:
(b) 0,2
Сначала умножим 25 на 8.
∴ 25 × 8 = 200
Сумма десятичных знаков в заданных десятичных разрядах = (2 + 1) = 3
∴ 0,25 × 0,8 = 0,200 [3 десятичных знака]
= 0,2
Страница № 51:
Вопрос 14:
Отметить (✓) против правильного ответа
0,4 × 0,4 × 0,4 =?
(a) 6.4
(b) .64
(c) .064
(d) ни один из этих
Ответ:
(в).064
Сначала мы найдем произведение 4 × 4 × 4 = 64
Сумма десятичных знаков в заданных десятичных разрядах = (1 + 1 + 1) = 3
∴ 0,4 × 0,4 × 0,4 = 0,064 (3 знака после запятой. )
Страница № 51:
Вопрос 15:
Отметить (✓) против правильного ответа
1,1 × 0,1 × 0,01 =?
(a) .011
(b) .0011
(c) .11
(d) ни один из этих
Ответ:
(б).0011
Сначала найдем произведение 11 × 1 × 1.
Сумма десятичных знаков в заданных десятичных разрядах = (1 + 1 + 2) = 4
∴ 1,1 × 0,1 × 0,01 = 0,0011 (4 десятичных знака)
Страница № 51:
Вопрос 16:
Отметить (✓) против правильного ответа
2,08 ÷ (0,16) =?
(a) 13
(b) .13
(c) 1,3
(d) ни один из этих
Ответ:
(а) 13
2.08 ÷ 0,16 = 2,080,16 = 2,08 × 1000,16 × 100 = 20816 = 13
Страница № 51:
Вопрос 17:
Отметить (✓) против правильного ответа
1,02 ÷ 6 =?
(а) 1,7
(б) 0,17
(в) 0,017
(г) ни один из этих
Ответ:
(б) 0,17
1,02 ÷ 6 = 1,026 = 1,02 × 1006 × 100 = 1026 × 100 = 17100 = 0.17
Страница № 51:
Вопрос 18:
Отметить (✓) против правильного ответа
30,94 ÷ 0,7 =?
(а) 44,2
(б) 4,42
(в) 442
(г) 0,442
Ответ:
(а) 44,2
30,94 ÷ 0,7 = 30,9 40,7 = 30,94 × 1000,7 × 100 = 309470 = 44,2
Страница № 51:
Вопрос 19:
Отметьте (✓) против правильного ответа
2.73 ÷ 1,3 =?
(a) 21
(b) 2,1
(c) 0,21
(d) ни один из этих
Ответ:
(б) 2,1
2,73 ÷ 1,3 = 2,731,3 = 2,73 × 1001,3 × 100 = 27313 × 10 = 2110 = 2,1
Страница № 51:
Вопрос 20:
Отметить (✓) против правильного ответа
89,1 ÷ 2,2 =?
(а) 40.5
(б) 4,05
(в) 41
(г) 41,5
Ответ:
(а) 40,5
89,1 ÷ 2,2 = 89,12,2 = 89,1 × 102,2 × 10 = 89122 = 40,5
Страница № 51:
Вопрос 21:
Отметить (✓) против правильного ответа
0,5 × 0,05 =?
(а) 0,25
(б) 2,5
(в) 0,025
(г) ни один из этих
Ответ:
(в) 0.025
Сначала мы умножим 5 на 5.
т.е. 5 × 5 = 25
Сумма десятичных знаков в заданных десятичных разрядах = (1 + 2) = 3
∴ 0,5 × 0,05 = 0,025 (3 десятичных знака)
Страница № 53:
Вопрос 1:
Если стоимость ручки составляет 32,50 рупий, найдите стоимость 24 таких ручек.
Ответ:
Стоимость 1 ручки = 32,50 рупий
∴ Стоимость 24 таких ручек = (32,50 рупий)50 × 24)
= 780
рупий Следовательно, стоимость 24 ручек составляет 780 рупий.
Страница № 53:
Вопрос 2:
Автобус может преодолеть 64,5 км за час. Какое расстояние он может преодолеть за 18 часов?
Ответ:
Расстояние, пройденное автобусом за 1 час = 64,5 км
∴ Пройденное расстояние за 18 часов = (64,5 × 18) км
= 1161 км
Таким образом, автобус может преодолеть расстояние в 1161 км за 18 часов.
Страница № 53:
Вопрос 3:
Найдите произведение 0,68 × 6,5 × 0,04.
Ответ:
Сначала мы найдем произведение 68 × 65 × 4.
Теперь 68 × 65 × 4 = 4420 × 4 = 17680
Сумма десятичных знаков в заданных десятичных разрядах = (2 + 1 + 2) = 5
Итак, у продукта пять знаков после запятой.
∴ 0,68 × 6,5 × 0,04 = 0.17680
= 0,1768
Страница № 53:
Вопрос 4:
Каждый мешок с цементом весит 48,5 кг. Сколько таких сумок будут весить 2231 кг?
Ответ:
Общий вес всех мешков = 2231 кг
Вес каждого мешка = 48,5 кг
Количество мешков = Общий вес Вес каждого мешка
= 223148.5 кг
= 2231 × 1048,5 × 10 = 22310485 = 46
Следовательно, 46 мешков цемента будут весить 2231 кг.
Страница № 53:
Вопрос 5:
Разделить:
(i) 0,196 на 1,4
(ii) 39,168 на 1,2
(iii) 0,228 на 0,38
Ответ:
(i) 0,196 ÷ 1,4 = 0,1961,4 = 0,196 × 101,4 × 10 = 1,9614 = 0.14
(ii) 39,168 ÷ 1,2 = 39,1681,2 = 39,168 × 101,2 × 10 = 391,6812 = 32,64
(iii) 0,228 ÷ 0,38 = 0,2280,38 = 0,228 × 1000,38 × 100 = 22,838 = 0,6
Страница № 53:
Вопрос 6:
Произведение двух десятичных знаков равно 1,824. Если один из них равен 0,64, найдите другой.
Ответ:
Произведение заданных десятичных знаков = 1.824
Одно десятичное число = 0,64
Другое десятичное число = 1,824 ÷ 0,64
= 1,8240,64 = 1,824 × 1000,64 × 100 = 182,464 = 2,85
Следовательно, второе десятичное число равно 2,85.
Страница № 53:
Вопрос 7:
Сколько кусков фанеры толщиной 0,45 см необходимо для изготовления стопки высотой 2,43 м?
Ответ:
Толщина ворса фанеры = 2.43 м = 2,43 × 100 см = 243 см
Толщина одного куска фанеры = 0,45 см
∴ Необходимое количество кусков фанеры = 2430,45 = 243 × 1000,45 × 100 = 2430045 = 540
Отсюда необходимое количество штук фанеры 540.
Страница № 53:
Вопрос 8:
Каждая сторона многоугольника имеет длину 3,8 см и периметр 22,8 см. Сколько сторон у многоугольника?
Ответ:
Пусть количество сторон многоугольника равно n .
Длина каждой стороны многоугольника = 3,8 см
∴ Периметр многоугольника = (3,8 × n ) см
Но при условии, что его периметр равен 22,8 см.
∴ (3,8 × n ) см = 22,8 см
⇒ n = 22,83,8 = 22838 = 6
Следовательно, данный многоугольник имеет шесть сторон.
Страница № 53:
Вопрос 9:
Отметить (✓) против правильного ответа
2125 =?
(а) 2.4
(b) 2,04
(c) 2,004
(d) ни один из этих
Ответ:
(б) 2,04
2125 = 5125 = 2,04
Страница № 53:
Вопрос 10:
Отметить (✓) против правильного ответа
1,008 =?
(a) 1225
(b) 11125
(c) 12125
(d) ни один из этих
Ответ:
б 11125
1.008 = 1,008 × 10001 × 1000 = 10081000 = 1008 ÷ 41000 ÷ 4 = 126125 = 11125
Страница № 53:
Вопрос 11:
Отметить (✓) против правильного ответа
2 кг 5 г =?
(a) 2,5 кг
(b) 2,05 кг
(c) 2,005 кг
(d) ни один из этих
Ответ:
(c) 2,005 кг
2 кг 5 г = (2 × 1000) г + 5 г = (2005) г
= 20051000 кг = 2.005 кг
Страница № 53:
Вопрос 12:
Отметить (✓) против правильного ответа
0,12 ÷ 0,15 =?
(а) 0,8
(б) 0,08
(в) 0,008
(г) ни один из этих
Ответ:
(б) 0,08
Имеем:
0,012 ÷ 0,15 = 0,0120,15 = 0,012 × 1000,15 × 100 = 1,215 = 0.08
Страница № 53:
Вопрос 13:
Отметить (✓) против правильного ответа
1,1 × 0,1 × 0,01 =?
(a) .11
(b) .011
(c) .0011
(d) ни один из этих
Ответ:
(c) .0011
Сначала мы найдем произведение 11 × 1 × 1.
то есть, 11 × 1 × 1 = 11 × 1 = 11
Сумма десятичных знаков в заданных десятичных разрядах = (1 + 1 + 2 ) = 4
∴ 1.1 × 0,1 × 0,01 = 0,0011 [4 десятичных знака]
Страница № 53:
Вопрос 14:
Отметить (✓) против правильного ответа
4,669 ÷ 2,3 =?
(a) 2,3
(b) 2,03
(c) 2,003
(d) ни один из этих
Ответ:
(б) 2,03
4,669 ÷ 2,3 = 4,6692,3 = 4.669 × 102,3 × 10 = 46,6923 = 2,03
Страница № 53:
Вопрос 15:
Отметить (✓) против правильного ответа
Что нужно добавить к 2.06, чтобы получить 3.1?
(a) 1,4
(b) 1,24
(c) 1,04
(d) ни один из этих
Ответ:
Вариант (c) правильный.
Пусть добавляемое число будет x.
Имеем:
2,06 + x = 3,1
⇒ x = 3,1 — 2,06
Преобразуя данные десятичные дроби в аналогичные десятичные, получаем:
2,06 и 3,10
Таким образом, необходимое число = (3,10 — 2,06) = 1.04
Следовательно, 1.04 нужно добавить к 2.06, чтобы получить 3.1.
Страница № 53:
Вопрос 16:
Отметить (✓) против правильного ответа
Из чего следует вычесть.1, чтобы получить 0,04?
(a) 0,6
(b) 0,06
(c) 0,006
(d) ни один из этих
Ответ:
(b) 0,06
Имеем:
0,1 — x = 0,04
⇒ x = 0,1 — 0,04
Преобразуя данные десятичные дроби в аналогичные десятичные, получаем:
0,10 и 0,04
Таким образом, необходимое число = (0,10 — 0,04) = 0,06
Следовательно, из 0,1 следует вычесть 0,06, чтобы получить 0,04.
Страница № 53:
Вопрос 17:
Заполните пустые поля.
(i) 1,001 ÷ 14 = ……
(ii) 204 ÷ 0,17 = ……
(iii) 0,47 × 5,3 = ……
(iv) 0,023 × 0,03 = ……
(v) (0,7) 2 = ……
(vi) (0,05) 3 = ……
Ответ:
(i) 1,001 ÷ 14 = 0,0715
Объяснение: 1,00114 = 0,0715
(ii) 204 ÷ 0,17 = 1200
Пояснение: 2040.17 = 204 × 1000,17 × 100 = 204 × 10017 = 12 × 100 = 1200
(iii) 0,47 × 5,3 = 2,491
Пояснение: Сначала мы умножим 47 на 53.
∴ 47 × 53 = 2491
Сумма десятичных знаков в заданных десятичных разрядах = (2 + 1) = 3
∴ 0,47 × 5,3 = 2,491
(iv) (0,7) 2 = 0,49
Пояснение: (0,7) 2 = 0,7 × 0,7
Сначала найдем произведение 0.7 × 0,7.
Теперь 7 × 7 = 49
Сумма десятичных знаков в заданных десятичных разрядах = (1 + 1) = 2
Итак, произведение должно иметь два десятичных знака.
∴ (0,7) 2 = 0,7 × 0,7 = 0,49
(v) (0,05) 3 = 0,000125
Пояснение: Сначала найдем произведение 0,05 × 0,05 × 0,05.
Итак, 5 × 5 × 5 = 125
Сумма десятичных знаков в заданных десятичных разрядах = (2 + 2 + 2) = 6
Итак, произведение должно иметь шесть десятичных знаков.
∴ (0,05) 3 = 0,05 × 0,05 × 0,05 = 0,000125
Страница № 53:
Вопрос 18:
Напишите «T» для истинного и «F» для ложного
(i) 0,5 × 0,05 = 0,25
(ii) 0,25 × 0,8 = 0,2
(iii) 0,35 ÷ 0,7 = 0,5
(iv). 4 × 0,4 × 0,4 = 0,64
(v) 6 см = 0,06 м
Ответ:
(i) T
Имеем:
0.5 × 0,05
Теперь 5 × 5 = 25
Сумма десятичных знаков в заданных десятичных разрядах = (1 + 2) = 3
∴ 0,5 × 0,05 = 0,025
(ii) T
Мы имеем:
0,25 × 0,8
Теперь 25 × 8 = 200
Сумма десятичных знаков в заданных десятичных разрядах = (2 +1) = 3
∴ 0,25 × 0,8 = 0,200 = 0,2
(iii) T
Мы имеем:
0,35 ÷ 0,7 = 0,350. 7 = 0,35 × 100,7 × 10 = 3,57 = 0,5
(iv) F
Мы имеем:
0,4 × 0,4 × 0,4
Итак, 4 × 4 × 4 = 64
Сумма десятичных разрядов в заданных десятичных разрядах = (1 + 1 +1) = 3
∴ 0.4 × 0,4 × 0,4 = 0,064
(v) T
6 см = 6100 м = 0,06 м
Просмотреть решения NCERT для всех глав класса 7
Совместимые числа для третьего класса по математике
В третьем классе учителя в основном подчеркивают совместимые числа в сложении и вычитании. Совместимые числа — это числа, с которыми легко работать мысленно, например, части 10. Учащимся, которые запоминают 8 + 2 = 10, легче понять, что 10 — 2 = 8.К третьему классу ученики также могут быстро ответить на 80 + 20 или 100-20, распознавая совместимые числа.
TL; DR (слишком долго; не читал)
Совместимые числа позволяют учащимся быстро выполнять в уме математические вычисления и служат строительными блоками для абстрактных рассуждений. Учащиеся начинают развивать этот навык в детском саду с частей простых чисел и со временем добавляют другие знания, включая части от 10, части от 20 и контрольные числа.
Дружественные числа
Совместимые числа — это «дружественные числа», которые позволяют быстрее решать проблемы.К пятому классу ученики могут найти, какие дружественные числа использовать для оценки ответа на такие вопросы, как 2 012 ÷ 98. Те, кто понимает оценку, используют 2 000 ÷ 100 для приблизительного ответа. Когда ученик понимает части каждого числа от 1 до 20, это знание позже становится дружелюбным помощником, когда ему приходится решать более сложные вопросы, такие как 33 + 16.
Игра в поиск совместимых чисел
Навык определения совместимых чисел начинается в детском саду. или раньше, когда дети выучивают части чисел от 3 (1 + 1+ 1 или 1 + 2) до 10.Распространенный способ выучить совместимые части маленьких чисел в детском саду и в первом классе — сыграть в «игру в прятки». Показав шесть кубиков, игрок держит их за спиной, достает два и спрашивает другого игрока, сколько из них «спрятано».
Совместимые числа для контрольных тестов
Контрольные числа — это еще одна форма совместимых чисел, которую следует знать третьеклассникам. Эти числа заканчиваются на 0 или 5 и значительно упрощают процесс оценки; например, учащиеся могут использовать 25 + 75, чтобы приблизительно получить сумму 27 + 73.

 Уровень 4. Рабочая тетрадь» от Kumon
Уровень 4. Рабочая тетрадь» от Kumon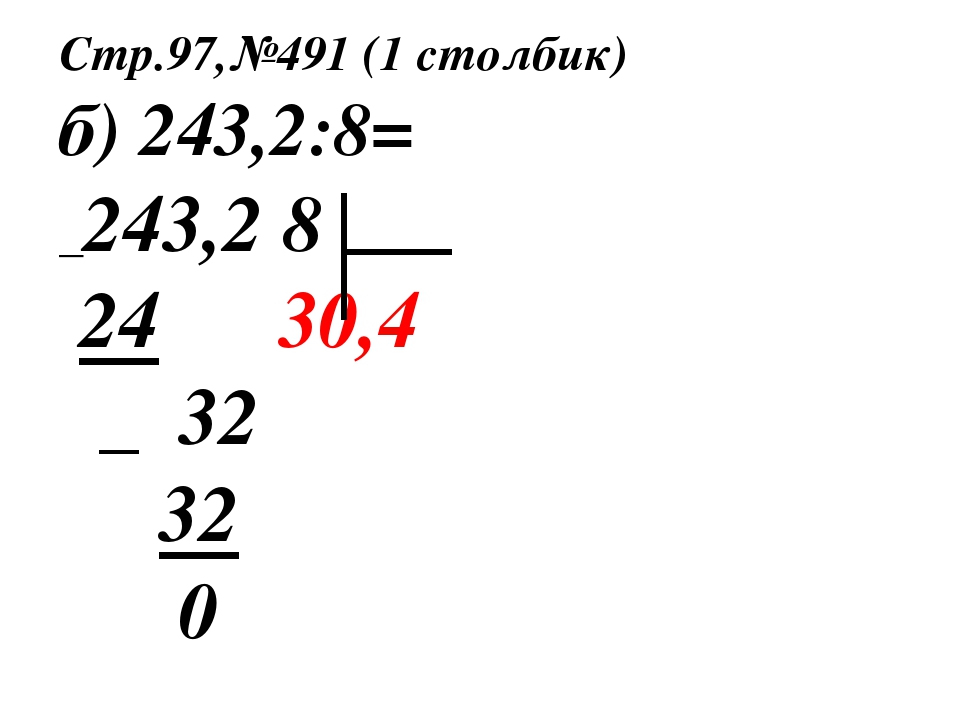 Сколько раз делитель может содержаться в делимом?
Сколько раз делитель может содержаться в делимом?