Логические задачи для тренировки — Школа 52, Владивосток
Страница 1 из 2
Задачи для подготовки к самостоятельной работе.
1. Министры иностранных дел России, США и Китая обсудили за закрытыми дверями проекты соглашения о полном разоружении, представленные каждой из стран. Отвечая затем на вопрос журналистов: «Чей именно проект был принят?», министры дали такие ответы:
Россия — «Проект не наш, проект не США»;
США — «Проект не России, проект Китая»;
Китай — «Проект не наш, проект России».
Один из них (самый откровенный) оба раза говорил правду; второй (самый скрытный) оба раза говорил неправду, третий (осторожный) один раз сказал правду, а другой раз — неправду.
Определите, представителями каких стран являются откровенный, скрытный и осторожный министры.
2. В 8, 9 и 10-ом классах учатся три товарища: Наиль, Зиннур и Альберт. Один из них занимается в кружке информатики, другой -радиолюбитель, третий – авиамоделист. Скажите, в каком классе учится и в каком кружке занимается каждый из них, если известно, что:
8-й класс посетил лесхоз, 9-й – кондитерскую фабрику,
10-й класс — автозавод;
во время посещения лесхоза Зиннур опасался, как бы не разбить лежавшую в кармане радиолампу;
Наиль ушёл на стадион один, так как его товарищ был занят налаживанием своей модели самолёта;
4) товарищ авиамоделиста очень заинтересовался конвейером на автозаводе.
3. Однажды в международном лагере отдыха за круглым столом оказалось пятеро парней из Москвы, Санкт-Петербурга, Новгорода, Казани и Уфы. Их имена: Саша, Никита, Руслан, Петя и Миша.
Москвич сидел между уфимцем и Мишей, санкт-петербужец – между Сашей и Никитой, а напротив него сидели казанец и Руслан. Петя никогда не был в Санкт-Петербурге, а Саша не бывал в Москве и Уфе. Уфимец с Никитой регулярно переписываются.
В каком городе живёт каждый из ребят?
4. Лауреатом женского поэтического конкурса стали пять поэтесс.
1-е место заняла мисс Мартин. Бетти Мун не писала стихотворение «Сорока». Своё стихотворение Мэри сочинила в мае. «Муза» была написана в сентябре. Джастина Моран написала «Зрелый день». Стихотворение «Человек» принадлежит перу Кэт. «Муссон» был создан Сюзан в марте. Мисс Мегге написала своё стихотворение в апреле. Фамилия Мэри не Мульдон, а одно из стихотворений написано в октябре.
Бетти Мун не писала стихотворение «Сорока». Своё стихотворение Мэри сочинила в мае. «Муза» была написана в сентябре. Джастина Моран написала «Зрелый день». Стихотворение «Человек» принадлежит перу Кэт. «Муссон» был создан Сюзан в марте. Мисс Мегге написала своё стихотворение в апреле. Фамилия Мэри не Мульдон, а одно из стихотворений написано в октябре.
Назовите имя и фамилию каждой поэтессы, название стихотворения, которое она написала, а также время его создания.
5. Три свидетеля дорожного происшествия сообщили сведения о скрывшемся нарушителе. Боб утверждает, что тот был на синем «Рено». Джон сказал, что нарушитель ехал на черной «Тойоте», а Сэм сказал, что машина была точно не синяя, и, по всей видимости, это был «Форд». Когда удалось отыскать машину, выяснилось, что каждый из свидетелей точно определил только один из параметров автомобиля, а в другом ошибся. Машина какой марки и какого цвета была у нарушителя?
6. Внимание Андрея, Дениса и Марата привлек промчавшийся мимо них автомобиль.
— Это английская машина марки «Феррари» — сказал Андрей.
— Нет, машина итальянская марки «Понтиак», — возразил Денис.
— Это «Сааб», и сделан он не в Англии, — сказал Марат.
Оказавшийся рядом знаток автомобилей сказал, что каждый из них прав только в одном из двух высказанных предположений.
Какой же марки этот автомобиль и в какой стране изготовлен?
7. Трое друзей, болельщиков автогонок «Формула-1», спорили о результате предстоящего этапа гонок.
— Вот увидишь, Шумахер не придет первым, — сказал Джон. — Первым будет Хилл.
— Да нет же, победителем будет, как всегда, Шумахер! — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?
8 Три дочери писательницы Дорис Кей — Джуди, Айрис и Линда тоже очень талантливы. Они приобрели известность в разных видах искусств — пении, балете и кино. Все они живут в разных городах, поэтому Дорис часто звонит им в Париж, Рим и Чикаго, Известно, что:
Они приобрели известность в разных видах искусств — пении, балете и кино. Все они живут в разных городах, поэтому Дорис часто звонит им в Париж, Рим и Чикаго, Известно, что:
1) Джуди живет не в Париже, а Линда — не в Риме;
2) Парижанка не снимается в кино;
З) Та, кто живет в Риме, певица;
4) Линда равнодушна к балету.
Где живет Айрис и какова ее профессия?
9 В симфонический оркестр приняли на работу трех музыкантов — Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе. Известно, что:
1) Смит — самый высокий;
2) играющий на скрипке меньше ростом играющего на флейте;
З) играющие на скрипке и флейте и Браун любят пиццу;
4) когда между альтистом и трубачом возникает ссора, Смит мирит их;
5) Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
10. После традиционного вечера встречи с бывшими выпускниками школы в стенгазете появилась заметка о трех наших бывших учениках. В этой заметке было написано, что Иван, Андрей и Борис стали учителями. Теперь они преподают разные дисциплины: один — математику, второй — физику, а третий — химию. Живут они тоже в разных городах: Минске, Витебске и Харькове. В заметке было еще написано, что первоначальные их планы осуществились не полностью: Иван работает не в Минске, Андрей — не в Витебске; житель Минска преподает не математику, Андрей преподает не физику. Повезло только жителю Витебска: он преподает любимую им химию. Кто где живет и что преподает?
11. В педагогическом институте Казакова, Андреева, Покатина, Галеев, Шакиров и Веселов преподают философию, математику, английский язык, французский язык, немецкий язык, историю.
Преподаватель немецкого языка и преподаватель математики в студенческие годы занимались художественной гимнастикой.
Шакиров старше Веселова, но стаж работы у него меньше, чем у преподавателя философии.
Будучи студентками, Казакова и Андреева учились вместе в одном университете. Все остальные окончили педагогический институт.
Все остальные окончили педагогический институт.
Веселов – отец преподавателя французского языка.
Преподаватель английского языка – самый старший из всех по возрасту и по стажу работы. Он работает в этом институте с тех пор, как окончил его. Преподаватели математики и истории – его бывшие студенты.
Казакова старше преподавателя немецкого языка.
Кто какой предмет преподаёт?
12. Одиннадцать ребят: Александр, Борис, Василий, Георгий, Дмитрий, Евгений, Захар, Иван, Кирилл, Леонид и Михаил – учатся все в разных классах одной школы.
Старший брат Дмитрия оканчивает 7-й класс, а младший брат Евгения учится в 5-ом классе. Александр старше Кирилла на один класс, Леонид старше Евгения на два класса, а самый старший из мальчиков Михаил. Борис помогает в учёбе Евгению, Дмитрий – Ивану, Георгий – Александру.
Иван при окончании 4-го класса получил похвальную грамоту.
3) Борис – вожатый в 5-ом классе, а Василий – в 4-ом классе.
4) Александр, Кирилл и шестиклассник занимаются в гимнастической секции, а одновременно с ними тренируются баскетболисты, среди которых всегда Борис, Евгений и восьмиклассник.
5) Александр и семиклассник живут на улице Лесной, Георгий и пятиклассник – на улице Красивой, Дмитрий, первоклассник и восьмиклассник – на Садовой, а Кирилл и десятиклассник – на Солнечной.
Кто из них в каком классе учится?
13. Три одноклассника — Влад, Тимур и Юра, встретились спустя 10 лет после окончания школы.
Выяснилось, что один из них стал врачом, другой физиком, а третий юристом.
Один полюбил туризм, другой бег, страсть третьего — регби.
Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист.
Врач сказал, что он разделяет увлечение коллеги.
Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Определите, кто чем любит заниматься в свободное время и у кого какая профессия.
Математика.
 Логические задачи.
Логические задачи.
Методы решения логических задач
Пример. Имеются два сосуда — трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 1, 2, 3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду.
Решение. В рассматриваемой задаче стороны параллелограмма должны иметь длины 3 и 5 единиц. По горизонтали будем откладывать количество воды в литрах в 5-литровом сосуде, а по вертикали – в 3-литровом сосуде. На всем параллелограмме нанесена сетка из одинаковых равносторонних треугольников.
Метод рассуждений
Метод таблиц
Метод кругов Эйлера
Идея метода: состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи.
Идея метода: оформлять результаты логических рассуждений в виде таблицы
Идея метода : определить количество элементов, обладающих общими свойствами.
Пример. Владимир, Игорь и Сергей преподают математику, физику и литературу, а живут они в Рязани, Туле и Ярославле. Известно также, что Владимир живет не в Рязани, Игорь живет не в Туле, рязанец – не физик, Игорь – не математик, туляк преподает литературу. Кто где живет и что преподает?
Решение. Составим таблицу 3 х 3, выбрав основными параметрами имена и города. Тогда, учитывая, что рязанец – не физик, а туляк – литератор, получаем, что рязанец – математик, а житель Ярославля – физик.
Ответ: Сергей живет в Рязани – он математик, Владимир живет в Туле – он преподает литературу, Игорь живет в Ярославле – он физик.
Пример : Коренными жителями острова являются рыцари света и рыцари тьмы. Рыцари света всегда говорят правду, а рыцари тьмы всегда лгут. Рыцарь А говорит: «Я – лжец». Является ли он уроженцем острова рыцарей света и рыцарей тьмы?
Рыцари света всегда говорят правду, а рыцари тьмы всегда лгут. Рыцарь А говорит: «Я – лжец». Является ли он уроженцем острова рыцарей света и рыцарей тьмы?
Решение:
Пусть А сказал правду, значит, он – рыцарь тьмы. Но он не может быть рыцарем тьмы, так как рыцари тьмы всегда лгут. Пусть А сказал ложь, тогда он рыцарь света. Но рыцари света говорят правду. Опять не получается. Значит, А не может быть уроженцем острова рыцарей света и рыцарей тьмы.
Ответ: А не является уроженцем острова.
Пример : На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?
Решение: По условию задачи нарисуем чертёж.Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно,
26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только Рон.
Ответ: 8 книг прочитал только Рон .
Метод графов
Идея метода: объекты представляются в графе вершинами Связи между объектами представляются, если связь однонаправленная (обозначается на схеме пунктирными линиями) или ребрами, если связь между объектами двусторонняя (обозначается сплошными линиями).
Пример : Атос, Портос и Арамис в соревновании по фехтованию заняли три первых места. Какое место занял каждый из них, если Портос занял не второе и не третье место, а Арамис – не третье?
Решение : Учитывая условия задачи, сразу делаем вывод, что Портос занял первое место. Значит, Арамис занял второе место, и Атос – третье место. Решение задачи показано на чертеже:
Ответ: Арамис – второе место; Атос – третье место; Портос – первое место.
Логические задачи с ответами 3 класс ( задачи на логику по математике)
Дата: 22 декабря 2013 Автор: Алина Рубрика: Викторины,Школа
Логические задачи для 3 класса
составленные в виде вопросов и ответов
Задача 1. Ребята измеряли шагами длину игровой площадки. У Лизы получилось 25 шагов, у Полины – 27, у Максима – 22, а у Юры – 24. У кого из ребят самый короткий шаг? (У Полины)
Задача 2. На часах было 11:45, когда начался мультфильм. Он длился 50 минут. Точно в середине просмотра пришла мама и позвала обедать. Какое время показывали часы в этот момент? (12:10)
Задача 3. Четыре девочки ели конфеты. Аня съела больше, чем Юля. Ира – больше, чем Света, но меньше, чем Юля. Расставь имена девочек в порядке возрастания количества съеденных конфет. (Света, Ира, Юля, Аня)
Задача 4. У сороконожки 90 ножек. Она купила 13 пар сапожек. Но при этом 16 ног остались босыми. Сколько пар старых сапожек было на сороконожке до покупки новых сапожек? (24)
Задача 5. Петя и Коля живут в одном многоэтажном доме. Квартира Коли на 12 этажей выше, чем Пети. Вечером Петя поднимался по лестнице к Коле. Когда он прошёл половину пути, то оказался на 8 этаже. На каких этажах квартиры мальчиков? (П-2, К-14)
Задача 6. Из 64 маленьких кубиков составили большой куб. Синей краской покрасили пять граней большого куба. Назови количество маленьких кубиков с тремя синими гранями. (4 – по углам)
Задача 7. На пароме помещается или 6 грузовиков, или 10 легковушек. В четверг паром, полностью загруженный, 5 раз пересек реку и переправил 42 машины. Сколько было среди них грузовиков? (12)
Задача 8. Речь пойдёт про единицы времени. Что можно узнать, данным произведением 60 х 60 х 24 х 7? (Количество секунд в неделю)
Задача 9. Брату и сестре 2 года назад вместе было 15 лет. Сейчас сестре 13 лет. Сколько должно пройти лет, чтобы брату исполнилось 9 лет? (3 года)
Сейчас сестре 13 лет. Сколько должно пройти лет, чтобы брату исполнилось 9 лет? (3 года)
Задача 10. В гости к Игорю пришли друзья. Сколько их было, если каждый из них сложил из даты своего рождения число и номер месяца и получил 35? Причём даты рождения у всех гостей разные. (8)
Автор: Анна Круглова
Копилка викторин для школьников
Оцените статью: Поделитесь с друзьями!
Метки:
Сборник математических и логических задач для 1–4 классов. Электронная книга
Описание
В книге представлены 10 готовых комплектов заданий, разработанных под руководством Марины Анатольевны Поповой – педагога высшей квалификационной категории с более чем 20-летним стажем, неоднократным победителем конкурсов профессионального мастерства педагогов, имеющей награды комитета образования администрации Псковской области.
Задания можно использовать для проведения олимпиад и других занятий по решению логических задач и задач на внимательность для учеников 1–4 класса в качестве внеурочной деятельности педагога. Также они могут быть использованы в качестве подготовки к участию в районных и городских олимпиадах, для проведения контрольных, проверочных работ, а также для тестирования учеников. Также задания годятся для самостоятельной подготовки учеников в домашних условиях.
Книга будет интересна педагогам, руководителям кружков и факультативов, а также активным родителям.
Задания представлены в виде теста – 10 вопросов и по 5 вариантов ответов к каждому вопросу. Необходимо выбрать и указать только 1 правильный ответ в каждом вопросе.
Данная форма тестирования широко применяется при оценке знаний учеников и, с учётом развития компьютерных технологий в обучении, будет применяться ещё шире.
В конце книги приведены ответы, позволяющие легко проверить работы.
Задания предложены в форме, которая позволяет раздать готовые материалы для работы в классе или в качестве домашнего задания.
Содержание издания
1. Веселые олимпиадные и развивающие задания по математике для 1 класса.
Веселые олимпиадные и развивающие задания по математике для 1 класса.
2. Логические задания по математике для 1 класса.
3. Сказочные олимпиадные задания по математике для 1 класса.
4. Логические и развивающие задания по математике для 2 класса.
5. Логические задания по математике для 2 класса.
6. Развивающие задания по математике для 3 класса.
7. Олимпиадные задания с величинами по математике для 3 класса.
8. Исторические задачи по математике для 3 класса.
9. Исторические развивающие задания по математике для 4 класса.
10. Логические задания по математике для 4 класса.
Технические характеристики
Книга представлена в электронном виде в формате .pdf. Данный тип файлов открывают все браузеры и электронные книги. Также можно использовать программу Acrobat Reader или аналог.
Оплата и доставка
– Методы оплаты
Вы можете выбрать наиболее удобный для Вас способ оплаты. Интернет-магазин «Интеграл» предлагает Вам следующие варианты оплаты:
- Банковские карты.
- Интернет-банкинг – онлайн платежи.
- Терминалы оплаты.
- Банковские переводы.
- Электронные деньги.
Более подробнее о методах оплаты.
– Доставка
Электронная доставка бесплатная. Ссылка на скачивание высылается на e-mail заказчика после оплаты.
На текущий момент мы не пересылаем покупателям коробочные версии или программы, записанные на CD или DVD носителях.
По всем вопросам обращайтесь на наш контактный e-mail: [email protected].
Отзывы покупателей о программе
Отзывов пока нет!
Занимательные задачи
1 260
Занимательные задачи!
Чем хороши занимательные задачи — ими можно интересно занять детей по в дороге, по пути в школу или устроить конкурс на школьном празднике. Обратите внимание, что мало кто сможет дать правильный ответ сразу, потому не забывайте о маленьких подсказках, разгадывание задачек от этого будет не менее интересным.
Занимательные задачи по математике
1.В каждом из 4 углов комнаты сидит кошка. Напротив каждой из этих кошек сидят три кошки. Сколько всего в этой комнате кошек?
2. У отца шесть сыновей. Каждый сын имеет сестру. Сколько всего детей у этого отца?
3. В мастерской по пошиву одежды от куска сукна в 200 м ежедневно, начиная с 1 марта, отрезали по 20 м. Когда был отрезан последный кусок?
4. В клетке находятся 3 кролика. Три девочки попросили дать им по одному кролику. Каждой девочке дали кролика. И все же в клетке остался один кролик. Как так получилось?
5. 6 рыбаков съели 6 судаков за 6 дней. За сколько дней 10 рыбаков съедят 10 судаков?
6. На одном дереве сидело 40 сорок. Проходил охотник, выстрелил и убил 6 сорок. Сколько сорок осталось на дереве?
7.Два землекопа за 2 часа работы выкопают 2 м канавы. Сколько нужно землекопов, чтобы они за 100 часов работы выкопали 100 м такой же канавы?
8. Два отца и два сына разделили между собой 3 апельсина так, что каждому досталось по одному апельсину. Как это могло получиться?
9. По стеблю растения, высота которого 1 м, от земли ползет гусеница. Днем она поднимается на 3 дм, а ночью опускается на 2 дм. Через сколько суток гусеница доползет до верхушки растения?
10. Есть два ведра емкостью 4 и 9 литров. Как с их помощью принести из речки ровно 6 литров воды?
Ответы:
1.4
2.Одной девочке дали клетку с кроликом.
3.9марта
4.7
5. 6 рыбаков за день едят 1 судака.
Один рыбак есть 1/6 судака в день.
10 рыбаков едят за день 10/6 судака.
10 судаков делим на 10/6 судака = 6 дней
6.Все улетели
7. 2
8. Дед, отец и внук = 2 отца и 2 сына
Дед, отец и внук = 2 отца и 2 сына
9.Через 7/12 суток.
10. Из полного девятилитрового ведра нужно вылить в реку 8литров воды, пользуясь ведром в 4 литра. Затем литр, оставшийся в большом ведре, нужно перелить в пустое четырехлитровое ведро. Если в него теперь добавить три литра из полного большого ведра, то в девятилитровом ведре как раз останется шесть литров воды.
Подумай и сосчитай
Чтоб одеть тепло сыночков,
Не хватает двух носочков.
Сколько же в семье сынков,
Если в доме шесть носков?
Ответ:четверо
Столько книжек у ребяток,
Сколько у Алеши пяток.
Принесла ребяткам Галя
Мячик, книжку, мишек.
Вы, ребята, посчитали,
Сколько стало книжек?
Ответ: три
******************
К трем лягушкам у болота
Прибежали два енота,
Прискакала тетя жаба
И пришла наседка Ряба.
Сколько в камышах болотных
Оказалось земноводных?
Ответ: четверо
Задачи на внимание
1. Подумай и скажи — кто быстрее переплывет речку — утята или цыплята?
2. Подумай и скажи — какого цвета волосы у колобка?
3. Отгадай загадку:
Лежали конфетки в кучке.
Две матери, две дочки
Да бабушка с внучкой
Взяли конфет по штучке,
И не стало этой кучки.
Сколько конфет было в кучке?
4. Росли 5 берез. На каждой березе по 5 больших веток. На каждой ветке по 5 маленьких веток. На каждой маленькой ветке — по 5 яблок. Сколько всего яблок?
5. Подумай и скажи — что помогает выжить белым медведям в пустыне, где нет воды?
6. На каких деревьях вьют свои гнезда страусы?
7. На столе лежит 2 яблока и 4 груши. Сколько всего овощей лежит на столе?
8. Подумай и скажи — кто громче рычит: тигр или буйвол?
9. Посмотрел Ваня утром в окно и говорит:
Посмотрел Ваня утром в окно и говорит:
— А на улице, оказывается, очень сильный ветер. Нужно теплее одеваться.
Как он догадался, что на улице ветер? Что он увидел?
10. Пошли 2 девочки в лес за грибами, а навстречу 2 мальчика. Сколько всего детей идет в лес? (подсказка: 2 — остальные идут обратно)
11. В комнате горело 5 свечей. Зашел человек, потушил 2 свечи. Сколько осталось? ( подсказка: 2- остальные сгорели)
12. Бревно распилили на 4 части. Сколько сделали распилов?
13. Прочитай слова и скажи — какое слово лишнее в каждом ряду?
— диван, стул, шкаф, конура, тумбочка,
— гвоздика, ромашка, камыш, лилия, астра,
— боровик, мухомор, сыроежка, подберезовик, лисичка.
14. Подумай и скажи — сколько земли будет в яме глубиной 1 метр, длиной 1 метр и шириной 1 метр?
15. У шестилетней девочки была кошка с коротким хвостом. Она съела мышку с длинным хвостом, а мышка проглотила 2 зернышка и съела тонкий кусочек сыра. Скажи, сколько лет было девочке, у которой была кошка?
16. На одном берегу реки стоит петух, а на другом индюк. Посреди реки — островок. Кто из этих птиц быстрее долетит до островка?
17. Скажи сколько грибов можно вырастить из 5 семечек?
18. Скажи, кто обитает в море на большей глубине: щука, рак или форель?
19. Гусь на двух ногах весит 2 кг. Сколько он будет весить, стоя на одной ноге?
20. На клене 5 веток. На каждой ветке по 2 яблока. Cколько яблок на клене?
Мой блог находят по следующим фразам
Логические задачи для 6-7 классов
“ Логические задачи ”
Выполнили: ученицы 7 математического класса УВК-лицея №100 г. Днепропетровска
Русина Маргарита и Кирсанова Дарья
Руководитель: учитель высшей категории УВК-лицея №100
г. Днепропетровска Гончарова Елена Александровна
Днепропетровска Гончарова Елена Александровна
Логика
- Логика (греч. logike ), наука о способах доказательств и опровержений; совокупность научных теорий, в каждой из которых рассматривается определённые способы доказательств и опровержений. Основателем логики считается Аристотель.
Особую роль в ускорении научно-технического прогресса играют приложения логики в вычислительной математике, теории автоматов, лингвистике, информатике и др.
Логика
- «Логика — это наука о законах правильного мышления, о требованиях, предъявляемых к последовательному и доказательному рассуждению»
Немецкий философ И. Кант
Методы решений логических задач
- Метод первый: Метод рассуждений
- Способ рассуждений — самый примитивный способ. Этим способом решаются самые простые логические задачи. Его идея состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи.
- Метод второй: Метод таблиц
Основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи.
ЗАДАЧА 1: «СКАНДАЛ В ГАРАЖЕ»
Послушайте, что говорят постояльцы отеля:
-Это не я! – Анри де Сезар
-Это не Долорес! – Лорд
-Это сделала женщина! – Дик
Среди этих высказываний верно только одно.
КТО УГНАЛ МАШИНУ?
Вот задача: В дорожном отеле
Появились на прошлой неделе
Постояльцы — профессор Брезак
(Он недавно купил «Кадиллак»),
Славный парень по имени Дик,
У которого есть грузовик,
Некто в сером – Анри де Сезар, —
У которого есть «Ягуар»,
Старый лорд из далёкого порта
(Лорд – владелец огромного «Форда»)
И весёлая мисс Долорес
(Не забудь у неё «Мерседес»!).
А вчера поздно вечером леди
Прикатила в «Рено» цвета меди.
И наутро профессор Брезак
Не нашёл в гараже «Кадиллак»…
РЕШЕНИЕ
Предположим, слова Анри де Сезара правда. Значит слова Дика и лорда – ложь. Машину угнала угнала не женщина. Машину угнала Долорес. Получаем противоречие.
Предположим, что слова Дика правда и угонщик – женщина. Но тогда, посчитав слова Анри и лорда ложью, получаем, что угонщики – Долорес и Анри. Приходим к противоречию.
Предположим, что правду сказал лорд. Угонщик – не Долорес. Тогда слова «Это не я!» Анри де Сезара – ложь. И слова Дика о том, что это сделала женщина, — тоже ложь. Никакого противоречия.
Выходит машину украл Анри де Сезар.
ЗАДАЧА 2: «О КРОКОДИЛЕ»
В жаркой солнечной Уганде,
Где берёт начало Нил,
В сочных зарослях осоки
Притаился крокодил.
Он лежит зелёный, милый.
От жары прикрыл глаза…
Берегитесь крокодила!
Доверять ему нельзя!
Сейчас крокодил крадётся к бабочке… За минуту он приближается к ней на два метра. А всю следующую минуту ползёт назад и отползает на один метр. В течении следующей минуты опять приближается к бабочке на два метра. Потом отползает на метр. Ну, итак далее… Расстояние между бабочкой и крокодилом 10 метров.
ЗА КАКОЕ ВРЕМЯ КРОКОДИЛ ДОБЕРЁТСЯ ДО БАБОЧКИ?
РЕШЕНИЕ
За 2 минуты крокодил подкрадётся к бабочке на 1 метр, за 4 минуты – на 2 метра, за 6 минут – на 3 метра… За 16 минут на 8 метров. А за следующую минуту крокодил проползёт 2 метра и доберётся до бабочки. Таким образом, крокодилу понадобится 17 минут.
ЗАДАЧА 3: «О КЕНГУРУ»
На поляне по утру
Встретил стадо кенгуру.
В стаде тридцать пять голов
(Я поклясться в том готов!)
Ног – сто двадцать! Как же, братцы?
Помогите разобраться!
СКОЛЬКО В СТАДЕ МАМ-КЕНГУРУ, СКОЛЬКО ПАП-КЕНГУРУ И СКОЛЬКО КЕНГУРЯТ?
У кенгуру четыре ноги. Две задних и две передних. Об этом надо помнить, решая задачу. У кенгурёнка, который сидит в маминой сумке тоже четыре, однако задние ноги кенгурят не видны…
Две задних и две передних. Об этом надо помнить, решая задачу. У кенгурёнка, который сидит в маминой сумке тоже четыре, однако задние ноги кенгурят не видны…
РЕШЕНИЕ
Ног должно быть 35*4=140. Двадцать недостающих ног принадлежат кенгурятам (их задние ноги не видны).
В стаде 10 кенгурят, 10 мам-кенгуру и 15 пап-кенгуру.
ЗАДАЧА 4: «О ДРАЧЛИВЫХ БРАТЬЯХ»
В семье Капулетти
Драчливые дети.
Нет братьев на свете драчливее этих!
Чезаре, Сантино,
Роберто и Джонни.
Однажды их мама –
Усталая Конни –
Пирог испекла.
А Джузеппе-отец
Съел четверть его
И лёг спать наконец.
Остаток увидев,
Расплакалась мама…
В семействе сейчас
Разыграется драма!
Задача для мамы
И впрямь не легка:
Ну, как разделить ей
Кусок пирога,
Чтобы не стали драться
Четыре упряменьких братца?
Придётся разделить пирог на четыре куска, одинаковых не только по весу, но и по форме.
РЕШЕНИЕ
ЗАДАЧА 5: «О ТРЁХ ЛЫЖНИКАХ»
Три товарища –
Илья, Ваня и Федот
Стали спорить у лыжни,
Кто за кем пойдёт.
Первым, верно, буду я, —
Говорит Илья. –
Следом Ваня. А Федот
Третьим пусть идёт.
-Ну, уж нет! – сказал Федот. –
Всё наоборот:
Первым точно буду я.
А вторым Илья.
-Нет, так дело не пойдёт! –
Ваня им ответил.
Ваня хочет первым быть,
Но никак не третьим…
Сколько всего вариантов встать на лыжню было у трёх лыжников?
РЕШЕНИЕ
Ваня Илья Федот; Ваня Федот Илья; Илья Ваня Федот;
Илья Федот Ваня; Федот Илья Ваня; Федот Ваня Илья.
Всего 6 способов.
Расставьте скобки и математические знаки так, чтобы равенство было верным: 9999999 = 100
Решение
- Это можно сделать множеством способов, вот некоторые из них: (99-9):9 + (99-9) = 100 (99-99)* 999 = 10*0 999/9-99/9=100 (9*9+9)/9+99-9=100
Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский».
На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский».
Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?
Решение
- 1. Вадим изучает китайский;
- 2. Сергей не изучает китайский;
- 3. Михаил не изучает арабский.
- Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно.
- Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно.
- Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
- Четверо друзей-рыбаков Алан, Боб, Сэм и Дэн (сокращённо А, В, С и D) традиционно взвесив свой улов после рыбалки, обнаружили следующее: 1. D поймал больше, чем С. 2. А и В вместе поймали столько же, сколько С и D вместе 3. A и D вместе поймали меньше, чем В и С вместе. Разместите результаты взвешиваний в убывающем порядке.
Решение
- Результаты взвешивания уловов а, b, с и d удовлетворяют соотношения: c
- Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Леонард Эйлер
- Некоторые ребята из класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?
- Истинностные задачи – это задачи, в которых требуется установить истинность или ложность высказываний.

- Украли у Ивана Царевича Василису Прекрасную. Поехал он выручать ее. Поймал Змея Горыныча, Бабу Ягу, Кощея Бессмертного и Лешего – Иван Царевич знал, что один из них украл ее. И спрашивает: «Кто украл Василису?» Змей Горыныч, Баба Яга и Кощей Бессмертный ответили: «Не я», а Леший – «Не знаю». Потом оказалось, что двое из них сказали правду, а двое – неправду. Знает ли Леший, кто украл Василису?
- Начнем рассуждать с ответов Змея Горыныча, Бабы Яги, Кощея Бессмертного. Так как украл Василису Прекрасную кто-то один, то среди ответов Змея Горыныча, Бабы Яги, Кощея Бессмертного может быть лишь один ложный, иначе при двух ложных ответах получается, что украли ее двое. Тогда вторым ложным ответом будет ответ Лешего, так как всего ложных ответов два. Поэтому Леший знал, кто украл Василису Прекрасную.
- Ответ: Леший знал, кто украл Василису Прекрасную.
Логические задачи по математике для 5 класса
Автор Administrator На чтение 2 мин. Опубликовано
Логические задачи по математике с картинками сделают урок по-настоящему увлекательным. Сборник, над которым надо как следует подумать, выручит педагога и на простом уроке, когда дети устали, и на открытом, когда надо показать свое педагогическое мастерство.
Логические задачи по математике с картинками сделают урок по-настоящему увлекательным. Сборник, над которым надо как следует подумать, выручит педагога и на простом уроке, когда дети устали, и на открытом, когда надо показать свое педагогическое мастерство.
Логика и математика — это две взаимосвязанные дисциплины. Обучаясь математике, ребенок развивает логику. Осваивая логику, школьник быстрее справляется с математикой. Дети очень любят задания логической направленности. Тем более, если в них есть изюминка – например, они тесно связаны с житейским опытом детей. Во всех представленных заданиях есть секрет – для их решение требуются либо дополнительные сведения из математики, либо неожиданно простые вычисления.
Во всех представленных заданиях есть секрет – для их решение требуются либо дополнительные сведения из математики, либо неожиданно простые вычисления.
Данные логические задачи по математике для 5 класса имеют ответы и объяснения решений. Всего в книге дано 16 задач. Сборник может быть полезен и на досуге. Решая «хитрые» задачки со своим ребенком, взрослые воспитают его пытливым и умным. Дети увлеченно решают логические задачки в компании сверстников. Также эта книга буде уместна при подготовке класса к олимпиадному конкурсу или после каникул для быстрой адаптации к работе в школе.
Издательство: Все Для Детей
Год издания: 2014
Автор: Все Для Детей
Формат: PDF
Количество страниц: 23
Язык: Русский
Скачать бесплатно logicheskie-zadachi-matematika-5-klass-uchebnik.pdf
Вы здесь: На главную → Интернет-ресурсы → Любимые головоломки В феврале 2014 года я попросил своих подписчиков назвать их любимую математическую головоломку. Результатом стал сборник — список головоломок, подобранный учителями и родителями! На этой странице перечислены наиболее сложные головоломки. Самые простые из них перечислены на этой странице.
См. Также: Любимые математические головоломки для детей — самые простые головоломки, собранные в моем конкурсе.Большинство из них требует только четырех основных операций или даже не этого, поэтому они хорошо подходят для детей младшего школьного возраста и выше. |
Стандарты математической практики | Инициатива Common Core State Standards
Стандарты математической практики описывают различные виды знаний, которые преподаватели математики на всех уровнях должны стремиться развивать у своих учеников. Эти практики опираются на важные «процессы и навыки», имеющие давнюю важность в математическом образовании.Первыми из них являются стандарты процесса NCTM для решения проблем, обоснования и доказательства, коммуникации, представления и связей. Вторые — это направления математической подготовки, указанные в отчете Национального исследовательского совета Adding It Up : адаптивное мышление, стратегическая компетентность, концептуальное понимание (понимание математических понятий, операций и отношений), беглость процедур (умение гибко выполнять процедуры, точно, эффективно и уместно) и продуктивному расположению (привычная склонность считать математику разумной, полезной и стоящей, в сочетании с верой в усердие и собственную эффективность).
Стандарты в этой области:
CCSS.Math.Practice.MP1 Разбирайтесь в проблемах и настойчиво их решайте.
Учащиеся со знанием математики начинают с объяснения себе значения проблемы и поиска точек входа для ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто предпринимают попытки решения. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной проблемы, чтобы получить представление о ее решении.Они отслеживают и оценивают свой прогресс и при необходимости меняют курс. Старшие ученики могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или изменять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую информацию. Математически опытные студенты могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и отношений, графических данных и искать закономерности или тенденции. Младшие ученики могут полагаться на использование конкретных предметов или изображений, чтобы помочь осмыслить и решить проблему.Математически опытные ученики проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?» Они могут понимать подходы других к решению сложных проблем и определять соответствия между разными подходами.
Математически опытные студенты могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и отношений, графических данных и искать закономерности или тенденции. Младшие ученики могут полагаться на использование конкретных предметов или изображений, чтобы помочь осмыслить и решить проблему.Математически опытные ученики проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?» Они могут понимать подходы других к решению сложных проблем и определять соответствия между разными подходами.
CCSS.Math.Practice.MP2 Размышляйте абстрактно и количественно.
Учащиеся со знанием математики понимают величины и их отношения в проблемных ситуациях. Они привносят две взаимодополняющие способности для решения проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать символами представления, как если бы они жили своей собственной жизнью, не обязательно обращая внимание на их референтов. — и возможность контекстуализировать , останавливаться по мере необходимости во время процесса манипуляции, чтобы исследовать референты для задействованных символов.Количественные рассуждения влекут за собой привычку создавать связное представление о рассматриваемой проблеме; с учетом задействованных единиц; внимание к значению количеств, а не только к тому, как их вычислить; знание и гибкое использование различных свойств операций и объектов.
CCSS.Math.Practice.MP3 Создавайте жизнеспособные аргументы и критикуйте рассуждения других.
Студенты со знанием математики понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов.Они делают предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они умеют анализировать ситуации, разбивая их на случаи, а также могут распознавать и использовать контрпримеры. Они оправдывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, приводя правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Математически опытные учащиеся также могут сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и — если в аргументе есть изъян — объяснять, что это такое.Учащиеся начальной школы могут строить аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не принимаются формально до более поздних оценок. Позже студенты учатся определять области, к которым применим аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
Они оправдывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, приводя правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Математически опытные учащиеся также могут сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и — если в аргументе есть изъян — объяснять, что это такое.Учащиеся начальной школы могут строить аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не принимаются формально до более поздних оценок. Позже студенты учатся определять области, к которым применим аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
CCSS.Math.Practice.Модель MP4 с математикой.
Учащиеся со знанием математики могут применять полученные знания для решения проблем, возникающих в повседневной жизни, в обществе и на рабочем месте. В младших классах это может быть так же просто, как написать дополнительное уравнение для описания ситуации. В средних классах учащийся может применять пропорциональное рассуждение для планирования школьного мероприятия или анализа проблемы в сообществе. В старшей школе ученик может использовать геометрию для решения проектной задачи или использовать функцию, чтобы описать, как одна интересующая величина зависит от другой.Математически опытные студенты, которые могут применять то, что они знают, комфортно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что они могут потребовать пересмотра позже. Они могут определять важные величины в практической ситуации и отображать свои отношения с помощью таких инструментов, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически проанализировать эти отношения, чтобы сделать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не служит своей цели.
Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не служит своей цели.
CCSS.Math.Practice.MP5 Стратегически используйте соответствующие инструменты.
Учащиеся со знанием математики рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Опытные студенты в достаточной мере знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как понимание, которое необходимо получить, так и их ограничения.Например, старшеклассники со знанием математики анализируют графики функций и решений, сгенерированные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценки и другие математические знания. Создавая математические модели, они знают, что технологии могут позволить им визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Учащиеся с математическими знаниями в различных классах могут определять соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач.Они могут использовать технологические инструменты для изучения и углубления понимания концепций.
CCSS.Math.Practice.MP6 Внимание к точности.
Учащиеся со знанием математики стараются общаться с другими именно так. Они пытаются использовать четкие определения в обсуждениях с другими и в своих собственных рассуждениях. Они заявляют значение выбранных символов, в том числе используют знак равенства последовательно и надлежащим образом. Они осторожны при указании единиц измерения и маркировке осей, чтобы уточнить соответствие количеству в проблеме. Они производят точные и эффективные вычисления, выражают числовые ответы со степенью точности, соответствующей контексту проблемы. В начальных классах ученики дают друг другу тщательно сформулированные объяснения. К моменту поступления в среднюю школу они научились проверять утверждения и четко использовать определения.
Они производят точные и эффективные вычисления, выражают числовые ответы со степенью точности, соответствующей контексту проблемы. В начальных классах ученики дают друг другу тщательно сформулированные объяснения. К моменту поступления в среднюю школу они научились проверять утверждения и четко использовать определения.
CCSS.Math.Practice.MP7 Ищите и используйте структуру.
Студенты, разбирающиеся в математике, внимательно приглядываются, чтобы различить образец или структуру. Молодые студенты, например, могут заметить, что еще три и семь — это столько же, сколько еще семь и три, или они могут отсортировать набор фигур в зависимости от того, сколько сторон у этих фигур.Позже учащиеся увидят, что 7 × 8 равно хорошо запоминающимся 7 × 5 + 7 × 3, при подготовке к изучению свойства распределения. В выражении x 2 + 9 x + 14 старшие ученики могут видеть 14 как 2 × 7 и 9 как 2 + 7. Они осознают значение существующей линии в геометрической фигуре и могут использовать стратегия рисования вспомогательной линии для решения задач. Они также могут сделать шаг назад для обзора и изменения перспективы. Они могут видеть сложные вещи, такие как некоторые алгебраические выражения, как отдельные объекты или как составленные из нескольких объектов.Например, они могут видеть 5 — 3 ( x — y ) 2 как 5 минус положительное число, умноженное на квадрат, и использовать это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x . и и .
CCSS.Math.Practice.MP8 Ищите и выражайте закономерность в повторяющихся рассуждениях.
Студенты со знанием математики замечают, если вычисления повторяются, и ищут как общие методы, так и ярлыки. Ученики старших классов могут заметить при делении 25 на 11, что они повторяют одни и те же вычисления снова и снова, и придут к выводу, что у них есть повторяющаяся десятичная дробь.Обращая внимание на вычисление наклона, поскольку они неоднократно проверяют, находятся ли точки на прямой, проходящей через (1, 2) с наклоном 3, ученики средней школы могут абстрагироваться от уравнения ( y — 2) / ( x — 1) = 3. Обратите внимание на закономерность в том, как условия отменяются при раскрытии ( x — 1) ( x + 1), ( x — 1) ( x 2 + x + 1), и ( x — 1) ( x 3 + x 2 + x + 1) может привести их к общей формуле для суммы геометрического ряда.Работая над решением задачи, ученики с математическими навыками следят за процессом, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
Обратите внимание на закономерность в том, как условия отменяются при раскрытии ( x — 1) ( x + 1), ( x — 1) ( x 2 + x + 1), и ( x — 1) ( x 3 + x 2 + x + 1) может привести их к общей формуле для суммы геометрического ряда.Работая над решением задачи, ученики с математическими навыками следят за процессом, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
Соединение стандартов математической практики со стандартами математического содержания
Стандарты математической практики описывают способы, с помощью которых развивающиеся студенты, практикующие математическую дисциплину, должны все активнее заниматься этим предметом по мере того, как они растут в математической зрелости и опыте на протяжении младших, средних и старших классов школы.Разработчики учебных программ, оценок и повышения квалификации должны уделять внимание необходимости увязать математические практики с математическим содержанием в обучении по математике.
Стандарты математического содержания представляют собой сбалансированное сочетание процедуры и понимания. Ожидания, начинающиеся со слова «понять», часто являются особенно хорошей возможностью связать практики с содержанием. Студенты, которым не хватает понимания темы, могут слишком сильно полагаться на процедуры.Без гибкой основы для работы они с меньшей вероятностью будут рассматривать аналогичные проблемы, связно представлять проблемы, обосновывать выводы, применять математику к практическим ситуациям, осознанно использовать технологии для работы с математикой, точно объяснять математику другим ученикам, сделайте шаг назад, чтобы получить обзор, или отклонитесь от известной процедуры, чтобы найти ярлык. Короче говоря, непонимание фактически мешает студенту заниматься математической практикой.
В этом отношении те стандарты содержания, которые устанавливают ожидания понимания, являются потенциальными «точками пересечения» между Стандартами математического содержания и Стандартами математической практики. Эти точки пересечения предназначены для взвешивания по отношению к центральным и генеративным концепциям школьной программы математики, которые в наибольшей степени заслуживают времени, ресурсов, инновационной энергии и сосредоточения, необходимых для качественного улучшения учебной программы, обучения, оценивания, профессионального развития и успеваемости учащихся в школе. математика.
Эти точки пересечения предназначены для взвешивания по отношению к центральным и генеративным концепциям школьной программы математики, которые в наибольшей степени заслуживают времени, ресурсов, инновационной энергии и сосредоточения, необходимых для качественного улучшения учебной программы, обучения, оценивания, профессионального развития и успеваемости учащихся в школе. математика.
4 СТРОКИ МАТЕМАТИЧЕСКИХ ЗНАНИЙ | Подводя итог: помощь детям в изучении математики
Фусон, К.К., & Бургхардт, Б. (1993). Групповые тематические исследования второклассников, изобретающих многозначные процедуры сложения десятичных блоков и письменных оценок. В J.R.Becker & B.J.Pence (Eds.), Proceedings of the пятнадцатого ежегодного собрания Североамериканского отделения Международной группы психологии математического образования (стр. 240–246). Сан-Хосе, Калифорния: Государственный университет Сан-Хосе. (Услуга размножения документов ERIC № ED 372 917).
Fuson, K.C., Carroll, W.M.И Лэндис Дж. (1996). Уровни осмысления и решения сложения и вычитания сравнивают словесные задачи. Познание и обучение , 14 , 345–371.
Гири, округ Колумбия (1995). Отражения эволюции и культуры в детском познании. Американский психолог , 50 (1), 24–37.
Грино Дж. Г., Пирсон П. Д. и Шонфельд А. Х. (1997). Последствия для NAEP исследований в области обучения и познания.В: Р. Линн, Р. Глейзер и Г. Борнштедт (редакторы), Оценка в переходный период: мониторинг прогресса в области образования в стране (Справочные исследования, стр. 151–215). Стэнфорд, Калифорния: Национальная академия образования.
Hagarty, M., Mayer, R.E., & Monk, C.A. (1995). Понимание арифметических словесных задач: сравнение успешных и неудачных решателей задач. Журнал педагогической психологии , 87 , 18–32.
Хатано, Г. (1988, осень). Социальные и мотивационные основы математического понимания. Новые направления развития ребенка , 41 , 55–70.
(1988, осень). Социальные и мотивационные основы математического понимания. Новые направления развития ребенка , 41 , 55–70.
Хиберт, Дж. (Ред.). (1986). Концептуальные и процедурные знания: пример математики . Хиллсдейл, Нью-Джерси: Эрлбаум.
Хиберт Дж. И Карпентер Т. (1992). Учиться и преподавать с пониманием. В D. A.Grouws (Ed.), Справочник по исследованиям в области преподавания и обучения математике (стр.65–97). Нью-Йорк: Макмиллан.
Хиберт, Дж., Карпентер, Т.П., Феннема, Э., Фусон, К.С., Вирн, Д., Мюррей, Х., Оливье, А., и Хумэн, П. (1997). Осмысление: преподавание и изучение математики с пониманием . Портсмут, Нью-Хэмпшир: Heinemann.
Хиберт Дж. И Уирн Д. (1986). Процедуры над понятиями: приобретение знаний о десятичных числах. В J.Hiebert (Ed.), Концептуальные и процедурные знания: случай математики (стр.199–223). Хиллсдейл, Нью-Джерси: Эрлбаум.
Хиберт Дж. И Уирн Д. (1996). Обучение, понимание и навыки сложения и вычитания многозначных чисел. Познание и обучение , 14 , 251–283.
Хилгард, Э. Р. (1957). Введение в психологию (2-е изд.). Нью-Йорк: Харкорт Брейс.
Инелдер Б. и Пиаже Дж. (1958). Развитие логического мышления с детства до юности . Нью-Йорк: Основные книги.
Катона, Г. (1940). Организация и запоминание . Нью-Йорк: издательство Колумбийского университета.
Килпатрик Дж. (1985). Заниматься математикой, не понимая ее: комментарий к Хигби и Кунихире. Психолог-педагог , 20 (2), 65–68.
Кнапп, М.С., Шилдс, П.М., и Тернбулл, Б.Дж. (1995). Академическая задача в классах с высоким уровнем бедности. Дельта Фи Каппан , 76 , 770–776.
Куба В.Л., Карпентер Т. П. и Сваффорд Дж. (1989). Количество и операции. В М. М. Линдквисте (ред.), Результаты четвертой математической оценки Национальной оценки успеваемости (стр. 64–93). Рестон, Вирджиния: Национальный совет учителей математики.
П. и Сваффорд Дж. (1989). Количество и операции. В М. М. Линдквисте (ред.), Результаты четвертой математической оценки Национальной оценки успеваемости (стр. 64–93). Рестон, Вирджиния: Национальный совет учителей математики.
Математические и логические головоломки на тему мистера Бартона Maths
arrow_back
Вернуться домой
Математические и логические головоломки
Я обожаю хорошие математические или логические головоломки.Этот
страница — это коллекция некоторых из моих любимых, которые я выполнил
с годами. Некоторые вы будете знать, но, надеюсь, некоторые вы узнаете
нет. Многие пришли из выдающейся игры Numberplay
Блог из New York Times.
Головоломки не сгруппированы по темам (это может выдать
некоторые секреты их решения) или по возрасту или сложности,
потому что это очень сильно зависит от самого решателя головоломки.
Пожалуйста, не присылайте мне какие-либо ответы по электронной почте, так как я боюсь
У меня нет времени отвечать. В любом случае, это испортило бы удовольствие. Но
Я полагаю, что за относительно большие суммы денег у меня может возникнуть соблазн
разгласить некоторую информацию. И если у вас есть любимая головоломка,
вы думаете, хорошо впишется в эту коллекцию, пожалуйста, дайте мне знать
через
Twitter
Содержание
1.Круг смерти
keyboard_arrow_up
В начало
Сто человек стоит в кругу. Они считают
начиная с одного и заканчивая сотней. Поскольку они находятся в
круг, ОДИН рядом с ДВЕ и ОДНОЙ СТО. У ОДНОГО есть меч и
убивает ДВОИХ. Он передает меч ТРИ, которые убивают ЧЕТЫРЕХ. И другие
И другие
вперед. ДЕВЯТЬ ДЕВЯТЬ убивает ОДНУ СОТНУ и передает меч ОДНОМУ.Затем ОДИН убивает ТРИ и передает меч ПЯТЬ. Это продолжается
пока не останется только один человек. Какой он номер?
2. Проблема 4 монет
keyboard_arrow_up
В начало
Вы создаете новую систему монет для своей страны. Вы должны использовать
только четыре достоинства монеты, и вы должны иметь возможность создавать значения 1
через 10, используя минимум одну монету и максимум две монеты.Какие
4 монеты вы выбираете, и можете ли вы придумать второй набор из 4
монеты, которые достигают той же цели?
3. Обручальное кольцо
keyboard_arrow_up
В начало
В некоторых сельских районах России собиралась невеста.
шесть длинных кусочков соломы или травы и возьмите их в руку. Она
затем случайным образом завязывал пары узлов сверху и снизу.Поскольку сверху и снизу торчат шесть травинок,
руку, она завяжет три узла сверху и три узла на
дно. История гласит, что если она образовала одно большое кольцо, она
скоро выйдет замуж. Какова вероятность, что она получит
в браке?
4. Задача средних значений
keyboard_arrow_up
В начало
Рассмотрите список всех способов, которыми вы могли бы взять четыре различных
цифры от 1 до 9 и расположите их так, чтобы получилась сумма двух двузначных
числа.Некоторые числа могут встречаться несколько раз: 134, для
Например, 93 + 41, а также 91 + 43.
Каковы среднее значение, медиана и мода всех чисел на этом
список? (Среднее — это сумма всех чисел, деленная на количество
чисел, медиана — это среднее значение в отсортированном списке
числа, а режим — это число, которое встречается чаще всего. )
)
5. Как избежать тролля
keyboard_arrow_up
В начало
Каждый день вы совершаете поездку из пункта А в пункт Б, расстояние до которого составляет 2 мили.Но твой
поездка непредсказуема.
В 50% дней вы можете ходить между А и Б без каких-либо
препятствие.
В остальных 50% случаев тролль появляется на полпути,
блокируя вашу поездку. Тролль также активирует невидимый барьер.
который блокирует 1 милю перпендикулярно в обоих направлениях, заставляя вас
обойти его, чтобы завершить поездку.
Вы не сможете увидеть тролля или барьер, пока не окажетесь на полпути от
От A до B, поэтому вы не можете заранее спланировать, нужно ли вам ходить
вокруг шлагбаума.Вы знаете, что тролль появляется случайно в 50% случаев.
время.
Если вы можете идти по прямой до любых точек между A и B,
какова ваша лучшая стратегия, чтобы вы прошли наименьшее расстояние
в среднем? Что это за расстояние?
6. Пещера Али-Бабы
keyboard_arrow_up
В начало
Али-Баба нашел пещеру, полную золота и алмазов. Сумка, полная
золото весит 200 килограммов, мешок с бриллиантами весит 40
килограммы.Али-Баба может нести за один раз только 100 килограммов. А
килограмм золота стоит 20 долларов, а килограмм бриллиантов — 60 долларов.
Какую самую большую сумму денег Али-Баба может заработать за
золото и бриллианты он может унести сразу (за одну попытку за одну
мешок)?
7. Игра-головоломка «Напиток»
keyboard_arrow_up
В начало
Игра начинается с 6 пустых стаканов подряд, пронумерованных от 1 до 6.Вы бросаете стандартный кубик. Если номер стакана пустой,
Если номер стакана пустой,
затем стакан наполняется. Если номер стакана полный,
затем вы выпиваете этот стакан, и он становится пустым.
Есть особое правило, когда 5 стаканов полны. Если вы катите
номер для одинокого пустого стакана, затем последний стакан наполняется
и надо выпить все 6 стаканов. На этом игра заканчивается.
Среднее количество бросков с начала игры
пока игра не закончится?
8.Жемчуг раджи
keyboard_arrow_up
В начало
Раджа по своей воле оставил своим дочерям определенное количество
жемчуг с инструкциями по их разделению следующим образом: Самый старый
дочь должна была получить 1 жемчужину плюс 1/7 того, что осталось. В
следующая старшая дочь должна была получить 2 жемчужины плюс 1/7 из них
оставил. Следующая старшая дочь должна была получить 3 жемчужины плюс 1/7
что осталось, и так далее таким же образом.Младшая дочь
получил то, что осталось после всех остальных дивизий.
Сначала младшая дочь думала, что раздача
несправедливо, но после тщательных расчетов она пришла к выводу, что все
дочери получат столько же жемчуга.
Сколько всего было жемчуга и дочерей?
9. Санкт-Петербургская лотерея
keyboard_arrow_up
В начало
Предположим, мы играем в следующую игру.Я постоянно подбрасываю монету
пока не поднимется голова. Если выпадет орел при первом броске, я
заплатить вам 2 доллара. Если он появится при втором броске, я даю вам 4 доллара; если
на третьем я плачу 8 долларов и так далее, каждый раз удваивая.
Сколько вы готовы заплатить мне за эту игру?
10. День рождения Шерил
keyboard_arrow_up
В начало
Альберт и Бернард только что подружились с Шерил, и они хотят
узнать, когда у нее день рождения. Шерил дает им список из 10
Шерил дает им список из 10
возможные даты.
15 мая 16 мая 19 мая
17 июня 18 июня
14 июля 16 июля
14 августа 15 августа
Затем Шерил сообщает Бернарду и Альберту месяц и месяц.
день ее дня рождения соответственно.
Альберт: Я не знаю, когда у Шерил день рождения, но я знаю, что
Бернар тоже не знает.
Бернард: Сначала я не знаю, когда у Шерил день рождения, но я
знать сейчас.
Альберт: Тогда я также знаю, когда у Шерил день рождения.
Когда у Шерил день рождения?
11. Возраст детей
keyboard_arrow_up
В начало
На улице встречаются 2 математика, и один говорит другому: «Я
Спорим, ты не можешь угадать возраст моих троих детей «(все целые возрасты).
Второй математик говорит:» Я приму вашу ставку, но только если вы
дайте мне достаточно информации, чтобы решить эту проблему.
Первый соглашается и говорит: «Продукт возраста моих трех детей —
36. «
» Этой информации недостаточно. «
« Верно! »- он оглядывается, шпионит за адресом в здании.
и говорит: «Суммарный возраст моих детей совпадает с адресом
вон там. «
Немного подумав;» Этой информации все еще недостаточно «.
» Вы снова правы! У моего старшего сына рыжие волосы ».
Подумав, второй математик выиграл пари.
12. Кольцо вокруг Земли
keyboard_arrow_up
В начало
Представьте себе стальную полосу вокруг экватора Земли,
красиво и уютно (~ 25 000 миль). Если вы затем добавите один фут стали к
эта группа, насколько она поднята над землей? Достаточно высок
подсунуть под него волосы? Твоя рука? Достаточно высоко, чтобы под ним пройти?
13. Школьные шкафчики
keyboard_arrow_up
В начало
Имеется школа на 1000 учеников и 1000 шкафчиков. На
На
в первый день семестра директор просит первого ученика уйти
и открыть каждый шкафчик, он просит второй пойти в
каждый второй шкафчик и закрыть его, третий перейти к каждому третьему
шкафчик и закройте его, если он открыт, или откройте, если он закрыт,
четвертый, чтобы перейти к четвертому шкафчику и так далее. Процесс
укомплектован тысячным учеником. Сколько шкафчиков открыто
в конце?
14.Ставка дьявола
keyboard_arrow_up
В начало
Ты умрешь, а дьявол говорит, что отпустит тебя на небеса, если ты побьешь
его в игре. Он усаживает вас за круглый стол. Он делит
большая куча четвертей пополам, чтобы у вас обоих было одинаковое количество
кварталы в собственной куче. Он говорит: «Хорошо, мы по очереди
положить четверти вниз, перекрытия не допускаются, а четверти
должен опираться на поверхность стола.Первый парень, который не умеет
четверть вниз проигрывает. Вы не можете сдвинуть или попытаться сжать любую четверть
в пространство, которое переместится еще на четверть «. Дьявол говорит, что хочет
идти первым.
Вы понимаете, что если дьявол пойдет первым, у него, вероятно, есть стратегия, чтобы
выиграть. У вас еще не было времени подумать об этом, поэтому вы спрашиваете
какое-то время обдумывать ваши варианты. Он дает вам 15 минут.
По прошествии этого времени вы знаете, как победить его … но вы также
знайте, что вы должны пойти первым, чтобы ваша стратегия выиграла.Ты убедишь его
чтобы отпустить вас первым, сказав, что у вас действительно не хватило времени, чтобы
продумайте стратегию, так что вы должны, по крайней мере, пойти первым. Какая у тебя
выигрышная стратегия?
15.
 Половина яйца keyboard_arrow_up
Половина яйца keyboard_arrow_up
В начало
Крестьянка пришла на рынок продать яиц. Первый покупатель
взяла половину ее яиц плюс 1/2 яйца. То же произошло и с
оставшиеся яйца: второй покупатель-покупатель взял половину своих яиц плюс 1/2
яйцо.Третий купил только то, что осталось: 1 яйцо.
Сколько яиц было изначально?
16. Сделайте 6
keyboard_arrow_up
В начало
Можно использовать только два математических символа (включая факториалы и
квадратные корни), чтобы получить 6
0 0
0 = 6
1 1
1 = 6
2 2
2 = 6
3 3
3 = 6
4 4
4 = 6
5 5
5 = 6
6 6
6 = 6
7 7
7 = 6
8 8
8 = 6
9 9
9 = 6
17.Три лжеца подбрасывают монету
keyboard_arrow_up
В начало
Три человека имеют тенденцию лгать 1/3 времени. Там
это подбрасывание монеты, которое все видят. Все говорят, что это головы. Что такое
вероятность, что это на самом деле Головы?
18. Освободить узников
keyboard_arrow_up
В начало
По прибытии надзиратель встречает 23 новых заключенных.Он говорит
им: «Вы можете встретиться сегодня и спланировать стратегию. Но после сегодняшнего дня
вы будете в изолированных камерах и не будете иметь связи с
друг друга.
«В тюрьме есть коммутатор, в котором есть два светильника.
переключатели с обозначениями 1 и 2, каждый из которых может быть как в верхнем, так и в верхнем положении.
нижнее положение. Я не говорю вам об их нынешнем положении. В
переключатели ни к чему не подключены.
«После сегодняшнего дня, время от времени, когда мне так хочется, я
случайным образом выберет одного заключенного и сопроводит его к выключателю
номер.Этот заключенный выберет один из двух переключателей и
изменить свое положение. Он должен щелкнуть одним переключателем, когда посещает
коммутатор, и может щелкнуть только один из переключателей. Тогда он будет
привел обратно в свою камеру.
«Никому другому не разрешат менять переключатели, пока я не приведу
следующий заключенный в рубку. Я собираюсь выбрать
заключенные наугад. Я могу выбрать одного и того же парня три раза за
грести, или я могу прыгнуть и вернуться.Я не буду трогать
выключатели, если бы я хотел, чтобы ты умер, ты был бы уже мертв.
«Если у вас будет достаточно времени, все в конечном итоге посетят выключатель
номер столько же раз, сколько и все остальные. В любое время,
любой может заявить мне: «Мы все посетили коммутатор».
«Если это правда, то вы все будете освобождены. Если это ложь, и
кто-то еще не посетил коммутатор, вы все умрете
ужасно.За вами будут внимательно наблюдать, и любая попытка
нарушение любого из этих правил приведет к мгновенной смерти всех
ты »
Какую стратегию они придумали, чтобы быть свободными?
19. Горящие веревки для измерения времени
keyboard_arrow_up
В начало
Разминка: вам дается коробка спичек и кусок
веревка. Веревка горит со скоростью одна веревка в час, но
он не может гореть равномерно.Например, если вы зажжете
веревку на одном конце, пройдет ровно 60 минут, прежде чем вся
веревка сгорела, но, возможно, первая 1/10 веревки
нужно 50 минут, чтобы сжечь оставшиеся 9/10 веревки
горение занимает всего 10 минут. Как можно измерить период
Как можно измерить период
ровно 30 минут? Вы можете выбрать стартовый
время. Точнее, учитывая спички и веревку, вы
должны произнести слова «начало» и «готово» с интервалом ровно 30 минут.
Актуальная проблема: Учитывая коробку спичек и две такие
веревки, не обязательно одинаковые, измеряются за 15 минут.
20. Минимальное количество самолетов
keyboard_arrow_up
В начало
На острове Бэгшот есть аэропорт. Аэропорт — это
база неограниченного количества одинаковых самолетов. Каждый
у самолета есть запас топлива, чтобы он мог лететь ровно на половину пути
по всему миру, по большому кругу.Самолеты имеют
возможность дозаправки в полете без потери скорости и утечки
топливо. Хотя количество топлива не ограничено, остров является единственным источником
топлива.
Какое наименьшее количество самолетов необходимо для получения одного самолета?
по всему миру при условии, что все самолеты
должны благополучно вернуться в аэропорт? Как вы пришли к своему ответу?
Примечания:
(a) Каждый самолет должен вылетать и возвращаться в один и тот же аэропорт, и
это единственный аэропорт, в котором они могут приземлиться и заправиться на земле.
(b) У каждого самолета должно быть достаточно топлива для возврата в аэропорт.
(c) Время и расход топлива заправки можно не учитывать. (так
мы также можем предположить, что один самолет может заправить более одного
самолетов в воздухе одновременно.)
(d) Количество топлива, перевозимого самолетами, может быть равно нулю, пока
другой самолет заправляет эти самолеты. Что это
наименьшее количество самолетов и количество топливных баков, необходимых для
выполнить эту работу? (нам нужен только самолет, чтобы облететь
мир)
21.
 Минимальное количество весов keyboard_arrow_up
Минимальное количество весов keyboard_arrow_up
В начало
Однажды ко мне пришел оптовый торговец и задал мне эту проблему.
Каждый день в своем бизнесе он должен взвешивать суммы от одного фунта
до ста двадцати одного фунта, с точностью до фунта. Делать
это, какое минимальное количество гирь ему нужно и насколько тяжелый
должен быть каждый вес?
22.Относительно Prime Bet
keyboard_arrow_up
В начало
Есть ящик, в котором хранились шары с разными номерами.
Вы должны случайным образом выбрать из лота два шара.
Если кто-то предлагает вам шанс 2 к 1, то числа будут
относительно простое число, например
. Если выбранные вами шары имеют числа 6 и 13, вы теряете 1 доллар.
Если выбранные вами шары имеют номера 5 и 25, вы выигрываете 2 доллара.
Вы примете эту ставку?
23. Переход через мост
keyboard_arrow_up
В начало
Четыре человека должны перейти ночью по шаткому мосту.
К сожалению, у них всего один факел, да и мост тоже
опасно переходить без него. Мост достаточно крепкий
для поддержки двух человек одновременно. Не все люди занимают одно и то же время
перейти мост.Время для каждого человека: 1 мин., 2 мин., 7 мин.
и 10 мин. Какое кратчайшее время нужно всем четверым
перейти мост?
24. 25 лошадей, 5 треков
keyboard_arrow_up
В начало
У мистера Джона 25 лошадей, и он хочет выбрать 3 самых быстрых лошади.
из этих 25. У него всего 5 гусениц, то есть всего 5 лошадей.
может работать одновременно. У него даже секундомера нет. Что это
Что это
минимальное количество скачек, необходимое для поиска 3-х самых быстрых лошадей?
25. Головоломка с переворачивающимися монетами
keyboard_arrow_up
В начало
На столе лежит двадцать монет, десять
в настоящее время решки и десятки. Вы сидите в
стол с завязанными глазами и в перчатках. Ты умеешь чувствовать
где находятся монеты, но не могут увидеть или почувствовать, направляются ли они
или решки.Вы должны создать два набора монет. Каждый набор должен иметь
такое же количество орлов и решек, что и в другой группе. Ты можешь
только перемещайте или подбрасывайте монеты, вы не можете определить их
Текущее состояние.
Как создать две четные группы монет с одинаковым номером?
орла и решки в каждой группе?
26. Случайные места в самолетах
keyboard_arrow_up
В начало
Люди ждут в очереди на посадку в 100-местный самолет.Стив
первый человек в очереди. Он садится в самолет, но внезапно
не может вспомнить номер его места, поэтому выбирает место на
случайный. После этого каждый человек, попавший в самолет, садится в
назначенное им место, если оно доступно, в противном случае они выберут
произвольно открытое место для сидения.
Рейс заполнен, вы последний в очереди. Что это
вероятность того, что вы сядете на отведенное вам место?
27.Доля девочек и мальчиков
keyboard_arrow_up
В начало
В стране, где все хотят мальчика, каждая семья продолжает
иметь детей, пока не родится мальчик. Через некоторое время какой
соотношение мальчиков и девочек в стране? (Предполагая, что вероятность
иметь мальчика или девочку — одно и то же)
28.
 Шляпы и монстр keyboard_arrow_up
Шляпы и монстр keyboard_arrow_up
В начало
Есть остров с 10 жителями.Однажды приходит монстр
и говорит, что намерен съесть каждого из них, но даст
у них шанс выжить следующим образом:
Утром монстр выстроит в очередь всех людей — одиночные
файл так, чтобы последний человек видел оставшиеся 9, следующий человек
видит оставшиеся 8 и так далее, пока первый человек, который
очевидно никого не видит перед собой. Тогда монстр
случайным образом надеть им на голову черные или белые шляпы (все они могут быть
белый, полностью черный или любое их сочетание).
Монстр предложит каждому человеку, начиная с последнего (кто
видит чужие шляпы), чтобы угадать цвет своей шляпы.
Ответом может быть только одно слово: «белый» или «черный». Монстр
съест всех десяти заложников, как только второй пленник ответит
неправильно. Все остальные люди услышат предположение, но не
результат предположения. Затем монстр перейдет к следующему
до последнего человека (который видит только 8 человек) и так до конца.
Чудовище дает им подумать всю ночь.
Задача:
Разработайте стратегию, которая гарантирует выживание всех пленников.
Допущения:
1) Все 10 человек могут легко понять вашу стратегию и будут
выполнить его с безупречной точностью.
2) Если монстр подозревает, что кто-то из людей раздает
информация любому из оставшихся членов команды интонацией
слова при ответе, или любые другие знаки, или наощупь, он съест
все.
3) Единственно допустимый ответ — короткий, бесстрастный «белый» или
«чернить».
29. Яйца из здания
keyboard_arrow_up
В начало
Предположим, что есть 100-этажное здание. Вам дано 2
Вам дано 2
одинаковые яйца. Самым интересным свойством яиц является то, что
у каждого яйца есть свой «пороговый» этаж. Назовем этот этаж N.
Это означает, что яйцо не разобьется при падении с
любого этажа ниже этажа N, но яйцо обязательно сломается от
любой этаж выше этажа N, включая сам этаж N.
Например, если свойство яиц таково, что N равно 15,
эти яйца всегда будут разбиваться на любом этаже выше или равном
15-й этаж, но эти яйца никогда не разобьются ни на одном этаже ниже
этаж 15. То же самое верно и для других яиц, поскольку они
идентичный.
Это очень крепкие яйца, потому что их можно уронить несколько раз.
раз, не ломаясь, пока они падают с пола
ниже их «порогового» этажа, этаж N.Но как только яйцо упало
этажом выше порога этажа
Вот загадка: какую стратегию следует предпринять, чтобы
минимизировать количество капель яиц, используемых для поиска этажа N (
пол порога) для яйца? Кроме того, каково минимальное количество
падает в худшем случае, используя эту стратегию?
Помните, что вам дается 2 одинаковых яйца, у каждого из которых есть
такой же точный порог пола.
30.5 пиратов, 100 золотых монет
keyboard_arrow_up
В начало
Пять корабельных пиратов получили 100 золотых монет и должны
поделить добычу. Пираты все очень умны,
коварный и эгоистичный (особенно капитан).
Капитан всегда предлагает распределить добычу. Все
пираты голосуют за предложение, и если половина экипажа или больше уходит
«Да», добыча делится, как было предложено, так как ни один пират не будет
готовы сразиться с капитаном без превосходящей силы на их
боковая сторона.
Если капитан не заручился поддержкой хотя бы половины своей команды
(включая его самого), ему грозит мятеж, и все пираты
повернуться против него и заставить его ходить по доске. Пираты начинают
снова со следующим старшим пиратом в качестве капитана.
Какое максимальное количество монет капитан может оставить без
рискуя своей жизнью?
Математические приложения для 8-х классов для iPad, iPhone, Android, Windows 8
iTooch 8-й класс MathApp Store 4.8
Откройте для себя наше математическое приложение для восьмиклассников
В большинстве школ США восьмой класс является мостом между средней и старшей школами. Соответственно, учащимся восьмых классов необходимо улучшить свое понимание основ математики, развить логические и логические навыки, а также интерпретировать графики, диаграммы и данные. Приложение iTooch для 8-х классов по математике, разработанное в соответствии с Общими основными стандартами, подчеркивает точность и мастерство. Пять его разделов — «Функции», «Алгебраические структуры», «Свойства и операции», «Статистика и вероятность» и «Геометрия» — предоставляют учащимся как обзор, так и задачи, а также возможность использования уникального форума iPad для облегчения обучения и улучшения визуальных характеристик.Учащиеся средней и старшей школы могут использовать iTooch для 8-х классов математики, чтобы проверить свое понимание, потренироваться перед тестами и викторинами, а также перейти на следующие уровни математики при переходе в старшую школу.
Свойства и операции
- Генерация эквивалентных числовых выражений
- Десятичное разложение до рациональных чисел
- Процент уменьшения и увеличения
- Пропорции и проценты
- Похожие изображения
- Рациональные и иррациональные числа
- Оценка ценности выражений
- Научная запись
- Квадраты и квадратные корни
- Кубических корней
Алгебраические структуры
- Что такое полиномы
- Работа с экспонентами
- Упрощающие полиномы
- Добавление полиномов
- Вычитание полиномов
- Умножение многочленов на одночлены
- Паттерны в умножении многочленов
- Использование метода FOIL для умножения биномов
- Факторинг мономов
- Факторинговые многочлены
- Делительные многочлены
- Решение неравенств и построение графиков
- Уравнения с переменными с обеих сторон
Статистика и вероятность
- Теоретическая и экспериментальная вероятность
- Стеблево-листовые делянки
- Построение точечных диаграмм
- Ящики и усы
- Перестановки и комбинации
- Линейные графики
- Круговые диаграммы
- Таблицы частот, гистограммы и линейные графики
- Среднее значение, Медиана, Режим, Диапазон
- Гистограммы и двойные столбиковые диаграммы
Функции
- Определение функций
- Уклон прямой
- Интерпретация уклона — форма пересечения
- Форма остроконечного откоса
- Описание упорядоченных пар
- Таблицы и графики
- Координатная плоскость
- Графические линейные функции
- Нелинейные функции
Геометрия
- Основы треугольников и многоугольников
- Построение сетей трехмерных фигур
- Угловые отношения и классификационные линии
- Площадь пирамид и конусов
- Площадь призм и цилиндров
- Объем призм и цилиндров
- Объем пирамид и конусов
- Преобразования
- Круги и окружность
- Сферы
- Теорема Пифагора
Характеристики
Загруженные тысячами вопросов, приложения охватывают официальные образовательные программы и соответствуют Общим основным государственным стандартам.
Это приложение создает отличную игровую динамику и стимулы, так что пользователь всегда хочет развиваться дальше в приложении.
Приложения включают в себя доску и калькулятор, чтобы учащиеся могли писать и вычислять прямо на экране, не выходя из приложения.
К каждой главе прилагается краткое содержание урока, чтобы подчеркнуть основные концепции, которые студенты должны знать, чтобы отвечать на вопросы.
Мгновенно переходите от одного экрана к другому. Перестаньте ждать загрузки информации с сервера: пропускная способность больше не является проблемой.
Приложения автоматически синхронизируются в фоновом режиме, чтобы загружать новые действия при наличии подключения к Интернету.
Право на участие в программе оптовых закупок Apple
(только для iOS)
Вы представитель школы и хотите купить iTooch 8th Grade Math для всей организации? Хорошие новости! iTooch 8th Grade Math имеет право на участие в программе Apple Volume Purchase Program (VPP) для образовательных учреждений. Мы предложим вам специальные цены при покупке 20 и более приложений.Чтобы воспользоваться этим предложением, вы можете купить наше приложение iTooch по математике для 8-х классов вместо покупки контента в нашем приложении для средней школы iTooch. Дополнительную информацию о программе оптовых закупок можно найти на веб-сайте Apple. Есть вопросы? Не стесняйтесь связаться с нами.
Познакомьтесь с учителями математики в 8-м классе:
Нина Берлер
Соавтор
iTooch по математике в 8-м классе, Нина Берлер преподавала английский язык и математику в средней школе и работала один на один с многочисленными учениками средних и старших классов, чтобы улучшить навыки письма, улучшить учебные привычки, подготовиться к стандартным тестам и собеседованиям, а также подавать заявление в независимые школы и колледжи.Она также является независимым подрядчиком eduPad, Службы образовательного тестирования и Wall Street Journal Classroom Edition. На протяжении своей корпоративной карьеры Нина работала в компании KPMG, предоставляющей профессиональные услуги, где она руководила программным подразделением Executive Education и руководила инициативами в области маркетинговых коммуникаций. Нина имеет степень бакалавра гуманитарных наук с отличием Университета Брауна и степень магистра делового администрирования Школы бизнеса Стерна Нью-Йоркского университета. В настоящее время она проходит сертификационную программу Калифорнийского университета в Лос-Анджелесе по консультированию колледжей. Нина является членом Национальной ассоциации консультирования при поступлении в колледж (NACAC) и Комитета школ выпускников Брауна.
На протяжении своей корпоративной карьеры Нина работала в компании KPMG, предоставляющей профессиональные услуги, где она руководила программным подразделением Executive Education и руководила инициативами в области маркетинговых коммуникаций. Нина имеет степень бакалавра гуманитарных наук с отличием Университета Брауна и степень магистра делового администрирования Школы бизнеса Стерна Нью-Йоркского университета. В настоящее время она проходит сертификационную программу Калифорнийского университета в Лос-Анджелесе по консультированию колледжей. Нина является членом Национальной ассоциации консультирования при поступлении в колледж (NACAC) и Комитета школ выпускников Брауна.
Уильям Скотт Стоун
iTooch 8-й класс по математике, Уильям Скотт Стоун, имеет степень бакалавра компьютерных наук в Францисканском университете Стьюбенвилля, штат Огайо, и работал программистом в Northrop Grumman. Он также имеет степень бакалавра педагогического образования в Стоктонском колледже Понома, штат Нью-Джерси. Он был педагогом в течение пяти лет, преподавая математику и общественные науки в средней школе. Он полностью переработал веб-сайт школьного округа с учетом потребностей учителей и простоты использования.
До образования он восемь лет служил в армии США, в течение которых был направлен в «Бурю в пустыне» (1-я война в Ираке, 1991 г.). Во время службы он работал и управлял различными военными автомобилями. Большая часть его службы была завершена в форте Кэмпбелл Кентукки (101-я воздушно-десантная дивизия), где он получил свои крылья и был повышен до Сарджента.
Эйлин Хейес
Айлин Хейес, редактор 8-го класса по математике iTooch, имеет степень бакалавра журналистики Калифорнийского государственного университета в Лонг-Бич.Она писала и редактировала в газетах 30 лет, пытаясь решить, кем она хотела бы стать, когда вырастет. Она является автором трех научно-популярных книг для подростков и двух загадок для детей. Изучая искусство повествования, она изучала сценарии и импровизацию, получила сертификат документального искусства и вызвалась участвовать в уличных актерах ярмарки эпохи Возрождения. Она берет все это обратно в класс в качестве писателя в резиденции Объединенного совета искусств округа Уэйк, Северная Каролина.Родом из Лос-Анджелеса, она сейчас живет в Роли со своим блестящим мужем и одним из двух интересных, красноречивых сыновей.
Она берет все это обратно в класс в качестве писателя в резиденции Объединенного совета искусств округа Уэйк, Северная Каролина.Родом из Лос-Анджелеса, она сейчас живет в Роли со своим блестящим мужем и одним из двух интересных, красноречивых сыновей.
Вам также могут понравиться эти другие приложения для 8-го класса:
8 класс / Искусство английского языка / Средняя школа
7 класс / 8 класс / Музыка
Тысячи бесплатных заданий по математике, головоломок по математике и образовательных ресурсов по математике для учащихся начальных классов, основанных на сингапурской учебной программе по математике.
Mathinenglish.com, математический сайт с тысячами бесплатных и составленных учителями заданий по математике, рабочих тетрадей, математических головоломок и головоломок для детей.
в начальном математическом образовании.
Математика космической свиньи
Space Pig Math — это видеоигра в жанре экшн для отработки таблицы умножения — до 12×12
Полностью удовлетворяющая и захватывающая игра на умножение с интуитивной обратной связью, визуальными эффектами и звуками в ретро-стиле.
Прорывайтесь сквозь волны астероидов и пришельцев, чтобы спасти друзей космической свиньи —
они, в свою очередь, дадут вам потрясающие бонусы, которые помогут вам! Более
100 новых головоломок по математике!
Мы недавно добавили 400 новых распечатываемых математических головоломок IQ, которые вы должны решить.Повысьте свой IQ и умственные способности.
Наши математические и числовые головоломки имеют 4 уровня сложности и могут быть довольно сложными. Вы можете распечатать тизеры IQ или загрузить файл Powerpoint.
Хотите узнать больше? Кликните сюда.
Какое натуральное число следует заменить
знак вопроса?
Какое натуральное число следует заменить
знак вопроса?
Достаточно ли хороши ваши математические и числовые навыки, чтобы видеть закономерность?
Хотите узнать ответ? Кликните сюда.
Какая костяшка завершает ряд?
Какое домино завершит этот узор? Используйте свои математические и логические навыки, чтобы решить эту головоломку IQ.
Можете ли вы решить нашу математическую головоломку IQ для детей?
Хотите узнать ответ? Кликните сюда.
Новый внедорожник LEGO 4×4
Lego, наконец, представила новый крутой внедорожник 4×4 X-treme.
Чтобы увидеть, что можно сделать с этим супер крутым внедорожником, некоторые фанаты Lego построили непревзойденную полосу препятствий.Посмотрите удивительное испытание Lego. Более
Коровы и фермеры
Есть несколько коров и
некоторые фермеры в
луг.
Всего у них 22 головы и 72 ноги. Сколько коров и фермеров на лугу?
Нажмите здесь, чтобы ответить
Сколько яиц?
Петух отложил 9 яиц, и жена фермера взяла 5 из них, чтобы приготовить омлет.
Другой петух отложил 10 яиц, но 5 были гнилыми, и их пришлось выбросить. Сколько яиц осталось?
Нажмите здесь, чтобы ответить
Стоимость кролика?
Сможете ли вы решить эту загадку алгебры животных? В чем ценность кролика?
Используйте свои математические навыки и найдите значение кролика, жирафа, русалки и лягушки. Вы достаточно умны? Эта головоломка с картинками включает в себя все основные операции сложения, вычитания, умножения и деления.Очень сложно для молодых учеников. Более
Какой фильм или песня?
Математика — это больше, чем просто числа и символы. Этот знаменитый математический символ обозначает известный фильм и песню. Который из?
Этот очень забавный фильм был выпущен в 1999 году и до сих пор имеет 3 продолжения. Песня вышла в 1971 году, ее написал и спел Дон Маклин.
Нажмите здесь, чтобы ответить
Чтение мыслей
Выберите число и соответствующий символ, и пусть математический магический хрустальный шар угадает его.
Это фантастический сложный математический трюк. Вашим ученикам понравятся удивительные способности синего хрустального шара. Загрузите версию этого классического математического трюка в формате PowerPoint.
Mathinenglish предлагает тысячи легко усваиваемых заданий по математике и множество математических головоломок для детей и учеников начальных классов.
Наши рабочие листы по математике основаны на сингапурской программе математики и подходят для начальных классов математики с 1 по 6.Мы верим
что язык, используемый в рабочих таблицах и головоломках для детей, должен быть простым и не отвлекать внимание от реальной проблемы:
понимание математики.
Не стесняйтесь загружать наши рабочие листы по математике в формате pdf и использовать их на уроках математики или на домашнем обучении.
Наши математические ресурсы созданы учителями и используются их учениками-математиками.
Наши новые материалы? Подписывайтесь на нас.
Рабочие листы с заданиями по математике для 8-х классов
Решение математических задач может напугать восьмиклассников.Не должно. Объясните учащимся, что вы можете использовать основы алгебры и простые геометрические формулы для решения, казалось бы, неразрешимых задач. Ключ состоит в том, чтобы использовать предоставленную вам информацию, а затем изолировать переменную для алгебраических задач или знать, когда использовать формулы для геометрических задач. Напомните учащимся, что всякий раз, когда они решают задачу, что бы они ни делали с одной стороной уравнения, они должны делать с другой. Итак, если они вычтут пять из одной части уравнения, им нужно будет вычесть пять из другой.
Бесплатные распечатанные рабочие листы, представленные ниже, дадут студентам возможность решить задачи и заполнить свои ответы в отведенных для этого пустых местах.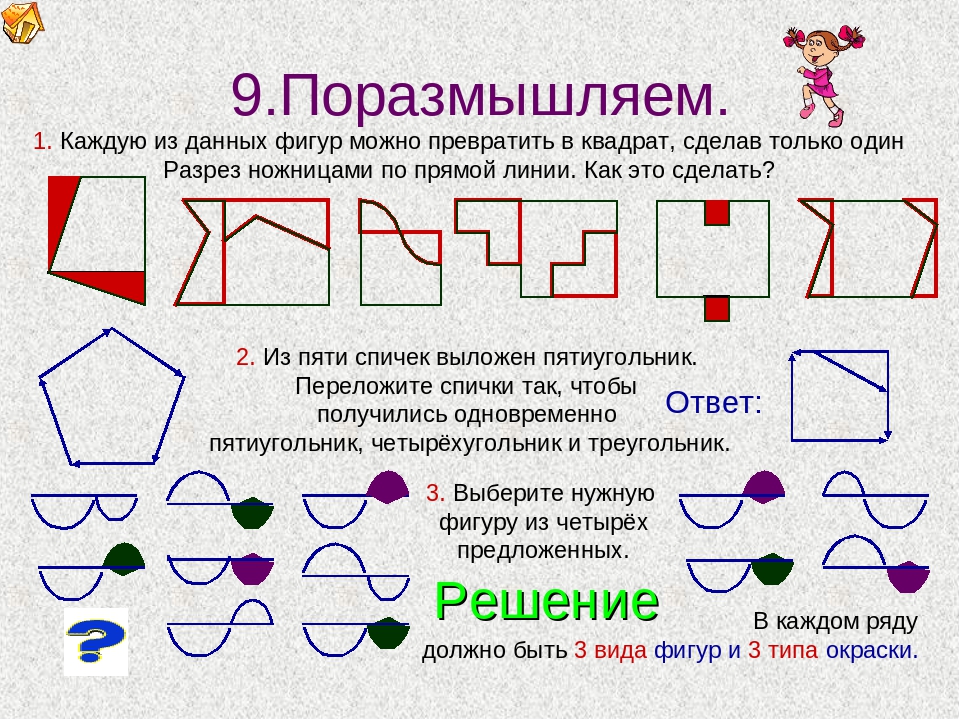 После того, как учащиеся завершат работу, используйте рабочие листы для быстрой формирующей оценки для всего класса математики.
После того, как учащиеся завершат работу, используйте рабочие листы для быстрой формирующей оценки для всего класса математики.
Рабочий лист № 1
Деб Рассел
Распечатать PDF : Рабочий лист № 1
В этом PDF-файле ваши ученики будут решать такие задачи, как:
«5 хоккейных шайб и три клюшки стоят 23 доллара.5 хоккейных шайб и 1 клюшка стоят 20 долларов. Сколько стоит 1 хоккейная шайба? »
Объясните ученикам, что им нужно будет учитывать то, что они действительно знают, например, общую стоимость пяти хоккейных шайб и трех хоккейных клюшек (23 доллара США), а также общую стоимость пяти хоккейных шайб и одной клюшки (20 долларов США). Укажите студентам, что они начнут с двух уравнений, каждое из которых дает общую цену, а каждое включает пять хоккейных клюшек.
Рабочий лист № 1 Решения
Деб Рассел
Распечатать PDF : Рабочий лист №1 Решения
Чтобы решить первую проблему на листе, настройте ее следующим образом:
Пусть «P» представляет переменную для «шайбы».
Пусть «S» представляет переменную для «палки».
Итак, 5P + 3S = 23 доллара, а 5P + 1S = 20 долларов.
Затем вычтите одно уравнение из другого (поскольку вы знаете сумму в долларах):
5P + 3S — (5P + S) = 23 — 20 долларов.
Таким образом:
5P + 3S — 5P — S = 3 доллара. Вычтем 5P из каждой части уравнения, что даст: 2S = 3 доллара.Разделите каждую часть уравнения на 2, и получится, что S = 1,50 доллара.
Затем подставьте 1,50 доллара США вместо S в первом уравнении:
5P + 3 (1,50 доллара) = 23 доллара, что дает 5P + 4,50 доллара = 23 доллара. Затем вы вычитаете 4,50 доллара из каждой части уравнения, получая: 5P = 18,50 доллара.
Разделите каждую часть уравнения на 5, чтобы получить:
P = 3,70 долл.
США
Обратите внимание, что ответ на первый вопрос на листе ответов неверен. Это должно быть 3,70 доллара. Остальные ответы на листе решения верны.
Рабочий лист № 2
Деб Рассел
Распечатать PDF : Рабочий лист № 2
Чтобы решить первое уравнение на рабочем листе, учащимся необходимо знать уравнение для прямоугольной призмы (V = lwh, где «V» означает объем, «l» означает длину, «w» означает ширину, а «h». равна высоте). Проблема заключается в следующем:
«На вашем заднем дворе ведутся раскопки для бассейна. Его размеры 42F x 29F x 8F. Грязь вывозят на грузовике, который вмещает 4 человека.53 кубических фута Сколько грузовиков с землей увезут? »
Рабочий лист № 2 Решения
Деб Рассел
Печать PDF : Рабочий лист № 2 Решения
Для решения задачи сначала рассчитайте общий объем бассейна. Используя формулу для объема прямоугольной призмы (V = lwh), вы получите:
V = 42F x 29F x 8F = 9744 кубических футов
Затем разделите 9744 на 4,53, или:
9744 кубических футов ÷ 4.53 кубических фута (на грузовик) = 2151 грузовик
Вы даже можете облегчить атмосферу в своем классе, воскликнув: «Вам придется потратить немало грузовиков, чтобы построить этот пул».
Обратите внимание, что ответ на листе решения этой проблемы неверен. Это должно быть 2151 кубический фут. Остальные ответы на листе решения верны.
.

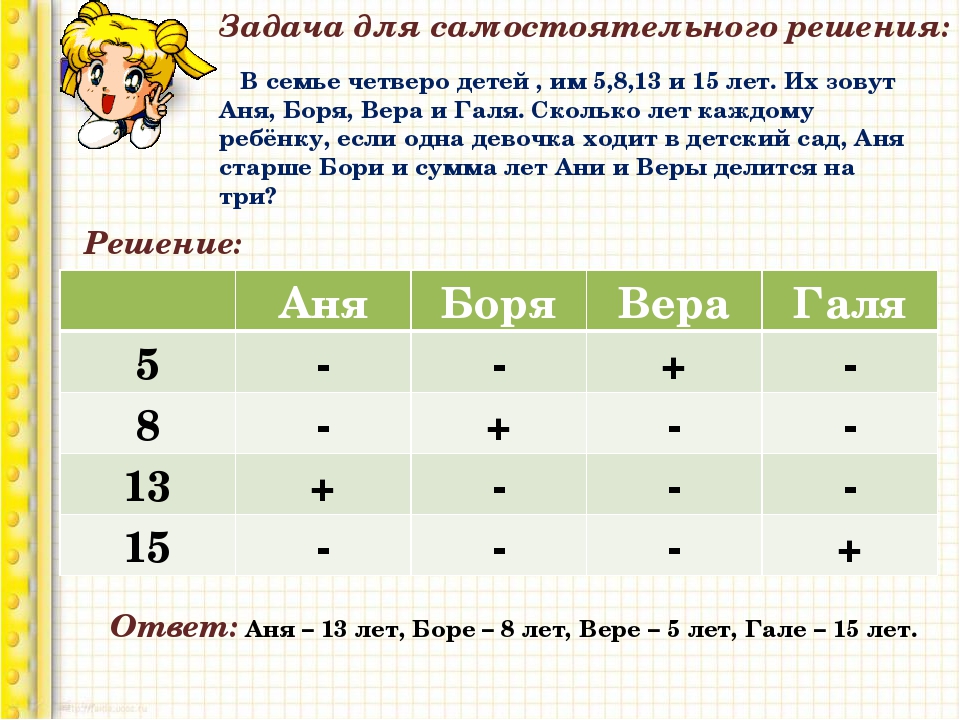
 .. где еще 1 доллар ???
.. где еще 1 доллар ???
 Вы можете написать автору для решения.Источник: Математические загадки Стива Миллера
Вы можете написать автору для решения.Источник: Математические загадки Стива Миллера Это будет , также означало бы, что число НЕ может делиться на 10, 15, 20, 25 или на 12, 18, 24 или 30. Таким образом, студенты, которые сказали, что оно делится на 10, на 15 и т. Д., Также сказали бы неправильный. Итак, два числа не могут быть 5 и 6.
Это будет , также означало бы, что число НЕ может делиться на 10, 15, 20, 25 или на 12, 18, 24 или 30. Таким образом, студенты, которые сказали, что оно делится на 10, на 15 и т. Д., Также сказали бы неправильный. Итак, два числа не могут быть 5 и 6.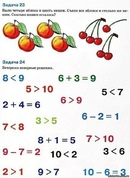 1, на котором есть коза.
1, на котором есть коза. Каково оптимальное количество учителей, сопровождающих и студентов, которые пойдут, если все 100 мест должны быть заполнены и все 100 долларов должны быть потрачены?
Каково оптимальное количество учителей, сопровождающих и студентов, которые пойдут, если все 100 мест должны быть заполнены и все 100 долларов должны быть потрачены?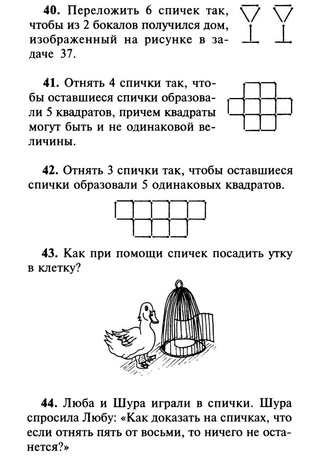 Туземец встал, перешел дорогу, и двое туземцев минутку болтали. Затем туземец, который перешел дорогу, вернулся и сказал миссионеру: «Он сказал, что он с западной стороны острова».
Туземец встал, перешел дорогу, и двое туземцев минутку болтали. Затем туземец, который перешел дорогу, вернулся и сказал миссионеру: «Он сказал, что он с западной стороны острова».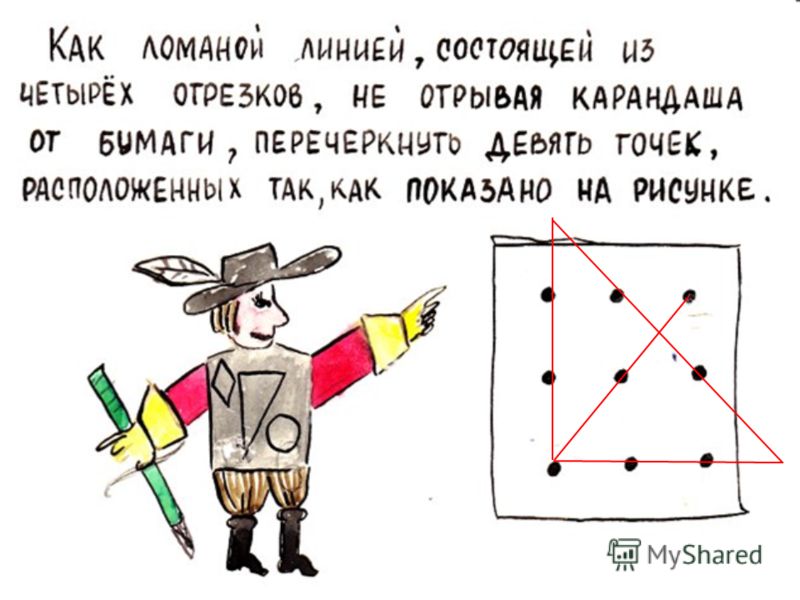
 США
США