Задачи на двузначные числа во 2 классе. Задачи по математике
Дата публикации: .
Сложение и вычитание двузначных чисел
1. Выбери двузначные числа из числового ряда.
а) 1, 23, 341, 29, 3, 396, 58, 293, 482
б) 12, 48, 671, 38, 592, 4, 39, 219
2. Сложи двузначные числа.
| 35 + 14 = | 54 + 28 = | 14 + 72 = |
| 27 + 31 = | 19 + 16 = | 54 + 48 = |
| 83 + 14 = | 32 + 38 = | 44 + 27 = |
| 17 + 31 = | 69 + 16 = | 74 + 48 = |
3. Выполни вычитание двузначных чисел.
| 35 — 14 = | 54 — 28 = | 84 — 67 = |
| 47 — 10 = | 69 — 68= | 54 — 48 = |
| 76 — 19 = | 89 — 58 = | 45 — 45 = |
| 90 — 20 = | 74 — 59= | 66 — 55 = |
4. Реши уравнения.
| 18 + x = 73 | 93 — x = 51 |
| 45 + x = 63 | 48 — x = 21 |
| 67 + x = 89 | 37 — x = 21 |
5. Реши примеры и найди значения х. Распиши ответы после каждого действия.
Реши примеры и найди значения х. Распиши ответы после каждого действия.
а) x — 14 + 17 — 38 + 22 = 18
1. ______________ 2. ________________ 3. _______________ 4. ________________
б) x — 87 + 15 — 10 + 14 = 98
1. ______________ 2. ________________ 3. _______________ 4. ________________
6. Раскрой скобки и реши числовые выражения.
а) 44 — ( 53 — 34 ) + ( 47 — 14 ) =
б) 67 — ( 15 — 11 ) + ( 93 — 57 ) =
в) 63 + ( 12 — 10 ) + ( 37 + 41 ) =
Текстовые задачи с двузначными числами
1) 18 самолётов прилетели вовремя, а 10 самолётов опоздали. Сколько самолётов приземлилось в аэропорту?
2) Ребята играли в снежки. Коля кинул 15 снежков, 11 из них не попали в цель. Миша кинул 23 снежка, 12 из них не попали в цель. Сколько всего снежков попали в цель, а сколько в цель не попали?
3) Папа получил 24 письма за рабочий день, мама получила на 11 писем меньше. Сколько всего писем получили папа и мама за рабочий день?
Тренажеры по математике 2 класс (задачи и примеры)
В математике, конечно же, важно уметь думать и мыслить логически, но не менее важна в ней практика. Половина ошибок на экзаменах по математике делается из-за неправильного вычисления простых действий с числами — сложение, вычитание, умножение, деление. А отработать эти навыки важно еще в начальной школе. Чтобы ничего не упустить, необходимо систематически заниматься с ребенком по специальным тетрадям — тренажерам. Они позволяют отработать математические навыки и умения и довести их до автоматизма. Тренажеры разнообразные, не обязательно скачивать их все, достаточно одного-двух понравившихся. Пособия можно использовать в работе с младшими школьниками не зависимо от программы, по которой ведется обучение.
Половина ошибок на экзаменах по математике делается из-за неправильного вычисления простых действий с числами — сложение, вычитание, умножение, деление. А отработать эти навыки важно еще в начальной школе. Чтобы ничего не упустить, необходимо систематически заниматься с ребенком по специальным тетрадям — тренажерам. Они позволяют отработать математические навыки и умения и довести их до автоматизма. Тренажеры разнообразные, не обязательно скачивать их все, достаточно одного-двух понравившихся. Пособия можно использовать в работе с младшими школьниками не зависимо от программы, по которой ведется обучение.
Один из самых важных моментов математики за 2 класс — отработать до автоматизма таблицу умножения. Отводим этой теме целую страницу. Чтобы перейти на нее и скачать тренажер на таблицу умножения, кликните по картинке:
Далее для ознакомления приведем список пособий, которые возможно купить в книжных магазинах. Пособия расположены сверху вниз в порядке увеличения сложности.
Математика. Решаем примеры с переходом через десяток.
Тетрадь для отработки навыков сложения и вычитания с переходом через десяток. Не просто примеры, а интересные игры и задания.
Карточки-задания. Математика. Сложение и вычитание. 2 класс
Удобные карточки для учителя второклашек. 2 варианта на сложение и вычитание одного вида. Подойдут для организации самостоятельной работы по математике в зависимости от продвижения по программе.
Математика. Сложение и вычитание в пределах 20. 1-2 классы. Е.Э.Кочурова
В разных курсах математике тема сложения и вычитание в пределах 20 изучается или в конце 1 класса, или в начале 2-го. В любом случае пособие поможет закрепить изученные способы манипуляций с числами, в некоторых заданиях эти способы представлены в виде своеобразных подсказок. В ходе самостоятельной работы с тетрадью ребенок ориентируется на образец выполнения и алгоритмические предписания. Умение пользоваться такими подсказками в учебе позволит ученику не только находить и использовать нужную информацию в ходе выполнения задания, но и осуществлять самопроверку.
Начинается тетрадь с отработки навыков сложения и вычитание в пределах 10, эта часть подойдет и для первоклашек.
Математика тренажерная тетрадь для 2 класса
Тетрадь содержит не только примеры на сложение и вычитание, но и перевод единиц друг в друга, и сравнение результатов вычисления (больше-меньше).
3000 примеров по математике (счет в пределах 100 часть 1)
Тренажер со счетом на время. Время засекать на решение одной колонки примеров и записывать внизу в окошечке. Обратите внимание на колонки, которые ребенок решал более 5 минут, значит у него возникли сложности по этому виду примеров. Приведены примеры на сложение и вычитание в пределах десяти и с переходом через десяток, сложение и вычитание десятков, манипуляции в пределах сотни.
Счет от 0 до 100
В этой прописи дается много примеров на сложение и вычитание, чтобы закрепить навыки устного счета в пределах 100.
Считаем правильно. Рабочая тетрадь по математике.
 Г.В.Белых
Г.В.Белых
Тетрадь также выполнена в виде тренажера, сплошные примеры и уравнения. Начинается со счета в пределах десяти, далее — в пределах сотни (сложение, вычитание, умножение и деление), заканчивается сравнением уравнений (примеры со знаками больше, меньше, равно).
Пособия пригодятся и учителям начальных классов в их работе, и родителям для занятий дома с детьми, в частности, в летние каникулы. Задания разных уровней сложности позволят осуществить дифференцированный подход к обучению.
А еще у нас есть отличный онлайн тренажер по математике! Родителям не нужно ничего распечатывать и проверять, все это за вас совершенно бесплатно сделаем мы! Выбирайте режим и вперед >>
Тесты онлайн по математике для 2 класса
Здесь выложены онлайн тесты по математике за 2 класс на тему «Математические задачи, Сложение и вычитание до 100, и Умножение и деление» и другие. Тесты составлены с учетом школьной программы по математике для 2 класса на основе того, что должен знать и уметь ребенок в этом возрасте. А именно:
А именно:
Математические задачи для 2 класса. Задачи на нахождение неизвестного слагаемого, неизвестного уменьшаемого и неизвестного вычитаемого. Решение задач в 2 действия на сложение и вычитание. Решение задач в одно действие на умножение и деление (с числами 2 и 3 из таблицы умножения). Порядок выполнения действий в выражениях, содержащих 2-3 действия (со скобками и без них). При этом, кроме простых выражений из программы 1 класса, в этих задачах используются новые (более сложные) выражения: прибавление одноцифрового числа к двухцифровому (45+7), отнимание одноцифрового числа от двухцифрового (45-7), прибавление и отнимание двухцифровых чисел (45+27, 45-27). Также в этих задачах используются меры длины (миллиметры, сантиметры, дециметры, метры), разменная монета (рубли, копейки), единицы измерения веса (киллограмм, центнер), единицы измерения ёмкости (литр).
Сложение и вычитание до 100 для 2 класса. Новая счетная единица – десяток.. Счет десятками. Образование и названия чисел, их десятичный состав. Запись и чтение чисел. Числа однозначные и двузначные. Порядок следования чисел при счете. Сравнение чисел. Единицы длины: сантиметр, дециметр, миллиметр, метр. Соотношения между ними. Единицы времени: час, минута. Соотношение между ними. Определение времени по часам с точностью до минуты. Монеты (набор и размен). Задачи на нахождение неизвестного слагаемого, неизвестного уменьшаемого и неизвестного вычитаемого. Решение задач в 2 действия на сложение и вычитание. Устные и письменные приемы сложения и вычитания чисел в пределах 100. Числовое выражение и его значение. Порядок действий в выражениях, содержащих 2 действия (со скобками и без них). Сочетательное свойство сложения. Использование переместительного и сочетательного свойств сложения для рационализации вычислений.
Образование и названия чисел, их десятичный состав. Запись и чтение чисел. Числа однозначные и двузначные. Порядок следования чисел при счете. Сравнение чисел. Единицы длины: сантиметр, дециметр, миллиметр, метр. Соотношения между ними. Единицы времени: час, минута. Соотношение между ними. Определение времени по часам с точностью до минуты. Монеты (набор и размен). Задачи на нахождение неизвестного слагаемого, неизвестного уменьшаемого и неизвестного вычитаемого. Решение задач в 2 действия на сложение и вычитание. Устные и письменные приемы сложения и вычитания чисел в пределах 100. Числовое выражение и его значение. Порядок действий в выражениях, содержащих 2 действия (со скобками и без них). Сочетательное свойство сложения. Использование переместительного и сочетательного свойств сложения для рационализации вычислений.
Умножение и деление для 2 класса. Конкретный смысл и названия действий умножения и деления. Знаки умножения • (точка) и деления : (две точки). (В тестах знак умножения заменяется на «х»). Названия компонентов и результата умножения (деления), их использование при чтении и записи выражений. Переместительное свойство умножения. Взаимосвязи между компонентами и результатом действия умножения; их использование при рассмотрении деления с числом 10 и при составлении таблиц умножения и деления с числами 2, 3. Порядок выполнения действий в выражениях, содержащих 2-3 действия (со скобками и без них). Периметр прямоугольника (квадрата). Решение задач в одно действие на умножение и деление.
(В тестах знак умножения заменяется на «х»). Названия компонентов и результата умножения (деления), их использование при чтении и записи выражений. Переместительное свойство умножения. Взаимосвязи между компонентами и результатом действия умножения; их использование при рассмотрении деления с числом 10 и при составлении таблиц умножения и деления с числами 2, 3. Порядок выполнения действий в выражениях, содержащих 2-3 действия (со скобками и без них). Периметр прямоугольника (квадрата). Решение задач в одно действие на умножение и деление.
Дальше вы можете пройти по порядку (или вразброс) тесты по математике за 2 класс. Желаем успехов!
Тесты
В этом тесте тебе нужно решить 10 математических задач на нахождение суммы для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на нахождение суммы для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на нахождение суммы для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на нахождение остатка для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на нахождение остатка для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на нахождение остатка для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на тему «Больше, меньше» для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на тему «Больше, меньше» для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного слагаемого и вычитаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного слагаемого и вычитаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного слагаемого и вычитаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного слагаемого и вычитаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного третьего слагаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного третьего слагаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного уменьшаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с нахождением неизвестного уменьшаемого для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на разностное сравнение для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на разностное сравнение для 2 класса.
В этом тесте тебе нужно решить 10 математических задач на разностное сравнение для 2 класса.
В этом тесте тебе нужно решить 10 математических задач с косвенными вопросами для 2 класса.
В этом тесте тебе нужно решить все примеры на сложение в пределах 100 для 2 класса.
В этом тесте тебе нужно решить все примеры на сложение в пределах 100 для 2 класса.
В этом тесте тебе нужно решить все примеры на сложение в пределах 100 для 2 класса.
В этом тесте тебе нужно решить все примеры на сложение с переходом через десяток в пределах 100 для 2 класса.
В этом тесте тебе нужно решить все примеры на вычитание в пределах 100 для 2 класса.
В этом тесте тебе нужно решить все примеры на вычитание в пределах 100 для 2 класса.
В этом тесте тебе нужно решить все примеры на вычитание в пределах 100 для 2 класса.
В этом тесте тебе нужно решить все примеры на вычитание с переходом через десяток для 2 класса.
В этом тесте тебе нужно решить все примеры на вычитание с переходом через десяток для 2 класса.
В этом тесте тебе нужно проверить свои знания таблицы умножения с числами «2» и «3» для 2 класса.
В этом тесте тебе нужно увеличивать или уменьшать число «2» в заданное количество раз, а также увеличивать и уменьшать другие числа в 3 раза
В этом тесте тебе нужно увеличивать или уменьшать число «3» в заданное количество раз, а также увеличивать и уменьшать другие числа в 3 раза
В этом тесте тебе нужно пройти математический диктант, в котором нужно решать выражения с числом «2».
В этом тесте тебе нужно пройти математический диктант, в котором нужно решать выражения с числом «3».
В этом тесте тебе нужно решить примеры, состоящие из нескольких действий, руководствуясь при этом правилом порядка математических действий.
В этом тесте тебе нужно решить 10 математических заданий, в которых ты сможешь проверить не только математические способности, но и логическое мышление.
Задачи в 2 действия. Математика 2 класс Богданович. ГДЗ, решебник.
Категория: —>> Математика 2 класс Богданович
Задание: —>> 164 — 191
наверх
Задание 164.
Мама порвала с одного куста 5 помидоров с другого 4. Детям она отдала 6 помидоров. Сколько помидоров осталось?
Решение:
- 5 + 4 = 9 всего собрала
- 9 — 6 = 3 осталось
- Ответ: 3 помидора осталось
Задание 165.
На тарелке было 6 жёлтых яблок и 4 красных. Съели 7 яблок. Сколько яблок осталось на тарелке?
Решение:
- 6 + 4 = 10
- 10 — 7 = 3
- Ответ: 3 яблока осталось на тарелке.
Задание 166.
Решение:
| 8 + 8 + 1= 17 | 7 + 7 — 1= 13 | 13 — 8 — 5 = 0 | 12 — 7 — 5 = 0 |
| 9 + 8 — 10 = 7 | 8 + 3 — 5 = 6 | 11 — 8 — 0 = 3 | 16 — 7 + 6 = 15 |
Задание 167.

К числу 5 прибавили 2, а потом ещё 6.На сколько увеличилось число 5?
Решение:
- 5 + 2 = 7
- 7 + 6 = 13
- 13 — 5 = 8
- Ответ:число 5 увеличелось на 8.
Задание 168.
Марина написала неизвестное число. Если к нему прибавить 8, то получится 10. Какое число написала Марина?
Решение:
- 10 — 8 = 2
- Ответ:Марина написала число 2.
Задание 169.
Найди разность 14 — а, если а = 8, а = 5.
Решение:
- Если а = 8, то 14 — а = 6
- Если а = 5, то 14 — а = 9
Задание 170.
Составь задачу по таблице. Реши её.
| Было | Истратили | Осталось |
| ? | 8 грн. | 9 грн. |
Решение:
Петя в магазине потратил на игрушки 8 гривен и у него осталось 9 гривен. Сколько денег было у Пети до покупки игрушек?
Сколько денег было у Пети до покупки игрушек?
- 1) 8 + 9 = 17
- Ответ: 17 гривен.
Задание 171.
Задание 172.
Сумма длин всех сторон многоугольника
периметр многоугольника.
- 2 + 5 + 2 + 4 = 13 (см)
- Ответ: 13 см.
- Проверь, правильно ли найден периметр четырёхугольника. Найди самостоятельно периметр треугольника.
Решение:
- 1) Периметр четырехугольника найден верно.
- 2) P = 3 + 4 + 5 = 12
- Ответ: Периметр треугольника равен 12 см.
Задание 173.
Реши примеры.
Решение:
| 2 + 9 — 7 = 4 | 16 — 8 + 5 = 13 | 14 — 9 + 6 = 11 | 8 + 8 — 9 = 7 |
| 13 — 9 + 8 = 12 | 9 + 9 — 8 = 10 | 15 — 8 — 6 = 1 | 9 — 9 + 5 = 5 |
Задание 174.
На урок труда принесли 7 листов зелёной бумаги и 5 жёлтой. На изготовление коробки израсходовали 4 листа. Сколько листов бумаги осталось?
На изготовление коробки израсходовали 4 листа. Сколько листов бумаги осталось?
| Было | Израсходовали | Осталось |
| 7 зеленых 5 желтых | 4 | ? |
Решение
- 1) 7 + 5 = 12 (л.)
- 2) 12 — 4 = 8 (л.)
- Ответ: 8 листов.
Как решить задачу другим способом?
Решение:
- 1) 5 — 4 = 1
- 2) 7 + 1 = 8
Задание 175.
Реши примеры.
Решение:
| 8 — 2 + 7 = 13 | 10 + 5 — 9 = 6 | 14 — 7 + 2 = 9 |
| 9 — 4 + 7 = 12 | 13 — 4 + 5 = 9 | 12 — 9 + 8 = 11 |
Задание 176.
В ящике было 12 кг картофеля. На приготовление завтрака использовали 2 кг картофеля, а на приготовление обеда — 3 кг. Сколько килограммов картофеля осталось в ящике?
План решения
- 1) Сколько всего килограмм картофеля использовали на приготовление завтрака и обеда?
- 2) Сколько килограммов картофеля осталось в ящике?
Решение:
- 1) 2 + 3 = 5
- 2) 12 — 5 = 7
- Ответ: 7 кг.

Задание 177.
Реши примеры.
Решение:
| 13 — 7 = 6 | 12 — 5 = 7 | 7 + 4 — 5 = 6 | 12 — 6 + 7 = 13 |
Задание 178.
Решение:
|
|
Задание 179.
Составь задачу по рисунку и реши её устно.
Решение:
У мамы было 10 метров ткани. На пошивку платья она израсходовала 2 м. ткани, а на пошивку юбки 1 м. Сколько ткани осталось у мамы?
- 1) 2 + 1 = 3
- 2) 10 — 3 = 7
- Ответ: 7 метров.
Задание 180.
У Максима было 12 наклеек. В один конверт он положил 4 наклейки, а в другой 3. Сколько наклеек осталось положить в конверт?
В один конверт он положил 4 наклейки, а в другой 3. Сколько наклеек осталось положить в конверт?
План решения
- 1) Сколько всего наклеек Максим уже положил в конверт?
- 2) Сколько наклеек осталось положить в конверт?
Решение:
- 1) 4 + 3 = 7
- 2) 12 — 7 = 5
- Ответ: 5 наклеек.
Задание 181.
На прогулку вывели 7 девочек, а мальчиков на 3 меньше. Сколько мальчиков вышло на прогулку? Сколько всего детей вышло на прогулку?
Решение:
- 1) 7 — 3 = 4
- 2) 7 + 4 = 11
- Ответ: 4 мальчика вышло на прогулку, 11 детей всего вышло на прогулку.
Задание 182.
Рассмотри таблицу сложения и вычитания чисел. Объясни, как находить ответы при сложении и вычитании.
Найди по таблице сумму 7 + 9 и разность 15 — 6.
Решение:
Для того что бы выполнить сложение при помощи таблицы, нужно провести воображаемые линии от цифр, которые мы собираемся складывать(вниз от верхнего числа и вправо от цифры, которая расположена в крайней левой колонке). Результатом пересечения этих воображаемых линий будет сумма, выбранных нами цифр.
Результатом пересечения этих воображаемых линий будет сумма, выбранных нами цифр.
При вычитании, выбираем вычитаемое из нижнего ряда (выделено синим), уменьшаемое находим в той же колонке, что и вычитаемое. Разность в крайней левой колонке, в том же ряду что и уменьшаемое.
- 1) 7 + 9 = 16
- 2) 15 — 6 = 9
Задание 183.
Числа 13, 16, 18 разложи на два слагаемых так, чтобы одним из слагаемых было число 9.
Образец. 14 = 9 + 5.
Решение:
- 1) 13 = 9 + 4
- 2) 16 = 9 + 7
- 3) 18 = 9 + 9
Задание 184.
Решение:
| 1) Дополни до 12. | 2) Увеличь на 7 |
Задание 185.
Из каждой пары выражений выпиши выражение с меньшим значением:
| 17 — 9 и 12 — 3 | 16 — 7 и 12 — 9 |
| 3 + 9 и 4 + 8 | 9 + 4 и 9 + 7 |
Решение:
| 17 — 9 | 12 — 9 |
| 3 + 9 = 4 + 8 | 9 + 4 |
Задание 186.

Найди периметры треугольников.
Периметр какого треугольника больше и на сколько?
Задание 187.
У Толи было 8 тетрадей в клетку и 7 тетрадей в линейку. 5 тетрадей в линейку он отдал другу. Сколько тетрадей осталось у Толи? Реши задачу двумя способами.
Решение:
- 1 способ:
1) 8 + 7 = 15 (тетрадей) всего было у Толи;
2) 15 — 5 = 10 (тетрадей). - 2 способ:
1) 7 — 5 = 2 (тетради) в линейку осталось у Толи;
2) 2 + 8 = 10 (тетрадей). - Ответ: у Толи осталось 10 тетрадей.
Задание 188.
На аэродроме было 12 самолётов. Сначала взлетело 2 самолёта, а потом ещё 3. Сколько самолётов осталось на аэродроме?
Решение:
- 1) Способ: сначала вычисляем сколько всего взлетело самолетов, то что получилось, отнимает от количества самолетов, которое стояло сначала на аэродроме.
- 2) Способ: отнимаем количество самолетов, которое сначала взлетело, затем отнимаем самолеты, которые взлетели после них.

Задание 189.
Решение:
| 17 — 9 = 8 | 4 + 8 — 9 = 12 — 9 = 3 | 16 — 9 = 7 | 5 + 9 — 6 = 14 — 6 = 8 |
| 13 — 8 = 5 | 4 + 8 — 9 = 12 — 9 = 4 | 13 — 7 = 6 | 12 — 5 + 8 = 7 + 8 = 15 |
Задание 190.
В ящике было 12 кг лука. В первый день продали 4 кг лука, а во второй 5 кг. Сколько килограммов лука осталось в ящике?
- 1) 12 — 4 = 8 (кг) осталось лука после продажи в первый день;
- 2) 8 — 5 = 3 (кг) осталось лука после продажи во второй день.
- Ответ: осталось 3 кг лука.
Решение:
Сначала узнаем сколько лука осталось в первый день, затем от полученного результата отнимаем лук, проданный во второй день.
- Второй способ:
- 1) 4 + 5 = 9 (кг) лука продали за 2 дня;
- 2) 12 — 9 = 3 (кг).
Задание 191.
Решение:
- 1) На странице было изображено 2 треугольника, а кругов на 8 больше.
 Сколько кругов было на странице?
Сколько кругов было на странице?- 1) 2 + 8 = 10 (кругов).
- Ответ: на странице было изображено 10 кругов.
- 2)
- 14 — 10 + 4 = 4 + 4 = 8
- 17 — 10 + 4 = 7 + 4 = 11
- 19 — 10 + 3 = 9 + 3 = 12
- 20 — 10 + 3 = 10 + 3 = 13
Задание: —>> 164 — 191
Задачи в два действия — урок. Математика, 2 класс.
Карлсон за один день съел \(10\) банок варенья, а за второй день съел на \(3\) банки меньше. Сколько всего банок варенья съел Карлсон за два дня вместе?
По условию составим запись и выработаем план решения:
1 день −10 банок 2 день −? на 3 банки меньше, чем в 1 день − за 2 дня вместе?
Обрати внимание!
Анализируя эту схему, делаем вывод, что задача решается двумя действиями.
Сначала найдём ответ на вопрос:
1) сколько банок варенья съел Карлсон за второй день?
На \(3\) банки меньше — это значит, следует отнять \(3\)!
\(10 — 3 = 7\) (б. ) — столько банок варенья съел Карлсон за второй день.
) — столько банок варенья съел Карлсон за второй день.
Теперь знаем количество банок варенья, которое съел Карлсон за первый день и за второй день. Поэтому можно ответить на вопрос задачи.
2) Сколько всего банок варенья съел Карлсон за два дня вместе?
Вместе — это значит, следует сложить!
\(10 + 7 = 17\) — столько банок варенья съел Карлсон за два дня вместе.
Ответ: за \(2\) дня Карлсон съел \(17\) банок варенья.
Можно решение этой задачи записать и одним примером:
\((10 — 3) + 10 = 17\).
Первым действием в скобках ответим на первый вопрос, а вторым действием ответим на вопрос задачи.
Пример:
в клетке было \(7\) синих попугаев и \(8\) зелёных попугаев.
Продали \(5\) птиц. Сколько попугаев осталось в клетке?
Сразу на вопрос задачи ответить нельзя.
В ходе решения составим такую запись:
1) \(7 + 8 = 15\) п.,
2) \(15 — 5 = 10\) п.
Ответ: \(10\) попугаев осталось в клетке.
Первым действием узнали общее количество птиц в клетке.
Вторым действием ответили на вопрос задачи, т. е. узнали количество попугаев, оставшихся в клетке.
Задачи в два действия — это составные задачи, в которых для нахождения искомого ответа нужно сначала вычислить одно неизвестное по имеющимся данным.
примеры и способы решения математических задач для родителей
На протяжении всего обучения школьникам приходится решать задачи — в начальной школе по математике, а затем по алгебре, геометрии, физике и химии. И хотя условия задач в разных науках отличаются, способы решения основаны на одних и тех же логических принципах. Понимание того, как устроена простая задача по математике, поможет ребёнку разработать алгоритмы для решения задач из других областей науки. Поэтому учить ребёнка решать задачи необходимо уже с первого класса.
Нередки случаи, когда точные науки вызывают у детей сопротивление. Видя это, учителя и родители записывают таких детей в «гуманитарии», из-за чего они только укрепляются во мнении, что точные науки — это не для них. Преподаватель математики Анна Эккерман уверена, что проблемы с математикой часто имеют исключительно психологический характер:
Преподаватель математики Анна Эккерман уверена, что проблемы с математикой часто имеют исключительно психологический характер:
Детям вбивают в голову, что математика — это сложно. К длинным нудным параграфам в учебнике сложно подступиться. Учитель ставит на ребёнке клеймо «троечника» или «двоечника». Если не внушать детям, что они глупые и у них ничего не получится, у них получится ровно всё.
Чтобы ребёнку было интересно учить математику, он должен понимать, как эти знания пригодятся ему, даже если он не собирается становиться программистом или инженером.
Математика ежедневно помогает нам считать деньги, без умения вычислять периметр и площадь невозможно сделать ремонт, а навык составления пропорций незаменим в кулинарии — используйте это. Превращайте ежедневные бытовые вопросы в математические задачи для ребёнка: пусть польза математики станет для него очевидна.
Конечно, найти в быту применение иррациональным числам или квадратным уравнениям не так просто. И если польза этих знаний вызывает у подростка вопросы, объясните ему, что с их помощью мы тренируем память, развиваем логическое мышление и остроту ума — навыки, в равной степени необходимые как «технарям», так и «гуманитариям».
И если польза этих знаний вызывает у подростка вопросы, объясните ему, что с их помощью мы тренируем память, развиваем логическое мышление и остроту ума — навыки, в равной степени необходимые как «технарям», так и «гуманитариям».
Как правильно научить ребёнка решать задачи
Если ребёнок только начинает осваивать навык решения задач, приучите его придерживаться определённого алгоритма.
1. Внимательно читаем условия
Лучше вслух и несколько раз. После того как ребёнок прочитал задачу, задайте ему вопросы по тексту и убедитесь, что ему понятно, что вычислять нужно количество грибов, а не огурцов. Старайтесь не нервничать, если ребёнок упустил что-то из вида. Дайте ему разобраться самостоятельно. Если в условиях упоминаются неизвестные ребёнку реалии — объясните, о чём идёт речь.
Особую сложность представляют задачи с косвенным вопросом, например:
«Один динозавр съел 16 деревьев, это на 3 меньше, чем съел второй динозавр. Сколько деревьев съел второй динозавр?». Невнимательно прочитав условия, ребёнок посчитает 16−3, и получит неправильный ответ, ведь эта задача на самом деле требует не вычитания, а сложения.
Невнимательно прочитав условия, ребёнок посчитает 16−3, и получит неправильный ответ, ведь эта задача на самом деле требует не вычитания, а сложения.
2. Делаем описание задачи
В решении некоторых задач поможет представление данных в виде схемы, графика или рисунка. Чем ярче сложится образ, тем проще будет его осмыслить. Наглядная запись позволит ребёнку не только быстро разобраться в условиях задачи, но и поможет увидеть связь между ними. Часто план решения возникает уже на этом этапе.
Ребёнок должен чётко понимать значения словесных формул и знать, какие математические действия им соответствуют.
Формы краткой записи условий задач / shkola4nm.ru
3. Выбор способа решения
Наглядно записанное условие должно подтолкнуть ребёнка к нахождению решения. Если этого не произошло, попробуйте задать наводящие вопросы, проиллюстрировать задачу при помощи окружающих предметов или разыграть сценку. Если один из способов объяснения не сработал — придумайте другой. Многократное повторение одного и того же вопроса неэффективно.
Многократное повторение одного и того же вопроса неэффективно.
Все, даже самые сложные, математические задачи сводятся к принципу «из двух известных получаем неизвестное». Но для нахождения этой пары чисел часто требуется выполнить несколько действий, то есть разложить задачу на несколько более простых.
Ребёнок должен знать способы получения неизвестных данных из двух известных:
- слагаемое = сумма − слагаемое
- вычитаемое = уменьшаемое − разность
- уменьшаемое = вычитаемое + разность
- множитель = произведение ÷ множитель
- делитель = делимое ÷ частное
- делимое = делитель × частное
После того как план действий найден, подробно запишите решение. Оно должно отражать всю последовательность действий — так ребёнок сможет запомнить принцип и пользоваться им в дальнейшем.
4. Формулировка ответа
Ответ должен быть полным и точным. Это не просто формальность: обдумывая ответ, ребёнок привыкает серьёзно относиться к результатам своего труда. А главное — из описания должна быть понятна логика решения.
А главное — из описания должна быть понятна логика решения.
Задание из базового курса алгебры домашней онлайн-школы «Фоксфорда», 7 класс
Одна из самых распространённых ошибок — представление в ответе не тех данных, о которых спрашивалось изначально. Если такая проблема возникает, нужно вернуться к первому пункту.
5. Закрепление результата
Не стоит думать, что выполнив задание один раз, ребёнок сразу научится решать задачи. Полученный результат нужно зафиксировать. Для этого подумайте над решённой задачей ещё немного: предложите ребёнку поискать другой способ решения или спросите, как изменится ответ при изменении того или иного параметра в условии.
Важно, чтобы у ребёнка сложился чёткий алгоритм рассуждений и действий в каждом из вариантов.
В нашей онлайн-школе, помимо уроков, ученики могут закреплять свои знания на консультациях в формате открытых часов, где учителя разбирают темы, вызвавшие затруднения, показывают необычные задачи и различные способы их решения.
Что поможет ребёнку решать задачи
В заключение расскажем о том, как сделать процесс решения задач проще и интереснее:
- Для того чтобы решать задачи, необходимо уметь считать. Следует выучить с ребёнком таблицу умножения, освоить примеры с дробями и простые уравнения.
- Чтобы решение задач не превратилось для ребёнка в рутину, проявите фантазию. Меняйте текст задания в соответствии с интересами ребёнка. Например, решать задачи на движение будет куда интереснее, если заменить банальные поезда трансформерами, летящими навстречу друг другу в эпической схватке.
- Дети с развитой логикой учатся решать задачи быстрее. Советуем разбавлять чисто математические задания логическими. Задачи «с подвохом» избавят ребёнка от шаблонного мышления, а задания с большим количеством лишних данных научат выделять главное из большого количества условий.
<<Блок перелинковки>>
После того как ребёнок решит достаточно задач одного типа, предложите ему самому придумать задачу. Это позволит ему не только закрепить материал, но и проявить творческие способности.
Это позволит ему не только закрепить материал, но и проявить творческие способности.
ГДЗ по математике 2 класс Моро учебник
ГДЗ по математике – залог успеха второклассника!
Второклассникам приходится считать много и постоянно! Еще бы, ведь содержание курса математики включает в себя не только сухие примеры. В теме «Рубль. Копейка» ребятам предстоит считать деньги. В темах, посвященных нумерации, они переводят метры в миллиметры. Часам и секундам тоже нашлась специальная тема. А ведь при этом приходится еще делать вычисления с переходом за десяток, учиться выполнять действия в скобках, разбираться, откуда в уравнениях взялись буквы и что они обозначают, выполнять множество других заданий. Задача учителя и родителей – сформировать прочные навыки выполнения арифметических действий, без которых невозможно успешное изучение большинства школьных наук. Для поиска требуемого задания или упражнения по математике для второго класса необходимо выбрать соответствующую часть: первую или вторую, найти искомый номер страницы из учебника, перейти по ссылке на страницу с решением и найти искомый ответ на номер своего примера или задачи.
Учебник часть 1 (страницы)
4567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495
Учебник часть 2 (страницы)
456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111
Смотреть ГДЗ к рабочей тетради по математике за 2 класс Моро
Почему второкласснику трудно дается математика
Школьник тоже осознает необходимость серьезного отношения к важному предмету. И очень хочет, чтобы у него все получалось. Но путь к желанному результату для многих детей оказывается довольно сложным.
Не все ребята сформировали навыки абстрактного мышления, не каждый в дошкольном детстве подготовил свою память и внимание к усвоению большого количества информации.
Родители могут помочь ребенку. Ведь они, как никто другой, заинтересованы в успехах собственного чада. Но мамы и папы не знают современных подходов к обучению в младшей школе, им неизвестны требования к оформлению практических работ разного вида.
Ведь они, как никто другой, заинтересованы в успехах собственного чада. Но мамы и папы не знают современных подходов к обучению в младшей школе, им неизвестны требования к оформлению практических работ разного вида.
ГДЗ поможет всем!
Проблему снимает обращение к дополнительному образовательному ресурсу – готовым заданиям по математике, специально составленным к учебнику М.И.Моро.
Здесь собраны все те работы, которые включены в 1 и 2 части учебного пособия. Но если в учебнике они представлены в виде пособий, то в решебнике под каждым номером содержится правильный ответ, подробное решение, грамотное оформление работы.
Теперь при любом затруднении ученика он сможет увидеть, как работать со схемой или рисунком, как решить уравнение и задачу, как представить ответ в виде чертежа и дать к нему объяснения. Наглядный пример очень важен для детей, у которых еще не полностью сформировано абстрактное мышление.
Взрослые тоже не могут обойтись без ГДЗ. Если малыш не разберется в задаче самостоятельно, он придет к маме. Ей понадобится пара минут, чтобы с помощью решебника понять логику поиска ответа.
Ей понадобится пара минут, чтобы с помощью решебника понять логику поиска ответа.
Педагог, вооружив родителей готовыми домашними заданиями, получает армию консультантов, которые восполнят нехватку времени на уроке.
ГДЗ по математике – залог успеха второклассника!
Решение задач: 2 класс по математике
Приборная панель
Математика 2 класс
Решение проблем
Перейти к содержанию
Приборная панель
Авторизоваться
Приборная панель
Календарь
Входящие
История
Помощь
Закрывать
-
Мой Dashboard
- 2 класс Математика
- Страницы
- Решение задач
NE
- Дом
- Процедуры
- Закрытие
- Банк ресурсов
- Курс 1-го класса
- Курс 3-го класса
- Учебный план 2-го класса Сообщество
- Семья и сообщество 2-го класса
- Сотрудничество
- Google Диск
Распечатанные рабочие листы для задач по математике для второго класса
Проблемы со словами могут быть сложной задачей для учащихся, особенно для второклассников, которые, возможно, еще учатся читать. Но вы можете использовать базовые стратегии, которые будут работать практически с любым учеником, даже с теми, кто только начинает изучать письменные навыки.
Но вы можете использовать базовые стратегии, которые будут работать практически с любым учеником, даже с теми, кто только начинает изучать письменные навыки.
Инструкции и стратегии
Чтобы помочь второклассникам научиться решать задачи со словами, научите их выполнять следующие действия:
- Изучите математическую задачу: Прочтите слово «задача», чтобы понять ее общий характер. Поговорите со своими учениками о проблеме и обсудите, какие части являются наиболее важными.
- Прочтите математическую задачу: Прочтите вопрос еще раз. На этот раз сосредоточьтесь на конкретных деталях проблемы. Какие части проблемы связаны друг с другом?
- Задайте вопросы о задействованных операциях: Поразмышляйте еще раз. Определите конкретные математические операции, которые вам нужно выполнить, и перечислите их на бумаге в порядке их выполнения.
- Спросите себя о предпринятых шагах: Просмотрите каждый сделанный шаг.
 Определите, кажется ли ваш ответ разумным. Если возможно, сравните свой ответ с ответами в книге, чтобы определить, на правильном ли вы пути.
Определите, кажется ли ваш ответ разумным. Если возможно, сравните свой ответ с ответами в книге, чтобы определить, на правильном ли вы пути. - Завершите: Просмотрите текст словесных задач, которые вы будете решать, чтобы определить любые слова, которые вы не узнаете. Перечислите их и определите их значение, прежде чем решать проблемы. Напишите краткие определения терминов для справки при решении проблем.
Решение проблем
Изучив эти стратегии, используйте следующие бесплатные распечатки задач со словами, чтобы студенты могли практиковать то, что они узнали.Есть только три рабочих листа, потому что вы не хотите перегружать своих второклассников, когда они только учатся решать задачи со словами.
Начните медленно, при необходимости повторите шаги и дайте своим ученикам возможность усвоить информацию и научиться словесным методам решения проблем в расслабленном темпе. В печатных материалах содержатся термины, которые будут знакомы молодым студентам, такие как «треугольник», «квадрат», «лестница», «десять центов», «пятак» и дни недели.
Д. Рассел
В эту распечатку включены восемь математических задач, которые покажутся второклассникам многословными, но на самом деле они довольно просты.Задачи на этом листе включают задачи со словами, сформулированные в виде вопросов, например: «В среду вы видели 12 малиновок на одном дереве и 7 на другом дереве. Сколько всего малиновок вы видели?» и «У всех ваших 8 друзей есть двухколесные велосипеды, сколько всего это колес?»
Если студенты озадачены, прочитайте задачи вслух вместе с ними. Объясните: если вы вычеркнете слова, это будут простые задачи на сложение и умножение, где ответ на первый будет следующим: 12 робинов + 7 робинов = 19 робинов; а ответ на второй будет: 8 друзей x 2 колеса (для каждого велосипеда) = 16 колес.
Д. Рассел
Эта последняя печатная форма в наборе содержит немного более сложные задачи, такие как эта, связанная с деньгами: «У вас есть 3 квартала, и ваша выписка обошлась вам в 54 цента. Сколько денег у вас осталось?»
Чтобы ответить на этот вопрос, предложите учащимся изучить проблему, а затем прочитать ее всем классом. Задайте такие вопросы, как: «Что может помочь нам решить эту проблему?» Если учащиеся не уверены, возьмите три четверти и объясните, что они равны 75 центам. Тогда задача превращается в простую задачу вычитания, поэтому завершите ее, указав числовую операцию на доске следующим образом: 75 центов — 54 цента = 21 цент.
Задайте такие вопросы, как: «Что может помочь нам решить эту проблему?» Если учащиеся не уверены, возьмите три четверти и объясните, что они равны 75 центам. Тогда задача превращается в простую задачу вычитания, поэтому завершите ее, указав числовую операцию на доске следующим образом: 75 центов — 54 цента = 21 цент.
Задачи по обучению словарю во 2-м классе
Если вы ищете лучший способ научить словесным задачам и, что более важно, хотите, чтобы ваши ученики были более успешными в решении текстовых задач, я здесь, чтобы помочь. Учить словесные задачи во 2-м классе не должно быть проблемой.
Почему так сложно учить задачи по словам во 2-м классе?
Когда я только начал преподавать, я учил своих учеников использовать ключевые слова, подчеркивать и обводить, выделять и вставлять рамку… и, тем не менее, это не помогло.Они все еще не знали, когда складывать, а когда убирать.
И мои ученики не понимали и не успевали лучше.
Не помогло то, что я не преподавал постоянно и не позволял своим ученикам практиковаться в решении словесных задач.
Задачи со словом всегда были источником разногласий для моих учеников, независимо от того, в каком классе я преподавал (1-й, 2-й и 4-й), и всегда были тем, что я преподавал наугад в рамках принятой математической программы.
Большинство учебных программ по математике предлагают следующее:
- Задачи на 1 или 2 слова в конце каждого урока, но на самом деле не предлагают способ научить студентов решать задачи со словами
- 1 глава о «решении задач»
И серьезно, ни один из них полезно.
Я хотел, чтобы мои ученики ежедневно практиковались в стратегических задачах по решению словесных задач.
И знаете что? Когда я начал последовательно и стратегически преподавать задачи со словами во 2-м классе, мои ученики были менее разочарованы и гораздо более искусно решали задачи со словами.
Итак, какое решение?
Сейчас я следую 4-дневному плану обучения и оцениваю его на 5-й день.
Я больше не учу ключевые слова или подчеркивание, обводку, выделение и / или бокс… вместо этого я учу своих учеников искать закономерности в том, как структурированы проблемы со словами… ситуации со словами.
Кроме того, я посвящаю 5-10 минут каждый день обучению и практике словесных задач.
Как я узнаю, чему учить?
Начну со стандарта.
Честно говоря, что бы я ни преподаю, именно здесь я начинаю. Мне нужно точно знать, чего я ожидаю, чтобы потом я мог помочь своим ученикам справиться с этим.
Стандарт Common Core для 2-го класса гласит:
CCSS.MATH.CONTENT.2.OA.A.1
- Используйте сложение и вычитание в пределах 100 для решения одно- и двухэтапных задач со словами, включающих ситуации сложения, взятия из, сложения, разделения и сравнения с неизвестными во всех позициях, e.g., используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему.
Хотя многие штаты больше не используют термин «Common Core», многие принятые ими стандарты совпадают или, по крайней мере, схожи.
MAFS.2.OA.1.1 (стандарты Флориды)
- Используйте сложение и вычитание в пределах 100 для решения одно- и двухэтапных задач со словами, включающих ситуации сложения, взятия из, сложения, разделения и сравнения с неизвестными во всех позициях, e.g., используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему.
Итак, вот что нужно уметь решать второклассникам:
- Сложение / вычитание в пределах 100
- Одно- и двухступенчатое
- Добавить к
- Взять из
- Соединить
- Разобрать
- Сравнить
Когда вы посмотрите на то, что должны делать второклассники, неудивительно, что учить словесные задачи так сложно, не говоря уже о том, что студенты действительно их осваивают.
Как я учу задачи по слову во 2-м классе:
В начале года ученики знакомятся с нашей рутинной задачей со словом после первых двух недель в школе.
Я объясняю, что словесные задачи подобны историям, которые мы должны читать и понимать, что происходит в рассказе. Мы называем эти слова «проблемными ситуациями».
Мы называем эти слова «проблемными ситуациями».
Затем я учу студентов, что есть 4 вещи, которые они всегда должны делать, решая задачу со словами:
- Напишите числовое предложение
- Используйте стратегию для решения
- Я объясняю студентам, что я не могу залезть в их мозг, чтобы увидеть, что они думают, и если я не знаю, о чем они думают, я не может помочь им лучше решать проблемы со словами.
- Учащиеся могут нарисовать картинку, использовать семейство фактов, базовые 10 блоков и / или стандартный алгоритм.
- Вычисление
- Я смотрю, чтобы убедиться, что ученик дал правильный ответ.
- Ответ в предложении
- Например, вместо того, чтобы просто сказать «4», мои ученики пишут: «У Шайенна 4 собаки». Это важно для соединения математики и письма, но также помогает учащимся проверить, действительно ли их ответ отвечает на вопрос, заданный в словесной задаче.
Запуск рутинной задачи Word — это все о моделировании и рутине. Студентам не нужно много времени, чтобы научиться этому.
Студентам не нужно много времени, чтобы научиться этому.
Я проделал для вас тяжелую работу — у меня на весь год есть задачи по словам во 2-м классе, готовые для вас!
Что такое рутинная задача для 2-х классов?
По понедельникам я использую слово «проблемная ситуация». Я считаю полезным, чтобы студенты «разыгрывали» ситуацию. Используйте пример на ситуационном плакате / диаграмме привязки, чтобы показать учащимся образец.(Я учу студентов, что подчеркнутые части числового предложения — это известные нам части, а квадрат представляет неизвестное.)
Смоделируйте и решите практическую задачу со словами и поделитесь своими отзывами со студентами.
В течение следующих 3 дней мы моделируем и решаем задачу со словом, которая имеет ту же ситуацию, что и понедельник. Так что мы не скучаем. Это очень систематично.
Наконец, по пятницам ученики самостоятельно решают 2 задачи со словами, следуя той же ситуации, которую мы использовали всю неделю.
Для дифференциации или расширения учащиеся могут написать задачу на обратной стороне своего экзамена, которая соответствует той же ситуации, которую они изучали на этой неделе. Это отличный способ узнать, действительно ли студенты понимают ситуацию, которую мы узнали на той неделе.
Возможно вам понравится:
Давайте подключимся!
Instagram // Pinterest // Facebook // Учителя платят учителям
Реальный мир Решение задач по математике для второго класса
Edgewood Magnet School в Нью-Хейвене, штат Коннектикут, — это школа-магнит, которая объединяет искусство в учебную программу.Студентам в этой среде рекомендуется использовать стратегии наблюдения, интерпретации и анализа, чтобы улучшить свои мыслительные способности по каждому предмету. Выполняя эту миссию, и учителя, и ученики используют уникальные и захватывающие подходы к «основам» и работают вместе, чтобы обеспечить включение всех учащихся.
Для большинства второклассников начало года — время освежить знания и навыки первого класса. Лето вдали от прямого обучения и возможностей для практики и руководства иногда означает потерю твердого понимания усвоенных концепций математики.Этот трех-четырехнедельный блок предназначен для обзора и построения нового понимания одноэтапного решения словесных задач с использованием сложения и вычитания по мере того, как учащиеся развивают навыки и стратегии, которые они будут использовать в течение всего года. Учащиеся с помощью серии математических сценариев будут использовать типы задач, указанные в Таблице 1 Общего основного математического глоссария, который охватывает сложение и вычитание. 1
Common Core концентрируется на четком наборе математических навыков и концепций. Учащиеся изучают концепции организованным образом в течение учебного года, а также между классами.Стандарты побуждают студентов решать реальные проблемы. 2
Common Core требует большего внимания к математике. Вместо того, чтобы стремиться охватить множество тем в учебной программе шириной в милю и глубиной в дюйм, стандарты просят учителей математики значительно сузить и углубить то, как время и энергия тратятся в классе. Это означает четкое сосредоточение внимания на основной работе каждого класса, которая для классов от детского сада до второго класса включает в себя концепции, навыки и решение проблем, связанных с сложением и вычитанием.
Вместо того, чтобы стремиться охватить множество тем в учебной программе шириной в милю и глубиной в дюйм, стандарты просят учителей математики значительно сузить и углубить то, как время и энергия тратятся в классе. Это означает четкое сосредоточение внимания на основной работе каждого класса, которая для классов от детского сада до второго класса включает в себя концепции, навыки и решение проблем, связанных с сложением и вычитанием.
Округ государственных школ Нью-Хейвена использует сингапурский подход Math in Focus, — учебную программу на основе Common Core для учащихся от детского сада до пятого класса. Учебники и рабочие тетради для учащихся следуют учебному плану, который включает изучающих концепций и навыков с помощью наглядных уроков и инструкций учителя для понимания того, как и почему; объединение концепций и навыков посредством практики, занятий и математических журналов для глубокого понимания математики, практической работы в парах и в небольших группах; и, , применение концепций и навыков посредством обширной практики решения проблем и задач для создания специалистов по решению проблем в реальном мире. 3
3
Этот подход включает решение проблем на протяжении каждого урока и поощряет частую практику как в вычислениях, так и в решении проблем. Словесные задачи появляются в каждой главе и переходят от 1-го шага к 2-шагному и многоступенчатому. Каждая глава завершается сложной задачей или набором задач, которые требуют от студентов решения некоторых нестандартных вопросов. Для решения этих проблем учащимся необходимо использовать свои глубокие предыдущие знания, а также недавно приобретенные концепции и навыки, сочетая стратегии решения проблем с навыками критического мышления, включая классификацию, сравнение, упорядочение, идентификацию частей и целого, выявление закономерностей и взаимосвязей, индукция и дедукция и пространственная визуализация.
Текст для второго класса начинается с цифр до 1000. Учащиеся начинают с выражения чисел в стандартной форме (231), развернутой форме (200 + 30 + 1) и словарной форме (двести тридцать один). Это сопровождается конкретными представлениями через базовые десять блоков, а для двухзначных чисел и нескольких трехзначных чисел — представление цепочками стержней длиной 1, 10 и 100. Эта начальная глава также включает в себя последовательность чисел и сравнение с использованием большего, чем и меньше терминологии, а затем сразу перейдем к сложению и вычитанию двух- и трехзначных чисел.Здесь должен быть вывод, если у вас есть еще сотни, десятки и единицы не имеют никакого / большого значения; и если у вас столько же сотен, но больше десятков, то единицы не имеют большого значения. Большинство моих учеников (если не все) борются с самого начала! Похоже, у них нет прочного основания для понимания чисел до 100 или концепции разряда в целом. Этот модуль разработан для того, чтобы опередить разочарование, которое студенты испытывают, когда их слишком быстро подталкивают, прежде чем они получат твердое представление о принципах позиционной ценности и свойствах операций.
Эта начальная глава также включает в себя последовательность чисел и сравнение с использованием большего, чем и меньше терминологии, а затем сразу перейдем к сложению и вычитанию двух- и трехзначных чисел.Здесь должен быть вывод, если у вас есть еще сотни, десятки и единицы не имеют никакого / большого значения; и если у вас столько же сотен, но больше десятков, то единицы не имеют большого значения. Большинство моих учеников (если не все) борются с самого начала! Похоже, у них нет прочного основания для понимания чисел до 100 или концепции разряда в целом. Этот модуль разработан для того, чтобы опередить разочарование, которое студенты испытывают, когда их слишком быстро подталкивают, прежде чем они получат твердое представление о принципах позиционной ценности и свойствах операций.
Этот модуль открывает учебный год с одноступенчатых задач на сложение и вычитание всех типов с использованием чисел до 10. Цель состоит в том, чтобы потратить время на отработку основных вычислений с числами, с которыми ученик может комфортно работать, прежде чем сразу перейти к школьной программе. Как только будет достигнут уровень понимания этих наборов задач (числа до 10), учащиеся перейдут к решению одноэтапных задач с использованием чисел для подростков, а затем к числам до 100. Большинство задач по учебной программе в начале года требуют добавления и вычитание 3-значных чисел.Некоторые учащиеся быстро перейдут к заданиям с числами до 100 и будут готовы работать по обычной учебной программе.
Как только будет достигнут уровень понимания этих наборов задач (числа до 10), учащиеся перейдут к решению одноэтапных задач с использованием чисел для подростков, а затем к числам до 100. Большинство задач по учебной программе в начале года требуют добавления и вычитание 3-значных чисел.Некоторые учащиеся быстро перейдут к заданиям с числами до 100 и будут готовы работать по обычной учебной программе.
На протяжении всего курса основное внимание будет уделяться решению, а затем и построению набора словесных задач, обеспечивающих надежную и сбалансированную практику. Наборы задач будут основаны на сценарии, который раскрывает суть истории. Каждый сценарий позволит нам решить несколько проблем, изменив числа и убедившись, что каждый набор чисел представляет собой разумную проблему.Эта идея выглядит так: У Джона в коробке 8 мелков. Он делит 3 с Сэмом. Сколько мелков осталось у Джона в коробке? В коробке у Джона есть мелки. Он делит 3 с Сэмом. В коробке у Джона осталось 5 мелков. Сколько мелков начал Джон? У Джона 5 цветных карандашей. У Сэма на 2 меньше, чем у Джона. Сколько мелков у Сэма? Джон и Сэм делятся мелками. У Джона их 5, а у Сэма 3. Сколько мелков у друзей вместе? Двое учащихся участвуют в нескольких рассказах об обмене цветными карандашами, в которых используется один и тот же набор чисел, но в немного разных ситуациях.Некоторые ситуации более очевидны и понятны, в то время как другие требуют больше размышлений. Важно предоставить учащимся возможность работать и решать различные типы задач, которые можно создать из одного набора чисел. 4
Сколько мелков начал Джон? У Джона 5 цветных карандашей. У Сэма на 2 меньше, чем у Джона. Сколько мелков у Сэма? Джон и Сэм делятся мелками. У Джона их 5, а у Сэма 3. Сколько мелков у друзей вместе? Двое учащихся участвуют в нескольких рассказах об обмене цветными карандашами, в которых используется один и тот же набор чисел, но в немного разных ситуациях.Некоторые ситуации более очевидны и понятны, в то время как другие требуют больше размышлений. Важно предоставить учащимся возможность работать и решать различные типы задач, которые можно создать из одного набора чисел. 4
Таксономия типов задач на сложение и вычитание, определенная в Глоссарии общих основных государственных стандартов математики, представляет собой структуру, которая разделяет одноэтапные задачи на три широких класса: изменить , сравнение и частично частично .Затем каждый из трех классов разделяется на 14 типов задач, отсортированных следующим образом: изменение , в котором некоторое количество либо добавляется к другому количеству, либо отнимается от него с течением времени; сравнение , в котором одна сумма описывается как больше или меньше другой суммы; и частично-частично-целое , в котором сумма состоит из двух частей. 5
5
В группе проблем изменения есть две подгруппы: изменение-увеличение , в которой количество прибавляется к начальной сумме, и изменение-уменьшение , в которой количество берется из начальной суммы.Мы могли бы распознать эти подгруппы более привычно как «добавить к» или «взять от». Кроме того, в каждой из этих подгрупп существует три возможных неизвестных величины. Один сценарий, показывающий изменение-увеличение : 2 котенка играли с пряжей. К ним присоединяются еще 3 котенка. Сейчас 5 котят играют с пряжей. Используя эти количества, неизвестное может быть результатом (2 + 3 =?), Неизвестной величиной изменения (2 +? = 5) или неизвестной начальной суммой (? + 3 = 5). В подгруппе изменение-уменьшение снова есть три возможных неизвестных.Сценарий для этого примера: на ветке сидят 5 птиц. 2 улетают. Теперь на ветке сидят 3 птицы. Здесь ученики снова могут решить окончательную сумму (5 — 2 =?), Сумму сдачи (5 -? = 3) или начальную сумму (? — 2 = 3). Это дает все шесть типов проблем с изменениями.
Это дает все шесть типов проблем с изменениями.
Аналогичным образом проблемы сравнение также можно разделить на две подгруппы: сравнение-больше , в котором одна величина описывается как больше или больше, чем другая, и сравнения-меньше, , в которой одна величина описывается как меньше или меньше чем другой.Здесь снова каждая из этих двух подгрупп имеет три возможных неизвестных, всего 6 типов. У Сэма 6 шариков. У Джеймса 8 шариков. У Джеймса на 2 шарика больше, чем у Сэма. Неизвестным количеством может быть меньшее количество (? + 2 = 8), неизвестное большее количество
(6 + 2 =?), Или неизвестная разница (8-6 =?), Одна величина больше, а другая меньше. Используя тот же сценарий для набора задач без сравнения , язык необходимо изменить с «больше чем» на «меньше чем».Вот как можно представить этот набор с языковыми настройками: у Сэма 6 шариков. У Джеймса 8 шариков. У Сэма на 2 шарика меньше, чем у Джеймса.
Часть-часть-целое задачи — это набор двух величин, частей, которые вместе составляют целое количество. Этот тип проблемы кажется очень похожим на категорию , изменяющую категорию , но в этом типе проблемы нет никаких изменений с течением времени. Две части играют эквивалентные роли, что позволяет использовать только две возможные неизвестные категории: либо часть неизвестна, либо неизвестно целое.Есть 4 большие собаки и 3 маленькие собаки. Всего 7 собак. Одна из частей может быть неизвестной (4 +? = 7 или? + 3 = 7) или неизвестным может быть размер целого (4 + 3 =?). Поскольку детали взаимозаменяемы, в этом классе задач всего 2 типа.
Этот тип проблемы кажется очень похожим на категорию , изменяющую категорию , но в этом типе проблемы нет никаких изменений с течением времени. Две части играют эквивалентные роли, что позволяет использовать только две возможные неизвестные категории: либо часть неизвестна, либо неизвестно целое.Есть 4 большие собаки и 3 маленькие собаки. Всего 7 собак. Одна из частей может быть неизвестной (4 +? = 7 или? + 3 = 7) или неизвестным может быть размер целого (4 + 3 =?). Поскольку детали взаимозаменяемы, в этом классе задач всего 2 типа.
Следующая диаграмма сортирует эти классы и категории в структуру. В Приложении А к этому модулю приведен набор примеров проблем, иллюстрирующих каждый из этих 14 типов.
Тип проблемы | Сумма неизвестна | ||||
Изменение | Увеличение Дополнение к | Начальный | Изменение | Финал | |
Уменьшение Вычесть из | Начальный | Изменение | Финал | ||
Сравнение | Большой / Подробнее | Меньший | Большой | Разница | |
Меньше / Меньше | Меньший | Большой | Разница | ||
Частично-частично-целое | Часть | Всего | |||
Сценарии проблем
Для второклассников школьная жизнь — это большая часть их мира. Большинство моих учеников приехали в Эджвуд на год детского сада и остались там до первого класса, так что год во втором классе, по сути, стал их третьим годом в той же школе. Им комфортно в здании, и они знают многих других студентов. Они станут активными участниками математических историй, которые мы будем строить вместе. Действия, которые происходят в классе, в кафетерии, на детской площадке и в автобусе, кажутся узнаваемыми ситуациями, которые помогут вам получить базовое понимание контекста.
Большинство моих учеников приехали в Эджвуд на год детского сада и остались там до первого класса, так что год во втором классе, по сути, стал их третьим годом в той же школе. Им комфортно в здании, и они знают многих других студентов. Они станут активными участниками математических историй, которые мы будем строить вместе. Действия, которые происходят в классе, в кафетерии, на детской площадке и в автобусе, кажутся узнаваемыми ситуациями, которые помогут вам получить базовое понимание контекста.
Кроме того, у учащихся есть возможность включить темы и изучить другие предметы, такие как наука, общественные науки, грамотность, искусство, музыка и, в нашей школе, танцы и драма. Одним из примеров может быть создание набора задач-рассказов, посвященных жизненному циклу бабочки, единице изучения каждый год во втором классе. Обладая общими знаниями, которые получат учащиеся, этот контент может стать сценарием текстовых задач. Примером может быть: Семь гусениц поднялись по ветке и образовали куколки. Позже в тот же день еще три гусеницы поднялись по ветке и образовали куколки. Сколько кукол свешивается с ветки? Точно так же использование персонажей в книге, прочитанной вместе в качестве класса, может дать персонажам новый набор задач. Любопытный Джордж съел связку бананов. Он съел 4 из них. Теперь у него 3. Сколько бананов начал любопытный Джордж? Использование общего или тематического контента не только объединит все мышление и практику, но и предоставит осязаемые и реальные ситуации.При наличии установленного сценария учащиеся будут работать с набором чисел, определяя неизвестное в рамках каждого типа задач.
Позже в тот же день еще три гусеницы поднялись по ветке и образовали куколки. Сколько кукол свешивается с ветки? Точно так же использование персонажей в книге, прочитанной вместе в качестве класса, может дать персонажам новый набор задач. Любопытный Джордж съел связку бананов. Он съел 4 из них. Теперь у него 3. Сколько бананов начал любопытный Джордж? Использование общего или тематического контента не только объединит все мышление и практику, но и предоставит осязаемые и реальные ситуации.При наличии установленного сценария учащиеся будут работать с набором чисел, определяя неизвестное в рамках каждого типа задач.
Создание проблем
Часто задаваемый вопрос: «Что мы должны сделать, чтобы ответить на вопрос, чтобы решить проблему со словом?» Фундаментальное понимание того, что задают, не очевидно для студентов, что делает решение недоступным. Большинство первоклассников, поступающих во второй класс, имеют базовое понимание, когда история (проблема) классифицируется как окончательный неизвестный или полностью неизвестный , но большинство других компонентов таксономии им незнакомы или их просто слишком сложно расшифровать. Чтобы помочь им в их мышлении, они будут использовать конкретные модели, такие как они сами (2 ребенка сидят за столом для чтения, еще 4 присоединяются к ним), разыгрывая сценарии. Многие основные материалы в классе — карандаши, записные книжки, папки, мелки — можно использовать для создания и разработки сценариев с учетом каждого типа проблемы.
Чтобы помочь им в их мышлении, они будут использовать конкретные модели, такие как они сами (2 ребенка сидят за столом для чтения, еще 4 присоединяются к ним), разыгрывая сценарии. Многие основные материалы в классе — карандаши, записные книжки, папки, мелки — можно использовать для создания и разработки сценариев с учетом каждого типа проблемы.
Решение проблем
Следуя общему плану сингапурской математической программы, студенты будут решать задачи, используя конкретный, графический и абстрактный подход.Поскольку это стандартный подход к преподаванию математики в нашем округе в течение года, учащиеся начнут с этого набора стратегий для решения наборов задач.
Задачи со словом пишутся в виде рассказов и сценариев, поэтому язык необходимо учитывать при составлении задач для начинающих второклассников. Задачи со словом связаны не только с языком и чтением, но и с математикой. Если рассказ непонятен, как студенты могут начать понимать, что им делать с числами, которые им дали, и вопросом, который им задали? Таким образом, слова и словарный запас должны быть подходящими и полезными для разных уровней чтения поступающих студентов. Структура словесных задач должна быть понятной и ясной, доступной как в языке, так и в цифрах. Кроме того, следует обсудить язык, особенно слова, которые выражают взаимосвязь между задействованными величинами, чтобы убедиться, что он знаком всем учащимся.
Структура словесных задач должна быть понятной и ясной, доступной как в языке, так и в цифрах. Кроме того, следует обсудить язык, особенно слова, которые выражают взаимосвязь между задействованными величинами, чтобы убедиться, что он знаком всем учащимся.
Это явная интеграция языковых искусств и математики и метода, с помощью которого учащиеся могут связать математику с реальным миром, в данном случае, посредством занятий, которыми они занимаются в школе. Навыки чтения и вычисления сочетаются даже с простейшими задачами со словами.
Структура коллекции задач
Введение в содержание этого раздела включает в себя определенную последовательность и основы, которые помогут студентам решить 14 типов задач. Чтобы начать раздел, учащиеся будут работать только с числами до 10. Это важная отправная точка для обеспечения понимания. Большинство моих второклассников умеют складывать и вычитать до 10, но не очень хорошо владеют языком проблемных слов. Итак, во-первых, ученикам будет больше интересна язык, чем арифметика. Студенты будут практиковаться в выяснении того, что именно задают проблемы, с проблемами, с которыми они знакомы, прежде чем перейти к новому этапу. Выполнение всех типов задач улучшит и увеличит стратегию и уверенность!
Студенты будут практиковаться в выяснении того, что именно задают проблемы, с проблемами, с которыми они знакомы, прежде чем перейти к новому этапу. Выполнение всех типов задач улучшит и увеличит стратегию и уверенность!
После того, как освоено сложение и вычитание в пределах 10, следующая фаза единицы переходит к числам до 20. Ключевым моментом является продолжение сценариев, которые очевидны и повторяются по мере введения новых чисел. Примером этого перехода могут быть следующие параллельные задачи:
На первой остановке в автобус сели 6 студентов.На второй остановке в автобус сели 3 студента. Сколько студентов в автобусе после второй остановки? ( изменение-увеличение, окончательное неизвестно)
Некоторые студенты сели в автобус на первой остановке. На второй остановке в автобус сели 3 студента. Сейчас в автобусе 9 студентов. Сколько студентов сели на первую остановку? ( изменение-прибавка, изначально неизвестно)
Теперь они становятся:
На первой остановке в автобус сели 11 студентов. На второй остановке в автобус сели 7 студентов.Сколько студентов в автобусе после второй остановки? ( изменение-увеличение, окончательное неизвестно)
На второй остановке в автобус сели 7 студентов.Сколько студентов в автобусе после второй остановки? ( изменение-увеличение, окончательное неизвестно)
Некоторые студенты сели в автобус на первой остановке. На второй остановке в автобус сели 7 студентов. Сейчас в автобусе 18 студентов. Сколько студентов сели на первую остановку? ( изменение-прибавка, изначально неизвестно)
При работе с числами до 20 важно, чтобы учащиеся понимали, что «подростковые» числа (11-19) на самом деле равны 10 и некоторым единицам. Студенты должны работать с числами в пределах 20, составляя уравнения, используя свои знания и умение составлять первую десятку.В случае 7 + 6 создание новой десятки выглядит так:
7 + 6 = 7 + 3 + 3 = 10 + 3 = 13
Поскольку 7 требует 3, чтобы получить десять, а 6 состоит из 3 + 3, это уравнение показывает, как получается 10 и еще несколько. Практика этого метода с использованием двух десятков фреймов наглядно демонстрирует процесс. В приведенном выше примере учащиеся используют десять кадров, чтобы показать 7 и 6 отдельно. Чтобы получить новые 10, ученики переместят 3 из 6, которые теперь показывают 10 и еще 3 или 13.
В приведенном выше примере учащиеся используют десять кадров, чтобы показать 7 и 6 отдельно. Чтобы получить новые 10, ученики переместят 3 из 6, которые теперь показывают 10 и еще 3 или 13.
Как упоминалось ранее, очевидно, что наиболее доступными типами задач для учеников, поступающих во второй класс, являются изменение-увеличение или изменение-уменьшение, результат неизвестен и частично-частично-целое, целое неизвестно. Общая стратегия решения задачи со словами, кажется, состоит в том, чтобы просто взять два числа, которые вы видите, и сложить их вместе или, возможно, вычесть их, но часто ученики просто не уверены. Кажется, что это наиболее часто используемые типы задач, что оставляет учащихся без сбалансированного опыта работы со всеми 14 типами и, в конечном итоге, без некоторых стратегий, которые можно использовать при решении задач.Студентам необходимо увидеть широкий круг задач, чтобы получить четкое представление о том, как используются сложение и вычитание и как они связаны друг с другом. Понятие достаточности примеров означает, что учащимся следует познакомиться с широким спектром примеров, чтобы обеспечить всестороннюю практику с концепцией. 6
Понятие достаточности примеров означает, что учащимся следует познакомиться с широким спектром примеров, чтобы обеспечить всестороннюю практику с концепцией. 6
Подходы к данной учебной программе различаются в зависимости от стиля обучения всех учащихся.
Общий формат основан на модели мастерской. Концепции и навыки преподаются с помощью серии мини-уроков, посвященных цели, с использованием следующих методов:
Эмпирическое обучение: Большинству молодых студентов необходимо начинать с практического обучения.Использование конкретных моделей для разработки математических историй позволяет учащимся увидеть проблему и манипулировать элементами по мере развития рассказа. Этот тип обучения — важный первый шаг.
Дифференцированное обучение: уроки и упражнения будут нацелены на максимальное обучение. Студенты будут использовать различные подходы, работая иногда индивидуально, а иногда в небольших группах, в зависимости от сложности работы. Некоторые студенты будут двигаться быстрее по мере овладения навыками, а некоторым потребуется больше возможностей для практики.
Совместное обучение: учащимся будет предоставлена возможность работать в совместных группах над созданием математических рассказов для представления классу. Эта стратегия позволит студентам работать совместно, выполняя различные роли, необходимые для завершения работы, с акцентом на успех для всех.
Задание 1: Упорядоченные типы проблем — проблемы до 10
Вводная (и обзорная) часть модуля охватывает все типы проблем, но в определенной последовательности. Цель состоит в том, чтобы учащиеся прочитали и интерпретировали словесную задачу с помощью инструкций, а затем самостоятельно попрактиковались.Из-за множества типов задач эта часть займет несколько дней, прежде чем студенты научатся писать свои собственные наборы задач. Исходя из потребностей учащихся и темпа понимания, я ожидаю, что этот раздел будет продолжаться от четырех до шести дней, а при необходимости и больше.
Последовательность следующая: часть-часть-целое ; изменение-увеличение и изменение-уменьшение ; и, наконец, сравните больше и сравните меньше .Следующие вводные занятия разработаны как групповое мероприятие, когда студенты сидят за партами или собираются на ковре рядом с доской или мольбертом. Вся групповая часть должна составлять максимум 20 минут. В конце каждой сессии я предлагаю студентам решить от 5 до 10 похожих задач. Более способные студенты могут начать создавать свои собственные проблемы во время самостоятельной работы.
Начало с основ дает хорошую возможность познакомиться с навыками студентов, что помогает при подготовке дифференцированной работы и создании групп,
На этом уроке учащиеся будут интерпретировать проблемы реального мира и с помощью манипуляторов и картинок решать истории частично-частично-целиком, используя сложение и вычитание.
Играют 6 девочек
С ними играют 3 мальчика.
Сколько всего детей играет?
Начните рассказ со всего неизвестного, как в этом примере. Этот тип историй идеально подходит для того, чтобы учащиеся разыгрывали прямо в классе. Напишите историю на доске или листе с диаграммами и попросите учащихся выступить в качестве актеров. Когда ученики решат задачу, напишите математическое предложение, чтобы показать, что произошло: 6 + 3 = 9 учеников. Объясните, что две части (мальчики и девочки) составили одно целое (детей).Пока студенты все еще находятся в актерской позиции, представьте новый подход к этому сценарию:
Играют 9 учеников.
Из них 6 девочек.
Сколько мальчиков играет?
На этом наглядном примере ученики должны сразу увидеть, сколько. Важная концепция, которую следует продемонстрировать, заключается в том, что части могут быть определены, когда известны целое и одна часть, в этом случае 9 известно как целое, а 6 — как одна часть. Опять же, напишите математическое предложение, чтобы показать этот расчет: 6 +? = 9 и включите стратегию начала с целого, чтобы определить недостающую часть как предложение вычитания 9-6 = 3.Практика обоих подходов к решению поможет учащимся соединить сложение и вычитание и понять, как они используются вместе.
Поскольку на этом уроке учащиеся должны читать задачи-рассказы, я объединю беглых читателей с теми, кто не владеет свободно, предоставлю счетчики тем, кто их хочет, и позволю партнерам работать вместе над решением проблем и поделиться стратегиями, которые они использовали.
Я воспользуюсь еще двумя примерами, подобными приведенным ниже, чтобы продемонстрировать, не забывая писать на доске слово «задача», а также математическое предложение.Я также перефразирую проблемы, чтобы часть была неизвестной.
У Ханны 5 красных маркеров.
У нее 3 синих маркера
Сколько всего маркеров у Ханны?
7 учеников рисуют мелками.
2 ученика рисуют цветными карандашами.
Сколько учеников рисуют?
Продолжая эту же идею, следующий набор типов задач включает изменение-увеличение и изменение-уменьшение .Хотя часть-часть-целое — это язык, который учащиеся могут усвоить и использовать при обсуждении своей работы, язык изменение-увеличение и изменение уменьшение немного сложнее. Использование слова изменение больше подходит для студентов, чтобы продемонстрировать, что некоторая сумма была либо добавлена, либо вычтена из начальной суммы.
Введите слово «проблема» ниже, которое является примером неизвестного результата в категории «изменение-увеличение».
У Джейсона в начале дня на графике было 8 наклеек «пойманный на хорошем».
За школьный день он заработал еще 2 стикера.
Сколько наклеек у Джейсона на графике в конце дня?
Учащийся может решить задачу, как написано, и, используя тот же сценарий, предложить им создать историю без изменений и начальная неизвестная история . Одним из примеров может быть:
У Джейсона на графике
было несколько наклеек «пойманный на хорошем».
начало дня.
За школьный день он заработал еще 2 стикера.
В итоге у него 10 наклеек.
Сколько наклеек было у Джейсона в начале дня?
Это устное задание, в котором я написал скорректированную версию по всем направлениям, поместив математическое предложение внизу. Важно позволить студентам поработать над составлением задачи, чтобы они могли начать видеть взаимосвязь между проблемами и тем, что они задают.
Результат Неизвестно Версия 8 + 2 =? | Изменение Неизвестно Версия 8+? = 10 | Начальный Неизвестно Версия ? + 2 = 10 |
Цель состоит в том, чтобы учащиеся понимали, а не просто решали.Я могу неформально оценить во время обсуждения переписывания текста слово «проблема», с более формальной оценкой позже в разделе.
Следующая категория — это типов задач «изменение-уменьшение», . Следуя тому же формату, что и раньше, я представлю результат неизвестный, заменим неизвестный , а затем начальный неизвестный.
Кристалл собрала 7 листов для своего проекта.
2 листа унесло ветром.
Сколько листьев у Кристалл осталось для своего проекта?
Результат Неизвестно 7 — 2 =? | Изменение Неизвестно 7 -? = 5 | Начальный Неизвестно ? — 2 = 5 |
Опять же, цель состоит в том, чтобы учащиеся понимали, а не просто решали.
Третий широкий класс, сравните, труднее для моих 2 и учеников. Это требует, чтобы текст словесных задач был очень простым. Студенты не должны путаться, когда они учатся извлекать данные из задачи. Помните, что использование точной терминологии — это не цель, а, скорее, понимание сути проблемы. Вот три способа, которыми я представлю сценарий, который показывает типы задач сравнение-больше , и три способа показать без сравнения. Студенты должны иметь возможность практиковать все типы. Конечно, не все эти примеры следует использовать одновременно. Когда я записываю задачи на листе с диаграммами и вывешиваю их в классе, ученики могут начать видеть и проводить собственные сравнения и противопоставления, поскольку один сценарий объясняется по-разному. Использование слов «больше» и «меньше» должно быть выделено и объяснено по мере введения и работы над набором проблем. Моя роль здесь состоит в том, чтобы позволить ученикам начать замечать тонкие различия в формулировках и в том, как они меняют мышление.Лучше начать с простого!
У Оливии на 4 ластика больше, чем у Джона. У Джона 2 ластика. Сколько ластиков у Оливии? (сравнение-больше, большее неизвестно) 2 + 4 =? | У Джона на 4 ластика меньше, чем у Оливии. У Джона 2 ластика. Сколько ластиков у Оливии? (без сравнения, большее неизвестно) 4 + 2 =? |
У Оливии на 4 ластика больше, чем у Джона. У Оливии 6 ластиков. Сколько ластиков у Джона? (сравнение больше, меньше неизвестно) 6 — 4 =? | У Джона на 4 ластика меньше, чем у Оливии. У Оливии 6 ластиков. Сколько ластиков у Джона? (без сравнения, меньше неизвестно) 6 — 4 =? |
У Оливии 6 ластиков. У Джона 2 ластика. На сколько ластиков у Оливии больше, чем у Джона (сравнение-больше, разница неизвестна 6 — 2 =? 2+? = 6 | У Джона 2 ластика. У Оливии 6 ластиков. На сколько ластиков у Джона меньше, чем у Оливии? (без сравнения, разница неизвестна) 6 — 2 =? |
На протяжении этих вводных занятий мы со студентами будем обсуждать сценарии, которые в конечном итоге можно будет использовать в собственных текстовых задачах.Идеи должны генерироваться на основе школьных мероприятий и материалов, побуждая учащихся задуматься о том, что ученики могут фактически использовать для манипуляций или, как в первом сценарии, уметь действовать, чтобы решить. Сохраняя список идей на бумаге с диаграммами в качестве справочного материала, учащиеся не будут испытывать затруднений со словарным запасом или подходящими сценариями; им предстоит решить свои проблемы. Этот список подготовит студентов ко второй части модуля.
Задание 2: Классные / школьные сценарии
Как указывалось ранее, слова и словарный запас должны быть доступны для учащихся, а не должны быть проблемой или препятствием.Цель состоит в том, чтобы научиться обдумывать истории и использовать информацию, собранную во время сеанса мозгового штурма. Чтобы начать эту часть, просмотрите диаграммы и добавьте больше, если у учащихся появятся новые идеи. Для составления задач со словами может быть полезно иметь информацию в категориях, например:
Используемые нами материалы
Занятия, которые мы посещаем
Занятия в школе
Имена одноклассников
Я создам группы из двух или трех учеников, чтобы они написали свои собственные задачи и поделились с классом.Поскольку этот урок требует, чтобы учащиеся читали и писали задачи-рассказы, опять же, беглые читатели и писатели с теми, кто не владеет свободно, предоставляют счетчики для тех, кто их хочет, и позволяют партнерам работать вместе над решением проблем и делиться стратегиями, которые они использовали. .
Цель в этот период времени — предложить учащимся написать ту же задачу, но попробовать ее по-другому, выбрать другой тип, когда они рассказывают историю. Время для совместной работы групп студентов будет во время прибытия в качестве утренней работы и во время части математического семинара по математике.Это позволит учащимся работать со своими партнерами по 30 минут в день над созданием математических рассказов.
Я подчеркну, что важно хранить их коллекцию вместе, поскольку большая часть их работы станет частью рабочей тетради, которую они создадут в конце этого раздела. Папки и математические журналы могут быть полезны, или мой ежедневный сбор незавершенной работы — еще один вариант.
Мероприятие 3: Научные сценарии
Первым разделом в науке 2 nd является исследование жизненного цикла бабочки.Студенты получают гусениц в начале семестра и наблюдают и записывают изменения в жизни гусениц. Работа, которую студенты выполняют на уроках естествознания, может стать информацией и сценариями, которые они могут использовать для составления текстовых задач.
Используя все типы задач, мы напишем несколько вместе как класс. Это дополнительная возможность очень конкретно интегрировать математику в наши научные исследования и работу. Студентам важно осознавать, что, хотя их обучение было разделено на предметные области, по существу невозможно разделить все это на категории.Таким образом, в этой части модуля используются математика, естественные науки и чтение, чтобы помочь учащимся узнать о жизненном цикле бабочки (а также других животных).
Учащиеся будут создавать наборы задач, используя свой ежедневный опыт отслеживания своих гусениц. У каждого ученика есть 2-3 гусеницы, за которыми можно наблюдать и записывать информацию, что может стать началом словесных задач. Примеры для начала: если в таблице 3 8 гусениц и 2 гусеницы присоединяются к этой группе, сколько гусениц наблюдается в таблице 3? В классе 28 учеников.Каждому ученику понадобится одна чашка еды для гусениц. Есть 30 чашек корма для гусениц. На сколько чашек еды больше, чем у студентов?
Часто встречаются студенты, которые проявляют большой интерес к другим областям науки. Это область, которую следует поощрять, если учащиеся рады поделиться своими знаниями. Некоторые учащиеся будут более склонны использовать единицу обучения, проводимую в классе, но в течение дня, посвященного грамотности, учащиеся знакомятся с большим количеством научно-популярной литературы или информационного текста, который, безусловно, может обогатить наши научные словесные задачи. .
На протяжении всего раздела по естествознанию студенты будут продолжать писать текстовые задачи различных типов, чтобы в конечном итоге включить их в наш последний проект — рабочую тетрадь. Эти задачи можно писать во время утренней рабочей сессии, во время семинара по математике и в конце урока естествознания. К концу раздела у каждого студента должно быть две задачи, которые нужно добавить в главу «Наука» в учебном пособии.
Мероприятие 4: Создание Рабочей тетради / Празднование публикации
Цель этой части модуля состоит в том, чтобы отсортировать словарные задачи по «главам» и создать рабочую тетрадь, которой можно поделиться на Празднике публикации.Главы будут названы по предметам или категориям, в зависимости от выбора ученика и предложения учителя. Идеи включают в себя рассказы для начинающих, занятия в классе, развлечения на детской площадке, науку и математику и связи с общественными исследованиями. Пусть студенты творчески подходят к названиям!
Студенты представят свои работы, которые будут включать как минимум одно словесное задание для каждой главы. Они также должны представить решения своих проблем, чтобы их можно было включить в ключ ответа. В каждой главе будет не менее 25 задач с примерами всех типов и с разным уровнем сложности.Задачи со словами могут быть напечатаны или написаны от руки для окончательной рабочей тетради, в зависимости от того, что учащиеся решат как класс. Для празднования необходимо будет скопировать и каким-либо образом переплести одну рабочую тетрадь на каждого учащегося.
За две недели до Праздника публикации студенты создадут приглашение, чтобы передать его семье и друзьям, приглашая их прийти на «Праздник решения проблем». Родители и другие VIP-гости потратят некоторое время на работу над задачами со словами, перемещаясь по комнате, навещая многих студентов.Студенты поделятся с гостями своей собственной работой (словесными задачами, которые они сами создали) и «помогут» посетителям найти ответы.
У каждого студента будет лист «Комментарии», который гости смогут подписать и оставить комментарии о своем опыте работы со студентом. Я рекомендую посетителям остановиться, чтобы поговорить с каждым студентом или с любым другим студентом во время их посещения.
Кроме того, это возможность предложить студентам работать редакторами и издателями.Создание рабочей книги потребует времени на просмотр и сборку, и эти задачи могут быть делегированы и разделены заинтересованными учащимися.
Общие государственные стандарты по математике,
http://www.corestandards.org/the-standards/mat Mathematics.
Фонг, Хо Кхеонг. Математика в фокусе Сингапура Математика Маршалла Кавендиша . Итоговая ред. Сингапур: Marshall Cavendish Education, 2015.
.
Фусон, Карен К. Математические выражения . Издание 2011 г. Орландо, Флорида: Houghton Mifflin Harcourt;, 2011.
Хау, Роджер. Три столпа математики для первого класса и не только
Howe, Roger, Самое важное, что нужно знать вашему ребенку об арифметике
Хау, Роджер и Гарольд Рейтер, Пять стадий разложения места
Ma, L. Знание и преподавание элементарной математики , Erlbaum Associates, Махва, Нью-Джерси, 1999.
Московские головоломки: 359 математических увлечений . Нью-Йорк: Dover Publications, 1992.
Поля, Георгий. Как решить: новый аспект математического метода . Издание Новой Принстонской научной библиотеки, 2014.
Изменение Увеличение / Результат Неизвестен
На занятиях 7 учеников. К ним присоединяются еще 2 студента. Сколько учеников сейчас в классе?
Изменение Увеличение / Изменение Неизвестно
На занятиях 7 учеников.К ним присоединяются еще несколько студентов. Тогда было 9 учеников. Сколько студентов попадает в первые 7 человек?
Увеличение изменения / начальное значение неизвестно
Некоторые ученики на занятиях. К ним присоединились еще 2 студента. Тогда было 9 учеников. Сколько студентов было в классе вначале?
Изменение Уменьшение / Результат Неизвестен
На занятиях находилось
учеников 9 человек. 2 студента ушли домой. Сколько учеников сейчас в классе?
Изменение Уменьшение / Изменение Неизвестно
На занятиях находилось
учеников 9 человек.Некоторые студенты разошлись по домам. Сейчас здесь 7 студентов. Сколько студентов ушли домой?
Изменение Уменьшение / Исходное значение Неизвестно
Несколько учеников были в классе. 2 студента ушли домой. Тогда в классе было 7 учеников. Сколько студентов было в классе вначале?
Сравнить больше / Разница неизвестна
У Сэма 10 картошек фри. У Эмили 6 картошек фри. Насколько больше у Сэма, чем у Эмили?
Сравнить Больше / Больше неизвестно
У Сэма на 4 картофеля фри больше, чем у Эмили.У Эмили 6 картошек фри. Сколько картофеля фри у Сэма?
Сравнить Больше / Меньше Неизвестно
У Сэма на 4 картофеля фри больше, чем у Эмили. У Сэма есть 10 картошек фри. Сколько картофеля фри у Эмили?
Сравнить Меньше / Различий неизвестно
У Сэма 10 картошек фри. У Эмили 6 картошек фри. Насколько у Эмили меньше, чем у Сэма?
Сравнить Меньше / Меньше Неизвестно
У Эмили на 4 картофеля фри меньше, чем у Сэма. У Сэма 10 картошек фри.Сколько картошки фри у Эмили?
Сравнить Меньше / больше Неизвестно
У Эмили на 4 картофеля фри меньше, чем у Сэма. У Эмили 6 картошек фри. Сколько картофеля фри у Сэма?
Частично-Частично-Целое / Целое Неизвестно
У Сэма 4 печенья на обед. У него есть еще 2 на ужин. Сколько файлов cookie у Сэма?
Частично-Частично-Целое / Целое Неизвестно
Сэм сегодня съел 6 печенек. У него было 4 штуки на обед. Сколько он ел на обед?
Этот модуль, естественно, объединяет грамотность и математику.Как чтение, так и письмо являются неотъемлемой частью способности учащихся решать словесные задачи, включающие как сложение, так и вычитание.
Ученики будут работать в соответствии с Общим основным государственным стандартом по математике, 2.OA.A.1, который гласит, что второклассники должны к концу года уметь «представлять и решать задачи, включающие сложение и вычитание, в пределах 100». для решения одноэтапных задач со словами, включающих ситуации сложения, взятия из, объединения, разборки и сравнения с неизвестными во всех позициях.Во время этого раздела учащиеся начнут решать и составлять словесные задачи с числами до 10, переходить к числам до 20 и переходить к 100 и до 1000 по мере того, как они усваивают концепцию разложения.
В этом разделе также рассматриваются Общие основные государственные стандарты чтения информационного текста, RI.2.1, в которых учащиеся работают над поиском ключевых идей и деталей, задавая и отвечая на такие вопросы, как кто, что, где, когда, почему и как продемонстрировать понимание ключевых деталей текста.На протяжении этого раздела, посвященного задачам со словами, учащиеся будут работать, задавая эти вопросы, чтобы определить, какую информацию дает математический рассказ. Когда они начнут писать свои собственные текстовые задачи, им нужно будет рассмотреть эти вопросы, чтобы составить содержательный рассказ для текста своей проблемы.
- Общие основные государственные стандарты по математике, http://www.corestandards.org/the-standards/mat Mathematics.
- Общие государственные стандарты по математике
- Хо Кхеонг Фонг, Математика в фокусе Сингапура Математика Маршалла Кавендиша , 8.
- Роджер Хоу, Три столпа математики для первого класса и не только, 2 .
- Роджер Хоу, Три столпа математики для первого класса и не только, 1 . Стандартные государственные стандарты по математике
- Роджер Хоу, Три столпа математики для первого класса и не только, 2
Область задачи умножения слов 2-й класс
Добро пожаловать на нашу страницу задач на умножение слов для второго класса.
Здесь вы найдете нашу подборку печатных задач умножения.
которые помогут вашему ребенку применять и практиковать свои навыки умножения и умножения для решения ряда «реальных» проблем.
Здесь вы найдете ряд рабочих листов для решения задач, связанных с умножением.
Каждый лист включает в себя решение ряда письменных задач на умножение.
Для каждого рабочего листа ниже есть 3 уровня сложности: A, B и C.
Рабочий лист А — самый простой уровень, подходящий для детей в начале их класса.
Рабочий лист B — это рабочий лист среднего уровня для детей, которые работают на ожидаемом уровне в своем классе.
Рабочий лист C задан на более сложном уровне, подходящем для более способных математиков.
Задачи на каждом листе похожи по формулировке, но их числа усложняются по мере того, как уровень становится сложнее.
Чтобы способствовать развитию навыков тщательной проверки и мышления, на каждом листе есть один «хитрый» вопрос, который не является проблемой умножения.Детям необходимо определить эту словесную проблему и решить, какую операцию им необходимо решить.
Использование этих листов поможет вашему ребенку:
- применять свои навыки умножения и умножения;
- применять свои знания таблицы умножения для выяснения связанных фактов;
- распознает проблемы с умножением и пытается обнаружить «хитрые» проблемы;
- решить ряд проблем «реальной жизни».
Некоторые листы имеют версию для Великобритании с набором орфографии для Великобритании.
В нашей области задач на умножение слов для 3-го класса вы найдете ряд задач на умножение слов, предназначенных для учеников 3-го класса.
Охватываются следующие области:
- основные информационные бюллетени по умножению;
- фактов умножения до 10х10;
- задач, для решения которых требуются письменные методы умножения (TU x U)
Взгляните на еще несколько наших рабочих листов, похожих на эти.
У нас есть ряд реальных проблем, связанных с различными измерениями,
типа самых быстрых насекомых, или длины разных динозавров!
Есть целый ряд различных навыков, от округления и разложения до использования сложения, вычитания и умножения.
Здесь вы найдете подборку таблиц времени умножения.
до 10×10 или 12×12, чтобы помочь вашему ребенку в изучении
Факты умножения.
Существует широкий выбор таблиц умножения, в том числе
цветные и черно-белые, диаграммы меньшего размера, диаграммы с заливкой
и пустые диаграммы.
Использование этих таблиц поможет вашему ребенку:
- Узнайте их факты умножения на 10х10 или 12х12;
- Попрактикуйтесь в их таблице умножения.
Все бесплатные печатные математические таблицы в этом разделе основаны на тестах Elementary Math Benchmarks.
Здесь вы найдете ряд бесплатных печатных игр на умножение.
Следующие игры развивают математические навыки умножения в увлекательной и мотивирующей форме.
Использование этих листов поможет вашему ребенку:
- узнать их факты умножения;
- попрактиковаться и улучшить свой отзыв таблицы умножения;
- развивают свои навыки стратегического мышления.
Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике.
и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.
задач со словами по типу задачи
Научите учащихся решать задачи со словами, понимая контекст задачи. Задачи соединения Word — это самый простой тип задачи Word, но они закладывают хорошую прочную основу для будущей работы над другими типами задач.
Ниже приведено видео Facebook Live, которое я записал по этой теме.В тексте есть некоторые моменты из видео, но видео идет более подробно.
Есть три типа проблем соединения. Я подробно расскажу о них в видео и в этом посте об использовании ключевых слов для решения словесных задач.
Вот три примера проблем соединения для трех типов проблем соединения. Они отличаются от словесных задач в видео.
JRU (Результат присоединения неизвестен)
На детской площадке было _____ детей. Еще ____ детей вышло на площадку.Сколько детей на детской площадке?
JCU (присоединиться к изменению неизвестно)
На детской площадке было ____ детей. Еще несколько ребят вышли на площадку. Сейчас на детской площадке ____ детей. Сколько детей пришло на детскую площадку?
JSU (Join Start Unknown)
Некоторые дети были на детской площадке. ____ детей вышли на площадку. Сейчас на детской площадке ____ детей. Сколько детей было на детской площадке вначале?
Есть несколько правил, которым я следую, когда преподаю студентам текстовые задачи.Один из ключей — это постоянство словарного запаса и распорядка.
Используйте согласованный словарь
При обучении задачам объединения и разделения слов я постоянно использую одни и те же три слова при обозначении и обсуждении задач со словами. Что это за три слова? Это начало, изменение и результат.
start довольно понятен. Здесь начинается проблема. Это начало проблемы.
Изменение — это то, что изменяется в рамках рабочей проблемы.Что добавляется или отнимается у человека или объекта в проблеме.
Результат — это не ответ, а результат изменения . Будьте осторожны при использовании слова «результат» и не указывайте «ответ» в задаче. Результат — это только ответ, когда он неизвестен.
Решить для неизвестного
Другая ключевая часть процедуры — всегда искать неизвестное . Неизвестное может быть любым из трех: начало, изменение или результат, и то, как ученик решает проблему, будет меняться в зависимости от размещения неизвестного.
Я постоянно использую ящик для неизвестного. Проходя через проблему, я помечу начальное изменение и результат и буду использовать поле для всего, что неизвестно. Это та часть, которую студенты должны выяснить.
Обозначьте слово «проблема»
Когда я прохожу слово «проблема» со студентами, я помечаю его буквами S, C и R, чтобы обозначить начало, изменение и результат проблемы. Такая маркировка также помогает поддерживать постоянный словарный запас.
Напишите уравнение
По мере того, как мы работаем над пониманием проблемы, мы пишем уравнение.До этого момента у учащихся не было никаких цифр в задаче. Вы можете узнать, почему я не использую числа в задачах со словами в этом сообщении в блоге.
Дайте учащимся числа
На этом этапе дайте учащимся номера для задачи. Поскольку есть пробелы, вы можете легко различить числа в задаче. Я разработал этот ресурс для использования в моем совмещенном классе первого и второго класса. Я легко смогла дать обоим классам одну и ту же задачу и различать числа для каждого класса.
Обязательно обратите внимание на результат и убедитесь, что он больше, чем начало или изменение.
Я знаю, что нам кажется, что мы проделываем большую работу над интерфейсом, прежде чем учащиеся приступят к решению уравнения. Я обещаю. Вся эта работа в конечном итоге окупится, поскольку студенты смогут перенести этот опыт на решение многоступенчатых задач со словами.
В этом видео я подробно рассказываю о каждом из перечисленных выше типов задач, а также моделирую, как я использую числовую линию при обучении и решении этих задач.Вы можете узнать больше о различных моделях и стратегиях, а также о числовых линиях в связанных сообщениях блога.
Free Word Задачи по типу задачи, включая задачи о соединении
Хотите бесплатный образец словарных задач, которые я использую в своем классе? Щелкните здесь или изображение ниже. БЕСПЛАТНЫЙ образец задач Word по типу задачи
Возможно, вас заинтересует. . .
задач Word: сравнение двух групп | Математика для 2-го класса
Как решать задачи со словами, сравнивающие две группы
Чарли в этом году прочитал 9 книг.Чарли в этом году прочитал на 5 книг меньше, чем Рик. Сколько книг Рик прочитал в этом году?
Это проблема со словами, в которой сравнивает две группы. Когда вы сравниваете две группы, вы либо прибавляете, либо вычитаете .
😀 Совет: в задачах этого типа используются слова больше, и меньше, . В этих задачах НЕ думает, что «больше » предназначено только для сложения, а «меньше» — только для вычитания. Оба слова могут использоваться как для сложения, так и для вычитания .
Итак, вам действительно нужно внимательно прочитать слово «проблема».
Попробуем решить эту проблему, выполнив 4 шага.
Шаг 1. Соберите улики.
Мы сравниваем книги, которые Чарли и Рик прочитали в этом году.
Чарли прочитал 9 книг.
Это на 5 меньше, чем количество книг, которые прочитал Рик.
Шаг 2. Нарисуйте картинку или модель.
Мы знаем, что Рик читал больше, чем Чарли.
Но сколько книг он на самом деле прочитал?
Что мы делаем, чтобы решить эту проблему?
Верно!
👉 Мы прибавляем 9 плюс 5 .
Шаг 3. Напишите уравнение.
9 + 5 = 14
Шаг 4. Напишите ответ словесным предложением.
В этом году Рик прочитал 14 книг.
Отличная работа! 👏 🎉
Другой пример
Давайте решим еще одну словесную задачу.
Дэн построил 10 стульев в понедельник. Во вторник он построил 14 стульев. На сколько стульев он построил во вторник больше, чем в понедельник?
Шаг 1. Соберите улики.
Сравним стулья, которые Дэн построил в понедельник и вторник.
Шаг 2. Нарисуйте картинку.
Мы видим, что во вторник он построил больше стульев, чем в понедельник.
Но сколько еще?
👉 Мы находим разницу путем вычитания.
Шаг 3. Напишите уравнение.
14-10 = 4
Шаг 4. Напишите ответ словесным предложением.
Дэн построил на стула на 4 больше во вторник, чем в понедельник.
Отличная работа! 🎉 👏
Смотри и учись
Теперь вы можете попробовать поработать на практике! 💪
.



 Сколько кругов было на странице?
Сколько кругов было на странице?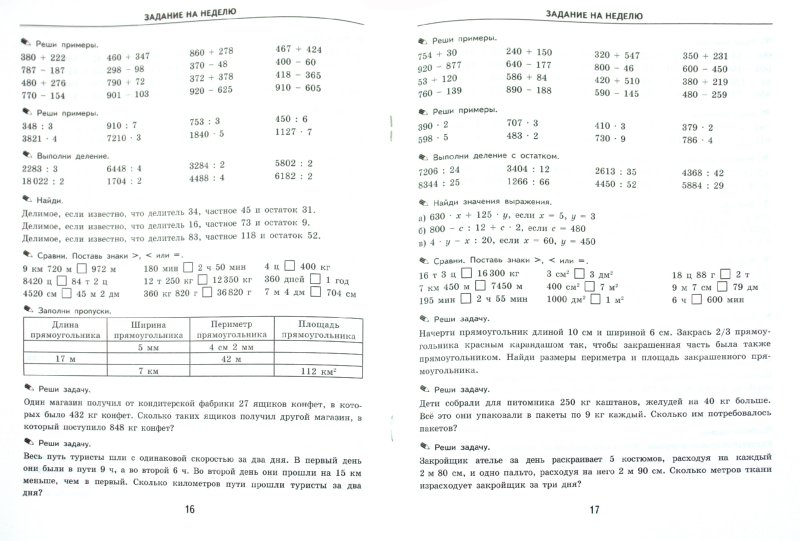 Определите, кажется ли ваш ответ разумным. Если возможно, сравните свой ответ с ответами в книге, чтобы определить, на правильном ли вы пути.
Определите, кажется ли ваш ответ разумным. Если возможно, сравните свой ответ с ответами в книге, чтобы определить, на правильном ли вы пути.