Страница 76 №244-251 ГДЗ к учебнику «Математика» 5 класс Бунимович, Дорофеев, Суворова
Ответы к упражнениям учебника
Задачи на части
Задание 244. Купили 1 кг 800 г сухофруктов из яблок, груш и слив. Яблок в них 4 части, груш − 3 части, слив − 2 части. Сколько граммов яблок, груш и слив в сухофруктах в отдельности?
Указание.
Выразите массу сухофруктов в граммах.
Решение задачи
1 кг 800 г = 1800 г
1) 3 + 4 + 2 = 9 (частей) − всего;
2) 1800 : 9 = 200 (г) − составляет одна часть;
3) 200 * 4 = 800 (г) − яблок в сухофруктах;
4) 200 * 3 = 600 (г) − груш в сухофруктах;
5) 200 * 2 = 400 (г) − слив в сухофруктах.
Ответ: 400 г слив, 600 г груш, 800 г яблок.
Задание 245. В сухофруктах яблоки составляют 7 частей, груши − 4 части, сливы − 5 частей. Сколько всего сухофруктов, если в них:
а) 160 г груш;
б) 280 г яблок;
в) 225 г слив?
Решение
а) 1) 160 : 4 = 40 (г) − составляет одна часть;
2) 7 * 40 = 280 (г) − яблок в сухофруктах;
3) 5 * 40 = 200 (г) − слив в сухофруктах;
4) 160 + 280 + 200 = 640 (г) − сухофруктов всего.
Ответ: 640 гб) 1) 280 : 7 = 40 (г) − составляет одна часть;
2) 40 * 4 = 160 (г) − груш в сухофруктах;
3) 40 * 5 = 200 (г) − слив в сухофруктах;
4) 280 + 160 + 200 = 640 (г) − сухофруктов всего.
Ответ: 640 гв) 1) 225 : 5 = 45 (г) − составляет одна часть;
2) 7 * 45 = 315 (г) − яблок в сухофруктах;
3) 4 * 45 = 180 (г) − груш в сухофруктах;
4) 225 + 315 + 180 = 720 (г) − сухофруктов всего.
Ответ: 720 г.
Задание 246. При пайке изделий из жести применяют сплав, содержащий 2 части свинца и 5 частей олова. Сколько свинца и олова содержит кусок сплава, в котором олова на 360 г больше, чем свинца?
Решите эту задачу по плану:
1) Сколько частей составляют 360 г?
2) Сколько граммов приходится на 1 часть?
3) Сколько свинца в сплаве?
4) Сколько олова в сплаве?
Решение
1) 5 − 2 = 3 (части) − составляют 360 г;
2) 360 : 3 = 120 (г) − приходится на 1 часть;
3) 120 * 2 = 240 (г) − свинца в сплаве;
4) 120 * 5 = 600 (г) − олова в сплаве.
Ответ: 240 г свинца и 600 г олова.
Задание 247. Купили 60 тетрадей, причем тетрадей в клетку в 2 раза больше, чем тетрадей в линейку (рис. 4.3). Сколько частей приходится на тетради в линейку? на тетради в клетку? на все тетради? Сколько купили тетрадей в линейку? Сколько − в клетку?
Решение задачи
1) 1 * 2 = 2 (части) − составляют тетради в клетку;
2) 1 + 2 = 3 (части) − всего;
3) 60 : 3 = 20 (тетрадей) − в линейку;
4) 20 * 2 = 40 (тетрадей) − в клетку.
Ответ: 20 тетрадей в линейку; 40 тетрадей в клетку.
Задание 248. а) На двух полках вместе 120 книг, причем на первой полке книг в 3 раза больше, чем на второй. Сколько книг на каждой полке?
б) В плацкартном вагоне в 3 раза больше спальных мест, чем в мягком вагоне. Всего в этих вагонах 72 места. Сколько спальных мест в мягком вагоне?
Решение задач
а) 1) 1 * 3 = 3 (части) − книг на первой полке;
2) 1 + 3 = 4 (части) − всего;
3) 120 : 4 = 30 (книг) − на второй полке;
4) 30 * 3 = 90 (книг) − на первой полке.
Ответ: 90 книг и 30 книг.б) 1) 1 * 3 = 3 (части) − спальных мест в плацкартном вагоне;
2) 1 + 3 = 4 (части) − всего;
3) 72 : 4 = 18 (мест) − в мягком вагоне;
4) 18 * 3 = 54 (места) − в плацкартном вагоне.
Ответ: 18 мест в мягком вагоне, 54 места в плацкартном вагоне.
Задание 249. а) Коля и Таня рвали в лесу орехи. Всего они сорвали 10 орехов. Таня сорвала в 2 раза меньше орехов, чем Коля. Сколько орехов было у Коли и сколько у Тани?
б) Алина прочитала в 3 раза меньше страниц, чем ей осталось прочитать. Всего в книге 176 страниц. Сколько страниц прочитала Алина?
Подсказка.
Переформулируйте каждую задачу, используя слово «больше».
Решение задач
а) Если Таня сорвала в 2 раза меньше орехов, то Коля собрал в 2 раз орехов больше, тогда:
1) 1 * 2 = 2 (части) − орехов собрал Коля;
2) 1 + 2 = 3 (части) − всего;
3) 120 : 3 = 40 (орехов) − собрала Таня;
4) 40 * 2 = 80 (орехов) − собрал Коля.
Ответ: 40 орехов собрала Таня; 80 орехов собрала Коля.б) Если Алина прочитала в 3 раза меньше страниц, чем ей осталось прочитать, то значит Алене осталось прочить в 3 раза больше, чем она прочитала, тогда:
1) 1 * 3 = 3 (части) − осталось прочитать Алине;
2) 1 + 3 = 4 (части) − всего;
3) 176 : 4 = 44 (страницы) − прочитала Алина.
Ответ: 44 страницы.
Задание 250. Дочка младше мамы в 4 раза и младше бабушки в 9 раз. Сколько лет каждой, если вместе им 98 лет?
Решение задачи
1) 1 + 4 + 9 = 14 (частей) − всего;
2) 98 : 14 = 7 (лет) − дочке;
3) 7 * 4 = 28 (лет) − маме;
4) 7 * 9 = 63 (года) − бабушке.
Ответ: 7 лет дочек, 28 лет маме, 63 года бабушке.
Задание 251. У Сережи в коллекции в 3 раза меньше марок, чем у Васи, а у Андрея в 2 раза больше, чем у Васи. Сколько марок у каждого, если у Андрея на 80 марок больше, чем у Сережи?
Решение задачи
1) 3 * 2 = 6 (раз) − больше у Андрея марок, чем у Сережи;
2) 6 − 1 = на 5 (частей) − больше у Андрея марок, чем у Сережи;
3) 80 : 5 = 16 (марок) − у Сережи;
4) 16 * 3 = 48 (марок) − у Васи;
5) 16 * 6 = 96 (марок) − у Андрея.
Ответ: 16 марок у Сережи, 48 марок у Васи, 96 марок у Андрея.
Страница не найдена
Новости
16 апр
Стали известны лауреаты конкурса «Молодые педагоги — московскому образованию». Его участниками стали более 900 учителей.
16 апр
Прокуратура Уссурийска (Приморский край) начала проверку сообщения об обрушении стены в школе села Воздвиженка.
16 апр
Доктор педагогических наук, профессор, эксперт по образованию Юлия Лях дала рекомендации по выбору школы для ребёнка.
16 апр
Роспотребнадзор подвёл предварительные итоги внеплановых проверок в учебных организациях и комбинатах Санкт-Петербурга, ответственных за организацию детского питания.
15 апр
Председатель комитета Совета Федерации по науке, образованию и культуре Лилия Гумерова прокомментировала в беседе с RT предложение ввести в школах России регулярные лекции диетологов в рамках курса «Здоровое питание и образ жизни».
15 апр
Уполномоченный по правам ребёнка в Республике Татарстан, основатель Национального родительского комитета Ирина Волынец предложила ввести в школах России регулярные лекции диетологов в рамках курса «Здоровое питание и образ жизни». Копии обращений на имя министра просвещения Сергея Кравцова и на имя министра здравоохранения Михаила Мурашко есть в распоряжении RT.
14 апр
Объявлена дата проведения праздника «Алые паруса» в Санкт-Петербурге. Мероприятие состоится 25 июня.
Мероприятие состоится 25 июня.
Формулы для решения задач на дроби для 5 класса
В 5 классе на уроках математики ученики знакомятся с дробями и процентами. В 6 классе эта тема повторяется, но изучается более глубоко. А встречаться дроби и проценты продолжат вплоть до задач внешнего тестирования (ЗНО) для 11 класса.
Обыкновенная дробь — это пара чисел, записанных через черту.
Число под чертой (знаменатель), показывает, на сколько частей разделили целое.
Число над чертой (числитель) показывает, сколько этих частей выбрано.
То есть дробь $\frac{3}{8}$ (три восьмых) означает, что целое было разделено на 8 частей, а взято из них три.
Существуют три класса задач на дроби: нахождение дроби от числа, нахождение числа по его дроби и выражение отношения чисел в виде дроби.
Как найти дробь от числа
В задачах на дробь от числа известно само число и дробь, которая от него взята. А найти требуется, какую величину составит эта дробь. Рассмотрим такую задачу
Пример 1.1.
В самолёте 120 пассажиров. $\frac{2}{5}$ (две пятых) из них летят в самолёте в первый раз. Сколько пассажиров летит в первый раз?
Это задача на нахождение дроби от числа.
Есть число: 120.
Есть дробь: $\frac{2}{5}$
Нужно найти, чему равны две пятых от 120.
Решаются задачи на нахождение дроби от числа так.
Решение
Задаём себе два вопроса:
1. Чему равна $\frac{1}{5}$ (одна пятая) от 120?
Для этого 120 делим на 5, получаем 24.
2. Чему равны $\frac{2}{5}$ (две пятых) от 120?
Результат 24, корый мы получили, нужно умножить на 2.
Получаем 48.
Значит, $\frac{2}{5}$ от 120 составляет 48.
Ответ: 48 пассажиров летят впервые.
Попробуем решить ещё одну задачу на нахождение дроби от числа.
Пример 1.2.
В городе живут 1 500 000 человек. Из них $\frac{3}{25}$ — школьники. Сколько в городе школьников?
Из них $\frac{3}{25}$ — школьники. Сколько в городе школьников?
Решение
1. Чему равна $\frac{1}{25}$ от 1 500 000?
1 500 000:25 = 60 000
2. Чему равны $\frac{2}{25}$ от 1 500 000?
60 000*3 = 180 000
Ответ: 180 000 школьников.
Когда вы набрались опыта решать такие задачи по вопросам, эти два вопроса можно свести в одно действие и использовать правило:
Чтобы найти дробь от числа, нужно это число умножить на дробь
Или, что то же самое:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби и умножить на её числитель
Пример 1.3.
В автосалон завезли 14 автомобилей. За месяц продали 2/7 этого количества. Сколько автомобилей продали?
Решение
Умножим 14 на $\frac{2}{7}$:
$14\cdot \frac{2}{7} = \frac{14\cdot 2}{7} = 2\cdot 2 = 4$
Ответ: 4 автомобиля.
Теперь рассмотрим задачи второго типа:
Как найти число по дроби
В задачах этого типа исходное число неизвестно. Зато известна величина некоторой части от этого числа и какую дробь составляет эта часть от исходного числа. Для удобства рассмотрим, как бы выглядели эти же три задачи, если бы в них требовалось найти число по дроби.
Пример 2.1.
В самолёте сидят пассажиры (сколько их неизвестно!). Известно, что 48 пассажиров или $\frac{2}{5}$ (две пятых) от их количества летят впервые. Нужно найти: сколько всего пассажирова в самолёте?
Решение
Эти 48 пассажиров, которые летят впервые, составляют две пятых ($\frac{2}{5}$) от общего количества пассажиров в салоне. Мы можем найти одну пятую?
Да, нужно 48 разделить на 2.
48:2 = 24.
Мы узнали, что одна пятая часть от всех пассажиров — это 24 человека. Сколько всего пассажиров? В пять раз больше, то есть 24х5 = 120.
Ответ: 120 пассажиров всегов самолёте
Понятно? Давайте разберём ещё одну задачу.
Пример 2.2.
Три двадцать пятых ($\frac{3}{25}$) населения города составляют школьники. Школьников в городе 180 000. Каково общее население города?
Школьников в городе 180 000. Каково общее население города?
Решение
Опять само число (то есть население города) на неизвестно, зато известно, чему равны $\frac{3}{25}$ от него.Значит, можно сначала найти, чему равна $\frac{1}{25}$ от населения города. Разделим 180 000 на 3:
180 000:3 = 60 000
Зная одну двадцать пятую, можно найти и целое, умножив 60 000 на 25.
60 000х25 = 1 500 000
Ответ: в городе 1 500 000 жителей
Когда будете уверенно решать задачи на нахождение числа по его дроби по вопросам, можно будет заменить эти вопросы одним действием и использовать правило:
Чтобы найти число по его дроби, известную величину нужно разделить на эту дробь
Или, что то же самое:
Чтобы найти число по его дроби, известную величину нужно разделить на числитель дроби и умножить на её знаменатель
Пример 2.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4, что составляет 2/7 всех автомобилей. Сколько автомобилей завезли в салон?
Решение
Разделим 4 на $\frac{2}{7}$:
$4: \frac{2}{7} = \frac{4\cdot 7}{2} = 2\cdot 7 = 14$
Ответ: 14 автомобилей завезли в салон.
И перейдём теперь к третьему типу задач на дроби, которые изучаются в математике 5 класса:
Как найти отношение двух чисел и выразить его в виде дроби
В задачах на нахождение отношения оба числа известны, а нужно найти, какую дробь второе число составляет от первого. Решаются они проще всего
Пример 3.1.
В самолёте 120 пассажиров. Из них 48 человек летят в первый раз. Какая часть пассажиров летит в первый раз?
Решение
Чтобы найти, какую дробь 48 составляет от общего количества пассажиров (120), нужно 48 разлелить на 120 и затем скоратить, что возможно.
Доля летящих впервые пассажиров составляет $\frac{48}{120}$.
И числитель, и знаменатель делятся на 2, значит, можно сократить на 2.
$\frac{48}{120}=\frac{24}{60}$
Сократим ещё раз на 2:
$\frac{24}{60} = \frac{12}{30}$
И ещё раз:
$\frac{12}{30} = \frac{6}{15}$
Теперь можно сократить на 3:
$\frac{6}{15} = \frac{2}{5}$
Больше сокращать не на что — это и можно записать как окончательный ответ задачи.
Ответ: $\frac{2}{5}$ пассажиров летят впервые.
Так что правило для решения задач на нахождение отношения чисел самое простое:
Чтобы найти, в виде какой дроби выражается отноешние двух чисел, нужно сначала записать дробь, в которой числитель и знаменатель — эти числа, а затем сократить её.
Обратите внимание, что дробь $\frac{A}{B}$ обозначает, какую долю величина А составляет от величины В и правильно записывайте величины в числитель и знаменатель.
Разберём ещё два примера.
Пример 3.2.
В городе с населением 1 500 000 жителей живут 180 000 школьников. Какую часть населения города составляют школьники?
Решение
Нужно найти, какую часть 180 000 составляет от 1 500 000?
Записываем дробь и сокращаем:
$\frac{180000}{1500000}=\frac{18}{150}=\frac{9}{75}=\frac{3}{25}$
Ответ: школьники составляют $\frac{3}{25}$ от общего населения города
Пример 3.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4. Какую часть от всех автомобилей это составляет, если всегов автомалон завезли 14 машин?
Решение
Точно так же, берём дробь $\frac{4}{14}$ и сокращаем:
$\frac{4}{14}=\frac{2}{7}$
Ответ: продали $\frac{2}{7}$ от общего количества автомобилей.
Вот как решаются задачи на дроби. Вы найдёте справочники по формулам математики 5, 6 и других классов в разделе «Математика в школе».
Математика 5 класс — Поурочные разработки
Глава 1. Линии
1.1. Разнообразный мир линий
УРОК 1. Линии на плоскости
1.2. Прямая. Части прямой. Ломаная
УРОК 2. Прямая. Отрезок и луч
УРОК 3. Ломаная
1.3. Длина линии
УРОК 4. Сравнение отрезков. Длина отрезка. Единицы длины
УРОК 5. Длина линии. Длина ломаной. Старинные единицы длины
1.4. Окружность
УРОК 6. Окружность. Круг
УРОК 7. Окружность и круг
Глава 2. Натуральные числа
2. 1. Как записывают и читают числа
1. Как записывают и читают числа
УРОК 8. Сопоставление десятичной системы записи чисел и римской нумерации
УРОК 9. Десятичная система записи чисел
2.2. Сравнение чисел
УРОК 10. Натуральный ряд чисел и его свойства
УРОК 11. Сравнение чисел. Двойное неравенство
2.3. Числа и точки на прямой
УРОК 12. Координатная прямая
УРОК 13. Изображение натуральных чисел точками на координатной прямой
2.4. Округление натуральных чисел
УРОК 14. Округление натуральных чисел
УРОК 15. Правило округления натуральных чисел
2.5. Перебор возможных вариантов
УРОК 16. Перебор возможных вариантов
УРОК 17. Дерево возможных вариантов
УРОК 18. Решение комбинаторных задач
УРОК 19. Логика перебора при решении комбинаторных задач
Глава 3. Действия с натуральными числами
3.1. Сложение и вычитание
УРОК 20. Сложение натуральных чисел
УРОК 21. Взаимосвязь между сложением и вычитанием натуральных чисел
УРОК 22. Нахождение неизвестных компонентов сложения и вычитания
УРОК 23. Прикидка и оценка результатов вычислений
УРОК 24. Решение текстовых задач
3.2. Умножение и деление
УРОК 25. Умножение натуральных чисел
УРОК 26. Умножение и деление натуральных чисел
УРОК 27. Нахождение неизвестных компонентов умножения и деления
УРОК 28. Умножение натуральных чисел. Прикидка и оценка результатов вычислений
УРОК 29. Деление натуральных чисел. Прикидка и оценка результатов вычислений
УРОК 30. Простейшие задачи на движение
УРОК 31. Решение задач на умножение и деление натуральных чисел
УРОК 32. Зачет 1. «Натуральные числа»
3.3. Порядок действий в вычислениях
УРОК 33. Порядок действий в вычислениях
УРОК 34. Порядок действий в выражениях, содержащих действия разных ступеней
УРОК 35. Порядок действий. Вычисления по схеме
УРОК 36. Порядок действий в вычислениях. Решение текстовых задач
3. 4. Степень числа
4. Степень числа
УРОК 37. Степень числа
УРОК 38. Квадрат и куб числа
УРОК 39. Порядок действий при вычислении значений выражений, содержащих степени
3.5. Задачи на движение
УРОК 40. Задачи на движение навстречу и в противоположных направлениях
УРОК 41. Задачи на движение навстречу и в одном направлении
УРОК 42. Задачи на движение по течению и против течения
УРОК 43. Различные задачи на движение
УРОК 44. Зачет 2. «Действия с натуральными числами»
Глава 4. Использование свойств действий при вычислениях
4.1. Свойства сложения и умножения
УРОК 45. Переместительное и сочетательное свойства сложения и умножения
УРОК 46. Преобразование выражений на основе свойств действий
4.2. Распределительное свойство
УРОК 47. Распределительное свойство
УРОК 48. Вынесение общего множителя за скобки
УРОК 49. Преобразование числовых выражений на основе распределительного закона
4.3. Задачи на части
УРОК 50. Задачи на части
УРОК 51. Задачи на части, в условии которых дается масса всей смеси
УРОК 52. Задачи на части, в которых части в явном виде не указаны
УРОК 53. Разные задачи на части
4.4. Задачи на уравнивание
УРОК 54. Как решать задачи на уравнивание
УРОК 55. Решение задач на уравнивание
УРОК 56. Зачет 3. «Использование свойств действий при вычислениях»
Глава 5. Многоугольники
5.1. Как обозначают и сравнивают углы
УРОК 57. Угол. Обозначение углов. Сравнение углов
УРОК 58. Виды углов. Биссектриса угла
5.2. Измерение углов
УРОК 59. Градус, транспортир, измерение углов
УРОК 60. Построение углов заданной градусной меры с помощью транспортира
УРОК 61. Построение углов
5.3. Ломаные и многоугольники
УРОК 62. Ломаные и многоугольники. Периметр многоугольника
УРОК 63. Многоугольники. Диагонали многоугольников
Глава 6. Делимость чисел
6. 1. Делители и кратные
1. Делители и кратные
УРОК 64. Делители числа. Наибольший общий делитель
УРОК 65. Делители и кратные числа. Наименьшее общее кратное
УРОК 66. Делители и кратные
6.2. Простые и составные числа
УРОК 67. Простые и составные числа
УРОК 68. Разложение составного числа на простые множители
6.3. Делимость суммы и произведения
УРОК 69. Делимость суммы и произведения
6.4. Признаки делимости
УРОК 70. Признаки делимости на 2, на 5, на 10
УРОК 71. Признаки делимости на 9 и на 3
УРОК 72. Признаки делимости чисел
УРОК 73. Делимость натуральных чисел. Урок-игра «Математический перекресток»
6.5. Деление с остатком
УРОК 74. Деление с остатком
УРОК 75. Нахождение неизвестных компонентов при делении с остатком
УРОК 76. Деление с остатком при решении задач
6.6. Разные арифметические задачи
УРОК 77. Решение задач арифметическим способом
УРОК 78. Зачет 4. «Делимость чисел»
Глава 7. Треугольники и четырехугольники
7.1. Треугольники и их виды
УРОК 79. Треугольники и их виды. Свойства равнобедренного треугольника
УРОК 80. Классификация треугольников по сторонам и углам
7.2. Прямоугольники
УРОК 81. Прямоугольники
УРОК 82. Прямоугольник. Свойства диагоналей прямоугольника
7.3. Равенство фигур
УРОК 83. Равные фигуры
УРОК 84. Равные фигуры
7.4. Площадь прямоугольника
УРОК 85. Площадь прямоугольника
УРОК 86. Площадь фигур, составленных из прямоугольников
7.5. Единицы площади
УРОК 87. Единицы площади
Глава 8. Дроби
8.1. Доли
УРОК 88. Как единица на доли делится
УРОК 89. Нахождение целого по его части
8.2. Что такое дробь
УРОК 90. Как из долей получаются дроби. Правильные и неправильные дроби
УРОК 91. Изображение дробей точками на координатной прямой
УРОК 92. Решение задач на нахождение дроби от числа
УРОК 93. Решение основных задач на дроби
Решение основных задач на дроби
8.3. Основное свойство дроби
УРОК 94. Основное свойство дроби
УРОК 95. Основное свойство дроби. Приведение дробей к новому знаменателю
УРОК 96. Основное свойство дроби. Сокращение дробей
УРОК 97. Преобразование дробей с помощью основного свойства
8.4. Сравнение дробей
УРОК 98. Сравнение дробей с одинаковыми знаменателями
8.5. Приведение дробей к общему знаменателю
УРОК 99. Приведение дробей к общему знаменателю
УРОК 100. Приведение дробей к общему знаменателю и их сравнение
УРОК 101. Сравнение дробей
УРОК 102. Различные приемы сравнения дробей
8.6. Натуральные числа и дроби
УРОК 103. Натуральные числа и дроби
УРОК 104. Натуральные числа и дроби
8.7. Случайные события
УРОК 105. Достоверные, невозможные и случайные события
УРОК 106. Случайные события
УРОК 107. Зачет 5. «Обыкновенные дроби»
Глава 9. Действия с дробями
9.1. Сложение дробей
УРОК 108. Сложение обыкновенных дробей с одинаковыми знаменателями
УРОК 109. Сложение дробей с разными знаменателями
УРОК 110. Сложение дробей. Прикидка оценка результатов
УРОК 111. Задачи на совместную работу
9.2. Сложение смешанных дробей
УРОК 112. Смешанные дроби
УРОК 113. Выделение целой части из неправильной дроби
УРОК 114. Сложение смешанных дробей
9.3. Вычитание дробных чисел
УРОК 115. Вычитание обыкновенных дробей
УРОК 116. Вычитание дроби из целого числа
УРОК 117. Вычитание чисел, одно из которых выражается смешанной дробью
УРОК 118. Рациональные приемы вычислений
УРОК 119. Вычитание смешанных дробей
УРОК 120. Игра «Биржа знаний»
УРОК 121. Зачет 6. «Сложение и вычитание дробей»
9.4. Умножение дробей
УРОК 122. Умножение обыкновенных дробей
УРОК 123. Умножение дроби на натуральное число
УРОК 124. Умножение смешанных дробей
УРОК 125. Решение задач, приводящих к умножению дробей
Решение задач, приводящих к умножению дробей
УРОК 126. Возведение в степень обыкновенных дробей. Применение свойств умножения для упрощения вычислений
9.5. Деление дробей
УРОК 127. Деление обыкновенных дробей
УРОК 128. Деление обыкновенной дроби на натуральное число и числа на дробь
УРОК 129. Деление смешанных дробей
УРОК 130. Все случаи деления обыкновенных дробей
УРОК 131. Решение задач, приводящих к делению дробей
УРОК 132. Действия с обыкновенными дробями
9.6. Нахождение части целого и целого по его части
УРОК 133. Нахождение дроби от числа и числа по его дроби
УРОК 134. Нахождение части целого на основе формального правила
УРОК 135. Нахождение целого по его части на основе формального правила
УРОК 136. Решение задач на нахождение дроби от числа и числа по его дроби
УРОК 137. Решение задач на нахождение дроби от числа и числа по его дроби
9.7. Задачи на совместную работу
УРОК 138. Задачи на совместную работу
УРОК 139. Задачи на совместную работу
УРОК 140. Задачи на совместную работу
УРОК 141. Обыкновенные дроби
УРОК 142. Зачет 7. «Умножение и деление дробей»
Глава 10. Многогранники
10.1. Геометрические тела и их изображение
УРОК 143. Знакомство с геометрическими телами. Многогранники. Цилиндр. Конус. Шар
УРОК 144. Геометрические тела и их изображение
10.2. Параллелепипед
УРОК 145. Прямоугольный параллелепипед. Куб
УРОК 146. Прямоугольный параллелепипед. Куб
10.3. Объем параллелепипеда
УРОК 147. Объем прямоугольного параллелепипеда. Единицы объема
УРОК 148. Объем прямоугольного параллелепипеда
УРОК 149. Решение задач на вычисление объемов
10.4. Пирамида
УРОК 150. Пирамида и ее элементы
10.5. Развертки
УРОК 151. Развертки параллелепипеда и куба
УРОК 152. Развертки поверхностей геометрических тел
Глава 11. Таблицы и диаграммы
11. 1. Чтение и составление таблиц
1. Чтение и составление таблиц
УРОК 153. Чтение таблиц
УРОК 154. Чтение и составление турнирных и частотных таблиц
УРОК 155. Построение таблиц
11.2. Чтение и построение диаграмм
УРОК 156. Чтение и построение столбчатых диаграмм
УРОК 157. Столбчатые и круговые диаграммы
11.3. Опрос общественного мнения
УРОК 158. Опрос общественного мнения
УРОКИ 159-160. Опрос общественного мнения
| Класс | Название урока | Ссылка на учебные материалы |
| 5 | Ряд натуральных чисел. Десятичная система записи натуральных чисел | https://resh.edu.ru/subject/lesson/7719/main/234018/ |
| 5 | Сравнение натуральных чисел | https://resh.edu.ru/subject/lesson/7718/main/235258/ |
| 5 | Сравнение именованных чисел | https://interneturok.ru/lesson/matematika/5-klass/bnaturalnye-chislab/izmerenie-velichin-edinitsy-izmereniya?block=player |
| 5 | Измерение отрезков | https://resh.edu.ru/subject/lesson/7740/main/234855/ |
| 5 | Длина отрезка | https://resh.edu.ru/subject/lesson/6914/main/235937/ |
| 5 | Прямая, луч, отрезок | https://resh.edu.ru/subject/lesson/7741/main/235227/ |
| 5 | Координатный луч | https://resh.edu.ru/subject/lesson/7756/main/234421/ |
| 5 | Представление натуральных чисел на координатном луче | https://resh.edu.ru/subject/lesson/7738/main/233801/ |
| 5 | Сложение натуральных чисел. Законы сложения | https://resh.edu.ru/subject/lesson/7723/main/ |
| 5 | Арифметические действия с натуральными числами | https://mosobr. tv/release/7856 tv/release/7856 |
| 5 | Вычитание | https://resh.edu.ru/subject/lesson/7717/main/235289/ |
| 5 | Правила вычитания суммы из числа и числа из суммы | https://znaika.ru/catalog/5-klass/matematika/Svoystva-vychitaniya-naturalnykh-chisel.html |
| 5 | Решение текстовых задач с помощью сложения и вычитания | https://resh.edu.ru/subject/lesson/7716/main/233832/ |
| 5 | Числовые выражения | https://resh.edu.ru/subject/lesson/7708/main/266123/ |
| 5 | Углы. Измерение углов | https://resh.edu.ru/subject/lesson/589/ |
| 5 | Углы. Измерение углов | https://resh.edu.ru/subject/lesson/7735/main/234886/ |
| 5 | Многоугольники | https://resh.edu.ru/subject/lesson/7727/main/267638/ |
| 5 | Треугольники | https://resh.edu.ru/subject/lesson/7734/main/234917/ |
| 5 | Четырёхугольники | https://resh.edu.ru/subject/lesson/7733/main/233522/ |
| 5 | Симметрия относительно точки, относительно прямой и относительно плоскости | https://resh.edu.ru/subject/lesson/983/ |
| 5 | Умножение. Законы умножения | https://resh.edu.ru/subject/lesson/7722/main/235069/ |
| 5 | Распределительный закон | https://resh.edu.ru/subject/lesson/7724/main/266247/ |
| 5 | Умножение. Законы умножения | https://resh.edu.ru/subject/lesson/7712/main/235041/ |
| 5 | Деление нацело | https://resh.edu.ru/subject/lesson/7712/main/235041/ |
| 5 | Деление с остатком | https://resh.edu.ru/subject/lesson/7709/main/235165/ |
| 5 | Степень с натуральным показателем | https://resh. edu.ru/subject/lesson/7713/main/234793/ edu.ru/subject/lesson/7713/main/234793/ |
| 5 | Решение текстовых задач с помощью умножения и деления | https://resh.edu.ru/subject/lesson/7711/main/234760/ |
| 5 | Площадь прямоугольника. Единицы площади | https://resh.edu.ru/subject/lesson/7732/main/233181/ |
| 5 | Прямоугольный параллелепипед | https://resh.edu.ru/subject/lesson/7731/main/234669/ |
| 5 | Объём прямоугольного параллелепипеда. Единицы объёма | https://resh.edu.ru/subject/lesson/7730/main/272356/ |
| 5 | Объём прямоугольного параллелепипеда | https://resh.edu.ru/subject/lesson/7753/main/234824/ |
| 5 | Понятие дроби | https://resh.edu.ru/subject/lesson/7782/main/233643/ |
| 5 | Сравнение обыкновенных дробей | https://resh.edu.ru/subject/lesson/16/ |
| 5 | Задачи на дроби (нахождение части целого) | https://resh.edu.ru/subject/lesson/7780/main/234203/ |
| 5 | Дроби и деление натуральных чисел | https://znaika.ru/catalog/5-klass/matematika/Delenie-i-drobi.html |
| 5 | Нахождение целого по его части | https://resh.edu.ru/subject/lesson/7779/main/233956/ |
| 5 | Задачи на дроби (нахождение части целого) | https://resh.edu.ru/subject/lesson/7780/main/234203/ |
| 5 | Сложение дробей с одинаковым знаменателем | https://resh.edu.ru/subject/lesson/7774/main/233212/ |
| 5 | Понятие смешанной дроби | https://resh.edu.ru/subject/lesson/7761/main/233026/ |
| 5 | Сложение смешанных дробей | https://resh.edu.ru/subject/lesson/7760/main/233336/ |
| 5 | Вычитание смешанных дробей | https://resh. edu.ru/subject/lesson/7759/main/233615/ edu.ru/subject/lesson/7759/main/233615/ |
| 5 | Понятие положительной десятичной дроби | https://resh.edu.ru/subject/lesson/6903/main/235413/ |
| 5 | Сравнение положительных десятичных дробей | https://resh.edu.ru/subject/lesson/6902/main/236096/ |
| 5 | Округление натуральных чисел. Теоретическая часть | https://resh.edu.ru/subject/lesson/23/ |
| 5 | Округление десятичных дробей | https://resh.edu.ru/subject/lesson/27/ |
| 5 | Чтение и запись десятичных дробей | https://video-ypoku.com/dlya-detej-i-roditelej/shkolnikam/1383-matematika-5-klass-desyatichnye-drobi |
| 5 | Сложение положительных десятичных дробей | https://resh.edu.ru/subject/lesson/6901/main/236064/ |
| 5 | Вычитание положительных десятичных дробей | https://resh.edu.ru/subject/lesson/6900/main/236033/ |
| 5 | Сложение и вычитание десятичных дробей | https://resh.edu.ru/subject/lesson/719/ |
| 5 | Умножение и деление десятичной дроби на 10, 100, 1000 | https://resh.edu.ru/subject/lesson/720/ |
| 5 | Умножение положительных десятичных дробей. Часть 1 | https://resh.edu.ru/subject/lesson/6898/main/235559/ |
| 5 | Умножение положительных десятичных дробей. Часть 2 | https://resh.edu.ru/subject/lesson/6897/main/236204/ |
| 5 | Деление натуральных чисел | https://mosobr.tv/release/7932 |
| 5 | Деление десятичной дроби на целое число | https://resh.edu.ru/subject/lesson/722/ |
| 5 | Умножение и деление десятичной дроби на 10, 100, 1000 | https://resh. edu.ru/subject/lesson/720/ edu.ru/subject/lesson/720/ |
| 5 | Деление положительных десятичных дробей. Часть 1 | https://resh.edu.ru/subject/lesson/6896/main/236240/ |
| 5 | Деление положительных десятичных дробей. Часть 2 | https://resh.edu.ru/subject/lesson/6895/main/237500/ |
| 5 | Среднее арифметическое | https://resh.edu.ru/subject/lesson/715/ |
| 5 | Среднее арифметическое нескольких чисел | https://resh.edu.ru/subject/lesson/22/ |
| 5 | Понятие о проценте | https://resh.edu.ru/subject/lesson/6846/main/237181/ |
| 5 | Проценты. Вычисление процентов от числа и числа по известному проценту, выражение отношения в процентах | https://resh.edu.ru/subject/lesson/1060/ |
| 5 | Задачи на проценты. Часть 1 | https://resh.edu.ru/subject/lesson/6848/main/237738/ |
| 5 | Задачи на проценты. Часть 2 | https://resh.edu.ru/subject/lesson/6839/main/237149/ |
| 5 | Занимательные задачи по теме «Смешанные дроби» | https://resh.edu.ru/subject/lesson/7752/main/233553/ |
| 5 | Итоговое обобщение и систематизация знаний по темам «Делимость натуральных чисел» | https://resh.edu.ru/subject/lesson/7790/main/234080/ |
| 5 | Итоговое обобщение и систематизация знаний по темам «Обыкновенные дроби и смешанные дроби» | https://resh.edu.ru/subject/lesson/7789/main/266061/ |
| 5 | Единицы длины | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/687915 |
| 5 | Шкала. Примеры шкал | https://infourok.ru/videouroki/2947 |
| 5 | Буквенное выражение и его значение | https://infourok. ru/videouroki/2952 ru/videouroki/2952 |
| 5 | Формулы | https://infourok.ru/videouroki/2922 |
| 5 | Уравнение | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/4369029 |
| 5 | Биссектриса угла | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/2680471 |
| 5 | Равные фигуры | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/4909803 |
| 5 | Прямоугольник. Периметр прямоугольника | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/1299188 |
| 5 | Порядок действий | https://infourok.ru/videouroki/2920 |
| 5 | Понятие площади | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/856976 |
| 5 | Пирамида | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/3149941 |
| 5 | Ломаная. Длина ломаной | https://uchebnik.mos.ru/moderator_materials/material_view/atomic_objects/4454434 |
| 5 | Развёртки геометрических фигур | https://uchebnik.mos.ru/moderator_materials/material_view/atomic_objects/5795070 |
| 5 | Округление чисел. Прикидки | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/5206540 |
| 5 | Умножение десятичных дробей на 0,1, 0,01, 0,001 и т. д. | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/439985 |
| 5 | Деление десятичной дроби на 0,1, 0,01, 0,001 и т. д. | https://znaika.ru/catalog/5-klass/matematika/Delenie-na-desyatichnuyu-drob.html |
| 6 | Делители натурального числа | https://resh. edu.ru/subject/lesson/694/ edu.ru/subject/lesson/694/ |
| 6 | Признаки делимости | https://resh.edu.ru/subject/lesson/7750/main/234576/ |
| 6 | Простые и составные числа | https://resh.edu.ru/subject/lesson/7749/main/234979/ |
| 6 | Наибольший общий делитель (НОД) | https://resh.edu.ru/subject/lesson/7747/main/233739/ |
| 6 | Наименьшее общее кратное (НОК) | https://resh.edu.ru/subject/lesson/7746/main/234266/ |
| 6 | Равенство дробей | https://resh.edu.ru/subject/lesson/7781/main/269492/ |
| 6 | Понятие дроби | https://resh.edu.ru/subject/lesson/7782/main/233643/ |
| 6 | Приведение дробей к общему знаменателю. Сокращение дробей | https://resh.edu.ru/subject/lesson/7777/main/233115/ |
| 6 | Приведение дробей к общему знаменателю. Сокращение дробей | https://resh.edu.ru/subject/lesson/7778/main/233708/ |
| 6 | Сравнение дробей | https://resh.edu.ru/subject/lesson/7776/main/233243/ |
| 6 | Сравнение дробей. Сравнение с единицей. Сравнение остатков до единицы | https://resh.edu.ru/subject/lesson/7775/main/233398/ |
| 6 | Сложение дробей с одинаковым знаменателем | https://resh.edu.ru/subject/lesson/7774/main/233212/ |
| 6 | Сложение дробей с разными знаменателями | https://resh.edu.ru/subject/lesson/7773/main/233057/ |
| 6 | Вычитание дробей | https://resh.edu.ru/subject/lesson/7771/main/233150/ |
| 6 | Решение задач с использованием вычитания дробей | https://resh.edu.ru/subject/lesson/7770/main/233925/ |
| 6 | Умножение натурального числа на дробь | https://resh. edu.ru/subject/lesson/7769/main/234483/ edu.ru/subject/lesson/7769/main/234483/ |
| 6 | Законы умножения. Распределительный закон | https://resh.edu.ru/subject/lesson/7767/main/234545/ |
| 6 | Нахождение части целого и целого по его части | https://resh.edu.ru/subject/lesson/7764/main/233584/ |
| 6 | Решение задач на применение умножения дроби на натуральное число и умножение дробей | https://resh.edu.ru/subject/lesson/7768/main/234142/ |
| 6 | Умножение и деление обыкновенной дроби на обыкновенную дробь | https://resh.edu.ru/subject/lesson/710/ |
| 6 | Деление дробей | https://resh.edu.ru/subject/lesson/7766/main/234948/ |
| 6 | Свойства деления | https://znaika.ru/catalog/5-klass/matematika/Delenie-naturalnykh-chisel-i-ego-svoystva.html |
| 6 | Понятие положительной десятичной дроби | https://resh.edu.ru/subject/lesson/6903/main/235413/ |
| 6 | Бесконечные периодические десятичные дроби | https://resh.edu.ru/subject/lesson/6915/main/236435/ |
| 6 | Разложение положительной обыкновенной дроби в конечную десятичную дробь | https://resh.edu.ru/subject/lesson/6919/main/237273/ |
| 6 | Отношение чисел и величин | https://resh.edu.ru/subject/lesson/6844/main/235847/ |
| 6 | Пропорции | https://resh.edu.ru/subject/lesson/6841/main/237211/ |
| 6 | Проценты. Вычисление процентов от числа и числа по известному проценту, выражение отношения в процентах | https://resh.edu.ru/subject/lesson/1060/ |
| 6 | Прямая и обратная пропорциональность | https://resh.edu.ru/subject/lesson/6849/main/237769/ |
| 6 | Деление числа в данном отношении | https://resh. edu.ru/subject/lesson/6842/main/235816/ edu.ru/subject/lesson/6842/main/235816/ |
| 6 | Окружность и круг. Сфера и шар | https://resh.edu.ru/subject/lesson/588/ |
| 6 | Длина окружности. Площадь круга | https://resh.edu.ru/subject/lesson/6913/main/236498/ |
| 6 | Куб, шар, пирамида, цилиндр, конус | https://resh.edu.ru/subject/lesson/557/ |
| 6 | Столбчатые и круговые диаграммы | https://resh.edu.ru/subject/lesson/1228/ |
| 6 | Отрицательные целые числа | https://resh.edu.ru/subject/lesson/6872/main/237087/ |
| 6 | Координатная ось. Часть 1 | https://resh.edu.ru/subject/lesson/6912/main/236158/ |
| 6 | Представление целых чисел на координатной оси | https://resh.edu.ru/subject/lesson/6866/main/236343/ |
| 6 | Координатная ось. Часть 2 | https://resh.edu.ru/subject/lesson/6920/main/236020/ |
| 6 | Противоположные числа. Модуль числа | https://resh.edu.ru/subject/lesson/6862/main/237056/ |
| 6 | Сравнение целых чисел | https://resh.edu.ru/subject/lesson/6861/main/237025/ |
| 6 | Сложение целых чисел. Часть 1 | https://resh.edu.ru/subject/lesson/6863/main/236994/ |
| 6 | Сложение целых чисел. Часть 2 | https://resh.edu.ru/subject/lesson/6864/main/236963/ |
| 6 | Сложение целых чисел. Часть 3 | https://resh.edu.ru/subject/lesson/6865/main/236933/ |
| 6 | Законы сложения целых чисел | https://resh.edu.ru/subject/lesson/6860/main/237335/ |
| 6 | Рациональное вычисление значений арифметических выражений с применением вычитания, как алгебраического сложения. Часть 1 (теория) Часть 1 (теория) | https://resh.edu.ru/subject/lesson/1380/ |
| 6 | Разность целых чисел. Часть 1 | https://resh.edu.ru/subject/lesson/6859/main/237552/ |
| 6 | Разность целых чисел. Часть 2 | https://resh.edu.ru/subject/lesson/6858/main/236901/ |
| 6 | Произведение целых чисел. Часть 1 | https://resh.edu.ru/subject/lesson/6857/main/236870/ |
| 6 | Произведение целых чисел. Часть 2 | https://resh.edu.ru/subject/lesson/6856/main/237301/ |
| 6 | Произведение целых чисел. Часть 1 | https://resh.edu.ru/subject/lesson/6857/main/236870/ |
| 6 | Распределительный закон | https://resh.edu.ru/subject/lesson/6871/main/236746/ |
| 6 | Раскрытие скобок и заключение в скобки | https://resh.edu.ru/subject/lesson/6855/main/235382/ |
| 6 | Частное целых чисел. Часть 1 | https://resh.edu.ru/subject/lesson/6869/main/237521/ |
| 6 | Частное целых чисел. Часть 2 | https://resh.edu.ru/subject/lesson/6870/main/236808/ |
| 6 | План и этапы решения задачи. Анализ решения, Проверка решения, проверка обратным действием | https://resh.edu.ru/subject/lesson/608/ |
| 6 | Зависимости между величинами: скорость, время, расстояние; производительность, время, работа; цена, количество, стоимость | https://resh.edu.ru/subject/lesson/346/ |
| 6 | Использование таблиц, схем, чертежей, других средств представления данных при решении задачи | https://resh.edu.ru/subject/lesson/340/ |
| 6 | Построение фигур, симметричных относительно заданной точки или прямой. Часть 1 Часть 1 | https://resh.edu.ru/subject/lesson/1392/ |
| 6 | Построение фигур, симметричных относительно заданной точки или прямой. Часть 2. | https://resh.edu.ru/subject/lesson/1120/ |
| 6 | Декартова система координат на плоскости | https://resh.edu.ru/subject/lesson/6921/main/236560/ |
| 6 | Столбчатые диаграммы. Графики | https://resh.edu.ru/subject/lesson/6911/main/235706/ |
| 6 | Построение столбчатых диаграмм. Чтение графиков | https://resh.edu.ru/subject/lesson/6922/main/236622/ |
| 6 | Обобщение и систематизация знаний по теме «Декартова система координат на плоскости» | https://resh.edu.ru/subject/lesson/6917/main/236653/ |
| 6 | Занимательные задачи на проценты | https://resh.edu.ru/subject/lesson/6918/main/235909/ |
| 6 | Сложные задачи на проценты | https://resh.edu.ru/subject/lesson/6910/main/236839/ |
| 6 | Обобщение и систематизация знаний по темам «Десятичные дроби, проценты, решение задач на проценты» | https://resh.edu.ru/subject/lesson/6923/main/236777/ |
| 6 | Случайные события | https://znaika.ru/catalog/6-klass/matematika/Pervoe-znakomstvo-s-ponyatiem-veroyatnost.html |
| 6 | Вероятность случайного события | https://znaika.ru/catalog/6-klass/matematika/Pervoe-znakomstvo-s-ponyatiem-veroyatnost.html |
| 6 | Арифметические действия с рациональными числами | https://clck.ru/MWVCo |
| 6 | Свойства умножения рациональных чисел | https://uchebnik.mos.ru/catalogue/material_view/atomic_objects/4033089 |
| 6 | Свойства вычитания рациональных чисел | https://uchebnik. mos.ru/catalogue/material_view/atomic_objects/4368360 mos.ru/catalogue/material_view/atomic_objects/4368360 |
| 6 | Коэффициент | https://infourok.ru/videouroki/2988 |
| 6 | Перпендикулярные прямые | https://infourok.ru/videouroki/2991 |
| 6 | Параллельные прямые | https://infourok.ru/videouroki/2992 |
|
Математика 5 класс. Ответы на задачи учебника Бунимовича
Бунимович Е.А. Дорофеев Г.В. Суворова С.Б.
гдз решебник математика 5 класс
ответы готовые домашние задания
УЧЕБНИК
БЫСТРЫЙ ПЕРЕХОД К ЗАДАЧАМ
ГЛАВА 1
ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 1
ЗАДАЧИ 1-54
ПОДВЕДЕМ ИТОГИ — ГЛАВА 1
ГЛАВА 2
ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 2
| 5. КАК ЗАПИСЫВАЮТ И ЧИТАЮТ ЧИСЛА | ОТВЕТ |
| 6. НАТУРАЛЬНЫЙ РЯД. СРАВНЕНИЕ… | ОТВЕТ |
| 7. ОКРУГЛЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ | ОТВЕТ |
| 8. КОМБИНАТОРНЫЕ ЗАДАЧИ | ОТВЕТ |
ЗАДАЧИ 55-121
ПОДВЕДЕМ ИТОГИ — ГЛАВА 2
ГЛАВА 3
ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 3
9. СЛОЖЕНИЕ И ВЫЧИТАНИЕ СЛОЖЕНИЕ И ВЫЧИТАНИЕ | ОТВЕТ |
| 10. УМНОЖЕНИЕ И ДЕЛЕНИЕ | ОТВЕТ |
| 11. ПОРЯДОК ДЕЙСТВИЙ В ВЫЧИСЛЕНИЯХ | ОТВЕТ |
| 12. СТЕПЕНЬ ЧИСЛА | ОТВЕТ |
| 13. ЗАДАЧИ НА ДВИЖЕНИЕ | ОТВЕТ |
ЗАДАЧИ 122-212
ПОДВЕДЕМ ИТОГИ — ГЛАВА 3
ГЛАВА 4
ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 4
| 14. СВОЙСТВА СЛОЖЕНИЯ И УМНОЖЕНИЯ | ОТВЕТ |
| 15. РАСПРЕДЕЛИТЕЛЬНОЕ СВОЙСТВО | ОТВЕТ |
| 16. РЕШЕНИЕ ЗАДАЧ | ОТВЕТ |
ЗАДАЧИ 213-262
ПОДВЕДЕМ ИТОГИ — ГЛАВА 4
ГЛАВА 5
ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 5
| 17. КАК ОБОЗНАЧАЮТ СРАВНИВАЮТ УГЛЫ | ОТВЕТ |
| 18. ИЗМЕРЕНИЕ УГЛОВ | ОТВЕТ |
| 19. МНОГОУГОЛЬНИКИ | ОТВЕТ |
ЗАДАЧИ 263-309
ПОДВЕДЕМ ИТОГИ — ГЛАВА 5
ГЛАВА 6
ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 6
20. ДЕЛИТЕЛИ И КРАТНЫЕ ДЕЛИТЕЛИ И КРАТНЫЕ | ОТВЕТ |
| 21. ПРОСТЫЕ ЧИСЛА | ОТВЕТ |
| 22. ДЕЛИМОСТЬ СУММЫ И ПРОИЗВЕДЕНИЯ | ОТВЕТ |
| 23. ПРИЗНАКИ ДЕЛИМОСТИ | ОТВЕТ |
| 24. ДЕЛЕНИЕ С ОСТАТКОМ | ОТВЕТ |
ЗАДАЧИ 310-403
ПОДВЕДЕМ ИТОГИ — ГЛАВА 6
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 |
ГЛАВА 7
ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 7
| 25. ТРЕУГОЛЬНИКИ И ИХ ВИДЫ | ОТВЕТ |
| 26. ПРЯМОУГОЛЬНИКИ | ОТВЕТ |
| 27. РАВЕНСТВО ФИГУР | ОТВЕТ |
| 28. ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА | ОТВЕТ |
ЗАДАЧИ 404-463
ПОДВЕДЕМ ИТОГИ — ГЛАВА 7
ГЛАВА 8
ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 8
29. ДОЛИ И ДРОБИ ДОЛИ И ДРОБИ | ОТВЕТ |
| 30. ОСНОВНОЕ СВОЙСТВО ДРОБИ | ОТВЕТ |
| 31. СРАВНЕНИЕ ДРОБЕЙ | ОТВЕТ |
| 32. НАТУРАЛЬНЫЕ ЧИСЛА И ДРОБИ | ОТВЕТ |
ЗАДАЧИ 464-543
ПОДВЕДЕМ ИТОГИ — ГЛАВА 8
ГЛАВА 9
ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 9
| 33. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ | ОТВЕТ |
| 34. СЛОЖ. И ВЫЧИТ. СМЕШАННЫХ ДРОБЕЙ | ОТВЕТ |
| 35. УМНОЖЕНИЕ ДРОБЕЙ | ОТВЕТ |
| 36. ДЕЛЕНИЕ ДРОБЕЙ | ОТВЕТ |
| 37. НАХОЖДЕНИЕ ЧАСТИ ЦЕЛОГО… | ОТВЕТ |
| 38. ЗАДАЧИ НА СОВМЕСТНУЮ РАБОТУ | ОТВЕТ |
ЗАДАЧИ 544-672
ПОДВЕДЕМ ИТОГИ — ГЛАВА 9
ГЛАВА 10
ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 10
| 39. ГЕОМЕТРИЧЕСКИЕ ТЕЛА И ИХ ИЗОБРАЖЕНИЕ | ОТВЕТ |
| 40. ПАРАЛЛЕЛЕПИПЕД И ПИРАМИДА | ОТВЕТ |
41. ОБЪЕМ ПАРАЛЛЕЛЕПИПЕДА ОБЪЕМ ПАРАЛЛЕЛЕПИПЕДА | ОТВЕТ |
| 42. РАЗВЕРТКИ | ОТВЕТ |
ЗАДАЧИ 673-722
ПОДВЕДЕМ ИТОГИ — ГЛАВА 10
ГЛАВА 11
ВОПРОСЫ И ЗАДАНИЯ К ГЛАВЕ 11
| 43. ЧТЕНИЕ И СОСТАВЛЕНИЕ ТАБЛИЦ | ОТВЕТ |
| 44. ДИАГРАММЫ | ОТВЕТ |
| 45. ОПРОС ОБЩЕСТВЕННОГО МНЕНИЯ | ОТВЕТ |
ЗАДАЧИ 723-739
ПОДВЕДЕМ ИТОГИ — ГЛАВА 11
Air Jordan
4 шага к успеху ваших учеников
«Они знают математику. Они просто не умеют решать задачи со словами. Это их понимание прочитанного.
Мисс Хартвелл объясняла, почему ее ученики не справились с государственными тестами. Она знала своих учеников и провела всестороннюю оценку. Она была уверена, что их трудности связаны с неграмотностью.
«Я не понимаю, почему они так усложняют чтение. Дети уже сдают тест по языку ».
Меня подобрали с г-жойХартвелл (и другие в ее школе) в рамках программы Нью-Йорка по повышению успеваемости по математике. Целью было привнести концептуальную математику в школы уровня 1. Школы первого уровня были школами, которые возглавляли город в трех областях. Самый низкий доход, самые низкие результаты тестов и самый высокий процент цветных студентов.
Я слышал объяснение «грамотности» от других учителей программы. И это имело смысл. Если учащиеся знали математику, почему еще они не справлялись с тестом, в котором было много проблем со словами?
Но тут была загвоздка.За последние три года уровень грамотности снизился с 30% до 40% по всему городу. За тот же период результаты по математике в основном оставались неизменными.
Если бы это была проблема с чтением, повышение оценок по чтению должно открыть взрывной рост в математике. Кроме того, язык слов «проблемы» просто не казался достаточно сложным, чтобы вызывать проблемы.
В следующий урок я должен был посетить класс мисс Хартвелл. Она запланировала урок по проблемам со словами, чтобы я мог увидеть проблему из первых рук.
Проблемы со словами, связанные с перекрытием строительных лесов
Студенты сели за круглые столы, а она стояла впереди. У нее и ее учеников были портативные доски.
Они открыли свои учебники на 47 странице, и она прочитала вслух задачу со словом. «У Сары 40 фунтов. моркови для ее лошадей. Если у нее 100 лошадей, сколько фунтов получит каждая лошадь? »
«Хорошо, класс, у нее есть 40 фунтов, которые она даст каждой лошади. Так какая операция нам нужна? »
Она указала на таблицу привязок, в которой перечислены «ключевые слова» для каждой операции.«Каждый» был в верхней части списка деления.
«Дивизия!» класс ответил.
«Верно. Так как же разделить небольшое число на большое? »
В классе было тихо. Мисс Хартвелл нарисовала на своей доске винкулум (дом с длинными перегородками). Студенты копировали, когда она положила 40 под домом и 100 снаружи.
«Теперь 100 не вписывается в 40, поэтому нам нужно добавить десятичную дробь». Она изменила 40 на 40.0. «Сколько раз 100 превратится в 400?»
Несколько студентов крикнули: «Четыре!»
КУБИКИ «Стратегия» может сбить с толку студентов
«Совершенно верно.Теперь нам нужно добавить десятичную дробь в наше частное. Наш окончательный ответ? »
Класс зачитал с доски ответ «0,4».
Она назначила аналогичную задачу и указала на плакат «КУБИКИ» на стене. «Не забудьте обвести числа и ключевые слова в квадрат».
Она разошлась по мере работы студентов. Некоторые спрашивали, где поставить десятичную дробь. У других возникли проблемы с построением части вычитания в длинном делении. Некоторые ученики работали в парах, один занимался счетами, а другой копировал.
К концу урока у каждого был правильный ответ на листке. «Видеть?» Мисс Хартвелл заметила: «Все они знают математику».
Что пошло не так?
Хотя это крайний пример, многие ошибки, совершенные мисс Хартвелл, на самом деле довольно распространены.
Излишние строительные леса возникают, когда мы оказываем студентам слишком большую поддержку. Педагогам свойственно гордиться тем, что они оказывают студентам «столько поддержки, сколько им нужно», но чрезмерные строительные леса — это другое дело.
Термин «строительные леса» происходит от Льва Выготского. Он ввел термин «зона ближайшего развития». ZPD включает в себя вещи, которые просто недоступны для учащихся. Они не могут сделать это самостоятельно, но они могут сделать это при поддержке. С помощью «строительных лесов» мы можем превратить эти навыки в основной набор навыков учащегося.
Зона ближайшего развития Выготского
Часто упускается из виду то, что строительные леса применимы только к навыкам, уже имеющимся в ZPD учащегося. Есть целый ряд навыков, которые в настоящее время недоступны для учащихся.Когда мы пытаемся укрепить эти навыки, мы приносим больше вреда, чем пользы.
Одна из проблем с чрезмерным использованием строительных лесов заключается в том, что учащиеся никогда не усваивают целевые навыки. Когда мы помогаем студенту в чем-то, кроме его ZPD, он всегда будет нуждаться в нашей помощи. По крайней мере, до тех пор, пока мы не определим промежуточные навыки, что — это в их ZPD.
Другая проблема заключается в том, что чрезмерные строительные леса дают нам ложное ощущение успеха. В этом случае г-жа Хартвелл считала, что ее ученики могут «вычислить» в словесной задаче.На самом деле они просто имитировали ее действия. Не было никаких оснований полагать, что они смогут найти подобное решение самостоятельно.
Она также убрала весь процесс «формулирования» из процесса решения проблем. Многие преподаватели считают понимание и формулировку одним и тем же, но формулировка — это отдельная математическая компетенция.
И это может быть просто отсутствующий ингредиент из того способа, которым вы сейчас преподаете задачи со словом.
Классные ресурсы и профессиональное обучение
Формулировка
: ключ к успеху в решении проблем со словами
Формулирование словесных задач требует их понимания.Но это выходит за рамки этого. Формулировка больше похожа на перевод, чем на понимание.
Когда ученик читает словесную задачу, сначала он должен превратить буквы в звуки (расшифровка). Затем им нужно понять, что означают слова (словарный запас). Им нужно понимать, как слова сочетаются друг с другом в предложении (синтаксисе). Наконец, понимание приходит, когда эти части соединяются вместе, чтобы придать смысл.
Большинство учеников 6-х классов могли прочитать задачу мисс Хартвелл и легко понять, что Сара раздает морковку своим лошадям.Но гораздо меньше людей будут связывать «деление» моркови с делением.
Это часть, которая сбивает с толку многих преподавателей. Нам это кажется таким очевидным. «Она , буквально делит морковь. Как они могли не видеть, что это разделение ».
Они просто не делают. Если бы они это сделали, вы бы не увидели таблицы ключевых слов, висящие в классах математики. И все это восходит к тому моменту, когда мы впервые обучаем операциям.
Почему студенты борются с формулировкой
Многие учителя во многих школах учат учеников, что математика является предметом осмысления.Но в других математика преподается как предмет запоминания.
Пример «математика как запоминание» — это когда учащиеся запоминают математические факты. Но алгоритмы также связаны с запоминанием. Положите 120 поверх 47. Выполните следующие действия, чтобы сложить, эти — вычесть, вычесть, а эти — умножить.
Учащиеся могут повторять эти шаги, не понимая размера чисел или даже того, что означают операции.
Когда мы начинаем с концепций (используя визуальные модели или числовые предложения), студенты узнают, что означают операции.Когда мы переходим непосредственно к алгоритму, студенты думают об операциях как о серии случайных шагов.
Год за годом студенты запоминают и повторяют. Они выполняют один и тот же алгоритм 30 раз для домашнего задания. Измените числа, и процесс останется прежним. Но дайте им слово «проблема», и теперь они должны иметь смысл.
Что тесты говорят нам о рассуждениях
Мы могли бы дать нашим студентам 10 задач с заголовком «Задачи с разделением слов», чтобы упростить задачу.Им даже не нужно будет читать задачи. Им просто нужно выяснить (или угадать), какое число является делителем, а какое — делимым.
Но когда учащиеся сдают государственный тест, цель не в том, чтобы облегчить задачу. Цель состоит в том, чтобы оценить, что они могут делать самостоятельно.
Создатели тестов не хотят указывать им, какую операцию использовать. Они даже добавят ключевые слова для разделения и сложения в одной и той же задаче. «В классе 20 учеников. Если у каждого ребенка есть три доллара, сколько у них всего ? »
Итак, когда учащиеся борются с проблемами со словами, речь идет не только о задачах со словами.Обычно это означает, что они занимаются математикой по памяти. Нам нужно научить их тому, что математика имеет смысл.
Студентам нужны стратегии и способы решения проблем со словами
Отчасти проблема такой системы, как CUBES , заключается в том, что она называет себя стратегией, но на самом деле это процесс.
Процесс — это последовательность шагов. Определив эффективный процесс, вы можете повторять его снова и снова, не особо задумываясь. Алгоритмы — это процесс. Как и выстраивание в очередь от самого высокого к самому короткому на прогулке до обеда.
А стратегия другая. Стратегии требуют глубокого понимания. И умение применять понимание в новых ситуациях.
Мы не можем подготовить учащихся к каждому сценарию, с которым они столкнутся в словесной задаче. Некоторые требуют, чтобы они сочетали различные математические навыки, которых никогда раньше не объединяли. Или они могут потребовать, чтобы учащиеся изменили порядок шагов, чтобы прийти к правильному решению.
Рассмотрим следующее:
У вас есть 5 галлонов сока на школьное мероприятие с участием 100 учеников.Если каждая чашка вмещает 3 унции, сколько чашек может выпить каждый студент? Сколько еще останется.
Процесс решения проблем может помочь учащимся приступить к решению этой проблемы. «Определите, о чем спрашивают». «Подумайте, какая информация предоставляется».
Но не существует установленного процесса, который мы могли бы научить их решать. Вот тут-то и пригодится стратегия. Им нужно конвертировать единицы. Осознайте, что мы делим остатками, а не делим полностью. Им также, вероятно, следует изменить порядок операций, разделив сок на чашки, прежде чем разделить на количество студентов.
Нет никакого «трюка», который приведет студентов туда. Им нужно понимать смысл операций. Им нужно понимать математику как объект смысла. И им нужна постоянная практика применения стратегического мышления к текстовым задачам.
Процесс Polya для решения проблем со словами
Джордж Полиа был влиятельным венгерским математиком и профессором Стэнфорда, который нашел процесс, который можно использовать для решения любой задачи. Его работа затронула бесчисленное количество математиков и педагогов, большинство из которых не знают его имени.
Фактически, CUBES и другие так называемые стратегии решения проблем во многом основаны на его работе. Проблема в том, что они пытаются его упростить. В процессе они удаляют все, что напоминает глубокое размышление.
Поля считала, что любую проблему можно решить в четыре этапа: понять, спланировать, решить и осмыслить. Я думаю, что первоначальный четырехэтапный процесс Поли вполне подходит для использования в школах.
Чтобы понять проблему, мы определяем, какая информация предоставляется и что мы хотим найти.Отсюда берутся буквы «C» и «U» в кубах. Если учащиеся хотят обвести числа и подчеркнуть вопрос, хорошо. Я предпочитаю писать их (с единицами) в графическом органайзере, по крайней мере, сначала. Это помогает им обрабатывать то, что они читают. Это также помогает мне, как учителю, оценивать их понимание, когда я хожу по комнате.
Далее идет сложная часть. «План» — это то место, где мы формулируем проблему. Мы берем сценарий реального мира и превращаем его в другое математическое представление.
Третий шаг — решить. Если мы правильно сформулировали, то здесь мы и рассчитаем. Студенты обычно используют алгоритм, но я также рекомендую использовать уравнения и визуальные модели.
Наконец, студенты оглядываются и проверяют свою работу. Им также следует задуматься над своим процессом. Если я ошибся, то почему? Может ли эта стратегия помочь мне решить подобные проблемы в будущем?
Стратегии решения проблем со словами
Определенно полезно иметь процесс решения проблем со словами.Но мы не можем притворяться, что значимую математику можно выучить, просто следуя шагам. Весь смысл задач со словами состоит в том, чтобы расширить математику за пределы «математических фактов» и алгоритмов.
Есть несколько полезных стратегий, которые помогут студентам с формулировкой. Сначала я открыто обучаю нескольким различным стратегиям.
Когда я преподаю стратегии, мои ученики решают задачи, которые хорошо сочетаются с этой стратегией. Некоторые типы задач хорошо сочетаются с «Угадай и проверь».Другие больше подходят для «Нарисуй картинку».
В конце концов, я даю им сложные задачи со словами, которые можно решить несколькими способами. Когда инструменты будут в их поясах, они смогут выбрать наиболее подходящий для ситуации.
Комбинирование стратегий также может быть очень эффективным. Например, рисование картинки часто может помочь с формулировкой. Если у фермера 18 рядов моркови и 10 морковок в каждом ряду, ученик может начать с рисования поля. В какой-то момент они могут подумать: «Ого, это массив», и понять, что они могут умножать, используя мысленную математику, выражение или алгоритм.
В других случаях учащиеся могут использовать визуальные модели, чтобы сформулировать и решить задачу.
Помогите своим ученикам решить сложные задачи со словами
Если вы похожи на многих учителей, вы, возможно, беспокоитесь о том, как ваши ученики со всем этим справятся. Процессы, стратегии, критическое мышление … здесь много всего.
Возможно, вы даже думаете, что до этой статьи задачи со словами казались проще. Если так, прошу прощения.
Ключ в том, чтобы не перегружаться, пытаясь сделать все сразу.Начните с решения простой задачи со словами, используя метод Полии. Затем каждую неделю вводите новую стратегию. К концу года вы будете поражены тем, как далеко они продвинулись.
Может быть, вы хотите глубже творчески решать проблемы. Подумайте о том, чтобы посетить практический математический семинар или поработать с онлайн-тренером.
Если вы готовы принести завтра в класс Полиу, этот графический органайзер — отличный способ начать. Это построит четырехэтапный процесс и поможет вам определить, где ваши ученики сбиваются с пути.
Организатор задач Free Word
Об авторе
Джефф Лисиандрелло — основатель Room to Discover и консультант по образованию, специализирующийся на обучении, ориентированном на учащихся. Его 3-мостовой дизайн для обучения помогает школам изучать инновационные методы в традиционных условиях. Ему нравится помогать педагогам применять индивидуальный подход к обучению, основанный на запросах. Вы можете связаться с ним через Twitter @EdTechJeff
Порядок операций Слово Проблемы с решениями
Научитесь записывать задачи о порядке операций в числовые
выражения и узнайте, как их решать, используя порядок операций.
Другие задачи по порядку операций со словами
Пример № 1:
Сильвия купила 4 банана по 50 центов каждый и 1 яблоко за 80 центов. Напишите числовое выражение, чтобы представить эту ситуацию, а затем найдите общую стоимость в долларах.
Решение
4 × 50 + 80
= 200 + 80
= 280 центов или 2,80 доллара
Общая стоимость 2,80 доллара
Пример № 2:
Роберт купил 2 гамбургера за 3 доллара.50 каждый и 3 средних картофеля фри по 1,20 доллара за штуку. Напишите числовое выражение, чтобы представить эту ситуацию, а затем найдите стоимость.
Решение
2 × 3,50 + 3 × 1,20
= 7 + 3,60
= 10,60
Пример № 3:
Марта платит 20 долларов за материалы для изготовления серег. Она делает 10 серег и продает 7 за 5 долларов и 3 за 2 доллара. Напишите числовое выражение для представления этой ситуации, а затем найдите прибыль Марты?
Решение
7 × 5 + 3 × 2 — 20
= 35 + 6 — 20
= 41 — 20
= 21
Пример № 4:
Джон купил 3 штана по 25 долларов каждый и оплачивается стодолларовой купюрой.Напишите числовое выражение для представления этой ситуации, а затем выясните, сколько денег Джон получит обратно от кассира?
Решение
100-3 × 25
= 100-75
= 25
Хитрый порядок операций задачи со словами
Пример № 5:
Цена рубашки 100 долларов. Менеджер магазина дает скидку 50 долларов. Мужчина и его брат купили 4 рубашки, а затем разделили их стоимость со своим братом. Напишите числовое выражение, чтобы представить эту ситуацию, а затем найдите цену, которую заплатил каждый из братьев.
Решение
(100-50) × 4 ÷ 2
= (50) × 4 ÷ 2
= 200 ÷ 2
= 100
Цена, заплаченная каждым братом, составляет 100 долларов
Пример # 6:
Питер снял сегодня 1000 долларов со своего банковского счета. Он использует 500, чтобы починить свою машину. Затем он разделил деньги на 5 равных частей и раздал 4 части, а 1 часть оставил себе. В конце концов, он повел жену в ресторан и потратил 60 долларов на еду. Напишите числовое выражение, чтобы представить эту ситуацию, а затем найдите, сколько денег у Питера сейчас?
Решение
(1000-500) ÷ 5-60
= (500) ÷ 5-60
= 100-60
= 40
У Питера осталось 40 долларов.
9 советов и приемов для решения задач со словами
Привет! Меня зовут Джо-Эллен из Love Believe Teach с Джо-Эллен Фуди, и я рада быть приглашенным блогером для Рэйчел Линетт.
Давайте поговорим о… проблемах со словами. Я могу начать с того, что скажу вам, что люблю учить детей решать задачи со словами, но не буду. Проблемы со словом сложны. Двухэтапные задачи со словами еще сложнее, и научить их решать, возможно, будет самым сложным навыком, которому вы обучаете в течение всего года.Хуже всего то, что вы ничего не можете с этим поделать. Неа! Нада! Задачи со словами есть в каждой математической программе, в каждом классе, в каждом стандартизированном математическом тесте, и они являются важным навыком, которым ученики должны овладеть, чтобы выжить в нашем мире. И это наша главная цель, верно?
Итак, вот что я нашел наиболее полезным и наименее болезненным для учащихся способом научиться решать сложные словесные задачи.
Не ожидайте 100% мастерства после одного урока.Этого просто не произойдет. Я знаю, что это может быть трудно понять, но этот навык требует ВРЕМЕНИ и очень много. К сожалению, от этого никуда не деться.
Признайте, что задачи со словом сложны и вашим ученикам потребуется много практики с ними. Почему-то произнесение этого вслух делает весь процесс немного менее пугающим.
Используйте много, много, много форм практики. Я не могу этого достаточно подчеркнуть. Если у вас нет ученика, обладающего сверхспособностью решать задачи с чудодейственным словом, вашим ученикам понадобится ОЧЕНЬ много практики.Студентам нужны непосредственные инструкции всего класса, время с партнером, самостоятельные занятия для практики, веселые игры «вставай и двигайся», центры карточек с заданиями и домашние задания. Да, вам нужно привлечь родителей ваших учеников к тому, чтобы помочь их детям справиться с этими трудными проблемами. Разнообразие важно для того, чтобы ваши ученики продолжали практиковаться и улучшать свои навыки.
Обучайте, переучивайте, а затем, по прошествии некоторого времени, переучивайте снова. Иногда детям нужно время, чтобы усвоить все трюки, которым вы их научили.Поэтому после первого вводного урока подождите немного и повторите его с помощью короткого мини-урока, чтобы освежить их сознание. Повторяйте мини-уроки столько раз, сколько нужно.
Ох, ох! Я сказал это. И да, я имел это в виду. От этого никуда не деться. Судя по моему опыту, да, у меня его более 18 лет, студентам нужно много-много практики, чтобы справиться с задачами со словом. Иногда, просто иногда, может помочь решить проблему за проблемой. Вы можете мне не поверить, но для детей они действительно воспринимают это как вызов.Поверьте мне!
Вот как я это делаю: сначала я раздаю лист с упражнениями №1 с одной или двумя задачами. Я даю студентам время закончить, и как только они заканчивают, они проверяют его. Если они все поймут правильно, я немедленно даю им страницу №2. Затем я повторяю процесс снова и снова, пока не почувствую, что они устают. Вы узнаете, когда ваш класс достигнет дневного максимума. Они начнут отказываться от задания, не будут работать так усердно, «веселье» больше не витает в воздухе, и вот тогда я понимаю, что пора переходить к следующему занятию.
Другой способ попрактиковаться — превратить его в игру, чтобы увидеть, сколько задач класс может правильно решить за x минут. Начните со слов: «Мы будем выполнять столько задач, сколько сможем за пять минут. На своей отметке, готовься, ВПЕРЕД! » Ваш класс будет думать, что они играют в игру, а не решают сложные задачи со словами. Вы можете легко отслеживать, сколько задач класс решил правильно в установленные сроки. Если вы повторите эту игру несколько раз, вы увидите, что их общее количество становится все выше и выше по мере роста их навыков.Затем посмотрите, как ваш класс отмечает свои достижения. Они это заслужили!
БЕСПЛАТНАЯ ЗАДАЧА, состоящая из двух слов, которая поможет вашим ученикам начать практиковаться и практиковаться. Я считаю, что наиболее эффективно начинать с одной проблемы на странице, а учащиеся решать до трех задач на странице.
Да, некоторым детям они нужны. Им нужна система, которой нужно следовать. Я обнаружил, что дать студентам одну простую и понятную стратегию — лучший способ помочь этим студентам.Для них это просто не так запутанно. Убедитесь, что вы выбрали удачную стратегию!
Вот слово «план атаки», которое я использую со своими второклассниками:
- Шаг 1. Прочтите проблему и подумайте: «В чем проблема?»
- Шаг 2. Перечитайте проблему и подумайте: «В чем проблема?»
- Шаг 3. Спланируйте свою «атаку» и подумайте: «Как лучше всего решить эту проблему?»
- Шаг 4. Решите проблему и подумайте: «Какую операцию мне следует использовать?»
- Шаг 5. Проверьте свой ответ и подумайте: «Имеет ли мой ответ смысл? Моя математика верна? »
Да, мы учителя и должны учить, но иногда дети просто не понимают, что мы говорим или как мы что-то объясняем.Это не делает нас плохими учителями; считайте это тайной юного ума. Все, что вам нужно сделать, это разделить студентов на пары, которые борются с кем-то, кто пытается справиться с проблемами. Прежде чем вы это узнаете, каждый с легкостью справится с этими проблемами со словами!
Попросите учащихся написать свои собственные задачи со словами, а затем попросите друга решить их. Как только ваши ученики научатся решать задачи со словами, вы увидите, как их понимание этих задач будет расти.
Поговорите о том, что есть много разных способов решить словесную задачу, и что на 100% нормально решать проблему с помощью стратегии, отличной от чьей-либо другой.Примите эту идею и скажите своим ученикам, что все наши умы уникальны и решение этих проблем просто должно иметь смысл для вас.
Итак, вот и все. Я искренне надеюсь, что вы сможете найти несколько идей, которые сможете сразу же реализовать в своем собственном классе. Для большинства студентов проблемы со словами являются сложной задачей, но они никуда не денутся. Итак, давайте просто сделаем их чем-то, над чем мы будем работать вместе. Если у вас есть какие-либо советы и приемы, которые сработали для ваших учеников, я хотел бы услышать о них в комментариях ниже.
Джо-Эллен Фуди преподает более 18 лет в классах K-3. Она замужем, у нее двое маленьких мальчиков. Джо-Эллен увлечена мотивацией студентов выходить за рамки того, что, по их мнению, было возможным. Ее магазин Teachers Pay Teachers называется Love Believe Teach with Jo-Ellen Foody и ориентирован на класс K-3. Вы можете найти ее в Facebook, Instagram, Pinterest, Twitter или по электронной почте.
.

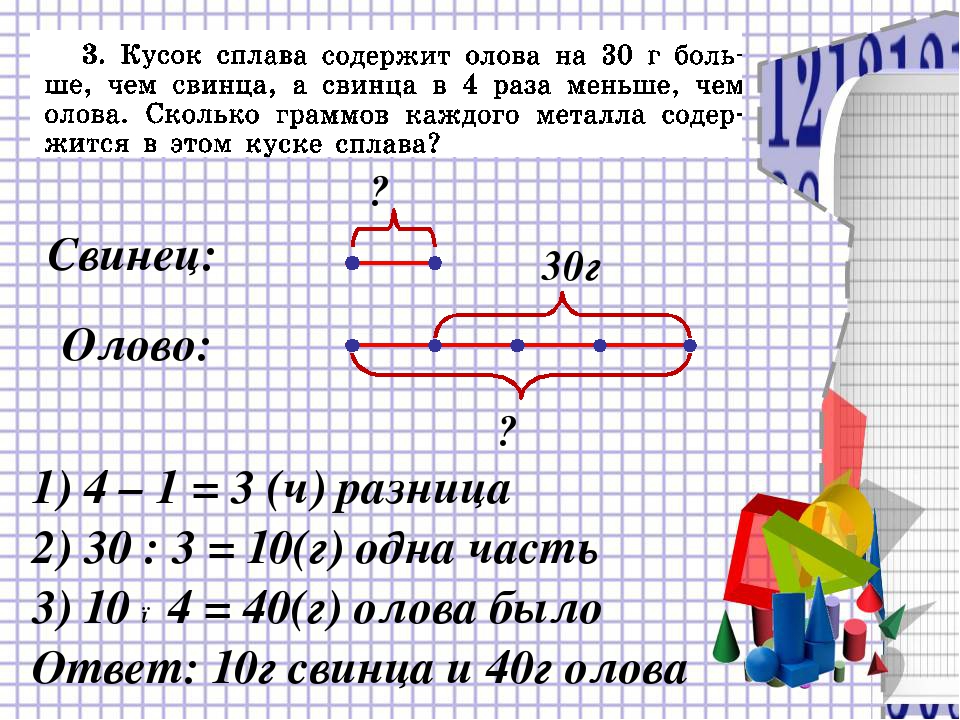

 Какова масса куска бронзы, если в ней олова меньше, чем меди, на 132 г?
Какова масса куска бронзы, если в ней олова меньше, чем меди, на 132 г?