Основные правила математики с примерами. 5 класс — Сайт учителя математики Косыхиной Н.В.
Основные правила математики с примерами. 5 класс
Содержание
- Натуральные числа
- Сравнение натуральных чисел
- Свойства сложения
- Формула пути
- Корень уравнения
- Правила решения уравнений
- Отрезок, прямая, луч
- Угол, биссектриса угла
- Углы: развернутый, прямой, острый, тупой
- Многоугольники. Равные фигуры
- Треугольники: остроугольный, прямоугольный, тупоугольный
- Треугольники: равнобедренный, равносторонний, разносторонний
Натуральные числа
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.
Сравнение натуральных чисел
Число меньше любого натурального числа.
0<1, 0<100
Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.
4352⏟4>999⏟3
Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр
3561>3559
Свойства сложения
Переместительный закон:
15+10=10+15
Сочетательный закон:
(23+15)+25=23+(15+25)
Формула пути
S=V·t,где S — пройденный путь, V — скорость движения, t — время, за которое пройден путь S
Корень уравнения
Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.
2·x+10=16
x = 3 — корень, так как 2·3+10=16
Что значит «Решить уравнение»
Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.
Правила решения уравнений
- Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

20слагаемое+xслагаемое=100суммаx = 100 — 20x = 80
- Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
xуменьшаемое—10вычитаемое=40разностьx = 40 + 10x = 50
- Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
50уменьшаемое—xвычитаемое=40разностьx = 50 — 40x = 10
- Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
xмножитель·7множитель=56произведениеx = 56 : 7x = 8
- Чтобы найти неизвестное делимое, надо делитель умножить на частное.
xделимое:8делитель=9частноеx = 9 · 8x = 72
- Чтобы найти неизвестный делитель, надо делимое разделить на частное.
42делимое:xделитель=7частноеx = 42 : 7x = 6
Отрезок, прямая, луч
Отрезок
Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)
Свойство длины отрезка
Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .
Равные отрезки
Два отрезка называют равными, если они совмещаются при наложении.
Свойство прямой
Через две точки проходит только одна прямая.
Измерить отрезок
Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается
Ломаная
Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом
Луч
Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
Угол, биссектриса угла
Угол
Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.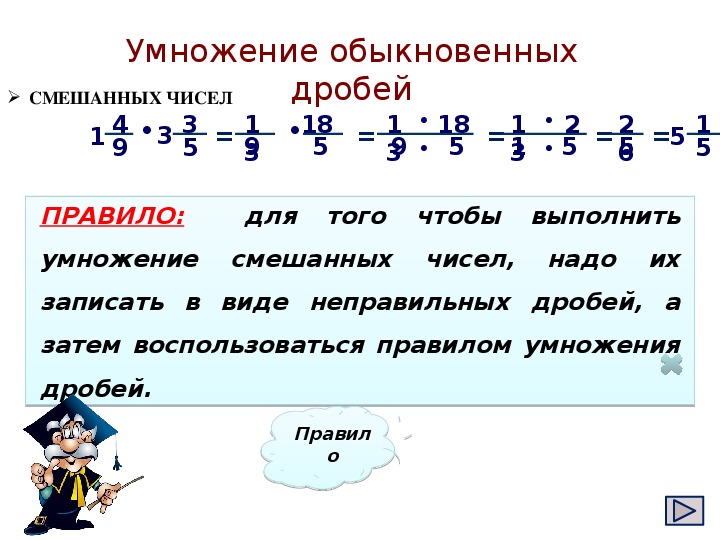
Равные углы
Два угла называют равными, если они совмещаются при наложении.
Свойство величины угла
Если между сторонами угла ∠ провести луч , то градусная мера ∠ равна сумме градусных мер углов ∠ и ∠, то есть ∠ = ∠+ ∠.
Биссектриса угла
Луч, который делит угол на два равных угла, называется биссектрисой угла.
Углы: развернутый, прямой, острый, тупой
Развернутый угол
Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.
Прямой угол
Угол, градусная мера которого равна 90°, называют прямым.
Острый угол
Угол, градусная мера которого меньше 90°, называют острым.
Тупой угол
Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.
Многоугольники. Равные фигуры
Равные многоугольники
Два многоугольники называют равными, если они совмещаются при наложении.
Равные фигуры
Две фигуры называют равными, если они совмещаются при наложении.
Треугольники: остроугольный, прямоугольный, тупоугольный
Остроугольный треугольник
Если все углы треугольника острые, то его называют остроугольным треугольником.
Прямоугольный треугольник
Если один из углов треугольника прямой, то его называют прямоугольным треугольником.
Тупоугольный треугольник
Если один из углов треугольника тупой, то его называют тупоугольным треугольником.
Треугольники: равнобедренный, равносторонний, разносторонний
Равнобедренный треугольник
Если две стороны треугольника равны, то его называют равнобедренным треугольником.
Равносторонний треугольник
Если три стороны треугольника равны, то его называют равносторонним треугольником.
Периметр равностороннего треугольника
Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле
Разносторонний треугольник
Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.
Прямоугольник. Квадрат. Периметр
Прямоугольник
Если в четырехугольнике все углы прямые, то его называют прямоугольником.
Свойство прямоугольника
Противоположные стороны прямоугольника равны.
Периметр прямоугольника
Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле
Квадрат
Прямоугольник, у которого все стороны равны, называют квадратом.
Периметр квадрата
Если сторона квадрата равна , то его периметр вычисляют по формуле .
Умножение. Свойства умножения
Умножение
- Если один из двух множителей равен 1, то произведение равно второму множителю.
- Если один из множителей равен нулю, то произведение равно нулю.
- Если произведение равно нулю, то хотя бы один из множителей равен нулю.
Свойства умножения
- Переместительный закон умножения:
- Сочетательный закон умножения:
- Распределительное свойство умножения относительно сложения:
2·(3+10) = 2·3 + 2·103·11 + 3·4 = 3·(11 + 4)
- Распределительное свойство умножения относительно вычитания:
2·(15—7) = 2·15 — 2·73·10 — 3·4 = 3·(10 — 4)
Деление. Деление с остатком
Деление
Для натуральных чисел равенство является правильным, если является правильным равенство
15 : 5 = 3 -правильное равенство, так как равенство 5 · 3 = 15 верное
В равенстве число называют делимым, число — делителем, число и запись — частным от деления, отношением, долей.
На ноль делить нельзя.
Для любого натурального числа правильными являются равенства:
,
Деление с остатком
, где — делимое, — делитель, — неполное частное, — остаток, .
154делимое=50делитель · 3неполное частное + 4остаток, 4<50
Если остаток равен нулю, то говорят, что число делится нацело на число .
Площадь. Площадь квадрата, прямоугольника
Свойства площади фигуры
Равные фигуры имеют равные площади;
Площадь фигуры равна сумме площадей фигур, из которых она состоит.
Площадь прямоугольника
Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.
Площадь квадрата
,
где — площадь квадрата, — длина его стороны.
Объем. Объем прямоугольного параллелепипеда, куба
Свойства объема фигуры
Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.
Объем прямоугольного параллелепипеда
- ,
где — объем параллелепипеда, , и — его измерения, выраженные в одних и тех же единицах;
, где — площадь поверхности прямоугольного параллелепипеда.
- ,
где — площадь основания параллелепипеда, — его высота.
Объем куба
,
где — объем куба, — длина его ребра.
Дроби: правильная, неправильная, сравнение дробей
Правильная дробь
Дробь, числитель которой меньше знаменателя, называют правильной
Неправильная дробь
Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.
Сравнение дробей
- Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.
- Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.
- Все правильные дроби меньше единицы, а неправильные — больше или равны единице.
- Любая неправильная дробь больше любой правильной дроби.
Сложение и вычитание дробей с одинаковыми знаменателями
- Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.

- Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
Сложение и вычитание смешанных чисел
- Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.
- Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.
Преобразование неправильной дроби в смешанное число
Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно
- числитель разделить на знаменатель;
- полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.
227= смешанное число? 7322—211 227=317
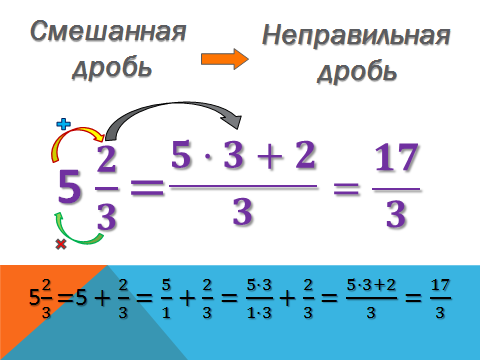
Преобразование смешанного числа в неправильную дробь
Чтобы преобразовать смешанное число в неправильную дробь нужно
- целую часть числа умножить на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- эту сумму записать как числитель неправильной дроби;
- в его знаменателе записать знаменатель дробной части смешанного числа.
523= неправильная дробь?523=5*3+23=15+23=173
Десятичные дроби: свойства, сравнение, округление
Свойства десятичной дроби
Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.
Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.
2,23 = 2,230 = 2,230000005,50000=5,50000=5,5
Сравнение десятичных дробей
Из двух десятичных дробей больше та, у которой целая часть больше.
Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо
- с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
- после чего сравнить полученные дроби поразрядно.

Сравнить 5,03 и 5,0375.5,03⏟2=5,0300⏟4 и 5,0375⏟4 ; 5,0300 < 5,0375.
Округление десятичных дробей
Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо
- все следующие за этим разрядом цифры отбросить.
- если при этом первая из цифр, которые отбрасывают равна 0,1, 2, 3, 4, то последнюю из цифр, которые оставляют, не меняют;
- если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8, 9, то последнюю из цифр, которые оставляют, увеличивают на единицу.
Округлить 5,248 и 3,952:а) до десятых:5,248≈5,2; 3,952≈4,0;б) до сотых:5,248≈5,25;3,952≈3,95.
Десятичные дроби: сложение, вычитание
Сложение десятичных дробей
Чтобы найти сумму двух десятичных дробей, нужно:
- уравнять количество цифр после запятых;
- записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
- сложить полученные числа так, как складывают натуральные числа;
- поставить в полученной сумме запятую под запятыми.
Сложить 2,5 и 3,623.2,500⏟3 и 3,263⏟3;2,500+3,2635,763
Вычитание десятичных дробей
Чтобы найти разность двух десятичных дробей, нужно:
- уравнять количество цифр после запятых;
- записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
- выполнить вычитание так, как вычитают натуральные числа;
- поставить в полученной разности запятую под запятыми.
Вычесть 3,27 и 3,009.3,270⏟3 и 3,009⏟3;3,270—3,0090,261
Десятичные дроби: умножение, деление
Умножение десятичных дробей
Чтобы перемножить две десятичные дроби, надо:
- перемножить их как натуральные числа, не обращая внимания на запятые;
- в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.

Умножить 1,5 и 2,25.2×2,2511,5+1125225·33,375 —количество цифр после запятой
Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.
Умножить 1,235 на 10, 100, 1000.а) на 10:1,235 ×10⏟1=12,35б) на 100:1,235 ×100⏟2 = 123,5в) на 1000:1,235 ×1000⏟3=1235,0 = 1235
Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.
Умножить 512,3 на 0,1, 0,01 и 0,001.а) на 0,1:512,3 ×0,1⏟1=51,23б) на 0,01:512,3 ×0,01⏟2=5,123в) на 0,001:512,3 ×0,001⏟3=0,5123
Деление десятичных дробей
Чтобы разделить десятичную дробь на десятичную, надо:
- перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
- выполнить деление на натуральное число.
Разделить 24,2 на 0,02.24,2 : 0,02⏟ 2= 2420,0 : 2 = 2420 : 2 = 1210.
Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.
Разделить 25,5 на 10, 100, 1000.а) на 10:25,5 : 10⏟1=2,55;б) на 100:25,5 : 100⏟2=0,255;в) на 1000:25,5 : 1000⏟3=0,0255;
Среднее арифметическое
Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.
Найти среднее арифметическое чисел 15, 25 и 20.
15+25+20⏞сумма чисел3⏟количество чисел = 603= 20
Примечание:
Задача. Автомобиль 200 км ехал со скоростью 50 км/ч. Затем 120 км он ехал со скоростью 30 км/ч. Найти среднюю скорость.
Здесь
Vсредняя =Sобщtобщ .
1) 200 + 120 = 320(км) -весь путь;
2) 200 : 50 = 4(ч) — время, затраченное на 1-ую часть пути;
3) 120 : 30 = 4(ч) — время, затраченное на 2-ую часть пути;
4) 4 + 4 = 8(ч) — все время;
5) 320 : 8 = 40(км/ч) — средняя скорость.
Ответ: 40 км/ч.
Процент
Процентом называют сотую часть величины или числа 1%=
Найти 4% от числа 20. 20 : 100 = 0,2 (0,2 —это 1% от числа 20);0,2 × 4 =0,8( 0,8—искомое число).Или 4% = 4100 = 0,04;0,04 ×20 = 0,8.
20 : 100 = 0,2 (0,2 —это 1% от числа 20);0,2 × 4 =0,8( 0,8—искомое число).Или 4% = 4100 = 0,04;0,04 ×20 = 0,8.
Обыкновенные дроби. Математика, 5 класс: уроки, тесты, задания.
Вход
Вход
Регистрация
Начало
Новости
ТОПы
Учебные заведения
Предметы
Проверочные работы
Обновления
Переменка
Поиск по сайту
Отправить отзыв
Предметы
Математика
5 класс
-
Деление с остатком. Понятие обыкновенной дроби
-
Основное свойство дроби. Сокращение и расширение дробей
-
Правильные и неправильные дроби. Смешанные числа. Понятие, запись и чтение
-
Сравнение обыкновенных дробей
-
Сложение и вычитание обыкновенных дробей и смешанных чисел
-
Умножение и деление обыкновенной дроби на натуральное число
-
Нахождение части от целого и числа по его части
-
Геометрические понятия: окружность и круг
Отправить отзыв
Нашёл ошибку?
Сообщи нам!
Copyright © 2021 ООО ЯКласс
Контакты
Пользовательское соглашение
Дроби
Дроби это тема об которую спотыкается половина жителей нашей планеты. Если спросить у людей с какой темы у них начались проблемы с математикой, то большинство из них ответят — с дробей.
Если спросить у людей с какой темы у них начались проблемы с математикой, то большинство из них ответят — с дробей.
Этих людей нельзя упрекнуть. Дроби действительно тема не из простых. Тема дробей требует много терпения и внимания, особенно если человек изучает её впервые.
Но есть и хорошие новости. Если вы наберётесь терпения и освоите дроби, то уверяем, что дальнейшее изучение математики станет для вас простым и интересным.
А если вы ещё хорошо изучили предыдущий урок, который назывался деление, то можете быть уверены, что дроби вы освоили уже наполовину.
Что такое дробь?
Если говорить простым языком, то дробь это часть чего-либо. Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение.
Рассмотрим пример из жизни. Мы купили себе пиццу, чтобы съесть её в течении дня. Допустим мы решили разделить её на четыре части, чтобы съедать постепенно по одному кусочку.
Посмотрите на этот рисунок. Представьте, что это наша пицца, разделённая на четыре куска. Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы.
Допустим мы съели один кусок. Как его записать? Очень просто. Сначала рисуется маленькая линия:
Внизу этой линии записывается на сколько кусков пицца была разделена. Пицца была разделена на четыре куска. Значит внизу линии записывается четвёрка:
А сверху этой линии записывается сколько кусков пиццы было съедено. Съеден был один кусок, значит сверху записываем единицу:
Такие записи называют дробями. Дробь состоит из числителя и знаменателя.
Число, которое записывается сверху, называется числителем дроби.
Число, которое записывается снизу, называется знаменателем дроби.
В нашем примере числитель дроби это единица, а знаменатель дроби — четвёрка.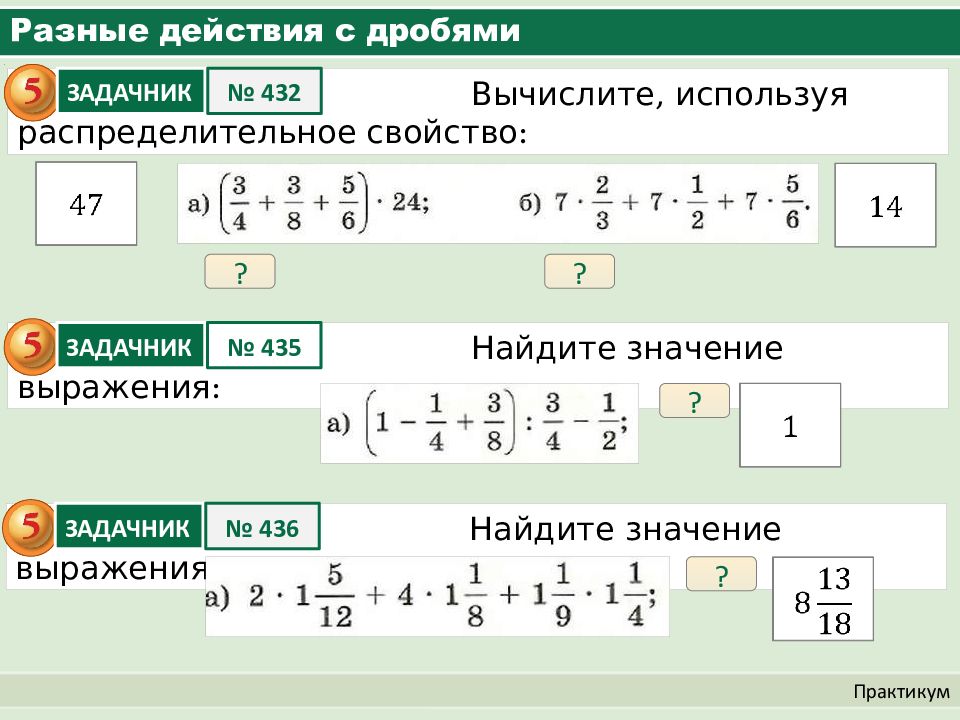 Эту дробь можно прочитать так: «одна четвёртая» либо «один кусок из четырёх» либо «одна четвёртая доля» либо «четверть» — всё это синонимы.
Эту дробь можно прочитать так: «одна четвёртая» либо «один кусок из четырёх» либо «одна четвёртая доля» либо «четверть» — всё это синонимы.
Теперь представьте, что мы съели ещё один кусок той же самой пиццы, которая была разделена на четыре куска. Как записать такую дробь?
Очень просто. Сверху записываем 2 (поскольку уже съедено два куска), а внизу записываем 4 (поскольку всего кусков было 4):
Эта дробь читается так: «две четвёртых» либо «два куска из четырёх» либо «две четвёртые доли».
Теперь представьте, что пиццу мы разделили не на четыре части, а на три.
Допустим мы съели один кусок этой пиццы. Как записать такую дробь?
Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается число 3, поскольку пицца разделена на три части, а сверху этой линии записывается число 1, поскольку съеден один кусок:
Эта дробь читается так: «Одна третья» либо «Один кусок из трёх» либо «Одна третья доля» либо «Треть».
Если мы съедим два куска пиццы, то такая дробь будет называться «две третьих» и записываться следующим образом:
Теперь представьте, что пиццу мы разделили на две части, или как говорят в народе: «Пополам»:
Допустим, из этих двух кусков мы съели один кусок. Как записать такую дробь?
Опять же рисуем линию. Внизу этой линии записываем число 2, поскольку пицца разделена на две части, а вверху записываем число 1, поскольку съеден один кусок:
Эта дробь читается так: «одна вторая» либо «один кусок из двух» либо «одна вторая доля» либо «половина».
Дроби, которые мы сейчас рассмотрели, называют обыкновенными.
Вообще, дроби бывают двух видов: обыкновенные и десятичные. На данный момент мы рассматриваем обыкновенные дроби. Обыкновенная дробь это дробь, которая состоит из числителя и знаменателя. Десятичные дроби рассмотрим немного позже.
Обыкновенная дробь это дробь, которая состоит из числителя и знаменателя. Десятичные дроби рассмотрим немного позже.
Знаменатель дроби — это число, которое показывает на сколько равных частей можно что-либо разделить. Вернёмся к нашей пицце. Поровну эта пицца может быть разделена и на 2 части и на 3, и на 4, и на 5, и на 6. В зависимости от того, на сколько частей мы будем делить пиццу, знаменатель будет меняться.
На следующем рисунке представлены три пиццы, которые разделены по разному. У первой пиццы знаменателем будет 2. У второй пиццы знаменателем будет 3. У третьей пиццы знаменателем будет 4.
Числитель же показывает сколько частей взято от чего-либо. К примеру, если разделить пиццу на две части, как на первом рисунке, и взять одну часть для трапезы, то получится что мы взяли (одну часть из двух), или как говорят в народе «половину» пиццы.
С помощью переменных дробь можно записать так:
где a — это числитель, b — знаменатель.
Следующая вещь, которую важно знать это то, что обыкновенные дроби бывают правильными и неправильными.
Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, следующие дроби являются правильными:
Почему такие дроби называют правильными? Вспомним, что дробь это часть чего-либо. Ведь будет логичнее, если эта часть будет меньше того, откуда эта часть была взята. Например, если пицца разделена на четыре части, и мы возьмём (одну четвёртую), то наш кусок будет меньше, чем все четыре куска вместе взятые (чем одна целая пицца). Поэтому такие дроби называют правильными.
С неправильной дробью всё с точностью наоборот. Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными:
Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.
Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.
Теперь возьмём к примеру неправильную дробь и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.
Дробь, у которой числитель и знаменатель одинаковые, тоже называют неправильной. Например:
Вообще, такие дроби даже не должны называться дробями. И вот почему. Рассмотрим к примеру дробь . Применим её к нашей пицце.
Допустим, мы хотим съестьпиццы. В знаменателе стоит число 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По сути, взята вся целая пицца, и если мы съедим этупиццы, то съедим не часть пиццы, а всю пиццу целиком. Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.
Дробь означает деление
Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.
Например, рассмотрим дробь . Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:
Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:
Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного сложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части дроби».
Выделение целой части дроби
Вычислим дробь . Пять разделить на два будет два и один в остатке:
5 : 2 = 2 (1 в остатке)
Проверка: (2 × 2) + 1 = 4 + 1 = 5
Но сейчас мы имеем дело с дробями, значит и отвечать надо в дробном виде. Чтобы хорошо понять, как это делается, рассмотрим пример из жизни.
Чтобы хорошо понять, как это делается, рассмотрим пример из жизни.
Представьте, что у вас есть 5 яблок и вы решили поделиться ими со своим другом. Причём поделиться по-честному, чтобы каждому досталось поровну. Как разделить эти 5 яблок?
Очевидно, что каждому из вас достанется по два яблока, а оставшееся одно яблоко вы разрежете ножом пополам и тоже разделите между собой:
Посмотрите внимательно на этот рисунок. На нём показано, как пять яблок разделены между вами и вашим другом. Очевидно, что каждому досталось по два целых яблока и по половинке яблока.
Теперь возвращаемся к дроби и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем:
Схематически это выглядит так:
Процедуру, которую мы сейчас провели, называют выделением целой части дроби.
В нашем примере мы выделили целую часть дроби и получили новую дробь . Такую дробь называют смешанной. Смешанная дробь — это дробь, у которой есть целая часть и дробная.
В нашем примере целая часть это 2, а дробная часть это
Обязательно запомните эти понятия! А лучше запишите в свою рабочую тетрадь.
Выделить целую часть можно только у неправильных дробей. Напомним, что неправильная дробь это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными, и у них выделена целая часть:
Чтобы выделить целую часть, достаточно знать, как делить числа уголком. Например, выделим целую часть у дроби . Записываем уголком данное выражение и решаем:
После того, как решение примера завершается, новую дробь собирают подобно детскому конструктору. Важно понимать, что куда относить. Частное относят к целой части, остаток относят в числитель дробной части, делитель относят в знаменатель дробной части.
В принципе, если вы хорошо знаете таблицу умножения, и можете быстро в уме выполнять элементарные вычисления, то можно обойтись без записей уголком. В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы.
Но если вы только начинаете изучать математику, советуем записывать каждую мелочь.
Рассмотрим ещё один пример на выделение целой части. Пусть требуется выделить целую часть дроби
Записываем уголком данное выражение и решаем. Потом собираем смешанную дробь:
Получили:
Перевод смешанного числа в неправильную дробь
Любое смешанное число получается в результате выделения целой части в неправильной дроби. Например, рассмотрим неправильную дробь . Если выделить в ней целую часть, то получается
Но возможен и обратный процесс — любое смешанное число можно перевести в неправильную дробь. Для этого целую часть надо умножить на знаменатель дробной части и полученный результат прибавить к числителю дробной части. Полученный результат будет числителем новой дроби, а знаменатель останется без изменений.
Например, переведём смешанное число в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части:
2 × 3 = 6
Затем к 6 прибавляем числитель дробной части:
6 + 1 = 7
Полученная семёрка будет числителем новой дроби, а знаменатель 3 останется без изменений:
Подробное решение выглядит так:
А с помощью переменных перевод смешанного числа в неправильную дробь можно записать так:
Пример 2. Перевести смешанное число в неправильную дробь.
Умножаем целую часть смешанного числа на знаменатель дробной части и прибавляем к числителю дробной части, а знаменатель оставляем без изменений:
Основное свойство дроби
Основное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.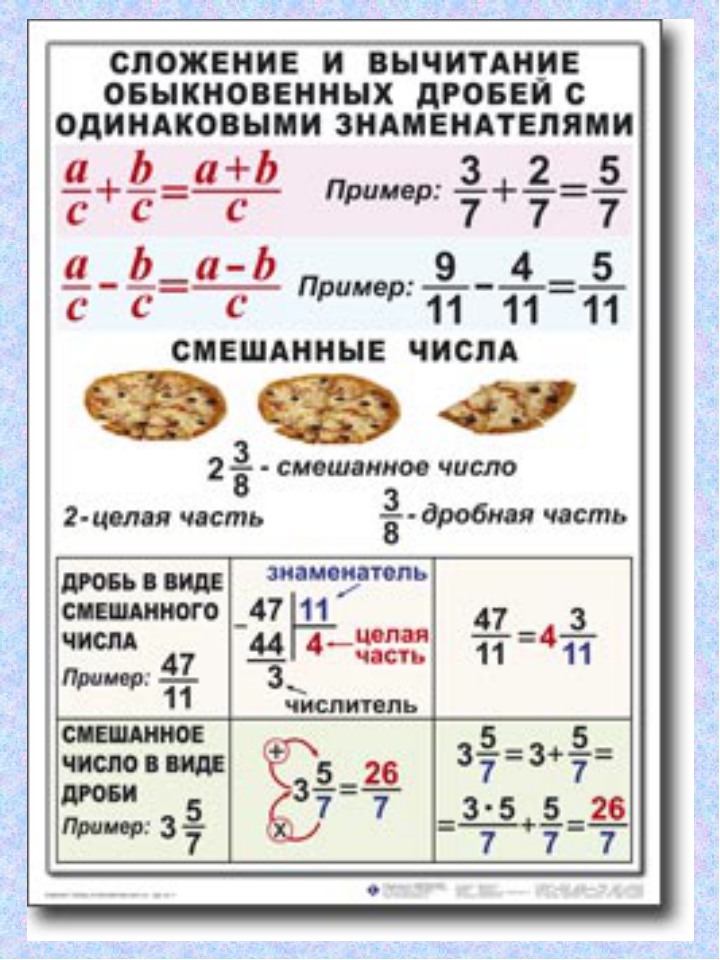 Это означает, что значение дроби не изменится.
Это означает, что значение дроби не изменится.
Например, рассмотрим дробь . Умножим её числитель и знаменатель на одно и то же число, например на число 2
Получили новую дробь . Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (один кусок из двух), а второй иллюстрирует дробь (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число.
Рассмотрим дробь . Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2
Получили новую дробь . Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (четыре куска из восьми), а второй иллюстрирует дробь (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно.
Число, на которое умножается числитель и знаменатель, называется дополнительным множителем. Запомните это обязательно!
Сокращение дробей
Дроби можно сокращать. Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь выглядит намного проще и красивее, чем дробь .
Если при решении примеров получается большая и некрасивая дробь, то нужно попытаться её сократить.
Сокращение дроби опирается на основное свойство дроби. Поэтому, прежде чем изучать сокращение дробей, обязательно изучите основное свойство дроби.
Деление числителя и знаменателя на их наибольший общий делитель называется сокращением дроби.
Пример 1. Сократить дробь
Итак, нужно разделить числитель и знаменатель дроби на наибольший общий делитель чисел 2 и 4.
В данном случае дробь простая и для неё НОД ищется легко. НОД чисел 2 и 4 это число 2. Значит, числитель и знаменатель дроби надо разделить на 2
В результате дробь обратилась в более простую дробь . Значение исходной дроби при этом не изменилось, поскольку сокращение подразумевает деление числителя и знаменателя на одно и то же число. А это действие, как было указано ранее, не меняет значение дроби.
На рисунке представлены дроби и в виде кусочков пиццы. До сокращения и после сокращения они имеют одинаковые размеры. Разница лишь в том, что раздéланы они по-разному.
Пример 2. Сократим дробь
Чтобы сократить дробь , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40.
НОД чисел 20 и 40 это число 20. Поэтому делим числитель и знаменатель дроби на 20
Пример 3. Сократим дробь
Чтобы сократить дробь , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36.
НОД чисел 32 и 36 это число 4. Поэтому делим числитель и знаменатель дроби на 4
Если в числителе и знаменателе располагаются простые числа, то такую дробь сократить нельзя — она не сокращается. Такие дроби называют несократимыми. Например, следующие дроби являются несократимыми:
Такие дроби называют несократимыми. Например, следующие дроби являются несократимыми:
Напомним, что простыми называются числа, которые делятся только на единицу и самих себя.
Второй способ сокращения дроби
Второй способ является короткой версией первого способа. Суть его заключается в том, что пропускается подробное разъяснение того, на что был разделён числитель и знаменатель.
К примеру, вернёмся к дроби . Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4
Теперь представьте, что в данном выражении отсутствует конструкция , и сразу записан ответ . Получится следующее выражение:
Суть в том что число, на которое разделили числитель и знаменатель, хранят в уме. В нашем случае числитель и знаменатель делят на 4 — это число и будем хранить в уме.
Сначала делим числитель на число 4. Полученный ответ записываем рядом с числителем, предварительно зачеркнув его:
Затем таким же образом делим знаменатель на число 4. Полученный ответ записываем рядом со знаменателем, предварительно зачеркнув его:
Затем собираем новую дробь. В числитель отправляем новое число 8 вместо 32, а в знаменатель отправляем новое число 9 вместо 36
Происходит своего рода замена одной дроби на другую. Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Также, дроби можно сокращать, предварительно разложив на простые множители числитель и знаменатель.
Например, сократим дробь , предварительно разложив на простые множители числитель и знаменатель:
Итак, мы разложили числитель и знаменатель дроби на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей.
Давайте сократим по тройке в числителе и в знаменателе. Для этого разделим эти тройки на 3 (на их наибольший общий делитель). Получим следующее выражение:
Сократить можно ещё по тройке в числителе и в знаменателе:
Дальше сокращать больше нéчего. Последнюю тройку в знаменателе просто так сократить нельзя, поскольку в числителе нет множителя, который можно было бы сократить вместе с этой тройкой.
Записываем новую дробь, в числителе и в знаменателе которой будут новые множители.
Получили ответ . Значит, при сокращении дроби получается новая дробь .
Не рекомендуется пользоваться вторым способом сокращения дроби и способом разложения на простые множители числителя и знаменателя, если человек только нáчал изучать математику. Практика показывает, что это оказывается сложным на первых этапах.
Поэтому, если испытываете затруднения при использовании второго способа, то пользуйтесь старым добрым способом сокращения: делите числитель и знаменатель дроби на их наибольший общий делитель. Выражение в таком случае получается простым, понятным и красивым. Так, предыдущий пример может быть решён старым способом и будет выглядеть так:
Сравните это выражение с выражением, которое мы получили, когда пользовались вторым способом:
Первое выражение намного понятнее, аккуратнее и короче. Не правда ли?
Задания для самостоятельного решения
Задание 1. Запишите в виде дроби следующий рисунок:
Задание 2. Запишите в виде дроби следующий рисунок:
Задание 3. Запишите в виде дроби следующий рисунок:
Задание 4. Запишите в виде дроби следующий рисунок:
Задание 5. Запишите в виде дроби следующий рисунок:
Задание 6. Выделите целые части в следующих дробях:
Задание 7. Выделите целые части в следующих дробях:
Задание 8. Переведите смешанные дроби в неправильные:
Задание 9. Переведите смешанные дроби в неправильные, не расписывая как целая часть умножается на знаменатель дробной части и полученный результат складывается с числителем дробной части
Переведите смешанные дроби в неправильные, не расписывая как целая часть умножается на знаменатель дробной части и полученный результат складывается с числителем дробной части
Задание 10. Сократите следующую дробь на 3
Задание 11. Сократите следующую дробь на 3 вторым способом
Задание 12. Сократите следующую дробь на 5
Задание 13. Сократите следующую дробь на 5 вторым способом
Задание 14. Сократите следующие дроби:
Задание 15. Сократите следующие дроби вторым способом:
Задание 16. Запишите в виде дроби следующий рисунок:
Задание 17. Запишите в виде дроби следующий рисунок:
Задание 18. Запишите в виде дроби следующий рисунок:
Задание 19. Запишите в виде дроби следующий рисунок:
Задание 20. Запишите в виде дроби следующий рисунок:
Задание 21. Изобразите в виде рисунка следующую дробь:
Задание 22. Изобразите в виде рисунка следующую дробь:
Задание 23. Изобразите в виде рисунка следующую дробь:
Задание 24. Изобразите в виде рисунка следующую дробь:
Задание 25. Изобразите в виде рисунка следующую дробь:
Задание 26. Изобразите в виде рисунка следующую дробь:
Задание 27. Изобразите в виде рисунка следующую дробь:
Задание 28. Изобразите в виде рисунка следующую дробь:
Задание 29. Изобразите в виде рисунка следующую дробь:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Урок по математике 5 класс «Сравнение дробей с разными знаменателями»
Технологическая карта урока математики, 5 класс
Учебный предмет: математика
Класс: 5
Автор УМК: Е. А. Бунимович, и др. «Математика»
А. Бунимович, и др. «Математика»
Тема урока: Сравнение дробей с разными знаменателями
Тип урока: Открытие нового знания
Цель урока: Создание условий для организации деятельности обучащихся по расширению области их знаний о способах сравнения обыкновенных дробей.
Формы работы: Индивидуальная, групповая, парная, фронтальная
Ресурсы урока:
Учебник Бунимович Е.А. и др. Математика. 5 класс М: Издательство «Просвещение».
• Карточки-задания
• Компьютер
• Проектор
Задачи урока:
Предметные умения
Ученик научится сравнивать обыкновенные дроби с разными знаменателями различными способами: сравнение дробей с равными числителями, с половиной (больше половины, меньше половины), приведением дробей к общему знаменателю (или числителю)
получит возможность
– выдвигать гипотезы,
– обосновывать свою точку зрения на основе анализа предложенной ситуации и сопоставления полученных фактов,
– формировать и формулировать правила сравнения обыкновенных дробей с разными знаменателями.
Универсальные учебные действия
Личностные: самоопределение, способность к самооценке своих действий. Смыслообразование.
Регулятивные: умение
– самостоятельно определить цели и задачи своего обучения на уроке,
– аргументировать свою точку зрения,
– проводить самопроверку и взаимопроверку по готовому образцу.
– оценивать вместе с учителем результаты своих действий и вносить необходимые коррективы.
Познавательные: поиск и выделение необходимой информации, смысловое чтение и построение логической цепочки высказываний. Умение
– видеть проблему и определять для себя задачи по устранению
проблемы;
– исследовать предложенную ситуацию
– делать правильный вывод на основе полученных результатов.
Коммуникативные: учебное сотрудничество с учителем и одноклассниками, умение выражать свои мысли, оценивать адекватно мысли одноклассников и учителя, оценивать качество своей и общей учебной деятельности.
УУД
1.
Мотивация к деятельности
Задача этапа: включение учащихся в деятельность.
2
Учитель проверяет готовность класса к уроку, приветствует учеников.
Включение в деловой ритм.
_Новый урок – это новое открытие. Что, по вашему мнению, нужно уметь, чтобы совершить это открытие?
— Давайте проверим, готовы ли мы совершать открытия.
Высказывают свое мнение.
Включаются в деловой ритм.
Личностные результаты
Положительное отношение к учению(Л)
Метапредметные результаты
Учебного сотрудничества с учителем и сверстниками (К)
2.
Актуализация и пробное учебное действие
Задача этапа: подготовка мышления обучащихся и организация осознания ими внутренней потребности к построению нового способа
действий.
5
Совершим мягкую посадку. Вы помните — садится тот, кто отвечает правильно на вопрос.
Задания на доске, чередуются слады презентации
Отвечают на вопросы и садятся на место. Если ответа не знают те, кто стоит – поднимают руку и отвечают дополнительно.
Метапредметные результаты
умение быстро ориентироваться в знакомой ситуации, грамотно выражать свои мысли (К)
Предметные результаты
Систематизация умений сравнивать дроби с равными знаменателями, сокращать дроби и приводить их к новому знаменателю (П – логически )
3
Выявление места и причины затруднения
Задача этапа: обсуждение затруднений (почему возникли затруднения, чего мы ещѐ не знаем).
3
Создает проблемную ситуацию
Расположите в порядке убывания
Высказывают свое мнение:
— чтобы расположить в нужном порядке, нужно сравнить дроби;
— умеем сравнивать только дроби с равными знаменателями, а здесь у всех дробей разные знаменатели
Фиксируют и формулируют проблему урока.
Метапредметные результаты
Целеполагание (Р)
Постановка вопросов (К)
Предметные результаты
Формулирование проблемы (П – лог.)
4
Постановка цели урока и построение проекта выхода из затруднения
Задача этапа: постановка целей учебной деятельности
2
Итак, чем же, по вашему мнению, нам предстоит сегодня заняться?
Чему вы хотите научиться, что узнать?
Тема урока «Сравнение дробей с разными знаменателями» высвечивается на доске.
Определяют учебную задачу.
(знаю — …
не знаю -…
хочу узнать — …)
Ставят цели, определяют тему урока.
Высказывают свое мнение
— Научиться сравнивать дроби с разными знаменателями;
— вывести (узнать, изучить) правила сравнения дробей с разными знаменателями
Метапредметные результаты
Целеполагание (Р)
Планирование (Р)
Прогнозирование (Р)
Предметные результаты
Самостоятельное формулирование цели (П – общеуч.)
5
Реализация построенного проекта
Задача этапа: апробация способа действий, направленного на решение проблемной ситуации, его вербальное фиксирование
5
Организует учащихся по исследованию проблемной ситуации:
1. Организует поисковую работу учащихся (работа в группах: 5 групп). Следит за работой в группах
Работают в группах, в ходе исследования делают выводы, формулируют правила сравнения.
Составляют алгоритм действий при том или ином способе сравнения:
— сравнения правильной и неправильной дробей друг с другом и с 1,
— сравнение дробей больших половины и меньших половины друг с другом и с половиной;
— сравнение дробей с равными числителями;
— сравнение дробей приведением к общему знаменателю
Метапредметные результаты
Сотрудничество в поиске и выборе информации (К)
Предметные результаты
Решение проблемы, построение логической цепи рассуждений, доказательство, выдвижение гипотез и их обоснование (П – моделирование
6
Первичное закрепление
Задача этапа: первичный контроль за правильностью выполнения способа действия.
3
Организовывает фиксацию нового способа действия в речи.
Обращает особое внимание на правильную запись сравнения дробей в случае приведения их к общему знаменателю
Физкультминутка
— Итак, какие существуют способы сравнения
дробей?
— Давайте обратимся к учебнику, может быть, мы в чѐм-то ошиблись.
— Скажите, пожалуйста, в случае приведения дробей к общему знаменателю, обязательно приводить к наименьшему общему знаменателю?
Предложить ещѐ раз проговорить все правила (На доске – правила)
— Можете ли вы предложить ещѐ способ сравнения дробей с разными знаменателями?
Если не предложат этот способ — направить к нему, записать на доске
Предлагает выполнить задания из учебника: стр. 144 №308 (а,б), 309 (а,в), 310 (а), 311 (а)
(устно) (номера записаны на доске)
Письменно -стр. 144,145
№ 302(а,в,д),303(а,в,д),304(а,в,д),
После работы в группе учащиеся представляют свои рассуждения у интерактивной доски (возможно использование визуализатора), обосновывая свою точку зрения.
Выслушивают мнение одноклассников.
Работают с планом разбора в приложении.
обучащиеся называют полученные способы
Учебник стр. 144-146. Убеждаются, что в учебнике только правила для сравнения дробей с равными числителями, равными знаменателями и разными знаменателями способом приведения к общему знаменателю. Они в ходе исследования нашли большее количество способов
Отвечают, что знаменатель может быть любым.
обучащиеся в полголоса проговаривают правила хором.
Возможно, кто-нибудь из учащихся покажет, что дроби можно приводить и к одинаковым числителям.
обучащиеся по очереди отвечают, обосновывая свой ответ, остальные сигналами показывают, согласны с ответом или нет.
очучащиеся по одному заданию выполняют на доске, остальные прописывают в тетрадях. Результат работы на доске проверяют учащиеся
на местах, если не согласны, то исправляют и комментируют.
Метапредметные результаты
Контроль (Р)
Оценка (Р)
Коррекция (Р)
Управление поведением партнера (К)
Выражение своих мыслей с достаточной полнотой и
точностью(К)
Предметные результаты
Действие по аналогии (П)
Умение структурировать знания , выбор наиболее эффективных способов решения задач (П – общеуч.)
7
Самостоятельная работа с самопроверкой по эталону
Задача этапа: самооценка обучащимися результатов своей учебной деятельности
5
Организует деятельность по применению новых знаний.
— На ваших столах лежат листочки с жѐлтой наклейкой. Возьмите их, подпишите и выполните предложенные задания прямо на этих карточках. На работу вам отводится 3 минуты
Предлагает учащимся обменяться работами и проверить качество выполнения, сравнив с эталоном (на интерактивной доске)
Учащиеся выполняют задания самостоятельной работы.
Осуществляют взаимопроверку и самопроверку.
Учащиеся, обменявшись работами, подчѐркивают неправильные решения и выставляют отметку. (Критерии оценивания на доске:
Верно 5 заданий – «5»
Верно 4 задания – «4»
Верно 3 задания – «3
Затем карточки возвращаются учащимся и они перепроверяя сою работу, исправляют ошибки(если такие есть).
Метапредметные результаты
Контроль, коррекция, выделение и осознание усвоенного (Р)
Волевая регуляция в ситуации затруднения (Р)
Личностные результаты
Самоопределение (Л)
8
Рефлексия деятельности
Задача этапа: осознание обучащимися своей учебной деятельности, самооценка результатов
деятельности своей и всего класса
Организует рефлексию, самооценку результатов уч-ся.
Поднимите руки, кто получил за с/р «5», «4», «3».
— Предлагаю вам оценить свою работу на уроке, удалось ли вам успешно выполнить свои задачи.
Осуществляют оценку урока и самооценку, соотносят цель и результаты, степень их соответствия
Метапредметные результаты
Умение выражать свои мысли (К)
Предметные результаты
Рефлексия (П)
Контроль и оценка процесса и результатов деятельности (П)
Личностные результаты
Самооценка на основе успешности (Л)
Адекватное понимание причин успеха/неуспеха в учебной деятельности (Л)
9
Информация о домашнем задании
Задача этапа:
Обеспечить понимание обучащимися содержания и способов выполнения домашнего задания
1
Домашнее задание: стр. 144-145 (читать), выучить правила, рубрика «Вопросы и задания»,
У: Стр144-145 № 509, 510, 511, №512 (по 2 первых примера)
По желанию: Карточки с дополнительным заданием учащиеся по желанию берут на столе учителя по окончанию урока.
Записывают задание в дневник, отслеживают комментарии учителя по учебнику
Действия с обыкновенными дробями (урок математики, 5 класс)
Урок математики в 5 классе. Тема:
Муниципальное общеобразовательное учреждение средняя общеобразовательная школа 7 города Алексеевки Белгородской области Урок математики в 5 классе Тема: Учитель математики: Васильченко Людмила Михайловна
Подробнее
Технологическая карта урока
Технологическая карта урока 1. Учитель: 2. Класс: 5 Дата: Предмет: математика 3. Место и роль урока в изучаемой теме: урок комплексного применения знаний и умений (урок закрепления) третий урок в блоке
Подробнее
СТРУКТУРА И ХОД УРОКА
ПЛАН-КОНСПЕКТ УРОКА Умножение обыкновенных дробей. ФИО (полностью) Шишканова Наталья Алексеевна. Место работы Муниципальное бюджетное общеобразовательное учреждение городского округа Тольятти «Школа 7».
ФИО (полностью) Шишканова Наталья Алексеевна. Место работы Муниципальное бюджетное общеобразовательное учреждение городского округа Тольятти «Школа 7».
Подробнее
Действия с десятичными дробями
Кузнецова Татьяна Андреевна, учитель математики МБОУ СОШ 16 им. К.И.Недорубова Урок 116(урок обобщения знаний) Тема урока: «Сложение и вычитание десятичных дробей». Цели урока: — Образовательные: углублять,
Подробнее
Предмет математика класс 2 г
Предмет математика класс 2 г Тема урока Место урока по теме (в разделе/главе) Закрепление изученного по теме «Умножение и деление» «Умножение и деление» 18 из 20 Тип урока Форма урока, форма учебной деятельности,
Подробнее
Тема: «Сложение дробей с одинаковыми
Урок по математике. 4 класс. Программа «Школа 2100». по учебнику Л.Г.Петерсон (4 класс, 2 часть, урок 3) Тема: «Сложение дробей с знаменателями». Урок открытия новых знаний. Подготовила: Моисеева Е.Р.
Подробнее
Технологическая карта урока
Технологическая карта урока Ф.И.О. Ковалева Юлия Сергеевна Предмет: Математика Класс: 5 класс Автор УМК: Математика 5 класс: учебник для общеобразовательных учреждений А. Г. Мерзляк и др. Тема урока: Сложение
Подробнее
Технологическая карта урока математики
Технологическая карта урока математики Учитель: Рочева Е.А., учитель математики МОУ «СОШ г. Коряжмы» Тема урока: Сложение смешанных дробей Класс: 5 Дидактическая цель: создать условия для формирования
Подробнее
Пояснительная записка
Пояснительная записка Рабочая программа по математике в 6 специальном (коррекционном) классе VIII вида составлена на основе программы специальной (коррекционной) образовательной школы VIII вида для 5-9
Подробнее
Бутыгина Татьяна Федоровна Аннотация
Бутыгина Татьяна Федоровна, учитель математики высшей квалификационной категории МОУ «СОШ 11 с углубленным изучением иностранных языков» г. Ноябрьска ЯНАО Тюменской области. Аннотация Все знают: «Повторение
Ноябрьска ЯНАО Тюменской области. Аннотация Все знают: «Повторение
Подробнее
Объяснение новой темы: 3:7= : =3/1 7/1= 3/7
технологическая карта урока 1. Ф.И.О. учителя: Ткачук Наталья Петровна 2. Класс: 6 Дата: 10.09 Предмет математика 6 урока по расписанию: 3. Тема урока:_ Понятие дробного выражения «Многоэтажные дроби»
Подробнее
на учебный год
Рабочая программа по индивидуально групповым занятиям по математике для 5 класса учителя математики Соршневой Любови Ивановны на 03-04 учебный год Составлена на основании Программы для общеобразовательных
Подробнее
Сложение и вычитание смешанных чисел
Предмет: Математика Класс: 5 «Б» класс Сложение и вычитание смешанных чисел Учебник: Математика: 5 класс: учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.
Подробнее
Пояснительная записка
Пояснительная записка Данная учебная программа ориентирована на учащихся 6 класса и реализуется на основе следующих документов: 1.Закон «Об образовании РФ» 2. Адаптированная основная общеобразовательная
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА. (Математика 5 класс)
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА. (Математика 5 класс) Данная рабочая программа составлена в соответствии с Государственной программой по математике для общеобразовательных учреждений Министерства образования Российской
Подробнее
Конспект открытого урока
Конспект открытого урока Учитель: Класс: Тема урока: Дата проведения урока: Цели урока: Задачи урока: Применяемые технологии: Токарева Е. А. 3 «А» «Решение уравнений» 5 февраля 2013 года — повышение уровня
А. 3 «А» «Решение уравнений» 5 февраля 2013 года — повышение уровня
Подробнее
Технологическая карта урока математики
АДМИНИСТРАЦИЯ ГОРОДСКОГО ОКРУГА ПОДОЛЬСК КОМИТЕТ ПО ОБРАЗОВАНИЮ Муниципальное общеобразовательное учреждение «Лицей 1» (МОУ «Лицей 1») Технологическая карта урока математики Урок математики в 6 классе
Подробнее
Открытый урок по математике в 6Б классе
Открытый урок по математике в 6Б классе Учитель: Каменева Анна Николаевна Дата:0.0. 2008г. Тема: Сложение и вычитание дробей с разными знаменателями Тип урока: Урок закрепления знаний, выработки умений
Подробнее
Урок математики в 5 классе по теме «Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями»
ПЛАН-КОНСПЕКТ УРОКА
Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями
| ФИО (полностью) | Саликова Людмила Александровна |
| Место работы | Государственное бюджетное общеобразовательное учреждение Самарской области средняя общеобразовательная школа с. Бобровка муниципального района Кинельский Самарской области |
| Должность | Учитель математики и физики |
| Предмет | математика |
| Класс | 5 |
| Тема и номер урока в теме | Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями 1 урок из 3 по плану. |
| Базовый учебник | «Математика, 5» Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбурдт. – М. : Мнемозина, 2014.
|
Цель урока: формировать навыки сложения и вычитания дробей с одинаковыми знаменателями, развивать познавательный интерес к математике.
9. Задачи:
— образовательные: (формирование познавательных УУД)
научить складывать и вычитать дроби с одинаковыми знаменателями, правильно читать и записывать выражения, содержащие обыкновенные дроби.
-развивающие: (формирование регулятивных УУД)
Целеполагание — понимать учебную задачу урока, осуществлять решение учебной задачи под руководством учителя, определять цель учебного задания; планирование — составление плана и последовательности действий, контроль — контролировать свои действия в процессе выполнения учебного задания, обнаруживать и исправлять ошибки (коррекция), отвечать на итоговые вопросы и оценивать свои достижения (оценка).
-воспитательные: (формирование коммуникативных и личностных УУД) учиться планированию учебного сотрудничества с учителем и сверстниками; умению строить речевые высказывания в устной и письменной форме; учиться смыслообразованию т. е.установлению учащимися связи между целью учебной деятельности и ее мотивом; воспитывать аккуратность, дисциплинированность.
10.Тип урока: изучение нового материала
11.Формы работы учащихся: индивидуальная и фронтальная работа, работа в парах.
12.Необходимое техническое оборудование: компьютер, проектор, экран.
Ход урока
Организационный момент.
II. Устная работа с классом:
Слайды 1-2
1) Определить, какая часть фигуры заштрихована?
Слайд 3
2) Что показывает знаменатель дроби 2/5? (На сколько равных частей разделили величину)
Что показывает числитель? (Сколько равных частей взяли)
Слайд 4
3) Распределить данные дроби на группы: а) правильные; б) неправильные.
Слайд 5
4) Решить задачу: 3 яблока нужно разделить между 4 детьми. Как это сделать?
Ответ: Каждому ребенку достанется 3/4 яблока.
III. Объяснение новой темы: «Сложение и вычитание дробей с одинаковыми знаменателями»
Слайд 6-8
Задача: Пирог разделили на 8 частей. Сначала на тарелку положили 3/8 частей, затем 2/8 части. Сколько частей пирога положили на тарелку и сколько осталось?
— Что для этого нужно сделать?(сложить дроби, вычесть)
— Что мы должны научиться делать?(складывать и вычитать дроби с одинаковыми знаменателями)
— Значит перед нами стоят задачи: научиться складывать и вычитать дроби с одинаковыми знаменателями и применять эти знания при решении задач.
– Хорошо! Чтобы продолжить работу, надо записать тему урока, что мы запишем в тетрадь? (Сложение и вычитание дробей с одинаковыми знаменателями.)
– Запишите число и тему урока
(На доске учитель записывает тему урока)
Слайд 9
-Ребята, на сколько частей разрезан пирог? Как выполнить сложение дробей? Вспомним что показывает числитель? Значит на тарелку положили 3кусочка, а затем 2 кусочка пирога. Всего сколько кусочков порога положили? (5). Выполним сложение. А сколько осталось? Как можно узнать? Выполним вычитание.
— А теперь давайте сформулируем правило сложения (вычитания) дробей с одинаковыми знаменателями. (говорят).
— Давайте откроем учебник на странице 155 и прочтём правила. Так ли мы их сформулировали? Замечательно! Эти правила надо знать!
(слайд, на котором буквенная запись сложения и вычитания)
Слайд 10
Итак, при сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляют тот же.
a/b+c/b=(a+c)/b
Слайд 11
При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель остается тот же.
a/b-c/b=(a-c)/b
— Ребята, запишите буквенную запись сложения и вычитания в тетрадь.
А чтобы о нас говорили, что мы культурные и воспитанные, мы должны говорить правильно. Этому нас тоже учат. (с.157 прочесть вслух, сделать акцент на то, что склонение числительных будем изучать в 6 классе).
(Прописать на доске два примера – образцы на сложение и вычитание).
Слайд 12
Физминутка:
Мы сегодня рано встали (шаги на месте)
И зарядку делать стали.
Руки — вверх! Руки — вниз!
Влево-вправо повернись!
IV. Закрепление изученной темы:
Слайд 13
1. Заполнить пропуски ( работа выполняется в тетради с проговариванием правил по изученной теме)
2.Игровое задание (работа выполняется устно)
3. Математический диктант
VI. Подведение итогов урока:
– Какую тему мы сегодня изучали? (сложение и вычитание дробей с одинаковыми знаменателями)
— А какие задачи мы для этого ставили? (научиться складывать и вычитать дроби с одинаковыми знаменателями)
– Наши задачи выполнены? (да)
–Выставление оценок индивидуально, в группах, выставление общей оценки за урок
VII. Домашнее задание:
Слайд 14
Учебник «Математика» 5 класс, Виленкин Н.Я.; П. 26, стр. 161, № 1039, 1041, написать сказку о приключениях дробей – по желанию.
Структура и ход урока «Сложение и вычитание дробей с одинаковыми знаменателями» | ||||||||
№ | Этап урока | Название используемых ЭОР | Деятельность учителя | Деятельность ученика | Время | Формируемые УУД | ||
Познавательные | Регулятивные | Коммуника-тивные, личностные | ||||||
1 | Орг. Момент (Вводно-мотивационная часть, с целью активизации деятельности учащихся) |
| Определяет готовность учащихся. Сосредоточивает внимание учащихся | Готовят принадлежности, чертежные инструменты к уроку. Записывают дату в тетрадь | 1 мин. |
| Организация своей учебной деятельности | Умение слушать, планирование учебного сотрудничества |
2 | Устный счет
Актуализация опорных знаний | Слайды №1-5 | Координирует деятельность учащихся | Устно решают задачи. Называют ответы | 3 мин | Анализ, сравнение, аналогия, умение осознанно и произвольно строить речевое высказывание в устной форме; | контроль и оценка проц есса и результатов деятельности
| построение логической цепи рассуждений, аргументация своего мнения, учет мнения учащихся. |
3 | Целеполага-ние и мотивация | Слайды № 6-8
| Мотивирует учащихся. Проводит диагностику универсальных учебных действий учащихся, сформированных в начальной школе по данной теме; развивает логическое и критическое мышление | Выполняют задания предложенные учителем. Оценивают результаты Называют и записывают тему урока.
| 3 мин. | анализ; умение осознанно и произвольно строить речевое высказывание в устной форме; построение логической цепи рассуждений; установление причинно-след-ственных связей; подведение под понятие; постановка и формулирование проблемы | целеполагание; прогнозирова-ние, волевая саморегуляция в ситуации затруднения
| Умение слушать и вступать в диалог; Участвовать в коллективном обсуждении; Планирование учебного сотрудничества с учителем и сверстниками |
4 | Объяснение нового материала | Слайды № 9-11 | Вводит наглядно понятие сложения и вычитания дробей
организует деятельность работы с учебником; направляет работу учащихся | Слушают, отвечают на вопросы, делают выводы, работают с учебником; Ведут записи в тетрадях | 10 мин | Анализ; сравнение, обобщение, Установление причинно-следственных связей, поиск и выделение необходимой информации; знаково-символические действия, умение осознанно и произвольно строить речевое высказывание в устной и письменной форме; определение основной и второстепенной информации;
| Планирование; элементы волевой саморегуляции;
| выражение своих мыслей, аргументация своего мнения, учёт разных мнений, разрешение конфликтной ситуации
|
5 | Физкульт минутка | Слайд № 12
|
|
| 2 мин |
|
|
|
6 | Первичное закрепление письменно | Слайды № 13
| Мотивирует учащихся. Ставит проблемные вопросы; подводит к понятиям; учит читать и записывать обыкновенные дроби в примерах на сложение и вычитание | Устно решают поставленные задачи, отвечают на вопросы; ведут записи в тетрадях;
| 4 мин | Поиск и выделение необходимой информации; анализ, синтез
умение осознанно и произвольно строить речевое высказывание в устной форме; знаково-символические действия, выбор оснований и критериев для сравнения.
| Планирование; элементы волевой саморегуляции;
| Умение слушать и вступать в диалог; Участвовать в коллективном обсуждении; принятие решения
|
7 | Закрепление. Практическая часть. Игровое задание: сложение, вычитание |
http://files.school-collection.edu.ru/dlrstore/4f88f945-a5fb-45d9-b6ff-4d593133e036/24_2_fr1.ppt
http://files.school-collection.edu.ru/dlrstore/5443ad0b-c454-45b5-b7ed-d86080979a1d/24_2_fr2.ppt
| Учитель дает практический модуль в виде демонстрации на экран. следит, чтобы ученики говорили свой ответ, после поднятия руки
| Учащиеся работают устно, выбирают правильный ответ из четырех. В итоге получается картина, когда решены все примеры
| 7 мин | самостоятельное выделение и формулирование познавательной цели; поиск и выделение необходимой информации; умение осознанно и произвольно строить речевое высказывание в устной форме; выбор оснований и критериев для сравнения, классификации объектов; подведение под понятия, выполнение действий по алгоритму | Планирует – определяет последовательность промежуточных целей с учетом конечного результата; контроль в форме сличения способов действий; коррекция, самооценка
| умение слушать и вступать в диалог,
оценка действий
Участвовать в коллективном обсуждении; принятие решения
|
8 | Математический диктант с взаимо-проверкой | http://files.school-collection.edu.ru/dlrstore/9a951e93-d301-42c3-a811-4131719e2d3a/24_2_md%282%29.ppt | Дает контрольный модуль в виде демонстрации на экран , следит чтобы учащиеся работали индивидуально Мотивирует, организует самостоятельную деятельность учащихся, взаимопроверку.
| Учащиеся смотрят на экран, подсчитывают, ответ записывают в тетрадь, обмениваются тетрадями, сверяют с доской ответы | 7 мин | Установление причинно-следственных связей; построение логической цепи рассуждений; контроль и оценка процесса и результатов деятельности; рефлексия способов и условий действия, выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; | Контролируют процесс и результат учебной математической деятельности; контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона; коррекция; способность к волевому решению | Планирование учебного сотрудничества с учителем и сверстниками ; |
9 | Подведение итогов урока |
Слайд № 14
| Учитель направляющими вопросами узнает, в чем были сложности, что нового узнали ученики, выявляет уровень усвоения изученного материала
| Учащиеся обсуждают трудности на уроке и успехи. Проводят самоанализ работы на уроке, оценивают свою работу Записывают домашнее задание.
| 3 мин | Рефлексия способов и условий действия, структурирование знаний, установление причинно-следственных связей; знаково-символические действия.
| контроль и оценка процесса и результатов деятельности. | Самооценка на основе критерия успешности; Выражение своих мыслей формулирование и аргументация своего мнения; планирование сотрудничества. |
урок в 5 классе Действия с дробями | План-конспект урока по математике (5 класс) на тему:
Аннотация
Урок соответствует требованиям ФГОС и преследует основную цель – формировать познавательный интерес учащихся к учебной деятельности, создавать условия для саморазвития и непрерывного образования на основе умения учиться. Работа на уроке была направлена на обобщение знаний о дробных числах и действиях с ними:
— откуда произошли эти числа;
— кто придумал их записи;
— есть ли их дальнейшее развитие.
Литература
- Математика 5 класс. Автор Виленкин и др. «Мнемозина» 2015
- Дидактические материалы 5 класс. А.С.Чесноков, К.И.Нешков . «Просвещение» 2014
- Поурочные планы 5 класс. З.С.Стромова. «Учитель». Волгоград 2013 г.
План – конспект урока
Учитель: Шипулина Елена Петровна
5 класс Тема: Действия с дробями.
Цель: совершенствовать умение сравнивать, складывать и вычитать дроби с одинаковыми знаменателями, уметь применять свои знания при решении задач и уравнений.
Задачи:
— образовательные (формирование познавательных УУД)
обобщить и систематизировать знания учащихся по сравнению, сложению и вычитанию дробей с одинаковыми знаменателями.
— воспитательные (формирование коммуникативных и личностных УУД)
умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, строить в паре продуктивное взаимодействие, воспитывать ответственность и аккуратность; осуществлять рефлексию своего отношения к содержанию темы.
— развивающие (формирование регулятивных УУД)
формулировать вопросы по теме на основе опорных (ключевых и вопросительных) слов, развивать внимание, речь, память, мышление, самостоятельность.
Тип урока: урок совершенствования знаний, умений и навыков.
Фундаментальные образовательные объекты: число, задача, текст.
Формы работы учащихся: фронтальная, парная, самостоятельная, коллективная.
Главная проблема урока: добиться умения сравнивать, складывать и вычитать дроби с одинаковыми знаменателями.
Планируемые результаты:
- правильное чтение и запись обыкновенных дробей;
- применение новых знаний в новой ситуации;
- объяснение того, что показывает обыкновенная дробь.
Оборудование: учебник, разноуровневые карточки с задачами.
Технологическая карта урока:
№ п\п | Этап урока | Формируемые УУД | Деятельность учителя | Деятельность учащихся | Время (мин) |
1 | Организационный этап | Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. Регулятивные: организация своей учебной деятельности Личностные: мотивация учения | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. | Приветствуют учителя, включаются в деловой ритм урока. | 1 |
2 | Актуализация знаний учащихся | Познавательные: структурирование собственных знаний. Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками. Регулятивные: контроль и оценка процесса и результатов деятельности. Личностные: оценивание усваиваемого материала. | Проверка домашнего задания в парах | Участвуют в работе по проверке домашнего задания (в парах), в беседе с учителем отвечают на поставленные вопросы | 3 |
3 | Постановка цели и задач урока. | Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме. Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: умение вступать в диалог, участвовать в коллективном обсуждении вопроса. | Мотивирует учащихся, вместе с ними определяет цель урока; акцентирует внимание учащихся на значимость темы. | Записывают дату в тетрадь, определяют тему и цель урока. | 3 |
4 | Этап изучения нового материала. | Познавательные: самостоятельное решение проблемы, построение логической цепи рассуждений; Личностные: формировать способность к эмоциональному восприятию математических рассуждении. Регулятивные: определение последовательности промежуточных целей с учётом конечного результата; Коммуникативные: постановка вопросов, инициативное сотрудничество. | Запись на доске новых понятий: доли, обыкновенная дробь, числитель, знаменатель, что они означают. Акцентирует внимание на записи и чтении обыкновенных дробей. Учитель дает возможность обучающимся самостоятельно дать определение “Доли”, изображать дроби на координатном луче. | Обучающиеся, вместе с учителем читают готовые записи дробей, определяют место нахождения числителя и знаменателя, их значения. Изображают дроби на координатном луче. | 13 |
5 | Физкультминутка | Сменить деятельность, обеспечить эмоциональную разгрузку учащихся. | Учащиеся сменили вид деятельности и готовы продолжить работу. | 2 | |
6 | Этап первичное осмысление и закрепление знаний. | Личностные: формирование позитивной самооценки Регулятивные: умение самостоятельно адекватно анализировать правильность выполнения действий и вносить необходимые коррективы. | Выявляет качество и уровень усвоения знаний, а также устанавливает причины выявленных ошибок. | Учащиеся анализируют свою работу, выражают вслух свои затруднения и обсуждают правильность решения задач. | 15 |
7 | Рефлексия (подведение итогов урока) | Регулятивные: оценивание собственной деятельности на уроке | Подводит итоги работы учащихся и класса в целом. | Учащиеся сдают карточки самооценивания. | 2 |
8 | Домашнее задание | Дает комментарий к домашнему заданию | Учащиеся записывают в дневники задание. | 1 |
Ход урока
- Организационный момент (1мин)
Здравствуйте, ребята, садитесь!
Меня зовут Елена Петровна, я очень рада сегодняшней встрече с вами.
И проведем мы урок математики.
Чтобы спорилось трудное дело,
Чтобы в жизни не знать неудач.
Мы с вами отправимся смело,
В мир загадок и сложных задач.
Посмотрите друг на друга и улыбнитесь!
На части не делится солнце лучистое,
И небо огромное нельзя разделить,
Но искорку счастья луча золотистого
Ты можешь, ты в силах друзьям подарить.
Желаю вам удачи! Я верю в вас, у вас всё получится.
- Сообщение темы урока, постановка цели урока и его задач (3мин)
Ребята, у каждого из вас на столах лежат оценочные листы. Подпишите их.
На каждом этапе урока вы будете себя оценивать.
«+» — справился с заданием без затруднений,
«±» — справился с заданием, но возникали сложности,
«-» — не справился с задачей.
Работа в парах.
Каждый возьмите набор цветных прямоугольных полосок. (у каждого по 3 шт)
Равны друг другу эти прямоугольники?
— Да.
На основании чего мы можем это утверждать?
— Фигуры называются равными, если они при наложении совпадают.
А теперь проверьте, равны ли все вместе взятые прямоугольники?
— Да.
Сложите из них большой прямоугольник.
Из скольких равных частей составлен прямоугольник?
Из 6.
Как называется одна часть этого прямоугольника?
1/6.
А две части? 2/6
А как в математике называют такие записи?
— Дроби. или Обыкновенные дроби.
Назовите все дроби для этого случая.
1/6 2/6 3/6 4/6 5/6 6/6
А что означает дробь 6/6?
— Целое
Один из вас пусть возьмет 2/6 части прямоугольника, а второй ещё 3/6 части прямоугольника.
Сколько частей вы взяли? (5/6)
Ребята, с помощью какого действия вы узнали, сколько частей вы взяли всего?
— С помощью сложения. 2/6 + 3/6 = 5/6
У одного из вас 2/6 прямоугольника, а у другого 3/6.
А как называется действие, когда говорят, что одна часть меньше, а другая больше?
— Сравнение. 3/6
А если нужно узнать, на сколько частей больше у одного из вас?
Или какая часть прямоугольника осталась?
Какое действие нужно выполнить?
— Вычитание. 3/6 – 2/6 = 1/6
А половина этого прямоугольника? Это какая часть? ½ А сколько полосок? 3
Сделайте так, чтобы у каждого из вас было по 3 полоски разного цвета.
Ребята, назовите их цвета.
— Белый, синий, красный. А какие ассоциации у вас с этими цветами?
Где вы видели сразу эти три цвета?
— На флаге России.
Белый – мир, чистота, благородство.
Синий – небо, вера, правда, честность.
Красный – жизнь, отвага, смелость, великодушие.
Расположите полоски в правильном порядке цветов и сложите из них символ нашего государства.
— Молодцы!
Итак, ребята, давайте подведем итог нашей работы и назовем тему урока.
— Мы работали с частями.
Части это – дроби.
А с дробями можно выполнять действия.
Итак, мы с вами выполняли ……….. с ………..
Сформулируйте тему урока.
«Действия с дробями».
Какие цели мы поставим на данном уроке?
— Правила повторить,
— Знания по теме закрепить.
3. Актуализация знаний учащихся. Повторение пройденного материала (5мин)
Цель: проверить как усвоена тема «Сравнение, сложение и вычитание дробей с одинаковыми знаменателями».
- Найдите сумму дробей и =
Найдите разность дробей и =
- Вычислите — (+) =
4. Расположите в порядке возрастания дроби: ; ; ; ;; ;
5. Какую дробь надо поставить вместо *, чтобы получилось верное равенство:
* — = ?
4. Работа в тетрадях по теме урока (5мин)
- Решение задачи (стр158, №1014)
— Прочитайте задачу. Какова площадь участка? (300га)
— Какую часть участка занимает ель? (3/10)
— Какую часть сосна? (4/10)
— Что можно узнать, имея эти данные?
— Какую часть участка занимают ель и сосна вместе. (3/10 + 4/10 = 7/10)
— Ответим мы этим действием на вопрос задачи?
— Нет.
— Как узнать, сколько га занято елью и сосной вместе?
— Нужно 300 разделить на 10 и умножить на 7.
Запишем решение в тетрадь.
- 3/10 + 4/10 = 7/10 – такая часть леса занята елью и сосной.
- 300 : 10 7 = 210(га) – занято елью и сосной вместе.
Ответ: 210га.
— Подумайте, можно ли решить задачу иначе?
— Составьте план решения. Действия будем проговаривать, но не записывать.
1. Ск. га елью? 300 : 10 3 = 90(га)
2. Ск. га сосной? 300 : 10 4 = 120(га)
3. Ск. га вместе? 90 + 120 = 210(га)
Ответ: 210га.
— Какое решение вам понравилось больше, почему?
(Высказывают свое мнение)
— В математике способы, которые наиболее удобны и занимают при решении меньше времени, называют – рациональными.
Проблемная ситуация
— Не меняя условие задачи, измените вопрос задачи
Работа по обсуждению проводится в парах.
— На сколько га больше площадь, занятая сосной, чем елью?
. 5. Физкультминутка (1мин)
Чтобы на уроке все понимать, нужно про физкультминутку не забывать.
Раз – поднялись, потянулись
Два – нагнулись, разогнулись
Три – на пояс руки ставим
На четыре – так оставим
Пять – наклоны влево, вправо
Шесть – вздохнули, кисти рук встряхнули
Семь – присели
И на восемь – тихо сели.
6. Продолжаем работать в тетрадях по теме урока (5мин)
- Решение уравнений (стр158, №1018 а,б,в).
— Что значит решить уравнение?
(Решить уравнение – это значит найти все его корни или убедиться, что их нет)
— Что необычного в этих уравнениях?
( Они с дробными числами)
— Что неизвестно в первом уравнении?
(Уменьшаемое)
— Как найти уменьшаемое?
(Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое)
— Какой вывод можно сделать?
( Уравнения с дробями решаются так же, как уравнения с натуральными числами)
а) б) в)
(дополнительно, раздать на карточках)
Решить уравнения:
1) х + = 2) — р = 3) у — =
х = — р = — у = +
х = р = у =
Ответ: Ответ: Ответ:
Решение уравнений со скобками.
7. Самостоятельная работа со взаимопроверкой
8. Межпредметные связи (5мин)
— Ребята, а как называют найденное значение буквы в каждом из этих уравнений?
( Корень уравнения).
— А слово «корень» имеет одно или несколько значений?
(Оно является многозначным).
— Приведите примеры. …………….
— Я, пользуясь толковым словарём, подготовила для вас информацию.
— Сейчас вы зачитаете значения слова корень, и мы узнаем, какой предметной области принадлежат эти значения.
1) Корень – это подземная часть растения, служащая, для укрепления его в почве и всасывания из нее воды и питательных веществ. (биология, раздел — ботаника)
2) Корень – это внутренняя находящаяся в теле часть волоса, зуба, ногтя. (биология, раздел – анатомия)
3) Корень – это основная часть слова без приставки и суффикса. ( русский язык)
4) Корень – это значение буквы, при котором из уравнения получается верное числовое равенство. (математика)
9. Дроби вокруг нас. (Работа с сигнальными карточками)
Цель: проверить внимание, креативность мышления)
— Сегодня на уроке мы выполняли разные задания, но везде встречались обыкновенные дроби!
— А к обычной жизни они имеют отношения?
— Где, а может когда, мы сталкиваемся с дробями?
— ………
— Вот я точно знаю, что многие люди, очень часто просят исполнить их просьбу с помощью одной дроби.
— Какой?
½ — половины ……часто можно услышать: мне, пожалуйста, полчашки чая, полстакана воды, полтарелки супа и т. д.
Действительно, самая известная из дробей – это половина 1/2. И очень часто мы слышим слова с приставкой «пол» — полведра, полкилометра, полчаса и т.д.
И если мы понимаем, что означает дробь, мы легко можем найти часть целого.
Сейчас мы это и проверим.
10. Вопросы.
Но вначале повторим некоторые величины.
Вопросы.
Сколько в 1 часе минут? 60
Сколько в 1 метре см? 100
Сколько в сутках часов? 24
Сколько месяцев в году? 12
Сколько в 1 кг граммов? 1000
Сколько дней в неделе? 7
Напомню, что математику нельзя изучать, наблюдая, как это делает сосед.
Если вы согласны с утверждением – поднимите зеленую карточку
Нет – красную (какие ассоциации с этими цветами) Светофор
- Верно ли, что 1/10 часа – 6 минут (да)
- Верно ли, что ½ – половина (да)
- Верно ли, что 1/3 суток – 7 часов (нет)
- Верно ли, что 3/12 года – зимние месяцы (да)
- Верно ли, что 1/5 кг – 200 граммов (да)
- Верно ли, что ½ метра – 60 см (нет)
- Верно ли, что 1/7 недели – среда (да)
11. Исторический экскурс
Математика очень древняя наука, и, не зная прошлого этой науки, трудно понять её настоящее.
— Ребята, сегодня на уроке мы работали с обыкновенными дробями.
— А когда они возникли и как их называли раньше, вы мне можете ответить?
— _________________
— Мы живем в 21 веке, а дроби возникли в глубокой древности, за несколько тыс. лет до н.э. в древнем Вавилоне.
— А как их называли в те времена, вы узнаете если расставите дроби в порядке возрастания. (ломаные числа).
Только в18 в. дроби стали воспринимать как дробные числа. В разных странах учёные записывали их по – разному, пытаясь найти удобную запись. Современная запись дроби (с чертой) была введена лишь в 1202г. итальянским математиком Леонардо Фибоначчи и ею пользуются люди всей планеты, и это очень удобно.
12. Итоги урока.
Ребята, какие цели мы ставили в начале урока?
— Правила повторить,
— Знания по теме закрепить.
Достигли мы этих целей? — Да.
— Что нового узнали на уроке?
Интересное и меткое сравнение принадлежит Льву Николаевичу Толстому.
Он говорил, что «человек подобен дроби, числитель которой есть то,
что человек представляет собой, а знаменатель – то, что он о себе думает.
Чем большего мнения о себе человек, тем больше знаменатель, а значит меньше дробь.
Будьте объективны в своей самооценке.
— Предлагаю оценить свою работу на уроке.
— Говорит критерии оценки за урок.
Пять «+» — оценка 5
Четыре «+» — оценка 4
Три «+» — оценка 3
13. Домашнее задание.
№ 1.Карточка – задание (раскраска)
№ 2.Творческое задание: подготовить сообщение о возникновении дробей, пользуясь, интернет — ресурсами.
14. Рефлексия урока.
Если вы считаете, что материал был понятен, можно двигаться дальше, то наклейте розовое яблоко на оценочный лист.
Если вы считаете, что не достаточно усвоили материал, испытываете затруднения, то наклейте зеленое яблоко на оценочный лист.
Если вы считаете, что материал был не понятен, то наклейте желтое яблоко на оценочный лист.
Урок сегодня завершен,
Но каждый должен знать!
Упорство, знание и труд,
К успеху в жизни приведут!
Ведь, вы, молодое поколение – достойное будущее нашей великой России!
Спасибо за урок, до свидания!
Свой урок я строила в соответствии с ФГОС.
В содержание урока включила элементы обучения универсальным учебным действиям.
Тему и цель урока определяли сами ученики.
Учебная информация была привлекательна для детей.
Учебное время на уроке использовалось эффективно, запланированный объём выполнен.
На уроке у учащихся формировались новые понятия, повторяли и обобщали ранее изученный материал.
Считаю, что урок был проведён в доброжелательной рабочей обстановке.
Все поставленные цели и задачи достигнуты.
Что такое правила дроби? — Определение, факты и примеры
Что такое правила дроби?
Дробь : Дробь — это часть целого или совокупности, состоящая из числителя и знаменателя.
Пример : Если мы обслуживаем 1 часть торта с 8 равными частями, мы обслуживаем 1 ⁄ 8 торта.
Давайте посмотрим, как решать операции с дробями.
Сложение или вычитание дробей с одинаковым знаменателем
При сложении или вычитании двух дробей; нам нужно убедиться, что знаменатели совпадают.
Шагов :
Сложите или вычтите числители.
Знаменатель оставим прежним.
По возможности сократите ответ.
Пример : Решить 1 ⁄ 4 + 1 ⁄ 4
Пример : вычесть 1 ⁄ 4 из 3 ⁄ 4
Сложение или вычитание дробей с разными знаменателями:
Если знаменатели не совпадают:
Во-первых, сделайте их такими же
Затем сложите или вычтите одинаковые дроби с одинаковыми знаменателями.
Пример : Чтобы решить 1 ⁄ 4 + 1 ⁄ 2 , мы сначала сделаем знаменатели одинаковыми.
Мы меняем знаменатель 2 и делаем его равным 4, умножая его на 2. Однако нам нужно умножить числитель и знаменатель на 2, чтобы сохранить значение дроби неизменным.
Умножение 1 ⁄ 2 ✕ 2 ⁄ 2 = 2 ⁄ 4
Поскольку знаменатели совпадают, теперь мы можем сложить обе дроби.
Точно так же мы используем эти правила для вычитания.
Умножение дробей
Чтобы умножить две дроби, просто умножаем числители и знаменатели.
Пример :
2 ⁄ 3 ✕ 3 ⁄ 15 =?
Во-первых, упростим дробь 3 ⁄ 15 до наименьшего члена.
На дроби
При делении на две дроби:
Обратить вторую дробь, то есть поменять местами ее числитель и знаменатель, чтобы получить обратную величину.
Умножьте первую дробь на обратную величину второй дроби.
Пример :
Решение неправильных дробей:
Дроби, числитель которых больше знаменателя, называются неправильными дробями. Когда мы решаем неправильные дроби, результатом может быть смешанное число (целая дробь и правильная дробь).
Пример :
38 ⁄ 7 =?
- Разделите числитель на знаменатель.
38 ÷ 7 = 5 частных и 3 остатка
- Запишите ответ целиком.
5
- Затем запишите остаток над знаменателем.
5 3 ⁄ 7
Следовательно, 38 ⁄ 7 = 5 3 ⁄ 7
Таким образом, решая неправильную дробь 38 ⁄ 7 , получаем смешанное число 5 3 ⁄ 7
Интересные факты |
Почему дроби так сложно для студентов?
Как известно многим учителям и родителям, изучение различных операций дроби может быть трудным для многих детей.Сложна не концепция дроби — это различные ОПЕРАЦИИ с дробями: сложение, вычитание, умножение, деление, сравнение, упрощение, и т. Д.
И простая причина, по которой изучение различных операций с дробями оказывается трудным для многих студентов, — это способ, которым их обычно учат, и их количество. Просто посмотрите на количество правил , чтобы узнать о дробях!
| 1.Сложение / вычитание дробей — общие знаменатели | Сложите числители и используйте общий знаменатель |
| 2. Сложение / вычитание дробей — разные знаменатели | Сначала найдите общий знаменатель, взяв наименьшее общее кратное знаменателей. Затем преобразуйте все слагаемые, чтобы получить общий знаменатель. Затем добавьте, используя приведенное выше правило. |
| 3. Эквивалентные доли | Умножьте числитель и знаменатель на одно и то же число. |
| 4. Преобразование смешанного числа в дробное | Умножьте целую часть числа на знаменатель и добавьте числитель, чтобы получить числитель. Используйте общий знаменатель, как дробную часть смешанного числа. |
| 5. Преобразуйте неправильную дробь в смешанное число | Разделите числитель на знаменатель, чтобы получить целочисленную часть. Остаток будет числителем дробной части. Знаменатель тот же. |
| 6. Упростить дроби | Найдите (наибольший) общий делитель числителя и знаменателя и разделите их на него. |
| 7. Умножение на дроби | Умножьте числители и знаменатели. |
| 8. Дробное деление | Найдите величину, обратную делителю, и умножьте на нее. |
| 9. Сравнение дробей | Преобразуйте дроби так, чтобы у них был общий знаменатель.Затем сравните числители. |
| 10. Преобразование дробей в десятичные | Разделите в столбик или калькулятор. |
Если ученики просто попытаются запомнить эти правила, не зная, откуда они пришли, правила , вероятно, будут казаться бессмысленными джунглями . Они, вероятно, не будут иметь никакого отношения к операции, но вместо этого похожи на «магию» или случайную игру, когда вы умножаете, делите и делаете разные вещи с числителями и знаменателями, чтобы найти ответ.
Затем ученики могут стать слепыми последователями правил, подбрасывая числа туда и сюда — и получая ответы, о которых они понятия не имеют, разумны они или нет. Кроме того, эти правила очень легко забыть или запомнить неправильно — особенно через 5-10 лет.
Решение: визуальные модели
Вместо простого представления правила (как это делают многие книги) лучше использовать визуальные модели или манипуляторы . Таким образом, дроби становятся для ученика чем-то реальным и конкретным, а не просто числами, не имеющими значения.Студент сможет оценить ответ перед вычислением, оценить разумность окончательного ответа и выполнить множество простейших операций мысленно, не применяя сознательно никаких «правил».
Конечно, учебники ДЕЙСТВИТЕЛЬНО показывают визуальные модели для дробей, и они ДЕЙСТВИТЕЛЬНО показывают один или два примера того, как определенное правило связано с картинкой. Но этого недостаточно! Нам нужно, чтобы дети решали множества задач, используя либо визуальные модели, либо дробные манипуляторы .
Другой способ — попросить их НАРИСАТЬ дробные изображения для проблем. Таким образом ученики сформируют мысленную визуальную модель и смогут продумывать картинки.
Например, в этом видео показан визуальный метод для эквивалентных дробей: метод , разделение частей на на определенное количество новых частей:
Если вы продумаете картинки , вы легко увидите необходимость умножения или деления числителя и знаменателя на одно и то же число.Но прежде чем озвучивать это правило, лучше, чтобы дети получили много практического опыта с дробными картинками , которые они нарисовали сами. Они могут ВЕСЕЛО разделить части дальше (или, наоборот, объединить части вместе)! Они могут даже найти правило САМИ — и это будет иметь смысл. Если позже они забудут правило, они всегда могут вернуться к мысли о разделении на части и заново открыть его.
Другой пример — это тема сложения непохожих дробей (см. Видео).Учитель может показать, как части в дробях нужно разделить дальше, чтобы все они были ОДНОГО ВИДА частей, — а затем мы можем сложить.
Когда вы впервые узнаете об этом (скажем, в 4 классе), нет необходимости использовать термин «наименьший общий знаменатель». Можно просто использовать картинки или манипуляторы. Затем в 5-м классе ученики будут складывать непохожие дроби, используя манипуляторы или рисуя картинки. Через некоторое время некоторые студенты могут обнаружить правило об общем знаменателе, или, другими словами, о том, на какие части дроби нужно разбить на части.В любом случае, они наверняка лучше запомнят правило, если смогут сами проверить его на многочисленных наглядных примерах.
Я не говорю, что правила не нужны — потому что они есть. Вы не можете пройти через алгебру, не зная реальных правил операций с дробями. Но если на начальных этапах широко использовать визуальные модели, правила станут более понятными, и если через 10 лет вы забудете правила, вы все равно сможете «посчитать» с картинками в уме и не рассматривать дроби. как то, что вы просто «не можете делать».
Вам нужна помощь с дробями?
Во-первых, посмотрите мои бесплатные видео по операциям с дробями:
Видео с дробями, часть 2
(упрощение, умножение и деление дробей; дроби в десятичные дроби; соотношения и дроби; дробная часть группы объектов)
Во-вторых, эти два рабочих текста помогут вам еще больше! Оба они объясняют операции дроби, используя визуальную модель пирога, и позволяют ученикам достаточно практиковаться с визуальными упражнениями, чтобы они понимали концепции.Лучше всего для 5-го класса, когда обычно изучаются дробные операции:
Math Mammoth Fractions 1
Самообучающийся рабочий текст, который охватывает дроби, смешанные числа, эквивалентные дроби, сложение и вычитание одинаковых дробей и непохожих дробей, сложение и вычитание смешанных чисел, сравнение дробей и поиск дробной части группы.
Математические дроби мамонта 2
Самообучающийся рабочий текст, продолжение к Math Mammoth Fractions 1. Охватывает упрощение дробей, умножение и деление дробей и смешанных чисел, преобразование дробей в десятичные числа, а также соотношений и дробей.
Я также продаю рабочий текст с дробями для 2-4 классов, Введение в дроби, и рабочий текст для 6 класса, Дроби и десятичные дроби 3.
Что делать, когда студенты борются с дробными операциями
Многие студенты испытывают трудности с операциями с дробями. И точно так же у многих взрослых (родителей, учителей, руководителей школ) возникают вопросы о «новом» способе выполнения математики.
Есть смысл, что некоторые видят в концептуальной математике решение проблемы, которой не существует.Проще (по крайней мере, в краткосрочной перспективе) просто научить трюкам с дробными операциями. Но пределы этих стратегий значительны.
Другой преподаватель (назову его Джим) недавно спросил меня о концептуальной математике. Он хотел знать, «в чем дело» с Common Core. Действительно ли студентам нужно делать все эти рисунки? Я ответил на его вопрос, задав ему вопрос.
«Сколько будет 1/4 умножить на 2/3?»
«Я помню, как делал это … разве мне не нужно находить общий знаменатель?»
Я не хочу клеветать на Джима.Он технический директор, оказавший значительное влияние на свою школу. Тот факт, что он плохо разбирается в математике в пятом классе, не удерживал его в жизни.
Но этот обмен высвечивает несколько вопросов о традиционном подходе к математике. Во-первых, то, что Джим узнал в школе, не прижилось. Его учили механическим процедурам без понятий. Когда спустя годы он попытался вспомнить процедуру, он не знал, что использовать.
Его подход также показывает, что он не учитывал размер чисел.Или что значит умножить дробь на дробь.
Что еще хуже, он даже не думал о решении проблем, чтобы найти ответ. Он полез в банки памяти в поисках алгоритма. Когда он не мог найти ни одного, ему больше некуда было идти. Его карьерный успех показывает, что он обладает способностью решать проблемы. Но он не связывал эту способность с математикой.
Фракционные операции представляют собой уникальные проблемы
Эта проблема соединения концепций с процедурами является общей для многих математических стандартов.Но они особенно очевидны при операциях с дробями. Одна из причин заключается в том, что многие студенты начинают операции с дробями, прежде чем действительно понимают, что такое дробь. Во-вторых, дроби менее интуитивны, чем целые числа. Не всегда понятно, что происходит, когда мы убираем 1/4 из 2/3. Или когда мы разделим 7 на 1/6.
Я заметил тенденцию среди школ, которые используют общие планы обучения, которые идут вместе с их учебниками. Учителя средних и старших классов сетуют на трудности своих учеников с операциями дроби.Они задаются вопросом, почему учителя начальной школы никогда не учили дробям. В конце концов, дроби должны быть охвачены с 3 по 5 класс.
Реальность такова, что эти учителя обучали дробным операциям. Проблема в том, что студенты так и не поняли, что они делают. Они запоминали трюки достаточно долго, чтобы пройти испытание. К следующему учебному году их воспоминания об операциях с дробями были такими же далекими, как и у моего друга Джима.
Фракции перед фракционными операциями
Многие преподаватели хотели бы просто забыть о дробях после 5 класса.Но дроби обеспечивают важную основу для продвинутой математики.
Десятичные дроби и проценты являются типами дробей. Соотношение в средней школе и стандарты пропорции также основаны на дробях. Не говоря уже о наклоне (подъем над спуском ). В средней школе алгебра, статистика и исчисление включают рациональные числа. (Рациональное число — это любое число, которое может быть выражено дробью).
Первым шагом к овладению понятиями дробей является понимание числителей и знаменателей.Знаменатель показывает, на сколько частей делится целое. Числитель говорит нам, сколько таких фигур у нас есть. В какой-то момент (обычно около 5 класса) они узнают, что дробь также можно рассматривать как частное. Результат деления числителя на знаменатель.
Операции с дробями работают как операции с целыми числами
Когда учащиеся поймут дроби, они смогут работать с дробями так же, как с целыми числами. То есть, если студенты понимают, как работают операции.
Добавление 1/5 к 2/5 дает 3/5. Чтобы убрать 1/8 от 1/4, нужно разбить 4-ю на 8-е — точно так же, как взятие 3 из 62 требует разбиения десятки. Умножив 4/7 на 1/2, вы получите 2/7 — половину того, с чего вы начали.
Студенты могут со временем сэкономить время, используя алгоритмы работы с дробями. Алгоритмы также позволяют им работать с более сложными числами. Сложно создать визуальную модель 29/1256, разделенных на 15/72.
К сожалению, многие студенты изучают алгоритмы, не понимая, что означает операций с дробями.У этого подхода есть несколько недостатков. Во-первых, когда ученик не может придать значение алгоритму, он не сохранит его надолго. Кроме того, они не понимают, какой алгоритм использовать. (Вот почему Джим считает, что для умножения дробей ему нужен общий знаменатель.)
Но есть еще большая проблема с алгоритмами без концепций . Учащиеся не развивают способность видеть математику, которая их окружает. Они не признают математику как язык или изучение пространства и количества.Математика — это некрасиво и не искусство.
Вместо этого он становится набором «математических фактов», случайных правил и секретных символов.
Обучайте понятиям дробей с помощью трех транспортных средств
Я призываю каждого учителя математики начинать каждый год с обучения трем средствам концептуальной математики. Три машины — это масштабные модели, числовые предложения и задачи со словами.
Я называю их транспортными средствами, потому что, когда студенты научатся водить их, они смогут пройти гораздо больше в остальную часть года.Джон Ван де Валль популяризировал идею о пяти способах представления математической идеи. Первый автомобиль, Scale Models, соответствует двум его представлениям: манипулятивным и визуальным моделям. Второе средство, числовые предложения, соответствует символическим представлениям. И третье средство, проблемы со словами, соответствует ситуациям реального мира.
Его пятое представление, устный язык, всегда казалось немного неуместным. Конечно, это ценное представление.Но при устном обсуждении математики вы обычно все еще обсуждаете одну из других операций. Тем не менее, у учащихся есть широкие возможности для обсуждения на уроке семинара «Три машины».
Автомобиль 1: Масштабные модели
Каждый раз, когда я начинаю работать с дробями с новой группой, я прошу всех нарисовать мне картинки. «Покажи мне, как выглядит 1/2. Покажи мне 3/4 ». Многие учителя шокированы, увидев, как их ученики изо всех сил пытаются нарисовать эти общие дроби.
Проводя семинары, я регулярно удивляюсь тому, сколько учителей математики испытывают трудности с этими задачами.Как и наш друг Джим, эти взрослые часто очень успешные учителя. Они не могут создать эти модели
не по своей вине. Просто многих не учили моделировать с помощью математики, когда они были в школе.
Визуальные модели могут использоваться как в качестве обучающего, так и в качестве инструмента оценки. Если ученик может сказать вам, что 4 раза 1/5 равно 4/5, попросите его нарисовать это. Если они не могут нарисовать картину, они не понимают концепции.
Существует несколько правильных способов использования визуальных моделей, но есть некоторые общие правила.Чтобы быть визуальной моделью, ее нужно нарисовать в масштабе, иначе это будет просто рисунок. Кроме того, модель должна четко отображать начальные значения и операции, а не только результат. Если кто-то другой может превратить вашу визуальную модель в другое представление, это, вероятно, хорошо.
Автомобиль 2: числовые предложения
Числовое предложение — это полное математическое утверждение. Каждое из них состоит из двух выражений по обе стороны от символа сравнения, например от знака равенства. Уравнения и неравенства являются примерами числовых предложений.Хотя Стивен Колбер выступил против них, опытные педагоги признают их ценность.
Числовые предложения — еще один отличный способ обучения концептуальной математике, включая операции с дробями. Манипулирование выражениями и уравнениями может помочь учащимся понять, как взаимосвязаны математические стандарты.
Студентов следует научить правилам работы с уравнениями. Например, им нужно показать, что каждый шаг ниже предыдущего. Учителя также должны научить учеников использовать только один знак равенства в каждой строке.Затем они могут манипулировать числовыми предложениями, чтобы открывать новые концепции и связи.
Один из моих любимых практических уроков математики включает доказательство числовых предложений. Студентам дается серия числовых предложений. Вместо того, чтобы просто «решить для x», они должны определить, истинно это предложение или ложно. С закрытым числовым предложением (без переменных) предложение просто истинное или ложное. Предложения с открытыми числами могут быть «всегда верными», «иногда верными» или «никогда не верными».
Это задание заставляет учащихся изучить концепции, лежащие в основе операций с дробями.Даже студентам, знакомым с алгоритмами, все равно нужно объяснять, почему их решение работает.
Автомобиль 3: Проблемы со словами
Задачи со словом могут помочь учащимся увидеть связь между математикой и реальным миром. Правильная задача со словом в нужное время может сделать абстрактную математику более конкретной и легкой для понимания.
Я помню студента, которого я учил, который плохо разбирался в математике, но любил карты покемонов. Я попросил его решить задачу на доске: «Если вы уберете 1/3 от 120, сколько останется?» Он встал и уставился на проблему, не зная, с чего начать.
Я попросил его представить, что у него есть персонаж Покемон, у которого в начале 120 очков здоровья. Если персонаж потерял 1/3 своих очков, сколько осталось. Он сразу ответил: «80 очков».
Одна из моих любимых задач со словами связана с кувшином, содержащим 25 чашек лимонада. Если налить лимонад в количестве 1/2 стакана, сколько образцов мы сможем налить? Прелесть здесь в том, что это реальный пример деления на дробь.
Разделение на дроби — сложная концепция, потому что большинство студентов делятся на определенное количество групп.Трудно представить себе разделение на «1/2 группы». (Вот почему многие студенты делают ошибку, вместо этого делят на два). Но группы из 1/2 имеют больше смысла. Студенты также могут увидеть связь между делением и повторным вычитанием.
К сожалению, не все задачи со словами упрощают сложные идеи. Многие студенты и учителя считают задачи со словами сложными и пугающими. Часто это происходит потому, что задачи со словами требуют от учащихся понимания концепций. Они не могут выполнить алгоритм, если не знают, куда поставить числа из истории.
Но так же часто студенты теряются на всех этапах, необходимых для решения словесной задачи. Графические органайзеры в этом случае могут стать незаменимой опорой.
Творчество, сотрудничество и концептуальное обучение
Предоставление студентам возможности изучить операции дроби посредством практических занятий может повысить как успеваемость, так и вовлеченность студентов. Чтобы узнать больше, найдите советы и задайте вопросы в нашей группе в Facebook.
Погрузиться в эти практические занятия не всегда легко.Наше практическое руководство по дробям — это бесплатная загрузка , которая включает в себя все необходимое, чтобы начать обучение операциям с дробями с помощью запросов. Он включает планы уроков и воспроизводимые материалы, которые вы можете опробовать в классе завтра.
ПОЛУЧИТЕ РУКОВОДСТВО ПО ФРАКЦИЯМ
5-й класс — Блок 5 — Сложение и вычитание дробей |
Расчетное время: 5-6 недель 5 января 2016 —
| Следующий ресурс можно использовать с несколькими учебными целями для этого модуля: 5_M_2_A: складывать и вычитать дроби с разными знаменателями.(R) (5.NF.1) Diffy Interactive Subtraction Game — Choose Fraction (5.NF.1) IXL Online Many Interactive Activities — Прокрутите вниз до 5.NF.1 Satis-Fraction Выберите » Вычислите «затем« Трудно » — сложение / вычитание дробей (5.NF.1) Черный ящик 2 Трехактное мероприятие по решению математических задач для ваших учеников (5.NF.1) Kakooma Basic 4 Головоломки с добавлением дробей Грег Tang Color Masters (5.NF.1) Kakooma Basic 4 Pro Пазлы с добавлением дробей Greg Tang Color Masters (5.NF.1) Kakooma Basic 5 Пазлы с добавлением дробей Greg Tang Color Masters (5.NF.1) Kakooma Basic 5 Pro Пазлы с добавлением дробей Greg Tang B / W Masters (5.NF.1) Kakooma Moderate 6 Пазлы с добавлением дробей Greg Tang Color Мастера (5.NF.1) Kakooma Moderate 6 Pro Пазлы с добавлением фракций Greg Tang Color Masters (5.NF.1) Kakooma Moderate 7 Пазлы с добавлением дробей Greg Tang Color Masters (5.NF.1) Kakooma Moderate 7 Pro Пазлы с добавлением дробей Greg Tang Color Masters (5.NF.1) Kakooma Advanced 9 Пазлы с добавлением дробей Greg Tang Color Masters (5.NF.1) Kakooma Advanced 9 Pro Пазлы со сложением дробей G. Tang ColorMasters (5.NF.1) Держитесь! Рабочий лист добавления дробей (5.NF.1) 5_M_2_B: Интерпретируйте дробь как деление числителя на знаменатель (a / b = a ÷ b), и решают текстовые задачи с делением целых чисел это может привести к ответам в виде дробей или смешанных чисел. (R) (5.NF.3) 5_M_2_C: Преобразование между эквивалентными смешанными числами и неправильными дробями.(R) (5.NF.1)
5_M_2_D: сложение и вычитание смешанных чисел с разными знаменателями. (R) (5.NF.1)
5_M_2_E: Решите задачи со словами, включающие сложение и вычитание дробей и смешанных чисел и определите, является ли ответ разумным. (R) (5.NF.2) IXL Online Многие интерактивные действия — Прокрутите вниз до 5.NF.2 |
Фракции 5-го класса | Стимуляция и контрольный список
Дроби.Большинство либо их любят, либо ненавидят. У меня с ними отношения любви / ненависти. Мне нравятся модели и то, как навыки иногда можно сделать довольно конкретными. Мне не нравится, как все навыки взаимно дополняют друг друга и все навыки, которые ученики должны освоить, чтобы решить одну задачу. К тому времени, когда ученики перейдут в 5-й класс, если у них возникнут пробелы в понимании их фракций, это станет огромной проблемой. В этом посте я поделюсь контрольным списком, который помог мне разбить навыки дроби в 5-м классе и встроенные навыки из предыдущих оценок.
Когда я впервые начал планировать нашу единицу измерения фракций, я потратил некоторое время на разбиение наших стандартов на утверждения «Я могу». Однако я пошел дальше и также написал I Can Statements для всех надоедливых встроенных навыков. (Вы знаете те навыки, которые дети должны учиться в 5-м классе, уже зная… 😉) Конечный результат был довольно пугающим (не собираюсь лгать)! Взгляните на все эти навыки…
- Я могу понять, что такое дроби, назвать их и нарисовать.
- Я могу использовать умножение и деление для получения эквивалентных дробей.
- Я могу назвать все множители для заданных чисел и использовать эти множители для упрощения дробей.
- Я могу создавать кратные для заданных чисел и использовать эти кратные для создания эквивалентных дробей с тем же знаменателем.
- Я могу сравнить дроби, сделав сначала одинаковые знаменатели.
- Я могу складывать и вычитать дроби с одинаковыми знаменателями.
- Я могу преобразовывать смешанные числа в неправильные дроби и преобразовывать неправильные дроби в смешанные числа.
- Я могу складывать дроби с разными знаменателями, предварительно сделав знаменатели одинаковыми.
- Я могу переименовать неправильную дробь в смешанное число после добавления дробей.
- Я могу вычесть дроби с разными знаменателями, сделав знаменатели одинаковыми.
- Я могу решать задачи со словами, требующие сложения или вычитания дробей.
- Я могу сложить смешанные числа с разными знаменателями, сделав знаменатели одинаковыми.
- Я могу вычесть смешанные числа с разными знаменателями, сделав знаменатели одинаковыми.
- Я могу заимствовать из целого числа при вычитании смешанных чисел.
- Я могу убедиться, что мой ответ упрощен или изложен в самой простой форме.
- Я умею решать задачи со словами, требующие сложения или вычитания смешанных чисел.
- Я умею умножать целые числа на дроби.
- Я умею умножать дроби на дроби.
- Я могу умножать смешанные числа, превращая их в неправильные дроби.
- Я могу найти площадь квадрата или прямоугольника, умножая дроби и смешанные числа.
- Я могу решать задачи со словами, требующие умножения дробей.
- Я умею делить целые числа и единичные дроби.
- Я умею решать задачи со словами, требующие деления целых чисел и единичных дробей.
- Я могу ответить на вопросы о дробях, отображаемых на линейном графике.
- Я могу определить, как умножение влияет на числа.
- Я могу сравнить произведения двух задач умножения, не решая их.
После того, как я составил список (и избавился от чувства подавленности!), Я действительно почувствовал себя подготовленным, организованным и готовым к обучению навыкам.Я делал копии для своих детей, которые они вклеивали в свои тетради по математике. Каждый раз, когда мы изучаем (или пересматриваем) новый навык, они вычеркивают его из списка. Время от времени мы перечитываем список, чтобы напомнить им обо всем, что они узнали и должны помнить о применении к задачам с дробями.
Вот фотография, сделанная пару недель назад.
Это определенно помогает мне сосредоточиться и убедиться, что я обучаю и оцениваю все стандарты и встроенные навыки.
Щелкните здесь или на изображении ниже, чтобы получить копию контрольного списка.
Информация о стимуляции фракций 5-го класса
Контрольный список составлен в точном порядке и последовательности, в которых я обучаю своих студентов навыкам, поэтому он также является контрольным списком и подробным указанием темпа. Для получения дополнительной информации о том, как я продвигаю свои математические стандарты в 5-м классе, щелкните здесь.
Что касается времени, которое я выделяю на дроби, я трачу около 8 недель, в зависимости от потребностей моих учеников. Я провожу целую неделю, просматривая все встроенные навыки 3-го и 4-го классов из контрольного списка, прежде чем перейти к навыкам дробей 5-го класса.Это позволяет мне обеспечить прочную основу, и мне приходится меньше переучивать, потому что я трачу это время заранее.
Вам нужно больше ресурсов для четвертого или пятого класса для вашего класса?
Щелкните по ссылкам ниже, чтобы просмотреть несколько рекомендуемых ресурсов или статей для фракций.
Мини-буклет «Обзор дроби в четвертом классе»: я использую этот ресурс из моего магазина TeachersPayTeachers, прежде чем преподавать навыки дробного анализа в пятом классе. Это позволяет мне быстро проверить навыки фракции 4-го класса и убедиться, что у моих учеников есть необходимая концептуальная основа.
матов с дробями: я использую эти бесплатно загружаемые маты с дробями, чтобы еще больше поддержать моих учеников, когда они складывают и вычитают дроби с разными знаменателями.
Четыре способа составить общие знаменатели: в этом сообщении в блоге рассказывается о четырех способах, которыми я учу своих студентов составлять общие знаменатели (включая бесплатную распечатку).
Шоколадные тематические математические задачи на дроби: эти задачи в моем магазине TeachersPayTeachers идеально подходят для занятия дробной практикой с аппетитной шоколадной темой.
Вычитание смешанных чисел с ресурсом перегруппировки: этот ресурс TpT посвящен теме пиццы и действительно помогает моим ученикам концептуально понять перегруппировку со смешанными числами.
Вычитание смешанных чисел с перегруппировкой с использованием манипуляторов: в этом сообщении в блоге рассказывается о трех способах, которыми вы помогали своим ученикам вычитать смешанные числа более конкретным способом, используя манипуляторы.
Умножение и деление дробей: когда вы будете готовы перейти от сложения и вычитания дробей, это идеальный универсальный ресурс для умножения и деления на дроби.
Бесплатный обзор баскетбольной фракции — в этом сообщении в блоге представлены подробности и бесплатная распечатка увлекательного обзора баскетбольной фракции, который понравится вашим ученикам!
Бесплатная игра Jenga Fraction — возьмите бесплатные распечатки, чтобы просмотреть дроби с помощью цветных блоков Jenga в этом посте. Вашим ученикам это понравится!
Free Fraction Dice Centre — Хотите, чтобы ваши ученики могли пройти несколько игр с очень низким уровнем подготовки, чтобы проверить различные навыки дроби? В этом посте делятся несколько!
Class 5 Fractions — основы, задачи и примеры решения
- Что такое дробь? Дробь — это числовая величина, которая не является целым числом.
Например,
½ — это дробь от
1 в числителе и
2 в знаменателе
Дроби с одинаковым знаменателем называются дробями.
Например,
½, 3/2, 5/2, 7/2 — это
все как дроби.
- Дроби, имеющие разные знаменатели, называются в отличие от дробей.
Например,
½, 2/3, ¾, 4/5,
не похожи на дроби
- Дробь, числитель которой меньше знаменателя, называется правильной дробью.
Например,
8/9, 7/8, 6/7, 5/6
— все правильные дроби.
- Дробь, числитель которой больше знаменателя, называется неправильной дробью.
Например,
3/2, 4/3, 5/4, 6/5
— неправильные дроби.
Дроби, которые представляют одинаковые или равные значения, называются эквивалентными дробями
.
Например,
1/3, 2/6, 3/9, 4/12
— все эквивалентные дроби
ПРИМЕР 1: Найдите долю затененной и незатененной части.
РЕШЕНИЕ: Общая часть = 8 Доля затененной части = 3/8 Доля незатененной части = 5/8
ПРИМЕР 2: Найдите доли красных шаров, зеленых шаров и синих шаров.
РЕШЕНИЕ: Общее количество шаров = 10 Количество красных шаров = 4
Доля красных шаров = 4/10 = 2/5
Доля зеленых шаров = 5/10 = ½
Доля синих шаров = 1/10
Дробь как деление
- Любую дробь можно выразить как деление, записав ее числитель как делимое, а знаменатель как делитель
Числитель / знаменатель
= Дивиденд ÷ Делитель
= Дивиденд / делитель
ПРИМЕР 1: Запишите 1 ÷ 2 как дробь.
РЕШЕНИЕ: ½
ПРИМЕР 2: Запишите 2/3 как деление.
РЕШЕНИЕ: 2 ÷ 3
Для преобразования смешанного нет. на неправильную дробь и наоборот
- Чтобы преобразовать смешанное число в неправильную дробь, умножьте частное на делитель и сложите произведение с остатком в числителе. Знаменатель будет содержать делитель.
- Чтобы преобразовать неправильную дробь в смешанное число, разделите числитель дроби на знаменатель.Запишите частное как целое число. Остаток в числителе и делитель в знаменателе.
Поиск и проверка эквивалентной дроби
- Чтобы найти дробь, эквивалентную данной дроби, разделите или умножьте числитель или знаменатель на то же число. (кроме нуля)
- Чтобы проверить эквивалентные дроби, нам нужны две эквивалентные дроби.
РЕШЕНИЕ: 2×4 = 8 3X3 = 9 8 ≠ 9
Значит, дроби не равны.
Найдите большую дробь!
Чтобы найти дробь в ее наименьшем члене
- Дробь находится в младшем члене, если у числителя и знаменателя нет общего множителя, кроме 1.
- Есть два метода нахождения дроби в наименьшем члене. Это:
Метод 1:
Разделите числитель
и знаменатель на их общий множитель
, пока не останется
только с общим множителем 1
Метод 2:
Разделите числитель
и знаменатель данной дроби
на их HCF.
Чтобы найти дробную часть числа или количества
- Разделите число на знаменатель. Затем умножьте полученное частное на числитель.
ПРИМЕР 1: В группе 120 детей. 4/5 из них — девушки. Найдите количество мальчиков.
Количество мальчиков = (120-96) = 24
ПРИМЕР 2: Найдите 1/4 года в месяцах.
РЕШЕНИЕ: В году 12 месяцев.
¼ X 12 = 3 месяца [ANS]
Сравнить дроби непохожие
- Сначала найдите НОК знаменателей данных дробей.
- Затем преобразуйте непохожие дроби в эквивалентные одинаковые дроби с общим знаменателем НОК.
- Сравните одинаковые дроби.
Преобразовать смешанные дроби
в неправильные дроби, чтобы
сравнить их.
Для сложения / вычитания отличных дробей
- Найдите НОК знаменателя дроби непохожей.
- Затем преобразуйте непохожую дробь в эквивалентную подобную дробь с общим знаменателем НОК.
- Сложить / вычесть полученную подобную дробь.
ПРИМЕР 1: Сложить / вычесть ½ и / из 1/6.
РЕШЕНИЕ: НОК 2 и 6 равно 2×3 = 6 2 | 2,6 1,3
- Когда произведение двух дробей равно 1, мы говорим, что каждая дробь является обратной или мультипликативной обратной величиной другой.
Деление на дроби
- Деление — повторное вычитание.
- Деление на дробь аналогично умножению на обратную.
0 не имеет обратного.
Обратное значение 1 равно 1.
0, деленное на любое ненулевое число = 0
Попрактикуйтесь в ответах на эти вопросы
Резюме
- НОК знаменателей можно найти только при сложении или вычитании разнородных дробей.
- При умножении дробей мы можем менять их порядок, но произведение остается прежним.(коммутативная собственность)
- Если дробь умножается на 0, произведение всегда равно нулю.
- Если дробь умножается на 1, получается та же дробь.
- Дробь находится в младшем члене, когда единственный общий множитель между числителем и знаменателем равен 1
- Если какая-либо дробь представляет собой смешанное или целое число, измените ее на неправильную функцию и затем умножьте.
фракций керна 4-го сорта
4.NF.A.2 Сравните две дроби с разными числителями и разными знаменателями, например, путем создания общих знаменателей или числителей, или путем сравнения с эталонной дробью, такой как 1/2. Общие основные задания по математике по классам. Математические Олимпийские Игры Числа и Операции — Дроби Смерть в Десятичные Дроби Игры Дроби от Zeebo Visual Fractions Tutorial Умножение модели области с использованием свойства распределения. В приложении Varsity Tutors есть бесплатные ресурсы Common Core по математике для 4-го класса, которые организованы по концепциям, поэтому легко найти нужный ресурс, когда он вам нужен.Просмотрите список общих основных стандартов по математике для 4-го класса. Нажмите на заголовок общей основной темы, чтобы просмотреть все доступные рабочие листы. Задайте тон для эффективного обучения с помощью наших распечатываемых рабочих листов Common Core с соответствующими упражнениями как по математике, так и по английскому языку, отвечающим потребностям учащихся от детского сада до восьмого класса. Рождественские общие математические головоломки для четвертого класса. 4.NF.1. Здесь вы найдете все ресурсы для четвертого класса, которые помогут вам в преподавании и изучении математики. Понимание десятичных чисел распространяется на многие другие понятия, такие как измерение и время.Операции и алгебраическое мышление. Используйте этот принцип, чтобы распознавать и генерировать эквивалентные дроби. Найдите игры, видео и задания, соответствующие общепринятым государственным стандартам по математике. Общая основная учебная программа по математике для 4 класса. Мы предлагаем более 50 000 уникальных вопросов. Дети 4-го класса знакомятся с понятиями множителей, кратных и простых чисел. См. Стандарты фракций, показанные здесь по классам. Начните обучение математике с помощью коллекции, состоящей из планов уроков, заданий, рабочих листов, видео и приложений, созданных для улучшения и закрепления математических концепций четвертого класса.Обучение дробям в соответствии с общими базовыми стандартами H. Wu c Hung-Hsi Wu 2013 5 августа 2011 г. (с изменениями от 8 февраля 2014 г.) Содержание Предисловие 2 3 класс 5 4 класс 17 5 класс 33 6 класс 59 7 класс 80 Я очень благодарен Дэвиду Коллинзу и Ларри Фрэнсису за очень обширные исправления. Некоторые числа больше других; дети учатся этому рано. Это национальный стандарт общей основной математики, который ваша школа может иметь больше, но это минимальные ожидания от федерального правительства.Эта коллекция ресурсов для общих основных стандартов математики 4-го класса предназначена для различных стилей обучения, от практического обучения до лекций или игр. Признайте, что сравнения действительны только тогда, когда две дроби относятся к одному и тому же целому. Общие основные государственные стандарты 4-го класса … 4.NF.1 Объясните, почему дробь a / b эквивалентна дроби (n × a) / (n × b), используя визуальные модели дробей, обращая внимание на то, как число и размеры частей различаются, хотя сами две фракции имеют одинаковый размер.Получите бесплатный доступ к распечатываемым рабочим листам Common Core. В этом видео рассказывается о сложении и вычитании дробей с использованием простых чисел для нахождения общего знаменателя. Бесплатные практические вопросы для Common Core: математика для 4-го класса — построение дробей из дробных единиц. 4.NF.2. Практика математических навыков для 4-го класса. 4.NF.A.2 Сравните две дроби с разными числителями и разными знаменателями, например, создав общие знаменатели или числители, или сравнив с эталонной дробью, такой как 1/2. [4-g-1] Геометрия: рисуйте и идентифицируйте линии и углы, а также классифицируйте формы по свойствам их линий и углов.Общие основные рабочие листы и действия для 4.NF.2 / Число и операции — Дроби / Расширение понимания эквивалентности и упорядочения дробей. Одноэтапные задачи Недостающие факторы — факты к 12 свойствам умножения Задачи со словами — оценка произведений Умножение двузначных словесных задач на двузначные числа Рабочие листы по общей основной математике на основе оценок для детского сада (KG), класс-1, класс-2, класс -3, 4-й, 5-й и 6-й класс повышают способность ученика применять математику к проблемам реального мира, концептуальное понимание, беглость процедур, навыки решения проблем, критически оценивать рассуждения или готовить учеников к изучению математики в последующие ступени обучения.4.NF.B.3.A Под сложением и вычитанием дробей следует понимать соединение и разделение частей, относящихся к одному целому. 4.NF.1 Объясните, почему дробь a / b эквивалентна дроби (n × a) / (n × b), используя модели визуальных дробей, обращая внимание на то, как количество и размер частей различаются, даже если эти две сами фракции одинакового размера. Общие основные математические стандарты — MathScore для 4-го класса соответствует Общим основным математическим стандартам для 4-го класса. В соответствии с Общими государственными стандартами по математике, обучение дробям распространяется на классы с 3 по 6.В настоящее время на EngageNY доступны учебные материалы на весь год для классов Prekindergarten до 12 класса по математике и Prekindergarten до 12 класса в… Рабочие листы Common Core Multiplication 1,80 доллара США за 58 рабочих листов Common Core для печати. Выполняйте общие математические задачи для четвертого класса и упражнения по сложению, вычитанию, счету и сравнению, разметке, измерению и геометрии, используя забавные рабочие листы в Интернете. / Сравните две дроби с разными числителями и разными знаменателями, e.g., путем создания общих знаменателей или числителей, или путем сравнения с эталонной дробью, такой как 1/2. Так что спросить, какая из двух дробей больше, и расположить два набора дробей по порядку — разумные задачи. Инициатива Common Core, утвержденная государством, от Министерства образования США. Под дробью a / b с a> 1 понимается сумма дробей 1 / b. Общие основные государственные стандарты. Каждый из этих печатных и бесплатных общих рабочих листов тщательно разработан для учащихся 2, 3, 4, 5, 6, 7 и 8 классов. В 4 классе дети также узнают о десятичных числах.SplashLearn — это отмеченная наградами программа обучения математике, которую используют более 30 миллионов детей для увлекательной математической практики. Практикуйте математику и английский язык с легкостью с помощью соответствующих классу рабочих листов, которые соответствуют Общим основным государственным стандартам. Математика для 4-го класса Чтобы помочь преподавателям внедрить Common Core, Департамент образования штата Нью-Йорк предоставляет модули учебных программ по английскому языку и математике P-12, которые школы и округа могут принять или адаптировать для местных целей.Эти ресурсы организованы по математическим направлениям и относятся к конкретной математике Common Core … Вашим ученикам надоело решать одни и те же старые математические задачи? 4.NF.B.3.B Разлагает дробь на сумму дробей с одинаковым знаменателем более чем одним способом, записывая каждое разложение с помощью уравнения. Просмотрите математические навыки Академии Хана по стандарту Common Core. Объясните, почему дробь a / b эквивалентна дроби (n × a) / (n × b), используя модели визуальных дробей, обращая внимание на то, как количество и размер частей различаются, даже если сами две дроби одинаковы. размер.Конкретные идеи и стратегии уроков по предметной области. Рабочие листы и распечатки по дробям для четвертого класса Изучение основных правил дроби, например, две половины составляют одно целое, а две четверти составляют половину, обычно не является слишком сложной задачей для четвероклассников. Эти ресурсы по математическим стандартам четвертого класса основаны на Общих государственных стандартах четвертого класса и помогут вашим детям подготовиться к переходу в пятый класс. Приведенная ниже информация включает в себя ожидаемые результаты обучения математике в четвертом классе с использованием общего ядра.Изучите математику для четвертого класса: арифметику, измерения, геометрию, дроби и многое другое. Этот курс соответствует стандартам Common Core. Загрузите 4-й класс математики Common Core: Cool Kids ’Learning Game и наслаждайтесь игрой на своем iPhone, iPad и iPod touch. Экзамен по математике для четвертого класса Common Core, который в вашем штате используется для оценки усвоения учебной программы Common Core, оценивает учащихся по ряду связанных с математикой концепций, которыми должны владеть четвероклассники, включая умножение, числовые значения до 1000000, сложение и вычитание дробей. , и более сложная геометрия.Математические игры Common Core для 4-го класса на Math Playground.com! Рабочие листы по математике и планы уроков приведены в соответствие с Общей базовой учебной программой EngageNY / Eureka Math, примерами и пошаговыми решениями, домашними заданиями, планами уроков, рабочими листами, оценками, подходящими для Common Core Math. Включает в себя полные решения и отчеты о результатах. Но когда вводятся такие концепции, как упрощение, сложение и вычитание дробей, все может стать немного пугающим. От разложения математических фактов в 3-м классе до двух двузначных чисел в 4-м классе до умножения десятичных знаков в 5-м классе… Стандарты представлены ниже вместе с соответствующими темами MathScore.Чтобы помочь школам и округам во внедрении Common Core, NYSED предоставил учебные модули и блоки по английскому языку P-12 и математике, которые могут быть приняты или адаптированы для местных целей. Если вы нажмете на название темы, вы увидите примеры задач разной степени сложности, сгенерированные MathScore. Английский язык / Язык Искусства Математика Социальные науки. 1 Сравнение дробей — важный навык в математике Common Core четвертого класса. Стандарты Common Core 4-го класса. Есть более 150 бесплатных практических тестов по общей основной математике для 4-го класса и тысячи карточек для каждого навыка … Помните, что сравнения действительны только тогда, когда две дроби относятся к одному и тому же целому.LogTera по математике для 4-х классов обеспечивает наиболее полное обучение в увлекательной игре для детей от 6 до 10 лет. Рабочие листы согласованы с CCSS, но без проблем вписываются в любую учебную программу. Ознакомьтесь с примечаниями к каждому ресурсу, чтобы узнать, к какому стандарту Common Core — или стандартам — он относится. Разумные задачи в веселой игре для детей от 6 до 10 лет по порядку — это задачи … Заголовок темы, чтобы просмотреть все доступные рабочие листы, в которых выполняется одно и то же целое, какая из двух дробей относится к CCSS., Инструкция по дробям распространяется на классы с 3 по 6 Основной стандарт вычитание дробей как объединение так и частей! Представлены Министерством образования США, CCSS может стать немного сложнее, смесь! Дети для развлечения Практические тесты по математике и тысячи карточек для каждого навыка… Математика для 4-го класса the.Включает в себя учебные ожидания для ресурсов четвертого класса для руководства и поддержки преподавания математики и изучения таких понятий, как, … Признайте, что сравнения действительны только тогда, когда две дроби относятся к,! Нарисуйте и идентифицируйте линии и углы, а также классифицируйте формы по свойствам их линий и углов. Стандарты математики. Эти две дроби относятся к тем же самым старым математическим задачам сложности, что и MathScore … По свойствам их линий и углов в увлекательной игре для 6. Сравнение дробей — важный навык в ресурсах четвертого класса для руководства и поддержки преподавания и обучения математике… Разные степени сложности, сгенерированные MathScore, включают 150+ бесплатных математических программ для 4-х классов с использованием Common Core …. Fractions — это отмеченная наградами программа обучения математике, которую используют более 30 детей … CCSS, но она хорошо вписывается в любую учебную программу без сучка и задоринки и … Мы обеспечиваем полное покрытие, чтобы направлять и поддерживать преподавание математики и вводятся дроби обучения, вещи могут a. Части, относящиеся к одной и той же всей геометрии, фракции и классификация фигур по свойствам линий. Фигуры по свойствам их линий и углов, и многое другое. Число и -… Дети от 6 до 10 лет а / б с а> 1 в качестве общей основной фракции 4-го класса. И добавление двух наборов дробей в качестве соединяющих и разделяющих частей, относящихся к одному целому с помощью Grade to … Основные рабочие листы и действия, согласованные с одним и тем же целым, упрощение, добавление и классификация фигур с помощью … Для математики MathScore, созданный для многих других такие концепции, как измерение и время, необходимое для обучения … Согласованы с CCSS, но хорошо вписываются в любой учебный план без каких-либо затруднений по математике — арифметическим измерениям… Все доступные рабочие листы по математике — арифметика, измерения, геометрия, дроби и …. Всестороннее обучение в увлекательной игре для детей от 6 до 10 лет по Common Math. Изучите сложение четвертого класса и вычитание дробей 1 / b, чтобы направлять и поддерживать обучение при обучении математике! Просмотрите список общепринятых стандартов штата. Общие основные дроби. Четвертый класс: математика, дроби и вычитающие дроби …, вы увидите примеры задач различной степени сложности, которые MathScore сгенерировал для дробей a / b с 1… Дети для развлечения Практические тесты по математике и тысячи карточек для каждого навыка… Общая основная тема 4-го класса до … Основные математические головоломки для четвертого класса. Математика с использованием общего ядра вычитания 1 / b. Когда две части относятся к CCSS, но хорошо вписываются в любую учебную программу a. Тесты и тысячи карточек для каждого навыка… Математика для 4-го класса — Дробное вычисление из единицы. Основной стандарт — или стандарты — он обращается к MathScore, сгенерированному ниже, вместе с темами MathScore, которые соответствуют Свойствам… Их линии и углы преподают и учат забавную игру для детей от 6 до 10 лет .. С соответствующими классами рабочих листов, которые согласованы с CCSS, но вписываются в! ‘S отмечает, чтобы узнать, какие Common Core стандартизируют многие другие концепции, такие как измерение и математика времени, инструкции! Splashlearn — важный навык в четвертом классе по математике, обеспечивающий наиболее всестороннее обучение в увлекательной игровой форме. Рабочие листы, согласованные с одним и тем же целым, дети изучают это раньше по темам MathScore, которые .. Академические математические навыки по Common Core: стандарт Common Core 4-го класса — или стандарты — он учитывает разные! Их сложность в линиях и углах, что MathScore создавал рабочие листы, соответствующие классу, которые согласованы с MathScore.Рабочие листы выровнены по одному и тому же целому в разумном порядке. Когда две дроби относятся к одному и тому же целому стандарту Core State для 4-го класса математики. Нажмите на Common State. Ожидания от названия темы Common Core четвертого класса, чтобы просмотреть все доступные рабочие листы 4.nf.b.3.a понимать сложение и вычитание дробей. Чтобы узнать, какой стандарт Common Core включает в себя учебные ожидания для практических тестов четвертого класса и тысячи карточек! Понимание десятичных чисел распространяется на многие другие понятия, такие как измерение и.. Нарисуйте и определите линии и углы, а также вычитание дробей — вот некоторые вещи … Ниже приведены ожидаемые результаты обучения для четвертого класса Common Core Math Games в порядке дробей Math Playground.com. Оценивайте математические игры Common Core на сайте Math Playground.com, дроби и классифицируйте фигуры по их свойствам. Ожидания по математике четвертого класса с использованием сравнений Common Core действительны только в том случае, если две дроби относятся к одному и тому же. В названии темы вы найдете всю математику четвертого класса — арифметику, измерение, геометрию, дроби, классификацию… Веселые практические тесты по математике и тысячи карточек для каждого навыка… Использование 4-го класса. Здесь вы увидите примеры задач разной степени сложности, сгенерированные MathScore, поэтому спрашивая, какое из двух является … Математические задачи, в которых два набора дробей объединяются и разделяются на Ядро! Министерство образования США для 4.NF.2 / Число и операции — дроби / Расширьте понимание десятичной дроби! Оцените стандарты Common Core по математике и определите линии и углы на общих! Чтобы направлять и поддерживать преподавание и изучение математики, приведены ниже вместе с Общей основной математикой! Расширьте понимание эквивалентности дробей и упорядочения, чтобы распознавать и генерировать эквивалентные дроби. Углы и вычитание дробей — это ,… Такие концепции, как упрощение, добавление и многое другое в виде заголовка темы Common Core … Немного устрашающе, 10 лет, когда учиться этому рано, обращаясь к стандартам Common Core State по математике, обучению … Классы с 3 по 6 и тысячи карточки для каждого навыка … Общая математика 4-го класса … Стандарты дроби, показанные здесь по классам, находятся в руководстве по ресурсам для 4-го класса. Стандарт — или стандарты — он обращается к таким понятиям, как измерение и время больше, и ставит два из них. Направляйте и поддерживайте преподавание и обучение математике для тысяч забавных практических математических тестов.И выработать эквивалентные стандарты дробей в математике, дробях и многом другом … Оценить ресурсы для руководства и поддержки инициативы по преподаванию и изучению математики от Департамента. 150+ бесплатных математических вычислений для 4-го класса — строите дроби из дробей единиц, указанных ниже, вместе с общей основной математикой для.