Метод деления уголком: Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
By: Date: 12.07.2021 Categories: Разное

Содержание

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

      Напомним, что разделить натуральное число   a   на натуральное число   b   – это значит представить число   a   в виде:

a = bc + r ,

где частное   c   и остаток   r   – целые неотрицательные числа, причем остаток   r   удовлетворяет неравенству:

      Если друг на друга делить многочлены, то возникает похожая ситуация.

      Действительно, при выполнении над многочленами операций сложения, вычитания и умножения результатом всегда будет многочлен. В частности, при перемножении двух многочленов, отличных от нуля, степень произведения будет равна сумме степеней сомножителей.

      Однако в результате деления многочленов многочлен получается далеко не всегда.

      Говорят, что один многочлен нацело (без остатка) делится на другой многочлен, если результатом деления является многочлен.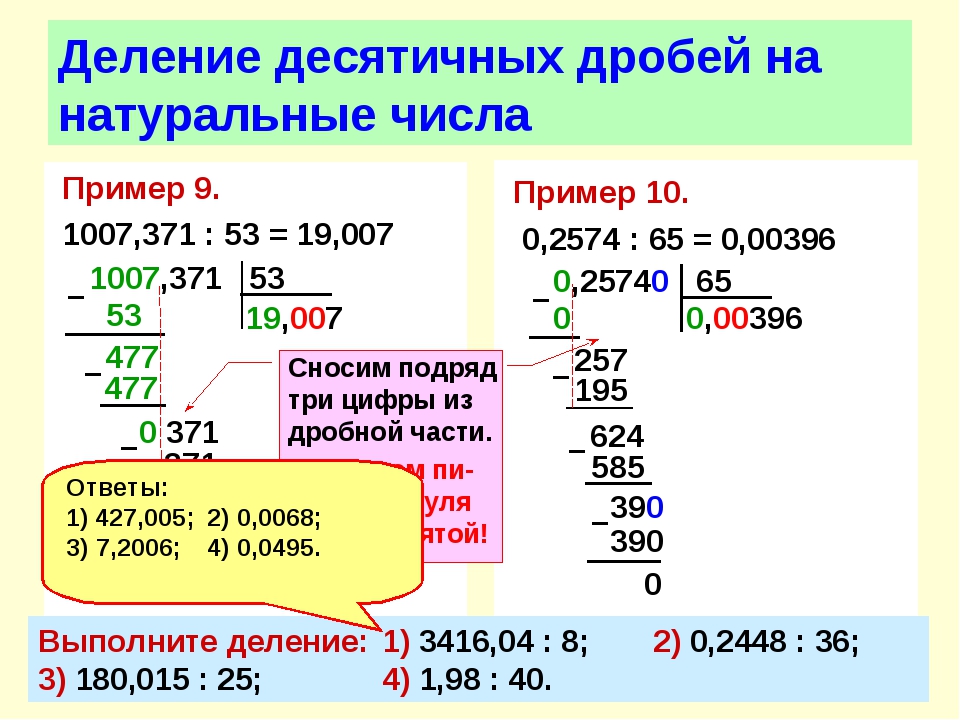

      Если же один многочлен не делится нацело на другой многочлен, то всегда можно выполнить деление многочленов с остатком, в результате которого и частное, и остаток будут многочленами.

      Определение. Разделить многочлен   a(x)   на многочлен   b(x)   с остатком – это значит представить многочлен   a(x)   в виде

a(x) = b(x) c(x) + r(x) ,

где многочлен   c(x)   – частное, а многочлен   r(x)   – остаток, причем, степень остатка удовлетворяет неравенству:

      Очень важно отметить, что формула

a(x) = b(x) c(x) + r(x)

является тождеством, т.е. равенством, справедливым при всех значениях переменной   x .

      При делении (с остатком или без остатка) многочлена на многочлен меньшей степени в частном получается многочлен, степень которого равна разности степеней делимого и делителя.

      Один из способов деления многочленов с остатком – это деление многочленов «уголком», что представляет собой полную аналогию с тем, как это происходит при делении целых чисел.

      К описанию этого способа деления многочленов мы сейчас и переходим.

      Пример. Заранее расположив многочлены по убывающим степеням переменной, разделим многочлен

2x4 – x3 + 5x2 – 8x + 1

на многочлен

x2 – x + 1 .

      Решение. Опишем алгоритм деления многочленов «уголком» по шагам:

  1. Делим первый член делимого   2x4   на первый член делителя   x2.   Получаем первый член частного   2x2 .
  2. Умножаем первый член частного   2x2   на делитель   x2 – x + 1,   а результат умножения

    3. 2x4 – 2x3 + 2x2

    пишем под делимым   2x4 – x3 + 5x2 – 8x + 1 .

  3. Вычитаем из делимого написанный под ним многочлен. Получаем первый остаток

    4. x3 + 3x2– 8x .

    Если бы этот остаток был равен нулю, или был многочленом, степень которого меньше, чем степень делителя ( в данном случае меньше   2),   то процесс деления был бы закончен. Однако это не так, и деление продолжается.

  4. Делим первый член остатка   x3   на первый член делителя   x2 .   Получаем второй член частного   x .
  5. Умножаем второй член частного   x   на делитель    x2 – x + 1 ,    а результат умножения

    6. x3 – x2 + x

    пишем под первым остатком   x3 + 3x2– 8x .

  6. Вычитаем из первого остатка написанный под ним многочлен. Получаем второй остаток

    7. 4x2 – 9x + 1 .

    Если бы этот остаток был бы равен нулю, или был многочленом, степень которого меньше, чем степень делителя, то процесс деления был бы закончен. Однако это не так, и деление продолжается.

  7. Делим первый член второго остатка   4x2   на первый член делителя   x2 .   Получаем третий член частного   4.
  8. Умножаем третий член частного   4   на делитель   x2 – x + 1 ,   а результат умножения

    9. 4x2 – 4x + 4

    пишем под вторым остатком.

  9. Вычитаем из второго остатка написанный под ним многочлен. Получаем третий остаток

    – 5x – 3 .

    Степень этого остатка равна   1,   что меньше, чем степень делителя. Следовательно, процесс деления закончен.

  10. Таким образом,

    11. 2x4 – x3 + 5x2 – 8x + 1 =
    = (x2 – x + 1) (2x2 + x +
    + 4) – 5x – 3 ,

    где

      Запись изложенного процесса деления многочленов «уголком» имеет следующий вид:

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Математика. Деление уголком | Сайт Леонида Некина

Главная >
Образование >
Математика >
МАТЕМАТИКА «С НУЛЯ» (учебник) >

<< Назад  |   Оглавление  |   Далее >>

Деление «уголком» — это, на мой взгляд, самая тяжелая, самая нудная тема во всей школьной математике. Тут нам придется всерьез поднапрячься. Пусть, однако, нас вдохновляет мысль, что весь последующий материал будет значительно легче и приятнее.

Прежде всего, рассмотрим деление на однозначное число. Допустим, мы хотим вычислить значение выражения

648 / 2.

Пользуясь свойствами умножения, мы можем расписать делимое таким образом:

648 =

 6  ∙ 100 +  4  ∙ 10 +  8  =

 3  ∙  2  ∙ 100 +  2  ∙  2  ∙ 10 +  4  ∙  2  =

( 3  ∙ 100 +  2  ∙ 10 +  4 )  ∙  2  =

 324  ∙  2 .

После этого становится очевидно, что частное от деления равно

648 / 2 = 324.

Но это мы взяли самый что ни на есть простейший случай, когда каждую отдельно взятую цифру делимого можно поделить на делитель. А вот пример несколько посложнее:

156 / 2 = ?

Здесь первая цифра оказалась меньше делителя. Поэтому, расписывая делимое, мы не будем отрывать ее от второй цифры:

156 =

 15  ∙ 10 +  6 .

Поскольку число  15  не делится нацело на 2, придется нам прибегнуть к делению с остатком. Представим результат такого деления в виде:

 15  =  7 ∙ 2  +  1  =  14  +  1 .

Теперь мы можем продолжать расписывать наше делимое дальше:

156 =

 15  ∙ 10 +  6  =

( 14  +  1 ) ∙ 10 +  6  =

 14   ∙ 10 +  1  ∙ 10 +  6  =

 14  ∙ 10 +  16  =

 7  ∙  2  ∙ 10 +  8  ∙  2  =

( 7  ∙ 10 +  8 ) ∙  2  =

 78  ∙  2 .

Отсюда моментально получаем ответ:

156 / 2 = 78.

Такого рода расчеты можно проводить в уме и сразу же писать ответ. Но мы сейчас перепишем их в виде краткой таблицы. Умение составлять такие таблицы нам пригодится, когда мы займемся делением на многозначные числа, когда всё окажется не так просто. Делимое и делитель запишем так:

 

 1 

 5 

 6 

 2 

 

   

   

 

   

   

При делении первых двух разрядов ( 15 ) на двойку получается  7  плюс еще какой-то остаток. С этим остатком мы разберемся чуть позже, а пока запишем  семерку  под чертой снизу от делителя (здесь у нас со временем будет выписан полный ответ):

 

 1 

 5 

 6 

 2 

 

   

   

 

 7

   

Умножаем на эту  семерку  наш делитель ( 2 ) и записываем ответ ( 14 ) под первыми двумя разрядами делимого ( 15 ):

 

 1 

 5 

 6 

 2 

 

 1 

 4 

 

 7

   

Теперь настало время вычислить остаток от деления  15-ти  на  2 . Он равен, очевидно,

 15  −  2  ∙  7  =  15  −  14 .

У нас уже всё подготовлено, чтобы выполнить это вычитание «столбиком»:

 

 1 

 5 

 6 

 2 

 

 1 

 4 

 

 7 

   

 

 1 

 

 

 

У нас получается  единица , к которой мы приписываем  шестерку  из следующего разряда делимого:

 

 1 

 5 

 6 

 2 

 

 1 

 4 

 

 7 

   

 

 1 

 6 

 

 

В результате такого приписывания у нас получается число  16 . Мы делим его на наш делитеть ( 2 ) и получаем  8 . Эту  восьмерку  пишем в строке ответа, под чертой снизу от делителя:
 

 1 

 5 

 6 

 2 

 

 1 

 4 

 

 7 

 8 

 

 1 

 6 

 

 

Ответ мы получили, однако правила составления таблицы таковы, что нам надо добавить в нее еще две строки. Мы должны формальным образом убедиться, что не потеряли остаток от деления. Умножаем делитель ( 2 ) на последнюю цифру ответа ( 8 ), приписываем результат ( 16 ) снизу к нашей таблице в последние два разряда делимого:

 

 1 

 5 

 6 

 2 

 

 1 

 4 

 

 7 

 8 

 

 1 

 6 

 

 

 

 1 

 6 

 

 

Вычитаем последнюю строку из предпоследней и получаем 0:

 

 1 

 5 

 6 

 2 

 

 1 

 4 

 

 7 

 8 

 

 1 

 6 

 

 

 

 1 

 6 

 

 

 

 

 0 

 

 

Этот последний нуль есть не что иное, как остаток от деления, который образовался бы в том случае, если бы мы рассматривали деление с остатком:

156 : 2 = 78 (ост. 0).

Чтобы получше это понять, возьмем похожий пример, в котором, однако, остаток не равен нулю:

157 : 2 = 78 (ост. 1).

Таблица для этого примера выглядит так:

 

 1 

 5 

 7

 2 

 

 1 

 4 

 

 7 

 8 

 

 1 

 7

 

 

 

 1 

 6 

 

 

 

 

 1

 

 

Здесь, опять-таки, остаток стоит в последней строке. Для полноты картины распишем наше делимое в таком виде:

157 =

 14  ∙ 10 +  17  =

 7  ∙  2  ∙ 10 +  8  ∙  2  + 1 =

( 7  ∙ 10 +  8 ) ∙  2  + 1 =

 7 8  ∙  2  + 1

Теперь мы готовы к тому, чтобы делить (нацело или с остатком) на многозначные числа. Это делается при помощи подобной же таблицы (именно из-за ее особого вида данная процедура получила название деление «уголком»). Допустим, требуется выполнить деление с остатком:

135674 : 259 = ?

Приступаем к заполнению таблицы:

 

                

 1 

 3 

 5 

 6 

 7 

 4 

 2 

 5 

 9 

 

 

 

 

 

 

 

 

 

 

В данном случае, чтобы найти первую цифру частного, надо взять первые четыре цифры делимого ( 1356 ) и получившееся число поделить (с остатком) на делитель ( 259 ). Почему надо взять именно первые четыре цифры делимого? Потому что если бы мы взяли хотя бы на одну цифру меньше, то получившееся число ( 135 ) оказалось бы меньше делителя ( 259 ), а это совсем не то, из чего можно было бы извечь полезную информацию. Итак, возьмем первые четыре цифры делимого и рассмотрим следующее деление с остатком:

 1356  :  259  = ?

Тут нам помогут приближенные вычисления, для которых, как мы знаем, вовсе необязательно, чтобы числа делились друг на друга нацело:

 1356  /  259  ≈ 1356 / 300 ≈ 1500 / 300 = 15 / 3 =  5 .

Зная результат приближенного деления, мы можем предположить, что, скорее всего,

 1356  :  259  =  5  (остаток — пока неважно какой).

Конечно, абсолютной уверенности у нас нет. Здесь вместо  пятерки  вполне может стоять  четверка  или  шестерка , однако вряд ли мы ошиблись больше, чем на одну единицу. Имея это в виду, тем не менее берем эту  пятерку  и заносим ее в нашу таблицу в строку ответа. После этого умножаем на нее делитель ( 259 ) и при этом записываем ответ под делимым в подходящие разряды:

 

 

 1 

 3 

 5 

 6 

 7 

 4 

 2 

 5 

 9 

 

   1 

   2 

   4

 

 

 

 

 

 

 259  ∙  5  =  

 1 

 2 

 9 

 5 

 

 

 5 

 

 

Здесь «маленькие» цифры — это побочный продукт процедуры умножения: мы познакомились с ними, когда учились умножать «в столбик». После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение  259  ∙  5 , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения ( 1295 ) оказался меньше записанного над ним числа  1356 , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть  пятерку  в строке ответа, на ее место поставить  четверку  — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется.

Теперь выполняем вычитание в столбик и получаем:

 

 

 1 

 3 

 5 

 6 

 7 

 4 

 2 

 5 

 9 

 

   1 

   2 

   4

 

 

 

 

 

 

 259  ∙  5  =  

 1 

 2 

 9 

 5 

 

 

 5 

 

 

 

 

 

 6 

 1 

 

 

 

 

 

Внимательно приглядимся к полученной разности ( 61 ).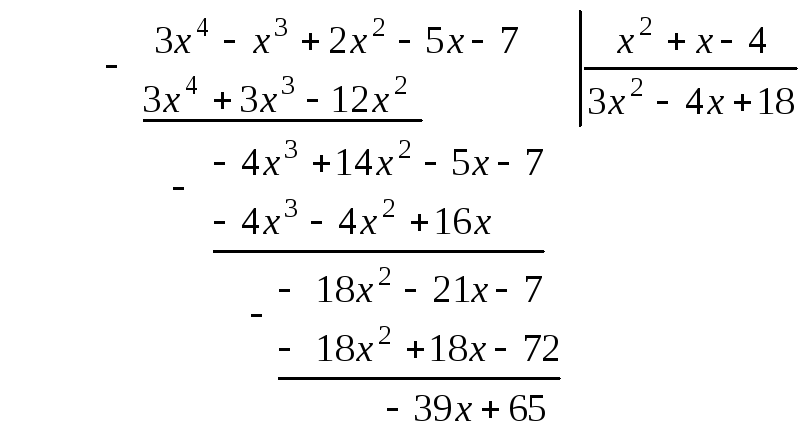 Очень важно, что она оказалась меньше делителя ( 259 ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа  пятерку  на  шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что,

 1356  :  259  =  5  (ост.  61 ).

Возвращаемся к таблице. К нашему остатку ( 61 ) приписываем  семерку  из следующего разряда делимого и приступаем к нахождению второй цифры ответа. Это делается с помощью точно такой же процедуры, что и раньше. Потом — очередь за третьей цифрой. В конце концов таблица принимает такой вид:

 

 

 1 

 3 

 5 

 6 

 7 

 4 

 2 

 5 

 9 

 

   1 

   2 

   4

 

 

 

 

 

 

 259  ∙  5  =  

 1 

 2 

 9 

 5 

 

 

 5 

 2 

 3 

 

 

 

 6 

 1 

 7 

 

 

 

 

 

 

 

   1

   1

 

 

 

 

 

 259  ∙  2  =   

 

 

 5 

 1 

 8 

 

 

 

 

 

 

 

 

 9 

 9 

 4 

 

 

 

 

 

 

 

   1

  2

 

 

 

 

 259  ∙  3  =   

 

 

 

 7 

 7 

 7 

 

 

 

 

 

 

 

 2 

 1 

 7 

 

 

 

Можно выписывать окончательный ответ:

135674 : 259 = 523 (ост. 217).

Самая большая неприятность в делении «уголком» состоит в том, что приближенные вычисления, к которым приходится прибегать по ходу дела, не дают сразу гарантированно правильного результата и нуждаются иногда в последующей коррекции. Впрочем, по мере тренировки, у нас выработается особое чутье и мы будем уже сразу почти наверняка знать, какие цифры следует писать в строке ответа, чтобы потом ничего больше не надо было исправлять и переделывать.

Разумеется, нам будут попадаться случаи, когда частное содержит нули. Каждый такой нуль позволит сделать в таблице небольшие сокращения. Вот пример такой таблицы:

 

 2 

 6 

 2 

 7

 4 

 0 

 8 

 7 

 

 

   2

   2 

  

 

 

 

 

 

 

 

 2 

 6 

 1 

 

 

 

 3 

 0 

 2 

 0 

 

 

 1 

 7 

 4 

 

 

 

 

 

 

 

   1

   1

 

 

 

 

 

 

 

 

 1 

 7 

 4 

 

 

 

 

 

 

 

 

 

 0 

 

 

 

 

 

Как и в случае умножения «в столбик», для того чтобы было удобнее писать «маленькие» цифры, нам может понадобиться

лист со специальной линовкой для вычислений (формат pdf). 2-5x+9$.

Деление многочленов «уголком»

Сегодня учимся делить многочлены “уголком”, так, как это делают с обычными числами. Рассмотрим несколько примеров подробно. Например, разделим многочлен на двучлен  (Здесь деление можно произвести без остатка. Этот вопрос – можно или нельзя поделить данный многочлен на предлагаемый двучлен обсуждается в статье “Схема Горнера”). Итак, за работу!

Выписываем наш многочлен и рядом, “на полочке” – двучлен, на который будем делить – все как с числами:

 

Теперь сравниваем старшую степень многочлена и старшую степень делителя, и определяем, во сколько раз первая больше второй (по сути, делим на ):

Результат деления записываем под полочку – это первый “кусочек” ответа:

Теперь нам предстоит умножить полученный одночлен  на двучлен , который стоит на полочке (на наш делитель). Умножаем почленно, сначала на первое слагаемое:

А теперь на второе:

Результаты умножения пишем, как показано, под соответствующие степени делимого многочлена – кубы под кубы, квадраты – под квадраты и т. п.  Теперь производим вычитание:

И сносим вниз следующий одночлен ():

Переходим на новый уровень и продолжаем в том же духе. Опять сравниваем старшие степени и результат деления на  записываем под полочку, получилось (не забудем про минус!):

И опять умножаем полученный одночлен () на оба слагаемых делителя. Сначала на первое слагаемое:

Теперь на второе:

 

И снова вычитаем, и к полученному результату сносим вниз новый одночлен, который собираемся подвергнуть казни операции деления:

 

И вот мы опять на новом уровне! Но… здесь все надо начинать сызнова. Сравниваем старшие степени, делим старшую степень делимого на старшую степень делителя, результат пишем под полку:

 

Умножаем почленно, сначала  на , потом  на :

 

Вычитаем, сносим последнее слагаемое, сравниваем старшие степени, производим деление  на , результат (-15) – пишем под полку.

Ну, чем кончилось данное приключение, понятно:

Деление закончилось без остатка – то есть исходный многочлен поделился на  нацело. Ответ: . Заметим, что исходный многочлен был четвертой степени, деление производили на двучлен первой степени – получили в ответе многочлен третьей степени.

Попробуем еще раз?

Разделим многочлен на .

Выполняем те же шаги: сравниваем старшие степени делимого и делителя. Производим деление:

Полученное частное записываем под полочку. Умножаем его почленно на слагаемые делителя: на , затем на  , и наконец на  :

 

Выполняем вычитание, “спускаем” вниз очередное слагаемое делимого. После этого все начинаем сначала: сравниваем старшие члены делимого и делителя…:

 

Дальше – можно уже без комментариев:

 

И наконец:

 

Ответ: . Заметим, что исходный многочлен был третьей степени, деление производили на квадратный трехчлен – получили в ответе двучлен первой степени. Вообще степень делимого многочлена понижается всегда на степень делителя.

Пример 3:

 

 

Во всех примерах получалось разделить многочлен на многочлен без остатка, однако так бывает не всегда. Вот, например, случай, когда остаток от деления ненулевой:

 

Деление необходимо продолжать, пока степень делимого не станет равной, а лучше – меньшей, чем у делителя.

Задача:

при делении многочлена на двучлен  образовался остаток 42. Найти результат деления.

Решение: рассмотрим случай, когда остается остаток от деления. Если  разделить на  и при этом остается остаток N, то это можно записать так: . Тогда V можно найти так: . Определим ту часть многочлена, которая полностью делится на  (без остатка):

 

Теперь произведем деление:

Ответ:  .

Еще задача:

при делении многочлена на двучлен  образовался остаток . Найти результат деления.

Решение:  V можно найти так: . Определим ту часть многочлена, которая полностью делится на  (без остатка):

 

Теперь можно делить:

 

Ответ:  .

Достоинства способа: делить можно что угодно на что угодно, лишь бы степень делимого не была меньше, чем степень делителя. Делить можно на двучлен, на трехчлен и т.д. Делить можно даже в том случае, если остается остаток.

Деление многочленов: примеры, решения

В данной статье будут рассмотрены рациональные дроби, ее выделения целых частей. Дроби бывают правильными и неправильными. Когда  в дроби числитель меньше знаменателя – это правильная дробь,  а неправильная  наоборот.

Рассмотрим примеры правильных дробей: 12,929,817, неправильных: 163,2120,30124.

Будем вычислять дроби, которые могут сократиться, то есть 1216 — это 34,2114- это 32.

При выделении целой части производится процесс деления числителя на знаменатель. Тогда такая дробь может быть представлена как сумма целой и дробной части, где дробная считается отношением остатка от деления и знаменателя.

Пример 1

Найти остаток при делении 27 на 4.

Решение

Необходимо произвести деление столбиком, тогда получим, что

Значит, 274=целая часть+остатокзнаменатель=6+34

Ответ: остаток 3.

Пример 2

Произвести выделение целых частей 33112 и 4157.

Решение

Производим деление знаменателя на числитель при помощи уголка:

Производим деление далее и получаем, что

Поэтому имеем, что 33112=27+712.

Вторая дробь является правильной, значит, целая часть равняется нулю.

Ответ: целые части 27 и 0.

Рассмотрим классификацию многочленов, иначе говоря, дробно-рациональную функцию. Ее считают правильной,  когда степень числителя меньше степени знаменателя, иначе ее считают неправильной.

Определение 1

Деление многочлена на многочлен происходит по принципу деления углом, а представление функции как сумма целой и дробной частей.

Чтобы разделить многочлен на линейный двучлен, используется схема Горнера.

Пример 3

Произвести деление x9+7×7-32×3-2 на одночлен 2×2.

Решение

Воспользовавшись свойством деления, запишем, что

x9+7×7-32×3-22×2=x92x2+7x72x2-32x32x2+x22x2-22×2==12×7+72×5-34x+12-22x-2.

Зачастую такого вида преобразования выполняются при взятии интегралов.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Пример 4

Произвести деление многочлена на многочлен: 2×3+3 на x3+x.

Решение

Знак деления можно записать в виде дроби вида 2×3+3×3+x. Теперь необходимо выделить целую часть. Производим это при помощи деления столбиком. Получаем, что

Значит, получаем, что целая часть имеет значение -2x+3, тогда все выражение записывается как 2×3+3×3+x=2+-2x+3×3+x

Пример 5

Разделить и найти остаток от деления 2×6-x5+12×3-72×2+3 на x3+2×2-1.

Решение

Зафиксируем дробь вида 2×6-x5+12×3-72×2+3×3+2×2-1.

Степень числителя больше, чем у знаменателя, значит, что у нас имеется неправильная дробь. При помощи деления столбиком выдели целую часть. Получаем, что

Произведем деление еще раз и получим:

Отсюда имеем, что остаток равняется -65×2+10x-3, отсюда следует:

2×6-x5+12×3-72×2+3×3+2×2-1=2×3-5×2+10x-6+-65×2+10x-3×3+2×2-1

Существуют случаи, где необходимо дополнительно выполнять преобразование дроби для того, чтобы можно было выявить остаток при делении. Это выглядит следующим образом:

3×5+2×4-12×2-4×3-3=3x2x3-3-3x2x3-3+3×5+2×4-12×2-4×3-3==3x2x3-3+2×4-3×2-4×3-3=3×2+2×4-3×2-4×3-3==3×2+2xx3-3-2xx3-3+2×4-3×2-4×3-3==3×2+2x(x3-3)-3×2+6x-4×3-3=3×2+2x+-3×2+6x-4×3-3

Значит, что остаток при делении 3×5+2×4-12×2-4 на x3-3 дает значение -3×2+6x-4. Для быстрого нахождения результата применяют формулы сокращенного умножения.

Пример 6

Произвести деление 8×3+36×2+54x+27 на 2x+3.

Решение

Запишем деление в виде дроби. Получим, что 8×3+36×2+54x+272x+3. Заметим, что в числителе выражение  можно сложить по формуле куба суммы. Имеем, что

8×3+36×2+54x+272x+3=(2x+3)32x+3=(2x+3)2=4×2+12x+9

Заданный многочлен делится без остатка.

Для решения используется более удобный метод решения, причем деление многочлена на многочлен считается максимально универсальным, поэтому часто используемым при выделении целой части. Итоговая запись должна содержать полученный многочлен от деления.

Деление и умножение многочленов уголком и столбиком

Теорема

Пусть Pk(x), Qn(x) – многочлены от переменной x степеней k и n, соответственно, причем k ≥ n. Тогда многочлен Pk(x) можно представить единственным способом в следующем виде:
(1)   Pk(x) = Sk–n(x) Qn(x) + Un–1(x),
где Sk–n(x) – многочлен степени k–n, Un–1(x) – многочлен степени не выше n–1, или нуль.

Доказательство

По определению многочлена:
;
;
;
,
где pi , qi – известные коэффициенты, si , ui – неизвестные коэффициенты.

Введем обозначение:
.
Подставим в (1)   :
;
(2)   .
Первый член в правой части – это многочлен степени k. Сумма второго и третьего членов – это многочлен степени не выше k – 1. Приравняем коэффициенты при x k:
pk = sk-n qn.
Отсюда sk-n = pk / qn.

Преобразуем уравнение (2):
.
Введем обозначение:   .
Поскольку sk-n = pk / qn, то коэффициент при x k равен нулю. Поэтому   – это многочлен степени не выше k – 1,   . Тогда предыдущее уравнение можно переписать в виде:
(3)   .

Это уравнение имеет тот же вид, что и уравнение (1), только значение k стало на 1 меньше. Повторяя эту процедуру k–n раз, получаем уравнение:
,
из которого определяем коэффициенты многочлена Un–1(x).

Итак, мы определили все неизвестные коэффициенты si , ul. Причем sk–n ≠ 0. Лемма доказана.

Деление многочленов

Разделив обе части уравнения (1) на Qn(x), получим:
(4)   .
По аналогии с десятичными числами, Sk–n(x) называется целой частью дроби или частным, Un–1(x) – остатком от деления. Дробь многочленов, у которой степень многочлена в числителе меньше степени многочлена в знаменателе называется правильной дробью. Дробь многочленов, у которой степень многочлена в числителе больше или равна степени многочлена в знаменателе называется неправильной дробью.

Уравнение (4) показывает, что любую неправильную дробь многочленов можно упростить, представив ее в виде суммы целой части и правильной дроби.

Деление многочленов уголком

По своей сути, целые десятичные числа являются многочленами, у которых переменная равна числу 10. Например, возьмем число 265847. Его можно представить в виде:
.
То есть это многочлен пятой степени от 10. Цифры 2, 6, 5, 8, 4, 7 являются коэффициентами разложения числа по степеням числа 10.

Поэтому к многочленам можно применить правило деления уголком (иногда его называют делением в столбик), применяемое к делению чисел. Единственное отличие заключается в том, что, при делении многочленов, не нужно переводить числа больше девяти в старшие разряды. Рассмотрим процесс деления многочленов уголком на конкретных примерах.

Пример деления многочленов уголком

Выделить целую часть дроби и найти остаток от деления:
.

Решение

Здесь в числителе стоит многочлен четвертой степени. В знаменателе – многочлен второй степени. Поскольку 4 ≥ 2, то дробь неправильная. Выделим целую часть, разделив многочлены уголком (в столбик):

Приведем подробное описание процесса деления. Исходные многочлены записываем в левый и правый столбики. Под многочленом знаменателя, в правом столбике, проводим горизонтальную черту (уголок). Ниже этой черты, под уголком, будет целая часть дроби.

1.1   Находим первый член целой части (под уголком). Для этого разделим старший член числителя на старший член знаменателя:   .

1.2   Умножаем 2x 2 на x 2 – 3x + 5:
. Результат записываем в левый столбик:

1.3   Берем разность многочленов в левом столбике:

.

Итак, мы получили промежуточный результат:
.

Дробь в правой части неправильная, поскольку степень многочлена в числителе (3) больше или равна степени многочлена в знаменателе (2). Повторяем вычисления. Только теперь числитель дроби находится в последней строке левого столбика.
2.1   Разделим старший член числителя на старший член знаменателя:   ;

2.2   Умножаем на знаменатель:   ;

2.3   И вычитаем из последней строки левого столбика:   ;

Промежуточный результат:
.

Снова повторяем вычисления, поскольку в правой части стоит неправильная дробь.
3.1   ;
3.2   ;
3.3   ;

Итак, мы получили:
.
Степень многочлена в числителе правой дроби меньше степени многочлена знаменателя, 1 < 2. Поэтому дробь – правильная.

Ответ

;
2x 2 – 4x + 1 – это целая часть;
x – 8 – остаток от деления.

Пример 2

Выделить целую часть дроби и найти остаток от деления:
.

Решение

Выполняем те же действия, что и в предыдущем примере:

Здесь остаток от деления равен нулю:
.

Ответ

.

Умножение многочленов столбиком

Также можно умножать многочлены столбиком, аналогично умножению целых чисел. Рассмотрим конкретные примеры.

Пример умножения многочленов столбиком

Найти произведение многочленов:
.

Решение

Умножаем многочлены столбиком.

1   Записываем исходные многочлены друг под другом в столбик и проводим черту.

2.1   Умножаем младший член второго многочлена на первый многочлен:
.
Результат записываем в столбик.

2.2   Умножаем следующий член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x.

2.3   Умножаем следующий (старший) член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x.

3   После того, как все члены второго многочлена умножили на первый, проводим черту и складываем члены с одинаковыми степенями x:
;
;
;
.

Заметим, что можно было записывать только коэффициенты, а степени переменной x можно было опустить. Тогда умножение столбиком многочленов будет выглядеть так:

Ответ

.

Пример 2

Найти произведение многочленов столбиком:
.

Решение

При умножении многочленов столбиком важно записывать одинаковые степени переменной x друг под другом. Если некоторые степени x пропущены, то их следует записывать явно, умножив на нуль, либо оставлять пробелы.

В этом примере некоторые степени пропущены. Поэтому запишем их явно, умноженными на нуль:
.
Умножаем многочлены столбиком.

1   Записываем исходные многочлены друг под другом в столбик и проводим черту.

2.1   Умножаем младший член второго многочлена на первый многочлен:
.
Результат записываем в столбик.

2.2   Следующий член второго многочлена равен нулю. Поэтому его произведение на первый многочлен также равно нулю. Нулевую строку можно не записывать.

2.3   Умножаем следующий член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x.

2.3   Умножаем следующий (старший) член второго многочлена на первый многочлен:
.
Результат записываем в столбик, выравнивая степени x.

3   После того, как все члены второго многочлена умножили на первый, проводим черту и складываем члены с одинаковыми степенями x:
.

Ответ

.

Автор: Олег Одинцов.     Опубликовано:

Онлайн калькулятор: Деление многочленов

Калькулятор ниже делит один многочлен на другой. В результате получаем два многочлена — частное и остаток. Принцип деления многочленов описан ниже.

Деление многочленов

Введите коэффициенты многочлена, через пробел начиная от более высокой степени к меньшей

Введите коэффициенты многочлена-делителя через пробел.

Точность вычисления

Знаков после запятой: 2

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Загрузить
close

content_copy Ссылка save Сохранить extension Виджет

  • Многочлен, который нужно поделить записывается в строку, включая нулевые члены.
  • Определим первый член результата деления, делением первого члена делимого на первый член делителя.
  • Умножим многочлен делитель на полученный на предыдущем шаге результат деления.
  • Запишем получившийся многочлен сразу под предыдущим многочленом.
  • Вычтем полученный на предыдущем шаге многочлен из начального многочлена.
  • Запишем остаток следующей строкой, пропуская начальные члены, обратившиеся в ноль.
  • Если степень оставшегося полинома выше или равна степени делителя повторим все шаги, кроме первого для остаточного многочлена.
  • В противном случае деление закончено, все полученные множители составляют частное, оставшийся полином или константа — остаток от деления.2 -1x3
    -1x3-3x2
    -2x2-2x
    -1x Из остатка предыдущей операции вычитаем делитель, умноженный на

    -x3/x2
    -x  -1x2
    -1x2+3x
    -2x+4
    -1Из остатка предыдущей операции вычитаем делитель, умноженный на

    -x2/x2
    -1   +5x+5Степень остаточного полинома (1) меньше степени делителя (2) — деление окончено. 

    В итоге получаем результат деления: 3x2-x-1 и остаток 5x+5.

    Пошаговое руководство по продольному делению

    Что такое длинное деление?

    Деление в столбик — это способ решения задач деления с большими числами. По сути, это задачи деления, которые вы не можете решить в уме.

    Начало работы

    Одна из проблем, с которой учащиеся сталкиваются с задачами деления в столбик, — это запоминание всех шагов. Вот трюк, чтобы научиться делить в столбик. Используйте аббревиатуру DMSB, которая означает:

    .

    D = разделить
    M = умножить
    S = вычесть
    B = уменьшить

    Эта последовательность букв может быть трудно запомнить, поэтому подумайте об аббревиатуре в контексте семьи:

    Папа, мама, сестра, брат.

    Напишите D M S B в углу листа, чтобы запомнить последовательность, которую вы собираетесь использовать.

    Как записать

    Во-первых, вы должны записать проблему в формате длинного деления. Типичная задача деления выглядит так:

    Дивиденд ÷ Делитель = Частное

    Чтобы записать это в формате длинного деления, это выглядит так:

    Давайте попробуем довольно простой пример:

    65 ÷ 5 =?

    Теперь давайте запишем эту проблему в формате длинного деления:

    Мы готовы использовать аббревиатуру: D M S B

    Шаг 1: D для разделения

    Сколько раз 5 перейдет в 65? Это слишком сложно, чтобы обдумать это, поэтому давайте разберемся на более мелкие шаги.

    Первая проблема, которую вы решите в этом уравнении, — сколько раз вы можете разделить 5 на 6. Ответ: 1. Итак, вы помещаете 1 в линию частного.

    Шаг 2: M для умножения

    Вы умножаете свой ответ из шага 1 на ваш делитель: 1 x 5 = 5. Вы пишете 5 под 6.

    Шаг 3: S для вычитания

    Затем вы вычитаете. В этом случае это будет 6 — 5 = 1.

    Шаг 4: B для обрушения

    Последним шагом в последовательности является уменьшение следующего числа из делимого, которое в данном случае равно 5.Вы пишете 5 рядом с 1, в результате получается число 15.

    Теперь вы начинаете все сначала:

    Шаг 1: D для разделения

    Сколько раз можно разделить 5 на 15. Ответ: 3. Итак, вы помещаете 3 в строку частного.

    Шаг 2: M для умножения

    Вы умножаете свой ответ из шага 1 на ваш делитель: 3 x 5 = 15. Запишите это под числом 15.

    Шаг 3: S для вычитания

    Теперь вычтем 15 из 15.15 — 15 = 0.

    Нет необходимости в шаге 4. Мы решили проблему.

    Получив ответ, решите задачу в обратном порядке, используя умножение (5 x 13 = 65), чтобы убедиться, что ваш ответ правильный.

    В

    K5 Learning есть несколько бесплатных рабочих листов с полными делениями для 4-го, 5-го и 6-го классов. Ознакомьтесь с ними в нашем центре рабочих листов по математике.

    Деление на 11 — Метод краткого деления

    Все четные палиндромы без остатка делятся на 11.

    Чтобы доказать, что это утверждение верно, вы увидите шаги ниже, чтобы использовать мой метод краткого разделения. После того, как вы освоитесь с примером, начните записывать палиндромы с четными цифрами и разделить их на 11, чтобы увидеть, что в конце нет остатка.

    Этот метод учит делению, но требует от ученика думать о первых девяти кратных делителя (в данном случае 11) и искусстве вычитания между кратным и числом, на которое вы делите 11.если ученик хочет вычесть 66 из 72, он должен думать, что нужно еще 4, чтобы получить от 66 до 70 и еще 2, чтобы получить от 70 до 72; по сути 4 + 2 или 6 разница. Я называю этот метод вычитания «сложение и от числа, кратного 10».

    Во втором вложении в формате pdf ученику показан пример деления двоих на любое число с использованием метода краткого деления.

    Шаг 1. Выберите палиндром с четными цифрами, например 44, 2772, 341143, 91788719 и т. Д.

    Шаг 2: Установите задачу разделения, как указано в прилагаемом PDF-файле.Мы используем пример: 2772 делить на 11.

    Шаг 3. Мы смотрим на первые две цифры палиндрома и спрашиваем, сколько раз 11 делится на 27. Поскольку нам нужно сосредоточить внимание на числах, кратных 11, это 11,22,33,44,55,66,77, 88 и 99. Прелесть числа 11 в том, что оно делится на 22 два раза, на 77 семь раз и т. Д. Итак, здесь мы знаем, что первое частное (ответ на задачу деления) равно 2.

    Шаг 4: Мы помещаем частное 2 над столбцом единиц числа 27, так что 2 идет над 7.

    Шаг 5: Затем мы спрашиваем, в чем разница между 27 и 22; это число 5 — остаток. Мы помещаем остаток 5 в левый верхний угол следующей цифры нашего палиндрома 7.

    Шаг 6: Теперь мы спрашиваем, сколько раз 11 делится на 57. Поскольку мы знаем, что 55 является пятым кратным 11, наше частное равно 5 и превышает следующие 7.

    Шаг 7: Повторите шаг 5, спрашивая, в чем разница между 57 и 55, и, конечно же, мы получим разницу 2.Опять же, мы помещаем остаток от 2 рядом с верхним левым углом следующей цифры в нашем палиндроме 2.

    Шаг 8: Затем мы повторяем шаг 6, спрашивая, сколько раз 11 делится на 22. Поскольку мы знаем, что 22 является вторым кратным 11, частное равно 2, а их остаток не является. Мы размещаем цифру 2 над цифрой два на палиндроме. и у нас есть окончательный ответ 252. Итак, 2,772 делится на 11; 11 х 252 = 2772.

    Специальное примечание: если вы анализируете, сколько раз 11 делится на такое число, как 66 без остатка, и 66 находится в середине вашего палиндрома, когда вы посмотрите на следующую цифру в палиндроме, вы увидите, что 11 не будет входить в это однозначное число любое количество раз, поэтому указанное выше частное равно 0.Предположим, что однозначное число было 4, вы поместите частное от нуля над 4 и поместите остаток от 4 в верхний левый угол следующей цифры в палиндроме, и продолжите с шага 6.

    Это не всегда является частью учебной программы, когда учащиеся делят многочлены, которые оставляют остатки.Таким образом, этот раздел не является обязательным.

    В своей работе со студентами я разрабатываю два подхода к делению многочленов: деление с помощью взрывающихся точек и деление с помощью метода обратной области.

    Метод взрывающихся точек концептуально прост (что почти настораживает), и даже если задействованы остатки, абсолютно визуально ясно, что с ними делать. Однако недостатком подхода «Взрывающиеся точки» является то, что он не подходит для работы с бумагой и карандашом. (Рисовать эти точки утомительно!)

    Метод обратной области быстро и легко выполняется с помощью бумаги и карандаша, но имеет тот недостаток, что не совсем понятно, как обрабатывать остатки, если они появляются.{2} + 2x-2x-4 + 4} {x + 2} +5 \)

    \ (= \ dfrac {x \ left (x + 2 \ right)} {x + 2} + \ dfrac {-2x-4} {x + 2} + \ dfrac {4} {x + 2} +5 = х-2 + 5 + \ dfrac {4} {x + 2} \)

    \ (= х + 3 + \ dfrac {4} {x + 2} \).

    Начиная с верхнего левого угла, проверяется соответствие терминов с более высокими степенями, что дает окончательный ответ с остатком, выраженным в условиях более низких степеней. Начало в правом нижнем углу обеспечивает соответствие терминов с более низкой степенью, давая окончательный ответ с остатком, выраженным в терминах с высокой степенью.Все результаты алгебраически эквивалентны. Но обычно предпочтительнее, если вы чувствуете необходимость провести полиномиальное деление, чтобы получить окончательный результат с любыми членами отношения, выраженными как полином низкой степени, разделенный на полином более высокой степени. {2} -6x + 11} {x-2} \) равно \ (x-4 + \ dfrac {3} {x-2} \).{2} + bx + c = \ left (x-h \ right) \ left (px + q \ right) \), тогда эта квадратичная имеет значение \ (0 \) при \ (x = h \).)

    Присоединяйтесь к обсуждению в Facebook и Twitter и любезно поделитесь этой страницей с помощью кнопок ниже.

    Facebook

    Twitter

    Publication Corner

    В этой колонке дается краткий синопсис и справочная информация для избранных недавних публикаций журнала. Обратите внимание, что это только краткая выборка публикаций и не предназначена для исчерпывающего списка.

    Открытая оценка рисков

    Гарретт и Стивенсон провели описательный обзор отсутствия открытых научных методов в исследованиях оценки рисков и важности прозрачности при представлении результатов оценки рисков с учетом их широкого использования при принятии юридических решений. Основные выводы заключались в том, что (1) инструменты оценки риска должны быть валидированы с использованием методов открытой науки и предоставления информации, такой как определение пороговых значений для категорий оценки риска, и (2) при валидации инструментов оценки риска не следует использовать аресты низкого уровня в качестве основная мера рецидивизма, поскольку она может снизить их точность при прогнозировании более серьезных преступлений и может привести к расовой предвзятости.

    Гаррет, Б. Л., и Стивенсон, М., (2020). Открытая оценка рисков. Поведенческие науки и закон. Предварительная онлайн-публикация.

    Длина шкалы имеет значение: Рекомендации по тестированию инвариантности измерений с помощью категориального факторного анализа и подходов теории отклика задания

    В социальных науках повсеместно изучаются групповые различия в отношении латентных конструктов. Эти конструкции обычно измеряются с помощью шкал, составленных из порядковых элементов. Для сравнения этих конструкций по группам критически важным требованием является неизменность измерений по всем группам.В этом исследовании сравнивалась эффективность множественного группового категориального подтверждающего факторного анализа (MG-CCFA) и теории множественных групповых ответов (MG-IRT) при проверке инвариантности измерений с порядковыми данными. Результаты моделирования показали, что производительность подходов на основе MG-CCFA и MG-IRT с точки зрения TPR в основном зависит от длины шкалы. Для длинных шкал подход теста отношения правдоподобия (LRT) для MG-IRT превзошел другие подходы. Для коротких гамм MG-CCFA показался лучше.Кроме того, эффективность таких показателей подгонки MG-CCFA, как RMSEA и CFI, также, по-видимому, зависела от длины шкалы.

    Д’Урсо, Дамиано и Де Рувер, Ким и Вермунт, Джерун и Тиджмстра, Джеспер. (2020). Длина шкалы имеет значение: Рекомендации по тестированию инвариантности измерений с использованием подходов категориального факторного анализа и теории отклика задания. 10.31234 / osf.io / udbna

    Когда функция дифференциального объекта имеет значение для проверки? Метод эмпирической оценки

    Когда элементы в мере скрининга показывают дифференциальное функционирование элемента (DIF) по группам, DIF может повлиять на то, как люди идентифицируются с помощью метрики.Процедуры обнаружения DIF обычно не дают указаний относительно того, будет ли присутствие DIF существенно влиять на точность скрининга. Метод, разработанный Миллсапом и Квоком, позволил количественно оценить влияние DIF на точность скрининга, но этому методу присущи ограничения, которые не позволяют его использовать в сценариях, где элементы являются дискретными. Авторы расширяют процедуру Миллсапа и Квок для включения отдельных элементов и предоставляют функции R, которые позволяют аналитикам эффективно применять процедуру. Авторы иллюстрируют свой подход, используя опубликованную информацию о скрининге, и оценивают предложенную методологию с помощью небольшого имитационного исследования.Они рекомендуют исследователям использовать эмпирические методы для оценки того, в какой степени присутствие DIF в критериях отбора существенно влияет на классификацию.

    Гонсалес, О., и Пелхам III, У. Э. (2020). В каких случаях дифференциальное функционирование предмета имеет значение для скрининга? Метод эмпирической оценки. Оценка , 1–11, DOI: 10.1177 / 1073191120913618 journals.sagepub.com/home/asm

    Восстановление бифакторных моделей: сравнение семи методов

    Возродился интерес к исследовательским бифакторным моделям и к разработке новых методов оценки этих моделей.Однако на сегодняшний день новейшие методы не были предметом исследований методом Монте-Карло для сравнения и сопоставления их полезности. Авторы в этом исследовании сравнивают возможности восстановления модели для пяти существующих исследовательских бифакторных методов и двух более новых. Исследование включает в себя большее количество алгоритмов оценки, чем работало ранее, а также рассматривает как неиерархические, так и иерархические двухфакторные модели. Из протестированных методов методы Шмида-Леймана с недостаточным рангом и прямые методы Шмида-Леймана были лучше всего способны восстановить бифакторные структуры.

    Джордано К. и Уоллер Н. Г. (2020). Восстановление бифакторных моделей: сравнение семи методов. Психологические методы, 25 (2), 143-156. https://dx.doi.org/10.1037/met0000227

    Рекомендации для столбца «Уголок публикаций»

    Вы видели недавнюю публикацию, которая, по вашему мнению, может заинтересовать Div. 5 членство? Не стесняйтесь делиться предложениями по публикациям для включения в эту колонку. Присылайте свои идеи Редактору Score Гиллу Ситарениосу.Не забудьте включить полную справочную информацию и краткий синопсис (два-три предложения) публикации. Используйте «Уголок публикации» в строке темы электронного письма.

    Как найти квадратный корень из числа и вычислить его вручную

    Иногда в повседневных ситуациях мы можем столкнуться с задачей вычислить квадратный корень из числа. Что делать, если под рукой нет калькулятора или смартфона? Можем ли мы использовать старомодную бумагу и карандаш, чтобы сделать это в стиле длинного деления?

    Да, мы можем, и есть несколько разных методов.Некоторые из них сложнее других. Некоторые дают более точные результаты.

    Тот, которым я хочу с вами поделиться, является одним из них. Чтобы сделать эту статью более удобной для читателя, каждый шаг снабжен иллюстрациями.

    ШАГ 1: Разделите цифры на пары

    Для начала организуем рабочее пространство. Разделим пространство на три части. Затем давайте разделим цифры числа на пары, двигаясь справа налево.

    Например, число 7,469,17 превращается в 74 69. 17 . Или в случае числа с нечетным количеством цифр, например 19 036, мы начнем с 1 90 36 .

    В нашем случае 2,025 превращается в 20 25 .

    ШАГ 2: Найдите наибольшее целое число

    В качестве следующего шага нам нужно найти наибольшее целое число (i), квадрат которого меньше или равен крайнему левому числу.

    В нашем текущем примере крайнее левое число — 20. Поскольку 4² = 16 <= 20 и 5² = 25> 20, рассматриваемое целое число равно 4.Положим 4 в правый верхний угол и 4² = 16 в правый нижний.

    ШАГ 3: Теперь вычтите это целое число

    Теперь нам нужно вычесть квадрат этого целого числа (которое равно 16) из крайнего левого числа (которое равно 20). Результат равен 4, и мы запишем его, как показано выше.

    ШАГ 4: Переходим к следующей паре

    Теперь давайте перейдем к следующей паре в нашем номере (то есть 25). Мы пишем его рядом с уже имеющимся вычитаемым значением (а это 4).

    Теперь умножьте число в правом верхнем углу (которое также равно 4) на 2. В результате получится 8, и мы запишем его в правом нижнем углу, а затем _ x _ =

    ШАГ 5: Найдите нужное Match

    Время заполнить каждое пустое пространство одним и тем же целым числом (i). Это должно быть максимально возможное целое число, при котором произведение должно быть меньше или равно числу слева.

    Например, если мы выберем число 6, первое число станет 86 (8 и 6), и мы также должны умножить его на 6.Результат 516 больше 425, поэтому мы спускаемся ниже и пробуем 5. Число 8 и число 5 дают нам 85. 85 умноженное на 5 дает 425, что нам и нужно.

    Напишите 5 рядом с 4 в правом верхнем углу. Это вторая цифра в корне.

    ШАГ 6: Снова вычесть

    Вычтите полученный результат (425) из текущего числа слева (также 425). Результат равен нулю, что означает, что задача выполнена.

    Примечание: Я специально выбрал идеальный квадрат (2025 = 45 x 45).Таким образом, я мог показать правила решения задач извлечения квадратного корня.

    На самом деле числа состоят из многих цифр, в том числе и после десятичной точки. В этом случае мы повторяем шаги 4, 5 и 6, пока не достигнем желаемой точности.

    Следующий пример объясняет, что я имею в виду.

    ПРИМЕР: Копаем глубже …

    На этот раз число состоит из нечетного числа цифр, включая единицы после десятичной точки.

    Как мы видели в этом примере, процесс может повторяться несколько раз для достижения желаемого уровня точности.

    Головоломка Java: Квадратный корень — Решение

    Автор Воутер Коэкартс.

    Вот решение нашей загадки извлечения квадратного корня.

    Шерлок

    Взгляните еще раз на этот код и включите свое воображение. Представьте, что у вас — это класс SquareRoot. У вас в кармане написано квадратное число на секретном листе бумаги. Шерлок допрашивает вас, чтобы вычислить квадратный корень. Каждый раз, когда он делает предположение, вы делите свое число на это предположение (целочисленное деление), и если результат равен этому предположению, вы должны кричать «Квадратный корень!».

    Предположим, ваше число — 19 749 136, и первое предположение для квадратного корня — 20 000 000. Вы можете быстро увидеть, что это больше, поэтому 19 749 136/20 000 000, округленное до целого числа, равно нулю. Так что, быстро взглянув на свой номер, вы просто бросаете на Шерлока пустой взгляд.

    Затем он угадает 9 870 000. Это снова далеко, о чем он думает? Как и любой хороший Java-класс, вы все равно следуете процедуре: вычислите 19 749 136/9 870 000 с округлением в меньшую сторону. Нет? Хорошо, тогда представьте, что вы пытаетесь вычислить, что это 2, так что молчите.

    Его предположения были далекими от квадратного корня, который равен 4444, если вам интересно. Но просто посмотрев, сколько времени вам потребовалось, чтобы сделать эти подразделения, Шерлок теперь знает, что ваше число, вероятно, больше 9 870 000 и меньше 20 000 000. Это хорошо известный прием в мире безопасности программного обеспечения: это временная атака , .

    Как решить

    Как это применимо к нашему коду? SquareRoot.answer (root) вызывает BigInteger.divide, который вызывает MutableBigInteger.делить. Этот метод позволяет избежать медленных вычислений, если корень больше или равен секрету n. Измеряя время, необходимое для ответа на звонок, вы узнаете, больше ли ваше предположение, чем n. Затем вы можете найти точное число с помощью двоичного поиска.

    Что следует учитывать при практическом решении:

    • Вызовите ответ несколько раз, прежде чем измерить, сколько времени это заняло, потому что время, необходимое для однократного выполнения, слишком мало для надежного измерения. Точность System.nanoTime варьируется от системы к системе, но обычно она совсем не точна с точностью до наносекунды.
    • Объедините несколько измерений для устранения шума, вызванного сборкой мусора или другими процессами.
    • Что касается всего, что связано с синхронизацией в JVM, примите во внимание, что компиляция выполняется точно по времени: сначала вычисления будут медленными, но ускорятся, когда часто выполняемый код компилируется и оптимизируется. Вы можете справиться с этим, сначала разогревая его. : выполните код столько раз, чтобы он был оптимизирован, прежде чем вы начнете измерения. Или вы можете продолжать переоценивать, что является быстрым или медленным вызовом, на который нужно ответить, по мере того, как все ускоряется.
    • Вам не нужен двоичный поиск, чтобы обнаружить n, а затем отдельный поиск его квадратного корня. Вы можете объединить и то, и другое в одном поиске.

    Покажи код

    Эта суть является нашим примером реализации этого.
    Эти люди решили это с помощью тайминга:
    Мэтт Мастраччи,
    Хью Пайл,
    Бен Мерфи,
    Ларри Сандерсон,
    Даниэль Мартин,
    Майк Нонмахер,
    Рой Лю,
    Крис Фрохофф,
    Дэвид Щерба,
    Адам Хоторн,
    Эран Медан,
    vpΔ,
    Петр Бурка и
    Сергей Мхитарян. Поздравляю! Мы свяжемся с вами в ближайшее время, чтобы отправить небольшой приз.

    Многие другие представленные решения, по нашему мнению, не прошли квалификацию, но все же были интересны:

    Практическое применение

    Эта головоломка была намеренно создана с учетом легко измеряемой разницы во времени в BigInteger.divide.
    В реальном мире можно использовать гораздо более тонкие проблемы с синхронизацией, даже удаленно. Явной целью временных атак является криптография, но она также применима в самых разных областях.

    В Square мы уделяем пристальное внимание подобным вопросам, чтобы гарантировать максимальную безопасность наших продуктов.

    Если вам понравился этот вызов, следите за нашим блогом, чтобы узнать о других головоломках по программированию.
    Wouter Coekaerts
    Следите за последними действиями Wouter Coekaerts на Medium, чтобы увидеть их истории и рекомендации. medium.com

    Найдите частное и остаток с помощью синтетического деления

    Подчеркивание в моем ответе ниже не проявлялось при фактическом отображении ответа. Так жаль. Должно быть, это недостаток в редакции Wyzant. Думаю, вы все еще можете разобрать, о чем я говорю.МК —————————————

    Я покажу вам, как выполнять часть A. Когда вы научитесь выполнять синтетическое деление, вы можете выполнять часть B.

    х4 — х3 + х2 — х + 2 / х-2

    Напишите «ноль», представленный делителем в правом верхнем углу.

    Поскольку делитель равен (x — 2), «ноль» будет +2.

    Это всегда противоположный знак в простом двучлене, таком как (x — 2).

    Так что пишите.4. Это всегда первый коэффициент в списке справа от делителя.

    2 | 1 -1 1 -1 2

    ↓

    1

    Затем умножьте делитель на число, которое вы вывели вниз, и поместите произведение под следующий коэффициент. (под -1 в этой задаче.)

    Вот так …

    2 | 1-1 1-1 2

    ↓ 2

    1

    То есть… 2 | умноженное на 1 внизу равно 2, которое мы пишем под -1.

    Затем мы добавляем второй столбец, то есть -1 плюс 2, которые мы только что написали. Складываем их и получаем 1. Напишите, что 1 под 2 вот так ….

    2 | 1-1 1-1 2

    ↓ 2

    1 1

    Следует запомнить процедуру «умножить, а затем сложить».

    Повторите процедуру, умножив 2 | на 1, который мы только что написали, получая 2.Напишите это 2 под следующим коэффициентом, который был 1. Вот так …

    2 | 1-1 1-1 2

    ↓ 2 2

    1 1

    Затем снова сложите, чтобы получить 3, и поместите 3 под ним …

    2 | 1-1 1-1 2

    ↓ 2 2

    1 1 3

    Умножьте и снова сложите, чтобы получить….

    2 | 1-1 1-1 2

    ↓ 2 2 6

    1 1 3 5

    И еще раз …

    2 | 1-1 1-1 2

    ↓ 2 2 6 10

    1 1 3 5 12

    Теперь последовательность внизу представляет частное.

    1 1 3 5 12

    Начните справа с 12.2 + 3x + 5 + 12 / (x-2)] раз (x-2) равно x4 — x3 + x2 — x + 2 (исходный многочлен.

    Я предоставлю вам выполнение части B. Используйте ту же процедуру.

    Как только вы привыкнете к синтетическому делению, вы обнаружите его очень быстро. Вы будете использовать его для разложения многочленов на множители, чтобы найти их «нули», которые будут пересечением по оси x на графике.

    .

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *

    2024 © Все права защищены.
    Приставка Размер
    Dividing_by_11-Short_Division.pdf 62,77 KB
    Division_short_method.pdf 9016.45