«Математические трюки для быстрого счета»

Фанат математики и научный журналист Ингве Фогт с детства увлекался числами и счетом. В книге «Математические трюки для быстрого счёта» (издательство «Альпина нон-фикшн»), переведенной на русский язык Анастасией Наумовой, Фогт собрал интересные способы быстро решать арифметические задачи. От читателя не требуется ничего, кроме знания базовых правил арифметики. N + 1 предлагает ознакомиться с отрывком, посвященным методу скоростного счета в уме, который был придуман бежавшим из России инженером и математиком Яковом Трахтенбергом.

Супербыстрый

швейцарский метод сложения

Я никогда не забуду ту радость, с которой получил от отца в подарок волшебную книгу Микаэля Шрёдера «Молниеносный счет в уме» (Lynregning). Мне было 14 лет, я все детство мечтал о волшебной книге, способной научить меня считать в уме, и теперь даже задрожал от восторга. Передо мной лежала книга, где рассказывалось о таких приемах, о которых я и не подозревал. Помимо прочего, там говорилось о способе складывать огромные числа без особого труда. Если в совершенстве овладеть этим способом, складывать числа можно намного быстрее и веселее, чем если пользоваться классическим школьным приемом.

Этот новый метод сложения был изобретен беженцем из России, которому лишь благодаря чуду удалось выжить в нацистском концлагере и добраться до Швейцарии. Бедный, как церковная крыса, Трахтенберг всего за несколько лет успел усовершенствовать методы расчетов, использовавшиеся в швейцарских банках. Яков Трахтенберг с детства имел склонность к математике. Он родился в 1888 г. в Одессе, в обеспеченной семье. В 1912-м Трахтенберг получил должность главного инженера на Обуховском заводе в Санкт-Петербурге, где строились военные суда для российского флота. В 1917-м к власти в России пришли коммунисты. Трахтенберг, убежденный пацифист, обрадовался, узнав, что теперь завод будет выпускать тракторы. Но спустя некоторое время Трахтенберга обвинили в пособничестве царскому режиму. Ему чудом удалось спастись: переодевшись крестьянином, он бежал из страны. В 1919 г. Яков приехал в Берлин и начал жизнь с чистого листа.

Через несколько лет он женился на еврейской девушке, но с приходом к власти Гитлера им пришлось бежать в Австрию. Здесь Яков Трахтенберг написал труд под названием «Министерство мира» — своего рода пародию на гитлеровскую автобиографию «Моя борьба», где высмеивал фюрера и его боевых соратников. Австрийские нацисты почувствовали себя невероятно оскорбленными. В 1938 г. за день до захвата нацистской Германией Австрии Трахтенберга арестовали. Он смог сбежать и добраться до Югославии, но его опять схватили и отправили в концентрационный лагерь Заксенхаузен. Чтобы не сломаться и сохранить рассудок, Трахтенберг, несмотря на постоянные пытки и допросы, придумывал новые методы счета. Он отрывал кусочки ногтей и выскребал ими примеры на стенах барака. Его целью было разработать новую систему счисления.

В конце войны его жена раздобыла фальшивые документы и добилась перевода Якова Трахтенберга в трудовой лагерь, расположенный в Южной Германии. Оттуда они вдвоем сбежали в Швейцарию. С момента злополучного ареста в Австрии прошло семь лет. Якову Трахтенбергу вновь пришлось начинать жизнь с чистого листа. Ему хотелось поделиться своими идеями о быстром счете с другими, однако они никого не интересовали, пока Трахтенберг не стал обучать математике сына местного полицмейстера. Мальчик, сперва совершенно безнадежный, после занятия с Трахтенбергом научился умножать огромные числа на 11. За несколько лет тысячи швейцарцев освоили новый метод счета, придуманный Трахтенбергом. Этот метод приобрел такую популярность, что математик основал собственный институт, где занимались счетом в уме. И первым преподавателем в этом институте стал — кто бы вы думали? Сын полицмейстера!

Один из многих методов Трахтенберга позволяет складывать множество многозначных чисел всего за несколько секунд, проверять верность полученного ответа и, что немаловажно, находить столбец, в котором прячется ошибка, если таковая имеется.

Давайте проверим метод Трахтенберга и сложим следующие числа:

Используя классический школьный метод сложения, мы, скорее всего, сначала сложили бы числа в правом столбце (4 + 7 + 8 + 9 + 8 + 5 = 41), после чего приступили бы к следу ющим столбцам. С сегодняшнего дня и с этого самого момента вам достаточно будет складывать числа только до 11. Иначе говоря, с бо́льшими числами мы вообще не будем иметь дела. Первое правило — выделим число 11. Каждый раз, досчитав до 11, сделаем отметку, вычтем одиннадцать из имеющейся суммы и продолжим.

Для начала посмотрим на правый столбец.

4 + 7 = 11. Сделаем отметку, вычтем 11 и продолжим.
8 + 9 = 17. Здесь тоже есть 11, и еще остается 6.
6 + 8 = 14. Снова 11, и еще осталось 3.
3 + 5 = 8.

Мы выделили три раза по 11, и еще в правом столбце у нас осталось 8. Запишем два этих важных числа друг под другом. Остаток, то есть 8, запишем в одной строке, а количество чисел 11 — в другой.

Проделаем то же самое с другими столбцами. Решайте сами, хотите ли двигаться слева направо или в противоположном направлении. От порядка действий ничего не зависит. Если хотите, можете сперва подсчитать количество чисел 11 во всех столбцах. Все зависит от вашего желания. Единственное, о чем необходимо помнить, — это делать отметку каждый раз, когда сумма составит 11.

У нас появилось две новых строки. В верхней — количество единиц, а в нижней — количество чисел 11 в каждом столбце. Эти числа, единицы и одиннадцатки, нужно сложить определенным образом.

Фокус в том, чтобы записать вычисления в виде буквы L. Это означает, что в каждом столбце мы не только складываем единицы и одиннадцатки, но также учитываем количество чисел 11 в правом столбце. И, пожалуйста, не забывайте про числа в уме.

(Складываем 8 и 3 — получаем 11. Записываем число 1 и держим 1 в уме.)

(Складываем 4, 2, 3 и 1 (в уме) — получаем 10. Записываем число 0 и держим 1 в уме.)

(Складываем 5, 3, 2 и 1 (в уме) — получаем 11. Записываем число 1 и держим 1 в уме.)

(Складываем 9, 1, 3 и 1 (в уме) — получаем 14. Записываем число 4 и держим 1 в уме.)

(Складываем 1 и 1 (в уме) — получаем 2.)

Возможно, кому-то покажется, что такие расчеты занимают столько же времени, сколько традиционный метод, но, когда метод Трахтенберга внедрили в швейцарских банках, скорость работы существенно возросла. Может, вовсе не удивительно, что Швейцария получила мировую известность благодаря своим банкам?

Основные преимущества нового метода заключаются в том, что с ним, во-первых, проще проверить правильность ответа, а во-вторых, понять, в каком столбце кроется ошибка. Следовательно, если вам не повезло и вы ошиблись, вовсе не обязательно считать все заново. Вместо этого вы сразу можете перейти к столбцу с ошибкой. Чтобы найти ошибку, надо сперва вычислить общую сумму чисел в каждом столбце. Как вы, возможно, помните, вычисляя общую сумму, можно выбросить все девятки.

Начнем с общей суммы чисел в правом столбце. Здесь у нас числа 4, 7, 8, 9, 8 и 5.

4 + 7 = 11. Общая сумма цифр в числе 11 равна 2.

2 + 8 = 10. Сумма цифр в числе 10 составляет 1.

1 + 8 = 9. Не забываем выбрасывать девятки. Тогда у нас остается 5.

Сокращенная сумма цифр во втором столбце справа будет следующей: 5 + 3 + 3 = 11. Сумма цифр в числе 11 равна 2. Следовательно, 2 + 1 + 5 = 8. Последняя цифра у нас 9. Ее можно отбросить. Сокращенная сумма цифр в этом столбце составляет 8. Сокращенная сумма цифр во всех четырех столбцах составляет:

2 2 8 5

Это называется контрольным числом для всех четырех столбцов. Главное — найти взаимосвязь между числами 1, 11 и теми, что у нас в столбцах. Наслаждайтесь моментом, потому что это настоящее волшебство метода Трахтенберга. Контрольные числа каждого столбца должны совпадать с сокращенной суммой единиц и удвоенных одиннадцаток.

9 5 4 8 (единицы)
1 3 2 3 (одиннадцатки)
2 2 8 5 (контрольные числа)

Пойдем справа.

8 + 3 + 3 = 14. Сумма цифр в числе 14 составляет 5. Этот же ответ мы получили, когда вычислили контрольное число для правого столбца.

4 + 2 + 2 = 8. Сокращенная сумма цифр во всем столбце тоже составляет 8.

5 + 3 + 3 = 11. Сумма цифр в числе 11 составляет 2. Значит, все верно.

9 + 1 + 1 = 11. Сумма цифр в числе 11 составляет 2. Значит, тут тоже все правильно.

Если бы в расчетах была ошибка, мы бы сразу же увидели, в каком она столбце. Вместо того чтобы складывать числа во всех столбцах заново, нам достаточно заново пересчитать лишь один столбец. Это позволяет здорово сэкономить время! Неудивительно, что метод Трахтенберга завоевал в свое время такую популярность, ведь тогда калькуляторы и счетные машинки еще не уничтожили необходимость считать в уме. Однако, если бы все владели методом Трахтенберга, стать чемпионом быстрого счета было бы непросто. Поэтому лучше придумать секретные правила, о которых никто больше не знает.

Подробнее читайте:
Фогт И. Математические трюки для быстрого счёта / Ингве Фогт ; Пер. с норв. [Анастасии Наумовой] — М.: Альпина Паблишер, 2020. — 183 с.

Эффективный счёт в уме или разминка для мозга / Хабр

Эта статья навеяна топиком «Как и насколько быстро вы считаете в уме на элементарном уровне?» и призвана распространить приёмы С.А. Рачинского для устного счёта.
Рачинский был замечательным педагогом, преподававшим в сельских школах в XIX веке и показавшим на собственном опыте, что развить навык быстрого устного счёта можно. Для его учеников не было особой проблемой посчитать подобный пример в уме:

Используем круглые числа

Один из самых распространённых приёмов устного счёта заключается в том, что любое число можно представить в виде суммы или разности чисел, одно или несколько из которых «круглое»:

Т. к. на 10, 100, 1000 и др. круглые числа умножать быстрее, в уме нужно сводить всё к таким простым операциям, как 18 x 100 или 36 x 10. Соответственно, и складывать легче, «отщепляя» круглое число, а затем добавляя «хвостик»: 1800 + 200 + 190.

Еще пример:

31 x 29 = (30 + 1) x (30 - 1) = 30 x 30 - 1 x 1 = 900 - 1 = 899. 

Упростим умножение делением

При устном счёте бывает удобнее оперировать делимым и делителем нежели целым числом (например, 5 представлять в виде 10:2, а 50 в виде 100:2):

68 x 50 = (68 x 100) : 2 = 6800 : 2 = 3400;
3400 : 50 = (3400 x 2) : 100 = 6800 : 100 = 68. 

Аналогично выполняется умножение или деление на 25, ведь 25 = 100:4. Например,

600 : 25  = (600 : 100) x 4 = 6 x 4 = 24;
24 x 25 = (24 x 100) : 4 = 2400 : 4 = 600. 

Теперь не кажется невозможным умножить в уме 625 на 53:

625 x 53 = 625 x 50 + 625 x 3 = (625 x 100) : 2 + 600 x 3 + 25 x 3 = (625 x 100) : 2 + 1800 + (20 + 5) x 3 = 
= (60000 + 2500) : 2 + 1800 + 60 + 15 = 30000 + 1250 + 1800 + 50 + 25 = 33000 + 50 + 50 + 25 = 33125. 2 = 17000 + 19000 + 2000 + 25 = 38025. 

Хм, я бы не сказала, что это сильно легче, чем возведение в столбик, но, возможно, со временем можно приноровиться.
И начинать тренировки, конечно, следует с возведения в квадрат двузначных чисел, а там уже и до дизассемблирования в уме можно дойти.

Умножение двузначных чисел

Этот интересный приём был придуман 12-летним учеником Рачинского и является одним из вариантов добавления до круглого числа.
Пусть даны два двузначных числа, у которых сумма единиц равна 10:

M = 10m + n, K = 10a + 10 - n.

Составив их произведение, получим:

Например, вычислим 77 x 13. Сумма единиц этих чисел равна 10, т.к. 7 + 3 = 10. Сначала ставим меньшее число перед большим: 77 x 13 = 13 x 77.

Чтобы получить круглые числа, мы забираем три единицы от 13 и добавляем их к 77. Теперь перемножим новые числа 80 x 10, а к полученному результату прибавим произведение отобранных 3 единиц на разность старого числа 77 и нового числа 10:

13 x 77 = 10 x 80 + 3 x (77 - 10) = 800 + 3 x 67 = 800 + 3 x (60 + 7) = 800 + 3 x 60 + 3 x 7 = 800 + 180 + 21 = 800 + 201 = 1001. 2 = 10000 + 9500 x 2 + 9025 = 10000 + (90+5) x 2 x 100 + 9000 + 25 = 
= 10000 + 19000 + 1000 +  8000  + 25 = 38025. 

Вместо заключения

Казалось бы, зачем уметь считать в уме в 21 веке, когда можно просто подать голосовую команду смартфону? Но если задуматься, что будет с человечеством, если оно будет взваливать на машины не только физическую работу, но и любую умственную? Не деградирует ли оно? Даже если не рассматривать устный счёт как самоцель, для закалки ума он вполне подходит.

Использованная литература:
«1001 задача для умственного счёта в школе С.А. Рачинского».

Как научиться считать в уме | Клуб любителей математики

Считать в уме, по мнению многих, в наше время уже неактуально, ведь калькулятор есть в каждом смартфоне, компьютере и ноутбуке. Однако калькулятор не будет сопровождать вас при каждом вашем шаге, а считать необходимо постоянно и много. Способность сосчитать в уме – умение весьма нужное даже в 21 веке. А тем более это нужно школьникам для решения примеров по математике из нелёгкой школьной программы. И им весьма полезно будет уметь считать быстро, не пребегая к электронным устройствам.

Опыт и постоянные тренировки играют важную роль в развитии любых способностей, но навык устного счета не состоит только лишь из опыта. Это могут доказать люди, умеющие считать в уме гораздо более сложные примеры: например, умножать и делить трех- и четырехзначные числа, находить суммы и разности огромных примеров.

Что необходимо знать и делать человеку, дабы повторить такое?

• Во-первых, концентрация или же умение ненадолго удерживать в памяти несколько вещей одновременно.

• Во-вторых, алгоритмы, специальные методы вычислений и математические уловки, значительно облегчающие процесс устного счёта.

• В-третьих, практика. Постоянные тренировки и постепенное усложнение решаемых задач позволят улучшить скорость и качество устного счета.

Важно отметить, что именно практика имеет наибольшее значение. Не обладая достаточным опытом, вы не сможете быстро применять удобные алгоритмы, подходящие под определённые ситуации. И помните, что максимальный эффект будет достигнут при оптимальном использовании всех трёх составляющих. Тренировать сразу все аспекты этого навыка Вы можете в онлайн тренажере устного счёта.

Внимание и концентрация

Чтобы максимально быстро считать в уме, необходимо уметь концентрироваться на конкретном примере. Этот навык полезен не только для совершения математических операций, но и для решения любых жизненных задач. Существует несколько способов улучшить свою внимательность и способность к концентрации:

При счете в уме, важно ясно представлять себе решаемый пример – визуализировать его. Запоминать промежуточные результаты нужно не на слух, а так как они выглядят в записи, например, на бумаге. Тренировать подобное восприятие можно разными способами, и отчасти визуализация решения приходит с опытом.

Старайтесь всегда находить что-то интересное в рутине, превращая действие в игру. Так поступают и некоторые родители, желающие, чтобы их ребёнок выполнил какую-либо скучную работу.

Огромное количество людей всегда хотят «быть лучше» соперника. Именно поэтому состязательность является еще одним способом развить свою внимательность. В устном счете Вы можете найти себе соперника и пытаться его в этом превзойти.

Еще одним фактором, создающим азарт при счете, может стать борьба с самим собой при достижении определенного результата, то есть личные рекорды. Их можно ставить, например, в скорости счета, в количестве решенных примеров и своей точности ответов.

Наконец, максимальная концентрация может быть достигнута при спонтанном увлечении процессом счета. Как пример, во время чтения Вы перестаёте думать об окружающих вас предметах, людях, ситуациях, полностью погружаетесь в книгу. Именно неподдельный интерес к чему-либо способен заставить вас приобрести наибольшую внимательность в этом деле.

Безусловно, все эти способы надо отрабатывать, практиковать. В этом могут помочь различные тренажеры зрительной памяти и улучшения внимательности.

Простые арифметические закономерности

Решение любой по сложности задачи всегда сводится к применению базовых принципов, и именно эти принципы и закономерности позволят вам быстро выполнять различного рода операции. Существует определенный набор таких правил и закономерностей, которые необходимо довести до автоматизма с помощью разных онлайн тренажеров по математике.

Вычитание 7, 8, 9. Чтобы вычесть 9 из любого числа, нужно вычесть из него 10 и прибавить 1. Чтобы вычесть 8 из любого числа, нужно вычесть из него 10 и прибавить 2. Чтобы вычесть 7 из любого числа, нужно вычесть из него 10 и прибавить 3. Если обычно вы считаете по-другому, то для лучшего результата вам необходимо привыкнуть к этому новому способу.

Таблица умножения. Для быстрого устного счета хорошо бы безупречно знать таблицу умножения, которая является основой счета. Если у Вас с этим еще проблемы, можете воспользоваться онлайн Тренажером таблицы умножения.

Умножение на 2. Для умножения на 2 некруглых чисел пробуйте округлять их до ближайших более удобных. Так 139×2 проще считать, если сначала умножить 140 на 2 (140×2=280), а потом вычесть 1×2=2 (именно 1 нужно прибавить к 139, чтобы получить 140). Итого: 140×2-1×2=280-2=278.

Деление на 2. Несмотря на то, что многим умножение и деление на 2 дается достаточно просто, в сложных случаях так же пытайтесь округлять числа. Например, чтобы разделить 198 на 2, нужно сначала разделить 200 (это 198+2) на 2 и отнять 2 деленое на 2. Итого: 198:2=200:2-2:2=100-1=99.

Деление и умножение на 4 и 8. Деление (или умножение) на 4 и на 8 являются двукратным или трехкратным делением (или умножением) на 2. Производить эти операции удобно последовательно. Например, 46×4=46×2×2=92×2=184.

Умножение на 5 и 25. Умножение на 5, и деление на 2 – практически одно и то же, поэтому всегда умножайте на 5, поделив число на 2 и умножив его на 10: 88×5=88:2×10=440. Умножение на 25 соответствует делению на 4 (с последующим умножением на 100). Так 120×25 = 120:4×100 = 30×100 = 3000.

Умножение на 9. Быстро умножить любое число на 9 можно следующим образом: сначала умножьте это число на 10, а затем вычтите из результата само число. Например: 89×9=890-89=801.

Умножение на 11. Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры. Например: 23×11= 2 (2+3) 3 = 253. Или если сумма чисел в центре дает результат больше 10: 29×11 = 2 (2+9) 9 = 2 (11) 9 = 319.

И наконец, полезно знать деление чисел, кратных 10 на числа, кратные двум: 1000 = 2×500 = 4×250 = 8×125 = 16×62,5.

Более сложные методики

Эффективность умножения в уме некоторых двузначных чисел может быть выше за счет меньшего количества действий, если использовать специальные алгоритмов. Ниже представлены три специальные методики, в том числе введение и использование опорного числа.

Квадрат суммы и квадрат разности

Для того чтобы возвести в квадрат двузначное число, можно воспользоваться формулами квадрата суммы или квадрата разности. Например:

23²= (20+3)² = 20² + 2×3×20 + 3² = 400+120+9 = 529

69² = (70-1)² = 70² – 70×2×1 + 1² = 4 900-140+1 = 4 761

Возведение в квадрат чисел, заканчивающихся на 5

Чтобы возвести в квадрат числа, заканчивающиеся на 5, необходимо число до последней пятерки, умножить на сумму этого же числа и единицы. К результату дописываем 25. Вот несколько примеров:

25² = (2×(2+1)) 25 = 625

85² = (8×(8+1)) 25 = 7 225

155² = (15×(15+1)) 25 = (15×16)25 = 24 025

Опорное число

Наиболее популярной методикой умножения больших чисел в уме является прием использования, так называемого, опорного числа. Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. А методика использования этого числа зависит от того, являются ли множители больше или меньше него самого.

Оба множителя меньше опорного. Допустим, мы хотим умножить 48 на 47. Эти числа находятся достаточно близко к числу 50, а следовательно удобно использовать 50 в качестве опорного числа. Далее действуем так: из 47 вычетаем столько, сколько не хватает 48 до 50 (либо из 48 вычетаем столько, сколько не хватает 47 до 50), полученный результат умножаем на опорное число и прибавляем к нему произведение разностей опроного числа с каждым сомножителем. Наглядный пример:

(48–(50-47))×50 + (50-47)×(50-48) = 2250 + 6 = 2256

Оба множителя больше опорного. Действовать нужно точно так же, но не вычитать недостаток, а прибавлять избыток:

(51+(63-50))×50 + (63-50)×(51-50) = 3200 + 13 = 3213

Один множитель меньше, другой больше опорного. Схема та же, но произведение недостатка и избытка нужно вычитать:

(45+(52-50))×50 – (52-50)×(50-45) = 2350 – 10 = 2340

В заключение

Как уже было сказано ранее, навык устного счета набирается из трех составляющих: это способность концентрироваться конкретном примере, грамотный подбор метода быстрого счета и, конечно, опыт. Запомните, даже зная наизусть все алгоритмы, упрощающие вам устный счет, вы не сможете сосчитать без пракики так же быстро, как если бы вы занимались этим каждый день уже несколько лет. Именно потоянные тренировки на разного рода тренажерах устного счета позволят вам отточить мастрство в этом деле и приобрести тот самый бесценный навык быстрого устного счета.

Быстрый счет в уме без калькулятора

Человек всегда стремился научиться легко и быстро производить операции с большими числами в уме. Несмотря на то, что сейчас почти у каждого есть возможность пользоваться таким благом цивилизации как калькулятор, многие люди все равно интересуются различными системами устных вычислений и хитрыми математическими приемами. Какую пользу они несут для детей и взрослых, и стоит ли их изучать?

Устный счет и его польза

У современного человека появилось немало новых повседневных задач, которые связаны с работой, учебой или иными видами деятельности. Чтобы эффективно справляться с ними, он должен обладать целым рядом определенных навыков. Одной из важнейших способностей можно назвать счет в уме, которому мы учимся еще в школе на уроках математики. В начальных классах малыши сначала осваивают сложение и вычитание небольших чисел, а затем более сложные операции – умножение и деление.

В первые годы учебы педагоги уделяют внимание развитию устного счета, учат считать без помощи калькулятора или иных подручных средств. Но в дальнейшем приоритеты школьной программы смещаются в сторону углубленного изучения каждой из дисциплин, и математика не является исключением. Постепенно ученики отказываются считать в уме, предпочитая производить операции с числами в столбик или пользоваться гаджетами. Отсутствие постоянной практики не дает детям полноценно развить свои навыки, а потому и во взрослом возрасте люди все чаще полагаются на умных помощников, а не на возможности собственного интеллекта.

Развитие технологий действительно сделало жизнь проще, но и у этого есть свои минусы. Чтобы добиться значительного успеха в любом начинании, человек постоянно должен самосовершенствоваться, работать над собой. Тренировка умения быстро считать в уме может стать отличным помощником для достижения этих целей, ведь повышение навыков работы с числами также является эффективным способом развития интеллекта. Конечно, речь идет не о базовых умениях, которые прививаются еще в детские годы, а о более углубленном изучении приемов быстрого счета без калькулятора. Поговорим о тех из них, которые известны уже давно, и о более новых, только набирающих популярность.

Примеры быстрого счета в уме без калькулятора

Ученые прошлого, чья жизнь и работа была неотрывно связана с точными науками, всегда стремились найти новые способы быстрого счета. В то время они отлично обходились без калькулятора. Благодаря их разработкам сегодня можно найти немало приемов, позволяющих считать с высокой скоростью даже большие числа. Рассмотрим несколько таких способов на примерах:

• умножение на 11. Чтобы быстро произвести данную операцию в уме, нужно умножить наше число на 10, а затем прибавить в нему это же число. К примеру, требуется произвести умножение 46 на 11. Число 46 мы умножаем на 10: 46*10=460. К этому новому значению прибавляем 46 и получаем следующее выражение: 460+46=506.
• деление на 5. Для решения такого выражения потребуется умножить делимое на 2, а затем перенести запятую на один знак влево. Рассмотрим этот способ на примере деления числа 643 на 5: 643*2=1286. Переносим запятую нашего нового числа на знак влево и получаем ответ: 128,6.
• умножение на полтора. Чтобы быстро произвести такое действие необходимо к нашему значению прибавить его половину. К примеру, нужно найти результат умножения 116 на 1,5. Делим 116 на 2, получается 58. Теперь к 116 прибавляем наше новое значение: 116+58=174.
• вычитание трехзначного числа из 1000. Для решения такого примера подойдет следующий способ: от числа 9 отнимаем каждую цифру вычитаемого, кроме последней – ее отнимаем от 10. Чтобы из 1000 вычесть 845 нужно произвести следующие действия: от 9 отнять 8, получается 1, от 9 отнять 4, получается 5, а от 10 отнять 5, получается 5. Последовательно записываем каждое новое значение и получаем верный ответ: 1000-845=155.

Несмотря на то, что перечисленные способы нельзя назвать кардинально новыми, их использование позволяет удивить окружающих своими интеллектуальными способностями. Особенно ярко данные приемы демонстрируют дети, которые участвуют в различных телевизионных программах в качестве гостей.

Удивительные люди

Основным плюсом математических хитростей является то, что освоить и научиться применять их на практике может даже ребенок. Малыши и подростки, которые в совершенстве овладели этими приемами, успешно выступают на телевидении, где удивляют зрителей умением складывать, вычитать, умножать и делить даже большие числа в уме. Но использование таких способов счета имеет и свои недостатки, главным из которых можно назвать невозможность применять один и тот же метод в различных случаях. Так правила умножения любого числа на 11 работают только в определенных условиях и не распространяются на те ситуации, где множителем выступает другое значение.

Именно поэтому в качестве альтернативы математическим хитростям многие люди находятся в поиске все новых и новых методов устных вычислений, которые удалось бы более широко применять на практике. Техникой, которая отвечает этим запросам и пользуется все большей популярностью с каждым годом, является ментальная арифметика. Поговорим о ее ключевых особенностях и о том, как она позволяет считать быстрее калькулятора даже маленькому ребенку.

Техника быстрого устного счета

Ментальная арифметика имеет совершенно другой подход, чем другие давно известные или более новые способы работы с числами. В ее основе лежат вычисления на абакусе – специальном инструменте, который представляет собой особые счеты. Обучение данной технике состоит из нескольких этапов. На первых занятиях студенты осваивают абакус и учатся складывать и вычитать на нем небольшие числа. Впоследствии им предстоит привыкнуть представлять эти счеты в своем воображении и научиться производить арифметические операции уже на них. Постепенно сложность тренировок повышается, и студенты также осваивают умножение и деление в уме.

В процессе тренировок удается добиться потрясающей скорости работы с числами. Однако, быстрый счет в уме — не главное и далеко не единственное преимущество ментальной арифметики. Ее важнейшая особенность – это разностороннее развитие интеллекта, благодаря которому удается совершенствовать память, концентрацию внимания, скорость реакции, а также логическое, аналитическое и творческое мышление. Все это делает занятия ментальной арифметикой эффективным способом саморазвития, который подходит и для детей, и для взрослых.

Теперь обучение ментальной арифметике доступно в режиме онлайн на платформе Amavit. Индивидуальные занятия с личным тренером, большое количество обучающих игр на платформе и специальное приложение с абакусом на смартфон сделают тренировки не только эффективными, но и интересными. Зарегистрируйтесь на сайте amavit.com, подберите удобный график занятий и начните совершенствовать навыки устного счета, которые пригодятся в любом возрасте.

Методика «быстрого» счета

Отработка вычислительных навыков обучающихся на уроках математики с помощью приемов «быстрого» счета.

Кудинова И.К., учитель математики

МКОУ Лимановской СОШ

Панинского муниципального района

Воронежской области

«Приходилось ли тебе наблюдать, как люди с природными способностями к счёту бывают восприимчивы, можно сказать, ко всем наукам? Даже все те, кто туго соображает, если они обучаются этому и упражняются, то хотя бы они не извлекали из этого для себя никакой пользы, всё же становятся более восприимчивы, чем были раньше»

Платон

Важнейшей задачей образования является формирование универсальных учебных действий, обеспечивающих школьникам умение учиться, способность к саморазвитию и самосовершенствованию. Качество усвоения знаний определяется многообразием и характером видов универсальных действий. Формирование способности и готовности учащихся реализовывать универсальные учебные действия позволяет повысить эффективность процесса обучения. Все виды универсальных учебных действий рассматриваются в контексте содержания конкретных учебных предметов.

Важную роль в формировании универсальных учебных действий играет обучение школьников навыкам рациональных вычислений. Ни у кого не вызывает сомнения, что, развитие умения рациональных вычислений и преобразований, а также развитие навыков решения простейших задач «в уме» — важнейший элемент математической подготовки учащихся. Важность и необходимость таких упражнений доказывать не приходиться. Значение их велико в формировании вычислительных навыков, и совершенствовании знаний по нумерации, и в развитии личностных качеств ребенка. Создание определенной системы закрепления и повторения изученного материала дает учащимся возможность усвоения знаний на уровне автоматического навыка.

Знание упрощенных приемов устных вычислений остается необходимым даже при полной механизации всех наиболее трудоемких вычислительных процессов. Устные вычисления дают возможность не только быстро производить расчеты в уме, но и контролировать, оценивать, находить и исправлять ошибки. Кроме того, освоение вычислительных навыков развивает память и помогает школьникам полноценно усваивать предметы физико-математического цикла.

Очевидно, что приемы рационального счета  являются  необходимым элементом  вычислительной  культуры  в жизни каждого человека,  прежде всего силу своей практической значимости, а обучающимся она необходима практически на каждом уроке.

Вычислительная культура является фундаментом изучения математики и других учебных дисциплин, т. к. кроме того, что вычисления активизируют память, внимание, помогают рационально организовать деятельность и существенно влияют на развитие человека.

В повседневной жизни, на учебных занятиях, когда ценится каждая минута, очень важно  быстро и рационально провести устные и письменные вычисления, не допустив при этом ошибок и не используя при этом никаких дополнительных вычислительных средств.

Анализ результатов экзаменов в 9-х и 11-х классах показывает, что наибольшее количество ошибок учащиеся допускают при выполнении заданий на вычисления. Нередко даже высокомотивированные учащиеся к выходу на итоговую аттестацию утрачивают навыки устного счета. Они плохо и нерационально считают, все чаще прибегая к помощи технических средств-калькуляторов. Главная задача учителя – не только сохранить вычислительные навыки, но и научить применять нестандартные приемы устного счета, которые позволили бы значительно сократить время работы над заданием.

Рассмотрим конкретные примеры различных приемов быстрых рациональных вычислений.

РАЗЛИЧНЫЕ СПОСОБЫ СЛОЖЕНИЯ И ВЫЧИТАНИЯ

СЛОЖЕНИЕ

Основное правило для выполнения сложения в уме звучит так:

Чтобы прибавить к числу 9, прибавьте к нему 10 и отнимите 1;чтобы прибавить 8, прибавьте 10 и отнимите 2; чтобы прибавить 7, прибавьте10 и отнимите 3 и т. д. Например:

56+8=56+10-2=64;

65+9=65+10-1=74.

СЛОЖЕНИЕ В УМЕ ДВУЗНАЧНЫХ ЧИСЕЛ

Если цифра единиц в прибавляемом числе больше5, то число необходимо округлить в сторону увеличения, а затем вычесть ошибку округления из полученной суммы. Если же цифра единиц меньше, то прибавляем сначала десятки, а потом единицы. Например:

34+48=34+50-2=82;

27+31=27+30+1=58.

СЛОЖЕНИЕ ТРЕХЗНАЧНЫХ ЧИСЕЛ

Складываем слева на право, то есть сначала сотни, потом десятки, а затем единицы. Например:

359+523= 300+500+50+20+9+3=882;

456+298=400+200+50+90+6+8=754.

ВЫЧИТАНИЕ

Чтобы вычесть два числа в уме, нужно округлить вычитаемое, а затем подкорректируйте полученный ответ.

56-9=56-10+1=47;

436-87=436-100+13=349.

Умножение многозначных чисел на 9

1. Число десятков увеличим на 1 и вычтем из множимого

2. К результату приписываем дополнение цифры единиц множимого до 10

Пример:

576 · 9 = 5184 379 · 9 = 3411

576 – (57 + 1) = 576 – 58 = 518 . 379 – (37 + 1) = 341 .

4 1

Умножение на 99

1. Из числа вычитаем число его сотен, увеличенное на 1

2. Находим дополнение числа, образованного двумя последними цифрами до 100

3. Приписываем дополнение к предшествующему результату

Пример:

27 · 99 = 2673 (сотен – 0) 134 · 99 = 13266

27 – 1 = 26 134 – 2 = 132 (сотня – 1 + 1)

100 – 27 = 73 66

Умножение на 999 любого числа

1. Из умножаемого вычитаем число тысяч, увеличенное на 1

2. Находим дополнение до 1000

23 · 999 = 22977 ( тысяч – 0 + 1 = 1)

23 – 1 = 22

1000 – 23 = 977

124 · 999 = 123876 ( тысяч – 0 + 1 = 1)

124 – 1 = 123

1000 – 124 = 876

1324 · 999 = 1322676 (тысяча – 1 + 1 = 2)

1324 – 2 = 1322

1000 – 324 = 676

Умножение на 11, 22, 33, …99

Чтобы двузначное число, сумма цифр которого не превышает 10, умножить на 11, надо цифры этого числа раздвинуть и поставить между ними сумму этих цифр:

72 ×11= 7 (7+2) 2 = 792;

35 ×11 = 3 (3+5) 5 = 385.

Чтобы умножить 11 на двузначное число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить единицу, а вторую и последнюю (третью) оставить без изменения:

94 ×11 = 9 (9+4) 4 = 9 (13) 4 = (9+1) 34 = 1034;

59×11 = 5 (5+9) 9 = 5 (14) 9 = (5+1) 49 = 649.

Чтобы двузначное число умножить на 22, 33. …99, надо последнее число представить в виде произведения однозначного числа (от 1 до 9) на 11, т.е.

44= 4 × 11; 55 = 5×11 и т. д.

Затем произведение первых чисел умножить на 11.

48 × 22 =48 × 2 × (22 : 2) = 96 × 11 =1056;

24 × 22 = 24 × 2 × 11 = 48 × 11 = 528;

23 ×33 = 23 × 3× 11 = 69 × 11 = 759;

18 × 44 = 18 × 4 × 11 = 72 × 11 = 792;

16 × 55 = 16 × 5 × 11 = 80 × 11 = 880;

16 × 66 = 16 × 6 × 11 = 96 × 11 = 1056;

14 × 77 = 14 × 7 × 11 = 98 × 11 = 1078;

12 × 88 = 12 × 8 × 11 = 96 × 11 = 1056;

8 × 99 = 8 × 9 × 11 = 72 × 11 = 792.

Кроме того, можно применить закон об одновременном увеличении в равное число раз одного сомножителя и уменьшении другого.

Умножение на число, оканчивающееся на 5

Чтобы четное двузначное число умножить на число, оканчивающееся на 5, следует применить правило: если один из сомножителей увеличить в несколько раз, а другой – уменьшить во столько же раз, произведение не изменится.

44 × 5 = (44 : 2) × 5 × 2 = 22 × 10 = 220;

28 × 15 = (28 : 2) × 15 × 2 = 14 × 30 = 420;

32 × 25 = (32 : 2) × 25 × 2 = 16 × 50 = 800;

26 × 35 = (26 : 2) × 35 × 2 = 13 × 70 = 910;

36 × 45 = (36 : 2) × 45 × 2 = 18 × 90 = 1625;

34 × 55 = (34 : 2) × 55 × 2 = 17 × 110 = 1870;

18 × 65 = (18 : 2) × 65 × 2 = 9 × 130 = 1170;

12 × 75 = (12 : 2) × 75 × 2 = 6 × 150 = 900;

14 × 85 = (14 : 2) × 85 × 2 = 7 × 170 = 1190;

12 × 95 = (12 : 2) × 95 × 2 = 6 × 190 = 1140.

При умножении на 65, 75, 85, 95 числа следует брать небольшие, в пределах второго десятка. В противном случае вычисления усложнятся.

Умножение и деление на 25, 50, 75, 125, 250, 500

Для того, чтобы устно научиться умножать и делить на 25 и 75, надо хорошо знать признак делимости и таблицу умножения на 4.

На 4 делятся те, и только те числа, у которых две последние цифры числа выражают число, делящееся на 4.

Например:

124 делится на 4, так как 24 делится на 4;

1716 делится на 4, так как 16 делится на 4;

1800 делится на 4, так как 00 делится на 4

Правило. Чтобы число умножить на 25, надо это число разделить на 4 и умножить на 100.

Примеры:

484 × 25 = (484 : 4) × 25 × 4 = 121 × 100 = 12100

124 × 25 = 124 : 4 × 100 = 3100

Правило. Чтобы число разделить на 25, надо это число разделить на 100 и умножить на 4.

Примеры:

12100 : 25 = 12100 : 100 × 4 = 484

31100 : 25 = 31100 :100 × 4 = 1244

Правило. Чтобы число умножить на 75, надо это число разделить на 4 и умножить на 300.

Примеры:

32 × 75 = (32 :4) × 75 × 4 = 8 × 300 = 2400

48 × 75 = 48 : 4 × 300 = 3600

Правило. Чтобы число разделить на 75, надо это число разделить на 300 и умножить на 4.

Примеры:

2400 : 75 = 2400 : 300 × 4 = 32

3600 : 75 = 3600 : 300 × 4 = 48

Правило. Чтобы число умножить на 50, надо это число разделить на 2 и умножить на 100.

Примеры:

432× 50 = 432 :2 × 50 × 2 = 216 × 100 = 21600

848 × 50 = 848 : 2 × 100 = 42400

Правило. Чтобы число разделить на 50, надо это число разделить на 100 и умножить на 2.

Примеры:

21600 : 50 = 21600 : 100 × 2 = 432

42400 : 50 = 42400 : 100 × 2 = 848

Правило. Чтобы число умножить на 500, надо это число разделить на 2 и умножить на 1000.

Примеры:

428 × 500 = (428 :2) × 500 × 2 = 214 × 1000 = 214000

2436 × 500 = 2436 : 2 × 1000 = 1218000

Правило. Чтобы число разделить на 500, надо это число разделить на 1000 и умножить на 2.

Примеры:

214000 : 500 = 214000 : 1000 × 2 = 428

1218000 : 500 = 1218000 : 1000 × 2 = 2436

Прежде чем научиться умножать и делить на 125, надо хорошо знать таблицу умножения на 8 и признак делимости на 8.

Признак. На 8 делятся те и только те числа, у которых три последние цифры выражают число, делящееся на 8.

Примеры:

3168 делится на 8, так как 168 делится на 8;

5248 делится на 8, так как 248 делится на 8;

12328 делится на 8, так как 324 делится на 8.

Чтобы узнать, делится ли трехзначное число, оканчивающееся цифрами 2, 4, 6. 8. на 8, нужно к числу десятков прибавить половину цифр единиц. Если полученный результат будет делиться на 8, то исходное число делится на 8.

Примеры:

632 : 8, так как т.е. 64 : 8;

712 : 8, так как т.е. 72 : 8;

304 : 8, так как т.е. 32 : 8;

376 : 8, так как т.е. 40 : 8;

208 : 8, так как т.е. 24 : 8.

Правило. Чтобы число умножить на 125, надо это число разделить на 8 и умножить на 1000. Чтобы число разделить на 125, надо это число разделить на 1000 и умножить

на 8.

Примеры:

32 × 125 = (32 : 8) × 125 × 8 = 4 × 1000 = 4000;

72 × 125 = 72 : 8 × 1000 = 9000;

4000 : 125 = 4000 : 1000 × 8 = 32;

9000 : 125 = 9000 : 1000 × 8 = 72.

Правило. Чтобы число умножить на 250, надо это число разделить на 4 и умножить на 1000.

Примеры:

36 × 250 = (36 : 4) × 250 × 4 = 9 × 1000 = 9000;

44 × 250 = 44 : 4 × 1000 = 11000.

Правило. Чтобы число разделить на 250, надо это число разделить на 1000 и умножить на 4.

Примеры:

9000 : 250 = 9000 : 1000 ×4 = 36;

11000 : 250 = 11000 : 1000 ×4 = 44

Умножение и деление на 37

Прежде чем научиться устно умножать и делить на 37, надо хорошо знать таблицу умножения на три и признак делимости на три, который изучается в школьном курсе.

Правило. Чтобы умножить число на 37, надо это число разделить на 3 и умножить на 111.

Примеры:

24 × 37 = (24 : 3) × 37 × 3 = 8 × 111 = 888;

27 × 37 = (27 : 3) × 111 = 999.

Правило. Чтобы число разделить на 37, надо это число разделить на 111 и умножить на 3

Примеры:

999 : 37 = 999 :111 × 3 = 27;

888 : 37 = 888 :111 × 3 = 24.

Умножение на 111

Научившись умножать на 11, легко умножить на 111, 1111. и т. д. число, сумма цифр которого меньше 10.

Примеры:

24 × 111 = 2 (2+4) (2+4) 4 = 2664;

36 ×111 = 3 (3+6) (3+6) 6 = 3996;

17 × 1111 = 1 (1+7) (1+7) (1+7) 7 = 18887.

Вывод. Чтобы число умножить на 11, 111. и т. д., надо мысленно цифры этого числа раздвинуть на два, три и т. д. шагов, сложить цифры и записать между раздвинутыми цифрами.

Умножение двух рядом стоящих чисел

Примеры:

Вывод. При умножении двух рядом стоящих чисел надо сначала перемножить цифры десятков, затем цифру десятков умножить на сумму цифр единиц и, наконец, надо перемножить цифры единиц. Получим ответ (см. примеры)

Умножение пары чисел, у которых цифры десятков одинаковые, а сумма цифр единиц составляет 10

Пример:

24 × 26 = (24 – 4) × (26 + 4) + 4 × 6 = 20 × 30 + 24 = 624.

Числа 24 и 26 округляем до десятков, чтобы получить число сотен, и к числу сотен прибавляем произведение единиц.

18 × 12 = 2 × 1 сот. + 8 × 2 = 200 + 16 = 216;

16 × 14 = 2 × 1 × 100 + 6 × 4 = 200 + 24 = 224;

23 × 27 = 2 × 3 × 100 + 3 × 7 = 621;

34 × 36 = 3 × 4 сот. + 4 × 6 = 1224;

71 × 79 = 7 × 8 сот. + 1 × 9 = 5609;

82 × 88 = 8 × 9 сот. + 2 × 8 = 7216.

Можно решать устно и более сложные примеры:

108 × 102 = 10 × 11 сот. + 8 × 2 = 11016;

204 × 206 = 20 × 21 сот. +4 × 6 = 42024;

802 × 808 = 80 × 81 сот. +2 × 8 = 648016.

Проверка:

× 802

808

6416

6416__

648016

Умножение двузначных чисел, у которых сумма цифр десятков равна 10, а цифры единиц одинаковые.

Правило. При умножении двузначных чисел. у которых сумма цифр десятков равна 10, а цифры единиц одинаковые, надо перемножить цифры десятков. и прибавить цифру единиц, получим число сотен и к числу сотен прибавим произведение единиц.

Примеры:

72 × 32 = (7 × 3 + 2)сот. + 2 × 2 = 2304;

64 × 44 = (6 × 4 + 4) × 100 + 4 × 4 = 2816;

53 × 53 = (5 × 5 +3) × 100 + 3 × 3 = 2809;

18 × 98 = (1 × 9 + 8) × 100 + 8 × 8 = 1764;

24 × 84 = (2 × 8 + 4) ×100+ 4 × 4 = 2016;

63 × 43 = (6 × 4 +3) × 100 +3 × 3 = 2709;

35 × 75 = (3 × 7 + 5) × 100 +5 × 5 = 2625.

Умножение чисел, оканчивающихся на 1

Правило. При умножении чисел, оканчивающихся на 1, надо сначала перемножить цифры десятков и правее полученного произведения записать под этим числом сумму цифр десятков, а затем перемножить 1 на 1 и записать еще правее. Сложив столбиком, получим ответ.

Примеры:

Умножение двузначных чисел на 101, трехзначных – на 1001

Правило. Чтобы двузначное число умножить на 101, надо к этому числу приписать справа это же число.

48 × 101 = 4848;

56 × 101 = 5656.

Правило. Чтобы трехзначное число умножить на 1001, надо к этому числу справа приписать это же число.

Примеры:

648 1001 = 648648;

999 1001 = 999999.

Приемы устных рациональных вычислений, используемые на уроках математики, способствуют повышению общего уровня математического развития;  развивают у учеников навык быстро выделять из известных им законов, формул, теорем те, которые следует применить для решения предложенных задач, расчетов и вычислений; содействуют развитию памяти, развивают способность зрительного восприятия математических фактов, совершенствуют пространственное воображение. 

Помимо этого, рациональный счет на уроках математики играет немаловажную роль в повышении у детей познавательного интереса к урокам математики, как одного из важнейших мотивов учебно-познавательной деятельности, развития личностных качеств ребенка. Формируя навыки устных рациональных вычислений, учитель тем самым воспитывает у учащихся навыки сознательного усвоения изучаемого материала, приучает ценить и экономить время, развивает желание поиска рациональных путей решения задачи. Иными словами формируются познавательные, включая логические, познавательные и знаково-символические универсальные учебные действия.

Цели и задачи школы кардинально меняются, осуществляется переход от знаниевой парадигмы к лично-ориентированному обучению. Потому важно не просто учить решать задачи по математике, а показывать действие основных математических законов в жизни, объяснять, как может учащийся применить полученные знания. И тогда у детей появится главное: желание и смысл учиться.

Список литературы

Минских Е.М. «От игры к знаниям», М., «Просвещение» 1982.

Кордемский Б.А., Ахадов А.А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986.

Совайленко ВК. Система обучения математике в 5-6 классах. Из опыта работы.- М.:Просвещение, 1991.

Катлер Э. Мак-Шейн Р. «Система быстрого счёта по Трахтенбергу» — М. Просвещение, 1967.

Хэндли Билл «Считать в уме как калькулятор» — Минск, Попурри, 2006.

Минаева С. С. «Вычисления на уроках и внеклассных занятиях по математике.» — М.: Просвещение, 1983. 

Сорокин А.С. «Техника счета (методы рациональных вычислений)», М, Знани», 1976

http://razvivajka.ru/ Тренировка устного счета

http://gzomrepus.ru/exercises/production/ Упражнения на продуктивность и быстрый устный счет

БЫСТРЫЙ СЧЁТ В УМЕ – ТРЕНИРОВКА ДЛЯ МОЗГА | АКАДЕМИЯ AMAKids

В век электронных технологий умение быстро выполнять арифметические действия в уме стало неким раритетом. Вместо собственных мозгов люди используют для подсчетов калькулятор или мобильный телефон. Подобная привычка неблаготворно отражается на умственной деятельности. Поэтому нужно обучить детей быстрому счёту в уме.

Без постоянных тренировок мыслительные процессы замедляются, интенсивность деятельности мозга снижается, поскольку его извилины требовательны к упражнениям не меньше, чем мышцы.

Люди, умеющие быстро считать в уме, – не гении, но они обладают иным уровнем управления реальностью: быстро ориентируются в нестандартных ситуациях, принимают нетривиальные решения, способны сконцентрироваться на важных моментах.

ПОЛЬЗА СЧЁТА В УМЕ

Быстрый счёт в уме для детей очень важен для их развития. Дело в том, что современные ученые провели исследование и сделали вывод: у наших малышей идет спад интеллектуальных способностей. Мы всё чаще считаем на калькуляторе, делая наш мозг ленивым. Иногда даже в пределах 20 ребенок достает телефон и считает на нём. Ему так проще, чем напрягать извилины. И задача родителей – предотвратить это. Мама с папой должны много времени уделять тренировкам мозга своего ребенка. И самое лучшее упражнение для этого – устный счёт.

Те же ученые доказали, что устный счёт повышает уровень мыслительной деятельности. Когда ребенок решает арифметические примеры, у него развиваются память, речь, концентрация внимания, сосредоточенность, быстрота реакции. Он лучше воспринимает сказанное на слух. То есть активизируются все те качества, которые важны для учёбы.

Секрет успеха прост: нужно всего лишь каждый день уделять 15 минут устному счёту. Даже простые примеры на сложение и вычитание одно- и двухзначных чисел приведут мозг сына или дочери в порядок. Главное – это считать быстро.

Если считать обычные примеры для малыша скучно, то пусть упражнение примет игровую форму. Выходя на улицу, можно посчитать между собой цифры на номерах машин. Или, зайдя в магазин, сложить все цены на покупки.

ТЕХНИКА БЫСТРОГО СЧЁТА В УМЕ

Способов быстрого счёта в уме множество. Для получения власти над числами достаточно одной десятиминутной тренировки в день. Результат зависит от индивидуальных способностей, но положительные изменения отметят все, кто начнет развивающие занятия.

Несколько простых, но очень эффективных упражнений:

• сложение и вычитание в уме двузначных чисел;
• заучивание таблицы умножения. Многие люди не запомнили ее в школе, и этот пробел сохраняется на протяжении всей жизни. Автоматическое извлечение из памяти результатов перемножения однозначных чисел позволит применять мнемонические правила и алгоритмы, легко перейти к большей разрядности;
• чтение книг. Оно загружает мозг новой информацией, тренирует память. Часто нелюбовь к этому занятию связана со слабой техникой. Для улучшения скорости чтения есть специальные эффективные программы, например, курс «Либерики» для детей и взрослых.
• метод Леушиной. Состоит в обучении на предметах (пальцах, спичках). Дети учатся по этапам. Вначале они изучают простой счёт, потом понятия «больше», «меньше», «столько же». Затем переходят на счёт наоборот, а уже после этого к сложению и вычитанию.
• способ Гленна Домана. Это схема обучения детей быстрому устному счёту с помощью карточек. На каждой из них изображено разное количество точек. Сначала ребенку показывают карточку, на которой не более пяти точек. Затем их количество увеличивают. Постепенно малыш начинает считать до ста, не привязываясь при этом к цифрам.

Методики быстрого счёта в уме и опыт имеют колоссальное значение для улучшения скорости и качества процесса. Но есть еще несколько факторов, влияющих на процесс:

• индивидуальные способности, склонность к логическому мышлению;
• возраст. Дети достигают результатов в обучении быстрее, чем взрослые;
• знание специальных техник и алгоритмов.

МЕТОДИКА БЫСТРОГО СЧЁТА В УМЕ

Люди придумали множество методик для упрощения устных вычислений. Среди них: правило умножения двузначных чисел на 11, поразрядное сложение и вычитание, действия с привлечением опорных чисел при умножении до ста и проч.

Эффективной, проверенной методикой быстрого счёта в уме является ментальная арифметика. Обучение устному счету проходит с использованием абакуса, который впоследствии заменяется ментальной картинкой. После окончания курса вместе с навыком быстрого устного счета отмечается скачок в интеллектуальном развитии.

Ментальная арифметика за счет визуализации математических примеров на абакусе гармонично развивает два полушария головного мозга: правое и левое. Уже в период обучения родители замечают, что их ребенок стал лучше учиться в школе по многим разносторонним предметам, поверил в свои силы. У детей после изучения ментальной арифметики развивается память, образное мышление, концентрация внимания, усидчивость. У них появляются способности к изучению иностранных языков и творческая жилка. Они умеют анализировать, сделать правильный вывод и найти нестандартный подход к решению любой задачи.

Желание пополнить своей персоной аудиторию людей с развитым интеллектом заслуживает уважения. Достичь цели может каждый человек, если выберет для себя приемлемый вариант тренировок, будет заниматься регулярно и продуктивно.

Техника быстрого счета для детей

Современные технологии позволяют выполнять сложные числовые операции за секунду: мы уже практически не считаем в уме, а все чаще используем для этих целей калькулятор. Для чего тогда во всем мире так пристально изучают вопрос обучения детей быстрому счету? Зачем формировать умение у маленьких детей действовать с двузначными и трехзначными числами в уме, не совершая при этом ошибок. В этой статье мы детально рассмотрим все вопросы, затрагивающие обучение детей быстрому счету.

Влияние обучения счету на развитие умственных способностей

Для многих из нас показателем одаренности является умение ребенка умножать двузначные числа. Это заблуждение, так как умение быстро считать – это прежде всего показатель правильного развития мыслительной деятельности. Люди, выполняющие сложные математические вычисления в уме, не являются гениями, но они обладают определенными качествами, среди которых:

• гибкость мышления, проявление креативности;
• умение выделять главное и концентрироваться на достижении результата;
• способность находить выход из нестандартных ситуаций.

Проведенные научные исследования за последние пять лет свидетельствуют о том, что интеллектуальное развитие детей не является динамичным. Для того чтобы умственное развитие ребенка соответствовало норме и не вызывало проблем в школьном обучении, родителям необходимо заниматься с ребенком и обучать его навыкам устного счета.

Обучение счету оказывает благоприятное влияние на развитие психических процессов, необходимых для успешного обучения в школе. В процессе обучения формируется активная речевая и мыслительная деятельность.

Техника быстрого счета

Для того чтобы научить ребенка счету в уме достаточно уделять этому занятию 10-15 минут в день. Результат обучения будет зависеть от индивидуальных возможностей, но при системном подходе к обучению положительная динамика будет отмечена у каждого ребенка. Существует многочисленные способы обучения счету в уме. Представляем вам несколько простых упражнений.

• Выполнение операций в уме с простыми числами на сложение и вычитание.
• Разучивание таблицы умножения (это позволит в дальнейшем перейти к более сложным математическим алгоритмам).
• Увеличение техники чтения (отсутствие интереса у детей к математике связано со слабой памятью, а книги отлично развивают память).

Методики обучения быстрому счету

Приведенные ниже методики позволят вам сформировать навыки элементарного счета у детей на самых ранних этапах обучения.

Методика Глена Домана

Занятия, построенные по этой методике, подходят для детей раннего возраста. Обучение осуществляется с помощью карточек, на которых изображено разное количество точек. Рассматривая карточки, дети знакомятся с множествами, вводятся понятия «меньше» и «больше, развивается память. Недостатком методики является статичность и необходимость постоянного закрепления изученного, так как полученный навык недостаточно устойчив.

Методика А. М. Леушиной

Автор методики выделяет шесть этапов развития навыков счета у детей, начиная с двухлетнего возраста. Первые этапы являются подготовительными (дочисловые) и помогают понять ребенку элементарные действия с множествами, где количество предметов оценивается «один», «много», «поровну», «больше», «меньше».

Дети в возрасте 4-5 лет знакомятся с образование числа, учатся сравнивать множества. Затем постепенно идет усложнение задач, формируется принцип понимания последовательности натуральных чисел, благодаря чему ребенок осваивает счет и овладевает навыками простых арифметический действий в уме.

Обучение счету на основе состава числа

Методика ориентирована на заучивание состава чисел с помощью таблиц или устного проговаривания. Имея представление о составе числа, ребенку значительно легче совершать операции на сложение и вычитание. Например, спросив у ребенка, сколько будет «пять плюс два», ребенок вспомнит, что 5 и 2 входят в состав числа 7. Недостатком методики является возникновение у детей сложностей, связанных с запоминанием.

Ментальная Арифметика

Эта методика достаточно эффективна и в настоящее время. На занятиях ребенок осваивает счет с помощью абакуса (счеты). Сначала ребенок учится принципу работы с абакусом: передвигая косточки, он знакомится с простыми математическими действиями «сложение» и «вычитание», а потом выполняет такие же действия в уме, представляя абакус перед собой. Такой способ хорошо развивает образное и логическое мышление, а также способствует выполнению сложных вычислительных операций в уме с шестизначными числами.

Как выбрать лучшую методику

Для того, чтобы начать обучение счету, ориентируйтесь на возраст ребенка. Если ваш ребенок еще совсем маленький, то для начала ему нужно сформировать представления о множествах. Для этого подойдут методики Леушиной и Домана.

Для обучения детей старшего возраста отдавайте предпочтение ментальной арифметике. Применение разнообразных игровых форм и получение быстрого результата помогут сформировать у ребенка мотивацию к дальнейшему обучению и освоить навыки быстрого счета.

Speed ​​Math — лучшие методы, чтобы быстрее считать в голове

Не знаю, когда я понял, что люблю считать в голове — вероятно, после того, как я бросил школу и мне больше не приходилось заниматься математикой «зарабатывать на жизнь». Как ни странно, любовь к истории и географии у меня не развивалась одновременно!

Я не гений чисел: если вы попросите меня умножить 172 на 47, ответ не слетит с моего языка. Это займет у меня несколько ударов, и, возможно, это сработает с первой попытки, если я устану.Напротив, есть молниеносные человеческие калькуляторы, которые мгновенно выдадут вам произведение двух трехзначных чисел. И есть вундеркинды (такие как Даниэль Таммет), которые совершают еще более выдающиеся подвиги. Тем не менее, по обычным меркам, мои мысленные вычисления довольно быстрые, поскольку они используют ряд простых приемов, на которые я наткнулся с детства. Например, для этого вопроса 172 умножить на 47 я мог бы заметить, что 47 близко к пятидесяти (47 минус 3), и решил сначала вычислить 50 умноженное на 172 (либо взяв пятьдесят процентов от 172 — i.е. половина, то есть 86, и умножение на 100, то есть 8600; или разбив его на 5×100 = 500, 5×70 = 350, 5×2 = 10, суммируя до 860, умножая на десять = 8600). Затем я бы вычитал 3 раза 172 (51 x 10 + 6 = 516), получая 8084 за несколько (долгих) секунд.

Услышав о молниеносных человеческих калькуляторах, о которых говорилось выше, меня всегда интересовало, как к ним приходят ответы. Были ли они аутичными учеными, получившими ответы из эфира? Похоже, что это так для некоторых из них.Были ли они «гениями» со сверхбыстрым умом, которые использовали вычислительные приемы гораздо более мощные, чем мои собственные маленькие уловки? Это казалось более частым случаем.

Сокровище: книга Артура Бенджамина
Одним ярким зимним днем, когда мне было за сорок, в нужное время мне в руки попала книга: « секретов ментальной математики», Артура Бенджамина и Майкла Шермера. Это книга с довольно непривлекательной обложкой, но многообещающим подзаголовком: The Mathemagician’s Guide to Lightning Calculation and Amazing Math Tricks .Книга выполняет свое обещание. Если у вас есть хотя бы отдаленный интерес к повышению скорости умственных вычислений, я настоятельно рекомендую вам купить себе копию, потому что эта книга — сокровище.

Читая первые главы, я с восторгом осознал, что главный автор (Артур Бенджамин) использовал многие из тех уловок, на которые я, естественно, наткнулся. Конечно, это не было совпадением, а скорее естественным результатом параллельного процесса исследования. Было не только приятно читать знакомые описания кого-то, кто бродил по тем же джунглям, но также было ясно, что этот исследователь был намного смелее меня. Он шел по тропам, к которым я никогда не подходил (например, по кубам и квадратным корням), у него был набор крутых техник, о которых я никогда не думал, и он был очень-очень-очень очень быстрым. В самом деле, если бы это не разбило мою метафору исследователя довольно уродливым образом, я бы сказал, что Артур Бенджамин оказался Тарзаном чисел.

Для меня книга Артура Бенджамина пришла в отличное время, так как я заметил, что в последнее время некоторые числа начали доставлять мне проблемы, с тревожной перекрестной связью с 24-часовым временем, которое было , которое никогда не беспокоило меня раньше.Например, число 13 (которое также соответствует 13:00) иногда становилось «размытым» в моем сознании, если вы можете понять это. Этот печальный упадок заставил меня начать сожалеть о своей короткой фазе экспериментов с галлюциногенами несколькими годами ранее. С другой стороны, это могло быть простым следствием возраста или снижения численной активности. Конечно, немного упражнений пойдет мне на пользу.

Приемы, которые имеют смысл
Что мне нравится в Secrets of Mental Math , так это то, что каждая техника, которую представляет Артур, «имеет смысл».Я имею в виду, что для меня все его методы укладываются в знакомый алгебраический контекст, так что каждый метод можно легко декодировать, проверить и понять. Другими словами, он произносит числа на моей волне.

Это контрастирует со многими трюками «быстрой арифметики», которые я читал на многочисленных веб-страницах при исследовании темы, трюки, которые часто кажутся слишком изолированными, слишком произвольными, слишком не имеющими контекста, чтобы щелкать так, чтобы стимулировать удержание. Возможно, в этом заключается разница между тем, кто предлагает рецепт, который он не понимает, и человеком, который экспериментировал с техникой до такой степени, что он владеет ею.

Классные заметки
Я собираюсь использовать эту страницу в качестве «заметок», где я обобщу советы, приемы и техники мысленных вычислений, о которых я не знал, чтобы я мог легко освежить свою память в любое время. Я надеюсь, что, поделившись этими заметками, некоторые уловки понравятся нескольким исследователям, отправляющимся в те же джунгли. Чтобы предоставить более полезный ресурс, на странице также показаны методы, которые использует Артур, которые мне давно знакомы, но, возможно, не вдаваясь в подробности.

Но помните, это только заметки класса. Они не включают богатую оригинальную презентацию, личность учителя, упражнения, которые помогут вам преобразовать идеи в знания. Для меня эта книга — сокровище, и я не могу настоятельно рекомендовать вам взять ее копию — если бы не вы, то одному из ваших детей или племянников. Проходите ли вы стандартизированный тест, сидите на собрании, делите счет в ресторане или занимаетесь деревообрабатывающим проектом, удобство вычислений в вашей голове — это секретное оружие, которое не так уж сложно приобрести и которое делает прекрасное подарок любящему цифры ребенку.

Краткое описание этой очень длинной страницы
Чтобы помочь вам сориентироваться, позвольте мне объяснить структуру страницы. Первые два раздела (которые составляют основную часть содержания) посвящены «знакомым методам» и «новым методам». Это различие, вероятно, для вас бессмысленно, поскольку то, что для меня является новым, может быть вам знакомо. Он предназначен только для того, чтобы помочь мне быстро найти материал, который я, возможно, захочу пересмотреть в один прекрасный день. Тем не менее, можно найти определенную логическую прогрессию от «знакомого» к «новому».

Далее мы переходим к тому, что я бы назвал техниками второго уровня, не потому, что им не хватает мощности, а потому, что я, вероятно, не буду их использовать.

Далее мы кратко поговорим о математических фокусах. Артур называет себя «математиком» и устраивает развлекательное шоу для самых разных зрителей. Артур объясняет свои уловки в книге. Меня не очень интересуют фокусы, поэтому я не делал заметок для этой части книги, за исключением одного очень крутого алгоритма для вывода кубического корня двузначного целого числа, которое было построено в кубе.

Далее мы обсудим простой способ вычисления дня недели любой даты. В этом разделе я попытался улучшить технику, объясненную Артуром, представив несколько замечательных быстрых клавиш. Я также представляю еще одну знаменитую технику «дня недели», которая может извлечь пользу из моего ярлыка, что делает ее намного проще в использовании, чем обычно, и дает вам два варианта на тот случай, если вы влюбитесь в эти удивительно простые методы … Ты можешь!

Затем мы рассмотрим некоторые другие книги по быстрой арифметике и в заключение приведем несколько ссылок.

Напомним, вот схема:

Итак, без лишних слов, давайте окунемся в мир быстрой мысленной математики.

Знакомые техники

Чтобы обеспечить некоторую структуру, в этом разделе я резюмирую несколько техник, которые долгое время были частью «хлеба с маслом» моих мысленных вычислений и которые Артур ясно объясняет в своей книге.

Слева направо
Как и я, Артур, кажется, считает в уме слева направо. Например, возьмите числа 84 и 53. Если бы вы сложили или умножили их на бумаге, вы бы начали с последних цифр (4 и 3), но в уме вы начинаете слева. Вот примеры того, как это работает.

• Сложение: 84 + 53 = 13 (8 плюс 5 слева), за которым следует 7 (4 плюс 3) = 137. Для такой небольшой операции я бы фактически пошел большими кусками, с 134 (84 + 50) плюс 3, или «увидеть» ответ.

• Умножение: 84 x 53 = 4 240 (80 x 50 + 80 x 3) + 212 (4 x 53) = 4 452.Мы могли бы выбрать «инвертировать» 84 и 53: 4200 (50 x 84) + 252 (3 x 84) = 4452.

• Вычитание: 84 — 53 = 3 (8 минус 5), за которым следует 1 (4 минус 3) = 31.

• Деление: 168/3 = 150/3 + 18/3 = 56. 84/53 также работает слева направо: 1 оставляет 31/53 (1 + 31/53), а 31/53 снова работает слева направо.

Это правило написания слева направо не означает, что вы строго разбиваете каждое число слева направо. Вам могут прийти в голову и другие ярлыки, которые заставят вас разбить числа, с которыми вы работаете, на более крупные куски.

Округление
Это метод, о котором я упоминал во введении, где для вычисления 172 x 47 мы округляем 47 до 50. Часто проще оперировать числом, которое вы округлили в большую или меньшую сторону, а затем добавить или вычесть разницу. Например,

• Сложение: 49 + 77 = 127 (50 + 77) минус 1 = 126;
• Умножение: 49 x 77 = делится на 50 x 70 = 3500, 50 x 7 = 350, в сумме получается 3850 минус 77, что составляет 3750 (3850 минус 100) плюс 23 (разница от округления 77), что дает 3773;
• Вычитание: 77 — 49 = 27 (77 — 50) плюс 1 = 28.
• Деление: 196/4 = (200/4) — 1 = 49.

Билл Хэндли описывает некоторые другие методы округления, которые я использую все время.

Дополнения
В этом методе округления еще больше. У меня никогда не было названия для этого, но имя Артура имеет смысл. Для двузначных чисел, например, вы можете «округлить» 37 до 100, чтобы вычесть быстрее, а затем прибавить разницу, 63. Вот как это работает: чтобы вычислить 414 минус 37, вы выполняете 314 (400 — 100) и прибавляем обратно 63, получая 377.

Разница между 100 и числом (в случае двузначных чисел) — это то, что Артур называет дополнением. Я давно заметил, что все эти дополнения заложены в моем сознании. Например, если вы скажете 34, мне не нужно вычислять дополнение (66). Это значительно ускоряет выполнение многих задач на вычитание.

Если вы много работаете с числами в голове, вам часто приходят в голову трехзначные числа (или более длинные дополнения). Например, для 1200 минус 625 я инстинктивно прибавил 375 к 200, получив 575.

Обратите внимание, что в случае 1200 минус 375, дополнение к 625 может появиться и дать вам 200 + 625 = 825, но в первую очередь может возникнуть конкурирующий метод 800 (1200 минус 400) плюс 25 = 825. Никогда не знаешь, какая стратегия бросится в глаза в первую очередь.

У Артура есть крутой метод еще более быстрого вычитания с помощью дополнений.

Выбор метода
Для меня часто значительная часть вычислительного времени уходит на выбор метода, особенно если есть два привлекательных метода, конкурирующих за внимание. Для некоторых проблем вы решаете, анализируя, для других вам лучше прыгнуть с первой атакой, которая приходит к вам.

Использование аппаратных операций
Иногда вам бросается в глаза, что проблема близка к операции, которая заложена в вас, и вы можете воспользоваться этим. Например, для 4 умножения на 127, вместо умножения слева направо, я замечаю близость к 4 x 125 (жестко запрограммировано как 500), поэтому я просто добавляю 8 (четыре раза по два, поскольку два — это расстояние до 127 от 125).Результат: 508.

Использование факторов
Часто вам бросается в глаза, что число является произведением других чисел. Например, 18 трижды шесть. Это часто дает вам альтернативный, более быстрый метод вычисления чего-либо.

• Умножение: для 16 x 18 вы можете вычислить 16 x 3 (48) умножить на 6 = 288.
• Деление: для 120/15 вы можете вычислить 120/3 (40), разделенное на 5 = 8. Или, заметив ноль в конце 120 и 5 в конце 15, вы можете умножить на два, чтобы получить ноль также отображается справа: 240/30. Когда вы упрощаете это до 24/3, что дает 8, вы используете множители, не задумываясь об этом: вы делите 30 на 10 x 3 и начинаете с деления 240 на десять, первого множителя.

Этот пример показывает, что иногда при делении вы умножаете, чтобы появился общий множитель. По сути, правило — «все работает». Другие примеры:

• чтобы разделить на 16, я часто делю на 2, четыре раза подряд.
• чтобы умножить или разделить на 12½, я буду рассматривать это число как 100/8, умножить на 100 и разделить на 8 или наоборот.Я думаю, вы могли бы назвать это обратным факторингом .

Работа с факторами часто экономит ваше время. Например, в задаче умножения, такой как 16 x 18, с помощью факторного метода мы просто умножаем дважды, тогда как при классической операции слева направо нам нужно было бы дважды умножить , а затем добавить (10 x 16 = 160, 8 x 16 = 128, 160 + 128 = 288) или дважды умножьте , затем вычтите (20 x 16 = 320, 2 x 16 = 32, 320-32 = 288).

Запомненные дроби
Я помню тот давний день, когда, скучая в классе, я решил запомнить все дроби с делителями до девяти и числителями до девяти.

Например, 1/9 = 0,111 повторения, 2/9 = 0,222 повторения и так далее. Это оказалось чрезвычайно полезным. Однажды я оказался на обеде, где нам пришлось разделить счет между семью людьми. Запомнив схему дроби от семи, я получил удовольствие от объявления результата: 23.4285714… К сожалению, деление на семь встречается не так часто.

Было приятно увидеть, что Артур использует одни и те же запомненные дроби. В книге даже перечислены дроби от 11, которые я однажды выучил, но забыл из-за неиспользования, поэтому я перечисляю их в разделе новых методов.

• Все дроби от 9 — это произведение 0,1111… (повторение последней цифры). Например, 6/9 равно 0,6666… Это может пригодиться, если вы разделите 120 на 18 и заметите, что 18 равно 2 умножить на 9. Вы мгновенно упростите до 60/9, что даст вам 6,6666…

• Дроби от 8. Разве вы не используете их все время? 0,125 для одной восьмой, 0,375 для трех восьмых, 0,875 для семи восьмых … Промежуточные части встречаются не так часто, потому что они упрощаются до одной четверти, одной половины и трех четвертей.

• Доли числа от 7.Я люблю это. Одна седьмая — 0,142857, затем повторяются эти числа: 0,14285714… Все дроби от двух седьмых до девяти седьмых используют один и тот же образец, начиная с другой цифры. Чтобы узнать, какая цифра, просто умножьте начало (14) на числитель. Две седьмых = 0,28571428… Три седьмых = 0,42857142… Четыре седьмых = 0,57142857… Пять седьмых = 0,71428571… Шесть седьмых = 0,85714285…

• Доли от 6. Они появляются постоянно. Одна шестая — 0,1666… (повторяется). Пять шестых — 0.8333… (повторяет). Промежуточные — трети или половина.

• Доли от 5. Они также появляются постоянно. Деление на пять — это то же самое, что умножение на два и деление на десять, так что просто имейте «рефлекс умножить на два». Например, для трех пятых вы делаете два раза по три, так что это шестой пункт. Одна пятая — 0,2, две пятых — 0,4, три пятых — 0,6, четыре пятых — 0,8.

Проверка делимости числа на 3
Этот трюк я помню со школы и постоянно использую.Чтобы проверить, делится ли число на 3, вы просто складываете все цифры, и, если результат делится на 3, то же самое и исходное число. Например, для 817 273 вы получите 28, что не делится на 3. (Повторно, если вы не уверены, делится ли ваш результат на 3, продолжайте складывать цифры: для 28 вы получите 10.) С другой стороны, для 817 272 вы получите 27, что делится на 3, и действительно, 817 272 — это трижды 272 424.

На самом деле, для многих чисел я не утруждаю себя сложением всех цифр: я игнорирую цифры, которые уже кратны 3, ищу пары, которые в сумме дают 3, не обращая внимания на них, а затем складываю оставшиеся цифры.Например, для 6 817 273 я игнорирую 6, игнорирую пару 8-1, игнорирую пару 7-2 и игнорирую последние 3, оставляя 7.

Мне нравится этот трюк, но есть еще кое-что! Артур представляет другие приемы, которые я либо забыл, либо никогда не знал, чтобы проверить их на делимость на другие числа.

Умножение двузначных чисел на одиннадцать
Это излюбленный прием учителей начальной школы. Чтобы умножить двузначное число (например, 42) на одиннадцать, вы складываете две цифры (4 + 2 = 6) и вставляете их посередине: 462.Если вам нужно нести (в 49 x 11, 4 + 9 дает 13), добавьте единицу к первой цифре: 49 x 11 = 539.

Вы можете расширить этот трюк, чтобы умножить более длинные числа на 11, но для меня это не работает с умом, поэтому я им не пользуюсь. Я считаю, что лучше пойти на бумагу: например, для 87 657 умножить на 11 я напишу число один раз, а затем напишу его снова, чуть ниже первого числа, но сдвинутое на один столбец влево, затем сложу два числа . Конечно, это именно то, что делает классическое умножение.

Обратная сторона конверта
Артур — большой поклонник предположений. Я тоже
Например, возьмите 7 896 и 4099.

• Сложение: что такое 7 896 плюс 4 099? Не знаю, но это около двенадцати тысяч (8000 + 4000).
• Умножение: сколько 7 896 умножить на 4 099? Я не знаю, но это близко к 32 миллионам (8000 x 4000).
• Разделение: что такое 7 896 против 4 099? Не знаю, но это близко к двум (8000/4000). Если бы я хотел точно настроить приближение, которое, как я знаю, слишком велико для двух учетных записей (первое 7896 меньше 8000, второе 4099 больше 4000), глядя на соотношение между 4000 и 4100, я мог бы сказать, что добавив десять процентов к 4000, в результате чего знаменатель 4400 удалит около десяти процентов ответа (0.2), поэтому с 4100 я бы снял только четверть этого (0,05), получив приблизительное число 1,95, что немного ближе к фактическому ответу (1,926).

Проверка результатов
• Добавление: при добавлении длинных списков чисел я люблю добавлять второй раз снизу вверх.
• Деление: иногда вы можете захотеть умножить результат на делитель, чтобы убедиться, что вы снова встаете на ноги.

Позже мы рассмотрим другие техники, которые использует Артур: выброс девяток (который я не использовал с младших классов) и выброс одиннадцати.

Новые методы

В этом разделе представлены техники, которым я научился в книге.

Умножение соседних чисел: метод привязки
Допустим, вы хотите умножить близлежащие числа, например 62 на 63. Вы заметили, что оба числа близки к шестидесяти. Разбив его на части, если мы запишем 62 как 60 + 2 и 63 как 60 + 3, проблема будет (60 + 2) x (60 + 3), которая уменьшится до 60x (60 + 2 + 3) + 2×3.

Если это жестко запрограммировано в вас, тогда, когда вы видите 62 x 63, вы сразу переходите к 60×65 плюс 6 = 3906.Аккуратный!

Другой пример: 84 x 87 = 80×91 + 28 = 7 308.

Используя этот метод, вы ищете удобную «привязку» для перестановки умножения. В первом примере (62 x 63) колышек был 60; во втором примере (84 x 87) колышек был 80.

Этот «метод привязки» окупается во многих ситуациях. Например, если вы хотите умножить трехзначные числа на нули в середине, такие как 105 и 106, вы быстро получите 100 x 111 + 30 = 11 130.

Этот метод еще проще, если сумма последних цифр равна десяти. Например, для 62 x 68 вы сразу перейдете к 60×70 + 16 = 4216.

Билл Хэндли, специалист по технике «близких чисел», использует ее даже в тех случаях, когда числа совсем не рядом. В конце концов, распределение работает независимо от того, рядом или далеко числа, поэтому вы можете использовать любую привязку, которая вам нравится. Например, для 75 x 25 Билл использует 5 в качестве привязки, что дает (5 x 95) + (70 x 20). В обзоре книги Билла я также покажу его вариант метода привязки для таких случаев, как 23 x 87, где вы можете взять 20 в качестве привязки и 4 в качестве множителя.

Если вы действительно внимательны, вы можете найти привязку, когда рядом будут следующие числа:

• под круглым числом: 58 x 59 = 60 x 57 + 2 = 3 422. Это упрощение (60-2) x (60-1).
• по обе стороны от круглого числа: 57 x 62 = 60×59 — 6 = 3,534. Это упрощение (60-3) x (60 + 2).

Исходные числа для умножения (например, 188×190) в сумме дают ту же сумму (378), что и новые числа для умножения (200×178), и это может быть полезно для быстрой проверки того, что вы умножаете правильные числа, или даже как ярлык для получения второго числа для умножения.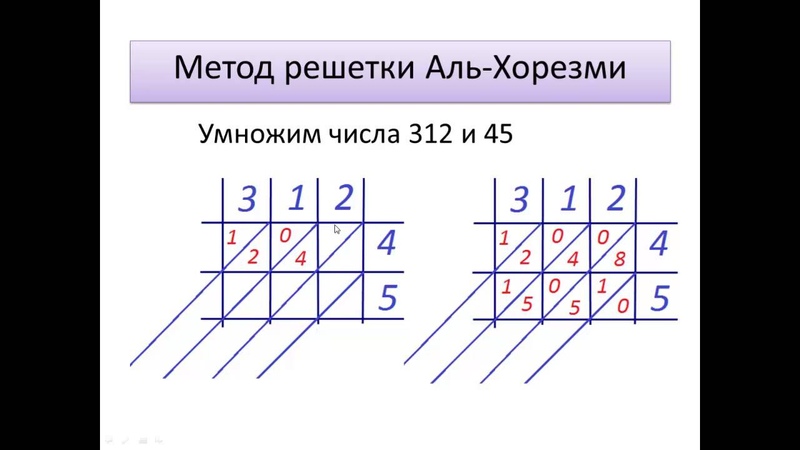

Если вы еще более внимательны, вы можете преобразовать некоторые проблемы в проблему с соседними номерами. Например, для 105 x 412, используя коэффициент 2, вы меняете задачу на 210 x 206, что дает 200×216 + 60 = 43 260. Для 104 x 927, используя коэффициент 3, вы меняете задачу на 312 x 309, что дает 300 x 321 + 108 = 96 408.

Возведение в квадрат методом колышка
• Особый случай «Легкий»: числа, оканчивающиеся на 5 (например, 75). Для двузначного числа возьмите первую цифру, умножьте ее на старшую цифру (7 x 8 = 56), закрепите 25 в конце: 5 625.2 = (a — b) x (a + b), при вычислении 38-квадрата a = 38 и b = 2.

• Трехзначные числа. Метод тот же. На этот раз мы находим ближайшее кратное 100. Например, в квадрате 211 ближайшее кратное равно 200, а число «на другой стороне» равно 222. Произведение равно 44 400, к которому вы добавляете квадрат расстояния. (11 квадратов — 121), что дает 44 521.

Приблизительные квадратные корни
Этот метод был откровением. Мы рассмотрим его для квадратных корней из двузначных чисел, но он работает и для больших чисел.Прежде чем мы рассмотрим алгоритм, рассмотрим общую идею. Мы пытаемся найти точное приближение. Возьмем 50. Мы знаем, что квадрат 7 равен 49, а квадрат 8 равен 64, поэтому ответ должен быть между 7 и 8, а 7 дает ближайший квадрат. Теперь рассмотрим 50/7. Поскольку 7 меньше нашей цели (квадратный корень из 50), это число (50/7) больше, чем цель. Другими словами, наша цель находится где-то между 7 и 50/7. Возьмите среднее из двух: это наше приближение. Один из способов вычислить среднее значение: (7 + 50/7) / 2 = 7.07. Другой способ — сказать, что среднее значение равно 7 плюс половина разницы, то есть 7 + (50/7 — 7) / 2, то есть 7 + (50 — 49) / 14, или 7 + 1/14.

Это алгоритм: возьмите число, которое дает ближайший квадрат. Затем добавьте начальную ошибку, деленную на двойное начальное приближение.

• Пример 1: квадратный корень из 90. Ближайший квадрат 9 (квадрат 9 — 81). Ошибка 9 (90 — 81). Наше окончательное приближение 9 + 9/18 = 9,5.
• Пример 2: квадратный корень из 78.Опять же, ближайшее приближение — 9. Ошибка -3 (78 — 81). Наше окончательное приближение 9 — 3/18, то есть 9 — 1/6, что составляет 8 + 5/6 (если вы обнаружите, что быстрее прибавить пять шестых к восьми, чем удалить одну шестую из девяти) = 8,83.

Насколько точен этот метод? Для чисел от 10 до 99 при сравнении приближения, округленного до второго десятичного знака, с фактическим квадратным корнем, округленным до второго десятичного знака, разница в восемьдесят раз составляет 0,01 или меньше, в восемь раз она равна 0,02, если она равна 0.03 (для 20) и сразу 0,04 (для 12). Для меня это очень-очень хорошо.

Кстати, чтобы улучшить ваше приближение, вы всегда можете взять второе приближение и повторить процедуру, добавив новую ошибку, разделенную на удвоенное приближение.

Артур не упоминает об этом, но я обнаружил, что этот метод можно легко преобразовать в процедуру для оценки кубических корней , хотя вычисления не так просты. Вот как это работает. Вы берете первую оценку и складываете ее в куб.Вторая оценка будет исходным приближением плюс начальная ошибка, деленная на удвоенный квадрат приближения . Обратите внимание, что по сравнению с алгоритмом вычисления квадратных корней, «квадрат» в делителе — единственное изменение.

Моя идея этой адаптации метода квадратного корня была вдохновлена ​​приложением к книге Билла Хэндли (рассмотрено ниже), где он представляет свой алгоритм вычисления кубических корней. Конечно, эти два понятия эквивалентны. Кстати, с чего вы начинаете — какова ваша первоначальная оценка? Билл указывает, что вы берете тройки цифр, начиная с правого, и заменяете каждую из них нулем.У вас останутся от одной до трех крайних левых цифр. Для вашего приближения вы берете ближайший куб целых чисел от 0 до 9. Их всего десять, некоторые из которых вы уже должны знать, а остальное вы запомните, если посмотрите на удивительный трюк Артура (не далеко ниже) для получение кубических корней из совершенных кубов двузначных целых чисел.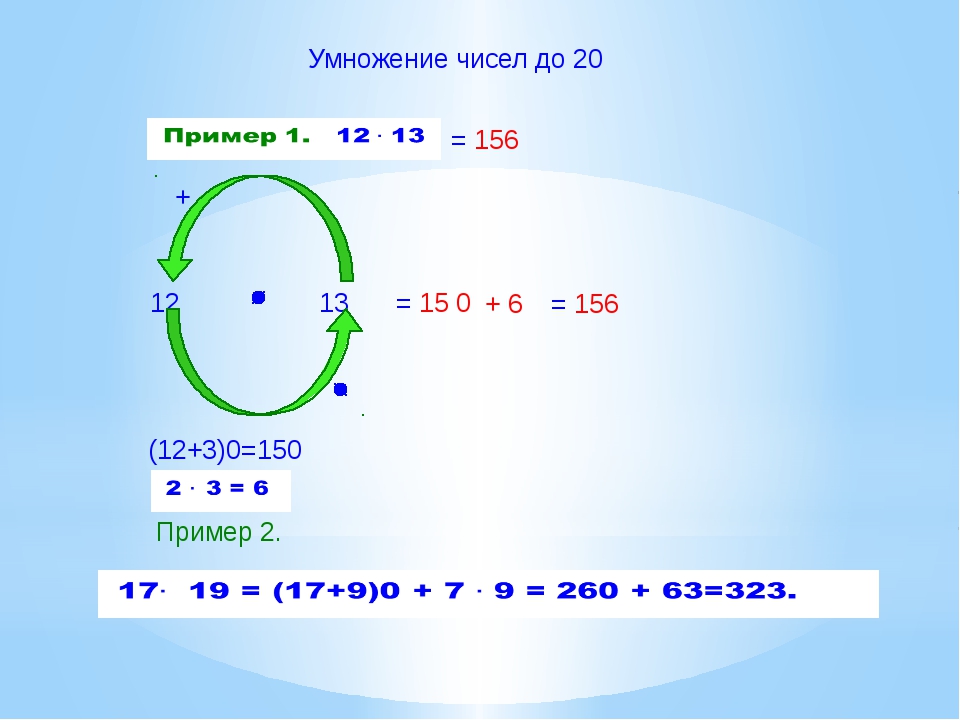 (0 ⇒ 0, 1 ⇒ 1, 2 ⇒ 8, 3 ⇒ 27, 4 ⇒ 64, 5 ⇒ 125, 6 ⇒ 216, 7 ⇒ 343, 8 ⇒ 512, 9 ⇒ 729.)

В своем обзоре книги Билла Хэндли я также упомяну его советы по вычислению квадратных корней из более длинных чисел.Ключевой трюк заключается в том, что при вычислении квадратного корня каждая пара цифр, начинающаяся справа, будет уменьшена до десяти (десять в квадрате — это сотня), за исключением крайнего левого префикса из одной или двух цифр. Используя обычный метод, вы оцениваете квадратный корень из этого однозначного или двузначного префикса, а затем настраиваете шкалу, умножая ее на десять.

Быстрое вычитание с дополнениями
Ранее мы говорили о комплементах. Напоминаем, что в случае двузначного числа, такого как 41, дополнение — это расстояние от сотни (здесь 59).Мы уже видели, как дополнения можно рассматривать как форму метода округления, которая может ускорить вычитание. Например, для 214 минус 41 вы удаляете 100 (114) и добавляете 41 (59), получая 173.

Артур представляет еще один метод, который мне никогда не приходил в голову и который может быть еще быстрее. Если взять 214 минус 41, опять же, вы знаете, что ответ будет сто с чем-то. В остальном вы вычисляете 41 минус 14 (27) и находите дополнение (73), снова возвращая 173. Это происходит сразу после появления водорослей, но мне никогда не приходило в голову.

Что быстрее? По-разному. В этом случае это близко. При первом способе вы находите дополнение, а затем добавляете. Во втором методе вы вычитаете, а затем находите дополнение. Если вычитание бросается в глаза, например, 44 минус 22, то второй метод, вероятно, быстрее. Например, в случае 122 минус 44, со вторым методом мы перескакиваем с 22 (разница) на 78 (дополнение и ответ), тогда как в первом методе мы переходим к 56 (дополнение), а затем добавляем его обратно к 22, чтобы найти 78.

Перекрестное умножение
Это отличный способ быстро умножать числа любого размера ручкой и бумагой. Я не буду это объяснять, потому что не хочу рисовать диаграммы. Объявление отличный повод купить книгу!

Разделение
Артур отмечает, что при мысленном делении полезно сначала выяснить, сколько цифр будет в ответе. Например, для 357/8 ответ состоит из двух цифр, потому что 100 будет слишком большим (8 x 100 = 800).Итак, когда вы начнете слева с 35 и обнаружите, что 4 работает (4 x 8 = 32), вы можете начать говорить «сорок» … Далее, 37 — это остаток, так что вы можете сказать «четыре». Затем вы можете продолжить с 50 и объявить «точка-шесть» (6 x 8 = 48) и так далее. (Или, в этом случае, идите прямо за деньгами, разделив 50 на 2 три раза подряд.)

Артур тоже предлагает этот отличный трюк. Допустим, вы хотите вычислить 230 из 24. Используя эту технику, вы сразу увидите, что 230 из 24 — это 9 + 14/24, и продолжите задачу оттуда.Как вы это видите? Во-первых, десять умножить на 24 равно 240, чуть больше 230, поэтому десять — это первое целое число над целой частью нашего ответа, и наш ответ должен быть «9 с чем-то». Пока чудес не было. Но крутая интуиция — очевидная, как только вы ее видите — состоит в том, чтобы посмотреть, насколько мы промахнемся, если умножим 23 на десять. Мы промахиваемся на десять (240 — 230 = 10). Итак, если мы умножим 24 на 9, мы получим короткую позицию на 14. Ответ: 9 + 14/24.

Вы бы не использовали эту технику каждый раз, но время от времени информация просто попадает вам в руки, потому что вы пытаетесь угадать целую часть деления, и ваше предположение «просто выходит за рамки» меньше, чем делитель.

На самом деле, если вы промахнулись еще больше, уловка по-прежнему доступна вам, хотя она может быть не такой немедленной. Предположим, что для 620 вместо 33 вы попробуете 20. У вас получится 660, так что вы увидите, что ваш множитель превысил два, и ответ должен быть «18 с чем-то». Так как 660 минус 33 равно 627, умножение 33 на 19 приведет к выходу за пределы 7. Умножение 33 на 18, следовательно, приведет к недостижению на 33 минус 7, что составляет 26. Это дает ответ 18 + 26/33.

Проверка на делимость
Ранее мы использовали уловку, чтобы проверить, делится ли число на 3.Вот аналогичные уловки, которые предлагает Артур для проверки делимости на другие числа.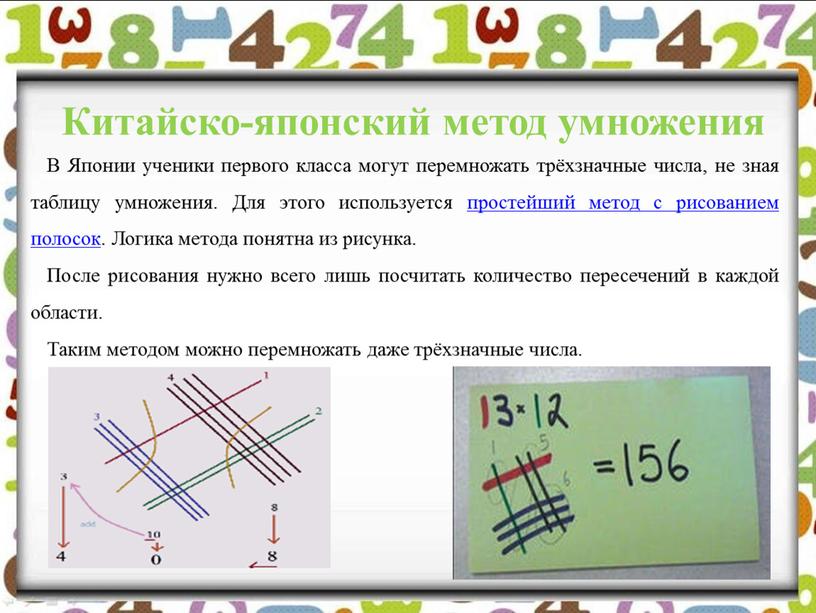

• Делимость на 4. Проверьте, делятся ли последние две цифры на 4. (Так как 4 x 25 равно 100, мы можем не учитывать цифры слева от двух последних). Если вам не сразу понятно, является ли 66 делится на 4, сначала разделите его на 2: вы получите нечетное число, поэтому это не сработает.

• Делимость на 8. Проверьте, делятся ли последние три цифры на 8. (Так как 8 x 125 равно 1000, мы можем не учитывать цифры слева от последних трех.)

• Делимость на 9. Проверьте, делится ли сумма цифр на 9. Например, 123 не делится на 9 (сумма цифр 6), тогда как 126 (сумма цифр 9). Чтобы понять, почему это работает, прочтите мою страницу о том, почему работает метод «изгнания девяток».

• Делимость на 6. Проверьте делимость на 2 и на 3. Duh…

• Делимость на 11. Поочередно складывайте и вычитайте цифры справа налево. Игнорируя любой отрицательный знак, если результат равен нулю или кратен 11, то исходное число делится на 11.Например, для 7 415 вычислите 5-1 + 4-7, получив -7, что не работает (7 не делится на 11). Для 9 273 вы вычисляете 3 — 7 + 2 — 9, что равно -11, и это работает, а 9 273 действительно одиннадцать умножить на 843.

• Делимость на другие нечетные числа. Обожаю эту технику. Допустим, вы хотите знать, делится ли 96 843 на 7. Добавляйте или вычитайте числа, кратные 7, пока в конце не получите ноль (добавление или удаление семерок, очевидно, не повлияет на делимость числа на семь). В этом случае мы можем добавить 7, чтобы получить 96 850.Вы можете убрать ноль, потому что деление на десять (то есть на 2 и 5) не влияет на то, является ли 7 множителем этого числа. Итак, у нас осталось 968. Делится на 7? Продолжайте добавлять или удалять семерки, чтобы получить нули. Здесь вы можете прибавить 42, получив 1010, или, проще говоря, удалить 28, получив 940. Удалите ноль. 94 делится на 7? Удалите 14, получив 80. Удалите ноль. Восемь не делится на 7, следовательно, и 96 843.

Давайте воспользуемся этой техникой, чтобы увидеть, делится ли 773 на 17. Складываем 17: 790.Убрать ноль. 79 не делится на 17 (слишком близко к 68), поэтому и 773 тоже.

Разное приближение
Вот несколько идей, которые упоминает Артур.

• Используйте известные фракции. Например, если вам нужно взять 7¾% от суммы, вы можете заметить, что эта доля близка к семи к девяти (7,77… повторение). Это дает вам быстрое приближение (умножение на 7, деление на 9, деление на сто), что особенно удобно, если вы живете в штате, где налог с продаж составляет 7¾%, например, в Калифорнии в старые добрые времена.

• Правило 70. Это интересная идея, о которой я впервые упомянул в великолепном выступлении Эла Бартлетта под названием Арифметика, население и энергия . Я никогда не использовал его, потому что слишком привык вычислять точный ответ с помощью логарифмов, но книга Артура убедила меня запомнить этот трюк из-за его скорости. Скажем, определенная сумма (например, население или денежная сумма) растет со скоростью i% в год. Сколько лет понадобится, чтобы удвоиться? Разделив 70 на i, вы получите хорошее приближение. y = 2. Следовательно, y.log (1 + i%) = log (2) и y = log (2) / log (1 + i%). Для i% = 7% получаем y = log (2) / log (1,07) = 10,24.

• Правило 110. Это та же идея, что и правило 70, но оно используется для оценки того, сколько времени потребуется, чтобы сумма сложного процента с определенной скоростью утроилась. Например, сумма, увеличивающаяся на 7% в год, утроится примерно за 16 лет (110/7 = 15,71). Чтобы получить точный ответ, вычислите log (3) / log (1.07) = 16,23.

Сохранение цифр на руках при вычислении
Хранение цифр на руке… Это странное выражение, но, как указывает Артур, цифры (одна, две, три…) называются цифрами не зря: наши пальцы — это оригинальная счетная машина.

Он дает уловку для запоминания цифр при выполнении многоступенчатых вычислений. За ноль сожмите кулак. У вас уже есть собственный способ представить цифры с первой по пятую с помощью пальцев. (Между прочим, какой бы метод ни использовали люди вокруг вас, это культурная традиция, и такие методы различаются в разных регионах мира. ) Для шести, семи, восьми и девяти коснитесь большим пальцем мизинца, безымянного пальца, среднего пальца и указателя. Палец. Обеими руками вы можете сохранить две цифры.

Запоминание больших чисел
Артур использует популярную (и древнюю) мнемоническую систему, называемую главной системой. Короче говоря, каждому числу присвоен согласный звук, так что числа можно закодировать словами. Например, «Сидней просто встряхнул Фабио» кодируется 0123456789:
.
0 в кодировке s или z,
1 кодируется t, d или th
2 кодируется n,
3 кодируется m,
4 кодируется r (как в четыре),
5 кодируется буквой L (римская цифра пятьдесят),
6 кодируется «влажными звуками», как в мягком g в «заработной плате», sh в «shush», ch в «зудящем»
7 кодируется K или жестким g в «go»,
8 кодируется f или v,
9 кодируется b или p.

Гласные ничего не кодируют. Обратите внимание, что система фонетическая: написание не имеет значения. Например, «itchy» кодирует только 1 (t является частью звука tch), а «garage» кодирует 746, поскольку два g произносятся по-разному.

Для телефонных номеров этот метод отлично работает, особенно если вы найдете забавные прозвища для кодирования номеров. Например, как можно забыть «большое лицо Джима» (у которого нет самого маленького лица) или «афродита на стенах» (у кого есть хорошая история на стенах, которую можно рассказать)?

Артур говорит, что использует эту технику для запоминания промежуточных результатов в середине длинных вычислений.Если вы планируете использовать такую ​​систему, то имеет смысл запомнить словарь для чисел от 00 до 99 (или даже от 000 до 999), чтобы слова были легко доступны для вас, когда они вам понадобятся.

Вот несколько кодировок, которые я придумал, которые могут вам понравиться:

• Квадратный корень из 2: Авторитарный снос, устав Микки Мауса.

• Корень квадратный из 3: Токийский мужчина доставляет неприятности повару.

• Первые десятичные знаки числа Пи: Вернитесь скоро, так как я собираюсь опубликовать свое потрясающее стихотворение для первых 100 десятичных знаков числа Пи.

Бесплатная программа 2Know может помочь вам кодировать числа. Этот онлайн-кодер крупной системы тоже неплох.

Методы, которые я, вероятно, не буду использовать

Вот несколько техник, которые упоминает Артур, и которые я, вероятно, не буду использовать, потому что они требуют запоминания определенных операций или потому, что я выполняю операцию так редко, что я ее не запомню. Чтобы узнать подробности, вы обязательно захотите прочитать книгу.

Обнаружение ошибок путем исключения девяти и одиннадцати
Эти два метода (ни один из которых не является полностью точным) используются для обнаружения ошибок в результатах ваших расчетов.Они могут сказать вам, что есть ошибка, но не могут сказать вам, что ошибки нет.

Мы научились методу «изгнания девяток» в начальной школе, но точный метод вскоре ускользнул из моей головы, и я сомневаюсь, что начну использовать любой из этих методов на этом позднем этапе.

Изгнание девяток (или одиннадцати) может выглядеть как магия, но причину, по которой это работает, действительно легко понять. Если вам интересно, посмотрите мою страницу, объясняющую, как и почему работает отбрасывание девяток. Здесь я просто резюмирую метод.

• Выброс девяток. Для каждого числа, с которым нужно работать, сложите все цифры, пока они не уменьшатся до одной цифры. Например, 859 дает 4 (8 + 5 + 9 = 22 и 2 + 2 = 4). Это называется модульной суммой, и это число по модулю 9 (остаток от деления на девять). Также вычислите мод-сумму для результата операции. Теперь выполните ту же операцию (сложение, вычитание или умножение) над модульными суммами, которую вы проделали с исходными числами. (Для разделения вам нужно сформировать тест определенным образом: см. Раздел о разделении на моей странице о том, как выбросить девятки и выбросить одиннадцать.)

Результат должен соответствовать третьей сумме модуляции. Например, для 859 x 17, если вы получаете 14 623, вы знаете, что допустили ошибку, потому что мод-сумма 859 равна 4, мод-сумма 17 равна 8, произведение равно 32, что дает модульную сумму 5. — тогда как мод-сумма 14 623 равна 7.

• Изгнание одиннадцати. Это дает число по модулю одиннадцать (остаток от деления на одиннадцать). Вы используете его как метод 9. Это означает, что когда вы складываете, вычитаете или умножаете модули, их модуль должен упроститься до модуля результата операции.Чтобы получить число по модулю 11, вы попеременно складываете и вычитаете все его цифры, начиная с самой правой цифры и двигаясь влево. Если вы получите отрицательное число, добавьте 11. Например, для 958 вы получите 9-5 + 8 = 12, тогда 2-1 = 1. И действительно, 957 равно 11 x 87, поэтому 958 больше 11 имеет остаток. of 1.

Если модули совпадают, метод исключения девяток имеет 8 шансов из 9 дать вам правильный совет («вероятно, без ошибок»). Если модули совпадают, метод «выбрасывания одиннадцати» имеет 10 шансов из 11 дать вам правильный совет («вероятно, без ошибок»).Если модули совпадают в обоих методах, метод имеет 98 шансов из 99 дать вам правильный совет.

Дружественные факторы
Артур дает список «дружественных факторов», которые он предлагает запомнить, чтобы, когда придет время, вы могли упростить свои вычисления. Например, 38 x 8 = 304, поэтому, если вам нужно было вычислить 38 x 24, вы могли бы решить пойти по пути факторинга, начиная с 8 (38 x 8 = 304), а затем умножив на 3, что легко, потому что «дружественный factor «имеет ноль посередине: 304 x 3 = 912.

Это круто, но я вряд ли вспомню длинный список дружественных факторов.

Еще одно изящное применение — сделать так, чтобы коэффициент дружелюбия появился путем деления большего числа: например, для 318 x 13 вы можете взять 3 x 106 x 13, что дает 3 x 1378 = 4 134.

Точные квадратные корни
Мне нравится метод Артура для приближения квадратных корней. Он также дает один для вычисления точных квадратных корней, но я не буду его использовать.

Кубинг
Мне почти никогда не нужно вычислять кубы, поэтому я никогда этого не вспомню.2) х 18 = 5832.

Волшебные трюки

Артур представляет ряд «фокусов». Для некоторых это может быть интересным, а для «фокусника» — развлечением, но меня они на самом деле не интересуют. Почему нет?

Представьте себе эту карикатуру на уловку. Придумайте любое число от одного до ста. Добавьте два. Вычтите свое число. А теперь позвольте мне угадать … результат два … верно?

Для меня большинство фокусов с числами — это вариации этого псевдотрюка. Если есть уловка, есть алгоритм — я могу не знать, какой из них, но этого достаточно, чтобы потерять интерес.Просто вопрос того, что заводит или выключает разных людей.

При этом трюки Артура очень эффективны для аудитории, поэтому, если у вас есть некоторая зрелищность и вы наслаждаетесь таким взаимодействием с людьми, то вам очень понравится эта часть книги. Я больше одиночка.

Тем не менее, был один трюк, который мне понравился: вот он.

Мгновенный корень куба
Это сверхбыстрый метод объявления кубического корня секретного двузначного числа, которое было построено в кубе.Для этого вам нужно знать первые десять кубиков: 1 → 1, 2 → 8, 3 → 27, 4 → 64, 5 → 125, 6 → 216, 7 → 343, 8 → 512, 9 → 729, 10 → 1000.

Все эти кубики оканчиваются на разные цифры от нуля до десяти, и это соотношение один к одному является отличной подсказкой, поскольку оно сообщает вам последнюю цифру двузначного числа, которое вы построили в кубе. Обратите внимание, что последняя цифра куба одинакова во всех случаях, за исключением двух пар, 2⇔8 и 3⇔7.

Допустим, зритель объявляет, что куб 42 875. Вы сразу же знаете, что последняя цифра 5, потому что 5 → 125.А как насчет первой цифры? Десять-куб — это тысяча, поэтому хитрость здесь заключается в том, чтобы не обращать внимания на все, что находится справа от запятой, и просто сосредоточиться на цифрах слева от запятой. Эти цифры (42) находятся между кубиками 3 и 4, поэтому первая цифра — 3. Секретное число — 35!

Метод Артура извлечения квадратного корня из квадратов двузначных целых чисел не так прост, но похож. Вы вычисляете первую цифру, игнорируя последние две цифры квадрата и сравнивая эти одну или две цифры с первыми десятью квадратами.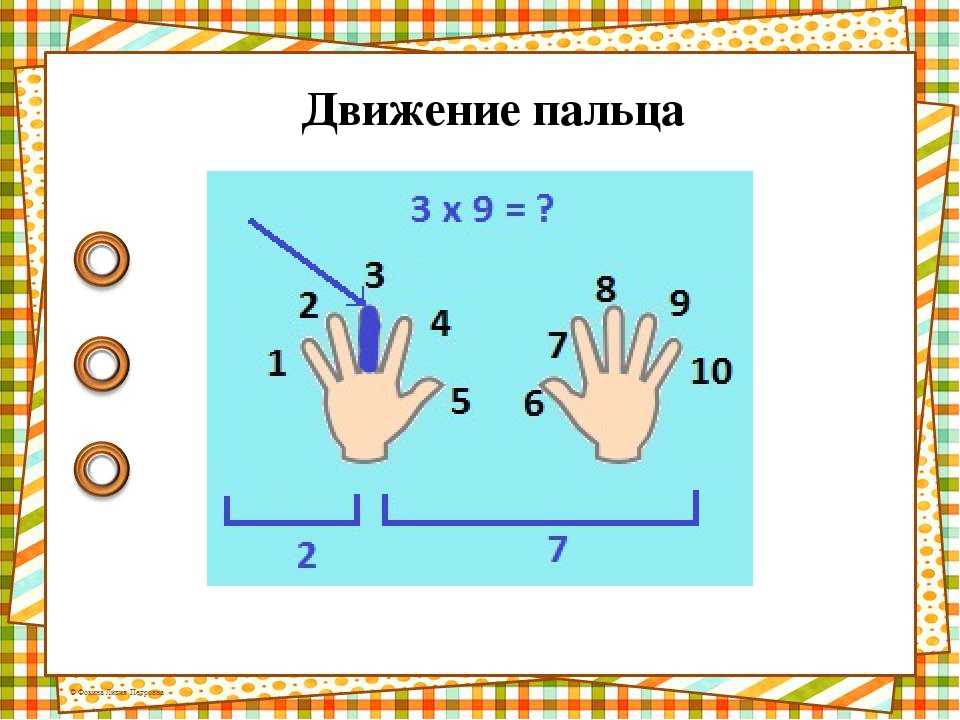 2 = 36). Чтобы решить, какое из них, вы возводите в квадрат число в середине (простой квадрат числа, оканчивающегося на пять) и смотрите, является ли ваш квадрат ниже или выше.

День недели любой даты

В «волшебной» части своей книги Артур представляет знаменитую технику определения дня недели любой даты в нашем григорианском календаре. Я не включил его в раздел, посвященный математической магии, потому что это полезный метод, который большинство из нас, вероятно, использует сотни раз, даже не демонстрируя его на сцене.

Я придумал улучшенную версию этой техники, сокращенное вычисление, которое упрощает весь процесс. Я скоро представлю его на отдельной веб-странице (по одному!)

Этот ярлык, который я использую, также ускоряет вычисление дня недели, если вы используете альтернативный метод, называемый алгоритмом Судного дня.

Прочие книги по ментальной математике

В этот раздел я планирую постепенно добавлять обзоры других книг о скоростных ментальных вычислениях.

Short-Cut Math , Джерард Келли.
Я считаю эту книгу в основном превосходной. Тон более академичный, чем в книге Артура, что можно объяснить как годом ее публикации (1969), так и тем фактом, что опыт Артура на сцене делает его беглым ведущим.

Я не встречал ни одного потрясающего трюка, но мне понравилось, что Джерард представил много маленьких техник, которые я тоже использую, техник, в которые Артур не входил. Например, Джерард находит время, чтобы описать некоторые разговоры, которые происходят в вашей голове, пока вы выполняете вычисления, а также общие методы, сочетающие мысленные вычисления с ручкой и бумагой, такие как поиск простых пар (например, 17 13) при суммировании столбцов чисел.

Джерард показывает добавления «без переноса», где вы суммируете каждый столбец цифр независимо, а затем складываете промежуточные суммы. Это особенно хорошо работает слева направо (записывая соответствующее количество нулей), поскольку вы получаете все более точные оценки.

На мой взгляд, у Джерарда была отличная интерпретация формулы n (n + 1) / 2, которую я всегда использовал для суммирования ряда последовательных цифр, начинающихся с 1. В его формуле сумма не должна начинаться с 1. Если F и L — первое и последнее число в ряду, вы берете среднее значение (F + L) / 2, а затем умножаете на количество чисел (L + 1-F).Легкий!

Джерард указывает, что если вы умножаете на бумаге, и это одно число имеет повторяющиеся цифры, например, как в 666 x 827, вам лучше поставить 666 в нижней части умножения, потому что все три прохода дадут то же число (здесь 4962), которое вы затем суммируете с соответствующими смещениями. Для чего-то вроде 248, отмечает Джерард, все цифры кратны друг другу, что дает нам быстрый способ записать строки 4x и 8x, если у нас есть строка 2x.

Я не поклонник раздела о возведении в квадрат, где Джерард вводит различные техники возведения в квадрат чисел, заканчивающихся на 1, 4 или 5. Хуже того, он опирается на свои правила возведения в квадрат, чтобы предоставить еще больше методов для умножения ближайших чисел, запутывая методы для действительно, помните, по сравнению с одним простым методом поблизости, описанным здесь.

Чтобы умножить на 45, Джерард предлагает умножить на 50 и вычесть десять процентов — прием, который я часто использовал при конвертации валют.Другой пример: умножение на 396 после умножения на 400, вместо четырехкратного вычитания числа, вы можете просто вычесть один процент. Еще один прекрасный пример: чтобы умножить 24 на 27,5, обратите внимание, что 27,5 равно 25 плюс десять процентов. Умножить 24 на 25 легко (25 — это четверть умножить на 100, так что 24/6 = 6 x 100 = 600). Добавьте десять процентов: 660.

В целом, для человека, который либо новичок в этой теме, либо очень ею интересуется, было бы обидно пропустить эту книгу. Я настоятельно рекомендую взять его в качестве дополнения к книге Артура.

Математика скорости , Билл Хэндли. Поначалу я думал, что мне эта книга понравится меньше, чем книга Джерарда Келли Short-Cut Math , но, дав ей шанс и прочитав ее до конца, она мне, вероятно, понравилась больше, чем книга Джерарда.

Одна вещь, которая сбила меня с толку, заключалась в том, что во введении Билл кланяется автору системы Трахтенберга, которая после беглого просмотра страницы Википедии меня не привлекает, поскольку она содержит слишком много «местных правил». Мне нравятся техники, которые прочно укоренились в алгебре, которую я могу сразу почувствовать. Тем не менее, Билл сказал, что его методы не совсем такие, как у Якова Трахтенберга.

Еще одна вещь, которая меня сначала оттолкнула, заключалась в том, что книга казалась более простой. Некоторые главы, казалось, были не столько о «арифметике скорости», сколько об обучении простой и понятной арифметике, то есть тому, как выполнять деление в столбик. Без сомнения, ценная информация, но это не то, что я искал, когда брал в руки книгу.

Первые семь глав представляют собой разработку близкого метода, который для моих нужд адекватно объяснен в нескольких абзацах выше.

Но затем Билл представил прекрасную вариацию этой техники. Считаем эти ароматы:
• Базовый аромат : 23 x 26 = 20 x (3 + 26) + 3 x 6 = 20×29 + 18 = 598
• Улучшенный вкус : 23 x 86 = 20 x (3 x4 + 86) + 3 x 6 = 20×98 + 18 = 1978

Обратите внимание, что в рецепте единственное изменение — это множитель x4, который равен множитель двух исходных чисел, округленный до ближайшего десяти.

Мне понравилось, что Билл указывает, что «соседние номера» совсем не обязательно должны быть рядом. Например, для 75 x 25 вы можете использовать 5 в качестве привязки, что даст 5 x 95 + 20 x 70 = 475 + 1400 = 1875.

Мне также понравилось, что Билл упомянул некоторые из моих любимых методов округления:
• Чтобы умножить на или на 90%, часто проще просто вычесть четверть или десять процентов.
• Чтобы умножить примерно на 19 и семь восьмых, умножьте на двадцать и вычтите восьмую.

Для приближения квадратных корней Билл использует почти ту же технику, представленную выше. Мне нравится, как он предлагает обращаться с числами, длина которых превышает две цифры. Допустим, вам нужен квадратный корень из 382 375. Вы начинаете с разбиения числа на пары из двух цифр, начиная с обратной стороны: 38 23 75. Ваше первое приближение фокусируется только на первой группе, которая будет состоять из одной или двух цифр. Для каждой из замыкающих групп вы просто умножаете на десять. Это означает, что каждое приближение сначала сводится к приближению квадратного корня из двузначного числа, что не так уж плохо … Используя более раннюю технику, 38 содержит шесть квадратов и остаток двух, что дает нам приближение 6 + 2/12 = 6.166 повторение. Следовательно, для нашего первого приближения к квадратному корню из 382 375 мы можем взять 616. Это неплохо, учитывая, что фактический ответ — это прикосновение к 618. Чтобы улучшить приближение, мы могли бы воспользоваться той же техникой, возведя в квадрат 616, а затем сложив остаток делится на (дважды 616). Это слишком много, чтобы делать в моей голове, но я просто дам вам знать, что это даст 618,369, неплохо, поскольку фактический ответ — 618,365. Другой способ точной настройки приближения, водорослево эквивалентный первому методу (который на самом деле обычно является сокращением этого метода), состоит в том, чтобы разделить 382 375 на первое приближение (616), а затем усреднить два числа.

В приложении Билл также упоминает метод аппроксимации кубических корней. Это вдохновило меня свести его к методу, который я представил выше, который эквивалентен водорослевым, но, на мой взгляд, более удобен для запоминания. Это почти тот же метод, что и для вычисления квадратных корней.

Билл упоминает технику, которую я никогда не осознавал, что использую. Чтобы вычесть 3745 из 10 000, я автоматически переключаюсь на какую-то технику дополнения, «завершая» все крайние левые цифры, чтобы они стали 9, и завершая последнюю цифру, чтобы она стала нулем: ведущая 3 дает 6 (3 + 6 = 9) , 7 дает 2, 4 дает 5, 5 дает 0, потому что 5 + 5 = 10.Ответ 6 255. Если бы мы вычитали из 100000 (дополнительный ноль), мы добавляем 9 впереди (и действительно, 9 завершает 0, чтобы получить 9).

Билл выполняет свое умножение крест-накрест (которое он называет «прямым методом») слева направо, что мне кажется сложнее, чем то, как это делает Артур, справа налево.

Он дает приближение для преобразования Фаренгейта в Цельсия (или наоборот), которое я считаю немного грубым: удалите 30, затем уменьшите вдвое, или удвойте, а затем добавьте 30. Я привык к C = (5/9) x (F- 32).Я запомнил, что 20C — это 68F (и большинство людей знают, что 0C — это 32F), но Билл также указывает, что 10C — это 50F и что каждое увеличение на 10C означает увеличение на 18F. Формула имеет смысл (в перевернутом виде это F = 1,8 C + 32), но я никогда не уделял времени, чтобы заметить, и это хорошо иметь в виду, поскольку это поможет в некоторых вычислениях. Например, для 15C просто добавьте 9 (половина 18) к 50 (значение 10), получив 59.

В целом, я очень рекомендую эту книгу, хотя для тех, кто уже разбирается в основах арифметики, я должен был выбрать только одну, мой выбор остается книгой Артура.

Самоучитель по высокоскоростной математике , Лестер Мейерс. Эта старинная книга давно распродана, но я заказал подержанный экземпляр. Я слышал об этом хорошее, и мне любопытно его просмотреть.

Ссылки

Сайт «Арифметическая игра» предлагает вам столько операций, сколько вы можете выполнить за две минуты. Вы устанавливаете диапазон чисел и типы операций.

Математик: веб-сайт Артура Бенджамина.

10 уловок для быстрого выполнения математических расчетов в голове

Не нужно быть учителем математики, чтобы знать, что многие ученики — и, вероятно, многие родители (это было давно!) — боятся математических задач, особенно если они включают большое количество.Изучение методов быстрого выполнения математики может помочь учащимся развить большую уверенность в математике, улучшить математические навыки и понимание, а также преуспеть в продвинутых курсах.

Получайте релевантные учебные материалы и обновления, доставляемые прямо в ваш почтовый ящик. Подпишитесь сегодня!

Присоединиться

Если это ваша работа — обучать их, вот вам отличное напоминание.

Быстрые математические приемы инфографики

10 уловок для быстрой математики

Вот 10 быстрых математических стратегий, которые учащиеся (и взрослые!) Могут использовать, чтобы вычислить в уме. Освоив эти стратегии, учащиеся должны иметь возможность точно и уверенно решать математические задачи, которые они когда-то боялись решать.

1. Добавление больших чисел

Сложить в уме большие числа может быть сложно. Этот метод показывает, как упростить этот процесс, сделав все числа кратными 10. Вот пример:

644 + 238

Хотя с этими числами сложно бороться, округление их в большую сторону сделает их более управляемыми. Итак, 644 становится 650, а 238 становится 240.

Теперь сложите 650 и 240 вместе. Итого 890. Чтобы найти ответ на исходное уравнение, необходимо определить, сколько мы прибавили к числам, чтобы округлить их в большую сторону.

650 — 644 = 6 и 240 — 238 = 2

Теперь сложите 6 и 2, чтобы получилось 8

Чтобы найти ответ на исходное уравнение, нужно вычесть 8 из 890.

890 — 8 = 882

Итак, ответ на 644 +238: 882.

2. Вычитая из 1 000

Вот основное правило вычитания большого числа из 1000: вычтите все числа, кроме последнего, из 9 и вычтите последнее число из 10.

Например:

1 000–556

Шаг 1: вычтем 5 из 9 = 4

Шаг 2: вычтем 5 из 9 = 4

Шаг 3: вычтем 6 из 10 = 4

Ответ 444.

3. 5-кратное умножение любого числа

Умножив число 5 на четное, можно быстро найти ответ.

Например, 5 x 4 =

• Шаг 1: Возьмите число, умноженное на 5, и разрежьте его пополам, в результате число 4 станет числом 2.
• Шаг 2: Добавьте ноль к числу, чтобы найти ответ. В данном случае ответ — 20.

5 х 4 = 20

При умножении нечетного числа на 5 формула немного отличается.

Например, рассмотрим 5 x 3.

• Шаг 1. Вычтите единицу из числа, умноженного на 5, в этом случае число 3 становится числом 2.
• Шаг 2: Теперь уменьшите число 2 вдвое, и оно станет числом 1. Сделайте 5 последней цифрой. Произведено число 15, и это и есть ответ.

5 x 3 = 15

4. Уловки деления

Вот быстрый способ узнать, когда число может быть равномерно разделено на эти определенные числа:

• 10, если номер заканчивается на 0
• 9, когда цифры складываются и общая сумма делится на 9
• 8, если последние три цифры делятся на 8 без остатка или равны 000
• 6, если это четное число и когда цифры складываются, ответ делится на 3 без остатка
• 5, если он заканчивается на 0 или 5
• 4, если оно заканчивается на 00 или двузначное число, которое делится на 4 без остатка
• 3, когда цифры складываются и результат делится без остатка на число 3
• 2, если он заканчивается на 0, 2, 4, 6 или 8

5.

Умножение на 9

Это простой метод, который помогает умножить любое число на 9. Вот как это работает:

Давайте возьмем пример 9 x 3.

Шаг 1 : вычтите 1 из числа, которое умножается на 9.

3 — 1 = 2

Число 2 — это первое число в ответе на уравнение.

Шаг 2 : Вычтите это число из числа 9.

9–2 = 7

Число 7 — второе число в ответе на уравнение.

Итак, 9 x 3 = 27

6. 10 и 11-кратные фокусы

Уловка для умножения любого числа на 10 состоит в том, чтобы добавить ноль в конец числа. Например, 62 x 10 = 620.

Существует также простой способ умножить любое двузначное число на 11. Вот оно:

11 х 25

Возьмите исходное двузначное число и поставьте между цифрами пробел. В данном примере это число 25.

2_5

Теперь сложите эти два числа и поместите результат в центр:

2_ (2 + 5) _5

2_7_5

Ответ на 11 x 25 — 275.

Если числа в центре складываются в число из двух цифр, вставьте второе число и прибавьте 1 к первому. Вот пример уравнения 11 x 88

8_ (8 +8) _8

(8 + 1) _6_8

9_6_8

Есть ответ на 11 x 88: 968

7. В процентах

Найти процентное значение числа может быть несколько сложно, но правильное понимание этого числа значительно упрощает понимание. Например, чтобы узнать, что составляет 5% от 235, воспользуйтесь этим методом:

• Шаг 1: Переместите десятичную запятую на одну позицию, 235 станет 23.5.
• Шаг 2: Разделите 23,5 на число 2, получится 11,75. Это также ответ на исходное уравнение.

8. Быстро возведите в квадрат двузначное число, которое заканчивается на 5

Давайте возьмем число 35 в качестве примера.

• Шаг 1. Умножьте первую цифру на себя плюс 1.
• Шаг 2: Поставьте 25 в конце.

35 в квадрате = [3 x (3 + 1)] & 25

[3 x (3 + 1)] = 12

12 и 25 = 1225

35 в квадрате = 1225

9.

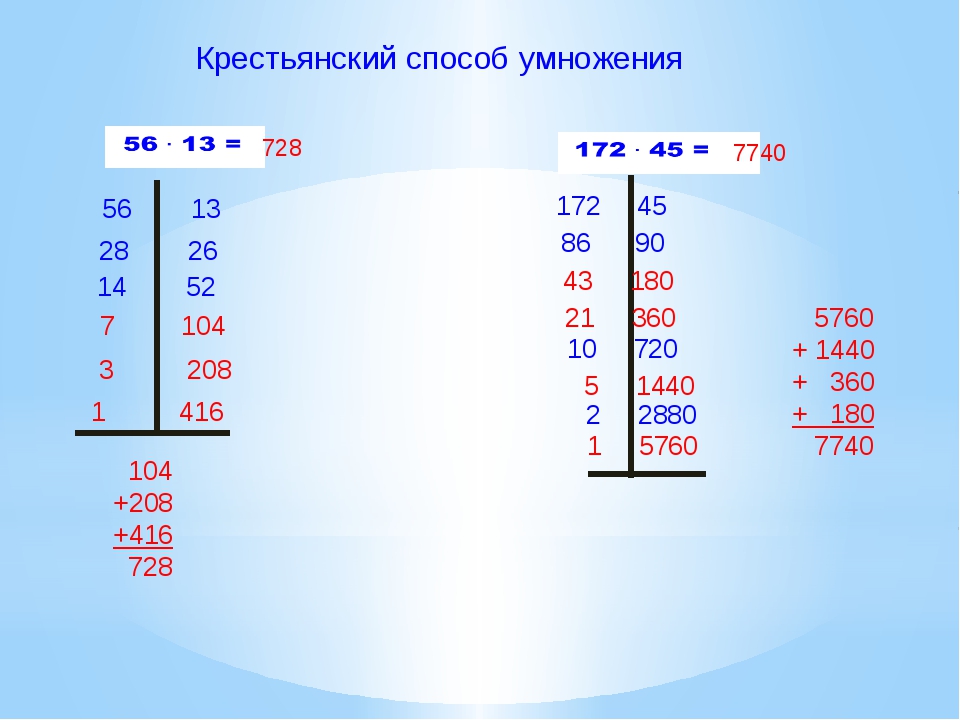Трудное умножение

При умножении больших чисел, если одно из чисел четное, разделите первое число пополам, а затем удвойте второе число. Этот метод быстро решит проблему. Например, рассмотрим

20 х 120

Шаг 1: разделите 20 на 2, получится 10. Удвойте 120, что равно 240.

Затем умножьте свои два ответа вместе.

10 х 240 = 2400

Ответ на 20 x 120: 2400.

10. Умножение чисел, оканчивающихся на ноль

Умножение чисел, оканчивающихся на ноль, на самом деле довольно просто.Это включает в себя умножение других чисел вместе, а затем добавление нулей в конце. Например, рассмотрим:

200 х 400

Шаг 1: Умножьте 2 на 4

2 х 4 = 8

Шаг 2: Поместите все четыре нуля после 8

80 000

200 x 400 = 80 000

Выполнение этих быстрых математических приемов может помочь как ученикам, так и учителям улучшить свои математические навыки и укрепить свои знания математики — и не бояться работать с числами в будущем.

Присоединяйтесь к Resilient Educator

Подпишитесь на нашу рассылку, чтобы получать контент, доставляемый в ваш почтовый ящик.Щелкните или коснитесь кнопки ниже.

Присоединиться

Вы также можете прочитать

Теги: Математика и естественные науки, Математика

10 советов, как улучшить свои умственные способности к математике

Иллюстрация: Елена Скотти / Gizmodo, Shutterstock

Калькуляторы — это здорово, но они не всегда удобны.Более того, никто не хочет, чтобы его видели, как он тянется к калькулятору на своем мобильном телефоне, когда пора вычислять 15-процентное вознаграждение. Вот десять советов, которые помогут вам вычислить числа в своей голове.

Мысленная математика не так сложна, как может показаться, и вы можете быть удивлены тем, насколько легко производить, казалось бы, невозможные вычисления, используя только свой прекрасный мозг. Вам просто нужно запомнить несколько простых правил.

Сложить и вычесть слева направо

Помните, как вас учили в школе складывать и вычитать числа справа налево (не забывайте носить одно!)? Это нормально, когда вы занимаетесь математикой с карандашом и бумагой, но при выполнении мысленной математики лучше делать это, двигаясь слева направо.Переключение порядка таким образом, чтобы вы начинали с самых больших значений, делает его немного более интуитивным и более легким для понимания. Итак, прибавляя 58 к 26, начните с первого столбца и вычислите 50 + 20 = 70, затем 8 + 6 = 14, что в сумме дает 84. Легко, легко.

Упростите для себя

Столкнувшись с трудным вычислением, попробуйте найти способ упростить задачу, временно изменив значения. Например, при вычислении 593 + 680 прибавьте 7 к 593, чтобы получить 600 (более управляемо).Вычислите 600 + 680, что составляет 1280, а затем уберите эти дополнительные 7, чтобы получить правильный ответ, 1273.

G / O Media может получить комиссию

Вы можете сделать то же самое с умножением. Для 89×6 вместо этого вычислите 90×6, а затем вычтите эти дополнительные 6, так что 540-6 = 534.

Запоминание строительных блоков

Примеры «строительных блоков». Подробнее см. Здесь.

Запоминание таблиц умножения — важный аспект умственной математики, и его нельзя сбрасывать со счетов.

Спенсер Гринберг, математик и основатель ClearerThinking.org, говорит, что, запоминая эти базовые «строительные блоки» математики, мы можем мгновенно получить ответы на простые задачи, которые встроены в более сложные. Так что, если вы забыли эти таблицы, было бы полезно поскорее освежить их в памяти. Пока вы это делаете, запоминайте свои таблицы 1 / n, чтобы вы могли быстро вспомнить, что 1/6 — это 0,166, 1/3 — это 0,333, а 3/4 — это 0,75.

Помните классные приемы умножения

Чтобы помочь вам выполнить простое умножение, важно запомнить некоторые изящные приемы.Одно из наиболее очевидных правил состоит в том, что любое число, умноженное на 10, просто должно иметь ноль в конце. При умножении на 5 ваш ответ всегда будет заканчиваться либо 0, либо 5.

Также, при умножении числа на 12, это всегда в 10 раз плюс вдвое больше этого числа. Например, при вычислении 12×4 сделайте 4×10 = 40 и 4×2 = 8, а затем 40 + 8 = 48. Один из моих любимых — умножение на 15: просто умножьте свое число на 10, а затем добавьте половину к ответу (например, 4×15 = 4×10 = 40, плюс половина этого ответа, 20, что даст вам 60).

Есть еще хитрый трюк для умножения на 16. Сначала умножьте рассматриваемое число на 10, а затем умножьте половину числа на 10. Затем сложите эти два результата вместе с самим числом, чтобы получить окончательный ответ. Итак, чтобы вычислить 16 x 24, сначала вычислите 10 x 24 = 240, затем вычислите половину 24, которая равна 12, и умножьте на 10, получив 120. Простая математика завершает это: 240 + 120 + 24 = 384.

Подобные уловки существуют и для других номеров, о которых вы можете прочитать здесь.

Квадраты — ваши друзья

Эти простые приемы хороши и хороши, но большие числа представляют собой другую проблему.Для этого физик с сайта askamathematician.com говорит, что неплохо было бы использовать разность квадратов (квадрат — это число, умноженное на само себя).

«Возьмите два числа, которые вы умножаете, и думайте о них как об их среднем, x, плюс и минус разница между каждым и их средним значением, ± y», — говорит он. «Эти два числа возведены в квадрат, поэтому вместо запоминания целых таблиц умножения вы запоминаете только квадраты».

Это может показаться сложной задачей, но запомнить все квадраты от 1 до 20 не так уж и плохо, как кажется.В конце концов, это всего лишь 20 чисел. Вооружившись этими предварительными знаниями, вы можете выполнить довольно невероятные вычисления.

Вот как это работает. Начнем с простого примера. Предположим на мгновение, что мы не знаем ответа на вопрос 10×4. Первый шаг — вычислить среднее число между этими двумя числами, которое равно 7 (т. Е. 10-3 = 7 и 4 + 3 = 7). Затем определите квадрат 7, который равен 49. Теперь у нас есть близкое, но недостаточно близкое число. Чтобы получить правильный ответ, мы должны возвести в квадрат разницу между средним (в данном случае 3) и получить 9.Последний шаг — выполнить простое вычитание, 49–9 = 40, и разве вы не знаете, что у вас есть правильный ответ.

Это может показаться окольным способом вычисления 10×4 (это так), но тот же метод работает для больших чисел. Возьмем, к примеру, 15×11. Еще раз, мы должны найти среднее число между этими двумя, которое равно 13. Квадрат 13 равен 169. Квадрат разницы среднего (2) равен 4. Наконец, 169-4 = 165, правильный ответ. .

Приблизительно

При выполнении мысленных вычислений, особенно для больших чисел, часто бывает хорошей идеей сделать обоснованную оценку и не беспокоиться о получении точного ответа. Например, еще во время Манхэттенского проекта физик Энрико Ферми хотел приблизительно оценить мощность атомного взрыва до получения диагностических данных. С этой целью он ронял листы бумаги, когда взрывная волна ударила его (с безопасного расстояния, курс). Измерив пройденное расстояние, он оценил силу взрыва примерно в 10 килотонн в тротиловом эквиваленте. Эта оценка была довольно точной, так как истинный ответ был 20 килотонн в тротиловом эквиваленте.

Этот метод, теперь известный как «оценка Ферми», работает, оценивая числа в степени десяти (подробнее см. Видео TED-Ed выше).Поэтому, когда вы пытаетесь придумать, казалось бы, невозможное решение, полезно разбивать элементы таким образом, а затем разбивать их на части. Например, при попытке оценить количество настройщиков пианино в вашем городе, сначала оцените население вашего города (например, 1000000), затем оцените количество пианино (10000), а затем количество настройщиков фортепиано (например, 100). Вы не получите точного ответа, но получите ответ быстро, причем часто достаточно близкий.

Если сомневаетесь, переставьте

Хорошей идеей будет использовать математические правила, чтобы преобразовать сложные задачи в более простую форму.Например, вычисление задачи 5x (14 + 43) само по себе является сложной задачей, но ее можно разбить на три довольно управляемых вычисления. Помня ваш порядок действий, эту проблему можно перефразировать как (5×14) + (5×40) + (5×3) = 285.

Превратите большую проблему в кучу мелких

Если есть сомнения, разбейте ее на части. «Для многих проблем способ быстро решить их — разбить их на подзадачи и решить их», — говорит Гринберг. «Когда вы сталкиваетесь с проблемой, которая кажется сложной, часто бывает полезно найти способы разбить ее на более простые проблемы, которые вы уже знаете, как решить.”

Например, вы можете умножить на 8, удвоив три раза. Поэтому вместо того, чтобы пытаться вычислить 12×8, просто удваиваю 12 три раза: 24, 48, 96. Или при умножении на 5 я начинаю с умножения на 10, так как это легко, затем делю на 2, поскольку это тоже обычно довольно легко. Например, для 5×18 вместо этого вычислите 10×18 и разделите на 2, где 180/2 = 90.

Используйте научную нотацию для неоправданно больших чисел

При вычислении больших чисел в уме помните, что вы можете сначала преобразовать их в экспоненциальную запись.Что получится 44 миллиарда разделить на 400 000? Простой способ справиться с этим — преобразовать 4 миллиарда в 10 ⁹ и 400000 в 10 ⁵ . Теперь мы можем выразить это как 44/4 и 10 ⁹ /10 ⁵ . Как указывает Гринберг, правило деления показателей требует от нас их вычитания (легко!), Поэтому мы получаем 11 x 10 ^(9-5) = 11 x 10 ⁴ = 110 000.

Простейший способ расчета чаевых

Наконец, несколько советов о том, как рассчитать чаевые в уме.Если вы можете подсчитать 10-процентные чаевые в уме (легко), то вы можете рассчитать и 20-процентные, и 15-процентные чаевые.

При расчете 10-процентных чаевых за обед, который стоит 112,23 доллара, просто переместите десятичную запятую на одну позицию влево, получив 11,22 доллара. При подсчете 20-процентных чаевых сделайте то же самое, но просто удвойте ответ (20-процентные чаевые вдвое больше, чем 10-процентные чаевые), который в данном случае составляет 22,44 доллара.

Для 15-процентных чаевых еще раз вычислите 10-процентные чаевые, а затем прибавьте половину (дополнительные 5 процентов составляют лишь половину от 10-процентной суммы).Итак, $ 11,22 + (11,22 / 2). Не волнуйтесь, если вы не можете получить точный ответ. Если не особо беспокоиться о десятичных точках, мы можем быстро подсчитать, что чаевые в размере 15% в размере 112,23 доллара равны 11 + 5,50 доллара, то есть 16,50 доллара. Достаточно близко. Добавьте четверть или две, если вы беспокоитесь о снижении производительности сервера.

Поделитесь, пожалуйста, другими интересными советами в комментариях!

Стратегия расчета на добавление

Хотите узнать больше о стратегии расчета на добавление?

Не смотрите дальше, я расскажу вам об этом прямо здесь и прямо сейчас.

На что рассчитывать на стратегию?

Расчет на — это стратегия, которую используют дети, как вы уже догадались… складывать числа. Дети начинают использовать эту стратегию, когда они способны осмыслять числа. Они переходят от подсчета всего или подсчета всего к расчету.

Эта стратегия сложения так важна, потому что это знак того, что ваши ученики начинают заниматься математикой в ​​уме. Дети должны уметь «удерживать» количество в уме, а затем прибавлять к нему.

Расчет на vs.Подсчет всего

Counting All — это именно то, что звучит. Дети считают каждое число, чтобы найти сумму. Обычно дети используют «Подсчет всего», если не могут представить себе, что представляет собой число.

Это нормально для детского сада и учеников 1-го класса. Хотя вы можете найти более добрых учеников, которые тоже могут рассчитывать на это.

В «Подсчете» дети начинают с заранее заданного числа и начинают считать.

Как это выглядит?

Это может выглядеть по-разному.Манипуляторы, математические модели и наглядные пособия — отличный способ для ваших детей изучить и понять эту стратегию. Вы можете использовать жетоны плюшевых мишек, соединяющие кубики, действительно все, что можно сгруппировать. Затем создайте визуальную модель.

Еще одна визуальная модель, которую можно использовать для представления подсчета, — это числовая линия. Используйте вопросы, чтобы направлять своих учеников и проиллюстрировать их мыслительный процесс.

Числовые пути также являются отличным инструментом для использования в детском саду, чтобы помочь ученикам визуализировать концепцию расчета на добавление.

Как только ученики по-настоящему научатся рассчитывать, они смогут делать это мысленно.

Шагая в расчет:

ШАГ 1 — Начните с дополнения

ШАГ 2 — Считайте или увеличивайте по единицам, пока не будет достигнуто второе слагаемое

Законченное число — это сумма.

( Совет учителя : Легче начать с большего слагаемого, потому что подсчитывать меньше. Это способствует отличному разговору по математике.«С какого числа вы начали и почему?»)

Я создал набор якорных диаграмм, чтобы осмыслить наиболее распространенные стратегии сложения, которые используют дети, включая «Расчет».

У каждой стратегии есть своя страница, так что вы можете добавлять их на лист диаграмм в течение учебного года.

Я также включил удобную для учащихся брошюру о стратегиях дополнения (включая все стратегии), чтобы ваши дети могли использовать ее за своими партами.

Брошюры также ОТЛИЧНЫ для родителей, так что они могут видеть, какие стратегии используют их дети.

244

стратегий вычитания мысленной математики — Шелли Грей

Итак, после выпуска моих дополнительных модулей «Ментальная математика» на сайте Teachers Pay Teachers у меня было много людей, интересующихся модулями стратегии вычитания. Я ТАК рад сообщить, что они официально ЗАВЕРШЕНЫ и опубликованы! Я искренне благодарен за все замечательные отзывы, которые я получил о дополнительных модулях, и я уверен, что набор вычитания так же великолепен!

Вычитание может быть очень сложной задачей для обучения.Для меня, как и для многих других, это потому, что мне лично не так комфортно вычитать, как сложение. Скорее всего, это верно для большинства ваших учеников. Поэтому чрезвычайно важно вооружить ваших учеников стратегиями, которые позволят им эффективно и результативно решать уравнения вычитания. Есть много-много умственных математических стратегий, которым вы можете научить своих учеников. Я разработал единицы для тех, которые я считаю наиболее важными, чтобы развить прочную основу для навыков вычитания.

Я загрузил на YouTube видео ниже, которое поможет вам немного понять каждую стратегию, а также почему так важно преподавать ментальную математику. Независимо от того, купили вы мои единицы или нет, я надеюсь, что это видео даст вам ценную информацию о стратегиях вычитания в уме. Для тех из вас, кто не хочет смотреть видео сегодня, я включил письменное описание каждой стратегии ниже.

1. Обратный отсчет и обратный отсчет: На самом деле это две отдельные стратегии, но они настолько тесно связаны, что я решил объединить их в один блок.Обратный отсчет обычно является первой стратегией, которую используют учащиеся, когда они учатся вычитать. Обратный отсчет означает просто начать с минимального числа (наибольшее число) и отсчитать, чтобы выяснить разницу. Например, в уравнении 13-2 ученик подумает: «13… 12, 11», чтобы получить ответ 11. Очень важно помнить, что обратный отсчет является эффективной стратегией только тогда, когда вычитание (число отнято) составляет 1, 2, 3 или 4. При вычитании, превышающем 4, учащиеся могут запутаться в своем подсчете и получить неправильные ответы.Как я упоминал ранее, обратный отсчет тесно связан с обратным отсчетом. При подсчете учащиеся начинают с вычитаемого и продолжают считать до уменьшенного. Например, в уравнении 10-7 ученик подумал бы: «7… 8, 9, 10», чтобы получить разницу в 3. Подсчет — эффективная стратегия только тогда, когда разница между уменьшаемым и вычитаемым составляет 1, 2, 3 или 4. Например, в уравнении 15-5 подсчет не будет эффективным, так как учащиеся, скорее всего, потеряют счет, сколько чисел было подсчитано.

2. Дополнение к мышлению : Дополнение к мышлению — еще одна стратегия, которую студенты обычно изучают на раннем этапе. Мышление «Сложение» просто означает, что между сложением и вычитанием существует обратная связь. Например, в уравнении 13–3 учащиеся должны подумать: «Что я могу добавить к 3, чтобы получить 13?» чтобы получить разницу на 10. Важным аспектом этой стратегии является изучение семейных фактов. Когда учащиеся понимают, что уравнения сложения и уравнения вычитания могут быть составлены с использованием одних и тех же трех чисел, они с большей вероятностью будут использовать одну операцию при работе с другой.

3. Использование парного разряда и развитие парного разряда : Двойной разряд — это один из самых простых фактов, которые нужно запомнить многим ученикам. Когда учащиеся достигли мастерства в сложении удвоений, они могут использовать их для решения уравнений вычитания, таких как 12-6 или 18-9. Развитие автоматизма с этими фактами сделает их легко узнаваемыми, так что учащиеся будут просто знать факт, а не думать об этом. Использование удвоений означает использование почти удвоений для решения уравнения вычитания.Например, для уравнения 15-7 ученики должны подумать: «Я знаю, что 15 на 1 больше, чем удвоение 7, поэтому ответ должен быть на 1 больше, чем 7.»

4. Использование десяти : десять иначе известно как «дружественное число» в математических терминах. Это потому, что с этим числом легко работать. С помощью стратегии «использовать десять» учащиеся учатся заменять десять другим числом, а затем корректировать ответ. Например, в уравнении 13-8 учащиеся сначала подумают «10-8», чтобы получить разницу 2, а затем сложат оставшиеся 3, взятые из исходного уравнения, чтобы получить общую разницу в 5.

5. Компенсация : Компенсация — одна из моих любимых стратегий вычитания, потому что, как только ученики узнают, как компенсировать, они могут начать использовать ее во многих различных математических ситуациях. Компенсация наиболее эффективно используется, когда результат вычитания уравнения равен 8 или 9. При использовании компенсации учащиеся меняют результат вычитания на 10, а затем корректируют ответ. Например, для уравнения 15–9 учащиеся сначала вычисляют разницу до 15–10, чтобы получить 5. Затем, поскольку 1 слишком много было вычтено из исходного уравнения, необходимо прибавить 1 к разнице, чтобы получить 6.

6. Расширение вычитаемого значения : Расширение вычитаемого значения — ценная стратегия при работе с многозначными уравнениями. Студенты используют расширенные обозначения для вычитания и вычитают их в два этапа. Например, в уравнении 45-21 учащиеся сначала выполняют 45-20, чтобы получить 25, а затем вычитают еще 1.

Как я уже упоминал в своем сообщении в блоге о стратегиях сложения, важно рассматривать каждую стратегию как инструмент, который вы даете каждому ученику в его наборе инструментов.Когда у учащихся есть все инструменты, они могут решить для себя, какой из них будет работать лучше всего. Однако, чтобы выбрать наиболее эффективный инструмент, они должны действительно хорошо понимать, как работает каждый из них. Вот почему так важно помочь ученикам развить мастерство на одном уровне, прежде чем переходить на следующий.

Мастерство означает, что учащиеся могут выполнять стратегию эффективно, без путаницы и неуверенности. Чтобы развить мастерство, важно преподавать каждую стратегию по отдельности, прежде чем объединять их вместе и ожидать, что ученики выберут лучшую для работы.Это означает, что если вы начинаете со стратегии обратного отсчета, вы должны обучать ее полностью, пока ученики не будут полностью освоены с ней. Затем, когда они почувствуют себя комфортно и вы почувствуете, что они достигли мастерства, пора переходить к подсчету, продолжая пересчитывать обратный отсчет. После достижения мастерства в подсчете учащиеся готовы изучать сложение мышления, и процесс продолжается. Ваша конечная цель при обучении стратегиям ментальной математики должна заключаться в том, чтобы научить учащихся изучать уравнение и использовать эффективную стратегию для его решения.Однако они не смогут этого сделать, если вы не позволите им овладеть каждой стратегией и широко использовать ее, прежде чем переходить к другой.

Один момент, на котором я действительно хочу выделить время, — это использование математического языка в вашем обучении. Если вы используете математический язык в своем обучении, ваши ученики тоже будут использовать его, независимо от их возраста. В уравнении вычитания уменьшаемое — это наибольшее число, вычитаемое — это убываемое число, а ответ называется разностью.Используйте эти слова ВСЕГДА, когда смотрите на уравнение или записываете уравнение на доске. Вы обнаружите, что ваши ученики начнут использовать эти слова в кратчайшие сроки! Кроме того, научите студентов использовать термин «наиболее эффективная стратегия» или «наиболее эффективная стратегия», когда они говорят о математике. Когда они видят уравнение, вы хотите, чтобы они подумали, какая стратегия будет наиболее эффективной или действенной. Спросите их, почему. Например, в уравнении 8-4 учащиеся должны понимать, что использование удвоения более эффективно, чем обратный отсчет.

Если вы начнете делать математические дискуссии частью своей повседневной жизни, вы, вероятно, начнете замечать, как студенты разрабатывают собственные математические стратегии, а это именно то, что вы хотите! Когда вы обеспечите им прочную основу, студенты, естественно, будут использовать свои знания, чтобы изобретать другие стратегии, которые им подходят. А если серьезно, как это здорово ?! Даже если вы не понимаете мышления ученика, если это работает для него, тогда это фантастика! Это означает, что вы не должны заставлять учащихся использовать одну конкретную стратегию после того, как они освоили все из них.Как только вы усвоите материал и овладеете им, позвольте учащимся использовать наиболее эффективную для них стратегию.

Я надеюсь, что это обсуждение было для вас полезным. Если у вас есть какие-либо вопросы об этих стратегиях или вам нужна дополнительная информация о том, как их преподавать, пожалуйста, оставьте комментарий ниже или свяжитесь со мной через мою страницу в Facebook «Учебные материалы Шелли Грей».

Кроме того, вот несколько ссылок, которые могут оказаться полезными при обучении мысленной математике:

Большое спасибо за чтение! Удачного дня,

Стратегии сложения умственной математики для свободного владения математическими фактами

Свободное владение математикой — это гораздо больше, чем просто скорость и точность.Истинная беглость также включает гибкость и правильное использование стратегии. Когда мы применяем мысленный математический подход к математическим фактам, мы поощряем студентов мыслить гибко, которые способны построить собственное понимание и использовать это понимание для решения более сложных задач.

Мы знаем, что способность гибко мыслить более эффективно, чем запоминание математических фактов. Это было глубоко изучено многими исследователями-математиками. Но иногда, когда мы начинаем обучать стратегиям, мы «обучаем» стратегиям запоминания.Например: «Каждый раз, когда вы видите числа, которые отличаются на 1, вы можете использовать стратегию удвоения плюс один». Вместо того, чтобы «обучать» стратегиям, в идеале мы хотим, чтобы учащиеся открывали их и строили собственное понимание. Лучший способ добиться этого — много-много работать с манипуляторами. И да, даже если вы преподаете старшие классы, ваши ученики должны использовать манипуляторы!

Тем не менее, иногда все же полезно иметь руководство по тому, к каким стратегиям направлять наших учеников.

Ниже я выделил семь различных стратегий сложения в уме, которые вы можете смоделировать в своем классе, чтобы помочь учащимся развить свое понимание.Я также включил видео для некоторых из них.

Рассчитывая — Рассчитывая на — это начальная математическая стратегия в уме. Подсчет на означает, что вы начинаете с наибольшего числа в уравнении, а затем начинаете считать. Например, в уравнении 5 + 3 вы хотите, чтобы учащиеся начинали с цифры «5» в голове, а затем считали «6, 7, 8». Это сделано для того, чтобы учащиеся не считали «1, 2, 3, 4, 5… .,6, 7, 8». Студенты также должны понимать свойство коммутативности сложения, когда, если уравнение выглядит так: «2 + 6», им все равно следует начинать с большего числа (в данном случае 6) и считать «7, 8».”

Вот видео, которое объяснит эту стратегию более подробно, или найдите модуль для обучения счету по стратегии ЗДЕСЬ.

Двойники — Двойники не обязательно являются стратегией , а скорее набором фактов, которые легко усвоить и запомнить. Двойники вокруг нас; представьте себе пальцы рук и ног — 5 + 5, колеса автомобиля — 2 + 2 или яйца в коробке — 6 + 6. Создание прочного фундамента для парных занятий поможет студентам в следующей стратегии — «Двойные игры плюс один».

Найдите модуль для обучения двойным фактам ЗДЕСЬ.

Ближайшие парные игры — Эта стратегия является естественным продолжением парных игр. Это включает использование известного факта и построение на нем. Например, чтобы решить 5 + 6, ученик может подумать: «Я знаю, что 5 + 5 дает 10, а еще один — 11». Эту стратегию лучше всего смоделировать с десятью кадрами, поэтому ее так легко увидеть! И помните, мы должны дать нашим ученикам возможность ВИДЕТЬ математику, чтобы они могли углубить свое понимание!

Вот видео, которое объясняет стратегию близких удвоений более подробно или найдите модуль для обучения фактам близких удвоений ЗДЕСЬ.

Сделай десятку — Сделай десятку — это математическая стратегия в уме, в которой учащиеся используют числовые комбинации, составляющие десять, для установления связей и отношений с другими фактами. Сначала ученики должны выучить числовые комбинации, которые составляют 10. Затем они могут уверенно использовать эти комбинации. Например, чтобы решить 8 + 5, ученик может подумать: «Я могу взять два из 5 и передать их 8, чтобы получилась десятка, а затем сложить оставшиеся 3, чтобы получить 13.«Десять кадров — отличный способ проиллюстрировать эту стратегию.

Вот видео, в котором более подробно объясняется, как сделать десять стратегию или найти модуль для обучения сделать десять ЗДЕСЬ.

Получение кратных десяти — Эта стратегия является естественным продолжением создания десяти. Чтобы сделать кратными десяти , мы можем использовать числовые комбинации, которые составляют десять (6 + 4, 7 + 3 и т. Д.). Это помогает нам понять, что такие выражения, как 26 + 4, будут делиться на десять.Десять фреймов — отличный способ смоделировать мыслительный процесс. Например, когда мы моделируем 26 + 4 с десятью кадрами, легко видеть, что мы можем переместить 4 точки, чтобы полностью заполнить три десяти кадра и получить 30.

Найдите модуль для обучения стратегии умножения десяти ЗДЕСЬ.

Сложение слева направо — Сложение слева направо — это мощная математическая стратегия для сложения чисел, состоящих из двух или более цифр. Понимание поставленной ценности является ключевым моментом, так как студенты будут группировать десятки, а затем единицы.Например, чтобы решить 24 + 53, мы сначала сложим 20 + 50, чтобы получить 70, затем 4 + 3, чтобы получить 7, и, наконец, 70 + 7, чтобы получить 77. Сложение слева направо важно для обучения ДО того, как учащиеся научатся традиционный алгоритм. Это связано с тем, что сложение слева направо сосредоточено на концептуальном понимании, а не на запоминании серии шагов.

Вот видео, в котором более подробно объясняется сложение слева направо, или найдите модуль для обучения сложению слева направо ЗДЕСЬ.

Разбить на части / Разобрать — Разбиение слагаемого по разряду — мощная математическая стратегия для сложения чисел, состоящих из двух или более цифр.Хотя это похоже на сложение слева направо, некоторые студенты предпочитают его, потому что только одно добавление разлагается по разряду, а не оба. Например, чтобы решить 43 + 35, мы могли бы сначала разложить 35 на 30 и 5. Мы начинаем с добавления 43 + 30, чтобы получить 73, а затем оставшиеся 5, чтобы получить 78.

Вот видео, которое объясняет более подробно стратегию разделения на части или найдите раздел для обучения разделению ЗДЕСЬ.

Я надеюсь, что этот пост помог вам составить план обучения математическим стратегиям в вашем классе! Я знаю, что если вы не учились таким образом, это будет непростой переход.

Если вам нужна дополнительная поддержка по обучению стратегиям сложения в классе, ознакомьтесь с этим комплектом стратегий сложения умственной математики, который включает блоки для всех стратегий, которые обсуждались выше.

учителей математики должны поощрять своих учеников считать пальцами

Примечание: это гостевой пост Адитьи Сингхала.

Помните, когда родители ругали вас за то, что вы пользуетесь пальцами для математики? И мы привыкли рисовать в уме пальцы, когда связывали руки за спиной.Тогда было трудно сопротивляться использованию пальцев. Почему мы до сих пор учим студентов не пользоваться пальцами, когда знаем, что сами не могли устоять перед использованием этой техники?

Потому что это устоявшаяся конвенция?

Визуальное обучение

Подумайте об этом иначе. В последнее время возрастает важность использования наглядных пособий в обучении. Школы применяют методы умного класса для обучения учащихся визуальным способом, потому что было доказано, что наглядные материалы остаются в сознании учеников дольше.Одно исследование даже утверждает, что человеческий разум интерпретирует визуальные эффекты в 60 000 раз быстрее, чем текст. Обучение через визуальные эффекты стало успешным сдвигом парадигмы в мире образования.

Первые формы визуализации

Итак, что заставляет вас думать, что пальцы не являются визуальными элементами? Математика — один из самых сложных предметов, особенно на начальном этапе, когда мы учимся считать. Использование наглядных пособий для обучения математике — определенно способ облегчить выживание на этом этапе.Пальцы — это наиболее легкодоступные наглядные пособия, которые мы можем использовать при изучении математики.

Позволение нашим ученикам использовать пальцы не только поощряет их считать, но также может быть полезным в обучении основам сложения. Научные блоги находят пальцы альтернативой часто используемым счетам и объясняют, как пальцы могут быть использованы для обучения простому сложению.

Однако есть что-то, что не дает вам разрешить вашим ученикам использовать эту простую технику. Это что?

Споры вокруг пальцевой техники

Учителя всегда не одобряли использование пальцев на уроках математики.Техника пальца считается менее разумным способом счета и расчетов. Большинство взрослых думают об этом как о технике, которая может помешать развитию детского мозга, и считают это детской уловкой, которая дает ответы, но не помогает в понимании.

Многие школы по всему миру запретили использование пальцев на уроках математики, и это вызывает серьезную озабоченность , потому что этим мы ограничиваем возможности развития мозга наших учеников.

Противоречивые теории

Недавнее исследование, опубликованное правительством США, предполагает, что «представление пальцев и стратегии на основе пальцев играют важную роль в обучении и понимании арифметики». Это исследование объясняет, почему мы, будучи детьми, привыкли видеть мысленное представление пальцев во время счета, когда нам было запрещено пользоваться пальцами.

В другом исследовании, опубликованном правительством США, говорится, что через год преимущества использования пальцев в математике станут очевидны.Учащиеся, хорошо знающие пальцы в первом классе, лучше справляются с цифрами во втором классе. Было обнаружено, что если шестилетний ребенок учится восприятию пальцев и может эффективно изображать свои пальцы, он / она оказывается лучше в математике, особенно в счете и расстановке чисел.

Мало того, есть конкретные доказательства из исследований, доказывающих, что когда студентов обучают восприятию и представлению пальцев, и они оказываются хорошими в этом, это приводит к более высоким математическим достижениям.Нейробиологи предлагают школам обучать учеников распознаванию пальцев. Это революционное исследование, которое предполагает, что техника пальца полезна для когнитивного развития детей.

В дополнение к вышеизложенному исследованию, профессор Стэнфордского университета Джо Боулер также опубликовал исследование, подтверждающее технику изображения пальцами. Согласно ее исследованию, использование пальцев на уроках математики дает неврологические преимущества. Она утверждает, что использование пальцев является ключевым в обучении базовой математике и впоследствии приводит к более высокому математическому IQ.

Как рассчитать пальцами?

Почти все дети учатся считать и выполнять простое сложение и вычитание с помощью пальцев. Однако, когда они становятся старше, мы отговариваем их считать по пальцам, что считается менее разумным способом мышления.

Вот некоторые методы представления пальцев, которые можно использовать для решения основных математических задач.

до 10

Все мы знаем, как сосчитать до 10 по пальцам:

До 30

Многие из нас могут сосчитать до 30 с помощью пальцевых перегородок:

до 99

корейцев используют метод под названием Chisenbop Counting to count up to 99.10

Старый китайский метод позволяет нам считать до 100000 на одной руке и до 10 000 000 000 двумя руками , касаясь маркеров по мере необходимости:

Умножение на 6, 7, 8, 9 и 10

Держите ладони внутрь, считая снизу вверх как от 6 до 10. Теперь коснитесь пальцами цифр, которые вы хотите умножить. Выше вы можете увидеть, как палец номер 8 соприкасается с пальцем номер 7 для вычисления 8 × 7.

Добавьте соприкасающиеся пальцы и пальцы под ними. Это ваши десятки. В данном примере это в сумме 5 (и будет равно 50).

Теперь умножьте пальцы левой руки (над соприкасающимися пальцами) на пальцы правой руки (над соприкасающимися пальцами). В этом примере вы умножите 2 × 3 = 6.

Добавьте два, и вы получите ответ (50 + 6 = 56).

Пальцы как воображаемые счеты

Сначала посмотрите это видео:

Эти индийские дети используют старую азиатскую технику, когда они используют пальцы как воображаемые счеты и управляют ими для выполнения более сложных математических операций за считанные секунды.Требуется

Требуется время, чтобы овладеть этой техникой, но было обнаружено, что даже слабовидящий ребенок может эффективно использовать ее. От умножения строк из 10-значных чисел до нахождения квадратного корня из 6-значного числа — эта техника может помочь детям делать все, что мы можем делать со счетами. (В методике используется корейская система счета . )

UCMAS (Универсальная система умственной арифметики) обучает этой системе. Основанный в 1993 году, он имеет глобальную сеть из более чем 5 500 центров в 57 странах и уже обучил миллионы детей.Многие ведущие университеты, такие как Гарвард, Стэнфорд, Калифорнийский университет Сан-Диего (UCSD) и

Многие ведущие университеты, такие как Гарвард, Стэнфорд, Калифорнийский университет Сан-Диего (UCSD) и Чикагский университет в США; Хартумский университет в Судане; и Манчестерский университет в Великобритании исследовали эту систему и обнаружили, что она очень полезна для детей в возрасте от 4 до 13 лет.