Уравнения 5 класса | Математика

Сегодня мы рассмотрим более сложные уравнения 5 класса, содержащие несколько действий.  Чтобы найти неизвестную переменную, в таких уравнениях надо применить не одно, а два правила.

1) x:7+11=21

Выражение, стоящее в левой части — сумма двух слагаемых

Таким образом, переменная x является частью первого слагаемого. Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое:

x:7=21-11

x:7=10

Получили простое уравнение 5 класса, из которого надо найти неизвестное делимое. Чтобы найти неизвестное делимое, нужно частное умножить на делитель:

x=10∙7

x=70

Ответ: 70.

2) 65-5z=30

Правая часть уравнения представляет собой разность:

Переменная z является частью неизвестного вычитаемого. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность:

5z=65-30

5z=35

Получили простое уравнение, в котором z — неизвестный множитель. Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель:

z=35:5

z=7

Ответ: 7.

3) 120:y-23=17

В правой части уравнения — разность. Переменная y является частью неизвестного уменьшаемого.

120:y	—	23	=	17
ум.		в.		р.

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое:

120:y=17+23

120:y=40

Здесь y — неизвестный делитель. Чтобы найти неизвестный делитель, надо делимое разделить на частное:

y=120:40

y=3

Ответ: 3.

4) (48+k)∙8=400

Левая часть уравнения представляет собой произведение. Переменная k — часть первого множителя:

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель:

48+k=400:8

48+k=50

В новом уравнении k — неизвестное слагаемое:

k=50-48

k=2

Ответ: 2.

Здесь мы решали уравнения 5 класса без использования свойств сложения и вычитания.  В 6 классе правила раскрытия скобок упрощаются, и решать такие уравнения становится проще.

ГДЗ. Математика 5 класс Тарасенкова. Уравнения.

Категория: —>> Математика 5 класс Тарасенкова.

Задание:  —>>      553 — 569  570 — 586 



наверх

Задание 553.

Какое из чисел 4. 5, 8 и 10 является корнем уравнения:

Решение:

1) 5;

2) 10;

3) 4.

Задание 554.

Решите уравнение устно:

Решение:

Задание 555.

Можно ли решить уравнение:

Решение:

1) x = 0;
2) Не имеет решений;
3) x = 1;
4) Не имеет решений;



Задание 556.

Решите уравнение:

Решение:

Задание 557.

Решите уравнение:

Решение:

Задание 558.

Составьте уравнение, корнем которого является число:

Решение:

Задание 559.

Составьте уравнение, корнем которого является число.

Решение:

Задание 560.

Некоторое число увеличили на 67 и получили число 109. Найдите это число.

Решение:

• Некоторое число — x.
• x + 67 = 109;
• x = 109 — 67;
• x = 42.
• Ответ: число 42.

Задание 561.

К некоторому числу прибавили 38 и получили число 245. Найдите это число.

Решение:

• x + 38 = 245;
• x = 245 — 38;
• x = 207.
• Ответ: 207.

Задание 562.

Некоторое число увеличили в 24 раза и получили число 1968. Найдите это число.

Решение:

• 24x = 1968;
• x = 1968 : 24;
• x = 82.
• Ответ: 82.

Задание 563.

Некоторое число уменьшили в 18 раз и получили число 378. Найдите это число.

Решение:

• x : 18 = 378;
• x = 378 * 18;
• x = 6804.
• Ответ: 6408.

Задание 564.

Некоторое число уменьшили на 22 и получили число 105. Найдите это число.

Решение:

• x — 22 = 105;
• x = 105 + 22;
• x = 127.
• Ответ: 127.

Задание 565.

Из числа 128 вычли некоторое число и получили 79. Найдите это число.

Решение:

• 128 — x = 79;
• x = 128 — 79;
• x = 49.
• Ответ: 49.

Задание 566.

Составьте и решите уравнение:

• 1) сумма удвоенного числа х и числа 39 равна 81;
• 2) разность чисел 32 и y в 2 раза меньше числа 64;
• 3) частное суммы чисел х и 12 и числа 2 равно 40;
• 4) сумма чисел х и 12 в 3 раза больше числа 15;
• 5) частное разности чисел у и 12 и числа 6 равно 18;
• 6) утроенная разность чисел у и 17 равна 63.

Решение:

• 1) 2x + 39 = 81
  • 2x = 81 — 39;
  • 2x = 42;
  • x = 42 : 2;
  • x = 21;
• 2) (32 — y) * 2 = 64
  • 32 — y = 64 : 2;
  • 32 — y = 32;
  • y = 32 — 32;
  • y = 0;
• 3) (x + 12) : 2 = 40
  • x + 12 = 40 * 2;
  • x + 12 = 80;
  • x = 80 — 12;
  • x = 68;
• 4) (x + 12) : 3 = 15
  • x + 12 = 15 * 3;
  • x + 12 = 45;
  • x = 45 — 12;
  • x = 33;
• 5) (y — 12) : 6 = 18
  • y — 12 = 18 * 6;
  • y — 12 = 108;
  • y = 108 + 12;
  • y = 120;
• 6) (y — 17) * 3 = 63
  • y — 17 = 63 : 3;
  • y — 17 = 21;
  • y = 21 + 17;
  • y = 38;

Задание 567.

Составьте и решите уравнение:

• 1) разность утроенного числа у и числа 41 равна 64;
• 2) сумма чисел 9 и х в 5 раз меньше числа 80;
• 3) частное суммы чисел у и 10 и числа 4 равно 16;
• 4) разность утроенного числа х и числа 17 равна 10.

Решение:

• 1) 3y — 41 = 64
  • 3y = 64 + 41;
  • 3y = 105;
  • y = 105 : 3;
  • y = 15;
• 2) (9 + x) * 5 = 80
  • 9 + x = 80 : 5;
  • 9 + x = 16;
  • x = 16 — 9;
  • x = 7;
• 3) (y + 10) : 4 = 16
  • y + 10 = 16 * 4;
  • y + 10 = 64;
  • y = 64 — 10;
  • y = 54;
• 4) 3x — 17 = 10
  • 3x = 10 + 17;
  • 3x = 27;
  • x = 27 : 3;
  • x = 9;

Задание 568.

Некоторое число увеличили на 5 и полученное число удвоили.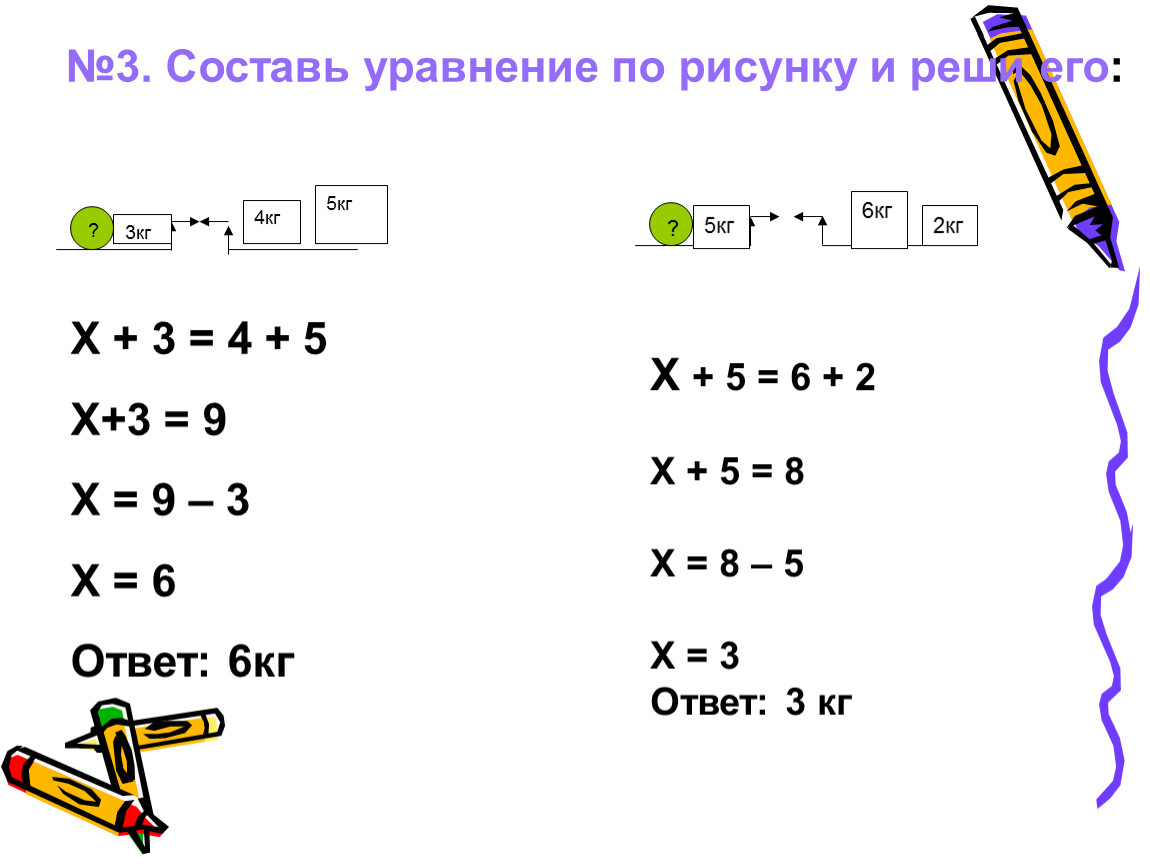 В результате получили число 22. Найдите неизвестное число.

Решение:

• (x + 5) * 2 = 22;
• x + 5 = 22 : 2;
• x + 5 = 11;
• x = 11 — 5;
• x = 6;

Задание 569.

Некоторое число увеличили в 7 раз и полученное число уменьшили на 54. В результате получили число 100. Найдите неизвестное число.

Решение:

• 7x — 54 = 100;
• 7x = 100 + 54;
• 7x = 154;
• x = 154 : 7;
• x = 22;



Задание:  —>>      553 — 569  570 — 586 

2 класс — уравнения. Как решить уравнение, примеры

Дата публикации: 13 апреля 2017.

Составление уравнений

1. Составь уравнение с числами 12, 34 и переменной x.

2. Составь уравнение с числами 7, 31 и переменной a.

3. Составь уравнение с числами 8, 54 и переменной b.

4. Составь уравнение с числами 5, 15 и переменной y.

5. Составь уравнение с числами 6, 24 и переменной c.

6. Составь уравнение с числами 3, 18 и переменной d.

7. Составь уравнение, используя рисунок.

а)
б)

9. Составь уравнения к текстовым задачам и реши их.

а) Бабушка к празднику испекла 20 пирожков. Гости съели 16 пирожков. Сколько пирожков осталось после праздника?

б) По плану автомобильный салон должен продать 34 автомобиля в месяц. К середине месяца было продано 19 автомобилей. Сколько автомобилей необходимо продать до конца месяца?

в) В оздоровительный лагерь приехало отдыхать 15 групп детей, но лагерь может принять ещё 8 групп. Сколько всего групп детей может принять лагерь?

Решение уравнений

1. Реши уравнения.

2. Заданы выражения: с + 12 и с — 12. Определи значение этих выражений при с = 34; c = 45; с = 59; c = 78.

3. Определи уравнения, в которых ответ равен 7.

4. Реши задачи, составив уравнения.

а) Длина школьного забора составляет 74 метра. Маляр покрасил 45 метров. Сколько метров забора осталось покрасить?

б) Расстояние от города до склада с песком составляет 93 км. До обеда грузовая машина, груженная песком, преодолела 56 км. Сколько километров ей надо преодолеть после обеда?

в) По плану заготовители должны собрать 30 кг клюквы. До обеда было собрано 19 кг клюквы. Сколько килограмм ягод необходимо собрать до конца рабочего дня?

г) В течении месяца механик отремонтировал 67 мотоциклов. Сколько мотоциклов ему осталось отремонтировать, если в начале месяца в мастерской находилось 77 мотоциклов?

Урок математики в 5-м классе по теме «Решение уравнений»

~ 1~

Лещёв Александр Сергеевич,учитель математики МБОУ «УстьМильская ООШ», с. УстьМильРС(Я)[email protected]

Урок математики в 5м классе по теме «Решение уравнений»

Аннотация.В статье представлено занятие по математике в 5 классе, которое рассчитано на 2 часа. Занятие содержит организационные моменты дополнительного математического образования учащихся.При проведении рекомендуется использовать презентацию с картинками, анимацией, звуками.Ключевые слова:математика, развитие творческих способностей, творческий подход, игровая ситуация, занимательная математика.

Цели:Обобщить и систематизировать материал по данной темеНаучить обобщать знания, осмысливать материал, делать выводы по материалу обязательного уровня. Провести диагностику усвоения системы знаний и умений и ее применения для выполнения практических зданий стандартного уровня с переходом на более сложный уровень.Содействовать рациональной организации труда; введением игровой ситуации снять нервнопсихическое напряжение; развивать познавательные интересы, память, воображение, мышление, внимание, наблюдательность, сообразительность; выработать самооценку в выборе пути, критерии оценки своей работы и работы товарища; повысить интерес учащихся к нестандартным задачам, сформировать уних положительный мотив учения[1]. Оформление:проектор, компьютер, раздаточный материал.

Ход урока1. Организационный моментМотивационная беседа.2. Сообщение правил игры–разбить класс на две команды;–выбрать название команды;–выигрывает та команда, которая набирает большее количество своих знаков;–команда, которая с очередным заданием справилась быстрее, имеет право выбораследующего задания;–главное условие игры –начинать с конкурса «Вспомнить»3. Актуализация опорных знанийВходной контроль.Конкурс «Вспомни»Каждой команде предлагается вспомнить правила нахождения неизвестных компонентов при решении уравнений, содержащих только действия первой ступени. Задание этого конкурса заключается в том, чтобы восстановить недостающие цифры в магическом шестиугольнике, решая различные уравнения. Эту фигуру составил любитель математики Адамс после 50 –летних проб. Требуется в клетках шестиугольника расставить числа от 1 до 19 так, чтобы сумма в любом ряду (по трем направлениям) всегда была равна 38.

~ 2~

Рис.1

4. Игровые действияСледующие конкурсы проходят в таком порядке, в котором их выбирают команды, проставляя в таблице названия своих команд, поэтому структура урока может измениться в ходе игры.Математическая шуткаТеорема: Ученики ничего не делают.Доказательство:1. По ночам занятий нет, значит, половина суток свободна. Остается 365 –182 = 183 (дня).2. В школе ученики занимаются половину дня, значит, вторая половина (т.е. четвертая часть суток) может быть свободна.Остается 183 –183: 4? 137 (дней). 3. В году 52 воскресенья. Из них наканикулы приходится? 15 дней, таким образом, выходных в учебном году 52 –15 = 37 (дней).Итого остается 137 37 = 100 (дней). 4. Но есть еще каникулы: осенние (? 5 дней), зимние (? 10 дней), весенние (? 7 дней), летние (? 78 дней).Всего 5 + 10 + 7 + 78 = 100 (дней). 5. Итак, школьники заняты в году 100 –100 = 0 (дней).ит.д.Вопрос: А когда же учиться?Где ошибка в рассуждениях?Ответ: Каникулы и воскресенья подсчитаны дважды[2].Конкурс «Загадай желание»Каждой команде предлагается загадать число, с помощью которого можно составить магический треугольник, при этом учесть, что числа от 1 до 6 уже расставлены определенным образом, запись задания ведется в тетрадь для последующего выполнения дома. Таким образом, учащиеся получают одно из домашних заданий.

Рис.2.

~ 3~

Конкурс «Переливания»Как с помощью семилитрового ведра и трехлитровой банки налить в кастрюлю ровно 5 литров воды?Решение. С помощью трехлитровой банки нальем 6 л воды в ведро.Еще раз нальем 3 л воды в банку и наполним семилитровое ведро доверху. Тогда в банке останется 2 л воды, которую выльем в кастрюлю. Добавим к ним 3 л воды с помощью банки, получим всего5 л воды. Возможны и другие варианты решения[4].Конкурс «Реши уравнение»

Каждой команде предлагается уравнение:21 + (16 + х) = 56248 : (41 –2х) = 8Конкурс «Составьзадачу по уравнению»

Каждой команде дается уравнение, по которому надо составить задачу.2х + 3 = 175х –2 = 48[3]Конкурс ««Перебор вариантов»1.Три богатыря–Илья Муромец, Добрыня Никитич и Алёша Попович, защищая от нашествия родную землю, срубили Змею Горынычу все 13 голов. Больше всех срубил Илья Муромец, а меньше всех –Алёша Попович. Сколько голов мог срубить каждый из них?2. На сколько частей можно разделить квадрат тремя прямыми линиями?3. В буфете продаются варенье, печенье, леденцы, халва и шоколад. Малыш хочет купить какието три различных сладости. Какие наборы сладостей он может приобрести? Выпиши все варианты[5, 6].Конкурс «!»Каждая команда, предварительно ознакомившись с текстом сообщения, содержащего сведения о симметричных числах, должна выполнить вычисления.Возьмите двузначное число из промежутка от 11 до 99. прибавьте к нему записанное справа налево исходное число (зеркальное). К результату прибавьте его зеркальное число, например: 39+93=132; 132+231=363. Получили число, которое называется симметричным. Из промежутка от11 до 99 лишь 4 числа более упрямы и для получения симметричных чисел требуют не одно сложение, а даже от одного до четырех сложений. Для двух самых упрямых чисел требуется даже 24! сложения. Сколько же это на самом деле? Попробуйте вычислить 24! Если число найдено, научите своего соседа выполнять такие вычисления.Конкурс «Черный ящик»

Каждой команде предлагается решить задачупомощью уравнения. «Периметр прямоугольника 288 см. Найдите стороны этого прямоугольника, если его ширина в 3 раза меньше длины»Конкурс «Эрудит»Почему одна из систем счисления носит название двенадцатеричная? Приведите примеры.5. Итог урокаПодвести итоги. Победителям выставить высшие баллы, а проигравшим на балл ниже. Учителю дается право оценить индивидуально нескольких учащихся в зависимости от их активности на уроке.6. Домашнее задание.Как дополнение к домашнему заданию, можно предложить творческую работу –придумать новые конкурсы, составить сценарийновой игры.7. Рефлексия.В конце урока опросить учеников, выяснить, что нового они узнали на уроке, чем можно дополнить урок, что изменить, чтобы стало еще лучше и интереснее.~ 4~

Ссылки на источники1.Математика. Итоговые уроки. 5 –9 классы/ Авт. –сост. О. В. Бощенко. –Волгоград: Учитель, 2005. –69 с.2.Дундина В. В. Система внеклассной и внеурочной работы по математике // Концепт: Актуальные вопросы основного и дополнительного математического образования. Выпуск 3. 2015. ART 65229. URL: http://ekoncept.ru/teleconf/65229.html Гос. рег. Эл № ФС 7749965. ISSN 2304120X. –[Дата обращения 6.05.2015]3.Виленкин Н. Я., Чесноков А. С., Шварцбурд С. И., Жохов В. И. Математика: учебник для 5 класса средней школы. –М.: Просвещение, 1990. –304 с4.Пукемова И. И. Внеклассное мероприятие по математике в 56 классах «Тропа семи испытаний» // Концепт: Актуальные вопросы основного и дополнительного математического образования. Выпуск 3. 2015. ART 65232. URL: http://ekoncept.ru/teleconf/65232.html Гос. рег. Эл № ФС 7749965. ISSN 2304120X.[Дата обращения 6.05.2015]5.Горев П. М. Уроки развивающей математики в 5–6х классах средней школы// Концепт.–2012.–№ 10 (октябрь).–ART12132.–0,6 п. л.–URL: http://www.covenok.ru/koncept/2012/12132.htm.–Гос. рег. Эл № ФС 7749965. –ISSN 2304120X [Дата обращения 6.05.2015]6.Горев П. М., Утёмов В. В. Уроки развивающей математики. 5–6 классы: Задачи математического кружка: Учебное пособие. Киров: Издво МЦИТО, 2014. –207 с.

Линейные уравнения для 5 класса

Одним из самых важных навыков при поступлении в 5 класс является умение решать простейшие уравнения. Так как 5 класс ещё не так далек от начальной школы, то и видов уравнений, которые может решать ученик не так уж и много. Мы познакомим Вас со всеми основными видами уравнений, которые необходимо уметь решать, если Вы хотите поступить в физико-математическую школу.

1 тип: «луковичные»
Это уравнения, которые почти со вероятностью встретятся Вам при поступлении в любую школу или кружок 5 класса как отдельное задание. Их легко отличить от других: в них переменная присутствует только 1 раз. Например, или .
Решаются они очень просто: необходимо просто «добраться» до неизвестной, постепенно «снимая» всё лишнее, что окружает её — как будто почистить луковицу — отсюда и такое название. Для решения достаточно помнить несколько правил из второго класса. Перечислим их все:

Сложение

1. слагаемое1 + слагаемое2 = сумма
2. слагаемое1 = сумма — слагаемое2
3. слагаемое2 = сумма — слагаемое1

Вычитание

1. уменьшаемое — вычитаемое = разность
2. уменьшаемое = вычитаемое + разность
3. вычитаемое = уменьшаемое — разность

Умножение

1. множитель1 * множитель2 = произведение
2. множитель1 = произведение : множитель2
3. множитель2 = произведение : множитель1

Деление

1. делимое : делитель = частное
2. делимое = делитель * частное
3. делитель = делимое : частное

Разберём на примере, как применять данные правила.

Заметим, что мы делим на и получаем . В этой ситуации мы знаем делитель и частное. Чтобы найти делимое, нужно делитель умножить на частное:

Мы стали немного ближе к самому . Теперь мы видим, что к прибавляется и получается . Значит, чтобы найти одно из слагаемых, нужно из суммы вычесть известное слагаемое:

И ещё один «слой» снят с неизвестной! Теперь мы видим ситуацию с известным значением произведения () и одним известным множителем ().

Теперь ситуация «уменьшаемое — вычитаемое = разность»

И последний шаг — известное произведение () и один из множителей ()

2 тип: уравнения со скобками
Уравнения данного типа чаще всего встречаются в задачах — именно к ним сводится 90% всех задач для поступления в 5 класс. В отличие от «луковичных уравнений» переменная здесь может встретиться несколько раз, поэтому решить её методами из предыдущего пункта невозможно. Типичные уравнения: или
Основная трудность — это правильно раскрыть скобки. После того, как удалось это верно сделать, следует привести подобные слагаемые (числа к числам, переменные к переменным), а после этого мы получаем самое простое «луковичное уравнение», которое умеем решать. Но обо всём по-порядку.

Раскрытие скобок. Мы приведём несколько правил, которыми следует пользоваться в данном случае. Но, как показывает практика, верно раскрывать скобки ученик начинает только после 70-80 прорешанных задач. Основное правило таково: любой множитель, стоящий за скобками необходимо умножить на каждое слагаемое внутри скобок. А минус, стоящий перед скобкой, меняет знак всех выражений, что стоят внутри. Итак, основные правила раскрытия:

Приведение подобных. Здесь всё гораздо легче: Вам необходимо путём переноса слагаемых через знак равенства добиться того, чтобы с одной стороны стояли только слагаемые с неизвестной, а с другой — только числа. Основное правило таково: каждое слагаемое, переносимое через , меняет свой знак — если оно было с ,то станет с , и наоборот. После успешного переноса необходимо сосчитать итоговое количество неизвестных, итоговое число стоящее с другой стороны равенства, нежели переменные, и решить простое «луковичное уравнение».

Приведём пример:
(раскроем скобки. Обратите внимание на смену знаков!)
(выполним умножения)
(перенесём , и через знак равенства — они «превратятся» в , и )
(посчитаем итоговое количество справа и число слева)
(ситуация «известный множитель и произведение»)

Освоив эти два типа уравнений, Вы можете быть уверенны, что сможете решить добрую половину всех заданий во вступительной олимпиаде в 5 класс.

Исследовательская работа «Происхождение уравнений»

Администрация г. Улан-Удэ

Комитет по образованию

Городская научно-практическая конференция для учащихся 5-7 классов Обыкновенное чудо

Тема работы: Происхождение уравнений

Номинация: математика

Автор: Хамаганова Ксения,6 б класс МАОУ СОШ №32

                   Консультант: Казазаева Е. Б., учитель математики МАОУ СОШ №32

г. Улан-Удэ

2019 г.

Оглавление.

1.Введение………………………………………………………………………………………..3

2.Происхождение уравнений……………………………………………………………………4

3. Решение уравнений……………………………………………………………………………6

4. Решение уравнений в Древней Греции и Индии……………………………………………7

5. Заключение…………………………………………………………………………………….8

6. Используемая литература…………………………………………………………………….9

1.Введение.

Тема происхождение уравнений выбрана мною потому, что в дальнейшем будут изучаться на уроках алгебры, которую будем изучать начиная с 7 класса. Алгебра − часть математики, принадлежащая, вместе с арифметикой и геометрией, к числу старейших разделов этой науки. Алгебра изучает общие свойства действий над различными величинами и решение уравнений, связанных с этими действиями. В отличие от арифметики, эти величины обозначаются буквами, а не цифрами.

В ходе работы над этой темой я попыталась выяснить историю уравнений, для чего нужны и значение их в математике.

Цель исследования: Выяснить историю происхождения уравнений и значение в нашей жизни.

Задачи исследования: Узнать происхождение уравнений, рассмотреть ряд уравнений.

2.Происхождение уравнений.

Кто и когда придумал первые уравнения? Что такое уравнение?

Уравнение – это равенство, содержащее неизвестное число, которое надо найти. Неизвестные числа в уравнениях принято обозначать с помощью маленьких латинских букв, например, p, t, u и т.п., но наиболее часто используются буквы x, y и z.

Задачи, приводящие к решению простейших уравнений, люди решали на основе здравого смысла. Еще 3-4 тысячи лет до нашей эры египтяне и вавилоняне умели решать простейшие уравнения, вид которых не был похож на современные.

Математика как наука родилась в Древней Греции. Греки унаследовали знания египтян, и пошли дальше. Алгебраические уравнения 1-й степени с одним неизвестным решали уже в Древнем Египте и Древнем Вавилоне. Вавилонские писцы умели решать и квадратные уравнения, а также простейшие системы линейных уравнений и уравнений 2-й степени. С помощью особых таблиц они решали и некоторые уравнения 3-й степени. В Древней Греции квадратные уравнения решали с помощью геометрических построений. Греческий математик Диофант (III в.) разработал методы решения алгебраических уравнений и систем таких уравнений со многими неизвестными в рациональных числах. Например, он решил в рациональных числах уравнение, систему уравнений, и т.д. (см. Диофантовы уравнения).

Большой вклад в развитие решения уравнений внес узбекский математик и астроном Мухаммед аль Хорезми (IX век). Кстати, название «алгебра» пошло от названия трактата Мухаммеда аль-Хорезми «Китаб аль-джебр валь-мукабала», где он дал общие правила для решения уравнений первой степени. Слово «аль-джебр» (восстановление), от которого алгебра получила своё название, означало перенос отрицательных членов уравнения из одной его части в другую с изменением знака. В алгебраическом трактате аль-Хорезми дается классификация линейных и квадратных уравнений.

Многие математики занимались решением уравнений. Одним из них был французский математик Франсуа Виет. Франсуа Виет жил в XVI веке. Он внес большой вклад в изучение различных проблем математики, астрономии, ввел буквенные обозначения в уравнении. Громкую славу Ф.Виет получил при короле Генрихе III во время франко-испанской войны. Испанские инквизиторы изобрели сложную тайнопись, благодаря которой они вели переписку с врагами Генриха III даже в самой Франции. Никто не мог найти шифр. Тогда обратились к Виету. Виет нашел решение за две недели непрерывной работы ключ к шифру, после чего Франция стала неожиданно выигрывать у Испании одно сражение за другим. Будучи уверенными, в том, что шифр разгадать невозможно, обвинили Виета в связи с дьяволом и приговорили к сожжению на костре. К счастью, он не был выдан инквизиторам и вошел в историю как великий математик. Более подробно познакомимся с Виетом в старших классах.

Алгебра как искусство решать уравнения зародились очень давно в связи с потребностью практики, в результате поиска общих приёмов решения однотипных задач. Самые ранние дошедшие до нас рукописи свидетельствуют о том, что в Древнем Вавилоне и Древнем Египте были известны приёмы решения линейных уравнений. Нильс Хенрик Абель (1802 – 1829) внес важный вклад в теорию уравнений. В 1824 году он опубликовал доказательство неразрешимости в радикалах общего буквенного выражения пятой степени.

Сейчас алгебра как наука значительно расширилась и усложнилась. Однако элементарная алгебра по-прежнему, как и во времена древних египтян, является наилучшим тренажёром для развития мышления.

3. Решение уравнений

Что значит решить уравнение? Решить уравнение (найти корни уравнения) это значит, что нужно найти значения неизвестных переменных, при которых это равенство достигается. Решить уравнение означает найти множество всех его решений (корней) или доказать, что корней нет.

Корень уравнения называется значение переменной, при котором уравнение обращается в верное равенство.

Давайте рассмотрим некоторые уравнения.

Например: Уравнение с одной переменной. Нам нужно найти число, при подстановке которого вместо «х» в уравнение, получится верное равенство. Такое число называют решением уравнения или корнем уравнения.

x:7+11=21

х:7=21-11

х:7=10

х=710

х=70 – корень уравнения. Проверим, подставив вместо х его числовое значение.

70:7+11=21

21=21 Уравнение решено верно.

Итак, при решении уравнений используются следующие свойства:

— Если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получится уравнение равносильное данному;

— Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Также с алгебраическими выражениями, входящими в уравнения, можно выполнять операции, которые не меняют его корней, в частности:

-В любой части уравнения можно раскрыть скобки.

-В любой части уравнения можно привести подобные слагаемые.

-К обеим частям уравнения можно прибавить одно и то же выражение.

-Из обеих частей уравнения можно вычесть одно и то же выражение.

4. Решение уравнений в Древней Греции и Индии

В «геометрической алгебре» древних греков решение уравнений сводилось к построению отрезков, представляющих положительные корни уравнений. Зачатки новой, арифметической алгебры встречаются лишь у Диофанта.

Вот пример задачи из «Арифметики» Диофанта.

«Если прибавить к 20 и отнять от 100 одно и то же число, то полученная сумма будет в 4 раза больше разности. Найти неизвестное.»

В 1881 г. Была найдена зарытой в земле близ Бахшали (северо-западная Индия) рукопись неизвестного автора, которая как полагают, относится к VI-VIII вв. В этом памятнике, написанном на березовой коре и известном в настоящее время под названием «Бахшалийской рукописи», содержится такая задача:

« Из четырех жертвователей второй дал вдвое больше первого, третий- втрое больше второго, четвертый вчетверо больше третьего, а все вместе дали 132. Сколько дал первый?»

Диофантовы уравнения (пример): 5x + 35y=40

Решение: Наибольший общий делитель (5, 35) = 5,

40 можно поделить на 5,

значит, у этого уравнения есть корни,

Например: x=1, y=1

Как бы мы могли решить это же уравнение в настоящее время:

5х+35у=40

выразим х через у и перенесем слагаемое 35у в правую часть уравнения, изменив знак на противоположный и получим

5х=40-35у разделим обе части этого уравнения на 5 (наибольший общий делитель)

х=8-7у Данное уравнение равносильно первому.

Решением данного уравнения с двумя переменными будет пара чисел, обращающих это уравнение в верное равенство. (х=1, у=1)

5. Заключение.

Таким образом, при изучении данной темы я узнала, что уравнения появились в жизни людей в далеком прошлом и по сей день являются неотъемлемой частью жизни человека будь то ремонт или приготовление пищи. Узнала, что алгебра — это часть (раздел) математики, посвященная изучению уравнений, содержащих цифры и буквенные обозначения, которые представляют величины, подлежащие определению. В современном мире на помощь человеку пришли калькуляторы и компьютеры, но без знания математики не обойтись. Она развивает наш ум и логику, память и внимание, помогает в решении жизненных задач.

6. Используемая литература.

Энциклопедический словарь юного математика/Сост. Э-68 А. П. Савин. — М.: Педагогика, 1989. — 352 с.

История математики в школе. IV—VI кл_Глейзер Г.И_1981

Алгебра 7 класс / Ю.Н.Макарычев –М. Просвещение 2009

Научно-технический энциклопедический словарь.

Автор материала: К. Хамаганова (6 класс)

5 класс. Математика. Ерина. Рабочая тетрадь №1. Ответы к стр. 26

Натуральные числа
Сложение и вычитание натуральных чисел
Уравнение

II. Находим информацию.
В папирусе Ахмеса есть специальный раздел «Вычисление кучи». Здесь под словом «куча» подразумевается неизвестная величина. Кто придумал обозначать неизвестную величину буквами, например, буквой х?

Трактат учёного-математика Аль-Хорезми (предположительно IX столетия) является первой дошедшей до нас книгой, в которой систематически изложена классификация уравнений и даны формулы их решения — первые зачатки алгебраического мышления. Неизвестная величина была обозначена как «шей» — по арабски «вещь». В XII веке в Испании при переводе трактата «шей» стали записывать как «xie», а далее слово сократилось до одной буквы «х».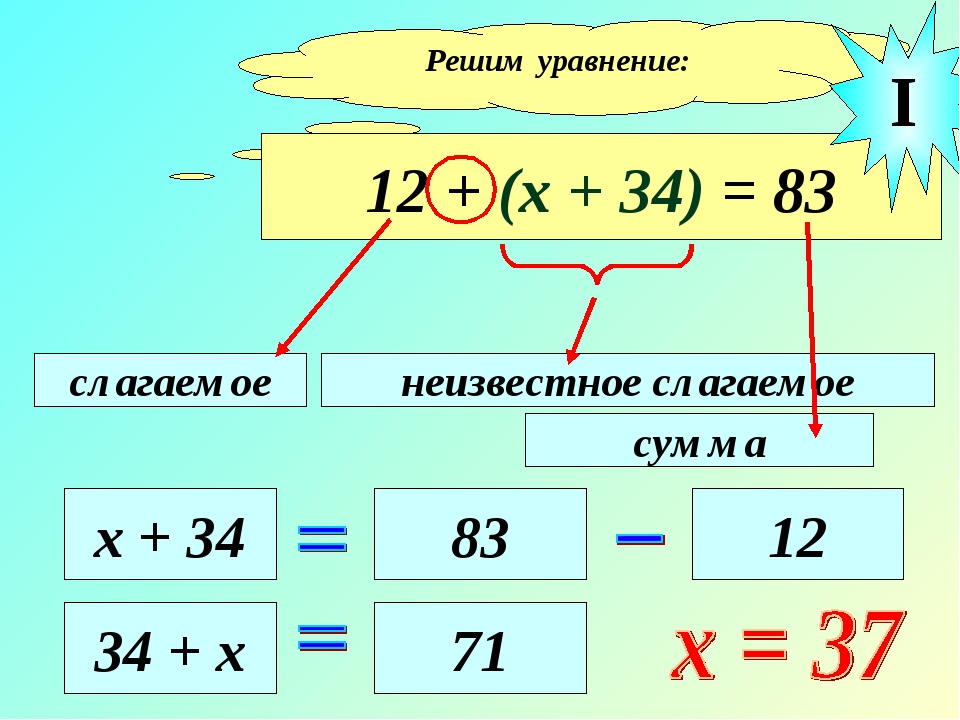

III. Анализируем, делаем выводы.
Какими натуральными числами необходимо заменить α и b, чтобы корнем уравнения
1) (16 — α) + (х — b) = 26 было число 12?

Р е ш е н и е:
1) (16 — α) + (х — b) = 26, при х = 12:
(16 — α) + (12 — b) = 26,
16 — α + 12 — b = 26,
16 + 12 — 26 = α + b,
2 = α + b, тогда α = 1 и b = 1;

2) (х — α) + (14 — b) = 21 было число 9?

Р е ш е н и е:
2) (х — α) + (14 — b) = 21, при х = 9:
(9 — α) + (14 — b) = 21,
9 — α + 14 — b = 21,
9 + 14 — 21 = α + b,
2 = α + b, тогда α = 1 и b = 1.

О т в е т: 1) α = 1 и b = 1, б) α = 1 и b = 1.

IV. Анализируем, строим умозаключения.
В городе жили 5 друзей: Макар, Егор, Аксён, Фрол и Филимон. Пофессии у низ разные: один мельник, другой маляр, третий — парикмахер. Егор и Фрол никогда не держали малярной кисти. Макар и Фрол не были на мельнице. Егор и Филимон жили в одном доме с почтальоном. Аксён гулял на свадьбе Егора и дочери парикмахера. Макар и Егор играли в городки с плотником и маляром. Фрол и Филимон брились в парикмахерской у друга, а почтальон брился сам. Кто есть кто?

Р е ш е н и е:
Егор не маляр, не почтальон, не парикмахер, не плотник.
Фрол не маляр, не мельник, не парикмахер.
Макар не мельник, не плотник, не маляр.
Филимон не почтальон, не парикмахер.
Аксён не парикмахер.
Тогда Егор — мельник.

Фрол или плотник или почтальон.
Макар или парикмахер или почтальон.
Филимон или маляр или плотник.
Аксён или маляр или плотник или почтальон.
Тогда Макар — парикмахер.

Фрол или плотник или почтальон.
Филимон или маляр или плотник.
Аксён или маляр или плотник или почтальон.
Если Фрол плотник, то Филимон — маляр, а Аксён — почтальон.
Если Фрол почтальон, то Филимон — или маляр или плотник, а Аксён — или маляр или плотник, то есть задача не имеет решения, поскольку невозможно однозначно определить, кто маляр, а кто плотник.
О т в е т: Егор — мельник, Макар — парикмахер, Фрол — плотник, Филимон — маляр, Аксён — почтальон.

Ответы по математике. Рабочая тетрадь. 5 класс. Часть 1. Ерина Т.М., Ерина М.Ю.

Математика. 5 класс

5 класс. Математика. Ерина. Рабочая тетрадь №1. Ответы к стр. 26

Оцените и поделитесь с друзьями!

уроков в классе | Математические решения

Черил начала урок с чтения Спагетти и фрикадельки для всех! вслух классу. По сюжету мистер и миссис Комфорт приглашают 32 члена семьи и друзей на встречу и устанавливают восемь квадратных столов, чтобы разместить по четыре человека за каждым, по одному в стороне. По мере того, как приходят гости, у всех есть свои идеи о том, как переставить столы, чтобы группы разного размера могли сидеть вместе. Миссис Комфорт протестует, зная, что позже возникнут проблемы с сиденьем, но ее протесты игнорируются.Вечеринка превращается в веселую смесь переставленных столов, стульев, тарелок, стаканов и еды. Однако, в конце концов, все сработает, когда миссис Комфорт оказалась права.

Когда Шерил закончила читать рассказ, она спросила класс: «О чем беспокоилась миссис Комфорт?»

Николь сначала ответила: «Здесь не будет достаточно места, потому что, когда вы складываете столы вместе, вы теряете стулья», — сказала она.

«Что ты имеешь в виду?» — спросила Черил.

«Это как если вы сложите два стола вместе, вы потеряете места там, где они соприкасаются.Это трудно объяснить.» Николь нарисовала в воздухе два стола, указывая на стороны, где они встретились. Черил нарисовала на доске два квадрата, нарисовав стрелку там, где стороны касались друг друга. «Вы имеете в виду потерять стулья здесь?» она спросила. Николь кивнула. (См. Рисунок 1).

Выслушав идеи других студентов о проблеме миссис Комфорт, Черил сказала: «Давайте использовать цветные плитки, чтобы изучить различные способы расстановки всего четырех столов. Начнем всего с четырех столов ».

Черил дала классным указаниям по расстановке квадратных «столов».«Когда плитки соприкасаются, — сказала она, — они должны касаться всей стороны. Прикосновение к частям сторон или только к углам недопустимо ». Она продемонстрировала на диапроекторе. (См. Рисунок 2.)

Шерил также разместила плитки таким образом, чтобы не следовать ее правилу, и попросила учеников объяснить, почему. (См. Рисунок 3.)

Затем она выполнила инструкции. «В своей группе поделитесь плитками, которые я положил на ваш стол, и найдите разные способы расставить четыре плитки.Обязательно следуй моему правилу ». Черил разложила около 70 плиток для каждой группы из четырех учеников.

Пока ученики работали, Черил ходила по классу, наблюдая за учениками и отвечая на вопросы по мере необходимости. Когда у всех была возможность поработать над проблемой, она прервала студентов и попросила их внимания.

«Что вы сделали?» — спросила Черил. «Кто бы хотел описать расположение, чтобы я мог построить его из плиток наверху?»

«Вы можете провести прямую линию», — сообщил Брэндон.

«Как это?» — спросила Черил, складывая четыре плитки в прямоугольник размером 1 на 4. Брэндон кивнул.

«Сделайте квадрат со всеми четырьмя из них», — сказала Рахиль. Черил построила квадрат из четырех плиток.

«Я сделала тройку и одну», — сказала Николь.

«Что ты имеешь в виду?» — спросила Черил.

«Один маленький столик, как у Натана, — пояснила Николь, — а затем столик 1 на 3».

«Вы можете сделать четыре отдельных стола», — сказал Натан.

«Ты мог бы поставить Т», — сказал Зак.«Положите три в ряд и один под средним».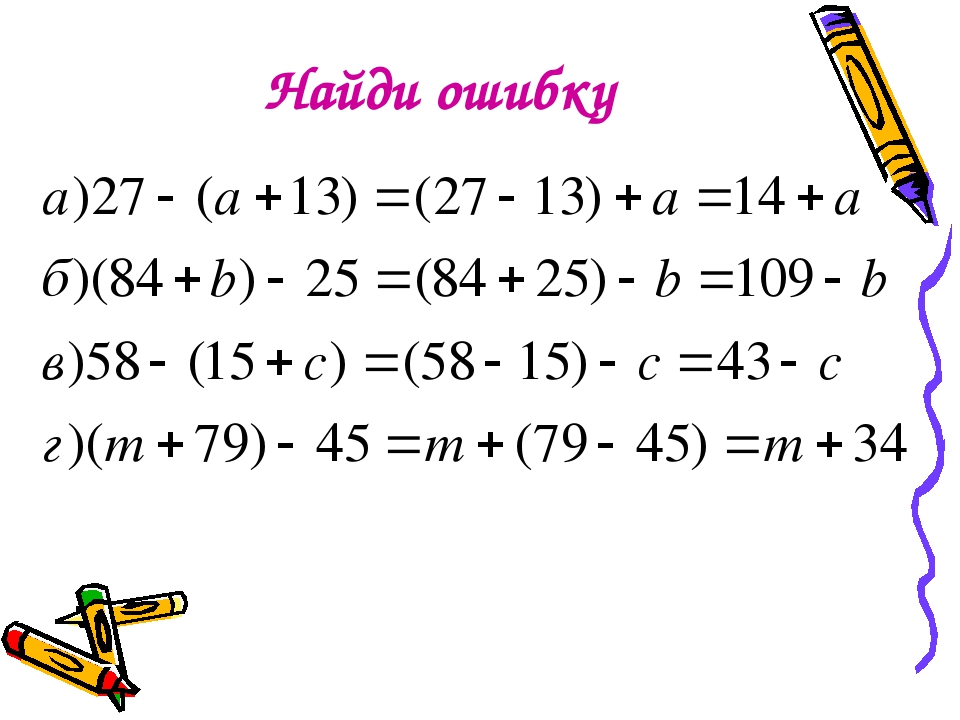

«Я тоже сделал это, но мой перевернут», — сказал Эрик.

Шерил построила аранжировку Эрика под руководством Зака ​​и указала классу, что когда вы можете перевернуть, повернуть или сдвинуть фигуру, чтобы она точно соответствовала другой фигуре, фигуры совпадают. «Мы будем считать конгруэнтные формы одинаковыми», — пояснила она.

Когда расположение студентов заполнило накладные расходы, Черил спросила: «Что, если бы мы использовали только отдельные прямоугольные столы, сделанные из четырех плиток? Какие формы мы должны удалить? »

«Я предложил четыре отдельные таблицы, — сказал Натан.

Рифка добавила: «И та, которая похожа на букву Т».

«Вы также должны снять мою», — сказала Николь. «Это не один прямоугольник».

Когда Малкия предложила убрать квадрат, разговор разгорелся. Некоторые ученики помнили, что квадрат — это прямоугольник, а другие — нет. Черил пояснила: «Квадрат — это особый вид прямоугольника, потому что все его стороны имеют одинаковую длину. Но, как и прямоугольник, квадрат по-прежнему имеет четыре угла в 90 градусов, а противоположные стороны параллельны.”

Шерил хотела убедиться, что ученики умеют маркировать построенные ими прямоугольники. Она нарисовала на доске прямоугольник размером 1 на 4. «Я могу записать это двумя способами», — сказала она и записала под прямоугольником:

Затем Черил нарисовала квадрат 2 на 2 и пометила его.

Черил указала на квадратный стол 2 на 2 и спросила: «Если один человек сидит сбоку от небольшого квадратного стола, и никто не сидит по углам или в щелях между столами, сколько людей может сидеть здесь? ”

«Легко, восемь», — ответила Николь.«Просто сосчитайте по два человека с каждой стороны, умноженные на четыре стороны».

«Когда вы подсчитываете количество людей, которые могут сесть за стол, вы фактически находите его периметр», — объяснила Шерил. «Это потому, что каждый человек сидит по одну сторону от меньшего квадрата и занимает одну единицу длины. Таким образом, периметр прямоугольника 2 на 2 составляет 8 единиц ».

«Периметр стола размером 1 на 4 равен 10», — заметил Эрик.

Черил попросила остальных проверить показания Эрика, а также изобразить периметр нескольких других прямоугольников.Затем она представила другую проблему.

— Давайте вспомним вечеринку мистера и миссис Комфорт, — начала Черил. «Предположим, миссис Комфорт решила, что все 32 человека должны сесть за один большой массивный прямоугольный стол, и она хотела выяснить, сколько маленьких квадратных столов можно арендовать. Посмотрите, сможете ли вы найти все возможные прямоугольные столы разных размеров и форм, на которых могут разместиться 32 человека ».

«Должен ли каждый стол вмещаться ровно 32?» JT хотел знать.

«Да», — ответила Черил.

«Сколько плиток мы используем?» — спросила Малкия.

«Это будет зависеть от столов, которые вы построите», — ответила Черил.

«Можем ли мы работать с партнером?» — спросила Николь.

«Да, — ответила Черил, — но веди свой личный учет».

Больше вопросов не было. Черил дала последнее указание. «Используйте плитки, но нарисуйте свои решения на листе бумаги. Обязательно запишите размеры каждого стола и количество людей, за которыми он может разместиться ».

Наблюдая за детьми

Остаток урока Черил наблюдала за учениками за работой и при необходимости оказывала помощь.

Она наблюдала, как Кэтлин составляла прямоугольник 16 на 2. «Хм, — громко сказала Кэтлин, работая, — давайте посмотрим, 32 человека. Это должно сработать, потому что 16 умножить на 2 будет 32 ». Кэтлин сосредоточенно нахмурилась, считая стороны квадратов. Затем она с удивлением посмотрела на Шерил.

«Я не понимаю», — сказала она. «Я насчитал 36 мест. Но в этом нет смысла, потому что 16 умножить на 2 равно 32. Может, я неправильно посчитал ». Она снова сосчитала стороны.

«Еще 36. Ага». Кэтлин пожала плечами, перемешала 16 плиток обратно в стопку в центре стола и начала строить еще один прямоугольник.

«Что ты делаешь?» — спросила ее Шерил.

«Что ж, я, должно быть, напортачила, потому что первая, которую я сделал, не сработала, поэтому я попробую что-нибудь еще», — ответила Кэтлин.

«Что ты собираешься попробовать?» — спросила Черил.

«Не знаю. Я просто собираюсь повозиться и посмотреть, что будет », — сказала она.

Черил наблюдала, как Кэтлин начала складывать плитки в длинный ряд шириной в один квадрат. Она продолжала считать стороны одну за другой каждый раз, когда добавляла новую плитку.Наконец она улыбнулась.

«Это работает! Этот вмещает 32 человека. Это 1 на 15. А теперь записать это ». Кэтлин начала рисовать прямоугольник на бумаге.

Алекс сидел напротив Кэтлин. «Я тоже нашел это», — сказал он. «Теперь я пробую что-то вдвое».

«О», — ответила Кэтлин и начала строить прямоугольник шириной в четыре квадрата.

Натан подошел к Шерил. «Я не рисую на бумаге прямоугольники, как все, — сказал он. «Вместо этого я решил использовать Xs. Но Люк сказал мне, что это неправильно. Разве я не могу нарисовать крестики, если захочу? » Натан показал Шерил свою газету.

Черил попросила Натана объяснить, что он сделал. Удовлетворенная тем, что он понимает, что делает, Шерил сказала: «То, что вы сделали, имеет для меня смысл».

Натан вернулся к Люку. «Я сказал вам, что она скажет, что все в порядке», — сказал он.

Черил пошла по классной комнате. К концу периода она увидела, что все студенты нашли некоторые прямоугольники, а некоторые нашли их все.Она попросила детей убрать плитку и собрала их бумаги. Шерил планировала продолжить урок на следующий день.

Следующий день

На следующее утро Черил дала классу возможность подумать над расширением. «Какой самый дешевый способ разместить 32 человека за одним большим прямоугольным столом? А какой самый дорогой способ? Чтобы ответить, некоторым из вас нужно будет найти дополнительные расстановки столов ».

Примерно через 10 минут Черил прервала учеников, чтобы начать обсуждение в классе. «Какие варианты есть у Comforts, чтобы посадить всех 32 человека за один стол?» — спросила Черил. Руки студентов вскинулись.

«У них будет группа, точнее, восемь», — сказала Рэйчел. Большинство студентов кивнули или пробормотали свое согласие.

«Может ли кто-нибудь описать размеры таблиц, которые будут работать?» — спросила Черил. «Я запишу их на доске».

Эрик сообщил: «Один раз-15, 2-раз-14, 3-раз-13, 4-раз-12, 5-раз-11, 6-раз-10, 7-раз-9 и-8-раз-8». . » После того, как Шерил записала размеры, она вернулась и зарисовала каждый соответствующий прямоугольник.

«О, я вижу закономерность!» — сказала Анферни. «Могу я показать это?» Черил кивнула, и Анферни подошла к доске. Она сказала, указывая: «Сверху вниз идет 1, затем 2, затем 3, затем 4, затем 5 и так далее, вплоть до 8».

«А другая сторона идет вниз», — добавила Анн Мария.

«О да, я этого не видела», — сказала Анферни. «Ага, 15, 14, 13 и так далее». Он снова сел.

«Разве список не должен продолжаться?» — спросила Черил. «Разве не следует прямоугольник 9 на 7?» (См. Рисунок 6.)

«Этот у тебя уже есть», — сказала Малкия.

«Да, 9 на 7 и 7 на 9 — это одно и то же, — добавила Николь.

«Все числа после 8-умножить на 8 — это повторения, — сказала Кирстен, — так что вы не можете их сосчитать».

«Давайте подумаем, сколько квадратных столов придется арендовать мистеру и миссис Комфорт на каждый большой прямоугольник», — сказала Шерил. «Сколько им придется арендовать за стол размером 15 на 1?»

«Пятнадцать. Легко, — ответили несколько студентов.

«А как насчет 2 на 14?» Черил продолжила.«Сколько столов придется арендовать Comforts для такой договоренности?»

«Двадцать восемь», — звали многие дети.

«А как насчет расположения 3х13?» — спросила Черил. Класс быстро понял, чем занимается Шерил.

«Вы просто размножаетесь», — сказала Рифка. «Просто сделай это для всех — 28, 39, 48, 55, 60, 63 и 64».

«Что вы заметили в форме столов?» Затем спросила Черил.

Малкия сказала: «Размер 8 на 8 — квадрат, а все остальные — прямоугольники.”

«Но ведь размер 8 на 8 тоже прямоугольник, помнишь?» Эрин напомнила Малкию.

«Смотрите, — сказал Брэндон. «Если они устроят длинный тонкий прямоугольник для 32 человек, то они смогут сделать это всего с 15 столами. Так дешевле всего.

«И они также сэкономили бы место, поскольку 1-умноженный на 15 занимает меньше всего места», — добавил Шарнет.

«Но вам понадобится длинная комната, — добавила Николь, — как для королевского банкета».

Затем Шерил остановила беседу и дала письменное задание оценить мышление каждого ученика.Она написала на доске три вопроса, чтобы дети могли ответить:

1. Какие шаблоны вам пригодились в работе?
2. Какие расстановки столов наиболее и наименее экономичны?
3. Что вы заметили в областях и периметрах выполненных вами мероприятий?

Учащиеся работали над заданием для остальной части класса.

Обучение линейным уравнениям в математике

Для многих учеников 8-х классов и выше числа и формы, которые они узнали, действительно начинают сходиться, когда они составляют и решают линейные уравнения.Эта тема объединяет идеи об алгебре, геометрии и функциях, и многим детям — и взрослым может быть трудно осмыслить. В этой статье объясняется, что такое линейное уравнение, и рассматриваются различные примеры. Затем он предлагает учащимся идеи уроков по введению и развитию концепции линейных уравнений с одной переменной.

Что такое линейное уравнение?

Как и любое другое уравнение, линейное уравнение состоит из двух равных друг другу выражений.Есть некоторые ключевые особенности, общие для всех линейных уравнений:

1. Линейное уравнение имеет только одну или две переменные.
2. Никакая переменная в линейном уравнении не возводится в степень больше 1 или не используется в качестве знаменателя дроби.
3. Когда вы находите пары значений, которые делают линейное уравнение истинным, и наносите эти пары на координатную сетку, все точки лежат на одной линии. График линейного уравнения представляет собой прямую линию.

Линейное уравнение с двумя переменными может быть описано как линейное соотношение между x и y , то есть двумя переменными, в которых значение одной из них (обычно y ) зависит от значение другого (обычно x ).В этом случае x является независимой переменной, а y зависит от нее, поэтому y называется зависимой переменной.

Независимая переменная, помеченная как x , обычно отображается по горизонтальной оси. Большинство линейных уравнений являются функциями. Другими словами, для каждого значения x существует только одно соответствующее значение y . Когда вы присваиваете значение независимой переменной x , вы можете вычислить значение зависимой переменной y .Затем вы можете нанести точки, названные каждой парой ( x , y ), на координатной сетке.

Описание линейных отношений

Студенты уже должны знать, что любые две точки определяют линию. Таким образом, для построения графика линейного уравнения на самом деле требуется всего лишь найти две пары значений и провести линию через точки, которые они описывают. Все остальные точки на линии предоставят значения x и y , которые удовлетворяют уравнению.

Графики линейных уравнений всегда представляют собой линии.Однако важно помнить, что не каждая точка на линии, которую описывает уравнение, обязательно будет решением проблемы, которую описывает уравнение. Например, проблема может не иметь смысла для отрицательных чисел (скажем, если независимая переменная — время) или очень больших чисел (скажем, чисел больше 100, если зависимая переменная — это оценка в классе).

Как выглядит линейное уравнение?

Пример 1: расстояние = скорость × время

В этом уравнении для любой заданной постоянной скорости соотношение между расстоянием и временем будет линейным. Однако расстояние обычно выражается положительным числом, поэтому на большинстве графиков этой взаимосвязи будут отображаться только точки в первом квадранте. Обратите внимание, что направление линии на графике ниже — снизу слева направо. Линии, идущие в этом направлении, имеют положительный наклон . Положительный наклон указывает, что значения на обеих осях увеличиваются слева направо.

Математика 7 класс, Раздел 6.7

Давайте посмотрим, насколько сбалансированная подвеска похожа на уравнение, а перемещение ее веса похоже на решение уравнения.

Цели обучения:

• Я могу объяснить, как сбалансированная подвеска и уравнение представляют одну и ту же ситуацию.
• Я могу найти неизвестный вес на диаграмме подвески и решить уравнение, которое представляет диаграмму.
• Я могу написать уравнение, описывающее веса на сбалансированной подвеске.

7.1 Схемы подвесов

На двух диаграммах все треугольники и квадраты одинаковы.

Для каждой диаграммы придумайте.. .

1. Одно, что должно быть правдой
2. То, что может быть правдой
3. То, что не может быть правдой

7.2 Соответствие подвеса и уравнения

Фигуры с одинаковой буквой на каждой сбалансированной вешалке имеют одинаковый вес.

• 2 \ в штучной упаковке {\ phantom {3}} + 3 = 5
• 3 \ в коробке {\ phantom {3}} + 2 = 3
• 6 = 2 \ в коробке {\ phantom {3}} + 3
• 7 = 3 \ в штучной упаковке {\ phantom {3}} + 1

1. Сопоставьте каждую подвеску с уравнением.Завершите уравнение, написав x, y, z или w в пустом поле.
2. Найдите решение каждого уравнения. Используйте вешалку, чтобы объяснить, что означает раствор.

7.3 Использование подвесок для понимания решения уравнений

Вот несколько уравновешенных вешалок, на каждой из которых указан ее вес. Для каждой диаграммы:

1. Напишите уравнение.
2. Объясните, как определить вес предмета, помеченного буквой, исходя из диаграммы.
3. Объясните, как вычислить вес предмета с буквой, рассуждая по уравнению.

Вы готовы к большему?

Когда у вас будет время, посетите сайт https://solveme.edc.org/Mobiles.html, чтобы решить несколько более сложных головоломок, в которых используются схемы вешалки, подобные приведенным в этом уроке. Вы даже можете построить новые. (Если вы хотите сделать это во время урока, сначала посоветуйтесь со своим учителем!)

Итоги урока 7

В этом уроке мы работали с двумя способами, чтобы показать, что две суммы равны: сбалансированная подвеска и уравнение.Мы можем использовать сбалансированную подвеску, чтобы подумать, как найти неизвестную сумму в соответствующем уравнении.

Подвеска показывает общий вес 7 единиц с одной стороны, который уравновешен 3 равными, неизвестными весами и 1-ю единицей веса с другой. Уравнение, которое представляет собой отношение: 7 = 3x + 1.

Мы можем снять по 1 шт. С каждой стороны, и подвеска останется в равновесии. Это то же самое, что вычесть 1 из каждой части уравнения.

Уравнение для новой подвески с балансировкой: 6 = 3x.

Таким образом, подвеска будет сбалансирована с \ frac13 веса с каждой стороны: \ frac13 \ boldcdot 6 = \ frac13 \ boldcdot 3x.

Две стороны вешалки уравновешивают следующие грузы: 6 гирь размером 1 единица с одной стороны и 3 гири неизвестного размера с другой стороны.

Вот краткий способ записать шаги, указанные выше:

\ begin {align} 7 & = 3x + 1 & \\ 6 & = 3x & \ text {после вычитания 1 с каждой стороны} \\ 2 & = x & \ text {после умножения каждой стороны на} \ tfrac13 \\ \ end {align}

Урок 7 Практические задачи

1. Существует пропорциональная зависимость между объемом пробы гелия в литрах и массой этой пробы в граммах. Если масса образца 5 граммов, то его объем составляет 28 литров. (5, 28) показано на графике ниже.

   1. Какова константа пропорциональности в этом соотношении?
   2. В этой ситуации, что означает число, которое вы нашли в части а?
   3. Добавьте еще как минимум три точки на график выше и пометьте их координатами.
   4. Напишите уравнение, которое показывает взаимосвязь между массой образца гелия и его объемом. Используйте m для массы и v для объема.

2. Объясните, как части сбалансированной подвески сравниваются с частями уравнения.

3. Вот вешалка:

   1. Напишите уравнение подвески.
   2. Нарисуйте еще вешалок, чтобы показать каждый шаг, который вы предпримете, чтобы найти x. Объясните свои рассуждения.
   3. Напишите уравнение для каждой нарисованной вешалки. Опишите, как каждое уравнение соответствует своей вешалке.

Четыре основных математических понятия, которые дети изучают в 5–6 классах | Scholastic

С пятого класса на шестой может произойти значительный скачок в знаниях математики, и мне нравится думать об этом как о переходе через мост.Чем больше мы соединим мост, тем лучше наши дети будут чувствовать себя в средней школе. Пятый класс — это кульминация всего, что ученики узнали на начальном уровне, а шестой класс можно рассматривать как отправную точку для средней школы. И независимо от того, как устроена средняя школа вашего ребенка, между этими оценками существует четкая связь. Чем более комфортно дети усваивают эти концепции к концу шестого класса, тем лучше они будут подготовлены к средней школе.

Вот четыре основных математических понятия, которые ваш ребенок усвоит в пятом и шестом классе:

1.Система счисления. В пятом классе ученики сосредотачиваются на сложении, вычитании, умножении и делении целых чисел, дробей и десятичных знаков. Ваш ребенок научится свободно вычислять эти типы чисел и понимать взаимосвязь между ними. Студенты также должны уметь использовать эти числа в реальных сценариях. В шестом классе дети продолжают понимать эти числа, а также знакомятся с отрицательными числами. Они начнут определять рациональные числа и целые числа в числовой строке, а также сравнивать их.Использование моделей значительно улучшит понимание ребенком этих концепций.

Поощряйте своего ребенка:

• Распознавайте и вычисляйте, используя дроби и десятичные дроби в реальном мире. Например, попросите ребенка вычислить скидку на распродаже; сумма налога при совершении покупок; найдите кончик счета или объясните спортивную статистику.
• Используйте дробные линейки для вычислений (сложение, вычитание, умножение или деление).

Изображение предоставлено: LearnZillion

• Найдите примеры положительных и отрицательных чисел в реальном мире (температура, расстояние, уровень моря и т. Д.)) и используйте модели, чтобы понять взаимосвязь между ними.

Изображение любезно предоставлено: положительное влияние Math

2. Коэффициенты. Ученики будут использовать свои знания о дробях и десятичных дробях в пятом классе для соотношения разума и оценки задач в шестом классе. Детям нужно будет связать свое понимание умножения и деления с реальными задачами с использованием соотношений. Они будут использовать модели (диаграммы, таблицы, двойные числовые линии и т. Д.), Чтобы помочь им установить эти связи и решить проблемы с удельной стоимостью.Студенты также узнают о процентах и ​​о том, как они соотносятся с дробями и десятичными знаками.

Поощряйте своего ребенка:

• Найдите примеры соотношений в реальном мире. Например, « Соотношение крыльев и клювов в скворечнике в зоопарке было 2: 1, потому что на каждые 2 крыла приходился 1 клюв».
• Используйте модели, чтобы понять проблемы соотношения и скорости:

Изображение предоставлено: 6-й класс мистера Пратта

Изображение предоставлено: nzmaths.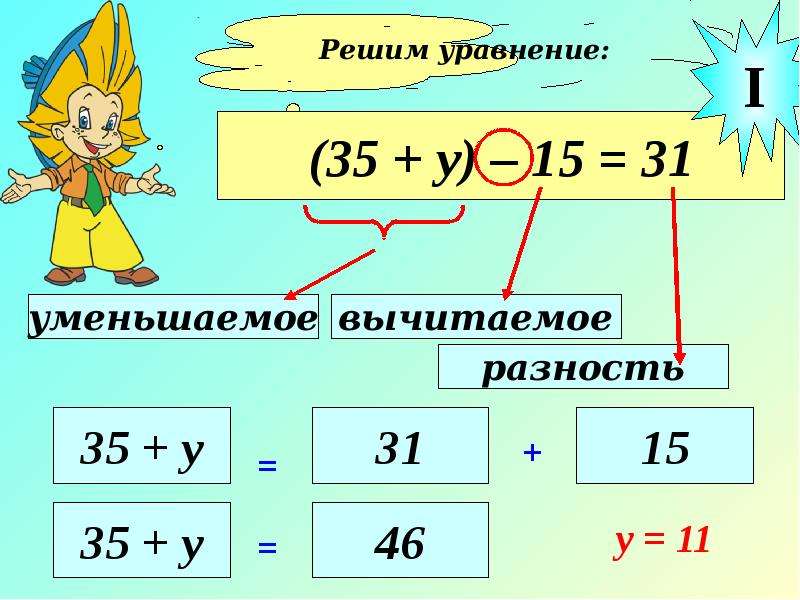

• Создавайте реальные проблемы, используя понимание соотношений. Например, « В этом рецепте соотношение 3 стакана муки к 4 стаканам сахара, поэтому на каждый стакан сахара приходится 3/4 стакана муки».

3. Выражения и уравнения. Учащиеся начинают понимать разницу между выражением и уравнением. Они используют переменные для представления неизвестного числа как в выражениях, так и в уравнениях. Ученики пятого и шестого классов следуют соответствующему порядку действий для решения задач, включая скобки и показатели.Ваши дети начинают читать, интерпретировать и писать выражения и уравнения, а также решать уравнения с одной переменной.

Поощряйте своего ребенка:

• Различайте выражение и уравнение и поймите значение знака равенства:

Выражение: 4y + 2
Уравнение: 4y + 2 = 14

• Решайте проблемы, используя аббревиатуру PEMDAS:

Изображение предоставлено coolmath. com

• С легкостью считайте и запишите выражение: Вычтите n из 8 дюймов как 8 — n.
• Создавайте и решайте реальные проблемы с помощью переменных. Например: « Аренда катка стоит 100 долларов плюс 5 долларов на человека. Напишите выражение, чтобы найти стоимость для любого количества (n) человек. Сколько стоит 25 человек? Ответ: 100 + 5n; так что для 25 человек = 100 + 5 (25) = 225 ».

4. Геометрия: Учащиеся продолжают классифицировать фигуры по категориям в зависимости от их свойств.Ваш ребенок научится находить площадь треугольников и некоторых четырехугольников. Они научатся вычислять объем трехмерных фигур, используя целые числа и дробные ребра. Учащиеся начинают использовать представление реальных проблем путем нанесения точек на координатную плоскость.

Поощряйте своего ребенка:

• Поймите разницу между поиском площади двухмерной фигуры и поиском объема трехмерной фигуры. Укажите на разные предметы и спросите, найдет ли ваш ребенок площадь или объем этой фигуры. Например, «Вы можете найти площадь или объем этого заднего двора?» Или: «Вы бы нашли объем этого бассейна?»
• Используйте соответствующий словарь при описании различных многоугольников и геометрических свойств. Например, «Что такое параллельные прямые?» Ответ: «Две линии на плоскости, которые никогда не пересекаются. Они всегда находятся на одинаковом расстоянии друг от друга».
• Используйте их обучение в третьем классе, чтобы понять, как найти площадь прямоугольника или найти значение треугольника:

Изображение предоставлено: Департамент математического образования Университета Джорджии

• Развивайте понимание координатной плоскости и начинайте наносить точки, используя реальные сценарии (используя миллиметровую бумагу).Например, «На карте библиотека расположена в (-2, 2), здание мэрии — в (0,2), а средняя школа — в (0,0). Представьте местоположения в виде точек на координатной сетке с единицей измерения 1 миля ».

Не волнуйтесь, если эти концепции поначалу кажутся немного пугающими. Помните, что вы не посещали ежегодные уроки математики, которые опираются друг на друга, как ваши дети. (Сначала может показаться, что ваши дети понимают это лучше, чем вы!)

Но в этом суть нашей серии блогов «Основные математические концепции».Мы хотим, чтобы и вы, , также обладали пониманием этих математических концепций. Вы можете быстро начать обучение своих детей, вы можете идти в ногу с ними, но это поможет вам больше общаться со своим ребенком по тому, что часто является сложным предметом.

У вас есть вопросы по этим концепциям или другие вопросы по математике вашего ребенка? Отправьте их Дженнифер здесь, чтобы она могла ответить в следующем блоге. Или поделитесь ими с нами на странице Scholastic Parents в Facebook.

Изображение предоставлено: © Oktay Ortakcioglu / iStockphoto

Промежуточная алгебра Урок 7: Линейные уравнения в одной переменной WTAMU > Виртуальная математическая лаборатория> Алгебра среднего уровня Цели обучения После изучения этого руководства вы сможете: Знайте, что такое линейное уравнение. Знайте, является ли значение решением или нет. Используйте свойства сложения, вычитания, умножения и деления равенств для решения линейных уравнений. Знайте, когда уравнение не имеет решения. Знайте, когда в уравнении все действительные числа являются решением. Введение Здесь мы начинаем вникать в суть того, что алгебра о — решение уравнений.В этом уроке мы будем искать конкретно при линейных уравнениях и их решениях. Мы начнем медленно а также решать уравнения, использующие только одно свойство, чтобы убедиться, что у вас есть физическое лицо понятий вниз. Тогда мы наберем темп и смешаем их там, где вам нужно использовать несколько свойств и шагов, чтобы выполнить работу. Уравнения могут быть использованы для решения различных проблемы. Позже учебные пособия, мы будем использовать их для решения текстовых задач.потом ты может ответить на эти сложные математические вопросы. Учебник Уравнение Два выражения равны друг другу Линейное уравнение Уравнение, которое можно записать в виде ax + b = c где a, b и c — константы Ниже приведен пример линейного уравнения: 3 x — 4 = 5 Решение Значение, такое, что при замене переменной на it, это делает уравнение верно. (левая сторона выходит равной правой) Набор решений Набор всех решений Пример 1 : Определите, соответствует ли какое-либо из следующих значений x решения к данному уравнению. 3 x — 4 знак равно 5; х = 3, 5. Проверка 3 3 x — 4 = 5 3 (3) — 4 = 5 9–4 = 5 5 = 5 Истинно 3 это решение Проверка 5 3 x — 4 = 5 3 (5) — 4 = 5 15 — 4 = 5 11 = 5 Ложь 5 не решение Решение линейного уравнения в целом Получите переменную, которую вы решаете, в одиночку с одной стороны и все else на другой стороне, используя ОБРАТНЫЕ операции. Следующее даст нам инструменты, которые нам нужны для решать линейные уравнения. Сложение и вычитание Свойства равенства Если a = b, то a + c = b + c Если a = b, то a — c = b — c Другими словами, если два выражения равны каждому другой и ты прибавлять или вычитать одно и то же к обеим сторонам, обе стороны будут оставаться равными. Обратите внимание, что сложение и вычитание являются обратными операции каждого Другие. Например, если у вас есть добавляемый номер, вам нужно перейти к другой стороне уравнения, тогда вы бы вычесть это с обеих сторон этого уравнения. Пример 2 : Найдите переменную. x — 5 = 2. x — 5 = 2 x — 5 + 5 = 2 + 5 x = 7 * Обратное от sub. 5 — доп. 5 Обратите внимание, что если вы вернете 7 для x дюйма исходной проблемы вы увидите, что 7 — это решение нашей проблема. Пример 3 : Найдите переменную. y + 4 = -7. y + 4 = -7 y + 4-4 = -7-4 y = -11 * Инверсия доп.4 является суб. 4 Обратите внимание, что если вы вернете -11 для y в исходной задаче, вы увидите, что -11 — это решение, которое мы находятся ищу . Умножение и деление Свойства равенства Если a = b, то a (c) = b (c) Если a = b, то a / c = b / c, где c — не равно 0. Другими словами, , если два выражения равны друг друга и ты умножить или разделить (кроме 0) одну и ту же константу на оба стороны, обе стороны останутся равными. Обратите внимание, что умножение и деление являются обратными операции каждого Другие.Например, если у вас есть число, которое умножается что вам нужно перейти к другой стороне уравнения, тогда вы бы разделите его с обеих сторон этого уравнения. Обратите внимание, что для умножения и деления это не гарантировал, что если вы умножаете на переменную, которую вы решаете, чтобы две стороны будет равным. Но гарантировано, что обе стороны пойдут быть равным, если вы умножаете или делите на константу или другое переменная, для которой вы не решаете.Мы поговорим подробнее о это в более позднем руководстве. Для этого урока просто обратите внимание, что вы можете использовать это свойство с константами и переменными, для которых вы не ищите. Пример 4 : Найдите переменную. х /2 = 5. * Обратно дел.на 2 это мульт. по 2 Если вы вернете 10 для x дюйма оригинал проблема, вы увидите, что 10 — это решение, которое мы ищем. Пример 5 : Найдите переменную.5 х = 7. * Инверсная по отношению к мульт. на 5 дел. по 5 Если вы вставите 7/5 обратно для x в оригинале проблема, вы увидите, что 7/5 — это решение, которое мы ищем. В приведенных выше примерах использовались только одно свойство за раз, чтобы помочь вам понять различные свойства, которые мы используем к решать уравнения.Однако в большинстве случаев нам приходится использовать несколько характеристики чтобы выполнить свою работу. Ниже приводится стратегия, которую вы можете использовать. чтобы помочь вам решить более сложные линейные уравнения. Стратегия решения линейного Уравнение Обратите внимание, что ваш учитель или книга ты Возможно, using сформулировал эти шаги немного иначе, чем я, но Это все сводится к одной и той же концепции — включите свою переменную один сторона и все остальное с другой, используя обратные операции. Шаг 1. При необходимости упростите каждую сторону. Это будет включать такие вещи, как удаление (), удаление дробей, добавление как термины и т. д. Чтобы удалить (): Просто используйте дистрибутив свойство, найденное в Уроке 5: Свойства действительных чисел. Чтобы удалить дроби : Поскольку дроби другой способ написать деление, а обратное деление — умножение, вы удаляете фракции умножив обе части на ЖК-дисплей всех ваших дробей. Шаг 2: Используйте Добавить. / Sub. Свойства для переместить переменную срок в одну сторону и все остальные условия в другую сторону. Шаг 3: Используйте Mult./Div. Свойства для удалить любые значения которые находятся перед переменной. Шаг 4. Проверьте свой ответ. Я считаю, что это самый быстрый и Самый простой способ приблизиться к линейным уравнениям. Пример 6 : Найдите переменную. 10 — 3 x = 7. * Инверсия доп. 10 является суб. 10 * Инверсная по отношению к мульт. на -3 — это div. по -3 Будьте осторожны, начиная со строки 4 к строке 5. Да, есть отрицательный знак. Но операция между -3 и x — это умножение, а не вычитание. Итак, если бы вы Добавлять 3 в обе стороны, вы бы получили -3 x + 3 вместо желаемых x . Если вы вернете 1 вместо x в исходной задаче, вы увидим, что 1 это решение, которое мы ищем. Пример 7 : Найдите переменную. 2 ( x + 5) — 7 = 3 ( x — 2). * Удалить () с помощью dist. опора * Получить все условия x с одной стороны * Инверсия доп. 3 является суб. 3 * Инверсная по отношению к мульт. на -1 — это div. по -1 Если вы вернете 9 вместо x в исходной задаче, вы увидим, что 9 — это решение, которое мы ищем. Пример 8 : Найдите переменную:. * Чтобы избавиться от дроби, мульт. с обеих сторон ЖК-дисплеем 4 * Получите все условия x на одной стороне * Инверсия доп.2 является суб. 2 * Инверсная по отношению к мульт. на -3 — это div. по -3 Если вы вернете 4/3 вместо x в исходной задаче вы увидите, что 4/3 это решение, которое мы ищем. Противоречие Противоречие — это уравнение с одной переменной, которая не имеет решения. Пример 9 : Найдите переменную. 4 x — 1 = 4 ( x + 3). * Удалить () с помощью dist. опора * Получите все условия x на одной стороне Куда делась наша переменная, x, ??? Он исчез на нас.Также обратите внимание, как мы получили ЛОЖЬ утверждение, -1 не равно 12. Это не означает, что x = 12 или x = -1. Когда ваша переменная падает из И вы закончите с ложным утверждением, то после всей вашей тяжелой работы есть НЕТ РЕШЕНИЕ. Итак, ответ — нет решения. Личность Тождество — это уравнение с одной переменной который имеет все действительные числа как решение. Пример 10 : Найдите переменную. 5 x + 10 = 5 ( x + 2). * Удалить () с помощью dist. опора * Получите все условия x на одной стороне На этот раз, когда наша переменная выпал, мы закончил с ИСТИННЫМ заявлением. Когда бы это ни случилось, твой ответ ВСЕ РЕАЛЬНЫЕ ЧИСЛА. Итак, ответ — все действительные числа . Практические задачи Это практические задачи, которые помогут вам следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти типы проблем. Math работает так же, как что-нибудь иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться Это. Даже лучшие спортсмены и музыканты получали помощь и много практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте. На самом деле не бывает слишком много практики. Чтобы получить максимальную отдачу от них, вы должны работать проблема на свой собственный, а затем проверьте свой ответ, щелкнув ссылку для ответ / обсуждение для этой проблемы .По ссылке вы найдете ответ а также любые шаги, которые позволили найти этот ответ. Практика Задачи 1a — 1e: Решите для переменной. Нужна дополнительная помощь по этим темам? Последний раз редактировал Ким Сьюард 1 июля 2011 г. Авторские права на все содержимое (C) 2002 — 2011, WTAMU и Kim Seward. Все права защищены.

5-классные школьные математические задачи, которые настолько сложны, что вы удивитесь, как вы вообще дошли до старшей школы

Математическая задача часто может выглядеть очень простой … прежде чем вы сядете за ее решение и обнаружите, что не знаете, как ее решить. Кроме того, есть задачи, которые заставят вас почувствовать себя математическим гением, когда вы решите их за 2 секунды — только для того, чтобы узнать, что ваш ответ — WAAAAY выключен.Вот почему математические задачи все время становятся вирусными, потому что они одновременно просты и в то же время не являются.

Вот пять проблем, подтверждающих эту точку зрения:

1. Что означает вопросительный знак?

Начнем с очень простого. Сможете ли вы решить, под каким числом должен стоять вопросительный знак?

Ответ: 6.

Объяснение: Сумма всех строк и столбцов должна составлять 15.

2. Летучая мышь и мяч

Бита и мяч в сумме стоят один доллар десять центов. Бита стоит на доллар дороже мяча. Сколько стоит мяч?

Getty Images

Вы ответили 10 центов? Это было бы неправильным !

Ответ: Мяч стоит 5 центов.

Пояснение: Когда вы читали математическую задачу, вы, вероятно, видели, что бита и мяч стоили в общей сложности доллар и десять центов, и когда вы обработали новую информацию о том, что бита на доллар больше, чем мяч, ваш мозг подскочил. к выводу, что мяч был десять центов, не выполняя математических расчетов.Но ошибка состоит в том, что когда вы действительно производите вычисления, разница между 1 и 10 центами составляет 90 центов, а не 1 доллар. Если вы потратите время на то, чтобы на самом деле посчитать, единственный способ, чтобы бита была на доллар больше, чем мяч, И общая стоимость, равная 1,10 доллара, — это если бейсбольная бита будет стоить 1,05 доллара, а мяч — 5 центов.

3. Переходить или не переходить

Представьте, что вы находитесь на игровом шоу, и вам предоставляется выбор из трех дверей: за одной дверью миллион долларов, а за двумя другими — ничего.Вы выбираете дверь №1, и ведущий, который знает, что за дверями, открывает другую дверь, скажем №3, и за ней ничего нет. Затем он говорит вам: «Вы хотите придерживаться своего выбора или переключиться?»

Итак, лучше ли придерживаться своего первоначального выбора или поменять свой выбор?

Getty Images

Большинство людей думают, что выбор не имеет значения, потому что у вас есть 50/50 шансов получить приз независимо от того, переключитесь вы или нет, поскольку осталось две двери, но на самом деле это не так!

Ответ: Всегда нужно менять свой выбор!

Объяснение: Когда вы впервые выбрали одну из трех дверей, у вас был 1 из 3 шансов выбрать дверь с призом за ней, что означает, что у вас был 2 из 3 шансов выбрать пустую дверь. Люди ошибаются здесь, когда думают, что, поскольку в игре осталось всего две двери, у вас есть 50% шанс, что ваш первый выбор был правильным. На самом деле ваши шансы никогда не менялись.

По-прежнему есть шанс 1 из 3, что вы выбрали правильную дверь, и шанс 2 из 3, что вы выбрали пустую дверь, что означает, что, когда хозяин открыл одну из пустых дверей, он исключил один из НЕПРАВИЛЬНЫХ вариантов и вероятность того, что приз за последней закрытой дверью по-прежнему 2 из 3 — вдвое больше, чем шансы, что вы выбрали правильную дверь вначале.Итак, в основном, переключая свой выбор двери, вы делаете ставку на 2 из 3 шансов, что сначала вы выбрали не ту дверь.

Конечно, вы не гарантированно выиграете, если переключитесь, но если вы будете играть в игру снова и снова, вы выиграете в 2/3 случаев, используя этот метод!

Все еще не уверены? Пусть гениальный профессор математики Калифорнийского университета в Беркли Лиза Голдберг еще лучше объяснит это с помощью набора диаграмм!

Этот контент импортирован с YouTube. Вы можете найти тот же контент в другом формате или найти дополнительную информацию на их веб-сайте.

4. Проблема PEMDAS

Когда вы решите эту, казалось бы, простую задачу, какой ответ вы получите?

Массы раскололись по поводу ответа на этот вопрос. Некоторые люди ПОЛОЖИТЕЛЬНЫ, ответ — 1, а некоторые абсолютно уверены, что ответ — 9.

Ответ: Победитель — 9!

Explanation: В удобном правиле порядка операций, которое вы выучили в начальной школе, PEMDAS, говорится, что вы должны решать проблему, перебирая круглые скобки, затем экспоненты, умножение и деление, а затем добавление и вычитание.Но суть PEMDAS в том, что некоторые люди интерпретируют его по-разному, и в этом заключается противоречие, стоящее за этой проблемой.

Некоторые люди думают, что все, что касается , касается скобок , следует решать ПЕРВЫМ. Это означает, что они упрощают задачу следующим образом: 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) = 6 ÷ 6 = 1.

Но то, что число касается скобок, не означает, что оно должно быть умножено перед делением, которое находится слева от него. PEMDAS предлагает решить все, что находится внутри скобок, затем экспоненты, а затем все умножение и деление слева направо в том порядке, в котором обе операции появляются (это ключ).Это означает, что как только вы решите все внутри скобок и упростите экспоненты, вы будете идти слева направо, несмотря ни на что. Это означает, что проблема фактически должна быть решена следующим образом: 6 ÷ 2 (1 + 2) = 6 ÷ 2 * (1 + 2) = 6 ÷ 2 * 3 = 3 * 3 = 9.

5. Проблема с кувшинками

В озере есть куст кувшинок. Каждый день нашивка увеличивается в размерах вдвое. Если заплатке потребуется 48 дней, чтобы покрыть все озеро, сколько времени потребуется, чтобы заплатка покрыла половину озера?

Getty Images

Заманчивый ответ — 24, но вы ошибаетесь, если это ваш окончательный ответ!

Ответ: Пятно на 47 день достигнет половины размера озера.

Пояснение: При всех разговорах об удвоении и половинках ваш мозг приходит к выводу, что для решения проблемы, когда кувшинок покрывает половину озера, все, что вам нужно сделать, это разделить количество дней, которое потребовалось для заполнения. озеро (48) пополам. Это понятно, но неправильно.

Проблема говорит о том, что патч УДВАИВАЕТСЯ в размере каждый день, а это значит, что в любой день участок лилии был вдвое меньше, чем накануне. Таким образом, если пятно достигает размера озера на 48-й день, это означает, что кувшинок был вдвое меньше озера на 47-й день.

Ноэль Дево
Редактор развлечений
Когда я не запираюсь в своей комнате из-за совершенно непродуктивного запоя Netflix или из-за того, что Tumblr преследует Тимоти Шаломе, я ищу потрясающие новости о знаменитостях, которые понравятся читателям Seventeen!

Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты. Вы можете найти больше информации об этом и подобном контенте на пианино.io

Книга по математике 5A для учащихся 5-х классов

Обязательно возьмите путеводители, потому что они милые, интересные, очаровательные и замечательные, и они заставят вашего ребенка влюбиться в математику (даже если он уже любит математику)

I ‘ m действительно впечатлен вниманием и деталями, не только математическим мышлением, но и визуальными эффектами, юмором и сюжетом.

… реакция, которую я видел, была действительно потрясающей. Что, кажется, выделяется … в этих книгах не преуменьшает объем работы и не разговаривает с ребенком свысока.

… каждый раз, когда ученики видят меня, они очень взволнованы и спрашивают, не сегодня ли «День Академии зверей». Им нравятся персонажи, им нравится юмор в Путеводителе, и они упорно стараются заполнить как можно больше материала из Практического пособия.

Моему сыну очень нравится эта программа … никогда не думал, что мне придется говорить ему, чтобы он сделал перерыв в математике, чтобы заняться другой работой.

Я почти уверен, что это самые увлекательные книги по математике, с которыми я когда-либо сталкивался, и они справляются с этим, совсем не разбавляя содержание (на самом деле, как раз наоборот).

Мне больше всего нравится то, что мои дети могут читать руководство и выполнять практическую работу самостоятельно, но я знаю, что им бросают вызов.

Слышать, как мой крохотный шестилетний ребенок объясняет, как возводить в квадрат числа, оканчивающиеся на 5, было потрясающе … Благодаря Beast Academy у меня теперь есть возможность наблюдать, как лицо моего сына загорается, когда я говорю, что пришло время для математики.

Академия зверей стала известна как «увлекательная математика» — полная сложных задач, которые заставляли их думать просто, чтобы усердно заниматься вычислениями.

Обожаю ваши книги! Это лучшее, что когда-либо случалось с математикой. Лиззи — мой любимый персонаж, потому что она очень похожа на меня. Она такая милая, нежная и не любит драконов!

Я упомянул, что [мой сын] почти готов перейти на следующий уровень Академии Зверей.