|
1. |
Верное решение
|
1 |
|
2. |
Делимое, делитель, частное
|
3 |
|
3. |
Значение буквенного выражения
|
2 |
|
4. 
|
Деление трёхзначного числа на двузначное (1)
|
1 |
|
5. |
Деление трёхзначного числа на двузначное (2)
|
1 |
|
6. |
Деление трёхзначного числа на двузначное (3)
|
1 |
|
7. 
|
Деление трёхзначного числа на 12 в столбик
|
4 |
|
8. |
Текстовая задача (цветы)
|
2 |
|
9. |
Текстовая задача (маргаритки и незабудки)
|
4 |
|
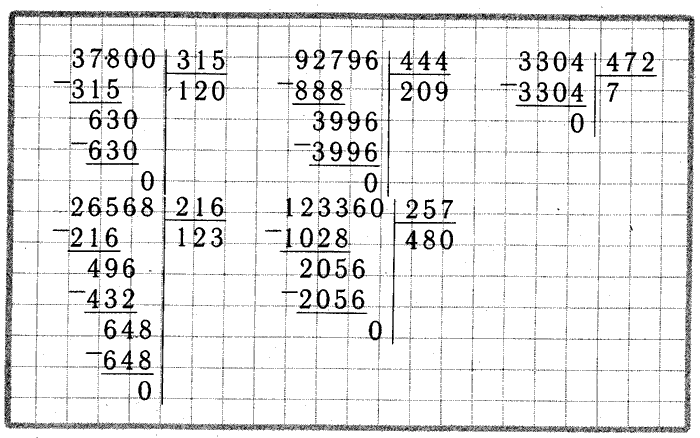
10. 
|
Значение числового выражения
|
3 |
|
11. |
Уравнение (сумма)
|
4 |
|
12. |
Составление и решение уравнения (произведение)
|
4 |
|
13. 
|
Составление и решение уравнения (частное)
|
4 |
Письменное деление на двузначное число (без остатка и с остатком)
Ой, здравствуйте, ребята!
Как давно мы с вами не
встречались! И вот, наконец, мы вместе.
Сегодня я хочу рассказать вам,
как выполнять письменное деление на двузначное число.
Ещё в третьем классе вы
знакомились с темой «Деление двузначного числа на двузначное» и знаете,
что такое деление выполняется методом подбора. Вот, например, при
делении восьмидесяти семи на двадцать девять мы сначала подбирали в качестве
частного число один.
Но, проверив деление умножением
и вычитанием, поняли, что остаток пятьдесят восемь больше делителя, что
недопустимо. Попробовали в качестве частного число два. Остаток получился
равным делителю. И только, когда попробовали число три, всё получилось.
А вот при делении числа
девяносто восемь на четырнадцать было просто сплошное мучение! – семь чисел
пришлось попробовать.
Вот одно из них:
Сегодня я расскажу вам о письменном
приёме деления трёхзначных чисел на двузначные и поделюсь небольшим
секретом, который поможет облегчить и ускорить процесс подбора нужного числа в частном.
Итак, приступим.
Предположим, надо разделить
триста сорок четыре на сорок три. А вот теперь – мой маленький секрет! Для
А вот теперь – мой маленький секрет! Для
того, чтобы делить было легче, вместо делителя, сорока трёх, возьмём
круглое число — сорок. Ведь вы помните, ребята, что сорок – это
произведение чисел десять и четыре. И мы можем делить последовательно на эти
множители. Делим триста сорок четыре на десять, а теперь тридцать четыре делим
на четыре. Получается восемь. Хочу предупредить вас, ребята, что это пока
только пробная цифра, поэтому в частное мы её не записываем, а умножаем
на неё делитель сорок три. Получается триста сорок четыре. Отлично, частное действительно
равно восьми.
Давайте попробуем разобрать ещё
один пример. Пятьсот тридцать четыре разделим на восемьдесят девять. Помните, сначала
делитель заменяем круглым числом – восемьдесят. Делим пятьсот
тридцать четыре на восемьдесят, то есть на десять, а потом пятьдесят три на
восемь. Получается примерно шесть. Не забываем! Пока мы не выполним проверку
умножением, взятая нами цифра только пробная, и записывать её в
частное ещё не нужно. Перемножаем восемьдесят девять и шесть. Ура! Получилось
пятьсот тридцать четыре. Частное равно шести.
Ну что же, я надеюсь, вы всё
поняли и сможете самостоятельно решить парочку примеров. Вот этих: 228 : 76 и 256
: 32.
Ну как, справились? У вас такое
решение?
А теперь давайте вместе найдём
частное чисел триста девяносто восемь и пятьдесят шесть:
Заменяем делитель круглым
числом пятьдесят. Триста девяносто восемь делим на десять, а
потом тридцать девять делим на пять. Кажется, получается по семь. Перемножаем пятьдесят
шесть и семь. Получается триста девяносто два. Так-так…
При умножении получилось не то
число, которое было в делимом. Может быть, я неправильно выполнила деление? Сейчас
проверю! Вычитаю из делимого полученное произведение — триста
девяносто два. Остаток – шесть, он меньше делителя. Значит, деление выполнено
Остаток – шесть, он меньше делителя. Значит, деление выполнено
верно, и в частное можно смело писать ответ семь.
Давайте попробуем найти частное
чисел сто шестьдесят два и тридцать девять. Вместо тридцати девяти берём
тридцать, сто шестьдесят два делим на десять и шестнадцать делим на три,
получается пять. Перемножаем пять и тридцать девять, получается… упс…сто
девяносто пять! Полученное число больше делимого! Такого быть не может!
Не зря я говорила, что пока в частное цифру писать не стоит – она пробная. Так
как полученное произведение больше делимого, пятёрку надо заменить на меньшее
число. Попробую умножить не на пять, а на четыре. Тридцать девять умножаю на
четыре, получается сто пятьдесят шесть. Уффф… это число меньше делимого. Теперь
узнаем на сколько. Вычитаем его из ста шестидесяти двух. Остаток
равен шести. Ну что же, частное чисел сто шестьдесят два и тридцать девять
равно четырём, остаток – шесть.
А теперь вы попробуйте сами
найти частные вот в таких примерах:
261 : 63; 376 : 68.
Итак, ребята, давайте проверим
вашу работу.
Конечно, со вторым примером
пришлось повозиться.
Но я надеюсь, что вы были
внимательны и справились с ним.
А теперь пришло время прощаться.
Удачи вам в освоении приёма письменного деления. Пока, ребята!
Презентация «Закрепление — Письменное деление на двузначное число»
Слайды и текст этой презентации
Слайд 1
Автор: Клюквина Надежда Алексеевна, учитель начальных классов г. Дзержинск Нижегородская область
Слайд 2
Все ли вы делаете зарядку по утрам?
А знаете ли вы, что есть зарядка для ума?
Догадались? Конечно, это………
математика
Слайд 3
Начинается урок. Он пойдет ребятам впрок.
Постарайтесь все понять,
Чтоб примеры и задачи
Без труда решать.
Он пойдет ребятам впрок.
Постарайтесь все понять,
Чтоб примеры и задачи
Без труда решать.
Слайд 4
450:50=
400:100=
75:25=
800:40=
150:30=
77:11=
640:80=
9
4
3
20
5
7
8
9 4 3 20 5 7 8
и е д е л е н
Д
Е
Л
Е
Н
И
Е
Слайд 5
Скорость Время Расстояние
15км/ч 3ч ?
? 2ч 6км
12 км/ч ? 36км
Слайд 6
Слайд 7
Классная работа. 22.04.
Слайд 8
Что общего в выражениях?
5 : 16 =
11 : 19 =
58 : 78 =
0 (ост. 5)
0 (ост. 11)
0 (ост. 58)
Как разделить меньшее число на большее?
Слайд 9
Задачи урока
Научиться выполнять деление на двузначное число в случаях, когда неполное делимое меньше делителя.
Слайд 10
ПАМЯТКА
Нахожу первое неполное делимое. Определяю количество цифр в частном. Определяю первую цифру частного (это пробная цифра). Пробую, подходит ли цифра…
Слайд 11
Какой пример решён верно?
Слайд 12
35210 70
143520 16
Определи количество цифр в частном
• • •
• • • •
Слайд 13
Выполните деление
16 238 23
Слайд 14
с. 65 (вверху)
Слайд 15
17640 35 96048 24 34860 42
• • • •
• • •
• • •
5 0 4
4 0 0 2
8 3 0
Уточните
тему урока
Случаи деления, когда в частном есть нули
Слайд 16
Закрепление Решение примеров
с. 65,№ 265(1столбик) – у доски
Слайд 17
с. 65 № 265 (2 столбик.)
Работа в паре.
Решить каждому по 1 примеру на деление, проверить пример, который решил сосед, действием умножения.
Проверка:
308
507
Самостоятельная работа
Слайд 18
Физминутка
Слайд 19
Привал
Потрудились мы немало. Настало время для привала.
Чтоб размяться нам в пути,
Ручками похлопали – раз, два, три.
Ножками потопали – раз, два, три.
Сели – встали, встали – сели.
И друг друга не задели.
Настало время для привала.
Чтоб размяться нам в пути,
Ручками похлопали – раз, два, три.
Ножками потопали – раз, два, три.
Сели – встали, встали – сели.
И друг друга не задели.
Слайд 20
М
О
Л
О
Д
Ы
Ц
!
Слайд 21
Показать
20 км
20 000 м
Задача № 266
Из двух посёлков, находящихся на расстоянии 20 км, вышли одновременно навстречу друг другу 2 лыжника. Они встретились через 40 минут. Один из них шёл со скоростью 240 м/мин.
С какой скоростью шёл второй лыжник?
1) :
2) —
Слайд 22
Задача № 266
Какова скорость сближения?
20 000 : 40 =500 (м/мин)
2) Какова скорость второго лыжника?
500 – 240 = 260 (м/мин)
20 000:40-240= 260(м/мин)
Ответ: 260 м/мин – скорость второго лыжника.
Слайд 23
Реши уравнения
с. 65, № 269
x·100 = 4 500 y:100 = 4 500
Слайд 24
Сегодня на уроке :
я повторил (а)… мне понравилось … мне было интересно… мне было трудно …
Я оцениваю свою деятельность …
Рефлексия
Слайд 25
Определи своё настроение
отличное
я был(а) уверен(а) в себе
мне было трудно
я устал(а)
Слайд 26
Домашнее задание На выбор: 1)Придумать 4 примера по теме урока 2)с. 65 № 268, 265 (3столбик) 3)р.т. с.64 №29
Слайд 27
Спасибо за урок!
Молодцы!
ДЕЛЕНИЕ НА 8: НАЦЕЛО И С ОСТАТКОМ
Благодарен вашему
журналу за публикацию моего
материала о признаке делимости
целых чисел на 7 (см. «Наука и
жизнь» № 10, 1997 г.). Рискну
предложить еще один новый признак
делимости, но уже на 8.
Я перелистал
много книг по занимательной
математике, но такого признака не
нашел нигде.
Общепринятый
признак делимости на 8 выглядит так:
число делится на 8 в том и только в
том случае, если его последние три
цифры образуют число, делящееся на
8.
Этот способ
деления основан на том, что все
числа, кратные 1000, делятся на 8 без
остатка.
Значит,
определение признака делимости на 8
любых многозначных целых чисел
сводится в итоге к определению
признака делимости на 8 трехзначных
чисел.
Трехзначные числа
и будем рассматривать.
Б. А. Кордемский
сводит делимость уже трехзначных
чисел к делимости двузначных
(образованных цифрами сотен и
десятков): «На 8 делится всякое
трехзначное число, у которого
двузначное число, образованное
цифрами сотен и десятков, сложенное
с половиной числа единиц, делится
на 4».
Он приводит
пример с числом 592. Применяя к нему
признак делимости, получаем:
59 + 1 = 60,
где 1 — это 2:2,
половина числа единиц.
Число 60 делится на
4, значит, число 592 делится на 8 без
остатка.
При данном методе
определения остатка от деления
надо учитывать, что трехзначные
числа, оканчивающиеся нечетной
цифрой (1, 3, 5, 7, 9), надо сначала
«округлить» в разряде единиц
до ближайшей большей или меньшей
четной цифры и в конечном
результате опять же учесть эту
единицу, то есть прибавить ее или
отнять. Это первое.
Второе: в
некоторых случаях сумма
двузначного числа, образованного
цифрами сотен и десятков, и
половины единиц будет также
трехзначным числом, что опять же не
совсем удобно. Это будет
происходить с рядом чисел в
промежутке от 968 до 999.
Однако всех этих
неудобств — прибавления (вычитания)
1 и оперирования трехзначными
числами — можно избежать.
Вспомним, что
четное число сотен — 2, 4, 6, 8 (200, 400, 600,
800) делится на 8 без остатка.
Следовательно, у таких, к примеру,
чисел, как 059, 237, 461, 632, 844, определить
остаток от деления на 8 можно сразу
по двузначному числу,
составленному из десятков и единиц,
то есть по числам 59, 37, 61, 32, 44.
Достаточно в уме разделить эти
двузначные числа на 8.
Если цифры сотен в
трехзначных исходных числах
нечетны (1, 3, 5, 7, 9), то опять же делим
на 8 двузначные числа, образованные
десятками и единицами, но в этом
случае прибавляем (или отнимаем) к
двузначным числам цифру 4. Этот факт
следует из того, что все целые
нечетные сотни (100, 300, 500, 700, 900) при
делении на 8 дают один остаток — 4.
Для примера
возьмем числа 165, 371, 587, 716, 923.
«Превратим» их в двузначные
числа, прибавляя (можно отнимая) 4:
69, 75, 91, 20, 27.
Делить эти
двузначные числа на 8 опять же
просто. Остатки от делений и будут
остатками от деления на 8 исходных
трехзначных чисел.
А как поступить,
если трехзначное число 997?
Выше говорилось,
что цифру 4 можно не только
прибавлять, но и отнимать от
двузначного числа. Значит, делить
на 8 будем уже число 93: 97- 4 = 93.
Так происходит
«избавление» от трехзначных
чисел.
Обобщая все
вышесказанное, алгоритм
упрощенного признака делимости на 8
целых чисел можно записать так:
отделяем, отсчитывая справа, три
цифры исходного числа; если третья
справа цифра четная (0, 2, 4, 6, 8), то
делим на 8 только число,
образованное двумя крайними
правыми цифрами; остаток от этого
деления и будет остатком от деления
на 8 всего исходного числа; если
третья справа цифра в исходном
числе нечетная (1, 3, 5, 7, 9), делим на 8 число,
образованное двумя крайними
правыми цифрами, плюс (минус) 4;
остаток от деления этой суммы и
даст остаток от деления на 8 всего
исходного целого числа.
Как видно, этот
признак делимости совсем прост, и
для его освоения понадобятся
минимальные усилия и знание
элементарной арифметики.
Литература
Кордемский Б. А. Математическая
смекалка. М., 1991.
М., 1991.
Воробьев Н. Н. Признаки
делимости. М., 1980.
Гарднер М. Математические
досуги. М., 1995.
II вариант | III вариант | |
1.Найди 3 от 808 8 2.Найди 5 от 459 9 3.Найди 4 от 497 7 4.Найди 3 от 255 5 | 309 : 3 + 819 246 : 3 + 278 208 : 4 + 129 696 : 3 + 148 | 1.Уменьши 287 в 7 раз. 2.Уменьши 568 в 8 раз. 3.Уменьши 189 в 3 раза. 4.Уменьши 546 в 6 раз. |
Как научить ребенка делить в столбик на однозначное, двузначное и трехзначное число | В помощь родителям младшего школьника
В конце 3 и 4 классов дети учатся делить в столбик. Если с умножением в столбик все достаточно понятно, то деление в столбик вызывает у детей замешательство. С первого раза с этой темой разобраться бывает сложно. В этой статье я расскажу, как научить ребёнка делить в столбик на однозначное, двузначное и трехзначное число.
Как научить делить в столбик на однозначное число
Разделим 938 на 2.
При записи деления в столбик знак деления записывают углом. Над чертой пишут делитель. Под чертой записывают ответ (частное).
1. Ищем первое неполное делимое. Т. е. число, которое мы будем делить первым.
Для этого существует правило: сколько цифр в делителе, столько цифр в первом неполном делимом.
В нашем примере делитель 2. Для записи этого числа используют одну цифру. Значит и первое неполное делимое будет состоять из одной цифры. Это 9.
2. 9 разделить на 2 без остатка нельзя. Ищу близкое к девяти число, которое делится без остатка на 2. Это число 8. 8 : 2 = 4. 4 записываю под чертой. Проверяю себя. 4 × 2 = 8. Но я делила 9. Из 9 вычитаю 8. Получается 1.
3. 1 нельзя разделить на два. Сношу следующую цифру (3) и записываю рядом с 1. Получилось число 13. Это второе неполное делимое.
4. 13: 2 без остатка нельзя. Близкое число, которое делится без остатка на 2, — 12. 12 : 2 = 6. 6 записываю под чертой. 6 × 2 = 12. Из 13 вычитаю 12. Получается 1.
5. 1 разделить на 2 нельзя. Сношу еще одну цифру. Это 8. Получилось число 18. 18- третье неполное делимое. 18 : 2 = 9. 9 × 2 = 18. 18 — 18= 0. Деление закончено.
938 : 2 = 469
Рассмотрим ещё один пример
4914 : 7
1. Сколько цифр в делителе, столько цифр в первом неполном делимом. Но 4 разделить на 7 нельзя. Поэтому первое неполное делимое — 49. 49 : 7 = 7. Проверяю себя. 7 ×7 = 49. 49 — 49 = 0. Но ноль в середине примера не пишем.
2. Сношу следующую цифру — 1. 1 на 7 не делится. В частном пишу 0.
Теперь внимательно! В в предыдущем примере мы не писали в частном 0 потому, что остался остаток при вычитании. В этом примере остатка при вычитании нет. Снесли цифру, число не разделилось. Пишем в частном 0.
Итак, 1 нельзя разделить на 7 без остатка. Пишу в частном 0.
3. Сношу следующую цифру — 4. Получилось число 14. 14 : 2 = 7. Проверяю себя. 7 × 2 = 14. 14 — 14 = 0. 4914 : 7 = 702.
Как делить в столбик на двузначное число
Потренируемся.
8508 : 12
1. В делителе две цифры. Поэтому первое неполное делимое — 85. Решаем методом подбора.
На сколько нужно умножить 12, чтобы получить число, близкое к 85? На 7. 12 × 7 = 84. 85 — 84 = 1.
2. 1 на 12 разделить нельзя. Сношу следующую цифру. Получилось число 10. 10 разделить на 12 нельзя. В частном пишу 0.
3. Сношу следующую цифру. Получилось число 108. 108 : 12 =9.
Как разделить в столбик на трехзначное число
Деление на трехзначное число происходит аналогично делению на двузначное число.
Разделим 29876 на 308.
1. Ищем первое неполное делимое. Сколько цифр в делителе, столько цифр в первом неполном делимом. Но 298 нельзя разделить на 308. Поэтому первое неполное делимое будет число 2987.
Поэтому первое неполное делимое будет число 2987.
2. Подбираем, на сколько нужно умножить 308, чтобы получилось число, близкое к 2987. Это число 9. 308 × 9 = 2772. 9 пишу в ответ. Из 2987 вычитаю 2772. Получается 215.
3. 215 нельзя разделить на 308. Сношу 6. Получилось число 2156. Оно делится на 308 без остатка. Получается 7. 7 пишу в ответ. Из 2156 вычитаю 2156. Получается 0. Деление закончено.
Делитесь своим мнением в комментариях, подписывайтесь на мой канал
Дошкольники и школьники: 1 уровень «Просто»
Дошкольники и школьники: 2 уровень «Помощь брата»
Дошкольники и школьники: 3 уровень «Помощь друга»
Дошкольники и школьники: 4 уровень «Микс формулы»
Дошкольники и школьники: 5 уровень «Анзан, сложение и вычитание без ограничений»
Дошкольники и школьники: 6 уровень «Умножение»
Дошкольники и школьники: 7 уровень «Деление»
Школьники: 8 уровень «Дроби»
Школьники: 9 уровень «Отрицательные числа»
Школьники: 10 уровень «Квадратные корни»
Дошкольники: 8-10 уровень решебник «Умножение и деление»
Краткосрочный интенсив «Простое сложение и вычитание»
Экспресс курс «Умножение»
Экспресс курс «Деление»
|
Как сделать двузначное и трехзначное деление
В этом посте мы узнаем, как сделать двузначное и трехзначное деление.
Чтобы выполнить деление на 2 и 3 цифры, выполните следующие действия:
- Сначала возьмите столько цифр делимого, сколько имеет делитель. Если цифры делимого меньше делителя, возьмите еще одну цифру делимого.
Например, если мы хотим разделить 5738/73, первое, что нам нужно сделать, это взять первые две цифры из делимого, 57, но поскольку 57 меньше 73, мы должны взять еще одну цифру из делимого. ; следовательно, это 573.
- Во-вторых, разделите первое число делимого (или первые два, если нам нужно взять другую цифру) на первое число делителя и проверьте, делится ли оно равномерно. Если он не делится равномерно, проверьте предыдущее число.
Если мы последуем предыдущему примеру, мы должны разделить 57 на 7. Поскольку 8 x 7 = 56, мы попробуем с 8. Мы умножаем 73 x 8 = 584, и поскольку 584 больше 573, 8 не делить равномерно, поэтому мы должны попробовать это с предыдущим числом.
73 x 7 = 511, а поскольку 511 меньше 573, 7 делится поровну, и мы сможем вычесть 573-511 = 62
- В-третьих, опустите следующую цифру и разделите, как в предыдущем шаге, пока не кончатся цифры.
Следуйте нашему примеру с двузначным делением. Следующее число, которое нам нужно выпустить, — это 8. Для этого мы должны разделить 628 на 73.
Мы берем новые первые две цифры, 62, и должны разделить их на 7.Так как 8 x 7 = 56, мы записываем 8 в частном и умножаем 73 x 8 = 584. Поскольку 584 меньше 628, мы можем продолжить вычитание 628 — 584 = 44. Поскольку больше нет чисел, которые нужно опускать. , мы закончили разделение. Решение — 78 с остатком 44.
Вы можете узнать больше о делении в нашем предыдущем посте, как решить двузначное деление.
Если вы хотите узнать больше о математике, зарегистрируйтесь на Smartick и попробуйте бесплатно.
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
3-значное на 2-значное длинное деление с остатками и шагами, указанными на ключе ответа (A)
Добро пожаловать в Трехзначное деление на 2-значное длинное число с остатками и шагами, указанными в ключе для ответа (A) Рабочий лист по математике со страницы рабочих листов для деления на Math-Drills.com. Этот математический лист был создан 2017-05-29 и был просмотрен 229 раз на этой неделе и 336 раз в этом месяце.Его можно распечатать, загрузить или сохранить и использовать в классе, домашней школе или в другой образовательной среде, чтобы помочь кому-то выучить математику.
Учителя могут использовать рабочие листы по математике в качестве тестов, практических заданий или учебных пособий (например, при групповой работе, на строительных лесах или в учебном центре). Родители могут работать со своими детьми, чтобы дать им дополнительную практику, помочь им освоить новые математические навыки или сохранить свои навыки свежими во время школьных каникул. Студенты могут использовать рабочие листы по математике для овладения математическими навыками на практике, в учебной группе или для взаимного обучения.
Используйте кнопки ниже, чтобы распечатать, открыть или загрузить версию PDF 3-значное 2-значное длинное деление с остатками и шагами, указанными в ответе Клавиша (A) математический лист . Размер файла PDF составляет 28652 байта. Показаны изображения для предварительного просмотра первой и второй (если есть одна) страниц. Если существует больше версий этого рабочего листа, другие версии будут доступны под изображениями для предварительного просмотра. Для более того, используйте строку поиска для поиска некоторых или всех этих ключевых слов: математика , деление, делитель, делимое, частное, остаток, шаги, стандарт, алгоритм .
Кнопка Печать запускает диалоговое окно печати вашего браузера. Кнопка Открыть откроет полный PDF-файл в новой вкладке вашего браузера. Кнопка Teacher инициирует загрузку полного файла PDF, включая вопросы и ответы (если таковые имеются). Если присутствует кнопка Студент , она инициирует загрузку только страниц с вопросами. Дополнительные параметры могут быть доступны, щелкнув кнопку правой кнопкой мыши (или удерживая нажатой кнопку на сенсорном экране).Я не вижу кнопок!
Деление из 3 цифр на 2 цифры в длину с остатками и шагами, указанными в ключе ответа (A) Рабочий лист по математике, страница 1 Деление из 3 цифр на 2 цифры в длину с остатками и шагами, указанными в ключе ответа (A) Рабочий лист по математике, страница 2
Другие версии:
Другие рабочие листы по разделам
Рабочих листов с длинным разделением для 4-6 классов
Вы здесь: На главную → Рабочие листы → Полное деление
Создайте неограниченное количество листов для деления в столбик (классы 4-6), в том числе с 2-значными и 3-значными делителями.Рабочие листы могут быть выполнены в формате html или PDF — и то, и другое легко распечатать. Вы также можете настроить их, используя генератор ниже.
Рабочие листы на этой странице разделены на три основных раздела:
Обратите внимание: рабочие листы для
деление в столбик с остатками находится на отдельной странице. Все задачи в таблицах на этой странице делятся на точные части (без остатка).
Основные инструкции для рабочих листов
Каждый рабочий лист генерируется случайным образом и поэтому уникален.Ключ ответа генерируется автоматически и помещается на вторую страницу файла.
Вы можете создавать рабочие листы либо в формате html, либо в формате PDF — и то, и другое легко распечатать. Чтобы получить рабочий лист PDF, просто нажмите кнопку с названием « Создать PDF » или « Создать PDF-лист ». Чтобы получить рабочий лист в формате html, нажмите кнопку « Просмотреть в браузере » или « Сделать рабочий лист html ». Это имеет то преимущество, что вы можете сохранить рабочий лист прямо из браузера (выберите «Файл» → «Сохранить»), а затем отредактировать его в Word или другом текстовом редакторе.
Иногда сгенерированный рабочий лист не совсем то, что вам нужно. Просто попробуйте еще раз! Чтобы получить другой рабочий лист с теми же параметрами:
- Формат PDF: вернитесь на эту страницу и снова нажмите кнопку.
- Формат Html: просто обновите страницу рабочего листа в окне браузера.
Длинное деление с однозначным делителем
Проблемы с делением — настройте длинное деление самостоятельно
На этих листах ученик должен сам настроить длинное деление (задача деления написана горизонтально вверху рабочего поля).
Длинное деление с двузначным делителем
Трехзначные делители
Следующие таблицы предназначены для трехзначных делителей. Деления точные. Если вы ищете разделение с остатками, вы можете создавать рабочие листы, используя генератор ниже, или перейти на эту страницу, чтобы найти готовые рабочие листы.
Генератор листов деления
Используйте генератор для создания настраиваемых рабочих листов, включая горизонтально написанные задачи, деление столбиком и деление с остатками.
Генератор листов деления
NumberNut.com: Раздел: 3-значные числа
Вы начали понимать деление в столбик и деление двузначных чисел. Давайте сделаем несколько примеров с двузначными и трехзначными числами. Если вы можете это сделать, вы можете разделить любые числа меньше одной тысячи.
Пример:
84 ÷ 6 =?
Шаг 1: 6 переходит в 8? Да, однажды. (Напишите 1 в вашем частном.)
Шаг 2: 6 x 1 = 6
Шаг 3: 8 — 6 = 2 Это значение 2 является вашим остатком.(Запишите 1 в своем частном.)
Шаг 4: Отнесите 4 вниз от делимого, чтобы получить 24.
Шаг 5: Переходит ли 6 в 24? Да, четыре раза. (Напишите 4 в вашем частном)
Шаг 6: 6 x 4 = 24
Шаг 7: 24 — 24 = 0
Поскольку разница равна 0 и в дивиденде больше нет значений, все готово.
84 ÷ 6 = 14
— или —
| 14 6) 84 -6 24 -24 0 |
Пример:
648 ÷ 4 =?
4 переходит в 6? Да, однажды.Напишите 1 в своем частном.
4 x 1 = 4
6 — 4 = 2
Вниз 4, чтобы получить 24.
Переходит ли 4 в 24? Да, шесть раз. Напишите 6 в вашем частном.
4 x 6 = 24
24 — 24 = 0 (Продолжайте, поскольку в делимом все еще есть числа.)
Опустите 8, чтобы получить 8.
Переходит ли 4 в 8? Да, два раза. Напишите 2 в вашем частном.
4 x 2 = 8
8-8 = 0 (без остатка и без числа в делимом)
648 ÷ 4 = 162
— или —
| 162 4) 648 — 4 24 — 24 8 — 8 0 |
Давайте попробуем пример с трехзначным делимым и двузначным делителем .Вы проделаете все те же шаги, но вам нужно будет работать с двузначными числами и подумать, сколько раз они войдут в значения делимого . Вы даже можете обнаружить, что они работают быстрее, чем вы ожидаете. Мы с тобой будем полегче.
Пример:
156 ÷ 12 =?
Переходит ли 12 в 1? Нет. Посмотрите на следующую цифру в делимом.
12 переходит в 15? Да, однажды. Напишите 1 в своем частном.
12 x 1 = 12
15 — 12 = 3
Опустите 6, чтобы получилось 36.
12 входит в 36? Да, трижды. Напишите 3 в своем частном.
12 x 3 = 36
36 — 36 = 0 (без остатка и без числа в делимом)
156 ÷ 12 = 13
— или —
| 13 12) 156 — 12 36 — 36 0 |
Мы приводили вам простые примеры. Давайте закончим с задачей, у которой есть остаток . Вы получите остаток, когда ваше окончательное вычитание не закончится на 0.Все, что останется, будет остатком.
Пример:
217 ÷ 14 =?
14 переходит в 21? Да, однажды. Напишите 1 в своем частном.
14 x 1 = 14
21 — 14 = 7
Убавьте 7 из дивиденда, чтобы получить 77.
Переходит ли 14 в 77? Да, пять раз. Напишите 5 в своем частном.
14 x 5 = 70
77 — 70 = 7
Поскольку в дивиденде больше нет значений, которые нужно уменьшить, у вас остается значение 7. Это 7 — ваш остаток.
Итак …
217 ÷ 14 = 15 r 7
— или —
| 15r7 14) 217 -14 77 -70 7 |
Мы собираемся остановиться на трехзначных числах, но было бы хорошо, если бы вы попрактиковались с более крупными значениями.Мы знаем, что они будут на ваших тестах, поэтому практика длинного деления только поможет вашим оценкам. Удачи!
Связанные виды деятельности
Урок для четвертого класса Разделение трехзначных чисел на однозначные
Я призываю учеников к ковру, пока мы готовимся к обсуждению в классе. Точка питания деления 3-значных на 1-значные числа уже установлена на смарт-плате. Мне нравится, когда мои ученики находятся рядом, чтобы я мог полностью сосредоточиться на них, пока я нахожусь на доске Smart.
Я начну с перебора важной лексики для этого урока. Студентам необходимо знать эти термины, чтобы понять урок.
Словарь:
частное — ответ на задачу деления
делитель — число, на которое делится другое число
дивиденды — сумма, которую вы хотите разделить
остаток — часть, которая останется после деления
Задача 1:
125 ÷ 3 =
Мы можем смоделировать это, используя блоки размеченных значений.
Попробуйте разделить сотни на 3 группы. Ты не можешь это делать. Следовательно, 1 сотню нужно перегруппировать в 10 десятков. Складываем 10 десятков + 2 десятка = 12 десятков. Мы можем разделить эти 12 десятков на 3 группы. В каждой группе будет по 4 десятка.
Теперь мы должны разделить 5 единиц на 3 группы.
В каждой группе будет по 1 игроку. Остается 2,
.
Частное для 125 ÷ 3 = 41 r 2.
Стандартный алгоритм — это способ решения задач деления.
D-Divide
M-Умножение
S-вычитание
B-Bring Down (Если вы опускаете число, вы должны начать процесс заново.)
Поскольку у нас нет как минимум 3 сотен, мы должны разделить 3 на 12 (то есть 120). Используйте умножение, чтобы помочь. Умножаем 3 x 4 = 12. Итак, получаем 4 десятки из 120. Затем вычтите 12 — 12 = 0. Убавьте 5. Теперь мы работаем с 5 единицами. Разделите 3 на 5, получится 1. Остаток будет 2, потому что 3 x 1 = 3 и 5 — 3 = 2.
Частное 41 с остатком 2.
Давайте попробуем вместе
Задача 2:
143 ÷ 4 =
Как мы узнаем, что в этой проблеме будет остаток?
AAA Сейчас
- AAAKnow имеет полный набор из тысяч
интерактивные уроки арифметики . - бесплатно или регистрация требуется, чтобы практиковать свой
математика на AAAKnow.com веб-сайт. - Неограниченная практика доступна по каждой теме, что позволяет
доскональное владение концепциями. - Широкий выбор уроков (от детского сада до восьмого класса).
level) позволяет обучению или обзору происходить на текущем уровне каждого человека. - Немедленная обратная связь предотвращает неправильную практику и обучение
методы, что является обычным результатом традиционных домашних заданий и рабочих листов.Практика может продолжаться сколько угодно долго в безопасном формате, который
помогает повысить самооценку и уверенность в себе. - Пожалуйста, попробуйте уроки , нажав на один из
оценки вверху или в области темы в левой части страницы. - Не забудьте добавить сайт в «Любимые места» и рассказать другим о
сайт. — отличный способ выучить или повторить математику. .
Что нового в AAA Know?
Веб-сайт AAAMath.com начал свою работу в 2000 году и предлагал бесплатные интерактивные уроки математики по основам арифметики и связанным с ней темам математики для K-8. Мы считали, что этот подход лучше, чем традиционные рабочие листы, потому что он обеспечивает немедленную обратную связь, тогда как рабочие листы позволяют студентам неоднократно практиковать неправильные методы, прежде чем они будут оценены.
AAAKnow.com был зеркалом AAAMath.com, который использовался для обработки высоких нагрузок трафика. По сути, они были одинаковыми. Когда переписывание AAAMath.com в современный формат было завершено, мы решили разместить его на сайте AAAKnow.com. Таким образом, люди по-прежнему могут использовать формат AAAMath.com, если они предпочитают его, и могут опробовать и использовать новый формат, если они предпочитают тот.
AAAMath.com
- Использует старый веб-формат.
- Оригинальные уроки
- Не работает с мобильными устройствами
- В основном для настольных компьютеров
- Новые уроки будут ссылками на AAAKnow.com
- Все уроки старого формата будут по-прежнему доступны
- Интерактивные уроки математики
- Без оплаты или регистрации
- Безлимитная практика
- Мгновенная обратная связь предотвращает отработку неправильных методов.
- Отличный способ выучить математику
- В будущем возможен переход на новый формат
AAAKnow.com
- Использует современный веб-формат.
- Практически одинаковые уроки
- Хорошо работает с мобильными устройствами
- Для любого типа компьютера
- На сайте будут разработаны новые уроки
- Все уроки старого формата будут по-прежнему доступны
- Интерактивные уроки математики
- Без оплаты или регистрации
- Безлимитная практика
- Мгновенная обратная связь предотвращает отработку неправильных методов.
- Отличный способ выучить математику
- Будет и дальше развиваться
Пожалуйста, дайте нам знать, если у вас есть какие-либо предложения или комментарии о веб-сайте AAAKnow.com, используя форму обратной связи для анонимных комментариев.
Как разделить любое число на 2- или 3-значное число? (С пошаговой инструкцией)
Теперь мы переходим к ускоренному математическому разделению на месте, основанному на давно установившемся ведическом процессе математических вычислений.Его можно сразу применить во всех случаях, и его можно охарактеризовать как «жемчужину всего» за универсальность его применения.
Чтобы понять визуальный мысленный метод однострочного деления, мы должны взять пример и его объяснение.
Подразделение Bya 2-значный номер :
Пример 1.
Разделим 38982 на 73.
Решение:
Шаг I.
Из делителя 73 записываем только первую цифру, т.е.например, 7 в столбце делителя и поместите другую цифру, то есть 3, «поверх флага», как показано на диаграмме ниже.
7 3 38 9 8 2
Весь дивизион будет к 7.
Шаг II.
Когда одна цифра (3) была поставлена сверху, мы выделяем одно место на правом конце делимого для оставшейся позиции ответа и отмечаем его от цифр вертикальной линией.
Шаг III.
Поскольку первая цифра слева от делимого (3) меньше 7, мы берем 38 в качестве нашего первого дивиденда.Когда мы разделим 38 на 7, мы получим 5 как частное и 3 как остаток. Мы записываем 5 как первую цифру частного и просто добавляем остаток 3 перед 9 делимого.
Шаг IV.
Теперь наш дивиденд равен 39. Из этого, однако, мы вычитаем произведение проиндексированной 3 и первой частной цифры (5), т. Е. 3 × 5 = 15. Остаток 24 — это наш фактический чистый дивиденд. Затем он делится на 7 и дает нам 3 в качестве второй цифры частного и 3 в качестве остатка, которые нужно разместить на своих местах, как это было сделано на третьем шаге.
Шаг V.
Теперь наш дивиденд равен 38. Из этого мы вычитаем произведение индекса (3) и 2-го частного (3), то есть 3 x 3 = 9. Остаток 29 является нашим следующим действительным дивидендом и делим его на 7. Мы получаем 4 как частное и 1 как остаток. Мы помещаем их на свои места.
Шаг VI.
Наш следующий дивиденд — 12, из которого, как и раньше, мы вычитаем 3 × 4, т. Е. 12, и получаем 0 и остаток
.
Таким образом мы говорим:
Частное (Q) равно 534, а остаток (R) равно 0.И на этом завершается вся процедура; и все это — однострочная ментальная арифметика, в которой все фактическое деление выполняется однозначным делителем 7. Процедура очень проста и не требует дальнейшего объяснения и объяснения. Еще несколько иллюстраций с текущими комментариями будут полезны и полезны, поэтому они приведены ниже:
Пример 2:
Разделите 163 84 на 128 (поскольку 12 — небольшое число, с которым нужно работать, мы можем рассматривать 128 как двузначное число).
Решение:
Шаг I.
Делим 16 на 12. Q = 1 & R = 4.
Шаг II.
43 — 8 X 1 = 35 — это наш следующий дивиденд.
Делим на 12, Q = 2, R = 11.
Шаг III.
118-8 X 2 = 102 — это наш следующий дивиденд.
Делим на 12,
Q = 8, R = 6 Шаг IV. 64 — 8 Х 8 = 0
Тогда наше окончательное частное = 128 и остаток = 0 Пример 3: Разделите 601325 на 76.
Решение:
Шаг I.
Здесь, при первом делении на 7, если мы поместим 8 в качестве первой цифры частного, оставшийся остаток будет слишком мал для вычитания, ожидаемого на следующем шаге. На следующем этапе мы получаем -ve дивидендов, что абсурдно. Итак, мы берем 7 как частную цифру и префикс остатка 11 перед следующей цифрой делимого.
Все остальные шаги аналогичны шагам, упомянутым ранее в примерах 1 и 2.Наше окончательное частное составляет 7912, а остаток равен 13. Если мы хотим, чтобы значения были десятичными, мы продолжаем делить согласно правилу вместо того, чтобы записывать остаток. Такие как;
Примечание:
Вертикальная линия, отделяющая остаток от частного, может быть разграничительной точкой для десятичной дроби.
Пример 4: Разделите 7777777 на 38
Решение:
Вы должны выполнить все шаги вышеуказанного решения.Попробуйте решить это. Вы заметили разницу?
Пример 5: Разделите 8997654 на 99. Попробуйте пошагово.
Пример 6: (i) Разделите 710,014 на 39 (до 4 знаков после запятой)
(ii) 718,589 ÷ 23 =?
(iii) 718,589 ÷ 96 =?
Решение. (i) Поскольку имеется одна флаговая цифра, вертикальная линия проводится так, что одна цифра перед десятичной дробью находится под остатком.
Для последнего раздела у нас было 64-45 = 19 в качестве нашего дивиденда, разделив на 3, мы выбрали 4 в качестве подходящего частного.Если мы возьмем 5 как частное, останется 4 в качестве остатка (19-15). Теперь следующий дивиденд будет 40 — 9 x 5 = -5, что недопустимо.
Вертикальная линия, отделяющая остаток от частного, может быть демаркационной точкой для десятичной дроби. Следовательно, ans = 18,2054
Разделение на 3-значный номер
Пример 8: Разделите 7031985 на 823.
Решение:
Шаг I.
Здесь делитель трехзначный. Все, что мы делаем, это ставим две последние цифры (23) делителя сверху. Поскольку есть две цифры флага (23), мы разделим две цифры (85) для остатка.
Шаг II.
Делим 70 на 8 и ставим 8 и 6 на свои места.
Шаг III.
Теперь наш валовой дивиденд равен 63. Из этого мы вычитаем 16, произведение десятков цифр флага, т. Е. 2, и первую частную цифру, т. Е. 8, и получаем остаток 63 — 16 = 47 как фактический дивиденд.И, разделив его на 8, мы получим 5 и 7 в качестве вопросов и ответов соответственно и поместим их на свои места.
Шаг IV.
Теперь наш валовой дивиденд равен 71, и мы вычитаем перекрестное произведение двух флаговых цифр 23 и двух частных цифр (8 и 5), то есть 2 x 5 + 3 x 8 = 10 + 24 = 34; и наш остаток равен 71 — 34 = 37. Затем мы продолжаем делить 37 на 8. Получаем Q = 4 & R = 5
Шаг V.
Теперь наш общий дивиденд составляет 59.Фактический дивиденд равен 59 минус произведение 23 и 54, то есть 59 — (2 x 4 + 3 x 5) = 59 — 23 = 36.
Делим 36 на 8, получаем Q = 4 и R = 4.
Вертикальная линия, отделяющая остаток от частного, может быть демаркационной точкой для десятичной дроби.
Ответ = 8544,33
Наш ответ может быть 8544,33, но если мы хотим получить частное и остаток, процедура несколько иная. В этом случае нам не нужны два последних шага, т.е. расчет до этапа
.
Перекрестное умножение двух флаговых цифр и двух последних цифр частного.

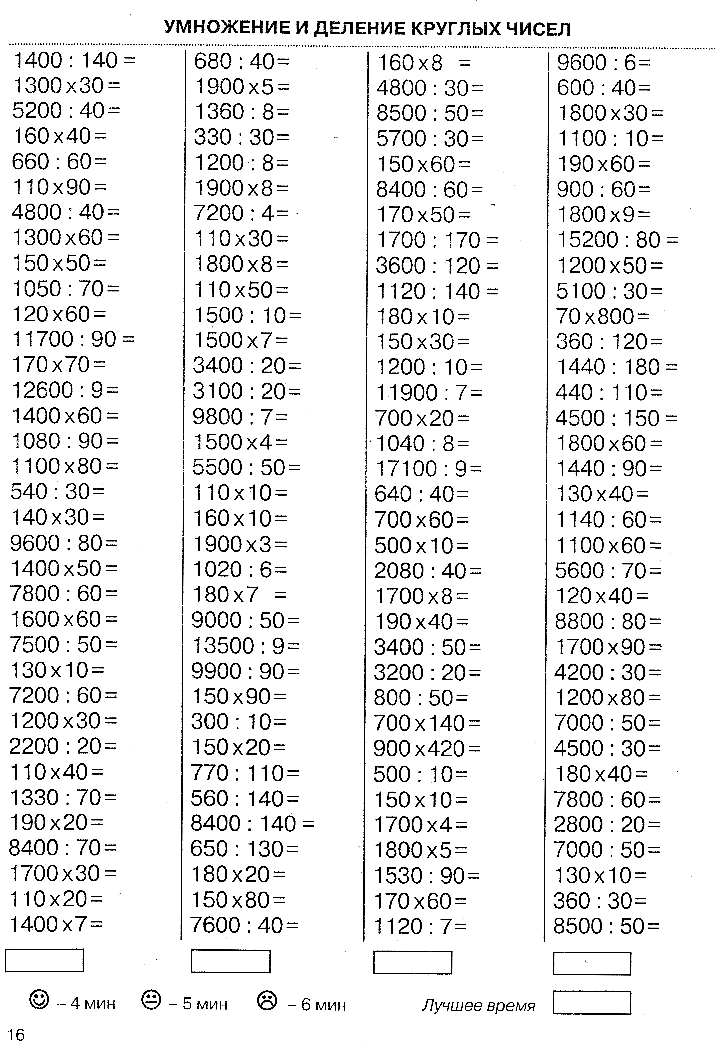

 Деление закончено.
Деление закончено.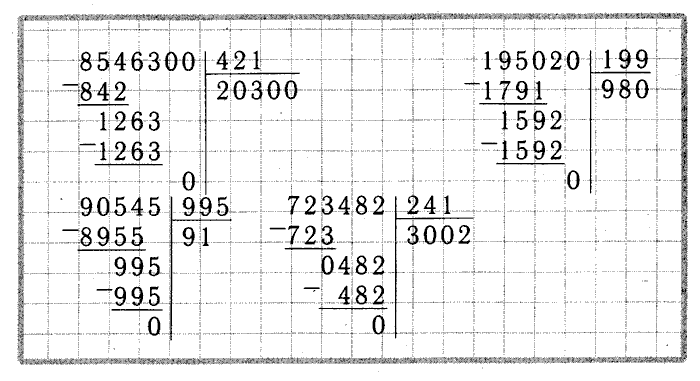
 Оценки и их комментирование
Оценки и их комментирование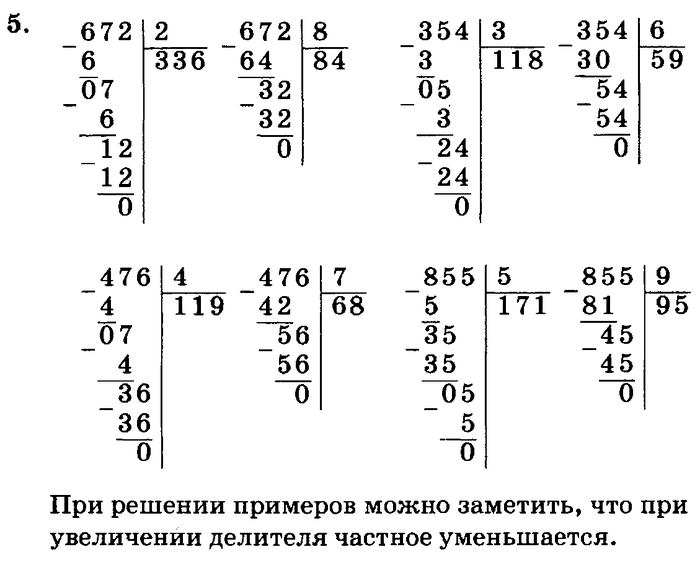 Исходя из этой цели, была сформулирована дополнительная образовательная цель – учить учащихся правильно и осмысленно выполнять действие деления трехзначного числа на однозначное число с переходом через разряд, через отработку алгоритма.
Исходя из этой цели, была сформулирована дополнительная образовательная цель – учить учащихся правильно и осмысленно выполнять действие деления трехзначного числа на однозначное число с переходом через разряд, через отработку алгоритма.
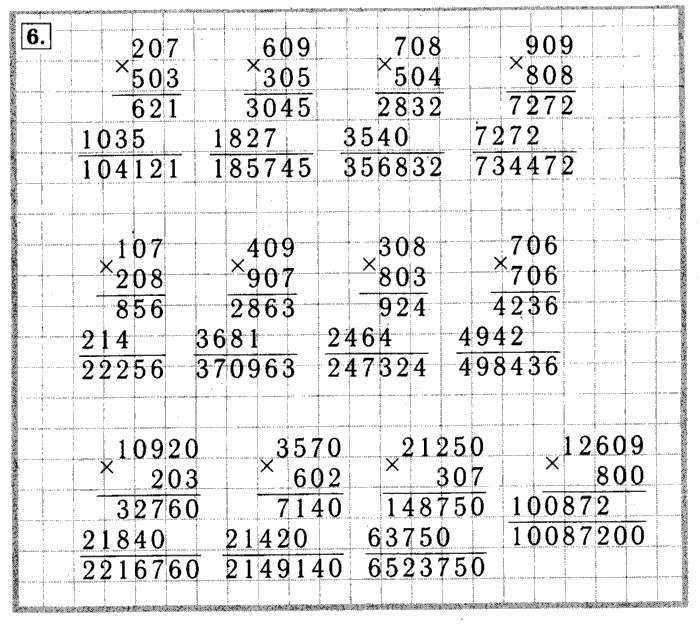 Логика. Развитие внимания. Нейрогимнастика. 8 листов.
Логика. Развитие внимания. Нейрогимнастика. 8 листов. д.)
д.)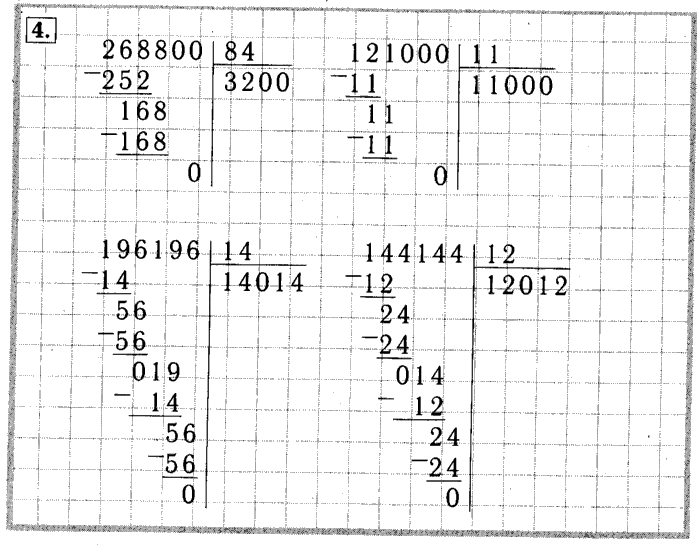 Каллиграфия цифр. 8 листов.
Каллиграфия цифр. 8 листов.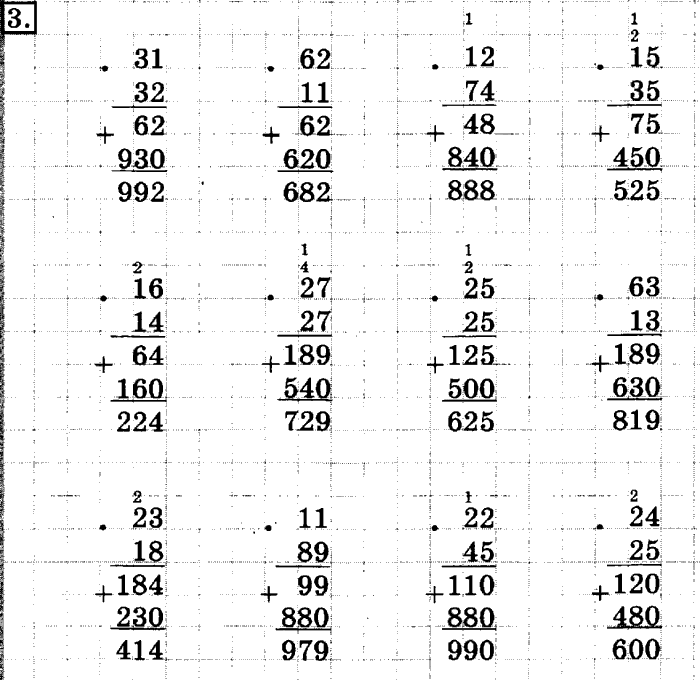 Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Каллиграфия чисел. 8 листов.
Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Каллиграфия чисел. 8 листов.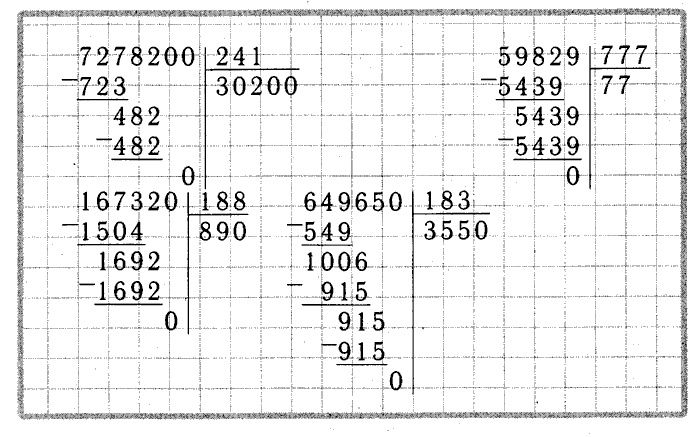 Счет в сотне. Логика. Основы математических представлений. Графомоторика в клетке. 8 листов.
Счет в сотне. Логика. Основы математических представлений. Графомоторика в клетке. 8 листов. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов.
Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов.
Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов. д.)
д.)