| Числа от 1 до 100 | ||
| 1.1 | Табличное умножение и деление. Уравнения | Тренажер mobil |
| 1.2 | Табличное умножение и деление (разные задания) | Тест |
| 1.3 | Табличное умножение на 2 и на 3 | Тест |
| 1.4 | Табличное умножение и деление на 4, 5, 6, 7 | Тест |
| 1.5 | Во сколько раз больше или меньше | Тест mobil |
| 1.6 | Сложение и вычитание. Разные виды примеров | Тренажер mobil |
| 1.7 | Сложение и вычитание в пределах 100 | Тест |
| 1.8 | Умножение двузначного числа на однозначное в уме | Обучающая игра — тренажер с анимацией |
| 1.9 | Деление двузначного числа на однозначное в уме | Обучающая игра — тренажер с анимацией |
| 1.10 | Внетабличное умножение и деление | Статья |
| 1.11 | Внетабличное умножение и деление. Примеры вида 30 · 2 , 80 : 40 | Тренажер mobil |
| 1.12 | Внетабличное умножение и деление. Уравнения | Тренажер mobil |
| 1.13 | Внетабличное умножение. Примеры вида 32 · 3 , 4 · 24 | Тренажер mobil |
| 1.14 | Внетабличное деление в пределах 100 вида 64 : 4 | Тренажер mobil |
| 1.15 | Внетабличное деление. Примеры вида 78 : 3, 84 : 7 | Тренажер mobil |
| 1.16 | Внетабличное умножение и деление. | Тест |
| Уравнения | ||
| 2.1 | Уравнения с пошаговой проверкой. (4 действия +, –, ·, : ) (записываем решение уравнения) | Тренажер |
| 2.2 | Выражение с буквой. Уравнение. | Тест |
| Деление с остатком | ||
3.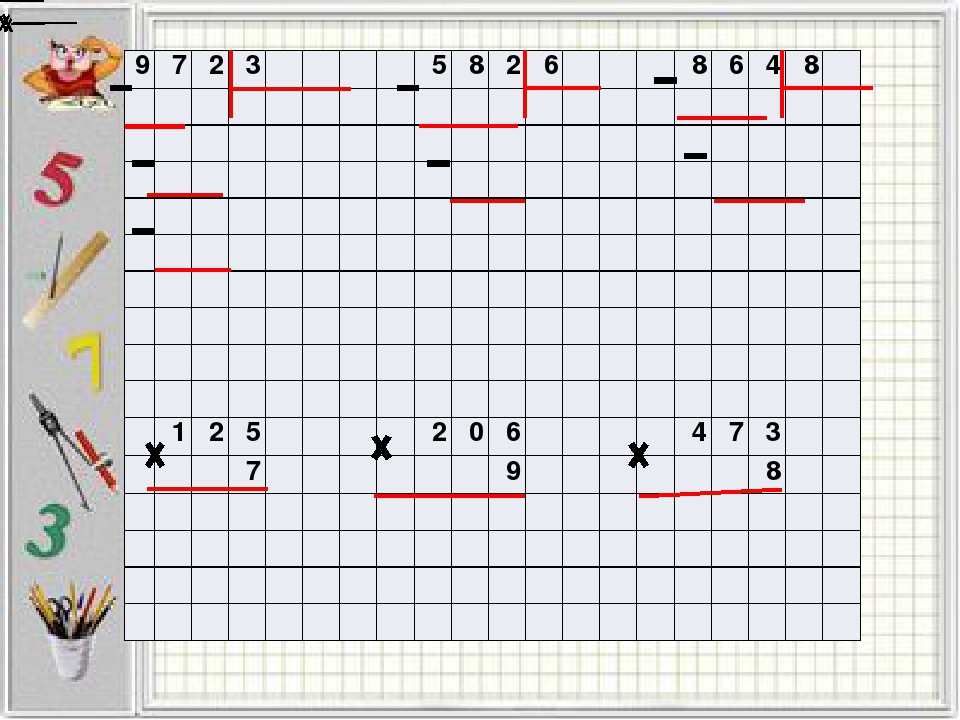 1 1 | Найди ближайшее число, которое делится на … | Упражнение mobil |
| 3.2 | Найди неполное частное или остаток | Упражнение mobil |
| 3.3 | Вставь пропущенное число (делитель) | Упражнение mobil |
| 3.4 | Деление с остатком. Напиши неполное частное и остаток | Тренажер mobil |
| 3.5 | Деление с остатком (различные задания) | Тест |
| Задачи | ||
| 4.1 | Решение задач | Тест 1 |
| 4.2 | Решение задач | Тест 2 |
| 4.3 | Во сколько раз больше или меньше | Тест |
| 4.4 | Нахождение доли от числа и числа по доле | Статья + тренажер |
| 4.5 | Задачи на доли | Тест |
| 4.6 | Периметр и площадь | Тест |
| 4.7 | Периметр и площадь — 100 заданий разного типа | Тренажер mobil |
| 4.8 | Периметр и площадь — 40 задач | Тренажер mobil |
| Порядок действий | ||
| 5.1 | Расставь порядок действий (буквенные выражения) | Тренажер mobil |
| 5.2 | Расставь порядок действий и реши примеры | Тренажер mobil |
| Числа от 1 до 1000 | ||
| 6.1 | Интерактивная таблица разрядов и классов | Интерактивная таблица |
| 6.2 | Напиши соседей числа (до 1000) | Тренажер mobil |
| 6.3 | Вставь пропущенные числа (до 1000) | Тренажер mobil |
| 6.4 | Сравни числа до 1000 | Тренажер |
| 6.5 | Представь число в виде суммы разрядных слагаемых | Тренажер |
| 6.6 | Чтение и запись трехзначных чисел | Тест |
6. 7 7 | Прибавление и вычитание разрядных единиц. Примеры вида: 657 + 200, 435 + 40, 346 + 2 | Тренажер mobil |
| 6.8 | Вычитание из круглых чисел до 1000. Примеры типа: 1000 — 300 , 800 — 20 , 500 — 3 , 800 — 230 , 600 — 234 | Тренажёр mobil |
| 6.9 | Устные приемы сложения и вычитания (до 1000) | Тест |
| 6.10 | Внетабличное умножение и деление в пределах 1000 (устный счет) | Тренажер mobil |
| 6.11 | Умножение и деление круглых чисел | Статья + тренажер |
| Сложение и вычитание трехзначных чисел столбиком | ||
| 7.1 | Сложение двух чисел столбиком (с пошаговой проверкой) | Тренажер |
| 7.2 | Сложение трех чисел столбиком (с пошаговой проверкой) | Тренажер |
| 7.3 | Вычитание столбиком (с пошаговой проверкой) | Тренажер |
| 7.4 | Сложение трехзначных чисел столбиком без перехода через разряд | Тренажер mobil |
| 7.5 | Сложение столбиком с переходом через разряд, типа 738 + 146 | Тренажер mobil |
| 7.6 | Вычитание столбиком с переходом через разряд, типа 523 — 375 | Тренажер mobil |
| 7.7 | Сложение и вычитание столбиком без перехода, типа 453 + 231, 467 — 322 | Тренажер mobil |
| 7.8 | Письменные приемы сложения и вычитания | Тест |
Для самостоятельной работы по математике 3 класс Решение примеров столбиком. | Тест по математике (3 класс) на тему:
1.Запиши примеры в столбик и вычисли:
268 + 556 742 -384 354 + 378 463 – 389
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
1. Запиши примеры в столбик и вычисли:
Запиши примеры в столбик и вычисли:
268 + 556 742 -384 354 + 378 463 – 389
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
1.Запиши примеры в столбик и вычисли:
268 + 556 742 -384 354 + 378 463 – 389
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
1.Запиши примеры в столбик и вычисли:
268 + 556 742 -384 354 + 378 463 – 389
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
1.Запиши примеры в столбик и вычисли:
268 + 556 742 -384 354 + 378 463 – 389
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
1.Запиши примеры в столбик и вычисли:
268 + 556 742 -384 354 + 378 463 – 389
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2. Запиши примеры в столбик и вычисли:
Запиши примеры в столбик и вычисли:
197 + 226 926 – 648 858 – 599 268 + 169
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2.Запиши примеры в столбик и вычисли:
197 + 226 926 – 648 858 – 599 268 + 169
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2.Запиши примеры в столбик и вычисли:
197 + 226 926 – 648 858 – 599 268 + 169
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2.Запиши примеры в столбик и вычисли:
197 + 226 926 – 648 858 – 599 268 + 169
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2.Запиши примеры в столбик и вычисли:
197 + 226 926 – 648 858 – 599 268 + 169
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2.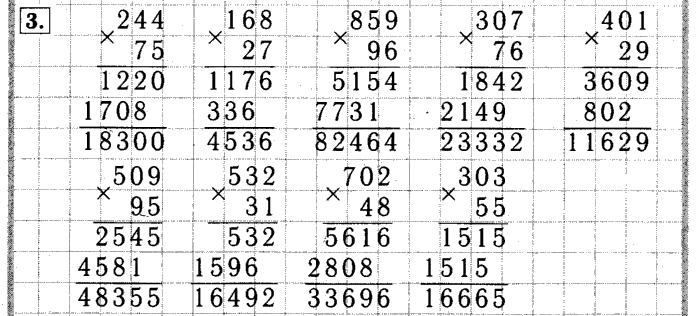 Запиши примеры в столбик и вычисли:
Запиши примеры в столбик и вычисли:
197 + 226 926 – 648 858 – 599 268 + 169
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
3000 примеров по математике с ответами и методическими рекомендациями. Решаем в столбик. 3 класс — Узорова О.В. | 978-5-17-115362-5
Стоимость товара может отличаться от указанной на сайте!
Наличие товара уточняйте в магазине или по телефону указанному ниже.
г. Воронеж, площадь Ленина, д.4
8 (473) 277-16-90
г. Богучар, ул. Дзержинского, д.4
8 (47366) 2-12-90
г. Воронеж, ул. Г. Лизюкова, д. 66 а
8 (473) 247-22-55
г.Поворино, ул.Советская, 87
8 (47376) 4-28-43
г. Воронеж, ул. Плехановская, д. 33
Воронеж, ул. Плехановская, д. 33
8 (473) 252-57-43
г. Воронеж, ул. Ленинский проспект д.153
8 (473) 223-17-02
г. Нововоронеж, ул. Ленина, д.8
8 (47364) 92-350
г. Воронеж, ул. Хользунова, д. 35
8 (473) 246-21-08
г. Россошь, Октябрьская пл., 16б
8 (47396) 5-29-29
г. Россошь, пр. Труда, д. 26А
8 (47396) 5-28-07
г. Лиски, ул. Коммунистическая, д.7
8 (47391) 2-22-01
г. Белгород, Бульвар Народный, 80б
Белгород, Бульвар Народный, 80б
8 (4722) 42-48-42
г. Курск, пр. Хрущева, д. 5А
8 (4712) 51-91-15
г. Губкин, ул. Дзержинского,д. 115
8 (47241) 7-35-57
г.Воронеж, ул. Жилой массив Олимпийский, д.1
8 (473) 207-10-96
г. Старый Оскол, ул. Ленина, д.22
8 (4725) 23-38-06
г. Воронеж, ул. Пушкинская, 2
8 (473) 300-41-49
г. Липецк, ул.Стаханова,38 б
8 (4742) 78-68-01
г. Курск, ул.Карла Маркса, д.6
Курск, ул.Карла Маркса, д.6
8 (4712) 54-09-50
г. Воронеж, Московский пр-т, д. 129/1
8 (473) 269-55-64
ТРЦ «Московский Проспект», 3-й этаж
Умножение в столбик — как умножать в столбик в 3 и 4 класс
Основные понятия
Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.
Название числа напрямую зависит от количества знаков.
- Однозначное — состоит из одного знака
- Двузначное — из двух
- Трехзначное — из трех и так далее.
Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитываются с конца.
Разряд единиц — то, чем заканчивается любое число. Разряд десятков — то, что находится перед разрядом единиц. Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.
- В числе 429 содержится 0 тысяч, 4 сотни, 2 десятка и 9 единиц.
Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.
Свойства умножения1. От перестановки множителей местами произведение не меняется. 2. Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением.
Самое главное в процессе вычисления — это знание таблицы умножения. |
Важно помнить правило: умножение в столбик с нулями дает в результате ноль
- а * 0 = 0, где а — любое натуральное число.
Алгоритм умножения в столбик
Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:
1. Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.
2. Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения. Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д.
3. Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.
Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.
4. После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.
5. Складываем то, что нашли и получаем ответ.
Умножение на однозначное число
Для решения задачи по произведению двух натуральных чисел, одно из которых однозначное, а другое — многозначное, нужно использовать способ столбика. Для вычисления воспользуемся последовательностью шагов, которую рассмотрели выше.
Возьмем пример 234 * 2:
1. Запишем первый множитель, а под ним второй. Соответствующие разряды расположены друг под другом. Двойка находится под четверкой.
2. Последовательно умножаем каждое число в первом множителе на второй, начиная с единиц и продвигаясь к десяткам и сотням.
3. Ответ запишем под чертой:
Производить действия необходимо в следующей последовательности:
Умножение двух многозначных чисел
Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.
Рассмотрим пример 207 * 8063:
- Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:
- Последовательно перемножаем значения разрядов. Результатом является неполное произведение.
- Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т.д. Результат запишем под чертой.
- По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:
- Далее складываем два произведения в столбик.
- Получившееся семизначное число — результат умножения исходных натуральных чисел.
Ответ: 8 063 * 207 = 1669041.
Примеры на умножение в столбик
Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость. Неважно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем.
Повтори тему — деление в столбик, она очень полезная!
Чтобы запомнить все правила, повторите метод сложения столбиком, так как один из этапов умножения состоит из сложения промежуточных результатов. А еще лучше — приходите заниматься увлекательной математикой в детскую школу Skysmart.
Вместо скучных параграфов ученики решают интерактивные задачки и головоломки с мгновенной автоматической проверкой, а еще чертят фигуры на онлайн-доске вместе с преподавателем.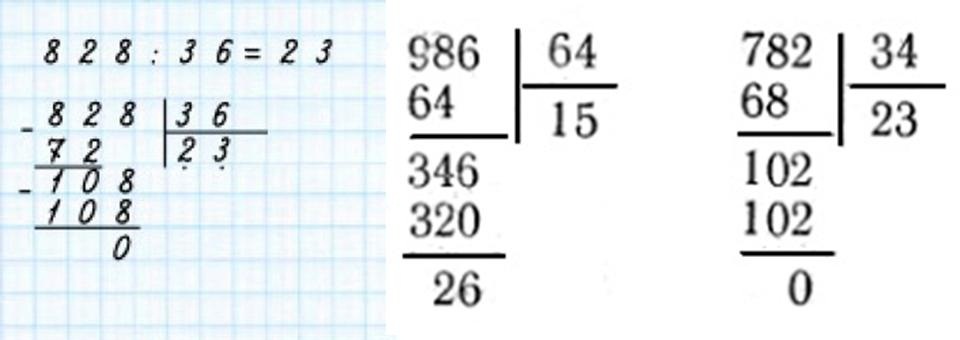
Игры примеры в столбик решать. Сложение столбиком
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1
. Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2
. На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3
. Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4
. Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг
. Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг
. Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг
. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг
. Ставим точку под делителем.
5 шаг
. После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг
. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг
. Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг
. Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг
*. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг
Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка.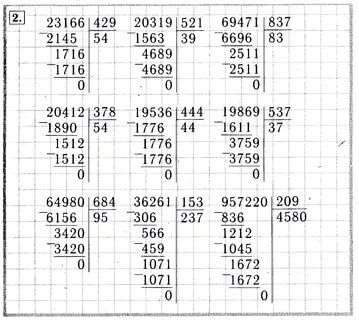 Если бы делили число 513, то в остатке была бы единица.
Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3)
(4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления.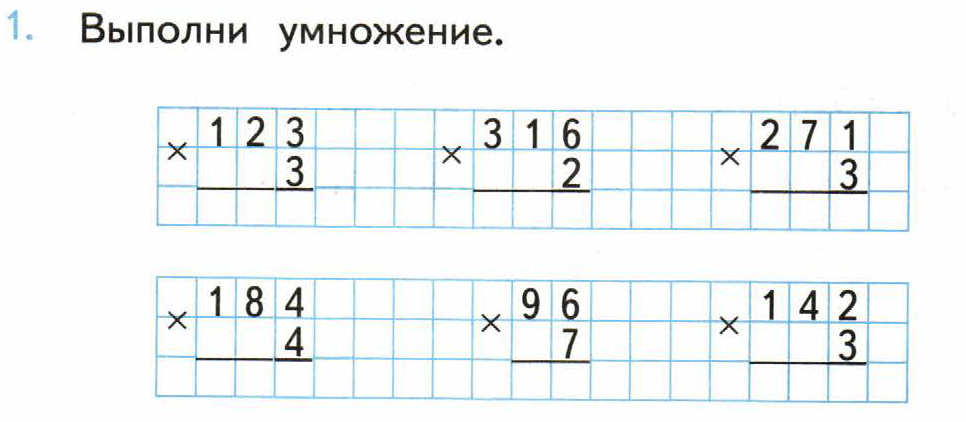 Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются.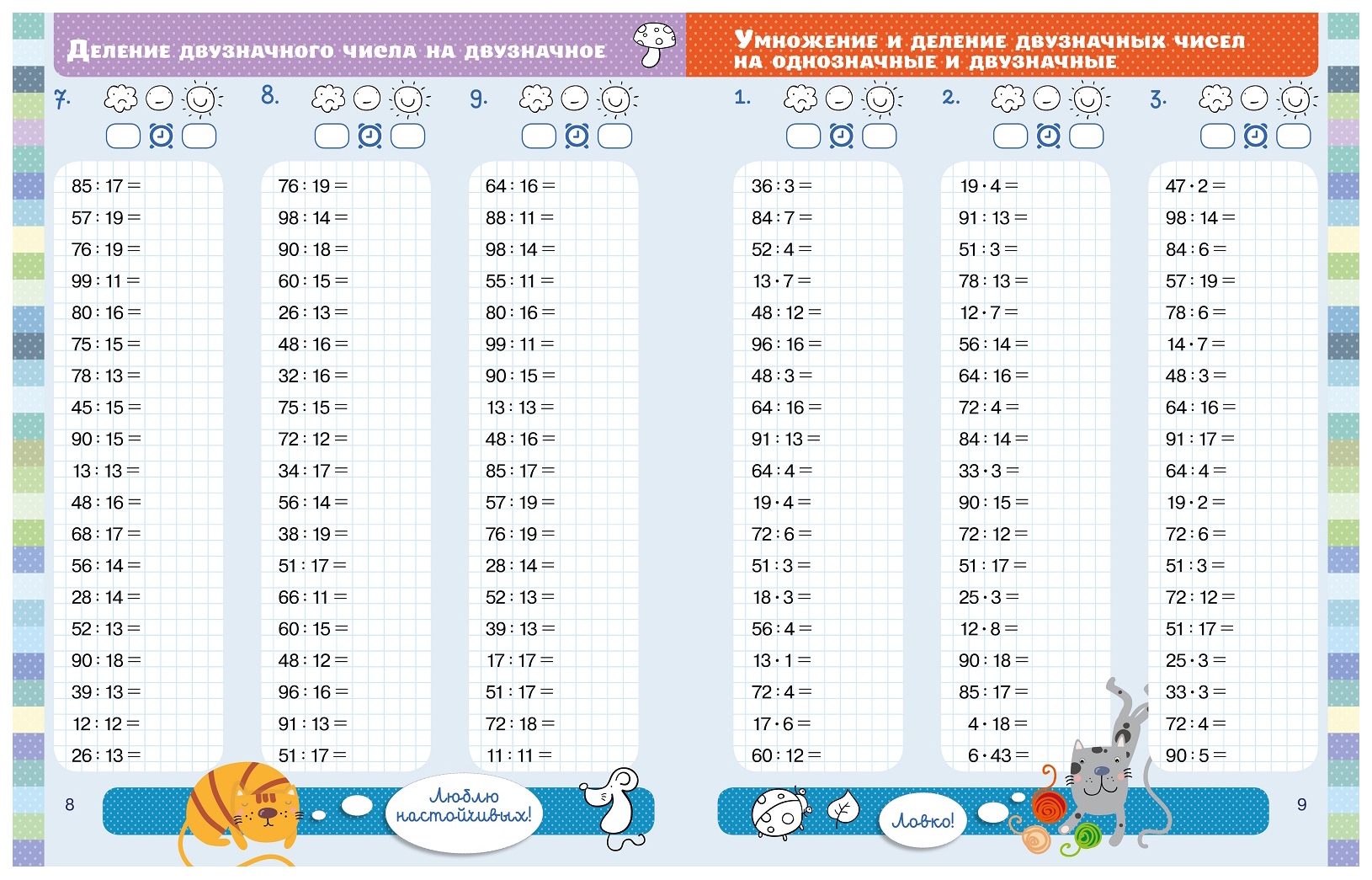 Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Онлайн игра-тренажёр «Умножение столбиком» помогает научиться умножать двух- и трёхзначные числа. Эта игра ориентирована на детей от 7 до 10 лет.
Умножение чисел столбиком — это программа математики за 3 класс школы. Но в этом действии нет ничего сложного, поэтому освоить умножение в столбик можно и раньше.
Но в этом действии нет ничего сложного, поэтому освоить умножение в столбик можно и раньше.
Как научиться умножать столбиком?
В игре представлены три уровня: умножение двузначного числа на двузначное (числа от 10 до 99), умножение трёхзначного числа на трёхзначное (числа от 100 до 999) и микс. В миксе трёхзначное число умножается на двузначное или двузначное умножается на трёхзначное.
Чтобы правильно умножать двух- и трёхзначные числа надо хорошо знать и .
Надеюсь, ты помнишь, что числа, которые умножаются друг на друга называются множителями: первый множитель, второй множитель и так далее. Результат умножения называется произведением. Также полагаю, что тебе известно, что в числах есть разряды: единицы (самый маленький), десятки, сотни, тысячи…
Итак, приступим. Начать умножение в столбик надо с того, что расположить множители таким образом, чтобы друг под другом оказались числа одинаковых разрядов: единицы под единицами, десятки под десятками и так далее. На следующем шаге берём цифру из разряда единиц второго множителя и умножаем её по очереди на каждую цифру первого множителя. Результат умножения каждой пары цифр записываем в верхнюю строку под соответствующим разрядом.
За каждый правильный ответ начисляется 1 балл. За неправильный — отнимается 3 балла.
Если тебе понравилась эта игра, обязательно поделись ею со своими друзьями. Ведь им она тоже может понравиться:-)
Эта игра предназначена и чрезвычайно полезна для мальчиков и девочек от 7 до 10 лет.
С лучшей бесплатной игрой учится очень быстро. Проверьте это сами!
Учить таблицу умножения — игра
Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа. Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять). Игровая форма тренажера подходит как для мальчиков, так и для девочек.
Игровая форма тренажера подходит как для мальчиков, так и для девочек.
Смотрите ниже шпаргалки в полной форме.
Умножение прямо на сайте (онлайн)
*
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 216 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Как умножать числа столбиком (видео по математике)
Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.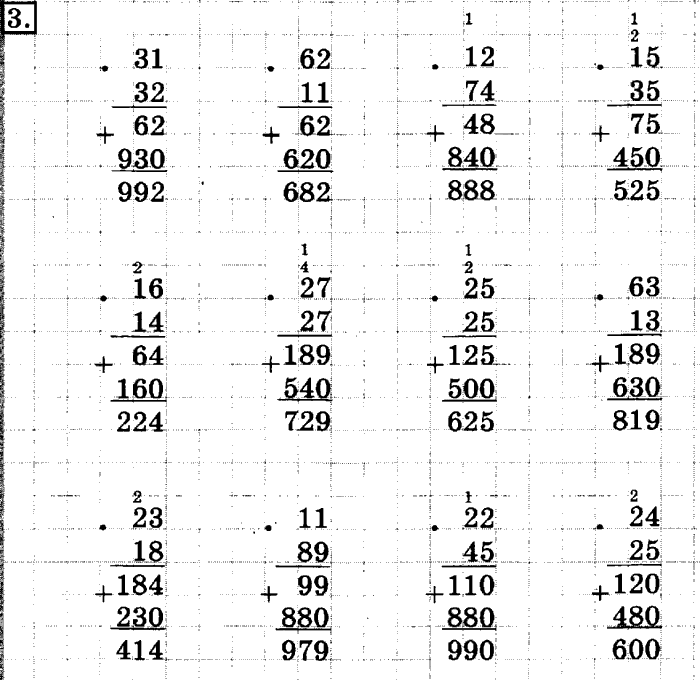
В этой игре мы будем учиться складывать столбиком числа до 100. Яркие картинки и подробные пояснения помогут легко понять и запомнить алгоритм сложения столбиком. А тренажер поможет закрепить тему.
Прежде всего нужно запомнить, что при решении примеров на сложение столбиком большее число записывается сверху, а меньшее — под ним. Числа записываются так, чтобы единицы были под единицами, а десятки (если они есть) — под десятками.
Сначала складывают единицы, а затем десятки, при этом возможно 2 варианта:
Если при сложении единиц получается однозначное число, мы просто записываем его под чертой под единицами. Если же при сложении единиц получается двузначное число, включая 10, мы записываем под единицами только вторую цифру(единицы), а 1 (десяток) прибавляем к десяткам.
Первый вариант описан и проиллюстрирован в уроке 1, а второй вариант — в уроке 2 нашей обучающей онлайн игры «Сложение столбиком». После просмотра уроков порешайте примеры на сложение столбиком самостоятельно в разделе «Тренажер»
Предыдущая статья: Компьютеры на электронных лампах
Следующая статья: Типы данных и их размер. Типы данных. Приставки целочисленных типов данных
3 класс, часть 1 – 2 Консультация 3. Уроки 1 – 13.
3 класс, часть 1 – 2
Консультация 3. Уроки 1 – 13.
На уроках 1 – 5 систематизируются знания учащихся о единицах измерения длины и массы, вводятся новые единицы измерения массы: грамм, центнер, тонна, закрепляются соотношения между единицами измерения длины, массы, умение выражать значения величин в разных единицах измерения. Также повторяются и закрепляются нумерация и действия с многозначными числами, решение текстовых задач, уравнений, примеров на порядок действий, умножение чисел в столбик, измерение отрезков и построение отрезков данной длины, понятие объема прямоугольного параллелепипеда, отрабатываются вычислительные навыки.
На уроке 1 воспроизводится таблица, устанавливающая соотношение между единицами длины, с которой учащиеся уже встречались раньше:
Теперь область применения этой таблицы существенно расширяется.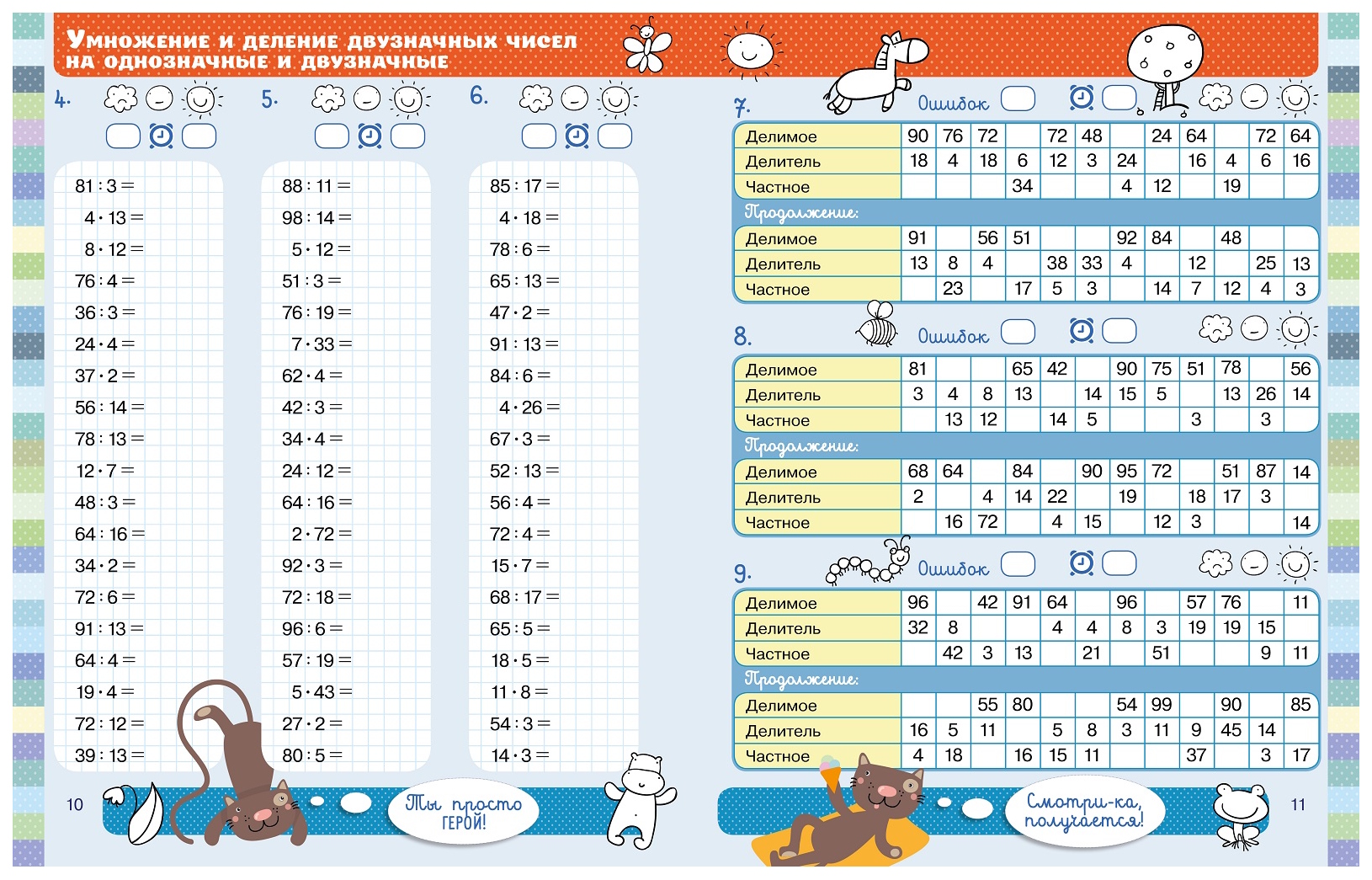 В №1, стр. 95 проговариваются все возможные соотношения между этими единицами. Например, устанавливается, что 1 км = 1000 м = 10 000 дм = 100 000 см = 1 000 000 мм и т. д. При этом надо вспомнить правило: при переходе к меньшим меркам выполняется умножение, а при переходе к большим меркам – деление. Соответствующие коэффициенты перехода (числа, на которые надо умножать или делить при переходе от одной единицы измерения к другой) записаны под дугами.
В №1, стр. 95 проговариваются все возможные соотношения между этими единицами. Например, устанавливается, что 1 км = 1000 м = 10 000 дм = 100 000 см = 1 000 000 мм и т. д. При этом надо вспомнить правило: при переходе к меньшим меркам выполняется умножение, а при переходе к большим меркам – деление. Соответствующие коэффициенты перехода (числа, на которые надо умножать или делить при переходе от одной единицы измерения к другой) записаны под дугами.
В № 2–4, стр. 95 учащиеся используют установленные соотношения и аналогию с десятичной системой записи чисел для перевода длин из одних единиц измерения в другие. Решение примеров записывается в тетради в клетку и проговаривается вслух. Способ обоснования может быть различным – на основе установленного правила либо на основе аналогии с десятичной системой записи чисел, например:
а) 7 м = 700 см, так как в 1 метре 100 сантиметров, а 100 · 7 = 700,
или
7 м = 700 см, так как 7 метров – это 7 сотен сантиметров;
б) 16 000 мм = 1600 см, так как в 1 сантиметре 10 миллиметров, а
16 000 : 10 = 1600,
или
16 000 мм = 1600 см, так как в 16 000 содержится 1600 десятков;
в) 12 км 50 м = 12 050 м, так как в 1 километре 1000 метров, значит,
в 12 км – 12 000 м, да еще 50 м, всего получится 12 050 метров,
или
12 км 50 м = 12 050 м, так как 12 км 50 м – это 12 тысяч 50 метров.
Основным способом является первый, так как он универсальный и используется, например, и при преобразовании единиц времени, где соотношения между единицами не являются десятичными. Однако акцент на аналогию системы мер длины и массы с десятичной системой записи чисел не только поможет закрепить знание нумерации, но и покажет связь изучения чисел с практическими задачами. Каждый из учеников может выбрать тот способ обоснования, который ему удобен, а в классе должны звучать оба способа.
Перед выполнением заданий № 5–6, стр. 96 надо повторить с учащимися правило о том, что величины можно сравнивать, складывать и вычитать только тогда, когда они выражены в одних и тех же единицах измерения. Поэтому для сравнения, сложения и вычитания величин в этих заданиях надо их сначала выразить в одинаковых мерках.
На уроке 2 в №1–2, стр. 98 учащиеся решают практические задачи, связанные с построением отрезков и измерением их длин. В №1 они устанавливают, что если точки A, B и C лежат на одной прямой, то длина AC равна сумме длин AB и BC, а если нет, то длина AC меньше суммы длин AB и BС. Другими словами, прямая линия, соединяющая две точки A и C, короче ломаной ABC. В №2 они строят планы земельных участков треугольной и четырехугольной формы и вычисляют их периметры. Таким образом, их внимание еще раз обращается на то, что числа возникли для решения практических задач, поэтому естественно, что соотношения между единицами измерения величин аналогичны принципу нумерации. Эта аналогия еще раз подчеркивается в №3, стр. 98. В заданиях №4–5, стр. 98 рассматриваются более сложные случаи перевода единиц длины.
На уроках 3–4 аналогичным образом рассматриваются единицы массы и соотношения между ними:
Правило перевода единиц и способы перевода остаются прежними, изменяются лишь названия единиц и переводные коэффициенты. Кроме того, рассматриваются виды гирь, которые обычно используются при взвешивании, и способы уравновешивания предметов на чашечных весах.
Хотим отметить, что при выполнении №10, стр. 99 следует обратить внимание на некоторые моменты. К настоящему времени дети уже знают, что одни и те же математические выражения могут описывать разнообразные жизненные ситуации. Так, выражение 2 + 3 может быть суммой игрушек, ручек, тракторов и еще чего угодно, в том числе «шклидулок». И от того, что мы не знаем, что такое «шклидулка», суть вычислений не изменится – мы все равно получим в ответе 5.
И от того, что мы не знаем, что такое «шклидулка», суть вычислений не изменится – мы все равно получим в ответе 5.
В задаче предлагается вымышленная ситуация – о шклидулках и бримазятах. Математическая структура задачи не представляет для учеников труда, но здесь они должны суметь перенести ее на абстрактное для них содержание и провести рассуждения во всей полноте.
– Чтобы ответить на первый вопрос задачи, можно сложить шклидулки, которые нашли бримазище и бримазенок. (Ищем целое.) Для этого сначала из 96 вычтем 64 и узнаем, сколько шклидулок нашел бримазенок. Чтобы узнать, во сколько раз больше шклидулок нашел бримазище, чем бримазенок, надо первое число разделить на второе.
1) 96 – 64 = 32 (ш.) – нашел бримазенок.
2) 96 + 32 = 128 (ш.).
3) 96 : 32 = 3 (раза).
Ответ: вместе они нашли 128 шклидулок, бримазище – в 3 раза больше бримазенка.
При выполнении №12, стр. 103 следует рассуждать так:
Р – 70 Г – 200 С – 40
И – 80 К – 5400 Б – 400
П – 50 О – 4800 Н – 100
СПРИНГБОК. Один из интереснейших видов газелей, обитающий в Южной Африке. Верхняя сторона тела – желто‑коричневая, нижняя сторона – белая, на границе проходит контрастная буровато‑черная полоса. Но самая замечательная особенность спрингбока – обширная продольная кожная складка на спине. Когда животное спокойно, складку не видно. Но, почувствовав опасность, спрингбок начинает подпрыгивать на месте, отталкиваясь одновременно всеми ногами, без видимых усилий, как резиновый мяч.
Прыжки спрингбока колоссальны: до 2 м в высоту. При этом края кожной складки расходятся, и выстилающий ее белый мех начинает ослепительно сверкать. Для всех обитателей саванны прыжки спрингбока служат сигналом опасности.
Спрингбок знаменит своими странствиями. К сожалению, говорить о них приходится лишь в прошедшем времени: они прекратились вместе с резким уменьшением численности спрингбока. Во время последнего крупного переселения спрингбоков в 1896 году животные плотной массой покрывали участок шириной около 25 км, а длина колонны составляла 220 км!
Во время последнего крупного переселения спрингбоков в 1896 году животные плотной массой покрывали участок шириной около 25 км, а длина колонны составляла 220 км!
Во второй части учебника закрепляются нумерация, сложение и вычитание многозначных чисел, вводится умножение и деление многозначного числа на однозначное, рассматриваются некоторые преобразования на плоскости (параллельный перенос, симметрия), меры времени и календарь, на основе некоторых логических понятий (высказывание, истинное и ложное высказывание) уточняется понятие уравнения и рассматриваются новые их виды. Учащиеся знакомятся с понятиями переменной и выражения с переменной, учатся находить значения выражений с переменной, строить формулы зависимостей между величинами.
На уроках 6 – 9 у учащихся формируется умение умножать многозначные числа на однозначные и умножать круглые числа в случаях, сводящихся к умножению на однозначное число, учатся решать задачи на нахождение значений величин по их сумме и разности. Ученики повторяют и закрепляют нумерацию, сложение и вычитание многозначных чисел, решение текстовых задач, решение уравнений с комментированием по компонентам действий, сравнение выражений, действия с единицами длины и массы.
Простейшие случаи умножения многозначного числа на однозначное (27 · 5, 140 · 3 и т. д.) и их запись в столбик уже встречались учащимся. На данном этапе обучения они должны распространить известный им способ умножения в столбик на общий случай умножения многозначного числа на однозначное, и отработать его для сложных случаев. Работа ведется, как обычно, деятельностным методом.
На уроке 6 на этапе актуализации знаний с учащимися нужно вспомнить распределительное свойство умножения. Для этого можно рассмотреть с ними различные способы нахождения площади прямоугольников для случаев, когда прямоугольник разбит на 2 части и на 3 части:
По данным рисункам ставятся вопросы:
1) Чем похожи и чем отличаются эти задачи? (В первой задаче прямоугольник разбит на две части, а во второй – на три.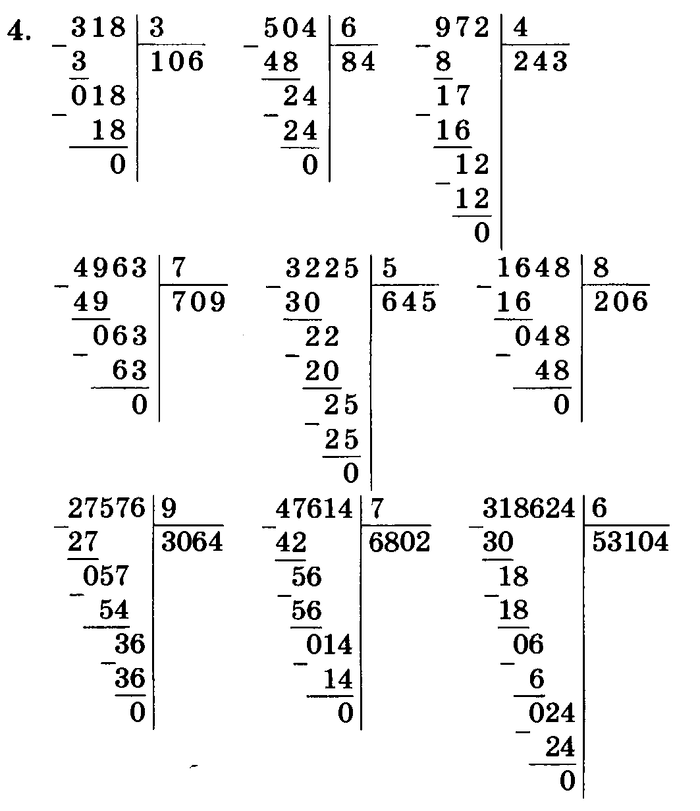 )
)
2) Как называется первое равенство? (Правило умножения суммы на число, или распределительное свойство умножения.)
3) Можно ли распространить это правило на сумму трех слагаемых? (Из второго равенства следует, что да.)
4) Можно ли его распространить на сумму большего числа слагаемых? (Да, ведь прямоугольник можно разбить на большее число частей.)
Чтобы поставить проблему, учащимся можно сначала предложить решить в тетрадях в клетку следующие примеры и выявить в них закономерности:
Ученики могут заметить, что:
1) все примеры – на умножение;
2) первый множитель увеличивается, а второй не изменяется;
3) с увеличением первого множителя произведение увеличивается;
4) если первый множитель увеличивается в 10 раз, то и все произведение
увеличивается в 10 раз.
Затем учитель предлагает, воспользоваться тем же вычислительным приемом и решить пример
При решении примера, вероятно, возникнет затруднение: могут получиться разные ответы, кто‑то из детей не решит его и т. д. Возникшая проблемная ситуация и мотивирует поиск нового способа действий.
В случае, если с последним примером справятся все обучающиеся, можно попросить их обосновать решение. Главное – дети должны заметить, что для решения данного примера используется другой вычислительный прием. Этот признак отличия они должны проговорить вслух: в первых четырех примерах требуется умножить двузначное число на однозначное, а в последнем примере – трехзначное на однозначное.
После этого цель урока может быть сформулирована следующим образом: установить, как умножается любое многозначное число на однозначное. Если последний пример выполнят все ученики, то цель урока мотивируется необходимостью обосновать правомерность используемого приема.
Этап «открытия» нового знания начинается с выбора метода рассуждений. Рассмотренная в начале урока задача о вычислении площадей прямоугольников должна помочь учащимся вспомнить, что алгоритм умножения двузначного числа на однозначное был установлен на основе правила умножения суммы на число (распределительного свойства умножения), и сориентироваться на это свойство.
В № 1, стр. 1 еще раз проговаривается формулировка правила умножения суммы на число и возможность его распространения на любое число слагаемых. Затем в № 2 (а), стр. 1 данное число 576 разбивается на удобные слагаемые 500 + 70 + 6 и на основе этого правила выполняются преобразования:
Очевидно, что такая запись является слишком громоздкой, неудобной, – это учащиеся скажут сразу. Тогда ставится задача найти более короткий способ записи по аналогии с умножением на двузначное число. Если самостоятельно ученики затруднятся это сделать, можно предложить им проанализировать слагаемые суммы по рисунку №2 (б), стр. 1. Дети должны заметить, что при вычислении суммы сначала подсчитывается число единиц, затем число десятков и число сотен (нули при сложении результата не изменяют). И поскольку все эти числа всегда являются двузначными (значения табличных произведений), то удобнее число единиц следующего разряда, которое «запоминается», писать вверху над соответствующим разрядом первого множителя, как при умножении двузначных чисел. Подвести учащихся к этому выводу можно следующей последовательностью вопросов:
1) Как получили слагаемые суммы? (6 единиц умножили на 9, потом 7 десятков умножили на 9, а потом 5 сотен умножили на 9.)
2) Всегда ли во втором слагаемом на конце будет нуль? Почему? (Всегда, так как считаем число десятков.)
3) Всегда ли в третьем слагаемом на конце 2 нуля? Почему? (Всегда, так как считаем число сотен.)
4) Почему во втором столбике нули зачеркнуты? (Они не изменяют значение суммы.)
5) Может ли число единиц, десятков или сотен «заходить» не на один следующий разряд, а на 2 или 3 разряда? (Нет, перемножаем однозначные числа, поэтому в произведении не может быть больше двух знаков.)
6) Сравните запись умножения во втором и третьем столбике – какая из записей удобнее? (В третьем столбике.)
7) Догадайтесь, как она получается из предыдущей? (Сначала умножаем единицы: 6 · 9 = 54, 4 единицы пишем, а 5 десятков запоминаем – записываем над числом десятков первого множителя. Потом умножаем десятки: 7 · 9 = 63, 63 + 5 = 68, 8 десятков пишем, а 6 сотен запоминаем. А потом умножаем сотни: 5 · 9 = 45, 45 + 6 = 51, записываем 51 сотню. – «Открытие».)
Потом умножаем десятки: 7 · 9 = 63, 63 + 5 = 68, 8 десятков пишем, а 6 сотен запоминаем. А потом умножаем сотни: 5 · 9 = 45, 45 + 6 = 51, записываем 51 сотню. – «Открытие».)
Пишу: множитель 9 под разрядом единиц множителя 576.
Умножаю единицы: 6 · 9 = 54 ед., пишу 4 в разряде единиц,
а 5 д. запоминаю.
Умножаю десятки: 7 · 9 = 63 д., 63 + 5 = 68 д., пишу 8 в разряде
десятков, а 6 с. запоминаю.
Умножаю сотни: 5 · 9 = 45 с., 45 + 6 = 51 с., пишу 1 в разряде
сотен, а 5 – в разряде тысяч.
Ответ: 5184.
В завершение учитель спрашивает у детей, изменятся ли рассуждения при умножении на однозначное число четырехзначного, пятизначного, шестизначного и т. д. числа. Как правило, дети легко распространяют полученный вывод на любое многозначное число. Тогда в тетради в клетку надо записать, решить и прокомментировать (с возможной помощью учителя) более сложный случай умножения, например, 5 · 20 156. Внимание детей обращается на порядок множителей и на то, что в данном случае также удобно писать однозначный множитель под разрядом единиц многозначного множителя.
Если у учащихся все же возникнет сомнение в правомерности распространения полученного вывода на случай умножения любого многозначного числа на однозначное, то можно рассмотреть аналогичным образом умножение четырехзначного числа на однозначное или предложить учащимся сделать это дома самостоятельно.
Примеры для этапа первичного закрепления подбираются в зависимости от уровня подготовленности класса. Можно, например, решить с подробным комментированием в громкой речи № 3 (а), стр. 1, а для этапа самоконтроля использовать № 3 (б), стр. 1. После выполнения самостоятельной работы ученики сопоставляют свое решение с образцом, предъявленным учителем, и убеждаются в том, что новый вычислительный прием ими освоен. Напомним, что при изучении нового материала первостепенное значение имеет создание ситуации успеха для каждого ребенка. Возможные ошибки должны здесь же исправляться, а материалы дорабатываться индивидуально, пока остальные учащиеся класса решают задачи на повторение.
Возможные ошибки должны здесь же исправляться, а материалы дорабатываться индивидуально, пока остальные учащиеся класса решают задачи на повторение.
На этапе повторения новое знание включается в систему знаний, а также решаются задания, обеспечивающие непрерывность развития содержательно‑методических линий курса. Так, на рассматриваемом уроке умножение многозначного числа на однозначное встречается при решении текстовых задач № 4–5, стр. 2, в уравнении № 6, стр. 2 и при работе с буквенными выражениями в № 7, стр. 2. Далее в задании № 8, стр. 2 повторяется правило порядка действий в выражениях и отрабатываются вычислительные навыки. В № 9, стр. 2 повторяются действия с многозначными числами, в № 10–11, стр. 2 – понятия равенства и пересечения множеств, которые связываются с рисованием геометрических фигур и перебором вариантов, а в № 12, стр. 2 предлагается логическая задача. Учитель на уроке введения нового знания выбирает для оставшихся 5–10 минут урока из этих заданий те, в которых учащиеся его класса испытывают больше затруднений.
Сделать этот выбор более осознанным и обоснованным позволяют «Электронные приложения к учебникам».
С другой стороны, методическим приемом, который позволяет существенно увеличить число решенных в классе примеров без перегрузки детей, является решение задач по выбору учащихся. Так, например, на данном уроке учитель может предложить учащимся на этапе повторения решить по выбору одно из заданий № 5–9, стр. 2. Учащиеся в течение 3–4 минут решают по одному выбранному ими заданию, а затем проговаривают их решение в течение следующих 5 минут. Таким образом, все задания воспроизведены в памяти детей, т. е. цель повторения достигнута. При этом в классе создается атмосфера психологической комфортности, так как каждый ребенок решает задание, которое он выбрал сам, а значит, то, которое ему больше понравилось. Задачи по выбору можно предлагать и для домашней работы.
Задачи по выбору можно предлагать и для домашней работы.
При подведении итога урока учитель обсуждает с учениками вопросы:
– Что нового узнали? (Научились умножать любое многозначное число на однозначное.)
– Какое математическое свойство для этого использовали? (Распределительное свойство умножения.)
– Кто уже чувствует себя уверенно в решении новых примеров?
– Что повторили? Что больше всего понравилось?
– Кто сегодня нам помогал на уроке?
– Как оцениваете свою работу?
Для домашней работы можно предложить учащимся придумать и решить свой пример на умножение многозначного числа на однозначное, решить задачу № 4, стр. 2 и по желанию – одно из заданий № 10–12, стр. 2. Таким образом, обязательное задание не займет у обучающихся больше 10–15 мин самостоятельной работы. При таком подходе исключена перегрузка детей, каждому из них обеспечивается возможность успешного усвоения необходимого минимума, и в то же время каждому предоставляется возможность обучения на высоком уровне за счет активного включения в деятельность на уроке и решения дополнительных развивающих заданий.
На уроках 7–8 рассматриваются более сложные случаи умножения многозначного числа на однозначное и случаи умножения круглых чисел, сводящиеся к ним. Так, в № 1, стр. 6 учащиеся распространяют на множество многозначных чисел изученное ранее правило: чтобы умножить круглые числа, надо выполнить умножение, не глядя на нули, а потом к полученному произведению приписать столько нулей, сколько в обоих множителях вместе. На основании этого правила при записи умножения круглых чисел в столбик для удобства вычислений нули мысленно отбрасываются и полученное однозначное число записывается в разряде единиц многозначного множителя:
На последующих уроках умножение многозначного числа на однозначное отрабатывается в основном в процессе выполнения проверки примеров на деление.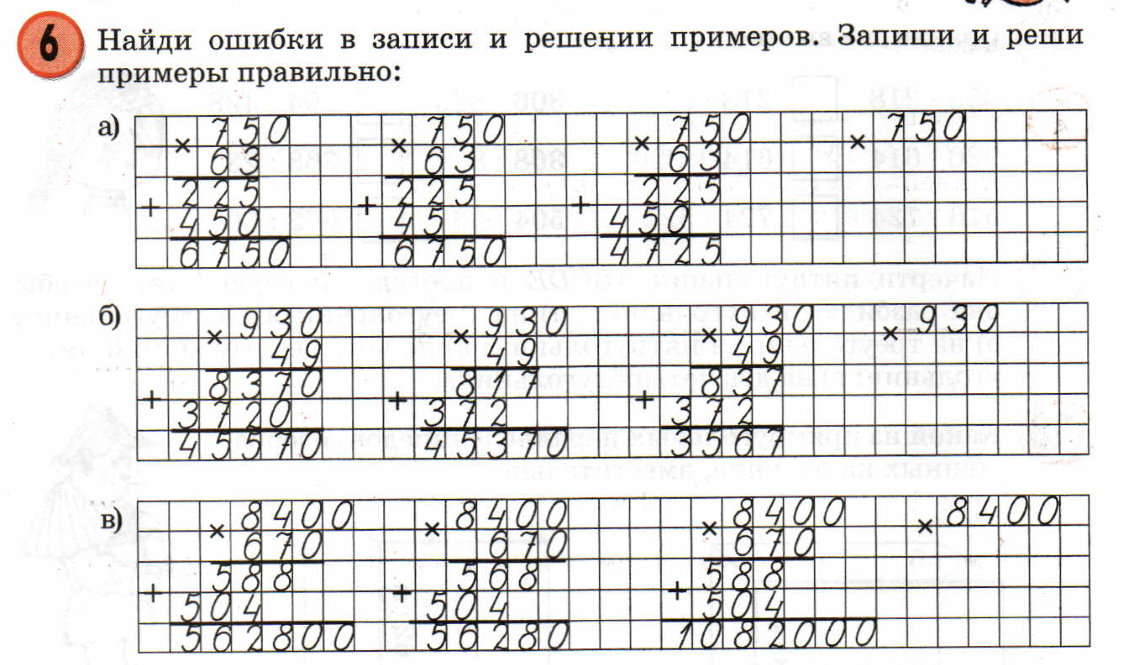
На уроке 8 рассматривается новый тип задач – задачи на нахождение величин по их сумме и разности. На основе предметных действий с моделями полосками ученики догадываются, что при вычитании из суммы двух чисел их разности получается удвоенное меньшее число, а при сложении суммы и разности – удвоенное большее число. Поэтому решить задачу, например, № 1, стр. 8 можно двумя способами:
Для этапа первичного закрепления предназначены задания № 3–4, стр. 8–9, а для этапа самостоятельной работы с самопроверкой в классе – № 2, стр. 8. Дома можно предложить им придумать и решить свои задачи на нахождение величин по их сумме и разности.
На всех данных и последующих уроках особое внимание уделяется комментированию решения уравнений по компонентам действий (№ 6, стр. 2; № 6, стр. 4; № 6, стр. 9; № 7, стр. 18; № 5, стр. 20; № 4, стр. 25 и т. д.). Это связано с подготовкой детей к изучению темы «Уравнения» на уроке 27 данной части учебника. К этому времени обучающиеся должны не только уметь на автоматизированном уровне верно находить неизвестные компоненты действий, но и комментировать решение по образцу, приведенному на стр. 77 учебника.
На уроках 9 – 12 формируется умение делить многозначные числа на однозначные и делить круглые числа, сводящиеся к делению на однозначное число, умение делать проверку деления умножением, а также повторяются и закрепляются нумерация, сложение и вычитание многозначных чисел, умножение многозначного числа на однозначное, решение текстовых задач. Учащиеся решают уравнения с комментированием по компонентам действий, повторяют понятие периметра треугольника, понятие числового луча, действия с единицами длины и массы, читают и записывают выражения.
При изучении внетабличного деления в пределах 100 учащиеся знакомились с правилом деления суммы на число. Сейчас это правило используется для построения алгоритма деления многозначного числа на однозначное. В итоге обсуждения учащиеся должны выявить и осмыслить основную идею, основной принцип деления многозначных чисел: сначала делится более крупная счетная единица, затем остаток дробится и делится следующая по величине счетная единица и так далее до конца. Новый материал вводится в обучение деятельностным методом.
Сейчас это правило используется для построения алгоритма деления многозначного числа на однозначное. В итоге обсуждения учащиеся должны выявить и осмыслить основную идею, основной принцип деления многозначных чисел: сначала делится более крупная счетная единица, затем остаток дробится и делится следующая по величине счетная единица и так далее до конца. Новый материал вводится в обучение деятельностным методом.
На уроке 9 на этапе актуализации знаний с учащимися нужно вспомнить взаимосвязь между умножением и делением (a : b = c ⇔ b · c = a, b 0), алгоритм деления с остатком и правило деления суммы на число, распространив его, как и в предыдущем случае, на сумму трех и более слагаемых.
На этапе постановки проблемы детям можно предложить в течение 2–3 минут в тетрадях в клетку самостоятельно решить примеры «по частям», т. е. используя правило деления суммы на число, и выявить в них закономерности:
Учащиеся могут заметить, что:
1) все примеры – на деление;
2) делимое увеличивается, а делитель не изменяется;
3) с увеличением делимого частное увеличивается;
4) если делимое увеличивается в 10 раз, то и частное увеличивается в 10 раз.
При решении последнего примера обычно возникает затруднение, которое мотивирует поиск нового способа действий (если и последний пример выполнят все ученики, можно попросить их найти лишний пример).
Далее учитель подводит учащихся к выявлению существенного для данного урока признака отличия последнего примера от предыдущих: первые четыре примера сводятся к делению двузначного числа на однозначное, а в последнем примере – деление трехзначного числа на однозначное. Этот признак отличия учащиеся должны проговорить вслух.
Таким образом, ставится цель урока – установить, как делится многозначное число на однозначное. (Если затруднений в решении последнего примера у обучающихся не возникнет, слово установить заменяется словом обосновать – ведь подобные примеры в классе ранее не рассматривались. )
)
На этапе «открытия» нового знания детям вначале предоставляется возможность выбрать метод рассуждений. Задания, рассмотренные в начале урока, должны сориентировать их на выбор правила деления суммы на число, распространенного на случай нескольких слагаемых. Для подбора слагаемых для вычисления частного 536 : 4 можно использовать графическую модель. Учитель рисует ее на доске, а учащиеся – в тетради:
Рассматривая ее, ученики должны догадаться, что для нахождения частного вначале надо разделить сотни (коробки), затем оставшуюся сотню перевести в десятки и делить все имеющиеся десятки (пачки) и, наконец, оставшийся десяток раздробить в единицы (штуки) и делить единицы. В менее подготовленных классах поиск решения целесообразно сопровождать не только графическим моделированием, но и предметным – работой с конкретными коробками, пачками и единицами предметов.
Получившиеся группы обводятся овалами – это «удобные слагаемые»:
Из приведенных рассуждений следует, что каждый получил 1 сотню, 3 десятка и 4 штуки, или 134 штуки предметов. На математическом языке проведенные рассуждения можно записать так:
536 : 4 = (400 + 120 + 16) : 4 = 400 : 4 + 120 : 4 + 16 : 4 = 100 + 30 + 4 = 134.
Эта цепочка преобразований записывается в тетрадь, и еще раз проговаривается полученный вывод: чтобы разделить многозначное число на однозначное, можно делимое разбить на сумму «удобных» слагаемых и делить «по частям», то есть по правилу деления суммы на число.
Применение этого способа действий весьма ограничено, но проведенные рассуждения помогут учащимся в дальнейшем осмыслить общий принцип деления многозначных чисел. Для перехода к делению углом надо показать им неудобство построенного способа действий, предложив, например, найти частное 11 768 : 4.
Понятно, что попытки найти «удобные» слагаемые вряд ли закончатся успехом, и тогда можно попросить детей еще раз вернуться к рисунку:
– Рассмотрите, с каких единиц мы начинали деление – с мелких или с крупных? (С крупных. )
)
– Конечно, ведь удобнее сначала раздать более крупные счетные единицы – коробки. Но вот у нас 1 коробка осталась, что нам пришлось сделать? (Достать пачки и делить уже пачки.)
– Правильно, нам пришлось раздробить сотни в десятки. А когда и десятки у нас закончились, что мы сделали? (Стали делить единицы.)
– Кто теперь догадается, как можно делить любое многозначное число, не подбирая слагаемые? (Делить сначала самые крупные счетные единицы, затем остаток дробить и делить более мелкие единицы.)
На доске в процессе беседы учитель кратко записывает суть выполняемых преобразований:
1) 5 с. : 4 = 1 с. (ост. 1 с.)
2) 13 д. : 4 = 3 д. (ост. 1 д.)
3) 16 ед. : 4 = 4 ед. Итак, 536 : 4 = 134.
Аналогично записывается решение примера 11 768 : 4, предложенного учителем:
1) 11 т. : 4 = 2 т. (ост. 3 т.)
2) 37 с. : 4 = 9 с. (ост. 1 с.)
3) 16 д. : 4 = 4 д.
4) 8 ед. : 4 = 2 ед. Итак, 11 768 : 4 = 2942.
Таким образом, поставленная проблема решена: найден общий способ деления многозначного числа на однозначное. Он заключается в делении с остатком возможно более крупных счетных единиц и последовательном переходе к делению более мелких счетных единиц. Однако остается проблема записи деления. На вопрос учителя: «Удобная ли запись деления?» – ответ всегда одинаковый: неудобная, громоздкая. Тогда можно предложить учащимся попробовать придумать свою запись, более короткую и удобную. Для этой цели лучше использовать первый пример – 536 : 4.
Только после того как дети предложат свои версии, следует показать им «свернутый» способ записи приведенных рассуждений – уголком, и прокомментировать его:
Проверку деления удобно делать умножением на основании взаимосвязи:
Так, для проверки выполненного деления можно число 2942 умножить на 4.
Учитель обращает внимание учащихся на то, что при комментировании примеров надо вначале указать первое неполное делимое, потом определить число цифр в частном, а затем рассказать, как находятся цифры в каждом разряде частного. При этом надо постоянно помнить о том, что на каждом шаге мы фактически выполняем деление с остатком, и поэтому получаемые остатки должны быть меньше делителя. Проверку решения удобно делать умножением.
При этом надо постоянно помнить о том, что на каждом шаге мы фактически выполняем деление с остатком, и поэтому получаемые остатки должны быть меньше делителя. Проверку решения удобно делать умножением.
Алгоритм письменного деления фиксируется с помощью блок-схемы:
Проблема разрешена.
Для проведения этапа первичного закрепления можно использовать задания № 3–6, стр. 11–12, которые решаются с проговариванием в громкой речи. В № 3 учащиеся находят частное всеми тремя рассмотренными способами. В № 4 внимание детей еще раз фиксируется на том, что остаток от деления всегда должен быть меньше делителя, проговариваются основные этапы деления многозначного числа на однозначное, выделенные в рамке на стр. 11. Примеры № 5–6 записываются в тетради в клетку и решаются по выбору. Здесь возможно комментирование в паре, в группе, создание игровых ситуаций. Достаточно, если каждый ребенок решит 2–3 примера. Параллельно проговаривается способ проверки деления умножением, зависимость между компонентами деления.
Задание № 2, стр. 10 целесообразно использовать на этапе самостоятельной работы с самопроверкой в классе. Оно менее сложное, чем примеры, решенные на предыдущем этапе урока, и содержит наглядную опору, которая поможет обучающимся лучше представить каждый этап деления.
На этапе повторения по выбору можно решить задания № 7 (а), стр. 12 и №9 (а), стр. 12.
При подведении итога урока обсуждаются вопросы:
– Что нового узнали? (Научились делить многозначное число на однозначное, записывать деление «углом».)
– Какой прием используется для устного деления? (Деление «по частям».)
– С каких единиц начинаем письменное деление? (С самых крупных.) А потом? (Делим по очереди более мелкие единицы.)
– Кто сегодня нам хорошо помогал?
– Кто доволен своей работой?
– Что повторили? Что больше всего понравилось?
В домашней работе можно предложить учащимся самостоятельно составить и решить пример на деление трехзначного числа на однозначное, построить его графическую модель и выполнить деление тремя способами по аналогии с тем, как это сделано в учебнике. Кроме того, решить по собственному выбору одно из заданий № 7 (б), 9 (б), стр. 12. В качестве дополнительного задания, которое выполняется по желанию, – одно из заданий №8, 10, стр. 12.
Кроме того, решить по собственному выбору одно из заданий № 7 (б), 9 (б), стр. 12. В качестве дополнительного задания, которое выполняется по желанию, – одно из заданий №8, 10, стр. 12.
На последующих уроках рассматриваются более сложные случаи деления: делимое содержит большее число цифр (урок 10), в частном получаются нули в середине и на конце (уроки 11–13).
Чтобы переварить знания, надо поглощать их с аппетитом.
(А. Франц)
Желаем Вам удачи и творческих успехов!
Мы вместе, значит, у нас все получится!
3 класс — деление, примеры и задачи на деление чисел и проверка.
Дата публикации: .
Задачи на тему: «Принципы, свойства и проверка результатов деления»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать:
Деление двузначного числа на однозначное (PDF)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Л.Г.Петерсон
М.И.Моро
Т.Е.Демидовой
Деление двухзначного числа на однозначное
1. Реши примеры.
| 21 : 7 = | 27 : 9 = | 32 : 4 = |
| 45 : 9 = | 49 : 7 = | 56 : 8 = |
| 36 : 6 = | 64 : 8 = | 63 : 3 = |
| 35 : 5 = | 42 : 6 = | 25 : 5 = |
| 36 : 9 = | 27 : 3 = | 72 : 8 = |
| 18 : 3 = | 36 : 3 = | 91 : 7 = |
| 15 : 5 = | 10 : 10 = | 10 : 2 = |
| 81 : 9 = | 9 : 3 = | 50 : 10 = |
2. Выполни деление и проверь результат умножением.
Выполни деление и проверь результат умножением.
| 12 : 2 = | 24 : 6 = | 14 : 7 = |
| 20 : 2 = | 60 : 4 = | 40 : 5 = |
3. Реши примеры, правильно выполняя последовательность действий.
72 : 8 + 22 * 4 — 28 : 4 =
36 — 81 : 9 + 12 : 6 * 7 =
17 + 7 * 5 — 48 : 4 =
90 : 3 — 24 + 11 * 5 =
4. Составь числовые выражения, содержащие операцию деления, и реши их.
4.1. Используй числа: 5, 9, 12, 17, 34, 58.
4.2. Используй числа: 6, 12, 16, 18, 24, 32.
5. Запиши заданные предложения в виде числовых выражений и реши их.
3.1. К числу 27 прибавь частное чисел 64 и 8.
3.2. К числу 43 прибавь частное чисел 33 и 3.
3.3. Из числа 36 вычти частное чисел 45 и 9.
3.3. Из числа 89 вычти частное чисел 72 и 8.
Решение текстовых задач на деление
1. Необходимо разложить 56 кг пряников в 8 пакетов. Сколько кг поместится в один пакет?
2. Рабочие построили 3 метра стены. Для этого им потребовалось 63 кирпича. Сколько кирпичей необходимо для строительства 1 метра стены?
3. На новый год 3 классу раздали 99 конфет. Сколько конфет досталось каждому ученику, если в классе учится 11 детей?
4. Ваня, Сережа и Маша сорвали с яблони 27 яблок. Можно ли разделить яблоки поровну между ребятами? Сколько яблок будет у каждого? Сколько еще яблок надо сорвать, чтобы у каждого было по 14 яблок?
Обзор сложения, вычитания, умножения и деления — математика для 3-го класса
Обзор фактов сложения, вычитания, умножения и деления
В математике есть 4 основных операции: сложение, вычитание, умножение и деление.
🤓 Вы проделали большую работу, изучая каждую из них.
В этом уроке давайте рассмотрим то, что вы узнали. 🤗
Обзор дополнения
Объединение двух или более чисел называется сложением .
✅ Уравнение сложения состоит из двух или более сложений, символа плюса (+), символа равенства (=) и суммы.
Попробуем сложить числа.
Пример добавления 1
4,255 + 3,104 =?
Давайте сложим числа, используя форму столбца .
Итак, каков ответ? 🤓
Верно! Это 7359.
4,255 + 3,104 = 7,359
Отличная работа! 👌
Пример добавления 2
675 + 198 =?
Добавляем! (Используйте перегруппировку , при необходимости .)
Какая сумма?
Очень хорошо! Это 873.
675 + 198 = 873
Отлично! 😎
Теперь перейдем к вычитанию.
Обзор вычитания
Вы помните, что такое вычитание? 🤔
Вычитание убирает часть числа.
✅ Уравнение вычитания состоит из , вычитаемого , вычитаемого , , символа минуса (-), символа равенства (=) и разности . Давайте теперь попробуем вычесть несколько чисел.
Пример вычитания 1
497 — 251 =?
Давайте вычтем числа, используя форму столбца .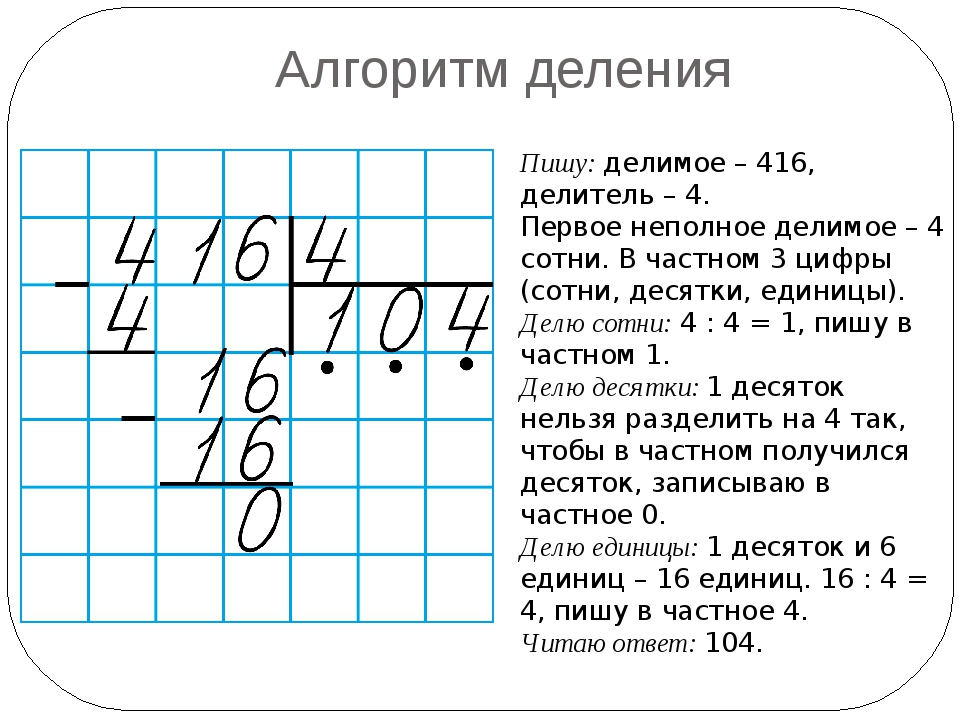
В чем разница? 🤓
497 — 251 = 246
Отличная работа! 👏
Пример вычитания 2
7 301 — 6 361 =?
Давайте вычесть! Используйте перегруппировку , при необходимости .
Какая разница у тебя? 😃
7 301 — 6 361 = 940
Вперед! 🤗
Давайте теперь рассмотрим умножение и деление.
Обзор умножения
Сложение равных групп снова и снова называется умножением .
👉 Например, когда мы умножаем 2 круга 5 раз, мы получаем 10 кругов.
5 × 2 = 10
✅ Уравнение умножения состоит из множителя , множителя , символа умножения (×), равно символу (=) и произведению .
Множитель и множимое также называются множителями .
Давайте теперь рассмотрим несколько примеров.
Пример умножения 1
9 × 8 =?
Давайте умножим эти числа, используя повторное сложение .
✅ Мы можем прибавить 9 к себе 8 раз, или прибавить 8 к себе 9 раз.
9 × 8 = 9 + 9 + 9 + 9 + 9 + 9 + + 9000 9 = 72
Итак,
9 × 8 = 72
Отличная работа! 👌
Пример умножения 2
256 × 3 =?
Давайте попробуем умножить эти числа, используя форму столбца .
✅ Сначала мы умножаем цифру в разряде единиц на 3.
✅ Затем мы умножаем цифру в разряде десятков на 3 и складываем перенос.
✅ Наконец, мы умножаем цифру в разряде сотен на 3 и складываем перенос.
Какой ответ вы получили?
256 × 3 = 768
Отличная работа! 👏
Подразделение Обзор
Вы помните, что такое деление? 🤓
Верно!
Раздел разбивает номер на равные группы.
👉 Например, когда мы разбиваем 10 кругов на 5 равных групп, мы получаем 2 круга в каждой группе.
10 ÷ 5 = 2
✅ Уравнение деления состоит из деления , делителя , символа деления (÷ или ⟌) и частного .
Давайте теперь рассмотрим несколько примеров деления.
Пример отдела 1
30 ÷ 6 =?
Давайте решим эту задачу деления, используя повторное вычитание .
✅ Мы начинаем с 30 и снова и снова вычитаем 6, , пока не дойдем до 0. Количество вычитаний — это наш ответ.
Сколько раз вы вычитали?
Правильно! 5 раз.
Итак,
30 ÷ 6 = 5
Отлично! 🤗
Совет: Думайте о делении как о противоположности умножения. Если вы видите 30 ÷ 6 =? подумайте: какое число, умноженное на 6, равно 30?
Если вы видите 30 ÷ 6 =? подумайте: какое число, умноженное на 6, равно 30?
6 х? = 30
И вы получите тот же ответ: 5!
Пример отдела 2
882 ÷ 7 =?
Давайте решим этот вопрос, используя длинное деление .
✅ Начнем с расстановки чисел в форме столбца.
✅ Теперь, посмотрим на первую цифру.
Вы можете сказать, сколько семерок поместится в восьмерку? 🤔
Очень хорошо! 1.
Напишите сверху 1 , как частное и запишите произведение от 1 и 7 под 8.
Теперь вычтите этот продукт из 8 , чтобы получить остаток.
Отлично! 😎
✅ Затем уберите следующую цифру и повторите процесс .
✅ Наконец, опустите последнюю цифру и повторите процесс .
Какой ответ вы получили?
882 ÷ 7 = 126
Отличная работа! 👏
🎉 Вы только что рассмотрели наиболее важные моменты, касающиеся сложения, вычитания, умножения и деления.
А теперь начните практику ниже.
Математика для 3-го класса — Блок 2: Умножение и деление, Часть 1
Сводка по агрегату
Модуль 2 открывает учащимся глаза на некоторые из самых важных материалов, которые они усвоят в 3-м классе — умножение и деление. В этом разделе «учащиеся начинают развивать эти концепции, работая с числами, с которыми они более знакомы, такими как 2, 5 и 10, в дополнение к числам, которые легко пропустить, например, 3 и 4», позволяя познавательным требуют использования самих понятий умножения и деления, а не чисел (CCSS Toolbox, Sequenced Units for Common Core State Standards in Mathematics Grade 3). Затем в Модуле 3 студенты будут работать над более сложными модулями 0, 1, 6–9 и кратными 10.
В этом разделе «учащиеся начинают развивать эти концепции, работая с числами, с которыми они более знакомы, такими как 2, 5 и 10, в дополнение к числам, которые легко пропустить, например, 3 и 4», позволяя познавательным требуют использования самих понятий умножения и деления, а не чисел (CCSS Toolbox, Sequenced Units for Common Core State Standards in Mathematics Grade 3). Затем в Модуле 3 студенты будут работать над более сложными модулями 0, 1, 6–9 и кратными 10.
Во 2-м классе ученики научились считать объекты в массивах, используя повторное сложение (2.OA.4), чтобы получить основу для умножения. Они также проделали обширную работу над одно- и двухэтапными задачами со словами, включающими сложение и вычитание, освоив все типы задач, связанных с этими операциями (2.OA.1). Таким образом, учащиеся развили сильную склонность к решению проблем и имеют базовое содержание, необходимое для того, чтобы сразу приступить к умножению и делению в этом разделе.
В начале этого раздела учащиеся получают понимание умножения и деления в контексте задач равных групп и массивов в Теме A. Чтобы сосредоточиться на концептуальном понимании умножения и деления (3.OA.1, 3. OA.2), в теме A не обсуждаются конкретные стратегии решения, и поэтому учащиеся могут подсчитать все объекты (стратегия уровня 1) или запомнить их подсчет пропусков и повторное добавление (стратегии уровня 2) из класса 2, чтобы найти продукт. Тем не менее, в темах B и C основное внимание уделяется разработке более эффективных стратегий решения умножения и деления, включая подсчет пропусков и повторное сложение (стратегии уровня 2), а также «простое знание» фактов, которое способствует достижению цели. «К концу 3 класса [ученики] знают по памяти все произведения двух однозначных чисел и связанные с ними факты деления» (3.OA.7). Как говорится в разделе «Операции и прогрессирование алгебраического мышления», «освоение этого материала и достижение беглости в однозначном умножении и соответствующем делении может занять довольно много времени, потому что не существует общих стратегий для умножения или деления всех однозначных чисел, как это есть для сложения или сложения. вычитание »(OA Progression, стр. 22). Таким образом, поскольку «существует множество моделей и стратегий, зависящих от конкретных чисел», они сначала работают с факторами 2, 5 и 10 в теме B, поскольку они выучили эти последовательности подсчета пропусков во 2 классе.Затем в теме C они работают с новыми факторами 3 и 4. Только тогда, когда учащиеся лучше познакомятся с этими факторами, они смогут решать с ними более сложные и / или абстрактные задачи, включая определение неизвестного целого числа в таблице. уравнение умножения или деления, связывающее три целых числа (3.OA.4) и решение двухэтапных задач со словами с использованием всех четырех операций (3.OA.3, 3.OA.8), оценивая разумность их ответов для различных типы проблем в теме D.
вычитание »(OA Progression, стр. 22). Таким образом, поскольку «существует множество моделей и стратегий, зависящих от конкретных чисел», они сначала работают с факторами 2, 5 и 10 в теме B, поскольку они выучили эти последовательности подсчета пропусков во 2 классе.Затем в теме C они работают с новыми факторами 3 и 4. Только тогда, когда учащиеся лучше познакомятся с этими факторами, они смогут решать с ними более сложные и / или абстрактные задачи, включая определение неизвестного целого числа в таблице. уравнение умножения или деления, связывающее три целых числа (3.OA.4) и решение двухэтапных задач со словами с использованием всех четырех операций (3.OA.3, 3.OA.8), оценивая разумность их ответов для различных типы проблем в теме D.
На протяжении этого раздела студенты занимаются различными математическими упражнениями.В блоке особое внимание уделяется абстрактному и количественному мышлению, поскольку учащиеся начинают понимать значение умножения и деления, а также абстрактные символы, используемые для их представления (МР.2). Кроме того, учащиеся моделируют математику с помощью этих новых операций, решая с их помощью одно- и двухшаговые уравнения (МР.4).
Это введение в умножение и деление будет углублено в Блоке 3, когда студенты будут изучать более сложные множители 0, 1, 6–9 и кратные 10.Затем, в Модуле 4, студенты будут изучать область как приложение умножения. В 4 классе их понимание умножения и деления станет еще более тонким, когда они придут к пониманию мультипликативного сравнения и решат связанные с ним словесные задачи (4.OA.1, 4.OA.2). Кроме того, они будут решать многоступенчатые задачи со словами, включающие все четыре операции, иногда при необходимости интерпретировать остаток в контексте задачи (4.OA.3). Наконец, студенты станут более свободно владеть умножением и делением, умножением целого числа до четырех цифр на однозначное целое число и два двузначных числа, а также деление до четырехзначных дивидендов на однозначное число. делитель (4.NBT.5, 4.NBT.6). Умножение и деление обеспечивают основу для множества алгебраических и геометрических тем, от линейных функций до тригонометрии, и, таким образом, это содержание имеет решающее значение для всего будущего математического обучения.
делитель (4.NBT.5, 4.NBT.6). Умножение и деление обеспечивают основу для множества алгебраических и геометрических тем, от линейных функций до тригонометрии, и, таким образом, это содержание имеет решающее значение для всего будущего математического обучения.
Темп: 19 учебных дней (16 уроков, 2 гибких дня, 1 контрольный день)
Инструкции по корректировке темпа на 2020-2021 учебный год в связи с закрытием школ см. В нашем разделе «Рекомендуемые корректировки для 3-го класса и последовательности».
Задания по математике
Дополнение
На этой странице указателя вы найдете ссылки на все типы рабочих листов, включая основные факты, двухзначные дополнения, трехзначные дополнения, четырехзначные дополнения, сложение дробей, десятичное сложение, семейства фактов и денежное добавление. .
Дополнение: основные факты
Рабочие листы с основными однозначными фактами сложения (суммы до 18).
Дополнение: 3-значные добавления
Практикуйтесь в сложении 3-значных чисел вместе с этими печатными листами, карточками задач и играми.
Сложение: 4- и 5-значные слагаемые
Предложите своим ученикам решить задачи на сложение с 4- и 5-значными числами.
Сложение: 3 или более слагаемых
Проблемы с добавлением столбца с 3 или более слагаемыми 1, 2, 3 и 4-значными числами.
Сочетание сложения и вычитания: базовое
Рабочие листы, карточки и числовые строки на этой странице содержат сочетание основных задач сложения и вычитания с однозначными числами.
Сложение: Дроби
Сложите дроби и смешанные числа с одинаковыми знаменателями, а также с разными знаменателями.
Свойства сложения
Эти рабочие листы были созданы для обучения студентов коммутативным и ассоциативным свойствам сложения.
Квадраты сложения
Развивайте навыки логического мышления с этими рабочими листами сложения квадратов.
Семейства фактов сложения-вычитания
Треугольники семейства основных фактов, числовые связи и таблицы фактов для сложения и вычитания.
Дополнение: игра на сумму (базовое дополнение)
На этих печатных игровых досках учащиеся раскрашивают пары чисел, которые равны заданной сумме.
Алгебра и предварительная алгебра
Напишите алгебраические выражения, научитесь определять независимые / зависимые переменные, находить переменные в уравнениях, работать с неравенствами и т. Д.
Углы: типы и измерение
Использование транспортира для измерения прямых, острых и тупых углов.
Углы: дополнительные, дополнительные, вертикальные
Загрузите рабочие листы, чтобы попрактиковаться в геометрических концепциях, связанных с вертикальными, дополнительными и дополнительными углами.
Площадь треугольников
Используйте формулу A = 1/2 x (b x h) для вычисления площади треугольников
Рабочие листы с площадью
Вычислите площадь (в квадратных единицах) фигур на этих листах.
Ящичковые диаграммы (диаграммы «ящик и усы»)
Используйте эти рабочие листы, чтобы помочь студентам узнать о статистике и создании диаграмм с ячейками и усами. Существуют также рабочие листы по вычислению Q1, Q3, медианы, минимального и максимального значений.
Календари (математика)
Календари, чтобы помочь студентам с годами, месяцами, неделями и днями в календаре.
Рабочие листы вместимости
Рабочие листы объема или вместимости (галлоны, кварты, пинты и чашки).
Круги: радиус, диаметр, окружность
Вычислите диаметр и радиус окружности; также включает рабочие листы окружности и площади.
Рабочие листы для раскраски по номерам
Раскрасьте загадочные картинки в соответствии с цифровой клавишей внизу.
Подсчет денег (австралийский)
Используйте эти рабочие листы, чтобы попрактиковаться в подсчете австралийских денег.
Подсчет денег (канадский)
Подсчитайте мультяшек, психов, четвертаков, пятак и десятицентовиков с помощью этих рабочих листов канадской валюты.
Подсчет денег (британские фунты)
Научитесь считать фунты и пенсы, монеты, используемые в Соединенном Королевстве.
Подсчет денег (США)
Практикуйтесь в подсчете американских денег (пенни, пятак, десять центов и четвертаки).
Рабочие листы подсчета 0–30 (очень простой)
Научитесь считать и записывать числа до 30.
Рабочие листы счета (более продвинутый уровень)
Узнайте, как точно считать двух-, трех- и четырехзначные числа. Заполните числовые строки, скажите, какое число идет раньше, и пропустите счет.
Daily Math Review
На этой странице вы найдете более 100 рабочих листов для ежедневного повторения («Math Buzz»), рассчитанных для классов с 1 по 5.
Ежедневные словесные задачи
В этой области есть ежедневные словесные задачи по математике для учащихся с 1 по 5. Есть сотни графических текстовых задач, которые нужно решить учащимся, и достаточно места для демонстрации своей работы.
Сложение и вычитание десятичных чисел
Сложение и вычитание десятичных чисел с разрядами десятых, сотых и тысячных долей.
Десятичное деление
Практикуйте деление в столбик с десятичными числами.
Десятичное умножение
Практикуйтесь в задачах умножения с десятичными множителями и произведениями.
Десятичные рабочие листы
Присвоение имен и работа с десятичными числами.
Рабочие листы деления: базовые
Рабочие листы основных разделов, игры и мероприятия.
Рабочие листы деления: длинные деления
Рабочие листы длинного деления с 2, 3 и 4-значными дивидендами.
Уравнения (базовая алгебра)
Научитесь балансировать простые алгебраические уравнения и находить значения переменных.
Четные и нечетные рабочие листы
Определение нечетных и четных чисел
Рабочие листы с экспонентами
Найдите экспоненты однозначных чисел на этих печатных рабочих листах и карточках задач.
Рабочие листы факторинга
Полное дерево факторов, найдите наибольшие общие множители и наименьшие общие множители.
Рабочие листы дробей (продвинутый уровень)
Сокращение дробей, упорядочивание дробей, эквивалентные дроби и сравнение дробей.
Рабочие листы фракций (базовые)
Определение основных фракций, полос фракций, манипуляторов дробей.
Дроби: сложение
Найдите суммы дробей и смешанных чисел. Включает в себя рабочие листы с дробями с одинаковым знаменателем, а также с дробями с одинаковым знаменателем.
Дроби: деление
Делите дроби и смешанные числа. Многие из этих рабочих листов включают в себя иллюстрированные задачи, задачи с графической моделью, а также текстовые задачи.
Дроби: смешанные числа
Практикуйте базовые навыки смешанного числа.
Дроби: Умножение
Умножайте дроби и смешанные числа. Многие рабочие листы включают модели и диаграммы, а также текстовые задания.
Дроби: обратные дроби
Распечатайте эти рабочие листы, чтобы помочь учащимся узнать о взаимных дробях.
Дроби: вычитание
Практикуйтесь в вычитании дробей и смешанных чисел. Включает подобные и непохожие знаменатели.
«Рамки и стрелки».
Используйте упражнения «Рамки и стрелки» для развития навыков логического мышления.
Графики: гистограммы
Прочтите гистограммы на рабочих листах и ответьте на вопросы.
Построение графиков: линейные графики
Расскажите о линейных графиках на рабочих листах и ответьте на вопросы.
Графики: линейные графики
Линейные графики — это особый тип числовой линии, который представляет частоту данных.
Графики: пиктограммы
Изучите пиктограммы на рабочих листах и ответьте на вопросы.
Графики: круговые диаграммы
Анализируйте круговые диаграммы на рабочих листах и отвечайте на вопросы.
Больше, меньше рабочих листов
Сравните числа больше, меньше и равные.
Таблицы сотен
Воспользуйтесь этими полезными таблицами разрядов, сотнями и девяноста девятками.
Ящики ввода и вывода
Заполните эти поля ввода и вывода для печати или поля правил.
Неравенства
Решите неравенства и изобразите их на графике.Включает неравенства с одной переменной, одноэтапным и двухэтапным неравенством.
Целые числа (базовые)
Сравните, упорядочите, сложите и вычтите положительные и отрицательные числа.
Наименьшее общее кратное (НОК)
Определите наименьшее общее кратное для каждого набора чисел
Линии, сегменты, лучи
Узнайте о прямых, линейных сегментах, лучах, параллельных и перпендикулярных прямых.
Математические кроссворды
Решайте математические задачи и разгадывайте кроссворды, используя ответы.
Загадки по математике
Решайте математические задачи, чтобы расшифровать ответ на забавные загадки.Включает в себя широкий спектр математических навыков, включая сложение, вычитание, умножение, деление, разметку, округление и многое другое.
Отрывки для математических рассказов
На этой странице есть отрывки для чтения целиком. Учащиеся используют информацию из отрывков для решения математических задач. Они намного длиннее, чем «обычные» задачи со словами.
Рабочие листы для средних (средних) значений
Вычислите среднее или среднее значение чисел.
Среднее значение, Медиана, Режим и Диапазон
Вычислите режим, медиану, среднее значение и диапазон заданных чисел.
Measurement Index
Выберите типы таблиц измерений, которые вам нужны, включая линейные измерения, емкость и температуру.
Измерение: CM, MM и M
Практикуйте метрические линейные измерения: сантиметры, миллиметры и метры.
Измерение: футы, ярды, дюймы
Изучение американских линейных измерений; дюймы, футы и ярды.
Измерение: граммы и килограммы
Измерение веса и преобразование в граммы и килограммы и обратно.
Измерение: литры и миллилитры
Оцените и преобразуйте измерения емкости в литры и миллилитры.
Измерение: фунты и унции
Измерьте вес и преобразуйте его в унции и фунты и обратно.
Математика в средней школе
Эта индексная страница свяжет вас с десятками тем по математике в средней школе на этом сайте. Темы включают неравенство, абсолютное значение, алгебру и многое другое.
Minute Math Drills
Листы упражнений и упражнений для базового сложения, вычитания, умножения и деления.
Кратные
Эти рабочие листы помогут студентам научиться находить и определять кратные числа.
Умножение (Свойства)
Узнайте об ассоциативных, распределительных, коммутативных и тождественных свойствах умножения.
Таблицы умножения
Распечатайте эти таблицы и таблицы умножения, чтобы студенты могли использовать их в качестве справки.
Рабочие листы умножения: Advanced
Решайте задачи двузначного и трехзначного умножения.
Рабочие листы умножения: Basic
Изучите основные факты умножения с помощью этих рабочих листов, загадочных картинок и игр.
Семейства фактов с делением-умножением
Базовые числовые связи, рабочие листы семейства фактов и треугольники для деления и умножения.
Умножение: сеточное умножение
Умножение на 2-, 3- или 4-значные числа с решетчатой сеткой.
Mystery Graph Art
Постройте упорядоченные пары, чтобы раскрыть загадочные картинки.
Mystery Math Pictures
Решите факты сложения, вычитания, умножения и деления, чтобы раскрыть загадочную картинку.
Детектив по числам (секретные числа)
Студенты будут использовать подсказки, размещаемые каждый день, чтобы вычислить еженедельное секретное число.
Числовые строки
Печатные рабочие листы числовых строк для обучения счету, сложению, вычитанию, шаблонам чисел, дробям и десятичным знакам.
Порядок операций
Практический порядок операций: скобки и показатели, затем умножение и деление, затем сложение и вычитание.
Заказанные пары; Координатные плоскости
Координатные плоскости и рабочие листы заказанных пар.
Порядковые номера
Порядковые номера определяют позицию в серии. (примеры: первый, второй, третий, четвертый и т. д.)
Шаблоны: Число
Учащиеся должны указать числа, которые идут следующими в этих шаблонах.
Выкройки: Рисунок
Учащиеся определяют, какие изображения будут следующими в выкройках.
Рабочие листы с процентами
Преобразование десятичных чисел и дробей в проценты.
Рабочие листы периметра
Добавьте, чтобы найти периметры многоугольников на этих листах.
Рабочие листы для разметки
Нахождение значения подчеркнутой цифры; стандартная и развернутая форма; округление.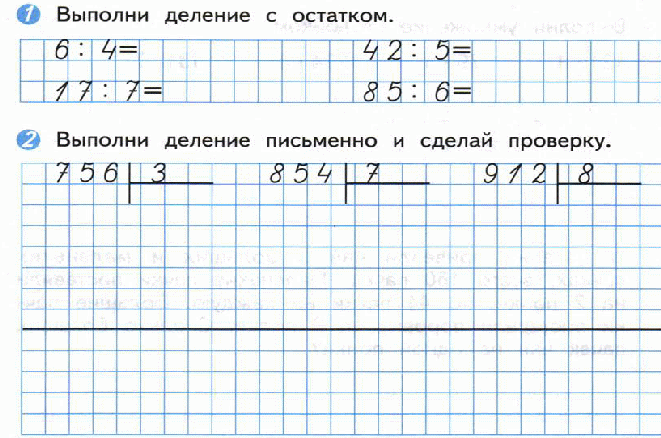
Простые и составные числа
Узнайте о различиях между простыми и составными числами. Кроме того, научитесь определять и находить простые числа путем факторизации или с помощью решета Эратосфена.
Рабочие листы с полигонами
Определение многоугольников и работа с ними.
Таблицы вероятностей
Определите вероятность определенных результатов.
Puzzle Match Math Games
Пазлы для печати, которые вы можете вырезать, чтобы учащиеся соответствовали друг другу. Отлично подходит для учебных центров, занятий в небольших группах и самостоятельной практики.
Теорема Пифагора
Найдите длины сторон прямоугольного треугольника по формуле теоремы Пифагора.
Рабочие листы с QR-кодами
Учащиеся используют iPad или смартфон для сканирования QR-кодов, чтобы заполнить или проверить задачи на каждой из этих математических листов.
Коэффициенты
Практикуйтесь в сравнении пар величин с помощью соотношений.
Отражение, вращение и перенос
Определите отраженные, повернутые и перемещенные формы.
Римские цифры
Научитесь читать и писать римские цифры с помощью этих распечатываемых листов и заданий.
Рабочие листы округления чисел
Округление чисел до ближайших десятков и сотен.
Научное представление
Научитесь записывать числа в экспоненциальном представлении.
Математика секретного кода
На этих листах студенты будут использовать ключ для декодирования секретных чисел в каждой задаче сложения, вычитания, умножения или деления.
Подобные и совпадающие рабочие листы
Определите похожие и совпадающие формы.
Счет с пропуском на 100 секунд
Используйте эти рабочие листы, чтобы научить студентов считать, пропускать сотни.
Пропустить счет по 10 с
Просмотрите счет по десяткам с помощью этих печатных форм.
Пропустить счет на 11 секунд
Подсчитать одиннадцать, умножить на одиннадцать и заполнить пропущенные числа.
Пропуск подсчета по 12 с.
Заполните пустые поля и задачи со словами, считая по двенадцати.
Пропустить счет на 25 секунд
Пропустить счет на двадцать пять очень важно, если вы учите своих учеников считать деньги.
Пропуск счета на 2 секунды
Используйте эти распечатки, чтобы научить студентов пропускать счет с интервалом в два.
Пропустить счет на 3 секунды
Набор рабочих листов на этой странице поможет студентам научиться считать по тройкам.
Пропустить счет по 4 секунды
Если вы учите студентов считать по четыре, попробуйте эти рабочие листы.
Пропустить счет на 5 секунд
Когда вы учите студентов считать по пятакам или по пятеркам, эти рабочие листы могут быть вам полезны.
Рабочие листы «Слайды, переворачивания и повороты»
Сообщите, были ли формы перевернуты, сдвинуты или повернуты.
Уклон
На этих рабочих листах учащиеся будут использовать графики, упорядоченные пары и таблицы для вычисления наклона прямых линий.
Рабочие листы твердых форм
Назовите твердые геометрические формы: прямоугольные призмы, кубы, сферы и цилиндры.
Специальные числа
Эти рабочие листы охватывают множество концепций разряда, включая четное / нечетное, определение значения цифр и запись чисел в развернутой форме.
Вычитание
Вычитание однозначных и многозначных чисел. Включает 1, 2, 3 и 4-значные числа.Также есть ссылки на десятичную дробь и вычитание денег.
Вычитание: базовое
Практикуйте основные факты однозначного вычитания; рабочие листы концепции и сверления.
Вычитание дробей
Практикуйтесь в вычитании дробей и смешанных чисел с помощью этих распечатываемых листов и карточек задач.
Площадь поверхности
Вычислите площадь поверхности прямоугольных призм и других трехмерных форм.
Рабочие листы симметрии
Найдите линии симметрии, определите симметричные фигуры и завершите симметричные формы.
Tally Marks
Научитесь считать объекты с помощью счетных меток.
Таблицы температуры
Считайте показания термометров Цельсия и Фаренгейта и укажите температуру.
Математика с десятью кадрами
Печатные задания с десятью кадрами для обучения счету, основному сложению и простому вычитанию.
Рабочие листы тесселяции
Научите учащихся распознавать геометрическую мозаику двумерных фигур.
Таблицы времени
Узнайте, как определять время с точностью до минуты, часа и четверти часа.
Время: прошедшее время
Определите количество прошедшего времени.
Диаграммы Венна (математика)
На этой странице есть рабочие листы математических диаграмм Венна.
Объем — Градуированные цилиндры
Эти рабочие листы содержат изображения градуированных цилиндров. Студенты должны указать правильный объем в миллилитрах.
Рабочие листы по объему
Вычислите объем твердых фигур. Включает объемные «счетные кубики», прямоугольные призмы, конусы, цилиндры и сферы.
Рабочие листы задач со словами (по типам)
Практикуйте задачи со словами на сложение, вычитание, умножение и деление.
Рабочие листы для задач со словами (смешанные)
Проанализируйте навыки работы со смешанными словами на разных уровнях обучения.
Задачи со словами (несколько шагов)
Эти задачи со словами состоят из нескольких этапов и требуют от учащихся навыков критического мышления.
Рабочие листы сложения
Здесь вы можете ссылаться на все типы рабочих листов сложения, включая основные факты, сложение дробей, 2-значное, 3-значное и 4-значное сложение.
Рабочие листы дробей
Указатель наших рабочих листов базового и продвинутого уровней.
Рабочие листы по геометрии
Изучите площадь, периметр, симметрию, многоугольники, твердые фигуры и многое другое.
Рабочие листы для построения графиков
Выберите круговые диаграммы, гистограммы и линейные диаграммы.
Пропуск рабочих листов
Подсчет по 2, 3, 4, 5, 10, 25 или 100 секунд.
Рабочие листы вычитания
Вот индексная страница, которая ссылается на все разделы вычитания нашего веб-сайта.
Рабочие листы по математическим навыкам
Эта страница содержит только частичный указатель заданий по математическим навыкам на S.T.W.
Полный указатель веб-сайта
Просмотрите полный указатель всех рабочих листов по математике, английскому языку, правописанию, фонетике, грамматике, естественным наукам и общественным наукам, которые можно найти на этом веб-сайте.
Массивы, умножение и деление
Массивы, умножение и деление
Дженни Пеннант с помощью Дженни Уэй и Майка Аскью исследует, как использовать массив в качестве инструмента мышления, чтобы помочь детям развить глубокое понимание умножения и деления.
Использование массивов для исследования чисел
Массивы — это полезные модели для умножения, которые можно использовать по-разному, от высоко структурированных уроков до игр и открытых исследований.
Массив формируется путем размещения набора объектов в строки и столбцы. Каждый столбец должен содержать такое же количество объектов, что и другие столбцы, и каждая строка должна иметь то же количество объектов, что и другие строки.
Следующий массив, состоящий из четырех столбцов и трех строк, может использоваться для представления числового предложения 3 x 4 = 12, 4 x 3 = 12, 3 + 3 + 3 + 3 = 12 и 4 + 4 + 4 = 12.
Построение фактов и таблиц умножения
Массивы можно использовать для конструктивного построения фактов умножения.Прежде чем сверлить и запоминать таблицы, дети должны понять, как эти факты выводятся. Например, постепенно добавляя еще один столбец из трех объектов, дети могут построить себе трехкратные таблицы. Это представление не только помогает понять процесс, но и дает визуальное изображение для
детей, на которых можно рисовать, когда они начнут использовать и запоминать основные числовые факты.
Использование массивов для исследования больших чисел
Массивы могут быть полезны для изучения вычислений, таких как 13 x 5, где массив можно разделить на полезные части, такие как 10 и 3.Это означает, что дети могут использовать свои известные числовые факты для вычислений.
Здесь 13 x 5 = (10 x 5) + (3 x 5).
Через некоторое время рисование всех точек может стать очень утомительным! Пустой массив становится очень полезным инструментом, помогающим детям моделировать свое мышление и разрабатывать более сложные операции умножения в неформальной обстановке.
Вот ребенок, использующий пустой массив в качестве инструмента мышления, чтобы помочь им вычислить 15 x 14.
Пустой массив помогает детям использовать другие стратегии, такие как компенсация, при выполнении умножения.Здесь, чтобы вычислить 34 x 9, ребенок решил сделать 34 x 10, а затем снять 34 x 1.
Помимо пустого массива, эта стратегия «деления умножения на простые части» может быть формализована в виде сеточный метод. Дети могут видеть, как «абстрактный» метод сетки накладывает на массив и формализует пустой массив в стандартной форме.
Деление как обратная операция умножения
Из четырех операций деление является наиболее сложной задачей для молодых студентов.Полное понимание деления обычно сильно отстает от других операций. Для многих детей возможности исследовать концепцию на конкретных материалах ограничиваются задолго до того, как они осознают взаимосвязь между разделением и тремя другими операциями. Одна из таких отношений, обратная связь
Между делением и умножением можно эффективно проиллюстрировать использование массивов.
Например; 3 × 5 = 15 или 3 строки из 5 составляют 15, могут быть представлены следующим массивом.
Если взглянуть на массив по-другому, можно увидеть обратное, то есть
15 ÷ 3 = 5 или 15, помещенные в 3 строки, дают 5 столбцов — или 5 в каждой строке.
Язык явно играет важную роль в способности выражать математические взаимосвязи, и физический массив поддерживает этот аспект понимания, давая детям конкретный образ для разговора.
Размещение математики в контексте реальной жизни с помощью словесных задач может облегчить как понимание взаимосвязи, так и ее выражение в словах.
Например, «Садовник посадил 3 ряда по 5 семян. Сколько семян она посадила?» представляет собой совсем другую проблему, чем «Садовник посадил 15 семян в 3 равных ряда. Сколько семян в каждом ряду?» тем не менее, обе эти проблемы со словами можно смоделировать с использованием одного и того же массива.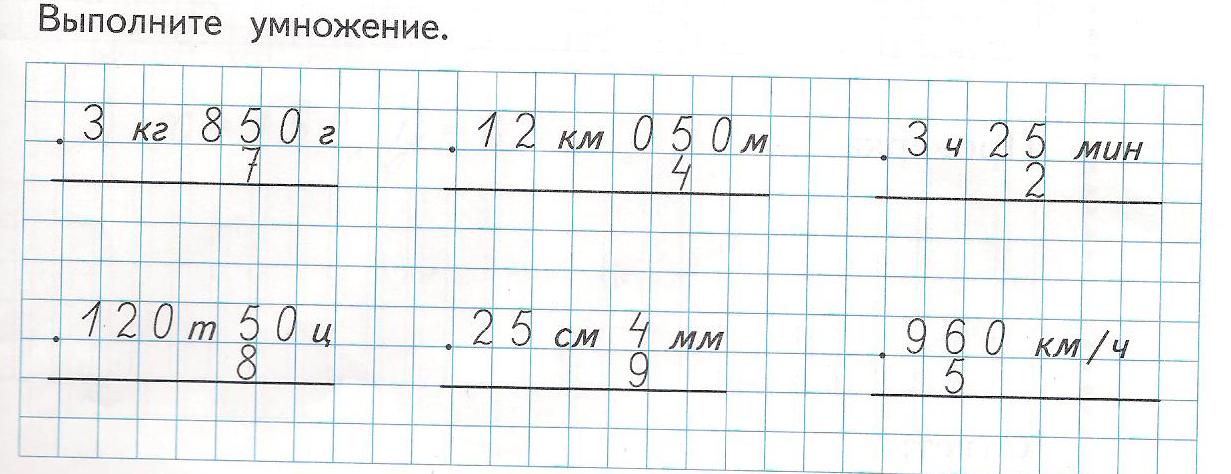
Дальнейшее изучение массива обнаруживает еще два способа выражения обратных отношений: 5 × 3 = 15 и 15 ÷ 3 = 5.
Слова «проблемы» могут быть адаптированы для описания этих операций и выделения сходств и различий между четырьмя выражениями, смоделированными одним массивом.
Использование пустого массива
Предположим, вы хотите вычислить 176 ÷ 8. Мы можем настроить его как массив с отсутствующим значением одной стороны.
Используя известные факты умножения, можно построить значение отсутствующей стороны.
Итак, ребенок может видеть, что 22 лота из 8 — это то же самое, что и 176.
Массив — очень мощный инструмент для поддержки развития детского мышления как в отношении умножения, так и деления.
Дополнительная литература
Чтобы прочитать об использовании массивов для иллюстрации числовых свойств, перейдите сюда, чтобы прочитать статью Дженни Уэй, озаглавленную «Иллюстрирование числовых свойств с помощью массивов».
Вот версия этой статьи в формате PDF.
Подразделение ÷ | Основы арифметики
На этой странице представлены основные сведения о Дивизионе (÷) .
См. Другие наши арифметические страницы для обсуждения и примеров: Сложение ( + ), Вычитание (-) и Умножение ( × ).
Отдел
Обычный письменный символ деления — (÷). В электронных таблицах и других компьютерных приложениях используется символ «/» (косая черта).
Деление — это противоположность умножения в математике.
Деление часто считается самой сложной из четырех основных арифметических функций. На этой странице объясняется, как выполнять расчеты деления. Когда мы хорошо разбираемся в методе и правилах, мы можем без ошибок использовать калькулятор для более сложных вычислений.
Дивизион
позволяет нам делить или «делиться» числами, чтобы найти ответ. Например, давайте посмотрим, как мы можем найти ответ на 10 ÷ 2 (десять, разделенные на два).Это то же самое, что «разделить» 10 сладостей между 2 детьми. У обоих детей должно получиться одинаковое количество конфет. В этом примере ответ — 5.
Например, давайте посмотрим, как мы можем найти ответ на 10 ÷ 2 (десять, разделенные на два).Это то же самое, что «разделить» 10 сладостей между 2 детьми. У обоих детей должно получиться одинаковое количество конфет. В этом примере ответ — 5.
Некоторые быстрые правила о делении:
Если вы разделите 0 на другое число, ответ всегда будет 0. Например: 0 ÷ 2 = 0. То есть 0 сладостей, разделенных поровну между 2 детьми — каждый ребенок получает 0 сладостей.
Когда вы делите число на 0, вы вообще не делите (это большая проблема в математике).2 ÷ 0 невозможно. У вас есть 2 сладости, но нет детей, чтобы разделить их между собой. Нельзя делить на 0.
Когда вы делите на 1, ответ будет таким же, как и число, которое вы делили. 2 ÷ 1 = 2. Две сладости, разделенные на одного ребенка.
Когда вы делите на 2, вы уменьшаете число вдвое. 2 ÷ 2 = 1.
Любое число, разделенное на такое же число, равно 1. 20 ÷ 20 = 1. Двадцать конфет, разделенных на двадцать детей — каждый ребенок получает по одной конфете.
Номера должны быть разделены в правильном порядке. 10 ÷ 2 = 5, тогда как 2 ÷ 10 = 0,2. Десять сладостей, разделенных на двоих детей, сильно отличаются от двух сладостей, разделенных на 10 детей.
Все дроби, такие как ½, ¼ и ¾, являются суммами деления. ½ — это 1 ÷ 2. Одна конфета, разделенная на двоих детей. Смотрите нашу страницу Дроби для получения дополнительной информации.
Множественное вычитание
Так же, как умножение — это быстрый способ вычисления множественных сложений, деление — это быстрый способ выполнения множественных вычитаний.
Например:
Если у Джона есть 10 галлонов топлива в машине и он использует 2 галлона в день, сколько дней до того, как у него закончится топливо?
Мы можем решить эту проблему, выполнив серию вычитаний или посчитав в обратном порядке с шагом 2.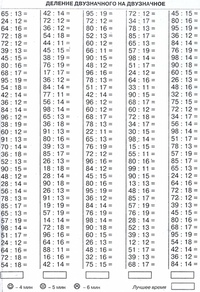
- В день 1 Джон начинает с 10 галлонов и заканчивается 8 галлонов. 10-2 = 8
- В день 2 Джон начинает с 8 галлонов и заканчивается 6 галлонов. 8–2 = 6
- В день 3 Джон начинает с 6 галлонов и заканчивается 4 галлонов. 6–2 = 4
- В день 4 Джон начинает с 4 галлонов и заканчивается 2 галлонов. 4–2 = 2
- В день 5 Джон начинает с 2 галлонов и заканчивается 0 галлонами. 2–2 = 0
У Джона заканчивается топливо на 5-й день.
Более быстрый способ выполнить это вычисление — разделить 10 на 2. То есть сколько раз 2 уходит в 10 или сколько партий по два галлона в десяти галлонах? 10 ÷ 2 = 5.
Таблица умножения (см. Умножение) может помочь нам найти ответ на простые вычисления деления.
В приведенном выше примере нам нужно было вычислить 10 ÷ 2 . Для этого с помощью таблицы умножения найдите столбец для 2 (заштрихованный красным заголовок).Двигайтесь вниз по столбцу, пока не найдете искомый номер: 10 . Переместитесь по строке влево, чтобы увидеть ответ (заштрихованный красным заголовок) 5 .
Таблица умножения
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Мы можем выполнить другие простые вычисления деления, используя тот же метод. Например, 56 ÷ 8 = 7 . Найдите 7 в верхней строке, посмотрите вниз по столбцу, пока не найдете 56 , затем найдите соответствующий номер строки, 8 .
Например, 56 ÷ 8 = 7 . Найдите 7 в верхней строке, посмотрите вниз по столбцу, пока не найдете 56 , затем найдите соответствующий номер строки, 8 .
Если возможно, вам следует попытаться запомнить приведенную выше таблицу умножения, потому что она значительно ускоряет решение простых вычислений умножения и деления.
Деление больших чисел
Вы можете использовать калькулятор для вычисления деления, особенно когда вы делите большие числа, которые труднее вычислить в уме.Однако важно понимать, как выполнять расчеты деления вручную. Это полезно, когда у вас нет под рукой калькулятора, но также важно для того, чтобы вы правильно использовали калькулятор и не допускали ошибок. Деление может показаться устрашающим, но на самом деле, как и в большинстве арифметических операций, оно логично.
Как и во всей математике, проще всего понять, если мы рассмотрим пример:
Машине Дэйва нужны новые шины. Ему нужно заменить все четыре шины на машине, а также запасную.
Дэйв получил предложение в местном гараже на сумму 480 фунтов стерлингов, включая шины, установку и утилизацию старых шин. Сколько стоит каждая шина?
Задача, которую нам нужно вычислить, — это 480 ÷ 5 . Это то же самое, что сказать, сколько раз 5 перейдет в 480?
Условно мы пишем это как:
Мы работаем слева направо в логической системе.
Мы начинаем с деления 4 на 5 и сразу решаем задачу. 4 не делится на 5, чтобы получить целое число, так как 5 больше 4.
Язык, который мы используем в математике, может сбивать с толку. Другой способ взглянуть на это — спросить: «Сколько раз 5 переходит в 4?».
Мы знаем, что 2 переходит в 4 дважды (4 ÷ 2 = 2), и мы знаем, что 1 переходит в 4 четыре раза (4 ÷ 1 = 4), но 5 не переходит в 4, потому что 5 больше 4.
Число, на которое мы делим (в данном случае 5), должно войти в число, на которое мы делим (в данном случае 4) целое количество раз. Как вы увидите, это необязательно должно быть точное целое число.
Как вы увидите, это необязательно должно быть точное целое число.
Так как 5 не входит в 4, мы помещаем 0 в первый столбец (сотни). Для получения помощи с столбцами сотен, десятков и единиц см. Нашу страницу на числах .
| Сот | Десятки | шт. | |
| 0 | |||
| 5 | 4 | 8 | 0 |
Затем мы переместимся вправо, чтобы включить столбец десятков.Теперь мы можем увидеть, сколько раз 5 переходит в 48.
5 действительно переходит в 48, поскольку 48 больше 5. Однако нам нужно выяснить, сколько раз оно идет.
Если мы обратимся к нашей таблице умножения, мы увидим, что 9 × 5 = 45 и 10 × 5 = 50 .
48 , число, которое мы ищем, находится между этими двумя значениями. Помните, что нас интересует целое число , умноженное на , когда 5 переходит в 48. Десять раз — это слишком много.
Мы можем видеть, что 5 переходит в 48 целое число (9) раз, но не точно, с оставшимися 3.
9 × 5 = 45
48-45 = 3
Теперь мы можем сказать, что 5 делится на 48 девять раз, но с остатком 3. Остаток — это то, что остается, когда мы вычитаем найденное число из числа, на которое делим: 48-45 = 3 .
Итак, 5 × 9 = 45, + 3, чтобы получить 48.
Мы можем ввести 9 в столбец десятков в качестве ответа на вторую часть вычисления и поставить наш остаток перед нашим последним числом в столбце единиц.Наше последнее число становится 30.
| Сот | Десятки | шт. | |
| 0 | 9 | ||
| 5 | 4 | 8 | 30 |
Теперь разделим 30 на 5 (или узнаем, сколько раз 5 делится на 30). Используя нашу таблицу умножения, мы можем увидеть, что ответ — ровно 6 без остатка. 5 × 6 = 30. Мы пишем 6 в столбце единиц нашего ответа.
Используя нашу таблицу умножения, мы можем увидеть, что ответ — ровно 6 без остатка. 5 × 6 = 30. Мы пишем 6 в столбце единиц нашего ответа.
| Сот | Десятки | шт. | |
| 0 | 9 | 6 | |
| 5 | 4 | 8 | 30 |
Так как остатков нет, расчет закончен и мы получили ответ 96 .
Новые шины
Дэйва будут стоить 96 фунтов каждая. 480 ÷ 5 = 96 и 96 × 5 = 480 .
Отдел рецептов
Наш последний пример деления основан на рецепте. Часто во время готовки рецепты сообщают вам, сколько еды они собираются приготовить, например, чтобы накормить 6 человек.
Указанные ниже ингредиенты необходимы для изготовления 24 сказочных лепешек, однако мы хотим приготовить только 8 сказочных лепешек. Мы немного изменили ингредиенты для удобства этого примера (оригинальный рецепт на BBC Food).
Первое, что нам нужно определить, это сколько восьмерок в 24 — используйте приведенную выше таблицу умножения или свою память.3 × 8 = 24 — если мы разделим 24 на 8, мы получим 3. Следовательно, нам нужно разделить каждый ингредиент, указанный ниже, на 3, чтобы получить необходимое количество смеси для изготовления 8 сказочных лепешек.
Состав
- 120 г сливочного масла, размягченного при комнатной температуре
- 120 г сахарной пудры
- 3 яйца от кур на свободном выгуле, слегка взбитые
- 1 чайная ложка ванильного экстракта
- 120 г муки самоподнимания
- 1-2 столовые ложки молока
Количество масла, сахара и муки все одинаково, 120гр.Поэтому необходимо всего один раз проработать 120 ÷ 3, поскольку для этих трех ингредиентов ответ будет одинаковым.
Как и раньше, мы начинаем с левого столбца (сотни) и делим 1 на 3.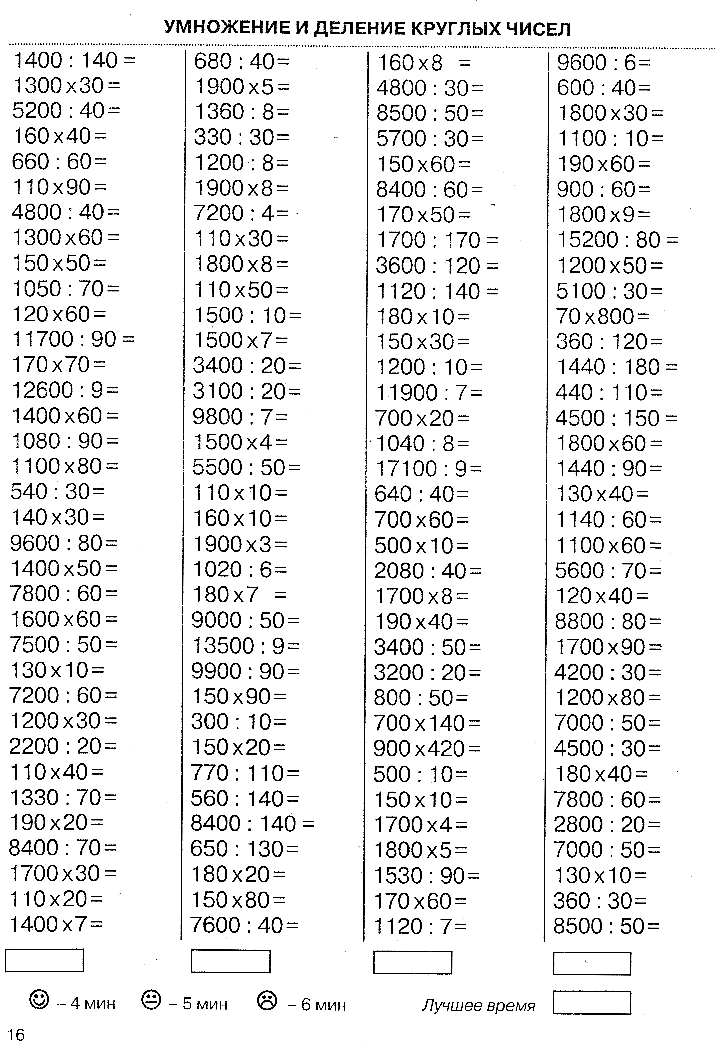 Однако 3 ÷ 1 не идет, так как 3 больше 1. Затем мы смотрим, сколько умножений 3 получается в 12. Используя таблицу умножения если необходимо, мы можем увидеть, что 3 переходит в 12 ровно 4 раза по без остатка.
Однако 3 ÷ 1 не идет, так как 3 больше 1. Затем мы смотрим, сколько умножений 3 получается в 12. Используя таблицу умножения если необходимо, мы можем увидеть, что 3 переходит в 12 ровно 4 раза по без остатка.
120 г ÷ 3, следовательно, 40 г. Теперь мы знаем, что нам понадобится 40 г масла, сахара и муки.
Исходный рецепт требует 3 яйца, и мы снова делим на 3. Итак, 3 ÷ 3 = 1, поэтому необходимо одно яйцо.
Следующий рецепт требует 1 чайная ложка ванильного экстракта. Нам нужно разделить одну чайную ложку на 3. Мы знаем, что деление можно записать в виде дроби, поэтому 1 ÷ 3 то же самое, что third (одна треть). Вам понадобится чайной ложки ванильного экстракта, хотя на самом деле сложно точно отмерить чайной ложки!
Оценка может быть полезной, а единицы измерения можно изменить!
Мы можем взглянуть на это с другой стороны, если мы знаем, что одна чайная ложка равна 5 мл или 5 миллилитрам.(Если вам нужна помощь с единицами измерения, см. Нашу страницу о «Системы измерения ».) Если мы хотим быть более точными, мы можем попробовать разделить 5 мл на 3. 3 делится на 5 один раз (3) с оставшимися 2. 2 ÷ 3 — это то же самое, что и so, поэтому 5 мл, разделенное на 3, дает 1 ⅔ мл, что в десятичных дробях составляет 1,666 мл. Мы можем использовать наши навыки оценки и сказать, что одна чайная ложка, разделенная на три, немного больше полутора миллилитров. Если у вас на кухне есть крошечные мерные ложки, вы можете быть очень точными!
Мы можем оценить ответ, чтобы убедиться, что мы правы.Три партии по 1,5 мл дают нам 4,5 мл. Итак, три партии «чуть больше 1,5 мл» дают нам около 5 мл. Рецепты редко являются точной наукой, поэтому небольшие оценки могут быть забавой и хорошей практикой для нашей ментальной арифметики.
Следующий рецепт требует 1-2 ст. Л. Молока. Это от 1 до 2 столовых ложек молока. У нас нет точного количества, и то, сколько молока вы добавите, будет зависеть от консистенции вашей смеси.
Мы уже знаем, что 1 ÷ 3 — это, а 2 ÷ 3 -.Поэтому нам понадобится – столовой ложки молока, чтобы испечь восемь сказочных лепешек. Давайте посмотрим на это с другой стороны. Одна столовая ложка равна 15 мл. 15 ÷ 3 = 5, поэтому ⅓ – столовой ложки равно 5–10 мл, что соответствует 1–2 чайным ложкам!
Дополнительные материалы по навыкам, которые вам нужны
Основы счета
Часть необходимых навыков Руководство по счету
Эта электронная книга содержит рабочие примеры и простые для понимания объяснения, чтобы показать вам, как использовать основные математические операции и начать манипулировать числами.Он также включает в себя примеры из реальной жизни, чтобы прояснить, насколько эти концепции полезны в реальной жизни.
Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.
Отдел
Дивизия делится на равные части или группы.
Это результат «честного обмена».
Пример: есть 12 шоколадных конфет, и 3 друга хотят ими поделиться, как они делят шоколадные конфеты?
12 конфет
12 шоколадных конфет, разделенных на 3
Ответ: 12 разделить на 3 равно 4.Они получают по 4 штуки.
Символы
÷ /
Мы используем символ ÷ или иногда символ / для обозначения деления:
Давайте использовать здесь оба символа, чтобы мы к ним привыкли.
Другие примеры
Вот еще несколько примеров:
Противоположность умножению
Деление
— это , противоположное умножению . Когда мы знаем факт умножения, мы можем найти факт деления:
Пример: 3 × 5 = 15, поэтому 15/5 = 3.
Также 15/3 = 5.
Почему? Что ж, подумайте о числах в строках и столбцах, как на этой иллюстрации:
| Умножение … | … Подраздел | |
|---|---|---|
3 группы по 5 составляют 15 . .. .. | … значит 15 делить на 3 дает 5 | |
а также: | ||
| 5 групп по 3 составляют 15… | … 15 разделить на 5 равно 3. | |
Итак, есть четыре связанных факта :
- 3 × 5 = 15
- 5 × 3 = 15
- 15/3 = 5
- 15/5 = 3
Знание таблицы умножения может помочь вам с делением!
Пример: что такое 28 ÷ 7?
Обыскивая таблицу умножения, мы обнаруживаем, что 28 равно 4 × 7, поэтому 28, разделенное на 7, должно быть равно 4.
Ответ: 28 ÷ 7 = 4
Имена
Для каждого числа в дивизионе есть специальные названия:
дивиденд ÷ делитель = частное
Пример: в 12 ÷ 3 = 4:
- 12 — дивиденд
- 3 — делитель
- 4 — частное
Но иногда он не работает идеально!
Иногда мы не можем точно разделить вещи… может быть что-то осталось.
Пример: Есть 7 костей, которые можно разделить с 2 щенками.
Но 7 нельзя разделить точно на 2 группы,
поэтому каждый щенок получает 3 кости,
, но останется 1 :
Мы называем это остатком .
Подробнее об этом читайте в разделе «Отделение и остатки»
.
Упражнения
Попробуйте эти листы деления.
Массивы
— 5 основных вещей, которые нужно знать об использовании массивов для моделирования умножения и деления
Топ 5 вещей, которые нужно знать об использовании массивов для моделирования умножения и деления:
1. Массив — это набор элементов, организованных в равные строки и равные столбцы, что создает прямоугольную форму. Строки представляют количество групп, а столбцы представляют количество в каждой группе.
Строки представляют количество групп, а столбцы представляют количество в каждой группе.
Инструменты, подходящие для моделирования массивов, включают: счетчики, квадратные плитки, миллиметровую бумагу и быстрые изображения. Используя массивы для моделирования задач деления или умножения, мы хотим перейти от конкретных манипуляций к быстрым картинкам, к абстрактному мышлению с использованием выражений или уравнений для описания массивов.
Это конкретная модель массива. Это может быть модель задачи деления, включающая 15 ÷ 5 или 15 ÷ 3. Это также может быть модель задачи умножения 5 x 3.
Массив миллиметровой бумаги.
Быстрое изображение массива со связанными уравнениями.
2. Массивы можно использовать для моделирования задач умножения и деления. Они помогают относиться к двум операциям.
Вот пример использования массива умножения для связи с делением. Как только сумма определена, учащиеся могут видеть, что они могут разделить на количество групп или строк, 2. Или они могут разделить на количество столбцов или количество в каждой строке, 3.
3. Полезно использовать задачи со словами, которые выявляют организацию объекта в равные строки или столбцы, чтобы побудить учащихся смоделировать массив.
Пример задачи умножения:
• «Райли сажал в своем томатном саду. Посадил 3 ряда томатов. В каждом ряду было по 5 растений. Сколько томатов посадил в своем саду Райли? »
• «Райли планировал в своем томатном саду. Он посадил по 3 куста томатов в каждом ряду.Посадил 5 одинаковых рядов помидоров. Сколько томатов посадил в своем саду Райли? »
Пример задач отдела:
• «У Рэйчел 15 кукол. У нее 5 полок для кукол. Она хочет, чтобы на каждой полке было одинаковое количество кукол. Сколько кукол Рэйчел ставит на каждую полку? »
• «У Рэйчел 15 кукол. Она размещает по 5 кукол в каждом ряду.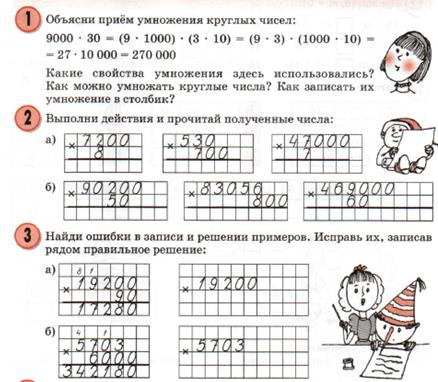 Сколько рядов нужно Рэйчел, чтобы разместить все куклы на полке? »
Сколько рядов нужно Рэйчел, чтобы разместить все куклы на полке? »
4.Массивы помогают обучать коммутативному свойству умножения, что приводит студентов к более эффективным стратегиям плавного умножения.
Эта модель показывает 3 ряда по 5 или 3 x 5.
Эта модель показывает 5 рядов по 3 или 5 x 3
На основе этих двух моделей учащиеся могут видеть, что итоговая сумма или продукт остается неизменной, поскольку вы не добавляете и не убираете квадратные плитки. Единственное, что изменилось, — это способ организации строк и столбцов или количество групп и их количество в каждой группе.
5. Понимание массива в 3-м классе важно для учащихся, которые развивают понимание области позже в 3-м классе и далее в 4-м классе. Он также готовит учащихся к моделированию больших задач умножения с использованием частичных произведений в 4-м классе.
Интересный способ изучить моделирование массивов с задачами умножения и деления — дать учащимся штампы бинго и попросить их штамповать массивы на плотной бумаге. Вы можете поставить задачу: «Было 24 ученика, которых нужно было распределить в равные ряды для собрания.Как их учитель мог организовать их в равные ряды? » Затем предложите студентам записать уравнения деления и умножения для каждой модели массива.
Отличная игра, которая побуждает студентов практиковаться в моделировании массивов, — это «Игра с массивами». Раздайте партнерам половину листа миллиметровой бумаги, карандаши двух разных цветов и кубик с цифрами 0–9. Попросите учащихся по очереди со своим партнером дважды повернуть числовой куб, чтобы определить количество строк и количество столбцов в своем массиве.Затем они создадут свой массив, записав соответствующее ему уравнение и закрасив его своим цветом. Игра продолжается до тех пор, пока человек не перестанет создавать свой массив. Тогда побеждает тот, у кого больше квадратов заштриховано цветным карандашом. (Это также можно изменить для деления, создав карточки задач деления, которые студенты могут вытащить, затем создать массив, соответствующий данной задаче, и решить для частного).

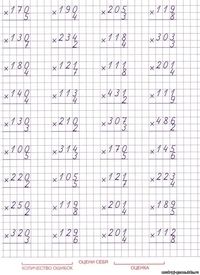 Это сделает подсчет упорядоченным и быстрым.
Это сделает подсчет упорядоченным и быстрым.