Урок математики в 3 классе «Записываем вычитание в столбик»
Урок математики в 3 классе
УМК «Планета знаний»
М. И. Башмаков, М. Г. Нефёдова
Тема: «Записываем вычитание в столбик»
Составила: учитель начальных классов
МБОУ «Тиксинская СОШ №2»
Огурцова Наталья Николаевна
Место в системе уроков:
Первый урок по теме: «Вычитаем числа».
Цель: сформировать умение вычитания чисел с переходом через разряд.
Задачи:
Образовательные:
познакомиться с алгоритмом письменных приёмов вычитания трёхзначных чисел, аналогичных таким же приёмам при вычитании двузначных чисел;
закрепить навык применения алгоритма письменного сложения и вычитания;
закрепить умение решать составные задачи;
Развивающие:
развивать навык устного счёта;
совершенствовать мыслительные операции: анализа, сопоставления;
развитие умения аргументировать своё мнение;
развивать интерес детей к математике, их математические способности;
развитие мыслительной деятельности, познавательной активности, мышления, наблюдательности, внимания, памяти;
развитие умения давать самооценку своей деятельности;
Воспитывающие:
воспитывать дисциплинированность, ответственность, способность сопереживать, самоуважение; активность, усидчивость, прилежание, любознательность, заинтересованность и пытливость в процессе учения;
воспитывать взаимопомощь, взаимовыручку;
воспитание и укрепление интереса к математике;
создание благоприятного психологического климата для возможности раскрытия потенциала каждого ребенка.
Планируемые результаты.
Предметные:
изучить способ вычитания чисел с переходом через разряд столбиком;
повторить разрядный состав двузначного и трехзначного числа.
Метапредметные:
определять цель деятельности на уроке с помощью учителя и самостоятельно.
высказывать свою версию, пытаться предлагать способ её проверки (на основе продуктивных заданий в учебнике).
развивать коммуникативные навыки (корректно излагать свое мнение, аргументировать свою позицию, уважать мнение партнера).
Личностные:
формирование познавательного интереса к новому учебному материалу;
определять успешность выполнения своего задания в диалоге с учителем.
самостоятельно определять и высказывать самые простые, общие для всех людей правила поведения при совместной работе и сотрудничестве (этические нормы).
Тип урока: урок «открытия» нового знания.
Оборудование, наглядность: учебник «Математика» (стр.46-47), тетрадь на печатной основе, персональный компьютер, проектор, раздаточный материал с заданиями, карточки для рефлексии.
Используемые методы и приемы:
метод эмоционального стимулирования,
словесный метод,
наглядный метод,
проблемно-поисковые методы,
практические методы,
самостоятельная работа,
элементы технологии коллективного взаимодействия.
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
Этап урока | Деятельность учителя | Деятельность учащихся | Формируемые УУД |
Осуществляемые действия | Осуществляемые действия | ||
I. Цель: Осознанный переход обучающихся из внеурочной жизнедеятельности в пространство учебной деятельности. | Эмоциональный настрой. Слайды 2- 3 Проговаривание стихотворения: Начинаем ровно в срок Мы – умные! Мы — дружные! Мы — внимательные и старательные! Будем слушать, отвечать, И пятёрки получать! Я желаю вам хорошего настроения и удачи на уроке. — Повернитесь друг к другу, улыбнитесь и скажите: «Я желаю тебе удачи». — Подумайте, что пригодится для успешной работы на уроке? — Предлагаю вам прочитать девиз нашего урока. Ребята, у вас на партах листы самооценки. На протяжении всего урока вы их будете заполнять. -Откройте тетради, запишите дату, классная работа. | Приготовление к уроку. Проговаривание стихотворения: — Вера в успех, внимание, трудолюбие, усердие, старание, знания. — «Мы пришли сюда учиться Не лениться, а трудиться, Только тот, кто много знает В жизни что-то достигает». | Личностные: Личностные Регулятивные |
II. Цель: Повторение изученного материала, необходимого для «открытия нового знания» и выявление затруднений в индивидуальной деятельности каждого учащегося. | СЛАЙД 5 (математическая разминка) Для начала проведём математическую разминку. Она нам поможет в нашей дальнейшей работе. 1.Таблица умножения Тренажер-презентация 2.Покажите числа, в которых: 4 сотни, 2 десятка 420 5 сотен 500 8 десятков, 3 сотни 380 4 сотни, 1 десяток 410 4 сотни, 2 десятка, 6 единиц 426 6 сотен, 7 десятков, 8 единиц 678 1 единица, 5 сотен, 3 десятка 531 3 десятка, 5 сотен, 4 единицы 534 (Числа записываются учениками на доске). Что объединяет эти числа? (Они трёхзначные). Из каких разрядов они состоят? (Единицы, десятки, сотни). Где пишутся единицы? Десятки? Сотни? Назовите числа, в которых отсутствуют единицы, десятки. Запишите ответы в тетрадях Увеличьте число 380 на 1 сотню. (480) Уменьшите число 531 на 1 единицу. (532) Увеличьте число 426 на 3 десятка. (456) Назовите наименьшее их этих чисел. (456) Назовите наибольшее из этих чисел. (532) Расположите данные числа в порядке возрастания. Откройте тетради, запишите там полученный ряд. (1 человек работает у доски) ПРОВЕРИМ! Устные вычисления Слайд 6 420+80=500 380+50=430 500-60=440 410-30=380 Прочитайте 1 выражение. Проверим. Слайд 7 Объясните, как вы считали. Какое правило помнили? Трёхзначные числа складываем и вычитаем по разрядам. Кто считал по-другому? — Молодцы! Вы хорошо потрудились. Оцените себя в листе самооценки. ПОКАЖИТЕ НАСТРОЕНИЕ | Показывают смайлики | |
III. Выявление места и причины затруднения. Цель: Обсуждение затруднений. 1 мин | СЛАЙД 8. Открытие новых знаний Слайд 63 -7 42-14 134-9 176 — 28 325-154 Прочитайте следующие выражения. Удобны ли известные вам приёмы вычисления при выполнении этого задания? Почему? Что же делать? Какой приём надо использовать, если трудно вычесть трёхзначные числа устно? — Умеем ли мы выполнять эти вычисления? | 176-28 325 -154 -Трудные случаи вычислений — Мы не умеем вычитать числа с переходом через разряд (Письменный приём, решение столбиком). | |
IV. Целеполагание и построение проекта выхода из затруднения. Цель: Обсуждение проекта выхода из затруднений. 2 мин. | Определите тему сегодняшнего урока. — Какое новое знание нам необходимо для дальнейшей работы? — Какую цель мы поставим? | «Записываем вычитание в столбик» — Научиться записывать и производить вычисления в столбик | |
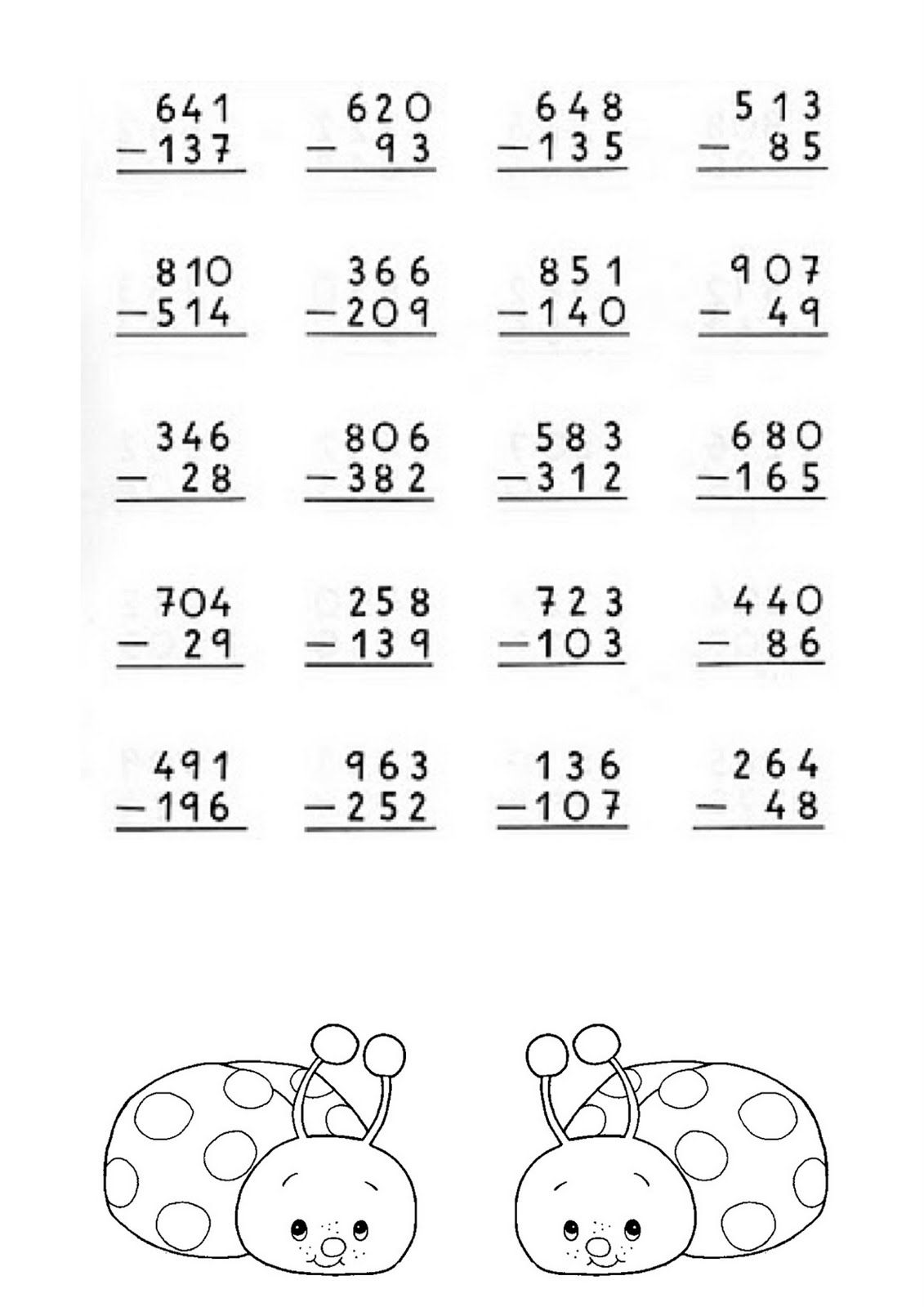
V. | (Слайд 9) Повторение алгоритма письменного вычитания А сможете ли вы самостоятельно объяснить, как вычитать эти числа столбиком? Отработка алгоритма письменного вычитания. 1)устная работа №1 , стр. 46 | Да, как вычитали двузначные числа. Будем учиться строить алгоритм вычитания чисел — По аналогии с алгоритмом вычитания двухзначных чисел — Так же, как и раньше: единицы под единицами, десятки под десятками, сотни под сотнями. Так же по разрядам. 2-й шаг – вычитаем единицы… 3-й шаг – вычитаем десятки… 4-й шаг – вычитаем сотни… 5-й шаг – читаем ответ. — Записываем единицы под единицами, десятки под десятками, сотни под сотнями… | Личностные: |
Физминутка. 1 мин | Музыкальная физминутка Слайд 10 | ||
VI. Первичное закрепление с комментированием во внешней речи. Цель: Проговаривание нового знания, запись в виде опорного сигнала (фронтальная работа, работа в парах). | Учебник с. 46 Сравните его с выводом, который мы составили сами. — Значит мы с вами вывели правильный алгоритм. — А научились мы им пользоваться? — Давайте будем совершенствовать новые знания Слайд 11 Пользуясь выведенным алгоритмом, выполним Задание №2 учебника. (с объяснением) — Объясни вычисления и выполни вычитание чисел (Один ученик у доски.) Два последних примера – самостоятельно. (Взаимопроверка.) ПОКАЖИТЕ НАСТРОЕНИЕ — Молодцы! Вы хорошо потрудились. Оцените друг друга в листе самооценки. | — Они одинаковы. — Нет, нужно потренироваться. Работаем в тетради. Используем таблицу алгоритм. Работа в парах | Познавательные УУД- построение логической цепи рассуждений. Коммуникативные — умение слушать, вступать в диалог Личностные: |
VII. Самостоятельная работа (работа в парах). Цель: Каждый для себя должен сделать вывод о том, что он уже умеет. | Самостоятельная работа (тест) Слайд 12 — Каким алгоритмом пользовались? Самопроверка Слайд 13 — Молодцы! Вы хорошо потрудились. Оцените себя в листе самооценки ПОКАЖИТЕ НАСТРОЕНИЕ | ||
Физминутка | Гимнастика для глаз | ||
VIII. | Где мы сможем применить полученные сегодня знания? Отправляемся в магазин за покупками. Стр. 47 № 4 (а) Задача Слайд 14 Разбор задачи. Прочитайте задачу. Покупатель купил шляпу за 448р. и шарф. У него было 975 р., а осталось 177р. Сколько он заплатил за шарф? Прочитайте условие задачи. Прочитайте вопрос задачи. Составим схему. — Слайд 15 Пригодились ли новые знания? — Молодцы! Оцените себя в листе самооценки ПОКАЖИТЕ НАСТРОЕНИЕ Игра «Волшебный квадрат» Ну а теперь проверим, какие вы трудолюбивые и внимательные. Решите данные на карточке примеры, если потребуется решить столбиком, вычисления выполните в тетрадях. Закрасьте ответы в волшебном квадрате, и вы узнаете, как вы потрудились. Проверка. СЛАЙД 17 | Было – 975р Купил -? 448р. и? р. Осталось – 177р. Было – Шляпа – Шарф = Осталось 975 – 448 -? =177 547 -? = 177 ? = 547 -177 Решают примеры ,закрашивают соответствующий квадратик в волшебном квадрате | |
IX. Рефлексия учебной деятельности (итог урока). Цель: Осознание учащимися учебной деятельности, самооценка результатов деятельности своей и всего класса. | СЛАЙД 18 -21 Завершается урок, Он пошёл ребятам впрок? Постарались всё понять? Учились тайны открывать? Ответы полные давали? На уроке не зевали? — Какую задачу ставили в начале урока? — Удалось ли решить поставленную задачу? — Каким способом? — Следовали составленному плану? Каким образом? — Какие получили результаты? — Что нужно сделать ещё? — Где можно применить новые знания? — Что на уроке у вас хорошо получилось? — Над чем ещё надо поработать? В листе самооценки выставите себе оценку за весь урок (критерии те же), вложите в тетрадь. ПОКАЖИТЕ НАСТРОЕНИЕ | — Научится решать примеры на сложение двух и трёхзначных чисел с переходом через разряд. — Да — Составили новый алгоритм. — Да. Мы сначала наблюдали, потом сравнивали, потом выводили алгоритм. — Закрепили умение применять новые знания на практике при решении примеров, задач. — Повторили единицы измерений и сложение именованных чисел. — Применяли логику, анализировали, сравнивали, оценивали себя и товарищей. — Потренироваться в решении примеров с переходом через разряд. — На уроке математике, в жизни при покупках и т.д. | |
Домашнее задание: | Домашнее задание: | Стр. |
Деление с остатком столбиком. Проверка деления с остатком
Привет,
друзья! А вот и я.
Опять
буду знакомить вас с новой темой. Я надеюсь, вы уже уверенно научились выполнять
деление с остатком? Помните, как мы шестнадцать делили на пять?
Вспоминаем
таблицу умножения и деления с числом пять. Находим число, которое делится на пять
без остатка и на числовом луче находится ближе остальных к числу шестнадцать.
Это пятнадцать. Пятнадцать делим на пять, получается три, а разницу
между шестнадцатью и пятнадцатью – один, записываем в остаток.
Вы
уже знаете, что знак умножения может записываться по-разному – иногда
точкой, иногда косым крестиком, а на клавиатуре компьютера или мобильного
телефона – звёздочкой. Но и знак деления тоже может выглядеть по-разному:
в тетрадях вы обычно пишете двоеточие, иногда этот знак выглядит как
горизонтальная черта, а над ней и под ней по точке. Но для письменного деления
Но для письменного деления
многозначных чисел используют знак деления, который похож на лежащую на боку
букву Т. И сегодня мы воспользуемся таким знаком деления для того, чтобы выполнять
деление с остатком столбиком.
Вот
посмотрите, допустим, нам надо разделить число двадцать пять на четыре.
Как
это записать, я покажу на разлиновке в клеточку. Ведь при таком
способе решения, как и при сложении и вычитании столбиком, очень важна
аккуратность записи. Итак, пишу делимое – число двадцать пять. Справа от него,
отступив одну клеточку, пишу делитель – четыре. Между ними ставлю знак деления
– вертикальная черта длиной в две клетки, а от неё – горизонтальная. Вот она,
буква Т. Вот делимое, вот делитель. Под чертой
место для частного.
Сначала
выясним, сколько раз число четыре содержится в двадцати пяти. Четыре
умножаем на нуль, равно нуль. Нуль меньше двадцати пяти. Так что нуль в качестве
Нуль меньше двадцати пяти. Так что нуль в качестве
частного нам уж точно не подходит.
Четыре
умножаю на один. Четыре. Это число тоже меньше двадцати пяти и тоже нас не
устраивает. Четыре умножаю на два – шесть. Оно тоже меньше двадцати пяти.
Четыре умножаю на три – двенадцать, четырежды четыре – шестнадцать, четырежды
пять – двадцать. Четыре умножить на шесть – двадцать четыре. На семь – двадцать
восемь. А двадцать восемь не меньше, а больше двадцати пяти.
Стоп!
Теперь получилось число, которое больше нашего делимого. Но это недопустимо.
Возвращаемся к шестёрке. Итак, четыре содержится в числе двадцать пять шесть
раз. Записываю в частном число шесть. А под делимым – то число, которое
получилось при умножении делителя и частного – двадцать четыре.
А
теперь вычитаю из делимого это полученное число двадцать четыре. Видите, получилось
вычитание столбиком. А результат вычитания – это остаток.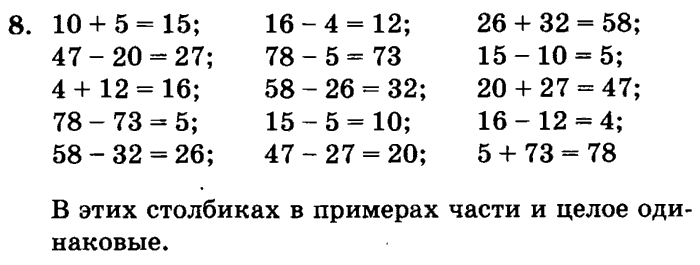
Я надеюсь, вы не забыли, что остаток обязательно должен быть меньше
делителя. В этом примере остаток один. Он меньше четырёх. Значит,
деление выполнено верно.
Запомните,
как расположены компоненты деления. Делимое и делитель находятся
на одной строчке, между ними пропускается одна клеточка. Частное расположено
под делителем, а под делимым – действие вычитания и остаток.
Конечно,
у нас получилось очень длинное вычисление. Методом проб и ошибок, начиная с
нуля, мы нашли нужное нам число. Но, если вы хорошо знаете таблицу умножения,
подбор нужного числа не будет столь долгим и утомительным.
Вот,
к примеру, надо сорок пять разделить на шесть. Вспомнив таблицу умножения
числа шесть, мы можем сказать, что ближайшими числами к делимому, которые
делятся на шесть, являются числа сорок два и сорок восемь. Сорок восемь получится
в результате умножения шести на восемь. Но число сорок восемь больше сорока
Но число сорок восемь больше сорока
пяти, и оно нам не подойдёт.
Сорок
два получится в результате умножения шести на семь. Сорок два меньше сорока
пяти. Значит, шесть содержится в сорока пяти семь раз. А остаток три. Наш остаток
меньше делителя, значит, деление выполнено верно.
Ну
а если, к примеру, надо число семь разделить на девять. Сколько раз число
девять содержится в семи? Ну конечно, нуль раз. В частном записываем нуль. Нуль
умножили на девять, тоже получился нуль, вычитаем… Остаток семь.
Если
делимое меньше делителя, то в ответе получится нуль, а остаток будет равен
делимому.
Ребята,
а вы знаете, несмотря на то, что вы вроде бы всё правильно делаете, при делении
с остатком случаются и ошибки. Как же проверить, правильно ли было выполнено
деление?
Ну
конечно обратными действиями. Мы выполняли деление и, чтобы найти остаток,
вычитание. Значит, для проверки нам понадобится умножение и сложение.
Значит, для проверки нам понадобится умножение и сложение.
Давайте
сейчас разделим число сорок три на одиннадцать. Запишем решение в строчку.
Сколько раз одиннадцать содержится в числе сорок три? Ну понятно, что не нуль и
не один раз. Если взять два, получится число двадцать два. Оно меньше сорока трёх.
Если взять три раза – это тридцать три. Оно тоже меньше сорока трёх. Возьмём
число четыре – получится сорок четыре. Оно больше сорока трёх. Стоп! Возвращаемся
к числу три. Число одиннадцать содержится в сорока трёх три раза и остаток
десять.
Вроде
бы всё правильно. Но убедиться в этом мы сможем, только выполнив проверку.
Сравниваем остаток с делителем. Десять меньше одиннадцати. Это правильно.
Теперь деление и вычитание проверяем умножением и сложением.
Делитель,
одиннадцать, умножаем на частное, три, и к результату прибавляем остаток,
десять. Одиннадцать умножить на три – тридцать три, и плюс десять – сорок три.
Ну,
вроде бы всё рассказал. Ну, а если что-то по рассеянности пропустил, вам
обязательно расскажет это ваш мудрый учитель.
А
теперь я предлагаю вам повторить то, о чём мы сегодня говорили.
*
Деление с остатком можно записывать как в строчку, так и столбиком.
*
При записи столбиком делимое и делитель находятся на одной строчке, между ними
пропускается одна клеточка, в которой записывается знак деления, похожий на
букву Т, лежащую на боку. Частное расположено под делителем, а под делимым –
действие вычитания и остаток.
Если
делимое меньше делителя, то в ответе получится нуль, а остаток будет равен
делимому.
Деление
с остатком можно проверить.
1.
Для этого сначала сравниваются остаток с делителем.
Важно!
Остаток должен быть меньше делителя!
После
сравнения остатка с делителем выполняем второй этап проверки.
2.
Умножить частное на делитель и к полученному произведению прибавить остаток.
Ну
вот и пришло время нам сегодня попрощаться. Хороших вам отметок, ребята! До
свидания!
Контрольные работы по математике для 3 класса — Математика 3 класс — 3 класс
КОНТРОЛЬНАЯ РАБОТА 5
Цель: проконтролировать усвоение приёма деления с остатком и его проверку, знание порядка действий в выражениях, умение решать задачи.
I вариант
1. Выполните деление с остатком и проверку к нему.
75 : 8 85 : 20 51 : 7
2. Вставьте числа в «окошки», чтобы получились верные равенства.
3. Найдите значения выражений.
56 : 2 – 36 : 12 (39 + 33) : 24 · 9
48 + 32 : (64 : 8) 93 – 3 · 8 : 6
4. Решите задачу.
Стекольщику нужно было вставить 96 стёкол. Он уже вставил в 14 окон по 3 стекла в каждое. Сколько стёкол осталось вставить стекольщику?
5. Решите задачу.
На тарелке было 48 блинов. Сколько блинов съели, если на тарелке осталось в 3 раза меньше блинов, чем было?
II вариант
1. Выполните деление с остатком и проверку к нему.
57 : 8 74 : 7 69 : 20
2. Вставьте числа в «окошки», чтобы получились верные равенства.
3. Найдите значения выражений.
80 + (24 – 4 · 5) 42 : 3 + 72 : 24
78 – 8 · 8 : 2 24 + 36 : (54 : 9)
4. Решите задачу.
В большой корзине было 95 тюльпанов. Продавец сделал из них 12 букетов, по 7 тюльпанов в каждом букете. Сколько осталось тюльпанов?
5. Решите задачу.
На столе стояло 52 стакана с соком. Сколько стаканов с соком выпили, если на столе осталось в 4 раза меньше стаканов с соком, чем было первоначально?
КОНТРОЛЬНАЯ РАБОТА 6
Цели: проверить усвоение нумерации трёхзначных чисел; проверить усвоение вычислительных приёмов; проконтролировать навыки решения задач, построения отрезков.
I вариант
1. а) Вставьте в «окошки» пропущенные числа.
б) Запишите цифрами:
9 сот. 2 дес. 8 сот.
4 сот. 3 ед. 5 сот. 1 дес. 7 ед.
в) Представьте числа в виде суммы разрядных слагаемых.
510, 742.
2. Решите задачу.
3 набора красок стоят 72 рубля. Сколько стоят 4 таких набора красок?
3. Решите примеры.
549 + 1 702 – 700 60 : (26 + 4) · 2
800 – 1 930 – 600 42 + 54 : 3 · 2
600 + 50 320 + 70 71 – (28 – 17) · 6
4. Заполните пропуски нужными числами.
5. Начертите отрезок АВ = 6 см, а отрезок ВС в 2 раза длиннее. На сколько см длина отрезка ВС больше длины отрезка АВ?
II вариант
1. а) Вставьте в «окошки» пропущенные числа.
б) Запишите цифрами:
7 сот. 5 сот 7 дес.
4 сот. 2 дес. 3 ед. 6 сот. 9 ед.
в) Представьте числа в виде суммы разрядных слагаемых.
490, 351.
2. Решите задачу.
72 стула расставили в 6 рядов, поровну в каждый ряд. Сколько стульев в 4 таких рядах?
3. Решите примеры.
659 + 1 805 – 800 96 : (41 – 9) · 3
900 – 1 760 – 500 36 + 60 : 4 · 2
400 + 80 980 – 30 72 – (44 + 16) : 4
4. Заполните пропуски нужными числами.
5. Начертите отрезок СД = 9 см, а отрезок АК в 3 раза короче. На сколько см длина отрезка СД больше длины отрезка АК?
КОНТРОЛЬНАЯ РАБОТА 7
Цель: проверить сформированность умений:
1) записывать и сравнивать трёхзначные числа;
2) складывать и вычитать трёхзначные числа;
3) решать задачи;
4) сравнивать единицы длины.
I вариант
1. а) Запишите число, в котором:
5 ед. III разряда и 2 ед. I разряда
7 ед. II разряда и 3 ед. I разряда
4 ед. III разряда
6 ед. III разряда и 9 ед. II разряда
б) Сравните числа:
567 … 601 300 … 299 110 … 101
2. Сравните (>, <, =).
5 м 4 дм … 540 см 8 м 1 см … 8 м 1 дм
9 дм 2 см … 1 м 604 см … 4 м 6 см
3. Решите примеры.
640 : 8 = 240 : 6 =
150 – 70 = 560 : 8 =
440 : 20 = 80 · 5 =
80 + 40 = 20 · 6 =
4. Решите задачу.
В соревнованиях участвуют 310 мальчиков и 270 девочек. Гимнастов среди них было 250 человек, а остальные пловцы. Сколько пловцов участвуют в соревнованиях?
5. Решите примеры столбиком.
535 + 65 756 – 628
198 + 672 963 – 817
189 + 467 707 – 629
II вариант
1. а) Запишите число, в котором:
9 ед. III разряда
7 ед. III разряда и 4 ед. II разряда
5 ед. II разряда и 2 ед. I разряда
8 ед. III разряда и 6 ед. I разряда
б) Сравните числа:
401 … 386 699 … 700 220 … 202
2. Сравните (>, <, =).
702 см … 2 м 7 см 6 м 9 дм … 690 см
8 дм 3 см … 1 м 4 м 5 см … 4 м 5 дм
3. Решите примеры.
630 : 7 = 90 + 7 =
210 : 3 = 560 : 4 =
2 · 70 = 360 : 4 =
170 – 80 = 30 · 5 =
4. Решите задачу.
В музей поехали 250 первоклассников и 320 второклассников. Мальчиков среди них было 300 человек. Сколько девочек поехало в музей?
5. Решите примеры столбиком.
652 + 265 683 – 134
363 + 498 712 – 243
548 + 152 622 – 355
Примеры в столбик по математике 3 класс распечатать :: piwedleostur
15.01.2017 10:05
Генератор случайных примеров по математике за класс на сложение и. Примеры по математике 3 класс. Тест по математике 3 класс на тему: Для самостоятельной работы по. Вы найдете разбор типовых примеров и задач. Примеры по математике 3 класс распечатать столбиком М 2, часть 1 Урок 5. Таблица деления математика для детей, 2, 3 класс Морфологический разбор слова с примерами и онлайн. Контрольные работы по математике для Примеры с решениями разной степени сложности. Сложение трехзначных чисел столбиком без перехода через разряд. В этой игре тренажёре предлагается решать задачи.
По математике для классов на сложение, вычитание, умножение,. За неправильныйотнимается 3 балла. Пособие содержит математических примеров по темам, изучаемым в 3 классе, в том. Вычисли, записывая решение столбиком.3. Реши уравнения, сделай проверку. ГДЗ по математике, 6 классВиленкин, Жохов, Чесноков, Шварцбурдонлайн решебник. Задания для детей 3 лет. Интересные рецензии пользователей на книгу 5000 примеров по математике. Скачать: Контрольные работы по математике для 3 класса по. Эти карточки я использую в течение года много раз, даже при проверке скорости счёта счёт в столбик.
По курсу математики за. Задачи на нахождение суммы двух произведений. Задачи на разностное и кратное сравнение. Примеры с решениями разной. Генератор случайных примеров по математике на деление столбиком поможет учителю подготовиться к уроку в 3 4 классах. Задачи на 3 действия. Поэтому займем десяток у соседа слева от 3. Рассмотрим пример: Урок: вычитание в столбик. Что мы должны помнить, садясь в школьный автобус. Сколько. За одну ночь он пробежал через 8 болот, 4 луга и 3 леса.3. Что такое сложение 3. Алгоритм решения выражений в столбик на сложение. Генератор случайных примеров.
Вместе с Примеры в столбик по математике 3 класс распечатать часто ищут
примеры для 3 класса на порядок действий
примеры по математике 3 класс на деление и умножение
задачи по математике 3 класс с ответами
задачи по математике 3 класс 1 четверть
примеры 3 класс сложение и вычитание трехзначных
задачи по математике 3 класс скачать бесплатно
примеры по математике 4 класс
примеры по математике 3 класс решать онлайн
Читайте также:
Спиши.ру учебник 5 класса бунеева русский язык
История 7 класс тесты и тренировочные задания по истории нового времени 1500-1800 к учебнику юдовской л.а гдз онлайн
Ответы на вопросы по истории по учебнику россия и мир10 класс данилов
Деление и умножение в столбик, правила, примеры видео
Умножение и деление однозначных чисел не составит труда для любого школьника, выучившего таблицу умножения. Она входит в программу математики за 2 класс. Другое дело – когда необходимо произвести математические действия с многозначными числами. Начинают такие действия на уроках математики в 3 классе. Разбираем новую тему «Деление и умножение в столбик»
Умножение многозначных чисел
Делить и умножать сложные числа проще всего столбиком. Для этого нужно разряды числа: сотни, десятки, единицы:
235 = 200 (сотни) + 30 (десятки) + 5 (единицы).
Это нам понадобится для правильной записи чисел при умножении.
При записи двух чисел, которые нужно перемножить, их записывают друг под другом, размещая числа по разрядам (единицы — под единицами, десятки под десятками). При умножении многозначного числа на однозначное трудностей не возникнет:
Правило умножения двухзначных чисел гласит, что сначала умножается первое из чисел на последнюю из цифр второго ряда (стоящую в разряде единиц), затем – оно же – на цифру из разряда десятков.
Запись ведется так:
Вычисление ведут с конца – с разряда единиц. При умножении на первую цифру – из разряда единиц – запись тоже ведут с конца:
- 3 х 5 = 15, записываем 5 (единицы), десятки (1) запоминаем;
- 2 х 5 = 10 и 1 десяток, который мы запомнили, всего 11, записываем 1 (десятки), сотни (1) запоминаем;
- поскольку дальше разрядов у нас в примере нет, записываем сотни (1 – которую запоминали).
Следующее действие – умножаем на вторую цифру (разряд десятков):
- 3 х 1 = 3;
- 2 х 1 = 2.
Поскольку умножали мы на цифру из разряда десятков, записывать начнем так же, с конца, начиная со второго места справа (там, где разряд десятков).
Запомнить правила умножения столбиком несложно:
1. записывать столбиком умножение нужно по разрядам;
2. вычисления производить, начиная с единиц;
3. записывать итог по разрядам – если умножаем на цифру из разряда единиц – запись начинаем с последнего столбика, из разряда – десятков – с этого столбца и ведем запись.
Правило, действующее для умножения в столбик на двухзначное число, действует и для чисел с большим количеством разрядов.
Чтобы легче было запомнить правила записи примеров умножения многозначных чисел в столбик, можно сделать карточки, выделив разными цветами разные разряды.
Если производится в столбик умножение чисел с нулями на конце, их не принимают во внимание при вычислении, а запись ведут так, чтобы значащая цифра была под значащей, а нули остаются справа. После проведения вычислений их количество дописывают справа:
Математик Яков Трахтенберг разработал систему быстрого счета. Метод Трахтенберга облегчает умножение, если применять определенную систему вычислений. Например, умножение на 11. Для получения результата нужно прибавить цифру к соседней:
2,253 х 11 = (0 + 2) (2 + 2) (2 + 5) (5 + 3) (3 + 0) = 2 + 4 + 7 + 8 + 3 = 24,783.
Доказать истинность просто: 11 = 10 + 1
2,253 х 10 + 2,253 = 22,530 + 2,253 = 24,783.
Алгоритмы вычислений для разных чисел разные, но они позволяют производить вычисления быстро.
Видео «Умножение столбиком»
Деление многозначных чисел
Деление столбиком может показаться детям сложным, однако запомнить алгоритм несложно. Рассмотрим деление многозначных чисел на однозначное число:
215 : 5 = ?
Записывается вычисление следующим образом:
Под делителем будем записывать результат. Деление выполняется следующим образом: сравниваем крайнюю левую цифру делимого с делителем: 2 меньше 5, разделить 2 на 5 мы не можем, поэтому берем еще одну цифру: 21 больше 5, при делении получается: 20 : 5 = 4 (остаток 1)
Сносим к полученному остатку следующую цифру: получаем 15. 15 больше 5, делим: 15 : 5 = 3
Решение будет выглядеть таким образом:
Так производится деление без остатка. По тому же алгоритму производится деление в столбик с остатком с той лишь разницей, что в последней записи будет указан не ноль, а остаток.
Если необходимо произвести деление трехзначных чисел в столбик на двухзначное, порядок действий будет таким же, как при делении на однозначное число.
Приведем примеры на деление:
Аналогично проводится вычисление при делении многозначного числа на двузначное с остатком: 853 : 15 = 50 и ( 3 ) остаток
Обратите внимание на эту запись: если при промежуточных вычислениях в результате получается 0, но пример не решен до конца, ноль не записывается, а сразу сносится следующая цифра, и вычисление производится дальше.
Поможет усвоить правила деления многозначных чисел в столбик видеоурок. Запомнив алгоритм и проследив последовательность записи вычислений, примеры на умножение и деление в столбик в 4 классе уже не будут казаться такими сложными.
Важно! Следите за записью: разряды должны записываться под разрядами, в столбик.
Видео «Деление в столбик»
Если во 2 классе ребенок выучил таблицу умножения, примеры на умножение и деление двузначного или трехзначного числа на уроках математики за 4 класс не вызовет у него трудностей.
Читайте так же:
Математика: сложение обыкновенных дробей
Математика: вычитание обыкновенных дробей
Быстрый способ выучить таблицу умножения
Калькулятор онлайн — Решение показательных уравнений
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Показательная функция, её свойства и график
Напомним основные свойства степени.n} \)
6) an > 0
7) an > 1, если a > 1, n > 0
8) anm, если a > 1, n
9) an > am, если 0
В практике часто используются функции вида y = ax, где a — заданное положительное число, x — переменная.
Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является
показатель степени, а основанием степени — заданное число.
Определение. Показательной функцией называется функция вида y = ax, где а — заданное число, a > 0, \( a \neq 1\)
Показательная функция обладает следующими свойствами
1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень ax где a > 0, определена для всех действительных чисел x.
2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение ax = b, где а > 0, \( a \neq 1\), не имеет корней,
если \( b \leqslant 0\), и имеет корень при любом b > 0.
3) Показательная функция у = ax является возрастающей на множестве всех действительных чисел, если a > 1, и
убывающей, если 0
Это следует из свойств степени (8) и (9)
Построим графики показательных функций у = ax при a > 0 и при 0 Использовав рассмотренные свойства отметим, что график функции у = ax при a > 0 проходит через точку (0; 1) и
расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.
График функции у = ax при 0
Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является
горизонтальной асимптотой графика.
Если х
Показательные уравнения
Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени.
Решение показательных уравнений часто сводится к решению уравнения ax = ab где а > 0, \( a \neq 1\),
х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \( a \neq 1\) равны
тогда и только тогда, когда равны их показатели.
Решить уравнение 23x • 3x = 576
Так как 23x = (23)x = 8x, 576 = 242, то уравнение можно записать в виде
8x • 3x = 242, или в виде 24x = 242, откуда х = 2.
Ответ х = 2
Решить уравнение 3х + 1 — 2 • 3x — 2 = 25
Вынося в левой части за скобки общий множитель 3х — 2, получаем 3х — 2(33 — 2) = 25,
3х — 2 • 25 = 25,
откуда 3х — 2 = 1, x — 2 = 0, x = 2
Ответ х = 2
Решить уравнение 3х = 7х
Так как \( 7^x \neq 0 \) , то уравнение можно записать в виде \( \frac{3^x}{7^x} = 1 \), откуда \( \left( \frac{3}{7} \right) ^x = 1 \), х = 0
Ответ х = 0
Решить уравнение 9х — 4 • 3х — 45 = 0
Заменой 3х = t данное уравнение сводится к квадратному уравнению t2 — 4t — 45 = 0.{x-2} = 1 \)
x — 2 = 0
Ответ х = 2
Решить уравнение 3|х — 1| = 3|х + 3|
Так как 3 > 0, \( 3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1)2 = (х + 3)2, откуда
х2 — 2х + 1 = х2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1
ГДЗ по математике 5 класс Чесноков дидактические материалы
Математика за 5 класс требует комплексного подхода к изучению. Очень многие дети, после младшей школы, испытывают некоторые трудности с этим предметом. Обусловлено это в первую очередь тем, что дисциплина становится более сложной, темы разнообразными. Они связаны между собой достаточно плотно, поэтому, если существовал пробел в знаниях по предыдущим разделам, то дальнейшее освоение будет затруднено. Чтобы этого избежать и не запустить ситуацию, рекомендуется использовать решебник по математике за пятый год обучения к дидактическим материалам автора Чеснокова и Нешкова.
Темы и разделы по предмету
- понятия точки, отрезка, луча и прямой;
- чтение и записывание больших натуральных чисел с разрядами и классами;
- сравнение десятичных дробей и их корректное изображение на числовой прямой. А также действия с ними;
- буквенные и цифровые выражения;
- объемы и площади простых геометрических фигур;
- понятие углов и единицы их измерения.
Как видно, добавляется достаточно много новых разделов. К тому же, некоторые из них формируют первые геометрические понятия. В связи с чем, требуется особое внимание при изучении данной дисциплины, как в школе, так и дома.
В чем помогут ГДЗ по математике к дидактическим материалам для 5 класса (авторы: А. С. Чесноков, К. И. Нешков)
Если школьник будет пользоваться готовыми домашними заданиями, то это обеспечит ему следующие преимущества:
- он сможет выполнять домашние задания самостоятельно;
- если что-либо останется непонятным, то можно нарешать некоторое количество номеров и упражнений по данной теме из аналогичной группы сложности;
- приобретенные навыки ребенок с успехом продемонстрирует во время проведения тестов и проверочных работ на уроке в классе. Он перестанет испытывать страх и неуверенность в себе. А это самым благотворным образом отразится не только на его психоэмоциональном состоянии, но также будет формировать лидерский характер;
- оценки за контрольные работы, четверти и год станут выше;
- и, что самое главное, грамотный подход с использованием решебника, позволит ему подготовить основу для дальнейшего освоения сложных тем по дисциплине в последующих классах. Результат – удачная сдача ОГЭ и ЕГЭ и планирование поступления в то учебное заведение, которое хочется.
Как избежать неудач
Некоторые дети, в силу своего характера и все-таки еще слишком юного возраста, не понимают всей меры ответственности по отношению к учебе, которая лежит на их плечах. Они просто бездумно списывают предложенные готовые ответы в этом информационном справочном материале. Этот подход только усугубляет ситуацию, так как не формирует нужные навыки. В этом случае роль родителей является ключевой и решающей. Они должны в первую очередь объяснить, как правильно использовать решебник, независимо от того, представлен он печатным изданием или используется в онлайн-режиме. И, чтобы избежать недоразумений и просчетов, им стоит контролировать учебный процесс, хотя бы периодически. Только в этом случае можно получить положительный эффект, и родители могут избежать нанимания репетитора.
Урок для третьего класса Массивы со строками и столбцами
Разминка этого урока — это обзор построения массивов и акцент на различии между столбцами и строками. Обсуждая план этого урока с помощью жестов, я перемещаю руку перед собой по горизонтали, когда использую словарный термин , строка , и держу руку перед собой вертикально, когда использую словарный термин , столбец. Поскольку это обзорный урок, я провожу быструю проверку понимания, используя вопрос «Можете ли вы назвать диаграмму, в которой используются строки и столбцы?» Ответ некоторых студентов — массивы.Я стараюсь повторить слово, а затем записать его на доске.
Я прошу учеников двигать руками по горизонтали и произносить ряд. Еще поясняю, что это по горизонтали как по горизонту. Затем я повторяю с вертикальными движениями и говорю, что это движение вертикальных , как их позвонки. Я использую этот словарь, потому что он связан с содержанием, которое мы рассмотрели в области науки в этом году.
Я повторяю жесты для строк и столбцов, сначала быстро произнося слова, чтобы увидеть жест, а затем переключаю их, чтобы дать жест, и ученики обеспечивают словарный запас.Вы также можете использовать учащихся, чтобы помочь им вести эту словарную деятельность.
Как только ученики научатся жестам и лексике, я объясняю, что они будут создавать массивы на миллиметровой бумаге с предложениями умножения чисел для отображения строк и столбцов. Учащиеся работают с партнером, используя кубики с числами до девяти (или можно использовать игральные карты) для создания каждого массива. Первое число, выбранное партнером A, будет использоваться для строк, а второе число, выбранное партнером B, будет числом для столбцов.Затем они записывают числовое предложение внутри массива и находят продукт.
Я использую особую структуру для создания числовых предложений, потому что хочу подчеркнуть разницу в словарном запасе. Стандарт Common Core не требует установленного порядка строк x столбцов или столбцов x строк, и учащиеся должны понимать, что порядок факторов не влияет на продукт. Но изначально это позволяет мне так структурировать мышление ученика, чтобы словарный запас «прижился». Я также применяю лексику к другим контекстам реального мира, включая сидение в ряду в кинотеатре и колонны, поддерживающие здание.
Определение и примеры матрицы, ее записей, строк, столбцов, обозначений матрицы. Матрица — это просто …
Матрица — это способ организации данных в столбцы и строки. В скобках [] пишется матрица. Посмотрите на картинку ниже, чтобы увидеть пример.
Каждый элемент в матрице называется записью.
Пример матрицы
Матрица, изображенная ниже, состоит из двух строк и трех столбцов.
- Его размеры 2 × 3
- Элементы матрицы ниже: 2, -5, 10, -4, 19, 4.
Размер матрицы
Размеры матрицы относятся к количеству строк и столбцов данной матрицы. По соглашению размер матрицы определяется числом строк • числом столбцов
Один из способов, которым некоторые люди помнят, что обозначение размеров матрицы — это строки за столбцами (а не столбцы за строками), — это вспомнить некогда популярную газировку:
RC Cola - строки перед столбцами!
Ниже вы можете увидеть два изображения одной и той же матрицы с выделенными строками и столбцами.
Размеры данной матрицы
- Размеры: 2 × 3
- 2 строки × 3 столбца
Матричное обозначение
Чтобы идентифицировать запись в матрице, мы просто пишем нижний индекс строки соответствующей записи, за которой следует столбец.
В матрице A слева мы пишем 23 для обозначения записи во второй строке и третьем столбце.
Один из способов запомнить, что в этой нотации на первом месте строки, а на втором — столбцы, — это думать об этом как о чтении книги. Вы всегда сначала читаете сбоку, так же как всегда сначала пишете строки. Продолжая аналогию, когда вы заканчиваете читать строку в книге, ваши глаза опускаются, как столбцы после строк. 23 указывает сначала номер строки, 2, затем номер столбца 3.
Практика определения записей
Практика 1
Шаг 1
Габаритные размеры
Размеры матрицы 3 × 3 (3 строки × 3 столбца)
Шаг 2
Найдите запись G 23 в матрице G слева.
Вход
G 23 — запись во второй строке и третьем столбце: 55.
Шаг 3
Габаритные размеры
Размеры
3 × 5 (3 строки × 5 столбцов)
Практика 2
Шаг 1
Отвечать
Запись j 34 — это запись в третьей строке и четвертом столбце.
Шаг 2
Отвечать
J 12 — число в первой строке и втором столбце: -5
Практика 3
Шаг 1
Отвечать
Размеры матрицы 4 × 5 (4 строки × 5 столбцов)
Шаг 2
Отвечать
Запись — 31 (строка 1 и столбец 4)
Шаг 3
Отвечать
v 45 обозначает запись в четвертой строке и пятом столбце, цифру 15 в правом нижнем углу.
Сложение и вычитание матриц
Вы можете складывать или вычитать матрицы, если каждая матрица имеет одинаковые размеры (другими словами, каждая из них должна иметь одинаковое количество столбцов и строк).
Чтобы сложить или вычесть матрицы, вы просто добавляете или вычитаете соответствующие записи (записи или числа, находящиеся в одном месте).
Почему для сложения и вычитания требуются одинаковые размеры?
Подумайте об этом: Поскольку добавление / вычитание матриц включает добавление / вычитание соответствующих записей. Что бы вы сделали с записями в одной матрице, которым нет соответствующей записи в другой?)
Рассмотрим пример, изображенный выше.. Матрица №1 имеет на один столбец больше, чем Матрица №2. Как бы вы сопоставили, не говоря уже о добавлении, записи в столбце 3 №1 с соответствующими записями в столбце №2. Что ж, ответ — вы не можете, поскольку вы не можете добавлять матрицы, если они не имеют одинакового количества строк и столбцов.
Дополнение + | Основы арифметики
Эта страница является частью нашей серии статей, посвященной основам арифметики — простейшему способу работы с числами.
Здесь вы узнаете основы сложения (+): как сложить, суммировать или объединить два или более чисел, чтобы получить новое число — итог.Умение «складывать» важно во всех сферах жизни, дома, в школе, на работе и в обществе.
См. Другие наши страницы, чтобы узнать о вычитании, умножении и делении.
Краткие сведения о добавлении:
- Сложение — это термин, используемый для описания сложения двух или более чисел.
- Знак плюс « + » используется для обозначения сложения: 2 + 2.
- При необходимости + можно использовать несколько раз: 2 + 2 + 2.
- Для более длинных списков чисел обычно проще записать числа в столбец и выполнить вычисление внизу.
- Слово «сумма» или символ ∑ также могут использоваться для сложения.
- Не имеет значения, в каком порядке вы складываете группу чисел, потому что ответ всегда будет одним и тем же:
1 + 2 + 3 + 4 дает тот же ответ (10), что и 4 + 2 + 1 + 3 - Добавление 0 к любому числу не имеет значения 2 + 0 = 2.
Базовое сложение — это шаг вперед от счета и обычно легко усваивается учащимися.
Как только ученик может сосчитать до десяти, он обычно может быстро прибавить до десяти.
Например, если учащемуся дают две стопки карт, одна стопка содержит 4 карты, а другая — 3 карты, он может пересчитать все карты и получить ответ: 7.
Использование пальцев — обычное дело при обучении счету и сложению. Добавление точек, нарисованных на листе бумаги, а затем использование «числовой линии» — это следующие шаги в обучении, на этот раз нет физических предметов, которые нужно было бы обрабатывать.
Наконец, когда цифры распознаны, можно вычислить ту же сумму, посмотрев на 3 + 4.
Сложить одно и то же число с собой (или удвоить) также довольно просто, если вы усвоили базовое понимание умножения, например, 3 + 3 = 6.
Сложить одно и то же число с собой аналогично умножению числа на 2:
3 + 3 также можно записать как
3 x 2 (устно 3 умножить на 2).
Добавление столбца
При сложении большого количества чисел полезно записывать их в столбцы, обозначая единицы, десятки и сотни (примеры см. На нашей странице чисел).Если нам нужно было добавить 4, 15, 23, 24, 35, 42
Шаг 1:
Расположите числа в столбцах, Сотни, Десятки и Единицы по мере необходимости:
| Десятки | Шт. |
| 4 | |
| 1 | 5 |
| 2 | 3 |
| 2 | 4 |
| 3 | 5 |
| 4 | 2 |
Сложите числа в правом столбце (единицы).Это должно дать вам ответ 23. Две десятки и три единицы. Напишите 3 в столбце «Единицы измерения».
Перенесите 2 десятка — это число обычно ставится под общей суммой, оно нам понадобится на следующем шаге.
| Десятки | Шт. | |
| 4 | ||
| 1 | 5 | |
| 2 | 3 | |
| 2 | 4 | |
| 3 | 5 | |
| 4 | 2 | |
| = | ||
| Всего | 3 | |
| Переносной | 2 |
Шаг 2:
Сложите числа в столбце десятков, не забывая включить 2, которые были перенесены.Вы должны получить ответ 14.
То есть 4 десятка (поскольку мы работаем в столбце десятков) и 1 для переноса в следующий столбец, сотни.
| Сот | Десятки | Шт. | |
| 4 | |||
| 1 | 5 | ||
| 2 | 3 | ||
| 2 | 4 | ||
| 3 | 5 | ||
| 4 | 2 | ||
| = | |||
| Всего | 4 | 3 | |
| Переносной | 1 | 2 |
Шаг 3:
Следующим шагом будет сложение чисел в столбце сотен.
В столбце сотен нет чисел, кроме 1, перенесенного из столбца десятков.
Так как больше добавить нечего, доведите до общей суммы.
У нас больше не осталось чисел, поэтому мы пришли к нашему ответу: 143 .
| Сот | Десятки | Шт. | |
| 4 | |||
| 1 | 5 | ||
| 2 | 3 | ||
| 2 | 4 | ||
| 3 | 5 | ||
| 4 | 2 | ||
| = | |||
| Всего | 1 | 4 | 3 |
| Переносной | 1 | 2 |
Вы можете использовать тот же метод для сложения все больших и больших чисел, добавляя дополнительные столбцы слева по мере необходимости для тысяч, десятков тысяч и т. Д.
Примеры добавления
Есть много примеров, когда сложение полезно в повседневных ситуациях. При разработке маршрута для путешествия вы можете сложить количество миль (или километров) для каждого шага путешествия, чтобы найти общее количество миль, которые вы пройдете. Это может помочь вам, например, спланировать остановки заправки.
Вы можете использовать сложение, чтобы вычислить, сколько времени потребуется. Например, если вы сядете в автобус в 11:00, а поездка займет 25 минут, во сколько вы приедете? Точно так же вы можете складывать дни, недели, месяцы или годы.
При добавлении минут или секунд всегда помните, что в минуте 60 секунд, а в часе 60 минут. Следовательно, 100 минут равны не часу, а 1 часу 40 минутам. См. Нашу страницу Расчет со временем для получения дополнительной информации.
Пожалуй, одно из самых распространенных повседневных применений сложения — работа с деньгами. Например, суммирование счетов и чеков. Следующий пример — типичный чек из супермаркета.Сложите все индивидуальные цены, чтобы найти общую стоимость посещения.
Поскольку SkillsYouNeed является британским сайтом, используется символ валюты — £ (фунты). Добавление в $ (доллары), € (евро) или любую другую валюту аналогично — просто измените символ валюты.
| Сыр Чеддер | £ 2,99 | |
| Простая мука | £ 0,79 | |
| Сахарный песок | £ 1.20 | |
| Сливочное масло | £ 1,24 | |
| Морковь | 0,16 фунта стерлингов | |
| Бытовая химия | £ 1,89 | |
| Молоко | £ 1,25 | |
| Молочный шоколад | 0,69 £ | |
| Моющее средство | £ 6.50 | |
| Яйца | £ 1.10 |
Добавьте цены в чек, как в предыдущем примере.
На этот раз у вас есть десятичная точка (.), Чтобы показать доли одной единицы (фунт £). При вычислении сложения столбцов вы можете игнорировать десятичную точку, пока не дойдете до конца. Начните с сложения чисел в правом столбце, как и раньше, работая по столбцам справа налево и перенося любые «десятки» в следующий столбец.
Не забудьте включить десятичную точку в конце ваших вычислений; у вас должно быть два столбца справа от него.Технически эти столбцы должны быть помечены как «Десятые» и «Сотые». Однако попробуйте складывать числа, не используя заголовки столбцов.
Возможно, вам будет проще написать или распечатать этот пример.
Ваш окончательный ответ должен быть: 17,81 фунта стерлингов.
Если вы пришли к другому ответу, проверьте свою работу и попробуйте еще раз.
Предупреждение!
Важно отметить, что не все мировые валюты основаны на десятичной системе счисления и не все валюты имеют два десятичных знака.Например, у некоторых есть ноль десятичных знаков (например, японская иена), а у некоторых — три десятичных разряда (например, динар во многих странах).
Примеров недесятичных валют очень мало. Мавритания (где 1 угия = 5 кумов) и Мадагаскар (где 1 ариари = 5 ираимбиланджа) только теоретически недесятичны, так как в обоих случаях стоимость каждой подъединицы слишком мала, чтобы иметь какое-либо практическое применение сегодня, а монеты Номиналы единиц больше не в обращении. Официальной валютой Суверенного военного Мальтийского ордена является мальтийское скудо, которое подразделяется на 12 тари, каждый из которых составляет 20 грани с 6 пикчоли на грано.
Все остальные мировые валюты либо десятичные, либо вообще не имеют подединиц, либо потому, что они были упразднены, либо потому, что они потеряли всякую практическую ценность и больше не используются. Для получения дополнительной информации о десятичной системе счисления см. Нашу страницу Системы измерения .
Стратегии умножения — Метод коробки
Когда я перешла в 3/4 класс, мне на колени оказался совершенно новый мир учебной программы. Поскольку я никогда раньше не учил умножению двойных и тройных цифр, я, естественно, начал учить своих учеников делать это именно так, как я научился.В методе алгоритма определенно нет ничего плохого, но со временем я обнаружил, что очень полезно изучить несколько других методов решения этих проблем. Этот пост посвящен моему новому фавориту…. Коробочный метод!
Первый шаг метода коробки — нарисовать коробку. Если вы умножаете две цифры на две цифры, ваше поле должно состоять из двух строк на два столбца. Для задачи три цифры на две цифры потребуются три строки и два столбца или две строки на три столбца (в любом случае работает из-за свойства коммутативности).
Затем вы расширяете каждый из факторов в соответствии с числовой стоимостью. Таким образом, 24 становится 20 + 4, а 35 становится 30 + 5. Каждая часть расширенной записи написана либо сверху, либо сбоку поля.
Шаг третий — умножить числа в сетке. Это похоже на магический квадрат. Умножьте верхнее число на число стороны и поместите ответ в поле, где пересекаются строка и столбец. На этом этапе я учу детей умножать числа, оканчивающиеся на ноль.Я заставляю их полностью игнорировать нули для начала. Поэтому вместо того, чтобы беспокоиться о 20 x 30, они просто работают с 2 x 3. После того, как они написали 6, они подсчитывают, сколько нулей они проигнорировали в первую очередь (2), и складывают их, получая 600. Это действительно дает смысл для них, и он охватывает еще один математический стандарт в процессе!
Последний шаг — сложить все числа в поле.
Вот и все! Как только дети поймут, как установить коробку, они отлично справятся с этой стратегией.Обучая методу ящика, я сначала позволяю детям использовать таблицу умножения, чтобы помочь им. Меня больше беспокоит их понимание процесса умножения двух или трех цифр. Как только они получают процесс, я даю им задачи обойтись без диаграммы, но я придерживаюсь цифр от 0 до 5 во всех местах. Они лучше пропускают счет с меньшими числами и, как правило, знают эти таблицы с меньшим умножением. Последний «уровень» — ввести в места более крупные цифры. Как только они смогут решать задачи типа 89 x 76, я знаю, что они понимают процесс и хорошо разбираются в своих таблицах умножения.
Вот еще несколько полных примеров:
Я планирую посвятить несколько постов другим стратегиям умножения и деления, которые я изучил за последние пару лет. Следующим будет…. Частичные продукты!
MAFS.2.G.1.2 | SMathSmarts
MAFS.2.G.1.2 Разделите прямоугольник на строки и столбцы квадратов одинакового размера и посчитайте, чтобы найти их общее количество.
Уровень когнитивной сложности: 1 отзыв
Студенты могут…
- Расскажите и покажите примеры строк и столбцов, разделяющих прямоугольник.
- Объясните, как фигура была разделена на квадраты, и посчитайте, чтобы найти общее количество квадратов.
Студенты могут… потому что учителя:
- Планируйте задачи, которые устанавливают связи между равным распределением и разделением с помощью прямоугольников.Эти связи начинают формировать концептуальное понимание умножения.
- Предоставьте учащимся возможность использовать плитки для покрытия прямоугольника. Они могут обсудить это, объяснив количество использованных рядов и столбцов квадратов. (Например, прямоугольник покрывали 2 ряда по 5 квадратов.)
- Помогите студентам установить связь между использованием физических плиток и графическим изображением, которое студенты затем могут нарисовать сами.
Вопросы для студентов:
- Задайте вопрос: дайте ученику прямоугольник и попросите его / ее покрыть его плиткой.Спросите учащегося, сколько плиток для этого нужно? Попросите учащегося использовать слова «строка» и / или «столбец» для описания количества использованных плиток.
- Пример ответа, свидетельствующего о понимании: учащийся будет использовать плитки, чтобы покрыть прямоугольник без перекрывающихся плиток или больших пространств. Студент правильно скажет количество использованных плиток. Тогда ученик сможет правильно использовать слова «строка» и «столбец». Например: есть 15 плиток. Есть 3 ряда по 5 плиток. ИЛИ Есть 5 столбцов по 3 плитки.
- Пример ответа, который указывает на неполное понимание или заблуждение: учащийся неправильно считает плитки и / или неправильно использует термины «строка» и «столбец». Например, в приведенной выше модели ученик может сказать, что есть 5 рядов по 3 плитки ИЛИ 3 столбца по 5 плиток.
Дополнительные ресурсы:
Дополнительные углубленные знания содержания
Видео: Разделите прямоугольники на квадраты одинакового размера, создав столбцы и строки
https: // learnzillion.ru / lesson_plans / 5598-разбиение прямоугольников на квадраты одинакового размера путем создания столбцов и строк
Образцы задач формирующего оценивания:
Ресурсы / задачи для поддержки вашего ребенка дома:
- Дайте ребенку учетную карточку или лист прямоугольной бумаги. Попросите их сложить его в равные строки и столбцы, например, 3 строки по 4. Попросите их описать, как прямоугольник был разложен, используя математический язык. Попросите их записать уравнение и общее количество квадратных единиц.
- Академия Хана: равные части окружностей и прямоугольников
Сложение слева направо: стратегия сложения
Сложение слева направо (также известное как внешнее сложение или метод частичных сумм) — одна из самых мощных математических стратегий в уме для обучения сложению двух- или трехзначных чисел.Однако многих сбивает с толку, почему это важно и почему оно может быть более эффективным, чем традиционное вертикальное добавление.
ПОЧЕМУ ЭТО ТАК ЭФФЕКТИВНО?
Самое лучшее в сложении слева направо — то, что эта стратегия способствует реальному пониманию.
Когда вы решаете уравнение с помощью стандартного алгоритма (вероятно, так, как вы научились складывать многозначные числа), вы используете серию шагов. Это включает в себя сначала добавление единиц, перенос при необходимости, затем добавление десятков, перенос при необходимости и т. Д.Эти шаги навсегда останутся в вашей памяти, и для тех, у кого есть отличные навыки запоминания, это может быть эффективным.
ОДНАКО стандартный алгоритм не способствует пониманию значения разряда и смысла числа. Это основная причина того, что современные инструкции по математике, как правило, уклоняются от традиционного алгоритма в младших классах. Мы хотим, чтобы наши студенты действительно понимали, что они делают. Когда учеников обучают методам, которые стимулируют мысленную математику, они могут более гибко думать не только об этой изолированной концепции, но и о других математических концепциях.
ПРИМЕРЫ
Давайте посмотрим на несколько примеров сложения слева направо в действии.
В этом примере мы складываем 25 + 34. Сначала мы складываем десятки: 20 + 30, чтобы получилось 50. Затем мы складываем единицы: 5 + 4, чтобы получить 9. Наконец, мы прибавляем 50 + 9, чтобы получить 59. Хотя это может показаться запутанным, если записано, как оно есть , этот процесс происходит очень быстро, когда учащийся понимает его — обычно это можно решить максимум за пару секунд.
Сложение слева направо также эффективно для добавления 3-значных плюс 3-значных чисел. В этом примере мы видим, что сначала складываем сотни, затем десятки, а затем единицы. Наконец, мы складываем все эти суммы вместе.
Когда учащиеся выполняют сложение таким образом, они хорошо понимают значение места и его значение. Например, в приведенном выше уравнении ученики видят «1» в 147 как 100, а не просто 1.«4» в 147 понимается как 40, а не просто 4. Это важное знание, если мы хотим, чтобы наши ученики стали эффективными математиками.
Всякий раз, когда мы преподаем математические стратегии, важно преподавать их таким образом, чтобы улучшить концептуальное понимание. Конкретно-репрезентативная абстрактная модель — отличная обучающая модель для этого. В видео ниже я подробнее расскажу о том, как можно обучить сложению слева направо с помощью модели CRA.
СЛЕДУЮЩИЕ ШАГИ:
- Если вам нужна полная поддержка для обучения стратегиям сложения в классе, ознакомьтесь с The Addition Station ЗДЕСЬ. Вы найдете стратегию сложения слева направо на дополнительных станциях для старших классов. Эти математические станции представляют собой станции для самостоятельного обучения, ориентированные на учащихся, для освоения основных математических стратегий. Студенты продвигаются по уровням в своем собственном темпе, гарантируя, что они всегда сталкиваются с проблемами, и работают в полную силу.
- Прочтите другие сообщения на этом сайте о стратегиях сложения. ЗДЕСЬ.
- Загрузите БЕСПЛАТНОЕ упражнение для отработки стратегии сложения слева направо. ЗДЕСЬ.
- Ознакомьтесь со стратегией добавления слева направо » ЗДЕСЬ.
- Найдите карточки с заданиями, чтобы усилить стратегию сложения слева направо, отдельно здесь:
Четыре основных математических понятия, которые ваши дети изучают в 3-4 классах | Scholastic
Третий и четвертый классы могут по-настоящему изменить правила игры для многих учеников. Вводится несколько новых тем, и темп обучения увеличивается одновременно с тем, как изучаемые концепции становятся более абстрактными.Решению проблем уделяется большое внимание, и выполнение многоэтапных задач может стать сложной задачей. Отличный способ помочь дома — ежедневно практиковать математические факты — складывать, вычитать, умножать и делить. Свободное владение языком очень важно в этом возрасте и действительно поможет вашему ребенку чувствовать себя более комфортно и уверенно в классе.
Вот четыре основных понятия, которые ваш ребенок усвоит в третьем и четвертом классе, а также способы, которыми вы можете закрепить обучение дома.
1. Умножение и деление .В третьем классе вводятся умножение и деление. Большую часть года уходит на понимание этих двух операций и взаимосвязи между ними. К концу третьего класса ваш ребенок должен выучить наизусть все факты умножения и деления (до 100). В четвертом классе ученики продолжают это понимание и начинают решать задачи двух- и трехзначного умножения и деления. На этом этапе понимания очень важно моделирование. Вы можете увидеть умножение и деление в группах, массивах и площадных моделях одинакового размера.
Поощряйте своего ребенка моделировать, используя:
- Группы одинакового размера: группы, содержащие одинаковое количество эквивалентных групп.
Изображение предоставлено: http://www.basic-math-explained.com
- Массивы: объекты или числа, расположенные в равные строки и столбцы.
Изображение предоставлено: http://eces.johnston.k12.nc.us
- Модель площади: модель, в которой длина и ширина прямоугольника представляют факторы.
Изображение предоставлено: http://mr-trex.weebly.com/blog/
2. Дроби: Ваш ребенок начнет понимать дроби, начиная с единичных дробей и используя визуальные модели дробей для представления части целого. Третьеклассники и четвероклассники находят эквивалентные дроби, упорядочивают дроби и сравнивают дроби, а также складывают и вычитают дроби с общими знаменателями. Студенты будут определять дроби, которые равны, меньше и больше единицы.
Поощряйте своего ребенка:
- Найдите дроби в реальном мире и поймите их значение.
- Используйте дроби при приготовлении пищи, покупках, еде, измерении и т. Д.
- Понимайте дробные единицы или дроби, где числитель равен 1.
Изображение предоставлено: http://www.mat Mathematicsdictionary.com
- Модель с дробями с использованием дробей шкала:
Изображение предоставлено: https: // www.eduplace.com
3. Измерения и данные . В третьем и четвертом классе ученики будут решать задачи измерения с использованием массы и объема. Третьеклассники и четвероклассники учатся определять время с точностью до минуты и решать задачи, используя прошедшее время. Они собирают данные и рисуют различные графики для представления данных. Студенты знакомятся с площадью и периметром и устанавливают связь между умножением и делением, а также как это связано с площадью.
Поощряйте своего ребенка:
- Оцените размеры предметов в реальном мире, используя литры, граммы и т. Д.
- Определите время с помощью аналоговых и цифровых часов.
- Выясните временные интервалы в своем дне; например, сколько часов или минут до следующего занятия.
- Читайте и интерпретируйте различные графики в газетах или в Интернете.
- Найдите площадь и периметр различных предметов в их доме, на улице или на детской площадке.
4. Геометрия. Студенты будут заниматься двухмерными фигурами. Третьеклассники и четвероклассники классифицируют, анализируют и сравнивают различные свойства двумерных полигонов.Они смотрят на количество сторон и углов и учатся определять эти многоугольники.
Поощряйте своего ребенка:
- Найдите двумерные полигоны в реальном мире, классифицируйте и определите их.
- Используйте соответствующий словарь при описании различных полигонов. Например: параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и равны.
- Свяжите дроби с геометрией.

 Мотивация к учебной деятельности.
Мотивация к учебной деятельности.
 Актуализация знаний и фиксирование затруднений в пробном учебном материале.
Актуализация знаний и фиксирование затруднений в пробном учебном материале.
 Выражения читайте по-разному.
Выражения читайте по-разному.
 Реализация построенного проекта.
Реализация построенного проекта.


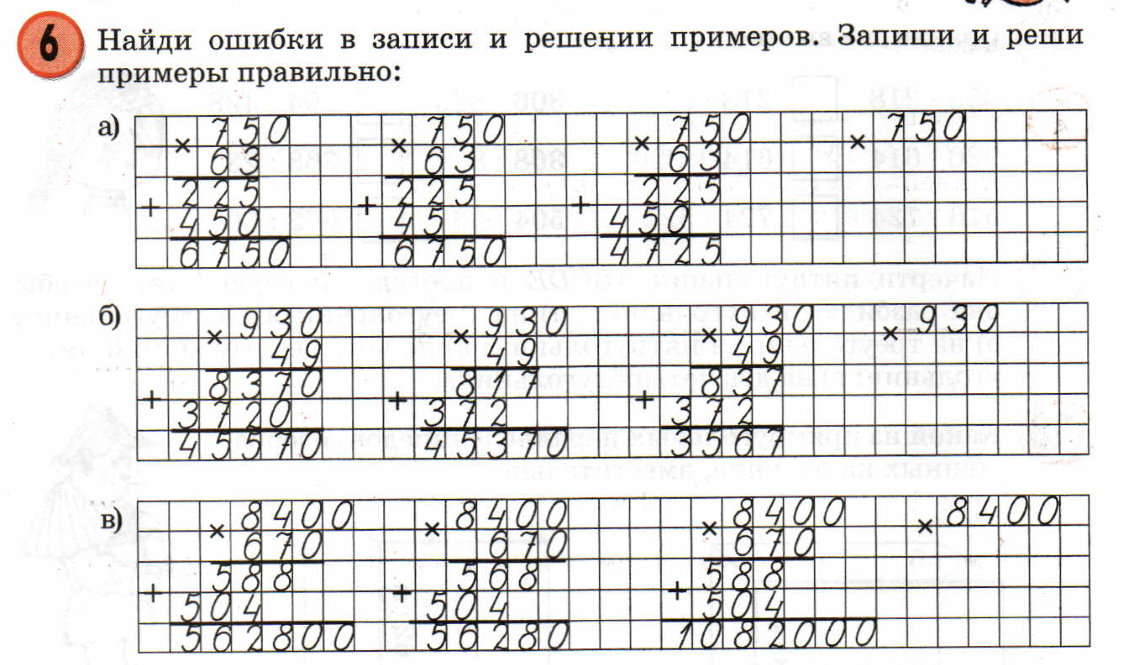
 Включение в систему знаний и повторение (предложить из набора заданий выбрать те, которые содержат новый алгоритм или новые понятия).
Включение в систему знаний и повторение (предложить из набора заданий выбрать те, которые содержат новый алгоритм или новые понятия). СЛАЙД 16.
СЛАЙД 16.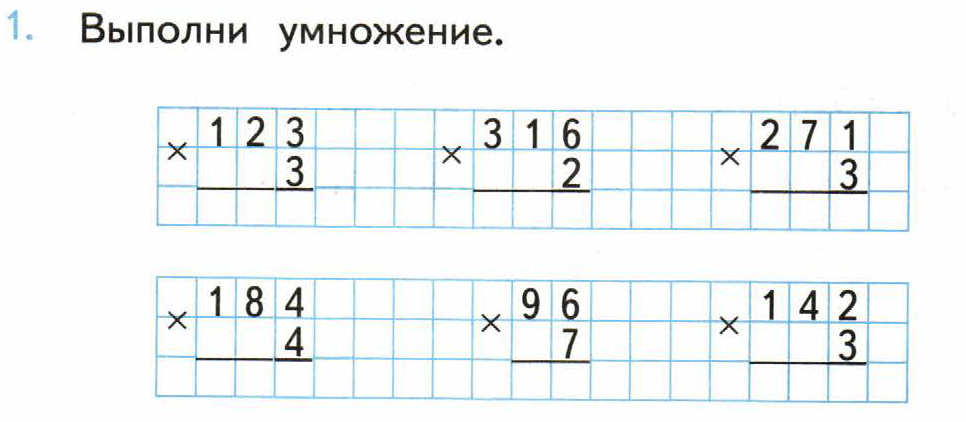 Я проверю, поставлю свою оценку. Если оценки совпадут, то вы научились правильно оценивать себя.
Я проверю, поставлю свою оценку. Если оценки совпадут, то вы научились правильно оценивать себя. 47 № 4(б), 6
47 № 4(б), 6