Развивающие задачи по математике 5 класс с решениями: Задачи на логику – 5 класс: ответы, решения, фото
By: Date: 04.08.2021 Categories: Разное

Содержание

Развивающие задачи по геометрии для 5 класса

Развивающие задачи по математике

для 5 класса

Задача 1

Определите, сколько отрезков с концами в отмеченных точках изображено на рисунке

Задача 2

Определите, сколько отрезков с концами в отмеченных точках изображено на рисунке

Задача 3

Определите, сколько отрезков с концами в отмеченных точках изображено на рисунке

Задача 4

Определите, сколько отрезков с концами в отмеченных точках изображено на рисунке

Задача 5

Сколько квадратов изображено на рисунке

Задача 6

Сколько квадратов изображено на рисунке

Задача 7

Сколько квадратов изображено на рисунке

Задача 8

Сколько прямоугольных треугольников изображено на рисунке

Задача 9

Сколько прямоугольных треугольников изображено на рисунке

Задача 10

Разрежьте фигуру на две равные части по линиям сетки так, чтобы в каждой из частей был кружок

Задача 11

Разрежьте фигуру на равные части по линиям сетки так, чтобы в каждой из частей был кружок

Задача 12

Разрежьте фигуру на равные части по линиям сетки так, чтобы в каждой из частей был кружок

Задача 13

Разрежьте фигуру на две равные части по линиям сетки так, чтобы в каждой из частей был кружок

Задача 14

Разрежьте фигуру на четыре равные части (Разрезать можно не только по сторонам клеток, но и по их диагоналям. )

Задача 15

Разделите фигуры на две равные части (Разрезать можно не только по сторонам клеток, но и по их диагоналям.)

ОТВЕТЫ

№1 Отрезков 30 штук

№2 Отрезков 35 штук

№3 Отрезков 40 штук

№4 Отрезков 44 штук

№5 Квадратов 14 штук

№6 Квадратов 11 штук

№7 Квадратов 20 штук

№8 Прямоугольных треугольников 11 штук

№9 Прямоугольных треугольников 14 штук

№10

№11

№12

№13

№14

№15

Нестандарные задачи, 5 класс | Презентация к уроку (5 класс) по теме:

Слайд 1

Математическая разминка

Слайд 2

Правильно ли решены примеры? 9+ 2= 3 9+ 2= 1 9+ 2= 1 5 + = 7 5+ = 7

Слайд 3

Толя выше Пети, Петя выше Саши, Дима ниже Саши. Кто из мальчиков самый высокий?

Слайд 4

Толя

Слайд 5

В двух коробках лежат шарики: в одной – только белые, в другой – только чёрные. Известно, что одна из надписей верна, другая – ложна. Какого цвета шарики в каждой коробке? Здесь лежат или белые, или чёрные шарики Здесь лежат чёрные шарики

Слайд 6

Чёрные шарики Белые шарики

Слайд 7

Что легче: яблоко или груша?

Слайд 8

Карлсон съел яблоко, грушу и персик. В каком порядке он мог их съесть, если каждый фрукт Карлсон ел отдельно? Перечисли все способы.

Слайд 9

Говорят, что черепаха Тортила отдала золотой ключик Буратино не так просто, а вынесла три коробочки. Тортила прочла надписи и сказала: « Действительно, в одной коробочке лежит золотой ключик, в другой – гадюка, а третья – пуста, но все надписи неверны». Где же лежит золотой ключик? «Здесь лежит золотой ключик» «Зелёная коробочка пуста» «Здесь сидит гадюка»

Слайд 10

Сколько весит кирпич? 1 кг

Слайд 11

Трое рыбаков поймали 75 окуней и стали варить уху. Когда один рыбак дал 8 окуней, другой 12, а третий 7, то окуней у них осталось поровну. Сколько окуней поймал каждый рыбак?

Слайд 12

Пришёл Иван-царевич в подземелье к Кощею Бессмертному Василису Прекрасную освобождать. В подземелье три темницы. В одной из них томится Василиса, в другой расположился Змей Горыныч, а третья темница – пустая. На дверях есть надписи, но все они ложные. В какой же темнице Василиса? «Здесь Василиса Прекрасная» «Темница 3 не пустая» «Здесь Змей Горыныч »

Слайд 13

Попрыгунья-Стрекоза половину времени каждых суток красного лета спала, третью часть времени каждых суток танцевала, шестую часть – пела. Остальное время она готовилась к зиме. Сколько часов в сутки Стрекоза готовилась к зиме?

Слайд 14

Расставь числа 1,2,3,4,5,6 в кружках так, чтобы сумма чисел вдоль каждой прямой равнялась 12.

Слайд 15

На трёх банках с вареньем наклеены надписи. Какого сорта варенье в каждой банке, если известно, что все надписи не верны? или

Слайд 16

Сколько треугольников содержит фигура?

Слайд 17

Однажды осенью в 11 часов вечера шёл сильный дождь. Как вы думаете. Возможна ли солнечная погода через 72 часа?

Слайд 18

Двое играли в шашки 4 часа. Сколько часов играл каждый из них?

Слайд 19

Улитка за день проползает по столбу 3 м вверх, а за ночь опускается на 2 м. За сколько дней она доберётся до вершины столба высотой 15 м?

Слайд 20

Поезд отходит из Санкт – Петербурга в Москву, а через час другой поезд отправляется из Москвы в Санкт – Петербург. Скорости поездов одинаковы. Какой из них в момент встречи будет находиться на меньшем расстоянии от Москвы?

Слайд 21

Петух, стоя на одной ноге, весит 3 кг. Сколько он будет весить, стоя на двух ногах?

Слайд 22

Имеются два сосуда вместимостью 3 л и 5 л. Как с помощью таких сосудов налить из водопроводного крана 4 л в третий сосуд?

Слайд 23

Как с помощью 7-литрового ведра и 3-литровой банки налить в кастрюлю ровно 5 л воды?

Слайд 24

Отцу 38 лет, а сыну 14. Во сколько раз отец был старше сына 6 лет назад?

Слайд 25

Ваня живёт выше Пети, но ниже Сени, а Вася живёт ниже Пети. Кто из них на каком этаже четырёхэтажного дома живёт?

Слайд 26

Во дворе гуляли кролики и куры. Всего 12 голов и 38 ног. Сколько было кроликов и сколько кур?

Слайд 27

Продолжите ряд: 2, 3, 4, 5, 6, … 10, 9, 8, 7, 6, 5, … 5, 10, 15, 20, … 24, 21, 18, 15, … 1, 2, 4, 8, 16, … 9, 1, 7, 1, 5, 1, … 1, 4, 9, 16, 25, … 1, 8, 27, 64, …

Слайд 28

Как расставить 16 стульев, чтобы у каждой из четырёх стен комнаты стояло: а) по 4 стула; б) по 5 стульев.

Слайд 29

Расставьте скобки 6 8 + 20 : 4 – 2 = 58 .

Урок-игра по математике для 5 класса

Задачи проведения урока- игры по математике в школе:

Учебные:

  1. Совершенствовать профессиональное мастерство педагогов в процессе подготовки, организации и проведения урока.

  2. Повысить уровень математического развития обучающихся и расширить их кругозор.

  3. Углубить представления обучающихся об использовании сведений из математики в повседневной жизни.

  4. Развитие у обучающихся умений работы с учебной информацией, развитие умений планировать и контролировать свою деятельность.

Развивающие:

  1. Развивать у обучающихся интерес к занятиям математикой.

  2. Выявлять учащихся, которые обладают творческими способностями, стремятся к углублению своих знаний по математике.

  3. Развивать речь, память, воображение и интерес через применение творческих задач и заданий творческого характера.

Воспитательные:

  1. Воспитывать самостоятельность мышления, волю, упорство в достижении цели, чувство ответственности за свою работу перед коллективом.

  2. Воспитание умений применять имеющиеся знания на практике.

  3. Воспитание умений защищать свои убеждения, делать нравственную оценку деятельности окружающих и своей собственной.

Ожидаемые результаты:

  1. Подтверждение имеющихся у обучающихся базовых знаний в соответствии с тематикой урока математики.

  2. Знакомство с видами творческой самостоятельной деятельности и развитие навыков её выполнения.

  3. Выявление круга учащихся, стремящихся к углублению знаний по математике.

  4. Вовлечение родителей в совместную с учащимися деятельность при проведении мероприятий.

  5. Расширение историко-научного кругозора учащихся в области математики.

  6. Развитие коммуникативных умений при общении с учениками разного возраста.

Формы поощрения активных и успешных участников:

  1. Награждение индивидуальных победителей грамотами образовательного учреждения и призами.

  2. Выставление хороших оценок в журнал активным и успешным обучающимся.

Мероприятия не должны быть затянуты по времени. Необходимо учитывать также то обстоятельство, что возрастает учебная нагрузка на детей. Содержание урока математики должно быть подобрано так, чтобы всем было интересно, а разноуровневые задания позволили бы каждому почувствовать себя успешным. Урок – игра по математике должна проходить под девизом: “Успех порождает успех!”

Итак, ученики делятся на две команды и выбирают себе командира.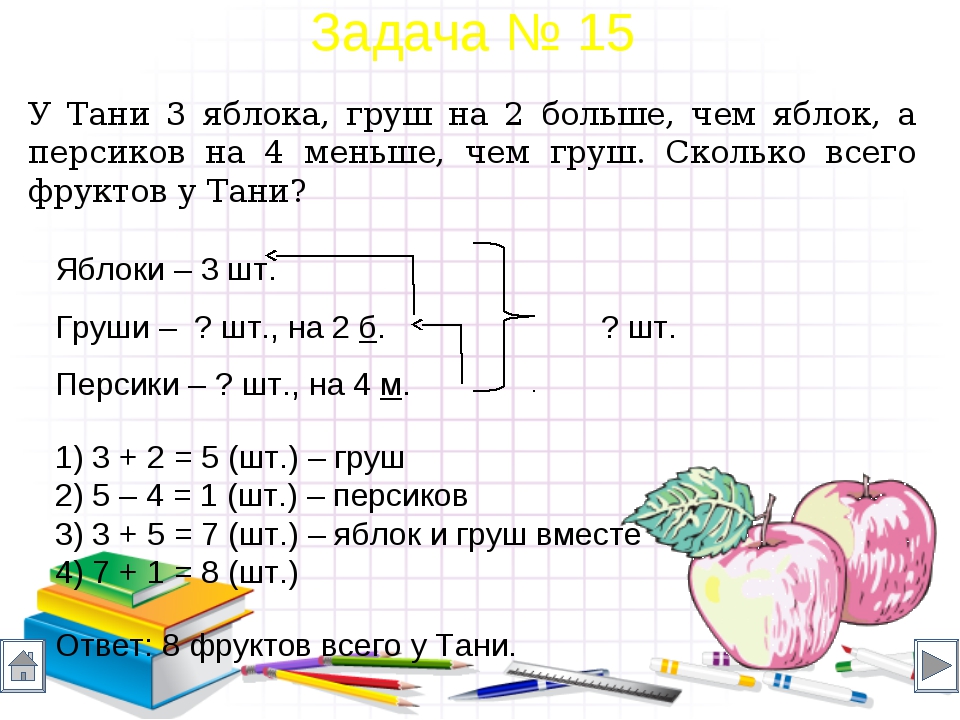

1-й конкурс «БЛИЦТУРНИР»

Командам предлагается решить пример, содержащий все математические действия, но выполнить это задание всей командой.

  • 1-й ученик – расставляет порядок действий.

  • 2-й ученик – выполняет первое действие.

  • 3-й ученик – выполняет второе действие.

  • 4-й ученик – выполняет третье действие.

  • 5-й ученик – выполняет четвертое действие.

  • 6-й ученик – выполняет пятое действие и записывает ответ.

Ряд 1: 14 + (36*18 – 522:87) – 21= 635

36*18=648; 2) 522:87=6; 3) 648 – 6 = 642; 4) 14+642=656; 5) 656 -21 = 635

Ряд 2: 23 + (468: 78 + 46 * 24) – 157 = 976

1) 468:78=6; 2) 46*24=1104; 3) 1104+6=1110; 4) 23+ 1110 = 1133;

5) 1133 – 157= 976

Ряд 3: 689 – (621: 69 + 35*18) + 57=107

621: 69 = 9; 2) 35*18=630; 4) 630 +9 = 639; 5) 689 -639 = 50: 6) 50+57=107  [5] 

2-й конкурс «ПОДУМАЙ»

Оценка: 5 баллов за правильно решенную задачу.

Коля, Боря, Вова и Юра заняли первые четыре места в соревнованиях. На вопрос, кто какое место занял, ребята ответили:

— Коля ни первое, ни четвертое.

— Боря занял второе место.

-Вова не был последним из четвертых.

— Кто какое место занял?

(1-Вова,2- Боря, 3- Коля,4-Юра) [4] 

3-й конкурс «ЗАДАНИЯ»

1)) Из разных цифр я сделал «бусы»

А в те кружки, где чисел нет,

Поставьте быстро вы ответ,

Чтоб данный нам открыть секрет

40 : 5
 

2) Буханка хлеба весит полкило и полбуханки. Сколько весит целая буханка? (ответ: 1 кг).

3) Число, увеличив себя вдвое, посмотрело на себя в зеркало и увидело там 906. Какое это число? (ответ: 453).

4) Восстановите стертые цифры 5* 683 <50 6*1.

5) В семье 6 дочерей. Каждая имеет брата. Сколько всего детей в семье? (ответ: 7)

6) Бревно пилят на 10 частей. Сколько надо сделать распилов? (ответ: 9) [2]  

4-й конкурс «ХУДОЖНИК»

На доске две одинаковые заготовки. Кто быстрее нарисует рисунок, соединив отрезками числа, делящиеся на 3. Участвуют по 2 человека от команды.

В это время проводится конкурс болельщиков 

5-й конкурс «БОЛЕЛЬЩИК»

1) Назови два числа, разность которых равна их сумме. (ответ: 0+0 = 0–0)

2) Какой цифрой заканчивается произведение всех чисел от 2 до 23? (ответ: 0) 

3) Что больше произведение или сумма всех цифр от 0 до 9? 

(ответ: сумма) 

4) Шел мужик в Москву и повстречал 7 женщин, у каждой из них по мешку, в каждом мешке по коту. Сколько существ направлялось в Москву? (один) 

5) Почему парикмахер в Женеве охотнее подстрижет двух французов, чем одного немца? (два человека заплатят больше, чем один)

6) Назовите два числа, сумма которых равна их произведению.

(ответ: 2 + 2 = 2 •2)

7) На двух руках 10 пальцев. Сколько пальцев на 10 руках? (ответ: 50)

8) Горело 5 свечей. Две из них погасло. Сколько свечей осталось?

(ответ: 5)

9) Одна сторона прямоугольника 8 см, а другая на 2 см больше. Какова площадь этого прямоугольника? (ответ: 80 кв. см)

10) Сумма двух чисел больше одного из них на 17 и больше другого на 13. Чему равны эти числа? (ответ: 13 и 17) [3]  

6-й конкурс «ВЫИГРАЙ ИГРАЮЧИ»

Лучший счетчик.

На доске написан ряд чисел, например: 24, 81, 49, 32, 72, 45, 56, 27 и 18. К доске выходят двое учащихся. По команде учителя один слева, другой справа пишут числа, при умножении которых получаются данные результаты. Тот, кто первым дойдет до середины и верно выполнит задание, считается победителем.

Считай – не зевай!

В игре участвуют две команды по пять человек. У играющих на груди таблички с двузначными числами. Таблички команд различаются только по цвету.
В 5-6 шагах перед каждой командой ставится стул. Учитель предлагает играющим какой-либо арифметический пример в два или три действия. Допустим: 36:4∙5 или: (29+25):6∙5. Играющие в уме подсчитывают результат. Тот, у кого окажется табличка с ответом (в данном случае 45), бежит к стулу и садится на него.
Примеры составляются заранее в зависимости от написанных на карточках чисел. Запомнить примеры на слух трудно, поэтому лучше написать их на табличках и показывать командам. Очко засчитывается той команде, представитель которой сядет на стул раньше.  [1] 

7-й конкурс «ВИКТОРИНА»

Вопросы для двух команд (1 балл за правильный ответ).

1.Высший балл в школах России (5)

2.Эффективный способ снять умственное и физическое напряжение, который надежно устраняет утомление, повышает защитные силы организма. (сон)

3.Назовите пословицу или поговорку про сон. (утро вечера мудренее!)

4.Сколько лет спал Илья Муромец. (33)

5.Наименьшее четное число (2)

6.Прямоугольник, у которого все стороны равны. (квадрат)

7.Масса кубического метра воды. (1000 кг.)

8.Геометрическая фигура, состоящая из точки и двух лучей, исходящих из этой точки. (угол)

9.Соперник нолика (крестик)

10.Если съесть одну сливу, что останется? (косточка) [3]  

8-й конкурс «ГОНКА ЗА ЛИДЕРОМ»

Право первого ответа имеет команда, набравшая меньшее количество баллов.

  1. Очень плохая оценка знаний. (Двойка.)

  2. Сколько козлят было у многодетной козы? (Семь.)

  3. Наименьшее составное число. (Два.)

  4. Сотая часть числа. (Процент.)

  5. Геометрическая фигура в любовных делах? (Треугольник.)

  6. Количество сторон в квартете. (Четыре.)

  7. Одно яйцо варят 4 минуты. Сколько нужно варить 5 яиц? (4 минуты)

  8. Назовите наименьшее натуральное число. (1)

  9. В семье 5 сыновей у каждого есть сестра. Сколько это человек? (6 человек)

  10. Какой знак надо поставить между двумя тройками, чтобы получить число больше двух, но меньше трех? (Запятую) [5]  

Итог урока.

Подсчет баллов. Оценивание учащихся, вручение медалей. 

Урок сегодня завершён, но каждый должен знать:

Что спорт, упорство, ум и труд
К успеху в жизни приведут!

Спасибо за урок! А сейчас у меня к вам небольшая просьба. На доске прикреплены изображения солнца и тучки. Возьмите себе на память об этом уроке то из них, которая на ваш взгляд олицетворяла урок. 

 

Урок по теме «Среднее арифметическое» 5 класс

Урок по теме «Среднее арифметическое» 5 класс

Автор: edu1

Методическая копилка —

Математика

Тема урока: «Среднее арифметическое»

Учебник:

Авт. Виленкин Н.Я. и др.

5 класс

учитель математики

МКОУ «Замостянская сош»

Селитренникова Галина Алексеевна

Цели урока

Образовательные:

  • ввести понятие среднего арифметического; вывести правило для его нахождения;

  • научить решать задачи, связанные с нахождением среднего арифметического;

  • отрабатывать навыки действий с десятичными дробями;

  • развивать умение составлять задачи, используя цифровые данные из жизни.

Развивающие:

  • содействовать развитию у школьников логического мышления, математической речи;

  • способствовать развитию познавательного интереса;

  • развивать умение анализировать, делать выводы на основе полученных результатов;

  • способствовать формированию правильной математической речи;

  • создать условия для развития у учащихся умений осуществлять самоконтроль и самооценку учебной деятельности.

Воспитательные:

  • содействовать осознанию учащимися ценности изучаемого предмета;

  • активизировать познавательную и творческую деятельность учащихся;

  • показать значение математических знаний в жизни, побудить применять эти знания в жизни.

Тип урока: урок открытия новых знаний.

Формы работы: индивидуальная, фронтальная, групповая.

Оборудование: презентация к уроку, проектор, экран.

Предварительная подготовка.

Для эффективности работы было дано предварительное домашнее задание:

  1. класс поделен на 3 группы по рядам;

  2. измерить и записать рост каждого обучающегося в группе.

Ход урока: 

 I. Мотивирование к учебной деятельности (организационный момент) — 1-2 минуты

 Посмотрите, всё ль в порядке:

Книжки, ручки и тетрадки.

Прозвенел сейчас звонок.

Начинается урок.

 Учитель приветствует обучающихся, проверяет готовность к уроку, отмечает отсутствующих.

Каждый ученик получает лист «Моё настроение», на котором отмечает смайлик, соответствующий его настроению.

II.Актуализация и фиксирование индивидуального затруднения в пробном учебном действии — 4-5 минут

1. Устное решение задач.

Задача 1.
У Иванова Ивана по математике в журнале стоят оценки

4   5   3   4   5   4   3  3   4

Как вы думаете, какую оценку в четверти получит Иван? И почему?

Задача 2.
К доске приглашаются три ученика.
Вопросы:
Кто самый высокий?
Кто самый низкий?
Кто средний по росту?

Какие «особенные слова» вы заметили в условиях всех задач?

     Часто мы и в жизни слышим фразы со словом “средний”, например: средний возраст, средний рост, средняя температура и т.д. Как вы понимаете эти выражения?

     В математике тоже есть свои понятия со словом “средний” и сегодня мы познакомимся с одним из этих  понятий. 

2. Устный счёт.
Тема сегодняшнего урока состоит из двух слов. Вы её сможете прочитать, если верно решите примеры и вставите буквы в таблицу ответов.

7,3 · 3          Е
64,24 : 8      А
12 – 2,6       И
68,2 : 2        О
45,4 + 0,6    С
12 · 0,1        Р
43,1 · 10      Д
81,1 : 0,1     Н
60 – 0,9       Ф
4,13 + 3,87  М
6,45 – 6,4    Т
0,1 · 0,1       К
7 · 0,01        Ч



46

1,2

21,9

431

811

21,9

21,9

 

 

 

 

 

 

 

 



8,03

1,2

9,4

59,1

8

21,9

0,05

9,4

0,07

21,9

46

0,01

34,1

21,9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

III. Постановка учебной задачи — 4-5 минут 

   Ребята, назовите тему урока. («Среднее арифметическое»)

   Запишем число и тему урока.
   Рассмотрим задачу:

У Ани 14 конфет, у Кати 9 конфет, а у Оли 10 конфет. Сколько конфет достанется каждой девочке, если конфеты разделить между ними поровну? 

Решение обсуждается с учащимися.
14 + 9 + 10 = 33 (конфеты)
33 : 3 = 11 (конфет)
Число 11 называют средним арифметическим чисел 14; 9 и 10.

Рассмотрим еще задачу :

Миша, Петя и Коля были в походе. Подойдя к лесу, они решили сделать привал. У Миши было 2 пирожка, у Пети 4 и у Коли 6. Все пирожки мальчики разделили поровну и съели. Сколько пирожков съел каждый?
Совместно с учащимися получается:
2 + 4 + 6 = 12 (пирожков)
12 : 3 = 4 (пирожка)
Число 4 называется средним арифметическим чисел 2; 4 и 6.

Ребята, что же называется средним арифметическим чисел? ( Ответы учащихся)

Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
Как найти среднее арифметическое нескольких чисел? (Ответы ребят)
Среднее арифметическое = (Сумма чисел) : (количество слагаемых)
(Учащиеся записывают в тетрадях)

IV. Открытие нового знания (построение  проекта выхода из затруднения)  7-8 минут

Из какой сказки вы прослушали отрывок?

 1.      Братья сеяли три поля по 200 га каждое. На первом поле собрали 7220ц пшеницы, на втором – 7560ц, а на третьем – 7090ц пшеницы. Определите урожайность на каждом поле и найдите среднюю урожайность.
Вопросы:
Как найти урожайность одного поля?
Как найти среднюю урожайность трёх полей?
7220 : 200 = 36,1(ц.) – урожайность на первом поле.
7560 : 200 = 37,8(ц.) – урожайность на втором поле.
7090 : 200 = 35,45(ц.) – урожайность на первом поле.
(36,1 + 37,8 + 35,45) : 3 = 36,45(ц.) – средняя урожайность трёх полей.

  1. Задание на сообразительность:

Подключите свои знания, смекалку, сообразительность, чувство юмора и попытайтесь отыскать «среднее арифметическое» не чисел, а предметов, которые нас окружают.

Итак, среднее арифметическое:

  • Велосипеда и мотоцикла. (Мопед.)

  • Трамвая и поезда. (Электричка.)

  • Апельсина и лимона. (Грейпфрут.)

  • Туфельки и сапога. (Ботинок.)

  • Пианино и баяна. (Аккордеон.)

  • Холодильника и вентилятора. (Кондиционер.)

  • Портфеля и рюкзака. (Ранец.)

  • Носка и чулка. (Гольф.)

 V. Первичное закрепление — 4-5 минут

1. Задача № 1502 (из учебника)

Участница соревнований по фигурному катанию на коньках получила оценки

5,3; 4,8; 5,4; 5,0; 5,3; 5,4; 5,3; 5,2; 5,1.
Найдите среднюю оценку этой участницы.
Как найти среднее арифметическое нескольких чисел?
Решение с коментированием:
(5,3 + 4,8 + 5,4 + 5,0 + 5,3 + 5,4 + 5,3 + 5,2 + 5,1) : 9 = 5,2

 2.Задача № 1504 (из учебника)

Поезд шёл 4 ч со скоростью 70 км/ч и 3ч со скоростью 84 км/ч. Найдите среднюю скорость поезда на пройденном за это время пути.

Как найти среднюю скорость?
Решение у доски по действиям или выражением:
(70 · 4 + 84 · 3) : 7 = 76(км/ч)

Средняя скорость =(Весь пройденный путь): (всё время движения).

 3. Игра – задание «Полёт в космос»

         А сейчас мы с вами отправимся в космос, посетим планету Меркурий. Но до полета надо размяться, привести себя в форму, космическую.

Физминутка

Быстро встали, улыбнулись
Выше-выше потянулись.
Ну-ка, плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
Сели, встали. Сели, встали.
И на месте побежали.

             Известно, что на планете Меркурий средняя температура +15°. Можно предположить, что возможна жизнь человека на этой планете. Но на самом деле температура на Меркурии колеблется от 150º мороза до 350°жары.

 VI. Самостоятельная работа с самопроверкой по образцу (эталону) — 4-5 минут.

Тест по теме: «Среднее арифметическое чисел»

Ответ на вопрос обведите кружком

 1. Найдите среднее арифметическое чисел 1,5 и 2,3

а) 1,9         б) 3,8     в) 3

2. Среднее арифметическое чисел 2, 4, 6, и 0 равно:

а) 3     б) 6     в) 4

3. Незнайка по математике получил следующие оценки 5, 3, 1, 4, 4, 1. Найдите среднюю оценку Незнайки.

а) 3   б) 4   в) 5

4. Вини — Пух съел 18 конфет, Пятачок — 9 конфет, Кролик — 3 конфеты. Сколько конфет в среднем съел каждый?

а) 12     б) 5     в) 10

5. Найдите среднее арифметическое чисел: 20,22 и 18,26

а) 23,78     б) 19,24     в) 12,43

VII.   Включение нового знания в систему знаний и повторение – 7-8 минут.

1.Задача.

1)Точка С – середина отрезка АВ. Найдите координату точки С.
2)Найдите среднее арифметическое чисел 12,36 и 22,57.

Сравните полученный результат

2. Практическая работа в группах.

 Предварительная подготовка.

Для эффективности работы было дано предварительное домашнее задание:

  1. класс поделен на 3 группы по рядам;

  2. измерить и записать рост каждого обучающегося в группе.

Вопрос:
Что мы можем определить, используя данные предварительного задания?
Ответ:
Мы можем определить средний рост в группе.
Что для этого нужно сделать?
Выполняйте задание.

 VIII. Рефлексия учебной деятельности на уроке (итог) — 2-3 минуты.

               Что нового вы узнали на уроке?

  • Сегодня я узнал…

  • Мне было интересно…

  • Я узнал и могу научить товарища…

  • Я понял, что…

  • Теперь я могу…

  • Меня удивило…

Каково ваше настроение в конце урока?

Домашнее задание.

   Учитель комментирует домашнее задание:
1. № 1524 (а/б), №1526

2. Вычислить средний возраст вашей семьи.

3. Узнать, где в жизни необходимо умение находить среднее   арифметическое  (подготовить сообщение по желанию).

     Итог урока. Выставление оценок. Спасибо Вам, дети, за урок. Я буду рада, если полученные на уроках математики знания помогут Вам в жизни при решении проблем. Вы – молодцы. Особо хочу отметить … Полные и правильные ответы давали …

 

Старинные задачи для учащихся 5 класса

Старинные задачи для учащихся 5 класса

Задачи из раздела «тексты старинных задач» интересны учащимся, как среднего возраста, так и старшего. Когда же решать старинные и занимательные задачи, развивающие логическое мышление, вызывающие большое любопытство у многих ребят? А что если сделать решение этих задач небольшой частью урока? Так «родилась» идея «Задача дня». Для неё отводится крайняя правая часть доски, на которой пишется задача «сегодняшнего дня». Ребята могут решать её, а могут и не решать. Просто те, кому она интересна, могут решить её дома или на перемене. На следующем уроке к этой задаче обязательно возвращаемся, уделяя её решению небольшую часть урока (а на доске может быть записана новая задача). Обычно решать её выходят 2-3 человека и предлагают иногда несколько способов решения одной и той же задачи – «бенефис одной задачи». Не беда, что кто-то не решил задачу, ведь он пытался это сделать, на уроке он увидит правильное решение.

Задачи на составление уравнения

1. «Кому пасти овец?» (задача из старинной русской рукописи XVII века).

 У пятерых крестьян — Ивана, Петра, Якова, Михея и Гаврилы — было 10 овец. Не могли они найти пастуха и решили пасти по очереди: по столько дней, сколько овец».

Известно, что у Ивана овец было вдвое меньше, чем у Петра, у Якова в два раза меньше, чем у Ивана, Михей имеет овец вдвое больше, чем Яков, а Гавриил — вчетверо меньше, чем Петр. Смекника-ка, по скольку дней следует пасти овец каждому?

2. Старинная задача.

Летела стая гусей, а навстречу ей – один гусь. Говорит гусь: «Здравствуйте, 100 гусей!» А вожак стаи в ответ: «Нас не 100 гусей. Вот было бы нас столько, сколько теперь, да еще столько, да ещё полстолька, да четверть столько, да еще ты, гусь, вот тогда нас было бы 100». Сколько в стае гусей?

3. Старинная русская задача.

Вопросил некто некого учителя: «Сколько имеешь учеников у себя, так как хочу отдать тебе сына в училище». Учитель ответил: «Если ко мне придёт учеников столько же, сколько имею, и полстолька, и четвертая часть, и твой сын, тогда будет у меня 100 учеников». Сколько было у учителя учеников?

4. Задача из «Курса чистой математики» Войтяховского (1811 г.).

Задумайте какое-нибудь число, умножьте его на 2, прибавьте к произведению 30, полученное число разделите на 2, от результата отнимите задуманное число, и тогда в ответе получится 15. Объясните, почему при любом заданном числе ответ всегда равен 15?

5. Задача из «Курса чистой математики» Войтяховского (1811 г.).

Бутылка с пробкой стоят 12 копеек. Бутылка стоит на 10 копеек дороже, чем пробка. Сколько стоит бутылка и сколько пробка?

6. Древнекитайская задача.

Некто подошел к клетке, в которой сидели фазаны и кролики. Сначала он сосчитал головы: их оказалось 15, затем он сосчитал ноги, их было 42. Сколько кроликов и сколько фазанов было в клетке?

7. Из учебника Эйлера «Основания алгебры» (1707-1773гг.)

Отец, у которого было трое сыновей, оставил им 1600 крон. Старший сын получил на 200 крон больше среднего, а средний – на 100 крон больше младшего. Сколько получил каждый из сыновей?

Задачи, решаемые с конца

8. «Мальчики и яблоки» (из «Арифметики» Л. Ф.Магницкого).

Трое мальчиков имеют по некоторому количеству яблок. Первый из мальчиков даёт двум другим столько яблок, сколько каждый из них имеет. Затем второй мальчик даёт двум другим столько яблок, сколько каждый из них имеет; в свою очередь, и третий даёт каждому из двух столько яблок, сколько есть у каждого в этот момент. После этого у каждого оказывается по 8 яблок. Сколько яблок было вначале у каждого мальчика?

9. Старая легенда гласит, что чешская королева Либуша обещала выйти замуж за того из трех добивавшихся её руки рыцарей, кто первый решит задачу: «Сколько слив помещается в корзине, из которой половину всего содержимого и одну сливу она отдаст первому, половину оставшегося и еще одну сливу – второму и, наконец, третьему – половину оставшихся и еще три сливы, после чего корзина опустела?»

10. Задача из «Курса чистой математики» Войтяховского(1811 г.).

Разносчик продал первому покупателю половину имевшихся у него апельсинов и ещё пол-апельсина, второму покупателю – половину оставшихся апельсинов и еще пол-апельсина; таким же образом продал он апельсины и остальным покупателям. Когда же подошел седьмой покупатель, то у разносчика уже ничего не осталось. Сколько апельсинов было у разносчика и сколько взял каждый из покупателей?

11. Из старинных рукописей.

В трёх кучках лежит 24 камешка. Если из первой кучки переложить во вторую столько, сколько находится во второй, а затем из второй в третью столько, сколько находится в третьей, наконец, из третьей в первую столько, сколько в первой осталось, то во всех кучках будет поровну. Сколько камешков в каждой кучке?

РЕШЕНИЯ, УКАЗАНИЯ, ОТВЕТЫ

1. Решение:

Пусть х овец – у Якова, 2х овец – у Ивана, 4х овец – у Петра, 2х овец – у Михея, х овец – у Гаврилы.

х + 2х + 4х + 2х + х = 10

х = 1

Ответ: Якову – 1 день, Ивану – 2 дня, Петру – 4 дня, Михею – 2 дня, Гавриле – 1 день.

2. Решение:

Пусть было х гусей.

х + х + 0,5х + 0,25х + 1 = 100

2,75 х = 99

х = 36

Ответ: 36 гусей.

3. Ответ: 36 учеников.

4. Решение:

Пусть х — задуманное число.

(х 2 + 30) : 2 – х = х + 15 – х = 15

5. Решение:

Пусть х коп. – пробка, тогда (х + 10) коп. – бутылка.

х + (х + 10) = 12

х = 1.

Ответ: пробка – 1 копейка, бутылка – 11 копеек.

6. Решение:

Пусть х – кроликов, тогда (15 – х) – фазанов.

4х + 2(15 – х) = 42

х = 6

Ответ: 6 кроликов, 9 фазанов.

7. Пусть х крон получил младший сын, тогда (х + 100) – средний, (х + 100) + +200 = (х + 300) крон – старший.

х + (х +100) + (х + 300) = 1600

х = 400

Ответ: 400, 500, 700 крон.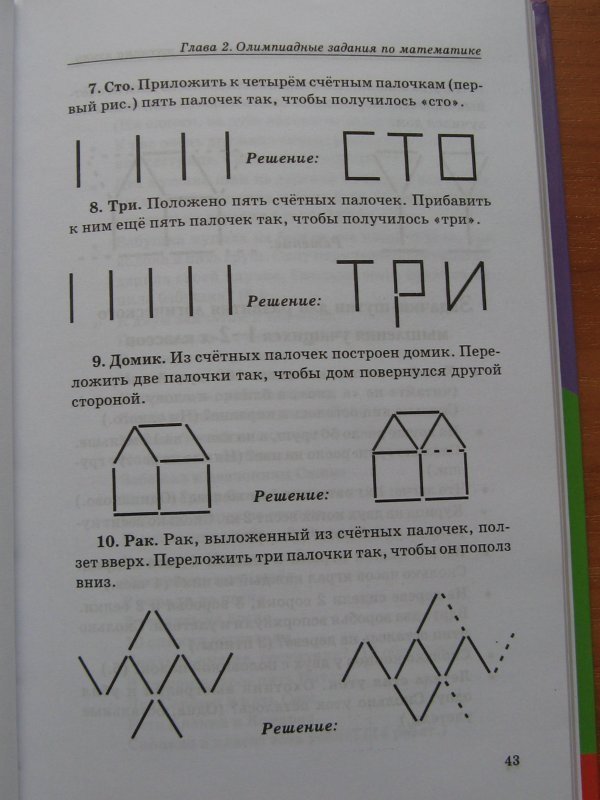

8. Решение:

Представим в виде таблицы и начнем ее заполнение с последней строки, зная, что у каждого мальчика оказывается по 8 яблок.

1 м. 2 м. 3 м.

13 7 4

2 14 8

4 4 16

8 8 8

Ответ: 13, 7, 4 яблока.

9. Решение:

((3 2 + 1) ) (слив).

Ответ: 30 слив.

10. Решение:

Всего было (((((0,5 2 +0,5) апельсина. Первый взял 63 : 2 + 0,5 = 32 апельсина, второй: 31 : 2 + 0,5 = 16, третий: 15 : 2 + 0,5 = 8, четвертый: 7 : 2 + 0,5 = 4, пятый: 3 : 2 + 0,5 = 2, шестой: 1

Ответ: 32, 16, 8, 4, 2, 1.

11. Решение:

Оформим в виде таблицы:

I II III

11 7 6

4 14 6

4 8 12

8 8 8

Ответ: 11, 7, 6 камешков.

Рабочая программа курса внеурочной деятельности «Занимательная математика» 5 класс


Муниципальное бюджетное
общеобразовательное учреждение
«Центр образования №6 «Перспектива»


 



РАССМОТРЕНО


на заседании  МО


 


Протокол  № 1


от   «1» сентября 2018г.


СОГЛАСОВАНО


заместитель директора


 


 


«1» сентября 2018г.


УТВЕРЖДАЮ


директор


МБОУ ЦО №6 «Перспектива»


 Ю. В.Евдокимова /_______/


        «1» сентября 2018г


 


РАБОЧАЯ ПРОГРАММА



по курсу внеурочной деятельности


«Занимательная математика»


 


для 5 класса


 


 


 


 


 


2018 год


 


Пояснительная записка


Программа  курса «Занимательная математика» предназначена для внеурочной работы и рассчитана на обучающихся 5-х классов, интересующихся математикой. Согласно ФГОС нового поколения проведение такого курса способствует самоопределению обучающихся при переходе к профильному обучению в средней и старшей школе.


Изучение курса составлено на основе авторской программы Е.Л. Мардахаевой «Занятия математического кружка. 5 класс»  с  использованием пособия: Горев П.М., Утёмов В.В. Уроки развивающей математики. 5-6 классы. Задачи математического кружка. – Киров: изд. МЦИТО, 2014.


Данный курс способствует развитию познавательной активности, формирует потребность в самостоятельном приобретении знаний и в дальнейшем автономном обучении, а также интеллектуальному, творческому, эмоциональному развитию учащихся.


Программа внеурочной деятельности содержит в основном традиционные темы занимательной математики: арифметику, логику, комбинаторику и т.д. Уровень сложности подобранных заданий таков, что к их рассмотрению можно привлечь значительное число учащихся, а не только наиболее сильных. В результате занятий учащиеся должны приобрести навыки и умения решать более трудные и разнообразные задачи, а так же задачи олимпиадного уровня.


При реализации содержания программы учитываются возрастные и индивидуальные возможности учащихся, создаются условия для успешности каждого ребёнка.


Обучение по программе осуществляется в виде теоретических и практических занятий. В ходе занятий учащиеся выполняют практические работы, готовят рефераты, выступления, принимают участия в конкурсных программах.


Курс позволяет обеспечить требуемый уровень подготовки школьников, предусматриваемый государственным стандартом математического образования, а также позволяет осуществлять при этом такую подготовку, которая является достаточной для углубленного изучения математики.


Таким образом, основной целью разработанной внеурочной деятельности является углубление  и расширение математических знаний  и умений, сохранение  и развитие интереса  учащихся к  математике.


Для достижения  поставленной  цели  необходимо решение  следующих учебных задач:


  1. в направлении личностного развития: развитие устойчивого интереса учащихся к математике и ее приложениям; формирование представлений о математике как части общечеловеческой культуры; значимости математики в развитии цивилизации и современного общества; развитие интереса к математическому творчеству и математических способностей;


  2. в метапредметном направлении: формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных  сфер человеческой деятельности; привитие учащимся определенных навыков научно-исследовательского характера; развитие у учащихся умения самостоятельно и творчески работать с учебной и научно-популярной литературой.


  3. в предметном направлении: создание фундамента для математического развития, формирование  механизмов мышления, характерных для математической деятельности, высокой культуры математического мышления; оптимальное развитие математических способностей у учащихся; расширение и углубление представлений учащихся о практическом значении математики.


  4. коммуникативные УУД: воспитание учащихся чувства коллективизма и умения сочетать индивидуальную работус коллективной; установление более тесных деловых контактов между учителем математики и учащимися и на этой основе более   глубокое изучение познавательных интересов и запросов школьников.


Основными педагогическими принципами, обеспечивающими реализацию программы, являются:


• учет возрастных и индивидуальных особенностей каждого ребенка;


• доброжелательный психологический климат на занятиях;


• личностно-деятельный подход к организации учебно-воспитательного процесса;


• оптимальное сочетание форм деятельности;


• доступность.


Эффективности   реализации  программы  курса способствует использование  различных форм проведения занятий, в частности  таких, как:


— эвристическая беседа;


— интеллектуальная игра;


— дискуссии;


— математические  состязания, турниры, конкурсы;


— творческие задания.


Оценка знаний и умений обучающихся проводится в виде  защиты исследовательских проектов, которые предполагают самостоятельную творческую работу обучающихся по предложенной тематике с последующей защитой их решения на занятиях, научно-практических конференциях. Предполагается, что знакомство учащихся с нестандартными (как по формулировке, так и по решению) задачами будет способствовать повышению их успеваемости на уроках математики и развитию у них интереса к предмету.


 


Предполагаемая результативность курса:


  •        усвоение основных базовых знаний по математике; её ключевых понятий;


  •        улучшение качества решения  задач различного уровня сложности учащимися;


  •        успешное выступление на олимпиадах, играх, конкурсах, научно-практических конференциях.


 


Результаты освоения содержания курса «Занимательная математика»


Личностными результатами изучения данного  курса являются:


  •    формирование целостного взгляда на мир в его органичном единстве и разнообразии природы, народов, культур и религий


  •    формирование уважительного отношения к иному мнению, истории и культуре других народов     


  •    овладение начальными навыками адаптации в динамично изменяющемся и развивающемся мире


  •    развитие любознательности, сообразительности при выполнении разнообразных заданий проблемного и эвристического характера;


  •    развитие внимательности, настойчивости, целеустремленности, умения преодолевать трудности — качеств весьма важных в практической деятельности любого человека;


  •    воспитание чувства справедливости, ответственности;


  •    развитие самостоятельности суждений, независимости и нестандартности мышления.


Метапредметными  результатами изучения курса является формирование универсальных учебных действий (УУД). По окончании обучения учащиеся должны уметь:


  • сравнивать разные приемы действий, выбирать удобные способы для выполнения конкретного задания.


  • использовать приобретённые математические знания для описания и объяснения окружающих предметов, процессов, явлений, а также для оценки их количественных и пространственных отношений.


  • моделировать в процессе совместного обсуждения алгоритм решения занимательных задач; использовать его в ходе самостоятельной работы.


  • применять изученные способы учебной работы и приёмы вычислений для работы с математическими головоломками.


  • включаться в групповую работу.


  • участвовать в обсуждении проблемных вопросов, высказывать собственное мнение и аргументировать его.


  • аргументировать свою позицию в коммуникации, учитывать разные мнения, использовать критерии для обоснования своего суждения.


  • контролировать свою деятельность: обнаруживать и исправлять ошибки.


Предметные результаты:


  • знают особые случаи устного счета


  • решают текстовые задачи, используя при решении таблицы и «графы»


  • знают разнообразные логические приемы, применяемые при решении задач.


  • решают  нестандартные задачи на разрезание


  • знают определения основных геометрических понятий


 


  • решают простейшие комбинаторные задачи путём систематического перебора возможных вариантов


  • измеряют геометрические величины, выражают одни единицы измерения через другие.


  • вычисляют значения геометрических величин(длин, углов, площадей, объемов)


 


Содержание курса «Занимательная математика»


Курс «Занимательная математика» входит во внеурочную деятельность по направлению общеинтеллектуальное развитие личности. Программа предусматривает включение задач и заданий, трудность которых определяется не столько математическим содержанием, сколько новизной и необычностью математической ситуации. Это способствует появлению желания отказаться от образца, проявить самостоятельность, формированию умений работать в условиях поиска, развитию сообразительности, любознательности.


В процессе выполнения заданий дети учатся видеть сходства и различия, замечать изменения, выявлять причины и характер этих изменений, на этой основе формулировать выводы. Совместное с учителем движение от вопроса к ответу – это возможность научить ученика рассуждать, сомневаться, задумываться, стараться и самому найти выход – ответ. Создание на занятиях ситуаций активного поиска, предоставление возможности сделать собственное «открытие», знакомство с оригинальными путями рассуждений, овладение элементарными навыками исследовательской деятельности, позволят обучающимся реализовать свои возможности, приобрести уверенность в своих силах.


Курс «Занимательная математика» предусматривает организацию подвижной деятельности учащихся, которая не мешает умственной работе. С этой целью включены подвижные математические игры, предусмотрена последовательная смена деятельности в течение одного занятия; передвижение по классу в ходе выполнения математических заданий на листах бумаги, расположенных на стенах классной комнаты и др. Во время занятий важно поддерживать прямое общение между детьми (возможность подходить друг к другу, переговариваться, обмениваться мыслями). При организации занятий целесообразно использовать принцип свободного перемещения по классу, работу в парах постоянного и сменного состава, работу в группах. Некоторые математические игры и задания могут принимать форму состязаний, соревнований между командами.


Место курса «Занимательная математика» в учебном плане


Программа рассчитана на 34 часа в год (1 час в неделю). Содержание курса «Занимательная математика» отвечает требованию к организации внеурочной деятельности: соответствует курсу «Математика», не требует от учащихся дополнительных математических знаний. Тематика задач и заданий отражает реальные познавательные интересы детей, содержит полезную и любопытную информацию, интересные математические факты, способные дать простор воображению.


Ценностные ориентиры содержания курса «Занимательная математика»


— формирование умения рассуждать как компонента логической грамотности;


— освоение эвристических приемов рассуждений;


— формирование интеллектуальных умений, связанных с выбором стратегии решения, анализом ситуации, сопоставлением данных;


— развитие познавательной активности и самостоятельности учащихся;


— формирование способностей наблюдать, сравнивать, обобщать, находить простейшие закономерности, использовать догадку, строить и проверять простейшие гипотезы;


— формирование пространственных представлений и пространственного воображения;


— привлечение учащихся к обмену информацией в ходе свободного общения на занятиях.


 


Тематическое планирование курса «Занимательная математика»


Содержание курса «Занимательная математика» направлено на воспитание интереса к предмету, развитию наблюдательности, геометрической зоркости, умения анализировать, догадываться, рассуждать, доказывать, умения решать учебную задачу творчески. Содержание может быть использовано для показа учащимся возможностей применения тех знаний и умений, которыми они овладевают на уроках математики.


Каждое занятие состоит из двух частей: задачи, решаемые с учителем, и задачи для самостоятельного (или домашнего) решения.  Учащиеся  знакомятся с интересными свойствами чисел, приемами устного счета, особыми случаями счета, с биографиями великих математиков, их открытиями. Большая часть занятий отводится решению олимпиадных задач.


Мир занимательных задач


Головоломки и числовые ребусы. Судоку. Старинные задачи. Задачи, решаемые способом перебора, «с конца». Логические задачи. Комбинаторные задачи. Графы. Круги Эйлера. Принцип Дирихле. Задачи на взвешивание. Задачи на переливание. Задачи на движение нестандартного характера.


Практика: Составление и решение ребусов, задач, загадок, связанных с математикой. Блиц-турнир по решению старинных занимательных задач. Задачи на сообразительность и смекалку «Затруднительные положения». Игра «Математический футбол» (игровой математический практикум по решению логических задач, головоломок). Соревнование «Кто больше». Турнир «Смекалистых»


 


 Как люди научились считать. Старинные системы записи чисел. Числа-великаны.


Как возникло слово «математика». Счёт у первобытных людей. Иероглифическая система древних египтян. Римские цифры. Славянские цифры. История возникновения названий – «миллион», «миллиард», «триллион». Числа великаны.


Практика: Занимательные задачи «Сколько?». Загадки о числах. Игра «Весёлый счёт». Задачи на смекалку «Цифры спрятались». Защита проекта «В мире чисел».


 


 


Математика вокруг нас


Что такое фольклорная математика? Освоение космического пространства человечеством. Роль математики в этом процессе. История строительства и развития города Липецка. Просмотр презентации «Наш город». Основы здорового образа жизни и математика.


Практика: Аукцион «Числа, спрятанные в пословицах и поговорках». Игра «Опознай пословицу». Конкурс частушек о математике. Задачи, связанные с историей освоения космоса. Игра-путешествие «Полёт на Марс». Практические задачи, связанные с городом. Конкурс задач с краеведческим содержанием, составленных детьми. Занимательные задачи, связанные со спортом, здоровым питанием, режимом дня. Сообщения о роли математики в формировании здорового образа жизни. Проект – выпуск газеты «Математика вокруг нас».


 


Блистательные умы


К.Гаусс. Л.Эйлер. Л.Ф.Магницкий. С.В. Ковалевская. Просмотр видеофильмов, содержащих информацию о великих учёных математиках России и Европы. Высказывания великих людей о значении математики.


Практика: Защита проектов «Великие математики».


 


Учебно-тематическое планирование


 








№ п/п


Название раздела


Количество часов в авторской рабочей программе


Кол-во часов в настоящей рабочей программе


1


Мир занимательных задач


17


17


2


Как люди научились считать. Старинные системы записи чисел.


5


5


3


Математика вокруг нас


7


7


4


Блистательные умы


5


5


 


Итого


34


34


 


 


 


 


 


 


 


 


 


 


 


 


 


 


 


 


 


Учебно-методическое и материально-техническое обеспечение образовательного процесса по курсу «Занимательная математика»


  1.       Библиотечный фонд


Методические пособия для учителя


  1. Горев П.М., Утёмов В.В. Уроки развивающей математики. 5-6 классы. Задачи математического кружка. – Киров: изд. МЦИТО, 2014


  2. Гусев А.А. Математический кружок. 5 класс. – М.: Мнемозина, 2013


  3. Киселёва Г.М. Математика. 5-6 классы. Организация познавательной деятельности. – Волгоград: Учитель, 2013


  4. Мардахаева Е.Л. Занятия математического кружка.–  М.: Мнемозина, 2012


  5. Математика. 5 класс: учебник для общеобразовательных учреждений / А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. −  М.: Вентана-Граф, 2015


  6. Олимпиадные задания по математике. 5-6 классы. Ю.В. Лепёхин – Волгоград: Учитель, 2011


  7. Факультативные занятия: Математика после уроков. Т.С.Безлюдова – Мозырь: Белый Ветер, 2013


  8. Математические олимпиады: методика подготовки.А.В. Фарков – М.: ВАКО, 2014


  9. Фарков А. В. Математические олимпиады в школе. 5-11 класс. – М.: Айрис-пресс, 2005


Справочные пособия, научно-популярная и историческая литература


  1. Баврин И.И., Фрибус Е.А. Старинные задачи. – М.: Просвещение, 1994.


  2. Гаврилова Т. Д. Занимательная математика. 5-11 класс. – Волгоград: Учитель, 2008.


  3. Депман И. Я., Виленкин Н. Я. За страницами учебника математики. 5-6 класс. – М.: Просвещение, 2004.


  4. Екимова М.А., Кукин Г.П. Задачи на разрезание. – М.: МЦНМО, 2002


  5. Левитас Г. Г. Нестандартные задачи по математике. – М.: ИЛЕКСА, 2007.


  6. Перли С.С., Перли Б.С. Страницы русской истории на уроках математики. – М.: Педагогика-Пресс, 1994


  7. Энциклопедия для детей. Математика. Том 11. – М.: Аванта+, 2003.


  8. Я познаю мир: математика/сост. А.П. Савин и др. – М.: АСТ, 1999


 


II. Печатные пособия


 Портреты выдающихся деятелей математики


 


III. Информационные средства. Интернет-ресурсы


http://www.edu.ru — Федеральный портал Российское образование


http://www.school.edu.ru — Российский общеобразовательный портал


www.1september.ru — все приложения к газете «1сентября»


http://school-collection.edu.ru – единая коллекция цифровых образовательных ресурсов


http://mat-game.narod.ru/ математическая гимнастика


http://mathc.chat.ru/ математический калейдоскоп


http://www.krug.ural.ru/keng/ Кенгуру


http://www.uroki.net/docmat.htm — для учителя математики, алгебры и геометрии


http://www.alleng.ru/edu/math2.htm — к уроку математики


http://www.uchportal.ru/ — учительский портал


http://mmmf.msu.ru/circles/z5/  — Малый Мехмат МГУ. Материалы занятий кружков


www.math—on—line.com – Занимательная математика – школьникам

Курчатовская школа. Подготовка к олимпиаде с репетитором

Сегодня в Москве существует несколько очень сильных физико- математических школ, для зачисления в которые недостаточно подачи заявления на прием. Многие проводят свои экзамены с олимпиадными задачами, к которым необходимо проводить специализированную подготовку. Одна из них — Курчатовская школа. Долгое время школа имела номер 1189 и до сих пор жива традиция называть ее именно так. Набор в 5 класс традиционно проходит в конце апреля — начале мая сразу по двум предметам: математика и русский язык. Работа по математике носит ярко выраженный олимпиадный характер и представляет из себя достаточно серьезное для среднего школьника испытание. Если Вы не поступили после 4 класса, можно дождаться соответствующей вступительной олимпиады через 2 года.

Варианты работ, предлагавшихся для поступления в 5 класс в последние годы:
Курчатовская олимпиада по математике от 18 апреля 2021 года
Пробная Курчатовская олимпиада по математике от 21 февраля 2021г
Удаленная Курчатовская олимпиада по математике для 4 класса от 24 мая 2020г. Основной тур.
Курчатовская олимпиада от 9 февраля 2020 года
Курчатовская олимпиада 2019г (20 апреля, основной тур)
Курчатовская олимпиада от 10 февраля 2019г (пробный тур)
Олимпиада по математике для 4 класса. Курчатовская школа, апрель 2018 г.
Олимпиада по математике в Курчатовской школе от 23 апреля 2017 г.
Курчатовская олимпиада по математике 2015

Почитать о формате проведения вступительного экзамена можно на отдельной странице Курчатовская олимпиада

Какую помощь в поступлении в 5 класс Курчатовской школы может оказать репетитор по математике?

Немного странно звучит «репетитор для 5-го класса». Неужели в таком возрасте родители тоже приглашают ребенку преподавателя? И каков в этом случае должен быть характер индивидуальных уроков?

Безусловно, нужно разбирать олимпиадные задачи для 4 класса на смекалку и логику. Привязка к возрасту и программе в них достаточно условная, ибо они проверяют не столько знания ученика, сколько его умение мыслить в нестандартных ситуациях. Способность к олимпиадным задачам отражает главным образом уровень развития школьника: силу его внимания, памяти, мышления, зрительного представления о рассматриваемых объектах. Поэтому главным направлением стратегии подготовки в школу имени Курчатова, принимаемая репетитором по математике, становится развивающая тематика заданий. Без развития (математического и общего интеллектуального) на экзамене будет очень сложно, ибо искать выход из нестандартных ситуации на олимпиаде придется «с чистого листа», без применения известных схем и типов задач.

Как проводит подготовку в Курчатовскую школу репетитор по математике?

Изучение ребенка

Нужно очень аккуратно и внимательно протестировать Курчатовского ученика, изучить его способности мышления и при получении неудовлетворительных результатов поставить родителей в известность о вероятных проблемах при поступлении. Не всем детям по зубам олимпиадный уровень, каким бы старательным, опытным и талантливым ни был ваш репетитор по математике. Чудеса случаются редко. Превратить троечника (или даже хорошиста) в маленького гения, — не сможет даже самый лучший преподаватель математики на планете. Поэтому реально оценивайте свои возможности.
Вы можете пройти мой предварительный олимпиадный тест для Курчатовской школы — 4 класс и прислать его результы мне на почту.

Оглядка на школу

Иногда требуется подготовительная школьная работа. Пятерки по математике тоже бывают разными. Репетитору необходимо быть на 100% уверенным в том, что все базовые навыки не просто присутствуют, но и могут с успехом работать в разнотипных задачах, нагруженных большим количеством операций (арифметических и логических). Для этого в начале процесса подготовки желательно уделить время последним (усложненным) номерам вариантов типовых контрольных работ. Они используются репетитором не только для подготовки к более серьезным задачам, но и для всестороннего изучения ученика.

Классификация задач репетитором по математике

На следующем этапе я бы советовал обратиться к классическим типовым задачам, традиционно включаемым в олимпиадные сборники. В них, как правило, рассматриваются ситуации, на базе которых можно составить еще с десяток аналогичных. На их основе репетитору по математике легче организовать самостоятельную работу ученика. Если задавать на дом только сложные, уникальные и нестандартные задачи, то должной логической нагрузки при выполнении домашней работы ребенок не получит, ибо просто не сможет ничего решить. Кроме этого нужно разделить задачи на группы: на движение, на пересчет, на монеты, на чистую логику, на переправы, на календарь, на числовые ребусы и др. Лучше их решать сначала раздельно, а затем вперемешку.

Мои материалы для Курчатовской школы

Долгие годы я изучал и сортировал всевозможные олимпиадные задачи из разных источников и для разных классов. Что то сразу отправлялось в мусорную корзину, что то восхищало и принималось «на ура». Сегодня я могу похвастаться огромной пачкой листов А4 с подготовленными для каждого олимпиадного урока задачами. В применении к Курчатовской школе — это кипа листов для поступающих в 5 класс. Вы их видите на соответствующем фото (кликните для увеличения). Помимо подготовленных комплектов по каждой теме отдельной стопкой хранятся листы с конкретными олимпиадами по математике прошлых лет. Все это богатство можно и нужно использовать. Я предлагаю подготовку не только в 5 класс, но и подготовку в 7 класс и далее советовал бы рассмотреть уроки с репетитором как минимум для контроля качества школьного обучения. Как известно кадры решают все и даже в хорошей с виду школе можно нарваться на проблемы.

О режиме занятий
Рекомендуемый график занятий при подготовке в Курчатовскую школу в течение года (начиная с сентября) – раз в неделю. Каждая сложная задача требует неспешного обдумывания и аккуратного оформления. Пауза в неделю – оптимальный режим. Ученик успеет поразмышлять в домашней работе над каждым заданным номером, а в случае возникновения сложностей будет иметь для их преодоления достаточный запас по времени. Опытные репетиторы по математике обычно говорят своим ученикам: «Не бросайте олимпиадную задачу, если она не получается. Отвлекитесь и попробуйте справиться с ней через час, на следующий день, через день, через два дня. И только тогда просите репетитора ее объяснить». Когда индивидуальные урока расположены близко, то времени на размышление не хватает.

Особенности перехода в Курчатовскую школу

Курчатовская школа работает только с 5 класса. Поэтому в нее попадают дети из разных школ, с разной предварительной подготовкой. Олимпиадные занятия у репетитора по математике в большинстве случаев проходят автономно, то есть без жесткой привязки к школьному учебнику, и поэтому после поступления в Курчатовскую школу может потребоваться определенная коррекция под смену программы. Например, если Вы переходите на учебник Петерсон с любого другого, то необходимо пройти темы «углы», «координатный луч», «задачи на проценты», «скорость сближения и удаления», а также еще несколько мелких тем. Для этого как раз есть время в мае, а в случае полнейшей неизвестности вплоть до 1 сентября придется увеличить частоту уроков в первый месяц нового учебного года. В любом случае не желательно прекращать контакты с репетитором по математике.

О гарантии подготовки
Процессы и объекты, которые описываются в условиях конкурсных задач по математике, сильно отклоняются от школьных стандартов и это отклонение на экзамене невозможно заранее предсказать. Поэтому гарантировать успех на олимпиаде в Курчатовской школе невозможно даже при грамотной работе репетитора. Если Вам это обещают, то будьте уверены как минимум в лукавстве преподавателя, преследующем цели повышения привлекательности его уроков.

В чем сложность работы репетитора по математике с олимпиадными задачами?

Главная проблема в решении и объяснении таких задач заключается в том, что рассматриваемые в них ситуации, вычислительные и логические операции, очень трудно отобразить на бумаге. Большую часть смысловых и даже вычислительных действий приходится обрабатывать в уме. Это сильно затрудняет репетитору комментирование решений и поиск ошибок. Чтобы раскрыть логически сложную математическую структуру объекта приходится приводить примеры максимально близких к ним моделей. Например, для анализа ситуаций с большим количеством элементов, репетитор по математике приводит примеры решений меньшим их количеством. Подмечаются закономерности на упрощенной модели, а затем они переносятся на исходную модель. Например, если ребенок не понимает, как репетитор математики складывает все натуральные числа от 1 до 100, лучше сначала рассмотреть пример с меньшим числом слагаемых, например 1+2+3+4+5+6+8+9+10. Упрощенная модель позволит увидеть все пары слагаемых с суммой 11 без непривычного для маленького ученика пропуска чисел в записи 1+2+3+…+100.

О проблемах учеников

Серьезную проблему при подготовке в Курчатовскую школу составляет отсутствие у ребенка практического опыта в работе с окружающими его объектами и процессами (в том числе и математическими). Составитель варианта может заложить в олимпиадную задачу какую-нибудь особенность, выявить которую без репетитора по математике ребенок сможет только проявив наблюдательность в процессе решения других задач (простых или сложных). Например, при ответе на вопрос о количестве нулей в произведении понадобиться не вычислительный опыт, а способность обращать внимание на то, как зависит результат от набора множителей. Правильный репетитор по математике раскрывает эти взаимосвязи в ходе практической работы с обычными не олимпиадными заданиями в уже 4 классе. Если ученик не запоминает указания репетитора, приходится заниматься весьма трудоемкой работой по подбору или составлению отдельных номеров на каждую подмеченную особенность. Проблем в олимпиадной подготовке имеется великое множество. Ребенок приходит к репетитору по математике в 4 классе не имея, порой даже навыков умножения или деления в столбик. А родители, тем не менее, болеют Курчатовской школой. Репетитору по математике приходится заниматься базовыми уроками и поднимать развивать простейшие практические навыки.

Связанные со школой странички сайта:
Курчатовская школа. Помощь в учебе

Немного о Курчатовской школе

Школа 1189 была создана в 1991 году усилиями И.Н. Полякова и М.Ю. Галицкого и сначала имела статус экспериментальной. Олимпиады по математике стали проводиться с 1993 года и в этот же год был создан первый физико-математический класс. Преподавателями школы — ведущие ученые Курчатовского института, с которыми дети общаются с ранних лет. Несмотря на богатую традициями историю, Школа 1189 всегда считалась одной из самых престижных в Москве. В 2006-м она вошла в пятерку ведущих школ по рейтингу «Известий» на основе результатов олимпиад в старших классах. В прошлом учебном году согласно новому рейтингу МИОО, составленного по тем же олимпиадам, Курчатовская школа из этой десятки, к сожалению, выпала, заняв не самое почетное для себя 12 место. Однако в СЗАО и уж точно в районе Строгино — м. Щукинкская лучшего места учебы не найти. По Москве в лидерах рейтинга идут 57-я школа и лицей «вторая школа».

В новейшей истории Курчатовской школы мы видим значительные изменения. Начиная с 26.09.2012 года по приказу Департамента образования г. Москвы произошло соединение сразу нескольких школ в районе м.Щукинская. Соединились 7-я, 77-я, 702-я, 703-я и 738-я школы. Далее с 28.08.2013 года по 04.03. 2015 года происходит целая серия реорганизации через соединение нескольких дошкольных (№2713 и № 2177) учреждений, в числе которых коррекционная общеобразовательная школа-интернат № 101, со сменой вывески на «Школа № 2077». Интересно, что старая добрая Курчатовская школа №1189 формально присоединилась к этому локомотиву последней, а именно в 2015 году. В общем, мутная история, в которую репетиторам по математике, занимающимся подготовкой Курчатовских учеников в 5 -7 классы, нет смысла вникать. По крайней мере у меня все происходит по тем же олимпиадным графикам и платам без оглядки на начальную школу. Раньше в 1189 ее не было, и сейчас, насколько я знаю, никто из обучающихся в присоединенных школах не имеет проходных льгот для поступления в 5 класс. Также проводится по математике олимпиада в 4 классе и также около 60 человек зачисляются (2 класса).

О курчатовском комплексе

Идея трансформации нескольких учреждений под единое управление на базе Курчатовского института создало для жителей района Октябрьское поле — м.Щукинская — Строгино полноценный образовательный комплекс со множеством направлений и дополнительных услуг. Чего только не встретишь: в одном крыле интернат, в другом коррекционные классы для детей с ограниченными возможностями, есть платные курсы для дошкольников и девятиклассников (с октября по апрель), встречаются даже курчатовские кадеты с изучением основ военной медицины. Надо сказать, что к созданному комплексу серьезно «приложился» МГМУ им. Сеченова и «Первый медицинский институт». Под их началом работают медико-биологическое направление, преподаватели институтов читают лекции. ведут курсы «младшая медицинская сестра». Медицине уделяется большое внимание. Все серьезно: переводные предпрофильные экзамены, лекции, переводные тесты.

Вернемся к математике

Если оценивать работу математической части школы по информации, предоставляемой репетитору его учениками, то какого-то серьезного послабления уровня не замечено. Механика отбора при поступлении сохранена: олимпиада по математике, с довольно высоким порогом даже для талантливых деток. С 7 класса принимаются профильные учебники, а в 5-6 классах обычные (Мерзляк, Полонский), но с профильным предметом ПРЗ (практикум по решению задач). Он сохраняется, насколько я знаю, вплоть до 9 класса. На нем детям дается дополнительная олимпиадная нагрузка (или близкая к ней).

Базовая математика в 5 классе раньше была посложней обычной школьной программы, но в основном за счет решения усложненных задач с вариантов «В» пособия Ершовой и Голобородько. Но все меняется и каждый преподаватель Курчатовской школы приносит в учебные планы свое видение профильного обучения. Посмотрим, что будет в 2018 -2019 году. В прошлые годы следили за строгостью в оформлении решений, а в задании на дом встречались интересные логические и занимательные задачки. Многие из них удавалось решить только с родителями или репетитором по математике. В связи с этим я бы советовал не полагаться только на школу и сохранить занятия у репетитора. За ребенком нужно следить постоянно.

Поучительный случай в Курчатовской школе

Лет 8 назад, еще в пору обособленной бытности Курчатовского обучения (до мании объединения), детей, поступивших в 5 класс, как обычно в соответствии с набранными баллами по вступительной олимпиаде, поделили на 2 класса: сильный и послабее. Более слабый класс занимался по обычной программе, а сильному предоставили «крутого» преподавателя из МФТИ, который больше внимания уделял не программе, а решал с детьми сложные олимпиадные задачки. В итоге на переводной контрольной работе в 6 класс «слабые дети» показали результаты лучше, чем «сильные». Вот так. Не стоит успокаиваться полностью доверять школе. Любой. Продолжайте занимайтесь с хорошим репетитором. В большинстве случаев это лучшее средство достижения высоких показателей по математике.

Раньше мне казался странным выбор учебника в 1189 для 5 класса, ибо в большем почете у математиков значился Петерсон, но после того, как на его программу 1-4 классов «накатили бочку» — он полностью сошел с тренда, уступив даже профильное первенство классической программе Виленкина и его производной — Мерзляку. Есть еще Никольский (лицей Вторая школа его принимает как базовый), но он мне еще больше не нравится. Лучший вариант в работе репетитора по математике, по крайней мере я так советую заниматься, — синтез Виленкина и Петерсон. Приезжайте ко мне в Строгино на уроки и я расскажу о своей системе подробнее.

Важная информация о школе

Адрес физико-математического корпуса : Москва, СЗАО, ул. маршала Василевского, дом 9, корпус 1.
Главный телефон школы (директор и администратор): (499) 194-10-44
Директор — Пушина Маргарита Алексеевна
Администратор — Болотина Инна Владимировна
Электронная почта [email protected]

Позиция рейтинга в списке лучших школ Москвы — 20 место
Начальная школа — есть. На физ-мат отделение нужно поступать по итогам апрельской олимпиады в конце 4 класса.

Местонахождение — недалеко от Строгино, поэтому Вам будет удобно заниматься у меня дома.

Если Вы когда-либо учились в 1189 — напишите свое мнение о Курчатовской школе.

Курчатовская школа на карте:

2 года назад Курчатовская школа объединилась со школой номер 2077, которая тоже стала именоваться Курчатовской, в связи с чем родители часто путают их географически.

Адрес второй Курчатовской школы таков:
Ул. Маршала Конева дом 10. Телефон (495) 194-10-44. Расположена школа дальше от м.Щукинская и Строгино чем ее приемная мама 1189, а именно в 600 метрах от м. Октябрьское поле.

На вступительных олимпиадах это не сильно отразилось. По прежнему в 5 класс проходит набор учеников через вступительное испытание. Правда несколько изменился характер задач. В 2016 и 2017 годах увеличилось число задач, пришедших на олимпиаду для 4 класса из обычных программ по математике для 5-6 класса. В 2018 году таких вольностей мной замечено не было. Каков будет баланс в следующем 2019 году — посмотрим.

Вопросы родителей по подготовке в Курчатовскую школу

Здравствуйте! Мы учимся в обычной школе, мальчик — отличник, 4 класс. В прошлом году прошел по конкурсу в математический лагерь под Костромой. Участвовал в олимпиаде за 4 класс осенью, в призеры не вышел, по баллам где-то 4 место. Заинтересован в математике. К сожалению в математический кружок пойти не удалось. Занимаемся дома. Подумываем попробовать силы в Курчатник. Не подскажете, пожалуйста, каких-нибудь методички, книжки, ссылки по Курчатовским задачкам (они отличаются от всех олимпиадных задачек, как я вижу)? Спасибо.

Репетитор по математике об олимпиадных материалах: специализированных методичек именно по Курчатовской — нет, как и критериев отбора задач (кроме их уровня и соответствия пройденному материалу в 1 — 4 классах). Я использую свою базу, наработанную за годы подготовки в 1189. В ней есть как редкие и уникальные задачи, так и достаточно распространенные типовые, ставшие олимпиадной классикой. Аналогичные материалы можно найти в различных сборниках, но, как правило, прежде чем садится решать все то, что в них имеется, нужно а) подготовить ребенка к восприятию сложных решений б) отсортировать материал по его тематической и программной пригодности. С сортировкой задач по классам дела обстоят неважно практически в любом пособии и это не принимая в расчет индивидуальные особенности маленького ученика. Часто в один список попадают задачи для разных классов. Работу по отбору задач должен выполнить репетитор по математике.

В случае отсутствия подготовленной дидактики репетитору нужно купить сразу несколько книжек и сначала перерешать задачи самостоятельно (без ребенка), а уже затем совместно. Надо иметь ввиду, что олимпиадные задачи для 4 — 5 класса часто заимствуются авторами пособий друг у друга и в среднем из 3-5 задач конкретному ученику может подойти лишь одна-две. Если взять какую-нибудь среднестатистическую олимпиадную подборку (на сайте или в книге), то наверняка половину имеющегося в ней материала придется отложить в сторону по причине несоответствия конкретному ученику и конкретной ситуации. Поэтому «сырье», из которого репетитор по математике подготавливает олимпиадный урок, должно быть куплено с большим запасом. Можно заказать книжечку Е.Г. Козловой «Сказки и подсказки» или Спивака «1001 задача по математике». Будет время — подготовлю страничку со ссылками на олимпиадные сайты, наиболее полезными и удобными для подготовки в Курчатовскую школу.

Подборка видео объяснений репетитора реальных задач с апрельского экзамена по математике в Курчатовскую школу в 2018г

Наконец дошли руки снять и разместить несколько примеров живых объяснений с последней Курчатовской олимпиады в 2018г. На первых двух видео — Ваш покорный слуга, на последнем (задача на куб) — мой хороший коллега, репетитор по математике, Валентин Юрьевич Колосов.

В шахматном турнире, сыгранном по принципу «каждый с каждым играет по 1 матчу» было сыграно 45 матчей. Сколько в этом турнире приняло участие шахматистов?

Для того, чтобы пронумеровать все страницы некоторой книжки потребовалось 354 цифры. Сколько было страниц?

Полный список задач варианта за 2018 год можно посмотреть по соответствующей ссылке в верхней части этой страницы.

О технических особенностях моих видеосъемок можно прочитать по ссылке Особенности записи видеоуроков репетитором по математике

Колпаков А.Н, Подготовка в Курчатовскую школу.

Решение задач: 5 класс по математике

    Приборная панель

    5 класс

    Решение проблем

    Перейти к содержанию

    Приборная панель

    • Авторизоваться

    • Панель приборов

    • Календарь

    • Входящие

    • История

    • Помощь

    Закрывать