Решаем в столбик
Уважаемые взрослые!
Счёт в столбик сам по себе несложен, но требует долговременной концентрации и внимания.
Очень часто дети-торопыжки, имеющие отличные оценки по математике, делают глупые и обидные ошибки. Например, вычитают из четырёх два и получают… один. Для детей и родителей это шок и полнейшее непонимание: «КАК такое может быть?». Знаете, может. И часто.
Как добиться автоматизированного счёта в столбик? Никого не удивлю своей позицией — нужна специальная отработка счёта в столбик. Когда-то давно у нас выходил сборник таких примеров. Сейчас его не издают. Но и мои ученики, и ученики многих моих коллег выучились быстрому и безошибочному счету в столбик по этому пособию.
Мне жалко, что хороший материал лежит столько лет, не принося никому пользы. Поэтому я решила выложить его на сайте до первого требования издателей убрать.
Как строится книга? На листочке в клеточку написаны примеры. На обратной стороне — примеры для работы над ошибками дома. Так как Ваши дети и так будут примеры решать дома — можете или решать всё подряд, или оставить примеры для работы над ошибками для будущего повторения. Потому что после того, как порешали примеры на умножение, хорошо бы вспомнить заново примеры и на сложение, и на вычитание.
Так как Ваши дети и так будут примеры решать дома — можете или решать всё подряд, или оставить примеры для работы над ошибками для будущего повторения. Потому что после того, как порешали примеры на умножение, хорошо бы вспомнить заново примеры и на сложение, и на вычитание.
В содержании написаны темы. Вот через тему я рекомендую не перешагивать и решать по 1-2 страницы на каждую. Весь материал дан в логической последовательности. В конце книги размещены самые распространенные математические ребусы счёта в столбик.
Для взрослых выходила даже книжка с ответами. Её я тоже выкладываю. Ответы на ребусы тоже есть.
P.S. Не увлекайтесь решением в столбик, если пример можно решить устно. В этой книге идёт отработка от простого к сложному. Поэтому здесь всё решаете в столбик. Когда научитесь — останавливайте детей: примеры, типа 83-56, 12х8, нужно решать устно. Необходимо постоянно тренировать приёмы счета, развивать мышление, память, внимание. Устный счёт очень полезен, очень развивает.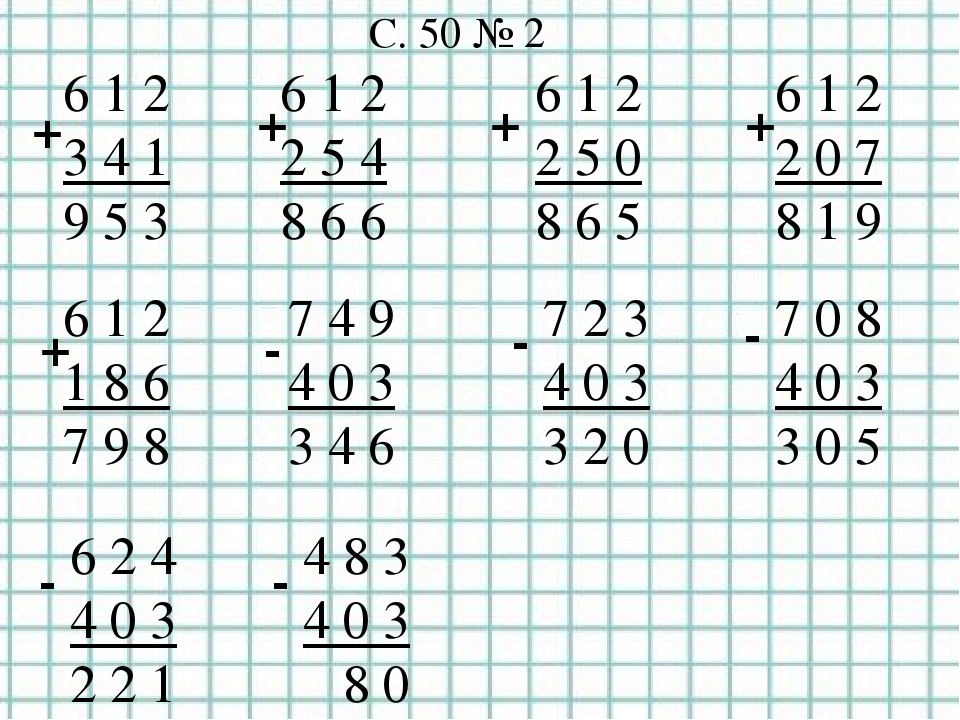
Помните, что счёт в столбик надо использовать только при необходимости.
Скачать/открыть книги Вы можете по ссылкам ниже:
Вычисления в столбик
Ответы на письменные вычисления
Деление десятичных дробей: правила, примеры
Основы деления десятичных дробей
Десятичные дроби — это дроби, у которых в знаменателе стоят числа, кратные 10. То есть 10, 100, 1000 и так далее.
Как делить десятичные дроби друг на друга — процесс представляет собой деление обыкновенных дробей. То есть для выполнения действий деления мы переписываем десятичную дробь в стандартный вид.
Рассмотрим пример: разделите 1,2 на 0,6
Как решаем Запишем десятичные дроби в виде обыкновенных. У нас получится: Таким образом, нам надо разделить
|
Ответ: 1,2÷0,6 = 2
Если для деления нам попадается периодические и непериодические дроби, то действуем следующим образом.
Периодические переводим в обыкновенную:
Если же встречается непериодическая десятичная дробь, то мы ее округляем до сотых и дальше делим, как обычно:
Как разделить целое число на десятичную дробь и наоборот
Здесь всё просто: приводим десятичную дробь к стандартному виду и натуральное число тоже представляем в виде дроби — само число нужно поделить на единицу.
Пример: 3,5 поделить на 55
Как решаем |
Ответ: 3,5÷55 = 0,063 (63)
Как разделить десятичную дробь на натуральное число столбиком
Делить столбиком можно не только натуральные числа, но и дроби. Алгоритм мы подробно опишем здесь. Итак, как делить десятичные дроби на натуральные числа в столбик:
1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
2. Выполнить деление по стандартной схеме. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.
Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться — получится периодическая дробь.
Пример: Разделить столбиком 49,14÷3
Как решаем
1. Делим столбиком, предварительно дописав два нуля к десятичной дроби.
2. После того, как мы поделили целую часть дроби и получили 16, отделяем ответ запятой (16) и продолжаем деление уже для дробной части
В конце у нас нулевой остаток, значит деление завершено. |
Ответ: 49,14÷3 = 16,38
Как разделить столбиком одну десятичную дробь на другую
Все просто: умножаем делимое и делитель на 10, 100 и так далее — так, чтобы делитель превратился в натуральное число. А потом решаем также, как в примере выше:
А потом решаем также, как в примере выше:
1. Переносим запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, дописываем в него нули с правой стороны.
2. После этого делим дробь столбиком на получившееся натуральное число.
Пример: поделить столбиком 63,42 на 2,1
Как решаем
Переносим запятую на один знак вправо, чтобы делитель (2,1) стало натуральным числом. Запятую переносим в обоих числах — у нас получается 634,2÷21. Затем производим деление |
Ответ: 63,42÷2,1 = 30,2
Как разделить десятичные дроби на 1000, 100, 10 и другие
Как вы уже заметили, есть основное правило деления десятичных дробей: по нему деление дроби на десятки, сотни, тысячи аналогично ее умножению на 1/1000, 1/100, 1/10 и другие.
Чтобы выполнить действие, нужно просто перенести запятую влево на нужное количество цифр (равное нулям). Если значений в числе не хватит для переноса — дописываем нужное количество нулей:
Как разделить десятичные дроби на 0,001, 0,01, 0,1 и другие
Правило из предыдущего пункта поможет нам без труда разделить дроби на указанные значения. Переводим эти числа в стандартные дроби и затем при делении действие будет аналогично умножению на 1000, 100, 10 (так как дробь, на которую делим переворачивается).
Чтобы найти ответ в подобных задачах, мы переносим запятую на одну, две, три цифры вправо (в зависимости от числа, на которое делим) и дописываем нули, если цифр в числе окажется недостаточно.
Как разделить смешанное число или обыкновенную дробь на десятичную и наоборот
Это действие мы также сводим к операциям с обыкновенными дробями. Вот как поступим со смешанным числом: записываем его в виде неправильной дроби, десятичную — в виде обычной дроби и делим по уже стандартной схеме.
В детской онлайн-школе Skysmart ученики решают такие задачки на интерактивной платформе. Внутри: автоматическая проверка, тысячи интересных задач и головоломок, онлайн-доска, на которой можно чертить и рисовать и поддержка чутких учителей. Запишите вашего ребенка на бесплатный вводный урок — мы покажем, как все проходит и вдохновим ребенка на дружбу с математикой.
Презентация «Сложение чисел в столбик с переходом через разряд»
Слайды и текст этой онлайн презентации
Слайд 1
Урок математики. 3 класс.
Презентацию разработала учитель начальных классов
БОУ г. Омска «СОШ №118».
Петрушина Татьяна Алексеевна
Слайд 2
Девиз урока
«Мы пришли сюда учиться Не лениться, а трудиться, Только тот, кто много знает В жизни что-то достигает».
Слайд 3
Математический диктант
— 45 увеличить на 33;
- 168 уменьшить на 130;
- 540 разделить на 90;
— найдите сумму чисел 72 и 24;
- 200 умножить на 5;
- частное чисел 800 и 8;
Уменьшаемое 127, вычитаемое 107, чему равна разность;
- 1 слагаемое 174, второе слагаемое 17, чему равна сумма;
78
38
6
96
1000
100
20
191
Слайд 4
Тема урока:
Наблюдать
Сравнивать
Делать выводы
Сложение чисел в столбик с переходом через разряд.
План урока:
Слайд 5
Слайд 6
Алгоритм сложения двузначных чисел с переходом через разряд. 1. Пишу… (единицы под единицами, десятки под десятками, сотни под сотнями) 2.Складываю единицы. (число единиц суммы — пишу под единицами, а 1дес. запоминаю) 3.Складываю десятки:…и увеличиваю количество десятков на 1. Пишу под десятками, а 1сот. запоминаю) 4. Складываю сотни: … и увеличиваю количество сотен на 1. Результат пишу под сотнями. 5. Ответ: …
Слайд 7
Самостоятельная работа.
Слайд 8
Самопроверка
Уровень А: 378, 389, 759
Уровень Б: 400, 760, 784
Уровень С:
253
459
712
+
286
316
602
+
326
481
807
+
1
1
1
1
1
Слайд 9
Повторяй! Не зевай!
До встречи!
Слайд 10
Задача.
Было –
Взяла –
Осталось —
? кг
?, 600г и 1 кг 500 г
900 г
1) 1500 + 600 = 2100 (г) — взяла
2) 2100 + 900 = 3000 (г) – 3 кг
Ответ: 3 кг муки было.
Слайд 11
Решаем уравнения.
А:
Х = 181
Х = 593
Б:
Х = 440
Х = 612
С: 234 – Х = 104
Х = 130
Х + 60 = 570
Х = 630
Слайд 12
Завершается урок, Он пошёл ребятам впрок? Постарались всё понять? Учились тайны открывать? Ответы полные давали? На уроке не зевали?
Слайд 13
— Какую задачу ставили в начале урока? Удалось ли решить поставленную задачу? Каким способом? Какие получили результаты? Что нужно сделать ещё? Где можно применить новые знания? Что на уроке у вас хорошо получилось? - Над чем ещё надо работать?
Слайд 14
Рефлексия
Я всё понял на уроке и могу
объяснить товарищу.
Я усвоил тему, но объяснить не могу.
Эта тема для меня трудная.
Слайд 15
Домашнее задание.
№ 3 стр.20 ( по желанию придумать два примера на новый способ)
Задача № 4 (а).
Слайд 16
Слайд 17
Использованные материалы.
Пятёрка. www.miranimashek.ru
Фон. http://tineydgers.at.ua/sova3.gif
http://www.mathknowledge.com/images/custom/LOGO.GIF
http://endem.ru/uploads/posts/2010-09/1285569710_osennie-listya.jpg
ttp://burla.su/uploads/posts/2010-05/1274360367_poslednii_zvonok.jpg
http://pochemuka.ru
http://aida.ucoz.ru
Конспект урока по математике «Запись вычитания столбиком» — 2 класс «Начальная школа 21 века» | План-конспект урока по математике (2 класс):
-Молодцы ребята, вы сегодня очень внимательны и активны. Теперь поработаем с нашими учебниками, открываем страницу 64 № 19. Эту задачу решаем устно.
-Слушаем внимательно условия задачи. Следим.
(Из аптеки вышли 5 человек. В ней осталось на 2 человека меньше, чем вышло. Сколько человек осталось в аптеке?)
-О чем эта задача?
-О чем нам говорит число 5?
-О чем нам говорит число 2?
-Сколько человек вышли из аптеки?
-Нам известно сколько человек осталось?
-Можно ли этот текст назвать задачей? Почему?
– Что вам известно? Что требуется узнать?
– Все ли данные понадобятся для решения этой задачи?
-Как будем решать?
Хорошо. Теперь ребят давайте попробуем изменить задачу, изменим так, слово «меньше» заменим словом «больше» и попробуем её решить
Теперь ребят давайте попробуем изменить задачу, изменим так, слово «меньше» заменим словом «больше» и попробуем её решить
(В аптеке было 5 человек. Через несколько минут стало на 2 человека больше. Сколько человек стало в аптеке?)
-О чем говорится в этой задаче?
-О чем нам теперь говорит число 5?
-А число 2 нам о чем говорит теперь?
-Что нам известно? Что изменилось?
-Что необходимо узнать?
-Как будем решать эту задачу?
-Чем отличается первая задача от второй?
-Молодцы ребята.
2 задание
-Вторую задачу будем решать письменно. Сначала слушаем условия задачи внимательно!
(Петя сорвал с одной яблони 12 яблок, а с другой 9. После того как он поделился с другом у него осталось 16. Сколько яблок Петя дал другу?)
-О чем говорится в задаче?
-О чем нам говорит число12?
-О чем нам говорит число 9?
-О чем нам говорит число 16?
-Что известно про 1 яблоню?
-Что нам известно про 2 яблоню?
-Что нам требуется узнать в этой задаче?
-Что нам известно? Составим краткую запись задачи.
-Это задача простая или составная? Почему? Сколько действий будем выполнять?
-Какое первое действие?
-Какое второе действие?
-Читаем ответ.
-Ребята, помните нашего друга Незнайку? Сегодня он с утра меня попросил передать Вам конверт. На этот раз Незнайка попробовал составить сам задачи. Задачи очень легкие, но у него и в составление задач возникли ошибки. Давайте постараемся найти ошибки и решить совсем легкие задачи. Вы решали сегодня задачи очень хорошо, поэтому, для вас не составит труда.
-Открывают учебники.
Да. Потому что даны условия, поставлен вопрос.
5-2=3 (человека осталось в аптеке)
5+2=7 (стало людей в аптеке)
В первой надо было отнять, во-второй прибавить.
Составная. Т.к. решается в несколько действий
1) 12 + 9 = 21 (всего яблок сорвал Петя)
2) 21 — 16 = 5
Ответ: Петя дал другу 5 яблок.
Решаем в столбик Узорова | DocumentBase.net: обмен учебными документами
Чтобы посмотреть этот PDF файл с форматированием и разметкой, скачайте его и откройте на своем компьютере.
x
****
*
* *8
x
7
*********
***
3
*
0
8
b d c e
b
b d a e
aaa a
a e c b e
aaa a
aaa a
baaa a
a b cdcd
c d bcd
e c
d
b cd
b cd
Мɚɬɟмɚɬичɟɫкиɟ
Оɞинɚкоɜыɟ
1
a b c d
*
a b c
a b
***
a
*****
4 3 2 1 2
00 4
3
****
***
1 9 7 1
5
x
***
1
0
164388:399
50127:231
544428:213
32032:208
62208:243
300202:574
89610:435
132840:328
35910:378
643926:214
118020:84
158050:58
208800:48
143115:47
171513:57
11840:37
93870:42
38608:76 16668:36
65664:19
11456:32
26220:46
5643:27
10810:47
54400:85
97760:65
49020:76
19950:38
60630:86
36990:54
32880:48
64524:76 57460:68
1428:42
7368:24
Пɪимɟɪы
поɜɬоɪɟния
813400:28
740160:36
Пɪимɟɪы
поɜɬоɪɟния
921570:51
681850:65
Пɪимɟɪы
поɜɬоɪɟния
90360:18
97120:16
9139:13 8512:14
9407:23
9315:45
612:36 792:22
805:35 828:36
759:23 936:36
989:43 986:34
992:31 975:13
702:18 936:78
714:34 938:14
252:14 342:18
221:17 988:52
688:16 703:19
841:29 702:18
684:12 884:17
864:36 468:13
646:19 925:25
899:31 888:74
832:16 266:14
957:29 949:73
987:47 713:31
455:13 924:77
476:34 555:37
576:16 962:26
Пɪимɟɪы
поɜɬоɪɟния
16560:90 8160:40
25120:80 5640:30
Пɪимɟɪы
поɜɬоɪɟния
16450:70 2160:40
46800:600 16680:60
Пɪимɟɪы
поɜɬоɪɟния
25560:60 37600:400
55200:300 13400:200
62040:3
83880:4
40350:5
63560:7
42630:7
36720:9
8320:2
9180:3
102620:4
213135:5
730548:9
208416:6
919884:7
118600:8
219400:8
48512:8 42120:8
86436:7
16245:5
27402:6
86544:9
23160:5 15630:5
25732:4
18932:4
66552:8
26712:9
9447:3
25338:6
7832:8
7038:6
5642:7
3184:4
7746:6
3685:5
4086:6
5526:6
23176:8
8632:4
62600:8 29296:4
24632:4
15048:8
67048:4
25032:8
370:5 835:5
348:6 378:7
536:4 672:7
356:4 456:6
265:5 272:4
645:5 348:6
834:6 895:5
785:5 388:4
287:7 544:8
676:4 625:5
455:7 596:4
976:8 684:6
492:4 525:3
585:5 896:8
368:4 882:9
595:5 856:4
681:3 784:7
957:3 654:3
Пɪимɟɪы
поɜɬоɪɟния
8656
2768
4036
Пɪимɟɪы
поɜɬоɪɟния
6464
5499
3015
Пɪимɟɪы
поɜɬоɪɟния
4823
2679
8006
869
597
788
386
294
665
932
364
728
293
246
589
648
752
345
19682
36 93458
27
54183
49 23456
68
6724
2657
65 3468
67
5864
72 4159
56
Пɪимɟɪы
28
25 51
68
56
92 38
75
44
19 25
25
46
39 52
43
16
26 74
35
52
47 27
43
65
29 76
36
54
57 27
39
99
49 45
37
33
27 36
55
59
42 46
45
54
28 84
25
70200
20 3500
3000
4060
200
10670
200 706000
300
50150
500 20700
300
37600
50240
31200
800 6510
700
5700
4000 10920
500
2843
5713
8000 3652
800
6273
5000 5842
9000
Пɪимɟɪы
поɜɬоɪɟния
5342
700 4794
9000
8354
500 7845
600
Пɪимɟɪы
поɜɬоɪɟния
702030 8
403709
306980 7
109640
38700 7
50904
49008 6
52078
Пɪимɟɪы
730700
5 290900
8
340200
6 400450
4
Пɪимɟɪы
поɜɬоɪɟния
4
6
80330
9 707300
5
936000
8 645000
6
Пɪимɟɪы
поɜɬоɪɟния
30900
4 88800
9
624000
7 208000
5
Пɪимɟɪы
поɜɬоɪɟния
204302
9 208406
3
92308
6 403209
5
9
38041
7 90604
5
30908
8 20503
6
70486
9
4
20702
3 90052
7
60944
8 87504
5
80069
6 5904
8
80037
9 43008
4
65784
72371
8 43582
6
58437
3 38756
9
82646
13478
8 34548
4
29898
9 35647
5
8524
4 36546
8
5368
7 4994
6
7
2647
8 4925
6
5894
3 9423
8
8
837
4 458
9
635
7 584
3
Пɪимɟɪы
9074065456358004702525
60047583727680005554
803070653245009032172
3320403176319565210405265846
64230253759586930502487654
3200241152357552131042103253
8005429 600449
5045857
606178 6023487
5406618 76023784
4203627
9003879 40342735
622356 9482643
81135207
93257587 422648
73285634 78214545
4615185
78655928 87563488
976523 5847525
76853554
83761324 569372
64785251 73476125
9915603
6946324 54871417
788527 62095105
7826703 44853261
586725
613531 4275234
3595779+37779189983065+6652195
7575139+63120661244385+3991528
5331368+65135891983405+3806
5292930+83345144896+3675
7844827+6842191345972+463428
4788287+12767652163787+4398546
3615+2039 2813+287
4328+3418
6026+1274 3308+4075
4665+3535 5713+2491
3219+615
6272+2367 4358+3326
8243+167 1186+8426
6918+2672 4213+3875
4862+768
2107+3908 2803+5370
6538+2250 1974+4025
3651+218
1724+5022 4533+56
9
7367+531 8212+1427
1945+34
3721+75 3197+4801
8
7
1076+6812
ɬɚкжɟ
коɬоɪых
ɫложɟниɟ
ɭчиɬɟлям
оɛъяɫнɟния
оɬɞɟльных
ɭчɟникоɜ
ɭчɚщихɫя
Кɚɪɬочки
Дɟлɟниɟ
4-, 5-, 6-
чɚюɬɫя
полɭчɚюɬɫя
нɭли
4-, 5-, 6-
97109 199
Мɚɬɟмɚɬичɟɫкиɟ
237
ɪɚɛоɬɚ
ɫɬɪ
Пɪɟɞиɫлоɜиɟ
5
Вычиɬɚниɟ
911 23
нɭли
мноɝознɚчноɝо
зɚпиɫи
пɟɪɜоɝо
множиɬɟля
нɭли
зɚпиɫи
пɟɪɜоɝо
множиɬɟля
нɭли
мноɝознɚчноɟ
зɚпиɫь
нɭля
мноɝознɚчноɝо
ɞɜɭзнɚчноɟ
чиɫло
чиɫло
нɭли
Приложенные файлы
- 8005895
Размер файла: 2 MB Загрузок: 0
Конспект урока по математике на тему «Запись вычитания столбиком» (2 класс)
Технологическая карта урока.
Тема:
Запись вычитания столбиком
Тип урока:
Урок отработки умений и рефлексии
Цели урока:
Закрепить пройденный материал.
Планированный результат.
Личностные результаты:
Предметные результаты:
Метапредметные результаты:
Фиксирование и преодоление затруднений при выполнении сложения и вычитания двузначных чисел.
Развитие мотивов учебной деятельности;
Развитие навыков конструктивного сотрудничества со сверстниками и учителем.
Оценка предметных результатов представляет собой оценку достижений планируемых результатов по всем учебным программам.
Оценивается способность к решению учебно-познавательных и учебно-практических задач, основанных на изучаемом учебном материале, с использованием способов действий
Формирование умения планировать, контролировать и оценивать учебные действия.
Ход урока.
Этап
Деятельность учителя
Деятельность учащихся
1.Самоопределение к деятельности.
Организационный момент.
Громко прозвенел звонок –
Начинается урок.
Наши ушки на макушке,
Глазки хорошо открыты.
Слушаем, запоминаем,
Ни минуты не теряем.
Здравствуйте, ребята! Садитесь. Меня зовут Клавдия Дмитриевна, и я проведу урок математики.
В тетрадях запишите число, классная работа. Сегодня 14 октября
Проверяют готовность к уроку.
Садятся за свои места.
Записывают дату, классная работа
2. Актуализация знаний
— Начнем наш урок с устного счета
Устный счет мы проведем с героями сказок. За каждый ваш ответ – герои сказок будут говорить, правильно ли вы ответили или нет.
— В каком числе 4 десятка и 7 единиц?
— Какое число меньше, чем 70,на 1?
— Найди сумму чисел 8 и 50.
— Найди разность чисел 94 и 4.
— Найди число, в котором 5 десятков и 3 единицы
— Какое число увеличили на 7, чтобы получить 30?
— Какое число уменьшили на 9, чтобы получить 21?
— Найдите значение выражения:
28 – 14; 46 + 23; 59 – 12.
Как удобнее записывать такие примеры?
— Какие правила нам понадобятся для того чтобы найти значение данных выражений?
— Давайте найдем значения этих выражений. Решите в тетради.
— Теперь проверяем ответы
— Если вы все решили правильно, то поднимите зеленый кружочек; если вы допустили 1 ошибку, то поднимите желтый кружочек; если у вас ничего не верно, то поднимите красный кружочек.
— Что это за слово столбик. Какое отношение оно имеет к математике?
-Что будем делать на уроке?
-Для чего нужно складывать столбиком?
— Когда мы используем запись столбиком?
— Как нужно записывать числа столбиком?
— С какого разряда мы начинаем сложение и вычитание столбиком?
47
69
58
90
53
23
30
Столбиком
Единицы складываем с единицами, десятки с десятками.
-Из единиц вычитаем единицы, из десятков вычитаем десятки.
28 46 59
—14 +23 —12
14 69 47
При помощи столбика решаем примеры.
Решать примеры столбиком
Это быстрый и легкий столбик решения примера.
Когда трудно вычислить, мы используем запись столбиком
Единицы под единицами, десятки под десятками.
С разряда единиц
3. Закрепление
пройденного
материала
Выполним № 4. Что нужно сделать?
— Давайте с вами условимся, как будем расставлять порядок действия?
— Все что мы можем вычислить – вычисляем устно, а если трудно – в столбик.
— При выполнении сначала будем правильно читать наши выражения.
— Выполним 1 выражение
— Прочитай его
— Запишите выражение.
— Какое действие будем выполнять первым?
— Давайте решим.
— Стоит ли выполнять столбиком 2 действие?
— Какой ответ получиться?
-Давайте посмотрим на 2 выражение, прочитайте его.
— Сколько действий?
— Какое действие будем выполнять первым?
— Давайте решим.
— Какой ответ получиться?
— Давайте посмотрим на 3 строчку, прочитайте его
— Сколько действий?
— Какое действие будем выполнять первым?
— Давайте решим
— Какой ответ получиться?
— Теперь выполняем самостоятельно
1 вариант выполняет 1 выражение из 2 столбика
2 вариант выполняет 2 выражение из 2 столбика
— Если вы все решили правильно, то поднимите зеленый кружочек; если вы допустили 1 ошибку, то поднимите желтый кружочек; если у вас ничего не верно, то поднимите красный кружочек.
Вычислить
1 действие будем выполнять в скобках, остальные по порядку
К разности чисел тридцати девяти и семнадцати прибавим двадцать
(39-17)+20=
В скобках
39
—17
22
-Нет, можно решить устно.
(39-17)+20= 42
Из пятидесяти девяти вычесть сумму чисел тридцати двух и тринадцати
2 действия
В скобках
32 59
+13 — 45
45 14
59 –(32+13)=14
Из суммы чисел шестидесяти семи и двенадцати вычесть пятьдесят пять
2 действия
В скобках
67 79
+12 — 55
79 24
(67+12)-55=24
1 вариант: 23+ (97-86) =34
2 вариант: (90-50)-10=30
4. Физкультминутка
Физкультминутка
Мы трудились очень много,
Отправляемся в дорогу.
(Ходьба на месте.)
Побываем тут и там,
Поглядим по сторонам.
(Повороты корпусом.)
Нам навстречу скачет зайка,
(Прыжки.)
В небе кружат птицы.
(Дети машут руками.)
Но пора вернуться в школу,
Нам надо учиться.
(Дети садятся за парты.)
5. Продолжение закрепления темы урока
— Выполним упражнение 6. Прочитайте его.
— Прочитайте 1 задание
— Вспомним правило, как узнать насколько одно число больше другого?
-Как будем решать?
— Как будем записывать?
-Решаем
— На сколько 38 больше 16?
— Прочитайте 2 задание
— Вспомним правило, как узнать насколько одно число меньше другого?
-Как будем решать?
— Как будем записывать?
— Решаем
— На сколько 75 меньше 98?
— Прочитайте 3 задание
— Как узнать насколько одно число меньше другого?
-Как будем решать?
— Как будем записывать?
— Решаем
— На сколько 7 меньше 27?
— Прочитайте 4 задание
— Как узнать насколько одно число больше другого?
-Как будем решать?
— Как будем записывать?
— Решаем
— На сколько 90 больше 60?
5 задание (30 меньше 80) выполняет 1 вариант
6 задание (56 больше 10) выполняет 2 вариант
— Если вы все решили правильно, то поднимите зеленый кружочек; если вы допустили 1 ошибку, то поднимите желтый кружочек; если у вас ничего не верно, то поднимите красный кружочек.
— Обратите внимание на 13 упражнение. Прочитайте его.
— О чем говорится в задаче?
— Куда отправились ученики?
— Сколько всего учеников?
— Сколько учеников пошло в кино?
— Сколько учеников пошло в музей?
— Сколько детей поехало в театр?
— Что нам нужно узнать?
— Давайте запишем краткую запись
— Какие слова возьмем для краткой записи?
— Как покажем общее количество детей?
К. – 30 уч.
М. – 23 уч. 95 уч.
Т.- ?
— Можем ли мы сразу ответить на вопрос задачи? Почему?
— Можем узнать?
— Что для этого мы сделаем?
Запишите решение
— Потом мы сможем узнать?
— Каким действием?
Запишите решение
— Как запишем ответ?
— Эту задачу можно решить и 2 способом.
Зная общее количество детей и детей, которые ушли в кино. Что мы можем узнать?
— Как мы узнаем? Каким действием?
— Запишите решение
— Если мы узнали сколько поехали в театр и музей, можем ли мы ответить на вопрос задачи? Каким образом?
— Запишите решение
— Как запишем ответ?
— Выполним упражнение 14.
— Как его будем выполнять?
— По цепочке решаем примеры
На сколько 38 больше 16
Чтобы узнать насколько одно число больше другого, нужно из большего числа вычесть меньшее
38-16=
Столбиком
38
—16
22
На 22, 38 больше 16
На сколько 75 меньше 98
Чтобы узнать насколько одно число меньше другого, нужно из большего числа вычесть меньшее
98-75=
Столбиком
98
—75
23
На 23, 75 меньше 98
На сколько 7 меньше 27
Чтобы узнать насколько одно число меньше другого, нужно из большего числа вычесть меньшее
27-7=
Устно
27-7=20
На 20, 7 меньше 27
На сколько 90 больше 60
Чтобы узнать насколько одно число больше другого, нужно из большего числа вычесть меньшее
90-60=
Устно
90-60=30
На 30, 90 больше 60
1 вариант: 80-30=50
2 вариант: 55-10=45
Об учениках
В кино, на экскурсию, в кукольный театр
95
30
23
Неизвестно
Сколько поехало в театр
К. – кино, М. – музей, Т. – театр
– кино, М. – музей, Т. – театр
С помощью фигурной скобки
Нет, мы не знаем сколько поехали вместе в кино и музей
Сложением
К количеству учеников, которые поехали в кино прибавим количество учеников, которые поехали музей
30+23= 53 (уч.) – поехали в кино и музей
Да
Из общего количества детей вычтем 1 действие
95-53=42(уч.)
Ответ: 42 ученика поехали в кукольный театр
Сколько детей поехало в театр и музей
Из общего количества детей вычтем количество детей, которые пошли в кино
95-30=65 (уч.) – поехали в музей и театр
Да, из количества учеников, которые поехали в театр и музей вычесть количество учеников, которые поехали в музей
65-23=42(уч.)
Ответ: 42 ученика поехали в кукольный театр
Устно
30+10=40 60+5=65 (40+40)-30=50
30-10=20 75-5= 70 (80-30)+20=70
90+10=100 88-8=80 (20+30)-10=40
90-10=80 96-6=90 (90-50)-30=10
6. Рефлексия.
Что мы сегодня с вами закрепили на уроке?
Были трудности?
Что вам понравилось на уроке?
Как вы оцениваете себя?
Все работали хорошо.
Решение примеров столбиком.
ОАОУ СПО «Астраханский социально – педагогический колледж»
Конспект пробного урока по математике, проведенного во 2 «Б» классе
Тема: «Запись вычитания столбиком»
Выполнила: Логинова К.Д.
Методист: Рябова Н.Ю.
Учитель: Ситалиева Д.С.
Подпись студента:________
Подпись учителя: ________
Подпись методиста: _______
Оценка за урок: __________
Дата: 14.10.15
Тема | Сложение и вычитание трёхзначных чисел в столбик. | ||
Цели | Образовательные:1) решать на новом числовом концентре текстовые задачи изученного вида; 2)учиться решат задачи, в которых значение величин находится через их сумму и отношение. Формировать УУД: — Личностные УУД: Самостоятельно определять и высказывать самые простые общие для всех людей правила поведения при общении и сотрудничестве. В самостоятельно созданных ситуациях общения и сотрудничества, опираясь на общие для всех простые правила поведения, делать выбор, какой поступок совершить. — Регулятивные УУД: самостоятельно формулировать цели урока после предварительного обсуждения. Учиться совместно с учителем находить и формулировать учебную проблему. Составлять план решения проблемы совместно с учителем. Работая по плану, сверять свои действия с целью и, при необходимости, исправлять ошибки с помощью учителя. В диалоге с учителем учиться вырабатывать критерии оценки и определять степень успешности выполнения своей работы и работы всех, исходя из имеющихся критериев. — Коммуникативные УУД: Донести свою позицию до других: высказывать свою точку зрения и пытаться её обосновать, приводя аргументы. Слушать других, пытаться принимать другую точку зрения, быть готовым изменить свою точку зрения. — Познавательные УУД: Самостоятельно предполагать, какая информация нужна для решения учебной задачи в один шаг. Решать задачи по аналогии. Строить аналогичные закономерности. | ||
Планируемый результат | Предметные: познакомиться с алгоритмами письменных приёмов сложения и вычитания трёхзначных чисел, аналогичных таким же приёмам при сложении и вычитании двузначных чисел. Знать Уметь Личностные: Объяснять самому себе: что во мне хорошо, а что плохо, что я хочу, что я могу. Метапредметные: формирование универсальных учебных действий (УУД): регулятивных, познавательных, коммуникативных. | ||
Основные понятия | Разрядные единицы, компоненты действий | ||
Межпредметные связи | чтение, окружающий мир | ||
Ресурсы:- основные — дополнительные | Методические рекомендации для учителя по курсу математики с элементами информатики 3 класс. С.А.Козлова, А.Г рубин, А.В.Горячев. | ||
Организация пространства | Парно-групповая, индивидуальная работа, фронтальная работа, самостоятельная работа. | ||
Этап | Деятельность учителя | Деятельность учащихся | УУД |
к деятельности | Прозвенел и смолк звонок. Запишите число. | запись числа, классной работы | Л:самоопределение К:взаимодействуют с учителем, слушают собеседника Р:целеполагание |
2 Актуализация знаний и фиксация затруднений в деятельности | Сегодня у нас будет урок-путешествие в царство… Но сначала математическая разминка игра «Цепочка». Итак, выполнив первое задание вы узнаете куда же мы отправимся. 1 слайд: Представьте в виде разрядных слагаемых: О 623= 600+ 20+3 Д 705= 700+5 А 920=900+20 П 78=70+8 Р 315=300+10+5 И 467=400+60+7 Р 509=500+9 Расставьте числа в порядке возрастания и вы узнаете название царства. 2 слай Совершенно верно «Природа» -поднимите сигнальные карточки, кому показалось трудным это задание? -Молодцы , сегодня на уроке вместе с выполнение математических задач мы узнаем некоторые интересные природные факты . 3 и 4 слайды | Все организованно работают и следят за правильностью ответов. Проверка: программа оценивает, ученик читает ответы, дети выполняют самооценку и сигнал – кружок (красный, желтый) -умножение и деление -При решении примеров, задач. Спрашиваю тех, кто поднимает руку.( Фронтальная работа.) | К: планирование учебного сотрудничества П: анализ объектов с целью выделения признаков |
3.Постановка учебной задачи | Открой те учебники на с .64 -Какая тема урока? -Какая цель нашего урока? -№1 ВЫПОЛНИТЕ ЗАДАНИЕ В ТЕТРАДЯХ. -Какая проблема возникла у нас? | СЛОЖЕНИЕ И ВЫЧИТАНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛ В СТОЛБИК. | Р:целеполагание К: постановка вопроса П: самостоятельное формулирование цели, проблемы |
4.Построение проекта выхода из затруднений | -Подумайте, как можно решить данные примеры? Поработайте в ПАРАХ. Коллективная проверка. — Проверим, как вы выполнили задание? — Кто рассуждал так же? — В №2 МИШКА ТОЖЕ ВЫПОЛНЯЛ ЭТИ ДЕЙСТВИЯ. -Что нового в его вычислениях? Итог:Сделайте вывод, как ВЫПОЛНИТЬ СЛОЖЕНИЕ И ВЫЧИТАНИЕ ТРЁХЗНАЧНЫХ ЧИСЕЛ В СТОЛБИК. -Сравним свой вывод с выводом учебника. 6 слайд -Скажите, знаете ли вы теперь, как выполнять действия сложения и вычитания в столбик. -Оцените свою работу (сигнальные карточки). Физминутка (упражнение для глаз) | Работают в ПАРАХ. 3 УЧЕНИКА РЕШАЮТ У ДОСКИ. Работа с учебниками. | Р: планирование, прогнозирование П: моделирование К: сотрудничество в поиске и выборе информации |
5.Первичное закрепление 5 или 4 5 или 4 | -Кто сможет теперь решить новые примеры? -комментировано примеры 874-265; 342-152; 548+72; 35+65; 170-78; 296+328. -Кто сможет самостоятельно решить примеры на стр.64, то выполните в паре (проговаривая алгоритм своему товарищу) -Назовите ответы (одна пара отвечает по очереди) Выберите 1 фразу для соседа по парте: Ты молодец.(зеленый) Я доволен твоей работой на уроке.(желтый) Ты мог бы поработать лучше.(красный) -Свою отметку поставьте на полях. Какой уровень? 7 слайд | Один ученик у доски, потом второй Работа в парах (нижние примеры) Программный | Р:контроль, оценка, коррекция П:умение произвольно строить речевые высказывания К: взаимодействуют с учителем, слушают собеседника, управление поведением партнера –контроль, оценка, коррекция |
7. Включение в систему знаний и повторение. 5 или 4 | Решение задачи. -Прочтите задачу про себя. Назовите ключевые фразы. — числовые данные задачи. -В парах выберите графическую схему к задаче и продумайте план решения задачи. 8 слайд -Решите задачу. 9 слайд Покажите свои круги-отметки и поставьте отметку на полях. Какой уровень или какая максимальная отметка? Почему ты поставила себе отметку 4? Вывод: — Какие знания и умения использовали? 10 слайд -с.64 №4 б) — прочитайте задачу. О ком в ней идёт речь? -Посмотрите на схему , заполните пустые клетки. — Что можем сказать о мышах? — Что можем сказать о хомяках? — Сколько им дают бобовых стеблей? — Что можем узнать? -А для чего это нужно? -Решите задачу. Оцените себя. 11 слад справка с мышах- полёвках и хомяках. 12 слайд Наш друг Мишка изучал поведение краснощёкого суслика… Прочитайте об этом поподробнее в №5 — какую схему мы нарисуем? 13 слайд Сравниваем. Самооценка. | Два ученика у доски: Ответы детей. 1) умения решать текстовые задачи; 2)табличное умножение; 3) умение составлять и решать выражения; 4) знание порядка действий в выражениях. Дети говорят, а я заполняю на слайде. Их одинаковое количество. Во 2 клетке на 2 больше. Сколь нужно б. с. Одному хомяку. Чтобы ответить на вопрос задачи. На слайде появляется решение по действиям. У доски отвечает 1 ученик. Фронтальная работа. На полях рисуют кружки соответствующего цвета. | Л:Самоопределение Р:Контроль, оценка, выделение и осознание того, что уж усвоено |
8.Рефлексия Деятельности д/з | — Достигли мы своей цели на уроке? -Чему научились? Кто считает, что он сегодня научился решать такие выражения? — А кто считает, что ему ещё нужна помощь? — Как складовать или вычитать трёхзначные числа. -Оцените свою работу на уроке с помощью цветных карточек -Покажите сигнальным знаком, какую отметку вы получили за сегодняшний урок. | 5 Зеленая карточка. Я удовлетворен уроком. Урок был полезен для меня. Я с пользой и хорошо работал на уроке. Я понимал все, о чем говорилось и что делалось на уроке. 4 Желтая карточка. Урок был интересен. Я принимал в нем участие. Урок был в определенной степени полезен для меня. Я отвечал с места, выполнил ряд заданий. Мне было на уроке достаточно комфортно. 3 Красная карточка. Пользы от урока я получил мало. Я не очень понимал, о чем идет речь. Мне это не нужно. К ответу на уроке я был не готов. | К:умение точно выражать свои мысли П: рефлексия Л:смыслообразование |
9 д/з | — 14 слайд А домашнее задание будет очень интересным: № 6,7 на с. |
Алгоритмы генерации столбцов — оптимизация
Авторы: Кедрик Дали (весна 2015 г.)
Стюарды: Даджун Юэ, Фэнци Ю
Алгоритмы генерации столбцов используются для проблем MILP. Формулировка была первоначально предложена Фордом и Фулкерсоном в 1958 г. [1]. Основное преимущество генерации столбцов состоит в том, что не все возможности нужно перечислять. Вместо этого проблема сначала формулируется как проблема с ограниченным ведущим (RMP). Этот RMP имеет как можно меньше переменных, и новые переменные вносятся в базис по мере необходимости, аналогично симплексному методу [2].Подобно симплексному методу, это означает, что если столбец с отрицательной приведенной стоимостью может быть найден, он добавляется в RMP, и этот процесс повторяется до тех пор, пока в RMP не перестанут быть добавлены столбцы.
Простая блок-схема создания столбца
Формулировка задачи создания столбцов зависит от типа проблемы. Один из распространенных примеров — проблема раскроя материала. Однако во всех случаях необходимо взять исходную проблему и сформулировать RMP, а также подзадачу.Решение RMP определяет некоторые параметры в подзадаче, тогда как подзадача будет использоваться, чтобы определить, есть ли какие-либо столбцы, которые могут войти в основу. Подзадача решает эту задачу с минимальными затратами. Если приведенная стоимость отрицательна, решение можно ввести в основу как новый столбец. Если приведенная стоимость больше или равна нулю, нижняя граница оптимального решения была найдена, хотя это может быть не целочисленное решение.
Один из распространенных примеров — проблема раскроя материала. Однако во всех случаях необходимо взять исходную проблему и сформулировать RMP, а также подзадачу.Решение RMP определяет некоторые параметры в подзадаче, тогда как подзадача будет использоваться, чтобы определить, есть ли какие-либо столбцы, которые могут войти в основу. Подзадача решает эту задачу с минимальными затратами. Если приведенная стоимость отрицательна, решение можно ввести в основу как новый столбец. Если приведенная стоимость больше или равна нулю, нижняя граница оптимального решения была найдена, хотя это может быть не целочисленное решение.
Проблема с режущим материалом (CSP)
В задаче раскроя заготовок цель состоит в том, чтобы свести к минимуму отходы, получаемые при нарезке валков фиксированного размера (так называемые «сырье») при выполнении заказов клиентов.
Например, у нас могут быть стальные стержни длиной L = 17 м, по заказу клиента двадцать пять стержней длиной 3 м, двадцать стержней длиной 5 м и пятнадцать стержней длиной 9 м.
Позвольте быть длиной, которую требует заказчик. Таким образом,
Пусть будет спрос на каждый кусок длины. Таким образом,
Традиционный состав IP
Традиционная формулировка целочисленного программирования для задач раскроя материала включает в себя минимизацию количества разрезаемых валков, чтобы удовлетворить ограничения спроса, а также общие ограничения размера.
Позвольте быть индекс имеющихся рулонов.
Пусть будет 1, если рулон обрезан, и 0 в противном случае.
Позвольте быть количеством раз, когда элемент разрезается на рулоне.
Тогда формулировка IP:
Однако эта формулировка неэффективна и ее трудно решить до оптимальности для большого числа переменных [3]. Алгоритмы генерации столбцов могут помочь быстро решить эту проблему за счет ограничения количества необходимых перечислений.
Состав для создания колонки
При создании колонки основное внимание уделяется различным схемам, по которым можно разрезать стержни [4].
Позвольте быть набором всех шаблонов, которые можно вырезать.
Позвольте быть количеством отрезков длины, вырезанных в выкройке p.
Позвольте быть количество раз, когда шаблон вырезан. Тогда столбцы поколения RMP и dual:
Теперь необходимо выбрать начальный набор столбцов. Это можно сделать, просто выбрав «фальшивые» столбцы, которые, как мы знаем, не попадут в раствор, или покрывая основу. В этом примере можно выбрать единичную матрицу. Лучше использовать исходную матрицу, покрывающую базис, потому что мы всегда можем вырезать по крайней мере такое количество баров из нашего исходного материала.Таким образом, наша исходная матрица:
Решение двойного RMP затем дает двойной множитель. Эти значения затем передаются в подзадачу, чтобы увидеть, будут ли добавлены какие-либо столбцы. Подзадача выглядит следующим образом:
Эта подзадача представляет собой задачу о рюкзаке, которая была тщательно изучена. Для решения этой задачи о рюкзаке можно использовать динамическое программирование (например, ветвление и границу) [5]. В конце этой подзадачи мы вычислим уменьшенную стоимость, чтобы определить, добавляем ли мы столбец решения в.Подобно симплексному алгоритму, если приведенная стоимость отрицательна, столбец добавляется в RMP, в противном случае мы завершаем добавление столбцов, и самое последнее первичное решение даст нам наше решение с нижней границей для RMP.
Для решения этой задачи о рюкзаке можно использовать динамическое программирование (например, ветвление и границу) [5]. В конце этой подзадачи мы вычислим уменьшенную стоимость, чтобы определить, добавляем ли мы столбец решения в.Подобно симплексному алгоритму, если приведенная стоимость отрицательна, столбец добавляется в RMP, в противном случае мы завершаем добавление столбцов, и самое последнее первичное решение даст нам наше решение с нижней границей для RMP.
Подстановка двойных переменных и других известных величин в подзадачу дает нам:
Решение которой дает
, со сниженной стоимостью
. Поскольку эта уменьшенная стоимость отрицательна, столбец добавляется в RMP, и он заменяет один из столбцов в основе.После добавления столбца
Решение двойного значения нового RMP дает двойной множитель.
. И снова эти значения передаются в подзадачу и становятся коэффициентами целевой функции. Решение второй итерации подзадачи дает снижение затрат на
. Поскольку эта уменьшенная стоимость отрицательна, столбец добавляется и алгоритм продолжается.
Новые двойные множители становятся, и после подстановки в подзадачу мы обнаруживаем, что столбец решения имеет уменьшенную стоимость, равную 0.Поскольку это не отрицательная приведенная стоимость, этот столбец не добавляется, и создание столбца прекращается. Затем можно найти оптимальное решение, используя самую последнюю версию и просто оптимизируя RMP. Результирующее решение для RMP:
что дает объективное значение.
Результатом является нижняя граница целочисленного решения для CSP и, как в этом случае, часто не является целым числом. В случае CSP простого округления часто бывает достаточно для получения приемлемого целочисленного решения, которое в данном случае будет 21 необработанной строкой для выполнения заказов.
Другие примеры
Другие приложения создания столбцов включают [6]:
- Планирование человеческих ресурсов
- Маршрутизация транспортных средств
- Планирование летных экипажей
Все эти приложения по-прежнему следуют базовому формату генерации столбцов. RMP формулируется и решается, а параметры отправляются в подзадачу. Затем подзадача решается, и если уменьшенная стоимость решения отрицательна, столбец добавляется к RMP, и цикл продолжается до тех пор, пока уменьшенная стоимость не станет неотрицательной.Формулировка каждой проблемы различается из-за разных параметров, но общий подход один и тот же.
RMP формулируется и решается, а параметры отправляются в подзадачу. Затем подзадача решается, и если уменьшенная стоимость решения отрицательна, столбец добавляется к RMP, и цикл продолжается до тех пор, пока уменьшенная стоимость не станет неотрицательной.Формулировка каждой проблемы различается из-за разных параметров, но общий подход один и тот же.
Алгоритмы генерации столбцов лучше всего использовать, когда имеется большое количество переменных, но не большое количество ограничений для сравнения. Перечисление всех возможностей при большом количестве переменных, часто из-за большого количества индексов, занимает много времени даже при эффективных методах решения. Алгоритмы генерации столбцов решают эту проблему, ограничивая то, что перечисляется, добавляя столбцы в основу только при необходимости.Когда столбцы переносятся в основу, также можно удалить любой столбец, который был заменен входящим столбцом, что может помочь сэкономить память при перечислении решений. Экономия времени и памяти — вот где сияют алгоритмы генерации столбцов, хотя они не лишены своих недостатков.
Одним из основных недостатков генерации столбцов является то, что может быть трудно определить, можно ли сформулировать проблему так, чтобы создание столбцов было выгодным. Обычно легче придумать стандартную модель MILP, чем эквивалент генерации столбцов, поскольку формулировки генерации столбцов не всегда очевидны.Однако, как только это начальное препятствие будет преодолено, создание столбцов станет полезным инструментом для решения проблем MILP.
Алгоритмы генерации столбцов наиболее полезны при работе с большим количеством переменных. Они эффективны, поскольку избегают перечисления всех возможных элементов традиционной формулировки MILP и вместо этого оценивают переменные только по мере необходимости. Это достигается за счет внесения столбцов в RMP, когда сниженная стоимость отрицательна. Процесс повторяется до тех пор, пока не будет достигнута неотрицательная уменьшенная стоимость, а затем можно будет решить самый последний первичный элемент, чтобы получить границу для проблемы MILP. Хотя первоначальная формулировка MILP с использованием алгоритмов генерации столбцов может быть трудно увидеть на первых порах, если формулировка может быть достигнута, использование алгоритма генерации столбцов дает много потенциальной экономии времени.
Хотя первоначальная формулировка MILP с использованием алгоритмов генерации столбцов может быть трудно увидеть на первых порах, если формулировка может быть достигнута, использование алгоритма генерации столбцов дает много потенциальной экономии времени.
[1] Л. Р. Форд, младший, Д. Р. Фулкерсон, (1958) Предлагаемое вычисление для максимальных потоков мульти-товарной сети. Наука управления 5 (1): 97-101. http://dx.doi.org/10.1287/mnsc.5.1.97
[2] Desrosiers, J., & Lübbecke, M. (2005). Учебник по созданию колонок.В: G. Desaulniers, J. Desrosiers & M. Solomon (Eds.), Column Generation (стр. 1-32): Springer US.
[3] (ноябрь 2012 г.) Лекция 8: Создание столбцов [PDF-документ] Получено с http://ocw.nctu.edu.tw/upload/classbfs1211073803.pdf
[4] Стейн, К. (2007) Создание столбцов: раскрой — очень прикладной метод [PDF-документ]. Получено с http://www.columbia.edu/~cs2035/courses/ieor4600.S07/columngeneration.pdf
[5] Создание столбцов [документ PDF]. Получено с http: // systemsbiology.ucsd.edu/sites/default/files/Attachments/Images/classes/convex_presentations/ColGen.pdf
Получено с http: // systemsbiology.ucsd.edu/sites/default/files/Attachments/Images/classes/convex_presentations/ColGen.pdf
[6] Ган, Х. (2008) Создание столбцов [документ PDF]. Получено с http://www.more.ms.unimelb.edu.au/students/operationsresearch/lecturenotes/620362_ColGen.pdf.
[7] Джованни Ригини. (Апрель 2013 г.) Создание столбцов [документ PDF]. Получено с http://homes.di.unimi.it/righini/Didattica/ComplementiRicercaOperativa/MaterialeCRO/CG.pdf.
Алгоритмы генерации столбцов — оптимизация
Авторы: Кедрик Дали (весна 2015 г.)
Стюарды: Даджун Юэ, Фэнци Ю
Алгоритмы генерации столбцов используются для проблем MILP.Формулировка была первоначально предложена Фордом и Фулкерсоном в 1958 г. [1]. Основное преимущество генерации столбцов состоит в том, что не все возможности нужно перечислять. Вместо этого проблема сначала формулируется как проблема с ограниченным ведущим (RMP). Этот RMP имеет как можно меньше переменных, и новые переменные вносятся в базис по мере необходимости, аналогично симплексному методу [2]. Подобно симплексному методу, это означает, что если столбец с отрицательной приведенной стоимостью может быть найден, он добавляется в RMP, и этот процесс повторяется до тех пор, пока в RMP не перестанут быть добавлены столбцы.
Подобно симплексному методу, это означает, что если столбец с отрицательной приведенной стоимостью может быть найден, он добавляется в RMP, и этот процесс повторяется до тех пор, пока в RMP не перестанут быть добавлены столбцы.
Простая блок-схема создания столбца
Формулировка задачи создания столбцов зависит от типа проблемы. Один из распространенных примеров — проблема раскроя материала. Однако во всех случаях необходимо взять исходную проблему и сформулировать RMP, а также подзадачу. Решение RMP определяет некоторые параметры в подзадаче, тогда как подзадача будет использоваться, чтобы определить, есть ли какие-либо столбцы, которые могут войти в основу. Подзадача решает эту задачу с минимальными затратами.Если приведенная стоимость отрицательна, решение можно ввести в основу как новый столбец. Если приведенная стоимость больше или равна нулю, нижняя граница оптимального решения была найдена, хотя это может быть не целочисленное решение.
Проблема с режущим материалом (CSP)
В задаче раскроя заготовок цель состоит в том, чтобы свести к минимуму отходы, получаемые при нарезке валков фиксированного размера (так называемые «сырье») при выполнении заказов клиентов.
Например, у нас могут быть стальные стержни длиной L = 17 м, по заказу клиента двадцать пять стержней длиной 3 м, двадцать стержней длиной 5 м и пятнадцать стержней длиной 9 м.
Позвольте быть длиной, которую требует заказчик. Таким образом,
Пусть будет спрос на каждый кусок длины. Таким образом,
Традиционный состав IP
Традиционная формулировка целочисленного программирования для задач раскроя материала включает в себя минимизацию количества разрезаемых валков, чтобы удовлетворить ограничения спроса, а также общие ограничения размера.
Позвольте быть индекс имеющихся рулонов.
Пусть будет 1, если рулон обрезан, и 0 в противном случае.
Позвольте быть количеством раз, когда элемент разрезается на рулоне.
Тогда формулировка IP:
Однако эта формулировка неэффективна и ее трудно решить до оптимальности для большого числа переменных [3]. Алгоритмы генерации столбцов могут помочь быстро решить эту проблему за счет ограничения количества необходимых перечислений.
Состав для создания колонки
При создании колонки основное внимание уделяется различным схемам, по которым можно разрезать стержни [4].
Позвольте быть набором всех шаблонов, которые можно вырезать.
Позвольте быть количеством отрезков длины, вырезанных в выкройке p.
Позвольте быть количество раз, когда шаблон вырезан. Тогда столбцы поколения RMP и dual:
Теперь необходимо выбрать начальный набор столбцов. Это можно сделать, просто выбрав «фальшивые» столбцы, которые, как мы знаем, не попадут в раствор, или покрывая основу. В этом примере можно выбрать единичную матрицу. Лучше использовать исходную матрицу, покрывающую базис, потому что мы всегда можем вырезать по крайней мере такое количество баров из нашего исходного материала.Таким образом, наша исходная матрица:
Решение двойного RMP затем дает двойной множитель. Эти значения затем передаются в подзадачу, чтобы увидеть, будут ли добавлены какие-либо столбцы. Подзадача выглядит следующим образом:
Подзадача выглядит следующим образом:
Эта подзадача представляет собой задачу о рюкзаке, которая была тщательно изучена. Для решения этой задачи о рюкзаке можно использовать динамическое программирование (например, ветвление и границу) [5]. В конце этой подзадачи мы вычислим уменьшенную стоимость, чтобы определить, добавляем ли мы столбец решения в.Подобно симплексному алгоритму, если приведенная стоимость отрицательна, столбец добавляется в RMP, в противном случае мы завершаем добавление столбцов, и самое последнее первичное решение даст нам наше решение с нижней границей для RMP.
Подстановка двойных переменных и других известных величин в подзадачу дает нам:
Решение которой дает
, со сниженной стоимостью
. Поскольку эта уменьшенная стоимость отрицательна, столбец добавляется в RMP, и он заменяет один из столбцов в основе.После добавления столбца
Решение двойного значения нового RMP дает двойной множитель.
. И снова эти значения передаются в подзадачу и становятся коэффициентами целевой функции. Решение второй итерации подзадачи дает снижение затрат на
Решение второй итерации подзадачи дает снижение затрат на
. Поскольку эта уменьшенная стоимость отрицательна, столбец добавляется и алгоритм продолжается.
Новые двойные множители становятся, и после подстановки в подзадачу мы обнаруживаем, что столбец решения имеет уменьшенную стоимость, равную 0.Поскольку это не отрицательная приведенная стоимость, этот столбец не добавляется, и создание столбца прекращается. Затем можно найти оптимальное решение, используя самую последнюю версию и просто оптимизируя RMP. Результирующее решение для RMP:
что дает объективное значение.
Результатом является нижняя граница целочисленного решения для CSP и, как в этом случае, часто не является целым числом. В случае CSP простого округления часто бывает достаточно для получения приемлемого целочисленного решения, которое в данном случае будет 21 необработанной строкой для выполнения заказов.
Другие примеры
Другие приложения создания столбцов включают [6]:
- Планирование человеческих ресурсов
- Маршрутизация транспортных средств
- Планирование летных экипажей
Все эти приложения по-прежнему следуют базовому формату генерации столбцов. RMP формулируется и решается, а параметры отправляются в подзадачу. Затем подзадача решается, и если уменьшенная стоимость решения отрицательна, столбец добавляется к RMP, и цикл продолжается до тех пор, пока уменьшенная стоимость не станет неотрицательной.Формулировка каждой проблемы различается из-за разных параметров, но общий подход один и тот же.
RMP формулируется и решается, а параметры отправляются в подзадачу. Затем подзадача решается, и если уменьшенная стоимость решения отрицательна, столбец добавляется к RMP, и цикл продолжается до тех пор, пока уменьшенная стоимость не станет неотрицательной.Формулировка каждой проблемы различается из-за разных параметров, но общий подход один и тот же.
Алгоритмы генерации столбцов лучше всего использовать, когда имеется большое количество переменных, но не большое количество ограничений для сравнения. Перечисление всех возможностей при большом количестве переменных, часто из-за большого количества индексов, занимает много времени даже при эффективных методах решения. Алгоритмы генерации столбцов решают эту проблему, ограничивая то, что перечисляется, добавляя столбцы в основу только при необходимости.Когда столбцы переносятся в основу, также можно удалить любой столбец, который был заменен входящим столбцом, что может помочь сэкономить память при перечислении решений. Экономия времени и памяти — вот где сияют алгоритмы генерации столбцов, хотя они не лишены своих недостатков.
Одним из основных недостатков генерации столбцов является то, что может быть трудно определить, можно ли сформулировать проблему так, чтобы создание столбцов было выгодным. Обычно легче придумать стандартную модель MILP, чем эквивалент генерации столбцов, поскольку формулировки генерации столбцов не всегда очевидны.Однако, как только это начальное препятствие будет преодолено, создание столбцов станет полезным инструментом для решения проблем MILP.
Алгоритмы генерации столбцов наиболее полезны при работе с большим количеством переменных. Они эффективны, поскольку избегают перечисления всех возможных элементов традиционной формулировки MILP и вместо этого оценивают переменные только по мере необходимости. Это достигается за счет внесения столбцов в RMP, когда сниженная стоимость отрицательна. Процесс повторяется до тех пор, пока не будет достигнута неотрицательная уменьшенная стоимость, а затем можно будет решить самый последний первичный элемент, чтобы получить границу для проблемы MILP. Хотя первоначальная формулировка MILP с использованием алгоритмов генерации столбцов может быть трудно увидеть на первых порах, если формулировка может быть достигнута, использование алгоритма генерации столбцов дает много потенциальной экономии времени.
Хотя первоначальная формулировка MILP с использованием алгоритмов генерации столбцов может быть трудно увидеть на первых порах, если формулировка может быть достигнута, использование алгоритма генерации столбцов дает много потенциальной экономии времени.
[1] Л. Р. Форд, младший, Д. Р. Фулкерсон, (1958) Предлагаемое вычисление для максимальных потоков мульти-товарной сети. Наука управления 5 (1): 97-101. http://dx.doi.org/10.1287/mnsc.5.1.97
[2] Desrosiers, J., & Lübbecke, M. (2005). Учебник по созданию колонок.В: G. Desaulniers, J. Desrosiers & M. Solomon (Eds.), Column Generation (стр. 1-32): Springer US.
[3] (ноябрь 2012 г.) Лекция 8: Создание столбцов [PDF-документ] Получено с http://ocw.nctu.edu.tw/upload/classbfs1211073803.pdf
[4] Стейн, К. (2007) Создание столбцов: раскрой — очень прикладной метод [PDF-документ]. Получено с http://www.columbia.edu/~cs2035/courses/ieor4600.S07/columngeneration.pdf
[5] Создание столбцов [документ PDF]. Получено с http: // systemsbiology.ucsd.edu/sites/default/files/Attachments/Images/classes/convex_presentations/ColGen.pdf
Получено с http: // systemsbiology.ucsd.edu/sites/default/files/Attachments/Images/classes/convex_presentations/ColGen.pdf
[6] Ган, Х. (2008) Создание столбцов [документ PDF]. Получено с http://www.more.ms.unimelb.edu.au/students/operationsresearch/lecturenotes/620362_ColGen.pdf.
[7] Джованни Ригини. (Апрель 2013 г.) Создание столбцов [документ PDF]. Получено с http://homes.di.unimi.it/righini/Didattica/ComplementiRicercaOperativa/MaterialeCRO/CG.pdf.
Алгоритмы генерации столбцов — оптимизация
Авторы: Кедрик Дали (весна 2015 г.)
Стюарды: Даджун Юэ, Фэнци Ю
Алгоритмы генерации столбцов используются для проблем MILP.Формулировка была первоначально предложена Фордом и Фулкерсоном в 1958 г. [1]. Основное преимущество генерации столбцов состоит в том, что не все возможности нужно перечислять. Вместо этого проблема сначала формулируется как проблема с ограниченным ведущим (RMP). Этот RMP имеет как можно меньше переменных, и новые переменные вносятся в базис по мере необходимости, аналогично симплексному методу [2]. Подобно симплексному методу, это означает, что если столбец с отрицательной приведенной стоимостью может быть найден, он добавляется в RMP, и этот процесс повторяется до тех пор, пока в RMP не перестанут быть добавлены столбцы.
Подобно симплексному методу, это означает, что если столбец с отрицательной приведенной стоимостью может быть найден, он добавляется в RMP, и этот процесс повторяется до тех пор, пока в RMP не перестанут быть добавлены столбцы.
Простая блок-схема создания столбца
Формулировка задачи создания столбцов зависит от типа проблемы. Один из распространенных примеров — проблема раскроя материала. Однако во всех случаях необходимо взять исходную проблему и сформулировать RMP, а также подзадачу. Решение RMP определяет некоторые параметры в подзадаче, тогда как подзадача будет использоваться, чтобы определить, есть ли какие-либо столбцы, которые могут войти в основу. Подзадача решает эту задачу с минимальными затратами.Если приведенная стоимость отрицательна, решение можно ввести в основу как новый столбец. Если приведенная стоимость больше или равна нулю, нижняя граница оптимального решения была найдена, хотя это может быть не целочисленное решение.
Проблема с режущим материалом (CSP)
В задаче раскроя заготовок цель состоит в том, чтобы свести к минимуму отходы, получаемые при нарезке валков фиксированного размера (так называемые «сырье») при выполнении заказов клиентов.
Например, у нас могут быть стальные стержни длиной L = 17 м, по заказу клиента двадцать пять стержней длиной 3 м, двадцать стержней длиной 5 м и пятнадцать стержней длиной 9 м.
Позвольте быть длиной, которую требует заказчик. Таким образом,
Пусть будет спрос на каждый кусок длины. Таким образом,
Традиционный состав IP
Традиционная формулировка целочисленного программирования для задач раскроя материала включает в себя минимизацию количества разрезаемых валков, чтобы удовлетворить ограничения спроса, а также общие ограничения размера.
Позвольте быть индекс имеющихся рулонов.
Пусть будет 1, если рулон обрезан, и 0 в противном случае.
Позвольте быть количеством раз, когда элемент разрезается на рулоне.
Тогда формулировка IP:
Однако эта формулировка неэффективна и ее трудно решить до оптимальности для большого числа переменных [3]. Алгоритмы генерации столбцов могут помочь быстро решить эту проблему за счет ограничения количества необходимых перечислений.
Состав для создания колонки
При создании колонки основное внимание уделяется различным схемам, по которым можно разрезать стержни [4].
Позвольте быть набором всех шаблонов, которые можно вырезать.
Позвольте быть количеством отрезков длины, вырезанных в выкройке p.
Позвольте быть количество раз, когда шаблон вырезан. Тогда столбцы поколения RMP и dual:
Теперь необходимо выбрать начальный набор столбцов. Это можно сделать, просто выбрав «фальшивые» столбцы, которые, как мы знаем, не попадут в раствор, или покрывая основу. В этом примере можно выбрать единичную матрицу. Лучше использовать исходную матрицу, покрывающую базис, потому что мы всегда можем вырезать по крайней мере такое количество баров из нашего исходного материала.Таким образом, наша исходная матрица:
Решение двойного RMP затем дает двойной множитель. Эти значения затем передаются в подзадачу, чтобы увидеть, будут ли добавлены какие-либо столбцы. Подзадача выглядит следующим образом:
Подзадача выглядит следующим образом:
Эта подзадача представляет собой задачу о рюкзаке, которая была тщательно изучена. Для решения этой задачи о рюкзаке можно использовать динамическое программирование (например, ветвление и границу) [5]. В конце этой подзадачи мы вычислим уменьшенную стоимость, чтобы определить, добавляем ли мы столбец решения в.Подобно симплексному алгоритму, если приведенная стоимость отрицательна, столбец добавляется в RMP, в противном случае мы завершаем добавление столбцов, и самое последнее первичное решение даст нам наше решение с нижней границей для RMP.
Подстановка двойных переменных и других известных величин в подзадачу дает нам:
Решение которой дает
, со сниженной стоимостью
. Поскольку эта уменьшенная стоимость отрицательна, столбец добавляется в RMP, и он заменяет один из столбцов в основе.После добавления столбца
Решение двойного значения нового RMP дает двойной множитель.
. И снова эти значения передаются в подзадачу и становятся коэффициентами целевой функции. Решение второй итерации подзадачи дает снижение затрат на
Решение второй итерации подзадачи дает снижение затрат на
. Поскольку эта уменьшенная стоимость отрицательна, столбец добавляется и алгоритм продолжается.
Новые двойные множители становятся, и после подстановки в подзадачу мы обнаруживаем, что столбец решения имеет уменьшенную стоимость, равную 0.Поскольку это не отрицательная приведенная стоимость, этот столбец не добавляется, и создание столбца прекращается. Затем можно найти оптимальное решение, используя самую последнюю версию и просто оптимизируя RMP. Результирующее решение для RMP:
что дает объективное значение.
Результатом является нижняя граница целочисленного решения для CSP и, как в этом случае, часто не является целым числом. В случае CSP простого округления часто бывает достаточно для получения приемлемого целочисленного решения, которое в данном случае будет 21 необработанной строкой для выполнения заказов.
Другие примеры
Другие приложения создания столбцов включают [6]:
- Планирование человеческих ресурсов
- Маршрутизация транспортных средств
- Планирование летных экипажей
Все эти приложения по-прежнему следуют базовому формату генерации столбцов. RMP формулируется и решается, а параметры отправляются в подзадачу. Затем подзадача решается, и если уменьшенная стоимость решения отрицательна, столбец добавляется к RMP, и цикл продолжается до тех пор, пока уменьшенная стоимость не станет неотрицательной.Формулировка каждой проблемы различается из-за разных параметров, но общий подход один и тот же.
RMP формулируется и решается, а параметры отправляются в подзадачу. Затем подзадача решается, и если уменьшенная стоимость решения отрицательна, столбец добавляется к RMP, и цикл продолжается до тех пор, пока уменьшенная стоимость не станет неотрицательной.Формулировка каждой проблемы различается из-за разных параметров, но общий подход один и тот же.
Алгоритмы генерации столбцов лучше всего использовать, когда имеется большое количество переменных, но не большое количество ограничений для сравнения. Перечисление всех возможностей при большом количестве переменных, часто из-за большого количества индексов, занимает много времени даже при эффективных методах решения. Алгоритмы генерации столбцов решают эту проблему, ограничивая то, что перечисляется, добавляя столбцы в основу только при необходимости.Когда столбцы переносятся в основу, также можно удалить любой столбец, который был заменен входящим столбцом, что может помочь сэкономить память при перечислении решений. Экономия времени и памяти — вот где сияют алгоритмы генерации столбцов, хотя они не лишены своих недостатков.
Одним из основных недостатков генерации столбцов является то, что может быть трудно определить, можно ли сформулировать проблему так, чтобы создание столбцов было выгодным. Обычно легче придумать стандартную модель MILP, чем эквивалент генерации столбцов, поскольку формулировки генерации столбцов не всегда очевидны.Однако, как только это начальное препятствие будет преодолено, создание столбцов станет полезным инструментом для решения проблем MILP.
Алгоритмы генерации столбцов наиболее полезны при работе с большим количеством переменных. Они эффективны, поскольку избегают перечисления всех возможных элементов традиционной формулировки MILP и вместо этого оценивают переменные только по мере необходимости. Это достигается за счет внесения столбцов в RMP, когда сниженная стоимость отрицательна. Процесс повторяется до тех пор, пока не будет достигнута неотрицательная уменьшенная стоимость, а затем можно будет решить самый последний первичный элемент, чтобы получить границу для проблемы MILP. Хотя первоначальная формулировка MILP с использованием алгоритмов генерации столбцов может быть трудно увидеть на первых порах, если формулировка может быть достигнута, использование алгоритма генерации столбцов дает много потенциальной экономии времени.
Хотя первоначальная формулировка MILP с использованием алгоритмов генерации столбцов может быть трудно увидеть на первых порах, если формулировка может быть достигнута, использование алгоритма генерации столбцов дает много потенциальной экономии времени.
[1] Л. Р. Форд, младший, Д. Р. Фулкерсон, (1958) Предлагаемое вычисление для максимальных потоков мульти-товарной сети. Наука управления 5 (1): 97-101. http://dx.doi.org/10.1287/mnsc.5.1.97
[2] Desrosiers, J., & Lübbecke, M. (2005). Учебник по созданию колонок.В: G. Desaulniers, J. Desrosiers & M. Solomon (Eds.), Column Generation (стр. 1-32): Springer US.
[3] (ноябрь 2012 г.) Лекция 8: Создание столбцов [PDF-документ] Получено с http://ocw.nctu.edu.tw/upload/classbfs1211073803.pdf
[4] Стейн, К. (2007) Создание столбцов: раскрой — очень прикладной метод [PDF-документ]. Получено с http://www.columbia.edu/~cs2035/courses/ieor4600.S07/columngeneration.pdf
[5] Создание столбцов [документ PDF]. Получено с http: // systemsbiology.ucsd.edu/sites/default/files/Attachments/Images/classes/convex_presentations/ColGen.pdf
Получено с http: // systemsbiology.ucsd.edu/sites/default/files/Attachments/Images/classes/convex_presentations/ColGen.pdf
[6] Ган, Х. (2008) Создание столбцов [документ PDF]. Получено с http://www.more.ms.unimelb.edu.au/students/operationsresearch/lecturenotes/620362_ColGen.pdf.
[7] Джованни Ригини. (Апрель 2013 г.) Создание столбцов [документ PDF]. Получено с http://homes.di.unimi.it/righini/Didattica/ComplementiRicercaOperativa/MaterialeCRO/CG.pdf.
Алгоритмы генерации столбцов — оптимизация
Авторы: Кедрик Дали (весна 2015 г.)
Стюарды: Даджун Юэ, Фэнци Ю
Алгоритмы генерации столбцов используются для проблем MILP.Формулировка была первоначально предложена Фордом и Фулкерсоном в 1958 г. [1]. Основное преимущество генерации столбцов состоит в том, что не все возможности нужно перечислять. Вместо этого проблема сначала формулируется как проблема с ограниченным ведущим (RMP). Этот RMP имеет как можно меньше переменных, и новые переменные вносятся в базис по мере необходимости, аналогично симплексному методу [2]. Подобно симплексному методу, это означает, что если столбец с отрицательной приведенной стоимостью может быть найден, он добавляется в RMP, и этот процесс повторяется до тех пор, пока в RMP не перестанут быть добавлены столбцы.
Подобно симплексному методу, это означает, что если столбец с отрицательной приведенной стоимостью может быть найден, он добавляется в RMP, и этот процесс повторяется до тех пор, пока в RMP не перестанут быть добавлены столбцы.
Простая блок-схема создания столбца
Формулировка задачи создания столбцов зависит от типа проблемы. Один из распространенных примеров — проблема раскроя материала. Однако во всех случаях необходимо взять исходную проблему и сформулировать RMP, а также подзадачу. Решение RMP определяет некоторые параметры в подзадаче, тогда как подзадача будет использоваться, чтобы определить, есть ли какие-либо столбцы, которые могут войти в основу. Подзадача решает эту задачу с минимальными затратами.Если приведенная стоимость отрицательна, решение можно ввести в основу как новый столбец. Если приведенная стоимость больше или равна нулю, нижняя граница оптимального решения была найдена, хотя это может быть не целочисленное решение.
Проблема с режущим материалом (CSP)
В задаче раскроя заготовок цель состоит в том, чтобы свести к минимуму отходы, получаемые при нарезке валков фиксированного размера (так называемые «сырье») при выполнении заказов клиентов.
Например, у нас могут быть стальные стержни длиной L = 17 м, по заказу клиента двадцать пять стержней длиной 3 м, двадцать стержней длиной 5 м и пятнадцать стержней длиной 9 м.
Позвольте быть длиной, которую требует заказчик. Таким образом,
Пусть будет спрос на каждый кусок длины. Таким образом,
Традиционный состав IP
Традиционная формулировка целочисленного программирования для задач раскроя материала включает в себя минимизацию количества разрезаемых валков, чтобы удовлетворить ограничения спроса, а также общие ограничения размера.
Позвольте быть индекс имеющихся рулонов.
Пусть будет 1, если рулон обрезан, и 0 в противном случае.
Позвольте быть количеством раз, когда элемент разрезается на рулоне.
Тогда формулировка IP:
Однако эта формулировка неэффективна и ее трудно решить до оптимальности для большого числа переменных [3]. Алгоритмы генерации столбцов могут помочь быстро решить эту проблему за счет ограничения количества необходимых перечислений.
Состав для создания колонки
При создании колонки основное внимание уделяется различным схемам, по которым можно разрезать стержни [4].
Позвольте быть набором всех шаблонов, которые можно вырезать.
Позвольте быть количеством отрезков длины, вырезанных в выкройке p.
Позвольте быть количество раз, когда шаблон вырезан. Тогда столбцы поколения RMP и dual:
Теперь необходимо выбрать начальный набор столбцов. Это можно сделать, просто выбрав «фальшивые» столбцы, которые, как мы знаем, не попадут в раствор, или покрывая основу. В этом примере можно выбрать единичную матрицу. Лучше использовать исходную матрицу, покрывающую базис, потому что мы всегда можем вырезать по крайней мере такое количество баров из нашего исходного материала.Таким образом, наша исходная матрица:
Решение двойного RMP затем дает двойной множитель. Эти значения затем передаются в подзадачу, чтобы увидеть, будут ли добавлены какие-либо столбцы. Подзадача выглядит следующим образом:
Подзадача выглядит следующим образом:
Эта подзадача представляет собой задачу о рюкзаке, которая была тщательно изучена. Для решения этой задачи о рюкзаке можно использовать динамическое программирование (например, ветвление и границу) [5]. В конце этой подзадачи мы вычислим уменьшенную стоимость, чтобы определить, добавляем ли мы столбец решения в.Подобно симплексному алгоритму, если приведенная стоимость отрицательна, столбец добавляется в RMP, в противном случае мы завершаем добавление столбцов, и самое последнее первичное решение даст нам наше решение с нижней границей для RMP.
Подстановка двойных переменных и других известных величин в подзадачу дает нам:
Решение которой дает
, со сниженной стоимостью
. Поскольку эта уменьшенная стоимость отрицательна, столбец добавляется в RMP, и он заменяет один из столбцов в основе.После добавления столбца
Решение двойного значения нового RMP дает двойной множитель.
. И снова эти значения передаются в подзадачу и становятся коэффициентами целевой функции. Решение второй итерации подзадачи дает снижение затрат на
Решение второй итерации подзадачи дает снижение затрат на
. Поскольку эта уменьшенная стоимость отрицательна, столбец добавляется и алгоритм продолжается.
Новые двойные множители становятся, и после подстановки в подзадачу мы обнаруживаем, что столбец решения имеет уменьшенную стоимость, равную 0.Поскольку это не отрицательная приведенная стоимость, этот столбец не добавляется, и создание столбца прекращается. Затем можно найти оптимальное решение, используя самую последнюю версию и просто оптимизируя RMP. Результирующее решение для RMP:
что дает объективное значение.
Результатом является нижняя граница целочисленного решения для CSP и, как в этом случае, часто не является целым числом. В случае CSP простого округления часто бывает достаточно для получения приемлемого целочисленного решения, которое в данном случае будет 21 необработанной строкой для выполнения заказов.
Другие примеры
Другие приложения создания столбцов включают [6]:
- Планирование человеческих ресурсов
- Маршрутизация транспортных средств
- Планирование летных экипажей
Все эти приложения по-прежнему следуют базовому формату генерации столбцов. RMP формулируется и решается, а параметры отправляются в подзадачу. Затем подзадача решается, и если уменьшенная стоимость решения отрицательна, столбец добавляется к RMP, и цикл продолжается до тех пор, пока уменьшенная стоимость не станет неотрицательной.Формулировка каждой проблемы различается из-за разных параметров, но общий подход один и тот же.
RMP формулируется и решается, а параметры отправляются в подзадачу. Затем подзадача решается, и если уменьшенная стоимость решения отрицательна, столбец добавляется к RMP, и цикл продолжается до тех пор, пока уменьшенная стоимость не станет неотрицательной.Формулировка каждой проблемы различается из-за разных параметров, но общий подход один и тот же.
Алгоритмы генерации столбцов лучше всего использовать, когда имеется большое количество переменных, но не большое количество ограничений для сравнения. Перечисление всех возможностей при большом количестве переменных, часто из-за большого количества индексов, занимает много времени даже при эффективных методах решения. Алгоритмы генерации столбцов решают эту проблему, ограничивая то, что перечисляется, добавляя столбцы в основу только при необходимости.Когда столбцы переносятся в основу, также можно удалить любой столбец, который был заменен входящим столбцом, что может помочь сэкономить память при перечислении решений. Экономия времени и памяти — вот где сияют алгоритмы генерации столбцов, хотя они не лишены своих недостатков.
Одним из основных недостатков генерации столбцов является то, что может быть трудно определить, можно ли сформулировать проблему так, чтобы создание столбцов было выгодным. Обычно легче придумать стандартную модель MILP, чем эквивалент генерации столбцов, поскольку формулировки генерации столбцов не всегда очевидны.Однако, как только это начальное препятствие будет преодолено, создание столбцов станет полезным инструментом для решения проблем MILP.
Алгоритмы генерации столбцов наиболее полезны при работе с большим количеством переменных. Они эффективны, поскольку избегают перечисления всех возможных элементов традиционной формулировки MILP и вместо этого оценивают переменные только по мере необходимости. Это достигается за счет внесения столбцов в RMP, когда сниженная стоимость отрицательна. Процесс повторяется до тех пор, пока не будет достигнута неотрицательная уменьшенная стоимость, а затем можно будет решить самый последний первичный элемент, чтобы получить границу для проблемы MILP. Хотя первоначальная формулировка MILP с использованием алгоритмов генерации столбцов может быть трудно увидеть на первых порах, если формулировка может быть достигнута, использование алгоритма генерации столбцов дает много потенциальной экономии времени.
Хотя первоначальная формулировка MILP с использованием алгоритмов генерации столбцов может быть трудно увидеть на первых порах, если формулировка может быть достигнута, использование алгоритма генерации столбцов дает много потенциальной экономии времени.
[1] Л. Р. Форд, младший, Д. Р. Фулкерсон, (1958) Предлагаемое вычисление для максимальных потоков мульти-товарной сети. Наука управления 5 (1): 97-101. http://dx.doi.org/10.1287/mnsc.5.1.97
[2] Desrosiers, J., & Lübbecke, M. (2005). Учебник по созданию колонок.В: G. Desaulniers, J. Desrosiers & M. Solomon (Eds.), Column Generation (стр. 1-32): Springer US.
[3] (ноябрь 2012 г.) Лекция 8: Создание столбцов [PDF-документ] Получено с http://ocw.nctu.edu.tw/upload/classbfs1211073803.pdf
[4] Стейн, К. (2007) Создание столбцов: раскрой — очень прикладной метод [PDF-документ]. Получено с http://www.columbia.edu/~cs2035/courses/ieor4600.S07/columngeneration.pdf
[5] Создание столбцов [документ PDF]. Получено с http: // systemsbiology.ucsd.edu/sites/default/files/Attachments/Images/classes/convex_presentations/ColGen.pdf
Получено с http: // systemsbiology.ucsd.edu/sites/default/files/Attachments/Images/classes/convex_presentations/ColGen.pdf
[6] Ган, Х. (2008) Создание столбцов [документ PDF]. Получено с http://www.more.ms.unimelb.edu.au/students/operationsresearch/lecturenotes/620362_ColGen.pdf.
[7] Джованни Ригини. (Апрель 2013 г.) Создание столбцов [документ PDF]. Получено с http://homes.di.unimi.it/righini/Didattica/ComplementiRicercaOperativa/MaterialeCRO/CG.pdf.
Алгоритмы генерации столбцов — оптимизация
Авторы: Кедрик Дали (весна 2015 г.)
Стюарды: Даджун Юэ, Фэнци Ю
Алгоритмы генерации столбцов используются для проблем MILP.Формулировка была первоначально предложена Фордом и Фулкерсоном в 1958 г. [1]. Основное преимущество генерации столбцов состоит в том, что не все возможности нужно перечислять. Вместо этого проблема сначала формулируется как проблема с ограниченным ведущим (RMP). Этот RMP имеет как можно меньше переменных, и новые переменные вносятся в базис по мере необходимости, аналогично симплексному методу [2]. Подобно симплексному методу, это означает, что если столбец с отрицательной приведенной стоимостью может быть найден, он добавляется в RMP, и этот процесс повторяется до тех пор, пока в RMP не перестанут быть добавлены столбцы.
Подобно симплексному методу, это означает, что если столбец с отрицательной приведенной стоимостью может быть найден, он добавляется в RMP, и этот процесс повторяется до тех пор, пока в RMP не перестанут быть добавлены столбцы.
Простая блок-схема создания столбца
Формулировка задачи создания столбцов зависит от типа проблемы. Один из распространенных примеров — проблема раскроя материала. Однако во всех случаях необходимо взять исходную проблему и сформулировать RMP, а также подзадачу. Решение RMP определяет некоторые параметры в подзадаче, тогда как подзадача будет использоваться, чтобы определить, есть ли какие-либо столбцы, которые могут войти в основу. Подзадача решает эту задачу с минимальными затратами.Если приведенная стоимость отрицательна, решение можно ввести в основу как новый столбец. Если приведенная стоимость больше или равна нулю, нижняя граница оптимального решения была найдена, хотя это может быть не целочисленное решение.
Проблема с режущим материалом (CSP)
В задаче раскроя заготовок цель состоит в том, чтобы свести к минимуму отходы, получаемые при нарезке валков фиксированного размера (так называемые «сырье») при выполнении заказов клиентов.
Например, у нас могут быть стальные стержни длиной L = 17 м, по заказу клиента двадцать пять стержней длиной 3 м, двадцать стержней длиной 5 м и пятнадцать стержней длиной 9 м.
Позвольте быть длиной, которую требует заказчик. Таким образом,
Пусть будет спрос на каждый кусок длины. Таким образом,
Традиционный состав IP
Традиционная формулировка целочисленного программирования для задач раскроя материала включает в себя минимизацию количества разрезаемых валков, чтобы удовлетворить ограничения спроса, а также общие ограничения размера.
Позвольте быть индекс имеющихся рулонов.
Пусть будет 1, если рулон обрезан, и 0 в противном случае.
Позвольте быть количеством раз, когда элемент разрезается на рулоне.
Тогда формулировка IP:
Однако эта формулировка неэффективна и ее трудно решить до оптимальности для большого числа переменных [3]. Алгоритмы генерации столбцов могут помочь быстро решить эту проблему за счет ограничения количества необходимых перечислений.
Состав для создания колонки
При создании колонки основное внимание уделяется различным схемам, по которым можно разрезать стержни [4].
Позвольте быть набором всех шаблонов, которые можно вырезать.
Позвольте быть количеством отрезков длины, вырезанных в выкройке p.
Позвольте быть количество раз, когда шаблон вырезан. Тогда столбцы поколения RMP и dual:
Теперь необходимо выбрать начальный набор столбцов. Это можно сделать, просто выбрав «фальшивые» столбцы, которые, как мы знаем, не попадут в раствор, или покрывая основу. В этом примере можно выбрать единичную матрицу. Лучше использовать исходную матрицу, покрывающую базис, потому что мы всегда можем вырезать по крайней мере такое количество баров из нашего исходного материала.Таким образом, наша исходная матрица:
Решение двойного RMP затем дает двойной множитель. Эти значения затем передаются в подзадачу, чтобы увидеть, будут ли добавлены какие-либо столбцы. Подзадача выглядит следующим образом:
Подзадача выглядит следующим образом:
Эта подзадача представляет собой задачу о рюкзаке, которая была тщательно изучена. Для решения этой задачи о рюкзаке можно использовать динамическое программирование (например, ветвление и границу) [5]. В конце этой подзадачи мы вычислим уменьшенную стоимость, чтобы определить, добавляем ли мы столбец решения в.Подобно симплексному алгоритму, если приведенная стоимость отрицательна, столбец добавляется в RMP, в противном случае мы завершаем добавление столбцов, и самое последнее первичное решение даст нам наше решение с нижней границей для RMP.
Подстановка двойных переменных и других известных величин в подзадачу дает нам:
Решение которой дает
, со сниженной стоимостью
. Поскольку эта уменьшенная стоимость отрицательна, столбец добавляется в RMP, и он заменяет один из столбцов в основе.После добавления столбца
Решение двойного значения нового RMP дает двойной множитель.
. И снова эти значения передаются в подзадачу и становятся коэффициентами целевой функции. Решение второй итерации подзадачи дает снижение затрат на
Решение второй итерации подзадачи дает снижение затрат на
. Поскольку эта уменьшенная стоимость отрицательна, столбец добавляется и алгоритм продолжается.
Новые двойные множители становятся, и после подстановки в подзадачу мы обнаруживаем, что столбец решения имеет уменьшенную стоимость, равную 0.Поскольку это не отрицательная приведенная стоимость, этот столбец не добавляется, и создание столбца прекращается. Затем можно найти оптимальное решение, используя самую последнюю версию и просто оптимизируя RMP. Результирующее решение для RMP:
что дает объективное значение.
Результатом является нижняя граница целочисленного решения для CSP и, как в этом случае, часто не является целым числом. В случае CSP простого округления часто бывает достаточно для получения приемлемого целочисленного решения, которое в данном случае будет 21 необработанной строкой для выполнения заказов.
Другие примеры
Другие приложения создания столбцов включают [6]:
- Планирование человеческих ресурсов
- Маршрутизация транспортных средств
- Планирование летных экипажей
Все эти приложения по-прежнему следуют базовому формату генерации столбцов. RMP формулируется и решается, а параметры отправляются в подзадачу. Затем подзадача решается, и если уменьшенная стоимость решения отрицательна, столбец добавляется к RMP, и цикл продолжается до тех пор, пока уменьшенная стоимость не станет неотрицательной.Формулировка каждой проблемы различается из-за разных параметров, но общий подход один и тот же.
RMP формулируется и решается, а параметры отправляются в подзадачу. Затем подзадача решается, и если уменьшенная стоимость решения отрицательна, столбец добавляется к RMP, и цикл продолжается до тех пор, пока уменьшенная стоимость не станет неотрицательной.Формулировка каждой проблемы различается из-за разных параметров, но общий подход один и тот же.
Алгоритмы генерации столбцов лучше всего использовать, когда имеется большое количество переменных, но не большое количество ограничений для сравнения. Перечисление всех возможностей при большом количестве переменных, часто из-за большого количества индексов, занимает много времени даже при эффективных методах решения. Алгоритмы генерации столбцов решают эту проблему, ограничивая то, что перечисляется, добавляя столбцы в основу только при необходимости.Когда столбцы переносятся в основу, также можно удалить любой столбец, который был заменен входящим столбцом, что может помочь сэкономить память при перечислении решений. Экономия времени и памяти — вот где сияют алгоритмы генерации столбцов, хотя они не лишены своих недостатков.
Одним из основных недостатков генерации столбцов является то, что может быть трудно определить, можно ли сформулировать проблему так, чтобы создание столбцов было выгодным. Обычно легче придумать стандартную модель MILP, чем эквивалент генерации столбцов, поскольку формулировки генерации столбцов не всегда очевидны.Однако, как только это начальное препятствие будет преодолено, создание столбцов станет полезным инструментом для решения проблем MILP.
Алгоритмы генерации столбцов наиболее полезны при работе с большим количеством переменных. Они эффективны, поскольку избегают перечисления всех возможных элементов традиционной формулировки MILP и вместо этого оценивают переменные только по мере необходимости. Это достигается за счет внесения столбцов в RMP, когда сниженная стоимость отрицательна. Процесс повторяется до тех пор, пока не будет достигнута неотрицательная уменьшенная стоимость, а затем можно будет решить самый последний первичный элемент, чтобы получить границу для проблемы MILP. Хотя первоначальная формулировка MILP с использованием алгоритмов генерации столбцов может быть трудно увидеть на первых порах, если формулировка может быть достигнута, использование алгоритма генерации столбцов дает много потенциальной экономии времени.
Хотя первоначальная формулировка MILP с использованием алгоритмов генерации столбцов может быть трудно увидеть на первых порах, если формулировка может быть достигнута, использование алгоритма генерации столбцов дает много потенциальной экономии времени.
[1] Л. Р. Форд, младший, Д. Р. Фулкерсон, (1958) Предлагаемое вычисление для максимальных потоков мульти-товарной сети. Наука управления 5 (1): 97-101. http://dx.doi.org/10.1287/mnsc.5.1.97
[2] Desrosiers, J., & Lübbecke, M. (2005). Учебник по созданию колонок.В: G. Desaulniers, J. Desrosiers & M. Solomon (Eds.), Column Generation (стр. 1-32): Springer US.
[3] (ноябрь 2012 г.) Лекция 8: Создание столбцов [PDF-документ] Получено с http://ocw.nctu.edu.tw/upload/classbfs1211073803.pdf
[4] Стейн, К. (2007) Создание столбцов: раскрой — очень прикладной метод [PDF-документ]. Получено с http://www.columbia.edu/~cs2035/courses/ieor4600.S07/columngeneration.pdf
[5] Создание столбцов [документ PDF]. Получено с http: // systemsbiology.ucsd.edu/sites/default/files/Attachments/Images/classes/convex_presentations/ColGen.pdf
Получено с http: // systemsbiology.ucsd.edu/sites/default/files/Attachments/Images/classes/convex_presentations/ColGen.pdf
[6] Ган, Х. (2008) Создание столбцов [документ PDF]. Получено с http://www.more.ms.unimelb.edu.au/students/operationsresearch/lecturenotes/620362_ColGen.pdf.
[7] Джованни Ригини. (Апрель 2013 г.) Создание столбцов [документ PDF]. Получено с http://homes.di.unimi.it/righini/Didattica/ComplementiRicercaOperativa/MaterialeCRO/CG.pdf.
Правило Крамера
Cramer’s
Правило
Дана система линейных
уравнения, правило Крамера — удобный способ решить только одну из переменных
без необходимости решать всю систему уравнений.Они обычно не
обучать правилу Крамера таким образом, но это должно быть суть
Правило: вместо решения всей системы уравнений можно использовать
Крамеру нужно найти всего одну переменную.
Воспользуемся следующим
система уравнений:
У нас есть левая часть
системы с переменными («матрица коэффициентов»)
а в правой части — значения ответов.Позволять
D
— определитель матрицы коэффициентов указанной выше системы, и
пусть D x
быть определителем, образованным заменой столбца x
значения со значениями столбца ответа:
система | коэффициент | ответ | D x : |
2 х |
Аналогично D y
и D z
тогда будет: Авторское право
Элизабет Стапель 2004-2011 Все права защищены
Оценка каждого детерминанта (с использованием метода, описанного здесь),
получаем:
Правило Крамера гласит, что x
= D x D ,
y =
D y D ,
и z
= D z D . То есть:
То есть:
х
= 3 / 3 = 1, y
= 6 / 3 = 2 ,
и z
= 9 / 3 = 3
Вот и все, что нужно для Cramer’s
Правило.Чтобы найти нужную вам переменную (назовите ее «» или «бета»),
просто оцените определяющее частное D
Д . (Пожалуйста
не просите меня объяснять, почему это работает. Просто поверьте мне, что детерминанты
может творить много видов магии.)
- Учитывая следующее
Система уравнений, найдите значение z .
Решить только для z ,
Сначала я нахожу определитель коэффициента.
Затем я формирую D z
заменив третий столбец значений столбцом ответов:
Затем я составляю частное |
Смысл правила Крамера
в том, что вам не нужно решать всю систему, чтобы получить одно значение
тебе нужно. Это сэкономило мне много времени на некоторых тестах по физике. я
Это сэкономило мне много времени на некоторых тестах по физике. я
забыть, над чем мы работали (я думаю, что-то с проводами и токами),
но правило Крамера было намного быстрее, чем любой другой метод решения (и
Видит Бог, мне нужно было дополнительное время). Не позволяйте всем нижним индексам и прочему
запутать вас; Правило действительно довольно простое. Вы просто выбираете переменную
вы хотите найти, замените столбец значений этой переменной в
определитель коэффициента со значениями столбца ответа, оцените, что
определитель и разделите на определитель коэффициента.Это все там
к нему.
Почти.
Что делать, если определитель коэффициента
ноль? Нельзя делить на ноль, что это значит? Я не могу пойти
в технические детали здесь, но « D
= 0 «означает, что
система уравнений не имеет единственного решения. Система может быть несовместимой
(никакого решения) или зависимое (бесконечное решение, которое может быть
выражается как параметрическое решение, например «( a ,
a + 3, a 4) «). С точки зрения правила Крамера: « D
С точки зрения правила Крамера: « D
= 0 «означает, что
вам придется использовать другой метод (например, матрицу
строковые операции) в
решить систему. Если D
= 0, вы не можете использовать Cramer’s
Правило.
Верх
| Вернуться к индексу
Цитируйте эту статью | Стапель, Елизавета.«Правило Крамера». Purplemath . Доступна с |
линейная алгебра — Найдите пространство столбцов, пустое пространство и специальное решение для матрицы.
Помните, у вас нет решения для системы, если, скажем, у вас есть система
$$
\оставил[
\ begin {array} {ccc c | c}
1 & 0 & 0 & 0 & a \\
0 & 1 & 0 & 0 & b \\
0 & 0 & 0 & 0 & c \\
\ end {массив}
\ right] $$
где $ c \ neq 0 $. Это потому, что система, по сути, говорит, что $ 0 = c $.
Это потому, что система, по сути, говорит, что $ 0 = c $.
Нулевое пространство — это подпространство всех решений $ A \ mathbf {x} = \ mathbf {0} $, а пространство столбцов — это промежуток между столбцами.
Чтобы найти пустое пространство, вы просто хотите определить основу для векторов решений однородной системы. Для уменьшенной ступенчатой формы вашей однородной системы у вас есть
$$
\оставил[
\ begin {array} {ccc c | c}
1 & 0 & 0 & 2 & 0 \\
0 & 1 & 0 & 0 & 0 \\
0 & 0 & 1 & 1 & 0 \\
\ end {массив}
\ right] $$
Допустим, каждый соответствующий столбец соответствует переменным $ x_ {1} $, $ x_ {2} $, $ x_ {3} $ и $ x_ {4} $.Поскольку столбец для $ x_ {4} $ не имеет ведущего $ 1 $, мы позволим $ x_ {4} $ быть свободной переменной.
Тогда RREF дает нам следующее решение однородной системы:
$$ x_ {1} + 2x_ {4} = 0 \ \ mathrm {или} \ x_ {1} = — 2x_ {4} $$
$$ x_ {2} = 0 $$
$$ x_ {3} + x_ {4} = 0 \ \ mathrm {или} \ x_ {3} = — x_ {4} $$
В векторной форме имеем
$$ \ begin {bmatrix} x_ {1} \\ x_ {2} \\ x_ {3} \\ x_ {4} \ end {bmatrix} = \ begin {bmatrix} -2x_ {4} \\ 0 \\ -x_ {4} \\ x_ {4} \ end {bmatrix} = \ begin {bmatrix} -2x_ {4} \\ 0x_ {4} \\ -x_ {4} \\ x_ {4} \ end {bmatrix } = \ begin {bmatrix} -2 \\ 0 \\ -1 \\ 1 \ end {bmatrix} x_ {4}. $$
$$
Таким образом, нулевое пространство исходной матрицы — это промежуток вектора $ \ begin {bmatrix} -2 \\ 0 \\ -1 \\ 1 \ end {bmatrix} $, поскольку $ x_ {4} $ может принимать любое значение.
Что касается пространства столбцов, вам нужно посмотреть столбцы в RREF, у которых в начале стоит $ 1 $. пространство столбцов будет диапазоном столбцов из исходной матрицы, у которых есть начальный $ 1 $ в RREF (т.е. пространство столбцов — это диапазон столбцов $ 1 $, $ 2 $ и $ 3 $).
Вы должны опубликовать исходную матрицу, с которой вы работаете, если собираетесь задать вопрос такого типа, чтобы мы могли полностью ответить на ваш вопрос и убедиться, что вы не допустили никаких ошибок после применения операций со строками.
.



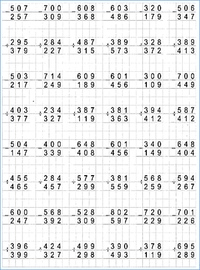 Учащиеся задают друг другу вопросы для проверки таблицы умножения.
Учащиеся задают друг другу вопросы для проверки таблицы умножения.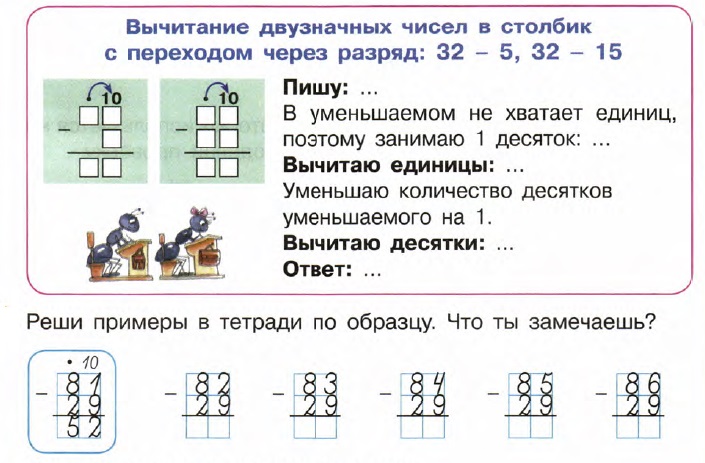


 в учебнике стр 64 №4
в учебнике стр 64 №4 Решаем задачу при помощи наводящих вопросов.
Решаем задачу при помощи наводящих вопросов.
 65.
65.