|
1. |
Запиши выражение и найди его значение (вычитание и сложение)
|
2 |
|
2. |
Запиши выражение и найди его значение (два вычитания)
|
2 |
|
3. 
|
Сравни выражения
|
1 |
|
4. |
Найди общее количество рабочих в двух автобусах
|
2 |
|
5. 
|
Количество автобусов
|
2 |
|
6. |
Сколько французских монет?
|
2 |
|
7. 
|
Число карасей
|
2 |
|
8. |
Хватит ли денег на покупку?
|
3 |
|
9. 
|
Число булочек у кондитера
|
3 |
|
10. |
Количество воды в баке
|
3 |
|
11. 
|
Выбери правильный ответ
|
3 |
Тест: Тест по математике «Решение задач»
Тест по математике «Решение задач»
Тест составлен для контроля и отработки умения решать текстовые задачи. Тест состоит из 18 вопросов. Выполняя тестовые задания, ученик должен выбрать один верный ответ из предложенных.
Математика 2 класс | Автор: Исаева Анжелика Владимировна | ID: 801 | Дата: 2. 1.2014
1.2014
«;} else {document.getElementById(«torf1″).innerHTML=»»;};
if (answ.charAt(1)==»1″) {document.getElementById(«torf2″).innerHTML=»»;} else {document.getElementById(«torf2″).innerHTML=»»;};
if (answ.charAt(2)==»1″) {document.getElementById(«torf3″).innerHTML=»»;} else {document.getElementById(«torf3″).innerHTML=»»;};
if (answ.charAt(3)==»1″) {document.getElementById(«torf4″).innerHTML=»»;} else {document.getElementById(«torf4″).innerHTML=»»;};
if (answ.charAt(4)==»1″) {document.getElementById(«torf5″).innerHTML=»»;} else {document.getElementById(«torf5″).innerHTML=»»;};
if (answ.charAt(5)==»1″) {document.getElementById(«torf6″).innerHTML=»»;} else {document.getElementById(«torf6″).innerHTML=»»;};
if (answ.charAt(6)==»1″) {document.getElementById(«torf7″).innerHTML=»»;} else {document.getElementById(«torf7″).innerHTML=»»;};
if (answ.charAt(7)==»1″) {document.getElementById(«torf8»). innerHTML=»»;} else {document.getElementById(«torf8″).innerHTML=»»;};
innerHTML=»»;} else {document.getElementById(«torf8″).innerHTML=»»;};
if (answ.charAt(8)==»1″) {document.getElementById(«torf9″).innerHTML=»»;} else {document.getElementById(«torf9″).innerHTML=»»;};
if (answ.charAt(9)==»1″) {document.getElementById(«torf10″).innerHTML=»»;} else {document.getElementById(«torf10″).innerHTML=»»;};
if (answ.charAt(10)==»1″) {document.getElementById(«torf11″).innerHTML=»»;} else {document.getElementById(«torf11″).innerHTML=»»;};
if (answ.charAt(11)==»1″) {document.getElementById(«torf12″).innerHTML=»»;} else {document.getElementById(«torf12″).innerHTML=»»;};
if (answ.charAt(12)==»1″) {document.getElementById(«torf13″).innerHTML=»»;} else {document.getElementById(«torf13″).innerHTML=»»;};
if (answ.charAt(13)==»1″) {document.getElementById(«torf14″).innerHTML=»»;} else {document.getElementById(«torf14″).innerHTML=»»;};
if (answ.charAt(14)==»1″) {document.getElementById(«torf15″).innerHTML=»»;} else {document.getElementById(«torf15″).innerHTML=»»;};
if (answ.charAt(15)==»1″) {document. getElementById(«torf16″).innerHTML=»»;} else {document.getElementById(«torf16″).innerHTML=»»;};
getElementById(«torf16″).innerHTML=»»;} else {document.getElementById(«torf16″).innerHTML=»»;};
if (answ.charAt(16)==»1″) {document.getElementById(«torf17″).innerHTML=»»;} else {document.getElementById(«torf17″).innerHTML=»»;};
if (answ.charAt(17)==»1″) {document.getElementById(«torf18″).innerHTML=»»;} else {document.getElementById(«torf18″).innerHTML=»»;};
}
}
Получение сертификата
о прохождении теста
|
|
ГДЗ по Математике 2 класс Моро учебник Решебник
Здесь представлен учебник по математике для самых маленьких школьников (2 класс) с готовыми ответами и правильными алгоритмами решения. Авторами выступили известные методисты М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова и С.В. Степанова. Готовые домашние задания (ГДЗ) облегчают задачу вхождения в учебный процесс и помогают быстрее приступить к конструктивному познанию основ этого важного и занимательного предмета. Изданием учебно-методического комплекса является «Школа России». На нашем сайте представлены только актуальные задания из указанного источника и правильные ответы к ним.
Авторами выступили известные методисты М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова и С.В. Степанова. Готовые домашние задания (ГДЗ) облегчают задачу вхождения в учебный процесс и помогают быстрее приступить к конструктивному познанию основ этого важного и занимательного предмета. Изданием учебно-методического комплекса является «Школа России». На нашем сайте представлены только актуальные задания из указанного источника и правильные ответы к ним.
Почему решебник по математике Моро нужен каждому второкласснику?
ГДЗ помогают ребенку мотивировать себя, чтобы заниматься самостоятельно, а также постоянно контролировать достигнутый уровень личного прогресса посредством решения проверочных упражнений. Со сборником по математике Моро, Бантовой, Бельтюковой, который полностью соответствуют ФГОС и повсеместно используются в рабочих программах педагогов, легко и удобно заниматься. Верные ответы онлайн имеют следующие преимущества перед иными видами пособий:
- наличие независимых вариантов выполнения многих примеров;
- примеры снабжены ценными методическими указаниями;
- сайт работает с персонального компьютера, ноутбука, планшета и смартфона;
- таблица номерных указателей позволяет быстро находить нужное задание.

С онлайн-решебником можно успешно готовиться к контрольным, проверочным, самостоятельным, и диагностическим работам, выполнять тесты и проходить внешнее независимое тестирование в конце учебного года.
Чем ГДЗ Моро, Бантовой превосходит другие учебники для 2 класса?
Чтобы хорошо успевать по математике и приносить домой исключительно отличные отметки, нужно приучить себя к систематической и тщательной работе. Это касается как отработки устного счета, так и формирования четкого понимания способов решения задач на одно и два действия. Во втором классе общеобразовательной школы ученики знакомятся лишь с самыми простыми понятия, но именно они станут залогом будущих успехов при изучении точных дисциплин. Ни в коем случае нельзя запускать предмет, а возникающие пробелы в знаниях, умениях и навыках необходимо ликвидировать в кратчайшие сроки. Сборник способен оказать значительную помощь в достижении следующих целей:
- повышение текущей успеваемости и степени уверенности в собственных силах на уроках;
- отработка практических навыков в области арифметики;
- формирование самостоятельности при подготовке к урокам;
- расширение кругозора и формирования навыков логического мышления.

Математика относится к тем предметам, которые непременно пригодятся будущему взрослому члену общества. Уметь произвести те или иные практически важные и полезные вычисления необходимо повсеместно. Поэтому пособие Моро для 2 класса рекомендовано наиболее широким массам учащихся, а также их неравнодушным родителям, которые хотели бы держать под контролем учебный прогресс своего сына или дочери.
Математика. 2 класс
Задачи:
1. Развитие умений решать задачи и составлять обратные, сравнивать величины, находить неизвестный множитель, познакомить с таблицей умножения на два.
2. Развитие логического мышления, внимания, памяти.
3. Воспитание интереса к математике, стремление использовать математические знания в повседневной жизни.
4. Повышение интереса к изучению ПДД через проведение интегрированного урока.
5. Повторение дорожных знаков.
Оборудование: стенды модульного кабинета ПДД, дорожные знаки, карточки, магнитофон.
Ход урока
1. ОРГМОМЕНТ
Приветствие, знакомство учащихся с целями и задачами урока.
2. СООБЩЕНИЕ ТЕМЫ
— Сегодня на уроке математики мы будем работать над таблицей умножения на два, решать и составлять обратные задачи, решать уравнения, находить сторону квадрата по известному периметру, а также повторим дорожные знаки, вспомним, что они обозначают.
(Класс сидит по группам.)
— Группы наши превращаются в экипажи машин дорожно-патрульной службы, а командиры будут штурманами. Штурман — это человек, который руководит всем движением.
Двигаться мы будем по городу. Городские дороги — это ваши тетради, в которых вы должны писать красиво, грамотно и аккуратно.
Откройте тетради, запишите дату.
Сядьте правильно, пристегнитесь ремнём безопасности.
Как вы думаете, зачем это необходимо сделать?
(Дети отвечают, поднимая руку. Добившись полного, правильного ответа, продолжаем. )
)
— Итак, мы отправляемся в путь! Будьте внимательны! Поехали!
3. УСТНАЯ РАБОТА
— Поехали и вдруг видим: на проезжей части дороги стоит человек. Кто это? Отгадайте?
(Учитель читает стихотворение.)
Кто-то запросто-непросто
Встал на нашем перекрёстке!
Быстро руку протянул,
Ловко палочкой взмахнул.
Вы видали?
Вы видали?
Все машины сразу встали!
Дружно встали в три ряда
И не едут никуда.
Ребята, кого мы увидели?
(Инспектора ГИБДД.)
Откройте конверт № 1.
(В конверте вопрос: «Как называется предмет, которым регулировщик управляет движением?».)
Для ответа слушайте задание. Вам надо решить выражения и значения расположить в порядке возрастания.
Какое слово у вас получилось? (Жезл.)
Задание в конверте:
83-67=15 (Е)
52-44=8 (Ж)
36+29=65 (З)
72+28=100 (Л)
Давайте вспомним, что обозначают сигналы регулировщика?
(Дети отвечают: если он стоит лицом или спиной с опущенными или вытянутыми в сторону руками — движение для транспорта и пешеходов запрещено. Если правая рука вытянута вперёд — путь пешеходам открыт за спиной регулировщика. Если рука поднята вверх — внимание! Движение всех запрещено!)
Если правая рука вытянута вперёд — путь пешеходам открыт за спиной регулировщика. Если рука поднята вверх — внимание! Движение всех запрещено!)
Справились! Молодцы!
(Регулировщик показывает: путь открыт. Едем дальше.)
Ребята, что за знак впереди? («Жилая зона».)
Как надо ехать? Почему? (Ответы детей: медленно, осторожно.)
Смотрите! На проезжую часть выбежал футболист. Найдите, под каким номером этот футболист. (Карточка № 1, в которой изображены геометрические фигуры.)
Как вы думаете, правильно ли поступил мальчик?
Почему?
А вы, водители, поступаете правильно? Молодцы!
4. РАБОТА НАД НОВЫМ МАТЕРИАЛОМ
Решение выражений
— Чтобы с вами не произошло таких историй, мы сейчас повторим знаки дорожного движения. Будьте внимательны! (Учитель показывает дорожные знаки, на которых записаны выражения. Дети пишут в тетрадях эти выражения и находят их значения.)
2*2= 3*2= 4*2=
5*2= 6*2= 7*2= 8*2=
Что обозначает этот знак?
Хорошо, вы вспомнили знаки, а сейчас включим музыку и постараемся запомнить слова, которые услышим в песне.
(Звучит песня «Таблица умножения».)
— Ребята, какие знаки вы знаете?
Что обозначает этот знак? (Звуковой сигнал запрещён.)
Геометрический материал
— Как называются геометрические фигуры, форму которых имеют знаки? (Треугольник, квадрат, круг, прямоугольник.)
Почему они разные?
(Знаки принадлежат к разным группам: предупреждающие, запрещающие, предписывающие, знаки приоритета, сервиса, информационо-указательные, знаки особых предписаний.)
— Назовите разрешающий знак, в котором есть буква?
Что это за буква? (Р)
Что обозначает этот знак? (Место стоянки.)
А в математике что обозначает эта буква? (Периметр.)
Нахождение периметра
— Что называется периметром?
Как найти периметр?
В какой геометрической фигуре находится эта буква? (В квадрате.)
Что вы знаете о квадрате?
Как найти периметр квадрата?
Откройте конверт № 2.
Найдите периметр квадрата.
Если дан периметр квадрата, как найти его сторону?
Запишите в тетрадях эту задачу. Чей экипаж справится с заданием, штурман поднимет руку.
Р=2+2+2+2 Р=8 см
а=8 см а=2 см
Устали? Поехали на парковку. Вышли из машин.
Физминутка.
Решение задач
— На этом стенде находятся машинки. Сосчитайте их и составьте условие задачи, которая решалась бы умножением.
(3*2= 6 машин.)
— Составьте обратные задачи (6:3=2; 6:2=3), запишите их в тетрадях.
Закончили? Садимся в машины.
К какому виду транспорта относятся ваши машины? (Специальный.)
Как передвигается спецтранспорт? (Едет с включённым звуковым сигналом, ему должны уступить дорогу даже на красный свет.)
Решение уравнений
Читает ученик:
— Эй, водитель, осторожно!
Ехать быстро невозможно,
Знают люди все на свете:
В этом месте ходят. .. дети.
.. дети.
Учитель:
— Найдите этот знак. Где его можно встретить?
(Дети отвечают: знак устанавливается около школ и предупреждает водителей, что в этом месте могут появиться на дороге дети. Но этот знак не разрешает переходить дорогу в том месте, где он установлен. Для перехода нужно поискать пешеходный переход, который обозначается знаком — синим квадратом с нарисованным внутри человечком.)
Учитель:
— Нашли карточку с легковой машинкой в круге с красным ободом?
Что означает этот знак?
(Дети отвечают.)
Как называются компоненты при умножении?
Как найти неизвестный множитель?
Решите уравнение, сделайте проверку. (а*9=18)
Сравнение выражений
— Отгадайте загадку:
Этот конь не ест овса,
Вместо ног — два колеса,
Сядь верхом и мчись на нём,
Только лучше правь рулём. (Велосипед.)
Кто знает, в каком году изобрели велосипед? Кто изобрёл?
(Первый прототип велосипеда был предложен великим итальянским учёным Леонардо да Винчи в 1495 году: показать иллюстрации. )
)
У кого из вас есть велосипед?
Какие правила для велосипедистов вы знаете?
Покажите предписывающий знак для велосипедиста.
И запрещающий. В чём их различие? (Дети отвечают устно.)
Выполним следующее задание. Сравните величины.
Вспомните, сколько сантиметров в 1 дециметре? А сколько миллиметров в 1 сантиметре?
(Дети записывают ответы в тетрадях.)
Чей экипаж справился с этим заданием? Молодцы!
5. ДОМАШНЕЕ ЗАДАНИЕ
Придумать разрешающий знак.
6. ЗАКЛЮЧИТЕЛЬНЫЙ ЭТАП УРОКА
Самый дружный, самый быстрый экипаж — это… (учитель называет лучшую группу). Молодцы!
Что нового узнали на уроке? Что запомнили?
Послушайте стихотворение
Читает ученик:
Правил дорожных
На свете немало,
Все бы их выучить
Нам не мешало,
Но основное из правил движения
Знать как таблицу
Должны умножения.
На проезжей части не шалить,
Не играть,
Не кататься,
Если хочешь целым быть
И живым остаться!
Учитель начальных классов, отличник народного просвещения Л.В. ШАШКОВА, МОУ Средняя общеобразовательная школа № 32, г. Красноярск
Этапы урока Цели | Форма организации учебной деятельности | Содержание взаимодействия с учащимися | Деятельность учащихся | Деятельность учителя |
I. Организация начала урока Цель: содействовать установлению нормального рабочего настроя у школьников и готовности к сотрудничеству. | 1.Приветствие учащихся; 2.Эмоциональный настрой на работу 3. Проверка готовности учащихся к уроку (Прием «Помощник учителя») | -Здравствуйте. — Сегодня у нас с вами необычный урок — открытый. Поздороваемся с нашими гостями. Я желаю вам успехов на нашем уроке. — Проверим готовность рабочего места. На каждом ряду проверит готовность. На столе у вас должны лежать учебник, тетрадь, пенал, полоска для рефлексии. — А теперь вспомним, как должен сидеть прилежный ученик. Не сутулиться, опираться на спинку стула и положить руки на парту перед собой. Молодцы, ребята! | Приветствуют учителя, эмоционально настраиваются на работу, проверяют готовность рабочего места к уроку. | Приветствует учащихся, содействует установлению нормального рабочего настроя у школьников и готовности к сотрудничеству, подготавливает учащихся к решению. |
II. Устный счет. Цель: актуализировать знания учащихся. | 1.Устное решение примеров. (М/П) 2. | — Начнем мы наш урок с разминки. Все внимание на слайд. (М/П) 1. Игра «Назови соседа» 2. Решите цепочку примеров. 3. Логическая задача 4. Лишняя фигура.
| Решают примеры и называют получившиеся ответы Находят значения выражений, осуществляют взаимопроверку | Проверяет ответы учащихся, исправляет ошибки. Контролирует выполнение заданий |
III. Сообщение темы и целей урока. Цель: сформировать у учащихся мотивацию по освоению нового материала | 1.Формулированеи темы и целей урока (решение Кроссворда) | — Посмотрите внимательно на доску. 1. Какая рыбка исполняла желания старухи в сказке А.С. Пушкин? (золотая) 2. Писательница, которая написала стихотворение «Идет бычок качается, вздыхает на ходу…» (Барто) 3. Населённый пункт, в котором земляные дороги, маленькое население и разводят животных? 4. Самая любимая оценка ученика (пятерка) 5. Медленное животное с панцирем (черепаха) 6. Средство передвижения, которое заправляется бензином. (машина) Какое слово получилось? Какая тема нашего урока? (Решение задач). Какие цели мы поставим перед собой? (решать задачи, решать примеры). Приступим к решению поставленных целей. | Работают над значением пословицы, определяют вид урока. Находят значение выражений, составляют тему урока из полученных букв, определяют цели урока. | Объясняет задание, задает вопросы, корректирует ответы учащихся. Осуществляет помощь при определение темы и целей урока. |
IV. Изучение нового материала. Цель: Обеспечить восприятие и первичное освоение учащимися изучаемого материала. | 1. Вступительная беседа 2. Минутка чистописания 3. С. 64 задача 1 4. С. 44 задача 3. | Вспомните, из чего состоит задача? (условие, вопрос, ответ, решение). Какие виды задач вы знаете? (простые, решаются в одно действие и составные, решаются в два действия). Пропишите в тетради 82, соблюдая наклон. Откройте учебник на странице 65. Прочитайте задание, записанное под цифрой 1? Что вы прочитали? Докажите. (есть условие и вопрос). Решим эту задачу. Что выполняют девочки в этой задаче? В чем измеряется расстояние в задаче? Какое расстояние прошла первая девочка? Вторая девочка? Что нужно узнать в задаче? Можем ли мы сразу ответить на главный вопрос задачи? Что нужно узнать? Какой это вид задачи? Какой это тип задачи? (составная задача, так как решается в два действия). Прочитайте условия задачи три. О чем говорится в задаче? Какая единица измерения используется для обозначения массы яблок? (кг). С чего мы начинаем решение задач? С краткой записи. Чтобы определить слова для краткой записи, вам нужно вспомнить, в чем хранятся яблоки. Какой это вид задачи? (простая задача, так как решается в одно действие). | Вспоминают структуру задачи, виды задач. Выполняют задание Решают задачу под руководством учителя Выполняют движения под руководством учителя | Обеспечивает восприятие и первичное освоение учащимися изучаемого материала. Контролирует действия учащихся, выполняя их корректировку Осуществляет профилактику переутомления |
V. Закрепление. Цель: закрепить полученные знания и умения. | 1. Карточки | У вас на столах карточки. | Решают примеры, записывают ответы в тетрадь | Следит за правильным решением примеров |
VI. Итог урока. Цель: подвести итоги. | 1. Беседа по теме урока | — Из чего состоит задача? -Какие виды задач вы знаете? — Что самое главное в решении задач? | Отвечают на вопросы учителя | Выставляет оценки, подводит итоги. |
2. Самооценка деятельности (рефлексия) | Оцените свою работу на уроке. У вас листочки трех цветов: Красные — вам было скучно, вы не работали на уроке. Желтые – вам было скучно, но вы работали на уроке. Зеленые – вам было интересно и вы достигли цели урока. | Учитель выявляет уровень усвоения нового материала. | Понимают причины успеха/неуспеха учебной деятельности. Самостоятельно оценивают свои достижения. | |
3. Д/з | Дома вам будет необходимо найти значение числовых выражений № 4 на с.65. Посмотрите на второй столбик, что это за примеры? Какой порядок действий в этих примерах? Откроем дневники и запишем д/з. Спасибо за урок, готовитесь к следующему. | Запоминают алгоритм выполнения домашнего задания | Проводит инструктаж по выполнению домашнего задания |
Презентация » Решение задач. Путешествие в космос» 2 класс
библиотека
материалов
Содержание слайдов
Номер слайда 1
Номер слайда 2
Номер слайда 3
Учитель начальных классов Хромова Светлана Николаевна Урок математики во 2 классе по УМК «Перспектива»
Номер слайда 4
В 1960 году Юрий Гагарин начал готовиться к полету в космос.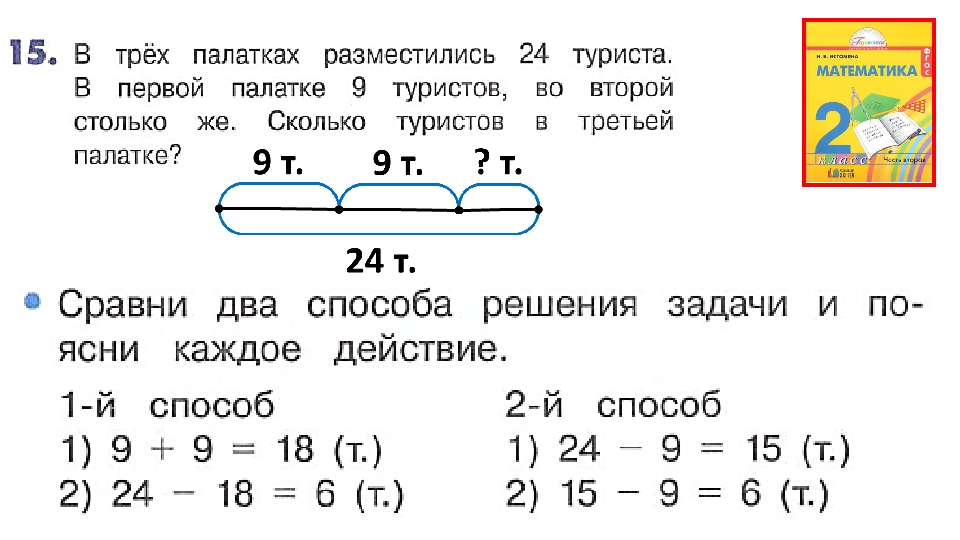 Работал упорно, с полной отдачей сил.
Работал упорно, с полной отдачей сил.
Номер слайда 5
. Чтоб сегодня наш урок, Всем пошёл ребятам впрок, Постарайтесь всё понять, Слушать, думать и вникать!
Номер слайда 6
БОРТОВОЙ ЖУРНАЛ Маршрутный лист 12 22 32 ……
Номер слайда 7
12 апреля 1961 года на старте прозвучало его знаменитое «Поехали»!
Номер слайда 8
КЛЮЧЕВОЕ СЛОВО УРОКА 29 — 19 = 4 + 3х6 = (80-70)+6= 26 + 14 = 40 – 35 = 90 : 10 =
Номер слайда 9
КЛЮЧЕВОЕ СЛОВО УРОКА 40-а 22-ч 16-а 10-д 9-а 5-з
Номер слайда 10
КЛЮЧЕВОЕ СЛОВО УРОКА ЗАДАЧА
Номер слайда 11
Номер слайда 12
Номер слайда 13
КЛАСТЕР ЗАДАЧА условие вопрос решение ответ
Номер слайда 14
СТАРТОВАЯ ПОДГОТОВКА
Номер слайда 15
СТАРТОВАЯ ПОДГОТОВКА
Номер слайда 16
СТАРТОВАЯ ПОДГОТОВКА
Номер слайда 17
И так! Внимание ! Взлёт! Наша ракета помчалась вперёд! Прощально мигнут и растают вдали Огни золотые любимой Земли!
Номер слайда 18
Номер слайда 19
Номер слайда 20
Номер слайда 21
. М.кратер- 15 ч. Б.кратер-? ч. на 65 > } ?Ч..
М.кратер- 15 ч. Б.кратер-? ч. на 65 > } ?Ч..
Номер слайда 22
ГАЛАКТИКА ЗАДАЧ Станция «Сочиняй-ка» Маленький кратер возьмёт в себя 15 человек. А большой кратер на 65 человек больше. Сколько человек возьмут в себя оба кратера?
Номер слайда 23
ГАЛАКТИКА ЗАДАЧ Станция «Сочиняй-ка» 15+65=80(ч.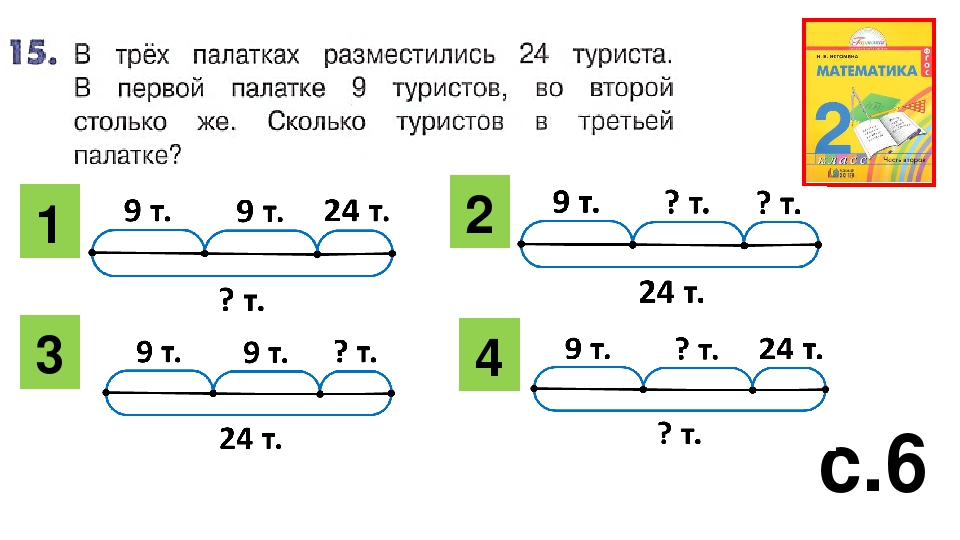 )-возьмёт большой кратер. 2) 15+80=95(ч.) Ответ: 95 человек возьмут оба кратера.
)-возьмёт большой кратер. 2) 15+80=95(ч.) Ответ: 95 человек возьмут оба кратера.
Номер слайда 24
ГАЛАКТИКА ЗАДАЧ Станция «Отдыхай-ка»
Номер слайда 25
ГАЛАКТИКА ЗАДАЧ Станция «Отдыхай-ка»
Номер слайда 26
К космическому полёту долго и упорно готовились 12 космонавтов. Они работали над собой, не покладая сил. Наконец, настал торжественный день отбора самых достойных космонавтов. Когда все построились, то выбрали самых сильных, ловких и умелых. А на Земле осталось 7 космонавтов. Сколько космонавтов были удостоены чести полететь в космос ?
Они работали над собой, не покладая сил. Наконец, настал торжественный день отбора самых достойных космонавтов. Когда все построились, то выбрали самых сильных, ловких и умелых. А на Земле осталось 7 космонавтов. Сколько космонавтов были удостоены чести полететь в космос ?
Номер слайда 27
К полёту готовились 12 космонавтов. Когда несколько космонавтов полетели , то на Земле осталось 7 . Сколько полетело в космос ?
Номер слайда 28
1) Осталось – 7 косм. Полетело — ? косм. 2) 12 косм.
3) ? косм. 7 ? 12
Полетело — ? косм. 2) 12 косм.
3) ? косм. 7 ? 12
Номер слайда 29
Решение: 12 –7= 5(косм.) Ответ: 5 космонавтов полетело в космос.
Номер слайда 30
Космонавт взял в космос 18 тюбиков картофельного пюре и 12 тюбиков мясного пюре.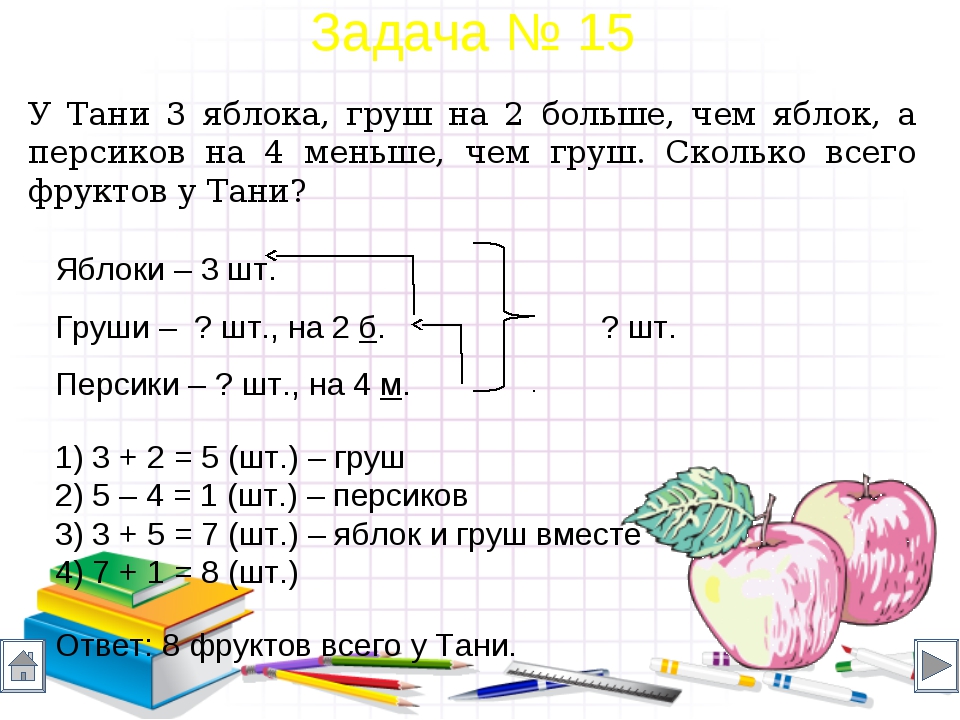 Съел он 20 тюбиков с космической пищей. Сколько тюбиков осталось?
Съел он 20 тюбиков с космической пищей. Сколько тюбиков осталось?
Номер слайда 31
1) 18 – 12 + 20 = 2) 20 – ( 18 – 12) = 3) 18 + 12 – 20 =
Номер слайда 32
18 + 12 – 20 = 20 (тюб. ) Ответ: 20 тюбиков осталось
) Ответ: 20 тюбиков осталось
Номер слайда 33
1) У Димы 27 марок на тему «Космос», а у Серёжи 10. Сколько марок у Димы? 2) Собаки Белка и Стрелка пробыли в космосе одни сутки. А собаки Ветерок и Уголёк 23 дня. Кто был в космосе больше и на сколько?
Номер слайда 34
108 минут длился первый полет в космос Космический корабль « ВОСТОК»
Номер слайда 35
1 вариант: стр.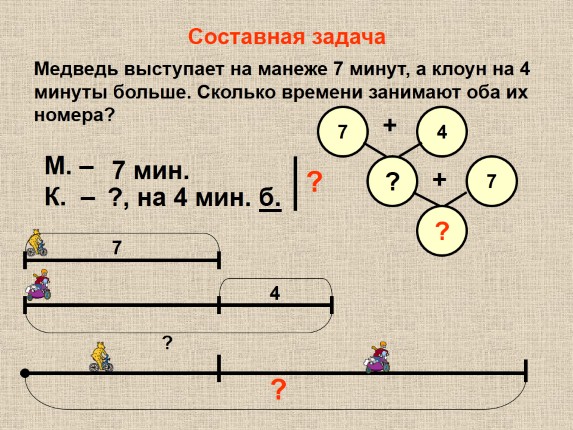 62 №3,6 2 вариант :стр.64 №3,4
62 №3,6 2 вариант :стр.64 №3,4
Номер слайда 36
РЕФЛЕКСИЯ Из полета возвратились Мы на землю приземлились. Как слетал ты? Расскажи! И звезду всем покажи!
Номер слайда 37
РЕФЛЕКСИЯ справился, всё решил сам решал с помощью было трудно
Номер слайда 38
РЕФЛЕКСИЯ справился, всё решил сам решал с помощью было трудно
Номер слайда 39
МОЛОДЦЫ!
Как превратить словесную задачу в сложную математическую задачу (часть первая)
Часть первая — создание задачи
Мышление о росте — это гораздо больше, чем модное слово, и нигде это не проявляется так очевидно, как в математике.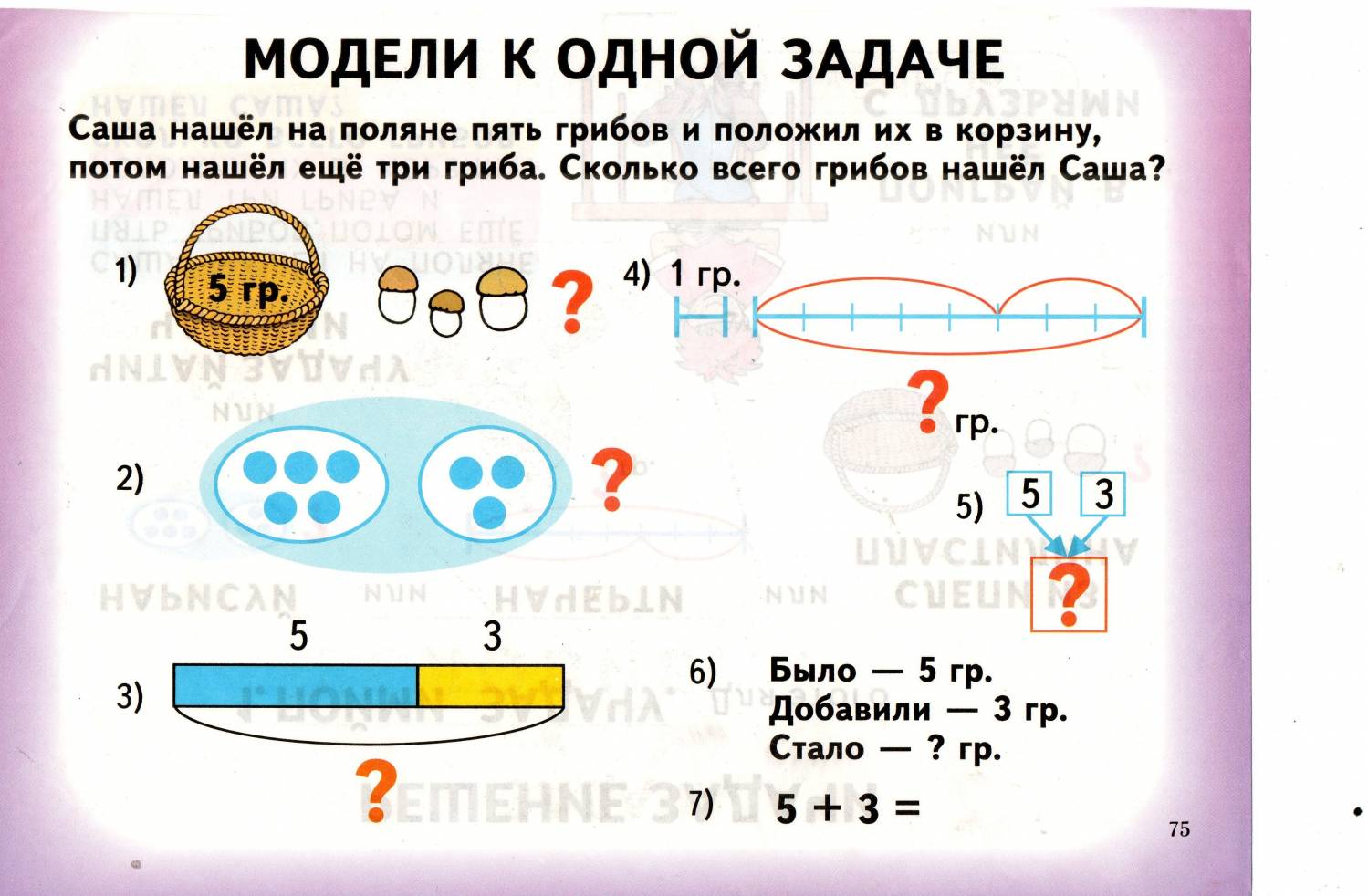 Результаты исследований в этой области меняют наши представления о передовых методах обучения математике. Оказывается, развитие математического мышления в большей степени связано с будущими успехами в математике, чем баллы по стандартным тестам!
Результаты исследований в этой области меняют наши представления о передовых методах обучения математике. Оказывается, развитие математического мышления в большей степени связано с будущими успехами в математике, чем баллы по стандартным тестам!
Один из способов развить у учащихся математический склад ума — это превратить традиционные задачи со словами в «сложные математические задачи».”
Я затронул тему сложных математических задач в своем недавнем вебинаре« Решение математических задач: образ мышления имеет значение, но я хочу немного больше углубиться в сложные математические задачи здесь, на Corkboard Connections ».
У сложных математических задач есть два важных компонента: ЧТО (проблема) и КАК (процесс).
В этом посте мы рассмотрим, как превратить скучную задачу со словами в сложную математическую задачу. В моем следующем посте я расскажу о стратегиях активного взаимодействия, которые вы можете использовать, чтобы помочь своим детям ускорить процесс решения проблем! Щелкните здесь, чтобы перейти ко второй части.
Чем проблема со словом отличается от задачи с богатой математикой
Простая задача со словом
Проблемы со словом на элементарном уровне, как правило, представляют собой простые задачи с единственным правильным ответом. Детей часто учат решать их, обучаясь определять ключевые слова и числа в задаче, а затем применяя необходимые математические операции. Например, простая задача со словами может выглядеть так: «Есть 10 яблок, и каждое яблоко очищается от кожуры за 2 минуты. Сколько всего минут нужно, чтобы очистить яблоки от кожуры? »
Типичный метод решения этой проблемы заключается в подчеркивании ключевых слов «каждый» и «во всех» и обведении цифр 10 и 2 в кружок.Ключевые слова говорят учащимся, что им нужно умножить числа, чтобы найти ответ, поэтому они умножают 10 и 2 и записывают число 20 в качестве ответа. Если вы попросите этих учеников нарисовать или смоделировать решения визуально, они будут в растерянности. Если вы попросите их пометить ответ единицей измерения, они с такой же вероятностью напишут «20 яблок», как и «20 минут».
Проблемы со словом не побуждают к глубокому размышлению, анализу или обсуждению, потому что решения довольно просты. Конечно, вы можете посоветовать своим ученикам поговорить с партнером о том, как они решили проблему, но их объяснения будут звучать так: «Сначала я подчеркнул ключевые слова, а затем обвел все числа.Затем я умножил числа, чтобы получить ответ ». Подобное объяснение вряд ли можно назвать «математической беседой»!
Rich Math Tasks
Rich математические задачи, с другой стороны, обычно более открыты и могут быть решены разными способами. Некоторые математические задачи представляют собой вопросы, основанные на запросах, которые содержат более одного правильного ответа, или задачи, требующие от учащихся использования практических материалов для поиска решений. Другие математические задачи на первый взгляд выглядят как обычные задачи со словами, но когда вы пытаетесь их решить, вы понимаете, что есть много способов найти ответ.В сложных математических задачах нет ключевых слов, которые можно было бы подчеркнуть, и обводка чисел не поможет, потому что для решения задачи вам могут даже не понадобиться все числа! Эти типы математических задач стимулируют обсуждение, вопросы и критическое мышление, поскольку учащиеся пытаются выбрать лучшую стратегию для решения проблемы.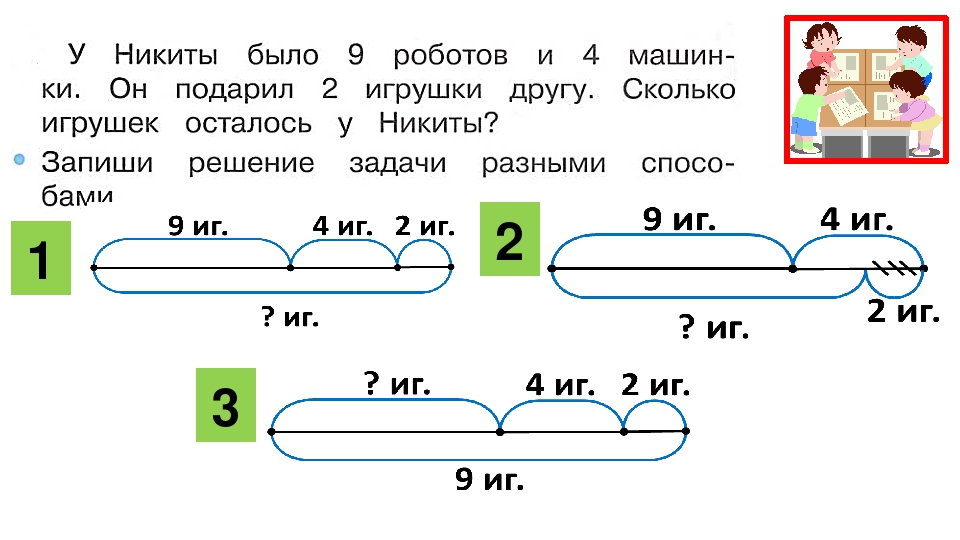
6 советов по созданию отличной математической задачи
Поиск или создание правильной математической задачи — первый шаг в разработке сложной математической задачи.Вот несколько советов, которые сделают процесс решения вашей проблемы намного проще.
1. Начните с визуальной задачи
Выберите словесную задачу, которую легко визуализировать, и попробуйте решить ее несколькими способами. Убедитесь, что ответ можно представить визуально, нарисовав его или используя физические модели. Если вы понимаете, что есть только один способ решить эту проблему или что будет сложно представить решения визуально, переписывайте проблему или найдите новую. Я воспользуюсь задачей Apple Peeling Word, описанной выше, чтобы продемонстрировать, как превратить простую задачу со словами в нечто гораздо более сложное и интересное.
2. Удалите ключевые слова
После того, как вы выбрали проблему, поищите такие ключевые слова, как «всего», «каждый», «за» и «всего». Если возможно, перепишите задачу, не используя ключевые слова, следя за тем, чтобы смысл не изменился. Удаление ключевых слов заставляет студентов ДУМАТЬ о том, какая операция необходима, вместо того, чтобы просто подчеркивать слова и бездумно выбирать операцию на основе этих слов.
Если возможно, перепишите задачу, не используя ключевые слова, следя за тем, чтобы смысл не изменился. Удаление ключевых слов заставляет студентов ДУМАТЬ о том, какая операция необходима, вместо того, чтобы просто подчеркивать слова и бездумно выбирать операцию на основе этих слов.
3. Добавьте дополнительные сведения и информацию
Затем добавьте сведения, которые на самом деле не нужны для поиска решения.Если учащихся научили подчеркивать ключевые слова и цифры в кружках, эти дополнительные детали их запутают. Им нужно будет подумать над задачей и решить, какие слова и числа на самом деле важны.
Давайте воспользуемся первыми тремя советами, чтобы переработать проблему Apple Peeling Word и превратить ее в Apple Peeling Challenge №1. Хотя проблема все еще довольно проста, отсутствие ключевых слов и лишних цифр делают ее более сложной. Студенты должны подумать о том, что им задают, и решить, как лучше их решить.Это хорошая начальная задача для ознакомления студентов с разнообразными математическими задачами, поскольку ее можно решить более чем одним способом с помощью визуальных моделей. Студенты могли рисовать круги вместо яблок, использовать круглые предметы, такие как пенни или фишки для бинго, или даже использовать настоящие яблоки!
Студенты могли рисовать круги вместо яблок, использовать круглые предметы, такие как пенни или фишки для бинго, или даже использовать настоящие яблоки!
Готовы поднять Apple Peeling Challenge №1 на новый уровень? Применение следующих 3 советов к этой задаче сделает ее еще более сложной и интересной!
4. Персонализируйте это и сделайте реальным
Чтобы сделать задачу более интересной, персонализируйте ее, добавив имя реального человека, возможно, даже имя одного из ваших учеников! Добавьте достаточно деталей, чтобы оживить или превратить в историю.В документе Apple Peeling Challenge № 2 , в том числе деталь о том, что Сэм чистит яблоки для пирога, делает проблему более значимой. Учитель из группы Mindset Connections в Facebook решил эту задачу и превратил ее в рассказ о приготовлении пирога на обед в честь Дня Благодарения!
5. Превратите это в многоэтапную задачу
Перепишите одноступенчатые задачи со словами, чтобы обеспечить выполнение нескольких шагов для ее решения. В информации в основной словарной задаче указано, что каждое яблоко очищается от кожуры за 2 минуты.Самый простой способ добавить еще один шаг — заменить эту деталь достаточной информацией, чтобы учащиеся могли рассчитать, сколько времени нужно, чтобы очистить каждое яблоко. Каждая задача будет немного отличаться, но всегда есть способ изменить задачу и превратить ее в многоступенчатую математическую задачу.
В информации в основной словарной задаче указано, что каждое яблоко очищается от кожуры за 2 минуты.Самый простой способ добавить еще один шаг — заменить эту деталь достаточной информацией, чтобы учащиеся могли рассчитать, сколько времени нужно, чтобы очистить каждое яблоко. Каждая задача будет немного отличаться, но всегда есть способ изменить задачу и превратить ее в многоступенчатую математическую задачу.
6. Изменение чисел
Часто можно усложнить задачу со словами, изменив числовые значения. Например, вместо того, чтобы чистить 10 яблок, Сэм может очистить 100 яблок, потому что он испекает 10 пирогов для банкета.Вы также можете использовать числа, которые дают дробные ответы. Например, в приведенном выше примере Apple Peeling Challenge № 2 Сэм может очистить 4 яблока за 6 минут, чтобы дети могли вычислить, сколько времени требуется, чтобы очистить одно яблоко. Но 6 не делится на 4, поэтому количество минут, необходимое для очистки одного яблока, не является целым числом. Вы видите, как небольшая настройка чисел может мгновенно усложнить задачу? Теперь у вас есть задача, которая идеально подходит для математического задания!
Вы видите, как небольшая настройка чисел может мгновенно усложнить задачу? Теперь у вас есть задача, которая идеально подходит для математического задания!
Почему бы не попробовать создать свой собственный Apple Peeling Challenge? На веб-семинаре «Решение математических задач: образ мышления» я поделился еще двумя проблемами с очисткой яблока, которые сильно отличаются от задач в этом посте.Готов поспорить, вы тоже можете придумать свои собственные проблемы с очисткой яблока!
Где найти редактируемые задачи со словами для сложных математических задач
Если вы не хотите создавать свои собственные многоступенчатые задачи со словами или у вас нет времени искать их, ознакомьтесь с моим новейшим продуктом, Math Mindset Проблемы. Это постоянно растущая коллекция редактируемых текстовых задач в нескольких различных форматах. Сами проблемы находятся в редактируемом документе PowerPoint, поэтому вы можете изменить формулировку и настроить их при необходимости.Все задачи были проверены учителями старших классов начальной школы, и они работают хорошо, как есть, но если вы используете другую систему измерения или хотите настроить проблемы, используя приведенные выше советы, вы легко можете это сделать. Если вы хотите познакомиться поближе, зайдите в мой магазин TpT и нажмите ссылку предварительного просмотра на странице продукта.
Если вы хотите познакомиться поближе, зайдите в мой магазин TpT и нажмите ссылку предварительного просмотра на странице продукта.
Показанный выше продукт Math Mindset Challenges включен в мой пакет веб-семинаров Math Mindset Challenges и в мой пакет решения математических задач.Оба пакета включают веб-семинар по профессиональному развитию Math Problem Solving: Mindsets Matter.
Далее — часть вторая: создание процесса
Помните, что сложные математические задачи состоят из двух основных компонентов: ЧТО и КАК. В этом посте я рассмотрел ЧТО, математическую задачу. Однако этого недостаточно, чтобы создать отличную словесную задачу; важно то, что вы делаете с этой проблемой! Щелкните здесь, чтобы прочитать Часть 2 «Создание процесса», в которой я подробно рассказал, КАК облегчить процесс решения проблем.Я поделился множеством активных стратегий взаимодействия, которые выведут решение проблем на совершенно новый уровень в вашем классе математики!
Word Стратегии решения задач для учащихся K – 4 классов [Бесплатные шаблоны]
Стратегии решения математических задач должны начинаться уже в детском саду или в первом классе! Поскольку в последние годы чтению научной литературы уделяется больше внимания, мы можем рассматривать текстовые задачи как часть жанра научной литературы. Загрузки для сегодняшнего сообщения включают несколько шаблонов или графических органайзеров, которые помогут студентам найти связь между задачами со словами и уравнениями, которые представляют эти проблемы.
Загрузки для сегодняшнего сообщения включают несколько шаблонов или графических органайзеров, которые помогут студентам найти связь между задачами со словами и уравнениями, которые представляют эти проблемы.
Как учитель математики, я много раз слышал, что «мы все учителя чтения», и этот пост покажет, как связаны эти две области, как математика, так и чтение, поскольку ученики создают представления, чтобы помочь им перейти от слов к уравнениям и наоборот. Кроме того, возьмите мои загружаемые шаблоны для нескольких представлений ниже! Используя эти шаблоны для разработки уроков, вы можете соответствовать многим Стандартам математической практики, которые лежат в основе стратегий решения математических задач.
- SMP 1: разбираться в проблемах и настойчиво их решать
- SMP 2: Размышляйте абстрактно и количественно
- SMP 4: Модель с математикой
- SMP 7: Найдите и используйте структуру
Манипулятивное и визуальное представление математических словесных задач тесно связаны. Эти представления представляют собой стратегии решения математических задач, которые могут использовать учащиеся. Я надеюсь, что вы терпите меня, когда я расскажу немного об истории того, что я узнал об обучении студентов с помощью манипуляций и репрезентаций.В 1960-х годах Джером Брунер ввел термины активный, иконический и символический, чтобы описать, как студенты продвигаются от использования манипуляторов к созданию рисунков, основанных на манипуляциях, к использованию только чисел и символов. Сегодня мы можем назвать эти шаги конкретными, репрезентативными (полубетонными) и абстрактными. Сингапурская математика использует термины конкретный, графический и абстрактный. Все эти три набора терминов относятся к одной и той же основной стратегии мастерского использования манипуляторов для демонстрации математической идеи, затем ученики излагают эту идею с помощью бумаги и карандаша (повторно представляют ее) и, наконец, используют только числа и символы для обозначения математической идеи.
Эти представления представляют собой стратегии решения математических задач, которые могут использовать учащиеся. Я надеюсь, что вы терпите меня, когда я расскажу немного об истории того, что я узнал об обучении студентов с помощью манипуляций и репрезентаций.В 1960-х годах Джером Брунер ввел термины активный, иконический и символический, чтобы описать, как студенты продвигаются от использования манипуляторов к созданию рисунков, основанных на манипуляциях, к использованию только чисел и символов. Сегодня мы можем назвать эти шаги конкретными, репрезентативными (полубетонными) и абстрактными. Сингапурская математика использует термины конкретный, графический и абстрактный. Все эти три набора терминов относятся к одной и той же основной стратегии мастерского использования манипуляторов для демонстрации математической идеи, затем ученики излагают эту идею с помощью бумаги и карандаша (повторно представляют ее) и, наконец, используют только числа и символы для обозначения математической идеи.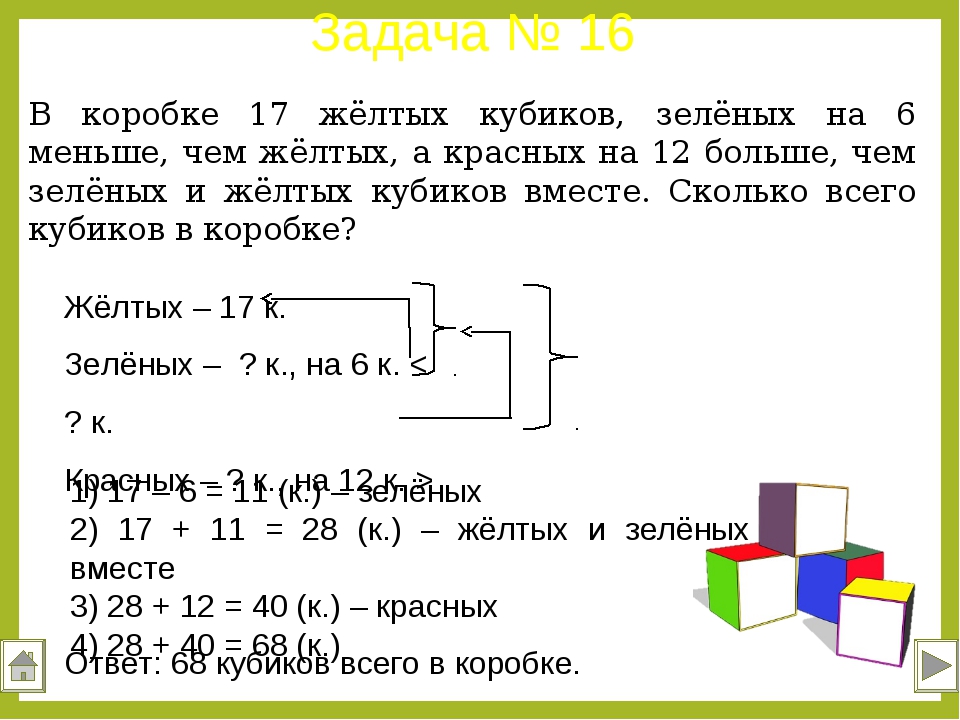 представляют это.
представляют это.
Я бы посоветовал студентам сначала поработать с такими манипуляторами, как счетчики плюшевых мишек, маленькие кубики или даже бобы. Они помогают показать взаимосвязь между ситуациями, о которых учащиеся читают в словесной задаче. Лучше всего, чтобы они использовали шаблон для представления своей идеи, используя десятикратную рамку, числовую связь, массив или модель области и ленточную диаграмму (полубетонные, графические или пиктограммы). Наконец, они поймут значение уравнения (абстрактное или символическое представление), когда они его напишут.
Если вы ищете стратегии решения задач по математике в детском саду до 4-го класса, вы найдете нижеприведенные загружаемые шаблоны очень полезными. Используя шаблоны, вы можете дать учащимся стратегии для чтения текстовых задач и создания представлений для их решения или даже дать им представление и предложить им создать текстовые задачи. Используйте эти загружаемые шаблоны, чтобы дать учащимся стратегии решения математических задач, включающие сложение, вычитание, умножение и деление.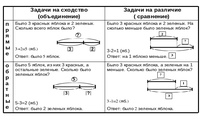 Распечатайте их и используйте сегодня в своем классе!
Распечатайте их и используйте сегодня в своем классе!
Детский сад и 1 класс — добавление
Ожидается, что в младших классах учащиеся только прибавят.Типичная проблема со словами может быть такой: «У Криса три апельсина и два яблока. Сколько фруктов у Криса вместе? » Студенты могут смоделировать задачу, используя кубики разного цвета. В загружаемом шаблоне есть место для вопроса, после чего учащиеся могут нарисовать рисунок на основе своих манипуляций. Ключевые полуабстрактные представления для этих студентов — десять рамок и числовые связи. В частности, с числовыми связями учащиеся должны думать о частях и итогах. Наконец, студенты пишут дополнительное предложение.
Для добавления доступны два шаблона. В первом есть один десятифрейм, предназначенный для детского сада, где ученики добавляют только в пределах десяти. Во втором есть две десятичные рамки, ориентированные на первый класс, где ученики складывают в пределах двадцати. Студентов продвинутого уровня можно подтолкнуть к представлению своих дополнительных предложений с помощью числовой линии, но это не входит в эту загрузку.
1 и 2 классы — Сложение и вычитание
По мере того, как учащиеся переходят в 1-й и 2-й классы, они узнают о взаимосвязи между сложением и вычитанием.Концептуально это отличается от ранней работы с простым добавлением. Стратегии решения проблем со сложением слов с двумя слагаемыми могут быть шаблонными. Два числа в задаче со словом необходимо сложить, но когда учащиеся сталкиваются с проблемами в словах с отсутствующей частью, у них должны быть стратегии и представления, чтобы думать о частях и целых.
В шаблоне для сложения и вычитания вы найдете числовые связи и ленточную диаграмму. Каждый шаблон имеет рамку с двумя числовыми связями, одна с удаленной «целиком», а другая — с одной из «частей».Учащимся необходимо прочитать задачу и решить, является ли проблема типом отсутствующей части или отсутствующей целой. Здесь нам нужно связать чтение с математикой. Точно так же учащиеся должны заполнить ленточную диаграмму, используя идеи части и целого, но на этот раз используя знак «?» или буква как переменная, обозначающая неизвестное.
Наконец, учащиеся должны написать хотя бы одно предложение сложения или вычитания, чтобы представить проблему с помощью знака «?» или переменная для неизвестного. Затем они могут написать числовое предложение, показывающее «решение», вместо вопросительного знака или переменной.Студентов продвинутого уровня можно подтолкнуть к представлению числовых предложений в числовой строке, но это не входит в эту загрузку.
Оценка 3 и 4 — Умножение и деление
Опираясь на работу во втором классе, учащиеся 3 и 4 классов должны применять стратегии решения словесных задач, включающие умножение и деление. Эти задачи требуют другого представления, чем стратегии математических задач со словами, включающие сложение и вычитание.
Загружаемый шаблон для классов 3 и 4 включает место для модели массива, модели области и ленточной диаграммы. Для ясности: учащиеся могут представлять задачи умножения и деления слов, используя любое из этих трех представлений:
Вы можете видеть, что эта серия абстрактных представлений умножения и деления переходит от более конкретных (полуабстрактных) версий, где вы можете считать точки или квадраты, к более абстрактным версиям, где студенты переходят от счета к поиску решений. Это также помогает учащимся на начальном этапе использовать переменные для представления неизвестных, поскольку они могут маркировать отсутствующие части модели области или массива буквой.
Это также помогает учащимся на начальном этапе использовать переменные для представления неизвестных, поскольку они могут маркировать отсутствующие части модели области или массива буквой.
В последнем поле загружаемого шаблона студентам предлагается написать уравнение, используя переменную или вопросительный знак для неизвестного, а затем «решить» его. Под решением я подразумеваю не использование алгебраических шагов (т. Е. Деление обеих сторон на три), а вместо этого просто написать «x = 7» в случае примера, приведенного непосредственно выше.Учащиеся могли использовать любую форму рассуждений, в том числе вернуться к использованию физических счетчиков и разделить их на равные группы.
Как стандарты математической практики связаны с использованием шаблонов
Я хочу поделиться некоторыми мыслями о том, как эти загружаемые шаблоны можно использовать для разработки стратегий учащихся по решению математических задач со словами и использования Стандартов математической практики (SMP).
SMP 1: разбираться в проблемах и настойчиво их решать.
Когда студентов просят составить схему, они должны четко понимать, что такое части и целое. Предоставление им представлений, таких как числовые связи, модели площадей и массивов или ленточные диаграммы, помогает им понять проблемы и взаимосвязи элементов, которые они обнаруживают при чтении слова «проблема».
SMP 2: Размышляйте абстрактно и количественно.
Когда учащиеся создают представление, такое как в Загрузке 4 (3 прямоугольника «x» равны 21), это абстрактное представление.Он ничего не говорит о том, в чем проблема. Когда ученики читают задачу о количестве (три игрушки общей стоимостью 21 доллар) и составляют ленточную диаграмму, они переходят от количеств к абстракциям. Другой способ использования этих шаблонов — заполнить ленточную диаграмму (или модель массива или области) и попросить учащихся заполнить остальные поля. Другими словами, ученики будут создавать свои собственные задачи с текстом из ленточной диаграммы. Они начинают с абстрактного представления и приходят к количественной идее (это может быть 21 яблоко и три человека или 21 шоколад и три коробки и т. Д.).
Они начинают с абстрактного представления и приходят к количественной идее (это может быть 21 яблоко и три человека или 21 шоколад и три коробки и т. Д.).
SMP 4: Модель с математикой.
Такие модели, такие как модели с областями и ленточные диаграммы, если они будут введены на раннем этапе, помогут учащимся, когда они используют модели с областями в старших классах для моделирования более сложных задач.
SMP 7: Ищите и используйте структуру.
Чтение задач со словами, а затем создание представлений с использованием шаблонов поможет учащимся искать ключевые слова и то, как они соотносятся со структурой частей и целых, строк и столбцов, факторов, итогов и делителей.Просмотр общих базовых структур с использованием числовых связей, десяти рамок, моделей площадей и массивов, а также ленточных диаграмм помогает укрепить общие базовые структуры, которые появляются в различных текстовых задачах.
Резюме
Загрузите и используйте мои бесплатные шаблоны, чтобы помочь студентам установить связь между задачами со словами и уравнениями, которые представляют эти проблемы. Когда вы это сделаете, вы будете вовлекать учащихся в использование изложенных выше Стандартов математической практики, давая им возможность представить себе в голове проблемы со словами и создать представления, которые показывают взаимосвязь задействованных количеств.
Когда вы это сделаете, вы будете вовлекать учащихся в использование изложенных выше Стандартов математической практики, давая им возможность представить себе в голове проблемы со словами и создать представления, которые показывают взаимосвязь задействованных количеств.
Решение вопросов Word
МНОГО примеров!
В алгебре мы часто задаем вопросы, например:
Пример: Сэм и Алекс играют в теннис.
В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр.
Сколько игр сыграл Алекс?
Как мы их решаем?
Уловка состоит в том, чтобы разбить решение на две части:
Превратите английский в алгебру.
Затем решите с помощью алгебры.
Превращение английского в алгебру
Превратить английский в алгебру помогает:
- Прочтите сначала все
- Сделайте эскиз , если возможно
- Назначьте букв для значений
- Найдите или разработайте формул
Вам также следует записать , что на самом деле требуется для , чтобы вы знали, куда вы собираетесь и когда вы прибыли!
Также ищите ключевые слова:
| Когда вы видите | Думаю | |
|---|---|---|
сложить, итого, сумма, увеличить, больше, вместе, вместе, плюс, более | + | |
минус, меньше, разница, меньше, уменьшено, уменьшено | – | |
умноженное на умножение на произведение, множитель | × | |
разделенное, частное, на, из, соотношение, соотношение, процент, ставка | ÷ | |
| увеличить или уменьшить | геометрия формулы | |
| Скорость, скорость | расстояние формулы | |
| Сколько дней, часов, минут, секунд | раз |
Мыслить ясно
Некоторые формулировки могут быть хитрыми, из-за чего трудно думать «правильно», например:
$
Пример: У Сэма на 2 доллара меньше, чем у Алекса.
 Как это записать в виде уравнения?
Как это записать в виде уравнения?
- Пусть S = долларов, у Сэма
- Пусть A = долларов у Алекса
Теперь … это то, что: S — 2 = A
или должно быть: S = A — 2
или должно быть: S = 2 — A
Правильный ответ: S = A — 2
( S — 2 = A — распространенная ошибка, так как в вопросе написано «Сэм … на 2 меньше … Алекс»)
Пример: на нашей улице собак вдвое больше, чем кошек.Как это записать в виде уравнения?
- Пусть D = количество собак
- Пусть C = количество кошек
Теперь … это то, что: 2D = C
или должно быть: D = 2C
Подумайте внимательно!
Правильный ответ: D = 2C
( 2D = C — распространенная ошибка, так как в вопросе написано «дважды … собаки … кошки»)
Примеры
Давайте начнем с очень простого примера , чтобы увидеть, как это делается:
Пример. Прямоугольный сад размером 12 х 5 м.
 Какова его площадь?
Какова его площадь?
Превратите английский в алгебру:
Эскиз:
.
Письма:
- Используйте w для ширины прямоугольника: w = 12 м
- Используйте h для высоты прямоугольника: h = 5 м
Формула для площади прямоугольника: A = w × h
Нас спрашивают о Районе.
Решить:
A = ш × в = 12 × 5 = 60 м 2
Площадь 60 кв.м .
Теперь попробуем пример сверху страницы:
Пример: Сэм и Алекс играют в теннис. В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр. Сколько игр сыграл Алекс?
Превратите английский в алгебру:
Письма:
- Используйте S , чтобы узнать, сколько игр Сэм сыграл
- Используйте A , чтобы узнать, сколько игр сыграл Алекс.
Мы знаем, что Сэм сыграл на 4 игры больше, чем Алекс, поэтому: S = A + 4
И мы знаем, что вместе они сыграли 12 игр: S + A = 12
Нас спрашивают, сколько игр сыграл Алекс: A
Решить:
Начать с: S + A = 12
S = A + 4 , поэтому мы можем
заменить S на «A + 4»: (A + 4) + A = 12
Упростить: 2A + 4 = 12
Вычтем 4 с обеих сторон: 2A = 12-4
Упростить: 2A = 8
Разделите обе части на 2: A = 4
Это означает, что Алекс сыграл 4 игры в теннис.
Проверка: Сэм сыграл на 4 игры больше, чем Алекс, поэтому Сэм сыграл 8 игр.
Вместе они сыграли 8 + 4 = 12 игр. Да!
Пример посложнее:
Пример: Алекс и Сэм также создают таблицы.
Вместе они делают 10 столов за 12 дней.
Алекс, работая в одиночку, может заработать 10 за 30 дней.
Сколько времени потребуется Сэму, работая в одиночку, чтобы сделать 10 столов?
Превратите английский в алгебру:
Письма:
- Используйте a для скорости работы Алекса
- Используйте с для скорости работы Сэма
12 дней Алекса и Сэма — это 10 столов, поэтому: 12a + 12s = 10
30 дней одного Алекса — это тоже 10 столов: 30a = 10
Нас спрашивают, сколько времени потребуется Сэму, чтобы сделать 10 столов.
Решить:
30a = 10 , поэтому ставка Алекса (столов в день): a = 10/30 = 1/3
Начать с: 12a + 12s = 10
Положите «1/3» для a: 12 (1/3) + 12s = 10
.
Упростить: 4 + 12s = 10
Вычтем 4 с обеих сторон: 12s = 6
Разделите обе стороны на 12: s = 6/12
Упростить: с = 1/2
Это означает, что ставка Сэма составляет половину стола в день (быстрее, чем у Алекса!).
Итак, 10 столов займет у Сэма всего 20 дней.
Интересно, стоит ли Сэму платить больше?
И еще пример «подстановки»:
Пример: Дженна усиленно тренируется, чтобы пройти квалификацию к Национальным играм.
У нее обычный еженедельный распорядок, в одни дни она тренируется по пять часов в день, а в другие — по 3 часа в день.
В общей сложности она тренируется 27 часов в семидневную неделю. Сколько дней она тренируется по пять часов?
Письма:
- Количество «5 часовых» дней: d
- Количество «3-х часовых» дней: e
Мы знаем, что в неделе семь дней, поэтому: d + e = 7
И она тренируется 27 часов в неделю, из которых d 5 часов в день и e 3 часа в день: 5d + 3e = 27
Нас спрашивают, сколько дней она тренируется по 5 часов: d
Решить:
d + e = 7
Итак: e = 7 — d
Положим в 5d + 3e = 27 5d + 3 (7 − d) = 27
Упростить: 5d + 21 — 3d = 27
Вычтем 21 с обеих сторон: 5d — 3d = 6
Упростить: 2d = 6
Разделим обе части на 2: d = 3
Количество «5 часовых» дней — 3
Проверка : Она тренируется по 5 часов 3 дня в неделю, поэтому она должна тренироваться по 3 часа в день в остальные 4 дня недели.
3 × 5 часов = 15 часов, плюс 4 × 3 часа = 12 часов дает в сумме 27 часов
Некоторые примеры из Geometry:
Пример: круг имеет площадь 12 мм
2 , каков его радиус?
Письма:
- Используйте A для площади: A = 12 мм 2
- Используйте r для радиуса
И формула для площади: A = π r 2
У нас спрашивают радиус.
Решить:
Нам нужно переставить формулу, чтобы найти площадь
Начать с: A = π r 2
Поменять местами стороны: π r 2 = A
Разделим обе части на π : r 2 = A / π
Извлечь квадратный корень из обеих частей: r = √ (A / π)
Теперь мы можем использовать формулу: r = √ (12/ π)
И получаем: r = 1.954 (до 3-х мест)
Пример: куб имеет объем 125 мм
3 , какова его площадь поверхности?
Сделайте быстрый набросок:
Письма:
- Используйте V для объема
- Используйте A для Area
- Используйте s для длины стороны куба
Формулы:
- Объем куба: В = с 3
- Площадь куба: A = 6s 2
У нас спрашивают площадь.
Решить:
Первая тренировка с по формуле объема:
Начать с: В = с 3
Поменять местами стороны: с 3 = V
Извлечь кубический корень с обеих сторон: s = ∛ (V )
И получаем: s = ∛ (125 ) = 5
Теперь мы можем рассчитать площадь поверхности:
Начать с: A = 6s 2
И получаем: А = 6 (5) 2
A = 6 × 25 = 150 мм 2
Пример о деньгах:
Пример: Джоэл работает в местной пиццерии.Когда он работает сверхурочно, он зарабатывает в 1¼ раза больше обычного.
Одну неделю Джоэл проработал 40 часов по обычной ставке, а также 12 часов сверхурочно. Если Джоэл заработал за эту неделю 660 долларов, какова его нормальная ставка заработной платы?
Письма:
- Обычная ставка оплаты труда Джоэля: N $ в час
Формулы:
- Джоэл работает 40 часов по цене N долларов в час = 40 долларов США
- Когда Джоэл работает сверхурочно, он зарабатывает в 1¼ раза больше обычной ставки = 1 доллар.
 25N в час
25N в час - Джоэл работает 12 часов по цене 1,25 доллара в час = (12 × 1 фунт) = 15 долларов
- А вместе он заработал 660 долларов, итак:
$ 40N + $ (12 × 1¼N) = 660 $
У нас спрашивают нормальную ставку зарплаты Джоэла в $ N.
Решить:
Начните с $ 40N + $ (12 × 1¼N) = 660 $
Упростить: 40N + 15N = 660 $
Еще более упростите: 55 долларов США = 660 долларов США
Разделим обе стороны на 55: $ N = 12 $
Итак, обычная ставка оплаты труда Джоэла составляет 12 долларов в час.
Чек
Обычная ставка оплаты труда Джоэла составляет 12 долларов в час, поэтому его сверхурочная ставка составляет 1¼ × 12 долларов в час = 15 долларов в час.Таким образом, его обычная зарплата 40 × 12 = 480 долларов плюс его сверхурочная работа в размере 12 × 15 долларов = 180 долларов дает нам в сумме 660
долларов.
Подробнее о деньгах на этих двух примерах, связанных со сложным процентом
Пример: Алекс кладет 2000 долларов в банк под 11% годовых.
 Сколько это будет стоить через 3 года?
Сколько это будет стоить через 3 года?
Это формула сложных процентов:
Итак, мы будем использовать эти буквы:
- Текущая стоимость PV = 2000 долларов США
- Процентная ставка (в десятичном формате): r = 0.11
- Количество периодов: n = 3
- Future Value (значение, которое мы хотим): FV
Нас спрашивают о будущей стоимости: FV
Решить:
Начать с: FV = PV × (1 + r) n
Добавьте то, что мы знаем: FV = $ 2000 × (1 + 0,11) 3
Вычислить: FV = $ 2000 × 1,367631
Вычислим: FV = 2735 долларов.26 (с точностью до цента)
Пример: Роджер положил 1000 долларов на сберегательный счет. На заработанные деньги ежегодно начислялись проценты по той же ставке. Через девять лет депозит Роджера вырос до 1 551,33 доллара США
Какова была годовая процентная ставка по сберегательному счету?
Формула сложных процентов:
с:
- Текущая стоимость PV = 1000 долларов США
- Процентная ставка (желаемое значение): r
- Количество периодов: n = 9
- Будущая стоимость: FV = 1551 доллар.
 33
33
Нас спрашивают о процентной ставке:
р.
Решить:
Начать с: FV = PV × (1 + r) n
Добавьте то, что мы знаем: 1551,33 доллара = 1000 долларов × (1 + r) 9
Поменять стороны: 1000 $ × (1 + r) 9 = 1551,33 $
Разделите обе стороны на 1000: (1 + r) 9 = 1551,33 доллара США / 1000 долларов США
Упростить: (1 + r) 9 = 1.55133
Корень 9-й степени: 1 + r = 1,55133 (1/9)
Вычислить: 1 + r = 1.05
Вычислить: r = 0,05 = 5%
Таким образом, годовая процентная ставка составляет 5%
Чек : 1000 долларов × (1,05) 9 = 1000 долларов × 1,55133 = 1551,33 доллара
И пример вопроса о соотношении:
Пример: В начале года соотношение мальчиков и девочек в классе было 2: 1
Но теперь, полгода спустя, четыре мальчика покинули класс и появились две новые девочки. Соотношение мальчиков и девочек сейчас составляет 4: 3
Соотношение мальчиков и девочек сейчас составляет 4: 3
Сколько всего студентов сейчас?
Письма:
- Кол-во мальчиков сейчас: б
- Количество девочек сейчас: г
Коэффициент текущей ликвидности 4: 3
b г = 4 3
Который можно переставить на 3b = 4g
На начало года было (b + 4) мальчиков и (g — 2) девочек, и соотношение было 2: 1
б + 4 г — 2 = 2 1
, который можно переставить на b + 4 = 2 (g — 2)
Нас спрашивают, сколько всего сейчас студентов: b + g
Решить:
Начать с: b + 4 = 2 (г — 2)
Упростить: b + 4 = 2g — 4
Вычтем 4 с обеих сторон: b = 2g — 8
Умножаем обе стороны на 3 (получаем 3b): 3b = 6g — 24
Помните 3b = 4g : 4g = 6g — 24
Вычтем 6g с обеих сторон : −2g = -24
Разделим обе части на −2: г = 12
Всего девушек 12 !
И 3b = 4g , поэтому b = 4g / 3 = 4 × 12/3 = 16 , так что имеется 16 мальчиков
Таким образом, сейчас в классе 12 девочек и 16 мальчиков, всего человек — 28 человек — человек.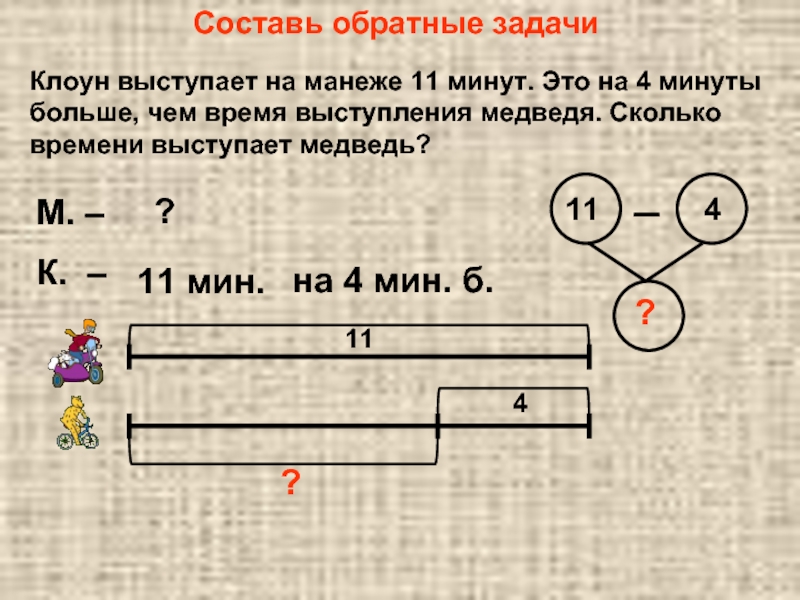
Чек
Сейчас 16 мальчиков и 12 девочек, поэтому соотношение мальчиков и девочек составляет 16: 12 = 4: 3.
В начале года было 20 мальчиков и 10 девочек, поэтому соотношение было 20: 10 = 2: 1
А теперь для некоторых квадратных уравнений:
Пример: произведение двух последовательных четных целых чисел равно 168. Что такое целые числа?
Последовательный означает один за другим. И они , даже , так что они могут быть 2 и 4, или 4 и 6 и т. Д.
Мы назовем меньшее целое число n , поэтому большее целое число должно быть n + 2
И нам говорят, что произведение (то, что мы получаем после умножения) равно 168, поэтому мы знаем:
п (п + 2) = 168
Нас спрашивают целые числа
Решить:
Начать с: n (n + 2) = 168
Развернуть: n 2 + 2n = 168
Вычтем 168 с обеих сторон: n 2 + 2n — 168 = 0
Это квадратное уравнение, и есть много способов его решить. Используя метод решения квадратного уравнения, мы получаем −14 и 12.
Используя метод решения квадратного уравнения, мы получаем −14 и 12.
Проверка −14: −14 (−14 + 2) = (−14) × (−12) = 168 ДА
Проверка 12: 12 (12 + 2) = 12 × 14 = 168 ДА
Итак, есть два решения: -14 и -12 — одно, 12 и 14 — другое.
Примечание: мы также могли попробовать «угадать и проверить»:
- Можно попробовать, скажем, n = 10: 10 (12) = 120 NO (слишком мало)
- Затем мы могли бы попробовать n = 12: 12 (14) = 168 ДА
Но если мы не вспомним, что умножение двух отрицаний дает положительный результат, мы можем пропустить другое решение (−14) × (−12).
А:
Пример: вы архитектор. Вашему клиенту нужна комната вдвое больше ширины. Им также нужна веранда шириной 3 метра по длинной стороне.
У вашего клиента 56 квадратных метров красивой мраморной плитки для покрытия всей площади.
Какой должна быть длина комнаты?
Давайте сначала сделаем набросок, чтобы все было правильно !:
Письма:
- длина помещения: л
- Ширина помещения: Вт
- Общая площадь с верандой: А,
Мы знаем:
- ширина комнаты равна половине ее длины: W = ½L
- общая площадь равна (ширина помещения + 3), умноженная на длину: A = (W + 3) × L = 56
Нас спрашивают о длине комнаты: L
Решить:
Начать с: (Ш + 3) × Д = 56
Заменитель W = ½L : (½L + 3) × L = 56
Упростить: ½L 2 + 3L = 56
Умножьте все члены на 2: L 2 + 6L = 112
Вычесть 112 с обеих сторон : L 2 + 6L — 112 = 0
Это квадратное уравнение , есть много способов его решить, на этот раз воспользуемся факторизацией:
Начать с: L 2 + 6L — 112 = 0
Два числа, которые умножаются и дают ac = −112,
и
сложить, чтобы получить b = 6, будут 14 и −8: L 2 + 14L — 8L — 112 = 0
Группа: L (L +14) — 8 (L + 14) = 0
Группа: (L — 8) (L + 14) = 0
Итак, L = 8 или -14
Есть два решения квадратного уравнения, но только одно из них возможно, так как длина комнаты не может быть отрицательной!
Так длина помещения 8 м
Чек
L = 8, поэтому W = ½L = 4
Итак, площадь прямоугольника = (W + 3) × L = 7 × 8 = 56
Вот и мы. ..
..
… Я надеюсь, что эти примеры помогут вам понять, как отвечать на словесные вопросы. А как насчет практики?
Стратегии решения задач — математика для учителей начальной школы
Вернитесь к первой задаче в этой главе, проблеме ABC. Что вы сделали, чтобы решить эту проблему? Даже если вы не разобрались с этим полностью самостоятельно, вы, вероятно, работали над решением и выяснили, что не работает.
В отличие от упражнений, простых рецептов решения проблемы не бывает. Вы можете становиться все лучше и лучше в решении проблем, как путем наращивания базовых знаний, так и просто практикуясь. По мере того, как вы решаете больше проблем (и узнаете, как их решали другие люди), вы изучаете стратегии и методы, которые могут быть полезны. Но ни одна стратегия не работает каждый раз.
Джордж Полиа был великим чемпионом в области , обучая навыкам эффективного решения проблем.Он родился в Венгрии в 1887 году, получил степень доктора философии. в Университете Будапешта и был профессором Стэнфордского университета (среди других университетов). Он написал множество статей по математике и три книги, самая известная из которых — «Как это решить». Полиа умерла в 1985 году в возрасте 98 лет.
в Университете Будапешта и был профессором Стэнфордского университета (среди других университетов). Он написал множество статей по математике и три книги, самая известная из которых — «Как это решить». Полиа умерла в 1985 году в возрасте 98 лет.
Джордж Полиа, около 1973 г.
В 1945 году Полиа опубликовал короткую книгу How to Solve It , в которой был дан четырехэтапный метод решения математических задач:
- Во-первых, вы должны понять проблему.
- Разобравшись, составьте план.
- Осуществите план.
- Оглянитесь на свою работу. Как могло быть лучше?
Это все хорошо, но как на самом деле сделать эти шаги?!?! Шаги 1 и 2 особенно загадочны! Как вы «составляете план»? Вот где вам понадобятся некоторые инструменты в вашем наборе инструментов и некоторый опыт, на который можно опираться.
С 1945 года было написано много, чтобы объяснить эти шаги более подробно, но правда в том, что они больше искусство, чем наука.Вот где математика становится творческим занятием (и становится таким увлекательным). Мы сформулируем некоторые полезные стратегии решения проблем, но такой список никогда не будет полным. Это действительно только начало, которое поможет вам на вашем пути. Лучший способ научиться решать проблемы — хорошо выучить справочный материал, а затем решить множество проблем!
Мы уже видели одну стратегию решения проблем, которую мы называем «желаемое за действительное». Не бойтесь менять проблему! Задайте себе вопросы «а что, если»:
- Что, если бы картина была другой?
- Что, если бы числа были проще?
- Что, если я просто придумал какие-то числа?
Вы должны обязательно вернуться к исходной проблеме в конце, но принятие желаемого за действительное может быть мощной стратегией для начала.
Это подводит нас к самой важной стратегии решения проблем:
Стратегия решения проблем 2 (Попробуйте что-нибудь!). Если вы действительно пытаетесь решить проблему, все дело в том, что вы не знаете, что делать прямо на старте. Вам нужно просто что-то попробовать! Приложите карандаш к бумаге (или стилус к экрану, или мел к доске, или что-то еще!) И попробуйте что-нибудь. Часто это важный шаг в понимании проблемы; просто немного повозитесь с этим, чтобы понять ситуацию и выяснить, что происходит.
И не менее важно: если то, что вы попробовали сначала, не работает, попробуйте что-нибудь другое! Поиграйте с проблемой, пока не почувствуете, что происходит.
Задача 2 (Окупаемость)
На прошлой неделе Алекс занял деньги у нескольких своих друзей. В конце концов, ему заплатили на работе, поэтому он принес в школу наличные, чтобы выплатить долги. Сначала он увидел Брианну и отдал ей четверть денег, которые принес в школу. Затем Алекс увидел Криса и отдал ему 1/3 того, что у него осталось после того, как он заплатил Брианне.Наконец, Алекс увидел Дэвида и отдал ему половину того, что у него осталось. Кто получил больше всего денег от Алекса?
Думать / Пара / Поделиться
После того, как вы некоторое время поработали над проблемой самостоятельно, обсудите свои идеи с партнером (даже если вы еще не решили ее). Что ты пробовал? Что вы узнали о проблеме?
Эта проблема поддается двум конкретным стратегиям. Пробовали ли вы что-нибудь из этого, когда работали над проблемой? Если нет, прочтите о стратегии, а затем попробуйте ее перед просмотром решения.
Стратегия решения проблем 3 (Нарисуйте картинку). Некоторые задачи, очевидно, связаны с геометрической ситуацией, и ясно, что вы хотите нарисовать картинку и пометить всю данную информацию, прежде чем пытаться ее решить. Но даже для не геометрической задачи, как эта, визуальное мышление может помочь! Можете ли вы изобразить что-то в ситуации картинкой?
Нарисуйте квадрат, представляющий все деньги Алекса. Затем заштрихуйте 1/4 квадрата — вот что он отдал Брианне.Как картинка может помочь решить проблему?
После того, как вы поработали над проблемой самостоятельно, используя эту стратегию (или если вы полностью застряли), вы можете посмотреть решение кого-то другого.
Стратегия решения проблем 4 (Сводные числа). Отчасти эта проблема усложняется тем, что она связана с деньгами, но цифры не приводятся. Это означает, что числа не должны иметь значения. Так что просто придумайте их!
Вы можете работать наперед: предположим, у Алекса была определенная сумма денег, когда он пришел в школу, скажем, 100 долларов.Затем выясните, сколько он дает каждому человеку. Или вы можете работать в обратном направлении: предположим, у него осталась какая-то определенная сумма в конце, например, 10 долларов. Поскольку он отдал Крису половину того, что у него осталось, это означает, что у него было 20 долларов, прежде чем он столкнулся с Крисом. Теперь поработайте в обратном направлении и выясните, сколько получил каждый человек.
Следите за решением только после того, как опробуете эту стратегию на себе.
Если вы используете стратегию «Прибавить числа», действительно важно помнить, о чем спрашивала исходная проблема! Не стоит отвечать примерно так: «У всех по 10 долларов.«Это не так в исходной задаче; это артефакт чисел, которые вы составили. Так что после того, как вы все проработаете, обязательно перечитайте задачу и ответьте на вопрос!
Задача 3 (Квадраты на шахматной доске)
Сколько квадратов любого возможного размера на шахматной доске 8 × 8? (Ответ не 64… Это намного больше!)
Помните, что первый шаг Поли — это понять проблему. Если вы не уверены, о чем спрашивают, или почему ответ не 64, обязательно спросите кого-нибудь!
Думать / Пара / Поделиться
После того, как вы некоторое время поработали над проблемой самостоятельно, обсудите свои идеи с партнером (даже если вы еще не решили ее).Что ты пробовал? Что вы узнали о проблеме, даже если не решили ее полностью?
Понятно, что вы хотите нарисовать картинку для этой проблемы, но даже с картинкой может быть трудно понять, нашли ли вы правильный ответ. Цифры становятся большими, и может быть трудно отслеживать свою работу. Ваша цель в конце — быть абсолютно уверенным в том, что вы нашли правильный ответ. Никогда не спрашивайте учителя: «Это правильно?» Вместо этого вы должны заявить: «Вот мой ответ, и вот почему я знаю, что он правильный!»
Стратегия решения проблем 5 (Попробуйте более простую задачу). Полиа предложил такую стратегию: «Если вы не можете решить проблему, вы можете решить более простую задачу: найти ее». Он также сказал: «Если вы не можете решить предложенную проблему, попробуйте сначала решить какую-нибудь связанную проблему. Можете ли вы представить себе более доступную связанную проблему? » В этом случае шахматная доска 8 × 8 довольно большая. Можете ли вы решить проблему для небольших плат? Как 1 × 1? 2 × 2? 3 × 3?
Конечно конечная цель — решить исходную проблему. Но работа с досками меньшего размера может дать вам некоторое представление и помочь разработать план (это шаг (2) Полии).
Стратегия решения проблем 6 (Работайте систематически). Если вы работаете над более простыми проблемами, полезно отслеживать, что вы выяснили и что меняется по мере усложнения проблемы.
Например, в этой задаче вы можете отслеживать, сколько квадратов 1 × 1 на каждой доске, сколько квадратов 2 × 2 на каждой доске, сколько квадратов 3 × 3 на каждой доске и т. Д. . Вы можете отслеживать информацию в таблице:
| размер платы | Количество квадратов 1 × 1 | Количество квадратов 2 × 2 | Количество квадратов 3 × 3 | Количество квадратов 4 × 4 | … |
| 1 по 1 | 1 | 0 | 0 | 0 | |
| 2 на 2 | 4 | 1 | 0 | 0 | |
| 3 на 3 | 9 | 4 | 1 | 0 | |
| … |
Стратегия решения проблем 7 (Используйте манипуляторы, чтобы помочь вам в расследовании). Иногда даже рисования изображения может быть недостаточно, чтобы помочь вам разобраться в проблеме. Наличие реальных материалов, которые вы перемещаете, иногда может очень помочь!
Например, в этой задаче может быть сложно отследить, какие клетки вы уже подсчитали. Вы можете вырезать квадраты 1 × 1, 2 × 2, 3 × 3 и так далее. На самом деле вы можете систематически перемещать меньшие клетки по шахматной доске, убедившись, что вы посчитаете все один раз и ничего не посчитаете дважды.
Стратегия решения проблем 8 (поиск и объяснение паттернов). Иногда числа в задаче настолько велики, что вы не можете сосчитать все вручную. Например, если бы задача в этом разделе касалась шахматной доски 100 × 100, вы бы не захотели пересчитывать все клетки вручную! Было бы гораздо более привлекательно найти узор на досках меньшего размера, а затем расширить этот узор, чтобы решить проблему для шахматной доски 100 × 100, просто вычислив.
Думать / Пара / Поделиться
Если вы еще этого не сделали, расширьте таблицу выше до шахматной доски 8 × 8, заполнив все строки и столбцы. Используйте свою таблицу, чтобы найти общее количество квадратов на шахматной доске 8 × 8. Тогда:
- Опишите все шаблоны, которые вы видите в таблице.
- Можете ли вы объяснить и обосновать любую из наблюдаемых закономерностей? Как вы можете быть уверены, что они продолжатся?
- Какой расчет вы бы сделали, чтобы найти общее количество клеток на шахматной доске 100 × 100?
(Мы скоро вернемся к этому вопросу.Так что, если вы прямо сейчас не уверены, как объяснить и обосновать обнаруженные вами закономерности, это нормально.)
Проблема 4 (Часы сломаны)
Эти часы разбиты на три части. Если вы сложите числа в каждой части, суммы будут последовательными числами. ( Последовательные числа — это целые числа, которые появляются одно за другим, например 1, 2, 3, 4 или 13, 14, 15.)
Можете ли вы разбить другие часы на другое количество частей, чтобы суммы были последовательными числами? Предположим, что на каждой части есть как минимум два номера и что ни один номер не поврежден (например,грамм. 12 не делится на две цифры 1 и 2.)
Помните, что ваш первый шаг — понять проблему. Разберитесь, что здесь происходит. Каковы суммы чисел на каждой фигуре? Они последовательные?
Думать / Пара / Поделиться
После того, как вы некоторое время поработали над проблемой самостоятельно, обсудите свои идеи с партнером (даже если вы еще не решили ее). Что ты пробовал? Какого прогресса вы добились?
Стратегия решения проблем 9 (Найдите математику, удалите контекст). Иногда проблема состоит из множества деталей, которые не важны или, по крайней мере, не важны для начала работы. Цель состоит в том, чтобы найти основную математическую задачу, затем вернуться к исходному вопросу и посмотреть, сможете ли вы решить ее с помощью математики.
В этом случае беспокоиться о часах и о том, как именно ломаются части, менее важно, чем беспокоиться о поиске последовательных чисел, суммирующих правильную сумму. Спросите себя:
- Какова сумма всех чисел на циферблате?
- Могу ли я найти два последовательных числа, которые дают правильную сумму? Или четыре последовательных числа? Или какую-то другую сумму?
- Как мне узнать, что я закончил? Когда мне перестать искать?
Конечно, решение вопроса о последовательных числах — это не то же самое, что решение исходной задачи.Вы должны вернуться и посмотреть, могут ли часы действительно разойтись, чтобы каждая часть давала вам одно из этих последовательных чисел. Возможно, вам удастся решить математическую задачу, но это не приведет к решению проблемы с часами.
Стратегия решения проблем 10 (проверьте свои предположения). При решении проблем легко ограничить свое мышление, добавив дополнительные предположения, которых нет в проблеме. Обязательно спросите себя: не слишком ли я ограничиваю свое мышление?
В задаче с часами, поскольку в первом решении часы сломаны радиально (все три части встречаются в центре, так что это похоже на разрезание пирога), многие люди предполагают, что именно так часы должны ломаться.Но проблема не требует, чтобы часы ломались радиально. Он может разбиться на такие части:
Вы предполагали, что часы сломаются определенным образом? Попробуйте решить проблему сейчас, если вы еще этого не сделали.
Вирусная математическая задача с двумя ответами разделяет Интернет
- Пользователь Twitter @pjmdoll поделился математической задачей: 8 ÷ 2 (2 + 2) =?
- Некоторые люди получили ответ 16, а некоторые — 1.
- Путаница связана с различием между современными и историческими интерпретациями порядка действий.
- Правильный ответ сегодня — 16. Ответ 1 был бы правильным 100 лет назад.
- Посетите домашнюю страницу INSIDER, чтобы узнать больше.
Известно, что вирусные математические уравнения разделяют людей в Интернете. Некоторые задачи настолько сложны, что кажутся невозможными, даже если они предназначены для учеников начальной школы.
Подробнее : 10 вирусных математических уравнений, которые поставили в тупик Интернет
Эта последняя вирусная проблема, о которой поделился пользователь Twitter @pjmdoll, является одним из таких уравнений.
—em ♥ ︎ (@pjmdolI) 28 июля 2019 г.
Уравнение: 8 ÷ 2 (2 + 2) =?
Каждый получает разные ответы.
—laur♏️ (@lauram_williams) 30 июля 2019 г.
—becca 10✧ * .✰LILY + BARBS DAY (@spaceywhy) 30 июля 2019 г.
—maggie (@BatmanOfficial_) 29 июля 2019 г.
—George W.Куш (@supermaddd) 29 июля 2019 г.
—Light💜 ᴮᵃⁿᵍᵗᵃⁿ ᶠᵒʳᵉᵛᵉʳ 💜 (@SakuraTsukimine) 29 июля 2019 г.
Вот правильный способ решения 8 ÷ 2 (2 + 2) =?
Сначала сложите числа в скобках.
8 ÷ 2 (4) =?
Теперь произведите умножение и деление слева направо.
8 ÷ 2 (4) = 4 (4) = 16.
Путаница вызвана различием между современными и историческими интерпретациями порядка операций, известными как PEMDAS:
- Круглые скобки
- Показатели
- Умножение и деление (слева направо)
- Сложение и вычитание (слева направо)
Похожая математическая задача стала вирусной в 2011 году, когда люди не могли прийти к единому мнению относительно ответа на 48 ÷ 2 (9 + 3).Преш Талвалкер, автор книги «Радость теории игр: введение в стратегическое мышление», объяснил противоречие на своем канале YouTube MindYourDecisions и в сообщении в своем блоге.
Люди, получившие число 1 как ответ на эту проблему, использовали устаревшую версию порядка операций, сначала умножая 2 (4), а затем деля 8 на 8, согласно Талуокеру. Этот ответ был бы правильным 100 лет назад. Но вставив уравнение в современный калькулятор, мы получим 16.Вы должны добавить еще один набор круглых скобок, чтобы получить ответ 1.
Люди получают разные ответы в зависимости от того, как они применяют порядок действий.
Талия Лакриц / ИНСАЙДЕР
Талуокер объясняет, что часть путаницы также вызвана тем, что в задаче двусмысленно установлен символ разделения.
«В учебниках всегда есть правильные скобки, или они объясняют, что нужно разделять», — пишет он в своем блоге. «Поскольку математический набор текста сегодня намного проще, мы почти никогда не видим ÷ как символ, вместо этого дроби записываются с числителем вертикально над знаменателем».
Вы можете посмотреть полное объяснение этого уравнения Талуокером ниже.
Решение проблем
Заявление об авторских правах для этой публикации услуг по оценке и оценке Авторизация Администратор Авторские права © 2000 | |||||||||||||||
HC1593866 — Карты для решения задач по математике HOPE Год 2 — Число и алгебра
Число надежды и алгебра — год 2
Стратегии решения проблем и навыки Карты по математике
Вставьте математическое решение задач и рассуждение.
Математические карточки «Стратегии решения проблем и навыки» предоставляют широкий спектр мотивирующих и интересных действий по решению проблем.
Для каждого уровня года, с 1 по 6 год, есть три поля, включающих:
• 30 карточек чисел и алгебры, плюс ответы
• 30 карточек измерений и геометрии, плюс ответы
• 30 карточек статистики и вероятностей, плюс ответы
Каждая коробка также включает карточку процесса решения проблем и карточку стратегии решения проблем, чтобы направлять и оказывать поддержку детям по мере их прохождения через каждый этап и набор коробок.
На лицевой стороне каждой карточки есть задача по математике, которую ученики должны решить, а на обратной стороне каждой карточки — дополнительное задание для более способных учеников. Задачи состоят из одного или нескольких шагов, требуют использования различных стратегий и навыков и сопровождаются красочными рисунками.
К функциям блоков «Решение проблем» относятся:
• Отличные ресурсы для поддержки решения проблем, важный компонент учебной программы по математике;
• Разнообразные, реальные и сложные задачи;
• Мероприятия, которые позволяют ученикам практиковать математические концепции, преподаваемые в классе, с помощью задач.

 ..» учителям
..» учителям ..» родителям
..» родителям
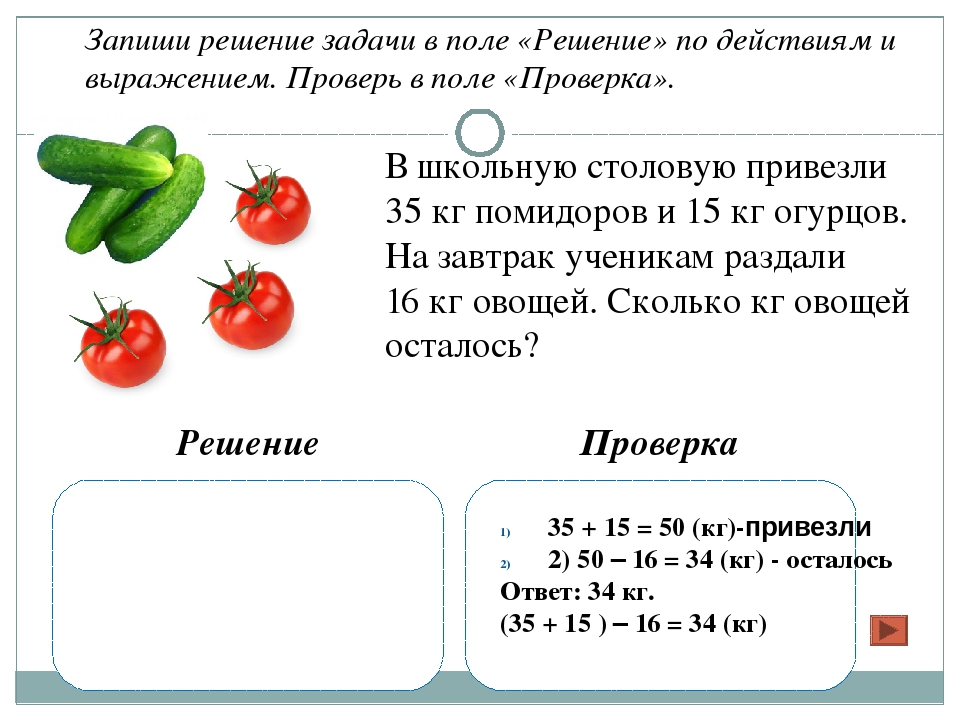


 Пора узнать тему нашего урока. Вам необходимо решить кроссворд.
Пора узнать тему нашего урока. Вам необходимо решить кроссворд.

 Белые карточки с не сложным заданием, нужно заполнить окошки. Зеленые карточки чуть по сложнее. Необходимо сравнить выражения. (Запись у доски).
Белые карточки с не сложным заданием, нужно заполнить окошки. Зеленые карточки чуть по сложнее. Необходимо сравнить выражения. (Запись у доски).
 25N в час
25N в час 33
33