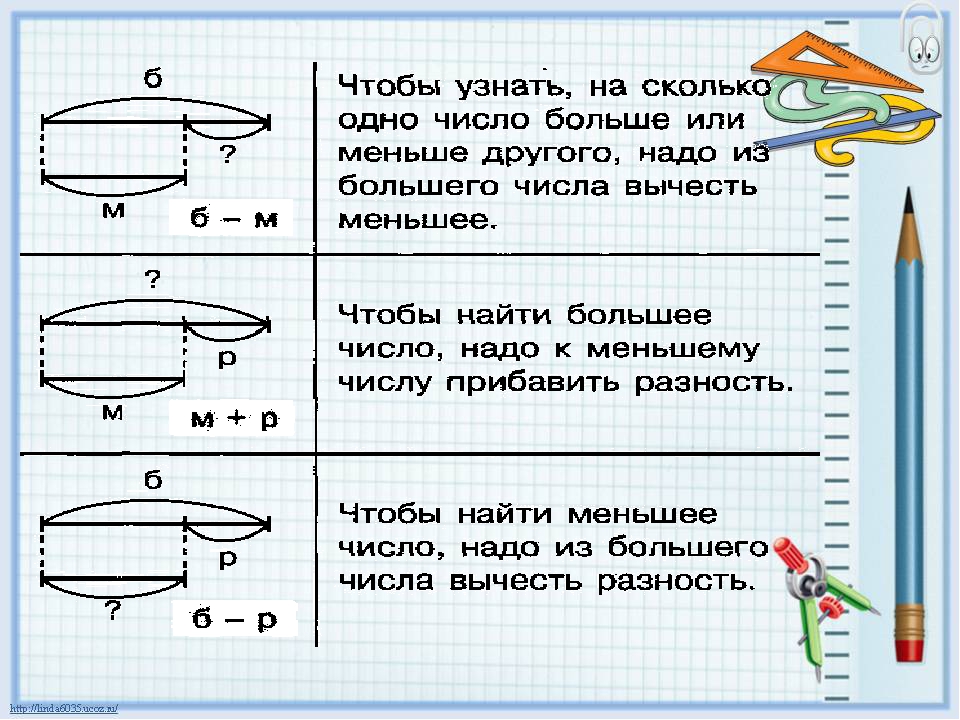
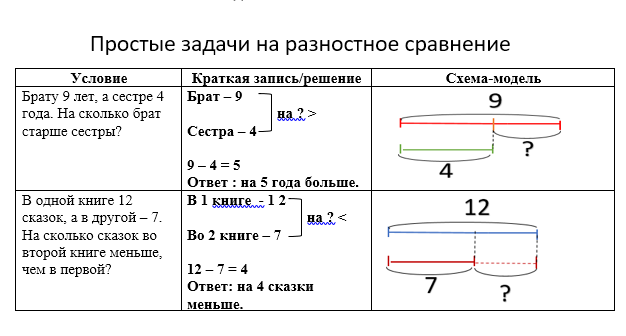
4 класс. Моро. Учебник №2. Ответы к стр. 60
Числа от 1 до 1000
Деление на двузначное и трёхзначное число
Письменное деление на двузначное число
Ответы к стр. 60
Объясни, как выполнено деление, по плану (с. 59).
_ 29736 |56 _ 136576 |64
280 |531 128 |2134
_173 _85
168 64
_56 _217
56 192
0 _256
256
0
Надо 29736 разделить на 56.
1) Выделяю первое неполное делимое. 297 (сотен).
2) Нахожу первую цифру частного. 297 : 56 = 5 (сотен).
3) Образую второе неполное делимое. 56 • 5 = 280, 297 — 280 = 17 (сотен). Добавляю оставшиеся 3 десятка — 173.
Добавляю оставшиеся 3 десятка — 173.
4) Нахожу вторую цифру частного. 173 : 56 = 3 (десятка).
5) Образую третье неполное делимое. 56 • 3 = 168, 173 — 168 = 5 (десятков). Добавляю оставшиеся 6 единиц — 56.
6) Нахожу третью цифру частного. 56 : 56 = 1.
Получилось частное 531.
Проверка. 56 • 531 = 29736 — деление выполнено верно, без остатка.
Надо 136576 разделить на 64.
1) Выделяю первое неполное делимое. 136 (тысяч).
2) Нахожу первую цифру частного. 136 : 64 = 2 (тысячи).
3) Образую второе неполное делимое. 64 • 2 = 128, 136 — 128 = 8 (тысяч). Добавляю оставшиеся 5 сотен — 85.
4) Нахожу вторую цифру частного. 85 : 64 = 1 (сотня).
5) Образую третье неполное делимое. 64 • 1 = 64, 85 — 64 = 21 (сотня). Добавляю оставшиеся 7 десятков — 217.
6) Нахожу третью цифру частного. 217 : 64 = 3 (десятка).
7) Образую четвёртое неполно делимое. 64 • 3 = 192, 217 — 192 = 25 (сотен).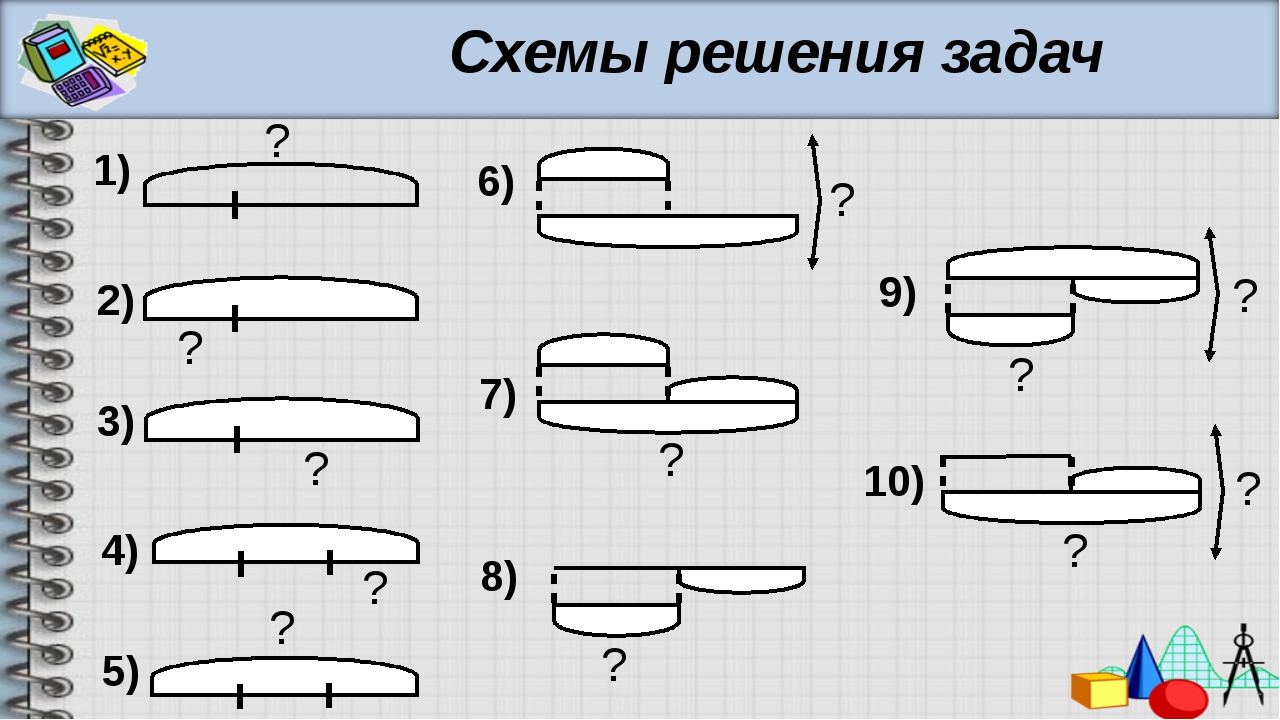 Добавляю оставшиеся 6 единиц — 256.
Добавляю оставшиеся 6 единиц — 256.
8) Нахожу четвёртую цифру частного. 256 : 64 = 4.
Получилось частное 2134.
Проверка. 64 • 2134 = 136576 — деление выполнено верно, без остатка.
226. 48984 : 52 91375 : 43 243144 : 72 351456 : 84
— 48984 |52 — 91375 |43
468 |942 86 |2125
_218 _53
208 43
_104 _107
104 86
0 _215
215
0
— 243144 |72 — 351456 |84
216 |3377 336 |4184
_271 _154
216 84
_554 _705
504 672
_554 _336
554 336
0 0
227. Реши задачи и сравни их решения.
Реши задачи и сравни их решения.
1) Теплоход за два дня прошёл 350 км. В первый день он был в пути 8 ч, а во второй — 6 ч. Какое расстояние он прошёл в каждый из дней, если шёл с одинаковой скоростью?
2) Теплоход в первый день был в пути 8 ч, а во второй — 6 ч, причём в первый день он прошёл на 50 км больше, чем во второй. Какое расстояние теплоход прошёл в каждый из этих дней, если шёл с одинаковой скоростью?
1-я задача
1) 8 + 6 = 14 (ч) — всего в пути
2) 350 : 14 = 25 (км/ч) — скорость теплохода
3) 25 • 8 = 200 (км) — прошёл теплоход в первый день
4) 25 • 6 = 150 (км) — прошёл теплоход во второй день
О т в е т: 200 км и 150 км.
2-я задача
1) 8 – 6 = 2 (ч) — больше шёл теплоход в первый день
2) 50 : 2 = 25 (км/ч) — скорость движения теплохода
3) 25 • 8 = 200 (км) — прошёл теплоход в первый день
4) 25 • 6 = 150 (км) — прошёл теплоход во второй день
О т в е т: 200 км и 150 км.
В обоих случаях находится скорость теплохода и вычисляется расстояние, которое он прошёл в каждый день. Но в первом случае скорость находится через общее время в пути, а во втором — через разницу во времени для первого и второго дня (разностное сравнение).
Но в первом случае скорость находится через общее время в пути, а во втором — через разницу во времени для первого и второго дня (разностное сравнение).
228. Фермеры продали 1364 т пшеницы, ржи — на 276 т меньше, чем пшеницы, а гречихи — в 8 раз меньше, чем ржи. Сколько тонн гречихи продали фермеры?
1) 1364 – 276 = 1088 (т) — ржи
2) 1088 : 8 = 136 (т) — гречихи
О т в е т: продали 136 т гречихи.
229. Проверь, верны ли равенства.
1428 : 42 = 2856 : 84 4507 • 18 = 81126
9408 – 936 = 8208 + 736 9512 : 29 = 328
1428 : 42 = 2856 : 84
34 = 34 — верно
9408 — 936 = 8208 + 736
8472 = 8944 — неверно
4507 • 18 = 81126
81126 = 81126 — верно
9512 : 29 = 328
328 = 328 — верно
230. Длина прямоугольника 8 см, периметр 24 см. Начерти такой же прямоугольник, раздели его на 2 равных треугольника. Найди площадь каждого треугольника.
Найди площадь каждого треугольника.
1) 24 : 2 – 8 = 4 (см) — ширина прямоугольника
2) 8 • 4 = 32 (см2) — площадь прямоугольника
3) 32 : 2 = 16 (см2) — площадь каждого треугольника
231. Один ученик умножил 1738 на 302 столбиком и получил в произведении 55516, другой на калькуляторе получил 524876. У кого из них верный ответ?
×1738
302
+ 3476
5214
524876 — правильный ответ получен на калькуляторе
Определи, сколько будет цифр в частном, и выполни деление. 17328 : 38
Первое неполное делимое 173, значит в частном будет 3 цифры.
— 17328 |38
152 |456
_212
190
_228
228
0
ЗАДАНИЕ НА ПОЛЯХ
ЦЕПОЧКА
РЕБУС
×487
45
+ 2435
1948
21915
ГДЗ по математике. Учебник. 4 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Учебник. 4 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 4 класс
4 класс. Моро. Учебник №2. Ответы к стр. 60
4.5 (89.74%) от 76 голосующих
ПНШ 4 класс. Математика. Учебник № 1, с. 16
Когда известен результат кратного сравнения
Ответы к с. 16
34. Рассмотри рисунок и скажи, на сколько равных частей разрезан торт. Какая часть торта лежит на лопатке?
Во сколько раз одна часть торта меньше, чем все оставшиеся части? Сколько граммов будет в одной части, если весь торт имеет массу 800 г? Запиши соответствующие вычисления.
Сколько граммов будет во всех оставшихся частях, кроме одной? Запиши соответствующие вычисления.
На 8 равных частей. Одна часть из восьми или одна восьмая часть.
Одна часть из восьми или одна восьмая часть.
Всего 8 частей: осталось 7 частей, 1 часть на лопатке. 7 : 1 = 7 – 1 часть торта меньше в 7 раз оставшихся частей.
Всего 8 частей, тогда 1 часть весит: 800 : 8 = 100 (г).
Вес оставшихся частей: 800 – 100 = 700 (г) или 100 • 7 = 700 (г).
35. Верёвку длиной 30 м нужно разрезать на две части так, чтобы одна часть была в 5 раз длиннее, чем другая. Сколько метров должно быть в каждой части?
Рассмотри схему к этой задаче и установи, какой из следующих вариантов решения является решением данной задачи.
1-й вариант 2-й вариант
1) 5 + 1 = 6 (ч.) 1) 30 м : 5 = 6 м
2) 30 м : 6 = 5 м 2) 30 м – 6 м = 24 м
3) 30 м – 5 м = 25 м
Перепиши выбранное решение с пояснением действий в тетрадь. Запиши ответ задачи.
Правильный первый вариант.
1) 5 + 1 = 6 (ч.) – количество частей верёвки
2) 30 м : 6 = 5 м – длина одной части верёвки (меньшей)
3) 30 м – 5 м = 25 м – длина пяти частей верёвки (большей)
О т в е т: меньшая часть 5 м, а большая – 25 м.
Ответы к заданиям. Математика. Учебник. Часть 1. Чекин А.Л. 2012 г.
Математика. 4 класс. Чекин А.Л.
4.8
/
5
(
50
голосов
)
Страница 37 — ГДЗ Математика 4 класс. Моро, Бантова. Учебник часть 2
Вернуться к содержанию учебника
Что узнали. Чему научились
Вопрос
22. 1) От двух противоположных берегов пруда навстречу друг другу поплыли одновременно два пловца и встретились через 10 мин. Первый плыл до встречи со скоростью 8 м/мин, второй — со скоростью 12 м/мин. Найди ширину пруда.
2) Измени задачу, чтобы она решалась так: 200 : 10 — 8 = 12. Ответ: 12 м/мин.
Ответ: 12 м/мин.
Подсказка
Повтори взаимосвязь между скоростью, временем и расстоянием.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
23. Составь задачу по чертежу и реши её.
Подсказка
Повтори взаимосвязь между скоростью, временем и расстоянием.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
24. Грузовая машина прошла 1500 км. Сколько горючего было израсходовано, если на каждые 50 км пути трубуется 16 л горючего?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
25.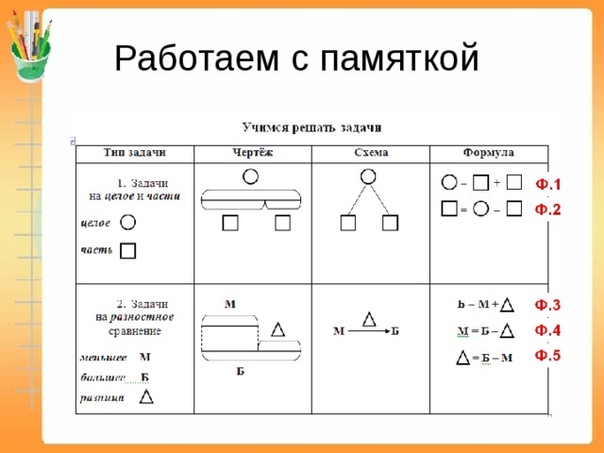 Площадь участка прямоугольной формы 3440 м2, его ширина 40 м. Найди длину участка.
Площадь участка прямоугольной формы 3440 м2, его ширина 40 м. Найди длину участка.
Составь и реши обратные задачи.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
26. В классе 20 парт. Длина крышки парты 110 см, ширина 50 см. Сколько нужно краски, чтобы покрасить крышки парт, если на 1 м2 требуется 100 г краски?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
27.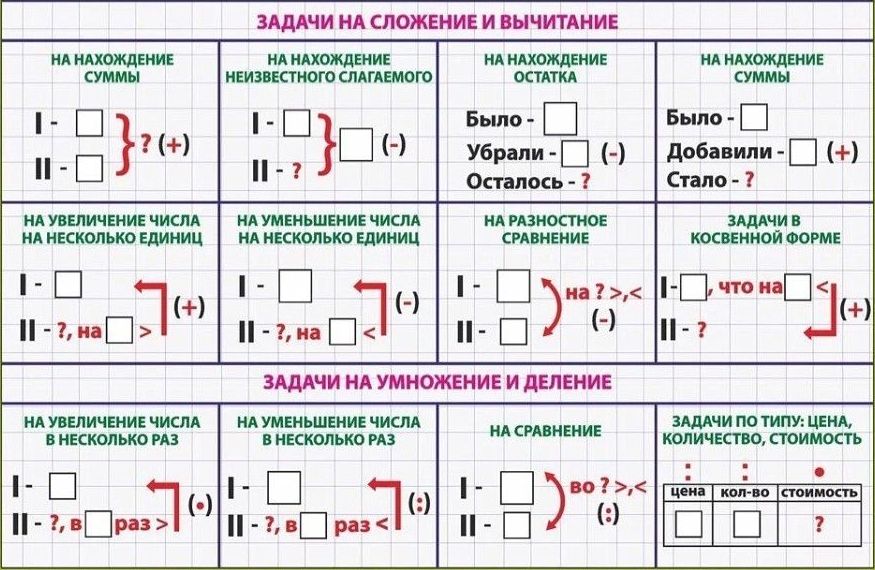 В трёх вагонах поезда едут 100 пассажиров. В первом и втором вагонах вместе 66 пассажиров, а во втором и третьем вагонах вместе 69 пассажиров. Сколько пассажиров в каждом вагоне?
В трёх вагонах поезда едут 100 пассажиров. В первом и втором вагонах вместе 66 пассажиров, а во втором и третьем вагонах вместе 69 пассажиров. Сколько пассажиров в каждом вагоне?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
28. Пройдя 2 м, девочка сделала 6 шагов. Сколько таких же шагов она сделает, пройдя 10 м? 100 м?
Подсказка
Повтори единицу длины — метр.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
1. Объясни на примере, как можно разделить число на произведение.
Объясни на примере, как можно разделить число на произведение.
Подсказка
Повтори, как делить на круглые числа.
Ты можешь составить другой пример.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
2. Составь пример, в котором нужно разделить на число, оканчивающееся нулём. Реши его с объяснением.
Подсказка
Повтори, как делить на круглые числа.
Ты можешь составить другой пример.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Магический квадрат
Подсказка
Магический квадрат — таблица, заполненная различными числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Ребус
Подсказка
Повтори алгоритм письменного деления многозначного числа.
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
© budu5.com, 2021
Пользовательское соглашение
Copyright
открытый урок по математике 4 класс
открытый урок по математике 4 класс
Автор: Любовь
Методическая копилка —
начальная школа
Математика, 4 класс
Учитель : Гусева Любовь Анатольевна
Раздел программы: « Деление на двузначное число»
Тема урока: Закрепление знаний и умений на деление на двузначное число.
Цели урока:
Совершенствовать навыки деления многозначных чисел на двузначное, умение читать многозначные числа, упражнять учащихся в переводе одних единиц длины в другие, вырабатывать навыки устного счёта;
Способствовать развитию мыслительных операций, воображения детей, интереса к предмету; на примере пчелы расширить представления детей о мире насекомых, о взаимосвязях в природе;
Создать условия для бережного отношения к окружающему нас животному миру.
Задачи урока:
Образовательные:
Закреплять знания деления многозначных чисел;
Развивать умения читать многозначные числа;
Развивающие:
Развитие памяти, внимания, творческого воображения, образного мышления;
Развитие речи, словарного запаса;
Воспитательные:
Воспитание стремления к получению новых знаний;
Воспитание коммуникативных качеств, умения слушать и высказывать своё
мнение;
Тип урока: Урок закрепления изученного материала.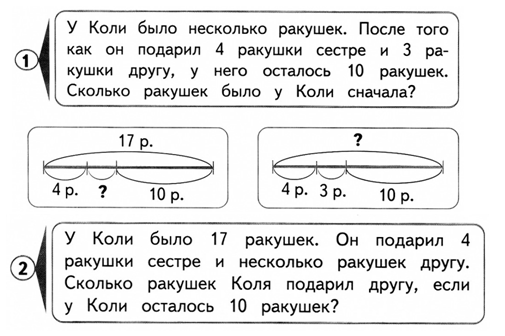
Методы обучения: словесный, наглядный;
Формы работы учащихся: индивидуальная, парная, фронтальная;
Приёмы: устный счёт, работа у доски, решение задач, примеров.
Технология: личностно- ориентированная.
Оборудование: пчела, « ульи», « пчелиные соты», карточки, учебники, письменные принадлежности, тетради.
Ход урока.
I.Организационный момент.
— Здравствуйте, ребята. Поприветствуйте гостей.
Посмотрите мне в глаза, улыбнитесь друг другу и тихонько сели.
Великая радость — работа.
В полях, за станком, за столом!
Работай до жаркого пота,
Работай без лишнего счёта-
Всё счастье земли – за трудом!
— Я не случайно начала наш сегодняшний урок стихотворением Валерия Яковлевича Брюсова. Сегодня нас ждёт большая работа. Справиться с ней смогут внимательные, любознательные, трудолюбивые и дружные ребята.
Справиться с ней смогут внимательные, любознательные, трудолюбивые и дружные ребята.
II.Устный счёт.
-Образцом трудолюбия , взаимовыручки нам будет служить маленькое существо, которое является одним из величайших тружеником во всём мире. А кто это, вы узнаете, разгадав русскую народную загадку «Лежит кучка поросят, кто ни тронет – завизжат». Сомневаетесь в ответе? А если вы решите устно примеры, а затем запишите ответы в порядке возрастания и соотнесите их с буквами, записанными около каждого примера, то получите ответ на загадку.
(Примеры записаны на доске)
Ы 4 · 8 – 27 : 3 = 23
Е 6 · (89-83) + 8 = 44
П 6 · 7 + 28 = 70
Ч 100 – 6 · 9 = 46
Л 90 – (3 6 + 30) = 24
70,46,44,24,23 /пчелы/
— Да, ребята, это пчелы – неутомимые труженики. Сегодня одна из них будет сопровождать нас на уроке.
— Пчелу почитали во все времена. Мед считали пищей богов.
Мед считали пищей богов.
III. Сообщение темы урока.
— Если заглянуть в улей, то можно увидеть, на первый взгляд, беспорядочно снующих пчел. Но это не так. Все в их жизни подчинено определенным законом, все находится в строгом порядке. Каждая пчела занимается своим делом, выполняя его на отлично. Пчелы хранят много тайны о себе, человек до сих пор не смог их всех разгадать.
Сегодня мы попробуем заглянуть в таинственный мир пчел. Но пчелы не расстаются со своими секретами легко, поэтому нам придется выполнить задания. Основными заданиями будут упражнение в делении на двузначное число. Справившись с ними, мы узнает много интересного. Итак, в путь за пчелой.
IV. Работа над закреплением пройденного материала.
— Её дорога начинается от улья. На пасеке обычно находится много ульев. Вот и мы у себя в классе «построим» пасеку.
(каждому надо решить пример, ответ будет номером улья. )
)
1189:41=29 2124:59=36
1530:34=45 3658:62=59
2. Задание на смекалку.
— Угадайте, сколько глаз у пчелки? У пчелы столько глаз, сколько у человека, ещё раз столько и еще раз полстолько. Сколько же глаз у пчёлки? (У пчелы 5 глаз.2 больших, состоящих в свою очередь из 10 тысяч глазков, и расположенных по бокам головы и 3 маленьких на лбу между ними).
3. Решение задачи на сравнение.
Рабочий день пчелы начинается с первым открывающимся цветком в 4 часа и закрывается в 20 часов. Рабочий день ученика длится с 8 до 12 часов. Во сколько раз больше работает пчела? На сколько часов ученик трудится меньше пчелы?
-Для удобства решения составим краткую запись.
-Выделим главные слова: о ком говорится в задаче?
Пчела-с 4ч. до 20ч.
Ученик- с 8ч до 12ч
В ? раз больше, на ? меньше
— Можем ли мы сразу ответить на вопрос задачи? (нет)
-Что нам нужно знать, чтобы ответить на него? (Нужно знать продолжительность рабочего дня пчелы и ученика?
-Можем мы узнать продолжительность рабочего дня пчелы, ученика? (Да) Как? Записываем первое действие. (20-4=16ч)-рабочий день пчелы.
(20-4=16ч)-рабочий день пчелы.
Записываем второе действие. (12-8=4ч)-рабочий день ученика.
-Теперь мы можем ответить на вопросы задачи? (Да)
Решаем дальше самостоятельно.(16:4=4 раза, 16-4=8часов)
4.Решение примеров
А сейчас несколько интересных чисел из мира пчёл.
1) За всю свою недолгую жизнь протяжённостью в 2 месяца пчела собирает несколько грамм нектара. А сколько — вы узнаете, решив пример
6750:45=150
2)В состав мёда входит много полезных для здоровья человека веществ. А сколько — вы узнаете, решив пример
16800:56=300
4) Пчела летит к цветку со скоростью 65 км/ч. Движение её крыльев незаметно для нас, так как она очень быстро ими машет. Сколько взмахов в секунду она совершает, вы тоже сейчас узнаете.
7480:17=440
(работа в парах)
V.Физкультминутка
1.Пчёлы в ульях сидят
И в окошко глядят,
Порезвиться захотели-
Друг за другом полетели.
VI.Этап контроля и самоконтроля
1. Перевод единиц длины.
-Все пчёлы летят на разное расстояние. Посмотрим на сколько мы «улетим». Переведите единицы длины, которые вы видите на карточке, в сантиметры.
3м=____см
1м05см=____см
4дм 6см=____см
2. Решение уравнений.
-Молодцы, ребята, вам всего по 10 лет, а вы уже многое знаете и умеете. Как вы думаете, в каком возрасте пчела начинает заниматься сбором нектара и пыльцы? Решив уравнения ,вы узнаете ещё одну тайну пчелы.
Х 81=486 180:х=15
29 х=551 403-х=377
(У доски )
От рождения до 6 дней- пчёлы убирают в улье.
От 6 до 12 дней- кормит личинок и матку.
От 12 до 19 дней- строит из воска соты.
От 19до 26 дней – охраняет улей, принимает нектар и пыльцу.
В возрасте 26 дней пчела вылетает на сбор нектара и пыльцы.
В почётном пенсионном возрасте , около 40 дней , пчела приносит в улей воду. Далеко от улья она уже не улетает.
Далеко от улья она уже не улетает.
3. Нахождение периметра шестиугольника.
Собрав нектар, пчела спешит в улей. Там она сливает его в соты, которые имеют форму шестиугольника. Пчелиные соты строятся из воска и имеют определённые размеры – диаметр5,4мм. Присутствующая у нас на уроке пчёлка больше настоящих пчёл, поэтому и «соты» наши большие. Длина стороны нашего шестиугольника равна 8 см. Давайте узнаем его периметр. Что называется периметром? Как его найти?
Найти периметр самостоятельно.
VII. Подведение итогов урока
-Наш необычный урок подходит к концу. Мы смогли заглянуть лишь одним глазком в жизнь этого удивительного насекомого, которое всю жизнь работает на благо других ничего не прося в замен.
Незаконченные предложения:
— Мы сегодня на уроке….
— Я закрепил(ла) …
— Я хотел(ла) бы больше…
— Мне понравилось….
— Оказывается , что. .
.
VIII. Дом. зад.
Страница 42 (учебник Моро 1 часть 4 класс) ответы по математике
185.
1) В магазин привезли 48 коробок с зелёным и чёрным виноградом. В 16 коробках был чёрный виноград, по 9 кг в каждой, а в остальных — зелёный, по 8 кг в каждой. Сколько всего килограммов винограда привезли в магазин?
2) В магазин привезли 400 кг зелёного и чёрного винограда. В нескольких коробках был чёрный виноград, по 9 кг в каждой, а в 32 коробках — зелёный виноград, по 8 кг в каждой. Сколько коробок чёрного винограда привезли в магазин?
1)
1) 9 * 16 = 144 кг черного винограда.
2) 48 — 16 = 32 коробки с зеленым виноградом.
3) 8 * 32 = 256 кг зеленого винограда.
4) 144 + 256 = 400 кг винограда привезли в магазин всего.Ответ: 400 кг.
2)
1) 8 * 32 = 256 кг зеленого винограда.
2) 400 — 256 = 144 кг черного винограда.
3) 144 : 9 = 16 коробок черного винограда.
Ответ: 16 коробок.
186. На своём приусадебном участке семья вырастила 56 кг огурцов, а перца — в 8 раз меньше, чем огурцов. На сколько килограммов перца было меньше, чем огурцов?
1) 56 : 8 = 7 кг перца вырастила семья.
2) 56 — 7 = 49 кг — на столько кг перца было меньше, чем огурцов.Ответ: 49 кг.
187. Сравни уравнения в каждом столбике и, не вычисляя, скажи, в котором из них неизвестное число больше. Проверь вычислением.
х = 78 — 37 = 41 х = 80 — 37 = 43
х = 90 — 47 = 43 > x = 90 — 50 = 40
x = 32 + 28 = 60 > x = 22 + 28 = 50
x = 63 — 45 = 18 x = 68 - 45 = 23
188.
1)
1000000 : 1000 — 999 = 1000 — 999 = 1
1000000 : 1000 + 1 = 1000 + 1 = 1001
420000 — 20000 = 400000
28000 : 4 * 100 = 7000 * 100 = 700000
2)
800 — 139 * 4 + 244 = 800 — 556 + 244 = 244 + 244 = 488
234 * 3 : 9 = 702 : 9 = 78
1000 — 678 = 322
189. Игра «Отгадай число».
Игра «Отгадай число».
Задумай любое однозначное число, кроме нуля. Умножь его на 5.
Произведение увеличь в 2 раза.
К результату прибавь 14.
Из суммы вычти 8.
Отбрось первую слева цифру результата.
Оставшееся число умножь на 7 и раздели на 2.
Объясни, почему в результате всегда будет 21.
Задуем, например, число 5.
5 * 5 = 25
25 * 2 = 50
50 + 14 = 64
64 — 8 = 56
56 → 6
6 * 7 — 42
42 : 2 = 21
Пусть х — задуманное число. Тогда по данному алгоритму можно записать:
(((х * 5) * 2 + 14 — 8 — 10 * х) * 7) : 2 = (10 * х + 6 — 10 * х) * 7 : 2 = 6 * 7 : 2 = 3 * 7 = 21.
190. Вычислительная машина работает так:
Составь план её работы.
Какое число будет получаться на выходе из машины, если на входе будет число: 7; 8; 10; 200; 12; 158?
План работы: на вход машины подается число. Это число сравнивается с числом 100. Если наше число меньше 100, тогда оно умножается на 6 и подается на выход машины. Если число больше 100, то оно сразу подается на выход машины.
Если число больше 100, то оно сразу подается на выход машины.
7 → 42; 8 → 48; 10 → 60; 200 → 200; 12 → 72; 158 → 158.
Задание под знаком вопроса.
900 — 756 : 9 — 84 = 900 — 84 — 84 = 732
906 : 6 * 100 = 151 * 100 = 15100
1000 — 806 = 194
Задание на полях.
Какая фигура лишняя.
Лишней фигурой может быть:
1) тупоугольный треугольник, так как остальные фигуры — остроугольные треугольники;
2) равносторонний треугольник, так как остальные треугольники — неравносторонние;
3) синий треугольник, так как остальные треугольники — зелёные.
ГДЗ: Математика 4 класс Башмаков, Нефедова
Математика 4 класс
Тип: Учебник
Авторы: Башмаков, Нефедова
Издательство: Дрофа
ЧТО ПРЕДСТОИТ ИЗУЧИТЬ В ЧЕТВЕРТОМ КЛАССЕ
В четвертом классе ребятам предстоит изучить много нового. Они будут проходить неравенства, решение самых простых уравнений с одним неизвестным, узнают новые термины и впервые познакомятся с важным разделом точных наук – геометрией. Всё это подробно изложено в «ГДЗ по Математике 4 класс Учебник Башмаков, Нефедова Планета знаний», выпущенном известным издательством Дрофа. Среди многочисленных тем и разделов этом учебнике есть и те, что могут даваться нелегко.
Они будут проходить неравенства, решение самых простых уравнений с одним неизвестным, узнают новые термины и впервые познакомятся с важным разделом точных наук – геометрией. Всё это подробно изложено в «ГДЗ по Математике 4 класс Учебник Башмаков, Нефедова Планета знаний», выпущенном известным издательством Дрофа. Среди многочисленных тем и разделов этом учебнике есть и те, что могут даваться нелегко.
ВАЖНАЯ РОЛЬ РОДИТЕЛЕЙ В ОБУЧЕНИИ
Освоить школьную программу будет легче, если всегда иметь под рукой «ГДЗ по Математике 4 класс Башмаков». В книге содержатся подробные ответы на все задания из учебника с примечаниями от авторов и дополнительными материалами. С помощью этого пособия можно проверять домашние задания и разбирать ошибки вместе с ребёнком. Помимо этого, можно вместе освоить тему, которую ученик пропустил в школе по уважительной причине, но необходимо «догнать» класс. К тому же, любой ребенок может, даже сидя на уроке, просто-напросто прослушать объяснения учителя, смотреть на него, но думать о своем, не слушая объяснение материала.
КОРОТКО О ПОСОБИИ
Издание состоит из двух частей, в первой сто девятнадцать, а во второй сто сорок две страницы. На них автору удалось разместить учебно-вспомогательный материал по всем темам основного курса математики для четвертого класса:
- Вычисление площади.
- Сложение тысяч и миллионов.
- Как складывать и вычитать разрядные слагаемые.
Каждое упражнение сопровождается подробным образцом решения, позволяющим понять и надежно запомнить все тем курса математики этого учебного года.
ПРЕИМУЩЕСТВА РЕШЕБНИКА
Безусловно, четвероклассник — это уже ученик настолько взрослый, что он в конце учебного года будет сдавать первые в своей жизни настоящие экзамены — всероссийские проверочные работы. Но при этом он находится еще в очень юном возрасте, не всегда может правильно координировать свою работу, и родители должны объяснить ребенку очень простые, но важные вещи:
- ГДЗ не может служить шпаргалкой;
- необходимо самостоятельно выполнить упражнения, прежде чем заглянуть в готовый ответ;
- если свой вариант отличается от варианта решебника, то нельзя копировать правильное решение, нужно самому найти и исправить ошибку.

Именно такой способ работы позволит освоить предмет надежно, но с минимальными затратами времени.
Конспект урока по математике «Задачи на движение» 4 класс
Конспект урока в 4 классе по УМК «Начальная школа XXI века».
Математика.
Тема. Решение разных видов задач на движение.
Форма урока: урок-путешествие
Тип урока: обобщающий урок.
Цель урока: использовать разные виды задач на движение как способ формирования метапредметных УУД на уроке.
Задачи урока:
-
Предметные:
-совершенствовать умение решать разные виды задач на движение
-совершенствовать умение использовать разные формы работы с арифметическими задачами в зависимости от цели работы
-совершенствовать умение составлять условие задачи по схеме, чертежу, текстовому материалу
-совершенствовать умение использовать данные диаграммы для решения задач
-
Метапредметные:
Познавательные УУД
-продолжить формирование действия анализа и синтеза в процессе работы над арифметическими задачами
— продолжить формирование умения делать умозаключения
— продолжить обучать действию моделирования
Регулятивные УУД
-формировать действие планирования при составлении плана решения задач
— продолжить формировать действия самоконтроля
-формировать действия оценки по заданным критериям
-совершенствовать умение применять общие способы действия в различных частных ситуациях
— продолжить формирование действия прогнозирования
Коммуникативные УУД
-формировать умение определять способ взаимодействия с одноклассниками,
-учить инициативному сотрудничеству в поиске решения задачи,
-учить слушать собеседника, задавать вопросы и отвечать на них
3. Личностные:
Личностные:
-формировать внутреннюю позицию обучающегося, которая
находит отражение в эмоционально-положительном отношении
обучающегося к уроку,
-формировать самооценку, включая осознание своих возможностей в учении, уважать себя и верить в успех
Оборудование урока: презентация к уроку; у учащихся – лист самооценки, раздаточный материал.
Ход урока.
|
| ||||
|
|
| |||
|
|
| |||
|
| ||||
|
|
| |||
|
| ||||
|
|
| |||
|
| ||||
|
|
| |||
|
| ||||
|
|
| |||
|
| ||||
|
|
| |||
|
| ||||
|
|
| |||
Приложения:
Лист №1. ( Скорости различных объектов)
Поезд «Сапсан» может развивать скорость до 350км/ч, а птица сапсан,
в честь которой и назван поезд, может развивать скорость до 322км/ч
Самая быстрая река в мире – Амазонка. Скорость течения 15км/ч
Скорость течения 15км/ч
Самая быстрая птица в мире сапсан. Он может развивать скорость до 322 км\ч, а на втором месте – черный стриж. Его скорость 160км/ч
Рыба-меч может развивать скорость до 130км/ч. Это позволяет ей легко обгонять морские лайнеры.
Самое быстрое насекомое в воздухе – Австралийская стрекоза. Она способна развить скорость до 58км/ч
Самая быстрая змея в мире черная мамба. Ее скорость 23км\ч
Кит-касатка может плыть со скоростью до 55км/ч
Шмель машет крыльями 160 раз в секунду
Самое медленное млекопитающее – ленивец. Скорость его передвижения около 2м/мин
Лист №2. Таблица самоконтроля.
Фамилия, имя ученика_______________________________________
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заполняя последнюю графу, используй цветные карандаши. Зеленый цвет показывает, что с заданием ты справился отлично, желтый – хорошо, а если ты считаешь, что какой- то вид работы на уроке получался у тебя не очень хорошо, то оставь кружок не закрашенным.
Зеленый цвет показывает, что с заданием ты справился отлично, желтый – хорошо, а если ты считаешь, что какой- то вид работы на уроке получался у тебя не очень хорошо, то оставь кружок не закрашенным.
Лист №3.
На диаграмме показаны скорости ковра-самолета, сапог-скороходов, верного коня и корабля. Известно, что самую большую скорость развивает ковер-самолет, медленнее всех движутся сапоги скороходы, а верный конь быстрее корабля. Укажите на диаграмме скорость движения каждого вида транспорта.
Планы уроков математики для четвертого класса
Посмотреть демо наших уроков
Учебная программа по математике Time4Learning доступна для учащихся от дошкольных учреждений до двенадцатых классов. Родители могут ожидать, что они увидят такие темы, как определение свойств форм, определение единиц длины, алгебраические выражения и многое другое.
Подробные планы уроков, представленные ниже, содержат подробный список учебной программы четвертого класса Time4Learning по математике.
Участники
часто используют эту страницу как ресурс для более подробного планирования, как руководство, помогающее выбрать конкретные занятия с помощью средства поиска занятий или сравнить нашу учебную программу с государственными стандартами и законами о домашнем обучении.
Что входит в план урока Time4Learning?
- Полная учебная программа для четвертого класса по математике с 18 главами, 376+ заданиями, рабочими листами и викторинами. Вот бесплатный лист для печати, которым можно поделиться со своим учеником.
- Глава уроки с подробным описанием пройденного содержания
- Несколько типов заданий для развития навыков, включая задания без баллов, викторины и распечатанные ключи ответов в викторинах
- Рабочие листы уроков и ключи для ответов на представленные материалы
- Легкий доступ к дополнительным главам по каждой теме
- Time4MathFacts, который использует забавные игры, чтобы вовлечь вашего ребенка в изучение основ математики
Учащиеся четвертого класса математической программы Time4Learning будут иметь доступ к урокам как третьего, так и пятого классов в рамках своего членства, так что они смогут продвигаться вперед или делать повторения в своем собственном темпе.
План урока математики — Учебный план четвертого класса
Преобразует числа, содержащие от двух до девяти цифр, из стандартной формы в развернутую и наоборот.
Записывайте числа до девяти цифр, используя устные и письменные подсказки.
Заказывайте номера до девяти цифр и сравнивайте номера с помощью символов и =.
Круглые числа до ближайших десяти, сотен, тысяч, десяти тысяч и сотен тысяч.
Сложите целые числа (4-значные, до 3-х чисел).
Вычтите 4-значные числа с несколькими нулями.
Оценивайте суммы и разницы, используя округление и совместимые числа.
Определить кратные и перечислить кратные данного числа. Определите общие кратные двух заданных чисел.
Умножение будет использоваться для решения задач.
Интерпретируйте уравнение умножения.
Умножение однозначных чисел на двузначные и трехзначные числа. Используйте в качестве стратегий частичные произведения и умножение в уме.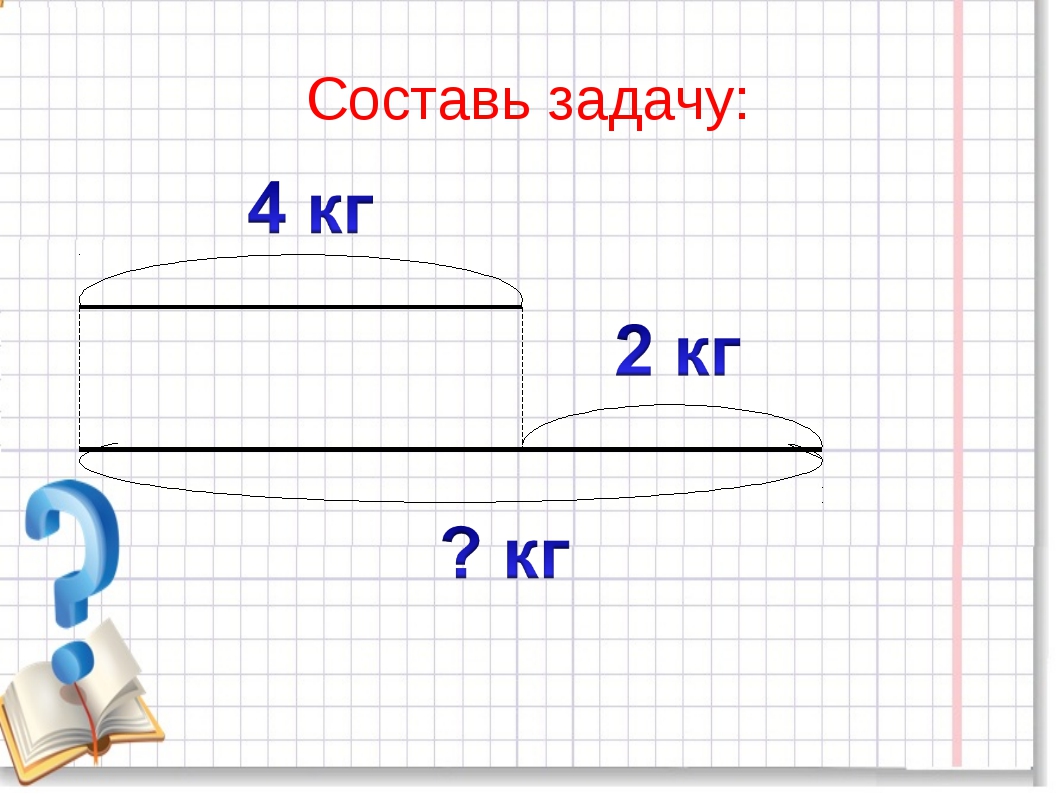
Умножение двузначных чисел на двузначные и трехзначные числа.
Умножьте несколько множителей.
Определите множители заданного числа и общие множители двух заданных чисел.
Найдите частные целых чисел и остатки с однозначными делителями. Проиллюстрируйте и объясните расчет с помощью уравнений, стандартных алгоритмов и моделей
Разделите двузначные дивиденды на однозначные делители с остатками и без них.
Найдите частные целых чисел и остатки с однозначными делителями, используя стратегии, основанные на разрядах, свойствах операций и / или взаимосвязи между умножением и делением.
Делите дивиденды до четырехзначных на однозначные с остатками и без них (включая частные с нулями).
Решайте одноэтапные и двухэтапные задачи со словами, в которых необходимо интерпретировать остатки.
Дивизион будет использован для сравнения.
Решает задачи двузначного деления с остатками и без них.
Применяйте понимание разряда при решении задач, включающих умножение на 10 или 100 и деление на 10 или кратное 10.
Найдите среднее значение набора чисел.
Сопоставьте части множества и части целого с эквивалентными дробями со знаменателем до 12.
Выявление неправильных дробей и преобразование неправильных дробей в смешанные числа.
Выразите дробь со знаминателем 10 как эквивалентную дробь со знаминателем 100.
Распознавать эквивалентные дроби. Сократите дроби до наименьших значений.
Преобразуйте неправильные дроби в целые числа с помощью моделей.
Исследуйте дроби, которые превращаются в целые числа.
Исследуйте дроби, которые превращаются в целые числа.
Порядок дробей с одинаковыми и непохожими знаменателями от 1 до 12 и сравнение дробей с помощью символов и =.
Узнайте, как сложение дробей объединяет части, относящиеся к одному целому, и как вычитание дробей разделяет части, относящиеся к одному целому.
Решайте задачи со словами, включающие сложение дробей с одинаковыми знаменателями, используя модели дробей и уравнения.
Решайте задачи со словами, связанные с вычитанием дробей с одинаковыми знаменателями, используя модели дробей и уравнения.
Разложите дробь на сумму дробей с одинаковым знаменателем более чем одним способом, используя визуальную модель дробей.
Разложите неправильную дробь на сумму дробей с одинаковым знаменателем более чем одним способом и запишите каждое разложение с помощью уравнения.
Сложить и вычесть дроби с одинаковыми знаменателями.
Сложить и вычесть смешанные числа с одинаковыми знаменателями.
Сложить и вычесть дроби с разными знаменателями до 12.
Складываем две дроби со знаменателями 10 и 100 соответственно.
Сложите единицу дроби несколько раз.
Распознавать кратные дроби.
Умножьте дробь на целое число, используя наглядные модели и уравнения.
Решайте задачи со словами, включающие умножение дроби на целое число, используя визуальные модели дробей и уравнения для представления проблемы.
Упорядочите десятичные дроби и сравните значения двух десятичных знаков, используя знаки, и = с точностью до тысячных.
Чтение и запись десятичных знаков как дробей.
Сложить и вычесть десятичные дроби до тысячных.
Считайте и обменивайте деньги на суммы до 100 долларов США. Решайте проблемы, требующие внесения изменений в сумме до 100,00 долларов США.
Решает задачи на сложение и вычитание, связанные с деньгами.
Решайте задачи умножения и деления, связанные с деньгами.
Определение и применение шаблонных правил с использованием последовательностей связанных чисел (арифметические, геометрические).
Примените соответствующее правило, чтобы заполнить диаграмму, включая таблицы ввода / вывода. Решайте проблемы, связанные с заданными отношениями, используя таблицу значений.
Представляет записанные отношения в виде выражений и использует переменную для представления неизвестной величины в выражении.
Изучите идею переменной, решив неизвестную величину в уравнении.Пример: 3 + a = 7.
Используйте коммутативные и ассоциативные свойства сложения и умножения, чтобы найти эквивалентные выражения или уравнения, содержащие неизвестную величину.
Определите, назовите и идентифицируйте точки, линии, линейные сегменты, лучи и углы.
Определяет и классифицирует углы как прямые, тупые или острые.
Поймите, что угол состоит из серии поворотов на один градус.
Узнайте, как рисовать углы заданной меры с помощью транспортира.
Узнайте, как измерять острые углы с помощью транспортира.
Научитесь измерять тупые углы с помощью транспортира.
Определение многоугольников, правильных многоугольников и неполигонов и их атрибутов (стороны, углы и вершины). Классифицируйте многоугольники на подмножества.
Классифицируйте многоугольники на подмножества.
Классифицируйте двумерные фигуры на основании наличия или отсутствия параллельных или перпендикулярных линий либо наличия или отсутствия углов определенного размера.
Классифицируйте треугольники по размеру угла (прямой, острый, тупой) и длине сторон (равносторонний, равнобедренный, разносторонний).
Определите радиус и диаметр круга и вычислите один, если задан другой.
Определите атрибуты твердых фигур, таких как кубы, призмы, пирамиды, конусы, цилиндры и сферы. (ребра, вершины и грани) Идентифицируйте и создайте двумерное представление трехмерного объекта.
Постройте точку из упорядоченной пары или запишите упорядоченную пару точек, показанных на координатной сетке. (Только 1-й квадрант)
После получения расстояния и навигационных направлений от начальной точки в первом квадранте запишите упорядоченную пару конечной точки.
Для плоской фигуры найдите похожую или совпадающую фигуру.
Применяет перенос, отражение или поворот к плоской фигуре. Предскажите результат. Определите изображение плоской фигуры как перемещение, отражение или вращение.
Классифицируют плоские фигуры как имеющие линейную симметрию, точечную симметрию, обе или не имеющие.
Сообщает и показывает время с 5-минутным и 1-минутным интервалами.
Найдите прошедшее время в днях и неделях.
Расшифровка расписания с использованием минут, часов, дней и недель.
Определите единицы длины. (дюйм, фут, ярд, миля) Оцените и сравните длину. Измерьте с точностью до четверти дюйма.
Преобразовать измерения длины в новые единицы.
После получения навигационных указаний от начальной точки определите упорядоченную пару конечной точки.
Определите единицы мощности. (чашка, пинта, кварта, галлон) Оцените и сравните вместимость.
Преобразовать измерения емкости в новые единицы.
Определите единицы веса (унция, фунт, тонна). Оцените и сравните вес.
Преобразование единиц веса в новые единицы.
Считайте показания термометра с точностью до ближайшего 2-градусного интервала. Вычислите изменение температуры.
Определите единицы длины (сантиметр, дециметр, метр). Оцените и сравните длину. Измерьте с точностью до сантиметра.
Преобразовать измерения длины в новые единицы.
Определите единицы объема (миллилитр, литр). Оцените и сравните емкость.
Преобразовать измерения емкости в новые единицы.
Определите единицы массы. (грамм, килограмм) Оценить и сравнить массу.
Преобразование единиц массы в новые единицы.
Считайте показания термометра с точностью до ближайшего 2-градусного интервала. Вычислите изменение температуры.
Найдите периметр, посчитав единицы и прибавив длины. Измерьте, чтобы найти периметр. Выберите соответствующую метку для измерения.
Выберите соответствующую метку для измерения.
Найдите область, считая единицы. Умножьте, чтобы найти площадь. Выберите соответствующие метки измерения.
Сравните периметр и площадь.
Найдите объем, считая единицы. Умножьте, чтобы найти объем. Выберите соответствующие метки измерения.
Отображение и интерпретация данных в таблицах частоты и совокупной частоты, сравнение данных и выводы.
Отображение и интерпретация данных в виде гистограмм и двойных гистограмм, сравнение данных и выводы.
Отображение и интерпретация данных на линейных диаграммах и диаграммах «стебель-лист», сравнение данных и выводы.
Отображайте и интерпретируйте данные в виде линейного графика, сравнивайте данные и делайте выводы.
Определите среднее значение, медианное значение, режим и диапазон на основе набора данных или графика.
Определите достоверность, вероятность и справедливость событий.
Определите и перечислите возможные комбинации события.
Вычислить вероятность в виде дроби.
Решите многоступенчатые задачи со словами, используя четыре операции. Представьте эти задачи с помощью уравнений с буквой, обозначающей неизвестную величину. Оцените разумность ответов.
Объем и последовательность Авторские права © 2017 Edgenuity, Inc. Все права защищены.
Инструмент поиска учебных занятий
Поиск занятий в уроке — один из многих полезных инструментов, которые Time4Learning предлагает своим участникам. Средство поиска занятий — это ярлык, с помощью которого родители могут легко просмотреть уроки или найти дополнительную практику для своего ребенка.
Каждому уроку в учебной программе присвоен уникальный номер занятия, который в планах уроков называется «номером LA». Эти номера можно найти либо на страницах содержания и последовательности, либо в планах уроков на родительской информационной панели.
Для получения дополнительной информации посетите наш раздел подсказок и помощи, в котором есть более подробная информация о поисковике действий.
Дополнительные ресурсы по математике для четвертого класса
Если вас интересуют планы уроков математики для четвертого класса, вас также могут заинтересовать:
Онлайн-программа для домашнего обучения, послешкольного и летнего использования
Если вы только изучаете Time4Learning, мы рекомендуем сначала посмотреть наши интерактивные демонстрации уроков.
Зарегистрируйтесь на Time4Learning и получите доступ к разнообразным образовательным материалам, которые увлекут вашего ребенка и побудят его добиться успеха. Сделайте Time4Learning частью ресурсов для домашнего обучения ваших детей.
Rich Tasks and Contexts
Здесь можно найти серию ресурсов для профессионального развития, предназначенных для поддержки включения сложных задач в учебную программу.
В последнее время я прочитал несколько статей, в которых упоминаются «сложные задачи», но ни одна из них, похоже, не говорит мне, что автор считает «сложной задачей». Я нашел это несколько разочаровывающим, и затем меня осенило, что веб-сайт NRICH полон вещей, которые мы могли бы описать как «сложные задачи» или проблемы, но, как и многие другие авторы, мы не сказали прямо, что мы могли бы иметь в виду под «хорошим».
Я нашел это несколько разочаровывающим, и затем меня осенило, что веб-сайт NRICH полон вещей, которые мы могли бы описать как «сложные задачи» или проблемы, но, как и многие другие авторы, мы не сказали прямо, что мы могли бы иметь в виду под «хорошим».
проблемы »или« сложные задачи ». Итак, что такое« сложные задачи »и почему они важны?
Я бы описал сложную задачу как имеющую ряд характеристик, которые вместе предлагают разные возможности для удовлетворения различных потребностей учащихся в разных условиях. раз.Для меня также очевидно, что большая часть того, что требуется для того, чтобы сделать сложную задачу «насыщенной», — это среда, в которой она представлена, включая поддержку и вопросы, используемые учителем, и роли, которые учащиеся
поощряются к усыновлению. То есть среда, в которой учащиеся являются не пассивными получателями знаний, принимающими то, что им дано, а независимыми напористыми конструкторами своего собственного понимания, которые бросают вызов и размышляют. Сама по себе богатая задача не богата — только то, что из нее сделано, позволяет ей реализовать свой потенциал.Имея это в виду, было бы полезно перечислить некоторые из
Сама по себе богатая задача не богата — только то, что из нее сделано, позволяет ей реализовать свой потенциал.Имея это в виду, было бы полезно перечислить некоторые из
вещи, которые я мог бы сказать, описывая сложную задачу. Богатые задачи (или хорошие задачи):
- доступны широкому кругу учащихся,
- может быть установлен в контекстах, которые вовлекают учащегося в математику, либо потому, что отправная точка интригует, либо потому, что возникающая математика интригует,
- доступны и предлагают возможности для первоначального успеха, побуждая учащихся думать самостоятельно,
- предлагают разные уровни сложности, но независимо от уровня учащегося возникает реальная проблема, и, следовательно, есть потенциал для расширения круга тех, кто нуждается в большем и требует большего (низкий порог — задачи с высоким потолком),
- позволяют учащимся ставить свои собственные проблемы,
- допускают разные методы и разные ответы (разные начальные точки, разные середины и разные концовки),
- предлагает возможности для поиска элегантных или эффективных решений,
- имеют потенциал для расширения навыков студентов и / или углубления и расширения знаний по математическому содержанию,
- поощряют творчество и творческое применение знаний.

- могут выявить закономерности или привести к обобщениям или неожиданным результатам,
- могут раскрыть основные принципы или установить связи между областями математики,
- поощрять сотрудничество и обсуждение,
- побуждает учащихся развивать уверенность и независимость, а также критически мыслить.
Не все сложные задачи будут выполнять все эти задачи, но они определенно справятся с некоторыми из них, если их использовать таким образом, чтобы ценить обсуждение, различия и критическую оценку.Учитель должен посмотреть на задачу и признать ее потенциал для выполнения некоторых или всех вышеперечисленных задач и представить ее таким образом и на форуме, которые сделают ее «богатой».
В руководящем документе «Математика на ключевом этапе 4: разработка схемы работы» вторичная национальная стратегия описывает сложную задачу как:
- доступный и расширяемый,
- тот, который позволяет учащимся принимать решения,
- вовлечение учащихся в тестирование, доказательство, объяснение, размышление и интерпретацию,
- содействие дискуссии и коммуникации,
- поощряя оригинальность и изобретательность,
- , поощряющие вопросы «а что, если» и «что, если нет»,
- приятен и содержит возможность удивить.

Кроме того, на странице 20 книги «Лучшая математика: исследование разработки учебной программы» Афзал Ахмед из Института высшего образования Западного Суссекса предложил следующие критерии для определения «богатой математической деятельности» в 1987 году:
- должен быть доступен всем на старте
- должен позволять решать дополнительные задачи и быть расширяемым
- должен побуждать детей к принятию решений
- должно привлекать детей в
- спекулируя
- Формирование и проверка гипотез
- доказательство или объяснение
- отражающий
- устный перевод
- не должен ограничивать детей от поиска в других направлениях
- должен способствовать обсуждению и общению
- должно поощрять оригинальность / изобретательность
- должен поощрять «а что, если?» и «а если нет?» вопросы
- должен иметь элемент неожиданности
- должно доставлять удовольствие.

Оба эти списка очень похожи на тот, с которого я начал эту статью, и, как и этот первый список, приведенный выше предполагает, что сложная задача зависит не только от самой задачи, но и от того, что с ней делается. Правильно выполненные сложные задачи позволяют всем учащимся найти что-то сложное для своего уровня, над которым можно работать.
В основе сложных заданий может лежать возможность развить понимание, изучить или использовать математические концепции, которые являются частью обычной учебной программы.Богатые задания и охват учебной программы или даже тестирование не противоречат друг другу. Природа сложных заданий дает учащимся возможность не только задавать вопросы и развивать свое понимание математических идей.
но также обрести уверенность в том, что они могут применять свои знания в различных контекстах, даже в незнакомых. У них также есть возможность удовлетворить потребности учебной программы по функциональной математике.
Иногда, возможно, лучшим описанием было бы «богатые контексты».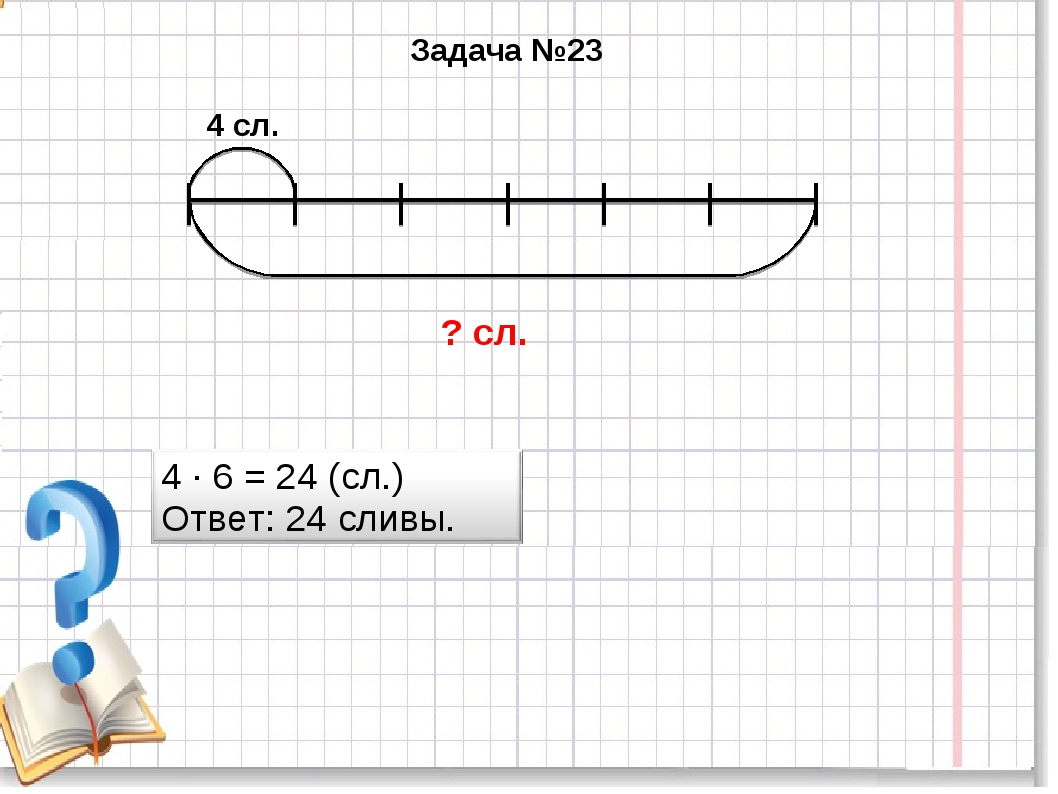 Контекст может быть проблемой, но это также может быть серия связанных задач или открытая среда, богатая многими из описанных выше смыслов. Примером богатой среды на сайте NRICH может быть среда Geoboard. Ряд разнообразных задач может включать в себя игру «квадрат», задачи «квадратные координаты» и «наклонные квадраты». Все это закрепляет и развивает идею квадрата, связывает эту идею с узором и
Контекст может быть проблемой, но это также может быть серия связанных задач или открытая среда, богатая многими из описанных выше смыслов. Примером богатой среды на сайте NRICH может быть среда Geoboard. Ряд разнообразных задач может включать в себя игру «квадрат», задачи «квадратные координаты» и «наклонные квадраты». Все это закрепляет и развивает идею квадрата, связывает эту идею с узором и
координаты и теорема Пифагора. Довольно богато, и все основано на рисовании квадратов на точечной сетке!
Чтобы помочь учителям в принятии решений о том, какие обширные задачи и где применять, веб-сайт NRICH предлагает ряд механизмов поддержки:
- публикуем богатые задачи и контексты!
- мы даем заметки и подсказки, чтобы помочь учителям увидеть некоторый потенциал задач или проблем, которые мы предлагаем,
- мы связываем все наши проблемы с темами содержания учебной программы,
- мы связываем некоторые проблемы непосредственно с документами учебного плана, чтобы было возможно «быстрое сопоставление».

Но мы не говорим учителям, как использовать задачи, давая подробные планы уроков, и это потому, что природа насыщенной задачи включает в себя «отпустить» и подготовиться к ряду потребностей ваших собственных учеников и к тому, где они могут идти. Любое предположение о том, что мы можем начать сомневаться в том, что лучше всего отвечает потребностям учащихся в каждом классе, будет неуместным. Тем не менее
Следующие основные идеи могут быть полезны при планировании работы с учащимися:
- попробуйте оценить то, что ваши ученики уже знают.При этом насыщенные задачи предлагают возможности узнать, что они действительно знают, и выявить сильные и слабые стороны и уровни уверенности учащихся, работающих над задачей. Богатые задачи, безусловно, являются отличным инструментом для поддержки оценки.
- имеют представление об основных требованиях вашей комплексной задачи — на какой минимальный результат вы надеетесь? Это также заставит вас рассмотреть ряд возможных результатов, которых вы можете ожидать.
 Но будьте готовы удивиться — ваши ученики, вероятно, придумают лучшие идеи и вопросы, чем вы можете придумать.
Но будьте готовы удивиться — ваши ученики, вероятно, придумают лучшие идеи и вопросы, чем вы можете придумать. - будьте готовы поощрять настойчивость. Это будет сложно, если ваши ученики не привыкли брать на себя ответственность за собственное обучение, но станет легче, когда они лучше ознакомятся с идеей и приобретут уверенность. Один из способов сделать это — ответить на просьбу об ответе вопросом … «Что мне делать дальше?» … «Что ты пробовал?»
- старается не вести учащихся по альтернативному пути, потому что они начали исследовать область темы, которую вы не ожидали — и это может означать: «Я не знаю».Учащиеся могут узнать больше из задачи, которую они считают «своей».
- помните, что учащиеся могут многому, а иногда и большему, научиться у своих сверстников, как и у вас.
По сути, сложные задания побуждают детей мыслить творчески, работать логически, обмениваться идеями, синтезировать их результаты, анализировать различные точки зрения, искать общие черты и оценивать результаты. Однако то, что нам действительно нужно, — это богатые классы: сообщества исследования и сотрудничества, способствующие общению и воображению.
Однако то, что нам действительно нужно, — это богатые классы: сообщества исследования и сотрудничества, способствующие общению и воображению.
Список литературы
Вторичная национальная стратегия, 2007, Математика на ключевом этапе 4: разработка вашей схемы работы, DfES.
4 Оценивание для поддержки изучения математики | Измерение того, что имеет значение: концептуальное руководство для оценки по математике
, как правило, путем подсчета количества вопросов, на которые даны правильные ответы, и сравнения баллов одного человека с баллами другого на основании их относительного процентильного ранга. Так называемые оценки с привязкой к норме уже много лет беспокоят педагогов.Несмотря на то, что высказывались различные критические замечания по поводу ссылки на нормы, основная проблема образования заключается в том, что такая информация недостаточно полезна для улучшения преподавания и обучения и может, фактически, иметь контрпродуктивные образовательные последствия. В классе учителя и ученики должны знать, что ученики понимают хорошо, что они понимают хуже, и какими должны быть следующие шаги обучения. Относительные рейтинги протестированных студентов могут быть использованы вне контекста класса, но в этом контексте необходимы формы результатов, полезные для процесса преподавания и обучения.
В классе учителя и ученики должны знать, что ученики понимают хорошо, что они понимают хуже, и какими должны быть следующие шаги обучения. Относительные рейтинги протестированных студентов могут быть использованы вне контекста класса, но в этом контексте необходимы формы результатов, полезные для процесса преподавания и обучения.
Программы оценивания должны информировать учителей и учеников о том, что ученики узнали, как они учатся и как они думают о математике. |
Например, чтобы спланировать свое обучение, учителя должны знать о текущем понимании каждым учеником того, чему будут учить. Таким образом, программы оценки должны информировать учителей и учеников о том, что ученики узнали, как они учатся и как они думают о математике.Чтобы эта информация была полезной для учителей, она должна включать анализ конкретных сильных и слабых сторон понимания учащимся, а не только оценок вне контекста.
Чтобы обучение было эффективным, результаты оценки должны быть своевременными. 35 Учебе учащихся не способствуют компьютерные распечатки, отправляемые учителям после того, как классы закончились в течение года и ученики ушли, а также учителя, которые уделяют слишком много времени оценке оценок.В частности, необходимо найти новые способы дать учителям и ученикам более непосредственные знания об успеваемости учеников по оценкам, предписанным внешними властями, чтобы эти оценки, а также собственные оценки учителя могли использоваться для улучшения обучения. Даже если основной целью оценки является определение достижений школы, штата или страны, оценка должна предоставлять учащимся и учителям отчеты об их успеваемости. Школьное время дорого.Когда учащимся не сообщают об их ошибках и заблуждениях, не говоря уже о том, чтобы помочь их исправить, оценка может как усилить недопонимание, так и потратить драгоценное учебное время впустую.
Когда форма оценивания незнакома, учителя несут особую ответственность перед своими учениками, чтобы сообщить им заранее.
(PDF) Отличительные схемы и задания в развитии мультипликативного мышления у детей
Отличительные схемы и задания…
PNA 7 (3)
Simon, M.A., & Blume, G. W. (1994). Построение и понимание мультипликативных отношений
: исследование потенциальных учителей начальных классов. Журнал
Исследования в области математического образования, 25 (5), 472-494.
Саймон М.А., Цур Р., Хайнц К., Кинзель М. и Смит М.С. (2000).
Характеристика перспективы, лежащей в основе практики учителей математики
в переходный период. Журнал исследований в области математического образования, 31 (5), 579-601.
Стеффе, Л. П. (1990). Обучение адаптивной математике. В Т. Дж. Куни и К. Р.
Хирш (ред.), Преподавание и изучение математики в 1990-е годы (стр. 41-51).
Рестон, Вирджиния: Национальный совет учителей математики.
Стеффе, Л. П. (1992). Схемы действия и работы с составными агрегатами.
Обучение и индивидуальные различия, 4 (3), 259-309. DOI: 10.1016 / 1041-
DOI: 10.1016 / 1041-
6080 (92)
-Y
Steffe, L.П. и Кобб П. (1998). Мультипликативные и делительные схемы. Сосредоточьтесь на
учебных задачах по математике, 20 (1), 45-62.
Стеффе, Л. П., и Олив, Дж. (2010). Детское дробное знание. Нью-Йорк,
Нью-Йорк: Спрингер.
Стеффе, Л. П., и фон Глазерсфельд, Э. (1985). Помогаем детям зачать номер
. Recherches en Didactique des Mathematiques, 6 (2-3), 269-303.
Штеффе, Л. П., фон Глазерсфельд, Э., Ричардс Дж. И Кобб П. (1983). Детская
Виды счета. Нью-Йорк, штат Нью-Йорк: Praeger.
Томпсон, П. В., и Салднха, Л. (2003). Дроби и мультипликативное рассуждение.
В J. Kilpatrick & G. Martin (Eds.), Научный сотрудник по стандартам NCTM
(стр. 95-113). Вашингтон, округ Колумбия: Национальный совет учителей математики
.
Цур Р. и Ламберт М. А. (2011). Промежуточные этапы участия как зона ближайшего развития
коррелируют при построении расчетов: правдоподобный концептуальный источник
для преходящего «регресса» детей к тому, чтобы считать все. Журнал
Журнал
для исследований в области математического образования, 42 (5), 418-450.
Цур Р. и Саймон М. А. (2004). Различают два этапа концептуального обучения математике
. Международный научно-математический журнал
Образование, 2 (2), 287-304. DOI: 10.1007 / s10763-004-7479-4
Цур, Р., Синь, Ю. П., Си, Л., Кенни, Р., и Геберт, А. (2010, апрель и май).
Учащиеся с нарушением обучаемости по математике остаются позади в мультипликативном мышлении
? Число как абстрактная составная единица — вероятный «виновник».Документ
, представленный Американской ассоциацией исследований в области образования, Денвер, Колорадо.
Цур, Р., Синь, Ю. П., Си, Л., Вудворд, Дж., И Джин, X. (2009). Содействие переходу
от этапа участия к этапу упреждения: случай мультипликативной смешанной координации в Чаде —
единиц (MMUC). В М. Цекаки, М. Калдримиду и Х. Саконидис
(ред.), Труды 33-й конференции Международной группы
Психология математического образования (т. 5. С. 249-256). Салоники,
5. С. 249-256). Салоники,
Греция: PME.
Математика — четвертый класс — 5012060
Общие примечания
MAFS.4
В 4 классе учебное время должно быть сосредоточено на трех критических областях: (1) развитие понимания и беглости с помощью многозначного умножения и развитие понимания деления для нахождения частных, включающих многозначные дивиденды; (2) развитие понимания эквивалентности дробей, сложения и вычитания дробей с одинаковыми знаменателями и умножения дробей на целые числа; (3) понимание того, что геометрические фигуры можно анализировать и классифицировать на основе их свойств, таких как наличие параллельных сторон, перпендикулярных сторон, определенных угловых размеров и симметрии.
(1) Учащиеся обобщают свое понимание разряда до 1 000 000, понимая относительные размеры чисел в каждом разряде.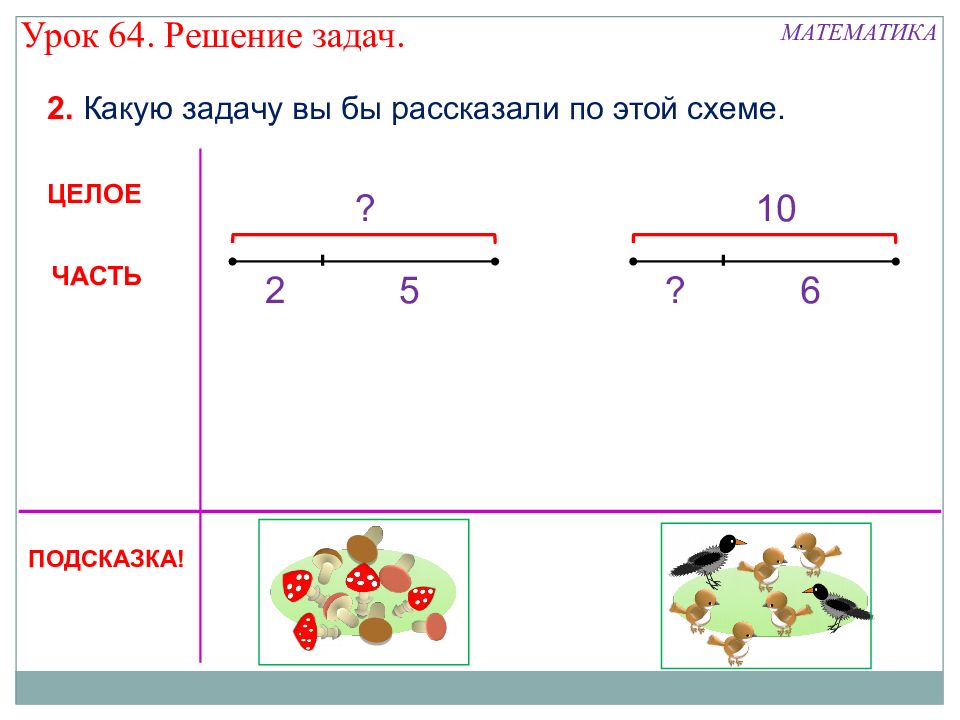 Они применяют свое понимание моделей умножения (группы равного размера, массивы, модели площадей), разметки и свойств операций, в частности свойства распределения, при разработке, обсуждении и использовании эффективных, точных и обобщающих методов для вычислять произведения многозначных целых чисел. В зависимости от цифр и контекста они выбирают и точно применяют соответствующие методы для оценки или мысленного расчета продуктов.Они развивают беглость с помощью эффективных процедур умножения целых чисел; понимать и объяснять, почему процедуры работают на основе числовой стоимости и свойств операций; и использовать их для решения проблем. Учащиеся применяют свое понимание моделей деления, разметки, свойств операций и отношения деления к умножению по мере того, как они разрабатывают, обсуждают и используют эффективные, точные и обобщающие процедуры, чтобы найти частные, включающие многозначные дивиденды. Они выбирают и точно применяют подходящие методы для оценки и мысленного вычисления частных, а также интерпретируют остатки в зависимости от контекста.
Они применяют свое понимание моделей умножения (группы равного размера, массивы, модели площадей), разметки и свойств операций, в частности свойства распределения, при разработке, обсуждении и использовании эффективных, точных и обобщающих методов для вычислять произведения многозначных целых чисел. В зависимости от цифр и контекста они выбирают и точно применяют соответствующие методы для оценки или мысленного расчета продуктов.Они развивают беглость с помощью эффективных процедур умножения целых чисел; понимать и объяснять, почему процедуры работают на основе числовой стоимости и свойств операций; и использовать их для решения проблем. Учащиеся применяют свое понимание моделей деления, разметки, свойств операций и отношения деления к умножению по мере того, как они разрабатывают, обсуждают и используют эффективные, точные и обобщающие процедуры, чтобы найти частные, включающие многозначные дивиденды. Они выбирают и точно применяют подходящие методы для оценки и мысленного вычисления частных, а также интерпретируют остатки в зависимости от контекста.
(2) Студенты развивают понимание эквивалентности дробей и операций с дробями. Они признают, что две разные дроби могут быть равными (например, 15/9 = 5/3), и разрабатывают методы для создания и распознавания эквивалентных дробей. Студенты расширяют предыдущие представления о том, как дроби строятся из единичных дробей, составляя дроби из единичных дробей, разлагая дроби на единичные дроби и используя значение дробей и значение умножения для умножения дроби на целое число.
(3) Учащиеся описывают, анализируют, сравнивают и классифицируют двухмерные формы. Создавая, рисуя и анализируя двумерные формы, учащиеся углубляют свое понимание свойств двумерных объектов и их использования для решения задач, связанных с симметрией.
Развитие английского языка Стандарты ELD Особые примечания Раздел:
Учителя обязаны проводить обучение аудированию, устной речи, чтению и письму, которое позволяет изучающим английский язык (ELL) обмениваться информацией, идеями и концепциями для академического успеха в предметной области математики . Для заданного уровня владения английским языком и с визуальной, графической или интерактивной поддержкой учащиеся будут взаимодействовать со словами, выражениями, предложениями и речами на уровне своего класса, чтобы обрабатывать или воспроизводить язык, необходимый для академической успеваемости. Стандарт ELD должен определять соответствующую концепцию области содержания или тему исследования, выбранную разработчиками учебных программ и учителями, которая максимизирует потребность ELL в коммуникативных и социальных навыках. Чтобы получить доступ к вспомогательному документу ELL, в котором описаны определения и дескрипторы производительности, щелкните следующую ссылку:
Для заданного уровня владения английским языком и с визуальной, графической или интерактивной поддержкой учащиеся будут взаимодействовать со словами, выражениями, предложениями и речами на уровне своего класса, чтобы обрабатывать или воспроизводить язык, необходимый для академической успеваемости. Стандарт ELD должен определять соответствующую концепцию области содержания или тему исследования, выбранную разработчиками учебных программ и учителями, которая максимизирует потребность ELL в коммуникативных и социальных навыках. Чтобы получить доступ к вспомогательному документу ELL, в котором описаны определения и дескрипторы производительности, щелкните следующую ссылку:
https: // cpalmsmediaprod.blob.core.windows.net/uploads/docs/standards/eld/ma.pdf
Руководство по внедрению стандартов Флориды Фокус Раздел:
Руководство по внедрению стандартов Mathematics Florida было создано для поддержки преподавания и изучения стандартов Mathematics Florida. Руководство разделено на три компонента: фокус, согласованность и строгость. Фокус означает сужение объема содержания в каждом классе или курсе, чтобы учащиеся достигли более высокого уровня понимания и более глубоко усвоили математические концепции.Стандарты математики позволяют преподавать и изучать математические концепции, сосредоточенные вокруг основных кластеров на каждом уровне обучения, усиленные за счет поддержки и дополнительных кластеров. Определяются основные, вспомогательные и дополнительные кластеры применительно к каждому классу или курсу. Обозначения кластеров для этого курса приведены ниже.
Руководство разделено на три компонента: фокус, согласованность и строгость. Фокус означает сужение объема содержания в каждом классе или курсе, чтобы учащиеся достигли более высокого уровня понимания и более глубоко усвоили математические концепции.Стандарты математики позволяют преподавать и изучать математические концепции, сосредоточенные вокруг основных кластеров на каждом уровне обучения, усиленные за счет поддержки и дополнительных кластеров. Определяются основные, вспомогательные и дополнительные кластеры применительно к каждому классу или курсу. Обозначения кластеров для этого курса приведены ниже.
Основные кластеры
MAFS.4.OA.1 Используйте четыре операции с целыми числами для решения задач.
MAFS.4.NBT.1 Обобщение понимания разрядов для многозначных целых чисел.
MAFS.4.NBT.2 Используйте понимание разряда и свойства операций для выполнения многозначной арифметики.
MAFS.4.NF.1 Расширить понимание эквивалентности дробей и упорядочения.
MAFS.4.NF.2 Построение дробей из единичных дробей, применяя и расширяя предыдущие представления об операциях с целыми числами.
MAFS.4.NF.3 Разберитесь в десятичной системе счисления для дробей и сравните десятичные дроби.
Поддерживающие кластеры
MAFS.4.OA.2 Ознакомьтесь с факторами и мультипликаторами.
MAFS.4.MD.1 Решает проблемы, связанные с измерением и преобразованием измерений из более крупной единицы в меньшую.
MAFS.4.MD.2 Представление и интерпретация данных.
Дополнительные кластеры
MAFS.4.OA.3 Создание и анализ шаблонов.
MAFS.4.MD.3 Геометрические измерения: понимание понятий угла и углов измерения.
MAFS.4.G.1 Нарисуйте и идентифицируйте линии и углы, а также классифицируйте формы по свойствам их линий и углов.
Примечание: Кластеры не следует сортировать от основных к вспомогательным, а затем обучать в этом порядке. Это нарушит последовательность математических идей и упустит возможность улучшить основную работу класса с помощью вспомогательных и дополнительных кластеров.
Это нарушит последовательность математических идей и упустит возможность улучшить основную работу класса с помощью вспомогательных и дополнительных кластеров.
бесплатных сложных заданий по математике по программе Mr Barton Maths
arrow_back
Вернуться к богатым задачам
Богатые задачи мистера Бартона
На этой странице я собрал свои любимые насыщенные задания
которые я использовал в течение последних 11 лет в доступном, легком
использовать формат.Я также приглашаю учителей поделиться своими идеями относительно
интересные вопросы и направления запросов для студентов
расследовать.
Содержание
Фон
keyboard_arrow_up
В начало
Для меня сложная задача — это одновременно увлекательная и трудная задача.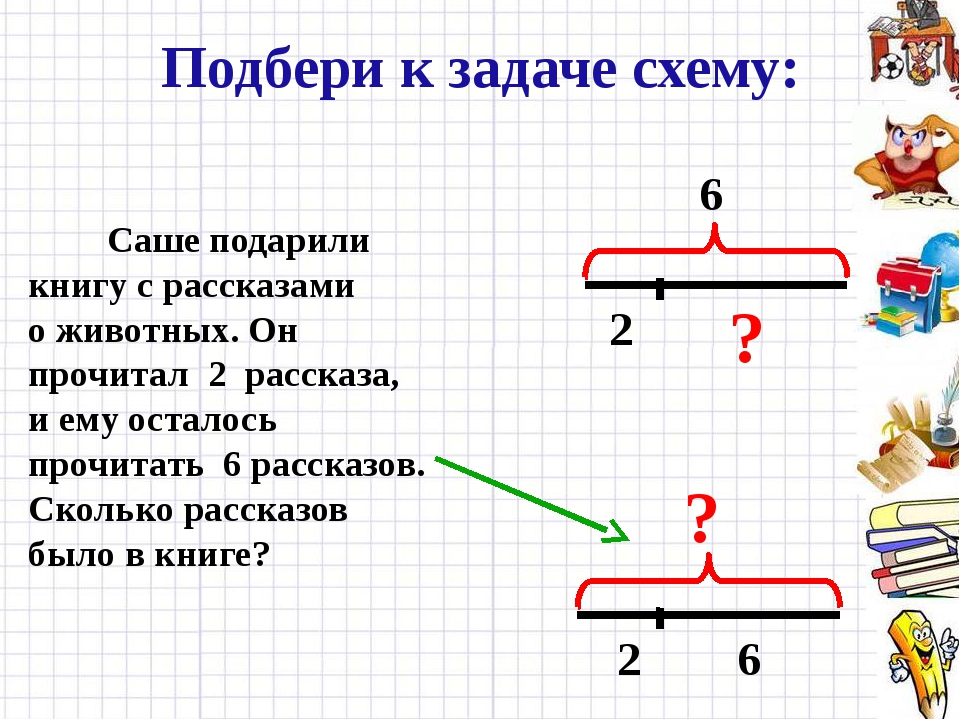
студенты с широким уровнем математических способностей. Им нужно
быть «низкий барьер, высокий потолок», под этим я подразумеваю, что студенты должны
добились успеха / достигли прогресса в выполнении задачи в течение первых 30
секунд, но мяса еще достаточно, чтобы заставить их думать
30 минут (а то и 3 урока) позже.
Я считаю, что такие занятия имеют решающее значение для учащихся.
математическое развитие. Они позволяют им проявлять творческий подход и работать
вместе значимым и позитивным образом. При разработке наших
Схема работы (вы можете прочитать мою серию
сообщений об этом в блогах), мы решили включить обязательный
богатая задача для всех студентов по каждому разделу темы, и многие из них могут
можно найти ниже.
Ключом к хорошей сложной задаче являются вопросы, которые ее сопровождают. Вот где происходит эффективное дифференцирование. Все студенты
Вот где происходит эффективное дифференцирование. Все студенты
начать задачу точно так же, но однажды начальный этап
была достигнута, студенты (индивидуально или в группах) могут свободно
проводить различные расследования, зондирующие вопросы и направления
расследование. Их может предоставить учитель или даже
сами студенты.
Сила богатой задачи заключается в этих вопросах.Так вот
мой план: я собираюсь поделиться как можно большим количеством моих любимых насыщенных задач
насколько это возможно, и мы надеемся, что учителя со всего мира
собираюсь предоставить вопросы. Это могут быть направления расследования,
исследования, подсказки, гипотезы, расширения, упрощения,
модификации, какие угодно. Важно то, что вам не нужно
знаете ответ сами. Просто выбрось это! Там будет
место для них в разделе комментариев внизу каждого TES
Страница ресурсов, и я всегда буду работать с несколькими
мои собственные вопросы.
Пожалуйста, присоединяйтесь. Расскажите, пожалуйста. Пожалуйста, просто поделитесь даже
один вопрос. И тогда задачи будут улучшаться, и
лучше и лучше.
Расширенные задачи
keyboard_arrow_up
В начало
Задача
1 — Положительные различия
Краткое описание: Учащиеся строят пирамиды простых чисел с помощью
взятие положительной разности пар чисел
Возможные навыки: Арифметика, дроби, десятичные дроби,
Написание выражений, доказательство
Задача
2 — Игра на множители и множители
Краткое описание: Студенты играют в стратегическую игру на
Числовая сетка 1-100, коэффициенты вычеркивания и множители
Вовлеченные потенциальные навыки: Арифметика, множители, умножители,
Простые числа, Proof
Задача
3 — Выберите 3 числа
Краткое описание: Учащиеся пытаются угадать друг друга
начальные числа, работая в обратном порядке от сумм пар
числа
Возможные навыки: Арифметика, написание выражений,
Решение уравнений
Задача
4 — Они встретятся?
Краткое описание: Можете ли вы помочь Ромео и Джульетте вернуться?
вместе в моем первом в истории романтическом задании по математике?
Вовлеченные потенциальные навыки: Расширение, векторы, аналогичные
Фигуры, вращение
Задача
5 — Номерные хижины
Краткое описание: Можете ли вы выяснить, как количество
эти лачуги сформированы и используют это, чтобы предсказывать ответы и определять
шаблоны?
Возможные навыки: Арифметика, написание выражений
Задача
6 — Усреднение
Краткое описание: Что происходит, когда мы постоянно принимаем
среднее значение наборов чисел?
Вовлеченные потенциальные навыки: в среднем, ИКТ
Задача
7 — Расположение дробей
Краткое описание: Вы можете заказать разные цифры для
дать самые большие и самые маленькие ответы на эти
проблемы с дробями?
Возможные навыки: Операции с дробями
Задача
8 — Diffy
Краткое описание: Первый урок нашей новой связки Года
7s, и один из моих фаворитов на все времена
Вовлеченные потенциальные навыки: Арифметика, написание выражений,
Доказательство
Задача
9 — Лестница одновременных уравнений
Краткое описание: Почему все получают одинаковый ответ на
эти проблемы с одновременным уравнением?
Вовлеченные потенциальные навыки: Одновременные уравнения, доказательство
Задача
10 — Сколько углов?
Краткое описание: С помощью геоборда, сколько углов
от 10 до 180 вы можете заработать?
Вовлеченные потенциальные навыки: Угловые факты, круговые теоремы
Задача
11 — Номер в обратном порядке
Краткое описание: Что происходит, когда мы меняем местами цифры
чисел и выполнять над ними операции?
Возможные навыки: Арифметика, написание выражений,
Доказательство
Задача
12 — Уменьшение умножения
Краткое описание: Следуйте правилу, чтобы уменьшить число в
размер с помощью умножения. Что-нибудь интересное происходит?
Что-нибудь интересное происходит?
Возможные навыки: Арифметика, написание выражений
Задача
13 — Сколько четырехугольников?
Краткое описание: Используя geoboard, сколько разных
четырехугольники можно сделать?
Возможные навыки: Свойства форм, угол
факты
Задача
14 — 1089
Краткое описание: Почему число 1089 такое особенное?
Возможные навыки: Арифметика, написание выражений,
Доказательство
Задача
15 — Координаты квадрата
Краткое описание : Что означают координаты углов
квадратов есть общего?
Вовлеченные потенциальные навыки: Координаты, свойства
фигуры, Векторы, Проба
Задача
16 — Белые медведи
Краткое описание : Можете ли вы выяснить, как получить итоговые значения?
в этой игре в кости?
Возможные навыки: Арифметика
Задача
17 — Треугольник Паскаля
Краткое описание : Какую математику вы можете обнаружить, скрываясь в
Треугольник Паскаля?
Потенциальные задействованные навыки: Последовательности
Задача
18 — Ловушка
Краткое описание : увлекательная стратегическая игра, в которой используются все
трансформации
Вовлеченные потенциальные навыки: Отражение, вращение,
Перевод, расширение
Задача
19 — Пожарные гидранты
Краткое описание : Где лучше всего разместить
эти пожарные гидранты для максимального охвата?
Привлекаемые потенциальные навыки: Геометрическое мышление
Задача
20 — Диагонали прямоугольников
Краткое описание : Сколько квадратов составляет диагональ
прямоугольник пройти?
Возможные навыки: Арифметика, последовательности, факторы,
Кратные, простые числа
Задача
21 — T-total
Краткое описание : Как рассчитать T-номер в
эта классическая курсовая работа по математике?
Возможные навыки: Арифметика, написание выражений,
Доказательство
Задача
22 — Число змей
Краткое описание : Какая самая длинная числовая змея вы можете
сделать, используя эти простые правила?
Возможные навыки: Арифметика, свойства
Числа, написание выражений
Задача
23 — Суммирование последовательных чисел
Краткое описание : Какие числа можно составить, используя суммы
последовательных номеров?
Возможные навыки: Арифметика, написание выражений
Задача
24 — NIM
Краткое описание : Замечательная стратегическая игра с использованием свай.
счетчиков
Вовлеченные потенциальные навыки: Стратегия, факторы, множественные,
Простые числа
Задача
25 — Функциональные машины
Краткое описание : Почему эти функциональные машины кажутся
дать такую же разницу?
Возможные навыки: Арифметика, порядок операций,
Написание выражений, раскрывающие скобки
Задача
26 — Leap Frog
Краткое описание : Если вы перепрыгнете через этот набор из 3 точек
достаточно раз, что вы замечаете?
Возможные навыки: Координаторы, строительство,
Векторы
Задача
27 — Решение линейных уравнений
Краткое описание : Путем упорядочивания наборов цифр, какие типы
решений можно сгенерировать для этого простого линейного уравнения
проблемы?
Возможные навыки: Решение линейных уравнений
Задача
28 — Десятичная арифметика
Краткое описание : Вы можете
сделать возможными самые большие и самые маленькие десятичные суммы?
Возможные навыки: Арифметика, десятичные дроби, место
Стоимость
Задача
29 — 24 кубика
Краткое описание : Какие разные 3D-объекты вы можете создавать
с 24 кубиками, и что вы заметили в их свойствах?
Вовлеченные потенциальные навыки: Площадь поверхности, объем, сходство
Задача
30 — Квадраты с наклоном
Краткое описание : Сколько квадратов с площадью 1-20 вы можете
Создайте?
Возможные навыки: Area, Pythagoras
Часто задаваемые вопросы
keyboard_arrow_up
В начало
Вы говорите, что мы должны делать это на каждом уроке?
№Точно нет. Я остро осознаю необходимость для студентов
Я остро осознаю необходимость для студентов
получить практику в ключевых математических навыках. Но я сильно
считают, что такие регулярные уроки не менее важны для
математическое развитие учащихся и получение им большего удовольствия
в теме. Их не следует рассматривать как разовые. Оба студента
учителя должны ценить их так же высоко, как и любой другой урок.
Что мне делать, если ребенок не занимается определенным
вопрос или направление расследования?
Простой ответ — даю им еще одну! Я должен сделать
призыв к суждению относительно того, действительно ли студент пытался и
не просто так легко сдаться.Но если по какой-то причине
вопрос или направление расследования не нашли отклика
студент, тогда я отправлю их на что-нибудь другое. Действительно,
Красота того, что у вас в рукаве много вопросов, заключается в том, что вы
гораздо больше шансов найти те, которые заинтересуют ваших учеников, чем если бы вы
просто проведите одно расследование, что весь класс
следующий.
Вы бы сделали такой урок для наблюдения?
Да, определенно буду.100%. Конечно, таких уроков немного
на рискованной стороне, так как вы не знаете, что произойдет. Но
они также невероятно гибкие. Представьте, что вы тщательно
запланировал урок с 40 слайдами PowerPoint и 5 красиво
подготовленные дифференцированные рабочие листы. И тогда вы обнаружите, что
студенты не понимают даже основ. Или они понимают далеко
больше, чем вы ожидали. У вас могут быть небольшие неприятности.Но
с уроком, набитым пробными вопросами, вы можете просто попробовать
их по другой линии расследования. Или, еще лучше, заставьте их
придумывают свои.
Решайте многоступенчатые задачи со словами, поставленные с целыми числами и имеющие ответы с целыми числами, используя четыре операции, включая задачи, в которых необходимо интерпретировать остатки.
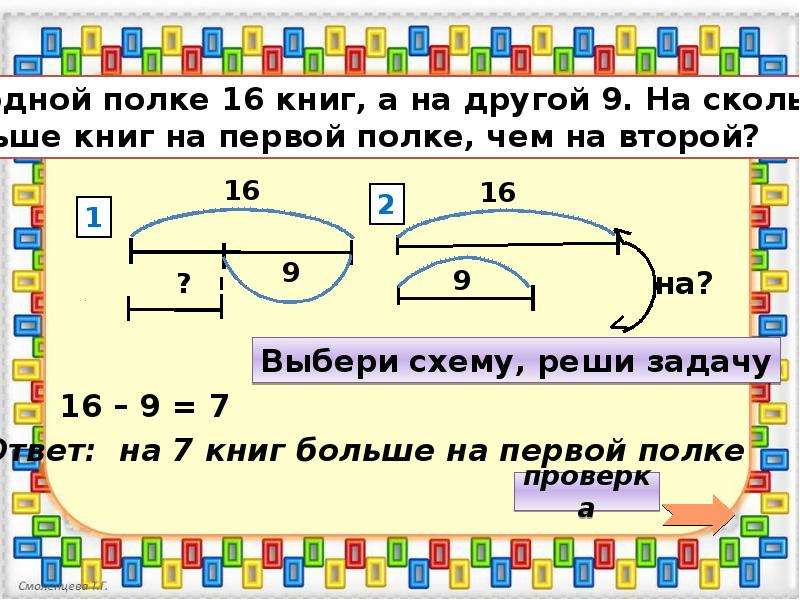 Представьте эти задачи с помощью уравнений с буквой, обозначающей неизвестную величину.Оцените разумность ответов с помощью мысленных вычислений и стратегий оценки, включая округление.
Представьте эти задачи с помощью уравнений с буквой, обозначающей неизвестную величину.Оцените разумность ответов с помощью мысленных вычислений и стратегий оценки, включая округление.
Планировщик воздушных шаров на день рождения:
Учащиеся разработают модель выбора планировщика вечеринок с воздушным шаром и ранжируют их от лучших к худшим.
Учащиеся смогут использовать предварительные знания сложения многозначных целых чисел, фактов и концепций умножения и деления, математических расчетов с деньгами и временем, понимания дробей и навыков решения проблем для решения нестандартных MEA (Model Eliciting). Activity), который требует практического применения математических навыков.
Рыба Ахой Рыба:
Студенты будут работать в группах, чтобы помочь клиенту в покупке различной рыбы для пруда. Из таблицы данных им нужно будет решить, какой вид рыбы и сколько рыбы купить в зависимости от размера каждого пруда. После этого им нужно будет еще раз просмотреть пересмотренную таблицу данных, чтобы сделать другой выбор рыбы и рассчитать затраты на ее покупку.
Из таблицы данных им нужно будет решить, какой вид рыбы и сколько рыбы купить в зависимости от размера каждого пруда. После этого им нужно будет еще раз просмотреть пересмотренную таблицу данных, чтобы сделать другой выбор рыбы и рассчитать затраты на ее покупку.
Новый слой краски:
В этом MEA студенты будут работать в совместных группах для решения многоступенчатых задач с целыми и десятичными числами, используя различные математические операции, такие как сложение, вычитание, умножение и деление. Студентов попросят помочь владельцу собственности, который планирует отремонтировать свою новую собственность, в покупке подходящей краски для наружного применения.Им нужно будет прочитать таблицу данных, расположить краски в порядке убывания, рассчитать необходимое количество галлонов в соответствии с площадью поверхности и общую стоимость каждой краски. К проблеме добавляется изюминка, когда одна из красок недоступна, но добавляются две другие, а также владелец хочет покрасить перегородки снаружи.
Планировка парка:
Студентам будет предложено спланировать игровую площадку, используя не более 30% площади парка.Они проанализируют наилучшее использование оборудования игровых площадок, используя таблицу данных о требованиях к площади, и сделают выбор на основе наименьшей площади, используемой для наибольшего количества оборудования (не превышая 30% от общей площади парка).
Требуются организаторы вечеринок:
В этом MEA студенты будут работать в совместных группах для решения многоступенчатых задач с целыми и десятичными числами, используя различные математические операции, такие как сложение, вычитание, умножение и деление.Студентов попросят помочь бизнесмену, который планирует вечеринку для своих сотрудников. Им нужно будет прочитать несколько объявлений и решить, какая компания предлагает лучшее предложение по аренде столов, стульев и скатертей для клиента. Им нужно будет принять во внимание количество гостей, пришедших на вечеринку, и разрешенный бюджет. К проблеме добавляется изюминка, когда студентов просят рассмотреть дополнительное объявление и тот факт, что список гостей теперь немного больше.
Pickle Pick:
В рамках этого типового задания (MEA) студентов просят разработать процедуру выбора марки солений для магазина сэндвичей.Студентам необходимо будет учитывать внешний вид, текстуру, цену, вкус, срок хранения и оценку стоимости доставки. Во второй части постановки задачи учащимся нужно будет найти компромисс между тем, что они ранее рассматривали, и придать больше значения расчетным расходам на доставку, добавив при этом еще три бренда для рассмотрения. Учащиеся завершат завершающее задание по созданию рекламного ролика для рекламы выбранного ими бренда. Студенты должны будут работать вместе и использовать стандартные письменные правила, чтобы писать и исполнять свои рекламные ролики для других групп.
Пионерский город МЭС:
Этот MEA разработан таким образом, чтобы учащиеся могли создать процесс выбора «Лучшего города для пионеров» во Флориде на основе определенных критериев. Студентам придется переформулировать свой процесс после того, как им будут предоставлены дополнительные критерии, на которых они будут основывать свою модель.
Робототехника с ограниченным бюджетом:
The P.T.A. Президенту ABC Elementary нужна помощь ваших учеников в выборе модели робототехники, которая соответствует потребностям учеников и программе внешкольного обогащения. Студенты должны придерживаться бюджета в 2000 долларов. Студентам будет предложено оценить модели 4 на основе заданных им критериев и бюджета.Студентам будет предоставлен набор данных, который поможет им разработать процедуру для этого. В своих командах они напишут письмо президенту P.T.A с описанием своих процедур и объяснением стратегии, которую они использовали. Студенты будут практиковаться в сложении, вычитании и умножении чисел на тысячи, чтобы рассчитать количество моделей определенной модели, которые можно купить, не выходя за рамки бюджета. Рубрики включены, чтобы помочь учащимся.
Талантливые дивы МЭА:
Это Типовое задание на выявление (MEA) написано на уровне 5-го класса.Этот MEA просит студентов выбрать футболку для талантов, которая обеспечит талантливым дивам лучшее соотношение цены и качества. Студентов просят расположить Talent Shirt Company от лучшего к худшему. Студенты должны предоставить талантливым дивам футболки с надписью «Best Value» и объяснить, как они пришли к своему решению.
Путешествия и многое другое MEA:
В этом Типовом мероприятии по выявлению (MEA) студентам необходимо будет помочь туристическому агенту подобрать лучший пакет для отдыха в отеле для семьи из четырех человек.Им необходимо принять во внимание все удобства, цены, льготы и отзывы. Изюминка наступает, когда туристическому агенту нужно будет предоставить путевки в гостиницу для семей из 5 человек.
Идти по этому пути:
Ученикам будет предложено расположить разные плитки пола для игровых комнат в центрах активности в общественных парках.Им нужно будет принять во внимание определенные факторы при составлении рейтинга. Им также необходимо будет рассчитать затраты на укладку напольной плитки, используя заданные размеры игровой комнаты и напольной плитки. «Изюминка» будет в том, что теперь клиенту необходимо включить складское помещение для некоторого оборудования игровой. Им нужно будет решить, использовать ли ту же плитку для пола или отличную от игровой, а также о дополнительных затратах на кладовку. После они добавят общую стоимость игровой комнаты и кладовой.Они сообщат о своих выводах и причинах в письмах клиенту.
Ярды в Ярды:
В этом MEA студенты будут работать в совместных группах для решения многоступенчатых задач со словами, поставленных с целыми числами. Студентов попросят помочь ландшафтной компании решить, какие изгороди лучше всего использовать для замены существующих живых изгородей, которые в настоящее время не процветают из-за заражения насекомыми.

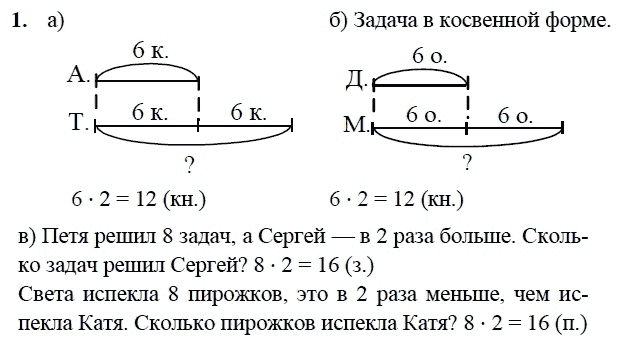
 Давайте с хорошим настроением начнем нашу работу.
Давайте с хорошим настроением начнем нашу работу.
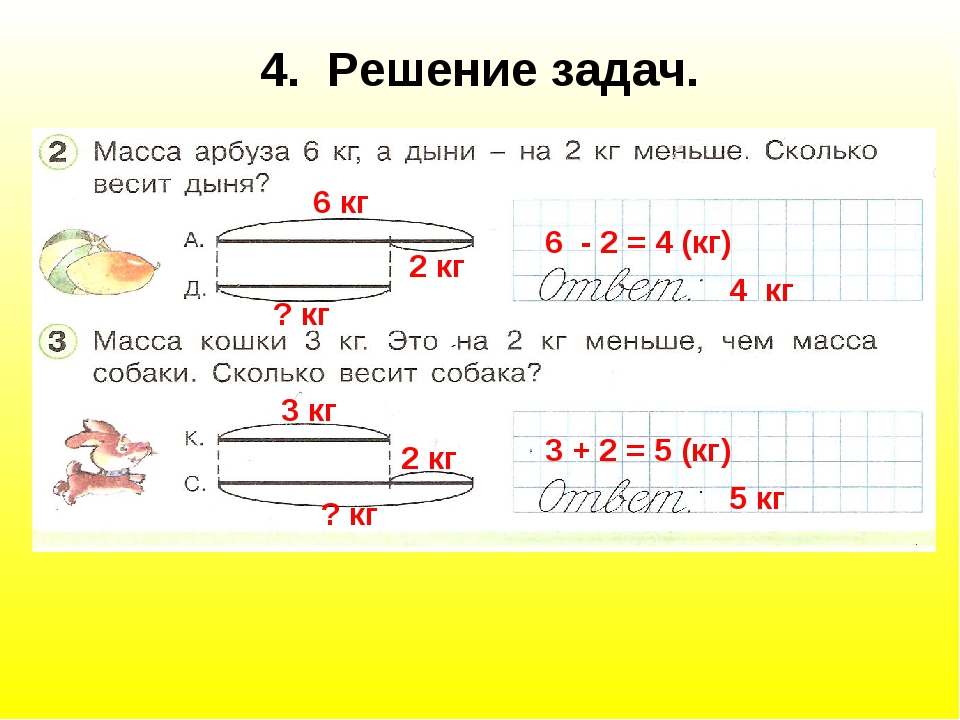

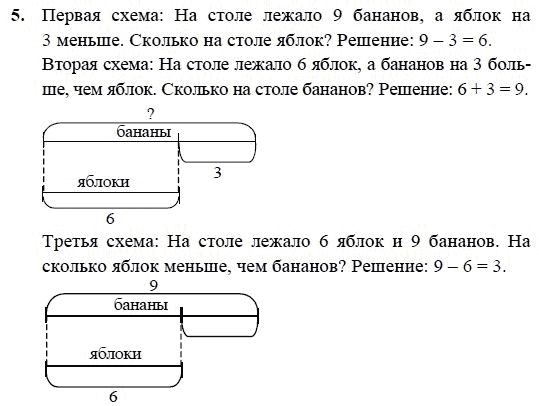
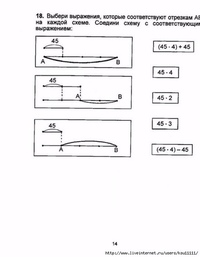 д. )
д. )

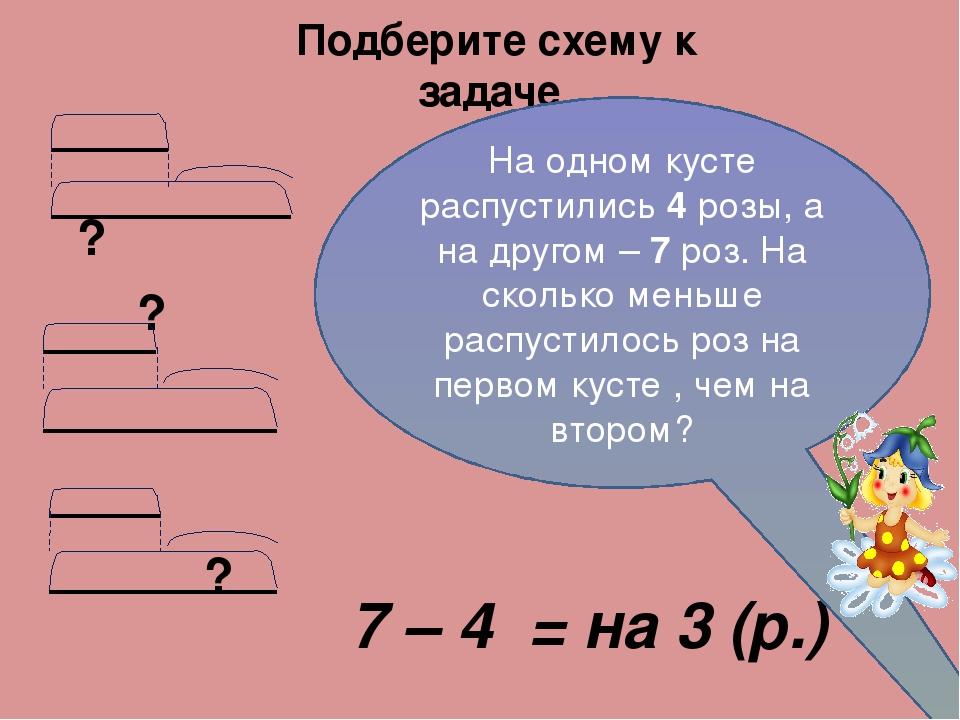
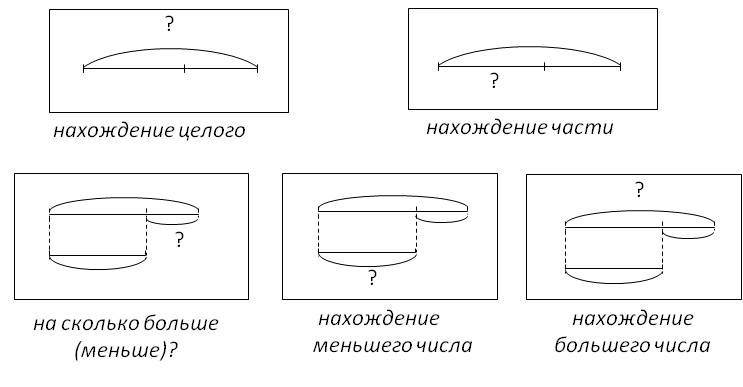 Известно, что самую большую скорость развивает ковер-самолет, медленнее всех движутся сапоги скороходы, а верный конь быстрее корабля. Укажите на диаграмме скорость движения каждого вида транспорта. Предлагаю вам эту работу выполнить в паре.
Известно, что самую большую скорость развивает ковер-самолет, медленнее всех движутся сапоги скороходы, а верный конь быстрее корабля. Укажите на диаграмме скорость движения каждого вида транспорта. Предлагаю вам эту работу выполнить в паре.
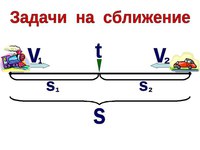

 7 минут.
7 минут.
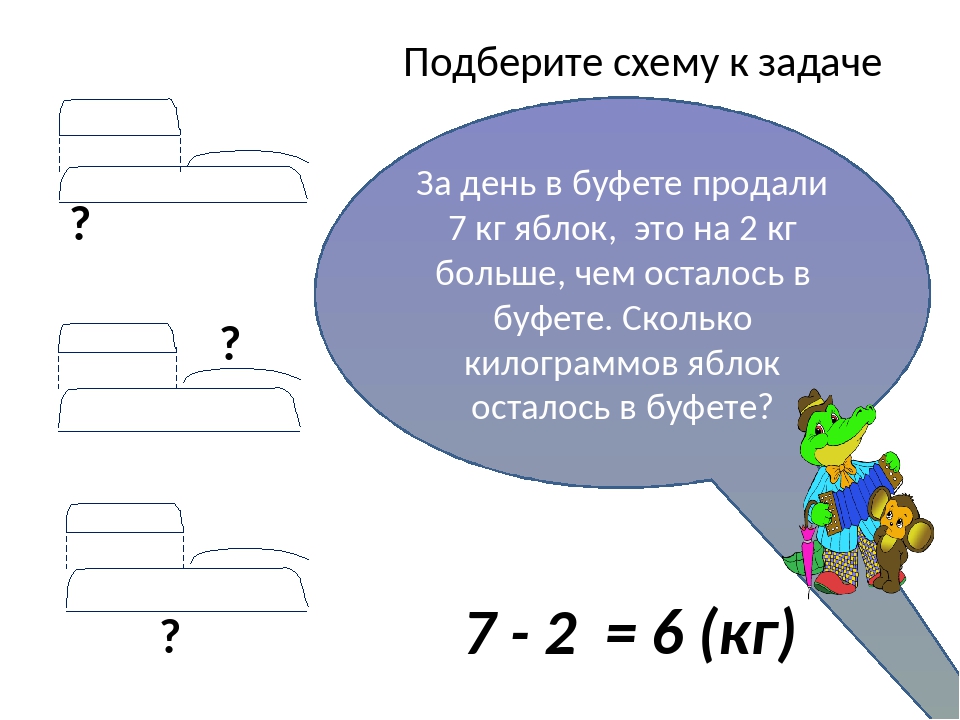
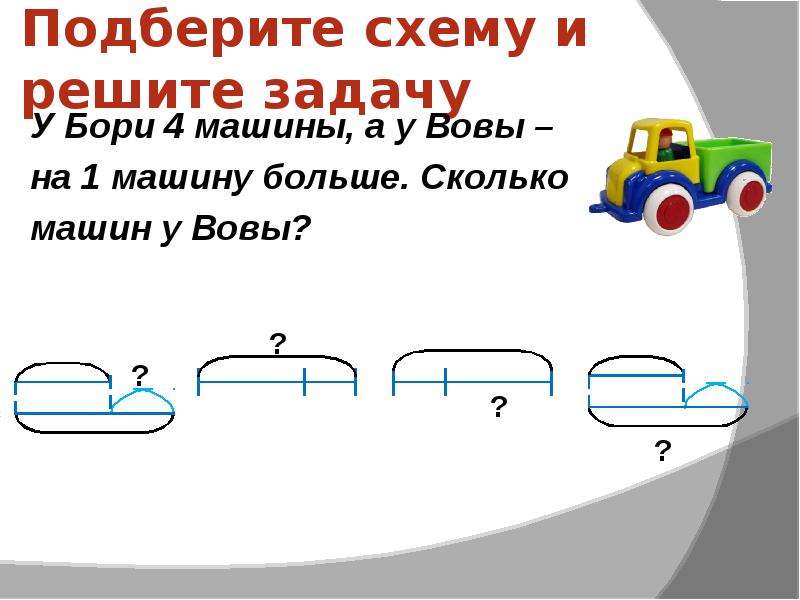 3 минуты
3 минуты
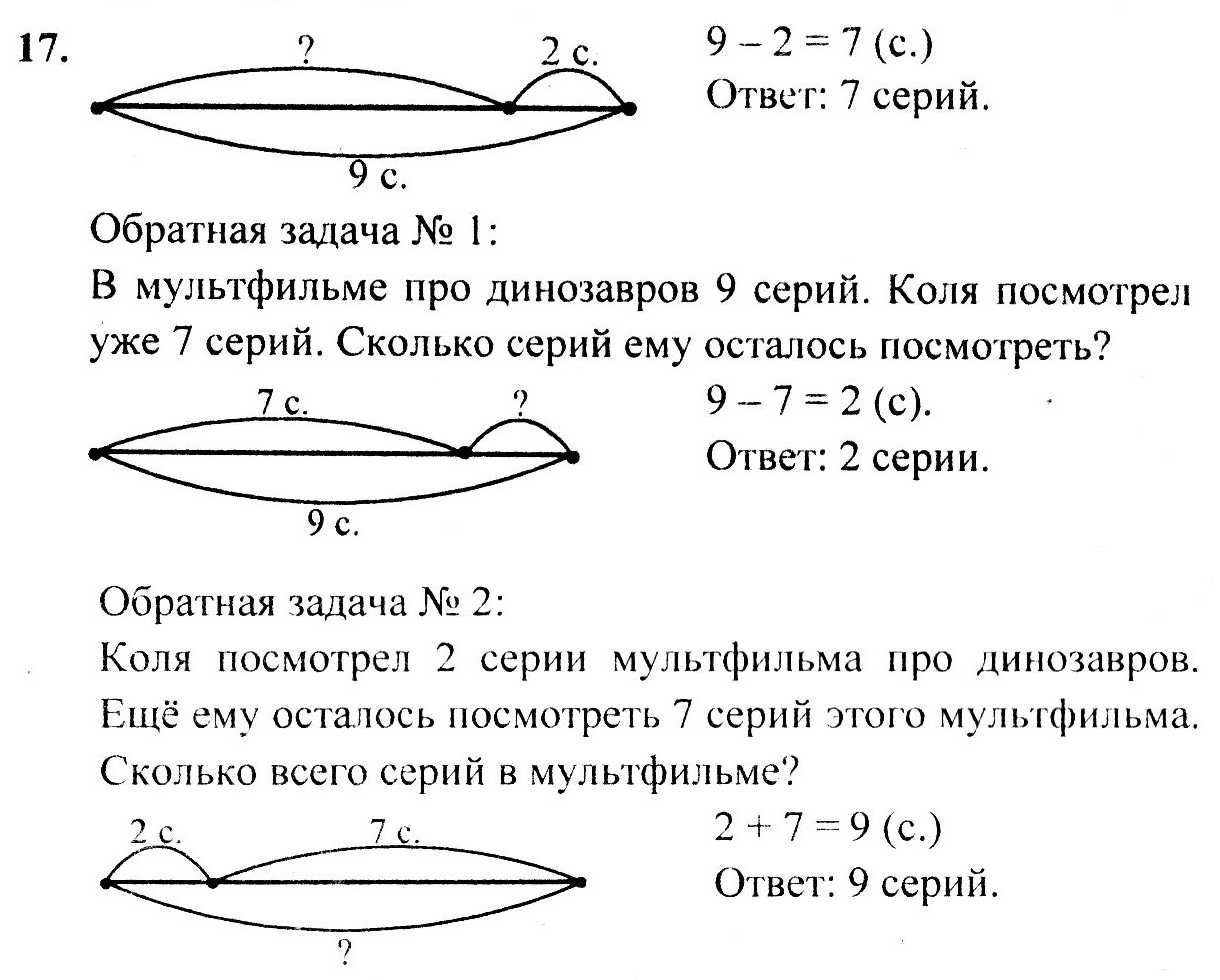
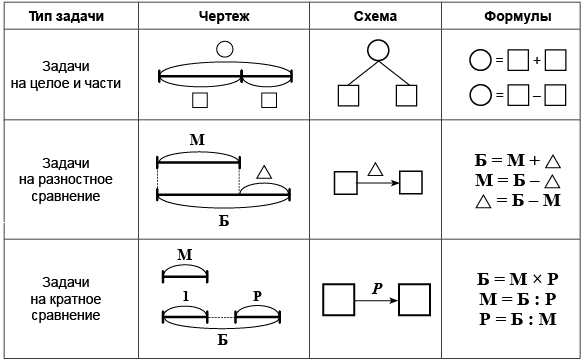
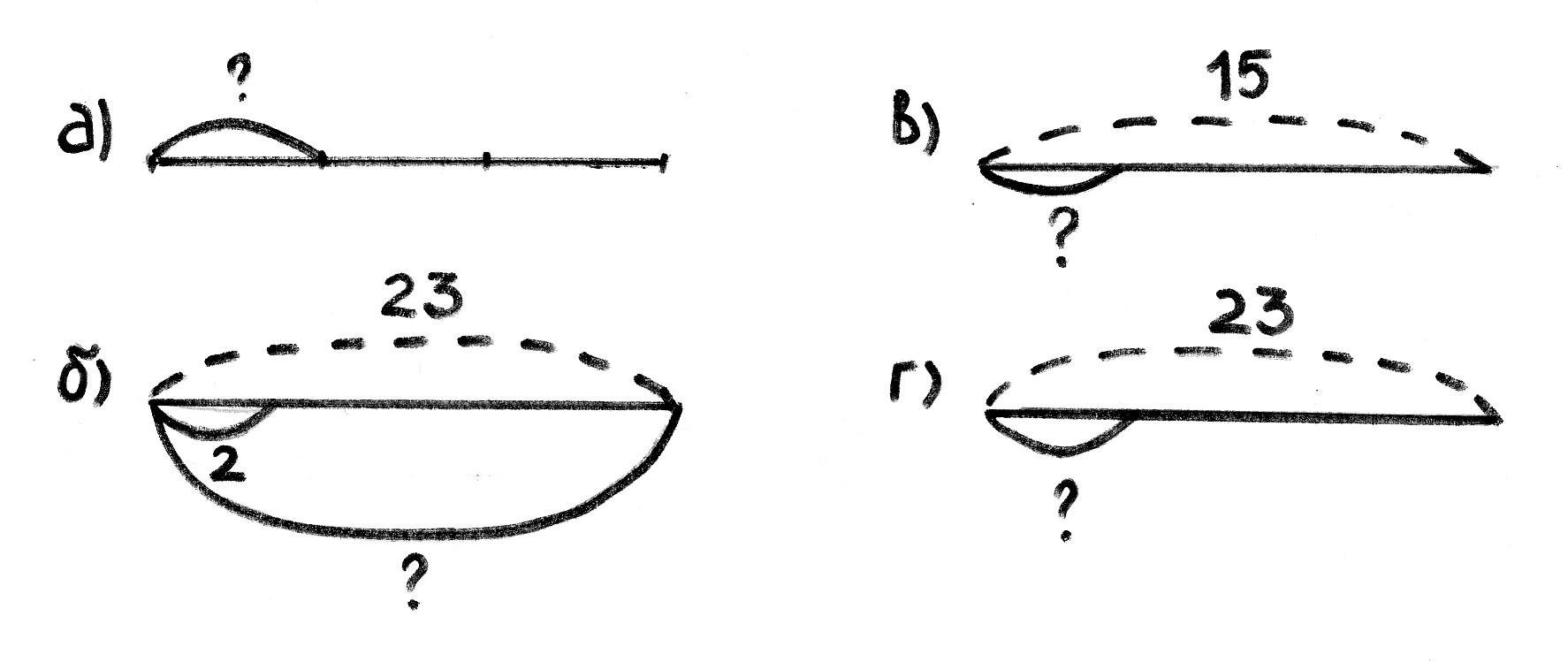
 Но будьте готовы удивиться — ваши ученики, вероятно, придумают лучшие идеи и вопросы, чем вы можете придумать.
Но будьте готовы удивиться — ваши ученики, вероятно, придумают лучшие идеи и вопросы, чем вы можете придумать.