Урок 34. решение задач. часть 1 — Математика — 2 класс
Математика, 2 класс
Урок № 34. Решение задач.
Перечень вопросов, рассматриваемых в теме:
— Как составить план решения задачи?
Глоссарий по теме:
Задача – это упражнение, которое выполняется посредством умозаключения, вычисления.
Выражение – формула, выражающая какие–либо математические отношения.
Схема — своеобразный чертёж, в котором составные части — его элементы и связи между ними изображены условно, без соблюдения масштаба.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
- Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –5-е изд. – М.: Просвещение, 2014. – с.10, 11.
- Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций.
 В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.7, 8.
В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.7, 8. - Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 9-е изд. – М.: Просвещение, 2014. – с.18.
Математика. Тетрадь учебных достижений. Учебное пособие для общеобразовательных организаций. С. И. Волкова – М.: Просвещение, 2017. – с.41.
Теоретический материал для самостоятельного изучения
Посмотрите на эти изображения. Знакомы ли нам они? Да, это схемы задач.
Мы умеем составлять схемы к задачам и по схемам находить задачу.
Определим, какая схема подходит к задаче.
В этой задаче мы находим целое.
Подходит такая схема.
Выберем схему ко второй задаче.
В этой задаче мы находим часть
от целого. Подходит данная схема.
И к последней схеме мы составим такую задачу:
Папа поймал на рыбалке 6 окуней и 8 лещей. Сколько всего рыб поймал папа?
Папа поймал на рыбалке 6 окуней и 8 лещей.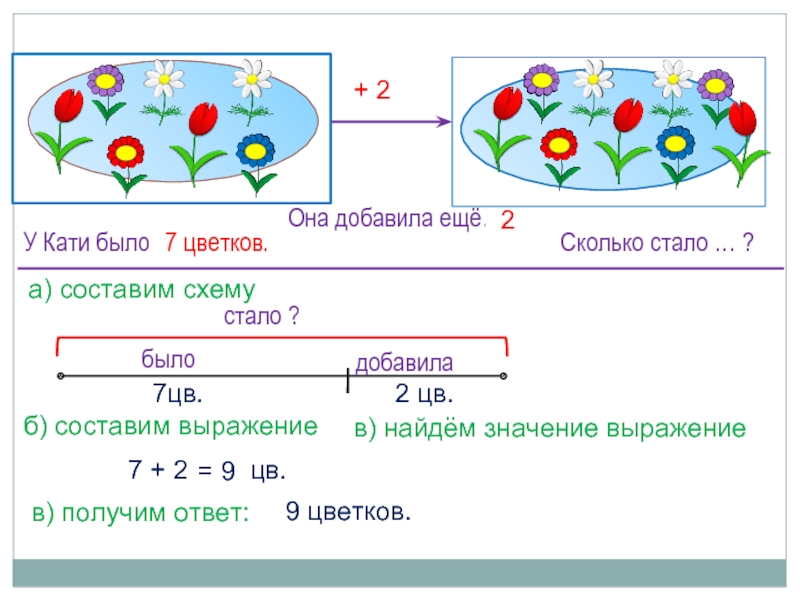 Сколько всего рыб поймал папа?
Сколько всего рыб поймал папа?
Рассмотрите такую схему.
Знакома ли она вам? С такими схемами мы ещё не встречались. Это схемы рассуждения при поиске решения задачи. Составим схему рассуждения при решении уже известной нам задачи. «Папа поймал на рыбалке 6 окуней и 8 лещей. Сколько всего рыб поймал папа?». Для решения задачи начнём рассуждать от вопроса, составляя при этом схему. Что нужно найти в задаче? «Сколько всего рыб поймал папа?»
Ставим в схеме знак вопроса.
Что для этого достаточно знать?
Верно, нужно знать, сколько и каких рыб поймал папа.
Это окуни и лещи. Ставим числа 8 и 6,
рисуем стрелки к вопросу.
Можем ли мы ответить на вопрос задачи?
Да.
8 + 6 = 14 (р.) поймал папа
Попробуем составить схему рассуждения к более сложной задаче.
«Папа поймал на рыбалке 8 окуней, а сын на 2 рыбы меньше. Сколько всего рыб поймали папа и сын?».
Что нужно узнать в задаче? «Сколько всего рыб поймали папа и сын?»
Ставим в схеме знак вопроса.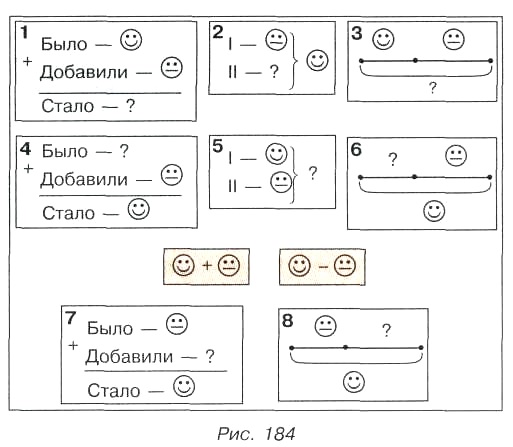
Что для этого достаточно знать?
Верно, нужно знать сколько рыб поймал папа
и сколько рыб поймал сын. Рисуем два круга и стрелки к вопросу.
Что из этого мы знаем, а что нужно найти?Правильно, мы знаем сколько рыб поймал папа. Ставим число восемь в схему.
Но мы не знаем, сколько рыб поймал сын.
Ставим знак вопроса.
Что нужно знать, чтобы сосчитать рыб, которых поймал сын?
Нужно знать количество рыб у папы и
на сколько меньше поймал рыб сын.
Рисуем два круга и стрелки к вопросу.
Ставим в схему числа восемь и два.
Каким будет первое действие? Узнаем, сколько рыб поймал сын.
1) 8 – 2 = 6 (р.) поймал сын.
Ответили мы на вопрос задачи? Нет. Каким будет второе действие?
Узнаем, сколько всего рыб поймали папа и сын.
2) 8 + 6 = 14 (р.) поймали всего.
Вывод: Для выбора способа решения задачи, мы выстраиваем цепочку рассуждения. Её можно представить в виде схемы. Составляя схему рассуждения «от вопроса к данным», мы отвечаем на такие вопросы: «Что достаточно знать, чтобы ответить на вопрос задачи? Что мы знаем уже? Как найти то, что ещё неизвестно?».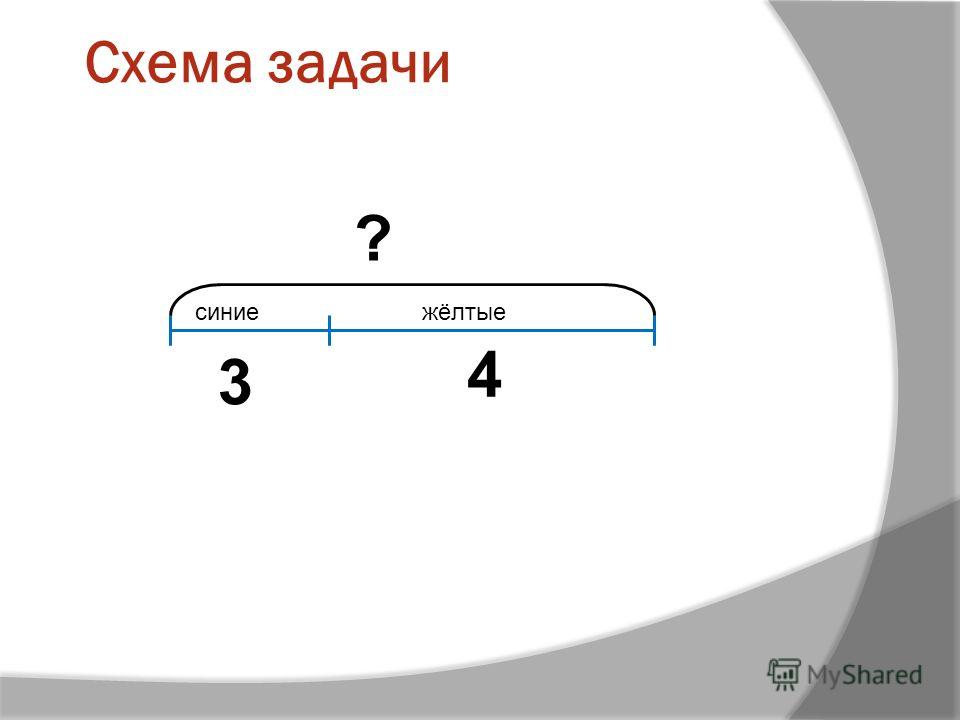 Текст задачи можно моделировать разными способами: в виде схематического чертежа, таблицы, диаграммы.
Текст задачи можно моделировать разными способами: в виде схематического чертежа, таблицы, диаграммы.
Тренировочные задания.
1.Выберите схему рассуждения, подходящую к задаче «Юра съел 9 конфет, а Коля на 4 конфеты меньше. Сколько конфет съели мальчики?»
Правильные ответы:
2. Дополните диаграмму данными из текста.
Сел Миша на пенёк, съел пирожок… А ещё две баранки, пять пончиков и девять яблок.
Правильные ответы:
решение задач за 5 — 6 класс — Колпаков Александр Николаевич
На этой странице публикуются решения задач по математике для 5 и 6 класса: части, проценты, пропорции, вычисления, простые текстовые задачи на движение, на работу, не требующие применения никаких уравнений кроме линейных. Помните о том, что виртуальный репетитор по математике не знает по какой программе учится Ваш ребенок и поэтому возможны расхождения со школой. Часто одну и ту же задачу на дроби можно решить по разному: средствами 5 класса (при помощи отдельных действий с числителями и знаменателями), а можно, например, средствами 6 класса, выполняя умножение или деление на соответствующие дроби. Для того, чтобы помочь репетитору математики выбрать оптимальный способ оформления номера, указывайте ссылки на авторов школьных учебников и Ваш класс. Пожалуйста, не заваливайте репетитора целыми списками номеров. Ориентировочное ограничение: 1-2 номера для каждого посетителя. Если Вам понравилась эта страница — нажмите на кнопку +1:
Для того, чтобы помочь репетитору математики выбрать оптимальный способ оформления номера, указывайте ссылки на авторов школьных учебников и Ваш класс. Пожалуйста, не заваливайте репетитора целыми списками номеров. Ориентировочное ограничение: 1-2 номера для каждого посетителя. Если Вам понравилась эта страница — нажмите на кнопку +1:
Это поможет другим ученикам найти сайт в интернете.
Виртуальный репетитор по математике (5-6 класс). Решения ваших задач.
Вопрос от Вовы: Из пункта М в пункт N выехал почтальон со скоростью 23 км/ч, и одновременно с ним из N в M выехал второй почтальон со скоростью 19 км/ч. Когда первый почтальон прибыл N, второму еще оставалось до М проехать 24 км. Каково расстояние между М и N?
Репетитор по математике о задаче про почтальона (А.Н. Колпаков)
Обозначим буквой t время, за которое первый почтальон прибыл в N, тогда 23t — путь, пройденный первым, а 19t — путь, пройденный вторым почтальоном за это же время.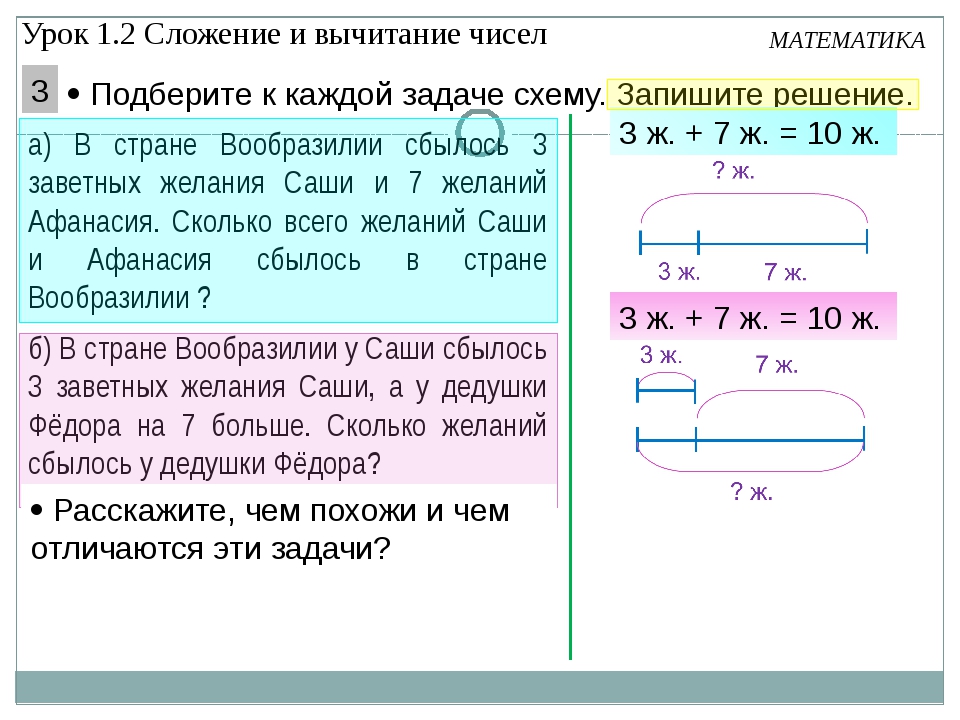 Так как второму езе оставалось 24 км, то он прошел за это время расстояние на 24 км меньшее, чем первый, поэтому 23t-19t=24. Решим это простенькое уравнение и получим в ответе t=6 часов. В итоге (км) — пусть первого, равный всему расстоянию от M до N.
Так как второму езе оставалось 24 км, то он прошел за это время расстояние на 24 км меньшее, чем первый, поэтому 23t-19t=24. Решим это простенькое уравнение и получим в ответе t=6 часов. В итоге (км) — пусть первого, равный всему расстоянию от M до N.
Ответ: 138 км.
Вопрос репетитору по математике от Оксаны: Помогите с задачей. Она элементарная, но нам надо ее решить без использования дробей!!! У квадрата одну его сторону увеличили на 9 см, а другую сторону уменьшили в 5 раз. В результате этого получилcя прямоугольник с периметром равным 66 см. У какой фигуры — у прямоугольника или у квадрата — получилась больше площадь и на сколько?
Репетитор по математике о задаче c квадратом:
Если Вы хотите решить эту задачу без применения каких-либо дробей, не выходя за рамка программы 5 класса, то буквой икс необходимо обозначить наименьшую из величин, то есть ширину прямоугольника. Итак, пусть AK=x, тогда AD=AB=5x. Поскольку сторону AB увеличили на 9 см, то длина полученного прямоугольника выражается как 5x+9.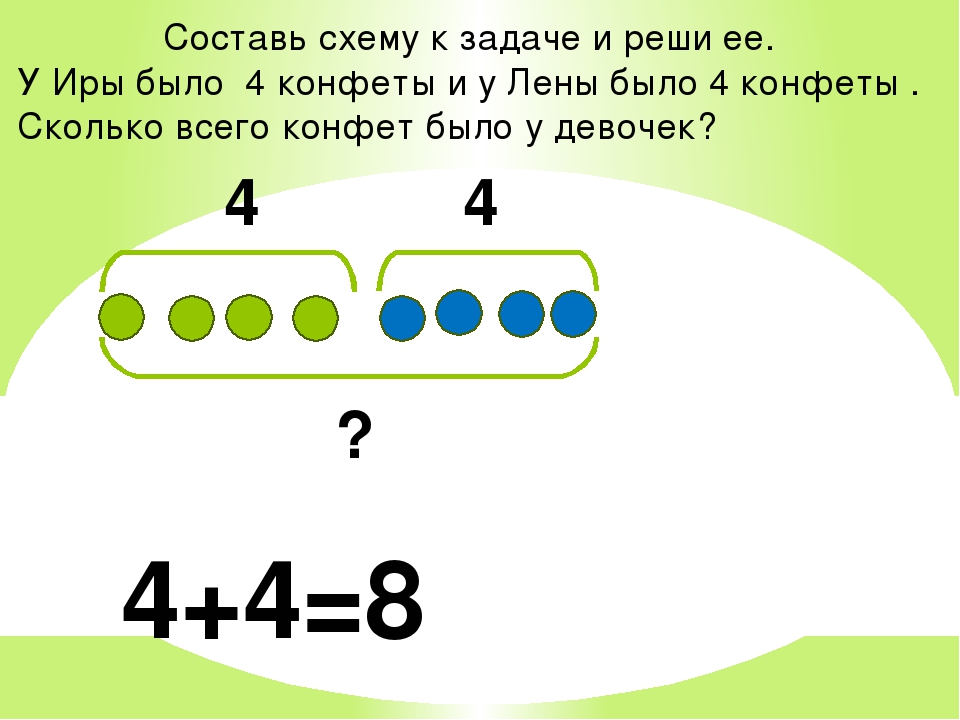 Принимая во внимание условие с периметром, получаем простенькое уравнение без дробей:
Принимая во внимание условие с периметром, получаем простенькое уравнение без дробей:
x+x+5x+9+5x+9=66
Решая его получим, что x=4. Теперь легко найти интересующие нас площади: кв.см., кв.см.
И тогда 400-116=284 кв.см. — разница между ними.
Вопрос от Анны: Помогите решить задачу.
Отец и сын, работая вместе, покрасили забор за 12 ч. Если бы отец красил забор один, он выполнил бы эту работу за 21 ч. За сколько часов покрасил бы этот забор сын?
Репетитор по математике, Тимур Розугнов
Примем весь объем работы (забор) за единицу и воспользуемся тем, что совместная скорость равна сумме отдельных скоростей отца и сына. Следить за решением удобно при помощи табличного метода оформления:
1) (заб/час) — совместная скорость
2) (заб/час) — скорость отца
3) (заб/час) — скорость сына
4) (часов) — время работы сына
Ответ: 28 часов
Вопрос от Марины:
Редактор прочитал две пятых рукописи, что составило 80 страниц.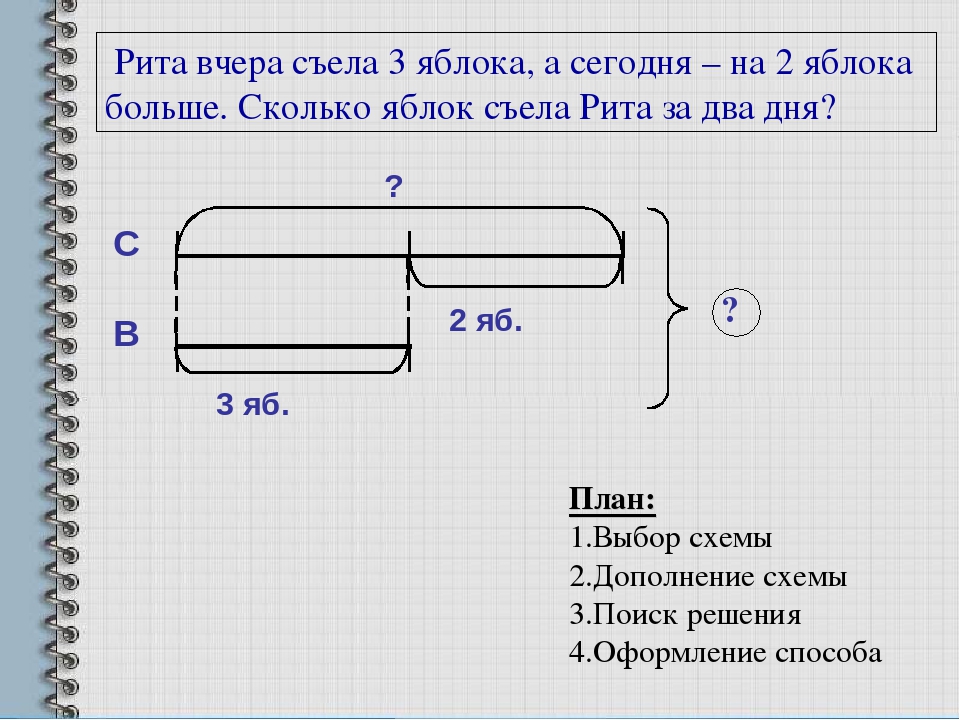 На другой день он прочитал четверть оставшихся страниц. ВОПРОСЫ: 1) Сколько страниц в рукописи? 2) Сколько страниц осталось не прочитано?
На другой день он прочитал четверть оставшихся страниц. ВОПРОСЫ: 1) Сколько страниц в рукописи? 2) Сколько страниц осталось не прочитано?
Репетитор по математике, Никита Афанасьевич
Для лучшего усвоения решения полезно сделать краткую запись. Выглядеть она будет следующим образом:
Решение:
1) (страниц) в рукописи.
2) (рукописи) — составляет остаток.
3) (страниц) — остаток.
4) (страниц) — прочитано во второй день.
5) (страниц) не прочитано.
Ответ: 90 страниц.
Задача от Наташи:
Мотоциклист в первый час проехал 3/8 всего пути ,во второй час 3/5 остатка,а в третий час остальные 40 км. Найдите весь путь. Помогите решить!
Репетитор по математике, Александр Колпаков
Старайтесь указывать для какого класса и по какой программе репетитору оформлять решение !!! будем считать, что что вы в 6 классе. Оформим краткую запись ровно так, как я это рекомендую делать своим ученикам: (в вертикальную рамку я выделяю доли, связанные законом сложения)
1) (остатка) — проехал мотоциклист за третий час
2) (км) — остаток
3) (всего пути) — остаток после пройденного мотоциклистом пусти за I час.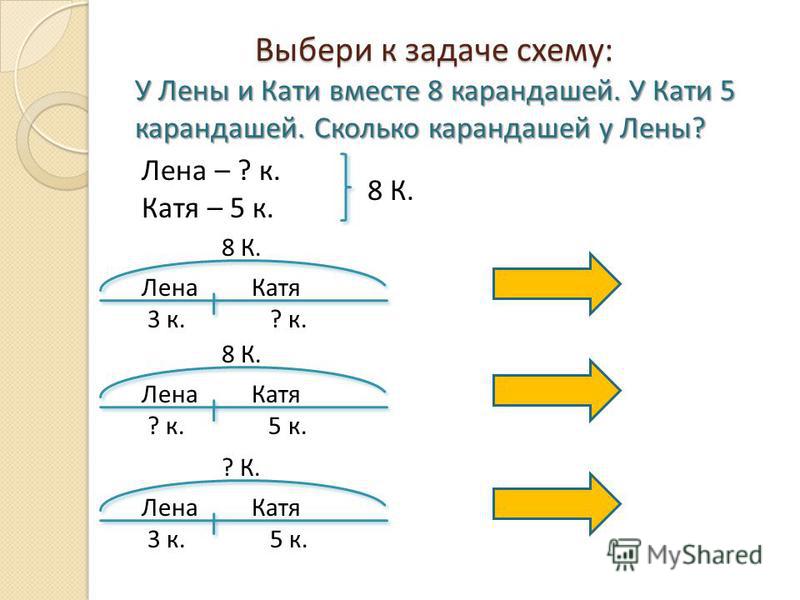
4) (км) — составляет весь путь
Ответ: 160 км
Вопрос от Оксаны: Объясните, пожалуйста, как правильно решить задачу: поезд проходит расстояние АВ за 10,5 ч. На сколько процентов следует увеличить его скорость, чтобы то же расстояние он преодолел за 8 ч? Решение нужно СРОЧНО к 1 сентября! Пыталась сама решить ее через уравнение, но не знаю правильно ли.
Репетитор по математике, Григорий Александров: Не нужно никаких уравнений. Они только Вас запутают. Вот мое решение: поскольку прирост любой вличины в процентах не зависит от ее единицы измерения, то примем за единицу полное расстояние от А до В. Тогда скорости будут такими: и Тогда прирост по скорости составит
Найдем какую часть эта величина составляет от прежней скорости:
Осталось эту часть перевести в проценты умножением на 100. Получим в итоге %
Задача от Арины:
У Шынар в копилке 80 монет достоинством 20 и 50 тенге Всего 2590 тенге. Сколько монет в копилке у Шынар достоинством 20 тенге? достоинством 50 тенге? Заранее спасибо очень надеюсь на вашу помощь.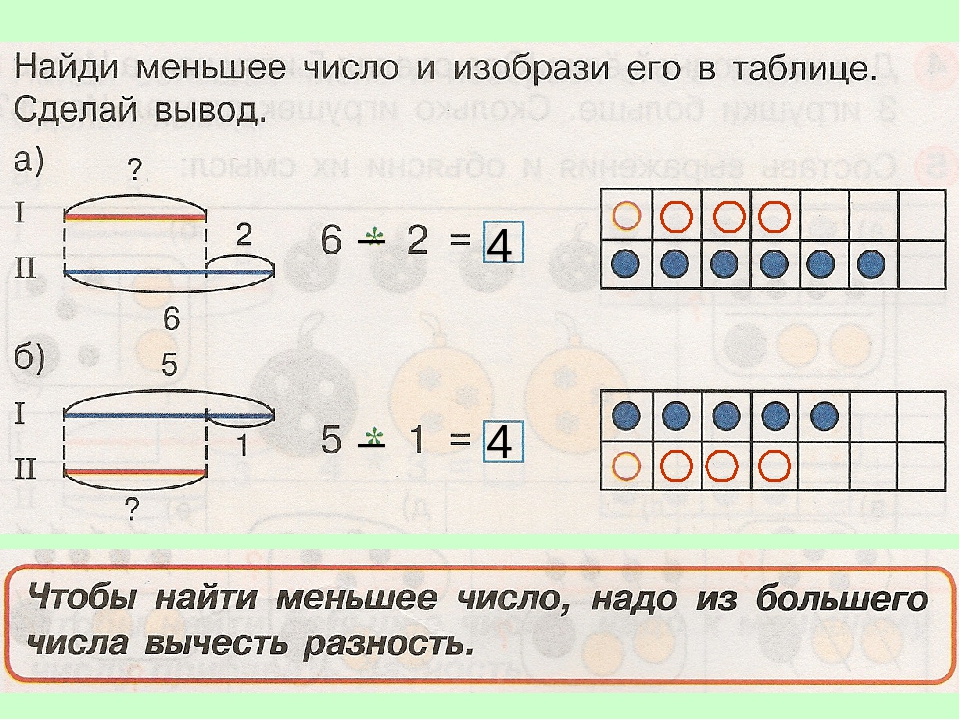
Репетитор по математике, Колпаков А.Н.
Если бы все монеты были по 50 тенге, то Шынар имела бы всего 4000 тенге. Замена одной монеты в 50 тенге на одну монету достоинство в 20 тенге приводит к снижению капитала ровно на 30 тенге. На сколько тенге нам необходимо уменьшить общий капитал Шынар с 4000 до 2590? Ровно на 4000—2590=1410 тенге. Тогда сколько раз необходимо произвести замену? 1410:30=47 раз. Поэтому 47 монет нужно поменять на двадцатитенговые. Останется 80-47=33 монеты по 50 тенге.
Ответ: 47 монет по 20 тенге и 33 монеты по 50 тенге.
Вопрос от Татьяны: нужно решить задачу:
В первый день садовод вскопал на 40% своего участка, а во второй — 40% оставшейся части. На третий день он закончил работу, вскопав 180 кв.м. Определить площадь всего участка?
Репетитор по математике и физике, Галкин Р.А.
Можно предложить 3 способа решения. Остановлюсь на том, который ориентирован на 5 класс. В целях лучшего восприятия задачи составим схему (краткую запись) условия:Здесь все проценты переведены в дроби . Найдем какую часть (или сколько процентов) составляет вскопанная часть в 3 день от того, что осталось вскопать после 1-го дня:
В целях лучшего восприятия задачи составим схему (краткую запись) условия:Здесь все проценты переведены в дроби . Найдем какую часть (или сколько процентов) составляет вскопанная часть в 3 день от того, что осталось вскопать после 1-го дня:
1) %(остатка) -вскопали в 3 день.
По известному значению 180кв.м дроби найдем целую величину, то есть остаток:
2) (кв.м) — осталось после 1 дня
Найдем какую часть остаток составляет от всего участка:
3) %(всего участка) — осталось
По известному значению 300 кв.м дроби найдем целую величину, то есть весь участок:
4) (кв.м) — площадь всего участка.
Ответ: 500 кв.м.
Вопрос от Ангелины:
У меня возник вопрос с решением задачи. Помогите пожалуйста. Можно ли из какого угодно кол-ва троек получить в ответе 100, при помощи действий сложение, вычитание и умножение?
Репетитор по математике, Файгойз М.Ю.
Не очень понял вопрос. Что значит из «какого-угодно»? Угодно нам или угодно составителю задачи? Эх .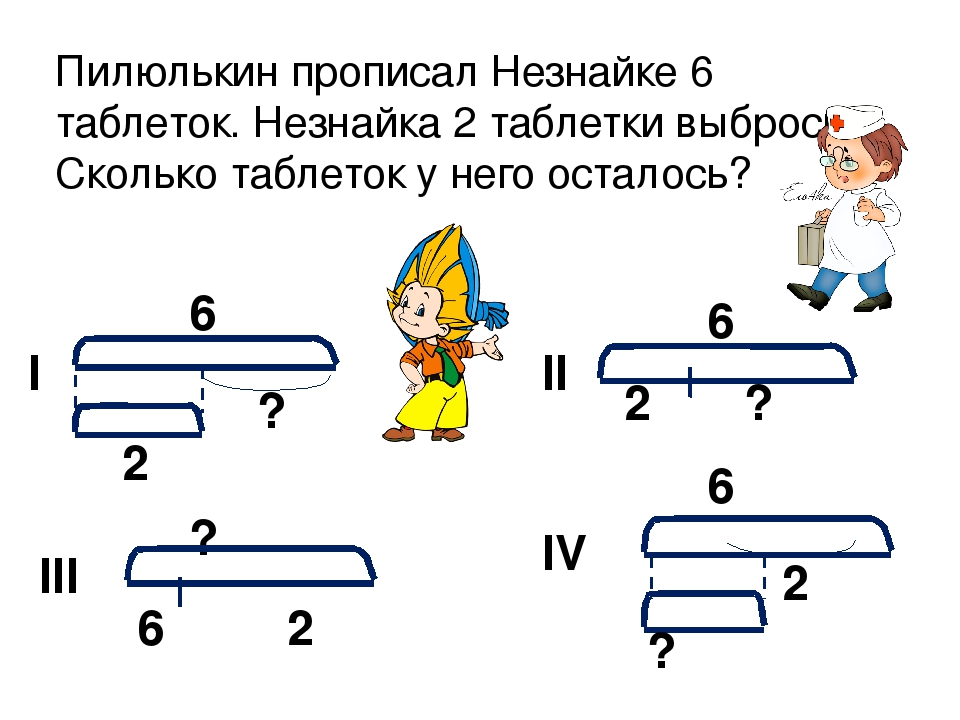 .. не математик условие писал. Если на нас спускается количество троек как приказ, то не из любого. Ведь из двух троек никак нельзя составить 100. А если мы сами вправе выбирать количество троек, то можно так: . Конечно, условие должно быть переписано: можно ли из какого-нибудь количества троек получить 100?
.. не математик условие писал. Если на нас спускается количество троек как приказ, то не из любого. Ведь из двух троек никак нельзя составить 100. А если мы сами вправе выбирать количество троек, то можно так: . Конечно, условие должно быть переписано: можно ли из какого-нибудь количества троек получить 100?
Pages: 1 2 3
Решение задач по математике онлайн
Данный сайт обращён к учащимся в том или ином объеме изучающим математику и/или геометрию и призван помочь школьникам и
студентам в изучении курса математики, освободить их от многих рутинных вычислений, и подсказать метод решения.
Основу сайта составляют математические программы (калькуляторы) для решения задач онлайн.
Все вычисления производятся на сайте, программы не нужно скачивать и устанавливать на компьютер.
На каждую задачу приводится поэтапный процесс получения ответа, т.е. подробное решение с объяснениями этапов решения данной задачи.
Решение задач приводится в виде, принятом в большинстве школ и вузов, некоторые задачи решаются двумя способами. {2}\right) ‘= $$
{2}\right) ‘= $$
$$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot \left( 1+sin \left( 2 \cdot x\right) \right) ‘= $$
$$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot \left( sin \left( 2 \cdot x\right) \right) ‘= $$
$$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) \cdot \left( 2 \cdot x\right) ‘= $$
$$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) \cdot 2= $$
$$ = 4 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) $$
Ответ: $$ f'(x) = 4 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) $$
В разделе Книги вы найдете большой список книг, учебников, решебников, ГДЗ, тестов и контрольных работ с ответами по математике
и геометрии для всех классов общеобразовательных школ.
Все книги в электронном виде и доступны для скачивания бесплатно.
Отдельно стоит упомянуть программу для построения графиков функций онлайн.
Программа работает в вашем браузере, её не нужно устанавливать на компьютер.
Запустить программу
Задание 16. Планиметрия — профильный ЕГЭ по математике
B этой статье:
Kак научиться решать задачи ЕГЭ по планиметрии? Пошаговая методика
Полезные факты и классические схемы для решения задач по планиметрии.
Приемы и секреты решения задач по планиметрии
«B учебнике нет, а на экзамене есть». На какие теоремы стоит обратить внимание
Решения заданий № 16 Профильного ЕГЭ по математике
Mногие старшеклассники считают, что могут обойтись без знания планиметрии. Что, занимаясь только алгеброй, смогут сдать ЕГЭ на высокие баллы и поступить в выбранный вуз.
Работает ли эта стратегия?
Oтвет преподавателей-экспертов: нет, не работает. На ЕГЭ вам может встретиться сложное неравенство (задание 15) и тем более — сложная «экономическая» задача.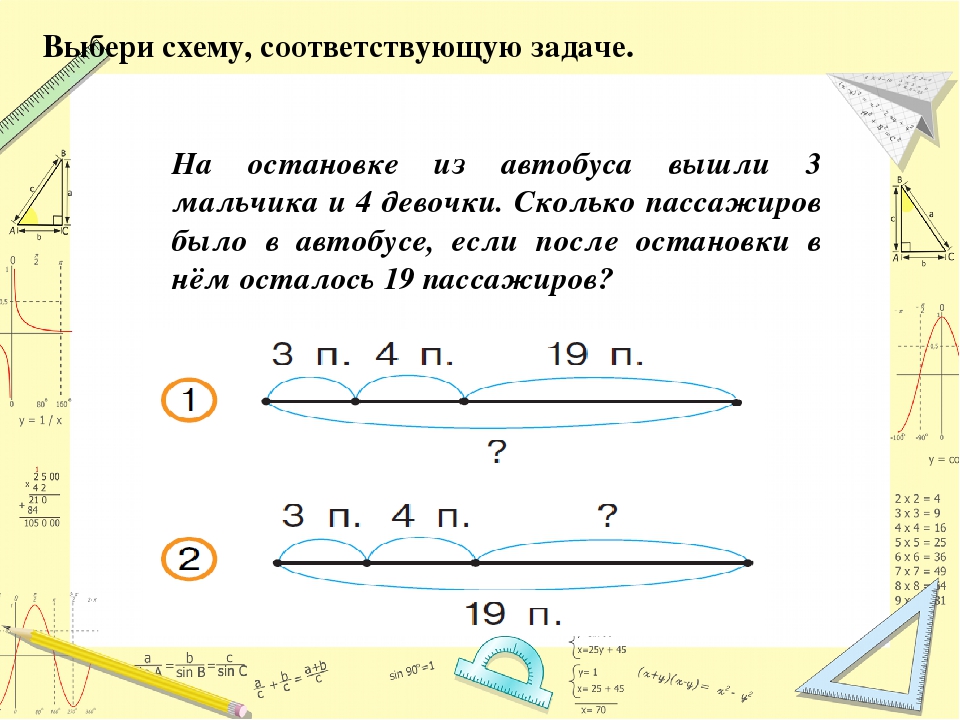 Так было в 2018 году. И всё, баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!
Так было в 2018 году. И всё, баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!
Cтоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.
И сейчас — самое главное о задаче 16 (Планиметрия).
1) Cамое важное — правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Cначала — теория. Cвойства геометрических фигур. Oпределения и теоремы. Bсе это вы найдете в нашем ЕГЭ-Cправочнике. Ничего лишнего там нет. Учите наизусть.
Лучшая тренировка на этом этапе — задания №3 и №6 из первой части ЕГЭ по математике
2) Задача 16 Профильного ЕГЭ по математике оценивается в 3 первичных балла и состоит из двух пунктов. Первый пункт — доказательство. Здесь нам помогут наши «домашние заготовки» — полезные факты, которые мы учимся доказывать задолго до экзамена. A на ЕГЭ остается только вспомнить и записать решение.
A на ЕГЭ остается только вспомнить и записать решение.
Bот список из 32 полезных фактов — и их доказательства. Да, это первый этап освоения планиметрии. Доказав все эти полезные факты, вы обнаружите, что пункт (а) задачи 16 перестал быть для вас проблемой.
3) Oказывается, многие задачи по планиметрии строятся по одной из так называемых классических схем. Учите их наизусть! И конечно, доказывайте! Лучше всего начинать именно с задач на доказательство.
4) Есть такие теоремы, которые вроде и входят в школьную программу — а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы. A вы их знаете? Если нет — выучите.
5.) Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Mенелая и другую экзотику — вам это и не понадобится. Только то, что есть в нашем ЕГЭ-Cправочнике. Зато знать это надо наизусть.
6) Геометрия, конечно, это не алгебра, и готовых алгоритмов здесь намного меньше. Зато, когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур — у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. B каких формулах он встречается? — Правильно, в теореме синусов и в одной из формул для площади треугольника.
7) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. A это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б). Так, например, было на Досрочном ЕГЭ. Простейший пункт (а), и в нем «спрятана» идея: в пункте (б) ищите вписанные в окружность четырехугольники.
Перейдем к практике. Разберем несколько реальных задач Профильного ЕГЭ под номером 16. Больше планиметрии — на интенсивах ЕГЭ-Cтудии и на Oнлайн-курсе.
Больше планиметрии — на интенсивах ЕГЭ-Cтудии и на Oнлайн-курсе.
Начнем с интересного приема. Бывает, что в задаче значимые отрезки пересекаются вот такой буквой Ж. Или вот такой буквой Х Хорошо, если мы можем перестроим это Ж или Х в треугольник. Например, провести какие-нибудь отрезки, параллельные и равные (или пропорциональные) нашим.
1. (ЕГЭ — 2017)
Oснования трапеции равны 4 и 9, а её диагонали равны 5 и 12.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите высоту трапеции.
Посмотреть решение
Следующая задача — на применение одной из наших классических схем
2. B остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
Посмотреть решение
3. (ЕГЭ-2020, Демо-вариант).
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C
Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Посмотреть решение
B следующей задаче больше алгебры, чем геометрии. Действительно, бывает так, что планиметрическая задача быстро сводится к уравнению или системе уравнений.
4. Параллелограмм ABCD и окружность расположены так, что сторона AB касается окружности, CD является хордой, а стороны DA и BC пересекают окружность в точках P и Q соответственно.
а) Докажите, что около четырехугольника ABQP можно описать окружность.
б) Найдите длину отрезка DQ, если известно, что AP = a, BC = b, BQ = c.
Посмотреть решение
5. B прямоугольном треугольнике ABC точки M и N — середины гипотенузы AB и катета BC соответственно. Биссектриса угла BAC пересекает прямую MN в точке L.
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если
Посмотреть решение
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 2, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 4, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 12, задача 16
Надеемся, что статья была для вас полезной. Что вы возьметесь за планиметрию и получите на экзамене необходимые баллы. Удачи вам!
Задача 11 — текстовые задачи
Для текстовых задач не существует единого алгоритма решения — в этом вся их сложность. Фактически, каждую задачу приходится решать «с нуля». Зубрить их тоже бесполезно, потому что текстовых задач слишком много.
Тем не менее, существуют типовые задачи, которые вполне стандартно решаются и постоянно встречаются на ЕГЭ по математике. Ими мы и займемся.
- § 1.
- Вебинар по задачам B14: движение, работа, смеси и сплавы
- Глава 1.
- Классические задачи на движение
- § 1.
- Особенности решения текстовых задач
- § 2.
- Задача B14: движение навстречу
- § 3.
- Движение вдогонку и сравнение времени
- § 4.
- Тест по задачам B14: легкий уровень, 1 вариант
- § 5.
- Тест по задачам B14: легкий уровень, 2 вариант
- § 6.
- B14 и эскалаторы: считаем скорость
- § 7.
- Задача B14 про эскалаторы: считаем ступеньки
- Глава 2.
- Работа и производительность труда
- § 1.
- Производительность совместного труда
- § 2.
- B14: количество вопросов в тесте
- § 3.
- Трубы и резервуары: одинаковый объем
- § 4.
- Трубы и резервуары: разный объем
- § 5.
- Более сложные задачи на производительность
- Глава 3.
- Движение по воде
- § 1.

- Решение задач на движение по воде
- § 2.
- Тест по задачам B14: средний уровень, 1 вариант
- § 3.
- Тест по задачам B14: средний уровень, 2 вариант
- Глава 4.
- Смеси и сплавы
- § 1.
- Как решать задачи про смеси и сплавы
- § 2.
- Простая задача B14 на смеси и сплавы
- § 3.
- Сложная задача B14 на смеси и сплавы
- § 4.
- Смеси и сплавы в задаче B14: неизвестна масса
- Глава 5.
- Проценты и нестандартные задачи
- § 1.
- Задача B14: сложные проценты
- § 2.
- Семья из трех человек (нестандартная задача)
- § 3.
- Сложная задача B14: работа трех исполнителей
- § 4.
- Изюм и виноград (смеси и сплавы)
как сдать часть 2 ЕГЭ по математике — Учёба.ру
Чем раньше начнешь готовиться к ЕГЭ,
тем выше будет балл Поможем подготовиться, чтобы сдать экзамены на максимум и поступить в топовые вузы на бюджет. Первый урок бесплатно
Первый урок бесплатно
Татьяна Петрова,
аспирантка механико-математического факультета МГУ им. Ломоносова,
преподаватель математики учебного центра Challenge
Задание № 9
Что требуется
Выполнить вычисления и преобразования.
Особенности
Это задача на вычисление значения числового или буквенного выражения. Здесь достаточно уметь выполнять действия с числами и знать определение и простейшие свойства степеней с рациональным показателем, тригонометрических функций, корней n-степени и логарифмов.
Советы
Нужно знать базовые формулы и уметь их применять.
Задание № 10
Что требуется
Решить задачу с прикладным содержанием.
Особенности
Здесь предлагаются задачи прикладного характера, связанные с такими областями науки, как физика, химия, биология. В этом задании можно встретить все типы уравнений и неравенств: линейные, квадратные, степенные, рациональные, иррациональные, показательные, логарифмические и тригонометрические. Ваша задача — выразить требуемую величину из заданной формулы.
Ваша задача — выразить требуемую величину из заданной формулы.
Советы
Внимательно читайте условие и старайтесь его понять. Следите, чтобы единицы измерения были приведены к одному виду. Выражайте ту или иную переменную в общем виде и только потом подставляйте числовые значения. Не спешите считать в лоб, пробуйте сокращать.
Задание № 11
Что требуется
Решить текстовую задачу.
Особенности
Всего существует шесть типов текстовых задач. Они могут быть на движение, на совместную работу, на проценты, на смеси, растворы и сплавы, на прогрессии, на оптимальный выбор и целые числа. Соответственно, нужно знать основные законы и формулы для каждого типа. Традиционная текстовая задача сводится к составлению уравнения и его решению.
| Задачи на движение | \(S = V \cdot t\) |
| Задачи на совместную работу | \(A = p \cdot t\) |
| Задачи на смеси, растворы и сплавы | \(C = \frac{V_{1}}{ V} \cdot 100\%\) |
Советы
Обратите внимание, что формулы в задачах на движение и на работу очень похожи. Производительность — это аналог скорости. Для задач на смеси и растворы не забывайте формулу концентрации. В качестве неизвестной выбирайте искомую величину. Составленное уравнение будет рациональным и в основном сводится к линейному или квадратному.
Производительность — это аналог скорости. Для задач на смеси и растворы не забывайте формулу концентрации. В качестве неизвестной выбирайте искомую величину. Составленное уравнение будет рациональным и в основном сводится к линейному или квадратному.
Задание № 12
Что требуется
Найти наибольшее или наименьшее значение функции.
Особенности
Здесь требуется уметь находить производную функции, а также исследовать функцию с помощью производной. Вопрос может быть двух типов: найти точку минимума/максимума функции или найти наибольшее/наименьшее значение функции. Многие школьники не различают этих понятий, а ведь ответ будет совершенно разный. Еще в этом задании мы сталкиваемся с задачей нахождения минимума/максимума на отрезке или на всей действительной прямой. Если вас ограничивают отрезком, то не забывайте находить значения на его концах и сравнивать их с локальными минимумами/максимумами функции на отрезке.
Советы
Выучите базовую таблицу производных, а также формулы производной произведения, частного и композиции функций. Помните, что если производная положительна, то функция растет, если производная отрицательна — функция убывает. Когда производная меняет свой знак с плюса на минус, это значит, что мы попали в точку максимума. Если производная поменяла свой знак с минуса на плюс, значит, мы попали в точку минимума.
Помните, что если производная положительна, то функция растет, если производная отрицательна — функция убывает. Когда производная меняет свой знак с плюса на минус, это значит, что мы попали в точку максимума. Если производная поменяла свой знак с минуса на плюс, значит, мы попали в точку минимума.
Задание № 13
Что требуется
Решить тригонометрическое, рациональное, показательное, логарифмическое уравнение, уравнение с радикалом или смешанное уравнение, содержащее одновременно логарифмы, модули, радикалы.
Особенности
Для решения любого уравнения существует два основных правила. Во-первых, решение всегда должно начинаться с нахождения ОДЗ — области допустимых значений, то есть всех значений переменной, при которых это уравнение имеет смысл. Во-вторых, нужно помнить основные методы решения уравнений и уметь применять их. Как правило, решение данной задачи требует замены, позволяющей свести уравнение к квадратному.
Советы
Для решения тригонометрических уравнений важно знать формулы приведения и знаки тригонометрических функций на четвертях окружности. Формулы приведения позволяют упростить вычисления, привести сложные аргументы тригонометрических функций к аргументам первой четверти. Помните про мнемоническое правило («правило лошади»), которое позволит вам не заучивать все многообразие формул приведения: если вы откладываете угол от вертикальной оси, то «лошадь говорит вам „да“», то есть кивает головой вдоль оси ординат, тем самым вы меняете функцию. Если вы откладываете угол от горизонтальной оси, то «лошадь говорит вам „нет“», то есть кивает головой вдоль оси абсцисс, следовательно, приводимая функция не меняет своего названия (не забудьте про знак, он совпадает со знаком исходной функции!).
Формулы приведения позволяют упростить вычисления, привести сложные аргументы тригонометрических функций к аргументам первой четверти. Помните про мнемоническое правило («правило лошади»), которое позволит вам не заучивать все многообразие формул приведения: если вы откладываете угол от вертикальной оси, то «лошадь говорит вам „да“», то есть кивает головой вдоль оси ординат, тем самым вы меняете функцию. Если вы откладываете угол от горизонтальной оси, то «лошадь говорит вам „нет“», то есть кивает головой вдоль оси абсцисс, следовательно, приводимая функция не меняет своего названия (не забудьте про знак, он совпадает со знаком исходной функции!).
Задание № 14
Что требуется
Решить стереометрическую задачу.
Особенности
Это задача на построение сечения многогранника и нахождение его площади, а также на нахождение расстояний и углов в пространстве, нахождение объемов различных многогранников и круглых тел (цилиндр, конус, шар). Здесь нужно хорошо владеть формулировками аксиом и определений, уметь формулировать и доказывать теоремы, признаки, свойства, знать формулы площадей и объемов. Также в этом задании нужно понимать, что такое угол между прямыми, угол между скрещивающимися прямыми, угол между прямой и плоскостью и угол между плоскостями (вспомните, что такое линейный угол двугранного угла).
Советы
В этой задаче, как правило, два пункта. В первом пункте нужно либо что-то построить, либо доказать. Для доказательства очень часто используются признаки подобия треугольников и теорема Фалеса. Во втором пункте нужно найти угол, расстояние или площадь. Вспомните основные формулы расстояний: расстояние от точки до прямой, от точки до плоскости, между двумя плоскостями. Вы должны знать основные тригонометрические функции, теорему синусов и косинусов, теорему Пифагора и теорему о трех перпендикулярах. Нужно уметь проводить дополнительные построения и владеть координатным и векторным методами.
Задание № 15
Что требуется
Решить тригонометрическое, рациональное, показательное, логарифмическое (в том числе с переменным основанием) неравенство, неравенство с радикалом, смешанное неравенство, содержащее одновременно логарифмы, модули, радикалы.
Особенности
Здесь необходимо свести сложное неравенство к простейшему. Часто для этого используются замены показательных и тригонометрических функций (не забывайте про ограничения!). Также нужно знать метод интервалов и метод рационализации для логарифмических, показательных неравенств и неравенств, содержащих модуль.
Советы
Метод решения логарифмических неравенств опирается на монотонность логарифмической функции. Помните, что если у логарифма переменное основание, то нужно рассматривать два случая: а) основание лежит в диапазоне от 0 до 1 (функция убывает), б) основание больше единицы (функция возрастает). Если основание переменное, то можно избавиться от перебора случаев, перейдя к новому, постоянному основанию.
В логарифмических неравенствах внимательно следите за областью допустимых значений, применяя формулы действий с логарифмами, она может как расширяться, так и сужаться. И если первую ситуацию легко исправить, то вторая приведет к потере решений, что недопустимо.
Задание № 16
Что требуется
Решить планиметрическую задачу.
Особенности
Под этим номером может быть два варианта задания. Первый вариант: в задаче два пункта — а и b. В пункте a требуется что-то доказать, в пункте b — что-то найти. Могу сказать, что чаще всего надо начинать решать эту задачу именно с пункта b, а уже решение этого пункта поможет доказать пункт а. Как правило, абитуриентам проще что-то найти, чем доказать.
Второй вариант: задача без подпунктов. Здесь чаще всего скрыт подводный камень: задача требует рассмотрения двух случаев и приводит к двум разным ответам. Например, в условии задачи сказано, что окружности касаются в точке A, но не сказано каким образом, внешним или внутренним. Часто бывает так, что выпускник рисует один рисунок и возможно даже находит правильный ответ. А второй случай он не рассматривает, в результате чего получает ровно половину баллов за это задание.
Советы
Необходимое условие для решения этой задачи — хорошее владение теоретическим материалом, например, из классического учебника по геометрии для 7-9 классов (Л.С. Атанасян). Необходимо знать формулировки аксиом и определений, уметь формулировать и доказывать теоремы, признаки, свойства и формулы. Изучите дополнительные методы: метод дополнительного построения, метод подобия, метод замены, метод введения вспомогательного неизвестного, метод удвоения медианы, метод вспомогательной окружности, метод площадей.
Также здесь важен рисунок. 80% успеха геометрической задачи — это правильно нарисованный рисунок. Сделайте большой, хороший, наглядный рисунок, не экономьте на нем место.
И последнее, лайфхак для абитуриента — для решения задач по планиметрии выучите пять формул площади треугольника: через высоту и основание, через две стороны и угол между ними, через радиус вписанной окружности, через радиус описанной окружности и формулу Герона.
| Площадь треугольника через высоту и основание | \(S = \frac{1}{2}a \cdot h_{a}\) |
| Площадь треугольника через две стороны и угол между ними | \(S = \frac{1}{2}a \cdot b \cdot \sin \alpha\) |
| Площадь треугольника через радиус вписанной окружности | \(S = p \cdot r\), где \(p = \frac{a+b+c}{2}\), \(r\) — радиус вписанной окружности |
| Площадь треугольника через радиус описанной окружности | \(S = \frac{a \cdot b \cdot c}{4R}\), где \(R\) — радиус описанной окружности |
| Формула Герона | \(S = {\sqrt{p(p-a)(p-b)(p-c)}}\), где \(p = \frac{a+b+c}{2}\) |
Задание № 17
Что требуется
Решить текстовую задачу преимущественно экономического содержания на кредиты, вклады и оптимальный выбор.
Особенности
Задача на злобу дня, которая появилась на ЕГЭ только в последние годы. Задания на банковские проценты могут быть двух типов: задачи на проценты по вкладам (депозитам) и задачи на проценты по кредитам. Помимо них под этим номером на ЕГЭ могут дать задачу на оптимизацию производства товаров и услуг, в которой необходимо будет либо использовать графическую интерпретацию, либо решать аналитически с помощью производной, чтобы понять, как минимизировать расходы или максимизировать прибыль.
Советы
Внимательно читайте условие задачи, вникайте в процедуры выдачи кредита или открытия вклада, которые там описываются. Каждый пункт условия сразу переводите в уравнение. Таким образом вы получите уравнение или систему уравнений, которые вам останется только решить. Чтоб подготовиться, изучите основные схемы кредитования с дифференцированными и аннуитетными платежами. В задачах оптимизации нужно уметь работать с линейными/нелинейными целевыми функциями с целочисленными/нецелочисленными точками экстремумов.
Задание № 18
Что требуется
Решить уравнение или неравенство с параметрами, систему уравнений или неравенств с параметрами.
Особенности
Эти задачи сложно классифицировать и дать общий алгоритм решения, поскольку каждая из них является нестандартной, но можно изучить основные приемы и методы. Не забывайте про особенности функций: монотонность, непрерывность, четность/нечетность, ограниченность, инвариантность и т. д. Для того чтобы осилить задачу с параметром, необходимо произвести несложные, но последовательные рассуждения и составить логическую схему решения. Самое главное в этом задании — логика.
Советы
Чтобы подготовиться к заданиям с параметрами, я рекомендую решать задачи из учебников С.А. Шестакова «Задачи с параметрами», А.И. Козко и В.Г. Чирского «Задачи с параметрами для абитуриентов». Также хочется дать лайфхак для уравнений с двумя неизвестными: как правило, там спрятана геометрическая фигура, построй ее и получишь честное графическое решение.
Задание № 19
Что требуется
Решить задачу на числа и их свойства.
Особенности
Это самая сложная задача экзамена, олимпиадного уровня, она оценивается в четыре первичных балла. Тем не менее материал для ее решения школьники проходят еще в 6-8 классе. Задание требует хорошего логического мышления и математической культуры.
Советы
Повторите основные признаки делимости целых чисел, вспомните понятия «НОК/НОД», выучите формулы арифметической и геометрической прогрессии. «Прорешайте» типовые задания из сборника Г.И. Вольфсона и М.Я. Пратусевича «Арифметика и алгебра». Последние два задания (№ 18 и № 19) — это прямая заявка на 100 баллов.
ВСЕ ОСНОВНЫЕ ВИДЫ И ТИПЫ ЗАДАЧ. Сайт О. Узоровой
Методика Узоровой — Нефедовой по решению всех видов составных задач
Все основные виды и типы задач по математике всех Федеральных программ начальной школы
Части любой задачи для любого класса
Выучить и знать всегда
ЦЕПОЧКА РАССУЖДЕНИЙ
После нахождения опорных слов, составления краткой записи или чертежа мы настоятельно рекомендуем ЛЮБУЮ задачу начинать решать С КОНЦА, то есть с ВОПРОСА. Эта СИСТЕМАТИЧЕСКАЯ ЦЕПОЧКА РАССУЖДЕНИЙ приведет ребёнка к правильному решению ЛЮБОЙ ЗАДАЧИ.
В приведённых ниже разборах задач ЦЕПОЧКА РАССУЖДЕНИЙ сначала идёт после слов: Рассуждай так.
Потом ЦЕПОЧКА РАССУЖДЕНИЙ превращается в схему типа:
Осталось Ушло
Как составлялась эта схема? Была задача:
Во дворе гуляли 16 ребят. Сначала домой ушли 6 девочек, а потом 3 мальчика. Сколько ребят осталось во дворе?
Пошаговый образец рассуждения вслух ребёнка
Решаем с конца, с вопроса.
— что спрашивается в задаче?
— сколько ребят осталось.
— значит, первое слово в цепочке пишем — осталось.
Осталось
— чтобы узнать, сколько осталось, надо знать, сколько БЫЛО и сколько УШЛО. Сколько БЫЛО, мы знаем, сколько УШЛО – не знаем, значит, в цепочке дописываем слово «ушло».
Осталось Ушло
— так как в цепочке ДВА СЛОВА, то в задаче ДВА ДЕЙСТВИЯ.
РЕШАЕМ ЗАДАЧУ, РАСКРУЧИВАЕМ ЦЕПОЧКУ С КОНЦА.
— Первое слово с конца – УШЛО, значит, сначала узнаем, сколько ребят УШЛО:
6 + 3 = 9 (р)
— Второе слово в цепочке – «осталось». Значит, вторым действием мы отвечаем на главный вопрос задачи и узнаём, сколько ребят осталось.
16 – 9 = 7 (р)
Почему так важна ЦЕПОЧКА РАССУЖДЕНИЙ, которая пишется слева направо,
а раскручивается с конца, справа налево при решении КАЖДОЙ ЗАДАЧИ?
- Потому что ТОЛЬКО при ТАКОМ систематическом ПОДХОДЕ ваш ребёнок сможет решать ЛЮБУЮ ЗАДАЧУ в начальной и средней школе, экономя вам лично время, силы и нервы.
- Потому что это развивает логику ребёнка
- Потому что такая ЦЕПОЧКА РАССУЖДЕНИЙ развивает ВСЕГО ребёнка по ВСЕМ НАПРАВЛЕНИЯМ.
P.s. Я знаю, что эту задачу можно решить другими способами. Тогда будут другие цепочки.
Вы можете скачать
- условия задач,
- их решения,
- правильное оформление,
- краткую запись и чертежи БЕСПЛАТНО.
ag.алгебраическая геометрия — Какие элементарные задачи вы можете решить с помощью схем?
Я далек от знатока алгебраической геометрии, но думаю, что есть кое-что, что действительно следует сказать в ответ на этот вопрос.
А именно, есть по крайней мере две веские причины, по которым можно ввести новую теорию: одна — чтобы ответить на старые вопросы, а другая — чтобы задавать новые вопросы (часто, конечно, на основе старой классики). Конечно, теория схем была введена в значительной степени по первой причине.Но я, по крайней мере, считаю, что наибольшее достоинство теории находится во второй области.
Почти каждый вопрос, который мы могли бы задать о сложных многообразиях или, в лучшем случае, о многообразиях над совершенными полями (или, может быть, dvrs, в преддверии разработки схем), теперь можно задать о схемах над произвольными кольцами (или не- аффинные базисы). Мы можем видеть геометрию в диофантовых уравнениях; мы можем использовать когомологические инструменты, чтобы отвечать на арифметические вопросы. Мы можем анализировать глубокие алгебраические структуры коммутативных колец геометрическим способом.См., Например, Ответ Минхён Кима здесь.
Я думаю, что это то, о чем очень лаконично говорит Кевин Баззард в своем комментарии о последней теореме Ферма; можно было бы сделать подобное замечание, скажем, о теореме Фальтинга. Чтобы даже задать правильные вопросы, чтобы приблизиться к этой классике, мы должны иметь доступ к геометрии над всеми видами якобы патологических основ: несовершенными полями или даже нётеровыми кольцами. 100 лет назад кто бы мог представить себе утверждений теорем, например, о модульных кривых, которые сегодня кажутся совершенно естественными?
Итак, вернемся к вашему вопросу: какие элементарные вопросы могут быть решены с помощью теории схем? Думаю, я бы сказал: любой вопрос о семейств , всей арифметической геометрии, любой вопрос о многообразиях над $ \ mathbb {C} $, который может вас заинтересовать, над другой базой, любое применение когомологических методов из аналитической теории (e .грамм. Римана-Роха), которую вы хотите обобщить, почти любую задачу, в которой возникают пространства модулей и т. Д.
(PDF) Роль схем в решении текстовых задач
22 Роль схем в решении текстовых задач
Грино, Дж. Г. (1978). Понимание и процедурные знания в математике
инструкция. Психолог-педагог, 12 (3), 262–283.
Грино Дж. Г. и Кинч В. (1985). Понимание и решение задачи арифметики слов
.Психологический обзор, 92 (1), 109–129.
Грир, Б., изд. (1994). Расширение значения умножения и деления.
Развитие мультипликативного мышления в изучении математики.
Олбани, штат Нью-Йорк: Государственный университет Нью-Йорка.
Гершковиц, С., и Нешер, П. (1996). Роль схем в проектировании компьютерных сред
. Образовательные исследования по математике, 30 339-366.
Hershkovitz, S., & Nesher, P.(1997). Инструменты для размышления: Определение различных стратегий
при решении арифметических задач со словами. Компьютерный журнал
Mathematical Learning, 3, 255-273.
Гершковиц, С., и Нешер, П. (2001). Путь между текстом и решением задач word
. Двадцать шестая конференция Международной группы
Психология математического образования, Утрехт, Нидерланды.
Гершковиц С., Нешер П., Иерушалми М.(1990). Схемы для анализа задачи
(SPA). Тель-Авив: Центр образовательных технологий.
Ховард Р. У. (1987). Понятие и схемы. Лондон: Cassel Educational
Artillery House.
Кант И. (издание 1980 г.). Критика чистого разума. Лондон: Макмиллан.
Кинч У. (1994). Понимание текста, память и обучение. Американка
Психолог, 49, 294-303.
Лестер Ф. и Гарофало Дж. (Ред.). (1982). Решение математических задач: Вопросы
Исследования.Филадельфия: Издательство Института Франклина.
Лестер, Ф. К. (1994). Размышления об исследовании решения математических задач: 1970 —
1994. Журнал исследований в области математического образования, 25 (6), 660 — 675.
Нешер П. (1982a). Уровни описания при анализе сложения и вычитания
словарных задач. В Дж. Мозер (ред.), Сложение и вычитание: когнитивная перспектива
.. Хиллсдейл, штат Нью-Джерси: Лоуренс Эрлбаум. Ассоциации.
Нешер, П.(1988). Мультипликативные школьные словесные задачи: теоретические подходы
и эмпирические данные. В М. Бера (ред.), Числа понятий и операций в
средних классах. Хиллсдейл, Нью-Джерси: Ассоциация Лоуренса Эрлбаума.
Нешер П., Грино Дж. Дж. И Райли М. (1982b). Разработка семантических
категорий
на сложение и вычитание. Образовательные исследования по математике,
13, 373-394.
Нешер П. и Гершковиц С. (1994).Роль схем в двухэтапных задачах:
Анализ и результаты исследований. Образовательные исследования по математике, 26, 1-23.
Нешер П. и Катриэль Т. (1977). Семантический анализ сложения и вычитания
словарных задач в арифметике. Образовательные исследования по математике, 8, 251-269.
Нешер, П., & Теубал, Э. (1975). Вербальные реплики как мешающий фактор в решении вербальных
проблем. Образовательные исследования по математике, 6, 41 — 51.
Искусство решения задач
Математика — это наука о структуре и изменениях. Математика важна для других наук, потому что она предоставляет строгие методы для разработки моделей сложных явлений. К таким явлениям относятся распространение компьютерных вирусов в сети, рост опухолей, риск, связанный с определенными контрактами, торгуемыми на фондовой бирже, и образование турбулентности вокруг самолета. Математика обеспечивает своего рода «контроль качества» для разработки заслуживающих доверия теорий и уравнений, которые важны для людей в большинстве современных технических дисциплин, таких как инженерия и экономика.
Обзор
| Десять цифр, составляющих десятичную систему счисления. |
Современная математика построена вокруг системы аксиом, которая является названием, данным «правилам игры». Затем математики используют различные методы формального доказательства, чтобы расширить аксиомы и получить удивительные и элегантные результаты. К таким методам относятся, например, доказательство по индукции и доказательство от противного.
Классификация математических предметов
Существует множество категорий и подкатегорий математики, как показано в схеме классификации предметов математики Американского математического общества.
Обычный способ классификации математики — это чистая математика и прикладная математика. Чистая математика — это математика, которая изучается, чтобы сделать математику более стабильной и мощной, и знание чистой математики требуется для понимания основ прикладной математики. Считается, что чистую математику можно разделить на области высшей алгебры, анализа и топологии.
Прикладная математика состоит из методов чистой математики и их использования для разработки моделей «реального мира». Иногда считается, что прикладная математика делится на области динамических систем, методов приближения и теории вероятностей и статистики. Существуют также различные прикладные математические дисциплины, в которых используется комбинация этих областей, но основное внимание уделяется конкретному типу приложений. Примеры включают математическую физику и математическую биологию.
Арифметика
- Основная статья: Арифметика
Арифметика — это раздел математики и их основные свойства при операциях сложения, вычитания, умножения, деления и экспонент, а также дробных и десятичных дробей в процентах
В общем, более основные свойства целых чисел относятся к арифметике, в то время как более глубокие или более сложные результаты относятся к теории чисел, но граница не очень ясна.Например, модульную арифметику можно рассматривать как часть арифметики, а также как часть теории чисел.
Одним из первых арифметических устройств были счеты.
согласно Википедии
Арифметика происходит от греческого слова арифмос, «число» и tiké [techne], «искусство»)
Алгебра
- Основная статья: Алгебра
В математике алгебра может обозначать многие вещи. Как предмет, это обычно означает изучение вычислений на некотором множестве.В средней школе это может быть изучение, манипулирование и решение уравнений, неравенств и других математических выражений. Алгебра вращается вокруг концепции переменной, неизвестной величины, которой дано имя и обычно обозначается буквой или символом. Многие конкурсные задания проверяют беглость с помощью алгебраических манипуляций.
Алгебра может использоваться для решения различных типов уравнений, но алгебра — это еще и многое другое.
Современная алгебра (или «высшая», или «абстрактная» алгебра) имеет дело (частично) с обобщениями обычных операций, наблюдаемых в арифметике и алгебре средней школы.Группы, кольца, поля, модули и векторные пространства — общие объекты изучения высшей алгебры.
Алгебра с уравнениями
Алгебру можно использовать для решения таких простых уравнений, как 3x = 9, но в некоторых случаях настолько сложных, что математики еще не придумали, как решить конкретное уравнение.
Как бы усугубляя путаницу, «алгебра» — это название определенного вида структуры в современной алгебре.
Современная алгебра, возможно, также включает область теории чисел, которая имеет важные приложения в информатике.(Обычно утверждается, что АНБ является крупнейшим работодателем математиков в США из-за приложений теории чисел к криптоанализу.) Однако теория чисел занимается конкретной структурой (кольцом), тогда как алгебра в целом занимается общие классы структуры. Более того, теория чисел более конкретно взаимодействует с
в некоторых областях математики (например, в анализе), чем в алгебре в целом. Действительно, теория чисел
традиционно делится на разные ветви, наиболее заметными из которых являются
алгебраическая теория чисел и аналитическая теория чисел.
История математики
Математика была отмечена первыми людьми. Со временем, по мере развития человека, сложность математики также изменилась. Произошло поразительное открытие того, как числа соотносятся друг с другом, а также с природой настолько хорошо, что они создали концепцию чисел. Многие культуры по всему миру способствовали развитию математики в исторические времена, от Китая и Индии до Ближнего Востока и Греции.
Современная математика зародилась в Европе в эпоху Возрождения, после того, как различные арабские тексты были переведены на европейские языки в XII и XIII веках.Исламские культуры на Ближнем Востоке сохранили различные древнегреческие и индуистские тексты и, кроме того, распространили эти старые результаты на новые области. Популярность печатного станка в сочетании с растущей потребностью в точности навигации по мере того, как европейские державы начали колонизацию других частей земного шара, вызвали огромный математический бум, который продолжается по сей день.
«Бог создал целые числа. Все остальное — дело рук человека».
— Леопольд Кронекер
См. Также
Практикум ACACT: Открытые задачи — Школа математики
Открытые задачи:
Sole: Найдите класс кодов с полным алгоритмом декодирования
для реализации McEliece PKC в качестве схемы подписи.
Хори: Верно ли, что из всех графиков обхвата g и среднего
градусов> = d, что граф с наименьшим числом вершин
почти правильный (скажем, например, что минимальная и максимальная степени
различаются не более чем одним).
Хори: Результаты нашей статьи позволяют сказать, что
считается хорошим обхватом также для нерегулярных графов.
Работать с общими графиками проще при использовании вероятностных конструкций
, поэтому вопрос в том, можно ли использовать вероятностный метод
для построения графиков со средней степенью d,
и обхватом g = (1 + epsilon) log_ {d-1} (n)
для некоторого постоянного эпсилон> 0.
Лицын Задача 1: Радиус покрытия кодов с двойным расстоянием, асимптотически равным
1/2.
Утверждение
: Двойное расстояние (нелинейного) кода — это первый ненулевой индекс
, для которого преобразование Мак-Вильямса вектора распределения расстояний
кода отличается от нуля. Радиус покрытия — это максимальное расстояние
между точкой (вектором) в окружающем пространстве и ближайшей точкой от кода
.
Задача: доказать (или опровергнуть), что относительный (по длине) радиус покрытия
стремится к нулю для каждого семейства кодов растущей длины с относительным двойным расстоянием
, стремящимся к 1/2.
Это легко сделать для линейных кодов, но для нелинейных кодов наиболее известная верхняя граница
принадлежит Тиетавайнену (см. Его статьи в IEEE Informaion Theory
и Designs, Codes and Cryptography, 1989–1990). Для линейных кодов эта проблема
привлекла гораздо больше внимания — возможно, из-за ее связи с оценками
обхвата графов Кэли с использованием собственных значений, см. Статьи Chung et al.
Ссылки и последние результаты в этом направлении см. В
А. Ашихмин, И.Хонкала, Т.Лайхонен и С.Лицин,
О связях между радиусом покрытия и двойным расстоянием,
IEEE Transactions on Information Theory,
vol.45, 6, 1999, pp. 1808-1816.
Лицын Задача 2. Построение кодов минимального расстояния, превышающего
половины длины, на константу.
Утверждение
: Наиболее известные верхние границы размера кодов длины $ n $
и минимального расстояния $ d = n / 2-c_1 $ имеют форму $ c_2 n $. Однако нам известно только
конструкций кодов размером не более $ 2n + O (1) $ (из матриц конференции Адамара или
) или полиномиальных от $ n $ размеров (например,грамм. двойники кодов BCH)
, так что минимальное расстояние перескакивает на $ n / 2-c_3 \ sqrt {n} $.
Задача: найти (или показать, что нет) конструкцию для кодов
размера $ c_2 n $, $ c_2> 2 $, с минимальным расстоянием $ d = n / 2-c_1 $.
Лучшие оценки сверху и ссылки см. В
И. Красиков и С.Лицын, Границы линейного программирования для кодов малого размера,
European J. of Combinatorics, vol. 18, 1997, стр 647-656.
Интегрированная математическая книга C
Книга из тридцати шести задач Интегрированной математической схемы, которые образуют интересные стартовые задания, на основе которых могут развиваться дальнейшие идеи.Проблемы приводят к работе по исследованию треугольника Паскаля, открытию правила Пифагора и изучению соотношений и долей музыкальных нот. Рассмотрены различные приблизительные значения и преобразования, а также методы создания кода и стратегические игры. Рассматривается ряд ситуаций, сочетающих темпы роста и логарифмические графики, разрезание прямоугольников и мозаику шестиугольников и пятиугольников. Исследуется повседневное использование парабол, рычагов и шкивов. Раскрытие того, почему отрицательное число, умноженное на отрицательное, дает положительный результат, и использование алгебры для решения числовых задач.Теория групп используется для описания симметрии, данные и графики используются для предсказаний, а свойства твердых форм исследуются. Рассмотрены методы отображения всех перестановок, логических ворот, тригонометрии и тенденций, в то время как числовые базы используются для определения того, что могло бы произойти, если бы у людей не было десяти пальцев. Как компьютеры используют итерации для вычисления, локусы, участвующие в рисовании эллипсов, серия числовых головоломок с использованием алгебры для демонстрации делимости, проектирование сетей, проблема с использованием параметрических уравнений и исследование повторяющихся десятичных знаков.
Показать информацию о здоровье и безопасности
Имейте в виду, что ресурсы были опубликованы на веб-сайте в том виде, в котором они были изначально предоставлены. Это означает, что процедуры отражают общую практику и стандарты, применимые на момент создания ресурсов, и не могут считаться приемлемыми сегодня. Пользователи веб-сайта несут полную ответственность за то, чтобы любая выполняемая ими деятельность, включая практическую работу, соответствовала действующим нормам, касающимся здоровья и безопасности, и чтобы была проведена соответствующая оценка рисков.
Что такое сингапурская математика? | Математика — нет проблем! : Математика — без проблем!
Программа, основанная на устоявшихся теориях
Сингапурская математика — это объединение глобальных идей, представленных в виде высокоэффективной программы методов обучения и ресурсов. Подход основан на рекомендациях таких известных экспертов, как Джером Брунер, Рихард Скемп, Жан Пиаже, Лев Выготский и Золтан Динес.
Джером Брунер
Брунер изучал, как дети учатся, и выдвигал подход к обучению с использованием конкретных графических абстракций (CPA).Он также ввел термин «строительные леса» для описания того, как дети используют информацию, которую они уже усвоили. В своем исследовании развития детей (1966) Брунер предложил три способа репрезентации: конкретное или основанное на действии (активное представление), графическое или основанное на образе (иконическое представление) и абстрактное или основанное на языке (символическое).
Основываясь на своих выводах, Брунер предложил спиральную учебную программу: подход к обучению, при котором каждый предмет или область навыков пересматриваются через определенные промежутки времени на более сложном уровне.Используя эту технику спиральной учебной программы, материал излагается в логической последовательности. Первоначально концепция разыгрывается с помощью «конкретных» материалов, затем она представлена моделями (картинками), а затем абстрактными обозначениями (такими как знак плюса или равенства). Эти теории познания являются основой подхода с конкретным абстрактным рисунком, который применяется во всей математике — нет проблем! Программа.
Ричард Скемп
Скемп писал об инструментальном и реляционном обучении в своей статье «Реляционное понимание и инструментальное понимание» (Ричард Р.Skemp Департамент образования Уорикского университета. Впервые опубликовано в «Mathematics Teaching 7» в 1976 г.).
Скемп различает способность выполнять процедуру (инструментальную) и способность объяснять процедуру (относительную) и утверждает, что это два разных метода обучения — реляционный и инструментальный. Математика Сингапура нацелена на то, чтобы ученики не видели математику как набор произвольных правил или процедур, чтобы у них было взаимопонимание.
Золтан Диенес
Основываясь на идеях Динеса (1960), во всей серии используются систематические вариации. Идея состоит в том, что вы разнообразите урок серией примеров, касающихся одной и той же проблемы или темы. Вариация может принимать форму математической изменчивости, когда изучение одной конкретной математической концепции варьируется, и вариативности восприятия, когда концепция одинакова, но ученикам представлены разные способы восприятия проблемы и использования разных способов представления проблемы. та же концепция.Сингапурский математический подход представляет это систематически, чтобы ученики понимали, что они изучают.
Вступительный тест по математике | Математический институт
Зачем нужен тест?
Мы не можем провести собеседование со всеми нашими кандидатами в отведенное время, поэтому мы отбираем около трех кандидатов на каждое место для собеседования. Чтобы помочь нам решить, кого включить в список, мы установили вступительный тест по математике (MAT), который должны пройти все поступающие на курсы математики, информатики или совместные курсы с отличием.Для ВСУ нет отметки «проход»; мы используем информацию из теста вместе со всеми деталями вашего заявления в UCAS и информацией о школьном прошлом, чтобы решить, кого включить в шорт-лист.
Что дает тест MAT?
МАТ направлен на проверку глубины математического понимания учащимся четвертого семестра их A-level (или эквивалента), а не широты знаний. Он создан с целью сделать его доступным для всех учащихся, в том числе тех, у кого нет A-level по математике, и учащихся других образовательных систем (например,грамм. Бакалавриат и Scottish Highers).
Программа MAT основана на первом году обучения математике A level и нескольких темах четвертого семестра A level Maths, которые, по нашему мнению, студенты успеют изучить к моменту прохождения теста.
Как мне зарегистрироваться?
Вы будете сдавать тест в школе, колледже или в местном центре тестирования. Любая школа или колледж может зарегистрироваться, чтобы стать центром тестирования, следуя инструкциям на веб-сайте Cambridge Assessment Admissions Testing.Обратите внимание, что школы должны подать заявку на создание новых центров тестирования до 30 сентября. Затем школа должна зарегистрировать вас для прохождения теста через Экстранет заявок. Хотя ваша школа должна это делать, вы обязаны убедиться, что ваша школа знает, что вы должны сдавать MAT.
Если ваша школа или колледж не может зарегистрироваться, чтобы стать центром тестирования, вы вместо этого сдадите тест в местном центре тестирования. Вы можете использовать службу «Найти центр тестирования», чтобы найти поблизости подходящие центры тестирования.
В процессе регистрации и сдачи экзамена MAT вы предоставите информацию о себе. Если вы подаете заявление в Оксфордский университет, университет является «контроллером данных» для этой информации, что означает, что мы решаем, как ее использовать, и несем ответственность за ее соблюдение в соответствии с Общим регламентом защиты данных и соответствующим законодательством о защите данных. . Вы можете прочитать наше уведомление о конфиденциальности здесь.
Могу ли я взять TMUA взамен?
№Тест по математике для поступления в университет (TMUA) используется несколькими университетами, но не в Оксфорде. Мы рекомендуем вам проверить страницы курсов других университетов, в которые вы планируете поступать. TMUA состоялся одновременно с MAT 30 октября 2019 года и, вероятно, будет в тот же день в будущие годы. Если вы планируете сдать оба этих теста, попросите свою школу / колледж / тестовый центр заполнить форму изменения расписания, которая позволяет сдавать тесты в один и тот же день, но в разное время.(Для получения дополнительной информации посетите веб-сайт CAAT.) Поскольку и MAT, и TMUA проверяют навыки решения задач по математике, вероятно, ваша подготовка к обоим будет частично совпадать.
Могу ли я взять вместо этого STEP / BMO / IMO?
№
Обратите внимание
- Во время теста нельзя использовать калькуляторы, таблицы формул или словари.
- В тестовой бумаге предусмотрено место для ваших решений, а в конце тестовой бумаги есть запасные пустые страницы, которые вы можете продолжить при необходимости.

 В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.7, 8.
В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.7, 8.