Умножение на четыре. Умножение на четыре Таблицу умножения на 2.3 4.5 6.7 8.9
На данном уроке будет рассмотрено, как выполнять умножение и деление на числа вида 10, 100, 0,1, 0,001. Также будут решены различные примеры на данную тему.
Упражнение.
Как умножить число 25,78 на 10?
Десятичная запись данного числа — это сокращенная запись суммы. Необходимо расписать ее более подробно:
Таким образом, нужно умножить сумму. Для этого можно просто умножить каждое слагаемое:
Выходит, что.
Можно сделать вывод, что умножить десятичную дробь на 10 очень просто: нужно запятую сдвинуть вправо на одну позицию.
Упражнение.
Умножить 25,486 на 100.
Умножить на 100 — это то же самое, что и умножить два раза на 10. Иными словами, необходимо сдвинуть запятую вправо два раза:
Упражнение.
Разделить 25,78 на 10.
Как и в предыдущем случае, необходимо представить число 25,78 в виде суммы:
Так как нужно поделить сумму, то это эквивалентно делению каждого слагаемого:
Выходит, чтобы разделить на 10, нужно запятую сдвинуть влево на одну позицию.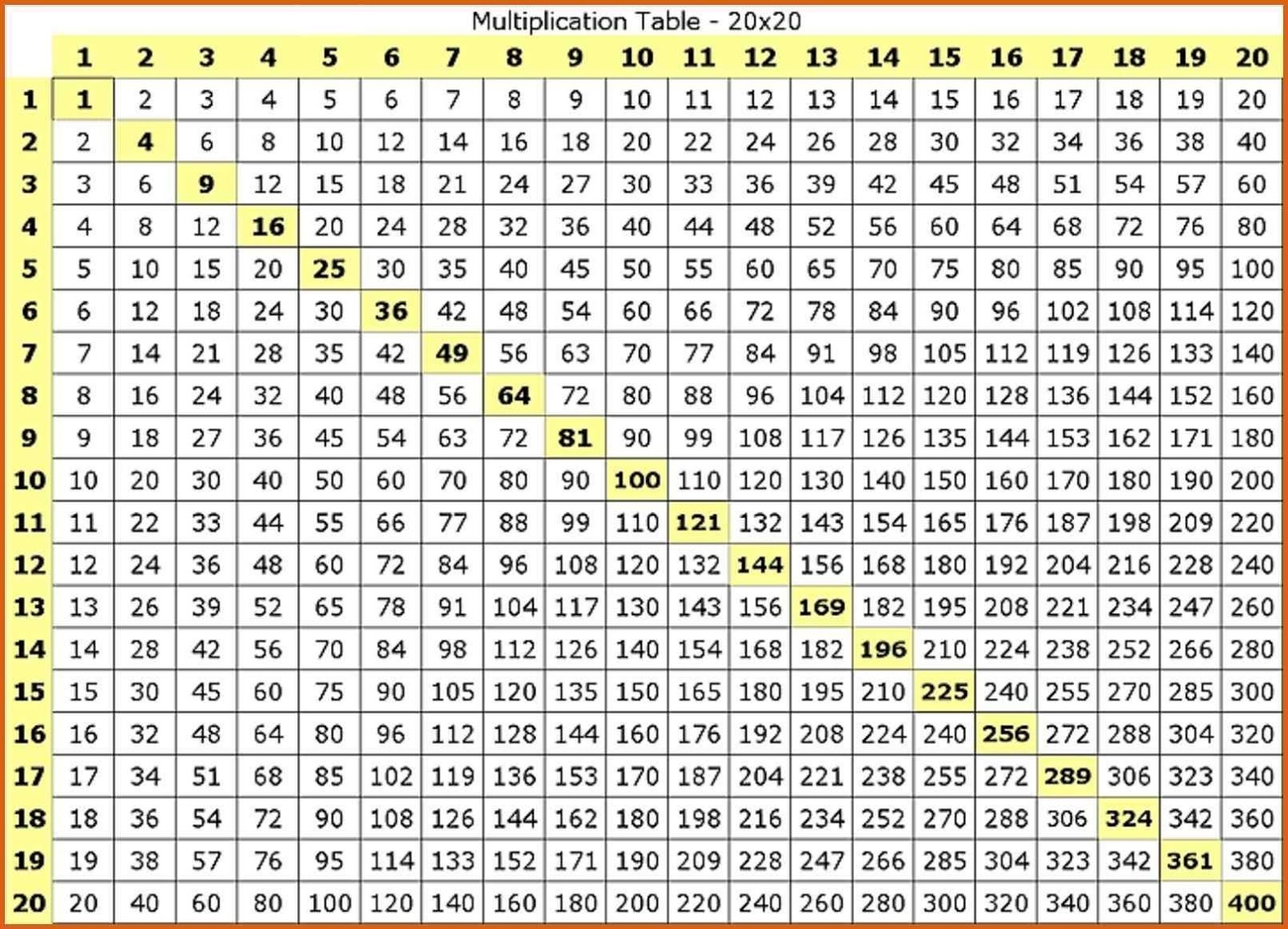 Например:
Например:
Упражнение.
Разделить 124,478 на 100.
Разделить на 100 — это то же самое, что два раза разделить на 10, поэтому запятая сдвигается влево на 2 позиции:
Если десятичную дробь нужно умножить на 10, 100, 1000 и так далее, нужно запятую сдвинуть вправо на столько позиций, сколько нулей у множителя.
И наоборот, если десятичную дробь нужно поделить на 10, 100, 1000 и так далее, нужно запятую сдвинуть влево на столько позиций, сколько нулей у множителя.
Пример 1
Умножить на 100 значит сдвинуть запятую вправо на две позиции.
После сдвига можно обнаружить, что после запятой уже нет цифр, а это значит, что дробная часть отсутствует. Тогда и запятая не нужна, число получилось целое.
Пример 2
Сдвигать нужно на 4 позиции вправо. Но цифр после запятой всего две. Стоит вспомнить, что для дроби 56,14 есть эквивалентная запись.
Теперь умножить на 10 000 не составляет труда:
Если не очень понятно, почему можно дописать два нуля к дроби в предыдущем примере, то дополнительное видео по ссылке сможет помочь в этом.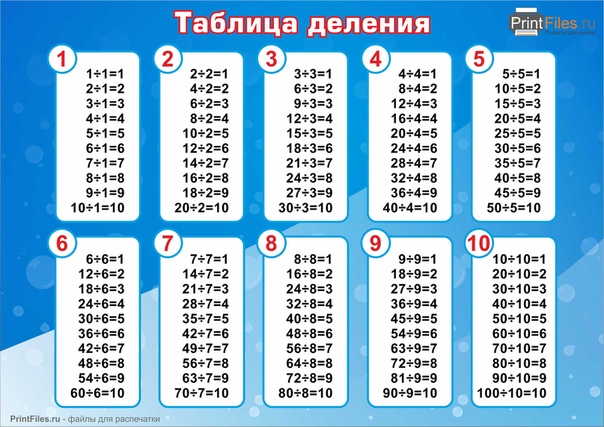
Эквивалентные десятичные записи
Запись 52 означает следующее:
Если впереди поставить 0, получим запись 052. Эти записи эквивалентны.
Можно ли поставить два нуля впереди? Да, эти записи эквивалентны.
Теперь посмотрим на десятичную дробь:
Если приписать ноль, то получается:
Эти записи эквивалентны. Аналогично можно приписать несколько нулей.
Таким образом, к любому числу можно приписать несколько нулей после дробной части и несколько нулей перед целой частью. Это будут эквивалентные записи одного и того же числа.
Пример 3
Так как происходит деление на 100, то необходимо сдвинуть запятую на 2 позиции влево. Слева от запятой не осталось цифр. Целая часть отсутствует. Такую запись часто используют программисты. В математике же, если целой части нет, то ставят ноль вместо нее.
Пример 4
Сдвигать нужно влево на три позиции, но позиций всего две. Если перед числом написать несколько нулей, то это будет эквивалентная запись.
То есть при сдвиге влево, если цифры кончились, необходимо восполнить их нулями.
Пример 5
В данном случае стоит помнить, что запятая всегда стоит после целой части. Тогда:
Умножение и деление на числа 10, 100, 1000 — очень простая процедура. Точно так же дело обстоит и с числами 0,1, 0,01, 0,001.
Пример
. Умножить 25,34 на 0,1.
Выполним запись десятичной дроби 0,1 в виде обыкновенной. Но умножить на — то же самое, что разделить на 10. Поэтому необходимо сдвинуть запятую на 1 позицию влево:
Аналогично умножить на 0,01 — это разделить на 100:
Пример.
5,235 разделить на 0,1.
Решение данного примера строится аналогичным образом: 0,1 выражается в виде обыкновенной дроби, а делить на — это все равно, что умножить на 10:
То есть чтобы поделить на 0,1, нужно запятую сдвинуть вправо на одну позицию, что равносильно умножению на 10.
Умножить на 10 и разделить на 0,1 — это одно и то же. Запятую нужно сдвинуть вправо на 1 позицию.
Разделить на 10 и умножить на 0,1 — это одно и то же. Запятую нужно сдвинуть вправо на 1 позицию:
Ребята, мы вкладываем душу в сайт. Cпасибо за то,
что открываете эту
красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook
и ВКонтакте
Таблица умножения — базовое понятие в математике, с которым мы знакомимся еще в начальной школе и которое потом используем всю жизнь вне зависимости от профессии. Вот только дети не спешат заучивать бесконечные столбики наизусть, особенно если задание пришлось на каникулы.
сайт
даст советы, как легко выучить таблицу вместе с детьми и сделать этот процесс увлекательным.
Таблица Пифагора
Несмотря на то что задача — выучить, то есть заучить, таблицу наизусть, прежде всего важно понять суть самого действия. Для этого можно заменить умножение сложением: одинаковые числа складываются столько раз, на сколько мы умножаем.
Например, 6×8 — это сложить 8 раз по 6.
Выделяем цветом одинаковые значения
Отличным помощником для изучения умножения станет таблица Пифагора, которая также демонстрирует некоторые закономерности. Например то, что от перемены мест множителей произведение не меняется: 4×6 = 6×4.
Например то, что от перемены мест множителей произведение не меняется: 4×6 = 6×4.
Отметьте такие «зеркальные» ответы определенным цветом — это поможет запомнить и не запутаться при повторении.
Начинать изучение таблицы Пифагора лучше с самых простых и понятных частей: умножения на 1, 2, 5 и 10.
При умножении на единицу число остается неизменным, а умножение на 2 дает нам удвоенное значение. Все ответы умножения на 5 оканчиваются либо на 0, либо на 5. А вот умножив на 10, в ответе мы получим двузначное число из цифры, которую умножали, и нуля.
Таблица для закрепления результата
Для закрепления результатов нарисуйте с ребенком пустую таблицу Пифагора и предложите ему заполнить клеточки правильными ответами. Для этого вам понадобится всего лишь листок бумаги, карандаш и линейка. Нужно нарисовать квадрат и поделить его на 10 частей по вертикали и горизонтали. А затем заполнить верхнюю строчку и крайний левый столбик числами от 1 до 9, пропустив первую клетку.
Конечно, все дети индивидуальны и универсального рецепта не существует. Главная задача родителя — найти подход и поддержать свое чадо, ведь все мы когда-то начинали с таких одновременно простых и сложных шагов.
Когда перед школьником становится задача учить таблицу умножения, то, конечно же, родители хотят ему помочь и ищут, какой самый быстрый способ выучить таблицу умножения. Методик великое множество, но во всем нужен индивидуальный подход к вашему карапузу. Мы расскажем вам о том, как можно легко объяснить ребенку принципы перемножения чисел и поспособствовать тому, чтобы он его запомнил в самые короткие сроки.
Скорее все, школьнику множить на 1 и 10 будет проще всего. Этот счет дается очень легко малышам, так как тут нет ничего страшного и трудного. Попробуйте нарисовать перед крохой несколько примеров, таких как 1*2=2, 1*5=5, 8*1=8. В любом случае число останется неизменным.
С 10-ой будет чуть-чуть посложнее, но если вы все нормально объясните ребенку 8-9 лет, что умножение на 10 похоже на принцип на 1, но к результату нужно добавить 0, то малыш это запомнит очень легко. Обязательно скажите вашему школьнику, что, выучив умножение на 1 и на 10 он уже будет знать первую и последнюю строчку во всех других столбцах.
Обязательно скажите вашему школьнику, что, выучив умножение на 1 и на 10 он уже будет знать первую и последнюю строчку во всех других столбцах.
Умножение на 2
С двойкой тоже будет легко, так как вы скажите малышу, что правильный результат можно получить, если сложить два предложенных числа. К примеру, если у ребенка есть пример 2*6, то ему всего лишь нужно сложить между собой 6+6 и получиться 12. После каждого занятия, обязательно делайте перерыв, минимум на час, а лучше всего продолжать занятия через сутки.
Умножение на 3
С умножением на тройку можно попробовать тот же способ, что и с двойкой. Нужно всего лишь пояснить ребенку, что 3*4 и 4+4+4 будут одинаково равняться 12. Если же этот способ вашему малышу абсолютно не подходит, то попробуйте поиграть с ассоциациями. Сначала попросите малыша, чтобы он пофантазировал и зарисовал свои ассоциации к цифрам от 1 до 9.
После этого начните придумывать историю по каждый пример, и так школьник запомнит табличку на 3 намного быстрее. Разрешите малышу играть с этими рисунками и придумывать к ним истории самостоятельно. Можете нарисовать к каждому примеру свою историю, так запомнится намного легче.
Разрешите малышу играть с этими рисунками и придумывать к ним истории самостоятельно. Можете нарисовать к каждому примеру свою историю, так запомнится намного легче.
Умножение на 4
Чтобы ваш малыш легко запомнил умножение на 4, напомните ему про принцип, которым пользовались, когда изучали столбцы с двойкой. Но только сейчас нам нужно будет удвоить нужное число и результат увеличить вдвое. К примеру, 4*4= 4*2=8*2=16.
Таблица умножения 4
Умножение на 5
При изучении действия на 5, вы должны сразу обратить внимание вашего ребенка 8-9 лет на то, что на результате умножения в этом столбце все результаты будут заканчиваться или на 5 или на ноль. Также обратите внимание на то, что 5 – это половинка десятки. Поэтому ответы проще будет умножать число не на 5, а на 10 и потом делить результат пополам. К примеру, нам нужно найти ответ на пример 7*5. Попробуйте 7*10, будет 70. Теперь 70 поделите на 2 – будет 35.
Умножение на 6
Для шестерки тоже есть способ, чтобы запоминание прошло легко для детей 8 лет, и этот столбец таблички был выучен за час. Попробуйте напомнить малышу, как он учил табличку на 3 и предложите ему к результату добавлять то же самое число. К примеру, 3*5=15, значит 6*5=3*5+15=30.
Попробуйте напомнить малышу, как он учил табличку на 3 и предложите ему к результату добавлять то же самое число. К примеру, 3*5=15, значит 6*5=3*5+15=30.
Таблица умножения 6
Умножение на 7
Если умножение до 6 уже не составляет для ребенка 8 лет большого труда, то понять, как умножать на 7 будет для него проще простого. Если нужно 7* 2 – значит нужно просто сложить 7 и 7, получится 14. Пример 7*4 будет означать, что цифру нужно удвоить дважды и так далее. Отдельно записать и выучить нужно будет лишь умножение на 7, 8 и 9.
Умножение на 8
По аналогии с предыдущими методами, умножение на 8 можно сравнить с четверкой, только результат нужно будет удваивать трижды. Если у нас в примере написано, что 4*8, то значит 2 множим на 4, получившуюся восьмерку еще на два, получаем 16 и потом этот результат множим еще на 2 и получаем 32.
Таблица умножения 8
Умножение на 9
Существует простой и очень легкий метод умножения на 9 на пальцах. Он определенно понравиться детям 8-9 лет, так как обучиться ему можно всего лишь за несколько минут, а не за час или два.
Он определенно понравиться детям 8-9 лет, так как обучиться ему можно всего лишь за несколько минут, а не за час или два.
Попросите школьника положить ручки на стол ладошками вниз. Считайте пальчики слева направо. Итак, к примеру, у нас есть пример 7*9. Отсчитываем 7 пальчиков справа. Загибаем палец, на котором остановили счет. Сколько пальчиков не загнуто слева от седьмого – шесть.
Значит, у нас в ответе будет шесть десятков. Сколько пальчиков справа от загнутого – три. Это будет число единиц в ответе. Так мы поняли что ответ – 63. Такое изучение таблички умножения на пальцах будет полезным. Не стоит ругать кроху, что он пользуется этим методом слишком долго. Именно такой метод позволит малышу крепко-накрепко запомнить умножение на 9.
Таблица умножения 9
Как умножать числа столбиком
Конечно же, после того, как ребенок 9 лет хорошо выучит табличку умножения, его нужно будет научить умножать в столбик двухзначные, а потом и трехзначные числа. Числа, которые умножаются друг на друга называются множителями. Их именуют первый множитель, второй множитель и так далее. Результат умножения будет носить название «произведение».
Числа, которые умножаются друг на друга называются множителями. Их именуют первый множитель, второй множитель и так далее. Результат умножения будет носить название «произведение».
Чтобы перемножить два числа, нужно будет расположить их в столбик друг над другом так, чтобы единицы были над единицами, десятки над десятками и так далее. Следующим этапом будет то, что верхнее число нужно будет умножить на цифру нижнего числа. Сначала умножаются единица, потом десятки, сотни и так далее. Результат обязательно нужно записать внизу под чертой.
Если в результате умножения у вас получилось число, которое больше десяти, что под черту идет только последняя цифра результата, а десяток, если он есть, записывается сверху. Потом этот десяток должен быть приплюсован к результату умножения десятка на единицу. Перемножение верхнего числа на десятки и сотни нижнего происходит по тем же правилам.
Если вы дадите вашему ребенку возможность спокойно усвоить тот или иной метод запоминания таблицы умножения, то он достаточно быстро начнет считать. Не настаивайте, если у малыша нет желания заниматься. Вы вполне можете идти на поводу у ребенка, позволяя ему не повторять таблицу.
Не настаивайте, если у малыша нет желания заниматься. Вы вполне можете идти на поводу у ребенка, позволяя ему не повторять таблицу.
Показывайте ему конкретные примеры в жизни, где таблица ему может пригодиться. К примеру, попросите дочь посчитать, столько конфет нужно купить, чтобы ее подружкам всем досталось по три. Девочке будет легко и интересно находить ответ, так как это непосредственно касается практики и жизни.
Математика является одной из самых важных и необходимых наук для вашего ребенка.
Без знания математики, вы не сможете посчитать, решить пример, задачку, уравнение.
В математике есть четыре вида арифметических действий: сложение, вычитание, умножение, деление.
Что такое умножение?
Это умное сложение
Ведь умней умножить раз,
Чем слагать все целый час.
Рассмотрим сегодня арифметическое действие, умножение, очень важно объяснить и научить умножать каждого ребенка, для этого мы рассмотрим, как можно умножить разные числа на 4.
##Умножение разных чисел на четыре
Рассмотрим, что получится, если умножить число четыре на разные числа.
###Умножим число четыре на два
Давайте посмотрим следующий пример, в этом примере два слагаемых 4, 4. Сложим эти два слагаемых, что мы получим? Мы получим ответ 8.
4 + 4 = 8
То есть сумма двух четверок равна восьми.
Теперь посмотрим, как можно получить число восемь путем умножения?
Посмотрите на пример, который написан выше. В примере два слагаемых, чтобы получить число восемь, надо цифру четыре, умножить на количество слагаемых. То есть четыре умножить на два — это сумма двух четверок.
4 * 2 = 8
Умножаем четыре, на два получается восемь.
Четырежды два восемь
###Умножим число четыре на три
Давайте посмотрим следующий пример, в этом примере три слагаемых 4, 4, 4. Сложим эти три слагаемых, что мы получим? Мы получим ответ 12.
4 + 4 + 4 = 12
То есть сумма трех четверок равна двенадцати.
Теперь посмотрим, как можно получить число двенадцать путем умножения?
Посмотрите на пример, который написан выше. В примере три слагаемых, чтобы получить число двенадцать, надо цифру четыре, умножить на количество слагаемых.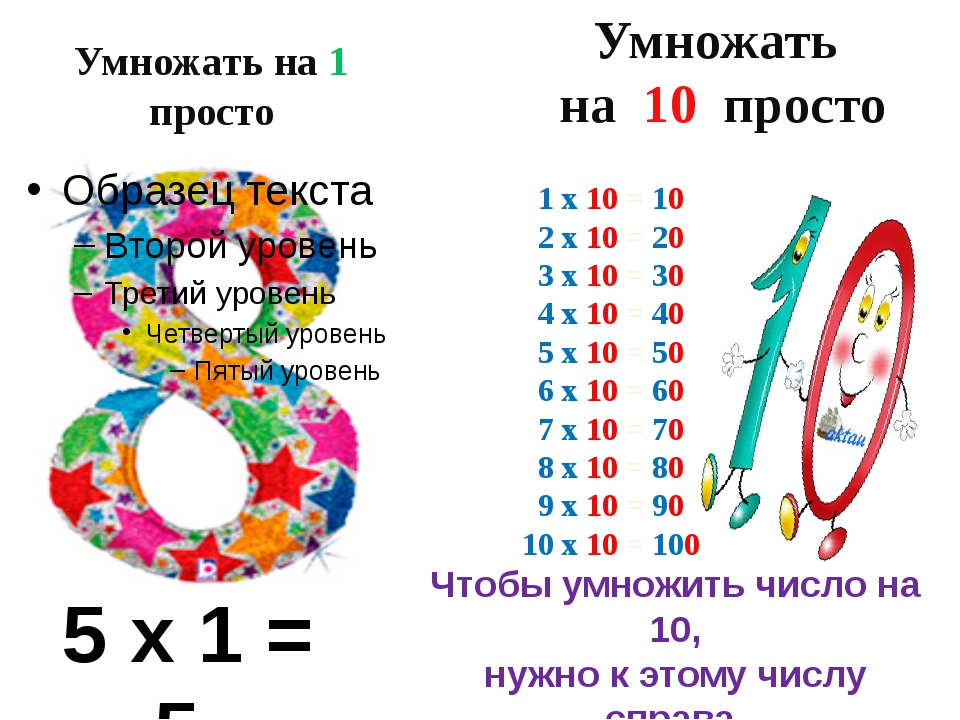 То есть четыре умножить на три — это сумма трех четверок.
То есть четыре умножить на три — это сумма трех четверок.
4 * 3 = 12
Умножаем четыре, на три получается двенадцать.
Четырежды три двенадцать
###Умножим число четыре на четыре
Давайте посмотрим следующий пример в этом примере четыре слагаемых 4, 4, 4, 4. Сложим эти четыре слагаемых, что мы получим? Мы получим ответ 16.
4 + 4 + 4 + 4 = 16
То есть сумма четырех четверок равна шестнадцати.
Теперь посмотрим, как можно получить число шестнадцать путем умножения?
Посмотрите на пример, который написан наверху, у нас в примере четыре слагаемых, чтобы получить число шестнадцать, нам надо цифру четыре, умножить на количество слагаемых, то есть на четыре получаем шестнадцать.
4 * 4 = 16
Умножаем четыре, на четыре получается шестнадцать.
Четырежды четыре шестнадцать
###Умножим число четыре на пять
Давайте посмотрим следующий пример в этом примере пять слагаемых 4, 4, 4, 4, 4. Сложим эти пять слагаемых, что мы получим? Мы получим ответ 20.
4 + 4 + 4 + 4 + 4 = 20
То есть сумма пяти четверок равна двадцати.
Теперь посмотрим, как можно получить число двадцать путем умножения?
Посмотрите на пример, который написан наверху, у нас в примере пять слагаемых, чтобы получить число двадцать, нам надо цифру четыре, умножить на количество слагаемых, то есть на пять получаем двадцать.
4 * 5 = 20
Умножаем четыре, на пять получается двадцать.
Четырежды пять двадцать
###Умножим число четыре на шесть
Давайте посмотрим следующий пример в этом примере шесть слагаемых 4, 4, 4, 4, 4, 4. Сложим эти шесть слагаемых, что мы получим? Мы получим ответ 24.
4 + 4 + 4 + 4 + 4 + 4 = 24
То есть сумма шести четверок равна двадцати четырем.
Теперь посмотрим, как можно получить число двадцать четыре путем умножения?
Посмотрите на пример, который написан наверху, у нас в примере шесть слагаемых, чтобы получить число двадцать четыре, нам надо цифру четыре, умножить на количество слагаемых, то есть на шесть получаем двадцать четыре.
4 * 6 = 24
Умножаем четыре, на шесть получается двадцать четыре.
Четырежды шесть двадцать четыре
###Умножим число четыре на семь
Давайте посмотрим следующий пример в этом примере семь слагаемых 4, 4, 4, 4, 4, 4, 4. Сложим эти семь слагаемых, что мы получим? Мы получим ответ 28.
Сложим эти семь слагаемых, что мы получим? Мы получим ответ 28.
4 + 4 + 4 + 4 + 4 + 4 + 4 = 28
То есть сумма семи четверок равна двадцати восьми.
Теперь посмотрим, как можно получить число двадцать восемь путем умножения?
Посмотрите на пример, который написан наверху, у нас в примере семь слагаемых, чтобы получить число двадцать восемь, нам надо цифру четыре, умножить на количество слагаемых, то есть на семь получаем двадцать восемь.
4 * 7 = 28
Умножаем четыре, на семь получается двадцать восемь.
Четырежды семь двадцать восемь
###Умножим число четыре на восемь
Давайте посмотрим следующий пример в этом примере восемь слагаемых 4, 4, 4, 4, 4, 4, 4, 4. Сложим эти восемь слагаемых, что мы получим? Мы получим ответ 32.
4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32
То есть сумма восьми четверок равна тридцати двум.
Теперь посмотрим, как можно получить число тридцать два путем умножения?
Посмотрите на пример, который написан наверху, у нас в примере восемь слагаемых, чтобы получить число тридцать два, нам надо цифру четыре, умножить на количество слагаемых, то есть на восемь получаем тридцать два.
4 * 8 = 32
Умножаем четыре, на восемь получается тридцать два.
Четырежды восемь тридцать два
###Умножим число четыре на девять
Давайте посмотрим следующий пример в этом примере девять слагаемых 4, 4, 4, 4, 4, 4, 4, 4, 4. Сложим эти девять слагаемых, что мы получим? Мы получим ответ 36.
4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 36
То есть сумма девяти четверок равна тридцати шести.
Теперь посмотрим, как можно получить число тридцать шесть путем умножения?
Посмотрите на пример, который написан наверху, у нас в примере девять слагаемых, чтобы получить число тридцать шесть, нам надо цифру четыре, умножить на количество слагаемых, то есть на девять получаем тридцать шесть.
4 * 9 = 36
Умножаем четыре, на девять получается тридцать шесть.
Четырежды девять тридцать шесть
###Умножим число четыре на десять
Давайте посмотрим следующий пример в этом примере десять слагаемых 4, 4, 4, 4, 4, 4, 4, 4, 4, 4. Сложим эти десять слагаемых, что мы получим? Мы получим ответ 40.
4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 40
То есть сумма десяти четверок равна сорока.
Теперь посмотрим, как можно получить число сорок путем умножения?
Посмотрите на пример, который написан наверху, у нас в примере десять слагаемых, чтобы получить число сорок, нам надо цифру четыре, умножить на количество слагаемых, то есть на десять получаем сорок.
4 * 10 = 40
Умножаем четыре, на десять получается сорок.
Четырежды десять сорок
Мы разобрали всю таблицу умножения на четыре, теперь посмотрим таблицу умножения на четыре всю целиком.
4 * 2 = 8
4 * 3 = 12
4 * 4 = 16
4 * 5 = 20
4 * 6 = 24
4 * 7 = 28
4 * 8 = 32
4 * 9 = 36
4 * 10 = 40
Таблицу умножения на четыре можно записать в другом порядке, поменяем множители местами и получим точно такой же ответ.
2 * 4 = 8
3 * 4 = 12
4 * 4 = 16
5 * 4 = 20
6 * 4 = 24
7 * 4 = 28
8 * 4 = 32
9 * 4 = 36
10 * 4 = 40
Чтобы хорошо запомнить таблицу умножения на четыре можно поиграть в следующие игры.
##Игры для запоминания таблицы умножения на четыре
###Игра первая «Ответь быстро»
В эту игру можно играть вдвоем, но лучше несколько человек, выбирается ведущий, это может быть взрослый, он дает задание и кто первый ответит правильно, тот человек набирает очки.
Такая игра научит вашего ребенка запоминать и отвечать быстро. Если играют нескольких человек, то у играющих появляется дух соревнования, и каждый будет пытаться ответить быстрее и набрать, как можно больше очков.
Вопрос 1. Четырежды два — ?
Вопрос 2. Четырежды восемь — ?
Вопрос 3. Четырежды пять — ?
Вопрос 4. Четырежды десять — ?
Вопрос 5. Четырежды три — ?
Вопрос 6. Четырежды семь — ?
Вопрос 7. Четырежды четыре — ?
Вопрос 8. Четырежды шесть — ?
Вопрос 9. Четырежды девять — ?
Вопросы можно менять метами до бесконечности, чем больше вы будете задавать такие вопросы, тем быстрее ребенок запомнит таблицу умножения и будет в ней хорошо ориентироваться.
###Игра вторая «Правильное ориентирование»
В эту игру лучше играть с несколькими детьми одновременно, выбираем ведущего, это может быть взрослый человек.
Ведущий берет мяч и встает в круг, задает вопрос по таблице умножения на четыре и кидает ребенку мяч, ребенок ловит этот мяч, быстро отвечает на вопрос и кидает обратно.
Если ребенок ответил неправильно, то ведущий кидает ему повторно мяч и задает уже другой вопрос.
При правильном ответе ребенка хвалят и кидают мяч другому ребенку.
Примерные вопросы:
— сколько будет четырежды девять;
— сколько получится, если шесть мы умножим на четыре;
— сколько будет четырежды три;
— сколько будет четырежды восемь;
— сколько будет пятью четыре;
— сколько будет, если семь мы умножим на четыре и так далее.
###Игра третья «Покажи быстро»
Для этой игры надо приготовить заранее карточки с цифрами от одного до сорока и раздать каждому ребенку, который будет участвовать в этой игре.
Ведущий задает вопросы по теме «умножение на четыре», а дети тихо с места отвечают при помощи этих карточек, поднимая их.
Ведущий проверяет правильность ответов и задает вопросы дальше.
Примерные вопросы для игры:
— какой получится ответ, если четыре умножить на семь;
— сколько будет пятью четыре;
— сколько будет восемью четыре;
— какой получится ответ, если четыре умножить на шесть;
— сколько получится, если четыре мы умножим на четыре;
— сколько будет четырежды три;
— сколько будет четырежды восемь;
— сколько будет девятью четыре;
— сколько будет, если семь мы умножим на четыре и так далее.
В этой игре меняйте формулировку вопроса, чтобы ребенок немного задумался.
###Игра четвертая «Быстрый ответ»
В этой игре ведущий читает стих на тему «изучение таблицы умножения на цифру четыре», а дети должны слушать внимательно и когда ведущий прочитает стих полностью или во время стиха, дети должны быстро дать ответ.
###Стих 1. Свинки
Четыре милых свинки
Плясали без сапог:
Четырежды четыре —
Сколько? Голых ног?
Ответ: шестнадцать голых ног.
###Стих 2. Мартышки
Четыре ученых мартышки
Ногами листали книжки…
На каждой ноге – пять пальцев:
Четырежды пять – догадайся?
Ответ: двадцать.
###Стих 3. Картошка
Шла на парад Картошка – в – мундире:
Четырежды шесть – будет …
Ответ: двадцать четыре.
###Стих 4. Сороки
Гуляли сорок сорок,
Нашли творожный сырок.
И делят на части творог:
Четырежды десять — …
Ответ: сорок.
##Домашнее задание
Для закрепления таблицы умножения на четыре мы предлагаем выполнить домашнее задание.
###Задание первое
После знака равно поставьте ответ, на выполнение задания дается тридцать секунд.
###Задание второе
В этом задании надо ответить на поставленные вопросы.
— сколько будет четырежды девять;
— сколько будет семью четыре;
— сколько получится, если девять умножить на четыре;
— сколько будет четырежды три;
— сколько будет четырежды пять;
— сколько будет четырежды шесть;
— сколько будет, если восемь умножить на четыре;
— сколько получится, если четыре умножить на четыре;
— сколько будет шестью четыре;
— сколько получится, если четыре умножить на десять.
###Задание третье
В этом задании даны несколько задачек их надо быстро и правильно решить.
Задача 1.
Четыре птички принесли в клюве по три ягодки. Сколько ягод принесли птички?
Задача 2.
У пяти белочек было по четыре шишки. Сколько шишек было у белочек?
Задача 3.
У каждого ежика в норке было по четыре гриба. Ежиков я насчитал шесть. Сколько всего грибов было у ежиков?
Задача 4.
К четырем зайчикам сегодня в гости придет столько же белочек. Сколько всего будет зверей?
Задача 5.
У Светы было четыре открытки, подружки подарили Свете еще столь же открыток. Сколько открыток стало у Светы?
Сколько открыток стало у Светы?
Задача 6.
В кружок рисования пришло записываться четыре девочки, а мальчиков в два раза больше. Сколько всего детей пришло записываться в кружок рисования?
###Задание четвертое
Посмотрите следующее задание, здесь даны примеры на умножение вам надо вместо точек поставить, цифру так, чтобы равенство получилось верным.
###Задание пятое
В этом задании даны два столбика, в первом столбике написаны примеры, а во втором написаны ответы.
Надо решить пример правильно, и найти нужный вам ответ, соедините пример и ответ стрелочкой.
###Задание шестое
В этом задании даны числа 8, 12,16, 20, 28, 24, 32, 36, 40.
Какое надо взять число, чтобы получилось следующее равенство?
Для лучшего усвоения математического счета и таблицы умножения мы предлагаем вам несколько развивающих игр для детей.
##Развивающие игры для детей
###Игра 1 «Сравнение цифр по памяти»
Игра «Сравнение цифр по памяти» развивает мышление и память.
Главная суть игры дано число его надо сравнить, с предыдущим числом.
В этой игре на несколько секунд на экране появляется цифра, ее надо запомнить, затем цифра исчезает и появляется другая цифра, ее надо сравнить с предыдущей, и ответить на вопрос «больше» или «меньше».
Если вы ответили правильно, вы набираете очки и играете дальше.
!.png)
Играть сейчас
###Игра 2 «Математические сравнения»
Игра «Математические сравнения» развивает мышление и память.
Главная суть игры сравнить числа и математические операции.
В этой игре надо сравнить два числа. На верху, написан вопрос, прочитайте внимательно вопрос.
Внизу расположены три кнопки «левое», «равно», «правое».
Ответить вы можете при помощи мышки, кликнув на нужную кнопку мышкой.
Если вы ответили правильно, вы набираете очки и играете дальше.
!.png)
Играть сейчас
##Курсы для развития интеллекта
Помимо игр, у нас есть интересные курсы, которые отлично прокачают Ваш мозг и улучшат интеллект, память, мышление, концентрацию внимания:
###Развитие памяти и внимания у ребенка 5-10 лет
Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.
После прохождения курса ребенок сможет:
1. В 2-5 раз лучше запоминать тексты, лица, цифры, слова
2. Научится запоминать на более длительный срок
3. Увеличится скорость воспоминания нужной информации
###Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
###Скорочтение за 30 дней
Вы бы хотели очень быстро прочитывать интересные Вам книги, статьи, рассылки и так далее.? Если Ваш ответ «да», то наш курс поможет Вам развить [скорочтение](/speedreading/) и синхронизировать оба полушария головного мозга.
При синхронизированной, совместной работе обеих полушарий, мозг начинает работать в разы быстрее, что открывает намного больше возможностей. **Внимание**, **концентрация**, **скорость восприятия** усиливаются многократно! Используя техники скорочтения из нашего курса вы сможете убить сразу двух зайцев:
1. Научиться очень быстро читать
Научиться очень быстро читать
2. Улучшить внимание и концентрацию, так как при быстром чтении они крайне важны
3. Прочитывать в день по книге и быстрее заканчивать работу
###Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Если вы хотите разогнать свой мозг, улучшить его работу, подкачать память, внимание, концентрацию, развить больше креативности, выполнять увлекательные упражнения, тренироваться в игровой форме и решать интересные задачки, тогда записывайтесь! 30 дней мощного фитнеса мозга Вам гарантированы:)
###Как улучшить память и развить внимание
Бесплатное практическое занятие от advance.
##Заключение
Регулярно занимайтесь со своими детьми, развивайте их, помогайте им понять главную суть математических операций, учите таблицу умножения вместе, помогите понять суть изучения таблицы умножения. Желаем вам удачи.
Если моя память мне не изменяет, таблица умножения до 5 включительно далась достаточно легко. Но вот с умножением на 6, 7, 8 и 9 возникали определенные трудности. Если бы я знала такой трюк раньше, домашнее задание выполнялось бы минимум в два раза быстрее;)
Если бы я знала такой трюк раньше, домашнее задание выполнялось бы минимум в два раза быстрее;)
Умножение на 6, 7 и 8
Поверните кисти ладонями к себе и присвойте каждому пальцу цифры от 6 и до 10 начиная с мизинца.
Теперь попробуем умножить, например, 7х8. Для этого соедините палец №7 на левой руке с пальцем №8 на правой.
А теперь считаем пальцы: количество пальцев под соединенными — это десятки.
(картинка кликабельна)
А пальцы левой руки, оставшиеся сверху, умножаем на пальцы правой — это и будут наши единицы (3х2=6). Итоге равен 56.
Иногда бывает так, что при умножении «единиц» результат получается больше 9. В таких случаях нужно плюсовать оба результата в столбик.
Например, 7х6. В этом случае получается, что «единицы» равны 12 (3х4). В десятки равны 3.
3 (десятки)
+
12 (единицы)
________
42
Умножение на 9
Снова поверните кисти ладонями к себе, но теперь нумерация пальцев будет идти по порядку с лева на право, то есть от 1 до 10.
Теперь умножаем, например, 2х9. Все то, что идет до пальца №2 — это десятки (то есть 1 в этом случае). А все то, что остается после пальца №2 — единицы (то есть 8). В итоге получаем 18.
Умножение десятичных дробей — примеры, правила как умножать в 5 классе
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
Вернемся к обыкновенным дробям позже, а сейчас обсудим десятичные дроби. Их знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Их знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
| Основные свойства |
|---|
|
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Как решаем:
- Знаменатель равен 10 — это один ноль.
- Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
- В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.
Ответ: 16/10 = 1,6.
Пример 2. Перевести 37/1000 в десятичную дробь.
Как решаем:
- Знаменатель равен 1000 — это три нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Так как в числителе только две цифры, то на пустующие места пишем нули.
- В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.
Ответ: 37/1000 = 0,037.
Приходите решать увлекательные задачки с красочными героями и в интерактивном формате. Запишите вашего ребенка на бесплатный вводный урок в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Принципы умножения десятичных дробей
С десятичными дробями можно производить те же действия, что и с любыми другими числами: складывать и вычитать, делить и умножать. В этом блоке узнаем, как умножать дроби.
В этом блоке узнаем, как умножать дроби.
| Свойства умножения десятичных дробей |
|---|
|
Умножение десятичных дробей друг на друга можно упростить и просто умножить натуральные числа. Главное — правильно поставить запятую в ответе.
Главное — правильно поставить запятую в ответе.
Если в задаче даны десятичные дроби с разными знаками — используем правило умножения отрицательных чисел. Как быстро запомнить:
| «−−» | минус на минус дает плюс |
| «−+» | минус на плюс дает минус |
| «+−» | плюс на минус дает минус |
| «++» | плюс на плюс дает плюс |
Числа с единицей и нулями (10, 100, 1000 и т. д.) называются разрядными единицами, так как цифра 1 — единственная значимая цифра в числе и от ее местоположения зависит количественное значение числа. Важно запомнить правила для умножения и деления на разрядную единицу:
- Чтобы умножить число на разрядную единицу, достаточно к числу справа дописать столько нулей, сколько их содержит разрядная единица.
- Чтобы разделить число на разрядную единицу, достаточно от числа справа отбросить столько нулей, сколько их содержит разрядная единица.

Как умножать десятичные дроби в столбик
Чтобы перемножить десятичные дроби нужно сделать три шага:
- Записать десятичные дроби в столбик и умножить друг на друга, как обыкновенные числа.
- Посчитать количество знаков после запятой у каждой дроби. Сложить их количество.
- Полученную цифру отсчитать справа налево и поставить запятую.
Пример 1. Перевести 5,4 в смешанное число.
Как решаем:
|
Ответ: 3,11 ∗ 0,01 = 0,0311.
| Примеры умножения десятичных дробей столбиком: |
|---|
Чтобы закрепить тему, смотрите видео «Умножение десятичных дробей».
Как умножать десятичные дроби на натуральные числа
Умножение десятичных дробей на обычные числа происходит так же, как и умножение между десятичными дробями. Чтобы считать быстрее, умножайте их в столбик по правилам выше. А вот и примерчики!
Пример 1. Умножить десятичную дробь 2,27 на целое число 15.
Как решаем:
умножить столбиком данные числа и отделить два знака запятой.
Ответ: 15 ∗ 2,27 = 34,05.
Пример 2. Умножить 11 на 0,005.
Как решаем:
умножить столбиком данные числа и отделить три знака запятой.
Ответ: 11 ∗ 0,005 = 0,055.
Пример 3. Умножить 0,1557.. на 3.
Как решаем:
- Округлить бесконечную дробь: 0,1557.
 .≈ 0,156
.≈ 0,156 - Полученное число умножить на 3: 0,156 ∗ 3 ≈ 0468.
Ответ: 0,1557.. ∗ 3 ≈ 0468..
Как умножать десятичные дроби на 10, 100, 1000
Чтобы умножить десятичную дробь на 10, 100, 1000, нужно просто перенести запятую в дроби вправо на столько знаков, сколько нулей стоит во втором множителе. Лишние нули слева можно отбросить. А если цифр не хватает — дописываем нули.
Примеры:
- 1,15 ∗ 10 = 11,5;
- 22,345 ∗ 100 = 2 234,5;
- 8,99 ∗ 1 000 = 8 990;
- 0,54678 ∗ 10 000 = 5467,8;
- 0,07 ∗ 1 000 = 70;
- 0,00033 ∗ 100 = 0,033.
Как умножать десятичные дроби на 0,1, 0,01, 0,001
Чтобы умножить десятичную дробь на 0,1, 0,01, 0,001, нужно перенести запятую в дроби влево на столько знаков, сколько нулей стоит перед единицей. Ноль целых — тоже считаем. Если цифр не хватает — просто дописываем дополнительный ноль — один или несколько — после запятой.
Примеры:
- 34,9 ∗ 0,1 = 3,49;
- 1,8 ∗ 0,1 = 0,18;
- 145,7 ∗ 0,01 = 1,457;
- 9655,1 ∗ 0,001 = 9,6551;
- 11,9 ∗ 0,0001 = 0,00119.

Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 3/5 на 0,9.
Как решаем:
Записать 0,9 в виде обыкновенной дроби:
0,9 = 9/10.
- Умножить числа по правилам
3/5 ∗ 9/10 = 27/50 = 0,54.
Ответ: 3/5 ∗ 0,9 = 0,54.
Пример 2. Умножить 0,18 на 3 1/4.
Как решаем:
Записать 3 1/4 в виде десятичной дроби:
3 1/4 = 3,25.
Произвести умножение в столбик или при помощи калькулятора:
0,18 ∗ 3,25 = 0,585.
Ответ: 0,18 ∗ 3 1/4 = 0,585.
А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.
Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.
Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.
Урок 27. решение уравнений вида: х ∙ 8 = 26 + 70, х : 6 = 18 ∙ 5, 80 : х = 46 – 30 — Математика — 4 класс
Математика, 4 класс
Урок № 27. Решение уравнений вида: х · 8 = 26 + 70, х : 6 = 18 · 5,80 : х = 46 – 30
Перечень вопросов, рассматриваемых в теме:
— как решать уравнения вида: x∙ 8 = 26 + 70, x : 6 = 18 ∙ 5, 80 : x = 46 – 30
— какой алгоритм решения данных уравнений?
Глоссарий по теме:
Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.
Алгоритм — последовательность действия (шагов)
Решить уравнение – это значит найти такое значение неизвестного числа, при котором равенство будет верным.
Основная и дополнительная литература по теме урока:
1. Моро М.И., Бантова М.А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.1 — М.; Просвещение, 2017. – с.80
2. Моро М.И., Волкова С.И. Математика. Рабочая тетрадь 4 класс. Часть 1. М.; Просвещение, 2016. – с.34,35
3. Волкова С.И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.44-45.
4. Волкова С.И. Математика. Тесты 4 класс. М.; Просвещение, 2017. – с.40-41.
5. Кочергина А.В. Учим математику с увлечением (Методическая библиотека). М.: 5 за знания, 2007. – с.159.
Теоретический материал для самостоятельного изучения
Вспомните, как связаны между собой числа при умножении.
Посмотрите, множитель 20, множитель 3, произведение 60.
Если 60 разделить на 20, получится 3.
Если 60 разделить на 3, получится 20.
Значит, если произведение разделить на один из множителей, то получится другой множитель. Это правило потребуется при решении уравнений, в которых неизвестен один из множителей.
20 ∙ 3 = 60
60 : 20 = 3
60 : 3 = 20
Решим уравнение:
произведение неизвестного числа и числа 7 равно числу 91. В нем неизвестен первый множитель. Как его найти? Для нахождения неизвестного первого множителя надо произведение 91 разделить на известный множитель 7. Делим 91 на 7 — получаем 13. Выполним проверку. Подставим в уравнение вместо икс число 13.
13 умножить на 7 получим 91. Получили верное равенство:
91 равно девяносто одному. Значит, решили правильно.
А теперь догадайтесь, как решить уравнение: произведение неизвестного числа и числа 7 равно сумме чисел восьмидесяти и одиннадцати. Найдем значение выражения в правой части уравнения: 80 плюс 11 равно 91. Тем самым мы получили уравнение, которое уже умеем решать. Посмотрите, как записывается решение этого уравнения и его проверка.
Вспомним, как связаны между собой числа при делении.
Посмотрите: делимое 15, делитель 3, частное равно пяти.
Если делитель 3 умножить на частное 5, получим делимое 15.
Если делимое 15 разделить на частное 5, получим делитель 3.
15 : 3 = 5
3 ∙ 5 = 15
15 : 5 = 3
Знание связей между делимым, делителем и частным потребуется для решения уравнений, в которых неизвестен один из компонентов: делимое или делитель. Посмотрите, как решаются такие уравнения. В первом уравнении неизвестно делимое. Чтобы его найти, нужно делитель 3 умножить на частное 9.
Во втором уравнении неизвестен делитель. Чтобы его найти, нужно делимое 45 разделить на частное 3.
А как решить такое уравнение? Вычислим произведение в правой части: 18 умножить на 5 получим 90. Получается уравнение, в котором неизвестно делимое. Вы уже знаете, как его решать. Выполним проверку решения уравнения. Подставим число 540 вместо икс, вычислим левую часть и правую часть выражения: 90 равно 90. Значит уравнение решили верно.
Задания тренировочного модуля:
1.К каждой позиции первого столбца подберите соответствующую позицию второго.
91 : х = 13 | x = 20 |
х : 21=4 | x = 7 |
24 ∙x = 96 | x = 84 |
x∙ 3 = 60 | x = 4 |
Правильный ответ:
91 : х = 13 | x = 7 |
х : 21= 4 | x = 84 |
24 ∙x = 96 | x = 4 |
x∙3 = 60 | x = 20 |
2. Выполните вычисления и выделите верный ответ:
7 ∙x = 140 : 2
Варианты ответов: 10, 400, 2
Правильный вариант:
10
3.Решите уравнение, подчеркните правильный ответ:
(80 : у) ∙ 700 = 2800
Варианты ответов:
2, 4, 20
Правильные варианты:
20
Умножение чисел. Множимое, множитель и произведение
Умножение — это арифметическое действие, с помощью которого находят сумму одинаковых слагаемых.
Пример. Во дворе посадили 3 ряда ёлок, по 4 ёлки в каждом ряду. Сколько ёлок посадили во дворе?
Чтобы ответить на этот вопрос, надо найти сумму 3 слагаемых, каждое из которых равно 4.
4 + 4 + 4 = 12.
Складывая 3 раза по 4 ёлки, мы получим общее количество ёлок во всех трёх рядах.
Умножить – значит повторить одно число слагаемым столько раз, сколько в другом содержится единиц.
Для записи умножения используется знак х
(косой крест) или ·
(точка), который ставится между числами. Например:
4 х 3 или 4 · 3
Эта запись означает, что 4 надо умножить на 3. Справа от записи умножения ставится знак =
(равно), после которого записывается полученный результат:
4 · 3 = 12.
Умножение – это краткая запись сложения одинаковых слагаемых.
Пример. Умножить 6 на 5 — это значит найти сумму пяти слагаемых, каждое из которых равно шести:
Умножить 6 на 5 — это значит найти сумму пяти слагаемых, каждое из которых равно шести:
6 + 6 + 6 + 6 + 6 = 30.
Сократим запись, заменив сложение на умножение:
6 · 5 = 30.
Оба выражения равны:
6 + 6 + 6 + 6 + 6 = 6 · 5 = 30,
но для краткости записей лучше всегда использовать умножение, когда число одинаковых слагаемых больше двух.
Множимое, множитель и произведение
Множимое — это число, которое умножают. Множитель — это число, на которое умножают. Например, в записи:
4 · 3,
4 — это множимое, 3 — множитель. Множимое является числом, которое выступает в качестве слагаемого. Множитель — это число, которое указывает количество одинаковых слагаемых.
Произведение — это число, которое получается в результате умножения. Например, в записи:
4 · 3 = 12,
12 — это произведение. При этом сама запись 4 · 3 тоже называется произведением.
При этом сама запись 4 · 3 тоже называется произведением.
Эту запись можно прочитать так: произведение четырёх и трёх равно двенадцати
, четыре умножить на три равно двенадцати
, по четыре взять три раза, получится двенадцать
.
Множимое и множитель иначе называются множителями или сомножителями.
Проверка умножения
Рассмотрим выражение:
4 · 3 = 12,
где 4 — это множимое, 3 — это множитель, а 12 — произведение. Чтобы узнать правильно ли было выполнено умножение, можно:
- Разделить произведение на множитель, если получится число, равное множимому, то умножение было выполнено верно:
12 : 3 = 4.
- Разделить произведение на множимое, если получится число, равное множителю, то умножение выполнено верно:
12 : 4 = 3.
Умножение двух чисел можно проверить делением, для этого произведение делят на один из сомножителей, если частное окажется равно другому сомножителю, то умножение выполнено верно.
Действия с дробями
Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе, всё что можно делать с обычными числами, можно делать и с дробями.
Сложение дробей с одинаковыми знаменателями
Сложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями;
- Сложение дробей с разными знаменателями.
Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.
Например, слóжим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.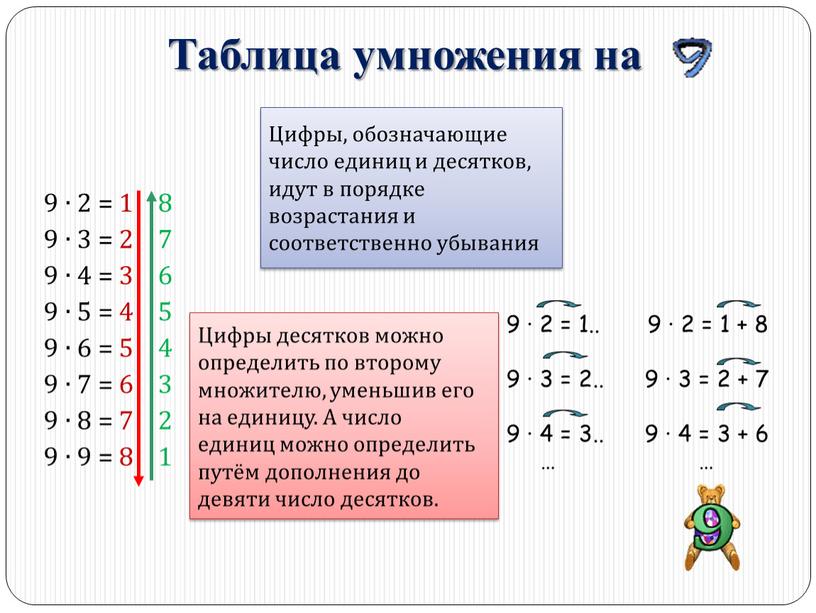
Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Сложение дробей с разными знаменателями
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1. Сложим дроби и
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби?«.
Поэтому на первых этапах советуем записывать каждую мелочь. Хвастаться можно лишь в будущем, когда будут усвоены азы.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателями
Вычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями.
Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1. Умножить дробь на число 1.
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2. Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Число, которое умножается на дробь, и знаменатель дроби разрешается сокращать, если они имеют общий делитель, бóльший единицы.
Например, выражение можно вычислить двумя способами.
Первый способ. Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:
Второй способ. Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4, поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
А вот к примеру выражение можно вычислить только первым способом — умножить число 7 на числитель дроби , а знаменатель оставить без изменений:
Связано это с тем, что число 7 и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробей
Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дроби
Любое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числа
Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Примеры:
- обратным числа 2 является дробь
- обратным числа 3 является дробь
- обратным числа 4 является дробь
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Примеры:
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2. Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
Получили ответ . Значит при делении половины на две части получается четверть.
Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:
Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:
Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь
В обоих случаях получился один и тот же результат.
Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь
Пример 2. Найти значение выражения
Умножим первую дробь на число, обратное делителю:
Допустим, имеется четверть пиццы и нужно разделить её на двоих:
Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:
Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5
10 : 2 = 5
Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь
Как видно результат не изменился. Мы снова получили ответ 5.
Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.
Пример 3. Найти значение выражения
Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь
Допустим, имелось пиццы:
Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков
Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет . Поэтому при делении на 6 получается
Деление числа на дробь
Правило деления числа на дробь такое же, как и правило деления дроби на число.
Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.
Например, разделим число 1 на .
Чтобы разделить число 1 на , нужно это число 1 умножить на дробь, обратную дроби . А обратная дроби это дробь
Выражение можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца:
Если зададим вопрос «сколько раз половина содержится в этой пицце», то ответом будет 2. Действительно, половина содержится в одной целой пицце два раза
Пример 2. Найти значение выражение
Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь
Допустим, у нас имеются две целые пиццы:
Если зададим вопрос «сколько раз половина содержится в двух пиццах», то ответом будет 4. Действительно, половина содержится в двух пиццах четыре раза:
Деление дробей
Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.
Например, разделим на
Чтобы разделить на , нужно умножить на дробь, обратную дроби . А обратная дроби это дробь
Допустим, имеется половина пиццы:
Если зададим вопрос «сколько раз четверть пиццы содержится в этой половине», то ответом будет 2. Действительно, четверть пиццы содержится в половине пиццы два раза:
Пример 1. Найти значение выражения
Умножаем первую дробь на дробь, обратную второй. Грубо говоря, умножаем первую дробь на перевёрнутую вторую:
Пример 2. Найти значение выражения
Умножаем первую дробь на дробь обратную второй:
Здесь советуем остановиться и потренироваться. Решите несколько примеров, приведенных ниже. Можете использовать материалы сайта, как справочник. Это позволит вам научиться работать с литературой.
Каждая следующая тема будет более сложной, поэтому нужно тренироваться.
Задания для самостоятельного решения:
Задание 1. Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Задание 6. Найдите значение выражения:
Решение:
Задание 7. Найдите значение выражения:
Решение:
Задание 8. Найдите значение выражения:
Решение:
Задание 9. Найдите значение выражения:
Решение:
Задание 10. Найдите значение выражения:
Решение:
Задание 11. Найдите значение выражения:
Решение:
Задание 12. Найдите значение выражения:
Решение:
Задание 13. Найдите значение выражения:
Решение:
Задание 14. Найдите значение выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Возведение в степень: правила, примеры, дробная степень
Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с формулирования базовых определений.
Определение 1
Возведение в степень — это вычисление значения степени некоторого числа.
То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0,5 в пятую степень», это следует понимать как «вычислите значение степени (0,5)5.
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n-ного числа множителей, каждый из которых равен a. Это можно записать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Пример 1
Условие: возведите -2 в степень 4.
Решение
Используя определение выше, запишем: (−2)4=(−2)·(−2)·(−2)·(−2). Далее нам нужно просто выполнить указанные действия и получить 16.
Возьмем пример посложнее.
Пример 2
Вычислите значение 3272
Решение
Данную запись можно переписать в виде 327·327. Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 327·327=237·237=52949=103949
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Пример 3
Выполните возведение в квадрат числа π.
Решение
Для начала округлим его до сотых. Тогда π2≈(3,14)2=9,8596. Если же π≈3.14159, то мы получим более точный результат: π2≈(3,14159)2=9,8695877281.
Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6)3 или преобразовать, если это возможно: 57=1255.
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
a1=a
Это понятно из записи .
От основания степени это не зависит.
Пример 4
Так, (−9)1=−9, а 73, возведенное в первую степень, останется равно 73.
Как возвести число в целую степень
Для удобства разберем отдельно три случая: если показатель степени — целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1. Ранее мы уже поясняли, что 0-я степень a может быть определена для любого действительного числа, не равного 0, и a0=1.
Пример 5
Примеры:
50=1, (-2,56)0=1230=1
00- не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1az, где а — любое число, а z — целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Пример 6
Возведите 2 в степень -3.
Решение
Используя определение выше, запишем: 2-3=123
Подсчитаем знаменатель этой дроби и получим 8: 23=2·2·2=8.
Тогда ответ таков: 2-3=123=18
Пример 7
Возведите 1,43 в степень -2.
Решение
Переформулируем: 1,43-2=1(1,43)2
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
В итоге у нас вышло (1,43)-2=1(1,43)2=12,0449. Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: (1,43)-2=1000020449
Отдельный случай — возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a-1=1a1=1a.
Пример 8
Пример: 3−1=1/3
913-1=13964-1=164 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: amn=amnпри любом положительном a, целом m и натуральном n.
Определение 2
Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n-ной степени.
У нас есть равенство amn=amn, которое, учитывая свойства корней, обычно применяется для решения задач в виде amn=anm. Это значит, что если мы возводим число a в дробную степень m/n, то сначала мы извлекаем корень n-ной степени из а, потом возводим результат в степень с целым показателем m.
Проиллюстрируем на примере.
Пример 9
Вычислите 8-23.
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8-23=8-23
Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8-23=1643=133643=133433=14
Способ 2. Преобразуем основное равенство: 8-23=8-23=83-2
После этого извлечем корень 83-2=233-2=2-2 и результат возведем в квадрат: 2-2=122=14
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Пример 10
Возведите 44,89 в степень 2,5.
Решение
Преобразуем значение показателя в обыкновенную дробь: 44,892,5=44,8952.
А теперь выполняем по порядку все действия, указанные выше: 44,8952=44,895=44,895=44891005=44891005=6721025=67105==1350125107100000=13 501,25107
Ответ: 13 501,25107.
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями — довольно сложная работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0mn можно придать такой смысл: если mn>0, то 0mn=0mn=0; если mn<0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0712=0, 0325=0, 00,024=0, а в целую отрицательную — значения не имеет: 0-43.
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a, то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Пример 11
Вычислите приближенное значение 2 в степени 1,174367….
Решение
Ограничимся десятичным приближением an=1,17. Проведем вычисления с использованием этого числа: 21,17≈2,250116. Если же взять, к примеру, приближение an=1,1743, то ответ будет чуть точнее: 21,174367…≈21,1743≈2,256833.
Числовые и буквенные выражения. Формула
Числовые и буквенные выражения.
Формула
Сложение, вычитание, умножение, деление — арифметические действия (или арифметические операции). Этим арифметическим действиям соответствуют знаки арифметических действий:
+ (читаем «плюс«) — знак операции сложения,
— (читаем «минус«) — знак операции вычитания,
∙ (читаем «умножить«) — знак операции умножения,
: (читаем «разделить«) — знак операции деления.
Запись, состоящая из чисел, связанных между собой знаками арифметических действий, называется числовым выражением. В числовом выражении могут присутствовать также скобки Например, запись 1290 : 2 – (3 + 20 ∙ 15) является числовым выражением.
Результат выполнения действий над числами в числовом выражении называется значением числового выражения. Выполнение этих действий называется вычислением значения числового выражения. Перед записью значения числового выражения ставят знак равенства «=». В таблице 1 приведены примеры числовых выражений и их значений.
Запись, состоящая из чисел и малых букв латинского алфавита, связанных между собой знаками арифметических действий называется буквенным выражением. В этой записи могут присутствовать скобки. Например, запись a + b – 3 ∙ c является буквенным выражением. Вместо букв в буквенное выражение можно подставлять различные числа. При этом значение букв может изменяться, поэтому буквы в буквенном выражении называют еще переменными.
Подставив в буквенное выражение числа вместо букв и вычислив значение получившегося числового выражения, находят значение буквенного выражения при данных значениях букв (при данных значениях переменных). В таблице 2 приведены примеры буквенных выражений.
Буквенное выражение может не иметь значения, если при подстановке значений букв получается числовое выражение, значение которого для натуральных чисел не может быть найдено. Такое числовое выражение называется некорректным для натуральных чисел. Говорят также, что значение такого выражения «не определено» для натуральных чисел, а само выражение «не имеет смысла». Например, буквенное выражение a – b не имеет значения при a = 10 и b = 17. Действительно, для натуральных чисел, уменьшаемое не может быть меньше вычитаемого. Например, имея всего 10 яблок (a = 10), нельзя отдать из них 17 (b = 17)!
В таблице 2 (колонка 2) приведён пример буквенного выражения. По аналогии заполните таблицу полностью.
Для натуральных чисел выражение 10 -17 некорректно (не имеет смысла), т.е. разность 10 -17 не может быть выражена натуральным числом. Другой пример: на ноль делить нельзя, поэтому для любого натурального числа b, частное b : 0 не определено.
Математические законы, свойства, некоторые правила и соотношения часто записывают в буквенном виде (т.е. в виде буквенного выражения). В этих случаях буквенное выражение называют формулой. Например, если стороны семиугольника равны a, b, c, d, e, f, g, то формула (буквенное выражение) для вычисления его периметра p имеет вид:
p = a + b + c + d + e + f + g
При a = 1, b = 2, c = 4, d = 5, e = 5, f = 7, g = 9, периметр семиугольника p = a + b + c + d + e + f + g = 1 + 2 + 4 + 5 +5 + 7 + 9 = 33.
При a = 12, b = 5, c = 20, d = 35, e = 4, f = 40, g = 18, периметр другого семиугольника p = a + b + c + d + e + f + g = 12 + 5 + 20 + 35 + 4 + 40 + 18 = 134.
Блок 1. Словарь
Составьте словарь новых терминов и определений из параграфа. Для этого в пустые клетки впишите слова из списка терминов, приведенного ниже. В таблице (в конце блока) укажите номера терминов в соответствии с номерами рамок. Рекомендуется перед заполнением клеток словаря еще раз внимательно просмотреть параграф.
- Операции: сложение, вычитание, умножение, деление.
2.Знаки «+» (плюс), «-» (минус), «∙» (умножить, «:» (разделить).
3.Запись, состоящая из чисел, которые связанны между собой знаками арифметических действий и в которой могут присутствовать также скобки.
4.Результат выполнения действий над числами в числовом выражении.
5. Знак, стоящий перед значением числового выражения.
6. Запись, состоящая из чисел и малых букв латинского алфавита, связанных между собой знаками арифметических действий (могут присутствовать также скобки).
7. Общее название букв в буквенном выражении.
8. Значение числового выражения, которое получается при подстановке переменных.в буквенное выражение.
9.Числовое выражение, значение которого для натуральных чисел не может быть найдено.
10. Числовое выражение, значение которого для натуральных чисел может быть найдено.
11. Математические законы, свойства, некоторые правила и соотношения, записанные в буквенном виде.
12. Алфавит, малые буквы которого используются для записи буквенных выражений.
Блок 2. Установите соответствие
Установите соответствие между заданием в левой колонке и решением в правой. Ответ запишите в виде: 1а, 2г, 3б…
Блок 3. Фасетный тест. Числовые и буквенные выражения
Фасетные тесты заменяют сборники задач по математике, но выгодно отличаются от них тем, что их можно решать на компьютере, проверять решения и сразу узнавать результат работы. В этом тесте содержится 70 задач. Но решать задачи можно по выбору, для этого есть оценочная таблица, где указаны простые задачи и посложнее. Ниже приведён тест.
- Дан треугольник со сторонами c, d, m, выраженными в см
- Дан четырехугольник со сторонами b, c, d, m, выраженными в м
- Скорость автомобиля в км/ч равна b, время движения в часах равно d
- Расстояние, которое преодолел турист за m часов, составляет с км
- Расстояние, которое преодолел турист, двигаясь со скоростью m км/ч, составляет b км
- Сумма двух чисел больше второго числа на 15
- Разность меньше уменьшаемого на 7
- Пассажирский лайнер имеет две палубы с одинаковым количеством пассажирских мест. В каждом из рядов палубы m мест, рядов на палубе на n больше, чем мест в ряду
- Пете m лет Маше n лет, а Кате на k лет меньше, чем Пете и Маше вместе
- m = 8, n = 10, k = 5
- m = 6, n = 8, k = 15
- t = 121, x = 1458
ТО:
- Значение данного выражения
- Буквенное выражение для периметра имеет вид
- Периметр, выраженный в сантиметрах
- Формула пути s, пройденного автомобилем
- Формула скорости v, движения туриста
- Формула времени t, движения туриста
- Путь, пройденный автомобилем в километрах
- Скорость туриста в километрах в час
- Время движения туриста в часах
- Первое число равно…
- Вычитаемое равно….
- Выражение для наибольшего количества пассажиров, которое может перевезти лайнер за k рейсов
- Наибольшее количество пассажиров, которое может перевезти лайнер за k рейсов
- Буквенное выражение для возраста Кати
- Возраст Кати
- Координата точки В, если координата точки С равна t
- Координата точки D, если координата точки С равна t
- Координата точки А, если координата точки С равна t
- Длина отрезка BD на числовом луче
- Длина отрезка CА на числовом луче
- Длина отрезка DА на числовом луче
Ответы (равно, имеет вид, не определено):
а)1; б) s=b ∙d; в) 9; г) 40; д) b + c + d + m; е) 7; ж) выражение не имеет смысла (некорректно) для натуральных чисел; з) 2 ∙ m (m + n) ∙ k; и) (m + n) – k; к) 6; л) 15; м) 3760; н) t – 3; о) фигура не может быть треугольником; п) 22; р) t – 3 ∙ 7; с) 0; т) 32; у) 59600; ф) 6019; х) 2880; ц) 10378; ч)1440; ш) на ноль делить нельзя; щ) 13; ы) 1800; э) 496; ю) 2; я) 12; аа) 14; бб) 5; вв) 35; дд) 79200; ее) 1900; жж) 118; зз) 18; ии) 12800; кк) 98; лл) 1458; мм) v = c : m; нн) 100; оо) 19900; пп) t = b : m; рр) 2520; сс) c + d + m; тт) x; уу) 1579; фф) t + 2; хх) 10206; цц) 135; чч) t + 2 ∙ 7; шш) 7 ∙ x; щщ) x – 2; ыы) 7 ∙ x – 2 ∙ 7; ээ) t + x ∙ 7; юю) 10192; яя) t + x; ааа) 123; ббб) 1456; ввв) 10327.
ПОКАЗАТЕЛИ ТЕСТА. Число задач 70, время выполнения 2 – 3 часа, сумма баллов: 1 ∙ 22 + 2 ∙ 24 + 3 ∙ 24 = 142. Для фасетного теста можно использовать следующую шкалу оценок.
Блок 4. Давайте поиграем
Блок 5. Обучающая игра «Уроки кота Леопольда»
Для учителя приводим ответы к блокам параграфа 6
Ответы к игре «Уроки Леопольда»
Западня 1 : 1/2, 1/3, 2/3, 7/8. Западня 2. 12, 2, 13 5. Западня 3. 6
Западня 4. 15. Западня 5. 396
Блок 1. Словарь
Блок 2. Установите соответствие.
Вариант 1: 1и, 2з, 3е, 4б, 5м, 6л, 7а, 8ж, 9в, 10д, 11г, 12к, 13т, 14н, 15ф, 16о, 17у, 18с, 19р, 20п
Вариант 2: 1д, 2е, 3к, 4а, 5г, 6з, 7и, 8б, 9ж, 10в
Блок 3. Фасетный тест. Числовые и буквенные выражения (ответы под заданиями)
Ответы к игре «Сокровища»
Деревянный – 10250. Оловянный – 21640. Медный – 50400. Серебряный – 191000. Золотой – 289800.
Калькулятор умножения
Добро пожаловать в калькулятор умножения Omni , где мы изучим одну из четырех основных арифметических операций: умножение . Короче говоря, мы используем его всякий раз, когда хотим добавить одно и то же число несколько раз. Например, 16 умножить на 7 (записано 16 * 7 ) — это то же самое, что сложить 16 семь раз или, что то же самое, добавить 7 шестнадцать раз. Удобно, что наш инструмент работает также как калькулятор умножения десятичных знаков .Более того, даже если у вас есть более двух чисел для умножения, вы все равно можете найти их произведение с помощью этого калькулятора.
Примечание : Если вы хотите увидеть пошаговые решения для умножения больших чисел, ознакомьтесь с калькулятором длинного умножения Omni.
Давайте не терять ни секунды и посмотрим , как умножать числа !
Произведение или умножение: как умножать числа
Произведение и умножение — это одно и то же: они являются результатом умножения чисел (или других объектов, если на то пошло).К счастью, процесс очень прост: он сводится к добавлению значения подходящее количество раз. Например, 24 умноженное на 5 означает, что мы добавляем 24 пять раз, то есть
24 * 5 = 24 + 24 + 24 + 24 + 24 = 120 .
Аналогично, 12 раз 20 преобразуется в сложение 12 двадцать раз:
12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 + 12 = 240 .
Однако обратите внимание, что мы всегда можем инвертировать процесс нахождения произведения с умножением. Другими словами, 24 , умноженное на 5 , также может означать двадцать четыре раза сложить 5 :
5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 120 ,
, и мы можем получить 12 умноженное на 20 , добавив 20 двенадцать раз:
20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 = 240 .
Мы всегда выбираем, как умножать числа, так как результат будет одинаковым в любом случае . С математической точки зрения это означает, что произведение или умножение равно , а коммутативная операция — . Обратите внимание, что то же самое верно и для сложения. С другой стороны, это не относится, скажем, к вычитанию.
Кроме того, наш калькулятор умножения работает только с числами , но математики придумали, как умножать другие объекты. Ниже мы перечислим еще несколько калькуляторов умножения от Omni.
Однако не всегда имеет дело с целыми числами , такими как 2 , 18 или 2020 . Мы узнали, как их умножить и что, скажем, 16 на 7 , но как найти произведение десятичных знаков? Например, сколько 0,2 умножить на 1,25 ? Наш калькулятор умножения также является калькулятором умножения десятичных знаков ?
Да, конечно!
Умножение десятичных знаков
По сути, десятичных знаков — это дроби .Следовательно, один из способов умножения десятичных дробей — преобразовать их в обычные дроби, а затем использовать основное правило умножения числителя на числитель на знаменатель на знаменатель . Например,
0,2 * 1,25 = (2/10) * (125/100) = (2 * 125) / (10 * 100) = 250/1000 = 0,25 .
Конечно, мы могли бы также найти более простые дроби, эквивалентные двум, указанным перед умножением. В этом случае мы могли бы сказать, что 0,2 = 1/5 и 1,25 = 5/4 , поэтому
0.2 * 1,25 = (1/5) * (5/4) = (1 * 5) / (5 * 4) = 5/20 = 1/4 .
Оба ответа верны ; как умножать десятичные дроби — это всегда ваш выбор. Однако, помимо двух упомянутых, есть еще .
При умножении десятичных знаков, скажем, 0,2 и 1,25 , мы можем начать с , забывая точки . Это означает, что для нахождения 0,2 * 1,25 мы начинаем с поиска 2 * 125 , что составляет 250 . Затем мы подсчитываем, сколько цифр справа от точек у нас было в общей сложности в числах, с которых мы начали (в данном случае это три: одна из 0.2 и два в 1,25 ). Затем мы записываем точку, которая представляет собой много цифр справа от в том, что мы получили. Для нас это означает размещение точки слева от 2 , что дает 0,250 = 0,25 (мы пишем 0 , если у нас нет числа перед точкой).
В общем, мы видели , как умножать десятичные дроби тремя способами . Честно говоря, первые два были почти одинаковыми; просто промежуточные шаги были в другом порядке.Тем не менее, на этом мы завершаем часть о том, как умножать без калькулятора. Теперь подробно опишем, как это сделать с одним, а точнее с калькулятором умножения Omni .
Пример: использование калькулятора умножения
Давайте найдем 2020 умножить на 12 с помощью калькулятора умножения. Вверху нашего инструмента мы видим формулу:
результат = a₁ * a₂ .
Это означает, что для расчета 2020 * 12 нам необходимо ввести:
a₁ = 2020 и a₂ = 12 .
В тот момент, когда мы даем второе число , калькулятор умножения выдаст ответ в поле Result .
результат = 2020 * 12 = 24240
Однако предположим, что вы хотите еще умножить результат на 1,3 (помните, что наш инструмент также работает как калькулятор умножения десятичных знаков).
Мы могли бы просто очистить поля и записать ответ сверху в один из факторов, т.е., введите a₁ = 24240 и a₂ = 1,3 . В качестве альтернативы, мы можем просто выбрать множества чисел под Умножить … , что позволит нам найти произведение умножения на большее количество чисел . Если мы это сделаем, мы получим возможность ввести a₁ , a₂ , a и так далее до a (обратите внимание, что изначально есть только a₁ и a more , но больше переменные появляются, когда вы начинаете заполнять поля).Затем достаточно ввести:
a₁ = 2020 , a₂ = 12 , a₃ = 1,3 ,
и зачитайте ответ снизу:
результат = 2020 * 12 * 1,3 = 31512 .
Что ж, этот калькулятор умножения действительно экономит много времени. Можете ли вы представить себе , написавшее две тысячи двадцать умноженное на число 12 , как мы это сделали в первом разделе? Мы, например, этого не делаем.
Умножение дробей и смешанных чисел
Умножение дробей
Если у вашей подруги четверть пирога, а она дает вам половину, сколько пирога у вас есть? Или, другими словами, какая половина от четверти? Или, чтобы выразить это в математической записи:
1 /2 x 1 /4 =?
Чтобы получить ответ, умножьте числители (верхние части) и знаменатели (нижние части) по отдельности.
В этом случае сначала мы умножаем числители:
1 x 1 = 1
Затем мы умножаем знаменатели:
2 x 4 = 8
В ответе числитель равен 1, а знаменатель — 8. Другими словами:
1 /2 x 1 /4 = 1 x 1 /2 x 4 = 1 /8
У вас одна восьмая часть пирога.
Другой пример
Попробуем другой.
2 /9 x 3 /4 =?
Сначала умножаем числители:
2 x 3 = 6
Затем умножаем знаменатели:
9 x 4 = 36
В ответе числитель 6 и знаменатель 36.Другими словами:
2 /9 x 3 /4 = 2 x 3 /9 x 4 = 6 /36
Это можно дополнительно уменьшить:
6 6 /36 6 = 1 /6
(См. Уменьшение дробей.)
Умножение смешанных чисел
Чтобы умножить два смешанных числа или смешанное число и дробь, сначала преобразуйте каждое смешанное число в дробь. Затем умножьте дроби.
Что такое 2 1 /3 x 1 /4 =?
Сначала запишем 2 1 /3 в виде дроби:
2 1 /3 = 7 /3
Затем умножаем дроби.
7 /3 x 1 /4 =?
Сначала умножаем числители:
7 x 1 = 7
Затем умножаем знаменатели:
3 x 4 = 12
В ответе числитель 7 и знаменатель 12. Другими словами:
2 1 /3 x 1 /4 = 7 x 1 /3 x 4 = 7 /12
Смешанные числа и неправильные дроби Обратные дроби
.com / ipa / 0/9/3 / 3/4/5 / A0933458.html
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами.Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т.е. для пяти сотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.
Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть 1 2/3 (с тем же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, т. Е. 1/2: 3 .
Десятичные числа (десятичные числа) вводятся с десятичной точкой . , и они автоматически переводятся в дроби — i.е. 1,45 .
Двоеточие : и косая черта / являются символом деления. Может использоваться для деления смешанных чисел 1 2/3: 4 3/8 или может использоваться для записи сложных дробей, например, 1/2: 1/3 . 1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное в дробное: 0.625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок или порядок, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Дроби в задачах со словами:
следующие математические задачи »
Умножение дробей — методы и примеры
Как умножать дроби?
В этой статье обсуждаются все шаги, которые необходимо знать при умножении дробей, включая умножение правильных и неправильных дробей, смешанных дробей и умножение дроби на целое число.Вот шаги для умножения дробей:
- Умножьте числители вместе и поместите произведение поверх получившейся дроби
- Умножьте знаменатели вместе и запишите результат внизу новой дроби
- Уменьшите или упростите дробь. результат, если возможно
Пример 1:
1/2 × 2/5
Шаг 1. Умножьте числители:
1/2 × 2/5 = 1 × 2 = 2
Шаг 2 .Умножьте знаменатели:
2 x 5 = 10
Шаг 3. Упростите дробь:
2/10 = 1/5
Пример 2:
1/3 × 9/16
Шаг 1. Умножьте числители:
1/3 × 9/16 = 1 × 9 = 9
Шаг 2. Умножьте знаменатели:
3 × 16 = 48
Шаг 3. Упростите дробь:
9 / 48 = 3/16
Пример 3:
Умножение: 4/5 x 7/6
Сначала умножьте числители, чтобы получить: 4 × 7 = 28.
Затем умножьте знаменатели, чтобы получить: 5 × 9 = 45.
Результат = 28/45
Поскольку нет общих делителей 28 и 45, эта дробь уже находится в самом низком значении. Окончательный ответ — 28/45.
Пример 4:
Умножение: 9/4 x 14/15
Вы можете выполнить все операции в одной строке математики. Не забудьте поставить числитель вверху, а знаменатели — внизу.
9/4 x 14/15 = (9 x 14) / (4 x 15) = 126/60
Умножение более чем на 2 дроби
Отмена — отличный способ умножения с более чем двумя множителями.
Пример 5:
Умножение (1/2) × (2/3) × (3/4) × (4/5).
Начните с исключения общих факторов.
(1/2) × (2/3) × (3/4) × (4/5).
= 1/5
Как умножить дроби на целые числа?
Дроби можно умножать на целые числа точно так же, как умножаются другие дроби.Самая важная процедура состоит в том, чтобы переписать целое число как дробь, введя знаменатель 1. Затем можно применить те же методы умножения дроби.
Целое число N можно преобразовать в дробь со знаменателем 1 следующим образом:
N = N / 1
Пример 6:
Умножение: 3/5 × 60.
3/5 × 60 = 3/5 x 60/1
Умножьте числители:
3 x 60 = 180
Умножьте знаменатели:
1 x 5 = 5
Результат 180/5, Упростите ответ до минимально возможного термины.
180/5 = 36.
Как умножить смешанные дроби?
Смешанная фракция — это фракция, состоящая из целой и дробной части. Например, 7½ — это смешанная дробь, состоящая из целого числа 7 и дробной части ½.
Ниже приведены ключевые шаги при умножении смешанных дробей или смешанной дроби на правильную или неправильную дробь:
- Первым шагом является преобразование всех дробей в неправильную дробь.
- Умножьте числители и поместите произведение вверху.
- Умножьте знаменатели и поместите произведение внизу.
- По возможности упростите результат.
Пример 7:
Умножение: 2 5 / 6 x 3 1 / 4
Начните с преобразования каждой смешанной дроби в эквивалентную неправильную дробь.
2 5 / 6 x 3 1 / 4 = 17/6 x 13/4 = 221/24
Окончательный ответ можно упростить или преобразовать обратно в смешанное число путем деления.Преобразование обратно в смешанную дробь похоже на деление с остатком. Частное становится целой частью, а остаток становится новым числителем.
Как умножить отрицательные дроби?
Те же правила умножения отрицательных чисел применяются при умножении дробей:
- + x + = +
- + x — = —
- — x — = +
Пример 8:
Умножение : 2/3 × (–3/4)
2/3 × (–3/4) = –6/12 = –1/2.
Пример 9:
Умножение: (–4/3) × (–7/5)
(–4/3) × (–7/5) = 28/15.
Практические вопросы
Умножьте следующие дроби:
- 1/3 × 4/5
- –3/7 × 2/11
- 9/10 × 35/36
- 3/8 × 10
- 5 / 3 × 7/2 × 6/7
- 6 × 4¾
- –11/3 × (–3/11)
- Мой грузовик проезжает 10 2 / 3 миль на галлон. Предположим, что бак пуст и я заправляю его 5 1 / 2 галлонов, как далеко я могу уехать с грузовиком?
- Рецепт требует 1/2 столовой ложки соли.Сколько нужно соли, чтобы приготовить 20 подобных рецептов?
Предыдущий урок | Главная страница | Следующий урок
Дроби: умножение и деление дробей
Урок 4: Умножение и деление дробей
/ ru / fractions / сложение-и-вычитание-фракции / content /
Умножение дробей
Дробь — это часть из целого . На последнем уроке вы узнали, как складывать и вычитать дроби.Но это не единственная математика, которую вы можете выполнять с дробями. Бывают случаи, когда будет полезно умножить и дроби.
Щелкните слайд-шоу, чтобы узнать, как написать задачу умножения с дробями.
Попробуй!
Попробуйте настроить задачу умножения ниже. Пока не беспокойтесь о ее решении!
Рецепт требует 2/3 стакана молока. Вы хотите разрезать рецепт пополам.
Примечание : Хотя наш пример говорит, что правильный ответ — 2/3 x 1/2, помните, что порядок умножения не имеет значения.1/2 x 2/3 тоже будет правильным.
Решение задач умножения с дробями
Теперь, когда мы знаем, как ставить задачи умножения с дробями, давайте попрактикуемся в решении некоторых. Если вы чувствуете себя комфортно, умножая целые числа, вы готовы умножать дроби.
Щелкните слайд-шоу, чтобы узнать, как умножить две дроби.
Попробуй!
Попробуйте решить приведенные ниже задачи умножения.
Умножение дроби на целое число
Умножение дроби и целого числа аналогично умножению двух дробей.Есть всего один дополнительный шаг: прежде чем вы сможете умножить, вам нужно превратить целое число в дробь. Это слайд-шоу покажет вам, как это сделать.
Щелкните слайд-шоу, чтобы узнать, как умножить дробь на целое число.
Умножим 2 раза на 1/3. Помните, это просто еще один способ спросить: «Что такое 1/3 из 2?»
Прежде чем мы начнем, мы должны убедиться, что эти числа готовы к умножению.
Мы не можем умножить целое число на дробь, поэтому нам придется записать 2 как дробь.
Как вы узнали из «Введение в дроби», мы также можем записать 2 как 2/1, потому что 2 можно дважды разделить на 1.
Теперь мы готовы к умножению!
Сначала мы умножим числителей: 2 и 1.
2 умножить на 1 равно 2. Мы выровняем 2 вместе с числителями.
Затем мы умножим знаменателя: 1 и 3.
1 умножим на 3 равно 3.Совместим тройку со знаменателями.
Таким образом, 2/1 умноженное на 1/3 равно 2/3. Мы также можем сказать, что 1/3 от 2 — это 2/3.
Давайте попробуем другой пример: 4 раза по 1/5.
Прежде чем мы начнем, нам нужно будет записать 4 в виде дроби.
Перепишем 4 как 4/1. Теперь мы готовы к размножению.
Сначала мы умножим числители: 4 и 1.
4 умножить на 1 равно 4, поэтому числитель нашего ответа будет 4.
Затем мы умножим знаменатели: 1 и 5.
1 умножить на 5 равно 5, поэтому 5 является знаменателем нашего ответа.
Итак, 4/1 умноженное на 1/5 равно 4/5.
Попробуй!
Попробуйте решить приведенные ниже задачи умножения.
Разделение на дроби
За последние несколько страниц вы узнали, как умножить дроби. Вы, наверное, догадались, что можно разделить и на дроби.Вы делите дроби, чтобы увидеть, сколько частей чего-то приходится на чего-то другого. Например, если вы хотите узнать, сколько четвертей дюйма в четырех дюймах, вы можете разделить 4 на 1/4.
Попробуем другой пример. Представьте, что рецепт требует 3 стакана муки, но ваш мерный стакан вмещает только 1/3, или 1/3 стакана. Сколько третей стакана нужно добавить?
Нам нужно выяснить, сколько третей чашки содержится в трех чашках.Другими словами, нам нужно разделить три на одну треть.
Задачу запишем так:
3 ÷ 1/3
Попробуй!
Попробуйте поставить эти задачи деления на дроби. Пока не беспокойтесь о их решении!
Рецепт требует 3/4 стакана воды. У вас есть только 1/8 мерного стакана.
Решение задач деления на дроби
Теперь, когда мы знаем, как писать задачи деления, давайте попрактикуемся в решении нескольких. Деление дробей во многом похоже на умножение.Требуется всего лишь один дополнительный шаг. Если вы умеете умножать дроби, вы можете и их делить!
Щелкните слайд-шоу, чтобы узнать, как разделить целое число на дробь.
Разделим 3 на 1/3. Помните, это просто еще один способ спросить: «Сколько третей в 3?»
В нашем уроке о делении вы научились писать знак деления следующим образом (/).
При делении дробей полезно использовать другой символ для деления (÷), чтобы не ошибочно принять его за дробь.
Как и в случае с умножением, мы начнем с поиска любых целых чисел в нашей задаче. Там один: 3.
Помните, 3 — это то же самое, что 3/1.
Прежде чем мы сможем разделить, нам нужно сделать еще одно изменение.
Мы заменим числителем и знаменателем дроби, которую мы делим на: 1/3 в этом примере.
Таким образом, 1/3 становится 3/1.
Это называется нахождением , обратного , или мультипликативного , обратного , дроби.
Поскольку мы меняем исходную дробь, мы также изменим знак деления (÷) на умножение знак (x).
Это потому, что умножение является обратным делению.
Теперь мы можем рассматривать это как обычную задачу умножения.
Сначала мы умножим числители: 3 и 3.
3 раза 3 равно 9, поэтому мы напишем это рядом с числителями.
Затем мы умножим знаменатели: 1 и 1.
1 умножить на 1 равно 1, поэтому мы запишем 1 рядом со знаменателем.
Как видите, 3/1 x 1/3 = 9/1.
Помните, любая дробь больше 1 также может быть выражена как целое число .Итак, 9/1 = 9.
3 ÷ 1/3 = 9. Другими словами, 9 третей в 3.
Давайте попробуем другой пример: 5 делится на 4/7.
Как всегда, перепишем любые целые числа, так что 5 станет 5/1.
Далее мы найдем , обратное от 4/7. Это дробь, на которую мы делим.
Для этого мы заменим числителем и знаменателем , так что 4/7 станет 7/4.
Затем мы изменим знак деления (÷) на умножение знак (x).
Теперь мы можем умножать как обычно. Сначала мы умножим числители: 5 и 7.
5 умножим на 7 равно 35, так что запишем это рядом с числителями.
Затем мы умножим знаменатели: 1 и 4.
1 умножить на 4 равно 4, поэтому мы запишем это рядом со знаменателями.
Итак, 5/1 x 4/7 = 35/4.
Как вы узнали ранее, мы можем преобразовать нашу неправильную дробь в смешанное число , чтобы наш ответ было легче читать.
35/4 = 8 3/4. Итак, 5 ÷ 4/7 = 8 3/4.
Попробуй!
Попробуйте решить эти проблемы с разделением. Не беспокойтесь пока о сокращении ответа .
Деление на две дроби
Мы только что научились делить целое число на дробь .Вы можете использовать тот же метод, чтобы разделить на две дроби .
Щелкните слайд-шоу, чтобы узнать, как разделить на две дроби.
Попробуем задачу с двумя дробями: 2/3 ÷ 3/4. Здесь мы хотим знать, сколько 3/4 в 2/3.
Сначала мы найдем , обратное дроби, на которую мы делим: 3/4.
Для этого мы заменим числителем и знаменателем .Таким образом, 3/4 становится 4/3.
Затем мы изменим знак деления (÷) на умножение знак (x).
Теперь умножим числители. 2 x 4 = 8, поэтому мы напишем 8 рядом с верхними числами.
Затем мы умножим знаменатели. 3 x 3 = 9, поэтому мы напишем 9 рядом с нижними числами.
Итак, 2/3 x 4/3 = 8/9.
Мы также можем записать это как 2/3 ÷ 3/4 = 8/9.
Давайте попробуем другой пример: 4/7 разделить на 2/9.
Целых чисел нет, поэтому мы найдем , обратное дроби, на которую мы делим. Это 2/9.
Для этого мы заменим числителем и знаменателем . Таким образом, 2/9 становится 9/2.
Теперь мы изменим знак деления (÷) на умножение Знак (x) и умножим как обычно.
Сначала умножим числители. 4 x 9 = 36.
Затем мы умножим знаменатели. 7 x 2 = 14.
Итак, 4/7 x 9/2 = 36/14. Как и раньше, вы можете преобразовать эту неправильную дробь в смешанное число.
Итак, 4/7 ÷ 2/9 = 2 8/14.
Попробуй!
Попробуйте решить эти проблемы с разделением. Не беспокойтесь пока о сокращении ответа .
Умножение и деление смешанных чисел
Как бы вы решили такую проблему?
Как вы узнали на предыдущем уроке, всякий раз, когда вы решаете задачу с смешанным числом , вам нужно сначала преобразовать его в неправильную дробь .Затем вы можете как обычно умножать или делить.
Использование отмены для упрощения задач
Иногда приходится решать такие задачи:
Обе эти дроби включают больших чисел . Эти дроби можно умножать так же, как и любые другие дроби. Однако такие большие числа трудно понять. Можете ли вы представить себе 21/50 или двадцать одна пятидесятая , ?
21/50 x 25/14 = 525/700
Даже ответ кажется сложным.Это 525/700, или пятьсот двадцать пять семисотых . Какой полный рот!
Если вам не нравится работать с большими числами, вы можете упростить такую задачу, используя метод под названием отмена . Когда вы отменяете дробей в задаче, вы уменьшаете их обеих одновременно.
Поначалу отмена может показаться сложной, но мы покажем вам, как это сделать шаг за шагом. Давайте еще раз посмотрим на только что рассмотренный пример.
Шаг 1
Сначала посмотрите на числитель первой дроби и знаменатель второй дроби. Мы хотим посмотреть, можно ли их разделить на на одно и то же число.
В нашем примере 21 и 14 можно разделить на 7.
Шаг 2
Затем мы разделим 21 и 14 на 7. Сначала разделим наше верхнее число слева: 21.
21 ÷ 7 = 3
Затем разделим нижнее число справа: 14.
14 ÷ 7 = 2
Мы напишем ответы на каждую задачу рядом с числами, которые мы разделили. Поскольку 21 ÷ 7 равно 3, запишем 3 вместо 21. 14 ÷ 7 равно 2, поэтому напишем 2 вместо 14. Мы можем зачеркнуть или отменить , числа, с которых мы начали.
Наша задача теперь выглядит намного проще, не так ли?
Шаг 3
Давайте посмотрим на другие числа дроби. На этот раз мы рассмотрим знаменатель первой дроби и числитель второй.Можно ли их разделить на на одно и то же число?
Обратите внимание, что их можно разделить на 25! Вы также могли заметить, что оба числа можно разделить на 5. Мы также можем использовать 5 , но обычно, когда вы отменяете, вы хотите найти наибольшее число , на которое можно разделить оба числа. Таким образом, вам не придется снова уменьшать дробь в конце.
Шаг 4
Затем мы отменим , как мы это делали на шаге 2.
Мы разделим наше нижнее число слева: 50.
50 ÷ 25 = 2
Затем разделим верхнее число справа: 25.
25 ÷ 25 = 1
Мы напишем ответы на каждую задачу рядом с числами, которые мы разделили.
Шаг 5
Теперь, когда мы отменили исходные дроби, мы можем умножить наши новые дроби, как обычно. Как всегда, сначала умножаем числители:
3 х 1 = 3
Затем умножьте знаменатели:
2 х 2 = 4
Итак, 3/2 x 1/2 = 3/4, или три четверти .
Шаг 6
Наконец, давайте еще раз проверим нашу работу. 525/700 был бы нашим ответом, если бы мы решили проблему без отмены. Если разделить 525 и 700 на 175, мы увидим, что 525/700 равно 3/4.
Можно также сказать, что мы уменьшаем 525/700 до 3/4. Помните, что отмена — это еще один способ уменьшить дроби перед решением проблемы. Вы получите один и тот же ответ, независимо от того, когда вы их уменьшите.
/ ru / дроби / преобразование-десятичные-дроби-и-дроби / содержание /
Умножение дробей на целые числа
Этот урок научит вас умножать дроби на целые числа на основе визуальных моделей.Мы просто находим общее количество частей путем умножения, что означает, что вы умножаете целое число и верхнее число (числитель) дроби. В уроке также есть много задач со словами.
В видео ниже я учу умножать дроби на целые числа, что является довольно простой концепцией. Вам просто нужно помнить, что 4 x (2/3) не рассчитывается как (4 x 2) / (4 x 3). В визуальной модели вы можете раскрасить две трети, четыре раза, чтобы получить ответ. Я также показываю интересную связь между (1/3) x 5 или одной третью пяти пирогов и 5 x (1/3), или пятью копиями 1/3.
Сколько пятых в
Наконец, мы даем ответ в виде смешанного числа : |
|
1.Неоднократно раскрашивайте детали, чтобы решить
умножения. Ответьте смешанным числом .
|
| ||||||
|
|
2. Заполнить.
а.
| г.
| г.
|
Решите, например, рисованием.
3. Высокие стаканы Эрики вмещают 3/8 литра каждый.
Сколько воды ей нужно налить
четверо из них?
| 4. Марлен хочет утроить этот рецепт (сделать его трижды). Сколько каждого ингредиента ей понадобится? |
|
| Чтобы умножить целое число на дробь, найдите общее количество «шт» (умножением). Это означает, что вы умножаете целое число на верхнее число. (числитель) фракции. | |||||||||||||
| |||||||||||||
Пример 2. Умножение можно производить в любом порядке.
|
5. Решить. Дайте свой ответ в минимальных выражениях
(упрощенно) и как смешанное число.Изучите пример.
|
| ||||||||||||
|
| ||||||||||||
|
| ||||||||||||
|
| ||||||||||||
|
|
6.Уильям спросил 20 пятиклассников, сколько времени
они потратили на работу по дому / работу по дому накануне. Затем он
округлил ответы до ближайшей 1/8 часа. В
линейный график показывает его результаты. Каждая x-отметка
соответствует одному пятикласснику.
а. Исключите трех студентов, которые сделали меньше всего
работа по дому и трое, которые сделали больше всего, и введите:
Большинство студентов использовали между
___________ и __________ часов для работы по дому и по дому.
г. Среднее значение для этих данных составляет 7/8 часов. Использовать это
подсчитать, сколько часов
эти 20 пятые
грейдеры, используемые для работы по дому в целом.
| НАПОМИНАНИЕ Дробь из число означает , что дробь ВРЕМЯ |
| |||||||||
Теперь вы уже научились находить
Оба метода по сути одинаковы: вы делите на 10 и умножаете на | ||||||||||
7. Найдите следующие величины.
а. 2/5 из 35 фунтов
г. 4/9 из 180 км
8. Папа строит полку длиной 4 метра. Он хочет использовать
2/5 из них для
садовые принадлежности и остальное для инструментов.
Какова длина этих двух частей?
полка?
( Подсказка: может помочь использование сантиметров.)
9. а. Джанет и Сэнди заработали 81 доллар за работу во дворе. Они разделили
денег поровну, так что Джанет получила 2/3, а Сэнди
получил
отдых. Сколько денег получила каждая девушка?
г. Что
происходит, если вместо этого они заработали 80 долларов?
10.
Энди нарисовал на бумаге прямоугольник размером 5 на 4 дюйма. Затем он нарисовал
второй прямоугольник, который был на 3/4 длины и ширины первого.
один.
а. Какой длины и ширины была секунда Энди
прямоугольник?
г. Нарисуйте оба прямоугольника (на отдельной бумаге).
| Эпилог: Есть кое-что интересное в умножении «дроби на целое». номер » или умножение «целого числа на дробь». Давайте сравним. | ||||||||||
|
, что дает 3 целых пирога. | |||||||||
выполняется в любом порядке. Но они означают разные вещи | ||||||||||
11. Заполните недостающие части.
| а. 2-я пятая часть 10 | 10 экз. Из 2/5 | |||||||||
, что равно . |
, что равно . |
| г. А ______________ часть 5 | 5 экземпляров 1/3 | |||||||||
, что равно . |
, что равно . |
| г. ____________________ из 7 | 7 экз. _______ | |||||||||
, что равно . |
, что равно . |
Здесь вы найдете бесплатные распечатанные рабочие листы для умножения дробей на целые числа.
Этот урок взят из книги Марии Миллер Math Mammoth Fractions 2 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
Сложение, вычитание, деление и умножение дробей
Руководство по эксплуатации
- Введите дроби в калькулятор выше.
- Выберите математическую операцию, которую вы хотите выполнить (сложение, вычитание, умножение, деление), используя серый раскрывающийся список выбора между двумя дробями.
- Результаты будут обновляться автоматически при изменении любого значения в калькуляторе.
- Флажок под калькулятором позволяет вам выбирать между уменьшением дроби до эквивалента наименьшего общего знаменателя (если установлен) или отказом от уменьшения (если не отмечен).
Как вычислить дроби вручную
Как складывать дроби
- Найдите наименьший общий знаменатель, умножив каждый знаменатель на другой.
- Умножьте каждый числитель на те же числа, на которые были умножены знаменатели.
- Сложите числители.
- Уменьшить результат до наиболее упрощенного числа.
Как вычесть дроби
- Найдите наименьший общий знаменатель, умножив каждый знаменатель на другой.
- Умножьте каждый числитель на те же числа, на которые были умножены знаменатели.
- Складываем второй числитель с первого.
- Уменьшить результат до наиболее упрощенного числа.
Как умножать дроби
- Умножьте числа сверху вместе.
- Умножьте числа внизу вместе.
- Уменьшить результат до наиболее упрощенного числа.
Как разделить дроби
- Переверните вторую дробь вверх дном, чтобы получить обратное число.
- Умножьте дроби вместе (как в разделе умножения выше).
- Уменьшить результат до наиболее упрощенного числа.
Дроби: история, актуальность и популярное использование
— Руководство Автор: Корин Б.Арены , опубликовано 22 октября 2019 г.
Практически каждый день мы имеем дело с дробями. Подумай об этом. Независимо от того, получаете ли вы четвертинки для разнообразия, покупаете одежду со скидкой 75% или готовите с половиной стакана масла, вы используете дроби.
В этом разделе мы поговорим о происхождении дробей, их важности при передаче информации и золотом сечении.
Что такое дроби?
Дроби
представляют части целого числа или любое количество равных частей.Он функционирует
чтобы описать, как части соотносятся с целым числом.
Для иллюстрации представьте целое число как торт. Если вы разрежете торт на 4 равные части, один кусок будет частью этого торта. В данном случае это 1/4 часть всего торта.
- 1 представляет один фрагмент или часть целого числа, которое называется числителем .
- 4 представляет, сколько всего частей содержится в целом числе, которое называется знаменателем .
Краткая история дробей
Слово Происхождение: Термин дробь происходит от латинского
слово fractio
что означает «сломать». В раннем английском языке это означает «сломанный кусок или
фрагмент ». Английское слово« разрушение »также
имеет то же происхождение слова.
Концепция дробей существует уже более 4000 лет. Но у разных цивилизаций есть свой способ стандартизации дробей для универсального использования.
Египтяне
Согласно Math Through the Ages : A Gentle History for Teachers and Others, египтяне были одними из первых, кто придумал форму дроби еще в 1800 г.C. Их концепция в основном ограничивалась частями, иначе известными как единичные дроби. Дроби единиц используют 1 в качестве числителя.
Египетские математики создали систему с основанием 10.
идея, которая похожа на системы счисления, которые мы используем сегодня. Цифра
иероглифы представляли их числа, что означает символы, соответствующие
определенное значение.
Поскольку числитель всегда равен 1, они должны были указать только знаменатель. Египтяне отметили знаменатель овалом или точкой над значением.Вот несколько примеров из книги Math Through the Ages :
Части были выражены как суммы долей единиц. Однако система не позволяла повторять дроби единиц в этой последовательности, что затрудняло выполнение расчетов. Чтобы решить эту проблему, египтяне создали обширные списки таблиц, в которых указаны двойные значения различных частей.
Вавилоняне
Другая цивилизация, создавшая сложную систему для
По словам преподавателя математики и автора Лиз Памфри, фракции принадлежали вавилонянам.
Вавилоняне организовали фракции в группы по 60 человек (основание 60). Сегодня мы обычно группируем числа в группы по 10. Но для вычислений, таких как углы и минуты для времени, мы также используем основание 60. Система сгруппировала дроби по 10 и использовала два символа, один для единицы, а другой для 10.
Ниже приведены символы, представляющие вавилонскую систему счисления от 1 до 20:
.
Однако у них не было символа нуля (который они позже добавили около 311 B.C.) или знак, который функционирует как десятичная точка для обозначения дробей целого числа. Это затрудняло интерпретацию чисел.
Например, цифры ниже читаются как 12 и 15.
По словам Памфри, символы также могут читаться как разные
значения:
| x60 | Квартир | Шестидесятых | Номер |
|---|---|---|---|
| 12 | 15 | ||
| 12 | 15 | 720 + 15 |
- 12 и 15 как отдельные номера
- 15/12
- 12 15/60
- 720 + 15
Как видите, отсутствие индикатора дроби делает его
трудно отделить целые числа от дробей.Скорее всего, они полагались на контекст, чтобы
разобраться в числовых значениях.
Как египетская, так и вавилонская системы были переданы позже людям в Греции, а затем и к средиземноморской цивилизации.
Греки
В Греции практика использования дробных величин в качестве сумм
единицы дроби были довольно распространены до средневековья. Например, Liber
Abbaci итальянского математика Фибоначчи — это
примечательный текст 13 века. В нем широко использовались дроби, описывающие
различные способы преобразования других дробей в суммы единичных дробей.
Чтобы лучше понять, ниже приведена таблица греческого языка.
цифровые символы. Обратите внимание, что они такие же, как буквы в греческом
алфавит:
| Значение | Шт. | Десятки | Сотни |
|---|---|---|---|
| 1 | α | ι | ρ |
| 2 | β | κ | σ |
| 3 | γ | λ | τ |
| 4 | δ | µ | υ |
| 5 | ε | ν | φ |
| 6 | ϝ | ξ | χ |
| 7 | ζ | ο | ψ |
| 8 | η | π | ω |
| 9 | θ | ϙ | ϡ |
Греческий
запись дробей требует от читателя понимания контекста для правильного
интерпретация.Чтобы выделить дробь, они ставят диакритический знак
знак (‘) после знаменателя дроби.
Например, число β (2) становится ½ при записи с
диакритический знак, β ’.
Аналогично, µβ (42) становится 1/42 при записи в µβ ’.
Однако здесь возникает путаница: µβ ’также может означать 40 ½. Вот почему понимание контекста имеет решающее значение при интерпретации греческих дробей.
Римлянам
У римлян дроби выражались только словами, которые
усложняли любые вычисления.
Их система была основана на единице веса, называемой «as».
При таком подходе 1 «as» равнялось 12 унций (римский
базовая единица измерения, основа современной унции). Таким образом, дроби
имеют знаменатели со значениями, кратными 12.
В таблице ниже указаны римские дроби.
с соответствующими условиями:
| Дробь | Римский термин |
|---|---|
| 11/12 | deunx for de uncia, забрал 1/12 |
| 10/12 | декстанов для декстанов, 1/6 отнято |
| 9/12 | dodrans for de quadrans, 1/4 забрано |
| 8/12 | bes — bi as for duae partes, 2/3 |
| 7/12 | перегородка для septem unciae |
| 6/12 | полуфабрикаты |
| 5/12 | quincunx для quinque unciae |
| 4/12 | триенс |
| 3/12 | квадранты |
| 2/12 | секстан |
| 1/12 | uncia |
| 1/24 | семунция |
| 1/48 | сицилийский |
| 1/72 | сценарий |
| 1/144 | сценарий |
| 1/288 | scrupulum |
китайский
Китайцы написали Девять
Главы по математическому искусству , датируемые примерно 100 годом до н. Э.С.
Он включает в себя текст о дробях, аналогичный тем, которые мы используем сегодня.
Согласно Math Through the Ages , он содержал большинство обычных правил вычисления с дробями, например, как складывать, делить и умножать дроби, а также сокращать дробь до наименьшего значения.
Однако в их системе не использовались неправильные дроби. Например, вместо неправильной дроби 9/4 они использовали бы ее эквивалентную смешанную дробь 2 1/4.
В отличие от западной математики, китайцы сосредоточились на практических приложениях, а не на теоретических рассуждениях и геометрии.
Индейцы
Индейцы разработали способ записи дробей,
ближе к тому, что мы используем сегодня.
До 1000 г. до н.э. индуистские мантры в ранний ведический период вызывали силы от десяти до ста и даже до триллиона, согласно сайту The Story of Mathematics. Это свидетельство того, что ранняя индийская цивилизация использовала сложные математические операции, включая дроби, квадраты, кубы и корни.
Около 500 г. до н. Э. Они изобрели систему письма, называемую брахми, которая состояла из 9 цифровых символов и нуля. Учитель математики и писатель Лиз Памфри отмечает, что эти числа во многом повлияли на современные числа, которые мы используем сегодня. См. Изображение ниже.
Индийская система записывала дроби, помещая одно значение поверх другого, точно так же, как сегодня числитель пишется над знаменателем. Однако они не поставили между ними черту. Например, дробь 4/5 будет выглядеть так:
Позже эту систему использовали арабы при торговле с индейцами.Именно арабы нарисовали черту, чтобы отличить верхнее число от нижнего числа в дроби. В конечном итоге это привело к тому, что в современную эпоху мы пишем дроби.
Как дроби улучшают способ передачи информации
По словам доктора Петерсона из MathForum.org: «дроби были изобретены, чтобы обеспечить способ работы с величинами меньше единицы».
Если люди использовали только целые числа, единственный способ сослаться на
меньшие количества — использовать меньшие единицы.Это то, что сделали римляне — они
использовали целые числа при измерении футов и использовали дюймы, когда им нужно было
учитывать меньшие единицы.
Например, вместо 1/12 фута они будут обозначать длину как 1 дюйм, а 1/4 фута будет 3 дюйма. Но что, если вы имеете в виду 2 с половиной фута? Как насчет 1 и 3/4 фута?
Если вы выбираете стандартную длину в соответствии с футами, это
сбивает с толку одновременное упоминание футов и дюймов. По сути,
фракции позволяют проводить измерения без необходимости создания
новые юниты.Было бы лучше учесть измерения в
последовательная мода.
США, как правило, больше используют дроби (английское измерение), поскольку они используют чашки, а не весы для измерения при приготовлении пищи и выпечке.
американцев еще не приняли метрическую систему, которая является
десятичная система, в которой используются единицы, относящиеся к десятичному коэффициенту.
Метрическая система обычно использует граммы и литры вместо американских единиц измерения.
за унции, чашки, пинты и так далее.
В таблице ниже показано преобразование объема из английской единицы измерения в ее метрический эквивалент:
США в метрические единицы преобразования объема
| Обычное количество в США (на английском языке) | Метрический эквивалент | ||||
|---|---|---|---|---|---|
| 1 чайная ложка | 5 мл | ||||
| 1 столовая ложка | 15 мл | ||||
| 60 мл | |||||
| 1/3 стакана | 80 мл | ||||
| 1/2 стакана или 4 жидких унции | 125 мл | ||||
| 2 / 3 стакана | 160 мл | ||||
| 3/4 стакана или 6 жидких унций | 180 мл | ||||
| 1 стакан или 8 жидких унций или 1/2 пинты | 250 мл | ||||
| 1 ½ стакана или 12 жидких унций | 375 мл | ||||
| 2 c ИБП или 1 пинта или 16 жидких унций | 500 мл | ||||
| 3 чашки или 1 ½ пинты | 700 мл | ||||
| 4 чашки или 2 пинты | или 950 мл | ||||
| 4 кварты или 1 галлон | 3.8 л | ||||
| 1 унция | 28 граммов | ||||
| 1/4 фунта (4 унции) | 112 грамм | ||||
| 1/2 фунта (8 унций) | 225 граммов | 3/4 фунта (12 унций) | 337 грамм | ||
| 1 фунт (16 унций) | 450 грамм |
Кроме того, сохранение измерений в одной единице позволяет нам складывать, вычитать, умножать и легко делить дроби.Это устраняет проблему преобразования, которая невозможна при измерении между двумя разными единицами.
Чтобы упростить вычисление дробей, воспользуйтесь калькулятором в верхней части этой страницы.
В то время как десятичные дроби предоставляют альтернативный способ обозначения
дроби (и более простой способ вычисления дробей с помощью калькулятора), это
необходимо понимать традиционные дроби и то, как их значения влияют на
целое число.
По данным Thoughtco.com,
студенты, которые не осваивают дроби в ранние годы, имеют тенденцию
запутаться и испытать математическое беспокойство.Они также упомянули половину американской восьмерки
грейдеры не могут расположить дроби по значению.
Интуитивное обучение дробям помогает детям развить более широкое понимание теоретических математических концепций, позволяя им использовать их в реальной жизни. Это намного лучше, чем запоминать таблицы с единицами измерения или символами.
Золотое сечение и последовательность Фибоначчи
В математике соотношение — это, по сути, сравнение двух
числа, которые зависят от типа сравниваемых чисел.
Вы можете встретить такой пример: 1: 3 или 1
из 3. Например, бутылка концентрата апельсинового сока состоит из 1 части апельсина.
сок и 3 части воды. Это также можно записать в виде дроби, 1/3.
Коэффициенты относятся к дробям, потому что они сравнивают разные
ценности, которые могут представлять собой целое. В этом примере бутылка целиком
апельсинового сока.
Золотое сечение
— специальное число, представленное греческим символом фи ( φ )
с приблизительным значением 1.618.
Получается путем разделения линии на 2 части, так что длинный отрезок
(а) деленная на короткую часть (б) равна всей длине, разделенной на
длинный раздел.
Чтобы лучше понять, вот иллюстрация со стандартным уравнением:
Исторически сложилось так, что соотношение соблюдалось в древних
такие сооружения, как Парфенон и пирамиды Египта. В Великой пирамиде
Гизы отношение основания к высоте примерно 1.5717, что является
близко к золотому сечению. Он также встречается в повторяющихся закономерностях в природе, таких как
как лепестки цветов, ракушки, ветви деревьев и спиральные галактики.
С другой стороны, Фибоначчи
последовательность — еще одна известная математическая формула. Последовательность получена из
сумма двух предшествующих чисел. Многие источники говорят, что Леонардо Фибоначчи
(Леонардо Пизанский) популяризировал его в своей книге Liber Abacci .
Но согласно Live Science,
математик Кейт Девлин, автор книги Finding Fibonacci: The Quest to
«Откройте для себя заново забытого математического гения, который изменил мир, », — говорится в сообщении.
что Леонардо Фибоначчи на самом деле не «открыл» последовательность.
Древние санскритские письма, в которых использовались индо-арабские цифры
системы были первыми, кто обсудил это за столетия до Леонардо Фибоначчи.
Последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610,
987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418,
317811 и так далее…
Когда математики создают квадраты на основе этой последовательности, они могут нарисовать спираль.
Как золотое сечение связано с последовательностью Фибоначчи?
Исследователи заметили, что когда вы берете любые два последовательных числа Фибоначчи, их отношение очень близко к золотому сечению.Итак, φ составляет примерно 1,618. Чтобы дать вам представление, см. Таблицу ниже.
| A | B | B / A | ||||
|---|---|---|---|---|---|---|
| 2 | 3 | 1,5 | ||||
| 3 | 5 | 1,661354 9661353 | 1,661354 9661353 | 1,661354 9661353 | ||
| 8 | 13 | 1,625 |
Итог
Понятие дроби разработали разные древние цивилизации.Одними из первых, кто изобрели дробную систему с обширными таблицами, были египтяне. Другие древние общества, такие как вавилоняне, греки, римляне и китайцы, также внесли свой вклад в его улучшение. Но на современные цифры и то, как мы пишем дроби, в основном повлияли индейцы, которые ввели индуистско-арабскую систему счисления.
Использование дробей помогает нам легко передавать информацию об измерениях. Это не позволяет людям использовать разные единицы измерения, что упрощает их расчет.
Наконец, дроби связаны со знаменитым золотым рационом и последовательностью Фибоначчи, которые во многом повлияли на то, как мы проектируем все виды структур.
Об авторе
Корин — страстный исследователь и автор финансовых тем, изучающий экономические тенденции, их влияние на население, а также то, как помочь потребителям принимать более мудрые финансовые решения. Другие ее тематические статьи можно прочитать на Inquirer.net и Manileno.com. Она имеет степень магистра творческого письма в Филиппинском университете, одном из ведущих учебных заведений в мире, и степень бакалавра коммуникационных искусств в колледже Мириам.



 .≈ 0,156
.≈ 0,156