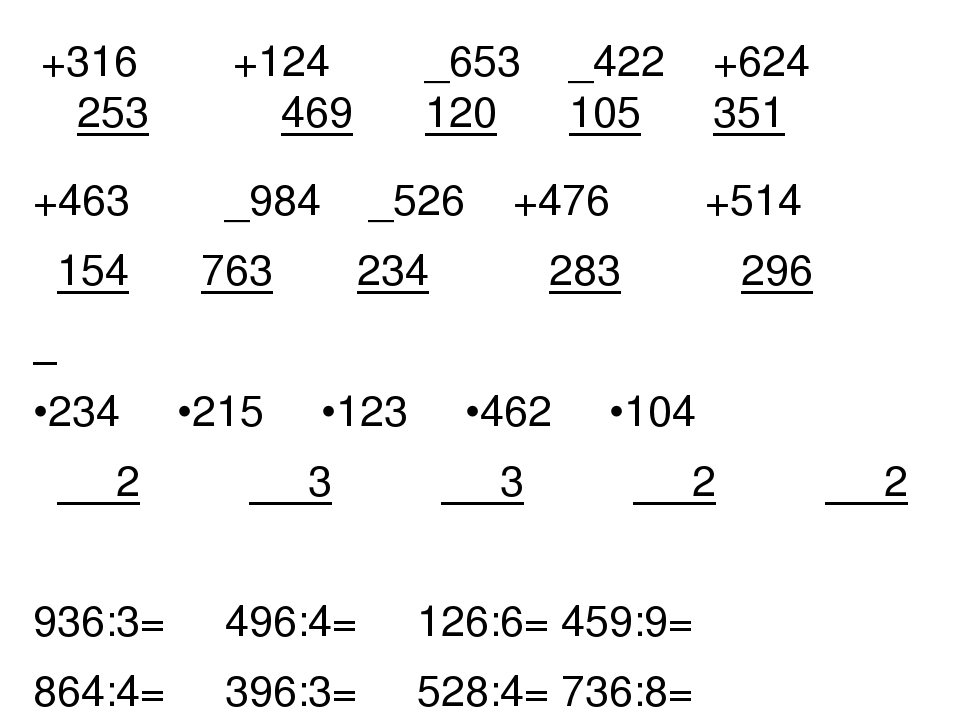Союз в русском языке (3 класс)

Союз — это сло­во, кото­рое соеди­ня­ет одно­род­ные чле­ны пред­ло­же­ния и части слож­ных предложений.

Объясним уче­ни­кам 3 клас­са, что такое союз в рус­ском язы­ке. Используем при­ме­ры про­стых и слож­ных пред­ло­же­ний и выяс­ним, для чего в них упо­треб­ля­ет­ся союз.

Союз в сложном предложении

Чтобы понять, что такое союз, нач­нем с того, что каж­дое пред­ло­же­ние име­ет свою грам­ма­ти­че­скую осно­ву. Основу состав­ля­ют глав­ные чле­ны пред­ло­же­ния — под­ле­жа­щее и сказуемое.

Рассмотрим два предложения:

Взошло солн­це.

В лесу запе­ли птицы.

В пер­вом пред­ло­же­нии (что?) «солн­це» — это подлежащее.

Солнце (что сде­ла­ло?) взо­шло.

Слово «взо­шло» обо­зна­ча­ет дей­ствие. Это сказуемое.

Подчеркнем грам­ма­ти­че­скую осно­ву предложения:

Взошло солн­це.

Во вто­ром пред­ло­же­нии (кто?) «пти­цы» — это под­ле­жа­щее, сло­во «запе­ли», кото­рое обо­зна­ча­ет дей­ствие, — это сказуемое.

Обозначим грам­ма­ти­че­скую основу:

В лесу запе­ли пти­цы.

Первое и вто­рое пред­ло­же­ние про­стые, так как в каж­дом из них име­ет­ся толь­ко одна грам­ма­ти­че­ская основа.

Определение

Предложение, в кото­ром содер­жит­ся одна грам­ма­ти­че­ская осно­ва, назы­ва­ет­ся про­стым.

А теперь объ­еди­ним эти пред­ло­же­ния в одно высказывание:

Взошло солн­це, в лесу запе­ли птицы.

Это слож­ное пред­ло­же­ние, состо­я­щее из двух частей. В каж­дой его части есть свои глав­ные чле­ны пред­ло­же­ния, своя грам­ма­ти­че­ская основа:

• солн­це взошло;
• пти­цы запели.

Исходя из этих наблю­де­ний, сде­ла­ем вывод:

Определение

Сложное пред­ло­же­ние — это пред­ло­же­ние, в кото­ром две и более грам­ма­ти­че­ские основы.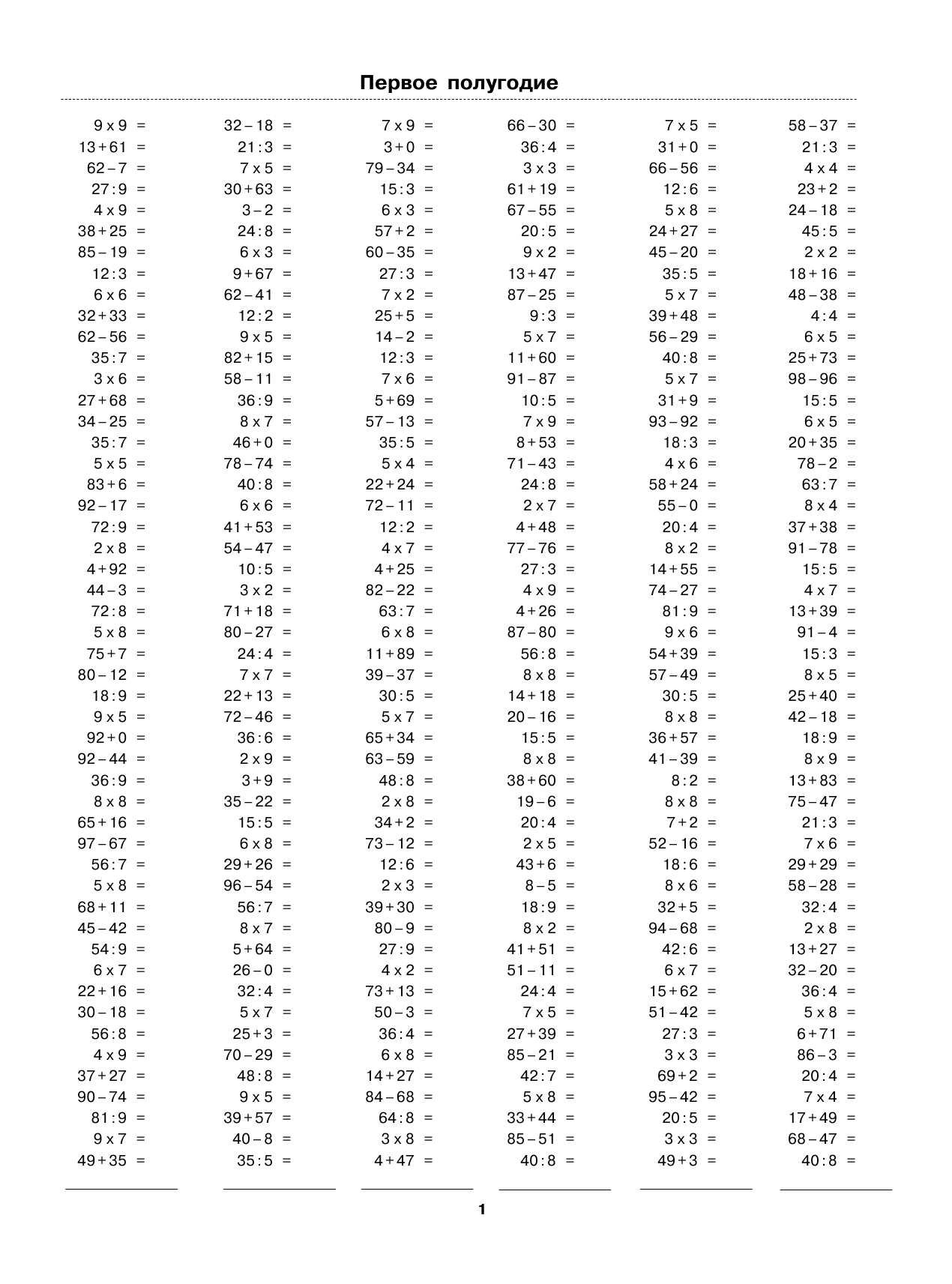

Рассмотрим еще примеры:

Подул ветер.

Тучи закры­ли солнце.

Начался мел­кий дождь.

Каждое про­стое пред­ло­же­ние опи­сы­ва­ет одно явле­ние при­ро­ды, содер­жит одну мысль, кото­рая оформ­ля­ет­ся завер­ша­ю­щей инто­на­ци­ей. В кон­це про­сто­го пред­ло­же­ния ста­вит­ся точка.

А теперь эти про­стые пред­ло­же­ния объ­еди­ним в сложное:

Подул ветер, тучи закры­ли солн­це, начал­ся мел­кий дождь.

Как видим, слож­ное пред­ло­же­ние состо­ит из несколь­ких про­стых. Сколько про­стых пред­ло­же­ний в соста­ве слож­но­го, столь­ко в нем частей. В этом слож­ном пред­ло­же­нии ука­жем три части. Части слож­но­го пред­ло­же­ния — это не про­сто пред­ло­же­ния. Объединившись в слож­ное, про­стые пред­ло­же­ния допол­ня­ют друг дру­га, пре­вра­ща­ют отдель­ные выска­зы­ва­ния в одну более пол­ную по содер­жа­нию мысль. На гра­ни­це частей слож­но­го пред­ло­же­ния отсут­ству­ет инто­на­ция завер­ше­ния мыс­ли, поэто­му меж­ду ними ста­вит­ся запятая.

Понаблюдаем, с помо­щью чего соеди­ня­ют­ся части слож­ных пред­ло­же­ний в еди­ное высказывание.

Сравним:

Пришла ночь, заси­я­ла луна на тём­ном небе.

Пришла ночь, и заси­я­ла луна на тём­ном небе.

В пер­вом слож­ном пред­ло­же­нии два про­стых пред­ло­же­ния соеди­ня­ют­ся толь­ко с помо­щью инто­на­ции. Между ними сто­ит запятая.

Во вто­ром пред­ло­же­ние появил­ся новый эле­мент — союз «и», кото­рый наря­ду с инто­на­ци­ей соеди­ня­ет про­стые пред­ло­же­ния в еди­ное целое.

Понаблюдаем:

Осенью пти­цы уле­та­ют на юг, а перед даль­ней доро­гой они поют на прощанье.

Дождь сту­чит по кры­ше, но небо уже свет­ле­ет.

Союзы «и», «а», «но» слу­жат сред­ством свя­зи меж­ду про­сты­ми пред­ло­же­ни­я­ми. С помо­щью сою­за «и» пере­чис­ля­ют­ся явле­ния или собы­тия, о кото­рых идет речь. Союзы «а» и «но» не толь­ко соеди­ня­ют части слож­ных пред­ло­же­ний, но и про­ти­во­по­став­ля­ют то, о чем сообщается.

Обратим вни­ма­ние, что в слож­ном пред­ло­же­нии перед сою­за­ми ста­вит­ся запя­тая, кото­рая отде­ля­ет части пред­ло­же­ния друг от друга.

Союз и однородные члены предложения

Союз может соеди­нять не толь­ко про­стые пред­ло­же­ния, но и отдель­ные сло­ва. У под­ле­жа­ще­го ино­гда быва­ет не одно, а два ска­зу­е­мых, а при ска­зу­е­мом может быть несколь­ко подлежащих:

В воз­ду­хе летят и кру­жат­ся жел­тые листья.

Березы и ели рас­тут вдоль дороги.

Такие чле­ны пред­ло­же­ния назы­ва­ют­ся одно­род­ны­ми. Однородные чле­ны пред­ло­же­ния отве­ча­ют на один и тот же вопрос и отно­сят­ся в пред­ло­же­нии к одно­му и тому же слову:

• листья (что дела­ют?) летят и (что дела­ют?) кружатся;
• (что?) бере­зы и (что?) ели рас­тут.

И в про­стом пред­ло­же­нии союз выпол­ня­ет одну и ту же роль. Он слу­жит сред­ством свя­зи одно­род­ных чле­нов предложения.

Обратим вни­ма­ние:

Союз «и» соеди­ня­ет одно­род­ные чле­ны пред­ло­же­ния, и тогда запя­тая перед ним не ста­вит­ся. Перед сою­за­ми «а» и «но» запя­тая ста­вит­ся всегда.

Одни и те же сою­зы «и», «а», «но» упо­треб­ля­ют­ся меж­ду одно­род­ны­ми чле­на­ми и в слож­ных пред­ло­же­ни­ях меж­ду их частями.

Примеры

Вспыхнул пер­вый луч солн­ца и осве­тил макуш­ки деревьев.

Над цве­та­ми жуж­жат насе­ко­мые, и гре­ют­ся на солн­це яще­ри­цы.

Пришла вес­на, но снег лежит еще повсюду.

Я знал ответ на этот вопрос, но про­мол­чал.

Вечерние тени сгу­сти­лись, а потом сра­зу насту­пи­ла лет­няя ночь.

Ветер затих, а затем сно­ва задул с новой силой.

Видеоурок

Скачать ста­тью: PDF

Более сложные примеры уравнений | Математика

52. Более сложные примеры уравнений.
Пример 1.

5/(x – 1) – 3/(x + 1) = 15/(x² – 1)

Общий знаменатель есть x² – 1, так как x² – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x² – 1. Получим:

или, после сокращения,

5(x + 1) – 3(x – 1) = 15

или

5x + 5 – 3x + 3 = 15

или

2x = 7 и x = 3½

Рассмотрим еще уравнение:

5/(x-1) – 3/(x+1) = 4(x² – 1)

Решая, как выше, получим:

5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.

Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.

Для первого примера получим:

Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.

Для второго примера получим:

5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0

Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.

Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.

Пример 2.

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:

(x + 3) (2x – 2) = (2x + 3) (x – 1)

или

2x² + 6x – 2x – 6 = 2x² + 3x – 2x – 3.

Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x². Однако, мы можем от обеих частей уравнения вычесть по 2x² — от этого уравнение не нарушится; тогда члены с x² уничтожатся, и мы получим:

6x – 2x – 6 = 3x – 2x – 3

Перенесем неизвестные члены влево, известные вправо — получим:

3x = 3 или x = 1

Вспоминая данное уравнение

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.

Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:

2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,

что невозможно.

Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:

(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)

Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:

6x + 10 = 2x + 18

или

4x = 8 и x = 2

Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:

или 11 = 11

Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:

(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x² + 4x – 10 = 2x² + 16x – 18.

Здесь уже члены с x² не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы

4x² – 12x = –8

или

x² – 3x = –2

Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:

1) 2² – 3 · 2 = –2 и 2) 1² – 3 · 1 = –2

Если мы вспомним начальное уравнение

(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),

то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.

Пример 3.

Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:

1) x² – 5x + 6 = x² – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),

2) x² – x – 2 = x² – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),

3) x² – 2x – 3 = x² – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).

Общий знаменатель равен (x – 3)(x – 2)(x + 1).

Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:

на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:

3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.

Отсюда получим:

–x = –13 и x = 13.

Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.

Если бы мы взяли уравнение:

то, поступая совершенно так же, как выше, получили бы

3(x + 1) – 2(x – 3) = x – 2

или

3x + 3 – 2x + 6 = x – 2

или

3x – 2x – x = –3 – 6 – 2,

откуда получили бы

0 = –11,

что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.

Задачи на пропорции по математике — примеры с ответами

Понятие пропорции

Чтобы решать задачи на тему пропорции, вспомним главное определение.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин.

Вывод из главного свойства пропорции:

• Крайний член равен произведению средних, которые разделены на другой крайний. То есть для пропорции a/b = c/d:
• Средний член равен произведению крайних, которые разделены на другой средний. То есть для пропорции a/b = c/d:

Решить пропорцию — значит найти неизвестный член. Свойство пропорции — главный помощник в решении.

Запомним!

Равенство двух отношений называют пропорцией.

Рассмотрим легкие и сложные задачи, которые можно решить с помощью пропорции. 5, 6, 7, 8 класс — неважно, всем школьникам полезно проанализировать занимательные задачки.

Задачи на пропорции с решением и ответами

Свойства пропорции придумали не просто так! С их помощью можно найти любой из членов пропорции, если он неизвестен. Решим 10 задач на пропорцию.

Задание 1. Найти неизвестный член пропорции: x/2 = 3/1

Как решаем:

В этом примере неизвестны крайние члены, поэтому умножим средние члены и разделим полученный результат на известный крайний член:

x = (2 * 3)/1 = 6

Ответ: x = 6.

Задание 2. Найти неизвестный член: 1/3 = 5/y

Как решаем:

y = (3 * 5)/1 = 15

Ответ: y = 15.

Задача 3. Решить пропорцию: 30/x = 5/8

Как решаем:

x = (30 * 8)/5 = 48

Ответ: x = 48.

Задание 4. Решить: 7/5 = y/10

Как решаем:

y = (7 * 10)/5 = 14

Ответ: y = 14.

Задание 5. Известно, что 21x = 14y. Найти отношение x — к y

Как решаем:

• Сначала сократим обе части равенства на общий множитель 7: 21x/7 = 14y/7.

  Получим: 3x = 2y.

• Теперь разделим обе части на 3y, чтобы в левой части убрать множитель 3, а в правой части избавиться от y: 3x/3y = 2y/3y.
• После сокращения отношений получилось: x/y = 2/3.

Ответ: 2 к 3.

На следующем примере мы узнаем как составить пропорцию по задаче💡

Задание 6. Из 300 подписчиков в инстаграм 108 человек — поставили лайк под постом. Какой процент всех подписчиков составляют те, кому понравился пост и они поставили лайк?

Как решаем:

• Примем всех подписчиков за 100% и запишем условие задачи кратко:

  300 — 100%

  108 — ?%

• Составим пропорцию: 300/108 = 100/x.
• Найдем х: (108 * 100) : 300 = 36.

Ответ: 36% всех подписчиков поставили лайк под постом.

Задание 7. Подруга Гарри Поттера при варке оборотного зелья использовала водоросли и пиявки в отношении 5 к 2. Сколько нужно водорослей, если есть только 450 грамм пиявок?

Как решаем:

• Составим пропорцию: 5/2 = x/450.
• Найдем х: (5 * 450) : 2 = 1125.

Ответ: на 450 грамм пиявок нужно взять 1125 гр водорослей.

Задание 8. Известно, что арбуз состоит на 98% из воды. Сколько воды в 5 кг арбуза?

Как решаем:

Вес арбуза (5 кг) составляет 100%. Вода — 98% или х кг.

Составим пропорцию:

5 : 100 = х : 98

х = (5 * 98) : 100

х = 4,9

Ответ: в 5 кг арбуза содержится 4,9 кг воды.

Перейдем к примерам посложнее. Рассмотрим задачу на пропорции из учебника по алгебре за 8 класс.

Задание 9. Папин автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Как рассуждаем:

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Обозначим:

• v1 = 75 км/ч
• v2 = 52 км/ч
• t1 = 13 ч
• t2 = х

Как решаем:

1. Составим пропорцию: v1/v2 = t2/t1.

   Соотношения равны, но перевернуты относительно друг друга.

2. Подставим известные значения: 75/52 = t2/13

   t2 = (75 * 13)/52 = 75/4 = 18 3/4 = 18 ч 45 мин

Ответ: 18 часов 45 минут.

Задание 10. 24 человека за 5 дней раскрутили канал в телеграм. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

Как рассуждаем:

1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.

2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.

3. Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:

Как решаем:

1. Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию:

   30 : 24 = 5 : х

2. Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член:

   х = 24 * 5 : 30

   х = 4

3. Значит, 30 человек раскрутят канал за 4 дня.

Ответ: за 4 дня.

Давайте практиковаться еще! Приходите на интерактивные уроки по математике в онлайн-школу Skysmart. Мы создали тысячи увлекательных заданий, чтобы учеба не вгоняла в тоску, а вдохновляла и приносила приятные оценки в дневник.

На бесплатном вводном уроке расскажем, как у нас все устроено и наметим план развития школьника.

Что должен знать ребёнок в 3 классе

Советы для родителей… Что должен знать ребёнок во 3 классе. Если вы обладаете информацией, что должен знать и уметь ваш ребёнок, вам легче будет ему помогать, его контролировать и получать необходимый результат…

Ещё у нас есть Что должен знать ребёнок во 2 классе

Математика

• знать последовательность чисел от 0 до 1000000, разряды, классы

• знать названия компонентов сложения и вычитания

Сумма: Слагаемое + слагаемое = значение суммы.

Разность: Уменьшаемое – вычитаемое  = значение разности.

• знать названия компонентов умножения и деления

• Произведение: Множитель x множитель = значение произведения.

  Частное: Делимое : делитель = значение частного.

• знать понятия «периметр» и «площадь«:

Периметр — это сумма всех сторон Площадь — это величина, которая показывает сколько места занимает фигура.

• уметь находить периметр. Например, У прямоугольника длина 5 см, а ширина 3 см. Найди его периметр. «P = 5 + 5 + 3 + 3 = 16 cм ИЛИ P = ( 5 + 3) x 2 = 16 см»

Чтобы найти периметр, надо сложить все стороны ИЛИ сложить длину и ширину и всё это умножить на 2.  

P = (a + b) x 2, где a — это длина, а b — это ширина. 

• уметь находить площадь прямоугольника. Например, У прямоугольника длина 5 см, а ширина 3 см. Найди его площадь. (S = 5 х 3 = 15 кв. см)

Чтобы найти площадь, надо длину умножить на ширину. S = a x b, где a — это длина, а b — это ширина. 

• знать таблицу умножения и внетабличное умножение и деление (13х5, 205:5)
• вычислять многозначные числа
• вычислять значения числовых выражений, содержащих 2-3 действия (со скобками и без них)
• решать уравнения и неравенства;
• выражать длину, массу, площадь измеряемых объектов, используя разные единицы измерения;
• выражать время, используя различные единицы измерения
• решать составные задачи в 2-3 действия
• решать простые задачи на скорость

Решаем задачи по математике (3 класс) и Решаем задачи на нахождение площади и периметра

Русский язык

• должен знать и свободно определять части слова (корень, окончание, приставка, суффикс):

(например, подсказка, где а — окончание, подсказк — основа, сказ — корень, под — приставка, к — суффикс).

Корень — это общая часть всех родственных слов. Окончание — это изменяемая часть слова, или часть слова, которая изменяется. Например, подруга, нет подруги, думаю о подруге, гожусь подругой. Основа — это всё, кроме окончания. Приставка — это часть слова, которая стоит перед корнем. Суффикс — это часть слова. которая стоит после корня. 

• должен знать и свободно определять части речи (имя существительное, имя прилагательное, глагол, местоимение, предлог, союз):

Имя существительное— это часть речи, которое обозначает предмет и отвечает на вопросы кто? или что?. (например, кукла, радость, весна, стол, кошка)

Имя прилагательное — это часть речи, которое обозначает признак предмета и отвечает на вопросы какой?, какая?, какое? и другие. (например, у красивая, белая, пушистая, весёлый)

Глагол — это часть речи, которое обозначает действие предмета и отвечает на вопросы что делает?, что сделает? и другие.  (например, бежать, прыгать, учить, нарисовать)

Местоимение — это часть речи, которая указывает на предметы, признаки, количество, но не называет их, то есть заменяет существительное, прилагательное, числительное и глагол. (например, мы, ты, он)

Предлог — это служебная часть речи, которая связывает слова. (например, у дома, за подругой)

Союз — это служебная часть речи, которая связывает между собой части предложения. (например, На грядке созрели морковь и капуста. Зимой холодно, а летом жарко.)

• должен знать и свободно определять члены предложения (главные — подлежащее и сказуемое, второстепенные — дополнение, обстоятельство, определение, союз, предлог).

• должен знать и свободно определять склонения имён существительных

• должен знать и свободно определять падеж имён существительных

• знать орфограммы:

1. Написание слов с парными согласными на конце слова и в середине слова походка, ход — ходить
2. Правописание слов с удвоенными согласными: терраса, коллекция
3. Проверяемые безударные гласные в корне слова: потяжелел 
4. Разделительный Ь: вьюга, вьёт 
5. Разделительный твёрдый знак: (ъ) подъехал
6. Правописание слов с непроизносимыми согласными:  прелестный — прелесть
7. Правописание окончаний  имён существительных 1, 2, и 3 склонения в различных падежах:  

Главное: Ошибкоопасные окончания И или Е? Запомните: у существительных 1 склонения падежные окончания —Е, а в Р.п. —И; у существительных 2 склонения падежные окончания —Е; у существительных 3 склонения падежные окончания —И!

Слова на -ИЯ, -ИЕ склоняются по правилам 3 склонения, то есть падежные окончания -И (на лекции)

8. Сложные слова: вертолёт, землетрясение

9. Неизменяемые приставки на А и О: зашёл, подход

10. Написание суффиксов: маленький, белизна, высота, бабушка

11. Написание имен существительных с шипящей на конце: ночь, луч

12. Окончания имён прилагательных в ед.ч и мн.ч  в И.п.: синяя, синее, синий, синие

13. Родовые окончания глаголов: солнце встало, девочка встала, ученик встал, ребята встали

14. Приставки и предлоги (перед глаголами предлогов не бывает): поехал

15. НЕ с глаголами:  не видел, НО негодовал, ненавидел.

Примеры по математике — генератор примеров

Сколько всего нужно узнать и выучить ребенку за короткий срок:

выучить буквы и цифры, научиться читать, писать, считать и решать.

Притом, что способности у всех деток разные.

Кто-то схватывает все «на лету», кому-то требуется чуть больше времени.

Чтобы закрепить и улучшить начальные навыки счета у детей, на сайте  «Быть МАМОЙ» создан онлайн — Генератор, который создает примеры и уравнения по математике для детей дошкольного и младшего школьного возраста.

С помощью такого онлайн генератора вы можете абсолютно бесплатно создать, скачать и распечатать готовые примеры на сложение и вычитание, на умножение и деление.

Готовые примеры по математике генерируются на странице в клеточку, что позволяет ребенку тренировать не только устный  счет, но и правильное написание цифр.
Генератор примеров и уравнений, имеет внутренние настройки, изменяя которые вы сможете создать примеры для детей разного возраста и уровня подготовки ( от 5 лет до 2-3 класса).

Чтобы получить и распечатать примеры по математике, вам нужно:

1. Задать (выбрать) параметры для заданий

• по количеству примеров: 10, 20, 30, 60 (2листа), 90 (3 листа)
• по виду задания: пример или уравнение
• по функциям математических действий: сложение, вычитание, умножение и деление.
• по диапазону чисел: от 1 до 100 (например — от 5 до 10, от 10 до 50 и т.п.)

2. Распечатать полученый файл. Предварительно вы можете сохранить файл с заданиями на компьютер или флешку.

ГЕНЕРАТОР ПРИМЕРОВ И УРАВНЕНИЙ

* Если вы генерируете примеры в браузере «Firefox», возможно некорректное отображение pdf.файлов в результате генерации (генерируется пустая страница в клеточку, либо нет знаков математических действий)

В этом случае вам нужно:

1. Сохранить полученный (некорректный) документ на компьютер, а затем открыть и распечатать файл с примерами с вашего компьютера.
2. Открыть данную страницу в другом браузере (Chrome, Яндекс), скопировав адрес страницы и вставив его в адресную строку.

Используйте онлайн генератор примеров по математике, если:

— Ваш ребенок только начал изучать счет. Выберите самые начальные параметры для генерации. Чтобы получились самые простые примеры по математике.

— Вашему ребенку требуется дополнительная подготовка по математике.

— Вы собираетесь в длительную поездку. Решение примеров и уравнений будет  полезным занятием, которое поможет скоротать время в дороге.

Генератор примеров по математике будет очень удобен как для родителей, так и для учителей.  Благодаря  параметрам выбора  можно создать сколько угодно заданий разного уровня сложности для подготовки.

Преимущества генератора математических примеров.

— Не нужно заранее покупать задачники и пособия по математике с примерами и уравнениями.

— Чтобы получить примеры для решения, не нужно предварительно скачивать программу на компьютер. Все примеры генерируются онлайн.

— Вы можете скачать файл с примерами на компьютер и распечатать его в любое время.

— Примеры генерируются на странице в клеточку, что очень удобно для правильного написания цифр ребенком.

— Вы можете подобрать задания индивидуально для вашего ребенка в зависимости от его уровня подготовки.

Если у вас возникнут трудности или вопросы по использованию генератора примеров — не стесняйтесь, задавайте вопросы в комментариях.
Так же буду признательна за поддержку в развитии генератора :))

Читайте похожие записи:

7 способов помочь младшему школьнику с математикой

Предположим, что математика уже в начальной школе ребёнка идёт туго, со скрипом. Трудно и скучно складывать и вычитать, не говоря уже о чём-то более сложном. Новые темы никак не хотят укладываться в голове. Писательница и мама троих детей Ксения Букша рассказывает, основываясь на собственном опыте, как помочь ребёнку освоить математику.

Полезная рассылка «Мела» два раза в неделю: во вторник и пятницу

Раскладываем трудности по полочкам

На уровне 1–5-го классов неспособных к математике детей не бывает. Но бывают дети с конкретными трудностями, которые можно и нужно преодолеть. Подумаем, почему ребёнку трудно с математикой.

Вот возможные варианты или их комбинации.

• Плохо считает, нет навыка счёта. Не очень хорошо знаком с числами.
• Не может вникнуть в суть поставленной задачи, с трудом понимает, что надо делать. Пробует все варианты («Так неправильно? Тогда попробую разделить», «В три раза больше — здесь нужен плюс или минус?»).
• Усваивает шаблонное решение, но не может его доработать. Столкнувшись с малейшим изменением условий, впадает в ступор.
• Не умеет читать сложные тексты. В результате не понимает ни описания правил, ни текста задачи. Если на пальцах объяснить, что надо делать, сразу решает нормально.
• В голове не укладываются концепции. С трудом их понимает и быстро забывает. Такой ребёнок может сто раз услышать объяснение, что такое икс (неизвестное), но так и не понять.
• Не развит навык наглядного представления. Не может представить себе, нарисовать схематичную картинку, «увидеть в уме».
• Короткое внимание: всё понимает, но делает кучу ошибок, особенно в длинных сложных примерах.

Как видим, математика раскладывается на множество разных навыков. Когда мы выяснили, в чём проблема, мы можем её решать. Заранее прошу прощения у учителей и методистов: я всего лишь родитель, а мои мысли по этому поводу — всего лишь частное мнение, хотя я стараюсь его обосновывать.

Ждём, пока созреет способность абстрактно мыслить

Мозг нейротипичного ребёнка дозревает до абстрагирования и обобщения далеко не сразу. У некоторых это происходит раньше, у других позже. Например, не все дети могут соотнести число и количество. Для очень многих и во 2–3-м классе есть только «15 яблок», а просто «15» нет.

При этом они как-то привыкают оперировать числами, и пробел в базовом понимании не очень заметен, пока речь не заходит о чуть более сложных вещах. Например, именно им трудновато понять, почему не может быть «полтора» в ответе на вопрос «сколько землекопов?». А уж когда начинаются проценты или задачи на скорость и расстояние, становится совсем сложно.

Стоит вернуться назад к конкретике. Возможно, для понимания дробей пока нужно проговаривать «в числителе арбузы, в знаменателе мальчики; 21 арбуз достался 42 мальчикам — каждому по половинке арбуза». Даже в пятом классе почти все концепции ещё можно заземлить до конкретики.

Развиваем навыки счёта

Просто учиться считать — это скучно. Нам помогут всевозможные игры с числами. Для начала — усложнённые ходилки с 2–3 кубиками (когда за один ход максимум — 18 очков, а не 6), потом — разнообразные игры в кости, где нужно считать очки.

Самая простая игра известна мне под названием «единичка»: игроки по очереди бросают один кубик (или два, или три), пытаясь добраться до сотни очков. Серия прерывается, когда у игрока выпадает хотя бы одна единичка: в этом случае очки за эту серию сгорают, и нужно уметь остановиться вовремя.

Очень рекомендую покер на костях. В этой игре есть ряд комбинаций, каждую из которых надо выбросить за три попытки. Эти попытки можно копить. Игроки делают ходы по очереди, выигрывает тот, кто первым выполнит все комбинации. Помимо простого навыка складывания очков, покер постепенно развивает тонкое понимание случайности и вероятности, просчитываемого риска и шансов. В такой покер может научиться играть даже шести- или семилетка.

Для отработки деления и умножения мы с дочкой говорили о числах как о «родственниках». Например, у числа 72 очень большая «семья»: у него есть «детки» 24 и 36, есть «внуки» — 2, 3, 4, 6, 12, 18. А вот число 37 не завело себе никакой «семьи», оно простое. Зато если «поженить» его с другим «одиночкой» — 41, у них получится вместе 78, теперь можно «заводить детей и внуков». Это хорошо помогает ориентироваться в таблице умножения.

Учим видеть и наглядно обобщать задачу

Чтобы хорошо схематизировать, надо уметь выделять именно то, что важно для условия задачи, и схематично изображать это на картинке. Сначала мы учимся выделению главного. Это знаменитые игры «что лишнее?», в которых может быть и несколько ответов. Арбуз, аист, абрикос, виноград — что лишнее? Смотря по какому признаку.

В учебнике Петерсон есть чудесные задачи, загромождённые кучей ненужных данных или лишённые необходимых условий. В задании автор просит найти и выделить только те условия, которые нужны для решения, а если их нет — указать, чего не хватает. Научившись видеть задачу, можно перейти к схематизации.

Многие дети вообще не понимают, зачем рисовать схемы к задачам и почему это проще. Всё потому, что схемы эти даны готовыми. Но по какому принципу они строятся? Почему, например, неважно, какой длины сам поезд, если он едет из А в Б? Как нарисовать «3 часа»? А «все груши, посаженные мальчиками»?

Можно вместе рисовать схемы разных задач, а потом предлагать ребёнку придумывать похожие. Такие задания есть и в учебниках, но там их мало. Для некоторых эта трудность вообще определяет все отношения с математикой, да и вообще с упорядочиванием данных, абстрагированием, обобщением, поиском решения.

Оттачиваем логику

Логика — один из инструментов, которые нужны всем. Нет людей, которые были бы не склонны к логике, есть те, у кого она «не поставлена». Это как умение орудовать шуруповёртом: научиться может каждый, у кого есть руки. Вы можете сами оценить, насколько железная у вас логика. Я очень люблю вот этот чудесный тест.

Человека с логикой не способна заморочить никакая пропаганда или реклама, его не запутает недобросовестный банк, он гораздо лучше ориентируется в окружающем мире.

С детьми можно начать с простых силлогизмов, которые иногда звучат смешно, но приводят к пониманию очень важных штук. Например, услышав от кого-нибудь сентенцию «мальчики не плачут», ребёнок может уточнить: «некоторые или все?»

Если дети не проходят понятие множества, стоит хоть немножко вместе с ним порисовать «кружочки» (не обязательно сразу вводить все понятия) и порешать соответствующие задачи: вот мальчики, вот коты, а вот те, кого зовут Вася. Где мальчики, которых зовут не Вася? А где тут девочки? А где кот Барсик?

Развиваем воображение

Воображение необходимо для всего, что связано с математикой и логикой. (Я даже не пишу «как ни странно», потому что это совершенно не странно.) Особенно умение мыслить образами.

Я очень люблю игру, в которой родитель и ребёнок по очереди задают друг другу «графические загадки», не имеющие точного ответа. Каждый рисует серию непонятных геометрических фигур или их комбинаций (точка в треугольнике, молния и круг, несколько кругов, касательные…), а другой дорисовывает их так, чтобы получилась картинка. Чем остроумнее решение, тем больше удовольствия получают оба игрока.

Существует много древних и новых игр, в которых нужно складывать узоры из деталей и фрагментов яйца (колумбово яйцо), квадрата, по-разному раскрашенных граней кубика («Сложи узор»). Есть и трёхмерные наборы, например «Пентамино». Речь не о том, чтобы выполнять задания, хотя все эти наборы можно использовать и так, но именно о творчестве из имеющихся деталей и об умении увидеть образ.

А можно ещё вырезать снежинки, дорисовывать симметричных бабочек и человечков, придумывать шифры, рисовать лабиринты и карты. Всё это и есть развитие математического воображения.

Учим ребёнка вычленять, чего конкретно он не понимает (метакогниция)

Я уже не раз писала про неё — и в связи с математикой, и в связи с сочинениями. Вкратце метакогниция — это умение «понимать, как я думаю», «знать, чего именно я не знаю», осознание своего мыслительного процесса. Именно этому почти никогда не учат в школе, а иногда даже портят уже развитую способность. Предполагается ведь, что есть простые и сложные способы решения той или иной задачи. Часто это так и есть, но порой гораздо ценнее умение идти самому и по шагам проверять себя: «Так нужно делать? Я прав?»

Совместные рассуждения (и я не про математику) ценны и тем, что сближают ребёнка и родителя, и тем, что мы показываем, как проходит процесс думания. Он не должен быть гладким и автоматическим. В нём есть тупики, неожиданные повороты. «Наше первоначальное предположение неверно, а это значит, что нужно идти не по дороге 1, а по дороге 2». Кстати, это пригодится и в школьной математике, когда нужно будет понимать доказательства теорем. Ведь хорошо запоминается только то, что прошёл сам своим умом, когда смог повторить чужие рассуждения и знаешь в них каждый поворот.

Задачи на нахождение периметра и сторон геометрических фигур. 3 класс

 {module Адаптивный блок Адсенс в начале статьи}

ЗАДАЧИ НА НАХОЖДЕНИЕ ПЕРИМЕТРА И СТОРОН ГЕОМЕТРИЧЕСКИХ ФИГУР

3 КЛАСС

  1) Сторона квадрата равна 3 см. Чему равен периметр?

  2) Длина прямоугольника 5 см, а ширина 4 см. Чему равен периметр?

  3) Крышка стола имеет прямоугольную форму. Длина 90 см, а ширина 60 см. Чему равен периметр?

  4) Начертите квадрат со стороной 6 см. Найдите его периметр.

  5) Лист бумаги имеет квадратную форму. Его сторона равна 10 см. Чему равен периметр?

  6) Огород прямоугольной формы имеет границу в 1000 м. Какие размеры могут иметь длина и ширина огорода? (Привести несколько решений в целых числах.)

  7) Сторона прямоугольника а = 4 см, а b — на 2 см длиннее. Чему равен периметр?

  8) Сторона квадрата равна 6 см. Чему равен периметр?

  9) Начертите прямоугольник шириной 4 см, а длиной в два раза больше. Найдите его периметр.

  10) Сторона прямоугольника а = 4 см, а периметр равен 14 см. Чему равна сторона b?

  11) Периметр квадрата равен 24 см. Чему равна его сторона?

  12) Одна сторона прямоугольника 1 дм, это на 3 см больше его другой стороны. Узнайте периметр и начертите прямоугольник.

  13) Сторона прямоугольника а = 7 см, а b — на 2 см короче. Чему равен периметр прямоугольника?

  14) Сторона прямоугольника а = 5 см, Р = 16 см. Чему равна сторона b?

  15) Периметр прямоугольника 20 см. Длина его стороны 6 см. Узнайте ширину прямоугольника и начертите его.

  16) Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 24 см.

  17) Периметр квадрата равен 28см. Чему равна его сторона?

  18) Участок земли имеет форму прямоугольника, длина которого 69 м, а ширина 31 м. Какой длины забор окружает этот участок?

  19) Начертите квадрат со стороной 5 см. Найдите его периметр.

  20) Чему равна сторона классной доски, если её периметр 10 м, а ширина 20 дм?

  21) Периметр прямоугольника 64 см. Найдите его длину, если ширина 14 см.

  22) Чему равен периметр треугольника со сторонами 10 см, 18 см и 9 см?

  23) В парке прямоугольной формы длиной 160 м и шириной 80 м на расстоянии 2 м от ограды сделана аллея. Найдите ее длину.

  24) Узнайте периметр хоккейной коробки, если её длина 15 м, а ширина 90 дм.

  25) Участок земли имеет форму прямоугольника, ширина которого 28 м, а длина на 14 м больше. Он обнесён проволокой в 7 рядов. Сколько метров проволоки потребовалось?

  26) Сколько тесьмы нужно купить для обшивки ковра длиной 2 м и шириной 15 дм?

  27) Длина и ширина 1 листа кровельной стали вместе составляют 2130 мм. Какова длина и ширина листа, если длина в два раза больше ширины?

  28) Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 36 см (в целых числах).

  29) Начертите прямоугольник длиной 6 см, а шириной в два раза меньше. Чему равен его периметр?

  30) Какой участок земли имеет большую ограду: квадратный со стороной 40 м или прямоугольный со сторонами 40 м и 30 м?

  31) Сумма сторон треугольника с тремя равными сторонами 27 дм. Чему равна его сторона?

  32) Найдите периметр прямоугольника длиной 5 дм, шириной 7 см.

  33) Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 48 см (в целых числах).

  34) Комната имеет 8 м длину и 4 м ширину. Сколько нужно кусков бордюра для оклейки комнаты? Длина куска бордюра 12 м.

 {module Адаптивный блок Адсенс в конце статьи}

сложных предложений • Teacher Thrive

Описание

Этот ресурс включает в себя все необходимое для обучения подчинительным союзам и сложным предложениям.

Материалы позволят вам явно обучать, укреплять и оценивать подчиненные союзы и сложные предложения всего за несколько минут в день.

Что включено:

• Урок PowerPoint (понедельник)
• Версия для печати — Включена цифровая версия (вторник)
• 30 карточек задач — Включена цифровая версия (среда)
• Заметки к эскизу (четверг)

Оценка

• — Включена цифровая версия (пятница)
• БОНУС: интерактивное занятие в блокноте

Скачайте превью для детального обзора ресурса.

ПРИМЕЧАНИЕ: Этот ресурс был написан на основе стандартов содержания третьего уровня. Однако ни один из материалов для учащихся не имеет отметки об уровне обучения. Это позволит учителям использовать этот ресурс на всех уровнях обучения.

BYOB! Создайте свой собственный комплект

Выберите нужные грамматические единицы и получите скидку на комплект. Вы можете выбрать единицы грамматики для любого уровня обучения! Чем больше ты покупаешь, тем больше экономишь. Скидка появится в вашей корзине для всех подходящих количеств .Наборы уровней не включены.

5+ единиц = скидка 10%
10+ единиц = скидка 15%
15+ единиц = скидка 20%
20+ единиц = скидка 25%
25+ единиц = скидка 30%
30+ единиц = скидка 35%

Получите полный комплект грамматики для третьего класса ЗДЕСЬ!

Прочие грамматические единицы для третьего класса:

Получайте все последние новости Teacher Thrive!

Прочтите: Это цифровая загрузка с невозвращаемой оплатой.Пожалуйста, внимательно прочтите описание и изучите файл предварительного просмотра перед покупкой.

© Copyright 2018 M. Tallman. Все права защищены. Разрешается копировать страницы, специально предназначенные для использования студентами или преподавателями первоначальным покупателем или лицензиатом. Он предназначен для использования одним учителем, если не были приобретены дополнительные лицензии. Воспроизведение любой другой части этого продукта строго запрещено. Копирование любой части этого продукта и размещение его в Интернете в любой форме (даже на личном / классном веб-сайте) строго запрещено.Это дает возможность для поиска в Интернете бесплатно разместить документ в Интернете и является нарушением Закона о защите авторских прав в цифровую эпоху (DMCA).

• Всего страниц 40
• Ответный ключ включен
• Продолжительность обучения 1 неделя

Только вошедшие в систему клиенты, которые приобрели этот продукт, могут оставлять отзыв.

Рабочих листов простых, составных и сложных предложений

Добро пожаловать в еще один отличный набор рабочих листов в формате pdf для простых, составных, сложных и составно-сложных предложений, где мы объясняем типы предложений на основе структуры или количества предложений.Будь то разъяснение компонентов каждого типа предложений, их объяснение с помощью множества примеров или проверка успеваемости детей с помощью увлекательных упражнений, эти распечатываемые рабочие листы для классов с 3 по 7 содержат все необходимое и обязательно изменят процесс обучения детей предложениям. в совершенно другой жанр. Получите доступ к некоторым из этих листов бесплатно!

Таблица предложений

Предоставьте детям возможность испытать типы предложений на собственном опыте с помощью этой таблицы простых, сложных и составных предложений.Определения и примеры позволяют лучше понять тему.

Завершение простых предложений

Простое предложение — это независимое предложение, образованное подлежащим и сказуемым, и в нем нет других предложений. На этом рабочем листе в формате pdf учащиеся завершают каждое простое предложение подлежащим или сказуемым.

Составные предложения с «и»

Сложные предложения немного длиннее простых предложений, но они не являются крепкими орешками.Здесь дети соединяют два простых предложения с помощью «и» и составляют составные предложения.

Простые и составные предложения

Простое предложение не обязательно должно быть коротким. Наслаждайтесь вечеринкой, когда дети 3-го и 4-го классов отделяют простые предложения от составных. Их проницательность помогает им благополучно приземлиться на берегу!

Координационные союзы

Координационные союзы имеют решающее значение для создания составных предложений из двух простых предложений.В этом упражнении для печати дети 4 и 5 классов складывают вместе два простых предложения и составляют составные предложения.

Сложные приговоры

Оттачивайте свои навыки преобразования двух простых предложений в одно составное предложение, используя соответствующее координирующее соединение с этим рабочим листом составных предложений.

Сложные предложения

На самом деле в сложных предложениях нет ничего сложного. На этом листе в формате PDF дети удивляют вас, добавляя зависимое предложение к каждому простому предложению и написав сложное предложение.

Подчиненные союзы

Подчинительные союзы, такие как «если» и «хотя», имеют решающее значение для написания сложных предложений. Пусть ученики 6-го класса проявят свой калибр, переписав эти простые предложения в сложные.

Составные приговоры

Превратить сложное предложение в сложное — не такая уж трудная задача. Просто преобразуйте одно из независимых предложений в зависимое, и все.Вот еще практика.

Простой составной комплекс | MCQ

В этом упражнении для печати проявляется вся эйфория, связанная с типами предложений. Детям 5-го, 6-го и 7-го классов необходимо читать предложения и, руководствуясь своим обучением, решать, являются ли они простыми, сложными или составными.

Определение типов

Определение предложения на основе его придаточных предложений — изящное искусство. Здесь молодые мастера учатся различать простые, составные, сложные и составно-сложные предложения.

Сложные предложения

Использование разнообразных структур предложений, включая расширенные простые предложения и сложные предложения, позволяет создавать тексты, которые становятся более интересными и рисуют более яркую картину в голове читателя. Студенты могут уверенно улучшить свое письмо, понимая, как предложения структурированы для достижения эффекта.

Сложные предложения

Сложное предложение формируется путем добавления одного или нескольких подчиненных (зависимых) предложений к основным (независимым) предложений с использованием союзов и / или относительных местоимений.Предложение — это простое предложение. Простые предложения содержат только одно предложение (группу глаголов). Сложные предложения содержат более одного предложения (группы глаголов).

В технических, научных и математических письмах логические отношения между элементами, которые связывают союзы, не указываются явно и вносят сложности в понимание. Эти письменные жанры привносят сложные элементы незнакомой лексики, включая жаргонные и технические слова, лексически плотные предложения и элемент «угадывания» или интерпретации данных применительно к задаче.Для многих студентов концепции или предметы незнакомы и, следовательно, проблематичны.

Например:

Глаголы

1. Лед тает при повышении температуры. Ученики должны интерпретировать причинно-следственную связь в предложении «Лед тает при повышении температуры» как означающее, что события происходят одновременно, и повышение температуры вызывает таяние льда.

2. Сахар растворяется в воде. Это означает, что сахар растворяется, когда его помещают в воду, потому что вода является растворителем.Здесь многоточие ‘увеличивает трудность для студентов.

Ни одно из этих значений не передается явным образом, но должно быть «восстановлено». Причинно-следственная связь должна быть выведена из предложений с использованием знания грамматики учащимся, а вода, действующая как растворитель, должна быть выведена из контекстуальных знаний учащихся по предмету.

Составление сложных предложений

Сложные предложения возникают, когда другие более сложные устройства используются для соединения предложений; это означает, что подчиненное (зависимое) предложение объединено с основным (или независимым) предложением.

Есть три основных способа соединения предложений в сложные предложения. При использовании:

• Относительные местоимения — тот, который, кто, чей
• Союзы (подчиняющие) — while, потому что, хотя, as, when, until, if, through, by, Since, when, when, if, where, before, etc
• Глагольные структуры (нефинитные) — (причастия) глагольные формы, оканчивающиеся на –ing или –ed, или инфинитивная глагольная форма, такая как идти, становиться, видеть

Эта презентация PowerPoint, разработанная учителями, может помочь вашему ученику понять, как строятся сложные предложения.Простые сложные предложения (PPTX 1616.82KB)

Мероприятия в поддержку стратегии

Действие 1: моделирование статей посредством совместного и смоделированного чтения

Используйте текущие учебные тексты и / или выберите подходящие тексты в Интернете — см. Онлайн-ресурсы ниже.

• учащимся предлагается широкий спектр комбинаций предложений, прочитанных им с помощью качественных текстов с группировкой предложений, подчеркнутой интонацией и паузой
• учащихся идентифицируют простые, составные и сложные предложения (включая главное и придаточное предложение), когда они читают или когда предложения читаются учащимся
• учащихся определяют количество идей, содержащихся в смоделированных предложениях из текстов, а затем определяют, какая идея является основной (независимое предложение), которая может стоять сама по себе.

Задание 2: инновации в аутентичных текстах и ​​использование собственных работ студентов

• преобразовать два предложения в составное предложение
• преобразовать несколько предложений в одно сложное предложение
• добавить прилагательные, чтобы описать существительные и сделать предложение более интересным
• добавляет наречные придаточные предложения, чтобы изменить глаголы и сделать предложение более интересным.

Действие 3: рабочие листы для встроенных статей

Используйте следующий веб-сайт, чтобы получить доступ к рабочим листам, чтобы сначала обучать, а затем практиковаться в небольших группах.

Встроенные статьи — основные ресурсы (DOC 134 КБ)

Задание 4: игры с предложением работы

Используя нарезанные и ламинированные ресурсы, сначала явным образом научите их использовать, а затем, используя одну или несколько игральных костей, попросите группы учеников устно или в письменной форме следовать правилам игры.

Приговор рабочих игр (PDF 413.73KB)

Интернет-ресурсы

Детские новостные сайты — Writing Stimulus

Список литературы

Австралийская учебная программа

ACELA1507: Поймите разницу между основным и придаточным предложением и то, что сложное предложение включает как минимум одно придаточное предложение.ACELA1522: исследуйте, как сложные предложения могут использоваться различными способами для разработки, расширения и объяснения идей.

Программа

NSW

EN3-6B: Учащийся использует знание структуры предложения, грамматики, пунктуации и словарного запаса, чтобы отвечать и составлять четкие и связные тексты на различных носителях.

Сложные и сложные предложения

Бумажная копия этого задания была роздана в классе. Если вы отсутствовали, прочтите, пожалуйста, это.

Сложные приговоры

A составное предложение состоит из двух или более независимых предложений .Это означает, что в предложении есть как минимум две мыслительные единицы, каждая из которых может стоять сама по себе как собственное предложение. Предложения составного предложения либо разделяются точкой с запятой , (относительно редко), либо соединяются координирующим союзом (которому чаще всего предшествует запятая). И два наиболее распространенных координирующих соединения — это , и , но. (Остальные или, пока еще, и так.) Это самый простой способ комбинирования идей, который у нас есть:

• Мериуэзер Льюис справедливо известен своей экспедицией на территорию Закупки Луизианы и за ее пределы , но мало кто знает о его вкладе в естествознание.
• Льюис был хорошо обучен учеными в Филадельфии перед своей экспедицией , а он был любопытным человеком по натуре.

Обратите внимание, что и не более чем связывают одну идею с другой; , но также связывает, но он делает больше работы с точки зрения установления интересной взаимосвязи между идеями. и являются частью непосредственного языкового арсенала детей и сновидений: одно просто следует за другим, и логическая взаимосвязь между идеями не всегда очевидна или важна. Слово , но (и другие координаторы) находится на несколько более высоком уровне аргументации.

Предложения: простые, сложные и сложные

Распространенная слабость в письменной форме — отсутствие разнообразных предложений. Знание трех основных типов предложений — простых, сложных и сложных — может помочь вам разнообразить предложения в написании.

Для наиболее эффективного письма используются различные типы предложений, описанных ниже.

1. Простые предложения

Простое предложение имеет самые основные элементы, которые делают его предложением: подлежащее, глагол и завершенная мысль.

Примеры простых предложений включают следующее:

1. Джо ждал поезда. «Джо» = субъект, «ожидал» = глагол
2. Поезд опоздал. «Поезд» = субъект, «было» = глагол
3. Мэри и Саманта сели в автобус.«Мария и Саманта» = составное подлежащее, «взяла» = глагол
4. Я искал Мэри и Саманту на автовокзале. «I» = субъект, «посмотрел» = глагол
5. Мэри и Саманта прибыли на автовокзал рано, но ждали автобус до полудня. «Мария и Саманта» = составное подлежащее, «прибыл» и «ожидал» = составной глагол

Совет : Если вы используете много простых предложений в эссе, вам следует подумать о том, чтобы преобразовать некоторые предложения в составные или сложные предложения (объяснено ниже).

Использование составного подлежащего, составного глагола, предложных фраз (например, «на автобусной станции») и других элементов помогает удлинить простые предложения, но простые предложения часто бывают короткими. Использование слишком большого количества простых предложений может сделать письмо «прерывистым» и помешать написанию плавно.

Простое предложение также может именоваться независимым предложением . Оно называется «независимым», потому что, хотя оно может быть частью составного или сложного предложения, оно также может стоять само по себе как законченное предложение.

2. Сложные приговоры

Составное предложение относится к предложению, состоящему из двух независимых предложений (или полных предложений), связанных друг с другом согласованным соединением . Координационные союзы легко запомнить, если вспомнить слова «FAN BOYS»:

.

• F или
• A nd
• N или
• В ут
• O r
• Y и
• S или

Примеры составных предложений включают следующее:

1. Джо ждал поезда, но поезд опаздывал.
2. Я искал Мэри и Саманту на автобусной станции, но они прибыли на станцию ​​до полудня и уехали в автобусе до моего приезда.
3. Мэри и Саманта прибыли на автовокзал до полудня, и они уехали на автобусе до моего приезда.
4. Мэри и Саманта уехали на автобусе до того, как я приехал, , так что я не видел их на автобусной станции.

Совет : Если вы в значительной степени полагаетесь на составные предложения в эссе, вам следует подумать о том, чтобы преобразовать некоторые из них в сложные предложения (объяснено ниже).

Координационные союзы полезны для соединения предложений, но сложные предложения часто используются слишком часто. Хотя координирующие союзы могут указывать на некоторый тип отношений между двумя независимыми предложениями в предложении, они иногда не указывают на большую часть отношений. Слово «и», например, только добавляет одно независимое предложение к другому, не указывая, как две части предложения логически связаны. Слишком много составных предложений, в которых используется «и», могут ослабить написание.

Более четкие и конкретные отношения можно установить с помощью сложных предложений.

3. Комплексные предложения

Сложное предложение состоит из независимого предложения и одного или нескольких зависимых предложений , связанных с ним. Зависимое предложение похоже на независимое предложение или полное предложение, но в нем отсутствует один из элементов, которые сделали бы его полным предложением.

Примеры зависимых статей включают следующее:

• , потому что Мэри и Саманта прибыли на автовокзал до полудня
• пока ждал на вокзале
• после того, как уехали на автобусе

Зависимые предложения, такие как те, что выше , не могут стоять отдельно как предложение, но они могут быть добавлены к независимому предложению, чтобы сформировать сложное предложение.

Зависимые предложения начинаются с подчиненных союзов . Ниже приведены некоторые из наиболее распространенных подчинительных союзов:

• после
• хотя
• как
• потому что
• до
• хотя
• если
• с
• хотя
• , кроме

С

• по
• , когда
• всякий раз, когда
• тогда как
• везде
• , а

Сложное предложение объединяет независимое предложение с одним или несколькими зависимыми предложениями.

Зависимые предложения могут идти первым в предложении, за которым следует независимое предложение, как в следующем примере:

Совет : Когда зависимое предложение идет первым, для разделения этих двух предложений следует использовать запятую.

1. Поскольку Мэри и Саманта прибыли на автовокзал до полудня, я не увидел их на вокзале.
2. Пока он ждал на вокзале, Джо понял, что поезд опаздывает.
3. После того, как они уехали на автобусе, Мэри и Саманта поняли, что Джо ждет на вокзале.

И наоборот, независимые предложения могут идти первым в предложении, за ними следует зависимое предложение, как в следующем примере:

Совет : Когда независимое предложение идет первым, для разделения двух предложений следует использовать запятую , а не .

1. Я не видел их на вокзале, потому что Мэри и Саманта прибыли на автовокзал до полудня.
2. Джо понял, что поезд опаздывает, когда он ждал на вокзале.
3. Мэри и Саманта поняли, что Джо ждал на вокзале после того, как уехали на автобусе.

Сложные предложения часто более эффективны, чем составные предложения, потому что сложное предложение указывает на более четкие и конкретные отношения между основными частями предложения. Слово «до», например, говорит читателям, что одно происходит раньше другого. Такое слово, как «хотя», передает более сложные отношения, чем такое слово, как «и».

Простой

Моя собака любит поиграть. (простой) (независимый класс)

Соединение

Моя собака любит играть в фетч, поэтому я часто играю с ней в фетч (Compound) (2 независимых предложения)

Моя собака любит играть в фетч, и она часто играет в фетч на улице.(соединение)

Моя собака любит поиграть, но никогда не возвращает мяч. (соединение)

(FANBOYS) Координационные союзы, используемые в составных предложениях

Комплекс

Хотя моя собака редко возвращает мяч, моя собака любит поиграть. (сложный) (1 независимая статья, 1 зависимая статья)

Моя собака любит играть в мяч, хотя никогда не возвращает мяч (сложный) (1 зависимый, 1 независимый)

Когда подчиненный начинает предложение (Пример 1), после предложения ставится запятая.

Если подчиненный второй, запятая не нужна (пример 2).

Подчиненные союзы: хотя, потому что, поскольку, так, что, когда, пока, до, после, всякий раз, где угодно, если, тогда как

Простое предложение | Что такое простое предложение?

Наша история

Простое предложение

Простое предложение — это предложение, состоящее всего из одного независимого предложения. В простом предложении нет зависимых придаточных предложений.(Независимое предложение (в отличие от зависимого предложения) может стоять отдельно как предложение.)

Примеры простых предложений

Ниже приведены примеры простых предложений.

• Я не могу пить теплое молоко.
• День без солнечного света подобен ночи.
• Только посредственные всегда на высоте. (Писатель Жан Жиро)
• Реальность продолжает разрушать мою жизнь. (Карикатурист Билл Уоттерсон)

Сводка видео

Посмотрите видео, в котором резюмируется этот урок о простых предложениях.

Подробнее о простых предложениях

Простое предложение не всегда является коротким базовым предложением, как в четырех приведенных выше примерах. Простое предложение может иметь составное подлежащее (т.е. подлежащее с двумя или более простыми подлежащими). Например:

• Джек любит гулять.

(Это простое предложение с одним простым подлежащим («Джек»).)

• Джек и Джилл любят гулять.

(Это простое предложение со сложным подлежащим, состоящим из двух простых подлежащих («Джек» и «Джилл»).)

Простое предложение также может иметь составное сказуемое (когда два или более глагола имеют одно и то же подлежащее). Например:

• Джек любит рыбалку.

(Это простое предложение с обычным сказуемым, т.е. есть только один главный глагол («нравится»).)

• Джек любит рыбалку, но ненавидит охоту.

(Это простое предложение с составным сказуемым.Подлежащее «Джек» является предметом двух глаголов («любит» и «ненавидит»).

• Джек любит прогулки и рыбалку, но ненавидит бег и охоту.

(Это по-прежнему простое предложение с составным предикатом. Подлежащее «Джек» по-прежнему является субъектом двух глаголов («нравится» и «ненавидит»), но вы можете видеть, как простое предложение может стать довольно загруженным.)

Вот пример простого предложения с составным подлежащим, составным предикатом и прямых объектов с более чем одним элементом.

• Джек и Джилл любят прогулки и рыбалку, но ненавидят бег и охоту.

(Это все еще простое предложение. Здесь нет зависимых придаточных предложений.)

Вот реальный пример занятого простого предложения:

• Волки и европейские бурые медведи слишком поздно начали бояться людей и вымерли в британских дебрях, лесах и горах Европы в средневековье.

Четыре типа структуры предложения

Простое предложение — это одна из четырех структур предложений, все из которых показаны ниже.В этих примерах независимые предложения затенены.

Простое предложение . В простом предложении есть только одно независимое предложение. Например:

• Вы хороши ровно настолько, насколько хороша ваша последняя стрижка. (Автор Фрэн Лебовиц)

Сложное предложение . Сложное предложение имеет независимое предложение и по крайней мере одно зависимое предложение. Например:

• Когда вы пишете комикс, человек слева всегда говорит первым.(Комик Джордж Карлин)

Подробнее о сложных предложениях.

Составное предложение . В составном предложении есть как минимум два независимых предложения. Например:

• Я бегал трусцой, но кубики льда продолжали выпадать из моего стакана. (Певец Дэвид Ли Рот)

Подробнее о сложных предложениях.

Сложно-сложное предложение . Составно-сложное предложение имеет как минимум два независимых предложения и как минимум одно зависимое предложение.Например:

• Я перестал верить в Санта-Клауса, когда мама отвела меня к нему в универмаг, и он попросил у меня автограф. (Актриса Ширли Темпл)

Почему мне нужны простые предложения?

Вот хороший повод позаботиться о простых предложениях:

Четко укажите, когда следует использовать запятую перед «и».

Возможность определить простое предложение помогает расставить запятую. Писатели часто не уверены, когда использовать запятую перед такими словами, как «и», «или», «и», но (так называемые союзы).

Давайте посмотрим на несколько примеров:

• Джеку нравится цыпленка, а нравится цыпленка Нандо.
• Джеку нравится курица, но ненавидит индейка.

(Это оба примера простых предложений с составными предикатами. В каждом примере есть одно подлежащее, управляющее двумя глаголами. Обратите внимание, что перед «и» или «но» нет запятой.)

Сравните два приведенных выше примера с этими предложениями:

• Джеку нравится цыпленка, а ему нравится цыпленка Нандо.
• Джеку нравится цыпленка , но он ненавидит индейку.

(Они похожи, но это не простые предложения с составными предикатами. Есть два подлежащих («Джек» и «он»), каждое из которых управляет своим собственным глаголом. Это примеры составных предложений, а не простых предложений с составными предикатами. Каждое предложение имеет два независимых предложения, а не одно. Обратите внимание, что теперь перед «и» и «но» стоит запятая.)

Правило
Используйте запятую перед «и» (или «но», «или» и т. Д.), который объединяет два независимых предложения (т. е. предложения, которые могут стоять отдельно как предложения).

Помните, что с составным предикатом вторая половина предиката не может стоять отдельно как предложение, потому что у нее нет собственного подлежащего.

• Джеку нравится цыпленка, а нравится цыпленка Нандо.

(В этом примере простого предложения «любит Nando’s» не является независимым предложением. Вот почему перед «и» нет запятой.)

• Джеку нравится цыпленка, а ему нравится цыпленка Нандо.

(В этом примере составного предложения «он любит Nando’s» является независимым предложением. Вот почему перед «и» стоит запятая.)

Подробнее о сложных предложениях.
Подробнее о соединениях.

Ключевой момент

• Если в простом предложении есть составное сказуемое, не отделяйте подлежащее от второго глагола запятой.
• Моя собака любит тосты, но не ест хлеб.
• Моя собака любит тосты, но не ест хлеб.

Помогите нам улучшить грамматику Monster

• Вы не согласны с чем-то на этой странице?
• Заметили опечатку?

Сообщите нам, используя эту форму.

См. Также

Что такое приговор?
Что такое независимые статьи?
Что такое зависимые предложения?
Что такое сложное предложение?
Что такое простое предложение?
Словарь грамматических терминов

Используйте простые, составные, сложные и составно-сложные предложения: CCSS.ELA-LITERACY.L.7.1.B

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Научите студентов писать сложные предложения

Когда студенты, изучающие английский язык, учатся составлять сложные предложения, их грамматика становится чище, а письмо — более стильным.

Введение

Продолжительность урока (30-60 минут)

На этом уроке ваши ученики научатся распознавать и писать сложные предложения. Этот урок не является полным обзором сложных предложений. Он знакомит студентов с одной базовой структурой.

Зачем нужно учиться писать такие предложения?

• Поскольку они сжимают много информации на сравнительно небольшом пространстве, сложные предложения эффективны.
• Когда ученики научатся создавать эту форму, они смогут писать немного стиля за счет разнообразия предложений.
• При обучении формулировке причин и следствий сложные предложения позволяют учащимся нарисовать картину контрастов и изменений во времени.

Часть 1. Как выглядит сложное предложение?

Вот несколько примеров:

• Хотя было холодно и дождливо, мы решили прогуляться по парку.
• После окончания университета начала работать в торговой компании.
• Пока дети пели, матери обсуждали, куда пойти пообедать.
• Перед тем, как пойти на заправку, я проверил, сколько денег у меня в кошельке.

Более детальный взгляд

Сложные предложения состоят из трех частей:

1. соединительное слово
2. зависимая статья
3. независимая статья

Соединительное слово

Это слово может быть в начале предложения или в середине. Существует около 30 различных соединительных слов. Большинству студентов не нужно запоминать их все. Но они должны знать, как использовать 5-7:

.

• После, хотя, потому что, до, если, когда, а

Независимая оговорка

Это предложение само по себе.Независимость означает сама по себе или сама по себе.

Зависимая оговорка

В нем есть глагол и подлежащее, но это не полное предложение. Его нужно добавить в самостоятельную статью. Зависимость означает, что нужен другой человек или вещь.

Часть 2а. Практика письма

Вот шесть пословиц, в которых используется сложная форма предложения. Завершите предложение, добавив последнюю часть пословицы, которая оказывается независимым предложением. (См. Ответы внизу сообщения.)

1. Где дым,…
2. Если сначала не получится,…
3. Если не сломалось…
4. Если ты не можешь их победить…
5. Когда в Риме,…
6. Когда дела идут тяжело…

Часть 2б.Дополнительная письменная практика

Завершите сложное предложение, добавив независимое предложение, которое имеет смысл.

1. После завтрака,
2. Хотя было холодно,
3. Потому что моя бабушка очень хорошо готовит,
4. Перед входом на бейсбольный стадион,
5. Если бы я был тобой,
6. Когда она принесла праздничный торт,
7. Пока учителя не было,

Часть 3. Упражнение на свободное владение языком

Часть 1

Это письменное задание на время.

Учащиеся просматривают в общей сложности 7 картинок, каждая со словом подсказка (которое является соединительным словом).