Урок 10. порядок выполнения действий в числовых выражениях — Математика — 3 класс
Математика, 3 класс
Урок №10. Порядок выполнения действий в числовых выражениях
Перечень вопросов, рассматриваемых в теме:
— В какой последовательности выполняются действия в выражениях без скобок?
— В какой последовательности выполняются действия в выражениях со скобками?
Глоссарий по теме:
Если в выражение без скобок входят только сложение и вычитание или умножение и деление, то действия выполняются по порядку: слева направо.
Если в выражение без скобок входят не только сложение и вычитание, но и умножение или деление, то сначала выполняются по порядку умножение и деление, а затем сложение и вычитание также по порядку.
Если в выражение есть скобки, то сначала выполняются действия в скобках, а затем в установленном порядке сначала умножение и деление, затем сложение и вычитание
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 24.
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 3 класс. Часть 1. М.; Просвещение, 2016. – с. 15.
Теоретический материал для самостоятельного изучения
Выполним вычисления устно и расставим значения выражений в порядке возрастания.
Подсказка: Он должен быть в доме, в шкафу, на столе и даже в портфеле ученика.
В результате вычислений получилось:
Действительно во всём должен быть порядок и в математике тоже.
Выполняя задания, мы пользуемся законами и правилами математики. Эти правила и законы и поддерживают математический порядок.
Выполняя устные вычисления, мы выполняли действия по порядку. В выражениях использовали действия умножения и деления.
Рассмотрим выражения:
6 ∙ 3 + 4 : 2; 27 : 3 — 2 ∙ 2; 2 ∙ (5 + 4).
Это числовые выражения. Для их составления использовали числа и знаки действий.
Использовали не только умножение и деление, но и сложение, вычитание. В каком порядке будем выполнять действия?
В выражении 76 – 27 + 9 – 10 использовали знаки сложения и вычитания. Выполнять действия нужно по порядку: слева направо.
В выражении 80 : 8 ∙ 2 использовали знаки умножения и деления. Выполнять действия нужно также по порядку: слева направо.
Вывод: Если в выражениях только сложение и вычитание или умножение и деление, то действия выполняются по порядку слева направо.
Выражения могут содержать сложение и вычитание, и умножение, и деление. В этом случае сначала выполняются деление и умножение по порядку. В математике эти действия считаются сильными. А затем сложение и вычитание тоже по порядку.
В математике есть способ, который позволяет выделить какое-то действие. Это постановка скобок. Скобки показывают, что действие внутри них, выполняется в первую очередь.
Действия в числовых выражениях выполняются в следующем порядке:
- Действия записанные в скобках;
- Умножение иделение по порядку: слева направо;
- Сложение и вычитание по порядку: слева направо.
Знания этих математических правил позволит правильно находить значения выражений и не нарушать порядок.
Порядок действий в выражениях особый.
И в каждом случае, помните, он свой.
В порядке все действия выполняйте.
Сначала в скобках все посчитайте.
Потом чередом, умножайте или делите.
И, наконец, вычитайте или сложите.
Тренировочные задания.
1. Выберите действие, которое будет в выражение первым.
38 + 4 ∙ 7 + 19
Правильный ответ: умножение.
2. Выберите действие, которое в выражение будет последним.
40 : 5 + 12 – 8 : 2
Правильный ответ: вычитание.
Порядок выполнения математических действий | интернет проект BeginnerSchool.ru
Сегодня мы поговорим о порядке выполнения математических действий. Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.
Читаем выражение слева направо и выбираем порядок действий по приоритету. Сначала выполняем действия в скобках. Затем умножение и/или деление. Далее складываем и вычитаем.
Если скобки имеют несколько вложений, то есть если внутри скобок есть ещё скобки, то сначала выполняем действия во внутренних скобках. Для простоты понимания, выражение в скобках можно воспринимать как самостоятельное выражение, то есть как отдельный пример, который надо решить. Внутри скобок действия выполняются согласно тому же порядку: Действия в скобках, затем умножение/деление, затем сложение/вычитание.
Умножение и деление не имеет между собой приоритета и выполняются слева направо, также как и сложение с вычитанием.
Рассмотрим пример:
38 – (10 + 6) = 22;
Итак, вспомним о том, что сначала вычисляются выражения в скобках
1) в скобках: 10 + 6 = 16;
2) вычитание: 38 – 16 = 22.
Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.
10 ÷ 2 × 4 = 20;
Порядок выполнения действий:
1) слева направо, сначала деление: 10 ÷ 2 = 5;
2) умножение: 5 × 4 = 20;
10 + 4 – 3 = 11, т.е.:
1) 10 + 4 = 14;
2) 14 – 3 = 11.
Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.
18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7
Порядок выполнения действий:
1) 18 ÷ 2 = 9;
2) 2 × 3 = 6;
3) 12 ÷ 3 = 4;
4) 9 – 6 = 3; т. е. слева направо – результат первого действия минус результат второго;
е. слева направо – результат первого действия минус результат второго;
5) 3 + 4 = 7; т.е. результат четвертого действия плюс результат третьего;
Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.
30 + 6 × (13 – 9) = 54, т.е.:
1) выражение в скобках: 13 – 9 = 4;
2) умножение: 6 × 4 = 24;
3) сложение: 30 + 24 = 54;
Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:
1) действия, заключенные в скобках;
2) умножение и деление;
3) сложение и вычитание.
Если вы хотите получать анонсы наших статей подпишитесь на рассылку “Новости сайта“.
Понравилась статья — поделитесь с друзьями:
Оставляйте пожалуйста комментарии в форме ниже
Порядок выполнения действий: правила, примеры.
Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Порядок вычисления простых выражений
Определение 1
В случае выражений без скобок порядок действий определяется однозначно:
- Все действия выполняются слева направо.
- В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Пример 1
Условие: вычислите, сколько будет 7−3+6.
Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:
7−3+6=4+6=10
Ответ: 7−3+6=10.
Пример 2
Условие: в каком порядке нужно выполнять вычисления в выражении 6:2·8:3?
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Пример 3
Условие: подсчитайте, сколько будет 17−5·6:3−2+4:2.
Решение
Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:
Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:
17−5·6:3−2+4:2=17−10−2+2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17−10−2+2=7−2+2=5+2=7
Ответ: 17−5·6:3−2+4:2=7.
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
.
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
Определение 2
В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Порядок вычислений в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:
Определение 3
Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Проиллюстрируем нашу мысль примером.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Пример 4
Условие: вычислите, сколько будет 5+(7−2·3)·(6−4):2.
Решение
В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7−2·3. Здесь нам надо умножить 2 на 3 и вычесть результат из 7:
7−2·3=7−6=1
Считаем результат во вторых скобках. Там у нас всего одно действие: 6−4=2.
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5+(7−2·3)·(6−4):2=5+1·2:2
Начнем с умножения и деления, потом выполним вычитание и получим:
5+1·2:2=5+2:2=5+1=6
На этом вычисления можно закончить.
Ответ: 5+(7−2·3)·(6−4):2=6.
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Пример 5
Условие: вычислите, сколько будет 4+(3+1+4·(2+3)).
Решение
У нас есть скобки в скобках. Начинаем с 3+1+4·(2+3), а именно с 2+3. Это будет 5. Значение надо будет подставить в выражение и подсчитать, что 3+1+4·5. Мы помним, что сначала надо умножить, а потом сложить: 3+1+4·5=3+1+20=24. Подставив найденные значения в исходное выражение, вычислим ответ: 4+24=28.
Ответ: 4+(3+1+4·(2+3))=28.
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Допустим, нам надо найти, сколько будет (4+(4+(4−6:2))−1)−1. Начинаем с выражения во внутренних скобках. Поскольку 4−6:2=4−3=1, исходное выражение можно записать как (4+(4+1)−1)−1. Снова обращаемся к внутренним скобкам: 4+1=5. Мы пришли к выражению (4+5−1)−1. Считаем 4+5−1=8 и в итоге получаем разность 8-1, результатом которой будет 7.
Мы пришли к выражению (4+5−1)−1. Считаем 4+5−1=8 и в итоге получаем разность 8-1, результатом которой будет 7.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Пример 6
Условие: найдите, сколько будет (3+1)·2+62:3−7.
Решение
У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 62=36. Теперь подставим результат в выражение, после чего оно примет вид (3+1)·2+36:3−7.
Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.
(3+1)·2+36:3−7=4·2+36:3−7=8+12−7=13
Ответ: (3+1)·2+62:3−7=13.
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
Порядок выполнения действий без скобок и со скобками
Для правильного вычисления значений числовых выражений, в которых нужно произвести более одного действия, необходимо знать установленный порядок выполнения арифметических действий.
Порядок действий без скобок
Установленный порядок арифметических действий без скобок:
- Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо:
- Если выражение содержит только действия на умножение и деление, то действия выполняются в порядке следования — слева направо:
- Если в выражении присутствуют и умножение с делением, и сложение с вычитанием, то сначала выполняются умножение и деление в порядке их следования (слева направо), а затем сложение и вычитание в порядке их следования (слева направо):
Порядок действий со скобками
Если выражение содержит скобки, то сначала выполняются все действия внутри скобок, а затем все действия, находящиеся за скобками.
В числовых выражениях со скобками порядок выполнения арифметических действий такой же, как и в выражениях без скобок.
Скобки применяются для обозначения действий, которые нужно произвести раньше остальных. Скобки не влияют на порядок остальных действий в выражении, остальные действия выполняются в указанном порядке.
Дробная черта
Дробная черта в выражении может быть заменена на знак деления, в этом случае, всё что было над и под дробной чертой надо взять в скобки. Например:
| 13 + 2 | = (13 + 2) : (10 — 7). |
| 10 — 7 |
Знак деления в выражении можно заменить дробной чертой только в том случае, если это не нарушает порядок действий. Например, выражение:
20 : 4(2 + 3)
нельзя заменить на
потому что такая замена нарушит порядок действий в данном выражении.
| 20 : 4(2 + 3) ≠ | 20 | ; |
| 4(2 + 3) |
| 20 | = 20 : (4(2 + 3)). |
| 4(2 + 3) |
Дробная черта в выражении заменяет скобки и означает, что надо вычислить отдельно выражение, стоящее в числителе, и отдельно выражение, стоящее в знаменателе, и первый результат разделить на второй.
Порядок действий в Математике
Основные операции в математике
Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).
Операции действия:
- сложение (+)
- вычитание (-)
- умножение (*)
- деление (:)
Операции отношения:
- равно (=)
- больше (>)
- меньше (<)
- больше или равно (≥)
- меньше или равно (≤)
- не равно (≠)
Сложение — операция, которая позволяет объединить два слагаемых. 4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
При знаке квадратного корня показатель корня принято опускать: √16 = 4.
3√8 = 2 — корень третьей степени называется — кубическим.
Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
- действия выполняются по порядку слева направо
- сначала выполняется умножение и деление, а затем — сложение и вычитание.
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо. Сначала умножение или сложение? — Умножаем, потом складываем. |
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
Как решаем:
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Ответ: 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Как рассуждаем:
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Ответ: 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
- Действиями первой ступени называют сложение и вычитание, а умножение и деление — действиями второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:
8 — 2 * 3 = 8 — 6 = 2.
Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.
Подставляем полученные значения в исходное выражение:
10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.
Какое действие в полученном выражении делается первым, умножение или деление? Выполняем слева направо: умножение, деление, затем — вычитание. Получилось:
10 + 2 * 8 : 2 = 10 + 18 : 2 = 10 + 6 = 16.
На этом все действия выполнены.
Ответ: 10 + (7 — 2 * 3) * (12 — 4) : 2 = 16.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Как решаем:
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
2 + 3 = 5.
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 24, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 4 + (3 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
Пример 1. Вычислить (4 + 1) * 3 + 62 : 3 — 7.
Как решаем:
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
(4 + 1) * 3 + 36 : 3 — 7.
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
(4 + 1) * 3 + 36 : 3 — 7 = 3 * 3 + 36 : 3 — 7 = 9 + 12 — 7 = 14.
Ответ: (3 + 1) * 2 + 62 : 3 — 7 = 14.
У нас есть статья «знаки больше, меньше или равно», она может быть полезной для тебя!
Еще больше практики — в детской школе Skysmart. Ученики занимаются на интерактивной платформе, в комфортном темпе и с поддержкой внимательных учителей.
Чтобы ребенок занимался математикой в удовольствие и чувствовал себя увереннее в школе, запишите его на бесплатный вводный урок. Познакомим с форматом и вдохновим на учебу!
Порядок выполнения действий / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Порядок выполнения действий
В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.
1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.
Например,
В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:
Вычисляем:
1) 10 + 15 = 25
2) 25 — 6 = 19
3) 19 — 8 = 11
Полностью пример записываем так:
10 + 15 — 6 — 8 = 25 — 6 — 8 = 19 — 8 = 11
Например,
В числовом выражении 3 арифметических действия: деление, умножение и деление.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:
Вычисляем:
1) 15 : 5 = 3
2) 3 • 4 = 12
3) 12 : 6 = 2
Полностью пример записываем так:
15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2
2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.
1)15 : 3 = 5
2) 6 • 8 = 48
3) 10 — 5 = 5
4) 5 + 48 = 53
Полностью пример записываем так:
10 — 15 : 3 + 6 • 8 = 10 — 5 + 6 • 8 = 10 — 5 + 48 = 5 + 48 = 53
3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.
1) 25 — 10 = 15
2) 15 : 3 = 5
3) 6 • 8 = 48
4) 5 + 48 = 53
Полностью пример записываем так:
(25 — 10) : 3 + 6 • 8 = 15 : 3 + 6 • 8 = 5 + 6 • 8 = 5 + 48 = 53
Например,
В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.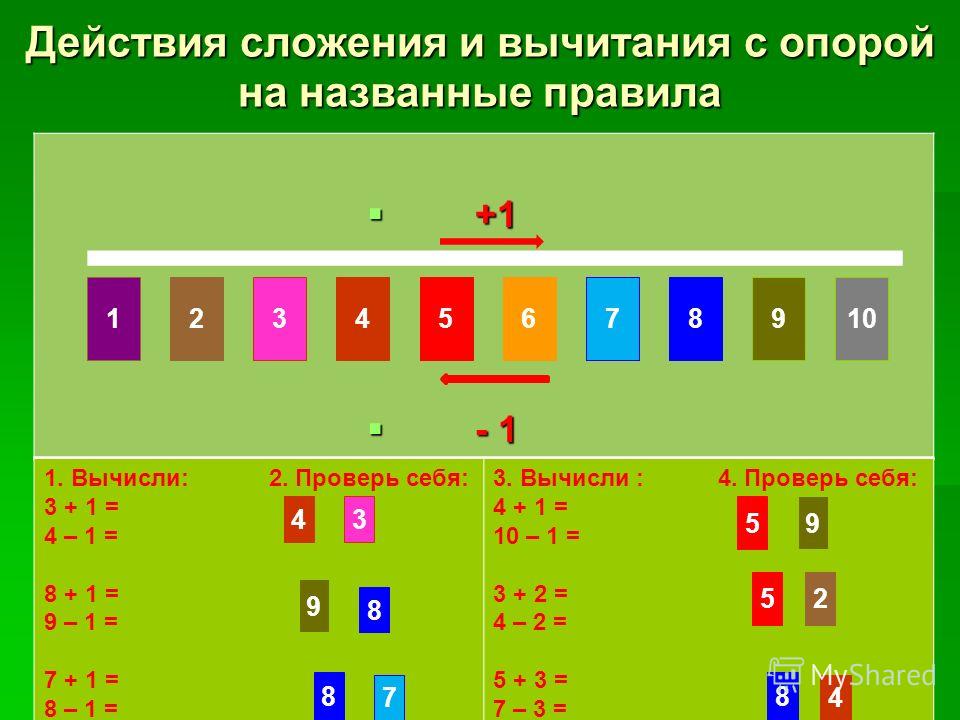
1) 12 : 4 = 3
2) 6 + 3 = 9
3) 18 : 9 = 2
4) 42 + 2 = 44
Полностью пример записываем так:
42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44
Вывод:
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Скобки
Правило встречается в следующих упражнениях:
2 класс
Страница 69. Вариант 2. Тест 1,
Моро, Волкова, Проверочные работы
Страница 26,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 48,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 52,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 59,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 69,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 81,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 50,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 64,
Моро, Волкова, Рабочая тетрадь, часть 2
3 класс
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 51,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 35. Вариант 2. № 3,
Вариант 2. № 3,
Моро, Волкова, Проверочные работы
Страница 45,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 47,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 64,
Моро, Волкова, Рабочая тетрадь, часть 2
4 класс
Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 68,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 23,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 66,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 57. Вариант 2. Проверочная работа 1,
Моро, Волкова, Проверочные работы
Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 58,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 75,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 9,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 63,
Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Номер 37,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 237,
Мерзляк, Полонский, Якир, Учебник
Номер 455,
Мерзляк, Полонский, Якир, Учебник
Номер 456,
Мерзляк, Полонский, Якир, Учебник
Номер 462,
Мерзляк, Полонский, Якир, Учебник
Номер 516,
Мерзляк, Полонский, Якир, Учебник
Номер 517,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 943,
Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 73,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 85,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 92,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 373,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 411,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 413,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 417,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 425,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 445,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 454,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
© budu5. com, 2021
com, 2021
Пользовательское соглашение
Copyright
3 класс. Моро. Учебник №1. Ответы к стр. 24
Числа от 1 до 100
Умножение и деление
Порядок выполнения действий
Ответы к стр. 24
Узнаем, в каком порядке выполняются действия в числовых выражениях.
1. Сравни выражения каждой пары: какие действия в них выполняются? В каком порядке выполняются эти действия и почему?
38 — 10 + 6 = 28 + 6 = 34 24 : 3 • 2 = 8 • 2 = 16
38 — (10 + 6) = 28 + 6 = 34 24 : (3 • 2) = 8 • 2 = 16
Прежде чем приступить к вычислениям, надо рассмотреть выражение: выяснить, есть ли в нём скобки, какие действия в нём имеются.
1) Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняются в том порядке, в каком они записаны: слева направо.
Если в выражение без скобок входят не только сложение и вычитание, но и умножение или деление или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
3) Если в выражении есть скобки, то сначала выполняют действия, записанные в скобках, по правилам пунктов 1 и 2.
Действия в числовых выражениях выполняют в следующем порядке:
1) действия, записанные в скобках;
2) умножение и деление;
3) сложение и вычитание.
В первой паре выполняется сложение и вычитание, во второй — деление и умножение. В первой случае сначала выполняется вычитание, а затем деление. Но при наличии скобок сначала выполняются действия в скобках — сложение, а затем вычитание.
Во втором случае сначала выполняется деление, а затем умножение. Но при наличии скобок сначала выполняются действия в скобках — умножение, а затем деление.
2.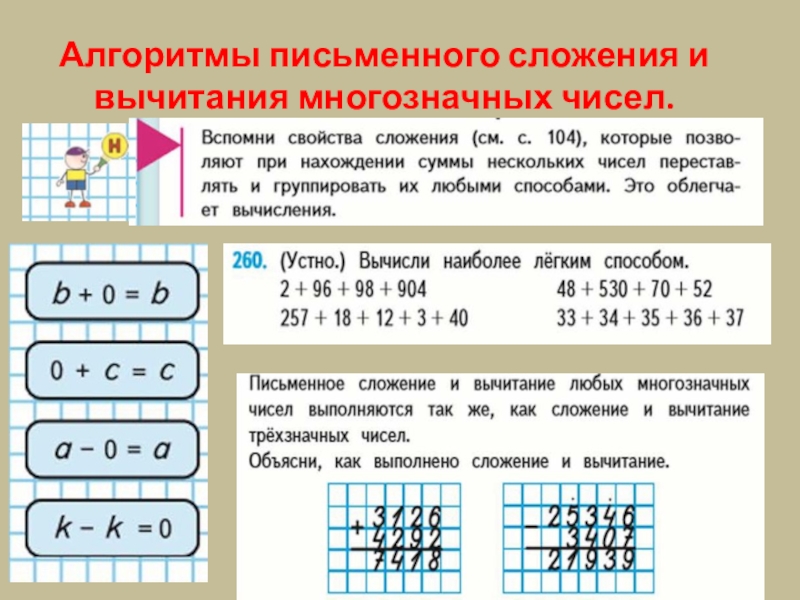 Объясни, как надо выполнять действия.
Объясни, как надо выполнять действия.
3 2 1
30 + 6 • (13 — 9) = 30 + 6 • 4 = 30 + 24 = 54
1 4 2 5 3
18 : 2 — 2 • 3 + 12 : 3 = 9 — 6 + 4 = 7
В первом выражении сначала выполняется действие в скобках — вычитание, затем умножение, а потом сложение.
Во втором выражении сначала выполняются действия деления и умножения, а затем действия вычитания и сложения — слева направо.
ГДЗ по математике. Учебник. 3 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 3 класс
3 класс. Моро. Учебник №1. Ответы к стр. 24
3.9 (78.46%) от 13 голосующих
Порядок действий: PEMDAS
Purplemath
Если вас просят упростить что-то вроде «4 + 2 × 3», естественно возникает вопрос: «Как мне это сделать? Потому что есть два варианта!» Я мог бы добавить первым:
4 + 2 × 3 = (4 + 2) × 3 = 6 × 3 = 18
…или можно сначала умножить:
4 + 2 × 3 = 4 + (2 × 3) = 4 + 6 = 10
Какой ответ правильный?
MathHelp.com
Кажется, ответ зависит от того, как вы смотрите на проблему. Но у нас не может быть такой гибкости в математике; математика не сработает, если вы не можете быть уверены в ответе или если можно вычислить одно и то же выражение, чтобы вы могли прийти к двум или более различным ответам.
Но у нас не может быть такой гибкости в математике; математика не сработает, если вы не можете быть уверены в ответе или если можно вычислить одно и то же выражение, чтобы вы могли прийти к двум или более различным ответам.
Чтобы устранить эту путаницу, у нас есть некоторые правила приоритета, установленные, по крайней мере, еще в 1500-х годах, которые называются «порядком операций». «Операции» — это сложение, вычитание, умножение, деление, возведение в степень и группирование; «порядок» этих операций указывает, какие операции имеют приоритет (выполняются) перед другими операциями.
Распространенным методом запоминания порядка действий является сокращение (или, точнее, «акроним») «PEMDAS», которое превращается в мнемоническую фразу «Пожалуйста, извините, моя дорогая тетя Салли». Эта фраза означает «круглые скобки, экспоненты, умножение и деление, сложение и вычитание» и помогает запомнить их порядок. Этот список показывает вам ранги операций: скобки опережают показатели, которые превосходят умножение и деление (но умножение и деление находятся в одном ранге), а умножение и деление превосходят сложение и вычитание (которые вместе находятся в нижнем ранге).Другими словами, приоритет:
- Круглые скобки (внутри них упростить)
- Экспоненты
- Умножение и деление (слева направо)
- Сложение и вычитание (слева направо)
Когда у вас есть несколько операций одного ранга, вы просто действуете слева направо. Например, 15 ÷ 3 × 4 не равно 15 ÷ (3 × 4) = 15 ÷ 12, а скорее (15 ÷ 3) × 4 = 5 × 4, потому что, двигаясь слева направо, вы попадаете в разделение подпишитесь первым.
Если вы не уверены в этом, проверьте это на своем калькуляторе, который был запрограммирован с иерархией порядка операций. Например, набрав это выражение в графическом калькуляторе, вы получите:
Например, набрав это выражение в графическом калькуляторе, вы получите:
Используя приведенную выше иерархию, мы видим, что в вопросе «4 + 2 × 3» в начале этой статьи ответ 2 был правильным, потому что мы должны выполнить умножение, прежде чем выполнять сложение.
(Примечание: носители британского английского часто вместо этого используют аббревиатуру «BODMAS», а не «PEMDAS». BODMAS означает «скобки, порядки, деление и умножение, а также сложение и вычитание». и «порядки» совпадают с показателями, два акронима означают одно и то же. Кроме того, вы можете видеть, что буквы «M» и «D» поменяны местами в британо-английской версии; это подтверждает, что умножение и деление равны того же «звания» или «уровня».Канадцы, говорящие по-английски, разделяют разницу, используя BEDMAS.)
Порядок операций был определен, чтобы предотвратить недопонимание, но PEMDAS может создать свою собственную путаницу; некоторые студенты иногда склонны применять иерархию, как будто все операции в задаче находятся на одном «уровне» (просто идут слева направо), но часто эти операции не «равны». Во многих случаях это помогает решать проблемы изнутри, а не слева направо, потому что часто некоторые части проблемы находятся «глубже», чем другие части.Лучший способ объяснить это — привести несколько примеров:
Мне нужно упростить термин с показателем, прежде чем пытаться добавить 4:
Я должен упростить в круглых скобках, прежде чем я смогу провести экспоненту. Только тогда я смогу добавить 4.
4 + (2 + 1) 2 = 4 + (3) 2 = 4 + 9 = 13
Упростить 4 + [–1 (–2 — 1)]
2 .

Я не должен пытаться делать эти вложенные круглые скобки слева направо; этот метод слишком подвержен ошибкам. Вместо этого я постараюсь работать изнутри. Сначала я упрощу внутри фигурных скобок, затем упрощу внутри квадратных скобок и только потом займусь квадратом. После этого я наконец могу добавить 4:
4 + [–1 (–2 — 1)] 2
= 4 + [–1 (–3)] 2
= 4 + [3] 2
= 4 + 9
= 13
Нет особого смысла в использовании квадратных скобок («[» и «]» выше) вместо скобок.Скобки и фигурные скобки (символы «{» и «}») используются, когда есть вложенные круглые скобки, как помощь в отслеживании того, какие круглые скобки к которым идут. Различные символы группировки используются только для удобства. Это похоже на то, что происходит в электронной таблице Excel, когда вы вводите формулу с использованием круглых скобок: каждый набор скобок имеет цветовую кодировку, поэтому вы можете определить пары:
Упростить
4 (–2 / 3 + 4 / 3 ).
Сначала я упрощу внутри скобок:
Итак, мой упрощенный ответ
8 / 3
На следующей странице есть еще примеры отработанных примеров ….
URL: https: // www.purplemath.com/modules/orderops.htm
Сначала умножить или сложить? Порядок обучения правилам операций
Когда дети сначала изучают сложение, вычитание, умножение и деление, они начинают с выполнения операций над двумя числами. Но что происходит, когда выражение требует нескольких операций? Со временем математики разработали набор правил, называемых порядком операций, чтобы определить, какую операцию выполнять в первую очередь.Правила такие:
Но что происходит, когда выражение требует нескольких операций? Со временем математики разработали набор правил, называемых порядком операций, чтобы определить, какую операцию выполнять в первую очередь.Правила такие:
- Умножайте и делите слева направо.
- Сложить и вычесть слева направо.
При упрощении выражения, такого как 12 ÷ 4 + 5 x 3-6, вы должны сначала вычислить 12 ÷ 4, поскольку порядок операций требует, чтобы вы начинали с левой стороны выражения и выполняли умножение или деление (в зависимости от того, что наступит раньше. ) перед сложением или вычитанием. После вычисления 12 ÷ 4 вы продолжаете движение слева направо в поисках умножения или деления.Итак, следующий шаг — вычислить 5 x 3. Теперь, когда все умножение и деление завершены, вы можете продолжить, добавляя или вычитая (в зависимости от того, что наступит раньше) слева направо. Шаги показаны ниже.
12 ÷ 4 + 5 x 3-6
3 + 5 x 3-6 (начиная с 12 ÷ 4 = 3)
3 + 15-6 (поскольку 5 x 3 = 15)
18-6 (поскольку 3 + 15 = 18)
12 (поскольку 18-6 = 12)
Группирующие символы, такие как круглые скобки (), квадратные скобки [] или фигурные скобки {}, позволяют определить порядок, в котором выполняются определенные операции.Посмотрите на это выражение:
6 + 4 x 7-3
6 + 28-3 (поскольку 4 x 7 = 28)
34-3 (поскольку 6 + 28 = 34)
31 (поскольку 34-3 = 31)
Что произойдет, если вы вставите круглые скобки в выражение? Скобки позволяют определить, какая операция выполняется в первую очередь. Порядок операций гласит, что операции внутри круглых скобок выполняются перед операциями вне скобок. Что произойдет, если мы заключим в скобки 6 + 4?
(6 + 4) x 7 — 3
10 x 7 — 3 (6 + 4 = 10, которое выполняется первым, потому что оно заключено в круглые скобки)
70 — 3 (нормальный порядок операций возобновляется, и 10 x 7 = 70)
67 (поскольку 70 — 3 = 67)
Обратите внимание, что ответ значительно отличается от предыдущего. Что, если мы заключим в скобки 7–3?
Что, если мы заключим в скобки 7–3?
6 + 4 x (7–3)
6 + 4 x 4 (На этот раз 7–3 в скобках, поэтому мы сделаем это в первую очередь.)
6 + 16 (Если скобки не осталось , мы продолжаем умножение перед сложением.)
22 (так как 6 + 16 = 22)
Этот набор скобок дает еще один ответ. Итак, когда используются круглые скобки, правила порядка операций следующие:
- Операции в скобках.
- Умножайте и делите слева направо.
- Сложить и вычесть слева направо.
Арифметика — можете ли вы опровергнуть это правило PEDMSA? — (деление перед умножением, вычитание перед сложением)
Чтобы расширить ответ Losethegame
Losethegame ответил: «Я попал сюда, погуглил тот же вопрос, хотя я не уверен, что (м) кто-либо из комментаторов ответил на него конкретно. Я думаю, вы правы в том, что ваше правило не может быть нарушено. Это, вероятно, может быть доказано алгебраически, потому что a * (b / c) = (a / c) * b и a + (bc) = (ac) + b…? «
Я согласен, что это, вероятно, может быть доказано алгебраически с помощью методов, подобных тому, о котором упоминает losethegame (хотя пример losethegame может быть ошибочным, поскольку, как указывает user21280, losethegame меняет местами операнды). Но, развивая идею алгебраического доказательства (и без замены операндов!), Я могу придумать некоторую алгебру, которая могла бы это доказать. (Aand предоставил user21280 считает, что мои примеры не учитывают все возможности. Его ответ с использованием логических формул мог бы).
Дано уравнение, в котором умножение идет текстуально перед делением, e.грамм. 3 * 4/2 неважно, что вы сделаете в первую очередь. Так что буквальные PEMDAS или PEDMAS подойдут. Принимая во внимание уравнение, в котором деление происходит текстуально перед умножением, например 6/2 * 3 , тогда имеет значение, что вы сделаете в первую очередь. Традиционное прочтение PEMDAS или PEDMAS дает это правильно (потому что они говорят, что сначала делайте первый, и это разделение), буквальное PEDMSA дает это правильно. Буквальное прочтение PEMDAS ошибочно.
Традиционное прочтение PEMDAS или PEDMAS дает это правильно (потому что они говорят, что сначала делайте первый, и это разделение), буквальное PEDMSA дает это правильно. Буквальное прочтение PEMDAS ошибочно.
Вычитание и раздел этой собственности.Итак, допустим, мы составляем небольшое уравнение той части уравнения, в которой операторы конкурируют друг с другом. Если вычитание конкурирует с сложением и вычитание происходит первым (текстуально, в уравнении), оно должно быть выполнено первым. Если деление соперничает с умножением, и деление идет первым, деление должно быть выполнено первым. В то время как если бы сложение конкурировало с вычитанием, то независимо от того, происходит ли оно первым в тексте, не имеет значения, выполняется ли сначала сложение или вычитание.Точно так же, если умножение конкурирует с делением, если умножение происходит сначала в текстовом виде, тогда не имеет значения, выполняется ли сначала деление или сначала выполняется умножение. Таким образом, литерал PEDMSA всегда работает (т.е. строго выполняет деление перед умножением, вычитание перед сложением). Как и традиционное / правильное чтение PEMDAS / PEDMAS, то есть чтение, в котором говорится, что умножение и деление имеют равный приоритет и сначала выполняют первое, аналогично сложению и вычитанию.
Так, например,
Принимая 1 * 2/3 , поэтому a * b / c
Следуя PEDMSA буквально дает 1 * (2/3) , поэтому a (b / c)
После PEDMSA традиционно получается (1 * 2) / 3 , поэтому (ab) / c
И мы знаем алгебраически, что a (b / c) = (ab) / c
1 * 2/3 а * б / с
знак равно
1 * 2/3 ab / c
Принимая 1/2 * 3 , поэтому a / b * c
Это оценивается одинаково независимо от того, следует ли строго упорядоченному PEDMSA или традиционному PEMDAS i.е. Независимо от того, делаете ли вы сначала деление, как правило, или первое из умножения и деления, это (a / b) * c в обоих случаях, так что очевидно одно и то же.
1/2 * 3 (а / б) * в
знак равно
1/2 * 3 (а / б) * в
С 1 + 2-3 , если мы выполним a + b-c , который заказан PEDMSA, то есть a + (b-c) , это будет тот же результат, что и при традиционном PEMDAS (a + b) -c. Мы знаем алгебраически a + (b-c) = a + b-c = (a + b) -c
Я вспоминаю, как мой учитель математики указывал на одну вещь, о которой вы хотите остерегаться / знать, — это
- (a + b) , который мы просверлили, был -a-b сильно отличается от -a + b .Вычитания всегда должны выполняться в первую очередь и по порядку … и если сначала выполняется вычитание или сначала первое из сложения и вычитания, то мы поддерживаем это правило.
1 + 2-3 а + (б-в)
знак равно
1 + 2-3 (а + б) -с
И для этого то же самое. алгебраически
1-2 + 3 (1-2) +3 (а-б) + в
знак равно
1-2 + 3 (1-2) +3 (а-б) + в
И я полагаю, наконец. 1-2-3 и 1/2/3 И независимо от того, выполняете ли строго заказанный PEDMSA или традиционный PEMDAS, это (1-2) -c и (1/2) / 3 так же там.
Я не уверен, все ли это возможности.
Это может оставить вопрос о том, что объясняет алгебру, например правило, что
a * (b / c) = (ab) / c
и
а + (b-c) = (a + b) -c
Также это соглашение о синтаксическом анализе, которое, кажется, разработано в конце 20 века, а не фундаментальное правило математики. https://www.quora.com/Is-the-order-of-operations-unclear-for-expressions-like-20-2-5+5
арифметических операций — Порядок работы — Имеет ли значение порядок..
Мы можем придумать любое правило, какое захотим. Пока мы в этом последовательны.
Так что такое 5 + 4×3 + 2?
Можно составить такое правило: 1) Вы всегда делаете это строго слева направо
Итак, 5 + 4×3 + 2 = 9×3 + 2 = 27 + 2 = 29.
Или мы могли бы составить правило, что: 2) Вы всегда сначала делаете сложение
Итак, 5 + 4×3 + 2 = 9×5 = 45.
Или мы могли бы составить такое правило: 3) Вы всегда сначала выполняете умножение
Итак, 5 + 4×3 + 2 = 5 + 12 + 2 = 19.
Или мы могли бы составить такое правило, что: 4) Вы всегда идете справа налево
Итак, 5 + 4×3 + 2 = 5 + 4×5 = 5 + 20 = 25.
Итак, какое правило лучше?
Ну, по многим причинам 3 лучше, а 1 и 4 — наихудшие. Но на самом деле мы, , могли бы обойтись с любым предоставленным, как только мы выберем тот, которого мы придерживаемся.
По многим причинам «Сначала умножение, потом сложение».
А как насчет скобок и скобок? Итак, вся причина, по которой у нас , скобок, а скобки указывают на то, что нам делать что-то в первую очередь.Они используются именно тогда, когда обычные правила — это , а не , что мы хотим сделать, поэтому мы добавляем их, чтобы указать, что что-то должно быть сделано в первую очередь.
Серьезно, если бы у нас было правило, что мы должны делать скобки на последние , вы можете видеть, что это не сработает. Как мы могли выразить «3 раза больше, чем 4 плюс 5», если у нас есть способ сказать «сначала сложите 4 и 5». «Сначала сложите 4 и 5» — это то, что 3x (4 + 5) означает .
Так почему мы сначала делаем умножение, а затем сложение? Или, если на то пошло, сначала силы, затем умножение и сложение?
Ну думаю это из-за «группировки».Когда мы добавляем вещи, мы группируем их, а не наборы единиц. 3 + 5 действительно означает «3 единицы, сгруппированные с 5, составляют 8 единиц». Когда мы множимся, мы группируемся по большим факторам, а не по маленьким единицам. 3×4 + 5×6 означает «у нас есть набор из 3 четверок и набор из 5 шестерок; это объединяет, и у нас есть 12 и 30, и мы объединяем их по единицам, чтобы получить 32». Я не знаю. Мне это кажется наиболее естественным способом. По-моему все равно ….
Я не знаю. Мне это кажется наиболее естественным способом. По-моему все равно ….
Итак, 3x (4 + 5) означает «хорошо, сначала мы специально группируем 4 и 5, а затем берем набор из 3 результатов из 9.Три девятки — это 27 дюймов.
И силы находятся в еще большей группировке.
Хорошо … так что насчет вычитания и деления.
Ну, сложение / вычитание — наоборот. 5 — 3 значит? + 3 = 5. Или, более алгебраически, 5 + [-3], где [-3] — это число, которое убирает 3. По сути, вычитание и сложение — это один и тот же уровень группировки. На самом деле не имеет значения, что вы сделаете в первую очередь. Я думаю, что мнемоника BODMAS не работает, так как с 3-4 +5 вы определенно не хотите, чтобы сложили 4 + 5, чтобы получить 3-4 + 5 = 3-7, прежде чем вычитаете.Вы действительно хотите подумать о том, чтобы вычитание складывалось с отрицательными числами 3–4 + 5 равно 3 + [-4] + 5, а теперь это просто сложение в любом порядке.
И аналогично деление, $ 8 \ div 4 $, является обратным умножению. $ 8 \ div 4 = 8 \ times \ frac 14 $.
Итак … нет. Различие между сложением и вычитанием не так важно, как все это. НО будьте осторожны. Если вы станете более наглым, будут случаться ошибки.
В любом случае, BODMAS — это просто вспомогательное средство памяти. На самом деле это не математическое правило.
развлекательной математики — BEDMAS, где порядок сложения перед вычитанием имеет значение?
Представьте себе мир, в котором BEDMAS не существует и где необходимо указать, в каком именно порядке оцениваются операции в выражении, используя круглые скобки. Допустимое выражение выглядит примерно так:
$$ ((a + b) \ times (c \ div (d — e))) $$
Посмотрите на это выражение. В нем четыре операции и четыре набора скобок. Каждый набор круглых скобок относится только к одной операции и наоборот.
$$ \ color {red} (\ color {orange} (3 \ color {orange} + 5 \ color {orange}) \ color {red} \ times \ color {blue} (6 \ color {blue} \ div \ color {# 00bf00} (9 \ color {# 00bf00} — 7 \ color {# 00bf00}) \ color {blue}) \ color {red}) $$
С этими круглыми скобками мы точно знаем, как вычислить это выражение. Результат этого выражения — 24 $.
Результат этого выражения — 24 $.
Теперь рассмотрим большое выражение. Что делать, если вы не хотите постоянно писать все эти скобки? Что, если вы хотите, чтобы большие выражения было легче читать? Не могли бы вы придумать способы уменьшить количество скобок и общих символов, которые вам нужны, чтобы полученное выражение оставалось однозначным? Что ж, математики сделали бы.И поэтому есть БЕДМЫ.
Сначала рассмотрим выражения, в которых используется только $ + $. Рассмотрим выражение $ ((a + b) + ((c + d) + e)) $. В этом выражении достаточно скобок для однозначного определения порядка операций. Но есть приятное свойство $ + $: для любых чисел $ a, b, c $ всегда так $ (a + b) + c = a + (b + c) $. Это называется законом ассоциативности . Теперь, если у нас есть несколько сумм сумм, мы можем просто опустить скобки между ними, потому что независимо от того, как вы их снова вставите, вы всегда получите один и тот же результат.Наше выражение упрощается до $ a + b + c + d + e $. Отлично, мы уже избавились от множества скобок.
Теперь давайте добавим $ \ times $ в бой. Закон ассоциативности также выполняется для $ \ times $, поэтому мы можем написать $ a \ times b \ times c \ times d \ times e $ вместо $ ((a \ times b) \ times ((c \ times d) \ раз е)) $. Теперь давайте посмотрим, что происходит, когда вы объединяете $ + $ и $ \ times $. Мы знаем, что $ a + (b \ times c) $ и $ (a + b) \ times c $ — разные выражения, поэтому мы не можем убрать круглые скобки в обоих случаях.Но вот новый закон: мы можем переписать $ (a + b) \ times c $ как $ (a \ times c) + (b \ times c) $. Это закон распределения . Это означает, что мы можем написать любое выражение, используя $ + $ и $ \ times $ как выражение, в котором вы всегда сначала выполняете все умножения, а только потом все сложения.
Как следствие, мы можем изобрести новый способ скрыть круглые скобки. В термине, где умножение и сложение находятся рядом друг с другом без скобок, мы согласны всегда сначала выполнять умножение. Это отличный способ, потому что, когда мы используем его, мы можем написать любой термин, используя $ + $ и $ \ times $, без каких-либо скобок!
Это отличный способ, потому что, когда мы используем его, мы можем написать любой термин, используя $ + $ и $ \ times $, без каких-либо скобок!
Пример:
Используя закон распределенности, мы можем переписать
$$ (a \ times (b + ((c + d) \ times (e + f)))) $$ к $$ ((a \ times b) + (((a \ times (c \ times e )) + (a \ times (c \ times f))) + ((a \ times (d \ times e)) + (a \ times (d \ times f))))) $$
Здесь много операторов, но если сначала договориться о умножении и запомнить закон ассоциативности, мы получим
$$ a \ times b + a \ times c \ times e + a \ times c \ times f + a \ times d \ times e + a \ times d \ times f $$
, который вообще не содержит скобок! Это не всегда было бы возможно, если бы мы выполняли вычисления слева направо или сложение перед умножением.
Теперь добавим вычитание. Во-первых, давайте вспомним, что слева от выражения стоит унарный знак минус, например $ -a $ — это сокращение для $ (0-a) $. Учитывайте срок сложения и вычитания:
$$ (a — (b — (c + (d — e)))) $$
Используя законы $ a + (b — c) = (a + b) — c $, $ ~ a — (b + c) = (a — b) — c $ и $ a — (b — c) = (ab) + c $, мы действительно можем переупорядочить эту последовательность операций так, чтобы скобки двигались как можно дальше влево, поэтому сложение и вычитание выполняются слева направо:
$$ ((((a — b) + c) + d) — e) $$
Итак, давайте просто согласимся, что сложение и вычитание без скобок выполняются слева направо.Получаем
$$ a — b + c + d — e $$
Это имеет то преимущество, что с этой нотацией вы можете фактически переписать вычитание как добавление отрицаний, используя унарный $ — $:
$$ a + (-b) + c + d + (-e) $$
Таким образом, этот метод делает термин намного более легким для чтения и понимания, и это позволяет нам намного проще переупорядочивать слагаемые в этой сумме.
Если мы хотим смешать умножение и вычитание, мы снова указываем, что умножение выполняется первым.
Теперь перейдем к разделению. Рассмотрим термин, смешивающий умножение и деление. Как и для сложения и вычитания, мы можем изменить порядок скобок так, чтобы операции выполнялись слева направо, используя совершенно аналогичные законы $ a \ times (b \ div c) = (a \ times b) \ div c $ , $ ~ a \ div (b \ times c) = (a \ div b) \ div c $ и $ a \ div (b \ div c) = (a \ div b) \ times c $.
Теперь мы согласны отказаться от скобок, когда операции фактически выполняются слева направо.Итак
$$ (a \ div (b \ times (c \ div (d \ div e)))) $$
становится
$$ ((((a \ div b) \ div c) \ times d) \ div e) $$
, который мы записываем как $$ a \ div b \ div c \ times d \ div e $$
Опять же, мы можем интерпретировать деление как умножение на обратное:
$$ a \ times (1 \ div b) \ times (1 \ div c) \ times d \ times (1 \ div e) $$
Так что с этим описанием намного проще работать, например, мы можем очень легко изменить его порядок.
Когда деление смешивается с сложением или вычитанием, мы говорим, что по умолчанию деление всегда выполняется первым.
Теперь обратите внимание, что термины, использующие $ \ div $, не всегда могут быть записаны без скобок, например $ a \ div (b + c) $.
Из-за этого математики фактически больше не используют символ $ \ div $. Вместо этого они используют обозначение дроби:
.
$$ a \ div b = \ frac {a} {b} $$. Приятно то, что мы можем рисовать горизонтальную линию посередине столько, сколько захотим, и что линия четко отделяет то, что находится над линией, от того, что под линией. Так что мы можем отбросить еще несколько скобок:
$$ a \ div (b + c) = \ frac {a} {b + c} $$
Сравните это с
$$ (a \ div b) + c = \ frac {a} {b} + c $$
Очевидно, мы можем заметить разницу.
Таким образом, мы можем написать любой термин, используя $ + $, $ — $, $ \ times $, $ \ div $, полностью без скобок!
Рассмотрим термин $ ((a + b) \ times (c \ div (d — e))) $ из начала моего ответа. Он имеет четыре набора круглых скобок, которых мы теперь технически можем избежать, используя правильную нотацию и расширяя с помощью закона распределения:
Он имеет четыре набора круглых скобок, которых мы теперь технически можем избежать, используя правильную нотацию и расширяя с помощью закона распределения:
$$ a \ times \ frac {c} {d — e} + b \ times \ frac {c} {d-e} $$
Обратите внимание, что это выражение обычно записывается как
$$ (a + b) \ times \ frac {c} {d — e} $$
, так как его на самом деле легче читать и понимать.В конце концов, у нас нет запретных скобок, мы просто нашли способы избежать их написания.
Теперь имейте в виду, что, поскольку никто вне школы на самом деле не использует $ \ div $, приоритет $ \ times $ и $ \ div $ на самом деле не известен общепринятым консенсусом. Это означает, что нам нужно использовать круглые скобки, когда $ \ div $ стоит перед $ \ times $, просто чтобы люди не запутались.
Теперь мы можем, наконец, взглянуть на термин на картинке вашего вопроса:
$$ 6-1 \ раз 0 + 2 \ div 2 $$
Если мы заменим круглые скобки по установленным нами правилам, мы получим
$$ ((6 — (1 \ times 0)) + (2 \ div 2)) = 7 $$
, который теперь должен быть совершенно однозначным.
Правила, которые мы установили, как вы уже могли догадаться, — это в точности BEDMAS (или, скорее, BDMAS, поскольку я не говорил об возведении в степень).
Обратите внимание, что если вы просто введете данный термин в калькулятор, вы не получите того же результата, потому что калькулятор оценивает операции в том порядке, в котором они вводятся, а не в порядке BEDMAS. Итак, калькулятор видит
$$ ((((6-1) \ times 0) + 2) \ div 2) = 1 $$
, что явно отличается от результата. Так что просто помните, что калькуляторы не умеют делать БЭДМЫ, и все готово.
Вот другое выражение:
$$ 24 \ дел 4 \ раз 3 $$
Каков результат этого выражения? По общему согласию, мы сначала делаем деление, но, опять же, технически мы должны были добавить скобки, потому что это соглашение не является общеизвестным. Или мы могли бы просто использовать обозначение дробей вместо $ \ div $, в этом случае мы получили бы два разных выражения:
Или мы могли бы просто использовать обозначение дробей вместо $ \ div $, в этом случае мы получили бы два разных выражения:
$$ \ frac {24} {4} \ times 3 \ neq \ frac {24} {4 \ times 3} $$
Итак, здесь мы можем ясно видеть предполагаемый порядок, и все снова в порядке.
Правило
PEMDAS — ChiliMath
Правило PEMDAS (аббревиатура от «Прошу прощения, дорогая тетя Салли») представляет собой набор правил, определяющих порядок вычислений, то есть какую операцию выполнять в первую очередь. В противном случае можно получить несколько или разные ответы. Мы не хотим, чтобы это произошло.
Ниже показан пример, в котором есть два возможных ответа. Первое решение дает неправильный ответ, поскольку вычисляет числовое выражение слева направо.В то время как второе решение является правильным, потому что оно следует правилам Порядка операций.
Упростите числовое выражение.
Неправильное решение:
Правильное решение:
Порядок операций
Шаг 1 : В верхней части списка помните, что ВСЕГДА упрощайте все внутри символов группировки. Примерами символов группировки являются круглые скобки (), квадратные скобки и фигурные скобки {}. Для вложенных группирующих символов проработайте это изнутри и снаружи.
Шаг 2 : Экспоненциальные выражения вычисляются или оцениваются перед выполнением любой из четырех основных арифметических операций, а именно: сложения, вычитания, умножения и деления.
Шаг 3 : Затем умножьте и / или разделите слева направо в зависимости от того, что наступит раньше, перед выполнением сложения и вычитания. Это говорит нам о том, что умножение и деление имеют более высокий уровень важности, чем сложение и вычитание.
Шаг 4 : Наконец, сложите и / или вычтите слева направо в зависимости от того, что идет раньше.
PEMDAS
PEMDAS — это мнемоническое устройство, которое может помочь нам запомнить уже известный порядок операций, который означает « P lease E xcuse M y D ear A Unt S союзник».
P — Круглые скобки
E — Показатели
M — Умножение
D — Раздел
A — Добавление
S операции умножения и деления имеют одинаковый уровень приоритета.Чтобы решить, когда умножать или делить, всегда выполняйте первое слева направо.
Таким же образом сложение и вычитание равны по важности. Выполните первую операцию слева направо.
Примеры применения правила PEMDAS
Пример 1 : Упростите следующее выражение, используя Порядок операций.
Решение : Обратите внимание, что здесь задействованы три операции.В зависимости от порядка операций умножение имеет приоритет перед сложением и вычитанием, поэтому мы будем умножать в первую очередь. Затем вычтите, затем добавьте, так как операция вычитания выполняется перед сложением слева направо.
Пример 2 : Упростите следующее выражение, используя Порядок операций.
Решение : символ группировки имеет наивысший приоритет, что означает, что мы должны сначала упростить все внутри. В скобках указаны операции деления и умножения.Поскольку они имеют одинаковую важность, порядок их появления слева для записи будет определять, что будет первым. В этом случае мы сначала делим, а затем умножаем.
После упрощения выражения внутри скобок у нас останется вычитание и деление. Очевидно, что деление должно быть вычислено перед вычитанием.
Пример 3 : Упростите следующее выражение, используя Порядок операций.
Решение : упростите выражение в скобках, затем оцените степени (члены с показателями).После этого у нас будет более простое выражение, включающее сложение, умножение и деление. Просматривая слева направо, мы видим, что сначала нужно умножить, затем разделить и, наконец, сложить.
Вас также может заинтересовать:
Порядок операций
Порядок операций
Если у вас есть математическая задача, которая включает более одной операции, например, сложение и вычитание или вычитание и Умножение ? Что делать в первую очередь?
Пример 1 : 6? 3 х 2 =?
- Вы делаете сначала вычитание (6? 3 = 3), а затем умножение (3 x 2 = 6 )?
- Или вы начнете с умножения (3 x 2 = 6), а затем вычтите (6? 6 = 0 )?
PEMDAS
В подобных случаях мы следуем порядку операций . Порядок, в котором должны выполняться операции, сокращенно обозначается как PEMDAS :
Порядок, в котором должны выполняться операции, сокращенно обозначается как PEMDAS :
- P аренты
- E xponents
- M ultiplication и D ivision (слева направо) A ddition и S ubtraction (слева направо)
(Один из способов запомнить это — вспомнить фразу P lease E xcuse M y D ear A Unt S союзник.)
- В приведенном выше примере мы имеем дело с умножением и вычитанием. Ультипликация M идет на шаг перед убиранием S , поэтому сначала мы умножаем 3 x 2, а затем вычитаем сумму из 6, получая 0.
Пример 2 : 30 5 x 2 + 1 =?
- Нет арентезов P .
- Нет компонентов E .
- Начнем с ultiplication M и D ivision, работая слева направо.
ПРИМЕЧАНИЕ: Несмотря на то, что умножение предшествует делению в PEMDAS, они выполняются в одном шаге слева направо. Сложение и вычитание также выполняются на одном этапе. - 30 5 = 6 , в результате чего 6 x 2 + 1 =?
- 6 x 2 = 12 , в результате чего 12 + 1 =?
- Затем мы выполняем сложение A : 12 + 1 = 13
Обратите внимание, что если бы мы выполняли умножение до деления, то получили бы неправильный ответ:
- 5 x 2 = 10 , оставляя 30 10 + 1 =?
- 30 10 = 3 , оставляя 3 + 1 =?
- 3 + 1 = 4 (меньше на 9!)
Последний пример для продвинутых студентов, использующий все шесть операций:
Пример № 3 : 5 + (4? 2) 2 х 3 6? 1 =?
- Начните с P арентезов: 4? 2 = 2 .(Несмотря на то, что вычитание обычно выполняется на последнем шаге, потому что оно указано в скобках, мы делаем это в первую очередь.) Остается 5 + 2 2 x 3 6? 1 =?
- Тогда E xponents: 2 2 = 4 .



