Умножения двузначных чисел в уме – искусство счета

Люди всегда стремились найти лучшие способы выполнения вычислений. Чем стремительнее развивается прогресс, тем более актуальными становятся высокие математические способности. Даже тот человек, карьера которого не предполагает работу с цифрами, ежедневно вынужден прибегать к счету в уме. Походы за покупками, оплата коммунальных счетов, планирование семейного бюджета – все это требует большого количество подсчетов. Конечно, можно полагаться на технику, ведь в каждом современном смартфоне присутствует калькулятор. Но все же стоит помнить, что умение быстро считать – это возможность существенно оптимизировать свои собственные ресурсы, поэтому развивать такие навыки важно.

Умножение в уме

В современном мире цифры окружают нас везде. Ежедневно мы не задумываясь выполняем десятки и даже сотни простых арифметических действий, но, стоит только столкнуться с более сложными числовыми операциями, и большинство людей машинально потянется к калькулятору. Мало кто хочет тратить время на сложные подсчеты в уме, когда с помощью информационных технологий произвести их можно за считанные секунды. Но что делать, если смартфона, калькулятора или листа бумаги с ручкой нет, а что-то посчитать нужно срочно? На помощь приходят методы счета в уме.

Складывать и вычитать устно – этому человек учится еще в школе. Со временем, удается научиться без труда производить вычисления даже с большими значениями. Конечно, это утверждение справедливо только для простых операций, таких как сложение и вычитание, а вот умножение освоить уже не так легко. В школе от детей требуется научиться умножать только на множитель от одного до десяти, а более сложные подсчеты допустимо производить на бумаге. Таким образом, ученикам не прививается умение выполнять умножение больших чисел в уме, этим навыкам можно обучиться только дополнительно.

Умение быстро считать очень полезно, так как оно используется ежедневно. Поэтому сегодня придумано множество подходов к счету. Чаще всего люди используют различные математические приемы, которые позволяют производить умножение устно. Они имеют свои плюсы и минусы, но все же позволяют получить правильный ответ без использования подручных средств. Чтобы определить, насколько эти способы эффективны и продуктивны в повседневных реалиях, нужно рассмотреть каждый из них отдельно.

Популярные методы устного умножения

Сегодня существует сразу несколько способов умножения в уме. Они не универсальны, но позволяют достаточно успешно производить операции с двузначными числами. Чтобы подобрать для себя оптимальный, лучше ознакомиться с самыми популярными из них:

Вариант 1. Умножение в столбик

Этот вариант отлично подходит тем, кто способен хорошо запоминать и удерживать в памяти сразу несколько промежуточных результатов вычислений. Благодаря этому подходу можно легко производить операции между двузначными числами. Рассмотрим данный вид счета на примере выражения 34*63.

Сначала необходимо умножить 34 на единицы второго числа: 34*3=102. Запоминаем это значение. Затем повторяем операцию уже с десятками множителя: 34*60=2040. Теперь требуется просто сложить результаты наших вычислений: 102+2040=2142

Вариант 2. Умножение с разложением на десятки и единицы

Этот вариант также требует хорошей памяти. Рассмотрим его на примере прошлого выражения 34*63.

Сначала требуется разложить числа на десятки и единицы, у нас получится: (30+4)*(60+3). Далее мы перемножаем между собой десятки: 30*60=1800. Запоминаем этот результат. Затем необходимо умножить десятки первого значения на единицы второго и наоборот: (30*3)+(60*4)=330. Теперь наступает самая сложная часть, главное – не сбиться. Нам нужно сложить результаты наших первых двух примеров и прибавить к ним произведение единиц перемножаемых чисел. Получится следующее выражение: 1800+330+4*3=2142.

Вариант 3. Умножение с большими числами

Этот вид вычислений больше подходит для тех двузначных чисел, которые близки к 100. Рассмотрим этот способ на примере выражения 88*95.

Сначала нужно представить каждое из этих значений как разность 100 и другого числа: 100-a=88 и 100-b=95, a=12, b=5. Так у нас получится (100-12)*(100-5). Теперь нужно произвести следующие вычисления: 88-b и 95-a, 88-5 и 95-12, получится 83 в обоих случаях. Это значение нужно запомнить. Теперь нам нужно найти a*b=12*5=60. Наш итоговый ответ будет состоять из четырех цифр от полученных ранее ответов: 83 и 60, получается 8360.

Иногда в результате подсчетов получается, что второе итоговое значение имеет три знака, а не два. Допустим, у нас получились числа 12 и 345. В этом случае нужно сложить вторую и третью цифру так, чтобы получилось 1545.

Это основные методы устного умножения. Но можно ли их назвать простыми? Несмотря на то, что при усердных тренировках удастся освоить любой из этих подходов, все же они будут требовать хорошей памяти и высокой концентрации. К тому же, не всегда допустимо проводить операции с многозначными числами с помощью данных методов. Лучше постараться найти для себя другие, более простые способы счета.

Быстрое умножение в уме больших чисел

Математики всех времен искали простые методы быстрого устного счета. Умножение и деление, в отличие от сложения и вычитания, являются более сложными операциями. Поэтому производить такие подсчеты в уме без должной подготовки сложно, тем более когда речь идет о многозначных числах. Проблема устного умножения в том, что не существует какого-либо универсального способа, который бы подходил вне зависимости от ситуации.

Мозг обычного человека не способен работать также быстро, как калькулятор. Мы склонны терять концентрацию, сбиваться, забывать результаты промежуточных операций. Поэтому стандартные способы устного умножения мало пригодны для повседневных задач. Они скорее являются хорошей разминкой для мозга, чем удобным инструментом. Но что делать, если быстро считать без подручных средств все же хочется?

Благодаря интернету можно найти немало информации по этому вопросу. Сегодня существует множество методик, позволяющих научиться складывать, вычитать, умножать и даже делить с моментальной скоростью. Но самым популярным направлением устного счета является ментальная арифметика. Ее неоспоримым плюсом является то, что она дается детям даже легче, чем взрослым.

Лучший способ научиться устному счету

Ментальная арифметика – это не только уникальный способ счета без подручных средств. В основе этой методики лежит равнозначное развитие как левого полушария мозга, отвечающего за логику и анализ, так и правого, которое контролирует работу воображения и фантазии. Несмотря на то, что освоить ментальную арифметику может любой желающий, она все же больше подходит для изучения в раннем возрасте. Именно в детстве можно приобрести навыки, которые не забудутся со временем и сохранятся на всю жизнь.

Обучение ментальной арифметике – длительный процесс, который требует усидчивости и нацеленности на результат. Пройдет немало времени, пока ребенок сможет полностью освоить программу и научиться не только складывать и вычитать, но и умножать и делить многозначные числа. Родителям не всегда удается контролировать периодичность занятий своего ребенка, а также следить за тем, чтобы он выполнял все необходимые упражнения. Этим обусловлен рост популярности групповых занятий ментальной арифметикой в центрах дополнительного развития детей.

Ученики, обучающиеся по этому направлению, сначала осваивают вычисления на древних счетах – абакусе. Когда базовые навыки закрепятся, наступает время для перехода к следующему, более сложному этапу. Теперь ученик постепенно привыкает представлять абакус в своем воображении и производить подсчеты уже на нем. Именно так и удается развить навык быстрого счета.

Благодаря занятиям ментальной арифметикой ребенок повышает успеваемость в школе, ведь теперь ему доступны не только простые вычисления в уме, но и быстрое умножение и деление. Количество времени, которое он тратит на выполнение домашних заданий, также сокращается. Так удается добиться большей продуктивности образовательного процесса в школе и дома. Навыки, приобретенные благодаря ментальной арифметике, сохранятся навсегда, что очень пригодится во взрослой жизни.

Как быстро умножать двузначные числа в уме?

Умение мгновенно считать в уме может стать бесценным подспорьем в работе и в условиях скоростных темпов жизни современного человека.

Как быстро умножать большие числа, как овладеть такими полезными навыками? У большинства вызывает затруднения устное перемножение двузначных чисел на однозначные. А о сложных арифметических расчетах и говорить нечего. Но при желании способности, заложенные в каждом человеке, можно развить. Регулярные тренировки, немного усилий и применение, разработанных учеными, эффективных методик позволят достичь потрясающих результатов.

Выбираем традиционные методы

Проверенные десятилетиями способы перемножения двузначных чисел не теряют своей актуальности. Простейшие приемы помогают миллионам обычных школьников, учащихся специализированных ВУЗов и лицеев, а также людям, занимающимся саморазвитием, усовершенствовать вычислительное мастерство.

Умножение с помощью разложения чисел

Наиболее легким способом, как быстро научиться умножать большие числа в уме, является перемножение десятков и единиц. Сначала умножаются десятки двух чисел, затем поочередно единицы и десятки. Четыре полученных числа суммируются. Для использования этого метода важно уметь запоминать результаты перемножения и складывать их в уме.

Например, для умножения 38 на 57 необходимо:

• разложить число на (30+8)*(50+7);
• 30*50 = 1500 – запомнить результат;
• 30*7 + 50*8 = 210 + 400 = 610 – запомнить;
• (1500 + 610) + 8*7 = 2110 + 56 = 2166

Естественно, необходимо отлично знать таблицу умножения, так как быстро умножать в уме этим способом не удастся без соответствующих умений.

Умножение в столбик в уме

Визуальное представление привычного перемножения в столбик многие используют при расчетах. Этот метод подойдет тем, кто умеет надолго запоминать вспомогательные числа и выполнять с ними арифметические действия. Но процесс значительно упрощается, если вы научились, как быстро умножать двузначные числа на однозначные. Для перемножения, например, 47*81 нужно:

• 47*1 = 47 – запомнить;
• 47*8 = 376 – запоминаем;
• 376*10 + 47 = 3807.

Запоминать промежуточные результаты поможет проговаривание их вслух с одновременным суммированием в уме. Несмотря на сложность мысленных вычислений, после непродолжительных тренировок этот метод станет вашим любимым.

Приведенные выше способы умножения универсальны. Но знание более эффективных алгоритмов для некоторых чисел намного сократит количество расчетов.

Умножение на 11

Это, пожалуй, самый простой способ, который используется для умножения любых двузначных чисел на 11.

Достаточно между цифрами множителя вставить их сумму:
13*11 = 1(1+3)3 = 143

Если в скобках получается число больше 10, то к первой цифре добавляется единица, а из суммы в скобках вычитается 10.
28*11 = 2 (2+8) 8 = 308

Умножение больших чисел

Очень удобно перемножать числа, близкие к 100 разложением их на составляющие. Например, необходимо умножить 87 на 91.

• Каждое число необходимо представить как разницу 100 и еще одного числа:
  (100 — 13)*(100 — 9)
  Ответ будет состоять из четырех цифр, две первые из которых – разница первого множителя и вычитаемого из второй скобки или наоборот – разница второго множителя и вычитаемого из первой скобки.
  87 – 9 = 78
  91 – 13 = 78
• Вторые две цифры ответа — результат перемножения вычитаемых из двух скобок.13*9 = 144
• В результате получаются числа 78 и 144. Если при записывании окончательного результата получается число из 5 цифр вторую и третью цифру суммируем. Результат: 87*91 = 7944.

Это самые простые способы перемножения. После многократного их применения, доведения вычислений до автоматизма можно осваивать более сложные техники. И через некоторое время проблема, как быстро умножить двузначные числа перестанет вас волновать, а память и логика существенно улучшатся.

умножаем большие числа в уме — Блог Викиум

В эру цифровых технологий у нас пропала необходимость запоминать телефоны и адреса, считать в голове. Даже ориентироваться на местности нам помогают гаджеты. Устный счет последний раз мы применяем в школе, а зря. Помимо удобства (ведь вы можете сами быстро все посчитать, не доставая смартфон), умение быстро умножать и делить здорово тренирует мозг. А если мозг не тренировать, он ленится, что приводит к ухудшению всех его функций и нашей продуктивности. Еще до времен повсеместного распространения вычислительных машин люди изобрели несколько лайфхаков устного счета. Рассмотрим их подробнее.

Гаусс — не только распределение

Еще когда будущий «король математиков» и автор закона, названного его именем, Карл Фридрих Гаусс отличался уникальными навыками. По легенде, примерно в возрасте 3 лет он заметил, что платежные ведомости его отца рассчитаны неправильно. После проверки оказалось, что мальчик был прав. В дальнейшем он продемонстрировал феноменальные математические способности. И некоторые лайфхаки устного счета называют тоже его именем.

Достаточно одной таблицы

Чтобы научиться перемножать любые числа, нам необходимо помнить таблицу умножения. Хитрость заключается в том, что любое большое число можно разложить на маленькие — те, что представлены в этой таблице. Суть умножения двух чисел заключается в многократном повторении одного из них. Например, 7 умножить на 3 — означает, что число 7 надо повторить 3 раза: 7+7+7 = 7*3 = 21.

Если перед нами стоит задача умножить однозначное число на многозначное, то достаточно разложить больше на маленькие по разрядам, т.е. сначала сотни, потом десятки, потом единицы. И по очереди их умножить на заданное число. Далее останется сложить эти произведения. Например, 254*7 = 200*7 + 50*7 + 4*7 = 1400 + 350 + 28 = 1778. Как мы видим, каждый разряд представляет собой однозначное число с определенным количеством нулей. Таким образом, нам нужно лишь помнить таблицу умножения, чтобы легко справиться с этой задачей.

Этот же способ применим для умножения двух двузначных чисел — их нужно так же разбить на однозначные и выполнить операцию последовательно. Допустим, наша задача умножить 67 на 43. 43 — это 40 + 3. А значит, 67 нужно умножить сначала на 40, затем на 3, и сложить эти произведения. Далее раскладываем 67 и производим ту же операцию. Получаем: 67*40 + 67*3 = 60*40 + 7*40 + 60*3 + 7*3 = 2400 + 280 + 180 + 21 = 2881.

Одиннадцать друзей умножения

Самый простой и интересный способ умножения двузначного числа — с использованием числа 11. Нужно всего лишь сложить между собой цифры, из которых состоит двузначное число. А по бокам поставить те же самые исходные 2 числа, которые мы складывали. Что получится, если 35 умножить на 11? Складываем 3 + 5 = 8, а по бокам ставим 3 и 5 — 385. Проверяем на калькуляторе. Но что делать, если сумма двух этих чисел больше 10? Куда что ставить? Нужно сделать все ровно так же, только при помощи наложения. Посмотрим на примере 83*11: 8 + 3 = 11. Посередине у нас стоит 11, справа 3, а к первому месту прибавляется 8, итого: 8 + 1 = 9 — это первое число. Далее у нас стояла единица, последней тройка. Собираем: 913. Проверяем. Вуаля!

Лайфхаки не тренировка

Конечно, само слово «лайфхак» подразумевает, что мы используем определенный прием, чтобы меньше напрягать мозг. При таком счете мозг тоже тренируется — ведь нам надо удерживать всю раскладку в голове, да еще и складывать эти элементы. Чтобы быстро выучить эти методики, а также дополнительно поддерживать функции мозга в тонусе, нам нужны полноценные тренировки. Они позволят освоить еще больше лайфхаков, быстро адаптироваться в незнакомых ситуациях и не теряться при виде больших данных.

Викиум разработал более 75 специальных — когнитивных тренажеров. Они развивают базовые (когнитивные) функции мозга комплексно, по запатентованной технологии. Программа составляет вам персональный план тренировок, следит за прогрессом, постепенно повышает нагрузку. Сами тренажеры выглядят как игровые задания с понятным интерфейсом — на них могут заниматься даже дети от 7 лет. В результате регулярных тренировок существенно увеличивается работоспособность мозга и ваша общая продуктивность. Занимайтесь каждый день всего по 10 минут и будьте в тонусе!

6 традиционных МЕТОДОВ УМНОЖЕНИЯ В УМЕ – выбери лучший!

Нам предстоит изучить только лучшие способы перемножения двухзначных чисел. Статья содержит наиболее распространенные и потому эффективные приёмы. В результате они позволят вам научиться умножать двухзначные числа в уме в разы быстрее. 

Способ №1 – разложение числа на десятки и единицы

Наиболее легким и понятным является методика перемножения двухзначных чисел из школьной программы. Суть этого способа заключается в разбиении множителей на десятки и единицы. Далее получившиеся четыре числа перемножаются между собой. Метод простой, но для его использования необходимо умение запоминать одновременно несколько числовых значений и производить с ними арифметические расчеты.

Например: 54*73 = (50+4)*(70+3) = 50*70 + 50*3 + 4*70 + 4*3 = 3500+150+280+12 = 3942

Проще всего подобные примеры решать в три действия. В первом действии перемножаются десятки, во втором — единицы с десятками и суммируются между собой, а в третьем действии к полученной сумме прибавляется произведение единиц.

Это выглядит так:
1. 50*70 = 3500 – запомнить в уме
2. 50*3+4*70 = 430 – запомнить в уме
3. (3500+430)+3*4 = 3942 – итоговый результат

Для того чтобы за максимально короткое время решать такие примеры, необходимо обладать достаточно прочными знаниями таблицы умножения и уметь суммировать однозначные и двузначные числа, а также обладать способностью быстрого переключения внимания между производимыми расчетами, запоминая их в уме. Этот навык можно натренировать с помощью визуального представления совершаемых арифметических вычислений. Как он осуществляется? При помощи представления картинки вашего решения и получившихся промежуточных результатов.

Как видно из примера, эту методику умножения нельзя назвать самой простой и эффективной, поэтому следует иметь в виду и другие, альтернативные ей способы.

Способ №2 – арифметические подгонки

Среди вариантов вычислений в уме этот способ можно считать одним из наиболее распространенных. Подгонка примера применяется в случае, если необходимо быстро вычислить примерный или точный результат. Этот способ наиболее широко применяется в школах и высших учебных заведениях с математическим уклоном. Школьников и студентов обучают искать наиболее простые алгоритмы вычислений. Далее представлено несколько примеров таких подгонок:
Подгонка примеров к соответствующему виду считается очень популярным способом подсчетов в уме. Она применяется, когда вам требуется в короткие сроки определить приблизительный или правильный ответ. Школьников и студентов обучают искать наиболее удобные алгоритмы вычислений для разнообразных задач. Варианты подгонок представлены ниже:

Пример 49*49 решается следующим образом: (49х100) / 2 — 49. В первую очередь 49 умножается на сто – 4900. Потом 5900 делится на два – 2450. Из полученного результата вычитается 49. В итоге получается 2401.

Произведение чисел 56х92 вычисляется следующим образом: 56х100-56х2х2х2. Из этого следует: 56х2 = 112х2 = 224х2 = 448. Далее из 5600 вычитается 448, получается 5152.

Подобный вариант решения может быть применим только тогда, когда вы способны в уме умножать двузначные и однозначные числа и запоминать все полученные результаты. Помимо этого, приходится постоянно подбирать правильный алгоритм решения каждого примера и следить за его соблюдением.

Вывод. Этот способ отлично подходит для тренировки умственных способностей и памяти, но вероятность получить неверный результат из-за неправильно выбранного алгоритма решения значительно выше, чем при применении способа №1.

Способ №3 — визуальное представление в уме перемножения в столбик

56х67 – произведем расчеты в столбик.

Сложность такого умножения заключается в необходимости постоянно держать в памяти несколько вспомогательных чисел, а количество арифметических действий значительно больше, чем у других методов. Но произведение расчетов можно сделать значительно проще. В ЭТОЙ статье мы говорили о важности умения быстро перемножать однозначные числа с двузначными. Если вы уже научились это делать, то вычислить в столбик в уме для вас не составит труда. Порядок действий следующий:

1. 56х7=350 + 42 = 392 – запоминаем.
2. 56х6 = 300 + 36 = 336 — запоминаем.
3. 336х10 + 392 = 3360 + 392 = 3752 – это уравнение сложнее, но вычисление можно сделать проще путем проговаривания числа, которое не вызывает у вас трудностей. Пока вы проговариваете, суммируйте 360 и 392.

В итоге мысленные вычисления в столбик напрямую сложны, но можно значительно упростить этот процесс, если натренировать способность быстрого перемножения двузначных и однозначных чисел. Проще говоря, умножение в столбик является более сложной вариацией способа №1. Что лучше – выбирать вам.

Главным плюсом 3-х способов перемножения двухзначных чисел для устного счета в уме, приведенных выше, является их универсальность — они могут применяться для различных вычислений. Имея достаточно навыка устных вычислений, и зная эти способы, вы сможете найти правильное решение соответствующей задачи. Но при использовании правильных алгоритмов решения, можно значительно сократить количество выполняемых при решении в уме действий.

Способ 4. При умножении на 11

Наиболее простым является умножение любого двухзначного числа на 11. Для вычисления между первыми двумя цифрами множителя, отличного от 11, ставится сумма этих чисел.
Например, при умножении 14 на 11,между 1 и 4 вставляем сумму этих чисел (1+4). В итоге получается: 14*11 = 1 (1+4) 4 = 154.
Если центральные цифры в сумме дают результат больше десяти, то к первой цифре следует добавить единицу, а вторую цифру надо заменить суммой цифр умножаемого числа с вычетом 10.

Например: 56*11 = 5 (5+6) 6 = 5 (11) 6 = 616.

Этот способ можно использовать для умножения на 11 любых двухзначных чисел. Можно привести дополнительные примеры:

73 * 11 = 7 (7+3)3 = 803
45 * 11 = 4 (4+5) 5 = 495

Быстро производить умножение двухзначных и любых других чисел на одиннадцать в уме легко.

Формулы сокращенного умножения: квадраты суммы и разности

Для возведения в квадрат двухзначных чисел хорошо подходят формулы квадратов суммы и разницы.

К примеру:
14²= (10+4)² = 10² + 4*2*10 + 4² = 100+80+16 = 196
78² = (80-2)² = 80² – 80*2*2 + 2² = 6400-320+4 = 6084

Способ 5. Возведение в квадрат чисел, которые заканчиваются на 5

Числа, заканчивающиеся на пять, возводятся в квадрат по очень простому алгоритму. Числа до конечной 5-ки умножаются на это же число, и добавляется единица. К оставшемуся числу прибавляется число 25.

35² = (3*(3+1)) 25 = 1225
45² = (4*(4+1)) 25 = 2025
75² = (7*(7+1)) 25 = 5625

Такой же алгоритм применяется для более сложных примеров:

355² = (35*(35+1)) 25 = (35*36)25 = 126025

Способ 6. Умножение чисел до 20

Этап № 1. В качестве примера будем использовать числа 15 и 19. К одному из чисел добавляем количество единиц другого. Получаем: 15+9=24
Этап № 2. Полученное число нужно умножить на 10. Получаем: 24*10=240
Этап № 3. Далее получившееся число складываем с произведением единиц 15 и 19 – 240+5*9=285
Данный пример можно «сократить» в записи:
15*19 = (15+9)*10+5*9 = 285

Доказать верность этого метода можно следующим образом: 15*19 = (10+5)*(10+9) = 10*10+10*5+10*9+5*9 = 10*(10+5+9) +5*9.

Фактически этот метод представляет собой способ применения для расчетов опорных чисел. В конкретном примере опорным числом является десятка. Последнее выражение наглядно показывает, что именно на это число мы и умножали расположенное внутри скобки. Вместо десяти опорным числом может выступать и любое другое число. Наиболее удобными принято считать числа 100, 50, 25 и 20. В ЭТОЙ статье более подробно рассматривается использование опорных чисел. Здесь же приведем только ознакомительное описание этой темы.

Применим методику опорного числа для перемножения чисел 14 и 16. Тут, так же как и в прошлом примере, удобнее будет использовать 10-ку как опорное число. 14 больше десяти на 4, а 16 – на 6. Для определения произведения этих чисел нужно произвести следующие действия:

К одному из множителей прибавляется число, на которое второй множитель больше опорного. А именно, 6 — к 14, или 4 — к 16 (не делайте этого одновременно!). В обоих случаях получается одно и то же: 20. Затем 20 умножаем на опорное число, то есть на 10. Результат: 200.
К 200 прибавляем произведение 4*6. Ответ: 224.

Похожие статьи

Please enable JavaScript to view the comments powered by Disqus.

Как быстро умножать числа без калькулятора

Не любишь математику? Ты просто не умеешь ею пользоваться! На самом деле, это увлекательная наука. И наша подборка необычных методов умножения подтверждает это.

Умножай на пальцах, как купец

Этот метод позволяет умножать числа от 6 до 9. Для начала согни обе руки в кулаки. Затем на левой руке отогни столько пальцев, на сколько первый множитель больше числа 5. На правой проделай то же самое для второго множителя. Посчитай количество разогнутых пальцев и умножь сумму на десять. А теперь перемножь сумму загнутых пальцев левой и правой руки. Сложив обе суммы, получишь результат.

Пример. Умножим 6 на 7. Шесть больше пяти на один, значит на левой руке отгибаем один палец. А семь – на два, значит на правой – два пальца. В сумме – это три, а после умножения на 10 – 30. Теперь перемножим четыре загнутых пальца левой руки и три – правой. Получим 12. Сумма 30 и 12 даст 42.

Вообще-то здесь речь идет о простой таблице умножения, которую хорошо бы знать наизусть. Но этот метод хорош для самопроверки, да и пальцы размять полезно.

Умножай, как Ферроль

Этот способ получил название по фамилии немецкого инженера, который им пользовался. Метод позволяет быстро перемножить числа от 10 до 20. Если потренируешься, то сможешь делать это даже в уме.

Суть простая. В итоге всегда будет получаться трехзначное число. Так что сначала считаем единицы, потом – десятки, затем – сотни.

Пример. Умножим 17 на 16. Чтобы получить единицы, умножаем 7 на 6, десятки – складываем произведение 1 и 6 с произведением 7 и 1, сотни – умножаем 1 на 1. В итоге получим 42, 13 и 1. Для удобства запишем их в столбик и сложим. Вот и итог!

Умножай, как японец

Этот графический способ, которым пользуются японские школьники, позволяет легко перемножить двух- и даже трехзначные числа. Чтобы опробовать его, приготовь бумагу и ручку.

Пример. Умножим 32 на 143. Для этого нарисуем сетку: первое число отразим тремя и двумя линиями с отступом по горизонтали, а второе – одной, четырьмя и тремя линиями по вертикали. В местах пересечения линий поставим точки. В итоге у нас должно получиться четырехзначное число, поэтому условно разделим таблицу на 4 сектора. И пересчитаем точки, попавшие в каждый из них. Получаем 3, 14, 17 и 6. Чтобы получить ответ, лишние единички у 14 и 17 прибавим к предыдущему числу. Получим 4, 5 и 76 – 4576.

Умножай, как итальянец

Еще один интересный графический способ используется в Италии. Пожалуй, он проще японского: точно не запутаешься при переносе десятков. Чтобы перемножить большие числа с его помощью, нужно начертить сетку. По горизонтали сверху записываем первый множитель, а по вертикали справа – второй. При этом на каждую цифру должна приходиться одна клетка.

Теперь перемножим цифры каждого ряда на цифры каждой колонки. Результат запишем в клетку (разделенную надвое) на их пересечении. Если получилось однозначное число, то в верхнюю часть клетки пишем 0, а в нижнюю – полученный результат.

Осталось сложить все числа, оказавшиеся в диагональных полосках. Начинаем с нижней правой клетки. Десятки при этом прибавляем к единицам в соседнем столбике.

Вот как мы умножили 639 на 12.

Весело, правда? Нескучной тебе математики! И помни, что гуманитарии в ИТ тоже нужны!

Эта инструкция научит вас умножать тысячи в уме. Сколько будет 5185 на 8018?

В школе всё время слышал «где мне пригодится эта математика?».

И сам задавался таким вопросом. А сейчас вот не хватает учебника для «раскачки» извилин. Например, было бы заметно удобнее считать утерянные цены на Apple или выравнивать пиксельную сетку для иллюстраций.

Но не всё потеряно. Умножать числа в любом возрасте считают проверенным способом подточить ум и даже улучшить психическое здоровье.

Ниже расскажу, где оно ещё может пригодиться и что за секретный способ умножения прокачает ваше знание цифр до уровня интуиции.

Крупный счёт прокачает решение бытовых вопросов

Как любому компьютеру нужно расширять оперативную память, так и нашему мозгу нужен отсек для быстрых операций.

Тренировки с умножением укрепят краткосрочную память. Вы перестанете забывать, закрыли ли дверь на ключ, сколько яиц лежало в холодильнике перед походом в магазин и о чём вели речь после того, как отвлеклись.

Не говоря о том, что будете мгновенно считать, во сколько обойдётся вон тот сочный кусок мяса на шашлык или заправка автомобиля, чтобы доехать до соседнего города.

Вам нужна только математика начальной школы

Чтобы умножать без бумаги, нужно на уровне рефлекса освоить два навыка:

I. Знать таблицу умножения
II. Складывать числа

Пункты важны, потому что будете десятки раз повторять операции. Получается просто, но много.

Отточить умножение поможет приложение УмноЖатель

Уделяйте тренировке не больше пяти минут за подход. Потом запоминать сложнее, а после тройки долгих сессий цифры начнут раздражать.

Быстро складывать получится точно таким же постоянным запоминанием.

Почти нигде не просят знать таблицу сложения, а она есть. Если до десяти цифры знают почти все, то после этого порога начинается ступор.

На лету вспомнить, какое число будет в следующем десятке полезнее в жизни, чем любое другое вычисление. Поэтому качайте и запоминайте.

Ещё один способ сложения, которого некоторые стесняются – довод до десятка. Это когда к одному числу сначала добавляют до круглого значения часть из второго, а потом плюсуют остаток:

8+5 = 8+2+3 = 10+3 = 13

В этом способе нет ничего стыдного, он эффективен, и с практикой доводится до автоматизма.

Когда научитесь на лету умножать и складывать элементарные значения, вставайте на продвинутый уровень: расчёты четырёхзначных чисел.

Операции с умножением тысячей в уме можно разделить на два типа: умножение на однозначные и многозначные числа.

Как умножить тысячи на однозначное число

Чтобы получить ответ на, допустим, пример 3864∙7, вам поможет система Разбить-умножить, разбить-сложить.

Так выглядит алгоритм:

1. Разбиваем большое число на единицы, десятки, сотни и так далее.

3864 = 3000 + 800 + 60 + 4

2. Умножаем каждый кусочек на второе число.

3000∙7 = 21000 | 800∙7 = 5600 | 60∙7 = 420 | 4∙7 = 28

3. Разбиваем результаты на простые группы одного размера.

21000 = 20000+1000 | 5600=5000+600 | 420 = 400+20 | 28 = 20+8

20000 | 1000+5000 | 600+400 | 20+20 | 8

4. Складываем группы с конца.

20000 + 1000+5000 + 600+400 + 20+20 + 8

20000 + 6000 + 1000 + 40 + 8

27048

Хотя на бумаге способ получается долгим, через несколько дней тренировка даст заметные результаты в скорости. У вас улучшится краткосрочная память, и вместимость чисел для сложения постепенно увеличится.

Важнее всего не потерять куски при последнем сложении. Этот этап доведёте до автомата постоянной практикой.

Отличие метода от привычного столбика в том, что мы постоянно дробим элементы на лёгкие частицы, которые быстро складываются.

Как умножить тысячи на многозначное число

Здесь поможет система Якова Трахтенберга. Во время заключения нацистами математик нашёл способ счёта особо крупных чисел в уме.

Предупреждаю, что способ подойдёт только тем, кто наработал краткосрочную память на большой массив чисел. Поскольку вам придётся долго держать остаток в уме и параллельно делать десяток сложений.

Запомните метод как Принцип снежинки.

В качестве примера решим 5362∙2934. Алгоритм такой:

0. Представьте числа привычным столбиком.

1. Перемножьте конечные (2∙4) цифры сверху и снизу.

Предпоследнюю цифру при наличии держим в уме (0), последнюю отправляем в результат (8): ** *** **8.

2. Перемножьте предпоследнюю цифру верхнего числа на последнюю нижнего (6∙4) и наоборот (3∙2).

Сложите результаты с тем, что храните в уме (24+6+0=30).

Держим остаток (3), а последнее число ставим в итог слева от предыдущего (0): ** *** *08.

3. Умножьте вторую цифру верхнего числа на последнюю нижнего (3∙4) и наоборот (9∙2).

Сложите результаты (12+18=30), а к ним добавьте умноженные друг на друга третьи цифры (6∙3) и остаток в уме (30+18+3=51).

Получили десяток в уме (5) и третью с конца цифру (1): ** *** 108.

4. Умножьте первую цифру сверху на последнюю снизу (5∙4) и наоборот (2∙2).

Умножьте вторую цифру сверху на третью снизу (3∙3) и наоборот (9∙6).

Сложите четыре числа и пятое из ума (20+4+9+54+5=92).

Получили десяток в уме (9) и четвёртую с конца цифру (2): ** **2 108.

5. Умножьте первую цифру верхнего числа на третью нижнего (5∙3) и наоборот (2∙6).

Сложите результаты, а к ним добавьте умноженные друг на друга вторые числа (3∙9) и остаток в уме (15+12+27+9=63).

Получили десяток в уме (6) и пятую с конца цифру (3): ** *32 108.

6. Умножьте первую цифру верхнего числа на вторую нижнего (5∙9) и наоборот (2∙3).

Сложите результаты с остатком в уме (45+6+6=57).

Получили десяток в уме (5) и пятую с конца цифру (7): ** 732 108.

7. Умножьте первую цифру верхнего числа на первую нижнего (5∙2).

Сложите результат с остатком в уме (10+5=15).

Запишите всё число перед итоговым: 15 732 108.

Вы получили ответ.

Если ваш множитель двух- или трёхзначный, то вместо недостающих цифр нижнего ряда подставляйте нули. В таком случае последним этапом будет тот, где вы умножаете максимальное количество пар.

Принцип снежинки намного проще, чем умножать столбиком. Вам не нужно держать в уме много крупных чисел сразу.

Важна только структура: запомните нарастающий порядок умноженных пар и что с чем нужно складывать.

Единственной сложностью останется запомнить результат, который вы постепенно выстраиваете.

Чаще тренируйте память вариантами проще, например, умножением двух- и трёхзначными числами в приложении Устный счёт.

И тогда сможете считать миллионы, не коснувшись бумаги.

🤓 Хочешь больше? Подпишись на наш Telegram.

… и не забывай читать наш Facebook и Twitter
🍒

В закладки

iPhones. ru

Превращаем мозг в суперкомпьютер.

Павел Телешевский

@Tinelray

У меня 4 новых года: обычный, свой, WWDC и сентябрьская презентация Apple. Последний — самый ожидаемый, и ни капли за это не стыдно.
Instagram/Telegram: @tinelray

• До ←
  

  Владельцы iPhone теперь могут использовать Face ID вместо пароля на сайтах

• После →
  

  Вы не сможете запустить Windows через Boot Camp на Mac с процессором Apple

Умножать двузначные числа на двузначные в уме, оказывается, просто! Используем метод Трахтенберга! | Техночтиво

Привет, друзья!

Продолжаем знакомиться с системой быстрого счета Якова Трахтенберга, и сегодня на очереди у нас умножение двузначных чисел.

Книга «Система быстрого счета» включает в себя множество методик умножения, придуманных Яковом Трахтенбергом, но, как показала практика, то ли я плохо пишу заголовки, то ли последняя из статей на эту тему зашла очень плохо, потому как привык народ все умножать на калькуляторе! Лентяи… А ведь система предлагает даже умножение четырехзначных чисел на четырехзначные без многоэтажных записей, но об этом я напишу в следующих статьях.

Ну, «Ближе к телу», как говорится.

Допустим, нужно умножить 44х23. Пока что мы не опытные в этих делах и пишем выражение на бумажке, обязательно добавив перед первым множителем два нуля (ноля). Ответ будет записываться под первым множителем.

Два нуля просто для удобства написания ответа.

Начинаем умножать.

На первый взгляд может показаться, что все это очень сложно и громоздко, но, порешав пару-тройку примеров, Ваши сомнения улетучатся, уверяю.

Шаг 1

Умножаем друг на друга две крайних цифры множителей: 4 х 3 = 12. Двойку записываем, единичку переносим.

Не забывайте о перенесенной единице!

Шаг 2

Перемножаем и складываем внешние и внутренние пары:

Не забываем перенести двойку!

Шаг 3

Осталось перемножить только первые цифры множителей.

Не забывайте про перенесенную двойку. Я вот постоянно теряю эти перенесенные цифры…

Если хорошенько потренироваться на бумаге, то Вы потом с удивлением заметите, что все операции можете проворачивать просто в уме, даже не записывая числа.

Несмотря на то, что моя память оставляет желать лучшего, у меня получилось умножать двузначные числа в уме практически безошибочно. Думаю, сможете и Вы! Главное — практика!

Из тех методов, о которых я писал ранее, этот, наверное, наиболее часто можно использовать в обычной жизни!

Надеюсь, статья была познавательной и интересной. Всего Вам доброго, друзья!

уловок и советов по умножению умножения, которые помогут быстрее вычислить в уме

Приемы умножения и советы в этом посте позволят вам выполнять вычисления в уме быстрее, чем калькулятор, находящийся в вашей голове. Существует множество умственных стратегий умножения, но описанные здесь стратегии умственного умножения могут применяться для умножения любого набора чисел. Изучение советов по умножению умственных способностей из этого поста будет похоже на обучение катанию на велосипеде. Как только вы выучите это, действительно очень трудно это забыть.

Прежде чем мы продолжим, вы, должно быть, освоили однозначное умножение. Обязательным условием является знание ваших таблиц однозначного умножения от 1 x 1 до 9 x 9, прежде чем вы начнете умножать большие числа в уме. Если вы немного подзабыли, добавьте этот пост в закладки и сначала убедитесь, что вы запомнили свои однозначные таблицы умножения. Если вы хорошо умеете умножать однозначные числа, можете читать дальше.

Этот пост является второй частью серии «Уловки с умственной математикой».Мы настоятельно рекомендуем вам прочитать первый пост из этой серии — «Уловки мысленной математики для скоростной математики», прежде чем приступить к изучению того, как выполнять мысленную математику при умножении.

Секрет умножения умножения

В первой части «Уловок ментальной математики» мы узнали, что математику в уме становится труднее выполнять, если вы считаете справа налево. Следовательно, секрет ментальной математики в том, чтобы делать обратное и вместо этого вычислять слева направо. Решая слева направо, вы начнете называть ответ до того, как закончите полный расчет.Вычисление слева направо сначала может показаться немного странным, но после небольшой практики это станет естественным. В этом посте мы увидим, как применить это к умственному умножению.

Что такое множимое и множитель?

Прежде чем мы перейдем к уловкам умножения для выполнения мысленных вычислений, давайте быстро определим, что такое множимое и множитель. Возьмем, к примеру, задачу умножения 43 x 23. Здесь число 43 — это множимое — число, которое умножается. Число 23 — это множитель — число, на которое умножается первое число.

В этом посте есть несколько приемов умножения для умственной математики. У каждого метода умственного умножения будет два примера. Первый пример, видимый всем, познакомит вас с уловкой умножения. Во втором примере, видимом только для вошедших в систему пользователей, будут варианты, не описанные в первом примере. Так что войдите в систему или зарегистрируйтесь бесплатно, чтобы получить доступ ко всему контенту.

Уловки умножения для однозначного числа

Общее умножение умножения на однозначное умножение

Общий мысленный метод умножения — умножение слева направо.Хотя общий метод может быть применен для любого числа, он работает лучше всего, когда числа не заканчиваются на 7, 8 и 9. У нас есть отдельный метод для чисел, заканчивающихся на 7, 8 и 9. А пока давайте применим умножение умножения умножить 5321 x 4.

Правило простое. Умножайте слева направо. По одной цифре за раз.

Умножение слева направо выполняется быстрее, потому что вам нужно запомнить меньше чисел, чтобы вызвать их и использовать позже. Вы сразу же начнете называть ответ с самого первого шага расчета.

Теперь попробуйте умножить 7142 x 6. Процедура такая же, как и раньше, и вы можете найти ее ниже:

Умножение в уме с округлением в большую сторону для однозначного множителя

Использование умножения в уме после округления полезно, когда числа заканчиваются на 7, 8 или 9. Это значительно упрощает умножение. Давайте посмотрим, как применить это на примере. Умножить 68 x 3.

1. Округлите число

2. Умножить слева направо

3. Умножьте округленную сумму в большую сторону.

4.Вычтите числа из двух предыдущих шагов

Если вы попытаетесь сделать это так, как вы обычно делаете это на бумаге, вы поймете, что на то, чтобы сделать это в уме, уходит больше времени, чем то, что вам нужно сейчас. Если у вас еще нет скорости, не волнуйтесь. Это придет с практикой. В конце есть практические упражнения и рабочие листы умножения, которые вы можете скачать и практиковать.

Теперь вы попробуйте умножить 96 x 7. Процедура такая же, как и раньше, и вы можете найти ее ниже:

Умножение 2-значных чисел в уме

Общие приемы умножения

Давайте теперь посмотрим, как умножать в уме двузначные числа. Уловки умножения, которые мы видели ранее, нужно немного изменить. Давайте посмотрим, как это сделать, на примере. Умножить 36 x 32.

1. Разбить множимое

2. Умножить слева направо

3. Сложите отдельные ответы, чтобы получить окончательный ответ

Вы можете решить ту же задачу, разбив множитель вместо множимого. Ваш выбор будет зависеть от того, что дает вам более простой процесс сложения на шаге 3. Постарайтесь выбрать число, которое имеет меньшую цифру, потому что в большинстве случаев это обычно приводит к добавлению меньших чисел.

Теперь вы попробуйте умножить 26 x 23. Процедура такая же, как и раньше, и вы можете найти ее ниже:

Округление в большую сторону для двухзначного множителя

Как и в случае однозначных множителей, округление и умножение полезно, когда числа заканчиваются на 7, 8 или 9. Давайте посмотрим, как это сделать, на примере. Умножить 87 x 99:

1. Округлить число

2. Умножьте округленное значение на сумму, округленную в большую сторону слева направо.

3. Вычтите два числа

Теперь попробуйте умножить 41 x 57.Процедура такая же, как и раньше, и вы можете найти ее ниже:

Умножение умножения с использованием множителей

Как и округление в большую сторону, один из приемов умножения состоит в том, чтобы разложить число на множители перед его умножением. Давайте посмотрим, как это сделать, попытавшись умножить 45 x 22.

1. Разложите на множители

.

2. Умножьте число на первый множитель (слева направо)

4. Умножьте произведение на второй множитель (слева направо)

В уловках умножения, которые мы видели ранее, вам нужно будет запомнить произведение первой цифры, чтобы добавить / вычесть произведение второй цифры.Однако при умножении с использованием множителей вы просто умножаете второй множитель на первое произведение, так что вам не нужно запоминать столько чисел при вычислении.

Теперь вы попробуете умножить 21 x 63 с помощью факторного метода. Процедура такая же, как и раньше, и вы можете найти ее ниже:

Рабочие листы по уловкам умственного умножения

Ниже вы можете скачать рабочие листы в формате PDF, чтобы применить описанные приемы умножения.

Калькулятор для превращения в человека

Вы узнали основные приемы умножения. Но Мы лишь поцарапали поверхность, и нам предстоит еще многое рассказать. Если вы действительно хотите стать человеком-калькулятором и поднять свои математические навыки на новый уровень, посмотрите это видео. В видео я поделюсь историей о том, как я на самом деле боролся с математикой и как я пришел к тому, где я сейчас. Вы узнаете секрет, который сократит вашу кривую обучения и ускорит ваш путь к математическому мастерству в уме.Чтобы посмотреть видео кликните здесь.

Заключение

Свои вопросы, пояснения и отзывы оставляйте в комментариях. Потребуется практика, прежде чем применение уловок умножения станет простым и легким. Поначалу вам будет сложно запомнить все числа в своей голове, когда вы будете считать. Но практика поможет вам улучшить кратковременную память на числа. Заставьте себя мысленно производить вычисления слева направо для повседневных вычислений и используйте калькулятор только для того, чтобы перепроверить свои числа.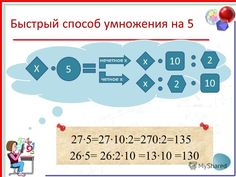 Чем больше вы практикуетесь, тем выше ваша скорость и способности.

Ненавижу математику? Эти умственные уловки заставят вас размножаться быстрее, чем когда-либо мог Эйнштейн! «Взломы разума :: WonderHowTo

2 + 2 = 4.

Это примерно столько математики, с которой я могу справиться без калькулятора каждый день. Я ненавижу заниматься математикой больше всего в жизни, в основном потому, что у меня это плохо получается — и я ненавижу делать то, что у меня не получается.

Итак, когда я натыкаюсь на классный математический трюк в Интернете, который утверждает, что облегчает жизнь таким людям, как я, я все слышу.Хотя вычисления (в основном) бесполезны для повседневной жизни среднего человека, умножение, сложение, вычитание и проценты — это все, что мы должны уметь делать — и без калькулятора.

Как большой поклонник TED Talks, я наткнулся на следующее видео, где Гаурав Текривал демонстрирует преимущества того, что называется ведической математикой, которая является базовым набором стратегий, помогающих упростить сложные вычисления.

Хотя происхождение этих учений несколько загадочно, стратегии весьма эффективны, и я буду помнить это каждый день. Может быть, математика все-таки не так уж сложна?

Вот несколько советов и приемов.

Как умножить двузначные числа на 11

Моя таблица умножения остановилась на 10, поэтому, помимо этого, я делаю вычисления, основываясь на памяти или подсчете в уме. Однако, используя ведическую математику, умножить на 11 совсем несложно.

Все, что вам нужно сделать, это сложить цифры числа, которое вы умножаете, на 11 и поместить его в середину исходного числа. Если сумма цифр 10 или больше, просто перенесите ее. Лучше увидеть, чем написать.

Видите, как легко это было? В принципе, если вы умеете складывать, вы знаете, как умножать на 11.

Теперь давайте посмотрим на другой пример.

Просто разделите умноженное число на 11 (в данном случае также 11 ), чтобы между ними оставалось место для вашего числа.Теперь просто сложите две цифры этого числа вместе ( 1 + 1 = 2 ) и бросьте сумму в то место, которое вы оставили открытым. Это дает вам 121 .

Просто добавьте 5 + 8 , что дает 13 . Вставьте его между 5 и 8 , и вы получите 5138 . Но это неправильно, так как вам нужно перенести это. Перенесите его, и вы получите 638 .

Излишне говорить, что теперь, когда я знаю это, я чувствую себя полным задирой.

Как умножать числа, близкие к степени 10

В этом базовом методе используются степени 10 (десятки, сотни, тысячи и т. Д.), А также перекрестное вычитание и умножение сумм. Опять же, гораздо лучше видеть, что я говорю, чем пытаться это прочитать. Вот пример умножения двух двузначных чисел (основание сотен).

То, что делает Гаурав, на самом деле довольно просто.

Он берет разность каждого числа из 100 и помещает эти числа в правый столбец ( 99-100 = -01 и 97-100 = -03 ).

Затем он складывает один набор чисел (подойдет любая пара), чтобы получить первое число ответа. Итак, 99 + -03 или 97 + -01 = 96 . Итак, это будет первая часть ответа.

Теперь умножьте два меньших числа ( -01 x -03 ), чтобы получить вторую часть ответа. -01 х -03 = 03 . Итак, это дает ответ 9603 .

Довольно круто, правда?

Тот же метод работает для любого основания из десяти. 999 x 987 или 9 878 x 9 999 все будут работать с базой 1000 и 10000 соответственно. Вы можете увидеть это примерно на отметке 3:45 на видео.

Как умножить двузначные числа на любые другие двузначные

Самое интересное в математике — наблюдать, как кажущиеся невозможными комбинации в конце концов выходят идеально. Выполняя определенные операции, вы можете превратить чрезвычайно сложные уравнения в простые пошаговые решения.

Используя вертикальный и крестообразный паттерны, мы можем легко умножать большие двузначные числа, как на изображении ниже.

Вместо того, чтобы использовать метод умножения стоя, мы собираемся разделить и победить.

Сначала умножаем вертикально вверх по правой стороне. 2 х 4 = 8 . Итак, 8 будет последней цифрой в нашем ответе.

Далее перемножаем крест-накрест. 3 x 2 = 6 и 4 x 1 = 4 . Теперь добавьте 6 + 4 , чтобы получить 10 . Перенесите 1 , как обычно, и у вас останется 0 , который будет перед уже имеющимся у нас 8 .

Итак, теперь у вас должно быть 08 в строке ответа.

Наконец, мы вертикально умножаем левую часть. 3 x 1 = 3 и прибавляем перенесенное 1 . Поместите это перед строкой ответа, и мы получим 408 .

Как умножать, используя линии вместо чисел

Если вы больше визуальный ученик, который действительно ненавидит числа, вы также можете использовать их по-японски и заменить эти цифры на строки, как это делает YouTuber kimelicious.Я не буду объяснять это — просто посмотрите, и вы увидите.

Разве вы не любите математику сейчас?

Есть несколько действительно удивительных математических трюков с использованием ведической математики, поэтому обязательно посмотрите полное видео, чтобы лучше понять это и начать использовать в своей повседневной жизни.

У вас есть какие-нибудь прикольные математические трюки? Дайте нам знать в комментариях.

Хотите освоить Microsoft Excel и вывести свои перспективы работы на дому на новый уровень? Начните свою карьеру с нашего пакета обучения Microsoft Excel Premium A-to-Z из нового магазина гаджетов и получите пожизненный доступ к более чем 40 часам инструкций от базового до расширенного по функциям, формулам, инструментам и многому другому.

Купи сейчас (97% скидка)>

Другие выгодные предложения, которые стоит проверить:

Оригинальные изображения обложек Джеймса Вестона / Shutterstock, Photosync / Shutterstock

случайных математических уловок (Часть 1): Умножение двузначных чисел | Тайсон Ву

Фото предоставлено: Unsplash

Пример 1

45 * 63 =?

Прежде чем искать лучший способ решения подобных проблем умножения, давайте посмотрим, как традиционный метод обучения в начальной школе будет подходить к этому вопросу:

Вертикальная форма

Когда нам нужно выполнить умножение двух двузначных чисел в, мы можем интуитивно разделить их на две задачи умножения двузначного и однозначного числа.В приведенном выше примере обычный способ выполнения математических вычислений — разбить его на 45 * 60 + 45 * 3.

Проблемы возникают при обычной практике

Однако, когда нам приходится выполнять математические вычисления без карандаша и бумаги, мы не можем отметить промежуточные результаты и часто забываем результат 45 * 60, когда переходим к вычислению 45 * 3. Не говоря уже о том, что мы должны сложить два результата, чтобы получить окончательный ответ. Мы должны найти лучший способ, который меньше полагается на запоминание промежуточных результатов.

Метод

«Практическое правило» выглядит так:

«Внешние * внутренние, десятки * десятки, единицы * единичные»

Вот объяснение:

• Умножьте две «внешние» цифры (4 и 3) и две «внутренние» цифры (5 и 6), затем сложите их: 4 * 3 + 5 * 6 = 42. Это первый промежуточный результат . Чтобы промежуточный результат не занимал ваши драгоценные слоты памяти, вы можете напомнить себе число 42, используя жест рукой, то есть 4 слева и 2 справа.

Ваша рука должна выглядеть так.

• Двигаясь дальше, мы смотрим на две цифры десятков и умножаем их. 4 * 6 = 24. Снова посмотрите на свою руку и представьте себе число 24. Совместите крайнюю правую цифру с десяткой на руке и сложите их, как показано ниже. У вас должно получиться число 282 , и это число, которое следует сейчас запомнить:

Посмотрите на свою руку и представьте, что эти числа парят в воздухе

• Наконец, мы смотрим на две цифры на единицы и умножаем их.5 * 3 = 15. Помните промежуточный результат 282 ? Совместите крайнюю левую цифру 15 с крайней правой цифрой промежуточного результата и сложите их. И это окончательный ответ: 2835.

Это рассматривается как улучшенный способ умножения двузначных чисел, поскольку нам нужно запомнить не более двух простых промежуточных результатов в любой момент. Кроме того, мы могли меньше запоминать с помощью жестов рук.

Пример 2

Давайте сделаем еще один пример:

79 * 23 =?

Число, которое проходит через вашу руку и голову, следует записывать следующим образом:

• Первый промежуточный результат «Outers * Inners» должен быть 39 .
• «Добавьте» 14 к первому промежуточному результату и получите 179.
• «Добавьте» 27 к 179, чтобы получить 1817.
• Готово!

Это то, что вы сделали в своей голове?

79 * 23 =?

Поначалу ваша скорость вычислений с использованием этого трюка может быть немного медленной, но я могу гарантировать, что после небольшой практики вы сможете придумать ответ быстрее, чем ваш друг, который пытается ввести числа в калькулятор. чтобы получить результат. Это уловка, которую определенно стоит потренировать!

Числовой трюк с чтением мыслей

Вы когда-нибудь думали о том, насколько ценны числовые уловки в классе? Представьте себе: ребенок слышит числовой трюк.Малыш любит числовые фокусы. Ребенок находит других детей, чтобы попробовать числовой трюк. Другие дети обожают числовые трюки. Дети повсюду находят больше числовых уловок и решают в уме математические вычисления, потому что числовые уловки — это очень весело. Я прав?

Почему бы не включить больше числовых трюков в свой класс математики в этом году? Я думаю, можно с уверенностью сказать, что дети будут с нетерпением ждать уроков, как никогда раньше!

Этот числовой трюк — забавный способ начать, и он существует всегда, потому что я помню его, когда был ребенком!

Вы думали о серых слонах в Дании? ВААА — ??! Вы были! Видите ли, я же говорил вам, что умею читать мысли!

Этот трюк работает, потому что в результате сложения цифр, кратных девяти, вы всегда получаете «9», поэтому вычитание 5 дает вам 4, что, в свою очередь, дает вам букву «D».Он основан на логическом предположении, что «жертва» числового трюка выберет Данию, когда ее попросят выбрать страну, начинающуюся с буквы «D». Также предполагается, что в качестве циркового животного будет выбран слон, начинающийся на букву «Е», и, конечно же, слоны серые. Это очень редко, но вы можете встретить одного или двух человек, которые МОГУТ сказать Доминиканская Республика вместо Дании. Я знаю это, потому что это случилось со мной, когда я попробовал этот трюк на своей дочери. Честно говоря, мне было интересно, может ли она сказать «Доминиканская Республика», потому что она любит географию, но я был уверен, когда она сказала: «Я не знаю, как произносить страну, которую я выбрал».Я быстро убедился, что она выбрала Доминиканскую Республику, а не Данию. Затем мой быстрый поиск в мозгу, чтобы найти животное, имя которого начинается с «О», заставил меня спросить ее: «Почему вы думаете об орангутанах в Доминиканской Республике?» Она была так потрясена, что я знал, что она думала об этом.

Чтобы узнать больше о математических хитростях, посетите «Учимся с математическими играми». Дай мне знать, если попробуешь это. Я хотел бы услышать, сработало ли это для вас и есть ли у вас кто-нибудь, кто выбрал бы Доминиканскую Республику!

Как умножить большие числа в уме (перекрестное умножение) — World Mental Calculation

Основной метод — для малых чисел

При вычислении умножения, когда одно из чисел маленькое, например, 68435 × 18 , может быть самым быстрым просто сложить кратные меньшего числа:

• 5 × 18 = 90 ⇒ ………… 0
• 9 + 3 × 18 = 63 ⇒ ……….30
• 6 + 4 × 18 = 78 ⇒ ……. 830
• 7 + 8 × 18 = 151 ⇒ …… 1830
• 15 + 6 × 18 = 123 ⇒ 1231830

На самом деле, когда я тренирую новичков по ментальной математике, одна из первых вещей, над которыми я работаю, — это расширение знаний о таблицах умножения на другие полезные числа, такие как 18, чтобы упростить выполнение этой задачи.

Но при использовании этого базового метода для больших умножений, такого как 29136 × 5847 , у нас не хватает рабочей памяти для вычисления каждого кратного e.грамм. 5847 , не забывая уже вычисленные числа! Итак, нам нужен другой метод — более эффективный с точки зрения памяти.

Ниже я покажу вам метод перекрестного умножения, который используют большинство продвинутых мысленных калькуляторов для умножения.

Метод перекрестного умножения

Некоторые приятные моменты в этом методе:

• Вам нужно знать только таблицу умножения до 9 × 9
• Какими бы большими ни были умножения, вам никогда не придется запоминать сразу много чисел
• Это очень просто, если вы знаете простой шаблон

Чтобы увидеть, как это работает, возьмем в нашем примере 29136 × 5847 :

1-я цифра — место единиц:

Для начала просто умножим 6 × 7 = 42 .Тогда самая правая цифра ответа — 2, и мы можем «перенести» 4 для следующего шага:

  29136
         × 5847
                    2  (неся 4 из 42) 

2-я цифра — множители с 10:

Далее мы рассматриваем 40 × 6 и 7 × 30, так как это числовые произведения (4 × 6 и 7 × 3), которые имеют коэффициент 10, точно так же, как 40, которое мы запомнили из предыдущего шага.

Самый быстрый способ — начать с 4 из 40, которые у нас есть, затем добавить 4 × 6 и 7 × 3:

• 4 + 4 × 6 = 28
• 28 + 7 × 3 = 49

Эти пары сложение-умножение быстро применимы на практике.

Опять же, мы можем записать «9» вместо десятков в окончательном ответе и оставить 4 для следующего шага.

  29136
         × 5847
                  92  (неся 4 из 49) 

3-я цифра — множители с 100:

Мы продолжаем с 800 × 6, 40 × 30 и 7 × 100, так как это цифровые продукты с коэффициентом 100.

Опять же — начните с 4 из 400, которые у нас есть, затем добавьте остальные продукты:

• 4 + 8 × 6 = 52
• 52 + 4 × 3 = 64
• 64 + 7 × 1 = 71

Запишите «1» в разряде сотен окончательного ответа и сохраните 7 для следующего шага:

  29136
         × 5847
                192  (несёт 7 из 71) 

Обратите внимание, что на каждом шаге порядок цветов вверху является зеркальным отображением цветов внизу, поскольку каждая совпадающая пара цифр должна представлять одну и ту же степень 10.

Вы можете складывать цифры в любом порядке, но я считаю полезным всегда начинать с нижнего левого и верхнего правого произведения (здесь 8 × 6) и систематически перемещаться одновременно вправо по нижнему числу и влево по номеру. верхний номер.

4-я цифра — множители с 1000:

К настоящему времени картина должна быть достаточно ясной, поэтому я продолжу с минимальными комментариями:

• 7 + 5 × 6 = 37
• 37 + 8 × 3 = 61
• 61 + 4 × 1 = 65
• 65 + 7 × 9 = 128

  29136
         × 5847
              8192  (несет 12 из 128) 

5-я цифра — множители с 10,000:

На этот раз обратите внимание, что цифра «6» уже умножена на каждую цифру нижнего числа, поэтому не будет активна до конца вычисления:

• 12 + 5 × 3 = 27
• 27 + 8 × 1 = 35
• 35 + 4 × 9 = 71
• 71 + 7 × 2 = 85

  29136
         × 5847
            58192  (таща 8 из 85) 

6-я цифра — множители на 100000:

С этого момента расчет становится проще, так как продуктов той же величины становится все меньше и меньше:

• 8 + 5 × 1 = 13
• 13 + 8 × 9 = 85
• 85 + 4 × 2 = 93

  29136
         × 5847
          358192  (несет 9 из 93) 

7-я цифра — множители на 1000000:

• 9 + 5 × 9 = 54
• 54 + 8 × 2 = 70

  29136
         × 5847
        0358192  (несущая 7 из 70) 

8-я цифра — множители с 10,000,000:

Поскольку это заключительный этап, нам не нужно ничего нести, а просто записываем оставшиеся цифры:

  29136
         × 5847
    170358192  

Резюме

Итак, это стандартный метод перекрестного умножения, используемый людьми-любителями-калькуляторами, а также нынешними и прошлыми мировыми рекордсменами по умножению, такими как Фреддис Рейес и Марк Джорнет Санс! (Jeonghee Lee предпочитает метод письма справа налево).

В заключение — метод в целом:

• Начинайте с крайней правой цифры каждого числа:
  • рассчитать свой продукт
  • запишите цифру единиц
  • переносят цифру десятков для следующего этапа
• За каждую последующую цифру ответа:
  • возьмите перенесенный номер до
  • систематически добавляйте все продукты той же величины
  • запишите цифру единиц в окончательном ответе
  • отнести остальное к следующему этапу

На соревнованиях Memoriad и на Кубке мира по интеллектуальным вычислениям участники должны умножить 8-значные числа, например, 12345678 × 98702468, и самые быстрые участники могут сделать это за 15-30 секунд!

Чтобы попрактиковаться в этом, вы можете использовать программное обеспечение Memoriad — хотя я рекомендую начать с продуктов меньшего размера, состоящих из 3- и 4-значных чисел, прежде чем двигаться дальше.

Чтобы связаться со мной (Дэниел Тиммс) по поводу тренировки мысленных вычислений или чего-либо на этом сайте, вы можете связаться со мной здесь.

Мы нашли более быстрый способ умножения действительно больших чисел

Умножение двух чисел — это просто, не так ли?

В начальной школе мы учимся выполнять долгое умножение следующим образом:

Долгий путь к умножению.
Дэвид Харви

Подобные методы существуют тысячи лет назад, по крайней мере, у древних шумеров и египтян.

Но действительно ли это лучший способ умножить два больших числа?

Читать далее:
Шесть изображений показывают, как мы «видим» данные и фиксируем невидимую науку.

При длинном умножении мы должны умножить каждую цифру первого числа на каждую цифру второго числа. Если каждое из двух чисел состоит из N цифр, это всего N ² (или N x N ) умножений.В приведенном выше примере N равно 3, и нам пришлось сделать 3 ² = 9 умножений.

Примерно в 1956 году известный советский математик Андрей Колмогоров предположил, что это наилучший из возможных способов умножения двух чисел .

Другими словами, независимо от того, как вы устроите свои расчеты, объем работы, которую вы должны сделать, будет пропорционален как минимум N ² . Двойное количество цифр означает , четыре — раз больше работы.

Колмогоров считал, что если бы короткий путь был возможен, то наверняка он уже был бы обнаружен. В конце концов, люди умножали числа на протяжении тысячелетий.

Это превосходный пример логической ошибки, известной как «аргумент от незнания».

Более быстрый путь

Всего несколько лет спустя гипотеза Колмогорова оказалась совершенно неверной.

В 1960 году Анатолий Карацуба, 23-летний студент-математик из России, открыл хитрый алгебраический трюк, который сокращает количество необходимых умножений.

Например, для умножения четырехзначных чисел вместо 4 ² = 16 умножений метод Карацубы обходится только девятью. При использовании его метода вдвое большее количество цифр означает только , три, раз больше работы.

Это дает впечатляющее преимущество по мере того, как числа становятся больше. Для чисел с тысячей цифр метод Карацубы требует примерно в 17 раз меньше умножений, чем длинное умножение.

Но с какой стати кому-то захочется перемножать такие большие числа вместе?

На самом деле приложений огромное количество.Один из наиболее заметных и экономически значимых — это криптография.

Большие числа в жизни

Каждый раз, когда вы участвуете в зашифрованном общении в Интернете — например, заходите на свой банковский веб-сайт или выполняете поиск в Интернете — ваше устройство выполняет головокружительное число умножений, включая числа с сотнями или даже тысячами цифр.

Скорее всего, ваше устройство использует уловку Карацубы для этой арифметики. Все это часть удивительной программной экосистемы, которая обеспечивает максимально быструю загрузку наших веб-страниц.

Для некоторых более эзотерических приложений математикам приходится иметь дело с еще большими числами, состоящими из миллионов, миллиардов или даже триллионов цифр. Для таких огромных чисел даже алгоритм Карацубы слишком медленный.

Настоящий прорыв произошел в 1971 году с работами немецких математиков Арнольда Шёнхаге и Фолькера Штрассена. Они объяснили, как использовать недавно опубликованное быстрое преобразование Фурье (БПФ) для эффективного умножения огромных чисел. Их метод сегодня регулярно используется математиками для обработки миллиардов цифр.

БПФ — один из важнейших алгоритмов 20 века. Одно приложение, знакомое в повседневной жизни, — это цифровое аудио: всякий раз, когда вы слушаете MP3, музыкальные потоковые сервисы или цифровое радио, FFT обрабатывают декодирование звука за кулисами.

Еще более быстрый способ?

В своей статье 1971 года Шёнхаге и Штрассен также сделали поразительную гипотезу. Чтобы объяснить, мне нужно на мгновение остановиться на технических деталях.

Первая половина их гипотезы состоит в том, что должно быть возможно умножить N -значных чисел, используя ряд основных операций, которые пропорциональны не более чем N log ( N ) (это N , умноженное на натуральное число). логарифм N ).

Их собственный алгоритм не совсем достиг этой цели; они были слишком медленными в логарифмическом масштабе (log N ) (логарифм логарифма N ). Тем не менее, их интуиция заставила их подозревать, что они чего-то упускают, и что N log ( N ) должно быть возможным.

За десятилетия, прошедшие с 1971 года, несколько исследователей нашли улучшения в алгоритме Шёнхаге и Штрассена. Примечательно, что алгоритм, разработанный Мартином Фюрером в 2007 году, очень близко подошел к неуловимому логарифму N ( N ).

Вторая (и гораздо более сложная) часть их гипотезы заключается в том, что N log ( N ) должно быть основным пределом скорости — что ни один из возможных алгоритмов умножения не может работать лучше этого.

Звучит знакомо?

Мы достигли предела?

Несколько недель назад мы с Йорисом ван дер Ховеном опубликовали исследовательскую статью, описывающую новый алгоритм умножения, который, наконец, достигает священного Грааля N log ( N ), тем самым решая «легкую» часть гипотезы Шёнхаге-Штрассена .

Статья еще не рецензировалась, поэтому следует соблюдать осторожность. Стандартной практикой в ​​математике является распространение результатов исследований до того, как они будут подвергнуты экспертной оценке.

Вместо использования одномерных БПФ — основного продукта всей работы над этой проблемой с 1971 года — наш алгоритм опирается на многомерных БПФ. В этих гаджетах нет ничего нового: широко используемый формат изображений JPEG зависит от двумерного БПФ, а трехмерное БПФ имеет множество применений в физике и технике.

В нашей статье мы используем БПФ с 1729 измерениями. Это сложно визуализировать, но математически не сложнее, чем в двухмерном случае.

Действительно большие числа

Новый алгоритм не совсем практичен в его нынешнем виде, потому что доказательство, приведенное в нашей статье, работает только для смехотворно больших чисел. Даже если бы каждая цифра была написана на атоме водорода, в наблюдаемой Вселенной не хватило бы места, чтобы записать их.

Читать далее:
Почему нам нужно знать простые числа с миллионами цифр?

С другой стороны, мы надеемся, что при дальнейших усовершенствованиях алгоритм может стать практичным для чисел, состоящих всего из миллиардов или триллионов цифр. В таком случае он вполне может стать незаменимым инструментом в арсенале вычислительной математики.

Если полная гипотеза Шёнхаге – Штрассена верна, то с теоретической точки зрения новый алгоритм — это конец пути — невозможно сделать лучше.

Лично я был бы очень удивлен, если бы предположение оказалось неверным. Но нельзя забывать, что случилось с Колмогоровым. Математика иногда преподносит сюрпризы.

Настоящая причина того, почему это работает, и исчезает конкретность

Японское умножение? Китайское умножение? Умножение строк?

Как бы это ни называлось, это всего лишь уловка, если вы просто запоминаете, не имея смысла.

Вы когда-нибудь задумывались, почему Японское умножение работает?

Я слышал, как некоторые называли это китайским умножением, умножением из Индии, ведическим умножением, умножением палками, умножением строк и многим другим.

Хотя многие могут спорить о происхождении этого трюка с умножением , я собираюсь утверждать, что он вполне мог возникнуть прямо здесь, в Онтарио, Канада, учитывая, что наша программа по математике в Онтарио с 1 по 8 классы предполагает, что мы могли бы пойти об обучении умножению.

Но, для протокола, я действительно понятия не имею, откуда это взялось, и меня это не волнует. Однако меня ДЕЙСТВИТЕЛЬНО волнует, ПОЧЕМУ работает этот метод. Если вы думаете, что это просто уловка, то это потому, что вы, вероятно, рассматриваете этот метод только с процедурной точки зрения.

Посмотрите полное объяснение в видео или перейдите к письменному / визуальному резюме под ним.

Чтобы понять, как работает Японское умножение , мы должны вернуться к старому доброму и надежному методу организации равных групп по строкам и столбцам. Вы правы, я говорю о массиве :

Когда мы говорим «3 раза по 2», это то же самое, что сказать «3 группы по 2», и мы можем показать эти три группы как 3 строки и 2 столбца или 3 столбца и две строки.

По мере того, как числа становятся больше, например, 6 групп по 7 человек, учащимся часто может быть полезно показать количество групп и количество элементов в каждой группе (также известные как факторы).

Обратите внимание, что расположение может показаться знакомым, так как часто мы традиционно организовываем наши таблицы умножения или таблицы умножения.

Мы также можем использовать массивы для отработки подсчета пропусков, визуализации «двойников», «троек» и всевозможных других полезных навыков, которые многие сторонники «возврата к основам» хотели бы улучшить у наших учеников.

Хотя массивы — это круто, мы здесь не для того, чтобы обсуждать преимущества использования массивов при обучении умножению. Они также могут помочь нам понять, почему Японское умножение действительно работает.

Мы подойдем ближе к причине, когда начнем рассматривать более крупные факторы, такие как 13 групп по 14. Но, черт возьми, было бы действительно отстой, если бы нам пришлось построить массив из 13 строк и 14 столбцов с отдельными плитками!

К счастью, кто-то придумал блоки с базой 10, чтобы упростить построение массивов с большими множителями!

Если вы действительно хотите углубиться в базовые десять блоков, подумайте о прочтении этого поста.

Чтобы построить массив из 13 групп по 14, мы можем использовать базовые десять блоков, чтобы представить 13 как «10 стержней» плюс 3 «единичных тайла». Это уменьшает количество управляемых частей с 13 штук, чтобы представить число 13, до 4 штук и с 14 штук, чтобы представить число 14, только до 5 штук.

Теперь мы можем размножать по частям, сосредоточившись в первую очередь на наших 10 стержнях.

Как и в случае с таблицей умножения, мы можем умножить 10 на 10 и увидеть, что произведение занимает 100 единиц.С базовыми десятью блоками мы можем использовать «100 плоских» вместо 100 отдельных блоков или 10 десяти стержней.

Затем мы можем взглянуть на пустое пространство в правом верхнем углу нашего массива и заметить, что теперь нам нужно умножить 10 (из множителя 13) на оставшиеся 4 единицы (из множителя 14), чтобы получить 4 десяти- стержней, или 40.

Повторяя ту же логику для оставшихся 3 стержней, формируя множитель 13, затем мы умножаем 3 на 10 стержней, чтобы получить 3 стержня с 10 стержнями или 30.

Наконец, мы умножаем 3 единицы на 4, чтобы получить 12 для конечного продукта 182.

Итак, давайте сделаем еще один, а затем подключим к японскому умножению .

На этот раз мы рассмотрим 12 x 15. Обратите внимание, что применяется та же логика:

Веселая штука, правда?

Теперь давайте подключимся к японскому методу умножения .

Я собираюсь скрыть значения базовых 10 блоков, чтобы очистить экран и избавиться от беспорядка. Теперь я собираюсь выделить «промежутки» между каждым базовым блоком из десяти частей с помощью линий (видите, куда это идет?):

Двигаясь вперед, я еще немного отделю наши факторы от массива, чтобы мы не запутались.Как вы увидите ниже, японское умножение на — это просто пропуск шага рисования блоков с базовыми 10, когда вы сосредотачиваетесь на пересечении блоков с базовыми 10 (или палочек / линий). Как вы можете видеть на анимированном гифке ниже, каждый блок из десяти базовых десяти заменяется пересечением линий, расположенных между каждым блоком из десяти базовых элементов:

Каждый шаг можно разбить следующим образом:

• В верхнем левом углу у нас есть десять стержней, умноженные на десять, чтобы получить 100.Обратите внимание, что это точка пересечения двух десяти стержней, которая представляет собой 100 плоскую.
• В правом верхнем углу у нас есть 5 единиц, умноженных на десять стержней, чтобы получить 5 десяти стержней или 5 точек пересечения, чтобы представить 50.
• В нижнем левом углу у нас есть десять стержней, умноженные на 2 единицы, чтобы получить 2 десяти стержня или 2 точки пересечения, чтобы представить 20.
• Наконец, в правом нижнем углу у нас есть 5 единиц, умноженных на 2 единицы, чтобы получить 10 единиц или 10 точек пересечения.

Рассматривая как массив с базовыми блоками десяти, так и японское умножение, оба метода автоматически разбивают наши множители на 12 и 15, чтобы использовать свойство распределения; 12 = 10 + 2 и 15 = 10 + 5.

Теперь, когда у вас была возможность испытать использование десяти базовых блоков в этом посте или более подробно здесь, вы, вероятно, сможете визуализировать базовые десять блоков, расположенные между линиями, которые используются в японском методе умножения .

Довольно круто, а?

Японское умножение — это всего лишь уловка, если вы не знаете, почему это работает!

Я видел множество сообщений в социальных сетях, в которых говорилось, что Японское умножение — это уловка умножения или своего рода «магия» или «уловка вудо».Это утверждение верно только в том случае, если вы никогда не пытаетесь понять, почему оно работает. Хотя в прошлом я обучал многим математическим приемам, таким как перекрестное умножение для решения пропорций и суммы и произведения для факторинга, за последние несколько лет я полностью отказался от этого подхода в своем обучении. Я должен быть осторожен здесь, потому что я не утверждаю, что перекрестное умножение или сумма и произведение — плохие методы для использования в математике; это больше о том, когда и как они возникают на уроках математики.

Развитие глубокого концептуального понимания приведет к процессуальной беглости

Я считаю, что не существует такой вещи, как «трюк» в классе математики, когда глубокое концептуальное понимание создается до введения процедурной беглости.В случае решения пропорций учащиеся должны уметь решать пропорции, используя противоположные операции и понимая, что эквивалентные относительные величины кратны друг другу. Понимание того, «во сколько раз больше» один «кусок» дроби, чем другой, очень важно, прежде чем просто дать студентам такой инструмент, как перекрестное умножение, чтобы просто «добраться до ответа» как можно быстрее. Я хотел бы думать, что если студенты выработали глубокое концептуальное понимание до перехода к процедурам и алгоритмам, вполне вероятно, что они лучше поймут, как эффективно использовать процедуру, а также смогут выбраться из затруднительного положения, если проблемы когда-либо возникают.

В случае японского умножения , я бы сказал, что это всего лишь трюк с умножением , если вы преподаете этот метод без того, чтобы студенты имели возможность работать с концептуальной основой, которая заставляет его работать безупречно. В частности, учащиеся должны иметь возможность потратить значительное количество времени на работу с конкретными материалами, такими как квадратные плитки и базовые десять блоков, чтобы построить массивы, чтобы добиться высокой беглости умножения, прежде чем подталкивать учащихся к иконическому или визуальному представлению, например, к рисованию базы. десять блоков или использование более абстрактного представления, такого как рисование пересекающихся линий.

Японское умножение: почему диагональные линии?

Вы можете спросить себя:

Почему я всегда вижу линии в японском методе умножения на диагонали?

Что ж, это вероятно потому, что большинство тех, кто использует и разделяет японский метод умножения , может не знать, почему он на самом деле работает. Если я не совсем уверен, почему это работает, и я пытаюсь научить кого-то еще, как это делать в процедурной манере, мне может потребоваться помощь, чтобы организовать решение как для меня, так и для ученика.

Теперь, когда линии отображаются по диагонали, в массиве блоков с десятичными основаниями точки пересечения упорядочиваются в порядке их числового значения. Посмотрите ниже:

Как вы можете видеть выше, возможность вернуться к разметке и важность понимания того, что в десятичной системе счисления мы не можем иметь какое-либо число больше 9 в любом столбце разряда. Вы заметите, что 10 удилищ нужно заменить на десятку.

Таким образом, хотя многие могут посчитать это довольно крутым «трюком», он будет намного эффективнее, если студенты смогут сформулировать, откуда берутся подобные процедуры и почему они работают.

Еще лучше, когда студенты получат полное представление о массивах с базовыми десятью блоками, я бы предпочел предложить им посмотреть, сможет ли они придумать более простой способ визуально представить их двузначное умножение на бумаге без необходимости нарисуйте связку прямоугольников и квадратов. Кто-то может использовать палки для базовых десяти блоков, и, может быть, кто-то из вашего класса может придумать что-то похожее на этот метод палки. Как здорово это будет?

Базовые десять блоковых массивов и японское умножение — стандартный алгоритм

О, и прежде чем вы уйдете, вы должны знать, что использование десятичных блоков или японского метода умножения — отличный способ объяснить, почему работают частичные произведения и стандартный алгоритм умножения.

Если мы посмотрим на массив и стандартный алгоритм бок о бок, мы сможем ясно увидеть каждый шаг алгоритма. Проверить это:

Если вас интересует больше о том, как связаны массивы, модели площадей и стандартный алгоритм, см. Этот пост.

Важность выцветания конкретности в математике

Затухание конкретности — теория, предполагающая, что математические концепции лучше всего изучать в три этапа; этап активизации, на котором учащиеся используют конкретные манипуляторы, которые представляют математическую концепцию, над которой они работают.

Со временем, после того как учащиеся накопят достаточный опыт физической работы с конкретными манипуляторами, они переходят к этапу пиктограмм, где они начинают (часто естественным образом) рисовать визуальное представление конкретного манипулятора вместо того, чтобы физически удерживать объект и манипулировать им. в их руках.

По мере того, как учащиеся все больше привыкают к иконическим или визуальным представлениям, имеет ли смысл для них начать использовать символы, которые представляют значение, лежащее в основе предыдущих визуальных и конкретных представлений.Этот этап считается наиболее абстрактным из трех этапов, потому что теперь числа и символы используются как более эффективный способ представления работы и опыта, которые были разработаны на предыдущих этапах.

Японский метод умножения и выцветание конкретности

Итак, как выглядит умножение, которое мы только что исследовали сегодня, по отношению к трем стадиям угасания конкретности?

Конкретность Затухание: умножение одной цифры на одну цифру

Когда дело доходит до умножения одной цифры на одну цифру с использованием отдельных плиток единиц, как мы делали в начале этого поста, этапы могут выглядеть следующим образом:

1. Активный / Бетонный: физическая организация квадратных плиток в массив.
2. Iconic / Visual: Рисование квадратов или точек в виде массива на бумаге или использование пространственных рассуждений для визуализации массива «мысленным взором».
3. Символический / абстрактный: Использование чисел и символов для представления вашего мышления в надежде, что вы сможете представить себе, что эти символы означают в своем уме.

Конкретность Выцветание: одно- или двузначное умножение на двузначное

По мере того, как мы переходим к умножению две цифры на одну цифру или две цифры на двузначное умножение, стадии исчезновения конкретности могут выглядеть следующим образом:

1. Активный / конкретный: использование физических базовых десяти блоков для создания массивов и со временем, возможно, переход к бесплатным виртуальным манипуляторам, таким как числовые элементы в центре математического обучения, приложение Mathies Color Tiles Министерства образования Онтарио или интерактивные манипуляторы, предлагаемые через бесплатный Инструмент Knowledgehook Gameshow.
2. Iconic / Visual: Рисование массива с использованием конфигурации base 10 на бумаге и / или визуализация в уме.
3. Символическое / абстрактное: Соединение конкретного и визуального с символической нотацией, такой как этот «концептуальный» алгоритм умножения (или «частичные произведения»).

Другая возможность может включать различные визуальные и символические представления, например:

1. Активный / Конкретный: Использование физических базовых десяти блоков для создания массивов.
2. Iconic / Visual: Рисование модели области на бумаге для демонстрации частичных продуктов и / или визуализации в их уме.
3. Symbolic / Abstract: Соединение конкретного и визуального с символической нотацией, такой как стандартный алгоритм умножения.

Наконец, другая возможность:

1. Активный / Конкретный: Использование физических базовых десяти блоков для создания массивов.
2. Iconic / Visual: Рисование модификации десятичного блочного массива с использованием японского метода умножения на бумаге и / или визуализация в уме.
3. Symbolic / Abstract: Соединение конкретного и визуального с символической нотацией с помощью умственных математических стратегий, таких как разложение и повторное составление чисел. В этом случае, мысленно используя свойство распределения, умножьте 10 на 15, а затем 2 на 15.

В то время как моим первоначальным намерением в этом видео и публикации была быстрая анимация, чтобы показать, что японский метод умножения на самом деле не уловка, а, скорее, упрощение того, что нас просят делать в учебной программе математики Онтарио, он превратился в монстр.Я надеюсь, что потраченные время и усилия, по крайней мере, заставят вас задуматься о том, как мы могли бы работать, чтобы углубить понимание учащимися умножения в сочетании с увяданием конкретности.

Я твердо верю, что по мере того, как мы открываем все больше способов представления концепций в математике, наше понимание этих концепций будет продолжать углубляться и со временем порождать все больше и больше связей. Я живое доказательство того, что это правда, потому что меня постоянно шокируют новые связи, которые кажутся мне с каждым днем ​​все меньше и меньше усилий.Давайте все сохраним открытую позицию в отношении обучения и продолжим налаживать все больше и больше связей в области математики, которые мы можем использовать в качестве инструментов в наших классах для удовлетворения потребностей учащихся в обучении.