Урок 45. решение уравнений на основе связи между результатами и компонентами умножения и деления — Математика — 3 класс
Математика 3 класс
Урок № 45. Решение уравнений на основе связи между
результатами и компонентами умножения и деления
Перечень вопросов, рассматриваемых в теме:
- Какие правила помогают решать уравнения? на основе взаимосвязи между
- Как связаны результаты и компоненты умножения и деления?
- Как проверить правильность решения уравнения?
Глоссарий по теме:
Уравнение – это равенство, содержащее переменную, значение которой надо найти
Множитель – это компонент умножения.
Произведение – это результат умножения и выражение а * b.
Делимое – компонент деления, число которое делят.
Делитель – компонент деления, число на которое делят.
Частное – это результат действия деления, а также выражение а : b
Обязательная литература и дополнительная литература:
- Моро М.
 И., Бантова М. А. и др. Математика 3 класс. Учебник для
И., Бантова М. А. и др. Математика 3 класс. Учебник для
общеобразовательных организаций М.; Просвещение, 2017. – с. 20.
- Математика. 3 класс. Часть 2. / Л. Г. Петерсон. – М.: Ювента, 2013 – 96 с.: ил. с. 77.
Теоретический материал для самостоятельного изучения
Неизвестное число в математике обозначают буквой латинского алфавита, например икс. В математике такое равенство с переменной называют уравнение. Уравнение – это равенство, содержащее переменную, значение которой нужно найти, чтобы равенство было верным.
Если в уравнении неизвестен делитель, то, чтобы найти делитель, нужно делимое разделить на частное.
90 : с = 5
С = 90 : 5
С = 18
Если в уравнении неизвестно делимое, то, чтобы его найти, нужно делитель умножить на частное.
Х : 23 = 4
Х = 23 ∙ 4
Х = 92
Если в уравнении неизвестен множитель, то, нужно произведение разделить на известный множитель.
7 ∙ х = 56
Х = 56 : 7
Х = 8
Выполним тренировочные задания
№1. Выберите уравнение из предложенных равенств:
1) 40 : 6 = 8;
2) 8 ∙ 6 = 48;
3) х ∙ 5 = 40;
Ответ: х ∙ 5 = 40 – уравнение.
№2. К каждому уравнению первого столбца подберите соответствующее значение х.
Правильный вариант:
№3. Выделите цветом уравнения, которые решаются делением.
Ответ:
№ 4. Расшифруйте фамилию писателя, расставляя ответы в порядке возрастания:
Ответ:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 класс — уравнения.
 Задачи на решение уравнеий по математике примеры
Задачи на решение уравнеий по математике примеры
Дата публикации: .
Уравнения на сложение и вычитание
1. Реши уравнения.
| 56 — х = 23 | х + 17 = 78 | у — 25 = 34 |
| 49 + y = 67 | 38 — y = 22 | y + 40 = 79 |
2. Заданы выражения: d + 45 и d — 25. Определи значения заданных выражений при:
2.1. d = 36;
2.2. d = 52;
2.3. d = 48;
2.4. d = 44.
3. Составь уравнения, содержащие операцию сложения или вычитания, и реши их.
3.1. Используй числа: 56, 78 и переменную X.
3.2. Используй числа: 6, 43 и переменную A.
3.3. Используй числа: 12, 54 и переменную В.
3.4. Используй числа: 34, 91 и переменную X.
3.5. Используй числа: 56, 32 и переменную A.
3.6. Используй числа 11, 17 и переменную В.
4. Выбери пример, решением которого является число 32.
| 67 — х = 24 | х + 56 = 98 | у — 5 = 27 |
10. Вставьте вместо … число так, чтобы получилось верное равенство.
Вставьте вместо … число так, чтобы получилось верное равенство.
| 12 + … = 67 | 56 — … = 48 | … + 23 = 92 | … — 45 = 32 |
| 45 — … = 11 | 59 — … = 29 | … + 32 = 94 | … + 53 = 88 |
11. Реши задачи.
11.1. До ремонта в школьной столовой находилось 34 стола. После ремонта привезли еще 46 столов. Сколько столов находится в столовой?
11.2. На складе находилось 12 мешков с мукой, затем привезли еще 58 мешков и ещё 14 мешков. Сколько мешков с мукой находится на складе?
11.3. Полина собрала с грядки 18 ягод клубники, затем ещё 32 ягоды. Сколько всего ягод клубники собрала Полина?
Уравнения на умножение и деление
1. Реши уравнения.
| 56 : х = 8 | х * 17 = 68 | у : 25 = 2 |
| 28 : y = 4 | 12 * y = 60 | y * 4 = 100 |
2. Реши задачи.
2.1. В кафе стояло 16 стульев. После ремонта кафе количество стульев увеличилось в 3 раза. Сколько стульев находится в кафе после ремонта?
Сколько стульев находится в кафе после ремонта?
2.2. В механическом цеху завода находилось 56 станков. Одну четвертую часть станков отправили на ремонт. Сколько станков отправили на ремонт и сколько осталось в цеху?
2.3. На рынке продавец продавал ягоды смородины, всего у него было 68 кг ягод. В течении дня он продал половину имеющихся у него ягод. Сколько кг ягод он продал?
3. Составь уравнения, содержащие операцию умножения или деления, и реши их.
3.1. Используй числа: 8, 56 и переменную X.
3.2. Используй числа: 6, 42 и переменную A.
3.3. Используй числа: 3, 69 и переменную В.
3.4. Используй числа: 4, 92 и переменную X.
3.5. Используй числа: 39, 3 и переменную A.
3.6. Используй числа: 18, 2 и переменную В.
неравенства | уравнения | |
Умею | Буду учиться | |
1.Что такое уравнение. | 1. Решать простые и осложненные уравнения без скобок. | ? Буду учиться решать осложненные уравнения со скобками | 1 Найди последнее действие |
(х+2)*5=30 | 2.Выделить неизвестный компонент | |
(х+2) =30:5 | 3.Применить правило | |
(х+2) =6 | 4. Упростить правую часть | |
х=4 | 5. Корень уравнения найден? | |
6. | 2 уровень | 3 уровень |
(у+3)•7 = 49 | у+25=25•2 | 5• х= 25 |
4 • (х-20)=16 | а – 100=200:2 | У- 50=150 | Умею | Буду учиться |
Что такое уравнение. | Решать простые и осложненные уравнения без скобок. | —- Буду учиться решать осложненные уравнения со скобками |
Урок математики, 3 класс. Тема: : «Решение уравнений»
МУНИЦИПАЛЬНОЕ КАЗЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ЯРАГКАЗМАЛЯРСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА им. М.ЯРАГСКОГО»
М.ЯРАГСКОГО»
План-конспект
открытого урока по математике
в 3 «б» классе
Дата: 08.02.2019г
Тема: «Решение уравнений»
Разработал учитель начальных классов ,
Имирсадыкова Рейганат Мирземетовна.
Директор МКОУ «Ярагказмалярская СОШ имени М.Ярагского»
Аюбова Фезина Михралиевна
2019г
математика: учебник для 3 класса в 2-х ч УМК «Школа России»
Школа: МКОУ «Ярагказмалярская СОШ им.М.Ярагского»
Учитель начальных классов: Имирсадыкова Рейганат Мирземетовна
Дата: 08.02.2019г
Класс: 3 «б»
Урок математики, 3 класс.
Тема: : «Решение уравнений»
Тип урока: урок введения новых знаний.
Цель: познакомить с уравнениями нового вида.
Задачи:
Учить решать уравнения нового вида, которые будут вводиться через текстовую задачу.
Развивать умение переносить ранее изученные знания на новый материал.
Развивать интеллектуальные и коммуникативные умения, умения
Планируемые результаты:
Предметные:
Понимать, что такое «уравнение», «решить уравнение». Знать способ решения уравнения (на основе взаимосвязи между компонентами).
Уметь решать простые уравнения. Уметь решать задачи способом составления уравнения, читать математические выражения, неравенства, равенства.
Личностные:
Уметь проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные:
Уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение (Регулятивные УУД).
Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им (Коммуникативные УУД).
Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке (Познавательные УУД).
Оборудование:
компьютер, телевизор, презентация.
Лист самооценки учащихся представлен в Приложение 1
Листики для работы в группах
Карточки с домашним заданием ( разноуровневые задания).
Ход урока
I. Организация класса.
Положительный настрой на работу.
II. Актуализация знаний.
Ребята, вы согласны, что сейчас период повышенного распространения вирусных заболеваний. И что важно заботиться о здоровье? На что, нужно обратить внимание?
(Здоровый образ жизни. Гигиена . Здоровое питание.)
Гигиена . Здоровое питание.)
Знать о пользе разных продуктов?
Вы любите ягоды? Не случайно вас спрашиваю. Вы сейчас потренируетесь в счёте и заодно узнаете о пользе и лечебных свойствах некоторых ягод и фруктов.
Работа в тетрадях.
Математическая разминка + тема здоровья
(лечебные свойства ягод, фруктов)
Послушайте задачи и запишите выражения в тетрадях:
а) Семья собрала летом с одного куста 2 кг черной смородины. Сколько всего кг смородины собрала семья с 11 таких кустов?
В плодах черной смородины много витамина Е, С в 20 раз больше, чем в яблоках и апельсинах. Витамины — необходимы для растущего организма.
б) Юля разделила поровну 30 мандаринов среди пяти своих подруг. Сколько мандаринов получила каждая из них?
При простуде и кашле — рекомендуется каждое утро выпивать по стакану мандаринового сока. Эфирное масло мандарина поднимает настроение.
в) На зиму заготовили 4 баночки малины, а клюквы в 6 раз больше. Сколько банок с клюквой заготовили на зиму?
Сколько банок с клюквой заготовили на зиму?
Раны и ожоги, промытые клюквенным соком, моментально заживают. Брусника повышает остроту зрения и рекомендуются пилотам, морякам, водителям, работающим с напряжением зрения и ученикам.
г) Масса арбуза 12 кг, Сколько кг в 2,…3… арбузах?
Арбузы прекрасно утоляют жажду и выводят из организма ядовитые вещества.
Проверьте. (Слайд № 2 по щелчку)
Дети выполняют отметку в листе самооценки. Приложение 1.)
Какие знания понадобились для решения задач? (Знания таблицы умножения и деления)
Отлично справились с заданием.
Продолжаем математическую разминку:
2. Игра.
На какие 2 группы можно разбить записи? (Слайд № 3 по щелчку)
505 — 5
Х+ 20= 70
Х- 40 =30
808 — 8
(Уравнения и числовые выражения)
(Равенство с неизвестным)
III. Подводящий диалог к формулированию новой темы.
Сообщение темы урока.
Составление целей урока:
Обучающие: учиться решать уравнение нового типа;
Развивающие: развивать речевой аппарат, внимание, память, логическое мышление, применять знания в повседневной жизни;
Воспитывающие: выполнять правила для учащихся, уметь слышать, слушать, комментировать;
Что такое уравнение? Уравнение – это математическое равенство, которое содержит неизвестное число. Неизвестное число обозначают буквами латинского алфавита.
Что значит «решить уравнение»?
Решить уравнение – значит найти такое числовое значение неизвестного, при котором равенство будет верным.
В математике говорят: решить уравнение – это значит найти корень уравнения.
Работа с компонентами ( сложение, вычитание, умножение, деление)
Решение уравнений по вариантам. (1 –В Х+ 20= 70; 2 –В Х- 40 =30)
Проверка решения уравнений по рядам. (Слайд № 4).
(Слайд № 4).
Оцените своё решение (Дети делают отметку в листе самооценки.Приложение 1.)
III. Подводящий диалог к формулированию новой темы.
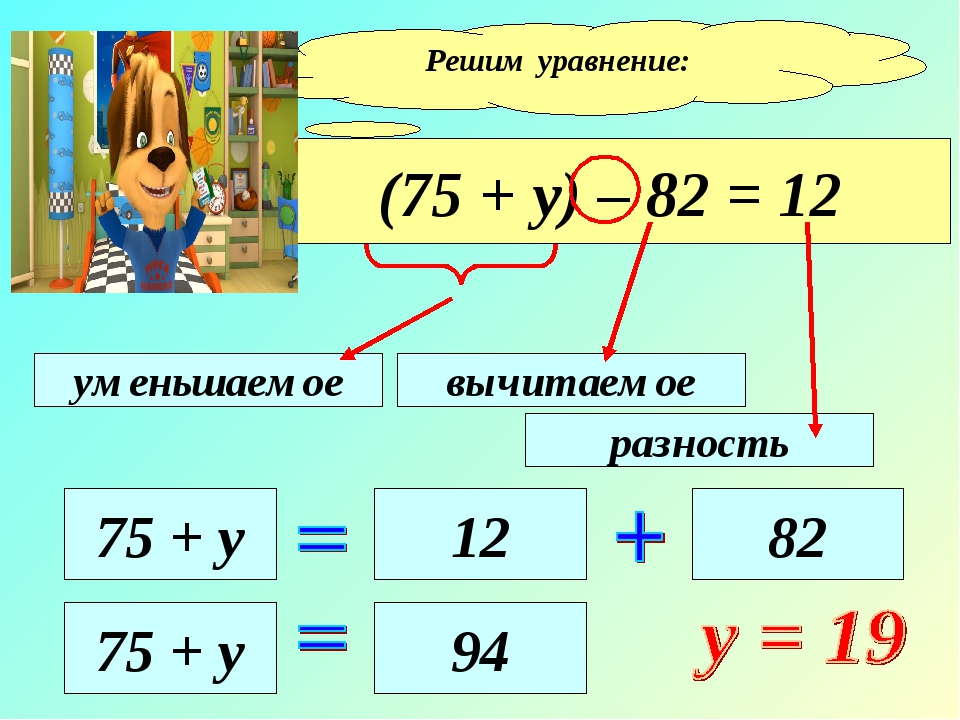
Работа с рисунками.
По этому рисунку давайте составим задачу и решим её. (слайд № 5 )
Ребята, перечислите предметы, которые здесь изображены художником? (Весы, гири, тыква).
Что за цифры на гирях. Зачем они? (Указывают массу гирь)
Скажите, в каком положении находятся весы (Весы находятся в равновесии)
Запишем то, что видите на картинке с помощью цифр, математических знаков(слайд № 6 по щелчку)
Что лежит сначала на левой чаше весов? (Тыква)
Какова её масса? (Неизвестна)
Как её можно обозначить?( Давайте обозначим массу тыкву буквой Х)
Что ещё находиться на этой же чаше? (Гиря массой в 2 кг)
Если это вместе на одной чаше весов, какой знак между числами поставим?
( х+2)
(Аналогично с правой чашей весов) Перечисляют и появляется запись: 5 5 5
Весы в равновесии, какой знак поставим между записями ? (Равенства)
Интересная запись! Х + 2 = 5 x 3
Давайте это запишем в тетрадь.
А я догадалась, как правую часть проще записать, а вы?
(5 x 3 сумма одинаковых слагаемых)
Х + 2 = 5 x 3
Что вы заметили? Что напоминает вам эта запись? (Похоже на уравнение)
А решали такие сложные уравнения? (Нет)
IV. Оздоровительная минутка.
Видеоролик «Фрукты»
V. Совместное «открытие» нового знания.
Работа в группах.
Проведём свои наблюдения, исследовательскую работу. Помогайте друг другу.
С чего бы вы начали решение этого уравнения?
Сделайте его проще!(Можно найти произведение 5 и 3. Мы получили уравнение, которое уже умеем решать: Х +2 = 15)
Неизвестно 1 слагаемое. Чтобы его найти, необходимо из суммы вычесть известное слагаемое.
Корень — 13 (слайд № 8 по щелчку)
Молодцы! Вы сделали открытие!
Смогли сами справиться с таким сложным заданием.
Сделайте отметку в листе самооценки. Делают отметку в листе самооценки.
(работа в группах)
Если уч-ся не смогут самостоятельно решить данное уравнение, то предложить готовое решение . ( № 1 стр. 88 учебника)
( № 1 стр. 88 учебника)
Откуда появляется число 15 в уравнении? (Произведение 5 и 3)
Витя решил уравнение так:
Х + 2 = 5 x 3
Х + 2 = 15
Х = 15 — 2
Х = 13
Ответ 13 килограммов масса камбалы.
Чему же равна масса рыбы?(Масса рыбы — 13 кг)
VI. Первичное закрепление.
Попытайтесь сами решить уравнение
Самостоятельная работа по вариантам (разно уровневая)(слайд № 11)
R + 10 = 43
2 х С = 24
х + 3 = 14 : 2
9 — у = 13 — 6
Проверка самостоятельной работы. (слайд № 12, 13)
VIII. Рефлексия.
IX. Итог урока.
Чему учились на уроке? (Учились решать сложные уравнения)
Проанализируйте свою деятельность.(лист самооценки) Вложите в свои тетради. (Заполненный лист самооценки вкладывают в тетради, тетради сдают).
Как работалось в команде?( Ответы детей)
О пользе каких ягод и фруктов вы узнали?(клюквы, черной смородины, арбуза, мандаринов, тыквы)
X. Домашнее задание. (дифференцированное)
Домашнее задание. (дифференцированное)
Чтобы научиться решать задачи с уравнениями, вы потренируйтесь в решении уравнений дома. Здесь и пригодятся полученные знания новой темы урока.
(Учащимся предлагаются разно уровневые карточки с уравнениями. Дети, оценивая степень усвоения, выбирают себе карточку легче по уровню или труднее)
1 уровень:
Х + 4= 3+3+3+3
3 + Х= 2 x 6
7+ у = 16 — 3
40 — а =30+ 8
*2 уровень
9 + у = 12 x 6
40 — а = 30 : 5
88 : с = 55 : 5
Х x 10 = 16 x 5
Дополнительный материал. (если останется время) Слайд № 13.
Игра.
Найдите зашифрованное слово.
12 х 2 = 24 ( З )
36 : 3 = 12 (Д)
40 : 10 = 4 (О)
18 + 12 = 30 (Р)
0 х 15 = 0 (О)
4 : 0 = нельзя (В)
1 х 35 = 35 (Ь)
16 : 2 = 8 (Я) Спасибо за урок!
Решение уравнений 3 класс — математика, уроки
Урок математики 3 класс
Тема урока: Решение уравнений.
Тип урока: урок закрепления, первичной проверки и коррекции знаний и умений.
Цели урока:
Личностные: создание педагогических условий для формирования у обучащихся положительной мотивацию к учению, умения преодолевать посильные трудности, чувства коллективизма, взаимовыручки и уважения друг к другу, умения вести диалог, аккуратности.
Метапредметные: формирование умения ставить цели и задачи, планировать и контролировать деятельность, умения классифицировать объекты, создавать, применять и преобразовывать модели, повышать алгоритмическую культуру обучающихся, развивать логическое мышление, познавательную активность и навыки научной речи.
Предметные: формирование умения построения математической модели, решения уравнений, содержащих одно или более одного арифметического действия и задач с помощью уравнений.
Методы обучения: наглядный, словесный, практический, частично-поисковый, репродуктивный.
Оборудование: презентация, музыкальное сопровождение, аншлаги, раздаточный материал, изображения талисманов, медали, смайлы.
ХОД УРОКА
1.Организационный момент
Рада видеть вас, друзья.
Поприветствуем гостей и за дело веселей.
Математика нас ждёт,
Начинаем наш урок.
I. Aктуализация знаний
-Ребята, а какое главное событие проходит сейчас в нашем крае?
1.Расшифруйте слово.
Задание: прочитать выражения разными способами.
13х3 – Л 15х6 – Д 49 : 7 – А
24 : 12 – П 9х4 – И 7х12 – М
56 : 8 – А 42 : 7 – О 6х6 – И
Ключ:
6
39 | 36 | 84 | 2 | 36 | 7 | 90 | 7 | |
О | Л | И | М | П | И | А | Д | А |
2. Математический диктант
Математический диктант
1. Найдите частное чисел 36 и 6.
2.Один множитель 9, другой 7. Найдите произведение.
3. Делимое 35, делитель 5. Найдите частное.
4. Во сколько раз 7 меньше 21?
5.Во сколько раз 16 больше 4?
6. На сколько 36 больше 9?
7. От пристани отплыли 6 лодок. В каждой лодке было по 4 весла. Сколько вёсел было в этих лодках?
8. В течение недели Витя читал книгу по 9 страниц в день. За это же время Коля прочитал на 15 страниц больше Вити. Сколько страниц прочитал Коля за неделю?
9. В классе 30 учеников, 2 ученика больны. Остальные дети разделились на группы по 4 человека для работы на уроке. Сколько групп получилось?
Ответы: 6, 63, 7, 3, 4, 27, 24, 78,7.
Итак, долгожданные XXII зимние Олимпийские Игры в г. Сочи 2014 уже в самом разгаре. Олимпийские игры – важнейшее событие в международной спортивной жизни. Они привлекают к себе пристальное внимание миллионов людей нашей планеты. Под олимпийскими знаменами собираются спортсмены всех континентов, потому что спорт сближает людей, помогает народам лучше понять и познать друг друга. Наверное, нет человека на земле, который был бы равнодушен к Олимпийским играм.
Наверное, нет человека на земле, который был бы равнодушен к Олимпийским играм.
Олимпийский флаг — это пять переплетенных колец на белом фоне. Эти кольца окрашены в синий, желтый, черный, зеленый и красный цвет, и переплетены друг с другом. Пять колец представляют пять частей света. Назовите 5 частей света. (Америка, Европа, Азия, Африка и Океания).
Сегодня вместе с нами на уроке Белый медведь, Леопард и Зайка – талисманы зимних Олимпийских Игр в Сочи. Талисман – это символ игр, приносящий удачу. Хочется верить, что эти герои тоже нам принесут сегодня удачу.
1.Верно ли утверждение?
Пятнадцать зимних спортивных дисциплин, объединённые в семь олимпийских видов спорта, включены в программу зимних Олимпийских игр 2014. Сегодня мы посетим некоторые спортивные площадки. Приближаемся на стадион, где будут проходить соревнования по конькобежному спорту. Все ли готово к соревнованиям?
Зайка приглашает нас на каток. Сейчас ученики 3 группы расскажут о соревнованиях на коньках. (Приложение 1)
(Приложение 1)
Задание Зайки. Если вы согласны с утверждением, ставим «+» в тетради. Если вы не согласны с утверждением, ставим «-».
Проверка.
Слагаемое + множитель = сумма
Уменьшаемое – вычитаемое = разность
Делимое : делитель = частное
Делимое – вычитаемое = разность
Множитель х делитель = произведение
Слагаемое + слагаемое = сумма
Уменьшаемое – слагаемое = разность
Множитель х множитель = произведение
Проверка. Один человек у доски. (- + + — — + — +)
Одну победу мы с вами одержали, правильно выполнив задание Зайки. Отметьте свою победу, нарисовав на полях тетради жёлтое кольцо — все ответы верны, ошибок нет; зелёное кольцо — 1-2 ошибки ; красное кольцо — 3-4 и более ошибок или затруднился выполнить заданеие.
( Дети оценивают себя сами: на партах у детей лежат фишки красного – «5», зеленого –«4», желтого –«3» цветов)
Учащиеся 4 группы расскажут нам о видах спорта на лыжах.(Приложение 1)
2. Дидактическая игра «Биатлон»(Приложение 2)
Дидактическая игра «Биатлон»(Приложение 2)
II.Постановка учебной задачи
Красная Поляна — популярный центр горнолыжного спорта. На склонах гор появились следы от лыж известных горнолыжников и сноубордистов. Задание Леопарда. Найди среди записей уравнение.
48 – 25 = 23
30 + х ? 40
36 : х = 9
Х х 5
Прочитайте. Докажите, что это уравнение.
Вставить пропущенное слово.
Уравнение – это ___________, в котором есть ______________ число.
Что такое уравнение? (Уравнение – это равенство, в котором есть неизвестное число).
Сформулируйте тему урока.
Какие задачи ставим перед собой? (знать способы решений уравнений на нахождение неизвестного делимого, делителя, множителя; уметь пользоваться математической терминологией, решать уравнения).
Для чего надо научиться решать уравнения?
III. Повторение изученного ранее
Подняться на вершину горы мы сможем по канатной дороге. Учащиеся 1 группы расскажут нам о новых видах зимних игр.
Работа в группах. Задание: восстановить последовательность этапов решения уравнений.
Каждая группа будет работать по заданному алгоритму. Не забывайте помогать друг другу: работа в группах – серьезный и ответственный труд.
Алгоритм
Запишите уравнения.
Найдите переменную.
Решите уравнение – найдите его корень.
Обсудите в группе, сделайте вывод.
1 группа:
Х + 28 = 53 28+х=53
Вывод: Чтобы найти неизвестное слагаемое, надо из ____________________________________________________________________
2 группа:
У-24=36
60-у=24
Вывод: Чтобы найти неизвестное уменьшаемое, надо к ____________________________________________________________________
Вывод: Чтобы найти неизвестное вычитаемое, надо из ____________________________________________________________________
3 группа:
Делимое делитель частное
b : 23 = 4
Делимое делитель частное
90 : c = 5
Вывод: Чтобы найти неизвестное делимое, надо ____________________________________________________________________
Вывод: Чтобы найти неизвестный делитель, надо ____________________________________________________________________
4 группа:
Множитель множитель произведение
7 * a = 56;
Множитель множитель произведение
a * 8 = 56
Вывод: Чтобы найти неизвестный множитель, надо ____________________________________________________________________
Защита работы групп. Взаимопроверка.
Взаимопроверка.
I. Закрепление.
Работа в парах.
Составить из данных чисел уравнение и решить их, объясняя друг другу в парах.
36, 12, 3, Х
12 х Х = 36
3 х Х = 36
Х х 12 = 36
Х х 3 = 36
36 : х = 12
36 : х = 3
IV.ФИЗКУЛЬТМИНУТКА для глаз
Зайка – самая активная жительница зимнего леса. Ее друзья всегда удивляются – и как она все успевает!? Ведь Зайка не только успевает учиться в Лесной Академии на “отлично”, помогать маме в семейном ресторанчике “Лесная запруда”, но и участвовать в различных спортивных соревнованиях. Зайка уверяет своих друзей, что у нее нет никакого секрета: просто она очень любит спорт. А еще она любит петь и танцевать
Всем полезно без сомненья
Всё, что связано с движеньем.
Вот, поэтому ребятки
Будем делать мы зарядку.
Скачут, скачут во лесочке (прыжки на месте)
Зайцы — серые клубочки.(руки возле груди, как лапки у зайцев, прыжки)
Прыг — скок, прыг – скок – (прыжки вперед-назад, вперед-назад)
Стал зайчонок на пенёк. (встать прямо, руки на пояс)
(встать прямо, руки на пояс)
Всех построил по порядку, (повернули туловище вправо, правую руку в сторону, затем влево и левую руку в сторону)
Стал показывать зарядку.
Раз! Шагают все на месте.(шаги на месте)
Два! Руками машут вместе, (руки перед собой, выполняем движение “ножницы”)
Три! Присели, дружно встали.(присесть, встать)
Все за ушком почесали.(почесать за ухом)
На “четыре” потянулись.(руки вверх, затем на пояс)
Пять! Прогнулись и нагнулись.(прогнуться, наклониться вперед)
Шесть! Все встали снова в ряд, (встать прямо, руки опустить)
Зашагали как отряд.(шаги на месте)
V. Работа над изученным материалом.
Решение задач
1. Первые Олимпийские игры прошли в Древней Греции более 1000 лет назад. Жители Древней Греции устраивали игры 1 раз в 4 года. Сколько месяцев проходило между двумя Олимпийскими играми?
2. В соревнованиях по биатлону приняли участие 51 спортсмен, а фигурном катании в 3 раза меньше. В кёрлинге приняли участие на 15 спортсменов больше, чем в фигурном катании, а в лыжных гонках в 3 раза больше, чем в кёрлинге. Сколько спортсменов приняли участие в лыжных гонках?
В кёрлинге приняли участие на 15 спортсменов больше, чем в фигурном катании, а в лыжных гонках в 3 раза больше, чем в кёрлинге. Сколько спортсменов приняли участие в лыжных гонках?
3. Конькобежец пробежал 1000 м за 4 мин. Сколько метров он пробежит за 9 мин?
4.Какая по счету Зимняя олимпиада будет в Сочи в XXI веке (после 2000 года)? В какие годы проводились зимние олимпиады, если они проводятся через 4 года, начиная c 2002, а Сочинская олимпиада будет в 2014 году?
Решение. пусть перед сочинской было х олимпиад.
Уравнение 2002+4х=2014
4х=2014-2002
4х= 12 х=3
Перед сочинской было 3 олимпиады, значит эта четвертая.
VIII. Итог урока.
Сегодня на уроке мы погрузились в неповторимую атмосферу Олимпийских игр, преодолели много трудностей и препятствий. Подошел к завершению наш урок. Посмотрите на свою шкалу, оцените свою работу на уроке.
IX. Домашнее задание.
Каждый участник соревнований, одержав победу, поднимается на пьедестал почета, чтобы получить заслуженную медаль. Сегодня вы тоже одержали победу, победу над собой. И тоже получаете медали за работу на уроке. На обратной стороне медали записаны 3 вида домашнего задания. 1задание необходимо выполнить всем, остальные задания выполнить по желанию.
Сегодня вы тоже одержали победу, победу над собой. И тоже получаете медали за работу на уроке. На обратной стороне медали записаны 3 вида домашнего задания. 1задание необходимо выполнить всем, остальные задания выполнить по желанию.
Методика «Незаконченное предложение»
3 класс. Моро. Учебник №1. Ответы к стр. 7
Числа от 1 до 100
Решение уравнений
Ответы к стр. 7
Будем учится решать уравнения с неизвестным слагаемым, которые подбором решить трудно.
4 + 3 = 7 5 + 4 = 9 3 + 6 = 9
7 — 4 = 3 9 — 5 = 4 9 — 6 = 3
7 — 3 = 4 9 — 4 = 5 9 — 3 = 6
Объясни, что получится, если из суммы двух слагаемых вычесть одно из них.
Закончи вывод.
Чтобы найти неизвестное слагаемое, надо из суммы двух слагаемых вычесть известное слагаемое.
1. Объясни решение уравнения и проверку.
х + 6 = 38 Проверка:
х = 38 — 6 32 + 6 = 38
х = 32 38 = 38
Для решения уравнения — нахождения неизвестного слагаемого — надо из суммы двух слагаемых вычесть известное слагаемое. Находим корень уравнения: х = 32. Для проверки решения подставим найденный корень в уравнение вместо неизвестного слагаемого. Получаем тождество: левая и правая части выражения равны, значит уравнение решено верно.
2. Реши уравнения с объяснением.
х + 18 = 42 Проверка:
х = 42 — 18 24 + 18 = 42
х = 24 42 = 42
64 + х = 82 Проверка
х = 82 — 64 64 + 18 = 82
х = 18 82 = 82
3. С одной грядки собрали 20 кг картофеля, а с другой — на 5 кг больше.
Объясни, что узнаешь, выполнив вычисления:
20 + 5 20 + (20 + 5)
20 + 5 = 25 (кг) — картофеля собрали с другой грядки
20 + (20 + 5) = 45 (кг) — картофеля собрали с двух грядок
4. Ваня собрал 8 стаканов малины, а его сестра — на 2 стакана меньше.
Ваня собрал 8 стаканов малины, а его сестра — на 2 стакана меньше.
Поставь вопрос так, чтобы задача решалась в два действия. Реши её.
Сколько стаканов малины всего собрали дети вместе?
1) 8 — 2 = 6 (с.) — собрала сестра Вани
2) 8 + 6 = 14 (с.) — собрали дети всего вместе
О т в е т: дети собрали 14 стаканов малины.
5. Вычисли, записывая решение столбиком.
75 — 49 64 + 28 93 — 57 56 + 16
— 75 + 64 — 93 + 56
49 28 57 16
26 92 36 72
Реши уравнение.
15 + х = 35
х = 35 — 15
х = 20
ЗАДАНИЯ НА ПОЛЯХ
Набери 15
| 7 | 6 | 2 | 4 |
| 8 | 2 | 7 | 4 |
| 7 | 5 | 6 | 1 |
| 4 | 9 | 1 | 2 |
15 = 7 + 6 + 2 = 4 + 8 + 2 + 1 = 7 + 4 + 4 = 9 + 6 = 7 + 5 + 2 + 1
ГДЗ по математике. Учебник. 3 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Учебник. 3 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 3 класс
3 класс. Моро. Учебник №1. Ответы к стр. 7
4.3 (85.38%) от 130 голосующих
Уравнений умножения для числовых линий — математика для 3-го класса
Узнайте, как умножить на числовой прямой
Итак, вы узнали, что умножение — это многократное сложение одного и того же числа.
Посмотрите на это уравнение умножения:
3 x 4 = ?
Мы выяснили, что существует 3 группы по 4 объекта.
Итак, как нам умножить, чтобы получить ответ?
Один из способов решения задач умножения — с использованием числовой прямой.
Это числовая строка:
Мы будем попрыгать на нем. 😎
Мы начинаем с нуля, затем на перескакиваем вперед на шагов.
Вернемся к нашему уравнению.
3 x 4 = ?
3 сообщает количество прыжков , которое мы должны сделать .
4 сообщает нам , насколько большим должен быть каждый прыжок.
Готовы?
Поехали!
Делаем 3 прыжка по 4 шага.
Итак, мы остановились на номере.
👍 При использовании числовой прямой для умножения ответом будет последнее число, на которое вы остановились.
😀 Важно : Никогда не считайте номер, с которого вы начинаете. Вы всегда начинаете отсчет со следующего числа.
Итак, каков ответ?
Верно! Это 12.
Отличная работа! 🎉
Давайте попробуем другое уравнение.
5 x 2 = ?
Сколько прыжков нам нужно сделать?
Да! 5 прыжков.
Насколько большим должен быть каждый прыжок?
Верно! 2 шага.
Поехали!
Где мы приземлились?
В 10!
Это наш ответ.
Отличная работа! 👏
Смотри и учись
youtube.com/embed/BsQo5SF-uLo» frameborder=»0″/>
Итак, почему бы вам не приступить к практике? 😎
PDST Математика после начального образования | Новые ресурсы: преподавание математики в среде DEIS
Этот веб-сайт использует Google Analytics для сбора анонимной информации, такой как количество посетителей сайта и наиболее популярные страницы.
Включение этого файла cookie помогает нам улучшать наш веб-сайт.
Пожалуйста, сначала включите строго необходимые файлы cookie, чтобы мы могли сохранить ваши предпочтения!
Показать детали
| Имя | Провайдер | Назначение | Срок действия |
|---|---|---|---|
| _ga | Файл cookie Google Analytics, который используется для расчета данных о посетителях, сеансах и кампании, а также для отслеживания использования сайта для аналитического отчета сайта. Файлы cookie хранят информацию анонимно и присваивают случайно сгенерированный номер для идентификации уникальных посетителей. Файлы cookie хранят информацию анонимно и присваивают случайно сгенерированный номер для идентификации уникальных посетителей.Отказаться на странице https://tools.google.com/dlpage/gaoptout | 730 дней | |
| _gat | Файл cookie Google Analytics, используемый для регулирования скорости запросов.Отказаться на странице https://tools.google.com/dlpage/gaoptout | 1 день | |
| _gid | Файл cookie Google Analytics используется для хранения информации о том, как посетители используют веб-сайт, и помогает в создании аналитического отчета о том, как работает веб-сайт.Собранные данные, включая количество посетителей, источник, откуда они пришли, и страницы, посещенные в анонимной форме. Отказаться на странице https://tools.google.  com/dlpage/gaoptout com/dlpage/gaoptout | 1 день | |
| NID | Содержит уникальный идентификатор, который Google использует для запоминания ваших предпочтений и другой информации, например, предпочитаемого вами языка (например,грамм. Английский), сколько результатов поиска вы хотите отображать на странице (например, 10 или 20) и хотите ли вы, чтобы фильтр безопасного поиска Google был включен. |
ресурсов по математике для домашнего обучения
Эти тщательно отобранные ресурсы предназначены для ознакомления студентов с ключевыми понятиями математики. Семейные письма и мероприятия могут быть хорошим началом, и вы можете продолжить занятия с учащимися, когда захотите.
- Семейные письма содержат справочную информацию о лексике и понятиях, а также включают задание, которое необходимо выполнить вместе с учащимся.
 (Доступно на английском и испанском языках.)
(Доступно на английском и испанском языках.) - Уроки учащихся можно выполнять независимо или вместе с вашей поддержкой, используя Руководство для учителя, которое включает дополнительные задания и ключи ответов.
- Мероприятия включают совместные игры и другие возможности для вашего ученика попрактиковаться в словарном запасе и навыках.
- Дополнительные мероприятия обеспечивают увлекательные и сложные действия, расширяющие понимание.
Советы для домашнего обучения содержит список советов для взрослых, которые можно использовать при работе с ребенком дома.
Выберите оценку, чтобы просмотреть доступные ресурсы:
Марка К | 1 класс | 2 класс | 3 класс | 4 класс | 5 класс | 6 класс | 7 класс | 8 класс
Марка К
Практика для печати: Урок для студентов | Руководство для учителя
1.
 Числа в пределах 5
Числа в пределах 5
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
2. Числа в пределах 10
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
3.Числа в пределах 100
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
4. Сложение и вычитание чисел
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
5.
 Описание фигур
Описание фигур
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
1 класс
Практика для печати: Урок для студентов | Руководство для учителя
1. Сложение и вычитание
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
2.Номера до 120
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
3.
 Измерение
Измерение
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
4.Фигуры
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
2 класс
Практика для печати: Урок для студентов | Руководство для учителя
1. Значение места
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
2.
 Сложение и вычитание
Сложение и вычитание
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
3. Концепции измерения
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
4.Концепции геометрии
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
3 класс
Практика для печати: Урок для студентов | Руководство для учителя
1.
 Умножение и деление
Умножение и деление
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
2.Фракции
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
3. Единицы площади и площади
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
4.Концепции геометрии
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
4 класс
Практика для печати: Урок для студентов | Руководство для учителя
1.
 Умножение целых чисел
Умножение целых чисел
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
2.Деление целых чисел
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
3. Операции с дробями
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
4.Концепции измерения и геометрии
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
5 класс
Практика для печати: Урок для студентов | Руководство для учителя
1.
 Объем и кубические единицы
Объем и кубические единицы
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
2.Умножение и деление на целые числа
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
3. Сложение и вычитание с дробями и десятичными знаками
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
4.Умножение и деление на дроби
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
6 класс
Практика для печати: Урок для студентов | Руководство для учителя
1.
 Выражения и уравнения
Выражения и уравнения
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
2.Деление на дроби
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
3. Положительные и отрицательные числа
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
4.Коэффициенты, ставки и проценты
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
5.
 Статистическое мышление
Статистическое мышление
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
7 класс
Практика для печати: Урок для студентов | Руководство для учителя
1.Пропорциональные отношения
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
2. Операции с рациональными числами
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
3.
 Выражения и уравнения
Выражения и уравнения
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
4. Геометрия
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
5.Популяции и выборки
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
8 класс
Практика для печати: Урок для студентов | Руководство для учителя
1.
 Выражения и уравнения
Выражения и уравнения
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
2.Функции
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
3. Преобразования
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
4.Геометрия
Инструкция: Семейные письма | Семейные письма на испанском языке | Студенческие уроки | Руководство для учителя
Мероприятие: Мероприятия | Ответные ключи
Пополнение: Активность | Ключ ответа
Фото:
Бесплатные занятия по математике в школе
Одна из лучших составляющих начала учебного года — это возможность узнать наших учеников и их интересы, в том числе их интересы по различным предметам. Мне нравится использовать задания, которые позволяют мне узнать интересы моих учеников, а также их математические навыки. В этом посте рассказывается о моих любимых заданиях по математике для 4–5 классов (скачать бесплатно в конце поста). Некоторые из заданий больше направлены на знакомство с вашими учениками и их математическими интересами, а некоторые помогут вам неформально оценить их математические навыки (вовлекая их).
Мне нравится использовать задания, которые позволяют мне узнать интересы моих учеников, а также их математические навыки. В этом посте рассказывается о моих любимых заданиях по математике для 4–5 классов (скачать бесплатно в конце поста). Некоторые из заданий больше направлены на знакомство с вашими учениками и их математическими интересами, а некоторые помогут вам неформально оценить их математические навыки (вовлекая их).
Партнерская деятельность по математике
Для этого простого задания для партнера по математике разделите своих учеников на пары.Затем попросите их по очереди задать друг другу вопросы на печатной форме, которые будут числовыми ответами. В каждом вопросе есть математическое задание, на которое учащиеся выполнят, получив ответ.
Вы можете попросить своих учеников по очереди задавать один вопрос за раз, а затем выполнять математическое задание с этим ответом. Или вы можете попросить их задать и ответить на все вопросы, а затем выполнить все математические вычисления сразу. Какой вариант лучше всего подходит вам и вашим ученикам.
Какой вариант лучше всего подходит вам и вашим ученикам.
Математические задания, включенные в это упражнение, представляют собой анализ математических навыков 4-го класса.
Math Обо мне
Мне нравится использовать задания «Математика обо мне», но к 4 и 5 классам мои ученики повторяли это снова и снова. Так что мне нужно немного «подрасти». Для этого я даю своим ученикам множество вариантов того, какими фактами они хотят поделиться, и прошу учеников писать уравнения вместо чисел.
Вы можете сделать это задание настолько простым или сложным, насколько это необходимо. Например, вы можете потребовать от учащихся составить двухэтапные уравнения или потребовать от них использовать каждую операцию хотя бы один раз.Или вы можете предоставить учащимся полный выбор с помощью уравнений, которые они создают.
После того, как учащиеся создали свои уравнения и факты (см. Пример ниже и в файле), вы можете попросить учащихся использовать липкие заметки или разрезать макулатуру, чтобы скрыть ответы. Затем либо развесьте бумаги, либо положите их на стол. Студенты могли ходить по комнате и выяснять факты о каждом человеке, решая уравнения, а затем проверяя ответы (поднимая стикер или клочок бумаги, чтобы найти ответ).
Затем либо развесьте бумаги, либо положите их на стол. Студенты могли ходить по комнате и выяснять факты о каждом человеке, решая уравнения, а затем проверяя ответы (поднимая стикер или клочок бумаги, чтобы найти ответ).
Я также моделирую это для студентов с моей собственной завершенной деятельностью. Это помогает обучать занятиям и позволяет студентам больше узнать обо мне.
Инвентарь / опрос по математике
Мне нравится узнавать, что мои ученики думают о предметах и как они считают себя учениками, используя вопросы инвентаризации интересов. Щелкните здесь, чтобы получить бесплатный инвентарь по интересам к чтению.
Это задание «Снова в школу» по математике включает 24 вопроса, которые помогут вам узнать чувства и отношение учащихся к математике.Вы можете использовать все вопросы или выбрать те, которые лучше всего подходят вашим ученикам.
Вот несколько вариантов использования этого задания:
Scoot Activity — Возьмите урок и предложите ученикам «поиграть» в SCOOT. Для этого просто разместите вопрос на каждом столе. Попросите учащихся вращаться (по вашему сигналу) по партам, пока они не ответят на все вопросы. Дайте студентам достаточно времени, чтобы прочитать вопрос и ответить на него, прежде чем они будут по очереди.
Для этого просто разместите вопрос на каждом столе. Попросите учащихся вращаться (по вашему сигналу) по партам, пока они не ответят на все вопросы. Дайте студентам достаточно времени, чтобы прочитать вопрос и ответить на него, прежде чем они будут по очереди.
Вокруг комнаты — Обмотайте вопросы лентой по комнате и попросите учащихся поработать парами или тройками, чтобы ответить на вопросы.Вы можете вращать учеников по вашему сигналу или позволить им свободно перемещаться. Если вы позволяете им свободно передвигаться, я рекомендую иметь правило, согласно которому за карточкой одновременно может находиться не более одной пары / триады учеников. В течение года я использую обзоры и задания «в классе», поэтому использование для этого вопросов для размышления также позволяет мне обучать процедурам и ожиданиям в отношении этого типа работы.
1-2 вопроса в день. Пусть ваши ученики поразмышляют и поделятся своими мыслями по математике в течение первой недели учебы.Вы можете предложить своим ученикам обсудить их ответы с группами или партнерами (им это нравится, и это вдвойне полезно для мозга).
Math Center или Station — Поместите вопросы по центру. Попросите учащихся ответить на вопросы на прилагаемом листе для записи (или на листе бумаги) или просто обсудить их ответы со своими группами.
Math Around the Room Activity
Для этого упражнения подготовьте проблемы, распечатав один комплект, вырезав проблемы (один разрез посередине) и заклеив проблемы по комнате.Распределите учеников по парам (рекомендуется) или по триадам. Поместите учащихся в исходные места и попросите их использовать листы для записей или листы бумаги для записи своей работы. Вы можете попросить учащихся передвигаться по комнате в своем темпе или по вашему сигналу.
Если вы заставляете учеников двигаться в своем темпе, я рекомендую иметь правило, согласно которому не более одной или двух пар могут одновременно решать задачу. Для студентов, которые заканчивают раньше, я проверяю их работу и отправляю их тем, которые они пропустили, для двойной проверки.Если вы перемещаете студентов по вашему сигналу, я рекомендую дать студентам время в конце, чтобы вернуться и закончить любые задачи, которые они не выполнили.
Мне нравится использовать это в качестве одного из моих заданий по математике в школе, потому что я часто использую этот тип задания в течение года для проверки и подготовки к тестам. Использование этого упражнения в качестве повторного занятия в школе позволяет мне представить упражнение и научить его ожиданиям и процедурам.
Это задание хорошо сочетается с любыми имеющимися у вас карточками заданий, если вы хотите продолжать его в течение учебного года.Нужны карточки задач? Щелкните по ссылкам ниже, чтобы увидеть наборы, которые есть в моем магазине.
Математика — Раскраска по ответам
Студенты по большей части любят раскрашивать. Это возвращение к школьной математике позволит им раскрасить, а вы получите некоторую ценную информацию об их математических навыках. Есть две версии этого задания: в одной рассматриваются математические навыки 3-го класса, а в другой — математические навыки 4-го класса. Рисунки и цвета такие же, поэтому убедитесь, что вы выбрали только тот, который подходит вашим ученикам.
Чтобы заполнить печатные формы, ученики решат каждое уравнение в таблице. Затем они выберут ответ из вариантов в таблице. Выбранному ими ответу присваивается цвет. Они раскрасят число (присвоенное задаче или уравнению) цветом, соответствующим правильному ответу.
Для подотчетности и для того, чтобы учащиеся не угадывали правильный цвет (возможно, только несколько чисел), убедитесь, что учащиеся показывают свои работы на обратной стороне листа или на отдельном листе.Другой вариант — попросить их проверить свои ответы (и работу) вами (или партнером), а затем раскрасить их картинку.
Получите бесплатные занятия по математике здесь
Щелкните здесь или на изображении ниже, чтобы получить бесплатные задания по математике в школе для 4–5 классов.
Вас интересуют математические центры? Получите бесплатные стартовые пакеты!
В дополнение к перечисленным выше занятиям по математике, мы также запускаем математические центры в первый месяц учебы в школе. Я делаю это с помощью своих бесплатных стартовых пакетов, которые отражают мои обычные математические центры.
Я делаю это с помощью своих бесплатных стартовых пакетов, которые отражают мои обычные математические центры.
Эти стартовые пакеты для математического центра позволяют мне:
- Познакомлю со всеми моими последовательными математическими центрами в первые две недели учебы.
- Обучайте и переобучайте ожиданиям центра значимым образом (используя фактические центры, которые студенты будут использовать в течение всего года).
- Убедитесь, что мои ученики точно знают, как заполнить каждый центр (качество и количество).
- Разберитесь с любыми неправильными представлениями об ожиданиях моего центра
Нажмите на свой уровень обучения, чтобы получить бесплатные стартовые комплекты.
Запуск математических центров для 3-х классов БЕСПЛАТНЫЙ стартовый пакет
Запуск математических центров для 4-х классов БЕСПЛАТНЫЙ стартовый пакет
Запуск математических центров для 5-х классов БЕСПЛАТНЫЙ стартовый пакет
Хотите снова вернуться к школьной математике?
Дополнительные мероприятия, бесплатные подарки и сообщения в блогах
Щелкните по ссылкам ниже, чтобы узнать о других занятиях и ресурсах, которые идеально подходят для возвращения в школу.
Бесплатное мероприятие по размышлению о возвращении в школу
Бесплатные распечатки с утренней работой в первый день в школе
Бесплатные занятия по возвращению в школу без подготовки для 3–5 классов
Бесплатные научные занятия для возвращения в школу
Снова в школу Читайте вслух с бесплатными печатными изданиями
Исследование интереса к бесплатному чтению
Бесплатные центры чтения и игры для открытия центров чтения
Решение двухэтапных уравнений — ChiliMath
Нет сомнений в том, что решить двухэтапное уравнение чрезвычайно просто.Как следует из названия, двухэтапные уравнения можно решить всего за два шага. Если вы впервые сталкиваетесь с двухэтапными уравнениями, не волнуйтесь, потому что мы рассмотрим достаточно примеров, чтобы вы познакомились с процессом.
Решая уравнение в целом, мы всегда помним о том, что все, что мы делаем с одной стороной уравнения, должно быть сделано и с другой стороной, чтобы уравнение оставалось сбалансированным.
Мы знаем, что мы полностью решили двухэтапное уравнение, если переменная, обычно представленная буквой в алфавите, изолирована на одной стороне уравнения (левой или правой), а число находится на противоположной стороне.
ОБЫЧНЫЙ способ решения двухэтапного уравнения:
Примечание : Это «обычный» метод, потому что таким образом решается большинство двухэтапных уравнений. Обратите внимание, что шаг 2 может быть заменен на шаг 3, который по сути тот же.
1) Сначала сложите или вычтите обе части линейного уравнения на одно и то же число.
2) Во-вторых, умножьте или разделите обе части линейного уравнения на одно и то же число.
3) * Вместо шага 2 всегда умножайте обе части уравнения на обратную величину коэффициента переменной.
Примеры решения двухэтапных уравнений
Пример 1: Решите приведенное ниже двухэтапное уравнение.
Как следует из названия этого линейного уравнения, для определения неизвестной переменной требуется два шага. Как правило, первый шаг заключается в том, чтобы избавиться от числа, «наиболее удаленного» от члена с решаемой переменной.Затем мы исключаем число, «ближайшее» к переменной. Число либо умножает, либо делит переменную. Его еще называют коэффициентом срока.
Здесь переменная x. Наша цель — решить x, изолировав его на одной стороне уравнения. Сохранение переменной слева или справа не имеет никакого значения. Это тебе решать! В этой задаче оставим его слева, так как он уже там.
Обратите внимание на то, что на той стороне (левая часть линейного уравнения), где находится переменная, 2 — «ближайшая» к переменной x, а 5 — «самая дальняя».
Это простое наблюдение позволяет нам решить, какое число удалить в первую очередь. Очевидно, +5, потому что это дальше между двумя. Противоположность +5 равна -5, это означает, что мы вычтем обе части уравнения на 5.
После исключения 5 в левой части уравнения путем вычитания обеих частей на 5, пришло время избавиться от числа, ближайшего к x или непосредственно связанного с ним, которое равно 2 в 2x. Поскольку 2 — это умножение переменной x, противоположная операция — деление на 2.
Разделив обе части на 2, мы получим окончательный ответ или решение данного двухшагового линейного уравнения.
Напоминаю, что это считается решенным, потому что коэффициент переменной просто положительный, +1.
Пример 2: Решите двухэтапное уравнение ниже.
Наша цель — сохранить переменную x на одной стороне уравнения. Неважно, на какой стороне, однако это «стандартная» практика — оставлять решаемую переменную в левой части.Некоторые учителя алгебры могут потребовать, чтобы переменная оставалась слева, и с этим ничего не поделаешь. Лично я не против, где вы храните переменную, левую или правую, при условии, что изолированная переменная на одной стороне уравнения имеет коэффициент +1.
Первый шаг включает удаление числа «дальше всего» от переменной x. Обратите внимание, что -3 «ближе всего» к x, а -8 «дальше». Итак, мы можем исключить -8, добавив к его противоположности, равному +8.
Второй шаг заключается в том, чтобы избавиться от числа, ближайшего к переменной x, равного -3.Поскольку -3 умножает переменную x, его противоположная операция — деление на -3. Разделив обе части на -3, мы решили линейное уравнение.
Быстрое напоминание: -3, деленное на -3, равно +1.
Пример 3: Решите двухэтапное уравнение ниже.
Вот ситуация, когда мы можем изолировать переменную x в правой части уравнения, поскольку она уже там есть.
Если посмотреть на правую часть уравнения, где находится переменная, число 3 ближе всего к x, потому что 3 делит переменную x.С другой стороны, число 26 — «дальше». Это означает, что нам придется иметь дело с +26, вычитая обе части уравнения на 26. Причина, по которой мы вычитаем, состоит в том, что аддитивная величина, обратная +26, равна -26.
Второй шаг — избавиться от знаменателя 3. Поскольку 3 делит x, противоположная операция — умножение на 3.
После умножения обеих частей на 3 мы пришли к окончательному ответу. Вы можете переписать свой окончательный ответ как x = -9.
Пример 4: Решите уравнение двух ниже.
Это может показаться многоступенчатым уравнением, но это не так. Это можно решить в два этапа. Не беспокойтесь о дробях, потому что с ними очень легко работать. В этом случае вы примените правило сложения дробей. Правило гласит, что если вы складываете две дроби с одинаковым знаменателем, просто сложите числители, а затем скопируйте общий знаменатель.
Вернемся к решению двухэтапного уравнения выше, чтобы удалить дробь в левой части, которая равна \ Large {- {3 \ over {10}}}, мы добавим \ Large {{3 \ over {10}}} к обеим сторонам уравнения.
Причина, по которой мы добавляем вместо вычитания, заключается в том, что аддитивная величина, обратная \ Large {- {3 \ over {10}}}, есть \ Large {+ {3 \ over {10}}}.
После добавления \ Large {{3 \ over {10}}} с обеих сторон, только {\ Large {{2 \ over 5}}} x остается с левой стороны.
Для правой части уравнения имеем \ Large {{9 \ over {10}} + {3 \ over {10}} = {{12} \ over {10}}}.
Все, что я сказал выше, — это только первый шаг. Теперь переходим ко второму шагу. Посмотрите на коэффициент переменной x.Это \ Large {{2 \ over 5}}, что означает, что его обратное значение равно \ Large {{5 \ over 2}}.
Чтобы окончательно решить данное уравнение, мы умножим обе части уравнения на обратную величину коэффициента рассматриваемой переменной. Вот полное пошаговое решение:
Практика с рабочими листами
12 необычных действий с уравнениями в один шаг
Мы ожидаем, что в 8-м классе ученики уже знают, как решать одношаговые уравнения.Многие из них делают это, но есть и другие, которые борются с ними. Я работаю со студентами, которые имеют право на математическую лабораторию, вторая доза математики в течение дня. Большинство моих учеников пропустили базовые понятия, когда они должны были выучить их в предыдущем классе. Итак, практика решения одношаговых уравнений работает как обзор для большинства студентов, но для других это кажется новой темой.
Большинство моих учеников пропустили базовые понятия, когда они должны были выучить их в предыдущем классе. Итак, практика решения одношаговых уравнений работает как обзор для большинства студентов, но для других это кажется новой темой.
Сегодня я поделюсь с вами 12 заданиями и идеями, которые помогут вашим ученикам понять и попрактиковаться в решении одношаговых уравнений.
За прошедшие годы я усвоил одну вещь: смотреть на навыки преподавания по-разному, в зависимости от того, что нужно ученикам. Для решения одношаговых уравнений это действительно должно быть автоматическим. Студентам не нужно много думать, решая их. Это должно стать естественным. Таким образом, практика решения одношаговых уравнений выглядит иначе, чем более сложные концептуальные темы. Ключ к тому, чтобы ученики свободно владели этими навыками, — это повторение, повторение, повторение.Я упоминал повторение?
В упражнениях, которые я собрал в этом списке, большое внимание уделяется практике беглости речи. Некоторые занятия проводятся с партнерами или небольшими группами. Другие отлично подходят для самостоятельной практики на математических станциях, выполнения домашних заданий и т. Д. В целом, если ваши ученики регулярно отрабатывают эти виды деятельности, они очень свободно овладевают этим навыком.
Некоторые занятия проводятся с партнерами или небольшими группами. Другие отлично подходят для самостоятельной практики на математических станциях, выполнения домашних заданий и т. Д. В целом, если ваши ученики регулярно отрабатывают эти виды деятельности, они очень свободно овладевают этим навыком.
Лабиринты с одношаговыми уравнениями
One Step Equations Pong
Игра в крестики-нолики
Доски для сотрудничества
Активность ловушки Кути для одношаговых уравнений
Equation Wheels
Снежный бой
Line Puzzle Activity
Подходящие карты
Kahoot для решения одношаговых уравнений
Викторина по Quizizz
Опасность
Давайте углубимся в деятельность
Давайте посмотрим на каждое из занятий и на то, что они могут предложить вашему классу.По мере того, как вы узнаете больше об упражнениях, вы будете видеть задания для всего класса, небольшой группы и самостоятельной практики. Кроме того, эти действия работают для звонков, практических занятий, а некоторые из них могут работать и для домашних заданий.
Кроме того, эти действия работают для звонков, практических занятий, а некоторые из них могут работать и для домашних заданий.
Если вы раньше не использовали математические лабиринты в классе, я предлагаю вам попробовать их. Я не всегда был верующим, но однажды я использовал их в отчаянии и никогда не оглядывался назад. Лабиринты отлично подходят для того, чтобы побудить студентов решать проблемы и практиковаться, не осознавая, сколько проблем они на самом деле решают.Каждый день в начале урока мы проходим один из этих лабиринтов. Вы можете положить их в конверт или карман для сухого стирания, если у вас несколько занятий в течение дня.
Я использую лабиринты с продвинутыми учениками, а также на уроках математики. Этот конкретный набор лабиринтов включает 4 лабиринта, и их сложность увеличивается от одного лабиринта к другому. Первый — это сложение и вычитание, второй — целые числа, третий — умножение и деление, а последний — смесь одношаговых уравнений со всеми операциями. Это упражнение — отличный способ постоянно практиковаться в этом навыке.
Это упражнение — отличный способ постоянно практиковаться в этом навыке.
Если вы хотите еще больше увлекательных математических лабиринтов, мы отправляем БЕСПЛАТНЫЙ лабиринт по математическим концепциям средней школы исключительно членам клуба «Лабиринт месяца». Если вы хотите присоединиться и получить БЕСПЛАТНЫЕ математические лабиринты, которых нет где-либо еще и , зарегистрируйтесь здесь:
Запишитесь в клуб «Лабиринт месяца».
Дети любят возвращаться к вещам очень давней давности (и я знаю некоторых учителей, которым это тоже нравится!).Забавно, как они думали, что 10 лет назад это были древние времена. Что ж, эта игра с уравнениями от XP Math восходит к временам Pong и добавляет в процесс решения одношаговых уравнений. Есть несколько способов настроить эту игру: по уровню математических задач и по уровню владения компьютером. Я бы посоветовал дать студентам калькулятор, потому что некоторые из используемых ими чисел не являются обычными числами.
Кроме того, вы можете сыграть в эту игру вместе со студентами, чтобы они соревновались с вами.Им это понравится, и они будут очень соревноваться.
Крестики-нолики — это интересный способ попрактиковаться в одношаговых уравнениях во многих различных формах. Эту игру можно использовать как совместную работу, игру, занятие в небольшой группе, для быстрого завершения или для всего класса. Моим ученикам нравится играть в крестики-нолики, и они забывают, что учатся решать одношаговые уравнения. Эта игра в крестики-нолики для одношаговых уравнений включает 8 игр, сложность которых возрастает от сложения и вычитания до целых чисел и умножения и деления.Это отличный способ повторить решение одношаговых уравнений.
Когда учащиеся играют вдвоем, каждый из них берет по символу x или o. Они ходят вперед и назад, решая уравнения, и, если они делают это правильно, помещают свой символ в квадрат. Мои дети действительно увлекаются этой игрой, и мне нравится слышать, как они рассказывают о проблемах, которые они решают.
Дети учатся решать одношаговые уравнения в совместной работе с классной доской, используя какую-либо доску общего вида и решая задачи на своем разделе / доске.Вы можете заставить их всех работать над одной и той же проблемой, а затем они сверится друг с другом, чтобы убедиться, что у них одинаковые ответы. Другой вариант — каждый работает над другой проблемой, но ответы на все проблемы одинаковы. Вы можете установить это в центрах и попросить учеников сменять друг друга.
Ссылка на эту идею ведет на сообщение в блоге с множеством идей для решения уравнений. В середине страницы она описывает то, что она называет «уравнениями салфеток», которые можно сделать с помощью рукавов для сухого стирания или больших студенческих досок.Вы можете скачать несколько бесплатных салфеток, но они представляют собой двухступенчатые уравнения. Если вам нужен набор задач для этого упражнения, вы можете щелкнуть эту ссылку, чтобы просмотреть список проблем, который вы могли бы использовать.
Несколько лет назад я попробовал ловушку для кути со своими учениками, и им это понравилось. Я не очень часто играю в эту игру со студентами, так что когда мы это делаем, это новость. Этот одношаговый уловитель кути включает в себя два разных уловителя кути. Один из них — ночь, а другой — день. Вы заставляете студентов сражаться друг с другом с помощью ловцов для кути.Если вы хотите, чтобы они просто выполнили задачи, они тоже могут это сделать. Убедитесь, что вы показываете им пример, прежде чем заставлять их играть.
Эта загрузка включает в себя 2 ловушки для кути с 8 одношаговыми уравнениями для каждой ловушки для кути, протокол учащегося, ключи ответов и наглядное руководство по складыванию ловушки для кути. Сами задачи не очень сложные, и лучше всего работает, когда учащиеся только изучают эти концепции.
Я хочу попробовать это упражнение Equations Wheels от мисс Calculate в моем классе математической лаборатории в качестве быстрого завершающего упражнения.Его можно использовать со многими другими темами, а не только с одношаговыми уравнениями. Вам понадобятся одношаговые уравнения и много прищепок. Вы пишете уравнения на колесе, а ответы на его обратной стороне. Также ответы будут написаны на обеих сторонах прищепок. Глядя на изображения в ее посте, я понял, как это работает. Вы также можете скачать пустое колесо из связанного сообщения в блоге.
Снежный бой
Снежный бой в классе украсит день каждого, независимо от времени года.Для создания снежного кома каждый должен написать на листе бумаги одноэтапное уравнение. Затем вы скомкаете бумагу в «снежный ком». Когда вы говорите «иди», все начинают кидать снежки, пока вы не скажете «Стоп». На этом этапе все разворачивают бумагу и решают задачу о снежном коме. Вы снова бросаете снежки, и все проверяют, правильный ли ответ.
Эта техника также работает с размышлениями или заданием вопросов. Это происходит из-за разлома мозга.Одна из лучших частей заключается в том, что никакой подготовки не требуется.
Это упражнение-головоломка — бесплатная игра, которую вы можете загрузить на TeachersPayTeachers. Аспект головоломки делает занятия с одношаговыми уравнениями увлекательными. Я никогда раньше не видел подобной головоломки. Убедитесь, что у ваших учеников есть линейка, когда они это сделают, чтобы ученики могли быть точными в своих ответах. Вы заметите, что некоторые ответы являются отрицательными целыми числами, поэтому ваши ученики должны быть знакомы с целыми числами для этого упражнения.Это отлично подходит в качестве практического занятия для учеников 7-8 классов.
Вы можете поймать бесплатный набор совпадающих карточек для практики решения одношаговых уравнений из блога Math in the Middle. В своем блоге она рассказывает о различных занятиях, которые вы можете попробовать с ними. Она предоставляет набор карточек, состоящий из 8 групп по четыре штуки. Эти карты можно использовать несколькими способами. Во-первых, вы можете дать каждому карточку по пути в комнату. Затем они должны посмотреть, смогут ли они найти трех других людей, у которых есть то же решение, что и у них.
Кроме того, вы можете попросить учащихся поработать в парах и попытаться найти 8 наборов совпадающих карточек. Кроме того, это действительно может быть использовано в качестве быстрого финишера.
Kahoot имеет несколько различных применений. Моя любимая часть в этом — возможность использовать эту игру для формирующего оценивания. В конце игры вы можете загрузить довольно подробный перечень данных на свой Google Диск.
Эта игра Kahoot состоит из 20 вопросов. 18 вопросов выглядят как простые выражения одношаговых уравнений.Последние два вопроса повышают уровень и представляют собой проблемы со словами. Эта игра отлично подходит как для предварительной оценки, так и для практики.
Quizizz похожа на Kahoot, за исключением того, что учащиеся могут идти в своем собственном темпе (я предпочитаю использовать вариант воспроизведения домашнего задания). Вы получите много отчетов об успеваемости учащихся от Quizizz. В этой игре-викторине есть множество одношаговых уравнений, которые я бы использовал в классе. В этой конкретной игре-викторине сочетаются как традиционные вопросы, так и задачи с парой слов.Мне нравится использовать Quizizz как разминку, циклический обзор для студентов. Можно пару недель заниматься одной и той же темой. Это дает студентам возможность улучшить свои навыки.
У
Jeopardy есть много особенностей, которые я ищу в игре-обзоре. Весь класс может играть одновременно, и вам не нужно проходить всю игру, чтобы она была эффективной. В моем классе, когда мы играем в Jeopardy, все отвечают на все вопросы. Я не играю в командном стиле. Кажется, что в командном стиле большинство детей не занимается.Я прошу студентов отслеживать свои собственные баллы и следить за тем, какие студенты получают их, а какие нет.
В этой конкретной игре Jeopardy вы найдете уравнения для решения следующих категорий: сложение, вычитание, умножение, деление и десятичные дроби. Всего 25 вопросов. Студентам придется работать с отрицательными числами, так что это лучше подходит для студентов с такими навыками.
Попробуй одно ..
Этот сборник одноэтапных упражнений с уравнениями поможет вам внести немного остроты в повседневную практику ваших учеников.Вам не нужно пытаться объединить все действия. Я бы начал с одного и посмотрел, как оно пойдет. Используйте один для циклического повторения для всего класса или для звонаря, когда они входят в класс. Помните, что практика одноэтапных вопросов заложит основу для многих других концепций, которым мы учим в средней школе. Эти занятия помогут вам дать им много-много возможностей для практики.
Большое спасибо за чтение. До скорого!
Связанные
Преподавание математики с помощью концептуальной мотивации и практического обучения
Это практический концептуальный документ, описывающий избранные средства для практического обучения и концептуальной мотивации на всех уровнях математического образования.В нем подробно описан подход, используемый авторами для разработки идей для практиков преподавания математики. В статье показано, что такой подход в математическом образовании, основанный на практическом обучении в сочетании с естественной мотивацией, проистекающей из здравого смысла, является эффективным. Кроме того, стимулирующие вопросы, компьютерный анализ (включая поиск в Интернете) и классические известные задачи являются важными инструментами мотивации в математике, которые особенно полезны в рамках практического обучения. Авторы утверждают, что вся учебная программа по математике K-20 под единым зонтом возможна, когда методы концептуальной мотивации и обучения действиям используются во всем этом широком спектре.Этот аргумент подтверждается различными примерами, которые могут быть полезны на практике школьным учителям и преподавателям вузов. Авторы нашли прагматическую причину для практического обучения в рамках математического образования практически на любом этапе академической жизни учащихся.
1. Введение
В настоящее время студентам требуется как познавательный, так и практический опыт на протяжении всего их математического образования, чтобы быть продуктивными гражданами 21 века. Происхождение этого утверждения можно проследить до работ Джона Дьюи, который подчеркивал важность образовательной деятельности, которая включает «развитие любого рода артистических способностей, особых научных способностей, эффективных гражданственности, а также профессиональных и деловых качеств». профессий »([1], с.307). Совсем недавно Биллетт [2], основываясь на своих исследованиях интеграции опыта обучения студентов высших учебных заведений в дисциплинах, связанных с сестринским уходом и аналогичными услугами в поддержку человеческих потребностей, предположил, что «возможно, можно полностью интегрировать практический опыт в совокупность опыта высшего образования, которая способствует развитию прочных и критических профессиональных знаний »(стр. 840). Главный аргумент данной статьи состоит в том, что в контексте математического образования практическое обучение (концепция, представленная в разделе 3) — это сам процесс передачи этого опыта в сочетании с концептуальной мотивацией (термин, введенный в разделе 2) при обучении математике. по всей учебной программе K-20.С этой целью в этом концептуальном документе, основанном на практических примерах, подробно описывается подход, использованный авторами для разработки идей для практикующих преподавателей математики, предлагается обзор избранных средств практического обучения в рамках формального континуума математического образования. В определенной степени эта статья продвигает идею обучения на практике [3] в контексте математического образования. Представлены аргументы, подтверждающие ценность практического обучения для всех вовлеченных лиц (на уровне колледжа, добавление к дуэту студента и преподавателя математики третьего сообщества или университетского профессионала, не являющегося математиком) (разделы 2–4).Также рассматривается интеграция компьютерной педагогики подписи (CASP) и нецифровой технологии, а также эффективное опросы с обучением действием (разделы 5 и 6).
Учащиеся могут с радостью получать формальное математическое образование в течение двадцати и более лет, и они могут быть мотивированы повсюду с помощью обширных учебных программ по математике. Практическое обучение в математическом образовании в сочетании с механической теорией переносит математические темы в реальный мир. Естественно, что примеры начального уровня имеют основополагающее значение, и это подкрепляется практическим обучением на вторичном уровне (разделы 4.1.1 и 4.1.2). Открытые проблемы математики часто могут быть представлены учащимся начальных, средних и высших учебных заведений (Раздел 7). Традиционно классические результаты и открытые задачи мотивируют не только студентов, но и самих педагогов. Поскольку необходимы эффективные учителя математики, практическое обучение следует использовать на всех уровнях математического образования, зная, что будущие преподаватели входят в число нынешних учащихся. Конечно, возможность участвовать в открытиях очень мотивирует всех, включая студентов и учителей математики, по крайней мере.
2. Любопытство и мотивация
Хотя необходимость изучения математики в начальной, средней и высшей школе общеизвестна, вопрос о том, как преподавать математику, остается спорным. Как более подробно описано в [4] со ссылками на [5–10], разногласия связаны с неоднородностью программ подготовки учителей, разногласиями между формализмом и смыслом между преподавателями математики и различными взглядами на использование технологий. Мы считаем, что надлежащий способ преподавания математики на всех уровнях — это делать это через приложения, а не использовать традиционные лекции, подчеркивая формализм математического аппарата.Реальные приложения поддерживают мотивацию заинтересованных людей при изучении математики. Эту естественную мотивацию можно рассматривать как зависящий от возраста процесс, простирающийся от естественного детского любопытства в начальной школе до истинного интеллектуального любопытства на уровне высшего образования. Независимо от возраста учащихся, любопытство можно рассматривать как мотивацию «приобретать или преобразовывать информацию в обстоятельствах, которые не представляют немедленной адаптивной ценности для такой деятельности» ([11], с. 76). То есть любопытство и мотивация — тесно связанные психологические черты.
Большинство исследований по развитию любознательности касается начального образования. Однако эти исследования могут помочь нам понять, как любопытство превращается в мотивацию стать высококлассным профессионалом. Например, Видлер [12] проводил различие между эпистемическим и перцептивным любопытством, которые проявляются, соответственно, «исследованием знания» и проявляются, например, когда ребенок ломает голову над какой-то научной проблемой, с которой он столкнулся… [и] повышенное внимание дается объектам в ближайшем окружении ребенка, например, когда ребенок дольше смотрит на асимметричную, а не на симметричную фигуру на экране »(стр.18). Точно так же взрослые учащиеся на высшем уровне могут быть мотивированы призывом своего учителя математики задать вопросы, касающимся информации, которой они поделились, или их опытом взаимодействия с окружающим миром, когда они пытаются интерпретировать «ткань мира … максимум и минимум »(Эйлер, цит. по [13], с. 121).
Связанный с высшим уровнем, Видлер [14] определил мотивацию достижения как «образец… действий… связанных со стремлением достичь некоего усвоенного стандарта качества» (стр.67). Есть также взрослые ученики, которые «заинтересованы в совершенстве ради него самого, а не ради вознаграждения, которое оно приносит» ([14], с. 69). Биггс [15] допускает, что внутренняя мотивация в изучении математики связана с «интеллектуальным удовольствием от решения проблем независимо от каких-либо вознаграждений, которые могут быть вовлечены… [предполагая, что] цели глубокого обучения и мотивации достижений в конечном итоге расходятся» (стр. 62). Классическим примером в поддержку этого предположения является решение гипотезы Пуанкаре (столетней давности), выполненное геометром Григорием Перельманом, который после почти десятилетия «глубокого обучения» отказался от нескольких международных наград за свою работу, включая медаль Филдса («Медаль Филдса»). Нобелевская премия ») и (1 миллион долларов) Clay Millennium Prize (https: // www.Claymath.org/).
Поскольку любопытство является источником мотивации к обучению, Мандельброт [16] в пленарной лекции по экспериментальной геометрии и фракталам на 7-м Международном конгрессе по математическому образованию посоветовал аудитории, состоящей в основном из преподавателей математики дошкольного образования, как сосредоточиться на любопытстве, когда преподавание математики: «Мотивируйте студентов тем, что увлекательно, и надейтесь, что возникающий энтузиазм создаст достаточный импульс, чтобы продвинуть их через то, что не весело, но необходимо» (стр.86). Именно такую мотивацию авторы называют концептуальной мотивацией. В частности, в этой статье термин «мотивация концепции» означает стратегию обучения, с помощью которой, используя любопытство учащихся в качестве стержня, введение новой концепции оправдывается использованием ее в качестве инструмента в приложениях для решения реальных проблем. Например, операция сложения может быть мотивирована необходимостью регистрации увеличения большого количества объектов другой такой величиной, концепция иррационального числа может быть мотивирована необходимостью измерения периметров многоугольных ограждений на плоскости решетки ( называется геодоска на начальном уровне), или концепция интеграла может быть мотивирована необходимостью найти области криволинейных плоских фигур.
Еще один математически значимый инструмент мотивации — конкретность. Согласно Дэвиду Гильберту, математика начинается с постановки задач в контексте конкретных действий, «подсказываемых миром внешних явлений» ([17], с. 440). Мы считаем, что «конкретность» является подходящим синонимом мотивации в отношении математического образования. Сам термин бетон указывает на то, что различные ингредиенты объединяются и синтезируются. Цель изучения математики — конкретизировать как теоретические, так и прикладные понятия.Полезно иметь четкое понимание чего-либо. Люди по своей природе хотят иметь «полное» знание определенных вещей. Зная детали и конкретизируя идеи, мы уменьшаем беспокойство, связанное с описанием и использованием этих идей. Конкретность мотивирует все стороны, участвующие в математическом образовании. Даже на административном уровне существует понимание того, что «основная учебная программа FKL [Основы знаний и обучения] предоставит вам возможность изучить множество жизненно важных областей обучения, сделав вас более осведомленными и вовлеченными в понимание проблем, которые глобальные реалий, которых требует »([18], курсив добавлено), где мы делаем упор на« реальности ».Это мотивация для всех, поскольку все мы хотели бы использовать математическую теорию или, по крайней мере, увидеть ее применение. Следовательно, мотивация у взрослых учеников пропорционально выше, чем у детей, которые могут не видеть «полезности» в математике. В Университете Южной Флориды преподавателей определенных курсов (например, последовательности исчисления) просят включить утверждение FKL в свои учебные планы.
До недавнего времени термины «промышленный» и «технический» имели довольно уничижительный оттенок в математическом образовании.Традиционное формальное чтение лекций по-прежнему доминирует в большинстве классных комнат. Однако при изучении математической теории часто используется некоторая «отрасль» или «техника», поэтому эти два понятия не дополняют друг друга. Трудно выделить часть огромного объема учебных программ по математике K-20, которая исключает использование теории или возможного практического применения. Кроме того, теория неявно включена в образование в области STEM из-за ее научного компонента.
В контексте подготовки учителей математики акцент на приложениях дает будущим учителям очень важную способность подавать примеры математических идей в удобных для использования формах.Затем эту способность можно передать своим ученикам. На уровне дошкольного образования можно понять, что математические знания возникают из необходимости разрешать реальные жизненные ситуации разной степени сложности. Принцип учебной программы, выдвинутый Национальным советом учителей математики [19], включает в себя представление о том, что всем учащимся на этом уровне следует предлагать опыт, «чтобы увидеть, что математика имеет мощное применение в моделировании и прогнозировании явлений реального мира» (стр. 15 -16). Этот акцент на приложениях выходит за рамки дошкольного уровня.Действительно, математика сильно развивалась и проникала во все сферы жизни, делая университетское математическое образование необходимым, но неоднозначным элементом современной культуры.
3. Обучение действиям
Многие люди прагматичны, делая то, что работает. Когда что-то не работает, человек вынужден задавать вопросы, как заставить это работать. Начиная с 1940-х годов Реджинальд Реванс начал разрабатывать концепцию обучения действием, метод решения проблем, характеризующийся действием и размышлением о результатах, в качестве педагогической педагогики для развития бизнеса и решения проблем [20, 21].С тех пор обучение действием стало описывать различные формы, которые оно может принимать, и контексты, в которых его можно наблюдать. В контексте достижения высокого качества университетского обучения «целью практического обучения является обучение отдельного учителя» ([22], с. 7). В общем контексте повышения профессиональной результативности Дилворт [23] утверждает, что практическое обучение начинается с исследования реальной проблемы, так что независимо от того, является ли проблема «тактической или стратегической… [процесс] обучения является стратегическим» (стр.36). Практическое обучение в математическом образовании можно определить как обучение через индивидуальную работу учащихся над реальной проблемой с последующим размышлением над этой работой. В большинстве случаев эту работу поддерживает «более знающий друг».
В математическом образовании практическое обучение, зародившееся в раннем детстве, имеет естественный уровень зрелости. Прежде чем мы займемся повседневными обязанностями, связанными с взрослой жизнью, мы можем свободно рассмотреть практическое обучение в игровой форме.Наша страсть к играм и изучению выигрышных стратегий переносится в более позднюю жизнь как средство развлечения и как инструмент для обучения следующего поколения детей. Мотивация к практическому обучению в математическом образовании постепенно меняется от выигрыша в играх к успеху в реальных предприятиях. Залог успеха — умение решать проблемы. Исследования показывают, что любопытство можно охарактеризовать как волнение по поводу необычных наблюдений и неожиданных явлений [24].Кроме того, «то, что будет интересно детям, во многом зависит от природы окружающего их мира и их предыдущего опыта» ([12], с. 33). Учащиеся на всех уровнях образования стремятся к конкретности, естественно интересуются реальным миром и пользуются преимуществами практического обучения, особенно когда они неоднократно используют его в математическом образовании. В частности, в программе послесреднего математического образования для нематематических специальностей проблемы должны иметь применимость к реальности. Интересно, что мы, кажется, возвращаемся к «играм», когда имеем дело с чистой теорией, поскольку мы можем искать абстрактное решение ради самого решения.
Макс Вертхаймер, один из основателей гештальт-психологии, утверждал, что для многих детей «имеет большое значение, есть ли реальный смысл вообще ставить проблему» ([25], с. 273). Он привел пример 9-летней девочки, которая не училась в школе. В частности, она не могла решать простые задачи, требующие использования элементарной арифметики. Однако, когда ей давали проблему, которая возникла из конкретной ситуации, с которой она была знакома и решение которой «требовалось ситуацией, она не сталкивалась с необычными трудностями, часто проявляя превосходный смысл» ([25], с.273-274). Другими словами, лучшая стратегия развития у студентов интереса к предмету — это сосредоточить преподавание на темах, которые находятся в их сфере интереса. Как сказал Уильям Джеймс, классик американской психологии, который первым применил его к обучению учителей, «Любой объект, не интересный сам по себе, может стать интересным, если он станет ассоциироваться с объектом, к которому интерес уже существует» ( [26], стр. 62). Интерес также можно использовать для развития мотивации в образовании, поскольку он «относится к модели выбора среди альтернатив — моделей, которые демонстрируют некоторую стабильность во времени и которые, по-видимому, не являются результатом внешнего давления» ([27], с.132).
Отражение так же важно, как и действие. Способность размышлять о выполняемых действиях составляет так называемый внутренний контроль, когда люди считают себя ответственными за собственное поведение, что отличается от внешнего контроля, когда они видят, что другие или обстоятельства являются основной мотивацией индивидуального поведения [28 ]. Процесс практического обучения при решении реальной проблемы обычно начинается с трех основных вопросов. Мы спрашиваем: во-первых, что должно происходить? Во-вторых, что нам мешает это сделать? В-третьих, что мы можем сделать?
Практическое обучение (часто называемое в академических кругах практическим исследованием [29, 30]) традиционно использовалось для обучения управлению бизнесом и социальным наукам [31, 32], проведению научных исследований [33] и повышению квалификации учителей [22, 34–36].В математическом образовании [4, 37] практическое обучение как метод обучения было принято как педагогика, ориентированная на самостоятельное решение реальных проблем с последующей рефлексией. Обучение — это основная цель, даже если решение проблем реально и важно. Обучение облегчается за счет отказа от устоявшихся мировоззрений, тем самым создавая несколько незнакомую обстановку для проблемы. Теперь у нас есть методика практического обучения с использованием технологий для преподавания математики через реальные проблемы под руководством инструкторов STEM и специалистов сообщества, использующих компонент проекта [4].Цифровые технологии видны, по крайней мере, в рамках необходимой типологии рукописей. Конечно, он может пойти намного дальше и включать в себя важную утилиту (например, числовой интегратор, электронную таблицу или специализированное программное обеспечение). Наконец, действие обучение (берущее начало в бизнес-образовании [20, 21]) обеспечивает эффективный и четкий подход к математическому образованию. Этот подход был разработан на основе различных (и, как упоминалось в начале раздела 2, иногда спорных) активных методов обучения , которые повсеместно используются преподавателями математики в различных контекстах обучения, ориентированных на конструктивизм и ориентированных на учащихся [38–41 ].
4. Практическое обучение на практике математического образования
Наша команда USF-SUNY [4] установила, что практическое обучение является положительной педагогической чертой на всех уровнях обучения (K-20). Кто-то может возразить, что, поскольку многие люди учатся на протяжении всей жизни, некоторые из нас могут использовать практическое обучение (возможно, в качестве преподавателей математики) за пределами K-20. Наша мотивация к практическому изучению математики может дать молодым ученикам возможность познакомиться с интересным, что известно о математике. Основные концепции могут быть довольно сложными, и студенты могут вернуться к идеям и развить их дальше по мере накопления опыта.Примеры практического обучения представлены в подразделах ниже по уровням обучения. Эти примеры даны с упором на конкретность, что, в свою очередь, мотивирует учащихся. Использование компонента проекта делает модель зонтика математики «один + два» доступной на высшем уровне (раздел 4.2.2).
4.1. Мотивация и обучение действиям на уровне начальной и средней школы
На уровне начальной школы математические концепции можно мотивировать с помощью надлежащим образом разработанных практических занятий, подкрепленных манипулятивными материалами.Такие действия должны объединять богатые математические идеи со знакомыми физическими инструментами. Как упоминалось выше, важным аспектом обучения действием является его ориентация на игру. Педагогическая характеристика игры в контексте обучения математике с помощью инструментов — это «нестандартное мышление», то есть то, что в присутствии учителя как «более знающего другого» открывает окно для будущего обучения учащихся. Тем не менее, отсутствие опоры можно наблюдать, как выразился Видлер [12], «когда ребенок дольше смотрит на асимметричную, а не на симметричную фигуру» (стр.18) интуитивно, через любопытство восприятия, осознавая, что устойчивость фигуры зависит от ее положения. То есть перцептивное любопытство в сочетании с творческим мышлением часто выходит за рамки деятельности, предназначенной для одного уровня, и сливается с изучением более продвинутых идей на более высоком когнитивном уровне. В следующих двух разделах показано, как использование двусторонних счетчиков и квадратных плиток, физических инструментов, обычно используемых в настоящее время в классе элементарной математики, может поддерживать, соответственно, введение чисел Фибоначчи, что позволяет с помощью вычислений открыть окно. к концепции золотого сечения и связать построение прямоугольников (из плиток) с обсуждением особых числовых соотношений между их периметрами и площадями.В обоих случаях переход от начального уровня к второстепенному может быть облегчен за счет использования цифровых технологий. То есть математические идеи, рожденные в контексте практического обучения с помощью физических инструментов, могут быть расширены на более высокий уровень с помощью вычислительных экспериментов, поддерживаемых цифровыми инструментами.
4.1.1. От двусторонних счетчиков к золотому сечению посредством обучения действием
Рассмотрим следующий сценарий обучения действиям:
Определите количество различных вариантов расположения одного, двух, трех, четырех и т. Д. На двусторонних (красных / желтых) счетчиках в котором не появляются две красные фишки подряд.
Экспериментально можно сделать вывод, что один счетчик можно расположить двумя способами, два счетчика — тремя способами, три счетчика — пятью и четыре счетчика — восемью (рис. 1). В частности, на рисунке 1 показано, что все комбинации с четырьмя счетчиками могут быть подсчитаны путем рекурсивного сложения 3 + 5 = 8, поскольку их можно разделить на две группы, так что в первой группе (с мощностью три) крайний правый счетчик равен красный, а во второй группе (мощность пять) крайний правый жетон желтый.Реализуя эту идею под руководством учителя, молодой ученик может обнаружить, что следующая итерация (пять счетчиков — 13 способов, так как 13 = 5 + 8) согласуется с описанием на рисунке 1. Увеличение для единообразия последовательность 2, 3, 5, 8, 13 двумя единицами (при условии, что пустой набор счетчиков имеет только одно расположение) позволяет описать завершение вышеупомянутого сценария обучения действиям (то есть размышления о результатах воздействия на конкретный материалов согласно определенному правилу) через последовательность 1, 1, 2, 3, 4, 5, 8, 13,…, (в которой первые два числа равны единице, а каждое число, начиная с третьего, является суммой два предыдущих числа) — одна из самых известных числовых последовательностей во всей математике, названная в честь Фибоначчи (1270–1350), самого выдающегося итальянского математика своего времени.В рамках размышления над сценарием юным студентам можно сказать, что, какими бы эзотерическими ни казались числа Фибоначчи, они, вероятно, столкнутся с ними снова.
Действительно, на вторичном уровне числа Фибоначчи можно исследовать в терминах отношений двух последовательных членов,. С этой целью можно использовать электронную таблицу, чтобы продемонстрировать, что отношения приближаются к числу 1,61803 по мере увеличения n , независимо от первых двух членов последовательности, и. Точное значение, число, известное как золотое сечение.Это пример того, как использование компьютера может предоставить ученикам и их учителям неформальный мост, соединяющий более низкий когнитивный уровень с более высоким. Без простоты вычисления соотношений двух последовательных чисел Фибоначчи, представленных в электронной таблице, было бы гораздо труднее связать простую обучающую деятельность по конкретному расположению двусторонних счетчиков с когнитивно более сложной идеей сходимости отношения к числу, известному с древности как золотое сечение.Золотое сечение, мотивируемое компьютером, может быть обнаружено в контексте изучения специальной числовой последовательности, описывающей задачу обучения действиям, подходящую для маленьких детей. Другими словами, компьютер может естественным образом открыть окно для будущего практического обучения учащихся (см. Примечание об исследовании болезни Альцгеймера в Разделе 6 ниже).
В связи с использованием двусторонних счетчиков в контексте чисел Фибоначчи следует отметить, что многие кандидаты в учителя считают, что конкретные материалы можно использовать только на элементарном уровне, а выше этого уровня они бесполезны.Имея это в виду, авторы хотели бы утверждать, что, как и в случае с числами Фибоначчи, конкретные материалы могут использоваться для введения довольно сложных понятий, чтобы добавить фактор конкретности в изучение абстрактных идей. В частности, двусторонние счетчики могут служить воплощением двоичной арифметики во вводном курсе информатики. Более конкретно, если записать первые 16 натуральных чисел в двоичной форме, то при поддержке двусторонних счетчиков можно увидеть следующее.Есть два однозначных числа, в которых в ряду не появляются никакие единицы (без красных жетонов подряд), три двузначных числа без единиц, стоящих подряд, пять трехзначных чисел, в которых в ряду не появляются никакие единицы, и восемь четырехзначных чисел, в которых подряд не появляются единицы. Числа 2, 3, 5 и 8 — это последовательные числа Фибоначчи, которые, таким образом, могут быть использованы в качестве фрагментов предыдущих знаний учащихся при разработке новых идей посредством практического обучения. Более подробные исследования вторичного (и третичного) уровня с числами Фибоначчи см. В [43].
Очевидно, что мотивация связана с ожидаемым будущим успехом как следствие подросткового возраста. Теперь студенты стремятся к большей конкретизации понятий. Когда учащиеся средней школы имеют сильную мотивацию к практическому обучению, они могут создавать проекты уровня бакалавриата, как описано для студентов в Разделе 4.2 ниже. При «зрелой» проектной работе появляется постепенное чувство «серьезности». Прекрасные примеры практического обучения учащихся средних школ, выступающих на уровне колледжа, можно увидеть в проекте Publix Лорен Вудбридж «Pallet Physics» ([44], v.3, 2 (8)), проект квантовых вычислений Бо Муна «Проблема суммы подмножеств: уменьшение временной сложности NP-полноты с помощью квантового поиска» ([44], т. 4, 2 (2)), ракетный проект Логана Уайта « Моделирование полета ракеты в приближении низкого трения »([44], v. 6, 1 (5)), и проект Рошана Вармана по спиновым вычислениям« Spintronic Circuits: The Building Blocks of Spin-based Computing »([44] , т. 7, 1 (1)).
4.1.2. Креативность и обучение действиям
Люди творческие, когда они мотивированы, и можно проявить больше творчества после общей, формирующей конкретизации идей.Важно рано распознавать творческие способности студентов. Педагоги рассматривают творчество как «один из важнейших навыков 21 века… жизненно важный для индивидуального и организационного успеха» ([45], стр. 1). Способность учителей распознавать творческие способности своих учеников, которые могут быть скрыты за их незрелой успеваемостью в классе, имеет решающее значение для успешного преподавания и продуктивного обучения. Если скрытые творческие способности учеников не признаются и не поддерживаются учителем, они, скорее всего, останутся бездействующими, если не исчезнут [46].Следующая история, взятая из класса второго класса, поддерживает идею о том, что учителя являются главными хранителями раскрытия творческого потенциала маленьких детей.
Кандидат в учителя начальных классов, работая индивидуально с учеником второго класса (под наблюдением классного руководителя), попросил его построить все возможные прямоугольники из десяти квадратных плиток (настоящая проблема для второго класса), ожидая, что ученик сможет Постройте два прямоугольника, 1 на 10 и 2 на 5, каждый из которых представляет собой факт умножения числа 10, что будет изучено позже (в третьем классе).Кандидат в учителя был удивлен, увидев три прямоугольника, как показано на рисунке 2. Большое количество обучающих идей для практического обучения может возникнуть из-за принятия прямоугольника с отверстием, которое демонстрирует скрытые творческие способности ребенка. Некоторые идеи могут быть связаны со вторичной математикой. Чтобы уточнить, подумайте о том, чтобы изучить взаимосвязь между площадью и периметром этого прямоугольника с отверстием, считая как внешний, так и внутренний периметры (размышление под руководством учителя о действиях ученика с использованием конкретных материалов).Видно, что площадь составляет 10 квадратных единиц, а периметр — 20 погонных единиц. То есть численно периметр в два раза больше площади. Сравнение площадей с периметрами прямоугольников известно еще со времен Пифагора [47]. В режиме обучения действием можно исследовать следующую ситуацию: существуют ли другие прямоугольники с прямоугольными отверстиями, у которых периметр в два раза больше площади? С этой целью на уровне средней школы можно ввести четыре переменные: a , b , c и d , как длину и ширину большего и меньшего прямоугольников.Отсюда следует соотношение ab — cd = a + b + c + d . Используя Wolfram Alpha — вычислительную машину знаний, доступную бесплатно в Интернете, — можно попросить программу решить указанное выше уравнение над положительными целыми числами. Результат будет следующим:
Если задать a = b = 3, можно выбрать c = 1, откуда d = 1. Это дает нам квадрат с квадратным отверстием (рисунок 3).Этот пример показывает, как знание алгебры и возможности использования технологий могут помочь практикующим учителям в работе с маленькими детьми по развитию критического мышления и развитию творческих способностей. То есть, опять же, технологии служат неформальным мостом, мотивирующим связующим звеном между двумя разными классами учебной программы по математике. Принимая во внимание, что учитель может не обязательно видеть богатую среду обучения за нетрадиционным ответом ученика, сам факт того, что такой ответ был принят и похвален, будет мотивировать этого и других учеников продолжать мыслить нестандартно.
В заключение этого раздела отметим, что тройку, ученика начальной школы, классного учителя и кандидата в учителя, можно сравнить в контексте практического обучения с учеником бакалавриата, математическим факультетом и предметом. Area Advisor, как описано ниже в Разделе 4.2.2. Сходство этих двух сред (с разницей в несколько лет) заключается в двойном наблюдении за учеником, изучающим математику, дуэтом «других более знающих».
4.2. Бакалавриат по математике и практическому обучению
4.2.1. Понимание абстрактности с обучением на практике
Язык математики абстрактный с большей абстракцией на более высоких уровнях. Традиционно университетская математика для нематематических специальностей преподается, дистанцируясь от реальности и не имея никакого отношения к профессиональным интересам студентов. В этом контексте многие будущие профессионалы не видят важности математики в своих перспективных областях [48]. Кроме того, абстрактность в обучении часто приводит к проблемам общения.Как отмечено в [49], в связи с преподаванием инженерной математики могут быть несоответствия между терминологией и идеями, используемыми математиком-преподавателем, и их интерпретацией студентами. Из-за того, что математическое образование на университетском уровне слишком теоретическое, оно становится неэффективным: нематематические специальности изучают предмет «потому что они должны». Альтернативный подход к математическому образованию основан на хорошо известном и прагматичном понятии «обучение на практике» (напр.ж., [50–54]), что делает возможным конструктивное взаимодействие чистых и прикладных идей. Этот подход имеет большой потенциал для внедрения экспериментального обучения в математику — базовую последовательность курсов в учебной программе по высшей математике.
4.2.2. Математическая модель зонтика
Вся университетская учебная программа по математике для нематематических специальностей может извлечь выгоду из практического обучения. Было обнаружено, что, особенно на университетском уровне, следует придерживаться «середины пути» в отношении относительных весов, придаваемых теории и применению.Математическая зонтичная группа (MUG) Университета Южной Флориды (USF), инициированная Аркадием Гриншпаном в 1999 году [55], занимает эту «позицию». Он устраняет разрыв между математическим образованием и приложениями, одновременно вдохновляя студентов STEM на приобретение математических навыков, необходимых для успеха в соответствующих дисциплинах. Эта инициатива привела к разработке модели «Зонтик математики» в образовании STEM, включающей сотни междисциплинарных (прикладных математических) студенческих проектов.За десять лет, прошедших с момента сообщения о том, что программа MUG была первой организацией, которая содействовала персонализированным математическим проектам, при поддержке консультантов по математике и предметным областям, для обучения нематематических дисциплин студентам STEM [56], MUG оставалась уникальной в этом отношении. Каждый проект выполняется под двойным контролем: консультант по математике (математический факультет) и консультант по предметной области (университетский или общественный специалист), который обычно предлагает проблему [4, 48, 55, 57–59].
Отличительной чертой MUG является уловка, заключающаяся в соединении одного студента бакалавриата с как минимум двумя специалистами. Ситуация проиллюстрирована на Рисунке 4. В результате ученики получают доступ к более широкому кругу знаний, чем обычно предоставляется одному преподавателю математики.
Еще одной сильной стороной является наличие связей с сообществом, которые возможны, или междисциплинарные связи, которые, по крайней мере, имеют место за пределами математического факультета вуза.Практическое обучение привносит «реальность» в абстракции математики. Даже когда преподаватели математики пытаются решить задачи с помощью приложений, полезность не осознается из первых рук, пока студенты не начнут применять ее. Это мотивационный подход для всех участников трио. Позже студенты могут решить провести исследование в связи с их опытом работы в проекте. Кроме того, они, вероятно, сохранят задействованные концепции дольше, чем при подходе «чистой лекции».
4.2.3. Практическое обучение на курсах математического анализа верхнего уровня
Практическое обучение является сильным мотивирующим фактором для всех участников, участвующих в математической группе Umbrella. Этот фактор, кажется, является общей нитью во всем спектре практического обучения K-20. Заинтересованность участников в практическом обучении может быть пропорциональна индивидуальному опыту. Преподаватели математики потенциально могут получить наибольшую пользу, но от студентов ожидается, что они будут знать теорию достаточно, чтобы их можно было мотивировать. Что касается программ бакалавриата по математике, таких как математический анализ II и III, считается, что учащимся достаточно пройти несколько небольших тестов и домашних заданий, а затем направить свою энергию на практическое обучение, а не требовать от них успешной сдачи выпускного экзамена.В частности, эта педагогика практического обучения помогает студентам, которые «незначительно преуспели», позволяя в их итоговые оценки включать компонент практического обучения, которому по праву придается значительный вес в общей оценке курса.
Чаще встречаются «успешные», которые могут быть очень продуктивными в своих проектах по обучению действиям. Есть вероятность, что работы студентов будут опубликованы или, возможно, даже отмечены [4, 57], как и многие студенты за последние два десятилетия.Это прекрасные мотиваторы для всех сторон, участвующих в практическом обучении. Поскольку действие проистекает из мотивации, важно осознавать роль «мотиваторов действия». Для студентов высших учебных заведений мощным мотиватором часто является изучение чего-то полезного и того, на чем можно построить или улучшить успешную карьеру.
Примечательно, что студенты естественным образом мотивированы успехом в изучении математики. Влияние практического обучения было проанализировано в Университете Южной Флориды на курсах инженерного исчисления, в которых участвовали тысячи студентов, прошедших эти курсы и последующие курсы с весны 2003 г. по весну 2015 г. [59].Некоторые результаты (сгруппированные по расе и этнической принадлежности) представлены на Рисунке 5 [59]. На этом рисунке показан эффект обучения действием, параллельных разделов обучения без действия и исторических (традиционных) разделов. В этой части исследования участвовали 1589 студентов, изучающих действие, и 1405 студентов, обучающихся на курсах, не использующих элемент обучения действием. Наконец, еще 2316 человек были отмечены как «исторические», что означает, что они прошли курс до весны 2003 г. (то есть до того, как было проведено различие в отношении использования или неиспользования практического обучения в своих курсах).Исследователи тщательно включили доверительные интервалы в свои результаты. Очевидно, что в этой относительно большой подгруппе из более крупного исследования все четыре категории расы / этнической принадлежности предпочитают быть участниками обучения действием. Для размышления есть много информации из [59]. Во всяком случае, этот и другие результаты демонстрируют академическое превосходство в действии над обучением без действия. Прагматический вывод состоит в том, чтобы обеспечить обучение действиям, поскольку это работает.
4.2.4. Практическое обучение как универсальная образовательная концепция
Мотивация преподавателей математики возникает в результате знакомства с новым опытом практического обучения. В настоящее время зарегистрированы многие сотни проектов практического обучения, представляющих широкий круг тем. Кроме того, всегда происходит обучение тонким действиям, которое никогда не документируется. Из тех проектов, которые доступны в Журнале бакалавриата по математическому моделированию: один + два (UJMM) [44], очевидно, что практически во всех областях можно использовать практическое обучение.Есть проекты, посвященные очень специфическим отраслям инженерии, например, биомедицинским нанотехнологиям. Есть также много других проектов, помимо «собственно инженерной мысли», например, связанных с музыкой или даже образованием. Другие — это кросс-полевые типы, которые не поддаются четкой классификации. Типы мостов часто представляют особый интерес. Это мотивирует преподавателей увидеть, что входит в смесь и какие области могут быть связаны посредством практического обучения. Это междисциплинарные особенности, желательные для всех учебных программ (в «вселенной учебных программ», то есть в образовании).Некоторые подробности доступны на главном веб-сайте Mathematics Umbrella Group (см. Центр промышленной и междисциплинарной математики). В журнале представлена избранная подгруппа из более чем 2400 студенческих проектов, представленных с 2000 года. Признак разнообразия тематики проектов и участников студенческих работ очевиден из разнообразия тем, рассматриваемых в последних изданиях UJMM ([44], v. 8 , 1-2): «Применение простых гармоник для моделирования толчка» Кая Раймонда, «Силы, действующие на парусную лодку» Келли Стукбауэр, «Оптимизация топливного элемента» Эдуардо Гинеса, «Анализ осадков в Тампе» Эми Полен, «Аппроксимация площади поверхности колеблющихся липидных листочков с помощью взвешенной сеточной мозаики» Анаф Сиддики, «Рудиментарная модель реакции глюкозы на стресс» Нашей Риос-Гусман, «Органический сельскохозяйственный анализ: эффективность общепринятой практики» Брэдли Биега, «Использование Баланс скорости энтропии для определения теплопередачи и работы во внутренне обратимом, политрофическом, установившемся процессе потока »Саванна Гриффин,« Модельная функция улучшения мирового рекорда женщин на 1500 м с течением времени »Энни Аллмарк , «Максимальная мощность солнечного модуля из поликристаллического кремния» Джейнил Патель, «Оптимизация реакции сдвига водяного газа» Али Албулуши и «Волны цунами» Саманты Пеннино.
Помимо множества опубликованных проектов бакалавриата, существуют «сценарии практического обучения», которые можно рассматривать как совокупность различных практических занятий. Этот смешанный опыт имеет несколько идеалистических проблем. Проблемы можно считать типичными для того, что может рассматриваться в проекте, а не реальными примерами. Эти сценарии мотивируют преподавателя математики включать практическое обучение в обычный теоретический курс.Этим опытом, вероятно, поделятся любые преподаватели математики, занимающие аналогичные должности в математическом образовании. Непосредственной мотивацией здесь является расширение нашего понимания взаимосвязи между теорией математики и решением актуальных проблем в реальном мире.
5. Мотивирующие вопросы как основное средство изучения математики
5.1. Вопросы как инструменты обучения действиям
Задаваемые вопросы обычно становятся более сложными по мере взросления учащихся.Преподаватели на всех уровнях математического образования используют знания и опыт, чтобы ответить на вопросы. Желательны конкретные и уверенные ответы, при этом иногда (как правило, на более высоких уровнях) вопросы могут потребовать дополнительных размышлений перед их изложением. В контексте постановки проблем и их решения важно различать два типа вопросов, которые могут быть сформулированы так, чтобы стать проблемой: вопросы, требующие получения информации, и вопросы, требующие объяснения полученной информации [60].Подобно двум типам знаков — символам первого порядка и символике второго порядка [61] — можно относиться к вопросам, ищущим информацию, как к вопросам первого порядка, а те, которые требуют объяснения, как к вопросам второго порядка [46]. В то время как на вопросы первого порядка можно ответить, используя разные методы, похоже, что не все методы могут быть использованы для объяснения того, что было получено при поиске информации, то есть для предоставления ответа на вопрос второго порядка. Часто просьба о объяснении является разумным размышлением о методе предоставления информации.
Что означает, что учителя должны обладать «глубоким пониманием» математики? Зачем им нужно такое понимание? У будущих учителей есть несколько причин, по которым они должны быть тщательно подготовлены к математике, чтобы иметь положительное влияние на успеваемость молодых изучающих математику. Во-первых, в современном классе математики ожидается, что ученики всех возрастов будут задавать вопросы, и их даже поощряют. В Соединенных Штатах национальные стандарты уже для классов до K-2 предполагают, что «необходимо воспитывать естественную склонность учащихся задавать вопросы… [даже] когда ответы не сразу очевидны» ([19], с.109). Это предложение подтверждается следующим комментарием кандидата в учителя начальной школы: «Не зная ответа на вопрос — это нормально, но нельзя оставлять этот вопрос без ответа». Кандидат описывает себя как «тот педагог, который всегда будет побуждать моих учеников задавать себе некоторые из тех же вопросов, которые позволят им участвовать в глубоком размышлении».
5.2. Международный характер обучения посредством задавания вопросов
Министерство образования Онтарио в Канаде, расположенное на границе с США, в рамках своей учебной программы по математике для младших классов ожидает, что учителя будут иметь возможность «задавать учащимся открытые вопросы … поощряйте студентов задавать себе подобные вопросы… [и] моделируйте способы, которыми можно ответить на различные вопросы »([62], с.17). Для развития такого мастерства «учителя должны знать способы использования математических рисунков, диаграмм, материалов для манипуляций и других инструментов для освещения, обсуждения и объяснения математических идей и процедур» ([63], с. 33). В Чили учителя математики должны «использовать представления, опираться на предварительные знания, задавать хорошие вопросы и стимулировать любознательное отношение и рассуждение учащихся» ([64], с. 37). В Австралии учителя математики знают, как мотивировать «любопытство, бросить вызов мышлению учащихся, обсудить математический смысл и моделировать математическое мышление и рассуждения» ([65], с.4). Репертуар возможностей обучения, которые преподаватели предлагают своим ученикам, включает постоянный поиск альтернативных подходов к решению проблем, а также помощь ученикам в изучении конкретной стратегии решения проблем, с которой они боролись. В национальной учебной программе по математике в Англии используются такие термины, как «практика со все более сложными задачами с течением времени… [и] может решать задачи… с возрастающей степенью сложности» ([66], стр. 1). С этой целью учителя должны быть готовы иметь дело с ситуациями, когда естественный поиск вопросов приводит учеников к этой изощренности и усложнению математических идей.Необходимость такой подготовки учителей подтверждается кандидатом в учителя, который сформулировал это следующим образом: «Если ученик спрашивает, почему, а учитель не может объяснить, как что-то произошло, ученик теряет всякую веру и интерес к предмету и уважение к учителю ».
На уровне бакалавриата часто обсуждаются вопросы второго порядка. Преподаватели математики знают, что такие вопросы могут быть полезны для стимулирования дальнейших исследований. Возможно, правда, что математика, с которой приходится сталкиваться на уровне начальной и средней школы, должна быть безупречно понята преподавателями математики и что учащиеся могут быть «уверены» в том, чему их учат.Когда мы начинаем заниматься, скажем, теорией множеств или двумерной / трехмерной геометрией, могут быть загадочные результаты, которые действительно побуждают учащихся задуматься об изучении высшей математики. Любопытство математики — это то, что учащиеся, вероятно, сочтут привлекательным. Конечно, преподавателю математики полезно иметь глубокое понимание темы; однако в ответе могут быть детали, которые не поддаются немедленному описанию. В некоторых редких случаях ответ даже не доступен. Ожидается, что зрелость студентов позволит им признать, что на более высоких уровнях математики они не должны терять веру и уважение к преподавателю, если объяснение откладывается.На более ранних этапах математического образования учащиеся верят, что математика идеальна. Однако математика так же несовершенна, как и все остальное, изобретенное людьми. Студенты должны это знать.
6. Компьютерная сигнатурная педагогика и модель обучения и преподавания 3P
Любопытство и мотивация также могут быть поддержаны использованием цифровых инструментов в качестве инструментов практического обучения. Как было показано на примерах из дошкольного математического образования, компьютеры могут способствовать переходу с одного познавательного уровня на другой (более высокий).Это согласуется с современным использованием компьютеров в математических исследованиях, когда новые результаты возникают в результате вычислительных экспериментов. Например, радость перехода от визуального к символическому, когда двухсторонние счетчики были предложены как средство рекурсивного построения чисел Фибоначчи, которые затем можно было смоделировать в электронной таблице, где, возможно, благодаря интуиции, определился определенный образец в поведении соотношений могут быть обнаружены два последовательных члена. Это открытие мотивирует формальное объяснение того, почему отношения ведут себя определенным образом.Точно так же переход от числового описания прямоугольников с точки зрения периметра и площади приводит к их формальному представлению. В то время как прямоугольник с отверстием был обнаружен путем мышления «нестандартно», наличие цифрового инструмента облегчает переход от визуального к символическому с последующим использованием последнего представления в ситуации математического моделирования.
Мощь компьютерного моделирования может служить мотивацией для разработки и последующего исследования более сложных рекуррентных соотношений, чем у чисел Фибоначчи.Как обсуждалось в [58], использование моделирования электронных таблиц может быть применено в контексте исследования болезни Альцгеймера для изучения популяции трансгенных мышей с упором на финансовую осуществимость покупки двух родительских мышей (самца и самку) и выращивания популяции мышей определенной размер. Эффективный подход к этой проблеме включает теорию рекуррентных соотношений, которые первоначально были введены на вторичном уровне через числа Фибоначчи. Результаты, полученные с помощью моделирования в электронной таблице, затем могут быть использованы для проверки теоретических результатов.Подробнее об этом проекте см. [55].
Все это приводит к понятию компьютерной сигнатурной педагогики (CASP), когда побуждает размышлять и поддерживать анализ действий, предпринятых учеником в контексте практического обучения, обеспечивает CASP глубинную (а не поверхностную) структуру обучения . [67] нанят учителем как «более знающий друг». Точно так же в более ранней публикации Биггс [15] проводил различие между поверхностной и глубинной структурой студенческих подходов к обучению , описывая первый подход с точки зрения студента, «вкладывающего минимальное время и усилия, чтобы соответствовать требованиям… [ тогда как последний подход] основан на интересе к предмету задачи; стратегия максимального понимания »(стр.6). Адаптировав модель обучения в классе, предложенную Данкином и Биддлом [68], Биггс [15] представил теперь известную 3P-модель обучения студентов, основанную на представлениях студентов об обучении в целом и их текущей учебной среде (предзнаменование), студенческий подход к обучению (процессу) и результат обучения студента (продукт). Исследование того, как первый P модели влияет на второй P и, как следствие, на третий P, было проведено Лиццио, Уилсоном и Саймонсом [69], которые выдвинули семь теоретических положений.Одно из этих предположений было основано на аргументе о том, что если студенты университетов воспринимают преподавание курсов их профессорами как надежное, то они с большей вероятностью выберут глубокий подход к обучению. Авторы пришли к выводу, что этот аргумент верен не только для учебных курсов по высшей математике, но и для курсов по методам математики для будущих школьных учителей. В современном преподавании математики правильное использование технологий является важной характеристикой учебной среды.В частности, в контексте студенческого подхода к обучению в глубокой структуре под эгидой CASP, можно расширить использование одного цифрового инструмента, такого как электронная таблица, другими современными технологиями, такими как Wolfram Alpha. С этой целью CASP, структурированный на основе глубоких подходов к преподаванию и обучению, может включать использование так называемых интегрированных электронных таблиц [70], которые поддерживают преподавание математики на всех образовательных уровнях с вычислительной надежностью обучения учащихся.
7.Проблемы и догадки, которые вдохновляют и мотивируют
Студент, изучающий математику (на любом уровне образования), скорее всего, столкнется с «тщетностью» математического совершенства. В математике есть легко выражаемые вопросы (предположения), на которые нет ответов (доказательство). Это похоже на принцип неопределенности Гейзенберга, где есть «пределы точности», например, при нахождении как положения, так и импульса. Важное понятие состоит в том, что не всегда есть «стандартные» решения математических задач.Зная это, учащиеся могут продолжить изучение математики для решения некоторых задач. В этих случаях действует «нестандартное» обучение действиям. Первоначальные размышления носят в основном теоретический характер, но в конечном итоге будет вызвано приложение. Заметьте, что проблему даже не нужно решать, многое предстоит узнать в этой попытке. Это мотивационный процесс. Кроме того, размышление привносит конкретность в концепции проблемы и относится к общей «природе» проблем и решению проблем.
Реальные приложения математики в значительной степени стимулируют различные виды исследований в предметной области, в которых участвуют как профессиональные математики, так и студенты разных специальностей. Это не означает, что прикладная математика является единственным значимым источником развития математической мысли. Действительно, в самой математике есть много проблем, которые раньше мотивировали и продолжают мотивировать тех, кто стремится получить полное представление о математике как о фундаментальной науке.Некоторые из этих задач (иногда называемых предположениями) можно рекомендовать для включения в учебную программу по математике для не математических специальностей, а также для кандидатов в учителя. Опыт авторов показывает, что теоремы и предположения, берущие начало как в чистой, так и в прикладной математике, могут запустить воображение и мыслительный процесс тех, чей ум открыт для оспаривания.
Например, формулировки и исторические подробности таких захватывающих проблем, как Великая теорема Ферма, доказанная Эндрю Уайлсом [71], и гипотеза Бибербаха, доказанная Де Бранжем [72] (см. Также [73]), могут быть включены в некоторые базовые курсы математики. для нематематических специальностей.Доказательства этих теорем требуют не только элементарных средств, но и чрезвычайно сложны. Однако, как заметил Стюарт [74], «тот факт, что доказательство важно для профессионального математика, не означает, что преподавание математики данной аудитории должно ограничиваться идеями, доказательства которых доступны этой аудитории» (стр. 187). . Давайте взглянем на них.
Последняя теорема Ферма утверждает, что уравнение не имеет ненулевых целочисленных решений для x, y и z при .В частности, эта теорема может быть представлена различным группам студентов-математиков как способ ответить на вопрос: Можно ли расширить интерпретацию троек Пифагора как разделение квадрата на сумму двух квадратов, чтобы включить аналогичные представления для более высоких степеней ? Как подробно описано в [75], использование электронной таблицы со второстепенными кандидатами в учителя позволяет визуализировать Великую теорему Ферма путем моделирования несуществующих решений вышеуказанного уравнения для почти таким же образом, как и для.Точно так же вполне возможно, что с помощью технологий или других средств естественный мост между утверждением Великой теоремы Ферма и некоторыми геометрическими свойствами модульных эллиптических кривых в доказательстве Уайлса станет доступным для будущих студентов-математиков.
Гипотеза Бибербаха утверждает, что для каждой аналитической функции, взаимно однозначной в единичном круге, неравенство выполняется. Один только этот легендарный результат с его ошеломляющими данными (см., Например, [76]) может вызвать у студентов интерес к изучению таких важных математических понятий, как взаимно однозначные функции, степенные ряды, сходимость и коэффициенты Тейлора, которые, в частности, являются целесообразно обсудить с инженерами-майорами.Здесь также стоит упомянуть о глубоких геометрических корнях гипотезы Бибербаха. Например, его доказательство для основано на представлении плоской заданной области как контурного интеграла и, таким образом, доступно для нематематических специальностей, зачисленных на курс исчисления верхнего уровня.
Существует также известная гипотеза Гольдбаха [77], которая утверждает, что каждое четное число больше двух может быть записано как сумма двух простых чисел (возможно, более чем одним способом). Было бы чудом, если бы эта гипотеза оказалась ложной.Пока встречных примеров не найдено. Хотя поиск противоположного примера кажется бесплодным, эмпирически было показано, что гипотеза Гольдбаха верна для всех четных чисел больше двух и меньше некоторого известного числа, состоящего из 17 цифр.
Еще одна известная, но легкая для понимания проблема — это гипотеза палиндрома [78]. Он имеет дело со свойством палиндромов (т. Е. Целых чисел, которые читаются так же, как вперед и назад) привлекать целые числа в соответствии со следующей процедурой: начать с любого целого числа, перевернуть его цифры и сложить два числа; повторите процесс с суммой и продолжайте видеть, что это приводит к палиндрому.Примечательно, что эта «игра с числами» недавно была упомянута как одна из двенадцати нерешенных проблем современной математики [79]. Именно эта проблема и, как отмечено в Принципах и стандартах школьной математики [19], ее образовательный потенциал для учащихся средних школ «ценить истинную красоту математики» (стр. 21) побудил кандидата в учителя средней школы работать с один из авторов по разработке вычислительных обучающих сред для учебных презентаций и экспериментов с большим классом развлекательных задач, как решенных, так и нерешенных [80].Как выразился Гаусс, «в арифметике самые элегантные теоремы часто возникают экспериментально в результате более или менее неожиданной удачи, а их доказательства лежат настолько глубоко погруженными в темноту, что опровергают самые острые вопросы» (цитируется в [81]. ], стр. 112).
Похоже, что использование технологий для значимых экспериментов с числами под эгидой CASP может вдохновить и мотивировать студентов уже на уровне дошкольного образования к новым открытиям в элементарной теории чисел.Каким-либо образом расширяя наше понимание математики, мы потенциально расширяем нашу способность «процветать». Это неотъемлемая ценность и мотивация для обучения действиям. Предполагается, что вся математика может иметь приложения. Нам нужно только иметь мотивацию для разработки этих приложений.
8. Заключение
В этой статье, используя опыт авторов в преподавании математики и надзоре за применением предмета в практике государственных школ и промышленности, представлена структура совместного использования практического обучения и концептуальной мотивации в контексте К-20 математического образования.Были представлены различные примеры практического обучения — индивидуальная работа над реальной проблемой с последующим размышлением под наблюдением «более знающего другого». Такой надзор может включать в себя «дуэт других» — классного учителя и кандидата в учителя в школе K-12, а также преподавателя математики и советника по предметной области в университете. В статье показано, что практическое изучение математики идет рука об руку с концептуальной мотивацией — методикой обучения, в которой введение математических концепций мотивируется (соответствующими классу) реальными приложениями, которые могут включать в себя действия учащихся над объектами, ведущие к формальному описанию этого. действие через символику математики.Этот подход основан на важных рекомендациях математиков [5, 16, 17] и педагогических психологов [1, 25, 26, 61].
Главный вывод статьи состоит в том, что за счет многократного использования концептуальной мотивации и практического обучения на всех уровнях математического образования общий успех учащихся имеет большой потенциал для улучшения. Это сообщение подкрепляется примерами творческого мышления молодых учащихся в классе, основанного на всестороннем сотрудничестве школьных учителей и преподавателей университета (в духе Группы Холмса [82]).Точно так же это сообщение было подкреплено примерами интереса студентов к изучению математического анализа посредством практического обучения в реальной жизни. Похоже, что растущий интерес студентов к математике связан с практическим обучением и концептуальной мотивацией, которые использовались для исправления широко распространенного формализма в преподавании математики, который, в частности, стал препятствием на пути к успеху STEM-образования [4, 7, 8] . Когда учащиеся имеют опыт практического изучения математики в школьные годы, они, вероятно, продолжат изучение предмета в том же духе, тем самым избежав многих препятствий на пути перехода от среднего образования к высшему.Как упоминалось в разделе 4.2.3, исследование по внедрению практического обучения инженерному исчислению с участием тысяч студентов Университета Южной Флориды [4, 59] показывает, что, хотя интерес студентов к практическому обучению может быть пропорционален индивидуальному опыту в этом случае их результаты обучения демонстрируют академическое превосходство практического обучения над другими педагогическими средствами проведения расчетов.
В начале формального математического образования школьники должны начать знакомство с педагогикой практического обучения и концептуальной мотивации, усиленной, в зависимости от обстоятельств, задаванием вопросов и ответами на них, а также обучением использованию технологий.Как было показано в статье, не только учебные программы по математике K-12 во многих странах поддерживают обучение учащихся, задавая вопросы, но и их будущие учителя ценят такое математическое обучение. Аналогичным образом, компьютерная сигнатурная педагогика [37] может использоваться для максимального понимания учащимися математики и поощрения их глубокого подхода к обучению [15]. У студентов университетов больше мотивации, чем у школьников, чтобы справляться с обязанностями взрослой жизни. Тем не менее, обе группы студентов все еще могут быть мотивированы своим естественным «бросающим вызов возрасту» любопытством.В этом отношении стимулирующие вопросы, склонность к использованию компьютеров и известные классические задачи являются важными инструментами мотивации при изучении математики. Объединение всей учебной программы по математике K-20 в единое целое возможно, когда методы концептуальной мотивации и обучения действиям используются во всем этом образовательном спектре. Наконец, очевидно, что есть прагматическая причина для того, чтобы знакомить учеников с радугой обучения действием, и это потому, что среди сегодняшних учеников есть завтрашние учителя.Процесс должен и дальше развиваться.

 И., Бантова М. А. и др. Математика 3 класс. Учебник для
И., Бантова М. А. и др. Математика 3 класс. Учебник для

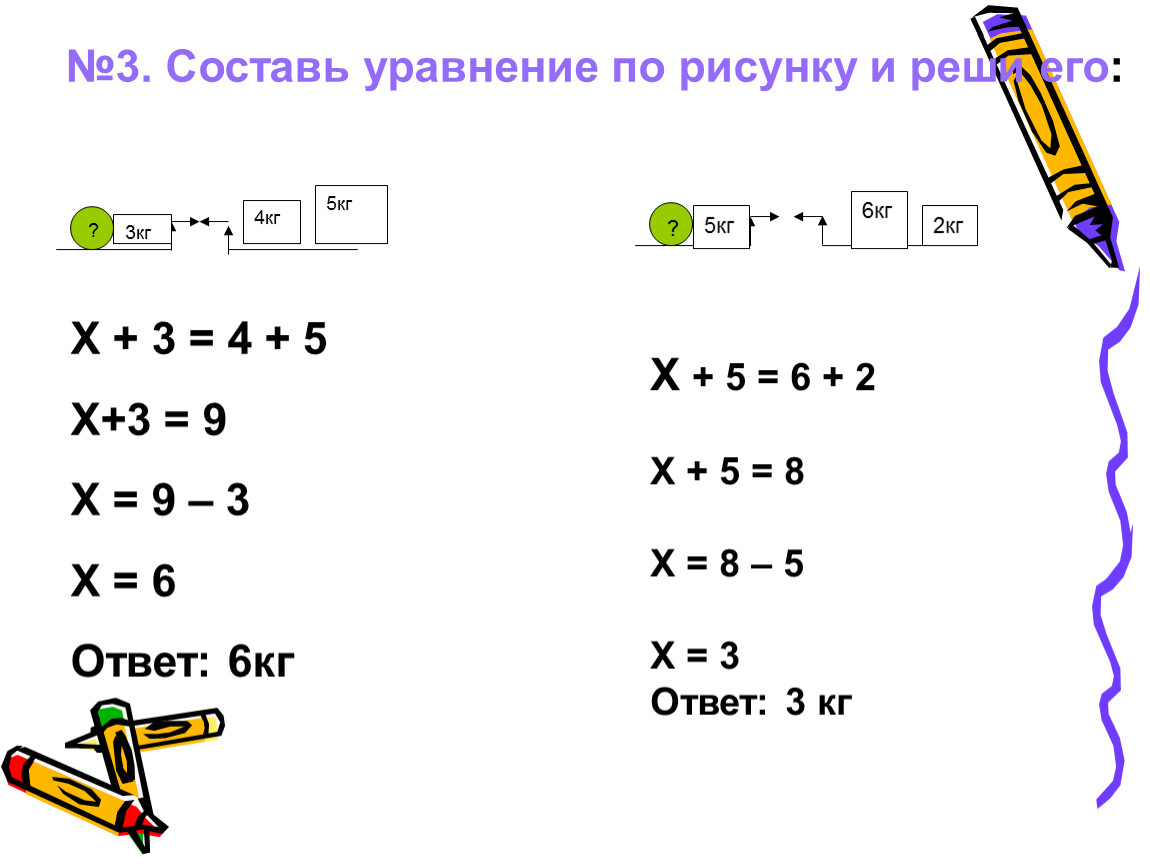
 применить правило нахождения неизвестного компонента
применить правило нахождения неизвестного компонента Сделай проверку.
Сделай проверку.
 (Доступно на английском и испанском языках.)
(Доступно на английском и испанском языках.)