Урок 42. уравнения первой степени с одним неизвестным. линейные уравнения с одним неизвестным — Алгебра — 7 класс

Алгебра

7 класс

Урок № 42

Уравнения первой степени с одним неизвестным. Линейные уравнения с одним неизвестным

Перечень рассматриваемых вопросов:

Линейные уравнения.

Корень уравнения.

Решение линейных уравнений.

Тезаурус:

Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.

Корень уравнения – это число, при подстановке которого в уравнение получается верное равенство.

Переменная – символ, используемый для представления величины, которая может принимать любое из ряда значений.

Свободный член – член уравнения, не содержащий неизвестного.

Решить уравнение – значит найти все его корни или установить, что их нет.

Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.

Линейное уравнение – уравнение вида ax = b, где x – переменная, a, b – некоторые числа.

Основная литература:

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

Дополнительная литература:

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Давайте посмотрим на 2 уравнения: 10x = 36 и 3x² = 2

Можем ли мы сказать, что оба уравнения являются линейными уравнениями первой степени?

Конечно, нет. Хотя, по определению линейных уравнений, оба уравнения подходят, у второго уравнения переменная входит в него во второй степени, а это противоречит отличительной особенности линейного уравнения первой степени.

Определение: Уравнение вида ax = b, где – x переменная, a, b – некоторые числа, называется линейным уравнением с одной переменной.

А что означает решить уравнение?

Решить уравнение – означает найти все его корни или доказать, что корней нет.

Линейными уравнениями называются не только уравнения вида ax + b = 0, но и любые уравнения, которые преобразованиями и упрощениями сводятся к этому виду.

Давайте подумаем, является ли уравнение 2(5x + 4) = 2x – 16 – линейным уравнением первой степени? Нет, так как оно не записано в виде ax = b. Можно ли привести его к такому виду?

Попробуем это сделать. Переменная x входит в это уравнение первой степени. Все такие уравнения можно преобразовать в вид ax + b = 0 с помощью тождественных преобразований. Для этого раскроем скобки в левой части уравнения, воспользовавшись распределительным законом умножения.

10x + 8 = 2x + 16

Вычтем из правой и левой частей уравнения 2x и 8.

Затем приведём подобные слагаемые в левой и правой частях уравнения и получим уравнение стандартного вида.

8x = 8

А как же проверить, является ли число корнем уравнения, не решая его?

В таком случае, нам достаточно подставить значение переменной в уравнение и проверить, выполняется равенство или нет.

Чтобы узнать, является ли число корнем уравнения, нужно:

— Подставить вместо переменной числовое значение.

— Упростить.

— Посмотреть, получилось верное равенство или нет.

Если верное, то число является корнем уравнения, в противном случае – нет.

Чётко распознать линейное уравнение можно в некоторых случаях. Скажем, если перед нами уравнения, в которых есть только неизвестные в первой степени и числа.

2(3x – 5) = x – 3

Приведём это уравнение к стандартному виду. В левой части раскроем скобки:

6x – 10 = x – 3

6x – x = 10 – 3

5x = 7

Линейное уравнение имеет вид:

ax = b, где a = 5 и b = 7.

Тренировочные задания.

Задание 1. Какое значение переменной удовлетворяет уравнению 4x – 2 = 14?

Варианты ответа:

x = 0

x = 2,5

x = 4

x = 0,1

Решение:

Для того чтобы определить, какое из значений удовлетворяет уравнению, нужно подставить вместо переменной соответствующее значение и проверить, получается ли истинное равенство. Соответственно, при истинности, значение переменной будет удовлетворять условию.

При x = 0 получаем: 4 · 0 – 2 = 14

–2 = 14 – ложь. Следовательно, x = 0 не удовлетворяет решению уравнения.

При x = 2,5 получаем: 4 · 2,5 – 2 = 14

3 = 14 – ложь. Следовательно, x = 2,5 не удовлетворяет решению уравнения.

При x = 4 получаем: 4 · 4 – 2 = 14

14 = 14 – истина. Следовательно, x = 4 удовлетворяет решению уравнения.

При x = 0,1 получаем: 4 · 0,1 – 2 = 14

–1,6 = 14 – ложь. Следовательно, x = 0,1 не удовлетворяет решению уравнения.

Ответ: x = 4

Задание 2. Уравнение 2(2x – 3) = 2x + 16 надо привести к стандартному виду.

Варианты ответа:

4x + 3 = 2x + 16

2x – 19 = 3x

4x = 22

2x = 22

Решение:

Для того чтобы определить, какое из значений является верным приведением уравнения к стандартному виду, нужно просто привести уравнение к стандартному виду.

2(2x – 3) = 2x + 16 – раскроем скобки, умножив число на разность;

4x – 6 = 2x + 16 – преобразуем уравнение, перенеся слагаемые, содержащие переменные в левую часть уравнения, а числа в правую, меняя при этом знак на противоположный;

4x – 2x = 16 – 6 – упростим выражение, приведя подобные слагаемые;

2x = 22 – полученное уравнение приведено к стандартному виду ax = b, где a = 1, b = 22

Ответ: 2x = 22

Решение линейных уравнений с примерами.

Уравнения онлайн Примеры уравнений 5

Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид

aх + b = 0
, где a и b произвольные числа, называется линейным уравнением

с одним неизвестным. Cегодня разберёмся, как эти линейные уравнения решать.

Например, все уравнения:

2х + 3= 7 – 0,5х; 0,3х = 0; x/2 + 3 = 1/2 (х – 2) — линейные.

Значение неизвестного, обращающее уравнение в верное равенство называется решением

или корнем уравнения

.

Например, если в уравнении 3х + 7 = 13 вместо неизвестного х подставить число 2 , то получим верное равенство 3· 2 +7 = 13. Значит, значение х = 2 есть решение или корень уравнения.

А значение х = 3 не обращает уравнение 3х + 7 = 13 в верное равенство, так как 3· 2 +7 ≠ 13. Значит, значение х = 3 не является решением или корнем уравнения.

Решение любых линейных уравнений сводится к решению уравнений вида

aх + b = 0.

Перенесем свободный член из левой части уравнения в правую, изменив при этом знак перед b на противоположный, получим

Если a ≠ 0, то х = ‒ b/a
.

Пример 1.

Решите уравнение 3х + 2 =11.

Перенесем 2 из левой части уравнения в правую, изменив при этом знак перед 2 на противоположный, получим
3х = 11 – 2.

Выполним вычитание, тогда
3х = 9.

Чтобы найти х надо разделить произведение на известный множитель, то есть
х = 9: 3.

Значит, значение х = 3 является решением или корнем уравнения.

Ответ: х = 3
.

Если а = 0 и b = 0
, то получим уравнение 0х = 0. Это уравнение имеет бесконечно много решений, так как при умножении любого числа на 0 мы получаем 0,но b тоже равно 0. Решением этого уравнения является любое число.

Пример 2.
Решите уравнение 5(х – 3) + 2 = 3 (х – 4) + 2х ‒ 1.

Раскроем скобки:
5х – 15 + 2 = 3х – 12 + 2х ‒ 1.

5х – 3х ‒ 2х = – 12 ‒ 1 + 15 ‒ 2.

Приведем подобные члены:
0х = 0.

Ответ: х — любое число
.

Если а = 0 и b ≠ 0
, то получим уравнение 0х = — b. Это уравнение решений не имеет, так как при умножении любого числа на 0 мы получаем 0, но b ≠ 0 .

Пример 3.
Решите уравнение х + 8 = х + 5.

Сгруппируем в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
х – х = 5 ‒ 8.

Приведем подобные члены:
0х = ‒ 3.

Ответ: нет решений.

На рисунке 1

изображена схема решения линейного уравнения

Составим общую схему решения уравнений с одной переменной. Рассмотрим решение примера 4.

Пример 4.

Пусть надо решить уравнение

1) Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12.

2) После сокращения получим
4 (х – 4) + 3·2 (х + 1) ‒ 12 = 6·5 (х – 3) + 24х – 2 (11х + 43)

3) Чтобы отделить члены, содержащие неизвестные и свободные члены, раскроем скобки:
4х – 16 + 6х + 6 – 12 = 30х – 90 + 24х – 22х – 86 .

4) Сгруппируем в одной части члены, содержащие неизвестные, а в другой – свободные члены:
4х + 6х – 30х – 24х + 22х = ‒ 90 – 86 + 16 – 6 + 12.

5) Приведем подобные члены:
‒ 22х = ‒ 154.

6) Разделим на – 22 , Получим
х = 7.

Как видим, корень уравнения равен семи.

Вообще такие уравнения можно решать по следующей схеме
:

а) привести уравнение к целому виду;

б) раскрыть скобки;

в) сгруппировать члены, содержащие неизвестное, в одной части уравнения, а свободные члены ‒ в другой;

г) привести подобные члены;

д) решить уравнение вида aх = b,которое получили после приведения подобных членов.

Однако эта схема не обязательна для всякого уравнения. При решении многих более простых уравнений приходится начинать не с первого, а со второго (Пример. 2
), третьего (Пример. 1, 3
) и даже с пятого этапа, как в примере 5.

Пример 5.
Решите уравнение 2х = 1/4.

Находим неизвестное х = 1/4: 2,
х = 1/8
.

Рассмотрим решение некоторых линейных уравнений, встречающихся на основном государственном экзамене.

Пример 6.
Решите уравнение 2 (х + 3) = 5 – 6х.

2х + 6 = 5 – 6х

2х + 6х = 5 – 6

Ответ: ‒ 0, 125

Пример 7.
Решите уравнение – 6 (5 – 3х) = 8х – 7.

– 30 + 18х = 8х – 7

18х – 8х = – 7 +30

Ответ: 2,3

Пример 8. Решите уравнение

3(3х – 4) = 4 · 7х + 24

9х – 12 = 28х + 24

9х – 28х = 24 + 12

Пример 9.
Найдите f(6), если f (x + 2) = 3 7-х

Решение

Так как надо найти f(6), а нам известно f (x + 2),
то х + 2 = 6.

Решаем линейное уравнение х + 2 = 6,
получаем х = 6 – 2, х = 4.

Если х = 4, тогда
f(6) = 3 7-4 = 3 3 = 27

Ответ: 27.

Если у Вас остались вопросы, есть желание разобраться с решением уравнений более основательно, записывайтесь на мои уроки в РАСПИСАНИИ . Буду рада Вам помочь!

Также TutorOnline советует посмотреть новый видеоурок от нашего репетитора Ольги Александровны, который поможет разобраться как с линейными уравнениями, так и с другими.

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Решаем дробно-рациональное уравнение 5/х = 100. Данное уравнение можно решить двумя способами. Давайте рассмотрим каждый из них.

План решения уравнения 5/x = 100

• найдем область допустимых значений для заданного уравнения;
• первый способ решения уравнения рассмотрев его как на пропорцию;
• второй способ решения уравнения, находя неизвестный делитель.

Находим неизвестный член пропорции

Сначала найдем ОДЗ уравнения. В левой части уравнения присутствует знак дроби и он равносилен знаку деления. Известно, что на ноль делить нельзя. Значит из ОДЗ мы должны исключить значения обращающие знаменатель в ноль.

ОДЗ: x принадлежит R \ {0}.

Теперь посмотрим на наше уравнение как на пропорцию.

Основное свойство пропорции.

Произведение крайних членов пропорции равно произведению ее средних членов.

Для пропорции a: b = c: d
или a/b = c/d
основное свойство записывается так: a · d = b · c.

Применим его и получим линейное уравнение:

100 * x = 5 * 1;

Разделим на 100 обе части уравнения, тем самым избавимся от коэффициента перед переменной х:

Находим неизвестный делитель

Посмотрим на уравнение как на частное. Где делимое равно 5, делитель x, а результат деления — частное равно 100.

Вспомним правило как найти неизвестный делитель — нужно делимое разделить на частное.

Найденный корень принадлежит ОДЗ уравнения.

Проверим найденное решение уравнения. Для этого подставим найденные корень в исходное уравнение и произведем вычисления:

Решение найдено верно.

Одним из самых важных навыков при поступлении в 5 класс
является умение решать простейшие уравнения. Так как 5 класс ещё не так далек от начальной школы, то и видов уравнений, которые может решать ученик не так уж и много. Мы познакомим Вас со всеми основными видами уравнений, которые необходимо уметь решать, если Вы хотите поступить в физико-математическую школу
.

1 тип: «луковичные»

Это уравнения, которые почти со вероятностью встретятся Вам при поступлении в любую школу
или кружок 5 класса как отдельное задание. Их легко отличить от других: в них переменная присутствует только 1 раз. Например, или .
Решаются они очень просто: необходимо просто «добраться» до неизвестной, постепенно «снимая» всё лишнее, что окружает её — как будто почистить луковицу — отсюда и такое название. Для решения достаточно помнить несколько правил из второго класса. Перечислим их все:

Сложение

1. слагаемое1 + слагаемое2 = сумма
2. слагаемое1 = сумма — слагаемое2
3. слагаемое2 = сумма — слагаемое1

Вычитание

1. уменьшаемое — вычитаемое = разность
2. уменьшаемое = вычитаемое + разность
3. вычитаемое = уменьшаемое — разность

Умножение

1. множитель1 * множитель2 = произведение
2. множитель1 = произведение: множитель2
3. множитель2 = произведение: множитель1

Деление

1. делимое: делитель = частное
2. делимое = делитель * частное
3. делитель = делимое: частное

Разберём на примере, как применять данные правила.

Заметим, что мы делим на и получаем . В этой ситуации мы знаем делитель и частное. Чтобы найти делимое, нужно делитель умножить на частное:

Мы стали немного ближе к самому . Теперь мы видим, что к прибавляется и получается . Значит, чтобы найти одно из слагаемых, нужно из суммы вычесть известное слагаемое:

И ещё один «слой» снят с неизвестной! Теперь мы видим ситуацию с известным значением произведения () и одним известным множителем ().

Теперь ситуация «уменьшаемое — вычитаемое = разность»

И последний шаг — известное произведение () и один из множителей ()

2 тип: уравнения со скобками

Уравнения данного типа чаще всего встречаются в задачах — именно к ним сводится 90% всех задач для поступления в 5 класс
. В отличие от «луковичных уравнений»
переменная здесь может встретиться несколько раз, поэтому решить её методами из предыдущего пункта невозможно. Типичные уравнения: или
Основная трудность — это правильно раскрыть скобки. После того, как удалось это верно сделать, следует привести подобные слагаемые (числа к числам, переменные к переменным), а после этого мы получаем самое простое «луковичное уравнение»
, которое умеем решать. Но обо всём по-порядку.

Раскрытие скобок
. Мы приведём несколько правил, которыми следует пользоваться в данном случае. Но, как показывает практика, верно раскрывать скобки ученик начинает только после 70-80 прорешанных задач. Основное правило таково: любой множитель, стоящий за скобками необходимо умножить на каждое слагаемое внутри скобок. А минус, стоящий перед скобкой, меняет знак всех выражений, что стоят внутри. Итак, основные правила раскрытия:

Приведение подобных
. Здесь всё гораздо легче: Вам необходимо путём переноса слагаемых через знак равенства добиться того, чтобы с одной стороны стояли только слагаемые с неизвестной, а с другой — только числа. Основное правило таково: каждое слагаемое, переносимое через , меняет свой знак — если оно было с ,то станет с , и наоборот. После успешного переноса необходимо сосчитать итоговое количество неизвестных, итоговое число стоящее с другой стороны равенства, нежели переменные, и решить простое «луковичное уравнение»
.

Приложение

Решение любого типа уравнений онлайн на сайт для закрепления изученного материала студентами и школьниками.. Решение уравнений онлайн. Уравнения онлайн. Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений.. Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней. Решение уравнений онлайн.. Уравнения онлайн. Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная.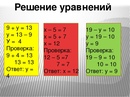 Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.

=

Решение уравнений 6 класс онлайн-подготовка на Ростелеком Лицей

 Решение уравнений

Уравнение, которое можно привести к виду ax = b, где a и b − некоторые числа

(a≠0), называется линейным уравнением с одним неизвестным.

Рассмотрим решение уравнения:

4·(х-5) = 16 (1)

х-5 = 16:4

х-5 = 4 (2)

х = 9

Уравнение (2) можно получить из уравнения (1), разделив обе части уравнения на 4.

4(х-5)=16 |:4   (1)                9 – корень уравнения (1), так как

4(x-5)4=164                          4(9-5) = 16 – верное равенство.

х-5 = 4  (2)                           9 – корень уравнения (2), так как

                                              9-5 = 4 – верное равенство.

Число 9 – это корень уравнения (1) и корень уравнения (2).

Сформулируем первое свойство уравнения.

Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю, и корни уравнения не изменятся.

Применим первое свойство к решению уравнения.

Пример 1. Решим уравнение 34x-98x=54-18.

Умножим обе части уравнения на 8. Тогда коэффициент перед x станет целым.

34x-98x = 54-18 |·8

3∙84x-9∙88x = 5∙84-1∙88

6x-9x = 10-1

-3x = 9

x = 9:(-3)

x = -3.

Пример 2. Решим уравнение 0,7x-0,2x = 5,5.

Умножим обе части уравнения на 10. Тогда коэффициенты перед x станут целыми.

0,7х-0,2х = 5,5 |·10

7х-2х = 55

5х = 55

x = 55:5

x = 11.

Пример 3. Решим уравнение -20x-50∙2 = 100.

Разделим обе части этого уравнения на 2.

(-20х-50)·2 = 10 |:2

-20х-50 = 50

-20х = 50+50

-20х = 100

x = 100:(-20)

x = -5.

Пример 4. Решим уравнение 2,1∙4-6y = -42.

Разделим обе части равенства на 2,1.

2,1·(4-6у) = -4 |:2,1

4-6у = -20

-6у = -24

y = -24:(-6)

y = 4.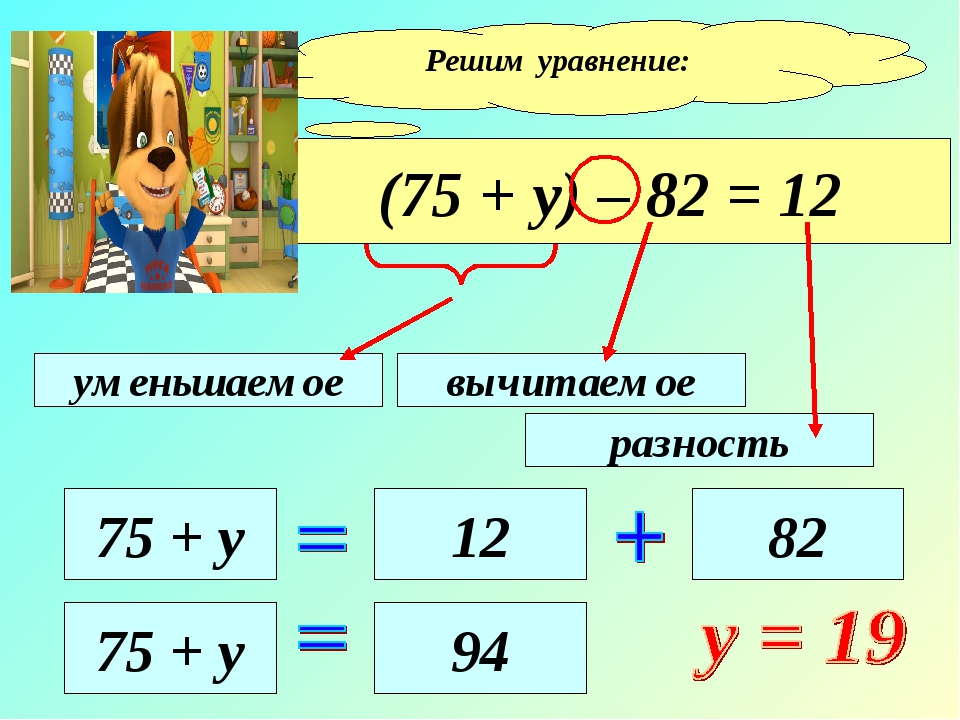

Пример 5. Решим уравнение 2х+5 = 17.

По правилу отыскания неизвестного слагаемого имеем 2х = 17-5; 2х = 12. Уравнения 2х+5 = 17 и 2х = 17-5 имеют один и тот же корень 6, т.к. 2·6+5 = 17 и 2·6 = 17-5.

Уравнение 2х = 17-5 можно записать так: 2х = 17+(-5).

Видим, что корень уравнения 2х+5 = 17 не изменяется, если перенести слагаемое 5 из левой части уравнения в правую, изменив его знак на противоположный.

Пример 6. Решим уравнение 5х = 2х+6.

Вычтем из правой и левой части равенства 2х.

5х-2х = 2х-2х+6

Или 5х-2х = 6

3х = 6

x = 2.

Уравнение 5х-2х = 6 можно получить из исходного, если слагаемое 2х перенести из правой части в левую, изменив его знак на противоположный.

Таким образом выполняется второе свойство уравнения:

Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знак.

Пример 7. Решим уравнение 13x+12 = x.

Умножим левую и правую часть равенства на 3.

13x+12 = x |·3

x+36 = 3x

Перенесем с противоположными знаками слагаемое 36 из левой части в правую, а слагаемое 3х из правой части в левую.

x-3x = -36

-2x = -36

x = -36:(-2)

x = 18

Рассмотрим сложные примеры.

Пример 8. Решим уравнение 12∙8x-4-5 = 6∙13x+12.

Сначала раскроем скобки.

12∙8x-12∙4-5 = 6∙13x+6∙12

4x-2-5 = 2x+3

Перенесем слагаемые, которые содержат неизвестное, в левую часть, а известные слагаемые в правую часть.

4х-2х = 3+2+5

2х = 10

x = 5

Пример 9. Решим уравнение 7-x6 = 19x-118.

Воспользуемся основным свойством пропорции: произведение средних равно произведению крайних.

8·(7-х) = 6·(19х-11)

Раскроем скобки в левой и в правой части уравнения.

8·7-8·х = 6·19х-6·11

56-8х = 114х-66

Перенесем неизвестное влево, а известное вправо.

-8х-114х = -66-56

-122х = -122

x = 1

Онлайн урок: Решение уравнений по предмету Математика 6 класс

Решить линейное уравнение с одним неизвестным вида a ∙ x = b — это значит найти все его корни или доказать, что корней нет.

Наличие и количество корней линейного уравнения зависит от значений коэффициента а и значения свободного члена уравнения b.

1. Линейное уравнение при a ≠ 0 и b — любое число, будет иметь один единственный корень; это значит, что неизвестная имеет единственное верное решение, при котором уравнение обращается в верное равенство.

Известно, что деление — это обратное действие умножению (т.е. по известному множителю и произведению можно определить неизвестный множитель).

Следовательно, решение уравнения a ∙ x = b, где a ≠ 0 выглядит так:

x = b ÷ a

или \(\mathbf{x = \frac{b}{a}}\) (это корень линейного уравнения).

2. Линейное уравнение при a = 0 и b ≠ 0 не имеет корней.

Если коэффициент а равен нулю, линейное уравнение запишется, как

0 ∙ x = b

Свойство умножения числа на нуль дает право утверждать, что при любом значении неизвестной х уравнение обращается в неверное равенство 0 = b.

Равенство 0 = b при b ≠ 0 неверно, а это значит, что в таком случае решения уравнения нет, т.е. уравнение не имеет корней.

3. Линейное уравнение при а = 0 и b = 0 имеет бесконечное множество корней, т.е. при любом значении неизвестной х уравнение обращается в верное равенство.

0 ∙ x = 0

0 = 0 (верное равенство)

Чтобы решить линейное уравнение необходимо выполнить ряд математических преобразований.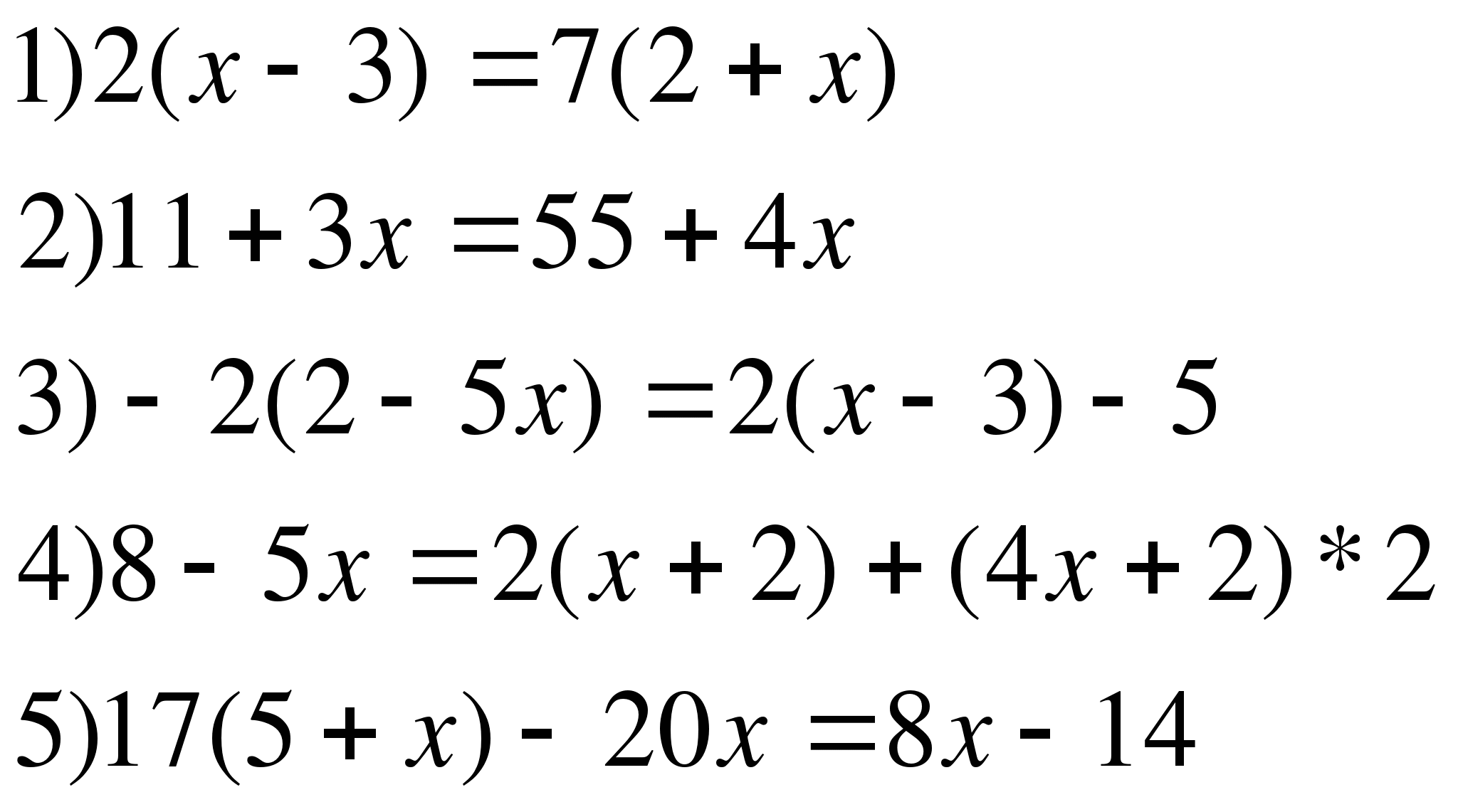

У меня есть дополнительная информация к этой части урока!

Закрыть

Некоторые математические преобразования позволяют перейти от решаемого уравнения к равносильному (эквивалентному), что порой упрощает решение первоначального уравнения.

Два уравнения равносильны, если у них одинаковые корни или оба не имеют корней, т.е. если определенное число является решением первого уравнения, то оно подойдет в качестве решения второму.

Например, равносильными можно считать уравнения:

Так как каждое из уравнений имеет только один корень, и он равен двум.

Равносильными, например, будут уравнения x ∙ 0 = 0 и х + 13 = 13 + х, так как решением этих уравнений может быть любое число, следовательно, решения их совпадают

Линейные уравнения обладают свойствами, которые позволяют совершать равносильные преобразования с различными уравнениями и сводить их к линейному уравнению с одной неизвестной стандартного вида, решать которое мы уже умеем.

Известно, что уравнение — это математическое равенство.

Если это равенство верно при определенных значениях неизвестной, то уравнение имеет верное решение.

Попробуем провести аналогию между уравновешенными весами и уравнением ax = b.

Как нам известно, уравновешенные весы нам показывают, что на каждой чаше весов находятся грузы равной массы.

Если весы были уравновешены, то добавив груз на одну чашу весов, необходимо добавить такой же по массе груз на вторую чашу, чтобы равновесие весов не было нарушено.

Аналогично, если убрать часть груза с одной чаши весов, то такую же часть груза нужно убрать со второй чаши, чтобы весы оставались уравновешенными.

А сейчас представим, что левая чаша весов — это левая часть линейного уравнения (ах), правая чаша весов — свободный член этого уравнения (b).

В таком случае получается, что если к левой и правой части уравнения прибавим (отнимем) одно и тоже число, то верное равенство не нарушится — получается уравнение равносильное исходному.

Добавлять к исходному можно любые числа, но необходимо выбирать то, которое упростит уравнение.

Рассмотрим пример:

Дано линейное уравнение 5х + 12 = 37

Для того, чтобы привести данное уравнение к стандартному виду: ax = b, прибавим к левой и правой части равенства —12 (противоположное числу 12, которое находится в правой части равенства, чтобы избавится в правой части от свободного члена уравнения),

5х + 12 + (-12) = 37 + (-12)

5х + 12 — 12 = 37 — 12

5х = 37 — 12

Если посмотреть внимательно на решение, то можно заметить, что число +12 исчезло из левой части исходного уравнения и появилось в правой части полученного после преобразований, при этом сменило знак и стало равным —12.

5х = 25 получили уравнение вида ax = b, так как a ≠ 0 и b ≠ 0 уравнение имеет единственный корень, найдем его:

х = 25/5

х = 5

Ответ: х = 5

Первое свойство равносильного преобразования уравнения

Любое слагаемое можно перенести из одно части уравнения в другую, при этом сменив знак этого слагаемого на противоположный, в результате получится новое уравнение, равносильное исходному.

Обычно слагаемые с неизвестным переносят в левую часть уравнения, а все остальные слагаемые в правую часть.

У меня есть дополнительная информация к этой части урока!

Закрыть

Чтобы лучше усвоить первое свойство равносильного преобразования уравнения, можно запомнить такое интересное сравнение.

Представьте ситуацию.

К хозяину дома приходит долгожданный гость.

Так как гость пришел с улицы, ему нужно уличную обувь переодеть на гостевые домашние тапочки.

Попробуем провести аналогию между рассмотренной ситуацией и первым свойством равносильного преобразования уравнения.

Например, возьмем уравнение 8х — 3 = 2х + 4.

Итак, в левой части уравнения слагаемое 8х является «хозяином» — он у себя «дома», «обувь» ему переодевать не нужно, значит, 8х знак свой не меняет.

Из правой части уравнения идет его «гость», слагаемое 2х. Ему как «гостю» приходится менять «обувь», т.е. менять свой знак на противоположный.

В правой части 2х был со знаком «+», при переходе меняет свой знак на противоположный и в левой части в «гостях» появляется со знаком «-».

Аналогично число 4 является «хозяином» в правой части уравнения, его знак остается неизменным, он у себя «дома».

Из левой части уравнения в «гости» идет слагаемое -3. Ему как «гостю» приходится менять «обувь», т.е. менять свой знак на противоположный.

В правой части слагаемое -3 было со знаком «-», при переходе знак меняется на противоположный и в левой части, в «гостях», становится знаком «+».

Получилось эквивалентное уравнение исходному, оно выглядит так:

8х — 2х =4 + 3

Приведем подобные, получим простейшее линейное уравнение.

6х = 7

\(\mathbf{x = \frac{7}{6}}\)

\(\mathbf{x =1 \frac{1}{6}}\)

Ответ: \(\mathbf{x =1 \frac{1}{6}}\)

Рассмотрим второе свойство равносильного преобразования уравнения.

Снова обратимся к аналогии с весами.

Для того, чтобы весы оставались в равновесии, увеличивая массу груза в 1,5 раза в одной из чаш, необходимо увеличить массу груза в 1,5 раза в другой чаше весов.

Увеличивая или уменьшая массу грузов на каждой чаше весов в одинаковое количество раз, равновесие весов будет сохраняться.

Так же происходит и с уравнением. Сформулируем второе свойство равносильного преобразования уравнения:

Разделив (или умножив) обе части на одно и тоже ненулевое число, равенство остается верным, получится уравнение равносильное исходному.

Рассмотрим пример

Дано уравнение 4 ∙ (2х — 1) = 16

Приведем данное уравнение к стандартному виду: ax =b

Раскрытие скобок только усложнит исходное уравнение.

Заметим, что левую и правую часть можем разделить на 4 (это наименьшее общее кратное чисел 4 и 16).

4 ∙ (2х — 1) = 16          |÷4

\(\mathbf{\frac{4 \cdot (2x — 1)}{4} = 16 \div 4}\)

2х — 1 = 4

Слагаемые с неизвестным оставляем в левой часть уравнения, а слагаемое -1 переносим в правую часть уравнения, сменив знак числа на противоположный, т.е. на «+».

2x = 4 + 1

2x = 5 получили уравнение вида ax = b

х = 5/2

x = 2,5

Ответ: х = 2,5

Решение линейных уравнений происходит с помощью нескольких преобразований, которые могут быть выполнены в любом порядке.

1. Освобождение от дробных членов уравнения (если такие есть) с помощью умножения левой и правой части уравнения на одно и тоже ненулевое число

2. Деление левой и правой части уравнения на одно и тоже ненулевое число

3. Раскрытие скобок (если они есть и это необходимо)

4. Перенос членов уравнения из одной части в другую со сменой их знаков на противоположные

5. Приведение подобных слагаемых

Завершая решение уравнения, стоит выполнить проверку, подставив в исходное уравнение найденное значение неизвестного. Если уравнение обратилось в верное равенство, значит, корень уравнения найден верно.

Итогом решения уравнения является ответ, в котором перечисляются все найденные корни уравнения.

Уравнения первой степени с одним неизвестным

(a + b)(a – b) = a² – b², (a + b)² = a² + 2ab + b²

и т. д. – это тождества. В § 41 мы установили, пользуясь основными законами арифметических действий, что всегда, какими бы ни были числа a и b, левая часть для каждого из этих равенств равна правой.

Равенство также есть тождество, так как при всяком допустимом значении a (а именно при ) левая его часть равна правой.

В § 24 и 45 мы встречались с другого рода равенствами, содержащими буквы, а именно с уравнениями. Рассмотренные нами в этих параграфах равенства содержали обозначенные буквами неизвестные числа, и нам требовалось решить уравнение, то есть выяснить, существуют ли такие значения неизвестного, при которых равенство будет верным, и найти эти значения неизвестного.

Пусть, например, даны два алгебраических выражения:

4x – 5 и 2x + 9.

Числовое значение каждого из этих выражений зависит от значения буквы x, как это видно из следующей таблицы, где в первой строке даны различные значения x, а во второй и третьей — соответствующие значения данных алгебраических выражений.

Поставим такой вопрос: найдутся ли такие значения x, при которых оба данных выражения будут иметь одно и то же значение?

Другими словами, при каких значениях x будет справедливо равенство:

4x – 5 = 2x + 9. (1)

Если продолжить эту таблицу, то окажется, что при x = 7 данные выражения имеют одно и то же значение 23. Однако из наших рассуждений не видно, существуют ли еще какие-нибудь значения x, при которых левая часть равенства (1) равна правой. Чтобы получить полный ответ, надо изучить свойства уравнений.

В настоящей главе мы изучим основные свойства уравнений и укажем способы их решения в простейших случаях.

Заметим, что уравнение, кроме букв, обозначающих неизвестные числа, может содержать и другие буквы, которые будут означать некоторые известные, определенные числа.

Приведем еще примеры уравнений с одним неизвестным.

Во всех этих уравнениях x является неизвестным числом, а там, где встречаются другие буквы (во втором и шестом уравнениях), мы считаем их известными.

Выражения, стоящие слева и справа от знака равенства, называются левой и правой частями уравнения.

1. Корни уравнения. Пусть дано уравнение:

3x – 7 = 29 – 6x.

Подставив в него вместо x число 4, получим:

3 * 4 – 7 = 5 и 29 – 6 * 4 = 5.

Обе части уравнения оказались равными одному и тому же числу. Получили верное равенство. Наоборот, если подставим вместо x любое другое число, например 5, то будем иметь:

3 * 5 – 7 = 8 и 29 – 6 * 5 = –1.

Левая часть оказалась равной 8, а правая –1.

Мы не получили равенства. Задача решения уравнения и состоит в том, чтобы определить, имеются ли такие значения неизвестного, при которых обе части уравнения равны одному и тому же числу (см. § 24), и найти эти значения.

Итак,

Решить уравнение с одним неизвестным — значит найти все те значения неизвестного, при которых уравнение обращается в верное равенство.

Все такие значения неизвестного называются его корнями или решениями.

Так, в предыдущем примере x = 4 является корнем, или решением, уравнения

3x – 7 = 29 – 6x.

Наоборот, например, значение x = 5 не является корнем этого уравнения.

2. Число корней уравнения. Уравнение может иметь единственный корень.

Например, уравнение

x + 3 = 7

имеет единственный корень: x = 4.

Действительно, подставив в уравнение 4 вместо x, получим

4 + 3 = 7

верное равенство. Подставив же в уравнение вместо x любое число, меньшее 4, получим в сумме с 3 число, меньшее 7, а подставив число, большее 4, получим в сумме с 3 число, большее 7. Значит, число 4 является единственным, которое в сумме с 3 дает 7, то есть обращает данное уравнение в верное равенство.

Уравнение может иметь несколько корней.

Так, уравнение

(x – 1)(x – 2)(x – 5) = 0

имеет три корня: x₁ = 1; x₂ = 2; x₃ = 5.

Действительно, при x = 1 обратится в нуль первый множитель в левой части, при x = 2 – второй множитель, при x = 5 — третий. А если хотя бы один из сомножителей равен нулю, то и все произведение равно нулю.

Если же мы подставим в уравнение вместо x любое другое число, то ни один из сомножителей в левой части не обратится в нуль. Следовательно, не будет равно нулю и их произведение.

Уравнение может совсем не иметь корней.

Возьмем, например, уравнение:

x + 5 = x + 1.

Какое бы значение мы ни давали букве x, левая часть этого уравнения всегда будет на 4 больше правой. Значит, нет таких значений x, которые обращали бы это уравнение в верное равенство. Уравнение не имеет корней.

Уравнение может иметь бесконечное множество корней.

Пусть дано уравнение:

5(x – 3) + 2 = 3(x – 4) + 2x – 1.

Подставляя вместо x любое число, убедимся, что левая и правая части уравнения будут равны. Значит, любое число является корнем этого уравнения. Покажем это.

Раскрыв скобки, получим:

5x – 15 + 2 = 3x – 12 + 2x – 1,

или

5x – 13 = 5x – 13.

В обеих частях оказалось одно и то же выражение.

Итак, данное уравнение оказалось равенством, справедливым при любых значениях буквы x.

Говорят, что данное уравнение удовлетворяется тождественно.

Проект по математике 5 класс по теме «Линейные уравнения и способы их решения».

Муниципальное Казённое Образовательное Учреждение

«Средняя общеобразовательная школа №4»

Научный проект по математике

«Виды линейных уравнений»

Автор проекта:

Ученица 5Г класса

Комарова Ксения

Руководитель проекта:

Чухманова Наталия

Викторовна

2016-2017 уч. год

Содержание.

1. Введение:

1.1 Возникновение проблемы.

1.2 Цель и задачи проекта.

2. Теоретическая часть:

2.1 Понятие линейного уравнения.

2.2 Случаи решения линейного уравнения.

3. Практическая часть:

3.1

3.3 Решение уравнений с дробными коэффициентами (с переносом

слагаемых).

Примеры решение уравнений.

3.4 Применение линейных уравнений при решении задач.

4. Заключение: Решение линейных уравнений, делением на коэффициент.

Примеры решение уравнений.

3.2 Решение линейных уравнений, способом переноса слагаемых

из одной части равнения в другую.

Примеры решение уравнений.

5. Самооценка.

6. Отзыв учителя.

7. Информационные ресурсы.

1. Введение.

   1. Возникновение проблемы.

Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.

Актуальность: чтобы перейти к исследованию данной темы, нам необходимо было ответить на вопрос «Зачем нужно изучать уравнения?». С линейными уравнениями мы знакомы из математики начальной школы, но в курсе 6 класса будет изучена новая тема — перенос слагаемых из одной части уравнения в другую и свойства уравнений. Этот материал в курсе математики -5 класса представляет некоторую сложность и научный интерес.

Проблема: углубить представления об уравнениях. Ответить на вопрос: «Какими способами можно решить уравнение и показать где, когда и какие уравнения приходится решать современному человеку.

Данная работа является попыткой обобщить и систематизировать изученный материал и изучить новый.

1. 2. Цель и задачи проекта.

Цель проекта: Рассмотреть различные виды линейных уравнений и способы их решений.

Задачи проекта:

1. Рассмотреть виды линейных уравнений.

2. Привести примеры различных способов решения уравнений..

3. Обобщить знания по этой теме.

4. Защитить проект и приготовить презентацию.

2. Теоретическая часть.

2.1 Понятие линейного уравнения.

Существуют уравнение в правах, уравнение времени (перевод истинного солнечного времени в среднее солнечное время, принятое в общежитии и в науке; астр.) и т.д..

В математике – это математическое равенство, содержащее одну или несколько неизвестных величин и сохраняющее свою силу только при определенных значениях этих неизвестных величин.

В уравнениях с одной переменной неизвестное обычно обозначают буквой «х».

Уравнения бывают разных видов:

ax + b = 0. — Линейное уравнение.

ax2 + bx + c = 0. — Квадратное уравнение.

ax3 + bx2 + cx + d = 0. — Кубическое уравнение.

ax4 + bx2 + c = 0. — Биквадратное уравнение.

Уравнение вида a·x=b, где x – переменная, a и b – некоторые числа, называется линейным уравнением с одной переменной.

Примеры линейных уравнений.

5·x=10 – это линейное уравнение с одной переменной x, здесь коэффициент a равен 5, а число b есть 10.

−2,3·y=0 – это тоже линейное уравнение, но с переменной y, в котором a=−2,3 и b=0.

А в линейных уравнениях x=−2 и −x=3,33 числовые коэффициенты a не присутствуют в явном виде и равны 1 и −1 соответственно, при этом в первом уравнении b=−2, а во втором — b=3,33.

А годом ранее в учебнике математики Виленкина Н. Я. линейными уравнениями с одним неизвестным помимо уравнений вида a·x=b считали и уравнения, которые можно привести к такому виду с помощью переноса слагаемых из одной части уравнения в другую с противоположным знаком, а также с помощью приведения подобных слагаемых. Согласно этому определению, уравнения вида 5·x=2·x+6, и т.п. тоже линейные.

2.2 Случаи решения линейного уравнения.

Рассмотрим способы решения линейных уравнений a·x+b=0. Выясним , имеет ли линейное уравнение корни, и если имеет, то сколько их и как их найти.

Наличие корней линейного уравнения зависит от значений коэффициентов a и b. При этом линейное уравнение a·x+b=0 имеет

• единственный корень при a≠0,

• не имеет корней при a=0 и b≠0,

• имеет бесконечно много корней при a=0 и b=0, в этом случае любое число является корнем линейного уравнения.

При a=0 линейное уравнение a·x+b=0 принимает вид 0·x+b=0. Из этого уравнения и свойства умножения чисел на нуль следует, что какое бы число мы не взяли в качестве x, при его подстановке в уравнение 0·x+b=0 получится числовое равенство b=0. Это равенство верное, когда b=0, а в остальных случаях при b≠0 это равенство неверное.

Следовательно, при a=0 и b=0 любое число является корнем линейного уравнения a·x+b=0, так как при этих условиях подстановка вместо x любого числа дает верное числовое равенство 0=0. А при a=0 и b≠0 линейное уравнение a·x+b=0 не имеет корней, так как при этих условиях подстановка вместо x любого числа приводит к неверному числовому равенству b=0.

Приведенные обоснования позволяют сформировать последовательность действий, позволяющую решить любое линейное уравнение. Итак, алгоритм решения линейного уравнения таков:

Сначала по записи линейного уравнения находим значения коэффициентов a и b.

Если a=0 и b=0, то это уравнение имеет бесконечно много корней, а именно, любое число является корнем этого линейного уравнения.

Если a=0 и b≠0, то исходное уравнение не имеет корней.

Если же a отлично от нуля, то

коэффициент b переносится в правую часть с противоположным знаком, при этом линейное уравнение преобразуется к виду a·x=−b,

после чего обе части полученного уравнения делятся на отличное от нуля число a, что и дает искомый корень исходного линейного уравнения .

Записанный алгоритм является исчерпывающим ответом на вопрос, как решать линейные уравнения.

Похожий алгоритм применяется для решения уравнений вида a·x=b. Его отличие состоит в том, что при a≠0 сразу выполняется деление обеих частей уравнения на это число, здесь b уже находится в нужной части уравнения и не нужно осуществлять его перенос.

Для решения уравнений вида a·x=b применяется такой алгоритм:

Если a=0 и b=0, то уравнение имеет бесконечно много корней, которыми являются любые числа.

Если a=0 и b≠0, то исходное уравнение не имеет корней.

Если же a отлично от нуля, то обе части уравнения делятся на отличное от нуля число a, откуда находится единственный корень уравнения, равный b/a.

3. Практическая часть:

3.1 Решение линейных уравнений, делением на коэффициент.

Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.

Примеры решение уравнений.

Решение уравнений с дробными коэффициентами (с переносом

слагаемых).

Применение линейных уравнений при решении задач.

Решение линейных уравнений, делением на коэффициент.

Решение линейных уравнений, способом переноса слагаемых

из одной части равнения в другую.

3.2 Решение линейных уравнений, способом переноса слагаемых

из одной части равнения в другую.

Корни уравнения не изменяются, если какое-нибудь слагаемое перевести из одной части уравнения в другую, изменив при этом его знак.

Переносите из левой части уравнения в правую то слагаемое, которое не содержит неизвестного:

а) 8х+5,9=7х+20

8х-7х=20-5,9

х=14,1

б) 6z-8=-5z-1.6

6z+5z=8-1.6

11z=6.4

z=6,4: 11

z= 0,58

Соберём в левой части уравнения все слагаемые, содержащие неизвестные, а в правой — не содержащие неизвестное:

в) 15y-8=-6y+4.6

15y+6y=8+4.6

21y= 12.6

У=12.6:21

У=0,6

г) -16n+1.7=2n-1

-16n-2n=-1.7-1

-18n=-2.7

18n=2.7

n=2,7:18

n=0,15

3.3 Решение уравнений с дробными коэффициентами (с переносом слагаемых).

Если в уравнении встречается дробный коэффициент – он него стараются избавиться – способном домножения на дробь обратную коэффициенту.

Примеры решение уравнений.

Решим уравнение 1/3х +12=х.

Решение. Умножим левую и правую части уравнения на 3 для того, чтобы освободится от дробного коэффициента. Получим х+36=3х. Перенесём с противоположными знаками слагаемое 36 из левой части в правую, а слагаемое 3х из правой части в левую: х-3х = -36. Упростим левую часть уравнения: -2х = -36. Теперь разделим обе части уравнения на -2, получим х=18.

Число 18 является корнем данного уравнения 1/3х + 12=х, так как верно равенство 1/3*18 + 12=18.

Уравнение, которое можно привести к такому виду с помощью переноса слагаемых и приведения подобных слагаемых, называют линейным уравнением с одним неизвестным.

3.4 Применение линейных уравнений при решении задач.

Решение линейных уравнений широко применяется при решении задач, рассмотрим примеры. Решим с помощью уравнения задачи.

Задача1.

На одной полке 42 книги, а на другой 34. Со второй полки сняли несколько книг, а с первой — столько, сколько осталось на второй. После этого на первой полке осталось 12 книг. Сколько книг сняли со второй полки ?

Пусть х книг сняли со второй полки, тогда на второй полке осталось 34-х книг. После того, как с первой полки сняли 34-х книг, на ней осталось 12 книг.

Составим уравнение:

42-(34-х)=12

42-34+х=12

х=4.

Ответ: со второй полки сняли 4 книги.

Задача2.

Стены дома 8 каменщиков сложили за 42 дня. Сколько нужно каменщиков, чтобы сложить стены такого же дома за 28 дней?

Пусть х — количество каменщиков, необходимое для того, чтобы сложить стены такого же дома за 28 дней. Составим и решим пропорцию:

8/х = 28/48

х = 8*42/28 = 12 каменщиков.

Ответ: 12 каменщиков.

Задача3.

Отрезок на плане, масштаб которого 2:7, изображается отрезок 4,2 см. Какой длины будет этот отрезок на плане, сделанном в масштабе 5:3?

Длина отрезка в натуре:

4,2: х = 2:7

х= 4,2*7/2

х = 14,7 см.

Длина отрезка на другом плане:

х : 14,7 = 5:3

х = 14,7*5

х=24,5 см

Ответ: 24,5 см.

Задача 4.

Длина отрезка АВ а 2 см больше, чем длина отрезка CD. Если длину отрезка АВ увеличить на 10 см, а длину отрезка CD увеличить в 3 раза, то получается равные результаты. Найдите длину отрезка АВ.

Пусть х — длина отрезка АВ, тогда длина отрезка CD равна х — 2 см. Если длину отрезка АВ увеличить на 10 см, а длину отрезка CD увеличить в 3 раза, то получается равные результаты.

Составим и решим уравнение:

х+10 = 3(х-2)

х+10 = 3х-6

-2х= -16

х=8 см.

Ответ: 8 см.

4.Заключение.

Самооценка

В целом, значение темы, кроме вышесказанного, заключается в том, что она применяется практически во всех современных технологиях (Физике, Химии и Алгебры, Геометрии), а так же открывает простор для созданий новых.

Работа над проектом, изучение линейных уравнений и их виды позволила более широко изучить данную тему.

По изученному мною материалу, использованного в процессе подготовке проекта можно сделать вывод о том, что большое количество людей знакомы с уравнениями и знают где можно применить в практической деятельности линейные уравнения. Это ещё раз говорит об актуальности данной темы.

6. Отзыв учителя.

7.Информационные ресурсы.

1. https://www.calc.ru/Lineynyye-Uravneniya-Vidy-Lineynykh-Uravneniy.html

2. http://www.grandars.ru/student/vysshaya-matematika/sistema-lineynyh-uravneniy.html

3. http://www.cleverstudents.ru/equations/linear_equations.html#definition

4. http://www.cleverstudents.ru/

Решение линейных уравнений с примерами

Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид  

aх + b = 0, где a и b произвольные числа, называется линейным уравнением с одним неизвестным. Cегодня разберёмся, как эти линейные уравнения решать.

Например, все уравнения:

2х + 3= 7 – 0,5х;  0,3х = 0;  x/2 + 3 = 1/2 (х – 2) — линейные.

Значение неизвестного, обращающее уравнение в верное равенство называется решением или корнем уравнения.

Например, если в уравнении 3х + 7 = 13 вместо неизвестного х подставить число 2 , то получим верное равенство 3· 2 +7 = 13. Значит, значение х = 2 есть решение или корень уравнения.

А значение х = 3 не обращает  уравнение  3х + 7 = 13 в верное равенство, так  как  3· 2 +7 ≠ 13. Значит, значение х = 3 не является решением или корнем уравнения.

Решение любых линейных уравнений сводится к решению уравнений вида

aх + b = 0.

Перенесем свободный член из левой части уравнения в правую, изменив при этом знак перед b на противоположный, получим

aх = ‒ b.

Если a ≠ 0, то х = ‒ b/a .

Пример 1. Решите уравнение 3х + 2 =11.

Перенесем 2 из левой части уравнения в правую, изменив при этом знак перед 2 на противоположный, получим 
3х = 11 – 2.

Выполним вычитание, тогда
3х = 9.

Чтобы найти х надо разделить произведение на известный множитель, то есть     
х = 9 : 3.

Значит, значение х = 3 является  решением или корнем уравнения.

Ответ: х = 3.

Если а = 0 и b = 0, то получим уравнение  0х = 0. Это уравнение имеет бесконечно много  решений, так как при умножении любого числа на 0 мы получаем 0,но b тоже равно 0. Решением этого уравнения  является любое число.

Пример 2. Решите уравнение 5(х – 3) + 2 = 3 (х – 4) + 2х ‒ 1.

Раскроем скобки:
5х – 15 + 2 = 3х – 12 + 2х ‒ 1.

Сгруппируем  в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
5х – 3х ‒ 2х =  – 12  ‒ 1 + 15 ‒ 2.

Приведем подобные члены:
0х = 0.

Ответ: х —  любое число.

Если а = 0 и b ≠ 0, то получим уравнение  0х = — b. Это уравнение решений не имеет, так как при умножении любого числа на 0 мы получаем 0, но  b ≠ 0 .

Пример 3. Решите уравнение х + 8 = х + 5.

Сгруппируем  в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
х – х = 5 ‒ 8.

Приведем подобные члены: 
0х = ‒ 3.

Ответ: нет решений.

На рисунке 1 изображена схема решения линейного уравнения

Составим общую схему решения уравнений с одной переменной. Рассмотрим решение примера 4.

Пример 4. Пусть надо решить уравнение 

1) Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12.

2) После сокращения получим
4 (х – 4) + 3·2 (х + 1) ‒ 12 = 6·5 (х – 3) + 24х – 2 (11х + 43)

3) Чтобы отделить члены, содержащие неизвестные и свободные члены, раскроем скобки:
4х – 16 + 6х + 6 – 12 = 30х – 90 + 24х – 22х – 86 .

4) Сгруппируем в одной части члены, содержащие неизвестные, а в другой – свободные члены:
4х + 6х – 30х – 24х + 22х = ‒ 90 – 86 + 16 – 6 + 12.

5) Приведем подобные члены:
‒ 22х = ‒ 154.

6) Разделим на  – 22 , Получим
х = 7.

Как видим, корень уравнения равен семи.

Вообще такие уравнения можно решать по следующей схеме:

а) привести уравнение к целому виду;

б) раскрыть скобки;

в) сгруппировать члены, содержащие неизвестное, в одной части уравнения, а свободные члены ‒ в другой;

г) привести подобные члены;

д) решить уравнение вида aх = b,которое получили после приведения подобных членов.

Однако эта схема не обязательна для всякого уравнения. При решении многих более простых уравнений приходится начинать не с первого, а со второго (Пример. 2),  третьего (Пример. 1, 3) и даже с пятого этапа, как в примере 5.

Пример 5. Решите уравнение 2х = 1/4.

Находим неизвестное  х = 1/4 : 2,
х = 1/8 .

Рассмотрим решение некоторых линейных уравнений, встречающихся на основном государственном экзамене.

Пример 6. Решите уравнение 2 (х + 3) = 5 – 6х.

Решение

2х + 6 = 5 – 6х

2х + 6х = 5 – 6

8х = ‒1

х = ‒1 : 8

х = ‒ 0, 125

Ответ: ‒ 0, 125

Пример 7. Решите уравнение – 6 (5 – 3х) = 8х – 7.

Решение

– 30 + 18х = 8х – 7

18х  – 8х =  – 7 +30

10х = 23

х = 23 : 10

х = 2,3

Ответ: 2,3

Пример 8. Решите уравнение

Решение:

3(3х – 4) = 4 · 7х + 24

9х – 12 = 28х + 24

9х – 28х = 24 + 12

-19х = 36

х = 36 : (-19)

х = — 36/19

Ответ: — . 

Пример 9. Найдите f(6), если f (x + 2) = 3^7-х

Решение

Так как надо найти f(6), а нам известно f (x + 2),
то х + 2 = 6.

Решаем линейное уравнение х + 2 = 6,
получаем х = 6 – 2, х = 4.

Если х = 4, тогда
f(6) = 3^7-4 = 3³ = 27

Ответ: 27.

Если у Вас остались вопросы, есть желание разобраться с решением уравнений более основательно, записывайтесь на мои уроки в РАСПИСАНИИ. Буду рада Вам помочь!

Также TutorOnline советует посмотреть новый видеоурок от нашего репетитора Ольги Александровны, который поможет разобраться как с линейными уравнениями, так и с другими.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Решение линейных уравнений с одним неизвестным

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Решение линейных уравнений с одной переменной

Линейное уравнение — это уравнение прямой, записанное с одной переменной. Единственная степень переменной — 1.Линейные уравнения с одной переменной могут иметь вид [latex] ax + b = 0 [/ latex] и решаются с использованием основных алгебраических операций.

Мы начинаем с классификации линейных уравнений с одной переменной как одного из трех типов: тождественные, условные или противоречивые. Уравнение тождества верно для всех значений переменной. Вот пример тождественного уравнения.

[латекс] 3x = 2x + x [/ латекс]

Набор решений состоит из всех значений, которые делают уравнение истинным.Для этого уравнения набором решений является все действительные числа, потому что любое действительное число, замененное на [латекс] x [/ латекс], сделает уравнение истинным.

Условное уравнение верно только для некоторых значений переменной. Например, если нам нужно решить уравнение [латекс] 5x + 2 = 3x — 6 [/ latex], мы получим следующее:

[латекс] \ begin {array} {l} 5x + 2 \ hfill & = 3x — 6 \ hfill \\ 2x \ hfill & = — 8 \ hfill \\ x \ hfill & = — 4 \ hfill \ end {array} [/ латекс]

Набор решений состоит из одного числа: [латекс] \ {- 4 \} [/ латекс].Это единственное решение, поэтому мы решили условное уравнение.

Несогласованное уравнение приводит к ложному утверждению. Например, если мы должны решить [латекс] 5x — 15 = 5 \ left (x — 4 \ right) [/ latex], мы получим следующее:

[латекс] \ begin {array} {ll} 5x — 15 = 5x — 20 \ hfill & \ hfill \\ 5x — 15 — 5x = 5x — 20 — 5x \ hfill & \ text {Subtract} 5x \ text {from обе стороны}. \ hfill \\ -15 \ ne -20 \ hfill & \ text {Ложный оператор} \ hfill \ end {array} [/ latex]

Действительно, [латекс] -15 \ ne -20 [/ латекс].Нет решения, потому что это противоречивое уравнение.

Решение линейных уравнений с одной переменной включает фундаментальные свойства равенства и основные алгебраические операции. Ниже приводится краткий обзор этих операций.

Общее примечание: линейное уравнение с одной переменной

Линейное уравнение с одной переменной можно записать в виде

[латекс] ax + b = 0 [/ латекс]

, где a и b — действительные числа, [латекс] a \ ne 0 [/ латекс].

Как сделать: дано линейное уравнение с одной переменной, используйте алгебру для его решения.

Следующие шаги используются для манипулирования уравнением и выделения неизвестной переменной, так что последняя строка читается как x = _________, если x — неизвестное. Нет установленного порядка, так как используемые шаги зависят от того, что указано:

1. Мы можем складывать, вычитать, умножать или делить уравнение на число или выражение, если мы делаем то же самое с обеими сторонами знака равенства.Обратите внимание, что мы не можем делить на ноль.
2. Примените свойство распределения по мере необходимости: [latex] a \ left (b + c \ right) = ab + ac [/ latex].
3. Выделите переменную на одной стороне уравнения.
4. Когда переменная умножается на коэффициент на последнем этапе, умножьте обе части уравнения на обратную величину коэффициента.

Пример 1: Решение уравнения с одной переменной

Решите следующее уравнение: [латекс] 2x + 7 = 19 [/ латекс].

Решение

Это уравнение может быть записано в виде [латекс] ax + b = 0 [/ латекс] путем вычитания [латекс] 19 [/ латекс] с обеих сторон.Однако мы можем перейти к решению уравнения в его исходной форме, выполнив алгебраические операции.

[латекс] \ begin {array} {ll} 2x + 7 = 19 \ hfill & \ hfill \\ 2x = 12 \ hfill & \ text {Вычтите 7 с обеих сторон}. \ Hfill \\ x = 6 \ hfill & \ text {Умножьте обе стороны на} \ frac {1} {2} \ text {или разделите на 2}. \ hfill \ end {array} [/ latex]

Решение [латекс] x = 6 [/ латекс].

Попробуйте 1

Решите линейное уравнение с одной переменной: [латекс] 2x + 1 = -9 [/ латекс].

Решение

Пример 2: Алгебраическое решение уравнения, когда переменная появляется с обеих сторон

Решите следующее уравнение: [латекс] 4 \ left (x — 3 \ right) + 12 = 15-5 \ left (x + 6 \ right) [/ latex].

Решение

Примените стандартные алгебраические свойства.

[латекс] \ begin {array} {ll} 4 \ left (x — 3 \ right) + 12 = 15-5 \ left (x + 6 \ right) \ hfill & \ hfill \\ 4x — 12 + 12 = 15 — 5x — 30 \ hfill & \ text {Применить свойство распределения}. \ Hfill \\ 4x = -15 — 5x \ hfill & \ text {Объединить похожие термины}. \ Hfill \\ 9x = -15 \ hfill & \ text {Поместите} x- \ text {термины на одну сторону и упростите}. \ hfill \\ x = — \ frac {15} {9} \ hfill & \ text {Умножьте обе стороны на} \ frac {1} {9 } \ text {, обратное 9}.\ hfill \\ x = — \ frac {5} {3} \ hfill & \ hfill \ end {array} [/ latex]

Анализ решения

Эта задача требует, чтобы свойство распределения применялось дважды, а затем свойства алгебры используются для достижения последней строки, [latex] x = — \ frac {5} {3} [/ latex].

Попробуй 2

Решите уравнение с одной переменной: [латекс] -2 \ left (3x — 1 \ right) + x = 14-x [/ latex].

Решение

Уравнений с переменными (предалгебра, введение в алгебру) — Mathplanet

В этом разделе вы узнаете, как решать уравнения, содержащие неизвестные переменные.Вы узнаете, как решать уравнения мысленно, используя таблицу умножения, и вы также узнаете, как найти решение уравнения с заданными числами, а также с помощью обратных операций.

Вы можете решить простое уравнение в уме с помощью таблицы умножения.

Пример

$$ \ begin {array} {lcl} 8x = 64 \ end {array} $$

$$ \ begin {array} {lcl} 8 \ cdot x = 64 \ end {array} $$

На какое число нужно умножить 8, чтобы получить произведение 64? Используя таблицу умножения, мы знаем, что число равно 8.

$$ 8 \ cdot 8 = 64 $$

Когда мы решаем уравнение, мы выясняем, какое значение x (или любой другой переменной) делает утверждение истинным (удовлетворяет уравнению).

Пример

Какое из следующих чисел является решением уравнения? х = 2, 7 или 8?

$$ 14-x = 7 $$

Здесь даны числа 2, 7 и 8. Одно из этих чисел удовлетворяет уравнению. Если вы не знаете решение прямо сейчас, вы можете исследовать, какое из приведенных чисел дает правильный ответ, подставляя различные значения x.

$$ \ begin {matrix} x = 2 \ Rightarrow & 14-2 = 12 & {\ color {red} {Wrong}} \: \: \\ x = 7 \ Rightarrow & 14-7 = 7 \: & { \ color {green} {Correct}} \\ x = 8 \ Rightarrow & 14-8 = 6 \: & {\ color {red} {Wrong}} \: \: \ end {matrix} $$

Ответ: x = 7

Вы уже решили уравнения, решения которых довольно легко увидеть, с помощью мысленной математики или шаблонов. Большинство уравнений труднее решить, и вам нужно упростить уравнение, прежде чем вы сможете увидеть решение.Один из способов сделать это — использовать обратные операции.

Операция — это, например, сложение, умножение, деление и вычитание. Обратная операция — это операция, которая обращает эффект другой операции. Сложение и вычитание противоположны друг другу, так же как деление и умножение — обратные.

Пример

С номерами

$$ 18 + 4 = 22 $$

$$ 18 + 4 {\ color {blue} \, — \, 4} = 22 {\ color {blue} \, — \, 4} $$

$$ 18 = 18 $$

С переменными и числами

$$ x + 4 = 22 $$

$$ x + 4 {\ color {blue} \, — \, 4} = 22 {\ color {blue} \, — \, 4} $$

$$ x = 18 $$

Отнимаем 4 с обеих сторон.

Пример

С переменными и числами

$$ x \ cdot 2 = 10 $$

$$ \ frac {x \ cdot 2} {{\ color {blue} 2}} = \ frac {10} {{\ color {blue} 2}} $$

$$ x = 5 $$

Делим обе стороны на 2

Видеоуроки

Решите следующее уравнение

$$ 8 \ cdot x-x = 21 $$

Решите следующее уравнение, используя обратные операции

$$ 6x + 4 = 28 $$

Как решать алгебру

г = 24 — 4x

Пояснение:

Как показано в приведенном выше примере, мы вычисляем значение переменной из одного уравнения и подставляем его в другое.

Нам дано, что

у = 24 — 4х —— (1)
2x + y / 2 = 12 —— (2)

Здесь мы выбираем уравнение (1) для вычисления значения x. Поскольку уравнение (1) уже находится в
самая упрощенная форма:

(Подставляя это значение y в уравнение (2), а затем решая для x
дает)

2x + (24-4x) / 2 = 12 —— (2) (∵ y = 24 — 4x)
2x + 24 / 2- 4x / 2 = 12
2x + 12 — 2x = 12
12 = 12

Вы можете подумать, что это тот же сценарий, что обсуждался выше (24 = 24).Но
ждать! Вы слишком рано пытаетесь сделать вывод. В предыдущем сценарии
результат 24 = 24 был получен потому, что мы поместили значение переменной в то же уравнение, что и
используется для его вычисления. Здесь мы этого не сделали.

Результат 12 = 12 имеет какое-то отношение к природе системы уравнений, которую мы
дано.Независимо от того, какой метод решения вы можете использовать, решение системы линейных
уравнения лежат в единственной точке, где их линии пересекаются. В этом сценарии две строки
в основном одинаковы (одна линия над другой. На следующем рисунке показан этот сценарий.

Такая система называется зависимой системой
уравнения.И решение такой системы — это вся линия (каждая точка на линии — это точка
пересечения двух линий)

Следовательно, решением данной системы уравнений является вся

строка: y = 24 — 4x

Другой возможный сценарий:

Подобно этому примеру, существует другой сценарий, в котором замена одной переменной
в уравнение 2 ^nd приводит к результату, аналогичному показанному ниже:

23 = –46

или

5 = 34

Такой сценарий возникает, когда не существует решения данной системы уравнений.Т.е.,
когда две линии вообще не пересекаются ни в одной точке.

Следовательно, в случае такого результата, когда кажется, что ваши основные математические правила не работают, простой вывод
заключается в том, что решения данной системы не существует. Такая система уравнений называется Несогласованная система .

уравнений в одной переменной — 6 класс

Внизу страницы представлены примеры и вопросы для 6-го класса по уравнениям и задачам в одной переменной с подробными решениями и пояснениями. Если вы обнаружите, что некоторые вопросы вызывают затруднения, не пропускайте
проводите с ними время и работайте в группах. Мы изучаем математику, решая сложные вопросы.

Больше математики в старших классах (10, 11 и 12 классы) — бесплатные вопросы и проблемы с ответами

Больше математики в средней школе (6, 7, 8, 9 классы) — Бесплатные вопросы и проблемы с ответами

Больше элементарной математики (4 и 5 классы) с бесплатными вопросами и проблемами с ответами

Домашняя страница

Решение линейных уравнений с одной переменной

Линейные уравнения с одной переменной — это уравнения, в которых переменная имеет показатель степени 1, который обычно не отображается (это понятно).Примером может быть что-то вроде \ (12x = x — 5 \). Для решения линейных уравнений есть одна основная цель: изолировать переменную . В этом уроке мы рассмотрим, как это делается, на нескольких примерах.

Содержание

1. Примеры решения одношаговых уравнений
2. Примеры решения двухэтапных уравнений
3. Примеры уравнений, в которых сначала необходимо упростить
4. Бесконечно много или нет решений
5. Сводка

реклама

Примеры решения одношаговых линейных уравнений

После всей вашей тяжелой работы над решением уравнения вы знаете, что хотите получить окончательный ответ, например \ (x = 5 \) или \ (y = 1 \).В обоих случаях переменная изолирована или сама по себе.

Итак, нам нужно выяснить, как изолировать переменную. Как мы это сделаем, зависит от самого уравнения! Если его на что-то умножили, поделим. Если к нему что-то добавили, мы вычтем. Поступая так, мы постепенно будем получать переменную сама по себе.

Давайте рассмотрим пример, чтобы увидеть, как это работает.

Пример

Решите уравнение: \ (4x = 8 \)

Решение

В этом примере 4 — это умножение на \ (x \).Следовательно, чтобы изолировать \ (x \), вы должны разделить эту сторону на 4. Делая это, вы должны помнить одно важное правило: что бы вы ни делали с одной стороной уравнения, вы должны делать с другой стороной. Итак, мы разделим обе стороны на 4.

\ (\ begin {align} 4x & = 8 \\ \ dfrac {4x} {\ color {red} {4}} & = \ dfrac {8} {\ color {red} {4}} \ end {align} \)

Упрощение:

\ (х = \ в коробке {2} \)

Вот и все, один шаг, и готово. (Вот почему подобные уравнения часто называют «одношаговыми» уравнениями)

Чек

Каждый раз, когда вы решаете линейные уравнения, вы всегда можете проверить свой ответ, подставив его обратно в уравнение.Если вы получите верное утверждение, значит, ответ правильный. Это не обязательно на 100% для каждой задачи, но это хорошая привычка, поэтому мы сделаем это для наших уравнений.

В этом примере наше исходное уравнение было \ (4x = 8 \). Чтобы проверить это, убедитесь, что верно следующее:

\ (\ begin {align} 4x & = 8 \\ 4 (2) & = 8 \\ 8 & = 8 \ end {align} \)

Это верное утверждение, поэтому наш ответ правильный.

Для любого уравнения любая операция, которую вы выполняете с одной стороной, должна выполняться и с другой стороной.

Давайте попробуем еще пару примеров, прежде чем переходить к более сложным уравнениям.

Пример

Решить: \ (3x = 12 \)

Решение

Поскольку \ (x \) умножается на 3, план состоит в том, чтобы разделить на 3 с обеих сторон:

\ (\ begin {align} 3x & = 12 \\ \ dfrac {3x} {\ color {red} {3}} & = \ dfrac {12} {\ color {red} {3}} \\ x & = \ в штучной упаковке {4} \ end {align} \)

Чек

Чтобы проверить наш ответ, мы позволим \ (x = 4 \) и подставим его обратно в уравнение:

\ (\ begin {align} 3x & = 12 \\ 3 (4) & = 12 \\ 12 & = 12 \ end {align} \)

Как и раньше, поскольку это истинное утверждение, мы знаем, что наш ответ правильный.

В следующем примере вместо умножения переменной на значение из переменной вычитается значение. Чтобы «отменить» это, мы добавим это значение обеим сторонам.

Пример

Решить: \ (y-9 = 21 \)

Решение

На этот раз из y вычитается 9. Итак, мы отменим это, добавив 9 к обеим сторонам.

\ (\ begin {align} y-9 & = 21 \\ y-9 \ color {red} {+ 9} & = 21 \ color {red} {+ 9} \\ y & = 30 \ end {align} \)

Далее мы рассмотрим то, что обычно называют «двухшаговыми» уравнениями.В этих уравнениях нам нужно будет отменить две операции, чтобы изолировать переменную.

Примеры двухступенчатых уравнений

В каждом из приведенных выше примеров нужно было выполнить один шаг, прежде чем мы получили ответ. В следующих примерах вы увидите, как работать с уравнениями, которые вместо этого состоят из двух шагов. Если выполняется более одной операции, важно помнить порядок операций PEMDAS. Поскольку вы отменяете операции с \ (x \), вы будете работать «снаружи внутрь».Это легче понять, когда вы увидите это на примере.

Пример

Решить: \ (2x-7 = 13 \)

Решение

Обратите внимание на две операции, происходящие с \ (x \): он умножается на 2, а затем вычитается 7. Нам нужно будет их отменить. Но только \ (x \) умножается на 2, поэтому первым шагом будет прибавление 7 к обеим сторонам. Тогда мы можем разделить обе части на 2.

Добавление 7 к обеим сторонам:

\ (\ begin {align} 2x-7 & = 13 \\ 2x-7 \ color {red} {+ 7} & = 13 \ color {red} {+ 7} \\ 2x & = 20 \ end {align} \ )

Теперь разделите обе стороны на 2:

.

\ (\ begin {align} 2x & = 20 \\ \ dfrac {2x} {\ color {red} {2}} & = \ dfrac {20} {\ color {red} {2}} \\ x & = \ в штучной упаковке {10} \ end {align} \)

Чек

Как и в случае с более простыми задачами, вы можете проверить свой ответ, подставив свое значение \ (x \) обратно в исходное уравнение.

\ (\ begin {align} 2x-7 & = 13 \\ 2 (10) — 7 & = 13 \\ 13 & = 13 \ end {align} \)

Это правда, значит, у нас есть правильный ответ.

Давайте посмотрим еще на один пример с двумя шагами, прежде чем мы снова будем преодолевать трудности. Убедитесь, что вы понимаете каждый показанный шаг и также работаете над проблемой.

Пример

Решить: \ (5w + 2 = 9 \)

Решение

Как и выше, есть две операции: \ (w \) умножается на 5, а затем к нему прибавляется 2.Мы отменим их, сначала вычтя 2 с обеих сторон, а затем разделив на 5.

\ (\ begin {align} 5w + 2 & = 9 \\ 5w + 2 \ color {red} {- 2} & = 9 \ color {red} {- 2} \\ 5w & = 7 \\ \ dfrac { 5w} {\ color {red} {5}} & = \ dfrac {7} {\ color {red} {5}} \\ w = \ boxed {\ dfrac {7} {5}} \ end {align} \)

Дробь справа не может быть упрощена, так что это наш окончательный ответ.

Чек

Пусть \ (w = \ dfrac {7} {5} \). Тогда:

\ (\ begin {align} 5w + 2 & = 9 \\ 5 \ left (\ dfrac {7} {5} \ right) + 2 & = 9 \\ 7 + 2 & = 9 \\ 9 & = 9 \ конец {align} \)

Итак, мы снова получили правильный ответ!

Упрощение перед решением

В следующих примерах есть больше изменяемых терминов и, возможно, необходимо некоторое упрощение.В каждом случае шаги будут заключаться в том, чтобы сначала упростить обе стороны, а затем использовать то, что мы делали, чтобы изолировать переменную. Сначала мы подробно рассмотрим пример, чтобы увидеть, как все это работает.

Чтобы понять этот раздел, вам должно быть удобно комбинировать похожие термины.

Пример

Решить: \ (3x + 2 = 4x-1 \)

Решение

Поскольку обе части упрощены (нет скобок, которые нам нужно вычислять, и нет одинаковых членов для объединения), следующим шагом будет получение всех x на одной стороне уравнения и всех чисел на другой стороне.Применяется то же правило — что бы вы ни делали с одной стороной уравнения, вы должны делать и с другой стороной!

Можно перемещать \ (3x \) или \ (4x \). Предположим, вы переместили \ (4x \). Поскольку он положительный, вы должны вычесть его с обеих сторон:

\ (\ begin {align} 3x + 2 & = 4x-1 \\ 3x + 2 \ color {red} {- 4x} & = 4x-1 \ color {red} {- 4x} \\ -x + 2 & = -1 \ end {align} \)

Теперь уравнение выглядит так же, как и раньше. Следующим шагом будет вычитание 2 с обеих сторон:

\ (\ begin {align} -x + 2 \ color {red} {- 2} & = -1 \ color {red} {- 2} \\ — x = -3 \ end {align} \)

Наконец, поскольку \ (- x = -1x \) (это всегда верно), разделите обе стороны на \ (- 1 \):

\ (\ begin {align} \ dfrac {-x} {\ color {red} {- 1}} & = \ dfrac {-3} {\ color {red} {- 1}} \\ x & = 3 \ end {выровнять}\)

Чек

Вы должны воспользоваться моментом и убедиться, что следующее утверждение является верным:

\ (3 (3) + 2 = 4 (3) — 1 \)

В следующем примере нам нужно будет использовать свойство распределения перед решением.Здесь легко ошибиться, поэтому убедитесь, что вы распределили число перед круглыми скобками для всех терминов внутри.

Пример

Решить: \ (3 (x + 2) -1 = x-3 (x + 1) \)

Решение

Сначала разложите 3 и –3 и соберите одинаковые термины.

\ (\ begin {align} 3 (x + 2) -1 & = x-3 (x + 1) \\ 3x + 6-1 & = x-3x-3 \\ 3x + 5 & = — 2x-3 \ end {выровнять}\)

Теперь мы можем прибавить 2x к обеим сторонам. (Помните, что вы получите тот же ответ, если вместо этого вычтете 3x с обеих сторон)

\ (\ begin {align} 3x + 5 \ color {red} {+ 2x} & = — 2x-3 \ color {red} {+ 2x} \\ 5x + 5 & = -3 \ end {align} \)

Отсюда мы можем решить, как и с другими двухэтапными уравнениями.

\ (\ begin {align} 5x + 5 \ color {red} {- 5} & = — 3 \ color {red} {- 5} \\ 5x & = — 8 \\ \ dfrac {5x} {\ color { красный} {5}} & = \ dfrac {-8} {\ color {red} {5}} \\ x & = \ dfrac {-8} {5} \\ & = \ boxed {- \ dfrac {8 } {5}} \ end {align} \)

Чек

Это был сложный вопрос, поэтому не забудьте проверить свой ответ и убедиться, что не было допущено никаких ошибок. Для этого вы убедитесь, что следующее утверждение является верным:

\ (3 \ left (- \ dfrac {8} {5} +2 \ right) -1 = \ left (- \ dfrac {8} {5} \ right) -3 \ left (- \ dfrac {8} { 5} +1 \ вправо) \)

(Примечание: это работает, но вы должны быть очень осторожны с скобками!)

Бесконечно много решений и нет решений

Бывают случаи, когда вы выполняете все эти шаги, и возникает действительно странное решение.Например, при решении уравнения \ (x + 2 = x + 2 \) с использованием описанных выше шагов в итоге получается \ (0 = 0 \). Это, конечно, правда, но что хорошего в этом?

Если вы получите подобное утверждение, это означает, что уравнение имеет бесконечно много решений. Любой \ (x \), о котором вы можете подумать, удовлетворял бы уравнению \ (x + 2 = x + 2 \). Подходящий ответ в этом случае — «бесконечно много решений».

Другая ситуация возникает, когда вы упрощаете уравнение до утверждения, которое никогда не бывает истинным, например \ (3 = 4 \) или \ (0 = 1 \).Это происходит с уравнением \ (x + 5 = x-7 \), которое приводит к \ (5 = -7 \), что, конечно, никогда не бывает истинным. Это означает, что никакое \ (x \) не удовлетворяет этому уравнению. Другими словами «нет решения». Итого:

• Если вы получите утверждение, которое всегда истинно, например \ (5 = 5 \) или \ (0 = 0 \), то существует бесконечно много решений.
• Если вы получаете утверждение, которое всегда ложно, например \ (10 ​​= 11 \) или \ (1 = 5 \), то решений нет.

реклама

Сводка

Решение линейных уравнений сводится к выделению переменной.В зависимости от уравнения это может занять от одного шага до многих. Всегда проверяйте, нужно ли вам сначала упростить одну или обе стороны уравнения, и всегда проверяйте свой ответ.

Подпишитесь на нашу рассылку новостей!

Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.

Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!

Связанные