Логические задачи для 5 класса по математике | Занимательные факты по алгебре (5 класс) по теме:
Логические задачи для 5-6 классов.
Предисловие.
Если логическое мышление, да еще и воображение хорошо развиты у человека, то он способен творчески мыслить и творчески подходить к поставленным задачам. Развитию логического мышления необходимо учиться. Нужно уметь пользоваться логическим мышлением и воображением. Нужно также развивать и всячески способствовать развитию логического мышления. Ведь это пригодится в жизни!
Для эффективного развития логического мышления можно и нужно решать различные ситуационные задачи и загадки. Как стандартные логические задачи головоломки, так и нестандартные. Это одновременно развивает логику, интеллект, воображение, фантазию.
Это всего лишь небольшой обзор тех увлекательных логических задач, которые могут быть использованы учителями во внеурочное время, а также при проведении внеклассных мероприятий.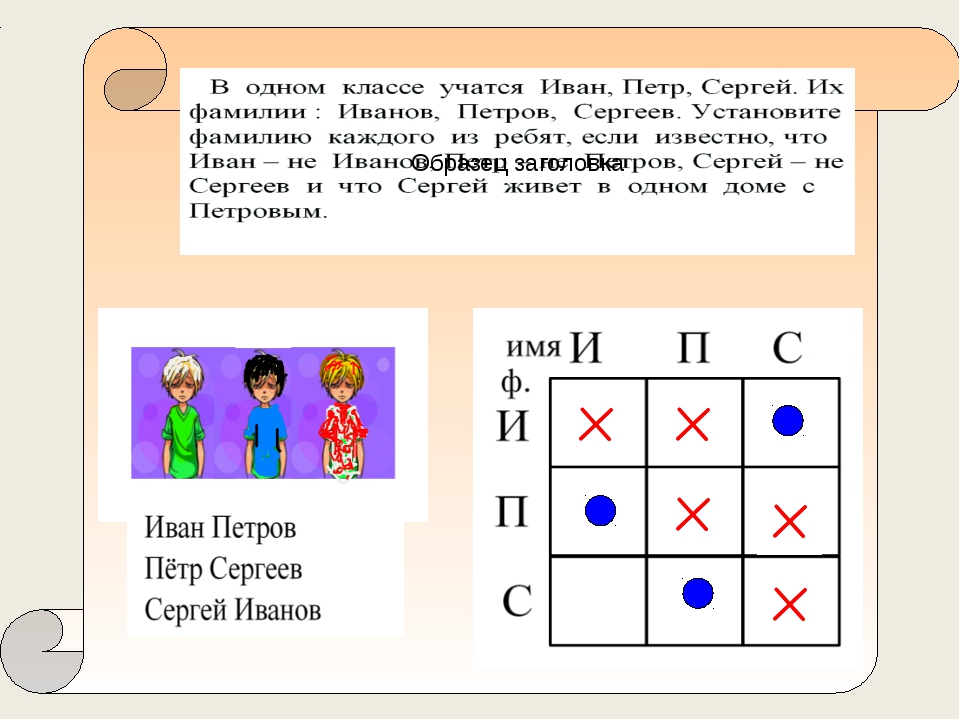
1.Шарики.
На столе стоят три одинаковых ящика. В одном из них 2 черных шарика, в другом 1 черный и 1 белый шарик, в третьем 2 белых шарика. На ящиках написано: «2 белых», «2 черных», «черный и белый». При этом известно, что ни одна из записей не соответствует действительности. Как, вынув только один шарик, определить правильное расположение надписей?
2.Про школьников.
В класе 35 учеников, из них 20 школьников занимаются в математическом круже, 11- в литературном, 10 ребят не посещают эти кружки. Сколько литераторов увлекаются математикой?
3.Тайный поклонник.
На парту Оли упал бумажный самолет с нарисованными красными сердечками. Оля развернула его и прочитала: «Ты — лучшая девочка в классе!» Она повернулась в сидящим за ней ребятам: Ивану, Сергею, Алексею. Все три мальчика покраснели.
— Кто из вас делает мне такие комплименты? — спросила Оля.
— Это Сергей! — сказал Иван.
— Я ничего такого не делал! — сказал Сергей.
— Не имею никакого представления, о чем ты говоришь! — сказал Алексей.
Подруга Оли Маша ухмыльнулась: «Двое из них лгут!» Однако она не хочет больше ничего говорить. Кто является тайным поклонником Оли?
4.Названия птиц.
Прочитайте названия птиц в этих анаграммах. Какое слово здесь лишнее?
ВОЛИГА, НИЦАСИ, ГАЙПОПУ, РОКАСО, ВЕЙЛОСО, РЕЦСКВО, ЗАНАС, УССТРА, ЛИНФИ, БЕЙРОВО
5.Кошки-мышки.
Если пять кошек ловят пять мышей за пять минут, то сколько времени нужно одной кошке, чтобы поймать одну мышку?
6.Опасная дорога.
Есть дорога по которой может проехать только одна машина. По дороге едут две машины: одна с горы, другая под гору. Как им разъехаться?
7.Бумажные стаканчики.
Имеются три бумажных стаканчика для мороженого. Требуется разложить по этим стаканчикам 10 монет так, чтобы в каждом стаканчике было нечетное число монет. Как это сделать?
Как это сделать?
8.Трудное наследство.
Один коневладелец оставил в наследство своим сыновьям конюшню. Он завещал старшему отдать половину, среднему треть, а младшему девятую часть всех лошадей. В конюшне на момент смерти владельца осталось 17 лошадей. Как можно не нарушив завещание поделить лошадей?
9.Двенадцать.
Как разделить пополам число двенадцать, что бы получилось семь?
10.Задача про велогонку.
Петя и Вася участвовали в велогонке. Все участники стартовали одновременно и показали на финише различное время. Петя финишировал сразу после Васи и оказался на десятом месте. Сколько человек участвовало в гонке, если Вася был пятнадцатым с конца?
11.Странное вычитание.
Можно ли от 29 отнять 1, чтобы при этом получилось 30?
12. Равенство
Равенство
9999999 = 100
Расставьте скобки и математические знаки так, чтобы равенство было верным.
13.Учащиеся
Из 38 учащихся 28 посещают хор и 17 лыжную секцию. Сколько лыжников посещает хор, если в классе нет учащихся , котрые не посещают хор или лыжную секицю?
14. Может ли такое быть?
Одного человека спросили:
— Сколько вам лет?
— Порядочно, — ответил он.
— Я старше некоторых своих родственников почти шестьсот раз. Может ли такое
15. Два числа.
Назовите два числа, у которых количество цифр равно количеству букв, составляющих название каждого из этих чисел.
16. Прилив.
С борта парохода был спущен стальной трап. Нижние 4 ступеньки трапа погружены в воду. Каждая ступенька имеет толщину в 5 см; расстояние между двумя соседними ступень ками составляет 30 см. Начался прилив, при котором уровень воды стал поднимается со скоростью 40 см в час. Как Вы считаете, сколько ступенек окажется под водой через 2 часа
Нижние 4 ступеньки трапа погружены в воду. Каждая ступенька имеет толщину в 5 см; расстояние между двумя соседними ступень ками составляет 30 см. Начался прилив, при котором уровень воды стал поднимается со скоростью 40 см в час. Как Вы считаете, сколько ступенек окажется под водой через 2 часа
Ответы. 1.Собственно ответ: Вытаскиваем шарик из коробки с надписью «белый и черный». Если шарик белый, то:
в коробке «белый и черный» — 2 белых шарика;
в коробке «2 белых» — 2 черных шарика;
в коробке «2 черных» — белый и черный шарики
Если шарик черный:
в коробке «белый и черный» — 2 черных шарика;
в коробке «2 белых» — белый и черный шарики;
в коробке «2 черных» — 2 белых шарика
2. Всего 35 учеников. 10 кружки не посещают. Значит, посещают кружки 35-10=25 учеников.
25 учеников посещают кружки. 20 учеников занимаются в математическом кружке. Значит, только литературный кружок посещают 25-20=5 человек.
В литературном кружке 11 человек. Лишь 5 из них посещают только литературный кружок. Значит, 11-5 = 6 человек-литераторов посещают ещё и математический кружок.
3.Алексей.
4.Иволга, синица, попугай, сорока, соловей, скворец, страус, филин, воробей. Лишнее слово здесь — «сазан», потому что это не птица, а рыба.
5..Пять
6.А зачем им разъезжаться? Они же обе вниз (под гору и с горы) едут.
7.Все дело в том, что один из стаканчиков можно вставить в другой. После этого в него можно положить любое нечетное число монет меньше 10. Например, 7. Оставшиеся монеты кладем в третий стаканчик.
8.Добавьте в конюшню еще одну лошадь. Теперь их получилось 18. Отдадим 9 лошадей старшему наследнику, 6 среднему и 2 младшему. Условия завещания выполнены. Можете забирать свою лошадь обратно.
9.Напишите это число римскими цифрами на листе бумаги и разрежьте его пополам.
10.Т.к. Петя финишировал сразу после Васи и оказался на 10-м месте, то Вася был девятым, т.е. перед ним было еще 8 участников. А раз известно, что Вася был пятнадцатым с конца, то всего было 15+8 = 23 участника.
11.Для того, чтобы на первый взгляд немыслимое стало естественным, нужно представить число 29 в римских цифрах. Тогда 29 — это XXIX. Отнимаем единицу, в данном случае I, и в результате получится XXX или 30.
12.(99-9):9 + (99-9) = 100
(99-99)* 999 = 10*0
999/9-99/9=100
(9*9+9)/9+99-9=100
(99-9)/9+(9-9)*9=10-0
(9*9+9)/9+(9-9)*9=10-0
99/99+(9-9)*9=1+0+0
(9*9+9)/9-9+9-9=1+0+0
13. 7 человек. Хор не посещают 10 человек, все они лыжники. Лыжников всего 17 человек, значит 7 человек надо «взять» из хора.
14.Может, например если человеку 50 лет, а его внуку или внучке 1 месяц.
15. «сто»-100 «миллион»-1000000
16.Через два часа под водой будут те же 4 ступеньки, потому что во время прилива лестница поднимается вместе с пароходом.
|
| ||
Рабочая программа курса внеурочной деятельности «Занимательная математика» 5 класс
Муниципальное бюджетное
общеобразовательное учреждение
«Центр образования №6 «Перспектива»
|
|
|
|
РАБОЧАЯ ПРОГРАММА
по курсу внеурочной деятельности
«Занимательная математика»
для 5 класса
2018 год
Пояснительная записка
Программа курса «Занимательная математика» предназначена для внеурочной работы и рассчитана на обучающихся 5-х классов, интересующихся математикой. Согласно ФГОС нового поколения проведение такого курса способствует самоопределению обучающихся при переходе к профильному обучению в средней и старшей школе.
Согласно ФГОС нового поколения проведение такого курса способствует самоопределению обучающихся при переходе к профильному обучению в средней и старшей школе.
Изучение курса составлено на основе авторской программы Е.Л. Мардахаевой «Занятия математического кружка. 5 класс» с использованием пособия: Горев П.М., Утёмов В.В. Уроки развивающей математики. 5-6 классы. Задачи математического кружка. – Киров: изд. МЦИТО, 2014.
Данный курс способствует развитию познавательной активности, формирует потребность в самостоятельном приобретении знаний и в дальнейшем автономном обучении, а также интеллектуальному, творческому, эмоциональному развитию учащихся.
Программа внеурочной деятельности содержит в основном традиционные темы занимательной математики: арифметику, логику, комбинаторику и т.д. Уровень сложности подобранных заданий таков, что к их рассмотрению можно привлечь значительное число учащихся, а не только наиболее сильных. В результате занятий учащиеся должны приобрести навыки и умения решать более трудные и разнообразные задачи, а так же задачи олимпиадного уровня.
В результате занятий учащиеся должны приобрести навыки и умения решать более трудные и разнообразные задачи, а так же задачи олимпиадного уровня.
При реализации содержания программы учитываются возрастные и индивидуальные возможности учащихся, создаются условия для успешности каждого ребёнка.
Обучение по программе осуществляется в виде теоретических и практических занятий. В ходе занятий учащиеся выполняют практические работы, готовят рефераты, выступления, принимают участия в конкурсных программах.
Курс позволяет обеспечить требуемый уровень подготовки школьников, предусматриваемый государственным стандартом математического образования, а также позволяет осуществлять при этом такую подготовку, которая является достаточной для углубленного изучения математики.
Таким образом, основной целью разработанной внеурочной деятельности является углубление и расширение математических знаний и умений, сохранение и развитие интереса учащихся к математике.
Для достижения поставленной цели необходимо решение следующих учебных задач:
-
в направлении личностного развития: развитие устойчивого интереса учащихся к математике и ее приложениям; формирование представлений о математике как части общечеловеческой культуры; значимости математики в развитии цивилизации и современного общества; развитие интереса к математическому творчеству и математических способностей; -
в метапредметном направлении: формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности; привитие учащимся определенных навыков научно-исследовательского характера; развитие у учащихся умения самостоятельно и творчески работать с учебной и научно-популярной литературой. -
в предметном направлении: создание фундамента для математического развития, формирование механизмов мышления, характерных для математической деятельности, высокой культуры математического мышления; оптимальное развитие математических способностей у учащихся; расширение и углубление представлений учащихся о практическом значении математики.
-
коммуникативные УУД: воспитание учащихся чувства коллективизма и умения сочетать индивидуальную работус коллективной; установление более тесных деловых контактов между учителем математики и учащимися и на этой основе более глубокое изучение познавательных интересов и запросов школьников.
Основными педагогическими принципами, обеспечивающими реализацию программы, являются:
• учет возрастных и индивидуальных особенностей каждого ребенка;
• доброжелательный психологический климат на занятиях;
• личностно-деятельный подход к организации учебно-воспитательного процесса;
• оптимальное сочетание форм деятельности;
• доступность.
Эффективности реализации программы курса способствует использование различных форм проведения занятий, в частности таких, как:
— эвристическая беседа;
— интеллектуальная игра;
— дискуссии;
— математические состязания, турниры, конкурсы;
— творческие задания.
Оценка знаний и умений обучающихся проводится в виде защиты исследовательских проектов, которые предполагают самостоятельную творческую работу обучающихся по предложенной тематике с последующей защитой их решения на занятиях, научно-практических конференциях. Предполагается, что знакомство учащихся с нестандартными (как по формулировке, так и по решению) задачами будет способствовать повышению их успеваемости на уроках математики и развитию у них интереса к предмету.
Предполагаемая результативность курса:
-
усвоение основных базовых знаний по математике; её ключевых понятий; -
улучшение качества решения задач различного уровня сложности учащимися; -
успешное выступление на олимпиадах, играх, конкурсах, научно-практических конференциях.
Результаты освоения содержания курса «Занимательная математика»
Личностными результатами изучения данного курса являются:
-
формирование целостного взгляда на мир в его органичном единстве и разнообразии природы, народов, культур и религий -
формирование уважительного отношения к иному мнению, истории и культуре других народов -
овладение начальными навыками адаптации в динамично изменяющемся и развивающемся мире -
развитие любознательности, сообразительности при выполнении разнообразных заданий проблемного и эвристического характера; -
развитие внимательности, настойчивости, целеустремленности, умения преодолевать трудности — качеств весьма важных в практической деятельности любого человека; -
воспитание чувства справедливости, ответственности; -
развитие самостоятельности суждений, независимости и нестандартности мышления.
Метапредметными результатами изучения курса является формирование универсальных учебных действий (УУД). По окончании обучения учащиеся должны уметь:
-
сравнивать разные приемы действий, выбирать удобные способы для выполнения конкретного задания. -
использовать приобретённые математические знания для описания и объяснения окружающих предметов, процессов, явлений, а также для оценки их количественных и пространственных отношений. -
моделировать в процессе совместного обсуждения алгоритм решения занимательных задач; использовать его в ходе самостоятельной работы. -
применять изученные способы учебной работы и приёмы вычислений для работы с математическими головоломками. -
включаться в групповую работу. -
участвовать в обсуждении проблемных вопросов, высказывать собственное мнение и аргументировать его.
-
аргументировать свою позицию в коммуникации, учитывать разные мнения, использовать критерии для обоснования своего суждения. -
контролировать свою деятельность: обнаруживать и исправлять ошибки.
Предметные результаты:
-
знают особые случаи устного счета -
решают текстовые задачи, используя при решении таблицы и «графы» -
знают разнообразные логические приемы, применяемые при решении задач. -
решают нестандартные задачи на разрезание -
знают определения основных геометрических понятий
-
решают простейшие комбинаторные задачи путём систематического перебора возможных вариантов -
измеряют геометрические величины, выражают одни единицы измерения через другие.
-
вычисляют значения геометрических величин(длин, углов, площадей, объемов)
Содержание курса «Занимательная математика»
Курс «Занимательная математика» входит во внеурочную деятельность по направлению общеинтеллектуальное развитие личности. Программа предусматривает включение задач и заданий, трудность которых определяется не столько математическим содержанием, сколько новизной и необычностью математической ситуации. Это способствует появлению желания отказаться от образца, проявить самостоятельность, формированию умений работать в условиях поиска, развитию сообразительности, любознательности.
В процессе выполнения заданий дети учатся видеть сходства и различия, замечать изменения, выявлять причины и характер этих изменений, на этой основе формулировать выводы. Совместное с учителем движение от вопроса к ответу – это возможность научить ученика рассуждать, сомневаться, задумываться, стараться и самому найти выход – ответ. Создание на занятиях ситуаций активного поиска, предоставление возможности сделать собственное «открытие», знакомство с оригинальными путями рассуждений, овладение элементарными навыками исследовательской деятельности, позволят обучающимся реализовать свои возможности, приобрести уверенность в своих силах.
Создание на занятиях ситуаций активного поиска, предоставление возможности сделать собственное «открытие», знакомство с оригинальными путями рассуждений, овладение элементарными навыками исследовательской деятельности, позволят обучающимся реализовать свои возможности, приобрести уверенность в своих силах.
Курс «Занимательная математика» предусматривает организацию подвижной деятельности учащихся, которая не мешает умственной работе. С этой целью включены подвижные математические игры, предусмотрена последовательная смена деятельности в течение одного занятия; передвижение по классу в ходе выполнения математических заданий на листах бумаги, расположенных на стенах классной комнаты и др. Во время занятий важно поддерживать прямое общение между детьми (возможность подходить друг к другу, переговариваться, обмениваться мыслями). При организации занятий целесообразно использовать принцип свободного перемещения по классу, работу в парах постоянного и сменного состава, работу в группах. Некоторые математические игры и задания могут принимать форму состязаний, соревнований между командами.
Некоторые математические игры и задания могут принимать форму состязаний, соревнований между командами.
Место курса «Занимательная математика» в учебном плане
Программа рассчитана на 34 часа в год (1 час в неделю). Содержание курса «Занимательная математика» отвечает требованию к организации внеурочной деятельности: соответствует курсу «Математика», не требует от учащихся дополнительных математических знаний. Тематика задач и заданий отражает реальные познавательные интересы детей, содержит полезную и любопытную информацию, интересные математические факты, способные дать простор воображению.
Ценностные ориентиры содержания курса «Занимательная математика»
— формирование умения рассуждать как компонента логической грамотности;
— освоение эвристических приемов рассуждений;
— формирование интеллектуальных умений, связанных с выбором стратегии решения, анализом ситуации, сопоставлением данных;
— развитие познавательной активности и самостоятельности учащихся;
— формирование способностей наблюдать, сравнивать, обобщать, находить простейшие закономерности, использовать догадку, строить и проверять простейшие гипотезы;
— формирование пространственных представлений и пространственного воображения;
— привлечение учащихся к обмену информацией в ходе свободного общения на занятиях.
Тематическое планирование курса «Занимательная математика»
Содержание курса «Занимательная математика» направлено на воспитание интереса к предмету, развитию наблюдательности, геометрической зоркости, умения анализировать, догадываться, рассуждать, доказывать, умения решать учебную задачу творчески. Содержание может быть использовано для показа учащимся возможностей применения тех знаний и умений, которыми они овладевают на уроках математики.
Каждое занятие состоит из двух частей: задачи, решаемые с учителем, и задачи для самостоятельного (или домашнего) решения. Учащиеся знакомятся с интересными свойствами чисел, приемами устного счета, особыми случаями счета, с биографиями великих математиков, их открытиями. Большая часть занятий отводится решению олимпиадных задач.
Мир занимательных задач
Головоломки и числовые ребусы. Судоку. Старинные задачи. Задачи, решаемые способом перебора, «с конца». Логические задачи. Комбинаторные задачи. Графы. Круги Эйлера. Принцип Дирихле. Задачи на взвешивание. Задачи на переливание. Задачи на движение нестандартного характера.
Судоку. Старинные задачи. Задачи, решаемые способом перебора, «с конца». Логические задачи. Комбинаторные задачи. Графы. Круги Эйлера. Принцип Дирихле. Задачи на взвешивание. Задачи на переливание. Задачи на движение нестандартного характера.
Практика: Составление и решение ребусов, задач, загадок, связанных с математикой. Блиц-турнир по решению старинных занимательных задач. Задачи на сообразительность и смекалку «Затруднительные положения». Игра «Математический футбол» (игровой математический практикум по решению логических задач, головоломок). Соревнование «Кто больше». Турнир «Смекалистых»
Как люди научились считать. Старинные системы записи чисел. Числа-великаны.
Как возникло слово «математика». Счёт у первобытных людей. Иероглифическая система древних египтян. Римские цифры. Славянские цифры. История возникновения названий – «миллион», «миллиард», «триллион». Числа великаны.
Числа великаны.
Практика: Занимательные задачи «Сколько?». Загадки о числах. Игра «Весёлый счёт». Задачи на смекалку «Цифры спрятались». Защита проекта «В мире чисел».
Математика вокруг нас
Что такое фольклорная математика? Освоение космического пространства человечеством. Роль математики в этом процессе. История строительства и развития города Липецка. Просмотр презентации «Наш город». Основы здорового образа жизни и математика.
Практика: Аукцион «Числа, спрятанные в пословицах и поговорках». Игра «Опознай пословицу». Конкурс частушек о математике. Задачи, связанные с историей освоения космоса. Игра-путешествие «Полёт на Марс». Практические задачи, связанные с городом. Конкурс задач с краеведческим содержанием, составленных детьми. Занимательные задачи, связанные со спортом, здоровым питанием, режимом дня. Сообщения о роли математики в формировании здорового образа жизни. Проект – выпуск газеты «Математика вокруг нас».
Сообщения о роли математики в формировании здорового образа жизни. Проект – выпуск газеты «Математика вокруг нас».
Блистательные умы
К.Гаусс. Л.Эйлер. Л.Ф.Магницкий. С.В. Ковалевская. Просмотр видеофильмов, содержащих информацию о великих учёных математиках России и Европы. Высказывания великих людей о значении математики.
Практика: Защита проектов «Великие математики».
Учебно-тематическое планирование
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учебно-методическое и материально-техническое обеспечение образовательного процесса по курсу «Занимательная математика»
-
Библиотечный фонд
Методические пособия для учителя
-
Горев П. М., Утёмов В.В. Уроки развивающей математики. 5-6 классы. Задачи математического кружка. – Киров: изд. МЦИТО, 2014
М., Утёмов В.В. Уроки развивающей математики. 5-6 классы. Задачи математического кружка. – Киров: изд. МЦИТО, 2014
-
Гусев А.А. Математический кружок. 5 класс. – М.: Мнемозина, 2013 -
Киселёва Г.М. Математика. 5-6 классы. Организация познавательной деятельности. – Волгоград: Учитель, 2013 -
Мардахаева Е.Л. Занятия математического кружка.– М.: Мнемозина, 2012 -
Математика. 5 класс: учебник для общеобразовательных учреждений / А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. − М.: Вентана-Граф, 2015 -
Олимпиадные задания по математике. 5-6 классы. Ю.В. Лепёхин – Волгоград: Учитель, 2011 -
Факультативные занятия: Математика после уроков. Т.С.Безлюдова – Мозырь: Белый Ветер, 2013 -
Математические олимпиады: методика подготовки.А.В. Фарков – М. : ВАКО, 2014
: ВАКО, 2014
-
Фарков А. В. Математические олимпиады в школе. 5-11 класс. – М.: Айрис-пресс, 2005
Справочные пособия, научно-популярная и историческая литература
-
Баврин И.И., Фрибус Е.А. Старинные задачи. – М.: Просвещение, 1994. -
Гаврилова Т. Д. Занимательная математика. 5-11 класс. – Волгоград: Учитель, 2008. -
Депман И. Я., Виленкин Н. Я. За страницами учебника математики. 5-6 класс. – М.: Просвещение, 2004. -
Екимова М.А., Кукин Г.П. Задачи на разрезание. – М.: МЦНМО, 2002 -
Левитас Г. Г. Нестандартные задачи по математике. – М.: ИЛЕКСА, 2007. -
Перли С.С., Перли Б.С. Страницы русской истории на уроках математики. – М.: Педагогика-Пресс, 1994 -
Энциклопедия для детей. Математика. Том 11. – М.: Аванта+, 2003.
Математика. Том 11. – М.: Аванта+, 2003.
-
Я познаю мир: математика/сост. А.П. Савин и др. – М.: АСТ, 1999
II. Печатные пособия
Портреты выдающихся деятелей математики
III. Информационные средства. Интернет-ресурсы
http://www.edu.ru — Федеральный портал Российское образование
http://www.school.edu.ru — Российский общеобразовательный портал
www.1september.ru — все приложения к газете «1сентября»
http://school-collection.edu.ru – единая коллекция цифровых образовательных ресурсов
http://mat-game.narod.ru/ математическая гимнастика
http://mathc. chat.ru/ математический калейдоскоп
chat.ru/ математический калейдоскоп
http://www.krug.ural.ru/keng/ Кенгуру
http://www.uroki.net/docmat.htm — для учителя математики, алгебры и геометрии
http://www.alleng.ru/edu/math2.htm — к уроку математики
http://www.uchportal.ru/ — учительский портал
http://mmmf.msu.ru/circles/z5/ — Малый Мехмат МГУ. Материалы занятий кружков
www.math—on—line.com – Занимательная математика – школьникам
Задачи на смекалку
Еще недавно третьеклашки решали такие задачи:
Ученик переписал числовое выражение, значение которого равно 58, но забыл поставить скобки. У него получилось:
6 ∙ 8 + 20 : 4 – 2
Где в этом выражении должны стоять скобки?
Применяя знаки арифметических действий и скобки можно восемью восьмерками записать число 1000:
888 + 88 + 8 + 8 + 8
Запишите:
а) семью семерками 700;
б) восемью семерками 700;
в) десятью четверками 500.
— Ну как получается? Идем в 4 класс.
Учащиеся решали задания из учебника, в котором требуется найти пропущенные числа:
У них получились разные ответы.
Найдите правила, по которым ребята заполнили клетки.
Трудно?
Придумайте свой вариант заполнения клеток.
.
В клетки таблицы по некоторому правилу записали несколько чисел.
Определите, что это за правило и заполните последние клетки.
Неужели это можно решить?…
Из спичек сложили шесть неверных равенств. Переложите одну спичку так, чтобы равенства стали верными.
XII + IX = II
X = VII — III
VI — VI = XI
И еще…
IV — V = I
X + X = I
IV — I + V = II
А теперь:
!
В чем его магия?
Попробуйте составить такой же, только 4×4 с числами от 1 до 16.
А тут ещё…
Выписали все натуральные числа от 1 до 99 без промежутков, получилось огромное число:
123456789101112131415161718…979899
а) Сколько раз в записи этого числа повторяется цифра 1? цифра 2?
б) Делится ли это число на 9 ?
Пора прощаться. Мы ещё порешаем!
И кубик Рубика научимся собирать!
Олимпиадные задания по математике 5 класс
Вар-т 1
Вар-т 2
Вар-т 3
Задание 1.
Расставьте в записи 7 х 9 + 12 : 3 — 2 скобки так,
чтобы значение получившегося выражения было равно 23.
Ответ:(7 х 9 + 2) : 3 — 2 = 23.
Задание 2.
В один сосуд входит 3 л, а в другой — 5л.
Как с помощью этих сосудов налить в кувшин 4л воды из водопроводного крана.
Ответ: Наполняем сосуд в 5л и отливаем в трехлитровый сосуд.
Оставшиеся 2 литра переливаем в кувшин.
Повторяя эту операцию, наливаем в кувшин 4 л воды.
Задание 3.
В оранжерее были срезаны гвоздики:
белых и розовых — 400 штук, розовых и красных — 300, белых и красных — 440.
Сколько гвоздик каждого цвета было срезано в оранжерее?
Ответ: Белых — 270, розовых — 130, красных — 170.
Сложить все данные числа и разделить результат на два;
получим количество гвоздик всех трех цветов,срезанных в оранжерее.
Задание 4.
Когда отцу было 27 лет, то сыну было только 3 года,
а сейчас сыну в три раза меньше лет, чем отцу. Сколько лет сейчас каждому из них?
Ответ: Пусть сейчас сыну — х лет, тогда отцу — 3х лет.
Поскольку разность возрастов отца и сына постоянна и равна по условию 24 годам,
то имеем уравнение: 3х — х = 24, откуда х = 12; 3х = 36.
Задание 5.
Принесли 5 чемоданов и 5 ключей от этих чемоданов, но неизвестно, какой ключ от какого чемодана.
Сколько проб придется сделать в самом худшем случае, чтобы подобрать к каждому чемодану свой ключ.
Ответ: Первым из ключей, которые мы будем подбирать к чемодану, в самом худшем случае придется сделать 4 пробы. (Если ключ не подошел к 4 чемоданам из 5, значит, он соответствует пятому).
Вторым ключом в самом худшем случае сделаем 3 пробы и т д.
Всего потребуется 10 проб (4 + 3 + 2 + 1 = 10
Задание 6.
Рыбак поймал рыбу. Когда у него спросили, колько весит пойманная рыба,
он сказал: «Я думаю, что ее хвост весит 1 кг, голова весит столько, сколько хвост и половина туловища,
а туловище — сколько голова и хвост вместе.»
Сколько же весит рыба?
Ответ: По условию туловище рыбы весит 1 кг ( вес хвоста) плюс вес головы,
а так как вес головы равен 1 кг (вес хвоста) и половине туловища,
то получается, что туловище рыбы весит 2 кг плюс половина туловища, т.е. туловище весит 4 кг.
Тогда голова весит 3 кг (сколько хвост и половина туловища), а вся рыба — 8 кг ( 3 + 4 + 1 = 8 ).
Олимпиадные задачи по математике 5 класс с ответами
Задача 1.
В корзине лежат яблоки, груши и персики – всего 37 плодов.
Яблок в корзине в два раза больше, чем персиков, и на 3 штуки больше, чем груш.
Сколько в корзине яблок, груш, персиков?
Задача 2.
Запишите все делители числа 24.
Запишите все числа, меньшие двухсот, которые кратны этому числу.
Задача 3.
Из двух городов, расстояние между которыми 100 км, одновременно выехали навстречу друг другу два велосипедиста,
скорости которых 12 км/ч и 14 км/ч.
Каким будет расстояние между велосипедистами через 3 часа после начала их движения?
Задача 4.
Начертите угол, который на 15 гр. меньше прямого угла.
Начертите угол, который на 65 гр. меньше развёрнутого угла.
На сколько градусов первый угол меньше второго?
Задача 5.
На стол положили ложки, вилки и ножи – всего 37 приборов.
При этом вилок положили в два раза больше, чем ножей и на 2 меньше, чем ложек.
Сколько положили на стол ложек, вилок, ножей?
Ответы:
1.
Яблок – 16, груш – 13, персиков – 8.
2.
Делители: 1, 2, 3, 4, 6, 8, 12, 24. Кратные: 24, 48, 72, 96, 120, 144, 168, 192.
3.
Искомое расстояние равно: 100 — (12 + 14) • 3 = 22 (км).
4.
Нужно начертить углы величиной в 75 гр. и 115 гр.. На 40 гр..
5.
Вилок – 14, ножей – 7, ложек – 16.
Олимпиадные задания по математике 5 класс с ответами
1. В выражении 4 + 32 : 8 + 4 • 3 расставьте скобки так, чтобы получилось число 28.
Ответ: 4 + (32 : 8 + 4) • 3.
2. Подберите корни уравнения: 15 : х = 16 — х
Ответ: 15, 1.
3. Необходимо получить число 16 с помощью четырех пятерок,
соединяя их знаками арифметических действий. Как это сделать?
Ответ: 55 : 5 + 5.
4. Чему равно значение выражения: 101101 • 999 — 101 • 999999?
Ответ: 0.
5. В семье трое братьев, каждый следующий брат вдвое младше предыдущего.
Сколько лет старшему, если всем им вместе 28 лет?
Ответ: 16.
6. Для нумерации страниц учебника потребовалось 324 цифры. Сколько страниц в этой книге?
Ответ: 144.
7. Напишите самое маленькое четырехзначное число, которое при делении на 6 дает в остатке 5.
Ответ: 1001.
8. У щенят и утят 42 ноги и 12 голов. Сколько щенят и сколько утят?
Ответ: 9 щенят, 3 утенка.
9. Напишите цифрами число, состоящее из 11 тысяч, 11 сотен и 11 единиц.
Ответ: 12111.
10. Сумма и произведение четырех натуральных чисел равны 8. Что это за числа?
Ответ: 1, 1, 4, 2.
11. Двумя прямыми линиями разделите циферблат часов на 3 части так,
чтобы после сложения чисел в каждой части получились 3 равные суммы.
Ответ: 1-ая сумма: 11, 12, 1, 2; 2-ая сумма: 10, 9, 3, 4; 3-я сумма: 8, 7, 6, 5.
Вар-т 1
Вар-т 2
Вар-т 3
Рабочая программа по математике 5 класс Никольский
|
«Рассмотрено»
Руководитель МО
МОУ СОШ №1 г.
________________________
Протокол №_____
от «____»_________2017 г.
|
«Согласовано»
Заместитель директора
по УВР
__________ Е.П. Матвеева
«____» ___________2017г
|
«Утверждено»
Директор МОУ СОШ №1 г.Свирска
__________ Л.А. Пазникова
«____» ___________2017г
|
|
Рабочая программа
по математике
для 5 класса
(уровень общеобразовательный)
Учитель Мордяшова Екатерина Анатольевна
Рабочая программа составлена на основе
Примерной государственной программы по математике
для общеобразовательных школ
2017/2018 учебный год
| ||
Рабочая программа по математике составлена на основе федерального компонента Государственного стандарта основного общего образования. Настоящая рабочая программа разработана применительно к авторской программе «Математика» С.М. Никольского и др. (М.: Просвещение, 2010) и ориентирована на использование учебно-методического комплекта:
Настоящая рабочая программа разработана применительно к авторской программе «Математика» С.М. Никольского и др. (М.: Просвещение, 2010) и ориентирована на использование учебно-методического комплекта:
- Математика 5 класс: учеб. для общеобразоват. учреждений / С.М. Никольский, М.К. Потапов, Н.И. Решетников, А.В. Шевкин. – М.: Просвещение, 2014.
2.Потапов М.К. Математика: дидактические материалы. 5 кл. / М.К. Потапов, А.В. Шевкин. – М.: Просвещение, 2012.
- Потапов М.К. Математика: рабочая тетрадь: 5 кл. / М.К. Потапов, А.В. Шевкин. – М.: Просвещение, 2008.
- Чулков П.В. Математика: тематические тесты: 5 кл. / П.В. Чулков, Е.Ф. Шершнев, О.Ф. Зарапина. – М.: Просвещение, 2009.
- Потапов М.К. Математика: книга для учителя 5-6 кл. / М.К. Потапов, А.В. Шевкин. – М.: Просвещение, 2010.
- Шарыгин, И.Ф. Задачи на смекалку. 5-6 классы: пособие для учащихся общеобразоват. учреждений / И.
 Ф. Шарыгин, А.В. Шевкин. – М.: Просвещение, 2010.
Ф. Шарыгин, А.В. Шевкин. – М.: Просвещение, 2010.
Главной целью образования является развитие ребенка как компетентной личности путем включения его в различные виды ценностной человеческой деятельности: Учеба, познание, коммуникации, профессионально-трудовой выбор, личностное саморазвитие, ценностные ориентации, поиск смыслов жизнедеятельности. С этих позиций обучение рассматривается как процесс овладения не только определенной суммой знаний и системой соответствующих умений и навыков, но и как процесс овладения компетенциями.
Это определило цели обучения математике:
- формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов; об идеях и методах математики;
- развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;
- овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
- воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики.

Согласно Федеральному базисному учебному плану данная рабочая программа предусматривает в 5 классе обучение в объеме 170 часов, 5 часов в неделю (контрольных работ – 9 ч.).
Планируемые предметные результаты освоения учебного курса
В результате изучения ученик должен:
знать/понимать:
— понятие натурального числа, десятичной дроби, обыкновенной дроби;
— правила выполнения действий с заданными числами;
— свойства арифметических действий;
— понятие буквенных выражений и уравнений, процентов;
— определение отрезка и луча, прямоугольного параллелепипеда и окружности;
уметь:
— выполнять арифметические действия с натуральными числами и десятичными дробями;
— применять свойства арифметических действий при решении примеров;
— решать уравнения, упрощать буквенные выражения;
— решать текстовые задачи, включая задачи, связанные с отношением и пропорциональностью величин, дробями и процентами;
— находить процент от числа и число по его проценту;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
— для решения несложных практических расчетных задач, в том числе с использованием при необходимости калькулятора;
— устной прикидки и оценки результата вычислений, проверки результата вычисления с использованием различных приемов;
владеть познавательными, коммуникативными и регулятивными универсальными действиями;
решать следующие жизненно-практические задачи:
— самостоятельно приобретать и применять знания в различных ситуациях для решения несложных практических задач, в том числе с использованием при необходимости справочных материалов, калькулятора и компьютера;
— работать в группах, аргументировать и отстаивать свою точку зрения;
— уметь слушать других, извлекать учебную информацию на основе сопоставительного анализа объектов;
— пользоваться предметным указателем энциклопедий и справочников для нахождения информации;
— самостоятельно действовать в ситуации неопределенности при решении задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Содержание учебного курса
- Натуральные числа и нуль
Ряд натуральных чисел. Десятичная запись, сравнение, сложение и вычитание натуральных чисел. Законы сложения. Умножение, законы умножения. Степень с
натуральным показателем. Деление нацело, деление с остатком. Числовые выражения. Решение текстовых задач арифметическими методами.
Основная цель — систематизировать и обобщить сведения о натуральных числах: об их сравнении, сложении и вычитании, умножении и делении, добиться осознанного овладения учащимися приемами вычислений с применением законов сложения и умножения, развивать навыки вычислений с натуральными числами.
При изучении данной темы вычисления выполняются сначала устно с опорой на законы сложения и умножения, на свойство вычитания, а потом столбиком. Большое внимание уделяется переместительному и сочетательному законам умножения и распределительному закону, их использованию для обоснования вычислений столбиком (на простых примерах), для рационализации вычислений. Тем самым закладывается основа осознанного овладения приемами вычислений. Вместе с тем достаточное внимание уделяется закреплению навыков вычисления столбиком, особенно в сложных случаях (нули в записи множителей или частного). Вводится понятие степени с натуральным показателем. При изучении числовых выражений закрепляются правила порядка действий.
Тем самым закладывается основа осознанного овладения приемами вычислений. Вместе с тем достаточное внимание уделяется закреплению навыков вычисления столбиком, особенно в сложных случаях (нули в записи множителей или частного). Вводится понятие степени с натуральным показателем. При изучении числовых выражений закрепляются правила порядка действий.
Изучение материала предусматривает систематическую работу по развитию у учащихся умения решать текстовые задачи арифметическими способами. Решение задач требует понимания отношений «больше на … (в …)», «меньше на … (в …)» и их связи с арифметическими действиями с натуральными числами, а также понимания стандартных ситуаций, в которых используются слова «всего», «осталось» и т. п. Типовые задачи «на части», на нахождение двух чисел по их сумме и разности рассматриваются в отдельных пунктах. Работа с арифметическими способами решения задач, нацеленная на развитие мышления и речи учащихся, продолжится при изучении следующих тем.
При наличии учебных часов рассматривается тема «Вычисления с помощью калькулятора».
- Измерение величин
Прямая, луч, отрезок. Измерение отрезков и метрические единицы длины. Представление натуральных чисел на координатном луче. Окружность и круг, сфера и шар. Углы, измерение углов. Треугольники и четырехугольники. Прямоугольный параллелепипед. Площадь прямоугольника, объем прямоугольного параллелепипеда. Единицы площади, объема, массы, времени. Решение текстовых задач арифметическими методами.
Основная цель — систематизировать знания учащихся о геометрических фигурах и единицах измерения величин, продолжить их ознакомление с геометрическими фигурами и с соответствующей терминологией.
Начальным этапом при изучении данной темы является измерение отрезков, изображение натуральных чисел на координатном луче — это освоение учащимися идеи числа как длины отрезка, точнее, как координаты точки на координатной прямой. Здесь же они вычисляют площадь прямоугольника и объем прямоугольного параллелепипеда, измерения которых — натуральные числа. Здесь вводятся единицы измерения длины, площади и объема, устанавливаются соотношения между единицами длины, единицами площади, единицами объема, изучаются единицы массы и времени. Введение градусной меры угла сопровождается заданиями на измерение углов и построение углов с заданной градусной мерой. При изучении данной темы решаются задачи на движение.
Здесь же они вычисляют площадь прямоугольника и объем прямоугольного параллелепипеда, измерения которых — натуральные числа. Здесь вводятся единицы измерения длины, площади и объема, устанавливаются соотношения между единицами длины, единицами площади, единицами объема, изучаются единицы массы и времени. Введение градусной меры угла сопровождается заданиями на измерение углов и построение углов с заданной градусной мерой. При изучении данной темы решаются задачи на движение.
При наличии учебных часов рассматривается тема «Многоугольники».
- Делимость натуральных чисел
Свойства и признаки делимости. Простые и составные числа. Делители натурального числа. Наибольший общий делитель, наименьшее общее кратное.
Основная цель — познакомить учащихся со свойствами и признаками делимости, сформировать навыки их использования.
При изучении данной темы значительное внимание уделяется формированию у учащихся простейших доказательных умений. Доказательства свойств и признаков делимости проводятся на характерных числовых примерах, но методы доказательства могут быть распространены на общий случай. При этом учащиеся получают первый опыт доказательства теоретических положений со ссылкой на другие теоретические положения. Понятия наибольшего общего делителя и наименьшего общего кратного вводятся традиционно, но следует учесть, что в дальнейшем не всегда требуется сокращать дробь на наибольший общий делитель ее числителя и знаменателя или приводить дроби обязательно к наименьшему общему знаменателю.
Доказательства свойств и признаков делимости проводятся на характерных числовых примерах, но методы доказательства могут быть распространены на общий случай. При этом учащиеся получают первый опыт доказательства теоретических положений со ссылкой на другие теоретические положения. Понятия наибольшего общего делителя и наименьшего общего кратного вводятся традиционно, но следует учесть, что в дальнейшем не всегда требуется сокращать дробь на наибольший общий делитель ее числителя и знаменателя или приводить дроби обязательно к наименьшему общему знаменателю.
При наличии учебных часов рассматривается тема «Использование четности при решении задач».
- Обыкновенные дроби
Понятие дроби, равенство дробей (основное свойство дроби). Приведение дробей к общему знаменателю. Сравнение, сложение и вычитание дробей. Законы сложения. Умножение дробей, законы умножения. Деление дробей. Смешанные дроби и действия с ними. Представление дробей на координатном луче. Решение текстовых задач арифметическими методами.
Основная цель — сформировать у учащихся умения сравнивать, складывать, вычитать, умножать и делить обыкновенные и смешанные дроби, вычислять значения выражений, содержащих обыкновенные и смешанные дроби, решать задачи на сложение и вычитание, на умножение и деление дробей, задачи на дроби, на совместную работу арифметическими методами.
Формирование понятия дроби сопровождается обучением решению простейших задач на нахождение части числа и числа по его части, а также задач, готовящих учащихся к решению задач на совместную работу. При вычислениях с дробями допускается сокращение дроби на любой общий делитель ее числителя и знаменателя (необязательно наибольший), а также приведение дробей к любому общему знаменателю (необязательно наименьшему). Но в том и в другом случаях разъясняется, когда вычисления будут наиболее рациональными.
При изучении данной темы решаются задачи на сложение и вычитание дробей, основные задачи на дроби. Операция умножения дробей вводится по определению, из которого получается правило умножения натурального числа на обыкновенную дробь. Особое внимание уделяется доказательствам законов сложения и умножения для дробей. Они проводятся на характерных числовых примерах с опорой на соответствующие законы для натуральных чисел, но методы доказательства могут быть распространены на общий случай. Деление дробей вводится как операция, обратная умножению. Смешанная дробь рассматривается как другая запись обыкновенной неправильной дроби. Отдельно изучаются вычисления со смешанными дробями. На характерных числовых примерах показывается, что площадь прямоугольника и объем прямоугольного параллелепипеда, измерения которых выражены рациональными числами, вычисляются по тем же правилам, что и для натуральных чисел.
Заключительный этап изучения темы — изображение дробей точками на координатной прямой. В данной теме решаются задачи на умножение и деление дробей, а также обращается особое внимание на то, что рассмотренные ранее задачи на дроби можно решать с помощью умножения и деления на дробь. Задачи на совместную работу выделены в отдельный пункт.
При наличии учебных часов рассматривается тема «Сложные задачи на движение по реке».
- Повторение
При организации текущего и итогового повторения используются задания из раздела «Задания для повторения» и другие материалы.
КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА ПО МАТЕМАТИКЕ
при 5 уроках в неделю (170 уроков за год)
|
Урок №
|
Номер пункта
|
Тема
|
Часы
|
Дата
|
Коррекция
| |
|
план.
|
факт.
| |||||
|
Глава 1. Натуральные числа и нуль
|
45
|
|
|
| ||
|
1
|
1.1
|
Ряд натуральных чисел
|
1
|
4.09.17-7.09.17
| ||
|
2
|
1.2
|
Десятичная система записи натуральных чисел
|
1
| |||
|
3
|
1.2
|
Десятичная система записи натуральных чисел
|
1
| |||
|
4
|
1.3
|
Сравнение натуральных чисел
|
1
| |||
|
5
|
1.3
|
Сравнение натуральных чисел
|
1
| |||
|
6
|
1.4
|
Сложение. Законы сложения
|
1
|
11.09-15.09
| ||
|
7
|
1.4
|
Сложение. Законы сложения
|
1
| |||
|
8
|
1.4
|
Сложение. Законы сложения
|
1
| |||
|
9
|
1.5
|
Вычитание
|
1
| |||
|
10
|
1.5
|
Вычитание
|
1
| |||
|
11
|
1.5
|
Вычитание
|
1
|
18.09-22.09
| ||
|
12
|
1.6
|
Решение текстовых задач с помощью сложения и вычитания
|
1
| |||
|
13
|
1.6
|
Решение текстовых задач с помощью сложения и вычитания
|
1
| |||
|
14
|
1.7
|
Умножение. Законы умножения
|
1
| |||
|
15
|
1.7
|
Умножение. Законы умножения
|
1
| |||
|
16
|
1.7
|
Умножение. Законы умножения
|
1
|
25.09-29.09
| ||
|
17
|
1.8
|
Распределительный закон
|
1
| |||
|
18
|
1.8
|
Распределительный закон
|
1
| |||
|
19
|
1.9
|
Сложение и вычитание чисел столбиком
|
1
| |||
|
20
|
1.9
|
Сложение и вычитание чисел столбиком
|
1
| |||
|
21
|
|
Контрольная работа №1
|
1
|
2.10-7.10
|
|
|
|
22
|
1.10
|
Умножение чисел столбиком
|
1
| |||
|
23
|
1.10
|
Умножение чисел столбиком
|
1
| |||
|
24
|
1.10
|
Умножение чисел столбиком
|
1
| |||
|
25
|
1.11
|
Степень с натуральным показателем
|
1
| |||
|
26
|
1.11
|
Степень с натуральным показателем
|
1
|
9.10-14.10
| ||
|
27
|
1.12
|
Деление нацело
|
1
| |||
|
28
|
1.12
|
Деление нацело
|
1
| |||
|
29
|
1.12
|
Деление нацело
|
1
| |||
|
30
|
1.13
|
Решение текстовых задач с помощью умножения и деления
|
1
| |||
|
31
|
1.13
|
Решение текстовых задач с помощью умножения и деления
|
1
|
16.10-21.10
| ||
|
32
|
1.14
|
Задачи «на части»
|
1
| |||
|
33
|
1.14
|
Задачи «на части»
|
1
| |||
|
34
|
1.14
|
Задачи «на части»
|
1
| |||
|
35
|
1.15
|
Деление с остатком
|
1
| |||
|
36
|
1.15
|
Деление с остатком
|
1
|
23.10-28.10
| ||
|
37
|
1.15
|
Деление с остатком
|
1
| |||
|
38
|
1.16
|
Числовые выражения
|
1
| |||
|
39
|
1.16
|
Числовые выражения
|
1
| |||
|
40
|
|
Контрольная работа №2
|
1
|
|
|
|
|
41
|
1.17
|
Нахождение двух чисел по их сумме и разноси
|
1
|
6.11-11.11
| ||
|
42
|
1.17
|
Нахождение двух чисел по их сумме и разноси
|
1
| |||
|
43
|
1.17
|
Нахождение двух чисел по их сумме и разноси
|
1
| |||
|
Дополнения к главе 1
| ||||||
|
1. Вычисления с помощью калькулятора
| ||||||
|
2. Исторические сведения
| ||||||
|
44
|
3. Занимательные задачи
|
1
| ||||
|
45
|
3. Занимательные задачи
|
1
| ||||
|
|
|
Глава 2. Измерение величин
|
30
|
|
|
|
|
46
|
2.1
|
Прямая. Луч. Отрезок
|
1
|
13.11-18.11
| ||
|
47
|
2.1
|
Прямая. Луч. Отрезок
|
1
| |||
|
48
|
2.2
|
Измерение отрезков
|
1
| |||
|
49
|
2.2
|
Измерение отрезков
|
1
| |||
|
50
|
2.3
|
Метрические единицы длины
|
1
| |||
|
51
|
2.3
|
Метрические единицы длины
|
1
|
20.11-25.11
| ||
|
52
|
2.4
|
Представление натуральных чисел на координатном луче
|
1
| |||
|
53
|
2.4
|
Представление натуральных чисел на координатном луче
|
1
| |||
|
54
|
|
Контрольная работа №3
|
1
|
|
|
|
|
55
|
2.5
|
Окружность и круг. Сфера и шар
|
1
| |||
|
56
|
2.6
|
Углы. Измерение углов
|
1
|
27.11-2.12
| ||
|
57
|
2.6
|
Углы. Измерение углов
|
1
| |||
|
58
|
2.7
|
Треугольники
|
1
| |||
|
59
|
2.7
|
Треугольники
|
1
| |||
|
60
|
2.8
|
Четырехугольники
|
1
| |||
|
61
|
2.8
|
Четырехугольники
|
1
|
4.12-9.12
| ||
|
62
|
2.9
|
Площадь прямоугольника. Единицы площади
|
1
| |||
|
63
|
2.9
|
Площадь прямоугольника. Единицы площади
|
1
| |||
|
64
|
2.10
|
Прямоугольный параллелепипед
|
1
| |||
|
65
|
2.10
|
Прямоугольный параллелепипед
|
1
| |||
|
66
|
2.11
|
Объем прямоугольного параллелепипеда. Единицы объема
|
1
|
11.12-16.12
| ||
|
67
|
2.11
|
Объем прямоугольного параллелепипеда. Единицы объема
|
1
| |||
|
68
|
2.12
|
Единицы массы
|
1
| |||
|
69
|
2.13
|
Единицы времени
|
1
| |||
|
70
|
2.14
|
Задачи на движение
|
1
| |||
|
71
|
2.14
|
Задачи на движение
|
1
|
18.12-23.12
| ||
|
72
|
2.14
|
Задачи на движение
|
1
| |||
|
73
|
|
Контрольная работа №4
|
1
|
|
|
|
|
Дополнения к главе 2
| ||||||
|
74
|
1. Многоугольники
|
1
| ||||
|
2. Исторические сведения
| ||||||
|
75
|
3. Занимательные задачи
|
1
| ||||
|
|
|
Глава 3. Делимость натуральных чисел
|
19
|
|
|
|
|
76
|
3.1
|
Свойство делимости
|
1
|
25.12-30.12
| ||
|
77
|
3.1
|
Свойство делимости
|
1
| |||
|
78
|
3.2
|
Признаки делимости
|
1
| |||
|
79
|
3.2
|
Признаки делимости
|
1
| |||
|
80
|
3.2
|
Признаки делимости
|
1
| |||
|
81
|
3.3
|
Простые и составные числа
|
1
|
15.01.18-20.01.18
| ||
|
82
|
3.3
|
Простые и составные числа
|
1
| |||
|
83
|
3.4
|
Делители натурального числа
|
1
| |||
|
84
|
3.4
|
Делители натурального числа
|
1
| |||
|
85
|
3.4
|
Делители натурального числа
|
1
| |||
|
86
|
3.5
|
Наибольший общий делитель
|
1
|
22.01-27.01
| ||
|
87
|
3.5
|
Наибольший общий делитель
|
1
| |||
|
88
|
3.5
|
Наибольший общий делитель
|
1
| |||
|
89
|
3.6
|
Наименьшее общее кратное
|
1
| |||
|
90
|
3.6
|
Наименьшее общее кратное
|
1
| |||
|
91
|
3.6
|
Наименьшее общее кратное
|
1
|
29.01-3.02
| ||
|
92
|
|
Контрольная работа №5
|
1
|
|
|
|
|
Дополнения к главе 3
| ||||||
|
1. Использование чётности и нечётности при решении задач
| ||||||
|
2. Исторические сведения
| ||||||
|
93
|
3. Занимательные задачи
|
1
| ||||
|
94
|
3. Занимательные задачи
|
1
| ||||
|
|
|
Глава 4. Обыкновенные дроби
|
65
|
|
|
|
|
95
|
4.1
|
Понятие дроби
|
1
| |||
|
96
|
4.2
|
Равенство дробей
|
1
|
5.02-10.02
| ||
|
97
|
4.2
|
Равенство дробей
|
1
| |||
|
98
|
4.2
|
Равенство дробей
|
1
| |||
|
99
|
4.3
|
Задачи на дроби
|
1
| |||
|
100
|
4.3
|
Задачи на дроби
|
1
| |||
|
101
|
4.3
|
Задачи на дроби
|
1
|
12.02-17.02
| ||
|
102
|
4.3
|
Задачи на дроби
|
1
| |||
|
103
|
4.4
|
Приведение дробей к общему знаменателю
|
1
| |||
|
104
|
4.4
|
Приведение дробей к общему знаменателю
|
1
| |||
|
105
|
4.4
|
Приведение дробей к общему знаменателю
|
1
| |||
|
106
|
4.4
|
Приведение дробей к общему знаменателю
|
1
|
19.02-24.02
| ||
|
107
|
4.5
|
Сравнение дробей
|
1
| |||
|
108
|
4.5
|
Сравнение дробей
|
1
| |||
|
109
|
4.5
|
Сравнение дробей
|
1
| |||
|
110
|
4.6
|
Сложение дробей
|
1
| |||
|
111
|
4.6
|
Сложение дробей
|
1
|
26.02-3.03
| ||
|
112
|
4.6
|
Сложение дробей
|
1
| |||
|
113
|
4.7
|
Законы сложения
|
1
| |||
|
114
|
4.7
|
Законы сложения
|
1
| |||
|
115
|
4.7
|
Законы сложения
|
1
| |||
|
116
|
4.7
|
Законы сложения
|
1
|
5.03-10.03
| ||
|
117
|
4.8
|
Вычитание дробей
|
1
| |||
|
118
|
4.8
|
Вычитание дробей
|
1
| |||
|
119
|
4.8
|
Вычитание дробей
|
1
| |||
|
120
|
4.8
|
Вычитание дробей
|
1
| |||
|
121
|
|
Контрольная работа №6
|
1
|
12.03-17.03
|
|
|
|
122
|
4.9
|
Умножение дробей
|
1
| |||
|
123
|
4.9
|
Умножение дробей
|
1
| |||
|
124
|
4.9
|
Умножение дробей
|
1
| |||
|
125
|
4.9
|
Умножение дробей
|
1
| |||
|
126
|
4.10
|
Законы умножения
|
1
|
19.03-24.03
| ||
|
127
|
4.10
|
Законы умножения
|
1
| |||
|
128
|
4.11
|
Деление дробей
|
1
| |||
|
129
|
4.11
|
Деление дробей
|
1
| |||
|
130
|
4.11
|
Деление дробей
|
1
| |||
|
131
|
4.11
|
Деление дробей
|
1
|
2.04-7.04
| ||
|
132
|
4.12
|
Нахождение части целого и целого по его части
|
1
| |||
|
133
|
4.12
|
Нахождение части целого и целого по его части
|
1
| |||
|
134
|
|
Контрольная работа №7
|
1
|
|
|
|
|
135
|
4.13
|
Задачи на совместную работу
|
1
| |||
|
136
|
4.13
|
Задачи на совместную работу
|
1
|
9.04-14.04
| ||
|
137
|
4.13
|
Задачи на совместную работу
|
1
| |||
|
138
|
4.14
|
Понятие смешенной дроби
|
1
| |||
|
139
|
4.14
|
Понятие смешенной дроби
|
1
| |||
|
140
|
4.14
|
Понятие смешенной дроби
|
1
| |||
|
141
|
4.15
|
Сложение смешенных дробей
|
1
|
16.04-21.04
| ||
|
142
|
4.15
|
Сложение смешенных дробей
|
1
| |||
|
143
|
4.15
|
Сложение смешенных дробей
|
1
| |||
|
144
|
4.16
|
Вычитание смешенных дробей
|
1
| |||
|
145
|
4.16
|
Вычитание смешенных дробей
|
1
| |||
|
146
|
4.16
|
Вычитание смешенных дробей
|
1
|
23.04-28.04
| ||
|
147
|
4.17
|
Умножение и деление смешенных дробей
|
1
| |||
|
148
|
4.17
|
Умножение и деление смешенных дробей
|
1
| |||
|
149
|
4.17
|
Умножение и деление смешенных дробей
|
1
| |||
|
150
|
4.17
|
Умножение и деление смешенных дробей
|
1
| |||
|
151
|
4.17
|
Умножение и деление смешенных дробей
|
1
|
30.04-5.05
| ||
|
152
|
|
Контрольная работа №8
|
1
|
|
|
|
|
153
|
4.18
|
Представление дробей на координатном луче
|
1
| |||
|
154
|
4.18
|
Представление дробей на координатном луче
|
1
| |||
|
155
|
4.18
|
Представление дробей на координатном луче
|
1
| |||
|
156
|
4.19
|
Площадь прямоугольника. Объём прямоугольного параллелепипеда
|
1
|
7.05-12.05
| ||
|
157
|
4.19
|
Площадь прямоугольника. Объём прямоугольного параллелепипеда
|
1
| |||
|
|
|
Дополнения к главк 4
|
|
|
|
|
|
1. Сложные задачи на движение по реке
| ||||||
|
2. Исторические сведения
| ||||||
|
158
|
3. Занимательные задачи
|
1
| ||||
|
159
|
3. Занимательные задачи
|
1
| ||||
|
|
|
Повторение
|
11
|
|
|
|
|
160
|
Повторение
|
1
| ||||
|
161
|
Повторение
|
1
|
14.05-19.05
| |||
|
162
|
Повторение
|
1
| ||||
|
163
|
Повторение
|
1
| ||||
|
164
|
Повторение
|
1
| ||||
|
165
|
Повторение
|
1
| ||||
|
166
|
Повторение
|
1
|
21.05-26.05
| |||
|
167
|
Повторение
|
1
| ||||
|
168
|
Повторение
|
1
| ||||
|
169
|
|
Итоговая контрольная работа №9
|
1
|
|
|
|
|
170
|
|
Обобщающий урок
|
1
|
|
|
|
В современном обществе возрастает значимость качества математического образования. Основой его высокого уровня является математическая грамотность подрастающего поколения. Поэтому обеспечение ею школьников – важная задача. Программа направлена на развитие математических способностей и формирование различных типов мышления. Правильное изучение математики приводит не только к умению считать, но и к умению логически мыслить, исследовать, конструировать, представлять себе сложные объекты, развивать познавательные виды деятельности, осваивать новые идеи, самостоятельно находить решения. Очень важно, что на занятиях основное внимание уделяется не заучиванию готовых определений, формул и методов, а пониманию материала. Под руководством учителя ребенок учится сам находить решения задач, а новые знания теории помогают ему в этом. В процессе занятий формируются и развиваются не только умения и навыки по математике, но и умение слушать, понимать, проверять свои и чужие действия, делать выводы, находить и исправлять ошибки, решать нестандартные задачи. Также происходит процесс развития интереса детей к математике и её приложениям в различных отраслях человеческой деятельности, формируется позитивная мотивация к занятиям и воспитывается стремление к сотрудничеству во время работы. Необходимо, чтобы учащийся мог проявить свои способности в разнообразных сферах деятельности, поэтому важный аспект – создание условий для такого развития и самореализации ребенка. Программа рассчитана на 40.5 часов (по 1.5 часа в неделю). Актуальность программы обусловлена тем, что в настоящее время увеличение умственной нагрузки на уроках математики заставляет задуматься над тем, как охранить у школьников интерес к изучаемому материалу, поддержать активность на протяжении всего занятия. В связи с этим ведутся поиски новых эффективных методов обучения и таких методических приемов, которые активизировали бы мышление обучающихся, стимулировали бы их самостоятельность в приобретении знаний. Имеется большое количество задач, для решения которых используют арифметические способы мышления, что позволяет развивать логику, интуицию и речь. Часть задач требует не долгих вычислений, а ясного взгляда и сосредоточенности, что развивает внимательность, смекалку, здравый смысл, способствует общему развитию детей. Нестандартные задачи и разные способы их решения способствуют развитию мышления и познавательного интереса. Практические задания подобраны таким образом, что постепенно и неоднократно повторяясь, осознаются и запоминаются основные принципы и методы решения задач, дети учатся анализировать и задавать правильные вопросы. Большое внимание уделяется геометрии, конструированию, моделированию и исследованию. Учебные занятия позволяют формировать интеллектуальное, научное и творческое мышления. Важное место в программе отведено знакомству, правилам проведения, подготовке к участию и разбору задач различных математических соревнований, проводимых в Москве и России: интернет-карусели, турниру Архимеда, Матпразднику, конкурсу Кенгуру и устной математической олимпиаде. Очень важно правильно подготовить детей к участию в этих конкурсах, объяснив особенности и правила их проведения и специфику предлагаемых задач. Цели и задачи программы
Ожидаемый результат
Учебный план
Содержание изучаемого курса
Литература
|
Задач по математике и логике в изобилии
Нонограммы для логических головоломок, здесь каждый найдет что-то для себя.
Ежедневные математические и логические задачи для всех
CryptoPics — интерактивные крипто-картинки для печати или японские логические головоломки — это увлекательное развлечение.
Magic Squares — Изучите историю этой головоломки и создавайте головоломки с магическими квадратами.
Праздничные пазлы — Веселые головоломки с символами праздников.
Логические головоломки — Используйте логику для решения этих словесных задач.
Головоломки с числами и словами — Бесплатные онлайн-головоломки с числами и словами.
Как решить проблемы со словами — Пошаговые инструкции по решению проблем со словами.
С Рождеством Христовым математические задачи — Решите эти словесные задачи для веселого веселья.
CRPuzzles — Интернет-журнал с множеством типов головоломок.
Моделирование математических задач — Узнайте, как решать текстовые задачи поэтапно.
Рисунок Это — математические задачи со словами бросят вызов всем членам семьи.
Brain Food — Сотни логических задач, головоломок и словесных игр для всех.
Brain Games — ссылки на забавные игры для мозга для студентов и семей.
Brain Games — Веселые интеллектуальные игры, включающие головоломки, логические игры и игры в слова.
Brain Teasers — Эти интерактивные головоломки разогреют ваш мозг до предела.
Puzzlers Paradise — Решайте логические задачи онлайн.
Nick’s Mathematical Puzzles — Сотни математических головоломок для проверки ваших логических и дедуктивных навыков.
Головоломки оригами на рассечение — Соберите многогранник оригами, чтобы решить головоломку.
Papyrus Puzzle Game — Сможете ли вы снова собрать папирус?
Задача недели — головоломки и словесные задачи для решения.
Задачи по математике и логике для детей
Interactive Fun Puzzles — Веселые головоломки для младших школьников.
Cool Math and Logic for Kids — Анимированные логические задачи, словесные задачи и головоломки для учеников начальной школы.
Logic Puzzles for Kids — Рабочие листы для печати для головоломок на логику и дивергентное мышление для детей младшего возраста.
Задачи с печатным текстом — Ресурсы по задачам с печатным текстом для классов с K по 12.
Задачи по слову для детей — Задачи со словом для 5–12 классов.
Математика и логика — Математические игры, задачи со словами и логические головоломки будут развлекать вас часами.
Головоломки — простые головоломки, которые помогут детям развить математические и логические навыки.
Math Gym — Интерактивная аркада с математическими и логическими играми.
Button Beach Challenge — Ментальная математика для начальных уровней.
Концептуальные задачи со словами — Интерактивные задачи со словами и учебные пособия по их решению для K-12.
Задачи по математике со словами — Помогите пчелам с проблемами со словами с медом.
Math Puzzles — Эти математические головоломки укрепляют словарный запас.
House of Math Word Problems — Тысячи словесных задач по математике для классов с 1 по 6; требуется членство.
K-12 Math Puzzles — Ссылки на математические задачи и головоломки.
Math Maven Mysteries — Используйте логику, чтобы разгадать эти загадки; проблемы варьируются от простых до сложных.
Задачи по математике и логике для подростков
Задачи геометрического слова — Решения и обучающие видео для задач геометрического слова.
Танграммы и другие логические головоломки — решайте математические головоломки, танграммы, логические головоломки и многое другое.
Квадратные уравнения — Задачи средней алгебры для старшеклассников.
Задачи по математике и логике для одаренных учеников — ссылки на головоломки, головоломки и логические игры.
Наибольшие проблемы со словом общего делителя — Бесплатные рабочие листы по алгебре.
Math Puzzles — множество математических головоломок для оттачивания логических навыков.
Танграммы — Используйте логические навыки, чтобы решить эти древние китайские головоломки.
Задачи со словами и физика — Узнайте, как задачи со словами могут помочь вам понять физику.
Судоку — Играйте в судоку онлайн и оттачивайте свои логические навыки.
Logics and Brain Teasers — Ссылки на логические задачи и головоломки.
Rebus Brainteasers — Веселые интерактивные ребусы.
Math and Logic Challengers — Открытые математические задачи.
Math and Logic Puzzles — Обострите смекалку с помощью забавных интерактивных головоломок.
Головоломки — математические, логические и другие головоломки.
Открытые математические задачи — задачи со словами и логические задачи помогают подготовить студентов к стандартному тестированию.
Математические и логические задачи для математиков и логиков
Nonogram Puzzles — попробуйте свои силы в решении этих головоломок.
Логические задачи со словами — Разгадайте загадку возраста трех дочерей и другие головоломки.
Нерешенные проблемы — Сможете ли вы решить одну из этих известных неразрешимых проблем?
Логический калькулятор
— Вычислите истинность логического утверждения с помощью этого онлайн-калькулятора логики.
Daily Translation Problem — Решите ежедневную задачу перевода, используя элементарную логику.
Задача занятого бобра. Если вы знаете, что такое машина Тьюринга, вы можете решить эту логическую задачу.
Популярные товары
Математическая логика и задачи со словами, гр. 5-6 — Creative Teaching Press
Более 100 воспроизводимых упражнений для совершенствования базовых навыков
Предназначен для развития математических знаний и развития навыков критического мышления. Действия сгруппированы по категориям, основанным на стандартах содержания NCTM — Алгебра, Геометрия, Измерение и Анализ данных и вероятность.Также включает:
- визуальных головоломок
- задачи со словами
- логических вызовов
- деятельность по формированию образцов
- многоступенчатые задачи
Серия Power Practice содержит несколько готовых к использованию страниц с упражнениями, чтобы студенты могли практиковать свои навыки. Веселые занятия можно использовать для дополнения и улучшения того, что вы преподаете в классе. Раздайте учащимся страницу с заданием в качестве самостоятельной классной работы или отправьте страницы домой в качестве домашнего задания, чтобы закрепить навыки, полученные в классе.Ключ ответа предоставляется для быстрого ознакомления.
Страницы упражнений в математической логике и задачах со словом 5-6 были специально разработаны для развития математических знаний и развития навыков критического мышления. Действия включают в себя визуальные головоломки, логические задачи, многоэтапные задачи и многое другое. Все мероприятия способствуют развитию творческого мышления и дают учащимся возможность применять различные стратегии решения проблем. Развитие навыков представлено на нескольких страницах, чтобы студенты могли повторно практиковаться с использованием определенной стратегии.
Действия сгруппированы по следующим математическим стандартам NCTM:
- число и операции
- алгебра
- геометрия
- измерение
- и анализ данных и вероятность
Перезарядка навыков с помощью Power Practice и дайте студентам возможность добиться успеха!
Характеристики логического развития пятиклассников через разделение обучения с десятичными знаками
Болл, Д.: 1990, «Понимание деления будущими учителями начальных и средних школ», Journal for Research in Mathematics Education , 21 (2), 132–144.
Google Scholar
Белл А., Свон М. и Тейлор Г.: 1981, «Выбор операции в вербальных задачах с десятичными числами», Образовательные исследования по математике , 12, 399–420.
Артикул
Google Scholar
Белл, А., Э. Фишбейн и Б. Грир: 1984, «Выбор операции в задачах вербальной арифметики: влияние размера числа, структуры задачи и контекста», Образовательные исследования по математике , 15, 129–147.
Артикул
Google Scholar
Белл, А., Грир, Б., Гримисон, Л. и Манган, К.: 1989, «Работа детей по мультипликативным задачам со словами: элементы описательной теории», Journal for Research in Mathematics Education , 20 (5), 434–449.
Google Scholar
Белл А. и Парди Д.: 1986, «Диагностическое обучение», Преподавание математики , 115, 39–41.
Google Scholar
Белл, А .: 1986, «Диагностическое обучение: 2 Уроки обсуждения конфликта», Преподавание математики , 116, 26–29.
Google Scholar
Белл, А.: 1987, «Диагностическое обучение: 3, провоцирующее обсуждение», Преподавание математики, , 118, 21–23.
Google Scholar
Браун, М .: 1981, «Числовые операции», в К. Харт (ред.), Понимание математики детьми: 11–16 , Джон Мюррей, Лондон, стр. 23–47.
Кобб П., Якель Э. и Вуд Т .: 1993, «Теоретическая ориентация», в T. Wood et al. (ред.), Rethinking Elementary School Mathematics: Insights and Issues , JRME Monography 6, Chap.3. С. 21–32.
Кобб, П.: 2000, «Проведение обучающих экспериментов в сотрудничестве с учителями», в А. Келли и Р. Леш (ред.), Справочник по планированию исследований в области математического и естественнонаучного образования . Hillsdale, Lawrence Erlbaum Associates, Нью-Джерси.
Де Корте, Э. и Вершаффель, Л .: 1996, «Эмпирический тест влияния примитивных интуитивных моделей операций на решение словесных задач с мультипликативной структурой», Learning and Instruction , 6 (3) , 219–242.
Артикул
Google Scholar
Де Корте, Э., Грир, Б. и Вершаффель, Л .: 1996, «Преподавание и изучение математики», в DC Berliner & RC Calfee (ред.), Handbook of Educational Psychology , Macmillan Publishing Company , Нью-Йорк, стр. 491–549.
Диксон, Л., Браун, М. и Гибсон, О.: 1984, Дети, изучающие математику: Руководство для учителей по последним исследованиям , Истборн, Холт, Райнхарт и Уинстон для Совета школ, Восточный Суссекс.
Dörfler, W .: 1991, «Формы и средства обобщения в математике», в A. J. Bishop et al. (ред.), «Математические знания: его рост через обучение», , Kluwer Academic Publishers, Dordrecht, стр. 61–85.
Фишбейн, Э., Дери, М., Нелло, М. и Марино, М .: 1985, «Роль неявных моделей в решении вербальных задач умножения и деления», Journal for Research in Mathematics Education , 16 (1), 3–17.
Google Scholar
Фишбейн, Э.: 1989, «Неявные модели и математические рассуждения», Для изучения математики , 9 (2), 9–14.
Google Scholar
Fischbein, E .: 1994, «Tacit models», в D. Tirosh (ed.), Implicit and Explicit Knowledge: An Educational Approach , Norwood, Ablex, New Jersey, pp. 96–110.
Гребер А. и Тирош Д.: 1988, «Умножение и деление с использованием десятичных чисел: деятельность и убеждения учителей начальных классов», Journal of Mathematical Behavior , 7, 263–280.
Google Scholar
Гравемейер, К. и Стивен, М .: 2002, «Новые модели как эвристика учебного дизайна», в K. Gravemeijer et al. (ред.), Символизация, моделирование и использование инструментов в математическом образовании , Kluwer Academic Publishers, Dordrecht, стр. 145–169.
Грир, Б .: 1987, «Несохранение умножения и деления с использованием десятичных знаков», Journal for Research in Mathematics Education , 18 (1), 37–45.
Google Scholar
Грир, Б.: 1988, «Несохранение умножения и деления: анализ симптома», Journal of Mathematical Behavior , 7, 281–298.
Google Scholar
Грир, Б .: 1992, «Умножение и деление как модели ситуаций», в Д. Гроуза (ред.), Справочник по исследованиям в области преподавания и обучения математике , Рестон, Национальный совет учителей математики, Вирджиния; Macmillan Publishing Company, Нью-Йорк, стр.276–295.
Грир, Б .: 1994, «Расширение значения умножения и деления», в Г. Харел и Дж. Конфри (ред.), Развитие мультипликативного мышления в изучении математики , Государственный университет им. Нью-Йорк Пресс, Олбани, стр. 61–85.
Харел, Г., Бер, М., Пост, Т. и Леш, Р .: 1994, «Влияние числового типа на решение задач умножения и деления: дополнительные соображения», в Г. Харел и Дж. Конфри (ред.), Развитие мультипликативного мышления в изучении математики , Государственный университет Нью-Йорка, Олбани, стр. 363–384.
Инелдер Б. и Пиаже Дж .: 1958, Развитие логического мышления от детства до подросткового возраста . (пер. А. Парсонс и С. Милгрэм), Basic Books.
Дженсон, Л .: 1986, «Иерархии логических рассуждений в математике», Журнал исследований в области математического образования , 17 (1), 3–20.
Google Scholar
Лимон, М .: 2001, «О когнитивном конфликте как обучающей стратегии концептуальных изменений: критическая оценка», Learning and Instruction , 11, 357–380.
Google Scholar
Манган, С .: 1989, «Умножение и деление как модели ситуаций: что исследование должно сказать учителю», в Б. Грире и Г. Малхерне (ред.), Новые направления в математическом образовании , Рутледж, Лондон, стр. 107–127.
Нешер, П.: 1988, «Мультипликативные школьные словесные задачи: теоретические подходы и эмпирические данные», в J. Hiebert и M. Behr (ред.), Числовые концепции и операции в средних классах . Hillsdale, Lawrence Erlbaum Associates, Нью-Джерси, стр. 41–52; Рестон, Национальный совет учителей математики, Вирджиния.
Окадзаки, М: 2003, «Характеристики логического развития пятиклассников посредством разделения обучения с десятичными знаками», на N.Pateman et al. (eds.), Proceedings of the 2003 Joint Meeting of PME and PMENA , Vol. 3. С. 413–419.
Piaget, J .: 1977, «Проблемы уравновешивания», М. Аппель и Л. Голдберг (ред.), Equilibration: Theory, Research, and Application , Plenum Press, New York, pp. 3 –13.
Пиаже, Дж .: 1985, Уравновешивание когнитивной структуры: центральная проблема интеллектуального развития , (перевод Т. Брауна и Л. Тэмпи), Издательство Чикагского университета.
Шварц, Дж .: 1988, «Интенсивные арифметические операции по преобразованию количества и референта», в J. Hiebert и M. Behr (ред.), Числовые концепции и операции в средних классах , Hillsdale, Lawrence Erlbaum Associates , Нью-Джерси, стр. 41–52; Рестон, Национальный совет учителей математики, Вирджиния.
Сфард, А .: 1991, «О двойственной природе математических концепций: размышления о процессах и объектах по разные стороны одной медали», Образовательные исследования по математике , 22, 1–36.
Артикул
Google Scholar
Шайер, М .: 2003, «Не только Пиаже; не только Выготский, и уж точно не Выготский как альтернатива Пиаже », Learning and Instruction , 13, 465–485.
Артикул
Google Scholar
Стеффе, Л .: 1990, «Несоответствия и когнитивный конфликт: взгляд конструктивиста», В центре внимания проблемы обучения математике , 12, 111–129.
Google Scholar
Стеффе, Л. и Томпсон, П. при участии фон Глазерсфельда, Э .: 2000, «Методология обучающего эксперимента: основные принципы и основные элементы», в А. Келли и Р. Леш (ред.), Справочник по дизайну исследований в области математического и естественнонаучного образования, , Махва, Lawrence Erlbaum Associates, Нью-Джерси, стр. 267–306.
Свон, М .: 1983, «Обучение десятичным разрядам: сравнительное исследование« конфликтного »и« только положительного »подходов», в R.Hershkowitz (ed.), Труды 7-й Международной конференции по психологии математического образования , стр. 211–216.
Свон, М .: 2001, «Работа с неправильными представлениями в математике», в П. Гейтсе (ред.), Issues in Mathematics Teaching , RoutledgeFalmer, pp. 147–165.
Тирош, Д .: 1990, «Несоответствия в математических построениях учащихся», Фокус на учебных задачах по математике , 12, 111–129.
Google Scholar
Тирош, Д.и Грэбер, А .: 1990, «Пробуждение когнитивного конфликта для изучения того, как учителя, работающие до службы, думают о разделении», Journal for Research in Mathematics Education , 21 (2), 98–108.
Google Scholar
Томпсон П. и Салдана Л .: 2003, «Дроби и мультипликативное мышление», в J. Kilpatrick et al. (ред.), Research Companion to the Principles and Standards for School Mathematics , Reston, National Council of Teachers of Mathematics, Virginia, pp.95–114.
Vergnaud, G .: 1983, «Мультипликативные структуры», в R. Lesh and M. Landau (ред.), Acquisition of Mathematical Concepts and Processes , Academic Press, New York, pp. 127–174.
Vergnaud, G .: 1988, ‘Мультипликативные структуры’, в J. Hiebert и M. Behr (ред.), Числовые концепции и операции в средних классах , Hillsdale, Lawrence Erlbaum Associates, Нью-Джерси, стр. 141–161; Рестон, Национальный совет учителей математики, Вирджиния.
Рабочие листы с задачами по математике | K5 Learning
Рабочие листы с задачами по слову для детского сада до 5 класса
Наши рабочие листы задач со словом лучше всего выполнять после того, как учащийся ознакомится с основным навыком. Мы включаем множество задач со смешанными словами или задач со словами с нерелевантными данными, чтобы учащиеся должны были тщательно обдумать проблему, а не просто применять формульное решение.
Выберите свою оценку / тему:
Детский сад:
Проблемы со сложением слов
Задачи на вычитание слов
Задачи 1 степени
Задачи со словами 2 степени
Задачи со словами 3 степени
Задачи со словами для 4-го класса
Задачи со словами 5-го класса
Темы включают:
- Простые задачи со сложением слов с 1-значным сложением
- Простые задачи со словами с вычитанием одной цифры
- Проблемы со сложением однозначных слов
- Сложение на суммы 50 и менее
- Добавление 3 или более чисел
- Вычитание однозначных чисел
- Вычитание чисел меньше 50
- Смешанное сложение и вычитание
- Время и прошедшее время
- Подсчет задач с денежным словом
- Задачи измерения слова (длины)
- Написание дробей из рассказа
- Проблемы со смешанными словами
- Задачи сложения 1,2- и 3-значных слов
- 1,2- и 3-значное вычитание
- Смешанное сложение и вычитание
- Умножение с точностью до 25
- Длина — сложение / вычитание / сравнение (обычная и метрическая)
- Время и прошедшее время (с интервалом 1/2 часа)
- Время и прошедшее время (интервалы 5 минут)
- Подсчет денег (монет и купюр)
- Задачи о словах с дробями
- Сравнение дробей
- Простые задачи сложения слов (числа до 100)
- Добавление в столбцы (числа до 1000)
- Ментальное вычитание
- Вычитание по столбцам (2-3 цифры)
- Смешанное сложение и вычитание
- Простое умножение (1 цифра на 1 или 2 цифры)
- Умножение числа, кратного 10
- Умножение в столбцах
- Простое деление
- Деление в столбик с остатками (числа 1-100)
- Смешанные задачи умножения и деления слов
- Определение, сравнение и упрощение дробей
- Сложение и вычитание дробей (как знаменатели)
- Проблемы с длиной слова
- Проблемы со словом времени (ближайшая 1 минута)
- Задачи о массе и весе слов
- Проблемы с объемом и емкостью слов
- Задачи Word с переменными
- Проблемы со смешанными словами
- Четыре операции (сложение, вычитание, умножение, деление)
- Оценка и округление
- Запись и сравнение дробей
- Сложение и вычитание дробей (как знаменатели)
- Умножение дробей на целые числа
- Сложение и вычитание десятичных знаков (до 3 членов)
- Задачи о длине слов (в обычных и метрических единицах)
- Задачи о массе и весе слов
- Проблемы с объемом и емкостью слов
- Проблемы со словом времени (включая утро и вечер)
- Задачи о деньгах (в десятичной системе счисления)
- Проблемы со словами при покупках
- Проблемы со смешанными словами
- Смешанные 4 операции (сложение, вычитание, умножение, деление)
- Оценка и округление слов задачи (на основе 4 операций)
- Сложить и вычесть дроби и смешанные числа (похожие и отличные от знаменателей)
- Умножение и деление дробей
- Смешанные операции с дробями (сложение, вычитание, умножение, деление)
- Задачи десятичных знаков (сложение, вычитание, умножение)
- Задачи длины слов (в обычных и метрических единицах)
- Задачи о массе и весе слов (унции, фунты / г, кг)
- Задачи по объему и объему слов
- Проблемы с переменными и выражениями со словами
- Словесные задачи с переменными и уравнениями
- Объем прямоугольной призмы
- Проблемы со словами GCF / LCM
- Проблемы со смешанными словами
Связанные темы
Рабочие листы с дробями
Рабочие листы по геометрии
Основные моменты домашней школы в 5-м классе: логика и критическое мышление
Один из принципов классического обучения — изучение логики.Это может показаться ошеломляющим для мамы, которая никогда официально не изучала эту тему, но это не обязательно!
Сегодня доступно множество отличных программ, которые помогут вам и вашим ученикам. Изучение логики и развитие сильных аргументов — важный и необходимый навык.
Головоломки и игры — отличный способ начать обучение логическому мышлению.
Думайте о них как о логической «разминке» — времени, когда ученики 5 и 6 классов могут выучить терминологию (силлогизмы? Заблуждения? — это как другой язык!) Логики, работая над головоломками и играми.
Это также идеальное время для ознакомления с рабочими тетрадями и программами критического мышления, которые укрепят способность учащихся к абстрактному мышлению.
В зависимости от роста и зрелости ребенка вы можете начать более формальную программу в 7-9 классах.
Когда учить детей логике
Есть несколько программ критического мышления, которые начинаются еще в детском саду и в первом классе.
Однако те ранние годы лучше всего посвятить основам — обучению чтению, началу письма и основам математики.
Несколько логических игр могут быть интересными, но не тратьте много времени на «критическое мышление» на этом этапе. Молодые мозги действительно не готовы к абстрактному мышлению, необходимому для истинного критического мышления.
Лучшее время для начала — это когда дети достигают той «дерзкой» стадии, которую Дороти Сэйерс упоминает в «Утраченных инструментах обучения», — когда они начинают сомневаться в том, что раньше считали само собой разумеющимся.
Сейчас самое время научить этому логическому мышлению — так что, пока они спорят с вами, по крайней мере, они будут логичны в этом!
Как научить детей логике
Как начать обучать логике?
С играми и головоломками!
Сохраните эти тяжелые курсы логики для старших классов.Ученики 5 и 6 классов только погружаются в воду логики, изучают терминологию и начинают развивать способность к абстрактному мышлению.
Итак, найдите программы, над которыми вы можете работать вместе. Обсудите текущие события. Если вы никогда не изучали логику формально, совместное обучение с ребенком может стать прекрасным инструментом для обсуждения.
Мне очень нравится серия Logic Liftoff для этих начальных этапов (Logic Countdown, Logic Liftoff и Orbiting with Logic), потому что она вводит широкий спектр головоломок логического и критического мышления.
В трех книгах этой серии вы затронете аналогии, последовательности, силлогизмы, нелогичные рассуждения и другие темы. Каждая книга охватывает одни и те же темы, и с каждым уровнем становится все сложнее.
Второй ресурс, который нам очень нравится, — Red Herring Mysteries. Нам нравится разгадывать несколько загадок за ужином всей семьей. Очень весело пытаться понять, что это за «отвлекающий маневр» в этой истории, и придумать правдоподобное решение.
Игры также являются отличным способом попрактиковаться в абстрактном мышлении.Я перечислил некоторые из наших любимых в этом посте о любимых математических и логических играх.
Логика обучения не должна пугать. Вам просто нужно желание учиться и план.
Рабочие листы по геометрии 5 класс
Jenette Héloïse 6 марта 2021 г. Рабочие листы
Почему родителям следует использовать рабочий лист — Хотя общеизвестно, что учителя используют этот инструмент в школе, многие из нас этого не делают Знаю, что родители также могут использовать его дома, чтобы дополнить обучение своего ребенка.С помощью письменного листа вы можете поощрять своего ребенка каждый день развивать свои навыки письма дома. Даже всего 30 минут ежедневной практики это может значительно улучшить навыки вашего ребенка. С письменным листом у вас также есть возможность воспользоваться расширенным рабочим листом, который поможет старшим детям с их способностями к письму и письму.
Расширение словарного запаса — Добавляя цвета для описания различных предметов, ваш ребенок также расширяет свой словарный запас.Обнаружение новых предметов определенного цвета помогает им выучить новые слова для обозначения предметов, например, красное яблоко, красная пожарная машина, красная рубашка и т. Д.
Развитие речи — Цвета часто являются первыми прилагательными, которые ваш ребенок выучит и будет использовать. Цвет используется для описания и обозначения определенных предметов, помогая вашему ребенку научиться произносить множество разных слов.
В раннем возрасте детей сначала учат писать буквы только на бумаге.Когда детям исполняется восемь-десять лет, их учат писать скорописью. Поначалу им это может показаться довольно трудным и скучным. Но один интересный способ научить их этому — также использовать рабочие листы. Основные листы скорописи, которые вы можете использовать: Rockin ’Round Letters, Climb’n’ Slide Letters, Loopy Letters, Lumpy Letters и Mix ’n’ Match.
Учителя используют листы писчей бумаги для печати. Они позволяют своим ученикам обводить цифры, буквы, слова или точки, поскольку это идеальный способ для ребенка практиковать контролируемые движения пальцев и запястья.Продолжая практиковаться или отслеживать, он скоро сможет писать более разборчиво и разборчиво.
Использование картинок — пока ваш ребенок еще учится распознавать буквы алфавита, вы можете использовать картинки (или сам предмет), чтобы помочь ему практиковать свои звуки. Найдите изображения птицы, мяча, летучей мыши, ванны, книги и т. Д., Чтобы практиковать букву ‘b’. Выберите букву на день и предложите ребенку найти в доме предметы, которые начинаются с этой буквы.На распечатываемых листах тоже должны быть полезные упражнения.
СВЯЗАННЫЕ СТАТЬИ
Рабочие листы по математике для четвертого класса для печати
21 апреля 2021 г.
Рабочие листы Glencoe Science Earth Science
21 апреля 2021 г. Рабочие листы для сложения и вычитания треугольников семейства фактов
21 апреля 2021 г.
Рабочие листы по математике для девяти классов Печатная версия
21 апреля 2021 г.
Рабочие листы по алгебре для четвертого класса
21 апреля 2021 г.
Задания по математике в детском саду, считая до 20
21 апреля 2021 г.
Фотографии заданий по математике по геометрии 5-й класс
ЗНАЧЕНИЕ РЕДАКТОРА
Диаграмма Венна Задания по математике 7-й класс
Умножение 907 на 21 апреля 2021 г.
21 апреля 2021 г.
Рабочий лист раскраски на испанском языке Ключ 9 0781
21 апреля 2021 г.
Задания по математике для первого класса вычитания
21 апреля 2021 г.
Оставьте свой ответ на заданиях по математике по геометрии 5-й класс
5 TED Talks вы должны показать свой урок математики | Блог
Ищете способ вдохнуть новую жизнь в уроки математики? Тогда мы предлагаем вам посмотреть отличные видеоролики с математическими загадками, снятые командой на TED-Ed.Благодаря очаровательной анимации и увлекательному стилю повествования эти видео не только занимательны; они идеально подходят для учителей, желающих отточить у своих учеников навыки решения проблем. Для вашего удовольствия, вот пять лучших математических видео от Whiz Education на TED-Ed!
1. Логическая головоломка зеленоглазых
Это интригующая логическая головоломка, рассказывающая историю отважного побега, устроенного группой из 100 человек, взятых в плен на необитаемом острове безумным диктатором. Он знакомит студентов с концепцией общих знаний философа Дэвида Льюиса и их ролью в решении проблем, хотя это не самый важный урок.Что еще более важно, он также учит студентов, что в математике всегда есть нечто большее, чем кажется на первый взгляд, и что вопросы, которые на первый взгляд кажутся неразрешимыми, могут быть решены, если они готовы продумать их систематически. Мы рекомендуем показать это ученикам 5 и 6 классов.
2. Переход через мост
Это простая задача, доступная для учащихся начальной школы любого возраста из-за низкого уровня входа в пол и высокого потенциала потолка.Цель состоит в том, чтобы перебросить четырех человек через шаткий мост за 17 минут или столкнуться с гневом некоторых довольно устрашающих зомби. Однако, как вы увидите в видео, эта задача далеко не проста. По сути, это простая задача сложения, которую также легко сформулировать и предпринять первые попытки, но она требует изрядного количества экспериментов. Мы думаем, что эту задачу было бы интересно воссоздать — возможно, попросите своих учеников попытаться выяснить, как перейти игровую площадку в отведенное время, а не через шаткий мост! Попробуйте это уже во 2-м классе.
3. Загадка о шляпе узника
10 человек похищены группой пришельцев, которые намереваются их съесть — если только люди не докажут, что они в высшей степени логичны! Люди помещаются в один ряд, от самого высокого до самого низкого, и каждому дается либо черная, либо белая шляпа. Начиная со спины, они должны угадать, какой цвет шляпы они носят, и они могут сделать только одну ошибку между собой, или они будут чау-чау-чау! Как они это сделают? Смотреть видео! Ключевые уроки здесь относятся к созданию кода и следованию логическим шаблонам.Решение основано на изящном применении паритета (шансы против эвенов). Помимо концепций, эта задача также служит отличным уроком командной работы: еще одна задача, которую стоит повторить в классе. Попробуйте вызвать 10 студентов на фронт и проверить, смогут ли они спастись от пришельцев. Отлично подходит для детей от 3 до 5 лет.
4. Загадка темной монеты
Это будет особенно интересно искателям приключений из вашего класса! В этом сценарии исследователю удается найти подземелье, полное ценных монет.К сожалению, монеты охраняет волшебник, который позволит исследователю уйти с добычей, только если он пройдет сложный тест. В этом видео рассматривается концепция «дополнительных мероприятий» — в ней также используется немного алгебры, поэтому оставьте ее для детей старшего возраста, которые готовятся к переходу в среднюю школу.
5. Загадка пароля
Еще одна проблема, связанная с антиутопическим будущим и людьми, попавшими в ловушку! (Здесь вроде возникает тема).На этот раз тиранические правители схватили трех борцов сопротивления. Их скармливают саламандрам-мутантам, если они не смогут угадать трехзначный код, необходимый для деактивации электрифицированной двери, используя три предоставленных математических подсказки. Это отличный вопрос для учителей, которые хотят развить у своих учеников беглость математики и смешать ее с решением задач, поскольку он включает в себя сложение, умножение и множество вычислений! Мы рекомендуем попробовать это с учениками 4 и 5 классов.
Хотите еще больше увлекательного материала по математике для ваших учеников?
Не ищите ничего, кроме наставника по математике! Благодаря красочной анимации, упражнениям и увлекательным наградам Maths-Whizz ваши ученики сразу же полюбят математику — это идеальный онлайн-сервис по математике для школ!
.

 Сборник, над которым надо как следует подумать, выручит педагога и на простом уроке, когда дети устали, и на открытом, когда надо показать свое педагогическое мастерство.
Сборник, над которым надо как следует подумать, выручит педагога и на простом уроке, когда дети устали, и на открытом, когда надо показать свое педагогическое мастерство. Выполнив похожие задания несколько раз подряд, дети почти наверняка усваивают алгоритм их решения.
Выполнив похожие задания несколько раз подряд, дети почти наверняка усваивают алгоритм их решения.
 Материалы охватывают весь курс и имеют большое воспитательное значение.
Материалы охватывают весь курс и имеют большое воспитательное значение. Они важны как для определения уровня ЗУН детей, так и для подготовки класса к более серьезному испытанию – ГИА. Обучившись работать с тестами дома, дети будут более уверены и продуктивны на проверочных уроках.
Они важны как для определения уровня ЗУН детей, так и для подготовки класса к более серьезному испытанию – ГИА. Обучившись работать с тестами дома, дети будут более уверены и продуктивны на проверочных уроках. Зачастую умные дети оказываются в рядах отстающих по весьма обидному поводу. Освоить азы математики, без которых «никуда», поможет сборник для решения примеров, составленный Узоровой О.
Зачастую умные дети оказываются в рядах отстающих по весьма обидному поводу. Освоить азы математики, без которых «никуда», поможет сборник для решения примеров, составленный Узоровой О.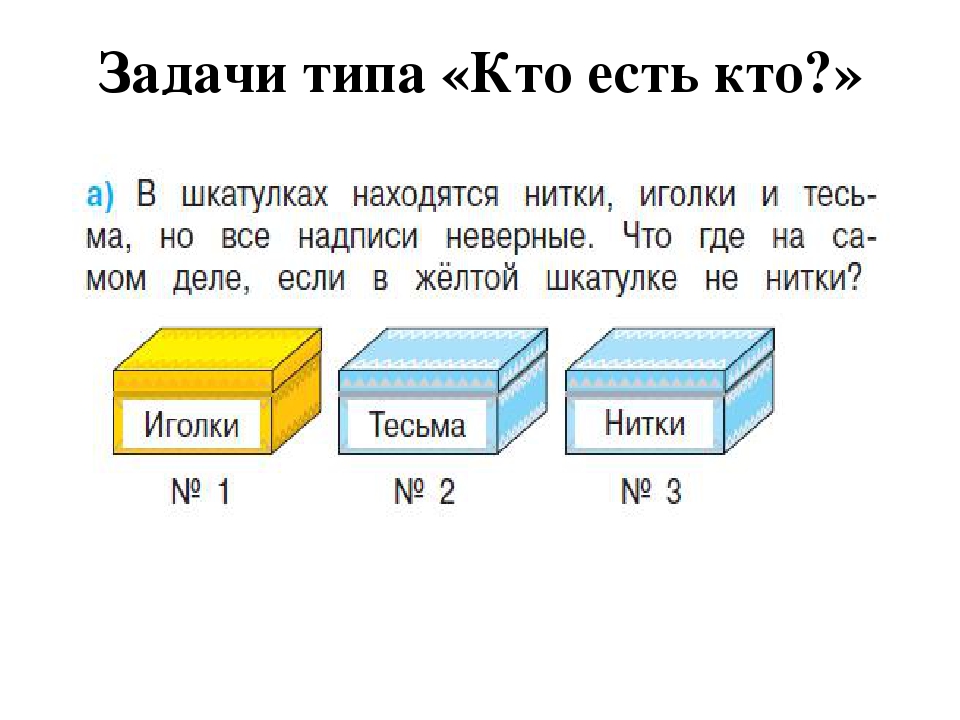 Контрольные работы по математике рекомендованы для качественной проверки навыков пятиклассников. В пособие вошли все необходимые работы, которые ученик должен выполнить в 5-ом классе.
Контрольные работы по математике рекомендованы для качественной проверки навыков пятиклассников. В пособие вошли все необходимые работы, которые ученик должен выполнить в 5-ом классе.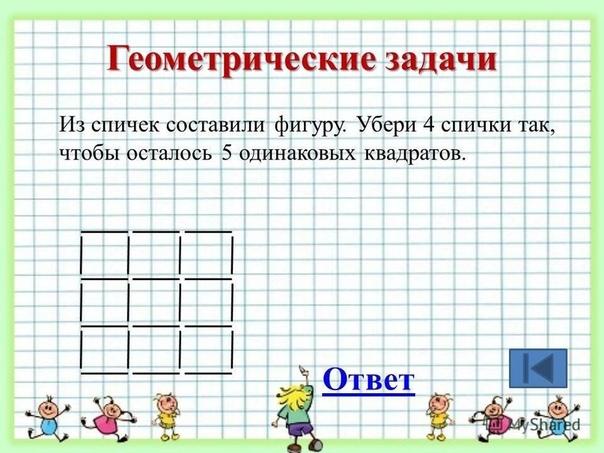 ..
..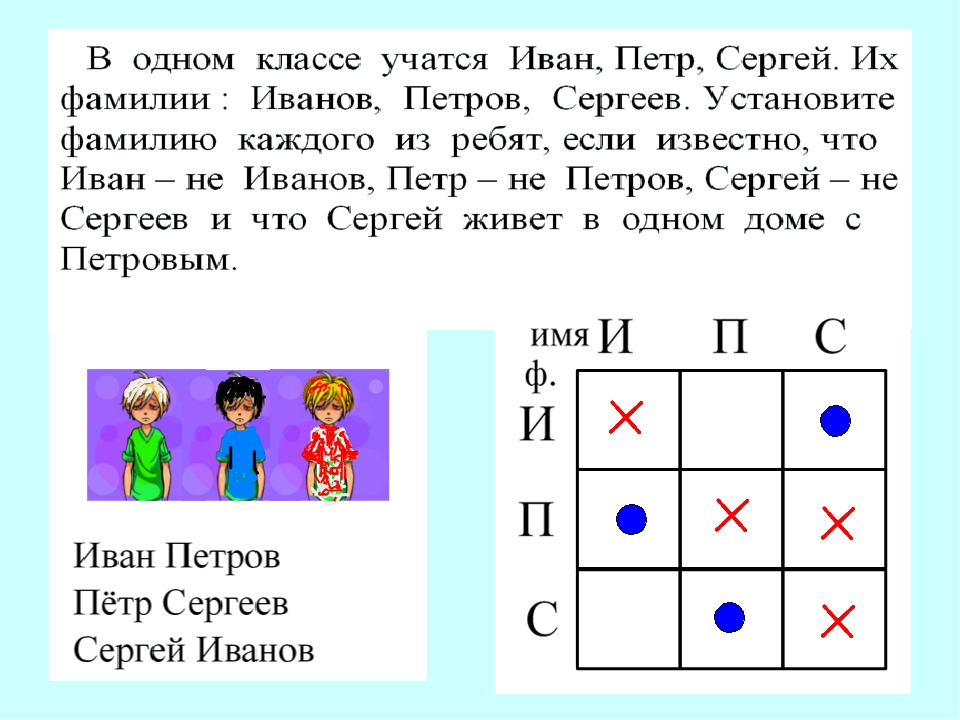 Скачать
Скачать



 Старинные системы записи чисел.
Старинные системы записи чисел.
 М., Утёмов В.В. Уроки развивающей математики. 5-6 классы. Задачи математического кружка. – Киров: изд. МЦИТО, 2014
М., Утёмов В.В. Уроки развивающей математики. 5-6 классы. Задачи математического кружка. – Киров: изд. МЦИТО, 2014
 : ВАКО, 2014
: ВАКО, 2014
 Математика. Том 11. – М.: Аванта+, 2003.
Математика. Том 11. – М.: Аванта+, 2003.
 Свирска
Свирска Ф. Шарыгин, А.В. Шевкин. – М.: Просвещение, 2010.
Ф. Шарыгин, А.В. Шевкин. – М.: Просвещение, 2010.