Тесты по Математике для 4 класса
Данный тест включает задания по теме «Единицы измерения массы».Проверяется умение переводить единицы, сравнивать, вычислять.
Математика 4 класс | Автор: Дементьев Вячеслав Сергеевич | ID: 12959 | Дата: 10.3.2021
выполнить умножение и деление многозначных чисел и внести результаты вычислений
Математика 4 класс | Автор: Кузнецова Лариса Николаевна | ID: 12323 | Дата: 7.5.2020
Источник: Математика. Тесты ФГОС. 4 класс / К.С. Мещерякова, В.В. Нестеркина. — Ростов-на-Дону : Феникс, 2016. — 31, [1] с. : ил. — (Тест-контроль)
Математика 4 класс | Автор: Мещерякова К.С. | ID: 12126 | Дата: 16.4.2020
Тестовая работа за курс 4 класса по математике. 11 вопросов с одним правильным ответом.
Математика 4 класс | Автор: Куркова О.А. | ID: 12125 | Дата: 7.4.2020
В первой половине теста будет проверка умений учащихся умножать и делить на круглые числа. В часте теста решение задач на нахождение Скорости, Времени и расстояния по двум известным.
В часте теста решение задач на нахождение Скорости, Времени и расстояния по двум известным.
Математика 4 класс | Автор: Сороконенко Тимофей Вадимович | ID: 11828 | Дата: 14.1.2020
Тест позволяет проверить умения:
Математика 4 класс | Автор: Баганова Татьяна Васильевна | ID: 11593 | Дата: 13.10.2019
Тест применяется на этапе актуализации на уроке «Сложение и вычитание величин»
Математика 4 класс | Автор: Владимирова Г. П. | ID: 11127 | Дата: 13.5.2019
Вопросы по математике для подготовки к ГКР
Математика 4 класс | Автор: Серебрякова М.Ю. | ID: 10810 | Дата: 27.3.2019
Цель: проверить сформированность представлений о скорости движения, умение решать задачи на встречное движение.
Математика 4 класс | Автор: Любовь | ID: 10811 | Дата: 22.2.2019
Проверить знания учащихся
Математика 4 класс | Автор: Тавасиева Диана Петровна | ID: 10812 | Дата: 29. 1.2019
1.2019
Страница 1 из 13
«Полный сборник задач по математике. 4 класс. Все типы задач. Контрольные работы. Карточки для работы над ошибками. Ответы» Узорова Ольга Васильевна, Нефедова Елена Алексеевна — описание книги | Академия начального образования
Алтайский край
Альметьевск
Ангарск
Астрахань
Белгород
Благовещенск
Братск
Брянск
Владивосток
Владимирская область
Волгоград
Волгоградская область
Воронеж
Воронежская область
Екатеринбург
Забайкальский край
Ивановская область
Иркутск
Кабардино-Балкарская Республика
Калужская
Кемерово
Кемеровская область
Киров
Кострома
Краснодарский край
Красноярск
Красноярский край
Курганская
Курск
Липецк
Москва
Московская область
Нижегородская область
Нижний Новгород
Нижний Тагил
Новосибирск
Новосибирская область
Омск
Оренбург
Оренбургская область
Орловская область
Пенза
Пермский край
Пермь
Приморский край
Республика Адыгея
Республика Башкортостан
Республика Бурятия
Республика Крым
Республика Мордовия
Республика Северная Осетия — Алания
Республика Татарстан
Республика Тыва
Республика Хакасия
Ростов-на-Дону
Ростовская область
Рязань
Самара
Самарская область
Саратов
Саратовская область
Севастополь
Смоленск
Ставрополь
Ставропольский край
Старый Оскол
Тамбов
Тамбовская область
Тверь
Томск
Тула
Тулун
Тульская область
Тюмень
Ульяновск
Ульяновская область
Хабаровск
Ханты-Мансийский автономный округ
Челябинск
Челябинская область
Чита
Чувашская Республика
Энгельс
Ямало-Ненецкий автономный округ
Ярославль
Тест №1 | Тест №2 | Тест №3 | Тест №4 | Тест №5 | |
1 | В | С | С | Д | С |
2 | В | В | С | А | С |
3 | С | Д | Д | В | Д |
4 | В | А | С | А | С |
5 | В | А | А | Д | В |
6 | С | Д | В | В | С |
7 | С | Д | В | С | А |
8 | Д | В | С | В | А |
9 | А | С | В | Д | В |
10 | В | В | Д | А | С |
11 | А | В | А | А | С |
12 | А | Д | А | Д | В |
13 | Д | В | В | С | В |
14 | С | С | В | Д | А |
15 | А | В | С | В | С |
16 | В | В | В | В | Д |
17 | В | С | А | Д | Д |
18 | С | А | В | С | С |
19 | В | В | Д | Д | А |
20 | А | С | А | А | Е |
Задачи олимпиады Кенгуру, решения и ответы
С 1997 по 2012 годы, за пятнадцать лет проведения в Украине олимпиады Кенгуру, собралась обширная база нестандартных математических задач. Они печатаются в ежегодном вестнике олимпиады, кроме того, к юбилею конкурса вышел сборник «10 років разом. Міжнародний математичний конкурс «Кенгуру»», в котором собраны условия всех задач за 1997-2006 годы.
Решение таких задач — хороший интеллектуальный досуг, вне зависимости от возраста. Помимо этого, в свете современных образовательных требований, решение задач Кенгуру может оказаться отличным подспорьем в подготовке к Независимому внешнему оцениванию.
Помимо этого, в свете современных образовательных требований, решение задач Кенгуру может оказаться отличным подспорьем в подготовке к Независимому внешнему оцениванию.
Здесь мы представляем свои варианты решения интересных на наш взгляд задач. Раздел регулярно пополняется. В пакет задач входит по одной задачи для каждого возраста, как правило, наивысшего (третьего) уровня сложности.
Краткие правила олимпиады
Участники олимпиады в зависимости от возраста делятся на следующие группы:
| Малюк | 3, 4 класс |
Школярик | 5, 6 класс |
Кадет | 7, 8, 9 класс |
Юніор | 10, 11 класс, 9 класс с углублённым изучением математики |
Студент | 10, 11 класс с углублённым изучением математики |
C 2007 года были введены уровни «Малюк 2»: 2 класс и «Випускник»: все 11-е классы.
Для каждой возрастной группы предлагаются задачи трёх уровней сложности:
| 1й уровень | 3 балла |
2й уровень | 4 балла |
3й уровень | 5 баллов |
Всего предлагется 30 задач, на решение отводится 75 минут. В ходе олимпиады запрещается пользоваться калькулятором и литературой.
Желаем успехов в решении!
Задачи на сайте формируются в виде пакетов. В каждый пакет входит по одной задаче каждого возрастного уровня. Уровень сложности, как правило, третий.
- Пакет 1: комбинаторика, логика, взвешивания
- Пакет 2: комбинаторика, логика, выражения
- Пакет 3: взвешивания, логика, делимость
- Пакет 4 : делимость, последовательности, рассуждения
- Пакет 5: вероятность, геометрия, логика
- Пакет 6: целая и дробная часть, делимость, цифры
- Пакет 7: комбинаторика, среднее арифметическое, дроби
- Пакет 8: числовые процессы, выбор, множества
- Пакет 9: комбинаторика, проценты, ребус
- Пакет 10: целые числа, уравнения, логика
- Пакет 11: целые числа, делимость, палиндромы
- Пакет 12: последовательности, проценты, уравнения
- Пакет 13: принцип Дирихле, цифры, множества
- Пакет 14: комбинаторика, делимость, геометрия
- Пакет 15: системы счисления, геометрия, арифметика
- Пакет 16: целые числа, логика, геометрия
- Пакет 17: тригонометрия, неравенства, геометрия
- Пакет 18: тригонометрия, последовательность, цифры
- Пакет 19: тригонометрия, последовательность, цифры
Далее>
Задайте вопрос на блоге о математике
Примеры, задачи и загадки по ТРИЗ с ответами
Говоря о разработанном Г. С. Альтшуллером алгоритме, мы отмечаем не только стройность научной теории, но и её способность без перебора многочисленных вариантов приводить к сильному решению. В этом несомненное преимущество ТРИЗ, ведь она располагает большим количеством практических инструментов для решения творческих задач и производственных кейсов любой сложности.
С. Альтшуллером алгоритме, мы отмечаем не только стройность научной теории, но и её способность без перебора многочисленных вариантов приводить к сильному решению. В этом несомненное преимущество ТРИЗ, ведь она располагает большим количеством практических инструментов для решения творческих задач и производственных кейсов любой сложности.
Чтобы наглядно это продемонстрировать, мы собрали задачи и упражнения и объяснили их решение, применяя методику ТРИЗ. Несмотря на то, что теория предназначена для работы с техническими задачами, примеры подобраны так, что даже человек без специального образования сможет по достоинству оценить её эффективность.
На этой странице приведены некоторые задачи и упражнения, которые Г. Альтов (псевдоним, под которым Г. С. Альтшуллер писал научную фантастику) публиковал в газете «Пионерская правда» для юных изобретателей. И, как часто бывает в таких случаях, не каждый взрослый мог справиться с этими задачами, в чём вы сможете убедиться самостоятельно. Подобраны и кейсы – описания реальных ситуаций, когда возникшие противоречия были решены при помощи ТРИЗ. Они более сложные для решения, но позволяют завершить представление о теории, как практическом инструменте.
Содержание
- Марсоход
- Вода в трубе
- Безопасный бассейн
- Лекарства для космонавтов
- Одуванчики
- Корм для рыбок
- Лёд на проводах
- Отзывы и комментарии
1
Марсоход
Условие. Во время научной экспедиции на Марс, космический корабль произвёл посадку в долине. Астронавты снарядили марсоход для лучшего изучения планеты, но как только покинули корабль, столкнулись с проблемой. Дело в том, что по поверхности было сложно передвигаться – этому мешали многочисленные холмы, ямы, большие камни. На первом же склоне колёсный вездеход с надувными шинами перевернулся на бок. С этой проблемой астронавты справились – они прицепили снизу груз, что усилило устойчивость машины, но стало причиной новой проблемы – груз задевал неровности, что усложняло движение. Итак, что нужно сделать, чтобы повысить проходимость марсохода? При этом у космонавтов нет возможности изменять его конструкцию.
Предполагаемое решение
Решение. Техническое противоречие сформулировано в условии задачи. Идеальный конечный результат – достичь абсолютной проходимости. При этом космонавты действуют в условиях Марса, у них нет возможности изменять конструкцию марсохода. Исходя из этого, ресурсом выступает груз. Не стоит также забывать и о законах развития технических систем, и следить за тем, чтобы изменение одной части не влияло на функционирование других элементов. Памятуя об этом, становится очевидным, что поднять груз в кабину или на крышу невозможно, так как произойдёт смещение центра тяжести и проблему решить не удастся. Спустить воздух из шин также нельзя – устойчивость немного повысится, но пострадает проходимость, усилится тряска.
Чтобы понять, как поступить с грузом, и получить сильное решение, нужно вспомнить, как мы обычно поступаем в условиях нехватки места? Стараемся разместить всё максимально компактно: объединить, сложить одно в другое. В ТРИЗ такой приём получил название «матрёшка». С её помощью задача про марсоход легко решаема: груз (металлические шарики, тяжёлая жидкость) нужно поместить внутрь шин. Этот способ имеет применение на практике, его предложил использовать японский изобретатель П. Шохо, для повышения устойчивости и проходимости кранов и погрузчиков.
2
Вода в трубе
Условие. Достаточно простая и известная задача. Есть металлическая труба, проложенная под землёй, по которой течёт вода. Для устранения неполадок в работе системы, часть трубы раскопали и столкнулись с необходимостью определить, в какую сторону движется вода. Попытки выяснить это путём простукивания, на слух, завершились неудачей. Вопрос: как понять в какую сторону течёт вода в трубе? Нарушать герметичность трубы (сверлить, резать) нельзя.
Предполагаемое решение
Решение. Эта задача решается очень просто. ТРИЗ предусматривает не только строгий алгоритм решения, но и чёткую проработку условий задания. Г. С. Альтшуллер всегда советовал перед началом работы попробовать сформулировать условия задачи другими словами. В нашем случае есть труба и вода, которая по ней движется. Воздействовать на трубу нельзя, значит нужно воздействовать на воду. Отсюда самое простое решение – нагреть трубу в одном месте, и по тому в какую сторону будет течь подогретая жидкость, нагревая и трубу, определить направление.
3
Безопасный бассейн
Условие. Это скорее не задача, а упражнение на способность находить эффективные творческие решения. Цель – предложить максимально безопасный бассейн для людей, которые не умеют плавать.
Предполагаемое решение
Решение. Используя метод системного анализа, можно найти ряд приемлемых решений, поскольку условия задачи не ограничивают нас в выборе средств. Так, можно построить бассейн уникальной конструкции (с небольшой глубиной, верёвочными ограждениями для каждой дорожки, выталкивающими фонтанами). Также можно снабжать пловцов вспомогательными плавсредствами, к примеру, спасательными жилетами. С точки зрения идеальности наиболее удачным вариантом можно считать предложение наполнить бассейн раствором концентрированной поваренной соли. В нём тело будет выталкиваться на поверхность без дополнительных усилий. Кстати, на эту тему существует загадка: «В каком море невозможно утонуть?». Поскольку физическую составляющую необходимого условия вы уже знаете, в качестве дополнения к упражнению подумайте над географической.
4
Лекарства для космонавтов
Условие. Не многим известно, что «морской болезнью» страдают не только моряки и путешествующие по морю, но и космонавты. Лекарства от данного недуга существуют, но есть оговорки по его применению в условиях космоса. Так, малые дозы нужно принимать часто, что неудобно, а большие – вредно. Как решить эту проблему?
Предполагаемое решение
Решение. Противоречие заключается в необходимости подачи в организм нужного количества лекарства без постоянного отвлечения на этот процесс космонавта. Для его решения был применён метод маленьких человечков. Лекарство представили как толпу людей, желающих попасть в нужное место. Очевидно, что для совершенствования этого процесса нужна определённая организация – очередь, постепенное продвижение. Эту идею реализовали в препарате, придя к выводу, что он должен усваиваться по частям, а не сразу. По этому принципу и были изобретены таблетки со скополамином, помогающие космонавтам справиться с «морской болезнью». Они имеют форму плоского диска, который, как пластырь, крепится за ухом. При этом активное вещество вследствие диффузии нормировано попадает в организм.
5
Одуванчики
Условие. Одуванчики имеют набор хромосом очень качественно близкий к человеческому. Как это можно использовать при контроле работы атомной электростанции?
Предполагаемое решение
Решение. Здесь, как видим, не совсем традиционная задача. Тем не менее, решается она достаточно просто, всё что нужно – применить один из законов развития ТС – закон согласования ритмики частей системы. И одуванчик, и человек – системы, а тот факт, что их хромосомы похожи, даёт возможность судить о достоверности результатов экспериментов на растениях и в случае с людьми. Но ритмика у одуванчика чаще (смена поколений раз в год), что за достаточно короткий период времени позволяет проследить генетические изменения экземпляров, растущих рядом с АЭС, и сделать соответствующие выводы и о влиянии на человека.
6
Корм для рыбок
Условие. У вас есть аквариум с рыбками, которые питаются циклопами. Вам нужно уехать на несколько дней и решить проблему с кормлением. Попросить помочь вы никого не можете. Запустить много циклопов за один раз нельзя – рыбки их съедят, и всё равно будут голодать. Как поступить в этом случае?
Предполагаемое решение
Решение. Бытовая ситуация, с которой (с возможными вариациями – кошки, попугаи и т.д. вместо рыбок) сталкивался каждый. По аналогии с предыдущей задачей становится очевидным, что приток корма в аквариум должен быть постоянным. Другими словами, в данном случае ИКР – независимое статическое поступление корма. Как это сделать? Знакомые с физикой, и в частности, с термодинамикой, должны найти решение достаточно быстро, используя описание мыслительного эксперимента Дж. Максвелла, известного как «Демон Максвелла». В переносе на наш случай решением может служить перегородка аквариума стенкой из органического стекла с небольшими отверстиями – достаточными для движения циклопов сквозь них и, в то же время, ограничивающие движения рыбок на «сторону циклопов».
7
Лёд на проводах
Условие. Напоследок сложная задача, с которой справляются очень немногие. В наших климатических условиях зимой существует опасность нарастания льда на проводах линии электропередач. Со временем образовавшаяся глыба может оборвать своей тяжестью провода, да ещё и повредить то, что находится на земле под ними. Какими методами бороться с обледенением?
Предполагаемое решение
Решение. Как и было анонсировано, решение данного кейса потребовало от изобретателей значительных усилий. Сначала высказывались предложения очищать провода внешними способами, например, с помощью человека. Но такие методы были откинуты в силу своей нецелесообразности. Появилась идея нагревать провода, пуская по них ток под сильным напряжением. Но это рождало новое противоречие, ведь в такое время пользователи не смогли бы пользоваться энергией. В данном случае сам ресурс (ток) был выбран правильно и учёные начали развивать идею нагрева проводов его посредством. Вскоре решение нашли – по всей линии на расстоянии в 5-6 м на провода надели специальные кольца из материала, обладающего магнитными свойствами – феррита. Под воздействием переменного тока магнит нагревался, что исключало обледенение.
Но и это решение не оказалось оптимальным. Дело в том, что провода продолжали греться и в тёплую пору, что было ненужным. Изобретение было усовершенствовано – кольца начали делать из магнита с точкой Кюри (П. Кюри первым заметил, что разные магниты сохраняют свои свойства до разных температур) равной нулю градусов. Такие магниты не грелись, когда температура воздуха поднималась выше 0°.
Больше интересных задач и кейсов по ТРИЗ ищите на официальном сайте фонда Г. С. Альтшуллера, на сайте «Креативный мир», в книге Н. и А. Нарбут «Учебник и сборник задач по ТРИЗ». Желаем вам успехов в практике решения изобретательских задач!
А также предлагаем сыграть в нашу игру на развитие нестандартного подхода в решении задач.
Сергей КрутькоДмитрий Гераськин
Вопросы-головоломки на собеседованиях с ответами. Часть 1 — Work.ua
Логические задачи кандидатам на вакансию задают, чтобы оценить их аналитические способности. С подобными вопросами может столкнуться каждый. Но даже, если с вами это не случится — изучить их для подготовки будет просто интересно.
Соискателям, столкнувшимся с головоломками в процессе собеседования, не стоит паниковать и теряться. Как правило, в большинстве случаев достаточно показать ход ваших мыслей и пути решения поставленной задачи. Вполне может быть, что у задачи и нет правильного решения или однозначного ответа. Ни в коем случае нельзя говорить «я не знаю» или «затрудняюсь ответить», просто размышляйте вслух.
Чтобы вы знали к чему быть готовыми и не растерялись, Work.ua собрал самые популярные вопросы-головоломки и подготовил ответы и рекомендации к ним. Кто знает, может вам попадутся именно эти задачи.
Все эти головоломки могут вам задать при собеседовании на вакансию программиста php.
Канализационные люки
Это, пожалуй, самый распространенный вопрос среди всех головоломок.
Вопрос: Почему канализационные люки круглые?
Ответ: Есть несколько вариантов. Так как диаметр круга одинаков, как его не крути, то круглый люк не может провалиться в колодец. У квадрата же, например, диагональ больше его сторон, поэтому крышка могла бы упасть. Также можно ответить, что круглые люки проще транспортировать и передвигать.
Лампочки
Вопрос: В закрытой комнате есть 3 лампочки, а в коридоре 3 выключателя. За какое минимальное открытие дверей можно определить какой выключатель к какой лампочке относится?
Ответ: За одно открытие. Включаем одновременно 2 выключателя, через некоторое время выключаем второй. Заходим в комнату: одна из лампочек осталась гореть — это первый выключатель, далее щупаем оставшиеся лампочки — теплая и будет вторым выключателем, а холодная соответственно третьим.
Торт
Вопрос: Как разделить торт на 8 равных частей тремя разрезами?
Ответ: Сперва нужно сделать 2 разреза крест на крест, поделив торт на 4 равных части. А затем разрезать торт горизонтально пополам. Ну и что, что куски стали невысокие, зато у вас 8 равных частей. Еще можно после первых двух разрезов сложить кусочки друг на друга и переполовинить одним разрезом.
Мертвый человек и спичка
Вопрос: Среди поля найден мертвый человек со спичкой в руках, следов нет. От чего он умер и при каких обстоятельствах?
Ответ: Человек умер от падения с самолета, который начал терять высоту, и авария была неизбежна. На всех пассажиров не хватило одного парашюта и они тянули жребий. Ему досталась короткая спичка, и он был вынужден прыгать без парашюта.
Автобус и мячи
Вопрос: Сколько теннисных мячей поместится в автобус?
Ответ: Точного правильного ответа не знает и сам рекрутер, так как не уточняется, что за мячи и автобус — их размеры не известны, и никто досконально это не проверял. Поэтому тут важен ход ваших мыслей, вы можете только предположить. Назовите примерные длину, ширину и высоту автобуса, размеры одного мяча. Посчитайте объем автобуса и мяча — так вы узнаете сколько мячей поместится в пустой автобус. Уменьшите примерно это значение с учетом сидений и других деталей автобуса, сделайте поправку на то, что мячи не квадратные и дайте ответ. В этом случае процесс поиска ответа важнее самого ответа. Варианты вопроса могут быть разные: мячи — футбольные, вместо автобуса — комната и т.п.
Таблетки
Вопрос: Доктор выдал пациенту 4 таблетки двух видов — по 2 таблетки каждого, которые нельзя отличить по внешнему виду. Таблетки надо выпить за два приема: утром по одной таблетке каждого вида и так же вечером. Если нарушить дозировку или не принять таблетки, то пациент умрет. Так вышло, что таблетки перемешались. Как пройти курс лечения и выжить?
Ответ: Конечно, можно сказать, что лучше пойти к врачу и попросить еще, все таки вопрос жизни и смерти. Но это могут быть единственные таблетки на Земле, доктор может исчезнуть при загадочных обстоятельствах и т.д. Так что ответить все же придется. К тому же все достаточно просто: нужно разделить каждую таблетку на 2 части и выпить по половинке каждой таблетки утром и вечером.
В заключение
Помните, что прежде всего такие задачи и головоломки предназначены для того, чтобы проверить поведение кандидата в нестандартных ситуациях, оценить способность к размышлению, творческому и логическому подходу. Увы, нередки случаи, когда интервьюер не может правильно интерпретировать результаты таких вопросов, или вовсе не понимает их предназначения. Но даже в этой ситуации уверенное поведение и стремление прийти к ответу покажут вас с лучшей стороны и увеличат шансы получить должность.
Читайте также: Вопросы-головоломки на собеседованиях с ответами. Часть 2
Чтобы оставить комментарий, нужно войти.
Контрольная работа по теме Решение задач. Логика.-пнш 4 класс
Данный урок является контрольным по теме «Решение задач. Логика»
Цель урока: проанализировать результаты усвоения темы, формирование навыка самоконтроля, самостоятельности.
Предметные УУД: произвольно и осознанно владеть общим умением решать конкретные учебные задачи.
Метапредметные: строить логическое рассуждение, включающее установление причинно-следственных связей; осуществлять взаимный контроль и оказывать в сотрудничестве необходимую помощь;
Личностные УУД: внутренней позиции школьника на уровне понимания необходимости учения, выраженного в преобладании учебно-познавательных мотивов
Просмотр содержимого документа
«Контрольная работа по теме Решение задач. Логика.-пнш 4 класс»
Контрольная работа по теме « Текстовые задачи. Логика»
Цель: проанализировать результаты усвоения темы, формирование навыка самоконтроля, самостоятельности.
Предметные УУД: произвольно и осознанно владеть общим умением решать конкретные учебные задачи.
Метапредметные: строить логическое рассуждение, включающее установление причинно-следственных связей; осуществлять взаимный контроль и оказывать в сотрудничестве необходимую помощь;
Личностные УУД: внутренней позиции школьника на уровне понимания необходимости учения, выраженного в преобладании учебно-познавательных мотивов
Оборудование: текст контрольной работы по вариантам.
План.
1.Орг. момент.
Встало солнышко давно,
Заглянуло к нам в окно,
На урок торопит нас –
Математика сейчас.
2.Сообщение темы и цели урока.
3.Работа по теме.
-Знакомство с текстом. Письмо контрольной работы.
1 вариант
Из чисел 34, 40, 500, 721, 63, 80 выбери и запиши:
«Круглые» и двузначные _______________________________
«Круглые» или двузначные _____________________________
Из чисел 5, 8, 12, 14, 16, 18, 20 выбери и запиши те, которые можно поставить вместо р, чтобы данная запись оказалась верной:
р ≥ 16 _________________________________________________________
8
Продолжи утверждения так, чтобы они были верными:
Если длина стороны квадрата меньше 12 см, то его площадь __________________________
Число 14 не только чётное, но и ___________________________________________________
Вычисли значение выражения
340 +9567– 60993 : 753
Реши задачу. Вычисли и запиши ответ.
От двух пристаней, находящихся на расстоянии 120 км друг от друга, отправляются одновременно навстречу друг другу два теплохода, скорость которых в стоячей воде одинаковая и равна 20 км/ч. Скорость течения реки 2 км/ч. Через сколько часов теплоходы встретятся?
Реши уравнение.
600-х=802:2
2 вариант
Из чисел 24, 60, 120, 512, 81, 20 выбери и запиши:
«Круглые» и двузначные _______________________________
«Круглые» или двузначные _____________________________
Из чисел 2, 6, 11, 13, 14, 17, 21 выбери и запиши те, которые можно поставить вместо р, чтобы данная запись оказалась верной:
р ≥ 14 _________________________________________________________
6
Продолжи утверждения так, чтобы они были верными:
Если длина стороны квадрата меньше 15 см, то его площадь равна __________________________
Число 13 не только нечётное, но и ___________________________________________________
Вычисли значение выражения
930 + 16974 : 414 – 804
Реши задачу. Вычисли и запиши ответ.
От двух пристаней, находящихся на расстоянии 180 км друг от друга, отправляются одновременно навстречу друг другу два катера, скорость которых в стоячей воде одинаковая и равна 30 км/ч. Скорость течения реки 3 км/ч. Через сколько часов катера встретятся?
Реши уравнение.
800-х=903:3
VI. Итоги урока. Рефлексия.
-Было ли вам трудно на уроке? Справились ли вы с заданиями? Свое состояние покажите по цветным карандашам.
VII. Дом. задание. Стр. 101№ 329-все решают, а те, которые считают, что математику знают на «5» еще № 334
Математика для четвертого класса Задачи по логике и рассуждению
Попросите вашего ребенка использовать свои знания четырех основных математических операций для решения приведенных ниже вопросов на логику и рассуждение. При решении вашему ребенку может быть полезно рисование картинки или использование таблицы.
Задачи на логику и рассуждение для четвероклассников
В четвертом классе ваш ребенок начнет применять свои математические знания для решения сложных задач. В этом классе успешное выполнение четырех основных математических операций (сложение, вычитание, умножение и деление) демонстрирует полное понимание вашим ребенком.Ваш ребенок также будет учиться оценивать, насколько разумны его или ее ответы, а также интерпретировать остатки, чтобы определить правильный ответ.
Задачи логики и рассуждения четвертого класса
1. Фермер каждый день кормит всех своих животных в одном и том же порядке. Используйте подсказки ниже, чтобы определить его ежедневный порядок.
- Цыплята кормили раньше свиней, но после коров.
- Коз кормили сразу после коров.
- Лошадей кормили вслед за свиньями.
- Чтобы определить порядок кормления, ваш ребенок должен начать с известной информации (коз кормят сразу после коров) и использовать подсказки для завершения упорядоченного списка. Правильный порядок — коровы, козы, цыплята, свиньи и лошади.
2. Класс мистера Смита совершил экскурсию в зоопарк. В зоопарке было четыре слона, за которыми класс наблюдал за обедом. Они обнаружили, что у каждого из слонов был любимый фрукт и любимое место для отдыха.Используйте подсказки ниже, чтобы выяснить имя каждого слона, его или ее любимые фрукты и место отдыха.
- Джаспер не любит бананы, но любит отдыхать на траве.
- Слон, отдыхавший у скал, съел яблоко.
- Слон, съевший грушу, не сел у дерева.
- Энджи села у воды, но груши не съела.
- Гарри не сидел у дерева, а Мак не любит апельсины.
- Ваш ребенок может захотеть создать таблицу для организации данной информации.Гарри любит есть яблоки у камней, Мак наслаждается бананом у дерева, Джаспер ест грушу на траве, а Энджи ест апельсин у воды.
3. Школьный автобус сделал три остановки по дороге в школу. На первую остановку сели 15 человек. На второй остановке четыре человека вышли и шесть человек сели. На третьей и последней остановке восемь человек вышли и 11 человек сели. Сколько человек было в автобусе к тому времени, как он добрался до школы?
- Это может помочь вашему ребенку нарисовать картинку, чтобы решить эту проблему.Чтобы вычислить ответ, ваш ребенок должен вычесть 15 — 4 = 11. Затем он или она должны сложить 11 + 6 = 17. В конце второй остановки в автобусе было 17 человек. Затем ваш ребенок должен вычесть 17-8 = 9, а затем сложить 9 + 11 = 20. К тому времени, как автобус прибыл в школу, в автобусе уже было 20 человек.
4. Город Франклин был создан по сетке. Есть 96 проспектов, которые идут с севера на юг. Есть 58 улиц, которые идут на восток и запад. Авеню пересекают улицы, и на каждом перекрестке есть светофор.Сколько светофоров во Франклине?
- Чтобы решить эту задачу, ваш ребенок должен умножить количество проспектов (96) на количество улиц (58), например: 96 x 58 = 5568.
Как решить задачи со словами за 3 простых шага
Проблемы со словами могут быть пугающими и подавляющими как для детей, так и для родителей. Они требуют, чтобы дети читали на уровне своего класса, решая сложную головоломку. Дайте ребенку возможность решать эти сложные проблемы, обучая их систематическому подходу к их решению.Будь то одноэтапная или многоэтапная задача со словами, простые стратегии, перечисленные ниже, позволят решить задачу наугад. 😉
1. Прочтите: Прочтите задачу и решите, о чем идет речь.
- Прочтите задачу 2 раза и более.
- Подчеркните или обведите ключевые слова, фразы и числа. Проведите черту через нерелевантную информацию.
2. План: Подумайте, что вас просят сделать в рассказе. Какая информация вам предоставляется и что вам нужно выяснить?
- Нарисуйте картинку.
- Обведите или подчеркните ключевые слова. (Используйте маркеры или цветные карандаши, чтобы обозначить ключевые числа и фразы цветом.)
- Напишите вопрос своими словами.
3. Решите: Какую стратегию вы могли бы использовать, чтобы найти недостающую информацию: сложение, вычитание, умножение или деление?
- Напишите числовое предложение и решите.
- Использовать счетчики.
- Создать диаграммы.
Проверьте свою работу, объяснив свои доводы.Ваш ответ имеет смысл?
Загрузите этот бесплатный контрольный список стратегии из Основы математики , чтобы помочь вашему ребенку решать задачи со словами.
Все учатся по-своему. То, что имеет смысл для одного человека, часто оказывается не самым легким вариантом для другого. Использование различных стратегий для решения словесных задач может помочь вашему ребенку понять, какая стратегия лучше всего подходит для него или для нее. Несколько советов по использованию:
1.Обведите цифры в рассказе и подчеркните ключевые фразы.
Цветовое кодирование — это забавный метод, который помогает детям решить, о какой операции задается вопрос. Назначьте цвет каждой операции и выделите фразу, которая ее идентифицирует. Например, красные ссылки на сложение и синие ссылки на вычитание.
2. Составьте список ключевых слов.
Списки ключевых слов лучше всего использовать для обучения детей младшего возраста решению словесных задач. По мере развития учебной программы по математике дети не должны зависеть от списка ключевых слов для решения задачи.Вопросы становятся сложнее.
Сложение
Всего
Вместе
Итого
Всего
Объединить
Сумма
Объединить
Вычитание
Разница
Меньше
Сколько больше
Сколько больше
Осталось
Осталось
Меньше
3. Визуальные эффекты
Если ваш ребенок учится наглядно, рисование картинки или использование счетчиков может помочь ему или ей понять, в чем проблема. Используйте числовые линии, диаграммы или счетчики или нарисуйте рисунок.
4. Напишите свою словесную задачу.
Знание того, что нужно для написания задачи, — это первый шаг в определении ключевых слов для решения истории. По очереди пишите вместе с ребенком свои словесные задачи и обменивайтесь ими, чтобы решить их.
5. Оставайтесь организованными.
Важно писать четко и содержать рабочее место в порядке, чтобы дети могли читать и выполнять свои собственные вычисления. Многим детям нужен отдельный лист бумаги, чтобы дать им достаточно места, чтобы решить и понять свой ответ.Графическая бумага — отличный вариант, чтобы помочь студентам записывать аккуратную работу.
Загрузите бесплатный образец задачи со словами из книги Основы математики , 1 класс.
В двухэтапной задаче со словами детям предлагается решить два связанных уравнения. Детям может быть сложно понять, когда они переходят от одношаговых задач к двухэтапным. Помогите своему ребенку понять его или ее отношения в двухэтапных задачах со словами с помощью следующих стратегий:
1.Обведите важную информацию.
Обведите числа и важные фразы, которые задают вопросы. Числовые предложения, необходимые для решения этих уравнений, скрыты в тех, кто задает вопросы. Определите первый и второй вопросы, которые необходимо решить.
2. Различайте две части проблемы.
Сначала определите первый шаг первой части слова «проблема». Напишите числовое предложение и решите.
3. Используйте ответ из первого шага решения всей проблемы.
Используйте ответ на первый вопрос, чтобы решить следующее уравнение. Какая операция требует ответа на второй вопрос?
Проверьте свою работу, объяснив свои доводы. На какой вопрос был дан ответ? Разумен ли ответ на заданный вопрос?
Загрузите бесплатный образец задачи с двумя стратегиями со словами из книги Основы математики , 2 класс
Загрузите бесплатный образец многостратегической задачи со словами из книги Основы математики , 4 класс
Evan-Moor’s Math Fundamentals — отличный ресурс для обучения студентов тому, как решать текстовые задачи за 3 простых шага.Он содержит пошаговые инструкции по решению вопросов и помогает детям использовать полезные наглядные пособия и ключевые фразы.
Ознакомьтесь с Daily Word Problems для последовательной практики решения текстовых задач.
Чтобы получить больше забавных советов и стратегий по математике, посетите нашу доску Pinterest по математике: идеи, занятия и уроки.
Сохраните эти советы и закрепите сейчас!
Хизер Фоуди — сертифицированный учитель начальных классов с более чем 7-летним опытом работы преподавателем и волонтером в классе.Ей нравится создавать содержательные и творческие уроки для учащихся. В настоящее время она работает в отделе маркетинга и коммуникаций Эван-Моора и любит создавать возможности для обучения, которые являются значимыми и творческими как для студентов, так и для учителей.
Категории: Для родителей, Домашнее обучение, Тенденции и советы, Без категорий |
Теги: сложение, общая математика, критическое мышление, математика Эврика, улучшение логических навыков детей, логика, математика, многоступенчатые рабочие задачи, умножение, обучение словесным задачам, текстовые задачи |
Постоянная ссылка
Mathwire.com | 100 логических плат
Стратегия: Учащиеся используют доску с сотнями, чтобы исключить числа после прочтения каждой подсказки. & nbsp Учащиеся должны применять свои знания о четно-нечетных, кратных и числовых значениях, чтобы успешно исключать числа, пока не будет найдено решение.
Материалы:
- Копия пакета «Сотня досок» для справки учителя
- Накладные расходы на роли совместного обучения (находятся в пакете учителя)
- Копии задач для каждой группы совместного обучения (находятся в пакете учителя)
- Сотня доска для каждой группы.& nbsp Поместите каждую таблицу в прозрачный защитный чехол, чтобы учащиеся могли использовать маркеры для сухого стирания, чтобы зачеркнуть числа после прочтения каждой подсказки.
- маркеров и ластиков сухого стирания для каждой группы
- Прозрачная таблица сотен досок или таблица сотен досок сухого стирания для использования в учебных целях
- Копии пустых сотен шаблонов логических задач на доске для студентов, чтобы они могли писать свои собственные задачи.
Знакомство с уроком:
`
- Определите совместные учебные группы из 3-4 учеников и назначьте роли или попросите учеников выбрать числа 1-4 и распределить роли, используя эти числа (например,грамм. все единицы — рекордер и т. д.)
- Используйте прозрачность для обсуждения ролей группы совместного обучения и ответственности каждого члена в процессе решения проблем
- Выберите по одной роли из каждой группы, чтобы сформировать «группу» класса, чтобы смоделировать первую задачу, которую ученики будут решать всем классом.
- Только у читателя есть копия задачи, которую он / она читает вслух классу, делая паузу после каждой подсказки, чтобы группа могла решить, какие числа вычеркнуть для этой подсказки.
- Регистратор вычеркивает числа на доске класса сотня, и шашки проверяют правильность выполнения всех операций.
- Ведущий задает вопросы или обсуждает, затем просит читателя прочитать следующую подсказку, и процесс повторяется.
- Когда группа закончила и пришла к одному ответу, модель предлагает читателю перечитать ключ за ключом к проблеме. Студенты должны показать большой палец вверх / большой палец вниз, что их ответ соответствует этой подсказке. Обсудите со студентами, что, если потратить время на проверку своей работы подсказки на подсказку, они не смогут получить неправильный ответ, потому что, если их ответ неправильный, одна из подсказок не сработает.
- Затем ведущий приносит заполненную доску с обведенным кружком ответом учителю для проверки. Если да, дайте группе следующую задачу. Если ответ неверен, обведите подсказку, которая не работает, и попросите группу решить проблему еще раз.
- При необходимости проверьте роли совместной группы.
Совместная учебная группа по решению проблем:
- Раздайте материалы всем группам.
- Раздайте каждому читателю копию следующей задачи и дайте указания группам приступить к работе.
- Обходите комнату, пока студенты работают, чтобы убедиться, что все студенты активно участвуют и соблюдают назначенные роли.
- По мере того, как группа дает правильный ответ и метку, дайте им следующую задачу.
Запись логических задач для сотни плат:
- Когда группа завершит все задачи, им нужно дать пустые шаблоны, чтобы они могли начать писать свои собственные задачи по образцу задач, решаемых в классе.Они начинают с короткой аннотации, выбирают ответ, а затем записывают подсказки по одной, пока их ответ не станет единственным оставшимся числом.
- Каждый студент должен обменяться своей проблемой с партнером для редактирования. Каждый ученик решает проблему своего партнера, чтобы увидеть, согласен ли он / она с ответом или есть несоответствия, которые необходимо разрешить.
- Попросите учеников опубликовать задачи со своими именами, классом и учебным годом, чтобы вы накопили банк этих задач для будущих учеников.
Дайте учащимся больше практики в использовании доски сотен для решения задач с числами. И снова ученики решают проблему ключ за ключом. Однако с этим набором учащиеся должны использовать умножение, деньги и факты измерения, чтобы правильно решить задачу и угадать число.
Пример задачи: Угадай число-1
- Число больше, чем количество пенсов в квартале.
- Число меньше, чем количество пенсов в пяти центов.
- Число нечетное.
- Если вы считаете по 5, вы произносите число.
- Сумма цифр 8.
- Какой номер?
Предлагаемое использование:
- Сделай сейчас! или разминка
- Деятельность математического центра
- Решение проблем в игровые дни
- Написание оригинальных задач «Угадай число» для коллекции классов
Книга по математике 4B для учащихся 4-х классов
Обязательно возьмите путеводители, потому что они милые, интересные, очаровательные и замечательные, и они заставят вашего ребенка влюбиться в математику (даже если он уже любит математику)
Я действительно впечатлен тщательностью и детализацией, не только математическим мышлением, но и визуальными эффектами, юмором и сюжетом.
… реакция, которую я видел, была действительно потрясающей. Что, кажется, выделяется … в этих книгах не преуменьшает объем работы и не разговаривает с ребенком свысока.
… каждый раз, когда ученики видят меня, они очень взволнованы и спрашивают, не «День Академии Зверей». Им нравятся персонажи, им нравится юмор в Путеводителе, и они упорно стараются заполнить как можно больше материала из Практического пособия.
Моему сыну очень нравится эта программа … никогда не думал, что мне придется говорить ему, чтобы он сделал перерыв в математике, чтобы заняться другой работой.
Я почти уверен, что это самые увлекательные книги по математике, с которыми я когда-либо сталкивался, и они справляются с этим, совсем не разбавляя содержание (на самом деле, как раз наоборот).
Самое лучшее для меня то, что мои дети могут читать руководство и выполнять практическую работу самостоятельно, но я знаю, что им бросают вызов.
Слышать, как мой крохотный шестилетний ребенок объясняет, как возводить в квадрат числа, оканчивающиеся на 5, было потрясающе … Благодаря Beast Academy у меня теперь есть возможность наблюдать, как лицо моего сына загорается, когда я говорю, что пора заниматься математикой.
Академия зверей стала известна как «увлекательная математика» — она была полна сложных задач, которые заставляли их думать просто, чтобы усердно заниматься вычислениями.
Обожаю ваши книги! Это лучшее, что когда-либо случалось с математикой. Лиззи — мой любимый персонаж, потому что она очень похожа на меня. Она такая милая, нежная и не любит драконов!
Я упомянул, что [мой сын] почти готов перейти на следующий уровень Академии Зверей. Сразу же [он] пошел и получил его, чтобы мы могли сразу начать, а затем попросил, чтобы я продолжал заниматься после первого раздела.
Обязательно возьмите путеводители, потому что они милые, интересные, очаровательные и замечательные, и они заставят вашего ребенка влюбиться в математику (даже если он уже любит математику)
Стратегии решения математических задач со словами
Математические задачи со словами могут быть непростыми, и зачастую их сложно решить. Использование метода SQRQCQ может упростить и упростить решение математических задач со словами.Метод SQRQCQ особенно полезен для детей с ограниченными возможностями обучения и может эффективно использоваться в программах специального образования. SQRQCQ — это сокращение от Survey, Question, Read, Question, Compute и Question.
Шаг 1. ИССЛЕДОВАНИЕ математической задачи
Первый шаг к решению задачи с математическим словом — прочитать задачу целиком, чтобы понять, что вас просят решить. Прочитав его, вы сможете решить, какие аспекты проблемы необходимо решить, а какие не имеют отношения к решению проблемы.Идея здесь в том, чтобы получить общее представление.
Шаг 2 — ВОПРОС
Как только у вас появится представление о том, что вы пытаетесь решить, вам нужно определить, какие формулы, шаги или уравнения следует использовать, чтобы найти правильный ответ. Невозможно найти ответ, если не можешь определить, что нужно решить. Собственно, какие вопросы задает проблема?
Шаг 3 — ПЕРЕЙТИ
Теперь, когда вы определили, что необходимо решить, перечитайте проблему и обратите особое внимание на конкретные детали.Определите, какие аспекты проблемы взаимосвязаны. Определите все относящиеся к делу факты и информацию, необходимые для решения проблемы. Как вы это делаете, запишите их.
Шаг 4 — ВОПРОС
Теперь, когда вы знакомы с конкретными деталями и тем, как взаимосвязаны различные факты и информация в рамках проблемы, определите, какие формулы или уравнения необходимо использовать для постановки и решения проблемы. Обязательно запишите, какие шаги или операции вы будете использовать для удобства.
Шаг 5 — ВЫЧИСЛИТЬ
Используйте формулы и / или уравнения, указанные на предыдущем шаге, для завершения расчетов. Обязательно следуйте указанным вами шагам при создании уравнения или использовании формулы. Выполняя каждый шаг, вычеркивайте его из своего списка.
Шаг 6 — ВОПРОС
После завершения расчетов проверьте окончательный ответ и убедитесь, что он правильный и точный. Если это не кажется логичным, просмотрите шаги, которые вы предприняли, чтобы найти ответ, и найдите ошибки расчетов или настройки.Пересчитайте числа или внесите другие изменения, пока не получите разумный ответ.
Как SQRQCQ помогает учащимся с ограниченными возможностями обучения?
Математические задачи со словами, как правило, являются особенно сложными для учащихся с ограниченными возможностями обучения (LD). Студентам LD часто не хватает «концептуальных образов» или способности визуализировать всю проблему, создавая законченный мысленный образ. Они часто сразу переходят к вычислениям и вычислениям, не понимая, в чем проблема или что они ищут.
Студенты LD также могут испытывать трудности с правильным пониманием слов или формулировок в математических задачах со словами. Неспособность правильно интерпретировать и понимать формулировки сильно влияет на их навыки математического мышления и часто приводит к неправильным расчетам и неправильным выводам.
Запоминание и манипулирование информацией и деталями в своей рабочей памяти — еще одна проблема, с которой сталкиваются некоторые студенты LD, пытаясь увидеть полную картину.Медленная обработка информации, сопровождаемая разочарованием и тревогой, часто побуждает студентов LD пытаться решать математические задачи как можно быстрее — вот почему они часто сразу переходят к вычислениям, пытаясь так быстро добраться до финиша. насколько возможно.
SQRQCQ — это метакогнитивное руководство, которое предоставляет студентам LD из логического порядка решения математических задач со словами. Он дает им достаточно направления, чтобы вести их через процесс рассуждений, не перегружая их.SQRQCQ — это также мнемоника, которую легко запомнить учащимся, и к которой они могут прибегнуть при выполнении домашних заданий или сдаче тестов.
Читайте также:
— Руководство по изучению математики
Что такое решение проблем? | NZ Maths
На этой странице мы обсуждаем «Что такое решение проблем?» под тремя заголовками: введение, четыре этапа решения проблем и научный подход.
Введение
Естественно, решение проблем — это решение проблем.И здесь мы ограничимся размышлениями о математических задачах, хотя решение задач в школе имеет более широкую цель. Если подумать, вся цель образования — научить детей решать проблемы. Таким образом, в учебной программе по математике решение проблем способствует развитию общих навыков решения проблем в рамках учебной программы Новой Зеландии.
Но решение задач также способствует развитию самой математики. Это часть единой области предмета, которая до недавнего времени оставалась незамеченной в школах по всему миру.Математика состоит из навыков и процессов. Навыки — это то, с чем мы все знакомы. К ним относятся основные арифметические процессы и связанные с ними алгоритмы. Они включают алгебру на всех ее уровнях, а также сложные области, такие как исчисление. Это сторона предмета, которая широко представлена в направлениях числа, алгебры, статистики, геометрии и измерения.
С другой стороны, математические процессы — это способы творческого использования навыков в новых ситуациях.Решение проблем — это математический процесс. Как таковое, его можно найти в Нити математических процессов вместе с логикой, рассуждением и коммуникацией. Это та сторона математики, которая позволяет нам использовать полученные навыки в самых разных ситуациях.
Прежде чем мы зайдем слишком далеко в обсуждение решения проблем, стоит отметить, что мы считаем полезным различать три слова «метод», «ответ» и «решение». Под «методом» мы подразумеваем средства, используемые для получения ответа.Обычно это включает одну или несколько стратегий решения проблем. С другой стороны, мы используем «ответ» для обозначения числа, количества или какой-либо другой сущности, о которой спрашивает проблема. Наконец, «решение» — это весь процесс решения проблемы, включая метод получения ответа и сам ответ.
метод + ответ = решение
Но как мы решаем проблемы? Кажется, есть четыре основных шага. Полиа провозгласил их в 1945 году, но все они были известны и использовались задолго до того.Мы имеем в виду , ну до этого. Древнегреческие математики, такие как Евклид и Пифагор, безусловно, знали, как это было сделано.
Четыре этапа решения проблем Поли перечислены ниже.
Четыре этапа решения проблемы
1. Понять и изучить проблему;
2. Найдите стратегию;
3. Используйте стратегию для решения проблемы;
4. Оглянитесь и подумайте над решением.
Хотя мы перечислили четыре этапа решения проблем по порядку, для сложных проблем может оказаться невозможным просто пройти их последовательно, чтобы получить ответ.Часто дети двигаются вперед и назад между ступенями и поперек них. Фактически, приведенная ниже диаграмма больше похожа на то, что происходит на практике.
Нет никаких шансов решить проблему, если вы не сможете сначала понять ее . Этот процесс требует не только знания того, что вам нужно найти, но и ключевых фрагментов информации, которые нужно каким-то образом объединить, чтобы получить ответ.
Дети (да и взрослые тоже) часто не могут усвоить всю важную информацию о проблеме за один раз.Практически всегда будет необходимо прочитать задачу несколько раз, как в начале, так и во время работы над ней. В процессе решения дети могут обнаружить, что время от времени им приходится возвращаться к исходному вопросу, чтобы убедиться, что они на правильном пути. С младшими детьми стоит повторить задачу, а затем попросить их сформулировать вопрос своими словами. Дети постарше могут использовать маркер, чтобы отметить и выделить наиболее полезные части проблемы.
Второй этап Полиа на поиск стратегии имеет тенденцию предполагать, что придумать подходящую стратегию довольно просто.Однако, безусловно, существуют проблемы, при которых дети могут счесть необходимым поиграть с информацией, прежде чем они смогут придумать стратегию, которая могла бы привести к решению. Эта исследовательская фаза также поможет им лучше понять проблему и может дать им представление о некоторой части информации, которой они пренебрегли после первого чтения.
Изучив проблему и определив план атаки, можно переходить к третьему этапу решения проблемы, решить проблему .Надеюсь, теперь проблема будет решена и ответ будет получен. На этом этапе детям важно следить за тем, что они делают. Это полезно, чтобы показать другим, что они сделали, а также для поиска ошибок, если правильный ответ не будет найден.
На этом этапе многие дети, особенно математически способные, останавливаются. Но стоит приучить их оглядываться назад на , что они сделали. Для этого есть несколько веских причин.Прежде всего, для них рекомендуется проверить свою работу и убедиться, что они не сделали никаких ошибок. Во-вторых, очень важно убедиться, что полученный ответ на самом деле является ответом на проблему, а не на проблему, которую, как они думали, задают. В-третьих, оглядываясь назад и немного подумав о проблеме, дети часто видят другой способ решения проблемы. Это новое решение может быть лучше, чем исходное, и может дать больше информации о том, что на самом деле происходит.Наконец, особенно лучшие ученики могут обобщить или расширить проблему.
Обобщение проблемы означает создание проблемы, в которой исходная проблема рассматривается как частный случай. Таким образом, задачу о трех свиньях можно превратить в одну с любым количеством свиней.
В задаче 4 раздела «Что такое проблема?» Есть проблема с башнями. Последняя часть этой задачи спрашивает, сколько башен можно построить для любой определенной высоты . Ответ на эту проблему будет содержать ответ на три предыдущих вопроса.Там нас спросили количество башен высотой один, два и три. Если у нас есть какая-то формула или выражение для любой высоты, то мы можем подставить в эту формулу, чтобы получить ответ, например, для высоты три. Таким образом, формула «любая» высота является обобщением случая высоты три. В качестве особого примера он содержит регистр высоты три.
Расширение проблемы — это родственная идея. Однако здесь мы сталкиваемся с новой проблемой, которая так или иначе связана с первой.Например, проблема, связанная с сложением, может быть рассмотрена, чтобы увидеть, имеет ли это какой-либо смысл с умножением. Хорошая задача — взять любое целое число и разделить его на два, если оно четное, умножить на три и добавить единицу, если оно нечетное. Продолжайте повторять эту манипуляцию. Ответ вы получите в конце концов 1? Приведем пример. Начнем с 34. Тогда получаем
34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1
Тогда мы, конечно, добрались до 1. Теперь выясняется, что никто в мире не знает, всегда ли вы доберетесь до 1 таким образом, независимо от того, с чего вы начнете.Вам есть о чем беспокоиться. Но причем тут расширение? Что ж, мы можем расширить эту проблему, сделать другую задачу, которая немного похожа на нее, просто изменив 3 на 5. Итак, на этот раз вместо деления на 2, если число четное, умножения его на три и добавления единицы, если оно нечетное, попробуйте деление на 2, если число четное, и умножение его на 5 и прибавление единицы, если оно нечетное. Эта новая проблема не рассматривает первую как частный случай, поэтому не является обобщением. Однако — это расширение — это проблема, которая тесно связана с оригиналом.Возможно, вы захотите увидеть, всегда ли эта новая проблема заканчивается цифрой 1. Или это просто?
Именно с помощью этого метода обобщения и расширения математика делает большие успехи. Вплоть до времен Пифагора было известно много прямоугольных треугольников. Например, было известно, что треугольник со сторонами 3, 4 и 5 был прямоугольным. Точно так же люди знали, что треугольники со сторонами 5, 12 и 13, а также 7, 24 и 25 имеют прямые углы. Обобщение Пифагора заключалось в том, чтобы показать, что КАЖДЫЙ треугольник со сторонами a, b, c был прямоугольным тогда и только тогда, когда a 2 + b 2 = c 2 .
Это подводит нас к аспекту решения проблем, о котором мы до сих пор не упоминали. То есть оправдание (или доказательство). Ваши ученики могут часто догадываться, каков ответ на проблему, но их решение не является полным, пока они не смогут обосновать свой ответ.
Сейчас некоторым проблемам трудно найти оправдание. В самом деле, вы можете поверить, что это не то, что может сделать никто из класса. Так что вы можете быть счастливы, что дети могут угадать ответ. Однако имейте в виду, что это оправдание отличает математику от любой другой дисциплины.Следовательно, этап обоснования важен, и его нельзя упускать слишком часто.
Научный подход
Другой способ взглянуть на процесс решения проблем — это то, что можно назвать научным подходом. Мы показываем это на диаграмме ниже.
Здесь задается проблема, и изначально идея состоит в том, чтобы поэкспериментировать с ней или изучить ее, чтобы получить некоторое представление о том, как действовать дальше. Через некоторое время есть надежда, что решатель сможет сделать предположение или угадать ответ.Если предположение верно, его можно будет доказать или оправдать. В этом случае начинается процесс оглядки назад, и делается попытка обобщить или расширить проблему. В этом случае вы, по сути, выбрали новую проблему, и поэтому весь процесс начинается заново.
Иногда, однако, предположение неверно, и поэтому находят контрпример. Это пример, противоречащий гипотезе. В этом случае ищется другая гипотеза, и вам нужно искать доказательство или другой контрпример.
Некоторые проблемы слишком сложны, поэтому необходимо отказаться от них. Теперь вы можете сдаться, чтобы отдохнуть, и в этом случае вы отказываетесь «на время». На самом деле это хорошая стратегия решения проблем. Часто, когда вы на какое-то время сдаетесь, ваше подсознание берет верх и придумывает хорошую идею, которой вы можете следовать. С другой стороны, некоторые проблемы настолько сложны, что в конце концов приходится «навсегда» отказаться от них. На протяжении всей истории математикам приходилось отказываться от множества сложных проблем.
Это приблизительный обзор того, что такое Решение проблем. Для простых задач четырехэтапный метод Полиа и научный метод можно выполнить без каких-либо затруднений. Но когда проблема сложна, часто требуется много усилий, прежде чем проблема будет окончательно решена — если это когда-либо произойдет!
Задачи с дробными словами | Примеры и решения
Сегодня мы рассмотрим несколько примеров словесных задач с дробями.
Хотя они могут показаться более сложными, на самом деле задачи со словами, включающие дроби, столь же просты, как и задачи с целыми числами.Единственное, что нам нужно сделать, это:
- Внимательно прочтите проблему.
- Подумайте, что он просит нас сделать.
- Подумайте, какая информация нам нужна.
- Реши.
- При необходимости упростите.
- Подумайте, имеет ли наше решение смысл (чтобы его проверить).
Как видите, единственная разница в задачах с дробными словами — это , шаг 5 (упрощение) .
Есть некоторые проблемы со словами, которые, в зависимости от предоставленной информации, мы должны выражать дробью.Например:
В моей корзине с фруктами 13 кусков фруктов, 5 из которых — яблоки.
Как можно выразить количество яблок дробью?
5 — Количество яблок (5) соответствует числителю (число, которое выражает количество частей, которые мы хотим представить).
13 — Общее количество плодов (13) соответствует знаменателю (число, которое выражает общее количество возможных частей).
Решением этой проблемы является неприводимая дробь (дробь, которую нельзя упростить). Поэтому делать нечего.
Word задачи с дробями: с участием двух дробей
В этих задачах мы должны помнить, как проводить операции с дробями.
Внимательно прочтите следующую проблему и шаги, которые мы предприняли для ее решения:
Мария потратила деньги, которые дали ей дедушка и бабушка, на книгу о приключениях.Также она потратила деньги на мешок конфет.
Какую часть платежа израсходовала Мария?
Находим общий знаменатель:
Рассчитываем:
Ответ:
Word задачи с дробями: с участием дроби и целого числа
Наконец, мы рассмотрим пример задачи со словами с дробью и целым числом.Теперь нам нужно будет преобразовать всю информацию в дробь с тем же знаменателем (как в примере выше), чтобы вычислить
.
Этим утром Мигель купил фунт анчоусов. Чтобы поесть вместе со своей семьей, он использовал фунт. Сколько у него осталось в холодильнике?
Преобразуем 1 в дробь с тем же знаменателем:
Рассчитываем:
Ответ:
Что вы думаете об этом сообщении? Вы видите, как легко решать задачи со словами с помощью дробей?
Чтобы продолжить обучение, попробуйте бесплатную пробную версию Smartick.

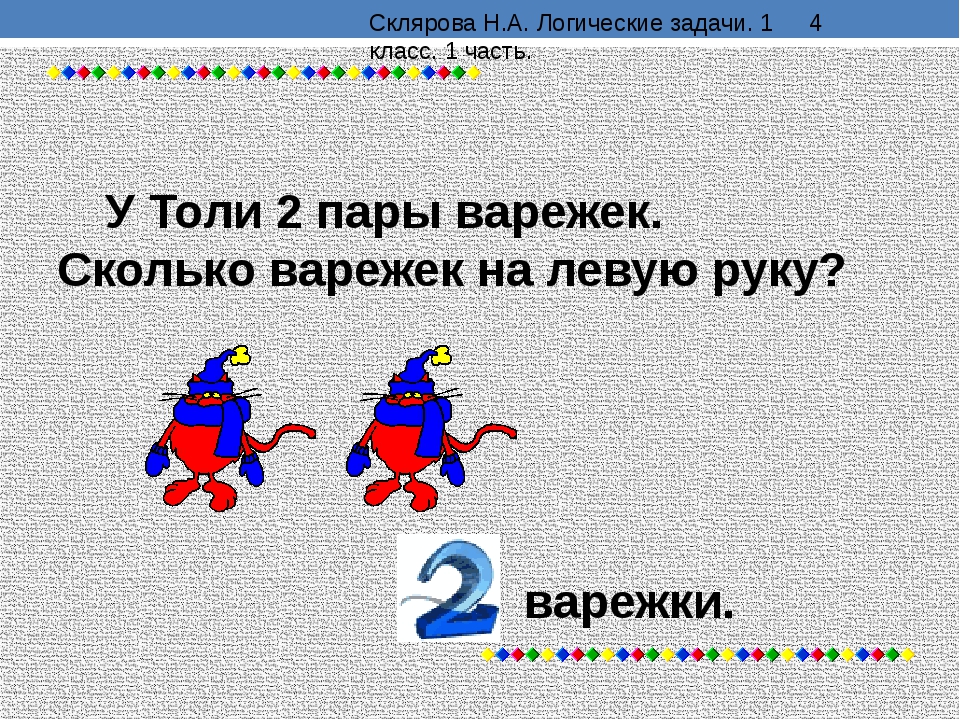

 Найди значение выражения (30 + 70) ∙ 6
Найди значение выражения (30 + 70) ∙ 6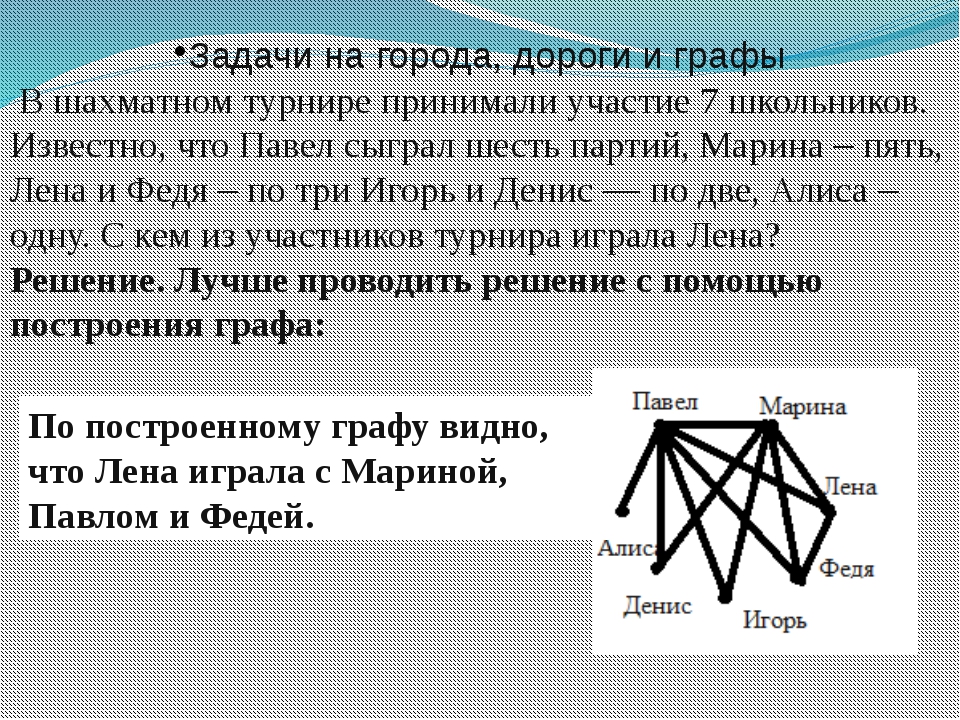
 Найди, какое расстояние пройдёт поезд за 7 ч, если его скорость всё время будет 80 км/ч
Найди, какое расстояние пройдёт поезд за 7 ч, если его скорость всё время будет 80 км/ч Выполни вычисления и выбери правильный ответ: 7961 х 84
Выполни вычисления и выбери правильный ответ: 7961 х 84 1км², 1м², 1см², 1мм², 1дм² – это единицы измерения…
1км², 1м², 1см², 1мм², 1дм² – это единицы измерения… Чему равен квадрат числа 6?
Чему равен квадрат числа 6? Динара купила 4 ручки по 50 тенге. Сколько тенге уплатила Динара за покупку?
Динара купила 4 ручки по 50 тенге. Сколько тенге уплатила Динара за покупку? Значение суммы чисел 52976 и 48679 равно
Значение суммы чисел 52976 и 48679 равно Укажи число, которое нужно вставить вместо пропуска: 3 т 35 кг = … кг
Укажи число, которое нужно вставить вместо пропуска: 3 т 35 кг = … кг Сколько времени затратил велосипедист, если он проехал 65 км с одной и той же скоростью 13 км/ч?
Сколько времени затратил велосипедист, если он проехал 65 км с одной и той же скоростью 13 км/ч? Чему равна ширина комнаты?
Чему равна ширина комнаты? . Выполни вычисления и выбери правильный ответ: 4524 х 56
. Выполни вычисления и выбери правильный ответ: 4524 х 56 В схеме выражения ∙ + : — надо выполнять действия в таком порядке:
В схеме выражения ∙ + : — надо выполнять действия в таком порядке: Укажи значение выражения 80 : а + 5, если а = 20.
Укажи значение выражения 80 : а + 5, если а = 20. 4 книги стоят 800 тенге. Сколько таких же книг можно купить на 1 200 тенге?
4 книги стоят 800 тенге. Сколько таких же книг можно купить на 1 200 тенге? Какое из этих равенств неверное?
Какое из этих равенств неверное? Какая пара наименований единиц величин сделает равенство 8__ = 800 __ верным, если наименования брать в том порядке, как они записаны?
Какая пара наименований единиц величин сделает равенство 8__ = 800 __ верным, если наименования брать в том порядке, как они записаны? Укажи значение неизвестного в уравнении 870 – х = 240 + 30.
Укажи значение неизвестного в уравнении 870 – х = 240 + 30. Найди площадь квадрата, периметр которого равен периметру прямоугольника со сторонами 15см и 5см.
Найди площадь квадрата, периметр которого равен периметру прямоугольника со сторонами 15см и 5см. Выполни вычитание 285960-63729
Выполни вычитание 285960-63729 Дидактический материал. Математика.
Дидактический материал. Математика.