100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?
— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.
Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.
— Расскажите поподробнее?
— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
— Система оценивания останется прежней?
— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.
— А апелляция?
— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.
— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?
— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?
— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
— На сколько процентов будет обновлена база вопросов?
— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.
Но по каждому предмету будут контекстные вопросы.
— По вашему мнению система справится с возможными хакерскими атаками, взломами?
— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.
— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?
— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.
— Сколько человек будет сидеть в одной аудитории?
— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.
— Будут ли ужесточены требования по дисциплине, запрещенным предметам?
— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.
— А наблюдатели будут присутствовать во время сдачи тестирования?
— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.
— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?
— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.
— Сколько средств выделено на проведение ЕНТ в этом году?
Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.
— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?
— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
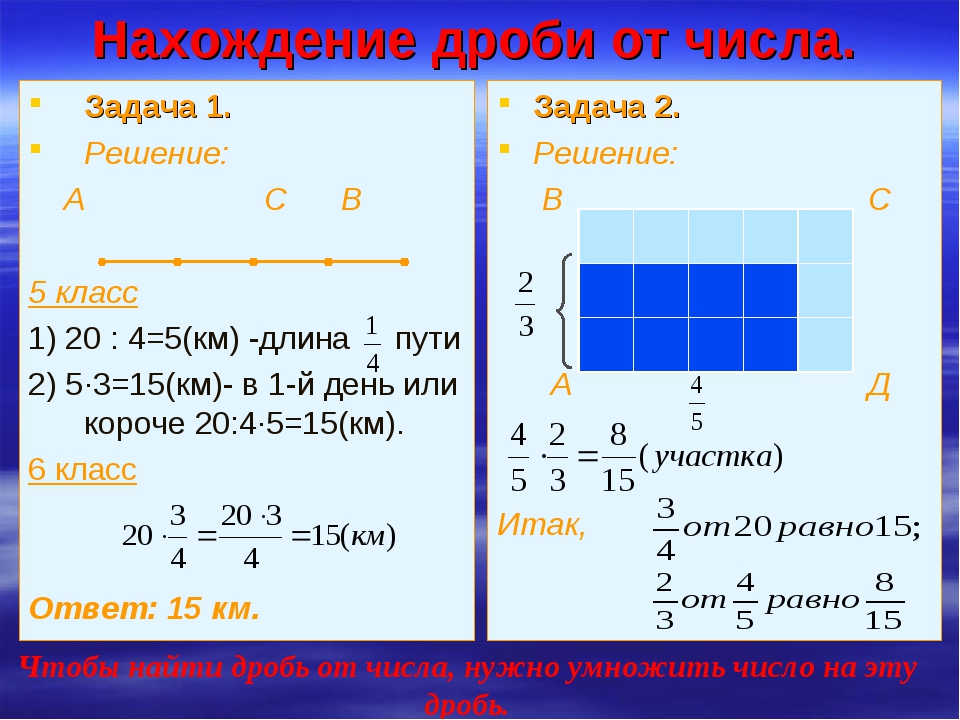
«Решение текстовых задач с помощью умножения и деления»
УРОК № 33 19.10.2017
Тема: Решение текстовых задач с помощью умножения и деления.
Цели:
-продолжить работу по приучению школьников к решению задач арифметическими способами;
-научить решать задачи с вопросами;
-формирование умение ставить цели учебной деятельности стремления добиваться их;
-развитие мышления.
Тип урока: урок открытия новых знаний
План урока
Организационный этап
Постановка цели и задач урока. Мотивация учебной деятельности учащихся
Открытие новых знаний
Первичное усвоение новых знаний
Физкультминутка
Первичное закрепление
Информация о домашнем задании, инструктаж по его выполнению
Рефлексия (подведение итогов занятия)
Ход урока
1.Организационный момент
Приветствие, проверка готовности к уроку
2. Постановка цели и задачей урока. Мотивация учебной деятельности учащихся
Тема нашего урока Решение задач. А что нужно уметь и знать для этого? (Складывать, вычитать, умножать, делить натуральные числа. Внимательно читать текст задачи).
А что нужно уметь и знать для этого? (Складывать, вычитать, умножать, делить натуральные числа. Внимательно читать текст задачи).
Создать условия для усвоения нового материала.
1).Устный счет (Вычислите наиболее рациональным способом)
26*11 63*11
6300:100 72:6
45*7*2 6800:200
520:26 510:17
210:30 170:10
900:100
3.Открытие новых знаний
Кто же поможет нам научиться решать задач?
Наш главный помощник-учебник по математике.
Откройте страницу 43 учебника. Разберите в парах решение задачи №1. Подготовьте выступление от пары объяснения решения этой задачи.
Самостоятельная работа в парах по изучению решения задачи №1
Задача №1: Число 50 увеличили в 3 раза, полученное число увеличили на 100. Во сколько раз увеличили число 50 за два раза?
Решение:
50*3=150-число, полученное после первого увеличения;
150+100=250-число, полученное после второго увеличения;
250:50=5 (раз)-во столько раз увеличили число 50 за два раза.

Ответ: в 5 раз.
4. Первичное усвоение новых знаний
А сейчас мы с вами научимся решать задачи с вопросами. Откройте задачи. Внимательно прочитайте условие задачи №1. (смотри приложение)
Что нужно найти в задаче?
Можно ли сразу ответить на вопрос задачи?
Что нужно найти в первом действии задачи? Первый вопрос к этой задаче сформулирован. Прочитайте его, запишите вопрос и ответьте на него.
Что нужно найти во втором действии задачи?
Запишите вопрос и ответьте на него. Запишите ответ к задаче
Один ученик работает у доски, остальные в тетради.
Решите задачу №2 самостоятельно с вопросами. Проверить устно
5. Физкультминутка
Видеоролик
6. Первичное закрепление
К выбору умножения и деления для решения задачи нужно подходить очень внимательно, так как, например, слова «в 3 раза больше» не всегда требует умножения.
Прочитайте внимательно задачу 2 из учебника на странице 44. Внимательно разберите решение задачи 2 из учебника, сформулируйте вопросы к действиям. Прочитайте эти вопросы.
Внимательно разберите решение задачи 2 из учебника, сформулируйте вопросы к действиям. Прочитайте эти вопросы.
Задача 2. Некто прочитал 90 страниц книги, это в 3 раза больше, чем ему осталось прочитать. Сколько страниц в книге?
Решение. Прочитано в 3 раза больше страниц, чем осталось прочитать, поэтому осталось прочитать в 3 раза меньше, чем уже прочитано.
Сколько страниц осталось прочитать?
1) 90:3=30(стр)-осталось прочитать
Сколько страниц в книге?
2) 90+30=120 (стр)-в книге
Ответ: 120 страниц
Найдите на карточке задачу, решаемую аналогично задаче2 из учебника. ( задача №3 (смотри приложение)). Решите эту задачу самостоятельно с вопросами. Двое решают за доской, остальные в тетради.
Прочитайте внимательно задачу №4 из карточки (смотри приложение). Чем похожа эта задача и чем отличается от задачи №3?
Какой можно задать 1 вопрос к задаче? Запишите вопрос.
Какой можно задать 2 вопрос к задаче? Запишите вопрос.
Прочитайте вопрос к задаче. Как на него ответить? Запишите вопрос.
Ответьте на вопросы к задаче. Запишите ответ. Проверить устно
Для тех, кто решает быстрее + № 198, 199, 207
7. Информация о домашнем задании, инструктаж по его выполнению
№ 201, 211 (для тех, у кого 5 +№ 214)
8.Рефлексия (подведение итогов занятия)
Что нового узнали на уроке?
Что вам показалось сложным на уроке?
Всегда ли в задачах слова «в 3 раза больше» требуют умножения?
Урок «Задачи на совместную работу» 5 класс
Задачи на совместную работу»
Тип урока: открытие новых знаний.
Основные цели:
- сформировать умение решать задачи на совместную работу по формуле и с использованием таблицы в простейших случаях;
- повторить и закрепить понятие степени числа, навыки вычисления в дробных выражениях.

Планируемые результаты:
Личностные
— развивать умение слушать; ясно, точно, громко излагать свои мысли в устной и письменной речи;
— развивать креативность мышления, инициативу, находчивость, активность при решении математических задач;
— формулировать представления о математике как способе познания.
Метапредметные: развивать умение видеть математическую задачу в конспекте проблемной ситуации в других дисциплинах, в окружающей жизни; формировать умение работать в группах.
Предметные: развивать умение работать с математическим текстом (анализировать, извлекать необходимою информацию).
Формы работы учащихся: групповая, индивидуальная.
Демонстрационные материалы: презентация, фрагмент мультфильма, шаги алгоритма, задачи на части(схемы).Приложение
Раздаточный материал: таблицы пустые 4 шт. для каждого ученика, цветные полоски для проведения рефлексии(по три цвета для каждого), маркеры( 1 на стол)Содержание:
для каждого ученика, цветные полоски для проведения рефлексии(по три цвета для каждого), маркеры( 1 на стол)Содержание:
Этап урока
Деятельность учителя
- Мотивация и самоопределение к учебной деятельности
Посмотрите всё ль в порядке ?
Книжка, ручка и тетрадка?
Все ли правильно сидят ?
Все ли правильно глядят ?
Прозвенел сейчас звонок –
начинается урок !
—Ребята! Сегодняшний урок я предлагаю вам провести в деревне Простоквашино с любимыми героями российского мультфильма.
-Откройте тетради, запишите дату, «Классная работа».
Записывают в тетрадях дату и «Классная работа».
-А начать урок я хочу словами французского философа и математика Рене Декарта:
«Для того чтобы усовершенствовать ум, надо больше размышлять, чем заучивать»
-Как вы думаете, почему он так сказал? Нам с вами нужно уметь размышлять?
-Потому что простое заучивание приносит меньше пользы, чем то знание, до которого додумываешься сам.
-Правильно. Если бы люди не размышляли, то никогда не сделали великих открытий — не полетели бы в космос, не изобрели бы компьютера и т. д.
-Поэтому нам с вами нужно уметь размышлять.
- А вы хотите узнавать новое?
- А как считаете,сможете это сделать?
- Актуализация и фиксирование индивидуального затруднения в пробном действии
-Чтобы узнать что-нибудь новое, надо вспомнить старые знания, которые пригодятся нам для открытия нового знания.
— Угадайте ключевое слово всех наших последних занятий. У меня есть три подсказки:
В словаре С.И. Ожегова о нем написано так:
– это частые прерывистые звуки…;
– это мелкие свинцовые шарики для стрельбы из охотничьего ружья…;
– она может быть правильной или неправильной, обыкновенной или десятичной.
Это слово: ДРОБЬ.
—
Решим несколько задач на дроби по готовым схемам: (схемы вывешиваю на магнитах на доску)
(остальные работают в тетрадях)
-Теперь вспомним как решать небольшие дробные выражения:(вывешиваю на магнитах на доску)
Далее три человека у доски решают дробные выражения:(остальные работают в тетрадях, проверяют отвечающих у доски)
-У вас в домашнем задании была задача на работу :
Героям «Простоквашино» надо заготовить на зиму 90 поленьев дров. Матроскин с д.Фёдором могут выполнить эту работу за 10 часов, а Шарик — за 15 часов. За какое время выполнят эту работу наши герои, если будут работать все вместе?
Матроскин с д.Фёдором могут выполнить эту работу за 10 часов, а Шарик — за 15 часов. За какое время выполнят эту работу наши герои, если будут работать все вместе?
—Справились? Заполните таблицу на экране. Объясните своё решение.
-Как называются задачи. Где кто-то выполняет некоторые действия, работает?
-Задачи на работу.
-А как назвать задачи,где идёт речь о работе сразу нескольких объектах?
-Задачи на совместную работу.
-Как вы считаете, в жизни встречаются такие ситуации, когда лучше работать вместе, чем по-одному?
-Да. Вместе работа выполняется быстрее, легче,веселее.
-Вот и кот Матроскин утверждает:
(видеофрагмент мультфильма «Совместный труд….»)
-Итак, запишите тему сегодняшнего урока «Задачи на совместную работу».
-Записывают тему урока в тетрадях.
-Если вы так успешно справились с домашней задачей, то может и со следующей справитесь быстро?
Почтальон Печкин может съесть коробку конфет за 2 минуты, Матроскин — за 3 минуты, а Галчонок — за 6 минут. За сколько минут они «уплетут» все конфеты вместе?
За сколько минут они «уплетут» все конфеты вместе?
-Пытаются решить задачу, используя таблицу.
-Что у вас получилось? (выслушиваю варианты ответов)
3.Выявление места и причины затруднения
-Почему ответы разные? В чём состоит затруднение?
-Мы не знаем объём работы
4.Построение проекта выхода из затруднения
-Тогда сформулируйте цель нашего урока.
- Вывести алгоритм решения задач на совместную работу, где неизвестен объём работы.
- Научиться решать задачи на совместную работу, где неизвестен объём работы.
5.Реализация построенного проекта
-Действительно, не всегда в задачах на совместную работу известен объём работы, или его невозможно выразить в каких-то единицах измерения. Например,построить дом, сделать домашнее задание, сделать уборку в квартире и т. д.
- Как же тогда можно обозначить всю целую выполненную работу?
- Её можно обозначить единицей.

- А чем тогда выразится производительность?
- Частью.
- Попробуйте теперь заполнить таблицу к предложенной задаче в пробном действии.
Заполняют таблицу, пробуют решить её.
- Теперь из предложенных шагов составьте алгоритм решения таких задач.
Выходят к доске. Расставляют шаги алгоритма в правильном порядке.
Физминутка
-Давайте немного отвлечёмся от математики и разомнём свои мышцы.
Выше, выше подтянитесь,
Ну — ка плечи распрямите,
Поднимите, отпустите,
Вправо, влево поверните,
Рук, коленями коснитесь…
И тихонечко садитесь.
6.Первичное закрепление с проговариванием во внешней речи.
-Итак, инструмент для решения таких задач у нас теперь есть. Значит ли, что мы уже умеем их решать?
-Нет. Надо потренироваться подействовать по этому алгоритму.
-Итак, решим следующие задачи, используя алгоритм и готовые пустые таблицы.
Корова сама может съесть стог сена за 3 месяца, а телёнку хватило бы его на 6 месяцев. Хватит ли им на двоих этого стога на два месяца?
Выходят к экрану, заполняют таблицу. Дорешивают задачи.
Дядя Фёдор сам может убрать дом за 12 часов, Матроскин — за 15 часов, а Шарик — за 20 часов.Узнав,что с курорта едут родители, они решили сделать уборку все вместе. Сколько времени у них уйдёт на это?
7.Самостоятельная работа с самопроверкой по эталону.
-Ну что? Научились?
-А как проверить?
—Решить самостоятельно.
-Правильно, следующую задачу вы решаете самостоятельно и затем сами себя проверите, сверившись с эталоном.
Папа может сам вымыть всю посуду за 12 минут, а мама — за 6 минут. За какое время они вымоют посуду, если объединят свои усилия?
Выполняют самостоятельную работу.
Проверяют себя по эталону.
-Молодцы! Почти все справились успешно.
8.Включение в систему знаний и повторение.
-В оставшееся время предлагаю повторить ранее пройденный материал.
№ 579 из учебника.
Дробное выражение, записанное заранее на доске:
(4 5/8 * 3 1/5 + 4 5/8 * 2 4/5) / ( 4 5/8 * 6/7)
Выставляем оценки.
9.Рефлексия учебной деятельности.
-Вспомните цель нашего урока.
-Достигли ли мы её?
-Запишите домашнее задание: № 612, 613; по желанию на отдельную оценку творческое задание «Придумать задачу на совместную работу с героями любимых мультфильмов и сделать к ней рисунок»
-А теперь вспомните весь сегодняшний урок, вспомните, как работали вы, что у вас получилось, что — нет, что было новым, а что просто вспомнили.
-Рефлексию урока предлагаю вам провести необычно.-На экране вы видите облако слов. Выберите из него одно или два слова, которые наиболее точно отражают ваши ощущения от урока.
-Напишите выбранное слово крупно печатными буквами на цветной полоске и прикрепите его на ватман.
Пишут маркерами на цветных полосках выбранные слова и приклеивают в листу ватмана.
-Таким образом у нас получилось «Облако слов» нашего урока.
-Спасибо всем за совместную работу!
Урок по теме «Среднее арифметическое» 5 класс
Урок по теме «Среднее арифметическое» 5 класс
Автор: edu1
Методическая копилка —
Математика
Тема урока: «Среднее арифметическое»
Учебник:
Авт. Виленкин Н.Я. и др.
5 класс
учитель математики
МКОУ «Замостянская сош»
Селитренникова Галина Алексеевна
Цели урока
Образовательные:
- ввести понятие среднего арифметического; вывести правило для его нахождения;
- научить решать задачи, связанные с нахождением среднего арифметического;
- отрабатывать навыки действий с десятичными дробями;
- развивать умение составлять задачи, используя цифровые данные из жизни.

Развивающие:
- содействовать развитию у школьников логического мышления, математической речи;
- способствовать развитию познавательного интереса;
- развивать умение анализировать, делать выводы на основе полученных результатов;
- способствовать формированию правильной математической речи;
- создать условия для развития у учащихся умений осуществлять самоконтроль и самооценку учебной деятельности.
Воспитательные:
- содействовать осознанию учащимися ценности изучаемого предмета;
- активизировать познавательную и творческую деятельность учащихся;
- показать значение математических знаний в жизни, побудить применять эти знания в жизни.
Тип урока: урок открытия новых знаний.
Формы работы: индивидуальная, фронтальная, групповая.
Оборудование: презентация к уроку, проектор, экран.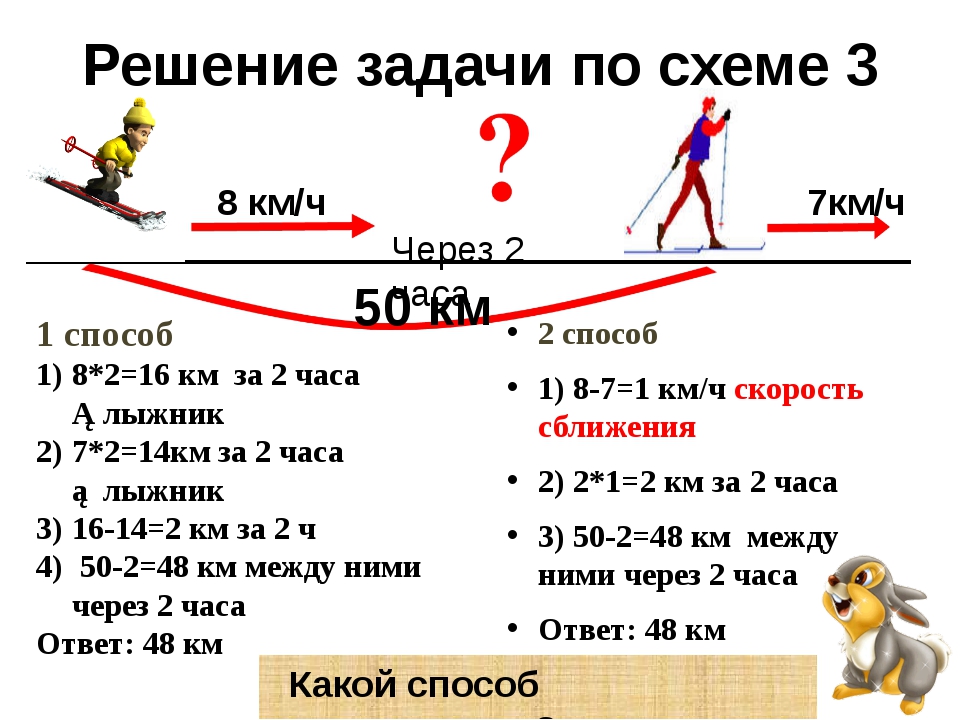
Предварительная подготовка.
Для эффективности работы было дано предварительное домашнее задание:
- класс поделен на 3 группы по рядам;
- измерить и записать рост каждого обучающегося в группе.
Ход урока:
I. Мотивирование к учебной деятельности (организационный момент) — 1-2 минуты
Посмотрите, всё ль в порядке:
Книжки, ручки и тетрадки.
Прозвенел сейчас звонок.
Начинается урок.
Учитель приветствует обучающихся, проверяет готовность к уроку, отмечает отсутствующих.
Каждый ученик получает лист «Моё настроение», на котором отмечает смайлик, соответствующий его настроению.
II.Актуализация и фиксирование индивидуального затруднения в пробном учебном действии — 4-5 минут
1. Устное решение задач.
Устное решение задач.
Задача 1.
У Иванова Ивана по математике в журнале стоят оценки
4 5 3 4 5 4 3 3 4
Как вы думаете, какую оценку в четверти получит Иван? И почему?
Задача 2.
К доске приглашаются три ученика.
Вопросы:
Кто самый высокий?
Кто самый низкий?
Кто средний по росту?
Какие «особенные слова» вы заметили в условиях всех задач?
Часто мы и в жизни слышим фразы со словом “средний”, например: средний возраст, средний рост, средняя температура и т.д. Как вы понимаете эти выражения?
В математике тоже есть свои понятия со словом “средний” и сегодня мы познакомимся с одним из этих понятий.
2. Устный счёт.
Тема сегодняшнего урока состоит из двух слов. Вы её сможете прочитать, если верно решите примеры и вставите буквы в таблицу ответов.
7,3 · 3 Е
64,24 : 8 А
12 – 2,6 И
68,2 : 2 О
45,4 + 0,6 С
12 · 0,1 Р
43,1 · 10 Д
81,1 : 0,1 Н
60 – 0,9 Ф
4,13 + 3,87 М
6,45 – 6,4 Т
0,1 · 0,1 К
7 · 0,01 Ч
|
46
|
1,2
|
21,9
|
431
|
811
|
21,9
|
21,9
|
|
|
|
|
|
|
|
|
|
8,03
|
1,2
|
9,4
|
59,1
|
8
|
21,9
|
0,05
|
9,4
|
0,07
|
21,9
|
46
|
0,01
|
34,1
|
21,9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
III. Постановка учебной задачи — 4-5 минут
Постановка учебной задачи — 4-5 минут
Ребята, назовите тему урока. («Среднее арифметическое»)
Запишем число и тему урока.
Рассмотрим задачу:
У Ани 14 конфет, у Кати 9 конфет, а у Оли 10 конфет. Сколько конфет достанется каждой девочке, если конфеты разделить между ними поровну?
Решение обсуждается с учащимися.
14 + 9 + 10 = 33 (конфеты)
33 : 3 = 11 (конфет)
Число 11 называют средним арифметическим чисел 14; 9 и 10.
Рассмотрим еще задачу :
Миша, Петя и Коля были в походе. Подойдя к лесу, они решили сделать привал. У Миши было 2 пирожка, у Пети 4 и у Коли 6. Все пирожки мальчики разделили поровну и съели. Сколько пирожков съел каждый?
Совместно с учащимися получается:
2 + 4 + 6 = 12 (пирожков)
12 : 3 = 4 (пирожка)
Число 4 называется средним арифметическим чисел 2; 4 и 6.
Ребята, что же называется средним арифметическим чисел? ( Ответы учащихся)
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
Как найти среднее арифметическое нескольких чисел? (Ответы ребят)
Среднее арифметическое = (Сумма чисел) : (количество слагаемых)
(Учащиеся записывают в тетрадях)
IV. Открытие нового знания (построение проекта выхода из затруднения) 7-8 минут
Из какой сказки вы прослушали отрывок?
1. Братья сеяли три поля по 200 га каждое. На первом поле собрали 7220ц пшеницы, на втором – 7560ц, а на третьем – 7090ц пшеницы. Определите урожайность на каждом поле и найдите среднюю урожайность.
Вопросы:
Как найти урожайность одного поля?
Как найти среднюю урожайность трёх полей?
7220 : 200 = 36,1(ц.) – урожайность на первом поле.
7560 : 200 = 37,8(ц.) – урожайность на втором поле.
7090 : 200 = 35,45(ц.) – урожайность на первом поле.
(36,1 + 37,8 + 35,45) : 3 = 36,45(ц.) – средняя урожайность трёх полей.
- Задание на сообразительность:
Подключите свои знания, смекалку, сообразительность, чувство юмора и попытайтесь отыскать «среднее арифметическое» не чисел, а предметов, которые нас окружают.
Итак, среднее арифметическое:
- Велосипеда и мотоцикла. (Мопед.)
- Трамвая и поезда. (Электричка.)
- Апельсина и лимона. (Грейпфрут.)
- Туфельки и сапога. (Ботинок.)
- Пианино и баяна. (Аккордеон.)
- Холодильника и вентилятора. (Кондиционер.)
- Портфеля и рюкзака. (Ранец.)
- Носка и чулка. (Гольф.)
V. Первичное закрепление — 4-5 минут
1. Задача № 1502 (из учебника)
Участница соревнований по фигурному катанию на коньках получила оценки
5,3; 4,8; 5,4; 5,0; 5,3; 5,4; 5,3; 5,2; 5,1.
Найдите среднюю оценку этой участницы.
Как найти среднее арифметическое нескольких чисел?
Решение с коментированием:
(5,3 + 4,8 + 5,4 + 5,0 + 5,3 + 5,4 + 5,3 + 5,2 + 5,1) : 9 = 5,2
2.Задача № 1504 (из учебника)
Поезд шёл 4 ч со скоростью 70 км/ч и 3ч со скоростью 84 км/ч. Найдите среднюю скорость поезда на пройденном за это время пути.
Как найти среднюю скорость?
Решение у доски по действиям или выражением:
(70 · 4 + 84 · 3) : 7 = 76(км/ч)
Средняя скорость =(Весь пройденный путь): (всё время движения).
3. Игра – задание «Полёт в космос»
А сейчас мы с вами отправимся в космос, посетим планету Меркурий. Но до полета надо размяться, привести себя в форму, космическую.
Физминутка
Быстро встали, улыбнулись
Выше-выше потянулись.
Ну-ка, плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
Сели, встали. Сели, встали.
И на месте побежали.
Известно, что на планете Меркурий средняя температура +15°. Можно предположить, что возможна жизнь человека на этой планете. Но на самом деле температура на Меркурии колеблется от 150º мороза до 350°жары.
VI. Самостоятельная работа с самопроверкой по образцу (эталону) — 4-5 минут.
Тест по теме: «Среднее арифметическое чисел»
Ответ на вопрос обведите кружком
1. Найдите среднее арифметическое чисел 1,5 и 2,3
а) 1,9 б) 3,8 в) 3
2. Среднее арифметическое чисел 2, 4, 6, и 0 равно:
а) 3 б) 6 в) 4
3. Незнайка по математике получил следующие оценки 5, 3, 1, 4, 4, 1. Найдите среднюю оценку Незнайки.
а) 3 б) 4 в) 5
4. Вини — Пух съел 18 конфет, Пятачок — 9 конфет, Кролик — 3 конфеты. Сколько конфет в среднем съел каждый?
а) 12 б) 5 в) 10
5. Найдите среднее арифметическое чисел: 20,22 и 18,26
а) 23,78 б) 19,24 в) 12,43
VII. Включение нового знания в систему знаний и повторение – 7-8 минут.
1.Задача.
1)Точка С – середина отрезка АВ. Найдите координату точки С.
2)Найдите среднее арифметическое чисел 12,36 и 22,57.
Сравните полученный результат
2. Практическая работа в группах.
Предварительная подготовка.
Для эффективности работы было дано предварительное домашнее задание:
- класс поделен на 3 группы по рядам;
- измерить и записать рост каждого обучающегося в группе.
Вопрос:
Что мы можем определить, используя данные предварительного задания?
Ответ:
Мы можем определить средний рост в группе.
Что для этого нужно сделать?
Выполняйте задание.
VIII. Рефлексия учебной деятельности на уроке (итог) — 2-3 минуты.
Что нового вы узнали на уроке?
- Сегодня я узнал…
- Мне было интересно…
- Я узнал и могу научить товарища…
- Я понял, что…
- Теперь я могу…
- Меня удивило…
Каково ваше настроение в конце урока?
Домашнее задание.
Учитель комментирует домашнее задание:
1. № 1524 (а/б), №1526
2. Вычислить средний возраст вашей семьи.
3. Узнать, где в жизни необходимо умение находить среднее арифметическое (подготовить сообщение по желанию).
Итог урока. Выставление оценок. Спасибо Вам, дети, за урок. Я буду рада, если полученные на уроках математики знания помогут Вам в жизни при решении проблем. Вы – молодцы. Особо хочу отметить … Полные и правильные ответы давали …
Мерзляк 5 класс — § 24. Комбинаторные задачи
Вопросы к параграфу
1. Какие задачи называют комбинаторными?
Комбинаторные задачи — это задачи, решение которых требует рассмотрения и подсчёта все возможных случаев (всех возможных комбинаций).
2. Как называют схему, с помощью которой удобно и наглядно решать комбинаторные задачи?
Дерево возможных вариантов.
Решаем устно
1. Одним слоем бумаги оклеили куб, длина ребра которого равна 3 дм. Сколько квадратных дециметров бумаги потребовалось на оклеивание куба?
Найдём площадь поверхности куба:
S = 6a² = 6 • 3² = 6 • 9 = 54 (дм²) — бумаги потребовалось для оклеивания куба.
Ответ: 54 дм².
2. Объём прямоугольного параллелепипеда равен 240 см³. Какая из следующих троек чисел может задавать измерения этого параллелепипеда:
1) 4 см, 6 см, 12 см
4 • 6 • 12 = 24 • 12 = 288 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.
2) 5 см, 6 см, 8 см
5 • 6 • 8 = 30 • 8 = 240 (см³) — да, эти числа могут быть измерениями данного прямоугольного параллелепипеда.
3) 3 см, 5 см, 10 см
3 • 5 • 10 = 15 • 10 = 150 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.
4) 10 см, 10 см, 24 см
10 • 10 • 24 = 100 • 24 = 2 400 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.
Ответ: числа 5 см, 6 см и 8 см.
3. Сколько центнеров пшеницы можно засыпать в бункер, имеющий форму прямоугольного параллелепипеда, если его длина равна 8 м, ширина — 2 м, высота — 1 м, а масса 1 м³ зерна составляет 8 ц?
1) 8 • 2 • 1 = 16 (м²) — объём бункера.
2) 16 • 8 = 128 (ц) — пшеницы можно засыпать в бункер.
Ответ: 128 центнеров.
4. Что больше и на сколько:
1) квадрат суммы чисел 4 и 3 или сумма их квадратов
(4 + 3)² > 4² + 3²
7² > 16 + 9
49 > 25
2) разность квадратов чисел 10 и 8 или квадрат их разности
10² — 8² > (10 — 8)²
100² — 64² > 2²
36 > 4
3) разность кубов чисел 5 и 3 или куб их разности
5³ — 3³ > (5 — 3)³
125 — 27 > 2³
98 > 8
Упражнения
645. Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 3 (цифры могут повторяться).
Таких двузначных чисел всего 9:
- 11, 12, 13
- 22, 21, 23
- 33, 31, 32
646. Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 0 (цифры могут повторяться).
Таких двузначных чисел всего 6:
647. У ослика Иа-Иа есть три надувных шарика: красный, зелёный и жёлтый. Он хочет подарить по одному шарику своим друзьям: Винни-Пуху, Пятачку и Кролику. Сколько у ослика Иа-Иа есть вариантов сделать подарки своим друзьям?
Решим задачу при помощи схемы «Дерево возможных вариантов».
Итак, у нас получилось шесть возможных вариантов:
Винни-Пуха | Пятачок | Кролик | |
Вариант 1 | Зелёный | Красный | Жёлтый |
Вариант 2 | Зелёный | Жёлтый | Красный |
Вариант 3 | Красный | Зелёный | Жёлтый |
| Вариант 4 | Красный | Жёлтый | Зелёный |
| Вариант 5 | Жёлтый | Зелёный | Красный |
| Вариант 6 | Жёлтый | Красный | Зелёный |
Ответ: 6 вариантов.
648. Сколько двузначных чисел, все цифры которых различны, можно составить из цифр 0, 1 и 2?
Таких двузначных чисел всего 4:
649. В футбольном турнире участвуют команды 5 «А» класса, 5 «Б» класса и 5 «В» класса. Сколько существует способов распределения первого и второго мест среди этих команд? Решение какой задачи из номеров 645—648 аналогично решению этой задачи?
Решим задачу при помощи схемы «Дерево возможных вариантов».
Итак, у нас получилось шесть возможных вариантов (последовательно места, занятые 5″А», 5″Б» и 5″В»):
Итак, у нас получилось шесть возможных вариантов (последовательно цвет шарика для Винни-Пуха, Пятачка и Кролика):
5″А» | 5″Б» | 5″В» | |
Вариант 1 | 1 | 2 | — |
Вариант 2 | 1 | — | 2 |
Вариант 3 | 2 | 1 | — |
| Вариант 4 | 2 | — | 1 |
| Вариант 5 | — | 1 | 2 |
| Вариант 6 | — | 2 | 1 |
Задача аналогична задаче № 647.
Ответ: 6 вариантов.
650. Запишите все трёхзначные числа, для записи которых используются только цифры (Цифры не могут повторяться.):
1) 3, 4 и 6
- 346, 364
- 436, 463
- 634, 643
2) 4, 7 и 0
651. Сколько различных трёхзначных чисел можно составить из цифр (Цифры могут повторяться.):
1) 1 и 2
- 111, 112, 121, 122
- 222, 221, 212, 211
Ответ: 8 чисел.
2) 0 и 1
Ответ: 4 числа.
652. Запишите все двузначные числа, в записи которых используются только цифры 2, 4, 9 и 0. (Цифры могут повторяться.)
- 22, 24, 29, 20
- 42, 44, 49, 40
- 92, 94, 99, 90
653. Сколько двузначных чисел можно составить из цифр 6, 7, 8 и 9 так, чтобы цифры были записаны в порядке возрастания?
Ответ: 6 чисел.
654. Сколько двузначных чисел можно составить из цифр 6, 7, 8 и 9 так, чтобы цифры были записаны в порядке убывания?
Ответ: 6 чисел.
655. Сколько существует двузначных чисел, сумма цифр которых равна 5?
Всего 5 чисел: 14, 23, 32, 41, 50.
Ответ: 5 чисел.
656. Сколько двузначных чисел, сумма цифр которых равна чётному числу, можно составить из цифр 1, 2, 3, 4 (цифры могут повторяться)?
Всего 8 чисел: 11, 13, 22, 24, 31, 33, 42, 44.
Ответ: 8 чисел.
657. Сколько двузначных чисел, сумма цифр которых равна нечётному числу, можно составить из цифр 0, 1,2, 3?
Всего 6 чисел: 10, 12, 21, 23, 30, 32.
Ответ: 6 чисел.
658. Кот Базилио и лиса Алиса решили украсть золотой ключик, который хранится в каморке папы Карло. Чтобы туда проникнуть, нужно подобрать двузначный код. Им известно, что дверь в каморку закрывает Буратино, который знает пока что только четыре цифры: 0, 1, 2 и 3. Какое наибольшее количество вариантов придётся перебрать коту и лисе, чтобы открыть дверь?
Составим таблицу:
- в первом столбце запишем возможные варианты первой цифры кода
- в верхней строке — возможные варианты второй цифры кода
- на пересечении строк и столбцов — возможные варианты кодов.
| 0 | 1 | 2 | 3 |
0 | 00 | 01 | 02 | 03 |
1 | 10 | 11 | 12 | 13 |
| 2 | 20 | 21 | 22 | 23 |
| 3 | 30 | 31 | 32 | 33 |
Итак, возможное количество вариантов кода — 16.
Ответ: 16 вариантов.
659. Сколько существует различных прямоугольников, периметры которых равны 24 см, а длины сторон выражены целым числом сантиметров?
P = (a + b) • 2
Если P = 24 см, то сумма длин сторон равна 24 : 2 = 12 см.
Существует 6 возможных вариантов таких прямоугольников. Длины сторон у них должны быть:
- 1 см и 11 см
- 2 см и 10 см
- 3 см и 9 см
- 4 см и 8 см
- 5 см и 7 см
- 6 см и 6 см (квадрат, который также соответствует определению прямоугольника).
Ответ: 6 прямоугольников.
660. У Ани есть 30 одинаковых кубиков. Сколько различных прямоугольных параллелепипедов она может из них составить, если для построения одного параллелепипеда надо использовать все имеющиеся 30 кубиков?
V = abc
Если V = 30, то можно подобрать 5 вариантов постройки прямоугольного параллелепипеда из одинаковых кубиков:
- 30 • 1 • 1 = 30
- 15 • 2 • 1 = 30
- 10 • 3 • 1 = 30
- 6 • 5 • 1 = 30
- 5 • 3 • 2 = 30
Ответ: 5 вариантов.
661. На прямой отметили четыре точки А, В, С и D. Сколько отрезков с концами в отмеченных точках можно провести? Какой из рисунков § 24 помогает решить эту задачу?
Для решения этой задачи можно ориентироваться на рисунок 184 § 24:
Но лучше сделать свой рисунок для этой конкретно задачи:
Ответ: 6 отрезков.
662. Подножие горы и её вершину связывают три тропы. Сколько существует маршрутов, ведущих от подножия к вершине и затем вниз к подножию?
Нарисуем эти три маршрута схематично, изобразив их в виде лучей, выходящих из единой точки, где:
- O — вершина горы
- A — первая точка у подножия горы
- B — вторая точка у подножия горы
- C — третья точка у подножия горы.
Тогда возможные следующие варианты маршрутов (начало маршрута — вершина — конец маршрута):
- AOA, AOB, AOC
- BOA, BOB, BOC
- COA, COB, COC
Итого — 9 вариантов маршрутов.
Ответ: 9 вариантов.
663. Спортивной команде предлагают футболки трёх цветов — красного, зелёного и синего, а шорты двух цветов — белого и жёлтого. Сколько вариантов выбора формы есть у команды?
Составим таблицу:
- в первом столбце запишем возможные варианты шорт
- в верхней строке — возможные варианты футболок
- на пересечении строк и столбцов — возможные варианты формы
Форма | Футболки | |||
| Красные | Зелёные | Синие | ||
Шорты | Белые | Красная футболка белые шорты | Зелёная футболка белые шорты | Синяя футболка белые шорты |
| Жёлтые | Красная футболка жёлтые шорты | Зелёная футболка жёлтые шорты | Синяя футболка жёлтые шорты | |
Итак, возможное количество вариантов формы — 6.
Ответ: 6 вариантов.
664. У Тани есть четыре платья и две пары туфель. Сколько у Тани есть вариантов выбора наряда?
Составим таблицу:
- в первом столбце запишем возможные варианты туфель
- в верхней строке — возможные варианты платьев
- на пересечении строк и столбцов — возможные варианты наряда
Наряд
| Платья | ||||
| 1 | 2 | 3 | 4 | ||
Туфли | 1 | Платье № 1 Туфли № 1 | Платье № 2 Туфли № 1 | Платье № 3 Туфли № 1 | Платье № 4 Туфли № 1 |
| 2 | Платье № 1 Туфли № 2 | Платье № 2 Туфли № 2 | Платье № 3 Туфли № 2 | Платье № 4 Туфли № 2 | |
Итак, возможное количество вариантов нарядов — 8.
Ответ: 8 вариантов.
665. В отряде космонавтов есть три пилота и два инженера. Сколько существует способов составить экипаж, состоящий из одного пилота и одного инженера?
Составим таблицу:
- в первом столбце запишем возможные варианты инженеров
- в верхней строке — возможные варианты пилотов
- на пересечении строк и столбцов — возможные варианты экипажа
Экипаж | Пилоты | |||
| 1 | 2 | 3 | ||
Инженеры | 1 | Пилот 1 Инженер 1 | Пилот 2 Инженер 1 | Пилот 3 Инженер 1 |
| 2 | Пилот 1 Инженер 2 | Пилот 2 Инженер 2 | Пилот 3 Инженер 2 | |
Итак, возможное количество вариантов нарядов — 6.
Ответ: 6 вариантов.
666. На рисунке 185 изображён план одного района города. Отрезками изображены улицы. Сколько существует маршрутов из точки А в точку В, если передвигаться разрешено по улицам, идущими вверх или вправо?
Существуют следующие варианты маршрутов:
- Вверх — вверх — вправо — вправо
- Вверх — вправо — вверх — вправо
- Вверх — вправо — вправо — вверх
- Вправо — вверх — вверх — вправо
- Вправо — вверх — вправо — вверх
- Вправо — вправо — вверх — вверх
Итак, возможное количество вариантов маршрутов — 6.
Ответ: 6 вариантов.
667. В записи 1 * 2 * 3 * 4 вместо каждой звёздочки можно поставить один из знаков «+» или «•». Чему равно наибольшее значение выражения, которое можно получить?
Наибольшее значение выражения можно получить, если расставить знаки в таком порядке:
1 + 2 • 3 • 4 = 1 + 6 • 4 = 1 + 24 = 25.
Упражнения для повторения
668. Расстояние между двумя сёлами равно 28 км. Из этих сёл одновременно в одном направлении выехали мотоциклист и автобус. Автобус ехал впереди со скоростью 42 км/ч, а мотоциклист ехал со скоростью 56 км/ч. Через сколько часов после начала движения мотоциклист догонит автобус?
1) 56 — 42 = 14 (км/ч) — скорость, с которой мотоциклист догоняет автобус — скорость сближения.
2) 28 : 14 = 2 (часа) — время, за которое мотоциклист догонит автобус.
Ответ: 2 часа.
669. Решите уравнение:
670. 1) Одно из слагаемых в 14 раз больше другого. Во сколько раз их сумма больше меньшего слагаемого?
Пусть х — первое слагаемое. Тогда второе слагаемое равно 14х.
(14х + х) : х = 15х : х = 15
Ответ: в 15 раз.
2) Вычитаемое в 12 раз больше разности. Во сколько раз уменьшаемое больше разности?
Пусть х — разность, тогда вычитаемое равно 12х, а уменьшаемое равно (12х + х).
(12х + х) : х = 13х : х = 13
Ответ: в 13 раз.
671. На ферме есть 156 коров, каждая из которых даёт в день 12 л молока. Молоко с фермы вывозят в бидонах ёмкостью 40 л. В некоторый день на ферме было в наличии 42 пустых бидона. Хватит ли бидонов, чтобы вывезти с фермы надоенное за день молоко?
1) 156 • 12 = 1 872 (литра) — молока надаивают на ферме за 1 день.
2) 42 • 40 = 1 680 (литров) — молока помещается в 42 пустых бидона.
3) 1 680 литров < 1 872 литра, значит 42 бидона не хватит для вывоза всего надоенного за день молока.
Ответ: Нет, не хватит.
672. Решите кроссворд.
По горизонтали:
2. Результат арифметического действия (Частное)
3. Единица измерения времени (Секунда)
4. Единица измерения углов (Градус)
5. Компонент умножения (Множитель)
6. Компонент сложения (Слагаемое)
По вертикали:
1. «Царица наук» (Математика)
Задача от мудрой совы
673. В классе 30 учащихся. Они сидят по двое за 15 партами так, что половина всех девочек сидит с мальчиками. Можно ли учеников класса пересадить так, чтобы половина всех мальчиков сидела с девочками?
1) Если половина всех девочек сидят с мальчиками, значит вторая половина девочек сидит друг с другом по двое за партой. Значит половина девочек — это чётное количество человек.
2) Если половина девочек — это чётное количество человек, то общее количество девочек (две половины) также будет чётным числом.
3) Предположим, что условие задачи выполнимо и половину мальчиков можно посадить с девочками. Это значит, что другая половина мальчиков будет сидеть по двое за партой. То есть половина мальчиков также должно быть чётным числом.
4) Половина мальчиков и половина девочек — это ровно половина класса. По нашему предположению это чётное количество человек, так как и половина мальчиков, и половина девочек чётные числа.
5) Но мы знаем, что в классе 30 учащихся, а половина от 30 человек — это 15 человек — нечётное число. Значит наше предположение о мальчиках было неверно и их нельзя посадить так, чтобы половина мальчиков сидела с девочками.
Ответ: Нет, нельзя.
Решение текстовых задач в 5-м классе
Состояние математического развития учащихся наиболее ярко характеризуется их умением решать задачи. Задачи – это основное средство оттачивания мысли каждого школьника. Научится решать задачи можно только, решая их.
Решение текстовых задач традиционно является одним из основных видов деятельности в 5–6 классах. На этом этапе у детей продолжается развитие логического мышления, элементарных навыков абстрагирования, математического моделирования и т.д. Основными этапами работы над текстовой задачей являются:
- чтение задачи;
- анализ условия задачи;
- построение математической модели;
- оформление решения;
- анализ полученного ответа.
Остановимся подробнее на каждом этапе.
ЧТЕНИЕ ЗАДАЧИ.
Дети вначале условие задачи читают самостоятельно, «про себя». Затем один из учеников читает вслух, так как некоторые дети обладают слабым навыком беглого чтения и с трудом воспринимают прочитанное. Если условие задачи не воспринимается большинством учащихся, то её необходимо прочитать учителю.
АНАЛИЗ УСЛОВИЯ ЗАДАЧИ.
Проводится в форме устного обсуждения, которое можно сопроводить краткой записью условия или графическим изображением. При работе над краткой записью необходимо учитывать, что она требует умозаключения, способствующие развитию логического мышления, приобретению навыков лаконичного и чёткого представления полученной информации. Удачно построенное краткое условие является , по существу, первым шагом построения математической модели задачи.
Например задача №238 .
За неделю собрали 6500 кг. винограда, из которых 650 кг. передали в детский сад, а остальной виноград отправили в город в ящиках. Сколько ящиков с виноградом отправили в город, если в каждом ящике было 13 кг. винограда?
В процессе обсуждения условие приводится к более привычному для детей виду:
Всего – 6500 кг.
Передали в детский сад — 650 кг.
Остальное — в ящики по 13 кг. в каждом}?
Я работаю в пятом классе по учебнику математики авторов Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова, С.И. Шваршбурда, поэтому все примеры взяты из этого учебника.
Творческий подход к работе над краткой записью позволит разрушить сложившийся у учащихся стереотип, при котором самым главным считается получение ответа. В связи с этим необходимо обратить внимание на встречающиеся методические недочёты. Не надо требовать от учащихся краткую запись к любой задаче. Иногда вполне достаточно просто обсудить условие. Не имеет смысла давать краткую запись к задачам, решаемым с помощью формулы (№716, 719, 720, 751, 752 и т.д.), а так же к задачам на движение в одну или противоположные стороны, к которым лучше сделать рисунок – схему. Она рассматривается как иллюстрация к условию, делающая его более наглядным и динамичным. Применение рисунков – схем имеет и ещё один важный аспект: развитие самостоятельной схематической интерпретации условия. В сознании детей происходит качественный скачёк от реального объекта к его символическому изображению.
Итак, к записи условий задачи целесообразно подходить по-разному. У одних задач устно обсудить условие, сделать краткую запись, рисунок – схему. У других, более сложных, к разбору их условия можно использовать одновременно и краткую запись, и рисунок – схему, и ещё какие – либо другие приёмы.
ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ – должно стать итогом разбора условия задачи. Основной целью работы учителя в этом направлении, по моему мнению, является воспитание у учащихся «чувства метода». Это приведёт к осознанному выбору арифметического или алгебраического метода решения задачи в каждом конкретном случае. На различных видах задач детям необходимо показать преимущество в использовании каждого метода.
Например, задача №489(б).
40 кг белил разлили в несколько банок, а потом в каждую банку добавили 2кг красной краски. В каждой банке оказалось 7кг краски. Сколько было банок?
Эту задачу не сложно решить арифметическим способом (состоит из двух шагов), поэтому алгебраический метод (предложен в учебнике) нецелесообразен.
Задача №468.
Во время уборки урожая с первого участка собрали 612т пшеницы, что в 4 раза больше, чем с третьего, а со второго – в 3 раза меньше, чем с первого. Сколько тонн пшеницы собрали с трёх участков?
Для решения этой задачи используется арифметический способ, но при составлении краткой записи использовать для большей наглядности рисунок – схему.
Для решения задач на части, с моей точки зрения, предпочтительнее алгебраический метод (составление уравнения), хотя арифметический тоже не вызывает особых затруднений. Нельзя настаивать на одном из этих методов, так как использование обеих позволит расширить математический кругозор учащихся и обогатит набор математических приёмов, применяемых в реальных жизненных ситуациях, позволит им выбрать оптимальный метод решения поставленной задачи.
ОФОРМЛЕНИЕ РЕШЕНИЯ ЗАДАЧИ вытекает из результата разбора условия задачи и выбора метода её решения.
Оформление задач, решаемых составлением уравнения, единообразно. Различия только в полноте даваемых разъяснений, но они не должны быть многословны.
Оформление задач, решаемых арифметическим способом, требует подробных записей. При решении в виде действий с пояснениями необходимо больше времени уделять насыщенности пояснений, так как именно они помогают ученику приобрести навык письменного оформления рассуждений. Если пояснение делать двумя – тремя словами, то задачу отличает от вычислительного упражнения только запись ответа. Через три – четыре урока дети не способны расшифровать смысл записанного числового выражения. Можно использовать и другой способ оформления – в вопросной форме. Эта форма обладает существенными преимуществами, но это не означает, что по вопросам нужно решать основную массу задач. Решение по вопросам требует значительных затрат времени, которого при пяти часах в неделю нет. Но всё равно решение некоторых задач оформляю в виде вопросов, так как они помогают представить решение задачи как целостную систему последовательных, логически взаимосвязанных шагов. Необходимость проводить обоснованные рассуждения развивает у детей способность чётко и лаконично выражать свои мысли, аргументировать свои действия, Постепенно снимает проблему «математического косноязычия».
Оформление задач, решаемых с помощью формул (площади, объёма, пройденного пути), единообразно. Запись условия и решения короткая, чёткая, позволяет экономить время, развивает навык работы с буквенными выражениями. В дальнейшем она используется при решении задач по геометрии и физике , начиная с седьмого класса.
АНАЛИЗ ПОЛУЧЕННОГО ОТВЕТА.
Обычно работа на этом этапе сводится к записи ответа. Иногда проводится проверка полученного числового результата подстановкой в условие задачи. А ведь только завершив решение, школьник может воспринять задачу, как единое целое, сделать некоторые общие выводы, критически оценить значение найденной величины, осмыслить её реальность с точки зрения здравого смысла.
Например, задача № 1527
Турист шёл 3,8 ч. со скоростью 1,2 м/с а затем 2,2 ч. со скоростью 0,9м/с Какова средняя скорость движения туриста на всём пути?
Она была дана на дом. Практически никто не обратил внимание на единицы скорости. Получили в ответе 1,308 км/ч. На следующем уроке я попросила поднять руки тех, у кого возникли затруднения при решении задачи №1527. Таких в классе не нашлось. Задача получилась у всех. Решение воспроизвели на доске. Проанализировали. Оказалось, что полученная скорость противоречит здравому смыслу. Прочитав ещё раз задачу, обратили внимание на единицы скорости, м/с. перевели в км/ч. Получили правильный ответ. И вообще при решении задач на движение, делаю акцент на полученном результате. Обращаю внимание на то, что скорость пешехода не может быть больше скорости велосипедиста, мотоциклиста и т.д.
Систематическая работа по анализу проведённого решения позволит со временем привить учащимся первичные навыки самоконтроля, обобщения и критической оценки полученного результата.
Очень полезно проводить уроки, посвящённые решению одной или двух задач разными способами. Это развивает математические способности и воспитывает интерес к математике, увеличивает запас различных приёмов решения.
Важным фактором успешной работы над задачей является уверенность учащегося в том, что он сможет её решить. Если задача трудная, то безрезультатность усилий снижает эффективность его мышления и ухудшает возможность дальнейшего обучения. Пятиклассники ещё не умеют долго думать над задачей, им хочется как можно быстрее увидеть положительный результат своего труда. Поэтому учителю необходимо им помочь умело поставленными наводящими вопросами, помогающими понять идею задачи.
Список литературы:
- Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. Математика 5 кл. МНЭМОЗИНА 2005 г.
- Т.В. Ахутина, Н.М. Пылаева Школа внимания. М., 1997 г.
- Материалы «Учительской газеты», библиотечка «Первого сентября», серия «Математика» 2000-2008 гг.
- Журналы «Математика в школе» разные годы издания.
ГДЗ по Математике 5 класс: Никольский С.М. Решебник
Решебник по математике для 5 класса Никольский – это онлайн-решебник, содержащий комплекс решенных примеров и задач по учебнику группы российских авторов Никольского С.М., Потапова М.К., Решетникова Н.Н. и Шевкина А.В. Его используют во многих общеобразовательных школах России в качестве пособия для обучения пятиклассников основам арифметики.
Готовые домашние задания по математике Никольского – стоит ли пятиклассникам ими пользоваться?
В 5 классе учебная программа не отличается повышенной сложностью, однако с ее усвоением нередко испытывают сложности даже ребята-отличники. Главная причина – переход из начальной школы в среднее звено. Родителям на этом этапе не следует сразу бросаться за помощью к репетиторам: надо позволять ребенку выбраться из сложной ситуации самостоятельно с опорой на готовые домашние задания.
ГДЗ по математике за 5 класс Никольский помогают разобрать примеры и задачи, которые ребенок не успел понять в классе, запомнить алгоритм их выполнения и особенности оформления. Родители на основе решебников могут проверять домашние работы и контролировать успеваемость своих детей.
Использование онлайн-ответов на упражнения учебника Никольского С.М. на сайте ГДЗ Путина обеспечивает к тому же и экономию времени:
- найти нужный ответ можно по его номеру в таблице;
- на одно упражнение может приходиться несколько вариантов решения;
- использовать базу ответов можно с любого устройства – телефона, планшета, ноутбука.
В дополнение – база решебников на сайте регулярно обновляется, оттого номера решений в таблице соответствуют упражнениям последних изданий учебников.
Какие задачи помогает выполнить решебник по математике за 5 класс от Никольского?
Несмотря на то, что в 5 классе учебная программа не отличается высоким уровнем сложности, однако спектр рассматриваемых тем чрезвычайно широк:
- натуральные числа, их свойства, математические действия с натуральными числами;
- прямая, отрезов, луч, угол и особенности их измерения;
- прямоугольники и треугольники, определение их площади;
- делимость натуральных числе и ее особенности, НОК и НОД;
- обыкновенные дроби, равенство дробей, их приведение к общему знаменателю, математические действия с дробями.
Особенностью учебника по математике для 5 класса Никольского С.М. в его 13-м издании 2014 года выступает наличие в нем нескольких видов задач – заданий для устной работы, повышенной трудности, старинных задач, а также задачек на построение. Любая из них найдет свое решение в решебнике по математике за 5 класс Никольский.
На основе готовых домашних заданий пятиклассники могут не только разобраться в практическом применении формул и теорем, но также подготовиться к самостоятельным и контрольным работам, олимпиадам и экзаменам.
Качественное усвоение учебной программы по математике в 5 классе – гарантия успеха в изучении предмета в последующие годы.
вопросов по математике для 5-го класса с ответами
МАТЕМАТИЧЕСКИЕ ВОПРОСЫ 5 КЛАССА С ОТВЕТАМИ
Математические вопросы с ответами для 5-го класса:
В этом разделе мы увидим некоторые практические задачи для учащихся 5-х классов.
Вопрос 1:
Внутренний круг треугольника ABC касается BC в точке D, AC в точке E и AB в точке F. Учитывая AF = 3, BD = 4 и CE = 6, найдите периметр треугольника ABC.
(А) 26 (В) 55 (В) 37
Решение
Вопрос 2:
Найдите сумму первых 16 членов арифметического ряда 5, 10, 15.. .
(A) 490 (B) 230 (C) 510
Решение
Вопрос 3:
Вычесть 573,9246 — 215,6
(A) 320,1046 (B) 125,3246 (C) 358,3246
Решение
Вопрос 4:
Вычислить 2 × 0 × 0 × 8 x 12 =
(A) 5 (B) 0 (A) 3
Решение
Вопрос 5:
Express 11/5 в десятичной форме
(А) 5.5 (B) 2,2 (C) 8,2
Решение
Вопрос 6:
Сумма углов треугольника составляет
(A) 180 градусов (B) 240 градусов (C) 360 градусов
Решение
Вопрос 7:
Диаметр круга 14 см. Тогда каким будет периметр окружности?
(A) 25π (B) 50π (C) 14π
Решение
Вопрос 8:
Разделите 0.4096 ÷ 0,032
(A) 12,8 (B) 15,3 (C) 10,1
Решение
Вопрос 9:
Сократить 45% на фракцию.
(A) 9/20 (B) 9/17 (C) 5/19
Решение
Вопрос 10:
Умножить 6a x 2a
(A) 8a (B) 12a 2 (C) 8a 2
Раствор
После того, как мы изучили все, что было сказано выше, мы надеемся, что студенты отработали бы задачи по рабочему листу.
Помимо материалов, представленных на этой веб-странице, если вам нужны другие сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь
Если у вас есть отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
07 Алгебра
07 Алгебра
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямой и обратной вариациям
Проблемы со словами по цене за единицу
Проблемы со словами по цене за единицу
Word задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами
Проблемы со словами с двойными фактами
Тригонометрические проблемы со словами
Проблемы с процентным соотношением слов
Проблемы со словами о прибылях и убытках
0
Задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи о словах с уравнениями
Проблемы со словами с линейными неравенствами
Ratio и Задачи
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Задачи со словами на возрастах
Проблемы со словами из теоремы Пифагора
Процент числового слова pr проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибылей и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Домен и диапазон рациональных функций
Область и диапазон рациональных функций
функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
Поиск квадратного корня с использованием длинного di видение
Л.Метод CM для решения временных и рабочих задач
Преобразование словесных задач в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении 17 в степени 23 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Mathwire.com | Решение проблем: Gr. 5-8
Решение задач: 5–8 классы
Эти задачи предназначены для учащихся 5-8 классов:
- Лист записи «Тринадцать способов» был разработан для учащихся, чтобы записать тринадцать способов закрасить диаграмму, чтобы представить 1/2, как указано на веб-сайте PBS Cyberchase, указанном в листе для записи.
- Туристическое агентство Bulldog просит студентов оценить планы аренды автомобилей от трех разных компаний и порекомендовать лучший вариант, учитывая разные планы семейных путешествий.
- Jen and Berry’s Ice Creamery требует, чтобы студенты написали правило прибыли для магазина, а затем использовали это правило (функцию) для оценки прибыли с учетом количества покупателей каждый день.
- Миссия на миллион долларов просит студентов решить, какая зарплата является лучшим предложением за один месяц работы: один миллион долларов или один цент в первый день, два цента во второй день, четыре цента в третий день и т. Д.
- TV Survey — это пример проблемы анализа данных с вопросами, разработанными для каждого уровня Таксономии Блума.
- Исследование игрушек с хлопьями имитирует получение учащимися одного из шести призов в коробке с хлопьями и просит учащихся оценить, сколько ящиков с хлопьями им нужно будет купить, прежде чем они получат все 6 различных игрушек. Учащиеся делают прогноз, проводят моделирование, систематизируют данные и анализируют данные, чтобы написать письмо миссис Оутс с подробным описанием ожидаемых результатов этой рекламной акции. Инструкции и все раздаточные материалы включены для этого упражнения.
- Онлайн-симулятор исследования игрушек из хлопьев был разработан, чтобы учащиеся могли проводить множество виртуальных испытаний для сбора данных на более крупной выборке после проведения эксперимента с подбрасыванием игральных костей.Обязательно прочтите инструкции перед загрузкой этого Java-апплета.
- Дополнительные игры и эксперименты см. В разделе Анализ данных: бросание двух игральных костей. Любая из этих игр становится упражнением по решению проблем, когда учащихся просят написать и защитить выигрышную стратегию, которую они разработали после игры и анализа лежащей в основе вероятности.
- Сколько разных способов сделать слово «СНЕГ»? легко решается со ссылкой на Треугольник Паскаля, но затем попробуйте показать каждый из различных путей.Для этого нужен организованный подсчет. Используйте рабочий лист записи, чтобы оценить использование учащимися техник систематического счета, чтобы найти все способы и связать их с соответствующей строкой треугольника Паскаля.
- Winter Paths требует от учащихся использовать методы систематического подсчета, чтобы найти все пути, которые означают ЗИМА, и соотнести решение с соответствующей строкой треугольника Паскаля.
Бесплатные задания по математике для пятиклассников
Ученики пятого класса, возможно, уже запомнили факты умножения в более ранних классах, но к этому моменту они должны понимать, как интерпретировать и решать словесные задачи.Задачи со словами важны в математике, потому что они помогают учащимся развивать мышление в реальном мире, одновременно применять несколько математических концепций и мыслить творчески, отмечает ThinksterMath. Задачи со словами также помогают учителям оценить истинное понимание математики учащимися.
Задачи для пятиклассников включают умножение, деление, дроби, средние значения и множество других математических понятий. В разделах №№ 1 и 3 представлены бесплатные рабочие листы, которые студенты могут использовать, чтобы практиковаться и оттачивать свои навыки решения текстовых задач.В разделах № 2 и 4 приведены соответствующие ключи ответов к этим рабочим листам для упрощения выставления оценок.
Смешайте математические задачи со словами
Распечатайте PDF-файл: Math Word Problems Mix
Этот рабочий лист представляет собой хорошее сочетание задач, включая вопросы, требующие от студентов демонстрации своих навыков умножения, деления, работы с долларовыми суммами, творческого мышления и нахождения среднего. Помогите своим пятиклассникам понять, что задачи со словами не должны быть пугающими, разрешив им хотя бы одну задачу.
Например, в задаче №1 спрашивается:
«Во время летних каникул ваш брат подрабатывает стрижкой газонов. Он косит шесть газонов в час, и ему нужно косить 21 газон. Сколько времени это у него займет?»
Брат должен быть Суперменом, чтобы косить шесть газонов в час. Тем не менее, поскольку это именно то, что указывает проблема, объясните учащимся, что они должны сначала определить, что они знают и что они хотят определить:
- Твой брат может косить шесть газонов в час.
- Ему нужно покосить 21 газон.
Чтобы решить задачу, объясните учащимся, что они должны записать ее в виде двух дробей:
6 газонов / час = 21 газон / x час
Затем они должны умножиться. Для этого возьмите числитель первой дроби (верхнее число) и умножьте его на знаменатель второй дроби (нижнее число). Затем возьмите числитель второй дроби и умножьте его на знаменатель первой дроби следующим образом:
6x = 21 час
Затем разделите каждую сторону на 6 , чтобы найти x: .
6x / 6 = 21 час / 6
х = 3.5 часов
Итак, вашему трудолюбивому брату потребуется всего 3,5 часа, чтобы косить 21 газон. Он быстрый садовник.
Смесь задач с математическим словом: решения
Распечатайте PDF: Смешивание задач по математическим словам: решения
В этом рабочем листе представлены решения проблем, с которыми учащиеся работали, в печатной форме на слайде № 1. Если вы видите, что учащиеся испытывают затруднения после того, как сдадут свою работу, покажите им, как решить одну или две задачи.
Например, проблема No.6 на самом деле представляет собой простую задачу деления:
«Твоя мама купила тебе годовой абонемент на плавание за 390 долларов. Она выплачивает 12 выплат из расчета, сколько денег нужно заплатить за абонемент?»
Объясните, что для решения этой проблемы вы просто разделите стоимость годичного плавательного пропуска, 390 долларов , на количество выплат, 12 , следующим образом:
390 долл. США / 12 = 32,50 долл. США
Таким образом, стоимость каждого ежемесячного платежа вашей мамы составляет 32,50 доллара.Обязательно поблагодарите маму.
Дополнительные математические задачи со словами
Распечатать PDF-файл: другие задачи по математике
Этот рабочий лист содержит задачи, которые немного сложнее, чем те, что были в предыдущей печатной форме. Например, проблема №1 гласит:
«Четверо друзей едят личную пиццу. У Джейн осталось 3/4, у Джилл осталось 3/5, у Синди осталось 2/3, а у Джеффа осталось 2/5. У кого осталось больше всего пиццы?»
Объясните, что сначала вам нужно найти наименьший общий знаменатель (ЖКД), нижнее число в каждой дроби, чтобы решить эту проблему.Чтобы найти ЖК-дисплей, сначала умножьте разные знаменатели:
4 х 5 х 3 = 60
Затем умножьте числитель и знаменатель на число, необходимое для каждого, чтобы получить общий знаменатель. (Помните, что любое число, разделенное само по себе, равно единице.) Итак, у вас будет:
- Джейн: 3/4 x 15/15 = 45/60
- Джилл: 3/5 x 12/12 = 36/60
- Синди: 2/3 x 20/20 = 40/60
- Джефф: 2/5 x 12/12 = 24/60
У Джейн осталось больше всего пиццы: 45/60, или три четверти.У нее будет много еды сегодня вечером.
Дополнительные математические задачи со словами: решения
Распечатайте PDF-файл: Дополнительные задачи с математическими словами: решения
Если учащиеся все еще не могут найти правильные ответы, пора применить несколько разных стратегий. Вы можете просмотреть все задачи на доске и показать учащимся, как их решать. Как вариант, разбейте студентов на группы — на три или шесть групп, в зависимости от того, сколько у вас студентов.Затем попросите каждую группу решить одну или две задачи, пока вы ходите по комнате, чтобы помочь. Совместная работа может помочь студентам мыслить творчески, когда они обдумывают одну или две проблемы; часто, как группа, они могут прийти к решению, даже если они изо всех сил пытались решить проблемы самостоятельно.
Рабочие листы с задачами о деньгах для 5 класса
Важные факты о денежной математике для 5 класса
Денежная математика — одна из тех математических концепций, в которых дети будут хвастаться своими математическими навыками сложения, вычитания, умножения и деления в реальной жизни.Это верно в отношении наших забавных денежных упражнений, в том числе:
Сложите и вычтите упражнения на сумму денег и задачи со словами, умножьте и разделите суммы денег на задачи со словами, прайс-лист, цену за единицу, цены продажи, найдите количество каждого типа монеты .
Как рабочие листы с задачами о деньгах для 5 класса могут помочь детям получить денежный опыт?
Как рабочие листы с задачами на слова «деньги» для 5 класса могут помочь детям получить денежный опыт?
Ваши дети будут иметь возможность овладеть множеством стратегий с денежным опытом, представленным в наших задачах с денежным словом с решениями и ответами.
Одна очень захватывающая стратегия, которая вызовет у детей любовь и интерес к этому ресурсу, — это простейший способ расчета продажной цены . Учитывая, что все предпочитают покупать вещи на распродаже, чтобы сэкономить, это упражнение будет иметь особое значение для ваших детей, поскольку они легко научатся рассчитывать скидки и цену продажи в любом месте и в любое время, даже без калькулятора.
Легко рассчитать продажную цену
Учитывая, например, что первоначальная цена товара составляет 40 долларов и действует скидка 25%, вы в первую очередь получите;
- Вычислите скидку , разделив 25 на 100, а затем умножив на 40,
i.е. 25 / 100 x 40 = 10 - Затем рассчитайте продажную цену, вычтя скидку из первоначальной цены,
, т.е. 40 долларов — 10 долларов = 30 долларов - Следовательно, ваша продажная цена составляет 30 долларов .
Ого, очень просто и быстро.
Проблема и решение | Электронные таблицы
Проблема и решение — это модель организации, в которой информация в отрывке выражается как дилемма или касается вопроса (проблемы), и что-то, что было, может или должно быть сделано для решения этой проблемы (решение или попытка решения).Может показаться, что структура текста проблемы и решения легко распознать, но это может быть довольно сложно идентифицировать, потому что ее часто путают с причинно-следственным паттерном организации, поскольку они оба имеют реляционные структуры; однако, если вы читаете отрывок и специально ищете как проблему, так и решение проблемы, вы обнаружите, что довольно легко отличить от причины и следствия, поскольку отрывки о причине и следствии не предлагают решений для каких-либо негативных явлений в пределах отрывка. а лучше просто объясните, почему и как они происходят.
Пример: Похоже, что в наши дни наблюдается всплеск подростковой беременности. Беременность в подростковом возрасте мешает молодым матерям реализовывать свои мечты и удовлетворять потребности младенца. К счастью, большинство подростковых беременностей можно легко предотвратить с помощью противозачаточных средств; однако даже противозачаточные средства не на 100% эффективны. Самый эффективный способ предотвратить беременность среди подростков — воздержание, которое на 100% эффективно.
Проблема и решение: Предлагаемые решения для подростковой беременности.
Есть также несколько сигнальных слов , которые могут указывать на то, что информация в отрывке упорядочена в структуре проблемы и решения организации: предложение, решение, ответ, проблема, проблема, проблематика, средство правовой защиты, предотвращение, и исправление. .
Вот простая таблица по проблеме и решению , если вашим ученикам нужно больше практики.
Вот более сложный набор из рабочих листов с текстовой структурой , если ваши ученики готовы к продвижению.
Подробнее о шаблонах организации
Шаблоны организации
Рабочие листы и задания со структурой текста
Практика по интерактивной структуре текста
Все рабочие листы для чтения
Задачи и решения по математическим словам
Проблема 1
Днем продавец продал в два раза больше груш, чем утром.
Если он продал в тот день 360 килограммов груш, сколько?
килограммов он продал утром, а сколько днем?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ — количество килограммов, которое он
продал утром.Затем днем он продал по 2 доллара за килограммы. Итак
итого $ x + 2x = 3x $. Это должно быть равно 360.
$ 3x = 360 $
$ x = \ frac {360} {3}
$ x = 120 $
Таким образом, продавец продал утром 120 кг, а 2 \ cdot 120 = 240 $ кг днем.
Задача 2 Мэри, Питер и Люси собирали каштаны. Мэри собрала в два раза больше каштанов, чем Питер. Люси выбрала
На 2 кг больше Питера. Вместе они втроем собрали 26 кг каштанов. Сколько килограммов набрал каждый из них?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет выбранной Питером суммой.Затем Мэри и Люси выбрали $ 2x $ и $ x + 2 $ соответственно.
Итак,
$ x + 2x + x + 2 = 26 $
$ 4x = 24 $
$ x = 6 $
Следовательно, Питер, Мэри и Люси выбрали 6, 12 и 8 кг соответственно.
Задача 3
София закончила $ \ frac {2} {3} $ книги. Она подсчитала, что закончила на 90 страниц больше, чем еще не прочитала. Как долго ее книга?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет общим количеством страниц в книге, тогда она закончила $ \ frac {2} {3} \ cdot x $ страниц.
Тогда у нее осталось $ x- \ frac {2} {3} \ cdot x = \ frac {1} {3} \ cdot x $ страниц.
$ \ frac {2} {3} \ cdot x- \ frac {1} {3} \ cdot x = 90 $
$ \ frac {1} {3} \ cdot x = 90 $
$ x = 270 $
Итак, в книге 270 страниц.
Задача 4
Сельскохозяйственное поле можно обработать 6 тракторами за 4 дня. Когда 6 тракторов работают вместе, каждый из них пашет.
120 га в сутки. Если два трактора были перемещены на другое поле,
тогда оставшиеся 4 трактора могут вспахать то же поле за 5 дней.Сколько гектаров в день будет обрабатывать один трактор?
Нажмите, чтобы увидеть решение
Решение:
Если каждый из тракторов за 6 долларов обрабатывает 120 гектаров в день, и они заканчивают работу за 4 доллара
дней, то все поле будет: 120 $ \ cdot 6 \ cdot 4 = 720 \ cdot 4 = 2880 $ га. Давайте
предположим, что каждый из четырех тракторов обрабатывал $ x $ гектаров в день. Таким образом, за 5 дней вспахано
$ 5 \ cdot 4 \ cdot x = 20 \ cdot x $ га, что равняется площади всего поля, 2880 га.
Итак, получаем $ 20x = 2880 $
$ x = \ frac {2880} {20} = 144 $. Таким образом, каждый из четырех тракторов будет обрабатывать 144 гектара в день.
Задача 5
Студент выбрал число, умножил его на 2, затем вычел 138 из результата и получил 102. Какое число он выбрал?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет выбранным им числом, тогда
$ 2 \ cdot x — 138 = 102 $
$ 2x = 240 $
$ x = 120 $
Задача 6
Я выбрал число и разделил его на 5.Затем я вычел из результата 154 и получил 6. Какое число я выбрал?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет выбранным мной числом, тогда
$ \ frac {x} {5} -154 = 6 $
$ \ frac {x} {5} = 160 $
$ x = 800 $
Задача 7
Расстояние между двумя городами 380 км. В этот же момент легковой автомобиль и грузовик начинают движение навстречу друг другу из
разные города. Они встречаются через 4 часа. Если автомобиль движется на 5 км / ч быстрее грузовика, какова их скорость?
Нажмите, чтобы увидеть решение
Решение:
Основная идея, используемая в задачах такого типа, заключается в том, что расстояние равно скорости, умноженной на время $ S = V \ cdot t $.
| В (км / ч) | т (час) | S (км) | |
| Автомобиль | х + 5 | 4 | 4 (х +5) |
| Грузовик | Х | 4 | 4x |
4 (x + 5) + 4x = 380
$ 4x + 4x = 380 — 20
$ 8x = 360
$ x = \ frac {360} {8}
$ x = 45
$
Следовательно, скорость грузовика составляет 45 долларов за км / час, а скорость автомобиля — 50 долларов за км / час.
Задача 8
Одна сторона прямоугольника на 3 см короче другой стороны. Если увеличить длину каждой стороны на 1 см, то площадь прямоугольника
увеличится на 18 см 2 . Найдите длины всех сторон.
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет длиной большей стороны $ x \ gt 3 $, тогда длина другой стороны будет $ x-3 $ см. Тогда площадь S 1 = x (x — 3) см 2 .
После увеличения длины сторон они станут $ (x +1) $ и $ (x — 3 + 1) = (x — 2) $ см в длину.2 + x — 2x — 2 $
$ 2x = 20 $
$ x = 10 $.
Итак, стороны прямоугольника равны $ 10 $ см и $ (10 — 3) = 7 $ см в длину.
Задача 9
В первый год две коровы дали 8100 литров молока. Второй год их производство увеличилось.
на 15% и 10% соответственно, а общее количество молока увеличилось до
9100 литров в год. Сколько литров молока давалось от каждой коровы за год?
Нажмите, чтобы увидеть решение
Решение:
Пусть x будет количеством молока первой коровы
произведен в течение первого года.Затем вторая корова в тот год произвела (8100 — x) литров молока. На второй год каждая корова произвела
такое же количество молока, как и в первый год, плюс увеличение на 15 \% $ или 10 \% $.
Итак, 8100 $ + \ frac {15} {100} \ cdot x + \ frac {10} {100} \ cdot (8100 — x) = 9100 $
Следовательно, 8100 $ + \ frac {3} {20} x + \ frac {1} {10} (8100 — x) = 9100 $
$ \ frac {1} {20} x = 190 $
$ x = 3800 $
Следовательно,
коровы дали 3800 и 4300 литров молока в первый год и 4370 долларов и 4730 долларов за литр молока во второй год, соответственно.
Проблема 10
расстояние между станциями A и B — 148 км. Экспресс отправился со станции A в сторону станции B со скоростью 80 км / ч. В то же
В это время товарный поезд покинул станцию B в сторону станции A со скоростью 36 км / час. Они встретились на станции C в 12 часов, и к тому времени
экспресс остановился на промежуточной станции на 10 мин, а грузовой поезд остановился на 5 мин. Найдите:
a) Расстояние между станциями C и B.
b) Время, когда грузовой поезд покинул станцию B.
Нажмите, чтобы увидеть решение
Решение
a) Пусть x будет расстоянием между
станции B и C. Тогда расстояние от станции C до станции A составляет $ (148 — x) $ км. К моменту встречи на станции C экспресс
ехал $ \ frac {148-x} {80} + \ frac {10} {60} $ часов, а грузовой поезд ехал $ \ frac {x} {36} + \ frac {5} {60} $ часов . Поезда ушли одновременно, так что:
$ \ frac {148 — x} {80} + \ frac {1} {6} = \ frac {x} {36} + \ frac {1} {12} $. Общий знаменатель чисел 6, 12, 36, 80 равен 720.Тогда
$ 9 (148 — x) +120 = 20x + 60 $
$ 1332 — 9x + 120 = 20x + 60 $
$ 29x = 1392 $
$ x = 48 $.
Следовательно, расстояние между станциями B и C составляет 48 км.
б) К моменту встречи на станции С фрахт
поезд ехал $ \ frac {48} {36} + \ frac {5} {60} $ часов, то есть 1 доллар в час и 25 долларов в минуту.
Следовательно, он покинул станцию B на отметке $ 12 — (1 + \ frac {25} {60}) = 10 + \ frac {35} {60} $ часов, то есть в 10:35.
Задача 11
Сьюзен едет из города А в город Б.После двух часов езды она
заметила, что она преодолела 80 км и подсчитала, что если она продолжит
двигаясь с той же скоростью, она опаздывала на 15 минут. Так
она увеличила скорость на 10 км / ч и прибыла в город B на 36 минут раньше
чем она планировала.
Найдите расстояние между городами A и B.
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет расстоянием между точками A и B. Поскольку Сьюзен преодолела 80 км за 2 часа, ее скорость составила $ V = \ frac {80} {2} = 40 $ км / час.
Если бы она продолжила движение с той же скоростью, то опоздала бы на 15 $ минут, т.е. запланированное время в пути составляет $ \ frac {x} {40} — \ frac {15} {60} $ hr.
Остальное расстояние $ (x — 80) $ км. $ V = 40 + 10 = 50 $ км / час.
Итак, она преодолела расстояние между A и B за $ 2 + \ frac {x — 80} {50} $ hr, и это оказалось на 36 минут меньше, чем планировалось.
Таким образом, запланированное время было $ 2 + \ frac {x -80} {50} + \ frac {36} {60} $.
Когда мы выравниваем выражения для запланированного времени, мы получаем уравнение:
$ \ frac {x} {40} — \ frac {15} {60} = 2 + \ frac {x -80} {50} + \ frac {36} {60} $
$ \ frac {x — 10} {40} = \ frac {100 + x — 80 + 30} {50} $
$ \ frac {x — 10} {4} = \ frac {x +50} {5} $
$ 5x — 50 = 4x + 200 $
$ x = 250 $
Итак, расстояние между городами A и B составляет 250 км.
Задача 12
Чтобы доставить заказ вовремя, компания должна производить 25 деталей в день. После изготовления 25 частей в день по 3
дней компания начала производить на 5 деталей больше в день, а к последнему дню работы было произведено на 100 деталей больше, чем планировалось.
Узнайте, сколько деталей изготовила компания и сколько дней это заняло.
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет количеством дней, в которых проработала компания. Тогда 25x — это
количество деталей, которые они планировали сделать.При новом уровне добычи они
сделано:
$ 3 \ cdot 25 + (x — 3) \ cdot 30 = 75 + 30 (x — 3)
$ Следовательно: 25 $ x = 75 + 30 (x -3) — 100 $
$ 25x = 75 + 30x -90 — 100 $
$ 190 -75 = 30x -25 $
$ 115 = 5x
$ x = 23 $
Итак, компания проработала 23 дня и заработала 23 $ \ cdot 25 + 100 = 675 $ штук.
Задача 13
В седьмом классе 24 ученика. Решили посадить на заднем дворе школы березы и розы. Пока каждая девочка посадила по 3
роз, каждые три мальчика посадили по 1 берёзе.К концу дня они посадили растения за 24 доллара. Сколько берез и роз было посажено?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет количеством роз. Тогда количество берез — 24 $ — x $, а количество мальчиков — $ 3 \ times (24-x) $. Если каждая девочка посадила 3
роз, в классе $ \ frac {x} {3} $ девочек.
Мы знаем, что в классе 24 ученика. Следовательно, $ \ frac {x} {3} + 3 (24 — x) = 24 $
$ x + 9 (24 — x) = 3 \ cdot 24 $
$ x +216 — 9x = 72 $
$ 216 — 72 = 8x $
$ \ frac {144} {8} = x
$ x = 18
$ Итак, ученики посадили 18 роз и 24 — x = 24 — 18 = 6 берез.
Задача 14
Автомобиль выехал из города A в сторону города B, двигаясь со скоростью V = 32 км / час. После 3 часов в пути водитель остановился на 15 минут в городе C.
на закрытой дороге ему пришлось изменить маршрут, увеличив поездку на 28 км. Он увеличил скорость до V = 40 км / час, но все равно опоздал на 30 минут. Находим:
а) Расстояние, которое преодолела машина.
б) Время, которое потребовалось, чтобы добраться от пункта C до пункта B.
Щелкните, чтобы увидеть решение
Решение:
Из постановки задачи мы не знаем, была ли 15-минутная остановка в городе C запланирована или она была запланирована.
непредвиденный.Итак, мы должны рассмотреть оба случая.
A
Остановка планировалась. Рассмотрим только поездку из C в B, и пусть $ x $ будет количеством часов, в течение которых водитель
потратил на эту поездку.
Тогда расстояние от C до B равно $ S = 40 \ cdot x $
км. Если бы водитель мог использовать первоначальный маршрут, ему потребовалось бы $ x — \ frac {30} {60} = x — \ frac {1} {2} $ часов, чтобы проехать от C до B. Расстояние от C до B.
согласно первоначальному маршруту $ (x — \ frac {1} {2}) \ cdot 32 $ км, и это
расстояние на $ 28 $ км короче, чем $ 40 \ cdot x $ км.Тогда у нас есть уравнение
$ (x — 1/2) \ cdot 32 + 28 = 40x $
$ 32x -16 +28 = 40x $
$ -8x = -12 $
$ 8x = 12 $.
$ x = \ frac {12} {8} $
$ x = 1 \ frac {4} {8} = 1 \ frac {1} {2} = 1 \ frac {30} {60} = 1 час. 30 минут.
Итак, автомобиль преодолел расстояние от C до B за 1 час 30 минут.
Расстояние от A до B составляет $ 3 \ cdot 32 + \ frac {12} {8} \ cdot 40 = 96 + 60 = 156 $ км.
B
Предположим, ему потребовалось $ x $ часов
чтобы добраться из C в B. Тогда расстояние $ S = 40 \ cdot x $ км.
Водитель не планировал остановку на C. Допустим, он остановился, потому что ему пришлось изменить маршрут.
Потребовалось $ x — \ frac {30} {60} + \ frac {15} {60} = x — \ frac {15} {60} = x — \ frac {1} {4} $ h, чтобы проехать от С к Б.
расстояние от C до B составляет 32 (x — \ frac {1} {4}) $ км, что на 28 $ км короче, чем $ 40 \ cdot x $, т.е.
$ 32 (x — \ frac {1} {4}) + 28 = 40x
долларов 32x — 8 +28 = 40x
долларов 20 = 8x
долларов x = \ frac {20} {8} = \ frac {5} {2} = 2 \ text {hr} 30 \ text {min}. $
Пройденное расстояние равно $ 40 \ умноженное на 2.5 = 110 км $.
Задача 15
Если фермер хочет вовремя вспахивать поле фермы, он должен вспахивать 120 гектаров в день. По техническим причинам он обрабатывал только 85 гектаров в день, следовательно, ему пришлось вспахивать на 2 дня больше, чем планировалось, и он
осталось еще 40 га. Какова площадь фермерского поля и сколько дней фермер изначально планировал работать?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет количеством дней в первоначальном плане.Таким образом, все поле составляет 120 $ \ cdot x $ га. Фермеру приходилось работать x + 2 доллара в день, и он
вспахали 85 долларов (x + 2) гектаров, оставив 40 гектаров невыпаханными. Тогда у нас есть уравнение:
$ 120x = 85 (x + 2) + 40 $
$ 35x = 210 $
$ x = 6 $.
Таким образом, фермер планировал завершить работу за 6 дней, а площадь фермерского поля составляет 120 $ \ cdot 6 = 720 $ га.
Задача 16
Столяр обычно делает определенное количество
запчасти за 24 дня. Но он смог увеличить свою производительность на 5 деталей в день, и поэтому он
не только закончил работу всего за 22 дня, но и сделал 80 дополнительных деталей.Сколько частей
плотник обычно делает в день, а сколько штук он делает за 24 дня?
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет количеством деталей, которые плотник обычно изготавливает за день. За 24 дня он заработал $ 24 \ cdot x $ штук. Его новая дневная норма производства составляет x + 5 долларов за штуку и в
$ 22 $ дней он сделал $ 22 \ cdot (x + 5) $ деталей. Это на 80 больше, чем $ 24 \ cdot x $. Следовательно
уравнение:
$ 24 \ cdot x + 80 = 22 (x +5) $
$ 30 = 2x
$ x = 15 $
Обычно он делает 15 частей в день, а за 24 дня он зарабатывает 15 $ \ cdot 24 = 360 $ частей.
Задача 17
Байкер преодолел половину расстояния между двумя городами за 2 часа 30 минут.
После этого он увеличил скорость на 2 км / час. Вторую половину дистанции он преодолел за 2 часа 20 минут. Найдите расстояние между двумя городами
и начальная скорость байкера.
Нажмите, чтобы увидеть решение
Решение:
Пусть x км / ч будет начальной скоростью
байкером, то его скорость во второй части поездки составляет x + 2 км / час.
Половина расстояния между двумя городами равна $ 2 \ frac {30} {60} \ cdot x $ км и $ 2 \ frac {20} {60} \ cdot (x + 2) $ км.Из уравнения: $ 2 \ frac {30} {60} \ cdot x = 2 \ frac {20} {60} \ cdot (x + 2) $
получаем $ x = 28 $ км / час.
Начальная скорость байкера 28 км / ч.
Половина расстояния между двумя городами составляет
$ 2 ч 30 мин \ умножить на 28 = 2,5 \ умножить на 28 = 70 $.
Таким образом, расстояние равно 2 $ \ 70 = 140 $ км.
Задача 18
Поезд преодолел половину расстояния между станциями A и B со скоростью 48 км / час, но затем ему пришлось остановиться на 15 мин. Составить
из-за задержки он увеличил свою скорость на $ \ frac {5} {3} $ м / сек и прибыл на станцию B вовремя.Найдите расстояние между двумя станциями и скорость поезда после остановки.
Нажмите, чтобы увидеть решение
Решение:
Сначала определим скорость поезда после остановки. Скорость
было увеличено на $ \ frac {5} {3} $ м / сек $ = \ frac {5 \ cdot 60 \ cdot 60} {\ frac {3} {1000}} $ км / час = $ 6 $ км / час. Следовательно
новая скорость 48 $ + 6 = 54 $ км / час. Если на покрытие первого
половины расстояния, то на преодоление расстояния требуется $ x — \ frac {15} {60} = x — 0,25 $ ч.
вторая часть.
Итак, уравнение: $ 48 \ cdot x = 54 \ cdot (x — 0,25) $
$ 48 \ cdot x = 54 \ cdot x — 54 \ cdot 0,25 $
$ 48 \ cdot x — 54 \ cdot x = — 13,5 $
$ -6x = — 13,5 $
$ x = 2,25 $ ч.
Все расстояние
$ 2 \ умножить на 48 \ умножить на 2,25 = 216 $ км.
Задача 19
Элизабет может выполнить определенную работу за 15 дней, а Тони — только 75%.
эта работа в одно и то же время. Тони работал один в течение нескольких дней, а затем к нему присоединилась Элизабет, так что они закончили остаток работы.
работа за 6 дней, работаем вместе.
Сколько дней проработал каждый из них и какой процент работы каждый из них выполнил?
Нажмите, чтобы увидеть решение
Решение:
Сначала мы найдем дневную производительность каждого рабочего. Если мы рассмотрим
вся работа как единица (1), Элизабет выполняет $ \ frac {1} {15} $ работы в день, а Тони выполняет 75 \% $ из $ \ frac {1} {15} $, т.е.
$ \ frac { 75} {100} \ cdot \ frac {1} {15} = \ frac {1} {20} $. Предположим, что Тони работал один
за $ x $ дней. Затем он в одиночку выполнил $ \ frac {x} {20} $ всей работы.За работой
вместе в течение 6 дней двое рабочих закончили $ 6 \ cdot (\ frac {1} {15} + \ frac {1} {20}) = 6 \ cdot \ frac {7} {60} = \ frac {7} { 10} $ работы.
Сумма $ \ frac {x} {20} $ и $ \ frac {7} {10} $ дает нам всю работу, т.е. $ 1 $. Получаем уравнение:
$ \ frac {x} {20} + \ frac {7} {10} = 1 $
$ \ frac {x} {20} = \ frac {3} {10} $
$. х = 6 $. Тони проработал 6 + 6 = 12 дней
и Элизабет работала за 6 долларов в день. Часть работы сделана
это $ 12 \ cdot \ frac {1} {20} = \ frac {60} {100} = 60 \% $ для Тони и $ 6 \ cdot \ frac {1} {15} = \ frac {40} {100} = 40 \% $ для Элизабет.
Задача 20
Фермер планировал вспахать поле, выполнив 120
га в сутки. После двух дней работы он увеличил свою дневную производительность на 25% и закончил работу на два дня раньше срока.
а) Какова площадь поля?
б) За сколько дней фермер выполнил свою работу?
c) За сколько дней фермер планировал завершить работу?
Нажмите, чтобы увидеть решение
Решение:
Прежде всего мы найдем новую суточную производительность
фермер в гектарах в сутки: 25% от 120 гектаров
$ \ frac {25} {100} \ cdot 120 = 30 $ га, поэтому 120 $ + 30 = 150 $ га
новая ежедневная продуктивность.Пусть x будет запланированным количеством
дней, отведенных на работу. Тогда хозяйство будет 120 \ cdot x $ га. На
с другой стороны, мы получим ту же площадь, если добавим 120 $ \ cdot 2 $ гектаров к
150 $ (х -4) $ га. Тогда мы получаем уравнение
$ 120x = 120 \ cdot 2 + 150 (x -4)
$ x = 12 $
Итак, работа изначально должна была занять 12 дней, но на самом деле поле было вспахано за 12-2. = 10 дней.
Площадь поля 120 $ \ cdot 12 = 1440 $ га.
Задача 21
Чтобы покосить травяное поле, бригада косилок планировала обрабатывать 15 гектаров в день.Через 4 рабочих дня они увеличили дневную производительность на
$ 33 \ times \ frac {1} {3} \% $ и закончил работу на 1 день раньше запланированного срока.
А) Какова площадь травяного поля?
Б) Сколько дней понадобилось, чтобы косить все поле?
C) Сколько дней изначально было запланировано для этой работы?
Подсказка : Посмотрите на проблему 20 и решите ее сами.
Ответ: А) 120 га; Б) 7 дней; В) 8 дней.
Задача 22
Поезд идет от станции A до станции B.Если поезд отправляется со станции А
и со скоростью 75 км / час прибывает на станцию B на 48 минут раньше запланированного. Если бы он двигался со скоростью 50 км / час, то к запланированному времени прибытия бы
осталось еще 40 км до станции B. Найти:
A) Расстояние между двумя станциями;
B) Время, за которое поезд следует из пункта А в пункт Б по расписанию;
C) Скорость поезда по расписанию.
Нажмите, чтобы увидеть решение
Решение:
Пусть $ x $ будет запланированным временем поездки из пункта А в пункт Б.Тогда расстояние
между A и B можно найти двумя способами. С одной стороны, это расстояние составляет $ 75 (x — \ frac {48} {60}) $ км. С другой стороны, это 50 $ + 40 $ км. Таким образом, мы получаем уравнение:
$ 75 (x — \ frac {48} {60}) = 50x + 40 $
$ x = 4 $ час — это запланированное время в пути. В
расстояние между двумя станциями составляет 50 $ \ cdot 4 + 40 = 240 $ км. Тогда скорость, которую поезд должен поддерживать, чтобы идти по расписанию, составляет $ \ frac {240} {4} = 60 $ км / час.
Задача 23
Расстояние между городами A и B составляет 300 км.Один поезд отправляется из города А, а другой — из города.
город B, оба уезжают в один и тот же момент времени и направляются друг к другу. Мы знаем, что один из них на 10 км / час быстрее другого. Находить
скорости обоих поездов, если через 2 часа после отправления расстояние между ними составляет 40 км.
Нажмите, чтобы увидеть решение
Решение:
Пусть скорость более медленного поезда будет $ x $ км / час. Тогда скорость
более быстрый поезд стоит (x + 10) $ км / час. За 2 часа они преодолевают 2x $ км и 2 (x +10) $ км соответственно.Поэтому, если они еще не встретились, весь
расстояние от A до B составляет $ 2x + 2 (x +10) +40 = 4x + 60 $ км. Однако если
они уже встретились и продолжили движение, расстояние будет $ 2x + 2 (x + 10) — 40 = 4x — 20 $ км.
Таким образом, мы получаем следующие уравнения:
$ 4x + 60 = 300 $
$ 4x = 240 $
$ x = 60 $ или
$ 4x — 20 = 300 $
$ 4x = 320 $
$ x = 80 $
Отсюда скорость более медленного поезда составляет 60 долларов США км / час или 80 долларов США км / час, а скорость
более быстрый поезд стоит 70 долларов за км / час или 90 долларов за км / час.
Задача 24
Автобус едет из города А в город Б.Если скорость автобуса составляет 50 км / час, он прибудет в город B на 42 минуты позже запланированного срока. Если автобус увеличивается
его скорость составляет $ \ frac {50} {9} $ м / сек, он прибудет в город B на 30 минут раньше запланированного срока. Находим:
A) Расстояние между двумя городами;
B) Планируемое время прибытия автобуса в пункт B;
C) Скорость автобуса по расписанию.
Нажмите, чтобы увидеть решение
Решение:
Сначала определим скорость автобуса после ее увеличения. Скорость
увеличено на $ \ frac {50} {9} $ м / сек $ = \ frac {50 \ cdot60 \ cdot60} {\ frac {9} {1000}} $ км / час $ = 20 $ км / час.Следовательно, новая скорость составляет $ V = 50 + 20 = 70 $ км / час. Если $ x $ — количество часов по расписанию, то со скоростью 50
км / ч автобус едет из пункта A в пункт B за $ (x + \ frac {42} {60}) $ час. Когда скорость автобуса составляет $ V = 70 $ км / ч, время в пути составляет $ x — \ frac {30} {60} $ час. потом
$ 50 (x + \ frac {42} {60}) = 70 (x- \ frac {30} {60}) $
$ 5 (x + \ frac {7} {10}) = 7 (x- \ frac { 1} {2}) $
$ \ frac {7} {2} + \ frac {7} {2} = 7x -5x $
$ 2x = 7 $
$ x = \ frac {7} {2} $ час.
Итак, автобус должен проделать путь за 3 доллара за час 30 долларов за минуту.
Расстояние между двумя городами составляет 70 долларов США (\ frac {7} {2} — \ frac {1} {2}) = 70 \ cdot 3 = 210 $ км, а запланированная скорость составляет $ \ frac {210} {\ гидроразрыв {7} {2}} = 60 $ км / час.
Эван Мур | Учебные материалы и планы уроков: Ежедневные задания Эвана-Мура 5 класс
Полностью пересмотренный в 2019 году с учетом стандартов на уровне класса Daily Word Problems — идеальный ресурс для улучшения навыков учащихся в решении проблем. Абсолютно НОВЫЕ текстовые задачи написаны для поддержки текущих математических стандартов и ожиданий и обеспечивают последовательный спиральный обзор математических понятий.Навыки решения проблем учащиеся улучшаются по мере того, как они участвуют в содержательной практической математической практике.
36 недель занятий дают возможность попрактиковаться в математических понятиях на уровне класса, таких как сложение, умножение, дроби, логика, алгебра и т. Д.
Каждую неделю посвящается теме и ежедневно решается проблема со словом в контексте реальной жизненной ситуации.
- Занятия с понедельника по четверг включают одно- или двухэтапную задачу.
- Пятничный формат более обширен и требует нескольких шагов.Многоступенчатые задачи требуют, чтобы учащиеся использовали навыки мышления более высокого порядка, применяя свое понимание в другом контексте.
- Воспроизводимые страницы предоставляют студентам достаточно места для решения, используя стратегию по своему выбору.
Что нового в обновленном издании Daily Word Problems ?
- Абсолютно новые задачи со словами для поддержки действующих стандартов
- Новые еженедельные темы, которые представляют проблемы в контексте реальной жизни
- Ежедневный список навыков, помогающий учителям определять применяемые навыки
Практика математических навыков 5-го класса включает :
- сложение и вычитание
- умножение
- деление
- оценка
- множители и кратные
- округление и оценка
- время
- деньги
- десятичные дроби (умножение и деление)
- сравнение дробей
- дроби вычитание, умножение и деление)
- логическое мышление
- шаблоны
- периметр и площадь
- объем жидкости, масса, измерение
- вес и емкость
- объем
- графики, диаграммы и карты
- координатные плоскости
- геометрия
Включает объем и последовательность диаграмма и ключ ответа.